Recommender system show formula with picture (#727)
* add formula pic * Add some notes and formula pictures * update README.cn.md
Showing
9.5 KB
8.1 KB
5.7 KB
* add formula pic * Add some notes and formula pictures * update README.cn.md
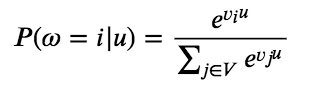
9.5 KB
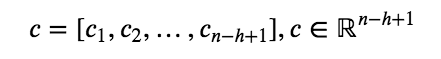
8.1 KB
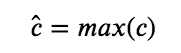
5.7 KB
