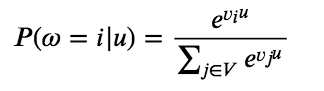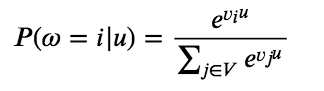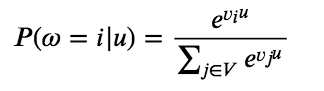diff --git a/05.recommender_system/README.cn.md b/05.recommender_system/README.cn.md
index 372e47dae0ae6b4e5def8f8643eac16fa13564b0..239cc9bed99f832b818814c28837d015e8436c04 100644
--- a/05.recommender_system/README.cn.md
+++ b/05.recommender_system/README.cn.md
@@ -2,6 +2,14 @@
本教程源代码目录在[book/recommender_system](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system),初次使用请您参考[Book文档使用说明](https://github.com/PaddlePaddle/book/blob/develop/README.cn.md#运行这本书)。
+### 说明: ###
+1. 硬件环境要求:
+本文可支持在CPU、GPU下运行
+2. Docker镜像支持的CUDA/cuDNN版本:
+如果使用了Docker运行Book,请注意:这里所提供的默认镜像的GPU环境为 CUDA 8/cuDNN 5,对于NVIDIA Tesla V100等要求CUDA 9的 GPU,使用该镜像可能会运行失败。
+3. 文档和脚本中代码的一致性问题:
+请注意:为使本文更加易读易用,我们拆分、调整了train.py的代码并放入本文。本文中代码与train.py的运行结果一致,可直接运行[train.py](https://github.com/PaddlePaddle/book/blob/develop/05.recommender_system/train.py)进行验证。
+
## 背景介绍
在网络技术不断发展和电子商务规模不断扩大的背景下,商品数量和种类快速增长,用户需要花费大量时间才能找到自己想买的商品,这就是信息超载问题。为了解决这个难题,个性化推荐系统(Recommender System)应运而生。
@@ -54,7 +62,9 @@ YouTube是世界上最大的视频上传、分享和发现网站,YouTube个性
对于一个用户$U$,预测此刻用户要观看的视频$\omega$为视频$i$的概率公式为:
-$$P(\omega=i|u)=\frac{e^{v_{i}u}}{\sum_{j \in V}e^{v_{j}u}}$$
+
+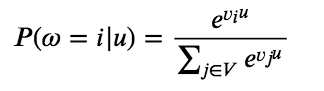
+
其中$u$为用户$U$的特征表示,$V$为视频库集合,$v_i$为视频库中第$i$个视频的特征表示。$u$和$v_i$为长度相等的向量,两者点积可以通过全连接层实现。
@@ -83,11 +93,15 @@ $$P(\omega=i|u)=\frac{e^{v_{i}u}}{\sum_{j \in V}e^{v_{j}u}}$$
其次,进行卷积操作:把卷积核(kernel)$w\in\mathbb{R}^{hk}$应用于包含$h$个词的窗口$x_{i:i+h-1}$,得到特征$c_i=f(w\cdot x_{i:i+h-1}+b)$,其中$b\in\mathbb{R}$为偏置项(bias),$f$为非线性激活函数,如$sigmoid$。将卷积核应用于句子中所有的词窗口${x_{1:h},x_{2:h+1},\ldots,x_{n-h+1:n}}$,产生一个特征图(feature map):
-$$c=[c_1,c_2,\ldots,c_{n-h+1}], c \in \mathbb{R}^{n-h+1}$$
+
+
+
接下来,对特征图采用时间维度上的最大池化(max pooling over time)操作得到此卷积核对应的整句话的特征$\hat c$,它是特征图中所有元素的最大值:
-$$\hat c=max(c)$$
+
+
+
#### 融合推荐模型概览
diff --git a/05.recommender_system/image/formula1.png b/05.recommender_system/image/formula1.png
new file mode 100644
index 0000000000000000000000000000000000000000..e3923ba2ec0080f0b4733f2781fff946ce076655
Binary files /dev/null and b/05.recommender_system/image/formula1.png differ
diff --git a/05.recommender_system/image/formula2.png b/05.recommender_system/image/formula2.png
new file mode 100644
index 0000000000000000000000000000000000000000..595205bf7af6e86ae02baca4f97c3439283a57f9
Binary files /dev/null and b/05.recommender_system/image/formula2.png differ
diff --git a/05.recommender_system/image/formula3.png b/05.recommender_system/image/formula3.png
new file mode 100644
index 0000000000000000000000000000000000000000..0443b979354d02881a10b332399a18ef2bb52dec
Binary files /dev/null and b/05.recommender_system/image/formula3.png differ
diff --git a/05.recommender_system/index.cn.html b/05.recommender_system/index.cn.html
index ea41aaa17231153901391b3116cc3987e986a8ab..186443b4cc6754483c8bc9d0c18b2c359cce7192 100644
--- a/05.recommender_system/index.cn.html
+++ b/05.recommender_system/index.cn.html
@@ -44,6 +44,14 @@
本教程源代码目录在[book/recommender_system](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system),初次使用请您参考[Book文档使用说明](https://github.com/PaddlePaddle/book/blob/develop/README.cn.md#运行这本书)。
+### 说明: ###
+1. 硬件环境要求:
+本文可支持在CPU、GPU下运行
+2. Docker镜像支持的CUDA/cuDNN版本:
+如果使用了Docker运行Book,请注意:这里所提供的默认镜像的GPU环境为 CUDA 8/cuDNN 5,对于NVIDIA Tesla V100等要求CUDA 9的 GPU,使用该镜像可能会运行失败。
+3. 文档和脚本中代码的一致性问题:
+请注意:为使本文更加易读易用,我们拆分、调整了train.py的代码并放入本文。本文中代码与train.py的运行结果一致,可直接运行[train.py](https://github.com/PaddlePaddle/book/blob/develop/05.recommender_system/train.py)进行验证。
+
## 背景介绍
在网络技术不断发展和电子商务规模不断扩大的背景下,商品数量和种类快速增长,用户需要花费大量时间才能找到自己想买的商品,这就是信息超载问题。为了解决这个难题,个性化推荐系统(Recommender System)应运而生。
@@ -96,7 +104,9 @@ YouTube是世界上最大的视频上传、分享和发现网站,YouTube个性
对于一个用户$U$,预测此刻用户要观看的视频$\omega$为视频$i$的概率公式为:
-$$P(\omega=i|u)=\frac{e^{v_{i}u}}{\sum_{j \in V}e^{v_{j}u}}$$
+
+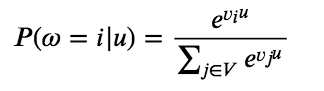
+
其中$u$为用户$U$的特征表示,$V$为视频库集合,$v_i$为视频库中第$i$个视频的特征表示。$u$和$v_i$为长度相等的向量,两者点积可以通过全连接层实现。
@@ -125,11 +135,15 @@ $$P(\omega=i|u)=\frac{e^{v_{i}u}}{\sum_{j \in V}e^{v_{j}u}}$$
其次,进行卷积操作:把卷积核(kernel)$w\in\mathbb{R}^{hk}$应用于包含$h$个词的窗口$x_{i:i+h-1}$,得到特征$c_i=f(w\cdot x_{i:i+h-1}+b)$,其中$b\in\mathbb{R}$为偏置项(bias),$f$为非线性激活函数,如$sigmoid$。将卷积核应用于句子中所有的词窗口${x_{1:h},x_{2:h+1},\ldots,x_{n-h+1:n}}$,产生一个特征图(feature map):
-$$c=[c_1,c_2,\ldots,c_{n-h+1}], c \in \mathbb{R}^{n-h+1}$$
+
+
+
接下来,对特征图采用时间维度上的最大池化(max pooling over time)操作得到此卷积核对应的整句话的特征$\hat c$,它是特征图中所有元素的最大值:
-$$\hat c=max(c)$$
+
+
+
#### 融合推荐模型概览