Merge branch 'develop' of https://github.com/PaddlePaddle/book into develop
Showing
01.fit_a_line/.run_ce.sh
0 → 100755
01.fit_a_line/_ce.py
0 → 100644
29.8 KB
22.9 KB
37.3 KB
27.8 KB
| W: | H:
| W: | H:


| W: | H:
| W: | H:


02.recognize_digits/.run_ce.sh
0 → 100755
02.recognize_digits/_ce.py
0 → 100644
02.recognize_digits/image/01.gif
0 → 100644
1.1 KB
02.recognize_digits/image/02.gif
0 → 100644
939 字节
02.recognize_digits/image/03.gif
0 → 100644
1.4 KB
02.recognize_digits/image/04.gif
0 → 100644
955 字节
02.recognize_digits/image/05.gif
0 → 100644
920 字节
03.image_classification/_ce.py
0 → 100644
04.word2vec/.run_ce.sh
0 → 100755
04.word2vec/_ce.py
0 → 100644
04.word2vec/image/Eqn1.gif
0 → 100644
397 字节
04.word2vec/image/Eqn2.gif
0 → 100644
991 字节
04.word2vec/image/Eqn3.gif
0 → 100644
1.1 KB
04.word2vec/image/Eqn4.gif
0 → 100644
1.4 KB
04.word2vec/image/Eqn5.gif
0 → 100644
1.2 KB
04.word2vec/image/Eqn6.gif
0 → 100644
982 字节
04.word2vec/image/Eqn7.gif
0 → 100644
1.1 KB
04.word2vec/image/Eqn8.gif
0 → 100644
1.5 KB
04.word2vec/image/Eqn9.gif
0 → 100644
1009 字节
05.recommender_system/.run_ce.sh
0 → 100755
05.recommender_system/_ce.py
0 → 100644
9.5 KB
8.1 KB
5.7 KB
06.understand_sentiment/README.cn.md
100644 → 100755
06.understand_sentiment/_ce.py
0 → 100644
13.3 KB
120.8 KB
19.0 KB
23.5 KB
07.label_semantic_roles/_ce.py
0 → 100644
28.3 KB
2.9 KB
1.6 KB
35.8 KB
7.7 KB
7.1 KB
17.3 KB
11.1 KB
16.5 KB
09.gan/.run_ce.sh
0 → 100755
09.gan/README.cn.md
0 → 100644
09.gan/_ce.py
0 → 100644
09.gan/dc_gan.py
0 → 100644
09.gan/image/01.gif
0 → 100644
2.2 KB
09.gan/image/dcgan_demo.png
0 → 100644
164.0 KB
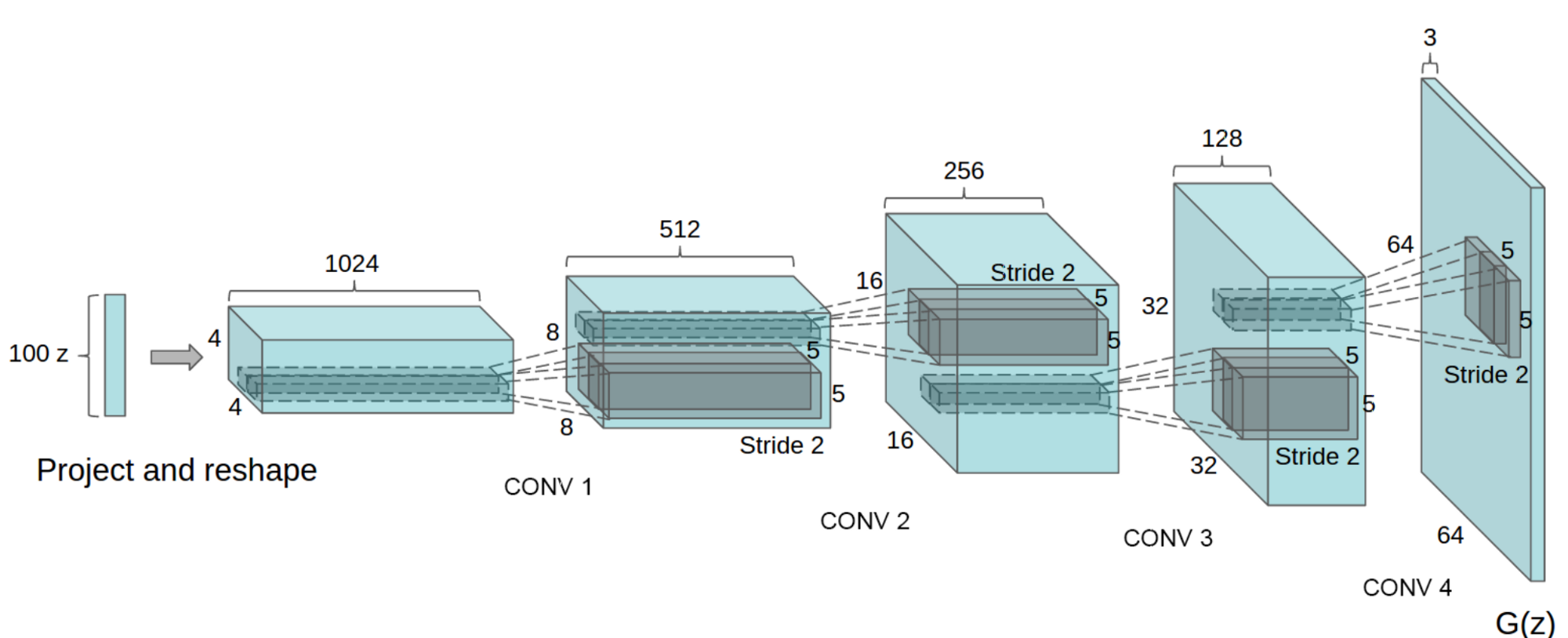
09.gan/image/dcgan_g.png
0 → 100644
231.8 KB
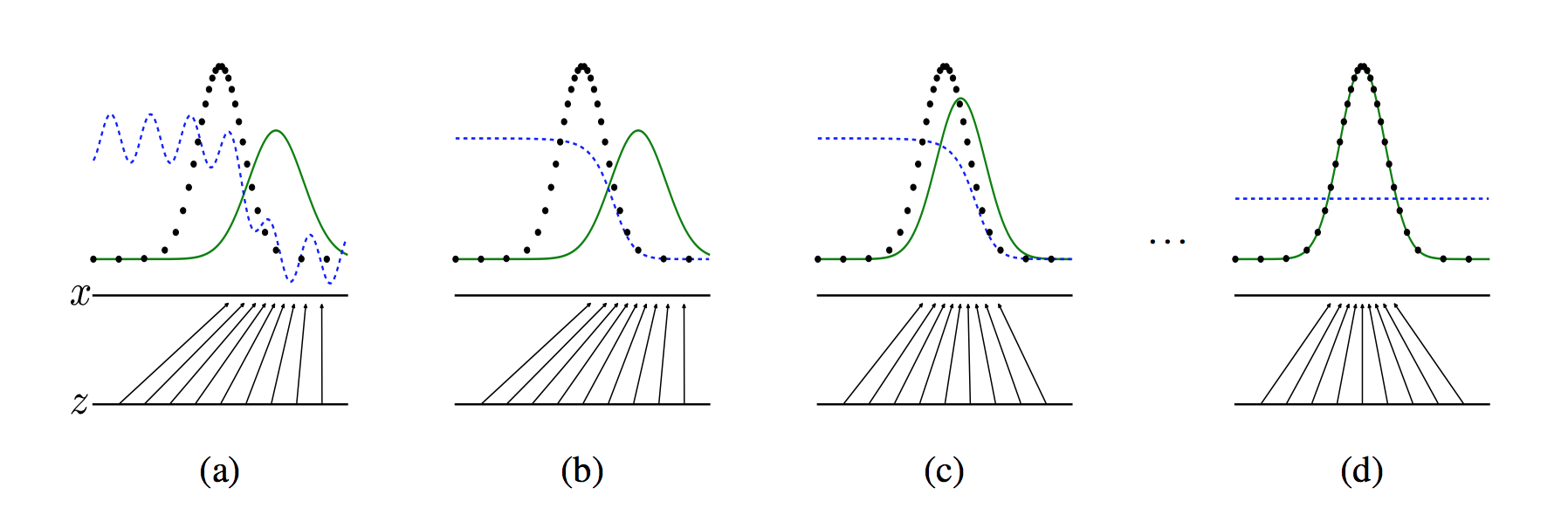
09.gan/image/process.png
0 → 100644
131.0 KB
09.gan/index.cn.html
0 → 100644
09.gan/network.py
0 → 100644
09.gan/utility.py
0 → 100644