update to v1.1.1
Showing
docs/Makefile
已删除
100644 → 0
docs/make.bat
已删除
100644 → 0
docs/requirements.txt
已删除
100644 → 0
docs/source/_static/logo.png
已删除
100644 → 0
12.1 KB
docs/source/conf.py
已删除
100644 → 0
docs/source/index.rst
已删除
100644 → 0
docs/source/introduction.rst
已删除
100644 → 0
docs/source/modules.rst
已删除
100644 → 0
docs/source/tutorial.rst
已删除
100644 → 0
文件已删除
此差异已折叠。
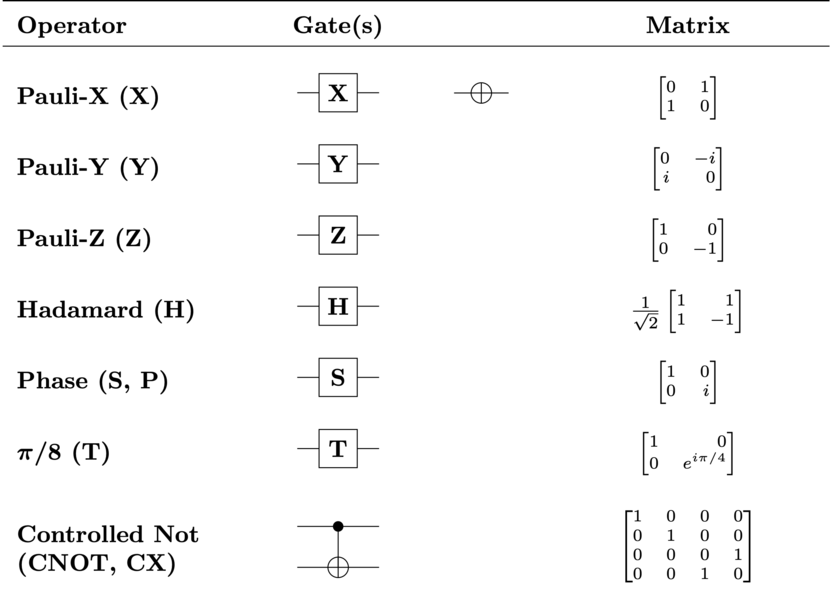
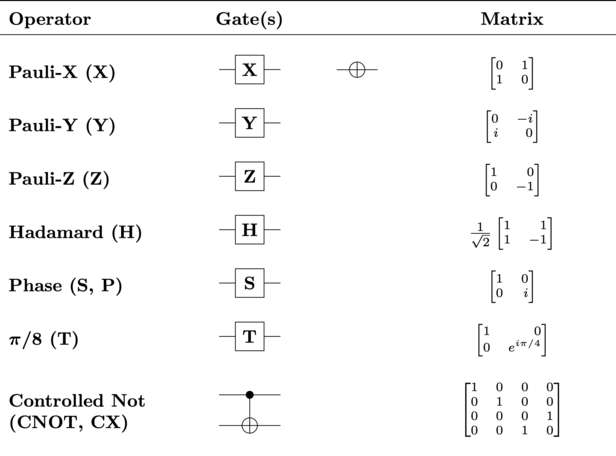
introduction/figures/gate.png
已删除
100644 → 0
59.9 KB
1.2 MB
969.5 KB
101.2 KB
文件已移动
264.9 KB
167.7 KB
42.2 KB
文件已移动
5.9 KB
5.6 KB
6.0 KB
5.6 KB
文件已移动
文件已移动
文件已移动
文件已移动
此差异已折叠。
此差异已折叠。
此差异已折叠。
文件已删除
文件已移动
文件已移动
文件已移动
1019.3 KB
文件已移动
20.8 KB
120.2 KB
文件已移动
1.5 MB
1.4 MB
文件已删除
文件已删除
此差异已折叠。
此差异已折叠。
此差异已折叠。
文件已移动
87.6 KB
此差异已折叠。
此差异已折叠。
此差异已折叠。
文件已移动
文件已移动
960.2 KB
7.5 KB
文件已移动
此差异已折叠。
此差异已折叠。
此差异已折叠。
tutorial/Q-GAN/QGAN_EN.ipynb
0 → 100644
此差异已折叠。
此差异已折叠。
文件已移动
文件已移动
此差异已折叠。
此差异已折叠。
文件已移动
tutorial/QAOA/QAOA.ipynb
已删除
100644 → 0
此差异已折叠。
tutorial/QAOA/QAOA.pdf
已删除
100644 → 0
此差异已折叠。
tutorial/QAOA/QAOA_CN.ipynb
0 → 100644
此差异已折叠。
tutorial/QAOA/QAOA_En.pdf
已删除
100644 → 0
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
tutorial/SSVQE/SSVQE_EN.ipynb
0 → 100644
此差异已折叠。
此差异已折叠。
tutorial/VQE/VQE_CN.ipynb
0 → 100644
此差异已折叠。
tutorial/VQE/VQE_EN.ipynb
0 → 100644
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
tutorial/VQSD/VQSD_EN.ipynb
0 → 100644
此差异已折叠。
此差异已折叠。
tutorial/VQSVD/VQSVD_CN.ipynb
0 → 100644
此差异已折叠。
tutorial/VQSVD/VQSVD_EN.ipynb
0 → 100644
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。