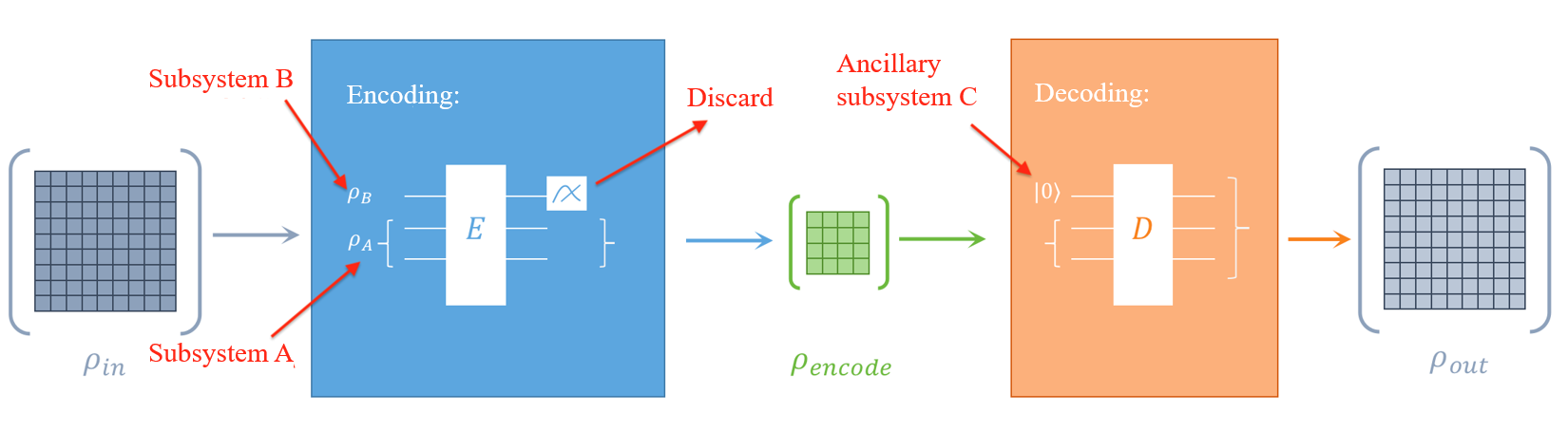
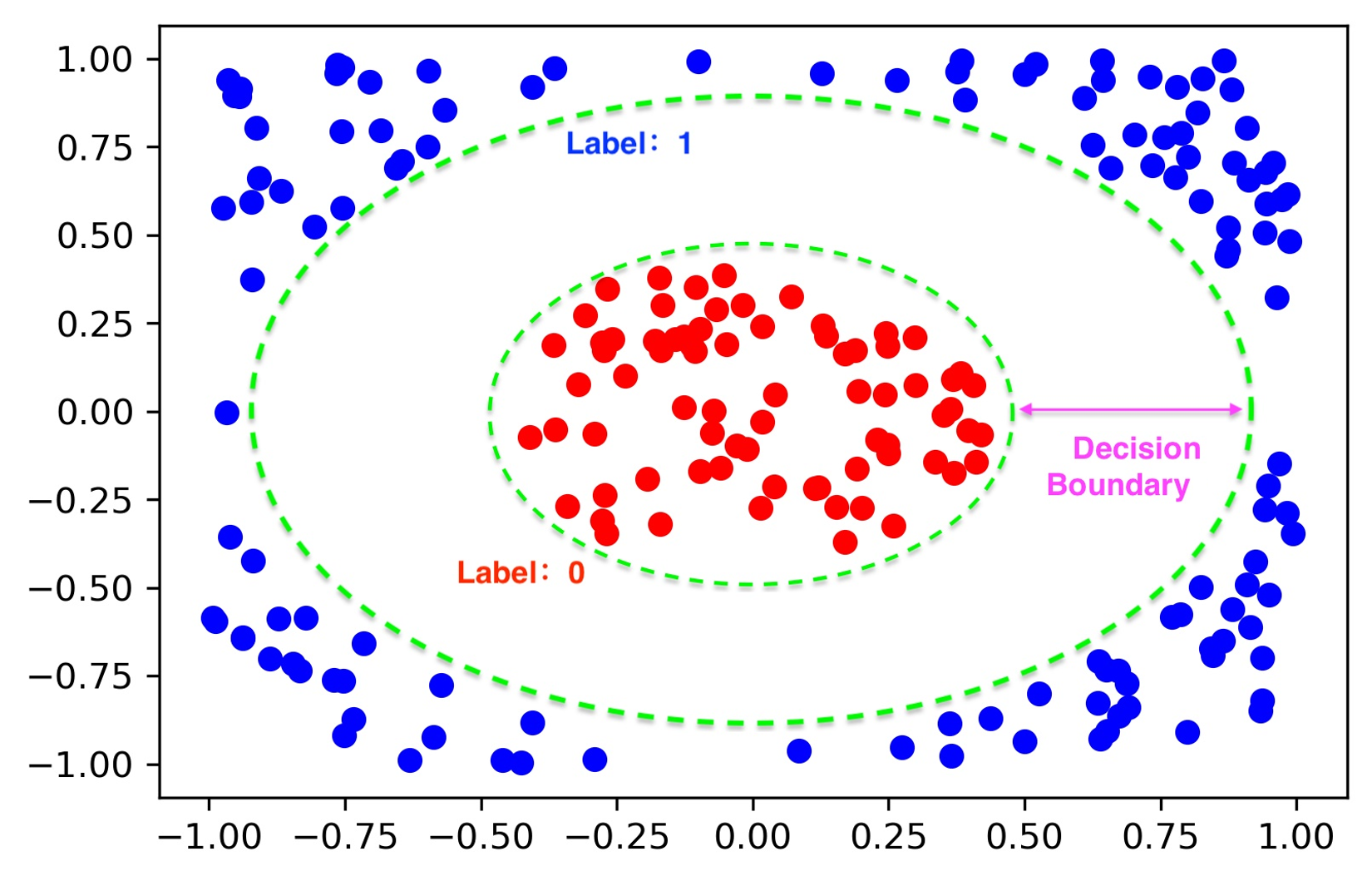
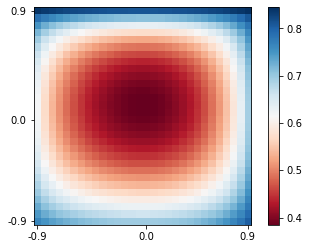
update to v1.1.1

README.md

 English | [简体中文](README_CN.md)
 
-# Paddle Quantum （量桨）
+# Paddle Quantum (量桨)
 
 - [Features](#features)
 - [Install](#install)
@@ -63,7 +63,7 @@ pip install -e .
 python -m pip install --upgrade -r requirements.txt
 ```
 
-### Use OpenFermion to read xyz molecule configuration file
+### Use OpenFermion to read .xyz molecule configuration file
 
 > Only macOS and linux users can use OpenFermion to read .xyz description files.
 

README_CN.md

@@ -168,9 +168,6 @@ Paddle Quantum 使用 setuptools 的 develop 模式进行安装，相关代码
 
     答：量桨是基于百度飞桨开发的量子机器学习工具集。飞桨作为国内首个开源开放的产业级深度学习平台，技术领先且功能完备。拥有飞桨的技术支持，特别是其强大的动态图机制，量桨可以方便地进行机器学习的优化以及 GPU 的加速。同时，基于百度量子计算研究所研发的高性能量子模拟器，量桨在个人笔记本电脑上也能支持20多个量子比特的运算。另外，量桨还有丰富的[量子机器学习案例](./tutorial)供大家参考和学习。
 
-5. 问：**非常想试用量桨，该怎么入门呢？**
-
-    答：建议新用户首先阅读量桨的[入门手册](./introduction)，它包含量桨详细的安装步骤以及入门教程。另外，量桨提供了丰富的[量子机器学习案例](./tutorial)，以 Jupyter Notebook 和 PDF 的方式呈现，方便用户学习和实践。如在学习和使用过程中遇到任何问题，欢迎用户通过 [Github Issues](https://github.com/PaddlePaddle/Quantum/issues) 以及技术交流QQ群（1076223166）与我们交流。
 
 ## Copyright and License
 

docs/Makefile

-# Minimal makefile for Sphinx documentation
-#
-
-# You can set these variables from the command line, and also
-# from the environment for the first two.
-SPHINXOPTS    ?=
-SPHINXBUILD   ?= sphinx-build
-SOURCEDIR     = source
-BUILDDIR      = build
-
-# Put it first so that "make" without argument is like "make help".
-help:
-	@$(SPHINXBUILD) -M help "$(SOURCEDIR)" "$(BUILDDIR)" $(SPHINXOPTS) $(O)
-
-.PHONY: help Makefile
-
-# Catch-all target: route all unknown targets to Sphinx using the new
-# "make mode" option.  $(O) is meant as a shortcut for $(SPHINXOPTS).
-%: Makefile
-	@$(SPHINXBUILD) -M $@ "$(SOURCEDIR)" "$(BUILDDIR)" $(SPHINXOPTS) $(O)

docs/make.bat

-@ECHO OFF
-
-pushd %~dp0
-
-REM Command file for Sphinx documentation
-
-if "%SPHINXBUILD%" == "" (
-	set SPHINXBUILD=sphinx-build
-)
-set SOURCEDIR=source
-set BUILDDIR=build
-
-if "%1" == "" goto help
-
-%SPHINXBUILD% >NUL 2>NUL
-if errorlevel 9009 (
-	echo.
-	echo.The 'sphinx-build' command was not found. Make sure you have Sphinx
-	echo.installed, then set the SPHINXBUILD environment variable to point
-	echo.to the full path of the 'sphinx-build' executable. Alternatively you
-	echo.may add the Sphinx directory to PATH.
-	echo.
-	echo.If you don't have Sphinx installed, grab it from
-	echo.http://sphinx-doc.org/
-	exit /b 1
-)
-
-%SPHINXBUILD% -M %1 %SOURCEDIR% %BUILDDIR% %SPHINXOPTS% %O%
-goto end
-
-:help
-%SPHINXBUILD% -M help %SOURCEDIR% %BUILDDIR% %SPHINXOPTS% %O%
-
-:end
-popd

docs/requirements.txt

-paddlepaddle>=1.8.3
-networkx>=2.4
-matplotlib>=3.3.0
-interval>=1.0.0
-progressbar>=2.5
-sphinx
-sphinx-rtd-theme
-PyStemmer
-readthedocs-sphinx-search
-jieba
\ No newline at end of file

docs/source/conf.py

-# -*- coding: utf-8 -*-
-# Configuration file for the Sphinx documentation builder.
-#
-# This file only contains a selection of the most common options. For a full
-# list see the documentation:
-# https://www.sphinx-doc.org/en/master/usage/configuration.html
-
-# -- Path setup --------------------------------------------------------------
-
-# If extensions (or modules to document with autodoc) are in another directory,
-# add these directories to sys.path here. If the directory is relative to the
-# documentation root, use os.path.abspath to make it absolute, like shown here.
-#
-import os
-import sys
-sys.path.insert(0, os.path.abspath('../..'))
-
-
-# -- Project information -----------------------------------------------------
-
-project = 'Paddle Quantum'
-copyright = u'2020, Institute for Quantum Computing, Baidu Inc.'
-author = u'Institute for Quantum Computing, Baidu Inc.'
-
-# The full version, including alpha/beta/rc tags
-release = '1.1.0'
-
-
-# -- General configuration ---------------------------------------------------
-
-# Add any Sphinx extension module names here, as strings. They can be
-# extensions coming with Sphinx (named 'sphinx.ext.*') or your custom
-# ones.
-extensions = [
-    'sphinx.ext.autodoc',
-    'sphinx.ext.napoleon',
-    'sphinx.ext.mathjax',
-    'sphinx_search.extension',
-]
-
-# Add any paths that contain templates here, relative to this directory.
-templates_path = ['_templates']
-
-# The language for content autogenerated by Sphinx. Refer to documentation
-# for a list of supported languages.
-#
-# This is also used if you do content translation via gettext catalogs.
-# Usually you set "language" from the command line for these cases.
-language = 'zh_CN'
-
-html_search_language = 'zh'
-
-# List of patterns, relative to source directory, that match files and
-# directories to ignore when looking for source files.
-# This pattern also affects html_static_path and html_extra_path.
-exclude_patterns = []
-
-
-# -- Options for HTML output -------------------------------------------------
-
-# The theme to use for HTML and HTML Help pages.  See the documentation for
-# a list of builtin themes.
-#
-html_theme = 'sphinx_rtd_theme'
-
-# Add any paths that contain custom static files (such as style sheets) here,
-# relative to this directory. They are copied after the builtin static files,
-# so a file named "default.css" will overwrite the builtin "default.css".
-html_static_path = ['_static']
-
-html_logo = '_static/logo.png'
-
-master_doc = 'index'
-
-# Autodoc
-autodoc_member_order = 'bysource'

docs/source/index.rst

-.. Paddle Quantum documentation master file, created by
-   sphinx-quickstart on Fri Aug 21 10:54:43 2020.
-   You can adapt this file completely to your liking, but it should at least
-   contain the root `toctree` directive.
-
-Welcome to Paddle Quantum's documentation!
-==========================================
-
-.. toctree::
-   :maxdepth: 2
-   :caption: Paddle Quantum 入门
-
-   introduction
-   tutorial
-
-.. toctree::
-   :maxdepth: 4
-   :caption: API 文档
-
-   modules

docs/source/introduction.rst

-.. _header-n0:
-
-Paddle Quantum （量桨）
-=======================
-
-`Paddle Quantum（量桨） <https://github.com/PaddlePaddle/Quantum>`__\ 是基于百度飞桨开发的量子机器学习工具集，支持量子神经网络的搭建与训练，提供易用的量子机器学习开发套件与量子优化、量子化学等前沿量子应用工具集，使得百度飞桨也因此成为国内首个目前也是唯一一个支持量子机器学习的深度学习框架。
-
-.. figure:: https://release-data.cdn.bcebos.com/Paddle%20Quantum.png
-   :target: https://github.com/PaddlePaddle/Quantum
-
-量桨建立起了人工智能与量子计算的桥梁，不但可以快速实现量子神经网络的搭建与训练，还提供易用的量子机器学习开发套件与量子优化、量子化学等前沿量子应用工具集，并提供多项自研量子机器学习应用。通过百度飞桨深度学习平台赋能量子计算，量桨为领域内的科研人员以及开发者便捷地开发量子人工智能的应用提供了强有力的支撑，同时也为广大量子计算爱好者提供了一条可行的学习途径。
-
-    关于量桨的更多内容可以查看 GitHub 页面：https://github.com/PaddlePaddle/Quantum
-
-.. _header-n6:
-
-特色
-----
-
-- 易用性
-
-  - 高效搭建量子神经网络
-  - 多种量子神经网络模板
-  - 丰富的量子算法教程（10+用例）
-
-- 可拓展性
-
-  - 支持通用量子电路模型
-  - 高性能模拟器支持20多个量子比特的模拟运算
-  - 提供多种优化工具和 GPU 加速
-
-- 特色工具集
-
-  - 提供组合优化和量子化学等前沿领域的计算工具箱
-  - 自研多种量子机器学习算法
-
-.. _header-n15:
-
-安装步骤
---------
-
-.. _header-n16:
-
-安装 PaddlePaddle
-~~~~~~~~~~~~~~~~~
-
-请参考
-`PaddlePaddle <https://www.paddlepaddle.org.cn/install/quick>`__
-安装配置页面。此项目需求 PaddlePaddle 1.8.3 或更高版本。
-
-.. _header-n19:
-
-下载 Paddle Quantum 并安装
-~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-.. code:: shell
-
-   git clone http://github.com/PaddlePaddle/quantum
-
-.. code:: shell
-
-   cd quantum
-   pip install -e .
-
-.. _header-n23:
-
-或使用 requirements.txt 安装依赖包
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-.. code:: shell
-
-   python -m pip install --upgrade -r requirements.txt
-
-.. _header-n25:
-
-使用 openfermion 读取 xyz 描述文件
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-
-.. note:: 仅在 macOS 和 linux 下可以使用 openfermion 读取 xyz 描述文件。
-
-VQE中调用 openfermion 读取分子 xyz 文件并计算，因此需要安装 openfermion 和
-openfermionpyscf。
-
-.. code:: shell
-
-   pip install openfermion
-   pip install openfermionpyscf
-
-.. _header-n29:
-
-运行
-~~~~
-
-现在，可以试着运行一段程序来验证量桨是否已安装成功。这里我们运行量桨提供的量子近似优化算法
-(QAOA) 的例子。
-
-.. code:: shell
-
-   cd paddle_quantum/QAOA/example
-   python main.py
-
-..
-
-.. note:: 关于 QAOA 的介绍可以参考我们的 `QAOA 教程 <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/QAOA>`__。
-
-.. _header-n51:
-
-交流与反馈
-----------
-
-- 我们非常欢迎您通过 `Github
-  Issues <https://github.com/PaddlePaddle/Quantum/issues>`__
-  来提交问题、报告与建议。
-- 技术交流QQ群：1076223166
-
-.. _header-n118:
-
-Copyright and License
----------------------
-
-Paddle Quantum 使用 `Apache-2.0 license <https://github.com/PaddlePaddle/Quantum/blob/master/LICENSE>`__ 许可证。

docs/source/modules.rst

-paddle_quantum
-==============
-
-.. toctree::
-   :maxdepth: 4
-
-   paddle_quantum

docs/source/paddle_quantum.circuit.rst

-paddle\_quantum.circuit module
-==============================
-
-.. automodule:: paddle_quantum.circuit
-   :members:
-   :undoc-members:
-   :show-inheritance:

docs/source/paddle_quantum.rst

-paddle\_quantum package
-=======================
-
-.. automodule:: paddle_quantum
-   :members:
-   :undoc-members:
-   :show-inheritance:
-
-Submodules
-----------
-
-.. toctree::
-   :maxdepth: 4
-
-   paddle_quantum.circuit
-   paddle_quantum.state
-   paddle_quantum.utils

docs/source/paddle_quantum.state.rst

-paddle\_quantum.state module
-============================
-
-.. automodule:: paddle_quantum.state
-   :members:
-   :undoc-members:
-   :show-inheritance:

docs/source/paddle_quantum.utils.rst

-paddle\_quantum.utils module
-============================
-
-.. automodule:: paddle_quantum.utils
-   :members:
-   :undoc-members:
-   :show-inheritance:

docs/source/tutorial.rst

-教程与案例
-=======================
-
-我们准备了入门教程和入门案例，来帮助用户快速学会如何使用量桨(Paddle Quantum)。
-
-.. _header-n33:
-
-入门教程
---------
-
-我们提供了一份 `Paddle Quantum 入门手册 <https://github.com/PaddlePaddle/Quantum/blob/master/introduction>`__\ 来方便用户快速上手
-Paddle Quantum。目前支持 PDF 阅读和运行 Jupyter Notebook
-两种方式。内容上，该手册包括以下几个方面：
-
-- Paddle Quantum 的详细安装教程
-- 量子计算的基础知识介绍
-- Paddle Quantum 的使用介绍
-- PaddlePaddle 飞桨优化器使用教程
-- 具体的量子机器学习案例—VQE
-
-入门案例
---------
-
-我们提供了涵盖量子优化、量子化学、量子机器学习等多个领域的案例供大家学习。与\ `入门手册 <https://github.com/PaddlePaddle/Quantum/blob/master/introduction>`__\ 类似，每个教程目前支持
-PDF 阅读和运行 Jupyter Notebook 两种方式。我们推荐用户下载 Notebook
-后，本地运行进行实践。
-
-1. `量子近似优化算法 (QAOA) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/QAOA>`__
-2. `变分量子特征求解器 (VQE) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/VQE>`__
-3. `量子神经网络的贫瘠高原效应 (Barren Plateaus) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/Barren>`__
-4. `量子分类器 (Quantum Classifier) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/Q-Classifier>`__
-5. `量子变分自编码器 (Quantum Autoencoder) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/Q-Autoencoder>`__
-6. `量子生成对抗网络 (Quantum GAN) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/Q-GAN>`__
-7. `子空间搜索 - 量子变分特征求解器 (SSVQE) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/SSVQE>`__
-8. `变分量子态对角化算法 (VQSD) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/VQSD>`__
-9. `吉布斯态的制备 (Gibbs State Preparation) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/Gibbs>`__
-10. `变分量子奇异值分解 (VQSVD) <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/VQSVD>`__
-
-此外，Paddle Quantum 也支持在 GPU
-上进行量子机器学习的训练，具体的方法请参考案例：`在 GPU 上使用 Paddle
-Quantum <https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/GPU>`__。

tutorial/GPU/GPU_Tutorial_CN.ipynb → introduction/PaddleQuantum_GPU_CN.ipynb

@@ -4,28 +4,34 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# 在 GPU 上使用 Paddle Quantum\n",
+    "# 在 GPU 上使用量桨\n",
     "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 1. 简介\n",
+    "## 简介\n",
     "\n",
     "> 注意，本篇教程具有时效性。同时不同电脑也会有个体差异性，本篇教程不保证所有电脑可以安装成功。\n",
     "\n",
-    "在深度学习中，大家通常会使用 GPU 来进行神经网络模型的训练，因为与 CPU 相比，GPU在浮点数运算方面有着显著的优势。因此，使用 GPU 来训练神经网络模型逐渐成为共同的选择。在 Paddle Quantum 中，我们的量子态和量子门也采用基于浮点数的复数表示，因此我们的模型如果能部署到 GPU 上进行训练，也会显著提升训练速度。\n",
-    "\n",
-    "## 2. GPU 选择\n",
+    "在深度学习中，大家通常会使用 GPU 来进行神经网络模型的训练，因为与 CPU 相比，GPU在浮点数运算方面有着显著的优势。因此，使用 GPU 来训练神经网络模型逐渐成为共同的选择。在 Paddle Quantum 中，我们的量子态和量子门也采用基于浮点数的复数表示，因此我们的模型如果能部署到 GPU 上进行训练，也会显著提升训练速度。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## GPU 选择\n",
     "\n",
-    "在这里，我们使用 Nvidia 的硬件设备，其 CUDA(Compute Unified Device Architecture) 对深度学习的框架支持比较好。我们的 PaddlePaddle 也可以比较方便地安装在 CUDA 上。\n",
+    "在这里，我们选择 Nvidia 的硬件设备，其 CUDA（Compute Unified Device Architecture）对深度学习的框架支持比较好，PaddlePaddle 也可以比较方便地安装在 CUDA 上。\n",
     "\n",
-    "## 3. 配置 CUDA 环境\n",
+    "## 配置 CUDA 环境\n",
     "\n",
-    "### 3.1 安装 CUDA\n",
+    "### 安装 CUDA\n",
     "\n",
     "这里，我们介绍如何在 x64 平台上的 Windows10 系统中配置 CUDA 环境。首先，在[CUDA GPUs | NVIDIA Developer](https://developer.nvidia.com/cuda-gpus)上查看你的GPU是否可以安装CUDA环境。然后，在[NVIDIA 驱动程序下载](https://www.nvidia.cn/Download/index.aspx?lang=cn)下载你的显卡的最新版驱动，并安装到电脑上。\n",
     "\n",
@@ -35,39 +41,38 @@
     "\n",
     "安装完成之后，打开 Windows 命令行，输入`nvcc -V`，如果看到版本信息，则说明 CUDA 安装成功。\n",
     "\n",
-    "### 3.2 安装 cuDNN\n",
+    "### 安装 cuDNN\n",
     "\n",
     "在[NVIDIA cuDNN | NVIDIA Developer](https://developer.nvidia.com/cudnn)下载 cuDNN，根据[飞桨的安装步骤](https://www.paddlepaddle.org.cn/install/quick)中的要求，我们**需要使用 cuDNN 7.6+** ，因此我们下载支持 CUDA 10.0 的最新版 cuDNN 即可。下载完成 cuDNN 后进行解压缩。然后，假设我们的 CUDA 的安装路径为`C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0`，我们将 cuDNN 解压缩后里面的`bin`、`include`和`lib`中的文件都替换 CUDA 的安装路径下的对应文件（如果文件已存在则进行替换，如果未存在则直接粘贴到对应目录中）。到这里，cuDNN 也就安装完成了。\n",
     "\n",
     "\n",
-    "### 3.3 配置环境变量\n",
+    "### 配置环境变量\n",
     "\n",
     "接下来还需要配置环境变量。右键电脑桌面上的“此电脑”（或“文件资源管理器”左栏的“此电脑”），选择“属性”，然后选择左侧的“高级系统设置”，在“高级”这一栏下选择“环境变量”。\n",
     "\n",
     "现在就进入到了环境变量的设置页面，在系统变量中选择`Path`，点击“编辑”。在出现的页面中，查看是否有`C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0\\bin`和`C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0\\libnvvp`这两个地址（其前缀`C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0`应该为你的 CUDA 的安装位置），如果没有，请手动添加。\n",
     "\n",
-    "### 3.4 验证是否安装成功\n",
+    "### 验证是否安装成功\n",
     "\n",
     "打开命令行，输入`cd C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0\\extras\\demo_suite`进入到 CUDA 安装路径（这里也应该为你的 CUDA 的安装位置）。然后分别执行`.\\bandwidthTest.exe`和`.\\deviceQuery.exe`，如果都出现`Result = PASS`，则说明安装成功。\n",
-    "\n",
-    "\n",
-    "## 4. 在 CUDA 环境上安装 PaddlePaddle\n",
-    "\n",
-    "根据[飞桨的安装步骤](https://www.paddlepaddle.org.cn/install/quick)中的说明，我们首先需要确定自己的python环境，用`python --version`来查看 python 版本，保证**python版本是3.5.1+/3.6+/3.7+**，并且用`python -m ensurepip`和`python -m pip --version`来查看 pip 版本，**确认是 9.0.1+**。然后，使用`python -m pip install paddlepaddle-gpu==1.8.4.post107 -i https://pypi.tuna.tsinghua.edu.cn/simple`来安装 GPU 版本的 PaddlePaddle。\n",
-    "\n",
-    "\n",
-    "## 5. 安装 Paddle Quantum\n",
-    "\n",
-    "下载 Paddle Quantum 的安装包，修改`setup.py`，将其中的`paddlepaddle`改为`paddlepaddle-gpu`，然后按照 Paddle Quantum 的安装要求，执行`pip install -e .`即可。\n",
-    "\n",
-    "> 如果你是在一个新的 python 环境中安装了 paddlepaddle-gpu 和 paddle_quantum，请在新 python 环境中安装 jupyter，并在新的 jupyter 下重新打开本教程并运行。"
+    "\n"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 6. 检测是否安装成功\n",
+    "## 在 CUDA 环境上安装 PaddlePaddle\n",
+    "\n",
+    "根据[飞桨的安装步骤](https://www.paddlepaddle.org.cn/install/quick)中的说明，我们首先需要确定自己的python环境，用`python --version`来查看 python 版本，保证**python版本是3.5.1+/3.6+/3.7+**，并且用`python -m ensurepip`和`python -m pip --version`来查看 pip 版本，**确认是 9.0.1+**。然后，使用`python -m pip install paddlepaddle-gpu==1.8.4.post107 -i https://pypi.tuna.tsinghua.edu.cn/simple`来安装 GPU 版本的 PaddlePaddle。\n",
+    "\n",
+    "## 安装 Paddle Quantum\n",
+    "\n",
+    "下载 Paddle Quantum 的安装包，修改`setup.py`，将其中的`paddlepaddle`改为`paddlepaddle-gpu`，然后按照 Paddle Quantum 的安装要求，执行`pip install -e .`即可。\n",
+    "\n",
+    "> 如果你是在一个新的 python 环境中安装了 paddlepaddle-gpu 和 paddle_quantum，请在新 python 环境中安装 jupyter，并在新的 jupyter 下重新打开本教程并运行。\n",
+    "\n",
+    "## 检测是否安装成功\n",
     "\n",
     "打开我们 GPU 版本的 PaddlePaddle 环境，执行下面的命令，若输出为`True`则表示当前 PaddlePaddle 框架可以在GPU上运行。"
    ]
@@ -76,7 +81,15 @@
    "cell_type": "code",
    "execution_count": 1,
    "metadata": {},
-   "outputs": [],
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "True\n"
+     ]
+    }
+   ],
    "source": [
     "import paddle \n",
     "from paddle import fluid\n",
@@ -87,37 +100,53 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 7. 使用教程和示例\n",
-    "\n",
-    "在 Paddle Quantum 中，我们使用动态图机制来定义和训练我们的参数化量子线路。在这里，我们依然使用动态图机制，只需要定义动态图机制的运行设备即可。方式如下：\n",
+    "## 使用教程和示例\n",
     "\n",
+    "在 Paddle Quantum 中，我们使用动态图机制来定义和训练我们的参数化量子线路。在这里，我们依然使用动态图机制，只需要定义动态图机制的运行设备即可。方式如下："
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "```python\n",
     "# 0 表示使用编号为0的GPU\n",
     "place = fluid.CUDAPlace(0)\n",
     "with fluid.dygraph.guard(place):\n",
     "    # build and train your quantum circuit model\n",
-    "```\n",
-    "\n",
-    "当我们想在 CPU 上运行时，也采用类似的方式，定义运行设备为CPU：\n",
+    "```"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "当我们想在 CPU 上运行时，也采用类似的方式，定义运行设备为CPU："
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "```python\n",
     "place = fluid.CPUPlace()\n",
     "with fluid.dygraph.guard(place):\n",
     "    # build and train your quantum circuit model\n",
-    "```\n",
-    "\n",
-    "我们可以在命令行中输入`nvidia-smi`来查看 GPU 的使用情况，包括有哪些程序在哪些 GPU 上运行，以及其显存占用情况。"
+    "```"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
+    "我们可以在命令行中输入`nvidia-smi`来查看 GPU 的使用情况，包括有哪些程序在哪些 GPU 上运行，以及其显存占用情况。\n",
+    "\n",
     "这里，我们以 [VQE](https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/VQE) 为例来说明我们该如何使用 GPU。首先，导入相关的包并定义相关的变量和函数。"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 3,
+   "execution_count": 2,
    "metadata": {},
    "outputs": [],
    "source": [
@@ -128,6 +157,7 @@
     "from paddle import fluid\n",
     "from paddle.complex import matmul, transpose\n",
     "from paddle_quantum.circuit import UAnsatz\n",
+    "\n",
     "import matplotlib.pyplot as plt\n",
     "import numpy\n",
     "from paddle_quantum.VQE.chemistrysub import H2_generator\n",
@@ -154,7 +184,7 @@
     "    # 量子神经网络作用在默认的初始态 |0000>上\n",
     "    cir.run_state_vector()\n",
     "\n",
-    "    # 计算给定哈密顿量的期望值\n",
+    "    # 计算给定 Hamilton 量的期望值\n",
     "    expectation_val = cir.expecval(Hamiltonian)\n",
     "\n",
     "    return expectation_val\n",
@@ -165,11 +195,13 @@
     "    Construct the model net\n",
     "    \"\"\"\n",
     "\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * PI), dtype=\"float64\"):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * PI), dtype=\"float64\"):\n",
     "        super(StateNet, self).__init__()\n",
     "\n",
     "        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.theta = self.create_parameter(\n",
+    "          shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
     "\n",
     "    # 定义损失函数和前向传播机制\n",
     "    def forward(self, Hamiltonian, N, D):\n",
@@ -192,18 +224,36 @@
   },
   {
    "cell_type": "code",
-   "execution_count": null,
+   "execution_count": 3,
    "metadata": {},
-   "outputs": [],
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 20 loss: -1.0599\n",
+      "iter: 20 Ground state energy: -1.0599 Ha\n",
+      "iter: 40 loss: -1.1229\n",
+      "iter: 40 Ground state energy: -1.1229 Ha\n",
+      "iter: 60 loss: -1.1347\n",
+      "iter: 60 Ground state energy: -1.1347 Ha\n",
+      "iter: 80 loss: -1.1359\n",
+      "iter: 80 Ground state energy: -1.1359 Ha\n"
+     ]
+    }
+   ],
    "source": [
     "# 0 表示使用编号为0的GPU\n",
     "place_gpu = fluid.CUDAPlace(0)\n",
-    "with fluid.dygraph.guard(palce_gpu):\n",
+    "with fluid.dygraph.guard(place_gpu):\n",
+    "  \n",
     "        # 确定网络的参数维度\n",
     "        net = StateNet(shape=[D + 1, N, 1])\n",
     "\n",
-    "        # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "        opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "        # 一般来说，我们利用Adam优化器来获得相对好的收敛\n",
+    "        # 当然你可以改成SGD或者是RMS prop.\n",
+    "        opt = fluid.optimizer.AdamOptimizer(\n",
+    "          learning_rate=LR, parameter_list=net.parameters())\n",
     "\n",
     "        # 记录优化结果\n",
     "        summary_iter, summary_loss = [], []\n",
@@ -226,11 +276,9 @@
     "            # 打印结果\n",
     "            if itr % 20 == 0:\n",
     "                print(\"iter:\", itr, \"loss:\", \"%.4f\" % loss.numpy())\n",
-    "                print(\"iter:\", itr, \"Ground state energy:\", \"%.4f Ha\" % loss.numpy())\n",
-    "\n",
-    "        # 储存训练结果到 output 文件夹\n",
-    "        os.makedirs(\"output\", exist_ok=True)\n",
-    "        savez(\"./output/summary_data\", iter=summary_iter, energy=summary_loss)"
+    "                print(\"iter:\", itr, \"Ground state energy:\", \n",
+    "                      \"%.4f Ha\" % loss.numpy())\n",
+    "\n"
    ]
   },
   {
@@ -249,14 +297,14 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "iter: 20 loss: -1.0669\n",
-      "iter: 20 Ground state energy: -1.0669 Ha\n",
-      "iter: 40 loss: -1.1129\n",
-      "iter: 40 Ground state energy: -1.1129 Ha\n",
-      "iter: 60 loss: -1.1163\n",
-      "iter: 60 Ground state energy: -1.1163 Ha\n",
-      "iter: 80 loss: -1.1172\n",
-      "iter: 80 Ground state energy: -1.1172 Ha\n"
+      "iter: 20 loss: -1.0865\n",
+      "iter: 20 Ground state energy: -1.0865 Ha\n",
+      "iter: 40 loss: -1.1153\n",
+      "iter: 40 Ground state energy: -1.1153 Ha\n",
+      "iter: 60 loss: -1.1338\n",
+      "iter: 60 Ground state energy: -1.1338 Ha\n",
+      "iter: 80 loss: -1.1359\n",
+      "iter: 80 Ground state energy: -1.1359 Ha\n"
      ]
     }
    ],
@@ -264,11 +312,14 @@
     "# 表示使用 CPU\n",
     "place_cpu = fluid.CPUPlace()\n",
     "with fluid.dygraph.guard(place_cpu):\n",
+    "  \n",
     "    # 确定网络的参数维度\n",
     "    net = StateNet(shape=[D + 1, N, 1])\n",
     "\n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛\n",
+    "    # 当然你可以改成SGD或者是RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(\n",
+    "      learning_rate=LR, parameter_list=net.parameters())\n",
     "\n",
     "    # 记录优化结果\n",
     "    summary_iter, summary_loss = [], []\n",
@@ -291,26 +342,20 @@
     "        # 打印结果\n",
     "        if itr % 20 == 0:\n",
     "            print(\"iter:\", itr, \"loss:\", \"%.4f\" % loss.numpy())\n",
-    "            print(\"iter:\", itr, \"Ground state energy:\", \"%.4f Ha\" % loss.numpy())\n",
-    "\n",
-    "    # 储存训练结果到 output 文件夹\n",
-    "    # os.makedirs(\"output\", exist_ok=True)\n",
-    "    # savez(\"./output/summary_data\", iter=summary_iter, energy=summary_loss)"
+    "            print(\"iter:\", itr, \"Ground state energy:\", \n",
+    "                  \"%.4f Ha\" % loss.numpy())"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 8. 总结\n",
+    "## 总结\n",
+    "\n",
+    "按照我们的测试，现在版本的 paddle_quantum 可以在 GPU 下运行，但是需要比较好的 GPU 资源才能体现出足够的加速效果。在未来的版本中，我们也会不断优化 paddle_quantum 在 GPU 下的性能表现，敬请期待。\n",
+    "\n",
+    "_______\n",
     "\n",
-    "实践证明，我们现在的 paddle_quantum 可以在 GPU 下运行，目前需要比较好的 GPU 资源才能体现出 GPU 的加速效果。在未来的版本中，我们也会不断优化 paddle_quantum 在 GPU 下的性能表现。"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
     "## 参考资料\n",
     "\n",
     "[1] [Installation Guide Windows :: CUDA Toolkit Documentation](https://docs.nvidia.com/cuda/cuda-installation-guide-microsoft-windows/index.html)\n",
@@ -337,7 +382,20 @@
    "name": "python",
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
-   "version": "3.7.7"
+   "version": "3.7.9"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
   }
  },
  "nbformat": 4,

introduction/PaddleQuantum_GPU_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Use Paddle Quantum on GPU\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Introduction\n",
+    "\n",
+    "> Note that this tutorial is time-sensitive. And different computers will have individual differences. This tutorial does not guarantee that all computers can install it successfully.\n",
+    "\n",
+    "In deep learning, people usually use GPU for neural network model training because GPU has significant advantages in floating-point operations compared with CPU. Therefore, using GPU to train neural network models has gradually become a common choice. In Paddle Quantum, our quantum states and quantum gates are also represented by complex numbers based on floating-point numbers. If our model can be deployed on GPU for training, it will also significantly increase the training speed.\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## GPU selection\n",
+    "\n",
+    "Here, we choose Nvidia's hardware devices, and its CUDA (Compute Unified Device Architecture) supports deep learning framework better. PaddlePaddle can also be easily installed on CUDA.\n",
+    "\n",
+    "## Configure CUDA environment\n",
+    "\n",
+    "### Install CUDA\n",
+    "\n",
+    "Here, we introduce how to configure the CUDA environment in Windows 10 on the x64 platform. First, check on [CUDA GPUs | NVIDIA Developer](https://developer.nvidia.com/cuda-gpus) to see if your GPU support the CUDA environment. Then, download the latest version of your graphics card driver from [NVIDIA Driver Download](https://www.nvidia.cn/Download/index.aspx?lang=cn) and install it on your computer.\n",
+    "\n",
+    "In [PaddlePaddle Installation Steps](https://www.paddlepaddle.org.cn/install/quick), we found that **Paddle Paddle only supports CUDA 9.0/10.0 single card mode under Windows; it does not support CUDA 9.1/9.2/10.1**, so we need to install CUDA10.0 (CUDA 9.0 is also possible in theory). Find the download link of CUDA 10.0 in [CUDA Toolkit Archive | NVIDIA Developer](https://developer.nvidia.com/cuda-toolkit-archive): [CUDA Toolkit 10.0 Archive | NVIDIA Developer](https://developer.nvidia.com/cuda-10.0-download-archive). After downloading CUDA, run the installation.\n",
+    "\n",
+    "During the installation process, select **Custom Installation** in the CUDA options, check all the boxes except for Visual Studio Integration (unless you are familiar with it). Then check CUDA option only. Then select the default location for the installation location (please pay attention to the installation location of your CUDA, you need to set environment variables later), and wait for the installation to complete.\n",
+    "\n",
+    "After the installation is complete, open the Windows command line and enter `nvcc -V`. If you see the version information, the CUDA installation is successful.\n",
+    "\n",
+    "### Install cuDNN\n",
+    "\n",
+    "Download cuDNN in [NVIDIA cuDNN | NVIDIA Developer](https://developer.nvidia.com/cudnn), according to [PaddlePaddle Installation Steps](https://www.paddlepaddle.org.cn/install/quick) requirements, we **need to use cuDNN 7.6+**, so we can download the latest version of cuDNN that supports CUDA 10.0. After downloading cuDNN, unzip it. Assuming the installation path of our CUDA is `C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0`. After decompressing cuDNN, we take the files in `bin`, `include` and `lib` and replace the corresponding original files in the CUDA installation path (if the file already exists, replace it, if it does not exist, paste it directly into the corresponding directory). At this point, cuDNN has been installed.\n",
+    "\n",
+    "### Configure environment variables\n",
+    "\n",
+    "Next, you need to configure environment variables. Right-click \"This PC\" on the desktop of the computer (or \"This PC\" in the left column of \"File Explorer\"), select \"Properties\", and then select \"Advanced System Settings\" on the left, under the \"Advanced\" column Select \"Environmental Variables\".\n",
+    "\n",
+    "Now you enter the setting page of environment variables, select `Path` in the `System variables`, and click `Edit`. In the page that appears, check if there are two addresses `C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0\\bin` and `C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0\\libnvvp`  (the prefix `C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0` should be your CUDA installation location), if not, please add them manually.\n",
+    "\n",
+    "### Verify that the installation is successful\n",
+    "\n",
+    "Open the command line and enter `cd C:\\Program Files\\NVIDIA GPU Computing Toolkit\\CUDA\\v10.0\\extras\\demo_suite` to enter the CUDA installation path (this should also be your CUDA installation location). Then execute `.\\bandwidthTest.exe` and `.\\deviceQuery.exe` respectively. If both `Result = PASS` appear, the installation is successful.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Install PaddlePaddle on CUDA environment\n",
+    "\n",
+    "According to the instructions in [PaddlePaddle Installation Steps](https://www.paddlepaddle.org.cn/install/quick), we first need to make sure our python environment is correct and use `python --version` to check the python version. Ensure that the **python version is 3.5.1+/3.6+/3.7+**, and use `python -m ensurepip` and `python -m pip --version` to check the pip version, **confirm it is 9.0.1+**. Then, use `python -m pip install paddlepaddle-gpu==1.8.4.post107 -i https://pypi.tuna.tsinghua.edu.cn/simple` to install the GPU version of PaddlePaddle.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Install Paddle Quantum\n",
+    "\n",
+    "Download the Paddle Quantum installation package, modify `setup.py`, change paddlepaddle` to `paddlepaddle-gpu`, and then execute `pip install -e .` according to the installation requirements of Paddle Quantum.\n",
+    "\n",
+    "> If you have installed paddlepaddle-gpu and paddle_quantum in a new python environment, please also install jupyter in the new python environment, and reopen this tutorial under the new jupyter notebook and run it."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Check if the installation is successful\n",
+    "\n",
+    "Open the new environment where we installed  the GPU version of PaddlePaddle and execute the following command. If the output is `True`, it means that the current PaddlePaddle framework can run on the GPU.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "True\n"
+     ]
+    }
+   ],
+   "source": [
+    "import paddle \n",
+    "from paddle import fluid\n",
+    "print(fluid.is_compiled_with_cuda())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Use tutorials and examples\n",
+    "\n",
+    "In Paddle Quantum, we use the dynamic graph mode to define and train our parameterized quantum circuits. Here, we still use the dynamic graph mode and only need to define the GPU core where we run the dynamic graph mode."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "```python\n",
+    "# 0 means to use GPU number 0\n",
+    "place = fluid.CUDAPlace(0)\n",
+    "with fluid.dygraph.guard(place):\n",
+    "    # build and train your quantum circuit model\n",
+    "```"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "If we want to run on CPU,  pretty much the same,  define the running device as CPU:"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "```python\n",
+    "place = fluid.CPUPlace()\n",
+    "with fluid.dygraph.guard(place):\n",
+    "    # build and train your quantum circuit model\n",
+    "```"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "We can enter `nvidia-smi` in the command line to view the usage of the GPU, including which programs are running on which GPUs, and its memory usage.\n",
+    "\n",
+    "Here, we take [VQE](https://github.com/PaddlePaddle/Quantum/blob/master/tutorial/VQE) as an example to illustrate how we should use GPU. First, import the related packages and define some variables and functions."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "import os\n",
+    "from numpy import concatenate\n",
+    "from numpy import pi as PI\n",
+    "from numpy import savez, zeros\n",
+    "from paddle import fluid\n",
+    "from paddle.complex import matmul, transpose\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "\n",
+    "import matplotlib.pyplot as plt\n",
+    "import numpy\n",
+    "from paddle_quantum.VQE.chemistrysub import H2_generator\n",
+    "from time import time\n",
+    "\n",
+    "Hamiltonian, N = H2_generator()\n",
+    "\n",
+    "\n",
+    "def U_theta(theta, Hamiltonian, N, D):\n",
+    "    \"\"\"\n",
+    "    Quantum Neural Network\n",
+    "    \"\"\"\n",
+    "    \n",
+    "    # Initialize the quantum neural network according to the number of qubits/network width\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Built-in {R_y + CNOT} circuit template\n",
+    "    cir.real_entangled_layer(theta[:D], D)\n",
+    "\n",
+    "    # Add in the last row a layer of R_y rotation gates\n",
+    "    for i in range(N):\n",
+    "        cir.ry(theta=theta[D][i][0], which_qubit=i)\n",
+    "\n",
+    "    # The quantum neural network acts on the default initial state |0000>\n",
+    "    cir.run_state_vector()\n",
+    "\n",
+    "    # Calculate the expected value of a given Hamiltonian\n",
+    "    expectation_val = cir.expecval(Hamiltonian)\n",
+    "\n",
+    "    return expectation_val\n",
+    "\n",
+    "\n",
+    "class StateNet(fluid.dygraph.Layer):\n",
+    "    \"\"\"\n",
+    "    Construct the model net\n",
+    "    \"\"\"\n",
+    "\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * PI), dtype=\"float64\"):\n",
+    "        super(StateNet, self).__init__()\n",
+    "\n",
+    "        # Initialize the theta parameter list and fill the initial value with the uniform distribution of [0, 2*pi]\n",
+    "        self.theta = self.create_parameter(\n",
+    "          shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "\n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self, Hamiltonian, N, D):\n",
+    "        # Calculate loss function/expected value\n",
+    "        loss = U_theta(self.theta, Hamiltonian, N, D)\n",
+    "\n",
+    "        return loss\n",
+    "\n",
+    "ITR = 80 # Set the total number of training iterations\n",
+    "LR = 0.2 # Set the learning rate\n",
+    "D = 2 # Set the depth of the repeated calculation module in the neural network"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "If you want to use GPU to train, run the following program:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 20 loss: -0.8634\n",
+      "iter: 20 Ground state energy: -0.8634 Ha\n",
+      "iter: 40 loss: -1.1203\n",
+      "iter: 40 Ground state energy: -1.1203 Ha\n",
+      "iter: 60 loss: -1.1350\n",
+      "iter: 60 Ground state energy: -1.1350 Ha\n",
+      "iter: 80 loss: -1.1359\n",
+      "iter: 80 Ground state energy: -1.1359 Ha\n"
+     ]
+    }
+   ],
+   "source": [
+    "# 0 means to use GPU number 0\n",
+    "place_gpu = fluid.CUDAPlace(0)\n",
+    "with fluid.dygraph.guard(place_gpu):\n",
+    "  \n",
+    "        # Determine the parameter dimension of the network\n",
+    "        net = StateNet(shape=[D + 1, N, 1])\n",
+    "\n",
+    "        # Generally speaking, we use Adam optimizer to get relatively good convergence\n",
+    "        # Of course, you can change to SGD or RMS prop.\n",
+    "        opt = fluid.optimizer.AdamOptimizer(\n",
+    "          learning_rate=LR, parameter_list=net.parameters())\n",
+    "\n",
+    "        # Record optimization results\n",
+    "        summary_iter, summary_loss = [], []\n",
+    "\n",
+    "        # Optimization cycle\n",
+    "        for itr in range(1, ITR + 1):\n",
+    "\n",
+    "            # Forward propagation to calculate loss function\n",
+    "            loss = net(Hamiltonian, N, D)\n",
+    "\n",
+    "            # Under the dynamic graph mechanism, back propagation minimizes the loss function\n",
+    "            loss.backward()\n",
+    "            opt.minimize(loss)\n",
+    "            net.clear_gradients()\n",
+    "\n",
+    "            # Update optimization results\n",
+    "            summary_loss.append(loss.numpy())\n",
+    "            summary_iter.append(itr)\n",
+    "\n",
+    "            # Print results\n",
+    "            if itr% 20 == 0:\n",
+    "                print(\"iter:\", itr, \"loss:\", \"%.4f\"% loss.numpy())\n",
+    "                print(\"iter:\", itr, \"Ground state energy:\",\n",
+    "                      \"%.4f Ha\"% loss.numpy())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "If you want to use CPU to train, run the following program:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 20 loss: -0.7789\n",
+      "iter: 20 Ground state energy: -0.7789 Ha\n",
+      "iter: 40 loss: -1.0741\n",
+      "iter: 40 Ground state energy: -1.0741 Ha\n",
+      "iter: 60 loss: -1.1271\n",
+      "iter: 60 Ground state energy: -1.1271 Ha\n",
+      "iter: 80 loss: -1.1351\n",
+      "iter: 80 Ground state energy: -1.1351 Ha\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Use CPU\n",
+    "place_cpu = fluid.CPUPlace()\n",
+    "with fluid.dygraph.guard(place_cpu):\n",
+    "  \n",
+    "    # Determine the parameter dimension of the network\n",
+    "    net = StateNet(shape=[D + 1, N, 1])\n",
+    "\n",
+    "    # Generally speaking, we use Adam optimizer to get relatively good convergence\n",
+    "    # Of course you can change to SGD or RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(\n",
+    "      learning_rate=LR, parameter_list=net.parameters())\n",
+    "\n",
+    "    # Record optimization results\n",
+    "    summary_iter, summary_loss = [], []\n",
+    "\n",
+    "    # Optimization cycle\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "\n",
+    "        # Forward propagation to calculate loss function\n",
+    "        loss = net(Hamiltonian, N, D)\n",
+    "\n",
+    "        # Under the dynamic graph mechanism, back propagation minimizes the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "\n",
+    "        # Update optimization results\n",
+    "        summary_loss.append(loss.numpy())\n",
+    "        summary_iter.append(itr)\n",
+    "\n",
+    "        # Print results\n",
+    "        if itr% 20 == 0:\n",
+    "            print(\"iter:\", itr, \"loss:\", \"%.4f\"% loss.numpy())\n",
+    "            print(\"iter:\", itr, \"Ground state energy:\",\n",
+    "                  \"%.4f Ha\"% loss.numpy())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Summary\n",
+    "\n",
+    "According to our test, the current version of paddle_quantum can run under GPU, but it needs better GPU resources to show sufficient acceleration. In future versions, we will continue to optimize the performance of Paddle Quantum under GPU. \n",
+    "\n",
+    "_______\n",
+    "\n",
+    "## Reference\n",
+    "\n",
+    "[1] [Installation Guide Windows :: CUDA Toolkit Documentation](https://docs.nvidia.com/cuda/cuda-installation-guide-microsoft-windows/index.html)\n",
+    "\n",
+    "[2] [Installation Guide :: NVIDIA Deep Learning cuDNN Documentation](https://docs.nvidia.com/deeplearning/cudnn/install-guide/index.html#installwindows)\n",
+    "\n",
+    "[3] [Getting Started PaddlePaddle](https://www.paddlepaddle.org.cn/install/quick)\n",
+    "\n"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.7.9"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

introduction/PaddleQuantum_Tutorial_CN.ipynb

@@ -6,7 +6,7 @@
    "source": [
     "# Paddle Quantum 入门手册\n",
     "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
    ]
   },
   {
@@ -22,8 +22,17 @@
    "source": [
     "这是一份简洁、实用的关于量子机器学习（Quantum Machine Learnig，QML）的介绍，面向读者包括但不限于物理、数学和计算机背景。本手册主要采用 Jupyter Notebook 的交互形式 (调用 Numpy, Matplotlib等 Python包以及飞桨Paddlepaddle深度学习框架来实现基于线性代数的量子运算和机器学习优化问题)。我们不仅提供了关于量子计算的一些基础教程同时还能手把手带你完成属于你自己的第一份量子机器学习算法。这并不是一份关于量子计算的百科全书，但我们涉及的案例经常出现在教科书中以及文献中。如果你想深入挖掘一些相关的基础知识，我们也提供了一些外部链接方便用户自己学习。\n",
     "\n",
+    "量子计算是由量子力学与计算理论交叉形成的新型学科，本质上是通过量子力学的基本规律去操控信息单元量子比特（quantum bit, qubit）的新型计算模式。与经典计算模型相比，在许多特定的信息处理任务上量子计算被普遍认为具有更强大的信息处理优势。关于量子计算的介绍与入门知识可以参考 [1-2]，想要系统性地学习量子计算学科的读者请参阅 Nielsen & Chuang 编写的经典教材 [3]。近期，量子计算领域中一个热门的课题是如何有效地结合量子计算和人工智能两者的潜能。量子机器学习便是这样一门结合了量子计算与机器学习的交叉学科，一方面研究者们希望利用量子计算的信息处理优势去促进人工智能的发展，另一方面也存在可能性去利用现有的人工智能的技术突破量子计算的研发瓶颈。关于量子机器学习的入门资料可以参考 [4-6]。\n",
     "\n",
-    "最后修改于: 2020年9月9日 由量桨 Paddle Quantum开发小组共同完成。\n",
+    "内容上，这份快速入门包括以下几个方面：\n",
+    "\n",
+    "- 量子计算和量子神经网络的基础知识介绍\n",
+    "- 量桨（Paddle Quantum）的使用介绍\n",
+    "- 飞桨（PaddlePaddle）优化器的使用教程\n",
+    "- 具体的量子机器学习案例—— 变分量子特征求解器（VQE）\n",
+    "\n",
+    "\n",
+    "最后修改于: 2021年1月9日 由量桨 Paddle Quantum 开发小组共同完成。\n",
     "\n",
     "<hr>"
    ]
@@ -83,12 +92,12 @@
    "source": [
     "我们推荐使用 [Anaconda](https://www.anaconda.com/download) 作为 Python3的开发环境，支持多种主流操作系统（Windows, MacOS, 以及 Linux）。Anaconda本身提供 Scipy, Numpy, Matplotlib等科学计算、作图包，最主要的是其自带 Python开发环境的管理器 conda，可以用来安装或者更新主流 Python包。这里我们提供一个例子来学习使用 conda创建和管理环境：\n",
     "\n",
-    "1. 首先进入命令行 (Terminal) 界面：Windows用户可以使用组合键 `win + R` 打开运行程序再输入 `cmd`/ Mac用户可以使用组合键 `command⌘ + 空格` 再输入 `Terminal`。\n",
+    "1. 首先进入命令行 (Terminal) 界面：Windows用户可以通过 `Anaconda Prompt`/ Mac用户可以使用组合键 `command⌘ + 空格` 再输入 `Terminal`。\n",
     "1. 进入 Terminal 后输入 `conda create --name paddle_quantum_env python=3.6` 创建名为 `paddle_quantum_env` 的 Python3.6 环境。\n",
     "1. 在 Terminal 内通过 `conda env list` 查看已有的环境，然后通过 `conda activate paddle_quantum_env ` 进入我们刚建立的环境。\n",
-    "1. 为了能正确运行 Jupyter Notebook 我们还需要安装 `conda install jupyter notebook`。安装完成之后，如果你想开启 Jupyter 只需要在Terminal内激活正确的环境然后输入 `jupyter notebook` 即可。\n",
+    "1. 为了能正确运行 Jupyter Notebook 我们还需要安装 `conda install jupyter notebook` 或者 `pip install jupyter notebook`。安装完成之后，如果你想开启 Jupyter 只需要在Terminal内激活正确的环境然后输入 `jupyter notebook` 即可。\n",
     "\n",
-    "<img src=\"figures/terminal.png\" width=\"650\" >\n",
+    "<img src=\"figures/intro-fig-terminal.png\" width=\"650\" >\n",
     "\n",
     "关于 conda 更多的本地指令请参考 [官方教程](https://docs.conda.io/projects/conda/en/latest/user-guide/getting-started.html)。\n",
     "<span class=\"blue\"> 此外，你也可以通过使用 <a href=\"https://docs.anaconda.com/anaconda/navigator/\"> Anaconda Navigator</a> 开启 jupyter notebook。\n",
@@ -96,7 +105,7 @@
     "以下是这个教程中你需要使用的包:\n",
     "<ul>\n",
     "    <li>Numpy\n",
-    "    <li>Paddlepaddle 1.8.3 以上\n",
+    "    <li>Paddlepaddle 1.8.5\n",
     "    <li>Paddle Quantum \n",
     "</ul>"
    ]
@@ -112,67 +121,18 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "接着我们先讲解下如何安装飞桨Paddlepaddle深度学习框架。用户需要再次打开 Terminal 界面，输入 `conda activate paddle_quantum_env `进入我们新建的Python 环境。接着输入 `conda install paddlepaddle` 安装最新的飞桨Paddle。如果你在按照以上方案安装 paddle-cpu 或者 paddle-gpu 遇到问题们可以参考 [官方链接](https://www.paddlepaddle.org.cn/documentation/docs/zh/install/install_Conda.html)。或者考虑以下备选方案：在 Terminal 界面输入 `pip install paddlepaddle` 或者开启 jupyter notebook 后运行以下的命令。"
+    "接着我们安装 Paddle Quantum 包，用户可以直接通过 `pip install paddle-quantum` 完成安装。关于本地安装方式，用户可以通过 Terminal 界面使用 git指令 `git clone http://github.com/PaddlePaddle/quantum` 或者直接下载 `zip` 压缩包，然后找到对应本地文件的路径输入 `cd quantum` 和 `pip install -e .` 完成安装。接着在 Terminal 界面输入`pip list`查看是否在正确的环境中安装完成。关于 git的使用和安装，请参考这篇 [教程](https://git-scm.com/book/zh/v2/%E8%B5%B7%E6%AD%A5-%E5%AE%89%E8%A3%85-Git)。此外，如果你需要更多的关于安装 Paddle Quantum 的帮助，可以参考我们的 [Github链接](https://github.com/PaddlePaddle/Quantum) 或者通过 Github Issues联系我们。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 1,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "from IPython.display import clear_output\n",
-    "\n",
-    "# 备用方法： 通过PyPI安装最新的飞桨Paddle\n",
-    "!pip install paddlepaddle\n",
-    "clear_output()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "在安装完成后，请通过以下代码段来检验是否成功安装 Paddle。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 2,
    "metadata": {
-    "colab": {},
-    "colab_type": "code",
-    "id": "HPV-UyAqsKFp"
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "Running Verify Fluid Program ... \n",
-      "Your Paddle Fluid works well on SINGLE GPU or CPU.\n",
-      "Your Paddle Fluid works well on MUTIPLE GPU or CPU.\n",
-      "Your Paddle Fluid is installed successfully! Let's start deep Learning with Paddle Fluid now\n"
-     ]
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:47:03.252187Z",
+     "start_time": "2021-01-09T12:46:59.940104Z"
     }
-   ],
-   "source": [
-    "from paddle import fluid\n",
-    "\n",
-    "# 检查飞桨Paddle是否成功安装\n",
-    "fluid.install_check.run_check()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "接着我们安装 Paddle Quantum包，很遗憾目前我们还不支持通过 pip安装。需要用户在 Terminal 界面通过 git指令 `git clone http://github.com/PaddlePaddle/quantum` 下载文件，然后输入 `cd quantum` 和 `pip install -e .` 完成安装。接着在 Terminal 界面输入`pip list`查看是否在正确的环境中安装完成。关于 git的使用和安装，请参考这篇 [教程](https://git-scm.com/book/zh/v2/%E8%B5%B7%E6%AD%A5-%E5%AE%89%E8%A3%85-Git)。此外，如果你需要更多的关于安装Paddle-Quantum 的帮助，可以参考我们的 [Github链接](https://github.com/PaddlePaddle/Quantum) 或者通过 Github Issues联系我们。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 3,
-   "metadata": {},
+   },
    "outputs": [],
    "source": [
     "import numpy as np\n",
@@ -210,7 +170,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "量子计算 (Quantum Computing QC )是利用量子物理中特有的现象 (量子叠加态，量子纠缠)来设计相应的量子算法以解决 (物理、化学、计算机等领域)特定的任务。现有的量子计算有好几种模型，比如有基于绝热定理的绝热计算模型以及基于测量的MBQC模型等等。在本手册中，我们主要讨论目前影响力最大、使用最广泛的量子电路（Quantum circuit）模型。在量子电路的框架下，运算最基本的组成单元是量子比特 (qubit)。这与经典计算机中比特 (bit) 的概念很相似。经典比特只能处于0和1两种状态中的某一种 (物理图景上可以对应高低电位)。与之不同的是，量子比特不仅可以处于两个状态$\\lvert {0}\\rangle$ 还有 $\\lvert {1}\\rangle$还可以处于两者的叠加态 (稍后我们来具体讲解下这一概念)。而常见的量子计算模型，就是利用量子逻辑门操控这些量子比特。逻辑门运算的基本理论是线性代数，在此我们假定读者已经具备一定的线性代数基础。"
+    "量子计算（Quantum Computing, QC）是利用量子物理中特有的现象（量子叠加态、量子相干性和量子纠缠等）来设计相应的量子算法以解决 （物理、化学、计算机等领域）特定的任务。现有的量子计算有存在几种模型，例如基于绝热定理的绝热量子计算模型（Adiabatic Quantum Computation, AQC）以及基于测量的量子计算模型（Measurement-Based Quantum Computation, MBQC）等等。在本介绍中，我们主要讨论目前影响力最大、使用最广泛的量子电路（Quantum Circuit）模型。在量子电路的框架下，运算最基本的组成单元是量子比特（qubit）。这与经典计算机中比特（bit）的概念很相似。经典比特只能处于0和1两种状态中的某一种（物理图景上可以对应晶体管的高低电位）。与之不同的是，量子比特不仅可以处于两个状态 $|0\\rangle$ 还有 $|1\\rangle$ 还可以处于两者的叠加态（稍后我们来具体讲解下这一概念）。在量子电路模型中，我们通过由一系列量子逻辑门构成的量子电路来操控这些量子比特的状态从而完成计算任务。逻辑门运算的基本理论是线性代数，在此我们假定读者已经具备一定的线性代数基础。"
    ]
   },
   {
@@ -226,22 +186,26 @@
    "source": [
     "### 数学表示\n",
     "\n",
-    "在量子力学中，一个微观粒子的量子态可以表示为由两个正规正交基线性组合得到的向量，这些基向量一般可以写为：\n",
+    "在量子力学中，一个二能级系统微观粒子（qubit）的量子态（quantum state）可以表示为由两个正规正交基线性组合得到的向量，这些基向量一般可以写为\n",
     "\n",
-    "$$ \\lvert {0}\\rangle := \\begin{bmatrix} 1 \\\\ 0 \\end{bmatrix}, \\quad \\lvert {1}\\rangle := \\begin{bmatrix} 0 \\\\ 1 \\end{bmatrix} $$\n",
+    "$$\n",
+    "|0\\rangle := \\begin{bmatrix} 1 \\\\ 0 \\end{bmatrix}, \\quad |1\\rangle := \\begin{bmatrix} 0 \\\\ 1 \\end{bmatrix}.\n",
+    "\\tag{1}\n",
+    "$$\n",
     "\n",
-    "我们这里向量的表示方法采用了量子物理上传统的狄拉克表示 (bra-ket)。这两个单位正交向量$\\{\\lvert {0}\\rangle, \\lvert {1}\\rangle \\}$，它俩一般被称为**计算基** (computational basis)。物理图景中我们可以认为 $\\lvert {0}\\rangle$ 和 $\\lvert {1}\\rangle$ 分别对应一个原子的能量基态和激发态或者其他一些二分类状态。 一个量子比特所有可能的态可以看作是二维希尔伯特空间中所有的归一化向量，这个希尔伯特空间的一组正规正交基正是$\\{\\lvert {0}\\rangle, \\lvert {1}\\rangle \\}$。而更多的量子比特系统也同样可以由高维度的希尔伯特空间中的的单位向量表示，而这个高维希尔伯特空间的正交基就是$\\{\\lvert {0}\\rangle, \\lvert {1}\\rangle \\}$的张量积。比如说，一个两量子比特 (2-qubit)系统可以被一个4维的希尔伯特空间里的单位复数向量表示，而这个希尔伯特空间的正规正交基是：\n",
+    "这里向量的表示方法采用了量子物理上传统的狄拉克表示（bra-ket）。这两个单位正交向量 $\\{|0\\rangle, |1\\rangle \\}$ 一般被称为**计算基**（computational basis）。物理图景中我们可以认为 $|0\\rangle$ 和 $|1\\rangle$ 分别对应一个原子的能量基态和激发态或者其他一些二分类状态。 一个量子比特所有可能的态可以看作是二维希尔伯特空间中所有的归一化向量，这个希尔伯特空间的一组正规正交基正是 $\\{|0\\rangle, |1\\rangle \\}$。更多的量子比特系统也同样可以由高维度的希尔伯特空间中的的单位向量表示，而这个高维希尔伯特空间的正交基就是 $\\{|0\\rangle, |1\\rangle \\}$ 的张量积。比如说，一个两量子比特（2-qubit）系统可以被一个4维的希尔伯特空间里的单位复数向量表示，而这个希尔伯特空间的正规正交基是\n",
     "\n",
-    "$$ \n",
-    "\\lvert {00}\\rangle = \\lvert {0}\\rangle\\otimes \\lvert {0}\\rangle := \\begin{bmatrix} 1 \\\\ 0 \\\\ 0 \\\\ 0 \\end{bmatrix}, \\quad \n",
-    "\\lvert {01}\\rangle = \\lvert {0}\\rangle\\otimes \\lvert {1}\\rangle := \\begin{bmatrix} 0 \\\\ 1 \\\\ 0 \\\\ 0 \\end{bmatrix}, \\quad\n",
-    "\\lvert {10}\\rangle = \\lvert {1}\\rangle\\otimes \\lvert {0}\\rangle := \\begin{bmatrix} 0 \\\\ 0 \\\\ 1 \\\\ 0 \\end{bmatrix}, \\quad\n",
-    "\\lvert {11}\\rangle = \\lvert {1}\\rangle\\otimes \\lvert {0}\\rangle := \\begin{bmatrix} 0 \\\\ 0 \\\\ 0 \\\\ 1 \\end{bmatrix}\n",
+    "$$\n",
+    "\\left\\{\n",
+    "|00\\rangle = |0\\rangle\\otimes |0\\rangle := \\begin{bmatrix} 1 \\\\ 0 \\\\ 0 \\\\ 0 \\end{bmatrix}, \\quad \n",
+    "|01\\rangle = |0\\rangle\\otimes |1\\rangle := \\begin{bmatrix} 0 \\\\ 1 \\\\ 0 \\\\ 0 \\end{bmatrix}, \\quad\n",
+    "|10\\rangle = |1\\rangle\\otimes |0\\rangle := \\begin{bmatrix} 0 \\\\ 0 \\\\ 1 \\\\ 0 \\end{bmatrix}, \\quad\n",
+    "|11\\rangle = |1\\rangle\\otimes |0\\rangle := \\begin{bmatrix} 0 \\\\ 0 \\\\ 0 \\\\ 1 \\end{bmatrix}\n",
+    "\\right\\}.\n",
+    "\\tag{2}\n",
     "$$\n",
     "\n",
-    "我们默认最左边的位置代表第一个量子比特，依此类推。其中符号 $\\otimes$ 是张量积运算。其工作原理大概如下：\n",
-    "给定两个矩阵$A_{m\\times n}$ 还有 $B_{p \\times q}$，那么$A,B$的张量积为\n",
-    "\n",
+    "我们默认最左边的位置代表第一个量子比特，依此类推。其中符号 $\\otimes$ 是张量积运算。其工作原理大概如下：给定两个矩阵 $A_{m\\times n}$ 还有 $B_{p \\times q}$，那么 $A,B$ 的张量积为\n",
     "\n",
     "$$\n",
     "A \\otimes B = \n",
@@ -250,17 +214,18 @@
     "\\vdots  & \\ddots & \\vdots \\\\\n",
     "a_{m1}B & \\cdots & a_{m n}B\n",
     "\\end{bmatrix}_{(mp)\\times (nq)}\n",
+    "\\tag{3}\n",
     "$$\n",
     "\n",
-    "一个单量子比特所处的任意量子态 $\\lvert {\\psi}\\rangle$可以写成基向量 $\\lvert {0}\\rangle$ 和 $\\lvert {1}\\rangle$ 的线性叠加，也就是说，它可以被描述成一个$\\lvert {0}\\rangle$ 和 $\\lvert {1}\\rangle$的线性组合\n",
+    "一个单量子比特所处的任意量子态 $|\\psi\\rangle$ 可以写成基向量 $|0\\rangle$ 和 $|1\\rangle$ 的线性叠加，也就是说，它可以被描述成一个 $|0\\rangle$ 和 $|1\\rangle$ 的线性组合：\n",
     "\n",
+    "$$\n",
+    "|\\psi\\rangle = \\alpha |0\\rangle  + \\beta |1\\rangle\n",
+    ":= \\begin{bmatrix} \\alpha \\\\ \\beta \\end{bmatrix}.\n",
+    "\\tag{4}\n",
+    "$$\n",
     "\n",
-    "$$\\lvert {\\psi}\\rangle = \\alpha \\lvert {0}\\rangle  + \\beta \\lvert {1}\\rangle\n",
-    ":= \\begin{bmatrix} \\alpha \\\\ \\beta \\end{bmatrix},\\,\\alpha, \\beta \\in \\mathbb{C}$$\n",
-    "\n",
-    "其中$\\alpha$ 和 $\\beta$ 可以是**复数**，他们表示概率振幅。这意味着当我们测量这个量子比特时，根据波恩法则，测量得到量子比特处于$\\lvert {0}\\rangle$ 状态的概率是$|\\alpha|^2$；而测量得到$\\lvert {1}\\rangle$的概率是$|\\beta|^2$。由于概率相加等于1，我们必须要加入如下的限制条件：\n",
-    "\n",
-    "$$|\\alpha|^2 + |\\beta|^2 = 1$$"
+    "其中 $\\alpha$ 和 $\\beta$ 可以是**复数**，他们表示概率振幅。这意味着当我们测量这个量子比特时，根据波恩法则，测量得到量子比特处于 $|0\\rangle$ 状态的概率是 $|\\alpha|^2$；而测量得到 $|1\\rangle$ 的概率是 $|\\beta|^2$。由于概率相加等于 1，我们必须要加入如下的限制条件：$|\\alpha|^2 + |\\beta|^2 = 1$。"
    ]
   },
   {
@@ -269,27 +234,18 @@
    "source": [
     "###  布洛赫球面 (Bloch Sphere) 表示\n",
     "\n",
-    "我们用一个球面上的点来表示一个量子比特可能处于的量子态，这个球面被称为**布洛赫球面**，(见图 1)\n",
+    "我们用一个球面上的点来表示一个量子比特可能处于的量子态，这个球面被称为**布洛赫球面**（Bloch Sphere），（见图1）\n",
     "\n",
-    "$$ \n",
-    "\\lvert {\\psi}\\rangle = \\alpha \\lvert {0}\\rangle  + \\beta \\lvert {1}\\rangle  \n",
-    "= \\cos\\bigg(\\frac{\\theta}{2}\\bigg) \\lvert {0}\\rangle +  e^{i\\varphi}\\sin\\bigg(\\frac{\\theta}{2}\\bigg) \\lvert {1}\\rangle\n",
+    "$$\n",
+    "|\\psi\\rangle = \\alpha |0\\rangle  + \\beta |1\\rangle  \n",
+    "= \\cos\\bigg(\\frac{\\theta}{2}\\bigg) |0\\rangle +  e^{i\\varphi}\\sin\\bigg(\\frac{\\theta}{2}\\bigg) |1\\rangle.\n",
+    "\\tag{5}\n",
     "$$\n",
     "\n",
-    "注意：多个量子系统的状态就无法用布洛赫球面来表示。如果是一个经典比特的话，那么它只有两个状态0和1，也就是布洛赫球面的北极和南极。这两个位置恰好对应着$\\lvert {0}\\rangle$ 和 $\\lvert {1}\\rangle$。**而一个量子比特不光可以处于两极，它可以在球面上任意一点，这样一种叠加的状态是经典比特做不到的**。举例来说，量子态 $\\frac{1}{\\sqrt{2}}\\big(\\lvert {0}\\rangle + i\\lvert {1}\\rangle\\big)$就处于球面赤道和 y-正半轴的交界处。"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "<img src=\"figures/bloch.png\" width=\"250\" >"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
+    "**注意**：多个量子系统的状态就无法用布洛赫球面来表示。如果是一个经典比特的话，那么它只有两个状态0和1，也就是布洛赫球面的北极和南极。这两个位置恰好对应着 $|0\\rangle$ 和 $|1\\rangle$。**而一个量子比特不光可以处于两极，它可以在球面上任意一点，这样一种叠加的状态是经典比特做不到的**。举例来说，量子态 $\\frac{1}{\\sqrt{2}}\\big(|0\\rangle + i|1\\rangle\\big)$就处于球面赤道和 $y$-正半轴的交界处。\n",
+    "\n",
+    "<img src=\"figures/intro-fig-bloch.png\" width=\"250\" >\n",
+    "\n",
     "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;  \n",
     "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;\n",
     "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;\n",
@@ -298,25 +254,17 @@
     "**图 1.** \n",
     "单量子比特的布洛赫球面表示. [[图片来源]](https://en.wikipedia.org/wiki/Qubit)\n",
     "\n",
-    "下面的内容面向对量子计算更熟悉的读者。如果你阅读这段感到困难，不用担心，您可以选择略过这一节，这不会对理解接下的内容产生影响。由于量子比特之间的交互以及去相干问题 (Decoherence)，因此，对于一个具有多量子比特的系统来说，它的单量子比特子系统将不再处于纯态 (pure state)，而是演变成混合态 (mixed state)。混合态可以看成不同纯态的按照一定概率的混合。\n",
-    " **单比特的混合态可以看成是布洛赫球内部的点，而不是存在于球表面**。通常来说，混合态需要用到量子力学的密度矩阵形式来描述，比如\n",
     "\n",
-    "$$ \n",
-    "\\rho_{\\text{mixed}} \n",
-    "= \\sum_i P_i \\lvert {\\psi_i}\\rangle\\langle{\\psi_i} \\lvert\n",
-    "= \\frac{1}{2} \\lvert {0}\\rangle \\langle{0} \\lvert  + \\frac{1}{2} \\lvert {1}\\rangle\\langle{1} \\lvert\n",
-    ":= \\frac{1}{2}  \\begin{bmatrix} 1 \\\\ 0\\end{bmatrix} \\begin{bmatrix} 1 & 0 \\end{bmatrix} +  \\frac{1}{2}  \\begin{bmatrix} 0 \\\\ 1\\end{bmatrix} \\begin{bmatrix} 0 & 1 \\end{bmatrix} \n",
-    "= \\frac{1}{2} \\begin{bmatrix} 1 & 0\\\\ 0 & 1 \\end{bmatrix}\n",
+    "下面的内容面向对量子计算更熟悉的读者。如果你阅读这段感到困难，不用担心，您可以选择略过这一节，这不会对理解接下的内容产生影响。由于量子比特之间的交互以及去相干问题 (Decoherence)，因此，对于一个具有多量子比特的系统来说，它的单量子比特子系统将不再处于纯态 (pure state)，而是演变成混合态 (mixed state)。混合态可以看成不同纯态的按照一定概率的混合。 **单比特的混合态可以看成是布洛赫球内部的点，而不是存在于球表面**。通常来说，混合态需要用到量子力学的密度矩阵形式来描述，比如以下量子态分别有 $1/2$ 的概率处于 $|0\\rangle$ 或 $|1\\rangle$ 态，\n",
+    "\n",
+    "$$\n",
+    "\\rho_{\\text{mixed}} = \\sum_i P_i |\\psi_i\\rangle\\langle\\psi_i| = \\frac{1}{2} |0\\rangle\\langle0| + \\frac{1}{2} |1\\rangle\\langle1| := \\frac{1}{2}  \\begin{bmatrix} 1 \\\\ 0\\end{bmatrix} \\begin{bmatrix} 1 & 0 \\end{bmatrix} +  \\frac{1}{2}  \\begin{bmatrix} 0 \\\\ 1\\end{bmatrix} \\begin{bmatrix} 0 & 1 \\end{bmatrix} = \\frac{1}{2} \\begin{bmatrix} 1 & 0\\\\ 0 & 1 \\end{bmatrix}.\n",
+    "\\tag{6}\n",
     "$$\n",
     "\n",
-    "其中行向量 (bra) $ \\langle{0} \\lvert $ 是列向量 (ket) $\\lvert {0}\\rangle$ 的复共轭转置。"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "**注：**如需更多信息，可参考维基百科 [链接](https://en.wikipedia.org/wiki/Qubit)"
+    "其中行向量（bra）$\\langle0|$ 是列向量 （ket）$|0\\rangle$ 的复共轭转置。\n",
+    "\n",
+    "**注：** 如需更多信息，可参考维基百科 [链接](https://en.wikipedia.org/wiki/Qubit)\n"
    ]
   },
   {
@@ -325,16 +273,16 @@
    "source": [
     "### <a name=\"gate\">什么是量子逻辑门?</a>\n",
     "\n",
-    "在经典计算机中，我们可以在经典比特上施加基本的逻辑运算( 非门 NOT, 与非门 NAND, 异或门 XOR, 与门 AND, 或门 OR)并组合成更复杂的运算。而量子计算则有完全不同的一套逻辑运算，它们被称为量子门 (quantum gate)。我们并不能在一个量子计算机上编译现有的C++程序。因为**经典计算机和量子计算机有不同的逻辑门构造，所以量子算法是需要利用这些量子门的特殊性来构造的**。\n",
+    "在经典计算机中，我们可以在经典比特上施加基本的逻辑运算（非门 NOT, 与非门 NAND, 异或门 XOR, 与门 AND, 或门 OR）并组合成更复杂的运算。而量子计算则有完全不同的一套逻辑运算，它们被称为量子门 (quantum gate)。我们并不能在一个量子计算机上编译现有的C++程序。因为**经典计算机和量子计算机有不同的逻辑门构造，所以量子算法是需要利用这些量子门的特殊性来构造的**。量子门在数学上可以被表示成酉矩阵（unitary matrix）。酉矩阵操作可以保证向量的长度不变，这是个很好的性质。不然我们对一个纯态量子比特进行操作，会让它劣化成混合态导致其无法接着很好地使用。酉矩阵定义为：\n",
     "\n",
-    "量子门在数学上可以被表示成酉矩阵 (unitary matrix)。酉矩阵操作可以保证向量的长度不变，这是个很好的性质。不然我们对一个纯态量子比特进行操作，会让它劣化成混合态导致其无法接着使用。那么什么是酉矩阵呢？\n",
-    "\n",
-    "$$ \n",
-    "U^{\\dagger}U = UU^{\\dagger} = I,\\,\n",
-    "\\Vert \\lvert {\\psi}\\rangle \\Vert  = \\Vert U\\lvert {\\psi}\\rangle\\Vert = 1\n",
+    "$$\n",
+    "U^{\\dagger}U = UU^{\\dagger} = I, \n",
+    "\\quad \\text{并且} \\quad \n",
+    "\\Vert |\\psi\\rangle \\Vert  = \\Vert U|\\psi\\rangle\\Vert = 1.\n",
+    "\\tag{7}\n",
     "$$\n",
     "\n",
-    "其中$U^{\\dagger}$是$U$的埃尔米特转置，$I$ 表示单位矩阵。但是酉矩阵作为量子门的物理意义是什么？这意味着**所有的量子门都必须是可逆的**。对于任何一个量子门运算，都可以找到一个与其对应的反向运算。除此之外，酉矩阵必须是个方阵。因为量子门的输入和输出要求有同样数量的量子比特。一个作用在 $n$ 量子比特的量子门可以写成一个 $2^n \\times 2^n$ 的酉矩阵。最常见的（也是物理上最容易实现的）量子门作用在一个或两个量子比特上，就像经典逻辑门那样。"
+    "其中 $U^{\\dagger}$ 是 $U$ 的 Hermite 转置，$I$ 表示单位矩阵。但是酉矩阵作为量子门的物理意义是什么？这意味着**所有的量子门都必须是可逆的**。对于任何一个量子门运算，都可以找到一个与其对应的反向运算。除此之外，酉矩阵必须是个方阵。因为量子门的输入和输出要求有同样数量的量子比特。一个作用在 $n$ 量子比特的量子门可以写成一个 $2^n \\times 2^n$ 的酉矩阵。最常见的（也是物理上最容易实现的）量子门作用在一个或两个量子比特上，就像经典逻辑门那样。"
    ]
   },
   {
@@ -343,35 +291,36 @@
    "source": [
     "### 单量子比特门\n",
     "\n",
-    "接下来，我们介绍在量子计算中非常重要的单量子比特门，包括泡利矩阵 $\\{X, Y, Z\\}$ 或 $\\{\\sigma_x, \\sigma_y, \\sigma_z\\}$、单比特旋转门 $\\{R_x, R_y, R_z\\}$ 和哈达玛门 $H$。有一个对于经典或量子计算都很重要的门是 **非门 (NOT gate)**，其可以表示成如下酉矩阵：\n",
-    "\n",
+    "接下来，我们介绍在量子计算中非常重要的单量子比特门，包括泡利矩阵 $\\{X, Y, Z\\}$、单比特旋转门 $\\{R_x, R_y, R_z\\}$ 和 Hadamard 门 $H$。其中 **非门（NOT gate）** 对于经典或量子计算都很重要，酉矩阵表示为：\n",
     "\n",
-    "$$ X := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix}$$\n",
-    "\n",
-    "这个量子门（酉矩阵）作用在单量子比特（一个复向量）上本质上的运算是**矩阵乘以向量**\n",
+    "$$\n",
+    "X := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix},\n",
+    "\\tag{8}\n",
+    "$$\n",
     "\n",
+    "这个量子门（酉矩阵）作用在单量子比特（一个复向量）上本质上的运算是**矩阵乘以向量**：\n",
     "\n",
-    "$$ \n",
-    "X \\lvert {0}\\rangle := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} \\begin{bmatrix} 1 \\\\0 \\end{bmatrix} \n",
-    "=\\begin{bmatrix} 0 \\\\1 \\end{bmatrix} = \\lvert {1}\\rangle \n",
-    "\\quad \\text{and} \\quad \n",
-    "X \\lvert {1}\\rangle := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} \\begin{bmatrix} 0 \\\\1 \\end{bmatrix} \n",
-    "=\\begin{bmatrix} 1 \\\\0 \\end{bmatrix}=\\lvert {0}\\rangle\n",
+    "$$\n",
+    "X |0\\rangle := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} \\begin{bmatrix} 1 \\\\0 \\end{bmatrix} \n",
+    "=\\begin{bmatrix} 0 \\\\1 \\end{bmatrix} = |1\\rangle, \n",
+    "\\quad \n",
+    "X |1\\rangle := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} \\begin{bmatrix} 0 \\\\1 \\end{bmatrix} \n",
+    "=\\begin{bmatrix} 1 \\\\0 \\end{bmatrix}=|0\\rangle.\n",
+    "\\tag{9}\n",
     "$$\n",
     "\n",
-    "回忆起前面的布洛赫球面表示，这个矩阵 $X$ 作用在一个量子比特（布洛赫球面上的一点）就相当于**关于布洛赫球的X轴旋转角度 $\\pi$**。这就是为什么\n",
-    " $X$ 可以表示成 $R_x(\\pi)$（只相差了一个无关紧要的全局相位 $e^{-i\\pi/2} = -i$ )。其他两个泡利矩阵 $Y$ 和 $Z$ 在这一点上也非常相似 （代表绕 Y和 Z轴旋转 $\\pi$运算 ）：\n",
-    "\n",
+    "回忆起前面的布洛赫球面表示，这个矩阵 $X$ 作用在一个量子比特（布洛赫球面上的一点）就相当于**关于布洛赫球的 $x$ 轴旋转角度 $\\pi$**。这就是为什么 $X$ 可以表示成 $R_x(\\pi)$（相差全局相位 $e^{-i\\pi/2} = -i$）。其他两个泡利矩阵 $Y$ 和 $Z$ 在这一点上也非常相似（代表绕 $y$ 和 $z$ 轴旋转 $\\pi$ 角度 ）：\n",
     "\n",
-    "$$ \n",
-    "Y := \\begin{bmatrix} 0 &-i \\\\ i &0 \\end{bmatrix}\n",
-    "\\quad \\text{and} \\quad \n",
-    "Z := \\begin{bmatrix} 1 &0 \\\\ 0 &-1 \\end{bmatrix}\n",
+    "$$\n",
+    "Y := \\begin{bmatrix} 0 &-i \\\\ i &0 \\end{bmatrix},\n",
+    "\\quad \n",
+    "Z := \\begin{bmatrix} 1 &0 \\\\ 0 &-1 \\end{bmatrix}.\n",
+    "\\tag{10}\n",
     "$$\n",
     "\n",
     "一般来说，任何一个在布洛赫球关于相应的轴旋转 $\\theta$ 角度的量子门可以表示为：\n",
     "\n",
-    "$$ \n",
+    "$$\n",
     "R_x(\\theta) := \n",
     "\\begin{bmatrix} \n",
     "\\cos \\frac{\\theta}{2} &-i\\sin \\frac{\\theta}{2} \\\\ \n",
@@ -388,13 +337,16 @@
     "\\begin{bmatrix}\n",
     "e^{-i\\frac{\\theta}{2}} & 0 \\\\ \n",
     "0 & e^{i\\frac{\\theta}{2}}\n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{11}\n",
     "$$\n",
     "\n",
-    "除了旋转门之外，最重要的单比特门就是哈达玛门了。对应的布洛赫球面解释是两个旋转组成的，先是按Z轴旋转$\\pi$，然后按Y轴旋转$\\pi/2$。它的矩阵表示是：\n",
+    "除了旋转门之外，最重要的单比特门就是 Hadamard 门了。对应的布洛赫球面解释是两个旋转组成的，先是按 $z$ 轴旋转 $\\pi$，然后按 $y$ 轴旋转 $\\pi/2$。它的矩阵表示是\n",
     "\n",
-    "$$H := \\frac{1}{\\sqrt{2}}\\begin{bmatrix} 1 &1 \\\\ 1 &-1 \\end{bmatrix} $$\n",
-    "\n"
+    "$$\n",
+    "H := \\frac{1}{\\sqrt{2}}\\begin{bmatrix} 1 &1 \\\\ 1 &-1 \\end{bmatrix}.\n",
+    "\\tag{12}\n",
+    "$$"
    ]
   },
   {
@@ -410,7 +362,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "<img src=\"figures/hardmad.png\" width=\"600\" >\n",
+    "<img src=\"figures/intro-fig-hadamard.png\" width=\"600\" >\n",
     "\n",
     "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;  \n",
     "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;\n",
@@ -424,7 +376,8 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "作用在两量子比特上的量子门可以表示成一个$4\\times4$酉矩阵\n",
+    "作用在两量子比特上的量子门可以表示成一个 $4\\times4$ 酉矩阵：\n",
+    "\n",
     "$$\n",
     "U = H \\otimes I \n",
     "= \\frac{1}{\\sqrt{2}} \\begin{bmatrix} 1 &1 \\\\ 1 &-1 \\end{bmatrix} \n",
@@ -436,56 +389,36 @@
     "1 &0 &-1 &0 \\\\\n",
     "0 &1 &0 &-1 \n",
     "\\end{bmatrix}\n",
-    "$$"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "另一种拓展方式是作用在全部两个量子比特上。比如CNOT，这个门会使得一个量子比特的状态影响到另一个量子比特的状态\n",
+    "\\tag{13}\n",
+    "$$\n",
+    "\n",
+    "另一种拓展方式是将逻辑门直接作用在两个量子比特上。比如受控非门 $\\text{CNOT}$，这个门会使得一个量子比特的状态影响到另一个量子比特的状态\n",
     "\n",
     "$$\n",
-    "CNOT := \n",
+    "\\text{CNOT} := \n",
     "\\begin{bmatrix} \n",
     "1 &0 &0 &0 \\\\ \n",
     "0 &1 &0 &0 \\\\\n",
     "0 &0 &0 &1 \\\\\n",
     "0 &0 &1 &0 \n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{14}\n",
     "$$\n",
     "\n",
-    "我们近距离观察一下它作用在不同的初始量子态上\n",
+    "我们观察一下它作用在不同的初始量子态上：\n",
     "\n",
     "$$\n",
-    "CNOT \\lvert {00}\\rangle = \\lvert {00}\\rangle, \\quad\n",
-    "CNOT \\lvert {01}\\rangle = \\lvert {01}\\rangle, \\quad\n",
-    "CNOT \\lvert {10}\\rangle = \\lvert {11}\\rangle, \\quad\n",
-    "CNOT \\lvert {11}\\rangle = \\lvert {10}\\rangle\n",
+    "\\text{CNOT} |00\\rangle = |00\\rangle, \\quad\n",
+    "\\text{CNOT} |01\\rangle = |01\\rangle, \\quad\n",
+    "\\text{CNOT} |10\\rangle = |11\\rangle, \\quad\n",
+    "\\text{CNOT} |11\\rangle = |10\\rangle.\n",
+    "\\tag{15}\n",
     "$$\n",
     "\n",
-    "也就是说，当第一个量子比特处于 $\\lvert {1}\\rangle$状态时，CNOT会在第二个量子比特上施加$X$门，如果第一个量子比特处于 $\\lvert {0}\\rangle$状态，那么第二个量子比特则不受任何影响。这也是为什么 CNOT 会被称为受控非门。下面是一些常见的量子门及它们的矩阵表示"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "<img src=\"figures/gate.png\" width=\"650\" >\n",
+    "也就是说，当第一个量子比特处于 $|1\\rangle$ 状态时，$\\text{CNOT}$ 会在第二个量子比特上施加 $X$ 门，如果第一个量子比特处于 $|0\\rangle$ 状态，那么第二个量子比特则不受任何影响。这也是为什么 $\\text{CNOT}$ 会被称为受控非门。下面是一些常见的量子门及它们的矩阵表示，**这些量子门都可以在量桨内被调用**。\n",
+    "\n",
+    "![intro-fig-gates](./figures/intro-fig-gates.png \"**图 3.** 常见的量子门. [[图片来源]](https://en.wikipedia.org/wiki/Quantum_logic_gate)\")\n",
     "\n",
-    "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;  \n",
-    "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;\n",
-    "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;\n",
-    "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;\n",
-    "&emsp;&emsp;\n",
-    "**图 3.** \n",
-    "常见的量子门. [[图片来源]](https://en.wikipedia.org/wiki/Quantum_logic_gate)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
     "**注**：更多信息可见如下维基百科 [链接](https://en.wikipedia.org/wiki/Quantum_logic_gate)"
    ]
   },
@@ -510,7 +443,7 @@
     "\n",
     "**注意:** 所有的单比特旋转门都按如下规定建立：\n",
     "\n",
-    "$$ \n",
+    "$$\n",
     "R_x(\\theta) := \n",
     "\\begin{bmatrix} \n",
     "\\cos \\frac{\\theta}{2} &-i\\sin \\frac{\\theta}{2} \\\\ \n",
@@ -527,16 +460,22 @@
     "\\begin{bmatrix}\n",
     "e^{-i\\frac{\\theta}{2}} & 0 \\\\ \n",
     "0 & e^{i\\frac{\\theta}{2}}\n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{16}\n",
     "$$\n",
     "\n",
-    "因此，我们不难看出 $X$ 门可以表示为$R_x(\\pi)$。以下是代码展示："
+    "因此，我们不难看出 $X$ 门可以表示为 $R_x(\\pi)$。以下是代码展示："
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 4,
-   "metadata": {},
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:47:08.582194Z",
+     "start_time": "2021-01-09T12:47:08.337302Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
@@ -578,14 +517,15 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "结果和$X (NOT)$门只相差一个全局相位$-i$\n",
+    "结果和 $X$（NOT）门只相差一个全局相位$-i$\n",
     "\n",
-    "\n",
-    "$$ \\text{output} = \\begin{bmatrix} 0 &-i \\\\ -i &0 \\end{bmatrix}\n",
-    "= -i\\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} = -i X\n",
+    "$$\n",
+    "\\text{output} = \\begin{bmatrix} 0 &-i \\\\ -i &0 \\end{bmatrix}\n",
+    "= -i\\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} = -i X.\n",
+    "\\tag{17}\n",
     "$$\n",
     "\n",
-    "有兴趣的话，你可以仔细思考一下为什么在量子计算中，全局相位并不重要。\n"
+    "有兴趣的话，你可以仔细思考一下为什么在量子计算中，全局相位并不重要。"
    ]
   },
   {
@@ -619,10 +559,11 @@
    "source": [
     "和原来一样，我们还是多了一个全局相位\n",
     "\n",
-    "\n",
-    "$$ \\text{output} = \\begin{bmatrix} 0 &-1 \\\\ 1 &0 \\end{bmatrix}\n",
-    "= -i\\begin{bmatrix} 0 &-i \\\\ i &0 \\end{bmatrix} = -i Y\n",
-    "$$\n"
+    "$$\n",
+    "\\text{output} = \\begin{bmatrix} 0 &-1 \\\\ 1 &0 \\end{bmatrix}\n",
+    "= -i\\begin{bmatrix} 0 &-i \\\\ i &0 \\end{bmatrix} = -i Y.\n",
+    "\\tag{18}\n",
+    "$$"
    ]
   },
   {
@@ -645,7 +586,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "经过上面的准备，你现在有一定的知识基础可以了解量子机器学习了。简单来说我们要做的就是利用量子电路来替代传统的神经网络来完成机器学习的任务。我们一般会准备一个可调节参数的量子电路（量子神经网络 QNN），很多时候也被称为模板 (Ansatz)，里面的参数是人为可调节的（这些参数其实就是旋转门的角度$\\theta$）。如果再加上一个精心设计的损失函数，就可以将一个量子计算问题转化为经典的寻找损失函数最小值问题。然后不断调节电路中的参数直到损失函数下降至收敛 (此时损失函数达到最优值或次优值)， 我们就完成优化了。\n"
+    "经过上面的准备，你现在有一定的知识基础可以了解量子机器学习了。简单来说，我们要做的就是利用参数化量子电路（Parametrized Quantum Circuit, PQC）来替代传统的神经网络来完成机器学习的任务。处理的对象可以是经典数据也可以是量子数据。我们一般会准备一个可调节参数的量子电路（PQC），也被称作量子神经网络（Quantum Neural Network, QNN）或者电路模板（ansatz），里面的参数是人为可调节的（这些参数大多数情况下就是旋转门的角度 $\\theta$）。例如上一节中看到的用参数 $\\pi$ 构造 $X$ 门，这其实就是最简单的量子神经网络。如果再加上一个精心设计的损失函数，就可以将一个计算问题转化为寻找损失函数的最值问题。然后不断调节电路中的参数直到损失函数下降至收敛（此时损失函数达到最优值或次优值），我们就完成了优化。这样的一种在量子设备上估值损失函数然后在经典设备上进行优化的框架被称为量子-经典混合优化，或者变分量子算法（Variational Quantum Algorithms, VQA）。"
    ]
   },
   {
@@ -654,27 +595,25 @@
    "source": [
     "### <a name=\"QNN\">示例: 如何创建量子神经网络 QNN?</a>\n",
     "\n",
-    "QNN通常可以表示为一些单比特量子旋转门和双比特门的组合。其中一个可以高效利用硬件的架构是只包含 $\\{R_x, R_y, R_z, \\text{CNOT} \\}$这四种量子门的模板。它们很容易在NISQ设备（通常是超导量子比特）上实现，因为CNOT只需要实施在相邻量子比特上。一个例子可见下图：\n"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "<img src=\"figures/gate1.png\" width=\"450\" >"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "通常来说，每条线代表一个量子比特。我们把图最上端的认为是第一个量子比特，依次往下。从左到右代表我们施加门的时间顺序，先施加最左边的量子门。接下来，我们来看看如何在量桨上建造这个简单的两比特量子神经网络\n"
+    "QNN 通常可以表示为一些单比特量子旋转门和双比特门的组合。其中一个可以高效利用硬件的架构是只包含 $\\{R_x, R_y, R_z, \\text{CNOT}\\}$ 这四种量子门的模板。它们很容易在 NISQ （Noisy-Intermidiate-Scale-Quantum）设备（通常是超导量子比特）上实现，因为 $\\text{CNOT}$ 只需要实施在相邻量子比特上。一个例子可见下图：\n",
+    "\n",
+    "\n",
+    "![intro-fig-gate1](./figures/intro-fig-gate1.png)\n",
+    "\n",
+    "通常来说，每条线代表一个量子比特。我们把图最上端的认为是第一个量子比特 $q_0$，依次往下。从左到右代表我们施加门的时间顺序，先施加最左边的量子门。接下来，我们来看看如何在量桨上建造这个简单的两比特量子神经网络\n",
+    "\n",
+    "\n"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 5,
-   "metadata": {},
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:47:11.924347Z",
+     "start_time": "2021-01-09T12:47:11.900263Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
@@ -727,7 +666,8 @@
     "-1 &0  &0 &0 \\\\\n",
     "0  &0  &1 &0 \\\\\n",
     "0  &0  &0 &1 \n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{19}\n",
     "$$"
    ]
   },
@@ -778,7 +718,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "<img src=\"figures/gate2.png\" width=\"450\" >\n"
+    "<img src=\"figures/intro-fig-gate2.png\" width=\"450\" >\n"
    ]
   },
   {
@@ -797,12 +737,17 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 7,
-   "metadata": {},
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:47:17.393379Z",
+     "start_time": "2021-01-09T12:47:16.964739Z"
+    }
+   },
    "outputs": [
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEPCAYAAABY9lNGAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZJElEQVR4nO3df5xddX3n8debn6JYfhmpkmhoidpQlGpEH+3WqijCY9VgBQ26FVwsdpVteai1cWtRqbuVVsW64tZ0URFXA0v9kS1RdEXrrhUkID8aIBL5GdQafiqyiJHP/nFOyM2dMzN3hty5l+T1fDzmMfee7zkz75k/5j3nfM+PVBWSJPXbadQBJEnjyYKQJHWyICRJnSwISVInC0KS1GmXUQfYVh73uMfVwoULRx1Dkh5RLrvsstural7X2HZTEAsXLmTNmjWjjiFJjyhJbp5szENMkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE7bzZXUD9fC5ReM7Hvf9L5/O+W42bqZbXbMNjuP5Gyz5R6EJKmTBSFJ6mRBSJI6WRCSpE5DLYgkRyZZl2R9kuUd489LcnmSTUmO6Vl+aJJvJ1mb5Kokrx5mTknSREMriCQ7A2cCRwGLgeOSLO5b7RbgBOAzfcvvA15XVQcDRwIfSrL3sLJKkiYa5mmuhwHrq+oGgCQrgaXANZtXqKqb2rEHezesqu/1vP5Bkh8D84C7h5hXktRjmIeYDgBu7Xm/oV02I0kOA3YDvt8xdlKSNUnWbNy4cdZBJUkTjfUkdZInAOcAr6+qB/vHq2pFVS2pqiXz5nU+UlWSNEvDLIjbgAU97+e3ywaS5FeAC4A/r6qLt3E2SdI0hlkQlwKLkhyYZDdgGbBqkA3b9T8PfKqqzh9iRknSJIZWEFW1CTgZuBC4FjivqtYmOS3JywGSPDvJBuBY4GNJ1rabvwp4HnBCkivaj0OHlVWSNNFQb9ZXVauB1X3LTu15fSnNoaf+7T4NfHqY2SRJUxvrSWpJ0uhYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jH+vCSXJ9mU5Ji+seOTXN9+HD/MnJKkiYZWEEl2Bs4EjgIWA8clWdy32i3ACcBn+rbdF3gX8BzgMOBdSfYZVlZJ0kTD3IM4DFhfVTdU1QPASmBp7wpVdVNVXQU82LftS4CvVtWdVXUX8FXgyCFmlST1GWZBHADc2vN+Q7tsm22b5KQka5Ks2bhx46yDSpImekRPUlfViqpaUlVL5s2bN+o4krRdGWZB3AYs6Hk/v1027G0lSdvAMAviUmBRkgOT7AYsA1YNuO2FwBFJ9mknp49ol0mS5sjQCqKqNgEn0/xhvxY4r6rWJjktycsBkjw7yQbgWOBjSda2294J/CVNyVwKnNYukyTNkV2G+cWrajWwum/ZqT2vL6U5fNS17ceBjw8znyRpco/oSWpJ0vBYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqdNABZHkd5I8pn3975J8MMmThxtNkjRKg+5B/DfgviTPAN4KfB/41HQbJTkyybok65Ms7xjfPcm57fglSRa2y3dNcnaSq5Ncm+Qdg/9IkqRtYdCC2FRVBSwFPlJVZwKPnWqDJDsDZwJHAYuB45Is7lvtROCuqjoIOAM4vV1+LLB7VR0CPAt44+bykCTNjUEL4qftf/F/AFyQZCdg12m2OQxYX1U3VNUDwEqagum1FDi7fX0+cHiSAAU8JskuwB7AA8BPBswqSdoGBi2IVwM/B/59Vf0ImA/8zTTbHADc2vN+Q7usc52q2gTcA+xHUxY/A34I3AK8v6ru7P8GSU5KsibJmo0bNw74o0iSBjFQQbSl8A/A7u2i24HPDysUzd7HL4EnAgcCb03yax25VlTVkqpaMm/evCHGkaQdz6BnMf0hzX/1H2sXHQB8YZrNbgMW9Lyf3y7rXKc9nLQXcAfwGuDLVfWLqvox8C1gySBZJUnbxqCHmN4M/A7tPEBVXQ88fpptLgUWJTkwyW7AMmBV3zqrgOPb18cAF7WT4bcALwRoT699LnDdgFklSdvAoAXx83aiGXjov/2aaoN2TuFk4ELgWuC8qlqb5LQkL29XOwvYL8l64C3A5lNhzwT2TLKWpmg+UVVXDfpDSZIevl0GXO+fkvwnYI8kLwbeBPyv6TaqqtXA6r5lp/a8vp/mlNb+7e7tWi5JmjuD7kEsBzYCVwNvpPmj/85hhZIkjd5AexBV9SDw9+2HJGkHMGVBJDmvql6V5Go65hyq6ulDSyZJGqnp9iD+pP380mEHkSSNlynnIKrqh+3LN1XVzb0fNBPVkqTt1KCT1C/uWHbUtgwiSRov081B/AeaPYVfS9J7HcJjaa5uliRtp6abg/gM8CXgr9hyERvAT7tunidJ2n5MVxBVVTcleXP/QJJ9LQlJ2n4NsgfxUuAymtNc0zNWwIQ7rEqStg9TFkRVvbT9fODcxJEkjYvpJqmfOdV4VV2+beNIksbFdIeYPjDFWNHekluStP2Z7hDTC+YqiCRpvEx3iOmFVXVRkt/vGq+qzw0nliRp1KY7xPR7wEXAyzrGCrAgJGk7Nd0hpne1n18/N3EkSeNioHsxJdkvyYeTXJ7ksiR/m2S/YYeTJI3OoDfrW0nzRLlXAse0r88dVihJ0ugN+kzqJ1TVX/a8f2+SVw8jkCRpPAy6B/GVJMuS7NR+vAq4cJjBJEmjNd1prj9lyz2YTgE+3Q7tBNwLvG2Y4SRJozPdWUyPnasgkqTxMugcBEn2ARYBj9q8rKq+OYxQkqTRG/Q01zcA36SZd3hP+/ndA2x3ZJJ1SdYnWd4xvnuSc9vxS5Is7Bl7epJvJ1mb5Ookj+rfXpI0PINOUv8J8Gzg5vb+TL8F3D3VBkl2Bs6keXb1YuC4JIv7VjsRuKuqDgLOAE5vt92FZr7jj6rqYOD5wC8GzCpJ2gYGLYj7q+p+aP7rr6rrgKdOs81hwPqquqGqHqC5lmJp3zpLgbPb1+cDhycJcARwVVVdCVBVd1TVLwfMKknaBgYtiA1J9ga+AHw1yReBm6fZ5gDg1t6v0S7rXKeqNgH3APsBTwEqyYXt1dtv7/oGSU5KsibJmo0bNw74o0iSBjHQJHVVvaJ9+e4kXwf2Ar48tFRNrn9Dc1jrPuBrSS6rqq/15VoBrABYsmRJDTGPJO1wBt2DIMkzk/wx8HRgQ3vYaCq3AQt63s9vl3Wu08477AXcQbO38c2qur2q7gNWA1M+3U6StG0NehbTqTRzBfsBjwM+keSd02x2KbAoyYFJdgOWAav61lkFHN++Pga4qKqK5iypQ5I8ui2O3wOuGSSrJGnbGPQ6iNcCz+iZqH4fcAXw3sk2qKpNSU6m+WO/M/Dxqlqb5DRgTVWtAs4CzkmyHriTpkSoqruSfJCmZApYXVUXzOYHlCTNzqAF8QOaC+Tub9/vzsTDRRNU1Wqaw0O9y07teX0/cOwk236aLbf2kCTNsenuxfRfaf6DvwdYm+Sr7fsXA98ZfjxJ0qhMtwexpv18GfD5nuXfGEoaSdLYmO5mfZsvYqOdaH5K+3ZdVXllsyRtxwaag0jyfJqzmG6iufX3giTHe7M+Sdp+DTpJ/QHgiKpaB5DkKcBngWcNK5gkabQGvVBu183lAFBV3wN2HU4kSdI4GHQP4rIk/50tp52+li0T2JKk7dCgBfFHwJuBP27f/x/go0NJJEkaC9MWRPtchyur6mnAB4cfSZI0Dqadg2ifw7AuyZPmII8kaUwMeohpH5orqb8D/Gzzwqp6+VBSSZJGbtCC+IuhppAkjZ3p7sX0KJoJ6oOAq4Gz2ie/SZK2c9PNQZwNLKEph6NoLpiTJO0ApjvEtLiqDgFIchbewVWSdhjT7UE8dEM+Dy1J0o5luj2IZyT5Sfs6wB7t+wBVVb8y1HSSpJGZ7nbfO89VEEnSeBn0Zn2SpB2MBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSeo01IJIcmSSdUnWJ1neMb57knPb8UuSLOwbf1KSe5O8bZg5JUkTDa0g2gcNnUlzD6fFwHFJFvetdiJwV1UdBJwBnN43/kHgS8PKKEma3DD3IA4D1lfVDVX1ALASWNq3zlKaGwICnA8cniQASY4GbgTWDjGjJGkSwyyIA4Bbe95vaJd1rtPe6+keYL8kewJ/Brxnqm+Q5KQka5Ks2bhx4zYLLkka30nqdwNnVNW9U61UVSuqaklVLZk3b97cJJOkHcSgT5SbjduABT3v57fLutbZkGQXYC/gDuA5wDFJ/hrYG3gwyf1V9ZEh5pUk9RhmQVwKLEpyIE0RLANe07fOKuB44NvAMcBFVVXA725eIcm7gXstB0maW0MriKralORk4EJgZ+DjVbU2yWnAmqpaBZwFnJNkPXAnTYlIksbAMPcgqKrVwOq+Zaf2vL4fOHaar/HuoYSTJE1pXCepJUkjZkFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jG+e5Jz2/FLkixsl784yWVJrm4/v3CYOSVJEw2tIJLsDJwJHAUsBo5LsrhvtROBu6rqIOAM4PR2+e3Ay6rqEOB44Jxh5ZQkdRvmHsRhwPqquqGqHgBWAkv71lkKnN2+Ph84PEmq6rtV9YN2+VpgjyS7DzGrJKnPMAviAODWnvcb2mWd61TVJuAeYL++dV4JXF5VP+//BklOSrImyZqNGzdus+CSpDGfpE5yMM1hpzd2jVfViqpaUlVL5s2bN7fhJGk7N8yCuA1Y0PN+frusc50kuwB7AXe07+cDnwdeV1XfH2JOSVKHYRbEpcCiJAcm2Q1YBqzqW2cVzSQ0wDHARVVVSfYGLgCWV9W3hphRkjSJoRVEO6dwMnAhcC1wXlWtTXJakpe3q50F7JdkPfAWYPOpsCcDBwGnJrmi/Xj8sLJKkibaZZhfvKpWA6v7lp3a8/p+4NiO7d4LvHeY2SRJUxvrSWpJ0uhYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jG+e5Jz2/FLkizsGXtHu3xdkpcMM6ckaaKhFUSSnYEzgaOAxcBxSRb3rXYicFdVHQScAZzebrsYWAYcDBwJfLT9epKkOTLMPYjDgPVVdUNVPQCsBJb2rbMUOLt9fT5weJK0y1dW1c+r6kZgffv1JElzZJchfu0DgFt73m8AnjPZOlW1Kck9wH7t8ov7tj2g/xskOQk4qX17b5J12yb6jD0OuH22G+f0bZhkIrPNjtlmx2yzM8psT55sYJgFMXRVtQJYMeocSdZU1ZJR5+hittkx2+yYbXbGNdswDzHdBizoeT+/Xda5TpJdgL2AOwbcVpI0RMMsiEuBRUkOTLIbzaTzqr51VgHHt6+PAS6qqmqXL2vPcjoQWAR8Z4hZJUl9hnaIqZ1TOBm4ENgZ+HhVrU1yGrCmqlYBZwHnJFkP3ElTIrTrnQdcA2wC3lxVvxxW1m1g5Ie5pmC22THb7JhtdsYyW5p/2CVJ2ppXUkuSOlkQkqROFoQkqZMF8TAk2TfJvqPOIUnDYEHMUJInJVmZZCNwCfCdJD9uly0ccbyxl2T/JM9sP/YfdZ7pJNlz1BmkUfEsphlK8m3gQ8D5m0+9bW8keCxwSlU9d4TxJpXk6qo6ZITf/1Dg72guhtx80eN84G7gTVV1+WiSTS3JLVX1pDHIsT9bbjdzW1X96yjzDCLJnlV174gzhOY+bg/97oDv1Bj/4UvytKq6btQ5wIKYsSTXV9WimY7NhSS/P9kQ8HdVNW8u82wVILkCeGNVXdK3/LnAx6rqGSMJ1mR4y2RDwJ9X1cgOIz5SixVGX65JjgA+ClzP1r+7g2h+d18ZVbapjPr31usRfS+mEbksyUdp7kK7+WaEC2iuCP/uyFI1zgX+B9DV+o+a4yz9HtNfDgBVdXGSx4wiUI//AvwNzUWZ/UZ9GPaTTF6snwBGVqxtjqnKddSH5/4WeFFV3dS7sL07w2rgN0YRqs3w4cmGgL3nMMqULIiZex3Ncyzew9a7rZuvDB+lq4D3V9W/9A8kedEI8vT6UpILgE+xdbG+DvjyyFI1Lge+UFWX9Q8kecMI8vQa52KF8S7XXWjuBN3vNmDXOc7S7/XAW4Gfd4wdN8dZJuUhpu1Ikt8Fbq6qWzrGllTVmhHE6s1wFM2zPrYq1qpaPbpUkOSpwB1VNeF2y0n2H+Xx/vY/zV+nu1hvrKqTR5UNIMk/A/9xknK9taoWdGw2J5K8A3gVzbNoen93y4DzquqvRpjtIuCdVfXPHWM3VtWBI4g1gQUxQ+1dZ08EjmbrP3RfBM6qql+MKJq2U+NarPBQud5ZVRs7xkZarm2G36D7d3fN6FI1p8gD91fVfaPMMR0LYoaSfJZmgvBstuy+zqeZg9i3ql49omi95fUK4Int4rEvryQrquqk6dece+OcTRo2C2KGknyvqp4y07G5MOblNdmZQAGurKr5c5lnqwDjnW0v4B00/wXvT3MCwo9pSv99VXX3qLLBVvmOBh7PmOWbTJIvVdVRo87RZZyyOUk9c3cmORb4h6p6ECDJTjTXQdw10mTwrI6C2gBcnOR7owjUYyNwM80f3c2qff/4kSTaYpyznQdcBLygqn4EkORXgRPasSNGFw3Yku/5ffmOZ8T5kjxzsiHg0DmMMjHAGGfr5R7EDLVXS58OvIDmv3VoTkv7OrC8qm4cSTAgycXAB+gur7dUVf8zwecy2/XA4ZNMoI96MnOcs62rqqfOdGyujHO+JL8E/omti3+z51bVHnMc6SHjnK2XexAzVFU3JXk3zTUPW01Sj7IcWstoyuvMJHe3y/amKa9lI8q02YeAfYAJf4SBv57bKBN8iPHNdnOStwNnb57wba+qPoEtZ+aM0jjnu5bmGpLr+weSmG0A7kHMUJI/o/lju5Ktr85cBqysqveNKhtMetbGF6vq2tGlaiR5Gt1nlJhtEkn2AZbTZNt8uOtfaa67eV9VjfSw5jjnS3IMcHVVresYO7qqvjD3qR76/mObrZcFMUPtsfyD+88Iap+7vXbEt9oY2/Jq/8t8TZutdwLdbLOU5PVV9YlR55jMOOcz22AsiBlKch3wkqq6uW/5k4GvjPiY6ziXl9m2sXG6Z0+Xcc5ntsE4BzFzpwBfayc2Nx8rfBLNDcBGelUr8CDN9Q839y1/Qjs2SmabhSRXTTZEc9rrSI1zPrM9fBbEDFXVl5M8hYm3EL508+2/R+gUxre8TsFss7E/8BImnkIdYMJtGkZgnPOZ7WGyIGahPYX04lHn6DfO5WW2WftHYM+quqJ/IMk35jzNROOcz2wPk3MQkqROo74dryRpTFkQkqROFoR2WEnmJ/likuuT3JDkI0l2H2C7zucsJzlt84OZkpyS5NGTrPfSJN9NcmWSa5K8sV1+dJLFA3z/gdaTHi4LQjukJAE+R/MkuUXAImAPHsatNarq1Kr63+3bU4AJBZFkV2AF8LL2Ody/BXyjHT4aGOQP/6DrSQ+Lk9TaISU5HHhXVT2vZ9mv0FwLsQA4Bliy+YltSf6R5nGu32j3IP6e5k6lPwKWVdXGJJ+kOTvlicD7gXXA7VX1gp7vsS9wHfDkqvp/Pct/u932nvbjlcALgZOA3YD1wB/Q3Omzfz2AM4F5wH3AH1bVddvkF6UdmnsQ2lEdDGz1mMyq+glwE831D1N5DLCmqg6muSPnu/q+zoeBH9DcovsFfWN30tyn6OYkn03y2iQ7tY+eXAX8aVUdWlXfBz5XVc9u9zSuBU6cZL0VNI/9fBbwNuCjM/5tSB28DkKauQeBc9vXn6Y5VDWwqnpDkkOAF9H8QX8xzd1P+/1mkvfS3JF3T+DC/hWS7An8NvA/m6NmAEw7jyINwoLQjuoamsNID2kPMf0qzaGh32TrPexHTfG1ZnyctqquBq5Ocg5wI90F8Ung6Kq6MskJwPM71tkJuLuqDp1pBmk6HmLSjuprwKOTvA4gyc40D1v6SDs3cBNwaJKdkiygucp6s53YUi6vAf5vx9f/KfDY/oVJ9kzy/J5Fh7LlHlD92zwW+GE7sf3arq/dHha7sX3KIWk8Y6ofXBqUBaEdUjVnZ7wCOKa9B9MdwINV9Z/bVb5F85/9NcCHgct7Nv8ZcFiSf6GZSD6t41usAL6c5Ot9ywO8Pcm6JFcA72HL3sNK4E/bU2B/HfgL4JI2S++kc/96rwVOTHIlsJbm2QzSw+ZZTBIPnUX0WeAVVXX5dOtLOwILQpLUyUNMkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKnT/weRuZs3hsDuNQAAAABJRU5ErkJggg==\n",
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEPCAYAAABY9lNGAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZJElEQVR4nO3df5xddX3n8debn6JYfhmpkmhoidpQlGpEH+3WqijCY9VgBQ26FVwsdpVteai1cWtRqbuVVsW64tZ0URFXA0v9kS1RdEXrrhUkID8aIBL5GdQafiqyiJHP/nFOyM2dMzN3hty5l+T1fDzmMfee7zkz75k/5j3nfM+PVBWSJPXbadQBJEnjyYKQJHWyICRJnSwISVInC0KS1GmXUQfYVh73uMfVwoULRx1Dkh5RLrvsstural7X2HZTEAsXLmTNmjWjjiFJjyhJbp5szENMkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE7bzZXUD9fC5ReM7Hvf9L5/O+W42bqZbXbMNjuP5Gyz5R6EJKmTBSFJ6mRBSJI6WRCSpE5DLYgkRyZZl2R9kuUd489LcnmSTUmO6Vl+aJJvJ1mb5Kokrx5mTknSREMriCQ7A2cCRwGLgeOSLO5b7RbgBOAzfcvvA15XVQcDRwIfSrL3sLJKkiYa5mmuhwHrq+oGgCQrgaXANZtXqKqb2rEHezesqu/1vP5Bkh8D84C7h5hXktRjmIeYDgBu7Xm/oV02I0kOA3YDvt8xdlKSNUnWbNy4cdZBJUkTjfUkdZInAOcAr6+qB/vHq2pFVS2pqiXz5nU+UlWSNEvDLIjbgAU97+e3ywaS5FeAC4A/r6qLt3E2SdI0hlkQlwKLkhyYZDdgGbBqkA3b9T8PfKqqzh9iRknSJIZWEFW1CTgZuBC4FjivqtYmOS3JywGSPDvJBuBY4GNJ1rabvwp4HnBCkivaj0OHlVWSNNFQb9ZXVauB1X3LTu15fSnNoaf+7T4NfHqY2SRJUxvrSWpJ0uhYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jH+vCSXJ9mU5Ji+seOTXN9+HD/MnJKkiYZWEEl2Bs4EjgIWA8clWdy32i3ACcBn+rbdF3gX8BzgMOBdSfYZVlZJ0kTD3IM4DFhfVTdU1QPASmBp7wpVdVNVXQU82LftS4CvVtWdVXUX8FXgyCFmlST1GWZBHADc2vN+Q7tsm22b5KQka5Ks2bhx46yDSpImekRPUlfViqpaUlVL5s2bN+o4krRdGWZB3AYs6Hk/v1027G0lSdvAMAviUmBRkgOT7AYsA1YNuO2FwBFJ9mknp49ol0mS5sjQCqKqNgEn0/xhvxY4r6rWJjktycsBkjw7yQbgWOBjSda2294J/CVNyVwKnNYukyTNkV2G+cWrajWwum/ZqT2vL6U5fNS17ceBjw8znyRpco/oSWpJ0vBYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqdNABZHkd5I8pn3975J8MMmThxtNkjRKg+5B/DfgviTPAN4KfB/41HQbJTkyybok65Ms7xjfPcm57fglSRa2y3dNcnaSq5Ncm+Qdg/9IkqRtYdCC2FRVBSwFPlJVZwKPnWqDJDsDZwJHAYuB45Is7lvtROCuqjoIOAM4vV1+LLB7VR0CPAt44+bykCTNjUEL4qftf/F/AFyQZCdg12m2OQxYX1U3VNUDwEqagum1FDi7fX0+cHiSAAU8JskuwB7AA8BPBswqSdoGBi2IVwM/B/59Vf0ImA/8zTTbHADc2vN+Q7usc52q2gTcA+xHUxY/A34I3AK8v6ru7P8GSU5KsibJmo0bNw74o0iSBjFQQbSl8A/A7u2i24HPDysUzd7HL4EnAgcCb03yax25VlTVkqpaMm/evCHGkaQdz6BnMf0hzX/1H2sXHQB8YZrNbgMW9Lyf3y7rXKc9nLQXcAfwGuDLVfWLqvox8C1gySBZJUnbxqCHmN4M/A7tPEBVXQ88fpptLgUWJTkwyW7AMmBV3zqrgOPb18cAF7WT4bcALwRoT699LnDdgFklSdvAoAXx83aiGXjov/2aaoN2TuFk4ELgWuC8qlqb5LQkL29XOwvYL8l64C3A5lNhzwT2TLKWpmg+UVVXDfpDSZIevl0GXO+fkvwnYI8kLwbeBPyv6TaqqtXA6r5lp/a8vp/mlNb+7e7tWi5JmjuD7kEsBzYCVwNvpPmj/85hhZIkjd5AexBV9SDw9+2HJGkHMGVBJDmvql6V5Go65hyq6ulDSyZJGqnp9iD+pP380mEHkSSNlynnIKrqh+3LN1XVzb0fNBPVkqTt1KCT1C/uWHbUtgwiSRov081B/AeaPYVfS9J7HcJjaa5uliRtp6abg/gM8CXgr9hyERvAT7tunidJ2n5MVxBVVTcleXP/QJJ9LQlJ2n4NsgfxUuAymtNc0zNWwIQ7rEqStg9TFkRVvbT9fODcxJEkjYvpJqmfOdV4VV2+beNIksbFdIeYPjDFWNHekluStP2Z7hDTC+YqiCRpvEx3iOmFVXVRkt/vGq+qzw0nliRp1KY7xPR7wEXAyzrGCrAgJGk7Nd0hpne1n18/N3EkSeNioHsxJdkvyYeTXJ7ksiR/m2S/YYeTJI3OoDfrW0nzRLlXAse0r88dVihJ0ugN+kzqJ1TVX/a8f2+SVw8jkCRpPAy6B/GVJMuS7NR+vAq4cJjBJEmjNd1prj9lyz2YTgE+3Q7tBNwLvG2Y4SRJozPdWUyPnasgkqTxMugcBEn2ARYBj9q8rKq+OYxQkqTRG/Q01zcA36SZd3hP+/ndA2x3ZJJ1SdYnWd4xvnuSc9vxS5Is7Bl7epJvJ1mb5Ookj+rfXpI0PINOUv8J8Gzg5vb+TL8F3D3VBkl2Bs6keXb1YuC4JIv7VjsRuKuqDgLOAE5vt92FZr7jj6rqYOD5wC8GzCpJ2gYGLYj7q+p+aP7rr6rrgKdOs81hwPqquqGqHqC5lmJp3zpLgbPb1+cDhycJcARwVVVdCVBVd1TVLwfMKknaBgYtiA1J9ga+AHw1yReBm6fZ5gDg1t6v0S7rXKeqNgH3APsBTwEqyYXt1dtv7/oGSU5KsibJmo0bNw74o0iSBjHQJHVVvaJ9+e4kXwf2Ar48tFRNrn9Dc1jrPuBrSS6rqq/15VoBrABYsmRJDTGPJO1wBt2DIMkzk/wx8HRgQ3vYaCq3AQt63s9vl3Wu08477AXcQbO38c2qur2q7gNWA1M+3U6StG0NehbTqTRzBfsBjwM+keSd02x2KbAoyYFJdgOWAav61lkFHN++Pga4qKqK5iypQ5I8ui2O3wOuGSSrJGnbGPQ6iNcCz+iZqH4fcAXw3sk2qKpNSU6m+WO/M/Dxqlqb5DRgTVWtAs4CzkmyHriTpkSoqruSfJCmZApYXVUXzOYHlCTNzqAF8QOaC+Tub9/vzsTDRRNU1Wqaw0O9y07teX0/cOwk236aLbf2kCTNsenuxfRfaf6DvwdYm+Sr7fsXA98ZfjxJ0qhMtwexpv18GfD5nuXfGEoaSdLYmO5mfZsvYqOdaH5K+3ZdVXllsyRtxwaag0jyfJqzmG6iufX3giTHe7M+Sdp+DTpJ/QHgiKpaB5DkKcBngWcNK5gkabQGvVBu183lAFBV3wN2HU4kSdI4GHQP4rIk/50tp52+li0T2JKk7dCgBfFHwJuBP27f/x/go0NJJEkaC9MWRPtchyur6mnAB4cfSZI0Dqadg2ifw7AuyZPmII8kaUwMeohpH5orqb8D/Gzzwqp6+VBSSZJGbtCC+IuhppAkjZ3p7sX0KJoJ6oOAq4Gz2ie/SZK2c9PNQZwNLKEph6NoLpiTJO0ApjvEtLiqDgFIchbewVWSdhjT7UE8dEM+Dy1J0o5luj2IZyT5Sfs6wB7t+wBVVb8y1HSSpJGZ7nbfO89VEEnSeBn0Zn2SpB2MBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSeo01IJIcmSSdUnWJ1neMb57knPb8UuSLOwbf1KSe5O8bZg5JUkTDa0g2gcNnUlzD6fFwHFJFvetdiJwV1UdBJwBnN43/kHgS8PKKEma3DD3IA4D1lfVDVX1ALASWNq3zlKaGwICnA8cniQASY4GbgTWDjGjJGkSwyyIA4Bbe95vaJd1rtPe6+keYL8kewJ/Brxnqm+Q5KQka5Ks2bhx4zYLLkka30nqdwNnVNW9U61UVSuqaklVLZk3b97cJJOkHcSgT5SbjduABT3v57fLutbZkGQXYC/gDuA5wDFJ/hrYG3gwyf1V9ZEh5pUk9RhmQVwKLEpyIE0RLANe07fOKuB44NvAMcBFVVXA725eIcm7gXstB0maW0MriKralORk4EJgZ+DjVbU2yWnAmqpaBZwFnJNkPXAnTYlIksbAMPcgqKrVwOq+Zaf2vL4fOHaar/HuoYSTJE1pXCepJUkjZkFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jG+e5Jz2/FLkixsl784yWVJrm4/v3CYOSVJEw2tIJLsDJwJHAUsBo5LsrhvtROBu6rqIOAM4PR2+e3Ay6rqEOB44Jxh5ZQkdRvmHsRhwPqquqGqHgBWAkv71lkKnN2+Ph84PEmq6rtV9YN2+VpgjyS7DzGrJKnPMAviAODWnvcb2mWd61TVJuAeYL++dV4JXF5VP+//BklOSrImyZqNGzdus+CSpDGfpE5yMM1hpzd2jVfViqpaUlVL5s2bN7fhJGk7N8yCuA1Y0PN+frusc50kuwB7AXe07+cDnwdeV1XfH2JOSVKHYRbEpcCiJAcm2Q1YBqzqW2cVzSQ0wDHARVVVSfYGLgCWV9W3hphRkjSJoRVEO6dwMnAhcC1wXlWtTXJakpe3q50F7JdkPfAWYPOpsCcDBwGnJrmi/Xj8sLJKkibaZZhfvKpWA6v7lp3a8/p+4NiO7d4LvHeY2SRJUxvrSWpJ0uhYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jG+e5Jz2/FLkizsGXtHu3xdkpcMM6ckaaKhFUSSnYEzgaOAxcBxSRb3rXYicFdVHQScAZzebrsYWAYcDBwJfLT9epKkOTLMPYjDgPVVdUNVPQCsBJb2rbMUOLt9fT5weJK0y1dW1c+r6kZgffv1JElzZJchfu0DgFt73m8AnjPZOlW1Kck9wH7t8ov7tj2g/xskOQk4qX17b5J12yb6jD0OuH22G+f0bZhkIrPNjtlmx2yzM8psT55sYJgFMXRVtQJYMeocSdZU1ZJR5+hittkx2+yYbXbGNdswDzHdBizoeT+/Xda5TpJdgL2AOwbcVpI0RMMsiEuBRUkOTLIbzaTzqr51VgHHt6+PAS6qqmqXL2vPcjoQWAR8Z4hZJUl9hnaIqZ1TOBm4ENgZ+HhVrU1yGrCmqlYBZwHnJFkP3ElTIrTrnQdcA2wC3lxVvxxW1m1g5Ie5pmC22THb7JhtdsYyW5p/2CVJ2ppXUkuSOlkQkqROFoQkqZMF8TAk2TfJvqPOIUnDYEHMUJInJVmZZCNwCfCdJD9uly0ccbyxl2T/JM9sP/YfdZ7pJNlz1BmkUfEsphlK8m3gQ8D5m0+9bW8keCxwSlU9d4TxJpXk6qo6ZITf/1Dg72guhtx80eN84G7gTVV1+WiSTS3JLVX1pDHIsT9bbjdzW1X96yjzDCLJnlV174gzhOY+bg/97oDv1Bj/4UvytKq6btQ5wIKYsSTXV9WimY7NhSS/P9kQ8HdVNW8u82wVILkCeGNVXdK3/LnAx6rqGSMJ1mR4y2RDwJ9X1cgOIz5SixVGX65JjgA+ClzP1r+7g2h+d18ZVbapjPr31usRfS+mEbksyUdp7kK7+WaEC2iuCP/uyFI1zgX+B9DV+o+a4yz9HtNfDgBVdXGSx4wiUI//AvwNzUWZ/UZ9GPaTTF6snwBGVqxtjqnKddSH5/4WeFFV3dS7sL07w2rgN0YRqs3w4cmGgL3nMMqULIiZex3Ncyzew9a7rZuvDB+lq4D3V9W/9A8kedEI8vT6UpILgE+xdbG+DvjyyFI1Lge+UFWX9Q8kecMI8vQa52KF8S7XXWjuBN3vNmDXOc7S7/XAW4Gfd4wdN8dZJuUhpu1Ikt8Fbq6qWzrGllTVmhHE6s1wFM2zPrYq1qpaPbpUkOSpwB1VNeF2y0n2H+Xx/vY/zV+nu1hvrKqTR5UNIMk/A/9xknK9taoWdGw2J5K8A3gVzbNoen93y4DzquqvRpjtIuCdVfXPHWM3VtWBI4g1gQUxQ+1dZ08EjmbrP3RfBM6qql+MKJq2U+NarPBQud5ZVRs7xkZarm2G36D7d3fN6FI1p8gD91fVfaPMMR0LYoaSfJZmgvBstuy+zqeZg9i3ql49omi95fUK4Int4rEvryQrquqk6dece+OcTRo2C2KGknyvqp4y07G5MOblNdmZQAGurKr5c5lnqwDjnW0v4B00/wXvT3MCwo9pSv99VXX3qLLBVvmOBh7PmOWbTJIvVdVRo87RZZyyOUk9c3cmORb4h6p6ECDJTjTXQdw10mTwrI6C2gBcnOR7owjUYyNwM80f3c2qff/4kSTaYpyznQdcBLygqn4EkORXgRPasSNGFw3Yku/5ffmOZ8T5kjxzsiHg0DmMMjHAGGfr5R7EDLVXS58OvIDmv3VoTkv7OrC8qm4cSTAgycXAB+gur7dUVf8zwecy2/XA4ZNMoI96MnOcs62rqqfOdGyujHO+JL8E/omti3+z51bVHnMc6SHjnK2XexAzVFU3JXk3zTUPW01Sj7IcWstoyuvMJHe3y/amKa9lI8q02YeAfYAJf4SBv57bKBN8iPHNdnOStwNnb57wba+qPoEtZ+aM0jjnu5bmGpLr+weSmG0A7kHMUJI/o/lju5Ktr85cBqysqveNKhtMetbGF6vq2tGlaiR5Gt1nlJhtEkn2AZbTZNt8uOtfaa67eV9VjfSw5jjnS3IMcHVVresYO7qqvjD3qR76/mObrZcFMUPtsfyD+88Iap+7vXbEt9oY2/Jq/8t8TZutdwLdbLOU5PVV9YlR55jMOOcz22AsiBlKch3wkqq6uW/5k4GvjPiY6ziXl9m2sXG6Z0+Xcc5ntsE4BzFzpwBfayc2Nx8rfBLNDcBGelUr8CDN9Q839y1/Qjs2SmabhSRXTTZEc9rrSI1zPrM9fBbEDFXVl5M8hYm3EL508+2/R+gUxre8TsFss7E/8BImnkIdYMJtGkZgnPOZ7WGyIGahPYX04lHn6DfO5WW2WftHYM+quqJ/IMk35jzNROOcz2wPk3MQkqROo74dryRpTFkQkqROFoR2WEnmJ/likuuT3JDkI0l2H2C7zucsJzlt84OZkpyS5NGTrPfSJN9NcmWSa5K8sV1+dJLFA3z/gdaTHi4LQjukJAE+R/MkuUXAImAPHsatNarq1Kr63+3bU4AJBZFkV2AF8LL2Ody/BXyjHT4aGOQP/6DrSQ+Lk9TaISU5HHhXVT2vZ9mv0FwLsQA4Bliy+YltSf6R5nGu32j3IP6e5k6lPwKWVdXGJJ+kOTvlicD7gXXA7VX1gp7vsS9wHfDkqvp/Pct/u932nvbjlcALgZOA3YD1wB/Q3Omzfz2AM4F5wH3AH1bVddvkF6UdmnsQ2lEdDGz1mMyq+glwE831D1N5DLCmqg6muSPnu/q+zoeBH9DcovsFfWN30tyn6OYkn03y2iQ7tY+eXAX8aVUdWlXfBz5XVc9u9zSuBU6cZL0VNI/9fBbwNuCjM/5tSB28DkKauQeBc9vXn6Y5VDWwqnpDkkOAF9H8QX8xzd1P+/1mkvfS3JF3T+DC/hWS7An8NvA/m6NmAEw7jyINwoLQjuoamsNID2kPMf0qzaGh32TrPexHTfG1ZnyctqquBq5Ocg5wI90F8Ung6Kq6MskJwPM71tkJuLuqDp1pBmk6HmLSjuprwKOTvA4gyc40D1v6SDs3cBNwaJKdkiygucp6s53YUi6vAf5vx9f/KfDY/oVJ9kzy/J5Fh7LlHlD92zwW+GE7sf3arq/dHha7sX3KIWk8Y6ofXBqUBaEdUjVnZ7wCOKa9B9MdwINV9Z/bVb5F85/9NcCHgct7Nv8ZcFiSf6GZSD6t41usAL6c5Ot9ywO8Pcm6JFcA72HL3sNK4E/bU2B/HfgL4JI2S++kc/96rwVOTHIlsJbm2QzSw+ZZTBIPnUX0WeAVVXX5dOtLOwILQpLUyUNMkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKnT/weRuZs3hsDuNQAAAABJRU5ErkJggg==\n",
       "text/plain": [
        "<Figure size 432x288 with 1 Axes>"
       ]
@@ -835,12 +780,17 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 8,
-   "metadata": {},
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:47:21.610944Z",
+     "start_time": "2021-01-09T12:47:21.228136Z"
+    }
+   },
    "outputs": [
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEPCAYAAABP1MOPAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAXIklEQVR4nO3dfbRddX3n8feHIGqF1gcitSQYqkGLT6gRXXWmRQsWlhawooZaFUfFjjKVZbUNU0VLnSlqdaxjbI31gbajEa3VtETR8aGd2kETEMUEIxGChNYaeVBbRzHynT/ODpycnHvvySX77Jvs92utu3L2/u1zzyf3j/u5e//2Q6oKSVJ/HdR1AElStywCSeo5i0CSes4ikKSeswgkqecO7jrA3jr88MNr2bJlXceQpP3K5Zdf/p2qWjxubL8rgmXLlrFx48auY0jSfiXJ9TONeWhIknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSem6/u7L4rli26pJOP3/bhU/t9PMlaRz3CCSp5ywCSeo5i0CSeq7VIkhycpItSbYmWTXDNs9KsjnJpiTvbzOPJGlPrU0WJ1kErAZOArYDG5Ksq6rNQ9ssB84DnlhVtyS5f1t5JEnjtblHcDywtaqurarbgLXAaSPbvBhYXVW3AFTVt1vMI0kao80iOBK4YWh5e7Nu2DHAMUk+n+SyJCeP+0ZJzk6yMcnGHTt2tBRXkvqp68nig4HlwAnAmcC7ktx7dKOqWlNVK6pqxeLFY5+0JkmapzaL4EZg6dDykmbdsO3Auqr6cVVdB3ydQTFIkqakzSLYACxPcnSSQ4CVwLqRbT7KYG+AJIczOFR0bYuZJEkjWiuCqtoJnANcClwNXFxVm5JckOTUZrNLgZuSbAY+C7yqqm5qK5MkaU+t3muoqtYD60fWnT/0uoBXNF+SpA50PVksSeqYRSBJPWcRSFLPWQSS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9ZxFIEk9ZxFIUs9ZBJLUcxaBJPWcRSBJPWcRSFLPWQSS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9ZxFIEk9ZxFIUs9ZBJLUc60WQZKTk2xJsjXJqjHjZyXZkeTK5utFbeaRJO3p4La+cZJFwGrgJGA7sCHJuqraPLLpB6vqnLZySJJm1+YewfHA1qq6tqpuA9YCp7X4eZKkeWizCI4Ebhha3t6sG/WMJF9J8uEkS8d9oyRnJ9mYZOOOHTvayCpJvdX1ZPHfAsuq6pHAp4CLxm1UVWuqakVVrVi8ePFUA0rSga7NIrgRGP4Lf0mz7g5VdVNV/ahZ/HPgsS3mkSSN0WYRbACWJzk6ySHASmDd8AZJHjC0eCpwdYt5JEljtHbWUFXtTHIOcCmwCHhPVW1KcgGwsarWAb+d5FRgJ3AzcFZbeSRJ47VWBABVtR5YP7Lu/KHX5wHntZlBkjS7rieLJUkdswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSem6iIkjyxCT3al7/ZpK3JHngBO87OcmWJFuTrJplu2ckqSQrJo8uSdoXJt0j+FPgB0keBfwO8A3gL2Z7Q5JFwGrgFOBY4Mwkx47Z7jDg5cAX9iK3JGkfmbQIdlZVAacBb6+q1cBhc7zneGBrVV1bVbcBa5v3j/pD4A3ADyfMIknahyYtgu8nOQ94LnBJkoOAu83xniOBG4aWtzfr7pDkMcDSqrpktm+U5OwkG5Ns3LFjx4SRJUmTmLQIng38CPhPVfUtYAnwprvywU2ZvIXBoaZZVdWaqlpRVSsWL158Vz5WkjRioiJofvn/NXD3ZtV3gL+Z4203AkuHlpc063Y5DHg48Lkk24AnAOucMJak6Zr0rKEXAx8G3tmsOhL46Bxv2wAsT3J0kkOAlcC6XYNV9d2qOryqllXVMuAy4NSq2rh3/wVJ0l0x6aGhlwFPBL4HUFXXAPef7Q1VtRM4B7gUuBq4uKo2JbkgyanzjyxJ2pcOnnC7H1XVbUkASHIwUHO9qarWA+tH1p0/w7YnTJhFkrQPTbpH8PdJ/itwzyQnAR8C/ra9WJKkaZm0CFYBO4CrgJcw+Cv/1W2FkiRNz0SHhqrqduBdzZck6QAyaxEkubiqnpXkKsbMCVTVI1tLJkmairn2CF7e/Pu0toNIkrox6xxBVf1L8/KlVXX98Bfw0vbjSZLaNulk8Ulj1p2yL4NIkrox1xzBf2bwl//PJ/nK0NBhwOfbDCZJmo655gjeD3wc+CMGp5Du8v2qurm1VJKkqZmrCKqqtiV52ehAkvtaBpK0/5tkj+BpwOUMTh/N0FgBP99SLknSlMxaBFX1tObfo6cTR5I0bXNNFj9mtvGqumLfxpEkTdtch4bePMtYAU/eh1kkSR2Y69DQk6YVRJLUjbkODT25qj6T5NfHjVfVR9qJJUmalrkODf0y8Bng18aMFWARSNJ+bq5DQ69t/n3BdOJIkqZt0ofX3y/J25JckeTyJH+S5H5th5MktW/Sm86tZfCEsmcAZzSvP9hWKEnS9Ez68PoHVNUfDi2/Psmz2wgkSZquSfcIPplkZZKDmq9nAZe2GUySNB1znT76fe68x9C5wF81QwcB/wa8ss1wkqT2zXXW0GHTCiJJ6sakcwQkuQ+wHLjHrnVV9Q9thJIkTc+kp4++CPgHBvMCf9D8+7oJ3ndyki1JtiZZNWb8t5JcleTKJP+Y5Ni9iy9JuqsmnSx+OfA44Prm/kOPBm6d7Q1JFgGrGTzb+FjgzDG/6N9fVY+oquOANwJvmTy6JGlfmLQIflhVPwRIcveq+hrwkDneczywtaqurarbGFyLcNrwBlX1vaHFezGYmJYkTdGkcwTbk9wb+CjwqSS3ANfP8Z4jgRuGvwfw+NGNmsdgvgI4hBlua53kbOBsgKOOOmrCyJKkSUy0R1BVT6+qW6vqdcBrgHcDp++LAFW1uqoeBPwe8OoZtllTVSuqasXixYv3xcdKkhp7c9bQY4D/wODwzeebwz2zuRFYOrS8pFk3k7XAn06aR5K0b0x61tD5wEXA/YDDgfcmGfvX+5ANwPIkRyc5BFgJrBv5vsuHFp8KXDNpcEnSvjHpHsFzgEcNTRhfCFwJvH6mN1TVziTnMDjVdBHwnqralOQCYGNVrQPOSXIi8GPgFuD58/6fSJLmZdIi+GcGF5L9sFm+O7Mf5gGgqtYD60fWnT/0+uUTfr4kqSVz3WvofzKYE/gusCnJp5rlk4Avth9PktS2ufYINjb/Xg78zdD6z7WSRpI0dXPddO6iXa+bCd9jmsUtVfXjNoNJkqZjojmCJCcwOGtoG4NbUi9N8nxvOidJ+79JJ4vfDDylqrYAJDkG+ADw2LaCSZKmY9J7Dd1tVwkAVNXXgbu1E0mSNE2T7hFcnuTPufMJZc/hzolkSdJ+bNIi+C3gZcBvN8v/B3hHK4kkSVM1ZxE0zxX4clU9FJ8XIEkHnDnnCKrqJ8CWJN7/WZIOQJMeGroPgyuLvwj8+66VVXVqK6kkSVMzaRG8ptUUkqTOzHWvoXswmCh+MHAV8O6q2jmNYJKk6ZhrjuAiYAWDEjiFwYVlkqQDyFyHho6tqkcAJHk33nFUkg44c+0R3HFjOQ8JSdKBaa49gkcl+V7zOsA9m+UAVVU/3Wo6SVLr5roN9aJpBZEkdWPSm85Jkg5QFoEk9ZxFIEk9ZxFIUs9ZBJLUcxaBJPVcq0WQ5OQkW5JsTbJqzPgrkmxO8pUkn07ywDbzSJL21FoRNA+0Wc3gHkXHAmcmOXZksy8BK6rqkcCHgTe2lUeSNF6bewTHA1ur6tqqug1YC5w2vEFVfbaqftAsXgYsaTGPJGmMNovgSOCGoeXtzbqZvBD4+LiBJGcn2Zhk444dO/ZhREnSgpgsTvKbDG53/aZx41W1pqpWVNWKxYsXTzecJB3gJn1C2XzcCCwdWl7SrNtNkhOB3wd+uap+1GIeSdIYbe4RbACWJzk6ySHASmDd8AZJHg28Ezi1qr7dYhZJ0gxaK4Lm+QXnAJcCVwMXV9WmJBck2fXQ+zcBhwIfSnJlknUzfDtJUkvaPDREVa0H1o+sO3/o9Yltfr4kaW4LYrJYktQdi0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp51otgiQnJ9mSZGuSVWPGfynJFUl2JjmjzSySpPEObusbJ1kErAZOArYDG5Ksq6rNQ5t9EzgLeGVbOfYXy1Zd0unnb7vwqTOOLeRsC5k/N+0vWisC4Hhga1VdC5BkLXAacEcRVNW2Zuz2FnNIkmbR5qGhI4Ebhpa3N+v2WpKzk2xMsnHHjh37JJwkaWC/mCyuqjVVtaKqVixevLjrOJJ0QGmzCG4Elg4tL2nWSZIWkDaLYAOwPMnRSQ4BVgLrWvw8SdI8tFYEVbUTOAe4FLgauLiqNiW5IMmpAEkel2Q78EzgnUk2tZVHkjRem2cNUVXrgfUj684fer2BwSEjSVJH9ovJYklSeywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6rmDuw4g3RXLVl3S6edvu/CpnX7+fC3kn9tCznagco9AknrOIpCknmu1CJKcnGRLkq1JVo0Zv3uSDzbjX0iyrM08kqQ9tVYESRYBq4FTgGOBM5McO7LZC4FbqurBwP8A3tBWHknSeG1OFh8PbK2qawGSrAVOAzYPbXMa8Lrm9YeBtydJVVWLuSRpXg7Uiey09Ts3yRnAyVX1omb5ucDjq+qcoW2+2myzvVn+RrPNd0a+19nA2c3iQ4AtrYSe2+HAd+bcqhtmmx+zzY/Z5qfLbA+sqsXjBvaL00erag2wpuscSTZW1Yquc4xjtvkx2/yYbX4WarY2J4tvBJYOLS9p1o3dJsnBwM8AN7WYSZI0os0i2AAsT3J0kkOAlcC6kW3WAc9vXp8BfMb5AUmartYODVXVziTnAJcCi4D3VNWmJBcAG6tqHfBu4C+TbAVuZlAWC1nnh6dmYbb5Mdv8mG1+FmS21iaLJUn7B68slqSeswgkqecsAknqOYtgAknum+S+XeeQpDZYBDNIclSStUl2AF8Avpjk2826ZR3HW/CSHJHkMc3XEV3nmUuSQ7vOIHXFs4ZmkOT/Am8FPlxVP2nWLQKeCZxbVU/oMN6MklxVVY/o8POPA/6MwcWBuy4gXALcCry0qq7oJtnsknyzqo5aADmOAI5sFm+sqn/tMs9ckhxaVf/WcYYwuLfZHT834IsL+ZqkJA+tqq91nWMXi2AGSa6pquV7OzYNSX59piHgz2a6n8g0JLkSeElVfWFk/ROAd1bVozoJNsjwipmGgN+vqs4O/1mg8/78pwDvAK5h95/bgxn83D7ZVbbZdP1zG7Vf3GuoI5cneQdwEXBDs24pgyuhv9RZqoEPAv8LGNfi95hyllH3Gi0BgKq6LMm9ugg05L8DbwJ2jhnr+jDp+5i5QN8LLNQC7fqQ2p8AJ1bVtuGVSY4G1gO/0EWoJsPbZhoC7j3FKHOyCGb2PAbPS/gDdt/l3HVFdJe+AvxxVX11dCDJiR3kGfbxJJcAf8HuBfo84BOdpRq4AvhoVV0+OpDkRR3kGWaBzs/BwPYx628E7jblLKNeAPwO8KMxY2dOOcusPDS0H0ryH4Hrq+qbY8ZWVNXGDmINZziFwbMmdivQqlrfXSpI8hDgptHbnDdjR3R5PL756/FBjC/Q64Zv395Btn8C/ssMBXpDVS0d87apSHIe8CxgLbv/3FYCF1fVH3WY7TPAq6vqn8aMXVdVR3cQayyLYAbN3VBfCJzO7r/QPga8u6p+3FE0HaAWeIHeXFU7xox1WqBNhl9g/M9t88zval9zyvkPq+oHXeaYhEUwgyQfYDBRdxF37nouYTBHcN+qenZH0YZL6unAzzWrF3xJJVlTVWfPveX0LeRsUtssghkk+XpVHbO3Y9OwwEtqpjNvAny5qpZMM89uARZ2tp8BzmPwl+0RDE4E+DaDcr+wqm5dANlOB+6/kLLNJsnHq+qUrnOMs9CyOVk8s5uTPBP466q6HSDJQQyuI7il02Tw2DFFtB24LMnXuwg0ZAdwPYNfrrtUs3z/ThLdaSFnuxj4DPCkqvoWQJKfBc5qxp7SXbQ7sp0wku35XWdL8piZhoDjphhlzwALONso9whm0Fw9/AbgSQz++obBKV+fBVZV1XWdBAOSXAa8mfEl9YqqenyH2a4BfmWGieyuJxYXcrYtVfWQvR2bhgWe7SfA37N7ue/yhKq655Qj3WEhZxvlHsEMqmpbktcxuGZgt8niLkugsZJBSa1Ocmuz7t4MSqrrh/u8FbgPsMcvW+CN042yh7eycLNdn+R3gYt2Tb42VxmfxZ1nw3RlIWe7msH1F9eMDiQx24TcI5hBkt9j8Et1LbtfsbgSWFtVF3aVDWY8U+JjVXV1d6kGkjyU8WdxmG0GSe4DrGKQbddhqn9lcN3KhVXV2eHIBZ7tDOCqqtoyZuz0qvro9FPd8fkLNtsoi2AGzbH2h42egdM8f3lTx7eYWLAl1fzl+BtNtuGJbLPNU5IXVNV7u84xjtnmZ6FlswhmkORrwK9W1fUj6x8IfLLj46ILuaTMto8ttPvSDDPb/Cy0bM4RzOxc4NPNBOOu43lHMbiZVWdXeTZuZ3D9wPUj6x/QjHXJbPOQ5CszDTE4nbQzZpufhZxtlEUwg6r6RJJj2PP2tht23Za6Q+eycEvqXMw2H0cAv8qepyYH2OMWBVNmtvlZyNl2YxHMojk187Kuc4xayCVltnn7O+DQqrpydCDJ56aeZndmm5+FnG03zhFIUs91fQtZSVLHLAJJ6jmLQAe0JEuSfCzJNUmuTfL2JHef4H1jn8Ob5IJdD/9Jcm6Sn5phu6cl+VKSLyfZnOQlzfrTkxw7wedPtJ20L1gEOmAlCfARBk8lWw4sB+7JXbidRFWdX1X/u1k8F9ijCJLcDVgD/FrzjOZHA59rhk8HJvkFP+l20l3mZLEOWEl+BXhtVf3S0LqfZnAdwVLgDGDFrqd/Jfk7Bo8A/VyzR/AuBnfW/Bawsqp2JHkfg7NBfg74Y2AL8J2qetLQZ9wX+BrwwKr6f0Prf7F573ebr2cATwbOBg4BtgLPZXBnytHtAFYDi4EfAC+uqq/tkx+Ues89Ah3IHgbs9njFqvoesI3BtQOzuRewsaoexuAOkq8d+T5vA/6ZwW2jnzQydjOD+/Bcn+QDSZ6T5KDmkYXrgFdV1XFV9Q3gI1X1uGbP4WrghTNst4bB4yIfC7wSeMde/zSkGXgdgTTe7cAHm9d/xeAQ08Sq6kVJHgGcyOAX90kM7tY56uFJXs/g7rGHApeObpDkUOAXgQ8NjnYBMOc8hzQpi0AHss0MDv/coTk09LMMDuk8nN33iu8xy/fa62OoVXUVcFWSvwSuY3wRvA84vaq+nOQs4IQx2xwE3FpVx+1tBmkSHhrSgezTwE8leR5AkkUMHujz9ubY/TbguCQHJVnK4IrjXQ7izhL5DeAfx3z/7wOHja5McmiSE4ZWHced9zcafc9hwL80E8zPGfe9m8NZ1zVPzCMDj5rtPy7tDYtAB6wanAnxdOCM5v5CNwG3V9V/azb5PIO/1DcDbwOuGHr7vwPHJ/kqgwndC8Z8xBrgE0k+O7I+wO8m2ZLkSuAPuHNvYC3wqubU0gcBrwG+0GQZnvwd3e45wAuTfBnYxODZANI+4VlD6o3mrJ0PAE+vqivm2l7qC4tAknrOQ0OS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9dz/B9VMzjhMqx3WAAAAAElFTkSuQmCC\n",
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEPCAYAAABP1MOPAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAXIklEQVR4nO3dfbRddX3n8feHIGqF1gcitSQYqkGLT6gRXXWmRQsWlhawooZaFUfFjjKVZbUNU0VLnSlqdaxjbI31gbajEa3VtETR8aGd2kETEMUEIxGChNYaeVBbRzHynT/ODpycnHvvySX77Jvs92utu3L2/u1zzyf3j/u5e//2Q6oKSVJ/HdR1AElStywCSeo5i0CSes4ikKSeswgkqecO7jrA3jr88MNr2bJlXceQpP3K5Zdf/p2qWjxubL8rgmXLlrFx48auY0jSfiXJ9TONeWhIknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSem6/u7L4rli26pJOP3/bhU/t9PMlaRz3CCSp5ywCSeo5i0CSeq7VIkhycpItSbYmWTXDNs9KsjnJpiTvbzOPJGlPrU0WJ1kErAZOArYDG5Ksq6rNQ9ssB84DnlhVtyS5f1t5JEnjtblHcDywtaqurarbgLXAaSPbvBhYXVW3AFTVt1vMI0kao80iOBK4YWh5e7Nu2DHAMUk+n+SyJCeP+0ZJzk6yMcnGHTt2tBRXkvqp68nig4HlwAnAmcC7ktx7dKOqWlNVK6pqxeLFY5+0JkmapzaL4EZg6dDykmbdsO3Auqr6cVVdB3ydQTFIkqakzSLYACxPcnSSQ4CVwLqRbT7KYG+AJIczOFR0bYuZJEkjWiuCqtoJnANcClwNXFxVm5JckOTUZrNLgZuSbAY+C7yqqm5qK5MkaU+t3muoqtYD60fWnT/0uoBXNF+SpA50PVksSeqYRSBJPWcRSFLPWQSS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9ZxFIEk9ZxFIUs9ZBJLUcxaBJPWcRSBJPWcRSFLPWQSS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9ZxFIEk9ZxFIUs9ZBJLUc60WQZKTk2xJsjXJqjHjZyXZkeTK5utFbeaRJO3p4La+cZJFwGrgJGA7sCHJuqraPLLpB6vqnLZySJJm1+YewfHA1qq6tqpuA9YCp7X4eZKkeWizCI4Ebhha3t6sG/WMJF9J8uEkS8d9oyRnJ9mYZOOOHTvayCpJvdX1ZPHfAsuq6pHAp4CLxm1UVWuqakVVrVi8ePFUA0rSga7NIrgRGP4Lf0mz7g5VdVNV/ahZ/HPgsS3mkSSN0WYRbACWJzk6ySHASmDd8AZJHjC0eCpwdYt5JEljtHbWUFXtTHIOcCmwCHhPVW1KcgGwsarWAb+d5FRgJ3AzcFZbeSRJ47VWBABVtR5YP7Lu/KHX5wHntZlBkjS7rieLJUkdswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSem6iIkjyxCT3al7/ZpK3JHngBO87OcmWJFuTrJplu2ckqSQrJo8uSdoXJt0j+FPgB0keBfwO8A3gL2Z7Q5JFwGrgFOBY4Mwkx47Z7jDg5cAX9iK3JGkfmbQIdlZVAacBb6+q1cBhc7zneGBrVV1bVbcBa5v3j/pD4A3ADyfMIknahyYtgu8nOQ94LnBJkoOAu83xniOBG4aWtzfr7pDkMcDSqrpktm+U5OwkG5Ns3LFjx4SRJUmTmLQIng38CPhPVfUtYAnwprvywU2ZvIXBoaZZVdWaqlpRVSsWL158Vz5WkjRioiJofvn/NXD3ZtV3gL+Z4203AkuHlpc063Y5DHg48Lkk24AnAOucMJak6Zr0rKEXAx8G3tmsOhL46Bxv2wAsT3J0kkOAlcC6XYNV9d2qOryqllXVMuAy4NSq2rh3/wVJ0l0x6aGhlwFPBL4HUFXXAPef7Q1VtRM4B7gUuBq4uKo2JbkgyanzjyxJ2pcOnnC7H1XVbUkASHIwUHO9qarWA+tH1p0/w7YnTJhFkrQPTbpH8PdJ/itwzyQnAR8C/ra9WJKkaZm0CFYBO4CrgJcw+Cv/1W2FkiRNz0SHhqrqduBdzZck6QAyaxEkubiqnpXkKsbMCVTVI1tLJkmairn2CF7e/Pu0toNIkrox6xxBVf1L8/KlVXX98Bfw0vbjSZLaNulk8Ulj1p2yL4NIkrox1xzBf2bwl//PJ/nK0NBhwOfbDCZJmo655gjeD3wc+CMGp5Du8v2qurm1VJKkqZmrCKqqtiV52ehAkvtaBpK0/5tkj+BpwOUMTh/N0FgBP99SLknSlMxaBFX1tObfo6cTR5I0bXNNFj9mtvGqumLfxpEkTdtch4bePMtYAU/eh1kkSR2Y69DQk6YVRJLUjbkODT25qj6T5NfHjVfVR9qJJUmalrkODf0y8Bng18aMFWARSNJ+bq5DQ69t/n3BdOJIkqZt0ofX3y/J25JckeTyJH+S5H5th5MktW/Sm86tZfCEsmcAZzSvP9hWKEnS9Ez68PoHVNUfDi2/Psmz2wgkSZquSfcIPplkZZKDmq9nAZe2GUySNB1znT76fe68x9C5wF81QwcB/wa8ss1wkqT2zXXW0GHTCiJJ6sakcwQkuQ+wHLjHrnVV9Q9thJIkTc+kp4++CPgHBvMCf9D8+7oJ3ndyki1JtiZZNWb8t5JcleTKJP+Y5Ni9iy9JuqsmnSx+OfA44Prm/kOPBm6d7Q1JFgGrGTzb+FjgzDG/6N9fVY+oquOANwJvmTy6JGlfmLQIflhVPwRIcveq+hrwkDneczywtaqurarbGFyLcNrwBlX1vaHFezGYmJYkTdGkcwTbk9wb+CjwqSS3ANfP8Z4jgRuGvwfw+NGNmsdgvgI4hBlua53kbOBsgKOOOmrCyJKkSUy0R1BVT6+qW6vqdcBrgHcDp++LAFW1uqoeBPwe8OoZtllTVSuqasXixYv3xcdKkhp7c9bQY4D/wODwzeebwz2zuRFYOrS8pFk3k7XAn06aR5K0b0x61tD5wEXA/YDDgfcmGfvX+5ANwPIkRyc5BFgJrBv5vsuHFp8KXDNpcEnSvjHpHsFzgEcNTRhfCFwJvH6mN1TVziTnMDjVdBHwnqralOQCYGNVrQPOSXIi8GPgFuD58/6fSJLmZdIi+GcGF5L9sFm+O7Mf5gGgqtYD60fWnT/0+uUTfr4kqSVz3WvofzKYE/gusCnJp5rlk4Avth9PktS2ufYINjb/Xg78zdD6z7WSRpI0dXPddO6iXa+bCd9jmsUtVfXjNoNJkqZjojmCJCcwOGtoG4NbUi9N8nxvOidJ+79JJ4vfDDylqrYAJDkG+ADw2LaCSZKmY9J7Dd1tVwkAVNXXgbu1E0mSNE2T7hFcnuTPufMJZc/hzolkSdJ+bNIi+C3gZcBvN8v/B3hHK4kkSVM1ZxE0zxX4clU9FJ8XIEkHnDnnCKrqJ8CWJN7/WZIOQJMeGroPgyuLvwj8+66VVXVqK6kkSVMzaRG8ptUUkqTOzHWvoXswmCh+MHAV8O6q2jmNYJKk6ZhrjuAiYAWDEjiFwYVlkqQDyFyHho6tqkcAJHk33nFUkg44c+0R3HFjOQ8JSdKBaa49gkcl+V7zOsA9m+UAVVU/3Wo6SVLr5roN9aJpBZEkdWPSm85Jkg5QFoEk9ZxFIEk9ZxFIUs9ZBJLUcxaBJPVcq0WQ5OQkW5JsTbJqzPgrkmxO8pUkn07ywDbzSJL21FoRNA+0Wc3gHkXHAmcmOXZksy8BK6rqkcCHgTe2lUeSNF6bewTHA1ur6tqqug1YC5w2vEFVfbaqftAsXgYsaTGPJGmMNovgSOCGoeXtzbqZvBD4+LiBJGcn2Zhk444dO/ZhREnSgpgsTvKbDG53/aZx41W1pqpWVNWKxYsXTzecJB3gJn1C2XzcCCwdWl7SrNtNkhOB3wd+uap+1GIeSdIYbe4RbACWJzk6ySHASmDd8AZJHg28Ezi1qr7dYhZJ0gxaK4Lm+QXnAJcCVwMXV9WmJBck2fXQ+zcBhwIfSnJlknUzfDtJUkvaPDREVa0H1o+sO3/o9Yltfr4kaW4LYrJYktQdi0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp51otgiQnJ9mSZGuSVWPGfynJFUl2JjmjzSySpPEObusbJ1kErAZOArYDG5Ksq6rNQ5t9EzgLeGVbOfYXy1Zd0unnb7vwqTOOLeRsC5k/N+0vWisC4Hhga1VdC5BkLXAacEcRVNW2Zuz2FnNIkmbR5qGhI4Ebhpa3N+v2WpKzk2xMsnHHjh37JJwkaWC/mCyuqjVVtaKqVixevLjrOJJ0QGmzCG4Elg4tL2nWSZIWkDaLYAOwPMnRSQ4BVgLrWvw8SdI8tFYEVbUTOAe4FLgauLiqNiW5IMmpAEkel2Q78EzgnUk2tZVHkjRem2cNUVXrgfUj684fer2BwSEjSVJH9ovJYklSeywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6rmDuw4g3RXLVl3S6edvu/CpnX7+fC3kn9tCznagco9AknrOIpCknmu1CJKcnGRLkq1JVo0Zv3uSDzbjX0iyrM08kqQ9tVYESRYBq4FTgGOBM5McO7LZC4FbqurBwP8A3tBWHknSeG1OFh8PbK2qawGSrAVOAzYPbXMa8Lrm9YeBtydJVVWLuSRpXg7Uiey09Ts3yRnAyVX1omb5ucDjq+qcoW2+2myzvVn+RrPNd0a+19nA2c3iQ4AtrYSe2+HAd+bcqhtmmx+zzY/Z5qfLbA+sqsXjBvaL00erag2wpuscSTZW1Yquc4xjtvkx2/yYbX4WarY2J4tvBJYOLS9p1o3dJsnBwM8AN7WYSZI0os0i2AAsT3J0kkOAlcC6kW3WAc9vXp8BfMb5AUmartYODVXVziTnAJcCi4D3VNWmJBcAG6tqHfBu4C+TbAVuZlAWC1nnh6dmYbb5Mdv8mG1+FmS21iaLJUn7B68slqSeswgkqecsAknqOYtgAknum+S+XeeQpDZYBDNIclSStUl2AF8Avpjk2826ZR3HW/CSHJHkMc3XEV3nmUuSQ7vOIHXFs4ZmkOT/Am8FPlxVP2nWLQKeCZxbVU/oMN6MklxVVY/o8POPA/6MwcWBuy4gXALcCry0qq7oJtnsknyzqo5aADmOAI5sFm+sqn/tMs9ckhxaVf/WcYYwuLfZHT834IsL+ZqkJA+tqq91nWMXi2AGSa6pquV7OzYNSX59piHgz2a6n8g0JLkSeElVfWFk/ROAd1bVozoJNsjwipmGgN+vqs4O/1mg8/78pwDvAK5h95/bgxn83D7ZVbbZdP1zG7Vf3GuoI5cneQdwEXBDs24pgyuhv9RZqoEPAv8LGNfi95hyllH3Gi0BgKq6LMm9ugg05L8DbwJ2jhnr+jDp+5i5QN8LLNQC7fqQ2p8AJ1bVtuGVSY4G1gO/0EWoJsPbZhoC7j3FKHOyCGb2PAbPS/gDdt/l3HVFdJe+AvxxVX11dCDJiR3kGfbxJJcAf8HuBfo84BOdpRq4AvhoVV0+OpDkRR3kGWaBzs/BwPYx628E7jblLKNeAPwO8KMxY2dOOcusPDS0H0ryH4Hrq+qbY8ZWVNXGDmINZziFwbMmdivQqlrfXSpI8hDgptHbnDdjR3R5PL756/FBjC/Q64Zv395Btn8C/ssMBXpDVS0d87apSHIe8CxgLbv/3FYCF1fVH3WY7TPAq6vqn8aMXVdVR3cQayyLYAbN3VBfCJzO7r/QPga8u6p+3FE0HaAWeIHeXFU7xox1WqBNhl9g/M9t88zval9zyvkPq+oHXeaYhEUwgyQfYDBRdxF37nouYTBHcN+qenZH0YZL6unAzzWrF3xJJVlTVWfPveX0LeRsUtssghkk+XpVHbO3Y9OwwEtqpjNvAny5qpZMM89uARZ2tp8BzmPwl+0RDE4E+DaDcr+wqm5dANlOB+6/kLLNJsnHq+qUrnOMs9CyOVk8s5uTPBP466q6HSDJQQyuI7il02Tw2DFFtB24LMnXuwg0ZAdwPYNfrrtUs3z/ThLdaSFnuxj4DPCkqvoWQJKfBc5qxp7SXbQ7sp0wku35XWdL8piZhoDjphhlzwALONso9whm0Fw9/AbgSQz++obBKV+fBVZV1XWdBAOSXAa8mfEl9YqqenyH2a4BfmWGieyuJxYXcrYtVfWQvR2bhgWe7SfA37N7ue/yhKq655Qj3WEhZxvlHsEMqmpbktcxuGZgt8niLkugsZJBSa1Ocmuz7t4MSqrrh/u8FbgPsMcvW+CN042yh7eycLNdn+R3gYt2Tb42VxmfxZ1nw3RlIWe7msH1F9eMDiQx24TcI5hBkt9j8Et1LbtfsbgSWFtVF3aVDWY8U+JjVXV1d6kGkjyU8WdxmG0GSe4DrGKQbddhqn9lcN3KhVXV2eHIBZ7tDOCqqtoyZuz0qvro9FPd8fkLNtsoi2AGzbH2h42egdM8f3lTx7eYWLAl1fzl+BtNtuGJbLPNU5IXVNV7u84xjtnmZ6FlswhmkORrwK9W1fUj6x8IfLLj46ILuaTMto8ttPvSDDPb/Cy0bM4RzOxc4NPNBOOu43lHMbiZVWdXeTZuZ3D9wPUj6x/QjHXJbPOQ5CszDTE4nbQzZpufhZxtlEUwg6r6RJJj2PP2tht23Za6Q+eycEvqXMw2H0cAv8qepyYH2OMWBVNmtvlZyNl2YxHMojk187Kuc4xayCVltnn7O+DQqrpydCDJ56aeZndmm5+FnG03zhFIUs91fQtZSVLHLAJJ6jmLQAe0JEuSfCzJNUmuTfL2JHef4H1jn8Ob5IJdD/9Jcm6Sn5phu6cl+VKSLyfZnOQlzfrTkxw7wedPtJ20L1gEOmAlCfARBk8lWw4sB+7JXbidRFWdX1X/u1k8F9ijCJLcDVgD/FrzjOZHA59rhk8HJvkFP+l20l3mZLEOWEl+BXhtVf3S0LqfZnAdwVLgDGDFrqd/Jfk7Bo8A/VyzR/AuBnfW/Bawsqp2JHkfg7NBfg74Y2AL8J2qetLQZ9wX+BrwwKr6f0Prf7F573ebr2cATwbOBg4BtgLPZXBnytHtAFYDi4EfAC+uqq/tkx+Ues89Ah3IHgbs9njFqvoesI3BtQOzuRewsaoexuAOkq8d+T5vA/6ZwW2jnzQydjOD+/Bcn+QDSZ6T5KDmkYXrgFdV1XFV9Q3gI1X1uGbP4WrghTNst4bB4yIfC7wSeMde/zSkGXgdgTTe7cAHm9d/xeAQ08Sq6kVJHgGcyOAX90kM7tY56uFJXs/g7rGHApeObpDkUOAXgQ8NjnYBMOc8hzQpi0AHss0MDv/coTk09LMMDuk8nN33iu8xy/fa62OoVXUVcFWSvwSuY3wRvA84vaq+nOQs4IQx2xwE3FpVx+1tBmkSHhrSgezTwE8leR5AkkUMHujz9ubY/TbguCQHJVnK4IrjXQ7izhL5DeAfx3z/7wOHja5McmiSE4ZWHced9zcafc9hwL80E8zPGfe9m8NZ1zVPzCMDj5rtPy7tDYtAB6wanAnxdOCM5v5CNwG3V9V/azb5PIO/1DcDbwOuGHr7vwPHJ/kqgwndC8Z8xBrgE0k+O7I+wO8m2ZLkSuAPuHNvYC3wqubU0gcBrwG+0GQZnvwd3e45wAuTfBnYxODZANI+4VlD6o3mrJ0PAE+vqivm2l7qC4tAknrOQ0OS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9dz/B9VMzjhMqx3WAAAAAElFTkSuQmCC\n",
       "text/plain": [
        "<Figure size 432x288 with 1 Axes>"
       ]
@@ -882,7 +832,7 @@
     "\\begin{bmatrix} \n",
     "\\cos \\frac{\\theta}{2} & -e^{i \\varphi}\\sin \\frac{\\theta}{2} \\\\ \n",
     "e^{i \\phi}\\sin \\frac{\\theta}{2} &e^{i (\\phi+\\varphi)} \\cos \\frac{\\theta}{2} \n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix},\\tag{20}\n",
     "$$\n",
     "\n",
     "$U_3$ 旋转门在效果上是等价于以下组合旋转门的,\n",
@@ -902,26 +852,30 @@
     "\\begin{bmatrix}\n",
     "e^{-i\\frac{\\varphi}{2}} & 0 \\\\ \n",
     "0 & e^{i\\frac{\\varphi}{2}}\n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix}.\\tag{21}\n",
     "$$\n",
     "\n",
     "感兴趣的读者不妨自行验证一下。\n",
     "\n",
-    "<img src=\"figures/complex_entangled_layer.png\" width=\"850\" >\n",
+    "<img src=\"figures/intro-fig-complex_entangled_layer2-cn.png\" width=\"850\" >\n",
     "\n",
     "特别地，当我们处理的任务不涉及虚数时，使用电路模板 `real_entangled_layer(theta, DEPTH)` 会更加高效 ($R_y$旋转门替代$U_3$)。"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 9,
+   "execution_count": 6,
    "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:47:40.125099Z",
+     "start_time": "2021-01-09T12:47:39.631740Z"
+    },
     "scrolled": true
    },
    "outputs": [
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAERCAYAAABhKjCtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAc2ElEQVR4nO3de5gddZ3n8fcn4aZcFCRehiQkahgFEdCWcccVb6DhQbmMOISLouJEhQzyqCNhdUDiZRFHV12DGtcoOivBu1mJICvgrrpIEq4mGgmRSyKMkYCgKBD47B9VIScn1aerO11dh+Tzep5+uqp+VXU+3WJ/U/X71a9km4iIiG7j2g4QERH9KQUiIiIqpUBERESlFIiIiKiUAhEREZVSICIiolKjBULSdEkrJK2UNLui/R2SbpJ0vaSfStq33D5F0l/K7ddL+nyTOSMiYnNq6jkISeOB3wCHAauBxcDxtpd37LOb7fvK5SOBU21PlzQF+IHt59X9vD333NNTpkwZxZ8gImLrt3Tp0j/YnlDVtl2Dn3swsNL2KgBJC4CjgMcKxIbiUNoZGHG1mjJlCkuWLBnp4RER2yRJtw3W1uQtpr2AOzrWV5fbNiHpNEm3AOcDp3c0TZV0naSfSHppgzkjIqJC653UtufafhZwJvCBcvOdwGTbBwHvBr4uabfuYyXNlLRE0pK1a9eOXeiIiG1AkwViDTCpY31iuW0wC4CjAWw/aPvucnkpcAuwT/cBtufZHrA9MGFC5S20iIgYoSYLxGJgmqSpknYAZgALO3eQNK1j9Qjg5nL7hLKTG0nPBKYBqxrMGhERXRrrpLa9XtIs4DJgPDDf9jJJc4AlthcCsyQdCjwM3AOcXB5+CDBH0sPAo8A7bK9rKmtERGyusWGuY21gYMAZxRQRMTySltoeqGprvZM6IiL6UwpERERUSoGIiIhKTT5JHaNkyuxLWvvsW887orXPjoh25QoiIiIqpUBERESlFIiIiKiUAhEREZVSICIiolIKREREVEqBiIiISikQERFRKQUiIiIqpUBERESlFIiIiKiUAhEREZVSICIiolIKREREVEqBiIiISikQERFRKQUiIiIqpUBERESlRguEpOmSVkhaKWl2Rfs7JN0k6XpJP5W0b0fbWeVxKyS9psmcERGxucYKhKTxwFzgcGBf4PjOAlD6uu39bR8InA98sjx2X2AGsB8wHbigPF9ERIyRJq8gDgZW2l5l+yFgAXBU5w627+tY3RlwuXwUsMD2g7Z/C6wszxcREWNkuwbPvRdwR8f6auDvuneSdBrwbmAH4JUdx17ddexezcSMiIgqrXdS255r+1nAmcAHhnOspJmSlkhasnbt2mYCRkRso5osEGuASR3rE8ttg1kAHD2cY23Psz1ge2DChAlbljYiIjbRZIFYDEyTNFXSDhSdzgs7d5A0rWP1CODmcnkhMEPSjpKmAtOAaxrMGhERXRrrg7C9XtIs4DJgPDDf9jJJc4AlthcCsyQdCjwM3AOcXB67TNI3gOXAeuA02480lTUiIjbXZCc1thcBi7q2nd2x/K4ex34E+Ehz6SIiopfWO6kjIqI/pUBERESlFIiIiKiUAhEREZVSICIiolIKREREVEqBiIiISikQERFRKQUiIiIqpUBERESlFIiIiKiUAhEREZVSICIiolIKREREVEqBiIiISkMWCEkvkbRzuXySpE9K2rv5aBER0aY6VxCfAx6QdADwHuAW4KuNpoqIiNbVKRDrbRs4Cvis7bnArs3GioiIttV55ej9ks4C3gi8VNI4YPtmY0VERNvqXEEcBzwIvNX2XcBE4OONpoqIiNYNWSDKovBtYMdy0x+A7zYZKiIi2ldnFNM/Ad8CvlBu2gv4XoOZIiKiD9S5xXQa8BLgPgDbNwNPrXNySdMlrZC0UtLsivZ3S1ou6UZJP+4cPivpEUnXl18L6/04ERExWup0Uj9o+yFJAEjaDvBQB0kaD8wFDgNWA4slLbS9vGO364AB2w9IeidwPkWfB8BfbB9Y+yeJiIhRVecK4ieS/gvwBEmHAd8E/leN4w4GVtpeZfshYAHFUNnH2L7S9gPl6tUUHeAREdEH6hSI2cBa4Cbg7cAi4AM1jtsLuKNjfXW5bTCnAD/sWN9J0hJJV0s6uuoASTPLfZasXbu2RqSIiKhryFtMth8Fvlh+NULSScAA8LKOzXvbXiPpmcAVkm6yfUtXtnnAPICBgYEhb3tFRER9gxYISd+w/Y+SbqKiz8H284c49xpgUsf6xHJb9+ccCrwfeJntBzvOv6b8vkrSVcBBFNN8RETEGOh1BfGu8vtrR3juxcA0SVMpCsMM4ITOHSQdRDF8drrt33ds3x14wPaDkvakGEV1/ghzRETECAzaB2H7znLxVNu3dX4Bpw51YtvrgVnAZcCvgG/YXiZpjqQjy90+DuwCfLNrOOtzgSWSbgCuBM7rGv0UERENqzPM9TDgzK5th1ds24ztRRSd2p3bzu5YPnSQ434O7F8jW0RENKRXH8Q7Ka4Uninpxo6mXYGfNR0sIiLa1esK4usUw07/K8VQ1w3ut72u0VQREdG6XgXCtm+VdFp3g6Q9UiQiIrZuQ11BvBZYSjHMVR1tBp7ZYK6IiGjZoAXC9mvL71PHLk5ERPSLXp3UL+h1oO1rRz9ORET0i163mD7Ro83AK0c5S0RE9JFet5heMZZBIiKiv/S6xfRK21dI+oeqdtvfaS5WRES0rdctppcBVwCvq2gzkAIREbEV63WL6Zzy+1vGLk5ERPSLIV8YJOkpkj4j6VpJSyV9WtJTxiJcRES0p84b5RZQvFHu9cCx5fLFTYaKiIj21ZnN9Rm2P9Sx/mFJxzUVKCIi+kOdK4gfSZohaVz59Y8U73iIiIitWK9hrvezcQ6mM4B/L5vGAX8C3tt0uIiIaE+vUUy7jmWQiIjoL3X6IDa8I3oasNOGbbb/T1OhIiKifUMWCElvA94FTASuB14M/D8yF1NExFatTif1u4AXAbeV8zMdBNzbZKiIiGhfnQLxV9t/BZC0o+1fA3/bbKyIiGhbnQKxWtKTge8Bl0v6PnBbnZNLmi5phaSVkmZXtL9b0nJJN0r6saS9O9pOlnRz+XVyvR8nIiJGy5B9ELaPKRc/KOlK4EnApUMdJ2k8MBc4DFgNLJa00Pbyjt2uAwZsPyDpncD5wHGS9gDOAQYohtouLY+9Zxg/W0REbIE6VxBIeoGk04HnA6ttP1TjsIOBlbZXlfsvAI7q3MH2lbYfKFevpugIB3gNcLntdWVRuByYXidrRESMjjqT9Z0NXAg8BdgT+LKkD9Q4917AHR3rq8ttgzkF+OEIj42IiFFW5zmIE4EDOjqqz6MY7vrh0Qoh6SSK20kvG+ZxM4GZAJMnTx6tOBERQb1bTL+j4wE5YEdgTY3j1gCTOtYnVh0n6VDg/cCRth8czrG259kesD0wYcKEGpEiIqKuXnMx/XeKDuI/AsskXV6uHwZcU+Pci4FpkqZS/HGfAZzQ9RkHAV8Aptv+fUfTZcBHyye4AV4NnFXrJ4qIiFHR6xbTkvL7UuC7HduvqnNi2+slzaL4Yz8emG97maQ5wBLbC4GPA7sA35QEcLvtI22vk/QhiiIDMMf2uro/VEREbLlek/VduGFZ0g7APuXqCtsP1zm57UXAoq5tZ3csH9rj2PnA/DqfExERo6/OXEwvpxjFdCvF1N+TJJ2cyfoiIrZudUYxfQJ4te0VAJL2AS4CXthksIiIaFedUUzbbygOALZ/A2zfXKSIiOgHda4glkr6H2x8o9yJbOzAjoiIrVSdAvEO4DTg9HL9/wIXNJYoIiL6Qs8CUU64d4Pt5wCfHJtIERHRD3r2Qdh+BFghKfNYRERsY+rcYtqd4knqa4A/b9ho+8jGUkVEROvqFIh/bTxFRET0nV5zMe1E0UH9bOAm4Eu2149VsIiIaFevPogLKabgvgk4nOKBuYiI2Eb0usW0r+39ASR9iXozuEZExFai1xXEYxPy5dZSRMS2p9cVxAGS7iuXBTyhXBdg27s1ni4iIlrTa7rv8WMZJGJbMmX2Ja199q3nHdHaZ8fjS53J+iIiYhuUAhEREZVSICIiolIKREREVOr1JPX9gAdrzyimiIitW69RTLsCSPoQcCfwNYohricCzxiTdBER0Zo6t5iOtH2B7ftt32f7c8BRTQeLiIh21SkQf5Z0oqTxksZJOpGOab97kTRd0gpJKyXNrmg/RNK1ktZLOrar7RFJ15dfC+v9OBERMVrqTPd9AvDp8svAz8ptPZVvo5sLHAasBhZLWmh7ecdutwNvBt5bcYq/2D6wRr6IiGjAkAXC9q2M7JbSwcBK26sAJC0oz/NYgSjPjaRHR3D+iIho0JC3mCTtI+nHkn5Zrj9f0gdqnHsv4I6O9dXltrp2krRE0tWSjh7GcRERMQrq9EF8ETiLcnZX2zcCM5oMVdrb9gDF7axPSXpW9w6SZpZFZMnatWvHIFJExLajToF4ou3ud0HUmf57DTCpY31iua0W22vK76uAq4CDKvaZZ3vA9sCECRPqnjoiImqoUyD+UP7r3QDlaKM7axy3GJgmaaqkHSiuOmqNRpK0u6Qdy+U9gZfQ0XcRERHNqzOK6TRgHvAcSWuA31I8LNeT7fWSZgGXAeOB+baXSZoDLLG9UNKLgO8CuwOvk3Su7f2A5wJfKDuvxwHndY1+ioiIhvUsEOVQ1VNtHyppZ2Cc7fvrntz2ImBR17azO5YXU9x66j7u58D+dT8nIiJGX88CYfsRSf+5XK71cFxERGwd6txiuq58kvmbdDxBbfs7jaWKiIjW1SkQOwF3A6/s2GYgBSIiYitW50nqt4xFkIiI6C9DFghJX6bivRC239pIooiI6At1bjH9oGN5J+AY4HfNxImIiH5R5xbTtzvXJV0E/LSxRBER0RdG8k7qacBTRztIRET0lzp9EN3vpr4LOLOxRBER0Rfq3GLadSyCREREf6nzPoiXlNNsIOkkSZ+UtHfz0SIiok11+iA+Bzwg6QDgPcAtwFcbTRUREa2rUyDW2zbF60I/a3sukNtOERFbuTrPQdwv6SzgJOAQSeOA7ZuNFRERbatTII6jeO3nKbbvkjQZ+HizsSIiNjdl9iWtffat5x3R2me3pc4opruAT3as3076ICIitnp1RjG9WNJiSX+S9JCkRyT9cSzCRUREe+p0Un8WOB64GXgC8DbggiZDRURE+2pNtWF7JTDe9iO2vwxMbzZWRES0rU4n9QOSdgCul3Q+cCcjm8MpIiIeR+r8oX9jud8sileOTgJe32SoiIhoX51RTLdJegLwDNvnjkGmeBzJsMOIrVedUUyvA64HLi3XD5S0sM7JJU2XtELSSkmzK9oPkXStpPWSju1qO1nSzeXXybV+moiIGDV1bjF9EDgYuBfA9vXA1KEOkjQemAscDuwLHC9p367dbgfeDHy969g9gHOAvys/+xxJu9fIGhERo6ROgXjYdvdzD5u9o7rCwcBK26tsPwQsoJjPaeNJ7Ftt3wg82nXsa4DLba+zfQ9wORk5FRExpuqMYlom6QRgvKRpwOnAz2sctxdwR8f6aoorgjqqjt2reydJM4GZAJMnT6556ojoJf1KsUGdK4h/BvYDHgQuAu4DzmgwU22259kesD0wYcKEtuNERGxV6oxiegB4f/k1HGsohsRuMLHcVvfYl3cde9UwPz8iIrbAoAViqJFKto8c4tyLgWmSplL8wZ9BMStsHZcBH+3omH41cFbNYyMiYhT0uoL4TxT9ABcBvwA0nBPbXi9pFsUf+/HAfNvLJM0BltheKOlFwHeB3YHXSTrX9n6210n6EEWRAZhje93wfrSIiNgSvQrE04HDKCbqOwG4BLjI9rK6J7e9CFjUte3sjuXFFLePqo6dD8yv+1kRETG6Bu2kLifmu9T2ycCLgZXAVeVVQUREbOV6dlJL2hE4guIqYgrwGYpbQhERsZXr1Un9VeB5FLeIzrX9yzFLFRERret1BXESxeyt7wJOlx7roxZg27s1nC0iIlo0aIGwnXc+RERsw1IEIiKiUgpERERUSoGIiIhKKRAREVEpBSIiIiqlQERERKUUiIiIqJQCERERlVIgIiKiUgpERERUGvKVoxERMbQpsy9p7bNvPe+IRs6bK4iIiKiUAhEREZVSICIiolIKREREVEqBiIiISo0WCEnTJa2QtFLS7Ir2HSVdXLb/QtKUcvsUSX+RdH359fkmc0ZExOYaG+YqaTwwFzgMWA0slrTQ9vKO3U4B7rH9bEkzgI8Bx5Vtt9g+sKl8sfXbGocdRoylJq8gDgZW2l5l+yFgAXBU1z5HAReWy98CXqWOl19HRER7miwQewF3dKyvLrdV7mN7PfBH4Cll21RJ10n6iaSXNpgzIiIq9OuT1HcCk23fLemFwPck7Wf7vs6dJM0EZgJMnjy5hZgREVuvJq8g1gCTOtYnltsq95G0HfAk4G7bD9q+G8D2UuAWYJ/uD7A9z/aA7YEJEyY08CNERGy7miwQi4FpkqZK2gGYASzs2mchcHK5fCxwhW1LmlB2ciPpmcA0YFWDWSMioktjt5hsr5c0C7gMGA/Mt71M0hxgie2FwJeAr0laCayjKCIAhwBzJD0MPAq8w/a6prJCRrxERHRrtA/C9iJgUde2szuW/wq8oeK4bwPfbjJbRET0liepIyKiUgpERERUSoGIiIhKKRAREVEpBSIiIiqlQERERKUUiIiIqJQCERERlVIgIiKiUgpERERUSoGIiIhKKRAREVEpBSIiIiqlQERERKUUiIiIqJQCERERlVIgIiKiUgpERERUSoGIiIhKKRAREVEpBSIiIiqlQERERKVGC4Sk6ZJWSFopaXZF+46SLi7bfyFpSkfbWeX2FZJe02TOiIjYXGMFQtJ4YC5wOLAvcLykfbt2OwW4x/azgf8GfKw8dl9gBrAfMB24oDxfRESMkSavIA4GVtpeZfshYAFwVNc+RwEXlsvfAl4lSeX2BbYftP1bYGV5voiIGCNNFoi9gDs61leX2yr3sb0e+CPwlJrHRkREg7ZrO8CWkDQTmFmu/knSipai7An8YaQH62OjmGRzyTYyyTYyyTYybWbbe7CGJgvEGmBSx/rEclvVPqslbQc8Cbi75rHYngfMG8XMIyJpie2BtnNUSbaRSbaRSbaR6ddsTd5iWgxMkzRV0g4Unc4Lu/ZZCJxcLh8LXGHb5fYZ5SinqcA04JoGs0ZERJfGriBsr5c0C7gMGA/Mt71M0hxgie2FwJeAr0laCayjKCKU+30DWA6sB06z/UhTWSMiYnON9kHYXgQs6tp2dsfyX4E3DHLsR4CPNJlvFLV+m6uHZBuZZBuZZBuZvsym4o5ORETEpjLVRkREVEqBiIiISikQERFR6XH9oFzbJO0BYHtd21keLyQ9jY1Pxa+x/R9t5hmKpF1s/6ntHBFtSCf1MEmaDJwPvAq4FxCwG3AFMNv2ra2F60HSTbb3b/HzDwQ+T/Ew5IaHHidS/A5PtX1tO8l6k3S77cl9kONxVVihP4prObfbwXT87oBr3Md/+CQ9x/av284BuYIYiYuBTwEnbng2o5xp9g0UExK+uK1gkv5hsCbg6WOZpcJXgLfb/kXnRkkvBr4MHNBGqDLDuwdrAnYZyyybBRiksEq6lz4urKXlQGvFVdKrgQuAm9n0HyXPlnSq7R+1lW0IP6LF31unFIjh29P2xZ0bykKxQNKHWsq0wcXA/wSq/nW00xhn6bZzd3EAsH21pJ3bCNTho8DHKR7K7NZ2P91X6NPCWubo2+IKfBo4tPuqvpydYRHw3DZClRk+M1gT8OQxjNJTCsTwLZV0AcU05RtmnJ1EMWXIda2lKtwI/JvtX3Y3SDq0hTydfijpEuCrbPp7exNwaWupCtcC37O9tLtB0ttayNOpnwsr9Hdx3Y5iJuhua4DtxzhLt7cA7wEerGg7foyzDCoFYvjeRPGio3PZ9L7mhqlD2nQGcN8gbceMYY7N2D5d0uEU7/ro/L3NLZ+4b9NbKCaJrNL2BGr9XFihv4vrfGCxpAVs+rubQfv/X10M/NL2z7sbJH1w7ONUSyd1RJ8bpLAu7IPCiqS/BdbZXlvR9rS2O9MlPZfq393y9lI9NgLyr7YfaDPHUFIghqmclvwU4Gg2/Y/u+8CXbD/cUrTObMcAf9NP2XqRNM/2zKH3HHv9nC2iaSkQwyTpIoqhmRey8f7mRIo+iD1sH9dStH7PtsdgTcANtieOZZ5NAvR3ticBZ1H8K/hpFAMQfk9R9M+zfW9b2WCTfEcDT6XP8g1G0g9tH952jir9lC19EMP3Qtv7dG1bDVwt6TdtBOrQz9nWArdR/NHdwOX6U1tJtFE/Z/sGxTM2r7B9F4CkpwNvLtte3V40YGO+l3flO5mW80l6wWBNwIFjGGXzAH2crVMKxPCtk/QG4Nu2HwWQNI7iOYh7Wk3W39lWAa+yfXt3g6Q7KvYfS/2cbYrtTV4oWf4hPk/SW1rK1GmwfB+T9NaWMm2wGPgJmxb+DZ48tlE208/ZHpMCMXwzgI8Bc8uHlaD4H/TKsq1N/ZztU8DuwGZ/hCmeTG/Tp+jfbLdJeh9w4YYO3/Kp6jezcWROm/o5368oniG5ubuhDwp/P2d7TPogRmCQkRHft/2r9lIV+jzbc6geUZJsg5C0OzCbItuG213/QTGs+jzbrV4Z9nM+SccCN9leUdF2tO3vjX2qxz6/b7N1avtBlscdSWcCX6e4R/2L8gvgIkmzWwtG32d7H8VUJKJ4v/g15XKy9WD7Httn2n6O7T3Kr+faPpOiY7hV/ZzP9req/gCXdh/TMF36OVunXEEMU9nZu1/3kFFJOwDLbE9rJ1myjVQ/Z+ulXyYSHEw/50u2etIHMXyPUjxjcFvX9meUbW1KtpHp22ySbhysiWLYa6v6OV+ybbkUiOE7A/ixpJvZ2Ak3GXg2MKutUKUzSLaROIP+zfY04DVsPgpNwGbTNLSgn/Ml2xZKgRgm25dK2ofN55hfvGH677Yk28j0czbgB8Autq/vbpB01Zin2Vw/50u2LZQ+iIiIqJRRTBERUSkFIiIiKqVAxDZL0kRJ35d0s6RVkj4raccax1W+Z1nSnA0vZpJ0hqQnDrLfayVdJ+kGScslvb3cfrSkfWt8fq39IrZUCkRskyQJ+A7Fy26mAdOAJ7AFU2vYPtv2/y5XzwA2KxCStgfmAa+zfQBwEHBV2Xw0UOcPf939IrZIOqljmyTpVcA5tg/p2LYbxbMQk4BjgQHbs8q2H1C8zvWq8griixQzld4FzLC9VtJXKEan/A3wb8AK4A+2X9HxGXsAvwb2tv2Xju1/Xx77x/Lr9cArgZnADsBK4I0UM3127wcwF5gAPAD8k+1fj8ovKrZpuYKIbdV+wCavybR9H3ArxfMPvewMLLG9H8WMnOd0neczwO8opuh+RVfbOop5im6TdJGkEyWNK189uRD4F9sH2r4F+I7tF5VXGr8CThlkv3nAP9t+IfBe4IJh/zYiKuQ5iIjhexS4uFz+d4pbVbXZfpuk/YFDKf6gH0Yx+2m350n6MMWMvLsAl3XvIGkX4O+BbxZ3zQAYsh8loo4UiNhWLae4jfSY8hbT0yluDT2PTa+wd+pxrmHfp7V9E3CTpK8Bv6W6QHwFONr2DZLeDLy8Yp9xwL22Dxxuhoih5BZTbKt+DDxR0psAJI0HPgF8tuwbuBU4UNI4SZMonrLeYBwbi8sJwE8rzn8/sGv3Rkm7SHp5x6YD2TgHVPcxuwJ3lh3bJ1adu7wt9tvyRVGocECvHzyirhSI2Ca5GJ1xDHBsOQfT3cCjtj9S7vIzin/ZLwc+A1zbcfifgYMl/ZKiI3lOxUfMAy6VdGXXdgHvk7RC0vXAuWy8elgA/Es5BPZZwL9STNn+M4qObQbZ70TgFEk3AMso3s0QscUyiimCx0YRXQQcY/vaofaP2BakQERERKXcYoqIiEopEBERUSkFIiIiKqVAREREpRSIiIiolAIRERGVUiAiIqLS/we/hA+xePQf4AAAAABJRU5ErkJggg==\n",
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAEPCAYAAABV6CMBAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAgq0lEQVR4nO3de5ydVX3v8c83ASIVUC7R0iSQVGIpiEYJkdML9QaGF0piBQlEAYtiD9LKy9YajhZqpKdQW7UcgxLL1QsB8UJOCaJHxHOqghkwEhJMGSBAItbhJigFDHzPH88a2NnZM/PsYfbsHfJ9v177Nc9e61lr//b8Mb951lrPemSbiIiIuiZ0O4CIiNi6JHFERERbkjgiIqItSRwREdGWJI6IiGjLdt0OYDzssccenj59erfDiIjYqtx00033257cXL5NJI7p06fT19fX7TAiIrYqku5uVZ6hqoiIaEsSR0REtKWjiUPSXEnrJPVLWtSi/oOS1kq6RdJ3JO3dUHeCpNvL64SG8gMlrS59nitJnfwOERGxuY4lDkkTgSXA4cB+wLGS9ms67cfAbNuvBK4E/rG03Q04E3gtMAc4U9Kupc1ngfcCM8trbqe+Q0REbKmTVxxzgH7bd9p+ElgGzGs8wfZ3bT9W3t4ATC3Hbwa+bftB2w8B3wbmStoT2MX2Da422boUmN/B7xAREU06mTimAPc2vN9QyoZyEnDNCG2nlOMR+5R0sqQ+SX0DAwNthh4REUPpiclxSe8EZgOfGKs+bS+1Pdv27MmTt1iGHBERo9TJxLERmNbwfmop24ykNwEfAY60/cQIbTfy7HDWkH1GRETndDJxrARmSpohaQdgAbC88QRJrwbOp0oav2iouhY4TNKuZVL8MOBa2/cBj0g6uKymOh64qoPfISIimnTsznHbmySdSpUEJgIX2l4jaTHQZ3s51dDUTsBXyqrae2wfaftBSR+nSj4Ai20/WI5PAS4GdqSaE7mGbdT0RVd37bPXn31E1z47Irqro1uO2F4BrGgqO6Ph+E3DtL0QuLBFeR/wijEMMyIi2tATk+MREbH1SOKIiIi2JHFERERbkjgiIqItSRwREdGWJI6IiGhLEkdERLQliSMiItqSxBEREW1J4oiIiLYkcURERFuSOCIioi1JHBER0ZYkjoiIaEtHt1WPbVeeFRLx/JUrjoiIaEsSR0REtKWjiUPSXEnrJPVLWtSi/hBJN0vaJOmohvLXS1rV8Hpc0vxSd7GkuxrqZnXyO0RExOY6NschaSKwBDgU2ACslLTc9tqG0+4BTgT+urGt7e8Cs0o/uwH9wLcaTvmQ7Ss7FXtERAytk5Pjc4B+23cCSFoGzAOeSRy215e6p4fp5yjgGtuPdS7UiIioq5NDVVOAexvebyhl7VoAXNZU9veSbpH0KUmTRhtgRES0r6cnxyXtCRwAXNtQfDqwL3AQsBvw4SHaniypT1LfwMBAx2ONiNhWdDJxbASmNbyfWsra8Q7g67Z/M1hg+z5XngAuohoS24LtpbZn2549efLkNj82IiKG0sk5jpXATEkzqBLGAuC4Nvs4luoK4xmS9rR9nyQB84FbxyDWIeVGtoiIzXXsisP2JuBUqmGm24ArbK+RtFjSkQCSDpK0ATgaOF/SmsH2kqZTXbF8r6nrL0laDawG9gDO6tR3iIiILXV0yxHbK4AVTWVnNByvpBrCatV2PS0m022/YWyjjIiIdvT05HhERPSeJI6IiGhLEkdERLQliSMiItqSxBEREW1J4oiIiLYkcURERFuSOCIioi1JHBER0ZYkjoiIaEsSR0REtCWJIyIi2pLEERERbUniiIiItiRxREREW0ZMHJL+UNILy/E7JX1S0t6dDy0iInpRnSuOzwKPSXoV8FfAHcClHY0qIiJ6Vp3Escm2gXnAZ2wvAXbubFgREdGr6iSORyWdDrwLuFrSBGD7Op1LmitpnaR+SYta1B8i6WZJmyQd1VT3lKRV5bW8oXyGpBtLn5dL2qFOLBERMTbqJI5jgCeAP7P9c6pnhH9ipEaSJgJLgMOB/YBjJe3XdNo9wInAl1t08V+2Z5XXkQ3l5wCfsr0P8BBwUo3vEBERY2TExFGSxVeBSaXofuDrNfqeA/TbvtP2k8AyquGuxr7X274FeLpOsJIEvAG4shRdAsyv0zYiIsZGnVVV76X6Q31+KZoCfKNG31OAexvebyhldb1AUp+kGyTNL2W7Aw/b3jRSn5JOLu37BgYG2vjYiIgYTp2hqvcDfwg8AmD7duAlnQyq2Nv2bOA44NOSXtZOY9tLbc+2PXvy5MmdiTAiYhtUJ3E8UYaaAJC0HeAa7TYC0xreTy1ltdjeWH7eCVwPvBp4AHhxiaHtPiMi4rmrkzi+J+l/ADtKOhT4CvC/a7RbCcwsq6B2ABYAy0doA4CkXSVNKsd7UF3xrC3Lgr8LDK7AOgG4qk6fERExNuokjkXAALAaeB+wAvjoSI3KPMSpwLXAbcAVttdIWizpSABJB0naABwNnC9pTWn++0CfpJ9QJYqzba8tdR8GPiipn2rO44J6XzUiIsbCdiOdYPtp4PPl1RbbK6gSTWPZGQ3HK6mGm5rb/QA4YIg+76RasRUREV0wZOKQdIXtd0haTYs5Dduv7GhkERHRk4a74vhA+fmW8QgkIiK2DkPOcdi+rxyeYvvuxhdwyviEFxERvabO5PihLcoOH+tAIiJi6zDcHMd/p7qy+F1JtzRU7Qx8v9OBRUQ8H0xfdHXXPnv92Ud0pN/h5ji+DFwD/APVktxBj9p+sCPRREREzxsucdj2eknvb66QtFuSR0TEtmmkK463ADdRLcdVQ52B3+1gXBER0aOGTBy231J+zhi/cCIiotcNNzn+muEa2r557MOJiIheN9xQ1T8PU2eqBypFRMQ2ZrihqtePZyAREbF1GG6o6g22r5P0p63qbX+tc2FFRESvGm6o6k+A64C3tqgzkMQREbENGm6o6szy893jF05ERPS6EfeqkrS7pHMl3SzpJkn/Imn38QguIiJ6T51NDpdRPQHw7VSPbB0ALu9kUBER0bvqJI49bX/c9l3ldRbw0jqdS5oraZ2kfkmLWtQfUq5kNkk6qqF8lqQfSloj6RZJxzTUXSzpLkmrymtWnVgiImJs1Ekc35K0QNKE8noH1XPEhyVpIrCEagv2/YBjJe3XdNo9wIlU25s0egw43vb+wFzg05Je3FD/IduzymtVje8QERFjZLjluI/y7B5VpwFfLFUTgF8Bfz1C33OA/vKMcCQtA+YBawdPsL2+1D3d2ND2fzQc/0zSL4DJwMMjf6WIiOik4Z4AuLPtXcrPCba3K68Jtnep0fcU4N6G9xtKWVskzQF2AO5oKP77MoT1KUmThmh3sqQ+SX0DAwPtfmxERAyhzlAVknaVNKfMSRwi6ZBOB1Y+d0/gC8C7bQ9elZwO7AscBOwGfLhVW9tLbc+2PXvy5MnjEW5ExDZhuBsAAZD0HuADwFRgFXAw8ENG3qtqIzCt4f3UUlaLpF2Aq4GP2L5hsLzhWehPSLqIkYfMIiJiDNW54vgA1X/3d5f9q15NvbmGlcBMSTMk7QAsAJbXCaqc/3XgUttXNtXtWX4KmA/cWqfPiIgYG3USx+O2HweQNMn2T4HfG6mR7U3AqVQrsG4DrrC9RtJiSUeW/g6StAE4Gjhf0prS/B3AIcCJLZbdfknSamA1sAdwVt0vGxERz92IQ1XAhrIU9hvAtyU9BNxdp3PbK4AVTWVnNByvpBrCam73RZ5dxdVcl+3cIyK6aMTEYftt5fDvJH0XeBHwzY5GFRERPavOFcfg0wD/iOq+ju/bfrKjUUVERM+qs8nhGcAlwO5UcwoXSfpopwOLiIjeVOeKYyHwqoYJ8rOpluVmUjq2StMXXd21z15/9hFd++yIsVJnVdXPgBc0vJ9EG/djRETE88twe1X9L6o5jV8CayR9u7w/FPjR+IQXERG9Zrihqr7y8yaqm/EGXd+xaCIioucN9+jYSwaPy53cLy9v19n+TacDi4iI3lRnr6rXUa2qWk+1xfo0SSfY/r8djSwiInpSnVVV/wwcZnsdgKSXA5cBB3YysIiI6E11VlVtP5g04JmHLG3fuZAiIqKX1bniuEnSv/Ls3lELeXbiPCIitjF1EsefA+8H/rK8/3/AeR2LKCIietqwiUPSROAntvcFPjk+IUVERC8bdo7D9lPAOkl7jVM8ERHR4+oMVe1Kdef4j4BfDxbaPrJjUUVERM+qkzj+tuNRRETEVmPIoSpJL5B0GtVjXfeleg7H9wZfdTqXNFfSOkn9kha1qD9E0s2SNkk6qqnuBEm3l9cJDeUHSlpd+jy3PHs8IiLGyXBzHJcAs6me7X041Y2AtZWJ9SWl7X7AsZL2azrtHuBE4MtNbXcDzgReC8wBzpS0a6n+LPBeYGZ5zW0nroiIeG6GG6raz/YBAJIuoP0dcecA/bbvLH0sA+YBawdPsL2+1D3d1PbNwLdtP1jqvw3MlXQ9sIvtG0r5pcB84Jo2Y4uIiFEa7orjmY0MbW8aRd9TgHsb3m8oZc+l7ZRyPGKfkk6W1Cepb2BgoHbQERExvOESx6skPVJejwKvHDyW9Mh4BThatpfanm179uTJk7sdTkTE88Zw26pPfI59bwSmNbyfSv0nB24EXtfU9vpSPnWUfUZExBios8nhaK0EZkqaUZ7nsQBYXrPttcBhknYtk+KHAdfavg94RNLBZTXV8cBVnQg+IiJa61jiKPMip1IlgduAK2yvkbRY0pEAkg6StIFqye/5ktaUtg8CH6dKPiuBxYMT5cApwL8C/cAdZGI8ImJc1bkBcNRsrwBWNJWd0XC8ks2HnhrPuxC4sEV5H/CKsY00IiLq6uRQVUREPA8NecVRVlJ5qHrbu3QkooiI6GnDraraGUDSx4H7gC9QPXN8IbDnuEQXERE9p85Q1ZG2z7P9qO1HbH+W6g7wiIjYBtVJHL+WtFDSREkTJC2kYXv1iIjYttRJHMcB7wD+s7yOLmUREbENGnE5btmIMENTEeNg+qKru/bZ688+omufHVuXEa84JL1c0nck3Vrev1LSRzsfWkRE9KI6Q1WfB06n7JZr+xaq7UMiImIbVCdx/Jbt5mdxjGab9YiIeB6okzjul/Qyys2A5RGv93U0qoiI6Fl19qp6P7AU2FfSRuAuqpsAIyJiGzRs4ijPDT/F9pskvRCYYPvR8QktIiJ60bCJw/ZTkv6oHOemv4iIqDVU9WNJy4Gv0HDHuO2vdSyqiIjoWXUSxwuAB4A3NJQZSOKIiNgG1blz/N3jEUhERGwdRkwcki6ixXM5bP9ZRyKKiIieVuc+jn8Dri6v7wC7AL+q07mkuZLWSeqXtKhF/SRJl5f6GyVNL+ULJa1qeD0taVapu770OVj3knpfNSIixkKdoaqvNr6XdBnw7yO1K0t5lwCHAhuAlZKW217bcNpJwEO295G0ADgHOMb2l4AvlX4OAL5he1VDu4Xl2eMRETHORvPM8ZlAnf/y5wD9tu+0/SSwjC132Z0HXFKOrwTeKElN5xxb2kZERA+oM8fR/OzxnwMfrtH3FODehvcbgNcOdY7tTZJ+CewO3N9wzjFsmXAukvQU8FXgLNtbzMFIOhk4GWCvvfaqEW5ERNRRZ6hq5/EIpBVJrwUes31rQ/FC2xsl7UyVON4FXNrc1vZSqq1SmD179haJJSIiRqfO8zj+sGw3gqR3SvqkpL1r9L0RmNbwfmopa3mOpO2AF1HdMzJoAXBZYwPbG8vPR4EvUw2JRUTEOKkzx/FZ4DFJrwL+CriDFv/ht7ASmClphqQdqJLA8qZzlgMnlOOjgOsGh50kTaB6ZO0z8xuStpO0RzneHngLcCsRETFu6iSOTeWP+TzgM7aXACMOX9neBJwKXAvcBlxhe42kxZKOLKddAOwuqR/4INC4ZPcQ4F7bdzaUTQKulXQLsIrqiuXzNb5DRESMkTpbjjwq6XTgncAh5Upg+zqd214BrGgqO6Ph+HHg6CHaXg8c3FT2a+DAOp8dERGdUSdxHAMcB5xk++eS9gI+0dmwIiLqm77o6q599vqzj+jaZ3dLnVVVPwc+2fD+HurNcURExPNQnVVVB0taKelXkp6U9FS53yIiIrZBdSbHP0N19/btwI7Ae4DzOhlURET0rlpbjtjuBybafsr2RcDczoYVERG9qs7k+GPlPoxVkv4RuI/R7XEVERHPA3USwLvKeadSPTp2GvD2TgYVERG9q86qqrsl7Qjsaftj4xBTRET0sDqrqt5KdZf2N8v7WZKatw6JiIhtRJ2hqr+j2kjwYYDyQKUZHYsoIiJ6Wp3E8RvbzfdtZJvyiIhtVJ1VVWskHQdMlDQT+EvgB50NKyIielWdK46/APYHnqB6NsYjwGkdjCkiInpYnVVVjwEfKa+IiNjGDZk4Rlo5ZfvI4eojIuL5abgrjv8G3Es1PHUjoHGJKCIietpwieO3gUOpNjg8DrgauMz2mvEILCIietOQk+NlQ8Nv2j6B6kl8/cD1kk6t27mkuZLWSeqXtKhF/SRJl5f6GyVNL+XTJf2XpFXl9bmGNgdKWl3anCspV0IREeNo2MlxSZOAI6iuOqYD5wJfr9OxpInAEqqrlg3ASknLba9tOO0k4CHb+0haAJxD9cRBgDtsz2rR9WeB91INn62g2qn3mjoxRUTEczfkFYekS4EfAq8BPmb7INsft72xZt9zgH7bd9p+ElgGzGs6Zx5wSTm+EnjjcFcQkvYEdrF9g21TPYlwfs14IiJiDAx3H8c7gZnAB4AfSHqkvB6V9EiNvqdQTa4P2lDKWp5jexPwS2D3UjdD0o8lfU/SHzecv2GEPgGQdLKkPkl9AwMDNcKNiIg6hhyqst3NZ27cB+xl+wFJBwLfkLR/Ox3YXgosBZg9e3a2SImIGCOdTA4bqZ7dMWhqKWt5jqTtgBcBD9h+wvYDALZvAu4AXl7OnzpCnxER0UGdTBwrgZmSZpQnCC4Amm8qXA6cUI6PAq6zbUmTy+Q6kn6XasjsTtv3AY9IOrjMhRwPXNXB7xAREU3qbHI4KrY3laW71wITgQttr5G0GOizvRy4APiCpH7gQarkAnAIsFjSb4CngT+3/WCpOwW4GNiRajVVVlRFRIyjjiUOANsrqJbMNpad0XD8OHB0i3ZfBb46RJ99wCvGNtKIiKirmxPgERGxFUriiIiItiRxREREW5I4IiKiLUkcERHRliSOiIhoSxJHRES0JYkjIiLaksQRERFtSeKIiIi2dHTLkYh4/pi+6Oquffb6s4/o2mfHlnLFERERbUniiIiItiRxREREW5I4IiKiLUkcERHRliSOiIhoS0cTh6S5ktZJ6pe0qEX9JEmXl/obJU0v5YdKuknS6vLzDQ1tri99riqvl3TyO0RExOY6dh+HpInAEuBQYAOwUtJy22sbTjsJeMj2PpIWAOcAxwD3A2+1/TNJr6B6bvmUhnYLyyNkIyJinHXyimMO0G/7TttPAsuAeU3nzAMuKcdXAm+UJNs/tv2zUr4G2FHSpA7GGhERNXUycUwB7m14v4HNrxo2O8f2JuCXwO5N57wduNn2Ew1lF5Vhqr+VpFYfLulkSX2S+gYGBp7L94iIiAY9PTkuaX+q4av3NRQvtH0A8Mfl9a5WbW0vtT3b9uzJkyd3PtiIiG1EJxPHRmBaw/uppazlOZK2A14EPFDeTwW+Dhxv+47BBrY3lp+PAl+mGhKLiIhx0snEsRKYKWmGpB2ABcDypnOWAyeU46OA62xb0ouBq4FFtr8/eLKk7STtUY63B94C3NrB7xAREU06ljjKnMWpVCuibgOusL1G0mJJR5bTLgB2l9QPfBAYXLJ7KrAPcEbTsttJwLWSbgFWUV2xfL5T3yEiIrbU0W3Vba8AVjSVndFw/DhwdIt2ZwFnDdHtgWMZY0REtKenJ8cjIqL3JHFERERbkjgiIqItSRwREdGWJI6IiGhLEkdERLQliSMiItqSxBEREW1J4oiIiLYkcURERFuSOCIioi1JHBER0ZYkjoiIaEsSR0REtCWJIyIi2pLEERERbUniiIiItiRxREREWzqaOCTNlbROUr+kRS3qJ0m6vNTfKGl6Q93ppXydpDfX7TMiIjqrY4lD0kRgCXA4sB9wrKT9mk47CXjI9j7Ap4BzStv9gAXA/sBc4DxJE2v2GRERHdTJK445QL/tO20/CSwD5jWdMw+4pBxfCbxRkkr5MttP2L4L6C/91ekzIiI6aLsO9j0FuLfh/QbgtUOdY3uTpF8Cu5fyG5raTinHI/UJgKSTgZPL219JWjeK7zAW9gDuH01DnTPGkWwpsY1OYhudxDY63Yxt71aFnUwcXWV7KbC023FI6rM9u9txtJLYRiexjU5iG51ejK2TQ1UbgWkN76eWspbnSNoOeBHwwDBt6/QZEREd1MnEsRKYKWmGpB2oJruXN52zHDihHB8FXGfbpXxBWXU1A5gJ/KhmnxER0UEdG6oqcxanAtcCE4ELba+RtBjos70cuAD4gqR+4EGqREA57wpgLbAJeL/tpwBa9dmp7zBGuj5cNozENjqJbXQS2+j0XGyq/sGPiIioJ3eOR0REW5I4IiKiLUkcERHRliSODpC0m6Tduh1HREQnJHGMEUl7SVomaQC4EfiRpF+UsuldDq/nSXqppNeU10u7Hc9IJO3U7RgiuiWrqsaIpB8CnwaubFg6PBE4GjjN9sFdDG9IklbbPqCLnz8L+BzVzZ+DN3NOBR4GTrF9c3ciG56ke2zv1e04oEq6PLslz0bb/9nNeEYiaSfbv+pyDKLa++6Z3xvwI/fwH0RJ+9r+abfjgCSOMSPpdtsz260bD5L+dKgq4HO2J49nPJsFIK0C3mf7xqbyg4Hzbb+qK4FVMXxwqCrgI7a7OhyZpDvqzz8MOA+4nc1/b/tQ/d6+1a3YhtPt31uj5+1eVV1wk6TzqHb7HdyIcRrVnfE/7lpUlcuBLwGt/kt4wTjH0uyFzUkDwPYNkl7YjYAa/E/gE1Q3oTbrhWHeixk66V4E9GrS7fYw378Ab7K9vrGw7FKxAvj9bgRVYjh3qCrgxeMYyrCSOMbO8VTPF/kYm1/+Dt4h3023AP9k+9bmCklv6kI8ja6RdDVwKZsn3OOBb3YtqsrNwDds39RcIek9XYinWZLu6GxHtbN2s43A9uMcS7N3A38FPNGi7thxjmVIGaraBkj6Y+Bu2/e0qJttu68LYTXGcDjVc1U2S7i2V3QvKpD0e8ADtrfY0lrSS7s9l1D+O30ZrZPuXbZP7WJsPwD+Yoike6/taS2ajQtJpwPvoHqeT+PvbQFwhe1/6GJs1wEftf2DFnV32Z7RhbC2kMQxRsruvicB89n8D+BVwAW2f9Ol0OJ5rMeT7oO2B1rU9ULS/X1a/97Wdi+qaik/8Ljtx7oZx0iSOMaIpMuoJiUv4dnL4KlUcxy72T6mS6E1JrW3Ab9Tins+qUlaavvkkc8cf70cW0SnJXGMEUn/Yfvl7daNhx5PakOtTBLwE9tTxzOezQLo4dgAJL0IOJ3qP+eXUi1++AXVPwRn2364B2KbD7ykl2IbjqRrbB/e7Tha6aXYMjk+dh6UdDTwVdtPA0iaQHUfx0NdjQwObJG4NgA3SPqPbgTUYAC4m+qP8SCX9y/pSkTP6uXYAK4ArgNeb/vnAJJ+Gzix1B3WvdCeie11TbGd0O3YJL1mqCpg1jiGsmUAPRxbo1xxjJFyd/g5wOup/ruHavncd4FFtu/qSmCApBuAf6Z1Uvug7ZbPbR+n2G4H3jjExH23J1F7NrYSwzrbv9du3Xjo8dieAr7H5v8QDDrY9o7jHNIzejm2RrniGCO210v6O6p7NjabHO9m0igWUCW1JZIeLmUvpkpqC7oU06BPA7sCW/xxBv5xfEPZwqfp3dgA7pb0N8Alg5PN5S7yE3l2tVC39HJst1Hd/3J7c4WkxFZDrjjGiKQPU/0RXsbmd6MuAJbZPrtbscGQq0iusn1b96KqSNqX1itcEtswJO0KLKKKb3Do7D+p7h0623bXhkh7PLajgNW217Wom2/7G+Mf1TOf37OxNUriGCNlrmD/5hVK5dnoa7q85UjPJrXyX+lxJbbGifvE9hxIerfti7odRyuJbXR6KbYkjjEi6afAm23f3VS+N/CtLo/p9nJSS2wd0Ev7GjVLbKPTS7FljmPsnAZ8p0yoDo5F7kW1cVrX7uAtnqa6f+PupvI9S103JbZRknTLUFVUy3O7JrGNTi/H1iiJY4zY/qakl7PlVs0rB7dZ76LT6N2kdhqJbbReCryZLZd7C9hiy4pxlthGp5dje0YSxxgqS11v6HYczXo5qSW25+TfgJ1sr2qukHT9uEezucQ2Or0c2zMyxxEREW3p9vbGERGxlUniiIiItiRxRDSRNFXSVZJul3SnpM9ImlSjXcvnaEtaPPjALEmnSfqtIc57i6QfS/qJpLWS3lfK50var8bn1zov4rlK4ohoIEnA16ie/DcTmAnsyHPYYsT2Gbb/T3l7GrBF4pC0PbAUeGt5zvqrgetL9XygTkKoe17Ec5LJ8YgGkt4InGn7kIayXaju5ZgGHAXMHny6nqR/o3os7/XliuPzVDu//hxYYHtA0sVUq2V+B/gnYB1wv+3XN3zGbsBPgb1t/1dD+R+Utr8sr7cDbwBOBnYA+oF3Ue2c2nwewBJgMvAY8F7bPx2TX1Rs03LFEbG5/YHNHndq+xFgPdX9G8N5IdBne3+qHU7PbOrnXOBnVNugv76p7kGqfZzulnSZpIWSJpRHiC4HPmR7lu07gK/ZPqhcmdwGnDTEeUupHt96IPDXwHlt/zYiWsh9HBFj52ng8nL8Raohr9psv0fSAcCbqP7QH0q1m2yzV0g6i2qH452Aa5tPkLQT8AfAV6rRNwBGnKeJqCOJI2Jza6mGo55Rhqp+m2qI6RVsfqX+gmH6ansc2PZqYLWkLwB30TpxXAzMt/0TSScCr2txzgTgYduz2o0hYiQZqorY3HeA35J0PICkiVQPwfpMmXtYD8ySNEHSNKq7ygdN4Nmkcxzw7y36fxTYublQ0k6SXtdQNItn98hqbrMzcF+ZUF/Yqu8yvHZXeSolqrxquC8eUVcSR0QDV6tF3gYcVfaoegB42vbfl1O+T3UlsBY4F7i5ofmvgTmSbqWawF7c4iOWAt+U9N2mcgF/I2mdpFXAx3j2amMZ8KGyVPdlwN8CN5ZYGie7m89bCJwk6SfAGqpnY0Q8Z1lVFTGMsqrpMuBttm8e6fyIbUESR0REtCVDVRER0ZYkjoiIaEsSR0REtCWJIyIi2pLEERERbUniiIiItvx/cLSMSvkFLhUAAAAASUVORK5CYII=\n",
       "text/plain": [
        "<Figure size 432x288 with 1 Axes>"
       ]
@@ -981,22 +935,27 @@
     "\n",
     "所谓的波函数模式也就是用复数向量表示和储存量子态。向量模式只能处理纯态，但这种模式在家用电脑硬件高效支持**20+量子比特**的运算。用户可以测试下自己电脑的极限在哪里。在这种表示下，量子门 (酉矩阵)作用在量子比特 (一个复向量)上本质上的运算是**矩阵乘以向量**：\n",
     "\n",
-    "$$\\lvert {\\psi}\\rangle = U \\lvert {\\psi_0}\\rangle$$\n",
+    "$$\\lvert {\\psi}\\rangle = U \\lvert {\\psi_0}\\rangle. \\tag{22}$$\n",
     "\n",
     "代码中，具体体现在 UAnsatz的调用 `cir.run_state_vector(input_state = None)`。如果我们不输入任何初始量子态，就会默认所有的量子比特都处于$\\lvert {0}\\rangle$态。接着来看个具体的例子："
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 10,
-   "metadata": {},
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:41.024881Z",
+     "start_time": "2021-01-09T12:47:50.905119Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "[[ 1.36742103e-03+0.j -1.15621578e-03+0.j  1.59433644e-03+0.j ...\n",
-      "   2.36662139e-04+0.j -2.47895067e-05+0.j -9.47071583e-04+0.j]]\n"
+      "[[-0.00172454+0.j -0.00029211+0.j  0.00071415+0.j ...  0.00040607+0.j\n",
+      "  -0.00104915+0.j  0.00085908+0.j]]\n"
      ]
     }
    ],
@@ -1039,24 +998,29 @@
     "\n",
     "同时 Paddle quantum也支持了密度矩阵运算模式，也就是用一个密度矩阵 $\\rho = \\sum_i P_i \\lvert {\\psi_i}\\rangle\\langle{\\psi_i} \\lvert$表示和储存量子态。该模式下可以根据算法需要支持**混合态模拟**。但是在密度矩阵模式下，家用电脑硬件只能运行10个左右的量子比特。请用户注意这方面的限制，我们也在不断优化这个模式下的模拟器性能。在这种表示下，量子门 (酉矩阵)作用在量子态(一个迹为1的厄尔米特矩阵)上本质上的运算是**矩阵乘法**：\n",
     "\n",
-    "$$\\rho = U \\rho_0 U^\\dagger$$\n",
+    "$$\\rho = U \\rho_0 U^\\dagger. \\tag{23}$$\n",
     "\n",
     "代码中，具体体现在 UAnsatz的调用 `cir.run_density_matrix()`。接着来看个具体的例子："
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 11,
-   "metadata": {},
+   "execution_count": 8,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:41.307338Z",
+     "start_time": "2021-01-09T12:48:41.028222Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "[[0.62679516+0.j 0.38101066+0.j 0.13601748+0.j 0.26505304+0.j]\n",
-      " [0.38101066+0.j 0.23160536+0.j 0.08268109+0.j 0.16111808+0.j]\n",
-      " [0.13601748+0.j 0.08268109+0.j 0.02951643+0.j 0.05751775+0.j]\n",
-      " [0.26505304+0.j 0.16111808+0.j 0.05751775+0.j 0.11208305+0.j]]\n"
+      "[[ 0.20642449+0.j -0.24205478+0.j -0.27795534+0.j  0.1672236 +0.j]\n",
+      " [-0.24205478+0.j  0.2838351 +0.j  0.32593235+0.j -0.19608755+0.j]\n",
+      " [-0.27795534+0.j  0.32593235+0.j  0.37427328+0.j -0.22517044+0.j]\n",
+      " [ 0.1672236 +0.j -0.19608755+0.j -0.22517044+0.j  0.13546713+0.j]]\n"
      ]
     }
    ],
@@ -1100,15 +1064,6 @@
     "如果你对源代码有兴趣，可以利用如下 magic command即时查看。或者关注我们的 [[Github]](https://github.com/PaddlePaddle/Quantum)！"
    ]
   },
-  {
-   "cell_type": "code",
-   "execution_count": 12,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "%psource density_op_random"
-   ]
-  },
   {
    "cell_type": "markdown",
    "metadata": {},
@@ -1125,7 +1080,7 @@
     "0 \\\\\n",
     "0 \\\\\n",
     "1\n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix}.\\tag{24}\n",
     "$$\n",
     "\n",
     "那么我们如何用量桨来制备一个贝尔态呢? 只需要如下的量子电路：\n"
@@ -1135,17 +1090,22 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "<img src=\"figures/bell2.png\" width=\"750\" >"
+    "<img src=\"figures/intro-fig-bell2.png\" width=\"750\" >"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 13,
-   "metadata": {},
+   "execution_count": 9,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:42.231220Z",
+     "start_time": "2021-01-09T12:48:41.331283Z"
+    }
+   },
    "outputs": [
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEJCAYAAACZjSCSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAV2klEQVR4nO3dfbRddX3n8fcn4VFBBYkPJcFQDWPRCmpEpnYpKnRgqYAFBXkYqVi0kgozfRCmFiu2axQrM+MQHWPVol2C+JxqhHFUOqOOmqAoBoxE5CEoNqggyvgQ+c4fZwcOl3vP3UnuPtd79/u11lk5e+/f2ed791q5n7t/v71/O1WFJKm/Fsx2AZKk2WUQSFLPGQSS1HMGgST1nEEgST1nEEhSz+002wVsq3322aeWLl0622VI0pxy1VVX3V5ViybbNueCYOnSpaxbt262y5CkOSXJTVNts2tIknrOIJCknjMIJKnnDAJJ6jmDQJJ6rtMgSHJkkg1JNiY5Z5LtpyXZnOTq5vXyLuuRJD1QZ5ePJlkIrASOADYBa5OsrqprJzT9QFWt6KoOSdJoXZ4RHAJsrKobquqXwKXAMR1+nyRpO3R5Q9m+wC1Dy5uAp0/S7rgkzwS+DfyHqrplkjbSnLf0nE/Odgmz7sY3Pm+2S9AkZnuw+J+BpVX1JODTwMWTNUpyRpJ1SdZt3rx5rAVK0nzX5RnBrcCSoeXFzbp7VdUPhxb/Abhgsh1V1SpgFcDy5ct9tuYs6ftftP41q/mqyzOCtcCyJPsn2QU4EVg93CDJo4cWjwau67AeSdIkOjsjqKotSVYAVwALgXdX1fok5wPrqmo18OokRwNbgB8Bp3VVjyRpcp3OPlpVa4A1E9adN/T+XODcLmuQJI0224PFkqRZZhBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST3XaRAkOTLJhiQbk5wzot1xSSrJ8i7rkSQ9UGdBkGQhsBI4CjgQeEmSAydptydwFvDlrmqRJE2tyzOCQ4CNVXVDVf0SuBQ4ZpJ2bwDeBPy8w1okSVPoMgj2BW4ZWt7UrLtXkqcAS6rqk6N2lOSMJOuSrNu8efPMVypJPTZtECR5RpIHN+9PSXJhksfs6BcnWQBcCPzZdG2ralVVLa+q5YsWLdrRr5YkDWlzRvB24O4kBzH4pf0d4L0tPncrsGRoeXGzbqs9gScCVya5ETgUWO2AsSSNV5sg2FJVxaB//6KqWsngl/h01gLLkuyfZBfgRGD11o1VdWdV7VNVS6tqKfAl4OiqWrfNP4Ukabu1CYK7kpwLnAp8sunS2Xm6D1XVFmAFcAVwHXBZVa1Pcn6So3ekaEnSzNmpRZsTgJOAl1XVbUn2A97cZudVtQZYM2HdeVO0PazNPiVJM2vaM4Kqug34MLBrs+p24KNdFiVJGp82Vw39MfAh4B3Nqn2Bj3VYkyRpjNqMEZwJPAP4CUBVXQ88osuiJEnj0yYIftHcGQxAkp2A6q4kSdI4tQmCf0nyn4DdkxwBfBD4527LkiSNS5sgOAfYDFwDvILBVUCv7bIoSdL4THv5aFXdA7yzeUmS5pkpgyDJZVX14iTXMMmYQFU9qdPKJEljMeqM4Kzm3+ePoxBJ0uyYcoygqr7fvH1VVd00/AJeNZ7yJEldazNYfMQk646a6UIkSbNj1BjBnzD4y/+3k3xjaNOewBe6LkySNB6jxgjeD3wK+M8MLiHd6q6q+lGnVUmSxmZUEFRV3ZjkzIkbkuxtGEjS/DDdGcHzgasYXD6aoW0F/HaHdUmSxmTKIKiq5zf/7j++ciRJ4zZqsPgpoz5YVV+d+XIkSeM2qmvoLSO2FfCcGa5FkjQLRnUNPXuchUiSZseorqHnVNVnk/zhZNur6iPdlSVJGpdRXUPPAj4LvGCSbQUYBJI0D4zqGnpd8+8fja8cSdK4tXl4/cOTvDXJV5NcleS/JXn4OIqTJHWvzaRzlzJ4QtlxwPHN+w90WZQkaXymfUIZ8OiqesPQ8t8mOaGrgiRJ49XmjOB/JjkxyYLm9WLgiq4LkySNx6jLR+/ivjmGzgb+qdm0APgp8OddFydJ6t6oq4b2HGchkqTZ0WaMgCR7AcuA3bauq6r/3VVRkqTxmTYIkrycwYPsFwNXA4cC/xfnGpKkeaHNYPFZwNOAm5r5h54M3NFlUZKk8WkTBD+vqp8DJNm1qr4F/Jtuy5IkjUubINiU5GHAx4BPJ/k4cFObnSc5MsmGJBuTnDPJ9lcmuSbJ1Uk+n+TAbSlekrTjph0jqKoXNm//JsnngIcCl0/3uSQLgZXAEcAmYG2S1VV17VCz91fV/2jaHw1cCBy5bT+CJGlHtL1q6CnA7zO4r+ALVfXLFh87BNhYVTc0+7gUOAa4Nwiq6idD7R/c7F+SNEZtJp07D7gYeDiwD/CeJK9tse99gVuGljc16ybu/8wk3wEuAF49RQ1nJFmXZN3mzZtbfLUkqa02YwQnA0+rqtc1U1MfCpw6UwVU1cqqeizwGmDSgKmqVVW1vKqWL1q0aKa+WpJEuyD4HkM3kgG7Are2+NytwJKh5cXTfO5S4NgW+5UkzaBRcw39dwZ99ncC65N8ulk+AvhKi32vBZYl2Z9BAJwInDThO5ZV1fXN4vOA65EkjdWoweJ1zb9XAR8dWn9lmx1X1ZYkKxjMVLoQeHdVrU9yPrCuqlYDK5IcDvwK+DHw0m2sX5K0g0ZNOnfx1vdJdgEOaBY3VNWv2uy8qtYAayasO2/o/VnbVK0kaca1mWvoMAZXDd3IYErqJUle6qRzkjQ/tLmP4C3AH1TVBoAkBwCXAE/tsjBJ0ni0uWpo560hAFBV3wZ27q4kSdI4tTkjuCrJP3DfE8pO5r6BZEnSHNcmCF4JnMl9d/3+H+BtnVUkSRqrkUHQTBz39ap6PIMJ4SRJ88zIMYKq+jWwIcl+Y6pHkjRmbbqG9mJwZ/FXgJ9tXVlVR3dWlSRpbNoEwV93XoUkadaMmmtoNwYDxY8DrgHeVVVbxlWYJGk8Ro0RXAwsZxACRzG4sUySNM+M6ho6sKp+FyDJu2g346gkaY4ZdUZw78RydglJ0vw16ozgoCRbnykcYPdmOUBV1UM6r06S1LlR01AvHGchkqTZ0WbSOUnSPGYQSFLPGQSS1HMGgST13Kg7i+8CaqrtXjUkSfPDqKuG9gRI8gbg+8D7GFw6ejLw6LFUJ0nqXJuuoaOr6m1VdVdV/aSq3g4c03VhkqTxaBMEP0tycpKFSRYkOZmh6aglSXNbmyA4CXgx8IPm9aJmnSRpHpj2eQRVdSN2BUnSvDXtGUGSA5J8Jsk3m+UnJXlt96VJksahTdfQO4FzaWYjrapvACd2WZQkaXzaBMGDqmriswicllqS5ok2QXB7ksfS3FyW5HgG9xVIkuaBNg+vPxNYBTw+ya3AdxncVCZJmgdGBkGShcCrqurwJA8GFlTVXeMpTZI0DiODoKp+neT3m/feRCZJ81CbMYKvJVmd5NQkf7j11WbnSY5MsiHJxiTnTLL9Pya5Nsk3mktUH7PNP4EkaYe0GSPYDfgh8JyhdQV8ZNSHmm6llcARwCZgbZLVVXXtULOvAcur6u4kfwJcAJywDfVLknZQmzuL/2g7930IsLGqbgBIcimDO5TvDYKq+txQ+y8Bp2znd0mSttO0QZDkPUzyXIKqetk0H90XuGVoeRPw9BHtTwc+NV09kqSZ1aZr6BND73cDXgh8byaLSHIKsBx41hTbzwDOANhvv/1m8qslqffadA19eHg5ySXA51vs+1ZgydDy4mbd/SQ5HPgr4FlV9YspaljF4F4Gli9fPuVT0yRJ2257nlm8DHhEi3ZrgWVJ9k+yC4P5iVYPN0jyZOAdDB5+86/bUYskaQe1GSOY+Ozi24DXTPe5qtqSZAVwBbAQeHdVrU9yPrCuqlYDbwb2AD6YBODmqjp6238MSdL2atM1tOf27ryq1gBrJqw7b+j94du7b0nSzGjzPIJnNNNLkOSUJBd645ckzR9txgjeDtyd5CDgz4DvAO/ttCpJ0ti0CYItVVUMbga7qKpWAtvdXSRJ+s3S5j6Cu5Kcy+Cu32cmWQDs3G1ZkqRxaXNGcALwC+D0qrqNwf0Ab+60KknS2LS5aug24MKh5ZtxjECS5o02Vw0dmmRtkp8m+WWSXye5cxzFSZK616Zr6CLgJcD1wO7Ay4G3dVmUJGl8Wk0xUVUbgYVV9euqeg9wZLdlSZLGpc1VQ3c3cwVdneQC4Pts3xxFkqTfQG1+oZ/atFsB/IzBjKLHdVmUJGl82lw1dFOS3YFHV9Xrx1CTJGmM2lw19ALgauDyZvngJKtHfkiSNGe06Rr6GwbPH74DoKquBvbvrCJJ0li1CYJfVdXE+wZ8SpgkzRNtrhpan+QkYGGSZcCrgS92W5YkaVzanBH8KfAEBvMNXQL8BDi7w5okSWPU5qqhuxk8XP6vui9HkjRuUwbBdFcG+WxhSZofRp0R/FvgFgbdQV8GMpaKJEljNSoIHgUcwWDCuZOATwKXVNX6cRQmSRqPKQeLmwnmLq+qlwKHAhuBK5OsGFt1kqTOjRwsTrIr8DwGZwVLgbcCH+2+LEnSuIwaLH4v8ERgDfD6qvrm2KqSJI3NqDOCUxjMNnoW8Ork3rHiAFVVD+m4NknSGEwZBFXlMwckqQf8ZS9JPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSz3UaBEmOTLIhycYk50yy/ZlJvppkS5Lju6xFkjS5zoIgyUJgJXAUcCDwkiQHTmh2M3Aa8P6u6pAkjdbmUZXb6xBgY1XdAJDkUuAY4NqtDarqxmbbPR3WIUkaocuuoX0ZPM9gq03NOknSb5A5MVic5Iwk65Ks27x582yXI0nzSpdBcCuwZGh5cbNum1XVqqpaXlXLFy1aNCPFSZIGugyCtcCyJPsn2QU4ERj5HGRJ0vh1FgRVtQVYAVwBXAdcVlXrk5yf5GiAJE9Lsgl4EfCOJD4GU5LGrMurhqiqNQwebDO87ryh92sZdBlJkmbJnBgsliR1xyCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknqu0yBIcmSSDUk2Jjlnku27JvlAs/3LSZZ2WY8k6YE6C4IkC4GVwFHAgcBLkhw4odnpwI+r6nHAfwHe1FU9kqTJdXlGcAiwsapuqKpfApcCx0xocwxwcfP+Q8Bzk6TDmiRJE+zU4b73BW4ZWt4EPH2qNlW1JcmdwMOB24cbJTkDOKNZ/GmSDZ1U3L19mPCzaZvM6vHL/Dhf9RjumLn8f/gxU23oMghmTFWtAlbNdh07Ksm6qlo+23XMVR6/Hecx3DHz9fh12TV0K7BkaHlxs27SNkl2Ah4K/LDDmiRJE3QZBGuBZUn2T7ILcCKwekKb1cBLm/fHA5+tquqwJknSBJ11DTV9/iuAK4CFwLuran2S84F1VbUaeBfwviQbgR8xCIv5bM53b80yj9+O8xjumHl5/OIf4JLUb95ZLEk9ZxBIUs8ZBJLUcwaBJPWcQdCRJDsleUWSy5N8o3l9Kskrk+w82/XNZUnm5ZUb0mzxqqGOJLkEuIPBXEqbmtWLGdw3sXdVnTBLpc0JSfaeahPw9apaPM565qIkDwXOBY4FHgEU8K/Ax4E3VtUds1bcHJfkU1V11GzXMVPmxBQTc9RTq+qACes2AV9K8u3ZKGiO2QzcxOAX/1bVLD9iViqaey4DPgscVlW3ASR5FIM/Ri4D/mAWa/uNl+QpU20CDh5jKZ0zCLrzoyQvAj5cVfcAJFkAvAj48axWNjfcADy3qm6euCHJLZO01wMtrar7TfPWBMKbkrxslmqaS9YC/8L9/xjZ6mHjLaVbBkF3TmTwfIWVSe5o1j0M+Bzz/w7qmfBfgb2ABwQBcMF4S5mzbkryl8DFVfUDgCSPBE7j/jMDa3LXAa+oqusnbphvf4w4RtChJL/D4JkL+zarbgU+XlXXzV5Vc0eSx/PA47fa49dOkr2Acxgcw63daT9gMMfXG6vKM9MRkhwPXFNVD5j2PsmxVfWx8VfVDa8a6kiS1wDvZ9Cv/eXmBXDJZI/t1P01f8leyuC0/CvNK3j8WquqH1fVa6rq8VW1d/P6nap6DYMBZI1QVR+aLAQae421mI55RtCRZkD4CVX1qwnrdwHWV9Wy2alsbvD4dSvJzVW132zXMVfNt+PnGEF37gF+i8GVL8Me3WzTaB6/HZTkG1NtAh45zlrmoj4dP4OgO2cDn0lyPfcNzO0HPA5YMVtFzSFn4/HbUY8E/h0PvEotwBfHX86c05vjZxB0pKouT3IAcAj3H+xcW1W/nr3K5gaP34z4BLBHVV09cUOSK8dezdzTm+PnGIEk9ZxXDUlSzxkEktRzBoHmtSSLk3w8yfVJbkhyUZJdW3zup1OsPz/J4c37s5M8aIp2z0/ytSRfT3Jtklc0649NcmCL72/VTpoJBoHmrSQBPgJ8rLnvYBmwOzswRUVVnVdV/6tZPBt4QBA004yvAl5QVQcBTwaubDYfC7T5Bd+2nbTDHCzWvJXkucDrquqZQ+sewuDehCXA8cDyqlrRbPsE8PdVdWVzRvBOBjN03gacWFWbk/wjg6tJfgv4e2ADcHtVPXvoO/YGvgU8pqr+39D632s+e2fzOg54DnAGsAuwETiVwcyWE9sBrAQWAXcDf1xV35qRA6Xe84xA89kTgKuGV1TVT4AbGdyPMMqDgXVV9QQGM1C+bsJ+3gp8D3j2cAg0237EYD6fm5JckuTkJAuq6ovN+r+oqoOr6jvAR6rqac2Zw3XA6VO0WwX8aVU9Ffhz4G3bfDSkKXgfgTS5e4APNO//iUEXU2tV9fIkvwsczuAX9xEMZv2c6IlJ/pbBzLR7AFdMbJBkD+D3gA8OersAmHacQ2rLINB8di2D7p97NV1Dj2LQpfNE7n9WvNuIfW1zH2pVXQNck+R9wHeZPAj+ETi2qr6e5DTgsEnaLADuqKqDt7UGqQ27hjSffQZ4UJJ/D5BkIfAW4KKm7/5G4OAkC5IsYXAX81YLuC9ETgI+P8n+7wL2nLgyyR5JDhtadTD3zZk08TN7At9vBphPnmzfTXfWd5sHHZGBg0b94NK2MAg0b9XgSogXAsc3cxb9ELinqv6uafIFBn+pXwu8Ffjq0Md/BhyS5JsMBnTPn+QrVgGXJ/nchPUB/jLJhiRXA6/nvrOBS4G/aC4tfSzw1wymKP8CgwFmpmh3MnB6kq8D6xk8Y0CaEV41pN5ortq5BHhhVX11uvZSXxgEktRzdg1JUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST13P8H+U8U+60bmLIAAAAASUVORK5CYII=\n",
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEJCAYAAACZjSCSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAV0ElEQVR4nO3de7QdZZ3m8e+TIBcFFSQqTaKh2zB2vKFG2ml7eYUeWCrggHJ1pMVGW9PK6pswbWOLPWu8tM60Q3QZb432koj3tCKMo9Iz6qgJimLANBFBgmIHFUQZL5Hf/LErsDmcs08lObW359T3s9ZeZ1fVu2v/UmvlPKfet+qtVBWSpP5aNOkCJEmTZRBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLP7THpAnbWgQceWMuXL590GZI0r1x++eU3V9WS6bbNuyBYvnw5GzdunHQZkjSvJLl+pm12DUlSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPWcQSBJPTfvbijT5Cw/+5OTLmGirnvdMyddgtQJzwgkqecMAknqOYNAknqu0yBIclSSzUm2JDl7mu2nJ9mW5Irm9aIu65Ek3VNng8VJFgNrgCOBrcCGJOur6qopTT9QVau7qkOSNFqXZwSHA1uq6tqq+iWwDji2w++TJO2CLoPgYOCGoeWtzbqpjk/yjSQfSrJsuh0lOTPJxiQbt23b1kWtktRbkx4s/mdgeVU9Gvg0cMF0japqbVWtqqpVS5ZM+4AdSdIu6jIIbgSG/8Jf2qy7U1X9sKp+0Sy+E3h8h/VIkqbRZRBsAFYkOSTJnsBJwPrhBkkOGlo8Bri6w3okSdPo7KqhqtqeZDVwKbAYeHdVbUpyHrCxqtYDL09yDLAd+BFwelf1SJKm1+lcQ1V1MXDxlHXnDr0/BzinyxokSaNNerBYkjRhBoEk9ZzTUEtj0vdpvMGpvH9TeUYgST1nEEhSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSzxkEktRzswZBkicluU/z/rQkb07y0O5LkySNQ5szgrcBtyd5DPDnwLeB97bZeZKjkmxOsiXJ2SPaHZ+kkqxqVbUkac60CYLtVVXAscD5VbUG2G+2DyVZDKwBjgZWAicnWTlNu/2AVwBf3pnCJUlzo00Q3JbkHOD5wCeTLALu1eJzhwNbquraqvolsI5BmEz1WuD1wM9b1ixJmkNtguBE4BfAC6vqJmAp8MYWnzsYuGFoeWuz7k5JHgcsq6pPjtpRkjOTbEyycdu2bS2+WpLU1qxB0Pzy/zCwV7PqZuCju/vFzZnFmxmMO8xWw9qqWlVVq5YsWbK7Xy1JGtLmqqE/Bj4EvL1ZdTDwsRb7vhFYNrS8tFm3w37AI4HLklwHPBFY74CxJI1Xm66hlwFPAn4CUFXXAA9s8bkNwIokhyTZEzgJWL9jY1XdWlUHVtXyqloOfAk4pqo27uS/QZK0G9oEwS+awV4AkuwB1GwfqqrtwGrgUuBq4KKq2pTkvCTH7GrBkqS5tUeLNv+S5D8D+yQ5Engp8M9tdl5VFwMXT1l37gxtn9pmn5KkudXmjOBsYBtwJfBiBr/YX9VlUZKk8Zn1jKCq7gDe0bwkSQvMjEGQ5KKqel6SK5lmTKCqHt1pZZKksRh1RvCK5uezxlGIJGkyZhwjqKrvN29fWlXXD78YDBhLkhaANoPFR06z7ui5LkSSNBmjxgj+hMFf/r+d5BtDm/YDvtB1YZKk8Rg1RvB+4FPAf2VwCekOt1XVjzqtSpI0NqOCoKrquiQvm7ohyQGGgSQtDLOdETwLuJzB5aMZ2lbAb3dYlyRpTGYMgqp6VvPzkPGVI0kat1GDxY8b9cGq+urclyNJGrdRXUNvGrGtgKfPcS2SpAkY1TX0tHEWIkmajFFdQ0+vqs8m+Y/Tba+qj3RXliRpXEZ1DT0F+Czw7Gm2FWAQSNICMKpr6NXNzz8aXzmSpHFr8/D6ByR5S5KvJrk8yT8kecA4ipMkda/NpHPrGDyh7HjghOb9B7osSpI0Pm2eWXxQVb12aPnvkpzYVUGSpPFqc0bwP5OclGRR83oecGnXhUmSxmPU5aO3cdccQ2cB/9RsWgT8FPiLrouTJHVv1FVD+42zEEnSZLQZIyDJ/sAKYO8d66rqf3dVlCRpfGYNgiQvYvAg+6XAFcATgf+Lcw1J0oLQZrD4FcATgOub+YceC9zSZVGSpPFpEwQ/r6qfAyTZq6q+Bfy7bsuSJI1LmzGCrUnuD3wM+HSSHwPXd1mUJGl8Zg2CqnpO8/Zvk3wOuB9wSadVSZLGpu1VQ48D/oDBfQVfqKpfdlqVJGls2kw6dy5wAfAA4EDgPUle1XVhkqTxaDNYfCrwhKp6dTM19ROB57fZeZKjkmxOsiXJ2dNsf0mSK5NckeTzSVbuXPmSpN3VJgi+x9CNZMBewI2zfSjJYmANcDSwEjh5ml/076+qR1XVYcAbgDe3KVqSNHdGzTX0PxiMCdwKbEry6Wb5SOArLfZ9OLClqq5t9rcOOBa4akeDqvrJUPv7NPuXJI3RqMHijc3Py4GPDq2/rOW+DwZuGFreCvze1EZJXgb8GbAnM9ytnORM4EyAhzzkIS2/XpLUxqhJ5y7Y8T7JnsChzeLmqvrVXBVQVWuANUlOAV4FvGCaNmuBtQCrVq3yrEGS5lCbuYaeyuCqoesYTEm9LMkLWkw6dyOwbGh5KaPHFtYBb5utHknS3GpzH8GbgD+sqs0ASQ4FLgQeP8vnNgArkhzCIABOAk4ZbpBkRVVd0yw+E7gGSdJYtQmCe+0IAYCq+tck95rtQ1W1PclqBk8zWwy8u6o2JTkP2FhV64HVSY4AfgX8mGm6hSRJ3WoTBJcneSd3PaHsVO4aSB6pqi4GLp6y7tyh969oWackqSNtguAlwMuAlzfL/wd4a2cVSZLGamQQNDeFfb2qHo43e0nSgjTyzuKq+jWwOYkX70vSAtWma2h/BncWfwX42Y6VVXVMZ1VJksamTRD8TedVSJImZtRcQ3szGCh+GHAl8K6q2j6uwiRJ4zFqjOACYBWDEDiawY1lkqQFZlTX0MqqehRAknfRbsZRSdI8M+qM4M6J5ewSkqSFa9QZwWOS7HheQIB9muUAVVX37bw6SVLnRk1DvXichUiSJqPNoyolSQuYQSBJPWcQSFLPGQSS1HOj7iy+DZjx+cBeNSRJC8Ooq4b2A0jyWuD7wPsYXDp6KnDQWKqTJHWuTdfQMVX11qq6rap+UlVvA47tujBJ0ni0CYKfJTk1yeIki5KcytB01JKk+a1NEJwCPA/4QfN6brNOkrQAzPo8gqq6DruCJGnBmvWMIMmhST6T5JvN8qOTvKr70iRJ49Cma+gdwDk0s5FW1TeAk7osSpI0Pm2C4N5VNfVZBE5LLUkLRJsguDnJ79DcXJbkBAb3FUiSFoA2D69/GbAWeHiSG4HvMLipTJK0AIwMgiSLgZdW1RFJ7gMsqqrbxlOaJGkcRgZBVf06yR80772JTJIWoDZdQ19Lsh74IEN3FFfVRzqrSpI0Nm2CYG/gh8DTh9YVYBBI0gLQ5s7iPxpHIZKkyZg1CJK8h2meS1BVL2zx2aOAfwAWA++sqtdN2f5nwIsY3JewDXhhVV3frnRJ0lxo0zX0iaH3ewPPAb4324eaK47WAEcCW4ENSdZX1VVDzb4GrKqq25P8CfAG4MS2xUuSdl+brqEPDy8nuRD4fIt9Hw5sqaprm8+tYzB53Z1BUFWfG2r/JeC0FvuVJM2hXXlm8QrggS3aHQzcMLS8tVk3kzOAT023IcmZSTYm2bht27bWhUqSZtdmjGDqs4tvAl45l0UkOQ1YBTxluu1VtZbB3c2sWrVqxucoS5J2Xpuuof12cd83AsuGlpc26+4myRHAXwNPqapf7OJ3SZJ2UZvnETypmV6CJKcleXOSh7bY9wZgRZJDkuzJYOrq9VP2/Vjg7Qyei/xvO1++JGl3tRkjeBtwe5LHAH8OfBt472wfqqrtwGrgUuBq4KKq2pTkvCTHNM3eCOwLfDDJFc0dzJKkMWpz+ej2qqokxwLnV9W7kpzRZudVdTFw8ZR15w69P2KnqpUkzbk2QXBbknMYXNr55CSLgHt1W5YkaVzadA2dCPwCOKOqbmIw6PvGTquSJI1Nm6uGbgLePLT8XVqMEUiS5oc2Vw09McmGJD9N8sskv05y6ziKkyR1r03X0PnAycA1wD4MJol7a5dFSZLGp9UUE1W1BVhcVb+uqvcAR3VbliRpXNpcNXR7c0PYFUneAHyfXZujSJL0G6jNL/TnN+1WM3hU5TLg+C6LkiSNT5urhq5Psg9wUFW9Zgw1SZLGqM1VQ88GrgAuaZYPcyoISVo42nQN/S2Dh8zcAlBVVwCHdFaRJGms2gTBr6pq6n0DPhNAkhaINlcNbUpyCrA4yQrg5cAXuy1LkjQubc4I/hR4BIP5hi4EfgKc1WFNkqQxanPV0O0MniD2192XI0katxmDYLYrg6rqmFHbJUnzw6gzgn8P3MCgO+jLQMZSkSRprEYFwYOBIxlMOHcK8EngwqraNI7CJEnjMeNgcTPB3CVV9QLgicAW4LIkq8dWnSSpcyMHi5PsBTyTwVnBcuAtwEe7L0uSNC6jBovfCzySwcPnX1NV3xxbVZKksRl1RnAag9lGXwG8PLlzrDhAVdV9O65NkjQGMwZBVfnMAUnqAX/ZS1LPGQSS1HMGgST1nEEgST1nEEhSzxkEktRzBoEk9ZxBIEk912kQJDkqyeYkW5KcPc32Jyf5apLtSU7oshZJ0vQ6C4Iki4E1wNHASuDkJCunNPsucDrw/q7qkCSN1ubh9bvqcGBLVV0LkGQdcCxw1Y4GVXVds+2ODuuQJI3QZdfQwQyecLbD1mbdTktyZpKNSTZu27ZtToqTJA3Mi8HiqlpbVauqatWSJUsmXY4kLShdBsGNwLKh5aXNOknSb5Aug2ADsCLJIUn2BE4C1nf4fZKkXdBZEFTVdmA1cClwNXBRVW1Kcl6SYwCSPCHJVuC5wNuTbOqqHknS9Lq8aoiqupjBoy6H15079H4Dgy4jSdKEzIvBYklSdwwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknqu0yBIclSSzUm2JDl7mu17JflAs/3LSZZ3WY8k6Z46C4Iki4E1wNHASuDkJCunNDsD+HFVPQz4b8Dru6pHkjS9Ls8IDge2VNW1VfVLYB1w7JQ2xwIXNO8/BDwjSTqsSZI0xR4d7vtg4Iah5a3A783Upqq2J7kVeABw83CjJGcCZzaLP02yuZOKu3cgU/5t2ikTPX5ZGOerHsPdM5//Dz90pg1dBsGcqaq1wNpJ17G7kmysqlWTrmO+8vjtPo/h7lmox6/LrqEbgWVDy0ubddO2SbIHcD/ghx3WJEmaossg2ACsSHJIkj2Bk4D1U9qsB17QvD8B+GxVVYc1SZKm6KxrqOnzXw1cCiwG3l1Vm5KcB2ysqvXAu4D3JdkC/IhBWCxk8757a8I8frvPY7h7FuTxi3+AS1K/eWexJPWcQSBJPWcQSFLPGQSS1HMGQUeS7JHkxUkuSfKN5vWpJC9Jcq9J1zefJVmQV25Ik+JVQx1JciFwC4O5lLY2q5cyuG/igKo6cUKlzQtJDphpE/D1qlo6znrmoyT3A84BjgMeCBTwb8DHgddV1S0TK26eS/Kpqjp60nXMlXkxxcQ89fiqOnTKuq3Al5L86yQKmme2Adcz+MW/QzXLD5xIRfPPRcBngadW1U0ASR7M4I+Ri4A/nGBtv/GSPG6mTcBhYyylcwZBd36U5LnAh6vqDoAki4DnAj+eaGXzw7XAM6rqu1M3JLlhmva6p+VVdbdp3ppAeH2SF06opvlkA/Av3P2PkR3uP95SumUQdOckBs9XWJPklmbd/YHPsfDvoJ4L/x3YH7hHEABvGG8p89b1Sf4KuKCqfgCQ5EHA6dx9ZmBN72rgxVV1zdQNC+2PEccIOpTkdxk8c+HgZtWNwMer6urJVTV/JHk49zx+6z1+7STZHzibwTHc0Z32AwZzfL2uqjwzHSHJCcCVVXWPae+THFdVHxt/Vd3wqqGOJHkl8H4G/dpfbl4AF0732E7dXfOX7DoGp+VfaV7B49daVf24ql5ZVQ+vqgOa1+9W1SsZDCBrhKr60HQh0Nh/rMV0zDOCjjQDwo+oql9NWb8nsKmqVkymsvnB49etJN+tqodMuo75aqEdP8cIunMH8FsMrnwZdlCzTaN5/HZTkm/MtAl40DhrmY/6dPwMgu6cBXwmyTXcNTD3EOBhwOpJFTWPnIXHb3c9CPgP3PMqtQBfHH85805vjp9B0JGquiTJocDh3H2wc0NV/Xpylc0PHr858Qlg36q6YuqGJJeNvZr5pzfHzzECSeo5rxqSpJ4zCCSp5wwCLWhJlib5eJJrklyb5Pwke7X43E9nWH9ekiOa92clufcM7Z6V5GtJvp7kqiQvbtYfl2Rli+9v1U6aCwaBFqwkAT4CfKy572AFsA+7MUVFVZ1bVf+rWTwLuEcQNNOMrwWeXVWPAR4LXNZsPg5o8wu+bTtptzlYrAUryTOAV1fVk4fW3ZfBvQnLgBOAVVW1utn2CeDvq+qy5ozgHQxm6LwJOKmqtiX5RwZXk/wW8PfAZuDmqnra0HccAHwLeGhV/b+h9b/ffPbW5nU88HTgTGBPYAvwfAYzW05tB7AGWALcDvxxVX1rTg6Ues8zAi1kjwAuH15RVT8BrmNwP8Io9wE2VtUjGMxA+eop+3kL8D3gacMh0Gz7EYP5fK5PcmGSU5MsqqovNuv/sqoOq6pvAx+pqic0Zw5XA2fM0G4t8KdV9XjgL4C37vTRkGbgfQTS9O4APtC8/ycGXUytVdWLkjwKOILBL+4jGcz6OdUjk/wdg5lp9wUundogyb7A7wMfHPR2ATDrOIfUlkGghewqBt0/d2q6hh7MoEvnkdz9rHjvEfva6T7UqroSuDLJ+4DvMH0Q/CNwXFV9PcnpwFOnabMIuKWqDtvZGqQ27BrSQvYZ4N5J/hNAksXAm4Dzm77764DDkixKsozBXcw7LOKuEDkF+Pw0+78N2G/qyiT7Jnnq0KrDuGvOpKmf2Q/4fjPAfOp0+266s77TPOiIDDxm1D9c2hkGgRasGlwJ8RzghGbOoh8Cd1TVf2mafIHBX+pXAW8Bvjr08Z8Bhyf5JoMB3fOm+Yq1wCVJPjdlfYC/SrI5yRXAa7jrbGAd8JfNpaW/A/wNgynKv8BggJkZ2p0KnJHk68AmBs8YkOaEVw2pN5qrdi4EnlNVX52tvdQXBoEk9ZxdQ5LUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST33/wHcMxRAFn2MEgAAAABJRU5ErkJggg==\n",
       "text/plain": [
        "<Figure size 432x288 with 1 Axes>"
       ]
@@ -1215,7 +1175,7 @@
     "\n",
     "$$\n",
     "\\min_{\\boldsymbol{\\theta}}\\mathcal{L}(\\theta_1, \\theta_2, \\theta_3)\n",
-    "= (\\theta_1)^2 + (\\theta_2)^2 + (\\theta_3)^2 + 10\n",
+    "= (\\theta_1)^2 + (\\theta_2)^2 + (\\theta_3)^2 + 10 \\tag{25}\n",
     "$$\n",
     "\n",
     "可以看出，只有当 $\\theta_1 = \\theta_2 = \\theta_3 = 0$ 的时候，$\\mathcal{L}$ 取最小值10。\n"
@@ -1223,8 +1183,13 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 14,
-   "metadata": {},
+   "execution_count": 10,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:42.863949Z",
+     "start_time": "2021-01-09T12:48:42.262829Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
@@ -1295,7 +1260,7 @@
     "\n",
     "接下来，我们试一个更复杂的损失函数。 首先我们介绍一个随机的埃尔米特矩阵 $H$ 其**特征值**为矩阵 $D$ 的对角元素。 \n",
     "\n",
-    "$$ D = \\begin{bmatrix} 0.2 &0 \\\\ 0 &0.8 \\end{bmatrix}  $$\n",
+    "$$ D = \\begin{bmatrix} 0.2 &0 \\\\ 0 &0.8 \\end{bmatrix}, \\tag{26}  $$\n",
     "\n",
     "不用担心，我们会帮你生成这个埃尔米特矩阵$H$. \n",
     "\n",
@@ -1315,14 +1280,14 @@
     "\\begin{bmatrix}\n",
     "e^{-i\\frac{\\theta_3}{2}} & 0 \\\\ \n",
     "0 & e^{i\\frac{\\theta_3}{2}}\n",
-    "\\end{bmatrix}\n",
+    "\\end{bmatrix}, \\tag{27}\n",
     "$$\n",
     "\n",
     "我们让这个矩阵（模板）乘以 $\\lvert {0}\\rangle$，得到一个新的2维复向量$\\lvert {\\phi}\\rangle$\n",
     "\n",
     "\n",
     "$$ \n",
-    "\\lvert {\\phi}\\rangle = U(\\theta_1, \\theta_2, \\theta_3)\\lvert {0}\\rangle\n",
+    "\\lvert {\\phi}\\rangle = U(\\theta_1, \\theta_2, \\theta_3)\\lvert {0}\\rangle, \\tag{28}\n",
     "$$\n",
     "\n",
     "然后，我们定义损失函数为：\n",
@@ -1330,7 +1295,7 @@
     "$$\n",
     "\\min_{\\boldsymbol{\\theta}}\\mathcal{L}(\\theta_1, \\theta_2, \\theta_3) \n",
     "= \\langle{\\phi} \\lvert H \\lvert {\\phi}\\rangle \n",
-    "=  \\langle{0} \\lvert  U^{\\dagger}H U \\lvert {0}\\rangle\n",
+    "=  \\langle{0} \\lvert  U^{\\dagger}H U \\lvert {0}\\rangle. \\tag{29}\n",
     "$$\n",
     "\n",
     "来看看优化后我们得到了什么！"
@@ -1338,16 +1303,21 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 15,
-   "metadata": {},
+   "execution_count": 11,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:43.137909Z",
+     "start_time": "2021-01-09T12:48:42.896539Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
      "output_type": "stream",
      "text": [
       "随机生成的矩阵 H 是:\n",
-      "[[ 0.55386934+2.77555756e-17j -0.282673  -8.48178487e-02j]\n",
-      " [-0.282673  +8.48178487e-02j  0.44613066+0.00000000e+00j]] \n",
+      "[[0.76063331+0.j         0.06546144+0.13336071j]\n",
+      " [0.06546144-0.13336071j 0.23936669+0.j        ]] \n",
       "\n",
       "不出所料，H 的特征值是:\n",
       "[0.2 0.8]\n"
@@ -1377,8 +1347,13 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 16,
-   "metadata": {},
+   "execution_count": 12,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:43.155166Z",
+     "start_time": "2021-01-09T12:48:43.146544Z"
+    }
+   },
    "outputs": [],
    "source": [
     "# 超参数设置\n",
@@ -1404,8 +1379,13 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 17,
-   "metadata": {},
+   "execution_count": 13,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:43.179953Z",
+     "start_time": "2021-01-09T12:48:43.161434Z"
+    }
+   },
    "outputs": [],
    "source": [
     "class Optimization_ex2(fluid.dygraph.Layer):\n",
@@ -1435,24 +1415,29 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 18,
-   "metadata": {},
+   "execution_count": 14,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:43.581225Z",
+     "start_time": "2021-01-09T12:48:43.201135Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "iter: 0   loss: 0.5581\n",
-      "iter: 1   loss: 0.3127\n",
-      "iter: 2   loss: 0.2455\n",
-      "iter: 3   loss: 0.2072\n",
-      "iter: 4   loss: 0.2010\n",
-      "iter: 5   loss: 0.2002\n",
-      "iter: 6   loss: 0.2000\n",
-      "iter: 7   loss: 0.2000\n",
-      "iter: 8   loss: 0.2000\n",
-      "iter: 9   loss: 0.2000\n",
-      "损失函数的最小值是:  0.20000008859899268\n"
+      "iter: 0   loss: 0.7653\n",
+      "iter: 1   loss: 0.5138\n",
+      "iter: 2   loss: 0.2556\n",
+      "iter: 3   loss: 0.2068\n",
+      "iter: 4   loss: 0.2030\n",
+      "iter: 5   loss: 0.2015\n",
+      "iter: 6   loss: 0.2007\n",
+      "iter: 7   loss: 0.2004\n",
+      "iter: 8   loss: 0.2002\n",
+      "iter: 9   loss: 0.2001\n",
+      "损失函数的最小值是:  0.20007871016474926\n"
      ]
     }
    ],
@@ -1494,7 +1479,7 @@
    "source": [
     "我们可以改变一下$H$的特征值。如果将它对角化后的的对角矩阵改变为\n",
     "\n",
-    "$$ D = \\begin{bmatrix} 0.8 &0 \\\\ 0 &1.2 \\end{bmatrix}  $$\n",
+    "$$ D = \\begin{bmatrix} 0.8 &0 \\\\ 0 &1.2 \\end{bmatrix}. \\tag{30}  $$\n",
     "\n",
     "你会发现我们仍然得到了$H$的最小特征值0.8, 你能找到背后的原因吗？还是说这背后隐藏着什么理论？\n"
    ]
@@ -1525,7 +1510,7 @@
     "\n",
     "假设我们想找到如下哈密顿量的基态：\n",
     "\n",
-    "$$ H = 0.4 \\, Z \\otimes I + 0.4 \\, I \\otimes Z + 0.2 \\, X \\otimes X$$\n",
+    "$$ H = 0.4 \\, Z \\otimes I + 0.4 \\, I \\otimes Z + 0.2 \\, X \\otimes X. \\tag{31}$$\n",
     "\n",
     "给定一种常见的量子神经网络架构"
    ]
@@ -1534,7 +1519,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "<img src=\"figures/vqeAnsatz.png\" width=\"450\" >"
+    "<img src=\"figures/intro-fig-vqeAnsatz.png\" width=\"450\" >"
    ]
   },
   {
@@ -1546,8 +1531,13 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 19,
-   "metadata": {},
+   "execution_count": 15,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:43.603696Z",
+     "start_time": "2021-01-09T12:48:43.592558Z"
+    }
+   },
    "outputs": [],
    "source": [
     "from paddle_quantum.utils import pauli_str_to_matrix\n",
@@ -1570,8 +1560,13 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 20,
-   "metadata": {},
+   "execution_count": 16,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:43.719137Z",
+     "start_time": "2021-01-09T12:48:43.608167Z"
+    }
+   },
    "outputs": [],
    "source": [
     "class vqe_demo(fluid.dygraph.Layer):\n",
@@ -1609,8 +1604,12 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 21,
+   "execution_count": 17,
    "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:48:46.185285Z",
+     "start_time": "2021-01-09T12:48:43.831438Z"
+    },
     "colab": {
      "base_uri": "https://localhost:8080/",
      "height": 1000
@@ -1689,13 +1688,23 @@
    "source": [
     "## <a name=\"References\">参考文献</a>\n",
     "\n",
-    "[1] [Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
+    "[1] Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information. (Cambridge university press, 2010).\n",
+    "\n",
+    "[2] Phillip Kaye, Laflamme, R. & Mosca, M. An Introduction to Quantum Computing. (2007).\n",
+    "\n",
+    "[3] Biamonte, J. et al. Quantum machine learning. [Nature 549, 195–202 (2017).](https://www.nature.com/articles/nature23474)\n",
+    "\n",
+    "[4] Schuld, M., Sinayskiy, I. & Petruccione, F. An introduction to quantum machine learning. [Contemp. Phys. 56, 172–185 (2015).](https://www.tandfonline.com/doi/abs/10.1080/00107514.2014.964942)\n",
     "\n",
-    "[2] [McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023 (2016).](https://iopscience.iop.org/article/10.1088/1367-2630/18/2/023023)\n",
+    "[5] Benedetti, M., Lloyd, E., Sack, S. & Fiorentini, M. Parameterized quantum circuits as machine learning models. [Quantum Sci. Technol. 4, 043001 (2019).](https://iopscience.iop.org/article/10.1088/2058-9565/ab4eb5)\n",
     "\n",
-    "[3] [Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).](https://www.nature.com/articles/nature23879)\n",
+    "[6] [Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
     "\n",
-    "[4] [Mitarai, K., Negoro, M., Kitagawa, M. & Fujii, K. Quantum circuit learning. Phys. Rev. A 98, 032309 (2018).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.98.032309)"
+    "[7] [McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023 (2016).](https://iopscience.iop.org/article/10.1088/1367-2630/18/2/023023)\n",
+    "\n",
+    "[8] [Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).](https://www.nature.com/articles/nature23879)\n",
+    "\n",
+    "[9] [Mitarai, K., Negoro, M., Kitagawa, M. & Fujii, K. Quantum circuit learning. Phys. Rev. A 98, 032309 (2018).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.98.032309)"
    ]
   },
   {
@@ -1729,6 +1738,24 @@
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
    "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {
+    "height": "calc(100% - 180px)",
+    "left": "10px",
+    "top": "150px",
+    "width": "426.667px"
+   },
+   "toc_section_display": true,
+   "toc_window_display": true
   }
  },
  "nbformat": 4,

introduction/PaddleQuantum_Tutorial_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Paddle Quantum Quick Start Manual\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "\n",
+    "# Overview\n",
+    "\n",
+    "Quantum computing (QC) is a new computing model laying in the intersection of quantum mechanics and theory of computation. QC follows the fundamental laws of quantum theory to manipulate quantum bits (qubits). For many specific computational tasks, it is widely believed that quantum algorithms exhibit advantages over classical algorithms at least in theory. For a systematic introduction to the subject of QC, we refer to [1-2].\n",
+    "\n",
+    "In recent years, one of the popular research topics in QC is combining the potential of quantum computing and artificial intelligence. Quantum machine learning (QML) is such an interdisciplinary subject. Researchers want to utilize the information processing advantages of quantum computing to promote the development of artificial intelligence. On the other side, it is also worth exploring the possibility of using artificial intelligence technology to break through the bottleneck of quantum computing research and development. For introductory materials about quantum machine learning, please refer to [3-5].\n",
+    "\n",
+    "Here, we provide a quick start for users to get started with Paddle Quantum. Currently, you can read all the content online or download the Jupyter Notebook from our [GitHub](https://github.com/PaddlePaddle/Quantum/tree/master/introduction). In terms of content, the quick start includes the following sections:\n",
+    "\n",
+    "- Introduction to quantum computing and quantum neural network (QNN)\n",
+    "- Introduction to Paddle Quantum\n",
+    "- PaddlePaddle optimizer tutorial\n",
+    "- A case study on quantum machine learning - Variational Quantum Eigensolver (VQE)\n",
+    "\n",
+    "**Latest version updated on:** Jan. 9th, 2021 by Paddle Quantum developers.\n",
+    "\n",
+    "---\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Quantum Computing Fundamentals\n",
+    "\n",
+    "Quantum Computing (QC) uses unique phenomena in quantum physics (quantum superposition, quantum interference, and quantum entanglement) to design algorithms and help solve specific tasks in physics, chemistry, and optimization theory. There are several existing quantum computation models including the Adiabatic Quantum Computation (AQC) based on the adiabatic theorem and Measurement-Based Quantum Computation (MBQC). This introduction will focus on the most widely used Quantum Circuit model. In quantum circuits, the basic computation unit is the quantum bit (qubit)， which is similar to the concept of bit in classical computers. Classical bits can only be in one of the two states, 0 or 1. By comparison, qubits can not only be in states $|0\\rangle$ and $|1\\rangle$ but also in a superposition state (we will explain this concept later). Quantum circuit model utilize quantum logic gates to manipulate the states of these qubits. The mathematics behind this process is linear algebra in the complex domain. Here we assume the readers are already familiar with linear algebra."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## What is a qubit?\n",
+    "\n",
+    "### Mathematical representation\n",
+    "\n",
+    "In quantum mechanics, the state of a two-level quantum system (e.g. electron spin) can be expressed as a state vector obtained through linear combinations of the following orthonormal basis,\n",
+    "\n",
+    "$$\n",
+    "|0\\rangle := \\begin{bmatrix} 1 \\\\ 0 \\end{bmatrix}, \\quad |1\\rangle := \\begin{bmatrix} 0 \\\\ 1 \\end{bmatrix}.\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "The vector representation here follows the Dirac notation (bra-ket) in quantum physics. This orthonormal basis $\\{|0\\rangle, |1\\rangle \\}$ is known as the **computational basis**. Physically, one could consider $|0\\rangle$ and $|1\\rangle$ as the energy ground state and excited state of an atom, respectively. All possible pure states of a qubit can be regarded as normalized vectors in the two-dimensional Hilbert space. Moreover, multi-qubit states can be represented by unit vectors in high-dimensional Hilbert space where the basis is the tensor product of  $\\{|0\\rangle, |1\\rangle\\}$. For example, a 2-qubit quantum state can be represented by a unit complex vector in a 4-dimensional Hilbert space with the orthonormal basis,\n",
+    "\n",
+    "$$\n",
+    "\\left\\{\n",
+    "|00\\rangle = |0\\rangle\\otimes |0\\rangle := \\begin{bmatrix} 1 \\\\ 0 \\\\ 0 \\\\ 0 \\end{bmatrix}, \\quad \n",
+    "|01\\rangle = |0\\rangle\\otimes |1\\rangle := \\begin{bmatrix} 0 \\\\ 1 \\\\ 0 \\\\ 0 \\end{bmatrix}, \\quad\n",
+    "|10\\rangle = |1\\rangle\\otimes |0\\rangle := \\begin{bmatrix} 0 \\\\ 0 \\\\ 1 \\\\ 0 \\end{bmatrix}, \\quad\n",
+    "|11\\rangle = |1\\rangle\\otimes |0\\rangle := \\begin{bmatrix} 0 \\\\ 0 \\\\ 0 \\\\ 1 \\end{bmatrix}\n",
+    "\\right\\}.\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "By convention, the leftmost position in ket notation represents the first qubit $q_0$, the second position represents the second qubit $q_1$, and so on. The symbol $\\otimes$ denotes the tensor product operation. It works as follows: Given two matrices $A_{m\\times n}$ and $B_{p \\times q}$, then the tensor product of $A, B$ is\n",
+    "\n",
+    "$$\n",
+    "A \\otimes B =\n",
+    "\\begin{bmatrix}\n",
+    "a_{11}B & \\cdots & a_{1 n}B\\\\\n",
+    "\\vdots & \\ddots & \\vdots \\\\\n",
+    "a_{m1}B & \\cdots & a_{m n}B\n",
+    "\\end{bmatrix}_{(mp)\\times (nq)}.\n",
+    "\\tag{3}\n",
+    "$$\n",
+    "\n",
+    "Any single qubit quantum state $|\\psi\\rangle$ can be written as a linear combination (superposition) of the basis vectors $|0\\rangle$ and $|1\\rangle$. \n",
+    "\n",
+    "$$\n",
+    "|\\psi\\rangle = \\alpha |0\\rangle + \\beta |1\\rangle\n",
+    ":= \\begin{bmatrix} \\alpha \\\\ \\beta \\end{bmatrix}.\n",
+    "\\tag{4}\n",
+    "$$\n",
+    "\n",
+    "where $\\alpha$ and $\\beta$ are **complex numbers** referred as the probability amplitudes. According to Born Rule, the probability to find the qubit in $|0\\rangle$ state is $|\\alpha|^2$; and the probability of $|1\\rangle$ is $|\\beta|^2$. Since the sum of probabilities equals to 1, one should introduce the constraint: $|\\alpha|^2 + |\\beta|^2 = 1$.\n",
+    "\n",
+    "\n",
+    "### Bloch sphere representation\n",
+    "\n",
+    "Geometrically, one can use a point on the unit sphere to represent the pure quantum state of a qubit. This sphere is called the **Bloch sphere**, (see Figure 1)\n",
+    "\n",
+    "$$\n",
+    "|\\psi\\rangle = \\alpha |0\\rangle + \\beta |1\\rangle\n",
+    "= \\cos\\bigg(\\frac{\\theta}{2}\\bigg) |0\\rangle + e^{i\\varphi}\\sin\\bigg(\\frac{\\theta}{2}\\bigg) |1\\rangle.\n",
+    "\\tag{5}\n",
+    "$$\n",
+    "\n",
+    "**Note**: The states of multi-qubit quantum systems cannot be directly represented by Bloch spheres. For a classical bit in state 0 or 1, it corresponds to the north or south pole of the Bloch sphere. **A qubit state can be at any point on the sphere. Such a superposition state is impossible for classical bits**. For example, the quantum state $\\frac{1}{\\sqrt{2}}\\big(|0\\rangle + i|1\\rangle\\big)$ is at the intersection of the equator and $+y$ axis.\n",
+    "\n",
+    "![intro-fig-bloch](./figures/intro-fig-bloch.png \"**Figure 1.** Bloch sphere representation of a single qubit. [[Image source]](https://en.wikipedia.org/wiki/Qubit)\")\n",
+    "\n",
+    "The following content is for readers who are more familiar with quantum computing. If you find it difficult to follow, don’t worry, you can skip it. Due to the interaction between qubits and decoherence, for a system with multiple qubits, its single-qubit subsystem will no longer stay in pure states, but a mixed state in general. The concept of mixed state can be regarded as a statistical mixture of multiple pure states. **The single-bit mixed state can be seen as a point inside the Bloch sphere**. The mixed state needs to be described in the density matrix formulation of quantum mechanics, for example the following mixed state has $1/2$ probability to be in $|0\\rangle$ or $|1\\rangle$,\n",
+    "\n",
+    "$$\n",
+    "\\rho_{\\text{mixed}} = \\sum_i P_i |\\psi_i\\rangle\\langle\\psi_i| = \\frac{1}{2} |0\\rangle\\langle0| + \\frac{1}{2} |1\\rangle\\langle1| := \\frac{1}{2}  \\begin{bmatrix} 1 \\\\ 0\\end{bmatrix} \\begin{bmatrix} 1 & 0 \\end{bmatrix} +  \\frac{1}{2}  \\begin{bmatrix} 0 \\\\ 1\\end{bmatrix} \\begin{bmatrix} 0 & 1 \\end{bmatrix} = \\frac{1}{2} \\begin{bmatrix} 1 & 0\\\\ 0 & 1 \\end{bmatrix}.\n",
+    "\\tag{6}\n",
+    "$$\n",
+    "\n",
+    "The row vector (bra) $\\langle0| = |0\\rangle^\\dagger$ is the conjugate transpose of the column vector (ket) $|0\\rangle$.\n",
+    "\n",
+    "**Note:** For more information, please refer to [Wikipedia](https://en.wikipedia.org/wiki/Qubit).\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## What is a quantum logic gate?\n",
+    "\n",
+    "In classical computers, we can apply basic logical operations (NOT gates, NAND gates, XOR gates, AND gates, and OR gates) on classical bits and combine them into more complicated operations. Quantum computing has a completely different set of logical operations, which are called quantum gates. We cannot compile existing C++ programs on a quantum computer. Because **classical computers and quantum computers have different logic gate structures, quantum algorithms need to be constructed using quantum gates**. Mathematically, a quantum gates can be expressed as a unitary matrix. Unitary operations could preserve vector length, which is a desirable property. Otherwise, if we operate on a pure state, it will be degraded into a mixed state, making it unreliable for the following running time. The unitary matrix is defined as:\n",
+    "\n",
+    "$$\n",
+    "U^{\\dagger}U = UU^{\\dagger} = I,\n",
+    "\\quad \\text{and} \\quad\n",
+    "\\Vert |\\psi\\rangle \\Vert = \\Vert U|\\psi\\rangle\\Vert = 1.\n",
+    "\\tag{7}\n",
+    "$$\n",
+    "\n",
+    "where $U^{\\dagger}$ is the conjugate transpose of $U$, and $I$ represents the identity matrix. But what is the physical meaning of representing quantum gates as unitary matrices? This implies that all quantum gates must be reversible. For any gate logic $U$, one can always find the corresponding reverse operation $U^\\dagger$. In addition, the unitary matrix must be a square matrix, because the input and output of the quantum operation require the same number of qubits. A quantum gate acting on $n$ qubits can be written as a $2^n \\times 2^n$ unitary matrix. The most common quantum gates act on one or two qubits, just like classical logic gates.\n",
+    "\n",
+    "### Single-qubit gate\n",
+    "\n",
+    "Next, we introduce single-qubit gates in quantum computing, including the Pauli matrices $\\{X, Y, Z\\}$, single-bit rotation gates $\\{R_x, R_y, R_z\\}$ and the Hadamard gate $H$. Firstly, **NOT gate** is important for both classical and quantum computing,\n",
+    "\n",
+    "$$\n",
+    "X := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix}.\n",
+    "\\tag{8}\n",
+    "$$\n",
+    "\n",
+    "This quantum gate (unitary matrix) acts on the state of a single qubit (a complex vector). The operation is essentially **multiplication between a matrix and a column vector**:\n",
+    "\n",
+    "$$\n",
+    "X |0\\rangle := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} \\begin{bmatrix} 1 \\\\0 \\end{bmatrix}\n",
+    "=\\begin{bmatrix} 0 \\\\1 \\end{bmatrix} = |1\\rangle,\n",
+    "\\quad \\text{and} \\quad\n",
+    "X |1\\rangle := \\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} \\begin{bmatrix} 0 \\\\1 \\end{bmatrix}\n",
+    "=\\begin{bmatrix} 1 \\\\0 \\end{bmatrix}=|0\\rangle.\n",
+    "\\tag{9}\n",
+    "$$\n",
+    "\n",
+    "Recall the Bloch sphere representation, this operation $X$ acting on a qubit state (a point on the Bloch sphere) is equivalent to **a rotation about the $x$ axis in the Bloch sphere with angle $\\pi$** . This is why $X$ can be expressed as $R_x(\\pi)$ (differ by a global phase $e^{-i\\pi/2} = -i$ ). The other two Pauli matrices $Y$ and $Z$ are very similar in this sense (representing rotation around the $y$ and $z$ axes with angle $\\pi$):\n",
+    "\n",
+    "$$\n",
+    "Y := \\begin{bmatrix} 0 &-i \\\\ i &0 \\end{bmatrix},\n",
+    "\\quad \\text{and} \\quad \n",
+    "Z := \\begin{bmatrix} 1 &0 \\\\ 0 &-1 \\end{bmatrix}.\n",
+    "\\tag{10}\n",
+    "$$\n",
+    "\n",
+    "Generally speaking, any quantum gate that rotates $\\theta$ on the corresponding axis on the Bloch sphere can be expressed as\n",
+    "\n",
+    "$$\n",
+    "R_x(\\theta) := \n",
+    "\\begin{bmatrix} \n",
+    "\\cos \\frac{\\theta}{2} &-i\\sin \\frac{\\theta}{2} \\\\ \n",
+    "-i\\sin \\frac{\\theta}{2} &\\cos \\frac{\\theta}{2} \n",
+    "\\end{bmatrix}\n",
+    ",\\quad \n",
+    "R_y(\\theta) := \n",
+    "\\begin{bmatrix}\n",
+    "\\cos \\frac{\\theta}{2} &-\\sin \\frac{\\theta}{2} \\\\ \n",
+    "\\sin \\frac{\\theta}{2} &\\cos \\frac{\\theta}{2} \n",
+    "\\end{bmatrix}\n",
+    ",\\quad \n",
+    "R_z(\\theta) := \n",
+    "\\begin{bmatrix}\n",
+    "e^{-i\\frac{\\theta}{2}} & 0 \\\\ \n",
+    "0 & e^{i\\frac{\\theta}{2}}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{11}\n",
+    "$$\n",
+    "\n",
+    "In addition to the rotation gates, the most important single-qubit gate is the Hadamard gate. The corresponding Bloch spherical interpretation consists of two separate rotations, first rotating $\\pi$ around the $z$-axis, and then rotating $\\pi/2$ around the $y$-axis. Its matrix representation is\n",
+    "\n",
+    "$$\n",
+    "H := \\frac{1}{\\sqrt{2}}\\begin{bmatrix} 1 &1 \\\\ 1 &-1 \\end{bmatrix}.\n",
+    "\\tag{12}\n",
+    "$$\n",
+    "\n",
+    "### Two-bit quantum gate\n",
+    "\n",
+    "We can expand the idea of single-qubit gates to multi-qubit. There are two ways to realize this expansion. The first is to apply single-qubit gates on selected qubits, while the other qubits are not operated. The figure below gives a concrete example:\n",
+    "\n",
+    "![intro-fig-hadamard](./figures/intro-fig-hadamard.png \"**Figure 2.** Circuit representation and interpretation of two-qubit logic operations. [[Picture source]](https://en.wikipedia.org/wiki/Quantum_logic_gate)\")\n",
+    "\n",
+    "The quantum gate acting on two-qubit system can be expressed as a $4\\times4$ unitary matrix\n",
+    "\n",
+    "$$\n",
+    "U = H \\otimes I \n",
+    "= \\frac{1}{\\sqrt{2}} \\begin{bmatrix} 1 &1 \\\\ 1 &-1 \\end{bmatrix} \n",
+    "\\otimes \\begin{bmatrix} 1 &0 \\\\ 0 &1 \\end{bmatrix} \n",
+    "= \\frac{1}{\\sqrt{2}} \\,\n",
+    "\\begin{bmatrix}\n",
+    "1 &0 &1 &0  \\\\ \n",
+    "0 &1 &0 &1  \\\\\n",
+    "1 &0 &-1 &0 \\\\\n",
+    "0 &1 &0 &-1 \n",
+    "\\end{bmatrix}.\n",
+    "\\tag{13}\n",
+    "$$\n",
+    "\n",
+    "Another way is to apply two-qubit gates directly. For example, $\\text{CNOT}$  gate will make the state of one qubit affect another qubit state.\n",
+    "\n",
+    "$$\n",
+    "\\text{CNOT} :=\n",
+    "\\begin{bmatrix}\n",
+    "1 &0 &0 &0 \\\\\n",
+    "0 &1 &0 &0 \\\\\n",
+    "0 &0 &0 &1 \\\\\n",
+    "0 &0 &1 &0\n",
+    "\\end{bmatrix},\n",
+    "\\tag{14}\n",
+    "$$\n",
+    "\n",
+    "When $\\text{CNOT}$  acts on the computational basis, we have\n",
+    "\n",
+    "$$\n",
+    "\\text{CNOT} |00\\rangle = |00\\rangle, \\quad\n",
+    "\\text{CNOT} |01\\rangle = |01\\rangle, \\quad\n",
+    "\\text{CNOT} |10\\rangle = |11\\rangle, \\quad\n",
+    "\\text{CNOT} |11\\rangle = |10\\rangle.\n",
+    "\\tag{15}\n",
+    "$$\n",
+    "\n",
+    "We can conclude that when the first qubit is in the $|1\\rangle$ state, $\\text{CNOT}$ will act $X$ gate on the second qubit. If the first qubit is in the $|0\\rangle$ state, then the second qubit is not affected in any way. This is why $\\text{CNOT}$ stands for the controlled-$\\text{NOT}$ gate. The following list contains frequently used quantum gates and their matrix representations. **All of these quantum gates can be called in Paddle Quantum**.\n",
+    "\n",
+    "![intro-fig-gates](./figures/intro-fig-gates.png \"**Figure 3.** List of common quantum gates. [[Image source]](https://en.wikipedia.org/wiki/Quantum_logic_gate)\")\n",
+    "\n",
+    "**Note**: For more information, please see the following Wikipedia [link](https://en.wikipedia.org/wiki/Quantum_logic_gate)."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## What is measurement in quantum mechanics?\n",
+    "\n",
+    "For a two-level quantum system, such as the spin of an electron, it can be spin up $\\uparrow$ or spin down $\\downarrow$, corresponding to state $|0\\rangle$ and state $|1\\rangle$. As mentioned before, the electron can be in a superposition state of spin up and down, which is $|\\psi\\rangle =\\alpha |0\\rangle + \\beta |1\\rangle$. The measurement will help us further understand what is a superposition state. It is worth noting that the measurement in quantum mechanics usually refers to a statistical result rather than a single measurement. This is due to the nature of measurements in quantum physics, which collapses the observed quantum state. For example, if we measure an electron in state $|\\psi\\rangle =\\alpha |0\\rangle + \\beta |1\\rangle$, we will have a probability of $|\\alpha|^2$ to obtain the measurement results of spin up, and after measurement, the quantum state collapses to the post-measurement state $ |0\\rangle$. Similarly, we also have a probability of $|\\beta|^2$ to get the spin down post-measurement state $|1\\rangle$. So if we want to get the value of $\\alpha$ accurately, one experiment is obviously not enough. We need to prepare a lot of electrons in the superposition state $\\alpha |0\\rangle + \\beta |1\\rangle$, measure the spin of each electron, and then count the frequency. Measurement has a special place in quantum mechanics. If the reader finds it difficult to understand, we refer to [Measurement in Quantum Mechanics](https://en.wikipedia.org/wiki/Measurement_in_quantum_mechanics) for more information."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Example and exercise\n",
+    "\n",
+    "### Example: Using Paddle Quantum to create a $X$ gate\n",
+    "\n",
+    "**Note:** All single-bit rotation gates are established as follows:\n",
+    "\n",
+    "$$\n",
+    "R_x(\\theta) :=\n",
+    "\\begin{bmatrix}\n",
+    "\\cos \\frac{\\theta}{2} &-i\\sin \\frac{\\theta}{2} \\\\\n",
+    "-i\\sin \\frac{\\theta}{2} &\\cos \\frac{\\theta}{2}\n",
+    "\\end{bmatrix}\n",
+    ",\\quad\n",
+    "R_y(\\theta) :=\n",
+    "\\begin{bmatrix}\n",
+    "\\cos \\frac{\\theta}{2} &-\\sin \\frac{\\theta}{2} \\\\\n",
+    "\\sin \\frac{\\theta}{2} &\\cos \\frac{\\theta}{2}\n",
+    "\\end{bmatrix}\n",
+    ",\\quad\n",
+    "R_z(\\theta) :=\n",
+    "\\begin{bmatrix}\n",
+    "e^{-i\\frac{\\theta}{2}} & 0 \\\\\n",
+    "0 & e^{i\\frac{\\theta}{2}}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{16}\n",
+    "$$\n",
+    "\n",
+    "Therefore, it is not difficult to see that the $X$ gate can be expressed as $R_x(\\pi)$. The following code will generate the $X$ gate:\n",
+    "\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:57:05.944723Z",
+     "start_time": "2021-01-09T12:57:02.038199Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The matrix representation of quantum gate is:\n",
+      "[[ 6.123234e-17+0.j -6.123234e-17-1.j]\n",
+      " [ 6.123234e-17-1.j  6.123234e-17+0.j]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "import numpy as np\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "\n",
+    "# Set the angle parameter theta = pi\n",
+    "theta = np.array([np.pi])\n",
+    "\n",
+    "# Initiate Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # We need to convert numpy.ndarray to variable supported in Paddle dynamic graph mode\n",
+    "    theta = fluid.dygraph.to_variable(theta)\n",
+    "    \n",
+    "    # Set the number of qubits required for calculation\n",
+    "    num_qubits = 1\n",
+    "    \n",
+    "    # Initialize our single-bit quantum circuit\n",
+    "    cir = UAnsatz(num_qubits)\n",
+    "    \n",
+    "    # Apply an Rx rotation gate to the first qubit (q0), the angle is pi\n",
+    "    which_qubit = 0\n",
+    "    cir.rx(theta, which_qubit)\n",
+    "    \n",
+    "    # Convert to numpy.ndarray\n",
+    "    # Print out this quantum gate\n",
+    "    print('The matrix representation of quantum gate is:')\n",
+    "    print(cir.U.numpy())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "There is a global phase $-i$ in front between the output and the $X$ (NOT) gate:\n",
+    "\n",
+    "$$\n",
+    "\\text{output} = \\begin{bmatrix} 0 &-i \\\\ -i &0 \\end{bmatrix}\n",
+    "= -i\\begin{bmatrix} 0 &1 \\\\ 1 &0 \\end{bmatrix} = -i X.\n",
+    "\\tag{17}\n",
+    "$$\n",
+    "\n",
+    "Can you figure out why such a global phase is not important in quantum computing? And not important in what sense?"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Exercise: Create a $Y$ gate\n",
+    "\n",
+    "Similar to the $X$ gate, try to create a $Y$ gate by filling the following code. "
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "theta = \"your code\"\n",
+    "\n",
+    "with fluid.dygraph.guard():    \n",
+    "    theta = fluid.dygraph.to_variable(theta)\n",
+    "    num_qubits = 1\n",
+    "    cir = UAnsatz(\"your code\")\n",
+    "    cir.ry(\"your code\")\n",
+    "    print(cir.U.numpy())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "As mentioned before, we have a global phase $-i$ in front:\n",
+    "\n",
+    "$$\n",
+    "\\text{output} = \\begin{bmatrix} 0 &-1 \\\\ 1 &0 \\end{bmatrix}\n",
+    "= -i\\begin{bmatrix} 0 &-i \\\\ i &0 \\end{bmatrix} = -i Y.\n",
+    "\\tag{18}\n",
+    "$$\n",
+    "\n",
+    "---"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Quantum Neural Network\n",
+    "\n",
+    "After the preparations above, we now have the necessary knowledge to have a taste on quantum machine learning (QML). QML uses quantum circuits to replace classical neural networks to complete machine learning tasks. So we need to prepare a parameterized quantum circuit (PQC), which is also called Quantum neural network (QNN) or Ansatz. The quantum circuit parameters are adjustable (usually these parameters are the angles $\\theta$ of rotation gates). As we have seen in the last section, using angle $\\pi$ to create a $X$ gate is probably the simplest QNN. If we design an appropriate loss function, then certain computational tasks can be transformed into optimization problems. Keep adjusting the parameters in PQC until the loss function convergences. "
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Example: How to create a quantum neural network?\n",
+    "\n",
+    "QNN can usually be expressed as a combination of single-qubit gates and two-qubit gates. One of the widely used circuit architectures is the hardware-efficient ansatz consists of $\\{R_x, R_y, R_z, \\text{CNOT}_{j,j+1} \\}$. They are easy to implement on near-term devices (usually superconducting qubits) because $\\text{CNOT}_{j,j+1} $ only works on adjacent qubits and hence mitigate the topological connectivity issues. The figure below gives us a concrete example:\n",
+    "\n",
+    "![intro-fig-gate1](./figures/intro-fig-gate1.png)\n",
+    "\n",
+    "Each horizontal line here represents a qubit. We define the upper qubit to be the first qubit $q_0$; the lower one is the second qubit $q_1$. From left to right, it represents the order that we apply quantum gates. The leftmost quantum gate will be applied first. Next, let’s take a look on how to build this simple two-qubit quantum neural network on Paddle Quantum."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:58:40.113133Z",
+     "start_time": "2021-01-09T12:58:40.081753Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The matrix representation of the quantum neural network U(theta=pi) in the figure is:\n",
+      "[[ 0.0000000e+00 -1.0000000e+00  6.1232340e-17 -6.1232340e-17]\n",
+      " [-1.0000000e+00  0.0000000e+00 -6.1232340e-17  6.1232340e-17]\n",
+      " [-6.1232340e-17  6.1232340e-17  1.0000000e+00  1.2246468e-16]\n",
+      " [ 6.1232340e-17 -6.1232340e-17 -1.2246468e-16  1.0000000e+00]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "import numpy as np\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "\n",
+    "# Set the angle parameter theta\n",
+    "theta = np.full([4], np.pi)\n",
+    "\n",
+    "# Start Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # We need to convert numpy.ndarray to variable supported in Paddle dynamic graph mode\n",
+    "    theta = fluid.dygraph.to_variable(theta)\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    num_qubits = 2\n",
+    "    cir = UAnsatz(num_qubits)\n",
+    "    \n",
+    "    # Add single-qubit rotation gates\n",
+    "    cir.ry(theta[0], 0)\n",
+    "    cir.ry(theta[1], 1)\n",
+    "\n",
+    "    # Add two-qubit gate\n",
+    "    cir.cnot([0, 1])\n",
+    "\n",
+    "    # Add single-qubit rotation gates\n",
+    "    cir.ry(theta[2], 0)\n",
+    "    cir.ry(theta[3], 1)\n",
+    "    \n",
+    "    print('The matrix representation of the quantum neural network U(theta=pi) in the figure is:')\n",
+    "    print(cir.U.numpy().real)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "$$\n",
+    "\\text{output} = \n",
+    "\\begin{bmatrix} \n",
+    "0  &-1 &0 &0 \\\\ \n",
+    "-1 &0  &0 &0 \\\\\n",
+    "0  &0  &1 &0 \\\\\n",
+    "0  &0  &0 &1 \n",
+    "\\end{bmatrix}.\n",
+    "\\tag{19}\n",
+    "$$\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Exercise\n",
+    "\n",
+    "Given the following code, can you work out the corresponding circuit?"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": null,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "theta = np.full([6], np.pi)\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    theta = fluid.dygraph.to_variable(theta)\n",
+    "    \n",
+    "    num_qubits = 3\n",
+    "    cir = UAnsatz(num_qubits)\n",
+    "    \n",
+    "    cir.ry(theta[0], 0)\n",
+    "    cir.ry(theta[1], 1)\n",
+    "    cir.ry(theta[2], 2)\n",
+    "    \n",
+    "    cir.cnot([0, 1])\n",
+    "    cir.cnot([1, 2])\n",
+    "\n",
+    "    cir.ry(theta[3], 0)\n",
+    "    cir.ry(theta[4], 1)\n",
+    "    cir.ry(theta[5], 2)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Answer:\n",
+    "\n",
+    "![intro-fig-gate2](./figures/intro-fig-gate2.png)\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Built-in circuit templates\n",
+    "\n",
+    "In the latest version of Paddle Quantum, we provide some built-in circuit templates to make users' life easier."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:59:37.481620Z",
+     "start_time": "2021-01-09T12:59:37.040582Z"
+    },
+    "scrolled": true
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEPCAYAAABY9lNGAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZJElEQVR4nO3df5xddX3n8debn6JYfhmpkmhoidpQlGpEH+3WqijCY9VgBQ26FVwsdpVteai1cWtRqbuVVsW64tZ0URFXA0v9kS1RdEXrrhUkID8aIBL5GdQafiqyiJHP/nFOyM2dMzN3hty5l+T1fDzmMfee7zkz75k/5j3nfM+PVBWSJPXbadQBJEnjyYKQJHWyICRJnSwISVInC0KS1GmXUQfYVh73uMfVwoULRx1Dkh5RLrvsstural7X2HZTEAsXLmTNmjWjjiFJjyhJbp5szENMkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE7bzZXUD9fC5ReM7Hvf9L5/O+W42bqZbXbMNjuP5Gyz5R6EJKmTBSFJ6mRBSJI6WRCSpE5DLYgkRyZZl2R9kuUd489LcnmSTUmO6Vl+aJJvJ1mb5Kokrx5mTknSREMriCQ7A2cCRwGLgeOSLO5b7RbgBOAzfcvvA15XVQcDRwIfSrL3sLJKkiYa5mmuhwHrq+oGgCQrgaXANZtXqKqb2rEHezesqu/1vP5Bkh8D84C7h5hXktRjmIeYDgBu7Xm/oV02I0kOA3YDvt8xdlKSNUnWbNy4cdZBJUkTjfUkdZInAOcAr6+qB/vHq2pFVS2pqiXz5nU+UlWSNEvDLIjbgAU97+e3ywaS5FeAC4A/r6qLt3E2SdI0hlkQlwKLkhyYZDdgGbBqkA3b9T8PfKqqzh9iRknSJIZWEFW1CTgZuBC4FjivqtYmOS3JywGSPDvJBuBY4GNJ1rabvwp4HnBCkivaj0OHlVWSNNFQb9ZXVauB1X3LTu15fSnNoaf+7T4NfHqY2SRJUxvrSWpJ0uhYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jH+vCSXJ9mU5Ji+seOTXN9+HD/MnJKkiYZWEEl2Bs4EjgIWA8clWdy32i3ACcBn+rbdF3gX8BzgMOBdSfYZVlZJ0kTD3IM4DFhfVTdU1QPASmBp7wpVdVNVXQU82LftS4CvVtWdVXUX8FXgyCFmlST1GWZBHADc2vN+Q7tsm22b5KQka5Ks2bhx46yDSpImekRPUlfViqpaUlVL5s2bN+o4krRdGWZB3AYs6Hk/v1027G0lSdvAMAviUmBRkgOT7AYsA1YNuO2FwBFJ9mknp49ol0mS5sjQCqKqNgEn0/xhvxY4r6rWJjktycsBkjw7yQbgWOBjSda2294J/CVNyVwKnNYukyTNkV2G+cWrajWwum/ZqT2vL6U5fNS17ceBjw8znyRpco/oSWpJ0vBYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqdNABZHkd5I8pn3975J8MMmThxtNkjRKg+5B/DfgviTPAN4KfB/41HQbJTkyybok65Ms7xjfPcm57fglSRa2y3dNcnaSq5Ncm+Qdg/9IkqRtYdCC2FRVBSwFPlJVZwKPnWqDJDsDZwJHAYuB45Is7lvtROCuqjoIOAM4vV1+LLB7VR0CPAt44+bykCTNjUEL4qftf/F/AFyQZCdg12m2OQxYX1U3VNUDwEqagum1FDi7fX0+cHiSAAU8JskuwB7AA8BPBswqSdoGBi2IVwM/B/59Vf0ImA/8zTTbHADc2vN+Q7usc52q2gTcA+xHUxY/A34I3AK8v6ru7P8GSU5KsibJmo0bNw74o0iSBjFQQbSl8A/A7u2i24HPDysUzd7HL4EnAgcCb03yax25VlTVkqpaMm/evCHGkaQdz6BnMf0hzX/1H2sXHQB8YZrNbgMW9Lyf3y7rXKc9nLQXcAfwGuDLVfWLqvox8C1gySBZJUnbxqCHmN4M/A7tPEBVXQ88fpptLgUWJTkwyW7AMmBV3zqrgOPb18cAF7WT4bcALwRoT699LnDdgFklSdvAoAXx83aiGXjov/2aaoN2TuFk4ELgWuC8qlqb5LQkL29XOwvYL8l64C3A5lNhzwT2TLKWpmg+UVVXDfpDSZIevl0GXO+fkvwnYI8kLwbeBPyv6TaqqtXA6r5lp/a8vp/mlNb+7e7tWi5JmjuD7kEsBzYCVwNvpPmj/85hhZIkjd5AexBV9SDw9+2HJGkHMGVBJDmvql6V5Go65hyq6ulDSyZJGqnp9iD+pP380mEHkSSNlynnIKrqh+3LN1XVzb0fNBPVkqTt1KCT1C/uWHbUtgwiSRov081B/AeaPYVfS9J7HcJjaa5uliRtp6abg/gM8CXgr9hyERvAT7tunidJ2n5MVxBVVTcleXP/QJJ9LQlJ2n4NsgfxUuAymtNc0zNWwIQ7rEqStg9TFkRVvbT9fODcxJEkjYvpJqmfOdV4VV2+beNIksbFdIeYPjDFWNHekluStP2Z7hDTC+YqiCRpvEx3iOmFVXVRkt/vGq+qzw0nliRp1KY7xPR7wEXAyzrGCrAgJGk7Nd0hpne1n18/N3EkSeNioHsxJdkvyYeTXJ7ksiR/m2S/YYeTJI3OoDfrW0nzRLlXAse0r88dVihJ0ugN+kzqJ1TVX/a8f2+SVw8jkCRpPAy6B/GVJMuS7NR+vAq4cJjBJEmjNd1prj9lyz2YTgE+3Q7tBNwLvG2Y4SRJozPdWUyPnasgkqTxMugcBEn2ARYBj9q8rKq+OYxQkqTRG/Q01zcA36SZd3hP+/ndA2x3ZJJ1SdYnWd4xvnuSc9vxS5Is7Bl7epJvJ1mb5Ookj+rfXpI0PINOUv8J8Gzg5vb+TL8F3D3VBkl2Bs6keXb1YuC4JIv7VjsRuKuqDgLOAE5vt92FZr7jj6rqYOD5wC8GzCpJ2gYGLYj7q+p+aP7rr6rrgKdOs81hwPqquqGqHqC5lmJp3zpLgbPb1+cDhycJcARwVVVdCVBVd1TVLwfMKknaBgYtiA1J9ga+AHw1yReBm6fZ5gDg1t6v0S7rXKeqNgH3APsBTwEqyYXt1dtv7/oGSU5KsibJmo0bNw74o0iSBjHQJHVVvaJ9+e4kXwf2Ar48tFRNrn9Dc1jrPuBrSS6rqq/15VoBrABYsmRJDTGPJO1wBt2DIMkzk/wx8HRgQ3vYaCq3AQt63s9vl3Wu08477AXcQbO38c2qur2q7gNWA1M+3U6StG0NehbTqTRzBfsBjwM+keSd02x2KbAoyYFJdgOWAav61lkFHN++Pga4qKqK5iypQ5I8ui2O3wOuGSSrJGnbGPQ6iNcCz+iZqH4fcAXw3sk2qKpNSU6m+WO/M/Dxqlqb5DRgTVWtAs4CzkmyHriTpkSoqruSfJCmZApYXVUXzOYHlCTNzqAF8QOaC+Tub9/vzsTDRRNU1Wqaw0O9y07teX0/cOwk236aLbf2kCTNsenuxfRfaf6DvwdYm+Sr7fsXA98ZfjxJ0qhMtwexpv18GfD5nuXfGEoaSdLYmO5mfZsvYqOdaH5K+3ZdVXllsyRtxwaag0jyfJqzmG6iufX3giTHe7M+Sdp+DTpJ/QHgiKpaB5DkKcBngWcNK5gkabQGvVBu183lAFBV3wN2HU4kSdI4GHQP4rIk/50tp52+li0T2JKk7dCgBfFHwJuBP27f/x/go0NJJEkaC9MWRPtchyur6mnAB4cfSZI0Dqadg2ifw7AuyZPmII8kaUwMeohpH5orqb8D/Gzzwqp6+VBSSZJGbtCC+IuhppAkjZ3p7sX0KJoJ6oOAq4Gz2ie/SZK2c9PNQZwNLKEph6NoLpiTJO0ApjvEtLiqDgFIchbewVWSdhjT7UE8dEM+Dy1J0o5luj2IZyT5Sfs6wB7t+wBVVb8y1HSSpJGZ7nbfO89VEEnSeBn0Zn2SpB2MBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSeo01IJIcmSSdUnWJ1neMb57knPb8UuSLOwbf1KSe5O8bZg5JUkTDa0g2gcNnUlzD6fFwHFJFvetdiJwV1UdBJwBnN43/kHgS8PKKEma3DD3IA4D1lfVDVX1ALASWNq3zlKaGwICnA8cniQASY4GbgTWDjGjJGkSwyyIA4Bbe95vaJd1rtPe6+keYL8kewJ/Brxnqm+Q5KQka5Ks2bhx4zYLLkka30nqdwNnVNW9U61UVSuqaklVLZk3b97cJJOkHcSgT5SbjduABT3v57fLutbZkGQXYC/gDuA5wDFJ/hrYG3gwyf1V9ZEh5pUk9RhmQVwKLEpyIE0RLANe07fOKuB44NvAMcBFVVXA725eIcm7gXstB0maW0MriKralORk4EJgZ+DjVbU2yWnAmqpaBZwFnJNkPXAnTYlIksbAMPcgqKrVwOq+Zaf2vL4fOHaar/HuoYSTJE1pXCepJUkjZkFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jG+e5Jz2/FLkixsl784yWVJrm4/v3CYOSVJEw2tIJLsDJwJHAUsBo5LsrhvtROBu6rqIOAM4PR2+e3Ay6rqEOB44Jxh5ZQkdRvmHsRhwPqquqGqHgBWAkv71lkKnN2+Ph84PEmq6rtV9YN2+VpgjyS7DzGrJKnPMAviAODWnvcb2mWd61TVJuAeYL++dV4JXF5VP+//BklOSrImyZqNGzdus+CSpDGfpE5yMM1hpzd2jVfViqpaUlVL5s2bN7fhJGk7N8yCuA1Y0PN+frusc50kuwB7AXe07+cDnwdeV1XfH2JOSVKHYRbEpcCiJAcm2Q1YBqzqW2cVzSQ0wDHARVVVSfYGLgCWV9W3hphRkjSJoRVEO6dwMnAhcC1wXlWtTXJakpe3q50F7JdkPfAWYPOpsCcDBwGnJrmi/Xj8sLJKkibaZZhfvKpWA6v7lp3a8/p+4NiO7d4LvHeY2SRJUxvrSWpJ0uhYEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKmTBSFJ6mRBSJI6WRCSpE4WhCSpkwUhSepkQUiSOlkQkqROFoQkqZMFIUnqNNSCSHJkknVJ1idZ3jG+e5Jz2/FLkizsGXtHu3xdkpcMM6ckaaKhFUSSnYEzgaOAxcBxSRb3rXYicFdVHQScAZzebrsYWAYcDBwJfLT9epKkOTLMPYjDgPVVdUNVPQCsBJb2rbMUOLt9fT5weJK0y1dW1c+r6kZgffv1JElzZJchfu0DgFt73m8AnjPZOlW1Kck9wH7t8ov7tj2g/xskOQk4qX17b5J12yb6jD0OuH22G+f0bZhkIrPNjtlmx2yzM8psT55sYJgFMXRVtQJYMeocSdZU1ZJR5+hittkx2+yYbXbGNdswDzHdBizoeT+/Xda5TpJdgL2AOwbcVpI0RMMsiEuBRUkOTLIbzaTzqr51VgHHt6+PAS6qqmqXL2vPcjoQWAR8Z4hZJUl9hnaIqZ1TOBm4ENgZ+HhVrU1yGrCmqlYBZwHnJFkP3ElTIrTrnQdcA2wC3lxVvxxW1m1g5Ie5pmC22THb7JhtdsYyW5p/2CVJ2ppXUkuSOlkQkqROFoQkqZMF8TAk2TfJvqPOIUnDYEHMUJInJVmZZCNwCfCdJD9uly0ccbyxl2T/JM9sP/YfdZ7pJNlz1BmkUfEsphlK8m3gQ8D5m0+9bW8keCxwSlU9d4TxJpXk6qo6ZITf/1Dg72guhtx80eN84G7gTVV1+WiSTS3JLVX1pDHIsT9bbjdzW1X96yjzDCLJnlV174gzhOY+bg/97oDv1Bj/4UvytKq6btQ5wIKYsSTXV9WimY7NhSS/P9kQ8HdVNW8u82wVILkCeGNVXdK3/LnAx6rqGSMJ1mR4y2RDwJ9X1cgOIz5SixVGX65JjgA+ClzP1r+7g2h+d18ZVbapjPr31usRfS+mEbksyUdp7kK7+WaEC2iuCP/uyFI1zgX+B9DV+o+a4yz9HtNfDgBVdXGSx4wiUI//AvwNzUWZ/UZ9GPaTTF6snwBGVqxtjqnKddSH5/4WeFFV3dS7sL07w2rgN0YRqs3w4cmGgL3nMMqULIiZex3Ncyzew9a7rZuvDB+lq4D3V9W/9A8kedEI8vT6UpILgE+xdbG+DvjyyFI1Lge+UFWX9Q8kecMI8vQa52KF8S7XXWjuBN3vNmDXOc7S7/XAW4Gfd4wdN8dZJuUhpu1Ikt8Fbq6qWzrGllTVmhHE6s1wFM2zPrYq1qpaPbpUkOSpwB1VNeF2y0n2H+Xx/vY/zV+nu1hvrKqTR5UNIMk/A/9xknK9taoWdGw2J5K8A3gVzbNoen93y4DzquqvRpjtIuCdVfXPHWM3VtWBI4g1gQUxQ+1dZ08EjmbrP3RfBM6qql+MKJq2U+NarPBQud5ZVRs7xkZarm2G36D7d3fN6FI1p8gD91fVfaPMMR0LYoaSfJZmgvBstuy+zqeZg9i3ql49omi95fUK4Int4rEvryQrquqk6dece+OcTRo2C2KGknyvqp4y07G5MOblNdmZQAGurKr5c5lnqwDjnW0v4B00/wXvT3MCwo9pSv99VXX3qLLBVvmOBh7PmOWbTJIvVdVRo87RZZyyOUk9c3cmORb4h6p6ECDJTjTXQdw10mTwrI6C2gBcnOR7owjUYyNwM80f3c2qff/4kSTaYpyznQdcBLygqn4EkORXgRPasSNGFw3Yku/5ffmOZ8T5kjxzsiHg0DmMMjHAGGfr5R7EDLVXS58OvIDmv3VoTkv7OrC8qm4cSTAgycXAB+gur7dUVf8zwecy2/XA4ZNMoI96MnOcs62rqqfOdGyujHO+JL8E/omti3+z51bVHnMc6SHjnK2XexAzVFU3JXk3zTUPW01Sj7IcWstoyuvMJHe3y/amKa9lI8q02YeAfYAJf4SBv57bKBN8iPHNdnOStwNnb57wba+qPoEtZ+aM0jjnu5bmGpLr+weSmG0A7kHMUJI/o/lju5Ktr85cBqysqveNKhtMetbGF6vq2tGlaiR5Gt1nlJhtEkn2AZbTZNt8uOtfaa67eV9VjfSw5jjnS3IMcHVVresYO7qqvjD3qR76/mObrZcFMUPtsfyD+88Iap+7vXbEt9oY2/Jq/8t8TZutdwLdbLOU5PVV9YlR55jMOOcz22AsiBlKch3wkqq6uW/5k4GvjPiY6ziXl9m2sXG6Z0+Xcc5ntsE4BzFzpwBfayc2Nx8rfBLNDcBGelUr8CDN9Q839y1/Qjs2SmabhSRXTTZEc9rrSI1zPrM9fBbEDFXVl5M8hYm3EL508+2/R+gUxre8TsFss7E/8BImnkIdYMJtGkZgnPOZ7WGyIGahPYX04lHn6DfO5WW2WftHYM+quqJ/IMk35jzNROOcz2wPk3MQkqROo74dryRpTFkQkqROFoR2WEnmJ/likuuT3JDkI0l2H2C7zucsJzlt84OZkpyS5NGTrPfSJN9NcmWSa5K8sV1+dJLFA3z/gdaTHi4LQjukJAE+R/MkuUXAImAPHsatNarq1Kr63+3bU4AJBZFkV2AF8LL2Ody/BXyjHT4aGOQP/6DrSQ+Lk9TaISU5HHhXVT2vZ9mv0FwLsQA4Bliy+YltSf6R5nGu32j3IP6e5k6lPwKWVdXGJJ+kOTvlicD7gXXA7VX1gp7vsS9wHfDkqvp/Pct/u932nvbjlcALgZOA3YD1wB/Q3Omzfz2AM4F5wH3AH1bVddvkF6UdmnsQ2lEdDGz1mMyq+glwE831D1N5DLCmqg6muSPnu/q+zoeBH9DcovsFfWN30tyn6OYkn03y2iQ7tY+eXAX8aVUdWlXfBz5XVc9u9zSuBU6cZL0VNI/9fBbwNuCjM/5tSB28DkKauQeBc9vXn6Y5VDWwqnpDkkOAF9H8QX8xzd1P+/1mkvfS3JF3T+DC/hWS7An8NvA/m6NmAEw7jyINwoLQjuoamsNID2kPMf0qzaGh32TrPexHTfG1ZnyctqquBq5Ocg5wI90F8Ung6Kq6MskJwPM71tkJuLuqDp1pBmk6HmLSjuprwKOTvA4gyc40D1v6SDs3cBNwaJKdkiygucp6s53YUi6vAf5vx9f/KfDY/oVJ9kzy/J5Fh7LlHlD92zwW+GE7sf3arq/dHha7sX3KIWk8Y6ofXBqUBaEdUjVnZ7wCOKa9B9MdwINV9Z/bVb5F85/9NcCHgct7Nv8ZcFiSf6GZSD6t41usAL6c5Ot9ywO8Pcm6JFcA72HL3sNK4E/bU2B/HfgL4JI2S++kc/96rwVOTHIlsJbm2QzSw+ZZTBIPnUX0WeAVVXX5dOtLOwILQpLUyUNMkqROFoQkqZMFIUnqZEFIkjpZEJKkThaEJKnT/weRuZs3hsDuNQAAAABJRU5ErkJggg==\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "N = 3 # Set the number of qubits\n",
+    "\n",
+    "# Start PaddlePaddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Apply Hadamard gate on each qubit\n",
+    "    cir.superposition_layer()\n",
+    "   \n",
+    "    # Prepare output state\n",
+    "    # If the user does not enter the initial quantum state, the default initial is |00..0>\n",
+    "    final_state = cir.run_state_vector()\n",
+    "    \n",
+    "    # Get the theoretical value of the probability distribution, set shots = 0\n",
+    "    cir.measure(shots = 0, plot = True)"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T12:59:50.443828Z",
+     "start_time": "2021-01-09T12:59:50.101308Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEPCAYAAABP1MOPAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAXIklEQVR4nO3dfbRddX3n8feHIGqF1gcitSQYqkGLT6gRXXWmRQsWlhawooZaFUfFjjKVZbUNU0VLnSlqdaxjbI31gbajEa3VtETR8aGd2kETEMUEIxGChNYaeVBbRzHynT/ODpycnHvvySX77Jvs92utu3L2/u1zzyf3j/u5e//2Q6oKSVJ/HdR1AElStywCSeo5i0CSes4ikKSeswgkqecO7jrA3jr88MNr2bJlXceQpP3K5Zdf/p2qWjxubL8rgmXLlrFx48auY0jSfiXJ9TONeWhIknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSem6/u7L4rli26pJOP3/bhU/t9PMlaRz3CCSp5ywCSeo5i0CSeq7VIkhycpItSbYmWTXDNs9KsjnJpiTvbzOPJGlPrU0WJ1kErAZOArYDG5Ksq6rNQ9ssB84DnlhVtyS5f1t5JEnjtblHcDywtaqurarbgLXAaSPbvBhYXVW3AFTVt1vMI0kao80iOBK4YWh5e7Nu2DHAMUk+n+SyJCeP+0ZJzk6yMcnGHTt2tBRXkvqp68nig4HlwAnAmcC7ktx7dKOqWlNVK6pqxeLFY5+0JkmapzaL4EZg6dDykmbdsO3Auqr6cVVdB3ydQTFIkqakzSLYACxPcnSSQ4CVwLqRbT7KYG+AJIczOFR0bYuZJEkjWiuCqtoJnANcClwNXFxVm5JckOTUZrNLgZuSbAY+C7yqqm5qK5MkaU+t3muoqtYD60fWnT/0uoBXNF+SpA50PVksSeqYRSBJPWcRSFLPWQSS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9ZxFIEk9ZxFIUs9ZBJLUcxaBJPWcRSBJPWcRSFLPWQSS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9ZxFIEk9ZxFIUs9ZBJLUc60WQZKTk2xJsjXJqjHjZyXZkeTK5utFbeaRJO3p4La+cZJFwGrgJGA7sCHJuqraPLLpB6vqnLZySJJm1+YewfHA1qq6tqpuA9YCp7X4eZKkeWizCI4Ebhha3t6sG/WMJF9J8uEkS8d9oyRnJ9mYZOOOHTvayCpJvdX1ZPHfAsuq6pHAp4CLxm1UVWuqakVVrVi8ePFUA0rSga7NIrgRGP4Lf0mz7g5VdVNV/ahZ/HPgsS3mkSSN0WYRbACWJzk6ySHASmDd8AZJHjC0eCpwdYt5JEljtHbWUFXtTHIOcCmwCHhPVW1KcgGwsarWAb+d5FRgJ3AzcFZbeSRJ47VWBABVtR5YP7Lu/KHX5wHntZlBkjS7rieLJUkdswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSem6iIkjyxCT3al7/ZpK3JHngBO87OcmWJFuTrJplu2ckqSQrJo8uSdoXJt0j+FPgB0keBfwO8A3gL2Z7Q5JFwGrgFOBY4Mwkx47Z7jDg5cAX9iK3JGkfmbQIdlZVAacBb6+q1cBhc7zneGBrVV1bVbcBa5v3j/pD4A3ADyfMIknahyYtgu8nOQ94LnBJkoOAu83xniOBG4aWtzfr7pDkMcDSqrpktm+U5OwkG5Ns3LFjx4SRJUmTmLQIng38CPhPVfUtYAnwprvywU2ZvIXBoaZZVdWaqlpRVSsWL158Vz5WkjRioiJofvn/NXD3ZtV3gL+Z4203AkuHlpc063Y5DHg48Lkk24AnAOucMJak6Zr0rKEXAx8G3tmsOhL46Bxv2wAsT3J0kkOAlcC6XYNV9d2qOryqllXVMuAy4NSq2rh3/wVJ0l0x6aGhlwFPBL4HUFXXAPef7Q1VtRM4B7gUuBq4uKo2JbkgyanzjyxJ2pcOnnC7H1XVbUkASHIwUHO9qarWA+tH1p0/w7YnTJhFkrQPTbpH8PdJ/itwzyQnAR8C/ra9WJKkaZm0CFYBO4CrgJcw+Cv/1W2FkiRNz0SHhqrqduBdzZck6QAyaxEkubiqnpXkKsbMCVTVI1tLJkmairn2CF7e/Pu0toNIkrox6xxBVf1L8/KlVXX98Bfw0vbjSZLaNulk8Ulj1p2yL4NIkrox1xzBf2bwl//PJ/nK0NBhwOfbDCZJmo655gjeD3wc+CMGp5Du8v2qurm1VJKkqZmrCKqqtiV52ehAkvtaBpK0/5tkj+BpwOUMTh/N0FgBP99SLknSlMxaBFX1tObfo6cTR5I0bXNNFj9mtvGqumLfxpEkTdtch4bePMtYAU/eh1kkSR2Y69DQk6YVRJLUjbkODT25qj6T5NfHjVfVR9qJJUmalrkODf0y8Bng18aMFWARSNJ+bq5DQ69t/n3BdOJIkqZt0ofX3y/J25JckeTyJH+S5H5th5MktW/Sm86tZfCEsmcAZzSvP9hWKEnS9Ez68PoHVNUfDi2/Psmz2wgkSZquSfcIPplkZZKDmq9nAZe2GUySNB1znT76fe68x9C5wF81QwcB/wa8ss1wkqT2zXXW0GHTCiJJ6sakcwQkuQ+wHLjHrnVV9Q9thJIkTc+kp4++CPgHBvMCf9D8+7oJ3ndyki1JtiZZNWb8t5JcleTKJP+Y5Ni9iy9JuqsmnSx+OfA44Prm/kOPBm6d7Q1JFgGrGTzb+FjgzDG/6N9fVY+oquOANwJvmTy6JGlfmLQIflhVPwRIcveq+hrwkDneczywtaqurarbGFyLcNrwBlX1vaHFezGYmJYkTdGkcwTbk9wb+CjwqSS3ANfP8Z4jgRuGvwfw+NGNmsdgvgI4hBlua53kbOBsgKOOOmrCyJKkSUy0R1BVT6+qW6vqdcBrgHcDp++LAFW1uqoeBPwe8OoZtllTVSuqasXixYv3xcdKkhp7c9bQY4D/wODwzeebwz2zuRFYOrS8pFk3k7XAn06aR5K0b0x61tD5wEXA/YDDgfcmGfvX+5ANwPIkRyc5BFgJrBv5vsuHFp8KXDNpcEnSvjHpHsFzgEcNTRhfCFwJvH6mN1TVziTnMDjVdBHwnqralOQCYGNVrQPOSXIi8GPgFuD58/6fSJLmZdIi+GcGF5L9sFm+O7Mf5gGgqtYD60fWnT/0+uUTfr4kqSVz3WvofzKYE/gusCnJp5rlk4Avth9PktS2ufYINjb/Xg78zdD6z7WSRpI0dXPddO6iXa+bCd9jmsUtVfXjNoNJkqZjojmCJCcwOGtoG4NbUi9N8nxvOidJ+79JJ4vfDDylqrYAJDkG+ADw2LaCSZKmY9J7Dd1tVwkAVNXXgbu1E0mSNE2T7hFcnuTPufMJZc/hzolkSdJ+bNIi+C3gZcBvN8v/B3hHK4kkSVM1ZxE0zxX4clU9FJ8XIEkHnDnnCKrqJ8CWJN7/WZIOQJMeGroPgyuLvwj8+66VVXVqK6kkSVMzaRG8ptUUkqTOzHWvoXswmCh+MHAV8O6q2jmNYJKk6ZhrjuAiYAWDEjiFwYVlkqQDyFyHho6tqkcAJHk33nFUkg44c+0R3HFjOQ8JSdKBaa49gkcl+V7zOsA9m+UAVVU/3Wo6SVLr5roN9aJpBZEkdWPSm85Jkg5QFoEk9ZxFIEk9ZxFIUs9ZBJLUcxaBJPVcq0WQ5OQkW5JsTbJqzPgrkmxO8pUkn07ywDbzSJL21FoRNA+0Wc3gHkXHAmcmOXZksy8BK6rqkcCHgTe2lUeSNF6bewTHA1ur6tqqug1YC5w2vEFVfbaqftAsXgYsaTGPJGmMNovgSOCGoeXtzbqZvBD4+LiBJGcn2Zhk444dO/ZhREnSgpgsTvKbDG53/aZx41W1pqpWVNWKxYsXTzecJB3gJn1C2XzcCCwdWl7SrNtNkhOB3wd+uap+1GIeSdIYbe4RbACWJzk6ySHASmDd8AZJHg28Ezi1qr7dYhZJ0gxaK4Lm+QXnAJcCVwMXV9WmJBck2fXQ+zcBhwIfSnJlknUzfDtJUkvaPDREVa0H1o+sO3/o9Yltfr4kaW4LYrJYktQdi0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp51otgiQnJ9mSZGuSVWPGfynJFUl2JjmjzSySpPEObusbJ1kErAZOArYDG5Ksq6rNQ5t9EzgLeGVbOfYXy1Zd0unnb7vwqTOOLeRsC5k/N+0vWisC4Hhga1VdC5BkLXAacEcRVNW2Zuz2FnNIkmbR5qGhI4Ebhpa3N+v2WpKzk2xMsnHHjh37JJwkaWC/mCyuqjVVtaKqVixevLjrOJJ0QGmzCG4Elg4tL2nWSZIWkDaLYAOwPMnRSQ4BVgLrWvw8SdI8tFYEVbUTOAe4FLgauLiqNiW5IMmpAEkel2Q78EzgnUk2tZVHkjRem2cNUVXrgfUj684fer2BwSEjSVJH9ovJYklSeywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6jmLQJJ6ziKQpJ6zCCSp5ywCSeo5i0CSes4ikKSeswgkqecsAknqOYtAknrOIpCknrMIJKnnLAJJ6rmDuw4g3RXLVl3S6edvu/CpnX7+fC3kn9tCznagco9AknrOIpCknmu1CJKcnGRLkq1JVo0Zv3uSDzbjX0iyrM08kqQ9tVYESRYBq4FTgGOBM5McO7LZC4FbqurBwP8A3tBWHknSeG1OFh8PbK2qawGSrAVOAzYPbXMa8Lrm9YeBtydJVVWLuSRpXg7Uiey09Ts3yRnAyVX1omb5ucDjq+qcoW2+2myzvVn+RrPNd0a+19nA2c3iQ4AtrYSe2+HAd+bcqhtmmx+zzY/Z5qfLbA+sqsXjBvaL00erag2wpuscSTZW1Yquc4xjtvkx2/yYbX4WarY2J4tvBJYOLS9p1o3dJsnBwM8AN7WYSZI0os0i2AAsT3J0kkOAlcC6kW3WAc9vXp8BfMb5AUmartYODVXVziTnAJcCi4D3VNWmJBcAG6tqHfBu4C+TbAVuZlAWC1nnh6dmYbb5Mdv8mG1+FmS21iaLJUn7B68slqSeswgkqecsAknqOYtgAknum+S+XeeQpDZYBDNIclSStUl2AF8Avpjk2826ZR3HW/CSHJHkMc3XEV3nmUuSQ7vOIHXFs4ZmkOT/Am8FPlxVP2nWLQKeCZxbVU/oMN6MklxVVY/o8POPA/6MwcWBuy4gXALcCry0qq7oJtnsknyzqo5aADmOAI5sFm+sqn/tMs9ckhxaVf/WcYYwuLfZHT834IsL+ZqkJA+tqq91nWMXi2AGSa6pquV7OzYNSX59piHgz2a6n8g0JLkSeElVfWFk/ROAd1bVozoJNsjwipmGgN+vqs4O/1mg8/78pwDvAK5h95/bgxn83D7ZVbbZdP1zG7Vf3GuoI5cneQdwEXBDs24pgyuhv9RZqoEPAv8LGNfi95hyllH3Gi0BgKq6LMm9ugg05L8DbwJ2jhnr+jDp+5i5QN8LLNQC7fqQ2p8AJ1bVtuGVSY4G1gO/0EWoJsPbZhoC7j3FKHOyCGb2PAbPS/gDdt/l3HVFdJe+AvxxVX11dCDJiR3kGfbxJJcAf8HuBfo84BOdpRq4AvhoVV0+OpDkRR3kGWaBzs/BwPYx628E7jblLKNeAPwO8KMxY2dOOcusPDS0H0ryH4Hrq+qbY8ZWVNXGDmINZziFwbMmdivQqlrfXSpI8hDgptHbnDdjR3R5PL756/FBjC/Q64Zv395Btn8C/ssMBXpDVS0d87apSHIe8CxgLbv/3FYCF1fVH3WY7TPAq6vqn8aMXVdVR3cQayyLYAbN3VBfCJzO7r/QPga8u6p+3FE0HaAWeIHeXFU7xox1WqBNhl9g/M9t88zval9zyvkPq+oHXeaYhEUwgyQfYDBRdxF37nouYTBHcN+qenZH0YZL6unAzzWrF3xJJVlTVWfPveX0LeRsUtssghkk+XpVHbO3Y9OwwEtqpjNvAny5qpZMM89uARZ2tp8BzmPwl+0RDE4E+DaDcr+wqm5dANlOB+6/kLLNJsnHq+qUrnOMs9CyOVk8s5uTPBP466q6HSDJQQyuI7il02Tw2DFFtB24LMnXuwg0ZAdwPYNfrrtUs3z/ThLdaSFnuxj4DPCkqvoWQJKfBc5qxp7SXbQ7sp0wku35XWdL8piZhoDjphhlzwALONso9whm0Fw9/AbgSQz++obBKV+fBVZV1XWdBAOSXAa8mfEl9YqqenyH2a4BfmWGieyuJxYXcrYtVfWQvR2bhgWe7SfA37N7ue/yhKq655Qj3WEhZxvlHsEMqmpbktcxuGZgt8niLkugsZJBSa1Ocmuz7t4MSqrrh/u8FbgPsMcvW+CN042yh7eycLNdn+R3gYt2Tb42VxmfxZ1nw3RlIWe7msH1F9eMDiQx24TcI5hBkt9j8Et1LbtfsbgSWFtVF3aVDWY8U+JjVXV1d6kGkjyU8WdxmG0GSe4DrGKQbddhqn9lcN3KhVXV2eHIBZ7tDOCqqtoyZuz0qvro9FPd8fkLNtsoi2AGzbH2h42egdM8f3lTx7eYWLAl1fzl+BtNtuGJbLPNU5IXVNV7u84xjtnmZ6FlswhmkORrwK9W1fUj6x8IfLLj46ILuaTMto8ttPvSDDPb/Cy0bM4RzOxc4NPNBOOu43lHMbiZVWdXeTZuZ3D9wPUj6x/QjHXJbPOQ5CszDTE4nbQzZpufhZxtlEUwg6r6RJJj2PP2tht23Za6Q+eycEvqXMw2H0cAv8qepyYH2OMWBVNmtvlZyNl2YxHMojk187Kuc4xayCVltnn7O+DQqrpydCDJ56aeZndmm5+FnG03zhFIUs91fQtZSVLHLAJJ6jmLQAe0JEuSfCzJNUmuTfL2JHef4H1jn8Ob5IJdD/9Jcm6Sn5phu6cl+VKSLyfZnOQlzfrTkxw7wedPtJ20L1gEOmAlCfARBk8lWw4sB+7JXbidRFWdX1X/u1k8F9ijCJLcDVgD/FrzjOZHA59rhk8HJvkFP+l20l3mZLEOWEl+BXhtVf3S0LqfZnAdwVLgDGDFrqd/Jfk7Bo8A/VyzR/AuBnfW/Bawsqp2JHkfg7NBfg74Y2AL8J2qetLQZ9wX+BrwwKr6f0Prf7F573ebr2cATwbOBg4BtgLPZXBnytHtAFYDi4EfAC+uqq/tkx+Ues89Ah3IHgbs9njFqvoesI3BtQOzuRewsaoexuAOkq8d+T5vA/6ZwW2jnzQydjOD+/Bcn+QDSZ6T5KDmkYXrgFdV1XFV9Q3gI1X1uGbP4WrghTNst4bB4yIfC7wSeMde/zSkGXgdgTTe7cAHm9d/xeAQ08Sq6kVJHgGcyOAX90kM7tY56uFJXs/g7rGHApeObpDkUOAXgQ8NjnYBMOc8hzQpi0AHss0MDv/coTk09LMMDuk8nN33iu8xy/fa62OoVXUVcFWSvwSuY3wRvA84vaq+nOQs4IQx2xwE3FpVx+1tBmkSHhrSgezTwE8leR5AkkUMHujz9ubY/TbguCQHJVnK4IrjXQ7izhL5DeAfx3z/7wOHja5McmiSE4ZWHced9zcafc9hwL80E8zPGfe9m8NZ1zVPzCMDj5rtPy7tDYtAB6wanAnxdOCM5v5CNwG3V9V/azb5PIO/1DcDbwOuGHr7vwPHJ/kqgwndC8Z8xBrgE0k+O7I+wO8m2ZLkSuAPuHNvYC3wqubU0gcBrwG+0GQZnvwd3e45wAuTfBnYxODZANI+4VlD6o3mrJ0PAE+vqivm2l7qC4tAknrOQ0OS1HMWgST1nEUgST1nEUhSz1kEktRzFoEk9dz/B9VMzjhMqx3WAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "N = 3 # Set the number of qubits\n",
+    "\n",
+    "# Start PaddlePaddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Apply Ry(pi/4) rotation gate on each qubit\n",
+    "    cir.weak_superposition_layer()\n",
+    "   \n",
+    "    # Prepare output state\n",
+    "    # If the user does not enter the initial quantum state, the default initial state is |00..0>\n",
+    "    final_state = cir.run_state_vector()\n",
+    "    \n",
+    "    # Get the theoretical value of the probability distribution, set shots = 0\n",
+    "    cir.measure(shots = 0, plot = True)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "The following figure depicts a handy circuit template `complex_entangled_layer(theta, DEPTH)` . Users can extend the circuit architecture by changing the circuit depth parameter `DEPTH`. Define generalized rotation gate $U_3$ as\n",
+    "\n",
+    "$$\n",
+    "U_3(\\theta, \\phi, \\varphi) :=\n",
+    "\\begin{bmatrix}\n",
+    "\\cos \\frac{\\theta}{2} & -e^{i \\varphi}\\sin \\frac{\\theta}{2} \\\\\n",
+    "e^{i \\phi}\\sin \\frac{\\theta}{2} &e^{i (\\phi+\\varphi)} \\cos \\frac{\\theta}{2}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{20}\n",
+    "$$\n",
+    "\n",
+    "The $U_3$ rotation gate is equivalent to the combination of three different rotation gates:\n",
+    "\n",
+    "$$\n",
+    "U_3(\\theta, \\phi, \\varphi) \n",
+    "= R_z(\\phi)*R_y(\\theta)*R_z(\\varphi)\n",
+    ":=\n",
+    "\\begin{bmatrix}\n",
+    "e^{-i\\frac{\\phi}{2}} & 0 \\\\ \n",
+    "0 & e^{i\\frac{\\phi}{2}}\n",
+    "\\end{bmatrix}\n",
+    "\\begin{bmatrix}\n",
+    "\\cos \\frac{\\theta}{2} &-\\sin \\frac{\\theta}{2} \\\\ \n",
+    "\\sin \\frac{\\theta}{2} &\\cos \\frac{\\theta}{2} \n",
+    "\\end{bmatrix}\n",
+    "\\begin{bmatrix}\n",
+    "e^{-i\\frac{\\varphi}{2}} & 0 \\\\ \n",
+    "0 & e^{i\\frac{\\varphi}{2}}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{21}\n",
+    "$$\n",
+    "\n",
+    "![intro-fig-complex_entangled_layer2](./figures/intro-fig-complex_entangled_layer2.png)\n",
+    "\n",
+    "When our task does not involve imaginary numbers, it is more efficient to use the circuit template `real_entangled_layer(theta, DEPTH)` ($R_y$ instead of $U_3$).\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:00:30.035538Z",
+     "start_time": "2021-01-09T13:00:29.585215Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAEPCAYAAABV6CMBAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAggUlEQVR4nO3dfZxdVX3v8c+XAIEKKA/R0iSQtIRakBpliNy2cn0Cw0uFWEGCkQdLjb1IKy9aa7gq1Ghvobbaco0PsTxaJSA+kFuC0SvibbVgJhgJAVOGECAR68izUsDA9/6x94STkzNn9pnMnnNgvu/X67xmn7X22ud3Aq/5zV5r7bVkm4iIiKp26nYAERHx3JLEERERHUniiIiIjiRxRERER5I4IiKiIzt3O4DxsN9++3nGjBndDiMi4jll9erVP7c9pbl8QiSOGTNm0N/f3+0wIiKeUyTd06o8XVUREdGRJI6IiOhIEkdERHQkiSMiIjqSxBERER1J4oiIiI4kcUREREeSOCIioiNJHBER0ZEJ8eR4ROy4GYuu69pnb7zgTV377Nhe7jgiIqIjSRwREdGRJI6IiOhIEkdERHSk1sQhaa6k9ZIGJC1qUX+OpNsl3Srp25IObKg7TdKd5eu0hvLDJa0tr3mRJNX5HSIiYlu1JQ5Jk4AlwLHAIcDJkg5pOu2HQJ/t3wWuAf62bLsPcD7wKmAOcL6kvcs2nwHeDcwqX3Pr+g4REbG9Ou845gADtjfYfgpYBhzfeILt79h+vHx7EzCtPH4j8C3bD9p+CPgWMFfS/sBetm+ybeAKYF6N3yEiIprUmTimAvc1vN9Ulg3nDOD6EdpOLY9HvKakhZL6JfUPDg52GHpERAynJwbHJb0T6AM+PlbXtL3Udp/tvilTttsyNyIiRqnOxLEZmN7wflpZtg1JbwA+CBxn+8kR2m7m2e6sYa8ZERH1qTNxrAJmSZopaVdgPrC88QRJrwA+R5E0ftZQtRI4RtLe5aD4McBK2/cDj0o6spxNdSpwbY3fISIimtS2VpXtLZLOokgCk4BLbK+TtBjot72comtqD+DL5azae20fZ/tBSR+lSD4Ai20/WB6fCVwG7E4xJnI9ERExbmpd5ND2CmBFU9l5DcdvaNP2EuCSFuX9wMvGMMyIiOhATwyOR0TEc0cSR0REdCSJIyIiOpLEERERHUniiIiIjiRxRERER5I4IiKiI0kcERHRkSSOiIjoSBJHRER0JIkjIiI6ksQREREdSeKIiIiOJHFERERHkjgiIqIjSRwREdGRWhOHpLmS1ksakLSoRf1Rkm6RtEXSCQ3lr5W0puH1hKR5Zd1lku5uqJtd53eIiIht1bYDoKRJwBLgaGATsErSctu3N5x2L3A68BeNbW1/B5hdXmcfYAD4ZsMp77d9TV2xR0TE8OrcOnYOMGB7A4CkZcDxwNbEYXtjWfdMm+ucAFxv+/H6Qo2IiKrq7KqaCtzX8H5TWdap+cCVTWV/LelWSZ+UNLlVI0kLJfVL6h8cHBzFx0ZERCs9PTguaX/gMGBlQ/G5wEuBI4B9gA+0amt7qe0+231TpkypPdaIiImizsSxGZje8H5aWdaJtwNfs/2roQLb97vwJHApRZdYRESMkzoTxypglqSZknal6HJa3uE1Tqapm6q8C0GSgHnAbTseakREVFVb4rC9BTiLopvpDuBq2+skLZZ0HICkIyRtAk4EPidp3VB7STMo7li+23TpL0paC6wF9gM+Vtd3iIiI7dU5qwrbK4AVTWXnNRyvoujCatV2Iy0G022/bmyjjDrMWHRd1z574wVv6tpnR0wEPT04HhERvSeJIyIiOpLEERERHUniiIiIjoyYOCT9vqQXlMfvlPQJSQfWH1pERPSiKnccnwEel/Ry4M+Bu4Arao0qIiJ6VpXEscW2KRYo/JTtJcCe9YYVERG9qspzHI9JOhc4BXi1pJ2AXeoNKyIielWVO46TgCeBP7L9U4oH9j5ea1QREdGzRkwcZbL4CjC0fPnPga/VGVRERPSuKrOq3g1cA3yuLJoKfL3GmCIioodV6ap6L/D7wKMAtu8EXlxnUBER0buqJI4nbT819EbSzoDrCykiInpZlcTxXUn/E9hd0tHAl4H/U29YERHRq6okjkXAIMX+F++hWCb9Q3UGFRERvWvE5zhsPwN8vnxFRMQEN+wdh6Sry59rJd3a/KpycUlzJa2XNCBpUYv6oyTdImmLpBOa6p6WtKZ8LW8onynp5vKaV5Xb0kZExDhpd8fxvvLnm0dzYUmTgCXA0cAmYJWk5bZvbzjtXuB04C9aXOK/bM9uUX4h8EnbyyR9FjiDYj2tiIgYB8Pecdi+vzw80/Y9jS/gzArXngMM2N5QzspaRrHeVeNnbLR9K/BMlWAlCXgdxXMlAJcD86q0jYiIsVFlcPzoFmXHVmg3Fbiv4f0mWuwh3sZukvol3SRpXlm2L/Cw7S0jXVPSwrJ9/+DgYAcfGxER7QzbVSXpf1DcWfxm05jGnsD36g4MOND2Zkm/CdwgaS3wSNXGtpcCSwH6+vry3ElExBhpN8bxJeB64G8opuQOecz2gxWuvRmY3vB+WllWie3N5c8Nkm4EXkGxZtaLJO1c3nV0dM2IiNhx7bqqbHsjxZIjjzW8kLRPhWuvAmaVs6B2BeYDy0doQ3n9vSVNLo/3o1jy5PZyX5DvAEMzsE4Drq1yzYiIGBvtEseXyp+rgf7y5+qG922VdwRnASuBO4Crba+TtFjScQCSjpC0CTgR+JykdWXz3wH6Jf2IIlFc0DAb6wPAOZIGKMY8Lq78bSMiYocN21Vl+83lz5mjvbjtFRRPmjeWnddwvIqiu6m53feBw4a55gaKGVsREdEF7QbHX9muoe1bxj6ciIjode0Gx/++TZ0pnqeIiIgJpl1X1WvHM5CIiHhuaNdV9TrbN0j6w1b1tr9aX1gREdGr2nVV/XfgBuAtLeoMJHFERExA7bqqzi9/vmv8womIiF434lpVkvaVdFG5/PlqSf8oad/xCC4iInpPlUUOl1HsAPg2iie2B4Gr6gwqIiJ614g7AAL72/5ow/uPSTqproAiIqK3Vbnj+Kak+ZJ2Kl9vp1hGJCIiJqB203Efo5g9JeBs4J/Lqp2AX9B6176IiHieazeras/xDCQiIp4bqoxxIGlvYBaw21CZ7f9XV1AREdG7Rkwckv4YeB/FKrZrgCOBfydrVUVETEhVBsffBxwB3FOuX/UK4OE6g4qIiN5VJXE8YfsJAEmTbf8Y+O16w4qIiF5VJXFskvQi4OvAtyRdC9xT5eKS5kpaL2lA0qIW9UeVT6RvkXRCQ/lsSf8uaZ2kWxufG5F0maS7Ja0pX7OrxBIREWNjxDEO228tD/9K0neAFwLfGKmdpEnAEuBoYBOwStLyhi1gAe4FTmf7qb2PA6favlPSbwCrJa20/XBZ/37b14wUQ0REt81YdF3XPnvjBW+q5bpVZ1W9EvgDiuc6vmf7qQrN5gAD5VavSFoGHA9sTRy2N5Z1zzQ2tP0fDcc/kfQzYAoZW4mI6LoqixyeB1wO7AvsB1wq6UMVrj0VuK/h/aayrCOS5gC7Anc1FP912YX1SUmTh2m3UFK/pP7BwcFOPzYiIoZRZYxjAXCE7fPLpdaPBE6pN6yCpP2BLwDvsj10V3Iu8FKKmV77AB9o1db2Utt9tvumTJkyHuFGREwIVRLHT2h48A+YDGyu0G4zML3h/bSK7QCQtBdwHfBB2zcNldu+34UngUspusQiImKctFur6n9TjGk8AqyT9K3y/dHADypcexUwS9JMioQxH3hHlaAk7Qp8DbiieRBc0v6275ckYB5wW5VrRkTE2Gg3ON5f/lxN8Ut8yI1VLmx7i6SzKFbSnQRcYnudpMVAv+3lko4or7038BZJH7F9KPB24ChgX0mnl5c83fYa4IuSplAsvrgG+JMq8URExNhot8jh5UPH5R3AweXb9bZ/VeXitlcAK5rKzms4XkXRhdXc7p95djXe5rosdRIR0UVV1qp6DcWsqo0Uf+VPl3RaFjmMiJiYqjzH8ffAMbbXA0g6GLgSOLzOwCIiojdVmVW1y1DSgK0P5+1SX0gREdHLqtxxrJb0Tzw75rCAZwfOIyJigqmSOP4EeC/wZ+X7fwU+XVtEERPY83Fdo3j+aZs4yoUKf2T7pcAnxiekiIjoZW3HOGw/DayXdMA4xRMRET2uSlfV3hRPjv8A+OVQoe3jaosqIiJ6VpXE8eHao4iIiOeMdmtV7UYxMH4QsBa42PaW8QosIiJ6U7sxjsuBPoqkcSzFg4ARETHBteuqOsT2YQCSLqbairgREfE81+6OY+tChumiioiIIe3uOF4u6dHyWMDu5XsBtr1X7dFFW3lYLCK6od2y6pPGM5CIiHhuqLLIYURExFa1Jg5JcyWtlzQgaVGL+qMk3SJpi6QTmupOk3Rn+TqtofxwSWvLa15UbiEbERHjpLbEUa5ztYRiKu8hwMmSDmk67V7gdOBLTW33Ac4HXgXMAc6XtHdZ/Rng3cCs8jW3pq8QEREt1HnHMQcYsL3B9lPAMuD4xhNsb7R9K/BMU9s3At+y/aDth4BvAXMl7Q/sZfsm2wauAObV+B0iIqJJuyfHHwM8XH2FWVVTgfsa3m+iuIOoolXbqeVrU4vy7UhaCCwEOOCArNEYETFW2s2q2hNA0keB+4EvUEzFXQDsPy7R7QDbS4GlAH19fcMmwIiI6EyVrqrjbH/a9mO2H7X9GZq6nIaxGZje8H5aWVbFcG03l8ejuWZERIyBKonjl5IWSJokaSdJC2hYXr2NVcAsSTMl7QrMB5ZXjGslcIykvctB8WOAlbbvBx6VdGQ5m+pU4NqK14yIiDFQJXG8A3g78J/l68SyrK1ymZKzKJLAHcDVttdJWizpOABJR0jaVF7zc5LWlW0fBD5KkXxWAYvLMoAzgX8CBoC7gOsrfteIiBgDI+7HYXsj1bqmWrVdAaxoKjuv4XgV23Y9NZ53CXBJi/J+4GWjiSciInbciHcckg6W9G1Jt5Xvf1fSh+oPLSIielGVrqrPA+dSrpZbPncxv86gIiKid1XZOvbXbP+gaWWPLLMez1lZVfj5J/9Nx1eVxPFzSb9F+TBguabU/bVG1UPyP2RExLaqJI73UjxI91JJm4G7KR4CjIiICaht4igXKjzT9hskvQDYyfZj4xNaRET0oraJw/bTkv6gPK7y0F9ERDzPVemq+qGk5cCXaXhi3PZXa4sqIiJ6VpXEsRvwAPC6hjIDSRwRERNQlSfH3zUegURExHPDiIlD0qW02JfD9h/VElFERPS0Kl1V/9JwvBvwVuAn9YQTERG9rkpX1Vca30u6Evi32iKKiIieNpo9x2cBLx7rQCIi4rmhyhhH897jPwU+UFtEERHR00a847C9p+29Gl4HN3dfDUfSXEnrJQ1IWtSifrKkq8r6myXNKMsXSFrT8HpG0uyy7sbymkN1ufuJiBhHVfbj+P1yuREkvVPSJyQdWKHdJGAJcCxwCHCypEOaTjsDeMj2QcAngQsBbH/R9mzbs4FTgLttr2lot2Co3vbPRvyWERExZqqMcXwGeFzSy4E/p9iu9YoK7eYAA7Y32H4KWMb2OwkeD1xeHl8DvF5N67cDJ5dtIyKiB1RJHFtsm+KX/KdsLwH2rNBuKnBfw/tNZVnLc8o9yh8B9m065yTgyqayS8tuqg+3SDQASFooqV9S/+DgYIVwIyKiiiqJ4zFJ5wLvBK6TtBOwS71hFSS9Cnjc9m0NxQtsHwa8unyd0qqt7aW2+2z3TZkyZRyijYiYGKokjpOAJ4EzbP8UmAZ8vEK7zcD0hvfTyrKW50jaGXghxbpYQ+bTdLdhe3P58zHgSxRdYhERMU6qzKr6qe1P2P7X8v29tquMcawCZkmaKWlXiiSwvOmc5cBp5fEJwA1ltxjlnc3baRjfkLSzpP3K412ANwO3ERER46bKrKojJa2S9AtJT0l6WtIjI7UrxyzOAlYCdwBX214nabGk48rTLgb2lTQAnAM0Ttk9CrjP9oaGssnASkm3Amso7lg+P/LXjIiIsVJlrapPUdwtfBnoA04FDq5ycdsrgBVNZec1HD8BnDhM2xuBI5vKfgkcXuWzIyKiHpWWHLE9AEyy/bTtS4G59YYVERG9qsodx+PlGMUaSX8L3M/o1riKiIjngSoJ4JTyvLMoto6dDrytzqAiIqJ3VVlW/R5JuwP72/7IOMQUERE9rMqsqrdQzGD6Rvl+tqTmabURETFBVOmq+iuKh+weBigXG5xZW0QREdHTqiSOX9lufm5juz3IIyJiYqgyq2qdpHcAkyTNAv4M+H69YUVERK+qcsfxp8ChFOtVXQk8CpxdY0wREdHDqsyqehz4YPmKiIgJbtjEMdLMKdvHtauPiIjnp3Z3HP+NYpOlK4GbgZYbJkVExMTSLnH8OnA0xdat7wCuA660vW48AouIiN407OB4uaDhN2yfRrFK7QBwo6Szxi26iIjoOW0HxyVNBt5EcdcxA7gI+Fr9YUVERK9qNzh+BfAyiv00PtK073dERExQ7Z7jeCcwC3gf8H1Jj5avxyQ9WuXikuZKWi9pQNKiFvWTJV1V1t8saUZZPkPSf0laU74+29DmcElryzYXScqgfUTEOBr2jsP2Du25IWkSsIRigH0TsErSctu3N5x2BvCQ7YMkzQcuBE4q6+6yPbvFpT8DvJtiptcKik2lrt+RWCMioro6N2SaAwzY3mD7KWAZcHzTOccDl5fH1wCvb3cHIWl/YC/bN9k2cAUwb8wjj4iIYdWZOKZSPAcyZFNZ1vIc21uAR4B9y7qZkn4o6buSXt1w/qYRrgmApIWS+iX1Dw4O7tg3iYiIrXp1C9j7gQNsvwI4B/iSpL06uYDtpbb7bPdNmTKlliAjIiaiOhPHZoptZodMK8taniNpZ+CFwAO2n7T9AIDt1cBdwMHl+dNGuGZERNSozsSxCpglaaakXYH5QPP6V8uB08rjE4AbbFvSlHJwHUm/STG7a4Pt+4FHJR1ZjoWcClxb43eIiIgmVfbjGBXbW8qnzFcCk4BLbK+TtBjot70cuBj4gqQB4EGK5AJwFLBY0q+AZ4A/sf1gWXcmcBmwO8VsqsyoiogYR7UlDgDbKyimzDaWnddw/ARwYot2XwG+Msw1+ykeTIyIiC7o1cHxiIjoUUkcERHRkSSOiIjoSBJHRER0JIkjIiI6ksQREREdSeKIiIiOJHFERERHkjgiIqIjSRwREdGRJI6IiOhIEkdERHQkiSMiIjqSxBERER1J4oiIiI4kcUREREdqTRyS5kpaL2lA0qIW9ZMlXVXW3yxpRll+tKTVktaWP1/X0ObG8ppryteL6/wOERGxrdp2ACz3DF8CHA1sAlZJWm779obTzgAesn2QpPnAhcBJwM+Bt9j+iaSXUWw/O7Wh3YJyJ8CIiBhndd5xzAEGbG+w/RSwDDi+6ZzjgcvL42uA10uS7R/a/klZvg7YXdLkGmONiIiK6kwcU4H7Gt5vYtu7hm3Osb0FeATYt+mctwG32H6yoezSspvqw5LU6sMlLZTUL6l/cHBwR75HREQ06OnBcUmHUnRfvaeheIHtw4BXl69TWrW1vdR2n+2+KVOm1B9sRMQEUWfi2AxMb3g/rSxreY6knYEXAg+U76cBXwNOtX3XUAPbm8ufjwFfougSi4iIcVJn4lgFzJI0U9KuwHxgedM5y4HTyuMTgBtsW9KLgOuARba/N3SypJ0l7Vce7wK8Gbitxu8QERFNaksc5ZjFWRQzou4Arra9TtJiSceVp10M7CtpADgHGJqyexZwEHBe07TbycBKSbcCayjuWD5f13eIiIjt1TYdF8D2CmBFU9l5DcdPACe2aPcx4GPDXPbwsYwxIiI609OD4xER0XuSOCIioiNJHBER0ZEkjoiI6EgSR0REdCSJIyIiOpLEERERHUniiIiIjiRxRERER5I4IiKiI0kcERHRkSSOiIjoSBJHRER0JIkjIiI6ksQREREdSeKIiIiO1Jo4JM2VtF7SgKRFLeonS7qqrL9Z0oyGunPL8vWS3lj1mhERUa/aEoekScAS4FjgEOBkSYc0nXYG8JDtg4BPAheWbQ+h2KP8UGAu8GlJkypeMyIialTnHcccYMD2BttPAcuA45vOOR64vDy+Bni9JJXly2w/aftuYKC8XpVrRkREjercc3wqcF/D+03Aq4Y7x/YWSY8A+5blNzW1nVoej3RNACQtBBaWb38haf0ovsNY2A/4+Wga6sIxjmR7iW10EtvoJLbR6WZsB7YqrDNxdJXtpcDSbschqd92X7fjaCWxjU5iG53ENjq9GFudXVWbgekN76eVZS3PkbQz8ELggTZtq1wzIiJqVGfiWAXMkjRT0q4Ug93Lm85ZDpxWHp8A3GDbZfn8ctbVTGAW8IOK14yIiBrV1lVVjlmcBawEJgGX2F4naTHQb3s5cDHwBUkDwIMUiYDyvKuB24EtwHttPw3Q6pp1fYcx0vXusjYS2+gkttFJbKPTc7Gp+AM/IiKimjw5HhERHUniiIiIjiRxRERER5I4aiBpH0n7dDuOiIg6JHGMEUkHSFomaRC4GfiBpJ+VZTO6HF7Pk/QSSa8sXy/pdjwjkbRHt2OI6JbMqhojkv4d+Afgmoapw5OAE4GzbR/ZxfCGJWmt7cO6+Pmzgc9SPPw59DDnNOBh4Ezbt3QnsvYk3Wv7gG7HAUXS5dkleTbb/s9uxjMSSXvY/kWXYxDF2ndb/92AH7iHfyFKeqntH3c7DkjiGDOS7rQ9q9O68SDpD4erAj5re8p4xrNNANIa4D22b24qPxL4nO2XdyWwIoZzhqsCPmi7q92RSbqj/vxjgE8Dd7Ltv9tBFP9u3+xWbO10+9+t0fN2raouWC3p0xSr/Q4txDid4sn4H3YtqsJVwBeBVn8l7DbOsTR7QXPSALB9k6QXdCOgBv8L+DjFQ6jNeqGb9zKGT7qXAr2adLvdzfePwBtsb2wsLFepWAH8TjeCKmO4aLgq4EXjGEpbSRxj51SK/UU+wra3v0NPyHfTrcDf2b6tuULSG7oQT6PrJV0HXMG2CfdU4Btdi6pwC/B126ubKyT9cRfiaZakOzo7U6ys3WwzsMs4x9LsXcCfA0+2qDt5nGMZVrqqJgBJrwbusX1vi7o+2/1dCKsxhmMp9lXZJuHaXtG9qEDSbwMP2N5uSWtJL+n2WEL51+lv0Trp3m37rC7G9n3gT4dJuvfZnt6i2biQdC7wdor9fBr/3eYDV9v+my7GdgPwIdvfb1F3t+2ZXQhrO0kcY6Rc3fcMYB7b/gK8FrjY9q+6FFo8j/V40n3Q9mCLul5Iur9D63+327sXVTGVH3jC9uPdjGMkSRxjRNKVFIOSl/PsbfA0ijGOfWyf1KXQGpPaW4HfKIt7PqlJWmp74chnjr9eji2ibkkcY0TSf9g+uNO68dDjSW24mUkCfmR72njGs00APRwbgKQXAudS/OX8EorJDz+j+IPgAtsP90Bs84AX91Js7Ui63vax3Y6jlV6KLYPjY+dBSScCX7H9DICknSie43ioq5HB4S0S1ybgJkn/0Y2AGgwC91D8Mh7i8v2LuxLRs3o5NoCrgRuA19r+KYCkXwdOL+uO6V5oW2N7TVNsp3U7NkmvHK4KmD2OoWwfQA/H1ih3HGOkfDr8QuC1FH/dQzF97jvAItt3dyUwQNJNwN/TOqmdY7vlvu3jFNudwOuHGbjv9iBqz8ZWxrDe9m93Wjceejy2p4Hvsu0fBEOOtL37OIe0VS/H1ih3HGPE9kZJf0XxzMY2g+PdTBql+RRJbYmkh8uyF1EktfldimnIPwB7A9v9cgb+dnxD2c4/0LuxAdwj6S+By4cGm8unyE/n2dlC3dLLsd1B8fzLnc0VkhJbBbnjGCOSPkDxS3gZ2z6NOh9YZvuCbsUGw84iudb2Hd2LqiDppbSe4ZLY2pC0N7CIIr6hrrP/pHh26ALbXesi7fHYTgDW2l7fom6e7a+Pf1RbP79nY2uUxDFGyrGCQ5tnKJV7o6/r8pIjPZvUyr9K31HG1jhwn9h2gKR32b6023G0kthGp5diS+IYI5J+DLzR9j1N5QcC3+xyn24vJ7XEVoNeWteoWWIbnV6KLWMcY+ds4NvlgOpQX+QBFAunde0J3tIzFM9v3NNUvn9Z102JbZQk3TpcFcX03K5JbKPTy7E1SuIYI7a/Ielgtl+qedXQMutddDa9m9TOJrGN1kuAN7L9dG8B2y1ZMc4S2+j0cmxbJXGMoXKq603djqNZLye1xLZD/gXYw/aa5gpJN457NNtKbKPTy7FtlTGOiIjoSLeXN46IiOeYJI6IiOhIEkdEE0nTJF0r6U5JGyR9StLkCu1a7qMtafHQhlmSzpb0a8Oc92ZJP5T0I0m3S3pPWT5P0iEVPr/SeRE7KokjooEkAV+l2PlvFjAL2J0dWGLE9nm2/2/59mxgu8QhaRdgKfCWcp/1VwA3ltXzgCoJoep5ETskg+MRDSS9Hjjf9lENZXtRPMsxHTgB6BvaXU/Sv1Bsy3tjecfxeYqVX38KzLc9KOkyitkyvwH8HbAe+Lnt1zZ8xj7Aj4EDbf9XQ/nvlW0fKV9vA14HLAR2BQaAUyhWTm0+D2AJMAV4HHi37R+PyT9UTGi544jY1qHANtud2n4U2Ejx/EY7LwD6bR9KscLp+U3XuQj4CcUy6K9tqnuQYh2neyRdKWmBpJ3KLUSXA++3Pdv2XcBXbR9R3pncAZwxzHlLKbZvPRz4C+DTHf9rRLSQ5zgixs4zwFXl8T9TdHlVZvuPJR0GvIHiF/3RFKvJNnuZpI9RrHC8B7Cy+QRJewC/B3y56H0DYMRxmogqkjgitnU7RXfUVmVX1a9TdDG9jG3v1Hdrc62O+4FtrwXWSvoCcDetE8dlwDzbP5J0OvCaFufsBDxse3anMUSMJF1VEdv6NvBrkk4FkDSJYhOsT5VjDxuB2ZJ2kjSd4qnyITvxbNJ5B/BvLa7/GLBnc6GkPSS9pqFoNs+ukdXcZk/g/nJAfUGra5fda3eXu1KiwsvbffGIqpI4Ihq4mC3yVuCEco2qB4BnbP91ecr3KO4EbgcuAm5paP5LYI6k2ygGsBe3+IilwDckfaepXMBfSlovaQ3wEZ6921gGvL+cqvtbwIeBm8tYGge7m89bAJwh6UfAOoq9MSJ2WGZVRbRRzmq6Enir7VtGOj9iIkjiiIiIjqSrKiIiOpLEERERHUniiIiIjiRxRERER5I4IiKiI0kcERHRkf8Pn0icmG2FlJwAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "N = 4 # Set the number of qubits\n",
+    "DEPTH = 6 # Set the quantum circuit depth\n",
+    "theta = np.random.randn(DEPTH, N, 3)\n",
+    "\n",
+    "# Start Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # We need to convert numpy.ndarray to variable supported in Paddle dynamic graph mode\n",
+    "    theta = fluid.dygraph.to_variable(theta)\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Add a complex strong entanglement structure QNN with depth D = 6 {Rz+Ry+Rz/U3 + CNOT's}\n",
+    "    cir.complex_entangled_layer(theta, DEPTH)\n",
+    "    \n",
+    "    # Prepare output state\n",
+    "    # If the user does not enter the initial quantum state, the default initial is |00..0>\n",
+    "    final_state = cir.run_state_vector()\n",
+    "    \n",
+    "    # Measure the output state [0, 1, 2] qubits 2048 times, and count the frequency of the measurement results\n",
+    "    cir.measure(shots = 2048, which_qubits = [0, 1, 2], plot = True)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "---\n",
+    "\n",
+    "# Operating Mode of Paddle Quantum\n",
+    "\n",
+    "## Wave function vector mode\n",
+    "\n",
+    "The so-called wave function mode is to use complex vectors to represent and store the quantum states. Vector mode can only handle pure states, but this mode efficiently supports **20+ qubit** operations on personal computer hardware. Users can test the limits of their computers. Under this representation, the essential operation of the quantum gate (unitary matrix) acting on qubits (a complex vector to describe the state) is **multiplying a matrix by a vector**:\n",
+    "\n",
+    "$$\n",
+    "|\\psi\\rangle = U |\\psi_0\\rangle.\n",
+    "\\tag{22}\n",
+    "$$\n",
+    "\n",
+    "A function `cir.run_state_vector(input_state = None)` will be used in the following code. If we don't enter any initial quantum state, all qubits will be set into the $\\lvert {0}\\rangle$ state by default. Let's take a specific example:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 8,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:02:13.332713Z",
+     "start_time": "2021-01-09T13:01:13.592149Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "[[ 0.00072194+0.j  0.00044133+0.j  0.00064311+0.j ... -0.00045617+0.j\n",
+      "   0.00025925+0.j  0.00080118+0.j]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "import numpy as np\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.state import vec, vec_random\n",
+    "\n",
+    "N = 20 # Set the number of qubits\n",
+    "DEPTH = 6 # Set the quantum circuit depth\n",
+    "theta = np.random.randn(DEPTH, N, 1)\n",
+    "\n",
+    "# Call the built-in |00..0> initial state\n",
+    "initial_state1 = vec(N)\n",
+    "# Call the built-in random quantum state |psi>\n",
+    "initial_state2 = vec_random(N)\n",
+    "\n",
+    "# Start Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # We need to convert numpy.ndarray to variable supported in PaddlePaddle dynamic graph mode\n",
+    "    theta = fluid.dygraph.to_variable(theta)\n",
+    "    initial_state = fluid.dygraph.to_variable(initial_state1)\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Add a real entanglement structure QNN {Ry+CNOT's} with depth of DEPTH\n",
+    "    cir.real_entangled_layer(theta, DEPTH)\n",
+    "    \n",
+    "    # Prepare output state\n",
+    "    # If the user does not enter the initial quantum state, the default initial state is |00..0>\n",
+    "    final_state = cir.run_state_vector(initial_state)\n",
+    "    print(final_state.numpy())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "\n",
+    "## Density matrix mode\n",
+    "\n",
+    "Paddle Quantum also supports the density matrix mode, which is to use density matrices $\\rho = \\sum_i P_i |\\psi_i\\rangle\\langle\\psi_i|$ to represent and store quantum states. This mode can supports **mixed state simulation** . But in density matrix mode, personal computer hardware can only support around 10 qubits. Please pay attention to this limitation. We are constantly optimizing the performance of the simulator in this mode. Under this representation, quantum gates (unitary matrices) acting on the quantum states (Hermitian matrix with a trace of 1) can be viewed as **matrix multiplication**:\n",
+    "\n",
+    "$$\n",
+    "\\rho = U \\rho_0 U^\\dagger.\n",
+    "\\tag{23}\n",
+    "$$\n",
+    "\n",
+    "Function `cir.run_density_matrix()` will be used in the following code. Here is an  example:\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 9,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:02:13.431007Z",
+     "start_time": "2021-01-09T13:02:13.337255Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "[[ 2.58020326e-01+0.j -3.54982418e-01+0.j  2.55776343e-01+0.j\n",
+      "   3.43259769e-03+0.j]\n",
+      " [-3.54982418e-01+0.j  4.88382132e-01+0.j -3.51895163e-01+0.j\n",
+      "  -4.72254201e-03+0.j]\n",
+      " [ 2.55776343e-01+0.j -3.51895163e-01+0.j  2.53551876e-01+0.j\n",
+      "   3.40274466e-03+0.j]\n",
+      " [ 3.43259769e-03+0.j -4.72254201e-03+0.j  3.40274466e-03+0.j\n",
+      "   4.56658865e-05+0.j]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "from paddle_quantum.state import density_op, density_op_random, completely_mixed_computational\n",
+    "\n",
+    "N = 2 # Set the number of qubits\n",
+    "DEPTH = 6 # Set the quantum circuit depth\n",
+    "theta = np.random.randn(DEPTH, N, 1)\n",
+    "\n",
+    "# Call the built-in |00..0><00..0| initial state\n",
+    "initial_state1 = density_op(N)\n",
+    "# Call the built-in random quantum state, you can specify whether to allow complex number elements and matrix rank\n",
+    "initial_state2 = density_op_random(N, real_or_complex=2, rank=4)\n",
+    "# Call the complete mixed state under the built-in calculation base\n",
+    "initial_state3 = completely_mixed_computational(N)\n",
+    "\n",
+    "# Start Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # We need to convert numpy.ndarray to variable supported in PaddlePaddle dynamic graph mode\n",
+    "    theta = fluid.dygraph.to_variable(theta)\n",
+    "    initial_state = fluid.dygraph.to_variable(initial_state1)\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Add a real number strong entanglement structure QNN {Ry+CNOT's} with depth of DEPTH\n",
+    "    cir.real_entangled_layer(theta, DEPTH)\n",
+    "    \n",
+    "    # Prepare output state\n",
+    "    # If the user does not enter the initial quantum state, the default initial is |00..0><00..0|\n",
+    "    final_state = cir.run_density_matrix(initial_state)\n",
+    "    print(final_state.numpy())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Exercise: How to prepare Bell states from computational basis\n",
+    "\n",
+    "Bell state is a widely used quantum entangled state, which can be expressed as\n",
+    "\n",
+    "$$\n",
+    "|\\Phi^+\\rangle = \\frac{1}{\\sqrt{2}} \\big(|00\\rangle + |11\\rangle\\big)\n",
+    "= \\frac{1}{\\sqrt{2}} \\,\n",
+    "\\begin{bmatrix}\n",
+    "1 \\\\\n",
+    "0 \\\\\n",
+    "0 \\\\\n",
+    "1\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{24}\n",
+    "$$\n",
+    "\n",
+    "So how do we use Paddle Quantum to prepare a Bell state? We can use the following quantum circuit :\n",
+    "\n",
+    "![intro-fig-bell2](./figures/intro-fig-bell2.png)"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 10,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:02:13.775333Z",
+     "start_time": "2021-01-09T13:02:13.434980Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEJCAYAAACZjSCSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAV4UlEQVR4nO3de7QlZX3m8e/TzVVBBWmVcLGJNmPQBNQWmZhRRMjAUgEDCnIZiRgw0hFmcgEmBiNm1niJzIxD69hGDZoliPeOIkxGJTPqqN0gFxtsaZFLo5hGRFBGsOE3f+xq2BzO2V3dfWofzqnvZ629elfVu+v8Tq3V59n1vlVvpaqQJPXXvJkuQJI0swwCSeo5g0CSes4gkKSeMwgkqecMAknqua1muoBNtcsuu9TChQtnugxJmlWuuOKKO6pqwWTbZl0QLFy4kJUrV850GZI0qyS5eaptdg1JUs8ZBJLUcwaBJPWcQSBJPWcQSFLPdRoESQ5NsjrJmiRnTbL9pCTrklzVvN7QZT2SpEfr7PLRJPOBpcAhwFpgRZLlVXXdhKafqKolXdUhSRqtyzOC/YE1VXVjVd0PXAQc0eHPkyRthi5vKNsNuHVoeS3wwknaHZXkxcD3gX9fVbdO0mZaLDzri13tela46R0vn+kSJD0GzfSdxf8IXFhV9yU5FbgAOGhioySnAKcA7LnnnuOtUNJjhl/muvky12XX0G3AHkPLuzfrHlJVP62q+5rFvwOeP9mOqmpZVS2uqsULFkw6VYYkaTN1GQQrgEVJ9kqyDXAssHy4QZJdhxYPB67vsB5J0iQ66xqqqvVJlgCXAfOBD1fVqiTnAiurajnw5iSHA+uBO4GTuqpHkjS5TscIquoS4JIJ684Zen82cHaXNUiSRvPOYknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5zoNgiSHJlmdZE2Ss0a0OypJJVncZT2SpEfrLAiSzAeWAocB+wCvTbLPJO12BE4HvtVVLZKkqXV5RrA/sKaqbqyq+4GLgCMmafd24J3ArzqsRZI0hS6DYDfg1qHltc26hyR5HrBHVX2xwzokSSPM2GBxknnAecCftmh7SpKVSVauW7eu++IkqUc2GgRJXpTk8c37E5Kcl+TpLfZ9G7DH0PLuzboNdgSeA1ye5CbgAGD5ZAPGVbWsqhZX1eIFCxa0+NGSpLbanBG8H7g3yb4Mvr3/APhoi8+tABYl2SvJNsCxwPING6vq51W1S1UtrKqFwDeBw6tq5ab+EpKkzdcmCNZXVTEY6D2/qpYy+DY/UlWtB5YAlwHXAxdX1aok5yY5fEuKliRNn61atLknydnAicC/afr2t26z86q6BLhkwrpzpmh7YJt9SpKmV5szgmOA+4DXV9XtDPr6391pVZKksdloEDR//D8NbNusugP4bJdFSZLGp81VQ38EfAr4QLNqN+BzHdYkSRqjNl1DpwEvAu4GqKobgKd0WZQkaXzaBMF9zRQRACTZCqjuSpIkjVObIPjnJP8R2D7JIcAngX/stixJ0ri0CYKzgHXAtcCpDC4HfUuXRUmSxmej9xFU1YPAB5uXJGmOmTIIklxcVa9Jci2TjAlU1e90WpkkaSxGnRGc3vz7inEUIkmaGVOOEVTVj5u3b6qqm4dfwJvGU54kqWttBosPmWTdYdNdiCRpZowaI/hjBt/8fzPJNUObdgS+3nVhkqTxGDVG8HHgS8B/ZnAJ6Qb3VNWdnVYlSRqbUUFQVXVTktMmbkiys2EgSXPDxs4IXgFcweDy0QxtK+A3O6xLkjQmUwZBVb2i+Xev8ZUjSRq3UYPFzxv1waq6cvrLkSSN26iuofeM2FbAQdNciyRpBozqGnrpOAuRJM2MUV1DB1XVV5L8wWTbq+oz3ZUlSRqXUV1DLwG+Arxykm0FGASSNAeM6hp6a/PvH46vHEnSuLV5eP2Tk7w3yZVJrkjy35I8eRzFSZK612bSuYsYPKHsKODo5v0nuixKkjQ+G31CGbBrVb19aPlvkhzTVUGSpPFqc0bwP5Mcm2Re83oNcFnXhUmSxmPU5aP38PAcQ2cA/9Bsmgf8AvizrouTJHVv1FVDO46zEEnSzGgzRkCSnYBFwHYb1lXV/+6qKEnS+Gw0CJK8gcGD7HcHrgIOAP4vzjUkSXNCm8Hi04EXADc38w89F7iry6IkSePTJgh+VVW/AkiybVV9D/hX3ZYlSRqXNkGwNsmTgM8B/5Tk88DNbXae5NAkq5OsSXLWJNvfmOTaJFcl+VqSfTaleEnSltvoGEFVvap5+9dJvgo8Ebh0Y59LMh9YChwCrAVWJFleVdcNNft4Vf2Ppv3hwHnAoZv2K0iStkTbq4aeB/weg/sKvl5V97f42P7Amqq6sdnHRcARwENBUFV3D7V/fLN/SdIYtZl07hzgAuDJwC7AR5K8pcW+dwNuHVpe26ybuP/TkvwAeBfw5ilqOCXJyiQr161b1+JHS5LaajNGcDzwgqp6azM19QHAidNVQFUtrapnAGcCkwZMVS2rqsVVtXjBggXT9aMlSbQLgh8xdCMZsC1wW4vP3QbsMbS8+0Y+dxFwZIv9SpKm0ai5hv47gz77nwOrkvxTs3wI8O0W+14BLEqyF4MAOBY4bsLPWFRVNzSLLwduQJI0VqMGi1c2/14BfHZo/eVtdlxV65MsYTBT6Xzgw1W1Ksm5wMqqWg4sSXIw8GvgZ8DrNrF+SdIWGjXp3AUb3ifZBti7WVxdVb9us/OqugS4ZMK6c4ben75J1UqSpl2buYYOZHDV0E0MpqTeI8nrnHROkuaGNvcRvAf4/apaDZBkb+BC4PldFiZJGo82Vw1tvSEEAKrq+8DW3ZUkSRqnNmcEVyT5Ox5+QtnxPDyQLEma5doEwRuB03j4rt//A7yvs4okSWM1MgiaieOurqpnMZgQTpI0x4wcI6iqB4DVSfYcUz2SpDFr0zW0E4M7i78N/HLDyqo6vLOqJElj0yYI/qrzKiRJM2bUXEPbMRgofiZwLfChqlo/rsIkSeMxaozgAmAxgxA4jMGNZZKkOWZU19A+VfXbAEk+RLsZRyVJs8yoM4KHJpazS0iS5q5RZwT7JtnwTOEA2zfLAaqqntB5dZKkzo2ahnr+OAuRJM2MNpPOSZLmMINAknrOIJCknjMIJKnnRt1ZfA9QU233qiFJmhtGXTW0I0CStwM/Bj7G4NLR44Fdx1KdJKlzbbqGDq+q91XVPVV1d1W9Hzii68IkSePRJgh+meT4JPOTzEtyPEPTUUuSZrc2QXAc8BrgJ83r1c06SdIcsNHnEVTVTdgVJElz1kbPCJLsneTLSb7bLP9Okrd0X5okaRzadA19EDibZjbSqroGOLbLoiRJ49MmCB5XVROfReC01JI0R7QJgjuSPIPm5rIkRzO4r0CSNAe0eXj9acAy4FlJbgN+yOCmMknSHDAyCJLMB95UVQcneTwwr6ruGU9pkqRxGBkEVfVAkt9r3nsTmSTNQW3GCL6TZHmSE5P8wYZXm50nOTTJ6iRrkpw1yfb/kOS6JNc0l6g+fZN/A0nSFmkzRrAd8FPgoKF1BXxm1IeabqWlwCHAWmBFkuVVdd1Qs+8Ai6vq3iR/DLwLOGYT6pckbaE2dxb/4Wbue39gTVXdCJDkIgZ3KD8UBFX11aH23wRO2MyfJUnaTBsNgiQfYZLnElTV6zfy0d2AW4eW1wIvHNH+ZOBLU9RwCnAKwJ577rmRHytJ2hRtuoa+MPR+O+BVwI+ms4gkJwCLgZdMtr2qljG4hJXFixdP+bAcSdKma9M19Onh5SQXAl9rse/bgD2Glndv1j1CkoOBvwReUlX3tdivJGkabc4zixcBT2nRbgWwKMleSbZhMD/R8uEGSZ4LfIDBw2/+ZTNqkSRtoTZjBBOfXXw7cObGPldV65MsAS4D5gMfrqpVSc4FVlbVcuDdwA7AJ5MA3FJVh2/6ryFJ2lxtuoZ23NydV9UlwCUT1p0z9P7gzd23JGl6tHkewYua6SVIckKS87zxS5LmjjZjBO8H7k2yL/CnwA+Aj3ZalSRpbNoEwfqqKgY3g51fVUuBze4ukiQ9trS5j+CeJGczuOv3xUnmAVt3W5YkaVzanBEcA9wHnFxVtzO4H+DdnVYlSRqbNlcN3Q6cN7R8C44RSNKc0eaqoQOSrEjyiyT3J3kgyc/HUZwkqXttuobOB14L3ABsD7wBeF+XRUmSxqfVFBNVtQaYX1UPVNVHgEO7LUuSNC5trhq6t5kr6Kok7wJ+zObNUSRJegxq8wf9xKbdEuCXDGYUParLoiRJ49PmqqGbk2wP7FpVbxtDTZKkMWpz1dArgauAS5vl/ZIsH/khSdKs0aZr6K8ZPH/4LoCqugrYq7OKJElj1SYIfl1VE+8b8HGRkjRHtLlqaFWS44D5SRYBbwa+0W1ZkqRxaXNG8CfAsxnMN3QhcDdwRoc1SZLGqM1VQ/cyeLj8X3ZfjiRp3KYMgo1dGeSzhSVpbhh1RvCvgVsZdAd9C8hYKpIkjdWoIHgacAiDCeeOA74IXFhVq8ZRmCRpPKYcLG4mmLu0ql4HHACsAS5PsmRs1UmSOjdysDjJtsDLGZwVLATeC3y2+7IkSeMyarD4o8BzgEuAt1XVd8dWlSRpbEadEZzAYLbR04E3Jw+NFQeoqnpCx7VJksZgyiCoKp85IEk94B97Seo5g0CSes4gkKSeMwgkqecMAknqOYNAknqu0yBIcmiS1UnWJDlrku0vTnJlkvVJju6yFknS5DoLgiTzgaXAYcA+wGuT7DOh2S3AScDHu6pDkjRam0dVbq79gTVVdSNAkouAI4DrNjSoqpuabQ92WIckaYQuu4Z2Y/A8gw3WNuskSY8hs2KwOMkpSVYmWblu3bqZLkeS5pQug+A2YI+h5d2bdZusqpZV1eKqWrxgwYJpKU6SNNBlEKwAFiXZK8k2wLHAyOcgS5LGr7MgqKr1wBLgMuB64OKqWpXk3CSHAyR5QZK1wKuBDyTxMZiSNGZdXjVEVV3C4ME2w+vOGXq/gkGXkSRphsyKwWJJUncMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5zoNgiSHJlmdZE2SsybZvm2STzTbv5VkYZf1SJIerbMgSDIfWAocBuwDvDbJPhOanQz8rKqeCfwX4J1d1SNJmlyXZwT7A2uq6saquh+4CDhiQpsjgAua958CXpYkHdYkSZpgqw73vRtw69DyWuCFU7WpqvVJfg48GbhjuFGSU4BTmsVfJFndScXd24UJv9s4Zfafb83o8ZsjPIZbZjb/H376VBu6DIJpU1XLgGUzXceWSrKyqhbPdB2zlcdvy3kMt8xcPX5ddg3dBuwxtLx7s27SNkm2Ap4I/LTDmiRJE3QZBCuARUn2SrINcCywfEKb5cDrmvdHA1+pquqwJknSBJ11DTV9/kuAy4D5wIeralWSc4GVVbUc+BDwsSRrgDsZhMVcNuu7t2aYx2/LeQy3zJw8fvELuCT1m3cWS1LPGQSS1HMGgST1nEEgST1nEHQkyVZJTk1yaZJrmteXkrwxydYzXd9slmROXrkhzRSvGupIkguBuxjMpbS2Wb07g/smdq6qY2aotFkhyc5TbQKurqrdx1nPbJTkicDZwJHAU4AC/gX4PPCOqrprxoqb5ZJ8qaoOm+k6psusmGJilnp+Ve09Yd1a4JtJvj8TBc0y64CbGfzh36Ca5afMSEWzz8XAV4ADq+p2gCRPY/Bl5GLg92ewtse8JM+bahOw3xhL6ZxB0J07k7wa+HRVPQiQZB7wauBnM1rZ7HAj8LKqumXihiS3TtJej7awqh4xTVkTCO9M8voZqmk2WQH8M4/8MrLBk8ZbSrcMgu4cy+D5CkuT3NWsexLwVeb+HdTT4b8COwGPCgLgXeMtZda6OclfABdU1U8AkjwVOIlHzgysyV0PnFpVN0zcMNe+jDhG0KEkv8XgmQu7NatuAz5fVdfPXFWzR5Jn8ejjt9zj106SnYCzGBzDDd1pP2Ewx9c7qsoz0xGSHA1cW1WPmvY+yZFV9bnxV9UNrxrqSJIzgY8z6Nf+VvMCuHCyx3bqkZpvshcxOC3/dvMKHr/WqupnVXVmVT2rqnZuXr9VVWcyGEDWCFX1qclCoLHTWIvpmGcEHWkGhJ9dVb+esH4bYFVVLZqZymYHj1+3ktxSVXvOdB2z1Vw7fo4RdOdB4DcYXPkybNdmm0bz+G2hJNdMtQl46jhrmY36dPwMgu6cAXw5yQ08PDC3J/BMYMlMFTWLnIHHb0s9Ffi3PPoqtQDfGH85s05vjp9B0JGqujTJ3sD+PHKwc0VVPTBzlc0OHr9p8QVgh6q6auKGJJePvZrZpzfHzzECSeo5rxqSpJ4zCCSp5wwCzWlJdk/y+SQ3JLkxyflJtm3xuV9Msf7cJAc3789I8rgp2r0iyXeSXJ3kuiSnNuuPTLJPi5/fqp00HQwCzVlJAnwG+Fxz38EiYHu2YIqKqjqnqv5Xs3gG8KggaKYZXwa8sqr2BZ4LXN5sPhJo8we+bTtpizlYrDkrycuAt1bVi4fWPYHBvQl7AEcDi6tqSbPtC8DfVtXlzRnBBxnM0Hk7cGxVrUvy9wyuJvkN4G+B1cAdVfXSoZ+xM/A94OlV9f+G1v9u89mfN6+jgIOAU4BtgDXAiQxmtpzYDmApsAC4F/ijqvretBwo9Z5nBJrLng1cMbyiqu4GbmJwP8IojwdWVtWzGcxA+dYJ+3kv8CPgpcMh0Gy7k8F8PjcnuTDJ8UnmVdU3mvV/XlX7VdUPgM9U1QuaM4frgZOnaLcM+JOqej7wZ8D7NvloSFPwPgJpcg8Cn2je/wODLqbWquoNSX4bOJjBH+5DGMz6OdFzkvwNg5lpdwAum9ggyQ7A7wKfHPR2AbDRcQ6pLYNAc9l1DLp/HtJ0DT2NQZfOc3jkWfF2I/a1yX2oVXUtcG2SjwE/ZPIg+HvgyKq6OslJwIGTtJkH3FVV+21qDVIbdg1pLvsy8Lgk/w4gyXzgPcD5Td/9TcB+SeYl2YPBXcwbzOPhEDkO+Nok+78H2HHiyiQ7JDlwaNV+PDxn0sTP7Aj8uBlgPn6yfTfdWT9sHnREBvYd9YtLm8Ig0JxVgyshXgUc3cxZ9FPgwar6T02TrzP4pn4d8F7gyqGP/xLYP8l3GQzonjvJj1gGXJrkqxPWB/iLJKuTXAW8jYfPBi4C/ry5tPQZwF8xmKL86wwGmJmi3fHAyUmuBlYxeMaANC28aki90Vy1cyHwqqq6cmPtpb4wCCSp5+wakqSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6rn/D+JaGszUWoXsAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The Bell state is:\n",
+      " [0.70710678+0.j 0.        +0.j 0.        +0.j 0.70710678+0.j]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Start Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    cir = UAnsatz(2)\n",
+    "\n",
+    "    # Add quantum gates\n",
+    "    cir.h(0)\n",
+    "    cir.cnot([0, 1])\n",
+    "    \n",
+    "    # If the user does not enter the initial quantum state, the default initial is |00..0>\n",
+    "    output_state = cir.run_state_vector()\n",
+    "    \n",
+    "    # We measure the output state 2048 times and obtain the frequency distribution of the measurement results\n",
+    "    cir.measure(shots = 2048, plot = True)\n",
+    "    \n",
+    "    print('The Bell state is:\\n', output_state.numpy())"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "---"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# PaddlePaddle Optimizer Tutorial\n",
+    "\n",
+    "## Example: Using gradient descent in PaddlePaddle to optimize multivariable functions\n",
+    "\n",
+    "\n",
+    "In this section, we will learn how to use the PaddlePaddle dynamic computational graph to find the minimum value of a multivariable function, for example,\n",
+    "\n",
+    "$$\n",
+    "\\min_{\\boldsymbol{\\theta}}\\mathcal{L}(\\theta_1, \\theta_2, \\theta_3)\n",
+    "= (\\theta_1)^2 + (\\theta_2)^2 + (\\theta_3)^2 + 10.\n",
+    "\\tag{25}\n",
+    "$$\n",
+    "\n",
+    "It is clear when $\\theta_1 = \\theta_2 = \\theta_3 = 0$, $\\mathcal{L}$ takes the minimum value of 10."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 11,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:03:57.626603Z",
+     "start_time": "2021-01-09T13:03:57.398028Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The minimum value of the loss function is: 10.000000020981819\n"
+     ]
+    }
+   ],
+   "source": [
+    "import numpy as np\n",
+    "from paddle import fluid\n",
+    "from paddle.complex import matmul\n",
+    "from paddle_quantum.utils import dagger\n",
+    "\n",
+    "# Set hyper parameter\n",
+    "theta_size = 3\n",
+    "ITR = 200 # Set the number of iterations\n",
+    "LR = 0.5  # Set the learning rate\n",
+    "SEED = 1  # Fix random number seed\n",
+    "\n",
+    "class Optimization_ex1(fluid.dygraph.Layer):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=-5., high=5., seed=SEED), dtype='float64'):\n",
+    "        super(Optimization_ex1, self).__init__()\n",
+    "        \n",
+    "        # Initialize a list of learnable parameters with length theta_size\n",
+    "        # Use the uniform distribution of [-5, 5] to fill the initial value\n",
+    "        self.theta = self.create_parameter(\n",
+    "        shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "\n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self):\n",
+    "        loss = self.theta[0] ** 2 + self.theta[1] ** 2 + self.theta[2] ** 2 + 10\n",
+    "        return loss\n",
+    "    \n",
+    "# Record intermediate optimization results\n",
+    "loss_list = []\n",
+    "parameter_list = []\n",
+    "\n",
+    "# Initialize paddle dynamic computational graph \n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # Define network dimensions\n",
+    "    myLayer = Optimization_ex1([theta_size])\n",
+    "    \n",
+    "    # Use Adam optimizer to get relatively good convergence\n",
+    "    # Of course you can change to SGD or RMSprop.\n",
+    "    optimizer = fluid.optimizer.AdamOptimizer(\n",
+    "    learning_rate = LR, parameter_list = myLayer.parameters())\n",
+    "    \n",
+    "    # Iteration of optimization\n",
+    "    for itr in range(ITR):\n",
+    "        \n",
+    "        # Forward propagation calculates the loss function\n",
+    "        loss = myLayer()[0]\n",
+    "        \n",
+    "        # Under the dynamic graph mode, backpropagation optimizes the loss function\n",
+    "        loss.backward()\n",
+    "        optimizer.minimize(loss)\n",
+    "        myLayer.clear_gradients()\n",
+    "        \n",
+    "        # Record the learning process\n",
+    "        loss_list.append(loss.numpy()[0])\n",
+    "        parameter_list.append(myLayer.parameters()[0].numpy())\n",
+    "        \n",
+    "    print('The minimum value of the loss function is:', loss_list[-1])"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Exercise: Finding Eigenvalues\n",
+    "\n",
+    "Next, let's try a more complicated loss function. First, we introduce a random Hermitian matrix $H$ whose **eigenvalues** are the diagonal elements of matrix $D$, where\n",
+    "\n",
+    "$$\n",
+    "D = \\begin{bmatrix} 0.2 &0 \\\\ 0 &0.8 \\end{bmatrix}.\n",
+    "\\tag{26}\n",
+    "$$\n",
+    "\n",
+    "Don't worry, we will help you generate this Hermitian matrix $H$.\n",
+    "\n",
+    "Initialize the parameter vector $\\boldsymbol{\\theta}$ to construct a simple linear operation $U(\\boldsymbol{\\theta}) = R_z(\\theta_1)*R_y(\\theta_2)*R_z(\\theta_3)$:\n",
+    "\n",
+    "$$\n",
+    "U(\\theta_1, \\theta_2, \\theta_3) =\n",
+    "\\begin{bmatrix}\n",
+    "e^{-i\\frac{\\theta_1}{2}} & 0 \\\\\n",
+    "0 & e^{i\\frac{\\theta_1}{2}}\n",
+    "\\end{bmatrix}\n",
+    "\\begin{bmatrix}\n",
+    "\\cos \\frac{\\theta_2}{2} &-\\sin \\frac{\\theta_2}{2} \\\\\n",
+    "\\sin \\frac{\\theta_2}{2} &\\cos \\frac{\\theta_2}{2}\n",
+    "\\end{bmatrix}\n",
+    "\\begin{bmatrix}\n",
+    "e^{-i\\frac{\\theta_3}{2}} & 0 \\\\\n",
+    "0 & e^{i\\frac{\\theta_3}{2}}\n",
+    "\\end{bmatrix}.\n",
+    "\\tag{27}\n",
+    "$$\n",
+    "\n",
+    "Multiply this matrix (ansatz) by $|0\\rangle$ to get a new 2-dimensional complex vector\n",
+    "\n",
+    "$$\n",
+    "|\\phi\\rangle = U(\\theta_1, \\theta_2, \\theta_3)|0\\rangle.\n",
+    "\\tag{28}\n",
+    "$$\n",
+    "\n",
+    "Then, we define the loss function as\n",
+    "\n",
+    "$$\n",
+    "\\min_{\\boldsymbol{\\theta}}\\mathcal{L}(\\theta_1, \\theta_2, \\theta_3)\n",
+    "= \\langle\\phi| H |\\phi\\rangle\n",
+    "= \\langle0| U^{\\dagger}H U |0\\rangle.\n",
+    "\\tag{29}\n",
+    "$$\n",
+    "\n",
+    "Let's see what we got after optimization!"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 12,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:04:24.823063Z",
+     "start_time": "2021-01-09T13:04:24.807113Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The randomly generated matrix H according to the spectral decomposition is:\n",
+      "[[0.30704576+0.j         0.06071073-0.22154654j]\n",
+      " [0.06071073+0.22154654j 0.69295424+0.j        ]] \n",
+      "\n",
+      "The eigenvalues of H are:\n",
+      "[0.2 0.8]\n"
+     ]
+    }
+   ],
+   "source": [
+    "from scipy.stats import unitary_group\n",
+    "\n",
+    "# V is a 2x2 random unitary matrix\n",
+    "V = unitary_group.rvs(2)\n",
+    "\n",
+    "# The diagonal elements in D are the eigenvalue of H\n",
+    "# You can change the diagonal element value here\n",
+    "D = np.diag([0.2, 0.8])\n",
+    "\n",
+    "# V_dagger is the Hermitian transpose of V\n",
+    "V_dagger = V.conj().T\n",
+    "\n",
+    "# @: Represents matrix multiplication\n",
+    "H = (V @ D @ V_dagger)\n",
+    "print('The randomly generated matrix H according to the spectral decomposition is:')\n",
+    "print(H,'\\n')\n",
+    "print('The eigenvalues of H are:')\n",
+    "print(np.linalg.eigh(H)[0])"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 16,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:05:28.870563Z",
+     "start_time": "2021-01-09T13:05:28.864497Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Hyper parameter settings\n",
+    "theta_size = 3 # set theta dimension\n",
+    "num_qubits = 1 # Set the number of qubits\n",
+    "ITR = 10 # Set the number of iterations\n",
+    "LR = 0.2 # Set the learning rate\n",
+    "SEED = 1 # Fix random seed for initializing theta parameter\n",
+    "\n",
+    "\n",
+    "# Set the circuit module separately\n",
+    "def U_theta(theta):\n",
+    "    \n",
+    "    # Initialize the circuit and add the quantum gates\n",
+    "    cir = UAnsatz(num_qubits)\n",
+    "    cir.rz(theta[0], 0)\n",
+    "    cir.ry(theta[1], 0)\n",
+    "    cir.rz(theta[2], 0)\n",
+    "    \n",
+    "    # Return parameterized matrix\n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 17,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:05:29.349729Z",
+     "start_time": "2021-01-09T13:05:29.340787Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class Optimization_ex2(fluid.dygraph.Layer):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0., high=2*np.pi, seed=SEED), dtype='float64'):\n",
+    "        super(Optimization_ex2, self).__init__()\n",
+    "        \n",
+    "        # Initialize a list of trainable parameters with length theta_size\n",
+    "        # And use the uniform distribution of [0, 2*pi] to fill the initial value\n",
+    "        self.theta = self.create_parameter(\n",
+    "        shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.H = fluid.dygraph.to_variable(H)\n",
+    "        \n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self):\n",
+    "        \n",
+    "        # Get the unitary matrix representation of the quantum neural network\n",
+    "        U = U_theta(self.theta)\n",
+    "        \n",
+    "        # Conjugate transpose operation\n",
+    "        U_dagger = dagger(U)\n",
+    "        \n",
+    "        # Calculate the loss function\n",
+    "        loss = matmul(U_dagger, matmul(self.H, U)).real[0][0]\n",
+    "        \n",
+    "        return loss"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 18,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:05:30.086892Z",
+     "start_time": "2021-01-09T13:05:29.956476Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 0 loss: 0.2064\n",
+      "iter: 1 loss: 0.2007\n",
+      "iter: 2 loss: 0.2033\n",
+      "iter: 3 loss: 0.2028\n",
+      "iter: 4 loss: 0.2013\n",
+      "iter: 5 loss: 0.2004\n",
+      "iter: 6 loss: 0.2008\n",
+      "iter: 7 loss: 0.2015\n",
+      "iter: 8 loss: 0.2016\n",
+      "iter: 9 loss: 0.2009\n",
+      "The minimum value of the loss function is: 0.20090539960637277\n"
+     ]
+    }
+   ],
+   "source": [
+    "loss_list = []\n",
+    "parameter_list = []\n",
+    "\n",
+    "# Initialize paddle dynamic graph mechanism\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    myLayer = Optimization_ex2([theta_size])\n",
+    "    \n",
+    "    # Generally speaking, we use Adam optimizer to get relatively good convergence\n",
+    "    # Of course you can change to SGD or RMS prop.\n",
+    "    optimizer = fluid.optimizer.AdamOptimizer(\n",
+    "    learning_rate = LR, parameter_list = myLayer.parameters())\n",
+    "    \n",
+    "    # Optimization cycle\n",
+    "    for itr in range(ITR):\n",
+    "        \n",
+    "        # Forward propagation calculates loss function\n",
+    "        loss = myLayer()[0]\n",
+    "        \n",
+    "        # Under the dynamic graph mechanism, back propagation minimizes the loss function\n",
+    "        loss.backward()\n",
+    "        optimizer.minimize(loss)\n",
+    "        myLayer.clear_gradients()\n",
+    "        \n",
+    "        # Record the learning curve\n",
+    "        loss_list.append(loss.numpy()[0])\n",
+    "        parameter_list.append(myLayer.parameters()[0].numpy())\n",
+    "        print('iter:', itr, 'loss: %.4f'% loss.numpy())\n",
+    "        \n",
+    "    print('The minimum value of the loss function is:', loss_list[-1])"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "We can change the eigenvalues of $H$. If the diagonal matrix after diagonalization is changed to\n",
+    "\n",
+    "$$\n",
+    "D = \\begin{bmatrix} 0.8 &0 \\\\ 0 &1.2 \\end{bmatrix}.\n",
+    "\\tag{30}\n",
+    "$$\n",
+    "\n",
+    "We still get the minimum eigenvalue of $\\lambda_{\\text{min}}(H)=0.8$. Can you find the reason behind it? Or is there any theory behind this?\n",
+    "\n",
+    "---"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Quantum Machine Learning Case Study\n",
+    "\n",
+    "## Variational Quantum Eigensolver - Unsupervised Learning\n",
+    "\n",
+    "At this stage, large-scale fault-tolerant quantum computers are still far from us. We can only build noisy intermediate-scale quantum (NISQ) computing devices. A promising type of algorithm suitable for NISQ devices is the quantum-classical hybrid algorithm, or variational quantum algorithms. People expect that this approach could surpass the performance of classical computers in certain applications. Among which, the Variational Quantum Eigensolver (VQE) is such an important application. It uses a parameterized circuit to search the vast Hilbert space and uses the gradient descent or other classical optimization methods to find the optimal parameters, which yield a state that is close to the ground state of a given Hamiltonian (find the minimum eigenvalue of a Hermitian matrix). Let's go through the following two-qubit example.\n",
+    "\n",
+    "Suppose we want to find the ground state of the following Hamiltonian:\n",
+    "\n",
+    "$$\n",
+    "H = 0.4 \\, Z \\otimes I + 0.4 \\, I \\otimes Z + 0.2 \\, X \\otimes X.\n",
+    "\\tag{31}\n",
+    "$$\n",
+    "\n",
+    "Given the following quantum neural network architecture\n",
+    "\n",
+    "![intro-fig-vqeAnsatz](./figures/intro-fig-vqeAnsatz.png)\n",
+    "\n",
+    "We have learned how to build this circuit. If you forget, please go to section **Quantum Neural Network**."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 35,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:08:40.727331Z",
+     "start_time": "2021-01-09T13:08:40.721736Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import numpy as np\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import pauli_str_to_matrix\n",
+    "\n",
+    "# First generate the Hamiltonian under Pauli string representation\n",
+    "# H_info is equivalent to 0.4*kron(I, Z) + 0.4*kron(Z, I) + 0.2*kron(X, X)\n",
+    "# Among them, X, Y, Z are the Pauli matrix and I is the identity matrix\n",
+    "H_info = [[0.4,'z0'], [0.4,'z1'], [0.2,'x0,x1']]\n",
+    "\n",
+    "# Set hyper parameter\n",
+    "num_qubits = 2\n",
+    "theta_size = 4\n",
+    "ITR = 10\n",
+    "LR = 0.6\n",
+    "SEED = 1\n",
+    "\n",
+    "# Convert the Hamiltonian into matrix representation\n",
+    "H_matrix = pauli_str_to_matrix(H_info, num_qubits)"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 36,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:08:41.137003Z",
+     "start_time": "2021-01-09T13:08:41.125057Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class vqe_demo(fluid.dygraph.Layer):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0., high=2*np.pi, seed=SEED), dtype='float64'):\n",
+    "        super(vqe_demo, self).__init__()\n",
+    "        \n",
+    "        # Initialize a list of learnable parameters with length theta_size\n",
+    "        # Use the uniform distribution of [0, 2*pi] to fill the initial value\n",
+    "        self.theta = self.create_parameter(\n",
+    "        shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        \n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self):\n",
+    "        \n",
+    "        # Initial quantum circuit\n",
+    "        cir = UAnsatz(num_qubits)\n",
+    "        \n",
+    "        # Add quantum gates\n",
+    "        cir.ry(self.theta[0], 0)\n",
+    "        cir.ry(self.theta[1], 1)\n",
+    "        cir.cnot([0, 1])\n",
+    "        cir.ry(self.theta[2], 0)\n",
+    "        cir.ry(self.theta[3], 1)\n",
+    "        \n",
+    "        # Choose state vector operation mode\n",
+    "        cir.run_state_vector()\n",
+    "        \n",
+    "        # Calculate the expected value of H_info in the current quantum state\n",
+    "        # The formula is given by <psi|H|psi>\n",
+    "        loss = cir.expecval(H_info)\n",
+    "        \n",
+    "        return loss"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 37,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T13:08:44.573571Z",
+     "start_time": "2021-01-09T13:08:41.546193Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 0 loss: 0.3195\n",
+      "iter: 1 loss: -0.4650\n",
+      "iter: 2 loss: -0.7123\n",
+      "iter: 3 loss: -0.7690\n",
+      "iter: 4 loss: -0.7925\n",
+      "iter: 5 loss: -0.8096\n",
+      "iter: 6 loss: -0.8186\n",
+      "iter: 7 loss: -0.8225\n",
+      "iter: 8 loss: -0.8239\n",
+      "iter: 9 loss: -0.8244\n",
+      "The calculated ground state energy is: -0.8243582047336566\n",
+      "The real ground state energy is: -0.8246211251235321\n"
+     ]
+    }
+   ],
+   "source": [
+    "loss_list = []\n",
+    "parameter_list = []\n",
+    "\n",
+    "# Initialize paddle dynamic computational graph\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # Define network dimensions\n",
+    "    vqe = vqe_demo([theta_size])\n",
+    "    \n",
+    "    # We usually use Adam optimizer to get relatively good convergence\n",
+    "    # Of course you can change it to SGD, Adagrad, or RMS prop as we did here.\n",
+    "    optimizer = fluid.optimizer.AdagradOptimizer(\n",
+    "      learning_rate = LR, parameter_list = vqe.parameters())\n",
+    "    \n",
+    "    # Optimization cycle\n",
+    "    for itr in range(ITR):\n",
+    "        \n",
+    "        # Forward propagation calculates loss function\n",
+    "        loss = vqe()\n",
+    "        \n",
+    "        # Under the dynamic graph mechanism, back propagation minimizes the loss function\n",
+    "        loss.backward()\n",
+    "        optimizer.minimize(loss)\n",
+    "        vqe.clear_gradients()\n",
+    "        \n",
+    "        # Record the learning curve\n",
+    "        loss_list.append(loss.numpy()[0])\n",
+    "        parameter_list.append(vqe.parameters()[0].numpy())\n",
+    "        print('iter:', itr, 'loss: %.4f'% loss.numpy())\n",
+    "    \n",
+    "    \n",
+    "    print('The calculated ground state energy is:', loss_list[-1])\n",
+    "    print('The real ground state energy is:', np.linalg.eigh(H_matrix)[0][0])"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## References\n",
+    "\n",
+    "[1] Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information. (Cambridge university press, 2010).\n",
+    "\n",
+    "[2] Phillip Kaye, Laflamme, R. & Mosca, M. An Introduction to Quantum Computing. (2007).\n",
+    "\n",
+    "[3] Biamonte, J. et al. Quantum machine learning. [Nature 549, 195–202 (2017).](https://www.nature.com/articles/nature23474)\n",
+    "\n",
+    "[4] Schuld, M., Sinayskiy, I. & Petruccione, F. An introduction to quantum machine learning. [Contemp. Phys. 56, 172–185 (2015).](https://www.tandfonline.com/doi/abs/10.1080/00107514.2014.964942)\n",
+    "\n",
+    "[5] Benedetti, M., Lloyd, E., Sack, S. & Fiorentini, M. Parameterized quantum circuits as machine learning models. [Quantum Sci. Technol. 4, 043001 (2019).](https://iopscience.iop.org/article/10.1088/2058-9565/ab4eb5)\n",
+    "\n",
+    "[6] [Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
+    "\n",
+    "[7] [McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023 (2016).](https://iopscience.iop.org/article/10.1088/1367-2630/18/2/023023)\n",
+    "\n",
+    "[8] [Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).](https://www.nature.com/articles/nature23879)\n",
+    "\n",
+    "[9] [Mitarai, K., Negoro, M., Kitagawa, M. & Fujii, K. Quantum circuit learning. Phys. Rev. A 98, 032309 (2018).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.98.032309)"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

paddle_quantum/GIBBS/HGenerator.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -28,18 +28,18 @@ def H_generator():
     Generate a Hamiltonian with trivial descriptions
     Returns: A Hamiltonian
     """
-    # 生成用泡利字符串表示的特定的哈密顿量
+    # Generate Pauli string representing a specific Hamiltonian
     H = [[-1.0, 'z0,z1'], [-1.0, 'z1,z2'], [-1.0, 'z0,z2']]
 
-    # 生成哈密顿量的矩阵信息
-    N_SYS_B = 3  # 用于生成吉布斯态的子系统B的量子比特数
+    # Generate the marix form of the Hamiltonian
+    N_SYS_B = 3  # Number of qubits in subsystem B used to generate Gibbs state
     hamiltonian = pauli_str_to_matrix(H, N_SYS_B)
 
-    # 生成理想情况下的目标吉布斯态 rho
-    beta = 1.5  # 设置逆温度参数 beta
+    # Generate the target Gibbs state rho
+    beta = 1.5  # Set inverse temperature beta
     rho_G = scipy.linalg.expm(-1 * beta * hamiltonian) / np_trace(scipy.linalg.expm(-1 * beta * hamiltonian))
 
-    # 设置成 Paddle quantum 所支持的数据类型
+    # Convert to the data type supported by Paddle Quantum
     hamiltonian = hamiltonian.astype("complex128")
     rho_G = rho_G.astype("complex128")
     return hamiltonian, rho_G
\ No newline at end of file

paddle_quantum/GIBBS/Paddle_GIBBS.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -27,7 +27,7 @@ from paddle_quantum.state import density_op
 from paddle_quantum.utils import state_fidelity, partial_trace
 from paddle_quantum.GIBBS.HGenerator import H_generator
 
-SEED = 14  # 固定随机种子
+SEED = 14  # Choose the seed for random generator
 
 __all__ = [
     "U_theta",
@@ -41,17 +41,17 @@ def U_theta(initial_state, theta, N, D):
     Quantum Neural Network
     """
 
-    # 按照量子比特数量/网络宽度初始化量子神经网络
+    # Initialize the quantum neural network by the number of qubits (width of the network)
     cir = UAnsatz(N)
 
-    # 内置的 {R_y + CNOT} 电路模板
+    # Use in-built template (R_y + CNOT)
     cir.real_entangled_layer(theta[:D], D)
 
-    # 铺上最后一列 R_y 旋转门
+    # Add a layer of R_y rotation gate
     for i in range(N):
         cir.ry(theta=theta[D][i][0], which_qubit=i)
 
-    # 量子神经网络作用在给定的初始态上
+    # Act quantum neural network on initilized state
     final_state = cir.run_density_matrix(initial_state)
 
     return final_state
@@ -65,28 +65,26 @@ class Net(fluid.dygraph.Layer):
     def __init__(self, N, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * PI, seed=SEED),
                  dtype='float64'):
         super(Net, self).__init__()
-
-        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值
+        # Initialize theta by sampling from a uniform distribution [0, 2*pi]
         self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)
-
-        # 初始化 rho = |0..0><0..0| 的密度矩阵
+        # Set the initial state as rho = |0..0><0..0|
         self.initial_state = fluid.dygraph.to_variable(density_op(N))
 
-    # 定义损失函数和前向传播机制
+    # Define the loss function and forward propagation mechanism
     def forward(self, H, N, N_SYS_B, beta, D):
-        # 施加量子神经网络
+        # Apply quantum neural network onto the initial state
         rho_AB = U_theta(self.initial_state, self.theta, N, D)
-
-        # 计算偏迹 partial trace 来获得子系统B所处的量子态 rho_B
+        
+        # Calculate the partial tarce to get the state rho_B of subsystem B
         rho_B = partial_trace(rho_AB, 2 ** (N - N_SYS_B), 2 ** (N_SYS_B), 1)
 
-        # 计算三个子损失函数
+        # Calculate the three components of the loss function
         rho_B_squre = matmul(rho_B, rho_B)
         loss1 = (trace(matmul(rho_B, H))).real
         loss2 = (trace(rho_B_squre)).real * 2 / beta
         loss3 = - ((trace(matmul(rho_B_squre, rho_B))).real + 3) / (2 * beta)
-
-        # 最终的损失函数
+        
+        # Get the final loss function
         loss = loss1 + loss2 + loss3
 
         return loss, rho_B
@@ -95,48 +93,46 @@ class Net(fluid.dygraph.Layer):
 def Paddle_GIBBS(hamiltonian, rho_G, N=4, N_SYS_B=3, beta=1.5, D=1, ITR=50, LR=0.5):
     r"""
     Paddle_GIBBS
-    :param hamiltonian: 哈密顿量
-    :param rho_G: 目标吉布斯态 rho
-    :param N: 量子神经网络的宽度
-    :param N_SYS_B: 用于生成吉布斯态的子系统B的量子比特数
-    :param D: 设置量子神经网络中重复计算模块的深度 Depth
-    :param ITR: 设置训练的总迭代次数
-    :param LR: 设置学习速率
-    :return: todo
+    :param hamiltonian: Hamiltonian
+    :param rho_G: Target Gibbs state rho
+    :param N: Width of QNN
+    :param N_SYS_B: Number of qubits in subsystem B used to generate Gibbs state
+    :param D: Depth of QNN
+    :param ITR: Number of iterations
+    :param LR: Learning rate
+    :return: State prepared by optimized QNN
     """
-    # 初始化paddle动态图机制
+    # Initialize PaddlePaddle dynamic graph machanism
     with fluid.dygraph.guard():
-        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable
+        # We need to convert Numpy array to variable supported in PaddlePaddle
         H = fluid.dygraph.to_variable(hamiltonian)
 
-        # 确定网络的参数维度
+        # Fix the dimensions of network
         net = Net(N, shape=[D + 1, N, 1])
 
-        # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.
+        # Usually, we recommend Adam optimizer for better results. If you wish, you could use SGD or RMS prop.
         opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())
 
-        # 优化循环
+        # Optimization iterations
         for itr in range(1, ITR + 1):
-            # 前向传播计算损失函数并返回生成的量子态 rho_B
+            # Run forward propagation to calculate loss function and obtain state rho_B
             loss, rho_B = net(H, N, N_SYS_B, beta, D)
 
-            # 在动态图机制下，反向传播极小化损失函数
+            # In dynamic graph, run backward propogation to minimize loss function
             loss.backward()
             opt.minimize(loss)
             net.clear_gradients()
-
-            # 转换成 Numpy array 用以计算量子态的保真度 F(rho_B, rho_G)
+            # Convert variable to Numpy array to calculate fidelity F(rho_B, rho_G)
             rho_B = rho_B.numpy()
             fid = state_fidelity(rho_B, rho_G)
-
-            # 打印训练结果
+            # Print results
             if itr % 5 == 0:
                 print('iter:', itr, 'loss:', '%.4f' % loss.numpy(), 'fid:', '%.4f' % fid)
     return rho_B
 
 
 def main():
-    # gibbs Hamiltonian preparing
+    # Generate gibbs Hamiltonian
     hamiltonian, rho_G = H_generator()
     rho_B = Paddle_GIBBS(hamiltonian, rho_G)
     print(rho_B)

paddle_quantum/GIBBS/example/main.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -23,18 +23,18 @@ from paddle_quantum.GIBBS.Paddle_GIBBS import Paddle_GIBBS
 
 
 def main():
-    # 生成用泡利字符串表示的特定的哈密顿量
+    # Generate Pauli string representing a specific Hamiltonian
     H = [[-1.0, 'z0,z1'], [-1.0, 'z1,z2'], [-1.0, 'z0,z2']]
 
-    # 生成哈密顿量的矩阵信息
-    N_SYS_B = 3  # 用于生成吉布斯态的子系统B的量子比特数
+    # Generate the marix form of the Hamiltonian
+    N_SYS_B = 3  # Number of qubits in subsystem B used to generate Gibbs state
     hamiltonian = pauli_str_to_matrix(H, N_SYS_B)
 
-    # 生成理想情况下的目标吉布斯态 rho
-    beta = 1.5  # 设置逆温度参数 beta
+    # Generate the target Gibbs state rho
+    beta = 1.5  # Set inverse temperature beta
     rho_G = scipy.linalg.expm(-1 * beta * hamiltonian) / np_trace(scipy.linalg.expm(-1 * beta * hamiltonian))
 
-    # 设置成 Paddle quantum 所支持的数据类型
+    # Convert to the data type supported by Paddle Quantum
     hamiltonian = hamiltonian.astype("complex128")
     rho_G = rho_G.astype("complex128")
 

paddle_quantum/QAOA/Paddle_QAOA.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/QAOA/QAOA_Prefunc.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/QAOA/benchmark.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/QAOA/example/main.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/SSVQE/HGenerator.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -26,10 +26,10 @@ def H_generator(N):
     Generate a Hamiltonian with trivial descriptions
     Returns: A Hamiltonian
     """
-    # 生成用泡利字符串表示的随机哈密顿量
+    # Generate the Pauli string representing a random Hamiltonian
     hamiltonian = random_pauli_str_generator(N, terms=10)
     print("Random Hamiltonian in Pauli string format = \n", hamiltonian)
 
-    # 生成哈密顿量的矩阵信息
+    # Generate the marix form of the Hamiltonian
     H = pauli_str_to_matrix(hamiltonian, N)
     return H

paddle_quantum/SSVQE/Paddle_SSVQE.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -25,7 +25,7 @@ from paddle_quantum.circuit import UAnsatz
 from paddle_quantum.utils import dagger
 from paddle_quantum.SSVQE.HGenerator import H_generator
 
-SEED = 14  # 固定随机种子
+SEED = 14  # Choose the seed for random generator
 
 __all__ = [
     "U_theta",
@@ -39,13 +39,13 @@ def U_theta(theta, N):
     Quantum Neural Network
     """
 
-    # 按照量子比特数量/网络宽度初始化量子神经网络
+    # Initialize the quantum neural network by the number of qubits (width of the network)
     cir = UAnsatz(N)
 
-    # 调用内置的量子神经网络模板
+    # Use a built-in QNN template
     cir.universal_2_qubit_gate(theta)
 
-    # 返回量子神经网络所模拟的酉矩阵 U
+    # Return the Unitary matrix simulated by QNN
     return cir.U
 
 
@@ -58,18 +58,19 @@ class Net(fluid.dygraph.Layer):
                  dtype='float64'):
         super(Net, self).__init__()
 
-        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值
+        # Initialize theta by sampling from a uniform distribution [0, 2*pi]
         self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)
-
-    # 定义损失函数和前向传播机制
+        
+    # Define the loss function and forward propagation mechanism
     def forward(self, H, N):
-        # 施加量子神经网络
+        # Apply QNN onto the initial state
         U = U_theta(self.theta, N)
 
-        # 计算损失函数
+        # Calculate loss function
         loss_struct = matmul(matmul(dagger(U), H), U).real
 
-        # 输入计算基去计算每个子期望值，相当于取 U^dagger*H*U 的对角元
+        # Use computational basis to calculate each expectation value, which is the same
+        # as a diagonal element in U^dagger*H*U
         loss_components = [
             loss_struct[0][0],
             loss_struct[1][1],
@@ -77,7 +78,7 @@ class Net(fluid.dygraph.Layer):
             loss_struct[3][3]
         ]
 
-        # 最终加权求和后的损失函数
+        # Calculate the weighted loss function
         loss = 4 * loss_components[0] + 3 * loss_components[1] + 2 * loss_components[2] + 1 * loss_components[3]
 
         return loss, loss_components
@@ -86,36 +87,37 @@ class Net(fluid.dygraph.Layer):
 def Paddle_SSVQE(H, N=2, THETA_SIZE=15, ITR=50, LR=0.3):
     r"""
     Paddle_SSVQE
-    :param H: 哈密顿量
-    :param N: 量子比特数/量子神经网络的宽度
-    :param THETA_SIZE: 量子神经网络中参数的数量
-    :param ITR: 设置训练的总迭代次数
-    :param LR: 设置学习速率
-    :return: 哈密顿量的前几个最小特征值
+    :param H: Hamiltonian
+    :param N: Number of qubits/Width of QNN
+    :param THETA_SIZE: Number of paramaters in QNN
+    :param ITR: Number of iterations
+    :param LR: Learning rate
+    :return: First several smallest eigenvalues of the Hamiltonian
     """
-    # 初始化paddle动态图机制
+    
+    # Initialize PaddlePaddle dynamic graph machanism
     with fluid.dygraph.guard():
-        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable
+        # We need to convert Numpy array to variable supported in PaddlePaddle
         hamiltonian = fluid.dygraph.to_variable(H)
 
-        # 确定网络的参数维度
+        # Fix the dimensions of network
         net = Net(shape=[THETA_SIZE])
-
-        # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.
+        
+        # Use Adagrad optimizer
         opt = fluid.optimizer.AdagradOptimizer(learning_rate=LR, parameter_list=net.parameters())
 
-        # 优化循环
+        # Optimization iterations
         for itr in range(1, ITR + 1):
 
-            # 前向传播计算损失函数并返回估计的能谱
+            # Run forward propagation to calculate loss function and obtain energy spectrum
             loss, loss_components = net(hamiltonian, N)
 
-            # 在动态图机制下，反向传播极小化损失函数
+            # In dynamic graph, run backward propogation to minimize loss function
             loss.backward()
             opt.minimize(loss)
             net.clear_gradients()
-
-            # 打印训练结果
+            
+            # Print results
             if itr % 10 == 0:
                 print('iter:', itr, 'loss:', '%.4f' % loss.numpy()[0])
     return loss_components

paddle_quantum/SSVQE/example/main.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/VQE/Paddle_VQE.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -39,21 +39,20 @@ def U_theta(theta, Hamiltonian, N, D):
     """
     Quantum Neural Network
     """
-
-    # 按照量子比特数量/网络宽度初始化量子神经网络
+    # Initialize the quantum neural network by the number of qubits (width of the network)
     cir = UAnsatz(N)
 
-    # 内置的 {R_y + CNOT} 电路模板
+    # Use built-in template (R_y + CNOT)
     cir.real_entangled_layer(theta[:D], D)
 
-    # 铺上最后一列 R_y 旋转门
+    # Add a layer of R_y rotation gates
     for i in range(N):
         cir.ry(theta=theta[D][i][0], which_qubit=i)
 
-    # 量子神经网络作用在默认的初始态 |0000>上
+    # Act QNN on the default initial state |0000>
     cir.run_state_vector()
 
-    # 计算给定哈密顿量的期望值
+    # Calculate the expectation value of the given Hamiltonian
     expectation_val = cir.expecval(Hamiltonian)
 
     return expectation_val
@@ -67,12 +66,12 @@ class StateNet(fluid.dygraph.Layer):
     def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * PI), dtype="float64"):
         super(StateNet, self).__init__()
 
-        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值
+        # Initialize theta by sampling from a uniform distribution [0, 2*pi]
         self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)
 
-    # 定义损失函数和前向传播机制
+    # Define the loss function and forward propagation mechanism
     def forward(self, Hamiltonian, N, D):
-        # 计算损失函数/期望值
+        # Calculate loss function (expectation value)
         loss = U_theta(self.theta, Hamiltonian, N, D)
 
         return loss
@@ -81,46 +80,47 @@ class StateNet(fluid.dygraph.Layer):
 def Paddle_VQE(Hamiltonian, N, D=2, ITR=80, LR=0.2):
     r"""
     Main Learning network using dynamic graph
-    :param Hamiltonian:
-    :param N:
-    :param D: 设置量子神经网络中重复计算模块的深度 Depth
-    :param ITR: 设置训练的总迭代次数
-    :param LR: 设置学习速率
-    :return: return: Plot or No return
+    :param Hamiltonian: Hamiltonian
+    :param N: Width of QNN
+    :param D: Depth of QNN
+    :param ITR: Number of iterations
+    :param LR: Learning rate
+    :return: No return
     """
 
-    # 初始化paddle动态图机制
+    # Initialize PaddlePaddle dynamic graph machanism
     with fluid.dygraph.guard():
+        # Determine the dimensions of network
         # 确定网络的参数维度
         net = StateNet(shape=[D + 1, N, 1])
 
-        # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.
+        # Usually, we recommend Adam optimizer for better result. If you wish, you could use SGD or RMS prop.
         opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())
 
-        # 记录优化结果
+        # Record optimization results
         summary_iter, summary_loss = [], []
-
-        # 优化循环
+        
+        # Optimization iterations
         for itr in range(1, ITR + 1):
 
-            # 前向传播计算损失函数
+            # Run forward propagation to calculate loss function
             loss = net(Hamiltonian, N, D)
 
-            # 在动态图机制下，反向传播极小化损失函数
+            # In dynamic graph, run backward propogation to minimize loss function
             loss.backward()
             opt.minimize(loss)
             net.clear_gradients()
 
-            # 更新优化结果
+            # Update optimized results
             summary_loss.append(loss.numpy())
             summary_iter.append(itr)
 
-            # 打印结果
+            # Print results
             if itr % 20 == 0:
                 print("iter:", itr, "loss:", "%.4f" % loss.numpy())
                 print("iter:", itr, "Ground state energy:", "%.4f Ha" % loss.numpy())
 
-        # 储存训练结果到 output 文件夹
+        # Save results in the 'output' directory
         os.makedirs("output", exist_ok=True)
         savez("./output/summary_data", iter=summary_iter, energy=summary_loss)
 

paddle_quantum/VQE/benchmark.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/VQE/chemistrygen.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -31,7 +31,7 @@ __all__ = [
 # todo
 def Hamiltonian_str_convert(qubit_op):
     '''
-    转换提供的哈密顿量信息成为我们熟悉的泡利字符串
+    Convert provided Hamiltonian information to Pauli string
     '''
     info_dic = qubit_op.terms
 
@@ -96,7 +96,7 @@ def calc_H_rho_from_qubit_operator(qubit_op, n_qubits):
 def read_calc_H(geo_fn, multiplicity=1, charge=0):
     """
     Read and calc the H and rho
-    return: H,rho matrix
+    Returns: H,rho matrix
     """
 
     if not isinstance(geo_fn, str):  # geo_fn = 'h2.xyz'
@@ -132,7 +132,6 @@ def read_calc_H(geo_fn, multiplicity=1, charge=0):
 def main():
     """
     The main function
-    Returns:
     """
 
     filename = 'h2.xyz'

paddle_quantum/VQE/chemistrysub.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/VQE/example/main.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/VQSD/HGenerator.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -26,12 +26,12 @@ __all__ = ["generate_rho_sigma", ]
 
 def generate_rho_sigma():
     scipy.random.seed(SEED)
-    V = scipy.stats.unitary_group.rvs(4)  # 随机生成一个酉矩阵
-    D = diag([0.5, 0.3, 0.1, 0.1])  # 输入目标态 rho 的谱
+    V = scipy.stats.unitary_group.rvs(4)  # Generate a random unitary martrix
+    D = diag([0.5, 0.3, 0.1, 0.1])  # Input the spectrum of the target state rho
     V_H = V.conj().T
-    rho = V @ D @ V_H  # 生成 rho
-    # print(rho)  # 打印量子态 rho
+    rho = V @ D @ V_H  # Generate rho
+    # print(rho)  # Print quantum state rho
 
-    # 输入用来标记的量子态sigma
+    # Input the quantum state sigma
     sigma = diag([0.1, 0.2, 0.3, 0.4]).astype('complex128')
     return rho, sigma

paddle_quantum/VQSD/Paddle_VQSD.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -37,14 +37,14 @@ def U_theta(theta, N):
     """
     Quantum Neural Network
     """
-
-    # 按照量子比特数量/网络宽度初始化量子神经网络
+    
+    # Initialize the quantum neural network by the number of qubits (width of the network)
     cir = UAnsatz(N)
 
-    # 调用内置的量子神经网络模板
+    # Use built-in template
     cir.universal_2_qubit_gate(theta)
 
-    # 返回量子神经网络所模拟的酉矩阵 U
+    # Return the Unitary matrix simulated by QNN
     return cir.U
 
 
@@ -56,23 +56,22 @@ class Net(fluid.dygraph.Layer):
     def __init__(self, shape, rho, sigma, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * numpy.pi, seed=SEED),
                  dtype='float64'):
         super(Net, self).__init__()
-
-        # 将 Numpy array 转换成 Paddle 动态图模式中支持的 variable
+        # Convert Numpy array to variable supported in PaddlePaddle
         self.rho = fluid.dygraph.to_variable(rho)
         self.sigma = fluid.dygraph.to_variable(sigma)
 
-        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值
+        # Initialize theta by sampling from a uniform distribution [0, 2*pi]
         self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)
 
-    # 定义损失函数和前向传播机制
+    # Define the loss function and forward propagation mechanism
     def forward(self, N):
-        # 施加量子神经网络
+        # Apply quantum neural network onto the initial state
         U = U_theta(self.theta, N)
 
-        # rho_tilde 是将 U 作用在 rho 后得到的量子态 U*rho*U^dagger
+        # rho_tilda is the quantum state obtained by acting U on rho, which is U*rho*U^dagger
         rho_tilde = matmul(matmul(U, self.rho), dagger(U))
-
-        # 计算损失函数
+        
+        # Calculate loss function
         loss = trace(matmul(self.sigma, rho_tilde))
 
         return loss.real, rho_tilde
@@ -81,35 +80,35 @@ class Net(fluid.dygraph.Layer):
 def Paddle_VQSD(rho, sigma, N=2, THETA_SIZE=15, ITR=50, LR=0.1):
     r"""
     Paddle_VQSD
-    :param rho: 待对角化的量子态
-    :param sigma: 输入用来标记的量子态sigma
-    :param N: 量子神经网络的宽度
-    :param THETA_SIZE: 量子神经网络中参数的数量
-    :param ITR: 设置训练的总的迭代次数
-    :param LR: 设置学习速率
-    :return: 优化之后量子态rho接近对角态的numpy形式
+    :param rho: Qauntum state to be diagonalized
+    :param sigma: Quantum state sigma
+    :param N: Width of QNN
+    :param THETA_SIZE: Number of parameters in QNN
+    :param ITR: Number of iterations
+    :param LR: Learning rate
+    :return: Diagonalized quantum state after optimization 
     """
-    # 初始化paddle动态图机制
+    # Initialize PaddlePaddle dynamic graph machanism
     with fluid.dygraph.guard():
-        # 确定网络的参数维度
+        # Fix the dimensions of network
         net = Net(shape=[THETA_SIZE], rho=rho, sigma=sigma)
 
-        # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.
+        # Use Adagrad optimizer
         opt = fluid.optimizer.AdagradOptimizer(learning_rate=LR, parameter_list=net.parameters())
 
-        # 优化循环
+        # Optimization iterations
         for itr in range(ITR):
-
-            # 前向传播计算损失函数并返回估计的能谱
+            
+            # Run forward propagation to calculate loss function and obtain energy spectrum
             loss, rho_tilde = net(N)
             rho_tilde_np = rho_tilde.numpy()
-
-            # 在动态图机制下，反向传播极小化损失函数
+            
+            # In dynamic graph, run backward propogation to minimize loss function
             loss.backward()
             opt.minimize(loss)
             net.clear_gradients()
 
-            # 打印训练结果
+            # Print results
             if itr % 10 == 0:
                 print('iter:', itr, 'loss:', '%.4f' % loss.numpy()[0])
     return rho_tilde_np

paddle_quantum/VQSD/example/main.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/__init__.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -15,3 +15,5 @@
 r"""
 Paddle Quantum Library
 """
+
+name = "paddle_quantum"

paddle_quantum/circuit.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -20,8 +20,6 @@ import numpy as np
 from numpy import binary_repr, eye, identity
 import matplotlib.pyplot as plt
 
-from Simulator.main import StateTranfer, init_state_gen, measure_state
-
 import paddle
 from paddle.complex import kron as pp_kron
 from paddle.complex import reshape as complex_reshape
@@ -33,6 +31,7 @@ from paddle.fluid import dygraph
 from paddle.fluid.layers import reshape, cast, eye, zeros
 from paddle.fluid.framework import ComplexVariable
 
+from paddle_quantum.simulator import StateTranfer, init_state_gen, measure_state
 from paddle_quantum.utils import dagger, pauli_str_to_matrix
 from paddle_quantum.intrinsic import *
 from paddle_quantum.state import density_op
@@ -44,7 +43,7 @@ __all__ = [
 
 
 class UAnsatz:
-    r"""基于Paddle的动态图机制实现量子线路的 ``class`` 。
+    r"""基于PaddlePaddle的动态图机制实现量子线路的 ``class`` 。
 
     用户可以通过实例化该 ``class`` 来搭建自己的量子线路。
 
@@ -95,11 +94,11 @@ class UAnsatz:
                 cir.ry(theta[1], 1)
                 cir.rz(theta[2], 1)
                 vec = cir.run_state_vector(input_state_var).numpy()
-                print(f"运行后的向量是 {vec}")
+                print(f"The output state vector is {vec}")
 
         ::
 
-            运行后的向量是 [0.17470783-0.09544332j 0.59544332+0.32529217j 0.17470783-0.09544332j 0.59544332+0.32529217j]
+            The output state vector is [0.17470783-0.09544332j 0.59544332+0.32529217j 0.17470783-0.09544332j 0.59544332+0.32529217j]
         """
         state = init_state_gen(self.n, 0) if input_state is None else input_state
         old_shape = state.shape
@@ -155,11 +154,11 @@ class UAnsatz:
                 cir.ry(theta[1], 0)
                 cir.rz(theta[2], 0)
                 density = cir.run_density_matrix(input_state_var).numpy()
-                print(f"密度矩阵是\n{density}")
+                print(f"The output density matrix is\n{density}")
 
         ::
 
-            密度矩阵是
+            The output density matrix is
             [[ 0.35403671+0.j         -0.47686058-0.03603751j]
             [-0.47686058+0.03603751j  0.64596329+0.j        ]]
         """
@@ -194,11 +193,11 @@ class UAnsatz:
                 cir.h(0)
                 cir.cnot([0, 1])
                 matrix = cir.U
-                print("生成贝尔态电路的酉矩阵表示为\n",matrix.numpy())
+                print("The unitary matrix of the circuit for Bell state preparation is\n",matrix.numpy())
 
         ::
 
-            生成贝尔态电路的酉矩阵表示为
+            The unitary matrix of the circuit for Bell state preparation is
             [[ 0.70710678+0.j  0.        +0.j  0.70710678+0.j  0.        +0.j]
             [ 0.        +0.j  0.70710678+0.j  0.        +0.j  0.70710678+0.j]
             [ 0.        +0.j  0.70710678+0.j  0.        +0.j -0.70710678+0.j]
@@ -234,7 +233,7 @@ class UAnsatz:
  
         Args:
             theta (Variable): 旋转角度
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
  
         ..  code-block:: python
 
@@ -265,7 +264,7 @@ class UAnsatz:
 
         Args:
             theta (Variable): 旋转角度
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
 
         ..  code-block:: python
         
@@ -286,17 +285,17 @@ class UAnsatz:
                                                     dygraph.to_variable(np.array([0.0]))]])
 
     def rz(self, theta, which_qubit):
-        r"""添加关于y轴的单量子比特旋转门。
+        r"""添加关于z轴的单量子比特旋转门。
  
         其矩阵形式为：
         
         .. math::
         
-            \begin{bmatrix} e^{-\frac{i\theta}{2}} & 0 \\ 0 & e^{\frac{i\theta}{2}} \end{bmatrix}
+            \begin{bmatrix} 1 & 0 \\ 0 & e^{i\theta} \end{bmatrix}
  
         Args:
             theta (Variable): 旋转角度
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
  
         ..  code-block:: python
         
@@ -319,7 +318,7 @@ class UAnsatz:
     def cnot(self, control):
         r"""添加一个CNOT门。
  
-        对于2量子比特的量子线路，当control为 ``[0, 1]`` 时，其矩阵形式为：
+        对于2量子比特的量子线路，当 ``control`` 为 ``[0, 1]`` 时，其矩阵形式为：
         
         .. math::
         
@@ -329,7 +328,7 @@ class UAnsatz:
             \end{align}
  
         Args:
-            control (list): 作用在的qubit的编号，``control[0]`` 为控制位，``control[1]`` 为目标位，其值都应该在 :math:`[0, n)`范围内， :math:`n` 为该量子线路的量子比特数
+            control (list): 作用在的qubit的编号，``control[0]`` 为控制位，``control[1]`` 为目标位，其值都应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
 
         ..  code-block:: python
         
@@ -356,7 +355,7 @@ class UAnsatz:
             \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}
  
         Args:
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
  
         .. code-block:: python
             
@@ -381,7 +380,7 @@ class UAnsatz:
             \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}
  
         Args:
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
  
         .. code-block:: python
             
@@ -406,7 +405,7 @@ class UAnsatz:
             \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}
  
         Args:
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
  
         .. code-block:: python
         
@@ -424,14 +423,14 @@ class UAnsatz:
     def h(self, which_qubit):
         r"""添加一个单量子比特的Hadamard门。
 
-        具体形式为
+        其矩阵形式为：
 
         .. math::
         
             H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1&1\\1&-1 \end{bmatrix}
 
         Args:
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
         """
         assert 0 <= which_qubit < self.n, "the qubit should >= 0 and < n(the number of qubit)"
         self.__history.append(['h', [which_qubit], None])
@@ -439,14 +438,14 @@ class UAnsatz:
     def s(self, which_qubit):
         r"""添加一个单量子比特的S门。
 
-        具体形式为
+        其矩阵形式为：
 
         .. math::
         
             S = \begin{bmatrix} 1&0\\0&i \end{bmatrix}
 
         Args:
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
         """
         assert 0 <= which_qubit < self.n, "the qubit should >= 0 and < n(the number of qubit)"
         self.__history.append(['u', [which_qubit], [dygraph.to_variable(np.array([0.0])),
@@ -456,14 +455,14 @@ class UAnsatz:
     def t(self, which_qubit):
         r"""添加一个单量子比特的T门。
 
-        具体形式为
+        其矩阵形式为：
 
         .. math::
 
             T = \begin{bmatrix} 1&0\\0&e^\frac{i\pi}{4} \end{bmatrix}
 
         Args:
-            which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+            which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
         """
         assert 0 <= which_qubit < self.n, "the qubit should >= 0 and < n(the number of qubit)"
         self.__history.append(['u', [which_qubit], [dygraph.to_variable(np.array([0.0])),
@@ -473,7 +472,7 @@ class UAnsatz:
     def u3(self, theta, phi, lam, which_qubit):
         r"""添加一个单量子比特的旋转门。
 
-        具体形式为
+        其矩阵形式为：
 
         .. math::
         
@@ -489,7 +488,7 @@ class UAnsatz:
               theta (Variable): 旋转角度 :math:`\theta` 。
               phi (Variable): 旋转角度 :math:`\phi` 。
               lam (Variable): 旋转角度 :math:`\lambda` 。
-              which_qubit (int): 作用在的qubit的编号，其值应该在[0, n)范围内，n为该量子线路的量子比特数
+              which_qubit (int): 作用在的qubit的编号，其值应该在 :math:`[0, n)` 范围内， :math:`n` 为该量子线路的量子比特数
         """
         assert 0 <= which_qubit < self.n, "the qubit should >= 0 and < n(the number of qubit)"
         self.__history.append(['u', [which_qubit], [theta, phi, lam]])
@@ -564,11 +563,11 @@ class UAnsatz:
         r"""对量子线路输出的量子态进行测量。
 
         Warning:
-            当plot为True时，当前量子线路的量子比特数需要小于6，否则无法绘制图片，会抛出异常。
+            当 ``plot`` 为 ``True`` 时，当前量子线路的量子比特数需要小于6，否则无法绘制图片，会抛出异常。
 
         Args:
             which_qubits (list, optional): 要测量的qubit的编号，默认全都测量
-            shots (int, optional): 该量子线路输出的量子态的测量次数，默认为1024次；若为0，则输出测量期望值的精确值
+            shots (int, optional): 该量子线路输出的量子态的测量次数，默认为1024次；若为0，则返回测量结果的精确概率分布
             plot (bool, optional): 是否绘制测量结果图，默认为 ``False`` ，即不绘制
         
         Returns:
@@ -586,11 +585,11 @@ class UAnsatz:
                 cir.cnot([0,1])
                 cir.run_state_vector()
                 result = cir.measure(shots = 2048, which_qubits = [1])
-                print(f"测量第1号量子比特2048次的结果是{result}")
+                print(f"The results of measuring qubit 1 2048 times are {result}")
 
         ::
 
-            测量第1号量子比特2048次的结果是{'0': 964, '1': 1084}
+            The results of measuring qubit 1 2048 times are {'0': 964, '1': 1084}
 
         .. code-block:: python
         
@@ -602,11 +601,11 @@ class UAnsatz:
                 cir.cnot([0,1])
                 cir.run_state_vector()
                 result = cir.measure(shots = 0, which_qubits = [1])
-                print(f"测量第1号量子比特的概率结果是{result}")
+                print(f"The probability distribution of measurement results on qubit 1 is {result}")
 
         ::
 
-            测量第1号量子比特的概率结果是{'0': 0.4999999999999999, '1': 0.4999999999999999}
+            The probability distribution of measurement results on qubit 1 is {'0': 0.4999999999999999, '1': 0.4999999999999999}
         """
         if self.__run_state == 'state_vector':
             state = self.__state
@@ -672,11 +671,11 @@ class UAnsatz:
                 cir.rx(theta[2], 2)
                 cir.run_state_vector(input_state_var)
                 expect_value = cir.expecval(H_info).numpy()
-                print(f'计算得到的{H_info}期望值是{expect_value}')
+                print(f'Calculated expectation value of {H_info} is {expect_value}')
         
         ::
         
-            计算得到的[[0.1, 'x1'], [0.2, 'y0,z4']]期望值是[0.05403023]
+            Calculated expectation value of [[0.1, 'x1'], [0.2, 'y0,z4']] is [0.05403023]
         
         .. code-block:: python
             
@@ -697,11 +696,11 @@ class UAnsatz:
                 cir.rz(theta[2], 2)
                 cir.run_density_matrix(input_state_var)
                 expect_value = cir.expecval(H_info).numpy()
-                print(f'计算得到的{H_info}期望值是{expect_value}')
+                print(f'Calculated expectation value of {H_info} is {expect_value}')
         
         ::
 
-            计算得到的[[0.1, 'x1'], [0.2, 'y0,z4']]期望值是[-0.02171538]
+            Calculated expectation value of [[0.1, 'x1'], [0.2, 'y0,z4']] is [-0.02171538]
         """
         if self.__run_state == 'state_vector':
             return vec_expecval(H, self.__state).real
@@ -731,17 +730,17 @@ class UAnsatz:
                 cir.superposition_layer()
                 cir.run_state_vector()
                 result = cir.measure(shots = 0)
-                print(f"测量全部量子比特的结果是{result}")
+                print(f"The probability distribution of measurement results on both qubits is {result}")
 
         ::
 
-            测量全部量子比特结果是{'00': 0.2499999999999999, '01': 0.2499999999999999, '10': 0.2499999999999999, '11': 0.2499999999999999}
+            The probability distribution of measurement results on both qubits is {'00': 0.2499999999999999, '01': 0.2499999999999999, '10': 0.2499999999999999, '11': 0.2499999999999999}
         """
         for i in range(self.n):
             self.h(i)
 
     def weak_superposition_layer(self):
-        r"""添加一层Hadamard的平方根门，即 :math:`\sqrt{H}` 门。
+        r"""添加一层旋转角度为 :math:`\pi/4` 的Ry门。
 
         代码示例:
 
@@ -754,18 +753,18 @@ class UAnsatz:
                 cir.weak_superposition_layer()
                 cir.run_state_vector()
                 result = cir.measure(shots = 0)
-                print(f"测量全部量子比特的结果是{result}")
+                print(f"The probability distribution of measurement results on both qubits is {result}")
 
         ::
 
-            测量全部量子比特的结果是{'00': 0.7285533905932737, '01': 0.12500000000000003, '10': 0.12500000000000003, '11': 0.021446609406726238}
+            The probability distribution of measurement results on both qubits is {'00': 0.7285533905932737, '01': 0.12500000000000003, '10': 0.12500000000000003, '11': 0.021446609406726238}
         """
         _theta = fluid.dygraph.to_variable(np.array([np.pi / 4]))  # Used in fixed Ry gate
         for i in range(self.n):
             self.ry(_theta, i)
 
     def real_entangled_layer(self, theta, depth):
-        r"""添加一层包含Ry门的强纠缠层。
+        r"""添加 ``depth`` 层包含Ry门和CNOT门的强纠缠层。
 
         Note:
             这一层量子门的数学表示形式为实数酉矩阵。
@@ -812,7 +811,7 @@ class UAnsatz:
             self.cnot([self.n - 1, 0])
 
     def complex_entangled_layer(self, theta, depth):
-        r"""添加一层包含U3门的强纠缠层。
+        r"""添加 ``depth`` 层包含U3门和CNOT门的强纠缠层。
 
         Note:
             这一层量子门的数学表示形式为复数酉矩阵。
@@ -967,7 +966,7 @@ class UAnsatz:
             self.__add_complex_block(theta[int((i - position[0]) / 2)], [i, i + 1])
 
     def real_block_layer(self, theta, depth):
-        r"""添加一层包含Ry门的弱纠缠层。
+        r"""添加 ``depth`` 层包含Ry门和CNOT门的弱纠缠层。
 
         Note:
             这一层量子门的数学表示形式为实数酉矩阵。
@@ -1014,7 +1013,7 @@ class UAnsatz:
                 self.__add_real_layer(theta[i][int((self.n - 1) / 2):], [1, self.n - 1])
 
     def complex_block_layer(self, theta, depth):
-        r"""添加一层包含U3门的弱纠缠层。
+        r"""添加 ``depth`` 层包含U3门和CNOT门的弱纠缠层。
         
         Note:
             这一层量子门的数学表示形式为复数酉矩阵。
@@ -1061,7 +1060,7 @@ class UAnsatz:
                 self.__add_complex_layer(theta[i][int((self.n - 1) / 2):], [1, self.n - 1])
 
 
-def local_H_prob(cir, hamiltonian, shots=1024):
+def __local_H_prob(cir, hamiltonian, shots=1024):
     r"""
     构造出Pauli测量电路并测量ancilla，处理实验结果来得到 ``H`` (只有一项)期望值的实验测量值。
 
@@ -1137,15 +1136,15 @@ def H_prob(cir, H, shots=1024):
             cir.rz(theta[2], 1)
             result_1 = H_prob(cir, H_info, shots = experiment_shots)
             result_2 = H_prob(cir, H_info, shots = 0)
-            print(f'消耗 {experiment_shots} 次测量后的期望值实验值是 {result_1}')
-            print(f'H期望值精确值是 {result_2}')
+            print(f'The expectation value obtained by {experiment_shots} measurements is {result_1}')
+            print(f'The accurate expectation value of H is {result_2}')
 
     ::
 
-        消耗 1024 次测量后的期望值实验值是 0.2326171875
-        H期望值精确值是 0.21242202548207134
+        The expectation value obtained by 1024 measurements is 0.2326171875
+        The accurate expectation value of H is 0.21242202548207134
     """
     expval = 0
     for term in H:
-        expval += term[0] * local_H_prob(cir, term[1], shots=shots)
+        expval += term[0] * __local_H_prob(cir, term[1], shots=shots)
     return expval

paddle_quantum/intrinsic.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.

paddle_quantum/state.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -57,7 +57,7 @@ def vec(n):
 
 
 def vec_random(n, real_or_complex=2):
-    r"""随机生成一个量子态，使用numpy形式。
+    r"""随机生成一个量子态的numpy形式。
 
     Args:
         n (int): 量子比特数量
@@ -152,7 +152,7 @@ def density_op_random(n, real_or_complex=2, rank=None):
     Args:
         n (int): 量子比特数量
         real_or_complex (int, optional): 默认为2，即生成复数组，若为1，则生成实数组
-        rank (int, optional): 矩阵的秩，默认为 :math:`2^n` （当rank为 ``None`` 时）
+        rank (int, optional): 矩阵的秩，默认为 :math:`2^n` （当 ``rank`` 为 ``None`` 时）
 
     Returns:
         numpy.ndarray: 一个形状为 ``(2**n, 2**n)`` 的numpy数组

paddle_quantum/utils.py

-# Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
+# Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
 #
 # Licensed under the Apache License, Version 2.0 (the "License");
 # you may not use this file except in compliance with the License.
@@ -59,10 +59,10 @@ def partial_trace(rho_AB, dim1, dim2, A_or_B):
         rho_AB (ComplexVariable): 输入的量子态
         dim1 (int): 系统A的维数
         dim2 (int): 系统B的维数
-        A_or_B (int): 1或者2，1表示去除A，2表示去除B
+        A_or_B (int): 1或者2，1表示计算系统A上的偏迹，2表示计算系统B上的偏迹
 
     Returns:
-        ComplexVariable: 量子态的偏迹
+        ComplexVariable: 输入的量子态的偏迹
 
     """
     if A_or_B == 2:
@@ -126,8 +126,8 @@ def gate_fidelity(U, V):
     :math:`U` 是一个 :math:`2^n\times 2^n` 的 Unitary 矩阵。
 
     Args:
-        U (numpy.ndarray): 量子门的酉矩阵形式
-        V (numpy.ndarray): 量子门的酉矩阵形式
+        U (numpy.ndarray): 量子门 :math:`U` 的酉矩阵形式
+        V (numpy.ndarray): 量子门 :math:`V` 的酉矩阵形式
 
     Returns:
         float: 输入的量子门之间的保真度
@@ -215,7 +215,7 @@ def NKron(matrix_A, matrix_B, *args):
         C = density_op_random(2)
         result = NKron(A, B, C)
 
-    ``result`` 应为： :math:`A \otimes B \otimes C`
+    ``result`` 应为 :math:`A \otimes B \otimes C`
     """
     return reduce(lambda result, index: np_kron(result, index), args, np_kron(matrix_A, matrix_B), )
 

setup.py

@@ -16,14 +16,30 @@
 Install library to site-packages
 """
 
-from setuptools import setup
+import setuptools
 
-setup(
-    name='paddle_quantum',
-    version='1.1.0',
-    description='Paddle Quantum circuit and function',
+with open("README.md", "r", encoding="utf-8") as fh:
+    long_description = fh.read()
+
+setuptools.setup(
+    name='paddle-quantum',
+    version='1.1.1',
     author='Institute for Quantum Computing, Baidu INC.',
     author_email='quantum@baidu.com',
-    url='http://quantum.baidu.com',
-    packages=['paddle_quantum'],
-    install_requires=['paddlepaddle==1.8.5', 'networkx>=2.4', 'matplotlib>=3.3.0', 'interval>=1.0.0', 'progressbar>=2.5'])
+    description='Paddle Quantum is a quantum machine learning (QML) toolkit developed based on Baidu PaddlePaddle.',
+    long_description=long_description,
+    long_description_content_type="text/markdown",
+    url='http://qml.baidu.com',
+    packages=['paddle_quantum', 'paddle_quantum.GIBBS', 'paddle_quantum.QAOA', 'paddle_quantum.SSVQE', 'paddle_quantum.VQE', 'paddle_quantum.VQSD',
+              'paddle_quantum.GIBBS.example', 'paddle_quantum.QAOA.example', 'paddle_quantum.SSVQE.example', 'paddle_quantum.VQE.example', 'paddle_quantum.VQSD.example'],
+    install_requires=['paddlepaddle==1.8.5', 'networkx>=2.4', 'matplotlib>=3.3.0', 'interval>=1.0.0', 'progressbar>=2.5'],
+    python_requires='>=3.6, <4',
+    classifiers=[
+        'Programming Language :: Python :: 3',
+        'License :: OSI Approved :: Apache Software License',
+        'Operating System :: OS Independent',
+    ],
+    project_urls={
+        'Documentation': 'https://qml.baidu.com/api/introduction.html',
+        'Source': 'https://github.com/PaddlePaddle/Quantum/',
+        'Tracker': 'https://github.com/PaddlePaddle/Quantum/issues'},)

tools/copyright.hook

@@ -9,7 +9,7 @@ import subprocess
 import platform
 
 COPYRIGHT = '''
-Copyright (c) 2020 Paddle Quantum Authors. All Rights Reserved.
+Copyright (c) 2021 Paddle Quantum Authors. All Rights Reserved.
 
 Licensed under the Apache License, Version 2.0 (the "License");
 you may not use this file except in compliance with the License.

tutorial/Barren/BarrenPlateaus_CN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# 量子神经网络的贫瘠高原效应\n",
+    "\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 概览\n",
+    "\n",
+    "在经典神经网络的训练中，基于梯度的优化方法不仅仅会遇到局部最小值的问题，同时还要面对鞍点等附近梯度近似于零的几何结构。相对应的，在量子神经网络中也存在着一种**贫瘠高原效应**（Barren plateaus）。这个奇特的现象首先是由 McClean et al. 在 2018 年发现 [[arXiv:1803.11173]](https://arxiv.org/abs/1803.11173)。简单来说，就是当你选取的随机电路结构满足一定复杂程度时优化曲面（Optimization landscape）会变得很平坦，从而导致基于梯度下降的优化方法很难找到全局最小值。对于大多数的变分量子算法（VQE等等），这个现象意味着当量子比特数量越来越多时，选取随机结构的电路有可能效果并不好。这会让你设计的损失函数所对应的优化曲面变成一个巨大的高原，让从而导致量子神经网络的训练愈加困难。你随机找到的初始值很难逃离这个高原，梯度下降收敛速度会很缓慢。\n",
+    "\n",
+    "![BP-fig-barren](./figures/BP-fig-barren-cn.png)\n",
+    "\n",
+    "图片由 [Gradient Descent Viz](https://github.com/lilipads/gradient_descent_viz) 生成\n",
+    "\n",
+    "本教程主要讨论如何在量桨（PaddleQuantum）平台上展示贫瘠高原这一现象。其中并不涉及任何算法创新，但能提升读者对于量子神经网络训练中梯度问题的认识。首先我们先引入必要的 library和 package：\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:14:18.886153Z",
+     "start_time": "2021-01-09T09:14:18.869759Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import time\n",
+    "import numpy as np\n",
+    "from matplotlib import pyplot as plt \n",
+    "import paddle.fluid as fluid\n",
+    "from paddle.fluid.framework import ComplexVariable\n",
+    "from paddle.complex import matmul, transpose   \n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import dagger\n",
+    "from paddle_quantum.state import density_op"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 随机的网络结构\n",
+    "\n",
+    "这里我们按照原作者 McClean (2018)论文中提及的类似方法搭建如下随机电路（目前我们不支持内置的 control-Z 门，方便起见用 CNOT 替代）：\n",
+    "\n",
+    "![BP-fig-Barren_circuit](./figures/BP-fig-Barren_circuit.png)\n",
+    "\n",
+    "首先作用在所有量子比特上绕布洛赫球的 Y-轴旋转 $\\pi/4$。\n",
+    "\n",
+    "其余的结构加起来构成一个模块（Block）, 每个模块共分为两层：\n",
+    "\n",
+    "- 第一层搭建随机的旋转门, 其中 $R_{\\ell,n} \\in \\{R_x, R_y, R_z\\}$。下标 $\\ell$ 表示处于第 $\\ell$ 个重复的模块， 上图中 $\\ell =1$。第二个下标 $n$ 表示作用在第几个量子比特上。\n",
+    "- 第二层由 CNOT 门组成，作用在每两个相邻的量子比特上。\n",
+    "\n",
+    "在量桨中, 我们可以这么搭建。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:06:50.244448Z",
+     "start_time": "2021-01-09T09:06:50.204352Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def rand_circuit(theta, target, num_qubits):\n",
+    "    # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
+    "    const = fluid.dygraph.to_variable(np.array([np.pi/4]))\n",
+    "    \n",
+    "    # 初始化量子电路\n",
+    "    cir = UAnsatz(num_qubits)\n",
+    "    \n",
+    "    # ============== 第一层 ==============\n",
+    "    # 固定角度的 Ry 旋转门\n",
+    "    for i in range(num_qubits):\n",
+    "        cir.ry(const, i)\n",
+    "\n",
+    "    # ============== 第二层 ==============\n",
+    "    # target是一个随机的数组,用来帮助我们抽取随机的单比特门 \n",
+    "    for i in range(num_qubits):\n",
+    "        if target[i] == 0:\n",
+    "            cir.rz(theta[i], i)\n",
+    "        elif target[i] == 1:\n",
+    "            cir.ry(theta[i], i)\n",
+    "        else:\n",
+    "            cir.rx(theta[i], i)\n",
+    "            \n",
+    "    # ============== 第三层 ==============\n",
+    "    # 搭建两两相邻的 CNOT 门\n",
+    "    for i in range(num_qubits - 1):\n",
+    "        cir.cnot([i, i + 1])\n",
+    "        \n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 损失函数与优化曲面 \n",
+    "\n",
+    "当我们确定了电路的结构之后，我们还需要定义一个损失函数（Loss function）来确定优化曲面（Optimization landscape）。按照原作者 McClean (2018)论文中提及的，我们采用 VQE算法中常用的损失函数：\n",
+    "\n",
+    "$$\n",
+    "\\mathcal{L}(\\boldsymbol{\\theta})= \\langle0| U^{\\dagger}(\\boldsymbol{\\theta})H U(\\boldsymbol{\\theta}) |0\\rangle,\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "其中的酉矩阵 $U(\\boldsymbol{\\theta})$ 就是我们上一部分搭建的带有随机结构的量子神经网络。对于其中的哈密顿量 $H$ 我们不妨先取最简单的形式 $H = |00\\cdots 0\\rangle\\langle00\\cdots 0|$。设定好这些后，我们就可以从最简单的两个量子比特的情形开始采样了 -- 生成 300 组随机网络结构和不同的随机初始参数 $\\{\\theta_{\\ell,n}^{(i)}\\}_{i=1}^{300}$。每次计算梯度都是按照 VQE 的解析梯度公式计算关于 **第一个参数 $\\theta_{1,1}$** 的偏导数。然后统计得到的这 300 个梯度的平均值和方差。其中解析梯度的公式为：\n",
+    "\n",
+    "$$\n",
+    "\\partial \\theta_{j} \n",
+    "\\equiv \\frac{\\partial \\mathcal{L}}{\\partial \\theta_j}\n",
+    "= \\frac{1}{2} \\big[\\mathcal{L}(\\theta_j + \\frac{\\pi}{2}) - \\mathcal{L}(\\theta_j - \\frac{\\pi}{2})\\big].\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "具体推导请参见：[arXiv:1803.00745](https://arxiv.org/abs/1803.00745)\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:06:59.420658Z",
+     "start_time": "2021-01-09T09:06:50.248652Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "主程序段总共运行了 9.145337104797363 秒\n",
+      "采样 300 个随机网络关于第一个参数梯度的均值是： 0.005925709445960606\n",
+      "采样 300 个随机网络关于第一个参数梯度的方差是： 0.028249053148446363\n"
+     ]
+    }
+   ],
+   "source": [
+    "# 超参数设置\n",
+    "np.random.seed(42)        # 固定 Numpy 的随机种子\n",
+    "N = 2                     # 设置量子比特数量 \n",
+    "samples = 300             # 设定采样随机网络结构的数量\n",
+    "THETA_SIZE = N            # 设置参数 theta 的大小\n",
+    "ITR = 1                   # 设置迭代次数\n",
+    "LR = 0.2                  # 设定学习速率\n",
+    "SEED = 1                  # 固定优化器中随机初始化的种子\n",
+    "\n",
+    "# 初始化梯度数值的寄存器\n",
+    "grad_info = []\n",
+    "\n",
+    "class manual_gradient(fluid.dygraph.Layer):\n",
+    "    \n",
+    "    # 初始化一个可学习参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * np.pi, seed=1),dtype='float64'):\n",
+    "        super(manual_gradient, self).__init__()\n",
+    "        \n",
+    "        # 将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
+    "        self.H = fluid.dygraph.to_variable(density_op(N))\n",
+    "        \n",
+    "    # 定义损失函数和前向传播机制    \n",
+    "    def forward(self):\n",
+    "        \n",
+    "        # 初始化三个 theta 参数列表\n",
+    "        theta_np = np.random.uniform(low=0., high= 2 * np.pi, size=(THETA_SIZE))\n",
+    "        theta_plus_np = np.copy(theta_np) \n",
+    "        theta_minus_np = np.copy(theta_np) \n",
+    "        \n",
+    "        # 修改用以计算解析梯度\n",
+    "        theta_plus_np[0] += np.pi/2\n",
+    "        theta_minus_np[0] -= np.pi/2\n",
+    "        \n",
+    "        # 将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
+    "        theta = fluid.dygraph.to_variable(theta_np)\n",
+    "        theta_plus = fluid.dygraph.to_variable(theta_plus_np)\n",
+    "        theta_minus = fluid.dygraph.to_variable(theta_minus_np)\n",
+    "        \n",
+    "        # 生成随机目标，在 rand_circuit 中随机选取电路门\n",
+    "        target = np.random.choice(3, N)      \n",
+    "        \n",
+    "        U = rand_circuit(theta, target, N)\n",
+    "        U_dagger = dagger(U) \n",
+    "        U_plus = rand_circuit(theta_plus, target, N)\n",
+    "        U_plus_dagger = dagger(U_plus) \n",
+    "        U_minus = rand_circuit(theta_minus, target, N)\n",
+    "        U_minus_dagger = dagger(U_minus) \n",
+    "\n",
+    "        # 计算解析梯度\n",
+    "        grad = (matmul(matmul(U_plus_dagger,self.H), U_plus).real[0][0] - matmul(matmul(U_minus_dagger, self.H), U_minus).real[0][0])/2  \n",
+    "\n",
+    "        return grad\n",
+    "\n",
+    "# 定义主程序段\n",
+    "def main():\n",
+    "    \n",
+    "    # 初始化paddle动态图机制\n",
+    "    with fluid.dygraph.guard():\n",
+    "        \n",
+    "        # 设置QNN的维度\n",
+    "        sampling = manual_gradient(shape=[THETA_SIZE])\n",
+    "        \n",
+    "        # 采样获得梯度信息\n",
+    "        grad = sampling()   \n",
+    "        \n",
+    "    return grad.numpy()\n",
+    "\n",
+    "\n",
+    "# 记录运行时间\n",
+    "time_start = time.time()\n",
+    "\n",
+    "# 开始采样\n",
+    "for i in range(samples):\n",
+    "    if __name__ == '__main__':\n",
+    "        grad = main()\n",
+    "        grad_info.append(grad)\n",
+    "\n",
+    "time_span = time.time() - time_start        \n",
+    "print('主程序段总共运行了', time_span, '秒')\n",
+    "print(\"采样\", samples, \"个随机网络关于第一个参数梯度的均值是：\", np.mean(grad_info))\n",
+    "print(\"采样\", samples, \"个随机网络关于第一个参数梯度的方差是：\", np.var(grad_info))"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 优化曲面的可视化\n",
+    "\n",
+    "接下来我们试着利用 Matplotlib来可视化这个优化曲面（Optimization landscape）。在**两个量子比特**的情况下，我们只有两个参数 $\\theta_1$ 和 $\\theta_2$, 并且第二层的随机电路电路总共有9种情况。这个很容易画出来：\n",
+    "\n",
+    "![BP-fig-landscape2](./figures/BP-fig-landscape2.png)\n",
+    "\n",
+    "可以看到的是最后一张图中 $R_z$-$R_z$ 结构所展示出的平原结构是我们非常不想见到的。在这种情况下，我们不能收敛到理论最小值。如果你想自己试着画一些优化曲面，不妨参见以下代码："
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:07:07.018008Z",
+     "start_time": "2021-01-09T09:06:59.426182Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAApoAAAEBCAYAAADYRQXiAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOz9d5wl2V3YDX9PhRs73c5penIOuxNXCANCZNtYtnkdwOAX8AsGzCPgASwbHkA2+AWcwIAMBhuDLEBgjEGYKKGExK5mdndy6umc482h4jnPH3Xvndu93dNhZnZmV/X9fO6n+96qOnUqnfOrXxRKKUJCQkJCQkJCQkKeNNqz7kBISEhISEhISMjbk1DQDAkJCQkJCQkJeSqEgmZISEhISEhISMhTIRQ0Q0JCQkJCQkJCngqhoBkSEhISEhISEvJUCAXNkJCQkJCQkJCQp8IzETSFEENCiKIQQt/l9kUhxIHnqU/PA0IIJYQ49Kz7sR2EED8hhFgRQiw8676EhIS89QnnladDOK+EPC7bEjSFEN8shLgphCgLIRaEEL8ohGjb7k6EEBNCiC+vfVdKTSmlmpRS/i76THXbsd1s+7T6tMW+3jIP6puBEGII+H7ghFKq9wm1qYQQpeqgPiuE+I+7GdyFEPuqbRWrnwkhxL/YZZ/eL4T40G62DQl5uxPOK49HOK+s5XmeV6ptvUsIIattFYQQ94UQ37LLttbcZ887WwqaQojvB34a+EGgFXgHsBf4qBAi8nS7F/I2ZQhYVUot7XRDIYTxiMUvKKWagC8B/gHwrbvsH0Bbta3/D/AjQoiveIy2nglbnKuQkGdGOK+EPAXeCvPKXLWtFuD7gF8RQhx9jPaeCTueW5RSm34ITkYR+Pvrfm8CloFvrX5/P/C7wG8DBeB1gosD8D8ACVSqbf1zYB+gAKO6zieBnwD+qrrOHwIdwG8AeeAKsK9h/wo4BPRX1699ysEhKYCDwMeBVWCl2lbbDvrUD3wESAMjwLc17P/9wO8AH6we723gwiPOowIObfD7pn2sLp8AfgC4AeSq5zfWsPwHgXlgjuDmr+8H+OvAnWr/ZoEfaNjuPcC16rkdBb66+vu3AHer24wB/7Rhm3cBM8APVfs6AfyjhuVR4N8DU8Ai8EtAfINj/vLqeZfVc/9r1d//VvU8Zqv3w/F15+F91fNg167Ro85x9fp8AIhUr+HphmXd1Xula4N21twH1d8uV891b3W7joZl5wieBXODtt4PfGiTe+JfVM99oXqd/k719y37C/zN6vXLEjwzZ3ZyrsJP+HmWH8J5JZxXHm7zLt6C80r1//Zq37+24f4dAf7xJtfrXcDMut+WgL9X/f+fs/a+c2vHsUFbE8CXb/B7Cvg/BM9Rpvr/YHXZ3wNeW7f+/w38wVbnuuE6vQ9YAP7Hjp75LQaErwa8TS7ArwO/1fCAuATaH5PgJh6nOvmuPylsPCCMEDwgrQQ38nD15jEIHrz/vo0H7Dca+nQI+IrqyesCPg387GYXaoM+fRr4z0AMeLF64d7dcLwWwUOnAz8JvLKLAWE7fbxMMDi1Ezys39FwbRaBU0AS+E3WDgjzwBc13Hznqv9fIhhcvoJAoz0AHKsu+xvVayAI3t7KDdu9q3ov/Mdqf78EKAFHq8t/hmAAbQeaCQb1n9zOAwccqbb1FQT3zz+v3g+RhvNwDdjDBoPM+nMMHKse//dVv/9n4Kcb1v0e4A83aWf9ffCO6nmoCYJ/DHxnw/o/A/z8Jm29n80Fzb9Xva4awVtyCejbqr/AWYLB6SWCe+//Wz0/0e2eq/ATfp7lh3BeCeeVt8G8Uv3tKwkEr27gV4DffcT1qveveo7+FoFgfHaDdfcQCPpfs0lbE2wsaHYAXwckqufrfwK/X10WJXjBaRS2rwJft9W5brhOP11tZ0dzy1YDwjcCC5ss+yngow0PyCsNy7R1N+Sak8LGA8IPNyz/D8CfNHz/WuDaox4wAkn7tUfcMH8buLqdAaF6kX2guWH5T/LwLen9wMcalp0AKjsdELbZx29s+P5vgV+q/v+rwE+te6gaH4op4J8CLev28V+An9nWzQG/D3zPuhst2bD8d4AfIRhASsDBhmVfAIxv9cBVv/8I8Dvr7p9Z4F0N5+Fbt+irIniTLlX//y0eCl8vVc+HqH5/lXXalA3ugyzBG7IieMurbfsPgM9W/9cJBplLm7T1fjYRNDdY9xrwnq36C/wi8OPrtr0PfMl2z1X4CT/P8kM4r4TzyttgXmlY5+eBm9W2Ox7R1rsIBMssgQbVB753g/Xi1XvufY9oa8199oj1XgQyDd9/Efg31f9PEmg9o1ud62rfHRo03zv5bOWjuQJ0bmKP76surzFd+0cpJQnUrP1btN/IYsP/lQ2+N222oRDiawi0Pn9bKVWp/tYjhPhw1YE3D3wI6NxmX/qBtFKq0PDbJMFbWo3GqLYyENup38I2+7h+P7Xz0E/DOa/2r5GvI3gznhRCfEoI8QXV3/cQmDU26s/XCCFeEUKkhRDZ6vaN/ckopUrr9tlP8NacAF4TQmSr2/5p9fft0N/Y/+r9M83a8z29fqMNOEdwfv4BgbCWrLb3OYJz9y4hxDGCN/6PVI+52PAZamirs9rW9xM8ZGb19z8ATggh9hO8KeeUUpe3eZx1hBD/WAhxreF8naru85H9JfBj+/7adtVt97D2WdvOuQoJeVaE88pDwnnlLTqvNPDLBOP3rymlVmFNtoGiEKLYsO6cUqqNwH3k54B3b7C//wbcV0r99Db6tgYhREII8V+EEJPVa/9poK0hgOnXgW8QQgjgmwgEcZvtnetlpZS10z7B1sFALxNI3n933cE0AV8D/EXDz3salmvAIIHqF4I3gadC1ZH21wk0Po03zf+/ut/TSqkWgrdo0bD8UX2aA9qFEM0Nvw0RvLE8Sbbq46OYp+GcE/SvjlLqilLqPQQq/d8neEuE4ME6uL4xIUQU+F8E2rue6sPwx+v6kxJCND5kQwTnaoVg0D6plGqrflpV4PS8HeYIBKhaX0T12BrP97buIRXwOwT37o82LPp1gvP7TQTmDau6flPDZ2pdW75S6j8SmLO+q/qbRXAua239j20eYx0hxF4CM8t3E7wBtwG3WHuuN+wvwfX7Nw3nuU0plVBK/VZj13fap5CQN5FwXnlIOK+8heeVqgD3ywRuGN9VywKgHmYbaNqov1Xh7n3AaSHE325o718QaJH/yTaPcT3fDxwFXqpe+y+uNV3d7ysEmskvAr6Bh/PXds71rp+3RwqaSqkc8K+AnxdCfLUQwhRC7CO4uWZYO8meF0L83erb1/cSDCSvVJctAk80PxmAEKKFQMP0w0qpz6xb3EzgUJsTQgwQODg3smmfqgPLXwE/KYSICSHOEFz4x0lVE6m2Vfvo2+jjo/gd4JuFECeEEAngx2oLhBARIcQ/EkK0KqVcAtW/rC7+b8C3CCG+TAihCSEGqlqzCIEKfRnwqm/zX7nBfv9Vtf0vIghK+Z/VN8VfAX5GCNFd7cOAEOKrdnAsf6PaJ5PgYbEJrsFu+Sng24QQtTQXHwL+DsGg+8FdtPXPhRCx6vcPAt9M4GOzlaCprbvuUYI3YkVwrhFBiotT67bbrL+/AnyHEOIlEZAUQvyNdZNXSMhzSzivhPPKBvt9q84rP0Qwln8r8O+AD4ptpj9SSjkE7hw/CnUN+nsJ4gEq22jCXHftDYJrXwGyQoh2Gq5fAx8EfgFwa/f3EzjXj2TL9EZKqX9LcDL/PcGN9TmCt5cvq0rlNf6AQLWcIdDC/N3qzQiBH8r/U1XJ/sCT6HiVcwTS+8+IN6qp/1V1eQ74I+D31m27VZ++nsC/Zg7438CPKaU+9hh9vU1wA9Q+37KNPm6KUupPgJ8liC4cqf5t5JuACRGoz78D+EfV7S5X9/0z1f1+CthbNee8l+DhzBC87XxkXZsL1WVzBA7y36GUuldd9r5qP16p7vNjBNdmO8dyn0Cg+nmCN6uvJYjkc7az/SZt3iQwG/xg9fs0QdSqAv5yh839EcFxf1u1rc8SDLCvK6XWm5bW8/Wsve6jSqk7BAPMywQT02ngs+v6v2F/lVKvVvvxC9U+jRAIvSEhbxnCeSWcVxp4S84rQojzBFHb/1gFeVJ/mmC83kne5V8FhoQQX0twn3cBdxvuu196xLZ/zNpr/36CaxcnON5XCMzf6/kfBIqN9S84uz7XW1ELNni8RoR4P4Gz8Dc+dmMhzyVCiHcRBLYMPuOu7BohxK8S+Mj8P0+grY8Dv6mU+q+P37NN9/HE+hsS8lYjnFfe/rwd5pW3GkKIOEHmknNKqQdvxj7DhM4hnxdUTXN/lyA90OO2dZFAY/Cex23rEfvYxxPqb0hISEhISJXvBK68WUImPKNa5yEhbyZCiB8nCLb5d0qp8cds69cJTArfuy569InxJPsbEhISEhICQelKgkwK3/+m7vdJmM5DQkJCQkJCQkJC1hNqNENCQkJCQkJCQp4KoaAZEhISEhISEhLyVHjSwUChHT4k5Omy3cTLISFvF8J5JSTk6fJU55VQoxkSEhISEhISEvJUCAXNkJCQkJCQkJCQp0IoaIaEhISEhISEhDwVQkEzJCQkJCQkJCTkqRAKmiEhISEhISEhIU+FUNAMCQkJCQkJCQl5KoSCZkhISEhISEhIyFMhFDRDQkJCQkJCQkKeCqGgGRISEhISEhIS8lQIBc2QkJCQkJCQkJCnQihohoSEhISEhISEPBVCQTMkJCQkJCQkJOSpEAqaISEhISEhISEhT4VQ0AwJCQkJCQkJCXkqhIJmSEhISEhISEjIU8F41h0IeTRKKXzfp1KpYJomhmGg6zpCiGfdtZCQkJCQtyBKKVzXxbbtcF4JeeqEguZzjFIKx3Hwfb/+qaHrejhAhISEhITsCCklruvieV79U5s/DMPANE10XQ/nlZAnhlBKPcn2nmhjn89IKXEcB6UUQggcx6k/9EoplFJIKRFCMDc3x549e0LB8/OD8MKGfL4RzitPgJp1zHXd+m+O46BpWn157eP7PsvLywwODtbnFU3Twnnl7ctTvbChRvM5Qym15i1T0zTWvwwIIerLAObn5xkYGKBSqdQHglDjGRISEhICD03lvu/X5w8p5Zp1ar9DoOhYWlqir68Pz/Pqyw3DqH9CwTNku4SC5nNEzVRe01Ru9yGuCZ2Nb6ZSyjWCZ+MAEQqeISEhIZ8frLeObWfsF0KglKrPKfBQCVLTiIaCZ8h2CQXN5wTLsnAcB9M0dyRkbsR6jWfNFFJ7M4WHvjjhABESEhLy9kMpRaVSwfd9TNNcIzTuhvXzUk1Lul7wrPl4hvNKSI1Q0HzG1N4S5+fnqVQqHDx48InvY6MBolHwXF5epq+vLxQ8Q0JCQt4G1KxjIyMjpFIpuru71yyXUjIyMsLq6iqpVIpUKkVLSwu6rgMPNZqPQghRX7+2z0bBc2lpicHBwboVLZxXPn8JBc1nSC36T0r52G+bO2G94Dk9PU1XV1foixMSEhLyFqfRVL7RvFKpVLhx4wYdHR2cPHmSfD5PPnOdlflpivYJ2traaW1t3VLQXM96wXN6epru7m5s267POTVlhmEYj225C3nrEAqaz4D10X81Qe4JZwDYEY3CZOiLExISEvLWYqNA0vXzyuLiIiMjI5w4cYLW1lZc16U/dQWj6TdRIgby/7BQ/nYWFvspFotcu3atrvFsbm7e0bi/kcbTcZw3CJ41U3soeL59CQXNN5mNov9ge6aKN4vQFyckJCTkrUOjdWyjeUVKyb1797Asi4sXLxKJRJB+kYj979HVOJqaQskKrv4SnfGfJXXgaymVznHs2DEymQwzMzMUi0VisVhd8Ewmk7sWPGtzneM4OI4DBMqO9fNKyNuDUNB8E3lU9N/zJGiuZytfHMuyiEajJJPJ0CQSEhIS8iax3jq20bxiWRaXL1+mr6+P48ePB8v9YYzyLyH819FYxWMIV+tH8/8SSKJ5H2Wo6wGx2AX6+vro6+urBxdls1kmJycpFoskEom64JlIJHaUKQV4pOBZKpVobm4mHo+HgudbnFDQfBPYyKSxno3yZT6vrBc8l5eXicVi9e+apoUmkZCQkJCnyPp5ZaMxtlAokM1mefHFF2ltbQVA2H+AXvkVhJpEEcHRvhDp30JTo0jtApp8FSWnwNSxrV8mGvv2YDshSCQSJBIJ+vv7UUpRLpfJZDKMjY1RLpdpamqqC547mc82EjynpqbYu3dvPd9nqPF86xIKmk+Z7ebG3CiB7luJ2iDQ+GZa88UJB4iQkJCQJ8dmpvIanudx9+5dSqUS+/fvD4RMVUQr/yy689soBL52Fs/XUP6nQTuMkjaafBVPvIMyS0TiwzjuErp+EMP8sjf0QQhBMpkkmUwyODiIUopisUg2m+XBgweUy2Xu3LlTFzwblRFb0Sh46rper1i03tTeWJQknFeeX0JB8yni+z7pdJqpqSlOnjz5SK3e82w634qaKwBszyQSCp4hISEhO6dmKp+amsLzPPbu3fuGdQqFAjdv3mRoaIiWlpZgfPXuYJR+ACGnkfpxpFT45FGsgNiHkPdRYj+23EtF3USIA+h6CUEHlcr7Seqn0LSeR/ZNCEFzczPNzc3s2bOHy5cvMzg4SCaT4d69eziOQ0tLS13wjEQiWx5r47yyPm5AKYVt29i2DTyshqfret2FK+T5IBQ0nwLrTRq1t85H8biCZuND+Sy234ztCp5SSpLJZCh4hoSEhGxAo3UMeIMFTCnF9PQ0s7OznDlzhqamJqampmjWfw+j8GugDSG140il8NUCiCEE91CqjOQwFZJ4Io+SeZS6imUNEYtNoWkXKVofoCXxr3fUXyEELS0ttLS01E3g+XyeTCbD3NwcnufR2tpKKpWira0N0zR31PZ6wVNKiWVZ9d9qQao1H89Q8Hx2hILmE2a9SaMmRG3Fs9RovpkP4EaCp1KK1157jfPnzwOhSSQkJCSkkfWBpLqur5lXXNfl1q1bRCIRLl26FIyvMkdv/McxxSxKPwneDTzjRRQ+qAz4y0jtAkqOUkbHl/MoNYWmX0D6r6IbeWCAonSw/Ntg/29aon9n18egaRptbW20tbUBgcUvl8uRzWaZmppCKbVG8NwJGwmelmVx//59Tp8+DTzUeIZlmN98QkHzCbFZ9N92BcjHETRr2z6rB+dx9t14nhp9cRpNIo2CZ2gSCQkJ+Xxhs0DSxvkim81y+/ZtDh48SG9vb7Dcu4pW/hk04WJqcyi/jGucBW8YSIN+AvxRPJnHEvvx/ZcRog9oQfqvomkv4Hmr2MY+iv4rGFo/K+WfI2l+KbrW9kSOTdd12tvbaW9vBwK/0lwuRyaTYWJignK5zNTUFF1dXbS2tq4JQN2KxjLMtXllvcYzFDzfPEJB8wmwWW5M2H40+ZMwnb8dCH1xQkJCQh4dSFpzyRofH2dpaYmzZ8+SSCRAKTTrvyO8zyD8e8T1CgXnDJGYDd4rILqAAZR3F9v4a1TcTwIKTTuJlLfRtBeQ8gYuSTJiGs1/hah2AlveIW5cZNX6AN2JH34qx2sYBh0dHXR0dABw7do1mpubWV1dZXR0FF3XaWtrI5VK0drauqWlaysfTykllUpljZUtFDyfDqGg+Zg8KjcmbD+a/HE1ms+Sp6lN3Y4vTjhAhISEvJ1YX5lt/Zjm+z7z8/P09vZy8eLFQOiSq2iVD6A5f4KgiKSbgnuKiPEy+BHQXwD/OlLbT1l7Adf9GJp2ASlfRcpZoB0px7DEl5J1P410D6EZeXyVAQws7xaOP0NL5BuJGW8MQnrSCCHo6Oigv78fCPz6s9ksS0tLjIyMYBjGmqpF6wXPR81LjRrP2rqh4Pn0CAXNXdJoKt8sNyZsX4B81Hr5fJ6RkRGamppob29/w0P1Vo5Y3ymbCZ7ZbJaZmRkOHToUDhAhISFvSbaTG3N1dZXh4WFaWlo4evRo8KN7BaP0owg1g6IZT3sJXy0SNf6KinuKuHkL/Nu4xhdScq8hRBlIIuWraPpZpH8V9C8g7U3hyatopDDiI3VtZky/gCOHscUL3C/9N15o3Vlg0G5pPP5IJEJ3dzfd3d0A2LZdDywqFApEo9G64NnU1LQjBchmgufc3ByWZdHf37+mDHM4r+yMUNDcBUop0uk0hUKB3t7eR95wjxMM1BhFeOjQISqVypqHqr29fceJcZ8Gz9I/tHEw9jyvfr7DN9OQkJC3ElJK5ufn6ybi9eOUlJLR0VGy2SzHjh1jdXUVlI9W+WU0+5eAGFK/gC9tpLwB2l6kihM3b6H0i1j4WM7L6PoefH8YOAXcwvfu44t3suq8TlQ/jZRXiekvYvkZJEVAw1cVlv39FP3XiGo95N1hWswjT/V8bDWvRaNRent7636ptapF09PTFAoFIpEInudRLBZ3VS6zNif7vo+mafi+j+d59XVqKfoMwwjLMG9BKGjukJoWs1KpkMvl6Ovre+T6u9Voep7H7du30XWdixcvIqWktbV1zUOVTqeZmJigUChw9+5dOjo6SKVSxOPxxzvIN5knISg3ui6EJpGQkJC3Co3WsZqAlEql1qxTqVS4efMmHR0dXLhwgVwuhyFW0Yv/BOHdRxnnwBvBw0eRBpLg30SyH8cv4oo0iCaggpQrSNWGJm7h+WcpejYlfwk96mG5D0C0YPnX8OwBiE6ha1/JiH2dNvMUyp8hqnUwWvpVzrb91FM/LzshHo8Tj8fr5TJXVlaYmppiYmKCUqlEMpmsazzj8fi2xn0pZV2IXG9JaxQ8hRBrNJ6h4LmWUNDcJutNGoZhbEtTuRuNZi3h7r59++qlvta3EY/HGRgYYGBggNdff509e/aQz+cZHh7Gtm2am5vrGs+tEuM+Ls9DDs/agLCe7QieoUkkJCTkWbA+kHSj4NGlpSUePHjAiRMn6gJohFc42PEfQfUDBvjTuFpfkLZIToBoB7EHV2oUvFZMcQ+QaNoZpLyB5x0iEklR1Aq4ZhndWCKqvYjNNXBPgHkH6WvknBcpiFFAI+fexRQpct4d4loPBW+UZuPgUz0/j5PNJBqNkkwmOXbsGEopSqUSmUyG0dHRN5TL3Ew5s9W8UqMmHzT61YaC50NCQXMbbFTuayfR5NuhJpBOT08zMzNTT7hb41HCmKZpJBIJ2traGBoaQkpJoVAgnU4zOzuL7/v1aL22tjYM4/m67E9C0NxuGxsJnjVtgu/7rKysMDg4GJpEQkJCniobBZI2KiaklNy/f59KpcLFixcDhYFy0Sq/QEJdRYkymv8ann4WXynwrwAm6GdQ3k0s4zAV/x6muYRhXMLzLuO6o2haikisnbyvY8krRPVT+P4SnppCkECZ94no55kjg04Mj2n0ygH8+BhRfz+uliGidTJR+g1Ot/7osz2Jj2B91HlTUxNNTU3s2bOnXi4zk8msUc7UBM9oNPqGNh7FowTPcrmMbdt0d3d/3gqez5fE8ZyxWW7M2v9Psja553kUCgVisdjDhLu7RNM0WltbaW1tZf/+/fi+TzabrecnE0LUH6jW1tbH7vvzrNHcisYB3nVd0uk0fX19a0wijab2z7cBIiQk5MmyWW5MoD4OlUolbt68SW9vL8eOHQvGHH8GzfoAmvMyOqu4IoljfAnK/ViwsXERvCtIf56K/hKO+ykEQ0gVxfMuU6kcIh6fxdXPsep8Ck00odGB7d8iqp/C9m8R0y/goVjyEzjmBHG9CXyBllhBqiiWGEfIJLnKLGOuTqx4i8H2g0/FXetpzitCPCyX2aicyWQy3LlzB9d1aW1txfd9mpubd7zvRlnBsiyKxSKpVOoNGs/GMsxv53klFDQ3Yavov+2axLdDoVDgxo0bGIYRVDHwbcTk76MtfgaVPIg/9Lch0rXp9lv5geq6viY/meu6ZDKZukmmUqkwNTVVj2h/s2/4N1Oj+ShqwmrjwB/64oSEhDwpHpUbE4J5JZvNMjc3x8mTJ+uKAOF8Ar38kwg1jyKKzUtY3jgx7WOgvwj+LfCu4BpfTMl9DeW9iqbtRcpJrMphEokHJJIGeXWEkvMp4uY5Ku7rRPWD2P4qvkojSFKSURbdJRw1gWb3UonO0mqcIufdos18gax7nZbIJW6VZmiJtvLA/STlYR/btndUx/zNYCdzQqNyZt++fUgpyeVyTE5OMjs7y8LCwq7LZdbmlUblUc1lwnGc+n2wvijJ22leCQXNDdjIVL6eJyVozszMMDU1xalTp7h37x64BfRXvwfhFRGFGaTnoF+5jHbw25G9F5/IzWea5po0EZcvXyYSiTAzM0OhUCCRSNQHjEQiseU+38oaza3aCH1xQkJCngQ169hmOZc9z2N6ehrXdXnppZcCFyfloJX/I7rzGygiSOM8vu+h5Oso1Qm0gn8NpZ3BIoLl/AWGcRbPew0pW5EyQiLxAIwvY8H+HDEjSIfkeGMIWrD960S0w/iqQIUvZMF5jTbzDI6bBgLByFEZACr+LKZ4iZvleVwlSfvTFPRlvuz0t2ISq9cxr7lrWZbFysrKrt21nuW8omkaqVSKXC5HIpGgo6OjXrWoVi6zMXn8o45vs3llveDpOM4bquHVNJ5vdcEzFDQbqF3sWjqDRwku2/XR3AzP87hz5w4Aly5dCgRX30e/9n6EW0BUppGtxxGlEbB9IsMfwo6moP3wG9p63DyamqbR29tbDzyqRbSPjY1RLpfX+K7EYrFd72cznjeN5qPYSPB0XXeN4Ol5Hs3NzZ8XJpGQkJBHU6tsVhujNhpjagGgqVSqXvEMfwKj9IPgTyONC+CN4ikPxRLQRjw6VU1h1EpJlUEASDzvJlIOoWlTKF4kZ3s48gaCCBXvOjHjDJZ3g4R5kbJ7BSV6mXIsYASNGDn3NlGtBzs6S1I/QMkfo804y4Kn4ag4lizRHz3GnH2PLnMfd0uf4MXmv1GvY15z17p8+TLZbHZDd63HVQps97w/qXllo3KZ2WyWdDrN+Pg4Qog1gmejELndeaW2TW0udxwHx3Hqyz3Po6WlpT6vvJUIBc0qNSHz5s2bDA0Nbem7+Dg+msVikRs3bjA0NMTAwEBdUOy1X0bLvoxMnUZUpkFIhFtAtZ8Fq4x5+4O47/hhMJ+8sFdDCEEikSCRSDA4OFh3mk6n09y7dw/HceomhFQqhWmab2uN5lZs9GZ67do1zp8/X1/emEopFDxDQj5/qFnHXn75Zd7xjne84dlvzJV85swZLMtidXUVYf8fdOsDKNGLQIA/j6t1g8yCnALaqDg9GLE4lgDPuwfY6MZFfO8KUtpo+gEK5KioCEJliJvnqbiv4ctlwKTi3gDxpTywbtBqHCfn3SVlvkjGvUZc78GWi+giQlw/wKyXZMYepdUI0usVvJXgr7/MzcJHeaHpr685tpqwfOjQIeCN7lq1FE7t7e00NTVtOCY+z/OKYRh0dnbS2dkJBMeXzWZZWVmpl8uszZG+7+/I1N6Yhq92HL7vc+PGDc6ePQsEyqH1Pp7PM6Ggydrov+2axHdrOp+dnWVycpLTp0+vcTIWXokOK9BwiuxdVLQdrXAfldiDsBfQCksow0e783vIF75hTZuPq9F8FI1O03v37q37rmQyGaanp+sPQTKZJJlM7iqI6a0saK6npvFsHCQ2Mom8XX1xQkJC3hhIquv6G8Zo13W5ffs2pmnWA0AdJ09v8pfR7DTILBozuPolpCqCfx2IgH4K5d0m5xwhZi6j1ByGcQ7Pex3XuQYMYka7yasElnoFtHYE8apP5iFsf4S48ddY8crYMvA9d1QeEBS80apW8y54zbh6kiknSdobpcPYw6o3TZe5n2V3nG7zAEvuGN3mAaasm+yNn9n0fKx317Isq26GLhaLdXet9vb2bee43M41eLMsZaZp0tXVRVdXEEvhOA6ZTIaFhQVWVlaIRCLYtl0XrHcyz9Tmd13X19xHjRrP513w/LwWNDeK/tN1/akImr7vc/fuXXzf59KlS2/w6dBGPkyrPYFKNCO8AjK5D5FNo+IdaKs3kG3HECqCkbmBk/tSaH10ovinRc13pZbPzfM8bt68ST6fZ2FhYc2bXEtLy7Zu+LeS6XynPMoXp9EJ/Nq1a7zzne98ovsOCQl581mfG7M2t/i+Xx8Lstkst2/f5uDBg/UiHPgPaBU/jxn/LJrvIOnB0V8E7xOABsYF8F5FyiXK2iWiiU8jxF6USuJ5r1MuHyWRGMfTD7HkvAJIDHEQTx8lbl6i7F4GBKZ2gik3g+0V8Zgioe+h7E/Tapwk592mzXyBvHufYvko9/1Z+iKBX6ehBSl/BOsCmOjiY6uX+SeDmwua64nFYvT19dWTq5fLZTKZDCMjI1iWRVNTU12Q2q271rOcEyKRCD09PfT09DA+Pk4sFkMIwezs7IblMrfqZ+O9s5HGszavNAqemqZx+/ZtXnrppR33/0nzeStobhb9txON5na1iDV/lcHBQQYHB994U3kVxNjvoeEgkyfQc68h8mMoEQGvgmdewC8KwEPIPPq9P8B/6Tvqmz9NjeZWGIZBLBZjcHCQ5ubmNW9yw8PD23qgntSA8LhtND7Mj8OjrsVmvjjf+Z3fybVr10LtZkjIW5iNcmPCw3lFKcXExARLS0ucPXuWRCIRbGj/H4zyv8akgqtaUPpZfDkZCJnVtEV4r+IZX0zRfR3FVRyni0hkEsc5TiRyl2STTUG9SNH5DIm6YOmhFFTc6xiiD090seqblLxbpCJnyThXMUQSAFflgr+yTNo/xrK5RIQEi84ocdHKkjNKUmtn2R2nSe8g482RFJf4y+wkrUYrWTdLm9m243MmhKhbxGruWrU80Hfv3sXzvF1FfD9PCoxayejGyn4baXQ3C8B91Ny0UdxArTLS+973Pj75yU8+Vv+fBJ+Xgub6qOHGi/Q4tck3Ym5ujkqlwjve8Q5aWlo2Xmni4ygpEYDITaCEgXDz+O1fhLx/Hbo70ZZuI6Pd+Mk+RH4R0hPQvq/exLOsd974MDa+ycEbH6iNyoA9qQHhcYXEJ2V+3+6xNE5CoQk9JOStS6OpfKOAH03TsCyL27dv09TUxMWLF4N1ZBG9/K/R3D9BiS5cdYiSaxHXXgXjJMh58K6g9AvYSCrOJ9H14/j+DSCOlBEikbtgfBlLzmsYelDko+Jew9T6ceUkyjmGiM1jay8yXblMXO8HNPLuXQxayHv3SOhDlP0pWswv4nppmg4zhdQW6YwcZs65Q8rsZ87J0Wr0UHLStOqDDNsWcc1Eoeg0O3k59zJf0/k1j30uhRC0tLQQjUY5e/Ysvu+/IeK7MbBos3H/ebFybdRGrVxmLQC3ptEdHx/fsFzmTvpRm0sqlQrJZPKx+v6k+LwSNLfKjQlPLm2R7/vcu3cP13VJJpOPTPoqhn8fmo5B7jWEk0V1nkT5BeRCBqEkqrSMQEFLF1pmGmmbiHufRL3zm4Ptn2MBZf0DVSsDVjORNDc31x+kx+F5GlR266caEhLy1mOr3JgQ+GPevHmTY8eO1f348G4HUeXoSP1MUKtc+EjlAgK810A/g/TnKclstVa5i++PolQvkcgCcA5Pj5B2rgEmtnePuHGBivcqhtaFK+eQ+Kz4Q+SdKySNIUreFKnIGTLODdrMo2Td6xiiBUN7iTHbxVE2JT8NCrLeHAKNtDeDhsGqO0WncYzrhTJ5r0xUd9HQWHQWSbtpvqrjq9DEk3U/2ijiO5PJ1ANvDMOoC2XNzc1rqr49LxrNR80rG2l018+TkUgEpRSWZW3blaAmsD4PfN4ImtvJjQlPRtAslUrcuHGDgYEB9uzZw+c+97nNb9j0MCI7hqq04GsmunDBLuHnNUR2EtW2F5GbRKYOouUmkI4LbYeRSzOwMoHo3Ac8PxrNRyHE2jJgtWoMCwsLZLNZrly58thJcR8HKeVjl+fcjaDpOM6OjjUkJOT5YDNTeePy0dFRSqUSp0+frkcpa9ZvIJw/RtGMJu8gtb14+jGEf4tkrAT6IfAXcJWNre3B814GBLp+Bt+/geelUKoDJ1rGkz5S5YibZ6m4GRx/FEGSincdTXs3M+IW7fpe8OfqZnLLXwYEOec+Jr3MOyZZWabor9BuDJL2Zki6PZTEIj3mYRbdB/RFjlGRMRbsGGlvnP2x/Yxb4+yL7WPCmmAoOsT98n2OJ48/1XNuGMaawBvbtslkMszNzdWr66VSKTzPeyLj+ePOK7V0idulNk8mEx77el9D+HcpFm0sq8zw/a/DssWG5TLXEwqabyK1t4B8Pr+t4JSa0/ZumZ+fZ2xsjFOnTj2s6lBNhbTRvsX4R4O/dp5ccoiUGkWKDpSyApfrSFUTqpsIpwidJxCuhW5V8K59AvHl3/JcazQfRa0aQ41Dhw6tMZEAm+YmW8/zEnW+00EFnq8BISQkZGuUUuTzeTzPI5lMbvjMW5bFjRs3aG9vr9e5RubQKj+H8K6gyXEAHOOLUO4NYATEAI5rYKpRbOMLqbh/BVQwjJfwvM/hOKMIEdQqn86Aod/B1PqAGBX3KlH9GLZ/j4T5DvK+IONlQfjk3WEM0UzOvUuTsY+iN4Fu7UWLaixZfSxp4zQ7gxABTQYvvTXVhYdNVGsi77VxtTBOXyQIRLWUFSxXD6umfS77uacuaK4nGo3S29tLb29vPQ90TeNp2zb5fL4e0b7TwKJnYSmTsgjubxGVr6DLByjtKG2xESYq/5wzL7z0hnKZtfyajSkHIUij2NTUtOP+CiG+GvhPBBn7/6tS6qfWLf8Z4EurXxNAt1Kq7VFtvq0FzVr0Xz6fZ3p6OijvuAW6rtf9N3eClJJ79+5h2zaXLl1ao6HaLHBIKYlKL1ITn6J2ARlPIKdmILU3+HF1BGXEIT2Cp8WRTgEjO4cf6UesjiOXZ59pMFBwHI+370clxd2OiaSxjW3uEKk+AuJlEIugzYOK0dMXxXO/DKW+FSF292jsJqCoVCrtakAICQl586lZx5aXl/F9f8Nnt5Yv8vjx47S3t3Pv3j00eRO98AtoMkhj5+vn8VDgfhxEDzCIUDM43h6cyBCu+xcP0xa5V7DtIWKxWaTxBczbn0JPaJjaEK6cqgf/KGwMbR+zbhnLd7DlMoazFy8ySXvkLGnnKp5jgAaR5CA3yhNEjVU0aVCJLGGSYNWfxJQJyuYicZXC8T2K3hHGK+N0mV3MO/PBX3ueDrODWXuWNqONaWsaQYSCV6HZePK1z7dDYx7o2pzQ0tJCJpOp54FuaWmhvb2dtra2LUtlvtkKDN+7gXD+K1HhoMkiSjsFQmO29NM4KggkWl8u0/f9elWm6elppJQUi0VefvnlHVvKhBA68AHgK4AZ4IoQ4iNKqTu1dZRS39ew/v8FnN2q3betoNlo0thuyiLYnem8XC5z48YN+vr6OH78+BsEnk2Tu8/fgek7yKYmNK9IzMviJ16CueuwNIJMtKA5ebKRPbR5U7jtR/AqNjnjEEroxGQZ//WPovZc2lF/nwZPI7Hudk0ktaS4Wz7MSqH8nwPjj0DPgOdBRAPNA9/AjJhEIx9Eid8E77sQxt/f8bHsZmAKNZohIc8/G+XGXK+UkFJy//59yuUyFy9eDAQZpehM/iHt/AZIkPo5pKwEUeXKA+0AyDEQ7TjiPBXtFlGlAyae9zqOc4pI5BbxRJSSeoG8/Unixnkq3mtoWhwkVNwbGKIbJTpI+y3k3OukIi9gO8tIrQxAzr0PMoYtZkH7Eq6Vh+s5MfsiR5l37tMfOcScc4euxD7m7DvE5BCv5ZdI+Q4YEJOBRrDFaGHZXSZlpFh1V+k0O2nWe1iqJPn06m3+Rs+FN/XabERt7q/lgR4aGkJKST6fJ51OMzMzg5SS1tbWuuC5XknwZgqavvPnCOd3ieoaQvkorRtBDCfyg9i+h6ZtLJc0phSEQNlx/fp17ty5w7Vr13jllVd43/vex3ve857tdPcSMKKUGgMQQnwYeA9wZ5P1vx74sa0afdsJmo+TGxN2LmguLCwwOjq6xlS+nk01juOfBbeCSp6E3GtINGROogFIj0pkiKSTp8WUyMheVDaCNjtP08Ax/MVZ/LZO1OQtCqKH++Uy3d3dtLe3k0wm31Lm9O1qIzczkUxMTJDJZCiVSlQqlXqk3hq8CTTnB/DNNIgC+BqYGqAQdhI8Cy3qgOYgXID/gKh8DBX5SdA7tn0su9VohoJmSMjzy0aBpOvnlVKpxM2bN+nt7eXYsWPBmCZX0Us/THfiGrY6SVSM4qOQaikI7lEjoCoo7RAWzdj+BCDx/fto2nmkfA3THAb9nSy7w5hGMBbZ/gjST2Jzn7hxFsu7ja+fZ7xymZjWhcAg69wipvViGQs0accoynskxXkmVYWorAbMVPtellkAcv48IMi686jSQa5rWRAa+UgeU5os+AvoSmeqPIUmNOasOSJEKHkJPrM6R39U8Rcr158bQXP9vKJpWr1UJgRWs1wuVy8l2ZgnuqWl5U0xnSul8OzfxPA/Q0QrI5SGEEGGGjv2oyCa8f3pbfub6rrOuXPn+Iqv+Aq+9Eu/lG/91m+lXC5vt7sDwHTD9xlgw0ScQoi9wH7g41s1+rYSNDeL/tN1fdt+l9sVNKWUWJbF3NzcG0zl225z8nPB3+VJZDxGQXQTn76H7OxDK85jlDJIJRBoWJlmWJ6A9gHIzCHsMrqKoDWlGKosYOy9gOu6TExM1E2xNTP0Zs7CT4pnUSqs0UQyMDDA3bt3SaVSOI7D8PAwtm3X/Vbam8eJ8T6U5kK0WjtWGcF3QHgaKqKBrSN0iebEAQ+0W2j230Ea/wEiF7fVr934aO7WlyYkJOTps1kgaeO8Mjc3x8TEBCdPnnzom+9eRqv8DBBDCBuDURz9CKgMqAVQUdBOIOUCZaJ4cgal5vC8IXS9jJSvAWdQZoKsl8ZTeTz3tbofpnSOoMWH8ZVNTp0kXWmMKn+RjHONuNGN5SxQttPEoy/wwKlQ8osICsS1VlbccVqNXnLeAp3mPlbcCfojpxiv+JQ9HctY5kD8AGOVsYd/E8HfPcYe0l4aWdjDZ9Qcg3qKGTvNgOhgurLyjK7WQ7YzrxiGQUdHBx0dgQC/Pg+0ZVnMzs4+slTmVjxK0PQ8F8f6VyS1NFFuo1QLmtCQYgA7+q9ABKZ93/d3PI8Xi0W6urpoaWnZPLXi4/EPgd9VSm0pXL1tBM2aSWOj6L8nLWjWTOVCCF588cUtBYuNNJpydRJRWAy+2EXoOo5azgCQs6OkANPOQO9xnPkKJKuCSKIJ0nOI3gPgu8ilOUxRwnynpKu/v55GqFafvOYs3GgeeNxIvCfNk3hrBEgmk/T29q4xkTi5P8GMfwBl2OAptHwczSujTBflJJHCQ0UDp3YR8dGKCoFCRVzwQOk+mvtDKPXDqOi7tuzDbqLOQx/NkJDnj+3kxvQ8j1u3bq2t+KZ8NOu/IdxPIfzbCBQl7zi+kES5DJigvwD+dVwhqIg+fO91NG0QRTOx2BQV6wTx+DwVEaHgjCJVZo0fJmjosREixhcxbk3QbPYDU/Wo8rI3jcAkY98CJ4WI72fONyj4Y/THjjNn3aUjMsiMlSOhtZFjAV0YtBsHmLWTTFoTpERgii375TV/LRmMlxEjyWRe0pNoglKOmB4BH3RL8uE7H+Odzh5KpdKGCcjfDHYzr6zPA/25z30O0zQfmQd6t/1wnQwV+/to06OYTKFEB5oq4ul/Czfy3dCwzW5M+OVyeTfzyiywp+H7YPW3jfiHwD/bTqPPl8SxCzYyla9nJ+bwrdZdXFxkZGSEkydPcu/evW0FwmwUDCRHriKaBtCKwTWUxRLRXCBoNldWULEYwrPwVAcycxPKNmgGrEyDZiB0DTU/DtFONOmibt+EdwUPx/r65LWEt+l0momJibp5oL29/ZH5PbfLs9Bormf9g6hpGu36x9ETPweOjnJNVJOLwAIlUFEFWJhFwAIvAcqo+ppqFsIOFA64EYSbQdg/ja91gPnogLLQdB4S8tZnO7kxbdtmYWGBo0ePMjAwUDWVL6GV/x26+6cA+GI/vtaHLj8bBH3q58B/HeXdwTa+hIr7MYRoRYhepJyhYh0mHiuQSApy/n7K3rV62qKKdxNddOL44yTMiyxkLbJJhavKFLwxdOLk3Lsk9f2U/HEM6wAqmmXFOsgSU3RHDgBQ9FYBWHGm0DBYdseIiiZcmeRuqULemyRlpMiQocPoYMFZoMvsYsFZoNPsZM6eY3/0NB9fXqDFaGKsPE+zHmfGSxMTJlnd5o5Y5AsYZGxsjEqlUk/H097evmUAzpO8ho87rwgh6G9Q4GyUB3qrNEO1dhqxnREs6/tp07swRAnFPjSVxTW/ES/ydW/Y/k2cV64Ah4UQ+wkEzH8IfMP6lYQQx4AU8PJ2Gn1LC5rbzY25k6jszQTNjZy8a+tudQNsFAwkx18H2tGqLwtFx8Qxe2lz5xCejUodA2sV5+4DtGgSYZeg7yAsjEDvIViagGgcvbMTPVuGB3dRX/xuxAaC9vpo7pp5oBZUUzMPdHR0bPst7UnyNBLritJHMYr/DmUKMCogkoCL8kDFquu5VWFSE2iuwMkl0FtLwTJDQzg6mgPCEQhtCX31+3E6fwOMrk37sdtgoFCjGRLyfLBVbkylFDMzM0xOTtLW1sbg4CAAwvkMevmHECqD1E8gfQdfGOC9jCOPEtVvg38NX3uJslrFc/8STduPlKMotR/QiMdGWMldwGu6QUTfAxhU3KvEjFNY3i0i5nEcH9J+hLQxA+4czcZBCt5oPaocGUzrkXgLw45GJbpATDSx5IyRMvrJeHP0RA+xaI/QGznKqjtJXHuRV3IPOBg/SM7L0W62k/EytBqtrHqr9eCfNqMN6XexYJl4StEfayddKLA30c2twiQnmvZwpzhNT6KPebPEXzv919aUlKxpf9va2jYNwHlSPClLWY3N8kA3phnajuXQsi5jOT9Ei94bhAnQjsDFNb8Z3/yqDbd5syxlSilPCPHdwJ8RpDf6VaXUbSHEvwZeVUp9pLrqPwQ+rLYpWL0lBc3a2+bS0hKdnZ1blu/byc22UeBQpVLhxo0bdHd3P3TyZvv1ztcLusqpoGaHQfr4fQPopVmMsofvNaxTyOPrneBOIvoPwNwdqPVLSfA9RP8gKrNINFfCMTzcO7eInDqzZX8azQNKKS5fvgyw5i2tvb2dVCq1rbfP502jKSp3iWR/GoSJMkooaaKiZURZgGxDaRkwBXoZVPU5FEhiooTIKfxWAZpEZEEYNkRAuQmEliey/N04fb+9aT9839/xG3upVHpYLSQkJOSZUHM5KpVKtLW1bfjC6Lout2/fxjAMXnjhBUZGRkC5aJWfR7N/G2UcAw+kcvFFHugGHKL6bSz3FHrUpeTfRdO6gQpKFZCyCU0bR2jvoEwFN34fQ6Rw/Mm6udxXOUDHlzar/hGy3j0M5yBebBSqlXgK7iioKCU1Ssz4Iq6VR+mNHqEk79MZ3cuMdZu43kLGm0NVw4CkglVniDkZ+FQuOUsIBPP2PEIJ5p15dHTm7DnajU6mSgbDxRWazQQCWLKzAGTd4AXdloHfu6Hp3PcCC10txVBLS0s9HU82myWdTjM2NlZPW1ezsD0p4fBJaTQ3Y6M0Q7U80BMTEwghaGtrw/O8ukayVPlzXOcnadKTxIQPKoauJrBjP4LUN48D2I3v/y5N5yil/hj443W//ei67+/fSZtvOUGzlhvTcRzGx8fp7u5+ou2vT9hey4d24sSJevqAGpumLdqgzcb15PRtkEGS23zJpDXRiTazShxQ/XsR2UmQErcYbCOL+SASfWkS4s2wPInq3ItHEyoWoZxyiBg6/t2bsA1Bc/0x6Lper2JUe0tLp9PMzs4ipay/fW6VNH23PFGNpqwQWfwhhJbBjyUQlQSaVYGkAqFQfgbdUpADSSvIHGgCYbUizCwKDeRxfOUTNe5RsveSSEyCqKAAIccwVn8Wr+N7N+zHbk0c+/bte6zjDwkJ2T015UWhUGBxcfENYz1ANpvlzp077N+/n76+PizLwtCW0IvfA6oCSHBfxzUuolQF5CwwC8ZFpPMqFSXRVQSllpHSAvpQah4pj6GbirQ3DaIZoVeI6EepeKt1c7nrz6CbX82D8qs0m0GwkR+ZRaeJgvuAJv0gRX+UmH+SvJmg4BsoFLYMBMBVZxoNg0VnNNBu2mP0Rs5xObdEm9FBxltgMDrIjD3D3theJq1JumQXy2KZfbF9OFKSsVLcLc5yJNnPcGmOQ4k+Rsrz7I13MVlZpi+aYry8SH80RbYc4fVCmvdJH1NbOx7qur4mAKeWtm5mZoZCoUAikaC9vf25KEu8E9ZbDl3XJZvNMjc3x+uvv04y9af0tn+UNtMnIXIocQ5NjWDFfx6lHX5k27vRaNZ8Sp8H3lKC5m5zY+6EmlAopeTBgwcUi8WH+dA2WXcr1ms05cSN+v/J/BKq6xS1NFVSNKEDntED0WqFhtV5VFcfIjsP7QP4roFdiOHfHoGWTlwzhnQlMW8Rf24Ovb//sY6/9pa2f/9+PM8jm82uSZpee5hqUXjPk0YzMv59aNo0ytHRPQdhusioBgKUJaCpeh1UBN3IQiaK29oGkSRCZhFINHscwSEAktFJfHEKzbiFV+7CsPOoyv9iemkv0Y4vXFOJobEfOyE0nYeEPDs8z6vnwzQM4w1julKKiYkJFhcXefHFF0kkEgCY8tMc6PwVhDeMQCHFflytF7xPAwKMi+BdQXqj5NQFMD6D70fR9cP4/gNsu4Vo1ECPtZHzFLYcJaLHUEqj4l0jZpzA8u4QMU+T8Q+QtoYRRMm792kxj5B3h2kxXyTjXqNctohGh1jU4yxZ8wAk9RRpd4aE20XZXKY/eow5+x59saMUvQjzTgJLusS1IBWcLgJBRlJVcIjgr0Yrn12Z5UBibfq+mgDZVE3O3hFpQaARc3v47MosB/VmPrs8wbt6Dj7y/K9PW1cul0mn01iWxeXLl+sJ1tePtVvxZgua6zFNk66uLiYmJjh87E8R/seIagpTQbG0H00vsGj9JC1t/SQSj+7rbivOPYkYjCfBW0LQ3Cz672lUw9E0Ddd1uXLlCl1dXZw7d+6x66I3mtht2yYzMcbD92WFZz0si6Xmx1FdvThjs4CGFokhXAsVb0Nk5/FkEuvmKFp3tUpARwpzYhrf1bGjg4jrN0juQtDc7FwahkFnZ2e9Rq9lWfUSkbU3Jtu2sW17107eT0qjGV387+jOLZSRQLgVaPZQtgatwbEJX0MRaKuFQ3D3mzZ6JYkyo1DrgtiHUVpFGlGEsNH8eZR+kqgzATRj+EUOyV/ibu4E09PTKKXqpTJd1w2jzkNC3gJslhuz0aLlOA43b94kmUxy6dKlYO5RDpr1i5j2fyWWAKXtx6UDKYdBjtQFTLwreMYXU3RfB/EyrnsI0xzBdTMoFScazePo7yZtfxxdtKLRhuNP4ltHMeL3kaqEqR1hys6BSODIbN0Ps2b6zjnDoKJEE93MuCYr7nQ9qjxl9lPyMwgVjEeWLBLTWlh24twqTBPTYhgYzNgzxEWcaWuapJZkxpqhRW8hr/J0cIq/WJqjzWxmrLxAykgyWl6gWY8zWl4gJkwmy0voaEipcWdR0R0PtKgukj+Zv7+loNmIEIJkMkkymWRhYYHz58/XE6zXxtpa8M1m7g2N1/dZ55OWUtLZ8/NocgJdM9FFAsPoRY8MkPO/E7/iMjY2RrlcXhNYtL5U5m4tZaGguU22E/23k7a22j6dTlMoFDh//nxdBb4ZO/HRlFKSyWS4f/U1js0uQ1sS7BLEmrHvDhPpTCHKmcBvM74f3EDDqe05hJq5i1qew+85SuXqGFpnF3JpAZHqQKWXwXUQfXvRNEHlzgzxL7HQEtuv6bqTcxqLxejr66Ovr68ehXfz5k1GRkZwXbcucKVSqW2nUXoSA4LhLRHL/CZKVwivjEqYCHyUFgWCdBwq1uADG48hsAEQohW9eIMce2lqnkQ4Ppo/gzLOAtcAH63UhCZL+JE9aHIFzTc5Ln4F+/y/r2t90+k0y8vL5PN5urq66kl/t3oT3a0vTUhIyO7YTm7M1dVV7t27x5EjRx76UPuTGKUfBP8+Uj+NXZnFiKeQ3utgnAZvNdBiahexhY/lfBzDOIPnraLr83heG4axgmZ8MavuKLbzaUx9H64/Qdw8T8V9DT06iUYKKfpI+wlK/nVazaB+eN4dRidJwX2AsHqR0VWikXdxrXSLvugRAEpeGoAlexyDKCVzkSa9A4VO2TvKSGWKvfG9TFYm67kxh+JDjFZG6Y32Vv8OcDWfR4+ZSBT9sRRpt8BAvINMYYq9iS5uFaY40bSHe8UZTieO8afTcxxu6uRBcYWBeCszlTxWZo6S55A0dqeE2CjBemNZYtM069rO9Xkun7Wg6XkVCuXvojU5hiFMJCZxfRAlunCi/5K4iDKYhMHBwXrAVGOpzNbW1vpcuhtLWaVSqWvfnzXPtaD5qNyYO2UrE2/NVJ7P5+s+Ittpc7vm+4WFBcrlMqfb4niWhUwdQFu4CW2DMDeNTB5ALwfO0+6qgxIaQklksVxXtFnZwEQhWtpQq8toqXb8sRH8zi506eDNr+CrBKVXbtD87qdflrIWhReLxTh16hSaptWdoScnJxFC1J28HyVwKaUeu8zXKfFfUJ6GMIooIgjdBk+AZaLlJVKLoEUFSlSQqU40sfDwONxZBB7NahapzqFbrwOg2dfw40cQXhy9/BrS7Ed37uFHjyG0HHrlClr+KkbL2brW13EcBgYG6qlPhoeHiUaj9QFjo6S/YXqjkJA3h/VlJNePO7qu43keDx48IJvNcv78+bp2STh/hF75BZToRZAAf4ayl6RJOYAN3quBP6Y3QkllgRjg43l3kXIQTZtBaIdR2hHm7ctEjRMgF9Gq03DFfZ2ofghLTuPrX8BY5XNEtQ4EEXLu3Xp0eatxhpx3A1SSjOyiaAX+lwv2CM16Jzlvke7IQZacUQZix5m17tJiHOUzmQn2xqvuWFWNaKacAQFZJxt89zIMRvdxK+ux4Nt4Tg6AJTv4u+oUAMi7QU5NV/p0a/uYLQTzYJMZCJS9sSZmKzkGEq18YnGUvzlw/Ilcv/VliS3LIp1O1y1sTU1N9TnnWQqajrNCqfLtmGRJmC6W0mnTHTR9P07kB+oBXDUaA6b27t2LlLI+l05PT1MsFhkbG6trcrej3fR9/7nJmf189GId28mNuVNqb6obtWVZFjdu3KCjo4Pz58/zyiuvbKvN7ZjOPc9jaWmJWCzGxYsXsf/PbwDgjEwT625FOkF/vOlpVCKK3tKO82CKyMEDqPkR5NIcek8vnt6JLAbryuUlFAKVqVZfiEZgbhEt1oqease5PwpvgqBZo/ZAb+QM3VhlIRaL1d8+G5P4Pu6AoE3/LhE/C7qBEOB7SbRVHSE0jFgR4qDsJJoeCPJYQyhjAPSbKL0Pw5kAQBcuWCaCFJBGoBCuiVa4g8BDau3gzyFw0OQ8MjJEZOY/YJ34UL0vtQoObW1t9aS/tVKZmyX9LRaLOzZxCCG+GvhPBCko/qtS6qfWLR8Cfh1oq67zL6rRhCEhn5fUAkl9399UceG6Lvl8nvb2di5cuBCsoypolf+E8G6CnENjBk9/EV9JmuKvgU/dXO7KPJZ2EM/7LGCi60fx/ft4nouut+CZLdjoKDxcOYcgie2P1GuXC9HOgq1w/FeJ671U/IW6uVwTgZCYtx8QN05zR+RIKJOyv0J/9Dhz9l1azG4K/kpdOVH28/ilg1y25kEJpipTJLQE05VpEjJBRsuQ0lKs+qu0eq1IJ8moZzLjZeilhQU3z/54N+OVpXrQz2CsgylrhSOJQcazipJjUfByJHWTkcIqBhqzlTwARc/mz+bvPzFBcz2xWGxNnstisVjXCubzeTzPo6enZ0cWthq7dc2znWHKle8hikWrXiDjJkmZNsr8pzjRb9lWG42lMAEuX75MW1tbPVK/Vt+8Fqm/Xq55Gm6Fj8NzJ2huNzdmje0KKZsJhSsrK9y/f59jx47Vo+C2y1aCZrFY5MaNGzQ1NdHT0xNUkpi4Hyx0XWTTAdzJqmbNsSh39JMwE0AJ6Tx0GaSpl8prk6Dp6Ik4qpBH6x9Azc+g9fRhZFdQmsDo68QvVPBmKlTujBE/cWBHx/OkMU2T7u5uuru767XJaw9KYxJf13V35OS9hsoKkekPoksb1VRCFlvQVRER85F2FFH1IBCyWN9E81bRymPIyB68pj5gAgClBHppEqV1oYwsQkiEo6PMM+C+hm7fwo/sQ3PHcaNfhGZbaN4SxvSH8PZ8I7BxdGA8Hicej2+Y9PcnfuInmJ2d5U//9E/5m3/zb9Lb27vlIQshdOADwFcQ1KK9IoT4iFLqTsNq/w/wO0qpXxRCnCBIV7FvN6c4JOStzla5MeFhhpFIJMKhQ0EwIN4oeuUn0bygXHAtAbvy/hKAXOkIrclhlPsqtvkuKs5HAYGun8L3b2HbS2hakkgkznxpAMF1hIhjiF48uUDCvEjZvYLjj2Po72DEmgK/F2VkiepdVPwFit54Vat5D93rR4vuYcVvwhErtGlJ8KHkB+byZXsckxiLzhjdkcNMVUwKvqRMJigdWR6jV+tlmmn6kn2MVkZpj7ZTsSs0xw7zqfQEByPBS6/uAzoY1broTXowmLaZSWIijlVuYao4y7nUAK9nZjmR6uFaZo6TrT3czi3Sp8cZKaxieR5Z26Itun13rt3QWKhkaGiI27dvk0qlyOfzO7Kw1diNAqRU+SSe+xOYQmLgseh1EaXCkvhnpKLf9FjH1hgrsT4Xds1q1t7eXreO7cYKvJUCo7rO3wfeDyjgulLqDQnd1/PcCJpKKSzLqpsRt3OStpswHd5YhlIpxcjICNlslgsXLuyqHvijBM35+XnGx8c5ffo0q6urKKVQlRJycaa+jpu2wYgClaCP2QJOLjDpeDPTmN0dUFjFLekooSN8H61nD3JyBBGJogAtmYR8HnfwIEJEUMoB38G6dvdNEzS380A21iYfHBxck0ZpYWEBIQTFYnFHpgGA6NUfRpN5PC2CnjEQuIi26nU2TcBCeQKSQToppbUiqhpMzZlGzyaQicNoPKDs9tHsLgCLeJGzICbRMncQWhwVa0XIwClfihfRS0sY5VH8yEmMpb/AG/gHoJlbOm2vT/r7oQ99iHe/+93Mzc3xTd/0TfzBH/zBdvxqLgEjSqmxapsfBt5DLXVBgAJqBW5bgbltndCQkLcRNS2X53nE4/ENhQspJcPDw5RKJS5evMirr74KgLB+D73yk4CN1M+gZAlPKPBerpaQvEprchipfwEluYznfBTdOI3vXcf3p3DdVkwzA8ZXsGh/FqKzRPVD2P4IpnEYz1ug7F7F1PdhM0BRJvCUja4XAY2sc4u4PkjFn8G0DyIjy6joCW6Vb5PU20FpLLtjNOkd68zlJ7Cly6rbw5T1gE4C4aTiB/NMzg/M4MvuMgJB2bcoWv2MOXNEhM6slyUqDJb1EhF0puwVDASjxXkMNBxL568Wc3RWfd5XncCMXvGCuUuvzgVNwiAVSTAgOvnzqTH+/uETT+06b0Zrayv91eDY9Ra2aDRat8BtVCZzp36Rxcr/xHd/AR0TgSAnmxFKcSX7hbxr/+6FzI1YXyqzZjWbmJggn8/zcz/3c/i+z/j4OPv3799Wm9tRYAghDgP/EvhCpVRGCLGt/JLPhaBZM5XncjlmZ2c5derUtrarCY/bEUoahcKaqXyNeWQXbFjDvFpByLKseu3bdDodvFFPTEA0BlbwwBNrQ0XaoJAFwDdiaGYngjwoBS29CF1QujmJsW8ANTOFLAWBLf7CHBgGnh8lN5NAk1Aam0Hr7sLs6kEspvFzRfTW5zPIpDGNkhCCaDSKaZprkviuT6P0hjZm/hxRmUOLO6iKgRb38D0dASgPRCzQYkoviRYNfIuksRfDvRn8r3WiW8MoO4bfdhDPfXgf6cXbeMmzmFwGWcLXzqLL10DGEJU8ujOBHz8UmNWwMe/9Iu6J9+54cKpF6v/Ij/zITu7DAWC64fsM8NK6dd4P/LkQ4v8CksCXb7tTISFvA2qBpIuLi0gp2bt37xvWKZfL3Lhxg56eHo4ePRq4AGkWeul9CPcVlHEK4d0MErCTB9oBB/xrYJwnW1iE2C10fRCQ+N4DfNmDri0SiZ7GIkbG/gRR/Qy2fwOFB2hUvBtEjZP4MkNJHWXOfhVdxDFFK66xSqtxipx3C10F2kUjGmXCGyTr3KHV6CbnLdEq95DTp2kzeyj6q1ULmMCRTbycmSSmuZiYrGqrNGlNzNvzpLQUGZlhIDbArDXLodhp/nJlmaFECxUrz/GmQe4WZ+oVfo4m+rlfnuNYcpCJyiJDcj+fWlxhSEswZRXZG21hspRhT7yVB4UV2iNxhvMrxDQDVypkIcK0UeRP7JE3XdBcrwBptLABayxstajvmmtXNBrdkUYzV/pl8H6DqAAdm6xsok0r8ke5d9FZ+ZqncXhraLSa1eSc9773vbz3ve8lmUzy4Q9/eDvNbEeB8W3AB5RSGQCl1NJ2Gn7mgmajqdwwjDVax63YSQ3zmlBaiyTcjal8q/1blsX169ffUEGoJpDawyPQcQBmbwPgFmzcuRUSXS2oYh5Xb0IvS2pGZG9+AdHdB2qaUqFMAvDnF6CtBb1UwBs6Q+nKFPR2oOaWEbEIZiqBNbVCoeBjnBim/avOPdYxbocnkUdzfRol27bXOHknk8n6IBCPx0H6mPd/DWF6+OVORDQbNFa1zkgrgp6wUQpU617wblX39lAIVMYeYBWhLLR8Gl22UD/5ykUrPry2eul2ELC1OoKKB+k6vLYvxev4W+CXMe98AOyHlTB2cuxPia8Hfk0p9R+EEF8A/A8hxCml1JNPPhsS8pzRGEhqGAaVSuUN69SsTidPnqS1tZoj0rvLiYH/Ar6GUGmUm8M1LqDkAsg5YAH0cyjvKpZSlKRGQq3geSWE2IdSEyjZAfoBsrKA0IIXfU/OomQMhwni5gUq7qsoUkw6BVz1Kk3GAYreGK2Ro6Sda9j+CihB0b9PXH8nNyqT9EaPkvUzJI0Oct4SngiOadmZwCBK1lskoV3ks5lJ9sT2MG1NczBxkNHyKEknSdEo0hHvIFPKENNiDEZPMlnWKUsPXwbzrlMtJGJVK/zUvutCB7uHXDV3ZqqllalsmaQeDJgxVyFRDESaueks8UWpA/zl6BwH21q5l1nF8yVL5RLdiTcv6HGreSkejzMwMMDAwMCaMpm1cpLNzc1rqvpsRqbwIxjyL2nRbUxcVv12WrQKv5P7apR3iuP61oHFj6LmRrhdNE3j6NGj9Pf384d/+Ic7mWO2o8A4AiCE+CyBef39Sqk/3arhZyZobpQbc6eC5npz+KMQQjA1NYVlWWsiCR+HRkGzJsAeP378DRHrtWpD7ugYztgUyb3dqEIWd3YZPB/VtheKdyBtIbNpxFBfkKTddSgsehhANJOHZAIqZWRzirLZRmWqQBSQmkD3fKIHB3DmV/BzNtGBPgqvTZH6yrPPPJfYVmw0IESj0TekUUqn0wwPD2PbNsfKf0Z3JYNyNPCL6AkPJTVE1MFPx1FeAuVoaIaEeAWl70c2dyD8wsOdVAdRAKW1EClIVFsMgYWMHMFYuobXdgrdvYVQDsrfgyanUaU72EPfg9f90DXFeeHH0ac/CmztY7meXfjSzAJ7Gr4PVn9r5J8AXw2glHpZCBEDOoFtvYGGhLwV2SiQdP084fs+d+/exfM8Ll68WPcPF/bvoVd+kfamBfDB18/jKQe8zwBR0M+AfwPpT1IxvgDH/QSxaARNO4SUI9h2GdOMYsZ6yPsxKv4raDKDIbrx1BK+fQwjfg/HGwX9ixmu3CYVOUPGuYFWTZaede4gZBOWtkDUP0ol0saSiiGRdT/MRXuEuNZCiRVS+iAZf4Y9sfPcKuRpqUZ915KvZytZAOyYDR7MWXM0682sWDHu5jO4yqOpmhMzZSQZKy/QbjYxUV6kmSgT1jInEvt4db6EQGfWX6HZiDBcWCGq6cy6JXQEeUOCB1m7zCHZxsRMDldBpBpd3Zts4s+mRvmmYzurXPc47EQBslGZzKWlJTKZDFevXkXTtLqio6WlpZpxxidX/A4Mholo4CmDokxSkAn+qPDFLNhNfFPqLG7Geqzj2G0OzVrKvCc8/xvAYeBdBPPOp4UQp5VS2Udt9Pjh3LukFgHYOMkahoHneVts+ZDtCpq2bbO8vIyUcttC5nbeAmoC5NjYGKOjo5vm3hRCoDwPZ3ISpMLTU2id/eAFfbdG59F6BhHZwNdFRdsAKDd14TnVRnwfrbsPAEOL4g8XiaSLqFgEbSWL0gTlfA6ZL2EOdaLFdNz5VQqvT255HI/L064MVPNrHBoa4oUXXuDCyf105K4hXdBEGVl9q3aKLaiVZnRPoGkumiGRZgrNmkEvzaGnV9Dnp/G18yiRRLPG6/uQoou4WkbJk8EPfvDmrZWzKAyk0YGxcgOpp/BbLuB1ff3aThoxZNtxNG9ng4pSajdazSvAYSHEfiFEBPiHwEfWrTMFfBmAEOI4ga53eac7Cgl5KyGlXJOAHdbOK4VCgcuXL9Pa2soLL7wQCJnKQS9+H0b5x0CtkC0dxhFn8Pw7IMdAPwrY4N/B1d9JXtk47sto+iE0zcHzsvh+nEgkh29+CfP2NUreq5j6viDpuh74COqxB0SME+TVfvIyEAjL3jwCk7z7gGbjEBIHrE4M2UPe7OJBZYpF6wFxrZWct0hP5DC+cumIBO+ZOhG6Iie5W/RYdPLMVGYwMJiqTBFXcVbVKs1+M1kvy1BsiKTejCYP83p2kYPJPjwl2RfvCrSR8Q4U0B/rQKLo0po5GBkiU06QdR32N7XjSJ+DTZ1UfJejzV3kXIsjLV0sWkVOtHSTUC1kbYNpp0JcaIzmMmjAVDbDHz64h2U9ntC1Ex5nXtJ1ndbWVpqbm7lw4QKnTp0iFosxNzfHlStXuH7zsyyl/wG6GkZDx5Zxsn4Ti16KP8h9FQtOE6dbDtMsEo+dNWe31eZ2kTJvOwqMGeAjSilXKTUODBMIno/kmQmamqahadqaG2EnGsrtrr+6usqrr75KKpWir69vWxdsI9/LjZBSMjU1heM4XLhwYVMBVtM0WFyEau42e2QW33wokCrbwTUfasLsiRk8PYLMC7TFDKI5iOmQxTKYJoUJG6O3C1yP6GAvmuOhDXZhruYRTTE85WGNz2EvZZj/i2sbmo2eJ3Y6IOiXfwUNC80I0hlpEYWz1ISyNDRcfN9AM4MBTcYGHu4n2oNQEmPpFtI+itIfllQTTuDPqedu4utn0HMTAGjOAjJyBqXtQ/hlZOQg9tAPwAb9ValDRJ3Mjo7dcZwdB6IppTzgu4E/A+4SRJffFkL8ayHE36qu9v3AtwkhrgO/BXyzet5yXoSEPGFqWsz184rneUxPT3Pz5k1OnTrFnj17Hq4jIvjx9yIj70EpgY9EqgWgFVQW/EmUdpyKfoai+zmElgIslMzheQk0bQUzeo4cg6zYnyCqHwM8tKofTsW7RlQ/jmvvIeP3sexOknXvENXaseUyqUjwcutVFQ/oMSa9FBPWKN3Rg/h4dEQGAZAEAnPanUFTJiU3ya2Cy5y9wEBsgIqsMBgdRCLpjgS+iAmC4MKYluJ6WlCoCt1FPxgjM14w9tVyZK44eaKaiW3H+MuFLCtWUOknUw36KfuB9sOrDicRTacv1kKT08ytxTQDTc24UjIYjVPyPY63d7HkWORdm7+8cZ0rV64wPDzMysrKjub7nfIkFSCRSITe3l6OHz/Oiy/0s2fPTxHXVzCVj+tKlHRIu0l+L/slzDkSTQm+rOOlXQmJ69mtRnMXguZ2FBi/T6DNRAjRSWBKH9uq4Wfuo9nIdivt1HiUoKmUYmxsjNXVVc6fP8/c3Ny2b+qaSfxRN0gtZUJHRwfHjh17ZHtCCMTs2hcDp7Q2nY+dVUhNR5N+IJAePIy8GkSoa119+IU8/sIS2uFjuJdniR3vAJaRToMGWCpie7qwxhbwNJ34gU6cpSz3X72JE4W2tjba29tpa2t7oolcH1d+2cmAoBYfYK5cQzoGZkcR6RmoChiGRFYrAPleHEME/xeKpXq5T+m71B9XP4rIuciuAwhvEaMwVd+HKGvgPzwmrThPtfwvKrYXFRva9Dg8swl8B/TtVcKo+Z/ulGpOzD9e99uPNvx/B/jCHTccEvIWZqNxRCnF6uoqQgheeumljSdtfT9+8idQ5nuI+v8MofIgWkDbj5RZyoDvLwBllMwBrSi1jOsdRDObWXZuYuqHAIVURcDA9h8QN89Rca/iiX7mtGvgXKv7YybM49hOmqI3DUqnwhQR40u5yT169CMUvRxKBXPWsjOBToRlZ5w2ow9HVZD2aa77sxxOHibn5YhqwQtrppwBHXIE0eUZLUO/cZKPLS4Q1SKMluZpjzQzUV6kN9LGrJWmP9rOnJ1mMNZJxXfolPt4tbDEUKyVqXKWPfFWxksZ+mPNPCis0BlNMFxYptmIIqWitCq4RxoBLJYDwdSuuoOb1Xm0r7mVqWSUdx87TS6XI51OMz4+vq3Az93wuILmRjKA7d6jbL2XuObSrudY9dvoNMq8XjnOby+exPVsULDXGMLN23ie90w0mrXk9TtBKeUJIWoKDB341ZoCA3hVKfWR6rKvFELcIcgg+4NKqdWt2n5mGk14fN+BzQRNx3F47bXX8H2/rmncSeDQVuvOzs5y+/ZthoaGtnUxNU1DLDa4xkUiFG5OYQwFaQdELEb5/hyVtoZMATKGqsYRuosZFAKRTGLlAwHGmV1BCQ13egGViMH8CiIeRZYr6G0tRI/uRTc0WMzRtyA4f/48nZ2dZLNZrl69ytWrV5mcnKRQKDy2oPhmlAatoX/uV0FpiKiG8sEtNqMbEt/T0OOBxlg0lDtrjT7U5qrSQ2HSt/IIt4hYzuNHzyB4eL2ViuHrDxMMK7MHqe9FCR1n4Bs37ZuUEj/aSkMG1C0J65yHhDw9crkct27dIhKJcOrUqS01QyJykQfzP4EUg6DyuKKFomjH9a6hKAMplFrGsjqAKA5xsr6Or8p4ch5BElfOkDCDIExPprHFOxmtXEO39wX7qPtj3iYiOnDkKgl1kpI4w7IfKA6y/iw6JsvOBCljAFuW6I0FuT2Tej8T5RRpGZTQXbAW0NCYKE8QUzFyeo7uSDdZN8vBxCHsSg+rTgRX+exPdiNRDMaCQNiuaGDVaTeDMajbTDGTiSFVoIhIRYJqdN2xYHlfvAUFDCVSeEpytnmQ6xNZBppaWbUqHE11MF3Ms6ephRm7QioaYzibJqJppK0Kd2eX64U9Dh06xMWLFzlx4gSRSISpqSkuX77M7du3mZ+f3/Z8vRlPQqPZKOCVrD+nUvlnRIRLTFgsel3EhcPHSxf548I7iUSbMOMxYpFB3t11jpWVFcbHx5mbm3usufZxfTR3glLqj5VSR5RSB5VS/6b6249WhUxUwP+tlDqhlDqtlNpWOPszFTQfl40EzXQ6zZUrV9i7dy9Hjhyp3yg7MctvJmj6vs+tW7dYWVnh4sWLJBKJbT0MQgicORuqN4vR3Qu+pLLighBo1e8q61C7DUujGczBwFzirWbR+/qRHYNYM4HQKfNlzKFekAq62sDzMQ8dIDtrkllsojAnmP9sEb9jD8Xhpboz80YPd7FY5O7du8zPz+M4zsYH8RTZ7oCgZm5AdhzhlpBSw8u3IozgnMrG1ESp6m9GG5o9H/wf6SVCYCJSGBiVQFss3BKVBYmnNZjRc4toq7fxzX3B+g6Iwgxex5ehYn2b9q8+IOjbTz4flp8MCXnyKKUYHx/n7t27nD59ekcFISS92MYvYRvvpui+ShDn0IqSizhOO0pBPG5R1t9JxbyHq8bQRApPLhM3gxQ+lnebqPEic66JTSCsSSML6BSq/pgKF7/SQkwcZlZEmLEXWbBHSagObFWiNxa4vsWNIMVR0VulM/ICL2eXsaViRa3QrrVT8At0yA4kkj3JwMWu1WylJ9JH2mpjzKtgyWBcz7iBtnHRzgIwawVayGlrhaOx/bwyX6DgOIwVA9/KyUo28LEsB+vPW0HFn6xT4Ux8kJkVKzD+VCeuhBGc555EEgkcaGmj7Llc6OrDTUsmlnJMZnJrznct8PPkyZNcunSJoaEhbNvGsiyuXLnCgwcPWF1d3bGZ/UloNGvb58u/hu/8BDoCgWDVb8dROh8rfQGfzB+n5NpoyqBktXKkeR8Hegc5cuQIe/fupa+vb40gfevWLebm5rbt0vYmms6fGm8bQVMpxejoKA8ePODcuXP1Wqg1dpoKaf265XKZK1eu0NzczJkzZzAMY9ttqkIZObqMticYOJQZDDzOfAYxMEQuHwwCer6C6hlE7+3DWS4ixUPNnIokyd1O42eLgYAJiJpAU3Gwe/aSnZDYixVifc2UR1cwWmIopZMdtUlfXmu6b3y4m5qaGBwcxLZtbt26xZUrVxgZGann/3zabLu608u/hlJBfjNV8tCUgyaqFX+0IPWoq/pQWj+ucR7XfBEvfgE/fggZ7am3I+P70HDr36PWMpVCG1LpVEQXmrWCQKKcJpTegpYdRXMyuF1/95H9exOdtkNCQjZACIHjOLz++uvYts2lS5fqaWq2i6ZpeLILM/F9CJFEyjkQAygFkcgomvnlLPlliu7rIFMoCkSNwDpVdq9iaoNo+mlWvA5Kfpq8ex9DNKOMLO2R00BgdUMJzGQ3DxyDJWeWvugRQBEjECwLXmCRXLRGaNI7cWQ/0xUTS9oMxgMlRLwqxBqRQAOZdoPIdE8aXE8LruWmiWMyXl6kM9LCTGWFgVgHi3aWfYke0m6BQ4k+UqKPxaLBqlPhaEsXWbfCXrOFrGtxpLmLZbvE4aYO5ioFTrX2IEsmCxmbB7k0HbE49zKrNBkmD7JpdCGYLVZrojsOp1JdeDnFYq5EKhbjz4ZHH3n9mpub2bt3L4lEgnPnztHe3k46neb111/n6tWrdeXIVtrBJ2U6z5X+E8r9b0TQiOBSlFFatBKvWO/gM/l9CAziepKpooEndb6274U1bawXpPft24fneQwPD3P58mXu37/P8vIyrus+sh874XmzlD1TH83Ngm52UlbS8zwcx+HmzZs0NTVx8eLFDS+KruvbjnirRZPXWF5eZnh4mJMnT9LW1rZl/9fjTy4CkL+5RMueFG7hodYwP1vE1Exqe/NsHaOtCShRGZ0j3tGMLBTw/Qi19wIRCXxx7MlFNNPAppnylI/MraC3xnFXCiAVif1tWHM5SvMOS38xQcdLgxv2r/Zwt7W11R+CbDbL8vIyIyMjW1ZQeFy2c73l2FXEagYzkccptxNrSuO7OpEWC+ULbK8FliPQ2YuYuBckbe86hUjfC7bvOouXOItevoHSWh62a3ZiVlYwgVLyKJGoCQRv7Xp+hGzTcdrUHfz4ADL16NQcb6aJIyQk5I34vs9rr73GwYMH64m5YWd+5DUFhmEcJtn0MxTy34bgDpp2EVfTWbU/h6GlglrlagBFhop7lYh+BFfO4IhTTFauINCJ631U/Pl6vfKSNwtKwxUrYLyL6+V7DMZOUrayWNUyuVkxQ4QkeW+R7sgBKrKIL49yvTDMvvg+ANJOGhQs+otERIQFb4GUmSLrZdkbOc/HFic53ryHu4Vp9og2xtUq/bF2Vpw8HZFmZq1VmowYKaMJzUnx8tIsL7RVs5pUUxIZWjAmx/RATGgyo+xPtBOrJLm6OseF7j5mSwX2t7Tx6tI8Jzs6ubq8yKn2Lm6ll+k3o7TpUebni0xaOeKGwVQ2T7Zi8e0vbZ3fWQiBrut0dHTUc15blkU6nWZiYoJSqVRPst7e3l4vftF4zR9L0FSSSNPPIrybpHQbHZ9Vv52UVuZ/F76ae5U2FBJPCZbLMXQhudi+j9aqIgneKCQ2VoYbGhpCSln3V52aCly7ajXOW1tb67LIbuaV7ZQzfrN4roKBoPEh37prhmGQy+W4cuUKhw8fXjOwrGc3Ppo1LWkmk+HixYtvuJG326Y/EZhvlePhRXqxpxbry0wtht6Wwl8NBhl/ZpmyrGYY8CVaTx+yXCI/UsAc7MUZmcKaWESPGCjbQT9zjMLHF4kc7URmKsSH2inenCU21IGfq+AsFWk60I09n8deLRPt2LK84RuSp6+vUd7S0lLPKbbrGuUNbEvQfPl/oePj2UlENYWQxMDJx/EKMeKtJRCgzIfXSLjZh//n5xELS/gdR1D+w2smI/3oVaf5RHocv2ttVaqoH0cqwbQ6zWQ1e0F7e3t9EFjTx106bYcazZCQJ4Ou67z00kuPFYBRm4M8z+PevU7a2r6W5qbPUaSM5ZVQVNC1fbhyDqUPo6uj+OI+mmhl1TfIO1doNg5T8B4Q1Tuo+PPk3LvgJ7BZpklcYNwvYVb9MZedoD55xp2ly9zHsjtBq9jHshrB0Nq5k3MxtQUEgqnKFC16C6vuKimZIqNn6knZuyO9lNwuFuxAqHareYILBL6cc1ag7ZwsL6EhKNsO8ysRRuU8ETTu5ZeIawb3CyskNJMpp0hU6AwXVogIDU1qzMw7rBoZBDBXCuasdLXSnV2Nmtc1DVPT6FExrj9Y4txAL0vFBc70dXNjfolUPMbw8ipHujYvmLLZi0EsFqO/v5/+/v41SdZv3bqF7/v18bmmENqtoOn7Hor30hKZJiYEjjKxZBNFGeN3Cl/JhBVHIDFFkumChisd4rq5RpsJW88JmqbVBUt4WCZzaWmJBw8eEI1G0XWdeDy+I8H5ebOUPXem8+3m0lRKsby8zPLyMufOnXukkAk799G0bZvXXnsNKSUXLlx4g5BZW287gqZXFTQBnLzEbX2oUdPb26ksu/V0OaIzhS8e3iD2bAZjaAhnpYJXDFTrynKJDPWjd6UozAeX0M8ED7tXCISwSCqONZ0h1t+M2axjTWWY/6ORbR3/emoVFE6fPs2FCxfo7e2lWCxy48YNXnvtNWzbJpfL7drMvtUD5F3/LFpmPljPddGT1WNWTWDpYDxMKyXcwGSj9AiiGLgLqEgLWrkajLU6B3M5/EQ19ZdsqBQkTFgpobRAeFZGksjyPWTiJN3n/jEvvPACLS0tLC0t8eqrr3L9+vU1ZpxQoxkS8uzZ6TO40fbFYpHLly/T1dXF0NC/I8cQBe8+WnVstry7xM2zAEhyGNolRqwZNK3mshWMhVnnNnF9EF9ZCKubmPYCY1KS9nIs2qO0Gr3YskxPLKg2pmuBgiWvFknpZ/nU6jRxvYm8l2dfYh8SScIJlAWJSPC35JfojQ5wLye5n88wWpojrkUYKy3QGWlhRRXpj6ZYcfIcSPSS88ocM/bxufky/U0d2EgON3VgS58BLY4tPfZEmrCVz6FkO5bvcallP6+MrXCgJVUP+pkrFTjQ0sZYPktfsonh7CptkShL5RLHjE6m08FclC5X56bq/NAUNfmz4S0z4mxJLcn6vn37OHfuHGfPnqWtrY2VlRVeffVVyuUy09PTlEqlHWm0PXeFQunriWgz6JpORcbJ+C2s+O38r8y7mbaaiAiTiGhlLK8w0EnqEc63HKI9sla426nyoVYm8+jRo1y6dIkjR44AQezJ5cuXuXPnDvPz89i2/ch2nrd55bmLOt+OQFjzwfE8j56enqAk4RbsRKPpui737t1jaGiII0eObCoEbadNpRTu5EL9e0FKvLwJenDqPVtgzWSJ7A9S5viJFkr3F9CSwSDipfPYbnDz2pMr6J1twXqOpOKlKN1fhoSJv1Qi2t+GNbGK2dmEPZsGDaI9TVRGV/CKNvkbC48dYa5pGm1tbRw4cIDz589z5swZhBD1RLY3b95kdnZ2R4l5txI05csfQcgKQgEodKOMlW1Dd0oIIfCrKZ6UpteFS9k0gKimBpGJ/of7aupHlDOoqRX85DFE+WE2ADsygJafx0+crm63H6F8lGpBJfoxTZOurq41g4BhGExMTHD58mXGx8epVCpbDgKNPG8DQkjI5zuFQoGpqSnOnDlDf38/QkToafkhQMP275MwLwDg+jOgmin7A6RVM55ysOUqoFHwRmkxjwEK3zIRyqQkmrlbKZJx5+mNBqmQknqgycq6C4Bg0R6jmT5KzgDLXgwFdESqZmM3GFOLZhGBYMFfIEaMiGhlutjMWHmVw8l+bOlxsKkPiaI/FuRrThnBGBPXI/T5/UzlfDxAVM3ksmomNxPBXOpXh+NSucwer435lSCISK8KTbWgn1QsWH8g2YynFKfbu9GygojSybsehzvamcjk6GtO8mA5TXMkwng6y8cePFrQ3I3Zu2aJO3LkCJcuXapnmxkbG+Py5cvcvXuXxcXFRwa82vYYxfK3YKgV4poPUiMiHAoyzh/kvpy0H8dVHspPsFDSMYVByXfATvLX+95Yy/1x82jG43Gam5sZGhri0qVL7NmzB8dxuHPnzpp8pOuVc7uZV4QQXy2EuC+EGBFC/IsNln+zEGJZCHGt+vn/bbft59Z0vhnZbJbbt29z6NAhotEos+vyU+62XQhu7pmZGdLp9JameNhe3k9nbhXlPdxvTE9QWVwmcnE/zsgY5cksAFZGogH2ioNyffT+QeSDB+ipFuz8w8ukt6fwV7IoEaGy4KA8SWSgHffBCkZ7EnsuS7SvleLNWRIHunEzJYz2BNFUC16+Qvpzc3S8Y4AnhWmaRCIRjh8/jlKKcrlcL8fpui6tra11M/tmmoZHDSru5b9Ac/I4bhtxcwVPxXGWohimjm4G59Vsq2ogm/sR5Wq1n0jDQ6Y9TIiuIikE8wjp4S/YaG3N1ArmqGpiY2ZHkN3dKFcgCPw7NyIejxOPx+tmnOnpaVZXV+u1ctva2kilUo/MW1oqlejr2zySPSQkZGds5Dtf++1Rwovv+9y5cwfLsti7d++aiTphvkh74ptIl38d2xtB0AyY5L1TpLlBxGtDI07FnycVeYGMcx2vmhBdGUUs8RLT+ij9kePMOXdxZbBs0X5AXGuh6K/SGz2MJS2ypV7G3Cn69UCIm6nMoKMz786TMlJkvAx743uZqczQ6h/kE0uLnG7ZB5WV+vEVvEq1/SwQRJWnjCRTiw4Tlo3QBE16hHv5JZqNKMOFZdrMGMOFZVJmnHEry5DZhFWKkrNcKl6euNC4t7pMRAiGM6sYQjBVCNyOFsslTqe6Kaw4LBfK9FRrmjdFg7G5v6WZ+UKJkx0prs0vsj/Vxu3ZZU4OrA3afZJomramlnk+nyedTjMzM4NS6g1uUJZ9jYr1A8SET0rLsuq1kjJLXHeO8ZHsJUqeiykMlNfKpCWRyiauRZBOkgOt3fQlmt/QBynlY2vYa8JqLZaiFizl+37dv3NiYqJuhvc8b8eCpghybn0A+AqC6j9XhBAfqeZjbuS3lVLfvdNjeMuYzpVSTExMcO/ePc6ePUtPT88TSVlUw/d9bt68STabZWBgYFu+h0G900drNPO35rA7HkY8uwuBX0v+QR5zsA+/EGi/KpNp5NAA7mywvDyZQWkaWlc3xftLaK1VreZMBkyD1VGPyGDwtuqXg/Nlz+dQgLtaJLq/GzfWwfRVyFdSpOdN5u/A7Kce+oc+aYQQJJNJhoaGePHFFzl37lw9d2ctYnCjfGKPmgC8Vz6O9EBV7wmnHCdieDjlYHslwdCC4B1iDQ+6fKhRrVX9CX5vuF7Rbvz5MjIWvFBoVrCekB6+6kVkghRI/sDWec+FEEQiETo6Ojh79mw9WjKbzXLt2jVef/11xsfHyeVya469XC7v2JdmqzfP6jp/XwhxRwhxWwjxmzvaQUjI24yt5oqaqTyVSjE0NLShAqE7+T3oWge+yhIxX2LS0ckyjKaacGSWtkiQe7fizwM6ZTlBk/YORr1mnGoGkbQ3i4bJqjtNR2SoWvUn8MkXpHg95zPpLWJgMGfN0R3ppiIrdBOMUZ2RwG9ex8RzhnhgBdV6xsuLGOiMlOZpMRJMlpfojbaxaGfp1VpJijheupVhq8LxVC+29DnS2oWnJIeaOvCV4kBTO75S7G9q50iyi1g5wXShxKG2dlwlOdbZja0kh1pSFD2XwUiM5UqZA8lmuvU4lRWXu4srdCbiDK+kiWqCsXQWTcBCIdCIVjyPPa0tJGyDP7v+YNPr8biBPOsRQtDa2sr+/fs5f/48L7744ho3qLvDP0+59F5MfEzhMuf1oAvFX+TP8bvp87hSJ6JHyFkJlqxAM9xmJlnKCoqOz9/eu3HRFt/3n1ploMZ8pLUymYlEgg9+8IN84hOf4H3vex//+T//ZwqFwnZ2cwkYUUqNKaUc4MPAex6r4w08d4LmRgOC67pcvXqVSqXCpUuXSCQSm667k3ZrlEolLl++THt7ez3n2nbM7FsJr67rMvHZm1h3injdKYzONrxc1V8lW8GPda5Z33YeugB4mRKRfUMUJy2UL4n0ddd/Nw8fwl60cFYDYcqbySNSMdyVEvH9nchkitX5OCuvptFMHbPJIH8/C7pG+laB8sKbU5Jyq8S8d+7cYWFhAd/3NxxU7Jc/AcU80pIYMYVVTqH7Qd+FFpx3P9GFUB6O2YYUzbitZ3FbziJpQTbtQwmjbk4HEKWH5b6VMhBWCb/Ygqe3YBYbkupXfPxIL7JlH6rpoen9UTQOCLVoycZBIB6PMzc3x+XLl7l58yaf+MQnWFlZ2ZGg2fDm+TXACeDrhRAn1q1zGPiXwBcqpU4C37vtHYSEvA2plaHciLm5OW7cuMGpU6cYHBzcML0dgK4105P8foT+hQyXb6GLZiQWERlYiPLuMDpJLH+JiLOfqP4SU76gIissWg+IyCSWzNMXDRKvmyLwLc+48zRp5/hUepKU2Y6tbHpEVTlRHapFNBgf5+w5BqJ7uZpxWHU8lv0CexNdFL0KR5r78ZTPvkQwV3RH2wBochPcWPKJJgMNl1et2FPyAhNywQuUHbmqaT6qItyeypN3g/my6AbrWV4QI6BVcxe3NrcQ0TR6SHBzbIWo9INa6U0JHN9nMBknZ9kc7epkNl9gb1srBgI9I7kztcRn7k3ivwnp8zbCMIy6G9TRk9fp7/kddBFc92UriZQ+H8+d4BPZY/hKx5IuZasFW5pIFJ6vyGQ1mowYL7T3cqA5teF+nkQJyu1qRSORCD09Pfz4j/84J06c4Md+7MeAbQdEDQDTDd9nqr+t5+uEEDeEEL8rhNizwfINee59NHO5HJcvX6a/v5/jx4+vuWhPQqO5uLjItWvXOHHiBIPVBOlCiG21+yhBs1gscuXKFSKLwUhRXtDRO9dG2ZVXQW99KGQ4OQE9D2uge55JZS7QslVm8yhAGDqlbPB2XJnOEulvAwV6ZxNoAtncwexn8kQ7E3hFl9ZjKQrDGfSIRsu+JKWZIqO/M77lsT0N1ucTGxwcxLIsCoUCN27cqEf41yL+3b/6JNIHDRtZcVC2ixkPBr1Is49SoFJ7KbsHkDMSOTmHHB7Dn80g7z7AfZDF9k7jNZ1AGfHAbF5pqJZVqSYOzixS9A+uqecjjWaUFcHve8e2j+9Rg0pjrdxLly5x4MAB5ufn+cxnPsP3fu/38u3f/u1MT09vuO06tvPm+W3AB5RSGQCl1BIhIZ8nbNf3v1aAY3l5uZ5vEx6mzduItvjXseK7KFziRiDQWdooUa0TTxURVi+aasKO9XOjPM2yM0G7uQcfj6QKzMQlPwPAoj1CZ2Q/GbeXnB8Ina1mUDiiJAMNYM7IERER5uxAu9lhDrFitbPilOmPBnNFs1H156/6pKerNcvnrDQDsp9XczYCjeHCCk16hPu5JdrMOMP5ZbqiSUaKq/REm5gu57iQ3MunR+fpTjQxXSnRHY3zIJumO5bgfjZNezTO/cwqzWaEpXKJI0YHI0sFNAH56lS4WlobhV5zGtrf3MrY8Ao9LU2UbZf25gSvjc9teJ6ftEZzM7Klf4vwPkSTJmkxKrgixkAsz1+VLvIX6X3kbAu7aLOcjTJTKlHxXJpEnHIxSsHzKHoOX7vnyKbtP6la5ztto1Kp8MILL/Bd3/VdTzIG4A+BfUqpM8BHgV/f7obPpUbT87y6qfzu3bucPXt2w5xQj6PRlFJy//59ZmZmuHjxIq2trWvW3a5GcyMTy8LCQvCGfOwE7nQwqKisiy0b/QYFhdEMek/w5ipMncpECU80aDVllMhAIJw6y0VUbxsMdpN+fRk9GQibRipo009bmIf2svi5HOiC8lRgThYo/LJH24kU5ZkClfkSq1dXkf7jBQU9Lo0Rg83NzZw6dWqNKWP4tz6MzGbQdQepxVFSR3oaQoDnavi+QcXag8zaaOkVvEgCUQrSd9DcoCnWYsjhcexcJ17L0frP0khA4WGQlioJ7KYDD7crFRHpKbyed277mLYbdV5zMfiGb/gGXnjhBT70oQ/xzd/8zfWJbgu28+Z5BDgihPisEOIVIcRXb/cYQkLejhiGsWb8r1mxWltb6wU4GtfdbPwXQuNoy3cAkHFuEaMfhEeEYBw34wZLcj/DlQfVBOwQ0YIxvaDNoxMh6y3QHTlAu7mfrDPIRGWVStVSM12ZxsQkK7L0RHqwlc1QfAhTmCS1fXxiaRm3Vv/cDcb40dI8UWEwUlwgZSaZsVY5GO+jkouzahlU8Dnc3Pn/svffUbKt6Vkn+Ns2Yoe36TNP5jmZx59zzz3m3jKSpkpdCCGQStMgQA0tmGk1zWqBxII1dNMzUz2DmrVgmGFYjSToxUwPRoMRjJqWQMiVqlRSVd063rv0PjO8j9j2mz/2zow8PvPcW1WXSz7/RGTkji+2fb/ne83zPhMuPxbP+q0koykAJqNpRrwcds+nBKNR3xaNRGP+dokknhBMJVPYnsc72UGoQliou17L7VabY5k06+0Ow/EoGz2TuK4xX6lyQo/w6MkWnge1gIhKwG/efbV4+7cTnudRbf40svtrxGULQ+rR8uIk5S6/1Pgit7pjGGqYeChBwUvioaK7EqLh8nSjRbtnElVULiVHOJsZfO3vfLtC569Dp9PZV5H0HqwDez2UY8FnuxBClIUQO5Wu/y/g0n4H/9gRTVVVsSyL27dv0+l0ngmVP4+37V++I12kKAoXL158a33M53M0hRA8ffqU9fV1rly5glLsIuw93tm5LqEj/ipYH8nitmwqt4touQT62ADC9DDnaqj5NMgStdkWRPrkVNGjNNYEwvZwsv4KuL1URQAialBbFdgNi8TJNGaxS/x4msbjClpSR1g2ve0uqVMpvLbN+m+/fCX5NviwlexCiBcqugeW53EdBRmLXk9DlgSEVISArpnFa0hIzTpS0w+Fu7FUf0BF3Ts4AFKrgVOWsRMXEJKMiI4iif61kzttvEIXoUYQWhSqG4hQDHLT+z6Ot+3gkE6n+cxnPvNMM4APCRWYAT4H/DjwDyVJ+sgGP8Qh/kPD3tD55uYmd+7c4cyZM4yPj7/gOXu+YcfzGDS+l7R+HhBoQfOHpvsEQ36fe702YdUnHjsC7Num39nHkUyyyhH/N6RBvlVrs9Rb8/MxzQ2fWHomOeEvlONB60lbuNjOET6obKKiMN/aJKvHKTlNRpUUXdfiWGzEb0Fp5BnWM9RKCnPdHknDj5iJ58LlNcsne8Vem6lIhkrFY7ZcZzPQxtzq+K+FIAe01PVf62aP8+kB2iWLcquLG9hXPSBCybBfeDmciOMJODmQ42goRUSJUutajKWiLJXqpA2dJxtlrs6t0bNe7Ijz7fRouk6PRutPo4k7qEh0RZiCk6XqRvhntR/hQSeJKRxsF4qdCCElhCNLJMJpLDlBPuqTbqdqMVyzdjv7vMwL/p0Mne+FEOKg37kGzEiSNCVJkg78SeBX9m4gSdLeqtUfAR7td/CPXejcNE2Wl5cZGhri9OnTbxQ73S/J2dm2Wq1y/fp1pqammJ6efuk+7Jdo7t3Osixu3LiBJElcvHgRTdNoP+3rZwpdob3aoFXRQZGRA++VcAQkswg9WH0IIJElNDGAWepRe1gAwyfCwlVw2oEMheN/5tR6OONxCvc8RMy/seRAOkmNqgjHIzGdpPG0RigXQo/IVB9UWP7VfYVpvyN43qi0fu8DpE4LxVDo9HKoQd8kgaBezeJ2BZIEXjQBnSD8re5ZLFjt/vtOtf++28KdXcA2ziHkfsqC0Ay0VgW508IxjuPFxpGEQIxcAGn/j8jbrDxbrdZBQxtvXHniezl/RQhhCyEWgaf4xPMQh/jE41Whc9u2efDgAdvb27z33nskEomXfHt/kbLjif8S8AmmZA2BcomiiOHiUrXXkVGo2usM6FMIPJJaEGb3WujSBX6vskhKS9NxOxyJ+ORTBAWOtuYTr5XeChPho9woW/RchZbTZSY+godgNOxHunTJL1q1PP87lulxf8tjzbORgSeNIiFkZtsVklp4N1w+3yozaiRIqxHsusrDcpnJeJL1dpPJRIq1VpPRcISNTpsj8QRLzTpj0TgZxaC63eNRoUzGMHhaLBPTNWZLFXRZZqnq90bfarbJ6hpySzC7Ut7thZ5N+LZuIp/G8TzSYZV/9Gu/w4MHD9jc3Hyt9NBHActcp9n+0yhiEwUJV6h0vBA9EeJ/rf9veNoLgQBDSrLeDtNwLTzPI06SQsOj6zqYwmVITTGZHuI//9znGBgYoNFocPv2bW7cuPFM0ed3I3T+No4fIYQD/AXgN/AJ5C8JIR5IkvTXJUn6kWCznw6KS+8APw382f2O/7HxaAohWFlZYX19nYGBgY9c8kUIgWmaPHnyZLca+lU4KNFsNBpcv36diYkJZmZmdg1dd63e//2MAR60lpuEZiZxuv2boXKnSHcPH2o8KGAqgRfXFhiTfjGKaYYIHwm69SzV0Yd9QymHsnhd6K50EBLUHpWRDJnG0yqSLmPX/STvxKkMrqKSuDCA1RPUF/dUY38X8TzR7P3O1/B6DnbLhW4PXe/iODJmRUX3LLSoT+as8B5Pd0AuhSRB3Q+JC82Ahu/x9CQZ6n7Fvbe4iGPFEAGJFPHR3fxMd2keV/iLAG/swoGO421DHPsMme/gjStP4N/gezORJCmHH0r/8ArJhzjEf6BwXZcnT54Qi8V45513Xtt5bj9EU7dOoPamUMlTtY7wpLtCwZwnJEXpuDWGwn7Y3K/dg4K5QEwMs9KL0nR1BGJXH7Nu+vNETasRkkKUnBIZMgzpxyj20tQdk4weeDeDbj9bpj9hrDtVQpLfy3yScb6yWWckmqJm9ziVHKTr2kyFk351eRAuPxJLIyMxEx7i+mKFTMi3oznDf80G2pipINKXM6KEFIXj4Qy3Z7cZTcTxhGAyk8T2PKazGTq2zfGBHJVuj+P5LDFNI9GWuTO/RT4eYXarQiyksVisocgShUZgrxWNkhdmYmIC0zS5f/8+169fZ2lpCcdx3roJyMtgWrN0ej+JLlUYUGuoeMTlNm3P4F/Vfoi6G0NBQSHGQkOgSyoxJYTdC7Net5CAjG4Q6moU6l2+/8gkiqKQTqc5duwYly9f5ty5c0Qikd2iz06nw+bmJt3u2xfgvs28IknSgT3CQohfE0IcF0IcE0L8jeCzLwkhfiV4/9eEEGeEEO8IIT4vhHi837E/FkTTcRzu3LlDs9l8oxfzw4zveR7vvffeG3MXDhI6t22b+/fvc/78+Rd0N9e/ViI85X/m7ZFLKt6u0630V25aOorp7vGwOS7lSv/3W2st1FyM0t0mnfVO/3vZBJHjgxSvdpDCCm7dJnEyC7YgciyB23aQx3S6kkcvm2X5hsnT32zSbimsXGtz+/+9/MZj3A8+bIhjL9HsfOsWot1CeA6K7CEkFc+TaLcHCYdtPE9Ck/1k90gi8AoDoZ5veHt6EimoohSJQaSdpXRiCIKwkUDCnVvCSfjC7ELu3w+SALclI5AQoxcOdBxvs3o9aC7NPleevwGUJUl6CHwF+D8IIcovH/EQh/hkY2tri62tLYaHhzly5Mgb7dWbiOba2hoPHjzgZPanmbMjbKurxJUctjDJhyYB6Dg1ALbNeRLqACltipI5TMFpIgKbtKOPWXJLDOqDWMJiPDKOLukIM89XCkUa9rPyRfPtLbJ6nIJZ50g4j4XDidgo0W6eRtefY7Jhfy5R5WBBHoTNd6rK61aP49oIDzZ9m7na8nM9lxp1JGA5eN3odpDww+VHRJL5Tf+Yii1/n2pdf7zuTsg48KQNhCOszVcxVBUBjGYS2K7LscEMja7J8eEsm7UWk/kUMVXj8b1NPEnb7fBz4cIFYrEYpmly/fp17t69y/r6+ociax3z63R7/xW6ZBKROpScNLpkc7t3nF+q/UG2LZuO20Ny42x2FGQJ2q6N2zUQrkZc05GQ6FRdcCQmkyk+f+TIC7+zU/m9U/Sp6zqe5/H06VOuXr36SoH11+GgaQRCiA+dzvZR47seOm80Gly9epWBgQHOnDmDpmn7LvDZD/a2EjMMY19EYD9E0/O8XVHy995774Xwp9O1ac1VqCxKqAkDZ88zomViCKMvh6APpancKSLnfQ+lNBjFXRbIYd9wmNst5KER8KC32SZyzPdqdpYbVDYUPNMjNOkbFymQnpAtCTWmoaeGWP9AQgqrtNd6GEcUGutN2hs9SnfrWK393/DfTuw8SI1f+12wTayegSxcf79rKdy2Tx69cBwpWNVLQXWlF0mjuP7/Q+l+YnbL7N9H7l4B9/ggWD3cp0u4mXOITv/iCCOJtziHO/5ZiPQVAPaDt1l5vkUuzX5WnkII8ZeFEKeFEOeEEP/iQD9wiEN8AuB5Ho8ePWJzc5OjR4++tI3wy/AqorlTpV6pVLhy5QpH0p8mqY2BJEgEofGytYqMSs3ZZEA/ioREWD7B16sVap5vr1a7q6TVNF2vuytjtJuP6bm0rVHumjUMWWelW2Q0nN0Nm4s9YXND1skQZW3T5kmnR13y7eJ8s4yCxON6gYiisWQ2SKoh5pplziaHaVYlGm2HjXaTY4k0hW6H48kMpV6HmZT/ejydpWpbXEzlaW9bqJ7EZrPFVDrJar3BeDLBQqXGUCzGbKlC2ggzW67w/sAw9x9tISNRbJtIQKnpE9NOkIupSDIScCQR58m9LfKpGL9zo98eWVVVMpkM8XicK1euMD09/QJZK5fL++YJrc4/xzH/Gorw55iim8YUIa72LvC/VN+h7XgYioFtJVlo23Qci5Cko3Zj1EyHmtXDdj2MXggVlZ7j8H0T47tdkl4FSZJQFIXx8XHeeecdLl26tKsrvaOtvLS0RKPReCMxPAjRNE2TcDj85g2/g/iuEs1er8eDBw92W33BwSrJd/Cqi7RT/X3u3DlGR/ffDedNRHMnH1PTNAzDeGkYpvmohHAFvbKJmxjELfYTnrV0jML1CsZRX+7CtmQQ0AqEIIxsDrthYUwH6QOyRKve94gKzTeY2nAaaadVZTtYtT6uIkdUzFIXK5Vn8ctVQhkda91GkgWpoTjdNZvYlE6j1ODL/8+rmKb5oVaLHxXaNx9jl5p4qKiG/2CZVQ8FG1X374nQSED+ZBkhJJz8OdrKOE1zgo55BKuXxk6ew82dJBbth9Z73b6Au6n0Sac9t4Vw+kRPJHzD7yqv7wr1Mhw0afvjtuo8xCE+CZAkiU6nw7Vr1zAMgwsXLqDr+oeSwtsZL5FIcO7cuV2bfyX1vwX8gp+wFKPrNRgK++nQihRCcIZr9WVCUoiGaDAkDyEQaL3Angfcd7W3ypHwDNdKJp6nY+FyLOrb/52wueP5+78TNrcsj5WKziOrTT4UZa1T52gsS83qcio1iOk5nEjm8RAcMVKcTgwR7kVYrTcZCIpMo7stJf3jiQVzS1TVOBlJIjUlyu0e8ZBPXNJB9CUf2NaRZAxPCI5l05yIZPDaHm3T5vhwlobpMD2UYa3SYDyTYG6rQi5usFSqcXFggMcPt5ElKFZb/NbVPtF8/lpGIpEXyFqlUuHmzZvcvn2blZWVF/qZ77xvdP4Bnv33CQGG3KPr6QyrZW6bM/xW4x1kKYwlHOo9g4atkFDDJNQImzVB3XLRZYWhcBypIVNudXE8l/FYgh88tv8i0R28TGA9HA6ztrbG1atXuX//PhsbGwdq3/wytFqtAzcB+Xbju9qCMhwO86lPfeoZtv6qzkCvwo5R2DvB70gX9Xo9rly58kyXn/24oV8nb1Sv17l//z7Hjx8nn8+zvf3yTjv1h33pwk7Rxc3HUJb9XBzH8n+/XVeRZYnarL/SdRZNmIxRX/VvtOZKB1mWiE7nWfmgRHIihrXdovG4QiRjsP3QJjzkG4becpfYcITedof0+QG25gVaKIxwWqSOx9n+oEz2XIrKgwZqVCE5GGXjapXmVUHi+2Fubg7LskilUmSzWVKp1IdunXVQ1H7195AlF7cLerJHx80R0isIIQhH/bC3rHiIwWlsK4b3aBZoIEZHkaoNPADNwC0GRVi5QUKD51Gqj4mKPtHfK+1khZOwbRMK6SieBcJ/JKSJUwfe/7fRO3ubXJpDHOIQr0aj0eDWrVucOXNmV8nheXmj1+H557FQKDA7O/vMeDuYiX6KsJOmp1YZCs+w1ntAx6mR0Y5wv2khANMzmY5MM9eZ8/dBgpbeQvGUXX3MkJSj0AvTdKtMGBHWzDLNQPJoqbONisx8e5OMFqNoNjguHeFrhSrHtCRzdoMjsTRFs006ZEDL9xoC9Fx/Lg15GrdXSwxF/XOw3Kz5Y7caSMBsreIXD1VKqJKE7io8XmsTVk0USWKxUkWWYKnmh9XXGv6ctd1sk4tEUNtwb7HI8SHf27rD+Qw9COfHI6xWGkzl0zS2O8gWNNomJyZyPFkpoakKS5tVJofTwfdfPk/vkLVMxnc49Ho9KpUKi4uLu/nu2WyWZDJJKvePwL5LXHYwpB6bTp68UudXmj/AB80BbGGiSzqOnaNmufRcGyFCWC2VpKpRl1tEJJ1ioUtU1UmGNWKofDo/SugjmBt3tJWHhoYQQtBut6lUKjx69Gi3hXEmkzmwQ+Jt+px/u/FdD50/fzMd1KP5/Pa9Xo9r164RCoW4cOHCMyTzIEU+L9uH9fV1Hj58yLvvvks+//oerfUH/Q40Wi5G474gPJYCoLkctKGcb6GdGsOuByRIgG3Eaa/6oYbeVpvoiWFsEQYB2kBQpGJ5aFPDdAoW1Qc1lJQGAsKjCZCg64YpP+3RWvMNVbfgE1dVk3A6LvlzCUr3amgxFVWS6NyVOHfuHJcuXSKbze6uFu/cucPq6iqdTue1N/tH4Zlr3VnEWd9GoCBkhV5Lp1f2kCQwrTCy5EAijdnQad8rIfZcHimQ6kBWEJWgb7kRRRQL9O6v0DHHEGrfuxly9lQ2GgmkRpOa8D2ZdqXkyx+Nvbyl2OvwNtWBh17NQxzio0UsFuPKlSvPkMLXdQZ6FXbk6lZWVl4YbweyrDDUuQhAxV5DRkGT82z08pTtFhndJ0RV2/dCliiRVJN0PL/aPCSHMKRJvlos0LB9O7YQEMvlToHhcIam02UmNoqHYNzIkzIH2W5LCCRsf3nNVtcnfnvD5lFFY7FV4awyyDdWSgxF46y3mhxNpCh02kxF4zQcm5PpLG3X4WQmhyME72gZbs5uMRIJ07JtZrJpaj2Tk/kslU6X47kshVab6WwKXVEYcsPcmttkKBVlbrtCOhpmdqtCWJWZ366gKTKr5TqjqTh2xWJltUqnF3QZCuxlMhbmN7719EDXB3xn1cjICGfPnuXy5cuMjIzQajXYKv0E2dhNJCFjCp0NZwBL6Pzrxg/zQXMITQ4RVxKsNDW2ej0QkFbjdFthGrZFzeoRchXsJkQUnbZtE/NUvIbLHz77aoH2t4UkScRiMSYmJp5pYVypVOh0Oq9s3/wytNvtj51H82NRDLQXb0M0d8hjpVLhxo0bTE9Pc/To0Zfqo71Na0nP83j48CHFYpErV668UtdzL+oP+h5NgQwOdLoG4dEkZtnc/V+15KIYfcey4yqEx/ri8WZLonDHNyK1xw3ksIqkSFRWg17frsAY9wloa6VF7PwQ879ZJToSprXaIXkiTmOhTeJYjPL9OnpSw6rZuD2PwcspXAHbH/R2cwWz2SwzMzNcuXKF48ePI8syc3NzXLt2jSdPnlAqlT7SHFrwDXrpX/wOwhModgdXqHiujKwH108PYUYm6NTi2IuBko8UPGyyhNrwjbiUyUGwgpdTe0XbDdqP6rgDZxFqGGr9a6Pgr0wjpRp2/iRKs0Yvnuf63Qc8fvz4lfpor8JBiGav1zuoqO4hDnGIN0BRlBfyMQ86r3iex/Xr15EkiUuXLr02vzPfPUtIjmF5XVLap/l6dRs5qDZf766joVG2y+TIISTBQGgnLUehaY7yrcoGuqTu5mN2PYsR/Dkgr/t5+x4eeS3JwqbJw3aXVaeNLims2C1yrwibn0uNMOTlcEx/X0Zj/lia7duzTCDKHgp0h6OqxrhIgPCPNRQ4aZxAcmjnNaz5441E45SWG7vh9uGkX41+JJfCdl1GEuEgjJ4jF42Qc3WeLBQZH0yxuFkhl4wwt1YmZugsblT43ZvzuK4/776NjqYsy0QjkMl/iUxsC11VEcjU7DCea/O/FC5xsxbD9hxsT7DR0ogoESKyTkSKslS2sVyXhB5iQInRbnjULQshBENKhFbN5NPTE0R07c07w4dzwOzMxceOHSMajb7QvnlHDso0zRe+e0g0X4KXkcGDXKCddmGLi4vMzs7ueuVehv0am+fF3a9fv45hGG+UxdiBWTNxu/1QbSfwKNbn2kgDz3YRUOwI0RP9rkfdinhGpJ1QCGPcNzpO0yY6kyN2aoDinQbxEyl//HUTASiGSmXTz/eMT/g3mp7wjYCR0/Esj9zZBEpKR38nw8LDLne/VqOw4LL1sPnCcRiGwejoKOfPn+fy5csMDAxQq9W4efMmt27demluzNtAXqrglitYdhgQOG2Bgodu2AgBva6BtVJHSe45Lx2/UlLOZJECcilF98gE6XuSocNR8ATdu+vY6Xd2Nd0AvEq/GNtth0ELETl+kcuXLzM0NPSCPtp+Erf3i4+jQTjEIT6JOAjRrFardDodJicnn5Gre+XY6Lyb+CItZ5qlwLO40l0hqSbpel3Sjh8ONjR/UbllbjEeOsY3ii0sT6Ht9piOPZuPaQXawSvdIjISluWxWdJ5arY5Fs/SdixOJvIIYDLmj58O+eMrkszRaJZuU2a2VKMW9CpfrvkL8oLnBOHyMook8bRW4UQyy/ZGm0KtzWypgqGqrDRbhBWZ9U6PsKqw2uqgSRJPCyVOGVEePNzEcTxWyn44fbPmR+oqLd8z27P9OTSl66w/LaMF4eZULIwQMJpPYjsuUyMZWl2L0XySWw/W9nWNXgbbXqfV+QlUscmA2sCQbQzZRVdk/mXzh1j0Ujieg9uWWNwWlNotKr0WumdQbUJKC+MJCDsa9ZqNISukQ2HClkK90iWsqvzI+RNv3pEAH4Xo/E5a4PPtm3fkoB4+fMi1a9eYm5ujUqnguu5bhc4lSfpBSZKeSJI0J0nSf/ua7f6oJElCkqTLBxn/u5qj+bbYewElSeLhw4e7FWpvEng/iEezVqvx4MEDTpw48VrdzedRvlOmQ4qQ4YDUD5UDNIoe8mAIb9tE1hWqT/z/ZUYjOD2HxqJJF5vsTILeeoNOHTy5v5puFyxMJ8gjDFZWva0eseMRas0QStz/rL7UBgkqDxsoYZnqoybpcylKVVi+Vmf802lqK11GzieobLX4+s8v8Sf+p34l/MvOSTqdJp32t9nJjVlYWKDb7fL48WOy2SzpdHpfZHwv1K8u4poymmbSsdMYRh3PkwhJHerNQSIpD9ogh9UgD1NFVEr+OYjFEbWdPNk9BNDuh8eF07/mVh3U3Gm00kOIJqHcJ9jCU3HT02jjJ5FkmVQqtRsusyyLarXK2toazWaTaDS6myu0U+F3UAL6cUzaPsQhPonYT47mjpbz5uYmkUjkQDb/ZPz7+cX138HDYzg0zKa5SUIkqFMHA7Bhw94gQoSkMsFmV6Xt1jkaTbJtVukFgus7+ZhbNMjpCUpWg5PKJF/dqvBuepRidYNUQFidwN4Vuv4cshCEzRVPZnvbYdbaIhc2WO20GNTDbPc6TCfTzNWrnM7meVguci47gOJJKE2JxXqN88MD3N0s8M7QAHe2CpzKpnlUru5+fmF4EKkHXtuhZbY5koqwXOswno6yWvUli5aKNUYzCTarDT49PsLdW+tEwzrza2XCusryVhVFltgo+c6CeqvH+EASqWbza7/5gMvnJw5M0nrWA3q9n0GTPMKSRdVJouAwZw3yO63PU3UUIqqHokR53LMIGSoRT6LbkZhvNnAkCKkaw0oSyxQokkzNdsiZCq7tEdY13pscJRF0PtoPvl1dgSRJIh6PE4/HmZycxHVdqtUqpVKJX/7lX+af/JN/Qj6f5/79+5w5c+aN5zF4Ln4e+AP4zT6uSZL0K0KIh8/9bhz4GeBbBz2O77pH860QPFjNZpNSqUQmk+HUqVNvvKgH8Wh2u93dPuuvMziSJL1AMEq3y1SftpGGBolMpGAPty3PN7HtOJIiEZ1M4fY83J6Hmk8THk+CJyE8gRSLo2cMCncblO5UCI/4KxQ5pO4Sz/K9OlrKf+9Gw5QedyndraMnVTqbPTJnktgth8y5FLETSWqOyuq1OgOn42zdaaDHFRRVorvtUZnvUF/ff+X5Tm7MjkDtXu/fzZs3951P0ry/ilzp4vUscF2ctoMsebiKQb2eAdeGtm+QCHIxlVwWdhYM8p6HqNMn9F69svteNPYI59suvYdrOANnIPHsdXWbbcyn64jRF1etO/pop0+f5r333mNychLHcXj8+DHXrl1jdnYWx3EOFJ77OCZtH+IQ/6HjVUUkr0uB2dFabrVavPfeeweW2Utrac4nzgNgBLq8RbeIjEzBLjAUGkKTNELWBL9b3N5dEq90iyjILLS3GNBTNJ0u0zFfgWU0nCVnDbPWEAgkyoH9e9osokoyTxoF4pLKSqfGZDRN3erx2dQxvrVQ4mgy44uqJwJvp+o7IFKBGHtYUZGAvBLh4Vxpd4pygtC1FdhXO3h1XI9UOETcUXk4t40SdJ+Lx337FTf8xbbs+oQ5FVKYChl4bRfH9ZgcStOzHI6NZmm0TWbGcxRrbY6NZojoKkZD8OjxFksrFcrVPZ3d9oFW99exej+FEsw1NTdOywtxvz3KrzY+x4bp0HK64EbZ6CjE1TACcN0ILTdEKh5nOJbE6GqsbtfZqlZxej0ypkq7bdK2LMKSwhfP7d+bCW/XOvJ57CfvX1EUcrkcx48f5yd/8if58R//ceLxOD/7sz/LP/2n//SNv3H16lWAOSHEghDCAv4F8MWXbPqzwN8CDlwW/10nmm/lWlY1Nucec+/ePQYGBvbdI/pt9DHflI/5fL9zgPJdn+RsXm8804NbTig4JY/GQpf4uRHkSD+8u3W1iuX2cz9KtyqEjw0gPPxCoNxOSCWECHJqPNsjdiyFltLYuOkQSqm4pkfqpB9qV3T/8nqGzv3fqeN0/f0MJ1TsjsvIuQSbt+tEBmXspsvX/t7ia4/1decglUrtdkc4c+YMuq6zvLzM1atXefToEdvb29j2iz1t1//RN8EDSVOwbRUpEkIIieJaCA2L8HiQBiGBV/a9mHJszzXpBh0mZBlR9f8vIjEIRIhFyEDU+22XvKr/vnt/FXtP+29XUfGKReSBYeTwm6/5TuL2hQsXuHjxIul0Gtd1n0kraLVaryXah6HzQxziO4PXORn2ai2fOXMGWZYPFGrfcTZ8Pvd5AJY6SxgY9OhxxPBFvRNqhkpvgHnTL/Sca22S1mLU7TYzAbEcCqcA8BAkRJiFzR73Wh2W7SZxNcRyu8qRaJqmbXI6OYgrBENBkeNAOM5xbYRKwyfTvYBUr9X8uagUEMD5WgUFiZVmnUvxEa7NbmCoym4rySelMolQiKelMnFNY6HWIBUO0bZsBhyDm083iRs6Tzf9Tj9zWxUMTWWp3EBXZUpdh0w0jNT02NjosLrppyaV6r4TYKev+Y5ZHIxHWblbIBH3w+kD+Ri/9dXHu+f1TWh2/jme9TcJSw4JpYntKYyoZZbtcf556R3ajoShhJHcNIstl5rVo+c6RNwUjq0RkhVs18NpySiSzlAqyXgmi9SSaXcdzG6PkOUwE4qgS96BolZvo0LysjEOSlY1TePzn/88//Jf/kt+4id+4o3br6+vA+ztSb0GPKMHKUnSRWBcCPHvDrQzAb7rRPNVeBUh9DyPR3ML1NaXuXLlCoZh7NsgvMl47FSsx2IxwuHwvi7wy8hr+U4/76+84qJP+yQxMdXPHV37ZoNuY89NK0s092pleoKuuYd43q4QnUywfq1J8U6d8IC/Mm0sdZBHElhVj9QJn2C2N/0E4dK9OplP57n378qkJg227zVJjofZul0nnFRpbvQQHsSGFAqPWqx8UKVd/vC9ZnfySc6ePct7773HyMgI7Xabu3fvPpPrWLm1hrlYQMOk2wshuw6S1aXSzBMJ2hBrQY6pkk1Br+frZ6oG7shpzOQJ2uUwNXOEbuIUdvo4YvQ4cq7fvlRK5fpWLRJHNBq7/+uu2ZDznyczkgJPoEy9vT6aYRhcuXKFU6dOoaoqS0tLXL16lYcPH7K1tfVCH9+PYy7NIQ7xScB+c/83NzdfqrV8EKK5Mwdke1mSbhJP8hiLjgFgC5vx8DTfLDWpWjZV0eFYdAgPj3HDj6h4u52CykiAZbtUajGemh1OJPJYnsvxhK9ykg+6/uwcSdOzGTWSVKsuD7bKPKqUMBSVx5USCVlly+oxYkQomT2Op7JUzR6XB0dI9UJggum4HM9l/VaSuQyu52tiup5gIuFrZJ4bGKCx1iYVDuN4HkfzaWzX5ehghp7tMDOUpWPaHB/KkgiHOBZKML9SYyQTptq2GR+Is1FqkY3rLKxXyMTDzK+XuTw5xINrqxghlaWVMrqmsLZR47e++nhf577e+jsI+xcwZJe41KHqphlQ6/y71qf4jfolECEsYdPoGRS6EFVDDOhxeu0wq40OVasDAlJ2FFXIOEJg2S5uzSUdiaCrCiOpDCErxBfeOcLS0hLXrl3j0aNHFAqFlzpO9uLbFTp/E96irfFrIUmSDPwd4K+87RgfS6L5qnyabrfL1atXiUQinPj055C3l97KILwM1WqVGzduMDMzw+Tk5L49rc+P2Vpr0yv6nmUBVOcabN8VyAM6QurfMLIm02r3cxkTMymKNxsoR/wVqjEUYfG3y0RGfMPimh5SLolwg0rzMZ+gSKpMo+5fxmYQ+q4vtkkdj5M+n6LZ8Y8jMep7T5MTEZyex9DZBLWlLiPvJOhsuYx+bxIvJfObf39+X8e9gzdJ9EiSRDKZ5OjRo1y6dIlz585hGAZra2s8+Xu/je1JdCwDTXHwhITtGSh2h7AehE+6vgdASSVh4iRtc5DmbJPmrU3suou9UUWqdvEshc6DLRo3S7RrCZz8aUhmkEJ7qrpT/U4/QlZwtgt0NgSEo7hBOoIyeexAx7+DvSvPvZIb7733HmNjY3S73d0+vvPz82xublKv1w/k0dyTS/OHgNPAj0uSdPr57T5MLs0hDvEfA3a6Bm1tbXHlypUXJuaDzisLCwssLi7yheEvAFC2ykhICC/J47pEze5yNOIXgoZk34GwI7w+19okpUWp2E1OqpN8a7NDSvHtdUT17VJ9R/qo6etdPm4UiKshdKGgtSM8LJY5mcnTcx2OxRN4CGayPpHNBxGaRCjE8VQWra2wUuoXNZrBce507mkGlcxN2+ZcOkN5vUXHdGh0/M9bpr9g7gbb73hPo5pOZ72N6/jjakF4PRX3bdzoQAYBDKajHDHCNLfqWJbL2EiSdsfi2FSeWr1LMmlw8+76K8+3EIJq8y8ju7+MLOk4QmPVHsDxFH619Qf4SuMYNafnt/p08jRtGQ+B5bhs1QV4CumQwUg4gVeXKDTbtG2bpKoT66nYtkuzZxHxJKyKxXsnJzgzc/Q5CaXWC46T5+fBj4Jovo1XtNPp7EsZZwfBAmt8z0djwN4LEAfOAl+VJGkJ+BTwKwdxYnzXiear8mmef8hLpRI3b97kxIkTTE5OIushRKuK4rkfyqO5kwD+5MmTXe2qg+D5lfJeb6aaU3FbHp4paNR0OqW+Ryt+LMnWrSaZi77UhRTxk4w7dRkkifBoAs8RaPkdQimx9dhEMfxLVn7QQDEURDKK5wXtG5e7ZE77rsDQQJiHHzSpBVqahYctZF2i8KCJEpKoLXcIp1X04RArVZuWENz7SpF7v1mgVT2YV/Mg6Q87IrXDbhq94YIrcLoyutSh0YygeiaOFEaRPJAlvHIZeXKabi9G/eYWbs/FLdcAUBJ7HqY9+yBMm/a9TerzEo4Uh50VodpPVZAzebAd3FobKzSGZPv3hTJ5cI8mvHrlKUkSiUSCqamp3T6+iUSCr371q3zpS1/il3/5l/mFX/gFNjY23vgb34lcmkMc4pOOnchVOBx+QWt5B69r2rEXjuPQarWwLItLly7xPfnvQZd0ep7JgPouXyttMxDyI01N138c59qbROUQBbPO0cggHh5HjAEGnBFW6wIPiXpQHPSkXiAsq8w1y4waCSpWh1PJQWzP5VJygsWiTSpYTO+IiLcDoli1/Nf1jr9oVz2JreUm9za2CasKj4slYrrWbyFZqpCLGMyXqwzFYySFRnmrw3yhylAyxmLRf13YrjKQiDK3VSGfiDC3VeG9I8M8uruBrqjMrZaIGToblS5GSGV+vYyuyixtVknHDfSezOZKk26gzFOt+c6EcsXPpbdMmw+uLb10XnGcLrXWn0MTNwjLAh2LrquTVZv8fvdTfKMxjCEbxOUom60QK50OXcciLOl43RgqKqbnInkSpWKPkKySNgwGQ1Ga2z3apk1IVckqIXp1FySJH/5UX1NZluVnHCfnz58nEonsdvfZKzv0URHNg3o0W63WgTyaV65cAZiRJGlKkiQd+JPAr+z8XwhRF0LkhBCTQohJ4APgR4QQ1/f7G991ovky7CWEQgjm5+dZXFzk8uXLu1XPAPKxC4QX7ry1R3Ond229Xt8Nwx8Uz+doVhfau2c1Npra/dxuS1h7RMMJKrPX73bQkzq1Fd8I9dZsEucHaGz5hmbrepXwUJT0mQzVuQ7ps/7xWw2HzKU8S9+sU7rfJjQUVKKHFLSYysqsiRpSqC13GTiXoFe1GXk3Ra9mM/xukshQCOV4hGu/sU0kp7D1uIUaktB0md/8uf17Nd9W6mfxF67htGwEIeSQhCUiSJpPtr1Ap81JJWireao3ioimbyy1wdRuKFxS9hYCdXbfuoHBwvFoP6nSVY9AIoUw9xDoSP9BNOe2sb0wUjaPHE+81fHsd+Wpqir5fJ4f//Ef56d/+qf5sR/7MYQQLCwsvPG734lcmkMc4pOAVy1+y+XybuRqamrqldu9qmnHXuzkdhqG4Ts/ZBlDMfje7PdT6uSo2r6dWu4UUJBZ7ZXIEcXyHI7GfEk7QwmR0WKsbJncabRZsVtEFY2C12MqlqHj2pxM+s6I4SCfSJdV3olMsFRo4yGxEhQ7PioX0CWJlV6HbNhgoV5lPJagYnZ5LzbAzcdbTGczdG2HEwM5bNfjeD6LKwRT6RQCmEgnieoaJyIpni5VGYz7c+JQynd4DKdjCGA0HUcAY5kE7w4PIjU9bNvjyFAK2/WYGslgu4Jjo1k6PZuZ8TzRsM7RaJynj7aYnspTLLU4eiRHsdxhYixNodRlMB/Fsy3mrq+wML/1jG6zY9dotf8MmjdHWm4TkiwcoWIoJv+8/sPcamfpeTYdx2GzHULDIKVGyKgJNipQ6HUwHYesGoGWgi6rtGwbQyi0i11SkTCaJGPYMk7TJaTKfOrEGNn4q72DmqY9UyQ6MTGBZVk8fPiQR48e0Wg0qFar+1q0vAxvQ1Y7nc6BUrIClZi/APwG8Aj4JSHEA0mS/rokST9yoB9/BT6WRHOnDaVt29y8eRPHcbh06RKh0LPSArKmIxwJr1F9xUjPYi+B7Xa7XLt2jWQyydmzZ9+6OmwveRVCcPtfL8ORKJIMktwfUx/WWPlmg8xl32jU1/3lXK/qEDqWo77Yr/hulT0qiz7x9ByBPhij2/UvVXWhAwHBavckhJBAgD7gr8qLt+tEz6QoLnQYOOeTKSUctCNr2EgykFC5db2K1fUQAuI5hVbZZupShqXrVe7+5jb1wv6dYQct6Kre2qC7UsX1JBSrDYqg09AQwSo+fSSMemQMjEHslSZCBmvLL/TxQv10A9H2yaWQwSsHou3RCF7QHg0jjFupY61WaG2HEd4er+fezkKZDO5yD+X42QMdx168zcqz2+1y9OhRfuqnforv+Z7veevf3sFHkUtziEN8EiGEwDRN5ubmuHTp0hsjV28KnW9vb+/mdsZisWe2PRe/zKbZZra1QUKNUHc6HI/568EY/hxWs33b1bEstothHvbaHI1lgv7k/hyR0X2CY3p+aHq1XSejR2g1BA83K8zWKmRUje1Om3HdoOd5nMn7RUJHk75DYiye4JSWwWoFEZsgnL1TXb4TBq92d7QvHXJ2mNVNn7wWm/48sBVoZG5Wg9dai7CmEjIlHt7fpFjzHQGVRpC+1fK/1+r644cUGWujg9UJNI+DOUPT/P2JRvwUgcnhDNuPqmRzCe5cL/V1m+/+e6rNP07b67HsjvN183v5963v5YF1lH9S+2Eetg0kIZFQUlS7CRq2TcMzkT2NjbpLOmSQ1SNklSjFYo9at4sQgmEtilWzsT1B27RICx2362G7LhFk/siV/XeI25EdOnLkCO+++y5Hjx4lHA5TKBS4fv06d+/eZW1tjW53/+oubzOvvE3uvxDi14QQx4UQx4QQfyP47EtCiF95ybafO4g3Ez4GRPNVofNGo8HVq1cZGxvjxIkTr2T10rn30G7tLxVthxTutFg8ceIEExMTH0pUdWdMx3G4ce0G9UddCjddYueG6GzvIWvBAzX/9Sbpc1lqC30PXK8nkwjE1wHUZIjU+X7hUH25Q23Tf2DbmybZ8yliEwaPf6tM7h2fTNafWqhRhczZBG3HP576ag8BbNyqEx0MUZ1vk/u+DNd+s8DI6ThrdxsMTkcpPbaJ5XRKix1kVUJXZf7d/2P2rc/Jm/Dk791Esh0kPQQS2D0VGY9oKMjHjMco327u8GlCwxmkwDDapv+QCgnsgp+m4Mbj4ASGNNv3eCu5vTmZOrVHPaQRPxXFrfX1M6V4HNly8TJH3vqY3mbl2W63P3a5NIc4xCcNtm1z69YtJEniwoULu7q3r8OriOZOW8q1tbXd3M7nI2Un42McjQzhCJfJiE8a3UCAfZsmKjKr3SIntEm+tdllNO7nUqYDYtm0fSfETjvJJ/Ui2VCEqKIz5GR5WKhwMuMXB+WCHM5sECq1AztZ6XUZjsQwaw6zW3VWGi0USeJJoYyhqjwplkmGQ7vh8sVqnYtDQxSWG8gurFebjKSiFFtdpvIptuotpvJptuotjg6ksRyXc8ksdx5sMDmUZrPUZGIwxVqxzvhgipXtGtm4ztJmlcszI8ze3CQa1llYKpFNR5hfKpJKGcwvlkgmDOaXSlyYHuL+1xeJRkMsL5Z5+rDM0OAYZ84pZCd+icfmNNcbY9woD/BBNcpcN84HrSsUrSiKpKBKER5WXUzXJaLoJL045ZaE5XqUzA6Gp9Go2WTCBqmwQdzVKBfbOJ4gaYSJ9RTq1S6eEKRknePpGKnE23du21EnOXHiBO+99x7T035a1tOnT7l69SpPnz59Y6e9t51XPm6yed91ovkytNttFhcXuXDhAoODg6/dVjEMhCMwl94cepRlmVKptNtBaG8Y/mXYT1hYlmU6nY5fpNRK4fb876zebKHm+xe7V/ENgNsTdDBQwv1VSq/l0WwIJDXItSw6bNxpoCV9L2VkPEZouF800i46SBkDhMRO4ZvTEWTfSbG6YrL9qImsSdRWugxf8HM9M8ejhM/GaXT9m1qP+L8fz+m4Nowcj1Hb7DH96SxEZe7c2mZ97sVuQS87Rwch6sWrW7SXm9giBGaXajuOgUXXVpElgXpimsoHW+CBW/MrxNVU/2EPWf6KWMmlkIIkdFvfs+LT+uL20p4JRU6nEKZN/VEPaWwKr7JH8sj1r5l+7O2J5icll+YQh/gkYMcm7TgsRkZGiMfj+071eRnRtCyLGzduIMsyFy9e3M3tfFk+5x8a8td2BdP3DM61tkhrMbrYHI+PMeSOsFUTuEBX+HZstllEk2RmmyUykk7N7nIyNYiH4Fx8hMX1LqrsR3R6jm/4S0FjivlGDU2WeVwpkQqF0SSFVDfE/bUiU6kELdvh1GCenuOHzR3P42gmjQCOpFO8OzhEqCPR7FgMJPy5JqoGWplh36YmDP81H4sQbgqk4PTEo76XNhnz7W0qeE1ENN6dHEKqOzi2y2Deb1E5PJTEdQVjwykc1+PIWJrpfAqp62BbLkcms1imSzYf4ctf+besm7/IqpvDVGPY+ii2kSWixdlqR5itVSi3qjhdhbWGQkLzf9uzQqw3PUzHIabqjMpJ2k0X2/Mod3tEHRWv45E0QoRVFbtsIXsSRkgjLlRUEy6f3r9g/8vwPEmMRCKMjY3xzjvvcPnyZXK53Aud9p6XxPtOeTS/3fhYEU3Xdbl37x6maTI9Pb2vilxFUWhduELnV//NG8deW1vDNE2uXLnyxlXty4TYX4Zer8fTp085e/Ys9kL/dCaOxXn85Sq59wbQoiqtlb5YsGUKkmd9b5sSktl60KQ63yb5ThYto7D1oIlZd4jOpAAoLvZYu1YjOuoTLrvj0jZ9Q1q41yRyxDd4tipT37bolG2G3/XzeQSABB0J5u/XWb5VJ5bXWblVJzUSZul6jUhOZu1eg6Pfl2F5q8mta9v0Wh7/6L+/+8bjPyie/NxtZARu18GTVeTA06tGVJzcBHZQbC5HdJxizX8f9DWXwvpuIZCW6hM0eU8nolattvveM/fITyj+ORKWQ6tsIO8R4XerLbxwCHUo/9bH9TYG4eOYS3OIQ3xSsLa2xoMHD7hw4QJDQ0MHqiR/fttGo8G1a9eYmJhgenr6mcX1y/I5vzDwDiFZY8usMmn4BT9jRo6I0KkUPW7V22wLEwWJ2UaR4XCchm3u5mPmgsJFVZK5GD/C7GYLy/V4WimjSQGhVDUqrs2xZJqmbXE6m8cRHpezIywv1kgH1eaxoE+7EuyzGSzQG6aJBESEysOHW2xUgvaZZZ8cb7d6yBIsleooksRCocrp4Rxrs2WaTZOF9QqaKrOw8ezr4kaFsK6gmYK5O5ssr1ZQFImVdb8j0Op6DUWWWNuokUyE8eomiw82WV+toigS62v+azj9iF7s/8umrdARUHGyVF1wcCm5cfRQinw8S1gdZKEtUWjXKTZq0FJptT0SqkZE1fDaElvlNj3HIabpjGDQbpq0LRvLdgl1JDRJxnJcYkLFbTp87v1jhPS3S6fbweu8kbIsk8lkmJ6e5sqVK5w+ffoZSbwdCSXLst6KaH6U8kYfBb7rRHPngd3xCiaTSUZHR/edPKsoCo6mIxkG7W9+8NJtdsZOJBJks9l9uaLfJO4uhGBxcZFms8nx48dJJBJsXO13o1ENn/w8/J0qmfcGYU9+YHmxw9zXquTezZA+mdwVUl+/0UQeC/lxYWD9ap38e1kqyz08RxAaCaSPpqJ0m33DFslFSRyJcP+rZUYvpQBoV3xjsnmnwfDn0tz9WokjF5O4lsfQiTieK8hORvAcQeqIin5Epy0c1uaanLicZeVRg0bJ5OZvb732PB3Eo7n25XWac3XsrodQJKy2hKo4CAEiEqEzW0dRfVIZGknsisV5jRZIoI4No0wdRToygy2n8IaPw/hxLELIgwMgSRh72k2a5b7X0mrtyYvRDZrbKlI8jhQx8Cp1vJH8h0qheNsQx0EF27/duTSHOMQnAQsLC1QqFd57773dZ2wn938/2Es019fXdwnrwMDAC9u+bK6IqQafzZ4CfP1GANOyKdei3Om0yOgGVavLqeSgX1wTTQF9fcySaxJTddyOwsP1KkuNGpOJFE3bYiIcwQOms/7COB3uR3zeT4+ysdHE9QRrdT8itFSr+5JIxRIRTeVpsUzGMNioN3kvO8zVe6uMZxNs1VtM5pKUW12O5pI0ejbHR3I0uiYnRnLM5DKEWlCpd5key9LuWUyPZml3LabHcrS7FjPjOYQQvDs8yOp8k+mpPM2WyczUAI1mj5mjA9QbXWaODqCpCkeTcZ7e3WD6+CC1aofpE0PUqh0+/YMNjn/mMb14kq2CxboZpeE6aJJBsZehbts03DamFaNkKuSMBOPJPBFpgJIlUTa7VHtdnJKF13VJhULENB2ralGt95CRGIhG0FvQapnIkkTCUehWeqQSYb7wmeP7uk9eh4PMCaFQaFcS78qVK7sSStvb27vSWS+TUHoZut3uvtJDvpP4rhNNgEKhwK1btzh9+jQTExP76ku7gx2DEP3ij9H58m+/8MCXSiVu3brFqVOnGBgYOBCBfdW2O57XTqfD8PDw7opj82pf2qhbC7xpQqJU8YhOB+GHiQjNQFB97XEXjL60ht1xae+xg67lYe/prbp2tUbqRJyFG3UKj1ukz/jEc/1GHWkwhOuAGYTGS7NtBs8lGLmSomH6x9Es+GGW1ft19IjMys0ak59OMr/YoVTsMn+rSjyrs/KoTiShUlzp8P/57+/sjvlh8ejn7uN6EqpnIiQFSXiEpC4FJ4HW8vMzvZ3q8lgQlsokcCMZWs4wnXaU0rcqVK6X6Kx3qd0pUblZwn7Uo3TXpi1PIJKDyIkYGCGU5p5K9MA7CtBrdrArXXrkkPN5EBLe2OtTNN6Etw1xfNxWnoc4xCcBk5OTnDt37pln8m08mg8fPqRYLHLlypVXLgpfNe4PDl4CYKG9xTF1lK9vtIjIITwER2N+Dr4cLG7X2jUAHtcLJLUwsiRxRAxya6PI8bS/bUb35wI95M8lpUBjeL5WIaHryG2ZudUKc+UKw/EYW80W07k0TctmMhHbFWd3heBELsOoFEMKhDhygdalEnQQigVd6zRZQZEl8iGDR3c3d4/NCwiPs9Oq0g6KfATkhU6j7O+bFaQ6mcH/zeBvTZVxt9s0a74DoN32d6TZ6DEyU2Do3F16iSjtjsvdFQ/H01GkGI+bYHoeUcVAsvMUuh49z6Zpm5Rq0LUFyZDBaCRJzovjoFG3LMrNFr3tJorlElYkoqpGY6uDJsvEjRBywwVLEAlr/KHPnkSW397psHuO3lLeaK+EUj6f59ixY89IKN2/f39XQul1Y3yc8F3fm1qtxsrKCleuXCGZDFonvoVB0PI53HCG+r/9DaDvcVxYWODy5cukUqmPRNy91+tx/fp1UqkUZ86cQVEUhBC0iibKgIGsSsiaTHm233e7VbLYXHaJTRhER/vFH52yTdPuXwIjr7NxzSI04xtHJSzz5PfKpE/64VXhChjQMFvBfgUC8APn4vSC52LzQZOBMz550RIq9+/XWLxZI5rRKC50mLiQpFtzGLuQZPhigobi0K65jByLYnZcJk4kaFVtps6lqG33yE9F+MW/c++V52m/Hs2F/98S3c0WEoK2nEB1etiaRs1NYERVhOkgGyrWZuCFlCUYP0bHyVP+Vgmr3IOdaycJ7O0aAPpAEskOzkfIoHy1RHnFQBo/jqT7ZFVOp5D2hNG9ik9mu4tVar2gV/zIi56Kg+CTkrR9iEN8EqAoygt26SD2fyfVyjAM3nnnnZ20lZfiVVJIF5JHGQ1nyTh5CjUFB4hIgVh7z58fHgXC61u9Jsfjfuj7neQo9YqM5Pn2vRXkYc5V/c5Bc40aCU1nqVFjQNUxVI3TWp4HqwWmcz4pHU36qVOJkE8YpcBXWmu3mUjE6ZUtVrdqbAZFkYsFPxpX6DqossTsVpmQqrBSrnM+k+PWrVVikRCzqyWS0TBza2XS8TDzaxWyyQjzGxXOHMlTnq/h9lwWV8ok4xqLK2UGcjEWl8sMDyRYXCnz7ukRFq6vkUiEWVkqMz6RYW2lwpGpLO3eKp/5sWXa4TCWqbHSi6HEFUrbNuvdMCE5jITMckNmvWvhCJeEEiFsp1HQkCQJSUCpZNLuOYRUlfFEiiE5gSyH6HkCxfZorNVwTItWu4fadFA9CQWJqVScSxcmDlx78DJ8VDqaoVDoGQmlycnJXQml69evMzc3tyuh9LZyg2/qOCdJ0p+XJOmeJEm3JUn6/Zc1CnkdvutEM5lMcunSJXS9X8TxtiGO1Bd/iOZXr2G22ty5c4der8fly5d3ZZH20+t8By8zHrVabVeDbWJiAujraC5/s8zDr1UwTqfInkng9Pzf0aIKpact7Jag1hFYVv9GSE1FmP1qiYFP+8YhOR1DeBJmU0MJS8SP6/SaLg3Tr16XFJi/Vyd1zA+VbN1rkj+foNxyWLpeI5b3z6EcVlDDMmvbHRJDYeyex3Ag5O4FXRtEWOL2zQILt2oYCZn5WzXSQyGeXquQHzcornaY+p4UX/7NFb7671a5d7W4r/P2MgghuPsPZnEsGQ8Py3SREbRNFb3tEs77BtUYTyDJMvqJKYp3TCo3qmjx/n3hVH2CqA8k8Xo+cVTSfS+DHCSrC8ulU5FpWoMooyPIqWR/m0QcWn01AK+qYA4OsKWI3YTsdrt94Af20KN5iEN8vLHfSFm1WmVubo5kMvlarc0dvCr6Zds2x9rjXK+1IPBCrjotwrLKWqfG0VgW23OZCdpLxjSdS8kJlre7dByP2XoFTZJ5Wi2TUXUarsOpTB7b85jJ+Dnmw1oYs+DsduNpB21uNwKJt7lSBUWSWGv3iGgqEVXHLlg8XC2Si4bYqrUYTUaodUyOD2Vo9ixOjOToWg7nJ4bIeTqaK2O7HkdH/BaVkyNpPE8wMZTGE4LxgRQnx/PETJl6rcvgQBwhIJ+L+a9ZfzGdThucnR7Eq5rYpkMi0OiMBMVEelhw/keeYhkq5W2JLS+KZ8tUSxoPyhYNq43rCTpmmpAcJa6GSCpRVsoe6+0WNauHhoLe0UlpYcKKSkzVKG+2MU2HSEhnJJJAaiuoukEqFiXakWhUW5itJk6xyWc/O4Hruh8bovn8GDuV7DsSShcuXCCVSlEoFLh27Rp//I//cTzPY3Fxcd+/sc+Oc/9MCHFOCHEB+L/hy+jtG991oinL8odaee4lj+GZSQQSj//Hf0w+n+fUqVPPXKQP49FcX1/n0aNHvPvuu89osO1st/yBvyJcuF7HSeqEM/7KNTUT2yV3jS2Lhg2y5h/vTnHP4vU60QmDTpB32VjvkbmYwRVB+7F5h+gpDWNaplUQuEafBGlZnc3ZNo7pkT3hP9BrN2sMfTbF2lyL2EBg4O7VCcUU1u43mPmDGb711U1GToWxuh5T5zI4psfQkRiuLRg5FWel2qRc7SFcgW25/M2/+A2a9Rc7Bu3ngbz1c08wyx2Ea+OYKrohaCoRIjHfSyC7/qJCTRqYxhDV2R5OLSCDgeClbGjYRT9JXc30yaWk9q+v2JOfKRyBVehQvNPD1VP965Xpv0eScLeb2N0EY1OTuz3KFxYWuHbtGo8fP6ZYLO5r0fO2Opoft1yaQxzik4BXyea97lne2yXu5MmTL+0Y9DK8bF5pNptcv36dLx69iIRfUT4UjmPi7Rb8pHXf/jfsLrqsgKlya6nMXK3CgB6mZVtMGlEEcCxoJxkOPKtNy+RKboStokWzZ+3KFs0WywzEomw0mhzNpGiYJicHcpiuy/tDo8zPVTiS9+evkUwgAC/tJMPvNEmByVwKqe6ysVHf1cKsNf0wdynQzNwq+2RWQ2L5zjar6zUkCRaXS8gybBc7aKrM0mqFUEhFc2Hl7ibzT7eJxULMPd0mmTKYfbJFLh8jcvabJKckNragnUrgKi42KUqWRsgNY27DWivMWqdFyWwieQqFhkQmFCEfjjIWTmLVodDqUDNNNCREzSNjGCiyREyodComEUMnEzUQFRtD1xnJZkhg8NnPTKPrLjdv3uTOnTtYlvVWTocdfCc6A6mqSi6X48SJE7z//vt86Utfotfr8TM/8zP8qT/1p/b1G/vpOCeEaOz5M0o/nXhf+K4TzZfhoIRw50YoFouUTh0ltrhJPvpih5eDejQ9z8PzPB4/fkyhUODKlSsv6B7ubLf0jX4hULXsYMY1ooMh1Gg/5JKcjjB/tUrusi+r1Kr4D7DddREJnY1H/WtZXGzTrPfDva2yAM3/7e37PeLHdCQVHj8skzvlG6ylmzUiWY2h8wnKQc7L4vUq6dEwnbrN+IUkR743zca2nz9TW3dQdYnZGxVSQ2EW79Y49YUcX/3tVY4cT7D4sM7Fz2ZQeuscn27xC1/6fWzbPlCXA6tj8/gfLyE7LpasoToOQnaxmwohs+ffgaUOxqlRmgWJ1lIbY6hPJJ2KH2IKDfeLgySlf9t67X6eilPtpyvYwffwoLFkI8amQZFB7U8e2kAKr2uhTPgFYjs9ys+dO8fly5cZGhqi0Whw+/Ztbt68yfLyMs1m86WG58Pk4xziEIf49uN188pO3n2j0di182/rlNja2uLevXucP3+e8+NHeS834XfRCQp+zGBhPdcsoUoyVavHcXWUb61scyoo8MkF+ZiKGuT/t3179rhSIqpqpAmztdGmatocz2V2ZYsEMB6EzVNGULkuy1zKDFHcaoGAUpC7vhzkrZdMD1WWWK600BWJbrNFd73F/blNMkmDxY0Kg5kYK9s1xgaSrBcbTA6nKVbbfHZ6jPsfrHDsSJZqrcPIQIRO1+H4sUG/COjoALbt8u7RQR59a4Wj0wNYlsvEVBbH8RgZS+F5gqnLLUZOtak0otT0CMJWKVWilBUZKQG9nsNs2UV1VXKhGENahnpLo2s7lHsdNE9hc7uFLsnkIgZDmoFX96h3TVo9k4wUxm46IEDyBF7FQlMUwoqKXe6Sz8b4kS9e2q0Cn5mZQZZl5ufnuXbtGk+ePHmj5uXz+HZ4NN+Eo0ePksvl+NVf/VV+8Rd/cV/f2U/HOQBJkn5KkqR5fI/mT+97p/gYE839hs6h36ZyaWmJsz/xx1BDMlv/8H996bgHMR6WZXHz5k1UVeXChQsvzdORZRmr67B2swaAJEPhaYvCQoemItFr939PT/vff/T7FUa/L8vmw75OpRJRGHiv7ylNTkZwDQURsKtwPATJPklSjDAj76dpbLtYO2LmHZf4MZW1Upv561VykwauI0hP+ETUU+HOzQKLd+uMnozRKNkcv5LF7nmMHY8TndLZ2GoR0h0+c/Qq//P/5d/y13/8F/g3f/df8Tf/zD/kZ/6T/zvdf/8TKCv/Crtbx7KsN57Pr/4397B7LrYnowuHrizhtVWy0zGE7REejWLn0qx/vYG57nssFV0KzomGVQi0NPeE0L1OQC4lgV0IzruhYRcbL7wXgLnVoHqzjJudwu30ybuS9D3A8uSLSgSyLJNKpTh27BiXL1/mzJkz6LrO8vLyM/ITdiBkelCP5kcRmjnEIQ6xf7wqdN7pdLh27RrpdHq3S9xB6wR28uNmZ2dZX1/nypUru/nXPzrudxxbDQp+njSK5EJR6naP97NHcGo6qufb9p3imvWu7zWcazVI6CHWWg2OJtMoksSVxAi35rYYCwhlJPC87sgWbbd8UrpQrpExwngNh8WVMnPbZfLxCKvlOgNRnXrPZmYoSzOoKjcdl89MjbO93GUsn0IISAVd5VLRQBg+4Ts7ktEwZwaydKuBLQ4W3+GgjfNOEZBlO0wkYmwuBDmgWw0kCdZXa2iazNJCmaHxMJmLN9msGBRt0AyFtbqGHY3gtDy0XoJiJ4KHxOp2CcnReVrq0XMcDFVlTE9iNyGqhei5LhFPpVrqokgSmahBytOpljpYtktC15AqfqqBIcl4NZNYWOOP/qfvomn9+V3TNAzD4Pz581y+fJmBgYFdzcvbt2+zurr6Rm+n53lv3XFwBwedV/YqmXzU84sQ4ueFEMeA/wb4Px3ku991ovmyk3GQqnPHceh2u9i2vdumMnT5fey5BTpzm89sexCPpuM4PHr0iPHx8Rd0057f/61bLVzLHzd3PIbZ8h+ydsNhfbtLYtx/+FrlPnmudF0yp/v5ed2ux+w3KmRP+Z9trXbYeNBk8EoQ3sjrLN2uE835D3xhtkUzCHUUZ3uMvuvnIdqKRKdnITxQE/4+zV+rMvO5LN/8vQ0Gpv2HaWelvPygzviZBI8XK5jCZTp2i3/0N36LP/+jX+PcsQKbxURw7mBhNcZwfJ3w/N8ncesvEi78FpVyGUVRsG0bx3GeOb+VuSbrv1dEklwsV0J2Xdx4BMUSGGkFJaIh5VI071hERmM4Td8L67Z84xUei/cd9HsLgQJyqWUTeB3/O/pAenfbve+1geTuNrX7FUw7BsGxi0BGSjqSe+OqMRQKMTw8zNmzZ3nvvfd25Sfu3r3LjRs3qNfr9Hq9A4VZDsnmIQ7xncPLyOOOKsnJkycZHx9/7bavgizLu92HhBDPiLkDfGH4OFFVZ7vXZFyN4iGYjKa5kBylXvUodbqsNGsAPKoUickKdddhOpHC8bzdqvNhI0bWjFBv+PZxq+k7KmbLFXRF5kkgW7RWbzKZThEP6cxoKZ6ulJkeyiIEDAZEcShIIYroO+RK4tLwEKV1XzC82fUX0G3bt09blTYS8HSlQDKi0yu0WZsvM7dYJGKoLKxUSCYMFpcr5LIxFpbLnJgepLvZAtNlc6PG0ZkBSsUmx08OU691mDk5TCwW4vQfWmStq+NlwriORLmRwZI1PNnDdQxWXQlLEfRaJu46bKz3yIcihBSVsK2zVmhT6fUwHYcRNYrTcomqGo4nkFoenukRM3TSegiraKIqMklFQWq5RFSZy++MMTH1bDGo53m7tlmWZdLp9K638+TJk/vydrqu+x33aLZarQNL5u2j49zz+BfAjx7kN77rRPNl2O9D3mq1uHr1Kpqm7V58gPyf+AJmS2LjH/ybtxq3UChQKpWYnJx8Y2ciWZbZeNQmPuyHKSL5vhxR9niM8lqPquWROKZTmtsjtyNgc71LdDREOKWxcq+O5wrqLZvs6QilJT8fZvNpl/SUweytKmbLIXXcNxSjl1OUtno7hee02zYDJ2M8vFpj7LQfmt940CM1oREblFmtlhACiksu0YTG0v06xy6lSQ8ZyAMytVKNv/RHfoP/63/xdVq1PvmZGa9jO/55ncg3gmP22ChrGI//NomFv8ep41O7VZ6u62LbNpZl8Wt/6Q52w8GyJRRD0AjHGAx6suM42JE0dsMn35GhoDpSAXOjBvQljrR8HKGGCJ04gn5qBnVshNDMOOpozg+HA3K0f973vlfT/apufSBB9VYZBo+AJGFXO/7/U8aBVo2SJO3KT1y6dIlz584hyzLb29tcvXqVhw8fsrW1hWW9mNO6g72G7BCHOMRHizflaAohWFhYeEaV5Plt90s0TdNke3ubkZERjh8//sJvG6rGD4ycACAsq8hI6G6Iawtl7peKJPQQ2502U5EYrhCczPmkJxKk+dTNHmfSedbXGmzXWjwulEgZYdbrTUYiYdqWzcl8Dk8IpgICOR6P09ro7hYJdYKe5ptV34avVprIEjzdKpOJhlE6HmtLFRY2ygykY6xu1xgfSLJdaXFsNEO9bXJiIk86HmEqEmNlscpANoRtu+QzYb84aMwvDhoeSDAxmibuQHG9jhF4Q3eknNpBupPneij6Fpu63ymuVfIohOI0ZBs1LGNVI7Qx8MoOBiq9lkYjpLNcqVDstEl6YeyuYCASIWcYJFydYrFFtdPF9TxyXggsgWW7xCQVt2YjyxJRFJymRUiCkWycL/zIhReuqRDilQQvHA4zOjr6Rm/nR0E04WCeybfRZn5Tx7lgH2b2/PmHgQP1qP5YEM23KQYqFArcvXuXc+fOoWnaM54kxdDRj0zSW6tS+kpfmudNF2zH+CwvLzM2NrZbrf46yLLMg6/U2OqajF5O0ev091sO+ae3utXDTMoYeX/1KCmw+bhJu2JjRxQGziV2DUJlpYuZ6Id3u3Wb2IkYdlDFPv9BhaF34izN1SkudZj6lB9uLy50UEdUhIC5axXSo2GEB+mRGA3hsvrAIj8Rptt0SB/xz4NQPOa2ayzfXeJv/YVv8anj8wDMDFXoWv6xx0I9nq77eUP5lMnsup+Urti+t3jQuk707s+iiQ66rqPrOpqmcf9fb1B/2sJRQO+4qKkQoY5Ld6lBeNCgsuxRn+tgbfohIlnxjz8ylkA4AmNmEFNEqTuDFJYNVr/SYO1rLVolhfXfa7L2+x0aJYNyOUsjPoDQI0jB6lw4e7yKUp9AqmnfW1y9XUWeOoa1VcM4PvKhc2l2jnmnp+3Y2Bi9Xo/79+9z/fp1FhYWqNfrz9yj3W73QH3OAX7913+dN0hQ/GVJkh5KknRXkqQvS5L09j01D3GITxh25hXHcbh9+zaWZT2jSrIX+41+FQoFZmdnSSaTDA0NvXK7L46fAaDodDmpjfC7C+scTab9CvKUb8MNxbdf1UBlZL5RQ5dl0qpBu2ixUW9xciCHKwTTWf878UDCzQ1sS6nT4dLgEHNzJXqmzZPNEtGQxtxWhbShU+5YTA2kqba7nBjOEw+HOBlPMztXZGokgxAwkvPtZCbwfhpBxXzc0DHXO9hBm+VeoKDSCua8xaUCkgS2adFaqvL4/gaxWIjZx1tkslHmnm4zMpZmbaXCxcsTrNxYYuA/q+BGPbRQmM1eDMUKIboSHTvGtizR0m1EUqG24aFqEajapGwV80mLWt2kaVkUOx20Lrgdl6RhMBiPITcEtbqJEIKMotMu9vCEIOJKuC0LQ5JJaip//H/3mZfygv1Gm17n7axUKiwtLR04t/PD4G0k8/bZce4vSJL0QJKk28BfBv7MQX7jY0E0n8feAp/nsZMHs7KywuXLl4nH4y81CsM/+QcRtsf2L319X+FM13W5e/cuvV6PS5cuoWnavm4Oz4G1O23adYc7d8rICQVZ8W/Q8krfg+nJKnUc9IxEclqnW/dX1oXZNmZ0TzszDTYeO4xe8UPhkgxz92uMXUoGxw9aXqNe8leFqw/rhJMqk59Ks/ikgRaWcSyP9KiBJEGh2UCLSwgPElk/hL/xxGb6/SS37xeZOdHjf/xzXyUd6kv+hHSP+/MpCo0kH9wZprUdp7WexCvG6JZSPLg3yMJSnPlCHgmXrY0yyjf+CtgtXxbKFnzjb88jXA8he2iTEdylHpkTUfR8GHkwSXu9R2QkjB3k+NjlNkpMRx7M0vByrHzTpPqwhVW1MfaE0OU9bcHcto1nephzLoV7FtVGDu34FE6j3wXIbfW9ikLuf7ddkNGnJzFOjH6kSduSJJFIJJicnOTixYu88847xGIxNjY2dsV219fXmZ2dPdDK03VdfuqnfgpeL0FxC7gshDgP/Gv8pO1DHOIQ+ETTNE2uXr3K0NDQM1Gw57Efp8T8/DzLy8ucP3/+jRGRS5kxLqbHkFsGwvJ/MxN09Nmq+drBy70OuiwzX68yFI5gug7fk5vg9pMtRgIZNDWI4FQ6QcSra/pdfwol4rpGBo3aVodKs8vx4RyW4zIUCyGAycFARs/wiXU8rCNVHJpBKL5c9+ertUIdCVjYqKAqMrOrRd49OsTTG+voqsLCcol0UqdQ6jA+mqZc7TI9lafVcbhwfJDFGxuk0zqW6TAynsTzBMMjKQASiTBnTg/TWK5gXKphuzbtUojFno6UAVOx8EhTLrtEXR15y0FuxLBVDVv20NJhakWTjidRLjRI6iEmpBhuz8PxPBzHxSqaGIpKLKxh2DJO0yES0giZAtnyiMoSEQn+5E9+llii31VpL952Ttjr7UwkEs/0M799+/Zby+ftF2+rzfymjnNCiJ8RQpwRQlwQQnxeCPHgION/LInmq2DbNjdv3kQI8Yz25ss8oNGjA0ipDFaxzdo/+f3Xjtvtdrl27RrZbJbTp08jy/K+V7Rrd1o4wQpv+ESCG7+7TfxclIGTMSorAeGRBMXFLq2CixPXCGf7K2gtLnH7y1ukLvir2bELKVo1m/X5JrFBnbGLKcobXQrrHUIJBVWXmX1Q4+hn/BVtu2ozeiHJowcVqls9pq74n89erTD8qRALj9tIsgaSYO5WlemLaYaOxmhLHrrU46987rcZz7eYylTZqvn5mMVGhE7VIN31uDTU5my+jCf8/RuNVTiaNnl/qE2jkODq/RGsTg21Ncudf/iX+G//ym/xs5/7LcqbXVpdl3w+TGo4BgIiGY1aSd296aIjQbg8IiNnElTKMdpFQa9ooad0zKJv+LRYP0nbbfeJY2/Tz1ESmkRvs4Vdt9m63qG8bhCaGUNIEuZmfXd7p9GvUJejIba+1SB0fPzbKkOhaRoDAwOcOnVqV2y3WCzy0z/909y5c4f/7r/777h58+Ybx7969SrT09O8QYLiK0KIndXNB/i5Noc4xH90eBlRrFarVKtVzp07x/Dw8FuP7TgOd+7c2a0LCIfDb3RKSJLEldhRtrsmVpBbP1spIQPrVo/RaJy2bXE664fNh8IGx6QUtWAhvtEIqs4LfhvJhUqV0WSchmlxajBPWFM5E0nzcK5ECN+J4QXV7W5gcbdq/hjzhSrnxwZZfFjAsz3m18vkU1HWCnUmBlOU6h1mxnM0O364/MxoHrXl6x+PDvsOj4GcP1fEY0F1vCLxzvQQrc0OwhNYpn/+N9ZqyAo8fbxJJKqheC6VhSLLi5sM/9EWtbpMO5HAa8roHYNOJ03V8/Ai0LNsmnqMmuuixnTCQiVUALUjoGlhbrcozdcoVNv0bIe4rhPpSHiuoGvaRGwJqechPIHedZFtD90RhCWJP/ZnPs3AaL/49nm8LnS+XwghnulnfvLkSRRF+VCV7G/C24TOvxP4WBDN/biom80m165dY3R09IU8mFcJ5g78ie9Fcky2fuUudvfl+XLVapWbN29y4sQJxsb68/J+iebc12u77yNZn/jO363hDatkZvzQw8DJOK2y//vllS4NW2AEOpv5k1E8B1bvmSROqDSClWq7ahMa0ukGN2F922TwbILxyymq2z0W7taIBxqZHcchMeg/8LM3KiSHdDKTKsWqDQhWnzY4+alccGASq7UGj25s8X/+s084MrAjqSRRbye5uzSM3lJ5f7TJYsFfGWkq3Fv23ycNl4cb/up6LF7nQq5JtONxeynHheE5vl/793QeddGjMscvpum1Zby2SWQsSuGRSbdo41T8Y5QVD3nCgLFBVr7axG66mCWfJ0XH9zwsTv9B7G345FLPR3aLh5RcCLyg6nEkQa9gsvb7XeSpmV0pJCHLmBt9+SjXdP3e6McGPhKiuZ9Qy47Y7oULF/j5n/95Pve5z/H++++zsrLyxvHX19efKVbgFRIUe/BfAP9+H7t+iEN8IrHzPAohePr0KVtbW8RisQ/VJGGnQj2fz+96RPebz/nFYycBmK1XSesh6rbF6YyfljQS8/fJ8TzGYwm6NZfFYoPHhRLJcIiNRpPpXNpvI5n3PZNDgefKUFUGHINaw0+5qpoCCVgs1gkpEsvlBtloiM1ak2ODaY5nM6gNj1bH4uhoEC7PB5JIsUASSZVRFZmUqvPoxjrVmm+XV1b9Nstrmw10TWFuoUg6GUGzBMWFCsuLJcaPZNjeajBzYpBW0+LkqRE8D2aOpHjyzUV0AzI/2KBWjVANRbAkF8KwJcI0XYHVdYg6IdoFlaino3U8oj2JXsWjgYecj+AASlvCLnaQmhaD0RidbZOu6aIrMqGWg9l0kSSJcM9D2C665RFV4Y/9xKcZn3597cVHkUP//LzyptzO572db+P1bLVaH8tucx8Lovkm7NUle1kezKtagA38wDkkVQHbZP7vfuWF/6+urvLkyRMuXrxIOp1+Ycx9Ec3fr+2+b1b6HrN2y2Zls8Xw5QSRXL8CcfBEjPkbVaQBFT0uUw3Eb4UHXVOitafZeb3cwQn3j2v+RpU2/t/dpkPyiMHwyTi3v7mN73AUWF0XPSeoWi5rTzuc+pRvyJaf1hmejjK/UWN8JsFf+kMPOB7fxLR9L5zrSRTXYELrYWhBDg79jjrJaP+m1wMJi7TRY7GSIhu2cVtJ5rbHmE4U+PwPzBNp+1XdZt3CbDi4WojWaodQWqW13ESNa5SqNtt3VPQg6V2Lq3Q3/POhGP1bc8ezGRqM4gSh8NDAHtH2aP/87pVB6rZU6mYWfTRDaCiJZ/bPbW+zRXQ6ixJSPxKiCQdP2k6n03zxi1/kR3/0Rz/0bz+3H38auAz87Y904EMc4j8wWJbFjRs3kCSJixcvfqiQ5U6F+unTp3cqdYH9zxUTiSQnY0lcIRjWfEKnBAvh1WZQaCkklJrEYrnJ0VQCx/OYzvmet512kt2gb/hqrc5MJs3GUp16o8tiscpIOk6l3WU0aWB7glNjgwhgMBFFliRipsPDuxu7vclrQZe09WIDCZhfr6CrChvFBmeyGW59a4nBfIz1zTr5bJhm2+b4sQHaHYuZowNomsKJoRRPb60xOBzILQXFmJYVOEnqXY6OJFm8vUkkFmKrWEWcVikJGVWWcSoKrW6KXtFC8ySoCQo9FSer01AdjGiIWskmJCmobQfWW6TtEEKR6Hgu9ZUK89dWiYdDGJpCZ71BPBQlm4qiNmw0SSJkeyimyX/6n73P4EQa13Vfe82+3c6Hl+V2Pu/tLBaLBya7H9e2xh9borlTwfzkyRM2Njae0SV7Hq9bUcY+92mE5VD/5gKdLd8b5rouDx8+pFKpcOXKFQzjxTyN/RiPTsOm7TnEB1WMpMrGY398RZNYfdzA7Lg8uFXGi/Rvlmjghdx42kQaFzS3+oYvMRHBlCXCST9UnBgzeHqjRnLSJ4PD5wyWF+oYwf/nb1TRRhQEsPKozlQghaREQ6SGfW/q8pM68YyOY3vEp8IUtjqM9W7yhy+ukgjbLJWHsF2ZB/M5Lg51ebTWF7rPan0P4JFEi7V6itlikm6rS6Xtk7uu6x/PkXSDGb2GIof54R/9Csd/wKNws8bAuQT1CkQCDdHMdJTYTJK6pNO4618zt+2vxONHYru5mKIXdAuKaZjbPvkM5fvXSdH33Lp7LtMzhUCyTHezx9YTBWUwt/uxmoliV7vET/thqo+KaB4EBzUIo6OjrK7u1dR9uQSFJElfAP6PwI8IIczn/3+IQ/zHgkajwbVr15iYmGBmZgZFUQ5MNIUQCCFYWlrarVBPJpPPbPO6moK9sG2by2H/mW8HWTaPyiUSms5Wp8XnByd5OldiJO7b4HAgw1br+mRwrlRGlSWeFsvkoxFGYwnCTYlyo8P0Tv5lyLez6YTvIW32/IV523Y5lUizttFFV2UWNipEwworWzWGMlFKtTYz4znaPYvzx4ZIWgohSUEISMZ94pjL+sftBdEj23FJC4XFxwUURWJhtkAkojP7eItcLs7yYokTp4dR2ia6BJ22ydSJQfgDNqahgyThdXWKkSh1xcZLK3RKNrYRR266xB2VRA3MdZuQptC1bWJ6CFk3MF0HTZJRCh3sup+bOXt7idK9LSJaGE1RoWoiuYL2cpnGapmf+EtfYOrM2G4E1HVdLMt6QZZv57p/FKog+x3jZd7OarVKu90+UG5np9P5WLY1/lgQzZddDEmSuHnzJoqi8O677762HdjriObE//5T2J6BZ5k8+NJvAXDjxg3C4fBrk7hfFY7fi7u/u82jW1XW610mvzfDDksaOR3HDITaUyNhrv72JqOfTSIrUNhTIBTLxIhPG6gh//iLGx0Kyx3iRw2iaY35Bw08F3qmTCynsbHeoV4wiQQR/snLSZ7crxJL+2Rv4X6dE9+b4fa1EsXtDqGIQrNqMTITJzNt8PUvr/H575X4iz9wv78PUo/FrUFOZP1wdnpPe8t02OR3HuR5sDJCq5hieSHJmCtxKiRT2BpmaSlHrSJT7hikjQ7b5QxTA1sUCuNcufgbhPMajiPR2TYRpoMkgxdRWbpuEc/7BldSoL0ctDKL969Fb8PPJ4qM9x8aeQ+5dPYIr3vNvqfSLPULgeygZabbdaltqRinfS+EPuCPGT/jh0++W0TzILk0V65cYXZ2ljdIULwL/E/4JLPwke7wIQ7xHxCEEKyurnLhwgUGBgbe/IWXQFEULMvi3r17tNvtV1ao7wetVotr167x/cMT6LLMcqPOZCKF5bmcyOS4khyhW3fwRL/QZ7HWJKQozJerjCZifj7mgL9gPpfJ8/DhFuGg6ry1I19UD/QuN8tEdI357Qonh3PIdQ/Jgk7PZmYijydgesw/LwkjEHzvdRnNRLFLPQqbDbaLvl1e26yjqjJziyVi0RDzS0XOnBiiMlcmoqtUK21mTgzR7dpMTefxPMHAcILBoQRhy2Fjvkil0PQLW1c3UN51MT0LxYlQ7OkYXRW54hGqhei6YSxXQELDKvXoKBqWoeAqMuGOQDQ8Ysi4bQtrs4URi2PEQpibDZSKjdmyKc0XWfn6HMt3V1m9tojUNvlrf/fHmZwZQVEUdF0nHA6j6/puE5YdWT7btnFd9yOTJnob7Hg7JyYmyGQyB8rtbLfbB1Yz+U7gY0E0n0ej0aDVajE8PPxasfQdvI5oahEdfWocyzFoz25S+91NxsbGOHr06GvHlSTpjUTz5m/7Ej+2JShWu4SOhcjNRNH3FK/kp3wy8eCbJYa/J0Wt2CdC9arF4t0a2bMxRs/H2V70PXcLd2qMfDqFGchGVLd6DF9MUC34xmT9ocnk+3EWFqs0yibRIZ8cGjGduuNvU9rocuyCH3JxVYGngSp7/MDQXXTVPy5PwNq6Qb3cvw0mkm02mxHuriVYWsuiW1GmQm0MxSNm9IngZgkGww6X0l0a2zkWVqYw7Sgg0d4EXW0z8+49yg8bKCGJXrGHMplg814TPIlwxD9HyakoTidIXg+8mOEhA8VQiZ3MoWbjxM6PEjs3CiGD6PE8ej6KuR20mNRkvJK/4pcNld5m8Lks0Vnrd17qlUxWvtbGOD2GCGREEt9FonnQXBpVVfm5n/s5eL0Exd8GYsC/kiTptiRJv/KK4Q5xiE80JEni7NmzH7ow4saNG6TTac6cOfPWNqJYLO5K8Q1nMnw67xci5Y0IqVCYsKlwZ2Gbp8UyuiKzUKkyHI3QdRxODgT5mPFgYY7EO8kBlpb9SvW5rQohVWFhu0I2FqbWtZgZymI6LjNDWY7l02Rcla3tBkbg7TSDrj3bQZvejYrfkzxqRHCLFk+fFvyq8mKTkcGo31IyaCU5NZFlZjJPqOPRqHTQA0m5VtMPnqytVNE0GbNrobVMHlxbYuJYnuJmnZPnx3E+10JzVOxWlG2h0wu7NDUbbJ2CkFGTYRRFJl6Xcbsyctkk4krIW10URcdSBQ3LIulphNBRXIFb6xJWwmiygtq16a7WkV0PqWkyOhDjZ//xT5IbfjY1DnxCp2kaoVBol3TuRDK73S5CiDeG2L+d2JmXDpLb2Wq1DuzR/E7I5n3siObGxgb3798nlUq9IKL7KrwpGfvkX/keZLODaSooX6mRSr553P0keF//9Q0ABIK1pw3WZ5ssLNdww4IdJZ12vV+EVG00UAdl4oM62SMGa4/90PTcrSrh8dDud5AEj+9XmP6sTxRlRWLuSY0Tn83ujiUbKuEgH3HtscnEhQhy2ubuB0VmLvk32t1vFLj4g0N86xsbLM/W+S8/v86loQrzZX8le30ux6mMier2CXfXVniwlGE6BENhh8lkf/9HQ3VM19/Jo/m+F9FxYwzrVUI9h0oly+B4BcPrcvTEIhG9QvSYRrnmUV3rYW/757QXeB53BO5DuTAYYdRjwzjpPEv3FOa+ZlFeEcx9ucXc77RY+GqLud+3KZTilCoJpMlRvMkYkurfxuHhvgxSeCSOZ/q/JYUUOmu+UV35WgtPCaFlDMIjfojqwxLNt0kc73Q6B86l+aEf+iHeIEHxBSHEYCBBcUEI8SOvH/EQhzjEy1CpVGg2m0xNTT1fhLdvCCFYXFxkcXHxGSm+PzA8AUDHtkm0db41v8FwPEbLsjg5EGgWR32vlB20F16tN8lFDKyqzdpGjfVqg6l8io5lMxz35YuO5HwyFQ7IX0RVKS7UWNn05Ypm18pEQhrz674o+1alybHRDK2uxfvTYyzd3mZ8OMgHDeYWNQjflyr+XKUIwertDWYfbxGJ6sw93WZgMM7aaoVjMwPUax0uvDvBxt01MkHUStH8MVZKW8jnXLqtMDVJw65ZxJ0Q7pKEp0TQGi6aKdBqgkbXQ84a2HEVqWIRScTxGiZ618Woe3Q7LnJUA9NBbnh4XQfN9jCLHaLREGrXYXw0yf/wT/8c8dSbFxuyLKOqKrquU6/XKZVKDA8P75LNHW/nd5J0vkzJ5HW5nX/1r/5Vbty4wZ07d2i32/v+je+EbN7HgmjueA8fP37M9vY277333r4kI3bwOlIohGBbruEkokgC3CY8/FtX3zjmm/JuFu5UKa35YfCBqRCNoKo8O27wra9sEpsJM3Y+wfLDvrxOsygoLPfoSC654333djihcuN3Nxm7nARJMHUpTWm9w/1vFZm8lOLY5TTbq23ufbPI0Ysp0kNh7lwtYLoWatAXPBQL07X8m3LhfpPsqMbQUZ1r19ZJ5UIMaRW+eHIJgLhn87g0yPkgXH4s3WOrHWWrFWazkGJccQB/3KRm8aTk50aGVVht++RswOhSMf0HOKL4HsVUrE23aNBs56mV4ySNDt//n9/C1TQ6RY/oqL9/WlymudRCUiWUqIY8OUC1F+Xpb9RZv9p8JueysxFUoY8Y2E0/XB4djtAtO2xc7eD08lSaaYwzE2iZvkFR0+Hd98ZoHOEG11KRWfm9BqnvPb77/4+CaB70+x/XpO1DHOKTjDdFqoQQrKys8PTpU7LZ7Fs/o57ncf/+fTqdDpcvX96V4pNlmcvpHJ8dHGd9uUEmHHR6C/qWe8Gcs9HyicKOPmZYlpmQ4ixuVDk26JPBaEAoNd1frK8FZPDpZpn3Jka4fWOVbDxCOZArMi2H6XG/FeVwIMpuhDQuTgxRWWsghGCr4M9XhVKPkK6wttkkk4pQLHc4O5nh4deXGBqJYvZsjkxl8TxBLr+zYBecOT3Myq0VPNdj9v4GqUyUxcdbDE4k6FxqYXfSFLoekgxChlJDopuJ0NAc5MEw1kYPBxXF8XCLHXJtFSNkYLV6KFEdr+GCJ5OIhXG32jglG1mVMYRAMT2SyQhSy+LkySH+xi/+V4TC/eLQ/WBzc5OVlRUuXrxINBp9xtu5t/PdToj920k89zOv7PV2/uzP/izpdJoHDx7wuc99jrW1tTf+xndKNu9jQTRN0+TGjRtomsaFCxdQVfVALcBete1OBwjHcZj589+HETKRHZut31mnudx4yUh9vKqSfQdXf3edqfdTSLIgN9IvoDECD/3K0wamYTF2KYaQBMMnopQ3fEJWK/RYWKgz8Y6fXD1+LonZdXl4tcTk+2naPZ9Qea5g8WmVblBp7nmC5bk6mekwZs+ltGZx7GKG7LDBvXslZE1CD8tYpkdqIErdcqlXbGIpwV/5T56iyL4RqzdlyusSO2QSJNbrSdxaiEHdYSjqstbtG1hX6xM4y+mvsFp2IIlhVOiavrHrmBGSXp1GNUoi0qRXMRk0ngKQTvpjxqbChE4Y1NGZ+3qDjZst4iP93Ccr8AKHcyG6Bf+cRYb7hUCe0n+4ZSTMhsviVxtUimEiZ8f8Hup7OgIpsf7YkfEYbteDRD+88GGlLF6lofk6fFz1zg5xiE8KXtWG8lV23fM8Hjx4QL1e58qVK+i6fiAiseOYME2Ta9eukUwmXwi5K4qCBBwPZ+lYDlpQdb5W9+ejHTmjUqfLiXwWDzibyVJZadFp+lGZcjNIsSpUUWWJ+UKNXDxCodHm5EiO05ksNF0QMJj17ZwWeCbrLT/EvbJVIxLSULoeq0+LLC6XGcjFKJXbTE1k6PYcpqcG8DzB2EiaMxN5pCDrS8bP6VxdLiPLvkZmMmUQ1RW62w3KhSbHz45hWw6D4/6EaGkC82ScbceBiILZcVCtJF4HYqZM2tJgtoemh3E7Npqho1gyliRhqRKu7SKvdohHDEJhlc5qDd1TicfDJBQNzZHQkbBqHaaOxfiTf/V7aTabByr+WltbY3Nz84WakB1v5w7p1DTtmYIi27ZfKCj6KATZDzqvhMNhZFnmS1/6EteuXXtGrvFV+E7J5n0siGa9XmdycpJjx47tGocPSzR39M4GBgY4efIko3/kBJ4agpCMXbf44K9+/bVjvq7qXAjBr/2zWa5f2yJ8VMfZQ3ya5f4NVqt0uX+9QmJGRt9TqDj5ToqNxRaPH5aZ/kyGwmbfzV2rm6hxhR0bOX42ycJcjfy4v/JNj4Z4OlcilvIfhPsfFBk+H6PdtFmdb3LsnQwhQ6Ha7pEdjgCCc8oqk4H3smPJqCJMTpN3pCeZLYeJ1Dxie+qtSs09kkG2wzcXkzzaHESp69S2UtS3UtiVECsb42xUxtkuBZWSoR4gkc93WZwdwog4TE8+QZZd2htd8u9nIRJj7VsumqZhlvwQfLvjG1FJgeai/z4+3ieXsta/VTvVfkFVt9jvaNRa77LwlSbVbhKh9vdf9KP8aEnf05k8l95dlcLBpImex9t6ND+O1YGHOMQnGa+aV3q9HteuXSMWi3H27FkURXmjs2EvJElCCEGj0eD69etMT08zMTHxwnY788oPn/Z7nz8ulIhqGlvNFjPZDI7ncSzrkzNDU7kyOExpq4vtCrbbNrois1ppkglrdGyXqVwSTwjGs0niYZ1BxeDRoy1aHX+xvrpdQ5Lg6WqJWCTE8laVsYEkAjiXz/L0/haTE36BUdAwCE0LWmHWO0QjOl7DZPH+JnNPtklnoqyuVJicytFqWpw4NYIQMDoQ5vE35rEsn8hurpbRdIWn99bJDyfpfEbCtiTkukukq9JphqgLDxFXcTWJriVhx3TMkAQhBVa7pAwDp9jG3WoSl8IQCWN5AopdYkYEPazhlTqY1S66ANVy+fz3n+Sv/8//NfF4nNXVVT744AMePHjA9vb2bp/7l2GnVeQ777yzWyD0MuzopmqatltQpCjKM97OnUr2j1qHcz/4dkbKPoxs3seCaA4ODpLP55/5TFXV194Ye/F8hXi5XObWrVucOnVqV+9MkiQyf/gK7SoYhkVztsqTfz73yjFfRjR38jWWnlSYf1Dzt1MkvvH7G6TPRjj5fVm2ln3SGM+pbC0ED92iydp2h8FTQXWf65Mj1xFUWz2SIyF2kgv1uMLdDwocez+DosHmeptGxaTnuiTyGtVOh1rBITUaRgvJnP5Mnm98eZ3jQeHPvatFzn5/noXZGvevF/m+70vxZ9/dYr7un99HGwkyqsNAxGW+kWShGiIjdAYjHo/KfWKXl7tstkPcWsuS7SgMaxHGZItBzaLuxJAlyKoN4nRIOU1cK8HTJyNEYyampRHRuyi2ghbWyaWbfOqPbVE3ZR5+pUZ7Mwi1T/Y9errphzii4zqu6Z93h35+qNXov/cCMq8YCu01/3xrMZV2EGbv1hxmf6tJ6MQoiqHS3eoTUyEkJFUmf2EARVHodDp4nvfSVel+8bYezcPQ+SEO8Z3Fy+aVWq3GjRs3mJ6eZnJycpcgqKp6IGfHTn3Bu+++Szabfel2O/PKmaEBjmWfFWCPhvz5odLposkyuiXzdLbASrnORDZJx7IZT/kOhyNDPjn0hG+vSpUaya7EnYfrGCGVxc0Kw9k4lUaXE+N5bMflWNAJZzgdJ9oSdIKGF5vbfmFRsWoR0n0R9lw2Rs+0mckmeHpnnZnjg7iux8iYT4K1oBVws9FjaijO0u0tEukIWyt1ho+kqJXb5MaiyBIMTERYGW7SCtmgKWy1JdSoAbZHDA1nvosomcRtGaXYI9aS0dMRaj2TUCKM5qp4TYuILKE1HbBlhAtuoY3btolqKnLX4Q/8kXP81//Dj6FpGkNDQ5w9e5ZPfepTjI6O0mw2uXnzJjdu3GB5eXk3h3GnlWiz2dxXK9GXXU9N09B1/RlvZ7VaRVXV78q8chAHxndKNu9jQTRfhoN4NHdWnjv5NXNzc1y6dOmFYqKTP3kOVVaptSMossvdv3uXbu3l5+x5oimEwPM8PM/jy7+8vPt5esD3kM0/rNLGYfxKgviAQn4ixI73/Ng7WbZXusw+bjPzuQybi/3Kc9PrcfPr20xdSTN0LMbjG37nhbsfFDj9/YMUAwHz4kaH2IREL3B+zj+sMfNehgf3CriuYHmuxsRMglOfyfHlX1/m/Pt+wc/73h0imsew1+YbiylOp/uyQJYZImSGCAchdV3bIcISm90U1UqKad1BkSUK3X6uS9P0CakiC6o931Wb1BsMpzqY5TCLiz6p7fZ0DLdL14szkpunudkilFCozvkeS1X1DboWVWgEBD0xvId8WcEJlAT1BT+0ZIyEsYMOGLEjMQI7S2zi/8/ef8fHdV9n/vj7lum9oVeCJMDeJIqqlnu35J7irGzHsZ3ibOJN/TlOnN0k6+/G68TJxqmb6mTjIsexJcUlki1ZskiKDSQAEgSI3qb3duvvj8EMQQokARJS5AjP68WXIHLm4s69dz7n+ZzznOdc9uD0dnswVJOZp3NU3CFEy+Uva2mphH/Aj9VlQ1EUzp8/38hgwPNtLtayQBiGsVk638QmXmJYS+l8bm6O8+fPr0oO15rRNE2TSqXC4uIihw8fvq69zMq4Us9qFpUa4RtPpLGKIulyhQO+CIOji2xvrRHKgKsWZ8xlSdB0IoMATCXz7O1oohLXcFqsVFWdZm9trQ4s+18K4rJ9XrrI9o4wi6MJCrkKE5MJfF4ryVSZLd1hSssm7IZp0t0eQEpXUco1Up5MLpfrx6I4XVbGRqNs296MUChjk0SUqkZHb+1chWVJVimj0dnp4Zg5jaMkIszp6GUXYkWAkooXK/mYitjsRvXIlHUdq8WBiYBZ0bCXdIzZci1r6LahzBfQMwoOuwU5r+C0WvHarUgVnbf/2GF+4pfe/LzrLQgCfr+frVu3cvjwYXbt2oUkSYyNjfHss89y7NgxstlsY/T0raCe7czn88zMzLBz585biis3QzSr1WpDD7wWvFi2ef8piKYkSWiaxvDwMJlMhttuuw273f6811k8Vhy3R5AlKBZlzEqF7/7M0VWPuXJBWEkyBUHg9A+iy6+B6bEaARIEmBzNcO5EnKVsBXvQgcNbS8FrKx4qRTewtVhp6XMTanMwc76WbRt+LoEcVnD4ag+WbBUYPhun90AAyQI2l8DclIIrYMXjtwIm8WyZ7t1+wKRU0LD5JBajBUwTBk/FeMu9Evf3ZgCoYkErOKjrMguKiJERKBmX9YvtUoWpoovFTJBeUydduvyQe+XLkgCHeDkjoKjLHd8WhVTRjUUykLAxNd6GJ6whizrlpEjIHWfn7kki2y6Tw9Ky/jLQ57rcrGNcJpeVhWWtZpsds7o8lst9+VrKbmnFz5dL5Vb/5c9kynZmxyW8O8NY/DbKCyWC+yMUCoWG5YjP57vC5sJisTTu/7U0OCtxM55rm6XzTWzixUc9rhiGwfnz50kkEtckh2uJQfU+AICdO3det+wKV8aVN+/YhigIjCVSNLldFBSFQ+1t+MoWRK22nlSXJ/iMLyUQBZhK5oh4nKQKZfrbwuxubcJZFikUFXye2mcQ5Nr6NxPNIgowOh3H67QSdNqR0yrJZJG+ngiGaRIJ1Ta7luXNeCpTYltPhLlzi1QKCpcuRmlq9hJdzLK1v5lyWWVLXxMtrT7cwOJEouGROTY0jy/kZGE6za5DnXhkAatVoni/Da0kkPW4yVtMzJAFQYdSCUTNRE+W8asSjqSBTTMRNAM9WQZNxh50o1dVjOkcVpsdV8CFtaRjkSQsmoFVN/jxj97H2z/yqjXc/ZqOsaOjg3379uHxeHA4HDidTo4fP87g4CDz8/NUqzc/5yIej3Pp0iUOHDiAw+G4blxRFOW6pPNmm1TX854Xyzbv+t+KFwmr7TxlWV7zDTcMg6WlJXp7e+nu7r6uNqLzoV4uHjuGYkhkEgLV0zFG/t8UO3+054rX1cvx9XJ5fVLA6aNRnnxqhoE9QdpbPTz3nZqXZt8eH6NnayWIrm1enn58Dl/Qxq5XRDj3TG0TIIgwM5EjvljCYhO589XtLDyWBwSCLXbOny7iDVgIdVpw+kXGhkoklsp0b3cRanJz8uklsqkqnX1eevf5ePbJmr3SwTtbmBvLMjmbRRCgtdPF0myet7VMND7P+JKDnT6N+aqLVmuR2ayHLrvOeNFGm71G+GbKboqKjX57bffausKbuEkuUtIknLJOQM6h6BaskopTuqwvrWg2oEDQX8CKRj5nJ1t10NyUY2kmQu+WJUrx2mttPpnsZBF7wIKjxY7FG0ZVoaiC0BWojaPMKBguDSEk4G32IgsmVrdEdGwJgFL+ckm8Wrj8rBj6ZVIs2WXUgs7YMzr9b26m9NQ8zh3uxkjTq7OK9S9pfSdZXxTqz0H957oup571WO/O82bsjTaxiU3cGmRZplKpcPLkSUKhEAMDA9eMFzcimuVymTNnztDd3b3m6UB1omGaJiGHncOdbRydmafT5yVkd6CmVaKpAkpVRxRgbCmJzyaTrWrsbI8wMh+nI+Qjni/R7HBx/Lkp2sI1ffz4bGK5bJ6mLexlIZFjR08T56dibAt7GTm9SGdbbc1JJDIAxBJlZFlkbCJGKOAk6HGgJUqkE0V27mln5Nw84SYPsWgOZXmEr6poaPEcQ+cXaOkMsjSbYsf+Ts6fmcUTsGG1yJRiWWIzcTIRCXvKS7oIPsGCUlGxaSbVooihK1jcVsxomapuIvvtFIoK1pyKx+7GUHW0TAmLKmJ1O2vNPot5EARciNgE+MCvvoG737h/HU/AZUcAt9tNb29vQ19bKpWIx+OcO3cOwzAIhUKEw2G8Xu+a9JaxWIypqalVB8xcK67UE1j156z+7/W4sp4BATc7zahum3fVsX5zxc+vWfdBr8IPfUYzl8tx4cIFXC7XFfqaa8HZ48HR70dVNVwekWpF4MRnhigmryS19RutaRqmaSKKIoIg8NW/HwXgwlCKpVQRe7tM32EvVe1yOdyxnF3LpqqUdBX/Fjs9u330HwoRX1ye222X+cH35uja58PfZKNlixtNNUjFqpQUE7vnsl6yUKwyPZfCF6qlxBVNZ3axQLil9pozx5foPRgkkyyTiJYplTXef79ENl/bKU2VfWz36IBAoSBzOuqhy1K7tl1WjZImcmLJQagiYhYv7658okpCq+2SRUEgXvURLbqZK4Q4NxFkKtVMuuxiNhGkqkpYpVpJ2y5XSWadeCwV5mYiqJoVQxGQJYOwdZzIfh/hI0GMVhfTizpLsypDj2eYGSpy6fsZFoaK6KZI7EKZxHkVUXUz+kSe4ccLzI0b5GUP7j3NuHwehOUnuDh/+frnlj0zAZTlqUGmDumYhGtPhKgtzr59+9ZUur6WBmflrlRV1XV/wddr2L6JTWxifVjtO6mqKmNjY/T09NxwaMf1YlA6nebUqVPs2LGDtra2NccrURTRNK3RLFIvn1sRmRpLMjIbI+B0kC6W6Ql6MUzoXdZj1s81nityoKmZ06dn8TitLCRy9LQGqCgaWztqr40se0cahsm+tiai0wUEYClWwm4TiacqhIM2cvkKW7qCGIZJf1eYi0enG6QoFs0hCDB2YQmf38HMVJJDh7qYOTVNW2cQ0wTPcnPl7GQM2SKCLuG1Ckyem2Prvk4yAy6SVhta0ELeYeAwLWQMEc0joztk9HgVj8ODXFLR40W8VRNUEQUTUxKwV8AsqMiGQHkui2iAUxdwyiI//98fXDfJ1HWdwcFBfD7fFfdfEIQGh7jttts4cOAAbrd7zQ1F0WiU6enpG04xXPkcrGYWX+cc9SraeuPKRo3O3Gj8UBPNxcVFhoaG2Llz55pubv24ze/qIuDSMFUNwzQpplS+/r4fNF5TL5Wbpsnw8DCxWAxN00hES3zzq5cAiDQ7GDmTYGm+yORkhtklhV33ROjY6uH86QQAVrvI2EiaqbEs54bjSH6R0DI57Nvtp1zSOD+YRPaLqOblz9ra5+LEs1EGDvsRJXB6HSxMldEEnUinBUWoMjWWRTVNurZ62XWkiSe/M0P/3jAOl4zPK3KPPEOrIDOVsWEtXj52Lidg1S7fdqtg8syMm+1WGVEQ6HXq5IzLGo+MYmM672Yi00wh48JWlPGWDVw2F35VJWiYpKNuikkfmaSduURNLF5Y1nRaZZ1C2ofktBAJlvE6pxg6kaOQNYhPlBEESF2qZUWDvZeJX7VymTiW4rVNgCBBZqJIIaYyc6bI2W8WKNh8BO5ogWXpqeyWqSzVXm8C6YnL04FKqQqz5yrc9urbbmpMV12Ds3KEmSiKxGIxHA7HujQ41Wr1psfZbWITm1g/FhcXicVidHR0PK/5dDVcKwbNzc0xOjp6RR/A9VxK6jBNE4vFQiaT4cKFCySTSe7f0s1dLe2cOjtPbziAbph0R2q6d2FZdL6UrW2cRxcTtAU8eFQJNa+gajpb2mq6Uo+ztpbkS7W1b2IhRcBtRyzopBbyJFNFeruDqJrBlp5lU/hlg/dcvkx30M7Qs5NYrRKXxqI0t/pIxPJs39GKqup0dIXYvbOV7GwKtaoxMx7D5rAwNrRApN1DIVtl3+Fe4qNzVIpVBAFOFKKYPgdiWsGvW7BPK5TTKq6ygZCsEihLOGU7pWoVwWtDKhpUiyYelx25UMVcqKCqJg6XDSFdxu1xYtcMPDaJX/7f72XvXVck4W6IusyhqamJ7u7rD7exWCw0Nzc3Goo6OjpWbSgyTZPFxUVmZ2fXTDKvxkqz+PofwzBIp9NYrdY1NxTdqk3fC4kfSqJpmiYXL15siK/dbve6Goc8h0P49jWjWk0cDgOqGtHBDN/73aEr9JiHDx+mu7ubYrHIyZMn+ePPPEH3DjdWm0hHnxd9uUS7ZXuIbLrKsWcW8LRb6bstSHOXi4GDYXLp2hd/6+4ATz8+RzRbZM8rIkyMpxvn5A3ZOXF0iYHDITq2ujh3olZfHjye4MCrm0kuT9FJJxSaev34QjWSlIyVwamQXl6Ihk7H2TLg47UtKQIWHatgEis14bfWzjOtSDRJNnTzMqG7WPXQaXez0lNzqVJbtKZLLso5F96KhYCq4NUrDQmlW7hMBK1OAVGAiEOlWvIwM9WEsSxab44UsKBQzeoIpolNUAkFcpQStesS6nM1so5W5+Xys5qtfalkh0hmspYF9ve60Mq1++zrrWUDs/MKyZhALG/Hf1sTvq3eRlOQu8uFvpyhNYUaSY0c9N3UYnAtXLhwgVAoRGtr66razuuRzv+oWbqb2MTLCaZpMjo6yuLiIr29vTfUUdZxdQyq6zqTySS33377FX0AN0qM1OOKxWLhyJEjtLS0kEwmOXvqJPZlKyKXvXZe84labJjNlPDYrSxlCmxtDtLkcdFr8zA1ncJhq23kk7na2jg+l8RulZlarNkXOawy231+psbitDbXSuuVSk0iFU/U5qGPT8aJhN34RCtWTaZS1ujo8mGaYLPVFtFctoQoCkiGwdzZOaZGo/Rsb6aQq7BloAWoyREG9rYz/OQILo+d+Usxdty2hfhdbjQZJJ+NYrSK7nFSdUtUPTL2KqimCJKAUNEwp/K47A5cThvleB49Z+JwWPHbrch5FVEUMHMlfE6ZX/jf76Bv1/o8w1VV5fTp07S3tzecaNYKQRDw+XyrNhQ9/fTTjI2NNeQTt4p6/BgaGqKvrw+/37/mhqJSqfSSbTB9SUS6a3UHrpam1jSN06dPA3DgwIGbMnc3MPDfsQVZcpHO6FhcApJV4MzfzjD5g3hjZyCKIl6vl76+PrZv28e//L9FBgeTSH6TaDZBa48Nr9/KyJlaBtPplhkZTHLi2UVmojlU2aC7f3l3KtU+Y7Wio+oGqmCy644Ibb1uzj5Xay46czyK6Vbp213baQYiNQKqmAYDB0L07vRz/AcLnD2V4MDdzfQO+BgfK3FhJMv2/W6cHpF0IsmrXDVN6ExepkutMpx1YJgwn7LjANpMjbhmYyTvoKVkEtB15sqXF18bEuO5EL6STLNWJa/XiJlDNklUahlZh6iSUWuE1CeXGgTUMGS8Dg2/qHFhsgndgETGRcijMJfsIOwvsmN7nOT4cpd5y+WsXiVdW3Alu0BhtpaiDK5oFHJFLmdarSsbgewi5YzGyHdy5AUHwQO1Xb4jcll+YG2VMKvg2WXj5MmTz7O5WC8Mw+DcuXP4/f7GIlPPdtb/SJK06gizl2p5YxOb+M8EQRBQVZWTJ08iSRIHDhzAZrOtL1YsB3NVVTl16hRWq3VVG5wb+S7XiYEgCEiSRDAYpL+/nyNHjvDOO/cBMLqQQBYgXqzSFfKh6Dp9LTVLoojbibJUIZaoJRXG5hI4bRbmYlm6W/yUqyrbOmtl87agBxIK+UyNWE5MxRFFWIqVCYfcxJMFtm1twu2ysSXgYXJkCduytVIupyIIsDBXwOuzE1vKsaXDycj3x2jrra2rxvJYzPHhBTx+B0G/C7NQolKoEmypxbtzySUIWJBECXdKwFQEhKyCqwrWqTJOuwPyFZR0CbthQXY5MSwSlUQBNzacdisWw6QSLSKaAvaqQWvEw3/7g3egmEWOHj3KyMgI8Xj8hvezWq1y+vRpenp6aGlpWdO9vx7qDUXhcBin08nAwADJZJJjx45x5syZW2ooqhPi3t5eIpHI80rs1zOLfyk7mbwkmoHgsuFtHat5mBWLRQYHB+nt7aW1tbXx92spW1z92v4f38Kp/z2CLewhn9GQ0VBLJv/yUyf56LOvwO6+sqz5B79zjFKxRnyDTTLnh2pf+IO3B1DKGql56N3m4/SxGuncfSjC0e/XmnXuflU7uVSNRPmCNkbOJijmVeLREne8sg3ZLjJxPkPndjvnBwtAgQOHm5EkkVNHlwAVRdXZeSiMZUpEL+uMXUjR3uclGLazOFfk0miRnbeFua8yhkM2MUwQRBsiBiFV5Piigz2uy1nLi3EbO20GdWf4iuAEcsxpboSkgN19eXJQRrfjWdZf5koiTcv8rWw68FPFbjFI5O1EvBVsci3TKYmAKpNKhSiUTZoBragTK/vY0p3ixHEDEDDVZU9MCyTHamXu8HYPiXO1bn67f0X2cYXWXl0hB6jkLm9ISimNS6cL9BwOwwpbI3+7j/Jsmt1v6qf5QIBKpUIikWBsbIxKpUIgECAcDhMIBG64M72aZF6N+vvr/61nyFfqOpPJ5CbZ3MQmXkDUTdj7+vpobm4Grp3AWA31BEbdoWLlca712qthmmbj9622rgiCwF07ttDqd7OYKbCjNcT5xSTW5Wlw8XSOPS1hxoaWMAyzQSynlzLs6Wvl3KVFvMvWR7lihV1dTcwMRVHKKpPZJKGgg2SqzI5tzZwfi9La5CWRLGCTJSwZhYlEFFkWGb8YJdLsIR7N07+zldGRRbp7w5SiOdTlSW2To0s4XBZmLsVp6fYQnS0wsLOV5x47gy/sxuGyMT44y/YD3Xx3ewGPIZNbrJA1RCxeG0pJQSqBHHSTqShYHBZcBdCqCi6PA6GoIGgyqq5jN3Sq6SpOhxVLUaG51cN//5sP4XTXgo9hGI2Z5JcuXcJmsxEOh4lEIldkmsvlMoODg2zfvp1gMLim+74WzMzMkEwm2b9/P5Ik0dTUtGpDUTAYJBKJrKmh6GqSeTVWNhRZLJbnNarOzMyQyWQ27DNuJF4SGc3VcPUXN5FIcObMjAPdwAAAecBJREFUGXbt2nUFyYQbzyVf7bj2oI2t7+zCLZpIRZ2SLlMVTNSMxt+967krjnf02XlODUfZcShIe4+NsQvLXdltbobO5hgaylMRdRLFIl0DNhxOgYmxemncZGmxyOBgjLbtHnYfjlAq1Ejbjv1hnv7uHMMXkvTsdWJ3XdYN6oLJ8Pk4++5sQhCgp9/H09+dwxO2MbAvRKDFwanjS6RSFW6/u4XuHT7Gj88S0Q0MEyZVN+HloeElwYJFvNx4EtdlWjUnlRX7jICmMa4EcGclXLLETPryl0JSL5N4j+PyPRGqKwieWcs2ei0VikrtuKouYkfFYgjEsl48tiIhRwVTsNDZVvMLTYwv+2N2SBjLnux27+Xz0qqXf3chenkKUHq5nM5ySfzqv586nmd2WsG+vXZepg6yUyKyp7bjru9K9+/fz+23304oFCIej3Ps2LHr2lzUSabP57uhzqeOlRocURT5yEc+whve8IY1vXcTm9jEzcFms7F///4ryOF6/ZlLpRKDg4Ps2bPnmiSz/tqrkx31xo56dexaWFxc5EBzbX2un1m0qGCRRMJWB9m5PMWySluwFh/qxDJbqG3q62XzoMOBEi2TzVboW9ZhBnw1YlYs1xbXiekE/VuamD2ziNNuIZsts22gBcMwiSzPLM/nKgRDLvJzadKLWeankmzd1YZa1enYUsuaqlWT1lY7z/3bGVp6Q2QTBXp2tgEwFU9gbnWRiVaRvE4Mi4haVgiUZFyCjJgu4ykbyAsVdARsQReVpRzVhIJkgMsUsCjg9zkQClX6toT4vX/8aINk1q93IBBg27ZtHDlyhP7+/kZPxbFjxxgfH2dpaYkzZ86wY8eODSWZU1NTpNNp9u3bd0Vme7WGopUTioaGhohGo6iq+rxj3ohkroaVjarFYpFf/dVf5d3vfveGfc6NxEsmo3k16guCaZpMT08Ti8W47bbbbrmBYuWCsOtD2xj9x0ma9vuZGytiVEQ0q0FsMM3ffvAEH/ib21mYz/MzH/4WCwsFZBm29AXYus+F3SIhaLC4UMts9mwN8NyxmtXRnXe3UC4pSFYDf8DK6HCNdOq6wePfmaKlw0VXp5elhcsEyeV1cep4lAN3NZNNVhkbTZHLKhx/dpF7X9vJwlwt27cwW6C5w4loyviDNrLpKmVVo1hU+cgukT6LxPmCn4hZBQk0E6oVOy26ScIq4xANqnk7XmCqaGGXW6eqw6LiRclohB01gh12W2B5Mk9IqlI1JRJ5CVW0E004CbolBMNgKm/HNEzyKgiEcQgFTJsdF1nc9tr7/S6VYsVJxSZhCjoOocqeO7KomW0UYmU0j44SMtGRsNkslG0CoTuDyGIt4epqsaGWdLJTNRLp7XSQnV2eLrTFRapehu90kJ6pLb4Wt0j8Qom4CQOvCFNYLNF8KIAoP3/BlySJcDhMOBzGNE2KxSKJROJ5Nhdut5vh4WF8Ph89PT3rfvY0TeNDH/oQd9xxB7/+67++7vdvYhObWDsEQXhe099aiaZpmiwsLJDP57n33ntvaIK98rhX+y5fK5NVn0pTLBb5yTe9gn+7+EXGlpJEPC6y5Qp3drTx3OlZ9m1tJZ5bRFk+7YszMSySwEw0Q2eTj/lEjru3dXLiB5PsGmhlbiFDbNm+aG4xj8NuYWYuTVdHAI/DirWoUypW6e4NsTCfIb1sxj42uoQ/4MA0TNq8Di6cmmbHgS5y6RmKuQoIcGl4ifbeELKq4XLZWTBBV3UEEc4/N0lnf4SZ3VYs8yaGYmIkSvgcdioZBd0poptmzVe6KmH3OhFUHW0mh1WwYvPZsVU0zKqORRQwcxV272nnE3/20A2rTE6nk66uLrq6utA0rWHEb7VamZubo1qtEgwG16zPvRYmJyfJ5/Ps2bPnhudUbyhqbm5ujCeNx+NMT08jSRKhUIhIJILFYuHMmTPrIpkrkc1mee9738snPvEJ3v72t9/sR3tB8ZIhmleXzleKYgVB4LbbbtsQse1KAuvb7qHl7gilxTK2ooHmkFA10C0ik4/H+Mufe45/HZ+kqcWKxeogEvFyYllPeedd7Zw4vciugxEiIQcnj9e8HXt6vZx4LoaqGPgDNrwWmR0HfUyN5lC0CrpuMj9boKXTRTSTZ/ftfkxN5uTRJXTd5MSzi+w4GGLb7iBjQynCLU6e/v4sqqJz8I4WnE4L3/9ebWSUx2Plvjd28eQT07SKGgd21zJw+YxMAYO9QZVJ1U2rAQgC0Yodo2LQvqwXjRgieV0gUXITVCEmWoBaltKnq+RkC4KmM19wopRFup0mNqAsWXBoNaKXE+34xTIuycQoCAiSi2zZTlkWafNnqWoWbKJK0bThryos5W30NWUoxUtUtCozw8vkMeRjYSIDaMRmKqhFE0+LheJSbffXd1cQF2DDxGKTGkTT1WRrEE13m71BNG2tIuWLtQ3F3GgZV8jCrvubbvh8CIKA2+3G7XbT09ODqqokk0lmZmZIJBI4nU6am5vRNG1di5au63z0ox9l165d/Pqv//pm2XwTm3iBcS1/5huVzg3DYHh4GNM08Xg8a5q0IooiqqqumWTqus7w8DAOh4O9e/fWYlxvO89NzNMT8ZOLlsgsN4FOLKSQJYHZWK7hj7mzO8LIdBxZ0Oh22JkdqzWQjk/EsVoEEqkK3Z1BpmdT7N7RxtD5BdqCHk59d4ymZu+ybVEUf8DB0mKWbQPNjF2IsnVrE6M/uIQlVMuwjg/P4w+7WZxN0bE1QCGtEPJYOfvUJDaHlUCTl/hchp2HtzAxNIdoFZiI1LTpssuBkVOoZDTsHgeVdAlZMQgIDqpKFRMNMafidDgQdRM9XqCsGHgcVsSyxoE7evn4Z370htf+ahSLxSumNGWzWeLxOJOTk1gsFiKRCOFwGIfDceODLcM0TSYmJiiXy+zevXvdXKTeUOTz1SpqdenWxYsXSaVSBIPBBudZz7Hz+Tzvec97+IVf+IWXLMmElxDRvBqVSoVSqURHRwddXV0bFpjrN7P+Z+dP9vHEB4/StD+AYYosnC+SKxkkNZ34P8xi+irMOkp0dvqZmsxxx5E2HA6Jo0cXUBSDaKzIxGSGUlll721N+H02kqkKqqLQ2+fn9IllYnpvO5WKhsVhQasqnDi2iGHA8HCa5nY3e+6IEJsr0dbl5tlnaqNG2zrchNscROMFMlUdTTd49ug8t93VytR4hu5tfr75bxM0NTv52R4T0YSFikC7KWIIDqZNK00Vs6HDTOetNNlN6mRSFESmy2Ha1VrmMWwYFA0Bl2hS1EQWVDfhkk5YEEhYRWC5lKybsCydrCoCWGs+mznBToAyNk3FYQrEk0FSFZ2B1ixaWUNyg1W0EU07sUoGfmUe8CEA8WWLo/AWJ8mJGvn0tdkaRLNcKTNxqkYut9wbxHPQj900r5RMiJefEV+Th8zFWibZ2+Vg9ngG/57Aup8Xi8VCU1MTsViMnp4eAoEAiUSCqakpZFluZEKvJ8LWdZ2PfexjdHd386lPfWqTZG5iEy8Srk5g3CijWa1WOXPmDC0tLbS3t3PixIk1/R5JkqhUKlcM97jW97xarXL27Fna2tqu6IB+y8F+FtN5yvEKs7MpECDsc5LIltjZ28zIZJSw38VCIkdJ0Qh4HNirFpaiWSpVjUjQTjxVYUuXn4mZDE7Hcmd6qsCenibOfv8S/qCTWDTHtoEWxi4s0d4ZIpOeo1JWGRhoYfTZS1gsEgvTSbbtbl+e9mMnkyhgkaxY9SJnnxpl275OxgZnae9rIh3LsTARo7e/iR8oCTxVO5WigqAY+CUHmqGhpIp4ZStlTackGVjdNuR4ueYK4rZgxIqgm3gdNihq3POq7Xzkt9+xpmu/EqlUiosXL7J///4GkfT7/Q0bqnK5TCKR4Pz586iq2tBQ+ny+62aex8fHURSFXbt2bcj6bbfbaW5uZmFhgd27dyPLMvF4nIsXL+JwOBpxZbUJh3UUi0Xe+9738pGPfIT3vOc9t3xOLyRekkQzm80yNDSEzWZbsw4O1mZWKooixWKRYrFYS7e/rg3PHa2IIhg5FX+Hg6agjVBa4dJsjpaSCx0Jp9VCV5cHSRZ48nuzOJ0W7ntFG4IIp09G0XUDBHj8iWksFpFXvr6LfFbB47PS2uri2NEFVNXA47UQDlvYd7iJmYkc4WYrI+cyTIxn6N/lJ1OqsmtfhNGRBG6flae+N4vTKXPfa7oYu5imWtE59oMFjtzbjqrptHe68efzbF+ec6+KDiTBBBMmpyzsD9VI5Sw2OlSZuGAStmkUNEirLqolDbzL1waBlOggrpjYClZEQ0C21rKCXk1Hl0ASICBp6Eat4ccpr/To1An4wCHppCsSAbuOVrYzk7DisOYwTfDKJQolOxabQqclySl8RLY4SV6q7d59rfYG0bQ7LmcSjOplLUx8Kktutva5ug75aLkrSOJ0hsz8ZSlCNXf5vESLiCgLdB5eP9GsZ9W9Xm+jXF6fnbuWhiLDMPj4xz9OMBjkd3/3dzdJ5iY28R+I6xHNXC7HuXPnGBgYIBQKNbKTa4EoiuRyOSqVynUzZfl8nuHh4VWbU165q5f/+5WjXEpl2dYZZmw2QXuTj0S2hKrVznliPolFFtE0g3bJwaVLcXYNtDJ8YRGHoxbOc4Va4mB0PErQb8elm+gFpfaejiCZVIlqpbaBH78Yxe224XPZUFIFyvkqvQe7GEnPkE0Xa9PsLibZfaiLyROX6O5vJTaVILGYxeGyMTE0x757tjF/fp7F8SjZ97agCwZ+h52yACVAttpgqUClouByWjAVDW1JxUTE7XMi5xQEpw1ZNRDKKm981yF+7Bdev6brvhLxeJyJiYmGu8BqcDgcdHZ20tnZiaZppFIp5ufnOX/+PB6Ph0gkQigUalSr6laKhmGwc+fODVu/VVXlzJkz9PT00NRUq7TVn7l6Q9Hw8DC6rq/aUFQqlfiRH/kRHnroId73vvdtyDm9kHjJEc2FhYWGw359huxaUM9UXm8UYH10YEdHBxcvXkRRlJoH4isCfP+T43i3u5FdFkxDp5go0tPtwXRZacoXyRQU4g6T8ZE0dx9px2ITGT6fJBYt4XLJ3PeKTioVneZmJ+0dHh5/fBpdN2nvcOPwWdl/qJnR8wkiTRYujZWYnChx5K42CgWVg4dbiEcLzM4WyOdqC8DhOyMIpozbayUYtPPciUWKBZX9tzfj81p54vEZAJxOmfdvtVMwFOZLAh1Cbfc+ZVjZKsvMCTr2aglbSQJRIKLAjCghGg48ioBHlkmJEDQ0ioLIzIzEdmftsfBhkkfEg4FVFEhhIYKKDCyVJdpdOi4UirqES9LxWC8vymXTQgAdv0PDYYBSdDFb0ukKF8lXrHhlAY+1iCzp+FodDaJpaJezD7nFWgZTEAUy07WfbR6J/Pyy76ZXYOpklinA1y4T9htIiwKGbjbskwAKsSqt+3xYXet73Osk0+PxrKrJrDcUdXR0oOs66XS6sSuVJIlnnnmGyclJ7HY7n/nMZzZ9Mzexif9gXItoLi0tMTExwf79+xvVibWSCl3X8Xq95PN5hoaGAIhEIjQ1NV2hEa3Pwd6zZ8+qFRCbReauXd386/dHsMi1ODYXq40VHp9L0BR0E0sVuHNHJxdOztPaXWvMicWzACzGynjcdhKpEtu2RIgnCnT7XQyfnKeppXYel8aiOBwWZqaS9PSFmZlMcmBPFye+PdJo9BkbWiAQcRObz7BlZxMSEsVYmmK2zOipKVp6QixNJRk41EMuVWBueBaLVWbSYWA3BbSkgqmDzyZTyBShZOB2ujHdUFVU5KSC025DFsBMlTBMAZsOVt3gwYeO8OBPrW1u+dX3b3Z2loMHD67ZJ1mWZZqamhod41drKMPhMPl8vuYTep1RpetFvfFnJcmso95QVG8qUlWVVCrF7Ows+XyefD7P9PQ0jzzyCO95z3t4//vfvyHn9ELjJUU0L1y4QLlc5vbbb0eWZQRBWLNmob6AXIto1n3MRFFskANN00gmk+TvXEJ2C4gWlYWTBWxdEp4uL6IsUkqpOA0Jl9dDR8RHR9hDIl8hES+jljRe+9peNM3gxIkF8nmVI3e2kUyWOXykjVyuSj6n8NzxWpPQ7j1eRMHG7Ud8GLrBc8cW0XUTr89GU6uT/tYwxaKCx23h+LM1zWdzqxVfWEK2Oxi7UEWyiHzniWn6tvlpjjjxJLNsLxos5l1IbsDQSZkiobIIAlhTAgnRSefyNVQRSKteutW6TkkgljEpOmTkgoNOUaAgG7i12sjKHBY8yyXzXN4k4oVMVSSjSGiGjKqB3WcnlS3htGkUVAm3RcfpqH0p3VadnGrHJamkSm6mohKSpOMUdeYzDnqasujVcOM+JZcbfpwBC8nlDvLIVhfxizXiGOlzMXumtrA2b/cxfSJT+xQOg/HTGt4mid4dHuafqnWz27wyqUtF7vy5LTd8hlZiJcns7e294euvbihaWlri6NGjDA4O0t7ezj/90z/9UOw8N7GJ/0xYTfu/8v/rZdFcLsftt9++rmEOK/WYsizT09NDT08P1WqVeDzO6OhoI5lhGAa5XI5Dhw5d93e8+e4d/Ov3RxibieN22khmS/R3RRididMa9NDidZGdzVMpq4xPJbBZReLJEr3dISankwxsa+bcyAIOmwVbQWM6kcRqk4gtlWjr8LMwl6Grx8vMlIqha2ztCjD8zDguj525iQRbd7UxPryA0yOTjoPLbmfixCWKuTL9h7oZPVkjYaIkUClV8TgtzA+liHQEyb2qGTNaxub1oCgqZUMjINmpWGsSJ7Ok4K4K6BYrkiihzGWRJRG7LCPrGne+qZetdzYRjUavyCreCPPz8ywtLTV8tW8GV2soy+UyQ0NDVKtVZFlmbGysUWK/lYTBapnM6+HqhqJz587x2c9+ltnZWb70pS8xMDDAK17xips+nxcLLxmiOTY2hizL7N+/v7FzqJPHtRLN1coc1xNny7LcuImZn7Jw7A8v4WgRkG2w8FwWe5cNb4cDj8WKoZsU4hqRoAOXz0rAYcNttaAWNGbmc/R0+QkE7SiqTiJRxjQhn1eQJYG9+3w4HDLPHU9iGLBzV4iZmTz9u0N43BaqVZ2TJ2taziN3tTE5meWOu9vI5xVSqTInT9asgA4c8lKulIhE7CTiZRSlyocMA6wiFZsTa8Ig6i6Sq0q01efVinasugByBd00WdTthHIii1aFVqtYG8FZseLRLFiXfTMXswbbljfcYklHcQrM5iUUVWJekbAi4pAEHJqGA0jFBCKyE6MK85IFp1XF6jWoomBDpyJZcJkqdoeBR5coWK1AFY9Hos8tcEmU6LzdDybEL9S66yN9LmaXSaQnYmsQTav78iNrsV/eVASb/aTHU+RiOtFOBXGbiDUn4IpYKA1p9NwTuuEzVEe9GWCtJHM1/MVf/AWhUIjJyUkKhQLxePymjrOJTWzihYGmaZw7dw6n08nBgwfXlbG6Xlyx2WyNZIaiKJw7d45yuYwkSVy6dImmpib8fv+qcW17V6RRNt/ZHmRwbBFBqMnsbYbIyJl5dN2krcXHwlKWrVuCjE+ksFpq6+LcfIatPWFmBhfwuu2k8wV27mln5Nw8bndN75dJq/j8Dox8hXxZoVxU2LKziYmRCrl0EQRYmMpy4HA3p799jh2393L+uUnmx2N4g07mL8W47VUDnP72WWRZoqkrxIxaxK5HMF1WtGwZh9WCkahQVQRcfidCVaeSN6notWYfLVrA7rBirRo4RIGf+v89wOFX72pkFaemptbUuHO1n+VGoO4GEAgE6OvrwzAMUqkUi4uLXLhwAbfb3Sixr2djUieZ3d3dayKZV0PTND796U/zwAMP8PGPf5zFxcV1H+M/Ci8Zorl169bneWHWieZah9RfXRKpLwZ1snqthcQwDPyv1RH/RKClx8/E0TSRHU40Q2f6WBopJODpsmP32dHLJpIg4HPYkYIChapGd7OPdKaCoEFiqcTOgRD5nEI45GB6KomqypwdTOIP2Lj99lYymSqaqjM5kaGr28uF8yl27Q7T1u5m8HSUWKyMoRvYbDI2m8ydd7VjtQk8+d05AAJBKy2tMgMI9ClQFgQcGRO7KDGv+WmRVTBMLpYNWjUREBi3g8PuwJ+vLW6mzYFiVpkpW2lSrczrVfpstesTFCQMNFK6QE61U8lKeJatvxQLWFUdu25SkEXcpoEbA92s6TfLRZWADpRFxqo+fBETpVIi5AWPqaDoEu6KzoWcn+3hDNWqyHPHF9BNgYE7w8yWKoTbHYhNMl33BlEzKrq2oiSfvexBllosXP77FabtFtHG1FgJi0NkYKeEIEHCPoV8qUg4HL6ueW6dZLrd7psimaZp8ulPf5q5uTn+/u//HkmSrtgpb2ITm/iPR7lc5syZM3R1da17JGHdIPtGTT+qqjI0NEQwGKSnpwfTNEmn00SjUUZHR/F4PDQ1NREKha4gSW+5ewd/8M/fJ5aqrW+Ti2kOdbRw7rkZdmxr4fzYErJUi3WFQm3dG5uIEfQ7aQl7sBRUZvJVurtDLC1miUdztS7z0SWaW32oikZPs5ezz4zTs72ZOHnmLqVweq3EFrJ094ewmAKJydqEuQsnp+jc1szsWJStezvp2NLEyX87Q8/OdibOzuL2O1EONiOaIoZuYIoCaqKCbLdj8VgoJgvYMho2iwW3y4aZ07C57ZiZKl6nhY/9ztvZfbgPoLFWbt26lXK5TDwebzTu1O2AvN5aU0F9E79v374NkyXV13+Xy8WWLbUqmCRJRCIRIpEIpmmSz+eJx+PMzMwgimKDDF+vIXQjSOZP/uRPcscdd/Dxj38cQRBoa2u76c/5YuMlQzRXm9iwFiuKle9fSTRXLgbXI5mqqnLu3DkC7QF2v7eDc/80h6/Tjk2SiY2U6Drop6rpzJ/PozmLWMMCriY7piEhGgIeuxWLJGC3SYhWgVyyQijgwG6ticOrKhiGyJG72rBZZZ5Yod3s6fGhqgZenxWv18p3vjWFIMAdd7TicFoYHU0xO5uhucXFk9+dY9v2AE1NdhYWsly8UOKhdhvYRBY0gVZRpICJMy0xh4HHpRAxnNSn+yiGC29avzzSPGswrMp0ibWGG7deG80pIlBCYCZjoV234UZg0ajistUWwkROw71cFk+VDdx2avpNHSKySdBSG+AjAKopYMuBaDi4qBh0B0okqxKtTg2lbGE87sUbEOn2lZnIOBujJhOLZSxuicWxAgIQbrPTdMiN0yaTXW4UkuyQma6V9GWbQOziMukUTOITtZ/VssHSoknr65s4fO9BkslkQ+vi8/kIh8NXLPIbQTL/4A/+gNHRUf7pn/5pw3bYm9jEJjYOmqZx6tQpdu3a1ehGvh5WNpmulWSWy2XOnj1LT09Pw+hdEARCoVCj6SOXyxGLxZiYmMBut9PU1EQ4HOY1t2/jT//lWRaTeXb2NGOkq4jV2tpYLNW06tF4BZfTylIsx9beCOOTcQa6w5z47hgdHbUmo/HRKD6/g3gsz8DOVi6MLNLa4mP27CzTqQIWq8TUxSi9/c1MjkaJdPjRqgYWA+ZGZqkUVbp2NjEzEqNaVrDYZKxWEbOqYGgGsZkkTZ1BFlI5lI521IqKoeh48iaSbEVGpDyXxiU5kHw2rAaosRKyLCGpOj6vlV/+7I/SM7A6YXI4HFd4Y65cvwGsVuuGk8z6MI5r+SQLgoDX622Mpq7LJFY2hEYikSsy1rdKMuvWeHv27OHXfu3XfigbSoW1TtRZI276YPUpCisxNDREZ2fnmrJBIyMjtLa2EggEbnoxSIwV+PKHT2MLWChlVWx+GUOH1EIZ2SNTLmnMzRYQPCaizwSHiWkRsXqslKs6WARUw8AQdS5NJkindQZ2hdEMnVJFY+hcgi1b/PT0ekmnK5w+Vdsx3nV3O5lMFZ/PRrGosLRYJBYrIQjwild2oVR1FhbygEk6VSab1Xhjd4A32jUMRcdelhEFkUtVaNFtGJgsOqF7eXFatAo4Uxbi9ipbZYG8RaCYt1C1m7SsmPozTwVdlQlpdmKodC2Ty7yhEV5u4ssbOqFlx4W0aRKRa+/P2GRCyzZJeVHGY2ikNQgsb2VSpozd0CiKCtsCVWJFC34r5KwiqazBNy+F8Yft5BJVnD6Zcl7DNKC510V8slY279zlY+FCjs7tDrx+iejxKrpq0rbHy/zyyMrwFifR5dfb3BLlssGrfmYL7/6fuxuf0zTNhrdaKpVqlGiSySRer7exk10PTNPkT/7kT3j22Wf54he/uCbvvZvED98qs4lN3BpuOq5omnZFAqJu5H333Xc/z8x9NRw7doxDhw41RiLfyB8TIJPJcP78eXbu3LnmSkaxWCQWi5FIJBAEgW+cWOL8TJo+j5czZ+bw+xzk8hUMw6S12ctiNMeeHa2cO7/Itr4m7KbA3PkomqZTrWj09kWYvBRn194Ohs/O0drux2G3kLi4hNttJ7aQYefBLkZOzdDc4SM6l8Xjd9DZ4mHk6HijXO5w25CtEoVMma17m7j4zCSSRaK9r5mZCwuE2vzk7mlhVqlgk2UERUBXavZF1oKCnjMRVB2HKKKkKjhsMpaqTtDv4JN/+l9o7li7pAlq6+zIyAiapuFwOEilUtjt9kZW8WYHuhiGwdmzZwkEAutyulmJlQ2hmUwGl8tFMBhkfn7+ig3Heo/5sY99jLa2thfateQFjSsvmYzmaljPuLD6a1cuBtfb6ay2GIS3ubG32hl+NIqj2YolKTE/nqf37iCTozn8XXa23hVEV03mZnIIooAomSyN5SgqKoFWO7MLRfwRiWLC5M67OtAxePK7M4QjTu69uwPZKvL9p+ZQVYO+rQF6en3Mz+W4cD7Fzt1h5mfzBEN27trWjs0u8d3l7vLt/T5KJYUdOyPk0lXuTFjQMxYu6CX2eEUyFomWUu12LsgivoSFMXsBv0vCnrIAAqGKlXF7GWfOgR0Ri2KQtOoEJJF5QNdcRLTaNQsLFlTZxKKZeESZos3AVTXwiBJZwUA2TSwWiahiIgKCaFLSwSlBvmzgsdVIZkUHuwSiRcKmGKiqnam8hTZHAUWz4qroFAVo7XMRvVTLVrZu83DpRM0DM9hqbxBNl9+CrptMnS8xcE+Ykr/KtoEANvly5tDbZm8Qzcg2N1Onswy84nKzEdR2pSu91UqlEmfPnkXTNKrVKoZhrHk+LdQWv7/8y7/kqaee4uGHH34hSeYmNrGJm4BhGIyOjlKtVvF6vWvW1tUrbfXG1BuRzMXFRWZnZzlw4MB1PRCvhsvlore3l97eXqrVKhXTzrljc5ydzONyWshky3S0uphbLBIMuFiM5liK5XHYZeSyTiZRpFioNvSY4rKn8KWxKC63Fb/XDrkypVyFzp4wsYUM02Mx7E4L0bksew73EL0wTyFdqwZdODlFV38LM6NLbN3bSVOLysVnJujZ08bUuQVicwmCbT48zU6G3AKiZkOLqUiShNttp7KQQ6kISDYZpyhCxcDvtVNNlmlp8/Jbf/lBfCH39S7J81CvODkcjiushorFYmO+uGmajZnnLpdrTeu3ruucPXuWcDhMZ2fnus5pJa5uCM1ms5w7dw5RFJmdnaVcLjdK7Gs5r7o1XigU4nd+53d+KDOZdbxkiObNTnGooz6Z4VYXg9f88jbO/esSkS4XF59NsvVIkNmzOUQb2G0ypx+PEt7ixOGzMjGeoXevn84tQcqaimpUiIQlTIuA328lmypx7nSSLb1+2ns8zMzlGLuYpqfXR/cWL6lUhce/MwXAfa/oRFV1pG4vs7M5XC4LQ88kaG52sq3fQyxaZGmxSiad4A1hPx4VEjaBnpyP6YyCLmi4ZEhYwZep3VYbTuIJhfZ6Y5CgU604CFIjZgIicc2kpMo4qzJgkrNpeE0J0RRYLCt0WWSqEkynVGymhEu2kUhV6ZBq1y2OSqtU+32zgoFTEijKKqqgEXSBZgG7qmJdnuLrliFXtjFXEXH6dIKCgq5YafGXiS7fA4v18gZBUy8nM9Lxy5rMfEohm1Q48UyMngM+2u72U5quoCqXM7RWl4woC2y969q75vrEh6amJrZs2dIo0czNzZHL5fB6vY0S+2odjaZp8rd/+7d885vf5Gtf+9otj0jdxCY2sbFQVZXBwUECgQADAwOcPn16zdr/OtGUJOmG4yQnJibI5/McPHjwlkYd2mw27rl9N19qOc/YRIxIyEGxpKIsV5/GLsVwu20oqsbO1hDnTsywc3cb0cUs0aUsoihwaSxGR2eAudk0Rw73cOLbw7R2BBEEuDg0T2tXkMWZFD0DYZSSQWoiSj5ZIFassuO2Hs6fmKJcqBJo8qDkS7i9tfV+cTxBZ38ri5NxgmEnF+w6YrSItSpid9nRgcpMFtliw+G3YK0aUNaQJREzp9DX4+e3/vqncDjXt07qus65c+fw+/3PK2uvtANSFIVEIsGlS5colUoND8prNV/pun6FQf9GQdd1xsbG2L59O83NzVSrVZLJZOO86iX2lZ7LK2EYBr/6q7+K3W7n93//93/orfFeMqVzwzCeN2x+YmICh8NBa2vr9X+paTIzM8PS0hIdHR2Ew+FrkoKJiQlyuRx79uy55mLw5w8cZex7CZxtNgzNJJ2q0HnQz8jRBJ2H/KTjFVKZMr37/FwcSuEMWxGsOtPTefoPhBk8EWP7fj9zi1kCzTKIAqdPZ7A7ZPbsj2C1SXz/yTk0zWDHrhCtnW7OnokRjZZoa3Pj89twu61ouoFpVDk7mMEwoLvHS0+7h9ed17BqJnkkHIrIJV0lrNsQmjWEhIAdiapski6AJAsE7SY5q4mZlJEQKXsqNKsyE1oVt2ZHtpk41dqDnHVpNKsiqmgyoyg4kHFrVioYuMWaqXvR1PEtzwxPmCoty9dxydCWSaeJIpjYEYibCsGQSYAquiHikmCmJNJmE8g5ZEL2AioyednB9y5ZqeR0vM0yuaiGKILTU5MxSFYAAV0xsTpFVNVEV01km4AJqFUD2SKw984ImQslctEqoW0u3CEbv/Lv917zuRkeHsbpdK5aLq/vShOJBMlkEovF0tgt17sgv/CFL/ClL32Jr3/962sqxW0Afni3tZvYxM3hpuNKNpvl1KlT9PX1NUqXg4OD9PX14XZfP6NWXx80TaO1tbUxJvBq6LrOyMgIVquV7du3b1jm6ZuPD/O5v/geXo+NQlGplc2b3CzGCvR1echOF/C47MzPZrBYJBxOK7lsmYFdbVwYXmD7jlaspsHM2XkEEYr5Kv17Oxg9O0dLt4+l6Sx9O1qoxrLMXYqy8/AWRo5P4HTbsTmtmKZJ95YQZ54YQRQFevd0cGlwllCbn5Z2P2e/f57Mu3cg2pwYVQ1JAGtGwWJImCaIOQWzrOF12xFKGn19IT75lx9YNwnXdZ3BwUGampro6OhY8/sMw2iUstPpNC6Xq1Fit1gsaJrGmTNnaGtr29DGGk3TOH36NF1dXauWy68+L6fT2Tgvq9WKYRh88pOfpFwu8/nPf/7FIpkvaFx5SRPNunHq9R6uuh7TMIyGziWZTGK1WmlqaiISiWC1Wte1GEweTfHHr36G7jsCjB1LseWeIBeeSdC8x0M6VqFQVWkf8DJ0PM72O4PMzWWwekSCrR4qmoYpQq6kMD2RpWe7j+eOLRGIWGjtsrKwWGFpoVrzwWx1kcxWOHc2jiDAffd3YhpwfiRBPF5m7z4fF87n2bkrgttjIRYt0TVV4c12D0sOAX9GImMHOSNhAjO6itVq0ClbSSFgK9Ye0FlbmbaqHZHa/5fsGlV03KXarjIhVuhebgqKmQqST0ZMikiI4Ad7TXuN5jVxFmq3uGo3cKkCOiaiZGJBICvp+I1atrToAk/JpGqaWAUBwzRIyVW2BgzSFZOwLFE1QNUERE8JuynwF1M2+veHcFgkzKqOVtGIXajpPlv67SyN1oTwPQf8TJzOANC918fk2drPrdvdzI3lsdol9h+OMH8qx6t/po+3/cbAqs9NvQzT19d3zWdhJerjy+LxOF/4whdYWFhgdnaWJ598stEJ+SJgk2hu4uWGm44rsVgMURTxeDyNv1uL9r8eV3RdbzTtpNNp3G53o2lHkiQURWFwcJCWlpZbKrteDUVROHHyNJ/9i0GKJZWBbc1cGIuyq7+FUklFT5SILWYxdJNwk5NErMT2gQgXL8RpafWRShXZ0uqjkCiwNJti16Fuhk9OE2rykE7mMXQ4eOcWBh8/R/e2FiaG5xElkfYtEWbHouy+Ywvz5+dILWbYcbiP88cvYXNa6epvIR/PkolmkQ52MOOSsFos2BwWlEQFVLBYZYREEVEHm0VCLKvs2dfBJz7//nWT8HojTUdHxw0TTteDaZoNm7m6DrZSqdDV1XXTmszVcCOSudp51Uv/iUSCz33uc5RKJWw2Gw8//PAtZcbXiZeHRnO1B3C1TvSVuLqzvN4NtnXr1gbpPHPmDIIgUK1WaWtrW1OjR++RINvuDxO9WGDrK4LoIvTcH6Cq6IiaSFvEy8VzKbbeE+DM8RgtWx3EYypltUA+r+AKWFiYzbN9f4hTx5e471WdVA2dp783SyBo59BtYSpqleeOL2CacNvBJrwBO08/PYdSNbDbJfYf9CEIMsGQg3JZZWoqg5bVeH0gQsYCroyAYhqoBQkZgahdJ5y3Y1YNzlaL9FHbrcccGp6Cg5RXJ1wUWaIKBRnBd/nWhwwrUZdOqWDg1m0kMlVaqZVK0nmFVmokNJNXcAq1cpNiEXCpICGQt5oEFPDqEhUM7IKIuXzbbIJATjTxGiKibiMeE6jYK/hlsImQ0QX8JRc5qUyzzcTilDn9g1qT1J67I8gVhXDAit12+fkQrZfjjsNzufzla7IxN5ZHqehkKgoFu8bO10VWfW7WSzLhyvFlo6Oj/NVf/RV79uzh7rvv5pvf/OaGll42sYlN3DpCodDzYsiNtP91SzyoybeCwSDBYPCK6TGTk5PIsky5XG6URzcKdc349m1beeNrdL7y9dNUqrUkjGBCZS5LMlFsZC6DQS+JWInpqTQ2m0g2U2Rru4eLJ2fYuquWqRsfWcATcJCM5dm2pxWLKDJ7bhrBhInhebYf6Obi6WmqFZWeHW1Mnp6ge6CN1GKGsTNT9O7uoJAuUEzmsNpkirkyWb8Nq9eOpmiYc3lEJDweB0JRQ3TYkXUT8hV2HWjl9R/Yw3PPPdewCVqLTlFRlHWZm18PgiDg8XjweDx0dnZy6tQpQqFQwx+zbp10vZnnN8J6SWb9vNxuN263m56eHrZu3crJkyfxer3ce++9PPPMMz/0ZXN4CWU0TdNEUZQr/m5paYlisbgqGahnMYHr3ohCocDZs2cJBoMUi0V0XW+MB7ue79XY0SS//don6TngZ+x0iv47QwwfjbPzngiDT8fYeruf0TMpmrc6ic1X8LXYSMYrBNvszE7m2HE4jGLoVFWdubkciwtFdu+PgGSiaAZjF1Ps2RchFi9gdwkMDWUJBK309/splSqcHax1UR842Ey5rBEM2mk7p7MtY2PaqGIXBewRiUBSIm3VkYsSIiJTlAnrdoSwiaoZWLISIGCIJnGxTFitlXcNTAxRw5ChbEJZM2gzaxlOXTKxArIhYGCCZGATRDKmhoaGzWkhV1CxSGC1ypSqKk6LgN0qIVkF/IaARTURBJBMWNI1WiQZXQBdA0kQKPnArZcoagKtFpH5qkHU1ClsDXPxdAqA5h4b0amahVF7nwc0k9ZmB0peZWG4lt0M99qITdZ+7trvY3IwA0D/kRAz57P87eQDSPLl5+NmSeZKPPLII/zhH/4hjz76KIFAYE264A3EZkZzEy83bGilbGxsDL/fTyRy5Sb0eibsVyOZTHLhwgVCoRC5XA5JkhrjDG9Fp11vUt29ezcej4dYIs8HPvYPGIbJ4d0dnHnqErv2XO4kX5zPIAjQ3OJjaTHL/oNdLI0ugqaTWKqVoprafcTms7T3+ViYyLJ7XwdTg1Pk0yV23rGFkWMTuH0ORFkk0hbAJpkMPzOGIAhsPdDN2Kkpune0YpUFRo9fwmK3ELp3GxMBK3pJQS4Y2B12EATERBHBEHDLEpQ1XvH6nfzkJ94G0NBPxuPxG+onK5UKZ86cYdu2bYRC6+tMvx7q5LW3t7dx/3VdJ5lMEo/HG7r8SCRCMBhcc0axXobv6OigpaVl3edVt8Y7d+4c//iP/4gsy2ueirhBeHmUzlcjmnUNw/bt26943XoWg7GxMXbv3t3Q49Qf9mg0SrVaJRwO09TUhMfjed6x/tc7nuHsd6J07PMydTZDy4CbpckCnhYbmXgZm9+CqpiYVlAVnUCnHbvPAlaT7z8+x4E7mzlzKoooiuw5FEFF5/SpKAM7Q+RyVcplDZtDRpIEPH4rsXiBXLZCMqnS1Gxn584gi4sVRi+k6HI7+dFcmJRFx12xUHSDmBNIiGWsskiTZiPtNbCkaw/mvFRGMKHddKBZTdJoGFXwSzKyLpARFFS3gDsvIyw/Y4LLwLFcbi8FdMo5FdEuITkkLAkBAYGKS8VTrGURVXft9QYmggySJpBBIYQVDZ2crNASsCKqGkF9WQNqEXBXIS2Du2pStCl026Gkm1RNgUcqoFR0nB6RctHANCDYYie1VCOTwRY76WiFbTsCBLw2pk5mUKsmsg10QFNqj6Cv2Ub/HSF+5Qt3X/HsjIyMYLfbb5pkfutb3+LTn/40jz322IYugOvAJtHcxMsNL7j2fz1xZXZ2lmg0yt69exsOE3Vz8Vgshmmaq846vxGi0ShTU1Ps27fviibV3/uDb5GN5TGLKqMji7jdNlRVp1rV2Lq9mfGLUQZ2tZHPliFTIpcqUC4qDT1ma7efxekMkizSs8XLpeMz9B/sZvTUNBarTKjVx9J0kkOv6OfUtwcxNIMdd/Rx/tglLDYLO27vYfToRTRVp3dPJxefm6D67v21JETBwCjruOwW1MU8oinisclYNIM3vfMg7/3Y61b9rLquk0qliMfjZLNZPB5PY9qOoiicPXuWgYGBNfmcrhXVapUzZ87Q19dHOBxe9TVXW99ZrdaGLv9aLgIbQTLr1nhf+tKX1jVtaAPx8iidr4bVTNjXsxgsLS1x8ODBK+xmrFZrQ/xb7zCenp6mUCgQDAYb48EEQeDdn9zJ2e9E0Uu1zKmgC+iqAaaKVoVmvx3DYuKO2JiZz7G0VERMCcQWi9x2pIUTzy7R1ecl3OZgYiKLbBHZvj3I6ZNRDh5uweU1UFWDobNxdu4Jkk6X6esL0tZh4rALfO+7CwD0bnHx6lQAUwCzKqBLUM7pOJCwOGyIBYFRW5mmdG0nvWCp4FWXu8L9KmQErMu3OuvUayPNcjJyAZaECq1mrbGlJBmUfSZqxURPm9ixIBVFtKKBCMgISIqEiYmAgKrrOBAREchLGj5NxosFVTCwmBKCKaPEJUBkzKHhQMPUTNyiFZduIggi7qqdKUGjzaqiyTKufBUFaNvqZvx0Lavb1utpEM36zxdH0uw8EqboMtl5exAJk5FnaplQf7tEer5C/13exq5wI0jmE088we/93u/x6KOP/keRzE1sYhO3iJuNK6ZpcvHiRRRF4cCBA1cMZFhpLq4oyhWzzuvJDLfbveqxTdNkenqaVCrV8OxciXe8fi+/+vP/D0kSCYZcpJJFdu1tZ/jsPIpSkwXoioaUK7Mwm2LXwS6GT82QjOWQJIHF6Qz9e9tRMkUqyTIAo6emad0SZHEihSiJ7Ly9hxOPnWbXndsYfnaMi6em6NvbhSiajB0fp31bC+Onprj43AR9b9vPGU1DilUBEa/XgZGp4nI5EEsqsmLw7g/ezVvev3oTZv0erJy2U9fBXrp0qaGdvNbYyZtBPUO6fft2gsHgNV+3mvVdIpFgeHgYXdcbJfZ6YmojSOZf/uVf8v3vf5+vfOUr/1Ek8wXHS4ZoXkujWV8Q1mrCvnIxOHjw4HWns6ycdX71PFOfz0dTZxOHH2zj+NcW2HFnmJFnE3QdcCCKNtr22DjxzCK9u/w8/cQc/fuDzIxnCUTsNLe7OftsjPte38n0XJYTx5bYf3szJ44uYo2JvPLVXczO5RkdrRGjO+9tIZ0poOsCZ07HOXRbC+Njae440gYCqBdLRFISU2aFFtNJwqrhUmVSHg1bTiYhVHFUbRTsoLt0PMmaaXvKrmDLSBguA1kRScsqUkGkbNEICzVS6nRayNo0Kmkda16iZFXwKzZEAVSfiZwBGZGkUKHZdGBRRZJClbBpw16WqYo6NlNCXr4dIgIpUyWCFZ9pQcdEQkCyWhCzFkqoJMMC3pJJ2tQICjL5kklMteJoEdjVauG5tI4sXf7CKdXLQWGlfZGhQy5T5egPFtl7d4T2O7xoaZ1gxE5mIUHrHpNjx47hdrsb/nk3Y8YO8NRTT/Fbv/VbPProo7esF7oWMpkMH/rQhxgaGkIQBP76r/+aO++88wX5XZvYxMsBGxVX6nPRfT7fDZtJrVYr7e3ttLe3o2kaiUSCyclJisUioVCIpqamhhbQNE1GR0fRdZ39+/evWiod2NlK/85WRkcWaW0PkEoWWZirZShnppLcdlsX5747ytadNT3mpQtLuL0OEks5urYFySQqUKkyd2EeVdEZuK2HCyemKOcVbE4LoqhSSNZ8i0eOjbPtYA9jp6awO2RKmQLFbImJwRl239OPrmk8F0sjulxYfS6sgoiQKmNBxKboWGWBh37hNdz31kPrukf165FIJNizZw+lUummfTGvRp1k9vf3EwgE1vVep9PZ2ECoqnpFYsrr9ZLL5eju7r5pkvliWOO9FOLKS6Z0DrWy9srzKRaLjI2NsW/fvnUtBnVCcbOaOdM0yWQyxGIxJodi/NOH4oR6LeCF6GKtqzwZK9O23c3E+Qy7jkQYPBpj9+EI556LMXBbCNEt8Mz35hnYEyK6WCSZKHP4nlaqhs6xZ2uZyn0Hm7C54OmnlwAIBu3s3ddELltleDhO39YA8zN57ssE8bosCIgUVBWzbGJ1iNiLVnIWFUmTEERISQp2Rcb0m6glHbsqYwomis8kmanQJDgQEDBsJhWbjpYzsCFTQcOLBdEUMEUT0zCxIGE4TUolBcki4vDImBqUiiqGaGA1JHTdxJAMXJIFTdGRBBOv1QKCSbBSyyKnBIWgaaUs6zi05UlDso5Ng4pVoUeykNZ1fFgomioVu8KTVo3OXh8el5XCUpXkXAWlomNz1Oa2V8s6kixgdcoUc7WyWLDFTnKptlu//ZWt+N02fv0L92AYBoODg2iahmEYyLLc2Emvdcf8gx/8gF/+5V/mkUceeUEbfh566CHuvfdePvShD6EoCqVSabXS0WbpfBMvN7wg2v+6by5cX+dfqVQ4e/YsXV1dN0Uo6qiXi2OxGLlcDp/PR6FQIBQK3TBePfv0GJ/+1Dew2S1YZJFCocqO3W3IhkkpmmN6PIYgCjS3+1maTdMzEGHqQpzOLWEolJi9uMSuO7YwfGwCp8eO1W6hkCmx784tnPi3QQC6d7cyPbSIbJXYfrCdoe+OIltlth3q5fyzY+y6axtT0QzZrS0YFQ2H1UI1VkSWRFymiMsi8tHfeAsHX7Fj3dcmnU4zOjrKvn37rliXV+o6y+XyFbrOtcT3crnM4ODghpfhFUXh5MmT2Gw2qtXq8yyK1oJ/+Id/4Mtf/vILbo33UogrL2miWalUGB4eZu/evcDaFoPOzs5bskG4Gpqm8blffILH/z5J524bU0MVuna4mTyfJ9zmJFesUK3otG/zUtV0mrqdPPmdGRwume5tPs6eiROK2NlxMMwTT0yjaQaHbm8hl69S1RXGx/P0bfXT3OIil60ydC4BwOE7WtF1g6ZFCy2XZPI2A71qYiAguAWUogF+0HUDsQQlXceJBcVnoBQMEE0kt4CaN5EMEUM0kUMCasnAWPY9t/hExCwYdqhKGoIuUKlqiBZwq7XdVUFQCBi1nzNClZBpr91lF0hFAdMColrLZOo+E2u2do90h4Fe1jElnTaLDXtFoiIb2DWReF3HaTFRNB2XRccpSdh0kYShkthl4dhw7TrsuT1CNlWltcWNU5YZ/F6tI71vX4CxwdouvGObh9mxWpndH7aRTlb4wCf28RO/tIeRkRFsNht9fX0NS4t4PE48HkdV1UYp5FpTgI4fP84v/MIv8PWvf52urq4Ne66uRjabZf/+/UxMTNxoAd0kmpt4uWFDiWbdqqhO7q73fctms4yMjLBjx44NJSqVSoVTp05hs9lQFAWPx0NTUxOhUGjVKpxhmPzcT/4t87Npdu3t4PzQPPt3tTH8zBi6brJlRwsT55fYurOV8ZFFRElgYG8HM2em6OiLcOHEVE2P2eJjaSbJ9v1dqMUyE2em2XlkKyNHx5GtEl39rcgSjJ+apKk3yMKFGGCy/9W7mBmeZb6rCVx2nJKInqrisMqYuSpBr41f/J/vpP9g77qvRd1g/Wpt6tW4WtdZb9q51jUrlUoMDg6uaxToWnB1ufxqiyKgkcxwOp2rPl9f/OIX+bu/+zseffTR6zYl3ypeKnHlJUs0TdNEVVWOHj1KKBSiubn5mruYF2oxqHuk+T1N/OabT5JLVmnb7mZmNE/XHjsT58r07HZTKmu4m2wsRIvMTeU5cKSZ08drc25uv7+VmYUsY6NpDh5uYWIig9dvJV0o0dTsoFgwMXQTRTVIJcvs3BUmGLJz9kycQqzKu5QOcnYdV1mm5DQQDYGyZqCIOhgCJVPDME3sPgnNNKAqoMs6hgaaCoqs4fXZqKRrpSLNouOwW1A1A1M30QUTubxM4F1gKdR+LqISpEYqRY+AlAcdA9kiIqoCeRT89S51r4k1J6ILJqJZK7WXHBrOslxrFJLA0HWqaLTbbFg0AVGvNRdl0PAgofp0IiWImzo0WfhOrPaF3XUowvDJOAB7DzeRS1dpjrhwyDJnnqyRzr13NzH4TO16774zwtlnY/z1s2+hbC5cQTKvRl2jG4/Hyefz+Hy+RrehJEmcOnWKn/3Zn+VrX/savb3rX0DXgzNnzvDhD3+YnTt3Mjg4yKFDh/jc5z632iK0STQ38XLDLcWVarV6+UDLesDBwcGGbOpa2sl6c87evXs3VC9YKBQYGhpq6AVXahSTySQOh6Ph1blSs/fEt4f53P/6Fv6Ak9aAk7GT0+zY38n5M7O094SYn0oC0N4bwG6zIVYqjJ2ZQRAEuvpbmL6wSHtfE8VsCZddxhd0MfzsGJJFonugjekLC2zb00alUGVicBpBENhx5zYq5RKXTkxjBF1wZDt2U4CijiSAkKsQ8Nj4tT/8Mbq2rz/BE41GmZ6eZv/+/esa3buyaSeZTGKz2RrXzGazUSwWOXv2bKN7f6NQJ5nt7e3XTGhdnYWtTwGqd9d/9atf5c///M957LHHNvTcVsNLJa68pIhmfYTkSnG2aZqk02lisRjZbBa/309TU1NjdNMLtRgUi0XOnTvXsFf41t9f4nMfO05rr5ul+QKCINC500PFVKmYZS6cLRKI2BAlgXi0wu7bwoh2gVMnomzfEWR6Nks6WeHQnS0UK0XOX8hRqRjs3BXCYpGw2yVGL6TYsSvMs8/MIwjwTnc3toIAZci7daSKSE5XMWQQDYGcoGBFAq9ApaQhOEHVdJx+K7JdwOYEw9Sx2CWsditOl41iTqNc0hBEqBZ0inmFUl7FZpPRVRNEqGRVLLKE02tBLehUqjqiAC67BUMGiylgaCYIoFdMTMMg4nagF00kl4CzIKMLJpg1n80MVYLY0GQDSRNQ0LHaDMJVG1mril+xUrEZmBUTh0PHqon8KyncXgvVqo5SNbA5JERBoFyqTQzyhxy0tLtwWSwUUyrz4zUrj759ASoljV/7u63XJZlXY+XC9fjjj/PFL36RWCzGF77wBe6+++4bvv9WceLECY4cOcIzzzzDHXfcwX/9r/8Vr9fL//gf/+Pql24SzU283LAhRHNlXKlb2sRiMUqlUkM7WR+8MDU1RTqdZs+ePRvaoJFKpbh48eIVTigrUc+OxWIxEokEsiw3Bo/IsoVf+tl/wsiW8HlsDJ+cIRB2U8iVURWd9i1+5icy7D/czbnvjqCrOtsPdHHx9AyR9gC5VAGP30Vbp4/B756vTfvZ3cmlszP4wm66tzdx5vFhZKvM9tu2cOnMFO1bm4lOx2jqCTMZ8kNVR8ur2C0ilqpB0Gfnt/7yAzS1X7vB5lpYWFhgYWGBffv23fI1XplR1DSNarXKzp07n2dhdSuoj6tsa2tbc9VU1/XGFKAvfOELnDp1isXFRb7zne9sqFH8tfBSiSsvOaJZ98dcrQPQMIyGdjKdTjf+7cCBAxsqpL3aywxqC8CvvPFxhp+Ns/cVTZQ1jflYgfhSkVJBY9ftIQafixOMWLB5RXRZwDAECnmVeLRMIGhj1+1hvvPtaQD8ARuHDrcycj7B3GweUYTDR9rJpCsEAnZcaRHLBYNiRUNyi+h5KIkaNo9MtaCj2w2sTgnJKdK9y0e4Dfbd4+GN7zh8RRnBNE3y+fwVE5Pqaf36NTNNk+hCgR88Mc+JpxeJLRRJLVTIxitUKhoWQcRmk6EIaKBZDWyKhCGbWHUJDMij4MWKhoEgCpi6idMp4TOtmKqJdXnEZW75dYrHgLyJjkabaEfUBfKihsMQEYMm59UioYM+Tv+glqnce7iJs8drGcyBfSEuDNZ2791bvSSTFQZ2BlGzBlMjWd7wUAvv+NmeNZPMqzEyMsLP/MzPcP/993PixAkeeughHnrooZt7mNaIpaUljhw5wtTUFADf//73+fSnP82jjz569Us3ieYmXm645UpZnVyupvNfSTrz+TymaeJyudi9e/d1m0nXi8XFRebm5ti7d++a41W5XCYWixGPx2sjlM9m+dLnn8XutCLLEoVcmYF97VwYnMcXdNLZFWToeyPsuL2X889N4gu50TWdQrbMgfu2M/7cOPlkseGPaXNa6dzeQimVIz6TpGtHO2OnJnH7nPTu7WBhMkpiOoVroI1C2I9ZUHG5bJi5Ki3Nbv7LJ+5H0cq43e6GRnEt3pOzs7PE43H27du3odc4n89z7tw5WlpayOVyVCqVhpvMrZix3wzJvBrf/OY3+cxnPsM999zDU089xR/+4R9y5MiRmzrWWvFSiSsvKaKpKAqqqt6w6ccwDEZGRtA0DYfDQSqVet5osJvF0tISMzMz7N2793l6kZnRLH/08ec4fzFBoMnO2HCa3bdFOHcihmQR2bLLj+gQWVjKoxs6czNFXB6Jrl4nFQNGhtP0bfXictmwuywcPTqPKArs2RshHHYyMZFhajLDnQfbcT4DBUHF7bJSLepoNgPRLqJoBs39LnYdCfPAB/vp3ubj/PnzyLK8pjm7pVKpsXAB1/V7m59b5NGvDpFecHLuRJzYYolqTkOvGDjcFpSijstlQUka2EQRWRJBhbyg4DNtYAVBMdFNA7vfgl0TkRGw5kV0TDRMLIhk5SoOTUACIqadmFChKOmYd8pYBAsLY3la2tyMnq2Ry713NHH2WI10Hri7mZPP1JqpDt7VTCpe4Bd/bxf3vmbPTS0qo6OjPPTQQ/zjP/4je/bsWff7bwX33nsvf/VXf0V/fz+f+tSnKBaL/P7v//7VL9skmpt4ueGWM5p1L83r6fzr/o1Op7NRzr66gnYzME2TyclJcrkce/bsuen4VK1WWVqK8j8++mXSsRJbdjYxMRLDapew2qx0dfoRVJXhYxM43DZsDiuZeJ7tB7pQqxqL5+foGmhl9MQkdpeNUJufcr6Cwy4higLTw3MIgsDe+3eQnEsye6HWtNp/5zbmbQ5UQ8CCiZ4p090V5L//zU9ic9gayYx6RnG1ZMZKrLwWG2lIXpfQ7du3rxHPrmXGfi1d52rYCJL5xBNP8Nu//ds89thjG5plXQteCnHlJUM0VVXlzW9+M695zWt48MEHaW9vX5UoKIrCuXPniEQidHZ2Niwi6lm7RCLR0LjUyg1rc3Ba6WW2d+/ea77v7z57lj/776cItTioVjRyGYUDdzczPpomssVFRdEYHkzg9ljp2eojnSmTq1ZweyARU8lmVfbf3kQyWaW52cXiYh6n08r5kSSiIHDXnW0IJwzsSIiaQFnSMZ1gyCY77w3z0H/bx9adtTKFrusMDQ3h9Xrp6elZN7Gq+73FYjEURWmUjzweD0tLS8zPzz+vrKEoGg///QVOPbvEhTNJkrNlLHYJNWsg2MCsmlhliYDdhlkwKQkqHsOKIutYNQnDMJHcJg5DxmKRsWQFsii4sYDFxFA1QqYVTYZvCouogklTixWP10Yk4CYXU4gvlFAqOqIE3qCdVLzWbd7e68DukPnyM++5KZJ56dIlfvzHf5y///u/Z//+/et+/63izJkzjc7ALVu28Dd/8zer2XFsEs1NvNxw03FlbGyMn//5n+eBBx7gLW95yzU9FOtSqb6+vgYRqFfQotEomUwGr9fbaNhZK0EyDIPz588jSRL9/f0bMj3sqcfO8blPfg1JFnG4ZcoFjW39AS48M4lskQi2+IjNptiyu4OJoTm27+9E1DTOH6vNKw+1BVgYj7JldwfoKuOnprA6LPTt7yG5kEItK5SLFTp3tCHLMnOpCnm3E4/NglHS2L69iU/82X+5ZowslUqNhsuV5vUOh4Px8fFGWXsjSWYmk+HChQvP61pfibo8KhaLkUqlsNvtDUJ8LX3oRpDMp556ik984hM8+uijt+RacLN4KcSVlwzRBJibm+OrX/0q//Iv/0K1WuUtb3kLDzzwQINE1UXUKxeD553AssYlGo02dld10nmth8kwDEZHRzFNk4GBget+AXTd4KNv/DeGjsfZvi9Ym3l+IIjkFjj61AJWm8TAniBnTsTYfVsY06pz+kQMVQWv18q+Q2GGRxLEY1WCISsulxVRFGlr9eB1W1DGVawLAorVpKhoOEIy9zzQyU/9xgHs9suET9O0hqC9o6PjVi5743j18lFdljAwMHDDRbWQr/L1L47x+COTTJ3PYWomatpAQUfWRUQRgj47Yhkqio5Tlxvlcw0DUzQJmDYki4BYEcgKVWymiNdt4VIpzyWpwKEjzZw8WiuhD+xxoZQFwkEXTtnCyeUmoOYOO9G5Cr/+mbt4z4d2rvvzT09P8yM/8iP83//7f7nttttu7iK+ONgkmpt4ueGW4srw8DAPP/wwjzzyCD6fjwceeIC3vvWthMNhBEFoTJDbtWvXNZsz6iQlGo2uuYKmaRpnz54lFArR1dW1YSNqTdPkF977p8xdStK/r51KIsfM+QXC7V7is1maewJEp9Ngwu2vHuC5R04jW2QinUEWxqN4Q27a+yJMnp4EoLk7zOS5Wdq3teBwW8kks8QnU2w92Mv0hQWq27rwuGyIJY19Bzr4pT9635o/y8pkRjabxW63s2PHjmu6fNwM6tZI+/fvv27X+tWo6zpXVvfqfp2wMSTzBz/4Ab/yK7/CN77xjRfUGm8D8PIhmo2DmCaxWIyvfvWrfPWrX2206J8/f54vf/nLDcH2WlAXVsfj8VXn0da9N/1+/5qzgoszBd7/im9QLWvsf3Uz33xsEkGAA3c0c+poFFGEe97QyTe/NYFumLR3uGlrd5HJK1w4n0IQ4K672wGDeLxAIacQ9NnIzGt0Vb0YJthCEm/8L338l1/e+zyiV5/X2t3dTXNz87qu7Y0wNTVFJpOhvb2dRCJBJpO5ofXGSly6mOaLfzPMyaeXyCcV1JxOpaIhayKCBHarhFO0YJRNLJpIFgWPaUXyC5gZA6so4tRldKtJyVCZDpUplhQqFR1JEog0O1laKALQ0+dAliXssojTZmF6tMy3z/8oLs/auxehtsF5z3vew5/+6Z++oEa2PT09eDweJElClmVOnDhxM4fZJJqbeLlhw+LK+Pg4Dz/8MF//+tex2Wx0dnaiKAqf//zn10xS6hW0aDR6RZf4ygpapVJhcHCQnp6eDV2jTdNkYmKCoRNTfOOvz2LTVZxOCxPDC7RtibA0ncDQTXp3t6BWqywMLxHpDLA0kcDfVCN3oWYP6YUUkkViaSKGKAocfM1uRp+7RC5Ra6rc98pdVIoVklY7FUPALFS56/5+fu733r3uc65L3SwWCz6fj0QiQT6fJxAINCbx3Wx2M5VKNby210Myr0a1WiWRSBCLxahWqwQCAdLpNJ2dnTdNEOvWeN/4xjfo7Oy86XO7HjYopsDLkWhejc997nP8n//zf9i2bRuxWIw3vvGNPPDAA+zYsWNdu6KVwmqAYDBILBaju7t73TuWZ/99jt/9tWeYvJTltrtbOPbMIoIAh+9pJVOucvpklC1bXZTKyxdFFpAkgZZWF9WKxsSlLNlsle4uL2iQmC+x1x5CE3X2vM7NR35rHy0tLc/TuNQNaOvd8BsF0zQb479WljXqWqW6/sZutzd28jeyo9B1g69/+SL/+v9GmR1LoxVENMVAqoiIDpAMAbfNipAD0wAFHRFw2WU8JQsZScFz0EHBrjFxPs22HUFOHq3pMXu3+ZkcywDgdImIksCb397Gz/3qoefZglwPi4uLvOtd7+Jzn/sc9913301fv7Wgp6eHEydOXHPO7hqxSTQ38XLDhscVXdf52Z/9WY4ePYrX68U0Td761rdeV7a16omtUkHzer1Eo1F27ty5oXZ7hmFw4cIFRFGkv7+fP/rlL/LUv5wk0h4gHcuhqTq77tjC+RNT9O/rIB/NMHtxCW/YharqlLMVBg53ER2LkVxI4/Q66BxowzQMLp2exGKX6dnVhcNtZ2F8CewWKsEQVDVe9cbdPPSrb7mpc64PUVlpEWcYRqMbO51ON2adr6fHIplMMj4+zv79+ze0Gbhuxi7LMpqmPc/2bi14sazxNiimwMudaJqmyec//3k+8IEP4HQ6SafTfOMb3+Dhhx9mZmaG1772tbz97W9ft7A4lUoxNDSE1VorXdcznetx6P/bPznL7//GUQAO3d3C9FQO02bi8sDYaA6latK/K4QvbGNsNEU0WuLgwWaGRxL4vDZ27QpTyCjIgoA0JdC81clv/MV9+MPSFZ2GdY1L/Uu70Qa09TFodenA9RbZleUGQRCu0N+shkKhwLlz59izZw9z0xW+8BdDDJ2Ik12soikGQgEUScchyrgdFsSMQAkV2RRxuyxoRYPjcgyP10L/jjBWSWTmUo72djdnT9U2DIfvbuXk0SX+9ckHsDrKJBKJK2bpXuvcotEo73znO/nMZz7Dq171qlu/kDfAJtHcxCZuChseV8rlMn/913/NT//0TyMIAgsLCzz88MP8y7/8C5VKpSHb6u3tXVcyY25ujkuXLmGz2a6Qbd0qEdJ1vTECs155Sy5m+PnXf4ZKscrOO7YwcmwCu8vG9l1tDH53mECzD1XRKKSLtG6J4As5GHlqFHfQic1lJTmbYeCOPsqFEsV8ifhkit33DDD09AVsbhuO/i0IArz1PYd558+sf33UdZ3BwUHC4fB1h12slsy4kXYyHo8zOTm5bv/NtZzzmTNnaG1tpa2trTElMB6Pk0qlcDgcN5wAdPbsWT784Q/z8MMPs23btg07t9WwSTRfBORyOR599FEefvhhxsbGePWrX82DDz7IwYMHr0s6r/Yyu7oppk6eVvM5uxqf+eRR/ub/nGXb3gCOgMwPvj+PaUJru5ut/X6ePbZAqaQhigKvelUXpbKGquq4HNZa97ZdRlvUec9P7+DB/zLwvONXq1Xi8TgLCwvk8/nGDN1rmQyvF6ZpMjIygtVqZevWres6Zv3cYrEYqqoSDocb100QBHK5XGOy09UGselUiX/48yF+8Pg8sakCehWMvEkFDbdoweO0Qg7Kssq8UWTHPWGO/qDWBbl7b5hcoUzQZ6WaF0hGK7z+bVv49B+/snH8qycA1eflejyexkzdd7zjHfzu7/4ur3/962/5Oq4Fvb29BAIBBEHgIx/5CB/+8Idv5jCbRHMTLze8aHFlNdnWm970Jh588EG2bdt23fVxbm6OpaUl9u7di9VqbVTQYrEYgiA0khnrLfHWB4e0t7fT1tZ2xb898jff529+5+uIksiW3e1Us0UKyTxKRaWQKdG5vZXYXJItO1tJL6YpZktk43ksNpntR3o4//QYumKAALvu6a91obsdJIs6FVHmvT91L2963/p9hFVVZXBwkLa2tued841wo2RGLBZrmLxvpMfp1STzalw9AUgQhEbMqyeoRkZG+OAHP8iXvvQlBgaeH883GhsUU2CTaK4NpVKJxx57jK985SsMDw9z//338+CDD3L48JW+kgsLC8zPz1/Ty0xV1YZWo1wuNx6kOkFZDX/+B6f4//7ns2iayfYdPrIplY4tPo4/t8CWPj/BkAO7TeLJ780CcN9dHUyMZhjoD9LfE+Rjv307/uC1zebrI7p27drV6K6vz329FX8wwzAYGhrC4/HcVNf6Smia1rhuxWIRl8tFLpfjwIEDNxyxVa1q/PPfnOfxr0+wNFlAyRmoRQPDNHEi4/ZYYI/I1ESWakXD5hKJRisAHLmzjWJB5R/+6a20tK2+MVBVtWFxMTQ0xGOPPcb4+Dif+tSnePvb337Tn3m9mJ+fp729nVgsxmtf+1r++I//+GbK9ZtEcxMvN/yHxZVEIsHXvvY1vvrVrxKLxXjDG97Agw8+eIVsqy47KpVK7Nq1a9XyarVabZBOwzCuayu3EnWp1NatW1fNWhmGwW/9+J+zOBUnGHSwOB6jmC3Ru7uDmdFFME323r2Voe+fp1pUCDT78Dd7cbjsDD99AVfQSfdAO4IsEJ1OIDtk3OEAGUXig7/0eu5+0/51X7ON7CG4Oplht9splUocOnRowzOZg4ODtLS0rJkY188tHo/zve99j5GREY4fP87DDz/cGJv9QmODYgpsEs31o1Kp8O1vf5svf/nLnD59mnvuuYe3ve1tfO973+P+++/n3nvvXZPWQtd1EokE0WiUYrHYsP+5mthVq1X+1+99h7/9sxlU1eDIfW2ohsn54QS5XJXb72jj2LML+HxWDu5p5vy5JK+4r4t3/sgA973h+vOz6ya/+/btu+KLdbXJ8Hr93nRdv6IjciORSqUYGRnB5/NRKBTW5V1mmiYP/+MFHvnncaLTRQpLCgYGOVWl4Fbp3+EBE9IpHV/AzrnBGL/76VfwwQ/tW9O5RaNRPvjBD+J0Opmbm+OjH/0oP/3TP70RH3td+NSnPoXb7eaXfumX1vvWTaK5iZcbXhJxZTXZ1pve9Cb++Z//mQ996ENr7hlYWUG7uhK0Evl8nqGhoRtKpWJzKf77j/wJC+NL9O3rYuLsDKYJOw73US0UGT85SWd/G/lskXwiz7aDPZSKZYq5EvlYgY7+Ni6dnqKltwlPxEfJauXVP7qL9v7QFROT1vLZqtUqZ86coa+vbyPKuVdgbm6OmZkZXC4XpVKJYDB4xWjHm0WdZDY3N99048/g4CC/+Iu/SCQSYWpqis9+9rO89rWvvelzuhncQkyBTaJ5a1AUhW9+85v80i/9EhaLhTvuuIO3v/3t3HfffetKu+u6TiqVIhaLkcvlGh1zVquVoaEh+vv7WVrQ+fz/OcWXv3QBALfbwsHbWmpaRBG8FiuaanLb7S184Of24fVfX7czMzNDIpG4rq8nrC6svl6XeN0aqaWlZcMtF662mrh6Jm1d4xKJRG54/U3T5Gv/PMq//uNFliaLmA6NWKXM4mKFHTtDaJrBG964hU/85tpKO7lcjne96138/M//PO95z3sapZC1SCRuFcViEcMw8Hg8FItFXvva1/Kbv/mbvOENb1jvoTaJ5iZebnjJxZVcLscXv/hFPvnJT9Ld3c3dd9/NAw88wKFDh9ZFeq5VQVMUhfHxcfbu3bumvoHj3zrL//f+v8A0TXbc0cfMhQUCAQd2l43JczOoVY1As4/evZ2c+vYgpgEun5O2rS1oqoYv7CU2n8Hf08QHP/V2tu3paiRa4vH4mrrE69nX/v7+1Xwabwnz8/MsLS2xf/9+JEnCMIxGPM5mszdlxA4bQzKvtsbTNA1VVTd0JPZq2MCYAptE89bxR3/0RxiGwc/8zM/w1FNP8ZWvfIWnn36aQ4cO8cADD/DKV75yXWLtOrGbnZ0lmUwSDodpb28nGAwiiiJPPD7FV754gUSizFNPztIUdnL7vla29gd470/sYMv2638J6xYWxWKR3bt3r2vhqgur6yMn69Yb9U7sut6nq6trw62RbtQFuFLjUrebqpeQrqdbqulIz/Pdx6IkkiIzM3l002TfwWZ+4b/djije+DtSKBR497vfzU/91E/xvve975Y+581gYmKiUabXNI0f+7Ef4xOf+MTNHGqTaG7i5YaXZFz52Mc+xutf/3pe9apX8dhjj/Hwww8zNDTE/fffzwMPPMAdd9yxbtKTSCSYnp4mn883/BvXKo360mf/jX/+X48QaPLStS3C6X8fAqBjeyuiJIJhMD0yR6DVR9eODgQgHcviDniQrDL+9hA/+qtvoa37+R7V9ZgXjUYbxG6leX2xWOTs2bMb3qgKNx5XebPJjI0gmXVrvD/7sz97wcdJXo0NjCmwSTRvHfWRliuh6zpPP/00X/nKV/jud7/Lnj17ePDBB3nNa16zpp1ILBZjcnKSvXv3UqlUiEajq2YT69d3PXYZFy7UMqI36gBfy7FWWm9IkkS5XGbr1q03bUB7LdR1pAcOHFizdqbesBOLxdB1vbGbd7lcV+ifRkdHEQRhTSM2V0OpVOI973kPP/ETP8EHPvCBdb//JYZNormJlxt+aOLKarKtBx98kLvuumtNU+qmpqZIp9Ps3LmTXC5HNBq9IptYb/y4Fv7+f/wL3/3CU6SXsgwc2crE4DROjwOX145kF8nHCsgWGV03SM6n2X54K5JFpntfNz/+aw/gDV5fT1//3PUJO8lkEpvNRqFQYN++fRtOMmdmZhrT+taacCkUCs9LZlztPrIRJPPFtMZ7EbBJNF9o6LrO0aNHefjhh/n3f/93tm/fztvf/nZe97rXrdrIUu8uvHo8Yz2bWDfydblcNDc3EwqF1rTI1JtzXC4XW7Zs2bDJCVAra5w+fZpAIEChUFiTNdFasRFWE1eXkOr6m6WlJURRvGmSWalU+JEf+RHe+c538uEPf3hDr+nV0HWd2267jfb2dh555JEX6tdsEs1NvNzwQxlXFEXh8ccf5ytf+QpHjx7lyJEjPPjgg6vKtkzT5OLFi2iaxo4dO64gVVdnE30+H83NzdfU4//tJ7/E1/7omwBsv60XSRIZ+cFFANq3tYJgYrVZCbYHmbsU5b5338l7/tubsNrW38GdTqcZGRkhFAqRzWbXNIlvrZiamiKbzd7STPTVkhmhUIjx8fFbko69WNZ4L1JMgU2i+eLCMAxOnTrFl7/8Zb71rW/R09PDAw88wBvf+EbcbjdHjx7F5XKxe/fu65ZFTNOkUCg0sol2u53m5uZrmonXx5XdyHPsZlCf47tjx47GjnNlN5+maatmE9eCaDTKzMzMhlpN1PWwY2NjKIrSWLjWY5gLtc/4vve9jze84Q383M/93AtKMgE++9nPcuLECXK53CbR3MQmNg4/9HFFVVWefPLJhmzr4MGDPPjgg7zyla/EMAyOHz9Oe3s7fX19112nTNMknU43RgV7PB6am5uftzY++aVn+fqffJvoVIx8skD79haau5so5csoJQV/awDDMLjnXUd47Y+v374IaIzuXDn6caU0ShTFNUmjVsPExASFQmHd0rHrQVVVYrEY4+PjCIJAS0vLTbm2vJjWeC9STIFNovkfh7pB+pe//GUee+wxqtVqbSLDH/0RwWBwXccqFArEYjESiQSyLNPc3NzY9dV1kx0dHRte0q53Lu7Zs+eaTS9XZxPX2mm4uLjI/Pw8+/fvX1PGdq2o7+4Btm3b1tDfpFIpnE5nwzD3esRWURTe//73c++99/Lxj3/8BSeZc3NzPPTQQ3ziE5/gs5/97CbR3MQmNg7/qeLKStnWv//7v6OqKm9961v5jd/4jXVVl64uYdcraPXpOvOTC/z1b/4To09O0LKlmamhWdSKysHX7SPSFeadv/hGmlfRY64FsViMqamp61axrs4m1knn9ezuVk6o27Vr14au2/VyeVNTE62traRSKeLxeCNLvJZkRiqV4h3veAe/9Vu/xZvf/OYNO7fV8CLGFNgkmv/x0DSNd7zjHfT19eH3+3n00UcJBAK87W1v4y1veQuRyPq+rKVS6YrJP9Vq9QXRTWYyGS5cuMCePXtu6GVZx9W2SdfqNFxYWGBxcZF9+/a9ICTTNE36+/uvWGjqWeK6Ya4syw39zcods6ZpfPCDH+TQoUP82q/92gtOMgHe9a538eu//uvk83k+85nPbBLNTWxi4/CfMq4kEgne/OY388ADD5BIJBqyrQcffJDXve5163LDqM9fX5nMKJVK7N27F4/Hy9zFRbKxHJ6Ak84d7ciWm1+z65Z766liKYrSSGZUKpVV/anrs+hVVV33eOkboW7nF4lE6OjouOLfVhL26yUzMpkM73znO/mVX/mVF8V/+UWMKbBJNF8aOHXqFAcPHgQufyG+8pWv8PWvfx2Hw8Hb3vY23va2t9Hc3LzmL0ixWGRwcJBQKEQ+n8c0zcb0iFvVTdanH60sa6wXdW1QLBYjk8k0Og3L5dqYx2t1Ad4srkcyV0O5XG6UaQzDQFVVrFYrf/qnf8rAwAC/+Zu/+aKQzEceeYTHHnuMz3/+83zve9/bJJqb2MTG4j9lXNE0jZGRkYa592qyrbe97W288Y1vXFeTTTKZ5MKFC4TDYbLZLBaLZcN0k3Nzc0Sj0VtKMGia1khmFAqFhh4/FoutaQzyenE9knk16g20Kwl7NpslEonw8Y9/vGGN90LjRY4psEk0X9owTZOpqanGnFxJknjrW9/Kgw8+SFtb2zW/MNlslpGRkStK2lfrJtdSalgN9eacffv23fKM3Trqu75Lly6RzWYJhUKNMs1GZDTXSzKvhqIoPPHEE/z2b//2/7+9ew+K8rr/B/5+BFEJcpdFIRUJUQw3I6hDQlBzIVHAXQxm1MlXIsRMq0nQYKP9kUmL04xJ2thaGW2JqY2JadXlorKIGDIqOorGhnRQTEHBAZSLgVXAhb2d3x/4POWqu8uz7LL7ec3sTCBy9uC6z+ez55zn80FzczNSUlKQmpqKWbNmjXhuj/Kb3/wGX331FRwdHdHd3Y179+5h+fLl+Prrr83xdJRoEntjd3GFP7Yll8tRVFQEiUQCqVSKhISEh9aobG5uFtoz8kll3x20cePGCYsZxsaGuro6KJVKhIWFibbAoNfrhbOe/Hl8Hx8foVSgGOP/+OOPBiWZQ1GpVDhw4AB27twJBwcHvPHGG0hLSxO9NOBAoxxTAEo0xw7GGBobG4WkU61WIzExEVKpFNOnTxeSJ/6NFRERMezKpUajQWtrK5qbm6FWqwf1ER9OU1MT6uvrRe8DC/QWpm1vb0dYWJhw8bpz586I7zQcaZIJ9F5QNm7cCDc3N2RlZaG0tBR+fn6IiooyeqyRoBVNQkRn93GlqqoKcrkchYWFcHd3F5LOvse2DFlt7O7uFlphGrqDxtd15ltsinVzDj/21atX4eTkhCeeeKLfFraLi4tQKtCUxYyRJplA/9J4y5Ytg0KhwOLFi/H444+bNJ4paEVzMLu+IPTFGENzczPy8vKQl5eHjo4OxMfHw9HREWq1Ghs3bjQ4KeP7iDc3Nz/0Zh0xtjWGU1tbi46OjiHvAuz7iZnjOOHiZciWPWMM1dXV0Ov1I0oy33//fTg4OGDnzp2iXgiNRYkmIaKjuPLAUMe2EhMTUV1djfnz5+PVV181eLXRkB00fhFAp9OJfm5Sr9fj6tWrmDRp0qByfgPPnE6cOFFYzDBkAYVPMr29vU1OCvnSeMnJyVi3bt2oHMMaCiWag5k8WHFxMdLT06HT6fDmm29i69atYs7L4lpbW5GRkSGstL3yyitYtmyZ0W9e/mad5uZm4XyLRCKBUqlEe3s7wsPDRT83acynWWPuNOSTTJ1OZ/K5HL1ejw8++ADd3d3YvXu3RZPMUUKJJrE3FFeGwF+b165di6amJvj6+hp0bGsow+2g3bx5E05OTnjyySdFTzIrKyvh4uKCwMDAR/55/twkX4SdTzqHWswQI8nkS+MtWbIEGzZssFiSOYpsP9HU6XSYOXMmTp48CX9/f8ybNw///Oc/8dRTT4k5N4tqamrC5s2bsXfvXqhUKhw9ehS5ubloaGjASy+9hKSkJKNrhvHnW65fvw6VSgWJRAJfX99he9Eaiy810dPTg6eeesroNxt/8RrqTkMAI04yGWPIyspCa2sr9u7dK2qCzevu7kZsbCx6enqg1WqRnJyMrKws0Z/HCDZ/xSNkAIorwzh79iwUCgU++ugj3Lp1q9+xrYSEBEilUgQEBBh1fdVqtUK9ScYYpk2bBolE0u8O8ZHgz5+6ubkhICDA6J/nt//5m0D5xQxnZ2dRkky1Wo2UlBQsXLgQmzZtMkuSaW9xxSoSzfPnz+N3v/sdTpw4AQDYvn07gN4DsbaOL8Sam5uLmpoavPjii5DJZHj66acfmSzyK4JarRazZs2CUqnsd4c4X8jXlKSz79hibJnwfXz5Ow05jsPEiRONai02cH7bt29HXV0dvvzyS7MkmfzzdHV1wcXFBRqNBjExMdi5c+eo97XtgxJNYm8orhhh4LGte/fuIT4+HjKZDEFBQY+8lvN3aXt6esLf37/fdZvfQTO2yPnAsb28vERpTKJWq4XFjJ6eHuh0Ovj4+Bj0ew5Fo9EgLS0NUVFR2LJli9lWMu0troh7kM9EjY2N/T59+Pv7o7y83IIzGj2urq5YvXo1Vq9ejc7OThw/fhzZ2dmoqqrCokWLIJPJMG/evEGJFH9A3MHBQUgEvby84OXlBcaYkHRWV1cP6r/+KHx/cQCinctxcHCARCKBj48Pqqur0dXVBScnJ5SXlwvFcr28vAxKOhlj2LFjB6qrq3HgwAGzJZlAb496viqARqOBRqOxh20UQsY8e40rfNeb9evXY/369WhtbUVBQQG2bt2K1tZWLFmyBFKpdMhru1arFXqA8zfQSCQSSCQSYQetsbERVVVVw9ZYHk7fgumm3pwzkJOTE/z8/DB16lRUVFRgwoQJUKlUuHDhgnAvg6FJsVarxS9/+UuEhYWZNckE7C+uWEWiSXq5uLhgxYoVWLFiBVQqFUpKSrBv3z68++67eO655yCTyRAdHQ2dTofvv/8evr6+Q/ZE5zgOHh4e8PDwEPqvt7S04MaNG3B2doaPj8+wZYn4BNbR0VH0czn8QXatVos5c+aA47h+SXFNTc0j7zRkjCE7Oxv//ve/cejQIdFvehqKTqdDZGQkampqsGHDBixYsMDsz0kIIWKYMmUK1q1bh3Xr1qG9vR1Hjx7Ftm3bUF9fj7i4OOHYFl8NJTAwEL6+voPG4VtKTpkypV//9Z9++umRO2g6nQ4VFRUj6i8+HL1eL9TJ5D9Y8G2M+aTY3d0dPj4+w/aH1+l0eOeddzBjxoxRq79sT3HFKhJNPz8/1NfXC183NDSI/o9xrJk0aRKkUimkUil6enpQWlqKgwcPCmdGXn75Zfz2t7995BuC4zi4ubnBzc0NQUFBQitM/pA33wpz/PjxQqmJCRMmPLLnrrGG6/owMCnm7zSsra3FhAkThFqdTk5OYIwhJydHaN8mdvmm4Tg4OKCiogJKpRJJSUmorKxEaGjoqDw3IcQ0FFcG8/DwQEpKClJSUoRjW3/4wx9QVVWF7u5uZGRkGLR9O27cOIN30LRaLSoqKoSVRzHxSaanp2e/1WsHB4d+STE/v//+97+D5qfX67Fp0yZMmTIFv//970dtZdGe4opVnNHUarWYOXOmcEf2vHnz8M033yAkJMTgMVJTU1FYWAgfHx9UVlaaMg2r19XVBZlMhpCQEHR3d+Ps2bOIioqCVCrFokWLjC7AO/BOPq1WCw8PD7OtZBrbWqzv/L744gvo9Xo0NjaiuLjY5G5HI7Vt2zY4Oztj8+bNFnl+0BlNYn8sElfsIaYAQH19vdDZ7tq1a7h69SoWL14MqVSK+fPnG3U0qe8O2s8//4yJEyeiq6sLAQEBZlvJ9PT0NPi8Z9/5tba24k9/+hPGjRsHX19f/O1vf7NY1RJbjytWkWgCQFFRETZu3AidTofU1FRkZmYa9fNnzpyBi4sL1qxZY7MXBY1Gg7KyMjz//PMAei+k/OreqVOnEB4eDplMhhdeeMGoFpb8nXqMMeh0OqNrYT6MWP1rs7OzcejQIUyePBkajQYKhcKotmymam1txfjx4+Hu7g6VSoW4uDhs2bIFCQkJZn/uYVCiSeyNReKKPcQUoLeBSG1trdDcoru7GydOnIBcLscPP/yAmJgYyGQyPPPMM0YdVVKr1bh8+TIee+wxqFQqTJgwwahamA/D37nu4eFh8k1Fer0e7733Hq5evQqdTodp06ZBLpePyoqmvcUVq0k0xVBXV4eEhASbvigMR6fT4cKFC5DL5fj2228RHBwMmUyGuLi4h7aw5D8Venh4YPr06QD618Lky0dIJBKj+6/z5ZHUavWIksyDBw/iyy+/hEKhwGOPPYa2tjZ4eHiMygXhP//5D1JSUqDT6aDX6/Haa6/hww8/NPvzPgQlmsTeWCyu2HNMASAc25LL5SgvL0d0dDRkMhmee+65hyaLarUaFRUVmDFjhtC9qO8OlaOjo7CYYWw3OVNWMgcaqjReW1sbPD09TRrPWPYWVyjRtEF6vR6XL1/G4cOHceLECQQGBkIqleKVV16Bq6ur8Of4UhMPqznWt3yERqOBt7c3JBLJI/uvi5Vk5uXlIScnBwqFQqi/aeco0ST2hhJNK6DRaHDq1Cnk5uairKwMUVFRkMlkg45t9fT0oKKiAkFBQfDy8hpyLJVKhebmZqH/Ol8L81E7aGKsZPKl8W7evIl//OMfZq1aMoZQomkouigMxn/6O3z4MI4fP45p06ZBKpVi4cKF2LdvH9auXWtwqQmNRiO0wuQLsEskkkH910da6J137Ngx/OUvf4FCoYC7u7tJY1gDvV4v5tkfSjSJvaFE08oMd2zriSeegEKhQGpqqsGrg0MVYB9qB41PMt3d3YXdN2PxpfEqKytx4MCBUalaYi5jKa5QovlAfX091qxZg+bmZnAch7feegvp6elmmKXl8HeVHzhwAJ9//jnmzJmDpKQkJCQkwNvb26ixtFqt0Arz/v37Qs2yyZMn48aNGyNOMouLi/Hpp59CoVAM+6l4pMz1miuVSuh0Ojg4OPRLkC9duoSuri7Mnz8fzs7Opg5PiSaxN2M20bSHuMIf2/r73/+O/Px8LFy4EMnJyY88tjUUtVqNlpaWQf3XJ02aJEqSmZ2djfLychw8eNBsVUsorgwxOCWavW7fvo3bt29j7ty56OjoQGRkJAoKCmyqXRlv1apVSExMRFRUFORyOY4dOyaUU0pMTIREIjGp/zp/p+H48eMRHBxs8jnK0tJSbNu2DUVFRcL5HnMwx2ve1NSExYsXIyoqCk5OTtiwYQPmzp2LI0eO4NChQ4iOjoanpydWr15t6lNQoknszZhNNO0lrmi1WsTGxuKzzz6Do6MjDh8+jJKSEsyYMQPLli3DkiVL+h3bMkTf/ut8t7uZM2cO2kEzBF8a77vvvkNubq7R50KNQXFliMFtJdFctWoVTp06hTt37kAikSArKwtpaWkmjyeVSvH222/jpZdeEnGW1kGlUvXblmCMoba2Frm5uSgoKICjoyMSExMhk8kwdepUg97U/HZ5d3c3fH190dLSgrt378LNzQ0SiWTYQrkDnTlzBpmZmVAoFEMWDTankb7mer0e6enp8PPzw6ZNm/DXv/4V5eXleOedd3DlyhXEx8ejsbERNTU1WLlyJTQajSmfqinRJPbGInFF7JgC2Fdc4Y9tyeVyFBUVYerUqZBKpYiPj4eHh4dBY/Lb5a6urpg0aRJaWlr67aC5uro+Mj4xxrBv3z4oFArk5+ePemk8iis2lGiKqa6uDrGxsaisrDT6U9hYxxhDQ0MDcnNzkZ+fD61Wi8TEREilUvziF78Y9k3NJ5l9t8sZY2hvb0dLSwva29vh6uoqFModKuk8d+4c3n//fRQWFo56YWWxXvPPPvsMS5cuxezZs7Fs2TI0Njbirbfewtq1a+Hk5ITa2lqcO3cOd+/eRUhICBYtWmTsU1CiSewNxZUxjj+2JZfLUVhYCE9PT0il0oce2+KTTDc3NwQEBAjf77uD1tHRAU9PT6EV5lDxaf/+/f127kYTxZUHg1Oi2V9nZycWLlyIzMxMLF++3NLTsSjGGJqampCXl4f8/Hx0dnYiPj4eUqm0X+egoZLMoca6e/eusL3Ot5r09vaGg4MDLl68iI0bN+LYsWPD3gFvLmK85owxcByH7du3Q6PRoK2tDSqVCgsXLsSuXbtQXFwMNzc3XLlyBStWrEBaWhoyMjJMeSpKNIm9obhiQxhjqK6ufuixLb1eLyRnfZPMgfR6Pdra2oQdtIGtJv/1r39h//79Qmm80URxpc/glGj+j0ajQUJCAl5++WW89957lp6O1WltbUV+fj7y8vLw888/Y+nSpaivr8eCBQvw+uuvG3xupm+ryfz8fJSUlODWrVsoKChARESEmX+L/sR+zZVKJWJiYiCRSFBaWgoAWLFiBV599VWsXLkSVVVVOHnyJN59910A/7uQGIESTWJvKK7YqIHHthwcHBAfH4/Tp09jy5YtmDdvnsFj9W01uWfPHtTU1KClpQWnT582+mbXkaK4MmBwSjR7McaQkpICT09P/PnPfzZpjO7ubsTGxqKnpwdarRbJycnIysoSd6JWoq2tDWlpaaisrMTkyZMRFxeHpKQkhISEGFVy4ccff0R6ejqio6Nx/vx5/OpXv8LatWvNOPP/EeM1Hzgex3HIycnBnTt3sHz5cgQHB+Pjjz9GUFAQkpOT+/15/g5CI1GiSeyN3cYVe4opjDHU1dUJq3/Ozs5ISEiAVCrF9OnTjUqcjhw5gl27dmHu3LkoKyvD7t278eyzz5pr6v1QXBkCY0zMx5hVVlbGALCwsDAWERHBIiIimEKhMGoMvV7POjo6GGOMqdVqNn/+fHb+/HlzTNfirl+/ztatW8e0Wi1TKpXs66+/ZklJSSwiIoJlZGSwsrIy1tHRwbq6uoZ9XLp0iYWGhrKqqiphXI1GM2q/gxiv+VCqq6tZeno6y8jIYDt27GChoaGsqKhIhBkzxsR9v9KDHmPhMWaN9BpjTzGFMcaOHz/OPvnkE6bX69mtW7dYdnY2e/7559n8+fNZVlYWq6ioYJ2dnQ+NK7m5uWzBggXszp07jLHev0OtVjtqvwPFlcEPWtE0k/v37yMmJgZ79uzBggULLD2dUdPZ2YmioiLI5XJcu3YNixcvhkwmw7x58/qtdF67dg1vvPEGvvnmG4SGhlpwxuZx/fp1XLhwAaWlpXjmmWfw5ptvijU0rWgSe0NxBfYbU4DeY1sFBQXIzc3FnTt3sHTpUkilUgQHB/db6Ryt0niWMlbjCiWaItPpdIiMjERNTQ02bNiATz75xNJTshiVSoUTJ05ALpejoqICsbGxkMlk8PHxwZo1a7B//37MmTPH0tMcNYwZfW5mKJRoEntj13GFYkp/bW1tOHr0KHJzc9HY2Cgc22pra8MHH3xgkdJ4ljQW4golmmaiVCqRlJSEXbt22eSKnbF6enrw7bff4vDhwzhy5AhKSkqMOuhtrNTUVBQWFsLHx8fW2sdRoknsDcUVUEwZyt27d1FYWIiDBw/iwoULqKiowLRp08z2fBRXTBycEk3z2bZtG5ydnbF582ZLT8WqaLVas/eYPXPmDFxcXLBmzRq6IBAytlFceYBiyvAoroyIWeOKaB3ZSe85EqVSCaB32/jkyZMIDg42ehydToenn34aCQkJIs/QOpj7YgAAsbGx8PT0NPvzEEKIuYgVUwCKK2KguGIa878yduT27dtISUmBTqeDXq/Ha6+9ZtKbeufOnZg9ezbu3btnhlkSQggZC8SKKQDFFWI5lGiKKDw8HD/88MOIxmhoaIBCoUBmZiZ27Ngh0swIIYSMNWLEFIDiCrEs2jq3Mhs3bsSnn35qVNFzQgghZDgUV4gl0b86K8LfzRYZGWnpqRBCCLEBFFeIpVGiaUXOnTuHo0ePIiAgACtXrsR3332H119/3aSxAgICEBYWhjlz5iAqKkrkmVq/VatWITo6Gj/99BP8/f3xxRdfWHpKhBAy6iiuiIfiimmovJEJRCqQ+lCnTp3CH//4RxQWFpr08wEBAfj+++/h7e0t8syIhVF5I2JvKK6IhOIKGQaVN7I2HMfh5s2blp4GIYQQG0FxhdgqSjQNxK/8Xrt2Dbt378b69evx5JNP4vPPPzfL8y1atMjkT51A70UrLi4OkZGRyMnJEXFmlldcXIxZs2YhKCgIH3/8saWnQwghJqG4Yj0orpgRY0zMh81LTk5meXl5jDHGDh06xH79618zlUpl4VkN1tDQwBhjrLm5mYWHh7PTp09beEbi0Gq1LDAwkF2/fp319PSw8PBwduXKFUtPazSJ/Z6lBz2s/WHzKK5YFsUV876HaUXTQPfv30dOTg6KiorAGENbWxtCQkJw8+ZNdHV1WXp6g/j5+QEAfHx8kJSUhIsXL1p4RuK4ePEigoKCEBgYCCcnJ6xcuRJHjhyx9LQIIcRoFFesA8UV86JE00Bnz55FTU0NMjMzcfLkScTExCAtLQ2+vr7w8vISOjdYg66uLnR0dAj/XVJSgtDQUJPGUiqVSE5ORnBwMGbPno3z58+LOVWjNTY24vHHHxe+9vf3R2NjowVnRAghprHHuGJtMQWguGJuYt91brM4jtsKQAsgmzHWzXHcWwBefPD1GcvOrj+O4wIB5D/40hHAN4yxj0wc60sAZYyxvRzHOQFwZowpxZmpSfNJBvAKY+zNB1//H4AFjLG3LTUnQggxhT3GFWuLKQ/mRHHFjKgFpQG43poTSgBTH1wMJAAyAGwB8BPHcR8A8AHwoaXfMADAGLsBIGKk43Ac5wYgFsAbD8ZVA1CPdNwRagTweJ+v/R98jxBCxgx7jCtWGlMAiitmRYmmARhjjOO4WwAyOY6bDMAFQC5jrAAAOI7bDeAra7gYiGwGgFYA+ziOiwBwGUA6Y8ySh4cuAXiS47gZ6L0QrASw2oLzIYQQo9lpXLHGmAJQXDErOqNpIMbYUQBSALcA7GaM/b8+//tZAD8CAMdxtvR36ghgLoA9jLGnAXQB2GrJCTHGtADeBnACQBWAQ4yxK5acEyGEmMIO44rVxRSA4oq50RnNEeA4bjwAPYCPABxmjF3mOI5jNvKXynGcL4ALjLGAB18/B2ArYyzeohMjhBAbZctxhWKKfbKVT0mjgnugz7dcAewBsAbANKB3O8QSczMHxlgTgHqO42Y9+NYLAK5acEqEEGJT7CmuUEyxT7SiKQKO454C8Bhj7JKl5yI2juPmANgLwAnADQBrGWPtFp0UIYTYOFuNKxRT7A8lmiNgK9sZhBBCrAPFFWJrKNEkhBBCCCFmQWc0CSGEEEKIWVCiSQghhBBCzIISTUIIIYQQYhaUaBJCCCGEELOgRJMQQgghhJgFJZqEEEIIIcQsKNEkhBBCCCFmQYkmIYQQQggxi/8Pag8GyxVm2AQAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 960x288 with 2 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "主程序段总共运行了 7.555869817733765 秒\n"
+     ]
+    }
+   ],
+   "source": [
+    "# 引入必要的 package\n",
+    "from matplotlib import cm\n",
+    "from mpl_toolkits.mplot3d import Axes3D\n",
+    "from matplotlib.ticker import LinearLocator, FormatStrFormatter\n",
+    "\n",
+    "time_start = time.time()\n",
+    "N = 2\n",
+    "\n",
+    "# 设置图像比例 竖：横 = 0.3 \n",
+    "fig = plt.figure(figsize=plt.figaspect(0.3))\n",
+    "\n",
+    "# 生成 x, y 轴上的点\n",
+    "X = np.linspace(0, 2*np.pi, 80)\n",
+    "Y = np.linspace(0, 2*np.pi, 80)\n",
+    "\n",
+    "# 生成 2D 网格 (mesh)\n",
+    "xx, yy = np.meshgrid(X, Y)\n",
+    "\n",
+    "\n",
+    "# 定义必要的逻辑门\n",
+    "def rx(theta):\n",
+    "    mat = np.array([[np.cos(theta/2), -1j*np.sin(theta/2)],\n",
+    "                    [-1j*np.sin(theta/2), np.cos(theta/2)]])\n",
+    "    return mat\n",
+    "\n",
+    "def ry(theta):\n",
+    "    mat = np.array([[np.cos(theta/2), -1*np.sin(theta/2)],\n",
+    "                    [np.sin(theta/2), np.cos(theta/2)]])\n",
+    "    return mat\n",
+    "\n",
+    "def rz(theta):\n",
+    "    mat = np.array([[np.exp(-1j*theta/2), 0],\n",
+    "                    [0, np.exp(1j*theta/2)]])\n",
+    "    return mat\n",
+    "\n",
+    "def CNOT():\n",
+    "    mat = np.array([[1,0,0,0],[0,1,0,0],[0,0,0,1],[0,0,1,0]])\n",
+    "    return mat\n",
+    "\n",
+    "# ============= 第一张图 =============\n",
+    "# 我们可视化第二层是 kron(Ry, Ry) 的情况\n",
+    "ax = fig.add_subplot(1, 2, 1, projection='3d')\n",
+    "\n",
+    "# 向前传播计算损失函数：\n",
+    "def cost_yy(para):\n",
+    "    L1 = np.kron(ry(np.pi/4), ry(np.pi/4))\n",
+    "    L2 = np.kron(ry(para[0]), ry(para[1]))\n",
+    "    U = np.matmul(np.matmul(L1, L2), CNOT())\n",
+    "    H = np.zeros((2 ** N, 2 ** N))\n",
+    "    H[0, 0] = 1\n",
+    "    val = (U.conj().T @ H@ U).real[0][0]\n",
+    "    return val\n",
+    "\n",
+    "# 画出图像\n",
+    "Z = np.array([[cost_yy([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))\n",
+    "surf = ax.plot_surface(xx, yy, Z, cmap='plasma')\n",
+    "#cset = ax.contourf(xx, yy, Z, zdir='z', offset=np.min(Z), cmap='viridis')\n",
+    "ax.set_xlabel(r\"$\\theta_1$\")\n",
+    "ax.set_ylabel(r\"$\\theta_2$\")\n",
+    "ax.set_title(\"Optimization Landscape for Ry-Ry Layer\")\n",
+    "#fig.colorbar(surf, shrink=0.5, aspect=5)\n",
+    "\n",
+    "# ============= 第二张图 =============\n",
+    "# 我们可视化第二层是 kron(Rx, Rz) 的情况\n",
+    "ax = fig.add_subplot(1, 2, 2, projection='3d')\n",
+    "\n",
+    "\n",
+    "def cost_xz(para):\n",
+    "    L1 = np.kron(ry(np.pi/4), ry(np.pi/4))\n",
+    "    L2 = np.kron(rx(para[0]), rz(para[1]))\n",
+    "    U = np.matmul(np.matmul(L1, L2), CNOT())\n",
+    "    H = np.zeros((2 ** N, 2 ** N))\n",
+    "    H[0, 0] = 1\n",
+    "    val = (U.conj().T @ H@ U).real[0][0]\n",
+    "    return val\n",
+    "\n",
+    "Z = np.array([[cost_xz([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))\n",
+    "surf = ax.plot_surface(xx, yy, Z, cmap='viridis')\n",
+    "#cset = ax.contourf(xx, yy, Z, zdir='z', offset=np.min(Z), cmap='viridis')\n",
+    "ax.set_xlabel(r\"$\\theta_1$\")\n",
+    "ax.set_ylabel(r\"$\\theta_2$\")\n",
+    "ax.set_title(\"Optimization Landscape for Rx-Rz Layer\")\n",
+    "\n",
+    "\n",
+    "plt.show()\n",
+    "\n",
+    "time_span = time.time() - time_start        \n",
+    "print('主程序段总共运行了', time_span, '秒')"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 更多的量子比特\n",
+    "\n",
+    "接着我们再看看不断的增加量子比特的数量，会对我们的梯度带来什么影响。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:13:19.968716Z",
+     "start_time": "2021-01-09T09:07:07.037371Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# 超参数设置\n",
+    "selected_qubit = [2, 4, 6, 8]\n",
+    "samples = 300\n",
+    "grad_val = []\n",
+    "means, variances = [], []\n",
+    "\n",
+    "\n",
+    "# 记录运算时长\n",
+    "time_start = time.time()\n",
+    "\n",
+    "# 不断增加量子比特数量\n",
+    "for N in selected_qubit:\n",
+    "    grad_info = []\n",
+    "    THETA_SIZE = N\n",
+    "    for i in range(samples):\n",
+    "        class manual_gradient(fluid.dygraph.Layer):\n",
+    "            # 初始化一个长度为 THETA_SIZE 的可学习参数列表\n",
+    "            def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * np.pi,seed=1),dtype='float64'):\n",
+    "                super(manual_gradient, self).__init__()\n",
+    "\n",
+    "                # 转换成 Paddle 动态图模式中支持的 variable\n",
+    "                self.H = fluid.dygraph.to_variable(density_op(N))\n",
+    "\n",
+    "            # 定义损失函数和前向传播机制    \n",
+    "            def forward(self):\n",
+    "\n",
+    "                # 初始化三个 theta 参数列表\n",
+    "                theta_np = np.random.uniform(low=0., high= 2 * np.pi, size=(THETA_SIZE))\n",
+    "                theta_plus_np = np.copy(theta_np) \n",
+    "                theta_minus_np = np.copy(theta_np) \n",
+    "\n",
+    "                # 修改用以计算解析梯度\n",
+    "                theta_plus_np[0] += np.pi/2\n",
+    "                theta_minus_np[0] -= np.pi/2\n",
+    "\n",
+    "                # 转换成 Paddle 动态图模式中支持的 variable\n",
+    "                theta = fluid.dygraph.to_variable(theta_np)\n",
+    "                theta_plus = fluid.dygraph.to_variable(theta_plus_np)\n",
+    "                theta_minus = fluid.dygraph.to_variable(theta_minus_np)\n",
+    "\n",
+    "                # 生成随机目标，在 rand_circuit 中随机选取电路门\n",
+    "                target = np.random.choice(3, N)      \n",
+    "                \n",
+    "                U = rand_circuit(theta, target, N)\n",
+    "                U_dagger = dagger(U) \n",
+    "                U_plus = rand_circuit(theta_plus, target, N)\n",
+    "                U_plus_dagger = dagger(U_plus) \n",
+    "                U_minus = rand_circuit(theta_minus, target, N)\n",
+    "                U_minus_dagger = dagger(U_minus) \n",
+    "\n",
+    "                \n",
+    "                # 计算解析梯度\n",
+    "                grad = ( matmul(matmul(U_plus_dagger, self.H), U_plus).real[0][0] - matmul(matmul(U_minus_dagger, self.H), U_minus).real[0][0])/2  \n",
+    "                \n",
+    "                return grad      \n",
+    "            \n",
+    "           \n",
+    "        # 定义主程序段    \n",
+    "        def main():\n",
+    "          \n",
+    "            # 初始化paddle动态图机制\n",
+    "            with fluid.dygraph.guard():\n",
+    "\n",
+    "                sampling = manual_gradient(shape=[THETA_SIZE])\n",
+    "                \n",
+    "                # 采样获得梯度信息\n",
+    "                grad = sampling()\n",
+    "                \n",
+    "            return grad.numpy()\n",
+    "        \n",
+    "        if __name__ == '__main__':\n",
+    "            grad = main()\n",
+    "            grad_info.append(grad)\n",
+    "            \n",
+    "    # 记录采样信息\n",
+    "    grad_val.append(grad_info) \n",
+    "    means.append(np.mean(grad_info))\n",
+    "    variances.append(np.var(grad_info))"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:13:21.355313Z",
+     "start_time": "2021-01-09T09:13:19.972155Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "我们接着画出这个采样出来的梯度的统计结果：\n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAzEAAAEWCAYAAABWoBknAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAABSnElEQVR4nO3dd3xV9f3H8dcnCRAgLBkKhCkQBFGGFXdRVNyi1eJqtVWpg5/W2jpbxVUXorZqW1TqqIK4cVS0aNwTpVVkuQXZQ4jIzOf3x/ck3ISMG3Jv7r3k/Xw87iNn3XM+9wbON5/zXebuiIiIiIiIZIqsVAcgIiIiIiJSE0piREREREQkoyiJERERERGRjKIkRkREREREMoqSGBERERERyShKYkREREREJKMoiZFtmpntbWZzzazIzIanOp5UMrOuZuZmllOX790aZvZvMzs1HWIRkfQQ3ce7pzqOeFjwTzNbYWbvpTqeVDOz+8zs2rp+71Zca18zm50OsUj1lMRIjZjZV2a23szalNv+UfSHZdcUhVaZq4E73D3P3Z8qv9PM/mVmC8xslZnNMbMzyu0famazzGyNmb1iZl1i9jUys/HRexea2e+S/3HqB3c/1N3vT/Z1zKyw/O9cRGrPzF4ws6sr2H50dL+s8UOI6D7+RWIiTLp9gIOAfHffvfxOM9vfzD42s5VmtszMnjSzjjH7qyxfqiqbZOu5++vuXpDs65jZEDObl+zrbOuUxMjW+BI4sWTFzPoBTVIXTpW6ADOq2H890NXdmwNHAdea2SCAKFF7AvgTsB3wAfBIzHtHAz2ja+wPXGRmhyT6A2xrVIMiUi/cD5xiZlZu+y+Ah9x9Y7wnytB7RhfgK3f/oZL9nwLD3L0l0AGYC/wtZv9oKilf4iibpAJR7Zj+7t2G6JcpW+NB4Jcx66cCD8QeED1FGmNm35jZIjP7u5k1jva1MrNnzWxJVNX+rJnlx7y30MyuMbM3zWy1mb1Yvuan3LXONLPPzGy5mU02sw7R9s+B7sAzUTOERuXf6+4z3H1dyWr02jFaPxaY4e6PuvtaQqGyq5n1jvnc17j7CnefCdwNnFZJjD3M7FUz+97MlprZIzH7bjezb6MnbtPMbN+YfaPN7NGoxmh19OSul5ldamaLo/cdXO67u97M3ovO97SZbVdJTC3M7N6oJmq+mV1rZtnRvuzo97fUzL4ADq/s+4+OHxjVxq2O4n3Eoir3kidOZnaxmS0E/hnnv4Ez4omlms9xmpm9Eb1/hZl9aWaHRvuuA/YF7oj+fdxR1WcUkRp5CmhN+D8GhHs/cATwgJntbmZvW6iJWGBmd5hZw5hj3czONbO5hD/wS7b1iJYPj+45q6L74OiY95Y0OT01KoOWmtnlMfuzzewyM/s8umdNM7NO0b7eZvZSVJ7MNrOfV/YBzaxDVOYsj8qgM6PtpwP3AHtG95aryr/X3Re5+3cxmzYBPWLWqypfqiubysd5cXRvXB19pqHR9nh+B+dYaJK92kK5vKOZvRV975NKjo+5z18Wfd9fmdnJVXx3R5jZ9Ojab5nZLjH7BpjZh9E1HwFyqzhPtpndEl3zSzMbZTHNjaOy5DozexNYA3Q3s1+Z2czo/F+Y2W9izlemhqS6WKr5HF+Z2e/N7H8Wyv5HzCzXzJoC/wY6RP8+iiz6u0VqyN310ivuF/AVcCAwG9gJyAbmEZ4WOaFWA+BWYDLhKVEz4Bng+mhfa+BnhNqbZsCjwFMx1ygEPgd6AY2j9RsqiecAYCkwEGgE/BV4rXy81Xymuwg3Nwc+BPKi7bcDfyt37CdR7K2i47eP2Xcc8HEl15gAXE54cJAL7BOz75ToO8kBLgQWArnRvtHAWmBYtP8BQk3Y5UAD4Ezgy3Lf3XxgZ6Ap8Djwr2hf1yjmnGj9SeAf0XHtgPeA30T7zgJmAZ2i3+Erse8t99kaAl8D50cxHQusB66N9g8BNgI3Rr+jxnH+Gzgjnliq+RynARui7ykbOBv4DrDy19FLL70S+yL84X1PzPpvgOnR8iBgj+i+1hWYCfw25lgHXor+zzeO2dYjWh4C9CPcU3cBFgHDo30l97q7o/vNrsA6YKdo/x+Aj4ECwKL9raN7yLfAr6K4BhDKlz6VfL7XCOVHLtAfWAIcEO07DXijmu+nM7ASKI7uU6dF26ssX6iibKrgGgXRZ+oQ893sWIPfwdNAc6Bv9B1OJTwcbEGoTTo15vexERhLuM//FPgBKIj238fmMmEAsBgYTLgvn0ooqxuxuTy5gFCeHBd9N9dW8h2eFcWRH31v/6Fs+VAIfBPFnxOd83DCw0qL4lwDDIz5HPOi5SpjqepzRPu/IpRHHQj/jmcCZ5W/jl61uMekOgC9MuvF5iTmj4SmWIcQCpqc6MbRNbox/FByo4zetycxf2yXO2d/YEXMeiHwx5j1c4AXKnnvvcBNMet50U2ma2y8cXyubEIb5j8CDWLOfUO5494kFE6dos+bG7PvIELzgYrO/wAwjtA+urpYVgC7RsujgZdi9h0JFAHZ0XqzKI6WMd/dDTHH9yEkFNnEJDHA9oQCqXHMsScCr0TLL5fcbKP1g6k8idmPkDhZzLY3KJvErI/9ruL8N3BGdbHE8TlOAz6L2dckeu8O5a+jl156JfYV3VNXsvmhzJvABZUc+1vgyZh1J0oIym3rUcn7bwNujZZL7nX5MfvfA06IlmcDR1dwjhHA6+W2/QO4soJjOxFqT5rFbLseuC9aPo1qkpiY920HXAzsEXPuSssXqiibKjh3D8If2gcSlW1VxFHR72DvmPVpwMUx67cAt0XLQwhJTNOY/ZOAP0XL97G5TPgboZYp9tqzCQnFfsQ8aIr2vUXlSczLRA+tovUD2TKJubqaz/0UcH7M5yhJYqqMparPES1/BZwSs+8m4O/lr6PX1r/UnEy21oPASYQb9QPl9rUl/LE4LapiXQm8EG3HzJqY2T/M7GszW0V4mtXSoiZAkYUxy2sIyUlFOhCelADg7kXAMqBjJcdXyN03ufsbhKc5Z0ebiwhPoGI1B1ZH+yi3v2RfRS4iJHfvmdkMM/t1yY6ounlmVN28kvCEK7b53KKY5R+Bpe6+KWYdyn4/38Ysf014glS+OV6XaPuCmN/RPwg1GRC+1/LnqUwHYL5Hd+YKYgBY4qHZAxD3v4HY81cWS3WfA2L+Lbn7mmixsn9PIpIg0T11KTDczHYEdgceBrDQLPZZC53WVwF/Zsv7VPn7SCkzG2yhQ/sSM/ue8ES+/PsrK0c6EWr7y+sCDC65l0T3k5OBHSo4tgOw3N1j7/lfU8OyB8DdlxP6ED0dNYOqrnypqmwqf+7PCMnJaGCxmU20zU2u4/kdlC9/yq/H3ktXeNk+QF8TvqfyugAXlvueO0XHVlSeVFf+xP47qejfTJltZnaomb1joRngSuAwtvzcJeeuKpaqPkeJeP+Wka2gJEa2irt/TWjWdBihg2GspYSbW193bxm9Wrh7yX/eCwlV3IM9dKjfL9pevgNoPL4j3EjCCUJb09aEmoGtkcPmPjEzCM0MYs+9I6Et8gpgQez+aLnCQQTcfaG7n+nuHQhNKu6y0E9mX0KC83OglYdOnt+zdd9FiU4xy50JNVNLyx3zLaEGo03M76i5u/eN9i+o4DyVWQB0NCvTgbdTuWO83HpN/g1UFUt1n6M65eMSkcR6gNCH8hRgiruX/BH8N0Iz0Z7RPeAytvz/X9X/z4cJTZY7uXsL4O8VvL8y37L5Pl9++6sx95KWHkZEO7uCY78DtjOzZjHbOlO7sqcd0DyO8qXSsqmiE7v7w+6+D5ubfd8Y7Yrnd1ATraJYSnQmfE/lfQtcV+57buLuE6i4PKmu/MmPWS9f9kDMvyMLfWMfB8YQmuu1BJ6n8rKnqliq+hzVUdmTAEpipDZOJ1T3lxl9xd2LCW2RbzWzdgBm1tHMhkWHNCMkOSstdDq/shYxTAB+ZWb9o5vTn4F33f2r6t5oZu3M7AQzy4s6Bw4jNEWaGh3yJLCzmf3MzHKBK4D/ufusaP8DwB8tdFLvTeh3cV8l1zreNndcX0G4gRUTvouNhLbUOWZ2BVs+YaupU8ysj5k1IQwx/VhMzQ0A7r4AeBG4xcyam1mWhQ6bP40OmQScZ2b5FjrjXlLF9d4mNKsYZWY5ZnY04YlrVWryb6DSWOL4HNVZRGjfLSLJ8QChic+ZhNqGEs2AVUBRdP+sKFGoSjNCTchaM9ud0DIgXvcA15hZTwt2MbPWwLNALzP7hZk1iF4/MbOdyp/A3b8lNC26PuqsvQuhTPxXPAGY2bFmVhDds9oS+pJ8FNXKQNXlS3VlU+x1CszsgKh8XEu47xZHu2v7O6jIVWbWMHpAdwShv2N5dwNnRbVpZmZNLQzU0IxQnmwk3PMbmNmxVF2eTALOj/7GaElolleVhoS+N0uAjRYGejm4kmOri6Wqz1GdRUBrM2sRx7FSCSUxstXc/XN3/6CS3RcDnwHvRNXU/yE8eYfQdrkxoXbgHUJTs62N4T+EYSYfJzw12RE4Id63E27a8wiJxRhCp8bJ0bmXEDqfXxftH1zu3FcSmiR8DbwK3OzulX2WnwDvmlkR4enh+R7mO5hC+PxzovOspYomFHF6kFDYLSR0OD2vkuN+Sbihf0r4fI8B7aN9d0ex/Zcw2EH52rZS7r6e0Jn/dEL791MIfwysq+w91OzfQHWxVPU5qnM7cJyFkcv+Eud7RCRO0QOltwid5ifH7Po9IfFYTfg/XtMhgs8Brjaz1YQ/4ifV4L1jo+NfJPwRfy+hX91qwh+0JxBqEBayeUCSipxI6H/zHSGxuDIqk+LRkXDfW00YZKAYOCZmf6XlSxxlU6xGwA2Ee+1CQm3PpdG+2v4OylsYxfMd8BChL+MWiVX0d8OZwB3R8Z8RjbwWU56cBiwn9FOqtPyJ4n4R+B/wEaFWZSPhwdoWot/xeYTf/wrC559cybFVxlLV56hO9L1MAL6ImqJpdLKtUDJCj4hsA8yskDAa2T0pjuNdQgfGf6YyDhERST4zG0Ioe/KrOTTZcRxKKHu6VHuwZDzVxIhIrZnZT81sh6g52amEIU+3uoZNRESkOmbW2MwOi8qejoQarCdTHZfUjbRKYszsEAsTMX1mZlu0wbcwgeIj0f53zaxrzL5dLEzaNMPChICVTo4kIglXQGjutZLQaf+4qL+KSMYys+4WJlJ9LNWxiEiFDLiK0JzrI8JcLFekNCKpM2nTnMzC0KpzCGOhzwPeB050909jjjkH2MXdzzKzE4Bj3H2EhSEJPwR+4e7/jTrorSzfmVlEROoHMxtP6Fi82N13jtl+CKEvVDZhIsYb4jjXY+5+XNKCFRGRGkunmpjdCZPSfRF1ppoIHF3umKPZPLrJY8BQMzNCR7z/uft/Adx9mRIYEZF67T7CZLyloodldwKHEiaCPTEaya+fhfkyYl/ttjyliIiki5xUBxCjI2VHZZpHGHGjwmPcfaOFCa5aA70AN7MphAkVJ7r7TRVdxMxGAiMBcnNzB3XuXNXw4+mhuLiYrKx0yjcrlilxQubEqjgTK1PihMyJdc6cOUvdvW2q4yjP3V+LbXIcKX1YBmBmEwkzt19PqLXZKipXkkdxJl6mxKo4EytT4oT4y5V0SmJqIwfYhzCM7RpgqplNc/ep5Q9093HAOICCggKfPXt2nQa6NQoLCxkyZEiqw6hWpsQJmROr4kysTIkTMidWM6tqNu10E8/DslJR0+TrgAFmdmmU7GxB5UryKM7Ey5RYFWdiZUqcEH+5kk5JzHzKzrSaz5Yz35YcMy/qB9MCWEYoiF5z96UAZvY8MJDNkxaKiIjUiLsvA85KdRwiIrKldKpXeh/oaWbdzKwhYeKm8hMQTQZOjZaPA172MDLBFKCfmTWJkpufEia+ExERKRHPwzIREckAaVMTE/VxGUVISLKB8e4+w8yuBj6IZlG/F3jQzD4jzJ56QvTeFWY2lpAIOfC8uz+Xkg8iIiLpqvRhGSF5OYEwY3etmdmRwJEdOmjibRGRupA2SQyAuz8PPF9u2xUxy2uB4yt577+AfyU1QBERyQhmNgEYArQxs3nAle5+b0UPyxJxPXd/BnimoKDgzEScT0Rqb8OGDcybN4+1a9cm7RotWrRg5syZSTt/oqRjnLm5ueTn59OgQYOten9aJTEiIiKJ4O4nVrJ9i4dlIrJtmjdvHs2aNaNr166EGTkSb/Xq1TRr1iwp506kdIvT3Vm2bBnz5s2jW7duW3WOdOoTIyIikpHM7EgzG1dUVJTqUEQksnbtWlq3bp20BEa2npnRunXrWtWSKYkRERGpJXd/xt1H5uXlpToUEYmhBCZ91fZ3oyRGREREREQyipIYEREREZEkuO666+jbty+77LIL/fv359133wVgyJAhfPDBB3UWx1dffcXgwYPp0aMHI0aMYP369Vsc89BDD9G/f//SV1ZWFtOnTwdg/fr1jBw5kl69etG7d28ef/zx0vdNmjSJPn360LdvX046qeyAj6tWrSI/P59Ro0Yl/DOpY7+IiIiISIK9/fbbPPvss3z44Yc0atSIpUuXVpg81IUrr7ySCy64gBNOOIGzzjqLe++9l7PPPrvMMSeffDInn3wyAB9//DHDhw+nf//+QEjG2rVrx5w5cyguLmb58uUAzJ07l+uvv54333yTVq1asXjx4jLn/NOf/sR+++2XlM+kmhgREZFaUsd+ESlvwYIFtGnThkaNGgHQpk0bKppLasKECfTr14+dd96Ziy++uHR7Xl4eF1xwAX379mXo0KEsWbIEgM8//5xDDjmEQYMGse+++zJr1qwq43B3Xn31VY477jgATj31VJ566qkq3zNhwgROOOGE0vXx48dz6aWXApCVlUWbNm0AuPvuuzn33HNp1aoVAO3atSt9z7Rp01i0aBEHH3xwldfaWkpiREREakkd+0UywJAhW77uuivsW7Om4v333Rf2L1265b5qHHzwwXz77bf06tWLc845h1dffXWLY7777jsuvvhiXn75ZaZPn877779fmmD88MMP7LbbbsyYMYOf/vSnXHXVVQCMHDmSv/71r0ybNo0xY8ZwzjnnVBnHsmXLaNGiBTk5oQFWfn4+8+fPr/I9jzzyCCeeGEaqX7lyJRBqVQYOHMjxxx/PokWLAJgzZw5z5sxh7733Zo899uCFF14AoLi4mAsvvJAxY8ZU+z1tLSUxIiIiIiIJlpeXx7Rp0xg3bhxt27ZlxIgR3FeSFEXef/99hgwZQtu2bcnJyeHkk0/mtddeA0KNx4gRIwA45ZRTeOONNygqKuKtt97i+OOPp3///vzmN79hwYIFCY373XffpUmTJuy8884AbNy4kXnz5rHXXnvx4Ycfsueee/L73/++dN/cuXMpLCxkwoQJnHnmmaxcuZK77rqLww47jPz8/ITGFkt9YkRERERk21dYWPm+Jk2q3t+mTdX7K5Gdnc2QIUMYMmQI/fr14/777+e0006r8XkgDElcXFxMy5YtSzvcV2bYsGEsWrSI3Xbbjbvvvpvvv/+ejRs3kpOTw7x58+jYsWOl7504cWJpLQxA69atadKkCcceeywAxx9/PPfeey8QanUGDx5MgwYN6NatG7169WLu3Lm8/fbbvP7669x1110UFRWxfv168vLyuOGGG7bqs1dENTEiIiK1pD4xIlLe7NmzmTt3bun69OnT6dKlS5ljdt99d1599VWWLl3Kpk2bmDBhAj/96U+B0CTrscceA+Dhhx9mn332oXnz5nTr1o1HH30UCP1d/vvf/25x7SlTpjB9+nTuuecezIz99tuv9Fz3338/Rx99dIUxFxcXM2nSpDL9YcyMI488ksIoiZs6dSp9+vQBYPjw4aXbly5dypw5c+jevTsPPfQQ33zzDV999RVjxozhl7/8ZUITGFASIyIiUmvqEyMi5RUVFXHqqafSp08fdtllFz799FNGjx5d5pj27dtzww03sP/++7PrrrsyaNCg0gSjadOmvPfee+y88868/PLLXHHFFUAYCvnee+9l1113pW/fvjz99NPVxnLVVVcxduxYevTowbJlyzj99NMBmDx5cul5AV577TU6depE9+7dy7z/xhtvZPTo0eyyyy48+OCD3HLLLUCo8WndujV9+vRh//335+abb6Z169Zb/Z3VhJqTiYiIiIgk2KBBg3jrrbcq3FcY0zTtxBNPLNN8K9bYsWO32NatW7fSDvTx6tatG++9994W24866iiOOuqo0vUhQ4bwzjvvbHFcly5dSvvqxDIzxo4dW2GcJU477bStbkJXFdXEiIiIiIhIRlESIyIiIiKSZtTHrmpKYkRERERkm+TuqQ5BKlHb342SGBERkVrS6GQi6Sc3N5dly5YpkUlD7s6yZcvIzc3d6nOoY7+IiEgtufszwDMFBQVnpjoWEQny8/OZN28eS5YsSdo11q5dW6s/xOtKOsaZm5tbq8kwlcSIiIiIyDanZALGZCosLGTAgAFJvUYiZEqcNaHmZCIiIiIiklGUxIiIiIiISEZREiMiIiIiIhlFSYyIiIiIiGQUJTEiIiK1pCGWRUTqlpIYERGRWnL3Z9x9ZF5eXqpDERGpF5TEiIiIiIhIRlESIyIiIiIiGSWtkhgzO8TMZpvZZ2Z2SQX7G5nZI9H+d82sa7n9nc2syMx+X2dBi4iIiIhIncpJdQAlzCwbuBM4CJgHvG9mk93905jDTgdWuHsPMzsBuBEYEbN/LPDvuopZREQkUxx2++t8umDV5g0vPAdAn/bNef78fVMUlYjI1kmnmpjdgc/c/Qt3Xw9MBI4ud8zRwP3R8mPAUDMzADMbDnwJzKibcEVERDLHwM4taZBtZbY1yDYGdmmVoohERLZeOiUxHYFvY9bnRdsqPMbdNwLfA63NLA+4GLiqDuIUERHJOOcN7UmWlU1iss04b2iPFEUkIrL10qY5WS2NBm519yIrd4Muz8xGAiMB2rZtS2FhYdKDq62ioiLFmWCZEqviTKxMiRMyK1bJDO2a53L8oHwe+eBbNmxyGmQbx+3WiXbNclMdmohIjaVTEjMf6BSznh9tq+iYeWaWA7QAlgGDgePM7CagJVBsZmvd/Y7yF3H3ccA4gIKCAh8yZEiCP0biFRYWojgTK1NiVZyJlSlxQmbFKmGyS+DIDh06pDqUKp03tCePTpsHuGphRCSjpVNzsveBnmbWzcwaAicAk8sdMxk4NVo+DnjZg33dvau7dwVuA/5cUQIjIiKSDJky2WW75rmcslNLLnj9IU7u00q1MCKSsdKmJsbdN5rZKGAKkA2Md/cZZnY18IG7TwbuBR40s8+A5YRER0REROJ03vrPaPHWBIrnToU118GvfgXZ2akOS0SkRtImiQFw9+eB58ttuyJmeS1wfDXnGJ2U4ERERLYBLX71C6at+4FBDz4IZ54Jd9wBt90Gar4oIhkknZqTiYiISB1Y3bs3vPEGTJwIK1bAjTemOiQRkRpREiMiIlIfmcGIETBrFowfH7Z9+SVccgmsWlX1e0VEUkxJjIiISH3WuDG0bx+Wp0yBm26Cnj3h7rth06bUxiYiUgklMSIiIhKcdRa8/z706gUjR8LAgfDKK6mOSkRkC0piREREZLNBg+C112DSJPj+e3jssVRHJCKyBSUxIiIiUpYZHH88zJwJ118ftr31Flx0UUhsRERSTEmMiIiIVKxxY2jePCy//jqMGRP6y4wbp/4yIpJSSmJERESkehdfDB98AL17w29+E/rLFBamOioRqaeUxIiIiEh8Bg6EV18N/WRWrQpJjYhICuSkOgAREZFMZ2ZHAkd26NAh1aEknxn87Gdw+OGQFT0LnTgxJDR//CO0bJnS8ESkflBNjIiISC25+zPuPjIvLy/VodSd3Fxo2DAsf/wxjB0b+sv84x+wcWNqYxORbZ6SGBEREamd664LNTF9+oS5ZgYODAMBiIgkiZIYERERqb2Sjv6PPQZFRbB4caojEpFtmPrEiIiISGKU9Jc54ojNTc1uugkWLoQrrlB/GRFJGNXEiIiISGI1ahQSGoDvvoPbboMePeBvf1N/GRFJCCUxIiIikjy33QYffgg77wznnAP9+8M776Q6KhHJcEpiREREJLn694dXXoEnnoB16yAnas3untKwRCRzKYkRERGR5DODY46BWbNgt93CtnPOgd/9DlasSG1sIpJxlMSIiIhI3cnODj+Li8PP224L88vceaf6y4hI3JTEiIiISN3Lygod/T/6CPr1g1GjYNddw7qISDWUxIiIiEjq7LorvPwyPPlkqKVp2zZsL6mpERGpgOaJERGRtGJmBpwMdHf3q82sM7CDu7+X4tAkWcxg+HA4+uiw7A6HHsqOzZuHJKdVq1RHKCJpRjUxIiKSbu4C9gROjNZXA3emLhypMyVzy6xfD926kf/EE2F+GfWXEZFylMSIiEi6Gezu5wJrAdx9BdAwtSFJnWrUCP7+dz4YNy4Mz1zSX2b27FRHJiJpQkmMiIikmw1mlg04gJm1BdRBoh76Yccd4T//gaefDn1lOnYMO9avT21gIpJySmJERCTd/AV4EmhnZtcBbwB/Tm1IkjJmcNRRUFgIeXkhgRkwAM47D5YvT3V0IpIiSmJERCStuPtDwEXA9cACYLi7P5raqCRtrFsH++0X+sn06AF//Sts2JDqqESkjimJERGRtOPus9z9Tne/w91npjoeSSPNmoX5ZaZPh4EDQ43MLrvAvHmpjkxE6lBaJTFmdoiZzTazz8zskgr2NzKzR6L975pZ12j7QWY2zcw+jn4eUOfBi4hIQpjZ/WbWMma9lZmNT0Ecw83s7qjcObiury/V6NcPXnoJJk8Oyx06hO1FRamNS0TqRNokMVEnzjuBQ4E+wIlm1qfcYacDK9y9B3ArcGO0fSlwpLv3A04FHqybqEVEJAl2cfeVJSvR6GQDanICMxtvZovN7JNy26t8WBbL3Z9y9zOBs4ARNbm+1BEzOPJImDQJsrJg2TLo3h3+7//Csohss+JOYqJakJPM7DIzu6LklcBYdgc+c/cv3H09MBE4utwxRwP3R8uPAUPNzNz9I3f/Lto+A2hsZo0SGJuIiNSdLDMrnd3QzLaj5pMz3wccEruhsodlZtbPzJ4t92oX89Y/onlqMoMZHHcc3HVX6C9z++3qLyOyjTJ3j+9AsxeA74FpwKaS7e5+S0ICMTsOOMTdz4jWf0GYK2BUzDGfRMfMi9Y/j45ZWu48Z7n7gZVcZyQwEqBt27aDJk2alIjwk6qoqIi8vLxUh1GtTIkTMidWxZlYmRInZE6s+++//zR33y2R5zSzXwKXA5MAA44D/uzuD9TwPF2BZ91952h9T2C0uw+L1i8FcPfrK3m/ATcAL7n7f6q4jsqVJNnaOJt++SU73nkn202bxppOnZh2111sSuLnzZTvEzInVsWZWJkSJ9SgXHH3uF7AJ/EeuzUvQiF1T8z6L4A7yscA5Mesfw60iVnvG23bMZ5r9urVyzPBK6+8kuoQ4pIpcbpnTqyKM7EyJU73zIkV+MCTUyb0AUYB5wJ9tvIcXWPLrnjKmXLvP4/w4O7vhIdjKlfqWK3iLC52f+YZ9wsu2LxtyZJax1SRTPk+3TMnVsWZWJkSp3v85UpN+sS8ZWb9anB8Tc0HOsWs50fbKjzGzHKAFsCyaD2fMK/AL9398yTGKSIiSRQ1B+4PNAdaA8cluPlyXNz9L+4+yN3Pcve/1/X1pZbM4IgjYOzYsD57NnTqBKNGwdKlVb9XRNJeTZKYfYBpUYfI/0Ujgf0vgbG8D/Q0s25m1hA4AZhc7pjJhI77EJ6ovezuHo1i8xxwibu/mcCYRESk7j1N6AO5Efgh5lVb8Tws2ypmdqSZjSvSyFjpq00bOP10+PvfoWdPuO22MHGmiGSkmnSUPDRpUQDuvtHMRgFTgGxgvLvPMLOrCdVKk4F7gQfN7DNgOSHRgdDkoAcQO9jAwe6+OJkxi4hIUuS7+yHVH1ZjpQ/LCMnLCcBJiTixuz8DPFNQUHBmIs4nSdC6NdxxB5x9NlxwQXjdey98+CE0aJDq6ESkhuJOYtz962i0mJ5AbsyurxMVjLs/DzxfbtsVMctrgeMreN+1wLWJikNERFLqLTPr5+4fb+0JzGwCMARoY2bzgCvd/d6KHpYlJGLJHH37wpQp8PzzoYlZSQLzzTfQuXNqYxORuMWdxJjZGcD5hOr36cAewNuAJpYUEZFE2gc4zcy+BNYRRihzd98l3hO4+4mVbN/iYZnUQ2Zw+OHhBTB1KgwbBr/5DVx1VWh6JiJprSZ9Ys4HfgJ87e77EyYeW5mMoEREpF47lFDrfzBwJHBE9DNtqU9MhuvfPzQz+8c/wvwyt96q/jIiaa4mfWLWuvtaM8PMGrn7LDMrSFpkIiJSL9VF8+VEU5+YDNe6Nfz1ryGR+d3vwuvRR+HNN0OtTQUOu/11Pl2wavOGF54DoE/75jx//r51EbVIvVaTJGZeNArYU8BLZraCNC5QREQkM6n5sqRMnz7wwgvw73/DqlUhgdm0CebMgZ12KnPowM4tmbt4NRs2bZ40vEG2MbBLq7qOWqReirs5mbsf4+4r3X008CfCSGHDkxSXiIjUX2q+LKl16KEwYkRYvv9+2HlnOOccWLKk9JDzhvYkq1wtTbYZ5w3tUZeRitRbcScxFpxiZle4+6uEp2P9kxWYiIjUW2uj0ShLmy8Dad18WX1itmHDh4cJMseNC/PLjB0L69fTrnkuxw/Kp0F2SGQaZBvH7daJds1yqz6fiCRETTr23wXsCZSM+LIauDPhEYmISH1Xvvny06R582V3f8bdR+bl5aU6FEm07baD22+Hjz+GvfaCCy+En/0MKFsbo1oYkbpVkz4xg919oJl9BODuK8ysYZLiEhGResrdj4kWR5vZK0AL4IUUhiQS+sQ8/3zoL9O4MQDtsjYyqs0axi7MVS2MSB2rSRKzwcyyAQcws7ZAcVKiEhERAaLmyyLp49BDNy/fcgujrr6abj8ZxuCRf09dTCL1UE2ak/0FeBJoZ2bXAW8Af05KVCIiUu+Y2RvRz9VmtirmtdrMVlX3fpE693//h40axWEfvEjbAf1gzBhYty7VUYnUC3HXxLj7Q2Y2DRhKmD15uLvPTFpkIiJSr7j7PmZmQF93/ybV8dSEmR0JHNmhQ4dUhyJ1Keov88GgQew+aRL84Q8wYwb885+pjkxkm1eT5mREI8TMSlIsIiJSz7m7m9lzQL9Ux1ITmuyyflvTuTM8+yxMmQL5+WHjvHmwbBnsumtqgxPZRlWbxJjZ5Kr2u/tRiQtHRESED83sJ+7+fqoDEamRYcM2L191FYwfD2ecAddcA+3apS4ukW1QPDUxewLfAhOAdwlNyURERJJlMHCymX0N/EAod9zdd0ltWCI1cNNNkJcHd9wBEybAn/4E550HjRqlOjKRbUI8ScwOwEGE+WFOAp4DJrj7jGQGJiIi9daw6g8RSXOtWsGtt8JZZ4W5ZS66KDQvu+GGVEcmsk2oNolx902E8flfMLNGhGSm0Myucvc7kh2giIjUL+7+tZm1AnoCsRNvpPWElyIVKijY3F+mf/+w7eOPobhY/WVEaiGuIZbNrJGZHQv8CziXzcMti4iIJJSZnQG8BkwBrop+jk5lTNUxsyPNbFxRUVGqQ5F0NWwYbL99WL70UhgwAEaOhEWLUhuXSIaqNokxsweAt4GBwFXu/hN3v8bd5yc9OhERqY/OB34CfO3u+wMDgJUpjaga7v6Mu4/My8tLdSiSCR58EC64IAzF3LNn6D+j+WVEaiSemphTCFX65wNvafKxuvPUR/PZ+4aXOe2FH9j7hpd56iPljSJSL6x197UQWgJEw/sXpDgmkcRp1QpuuSXMKbP//nDxxfCPf6Q6KpGMEk+fmLianEliPfXRfC594mN+3LAJgPkrf+TSJz4GYPiAjqkMTUQk2eaZWUvgKeAlM1uB+sPItqhXL3j6aXj5Zdhrr7DtlVegZcvQ3ExEKqUEJU3dPGV2aQJT4scNm7j+3zNx9xRFJSKSfO5+jLuvdPfRwJ+Ae4HhKQ1KJJkOOAByc8E91MoMGhTml1m4MNWRiaSteIZYlhT4buWPFW5ftGod/Ua/SO8dmtG7fTN679Ccndo3p/cOzWjaSL9OEclcZnYn8LC7v1myzd1fTWFIInXLDF58Ea69Fv7yF5g0CS6/HM4/PyQ5IlJKNTFpqkPLxhVub9m4AccO7IgZPP3Rd/zxqU/42d/e4l/vhJYWS4vWcetLc/h62Q91Ga6ISCLMAcaY2VdmdpOZqT2N1D8tW8KYMZv7y1xyCTz3XKqjEkk7enSfpv4wrKBMnxiAxg2yGX1U39I+Me7O/JU/MmvBanpuH0bEmbNoNX95eS5792hDl9ZNmTpzEXe88hm9d2hOn/bN6N2+OQU7NKN5boOUfC4Rkcq4++3A7WbWBTgBGG9mjYEJhEmW56Q0wCqY2ZHAkR06dEh1KLKt6Nkz9Jd5+23YY4+w7ZFHwvaBA1Mbm0gaiCuJiSYdOxI4BugFfAk8DTzt7ouTF179VZKo3DxlNvNX/kjHlo35w7CCMp36zYz8Vk3Ib9WkdNteO7bh06sOISfbAMgyo2F2Fs9/vIAJ731Telx+q8ZlEpshBW1p0lA5rYiknrt/DdwI3BjVxowHrgCyUxpYFdz9GeCZgoKCM1Mdi2xj9twz/Ny4ES67DL78En71K7juOthhh9TGJpJC1f7VamZPAK2A54CL3X2OmXUGjgb+ZWYN3X1IcsOsn4YP6MjwAR0pLCxkyJAhcb+vccPN5fz+vduxf+92uDsLV61l5oJVzFywmpkLVjFr4WpenrWIYoeP/nQQTRrCpA++5aNvVvLnY3bGzNiwqZgG2Wp1KCJ1x8xygEMJtTFDgULSfLJLkaTLyYFp00Lycvvtob/MZZeF+WbUX0bqoXgevf/a3VfGbnD3b4C/An+NhsGUNGdmtG/RmPYtGnNA7+1Lt6/dsInPlxTRqmlDAOav+JFZC1dhFmpyRj7wAbMXrg6DB5QOJNCMrq2bkqPkRkQSyMwOAk4EDgPeAyYCI91dnfxEIPSXuflm+M1v4Pe/D0nMAQfA4MGpjkykzsUzT8xKM+tNqHkpacs0H5js7jPLJzi1YWaHALcTmgzc4+43lNvfCHgAGAQsA0a4+1fRvkuB04FNwHnuPiVRcW3Lchtk07dDi9L1Cw7qxQUH9SpdP7DP9jRv3IBZC1bz6pwlbCwOwzs3ysmi1/bN6L1DM/bo3pqfDcqv89hFZJtzKfAwcKG7r0h1MCJpq0cPeOqp0Pm/b9+w7fbbYZ99wvDMIvVAPM3JLiY8GZtIeDIGkA9MMLOJ5RONrWVm2cCdwEHAPOB9M5vs7p/GHHY6sMLde5jZCYQ20yPMrA+h2UFfoAPwHzPr5e5lJ1qRGjt5cBdOHtwFgHUbN/HZ4iJmLVjNrIWhWdrLsxbz/Y8bSpOYY+96k4P67MDZQ3bE3flscRFd2zRVk7Rt1FMfzd/cb+udl7fotyVSE+5+QKpjEMkoJQlMURHceGNoWnbaaaHJWfv2KQ1NJNniaU52OtDX3TfEbjSzscAMICFJDLA78Jm7fxGdfyKh9ic2iTmaze2iHwPusNDu6WhgoruvA740s8+i872doNgEaJQTam1ia24gNEkDKHana+umtMkLTdOWFK3joFtfo2F2Fj3a5bFT+9AUraRJWuu8RnX+GSRxnvpofpkR9Oav/JFLn/gYQIlMLSgxFJEay8uDmTPhz3+G224r21+mccVTNohkuniSmGJC7cbX5ba3j/YlSkfg25j1eUD5Rp6lx7j7RjP7HmgdbX+n3HsrLPXNbCQwEqBt27YUFhYmIvakKioqyog41/zwA0dtb1C0ksLCz/lxozNyl0Z8u7qYb1f/wNQZq3n8Qy89vkUjo1NeFod1b0Cf1tmlTdVysizpsWbKd5oucRa78+NGWLPB+XFjWL7jo7X8uKHscT9u2MQ1T/+XhV/OYsmaYrKzjCyDLIPs6GfJcrYZO7UOg1As+qGY9cXQqVmosVv6YzEbi8seb9F7Yrc1zK7Zv5V0+T4r89Z3G7jvk/Wsj+6s81f+yEWPTufTmZ+yVwcNiy4iVWjRItTGjBwJf/gDXHMNnHwydOmS6shEkiKeJOa3wFQzm8vmJKMz0AMYlaS4ksbdxwHjAAoKCrwmo36lSk1HJ0uViuI8tNwxy4rWMWvh6tJR0mYtXMVOOxcwpKAdb362lNP++R4TR+7BoC7b8dXSH/hm+Rp6t29G27xGpYMNJCvWdJSIOIuLndXrNrJ67QZWr90YvcLy/r3b0aJxA975YhmT//sdVxzRh9wG2fzzzS+Z8N43pccXrdsY9/WWr3VmrNuOZz75rsrjmjbMZsbVQwE4b8JHfDz/e175/RAARvzjbd79cnmV7+/Wpmnp8SfdHZ5hPHxmmEvhqDve4Nvla8jOyiIny8iOXuvWZtEsz8jJMnbNb8mNx+1Sev0d2+Zx/oE9ATj7X9PYsKmYLDNyso3srKyQeGVlkZ0Vfg7o1JKf/6QTALe8OJsBnVtyQO/tWb+xmH+8+jnZ2eE6WRZ+ZmdnkR0tZ2UZBds3o19+CzZuKmbqrMX03qEZl7/zbmkCU2J9MTz3TTaXnTQkru9fROq5HXeEJ56Ar78OCYx7mDDz+ONht91SHZ1IwsTTsf8FM+tFaJ4V27H//QT3OZkPdIpZz4+2VXTMvGgIzhaEDv7xvFfSQOu8RuzdoxF792izxb7tm+dy+j7d6dYmTNz57P++Y8yLYW671k0bhhHSdgjz2vTeoRk9t8+jUU7aThuREMXurCpNPsr+XLV2I0N6taXTdk34ZP73jHvtC/4wrIBO2zXh6enzufHfs0ICsn4j7hWf/9n/24cWHVvw9bIfeHHGQn53UC9yG2TTonEDurfJo1luDs1yG0Q/c2jeuAHNo22/fWQ6S1av2+KcHVo25qqj+nLRsAI2FTsbi51idzZucjYVO5vc2VRc9i/1kft1Z/XazYnS+UN7sqRoXZn3bCx2iqPzbSouplnMhK1H7Vp2gsEDd9qeJavXhWtt2hzDdwvW0bptHpuKnbbNNjdnzIlqjEosK1rPD+s3hmtHr43llrOM0iTmwXe+ZmOxc0Dv7Vm7cRO3vFT9nIwj9+tOv/wWrNmwid88OI0/Hr4T3638scJjK9u+LcrUeck02aWknZIamO++g/vug5tuglNPpeERR6Q0LJFEiWt2Q3cvpmxzrWR4H+hpZt0ICcgJwEnljpkMnEro63Ic8LK7u5lNBh6O+ul0AHqyeRACyRA92uVxyaG9S9d/sUdXBnXZLprTJsxr8+A7X7NuY/gDODvL2LFtUx4/ey+a5Tbg2+VraJiTxfbNKx8vvy77GxQXOz+sD8lGRQnI6rUb2GvHNvTv1JJvl6/hyskzOGfIjuzWdTvemLuUs/81jaJ1G/EpL1Z6jb+dPJBO2zWhaN1G/jdvJavWhvZd7ZrlslePNqVJSPPcHJqXJiObk5KOrUJb6RE/6cyIn3QuPe+xA/M5dmDVI85dfthOZfrEADRukM0fhhWwXdOGbBcN2x2PnTuW7We1VwVJblVO2L1zmfXzhvas8LhQs7XlyD1jR/Qvsz7prD1rdP3pVxxcutysUQ5zrzu0TMJTHJsERYlVXm64/TZpkM1z5+1Du2a5/PPNr5hfQcLSoWX9aNOeyfOSabJLSVsdO8LcuaG/zK23MviRR2DWLLjwQvWXkYwWz+hknas7JrLS3VdtbSBRH5dRwBTCEMvj3X2GmV0NfODuk4F7gQejjvvLCYkO0XGTCIMAbATO1chkma9FkwbsuWNr9tyxdem2TcXOl0t/CEnNgtV8vXwNeY3CP+MxL87m/S+X89aloYnSpPe/BYOddmhOz+3zeOGThXF3RHd3fli/iVU/lk8+yjbJ6t+pJQf33YEf1m3ktH++x8mDuzB8QEc+W1zEQbe+WmkNSInLDjP6d2oJwOLVa1mzPsTWoWUuPxuUz/JF8+lX0KO0FqR8EtKqSUgU9ujemsI/7F963vLfWzKUfGelSWHLxuqETpiTqUG20SDOSsKc7KzSwTL+MKyg0sSwntC8ZCLJ0Lw53HADjBzJ8l/9irZ33gnnn5/qqERqJZ6amPvjOMaB+whzuGw1d38eeL7ctitiltcCx1fy3uuA62pzfUl/2VlGj3Z59GiXxxG7lN13+j7dOHKXzU057nnjC+YsKip9n0Hp4AElftywiZunzGb4gI4c//e32KdHW84/sCfrNhaz85VVTzWUnWX8eu+uHNx3BxrlZJX2uwBom9eIUfv3iKkJ2Zx4lNSMNMttQG6D0JG903ZNePb/9i09d/e2eYw+qi+FhUsYsl/3rf26km74gI4MH9AxY/oYpbv6nhjW5bxkIvVS9+7MuOoqhuy8MzRrBhs2wBlnwKhR8JOfpDo6kRqJJ4k5C5jjXt0zZZHU2iW/ZZn1f5+/H98sXxOaoy1YxV9e/qzC95X0N+jeJo92zUM/iUY5WVx+2E7kxSQezXJzSpOPZrk5NG6QXTrYQE52FhNHbm6C1KJJAy48uN48PZcEqs+JYV3NSyZS77WJmuzOnQtTpsADD8AvfxmanHWsHw9NJPPFk8Q8BnQxsznA/4CPS36mcydLkewso1ubpnRr05TD+rXn8Q/nV9nfoGSkKghNgs5M4xoQkW1UXc1LJiIAffrAnDlw/fUwdiw89lgYyezii6Fh/P0aRVKh2mnU3b0f0BY4mzBiTHfgMuB/ZrYwueGJJM4fhhXQuFxHhXrW30Ak3ZXMS1ZeouclE5ESzZuHJGbmTDjssJDIZG/bI3/KtiHe0cnWAe+bWZG7/1/J9mgoTJGMUN/7G4hkgN+yDc1LJpJRuneHRx+FoqKQxKxcCaecAn/6EwwuP/e4SOrFlcTEKNMvxt1XJDAWkaSrz/0NRNJdHc5LJiKVyQtztTF7NkybBnvsEZKZ66+H/KqH3hepS9U2JzOzO83sdDMbACRuynQREZFy3L3Y3d9x98ej1ztKYERSYPDg0F/m0ktDDU2vXnDVVVCslp2SHuKpifkv0B/4JdDMzD4ldLD8FPjU3R9JXngiIlJf1NW8ZCISp2bNwohlZ54ZOvt/8AFkVfv8W6ROVJvEuPu42HUzywf6AbsARwBKYkREJBHqbF4yEamBbt1g0iRYvz6sf/45/PrXcOONobmZSArUtE8M7j4PmAf8O/HhiIhIPaZ5yUTSWcmwy19/HZqa7bknnHxy6C/TqVNqY5N6J54+MZ3jfDWvi4BFRGSb9RjwvZl9YGbjzewCMxtqZu1SHVh1zOxIMxtXVFSU6lBEku+AA8JEmZdfHoZkLiiAa69NdVRSz8RTE6PqfRERSTp372dmjQjNlZ8HfiA0W+5rZrj7DikNsAru/gzwTEFBwZmpjkWkTuTlhcTljDNCf5nFMfOfu4NpLChJrnj6xOxfF4GIiIhoXjKRDNO1KzzyCGyKBhF87TW46CK47Tb1l5GkiqtPjJn1Bo6m7Lj9T7v7rGQFJiIi9ZrmJRPJJNnZ4efq1fDNN6G/zEknwQ03qL+MJEU8fWIuBiYS5oh5L3oZMNHMLklueCIiUl9oXjKRbcDhh4dO/3/8IzzxROgvM2ZMqqOSbVA8NTGnA33dfUPsRjMbS5gv5oZkBCYiIvWO5iUT2Rbk5cE114T+MpdcAjnRn5slE2VqrhlJgHiSmGKgA/B1ue3to30iIiK1pnnJRLYxXbrAhAmhoz/Agw/CnXeG/jJ77ZXS0CTzxZPE/BaYamZzgW+jbZ2BHsCoJMUlIiL1nOYlE9lGlIxU1qwZzJ8Pe+8NJ5wQJsvs3Dm1sUnGimd0shfMrBewO2U79r/v7puSGZyIiNQfZhbvXzMr3X1VUoMRkcQ79lg4+GC46Sa4+WZ46qnQX+bcc1MdmWSgapMYM8ty92LgnWr2i4iI1IbmJRPZ1uXlwdVXb+4v0zF6Pr5+feg7o/4yEqd4mpO9ZGZLgaeA59x9lZk1AQ4BjiG0V+6ftAhFRKRe0LxkIvVI587w8MOb1//8Z3juudBfZu+9UxaWZI54mpMNNbM+hHlinjOzhoQO/VOAW939wyTHKCIi9YTmJROpp3baCe65B/bZB0aMoNHw4amOSNJcXJNduvunhCEurzezxu7+Y3LDEhGR+iaal+xEwtxk70Wb8wnzkk10dw3pL7KtGjECjjgi9JW56SZ2f/JJWLsWTjst1ZFJmooriSnnUjPLAaYD0919TmJDEhGRekrzkonUZ02bwujRcPrpLP31r9l+113D9qIiaNJE/WWkjBr/a3D3K4Dbge+BY8zs7oRHJSIi9VHJvGTlaV4ykfqkUydmXn45DBgQ1keNgt13hzfeSG1cklbiGZ2sK3AusCOwnFAD84y7TyH0ixEREUmE36J5yUSkvGHDYOpU2Hdf+PnPw/wyXbumOipJsXhqYp4GZgF3AgcBuwKvmdmdZtYomcGJiEj94e4vAL2AqwgPyaYAo4GCaJ+I1EcnngizZoWmZs88A717wxNPpDoqSbF4kphsd7/X3acCy939TEKtzFfAuGQGJyIi9UfJvGPu/o67Px693imZWNnM1CBepL5q2hSuvBLmzIGTToI99gjbly6FYrU2rY/iKRD+Y2Yl1fgO4O4b3f1mYM9EBGFm25nZS2Y2N/rZqpLjTo2OmWtmp0bbmpjZc2Y2y8xmmJk6foqIZKaXzOwRMzvRzJpD6T3+WDN7EKjTIf3NbCcz+7uZPWZmZ9fltUWkEvn5MH48dOgA7nDssfCTn8Drr6c6Mqlj8SQxvwNamNkHQEczG2lmp5jZncCyBMVxCTDV3XsCU6P1MsxsO+BKYDCwO3BlTLIzxt17AwOAvc3s0ATFJSIidcTdhxKaknUlzEv2LqFM2IUwL1n/eM9lZuPNbLGZfVJu+yFmNtvMPjOzLcqacvHMdPezgJ8Dmn1PJB2dfTYsXgz77Rf6y3z5ZaojkjpSbRITVe1fB+wHnAnsAAwEPgESlSwcDdwfLd8PDK/gmGHAS+6+3N1XAC8Bh7j7Gnd/JYp1PeFJXX6C4hIRkTrk7p+6+/Xuvi8wxN33dPfRWzGx8n3AIbEbzCyb0L/zUKAPcKKZ9TGzfmb2bLlXu+g9RwHPAc/X9rOJSIKZhf4ys2fDVVfBc8+FSTOnTk11ZFIHzN2rPyh04L8I2AsoIiQKk9z984QEYbbS3VtGywasKFmPOeb3QK67Xxut/wn40d3HxBzTMortQHf/opJrjQRGArRt23bQpEmTEvERkqqoqIi8vLxUh1GtTIkTMidWxZlYmRInZE6s+++//zR33y0Z5zazqwmjaE5nK+Yli0bXfNbdd47W9wRGu/uwaP1SAHe/Po5zPefuh1eyT+VKkijOxMuUWLcmzoZLltB54kS+OPNMinNzabRwIevatoXs7CRFuW1/n6kSb7kS72SXNwNNCM28TgNaA+PN7G53/1c8JzCz/xBqccq7PHbF3d3Mqs+stjx/DjAB+EtlCUx0/nFEAxIUFBT4kCFDanqpOldYWIjiTKxMiVVxJlamxAmZFWuyuPsVZrY90J8wL1mPaHCZrdWRzUM3A8wjNFGukJkNAY4FGlFFTYzKleRRnImXKbFudZzHHx+a46xbB336QIsWcNttoblZEmzz32caizeJ2RU42t1Xmtnu7r53VDtTCMSVxLj7gZXtM7NFZtbe3ReYWXtgcQWHzQeGxKznR9cvMQ6Y6+63xROPiIikl3Sbl8zdCylbzohIpmjYEK67Di66CH76UzjuOLjpJujWLdWRSYLEO1zlzTHHLjWzscCpwLoExTE5Oh/Rz6crOGYKcLCZtYo69B8cbcPMrgVaECZKExGRzJTsecnmA51i1vOjbSKyrTGDE04I88tccw08/3yYX+ajj1IdmSRIXEmMuz/r7suj1eOBD4A84KQExXEDcFA0S/OB0TpmtpuZ3RPFsBy4Bng/el3t7svNLJ/QJK0P8KGZTTezMxIUl4iI1J1kz0v2PtDTzLqZWUPgBMJDtFozsyPNbFxRUVEiTiciidKkCfzxj2F+mUsvhV13Dds/+QQ2bUptbFIr8TYnKxWNAPZwIoNw92XA0Aq2fwCcEbM+Hhhf7ph5gCUyHhERSYn/mNkod7+DmHnJgJvNrKad+icQmiC3MbN5wJXufm8079kUIBsY7+4zEhG4uz8DPFNQUFCbPjsi9dpht7/OpwtWbd7wwnMA9GnfnOfP37d2J+/YEUaPDsvLl8M++0DXrqG/zDbWV6S+0OzHIiKSLhI2L5m7n+ju7d29gbvnu/u90fbn3b2Xu+8YTR8gImliYOeWNMgu+1y6QbYxsEuFc6BvvVat4B//gBUrYP/9w4SZnydkwF2pQ0piREQkLdTRvGRJoeZkIrV33tCeZFnZJCbbjPOG9kjshcxgxIjQX+baa+HFF8NIZt98k9jrSFIpiRERkbQRdeC/EDgb6AcsAV5095WpjKs67v6Mu4/MlHkYRNJRu+a5HD8ov7Q2pkG2cdxunWjXLDc5F2zcGC6/PPSXufVW6Nw5bH/rLfWXyQBKYkREJJ3cDHQhzEs2j83zkp2S0qhEpE7E1sYkpRamIh06wDnnhOXPPw9zygwaBK+8kvxry1ZTEiMiIulkV+D37v5fYHd3/z1hSP1zUxuWiNSFktoYg+TWwlSme3eYMAFWroQDDlB/mTSmJEZERNJJsuclE5E0d97QnvRslVU3tTDlmcHxx8PMmWGyzBdfhAED4Pvv6z4WqZKSGBERSRt1MC9ZUqhjv0jitGuey2WDG9d9LUysxo3hsstg7lwYPx5atAjbn3tO/WXShJIYERFJS+6+3t0fdvex7v5dquOpijr2i2yj2reH444Ly2+/DUccAQMHwssvpzYuURIjIiIiIlKtPfaARx+FVatg6FAYPpzG8+alOqp6S0mMiIiIiEh1zEKtzMyZcP31MHUq/S+4ADZsSHVk9ZKSGBERkVpSnxiReiQ3Fy65BObOZebll0ODBrBxIzz0UPgpdUJJjIiISC2pT4xIPbTDDqzs3z8sT54Mp5wSRjKbOjWlYdUXSmJERERERGrjmGPgscegqAgOPBCOPjqMbCZJoyRGRERERKQ2zOBnPwv9ZW64IYxe9vOfg3uqI9tmKYkREREREUmE3Fy4+OJQC3PffSG5WbUK7r5b/WUSTEmMiIiIiEgi7bAD7LprWH7oIRg5Evr3h5deSmlY2xIlMSIiIrWk0clEpFJnnQWPPw5r1sDBB8NRR8GcOamOKuMpiREREakljU4mIpUyg2OPDf1lbrwRCgvhd79LdVQZT0mMiIiIiEiyNWoEF10U+svccUfY9tVXcNdd6i+zFZTEiIiIiIjUle23h65dw/KDD8K554b+My++mNKwMo2SGBERERGRVPjjH+HJJ2HdOhg2DI44AmbPTnVUGSEn1QGIiIiIiNRLZjB8OBx6KPz1r3DNNXD77aGJWS0ddvvrfLpg1eYNLzwHQJ/2zXn+/H1rff5UU02MiIiIiEgqNWoEv/996C9zzTVh2zvvwJ13bnV/mYGdW9Ig28psa5BtDOzSqrbRpgUlMSIiIrWkIZZFJCHatYPWrcPyxIkwalToLzNlSo1Pdd7QnmRZ2SQm24zzhvZIRKQppyRGRESkljTEsogk3K23wlNPhf4yhxwChx8Os2bF/fZ2zXM5flB+aW1Mg2zjuN060a5ZbpICrltKYkRERERE0o0ZHH00zJgBY8bAG2/A5Mk1OkVsbcy2VAsDSmJERERERNJXo0Zw4YXw2Wdw/vlh2xNPhIEANmyo8q0ltTEG21QtDKRJEmNm25nZS2Y2N/pZYY8jMzs1OmaumZ1awf7JZvZJ8iMWEREREalDbduGhAZCjcx558Euu8C//13l284b2pOerbK2qVoYSJMkBrgEmOruPYGp0XoZZrYdcCUwGNgduDI22TGzYwH1qBQRERGRbds//xkSmU2b4LDDwquS/jLtmudy2eDG21QtDKRPEnM0cH+0fD8wvIJjhgEvuftyd18BvAQcAmBmecDvgGuTH6qIiIiISAqZwZFHwiefwC23wFtvwccfpzqqOpUuk11u7+4LouWFwPYVHNMR+DZmfV60DeAa4BZgTdIiFBERERFJJw0bwu9+B6edBq2iBkp//SsUF8M550CDBikNL5nqLIkxs/8AO1Sw6/LYFXd3M/ManLc/sKO7X2BmXeM4fiQwEqBt27YUFhbGe6mUKSoqUpwJlimxKs7EypQ4IbNiFRGRFNtuu/DTHV55BZ58Ev72Nxg7Fg49NLWxJUmdJTHufmBl+8xskZm1d/cFZtYeWFzBYfOBITHr+UAhsCewm5l9Rfg87cys0N2HUAF3HweMAygoKPAhQyo8LK0UFhaiOBMrU2JVnImVKXFCZsUqYbJL4MgOHTqkOhQRqc/M4PHH4bnnQg3N4YfDsGE0PumkVEeWcOnSJ2YyUDLa2KnA0xUcMwU42MxaRR36DwamuPvf3L2Du3cF9gHmVJbAiIiIJIMmuxSRtGEGRxwR+suMHQvvvUfOmm2vx0W6JDE3AAeZ2VzgwGgdM9vNzO4BcPflhL4v70evq6NtIiIiIiISq2FDuOAC+PZbVvfunepoEi4tOva7+zJgaAXbPwDOiFkfD4yv4jxfATsnIUQRERERkczTtGmqI0iKdKmJERERERERiYuSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDKKkhgREREREckoSmJERERERCSjKIkREREREZGMoiRGREREREQyipIYERGRWjKzI81sXFFRUapDERGpF5TEiIiI1JK7P+PuI/Py8lIdiohIvaAkRkREREREMoqSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDKKkhgREREREckoSmJERERERCSjKIkREREREZGMoiRGREREREQyipIYERERERHJKEpiREREREQkoyiJERERERGRjKIkRkREREREMoqSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDJKWiQxZradmb1kZnOjn60qOe7U6Ji5ZnZqzPaGZjbOzOaY2Swz+1ndRS8iItsqM2tqZh+Y2RGpjkVERDZLiyQGuASY6u49ganRehlmth1wJTAY2B24MibZuRxY7O69gD7Aq3UStYiIpCUzG29mi83sk3LbDzGz2Wb2mZltUdZU4GJgUnKiFBGRrZWT6gAiRwNDouX7gUJCwRFrGPCSuy8HMLOXgEOACcCvgd4A7l4MLE16xCIiks7uA+4AHijZYGbZwJ3AQcA84H0zmwxkA9eXe/+vgV2BT4HcOohXRERqIF2SmO3dfUG0vBDYvoJjOgLfxqzPAzqaWcto/RozGwJ8Doxy90UVXcjMRgIjo9V15Z/Spak2ZEZililxQubEqjgTK1PihMyJtSDVAVTE3V8zs67lNu8OfObuXwCY2UTgaHe/HtiiuVhUpjQl1PD/aGbPRw/Kyh+nciV5FGfiZUqsijOxMiVOiLNcqbMkxsz+A+xQwa7LY1fc3c3Ma3DqHCAfeMvdf2dmvwPGAL+o6GB3HweMi2L6wN13q8G1UkJxJl6mxKo4EytT4oTMidXMPkh1DDVQ0cOwwZUd7O6XA5jZacDSihKY6DiVK0miOBMvU2JVnImVKXFC/OVKnSUx7n5gZfvMbJGZtXf3BWbWHlhcwWHz2dzkDELiUggsA9YAT0TbHwVOT0TMIiIi7n5fqmMQEZGy0qVj/2SgZLSxU4GnKzhmCnCwmbWKOvQfDExxdweeYXOCM5TQhllERCTWfKBTzHp+tE1ERDJMuiQxNwAHmdlc4MBoHTPbzczuAYg69F8DvB+9ri7p5E8YBGC0mf2P0IzswjivOy5xHyGpFGfiZUqsijOxMiVOyJxYMyVOCGVHTzPrZmYNgRMID9ESKVO+D8WZWJkSJ2ROrIozsTIlTogzVgsVGSIiItsOM5tAqKFvAywCrnT3e83sMOA2wohk4939upQFKSIiW01JjIiIiIiIZJR0aU4mIiIiIiISl3qZxFQ2k3O6MbNOZvaKmX1qZjPM7PxUx1QRM8s1s/fM7L9RnFelOqaqmFm2mX1kZs+mOpbKmNlXZvaxmU1P9yFszaylmT1mZrPMbKaZ7ZnqmMozs4Louyx5rTKz36Y6roqY2QXR/6NPzGyCmaXlRItmdn4U44x0/S7risqUxFO5kniZUq5kQpkCKleSoablSr1sTmZm+wFFwAPuvnOq46lMNNx0e3f/0MyaAdOA4e6eVqOvmZkBTd29yMwaAG8A57v7OykOrULRXEK7Ac3dfYsJ7tKBmX0F7ObuaT8xlZndD7zu7vdEnaWbuPvKFIdVKQuzts8HBrv716mOJ5aZdST8/+nj7j+a2STg+XQb4tfMdgYmEiaPXA+8AJzl7p+lNLAUUZmSeCpXEi9TypVMK1NA5UoibE25Ui9rYtz9NWB5tQemmLsvcPcPo+XVwEzCZG1pxYOiaLVB9ErL7NjM8oHDgXtSHcu2wMxaAPsB9wK4+/p0L2wIw7B/nm4FTYwcoLGZ5QBNgO9SHE9FdgLedfc17r4ReBU4NsUxpYzKlMRTuVI/ZWiZAipXEqHG5Uq9TGIykZl1BQYA76Y4lApFVenTCROVvuTuaRknYVSii4AKZ95OIw68aGbTzGxkqoOpQjdgCfDPqCnFPWbWNNVBVeMEYEKqg6iIu88HxgDfAAuA7939xdRGVaFPgH3NrLWZNQEOo+z8K5Lm0r1MAZUrSZAJ5UomlimgciURalyuKInJAGaWBzwO/NbdV6U6noq4+yZ370+YPG73qFowrZjZEcBid5+W6ljisI+7DwQOBc6NmqukoxxgIPA3dx8A/ABcktqQKhc1TTgKeDTVsVTEwkS+RxMK8g5AUzM7JbVRbcndZwI3Ai8SqvynA5tSGZPELxPKFFC5kgSZUK5kVJkCKlcSZWvKFSUxaS5qC/w48JC7P5HqeKoTVfu+AhyS4lAqsjdwVNQueCJwgJn9K7UhVSx6coK7LwaeJLQRTUfzgHkxT0gfIxRA6epQ4EN3X5TqQCpxIPCluy9x9w3AE8BeKY6pQu5+r7sPcvf9gBXAnFTHJNXLtDIFVK4kSoaUK5lWpoDKlYSpabmiJCaNRR0b7wVmuvvYVMdTGTNra2Yto+XGwEHArJQGVQF3v9Td8929K6Hq92V3T7unEWbWNOp0S1SNfjChmjXtuPtC4FszK4g2DQXSrpNwjBNJ0yr/yDfAHmbWJPr/P5TQbyHtmFm76GdnQrvlh1MbkVQnU8oUULmSaJlSrmRgmQIqVxKmpuVKTl0ElW4sZiZnM5tHNJNzaqOq0N7AL4CPo3bBAJe5+/OpC6lC7YH7o9E5soBJ7p62w0xmgO2BJ8O9hhzgYXd/IbUhVen/gIeiKvUvgF+lOJ4KRQX3QcBvUh1LZdz9XTN7DPgQ2Ah8BIxLbVSVetzMWgMbgHMzpPNtUqhMSQqVK4mVSeVKRpQpoHIlCWpUrtTLIZZFRERERCRzqTmZiIiIiIhkFCUxIiIiIiKSUZTEiIiIiIhIRlESIyIiIiIiGUVJjIiIiIiIZBQlMSIJZmb5Zva0mc01sy/M7A4zaxTH+4oq2X61mR0YLf/WzJpUc55hZnaVmW1nZv/euk8hIiLpQuWKyJaUxIgkUDSR1BPAU+7eE+gJNAZu2tpzuvsV7v6faPW3QJWFDbAv8Fr0842tva6IiKSeyhWRimmeGJEEMrOhhInu9ovZ1hz4GugEHAfs5u6jon3PAmPcvTB6YnY3YSblhcAJ7r7EzO4DngU6AGOA2cBSd9+/3LVHAJcC3aPrbQ+sAj5196OS96lFRCRZVK6IVEw1MSKJ1ReYFrvB3VcBXwE9qnlvU+ADd+8LvApcWe48fwG+A/YvX9BE+x8BBgCfuHs/4GNggAoaEZGMpnJFpAJKYkTSRzHwSLT8L2CfrThHL+CLaLmpu69ORGAiIpKRVK7INktJjEhifQoMit0QVfvvQKiu30jZ/3e5VZyrRm09zewDYAowxMw+BQrMbLqZ7VuT84iISFpRuSJSASUxIok1FWhiZr8EMLNs4BbgDnf/kVD939/MssysE7B7zHuzCG2bAU6i4s6Tq4FmFV3Y3XcDngOOJnT4vNzd+7v767X+VCIikioqV0QqoCRGJIE8jJRxDHCcmc0FlgHF7n5ddMibwJeEJ2t/AT6MefsPwO5m9glwAHB1BZcYB7xgZq9UEsJAYDphBJlXa/dpREQk1VSuiFRMo5OJJJGZ7QVMAI5x9w+rO15ERKQqKldEAiUxIiIiIiKSUdScTEREREREMoqSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDKKkhgREREREcko/w87GcOGAHra8gAAAABJRU5ErkJggg==\n",
+      "text/plain": [
+       "<Figure size 960x288 with 2 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "grad = np.array(grad_val)\n",
+    "means = np.array(means)\n",
+    "variances = np.array(variances)\n",
+    "n = np.array(selected_qubit)\n",
+    "print(\"我们接着画出这个采样出来的梯度的统计结果：\")\n",
+    "fig = plt.figure(figsize=plt.figaspect(0.3))\n",
+    "\n",
+    "\n",
+    "# ============= 第一张图 =============\n",
+    "# 统计出随机采样的梯度平均值和量子比特数量的关系\n",
+    "plt.subplot(1, 2, 1)\n",
+    "plt.plot(n, means, \"o-.\")\n",
+    "plt.xlabel(r\"Qubit #\")\n",
+    "plt.ylabel(r\"$ \\partial \\theta_{i} \\langle 0|H |0\\rangle$ Mean\")\n",
+    "plt.title(\"Mean of {} sampled graident\".format(samples))\n",
+    "plt.xlim([1,9])\n",
+    "plt.ylim([-0.06, 0.06])\n",
+    "plt.grid()\n",
+    "\n",
+    "# ============= 第二张图 =============\n",
+    "# 统计出随机采样的梯度的方差和量子比特数量的关系\n",
+    "plt.subplot(1, 2, 2)\n",
+    "plt.semilogy(n, variances, \"v\")\n",
+    "\n",
+    "# 多项式拟合\n",
+    "fit = np.polyfit(n, np.log(variances), 1)\n",
+    "slope = fit[0] \n",
+    "intercept = fit[1] \n",
+    "plt.semilogy(n, np.exp(n*slope  + intercept), \"r--\", label=\"Slope {:03.4f}\".format(slope))\n",
+    "plt.xlabel(r\"Qubit #\")\n",
+    "plt.ylabel(r\"$ \\partial \\theta_{i} \\langle 0|H |0\\rangle$ Variance\")\n",
+    "plt.title(\"Variance of {} sampled graident\".format(samples))\n",
+    "plt.legend()\n",
+    "plt.xlim([1,9])\n",
+    "plt.ylim([0.0001, 0.1])\n",
+    "plt.grid()\n",
+    "\n",
+    "plt.show()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "要注意的是，在理论上，只有当我们选取的网络结构还有损失函数满足一定条件时 (2-design)详见论文 [[1]](https://arxiv.org/abs/1803.11173), 才会出现这种效应。接着我们不妨可视化一下不同量子比特数量对的优化曲面的影响：\n",
+    "\n",
+    "![BP-fig-qubit_landscape_compare](./figures/BP-fig-qubit_landscape_compare.png \"(a)不固定 z 轴尺度时，采样出的优化曲面分别从左至右对应2、4和6量子比特的情形。（b）同样的优化曲面但是固定 z 轴尺度作为对比。\")\n",
+    "<div style=\"text-align:center\">(a)不固定 z 轴尺度时，采样出的优化曲面分别从左至右对应2、4和6量子比特的情形。（b）同样的优化曲面但是固定 z 轴尺度作为对比。</div>\n",
+    "         \n",
+    "\n",
+    "画图时 $\\theta_1$ 和 $\\theta_2$ 是前两个电路参数, 剩余参数全部固定为 $\\pi$。不然我们画不出这个高维度的流形。\n",
+    "结果不出所料，陡峭程度随着 $n$ 的增大越来越小了，**注意到 Z 轴尺度的极速减小**。相对于2量子比特的情况，6量子比特的优化曲面已经非常扁平了。\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## 参考文献\n",
+    "\n",
+    "[1] McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. [Nat. Commun. 9, 4812 (2018).](https://www.nature.com/articles/s41467-018-07090-4)\n",
+    "\n",
+    "[2] Cerezo, M., Sone, A., Volkoff, T., Cincio, L. & Coles, P. J. Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks. [arXiv:2001.00550 (2020).](https://arxiv.org/abs/2001.00550)"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/Barren/BarrenPlateaus_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Barren Plateaus\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Overview\n",
+    "\n",
+    "In the training of classical neural networks, gradient-based optimization methods encounter the problem of local minimum and saddle points. Correspondingly, the Barren plateau phenomenon could potentially block us from efficiently training quantum neural networks. This peculiar phenomenon was first discovered by McClean et al. in 2018 [[arXiv:1803.11173]](https://arxiv.org/abs/1803.11173). In few words, when we randomly initialize the parameters in random circuit structure meets a certain degree of complexity, the optimization landscape will become very flat, which makes it difficult for the optimization method based on gradient descent to find the global minimum. For most variational quantum algorithms (VQE, etc.), this phenomenon means that when the number of qubits increases, randomly choose a circuit ansatz and randomly initialize the parameters of it may not be a good idea. This will make the optimization landscape corresponding to the loss function into a huge plateau, which makes the quantum neural network's training much more difficult. The initial random value for the optimization process is very likely to stay inside this plateau, and the convergence time of gradient descent will be prolonged.\n",
+    "\n",
+    "![BP-fig-barren](./figures/BP-fig-barren.png)\n",
+    "\n",
+    "The figure is generated through [Gradient Descent Viz](https://github.com/lilipads/gradient_descent_viz)\n",
+    "\n",
+    "This tutorial mainly discusses how to show the barren plateau phenomenon with Paddle Quantum. Although it does not involve any algorithm innovation, it can improve readers' understanding about gradient-based training for quantum neural network. We first introduce the necessary libraries and packages:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T08:57:15.883895Z",
+     "start_time": "2021-01-09T08:57:12.516705Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import time\n",
+    "import numpy as np\n",
+    "from matplotlib import pyplot as plt \n",
+    "import paddle.fluid as fluid\n",
+    "from paddle.fluid.framework import ComplexVariable\n",
+    "from paddle.complex import matmul, transpose   \n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import dagger\n",
+    "from paddle_quantum.state import density_op"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Random network structure\n",
+    "\n",
+    "Here we follow the original method mentioned in the paper by McClean (2018) and build the following random circuit (currently we do not support the built-in control-Z gate, use CNOT instead):\n",
+    "\n",
+    "![BP-fig-Barren_circuit](./figures/BP-fig-Barren_circuit.png)\n",
+    "\n",
+    "First, we rotate all the qubits around the $y$-axis of the Bloch sphere with rotation gates $R_y(\\pi/4)$.\n",
+    "\n",
+    "The remaining structure forms a block, each block can be further divided into two layers:\n",
+    "\n",
+    "- Build a layer of random rotation gates on all the qubits, where $R_{\\ell,n} \\in \\{R_x, R_y, R_z\\}$. The subscript $\\ell$ means the gate is in the $\\ell$-th repeated block. In the figure above, $\\ell =1$. The second subscript $n$ indicates which qubit it acts on.\n",
+    "- The second layer is composed of CNOT gates, which act on adjacent qubits.\n",
+    "\n",
+    "In Paddle Quantum, we can build this circuit with the following code:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T08:57:32.323084Z",
+     "start_time": "2021-01-09T08:57:32.307289Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def rand_circuit(theta, target, num_qubits):\n",
+    "\n",
+    "    # We need to convert Numpy array to variable supported in Paddle dynamic graph mode\n",
+    "    const = fluid.dygraph.to_variable(np.array([np.pi/4]))\n",
+    "    \n",
+    "    # Initialize the quantum circuit\n",
+    "    cir = UAnsatz(num_qubits)\n",
+    "    \n",
+    "    # ============== First layer ==============\n",
+    "    # Fixed-angle Ry rotation gates \n",
+    "    for i in range(num_qubits):\n",
+    "        cir.ry(const, i)\n",
+    "\n",
+    "    # ============== Second layer ==============\n",
+    "    # Target is a random array help determine rotation gates\n",
+    "    for i in range(num_qubits):\n",
+    "        if target[i] == 0:\n",
+    "            cir.rz(theta[i], i)\n",
+    "        elif target[i] == 1:\n",
+    "            cir.ry(theta[i], i)\n",
+    "        else:\n",
+    "            cir.rx(theta[i], i)\n",
+    "            \n",
+    "    # ============== Third layer ==============\n",
+    "    # Build adjacent CNOT gates\n",
+    "    for i in range(num_qubits - 1):\n",
+    "        cir.cnot([i, i + 1])\n",
+    "        \n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Loss function and optimization landscape\n",
+    "\n",
+    "After determining the circuit structure, we also need to define a loss function to determine the optimization landscape. Following the same set up with McClean (2018), we take the loss function from VQE:\n",
+    "\n",
+    "$$\n",
+    "\\mathcal{L}(\\boldsymbol{\\theta})= \\langle0| U^{\\dagger}(\\boldsymbol{\\theta})H U(\\boldsymbol{\\theta}) |0\\rangle,\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "The unitary matrix $U(\\boldsymbol{\\theta})$ is the quantum neural network with the random structure we built from the last section. For Hamiltonian $H$, we also take the simplest form $H = |00\\cdots 0\\rangle\\langle00\\cdots 0|$. After that, we can start sampling gradients with the two-qubit case - generate 300 sets of random network structures and different random initial parameters $\\{\\theta_{\\ell,n}^{( i)}\\}_{i=1}^{300}$. Each time the partial derivative with respect to the **first parameter $\\theta_{1,1}$** is calculated according to the analytical gradient formula from VQE. Then analyze the mean and variance of these 300 sampled partial gradients. The formula for the analytical gradient is:\n",
+    "\n",
+    "$$\n",
+    "\\partial \\theta_{j} \n",
+    "\\equiv \\frac{\\partial \\mathcal{L}}{\\partial \\theta_j}\n",
+    "= \\frac{1}{2} \\big[\\mathcal{L}(\\theta_j + \\frac{\\pi}{2}) - \\mathcal{L}(\\theta_j - \\frac{\\pi}{2})\\big].\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "For a detailed derivation, see [arXiv:1803.00745](https://arxiv.org/abs/1803.00745)."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T08:58:14.655001Z",
+     "start_time": "2021-01-09T08:58:05.939129Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The main program segment has run in total  8.693664789199829  seconds\n",
+      "Use  300  samples to get the mean value of the gradient of the random network's first parameter, and we have： 0.005925709445960606\n",
+      "Use  300 samples to get the variance of the gradient of the random network's first parameter, and we have： 0.028249053148446363\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Hyper parameter settings\n",
+    "np.random.seed(42)   # Fixed Numpy random seed\n",
+    "N = 2                # Set the number of qubits\n",
+    "samples = 300        # Set the number of sampled random network structures\n",
+    "THETA_SIZE = N       # Set the size of the parameter theta\n",
+    "ITR = 1              # Set the number of iterations\n",
+    "LR = 0.2             # Set the learning rate\n",
+    "SEED = 1             # Fixed the randomly initialized seed in the optimizer\n",
+    "\n",
+    "# Initialize the register for the gradient value\n",
+    "grad_info = []\n",
+    "\n",
+    "class manual_gradient(fluid.dygraph.Layer):\n",
+    "    \n",
+    "    # Initialize a list of learnable parameters and fill the initial value with a uniform distribution of [0, 2*pi]\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * np.pi, seed=1),dtype='float64'):\n",
+    "        super(manual_gradient, self).__init__()\n",
+    "        \n",
+    "        # Convert Numpy array to variable supported in Paddle dynamic graph mode\n",
+    "        self.H = fluid.dygraph.to_variable(density_op(N))\n",
+    "        \n",
+    "    # Define loss function and forward propagation mechanism  \n",
+    "    def forward(self):\n",
+    "        \n",
+    "        # Initialize three theta parameter lists\n",
+    "        theta_np = np.random.uniform(low=0., high= 2 * np.pi, size=(THETA_SIZE))\n",
+    "        theta_plus_np = np.copy(theta_np) \n",
+    "        theta_minus_np = np.copy(theta_np) \n",
+    "        \n",
+    "        # Modified to calculate analytical gradient\n",
+    "        theta_plus_np[0] += np.pi/2\n",
+    "        theta_minus_np[0] -= np.pi/2\n",
+    "        \n",
+    "        # Convert Numpy array to variable supported in Paddle dynamic graph mode\n",
+    "        theta = fluid.dygraph.to_variable(theta_np)\n",
+    "        theta_plus = fluid.dygraph.to_variable(theta_plus_np)\n",
+    "        theta_minus = fluid.dygraph.to_variable(theta_minus_np)\n",
+    "        \n",
+    "        # Generate random targets, randomly select circuit gates in rand_circuit\n",
+    "        target = np.random.choice(3, N)      \n",
+    "        \n",
+    "        U = rand_circuit(theta, target, N)\n",
+    "        U_dagger = dagger(U) \n",
+    "        U_plus = rand_circuit(theta_plus, target, N)\n",
+    "        U_plus_dagger = dagger(U_plus) \n",
+    "        U_minus = rand_circuit(theta_minus, target, N)\n",
+    "        U_minus_dagger = dagger(U_minus) \n",
+    "\n",
+    "        # Calculate the analytical gradient\n",
+    "        grad = (matmul(matmul(U_plus_dagger, self.H), U_plus).real[0][0]  - matmul(matmul(U_minus_dagger, self.H), U_minus).real[0][0])/2  \n",
+    "        return grad\n",
+    "\n",
+    "# Define the main block\n",
+    "def main():\n",
+    "    \n",
+    "    # Initialize paddle dynamic graph mode\n",
+    "    with fluid.dygraph.guard():\n",
+    "        \n",
+    "        # Set the dimension of QNN\n",
+    "        sampling = manual_gradient(shape=[THETA_SIZE])\n",
+    "        \n",
+    "        # Sampling to obtain gradient information\n",
+    "        grad = sampling()   \n",
+    "        \n",
+    "    return grad.numpy()\n",
+    "\n",
+    "\n",
+    "# Record running time\n",
+    "time_start = time.time()\n",
+    "\n",
+    "# Start sampling\n",
+    "for i in range(samples):\n",
+    "    if __name__ == '__main__':\n",
+    "        grad = main()\n",
+    "        grad_info.append(grad)\n",
+    "\n",
+    "time_span = time.time() - time_start        \n",
+    "print('The main program segment has run in total ', time_span, ' seconds')\n",
+    "print(\"Use \", samples, \" samples to get the mean value of the gradient of the random network's first parameter, and we have：\", np.mean(grad_info))\n",
+    "print(\"Use \", samples, \"samples to get the variance of the gradient of the random network's first parameter, and we have：\", np.var(grad_info))"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Visualization of the Optimization landscape\n",
+    "\n",
+    "Next, we use Matplotlib to visualize the optimization landscape. In the case of **two qubits**, we only have two parameters $\\theta_1$ and $\\theta_2$, and there are 9 possibilities for the random circuit structure in the second layer. \n",
+    "\n",
+    "![BP-fig-landscape2](./figures/BP-fig-landscape2.png)\n",
+    "\n",
+    "The plain structure shown in the $R_z$-$R_z$ layer from the last figure is something we should avoid. In this case, it's nearly impossible to converge to the theoretical minimum. If you want to try to draw some optimization landscapes yourself, please refer to the following code:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T08:58:53.124288Z",
+     "start_time": "2021-01-09T08:58:50.066333Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAApoAAAEBCAYAAADYRQXiAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOz9d5wl2V3YDX9PhRs73c5penIOuxNXCANCZNtYtnkdwOAX8AsGzCPgASwbHkA2+AWcwIAMBhuDLEBgjEGYKKGExK5mdndy6umc482h4jnPH3Xvndu93dNhZnZmV/X9fO6n+96qOnUqnfOrXxRKKUJCQkJCQkJCQkKeNNqz7kBISEhISEhISMjbk1DQDAkJCQkJCQkJeSqEgmZISEhISEhISMhTIRQ0Q0JCQkJCQkJCngqhoBkSEhISEhISEvJUCAXNkJCQkJCQkJCQp8IzETSFEENCiKIQQt/l9kUhxIHnqU/PA0IIJYQ49Kz7sR2EED8hhFgRQiw8676EhIS89QnnladDOK+EPC7bEjSFEN8shLgphCgLIRaEEL8ohGjb7k6EEBNCiC+vfVdKTSmlmpRS/i76THXbsd1s+7T6tMW+3jIP6puBEGII+H7ghFKq9wm1qYQQpeqgPiuE+I+7GdyFEPuqbRWrnwkhxL/YZZ/eL4T40G62DQl5uxPOK49HOK+s5XmeV6ptvUsIIattFYQQ94UQ37LLttbcZ887WwqaQojvB34a+EGgFXgHsBf4qBAi8nS7F/I2ZQhYVUot7XRDIYTxiMUvKKWagC8B/gHwrbvsH0Bbta3/D/AjQoiveIy2nglbnKuQkGdGOK+EPAXeCvPKXLWtFuD7gF8RQhx9jPaeCTueW5RSm34ITkYR+Pvrfm8CloFvrX5/P/C7wG8DBeB1gosD8D8ACVSqbf1zYB+gAKO6zieBnwD+qrrOHwIdwG8AeeAKsK9h/wo4BPRX1699ysEhKYCDwMeBVWCl2lbbDvrUD3wESAMjwLc17P/9wO8AH6we723gwiPOowIObfD7pn2sLp8AfgC4AeSq5zfWsPwHgXlgjuDmr+8H+OvAnWr/ZoEfaNjuPcC16rkdBb66+vu3AHer24wB/7Rhm3cBM8APVfs6AfyjhuVR4N8DU8Ai8EtAfINj/vLqeZfVc/9r1d//VvU8Zqv3w/F15+F91fNg167Ro85x9fp8AIhUr+HphmXd1Xula4N21twH1d8uV891b3W7joZl5wieBXODtt4PfGiTe+JfVM99oXqd/k719y37C/zN6vXLEjwzZ3ZyrsJP+HmWH8J5JZxXHm7zLt6C80r1//Zq37+24f4dAf7xJtfrXcDMut+WgL9X/f+fs/a+c2vHsUFbE8CXb/B7Cvg/BM9Rpvr/YHXZ3wNeW7f+/w38wVbnuuE6vQ9YAP7Hjp75LQaErwa8TS7ArwO/1fCAuATaH5PgJh6nOvmuPylsPCCMEDwgrQQ38nD15jEIHrz/vo0H7Dca+nQI+IrqyesCPg387GYXaoM+fRr4z0AMeLF64d7dcLwWwUOnAz8JvLKLAWE7fbxMMDi1Ezys39FwbRaBU0AS+E3WDgjzwBc13Hznqv9fIhhcvoJAoz0AHKsu+xvVayAI3t7KDdu9q3ov/Mdqf78EKAFHq8t/hmAAbQeaCQb1n9zOAwccqbb1FQT3zz+v3g+RhvNwDdjDBoPM+nMMHKse//dVv/9n4Kcb1v0e4A83aWf9ffCO6nmoCYJ/DHxnw/o/A/z8Jm29n80Fzb9Xva4awVtyCejbqr/AWYLB6SWCe+//Wz0/0e2eq/ATfp7lh3BeCeeVt8G8Uv3tKwkEr27gV4DffcT1qveveo7+FoFgfHaDdfcQCPpfs0lbE2wsaHYAXwckqufrfwK/X10WJXjBaRS2rwJft9W5brhOP11tZ0dzy1YDwjcCC5ss+yngow0PyCsNy7R1N+Sak8LGA8IPNyz/D8CfNHz/WuDaox4wAkn7tUfcMH8buLqdAaF6kX2guWH5T/LwLen9wMcalp0AKjsdELbZx29s+P5vgV+q/v+rwE+te6gaH4op4J8CLev28V+An9nWzQG/D3zPuhst2bD8d4AfIRhASsDBhmVfAIxv9cBVv/8I8Dvr7p9Z4F0N5+Fbt+irIniTLlX//y0eCl8vVc+HqH5/lXXalA3ugyzBG7IieMurbfsPgM9W/9cJBplLm7T1fjYRNDdY9xrwnq36C/wi8OPrtr0PfMl2z1X4CT/P8kM4r4TzyttgXmlY5+eBm9W2Ox7R1rsIBMssgQbVB753g/Xi1XvufY9oa8199oj1XgQyDd9/Efg31f9PEmg9o1ud62rfHRo03zv5bOWjuQJ0bmKP76surzFd+0cpJQnUrP1btN/IYsP/lQ2+N222oRDiawi0Pn9bKVWp/tYjhPhw1YE3D3wI6NxmX/qBtFKq0PDbJMFbWo3GqLYyENup38I2+7h+P7Xz0E/DOa/2r5GvI3gznhRCfEoI8QXV3/cQmDU26s/XCCFeEUKkhRDZ6vaN/ckopUrr9tlP8NacAF4TQmSr2/5p9fft0N/Y/+r9M83a8z29fqMNOEdwfv4BgbCWrLb3OYJz9y4hxDGCN/6PVI+52PAZamirs9rW9xM8ZGb19z8ATggh9hO8KeeUUpe3eZx1hBD/WAhxreF8naru85H9JfBj+/7adtVt97D2WdvOuQoJeVaE88pDwnnlLTqvNPDLBOP3rymlVmFNtoGiEKLYsO6cUqqNwH3k54B3b7C//wbcV0r99Db6tgYhREII8V+EEJPVa/9poK0hgOnXgW8QQgjgmwgEcZvtnetlpZS10z7B1sFALxNI3n933cE0AV8D/EXDz3salmvAIIHqF4I3gadC1ZH21wk0Po03zf+/ut/TSqkWgrdo0bD8UX2aA9qFEM0Nvw0RvLE8Sbbq46OYp+GcE/SvjlLqilLqPQQq/d8neEuE4ME6uL4xIUQU+F8E2rue6sPwx+v6kxJCND5kQwTnaoVg0D6plGqrflpV4PS8HeYIBKhaX0T12BrP97buIRXwOwT37o82LPp1gvP7TQTmDau6flPDZ2pdW75S6j8SmLO+q/qbRXAua239j20eYx0hxF4CM8t3E7wBtwG3WHuuN+wvwfX7Nw3nuU0plVBK/VZj13fap5CQN5FwXnlIOK+8heeVqgD3ywRuGN9VywKgHmYbaNqov1Xh7n3AaSHE325o718QaJH/yTaPcT3fDxwFXqpe+y+uNV3d7ysEmskvAr6Bh/PXds71rp+3RwqaSqkc8K+AnxdCfLUQwhRC7CO4uWZYO8meF0L83erb1/cSDCSvVJctAk80PxmAEKKFQMP0w0qpz6xb3EzgUJsTQgwQODg3smmfqgPLXwE/KYSICSHOEFz4x0lVE6m2Vfvo2+jjo/gd4JuFECeEEAngx2oLhBARIcQ/EkK0KqVcAtW/rC7+b8C3CCG+TAihCSEGqlqzCIEKfRnwqm/zX7nBfv9Vtf0vIghK+Z/VN8VfAX5GCNFd7cOAEOKrdnAsf6PaJ5PgYbEJrsFu+Sng24QQtTQXHwL+DsGg+8FdtPXPhRCx6vcPAt9M4GOzlaCprbvuUYI3YkVwrhFBiotT67bbrL+/AnyHEOIlEZAUQvyNdZNXSMhzSzivhPPKBvt9q84rP0Qwln8r8O+AD4ptpj9SSjkE7hw/CnUN+nsJ4gEq22jCXHftDYJrXwGyQoh2Gq5fAx8EfgFwa/f3EzjXj2TL9EZKqX9LcDL/PcGN9TmCt5cvq0rlNf6AQLWcIdDC/N3qzQiBH8r/U1XJ/sCT6HiVcwTS+8+IN6qp/1V1eQ74I+D31m27VZ++nsC/Zg7438CPKaU+9hh9vU1wA9Q+37KNPm6KUupPgJ8liC4cqf5t5JuACRGoz78D+EfV7S5X9/0z1f1+CthbNee8l+DhzBC87XxkXZsL1WVzBA7y36GUuldd9r5qP16p7vNjBNdmO8dyn0Cg+nmCN6uvJYjkc7az/SZt3iQwG/xg9fs0QdSqAv5yh839EcFxf1u1rc8SDLCvK6XWm5bW8/Wsve6jSqk7BAPMywQT02ngs+v6v2F/lVKvVvvxC9U+jRAIvSEhbxnCeSWcVxp4S84rQojzBFHb/1gFeVJ/mmC83kne5V8FhoQQX0twn3cBdxvuu196xLZ/zNpr/36CaxcnON5XCMzf6/kfBIqN9S84uz7XW1ELNni8RoR4P4Gz8Dc+dmMhzyVCiHcRBLYMPuOu7BohxK8S+Mj8P0+grY8Dv6mU+q+P37NN9/HE+hsS8lYjnFfe/rwd5pW3GkKIOEHmknNKqQdvxj7DhM4hnxdUTXN/lyA90OO2dZFAY/Cex23rEfvYxxPqb0hISEhISJXvBK68WUImPKNa5yEhbyZCiB8nCLb5d0qp8cds69cJTArfuy569InxJPsbEhISEhICQelKgkwK3/+m7vdJmM5DQkJCQkJCQkJC1hNqNENCQkJCQkJCQp4KoaAZEhISEhISEhLyVHjSwUChHT4k5Omy3cTLISFvF8J5JSTk6fJU55VQoxkSEhISEhISEvJUCAXNkJCQkJCQkJCQp0IoaIaEhISEhISEhDwVQkEzJCQkJCQkJCTkqRAKmiEhISEhISEhIU+FUNAMCQkJCQkJCQl5KoSCZkhISEhISEhIyFMhFDRDQkJCQkJCQkKeCqGgGRISEhISEhIS8lQIBc2QkJCQkJCQkJCnQihohoSEhISEhISEPBVCQTMkJCQkJCQkJOSpEAqaISEhISEhISEhT4VQ0AwJCQkJCQkJCXkqhIJmSEhISEhISEjIU8F41h0IeTRKKXzfp1KpYJomhmGg6zpCiGfdtZCQkJCQtyBKKVzXxbbtcF4JeeqEguZzjFIKx3Hwfb/+qaHrejhAhISEhITsCCklruvieV79U5s/DMPANE10XQ/nlZAnhlBKPcn2nmhjn89IKXEcB6UUQggcx6k/9EoplFJIKRFCMDc3x549e0LB8/OD8MKGfL4RzitPgJp1zHXd+m+O46BpWn157eP7PsvLywwODtbnFU3Twnnl7ctTvbChRvM5Qym15i1T0zTWvwwIIerLAObn5xkYGKBSqdQHglDjGRISEhICD03lvu/X5w8p5Zp1ar9DoOhYWlqir68Pz/Pqyw3DqH9CwTNku4SC5nNEzVRe01Ru9yGuCZ2Nb6ZSyjWCZ+MAEQqeISEhIZ8frLeObWfsF0KglKrPKfBQCVLTiIaCZ8h2CQXN5wTLsnAcB9M0dyRkbsR6jWfNFFJ7M4WHvjjhABESEhLy9kMpRaVSwfd9TNNcIzTuhvXzUk1Lul7wrPl4hvNKSI1Q0HzG1N4S5+fnqVQqHDx48InvY6MBolHwXF5epq+vLxQ8Q0JCQt4G1KxjIyMjpFIpuru71yyXUjIyMsLq6iqpVIpUKkVLSwu6rgMPNZqPQghRX7+2z0bBc2lpicHBwboVLZxXPn8JBc1nSC36T0r52G+bO2G94Dk9PU1XV1foixMSEhLyFqfRVL7RvFKpVLhx4wYdHR2cPHmSfD5PPnOdlflpivYJ2traaW1t3VLQXM96wXN6epru7m5s267POTVlhmEYj225C3nrEAqaz4D10X81Qe4JZwDYEY3CZOiLExISEvLWYqNA0vXzyuLiIiMjI5w4cYLW1lZc16U/dQWj6TdRIgby/7BQ/nYWFvspFotcu3atrvFsbm7e0bi/kcbTcZw3CJ41U3soeL59CQXNN5mNov9ge6aKN4vQFyckJCTkrUOjdWyjeUVKyb1797Asi4sXLxKJRJB+kYj979HVOJqaQskKrv4SnfGfJXXgaymVznHs2DEymQwzMzMUi0VisVhd8Ewmk7sWPGtzneM4OI4DBMqO9fNKyNuDUNB8E3lU9N/zJGiuZytfHMuyiEajJJPJ0CQSEhIS8iax3jq20bxiWRaXL1+mr6+P48ePB8v9YYzyLyH819FYxWMIV+tH8/8SSKJ5H2Wo6wGx2AX6+vro6+urBxdls1kmJycpFoskEom64JlIJHaUKQV4pOBZKpVobm4mHo+HgudbnFDQfBPYyKSxno3yZT6vrBc8l5eXicVi9e+apoUmkZCQkJCnyPp5ZaMxtlAokM1mefHFF2ltbQVA2H+AXvkVhJpEEcHRvhDp30JTo0jtApp8FSWnwNSxrV8mGvv2YDshSCQSJBIJ+vv7UUpRLpfJZDKMjY1RLpdpamqqC547mc82EjynpqbYu3dvPd9nqPF86xIKmk+Z7ebG3CiB7luJ2iDQ+GZa88UJB4iQkJCQJ8dmpvIanudx9+5dSqUS+/fvD4RMVUQr/yy689soBL52Fs/XUP6nQTuMkjaafBVPvIMyS0TiwzjuErp+EMP8sjf0QQhBMpkkmUwyODiIUopisUg2m+XBgweUy2Xu3LlTFzwblRFb0Sh46rper1i03tTeWJQknFeeX0JB8yni+z7pdJqpqSlOnjz5SK3e82w634qaKwBszyQSCp4hISEhO6dmKp+amsLzPPbu3fuGdQqFAjdv3mRoaIiWlpZgfPXuYJR+ACGnkfpxpFT45FGsgNiHkPdRYj+23EtF3USIA+h6CUEHlcr7Seqn0LSeR/ZNCEFzczPNzc3s2bOHy5cvMzg4SCaT4d69eziOQ0tLS13wjEQiWx5r47yyPm5AKYVt29i2DTyshqfret2FK+T5IBQ0nwLrTRq1t85H8biCZuND+Sy234ztCp5SSpLJZCh4hoSEhGxAo3UMeIMFTCnF9PQ0s7OznDlzhqamJqampmjWfw+j8GugDSG140il8NUCiCEE91CqjOQwFZJ4Io+SeZS6imUNEYtNoWkXKVofoCXxr3fUXyEELS0ttLS01E3g+XyeTCbD3NwcnufR2tpKKpWira0N0zR31PZ6wVNKiWVZ9d9qQao1H89Q8Hx2hILmE2a9SaMmRG3Fs9RovpkP4EaCp1KK1157jfPnzwOhSSQkJCSkkfWBpLqur5lXXNfl1q1bRCIRLl26FIyvMkdv/McxxSxKPwneDTzjRRQ+qAz4y0jtAkqOUkbHl/MoNYWmX0D6r6IbeWCAonSw/Ntg/29aon9n18egaRptbW20tbUBgcUvl8uRzWaZmppCKbVG8NwJGwmelmVx//59Tp8+DTzUeIZlmN98QkHzCbFZ9N92BcjHETRr2z6rB+dx9t14nhp9cRpNIo2CZ2gSCQkJ+Xxhs0DSxvkim81y+/ZtDh48SG9vb7Dcu4pW/hk04WJqcyi/jGucBW8YSIN+AvxRPJnHEvvx/ZcRog9oQfqvomkv4Hmr2MY+iv4rGFo/K+WfI2l+KbrW9kSOTdd12tvbaW9vBwK/0lwuRyaTYWJignK5zNTUFF1dXbS2tq4JQN2KxjLMtXllvcYzFDzfPEJB8wmwWW5M2H40+ZMwnb8dCH1xQkJCQh4dSFpzyRofH2dpaYmzZ8+SSCRAKTTrvyO8zyD8e8T1CgXnDJGYDd4rILqAAZR3F9v4a1TcTwIKTTuJlLfRtBeQ8gYuSTJiGs1/hah2AlveIW5cZNX6AN2JH34qx2sYBh0dHXR0dABw7do1mpubWV1dZXR0FF3XaWtrI5VK0drauqWlaysfTykllUpljZUtFDyfDqGg+Zg8KjcmbD+a/HE1ms+Sp6lN3Y4vTjhAhISEvJ1YX5lt/Zjm+z7z8/P09vZy8eLFQOiSq2iVD6A5f4KgiKSbgnuKiPEy+BHQXwD/OlLbT1l7Adf9GJp2ASlfRcpZoB0px7DEl5J1P410D6EZeXyVAQws7xaOP0NL5BuJGW8MQnrSCCHo6Oigv78fCPz6s9ksS0tLjIyMYBjGmqpF6wXPR81LjRrP2rqh4Pn0CAXNXdJoKt8sNyZsX4B81Hr5fJ6RkRGamppob29/w0P1Vo5Y3ymbCZ7ZbJaZmRkOHToUDhAhISFvSbaTG3N1dZXh4WFaWlo4evRo8KN7BaP0owg1g6IZT3sJXy0SNf6KinuKuHkL/Nu4xhdScq8hRBlIIuWraPpZpH8V9C8g7U3hyatopDDiI3VtZky/gCOHscUL3C/9N15o3Vlg0G5pPP5IJEJ3dzfd3d0A2LZdDywqFApEo9G64NnU1LQjBchmgufc3ByWZdHf37+mDHM4r+yMUNDcBUop0uk0hUKB3t7eR95wjxMM1BhFeOjQISqVypqHqr29fceJcZ8Gz9I/tHEw9jyvfr7DN9OQkJC3ElJK5ufn6ybi9eOUlJLR0VGy2SzHjh1jdXUVlI9W+WU0+5eAGFK/gC9tpLwB2l6kihM3b6H0i1j4WM7L6PoefH8YOAXcwvfu44t3suq8TlQ/jZRXiekvYvkZJEVAw1cVlv39FP3XiGo95N1hWswjT/V8bDWvRaNRent7636ptapF09PTFAoFIpEInudRLBZ3VS6zNif7vo+mafi+j+d59XVqKfoMwwjLMG9BKGjukJoWs1KpkMvl6Ovre+T6u9Voep7H7du30XWdixcvIqWktbV1zUOVTqeZmJigUChw9+5dOjo6SKVSxOPxxzvIN5knISg3ui6EJpGQkJC3Co3WsZqAlEql1qxTqVS4efMmHR0dXLhwgVwuhyFW0Yv/BOHdRxnnwBvBw0eRBpLg30SyH8cv4oo0iCaggpQrSNWGJm7h+WcpejYlfwk96mG5D0C0YPnX8OwBiE6ha1/JiH2dNvMUyp8hqnUwWvpVzrb91FM/LzshHo8Tj8fr5TJXVlaYmppiYmKCUqlEMpmsazzj8fi2xn0pZV2IXG9JaxQ8hRBrNJ6h4LmWUNDcJutNGoZhbEtTuRuNZi3h7r59++qlvta3EY/HGRgYYGBggNdff509e/aQz+cZHh7Gtm2am5vrGs+tEuM+Ls9DDs/agLCe7QieoUkkJCTkWbA+kHSj4NGlpSUePHjAiRMn6gJohFc42PEfQfUDBvjTuFpfkLZIToBoB7EHV2oUvFZMcQ+QaNoZpLyB5x0iEklR1Aq4ZhndWCKqvYjNNXBPgHkH6WvknBcpiFFAI+fexRQpct4d4loPBW+UZuPgUz0/j5PNJBqNkkwmOXbsGEopSqUSmUyG0dHRN5TL3Ew5s9W8UqMmHzT61YaC50NCQXMbbFTuayfR5NuhJpBOT08zMzNTT7hb41HCmKZpJBIJ2traGBoaQkpJoVAgnU4zOzuL7/v1aL22tjYM4/m67E9C0NxuGxsJnjVtgu/7rKysMDg4GJpEQkJCniobBZI2KiaklNy/f59KpcLFixcDhYFy0Sq/QEJdRYkymv8ann4WXynwrwAm6GdQ3k0s4zAV/x6muYRhXMLzLuO6o2haikisnbyvY8krRPVT+P4SnppCkECZ94no55kjg04Mj2n0ygH8+BhRfz+uliGidTJR+g1Ot/7osz2Jj2B91HlTUxNNTU3s2bOnXi4zk8msUc7UBM9oNPqGNh7FowTPcrmMbdt0d3d/3gqez5fE8ZyxWW7M2v9Psja553kUCgVisdjDhLu7RNM0WltbaW1tZf/+/fi+TzabrecnE0LUH6jW1tbH7vvzrNHcisYB3nVd0uk0fX19a0wijab2z7cBIiQk5MmyWW5MoD4OlUolbt68SW9vL8eOHQvGHH8GzfoAmvMyOqu4IoljfAnK/ViwsXERvCtIf56K/hKO+ykEQ0gVxfMuU6kcIh6fxdXPsep8Ck00odGB7d8iqp/C9m8R0y/goVjyEzjmBHG9CXyBllhBqiiWGEfIJLnKLGOuTqx4i8H2g0/FXetpzitCPCyX2aicyWQy3LlzB9d1aW1txfd9mpubd7zvRlnBsiyKxSKpVOoNGs/GMsxv53klFDQ3Yavov+2axLdDoVDgxo0bGIYRVDHwbcTk76MtfgaVPIg/9Lch0rXp9lv5geq6viY/meu6ZDKZukmmUqkwNTVVj2h/s2/4N1Oj+ShqwmrjwB/64oSEhDwpHpUbE4J5JZvNMjc3x8mTJ+uKAOF8Ar38kwg1jyKKzUtY3jgx7WOgvwj+LfCu4BpfTMl9DeW9iqbtRcpJrMphEokHJJIGeXWEkvMp4uY5Ku7rRPWD2P4qvkojSFKSURbdJRw1gWb3UonO0mqcIufdos18gax7nZbIJW6VZmiJtvLA/STlYR/btndUx/zNYCdzQqNyZt++fUgpyeVyTE5OMjs7y8LCwq7LZdbmlUblUc1lwnGc+n2wvijJ22leCQXNDdjIVL6eJyVozszMMDU1xalTp7h37x64BfRXvwfhFRGFGaTnoF+5jHbw25G9F5/IzWea5po0EZcvXyYSiTAzM0OhUCCRSNQHjEQiseU+38oaza3aCH1xQkJCngQ169hmOZc9z2N6ehrXdXnppZcCFyfloJX/I7rzGygiSOM8vu+h5Oso1Qm0gn8NpZ3BIoLl/AWGcRbPew0pW5EyQiLxAIwvY8H+HDEjSIfkeGMIWrD960S0w/iqQIUvZMF5jTbzDI6bBgLByFEZACr+LKZ4iZvleVwlSfvTFPRlvuz0t2ISq9cxr7lrWZbFysrKrt21nuW8omkaqVSKXC5HIpGgo6OjXrWoVi6zMXn8o45vs3llveDpOM4bquHVNJ5vdcEzFDQbqF3sWjqDRwku2/XR3AzP87hz5w4Aly5dCgRX30e/9n6EW0BUppGtxxGlEbB9IsMfwo6moP3wG9p63DyamqbR29tbDzyqRbSPjY1RLpfX+K7EYrFd72cznjeN5qPYSPB0XXeN4Ol5Hs3NzZ8XJpGQkJBHU6tsVhujNhpjagGgqVSqXvEMfwKj9IPgTyONC+CN4ikPxRLQRjw6VU1h1EpJlUEASDzvJlIOoWlTKF4kZ3s48gaCCBXvOjHjDJZ3g4R5kbJ7BSV6mXIsYASNGDn3NlGtBzs6S1I/QMkfo804y4Kn4ag4lizRHz3GnH2PLnMfd0uf4MXmv1GvY15z17p8+TLZbHZDd63HVQps97w/qXllo3KZ2WyWdDrN+Pg4Qog1gmejELndeaW2TW0udxwHx3Hqyz3Po6WlpT6vvJUIBc0qNSHz5s2bDA0Nbem7+Dg+msVikRs3bjA0NMTAwEBdUOy1X0bLvoxMnUZUpkFIhFtAtZ8Fq4x5+4O47/hhMJ+8sFdDCEEikSCRSDA4OFh3mk6n09y7dw/HceomhFQqhWmab2uN5lZs9GZ67do1zp8/X1/emEopFDxDQj5/qFnHXn75Zd7xjne84dlvzJV85swZLMtidXUVYf8fdOsDKNGLQIA/j6t1g8yCnALaqDg9GLE4lgDPuwfY6MZFfO8KUtpo+gEK5KioCEJliJvnqbiv4ctlwKTi3gDxpTywbtBqHCfn3SVlvkjGvUZc78GWi+giQlw/wKyXZMYepdUI0usVvJXgr7/MzcJHeaHpr685tpqwfOjQIeCN7lq1FE7t7e00NTVtOCY+z/OKYRh0dnbS2dkJBMeXzWZZWVmpl8uszZG+7+/I1N6Yhq92HL7vc+PGDc6ePQsEyqH1Pp7PM6Ggydrov+2axHdrOp+dnWVycpLTp0+vcTIWXokOK9BwiuxdVLQdrXAfldiDsBfQCksow0e783vIF75hTZuPq9F8FI1O03v37q37rmQyGaanp+sPQTKZJJlM7iqI6a0saK6npvFsHCQ2Mom8XX1xQkJC3hhIquv6G8Zo13W5ffs2pmnWA0AdJ09v8pfR7DTILBozuPolpCqCfx2IgH4K5d0m5xwhZi6j1ByGcQ7Pex3XuQYMYka7yasElnoFtHYE8apP5iFsf4S48ddY8crYMvA9d1QeEBS80apW8y54zbh6kiknSdobpcPYw6o3TZe5n2V3nG7zAEvuGN3mAaasm+yNn9n0fKx317Isq26GLhaLdXet9vb2bee43M41eLMsZaZp0tXVRVdXEEvhOA6ZTIaFhQVWVlaIRCLYtl0XrHcyz9Tmd13X19xHjRrP513w/LwWNDeK/tN1/akImr7vc/fuXXzf59KlS2/w6dBGPkyrPYFKNCO8AjK5D5FNo+IdaKs3kG3HECqCkbmBk/tSaH10ovinRc13pZbPzfM8bt68ST6fZ2FhYc2bXEtLy7Zu+LeS6XynPMoXp9EJ/Nq1a7zzne98ovsOCQl581mfG7M2t/i+Xx8Lstkst2/f5uDBg/UiHPgPaBU/jxn/LJrvIOnB0V8E7xOABsYF8F5FyiXK2iWiiU8jxF6USuJ5r1MuHyWRGMfTD7HkvAJIDHEQTx8lbl6i7F4GBKZ2gik3g+0V8Zgioe+h7E/Tapwk592mzXyBvHufYvko9/1Z+iKBX6ehBSl/BOsCmOjiY6uX+SeDmwua64nFYvT19dWTq5fLZTKZDCMjI1iWRVNTU12Q2q271rOcEyKRCD09PfT09DA+Pk4sFkMIwezs7IblMrfqZ+O9s5HGszavNAqemqZx+/ZtXnrppR33/0nzeStobhb9txON5na1iDV/lcHBQQYHB994U3kVxNjvoeEgkyfQc68h8mMoEQGvgmdewC8KwEPIPPq9P8B/6Tvqmz9NjeZWGIZBLBZjcHCQ5ubmNW9yw8PD23qgntSA8LhtND7Mj8OjrsVmvjjf+Z3fybVr10LtZkjIW5iNcmPCw3lFKcXExARLS0ucPXuWRCIRbGj/H4zyv8akgqtaUPpZfDkZCJnVtEV4r+IZX0zRfR3FVRyni0hkEsc5TiRyl2STTUG9SNH5DIm6YOmhFFTc6xiiD090seqblLxbpCJnyThXMUQSAFflgr+yTNo/xrK5RIQEi84ocdHKkjNKUmtn2R2nSe8g482RFJf4y+wkrUYrWTdLm9m243MmhKhbxGruWrU80Hfv3sXzvF1FfD9PCoxayejGyn4baXQ3C8B91Ny0UdxArTLS+973Pj75yU8+Vv+fBJ+Xgub6qOHGi/Q4tck3Ym5ujkqlwjve8Q5aWlo2Xmni4ygpEYDITaCEgXDz+O1fhLx/Hbo70ZZuI6Pd+Mk+RH4R0hPQvq/exLOsd974MDa+ycEbH6iNyoA9qQHhcYXEJ2V+3+6xNE5CoQk9JOStS6OpfKOAH03TsCyL27dv09TUxMWLF4N1ZBG9/K/R3D9BiS5cdYiSaxHXXgXjJMh58K6g9AvYSCrOJ9H14/j+DSCOlBEikbtgfBlLzmsYelDko+Jew9T6ceUkyjmGiM1jay8yXblMXO8HNPLuXQxayHv3SOhDlP0pWswv4nppmg4zhdQW6YwcZs65Q8rsZ87J0Wr0UHLStOqDDNsWcc1Eoeg0O3k59zJf0/k1j30uhRC0tLQQjUY5e/Ysvu+/IeK7MbBos3H/ebFybdRGrVxmLQC3ptEdHx/fsFzmTvpRm0sqlQrJZPKx+v6k+LwSNLfKjQlPLm2R7/vcu3cP13VJJpOPTPoqhn8fmo5B7jWEk0V1nkT5BeRCBqEkqrSMQEFLF1pmGmmbiHufRL3zm4Ptn2MBZf0DVSsDVjORNDc31x+kx+F5GlR266caEhLy1mOr3JgQ+GPevHmTY8eO1f348G4HUeXoSP1MUKtc+EjlAgK810A/g/TnKclstVa5i++PolQvkcgCcA5Pj5B2rgEmtnePuHGBivcqhtaFK+eQ+Kz4Q+SdKySNIUreFKnIGTLODdrMo2Td6xiiBUN7iTHbxVE2JT8NCrLeHAKNtDeDhsGqO0WncYzrhTJ5r0xUd9HQWHQWSbtpvqrjq9DEk3U/2ijiO5PJ1ANvDMOoC2XNzc1rqr49LxrNR80rG2l018+TkUgEpRSWZW3blaAmsD4PfN4ImtvJjQlPRtAslUrcuHGDgYEB9uzZw+c+97nNb9j0MCI7hqq04GsmunDBLuHnNUR2EtW2F5GbRKYOouUmkI4LbYeRSzOwMoHo3Ac8PxrNRyHE2jJgtWoMCwsLZLNZrly58thJcR8HKeVjl+fcjaDpOM6OjjUkJOT5YDNTeePy0dFRSqUSp0+frkcpa9ZvIJw/RtGMJu8gtb14+jGEf4tkrAT6IfAXcJWNre3B814GBLp+Bt+/geelUKoDJ1rGkz5S5YibZ6m4GRx/FEGSincdTXs3M+IW7fpe8OfqZnLLXwYEOec+Jr3MOyZZWabor9BuDJL2Zki6PZTEIj3mYRbdB/RFjlGRMRbsGGlvnP2x/Yxb4+yL7WPCmmAoOsT98n2OJ48/1XNuGMaawBvbtslkMszNzdWr66VSKTzPeyLj+ePOK7V0idulNk8mEx77el9D+HcpFm0sq8zw/a/DssWG5TLXEwqabyK1t4B8Pr+t4JSa0/ZumZ+fZ2xsjFOnTj2s6lBNhbTRvsX4R4O/dp5ccoiUGkWKDpSyApfrSFUTqpsIpwidJxCuhW5V8K59AvHl3/JcazQfRa0aQ41Dhw6tMZEAm+YmW8/zEnW+00EFnq8BISQkZGuUUuTzeTzPI5lMbvjMW5bFjRs3aG9vr9e5RubQKj+H8K6gyXEAHOOLUO4NYATEAI5rYKpRbOMLqbh/BVQwjJfwvM/hOKMIEdQqn86Aod/B1PqAGBX3KlH9GLZ/j4T5DvK+IONlQfjk3WEM0UzOvUuTsY+iN4Fu7UWLaixZfSxp4zQ7gxABTQYvvTXVhYdNVGsi77VxtTBOXyQIRLWUFSxXD6umfS77uacuaK4nGo3S29tLb29vPQ90TeNp2zb5fL4e0b7TwKJnYSmTsgjubxGVr6DLByjtKG2xESYq/5wzL7z0hnKZtfyajSkHIUij2NTUtOP+CiG+GvhPBBn7/6tS6qfWLf8Z4EurXxNAt1Kq7VFtvq0FzVr0Xz6fZ3p6OijvuAW6rtf9N3eClJJ79+5h2zaXLl1ao6HaLHBIKYlKL1ITn6J2ARlPIKdmILU3+HF1BGXEIT2Cp8WRTgEjO4cf6UesjiOXZ59pMFBwHI+370clxd2OiaSxjW3uEKk+AuJlEIugzYOK0dMXxXO/DKW+FSF292jsJqCoVCrtakAICQl586lZx5aXl/F9f8Nnt5Yv8vjx47S3t3Pv3j00eRO98AtoMkhj5+vn8VDgfhxEDzCIUDM43h6cyBCu+xcP0xa5V7DtIWKxWaTxBczbn0JPaJjaEK6cqgf/KGwMbR+zbhnLd7DlMoazFy8ySXvkLGnnKp5jgAaR5CA3yhNEjVU0aVCJLGGSYNWfxJQJyuYicZXC8T2K3hHGK+N0mV3MO/PBX3ueDrODWXuWNqONaWsaQYSCV6HZePK1z7dDYx7o2pzQ0tJCJpOp54FuaWmhvb2dtra2LUtlvtkKDN+7gXD+K1HhoMkiSjsFQmO29NM4KggkWl8u0/f9elWm6elppJQUi0VefvnlHVvKhBA68AHgK4AZ4IoQ4iNKqTu1dZRS39ew/v8FnN2q3betoNlo0thuyiLYnem8XC5z48YN+vr6OH78+BsEnk2Tu8/fgek7yKYmNK9IzMviJ16CueuwNIJMtKA5ebKRPbR5U7jtR/AqNjnjEEroxGQZ//WPovZc2lF/nwZPI7Hudk0ktaS4Wz7MSqH8nwPjj0DPgOdBRAPNA9/AjJhEIx9Eid8E77sQxt/f8bHsZmAKNZohIc8/G+XGXK+UkFJy//59yuUyFy9eDAQZpehM/iHt/AZIkPo5pKwEUeXKA+0AyDEQ7TjiPBXtFlGlAyae9zqOc4pI5BbxRJSSeoG8/Unixnkq3mtoWhwkVNwbGKIbJTpI+y3k3OukIi9gO8tIrQxAzr0PMoYtZkH7Eq6Vh+s5MfsiR5l37tMfOcScc4euxD7m7DvE5BCv5ZdI+Q4YEJOBRrDFaGHZXSZlpFh1V+k0O2nWe1iqJPn06m3+Rs+FN/XabERt7q/lgR4aGkJKST6fJ51OMzMzg5SS1tbWuuC5XknwZgqavvPnCOd3ieoaQvkorRtBDCfyg9i+h6ZtLJc0phSEQNlx/fp17ty5w7Vr13jllVd43/vex3ve857tdPcSMKKUGgMQQnwYeA9wZ5P1vx74sa0afdsJmo+TGxN2LmguLCwwOjq6xlS+nk01juOfBbeCSp6E3GtINGROogFIj0pkiKSTp8WUyMheVDaCNjtP08Ax/MVZ/LZO1OQtCqKH++Uy3d3dtLe3k0wm31Lm9O1qIzczkUxMTJDJZCiVSlQqlXqk3hq8CTTnB/DNNIgC+BqYGqAQdhI8Cy3qgOYgXID/gKh8DBX5SdA7tn0su9VohoJmSMjzy0aBpOvnlVKpxM2bN+nt7eXYsWPBmCZX0Us/THfiGrY6SVSM4qOQaikI7lEjoCoo7RAWzdj+BCDx/fto2nmkfA3THAb9nSy7w5hGMBbZ/gjST2Jzn7hxFsu7ja+fZ7xymZjWhcAg69wipvViGQs0accoynskxXkmVYWorAbMVPtellkAcv48IMi686jSQa5rWRAa+UgeU5os+AvoSmeqPIUmNOasOSJEKHkJPrM6R39U8Rcr158bQXP9vKJpWr1UJgRWs1wuVy8l2ZgnuqWl5U0xnSul8OzfxPA/Q0QrI5SGEEGGGjv2oyCa8f3pbfub6rrOuXPn+Iqv+Aq+9Eu/lG/91m+lXC5vt7sDwHTD9xlgw0ScQoi9wH7g41s1+rYSNDeL/tN1fdt+l9sVNKWUWJbF3NzcG0zl225z8nPB3+VJZDxGQXQTn76H7OxDK85jlDJIJRBoWJlmWJ6A9gHIzCHsMrqKoDWlGKosYOy9gOu6TExM1E2xNTP0Zs7CT4pnUSqs0UQyMDDA3bt3SaVSOI7D8PAwtm3X/Vbam8eJ8T6U5kK0WjtWGcF3QHgaKqKBrSN0iebEAQ+0W2j230Ea/wEiF7fVr934aO7WlyYkJOTps1kgaeO8Mjc3x8TEBCdPnnzom+9eRqv8DBBDCBuDURz9CKgMqAVQUdBOIOUCZaJ4cgal5vC8IXS9jJSvAWdQZoKsl8ZTeTz3tbofpnSOoMWH8ZVNTp0kXWmMKn+RjHONuNGN5SxQttPEoy/wwKlQ8osICsS1VlbccVqNXnLeAp3mPlbcCfojpxiv+JQ9HctY5kD8AGOVsYd/E8HfPcYe0l4aWdjDZ9Qcg3qKGTvNgOhgurLyjK7WQ7YzrxiGQUdHBx0dgQC/Pg+0ZVnMzs4+slTmVjxK0PQ8F8f6VyS1NFFuo1QLmtCQYgA7+q9ABKZ93/d3PI8Xi0W6urpoaWnZPLXi4/EPgd9VSm0pXL1tBM2aSWOj6L8nLWjWTOVCCF588cUtBYuNNJpydRJRWAy+2EXoOo5azgCQs6OkANPOQO9xnPkKJKuCSKIJ0nOI3gPgu8ilOUxRwnynpKu/v55GqFafvOYs3GgeeNxIvCfNk3hrBEgmk/T29q4xkTi5P8GMfwBl2OAptHwczSujTBflJJHCQ0UDp3YR8dGKCoFCRVzwQOk+mvtDKPXDqOi7tuzDbqLOQx/NkJDnj+3kxvQ8j1u3bq2t+KZ8NOu/IdxPIfzbCBQl7zi+kES5DJigvwD+dVwhqIg+fO91NG0QRTOx2BQV6wTx+DwVEaHgjCJVZo0fJmjosREixhcxbk3QbPYDU/Wo8rI3jcAkY98CJ4WI72fONyj4Y/THjjNn3aUjMsiMlSOhtZFjAV0YtBsHmLWTTFoTpERgii375TV/LRmMlxEjyWRe0pNoglKOmB4BH3RL8uE7H+Odzh5KpdKGCcjfDHYzr6zPA/25z30O0zQfmQd6t/1wnQwV+/to06OYTKFEB5oq4ul/Czfy3dCwzW5M+OVyeTfzyiywp+H7YPW3jfiHwD/bTqPPl8SxCzYyla9nJ+bwrdZdXFxkZGSEkydPcu/evW0FwmwUDCRHriKaBtCKwTWUxRLRXCBoNldWULEYwrPwVAcycxPKNmgGrEyDZiB0DTU/DtFONOmibt+EdwUPx/r65LWEt+l0momJibp5oL29/ZH5PbfLs9Bormf9g6hpGu36x9ETPweOjnJNVJOLwAIlUFEFWJhFwAIvAcqo+ppqFsIOFA64EYSbQdg/ja91gPnogLLQdB4S8tZnO7kxbdtmYWGBo0ePMjAwUDWVL6GV/x26+6cA+GI/vtaHLj8bBH3q58B/HeXdwTa+hIr7MYRoRYhepJyhYh0mHiuQSApy/n7K3rV62qKKdxNddOL44yTMiyxkLbJJhavKFLwxdOLk3Lsk9f2U/HEM6wAqmmXFOsgSU3RHDgBQ9FYBWHGm0DBYdseIiiZcmeRuqULemyRlpMiQocPoYMFZoMvsYsFZoNPsZM6eY3/0NB9fXqDFaGKsPE+zHmfGSxMTJlnd5o5Y5AsYZGxsjEqlUk/H097evmUAzpO8ho87rwgh6G9Q4GyUB3qrNEO1dhqxnREs6/tp07swRAnFPjSVxTW/ES/ydW/Y/k2cV64Ah4UQ+wkEzH8IfMP6lYQQx4AU8PJ2Gn1LC5rbzY25k6jszQTNjZy8a+tudQNsFAwkx18H2tGqLwtFx8Qxe2lz5xCejUodA2sV5+4DtGgSYZeg7yAsjEDvIViagGgcvbMTPVuGB3dRX/xuxAaC9vpo7pp5oBZUUzMPdHR0bPst7UnyNBLritJHMYr/DmUKMCogkoCL8kDFquu5VWFSE2iuwMkl0FtLwTJDQzg6mgPCEQhtCX31+3E6fwOMrk37sdtgoFCjGRLyfLBVbkylFDMzM0xOTtLW1sbg4CAAwvkMevmHECqD1E8gfQdfGOC9jCOPEtVvg38NX3uJslrFc/8STduPlKMotR/QiMdGWMldwGu6QUTfAxhU3KvEjFNY3i0i5nEcH9J+hLQxA+4czcZBCt5oPaocGUzrkXgLw45GJbpATDSx5IyRMvrJeHP0RA+xaI/QGznKqjtJXHuRV3IPOBg/SM7L0W62k/EytBqtrHqr9eCfNqMN6XexYJl4StEfayddKLA30c2twiQnmvZwpzhNT6KPebPEXzv919aUlKxpf9va2jYNwHlSPClLWY3N8kA3phnajuXQsi5jOT9Ei94bhAnQjsDFNb8Z3/yqDbd5syxlSilPCPHdwJ8RpDf6VaXUbSHEvwZeVUp9pLrqPwQ+rLYpWL0lBc3a2+bS0hKdnZ1blu/byc22UeBQpVLhxo0bdHd3P3TyZvv1ztcLusqpoGaHQfr4fQPopVmMsofvNaxTyOPrneBOIvoPwNwdqPVLSfA9RP8gKrNINFfCMTzcO7eInDqzZX8azQNKKS5fvgyw5i2tvb2dVCq1rbfP502jKSp3iWR/GoSJMkooaaKiZURZgGxDaRkwBXoZVPU5FEhiooTIKfxWAZpEZEEYNkRAuQmEliey/N04fb+9aT9839/xG3upVHpYLSQkJOSZUHM5KpVKtLW1bfjC6Lout2/fxjAMXnjhBUZGRkC5aJWfR7N/G2UcAw+kcvFFHugGHKL6bSz3FHrUpeTfRdO6gQpKFZCyCU0bR2jvoEwFN34fQ6Rw/Mm6udxXOUDHlzar/hGy3j0M5yBebBSqlXgK7iioKCU1Ssz4Iq6VR+mNHqEk79MZ3cuMdZu43kLGm0NVw4CkglVniDkZ+FQuOUsIBPP2PEIJ5p15dHTm7DnajU6mSgbDxRWazQQCWLKzAGTd4AXdloHfu6Hp3PcCC10txVBLS0s9HU82myWdTjM2NlZPW1ezsD0p4fBJaTQ3Y6M0Q7U80BMTEwghaGtrw/O8ukayVPlzXOcnadKTxIQPKoauJrBjP4LUN48D2I3v/y5N5yil/hj443W//ei67+/fSZtvOUGzlhvTcRzGx8fp7u5+ou2vT9hey4d24sSJevqAGpumLdqgzcb15PRtkEGS23zJpDXRiTazShxQ/XsR2UmQErcYbCOL+SASfWkS4s2wPInq3ItHEyoWoZxyiBg6/t2bsA1Bc/0x6Lper2JUe0tLp9PMzs4ipay/fW6VNH23PFGNpqwQWfwhhJbBjyUQlQSaVYGkAqFQfgbdUpADSSvIHGgCYbUizCwKDeRxfOUTNe5RsveSSEyCqKAAIccwVn8Wr+N7N+zHbk0c+/bte6zjDwkJ2T015UWhUGBxcfENYz1ANpvlzp077N+/n76+PizLwtCW0IvfA6oCSHBfxzUuolQF5CwwC8ZFpPMqFSXRVQSllpHSAvpQah4pj6GbirQ3DaIZoVeI6EepeKt1c7nrz6CbX82D8qs0m0GwkR+ZRaeJgvuAJv0gRX+UmH+SvJmg4BsoFLYMBMBVZxoNg0VnNNBu2mP0Rs5xObdEm9FBxltgMDrIjD3D3theJq1JumQXy2KZfbF9OFKSsVLcLc5yJNnPcGmOQ4k+Rsrz7I13MVlZpi+aYry8SH80RbYc4fVCmvdJH1NbOx7qur4mAKeWtm5mZoZCoUAikaC9vf25KEu8E9ZbDl3XJZvNMjc3x+uvv04y9af0tn+UNtMnIXIocQ5NjWDFfx6lHX5k27vRaNZ8Sp8H3lKC5m5zY+6EmlAopeTBgwcUi8WH+dA2WXcr1ms05cSN+v/J/BKq6xS1NFVSNKEDntED0WqFhtV5VFcfIjsP7QP4roFdiOHfHoGWTlwzhnQlMW8Rf24Ovb//sY6/9pa2f/9+PM8jm82uSZpee5hqUXjPk0YzMv59aNo0ytHRPQdhusioBgKUJaCpeh1UBN3IQiaK29oGkSRCZhFINHscwSEAktFJfHEKzbiFV+7CsPOoyv9iemkv0Y4vXFOJobEfOyE0nYeEPDs8z6vnwzQM4w1julKKiYkJFhcXefHFF0kkEgCY8tMc6PwVhDeMQCHFflytF7xPAwKMi+BdQXqj5NQFMD6D70fR9cP4/gNsu4Vo1ECPtZHzFLYcJaLHUEqj4l0jZpzA8u4QMU+T8Q+QtoYRRMm792kxj5B3h2kxXyTjXqNctohGh1jU4yxZ8wAk9RRpd4aE20XZXKY/eow5+x59saMUvQjzTgJLusS1IBWcLgJBRlJVcIjgr0Yrn12Z5UBibfq+mgDZVE3O3hFpQaARc3v47MosB/VmPrs8wbt6Dj7y/K9PW1cul0mn01iWxeXLl+sJ1tePtVvxZgua6zFNk66uLiYmJjh87E8R/seIagpTQbG0H00vsGj9JC1t/SQSj+7rbivOPYkYjCfBW0LQ3Cz672lUw9E0Ddd1uXLlCl1dXZw7d+6x66I3mtht2yYzMcbD92WFZz0si6Xmx1FdvThjs4CGFokhXAsVb0Nk5/FkEuvmKFp3tUpARwpzYhrf1bGjg4jrN0juQtDc7FwahkFnZ2e9Rq9lWfUSkbU3Jtu2sW17107eT0qjGV387+jOLZSRQLgVaPZQtgatwbEJX0MRaKuFQ3D3mzZ6JYkyo1DrgtiHUVpFGlGEsNH8eZR+kqgzATRj+EUOyV/ibu4E09PTKKXqpTJd1w2jzkNC3gJslhuz0aLlOA43b94kmUxy6dKlYO5RDpr1i5j2fyWWAKXtx6UDKYdBjtQFTLwreMYXU3RfB/EyrnsI0xzBdTMoFScazePo7yZtfxxdtKLRhuNP4ltHMeL3kaqEqR1hys6BSODIbN0Ps2b6zjnDoKJEE93MuCYr7nQ9qjxl9lPyMwgVjEeWLBLTWlh24twqTBPTYhgYzNgzxEWcaWuapJZkxpqhRW8hr/J0cIq/WJqjzWxmrLxAykgyWl6gWY8zWl4gJkwmy0voaEipcWdR0R0PtKgukj+Zv7+loNmIEIJkMkkymWRhYYHz58/XE6zXxtpa8M1m7g2N1/dZ55OWUtLZ8/NocgJdM9FFAsPoRY8MkPO/E7/iMjY2RrlcXhNYtL5U5m4tZaGguU22E/23k7a22j6dTlMoFDh//nxdBb4ZO/HRlFKSyWS4f/U1js0uQ1sS7BLEmrHvDhPpTCHKmcBvM74f3EDDqe05hJq5i1qew+85SuXqGFpnF3JpAZHqQKWXwXUQfXvRNEHlzgzxL7HQEtuv6bqTcxqLxejr66Ovr68ehXfz5k1GRkZwXbcucKVSqW2nUXoSA4LhLRHL/CZKVwivjEqYCHyUFgWCdBwq1uADG48hsAEQohW9eIMce2lqnkQ4Ppo/gzLOAtcAH63UhCZL+JE9aHIFzTc5Ln4F+/y/r2t90+k0y8vL5PN5urq66kl/t3oT3a0vTUhIyO7YTm7M1dVV7t27x5EjRx76UPuTGKUfBP8+Uj+NXZnFiKeQ3utgnAZvNdBiahexhY/lfBzDOIPnraLr83heG4axgmZ8MavuKLbzaUx9H64/Qdw8T8V9DT06iUYKKfpI+wlK/nVazaB+eN4dRidJwX2AsHqR0VWikXdxrXSLvugRAEpeGoAlexyDKCVzkSa9A4VO2TvKSGWKvfG9TFYm67kxh+JDjFZG6Y32Vv8OcDWfR4+ZSBT9sRRpt8BAvINMYYq9iS5uFaY40bSHe8UZTieO8afTcxxu6uRBcYWBeCszlTxWZo6S55A0dqeE2CjBemNZYtM069rO9Xkun7Wg6XkVCuXvojU5hiFMJCZxfRAlunCi/5K4iDKYhMHBwXrAVGOpzNbW1vpcuhtLWaVSqWvfnzXPtaD5qNyYO2UrE2/NVJ7P5+s+Ittpc7vm+4WFBcrlMqfb4niWhUwdQFu4CW2DMDeNTB5ALwfO0+6qgxIaQklksVxXtFnZwEQhWtpQq8toqXb8sRH8zi506eDNr+CrBKVXbtD87qdflrIWhReLxTh16hSaptWdoScnJxFC1J28HyVwKaUeu8zXKfFfUJ6GMIooIgjdBk+AZaLlJVKLoEUFSlSQqU40sfDwONxZBB7NahapzqFbrwOg2dfw40cQXhy9/BrS7Ed37uFHjyG0HHrlClr+KkbL2brW13EcBgYG6qlPhoeHiUaj9QFjo6S/YXqjkJA3h/VlJNePO7qu43keDx48IJvNcv78+bp2STh/hF75BZToRZAAf4ayl6RJOYAN3quBP6Y3QkllgRjg43l3kXIQTZtBaIdR2hHm7ctEjRMgF9Gq03DFfZ2ofghLTuPrX8BY5XNEtQ4EEXLu3Xp0eatxhpx3A1SSjOyiaAX+lwv2CM16Jzlvke7IQZacUQZix5m17tJiHOUzmQn2xqvuWFWNaKacAQFZJxt89zIMRvdxK+ux4Nt4Tg6AJTv4u+oUAMi7QU5NV/p0a/uYLQTzYJMZCJS9sSZmKzkGEq18YnGUvzlw/Ilcv/VliS3LIp1O1y1sTU1N9TnnWQqajrNCqfLtmGRJmC6W0mnTHTR9P07kB+oBXDUaA6b27t2LlLI+l05PT1MsFhkbG6trcrej3fR9/7nJmf189GId28mNuVNqb6obtWVZFjdu3KCjo4Pz58/zyiuvbKvN7ZjOPc9jaWmJWCzGxYsXsf/PbwDgjEwT625FOkF/vOlpVCKK3tKO82CKyMEDqPkR5NIcek8vnt6JLAbryuUlFAKVqVZfiEZgbhEt1oqease5PwpvgqBZo/ZAb+QM3VhlIRaL1d8+G5P4Pu6AoE3/LhE/C7qBEOB7SbRVHSE0jFgR4qDsJJoeCPJYQyhjAPSbKL0Pw5kAQBcuWCaCFJBGoBCuiVa4g8BDau3gzyFw0OQ8MjJEZOY/YJ34UL0vtQoObW1t9aS/tVKZmyX9LRaLOzZxCCG+GvhPBCko/qtS6qfWLR8Cfh1oq67zL6rRhCEhn5fUAkl9399UceG6Lvl8nvb2di5cuBCsoypolf+E8G6CnENjBk9/EV9JmuKvgU/dXO7KPJZ2EM/7LGCi60fx/ft4nouut+CZLdjoKDxcOYcgie2P1GuXC9HOgq1w/FeJ671U/IW6uVwTgZCYtx8QN05zR+RIKJOyv0J/9Dhz9l1azG4K/kpdOVH28/ilg1y25kEJpipTJLQE05VpEjJBRsuQ0lKs+qu0eq1IJ8moZzLjZeilhQU3z/54N+OVpXrQz2CsgylrhSOJQcazipJjUfByJHWTkcIqBhqzlTwARc/mz+bvPzFBcz2xWGxNnstisVjXCubzeTzPo6enZ0cWthq7dc2znWHKle8hikWrXiDjJkmZNsr8pzjRb9lWG42lMAEuX75MW1tbPVK/Vt+8Fqm/Xq55Gm6Fj8NzJ2huNzdmje0KKZsJhSsrK9y/f59jx47Vo+C2y1aCZrFY5MaNGzQ1NdHT0xNUkpi4Hyx0XWTTAdzJqmbNsSh39JMwE0AJ6Tx0GaSpl8prk6Dp6Ik4qpBH6x9Azc+g9fRhZFdQmsDo68QvVPBmKlTujBE/cWBHx/OkMU2T7u5uuru767XJaw9KYxJf13V35OS9hsoKkekPoksb1VRCFlvQVRER85F2FFH1IBCyWN9E81bRymPIyB68pj5gAgClBHppEqV1oYwsQkiEo6PMM+C+hm7fwo/sQ3PHcaNfhGZbaN4SxvSH8PZ8I7BxdGA8Hicej2+Y9PcnfuInmJ2d5U//9E/5m3/zb9Lb27vlIQshdOADwFcQ1KK9IoT4iFLqTsNq/w/wO0qpXxRCnCBIV7FvN6c4JOStzla5MeFhhpFIJMKhQ0EwIN4oeuUn0bygXHAtAbvy/hKAXOkIrclhlPsqtvkuKs5HAYGun8L3b2HbS2hakkgkznxpAMF1hIhjiF48uUDCvEjZvYLjj2Po72DEmgK/F2VkiepdVPwFit54Vat5D93rR4vuYcVvwhErtGlJ8KHkB+byZXsckxiLzhjdkcNMVUwKvqRMJigdWR6jV+tlmmn6kn2MVkZpj7ZTsSs0xw7zqfQEByPBS6/uAzoY1broTXowmLaZSWIijlVuYao4y7nUAK9nZjmR6uFaZo6TrT3czi3Sp8cZKaxieR5Z26Itun13rt3QWKhkaGiI27dvk0qlyOfzO7Kw1diNAqRU+SSe+xOYQmLgseh1EaXCkvhnpKLf9FjH1hgrsT4Xds1q1t7eXreO7cYKvJUCo7rO3wfeDyjgulLqDQnd1/PcCJpKKSzLqpsRt3OStpswHd5YhlIpxcjICNlslgsXLuyqHvijBM35+XnGx8c5ffo0q6urKKVQlRJycaa+jpu2wYgClaCP2QJOLjDpeDPTmN0dUFjFLekooSN8H61nD3JyBBGJogAtmYR8HnfwIEJEUMoB38G6dvdNEzS380A21iYfHBxck0ZpYWEBIQTFYnFHpgGA6NUfRpN5PC2CnjEQuIi26nU2TcBCeQKSQToppbUiqhpMzZlGzyaQicNoPKDs9tHsLgCLeJGzICbRMncQWhwVa0XIwClfihfRS0sY5VH8yEmMpb/AG/gHoJlbOm2vT/r7oQ99iHe/+93Mzc3xTd/0TfzBH/zBdvxqLgEjSqmxapsfBt5DLXVBgAJqBW5bgbltndCQkLcRNS2X53nE4/ENhQspJcPDw5RKJS5evMirr74KgLB+D73yk4CN1M+gZAlPKPBerpaQvEprchipfwEluYznfBTdOI3vXcf3p3DdVkwzA8ZXsGh/FqKzRPVD2P4IpnEYz1ug7F7F1PdhM0BRJvCUja4XAY2sc4u4PkjFn8G0DyIjy6joCW6Vb5PU20FpLLtjNOkd68zlJ7Cly6rbw5T1gE4C4aTiB/NMzg/M4MvuMgJB2bcoWv2MOXNEhM6slyUqDJb1EhF0puwVDASjxXkMNBxL568Wc3RWfd5XncCMXvGCuUuvzgVNwiAVSTAgOvnzqTH+/uETT+06b0Zrayv91eDY9Ra2aDRat8BtVCZzp36Rxcr/xHd/AR0TgSAnmxFKcSX7hbxr/+6FzI1YXyqzZjWbmJggn8/zcz/3c/i+z/j4OPv3799Wm9tRYAghDgP/EvhCpVRGCLGt/JLPhaBZM5XncjlmZ2c5derUtrarCY/bEUoahcKaqXyNeWQXbFjDvFpByLKseu3bdDodvFFPTEA0BlbwwBNrQ0XaoJAFwDdiaGYngjwoBS29CF1QujmJsW8ANTOFLAWBLf7CHBgGnh8lN5NAk1Aam0Hr7sLs6kEspvFzRfTW5zPIpDGNkhCCaDSKaZprkviuT6P0hjZm/hxRmUOLO6iKgRb38D0dASgPRCzQYkoviRYNfIuksRfDvRn8r3WiW8MoO4bfdhDPfXgf6cXbeMmzmFwGWcLXzqLL10DGEJU8ujOBHz8UmNWwMe/9Iu6J9+54cKpF6v/Ij/zITu7DAWC64fsM8NK6dd4P/LkQ4v8CksCXb7tTISFvA2qBpIuLi0gp2bt37xvWKZfL3Lhxg56eHo4ePRq4AGkWeul9CPcVlHEK4d0MErCTB9oBB/xrYJwnW1iE2C10fRCQ+N4DfNmDri0SiZ7GIkbG/gRR/Qy2fwOFB2hUvBtEjZP4MkNJHWXOfhVdxDFFK66xSqtxipx3C10F2kUjGmXCGyTr3KHV6CbnLdEq95DTp2kzeyj6q1ULmMCRTbycmSSmuZiYrGqrNGlNzNvzpLQUGZlhIDbArDXLodhp/nJlmaFECxUrz/GmQe4WZ+oVfo4m+rlfnuNYcpCJyiJDcj+fWlxhSEswZRXZG21hspRhT7yVB4UV2iNxhvMrxDQDVypkIcK0UeRP7JE3XdBcrwBptLABayxstajvmmtXNBrdkUYzV/pl8H6DqAAdm6xsok0r8ke5d9FZ+ZqncXhraLSa1eSc9773vbz3ve8lmUzy4Q9/eDvNbEeB8W3AB5RSGQCl1NJ2Gn7mgmajqdwwjDVax63YSQ3zmlBaiyTcjal8q/1blsX169ffUEGoJpDawyPQcQBmbwPgFmzcuRUSXS2oYh5Xb0IvS2pGZG9+AdHdB2qaUqFMAvDnF6CtBb1UwBs6Q+nKFPR2oOaWEbEIZiqBNbVCoeBjnBim/avOPdYxbocnkUdzfRol27bXOHknk8n6IBCPx0H6mPd/DWF6+OVORDQbNFa1zkgrgp6wUQpU617wblX39lAIVMYeYBWhLLR8Gl22UD/5ykUrPry2eul2ELC1OoKKB+k6vLYvxev4W+CXMe98AOyHlTB2cuxPia8Hfk0p9R+EEF8A/A8hxCml1JNPPhsS8pzRGEhqGAaVSuUN69SsTidPnqS1tZoj0rvLiYH/Ar6GUGmUm8M1LqDkAsg5YAH0cyjvKpZSlKRGQq3geSWE2IdSEyjZAfoBsrKA0IIXfU/OomQMhwni5gUq7qsoUkw6BVz1Kk3GAYreGK2Ro6Sda9j+CihB0b9PXH8nNyqT9EaPkvUzJI0Oct4SngiOadmZwCBK1lskoV3ks5lJ9sT2MG1NczBxkNHyKEknSdEo0hHvIFPKENNiDEZPMlnWKUsPXwbzrlMtJGJVK/zUvutCB7uHXDV3ZqqllalsmaQeDJgxVyFRDESaueks8UWpA/zl6BwH21q5l1nF8yVL5RLdiTcv6HGreSkejzMwMMDAwMCaMpm1cpLNzc1rqvpsRqbwIxjyL2nRbUxcVv12WrQKv5P7apR3iuP61oHFj6LmRrhdNE3j6NGj9Pf384d/+Ic7mWO2o8A4AiCE+CyBef39Sqk/3arhZyZobpQbc6eC5npz+KMQQjA1NYVlWWsiCR+HRkGzJsAeP378DRHrtWpD7ugYztgUyb3dqEIWd3YZPB/VtheKdyBtIbNpxFBfkKTddSgsehhANJOHZAIqZWRzirLZRmWqQBSQmkD3fKIHB3DmV/BzNtGBPgqvTZH6yrPPPJfYVmw0IESj0TekUUqn0wwPD2PbNsfKf0Z3JYNyNPCL6AkPJTVE1MFPx1FeAuVoaIaEeAWl70c2dyD8wsOdVAdRAKW1EClIVFsMgYWMHMFYuobXdgrdvYVQDsrfgyanUaU72EPfg9f90DXFeeHH0ac/CmztY7meXfjSzAJ7Gr4PVn9r5J8AXw2glHpZCBEDOoFtvYGGhLwV2SiQdP084fs+d+/exfM8Ll68WPcPF/bvoVd+kfamBfDB18/jKQe8zwBR0M+AfwPpT1IxvgDH/QSxaARNO4SUI9h2GdOMYsZ6yPsxKv4raDKDIbrx1BK+fQwjfg/HGwX9ixmu3CYVOUPGuYFWTZaede4gZBOWtkDUP0ol0saSiiGRdT/MRXuEuNZCiRVS+iAZf4Y9sfPcKuRpqUZ915KvZytZAOyYDR7MWXM0682sWDHu5jO4yqOpmhMzZSQZKy/QbjYxUV6kmSgT1jInEvt4db6EQGfWX6HZiDBcWCGq6cy6JXQEeUOCB1m7zCHZxsRMDldBpBpd3Zts4s+mRvmmYzurXPc47EQBslGZzKWlJTKZDFevXkXTtLqio6WlpZpxxidX/A4Mholo4CmDokxSkAn+qPDFLNhNfFPqLG7Geqzj2G0OzVrKvCc8/xvAYeBdBPPOp4UQp5VS2Udt9Pjh3LukFgHYOMkahoHneVts+ZDtCpq2bbO8vIyUcttC5nbeAmoC5NjYGKOjo5vm3hRCoDwPZ3ISpMLTU2id/eAFfbdG59F6BhHZwNdFRdsAKDd14TnVRnwfrbsPAEOL4g8XiaSLqFgEbSWL0gTlfA6ZL2EOdaLFdNz5VQqvT255HI/L064MVPNrHBoa4oUXXuDCyf105K4hXdBEGVl9q3aKLaiVZnRPoGkumiGRZgrNmkEvzaGnV9Dnp/G18yiRRLPG6/uQoou4WkbJk8EPfvDmrZWzKAyk0YGxcgOpp/BbLuB1ff3aThoxZNtxNG9ng4pSajdazSvAYSHEfiFEBPiHwEfWrTMFfBmAEOI4ga53eac7Cgl5KyGlXJOAHdbOK4VCgcuXL9Pa2soLL7wQCJnKQS9+H0b5x0CtkC0dxhFn8Pw7IMdAPwrY4N/B1d9JXtk47sto+iE0zcHzsvh+nEgkh29+CfP2NUreq5j6viDpuh74COqxB0SME+TVfvIyEAjL3jwCk7z7gGbjEBIHrE4M2UPe7OJBZYpF6wFxrZWct0hP5DC+cumIBO+ZOhG6Iie5W/RYdPLMVGYwMJiqTBFXcVbVKs1+M1kvy1BsiKTejCYP83p2kYPJPjwl2RfvCrSR8Q4U0B/rQKLo0po5GBkiU06QdR32N7XjSJ+DTZ1UfJejzV3kXIsjLV0sWkVOtHSTUC1kbYNpp0JcaIzmMmjAVDbDHz64h2U9ntC1Ex5nXtJ1ndbWVpqbm7lw4QKnTp0iFosxNzfHlStXuH7zsyyl/wG6GkZDx5Zxsn4Ti16KP8h9FQtOE6dbDtMsEo+dNWe31eZ2kTJvOwqMGeAjSilXKTUODBMIno/kmQmamqahadqaG2EnGsrtrr+6usqrr75KKpWir69vWxdsI9/LjZBSMjU1heM4XLhwYVMBVtM0WFyEau42e2QW33wokCrbwTUfasLsiRk8PYLMC7TFDKI5iOmQxTKYJoUJG6O3C1yP6GAvmuOhDXZhruYRTTE85WGNz2EvZZj/i2sbmo2eJ3Y6IOiXfwUNC80I0hlpEYWz1ISyNDRcfN9AM4MBTcYGHu4n2oNQEmPpFtI+itIfllQTTuDPqedu4utn0HMTAGjOAjJyBqXtQ/hlZOQg9tAPwAb9ValDRJ3Mjo7dcZwdB6IppTzgu4E/A+4SRJffFkL8ayHE36qu9v3AtwkhrgO/BXyzet5yXoSEPGFqWsz184rneUxPT3Pz5k1OnTrFnj17Hq4jIvjx9yIj70EpgY9EqgWgFVQW/EmUdpyKfoai+zmElgIslMzheQk0bQUzeo4cg6zYnyCqHwM8tKofTsW7RlQ/jmvvIeP3sexOknXvENXaseUyqUjwcutVFQ/oMSa9FBPWKN3Rg/h4dEQGAZAEAnPanUFTJiU3ya2Cy5y9wEBsgIqsMBgdRCLpjgS+iAmC4MKYluJ6WlCoCt1FPxgjM14w9tVyZK44eaKaiW3H+MuFLCtWUOknUw36KfuB9sOrDicRTacv1kKT08ytxTQDTc24UjIYjVPyPY63d7HkWORdm7+8cZ0rV64wPDzMysrKjub7nfIkFSCRSITe3l6OHz/Oiy/0s2fPTxHXVzCVj+tKlHRIu0l+L/slzDkSTQm+rOOlXQmJ69mtRnMXguZ2FBi/T6DNRAjRSWBKH9uq4Wfuo9nIdivt1HiUoKmUYmxsjNXVVc6fP8/c3Ny2b+qaSfxRN0gtZUJHRwfHjh17ZHtCCMTs2hcDp7Q2nY+dVUhNR5N+IJAePIy8GkSoa119+IU8/sIS2uFjuJdniR3vAJaRToMGWCpie7qwxhbwNJ34gU6cpSz3X72JE4W2tjba29tpa2t7oolcH1d+2cmAoBYfYK5cQzoGZkcR6RmoChiGRFYrAPleHEME/xeKpXq5T+m71B9XP4rIuciuAwhvEaMwVd+HKGvgPzwmrThPtfwvKrYXFRva9Dg8swl8B/TtVcKo+Z/ulGpOzD9e99uPNvx/B/jCHTccEvIWZqNxRCnF6uoqQgheeumljSdtfT9+8idQ5nuI+v8MofIgWkDbj5RZyoDvLwBllMwBrSi1jOsdRDObWXZuYuqHAIVURcDA9h8QN89Rca/iiX7mtGvgXKv7YybM49hOmqI3DUqnwhQR40u5yT169CMUvRxKBXPWsjOBToRlZ5w2ow9HVZD2aa77sxxOHibn5YhqwQtrppwBHXIE0eUZLUO/cZKPLS4Q1SKMluZpjzQzUV6kN9LGrJWmP9rOnJ1mMNZJxXfolPt4tbDEUKyVqXKWPfFWxksZ+mPNPCis0BlNMFxYptmIIqWitCq4RxoBLJYDwdSuuoOb1Xm0r7mVqWSUdx87TS6XI51OMz4+vq3Az93wuILmRjKA7d6jbL2XuObSrudY9dvoNMq8XjnOby+exPVsULDXGMLN23ie90w0mrXk9TtBKeUJIWoKDB341ZoCA3hVKfWR6rKvFELcIcgg+4NKqdWt2n5mGk14fN+BzQRNx3F47bXX8H2/rmncSeDQVuvOzs5y+/ZthoaGtnUxNU1DLDa4xkUiFG5OYQwFaQdELEb5/hyVtoZMATKGqsYRuosZFAKRTGLlAwHGmV1BCQ13egGViMH8CiIeRZYr6G0tRI/uRTc0WMzRtyA4f/48nZ2dZLNZrl69ytWrV5mcnKRQKDy2oPhmlAatoX/uV0FpiKiG8sEtNqMbEt/T0OOBxlg0lDtrjT7U5qrSQ2HSt/IIt4hYzuNHzyB4eL2ViuHrDxMMK7MHqe9FCR1n4Bs37ZuUEj/aSkMG1C0J65yHhDw9crkct27dIhKJcOrUqS01QyJykQfzP4EUg6DyuKKFomjH9a6hKAMplFrGsjqAKA5xsr6Or8p4ch5BElfOkDCDIExPprHFOxmtXEO39wX7qPtj3iYiOnDkKgl1kpI4w7IfKA6y/iw6JsvOBCljAFuW6I0FuT2Tej8T5RRpGZTQXbAW0NCYKE8QUzFyeo7uSDdZN8vBxCHsSg+rTgRX+exPdiNRDMaCQNiuaGDVaTeDMajbTDGTiSFVoIhIRYJqdN2xYHlfvAUFDCVSeEpytnmQ6xNZBppaWbUqHE11MF3Ms6ephRm7QioaYzibJqJppK0Kd2eX64U9Dh06xMWLFzlx4gSRSISpqSkuX77M7du3mZ+f3/Z8vRlPQqPZKOCVrD+nUvlnRIRLTFgsel3EhcPHSxf548I7iUSbMOMxYpFB3t11jpWVFcbHx5mbm3usufZxfTR3glLqj5VSR5RSB5VS/6b6249WhUxUwP+tlDqhlDqtlNpWOPszFTQfl40EzXQ6zZUrV9i7dy9Hjhyp3yg7MctvJmj6vs+tW7dYWVnh4sWLJBKJbT0MQgicORuqN4vR3Qu+pLLighBo1e8q61C7DUujGczBwFzirWbR+/qRHYNYM4HQKfNlzKFekAq62sDzMQ8dIDtrkllsojAnmP9sEb9jD8Xhpboz80YPd7FY5O7du8zPz+M4zsYH8RTZ7oCgZm5AdhzhlpBSw8u3IozgnMrG1ESp6m9GG5o9H/wf6SVCYCJSGBiVQFss3BKVBYmnNZjRc4toq7fxzX3B+g6Iwgxex5ehYn2b9q8+IOjbTz4flp8MCXnyKKUYHx/n7t27nD59ekcFISS92MYvYRvvpui+ShDn0IqSizhOO0pBPG5R1t9JxbyHq8bQRApPLhM3gxQ+lnebqPEic66JTSCsSSML6BSq/pgKF7/SQkwcZlZEmLEXWbBHSagObFWiNxa4vsWNIMVR0VulM/ICL2eXsaViRa3QrrVT8At0yA4kkj3JwMWu1WylJ9JH2mpjzKtgyWBcz7iBtnHRzgIwawVayGlrhaOx/bwyX6DgOIwVA9/KyUo28LEsB+vPW0HFn6xT4Ux8kJkVKzD+VCeuhBGc555EEgkcaGmj7Llc6OrDTUsmlnJMZnJrznct8PPkyZNcunSJoaEhbNvGsiyuXLnCgwcPWF1d3bGZ/UloNGvb58u/hu/8BDoCgWDVb8dROh8rfQGfzB+n5NpoyqBktXKkeR8Hegc5cuQIe/fupa+vb40gfevWLebm5rbt0vYmms6fGm8bQVMpxejoKA8ePODcuXP1Wqg1dpoKaf265XKZK1eu0NzczJkzZzAMY9ttqkIZObqMticYOJQZDDzOfAYxMEQuHwwCer6C6hlE7+3DWS4ixUPNnIokyd1O42eLgYAJiJpAU3Gwe/aSnZDYixVifc2UR1cwWmIopZMdtUlfXmu6b3y4m5qaGBwcxLZtbt26xZUrVxgZGann/3zabLu608u/hlJBfjNV8tCUgyaqFX+0IPWoq/pQWj+ucR7XfBEvfgE/fggZ7am3I+P70HDr36PWMpVCG1LpVEQXmrWCQKKcJpTegpYdRXMyuF1/95H9exOdtkNCQjZACIHjOLz++uvYts2lS5fqaWq2i6ZpeLILM/F9CJFEyjkQAygFkcgomvnlLPlliu7rIFMoCkSNwDpVdq9iaoNo+mlWvA5Kfpq8ex9DNKOMLO2R00BgdUMJzGQ3DxyDJWeWvugRQBEjECwLXmCRXLRGaNI7cWQ/0xUTS9oMxgMlRLwqxBqRQAOZdoPIdE8aXE8LruWmiWMyXl6kM9LCTGWFgVgHi3aWfYke0m6BQ4k+UqKPxaLBqlPhaEsXWbfCXrOFrGtxpLmLZbvE4aYO5ioFTrX2IEsmCxmbB7k0HbE49zKrNBkmD7JpdCGYLVZrojsOp1JdeDnFYq5EKhbjz4ZHH3n9mpub2bt3L4lEgnPnztHe3k46neb111/n6tWrdeXIVtrBJ2U6z5X+E8r9b0TQiOBSlFFatBKvWO/gM/l9CAziepKpooEndb6274U1bawXpPft24fneQwPD3P58mXu37/P8vIyrus+sh874XmzlD1TH83Ngm52UlbS8zwcx+HmzZs0NTVx8eLFDS+KruvbjnirRZPXWF5eZnh4mJMnT9LW1rZl/9fjTy4CkL+5RMueFG7hodYwP1vE1Exqe/NsHaOtCShRGZ0j3tGMLBTw/Qi19wIRCXxx7MlFNNPAppnylI/MraC3xnFXCiAVif1tWHM5SvMOS38xQcdLgxv2r/Zwt7W11R+CbDbL8vIyIyMjW1ZQeFy2c73l2FXEagYzkccptxNrSuO7OpEWC+ULbK8FliPQ2YuYuBckbe86hUjfC7bvOouXOItevoHSWh62a3ZiVlYwgVLyKJGoCQRv7Xp+hGzTcdrUHfz4ADL16NQcb6aJIyQk5I34vs9rr73GwYMH64m5YWd+5DUFhmEcJtn0MxTy34bgDpp2EVfTWbU/h6GlglrlagBFhop7lYh+BFfO4IhTTFauINCJ631U/Pl6vfKSNwtKwxUrYLyL6+V7DMZOUrayWNUyuVkxQ4QkeW+R7sgBKrKIL49yvTDMvvg+ANJOGhQs+otERIQFb4GUmSLrZdkbOc/HFic53ryHu4Vp9og2xtUq/bF2Vpw8HZFmZq1VmowYKaMJzUnx8tIsL7RVs5pUUxIZWjAmx/RATGgyo+xPtBOrJLm6OseF7j5mSwX2t7Tx6tI8Jzs6ubq8yKn2Lm6ll+k3o7TpUebni0xaOeKGwVQ2T7Zi8e0vbZ3fWQiBrut0dHTUc15blkU6nWZiYoJSqVRPst7e3l4vftF4zR9L0FSSSNPPIrybpHQbHZ9Vv52UVuZ/F76ae5U2FBJPCZbLMXQhudi+j9aqIgneKCQ2VoYbGhpCSln3V52aCly7ajXOW1tb67LIbuaV7ZQzfrN4roKBoPEh37prhmGQy+W4cuUKhw8fXjOwrGc3Ppo1LWkmk+HixYtvuJG326Y/EZhvlePhRXqxpxbry0wtht6Wwl8NBhl/ZpmyrGYY8CVaTx+yXCI/UsAc7MUZmcKaWESPGCjbQT9zjMLHF4kc7URmKsSH2inenCU21IGfq+AsFWk60I09n8deLRPt2LK84RuSp6+vUd7S0lLPKbbrGuUNbEvQfPl/oePj2UlENYWQxMDJx/EKMeKtJRCgzIfXSLjZh//n5xELS/gdR1D+w2smI/3oVaf5RHocv2ttVaqoH0cqwbQ6zWQ1e0F7e3t9EFjTx106bYcazZCQJ4Ou67z00kuPFYBRm4M8z+PevU7a2r6W5qbPUaSM5ZVQVNC1fbhyDqUPo6uj+OI+mmhl1TfIO1doNg5T8B4Q1Tuo+PPk3LvgJ7BZpklcYNwvYVb9MZedoD55xp2ly9zHsjtBq9jHshrB0Nq5k3MxtQUEgqnKFC16C6vuKimZIqNn6knZuyO9lNwuFuxAqHareYILBL6cc1ag7ZwsL6EhKNsO8ysRRuU8ETTu5ZeIawb3CyskNJMpp0hU6AwXVogIDU1qzMw7rBoZBDBXCuasdLXSnV2Nmtc1DVPT6FExrj9Y4txAL0vFBc70dXNjfolUPMbw8ipHujYvmLLZi0EsFqO/v5/+/v41SdZv3bqF7/v18bmmENqtoOn7Hor30hKZJiYEjjKxZBNFGeN3Cl/JhBVHIDFFkumChisd4rq5RpsJW88JmqbVBUt4WCZzaWmJBw8eEI1G0XWdeDy+I8H5ebOUPXem8+3m0lRKsby8zPLyMufOnXukkAk799G0bZvXXnsNKSUXLlx4g5BZW287gqZXFTQBnLzEbX2oUdPb26ksu/V0OaIzhS8e3iD2bAZjaAhnpYJXDFTrynKJDPWjd6UozAeX0M8ED7tXCISwSCqONZ0h1t+M2axjTWWY/6ORbR3/emoVFE6fPs2FCxfo7e2lWCxy48YNXnvtNWzbJpfL7drMvtUD5F3/LFpmPljPddGT1WNWTWDpYDxMKyXcwGSj9AiiGLgLqEgLWrkajLU6B3M5/EQ19ZdsqBQkTFgpobRAeFZGksjyPWTiJN3n/jEvvPACLS0tLC0t8eqrr3L9+vU1ZpxQoxkS8uzZ6TO40fbFYpHLly/T1dXF0NC/I8cQBe8+WnVstry7xM2zAEhyGNolRqwZNK3mshWMhVnnNnF9EF9ZCKubmPYCY1KS9nIs2qO0Gr3YskxPLKg2pmuBgiWvFknpZ/nU6jRxvYm8l2dfYh8SScIJlAWJSPC35JfojQ5wLye5n88wWpojrkUYKy3QGWlhRRXpj6ZYcfIcSPSS88ocM/bxufky/U0d2EgON3VgS58BLY4tPfZEmrCVz6FkO5bvcallP6+MrXCgJVUP+pkrFTjQ0sZYPktfsonh7CptkShL5RLHjE6m08FclC5X56bq/NAUNfmz4S0z4mxJLcn6vn37OHfuHGfPnqWtrY2VlRVeffVVyuUy09PTlEqlHWm0PXeFQunriWgz6JpORcbJ+C2s+O38r8y7mbaaiAiTiGhlLK8w0EnqEc63HKI9sla426nyoVYm8+jRo1y6dIkjR44AQezJ5cuXuXPnDvPz89i2/ch2nrd55bmLOt+OQFjzwfE8j56enqAk4RbsRKPpui737t1jaGiII0eObCoEbadNpRTu5EL9e0FKvLwJenDqPVtgzWSJ7A9S5viJFkr3F9CSwSDipfPYbnDz2pMr6J1twXqOpOKlKN1fhoSJv1Qi2t+GNbGK2dmEPZsGDaI9TVRGV/CKNvkbC48dYa5pGm1tbRw4cIDz589z5swZhBD1RLY3b95kdnZ2R4l5txI05csfQcgKQgEodKOMlW1Dd0oIIfCrKZ6UpteFS9k0gKimBpGJ/of7aupHlDOoqRX85DFE+WE2ADsygJafx0+crm63H6F8lGpBJfoxTZOurq41g4BhGExMTHD58mXGx8epVCpbDgKNPG8DQkjI5zuFQoGpqSnOnDlDf38/QkToafkhQMP275MwLwDg+jOgmin7A6RVM55ysOUqoFHwRmkxjwEK3zIRyqQkmrlbKZJx5+mNBqmQknqgycq6C4Bg0R6jmT5KzgDLXgwFdESqZmM3GFOLZhGBYMFfIEaMiGhlutjMWHmVw8l+bOlxsKkPiaI/FuRrThnBGBPXI/T5/UzlfDxAVM3ksmomNxPBXOpXh+NSucwer435lSCISK8KTbWgn1QsWH8g2YynFKfbu9GygojSybsehzvamcjk6GtO8mA5TXMkwng6y8cePFrQ3I3Zu2aJO3LkCJcuXapnmxkbG+Py5cvcvXuXxcXFRwa82vYYxfK3YKgV4poPUiMiHAoyzh/kvpy0H8dVHspPsFDSMYVByXfATvLX+95Yy/1x82jG43Gam5sZGhri0qVL7NmzB8dxuHPnzpp8pOuVc7uZV4QQXy2EuC+EGBFC/IsNln+zEGJZCHGt+vn/bbft59Z0vhnZbJbbt29z6NAhotEos+vyU+62XQhu7pmZGdLp9JameNhe3k9nbhXlPdxvTE9QWVwmcnE/zsgY5cksAFZGogH2ioNyffT+QeSDB+ipFuz8w8ukt6fwV7IoEaGy4KA8SWSgHffBCkZ7EnsuS7SvleLNWRIHunEzJYz2BNFUC16+Qvpzc3S8Y4AnhWmaRCIRjh8/jlKKcrlcL8fpui6tra11M/tmmoZHDSru5b9Ac/I4bhtxcwVPxXGWohimjm4G59Vsq2ogm/sR5Wq1n0jDQ6Y9TIiuIikE8wjp4S/YaG3N1ArmqGpiY2ZHkN3dKFcgCPw7NyIejxOPx+tmnOnpaVZXV+u1ctva2kilUo/MW1oqlejr2zySPSQkZGds5Dtf++1Rwovv+9y5cwfLsti7d++aiTphvkh74ptIl38d2xtB0AyY5L1TpLlBxGtDI07FnycVeYGMcx2vmhBdGUUs8RLT+ij9kePMOXdxZbBs0X5AXGuh6K/SGz2MJS2ypV7G3Cn69UCIm6nMoKMz786TMlJkvAx743uZqczQ6h/kE0uLnG7ZB5WV+vEVvEq1/SwQRJWnjCRTiw4Tlo3QBE16hHv5JZqNKMOFZdrMGMOFZVJmnHEry5DZhFWKkrNcKl6euNC4t7pMRAiGM6sYQjBVCNyOFsslTqe6Kaw4LBfK9FRrmjdFg7G5v6WZ+UKJkx0prs0vsj/Vxu3ZZU4OrA3afZJomramlnk+nyedTjMzM4NS6g1uUJZ9jYr1A8SET0rLsuq1kjJLXHeO8ZHsJUqeiykMlNfKpCWRyiauRZBOkgOt3fQlmt/QBynlY2vYa8JqLZaiFizl+37dv3NiYqJuhvc8b8eCpghybn0A+AqC6j9XhBAfqeZjbuS3lVLfvdNjeMuYzpVSTExMcO/ePc6ePUtPT88TSVlUw/d9bt68STabZWBgYFu+h0G900drNPO35rA7HkY8uwuBX0v+QR5zsA+/EGi/KpNp5NAA7mywvDyZQWkaWlc3xftLaK1VreZMBkyD1VGPyGDwtuqXg/Nlz+dQgLtaJLq/GzfWwfRVyFdSpOdN5u/A7Kce+oc+aYQQJJNJhoaGePHFFzl37lw9d2ctYnCjfGKPmgC8Vz6O9EBV7wmnHCdieDjlYHslwdCC4B1iDQ+6fKhRrVX9CX5vuF7Rbvz5MjIWvFBoVrCekB6+6kVkghRI/sDWec+FEEQiETo6Ojh79mw9WjKbzXLt2jVef/11xsfHyeVya469XC7v2JdmqzfP6jp/XwhxRwhxWwjxmzvaQUjI24yt5oqaqTyVSjE0NLShAqE7+T3oWge+yhIxX2LS0ckyjKaacGSWtkiQe7fizwM6ZTlBk/YORr1mnGoGkbQ3i4bJqjtNR2SoWvUn8MkXpHg95zPpLWJgMGfN0R3ppiIrdBOMUZ2RwG9ex8RzhnhgBdV6xsuLGOiMlOZpMRJMlpfojbaxaGfp1VpJijheupVhq8LxVC+29DnS2oWnJIeaOvCV4kBTO75S7G9q50iyi1g5wXShxKG2dlwlOdbZja0kh1pSFD2XwUiM5UqZA8lmuvU4lRWXu4srdCbiDK+kiWqCsXQWTcBCIdCIVjyPPa0tJGyDP7v+YNPr8biBPOsRQtDa2sr+/fs5f/48L7744ho3qLvDP0+59F5MfEzhMuf1oAvFX+TP8bvp87hSJ6JHyFkJlqxAM9xmJlnKCoqOz9/eu3HRFt/3n1ploMZ8pLUymYlEgg9+8IN84hOf4H3vex//+T//ZwqFwnZ2cwkYUUqNKaUc4MPAex6r4w08d4LmRgOC67pcvXqVSqXCpUuXSCQSm667k3ZrlEolLl++THt7ez3n2nbM7FsJr67rMvHZm1h3injdKYzONrxc1V8lW8GPda5Z33YeugB4mRKRfUMUJy2UL4n0ddd/Nw8fwl60cFYDYcqbySNSMdyVEvH9nchkitX5OCuvptFMHbPJIH8/C7pG+laB8sKbU5Jyq8S8d+7cYWFhAd/3NxxU7Jc/AcU80pIYMYVVTqH7Qd+FFpx3P9GFUB6O2YYUzbitZ3FbziJpQTbtQwmjbk4HEKWH5b6VMhBWCb/Ygqe3YBYbkupXfPxIL7JlH6rpoen9UTQOCLVoycZBIB6PMzc3x+XLl7l58yaf+MQnWFlZ2ZGg2fDm+TXACeDrhRAn1q1zGPiXwBcqpU4C37vtHYSEvA2plaHciLm5OW7cuMGpU6cYHBzcML0dgK4105P8foT+hQyXb6GLZiQWERlYiPLuMDpJLH+JiLOfqP4SU76gIissWg+IyCSWzNMXDRKvmyLwLc+48zRp5/hUepKU2Y6tbHpEVTlRHapFNBgf5+w5BqJ7uZpxWHU8lv0CexNdFL0KR5r78ZTPvkQwV3RH2wBochPcWPKJJgMNl1et2FPyAhNywQuUHbmqaT6qItyeypN3g/my6AbrWV4QI6BVcxe3NrcQ0TR6SHBzbIWo9INa6U0JHN9nMBknZ9kc7epkNl9gb1srBgI9I7kztcRn7k3ivwnp8zbCMIy6G9TRk9fp7/kddBFc92UriZQ+H8+d4BPZY/hKx5IuZasFW5pIFJ6vyGQ1mowYL7T3cqA5teF+nkQJyu1qRSORCD09Pfz4j/84J06c4Md+7MeAbQdEDQDTDd9nqr+t5+uEEDeEEL8rhNizwfINee59NHO5HJcvX6a/v5/jx4+vuWhPQqO5uLjItWvXOHHiBIPVBOlCiG21+yhBs1gscuXKFSKLwUhRXtDRO9dG2ZVXQW99KGQ4OQE9D2uge55JZS7QslVm8yhAGDqlbPB2XJnOEulvAwV6ZxNoAtncwexn8kQ7E3hFl9ZjKQrDGfSIRsu+JKWZIqO/M77lsT0N1ucTGxwcxLIsCoUCN27cqEf41yL+3b/6JNIHDRtZcVC2ixkPBr1Is49SoFJ7KbsHkDMSOTmHHB7Dn80g7z7AfZDF9k7jNZ1AGfHAbF5pqJZVqSYOzixS9A+uqecjjWaUFcHve8e2j+9Rg0pjrdxLly5x4MAB5ufn+cxnPsP3fu/38u3f/u1MT09vuO06tvPm+W3AB5RSGQCl1BIhIZ8nbNf3v1aAY3l5uZ5vEx6mzduItvjXseK7KFziRiDQWdooUa0TTxURVi+aasKO9XOjPM2yM0G7uQcfj6QKzMQlPwPAoj1CZ2Q/GbeXnB8Ina1mUDiiJAMNYM7IERER5uxAu9lhDrFitbPilOmPBnNFs1H156/6pKerNcvnrDQDsp9XczYCjeHCCk16hPu5JdrMOMP5ZbqiSUaKq/REm5gu57iQ3MunR+fpTjQxXSnRHY3zIJumO5bgfjZNezTO/cwqzWaEpXKJI0YHI0sFNAH56lS4WlobhV5zGtrf3MrY8Ao9LU2UbZf25gSvjc9teJ6ftEZzM7Klf4vwPkSTJmkxKrgixkAsz1+VLvIX6X3kbAu7aLOcjTJTKlHxXJpEnHIxSsHzKHoOX7vnyKbtP6la5ztto1Kp8MILL/Bd3/VdTzIG4A+BfUqpM8BHgV/f7obPpUbT87y6qfzu3bucPXt2w5xQj6PRlFJy//59ZmZmuHjxIq2trWvW3a5GcyMTy8LCQvCGfOwE7nQwqKisiy0b/QYFhdEMek/w5ipMncpECU80aDVllMhAIJw6y0VUbxsMdpN+fRk9GQibRipo009bmIf2svi5HOiC8lRgThYo/LJH24kU5ZkClfkSq1dXkf7jBQU9Lo0Rg83NzZw6dWqNKWP4tz6MzGbQdQepxVFSR3oaQoDnavi+QcXag8zaaOkVvEgCUQrSd9DcoCnWYsjhcexcJ17L0frP0khA4WGQlioJ7KYDD7crFRHpKbyed277mLYbdV5zMfiGb/gGXnjhBT70oQ/xzd/8zfWJbgu28+Z5BDgihPisEOIVIcRXb/cYQkLejhiGsWb8r1mxWltb6wU4GtfdbPwXQuNoy3cAkHFuEaMfhEeEYBw34wZLcj/DlQfVBOwQ0YIxvaDNoxMh6y3QHTlAu7mfrDPIRGWVStVSM12ZxsQkK7L0RHqwlc1QfAhTmCS1fXxiaRm3Vv/cDcb40dI8UWEwUlwgZSaZsVY5GO+jkouzahlU8Dnc3Pn/svffUbKt6Vkn+Ns2Yoe36TNP5jmZx59zzz3m3jKSpkpdCCGQStMgQA0tmGk1zWqBxII1dNMzUz2DmrVgmGFYjSToxUwPRoMRjJqWQMiVqlRSVd063rv0PjO8j9j2mz/2zow8PvPcW1WXSz7/RGTkji+2fb/ne83zPhMuPxbP+q0koykAJqNpRrwcds+nBKNR3xaNRGP+dokknhBMJVPYnsc72UGoQliou17L7VabY5k06+0Ow/EoGz2TuK4xX6lyQo/w6MkWnge1gIhKwG/efbV4+7cTnudRbf40svtrxGULQ+rR8uIk5S6/1Pgit7pjGGqYeChBwUvioaK7EqLh8nSjRbtnElVULiVHOJsZfO3vfLtC569Dp9PZV5H0HqwDez2UY8FnuxBClIUQO5Wu/y/g0n4H/9gRTVVVsSyL27dv0+l0ngmVP4+37V++I12kKAoXL158a33M53M0hRA8ffqU9fV1rly5glLsIuw93tm5LqEj/ipYH8nitmwqt4touQT62ADC9DDnaqj5NMgStdkWRPrkVNGjNNYEwvZwsv4KuL1URQAialBbFdgNi8TJNGaxS/x4msbjClpSR1g2ve0uqVMpvLbN+m+/fCX5NviwlexCiBcqugeW53EdBRmLXk9DlgSEVISArpnFa0hIzTpS0w+Fu7FUf0BF3Ts4AFKrgVOWsRMXEJKMiI4iif61kzttvEIXoUYQWhSqG4hQDHLT+z6Ot+3gkE6n+cxnPvNMM4APCRWYAT4H/DjwDyVJ+sgGP8Qh/kPD3tD55uYmd+7c4cyZM4yPj7/gOXu+YcfzGDS+l7R+HhBoQfOHpvsEQ36fe702YdUnHjsC7Num39nHkUyyyhH/N6RBvlVrs9Rb8/MxzQ2fWHomOeEvlONB60lbuNjOET6obKKiMN/aJKvHKTlNRpUUXdfiWGzEb0Fp5BnWM9RKCnPdHknDj5iJ58LlNcsne8Vem6lIhkrFY7ZcZzPQxtzq+K+FIAe01PVf62aP8+kB2iWLcquLG9hXPSBCybBfeDmciOMJODmQ42goRUSJUutajKWiLJXqpA2dJxtlrs6t0bNe7Ijz7fRouk6PRutPo4k7qEh0RZiCk6XqRvhntR/hQSeJKRxsF4qdCCElhCNLJMJpLDlBPuqTbqdqMVyzdjv7vMwL/p0Mne+FEOKg37kGzEiSNCVJkg78SeBX9m4gSdLeqtUfAR7td/CPXejcNE2Wl5cZGhri9OnTbxQ73S/J2dm2Wq1y/fp1pqammJ6efuk+7Jdo7t3Osixu3LiBJElcvHgRTdNoP+3rZwpdob3aoFXRQZGRA++VcAQkswg9WH0IIJElNDGAWepRe1gAwyfCwlVw2oEMheN/5tR6OONxCvc8RMy/seRAOkmNqgjHIzGdpPG0RigXQo/IVB9UWP7VfYVpvyN43qi0fu8DpE4LxVDo9HKoQd8kgaBezeJ2BZIEXjQBnSD8re5ZLFjt/vtOtf++28KdXcA2ziHkfsqC0Ay0VgW508IxjuPFxpGEQIxcAGn/j8jbrDxbrdZBQxtvXHniezl/RQhhCyEWgaf4xPMQh/jE41Whc9u2efDgAdvb27z33nskEomXfHt/kbLjif8S8AmmZA2BcomiiOHiUrXXkVGo2usM6FMIPJJaEGb3WujSBX6vskhKS9NxOxyJ+ORTBAWOtuYTr5XeChPho9woW/RchZbTZSY+godgNOxHunTJL1q1PP87lulxf8tjzbORgSeNIiFkZtsVklp4N1w+3yozaiRIqxHsusrDcpnJeJL1dpPJRIq1VpPRcISNTpsj8QRLzTpj0TgZxaC63eNRoUzGMHhaLBPTNWZLFXRZZqnq90bfarbJ6hpySzC7Ut7thZ5N+LZuIp/G8TzSYZV/9Gu/w4MHD9jc3Hyt9NBHActcp9n+0yhiEwUJV6h0vBA9EeJ/rf9veNoLgQBDSrLeDtNwLTzPI06SQsOj6zqYwmVITTGZHuI//9znGBgYoNFocPv2bW7cuPFM0ed3I3T+No4fIYQD/AXgN/AJ5C8JIR5IkvTXJUn6kWCznw6KS+8APw382f2O/7HxaAohWFlZYX19nYGBgY9c8kUIgWmaPHnyZLca+lU4KNFsNBpcv36diYkJZmZmdg1dd63e//2MAR60lpuEZiZxuv2boXKnSHcPH2o8KGAqgRfXFhiTfjGKaYYIHwm69SzV0Yd9QymHsnhd6K50EBLUHpWRDJnG0yqSLmPX/STvxKkMrqKSuDCA1RPUF/dUY38X8TzR7P3O1/B6DnbLhW4PXe/iODJmRUX3LLSoT+as8B5Pd0AuhSRB3Q+JC82Ahu/x9CQZ6n7Fvbe4iGPFEAGJFPHR3fxMd2keV/iLAG/swoGO421DHPsMme/gjStP4N/gezORJCmHH0r/8ArJhzjEf6BwXZcnT54Qi8V45513Xtt5bj9EU7dOoPamUMlTtY7wpLtCwZwnJEXpuDWGwn7Y3K/dg4K5QEwMs9KL0nR1BGJXH7Nu+vNETasRkkKUnBIZMgzpxyj20tQdk4weeDeDbj9bpj9hrDtVQpLfy3yScb6yWWckmqJm9ziVHKTr2kyFk351eRAuPxJLIyMxEx7i+mKFTMi3oznDf80G2pipINKXM6KEFIXj4Qy3Z7cZTcTxhGAyk8T2PKazGTq2zfGBHJVuj+P5LDFNI9GWuTO/RT4eYXarQiyksVisocgShUZgrxWNkhdmYmIC0zS5f/8+169fZ2lpCcdx3roJyMtgWrN0ej+JLlUYUGuoeMTlNm3P4F/Vfoi6G0NBQSHGQkOgSyoxJYTdC7Net5CAjG4Q6moU6l2+/8gkiqKQTqc5duwYly9f5ty5c0Qikd2iz06nw+bmJt3u2xfgvs28IknSgT3CQohfE0IcF0IcE0L8jeCzLwkhfiV4/9eEEGeEEO8IIT4vhHi837E/FkTTcRzu3LlDs9l8oxfzw4zveR7vvffeG3MXDhI6t22b+/fvc/78+Rd0N9e/ViI85X/m7ZFLKt6u0630V25aOorp7vGwOS7lSv/3W2st1FyM0t0mnfVO/3vZBJHjgxSvdpDCCm7dJnEyC7YgciyB23aQx3S6kkcvm2X5hsnT32zSbimsXGtz+/+9/MZj3A8+bIhjL9HsfOsWot1CeA6K7CEkFc+TaLcHCYdtPE9Ck/1k90gi8AoDoZ5veHt6EimoohSJQaSdpXRiCIKwkUDCnVvCSfjC7ELu3w+SALclI5AQoxcOdBxvs3o9aC7NPleevwGUJUl6CHwF+D8IIcovH/EQh/hkY2tri62tLYaHhzly5Mgb7dWbiOba2hoPHjzgZPanmbMjbKurxJUctjDJhyYB6Dg1ALbNeRLqACltipI5TMFpIgKbtKOPWXJLDOqDWMJiPDKOLukIM89XCkUa9rPyRfPtLbJ6nIJZ50g4j4XDidgo0W6eRtefY7Jhfy5R5WBBHoTNd6rK61aP49oIDzZ9m7na8nM9lxp1JGA5eN3odpDww+VHRJL5Tf+Yii1/n2pdf7zuTsg48KQNhCOszVcxVBUBjGYS2K7LscEMja7J8eEsm7UWk/kUMVXj8b1NPEnb7fBz4cIFYrEYpmly/fp17t69y/r6+ociax3z63R7/xW6ZBKROpScNLpkc7t3nF+q/UG2LZuO20Ny42x2FGQJ2q6N2zUQrkZc05GQ6FRdcCQmkyk+f+TIC7+zU/m9U/Sp6zqe5/H06VOuXr36SoH11+GgaQRCiA+dzvZR47seOm80Gly9epWBgQHOnDmDpmn7LvDZD/a2EjMMY19EYD9E0/O8XVHy995774Xwp9O1ac1VqCxKqAkDZ88zomViCKMvh6APpancKSLnfQ+lNBjFXRbIYd9wmNst5KER8KC32SZyzPdqdpYbVDYUPNMjNOkbFymQnpAtCTWmoaeGWP9AQgqrtNd6GEcUGutN2hs9SnfrWK393/DfTuw8SI1f+12wTayegSxcf79rKdy2Tx69cBwpWNVLQXWlF0mjuP7/Q+l+YnbL7N9H7l4B9/ggWD3cp0u4mXOITv/iCCOJtziHO/5ZiPQVAPaDt1l5vkUuzX5WnkII8ZeFEKeFEOeEEP/iQD9wiEN8AuB5Ho8ePWJzc5OjR4++tI3wy/AqorlTpV6pVLhy5QpH0p8mqY2BJEgEofGytYqMSs3ZZEA/ioREWD7B16sVap5vr1a7q6TVNF2vuytjtJuP6bm0rVHumjUMWWelW2Q0nN0Nm4s9YXND1skQZW3T5kmnR13y7eJ8s4yCxON6gYiisWQ2SKoh5pplziaHaVYlGm2HjXaTY4k0hW6H48kMpV6HmZT/ejydpWpbXEzlaW9bqJ7EZrPFVDrJar3BeDLBQqXGUCzGbKlC2ggzW67w/sAw9x9tISNRbJtIQKnpE9NOkIupSDIScCQR58m9LfKpGL9zo98eWVVVMpkM8XicK1euMD09/QJZK5fL++YJrc4/xzH/Gorw55iim8YUIa72LvC/VN+h7XgYioFtJVlo23Qci5Cko3Zj1EyHmtXDdj2MXggVlZ7j8H0T47tdkl4FSZJQFIXx8XHeeecdLl26tKsrvaOtvLS0RKPReCMxPAjRNE2TcDj85g2/g/iuEs1er8eDBw92W33BwSrJd/Cqi7RT/X3u3DlGR/ffDedNRHMnH1PTNAzDeGkYpvmohHAFvbKJmxjELfYTnrV0jML1CsZRX+7CtmQQ0AqEIIxsDrthYUwH6QOyRKve94gKzTeY2nAaaadVZTtYtT6uIkdUzFIXK5Vn8ctVQhkda91GkgWpoTjdNZvYlE6j1ODL/8+rmKb5oVaLHxXaNx9jl5p4qKiG/2CZVQ8FG1X374nQSED+ZBkhJJz8OdrKOE1zgo55BKuXxk6ew82dJBbth9Z73b6Au6n0Sac9t4Vw+kRPJHzD7yqv7wr1Mhw0afvjtuo8xCE+CZAkiU6nw7Vr1zAMgwsXLqDr+oeSwtsZL5FIcO7cuV2bfyX1vwX8gp+wFKPrNRgK++nQihRCcIZr9WVCUoiGaDAkDyEQaL3Angfcd7W3ypHwDNdKJp6nY+FyLOrb/52wueP5+78TNrcsj5WKziOrTT4UZa1T52gsS83qcio1iOk5nEjm8RAcMVKcTgwR7kVYrTcZCIpMo7stJf3jiQVzS1TVOBlJIjUlyu0e8ZBPXNJB9CUf2NaRZAxPCI5l05yIZPDaHm3T5vhwlobpMD2UYa3SYDyTYG6rQi5usFSqcXFggMcPt5ElKFZb/NbVPtF8/lpGIpEXyFqlUuHmzZvcvn2blZWVF/qZ77xvdP4Bnv33CQGG3KPr6QyrZW6bM/xW4x1kKYwlHOo9g4atkFDDJNQImzVB3XLRZYWhcBypIVNudXE8l/FYgh88tv8i0R28TGA9HA6ztrbG1atXuX//PhsbGwdq3/wytFqtAzcB+Xbju9qCMhwO86lPfeoZtv6qzkCvwo5R2DvB70gX9Xo9rly58kyXn/24oV8nb1Sv17l//z7Hjx8nn8+zvf3yTjv1h33pwk7Rxc3HUJb9XBzH8n+/XVeRZYnarL/SdRZNmIxRX/VvtOZKB1mWiE7nWfmgRHIihrXdovG4QiRjsP3QJjzkG4becpfYcITedof0+QG25gVaKIxwWqSOx9n+oEz2XIrKgwZqVCE5GGXjapXmVUHi+2Fubg7LskilUmSzWVKp1IdunXVQ1H7195AlF7cLerJHx80R0isIIQhH/bC3rHiIwWlsK4b3aBZoIEZHkaoNPADNwC0GRVi5QUKD51Gqj4mKPtHfK+1khZOwbRMK6SieBcJ/JKSJUwfe/7fRO3ubXJpDHOIQr0aj0eDWrVucOXNmV8nheXmj1+H557FQKDA7O/vMeDuYiX6KsJOmp1YZCs+w1ntAx6mR0Y5wv2khANMzmY5MM9eZ8/dBgpbeQvGUXX3MkJSj0AvTdKtMGBHWzDLNQPJoqbONisx8e5OMFqNoNjguHeFrhSrHtCRzdoMjsTRFs006ZEDL9xoC9Fx/Lg15GrdXSwxF/XOw3Kz5Y7caSMBsreIXD1VKqJKE7io8XmsTVk0USWKxUkWWYKnmh9XXGv6ctd1sk4tEUNtwb7HI8SHf27rD+Qw9COfHI6xWGkzl0zS2O8gWNNomJyZyPFkpoakKS5tVJofTwfdfPk/vkLVMxnc49Ho9KpUKi4uLu/nu2WyWZDJJKvePwL5LXHYwpB6bTp68UudXmj/AB80BbGGiSzqOnaNmufRcGyFCWC2VpKpRl1tEJJ1ioUtU1UmGNWKofDo/SugjmBt3tJWHhoYQQtBut6lUKjx69Gi3hXEmkzmwQ+Jt+px/u/FdD50/fzMd1KP5/Pa9Xo9r164RCoW4cOHCMyTzIEU+L9uH9fV1Hj58yLvvvks+//oerfUH/Q40Wi5G474gPJYCoLkctKGcb6GdGsOuByRIgG3Eaa/6oYbeVpvoiWFsEQYB2kBQpGJ5aFPDdAoW1Qc1lJQGAsKjCZCg64YpP+3RWvMNVbfgE1dVk3A6LvlzCUr3amgxFVWS6NyVOHfuHJcuXSKbze6uFu/cucPq6iqdTue1N/tH4Zlr3VnEWd9GoCBkhV5Lp1f2kCQwrTCy5EAijdnQad8rIfZcHimQ6kBWEJWgb7kRRRQL9O6v0DHHEGrfuxly9lQ2GgmkRpOa8D2ZdqXkyx+Nvbyl2OvwNtWBh17NQxzio0UsFuPKlSvPkMLXdQZ6FXbk6lZWVl4YbweyrDDUuQhAxV5DRkGT82z08pTtFhndJ0RV2/dCliiRVJN0PL/aPCSHMKRJvlos0LB9O7YQEMvlToHhcIam02UmNoqHYNzIkzIH2W5LCCRsf3nNVtcnfnvD5lFFY7FV4awyyDdWSgxF46y3mhxNpCh02kxF4zQcm5PpLG3X4WQmhyME72gZbs5uMRIJ07JtZrJpaj2Tk/kslU6X47kshVab6WwKXVEYcsPcmttkKBVlbrtCOhpmdqtCWJWZ366gKTKr5TqjqTh2xWJltUqnF3QZCuxlMhbmN7719EDXB3xn1cjICGfPnuXy5cuMjIzQajXYKv0E2dhNJCFjCp0NZwBL6Pzrxg/zQXMITQ4RVxKsNDW2ej0QkFbjdFthGrZFzeoRchXsJkQUnbZtE/NUvIbLHz77aoH2t4UkScRiMSYmJp5pYVypVOh0Oq9s3/wytNvtj51H82NRDLQXb0M0d8hjpVLhxo0bTE9Pc/To0Zfqo71Na0nP83j48CHFYpErV668UtdzL+oP+h5NgQwOdLoG4dEkZtnc/V+15KIYfcey4yqEx/ri8WZLonDHNyK1xw3ksIqkSFRWg17frsAY9wloa6VF7PwQ879ZJToSprXaIXkiTmOhTeJYjPL9OnpSw6rZuD2PwcspXAHbH/R2cwWz2SwzMzNcuXKF48ePI8syc3NzXLt2jSdPnlAqlT7SHFrwDXrpX/wOwhModgdXqHiujKwH108PYUYm6NTi2IuBko8UPGyyhNrwjbiUyUGwgpdTe0XbDdqP6rgDZxFqGGr9a6Pgr0wjpRp2/iRKs0Yvnuf63Qc8fvz4lfpor8JBiGav1zuoqO4hDnGIN0BRlBfyMQ86r3iex/Xr15EkiUuXLr02vzPfPUtIjmF5XVLap/l6dRs5qDZf766joVG2y+TIISTBQGgnLUehaY7yrcoGuqTu5mN2PYsR/Dkgr/t5+x4eeS3JwqbJw3aXVaeNLims2C1yrwibn0uNMOTlcEx/X0Zj/lia7duzTCDKHgp0h6OqxrhIgPCPNRQ4aZxAcmjnNaz5441E45SWG7vh9uGkX41+JJfCdl1GEuEgjJ4jF42Qc3WeLBQZH0yxuFkhl4wwt1YmZugsblT43ZvzuK4/776NjqYsy0QjkMl/iUxsC11VEcjU7DCea/O/FC5xsxbD9hxsT7DR0ogoESKyTkSKslS2sVyXhB5iQInRbnjULQshBENKhFbN5NPTE0R07c07w4dzwOzMxceOHSMajb7QvnlHDso0zRe+e0g0X4KXkcGDXKCddmGLi4vMzs7ueuVehv0am+fF3a9fv45hGG+UxdiBWTNxu/1QbSfwKNbn2kgDz3YRUOwI0RP9rkfdinhGpJ1QCGPcNzpO0yY6kyN2aoDinQbxEyl//HUTASiGSmXTz/eMT/g3mp7wjYCR0/Esj9zZBEpKR38nw8LDLne/VqOw4LL1sPnCcRiGwejoKOfPn+fy5csMDAxQq9W4efMmt27demluzNtAXqrglitYdhgQOG2Bgodu2AgBva6BtVJHSe45Lx2/UlLOZJECcilF98gE6XuSocNR8ATdu+vY6Xd2Nd0AvEq/GNtth0ELETl+kcuXLzM0NPSCPtp+Erf3i4+jQTjEIT6JOAjRrFardDodJicnn5Gre+XY6Lyb+CItZ5qlwLO40l0hqSbpel3Sjh8ONjR/UbllbjEeOsY3ii0sT6Ht9piOPZuPaQXawSvdIjISluWxWdJ5arY5Fs/SdixOJvIIYDLmj58O+eMrkszRaJZuU2a2VKMW9CpfrvkL8oLnBOHyMook8bRW4UQyy/ZGm0KtzWypgqGqrDRbhBWZ9U6PsKqw2uqgSRJPCyVOGVEePNzEcTxWyn44fbPmR+oqLd8z27P9OTSl66w/LaMF4eZULIwQMJpPYjsuUyMZWl2L0XySWw/W9nWNXgbbXqfV+QlUscmA2sCQbQzZRVdk/mXzh1j0Ujieg9uWWNwWlNotKr0WumdQbUJKC+MJCDsa9ZqNISukQ2HClkK90iWsqvzI+RNv3pEAH4Xo/E5a4PPtm3fkoB4+fMi1a9eYm5ujUqnguu5bhc4lSfpBSZKeSJI0J0nSf/ua7f6oJElCkqTLBxn/u5qj+bbYewElSeLhw4e7FWpvEng/iEezVqvx4MEDTpw48VrdzedRvlOmQ4qQ4YDUD5UDNIoe8mAIb9tE1hWqT/z/ZUYjOD2HxqJJF5vsTILeeoNOHTy5v5puFyxMJ8gjDFZWva0eseMRas0QStz/rL7UBgkqDxsoYZnqoybpcylKVVi+Vmf802lqK11GzieobLX4+s8v8Sf+p34l/MvOSTqdJp32t9nJjVlYWKDb7fL48WOy2SzpdHpfZHwv1K8u4poymmbSsdMYRh3PkwhJHerNQSIpD9ogh9UgD1NFVEr+OYjFEbWdPNk9BNDuh8eF07/mVh3U3Gm00kOIJqHcJ9jCU3HT02jjJ5FkmVQqtRsusyyLarXK2toazWaTaDS6myu0U+F3UAL6cUzaPsQhPonYT47mjpbz5uYmkUjkQDb/ZPz7+cX138HDYzg0zKa5SUIkqFMHA7Bhw94gQoSkMsFmV6Xt1jkaTbJtVukFgus7+ZhbNMjpCUpWg5PKJF/dqvBuepRidYNUQFidwN4Vuv4cshCEzRVPZnvbYdbaIhc2WO20GNTDbPc6TCfTzNWrnM7meVguci47gOJJKE2JxXqN88MD3N0s8M7QAHe2CpzKpnlUru5+fmF4EKkHXtuhZbY5koqwXOswno6yWvUli5aKNUYzCTarDT49PsLdW+tEwzrza2XCusryVhVFltgo+c6CeqvH+EASqWbza7/5gMvnJw5M0nrWA3q9n0GTPMKSRdVJouAwZw3yO63PU3UUIqqHokR53LMIGSoRT6LbkZhvNnAkCKkaw0oSyxQokkzNdsiZCq7tEdY13pscJRF0PtoPvl1dgSRJIh6PE4/HmZycxHVdqtUqpVKJX/7lX+af/JN/Qj6f5/79+5w5c+aN5zF4Ln4e+AP4zT6uSZL0K0KIh8/9bhz4GeBbBz2O77pH860QPFjNZpNSqUQmk+HUqVNvvKgH8Wh2u93dPuuvMziSJL1AMEq3y1SftpGGBolMpGAPty3PN7HtOJIiEZ1M4fY83J6Hmk8THk+CJyE8gRSLo2cMCncblO5UCI/4KxQ5pO4Sz/K9OlrKf+9Gw5QedyndraMnVTqbPTJnktgth8y5FLETSWqOyuq1OgOn42zdaaDHFRRVorvtUZnvUF/ff+X5Tm7MjkDtXu/fzZs3951P0ry/ilzp4vUscF2ctoMsebiKQb2eAdeGtm+QCHIxlVwWdhYM8p6HqNMn9F69svteNPYI59suvYdrOANnIPHsdXWbbcyn64jRF1etO/pop0+f5r333mNychLHcXj8+DHXrl1jdnYWx3EOFJ77OCZtH+IQ/6HjVUUkr0uB2dFabrVavPfeeweW2Utrac4nzgNgBLq8RbeIjEzBLjAUGkKTNELWBL9b3N5dEq90iyjILLS3GNBTNJ0u0zFfgWU0nCVnDbPWEAgkyoH9e9osokoyTxoF4pLKSqfGZDRN3erx2dQxvrVQ4mgy44uqJwJvp+o7IFKBGHtYUZGAvBLh4Vxpd4pygtC1FdhXO3h1XI9UOETcUXk4t40SdJ+Lx337FTf8xbbs+oQ5FVKYChl4bRfH9ZgcStOzHI6NZmm0TWbGcxRrbY6NZojoKkZD8OjxFksrFcrVPZ3d9oFW99exej+FEsw1NTdOywtxvz3KrzY+x4bp0HK64EbZ6CjE1TACcN0ILTdEKh5nOJbE6GqsbtfZqlZxej0ypkq7bdK2LMKSwhfP7d+bCW/XOvJ57CfvX1EUcrkcx48f5yd/8if58R//ceLxOD/7sz/LP/2n//SNv3H16lWAOSHEghDCAv4F8MWXbPqzwN8CDlwW/10nmm/lWlY1Nucec+/ePQYGBvbdI/pt9DHflI/5fL9zgPJdn+RsXm8804NbTig4JY/GQpf4uRHkSD+8u3W1iuX2cz9KtyqEjw0gPPxCoNxOSCWECHJqPNsjdiyFltLYuOkQSqm4pkfqpB9qV3T/8nqGzv3fqeN0/f0MJ1TsjsvIuQSbt+tEBmXspsvX/t7ia4/1decglUrtdkc4c+YMuq6zvLzM1atXefToEdvb29j2iz1t1//RN8EDSVOwbRUpEkIIieJaCA2L8HiQBiGBV/a9mHJszzXpBh0mZBlR9f8vIjEIRIhFyEDU+22XvKr/vnt/FXtP+29XUfGKReSBYeTwm6/5TuL2hQsXuHjxIul0Gtd1n0kraLVaryXah6HzQxziO4PXORn2ai2fOXMGWZYPFGrfcTZ8Pvd5AJY6SxgY9OhxxPBFvRNqhkpvgHnTL/Sca22S1mLU7TYzAbEcCqcA8BAkRJiFzR73Wh2W7SZxNcRyu8qRaJqmbXI6OYgrBENBkeNAOM5xbYRKwyfTvYBUr9X8uagUEMD5WgUFiZVmnUvxEa7NbmCoym4rySelMolQiKelMnFNY6HWIBUO0bZsBhyDm083iRs6Tzf9Tj9zWxUMTWWp3EBXZUpdh0w0jNT02NjosLrppyaV6r4TYKev+Y5ZHIxHWblbIBH3w+kD+Ri/9dXHu+f1TWh2/jme9TcJSw4JpYntKYyoZZbtcf556R3ajoShhJHcNIstl5rVo+c6RNwUjq0RkhVs18NpySiSzlAqyXgmi9SSaXcdzG6PkOUwE4qgS96BolZvo0LysjEOSlY1TePzn/88//Jf/kt+4id+4o3br6+vA+ztSb0GPKMHKUnSRWBcCPHvDrQzAb7rRPNVeBUh9DyPR3ML1NaXuXLlCoZh7NsgvMl47FSsx2IxwuHwvi7wy8hr+U4/76+84qJP+yQxMdXPHV37ZoNuY89NK0s092pleoKuuYd43q4QnUywfq1J8U6d8IC/Mm0sdZBHElhVj9QJn2C2N/0E4dK9OplP57n378qkJg227zVJjofZul0nnFRpbvQQHsSGFAqPWqx8UKVd/vC9ZnfySc6ePct7773HyMgI7Xabu3fvPpPrWLm1hrlYQMOk2wshuw6S1aXSzBMJ2hBrQY6pkk1Br+frZ6oG7shpzOQJ2uUwNXOEbuIUdvo4YvQ4cq7fvlRK5fpWLRJHNBq7/+uu2ZDznyczkgJPoEy9vT6aYRhcuXKFU6dOoaoqS0tLXL16lYcPH7K1tfVCH9+PYy7NIQ7xScB+c/83NzdfqrV8EKK5Mwdke1mSbhJP8hiLjgFgC5vx8DTfLDWpWjZV0eFYdAgPj3HDj6h4u52CykiAZbtUajGemh1OJPJYnsvxhK9ykg+6/uwcSdOzGTWSVKsuD7bKPKqUMBSVx5USCVlly+oxYkQomT2Op7JUzR6XB0dI9UJggum4HM9l/VaSuQyu52tiup5gIuFrZJ4bGKCx1iYVDuN4HkfzaWzX5ehghp7tMDOUpWPaHB/KkgiHOBZKML9SYyQTptq2GR+Is1FqkY3rLKxXyMTDzK+XuTw5xINrqxghlaWVMrqmsLZR47e++nhf577e+jsI+xcwZJe41KHqphlQ6/y71qf4jfolECEsYdPoGRS6EFVDDOhxeu0wq40OVasDAlJ2FFXIOEJg2S5uzSUdiaCrCiOpDCErxBfeOcLS0hLXrl3j0aNHFAqFlzpO9uLbFTp/E96irfFrIUmSDPwd4K+87RgfS6L5qnyabrfL1atXiUQinPj055C3l97KILwM1WqVGzduMDMzw+Tk5L49rc+P2Vpr0yv6nmUBVOcabN8VyAM6QurfMLIm02r3cxkTMymKNxsoR/wVqjEUYfG3y0RGfMPimh5SLolwg0rzMZ+gSKpMo+5fxmYQ+q4vtkkdj5M+n6LZ8Y8jMep7T5MTEZyex9DZBLWlLiPvJOhsuYx+bxIvJfObf39+X8e9gzdJ9EiSRDKZ5OjRo1y6dIlz585hGAZra2s8+Xu/je1JdCwDTXHwhITtGSh2h7AehE+6vgdASSVh4iRtc5DmbJPmrU3suou9UUWqdvEshc6DLRo3S7RrCZz8aUhmkEJ7qrpT/U4/QlZwtgt0NgSEo7hBOoIyeexAx7+DvSvPvZIb7733HmNjY3S73d0+vvPz82xublKv1w/k0dyTS/OHgNPAj0uSdPr57T5MLs0hDvEfA3a6Bm1tbXHlypUXJuaDzisLCwssLi7yheEvAFC2ykhICC/J47pEze5yNOIXgoZk34GwI7w+19okpUWp2E1OqpN8a7NDSvHtdUT17VJ9R/qo6etdPm4UiKshdKGgtSM8LJY5mcnTcx2OxRN4CGayPpHNBxGaRCjE8VQWra2wUuoXNZrBce507mkGlcxN2+ZcOkN5vUXHdGh0/M9bpr9g7gbb73hPo5pOZ72N6/jjakF4PRX3bdzoQAYBDKajHDHCNLfqWJbL2EiSdsfi2FSeWr1LMmlw8+76K8+3EIJq8y8ju7+MLOk4QmPVHsDxFH619Qf4SuMYNafnt/p08jRtGQ+B5bhs1QV4CumQwUg4gVeXKDTbtG2bpKoT66nYtkuzZxHxJKyKxXsnJzgzc/Q5CaXWC46T5+fBj4Jovo1XtNPp7EsZZwfBAmt8z0djwN4LEAfOAl+VJGkJ+BTwKwdxYnzXiear8mmef8hLpRI3b97kxIkTTE5OIushRKuK4rkfyqO5kwD+5MmTXe2qg+D5lfJeb6aaU3FbHp4paNR0OqW+Ryt+LMnWrSaZi77UhRTxk4w7dRkkifBoAs8RaPkdQimx9dhEMfxLVn7QQDEURDKK5wXtG5e7ZE77rsDQQJiHHzSpBVqahYctZF2i8KCJEpKoLXcIp1X04RArVZuWENz7SpF7v1mgVT2YV/Mg6Q87IrXDbhq94YIrcLoyutSh0YygeiaOFEaRPJAlvHIZeXKabi9G/eYWbs/FLdcAUBJ7HqY9+yBMm/a9TerzEo4Uh50VodpPVZAzebAd3FobKzSGZPv3hTJ5cI8mvHrlKUkSiUSCqamp3T6+iUSCr371q3zpS1/il3/5l/mFX/gFNjY23vgb34lcmkMc4pOOnchVOBx+QWt5B69r2rEXjuPQarWwLItLly7xPfnvQZd0ep7JgPouXyttMxDyI01N138c59qbROUQBbPO0cggHh5HjAEGnBFW6wIPiXpQHPSkXiAsq8w1y4waCSpWh1PJQWzP5VJygsWiTSpYTO+IiLcDoli1/Nf1jr9oVz2JreUm9za2CasKj4slYrrWbyFZqpCLGMyXqwzFYySFRnmrw3yhylAyxmLRf13YrjKQiDK3VSGfiDC3VeG9I8M8uruBrqjMrZaIGToblS5GSGV+vYyuyixtVknHDfSezOZKk26gzFOt+c6EcsXPpbdMmw+uLb10XnGcLrXWn0MTNwjLAh2LrquTVZv8fvdTfKMxjCEbxOUom60QK50OXcciLOl43RgqKqbnInkSpWKPkKySNgwGQ1Ga2z3apk1IVckqIXp1FySJH/5UX1NZluVnHCfnz58nEonsdvfZKzv0URHNg3o0W63WgTyaV65cAZiRJGlKkiQd+JPAr+z8XwhRF0LkhBCTQohJ4APgR4QQ1/f7G991ovky7CWEQgjm5+dZXFzk8uXLu1XPAPKxC4QX7ry1R3Ond229Xt8Nwx8Uz+doVhfau2c1Npra/dxuS1h7RMMJKrPX73bQkzq1Fd8I9dZsEucHaGz5hmbrepXwUJT0mQzVuQ7ps/7xWw2HzKU8S9+sU7rfJjQUVKKHFLSYysqsiRpSqC13GTiXoFe1GXk3Ra9mM/xukshQCOV4hGu/sU0kp7D1uIUaktB0md/8uf17Nd9W6mfxF67htGwEIeSQhCUiSJpPtr1Ap81JJWireao3ioimbyy1wdRuKFxS9hYCdXbfuoHBwvFoP6nSVY9AIoUw9xDoSP9BNOe2sb0wUjaPHE+81fHsd+Wpqir5fJ4f//Ef56d/+qf5sR/7MYQQLCwsvPG734lcmkMc4pOAVy1+y+XybuRqamrqldu9qmnHXuzkdhqG4Ts/ZBlDMfje7PdT6uSo2r6dWu4UUJBZ7ZXIEcXyHI7GfEk7QwmR0WKsbJncabRZsVtEFY2C12MqlqHj2pxM+s6I4SCfSJdV3olMsFRo4yGxEhQ7PioX0CWJlV6HbNhgoV5lPJagYnZ5LzbAzcdbTGczdG2HEwM5bNfjeD6LKwRT6RQCmEgnieoaJyIpni5VGYz7c+JQynd4DKdjCGA0HUcAY5kE7w4PIjU9bNvjyFAK2/WYGslgu4Jjo1k6PZuZ8TzRsM7RaJynj7aYnspTLLU4eiRHsdxhYixNodRlMB/Fsy3mrq+wML/1jG6zY9dotf8MmjdHWm4TkiwcoWIoJv+8/sPcamfpeTYdx2GzHULDIKVGyKgJNipQ6HUwHYesGoGWgi6rtGwbQyi0i11SkTCaJGPYMk7TJaTKfOrEGNn4q72DmqY9UyQ6MTGBZVk8fPiQR48e0Wg0qFar+1q0vAxvQ1Y7nc6BUrIClZi/APwG8Aj4JSHEA0mS/rokST9yoB9/BT6WRHOnDaVt29y8eRPHcbh06RKh0LPSArKmIxwJr1F9xUjPYi+B7Xa7XLt2jWQyydmzZ9+6OmwveRVCcPtfL8ORKJIMktwfUx/WWPlmg8xl32jU1/3lXK/qEDqWo77Yr/hulT0qiz7x9ByBPhij2/UvVXWhAwHBavckhJBAgD7gr8qLt+tEz6QoLnQYOOeTKSUctCNr2EgykFC5db2K1fUQAuI5hVbZZupShqXrVe7+5jb1wv6dYQct6Kre2qC7UsX1JBSrDYqg09AQwSo+fSSMemQMjEHslSZCBmvLL/TxQv10A9H2yaWQwSsHou3RCF7QHg0jjFupY61WaG2HEd4er+fezkKZDO5yD+X42QMdx168zcqz2+1y9OhRfuqnforv+Z7veevf3sFHkUtziEN8EiGEwDRN5ubmuHTp0hsjV28KnW9vb+/mdsZisWe2PRe/zKbZZra1QUKNUHc6HI/568EY/hxWs33b1bEstothHvbaHI1lgv7k/hyR0X2CY3p+aHq1XSejR2g1BA83K8zWKmRUje1Om3HdoOd5nMn7RUJHk75DYiye4JSWwWoFEZsgnL1TXb4TBq92d7QvHXJ2mNVNn7wWm/48sBVoZG5Wg9dai7CmEjIlHt7fpFjzHQGVRpC+1fK/1+r644cUGWujg9UJNI+DOUPT/P2JRvwUgcnhDNuPqmRzCe5cL/V1m+/+e6rNP07b67HsjvN183v5963v5YF1lH9S+2Eetg0kIZFQUlS7CRq2TcMzkT2NjbpLOmSQ1SNklSjFYo9at4sQgmEtilWzsT1B27RICx2362G7LhFk/siV/XeI25EdOnLkCO+++y5Hjx4lHA5TKBS4fv06d+/eZW1tjW53/+oubzOvvE3uvxDi14QQx4UQx4QQfyP47EtCiF95ybafO4g3Ez4GRPNVofNGo8HVq1cZGxvjxIkTr2T10rn30G7tLxVthxTutFg8ceIEExMTH0pUdWdMx3G4ce0G9UddCjddYueG6GzvIWvBAzX/9Sbpc1lqC30PXK8nkwjE1wHUZIjU+X7hUH25Q23Tf2DbmybZ8yliEwaPf6tM7h2fTNafWqhRhczZBG3HP576ag8BbNyqEx0MUZ1vk/u+DNd+s8DI6ThrdxsMTkcpPbaJ5XRKix1kVUJXZf7d/2P2rc/Jm/Dk791Esh0kPQQS2D0VGY9oKMjHjMco327u8GlCwxmkwDDapv+QCgnsgp+m4Mbj4ASGNNv3eCu5vTmZOrVHPaQRPxXFrfX1M6V4HNly8TJH3vqY3mbl2W63P3a5NIc4xCcNtm1z69YtJEniwoULu7q3r8OriOZOW8q1tbXd3M7nI2Un42McjQzhCJfJiE8a3UCAfZsmKjKr3SIntEm+tdllNO7nUqYDYtm0fSfETjvJJ/Ui2VCEqKIz5GR5WKhwMuMXB+WCHM5sECq1AztZ6XUZjsQwaw6zW3VWGi0USeJJoYyhqjwplkmGQ7vh8sVqnYtDQxSWG8gurFebjKSiFFtdpvIptuotpvJptuotjg6ksRyXc8ksdx5sMDmUZrPUZGIwxVqxzvhgipXtGtm4ztJmlcszI8ze3CQa1llYKpFNR5hfKpJKGcwvlkgmDOaXSlyYHuL+1xeJRkMsL5Z5+rDM0OAYZ84pZCd+icfmNNcbY9woD/BBNcpcN84HrSsUrSiKpKBKER5WXUzXJaLoJL045ZaE5XqUzA6Gp9Go2WTCBqmwQdzVKBfbOJ4gaYSJ9RTq1S6eEKRknePpGKnE23du21EnOXHiBO+99x7T035a1tOnT7l69SpPnz59Y6e9t51XPm6yed91ovkytNttFhcXuXDhAoODg6/dVjEMhCMwl94cepRlmVKptNtBaG8Y/mXYT1hYlmU6nY5fpNRK4fb876zebKHm+xe7V/ENgNsTdDBQwv1VSq/l0WwIJDXItSw6bNxpoCV9L2VkPEZouF800i46SBkDhMRO4ZvTEWTfSbG6YrL9qImsSdRWugxf8HM9M8ejhM/GaXT9m1qP+L8fz+m4Nowcj1Hb7DH96SxEZe7c2mZ97sVuQS87Rwch6sWrW7SXm9giBGaXajuOgUXXVpElgXpimsoHW+CBW/MrxNVU/2EPWf6KWMmlkIIkdFvfs+LT+uL20p4JRU6nEKZN/VEPaWwKr7JH8sj1r5l+7O2J5icll+YQh/gkYMcm7TgsRkZGiMfj+071eRnRtCyLGzduIMsyFy9e3M3tfFk+5x8a8td2BdP3DM61tkhrMbrYHI+PMeSOsFUTuEBX+HZstllEk2RmmyUykk7N7nIyNYiH4Fx8hMX1LqrsR3R6jm/4S0FjivlGDU2WeVwpkQqF0SSFVDfE/bUiU6kELdvh1GCenuOHzR3P42gmjQCOpFO8OzhEqCPR7FgMJPy5JqoGWplh36YmDP81H4sQbgqk4PTEo76XNhnz7W0qeE1ENN6dHEKqOzi2y2Deb1E5PJTEdQVjwykc1+PIWJrpfAqp62BbLkcms1imSzYf4ctf+besm7/IqpvDVGPY+ii2kSWixdlqR5itVSi3qjhdhbWGQkLzf9uzQqw3PUzHIabqjMpJ2k0X2/Mod3tEHRWv45E0QoRVFbtsIXsSRkgjLlRUEy6f3r9g/8vwPEmMRCKMjY3xzjvvcPnyZXK53Aud9p6XxPtOeTS/3fhYEU3Xdbl37x6maTI9Pb2vilxFUWhduELnV//NG8deW1vDNE2uXLnyxlXty4TYX4Zer8fTp085e/Ys9kL/dCaOxXn85Sq59wbQoiqtlb5YsGUKkmd9b5sSktl60KQ63yb5ThYto7D1oIlZd4jOpAAoLvZYu1YjOuoTLrvj0jZ9Q1q41yRyxDd4tipT37bolG2G3/XzeQSABB0J5u/XWb5VJ5bXWblVJzUSZul6jUhOZu1eg6Pfl2F5q8mta9v0Wh7/6L+/+8bjPyie/NxtZARu18GTVeTA06tGVJzcBHZQbC5HdJxizX8f9DWXwvpuIZCW6hM0eU8nolattvveM/fITyj+ORKWQ6tsIO8R4XerLbxwCHUo/9bH9TYG4eOYS3OIQ3xSsLa2xoMHD7hw4QJDQ0MHqiR/fttGo8G1a9eYmJhgenr6mcX1y/I5vzDwDiFZY8usMmn4BT9jRo6I0KkUPW7V22wLEwWJ2UaR4XCchm3u5mPmgsJFVZK5GD/C7GYLy/V4WimjSQGhVDUqrs2xZJqmbXE6m8cRHpezIywv1kgH1eaxoE+7EuyzGSzQG6aJBESEysOHW2xUgvaZZZ8cb7d6yBIsleooksRCocrp4Rxrs2WaTZOF9QqaKrOw8ezr4kaFsK6gmYK5O5ssr1ZQFImVdb8j0Op6DUWWWNuokUyE8eomiw82WV+toigS62v+azj9iF7s/8umrdARUHGyVF1wcCm5cfRQinw8S1gdZKEtUWjXKTZq0FJptT0SqkZE1fDaElvlNj3HIabpjGDQbpq0LRvLdgl1JDRJxnJcYkLFbTp87v1jhPS3S6fbweu8kbIsk8lkmJ6e5sqVK5w+ffoZSbwdCSXLst6KaH6U8kYfBb7rRHPngd3xCiaTSUZHR/edPKsoCo6mIxkG7W9+8NJtdsZOJBJks9l9uaLfJO4uhGBxcZFms8nx48dJJBJsXO13o1ENn/w8/J0qmfcGYU9+YHmxw9zXquTezZA+mdwVUl+/0UQeC/lxYWD9ap38e1kqyz08RxAaCaSPpqJ0m33DFslFSRyJcP+rZUYvpQBoV3xjsnmnwfDn0tz9WokjF5O4lsfQiTieK8hORvAcQeqIin5Epy0c1uaanLicZeVRg0bJ5OZvb732PB3Eo7n25XWac3XsrodQJKy2hKo4CAEiEqEzW0dRfVIZGknsisV5jRZIoI4No0wdRToygy2n8IaPw/hxLELIgwMgSRh72k2a5b7X0mrtyYvRDZrbKlI8jhQx8Cp1vJH8h0qheNsQx0EF27/duTSHOMQnAQsLC1QqFd57773dZ2wn938/2Es019fXdwnrwMDAC9u+bK6IqQafzZ4CfP1GANOyKdei3Om0yOgGVavLqeSgX1wTTQF9fcySaxJTddyOwsP1KkuNGpOJFE3bYiIcwQOms/7COB3uR3zeT4+ysdHE9QRrdT8itFSr+5JIxRIRTeVpsUzGMNioN3kvO8zVe6uMZxNs1VtM5pKUW12O5pI0ejbHR3I0uiYnRnLM5DKEWlCpd5key9LuWUyPZml3LabHcrS7FjPjOYQQvDs8yOp8k+mpPM2WyczUAI1mj5mjA9QbXWaODqCpCkeTcZ7e3WD6+CC1aofpE0PUqh0+/YMNjn/mMb14kq2CxboZpeE6aJJBsZehbts03DamFaNkKuSMBOPJPBFpgJIlUTa7VHtdnJKF13VJhULENB2ralGt95CRGIhG0FvQapnIkkTCUehWeqQSYb7wmeP7uk9eh4PMCaFQaFcS78qVK7sSStvb27vSWS+TUHoZut3uvtJDvpP4rhNNgEKhwK1btzh9+jQTExP76ku7gx2DEP3ij9H58m+/8MCXSiVu3brFqVOnGBgYOBCBfdW2O57XTqfD8PDw7opj82pf2qhbC7xpQqJU8YhOB+GHiQjNQFB97XEXjL60ht1xae+xg67lYe/prbp2tUbqRJyFG3UKj1ukz/jEc/1GHWkwhOuAGYTGS7NtBs8lGLmSomH6x9Es+GGW1ft19IjMys0ak59OMr/YoVTsMn+rSjyrs/KoTiShUlzp8P/57+/sjvlh8ejn7uN6EqpnIiQFSXiEpC4FJ4HW8vMzvZ3q8lgQlsokcCMZWs4wnXaU0rcqVK6X6Kx3qd0pUblZwn7Uo3TXpi1PIJKDyIkYGCGU5p5K9MA7CtBrdrArXXrkkPN5EBLe2OtTNN6Etw1xfNxWnoc4xCcBk5OTnDt37pln8m08mg8fPqRYLHLlypVXLgpfNe4PDl4CYKG9xTF1lK9vtIjIITwER2N+Dr4cLG7X2jUAHtcLJLUwsiRxRAxya6PI8bS/bUb35wI95M8lpUBjeL5WIaHryG2ZudUKc+UKw/EYW80W07k0TctmMhHbFWd3heBELsOoFEMKhDhygdalEnQQigVd6zRZQZEl8iGDR3c3d4/NCwiPs9Oq0g6KfATkhU6j7O+bFaQ6mcH/zeBvTZVxt9s0a74DoN32d6TZ6DEyU2Do3F16iSjtjsvdFQ/H01GkGI+bYHoeUcVAsvMUuh49z6Zpm5Rq0LUFyZDBaCRJzovjoFG3LMrNFr3tJorlElYkoqpGY6uDJsvEjRBywwVLEAlr/KHPnkSW397psHuO3lLeaK+EUj6f59ixY89IKN2/f39XQul1Y3yc8F3fm1qtxsrKCleuXCGZDFonvoVB0PI53HCG+r/9DaDvcVxYWODy5cukUqmPRNy91+tx/fp1UqkUZ86cQVEUhBC0iibKgIGsSsiaTHm233e7VbLYXHaJTRhER/vFH52yTdPuXwIjr7NxzSI04xtHJSzz5PfKpE/64VXhChjQMFvBfgUC8APn4vSC52LzQZOBMz550RIq9+/XWLxZI5rRKC50mLiQpFtzGLuQZPhigobi0K65jByLYnZcJk4kaFVtps6lqG33yE9F+MW/c++V52m/Hs2F/98S3c0WEoK2nEB1etiaRs1NYERVhOkgGyrWZuCFlCUYP0bHyVP+Vgmr3IOdaycJ7O0aAPpAEskOzkfIoHy1RHnFQBo/jqT7ZFVOp5D2hNG9ik9mu4tVar2gV/zIi56Kg+CTkrR9iEN8EqAoygt26SD2fyfVyjAM3nnnnZ20lZfiVVJIF5JHGQ1nyTh5CjUFB4hIgVh7z58fHgXC61u9Jsfjfuj7neQo9YqM5Pn2vRXkYc5V/c5Bc40aCU1nqVFjQNUxVI3TWp4HqwWmcz4pHU36qVOJkE8YpcBXWmu3mUjE6ZUtVrdqbAZFkYsFPxpX6DqossTsVpmQqrBSrnM+k+PWrVVikRCzqyWS0TBza2XS8TDzaxWyyQjzGxXOHMlTnq/h9lwWV8ok4xqLK2UGcjEWl8sMDyRYXCnz7ukRFq6vkUiEWVkqMz6RYW2lwpGpLO3eKp/5sWXa4TCWqbHSi6HEFUrbNuvdMCE5jITMckNmvWvhCJeEEiFsp1HQkCQJSUCpZNLuOYRUlfFEiiE5gSyH6HkCxfZorNVwTItWu4fadFA9CQWJqVScSxcmDlx78DJ8VDqaoVDoGQmlycnJXQml69evMzc3tyuh9LZyg2/qOCdJ0p+XJOmeJEm3JUn6/Zc1CnkdvutEM5lMcunSJXS9X8TxtiGO1Bd/iOZXr2G22ty5c4der8fly5d3ZZH20+t8By8zHrVabVeDbWJiAujraC5/s8zDr1UwTqfInkng9Pzf0aIKpact7Jag1hFYVv9GSE1FmP1qiYFP+8YhOR1DeBJmU0MJS8SP6/SaLg3Tr16XFJi/Vyd1zA+VbN1rkj+foNxyWLpeI5b3z6EcVlDDMmvbHRJDYeyex3Ag5O4FXRtEWOL2zQILt2oYCZn5WzXSQyGeXquQHzcornaY+p4UX/7NFb7671a5d7W4r/P2MgghuPsPZnEsGQ8Py3SREbRNFb3tEs77BtUYTyDJMvqJKYp3TCo3qmjx/n3hVH2CqA8k8Xo+cVTSfS+DHCSrC8ulU5FpWoMooyPIqWR/m0QcWn01AK+qYA4OsKWI3YTsdrt94Af20KN5iEN8vLHfSFm1WmVubo5kMvlarc0dvCr6Zds2x9rjXK+1IPBCrjotwrLKWqfG0VgW23OZCdpLxjSdS8kJlre7dByP2XoFTZJ5Wi2TUXUarsOpTB7b85jJ+Dnmw1oYs+DsduNpB21uNwKJt7lSBUWSWGv3iGgqEVXHLlg8XC2Si4bYqrUYTUaodUyOD2Vo9ixOjOToWg7nJ4bIeTqaK2O7HkdH/BaVkyNpPE8wMZTGE4LxgRQnx/PETJl6rcvgQBwhIJ+L+a9ZfzGdThucnR7Eq5rYpkMi0OiMBMVEelhw/keeYhkq5W2JLS+KZ8tUSxoPyhYNq43rCTpmmpAcJa6GSCpRVsoe6+0WNauHhoLe0UlpYcKKSkzVKG+2MU2HSEhnJJJAaiuoukEqFiXakWhUW5itJk6xyWc/O4Hruh8bovn8GDuV7DsSShcuXCCVSlEoFLh27Rp//I//cTzPY3Fxcd+/sc+Oc/9MCHFOCHEB+L/hy+jtG991oinL8odaee4lj+GZSQQSj//Hf0w+n+fUqVPPXKQP49FcX1/n0aNHvPvuu89osO1st/yBvyJcuF7HSeqEM/7KNTUT2yV3jS2Lhg2y5h/vTnHP4vU60QmDTpB32VjvkbmYwRVB+7F5h+gpDWNaplUQuEafBGlZnc3ZNo7pkT3hP9BrN2sMfTbF2lyL2EBg4O7VCcUU1u43mPmDGb711U1GToWxuh5T5zI4psfQkRiuLRg5FWel2qRc7SFcgW25/M2/+A2a9Rc7Bu3ngbz1c08wyx2Ea+OYKrohaCoRIjHfSyC7/qJCTRqYxhDV2R5OLSCDgeClbGjYRT9JXc30yaWk9q+v2JOfKRyBVehQvNPD1VP965Xpv0eScLeb2N0EY1OTuz3KFxYWuHbtGo8fP6ZYLO5r0fO2Opoft1yaQxzik4BXyea97lne2yXu5MmTL+0Y9DK8bF5pNptcv36dLx69iIRfUT4UjmPi7Rb8pHXf/jfsLrqsgKlya6nMXK3CgB6mZVtMGlEEcCxoJxkOPKtNy+RKboStokWzZ+3KFs0WywzEomw0mhzNpGiYJicHcpiuy/tDo8zPVTiS9+evkUwgAC/tJMPvNEmByVwKqe6ysVHf1cKsNf0wdynQzNwq+2RWQ2L5zjar6zUkCRaXS8gybBc7aKrM0mqFUEhFc2Hl7ibzT7eJxULMPd0mmTKYfbJFLh8jcvabJKckNragnUrgKi42KUqWRsgNY27DWivMWqdFyWwieQqFhkQmFCEfjjIWTmLVodDqUDNNNCREzSNjGCiyREyodComEUMnEzUQFRtD1xnJZkhg8NnPTKPrLjdv3uTOnTtYlvVWTocdfCc6A6mqSi6X48SJE7z//vt86Utfotfr8TM/8zP8qT/1p/b1G/vpOCeEaOz5M0o/nXhf+K4TzZfhoIRw50YoFouUTh0ltrhJPvpih5eDejQ9z8PzPB4/fkyhUODKlSsv6B7ubLf0jX4hULXsYMY1ooMh1Gg/5JKcjjB/tUrusi+r1Kr4D7DddREJnY1H/WtZXGzTrPfDva2yAM3/7e37PeLHdCQVHj8skzvlG6ylmzUiWY2h8wnKQc7L4vUq6dEwnbrN+IUkR743zca2nz9TW3dQdYnZGxVSQ2EW79Y49YUcX/3tVY4cT7D4sM7Fz2ZQeuscn27xC1/6fWzbPlCXA6tj8/gfLyE7LpasoToOQnaxmwohs+ffgaUOxqlRmgWJ1lIbY6hPJJ2KH2IKDfeLgySlf9t67X6eilPtpyvYwffwoLFkI8amQZFB7U8e2kAKr2uhTPgFYjs9ys+dO8fly5cZGhqi0Whw+/Ztbt68yfLyMs1m86WG58Pk4xziEIf49uN188pO3n2j0di182/rlNja2uLevXucP3+e8+NHeS834XfRCQp+zGBhPdcsoUoyVavHcXWUb61scyoo8MkF+ZiKGuT/t3179rhSIqpqpAmztdGmatocz2V2ZYsEMB6EzVNGULkuy1zKDFHcaoGAUpC7vhzkrZdMD1WWWK600BWJbrNFd73F/blNMkmDxY0Kg5kYK9s1xgaSrBcbTA6nKVbbfHZ6jPsfrHDsSJZqrcPIQIRO1+H4sUG/COjoALbt8u7RQR59a4Wj0wNYlsvEVBbH8RgZS+F5gqnLLUZOtak0otT0CMJWKVWilBUZKQG9nsNs2UV1VXKhGENahnpLo2s7lHsdNE9hc7uFLsnkIgZDmoFX96h3TVo9k4wUxm46IEDyBF7FQlMUwoqKXe6Sz8b4kS9e2q0Cn5mZQZZl5ufnuXbtGk+ePHmj5uXz+HZ4NN+Eo0ePksvl+NVf/VV+8Rd/cV/f2U/HOQBJkn5KkqR5fI/mT+97p/gYE839hs6h36ZyaWmJsz/xx1BDMlv/8H996bgHMR6WZXHz5k1UVeXChQsvzdORZRmr67B2swaAJEPhaYvCQoemItFr939PT/vff/T7FUa/L8vmw75OpRJRGHiv7ylNTkZwDQURsKtwPATJPklSjDAj76dpbLtYO2LmHZf4MZW1Upv561VykwauI0hP+ETUU+HOzQKLd+uMnozRKNkcv5LF7nmMHY8TndLZ2GoR0h0+c/Qq//P/5d/y13/8F/g3f/df8Tf/zD/kZ/6T/zvdf/8TKCv/Crtbx7KsN57Pr/4397B7LrYnowuHrizhtVWy0zGE7REejWLn0qx/vYG57nssFV0KzomGVQi0NPeE0L1OQC4lgV0IzruhYRcbL7wXgLnVoHqzjJudwu30ybuS9D3A8uSLSgSyLJNKpTh27BiXL1/mzJkz6LrO8vLyM/ITdiBkelCP5kcRmjnEIQ6xf7wqdN7pdLh27RrpdHq3S9xB6wR28uNmZ2dZX1/nypUru/nXPzrudxxbDQp+njSK5EJR6naP97NHcGo6qufb9p3imvWu7zWcazVI6CHWWg2OJtMoksSVxAi35rYYCwhlJPC87sgWbbd8UrpQrpExwngNh8WVMnPbZfLxCKvlOgNRnXrPZmYoSzOoKjcdl89MjbO93GUsn0IISAVd5VLRQBg+4Ts7ktEwZwaydKuBLQ4W3+GgjfNOEZBlO0wkYmwuBDmgWw0kCdZXa2iazNJCmaHxMJmLN9msGBRt0AyFtbqGHY3gtDy0XoJiJ4KHxOp2CcnReVrq0XMcDFVlTE9iNyGqhei5LhFPpVrqokgSmahBytOpljpYtktC15AqfqqBIcl4NZNYWOOP/qfvomn9+V3TNAzD4Pz581y+fJmBgYFdzcvbt2+zurr6Rm+n53lv3XFwBwedV/YqmXzU84sQ4ueFEMeA/wb4Px3ku991ovmyk3GQqnPHceh2u9i2vdumMnT5fey5BTpzm89sexCPpuM4PHr0iPHx8Rd0057f/61bLVzLHzd3PIbZ8h+ydsNhfbtLYtx/+FrlPnmudF0yp/v5ed2ux+w3KmRP+Z9trXbYeNBk8EoQ3sjrLN2uE835D3xhtkUzCHUUZ3uMvuvnIdqKRKdnITxQE/4+zV+rMvO5LN/8vQ0Gpv2HaWelvPygzviZBI8XK5jCZTp2i3/0N36LP/+jX+PcsQKbxURw7mBhNcZwfJ3w/N8ncesvEi78FpVyGUVRsG0bx3GeOb+VuSbrv1dEklwsV0J2Xdx4BMUSGGkFJaIh5VI071hERmM4Td8L67Z84xUei/cd9HsLgQJyqWUTeB3/O/pAenfbve+1geTuNrX7FUw7BsGxi0BGSjqSe+OqMRQKMTw8zNmzZ3nvvfd25Sfu3r3LjRs3qNfr9Hq9A4VZDsnmIQ7xncPLyOOOKsnJkycZHx9/7bavgizLu92HhBDPiLkDfGH4OFFVZ7vXZFyN4iGYjKa5kBylXvUodbqsNGsAPKoUickKdddhOpHC8bzdqvNhI0bWjFBv+PZxq+k7KmbLFXRF5kkgW7RWbzKZThEP6cxoKZ6ulJkeyiIEDAZEcShIIYroO+RK4tLwEKV1XzC82fUX0G3bt09blTYS8HSlQDKi0yu0WZsvM7dYJGKoLKxUSCYMFpcr5LIxFpbLnJgepLvZAtNlc6PG0ZkBSsUmx08OU691mDk5TCwW4vQfWmStq+NlwriORLmRwZI1PNnDdQxWXQlLEfRaJu46bKz3yIcihBSVsK2zVmhT6fUwHYcRNYrTcomqGo4nkFoenukRM3TSegiraKIqMklFQWq5RFSZy++MMTH1bDGo53m7tlmWZdLp9K638+TJk/vydrqu+x33aLZarQNL5u2j49zz+BfAjx7kN77rRPNl2O9D3mq1uHr1Kpqm7V58gPyf+AJmS2LjH/ybtxq3UChQKpWYnJx8Y2ciWZbZeNQmPuyHKSL5vhxR9niM8lqPquWROKZTmtsjtyNgc71LdDREOKWxcq+O5wrqLZvs6QilJT8fZvNpl/SUweytKmbLIXXcNxSjl1OUtno7hee02zYDJ2M8vFpj7LQfmt940CM1oREblFmtlhACiksu0YTG0v06xy6lSQ8ZyAMytVKNv/RHfoP/63/xdVq1PvmZGa9jO/55ncg3gmP22ChrGI//NomFv8ep41O7VZ6u62LbNpZl8Wt/6Q52w8GyJRRD0AjHGAx6suM42JE0dsMn35GhoDpSAXOjBvQljrR8HKGGCJ04gn5qBnVshNDMOOpozg+HA3K0f973vlfT/apufSBB9VYZBo+AJGFXO/7/U8aBVo2SJO3KT1y6dIlz584hyzLb29tcvXqVhw8fsrW1hWW9mNO6g72G7BCHOMRHizflaAohWFhYeEaV5Plt90s0TdNke3ubkZERjh8//sJvG6rGD4ycACAsq8hI6G6Iawtl7peKJPQQ2502U5EYrhCczPmkJxKk+dTNHmfSedbXGmzXWjwulEgZYdbrTUYiYdqWzcl8Dk8IpgICOR6P09ro7hYJdYKe5ptV34avVprIEjzdKpOJhlE6HmtLFRY2ygykY6xu1xgfSLJdaXFsNEO9bXJiIk86HmEqEmNlscpANoRtu+QzYb84aMwvDhoeSDAxmibuQHG9jhF4Q3eknNpBupPneij6Fpu63ymuVfIohOI0ZBs1LGNVI7Qx8MoOBiq9lkYjpLNcqVDstEl6YeyuYCASIWcYJFydYrFFtdPF9TxyXggsgWW7xCQVt2YjyxJRFJymRUiCkWycL/zIhReuqRDilQQvHA4zOjr6Rm/nR0E04WCeybfRZn5Tx7lgH2b2/PmHgQP1qP5YEM23KQYqFArcvXuXc+fOoWnaM54kxdDRj0zSW6tS+kpfmudNF2zH+CwvLzM2NrZbrf46yLLMg6/U2OqajF5O0ev091sO+ae3utXDTMoYeX/1KCmw+bhJu2JjRxQGziV2DUJlpYuZ6Id3u3Wb2IkYdlDFPv9BhaF34izN1SkudZj6lB9uLy50UEdUhIC5axXSo2GEB+mRGA3hsvrAIj8Rptt0SB/xz4NQPOa2ayzfXeJv/YVv8anj8wDMDFXoWv6xx0I9nq77eUP5lMnsup+Urti+t3jQuk707s+iiQ66rqPrOpqmcf9fb1B/2sJRQO+4qKkQoY5Ld6lBeNCgsuxRn+tgbfohIlnxjz8ylkA4AmNmEFNEqTuDFJYNVr/SYO1rLVolhfXfa7L2+x0aJYNyOUsjPoDQI0jB6lw4e7yKUp9AqmnfW1y9XUWeOoa1VcM4PvKhc2l2jnmnp+3Y2Bi9Xo/79+9z/fp1FhYWqNfrz9yj3W73QH3OAX7913+dN0hQ/GVJkh5KknRXkqQvS5L09j01D3GITxh25hXHcbh9+zaWZT2jSrIX+41+FQoFZmdnSSaTDA0NvXK7L46fAaDodDmpjfC7C+scTab9CvKUb8MNxbdf1UBlZL5RQ5dl0qpBu2ixUW9xciCHKwTTWf878UDCzQ1sS6nT4dLgEHNzJXqmzZPNEtGQxtxWhbShU+5YTA2kqba7nBjOEw+HOBlPMztXZGokgxAwkvPtZCbwfhpBxXzc0DHXO9hBm+VeoKDSCua8xaUCkgS2adFaqvL4/gaxWIjZx1tkslHmnm4zMpZmbaXCxcsTrNxYYuA/q+BGPbRQmM1eDMUKIboSHTvGtizR0m1EUqG24aFqEajapGwV80mLWt2kaVkUOx20Lrgdl6RhMBiPITcEtbqJEIKMotMu9vCEIOJKuC0LQ5JJaip//H/3mZfygv1Gm17n7axUKiwtLR04t/PD4G0k8/bZce4vSJL0QJKk28BfBv7MQX7jY0E0n8feAp/nsZMHs7KywuXLl4nH4y81CsM/+QcRtsf2L319X+FM13W5e/cuvV6PS5cuoWnavm4Oz4G1O23adYc7d8rICQVZ8W/Q8krfg+nJKnUc9IxEclqnW/dX1oXZNmZ0TzszDTYeO4xe8UPhkgxz92uMXUoGxw9aXqNe8leFqw/rhJMqk59Ks/ikgRaWcSyP9KiBJEGh2UCLSwgPElk/hL/xxGb6/SS37xeZOdHjf/xzXyUd6kv+hHSP+/MpCo0kH9wZprUdp7WexCvG6JZSPLg3yMJSnPlCHgmXrY0yyjf+CtgtXxbKFnzjb88jXA8he2iTEdylHpkTUfR8GHkwSXu9R2QkjB3k+NjlNkpMRx7M0vByrHzTpPqwhVW1MfaE0OU9bcHcto1nephzLoV7FtVGDu34FE6j3wXIbfW9ikLuf7ddkNGnJzFOjH6kSduSJJFIJJicnOTixYu88847xGIxNjY2dsV219fXmZ2dPdDK03VdfuqnfgpeL0FxC7gshDgP/Gv8pO1DHOIQ+ETTNE2uXr3K0NDQM1Gw57Efp8T8/DzLy8ucP3/+jRGRS5kxLqbHkFsGwvJ/MxN09Nmq+drBy70OuiwzX68yFI5gug7fk5vg9pMtRgIZNDWI4FQ6QcSra/pdfwol4rpGBo3aVodKs8vx4RyW4zIUCyGAycFARs/wiXU8rCNVHJpBKL5c9+ertUIdCVjYqKAqMrOrRd49OsTTG+voqsLCcol0UqdQ6jA+mqZc7TI9lafVcbhwfJDFGxuk0zqW6TAynsTzBMMjKQASiTBnTg/TWK5gXKphuzbtUojFno6UAVOx8EhTLrtEXR15y0FuxLBVDVv20NJhakWTjidRLjRI6iEmpBhuz8PxPBzHxSqaGIpKLKxh2DJO0yES0giZAtnyiMoSEQn+5E9+llii31VpL952Ttjr7UwkEs/0M799+/Zby+ftF2+rzfymjnNCiJ8RQpwRQlwQQnxeCPHgION/LInmq2DbNjdv3kQI8Yz25ss8oNGjA0ipDFaxzdo/+f3Xjtvtdrl27RrZbJbTp08jy/K+V7Rrd1o4wQpv+ESCG7+7TfxclIGTMSorAeGRBMXFLq2CixPXCGf7K2gtLnH7y1ukLvir2bELKVo1m/X5JrFBnbGLKcobXQrrHUIJBVWXmX1Q4+hn/BVtu2ozeiHJowcVqls9pq74n89erTD8qRALj9tIsgaSYO5WlemLaYaOxmhLHrrU46987rcZz7eYylTZqvn5mMVGhE7VIN31uDTU5my+jCf8/RuNVTiaNnl/qE2jkODq/RGsTg21Ncudf/iX+G//ym/xs5/7LcqbXVpdl3w+TGo4BgIiGY1aSd296aIjQbg8IiNnElTKMdpFQa9ooad0zKJv+LRYP0nbbfeJY2/Tz1ESmkRvs4Vdt9m63qG8bhCaGUNIEuZmfXd7p9GvUJejIba+1SB0fPzbKkOhaRoDAwOcOnVqV2y3WCzy0z/909y5c4f/7r/777h58+Ybx7969SrT09O8QYLiK0KIndXNB/i5Noc4xH90eBlRrFarVKtVzp07x/Dw8FuP7TgOd+7c2a0LCIfDb3RKSJLEldhRtrsmVpBbP1spIQPrVo/RaJy2bXE664fNh8IGx6QUtWAhvtEIqs4LfhvJhUqV0WSchmlxajBPWFM5E0nzcK5ECN+J4QXV7W5gcbdq/hjzhSrnxwZZfFjAsz3m18vkU1HWCnUmBlOU6h1mxnM0O364/MxoHrXl6x+PDvsOj4GcP1fEY0F1vCLxzvQQrc0OwhNYpn/+N9ZqyAo8fbxJJKqheC6VhSLLi5sM/9EWtbpMO5HAa8roHYNOJ03V8/Ai0LNsmnqMmuuixnTCQiVUALUjoGlhbrcozdcoVNv0bIe4rhPpSHiuoGvaRGwJqechPIHedZFtD90RhCWJP/ZnPs3AaL/49nm8LnS+XwghnulnfvLkSRRF+VCV7G/C24TOvxP4WBDN/biom80m165dY3R09IU8mFcJ5g78ie9Fcky2fuUudvfl+XLVapWbN29y4sQJxsb68/J+iebc12u77yNZn/jO363hDatkZvzQw8DJOK2y//vllS4NW2AEOpv5k1E8B1bvmSROqDSClWq7ahMa0ukGN2F922TwbILxyymq2z0W7taIBxqZHcchMeg/8LM3KiSHdDKTKsWqDQhWnzY4+alccGASq7UGj25s8X/+s084MrAjqSRRbye5uzSM3lJ5f7TJYsFfGWkq3Fv23ycNl4cb/up6LF7nQq5JtONxeynHheE5vl/793QeddGjMscvpum1Zby2SWQsSuGRSbdo41T8Y5QVD3nCgLFBVr7axG66mCWfJ0XH9zwsTv9B7G345FLPR3aLh5RcCLyg6nEkQa9gsvb7XeSpmV0pJCHLmBt9+SjXdP3e6McGPhKiuZ9Qy47Y7oULF/j5n/95Pve5z/H++++zsrLyxvHX19efKVbgFRIUe/BfAP9+H7t+iEN8IrHzPAohePr0KVtbW8RisQ/VJGGnQj2fz+96RPebz/nFYycBmK1XSesh6rbF6YyfljQS8/fJ8TzGYwm6NZfFYoPHhRLJcIiNRpPpXNpvI5n3PZNDgefKUFUGHINaw0+5qpoCCVgs1gkpEsvlBtloiM1ak2ODaY5nM6gNj1bH4uhoEC7PB5JIsUASSZVRFZmUqvPoxjrVmm+XV1b9Nstrmw10TWFuoUg6GUGzBMWFCsuLJcaPZNjeajBzYpBW0+LkqRE8D2aOpHjyzUV0AzI/2KBWjVANRbAkF8KwJcI0XYHVdYg6IdoFlaino3U8oj2JXsWjgYecj+AASlvCLnaQmhaD0RidbZOu6aIrMqGWg9l0kSSJcM9D2C665RFV4Y/9xKcZn3597cVHkUP//LzyptzO572db+P1bLVaH8tucx8Lovkm7NUle1kezKtagA38wDkkVQHbZP7vfuWF/6+urvLkyRMuXrxIOp1+Ycx9Ec3fr+2+b1b6HrN2y2Zls8Xw5QSRXL8CcfBEjPkbVaQBFT0uUw3Eb4UHXVOitafZeb3cwQn3j2v+RpU2/t/dpkPyiMHwyTi3v7mN73AUWF0XPSeoWi5rTzuc+pRvyJaf1hmejjK/UWN8JsFf+kMPOB7fxLR9L5zrSRTXYELrYWhBDg79jjrJaP+m1wMJi7TRY7GSIhu2cVtJ5rbHmE4U+PwPzBNp+1XdZt3CbDi4WojWaodQWqW13ESNa5SqNtt3VPQg6V2Lq3Q3/POhGP1bc8ezGRqM4gSh8NDAHtH2aP/87pVB6rZU6mYWfTRDaCiJZ/bPbW+zRXQ6ixJSPxKiCQdP2k6n03zxi1/kR3/0Rz/0bz+3H38auAz87Y904EMc4j8wWJbFjRs3kCSJixcvfqiQ5U6F+unTp3cqdYH9zxUTiSQnY0lcIRjWfEKnBAvh1WZQaCkklJrEYrnJ0VQCx/OYzvmet512kt2gb/hqrc5MJs3GUp16o8tiscpIOk6l3WU0aWB7glNjgwhgMBFFliRipsPDuxu7vclrQZe09WIDCZhfr6CrChvFBmeyGW59a4nBfIz1zTr5bJhm2+b4sQHaHYuZowNomsKJoRRPb60xOBzILQXFmJYVOEnqXY6OJFm8vUkkFmKrWEWcVikJGVWWcSoKrW6KXtFC8ySoCQo9FSer01AdjGiIWskmJCmobQfWW6TtEEKR6Hgu9ZUK89dWiYdDGJpCZ71BPBQlm4qiNmw0SSJkeyimyX/6n73P4EQa13Vfe82+3c6Hl+V2Pu/tLBaLBya7H9e2xh9borlTwfzkyRM2Njae0SV7Hq9bUcY+92mE5VD/5gKdLd8b5rouDx8+pFKpcOXKFQzjxTyN/RiPTsOm7TnEB1WMpMrGY398RZNYfdzA7Lg8uFXGi/Rvlmjghdx42kQaFzS3+oYvMRHBlCXCST9UnBgzeHqjRnLSJ4PD5wyWF+oYwf/nb1TRRhQEsPKozlQghaREQ6SGfW/q8pM68YyOY3vEp8IUtjqM9W7yhy+ukgjbLJWHsF2ZB/M5Lg51ebTWF7rPan0P4JFEi7V6itlikm6rS6Xtk7uu6x/PkXSDGb2GIof54R/9Csd/wKNws8bAuQT1CkQCDdHMdJTYTJK6pNO4618zt+2vxONHYru5mKIXdAuKaZjbPvkM5fvXSdH33Lp7LtMzhUCyTHezx9YTBWUwt/uxmoliV7vET/thqo+KaB4EBzUIo6OjrK7u1dR9uQSFJElfAP6PwI8IIczn/3+IQ/zHgkajwbVr15iYmGBmZgZFUQ5MNIUQCCFYWlrarVBPJpPPbPO6moK9sG2by2H/mW8HWTaPyiUSms5Wp8XnByd5OldiJO7b4HAgw1br+mRwrlRGlSWeFsvkoxFGYwnCTYlyo8P0Tv5lyLez6YTvIW32/IV523Y5lUizttFFV2UWNipEwworWzWGMlFKtTYz4znaPYvzx4ZIWgohSUEISMZ94pjL+sftBdEj23FJC4XFxwUURWJhtkAkojP7eItcLs7yYokTp4dR2ia6BJ22ydSJQfgDNqahgyThdXWKkSh1xcZLK3RKNrYRR266xB2VRA3MdZuQptC1bWJ6CFk3MF0HTZJRCh3sup+bOXt7idK9LSJaGE1RoWoiuYL2cpnGapmf+EtfYOrM2G4E1HVdLMt6QZZv57p/FKog+x3jZd7OarVKu90+UG5np9P5WLY1/lgQzZddDEmSuHnzJoqi8O677762HdjriObE//5T2J6BZ5k8+NJvAXDjxg3C4fBrk7hfFY7fi7u/u82jW1XW610mvzfDDksaOR3HDITaUyNhrv72JqOfTSIrUNhTIBTLxIhPG6gh//iLGx0Kyx3iRw2iaY35Bw08F3qmTCynsbHeoV4wiQQR/snLSZ7crxJL+2Rv4X6dE9+b4fa1EsXtDqGIQrNqMTITJzNt8PUvr/H575X4iz9wv78PUo/FrUFOZP1wdnpPe8t02OR3HuR5sDJCq5hieSHJmCtxKiRT2BpmaSlHrSJT7hikjQ7b5QxTA1sUCuNcufgbhPMajiPR2TYRpoMkgxdRWbpuEc/7BldSoL0ctDKL969Fb8PPJ4qM9x8aeQ+5dPYIr3vNvqfSLPULgeygZabbdaltqRinfS+EPuCPGT/jh0++W0TzILk0V65cYXZ2ljdIULwL/E/4JLPwke7wIQ7xHxCEEKyurnLhwgUGBgbe/IWXQFEULMvi3r17tNvtV1ao7wetVotr167x/cMT6LLMcqPOZCKF5bmcyOS4khyhW3fwRL/QZ7HWJKQozJerjCZifj7mgL9gPpfJ8/DhFuGg6ry1I19UD/QuN8tEdI357Qonh3PIdQ/Jgk7PZmYijydgesw/LwkjEHzvdRnNRLFLPQqbDbaLvl1e26yjqjJziyVi0RDzS0XOnBiiMlcmoqtUK21mTgzR7dpMTefxPMHAcILBoQRhy2Fjvkil0PQLW1c3UN51MT0LxYlQ7OkYXRW54hGqhei6YSxXQELDKvXoKBqWoeAqMuGOQDQ8Ysi4bQtrs4URi2PEQpibDZSKjdmyKc0XWfn6HMt3V1m9tojUNvlrf/fHmZwZQVEUdF0nHA6j6/puE5YdWT7btnFd9yOTJnob7Hg7JyYmyGQyB8rtbLfbB1Yz+U7gY0E0n0ej0aDVajE8PPxasfQdvI5oahEdfWocyzFoz25S+91NxsbGOHr06GvHlSTpjUTz5m/7Ej+2JShWu4SOhcjNRNH3FK/kp3wy8eCbJYa/J0Wt2CdC9arF4t0a2bMxRs/H2V70PXcLd2qMfDqFGchGVLd6DF9MUC34xmT9ocnk+3EWFqs0yibRIZ8cGjGduuNvU9rocuyCH3JxVYGngSp7/MDQXXTVPy5PwNq6Qb3cvw0mkm02mxHuriVYWsuiW1GmQm0MxSNm9IngZgkGww6X0l0a2zkWVqYw7Sgg0d4EXW0z8+49yg8bKCGJXrGHMplg814TPIlwxD9HyakoTidIXg+8mOEhA8VQiZ3MoWbjxM6PEjs3CiGD6PE8ej6KuR20mNRkvJK/4pcNld5m8Lks0Vnrd17qlUxWvtbGOD2GCGREEt9FonnQXBpVVfm5n/s5eL0Exd8GYsC/kiTptiRJv/KK4Q5xiE80JEni7NmzH7ow4saNG6TTac6cOfPWNqJYLO5K8Q1nMnw67xci5Y0IqVCYsKlwZ2Gbp8UyuiKzUKkyHI3QdRxODgT5mPFgYY7EO8kBlpb9SvW5rQohVWFhu0I2FqbWtZgZymI6LjNDWY7l02Rcla3tBkbg7TSDrj3bQZvejYrfkzxqRHCLFk+fFvyq8mKTkcGo31IyaCU5NZFlZjJPqOPRqHTQA0m5VtMPnqytVNE0GbNrobVMHlxbYuJYnuJmnZPnx3E+10JzVOxWlG2h0wu7NDUbbJ2CkFGTYRRFJl6Xcbsyctkk4krIW10URcdSBQ3LIulphNBRXIFb6xJWwmiygtq16a7WkV0PqWkyOhDjZ//xT5IbfjY1DnxCp2kaoVBol3TuRDK73S5CiDeG2L+d2JmXDpLb2Wq1DuzR/E7I5n3siObGxgb3798nlUq9IKL7KrwpGfvkX/keZLODaSooX6mRSr553P0keF//9Q0ABIK1pw3WZ5ssLNdww4IdJZ12vV+EVG00UAdl4oM62SMGa4/90PTcrSrh8dDud5AEj+9XmP6sTxRlRWLuSY0Tn83ujiUbKuEgH3HtscnEhQhy2ubuB0VmLvk32t1vFLj4g0N86xsbLM/W+S8/v86loQrzZX8le30ux6mMier2CXfXVniwlGE6BENhh8lkf/9HQ3VM19/Jo/m+F9FxYwzrVUI9h0oly+B4BcPrcvTEIhG9QvSYRrnmUV3rYW/757QXeB53BO5DuTAYYdRjwzjpPEv3FOa+ZlFeEcx9ucXc77RY+GqLud+3KZTilCoJpMlRvMkYkurfxuHhvgxSeCSOZ/q/JYUUOmu+UV35WgtPCaFlDMIjfojqwxLNt0kc73Q6B86l+aEf+iHeIEHxBSHEYCBBcUEI8SOvH/EQhzjEy1CpVGg2m0xNTT1fhLdvCCFYXFxkcXHxGSm+PzA8AUDHtkm0db41v8FwPEbLsjg5EGgWR32vlB20F16tN8lFDKyqzdpGjfVqg6l8io5lMxz35YuO5HwyFQ7IX0RVKS7UWNn05Ypm18pEQhrz674o+1alybHRDK2uxfvTYyzd3mZ8OMgHDeYWNQjflyr+XKUIwertDWYfbxGJ6sw93WZgMM7aaoVjMwPUax0uvDvBxt01MkHUStH8MVZKW8jnXLqtMDVJw65ZxJ0Q7pKEp0TQGi6aKdBqgkbXQ84a2HEVqWIRScTxGiZ618Woe3Q7LnJUA9NBbnh4XQfN9jCLHaLREGrXYXw0yf/wT/8c8dSbFxuyLKOqKrquU6/XKZVKDA8P75LNHW/nd5J0vkzJ5HW5nX/1r/5Vbty4wZ07d2i32/v+je+EbN7HgmjueA8fP37M9vY277333r4kI3bwOlIohGBbruEkokgC3CY8/FtX3zjmm/JuFu5UKa35YfCBqRCNoKo8O27wra9sEpsJM3Y+wfLDvrxOsygoLPfoSC654333djihcuN3Nxm7nARJMHUpTWm9w/1vFZm8lOLY5TTbq23ufbPI0Ysp0kNh7lwtYLoWatAXPBQL07X8m3LhfpPsqMbQUZ1r19ZJ5UIMaRW+eHIJgLhn87g0yPkgXH4s3WOrHWWrFWazkGJccQB/3KRm8aTk50aGVVht++RswOhSMf0HOKL4HsVUrE23aNBs56mV4ySNDt//n9/C1TQ6RY/oqL9/WlymudRCUiWUqIY8OUC1F+Xpb9RZv9p8JueysxFUoY8Y2E0/XB4djtAtO2xc7eD08lSaaYwzE2iZvkFR0+Hd98ZoHOEG11KRWfm9BqnvPb77/4+CaB70+x/XpO1DHOKTjDdFqoQQrKys8PTpU7LZ7Fs/o57ncf/+fTqdDpcvX96V4pNlmcvpHJ8dHGd9uUEmHHR6C/qWe8Gcs9HyicKOPmZYlpmQ4ixuVDk26JPBaEAoNd1frK8FZPDpZpn3Jka4fWOVbDxCOZArMi2H6XG/FeVwIMpuhDQuTgxRWWsghGCr4M9XhVKPkK6wttkkk4pQLHc4O5nh4deXGBqJYvZsjkxl8TxBLr+zYBecOT3Myq0VPNdj9v4GqUyUxcdbDE4k6FxqYXfSFLoekgxChlJDopuJ0NAc5MEw1kYPBxXF8XCLHXJtFSNkYLV6KFEdr+GCJ5OIhXG32jglG1mVMYRAMT2SyQhSy+LkySH+xi/+V4TC/eLQ/WBzc5OVlRUuXrxINBp9xtu5t/PdToj920k89zOv7PV2/uzP/izpdJoHDx7wuc99jrW1tTf+xndKNu9jQTRN0+TGjRtomsaFCxdQVfVALcBete1OBwjHcZj589+HETKRHZut31mnudx4yUh9vKqSfQdXf3edqfdTSLIgN9IvoDECD/3K0wamYTF2KYaQBMMnopQ3fEJWK/RYWKgz8Y6fXD1+LonZdXl4tcTk+2naPZ9Qea5g8WmVblBp7nmC5bk6mekwZs+ltGZx7GKG7LDBvXslZE1CD8tYpkdqIErdcqlXbGIpwV/5T56iyL4RqzdlyusSO2QSJNbrSdxaiEHdYSjqstbtG1hX6xM4y+mvsFp2IIlhVOiavrHrmBGSXp1GNUoi0qRXMRk0ngKQTvpjxqbChE4Y1NGZ+3qDjZst4iP93Ccr8AKHcyG6Bf+cRYb7hUCe0n+4ZSTMhsviVxtUimEiZ8f8Hup7OgIpsf7YkfEYbteDRD+88GGlLF6lofk6fFz1zg5xiE8KXtWG8lV23fM8Hjx4QL1e58qVK+i6fiAiseOYME2Ta9eukUwmXwi5K4qCBBwPZ+lYDlpQdb5W9+ejHTmjUqfLiXwWDzibyVJZadFp+lGZcjNIsSpUUWWJ+UKNXDxCodHm5EiO05ksNF0QMJj17ZwWeCbrLT/EvbJVIxLSULoeq0+LLC6XGcjFKJXbTE1k6PYcpqcG8DzB2EiaMxN5pCDrS8bP6VxdLiPLvkZmMmUQ1RW62w3KhSbHz45hWw6D4/6EaGkC82ScbceBiILZcVCtJF4HYqZM2tJgtoemh3E7Npqho1gyliRhqRKu7SKvdohHDEJhlc5qDd1TicfDJBQNzZHQkbBqHaaOxfiTf/V7aTabByr+WltbY3Nz84WakB1v5w7p1DTtmYIi27ZfKCj6KATZDzqvhMNhZFnmS1/6EteuXXtGrvFV+E7J5n0siGa9XmdycpJjx47tGocPSzR39M4GBgY4efIko3/kBJ4agpCMXbf44K9+/bVjvq7qXAjBr/2zWa5f2yJ8VMfZQ3ya5f4NVqt0uX+9QmJGRt9TqDj5ToqNxRaPH5aZ/kyGwmbfzV2rm6hxhR0bOX42ycJcjfy4v/JNj4Z4OlcilvIfhPsfFBk+H6PdtFmdb3LsnQwhQ6Ha7pEdjgCCc8oqk4H3smPJqCJMTpN3pCeZLYeJ1Dxie+qtSs09kkG2wzcXkzzaHESp69S2UtS3UtiVECsb42xUxtkuBZWSoR4gkc93WZwdwog4TE8+QZZd2htd8u9nIRJj7VsumqZhlvwQfLvjG1FJgeai/z4+3ieXsta/VTvVfkFVt9jvaNRa77LwlSbVbhKh9vdf9KP8aEnf05k8l95dlcLBpImex9t6ND+O1YGHOMQnGa+aV3q9HteuXSMWi3H27FkURXmjs2EvJElCCEGj0eD69etMT08zMTHxwnY788oPn/Z7nz8ulIhqGlvNFjPZDI7ncSzrkzNDU7kyOExpq4vtCrbbNrois1ppkglrdGyXqVwSTwjGs0niYZ1BxeDRoy1aHX+xvrpdQ5Lg6WqJWCTE8laVsYEkAjiXz/L0/haTE36BUdAwCE0LWmHWO0QjOl7DZPH+JnNPtklnoqyuVJicytFqWpw4NYIQMDoQ5vE35rEsn8hurpbRdIWn99bJDyfpfEbCtiTkukukq9JphqgLDxFXcTWJriVhx3TMkAQhBVa7pAwDp9jG3WoSl8IQCWN5AopdYkYEPazhlTqY1S66ANVy+fz3n+Sv/8//NfF4nNXVVT744AMePHjA9vb2bp/7l2GnVeQ777yzWyD0MuzopmqatltQpCjKM97OnUr2j1qHcz/4dkbKPoxs3seCaA4ODpLP55/5TFXV194Ye/F8hXi5XObWrVucOnVqV+9MkiQyf/gK7SoYhkVztsqTfz73yjFfRjR38jWWnlSYf1Dzt1MkvvH7G6TPRjj5fVm2ln3SGM+pbC0ED92iydp2h8FTQXWf65Mj1xFUWz2SIyF2kgv1uMLdDwocez+DosHmeptGxaTnuiTyGtVOh1rBITUaRgvJnP5Mnm98eZ3jQeHPvatFzn5/noXZGvevF/m+70vxZ9/dYr7un99HGwkyqsNAxGW+kWShGiIjdAYjHo/KfWKXl7tstkPcWsuS7SgMaxHGZItBzaLuxJAlyKoN4nRIOU1cK8HTJyNEYyampRHRuyi2ghbWyaWbfOqPbVE3ZR5+pUZ7Mwi1T/Y9errphzii4zqu6Z93h35+qNXov/cCMq8YCu01/3xrMZV2EGbv1hxmf6tJ6MQoiqHS3eoTUyEkJFUmf2EARVHodDp4nvfSVel+8bYezcPQ+SEO8Z3Fy+aVWq3GjRs3mJ6eZnJycpcgqKp6IGfHTn3Bu+++Szabfel2O/PKmaEBjmWfFWCPhvz5odLposkyuiXzdLbASrnORDZJx7IZT/kOhyNDPjn0hG+vSpUaya7EnYfrGCGVxc0Kw9k4lUaXE+N5bMflWNAJZzgdJ9oSdIKGF5vbfmFRsWoR0n0R9lw2Rs+0mckmeHpnnZnjg7iux8iYT4K1oBVws9FjaijO0u0tEukIWyt1ho+kqJXb5MaiyBIMTERYGW7SCtmgKWy1JdSoAbZHDA1nvosomcRtGaXYI9aS0dMRaj2TUCKM5qp4TYuILKE1HbBlhAtuoY3btolqKnLX4Q/8kXP81//Dj6FpGkNDQ5w9e5ZPfepTjI6O0mw2uXnzJjdu3GB5eXk3h3GnlWiz2dxXK9GXXU9N09B1/RlvZ7VaRVXV78q8chAHxndKNu9jQTRfhoN4NHdWnjv5NXNzc1y6dOmFYqKTP3kOVVaptSMossvdv3uXbu3l5+x5oimEwPM8PM/jy7+8vPt5esD3kM0/rNLGYfxKgviAQn4ixI73/Ng7WbZXusw+bjPzuQybi/3Kc9PrcfPr20xdSTN0LMbjG37nhbsfFDj9/YMUAwHz4kaH2IREL3B+zj+sMfNehgf3CriuYHmuxsRMglOfyfHlX1/m/Pt+wc/73h0imsew1+YbiylOp/uyQJYZImSGCAchdV3bIcISm90U1UqKad1BkSUK3X6uS9P0CakiC6o931Wb1BsMpzqY5TCLiz6p7fZ0DLdL14szkpunudkilFCozvkeS1X1DboWVWgEBD0xvId8WcEJlAT1BT+0ZIyEsYMOGLEjMQI7S2zi/8/ef8fHdV9n/vj7lum9oVeCJMDeJIqqlnu35J7irGzHsZ3ibOJN/TlOnN0k6+/G68TJxqmb6mTjIsexJcUlki1ZskiKDSQAEgSI3qb3duvvj8EMQQokARJS5AjP68WXIHLm4s69dz7n+ZzznOdc9uD0dnswVJOZp3NU3CFEy+Uva2mphH/Aj9VlQ1EUzp8/38hgwPNtLtayQBiGsVk638QmXmJYS+l8bm6O8+fPr0oO15rRNE2TSqXC4uIihw8fvq69zMq4Us9qFpUa4RtPpLGKIulyhQO+CIOji2xvrRHKgKsWZ8xlSdB0IoMATCXz7O1oohLXcFqsVFWdZm9trQ4s+18K4rJ9XrrI9o4wi6MJCrkKE5MJfF4ryVSZLd1hSssm7IZp0t0eQEpXUco1Up5MLpfrx6I4XVbGRqNs296MUChjk0SUqkZHb+1chWVJVimj0dnp4Zg5jaMkIszp6GUXYkWAkooXK/mYitjsRvXIlHUdq8WBiYBZ0bCXdIzZci1r6LahzBfQMwoOuwU5r+C0WvHarUgVnbf/2GF+4pfe/LzrLQgCfr+frVu3cvjwYXbt2oUkSYyNjfHss89y7NgxstlsY/T0raCe7czn88zMzLBz585biis3QzSr1WpDD7wWvFi2ef8piKYkSWiaxvDwMJlMhttuuw273f6811k8Vhy3R5AlKBZlzEqF7/7M0VWPuXJBWEkyBUHg9A+iy6+B6bEaARIEmBzNcO5EnKVsBXvQgcNbS8FrKx4qRTewtVhp6XMTanMwc76WbRt+LoEcVnD4ag+WbBUYPhun90AAyQI2l8DclIIrYMXjtwIm8WyZ7t1+wKRU0LD5JBajBUwTBk/FeMu9Evf3ZgCoYkErOKjrMguKiJERKBmX9YvtUoWpoovFTJBeUydduvyQe+XLkgCHeDkjoKjLHd8WhVTRjUUykLAxNd6GJ6whizrlpEjIHWfn7kki2y6Tw9Ky/jLQ57rcrGNcJpeVhWWtZpsds7o8lst9+VrKbmnFz5dL5Vb/5c9kynZmxyW8O8NY/DbKCyWC+yMUCoWG5YjP57vC5sJisTTu/7U0OCtxM55rm6XzTWzixUc9rhiGwfnz50kkEtckh2uJQfU+AICdO3det+wKV8aVN+/YhigIjCVSNLldFBSFQ+1t+MoWRK22nlSXJ/iMLyUQBZhK5oh4nKQKZfrbwuxubcJZFikUFXye2mcQ5Nr6NxPNIgowOh3H67QSdNqR0yrJZJG+ngiGaRIJ1Ta7luXNeCpTYltPhLlzi1QKCpcuRmlq9hJdzLK1v5lyWWVLXxMtrT7cwOJEouGROTY0jy/kZGE6za5DnXhkAatVoni/Da0kkPW4yVtMzJAFQYdSCUTNRE+W8asSjqSBTTMRNAM9WQZNxh50o1dVjOkcVpsdV8CFtaRjkSQsmoFVN/jxj97H2z/yqjXc/ZqOsaOjg3379uHxeHA4HDidTo4fP87g4CDz8/NUqzc/5yIej3Pp0iUOHDiAw+G4blxRFOW6pPNmm1TX854Xyzbv+t+KFwmr7TxlWV7zDTcMg6WlJXp7e+nu7r6uNqLzoV4uHjuGYkhkEgLV0zFG/t8UO3+054rX1cvx9XJ5fVLA6aNRnnxqhoE9QdpbPTz3nZqXZt8eH6NnayWIrm1enn58Dl/Qxq5XRDj3TG0TIIgwM5EjvljCYhO589XtLDyWBwSCLXbOny7iDVgIdVpw+kXGhkoklsp0b3cRanJz8uklsqkqnX1eevf5ePbJmr3SwTtbmBvLMjmbRRCgtdPF0myet7VMND7P+JKDnT6N+aqLVmuR2ayHLrvOeNFGm71G+GbKboqKjX57bffausKbuEkuUtIknLJOQM6h6BaskopTuqwvrWg2oEDQX8CKRj5nJ1t10NyUY2kmQu+WJUrx2mttPpnsZBF7wIKjxY7FG0ZVoaiC0BWojaPMKBguDSEk4G32IgsmVrdEdGwJgFL+ckm8Wrj8rBj6ZVIs2WXUgs7YMzr9b26m9NQ8zh3uxkjTq7OK9S9pfSdZXxTqz0H957oup571WO/O82bsjTaxiU3cGmRZplKpcPLkSUKhEAMDA9eMFzcimuVymTNnztDd3b3m6UB1omGaJiGHncOdbRydmafT5yVkd6CmVaKpAkpVRxRgbCmJzyaTrWrsbI8wMh+nI+Qjni/R7HBx/Lkp2sI1ffz4bGK5bJ6mLexlIZFjR08T56dibAt7GTm9SGdbbc1JJDIAxBJlZFlkbCJGKOAk6HGgJUqkE0V27mln5Nw84SYPsWgOZXmEr6poaPEcQ+cXaOkMsjSbYsf+Ts6fmcUTsGG1yJRiWWIzcTIRCXvKS7oIPsGCUlGxaSbVooihK1jcVsxomapuIvvtFIoK1pyKx+7GUHW0TAmLKmJ1O2vNPot5EARciNgE+MCvvoG737h/HU/AZUcAt9tNb29vQ19bKpWIx+OcO3cOwzAIhUKEw2G8Xu+a9JaxWIypqalVB8xcK67UE1j156z+7/W4sp4BATc7zahum3fVsX5zxc+vWfdBr8IPfUYzl8tx4cIFXC7XFfqaa8HZ48HR70dVNVwekWpF4MRnhigmryS19RutaRqmaSKKIoIg8NW/HwXgwlCKpVQRe7tM32EvVe1yOdyxnF3LpqqUdBX/Fjs9u330HwoRX1ye222X+cH35uja58PfZKNlixtNNUjFqpQUE7vnsl6yUKwyPZfCF6qlxBVNZ3axQLil9pozx5foPRgkkyyTiJYplTXef79ENl/bKU2VfWz36IBAoSBzOuqhy1K7tl1WjZImcmLJQagiYhYv7658okpCq+2SRUEgXvURLbqZK4Q4NxFkKtVMuuxiNhGkqkpYpVpJ2y5XSWadeCwV5mYiqJoVQxGQJYOwdZzIfh/hI0GMVhfTizpLsypDj2eYGSpy6fsZFoaK6KZI7EKZxHkVUXUz+kSe4ccLzI0b5GUP7j3NuHwehOUnuDh/+frnlj0zAZTlqUGmDumYhGtPhKgtzr59+9ZUur6WBmflrlRV1XV/wddr2L6JTWxifVjtO6mqKmNjY/T09NxwaMf1YlA6nebUqVPs2LGDtra2NccrURTRNK3RLFIvn1sRmRpLMjIbI+B0kC6W6Ql6MUzoXdZj1s81nityoKmZ06dn8TitLCRy9LQGqCgaWztqr40se0cahsm+tiai0wUEYClWwm4TiacqhIM2cvkKW7qCGIZJf1eYi0enG6QoFs0hCDB2YQmf38HMVJJDh7qYOTVNW2cQ0wTPcnPl7GQM2SKCLuG1Ckyem2Prvk4yAy6SVhta0ELeYeAwLWQMEc0joztk9HgVj8ODXFLR40W8VRNUEQUTUxKwV8AsqMiGQHkui2iAUxdwyiI//98fXDfJ1HWdwcFBfD7fFfdfEIQGh7jttts4cOAAbrd7zQ1F0WiU6enpG04xXPkcrGYWX+cc9SraeuPKRo3O3Gj8UBPNxcVFhoaG2Llz55pubv24ze/qIuDSMFUNwzQpplS+/r4fNF5TL5Wbpsnw8DCxWAxN00hES3zzq5cAiDQ7GDmTYGm+yORkhtklhV33ROjY6uH86QQAVrvI2EiaqbEs54bjSH6R0DI57Nvtp1zSOD+YRPaLqOblz9ra5+LEs1EGDvsRJXB6HSxMldEEnUinBUWoMjWWRTVNurZ62XWkiSe/M0P/3jAOl4zPK3KPPEOrIDOVsWEtXj52Lidg1S7fdqtg8syMm+1WGVEQ6HXq5IzLGo+MYmM672Yi00wh48JWlPGWDVw2F35VJWiYpKNuikkfmaSduURNLF5Y1nRaZZ1C2ofktBAJlvE6pxg6kaOQNYhPlBEESF2qZUWDvZeJX7VymTiW4rVNgCBBZqJIIaYyc6bI2W8WKNh8BO5ogWXpqeyWqSzVXm8C6YnL04FKqQqz5yrc9urbbmpMV12Ds3KEmSiKxGIxHA7HujQ41Wr1psfZbWITm1g/FhcXicVidHR0PK/5dDVcKwbNzc0xOjp6RR/A9VxK6jBNE4vFQiaT4cKFCySTSe7f0s1dLe2cOjtPbziAbph0R2q6d2FZdL6UrW2cRxcTtAU8eFQJNa+gajpb2mq6Uo+ztpbkS7W1b2IhRcBtRyzopBbyJFNFeruDqJrBlp5lU/hlg/dcvkx30M7Qs5NYrRKXxqI0t/pIxPJs39GKqup0dIXYvbOV7GwKtaoxMx7D5rAwNrRApN1DIVtl3+Fe4qNzVIpVBAFOFKKYPgdiWsGvW7BPK5TTKq6ygZCsEihLOGU7pWoVwWtDKhpUiyYelx25UMVcqKCqJg6XDSFdxu1xYtcMPDaJX/7f72XvXVck4W6IusyhqamJ7u7rD7exWCw0Nzc3Goo6OjpWbSgyTZPFxUVmZ2fXTDKvxkqz+PofwzBIp9NYrdY1NxTdqk3fC4kfSqJpmiYXL15siK/dbve6Goc8h0P49jWjWk0cDgOqGtHBDN/73aEr9JiHDx+mu7ubYrHIyZMn+ePPPEH3DjdWm0hHnxd9uUS7ZXuIbLrKsWcW8LRb6bstSHOXi4GDYXLp2hd/6+4ATz8+RzRbZM8rIkyMpxvn5A3ZOXF0iYHDITq2ujh3olZfHjye4MCrm0kuT9FJJxSaev34QjWSlIyVwamQXl6Ihk7H2TLg47UtKQIWHatgEis14bfWzjOtSDRJNnTzMqG7WPXQaXez0lNzqVJbtKZLLso5F96KhYCq4NUrDQmlW7hMBK1OAVGAiEOlWvIwM9WEsSxab44UsKBQzeoIpolNUAkFcpQStesS6nM1so5W5+Xys5qtfalkh0hmspYF9ve60Mq1++zrrWUDs/MKyZhALG/Hf1sTvq3eRlOQu8uFvpyhNYUaSY0c9N3UYnAtXLhwgVAoRGtr66razuuRzv+oWbqb2MTLCaZpMjo6yuLiIr29vTfUUdZxdQyq6zqTySS33377FX0AN0qM1OOKxWLhyJEjtLS0kEwmOXvqJPZlKyKXvXZe84labJjNlPDYrSxlCmxtDtLkcdFr8zA1ncJhq23kk7na2jg+l8RulZlarNkXOawy231+psbitDbXSuuVSk0iFU/U5qGPT8aJhN34RCtWTaZS1ujo8mGaYLPVFtFctoQoCkiGwdzZOaZGo/Rsb6aQq7BloAWoyREG9rYz/OQILo+d+Usxdty2hfhdbjQZJJ+NYrSK7nFSdUtUPTL2KqimCJKAUNEwp/K47A5cThvleB49Z+JwWPHbrch5FVEUMHMlfE6ZX/jf76Bv1/o8w1VV5fTp07S3tzecaNYKQRDw+XyrNhQ9/fTTjI2NNeQTt4p6/BgaGqKvrw+/37/mhqJSqfSSbTB9SUS6a3UHrpam1jSN06dPA3DgwIGbMnc3MPDfsQVZcpHO6FhcApJV4MzfzjD5g3hjZyCKIl6vl76+PrZv28e//L9FBgeTSH6TaDZBa48Nr9/KyJlaBtPplhkZTHLi2UVmojlU2aC7f3l3KtU+Y7Wio+oGqmCy644Ibb1uzj5Xay46czyK6Vbp213baQYiNQKqmAYDB0L07vRz/AcLnD2V4MDdzfQO+BgfK3FhJMv2/W6cHpF0IsmrXDVN6ExepkutMpx1YJgwn7LjANpMjbhmYyTvoKVkEtB15sqXF18bEuO5EL6STLNWJa/XiJlDNklUahlZh6iSUWuE1CeXGgTUMGS8Dg2/qHFhsgndgETGRcijMJfsIOwvsmN7nOT4cpd5y+WsXiVdW3Alu0BhtpaiDK5oFHJFLmdarSsbgewi5YzGyHdy5AUHwQO1Xb4jcll+YG2VMKvg2WXj5MmTz7O5WC8Mw+DcuXP4/f7GIlPPdtb/SJK06gizl2p5YxOb+M8EQRBQVZWTJ08iSRIHDhzAZrOtL1YsB3NVVTl16hRWq3VVG5wb+S7XiYEgCEiSRDAYpL+/nyNHjvDOO/cBMLqQQBYgXqzSFfKh6Dp9LTVLoojbibJUIZaoJRXG5hI4bRbmYlm6W/yUqyrbOmtl87agBxIK+UyNWE5MxRFFWIqVCYfcxJMFtm1twu2ysSXgYXJkCduytVIupyIIsDBXwOuzE1vKsaXDycj3x2jrra2rxvJYzPHhBTx+B0G/C7NQolKoEmypxbtzySUIWJBECXdKwFQEhKyCqwrWqTJOuwPyFZR0CbthQXY5MSwSlUQBNzacdisWw6QSLSKaAvaqQWvEw3/7g3egmEWOHj3KyMgI8Xj8hvezWq1y+vRpenp6aGlpWdO9vx7qDUXhcBin08nAwADJZJJjx45x5syZW2ooqhPi3t5eIpHI80rs1zOLfyk7mbwkmoHgsuFtHat5mBWLRQYHB+nt7aW1tbXx92spW1z92v4f38Kp/z2CLewhn9GQ0VBLJv/yUyf56LOvwO6+sqz5B79zjFKxRnyDTTLnh2pf+IO3B1DKGql56N3m4/SxGuncfSjC0e/XmnXuflU7uVSNRPmCNkbOJijmVeLREne8sg3ZLjJxPkPndjvnBwtAgQOHm5EkkVNHlwAVRdXZeSiMZUpEL+uMXUjR3uclGLazOFfk0miRnbeFua8yhkM2MUwQRBsiBiFV5Piigz2uy1nLi3EbO20GdWf4iuAEcsxpboSkgN19eXJQRrfjWdZf5koiTcv8rWw68FPFbjFI5O1EvBVsci3TKYmAKpNKhSiUTZoBragTK/vY0p3ixHEDEDDVZU9MCyTHamXu8HYPiXO1bn67f0X2cYXWXl0hB6jkLm9ISimNS6cL9BwOwwpbI3+7j/Jsmt1v6qf5QIBKpUIikWBsbIxKpUIgECAcDhMIBG64M72aZF6N+vvr/61nyFfqOpPJ5CbZ3MQmXkDUTdj7+vpobm4Grp3AWA31BEbdoWLlca712qthmmbj9622rgiCwF07ttDqd7OYKbCjNcT5xSTW5Wlw8XSOPS1hxoaWMAyzQSynlzLs6Wvl3KVFvMvWR7lihV1dTcwMRVHKKpPZJKGgg2SqzI5tzZwfi9La5CWRLGCTJSwZhYlEFFkWGb8YJdLsIR7N07+zldGRRbp7w5SiOdTlSW2To0s4XBZmLsVp6fYQnS0wsLOV5x47gy/sxuGyMT44y/YD3Xx3ewGPIZNbrJA1RCxeG0pJQSqBHHSTqShYHBZcBdCqCi6PA6GoIGgyqq5jN3Sq6SpOhxVLUaG51cN//5sP4XTXgo9hGI2Z5JcuXcJmsxEOh4lEIldkmsvlMoODg2zfvp1gMLim+74WzMzMkEwm2b9/P5Ik0dTUtGpDUTAYJBKJrKmh6GqSeTVWNhRZLJbnNarOzMyQyWQ27DNuJF4SGc3VcPUXN5FIcObMjAPdwAAAecBJREFUGXbt2nUFyYQbzyVf7bj2oI2t7+zCLZpIRZ2SLlMVTNSMxt+967krjnf02XlODUfZcShIe4+NsQvLXdltbobO5hgaylMRdRLFIl0DNhxOgYmxemncZGmxyOBgjLbtHnYfjlAq1Ejbjv1hnv7uHMMXkvTsdWJ3XdYN6oLJ8Pk4++5sQhCgp9/H09+dwxO2MbAvRKDFwanjS6RSFW6/u4XuHT7Gj88S0Q0MEyZVN+HloeElwYJFvNx4EtdlWjUnlRX7jICmMa4EcGclXLLETPryl0JSL5N4j+PyPRGqKwieWcs2ei0VikrtuKouYkfFYgjEsl48tiIhRwVTsNDZVvMLTYwv+2N2SBjLnux27+Xz0qqXf3chenkKUHq5nM5ySfzqv586nmd2WsG+vXZepg6yUyKyp7bjru9K9+/fz+23304oFCIej3Ps2LHr2lzUSabP57uhzqeOlRocURT5yEc+whve8IY1vXcTm9jEzcFms7F///4ryOF6/ZlLpRKDg4Ps2bPnmiSz/tqrkx31xo56dexaWFxc5EBzbX2un1m0qGCRRMJWB9m5PMWySluwFh/qxDJbqG3q62XzoMOBEi2TzVboW9ZhBnw1YlYs1xbXiekE/VuamD2ziNNuIZsts22gBcMwiSzPLM/nKgRDLvJzadKLWeankmzd1YZa1enYUsuaqlWT1lY7z/3bGVp6Q2QTBXp2tgEwFU9gbnWRiVaRvE4Mi4haVgiUZFyCjJgu4ykbyAsVdARsQReVpRzVhIJkgMsUsCjg9zkQClX6toT4vX/8aINk1q93IBBg27ZtHDlyhP7+/kZPxbFjxxgfH2dpaYkzZ86wY8eODSWZU1NTpNNp9u3bd0Vme7WGopUTioaGhohGo6iq+rxj3ohkroaVjarFYpFf/dVf5d3vfveGfc6NxEsmo3k16guCaZpMT08Ti8W47bbbbrmBYuWCsOtD2xj9x0ma9vuZGytiVEQ0q0FsMM3ffvAEH/ib21mYz/MzH/4WCwsFZBm29AXYus+F3SIhaLC4UMts9mwN8NyxmtXRnXe3UC4pSFYDf8DK6HCNdOq6wePfmaKlw0VXp5elhcsEyeV1cep4lAN3NZNNVhkbTZHLKhx/dpF7X9vJwlwt27cwW6C5w4loyviDNrLpKmVVo1hU+cgukT6LxPmCn4hZBQk0E6oVOy26ScIq4xANqnk7XmCqaGGXW6eqw6LiRclohB01gh12W2B5Mk9IqlI1JRJ5CVW0E004CbolBMNgKm/HNEzyKgiEcQgFTJsdF1nc9tr7/S6VYsVJxSZhCjoOocqeO7KomW0UYmU0j44SMtGRsNkslG0CoTuDyGIt4epqsaGWdLJTNRLp7XSQnV2eLrTFRapehu90kJ6pLb4Wt0j8Qom4CQOvCFNYLNF8KIAoP3/BlySJcDhMOBzGNE2KxSKJROJ5Nhdut5vh4WF8Ph89PT3rfvY0TeNDH/oQd9xxB7/+67++7vdvYhObWDsEQXhe099aiaZpmiwsLJDP57n33ntvaIK98rhX+y5fK5NVn0pTLBb5yTe9gn+7+EXGlpJEPC6y5Qp3drTx3OlZ9m1tJZ5bRFk+7YszMSySwEw0Q2eTj/lEjru3dXLiB5PsGmhlbiFDbNm+aG4xj8NuYWYuTVdHAI/DirWoUypW6e4NsTCfIb1sxj42uoQ/4MA0TNq8Di6cmmbHgS5y6RmKuQoIcGl4ifbeELKq4XLZWTBBV3UEEc4/N0lnf4SZ3VYs8yaGYmIkSvgcdioZBd0poptmzVe6KmH3OhFUHW0mh1WwYvPZsVU0zKqORRQwcxV272nnE3/20A2rTE6nk66uLrq6utA0rWHEb7VamZubo1qtEgwG16zPvRYmJyfJ5/Ps2bPnhudUbyhqbm5ujCeNx+NMT08jSRKhUIhIJILFYuHMmTPrIpkrkc1mee9738snPvEJ3v72t9/sR3tB8ZIhmleXzleKYgVB4LbbbtsQse1KAuvb7qHl7gilxTK2ooHmkFA10C0ik4/H+Mufe45/HZ+kqcWKxeogEvFyYllPeedd7Zw4vciugxEiIQcnj9e8HXt6vZx4LoaqGPgDNrwWmR0HfUyN5lC0CrpuMj9boKXTRTSTZ/ftfkxN5uTRJXTd5MSzi+w4GGLb7iBjQynCLU6e/v4sqqJz8I4WnE4L3/9ebWSUx2Plvjd28eQT07SKGgd21zJw+YxMAYO9QZVJ1U2rAQgC0Yodo2LQvqwXjRgieV0gUXITVCEmWoBaltKnq+RkC4KmM19wopRFup0mNqAsWXBoNaKXE+34xTIuycQoCAiSi2zZTlkWafNnqWoWbKJK0bThryos5W30NWUoxUtUtCozw8vkMeRjYSIDaMRmKqhFE0+LheJSbffXd1cQF2DDxGKTGkTT1WRrEE13m71BNG2tIuWLtQ3F3GgZV8jCrvubbvh8CIKA2+3G7XbT09ODqqokk0lmZmZIJBI4nU6am5vRNG1di5au63z0ox9l165d/Pqv//pm2XwTm3iBcS1/5huVzg3DYHh4GNM08Xg8a5q0IooiqqqumWTqus7w8DAOh4O9e/fWYlxvO89NzNMT8ZOLlsgsN4FOLKSQJYHZWK7hj7mzO8LIdBxZ0Oh22JkdqzWQjk/EsVoEEqkK3Z1BpmdT7N7RxtD5BdqCHk59d4ymZu+ybVEUf8DB0mKWbQPNjF2IsnVrE6M/uIQlVMuwjg/P4w+7WZxN0bE1QCGtEPJYOfvUJDaHlUCTl/hchp2HtzAxNIdoFZiI1LTpssuBkVOoZDTsHgeVdAlZMQgIDqpKFRMNMafidDgQdRM9XqCsGHgcVsSyxoE7evn4Z370htf+ahSLxSumNGWzWeLxOJOTk1gsFiKRCOFwGIfDceODLcM0TSYmJiiXy+zevXvdXKTeUOTz1SpqdenWxYsXSaVSBIPBBudZz7Hz+Tzvec97+IVf+IWXLMmElxDRvBqVSoVSqURHRwddXV0bFpjrN7P+Z+dP9vHEB4/StD+AYYosnC+SKxkkNZ34P8xi+irMOkp0dvqZmsxxx5E2HA6Jo0cXUBSDaKzIxGSGUlll721N+H02kqkKqqLQ2+fn9IllYnpvO5WKhsVhQasqnDi2iGHA8HCa5nY3e+6IEJsr0dbl5tlnaqNG2zrchNscROMFMlUdTTd49ug8t93VytR4hu5tfr75bxM0NTv52R4T0YSFikC7KWIIDqZNK00Vs6HDTOetNNlN6mRSFESmy2Ha1VrmMWwYFA0Bl2hS1EQWVDfhkk5YEEhYRWC5lKybsCydrCoCWGs+mznBToAyNk3FYQrEk0FSFZ2B1ixaWUNyg1W0EU07sUoGfmUe8CEA8WWLo/AWJ8mJGvn0tdkaRLNcKTNxqkYut9wbxHPQj900r5RMiJefEV+Th8zFWibZ2+Vg9ngG/57Aup8Xi8VCU1MTsViMnp4eAoEAiUSCqakpZFluZEKvJ8LWdZ2PfexjdHd386lPfWqTZG5iEy8Srk5g3CijWa1WOXPmDC0tLbS3t3PixIk1/R5JkqhUKlcM97jW97xarXL27Fna2tqu6IB+y8F+FtN5yvEKs7MpECDsc5LIltjZ28zIZJSw38VCIkdJ0Qh4HNirFpaiWSpVjUjQTjxVYUuXn4mZDE7Hcmd6qsCenibOfv8S/qCTWDTHtoEWxi4s0d4ZIpOeo1JWGRhoYfTZS1gsEgvTSbbtbl+e9mMnkyhgkaxY9SJnnxpl275OxgZnae9rIh3LsTARo7e/iR8oCTxVO5WigqAY+CUHmqGhpIp4ZStlTackGVjdNuR4ueYK4rZgxIqgm3gdNihq3POq7Xzkt9+xpmu/EqlUiosXL7J///4GkfT7/Q0bqnK5TCKR4Pz586iq2tBQ+ny+62aex8fHURSFXbt2bcj6bbfbaW5uZmFhgd27dyPLMvF4nIsXL+JwOBpxZbUJh3UUi0Xe+9738pGPfIT3vOc9t3xOLyRekkQzm80yNDSEzWZbsw4O1mZWKooixWKRYrFYS7e/rg3PHa2IIhg5FX+Hg6agjVBa4dJsjpaSCx0Jp9VCV5cHSRZ48nuzOJ0W7ntFG4IIp09G0XUDBHj8iWksFpFXvr6LfFbB47PS2uri2NEFVNXA47UQDlvYd7iJmYkc4WYrI+cyTIxn6N/lJ1OqsmtfhNGRBG6flae+N4vTKXPfa7oYu5imWtE59oMFjtzbjqrptHe68efzbF+ec6+KDiTBBBMmpyzsD9VI5Sw2OlSZuGAStmkUNEirLqolDbzL1waBlOggrpjYClZEQ0C21rKCXk1Hl0ASICBp6Eat4ccpr/To1An4wCHppCsSAbuOVrYzk7DisOYwTfDKJQolOxabQqclySl8RLY4SV6q7d59rfYG0bQ7LmcSjOplLUx8Kktutva5ug75aLkrSOJ0hsz8ZSlCNXf5vESLiCgLdB5eP9GsZ9W9Xm+jXF6fnbuWhiLDMPj4xz9OMBjkd3/3dzdJ5iY28R+I6xHNXC7HuXPnGBgYIBQKNbKTa4EoiuRyOSqVynUzZfl8nuHh4VWbU165q5f/+5WjXEpl2dYZZmw2QXuTj0S2hKrVznliPolFFtE0g3bJwaVLcXYNtDJ8YRGHoxbOc4Va4mB0PErQb8elm+gFpfaejiCZVIlqpbaBH78Yxe224XPZUFIFyvkqvQe7GEnPkE0Xa9PsLibZfaiLyROX6O5vJTaVILGYxeGyMTE0x757tjF/fp7F8SjZ97agCwZ+h52yACVAttpgqUClouByWjAVDW1JxUTE7XMi5xQEpw1ZNRDKKm981yF+7Bdev6brvhLxeJyJiYmGu8BqcDgcdHZ20tnZiaZppFIp5ufnOX/+PB6Ph0gkQigUalSr6laKhmGwc+fODVu/VVXlzJkz9PT00NRUq7TVn7l6Q9Hw8DC6rq/aUFQqlfiRH/kRHnroId73vvdtyDm9kHjJEc2FhYWGw359huxaUM9UXm8UYH10YEdHBxcvXkRRlJoH4isCfP+T43i3u5FdFkxDp5go0tPtwXRZacoXyRQU4g6T8ZE0dx9px2ITGT6fJBYt4XLJ3PeKTioVneZmJ+0dHh5/fBpdN2nvcOPwWdl/qJnR8wkiTRYujZWYnChx5K42CgWVg4dbiEcLzM4WyOdqC8DhOyMIpozbayUYtPPciUWKBZX9tzfj81p54vEZAJxOmfdvtVMwFOZLAh1Cbfc+ZVjZKsvMCTr2aglbSQJRIKLAjCghGg48ioBHlkmJEDQ0ioLIzIzEdmftsfBhkkfEg4FVFEhhIYKKDCyVJdpdOi4UirqES9LxWC8vymXTQgAdv0PDYYBSdDFb0ukKF8lXrHhlAY+1iCzp+FodDaJpaJezD7nFWgZTEAUy07WfbR6J/Pyy76ZXYOpklinA1y4T9htIiwKGbjbskwAKsSqt+3xYXet73Osk0+PxrKrJrDcUdXR0oOs66XS6sSuVJIlnnnmGyclJ7HY7n/nMZzZ9Mzexif9gXItoLi0tMTExwf79+xvVibWSCl3X8Xq95PN5hoaGAIhEIjQ1NV2hEa3Pwd6zZ8+qFRCbReauXd386/dHsMi1ODYXq40VHp9L0BR0E0sVuHNHJxdOztPaXWvMicWzACzGynjcdhKpEtu2RIgnCnT7XQyfnKeppXYel8aiOBwWZqaS9PSFmZlMcmBPFye+PdJo9BkbWiAQcRObz7BlZxMSEsVYmmK2zOipKVp6QixNJRk41EMuVWBueBaLVWbSYWA3BbSkgqmDzyZTyBShZOB2ujHdUFVU5KSC025DFsBMlTBMAZsOVt3gwYeO8OBPrW1u+dX3b3Z2loMHD67ZJ1mWZZqamhod41drKMPhMPl8vuYTep1RpetFvfFnJcmso95QVG8qUlWVVCrF7Ows+XyefD7P9PQ0jzzyCO95z3t4//vfvyHn9ELjJUU0L1y4QLlc5vbbb0eWZQRBWLNmob6AXIto1n3MRFFskANN00gmk+TvXEJ2C4gWlYWTBWxdEp4uL6IsUkqpOA0Jl9dDR8RHR9hDIl8hES+jljRe+9peNM3gxIkF8nmVI3e2kUyWOXykjVyuSj6n8NzxWpPQ7j1eRMHG7Ud8GLrBc8cW0XUTr89GU6uT/tYwxaKCx23h+LM1zWdzqxVfWEK2Oxi7UEWyiHzniWn6tvlpjjjxJLNsLxos5l1IbsDQSZkiobIIAlhTAgnRSefyNVQRSKteutW6TkkgljEpOmTkgoNOUaAgG7i12sjKHBY8yyXzXN4k4oVMVSSjSGiGjKqB3WcnlS3htGkUVAm3RcfpqH0p3VadnGrHJamkSm6mohKSpOMUdeYzDnqasujVcOM+JZcbfpwBC8nlDvLIVhfxizXiGOlzMXumtrA2b/cxfSJT+xQOg/HTGt4mid4dHuafqnWz27wyqUtF7vy5LTd8hlZiJcns7e294euvbihaWlri6NGjDA4O0t7ezj/90z/9UOw8N7GJ/0xYTfu/8v/rZdFcLsftt9++rmEOK/WYsizT09NDT08P1WqVeDzO6OhoI5lhGAa5XI5Dhw5d93e8+e4d/Ov3RxibieN22khmS/R3RRididMa9NDidZGdzVMpq4xPJbBZReLJEr3dISankwxsa+bcyAIOmwVbQWM6kcRqk4gtlWjr8LMwl6Grx8vMlIqha2ztCjD8zDguj525iQRbd7UxPryA0yOTjoPLbmfixCWKuTL9h7oZPVkjYaIkUClV8TgtzA+liHQEyb2qGTNaxub1oCgqZUMjINmpWGsSJ7Ok4K4K6BYrkiihzGWRJRG7LCPrGne+qZetdzYRjUavyCreCPPz8ywtLTV8tW8GV2soy+UyQ0NDVKtVZFlmbGysUWK/lYTBapnM6+HqhqJz587x2c9+ltnZWb70pS8xMDDAK17xips+nxcLLxmiOTY2hizL7N+/v7FzqJPHtRLN1coc1xNny7LcuImZn7Jw7A8v4WgRkG2w8FwWe5cNb4cDj8WKoZsU4hqRoAOXz0rAYcNttaAWNGbmc/R0+QkE7SiqTiJRxjQhn1eQJYG9+3w4HDLPHU9iGLBzV4iZmTz9u0N43BaqVZ2TJ2taziN3tTE5meWOu9vI5xVSqTInT9asgA4c8lKulIhE7CTiZRSlyocMA6wiFZsTa8Ig6i6Sq0q01efVinasugByBd00WdTthHIii1aFVqtYG8FZseLRLFiXfTMXswbbljfcYklHcQrM5iUUVWJekbAi4pAEHJqGA0jFBCKyE6MK85IFp1XF6jWoomBDpyJZcJkqdoeBR5coWK1AFY9Hos8tcEmU6LzdDybEL9S66yN9LmaXSaQnYmsQTav78iNrsV/eVASb/aTHU+RiOtFOBXGbiDUn4IpYKA1p9NwTuuEzVEe9GWCtJHM1/MVf/AWhUIjJyUkKhQLxePymjrOJTWzihYGmaZw7dw6n08nBgwfXlbG6Xlyx2WyNZIaiKJw7d45yuYwkSVy6dImmpib8fv+qcW17V6RRNt/ZHmRwbBFBqMnsbYbIyJl5dN2krcXHwlKWrVuCjE+ksFpq6+LcfIatPWFmBhfwuu2k8wV27mln5Nw8bndN75dJq/j8Dox8hXxZoVxU2LKziYmRCrl0EQRYmMpy4HA3p799jh2393L+uUnmx2N4g07mL8W47VUDnP72WWRZoqkrxIxaxK5HMF1WtGwZh9WCkahQVQRcfidCVaeSN6notWYfLVrA7rBirRo4RIGf+v89wOFX72pkFaemptbUuHO1n+VGoO4GEAgE6OvrwzAMUqkUi4uLXLhwAbfb3Sixr2djUieZ3d3dayKZV0PTND796U/zwAMP8PGPf5zFxcV1H+M/Ci8Zorl169bneWHWieZah9RfXRKpLwZ1snqthcQwDPyv1RH/RKClx8/E0TSRHU40Q2f6WBopJODpsmP32dHLJpIg4HPYkYIChapGd7OPdKaCoEFiqcTOgRD5nEI45GB6KomqypwdTOIP2Lj99lYymSqaqjM5kaGr28uF8yl27Q7T1u5m8HSUWKyMoRvYbDI2m8ydd7VjtQk8+d05AAJBKy2tMgMI9ClQFgQcGRO7KDGv+WmRVTBMLpYNWjUREBi3g8PuwJ+vLW6mzYFiVpkpW2lSrczrVfpstesTFCQMNFK6QE61U8lKeJatvxQLWFUdu25SkEXcpoEbA92s6TfLRZWADpRFxqo+fBETpVIi5AWPqaDoEu6KzoWcn+3hDNWqyHPHF9BNgYE7w8yWKoTbHYhNMl33BlEzKrq2oiSfvexBllosXP77FabtFtHG1FgJi0NkYKeEIEHCPoV8qUg4HL6ueW6dZLrd7psimaZp8ulPf5q5uTn+/u//HkmSrtgpb2ITm/iPR7lc5syZM3R1da17JGHdIPtGTT+qqjI0NEQwGKSnpwfTNEmn00SjUUZHR/F4PDQ1NREKha4gSW+5ewd/8M/fJ5aqrW+Ti2kOdbRw7rkZdmxr4fzYErJUi3WFQm3dG5uIEfQ7aQl7sBRUZvJVurtDLC1miUdztS7z0SWaW32oikZPs5ezz4zTs72ZOHnmLqVweq3EFrJ094ewmAKJydqEuQsnp+jc1szsWJStezvp2NLEyX87Q8/OdibOzuL2O1EONiOaIoZuYIoCaqKCbLdj8VgoJgvYMho2iwW3y4aZ07C57ZiZKl6nhY/9ztvZfbgPoLFWbt26lXK5TDwebzTu1O2AvN5aU0F9E79v374NkyXV13+Xy8WWLbUqmCRJRCIRIpEIpmmSz+eJx+PMzMwgimKDDF+vIXQjSOZP/uRPcscdd/Dxj38cQRBoa2u76c/5YuMlQzRXm9iwFiuKle9fSTRXLgbXI5mqqnLu3DkC7QF2v7eDc/80h6/Tjk2SiY2U6Drop6rpzJ/PozmLWMMCriY7piEhGgIeuxWLJGC3SYhWgVyyQijgwG6ticOrKhiGyJG72rBZZZ5Yod3s6fGhqgZenxWv18p3vjWFIMAdd7TicFoYHU0xO5uhucXFk9+dY9v2AE1NdhYWsly8UOKhdhvYRBY0gVZRpICJMy0xh4HHpRAxnNSn+yiGC29avzzSPGswrMp0ibWGG7deG80pIlBCYCZjoV234UZg0ajistUWwkROw71cFk+VDdx2avpNHSKySdBSG+AjAKopYMuBaDi4qBh0B0okqxKtTg2lbGE87sUbEOn2lZnIOBujJhOLZSxuicWxAgIQbrPTdMiN0yaTXW4UkuyQma6V9GWbQOziMukUTOITtZ/VssHSoknr65s4fO9BkslkQ+vi8/kIh8NXLPIbQTL/4A/+gNHRUf7pn/5pw3bYm9jEJjYOmqZx6tQpdu3a1ehGvh5WNpmulWSWy2XOnj1LT09Pw+hdEARCoVCj6SOXyxGLxZiYmMBut9PU1EQ4HOY1t2/jT//lWRaTeXb2NGOkq4jV2tpYLNW06tF4BZfTylIsx9beCOOTcQa6w5z47hgdHbUmo/HRKD6/g3gsz8DOVi6MLNLa4mP27CzTqQIWq8TUxSi9/c1MjkaJdPjRqgYWA+ZGZqkUVbp2NjEzEqNaVrDYZKxWEbOqYGgGsZkkTZ1BFlI5lI521IqKoeh48iaSbEVGpDyXxiU5kHw2rAaosRKyLCGpOj6vlV/+7I/SM7A6YXI4HFd4Y65cvwGsVuuGk8z6MI5r+SQLgoDX622Mpq7LJFY2hEYikSsy1rdKMuvWeHv27OHXfu3XfigbSoW1TtRZI276YPUpCisxNDREZ2fnmrJBIyMjtLa2EggEbnoxSIwV+PKHT2MLWChlVWx+GUOH1EIZ2SNTLmnMzRYQPCaizwSHiWkRsXqslKs6WARUw8AQdS5NJkindQZ2hdEMnVJFY+hcgi1b/PT0ekmnK5w+Vdsx3nV3O5lMFZ/PRrGosLRYJBYrIQjwild2oVR1FhbygEk6VSab1Xhjd4A32jUMRcdelhEFkUtVaNFtGJgsOqF7eXFatAo4Uxbi9ipbZYG8RaCYt1C1m7SsmPozTwVdlQlpdmKodC2Ty7yhEV5u4ssbOqFlx4W0aRKRa+/P2GRCyzZJeVHGY2ikNQgsb2VSpozd0CiKCtsCVWJFC34r5KwiqazBNy+F8Yft5BJVnD6Zcl7DNKC510V8slY279zlY+FCjs7tDrx+iejxKrpq0rbHy/zyyMrwFifR5dfb3BLlssGrfmYL7/6fuxuf0zTNhrdaKpVqlGiSySRer7exk10PTNPkT/7kT3j22Wf54he/uCbvvZvED98qs4lN3BpuOq5omnZFAqJu5H333Xc/z8x9NRw7doxDhw41RiLfyB8TIJPJcP78eXbu3LnmSkaxWCQWi5FIJBAEgW+cWOL8TJo+j5czZ+bw+xzk8hUMw6S12ctiNMeeHa2cO7/Itr4m7KbA3PkomqZTrWj09kWYvBRn194Ohs/O0drux2G3kLi4hNttJ7aQYefBLkZOzdDc4SM6l8Xjd9DZ4mHk6HijXO5w25CtEoVMma17m7j4zCSSRaK9r5mZCwuE2vzk7mlhVqlgk2UERUBXavZF1oKCnjMRVB2HKKKkKjhsMpaqTtDv4JN/+l9o7li7pAlq6+zIyAiapuFwOEilUtjt9kZW8WYHuhiGwdmzZwkEAutyulmJlQ2hmUwGl8tFMBhkfn7+ig3Heo/5sY99jLa2thfateQFjSsvmYzmaljPuLD6a1cuBtfb6ay2GIS3ubG32hl+NIqj2YolKTE/nqf37iCTozn8XXa23hVEV03mZnIIooAomSyN5SgqKoFWO7MLRfwRiWLC5M67OtAxePK7M4QjTu69uwPZKvL9p+ZQVYO+rQF6en3Mz+W4cD7Fzt1h5mfzBEN27trWjs0u8d3l7vLt/T5KJYUdOyPk0lXuTFjQMxYu6CX2eEUyFomWUu12LsgivoSFMXsBv0vCnrIAAqGKlXF7GWfOgR0Ri2KQtOoEJJF5QNdcRLTaNQsLFlTZxKKZeESZos3AVTXwiBJZwUA2TSwWiahiIgKCaFLSwSlBvmzgsdVIZkUHuwSiRcKmGKiqnam8hTZHAUWz4qroFAVo7XMRvVTLVrZu83DpRM0DM9hqbxBNl9+CrptMnS8xcE+Ykr/KtoEANvly5tDbZm8Qzcg2N1Onswy84nKzEdR2pSu91UqlEmfPnkXTNKrVKoZhrHk+LdQWv7/8y7/kqaee4uGHH34hSeYmNrGJm4BhGIyOjlKtVvF6vWvW1tUrbfXG1BuRzMXFRWZnZzlw4MB1PRCvhsvlore3l97eXqrVKhXTzrljc5ydzONyWshky3S0uphbLBIMuFiM5liK5XHYZeSyTiZRpFioNvSY4rKn8KWxKC63Fb/XDrkypVyFzp4wsYUM02Mx7E4L0bksew73EL0wTyFdqwZdODlFV38LM6NLbN3bSVOLysVnJujZ08bUuQVicwmCbT48zU6G3AKiZkOLqUiShNttp7KQQ6kISDYZpyhCxcDvtVNNlmlp8/Jbf/lBfCH39S7J81CvODkcjiushorFYmO+uGmajZnnLpdrTeu3ruucPXuWcDhMZ2fnus5pJa5uCM1ms5w7dw5RFJmdnaVcLjdK7Gs5r7o1XigU4nd+53d+KDOZdbxkiObNTnGooz6Z4VYXg9f88jbO/esSkS4XF59NsvVIkNmzOUQb2G0ypx+PEt7ixOGzMjGeoXevn84tQcqaimpUiIQlTIuA328lmypx7nSSLb1+2ns8zMzlGLuYpqfXR/cWL6lUhce/MwXAfa/oRFV1pG4vs7M5XC4LQ88kaG52sq3fQyxaZGmxSiad4A1hPx4VEjaBnpyP6YyCLmi4ZEhYwZep3VYbTuIJhfZ6Y5CgU604CFIjZgIicc2kpMo4qzJgkrNpeE0J0RRYLCt0WWSqEkynVGymhEu2kUhV6ZBq1y2OSqtU+32zgoFTEijKKqqgEXSBZgG7qmJdnuLrliFXtjFXEXH6dIKCgq5YafGXiS7fA4v18gZBUy8nM9Lxy5rMfEohm1Q48UyMngM+2u72U5quoCqXM7RWl4woC2y969q75vrEh6amJrZs2dIo0czNzZHL5fB6vY0S+2odjaZp8rd/+7d885vf5Gtf+9otj0jdxCY2sbFQVZXBwUECgQADAwOcPn16zdr/OtGUJOmG4yQnJibI5/McPHjwlkYd2mw27rl9N19qOc/YRIxIyEGxpKIsV5/GLsVwu20oqsbO1hDnTsywc3cb0cUs0aUsoihwaSxGR2eAudk0Rw73cOLbw7R2BBEEuDg0T2tXkMWZFD0DYZSSQWoiSj5ZIFassuO2Hs6fmKJcqBJo8qDkS7i9tfV+cTxBZ38ri5NxgmEnF+w6YrSItSpid9nRgcpMFtliw+G3YK0aUNaQJREzp9DX4+e3/vqncDjXt07qus65c+fw+/3PK2uvtANSFIVEIsGlS5colUoND8prNV/pun6FQf9GQdd1xsbG2L59O83NzVSrVZLJZOO86iX2lZ7LK2EYBr/6q7+K3W7n93//93/orfFeMqVzwzCeN2x+YmICh8NBa2vr9X+paTIzM8PS0hIdHR2Ew+FrkoKJiQlyuRx79uy55mLw5w8cZex7CZxtNgzNJJ2q0HnQz8jRBJ2H/KTjFVKZMr37/FwcSuEMWxGsOtPTefoPhBk8EWP7fj9zi1kCzTKIAqdPZ7A7ZPbsj2C1SXz/yTk0zWDHrhCtnW7OnokRjZZoa3Pj89twu61ouoFpVDk7mMEwoLvHS0+7h9ed17BqJnkkHIrIJV0lrNsQmjWEhIAdiapski6AJAsE7SY5q4mZlJEQKXsqNKsyE1oVt2ZHtpk41dqDnHVpNKsiqmgyoyg4kHFrVioYuMWaqXvR1PEtzwxPmCoty9dxydCWSaeJIpjYEYibCsGQSYAquiHikmCmJNJmE8g5ZEL2AioyednB9y5ZqeR0vM0yuaiGKILTU5MxSFYAAV0xsTpFVNVEV01km4AJqFUD2SKw984ImQslctEqoW0u3CEbv/Lv917zuRkeHsbpdK5aLq/vShOJBMlkEovF0tgt17sgv/CFL/ClL32Jr3/962sqxW0Afni3tZvYxM3hpuNKNpvl1KlT9PX1NUqXg4OD9PX14XZfP6NWXx80TaO1tbUxJvBq6LrOyMgIVquV7du3b1jm6ZuPD/O5v/geXo+NQlGplc2b3CzGCvR1echOF/C47MzPZrBYJBxOK7lsmYFdbVwYXmD7jlaspsHM2XkEEYr5Kv17Oxg9O0dLt4+l6Sx9O1qoxrLMXYqy8/AWRo5P4HTbsTmtmKZJ95YQZ54YQRQFevd0cGlwllCbn5Z2P2e/f57Mu3cg2pwYVQ1JAGtGwWJImCaIOQWzrOF12xFKGn19IT75lx9YNwnXdZ3BwUGampro6OhY8/sMw2iUstPpNC6Xq1Fit1gsaJrGmTNnaGtr29DGGk3TOH36NF1dXauWy68+L6fT2Tgvq9WKYRh88pOfpFwu8/nPf/7FIpkvaFx5SRPNunHq9R6uuh7TMIyGziWZTGK1WmlqaiISiWC1Wte1GEweTfHHr36G7jsCjB1LseWeIBeeSdC8x0M6VqFQVWkf8DJ0PM72O4PMzWWwekSCrR4qmoYpQq6kMD2RpWe7j+eOLRGIWGjtsrKwWGFpoVrzwWx1kcxWOHc2jiDAffd3YhpwfiRBPF5m7z4fF87n2bkrgttjIRYt0TVV4c12D0sOAX9GImMHOSNhAjO6itVq0ClbSSFgK9Ye0FlbmbaqHZHa/5fsGlV03KXarjIhVuhebgqKmQqST0ZMikiI4Ad7TXuN5jVxFmq3uGo3cKkCOiaiZGJBICvp+I1atrToAk/JpGqaWAUBwzRIyVW2BgzSFZOwLFE1QNUERE8JuynwF1M2+veHcFgkzKqOVtGIXajpPlv67SyN1oTwPQf8TJzOANC918fk2drPrdvdzI3lsdol9h+OMH8qx6t/po+3/cbAqs9NvQzT19d3zWdhJerjy+LxOF/4whdYWFhgdnaWJ598stEJ+SJgk2hu4uWGm44rsVgMURTxeDyNv1uL9r8eV3RdbzTtpNNp3G53o2lHkiQURWFwcJCWlpZbKrteDUVROHHyNJ/9i0GKJZWBbc1cGIuyq7+FUklFT5SILWYxdJNwk5NErMT2gQgXL8RpafWRShXZ0uqjkCiwNJti16Fuhk9OE2rykE7mMXQ4eOcWBh8/R/e2FiaG5xElkfYtEWbHouy+Ywvz5+dILWbYcbiP88cvYXNa6epvIR/PkolmkQ52MOOSsFos2BwWlEQFVLBYZYREEVEHm0VCLKvs2dfBJz7//nWT8HojTUdHxw0TTteDaZoNm7m6DrZSqdDV1XXTmszVcCOSudp51Uv/iUSCz33uc5RKJWw2Gw8//PAtZcbXiZeHRnO1B3C1TvSVuLqzvN4NtnXr1gbpPHPmDIIgUK1WaWtrW1OjR++RINvuDxO9WGDrK4LoIvTcH6Cq6IiaSFvEy8VzKbbeE+DM8RgtWx3EYypltUA+r+AKWFiYzbN9f4hTx5e471WdVA2dp783SyBo59BtYSpqleeOL2CacNvBJrwBO08/PYdSNbDbJfYf9CEIMsGQg3JZZWoqg5bVeH0gQsYCroyAYhqoBQkZgahdJ5y3Y1YNzlaL9FHbrcccGp6Cg5RXJ1wUWaIKBRnBd/nWhwwrUZdOqWDg1m0kMlVaqZVK0nmFVmokNJNXcAq1cpNiEXCpICGQt5oEFPDqEhUM7IKIuXzbbIJATjTxGiKibiMeE6jYK/hlsImQ0QX8JRc5qUyzzcTilDn9g1qT1J67I8gVhXDAit12+fkQrZfjjsNzufzla7IxN5ZHqehkKgoFu8bO10VWfW7WSzLhyvFlo6Oj/NVf/RV79uzh7rvv5pvf/OaGll42sYlN3DpCodDzYsiNtP91SzyoybeCwSDBYPCK6TGTk5PIsky5XG6URzcKdc349m1beeNrdL7y9dNUqrUkjGBCZS5LMlFsZC6DQS+JWInpqTQ2m0g2U2Rru4eLJ2fYuquWqRsfWcATcJCM5dm2pxWLKDJ7bhrBhInhebYf6Obi6WmqFZWeHW1Mnp6ge6CN1GKGsTNT9O7uoJAuUEzmsNpkirkyWb8Nq9eOpmiYc3lEJDweB0JRQ3TYkXUT8hV2HWjl9R/Yw3PPPdewCVqLTlFRlHWZm18PgiDg8XjweDx0dnZy6tQpQqFQwx+zbp10vZnnN8J6SWb9vNxuN263m56eHrZu3crJkyfxer3ce++9PPPMMz/0ZXN4CWU0TdNEUZQr/m5paYlisbgqGahnMYHr3ohCocDZs2cJBoMUi0V0XW+MB7ue79XY0SS//don6TngZ+x0iv47QwwfjbPzngiDT8fYeruf0TMpmrc6ic1X8LXYSMYrBNvszE7m2HE4jGLoVFWdubkciwtFdu+PgGSiaAZjF1Ps2RchFi9gdwkMDWUJBK309/splSqcHax1UR842Ey5rBEM2mk7p7MtY2PaqGIXBewRiUBSIm3VkYsSIiJTlAnrdoSwiaoZWLISIGCIJnGxTFitlXcNTAxRw5ChbEJZM2gzaxlOXTKxArIhYGCCZGATRDKmhoaGzWkhV1CxSGC1ypSqKk6LgN0qIVkF/IaARTURBJBMWNI1WiQZXQBdA0kQKPnArZcoagKtFpH5qkHU1ClsDXPxdAqA5h4b0amahVF7nwc0k9ZmB0peZWG4lt0M99qITdZ+7trvY3IwA0D/kRAz57P87eQDSPLl5+NmSeZKPPLII/zhH/4hjz76KIFAYE264A3EZkZzEy83bGilbGxsDL/fTyRy5Sb0eibsVyOZTHLhwgVCoRC5XA5JkhrjDG9Fp11vUt29ezcej4dYIs8HPvYPGIbJ4d0dnHnqErv2XO4kX5zPIAjQ3OJjaTHL/oNdLI0ugqaTWKqVoprafcTms7T3+ViYyLJ7XwdTg1Pk0yV23rGFkWMTuH0ORFkk0hbAJpkMPzOGIAhsPdDN2Kkpune0YpUFRo9fwmK3ELp3GxMBK3pJQS4Y2B12EATERBHBEHDLEpQ1XvH6nfzkJ94G0NBPxuPxG+onK5UKZ86cYdu2bYRC6+tMvx7q5LW3t7dx/3VdJ5lMEo/HG7r8SCRCMBhcc0axXobv6OigpaVl3edVt8Y7d+4c//iP/4gsy2ueirhBeHmUzlcjmnUNw/bt26943XoWg7GxMXbv3t3Q49Qf9mg0SrVaJRwO09TUhMfjed6x/tc7nuHsd6J07PMydTZDy4CbpckCnhYbmXgZm9+CqpiYVlAVnUCnHbvPAlaT7z8+x4E7mzlzKoooiuw5FEFF5/SpKAM7Q+RyVcplDZtDRpIEPH4rsXiBXLZCMqnS1Gxn584gi4sVRi+k6HI7+dFcmJRFx12xUHSDmBNIiGWsskiTZiPtNbCkaw/mvFRGMKHddKBZTdJoGFXwSzKyLpARFFS3gDsvIyw/Y4LLwLFcbi8FdMo5FdEuITkkLAkBAYGKS8VTrGURVXft9QYmggySJpBBIYQVDZ2crNASsCKqGkF9WQNqEXBXIS2Du2pStCl026Gkm1RNgUcqoFR0nB6RctHANCDYYie1VCOTwRY76WiFbTsCBLw2pk5mUKsmsg10QFNqj6Cv2Ub/HSF+5Qt3X/HsjIyMYLfbb5pkfutb3+LTn/40jz322IYugOvAJtHcxMsNL7j2fz1xZXZ2lmg0yt69exsOE3Vz8Vgshmmaq846vxGi0ShTU1Ps27fviibV3/uDb5GN5TGLKqMji7jdNlRVp1rV2Lq9mfGLUQZ2tZHPliFTIpcqUC4qDT1ma7efxekMkizSs8XLpeMz9B/sZvTUNBarTKjVx9J0kkOv6OfUtwcxNIMdd/Rx/tglLDYLO27vYfToRTRVp3dPJxefm6D67v21JETBwCjruOwW1MU8oinisclYNIM3vfMg7/3Y61b9rLquk0qliMfjZLNZPB5PY9qOoiicPXuWgYGBNfmcrhXVapUzZ87Q19dHOBxe9TVXW99ZrdaGLv9aLgIbQTLr1nhf+tKX1jVtaAPx8iidr4bVTNjXsxgsLS1x8ODBK+xmrFZrQ/xb7zCenp6mUCgQDAYb48EEQeDdn9zJ2e9E0Uu1zKmgC+iqAaaKVoVmvx3DYuKO2JiZz7G0VERMCcQWi9x2pIUTzy7R1ecl3OZgYiKLbBHZvj3I6ZNRDh5uweU1UFWDobNxdu4Jkk6X6esL0tZh4rALfO+7CwD0bnHx6lQAUwCzKqBLUM7pOJCwOGyIBYFRW5mmdG0nvWCp4FWXu8L9KmQErMu3OuvUayPNcjJyAZaECq1mrbGlJBmUfSZqxURPm9ixIBVFtKKBCMgISIqEiYmAgKrrOBAREchLGj5NxosFVTCwmBKCKaPEJUBkzKHhQMPUTNyiFZduIggi7qqdKUGjzaqiyTKufBUFaNvqZvx0Lavb1utpEM36zxdH0uw8EqboMtl5exAJk5FnaplQf7tEer5C/13exq5wI0jmE088we/93u/x6KOP/keRzE1sYhO3iJuNK6ZpcvHiRRRF4cCBA1cMZFhpLq4oyhWzzuvJDLfbveqxTdNkenqaVCrV8OxciXe8fi+/+vP/D0kSCYZcpJJFdu1tZ/jsPIpSkwXoioaUK7Mwm2LXwS6GT82QjOWQJIHF6Qz9e9tRMkUqyTIAo6emad0SZHEihSiJ7Ly9hxOPnWbXndsYfnaMi6em6NvbhSiajB0fp31bC+Onprj43AR9b9vPGU1DilUBEa/XgZGp4nI5EEsqsmLw7g/ezVvev3oTZv0erJy2U9fBXrp0qaGdvNbYyZtBPUO6fft2gsHgNV+3mvVdIpFgeHgYXdcbJfZ6YmojSOZf/uVf8v3vf5+vfOUr/1Ek8wXHS4ZoXkujWV8Q1mrCvnIxOHjw4HWns6ycdX71PFOfz0dTZxOHH2zj+NcW2HFnmJFnE3QdcCCKNtr22DjxzCK9u/w8/cQc/fuDzIxnCUTsNLe7OftsjPte38n0XJYTx5bYf3szJ44uYo2JvPLVXczO5RkdrRGjO+9tIZ0poOsCZ07HOXRbC+Njae440gYCqBdLRFISU2aFFtNJwqrhUmVSHg1bTiYhVHFUbRTsoLt0PMmaaXvKrmDLSBguA1kRScsqUkGkbNEICzVS6nRayNo0Kmkda16iZFXwKzZEAVSfiZwBGZGkUKHZdGBRRZJClbBpw16WqYo6NlNCXr4dIgIpUyWCFZ9pQcdEQkCyWhCzFkqoJMMC3pJJ2tQICjL5kklMteJoEdjVauG5tI4sXf7CKdXLQWGlfZGhQy5T5egPFtl7d4T2O7xoaZ1gxE5mIUHrHpNjx47hdrsb/nk3Y8YO8NRTT/Fbv/VbPProo7esF7oWMpkMH/rQhxgaGkIQBP76r/+aO++88wX5XZvYxMsBGxVX6nPRfT7fDZtJrVYr7e3ttLe3o2kaiUSCyclJisUioVCIpqamhhbQNE1GR0fRdZ39+/evWiod2NlK/85WRkcWaW0PkEoWWZirZShnppLcdlsX5747ytadNT3mpQtLuL0OEks5urYFySQqUKkyd2EeVdEZuK2HCyemKOcVbE4LoqhSSNZ8i0eOjbPtYA9jp6awO2RKmQLFbImJwRl239OPrmk8F0sjulxYfS6sgoiQKmNBxKboWGWBh37hNdz31kPrukf165FIJNizZw+lUummfTGvRp1k9vf3EwgE1vVep9PZ2ECoqnpFYsrr9ZLL5eju7r5pkvliWOO9FOLKS6Z0DrWy9srzKRaLjI2NsW/fvnUtBnVCcbOaOdM0yWQyxGIxJodi/NOH4oR6LeCF6GKtqzwZK9O23c3E+Qy7jkQYPBpj9+EI556LMXBbCNEt8Mz35hnYEyK6WCSZKHP4nlaqhs6xZ2uZyn0Hm7C54OmnlwAIBu3s3ddELltleDhO39YA8zN57ssE8bosCIgUVBWzbGJ1iNiLVnIWFUmTEERISQp2Rcb0m6glHbsqYwomis8kmanQJDgQEDBsJhWbjpYzsCFTQcOLBdEUMEUT0zCxIGE4TUolBcki4vDImBqUiiqGaGA1JHTdxJAMXJIFTdGRBBOv1QKCSbBSyyKnBIWgaaUs6zi05UlDso5Ng4pVoUeykNZ1fFgomioVu8KTVo3OXh8el5XCUpXkXAWlomNz1Oa2V8s6kixgdcoUc7WyWLDFTnKptlu//ZWt+N02fv0L92AYBoODg2iahmEYyLLc2Emvdcf8gx/8gF/+5V/mkUceeUEbfh566CHuvfdePvShD6EoCqVSabXS0WbpfBMvN7wg2v+6by5cX+dfqVQ4e/YsXV1dN0Uo6qiXi2OxGLlcDp/PR6FQIBQK3TBePfv0GJ/+1Dew2S1YZJFCocqO3W3IhkkpmmN6PIYgCjS3+1maTdMzEGHqQpzOLWEolJi9uMSuO7YwfGwCp8eO1W6hkCmx784tnPi3QQC6d7cyPbSIbJXYfrCdoe+OIltlth3q5fyzY+y6axtT0QzZrS0YFQ2H1UI1VkSWRFymiMsi8tHfeAsHX7Fj3dcmnU4zOjrKvn37rliXV+o6y+XyFbrOtcT3crnM4ODghpfhFUXh5MmT2Gw2qtXq8yyK1oJ/+Id/4Mtf/vILbo33UogrL2miWalUGB4eZu/evcDaFoPOzs5bskG4Gpqm8blffILH/z5J524bU0MVuna4mTyfJ9zmJFesUK3otG/zUtV0mrqdPPmdGRwume5tPs6eiROK2NlxMMwTT0yjaQaHbm8hl69S1RXGx/P0bfXT3OIil60ydC4BwOE7WtF1g6ZFCy2XZPI2A71qYiAguAWUogF+0HUDsQQlXceJBcVnoBQMEE0kt4CaN5EMEUM0kUMCasnAWPY9t/hExCwYdqhKGoIuUKlqiBZwq7XdVUFQCBi1nzNClZBpr91lF0hFAdMColrLZOo+E2u2do90h4Fe1jElnTaLDXtFoiIb2DWReF3HaTFRNB2XRccpSdh0kYShkthl4dhw7TrsuT1CNlWltcWNU5YZ/F6tI71vX4CxwdouvGObh9mxWpndH7aRTlb4wCf28RO/tIeRkRFsNht9fX0NS4t4PE48HkdV1UYp5FpTgI4fP84v/MIv8PWvf52urq4Ne66uRjabZf/+/UxMTNxoAd0kmpt4uWFDiWbdqqhO7q73fctms4yMjLBjx44NJSqVSoVTp05hs9lQFAWPx0NTUxOhUGjVKpxhmPzcT/4t87Npdu3t4PzQPPt3tTH8zBi6brJlRwsT55fYurOV8ZFFRElgYG8HM2em6OiLcOHEVE2P2eJjaSbJ9v1dqMUyE2em2XlkKyNHx5GtEl39rcgSjJ+apKk3yMKFGGCy/9W7mBmeZb6rCVx2nJKInqrisMqYuSpBr41f/J/vpP9g77qvRd1g/Wpt6tW4WtdZb9q51jUrlUoMDg6uaxToWnB1ufxqiyKgkcxwOp2rPl9f/OIX+bu/+zseffTR6zYl3ypeKnHlJUs0TdNEVVWOHj1KKBSiubn5mruYF2oxqHuk+T1N/OabT5JLVmnb7mZmNE/XHjsT58r07HZTKmu4m2wsRIvMTeU5cKSZ08drc25uv7+VmYUsY6NpDh5uYWIig9dvJV0o0dTsoFgwMXQTRTVIJcvs3BUmGLJz9kycQqzKu5QOcnYdV1mm5DQQDYGyZqCIOhgCJVPDME3sPgnNNKAqoMs6hgaaCoqs4fXZqKRrpSLNouOwW1A1A1M30QUTubxM4F1gKdR+LqISpEYqRY+AlAcdA9kiIqoCeRT89S51r4k1J6ILJqJZK7WXHBrOslxrFJLA0HWqaLTbbFg0AVGvNRdl0PAgofp0IiWImzo0WfhOrPaF3XUowvDJOAB7DzeRS1dpjrhwyDJnnqyRzr13NzH4TO16774zwtlnY/z1s2+hbC5cQTKvRl2jG4/Hyefz+Hy+RrehJEmcOnWKn/3Zn+VrX/savb3rX0DXgzNnzvDhD3+YnTt3Mjg4yKFDh/jc5z632iK0STQ38XLDLcWVarV6+UDLesDBwcGGbOpa2sl6c87evXs3VC9YKBQYGhpq6AVXahSTySQOh6Ph1blSs/fEt4f53P/6Fv6Ak9aAk7GT0+zY38n5M7O094SYn0oC0N4bwG6zIVYqjJ2ZQRAEuvpbmL6wSHtfE8VsCZddxhd0MfzsGJJFonugjekLC2zb00alUGVicBpBENhx5zYq5RKXTkxjBF1wZDt2U4CijiSAkKsQ8Nj4tT/8Mbq2rz/BE41GmZ6eZv/+/esa3buyaSeZTGKz2RrXzGazUSwWOXv2bKN7f6NQJ5nt7e3XTGhdnYWtTwGqd9d/9atf5c///M957LHHNvTcVsNLJa68pIhmfYTkSnG2aZqk02lisRjZbBa/309TU1NjdNMLtRgUi0XOnTvXsFf41t9f4nMfO05rr5ul+QKCINC500PFVKmYZS6cLRKI2BAlgXi0wu7bwoh2gVMnomzfEWR6Nks6WeHQnS0UK0XOX8hRqRjs3BXCYpGw2yVGL6TYsSvMs8/MIwjwTnc3toIAZci7daSKSE5XMWQQDYGcoGBFAq9ApaQhOEHVdJx+K7JdwOYEw9Sx2CWsditOl41iTqNc0hBEqBZ0inmFUl7FZpPRVRNEqGRVLLKE02tBLehUqjqiAC67BUMGiylgaCYIoFdMTMMg4nagF00kl4CzIKMLJpg1n80MVYLY0GQDSRNQ0LHaDMJVG1mril+xUrEZmBUTh0PHqon8KyncXgvVqo5SNbA5JERBoFyqTQzyhxy0tLtwWSwUUyrz4zUrj759ASoljV/7u63XJZlXY+XC9fjjj/PFL36RWCzGF77wBe6+++4bvv9WceLECY4cOcIzzzzDHXfcwX/9r/8Vr9fL//gf/+Pql24SzU283LAhRHNlXKlb2sRiMUqlUkM7WR+8MDU1RTqdZs+ePRvaoJFKpbh48eIVTigrUc+OxWIxEokEsiw3Bo/IsoVf+tl/wsiW8HlsDJ+cIRB2U8iVURWd9i1+5icy7D/czbnvjqCrOtsPdHHx9AyR9gC5VAGP30Vbp4/B756vTfvZ3cmlszP4wm66tzdx5vFhZKvM9tu2cOnMFO1bm4lOx2jqCTMZ8kNVR8ur2C0ilqpB0Gfnt/7yAzS1X7vB5lpYWFhgYWGBffv23fI1XplR1DSNarXKzp07n2dhdSuoj6tsa2tbc9VU1/XGFKAvfOELnDp1isXFRb7zne9sqFH8tfBSiSsvOaJZ98dcrQPQMIyGdjKdTjf+7cCBAxsqpL3aywxqC8CvvPFxhp+Ns/cVTZQ1jflYgfhSkVJBY9ftIQafixOMWLB5RXRZwDAECnmVeLRMIGhj1+1hvvPtaQD8ARuHDrcycj7B3GweUYTDR9rJpCsEAnZcaRHLBYNiRUNyi+h5KIkaNo9MtaCj2w2sTgnJKdK9y0e4Dfbd4+GN7zh8RRnBNE3y+fwVE5Pqaf36NTNNk+hCgR88Mc+JpxeJLRRJLVTIxitUKhoWQcRmk6EIaKBZDWyKhCGbWHUJDMij4MWKhoEgCpi6idMp4TOtmKqJdXnEZW75dYrHgLyJjkabaEfUBfKihsMQEYMm59UioYM+Tv+glqnce7iJs8drGcyBfSEuDNZ2791bvSSTFQZ2BlGzBlMjWd7wUAvv+NmeNZPMqzEyMsLP/MzPcP/993PixAkeeughHnrooZt7mNaIpaUljhw5wtTUFADf//73+fSnP82jjz569Us3ieYmXm645UpZnVyupvNfSTrz+TymaeJyudi9e/d1m0nXi8XFRebm5ti7d++a41W5XCYWixGPx2sjlM9m+dLnn8XutCLLEoVcmYF97VwYnMcXdNLZFWToeyPsuL2X889N4gu50TWdQrbMgfu2M/7cOPlkseGPaXNa6dzeQimVIz6TpGtHO2OnJnH7nPTu7WBhMkpiOoVroI1C2I9ZUHG5bJi5Ki3Nbv7LJ+5H0cq43e6GRnEt3pOzs7PE43H27du3odc4n89z7tw5WlpayOVyVCqVhpvMrZix3wzJvBrf/OY3+cxnPsM999zDU089xR/+4R9y5MiRmzrWWvFSiSsvKaKpKAqqqt6w6ccwDEZGRtA0DYfDQSqVet5osJvF0tISMzMz7N2793l6kZnRLH/08ec4fzFBoMnO2HCa3bdFOHcihmQR2bLLj+gQWVjKoxs6czNFXB6Jrl4nFQNGhtP0bfXictmwuywcPTqPKArs2RshHHYyMZFhajLDnQfbcT4DBUHF7bJSLepoNgPRLqJoBs39LnYdCfPAB/vp3ubj/PnzyLK8pjm7pVKpsXAB1/V7m59b5NGvDpFecHLuRJzYYolqTkOvGDjcFpSijstlQUka2EQRWRJBhbyg4DNtYAVBMdFNA7vfgl0TkRGw5kV0TDRMLIhk5SoOTUACIqadmFChKOmYd8pYBAsLY3la2tyMnq2Ry713NHH2WI10Hri7mZPP1JqpDt7VTCpe4Bd/bxf3vmbPTS0qo6OjPPTQQ/zjP/4je/bsWff7bwX33nsvf/VXf0V/fz+f+tSnKBaL/P7v//7VL9skmpt4ueGWM5p1L83r6fzr/o1Op7NRzr66gnYzME2TyclJcrkce/bsuen4VK1WWVqK8j8++mXSsRJbdjYxMRLDapew2qx0dfoRVJXhYxM43DZsDiuZeJ7tB7pQqxqL5+foGmhl9MQkdpeNUJufcr6Cwy4higLTw3MIgsDe+3eQnEsye6HWtNp/5zbmbQ5UQ8CCiZ4p090V5L//zU9ic9gayYx6RnG1ZMZKrLwWG2lIXpfQ7du3rxHPrmXGfi1d52rYCJL5xBNP8Nu//ds89thjG5plXQteCnHlJUM0VVXlzW9+M695zWt48MEHaW9vX5UoKIrCuXPniEQidHZ2Niwi6lm7RCLR0LjUyg1rc3Ba6WW2d+/ea77v7z57lj/776cItTioVjRyGYUDdzczPpomssVFRdEYHkzg9ljp2eojnSmTq1ZweyARU8lmVfbf3kQyWaW52cXiYh6n08r5kSSiIHDXnW0IJwzsSIiaQFnSMZ1gyCY77w3z0H/bx9adtTKFrusMDQ3h9Xrp6elZN7Gq+73FYjEURWmUjzweD0tLS8zPzz+vrKEoGg///QVOPbvEhTNJkrNlLHYJNWsg2MCsmlhliYDdhlkwKQkqHsOKIutYNQnDMJHcJg5DxmKRsWQFsii4sYDFxFA1QqYVTYZvCouogklTixWP10Yk4CYXU4gvlFAqOqIE3qCdVLzWbd7e68DukPnyM++5KZJ56dIlfvzHf5y///u/Z//+/et+/63izJkzjc7ALVu28Dd/8zer2XFsEs1NvNxw03FlbGyMn//5n+eBBx7gLW95yzU9FOtSqb6+vgYRqFfQotEomUwGr9fbaNhZK0EyDIPz588jSRL9/f0bMj3sqcfO8blPfg1JFnG4ZcoFjW39AS48M4lskQi2+IjNptiyu4OJoTm27+9E1DTOH6vNKw+1BVgYj7JldwfoKuOnprA6LPTt7yG5kEItK5SLFTp3tCHLMnOpCnm3E4/NglHS2L69iU/82X+5ZowslUqNhsuV5vUOh4Px8fFGWXsjSWYmk+HChQvP61pfibo8KhaLkUqlsNvtDUJ8LX3oRpDMp556ik984hM8+uijt+RacLN4KcSVlwzRBJibm+OrX/0q//Iv/0K1WuUtb3kLDzzwQINE1UXUKxeD553AssYlGo02dld10nmth8kwDEZHRzFNk4GBget+AXTd4KNv/DeGjsfZvi9Ym3l+IIjkFjj61AJWm8TAniBnTsTYfVsY06pz+kQMVQWv18q+Q2GGRxLEY1WCISsulxVRFGlr9eB1W1DGVawLAorVpKhoOEIy9zzQyU/9xgHs9suET9O0hqC9o6PjVi5743j18lFdljAwMHDDRbWQr/L1L47x+COTTJ3PYWomatpAQUfWRUQRgj47Yhkqio5Tlxvlcw0DUzQJmDYki4BYEcgKVWymiNdt4VIpzyWpwKEjzZw8WiuhD+xxoZQFwkEXTtnCyeUmoOYOO9G5Cr/+mbt4z4d2rvvzT09P8yM/8iP83//7f7nttttu7iK+ONgkmpt4ueGW4srw8DAPP/wwjzzyCD6fjwceeIC3vvWthMNhBEFoTJDbtWvXNZsz6iQlGo2uuYKmaRpnz54lFArR1dW1YSNqTdPkF977p8xdStK/r51KIsfM+QXC7V7is1maewJEp9Ngwu2vHuC5R04jW2QinUEWxqN4Q27a+yJMnp4EoLk7zOS5Wdq3teBwW8kks8QnU2w92Mv0hQWq27rwuGyIJY19Bzr4pT9635o/y8pkRjabxW63s2PHjmu6fNwM6tZI+/fvv27X+tWo6zpXVvfqfp2wMSTzBz/4Ab/yK7/CN77xjRfUGm8D8PIhmo2DmCaxWIyvfvWrfPWrX2206J8/f54vf/nLDcH2WlAXVsfj8VXn0da9N/1+/5qzgoszBd7/im9QLWvsf3Uz33xsEkGAA3c0c+poFFGEe97QyTe/NYFumLR3uGlrd5HJK1w4n0IQ4K672wGDeLxAIacQ9NnIzGt0Vb0YJthCEm/8L338l1/e+zyiV5/X2t3dTXNz87qu7Y0wNTVFJpOhvb2dRCJBJpO5ofXGSly6mOaLfzPMyaeXyCcV1JxOpaIhayKCBHarhFO0YJRNLJpIFgWPaUXyC5gZA6so4tRldKtJyVCZDpUplhQqFR1JEog0O1laKALQ0+dAliXssojTZmF6tMy3z/8oLs/auxehtsF5z3vew5/+6Z++oEa2PT09eDweJElClmVOnDhxM4fZJJqbeLlhw+LK+Pg4Dz/8MF//+tex2Wx0dnaiKAqf//zn10xS6hW0aDR6RZf4ygpapVJhcHCQnp6eDV2jTdNkYmKCoRNTfOOvz2LTVZxOCxPDC7RtibA0ncDQTXp3t6BWqywMLxHpDLA0kcDfVCN3oWYP6YUUkkViaSKGKAocfM1uRp+7RC5Ra6rc98pdVIoVklY7FUPALFS56/5+fu733r3uc65L3SwWCz6fj0QiQT6fJxAINCbx3Wx2M5VKNby210Myr0a1WiWRSBCLxahWqwQCAdLpNJ2dnTdNEOvWeN/4xjfo7Oy86XO7HjYopsDLkWhejc997nP8n//zf9i2bRuxWIw3vvGNPPDAA+zYsWNdu6KVwmqAYDBILBaju7t73TuWZ/99jt/9tWeYvJTltrtbOPbMIoIAh+9pJVOucvpklC1bXZTKyxdFFpAkgZZWF9WKxsSlLNlsle4uL2iQmC+x1x5CE3X2vM7NR35rHy0tLc/TuNQNaOvd8BsF0zQb479WljXqWqW6/sZutzd28jeyo9B1g69/+SL/+v9GmR1LoxVENMVAqoiIDpAMAbfNipAD0wAFHRFw2WU8JQsZScFz0EHBrjFxPs22HUFOHq3pMXu3+ZkcywDgdImIksCb397Gz/3qoefZglwPi4uLvOtd7+Jzn/sc9913301fv7Wgp6eHEydOXHPO7hqxSTQ38XLDhscVXdf52Z/9WY4ePYrX68U0Td761rdeV7a16omtUkHzer1Eo1F27ty5oXZ7hmFw4cIFRFGkv7+fP/rlL/LUv5wk0h4gHcuhqTq77tjC+RNT9O/rIB/NMHtxCW/YharqlLMVBg53ER2LkVxI4/Q66BxowzQMLp2exGKX6dnVhcNtZ2F8CewWKsEQVDVe9cbdPPSrb7mpc64PUVlpEWcYRqMbO51ON2adr6fHIplMMj4+zv79+ze0Gbhuxi7LMpqmPc/2bi14sazxNiimwMudaJqmyec//3k+8IEP4HQ6SafTfOMb3+Dhhx9mZmaG1772tbz97W9ft7A4lUoxNDSE1VorXdcznetx6P/bPznL7//GUQAO3d3C9FQO02bi8sDYaA6latK/K4QvbGNsNEU0WuLgwWaGRxL4vDZ27QpTyCjIgoA0JdC81clv/MV9+MPSFZ2GdY1L/Uu70Qa09TFodenA9RbZleUGQRCu0N+shkKhwLlz59izZw9z0xW+8BdDDJ2Ik12soikGQgEUScchyrgdFsSMQAkV2RRxuyxoRYPjcgyP10L/jjBWSWTmUo72djdnT9U2DIfvbuXk0SX+9ckHsDrKJBKJK2bpXuvcotEo73znO/nMZz7Dq171qlu/kDfAJtHcxCZuChseV8rlMn/913/NT//0TyMIAgsLCzz88MP8y7/8C5VKpSHb6u3tXVcyY25ujkuXLmGz2a6Qbd0qEdJ1vTECs155Sy5m+PnXf4ZKscrOO7YwcmwCu8vG9l1tDH53mECzD1XRKKSLtG6J4As5GHlqFHfQic1lJTmbYeCOPsqFEsV8ifhkit33DDD09AVsbhuO/i0IArz1PYd558+sf33UdZ3BwUHC4fB1h12slsy4kXYyHo8zOTm5bv/NtZzzmTNnaG1tpa2trTElMB6Pk0qlcDgcN5wAdPbsWT784Q/z8MMPs23btg07t9WwSTRfBORyOR599FEefvhhxsbGePWrX82DDz7IwYMHr0s6r/Yyu7oppk6eVvM5uxqf+eRR/ub/nGXb3gCOgMwPvj+PaUJru5ut/X6ePbZAqaQhigKvelUXpbKGquq4HNZa97ZdRlvUec9P7+DB/zLwvONXq1Xi8TgLCwvk8/nGDN1rmQyvF6ZpMjIygtVqZevWres6Zv3cYrEYqqoSDocb100QBHK5XGOy09UGselUiX/48yF+8Pg8sakCehWMvEkFDbdoweO0Qg7Kssq8UWTHPWGO/qDWBbl7b5hcoUzQZ6WaF0hGK7z+bVv49B+/snH8qycA1eflejyexkzdd7zjHfzu7/4ur3/962/5Oq4Fvb29BAIBBEHgIx/5CB/+8Idv5jCbRHMTLze8aHFlNdnWm970Jh588EG2bdt23fVxbm6OpaUl9u7di9VqbVTQYrEYgiA0khnrLfHWB4e0t7fT1tZ2xb898jff529+5+uIksiW3e1Us0UKyTxKRaWQKdG5vZXYXJItO1tJL6YpZktk43ksNpntR3o4//QYumKAALvu6a91obsdJIs6FVHmvT91L2963/p9hFVVZXBwkLa2tued841wo2RGLBZrmLxvpMfp1STzalw9AUgQhEbMqyeoRkZG+OAHP8iXvvQlBgaeH883GhsUU2CTaK4NpVKJxx57jK985SsMDw9z//338+CDD3L48JW+kgsLC8zPz1/Ty0xV1YZWo1wuNx6kOkFZDX/+B6f4//7ns2iayfYdPrIplY4tPo4/t8CWPj/BkAO7TeLJ780CcN9dHUyMZhjoD9LfE+Rjv307/uC1zebrI7p27drV6K6vz329FX8wwzAYGhrC4/HcVNf6Smia1rhuxWIRl8tFLpfjwIEDNxyxVa1q/PPfnOfxr0+wNFlAyRmoRQPDNHEi4/ZYYI/I1ESWakXD5hKJRisAHLmzjWJB5R/+6a20tK2+MVBVtWFxMTQ0xGOPPcb4+Dif+tSnePvb337Tn3m9mJ+fp729nVgsxmtf+1r++I//+GbK9ZtEcxMvN/yHxZVEIsHXvvY1vvrVrxKLxXjDG97Agw8+eIVsqy47KpVK7Nq1a9XyarVabZBOwzCuayu3EnWp1NatW1fNWhmGwW/9+J+zOBUnGHSwOB6jmC3Ru7uDmdFFME323r2Voe+fp1pUCDT78Dd7cbjsDD99AVfQSfdAO4IsEJ1OIDtk3OEAGUXig7/0eu5+0/51X7ON7CG4Oplht9splUocOnRowzOZg4ODtLS0rJkY188tHo/zve99j5GREY4fP87DDz/cGJv9QmODYgpsEs31o1Kp8O1vf5svf/nLnD59mnvuuYe3ve1tfO973+P+++/n3nvvXZPWQtd1EokE0WiUYrHYsP+5mthVq1X+1+99h7/9sxlU1eDIfW2ohsn54QS5XJXb72jj2LML+HxWDu5p5vy5JK+4r4t3/sgA973h+vOz6ya/+/btu+KLdbXJ8Hr93nRdv6IjciORSqUYGRnB5/NRKBTW5V1mmiYP/+MFHvnncaLTRQpLCgYGOVWl4Fbp3+EBE9IpHV/AzrnBGL/76VfwwQ/tW9O5RaNRPvjBD+J0Opmbm+OjH/0oP/3TP70RH3td+NSnPoXb7eaXfumX1vvWTaK5iZcbXhJxZTXZ1pve9Cb++Z//mQ996ENr7hlYWUG7uhK0Evl8nqGhoRtKpWJzKf77j/wJC+NL9O3rYuLsDKYJOw73US0UGT85SWd/G/lskXwiz7aDPZSKZYq5EvlYgY7+Ni6dnqKltwlPxEfJauXVP7qL9v7QFROT1vLZqtUqZ86coa+vbyPKuVdgbm6OmZkZXC4XpVKJYDB4xWjHm0WdZDY3N99048/g4CC/+Iu/SCQSYWpqis9+9rO89rWvvelzuhncQkyBTaJ5a1AUhW9+85v80i/9EhaLhTvuuIO3v/3t3HfffetKu+u6TiqVIhaLkcvlGh1zVquVoaEh+vv7WVrQ+fz/OcWXv3QBALfbwsHbWmpaRBG8FiuaanLb7S184Of24fVfX7czMzNDIpG4rq8nrC6svl6XeN0aqaWlZcMtF662mrh6Jm1d4xKJRG54/U3T5Gv/PMq//uNFliaLmA6NWKXM4mKFHTtDaJrBG964hU/85tpKO7lcjne96138/M//PO95z3sapZC1SCRuFcViEcMw8Hg8FItFXvva1/Kbv/mbvOENb1jvoTaJ5iZebnjJxZVcLscXv/hFPvnJT9Ld3c3dd9/NAw88wKFDh9ZFeq5VQVMUhfHxcfbu3bumvoHj3zrL//f+v8A0TXbc0cfMhQUCAQd2l43JczOoVY1As4/evZ2c+vYgpgEun5O2rS1oqoYv7CU2n8Hf08QHP/V2tu3paiRa4vH4mrrE69nX/v7+1Xwabwnz8/MsLS2xf/9+JEnCMIxGPM5mszdlxA4bQzKvtsbTNA1VVTd0JPZq2MCYAptE89bxR3/0RxiGwc/8zM/w1FNP8ZWvfIWnn36aQ4cO8cADD/DKV75yXWLtOrGbnZ0lmUwSDodpb28nGAwiiiJPPD7FV754gUSizFNPztIUdnL7vla29gd470/sYMv2638J6xYWxWKR3bt3r2vhqgur6yMn69Yb9U7sut6nq6trw62RbtQFuFLjUrebqpeQrqdbqulIz/Pdx6IkkiIzM3l002TfwWZ+4b/djije+DtSKBR497vfzU/91E/xvve975Y+581gYmKiUabXNI0f+7Ef4xOf+MTNHGqTaG7i5YaXZFz52Mc+xutf/3pe9apX8dhjj/Hwww8zNDTE/fffzwMPPMAdd9yxbtKTSCSYnp4mn883/BvXKo360mf/jX/+X48QaPLStS3C6X8fAqBjeyuiJIJhMD0yR6DVR9eODgQgHcviDniQrDL+9hA/+qtvoa37+R7V9ZgXjUYbxG6leX2xWOTs2bMb3qgKNx5XebPJjI0gmXVrvD/7sz97wcdJXo0NjCmwSTRvHfWRliuh6zpPP/00X/nKV/jud7/Lnj17ePDBB3nNa16zpp1ILBZjcnKSvXv3UqlUiEajq2YT69d3PXYZFy7UMqI36gBfy7FWWm9IkkS5XGbr1q03bUB7LdR1pAcOHFizdqbesBOLxdB1vbGbd7lcV+ifRkdHEQRhTSM2V0OpVOI973kPP/ETP8EHPvCBdb//JYZNormJlxt+aOLKarKtBx98kLvuumtNU+qmpqZIp9Ps3LmTXC5HNBq9IptYb/y4Fv7+f/wL3/3CU6SXsgwc2crE4DROjwOX145kF8nHCsgWGV03SM6n2X54K5JFpntfNz/+aw/gDV5fT1//3PUJO8lkEpvNRqFQYN++fRtOMmdmZhrT+taacCkUCs9LZlztPrIRJPPFtMZ7EbBJNF9o6LrO0aNHefjhh/n3f/93tm/fztvf/nZe97rXrdrIUu8uvHo8Yz2bWDfydblcNDc3EwqF1rTI1JtzXC4XW7Zs2bDJCVAra5w+fZpAIEChUFiTNdFasRFWE1eXkOr6m6WlJURRvGmSWalU+JEf+RHe+c538uEPf3hDr+nV0HWd2267jfb2dh555JEX6tdsEs1NvNzwQxlXFEXh8ccf5ytf+QpHjx7lyJEjPPjgg6vKtkzT5OLFi2iaxo4dO64gVVdnE30+H83NzdfU4//tJ7/E1/7omwBsv60XSRIZ+cFFANq3tYJgYrVZCbYHmbsU5b5338l7/tubsNrW38GdTqcZGRkhFAqRzWbXNIlvrZiamiKbzd7STPTVkhmhUIjx8fFbko69WNZ4L1JMgU2i+eLCMAxOnTrFl7/8Zb71rW/R09PDAw88wBvf+EbcbjdHjx7F5XKxe/fu65ZFTNOkUCg0sol2u53m5uZrmonXx5XdyHPsZlCf47tjx47GjnNlN5+maatmE9eCaDTKzMzMhlpN1PWwY2NjKIrSWLjWY5gLtc/4vve9jze84Q383M/93AtKMgE++9nPcuLECXK53CbR3MQmNg4/9HFFVVWefPLJhmzr4MGDPPjgg7zyla/EMAyOHz9Oe3s7fX19112nTNMknU43RgV7PB6am5uftzY++aVn+fqffJvoVIx8skD79haau5so5csoJQV/awDDMLjnXUd47Y+v374IaIzuXDn6caU0ShTFNUmjVsPExASFQmHd0rHrQVVVYrEY4+PjCIJAS0vLTbm2vJjWeC9STIFNovkfh7pB+pe//GUee+wxqtVqbSLDH/0RwWBwXccqFArEYjESiQSyLNPc3NzY9dV1kx0dHRte0q53Lu7Zs+eaTS9XZxPX2mm4uLjI/Pw8+/fvX1PGdq2o7+4Btm3b1tDfpFIpnE5nwzD3esRWURTe//73c++99/Lxj3/8BSeZc3NzPPTQQ3ziE5/gs5/97CbR3MQmNg7/qeLKStnWv//7v6OqKm9961v5jd/4jXVVl64uYdcraPXpOvOTC/z1b/4To09O0LKlmamhWdSKysHX7SPSFeadv/hGmlfRY64FsViMqamp61axrs4m1knn9ezuVk6o27Vr14au2/VyeVNTE62traRSKeLxeCNLvJZkRiqV4h3veAe/9Vu/xZvf/OYNO7fV8CLGFNgkmv/x0DSNd7zjHfT19eH3+3n00UcJBAK87W1v4y1veQuRyPq+rKVS6YrJP9Vq9QXRTWYyGS5cuMCePXtu6GVZx9W2SdfqNFxYWGBxcZF9+/a9ICTTNE36+/uvWGjqWeK6Ya4syw39zcods6ZpfPCDH+TQoUP82q/92gtOMgHe9a538eu//uvk83k+85nPbBLNTWxi4/CfMq4kEgne/OY388ADD5BIJBqyrQcffJDXve5163LDqM9fX5nMKJVK7N27F4/Hy9zFRbKxHJ6Ak84d7ciWm1+z65Z766liKYrSSGZUKpVV/anrs+hVVV33eOkboW7nF4lE6OjouOLfVhL26yUzMpkM73znO/mVX/mVF8V/+UWMKbBJNF8aOHXqFAcPHgQufyG+8pWv8PWvfx2Hw8Hb3vY23va2t9Hc3LzmL0ixWGRwcJBQKEQ+n8c0zcb0iFvVTdanH60sa6wXdW1QLBYjk8k0Og3L5dqYx2t1Ad4srkcyV0O5XG6UaQzDQFVVrFYrf/qnf8rAwAC/+Zu/+aKQzEceeYTHHnuMz3/+83zve9/bJJqb2MTG4j9lXNE0jZGRkYa592qyrbe97W288Y1vXFeTTTKZ5MKFC4TDYbLZLBaLZcN0k3Nzc0Sj0VtKMGia1khmFAqFhh4/FoutaQzyenE9knk16g20Kwl7NpslEonw8Y9/vGGN90LjRY4psEk0X9owTZOpqanGnFxJknjrW9/Kgw8+SFtb2zW/MNlslpGRkStK2lfrJtdSalgN9eacffv23fKM3Trqu75Lly6RzWYJhUKNMs1GZDTXSzKvhqIoPPHEE/z2b//2/7+9ew+K8rr/B/5+BFEJcpdFIRUJUQw3I6hDQlBzIVHAXQxm1MlXIsRMq0nQYKP9kUmL04xJ2thaGW2JqY2JadXlorKIGDIqOorGhnRQTEHBAZSLgVXAhb2d3x/4POWqu8uz7LL7ec3sTCBy9uC6z+ez55zn80FzczNSUlKQmpqKWbNmjXhuj/Kb3/wGX331FRwdHdHd3Y179+5h+fLl+Prrr83xdJRoEntjd3GFP7Yll8tRVFQEiUQCqVSKhISEh9aobG5uFtoz8kll3x20cePGCYsZxsaGuro6KJVKhIWFibbAoNfrhbOe/Hl8Hx8foVSgGOP/+OOPBiWZQ1GpVDhw4AB27twJBwcHvPHGG0hLSxO9NOBAoxxTAEo0xw7GGBobG4WkU61WIzExEVKpFNOnTxeSJ/6NFRERMezKpUajQWtrK5qbm6FWqwf1ER9OU1MT6uvrRe8DC/QWpm1vb0dYWJhw8bpz586I7zQcaZIJ9F5QNm7cCDc3N2RlZaG0tBR+fn6IiooyeqyRoBVNQkRn93GlqqoKcrkchYWFcHd3F5LOvse2DFlt7O7uFlphGrqDxtd15ltsinVzDj/21atX4eTkhCeeeKLfFraLi4tQKtCUxYyRJplA/9J4y5Ytg0KhwOLFi/H444+bNJ4paEVzMLu+IPTFGENzczPy8vKQl5eHjo4OxMfHw9HREWq1Ghs3bjQ4KeP7iDc3Nz/0Zh0xtjWGU1tbi46OjiHvAuz7iZnjOOHiZciWPWMM1dXV0Ov1I0oy33//fTg4OGDnzp2iXgiNRYkmIaKjuPLAUMe2EhMTUV1djfnz5+PVV181eLXRkB00fhFAp9OJfm5Sr9fj6tWrmDRp0qByfgPPnE6cOFFYzDBkAYVPMr29vU1OCvnSeMnJyVi3bt2oHMMaCiWag5k8WHFxMdLT06HT6fDmm29i69atYs7L4lpbW5GRkSGstL3yyitYtmyZ0W9e/mad5uZm4XyLRCKBUqlEe3s7wsPDRT83acynWWPuNOSTTJ1OZ/K5HL1ejw8++ADd3d3YvXu3RZPMUUKJJrE3FFeGwF+b165di6amJvj6+hp0bGsow+2g3bx5E05OTnjyySdFTzIrKyvh4uKCwMDAR/55/twkX4SdTzqHWswQI8nkS+MtWbIEGzZssFiSOYpsP9HU6XSYOXMmTp48CX9/f8ybNw///Oc/8dRTT4k5N4tqamrC5s2bsXfvXqhUKhw9ehS5ubloaGjASy+9hKSkJKNrhvHnW65fvw6VSgWJRAJfX99he9Eaiy810dPTg6eeesroNxt/8RrqTkMAI04yGWPIyspCa2sr9u7dK2qCzevu7kZsbCx6enqg1WqRnJyMrKws0Z/HCDZ/xSNkAIorwzh79iwUCgU++ugj3Lp1q9+xrYSEBEilUgQEBBh1fdVqtUK9ScYYpk2bBolE0u8O8ZHgz5+6ubkhICDA6J/nt//5m0D5xQxnZ2dRkky1Wo2UlBQsXLgQmzZtMkuSaW9xxSoSzfPnz+N3v/sdTpw4AQDYvn07gN4DsbaOL8Sam5uLmpoavPjii5DJZHj66acfmSzyK4JarRazZs2CUqnsd4c4X8jXlKSz79hibJnwfXz5Ow05jsPEiRONai02cH7bt29HXV0dvvzyS7MkmfzzdHV1wcXFBRqNBjExMdi5c+eo97XtgxJNYm8orhhh4LGte/fuIT4+HjKZDEFBQY+8lvN3aXt6esLf37/fdZvfQTO2yPnAsb28vERpTKJWq4XFjJ6eHuh0Ovj4+Bj0ew5Fo9EgLS0NUVFR2LJli9lWMu0troh7kM9EjY2N/T59+Pv7o7y83IIzGj2urq5YvXo1Vq9ejc7OThw/fhzZ2dmoqqrCokWLIJPJMG/evEGJFH9A3MHBQUgEvby84OXlBcaYkHRWV1cP6r/+KHx/cQCinctxcHCARCKBj48Pqqur0dXVBScnJ5SXlwvFcr28vAxKOhlj2LFjB6qrq3HgwAGzJZlAb496viqARqOBRqOxh20UQsY8e40rfNeb9evXY/369WhtbUVBQQG2bt2K1tZWLFmyBFKpdMhru1arFXqA8zfQSCQSSCQSYQetsbERVVVVw9ZYHk7fgumm3pwzkJOTE/z8/DB16lRUVFRgwoQJUKlUuHDhgnAvg6FJsVarxS9/+UuEhYWZNckE7C+uWEWiSXq5uLhgxYoVWLFiBVQqFUpKSrBv3z68++67eO655yCTyRAdHQ2dTofvv/8evr6+Q/ZE5zgOHh4e8PDwEPqvt7S04MaNG3B2doaPj8+wZYn4BNbR0VH0czn8QXatVos5c+aA47h+SXFNTc0j7zRkjCE7Oxv//ve/cejQIdFvehqKTqdDZGQkampqsGHDBixYsMDsz0kIIWKYMmUK1q1bh3Xr1qG9vR1Hjx7Ftm3bUF9fj7i4OOHYFl8NJTAwEL6+voPG4VtKTpkypV//9Z9++umRO2g6nQ4VFRUj6i8+HL1eL9TJ5D9Y8G2M+aTY3d0dPj4+w/aH1+l0eOeddzBjxoxRq79sT3HFKhJNPz8/1NfXC183NDSI/o9xrJk0aRKkUimkUil6enpQWlqKgwcPCmdGXn75Zfz2t7995BuC4zi4ubnBzc0NQUFBQitM/pA33wpz/PjxQqmJCRMmPLLnrrGG6/owMCnm7zSsra3FhAkThFqdTk5OYIwhJydHaN8mdvmm4Tg4OKCiogJKpRJJSUmorKxEaGjoqDw3IcQ0FFcG8/DwQEpKClJSUoRjW3/4wx9QVVWF7u5uZGRkGLR9O27cOIN30LRaLSoqKoSVRzHxSaanp2e/1WsHB4d+STE/v//+97+D5qfX67Fp0yZMmTIFv//970dtZdGe4opVnNHUarWYOXOmcEf2vHnz8M033yAkJMTgMVJTU1FYWAgfHx9UVlaaMg2r19XVBZlMhpCQEHR3d+Ps2bOIioqCVCrFokWLjC7AO/BOPq1WCw8PD7OtZBrbWqzv/L744gvo9Xo0NjaiuLjY5G5HI7Vt2zY4Oztj8+bNFnl+0BlNYn8sElfsIaYAQH19vdDZ7tq1a7h69SoWL14MqVSK+fPnG3U0qe8O2s8//4yJEyeiq6sLAQEBZlvJ9PT0NPi8Z9/5tba24k9/+hPGjRsHX19f/O1vf7NY1RJbjytWkWgCQFFRETZu3AidTofU1FRkZmYa9fNnzpyBi4sL1qxZY7MXBY1Gg7KyMjz//PMAei+k/OreqVOnEB4eDplMhhdeeMGoFpb8nXqMMeh0OqNrYT6MWP1rs7OzcejQIUyePBkajQYKhcKotmymam1txfjx4+Hu7g6VSoW4uDhs2bIFCQkJZn/uYVCiSeyNReKKPcQUoLeBSG1trdDcoru7GydOnIBcLscPP/yAmJgYyGQyPPPMM0YdVVKr1bh8+TIee+wxqFQqTJgwwahamA/D37nu4eFh8k1Fer0e7733Hq5evQqdTodp06ZBLpePyoqmvcUVq0k0xVBXV4eEhASbvigMR6fT4cKFC5DL5fj2228RHBwMmUyGuLi4h7aw5D8Venh4YPr06QD618Lky0dIJBKj+6/z5ZHUavWIksyDBw/iyy+/hEKhwGOPPYa2tjZ4eHiMygXhP//5D1JSUqDT6aDX6/Haa6/hww8/NPvzPgQlmsTeWCyu2HNMASAc25LL5SgvL0d0dDRkMhmee+65hyaLarUaFRUVmDFjhtC9qO8OlaOjo7CYYWw3OVNWMgcaqjReW1sbPD09TRrPWPYWVyjRtEF6vR6XL1/G4cOHceLECQQGBkIqleKVV16Bq6ur8Of4UhMPqznWt3yERqOBt7c3JBLJI/uvi5Vk5uXlIScnBwqFQqi/aeco0ST2hhJNK6DRaHDq1Cnk5uairKwMUVFRkMlkg45t9fT0oKKiAkFBQfDy8hpyLJVKhebmZqH/Ol8L81E7aGKsZPKl8W7evIl//OMfZq1aMoZQomkouigMxn/6O3z4MI4fP45p06ZBKpVi4cKF2LdvH9auXWtwqQmNRiO0wuQLsEskkkH910da6J137Ngx/OUvf4FCoYC7u7tJY1gDvV4v5tkfSjSJvaFE08oMd2zriSeegEKhQGpqqsGrg0MVYB9qB41PMt3d3YXdN2PxpfEqKytx4MCBUalaYi5jKa5QovlAfX091qxZg+bmZnAch7feegvp6elmmKXl8HeVHzhwAJ9//jnmzJmDpKQkJCQkwNvb26ixtFqt0Arz/v37Qs2yyZMn48aNGyNOMouLi/Hpp59CoVAM+6l4pMz1miuVSuh0Ojg4OPRLkC9duoSuri7Mnz8fzs7Opg5PiSaxN2M20bSHuMIf2/r73/+O/Px8LFy4EMnJyY88tjUUtVqNlpaWQf3XJ02aJEqSmZ2djfLychw8eNBsVUsorgwxOCWavW7fvo3bt29j7ty56OjoQGRkJAoKCmyqXRlv1apVSExMRFRUFORyOY4dOyaUU0pMTIREIjGp/zp/p+H48eMRHBxs8jnK0tJSbNu2DUVFRcL5HnMwx2ve1NSExYsXIyoqCk5OTtiwYQPmzp2LI0eO4NChQ4iOjoanpydWr15t6lNQoknszZhNNO0lrmi1WsTGxuKzzz6Do6MjDh8+jJKSEsyYMQPLli3DkiVL+h3bMkTf/ut8t7uZM2cO2kEzBF8a77vvvkNubq7R50KNQXFliMFtJdFctWoVTp06hTt37kAikSArKwtpaWkmjyeVSvH222/jpZdeEnGW1kGlUvXblmCMoba2Frm5uSgoKICjoyMSExMhk8kwdepUg97U/HZ5d3c3fH190dLSgrt378LNzQ0SiWTYQrkDnTlzBpmZmVAoFEMWDTankb7mer0e6enp8PPzw6ZNm/DXv/4V5eXleOedd3DlyhXEx8ejsbERNTU1WLlyJTQajSmfqinRJPbGInFF7JgC2Fdc4Y9tyeVyFBUVYerUqZBKpYiPj4eHh4dBY/Lb5a6urpg0aRJaWlr67aC5uro+Mj4xxrBv3z4oFArk5+ePemk8iis2lGiKqa6uDrGxsaisrDT6U9hYxxhDQ0MDcnNzkZ+fD61Wi8TEREilUvziF78Y9k3NJ5l9t8sZY2hvb0dLSwva29vh6uoqFModKuk8d+4c3n//fRQWFo56YWWxXvPPPvsMS5cuxezZs7Fs2TI0Njbirbfewtq1a+Hk5ITa2lqcO3cOd+/eRUhICBYtWmTsU1CiSewNxZUxjj+2JZfLUVhYCE9PT0il0oce2+KTTDc3NwQEBAjf77uD1tHRAU9PT6EV5lDxaf/+/f127kYTxZUHg1Oi2V9nZycWLlyIzMxMLF++3NLTsSjGGJqampCXl4f8/Hx0dnYiPj4eUqm0X+egoZLMoca6e/eusL3Ot5r09vaGg4MDLl68iI0bN+LYsWPD3gFvLmK85owxcByH7du3Q6PRoK2tDSqVCgsXLsSuXbtQXFwMNzc3XLlyBStWrEBaWhoyMjJMeSpKNIm9obhiQxhjqK6ufuixLb1eLyRnfZPMgfR6Pdra2oQdtIGtJv/1r39h//79Qmm80URxpc/glGj+j0ajQUJCAl5++WW89957lp6O1WltbUV+fj7y8vLw888/Y+nSpaivr8eCBQvw+uuvG3xupm+ryfz8fJSUlODWrVsoKChARESEmX+L/sR+zZVKJWJiYiCRSFBaWgoAWLFiBV599VWsXLkSVVVVOHnyJN59910A/7uQGIESTWJvKK7YqIHHthwcHBAfH4/Tp09jy5YtmDdvnsFj9W01uWfPHtTU1KClpQWnT582+mbXkaK4MmBwSjR7McaQkpICT09P/PnPfzZpjO7ubsTGxqKnpwdarRbJycnIysoSd6JWoq2tDWlpaaisrMTkyZMRFxeHpKQkhISEGFVy4ccff0R6ejqio6Nx/vx5/OpXv8LatWvNOPP/EeM1Hzgex3HIycnBnTt3sHz5cgQHB+Pjjz9GUFAQkpOT+/15/g5CI1GiSeyN3cYVe4opjDHU1dUJq3/Ozs5ISEiAVCrF9OnTjUqcjhw5gl27dmHu3LkoKyvD7t278eyzz5pr6v1QXBkCY0zMx5hVVlbGALCwsDAWERHBIiIimEKhMGoMvV7POjo6GGOMqdVqNn/+fHb+/HlzTNfirl+/ztatW8e0Wi1TKpXs66+/ZklJSSwiIoJlZGSwsrIy1tHRwbq6uoZ9XLp0iYWGhrKqqiphXI1GM2q/gxiv+VCqq6tZeno6y8jIYDt27GChoaGsqKhIhBkzxsR9v9KDHmPhMWaN9BpjTzGFMcaOHz/OPvnkE6bX69mtW7dYdnY2e/7559n8+fNZVlYWq6ioYJ2dnQ+NK7m5uWzBggXszp07jLHev0OtVjtqvwPFlcEPWtE0k/v37yMmJgZ79uzBggULLD2dUdPZ2YmioiLI5XJcu3YNixcvhkwmw7x58/qtdF67dg1vvPEGvvnmG4SGhlpwxuZx/fp1XLhwAaWlpXjmmWfw5ptvijU0rWgSe0NxBfYbU4DeY1sFBQXIzc3FnTt3sHTpUkilUgQHB/db6Ryt0niWMlbjCiWaItPpdIiMjERNTQ02bNiATz75xNJTshiVSoUTJ05ALpejoqICsbGxkMlk8PHxwZo1a7B//37MmTPH0tMcNYwZfW5mKJRoEntj13GFYkp/bW1tOHr0KHJzc9HY2Cgc22pra8MHH3xgkdJ4ljQW4golmmaiVCqRlJSEXbt22eSKnbF6enrw7bff4vDhwzhy5AhKSkqMOuhtrNTUVBQWFsLHx8fW2sdRoknsDcUVUEwZyt27d1FYWIiDBw/iwoULqKiowLRp08z2fBRXTBycEk3z2bZtG5ydnbF582ZLT8WqaLVas/eYPXPmDFxcXLBmzRq6IBAytlFceYBiyvAoroyIWeOKaB3ZSe85EqVSCaB32/jkyZMIDg42ehydToenn34aCQkJIs/QOpj7YgAAsbGx8PT0NPvzEEKIuYgVUwCKK2KguGIa878yduT27dtISUmBTqeDXq/Ha6+9ZtKbeufOnZg9ezbu3btnhlkSQggZC8SKKQDFFWI5lGiKKDw8HD/88MOIxmhoaIBCoUBmZiZ27Ngh0swIIYSMNWLEFIDiCrEs2jq3Mhs3bsSnn35qVNFzQgghZDgUV4gl0b86K8LfzRYZGWnpqRBCCLEBFFeIpVGiaUXOnTuHo0ePIiAgACtXrsR3332H119/3aSxAgICEBYWhjlz5iAqKkrkmVq/VatWITo6Gj/99BP8/f3xxRdfWHpKhBAy6iiuiIfiimmovJEJRCqQ+lCnTp3CH//4RxQWFpr08wEBAfj+++/h7e0t8syIhVF5I2JvKK6IhOIKGQaVN7I2HMfh5s2blp4GIYQQG0FxhdgqSjQNxK/8Xrt2Dbt378b69evx5JNP4vPPPzfL8y1atMjkT51A70UrLi4OkZGRyMnJEXFmlldcXIxZs2YhKCgIH3/8saWnQwghJqG4Yj0orpgRY0zMh81LTk5meXl5jDHGDh06xH79618zlUpl4VkN1tDQwBhjrLm5mYWHh7PTp09beEbi0Gq1LDAwkF2/fp319PSw8PBwduXKFUtPazSJ/Z6lBz2s/WHzKK5YFsUV876HaUXTQPfv30dOTg6KiorAGENbWxtCQkJw8+ZNdHV1WXp6g/j5+QEAfHx8kJSUhIsXL1p4RuK4ePEigoKCEBgYCCcnJ6xcuRJHjhyx9LQIIcRoFFesA8UV86JE00Bnz55FTU0NMjMzcfLkScTExCAtLQ2+vr7w8vISOjdYg66uLnR0dAj/XVJSgtDQUJPGUiqVSE5ORnBwMGbPno3z58+LOVWjNTY24vHHHxe+9vf3R2NjowVnRAghprHHuGJtMQWguGJuYt91brM4jtsKQAsgmzHWzXHcWwBefPD1GcvOrj+O4wIB5D/40hHAN4yxj0wc60sAZYyxvRzHOQFwZowpxZmpSfNJBvAKY+zNB1//H4AFjLG3LTUnQggxhT3GFWuLKQ/mRHHFjKgFpQG43poTSgBTH1wMJAAyAGwB8BPHcR8A8AHwoaXfMADAGLsBIGKk43Ac5wYgFsAbD8ZVA1CPdNwRagTweJ+v/R98jxBCxgx7jCtWGlMAiitmRYmmARhjjOO4WwAyOY6bDMAFQC5jrAAAOI7bDeAra7gYiGwGgFYA+ziOiwBwGUA6Y8ySh4cuAXiS47gZ6L0QrASw2oLzIYQQo9lpXLHGmAJQXDErOqNpIMbYUQBSALcA7GaM/b8+//tZAD8CAMdxtvR36ghgLoA9jLGnAXQB2GrJCTHGtADeBnACQBWAQ4yxK5acEyGEmMIO44rVxRSA4oq50RnNEeA4bjwAPYCPABxmjF3mOI5jNvKXynGcL4ALjLGAB18/B2ArYyzeohMjhBAbZctxhWKKfbKVT0mjgnugz7dcAewBsAbANKB3O8QSczMHxlgTgHqO42Y9+NYLAK5acEqEEGJT7CmuUEyxT7SiKQKO454C8Bhj7JKl5yI2juPmANgLwAnADQBrGWPtFp0UIYTYOFuNKxRT7A8lmiNgK9sZhBBCrAPFFWJrKNEkhBBCCCFmQWc0CSGEEEKIWVCiSQghhBBCzIISTUIIIYQQYhaUaBJCCCGEELOgRJMQQgghhJgFJZqEEEIIIcQsKNEkhBBCCCFmQYkmIYQQQggxi/8Pag8GyxVm2AQAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 960x288 with 2 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The main program segment has run in total  3.03204607963562  seconds\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Introduce the necessary packages\n",
+    "from matplotlib import cm\n",
+    "from mpl_toolkits.mplot3d import Axes3D\n",
+    "from matplotlib.ticker import LinearLocator, FormatStrFormatter\n",
+    "\n",
+    "time_start = time.time()\n",
+    "N = 2\n",
+    "\n",
+    "# Set the image ratio Vertical: Horizontal = 0.3\n",
+    "fig = plt.figure(figsize=plt.figaspect(0.3))\n",
+    "\n",
+    "# Generate points on the x, y axis\n",
+    "X = np.linspace(0, 2*np.pi, 80)\n",
+    "Y = np.linspace(0, 2*np.pi, 80)\n",
+    "\n",
+    "# Generate 2D mesh\n",
+    "xx, yy = np.meshgrid(X, Y)\n",
+    "\n",
+    "\n",
+    "# Define the necessary logic gates\n",
+    "def rx(theta):\n",
+    "    mat = np.array([[np.cos(theta/2), -1j*np.sin(theta/2)],\n",
+    "                    [-1j*np.sin(theta/2), np.cos(theta/2)]])\n",
+    "    return mat\n",
+    "\n",
+    "def ry(theta):\n",
+    "    mat = np.array([[np.cos(theta/2), -1*np.sin(theta/2)],\n",
+    "                    [np.sin(theta/2), np.cos(theta/2)]])\n",
+    "    return mat\n",
+    "\n",
+    "def rz(theta):\n",
+    "    mat = np.array([[np.exp(-1j*theta/2), 0],\n",
+    "                    [0, np.exp(1j*theta/2)]])\n",
+    "    return mat\n",
+    "\n",
+    "def CNOT():\n",
+    "    mat = np.array([[1,0,0,0],[0,1,0,0],[0,0,0,1],[0,0,1,0]])\n",
+    "    return mat\n",
+    "\n",
+    "# ============= The first figure =============\n",
+    "# We visualize the case where the second layer is kron(Ry, Ry)\n",
+    "ax = fig.add_subplot(1, 2, 1, projection='3d')\n",
+    "\n",
+    "# Forward propagation to calculate loss function：\n",
+    "def cost_yy(para):\n",
+    "    L1 = np.kron(ry(np.pi/4), ry(np.pi/4))\n",
+    "    L2 = np.kron(ry(para[0]), ry(para[1]))\n",
+    "    U = np.matmul(np.matmul(L1, L2), CNOT())\n",
+    "    H = np.zeros((2 ** N, 2 ** N))\n",
+    "    H[0, 0] = 1\n",
+    "    val = (U.conj().T @ H@ U).real[0][0]\n",
+    "    return val\n",
+    "\n",
+    "# Draw an image\n",
+    "Z = np.array([[cost_yy([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))\n",
+    "surf = ax.plot_surface(xx, yy, Z, cmap='plasma')\n",
+    "#cset = ax.contourf(xx, yy, Z, zdir='z', offset=np.min(Z), cmap='viridis')\n",
+    "ax.set_xlabel(r\"$\\theta_1$\")\n",
+    "ax.set_ylabel(r\"$\\theta_2$\")\n",
+    "ax.set_title(\"Optimization Landscape for Ry-Ry Layer\")\n",
+    "#fig.colorbar(surf, shrink=0.5, aspect=5)\n",
+    "\n",
+    "# ============= The second figure =============\n",
+    "# We visualize the case where the second layer is kron(Rx, Rz)\n",
+    "ax = fig.add_subplot(1, 2, 2, projection='3d')\n",
+    "\n",
+    "\n",
+    "def cost_xz(para):\n",
+    "    L1 = np.kron(ry(np.pi/4), ry(np.pi/4))\n",
+    "    L2 = np.kron(rx(para[0]), rz(para[1]))\n",
+    "    U = np.matmul(np.matmul(L1, L2), CNOT())\n",
+    "    H = np.zeros((2 ** N, 2 ** N))\n",
+    "    H[0, 0] = 1\n",
+    "    val = (U.conj().T @ H@ U).real[0][0]\n",
+    "    return val\n",
+    "\n",
+    "Z = np.array([[cost_xz([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))\n",
+    "surf = ax.plot_surface(xx, yy, Z, cmap='viridis')\n",
+    "#cset = ax.contourf(xx, yy, Z, zdir='z', offset=np.min(Z), cmap='viridis')\n",
+    "ax.set_xlabel(r\"$\\theta_1$\")\n",
+    "ax.set_ylabel(r\"$\\theta_2$\")\n",
+    "ax.set_title(\"Optimization Landscape for Rx-Rz Layer\")\n",
+    "\n",
+    "\n",
+    "plt.show()\n",
+    "\n",
+    "time_span = time.time() - time_start        \n",
+    "print('The main program segment has run in total ', time_span, ' seconds')"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## More qubits\n",
+    "\n",
+    "Then, we will see what happens to the sampled gradients when we increase the number of qubits"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:05:50.942581Z",
+     "start_time": "2021-01-09T08:59:20.037657Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Hyper parameter settings\n",
+    "selected_qubit = [2, 4, 6, 8]\n",
+    "samples = 300\n",
+    "grad_val = []\n",
+    "means, variances = [], []\n",
+    "\n",
+    "\n",
+    "\n",
+    "# Record operation time\n",
+    "time_start = time.time()\n",
+    "\n",
+    "# Keep increasing the number of qubits\n",
+    "for N in selected_qubit:\n",
+    "    grad_info = []\n",
+    "    THETA_SIZE = N\n",
+    "    for i in range(samples):\n",
+    "        class manual_gradient(fluid.dygraph.Layer):\n",
+    "            \n",
+    "            # Initialize a list of learnable parameters of length THETA_SIZE\n",
+    "            def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * np.pi,seed=1),dtype='float64'):\n",
+    "                super(manual_gradient, self).__init__()\n",
+    "\n",
+    "                # Convert to variable supported in Paddle dynamic graph mode\n",
+    "                self.H = fluid.dygraph.to_variable(density_op(N))\n",
+    "\n",
+    "            # Define loss function and forward propagation mechanism  \n",
+    "            def forward(self):\n",
+    "\n",
+    "                \n",
+    "                # Initialize three theta parameter lists\n",
+    "                theta_np = np.random.uniform(low=0., high= 2 * np.pi, size=(THETA_SIZE))\n",
+    "                theta_plus_np = np.copy(theta_np) \n",
+    "                theta_minus_np = np.copy(theta_np) \n",
+    "\n",
+    "                \n",
+    "                # Modify to calculate analytical gradient\n",
+    "                theta_plus_np[0] += np.pi/2\n",
+    "                theta_minus_np[0] -= np.pi/2\n",
+    "\n",
+    "                # Convert to variable supported in Paddle dynamic graph mode\n",
+    "                theta = fluid.dygraph.to_variable(theta_np)\n",
+    "                theta_plus = fluid.dygraph.to_variable(theta_plus_np)\n",
+    "                theta_minus = fluid.dygraph.to_variable(theta_minus_np)\n",
+    "\n",
+    "                # Generate random targets, randomly select circuit gates in rand_circuit\n",
+    "                target = np.random.choice(3, N)      \n",
+    "                \n",
+    "                U = rand_circuit(theta, target, N)\n",
+    "                U_dagger = dagger(U) \n",
+    "                U_plus = rand_circuit(theta_plus, target, N)\n",
+    "                U_plus_dagger = dagger(U_plus) \n",
+    "                U_minus = rand_circuit(theta_minus, target, N)\n",
+    "                U_minus_dagger = dagger(U_minus) \n",
+    "\n",
+    "                \n",
+    "                # Calculate analytical gradient\n",
+    "                grad = ( matmul(matmul(U_plus_dagger, self.H), U_plus).real[0][0]  - matmul(matmul(U_minus_dagger, self.H), U_minus).real[0][0])/2  \n",
+    "                \n",
+    "                return grad      \n",
+    "            \n",
+    "           \n",
+    "        # Define the main program segment    \n",
+    "        def main():\n",
+    "          \n",
+    "            # Initialize paddle dynamic graph mechanism\n",
+    "            with fluid.dygraph.guard():\n",
+    "\n",
+    "                sampling = manual_gradient(shape=[THETA_SIZE])\n",
+    "                \n",
+    "                \n",
+    "                # Sampling to obtain gradient information\n",
+    "                grad = sampling()\n",
+    "                \n",
+    "            return grad.numpy()\n",
+    "        \n",
+    "        if __name__ == '__main__':\n",
+    "            grad = main()\n",
+    "            grad_info.append(grad)\n",
+    "            \n",
+    "    # Record sampling information\n",
+    "    grad_val.append(grad_info) \n",
+    "    means.append(np.mean(grad_info))\n",
+    "    variances.append(np.var(grad_info))"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:05:51.863908Z",
+     "start_time": "2021-01-09T09:05:50.945336Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "We then draw the statistical results of this sampled gradient:\n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAzEAAAEWCAYAAABWoBknAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAABSnElEQVR4nO3dd3xV9f3H8dcnCRAgLBkKhCkQBFGGFXdRVNyi1eJqtVWpg5/W2jpbxVUXorZqW1TqqIK4cVS0aNwTpVVkuQXZQ4jIzOf3x/ck3ISMG3Jv7r3k/Xw87iNn3XM+9wbON5/zXebuiIiIiIiIZIqsVAcgIiIiIiJSE0piREREREQkoyiJERERERGRjKIkRkREREREMoqSGBERERERyShKYkREREREJKMoiZFtmpntbWZzzazIzIanOp5UMrOuZuZmllOX790aZvZvMzs1HWIRkfQQ3ce7pzqOeFjwTzNbYWbvpTqeVDOz+8zs2rp+71Zca18zm50OsUj1lMRIjZjZV2a23szalNv+UfSHZdcUhVaZq4E73D3P3Z8qv9PM/mVmC8xslZnNMbMzyu0famazzGyNmb1iZl1i9jUys/HRexea2e+S/3HqB3c/1N3vT/Z1zKyw/O9cRGrPzF4ws6sr2H50dL+s8UOI6D7+RWIiTLp9gIOAfHffvfxOM9vfzD42s5VmtszMnjSzjjH7qyxfqiqbZOu5++vuXpDs65jZEDObl+zrbOuUxMjW+BI4sWTFzPoBTVIXTpW6ADOq2H890NXdmwNHAdea2SCAKFF7AvgTsB3wAfBIzHtHAz2ja+wPXGRmhyT6A2xrVIMiUi/cD5xiZlZu+y+Ah9x9Y7wnytB7RhfgK3f/oZL9nwLD3L0l0AGYC/wtZv9oKilf4iibpAJR7Zj+7t2G6JcpW+NB4Jcx66cCD8QeED1FGmNm35jZIjP7u5k1jva1MrNnzWxJVNX+rJnlx7y30MyuMbM3zWy1mb1Yvuan3LXONLPPzGy5mU02sw7R9s+B7sAzUTOERuXf6+4z3H1dyWr02jFaPxaY4e6PuvtaQqGyq5n1jvnc17j7CnefCdwNnFZJjD3M7FUz+97MlprZIzH7bjezb6MnbtPMbN+YfaPN7NGoxmh19OSul5ldamaLo/cdXO67u97M3ovO97SZbVdJTC3M7N6oJmq+mV1rZtnRvuzo97fUzL4ADq/s+4+OHxjVxq2O4n3Eoir3kidOZnaxmS0E/hnnv4Ez4omlms9xmpm9Eb1/hZl9aWaHRvuuA/YF7oj+fdxR1WcUkRp5CmhN+D8GhHs/cATwgJntbmZvW6iJWGBmd5hZw5hj3czONbO5hD/wS7b1iJYPj+45q6L74OiY95Y0OT01KoOWmtnlMfuzzewyM/s8umdNM7NO0b7eZvZSVJ7MNrOfV/YBzaxDVOYsj8qgM6PtpwP3AHtG95aryr/X3Re5+3cxmzYBPWLWqypfqiubysd5cXRvXB19pqHR9nh+B+dYaJK92kK5vKOZvRV975NKjo+5z18Wfd9fmdnJVXx3R5jZ9Ojab5nZLjH7BpjZh9E1HwFyqzhPtpndEl3zSzMbZTHNjaOy5DozexNYA3Q3s1+Z2czo/F+Y2W9izlemhqS6WKr5HF+Z2e/N7H8Wyv5HzCzXzJoC/wY6RP8+iiz6u0VqyN310ivuF/AVcCAwG9gJyAbmEZ4WOaFWA+BWYDLhKVEz4Bng+mhfa+BnhNqbZsCjwFMx1ygEPgd6AY2j9RsqiecAYCkwEGgE/BV4rXy81Xymuwg3Nwc+BPKi7bcDfyt37CdR7K2i47eP2Xcc8HEl15gAXE54cJAL7BOz75ToO8kBLgQWArnRvtHAWmBYtP8BQk3Y5UAD4Ezgy3Lf3XxgZ6Ap8Djwr2hf1yjmnGj9SeAf0XHtgPeA30T7zgJmAZ2i3+Erse8t99kaAl8D50cxHQusB66N9g8BNgI3Rr+jxnH+Gzgjnliq+RynARui7ykbOBv4DrDy19FLL70S+yL84X1PzPpvgOnR8iBgj+i+1hWYCfw25lgHXor+zzeO2dYjWh4C9CPcU3cBFgHDo30l97q7o/vNrsA6YKdo/x+Aj4ECwKL9raN7yLfAr6K4BhDKlz6VfL7XCOVHLtAfWAIcEO07DXijmu+nM7ASKI7uU6dF26ssX6iibKrgGgXRZ+oQ893sWIPfwdNAc6Bv9B1OJTwcbEGoTTo15vexERhLuM//FPgBKIj238fmMmEAsBgYTLgvn0ooqxuxuTy5gFCeHBd9N9dW8h2eFcWRH31v/6Fs+VAIfBPFnxOd83DCw0qL4lwDDIz5HPOi5SpjqepzRPu/IpRHHQj/jmcCZ5W/jl61uMekOgC9MuvF5iTmj4SmWIcQCpqc6MbRNbox/FByo4zetycxf2yXO2d/YEXMeiHwx5j1c4AXKnnvvcBNMet50U2ma2y8cXyubEIb5j8CDWLOfUO5494kFE6dos+bG7PvIELzgYrO/wAwjtA+urpYVgC7RsujgZdi9h0JFAHZ0XqzKI6WMd/dDTHH9yEkFNnEJDHA9oQCqXHMsScCr0TLL5fcbKP1g6k8idmPkDhZzLY3KJvErI/9ruL8N3BGdbHE8TlOAz6L2dckeu8O5a+jl156JfYV3VNXsvmhzJvABZUc+1vgyZh1J0oIym3rUcn7bwNujZZL7nX5MfvfA06IlmcDR1dwjhHA6+W2/QO4soJjOxFqT5rFbLseuC9aPo1qkpiY920HXAzsEXPuSssXqiibKjh3D8If2gcSlW1VxFHR72DvmPVpwMUx67cAt0XLQwhJTNOY/ZOAP0XL97G5TPgboZYp9tqzCQnFfsQ8aIr2vUXlSczLRA+tovUD2TKJubqaz/0UcH7M5yhJYqqMparPES1/BZwSs+8m4O/lr6PX1r/UnEy21oPASYQb9QPl9rUl/LE4LapiXQm8EG3HzJqY2T/M7GszW0V4mtXSoiZAkYUxy2sIyUlFOhCelADg7kXAMqBjJcdXyN03ufsbhKc5Z0ebiwhPoGI1B1ZH+yi3v2RfRS4iJHfvmdkMM/t1yY6ounlmVN28kvCEK7b53KKY5R+Bpe6+KWYdyn4/38Ysf014glS+OV6XaPuCmN/RPwg1GRC+1/LnqUwHYL5Hd+YKYgBY4qHZAxD3v4HY81cWS3WfA2L+Lbn7mmixsn9PIpIg0T11KTDczHYEdgceBrDQLPZZC53WVwF/Zsv7VPn7SCkzG2yhQ/sSM/ue8ES+/PsrK0c6EWr7y+sCDC65l0T3k5OBHSo4tgOw3N1j7/lfU8OyB8DdlxP6ED0dNYOqrnypqmwqf+7PCMnJaGCxmU20zU2u4/kdlC9/yq/H3ktXeNk+QF8TvqfyugAXlvueO0XHVlSeVFf+xP47qejfTJltZnaomb1joRngSuAwtvzcJeeuKpaqPkeJeP+Wka2gJEa2irt/TWjWdBihg2GspYSbW193bxm9Wrh7yX/eCwlV3IM9dKjfL9pevgNoPL4j3EjCCUJb09aEmoGtkcPmPjEzCM0MYs+9I6Et8gpgQez+aLnCQQTcfaG7n+nuHQhNKu6y0E9mX0KC83OglYdOnt+zdd9FiU4xy50JNVNLyx3zLaEGo03M76i5u/eN9i+o4DyVWQB0NCvTgbdTuWO83HpN/g1UFUt1n6M65eMSkcR6gNCH8hRgiruX/BH8N0Iz0Z7RPeAytvz/X9X/z4cJTZY7uXsL4O8VvL8y37L5Pl9++6sx95KWHkZEO7uCY78DtjOzZjHbOlO7sqcd0DyO8qXSsqmiE7v7w+6+D5ubfd8Y7Yrnd1ATraJYSnQmfE/lfQtcV+57buLuE6i4PKmu/MmPWS9f9kDMvyMLfWMfB8YQmuu1BJ6n8rKnqliq+hzVUdmTAEpipDZOJ1T3lxl9xd2LCW2RbzWzdgBm1tHMhkWHNCMkOSstdDq/shYxTAB+ZWb9o5vTn4F33f2r6t5oZu3M7AQzy4s6Bw4jNEWaGh3yJLCzmf3MzHKBK4D/ufusaP8DwB8tdFLvTeh3cV8l1zreNndcX0G4gRUTvouNhLbUOWZ2BVs+YaupU8ysj5k1IQwx/VhMzQ0A7r4AeBG4xcyam1mWhQ6bP40OmQScZ2b5FjrjXlLF9d4mNKsYZWY5ZnY04YlrVWryb6DSWOL4HNVZRGjfLSLJ8QChic+ZhNqGEs2AVUBRdP+sKFGoSjNCTchaM9ud0DIgXvcA15hZTwt2MbPWwLNALzP7hZk1iF4/MbOdyp/A3b8lNC26PuqsvQuhTPxXPAGY2bFmVhDds9oS+pJ8FNXKQNXlS3VlU+x1CszsgKh8XEu47xZHu2v7O6jIVWbWMHpAdwShv2N5dwNnRbVpZmZNLQzU0IxQnmwk3PMbmNmxVF2eTALOj/7GaElolleVhoS+N0uAjRYGejm4kmOri6Wqz1GdRUBrM2sRx7FSCSUxstXc/XN3/6CS3RcDnwHvRNXU/yE8eYfQdrkxoXbgHUJTs62N4T+EYSYfJzw12RE4Id63E27a8wiJxRhCp8bJ0bmXEDqfXxftH1zu3FcSmiR8DbwK3OzulX2WnwDvmlkR4enh+R7mO5hC+PxzovOspYomFHF6kFDYLSR0OD2vkuN+Sbihf0r4fI8B7aN9d0ex/Zcw2EH52rZS7r6e0Jn/dEL791MIfwysq+w91OzfQHWxVPU5qnM7cJyFkcv+Eud7RCRO0QOltwid5ifH7Po9IfFYTfg/XtMhgs8Brjaz1YQ/4ifV4L1jo+NfJPwRfy+hX91qwh+0JxBqEBayeUCSipxI6H/zHSGxuDIqk+LRkXDfW00YZKAYOCZmf6XlSxxlU6xGwA2Ee+1CQm3PpdG+2v4OylsYxfMd8BChL+MWiVX0d8OZwB3R8Z8RjbwWU56cBiwn9FOqtPyJ4n4R+B/wEaFWZSPhwdoWot/xeYTf/wrC559cybFVxlLV56hO9L1MAL6ImqJpdLKtUDJCj4hsA8yskDAa2T0pjuNdQgfGf6YyDhERST4zG0Ioe/KrOTTZcRxKKHu6VHuwZDzVxIhIrZnZT81sh6g52amEIU+3uoZNRESkOmbW2MwOi8qejoQarCdTHZfUjbRKYszsEAsTMX1mZlu0wbcwgeIj0f53zaxrzL5dLEzaNMPChICVTo4kIglXQGjutZLQaf+4qL+KSMYys+4WJlJ9LNWxiEiFDLiK0JzrI8JcLFekNCKpM2nTnMzC0KpzCGOhzwPeB050909jjjkH2MXdzzKzE4Bj3H2EhSEJPwR+4e7/jTrorSzfmVlEROoHMxtP6Fi82N13jtl+CKEvVDZhIsYb4jjXY+5+XNKCFRGRGkunmpjdCZPSfRF1ppoIHF3umKPZPLrJY8BQMzNCR7z/uft/Adx9mRIYEZF67T7CZLyloodldwKHEiaCPTEaya+fhfkyYl/ttjyliIiki5xUBxCjI2VHZZpHGHGjwmPcfaOFCa5aA70AN7MphAkVJ7r7TRVdxMxGAiMBcnNzB3XuXNXw4+mhuLiYrKx0yjcrlilxQubEqjgTK1PihMyJdc6cOUvdvW2q4yjP3V+LbXIcKX1YBmBmEwkzt19PqLXZKipXkkdxJl6mxKo4EytT4oT4y5V0SmJqIwfYhzCM7RpgqplNc/ep5Q9093HAOICCggKfPXt2nQa6NQoLCxkyZEiqw6hWpsQJmROr4kysTIkTMidWM6tqNu10E8/DslJR0+TrgAFmdmmU7GxB5UryKM7Ey5RYFWdiZUqcEH+5kk5JzHzKzrSaz5Yz35YcMy/qB9MCWEYoiF5z96UAZvY8MJDNkxaKiIjUiLsvA85KdRwiIrKldKpXeh/oaWbdzKwhYeKm8hMQTQZOjZaPA172MDLBFKCfmTWJkpufEia+ExERKRHPwzIREckAaVMTE/VxGUVISLKB8e4+w8yuBj6IZlG/F3jQzD4jzJ56QvTeFWY2lpAIOfC8uz+Xkg8iIiLpqvRhGSF5OYEwY3etmdmRwJEdOmjibRGRupA2SQyAuz8PPF9u2xUxy2uB4yt577+AfyU1QBERyQhmNgEYArQxs3nAle5+b0UPyxJxPXd/BnimoKDgzEScT0Rqb8OGDcybN4+1a9cm7RotWrRg5syZSTt/oqRjnLm5ueTn59OgQYOten9aJTEiIiKJ4O4nVrJ9i4dlIrJtmjdvHs2aNaNr166EGTkSb/Xq1TRr1iwp506kdIvT3Vm2bBnz5s2jW7duW3WOdOoTIyIikpHM7EgzG1dUVJTqUEQksnbtWlq3bp20BEa2npnRunXrWtWSKYkRERGpJXd/xt1H5uXlpToUEYmhBCZ91fZ3oyRGREREREQyipIYEREREZEkuO666+jbty+77LIL/fv359133wVgyJAhfPDBB3UWx1dffcXgwYPp0aMHI0aMYP369Vsc89BDD9G/f//SV1ZWFtOnTwdg/fr1jBw5kl69etG7d28ef/zx0vdNmjSJPn360LdvX046qeyAj6tWrSI/P59Ro0Yl/DOpY7+IiIiISIK9/fbbPPvss3z44Yc0atSIpUuXVpg81IUrr7ySCy64gBNOOIGzzjqLe++9l7PPPrvMMSeffDInn3wyAB9//DHDhw+nf//+QEjG2rVrx5w5cyguLmb58uUAzJ07l+uvv54333yTVq1asXjx4jLn/NOf/sR+++2XlM+kmhgREZFaUsd+ESlvwYIFtGnThkaNGgHQpk0bKppLasKECfTr14+dd96Ziy++uHR7Xl4eF1xwAX379mXo0KEsWbIEgM8//5xDDjmEQYMGse+++zJr1qwq43B3Xn31VY477jgATj31VJ566qkq3zNhwgROOOGE0vXx48dz6aWXApCVlUWbNm0AuPvuuzn33HNp1aoVAO3atSt9z7Rp01i0aBEHH3xwldfaWkpiREREakkd+0UywJAhW77uuivsW7Om4v333Rf2L1265b5qHHzwwXz77bf06tWLc845h1dffXWLY7777jsuvvhiXn75ZaZPn877779fmmD88MMP7LbbbsyYMYOf/vSnXHXVVQCMHDmSv/71r0ybNo0xY8ZwzjnnVBnHsmXLaNGiBTk5oQFWfn4+8+fPr/I9jzzyCCeeGEaqX7lyJRBqVQYOHMjxxx/PokWLAJgzZw5z5sxh7733Zo899uCFF14AoLi4mAsvvJAxY8ZU+z1tLSUxIiIiIiIJlpeXx7Rp0xg3bhxt27ZlxIgR3FeSFEXef/99hgwZQtu2bcnJyeHkk0/mtddeA0KNx4gRIwA45ZRTeOONNygqKuKtt97i+OOPp3///vzmN79hwYIFCY373XffpUmTJuy8884AbNy4kXnz5rHXXnvx4Ycfsueee/L73/++dN/cuXMpLCxkwoQJnHnmmaxcuZK77rqLww47jPz8/ITGFkt9YkRERERk21dYWPm+Jk2q3t+mTdX7K5Gdnc2QIUMYMmQI/fr14/777+e0006r8XkgDElcXFxMy5YtSzvcV2bYsGEsWrSI3Xbbjbvvvpvvv/+ejRs3kpOTw7x58+jYsWOl7504cWJpLQxA69atadKkCcceeywAxx9/PPfeey8QanUGDx5MgwYN6NatG7169WLu3Lm8/fbbvP7669x1110UFRWxfv168vLyuOGGG7bqs1dENTEiIiK1pD4xIlLe7NmzmTt3bun69OnT6dKlS5ljdt99d1599VWWLl3Kpk2bmDBhAj/96U+B0CTrscceA+Dhhx9mn332oXnz5nTr1o1HH30UCP1d/vvf/25x7SlTpjB9+nTuuecezIz99tuv9Fz3338/Rx99dIUxFxcXM2nSpDL9YcyMI488ksIoiZs6dSp9+vQBYPjw4aXbly5dypw5c+jevTsPPfQQ33zzDV999RVjxozhl7/8ZUITGFASIyIiUmvqEyMi5RUVFXHqqafSp08fdtllFz799FNGjx5d5pj27dtzww03sP/++7PrrrsyaNCg0gSjadOmvPfee+y88868/PLLXHHFFUAYCvnee+9l1113pW/fvjz99NPVxnLVVVcxduxYevTowbJlyzj99NMBmDx5cul5AV577TU6depE9+7dy7z/xhtvZPTo0eyyyy48+OCD3HLLLUCo8WndujV9+vRh//335+abb6Z169Zb/Z3VhJqTiYiIiIgk2KBBg3jrrbcq3FcY0zTtxBNPLNN8K9bYsWO32NatW7fSDvTx6tatG++9994W24866iiOOuqo0vUhQ4bwzjvvbHFcly5dSvvqxDIzxo4dW2GcJU477bStbkJXFdXEiIiIiIhIRlESIyIiIiKSZtTHrmpKYkRERERkm+TuqQ5BKlHb342SGBERkVrS6GQi6Sc3N5dly5YpkUlD7s6yZcvIzc3d6nOoY7+IiEgtufszwDMFBQVnpjoWEQny8/OZN28eS5YsSdo11q5dW6s/xOtKOsaZm5tbq8kwlcSIiIiIyDanZALGZCosLGTAgAFJvUYiZEqcNaHmZCIiIiIiklGUxIiIiIiISEZREiMiIiIiIhlFSYyIiIiIiGQUJTEiIiK1pCGWRUTqlpIYERGRWnL3Z9x9ZF5eXqpDERGpF5TEiIiIiIhIRlESIyIiIiIiGSWtkhgzO8TMZpvZZ2Z2SQX7G5nZI9H+d82sa7n9nc2syMx+X2dBi4iIiIhIncpJdQAlzCwbuBM4CJgHvG9mk93905jDTgdWuHsPMzsBuBEYEbN/LPDvuopZREQkUxx2++t8umDV5g0vPAdAn/bNef78fVMUlYjI1kmnmpjdgc/c/Qt3Xw9MBI4ud8zRwP3R8mPAUDMzADMbDnwJzKibcEVERDLHwM4taZBtZbY1yDYGdmmVoohERLZeOiUxHYFvY9bnRdsqPMbdNwLfA63NLA+4GLiqDuIUERHJOOcN7UmWlU1iss04b2iPFEUkIrL10qY5WS2NBm519yIrd4Muz8xGAiMB2rZtS2FhYdKDq62ioiLFmWCZEqviTKxMiRMyK1bJDO2a53L8oHwe+eBbNmxyGmQbx+3WiXbNclMdmohIjaVTEjMf6BSznh9tq+iYeWaWA7QAlgGDgePM7CagJVBsZmvd/Y7yF3H3ccA4gIKCAh8yZEiCP0biFRYWojgTK1NiVZyJlSlxQmbFKmGyS+DIDh06pDqUKp03tCePTpsHuGphRCSjpVNzsveBnmbWzcwaAicAk8sdMxk4NVo+DnjZg33dvau7dwVuA/5cUQIjIiKSDJky2WW75rmcslNLLnj9IU7u00q1MCKSsdKmJsbdN5rZKGAKkA2Md/cZZnY18IG7TwbuBR40s8+A5YRER0REROJ03vrPaPHWBIrnToU118GvfgXZ2akOS0SkRtImiQFw9+eB58ttuyJmeS1wfDXnGJ2U4ERERLYBLX71C6at+4FBDz4IZ54Jd9wBt90Gar4oIhkknZqTiYiISB1Y3bs3vPEGTJwIK1bAjTemOiQRkRpREiMiIlIfmcGIETBrFowfH7Z9+SVccgmsWlX1e0VEUkxJjIiISH3WuDG0bx+Wp0yBm26Cnj3h7rth06bUxiYiUgklMSIiIhKcdRa8/z706gUjR8LAgfDKK6mOSkRkC0piREREZLNBg+C112DSJPj+e3jssVRHJCKyBSUxIiIiUpYZHH88zJwJ118ftr31Flx0UUhsRERSTEmMiIiIVKxxY2jePCy//jqMGRP6y4wbp/4yIpJSSmJERESkehdfDB98AL17w29+E/rLFBamOioRqaeUxIiIiEh8Bg6EV18N/WRWrQpJjYhICuSkOgAREZFMZ2ZHAkd26NAh1aEknxn87Gdw+OGQFT0LnTgxJDR//CO0bJnS8ESkflBNjIiISC25+zPuPjIvLy/VodSd3Fxo2DAsf/wxjB0b+sv84x+wcWNqYxORbZ6SGBEREamd664LNTF9+oS5ZgYODAMBiIgkiZIYERERqb2Sjv6PPQZFRbB4caojEpFtmPrEiIiISGKU9Jc54ojNTc1uugkWLoQrrlB/GRFJGNXEiIiISGI1ahQSGoDvvoPbboMePeBvf1N/GRFJCCUxIiIikjy33QYffgg77wznnAP9+8M776Q6KhHJcEpiREREJLn694dXXoEnnoB16yAnas3untKwRCRzKYkRERGR5DODY46BWbNgt93CtnPOgd/9DlasSG1sIpJxlMSIiIhI3cnODj+Li8PP224L88vceaf6y4hI3JTEiIiISN3Lygod/T/6CPr1g1GjYNddw7qISDWUxIiIiEjq7LorvPwyPPlkqKVp2zZsL6mpERGpgOaJERGRtGJmBpwMdHf3q82sM7CDu7+X4tAkWcxg+HA4+uiw7A6HHsqOzZuHJKdVq1RHKCJpRjUxIiKSbu4C9gROjNZXA3emLhypMyVzy6xfD926kf/EE2F+GfWXEZFylMSIiEi6Gezu5wJrAdx9BdAwtSFJnWrUCP7+dz4YNy4Mz1zSX2b27FRHJiJpQkmMiIikmw1mlg04gJm1BdRBoh76Yccd4T//gaefDn1lOnYMO9avT21gIpJySmJERCTd/AV4EmhnZtcBbwB/Tm1IkjJmcNRRUFgIeXkhgRkwAM47D5YvT3V0IpIiSmJERCStuPtDwEXA9cACYLi7P5raqCRtrFsH++0X+sn06AF//Sts2JDqqESkjimJERGRtOPus9z9Tne/w91npjoeSSPNmoX5ZaZPh4EDQ43MLrvAvHmpjkxE6lBaJTFmdoiZzTazz8zskgr2NzKzR6L975pZ12j7QWY2zcw+jn4eUOfBi4hIQpjZ/WbWMma9lZmNT0Ecw83s7qjcObiury/V6NcPXnoJJk8Oyx06hO1FRamNS0TqRNokMVEnzjuBQ4E+wIlm1qfcYacDK9y9B3ArcGO0fSlwpLv3A04FHqybqEVEJAl2cfeVJSvR6GQDanICMxtvZovN7JNy26t8WBbL3Z9y9zOBs4ARNbm+1BEzOPJImDQJsrJg2TLo3h3+7//Csohss+JOYqJakJPM7DIzu6LklcBYdgc+c/cv3H09MBE4utwxRwP3R8uPAUPNzNz9I3f/Lto+A2hsZo0SGJuIiNSdLDMrnd3QzLaj5pMz3wccEruhsodlZtbPzJ4t92oX89Y/onlqMoMZHHcc3HVX6C9z++3qLyOyjTJ3j+9AsxeA74FpwKaS7e5+S0ICMTsOOMTdz4jWf0GYK2BUzDGfRMfMi9Y/j45ZWu48Z7n7gZVcZyQwEqBt27aDJk2alIjwk6qoqIi8vLxUh1GtTIkTMidWxZlYmRInZE6s+++//zR33y2R5zSzXwKXA5MAA44D/uzuD9TwPF2BZ91952h9T2C0uw+L1i8FcPfrK3m/ATcAL7n7f6q4jsqVJNnaOJt++SU73nkn202bxppOnZh2111sSuLnzZTvEzInVsWZWJkSJ9SgXHH3uF7AJ/EeuzUvQiF1T8z6L4A7yscA5Mesfw60iVnvG23bMZ5r9urVyzPBK6+8kuoQ4pIpcbpnTqyKM7EyJU73zIkV+MCTUyb0AUYB5wJ9tvIcXWPLrnjKmXLvP4/w4O7vhIdjKlfqWK3iLC52f+YZ9wsu2LxtyZJax1SRTPk+3TMnVsWZWJkSp3v85UpN+sS8ZWb9anB8Tc0HOsWs50fbKjzGzHKAFsCyaD2fMK/AL9398yTGKSIiSRQ1B+4PNAdaA8cluPlyXNz9L+4+yN3Pcve/1/X1pZbM4IgjYOzYsD57NnTqBKNGwdKlVb9XRNJeTZKYfYBpUYfI/0Ujgf0vgbG8D/Q0s25m1hA4AZhc7pjJhI77EJ6ovezuHo1i8xxwibu/mcCYRESk7j1N6AO5Efgh5lVb8Tws2ypmdqSZjSvSyFjpq00bOP10+PvfoWdPuO22MHGmiGSkmnSUPDRpUQDuvtHMRgFTgGxgvLvPMLOrCdVKk4F7gQfN7DNgOSHRgdDkoAcQO9jAwe6+OJkxi4hIUuS7+yHVH1ZjpQ/LCMnLCcBJiTixuz8DPFNQUHBmIs4nSdC6NdxxB5x9NlxwQXjdey98+CE0aJDq6ESkhuJOYtz962i0mJ5AbsyurxMVjLs/DzxfbtsVMctrgeMreN+1wLWJikNERFLqLTPr5+4fb+0JzGwCMARoY2bzgCvd/d6KHpYlJGLJHH37wpQp8PzzoYlZSQLzzTfQuXNqYxORuMWdxJjZGcD5hOr36cAewNuAJpYUEZFE2gc4zcy+BNYRRihzd98l3hO4+4mVbN/iYZnUQ2Zw+OHhBTB1KgwbBr/5DVx1VWh6JiJprSZ9Ys4HfgJ87e77EyYeW5mMoEREpF47lFDrfzBwJHBE9DNtqU9MhuvfPzQz+8c/wvwyt96q/jIiaa4mfWLWuvtaM8PMGrn7LDMrSFpkIiJSL9VF8+VEU5+YDNe6Nfz1ryGR+d3vwuvRR+HNN0OtTQUOu/11Pl2wavOGF54DoE/75jx//r51EbVIvVaTJGZeNArYU8BLZraCNC5QREQkM6n5sqRMnz7wwgvw73/DqlUhgdm0CebMgZ12KnPowM4tmbt4NRs2bZ40vEG2MbBLq7qOWqReirs5mbsf4+4r3X008CfCSGHDkxSXiIjUX2q+LKl16KEwYkRYvv9+2HlnOOccWLKk9JDzhvYkq1wtTbYZ5w3tUZeRitRbcScxFpxiZle4+6uEp2P9kxWYiIjUW2uj0ShLmy8Dad18WX1itmHDh4cJMseNC/PLjB0L69fTrnkuxw/Kp0F2SGQaZBvH7daJds1yqz6fiCRETTr23wXsCZSM+LIauDPhEYmISH1Xvvny06R582V3f8bdR+bl5aU6FEm07baD22+Hjz+GvfaCCy+En/0MKFsbo1oYkbpVkz4xg919oJl9BODuK8ysYZLiEhGResrdj4kWR5vZK0AL4IUUhiQS+sQ8/3zoL9O4MQDtsjYyqs0axi7MVS2MSB2rSRKzwcyyAQcws7ZAcVKiEhERAaLmyyLp49BDNy/fcgujrr6abj8ZxuCRf09dTCL1UE2ak/0FeBJoZ2bXAW8Af05KVCIiUu+Y2RvRz9VmtirmtdrMVlX3fpE693//h40axWEfvEjbAf1gzBhYty7VUYnUC3HXxLj7Q2Y2DRhKmD15uLvPTFpkIiJSr7j7PmZmQF93/ybV8dSEmR0JHNmhQ4dUhyJ1Keov88GgQew+aRL84Q8wYwb885+pjkxkm1eT5mREI8TMSlIsIiJSz7m7m9lzQL9Ux1ITmuyyflvTuTM8+yxMmQL5+WHjvHmwbBnsumtqgxPZRlWbxJjZ5Kr2u/tRiQtHRESED83sJ+7+fqoDEamRYcM2L191FYwfD2ecAddcA+3apS4ukW1QPDUxewLfAhOAdwlNyURERJJlMHCymX0N/EAod9zdd0ltWCI1cNNNkJcHd9wBEybAn/4E550HjRqlOjKRbUI8ScwOwEGE+WFOAp4DJrj7jGQGJiIi9daw6g8RSXOtWsGtt8JZZ4W5ZS66KDQvu+GGVEcmsk2oNolx902E8flfMLNGhGSm0Myucvc7kh2giIjUL+7+tZm1AnoCsRNvpPWElyIVKijY3F+mf/+w7eOPobhY/WVEaiGuIZbNrJGZHQv8CziXzcMti4iIJJSZnQG8BkwBrop+jk5lTNUxsyPNbFxRUVGqQ5F0NWwYbL99WL70UhgwAEaOhEWLUhuXSIaqNokxsweAt4GBwFXu/hN3v8bd5yc9OhERqY/OB34CfO3u+wMDgJUpjaga7v6Mu4/My8tLdSiSCR58EC64IAzF3LNn6D+j+WVEaiSemphTCFX65wNvafKxuvPUR/PZ+4aXOe2FH9j7hpd56iPljSJSL6x197UQWgJEw/sXpDgmkcRp1QpuuSXMKbP//nDxxfCPf6Q6KpGMEk+fmLianEliPfXRfC594mN+3LAJgPkrf+TSJz4GYPiAjqkMTUQk2eaZWUvgKeAlM1uB+sPItqhXL3j6aXj5Zdhrr7DtlVegZcvQ3ExEKqUEJU3dPGV2aQJT4scNm7j+3zNx9xRFJSKSfO5+jLuvdPfRwJ+Ae4HhKQ1KJJkOOAByc8E91MoMGhTml1m4MNWRiaSteIZYlhT4buWPFW5ftGod/Ua/SO8dmtG7fTN679Ccndo3p/cOzWjaSL9OEclcZnYn8LC7v1myzd1fTWFIInXLDF58Ea69Fv7yF5g0CS6/HM4/PyQ5IlJKNTFpqkPLxhVub9m4AccO7IgZPP3Rd/zxqU/42d/e4l/vhJYWS4vWcetLc/h62Q91Ga6ISCLMAcaY2VdmdpOZqT2N1D8tW8KYMZv7y1xyCTz3XKqjEkk7enSfpv4wrKBMnxiAxg2yGX1U39I+Me7O/JU/MmvBanpuH0bEmbNoNX95eS5792hDl9ZNmTpzEXe88hm9d2hOn/bN6N2+OQU7NKN5boOUfC4Rkcq4++3A7WbWBTgBGG9mjYEJhEmW56Q0wCqY2ZHAkR06dEh1KLKt6Nkz9Jd5+23YY4+w7ZFHwvaBA1Mbm0gaiCuJiSYdOxI4BugFfAk8DTzt7ouTF179VZKo3DxlNvNX/kjHlo35w7CCMp36zYz8Vk3Ib9WkdNteO7bh06sOISfbAMgyo2F2Fs9/vIAJ731Telx+q8ZlEpshBW1p0lA5rYiknrt/DdwI3BjVxowHrgCyUxpYFdz9GeCZgoKCM1Mdi2xj9twz/Ny4ES67DL78En71K7juOthhh9TGJpJC1f7VamZPAK2A54CL3X2OmXUGjgb+ZWYN3X1IcsOsn4YP6MjwAR0pLCxkyJAhcb+vccPN5fz+vduxf+92uDsLV61l5oJVzFywmpkLVjFr4WpenrWIYoeP/nQQTRrCpA++5aNvVvLnY3bGzNiwqZgG2Wp1KCJ1x8xygEMJtTFDgULSfLJLkaTLyYFp00Lycvvtob/MZZeF+WbUX0bqoXgevf/a3VfGbnD3b4C/An+NhsGUNGdmtG/RmPYtGnNA7+1Lt6/dsInPlxTRqmlDAOav+JFZC1dhFmpyRj7wAbMXrg6DB5QOJNCMrq2bkqPkRkQSyMwOAk4EDgPeAyYCI91dnfxEIPSXuflm+M1v4Pe/D0nMAQfA4MGpjkykzsUzT8xKM+tNqHkpacs0H5js7jPLJzi1YWaHALcTmgzc4+43lNvfCHgAGAQsA0a4+1fRvkuB04FNwHnuPiVRcW3Lchtk07dDi9L1Cw7qxQUH9SpdP7DP9jRv3IBZC1bz6pwlbCwOwzs3ysmi1/bN6L1DM/bo3pqfDcqv89hFZJtzKfAwcKG7r0h1MCJpq0cPeOqp0Pm/b9+w7fbbYZ99wvDMIvVAPM3JLiY8GZtIeDIGkA9MMLOJ5RONrWVm2cCdwEHAPOB9M5vs7p/GHHY6sMLde5jZCYQ20yPMrA+h2UFfoAPwHzPr5e5lJ1qRGjt5cBdOHtwFgHUbN/HZ4iJmLVjNrIWhWdrLsxbz/Y8bSpOYY+96k4P67MDZQ3bE3flscRFd2zRVk7Rt1FMfzd/cb+udl7fotyVSE+5+QKpjEMkoJQlMURHceGNoWnbaaaHJWfv2KQ1NJNniaU52OtDX3TfEbjSzscAMICFJDLA78Jm7fxGdfyKh9ic2iTmaze2iHwPusNDu6WhgoruvA740s8+i872doNgEaJQTam1ia24gNEkDKHana+umtMkLTdOWFK3joFtfo2F2Fj3a5bFT+9AUraRJWuu8RnX+GSRxnvpofpkR9Oav/JFLn/gYQIlMLSgxFJEay8uDmTPhz3+G224r21+mccVTNohkuniSmGJC7cbX5ba3j/YlSkfg25j1eUD5Rp6lx7j7RjP7HmgdbX+n3HsrLPXNbCQwEqBt27YUFhYmIvakKioqyog41/zwA0dtb1C0ksLCz/lxozNyl0Z8u7qYb1f/wNQZq3n8Qy89vkUjo1NeFod1b0Cf1tmlTdVysizpsWbKd5oucRa78+NGWLPB+XFjWL7jo7X8uKHscT9u2MQ1T/+XhV/OYsmaYrKzjCyDLIPs6GfJcrYZO7UOg1As+qGY9cXQqVmosVv6YzEbi8seb9F7Yrc1zK7Zv5V0+T4r89Z3G7jvk/Wsj+6s81f+yEWPTufTmZ+yVwcNiy4iVWjRItTGjBwJf/gDXHMNnHwydOmS6shEkiKeJOa3wFQzm8vmJKMz0AMYlaS4ksbdxwHjAAoKCrwmo36lSk1HJ0uViuI8tNwxy4rWMWvh6tJR0mYtXMVOOxcwpKAdb362lNP++R4TR+7BoC7b8dXSH/hm+Rp6t29G27xGpYMNJCvWdJSIOIuLndXrNrJ67QZWr90YvcLy/r3b0aJxA975YhmT//sdVxzRh9wG2fzzzS+Z8N43pccXrdsY9/WWr3VmrNuOZz75rsrjmjbMZsbVQwE4b8JHfDz/e175/RAARvzjbd79cnmV7+/Wpmnp8SfdHZ5hPHxmmEvhqDve4Nvla8jOyiIny8iOXuvWZtEsz8jJMnbNb8mNx+1Sev0d2+Zx/oE9ATj7X9PYsKmYLDNyso3srKyQeGVlkZ0Vfg7o1JKf/6QTALe8OJsBnVtyQO/tWb+xmH+8+jnZ2eE6WRZ+ZmdnkR0tZ2UZBds3o19+CzZuKmbqrMX03qEZl7/zbmkCU2J9MTz3TTaXnTQkru9fROq5HXeEJ56Ar78OCYx7mDDz+ONht91SHZ1IwsTTsf8FM+tFaJ4V27H//QT3OZkPdIpZz4+2VXTMvGgIzhaEDv7xvFfSQOu8RuzdoxF792izxb7tm+dy+j7d6dYmTNz57P++Y8yLYW671k0bhhHSdgjz2vTeoRk9t8+jUU7aThuREMXurCpNPsr+XLV2I0N6taXTdk34ZP73jHvtC/4wrIBO2zXh6enzufHfs0ICsn4j7hWf/9n/24cWHVvw9bIfeHHGQn53UC9yG2TTonEDurfJo1luDs1yG0Q/c2jeuAHNo22/fWQ6S1av2+KcHVo25qqj+nLRsAI2FTsbi51idzZucjYVO5vc2VRc9i/1kft1Z/XazYnS+UN7sqRoXZn3bCx2iqPzbSouplnMhK1H7Vp2gsEDd9qeJavXhWtt2hzDdwvW0bptHpuKnbbNNjdnzIlqjEosK1rPD+s3hmtHr43llrOM0iTmwXe+ZmOxc0Dv7Vm7cRO3vFT9nIwj9+tOv/wWrNmwid88OI0/Hr4T3638scJjK9u+LcrUeck02aWknZIamO++g/vug5tuglNPpeERR6Q0LJFEiWt2Q3cvpmxzrWR4H+hpZt0ICcgJwEnljpkMnEro63Ic8LK7u5lNBh6O+ul0AHqyeRACyRA92uVxyaG9S9d/sUdXBnXZLprTJsxr8+A7X7NuY/gDODvL2LFtUx4/ey+a5Tbg2+VraJiTxfbNKx8vvy77GxQXOz+sD8lGRQnI6rUb2GvHNvTv1JJvl6/hyskzOGfIjuzWdTvemLuUs/81jaJ1G/EpL1Z6jb+dPJBO2zWhaN1G/jdvJavWhvZd7ZrlslePNqVJSPPcHJqXJiObk5KOrUJb6RE/6cyIn3QuPe+xA/M5dmDVI85dfthOZfrEADRukM0fhhWwXdOGbBcN2x2PnTuW7We1VwVJblVO2L1zmfXzhvas8LhQs7XlyD1jR/Qvsz7prD1rdP3pVxxcutysUQ5zrzu0TMJTHJsERYlVXm64/TZpkM1z5+1Du2a5/PPNr5hfQcLSoWX9aNOeyfOSabJLSVsdO8LcuaG/zK23MviRR2DWLLjwQvWXkYwWz+hknas7JrLS3VdtbSBRH5dRwBTCEMvj3X2GmV0NfODuk4F7gQejjvvLCYkO0XGTCIMAbATO1chkma9FkwbsuWNr9tyxdem2TcXOl0t/CEnNgtV8vXwNeY3CP+MxL87m/S+X89aloYnSpPe/BYOddmhOz+3zeOGThXF3RHd3fli/iVU/lk8+yjbJ6t+pJQf33YEf1m3ktH++x8mDuzB8QEc+W1zEQbe+WmkNSInLDjP6d2oJwOLVa1mzPsTWoWUuPxuUz/JF8+lX0KO0FqR8EtKqSUgU9ujemsI/7F963vLfWzKUfGelSWHLxuqETpiTqUG20SDOSsKc7KzSwTL+MKyg0sSwntC8ZCLJ0Lw53HADjBzJ8l/9irZ33gnnn5/qqERqJZ6amPvjOMaB+whzuGw1d38eeL7ctitiltcCx1fy3uuA62pzfUl/2VlGj3Z59GiXxxG7lN13+j7dOHKXzU057nnjC+YsKip9n0Hp4AElftywiZunzGb4gI4c//e32KdHW84/sCfrNhaz85VVTzWUnWX8eu+uHNx3BxrlZJX2uwBom9eIUfv3iKkJ2Zx4lNSMNMttQG6D0JG903ZNePb/9i09d/e2eYw+qi+FhUsYsl/3rf26km74gI4MH9AxY/oYpbv6nhjW5bxkIvVS9+7MuOoqhuy8MzRrBhs2wBlnwKhR8JOfpDo6kRqJJ4k5C5jjXt0zZZHU2iW/ZZn1f5+/H98sXxOaoy1YxV9e/qzC95X0N+jeJo92zUM/iUY5WVx+2E7kxSQezXJzSpOPZrk5NG6QXTrYQE52FhNHbm6C1KJJAy48uN48PZcEqs+JYV3NSyZS77WJmuzOnQtTpsADD8AvfxmanHWsHw9NJPPFk8Q8BnQxsznA/4CPS36mcydLkewso1ubpnRr05TD+rXn8Q/nV9nfoGSkKghNgs5M4xoQkW1UXc1LJiIAffrAnDlw/fUwdiw89lgYyezii6Fh/P0aRVKh2mnU3b0f0BY4mzBiTHfgMuB/ZrYwueGJJM4fhhXQuFxHhXrW30Ak3ZXMS1ZeouclE5ESzZuHJGbmTDjssJDIZG/bI3/KtiHe0cnWAe+bWZG7/1/J9mgoTJGMUN/7G4hkgN+yDc1LJpJRuneHRx+FoqKQxKxcCaecAn/6EwwuP/e4SOrFlcTEKNMvxt1XJDAWkaSrz/0NRNJdHc5LJiKVyQtztTF7NkybBnvsEZKZ66+H/KqH3hepS9U2JzOzO83sdDMbACRuynQREZFy3L3Y3d9x98ej1ztKYERSYPDg0F/m0ktDDU2vXnDVVVCslp2SHuKpifkv0B/4JdDMzD4ldLD8FPjU3R9JXngiIlJf1NW8ZCISp2bNwohlZ54ZOvt/8AFkVfv8W6ROVJvEuPu42HUzywf6AbsARwBKYkREJBHqbF4yEamBbt1g0iRYvz6sf/45/PrXcOONobmZSArUtE8M7j4PmAf8O/HhiIhIPaZ5yUTSWcmwy19/HZqa7bknnHxy6C/TqVNqY5N6J54+MZ3jfDWvi4BFRGSb9RjwvZl9YGbjzewCMxtqZu1SHVh1zOxIMxtXVFSU6lBEku+AA8JEmZdfHoZkLiiAa69NdVRSz8RTE6PqfRERSTp372dmjQjNlZ8HfiA0W+5rZrj7DikNsAru/gzwTEFBwZmpjkWkTuTlhcTljDNCf5nFMfOfu4NpLChJrnj6xOxfF4GIiIhoXjKRDNO1KzzyCGyKBhF87TW46CK47Tb1l5GkiqtPjJn1Bo6m7Lj9T7v7rGQFJiIi9ZrmJRPJJNnZ4efq1fDNN6G/zEknwQ03qL+MJEU8fWIuBiYS5oh5L3oZMNHMLklueCIiUl9oXjKRbcDhh4dO/3/8IzzxROgvM2ZMqqOSbVA8NTGnA33dfUPsRjMbS5gv5oZkBCYiIvWO5iUT2Rbk5cE114T+MpdcAjnRn5slE2VqrhlJgHiSmGKgA/B1ue3to30iIiK1pnnJRLYxXbrAhAmhoz/Agw/CnXeG/jJ77ZXS0CTzxZPE/BaYamZzgW+jbZ2BHsCoJMUlIiL1nOYlE9lGlIxU1qwZzJ8Pe+8NJ5wQJsvs3Dm1sUnGimd0shfMrBewO2U79r/v7puSGZyIiNQfZhbvXzMr3X1VUoMRkcQ79lg4+GC46Sa4+WZ46qnQX+bcc1MdmWSgapMYM8ty92LgnWr2i4iI1IbmJRPZ1uXlwdVXb+4v0zF6Pr5+feg7o/4yEqd4mpO9ZGZLgaeA59x9lZk1AQ4BjiG0V+6ftAhFRKRe0LxkIvVI587w8MOb1//8Z3juudBfZu+9UxaWZI54mpMNNbM+hHlinjOzhoQO/VOAW939wyTHKCIi9YTmJROpp3baCe65B/bZB0aMoNHw4amOSNJcXJNduvunhCEurzezxu7+Y3LDEhGR+iaal+xEwtxk70Wb8wnzkk10dw3pL7KtGjECjjgi9JW56SZ2f/JJWLsWTjst1ZFJmooriSnnUjPLAaYD0919TmJDEhGRekrzkonUZ02bwujRcPrpLP31r9l+113D9qIiaNJE/WWkjBr/a3D3K4Dbge+BY8zs7oRHJSIi9VHJvGTlaV4ykfqkUydmXn45DBgQ1keNgt13hzfeSG1cklbiGZ2sK3AusCOwnFAD84y7TyH0ixEREUmE36J5yUSkvGHDYOpU2Hdf+PnPw/wyXbumOipJsXhqYp4GZgF3AgcBuwKvmdmdZtYomcGJiEj94e4vAL2AqwgPyaYAo4GCaJ+I1EcnngizZoWmZs88A717wxNPpDoqSbF4kphsd7/X3acCy939TEKtzFfAuGQGJyIi9UfJvGPu/o67Px693imZWNnM1CBepL5q2hSuvBLmzIGTToI99gjbly6FYrU2rY/iKRD+Y2Yl1fgO4O4b3f1mYM9EBGFm25nZS2Y2N/rZqpLjTo2OmWtmp0bbmpjZc2Y2y8xmmJk6foqIZKaXzOwRMzvRzJpD6T3+WDN7EKjTIf3NbCcz+7uZPWZmZ9fltUWkEvn5MH48dOgA7nDssfCTn8Drr6c6Mqlj8SQxvwNamNkHQEczG2lmp5jZncCyBMVxCTDV3XsCU6P1MsxsO+BKYDCwO3BlTLIzxt17AwOAvc3s0ATFJSIidcTdhxKaknUlzEv2LqFM2IUwL1n/eM9lZuPNbLGZfVJu+yFmNtvMPjOzLcqacvHMdPezgJ8Dmn1PJB2dfTYsXgz77Rf6y3z5ZaojkjpSbRITVe1fB+wHnAnsAAwEPgESlSwcDdwfLd8PDK/gmGHAS+6+3N1XAC8Bh7j7Gnd/JYp1PeFJXX6C4hIRkTrk7p+6+/Xuvi8wxN33dPfRWzGx8n3AIbEbzCyb0L/zUKAPcKKZ9TGzfmb2bLlXu+g9RwHPAc/X9rOJSIKZhf4ys2fDVVfBc8+FSTOnTk11ZFIHzN2rPyh04L8I2AsoIiQKk9z984QEYbbS3VtGywasKFmPOeb3QK67Xxut/wn40d3HxBzTMortQHf/opJrjQRGArRt23bQpEmTEvERkqqoqIi8vLxUh1GtTIkTMidWxZlYmRInZE6s+++//zR33y0Z5zazqwmjaE5nK+Yli0bXfNbdd47W9wRGu/uwaP1SAHe/Po5zPefuh1eyT+VKkijOxMuUWLcmzoZLltB54kS+OPNMinNzabRwIevatoXs7CRFuW1/n6kSb7kS72SXNwNNCM28TgNaA+PN7G53/1c8JzCz/xBqccq7PHbF3d3Mqs+stjx/DjAB+EtlCUx0/nFEAxIUFBT4kCFDanqpOldYWIjiTKxMiVVxJlamxAmZFWuyuPsVZrY90J8wL1mPaHCZrdWRzUM3A8wjNFGukJkNAY4FGlFFTYzKleRRnImXKbFudZzHHx+a46xbB336QIsWcNttoblZEmzz32caizeJ2RU42t1Xmtnu7r53VDtTCMSVxLj7gZXtM7NFZtbe3ReYWXtgcQWHzQeGxKznR9cvMQ6Y6+63xROPiIikl3Sbl8zdCylbzohIpmjYEK67Di66CH76UzjuOLjpJujWLdWRSYLEO1zlzTHHLjWzscCpwLoExTE5Oh/Rz6crOGYKcLCZtYo69B8cbcPMrgVaECZKExGRzJTsecnmA51i1vOjbSKyrTGDE04I88tccw08/3yYX+ajj1IdmSRIXEmMuz/r7suj1eOBD4A84KQExXEDcFA0S/OB0TpmtpuZ3RPFsBy4Bng/el3t7svNLJ/QJK0P8KGZTTezMxIUl4iI1J1kz0v2PtDTzLqZWUPgBMJDtFozsyPNbFxRUVEiTiciidKkCfzxj2F+mUsvhV13Dds/+QQ2bUptbFIr8TYnKxWNAPZwIoNw92XA0Aq2fwCcEbM+Hhhf7ph5gCUyHhERSYn/mNkod7+DmHnJgJvNrKad+icQmiC3MbN5wJXufm8079kUIBsY7+4zEhG4uz8DPFNQUFCbPjsi9dpht7/OpwtWbd7wwnMA9GnfnOfP37d2J+/YEUaPDsvLl8M++0DXrqG/zDbWV6S+0OzHIiKSLhI2L5m7n+ju7d29gbvnu/u90fbn3b2Xu+8YTR8gImliYOeWNMgu+1y6QbYxsEuFc6BvvVat4B//gBUrYP/9w4SZnydkwF2pQ0piREQkLdTRvGRJoeZkIrV33tCeZFnZJCbbjPOG9kjshcxgxIjQX+baa+HFF8NIZt98k9jrSFIpiRERkbQRdeC/EDgb6AcsAV5095WpjKs67v6Mu4/MlHkYRNJRu+a5HD8ov7Q2pkG2cdxunWjXLDc5F2zcGC6/PPSXufVW6Nw5bH/rLfWXyQBKYkREJJ3cDHQhzEs2j83zkp2S0qhEpE7E1sYkpRamIh06wDnnhOXPPw9zygwaBK+8kvxry1ZTEiMiIulkV+D37v5fYHd3/z1hSP1zUxuWiNSFktoYg+TWwlSme3eYMAFWroQDDlB/mTSmJEZERNJJsuclE5E0d97QnvRslVU3tTDlmcHxx8PMmWGyzBdfhAED4Pvv6z4WqZKSGBERSRt1MC9ZUqhjv0jitGuey2WDG9d9LUysxo3hsstg7lwYPx5atAjbn3tO/WXShJIYERFJS+6+3t0fdvex7v5dquOpijr2i2yj2reH444Ly2+/DUccAQMHwssvpzYuURIjIiIiIlKtPfaARx+FVatg6FAYPpzG8+alOqp6S0mMiIiIiEh1zEKtzMyZcP31MHUq/S+4ADZsSHVk9ZKSGBERkVpSnxiReiQ3Fy65BObOZebll0ODBrBxIzz0UPgpdUJJjIiISC2pT4xIPbTDDqzs3z8sT54Mp5wSRjKbOjWlYdUXSmJERERERGrjmGPgscegqAgOPBCOPjqMbCZJoyRGRERERKQ2zOBnPwv9ZW64IYxe9vOfg3uqI9tmKYkREREREUmE3Fy4+OJQC3PffSG5WbUK7r5b/WUSTEmMiIiIiEgi7bAD7LprWH7oIRg5Evr3h5deSmlY2xIlMSIiIrWk0clEpFJnnQWPPw5r1sDBB8NRR8GcOamOKuMpiREREakljU4mIpUyg2OPDf1lbrwRCgvhd79LdVQZT0mMiIiIiEiyNWoEF10U+svccUfY9tVXcNdd6i+zFZTEiIiIiIjUle23h65dw/KDD8K554b+My++mNKwMo2SGBERERGRVPjjH+HJJ2HdOhg2DI44AmbPTnVUGSEn1QGIiIiIiNRLZjB8OBx6KPz1r3DNNXD77aGJWS0ddvvrfLpg1eYNLzwHQJ/2zXn+/H1rff5UU02MiIiIiEgqNWoEv/996C9zzTVh2zvvwJ13bnV/mYGdW9Ig28psa5BtDOzSqrbRpgUlMSIiIrWkIZZFJCHatYPWrcPyxIkwalToLzNlSo1Pdd7QnmRZ2SQm24zzhvZIRKQppyRGRESkljTEsogk3K23wlNPhf4yhxwChx8Os2bF/fZ2zXM5flB+aW1Mg2zjuN060a5ZbpICrltKYkRERERE0o0ZHH00zJgBY8bAG2/A5Mk1OkVsbcy2VAsDSmJERERERNJXo0Zw4YXw2Wdw/vlh2xNPhIEANmyo8q0ltTEG21QtDKRJEmNm25nZS2Y2N/pZYY8jMzs1OmaumZ1awf7JZvZJ8iMWEREREalDbduGhAZCjcx558Euu8C//13l284b2pOerbK2qVoYSJMkBrgEmOruPYGp0XoZZrYdcCUwGNgduDI22TGzYwH1qBQRERGRbds//xkSmU2b4LDDwquS/jLtmudy2eDG21QtDKRPEnM0cH+0fD8wvIJjhgEvuftyd18BvAQcAmBmecDvgGuTH6qIiIiISAqZwZFHwiefwC23wFtvwccfpzqqOpUuk11u7+4LouWFwPYVHNMR+DZmfV60DeAa4BZgTdIiFBERERFJJw0bwu9+B6edBq2iBkp//SsUF8M550CDBikNL5nqLIkxs/8AO1Sw6/LYFXd3M/ManLc/sKO7X2BmXeM4fiQwEqBt27YUFhbGe6mUKSoqUpwJlimxKs7EypQ4IbNiFRGRFNtuu/DTHV55BZ58Ev72Nxg7Fg49NLWxJUmdJTHufmBl+8xskZm1d/cFZtYeWFzBYfOBITHr+UAhsCewm5l9Rfg87cys0N2HUAF3HweMAygoKPAhQyo8LK0UFhaiOBMrU2JVnImVKXFCZsUqYbJL4MgOHTqkOhQRqc/M4PHH4bnnQg3N4YfDsGE0PumkVEeWcOnSJ2YyUDLa2KnA0xUcMwU42MxaRR36DwamuPvf3L2Du3cF9gHmVJbAiIiIJIMmuxSRtGEGRxwR+suMHQvvvUfOmm2vx0W6JDE3AAeZ2VzgwGgdM9vNzO4BcPflhL4v70evq6NtIiIiIiISq2FDuOAC+PZbVvfunepoEi4tOva7+zJgaAXbPwDOiFkfD4yv4jxfATsnIUQRERERkczTtGmqI0iKdKmJERERERERiYuSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDKKkhgREREREckoSmJERERERCSjKIkREREREZGMoiRGREREREQyipIYERGRWjKzI81sXFFRUapDERGpF5TEiIiI1JK7P+PuI/Py8lIdiohIvaAkRkREREREMoqSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDKKkhgREREREckoSmJERERERCSjKIkREREREZGMoiRGREREREQyipIYERERERHJKEpiREREREQkoyiJERERERGRjKIkRkREREREMoqSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDJKWiQxZradmb1kZnOjn60qOe7U6Ji5ZnZqzPaGZjbOzOaY2Swz+1ndRS8iItsqM2tqZh+Y2RGpjkVERDZLiyQGuASY6u49ganRehlmth1wJTAY2B24MibZuRxY7O69gD7Aq3UStYiIpCUzG29mi83sk3LbDzGz2Wb2mZltUdZU4GJgUnKiFBGRrZWT6gAiRwNDouX7gUJCwRFrGPCSuy8HMLOXgEOACcCvgd4A7l4MLE16xCIiks7uA+4AHijZYGbZwJ3AQcA84H0zmwxkA9eXe/+vgV2BT4HcOohXRERqIF2SmO3dfUG0vBDYvoJjOgLfxqzPAzqaWcto/RozGwJ8Doxy90UVXcjMRgIjo9V15Z/Spak2ZEZililxQubEqjgTK1PihMyJtSDVAVTE3V8zs67lNu8OfObuXwCY2UTgaHe/HtiiuVhUpjQl1PD/aGbPRw/Kyh+nciV5FGfiZUqsijOxMiVOiLNcqbMkxsz+A+xQwa7LY1fc3c3Ma3DqHCAfeMvdf2dmvwPGAL+o6GB3HweMi2L6wN13q8G1UkJxJl6mxKo4EytT4oTMidXMPkh1DDVQ0cOwwZUd7O6XA5jZacDSihKY6DiVK0miOBMvU2JVnImVKXFC/OVKnSUx7n5gZfvMbJGZtXf3BWbWHlhcwWHz2dzkDELiUggsA9YAT0TbHwVOT0TMIiIi7n5fqmMQEZGy0qVj/2SgZLSxU4GnKzhmCnCwmbWKOvQfDExxdweeYXOCM5TQhllERCTWfKBTzHp+tE1ERDJMuiQxNwAHmdlc4MBoHTPbzczuAYg69F8DvB+9ri7p5E8YBGC0mf2P0IzswjivOy5xHyGpFGfiZUqsijOxMiVOyJxYMyVOCGVHTzPrZmYNgRMID9ESKVO+D8WZWJkSJ2ROrIozsTIlTogzVgsVGSIiItsOM5tAqKFvAywCrnT3e83sMOA2wohk4939upQFKSIiW01JjIiIiIiIZJR0aU4mIiIiIiISl3qZxFQ2k3O6MbNOZvaKmX1qZjPM7PxUx1QRM8s1s/fM7L9RnFelOqaqmFm2mX1kZs+mOpbKmNlXZvaxmU1P9yFszaylmT1mZrPMbKaZ7ZnqmMozs4Louyx5rTKz36Y6roqY2QXR/6NPzGyCmaXlRItmdn4U44x0/S7risqUxFO5kniZUq5kQpkCKleSoablSr1sTmZm+wFFwAPuvnOq46lMNNx0e3f/0MyaAdOA4e6eVqOvmZkBTd29yMwaAG8A57v7OykOrULRXEK7Ac3dfYsJ7tKBmX0F7ObuaT8xlZndD7zu7vdEnaWbuPvKFIdVKQuzts8HBrv716mOJ5aZdST8/+nj7j+a2STg+XQb4tfMdgYmEiaPXA+8AJzl7p+lNLAUUZmSeCpXEi9TypVMK1NA5UoibE25Ui9rYtz9NWB5tQemmLsvcPcPo+XVwEzCZG1pxYOiaLVB9ErL7NjM8oHDgXtSHcu2wMxaAPsB9wK4+/p0L2wIw7B/nm4FTYwcoLGZ5QBNgO9SHE9FdgLedfc17r4ReBU4NsUxpYzKlMRTuVI/ZWiZAipXEqHG5Uq9TGIykZl1BQYA76Y4lApFVenTCROVvuTuaRknYVSii4AKZ95OIw68aGbTzGxkqoOpQjdgCfDPqCnFPWbWNNVBVeMEYEKqg6iIu88HxgDfAAuA7939xdRGVaFPgH3NrLWZNQEOo+z8K5Lm0r1MAZUrSZAJ5UomlimgciURalyuKInJAGaWBzwO/NbdV6U6noq4+yZ370+YPG73qFowrZjZEcBid5+W6ljisI+7DwQOBc6NmqukoxxgIPA3dx8A/ABcktqQKhc1TTgKeDTVsVTEwkS+RxMK8g5AUzM7JbVRbcndZwI3Ai8SqvynA5tSGZPELxPKFFC5kgSZUK5kVJkCKlcSZWvKFSUxaS5qC/w48JC7P5HqeKoTVfu+AhyS4lAqsjdwVNQueCJwgJn9K7UhVSx6coK7LwaeJLQRTUfzgHkxT0gfIxRA6epQ4EN3X5TqQCpxIPCluy9x9w3AE8BeKY6pQu5+r7sPcvf9gBXAnFTHJNXLtDIFVK4kSoaUK5lWpoDKlYSpabmiJCaNRR0b7wVmuvvYVMdTGTNra2Yto+XGwEHArJQGVQF3v9Td8929K6Hq92V3T7unEWbWNOp0S1SNfjChmjXtuPtC4FszK4g2DQXSrpNwjBNJ0yr/yDfAHmbWJPr/P5TQbyHtmFm76GdnQrvlh1MbkVQnU8oUULmSaJlSrmRgmQIqVxKmpuVKTl0ElW4sZiZnM5tHNJNzaqOq0N7AL4CPo3bBAJe5+/OpC6lC7YH7o9E5soBJ7p62w0xmgO2BJ8O9hhzgYXd/IbUhVen/gIeiKvUvgF+lOJ4KRQX3QcBvUh1LZdz9XTN7DPgQ2Ah8BIxLbVSVetzMWgMbgHMzpPNtUqhMSQqVK4mVSeVKRpQpoHIlCWpUrtTLIZZFRERERCRzqTmZiIiIiIhkFCUxIiIiIiKSUZTEiIiIiIhIRlESIyIiIiIiGUVJjIiIiIiIZBQlMSIJZmb5Zva0mc01sy/M7A4zaxTH+4oq2X61mR0YLf/WzJpUc55hZnaVmW1nZv/euk8hIiLpQuWKyJaUxIgkUDSR1BPAU+7eE+gJNAZu2tpzuvsV7v6faPW3QJWFDbAv8Fr0842tva6IiKSeyhWRimmeGJEEMrOhhInu9ovZ1hz4GugEHAfs5u6jon3PAmPcvTB6YnY3YSblhcAJ7r7EzO4DngU6AGOA2cBSd9+/3LVHAJcC3aPrbQ+sAj5196OS96lFRCRZVK6IVEw1MSKJ1ReYFrvB3VcBXwE9qnlvU+ADd+8LvApcWe48fwG+A/YvX9BE+x8BBgCfuHs/4GNggAoaEZGMpnJFpAJKYkTSRzHwSLT8L2CfrThHL+CLaLmpu69ORGAiIpKRVK7INktJjEhifQoMit0QVfvvQKiu30jZ/3e5VZyrRm09zewDYAowxMw+BQrMbLqZ7VuT84iISFpRuSJSASUxIok1FWhiZr8EMLNs4BbgDnf/kVD939/MssysE7B7zHuzCG2bAU6i4s6Tq4FmFV3Y3XcDngOOJnT4vNzd+7v767X+VCIikioqV0QqoCRGJIE8jJRxDHCcmc0FlgHF7n5ddMibwJeEJ2t/AT6MefsPwO5m9glwAHB1BZcYB7xgZq9UEsJAYDphBJlXa/dpREQk1VSuiFRMo5OJJJGZ7QVMAI5x9w+rO15ERKQqKldEAiUxIiIiIiKSUdScTEREREREMoqSGBERERERyShKYkREREREJKMoiRERERERkYyiJEZERERERDKKkhgREREREcko/w87GcOGAHra8gAAAABJRU5ErkJggg==\n",
+      "text/plain": [
+       "<Figure size 960x288 with 2 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "grad = np.array(grad_val)\n",
+    "means = np.array(means)\n",
+    "variances = np.array(variances)\n",
+    "n = np.array(selected_qubit)\n",
+    "print(\"We then draw the statistical results of this sampled gradient:\")\n",
+    "fig = plt.figure(figsize=plt.figaspect(0.3))\n",
+    "\n",
+    "\n",
+    "# ============= The first figure =============\n",
+    "# Calculate the relationship between the average gradient of random sampling and the number of qubits\n",
+    "plt.subplot(1, 2, 1)\n",
+    "plt.plot(n, means, \"o-.\")\n",
+    "plt.xlabel(r\"Qubit #\")\n",
+    "plt.ylabel(r\"$ \\partial \\theta_{i} \\langle 0|H |0\\rangle$ Mean\")\n",
+    "plt.title(\"Mean of {} sampled graident\".format(samples))\n",
+    "plt.xlim([1,9])\n",
+    "plt.ylim([-0.06, 0.06])\n",
+    "plt.grid()\n",
+    "\n",
+    "# ============= The second figure =============\n",
+    "# Calculate the relationship between the variance of the randomly sampled gradient and the number of qubits\n",
+    "plt.subplot(1, 2, 2)\n",
+    "plt.semilogy(n, variances, \"v\")\n",
+    "\n",
+    "# Polynomial fitting\n",
+    "fit = np.polyfit(n, np.log(variances), 1)\n",
+    "slope = fit[0] \n",
+    "intercept = fit[1] \n",
+    "plt.semilogy(n, np.exp(n*slope  + intercept), \"r--\", label=\"Slope {:03.4f}\".format(slope))\n",
+    "plt.xlabel(r\"Qubit #\")\n",
+    "plt.ylabel(r\"$ \\partial \\theta_{i} \\langle 0|H |0\\rangle$ Variance\")\n",
+    "plt.title(\"Variance of {} sampled graident\".format(samples))\n",
+    "plt.legend()\n",
+    "plt.xlim([1,9])\n",
+    "plt.ylim([0.0001, 0.1])\n",
+    "plt.grid()\n",
+    "\n",
+    "plt.show()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "It should be noted that, in theory, only when the network structure and loss function we choose meet certain conditions (unitary 2-design), see paper [[1]](https://arxiv.org/abs/1803.11173), this effect will appear. Then we might as well visualize the influence of choosing different qubits on the optimization landscape:\n",
+    "\n",
+    "![BP-fig-qubit_landscape_compare](./figures/BP-fig-qubit_landscape_compare.png \"(a) Optimization landscape sampled for 2,4,and 6 qubits from left to right in different z-axis scale. (b) Same landscape in a fixed z-axis scale.\")\n",
+    "<div style=\"text-align:center\">(a) Optimization landscape sampled for 2,4,and 6 qubits from left to right in different z-axis scale. (b) Same landscape in a fixed z-axis scale. </div>\n",
+    "\n",
+    "\n",
+    "$\\theta_1$ and $\\theta_2$ are the first two circuit parameters, and the remaining parameters are all fixed to $\\pi$. This way, it helps us visualize the shape of this high-dimensional manifold. Unsurprisingly, the landscape becomes more flat as $n$ increases. **Notice the rapidly decreasing scale in the $z$-axis**. Compared with the 2-qubit case, the optimized landscape of 6 qubits is very flat."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## References\n",
+    "\n",
+    "[1] McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. [Nat. Commun. 9, 4812 (2018).](https://www.nature.com/articles/s41467-018-07090-4)\n",
+    "\n",
+    "[2] Cerezo, M., Sone, A., Volkoff, T., Cincio, L. & Coles, P. J. Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks. [arXiv:2001.00550 (2020).](https://arxiv.org/abs/2001.00550)"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/Barren/BarrenPlateaus_Tutorial_CN.ipynb

-{
- "cells": [
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "# 量子神经网络的贫瘠高原效应 （Barren Plateaus）\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "\n",
-    "## 概览\n",
-    "\n",
-    "在经典神经网络的训练中，基于梯度的优化方法不仅仅会遇到局部最小值的问题，同时还要面对在鞍点附近梯度消失的问题。相对应的，在量子神经网络中也存在着一种**贫瘠高原效应**（Barren plateaus）。这个奇特的现象首先是由 McClean et al. 在 2018 年发现的 [1][[arXiv:1803.11173]](https://arxiv.org/abs/1803.11173)。简单来说，当你选取的随机电路结构满足一定复杂程度时，优化曲面（Optimization landscape）会变得很平坦, 从而导致基于梯度下降的优化方法很难找到全局最小值。对于大多数的变分量子算法（VQE等等），这个现象意味着当量子比特数量越来越多时，选取随机结构的电路有可能效果并不好。这会让你设计的损失函数所对应的优化曲面变成一个巨大的高原，从而导致量子神经网络的训练愈加困难。你随机找到的初始值很难逃离这个高原，梯度下降收敛速度会很缓慢。\n",
-    "\n",
-    "<img src=\"figures/barren.png\" width=\"680\" >\n",
-    "\n",
-    "&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;\n",
-    "图片由 [Gradient Descent Viz](https://github.com/lilipads/gradient_descent_viz) 生成\n",
-    "\n",
-    "本教程主要讨论如何在量桨（PaddleQuantum）平台上展示贫瘠高原这一现象。其中并不涉及任何算法创新，但能提升读者对于量子神经网络训练中梯度问题的认识。首先我们先引入必要的 library和 package："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 1,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "import time\n",
-    "import numpy as np\n",
-    "\n",
-    "from progressbar import ProgressBar\n",
-    "from matplotlib import pyplot as plt \n",
-    "from scipy.stats import unitary_group    \n",
-    "\n",
-    "import paddle.fluid as fluid\n",
-    "from paddle.fluid.framework import ComplexVariable\n",
-    "from paddle.complex import matmul, transpose   \n",
-    "from paddle_quantum.circuit import UAnsatz\n",
-    "from paddle_quantum.utils import dagger\n",
-    "from paddle_quantum.state import density_op"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 随机的网络结构\n",
-    "\n",
-    "这里我们按照原作者 McClean (2018)论文中提及的类似方法搭建如下随机电路（目前我们不支持内置的 control-Z 门，方便起见用 CNOT 替代）：\n",
-    "\n",
-    "<img src=\"figures/Barren_circuit.png\" width=\"400\" >\n",
-    "首先作用在所有量子比特上绕布洛赫球的 Y-轴旋转 $\\pi/4$。\n",
-    "\n",
-    "以上结构加起来构成一个模块（Block）, 每个模块共分为两层：\n",
-    "\n",
-    "- 第一层搭建随机的旋转门, 其中 $R_{\\ell,n} \\in \\{R_x, R_y, R_z\\}$。下标 $\\ell$ 表示处于第 $\\ell$ 个重复的模块， 上图中 $\\ell =1$。第二个下标 $n$ 表示作用在第几个量子比特上。\n",
-    "- 第二层由 CNOT 门组成，作用在每两个相邻的量子比特上。\n",
-    "\n",
-    "在量桨中, 我们可以这么搭建。\n"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 2,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "def rand_circuit(theta, target, num_qubits):\n",
-    "    \n",
-    "    # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "    const = fluid.dygraph.to_variable(np.array([np.pi/4]))\n",
-    "    \n",
-    "    # 初始化量子电路\n",
-    "    cir = UAnsatz(num_qubits)\n",
-    "    \n",
-    "    # ============== 第一层 ==============\n",
-    "    # 固定角度的 Ry 旋转门\n",
-    "    for i in range(num_qubits):\n",
-    "        cir.ry(const, i)\n",
-    "\n",
-    "    # ============== 第二层 ==============\n",
-    "    # target是一个随机的数组,用来帮助我们抽取随机的单比特门 \n",
-    "    for i in range(num_qubits):\n",
-    "        if target[i] == 0:\n",
-    "            cir.rz(theta[i], i)\n",
-    "        elif target[i] == 1:\n",
-    "            cir.ry(theta[i], i)\n",
-    "        else:\n",
-    "            cir.rx(theta[i], i)\n",
-    "            \n",
-    "\n",
-    "    # ============== 第三层 ==============\n",
-    "    # 搭建两两相邻的 CNOT 门\n",
-    "    for i in range(num_qubits - 1):\n",
-    "        cir.cnot([i, i + 1])\n",
-    "        \n",
-    "    return cir.U"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 损失函数与优化曲面 \n",
-    "\n",
-    "当我们确定了电路的结构之后，我们还需要定义一个损失函数（Loss function）来确定优化曲面（Optimization landscape）。按照原作者 McClean (2018)论文中提及的，我们采用 VQE算法中常用的损失函数：\n",
-    "$$\n",
-    "\\mathcal{L}= \\langle{0} \\lvert U^{\\dagger}(\\boldsymbol{\\theta})H U(\\boldsymbol{\\theta}) \\lvert {0}\\rangle\n",
-    "$$\n",
-    "\n",
-    "其中的酉矩阵 $U(\\boldsymbol{\\theta})$ 就是我们上一部分搭建的带有随机结构的量子神经网络。对于其中的哈密顿量 $H$ 我们不妨先取最简单的形式 $H = \\lvert {00\\cdots 0}\\rangle\\langle{00\\cdots 0} \\lvert$。设定好这些后，我们就可以从最简单的两个量子比特的情形开始采样了 -- 生成 300 组随机网络结构和不同的随机初始参数 $\\{\\theta_{\\ell,n}^{(i)}\\}_{i=1}^{300}$。每次计算梯度都是按照 VQE 的解析梯度公式计算关于**第一个参数 $\\theta_{1,1}$**的偏导数。然后统计得到的这 300 个梯度的平均值和方差。其中解析梯度的公式为：\n",
-    "\n",
-    "$$\n",
-    "\\partial \\theta_{j} \n",
-    "\\equiv \\frac{\\partial \\mathcal{L}}{\\partial \\theta_j}\n",
-    "= \\frac{1}{2} \\big[\\mathcal{L}(\\theta_j + \\frac{\\pi}{2}) - \\mathcal{L}(\\theta_j - \\frac{\\pi}{2})\\big]\n",
-    "$$\n",
-    "\n",
-    "具体推导请参见：[arXiv:1803.00745](https://arxiv.org/abs/1803.00745)"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 3,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "主程序段总共运行了 12.4281587600708 秒\n",
-      "采样 300 个随机网络关于第一个参数梯度的均值是： 0.005925709445960605\n",
-      "采样 300 个随机网络关于第一个参数梯度的方差是： 0.028249053148446363\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 超参数设置\n",
-    "np.random.seed(42)        # 固定 Numpy 的随机种子\n",
-    "N = 2                     # 设置量子比特数量 \n",
-    "samples = 300             # 设定采样随机网络结构的数量\n",
-    "THETA_SIZE = N            # 设置参数 theta 的大小\n",
-    "ITR = 1                   # 设置迭代次数\n",
-    "LR = 0.2                  # 设定学习速率\n",
-    "SEED = 1                  # 固定优化器中随机初始化的种子\n",
-    "\n",
-    "# 初始化梯度数值的寄存器\n",
-    "grad_info = []\n",
-    "\n",
-    "class manual_gradient(fluid.dygraph.Layer):\n",
-    "    \n",
-    "    # 初始化一个长度为 THETA_SIZE 的可学习参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
-    "        low=0.0, high=2 * np.pi, seed=1),dtype='float64'):\n",
-    "        super(manual_gradient, self).__init__()\n",
-    "        \n",
-    "        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "        self.H = fluid.dygraph.to_variable(density_op(N))\n",
-    "        \n",
-    "    # 定义损失函数和前向传播机制    \n",
-    "    def forward(self):\n",
-    "        \n",
-    "        # 初始化三个 theta 参数列表\n",
-    "        theta_np = np.random.uniform(\n",
-    "            low=0., high= 2 * np.pi, size=(THETA_SIZE))\n",
-    "        theta_plus_np = np.copy(theta_np) \n",
-    "        theta_minus_np = np.copy(theta_np) \n",
-    "        \n",
-    "        # 修改用以计算解析梯度\n",
-    "        theta_plus_np[0] += np.pi/2\n",
-    "        theta_minus_np[0] -= np.pi/2\n",
-    "        \n",
-    "        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "        theta = fluid.dygraph.to_variable(theta_np)\n",
-    "        theta_plus = fluid.dygraph.to_variable(theta_plus_np)\n",
-    "        theta_minus = fluid.dygraph.to_variable(theta_minus_np)\n",
-    "        \n",
-    "        # 生成随机目标，在 rand_circuit 中随机选取电路门\n",
-    "        target = np.random.choice(3, N)      \n",
-    "        \n",
-    "        U = rand_circuit(theta, target, N)\n",
-    "        U_dagger = dagger(U) \n",
-    "        U_plus = rand_circuit(theta_plus, target, N)\n",
-    "        U_plus_dagger = dagger(U_plus) \n",
-    "        U_minus = rand_circuit(theta_minus, target, N)\n",
-    "        U_minus_dagger = dagger(U_minus) \n",
-    "\n",
-    "        # 计算解析梯度\n",
-    "        grad = ( matmul(matmul(U_plus_dagger, self.H), U_plus).real[0][0]  \n",
-    "                - matmul(matmul(U_minus_dagger, self.H), U_minus).real[0][0])/2  \n",
-    "        return grad\n",
-    "\n",
-    "# 定义主程序段\n",
-    "def main():\n",
-    "    \n",
-    "    # 初始化paddle动态图机制\n",
-    "    with fluid.dygraph.guard():\n",
-    "        \n",
-    "        sampling = manual_gradient(shape=[THETA_SIZE])\n",
-    "        \n",
-    "        # 采样获得梯度信息\n",
-    "        grad = sampling()   \n",
-    "        \n",
-    "    return grad.numpy()\n",
-    "\n",
-    "\n",
-    "# 记录运行时间\n",
-    "time_start = time.time()\n",
-    "\n",
-    "# 开始采样\n",
-    "for i in range(samples):\n",
-    "    if __name__ == '__main__':\n",
-    "        grad = main()\n",
-    "        grad_info.append(grad)\n",
-    "\n",
-    "time_span = time.time() - time_start        \n",
-    "print('主程序段总共运行了', time_span, '秒')\n",
-    "print(\"采样\", samples, \"个随机网络关于第一个参数梯度的均值是：\", np.mean(grad_info))\n",
-    "print(\"采样\", samples, \"个随机网络关于第一个参数梯度的方差是：\", np.var(grad_info))"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 优化曲面的可视化\n",
-    "\n",
-    "接下来我们试着利用 Matplotlib来可视化这个优化曲面（Optimization landscape）。在**两个量子比特**的情况下，我们只有两个参数 $\\theta_1$ 和 $\\theta_2$, 并且第二层的随机电路电路总共有9种情况。这个很容易画出来：\n",
-    "\n",
-    "<img src=\"figures/landscape2.png\" width=\"1000\" >\n",
-    "\n",
-    "可以看到的是最后一张图中 $R_z$-$R_z$ 结构所展示出的高原结构是我们非常不想见到的。在这种情况下，我们不能收敛到理论最小值。如果你想自己试着画一些优化曲面，不妨参见以下代码："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 4,
-   "metadata": {},
-   "outputs": [
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAApoAAAEBCAYAAADYRQXiAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOz9d5QkWV6YDT83TNpyWd51tZ323TNtZ1kEuywsRgKtJF6JFwT6AB0hQJwFPkCrD4QT6ABCEgi7EgjBajFCEsIIu57dZWa7Z6a9qy7vbXoT9t7vj8jMzqqp6jLdPd09G885eaoyI+LGDXfvL35WKKUICQkJCQkJCQkJedxoT7sDISEhISEhISEhb09CQTMkJCQkJCQkJOSJEAqaISEhISEhISEhT4RQ0AwJCQkJCQkJCXkihIJmSEhISEhISEjIEyEUNENCQkJCQkJCQp4IT0XQFEIMCSGKQgh9l9sXhRAHnqU+PQsIIZQQ4tDT7sd2EEL8pBBiRQix8LT7EhIS8vwTzitPhnBeCXlUtiVoCiG+WQhxQwhRFkIsCCF+VQjRtt2dCCEmhBBfVvuulJpSSjUppfxd9JnqtmO72fZJ9WmLfT03D+pbgRBiD/B9wHGlVO9jalMJIUrVQX1WCPEfdzO4CyH2VdsqVj8TQoh/tcs+/ZgQ4sO72TYk5O1OOK88GuG8spZneV6ptvVuIYSstlUQQtwTQnzLLttac58962wpaAohvg/4GeAHgFbgHcBe4CNCiMiT7V7I25S9wKpSammnGwohjIcsflEp1QS8C/g64Ft32T+Atmpb/w/ww0KI9z5CW0+FLc5VSMhTI5xXQp4Az8O8MldtqwX4XuDXhBBHHqG9p8KO5xal1KYfgpNRBP7Rut+bgCXgW6vffwz4X8D/AArAGwQXB+C/AxKoVNv6l8A+QAFGdZ1PAj8J/E11nT8BOoDfBvLAZWBfw/4VcAjor65f+5SDQ1IAB4GPA6vASrWtth30qR/4YyANjAD/rGH/Pwb8PvCh6vHeAs4/5Dwq4NAGv2/ax+ryCeD7getArnp+Yw3LfwCYB+YIbv76foC/Ddyu9m8W+P6G7d4HXK2e21HgK6u/fwtwp7rNGPDPG7Z5NzAD/GC1rxPAP25YHgX+PTAFLAIfBOIbHPOXVc+7rJ7736z+/ner5zFbvR+OrTsPH6ieB7t2jR52jqvX55er/UoDpxqWdVf70LVBO2vug+pvl6rnupfgHutoWHYOWAbMDdr6MeDDm9wT/6p67gvV6/T3G87jQ/sLfHX1+mUJnpnTOzlX4Sf8PM0P4bwSzisPtnk3z+G8Uv2/vdr3r2m4f0eAf7LJ9Xo3MLPutyXgH1b//5esve/c2nFs0NYE8GUb/J4C/i/BnJSp/j9YXfYPgdfXrf99wB9uda4brtMHgAXgv+/omd9iQPhKwNvkAvwW8LsND4hLoP0xCW7icaqT7/qTwsYDwgjBA9JKcCMPV28eg+DB+2/beMB+u6FPh4D3Vk9eF/DXwM9vdqE26NOngF8BYsBL1Qv3pQ3HaxE8dDrwU8CruxgQttPHSwSDUzvBw/rtDddmETgJJIHfYe2AMA98UcPNd7b6/0WCweW9BBrtAeBoddnfqV4DQfD2Vm7Y7t3Ve+E/Vvv7LqAEHKku/3mCAbQdaCYY1H9qOw8ccLja1nsJ7p9/Wb0fIg3n4Sqwhw0GmfXnGDhaPf7vrX7/FeBnGtb9buBPNmln/X3wjup5qAmCfwZ8R8P6Pwf84iZt/RibC5r/sHpdNYK35BLQt1V/gbMEg9PLBPfe/6d6fqLbPVfhJ/w8zQ/hvBLOK2+DeaX625cTCF7dwK8B/+sh16vev+o5+rsEgvGZDdbdQyDo/+1N2ppgY0GzA/haIFE9X/+TtYJkmrXC9hXga7c61w3X6Weq7exobtlqQPhGYGGTZT8NfKThAXm1YZm27oZcc1LYeED4oYbl/wH484bvXwNcfdgDRiBpv/6QG+bvAVe2MyBUL7IPNDcs/ykevCX9GPDRhmXHgcpOB4Rt9vEbG77/O+CD1f9/A/jpdQ9V40MxBfxzoGXdPv4z8HPbujngD4HvXnejJRuW/z7wwwQDSAk42LDsC4DxrR646vcfBn5/3f0zC7y74Tx86xZ9VQRv0qXq/7/LA+HrZWAa0KrfX2OdNmWD+yBL8IasCN7yRHX51wGfrf6vEwwyFzdp68fYRNDcYN2rwPu26i/wq8BPrNv2HvCu7Z6r8BN+nuaHcF4J55W3wbzSsM4vAjcIBMOOh7T1bgLBMkugQfWB79lgvXj1nvvAQ9pac589ZL2XgEzD918F/m31/xMEWs/oVue62neHBs33Tj5b+WiuAJ2b2OP7qstrTNf+UUpJAjVr/xbtN7LY8H9lg+9Nm20ohPgqAq3P31NKVaq/dQshfq/qwJsHPgx0brMv/UBaKVVo+G2S4C2tRmNUWxmI7dRvYZt9XL+f2nnop+GcV/vXyNcSvBlPCiE+JYT4gurvewjMGhv156uEEK8KIdJCiGx1+8b+ZJRSpXX77Cd4a04ArwshstVt/6L6+3bob+x/9f6ZZu35nl6/0QacJTg/X0cgrCWr7X2O4CF6lxDiKMEb/x9Xj7nY8BlqaKuz2tb3EzxkZvX3PwKOV6NT3wvklFKXtnmcdYQQ/0QIcbXhfJ2s7vOh/SXwQ/q+2nbVbfew9lnbzrkKCXlahPPKA8J55TmdVxr4LwTj939TSq3CmmwDRSFEsWHdOaVUG4H7yC8A79lgf/8VuKeU+plt9G0NQoiEEOI/CyEmq9f+r4G2hgCm3wK+QQghgG8iEMRttneul5VS1k77BFsHA71CIHn/g3UHkwS+CvhYw897GpZrwCCBhA/Bm8AToepI+1sEGp/Gm+anqvs9rZRqIXiLFg3LH9anOaBdCNHc8NsQwdvQ42SrPj6MeRrOOUH/6iilLiul3keg0v9DgrdECB6sg+sbE0JEgf9NoL3rqT4Mf7auP6nqtW/c5xzBxFABTiil2qqfVhU4PW+HOQIBqtYXUT22xvO9rXtIBfw+wb37Iw2Lfovg/H4TgXnDqq7f1PCZWteWr5T6DwTmrO+s/mYRnMt/XG3rv2/zGOsIIfYSmFm+i+ANuA24ydpzvWF/Ca7fv204z21KqYRS6ncbu77TPoWEvIWE88oDwnnlOZ5XqgLcfyZww/iOWhYA9SDbQNNG/a0Kdx8ATgkh/l5De/8KOAL8020e43q+r7r9y9Vr/8W1pqv7fZVAM/lFwDfwYP7azrne9fP2UEFTKZUDfhz4RSHEVwohTCHEPgK7/wxrJ9lzQoh/UH37+h6CgeTV6rJF4LHmJwMQQrQQaJj+tVLqM+sWNxM41GaFEAMEDs6NbNqn6sDyN8BPCSFiQojTBBf+tx+hu5FqW7WPvo0+PozfB75ZCHFcCJEAfrS2QAgREUL8YyFEq1LKJVD919Jr/FfgW4QQXyqE0IQQA1WtWYRAhb4MeNW3+S/fYL8/Xm3/iwiCUv5n9U3x14CfE0J0V/swIIT4ih0cy9+p9skkeFhsgmuwW34a+DYhRC3NxX8H/j7BoPuhXbT1L4UQser3DwHfTOBjs1X6Im3ddY8SvBErgnONCFJcnFy33Wb9/TXg24UQL4uApBDi76ybvEJCnlnCeSWcVzbY7/M6r/xg9e+3EgjTHxLbTH+klHII3Dl+BOoa9PfToEHfAnPdtTcIrn2F4Nq303D9GvgQ8EuAV7u/H8O5fihbpjdSSv07gpP57wlurM8RvL18aVUqr/FHBKrlDIEW5h9Ub0YI3rD+dVUl+/2Po+NVzhJI7/9RvFlN/ePV5TngT4E/WLftVn36egL/mjng/wA/qpT6yCP09RbBDVD7fMs2+rgpSqk/J3De/TiBg/PH163yTcBEVX3+7QQCC1Uz77cQBLHkCJzT91bNOe8neDgzBG87f7yuzYXqsjmCwfHblVJ3q8s+UO3Hq9V9fpTg2mznWO5V+/eLBG9WX0MQyedsZ/tN2rxRPbYfqH6fIYhaVcCnd9jcnxIc9z+rtvVZAl+bN5RSE1ts+/Wsve6jSqnbBAPMKwQT0yngs+v6v2F/lVKvVfvxS9U+jRAIvSEhzw3hvBLOKw08l/OKEOIc8P8liDL3CQJlFEFGke3yG8CQEOJrCO7zLuBOw333wYds+2esvfY/RnDt4gTH+yqB+Xs9/51AsbHeGrfrc70VtQCHR2tEiB8jcBb+xkduLOSZRAjxboLAlsGn3JVdI4T4DQIfmX/9GNr6OPA7Sqlff/SebbqPx9bfkJDnjXBeefvzdphXnjeEEHGCzCVnlVL334p9hgmdQz4vqJrm/gFw5jG0dYFAY/C+R23rIfvYx2Pqb0hISEhISJXvAC6/VUImPKVa5yEhbyVCiJ8gCLb5WaXU+CO29VsEJoXvUWujRx8bj7O/ISEhISEhEJSuJMik8H1v6X4fh+k8JCQkJCQkJCQkZD2hRjMkJCQkJCQkJOSJEAqaISEhISEhISEhT4THHQwU2uFDQp4s2028HBLydiGcV0JCnixPdF4JNZohISEhISEhISFPhFDQDAkJCQkJCQkJeSKEgmZISEhISEhISMgTIRQ0Q0JCQkJCQkJCngihoBkSEhISEhISEvJECAXNkJCQkJCQkJCQJ0IoaIaEhISEhISEhDwRQkEzJCQkJCQkJCTkiRAKmiEhISEhISEhIU+EUNAMCQkJCQkJCQl5IoSCZkhISEhISEhIyBMhFDRDQkJCQkJCQkKeCKGgGRISEhISEhIS8kQIBc2QkJCQkJCQkJAnQihohoSEhISEhISEPBGMp92BkIejlML3fSqVCqZpYhgGuq4jhHjaXQsJCQkJeQ5RSuG6LrZth/NKyBMnFDSfYZRSOI6D7/v1Tw1d18MBIiQkJCRkR0gpcV0Xz/Pqn9r8YRgGpmmi63o4r4Q8NoRS6nG291gb+3xGSonjOCilEELgOE79oVdKoZRCSokQgrm5Ofbs2RMKnp8fhBc25PONcF55DNSsY67r1n9zHAdN0+rLax/f91leXmZwcLA+r2iaFs4rb1+e6IUNNZrPGEqpNW+Zmqax/mVACFFfBjA/P8/AwACVSqU+EIQaz5CQkJAQeGAq932/Pn9IKdesU/sdAkXH0tISfX19eJ5XX24YRv0TCp4h2yUUNJ8haqbymqZyuw9xTehsfDOVUq4RPBsHiFDwDAkJCfn8YL11bDtjvxACpVR9ToEHSpCaRjQUPEO2SyhoPiNYloXjOJimuSMhcyPWazxrppDamyk88MUJB4iQkJCQtx9KKSqVCr7vY5rmGqFxN6yfl2pa0vWCZ83HM5xXQmqEguZTpvaWOD8/T6VS4eDBg499HxsNEI2C5/LyMn19faHgGRISEvI2oGYdGxkZIZVK0d3dvWa5lJKRkRFWV1dJpVKkUilaWlrQdR14oNF8GEKI+vq1fTYKnktLSwwODtataOG88vlLKGg+RWrRf1LKR37b3AnrBc/p6Wm6urpCX5yQkJCQ55xGU/lG80qlUuH69et0dHRw4sQJ8vk8+cw1VuanKdrHaWtrp7W1dUtBcz3rBc/p6Wm6u7uxbbs+59SUGYZhPLLlLuT5IRQ0nwLro/9qgtxjzgCwIxqFydAXJyQkJOT5YqNA0vXzyuLiIiMjIxw/fpzW1lZc16U/dRmj6XdQIgby/7JQ/jYWFvspFotcvXq1rvFsbm7e0bi/kcbTcZw3CZ41U3soeL59CQXNt5iNov9ge6aKt4rQFyckJCTk+aHROrbRvCKl5O7du1iWxYULF4hEIki/SMT+9+hqHE1NoWQFV3+ZzvjPkzrwNZRKZzl69CiZTIaZmRmKxSKxWKwueCaTyV0LnrW5znEcHMcBAmXH+nkl5O1BKGi+hTws+u9ZEjTXs5UvjmVZRKNRkslkaBIJCQkJeYtYbx3baF6xLItLly7R19fHsWPHguX+MEb5gwj/DTRW8RjC1frR/E8DSTTvIwx13ScWO09fXx99fX314KJsNsvk5CTFYpFEIlEXPBOJxI4ypQAPFTxLpRLNzc3E4/FQ8HzOCQXNt4CNTBrr2Shf5rPKesFzeXmZWCxW/65pWmgSCQkJCXmCrJ9XNhpjC4UC2WyWl156idbWVgCE/UfolV9DqEkUERztC5H+TTQ1itTOo8nXUHIKTB3b+i9EY98WbCcEiUSCRCJBf38/SinK5TKZTIaxsTHK5TJNTU11wXMn89lGgufU1BR79+6t5/sMNZ7PL6Gg+YTZbm7MjRLoPk/UBoHGN9OaL044QISEhIQ8PjYzldfwPI87d+5QKpXYv39/IGSqIlr559Gd/4FC4Gtn8HwN5f81aC+gpI0mX8MT76DMEpH4MI67hK4fxDC/9E19EEKQTCZJJpMMDg6ilKJYLJLNZrl//z7lcpnbt2/XBc9GZcRWNAqeuq7XKxatN7U3FiUJ55Vnl1DQfIL4vk86nWZqaooTJ048VKv3LJvOt6LmCgDbM4mEgmdISEjIzqmZyqempvA8j717975pnUKhwI0bNxgaGqKlpSUYX73bGKXvR8hppH4MKRU+eRQrIPYh5D2U2I8t91JRNxDiALpeQtBBpfJjJPWTaFrPQ/smhKC5uZnm5mb27NnDpUuXGBwcJJPJcPfuXRzHoaWlpS54RiKRLY+1cV5ZHzeglMK2bWzbBh5Uw9N1ve7CFfJsEAqaT4D1Jo3aW+fDeFRBs/GhfBrbb8Z2BU8pJclkMhQ8Q0JCQjag0ToGvMkCppRienqa2dlZTp8+TVNTE1NTUzTrf4BR+E3QhpDaMaRS+GoBxBCCuyhVRvICFZJ4Io+SeZS6gmUNEYtNoWkXKFq/TEvi3+yov0IIWlpaaGlpqZvA8/k8mUyGubk5PM+jtbWVVCpFW1sbpmnuqO31gqeUEsuy6r/VglRrPp6h4Pn0CAXNx8x6k0ZNiNqKp6nRfCsfwI0ET6UUr7/+OufOnQNCk0hISEhII+sDSXVdXzOvuK7LzZs3iUQiXLx4MRhfZY7e+E9gilmUfgK863jGSyh8UBnwl5HaeZQcpYyOL+dRagpNP4/0X0M38sAARelg+bfA/j+0RP/+ro9B0zTa2tpoa2sDAotfLpcjm80yNTWFUmqN4LkTNhI8Lcvi3r17nDp1Cnig8QzLML/1hILmY2Kz6L/tCpCPImjWtn1aD86j7LvxPDX64jSaRBoFz9AkEhIS8vnCZoGkjfNFNpvl1q1bHDx4kN7e3mC5dwWt/HNowsXU5lB+Gdc4A94wkAb9OPijeDKPJfbj+68gRB/QgvRfQ9NexPNWsY19FP1XMbR+Vsq/QNL8EnSt7bEcm67rtLe3097eDgR+pblcjkwmw8TEBOVymampKbq6umhtbV0TgLoVjWWYa/PKeo1nKHi+dYSC5mNgs9yYsP1o8sdhOn87EPrihISEhDw8kLTmkjU+Ps7S0hJnzpwhkUiAUmjWf0N4n0H4d4nrFQrOaSIxG7xXQXQBAyjvDrbxt6i4nwQUmnYCKW+haS8i5XVckmTENJr/KlHtOLa8Tdy4wKr1y3QnfuiJHK9hGHR0dNDR0QHA1atXaW5uZnV1ldHRUXRdp62tjVQqRWtr65aWrq18PKWUVCqVNVa2UPB8MoSC5iPysNyYsP1o8kfVaD5NnqQ2dTu+OOEAERIS8nZifWW29WOa7/vMz8/T29vLhQsXAqFLrqJVfhnN+XMERSTdFNyTRIxXwI+A/iL415Dafsrai7juR9G080j5GlLOAu1IOYYlvoSs+9dI9xCakcdXGcDA8m7i+DO0RL6RmPHmIKTHjRCCjo4O+vv7gcCvP5vNsrS0xMjICIZhrKlatF7wfNi81KjxrK0bCp5PjlDQ3CWNpvLNcmPC9gXIh62Xz+cZGRmhqamJ9vb2Nz1Uz3PE+k7ZTPDMZrPMzMxw6NChcIAICQl5LtlObszV1VWGh4dpaWnhyJEjwY/uZYzSjyDUDIpmPO1lfLVI1PgbKu5J4uZN8G/hGl9Iyb2KEGUgiZSvoelnkP4V0L+AtDeFJ6+gkcKIj9S1mTH9PI4cxhYvcq/0X3mxdWeBQbul8fgjkQjd3d10d3cDYNt2PbCoUCgQjUbrgmdTU9OOFCCbCZ5zc3NYlkV/f/+aMszhvLIzQkFzFyilSKfTFAoFent7H3rDPUowUGMU4aFDh6hUKmseqvb29h0nxn0SPE3/0MbB2PO8+vkO30xDQkKeJ6SUzM/P103E68cpKSWjo6Nks1mOHj3K6uoqKB+t8l/Q7A8CMaR+Hl/aSHkdtL1IFSdu3kTpF7DwsZxX0PU9+P4wcBK4ie/dwxfvZNV5g6h+CimvENNfwvIzSIqAhq8qLPv7KfqvE9V6yLvDtJiHn+j52Gpei0aj9Pb21v1Sa1WLpqenKRQKRCIRPM+jWCzuqlxmbU72fR9N0/B9H8/z6uvUUvQZhhGWYd6CUNDcITUtZqVSIZfL0dfX99D1d6vR9DyPW7duoes6Fy5cQEpJa2vrmocqnU4zMTFBoVDgzp07dHR0kEqliMfjj3aQbzGPQ1BudF0ITSIhISHPC43WsZqAlEql1qxTqVS4ceMGHR0dnD9/nlwuhyFW0Yv/FOHdQxlnwRvBw0eRBpLg30CyH8cv4oo0iCaggpQrSNWGJm7i+WcoejYlfwk96mG590G0YPlX8ewBiE6ha1/OiH2NNvMkyp8hqnUwWvoNzrT99BM/LzshHo8Tj8fr5TJXVlaYmppiYmKCUqlEMpmsazzj8fi2xn0pZV2IXG9JaxQ8hRBrNJ6h4LmWUNDcJutNGoZhbEtTuRuNZi3h7r59++qlvta3EY/HGRgYYGBggDfeeIM9e/aQz+cZHh7Gtm2am5vrGs+tEuM+Ks9CDs/agLCe7QieoUkkJCTkabA+kHSj4NGlpSXu37/P8ePH6wJohFc52PEfQfUDBvjTuFpfkLZIToBoB7EHV2oUvFZMcReQaNpppLyO5x0iEklR1Aq4ZhndWCKqvYTNVXCPg3kb6WvknJcoiFFAI+fewRQpct5t4loPBW+UZuPgEz0/j5LNJBqNkkwmOXr0KEopSqUSmUyG0dHRN5XL3Ew5s9W8UqMmHzT61YaC5wNCQXMbbFTuayfR5NuhJpBOT08zMzNTT7hb42HCmKZpJBIJ2traGBoaQkpJoVAgnU4zOzuL7/v1aL22tjYM49m67I9D0NxuGxsJnjVtgu/7rKysMDg4GJpEQkJCnigbBZI2KiaklNy7d49KpcKFCxcChYFy0Sq/REJdQYkymv86nn4GXynwLwMm6KdR3g0s4wUq/l1McwnDuIjnXcJ1R9G0FJFYO3lfx5KXieon8f0lPDWFIIEy7xHRzzFHBp0YHtPolQP48TGi/n5cLUNE62Si9Nucav2Rp3sSH8L6qPOmpiaamprYs2dPvVxmJpNZo5ypCZ7RaPRNbTyMhwme5XIZ27bp7u7+vBU8ny2J4xljs9yYtf8fZ21yz/MoFArEYrEHCXd3iaZptLa20trayv79+/F9n2w2W89PJoSoP1Ctra2P3PdnWaO5FY0DvOu6pNNp+vr61phEGk3tn28DREhIyONls9yYQH0cKpVK3Lhxg97eXo4ePRqMOf4MmvXLaM4r6KziiiSO8S6U+9FgY+MCeJeR/jwV/WUc91MIhpAqiuddolI5RDw+i6ufZdX5FJpoQqMD279JVD+J7d8kpp/HQ7HkJ3DMCeJ6E/gCLbGCVFEsMY6QSXKVWcZcnVjxJoPtB5+Iu9aTnFeEeFAus1E5k8lkuH37Nq7r0traiu/7NDc373jfjbKCZVkUi0VSqdSbNJ6NZZjfzvNKKGhuwlbRf9s1iW+HQqHA9evXMQwjqGLg24jJP0Rb/AwqeRB/6O9BpGvT7bfyA9V1fU1+Mtd1yWQydZNMpVJhamqqHtH+Vt/wb6VG82HUhNXGgT/0xQkJCXlcPCw3JgTzSjabZW5ujhMnTtQVAcL5BHr5pxBqHkUUm5exvHFi2kdBfwn8m+BdxjW+mJL7Osp7DU3bi5STWJUXSCTuk0ga5NVhSs6niJtnqbhvENUPYvur+CqNIElJRll0l3DUBJrdSyU6S6txkpx3kzbzRbLuNVoiF7lZmqEl2sp995OUh31s295RHfO3gp3MCY3KmX379iGlJJfLMTk5yezsLAsLC7sul1mbVxqVRzWXCcdx6vfB+qIkb6d5JRQ0N2AjU/l6HpegOTMzw9TUFCdPnuTu3bvgFtBf+26EV0QUZpCeg375EtrBb0P2XngsN59pmmvSRFy6dIlIJMLMzAyFQoFEIlEfMBKJxJb7fJ41mlu1EfrihISEPA5q1rHNci57nsf09DSu6/Lyyy8HLk7KQSv/R3Tnt1FEkMY5fN9DyTdQqhNoBf8qSjuNRQTL+RiGcQbPex0pW5EyQiJxH4wvZcH+HDEjSIfkeGMIWrD9a0S0F/BVgQpfyILzOm3maRw3DQSCkaMyAFT8WUzxMjfK87hKkvanKejLfOmpb8UkVq9jXnPXsiyLlZWVXbtrPc15RdM0UqkUuVyORCJBR0dHvWpRrVxmY/L4hx3fZvPKesHTcZw3VcOraTyfd8EzFDQbqF3sWjqDhwku2/XR3AzP87h9+zYAFy9eDARX30e/+mMIt4CoTCNbjyFKI2D7RIY/jB1NQfsLb2rrUfNoappGb29vPfCoFtE+NjZGuVxe47sSi8V2vZ/NeNY0mg9jI8HTdd01gqfneTQ3N39emERCQkIeTq2yWW2M2miMqQWAplKpesUz/AmM0g+AP400zoM3iqc8FEtAG/HoVDWFUSslVQYBIPG8G0g5hKZNoXiJnO3hyOsIIlS8a8SM01jedRLmBcruZZToZcqxgBE0YuTcW0S1HuzoLEn9ACV/jDbjDAuehqPiWLJEf/Qoc/Zdusx93Cl9gpea/069jnnNXevSpUtks9kN3bUeVSmw3fP+uOaVjcplZrNZ0uk04+PjCCHWCJ6NQuR255XaNrW53HEcHMepL/c8j5aWlvq88jwRCppVakLmjRs3GBoa2tJ38VF8NIvFItevX2doaIiBgYG6oNhrv4KWfQWZOoWoTIOQCLeAaj8DVhnz1odw3/FDYD5+Ya+GEIJEIkEikWBwcLDuNJ1Op7l79y6O49RNCKlUCtM039Yaza3Y6M306tWrnDt3rr68MZVSKHiGhHz+ULOOvfLKK7zjHe9407PfmCv59OnTWJbF6uoqwv6/6NYvo0QvAgH+PK7WDTILcgpoo+L0YMTiWAI87y5goxsX8L3LSGmj6QcokKOiIgiVIW6eo+K+ji+XAZOKex3El3Dfuk6rcYycd4eU+RIZ9ypxvQdbLqKLCHH9ALNekhl7lFYjSK9X8FaCv/4yNwof4cWmv73m2GrC8qFDh4A3u2vVUji1t7fT1NS04Zj4LM8rhmHQ2dlJZ2cnEBxfNptlZWWlXi6zNkf6vr8jU3tjGr7acfi+z/Xr1zlz5gwQKIfW+3g+y4SCJmuj/7ZrEt+t6Xx2dpbJyUlOnTq1xslYeCU6rEDDKbJ3UNF2tMI9VGIPwl5AKyyhDB/t9h8gX/yGNW0+qkbzYTQ6Te/du7fuu5LJZJienq4/BMlkkmQyuasgpudZ0FxPTePZOEhsZBJ5u/rihISEvDmQVNf1N43Rruty69YtTNOsB4A6Tp7e5H9Bs9Mgs2jM4OoXkaoI/jUgAvpJlHeLnHOYmLmMUnMYxlk87w1c5yowiBntJq8SWOpV0NoRxKs+mYew/RHixt9ixStjy8D33FF5QFDwRqtazTvgNePqSaacJGlvlA5jD6veNF3mfpbdcbrNAyy5Y3SbB5iybrA3fnrT87HeXcuyrLoZulgs1t212tvbt53jcjvX4K2ylJmmSVdXF11dQSyF4zhkMhkWFhZYWVkhEolg23ZdsN7JPFOb33VdX3MfNWo8n3XB8/Na0Nwo+k/X9SciaPq+z507d/B9n4sXL77Jp0Mb+T1a7QlUohnhFZDJfYhsGhXvQFu9jmw7ilARjMx1nNyXQOvDE8U/KWq+K7V8bp7ncePGDfL5PAsLC2ve5FpaWrZ1wz9PpvOd8jBfnEYn8KtXr/LOd77zse47JCTkrWd9bsza3OL7fn0syGaz3Lp1i4MHD9aLcODfp1X8Imb8s2i+g6QHR38JvE8AGhjnwXsNKZcoaxeJJv4aIfaiVBLPe4Ny+QiJxDiefogl51VAYoiDePoocfMiZfcSIDC140y5GWyviMcUCX0PZX+aVuMEOe8WbeaL5N17FMtHuOfP0hcJ/DoNLUj5I1gXwEQXH129xD8d3FzQXE8sFqOvr6+eXL1cLpPJZBgZGcGyLJqamuqC1G7dtZ7mnBCJROjp6aGnp4fx8XFisRhCCGZnZzcsl7lVPxvvnY00nrV5pVHw1DSNW7du8fLLL++4/4+bz1tBc7Pov51oNLerRaz5qwwODjI4OPjmm8qrIMb+AA0HmTyOnnsdkR9DiQh4FTzzPH5RAB5C5tHv/hH+y99e3/xJajS3wjAMYrEYg4ODNDc3r3mTGx4e3tYD9bgGhEdto/FhfhQedi0288X5ju/4Dq5evRpqN0NCnmM2yo0JD+YVpRQTExMsLS1x5swZEolEsKH9fzHK/waTCq5qQeln8OVkIGRW0xbhvYZnfDFF9w0UV3CcLiKRSRznGJHIHZJNNgX1EkXnMyTqgqWHUlBxr2GIPjzRxapvUvJukoqcIeNcwRBJAFyVC/7KMmn/KMvmEhESLDqjxEUrS84oSa2dZXecJr2DjDdHUlzk09lJWo1Wsm6WNrNtx+dMCFG3iNXctWp5oO/cuYPnebuK+H6WFBi1ktGNlf020uhuFoD7sLlpo7iBWmWkD3zgA3zyk598pP4/Dj4vBc31UcONF+lRapNvxNzcHJVKhXe84x20tLRsvNLEx1FSIgCRm0AJA+Hm8du/CHnvGnR3oi3dQka78ZN9iPwipCegfV+9iadZ77zxYWx8k4M3P1AblQF7XAPCowqJj8v8vt1jaZyEQhN6SMjzS6OpfKOAH03TsCyLW7du0dTUxIULF4J1ZBG9/G/Q3D9HiS5cdYiSaxHXXgPjBMh58C6j9PPYSCrOJ9H1Y/j+dSCOlBEikTtgfClLzusYelDko+JexdT6ceUkyjmKiM1jay8xXblEXO8HNPLuHQxayHt3SehDlP0pWswv4lppmg4zhdQW6Yy8wJxzm5TZz5yTo9XooeSkadUHGbYt4pqJQtFpdvJK7hW+qvOrHvlcCiFoaWkhGo1y5swZfN9/U8R3Y2DRZuP+s2Ll2qiNWrnMWgBuTaM7Pj6+YbnMnfSjNpdUKhWSyeQj9f1x8XklaG6VGxMeX9oi3/e5e/curuuSTCYfmvRVDP8hNB2F3OsIJ4vqPIHyC8iFDEJJVGkZgYKWLrTMNNI2EXc/iXrnNwfbP8MCyvoHqlYGrGYiaW5urj9Ij8KzNKjs1k81JCTk+WOr3JgQ+GPeuHGDo0eP1v348G4FUeXoSP10UKtc+EjlAgK810E/jfTnKclstVa5i++PolQvkcgCcBZPj5B2rgImtneXuHGeivcahtaFK+eQ+Kz4Q+SdyySNIUreFKnIaTLOddrMI2TdaxiiBUN7mTHbxVE2JT8NCrLeHAKNtDeDhsGqO0WncZRrhTJ5r0xUd9HQWHQWSbtpvqLjK9DE43U/2ijiO5PJ1ANvDMOoC2XNzc1rqr49KxrNh80rG2l018+TkUgEpRSWZW3blaAmsD4LfN4ImtvJjQmPR9AslUpcv36dgYEB9uzZw+c+97nNb9j0MCI7hqq04GsmunDBLuHnNUR2EtW2F5GbRKYOouUmkI4LbS8gl2ZgZQLRuQ94djSaD0OItWXAatUYFhYWyGazXL58+ZGT4j4KUspHLs+5G0HTcZwdHWtISMizwWam8sblo6OjlEolTp06VY9S1qzfRjh/hqIZTd5Ganvx9KMI/ybJWAn0Q+Av4CobW9uD570CCHT9NL5/Hc9LoVQHTrSMJ32kyhE3z1BxMzj+KIIkFe8amvYeZsRN2vW94M/VzeSWvwwIcs49THqZd0yyskzRX6HdGCTtzZB0eyiJRXrMF1h079MXOUpFxliwY6S9cfbH9jNujbMvto8Ja4Kh6BD3yvc4ljz2RM+5YRhrAm9s2yaTyTA3N1evrpdKpfA877GM5486r9TSJW6X2jyZTHjs630d4d+hWLSxrDLD974WyxYblstcTyhovoXU3gLy+fy2glNqTtu7ZX5+nrGxMU6ePPmgqkM1FdJG+xbjHwn+2nlyySFSahQpOlDKClyuI1VNqG4inCJ0Hke4FrpVwbv6CcSXfcszrdF8GLVqDDUOHTq0xkQCbJqbbD3PStT5TgcVeLYGhJCQkK1RSpHP5/E8j2QyueEzb1kW169fp729vV7nGplDq/wCwruMJscBcIwvQrnXgREQAziugalGsY0vpOL+DVDBMF7G8z6H44wiRFCrfDoDhn4bU+sDYlTcK0T1o9j+XRLmO8j7goyXBeGTd4cxRDM59w5Nxj6K3gS6tRctqrFk9bGkjdPsDEIENBm89NZUFx42Ua2JvNfGlcI4fZEgENVSVrBcPaia9rns5564oLmeaDRKb28vvb299TzQNY2nbdvk8/l6RPtOA4uehqVMyiK4v0tUvoou76O0I7TFRpio/EtOv/jym8pl1vJrNqYchCCNYlNT0477K4T4SuA/EWTs/3Wl1E+vW/4DwD+ufjWAY0CXUiq9WZtva0GzFv2Xz+eZnp4Oyjtuga7rdf/NnSCl5O7du9i2zcWLF9doqDYLHFJKotKL1MSnqF1AxhPIqRlI7Q1+XB1BGXFIj+BpcaRTwMjO4Uf6EavjyOXZpxoMFBzHo+37YUlxt2MiaWxjmztEqj8G8QqIRdDmQcXo6YviuV+KUt+KELt7NHYTUFQqlXY1IISEhLz11Kxjy8vL+L6/4bNbyxd57Ngx2tvbuXv3Lpq8gV74JTQZpLHz9XN4KHA/DqIHGESoGRxvD05kCNf92IO0Re5lbHuIWGwWaXwB8/an0BMapjaEK6fqwT8KG0Pbx6xbxvIdbLmM4ezFi0zSHjlD2rmC5xigQSQ5yPXyBFFjFU0aVCJLmCRY9ScxZYKyuUhcpXB8j6J3mPHKOF1mF/POfPDXnqfD7GDWnqXNaGPamkYQoeBVaDYef+3z7dCYB7o2J7S0tJDJZOp5oFtaWmhvb6etrW3LUplvtQLD964jnF8nKhw0WURpJ0FozJZ+BkcFgUTry2X6vl+vyjQ9PY2UkmKxyCuvvLJjS5kQQgd+GXgvMANcFkL8sVLqdm0dpdTPAj9bXf9rgO99mJAJb2NBs9Gksd2URbA703m5XOb69ev09fVx7NixNwk8myZ3n78N07eRTU1oXpGYl8VPvAxz12BpBJloQXPyZCN7aPOmcNsP41VscsYhlNCJyTL+Gx9B7bm4o/4+CZ5EYt3tmkhqSXG3fJiVQvm/AMafgp4Bz4OIBpoHvoEZMYlGPoQSvwPedyKMf7TjY9nNwBRqNENCnn02yo25XikhpeTevXuUy2UuXLgQCDJK0Zn8E9r5bZAg9bNIWQmiypUH2gGQYyDaccQ5KtpNokoHTDzvDRznJJHITeKJKCX1Inn7k8SNc1S819G0OEiouNcxRDdKdJD2W8i510hFXsR2lpFaGYCcew9kDFvMgvYurpaH6zkx+yJHmHfu0R85xJxzm67EPubs28TkEK/nl0j5DhgQk4FGsMVoYdldJmWkWHVX6TQ7adZ7WKok+evVW/ydnvNv6bXZiNrcX8sDPTQ0hJSSfD5POp1mZmYGKSWtra11wXO9kuCtFDR9568Qzv8iqmsI5aO0bgQxnMgPYPsemraxXNKYUhACZce1a9e4ffs2V69e5dVXX+UDH/gA73vf+7bT3YvAiFJqDEAI8XvA+4Dbm6z/9cDvbtXo207QfJTcmLBzQXNhYYHR0dE1pvL1bKpxHP8suBVU8gTkXkeiIXMSDUB6VCJDJJ08LaZERvaishG02XmaBo7iL87it3WiJm9SED3cK5fp7u6mvb2dZDL5XJnTt6uN3MxEMjExQSaToVQqUalU6pF6a/Am0JzvxzfTIArga2BqgELYSfAstKgDmoNwAf4DovJRVOSnQO/Y9rHsVqMZCpohIc8uGwWSrp9XSqUSN27coLe3l6NHjwZjmlxFL/0Q3Ymr2OoEUTGKj0KqpSC4R42AqqC0Q1g0Y/sTgMT376Fp55DydUxzGPR3suwOYxrBWGT7I0g/ic094sYZLO8Wvn6O8colYloXAoOsc5OY1otlLNCkHaUo75IU55hUFaKyGjBT7XtZZgHI+fOAIOvOo0oHuaZlQWjkI3lMabLgL6ArnanyFJrQmLPmiBCh5CX4zOoc/VHFx1auPTOC5vp5RdO0eqlMCKxmuVyuXkqyMU90S0vLW2I6V0rh2b+D4X+GiFZGKA0hggw1duxHQDTj+9Pb9jfVdZ2zZ8/y3ve+ly/5ki/hW7/1WymXy9vt7gAw3fB9BtgwEacQIgF8JfBdWzX6thI0N4v+03V9236X2xU0pZRYlsXc3NybTOXbbnPyc8Hf5UlkPEZBdBOfvovs7EMrzmOUMkglEGhYmWZYnoD2AcjMIewyuoqgNaUYqixg7D2P67pMTEzUTbE1M/RmzsKPi6dRKqzRRDIwMMCdO3dIpVI4jsPw8DC2bdf9Vtqbx4nxAZTmQrRaO1YZwXdAeBoqooGtI3SJ5sQBD7SbaPbfRxr/ASIXttWv3fho7taXJiQk5MmzWSBp47wyNzfHxMQEJ06ceOCb715Cq/wcEEMIG4NRHP0wqAyoBVBR0I4j5QJlonhyBqXm8LwhdL2MlK8Dp1FmgqyXxlN5PPf1uh+mdA6jxYfxlU1OnSBdaYwqf4mMc5W40Y3lLFC208SjL3LfqVDyiwgKxLVWVtxxWo1ect4CneY+VtwJ+iMnGa/4lD0dy1jmQPwAY5WxB38Twd89xh7SXhpZ2MNn1ByDeooZO82A6GC6svKUrtYDtjOvGIZBR0cHHR2BAL8+D7RlWczOzj60VOZWPEzQ9DwXx/pxklqaKLdQqgVNaEgxgB39cRCBad/3/R3P48Vika6uLlpaWjZPrfhmNjrAzXzjvgb47FZmc3gbCZo1k8ZG0X+PW9CsmcqFELz00ktbChYbaTTl6iSisBh8sYvQdQy1nAEgZ0dJAaadgd5jOPMVSFYFkUQTpOcQvQfAd5FLc5iihPlOSVd/fz2NUK0+ec1ZuNE88KiReI+bx/HWCJBMJunt7V1jInFyf44Z/2WUYYOn0PJxNK+MMl2Uk0QKDxUNnNpFxEcrKgQKFXHBA6X7aO4PotQPoaLv3rIPu4k6D300Q0KePbaTG9PzPG7evLm24pvy0az/inA/hfBvIVCUvGP4QhLlEmCC/iL413CFoCL68L030LRBFM3EYlNUrOPE4/NURISCM4pUmTV+mKChx0aIGF/EuDVBs9kPTNWjysveNAKTjH0TnBQivp8536Dgj9EfO8acdYeOyCAzVo6E1kaOBXRh0G4cYNZOMmlNkBKBKbbsl9f8tWQwXkaMJJN5SU+iCUo5YnoEfNAtye/d/ijvdPZQKpU2TED+VrCbeWV9HujPfe5zmKb50DzQu+2H62So2N9Lmx7FZAolOtBUEU//u7iR74KGbXZjwi+Xy7uZV2aAPQ3fB4G5Tdb9f9mG2RzeBoLmRqby9ezEHL7VuouLi4yMjHDixAnu3r27rUCYjYKB5MgVRNMAWnE2+F4sEc0FgmZzZQUViyE8C091IDM3oGyDZsDKNGgGQtdQ8+MQ7USTLurWDXh38HCsr09eS3ibTqeZmJiomwfa29sfmt9zuzwNjeZ61j+ImqbRrn8cPfEL4Ogo10Q1uQgsUAIVVYCFWQQs8BKgjKqvqWYh7EDhgBtBuBmE/TP4WgeYDw8oC03nISHPP9vJjWnbNgsLCxw5coSBgYGqqXwJrfyz6O5fAOCL/fhaH7r8bBD0qZ8F/w2UdxvbeBcV96MI0YoQvUg5Q8V6gXisQCIpyPn7KXtX62mLKt4NdNGJ44+TMC+wkLXIJhWuKlPwxtCJk3PvkNT3U/LHMawDqGiWFesgS0zRHTkAQNFbBWDFmULDYNkdIyqacGWSO6UKeW+SlJEiQ4YOo4MFZ4Eus4sFZ4FOs5M5e4790VN8fHmBFqOJsfI8zXqcGS9NTJhkdZvbYpEvYJCxsTEqlUo9HU97e/uWATiP8xo+6rwihKC/QYGzUR7ordIM1dppxHZGsKzvo03vwhAlFPvQVBbX/Ea8yNe+afu3cF65DLwghNgPzBIIk9+wfiUhRCvwLuAbt9Pocy1objc35k6isjcTNDdy8q6tu9UNsFEwkBx/A2hHIxA0i46JY/bS5s4hPBuVOgrWKs6d+2jRJMIuQd9BWBiB3kOwNAHROHpnJ3q2DPfvoL74PYgNBO310dw180AtqKZmHujo6Nj2W9rj5Ekk1hWlj2AUfxZlCjAqIJKAi/JAxarruVVhUhNorsDJJdBbS8EyQ0M4OpoDwhEIbQl99ftwOn8bjK5N+7HbYKBQoxkS8mywVW5MpRQzMzNMTk7S1tbG4OAgAML5DHr5BxEqg9SPI30HXxjgvYIjjxDVb4F/FV97mbJaxXM/jabtR8pRlNoPaMRjI6zkzuM1XSei7wEMKu4VYsZJLO8mEfMYjg9pP0LamAF3jmbjIAVvtB5Vjgym9Ui8hWFHoxJdICaaWHLGSBn9ZLw5eqKHWLRH6I0cYdWdJK69xKu5+xyMHyTn5Wg328l4GVqNVla91XrwT5vRhvS7WLBMPKXoj7WTLhTYm+jmZmGS4017uF2cpifRx7xZ4m+d+ltrSkrWtL9tbW2bBuA8Lh6XpazGZnmgG9MMbcdyaFmXsJwfpEXvDcIEaEfg4prfjG9+xYbbvFWWMqWUJ4T4LuAvCdIb/YZS6pYQ4turyz9YXfXvA3+llCptp93nUtCsvW0uLS3R2dm5Zfm+ndxsGwUOVSoVrl+/Tnd39wMnb7Zf73y9oKucCmp2GKSP3zeAXprFKHv4XsM6hTy+3gnuJKL/AMzdhlq/lATfQ/QPojKLRHMlHMPDvX2TyMnTW/an0TyglOLSpUsAa97S2tvbSaVS23r7fNY0mqJyh0j2Z0CYKKOEkiYqWkaUBcg2lJYBU6CXQVWfQ4EkJkqInMJvFaBJRBaEYUMElJtAaHkiy9+F0/c/Nu2H7/s7fmMvlUoPqoWEhIQ8FWouR6VSiba2tg1fGF3X5datWxiGwYsvvsjIyAgoF63yi2j2/0AZR8EDqVx8kQe6AYeofgvLPYkedSn5d9C0bqCCUgWkbELTxhHaOyhTwY3fwxApHH+ybi73VQ7Q8aXNqn+YrHcXwzmIFxuFaiWegjsKKkpJjRIzvoir5VF6o4cpyXt0RvcyY90irreQ8eZQVbc7qWDVGWJOBj6VS84SAsG8PY9QgnlnHh2dOXuOdqOTqZLBcHGFZjOBAJbsLABZN5A3bBn4vRuazj0vsNDVUgy1tLTU0/Fks1nS6TRjY2P1tHU1C9vjEg4fl0ZzMzZKM1TLAz0xMYEQgra2NjzPq2skS5W/wnV+iiY9SUz4oGLoagI79sNIffM4gN34/u/SdI5S6s+AP1v32wfXff9N4De32+ZzJ2jWcmM6jsP4+Djd3d2Ptf31Cdtr+dCOHz9eTx9QY9O0RRu02bienL4FMkhymy+ZtCY60WZWiQOqfy8iOwlS4haDbWQxH0SiL01CvBmWJ1Gde/FoQsUilFMOEUPHv3MDtiForj8GXdfrVYxqb2npdJrZ2VmklPW3z62Spu+Wx6rRlBUiiz+I0DL4sQSikkCzKpBUIBTKz6BbCnIgaQWZA00grFaEmUWhgTyGr3yixl1K9l4SiUkQFRQg5BjG6s/jdXzPhv3YrYlj3759j3T8ISEhu6emvCgUCiwuLr5prAfIZrPcvn2b/fv309fXh2VZGNoSevG7QVUACe4buMYFlKqAnAVmwbiAdF6joiS6iqDUMlJaQB9KzSPlUXRTkfamQTQj9AoR/QgVb7VuLnf9GXTzK7lffo1mMwg28iOz6DRRcO/TpB+k6I8S80+QNxMUfAOFwpaBALjqTKNhsOiMBtpNe4zeyFku5ZZoMzrIeAsMRgeZsWfYG9vLpDVJl+xiWSyzL7YPR0oyVoo7xVkOJ/sZLs1xKNHHSHmevfEuJivL9EVTjJcX6Y+myJYjvFFI8wHpY2prx0Nd19cE4NTS1s3MzFAoFEgkErS3tz8TZYl3wnrLoeu6ZLNZ5ubmeOONN0im/oLe9o/QZvokRA4lzqKpEaz4L6K0Fx7a9m40mjWf0meB50rQ3G1uzJ1QEwqllNy/f59isfggH9om627Feo2mnLhe/z+ZX0J1naSWpkqKJnTAM3ogWq3QsDqP6upDZOehfQDfNbALMfxbI9DSiWvGkK4k5i3iz82h9/c/0vHX3tL279+P53lks9k1SdNrD1MtCu9Z0mhGxr8XTZtGOTq65yBMFxnVQICyBDRVr4OKoBtZyERxW9sgkkTILAKJZo8jOARAMjqJL06iGTfxyl0Ydh5V+d9ML+0l2vGFayoxNPZjJ4Sm85CQp4fnefV8mIZhvGlMV0oxMTHB4uIiL730EolEAgBT/jUHOn8N4Q0jUEixH1frBe+vAQHGBfAuI71Rcuo8GJ/B96Po+gv4/n1su4Vo1ECPtZHzFLYcJaLHUEqj4l0lZhzH8m4TMU+R8Q+QtoYRRMm792gxD5N3h2kxXyLjXqVctohGh1jU4yxZ8wAk9RRpd4aE20XZXKY/epQ5+y59sSMUvQjzTgJLusS1IBWcLgJBRlJVcIjgr0Yrn12Z5UBibfq+mgDZVE3O3hFpQaARc3v47MosB/VmPrs8wbt7Dj70/K9PW1cul0mn01iWxaVLl+oJ1tePtVvxVgua6zFNk66uLiYmJnjh6F8g/I8S1RSmgmJpP5peYNH6KVra+kkkHt7X3VacexwxGI+D50LQ3Cz670lUw9E0Ddd1uXz5Ml1dXZw9e/aR66I3mtht2yYzMcaD92WFZz0oi6Xmx1FdvThjs4CGFokhXAsVb0Nk5/FkEuvGKFp3tUpARwpzYhrf1bGjg4hr10nuQtDc7FwahkFnZ2e9Rq9lWfUSkbU3Jtu2sW17107ej0ujGV38b+jOTZSRQLgVaPZQtgatwbEJX0MRaKuFQ3D3mzZ6JYkyow8SO4h9GKVVpBFFCBvNn0fpJ4g6E0Azhl/kkPwgd3LHmZ6eRilVL5Xpum4YdR4S8hywWW7MRouW4zjcuHGDZDLJxYsXg7lHOWjWr2Lav04sAUrbj0sHUg6DHKkLmHiX8Ywvpui+AeIVXPcQpjmC62ZQKk40msfR30Pa/ji6aEWjDcefxLeOYMTvIVUJUzvMlJ0DkcCR2bofZs30nXOGQUWJJrqZcU1W3Ol6VHnK7KfkZxAqGI8sWSSmtbDsxLlZmCamxTAwmLFniIs409Y0SS3JjDVDi95CXuXp4CQfW5qjzWxmrLxAykgyWl6gWY8zWl4gJkwmy0voaEipcXtR0R0PtKgukj+fv7eloNmIEIJkMkkymWRhYYFz587VE6zXxtpa8M1m7g2N1/dp55OWUtLZ84tocgJdM9FFAsPoRY8MkPO/A7/iMjY2RrlcXhNYtL5U5m4tZaGguU22E/23k7a22j6dTlMoFDh37lxdBb4ZO/HRlFKSyWS4d+V1js4uQ1sS7BLEmrHvDBPpTCHKmcBvM74f3EDDqe05hJq5g1qew+85QuXKGFpnF3JpAZHqQKWXwXUQfXvRNEHl9gzxd1loie3XdN3JOY3FYvT19dHX11ePwrtx4wYjIyO4rlsXuFKp1LbTKD2OAcHwlohlfgelK4RXRiVMBD5KiwJBOg4Va/CBjccQ2AAI0YpevE6OvTQ1TyIcH82fQRlngKuAj1ZqQpMl/MgeNLmC5pscE7+Gfe7f17W+6XSa5eVl8vk8XV1d9aS/W72J7taXJiQkZHdsJzfm6uoqd+/e5fDhww98qP1JjNIPgH8PqZ/CrsxixFNI7w0wToG3GmgxtQvYwsdyPo5hnMbzVtH1eTyvDcNYQTO+mFV3FNv5a0x9H64/Qdw8R8V9HT06iUYKKfpI+wlK/jVazaB+eN4dRidJwb2PsHqR0VWikXdztXSTvuhhAEpekNZwyR7HIErJXKRJ70ChU/aOMFKZYm98L5OVyXpuzKH4EKOVUXqjvdW/A1zJ59FjJhJFfyxF2i0wEO8gU5hib6KLm4Upjjft4W5xhlOJo/zF9BwvNHVyv7jCQLyVmUoeKzNHyXNIGrtTQmyUYL2xLLFpmnVt5/o8l09b0PS8CoXyd9KaHMMQJhKTuD6IEl040f8fcRFlMAmDg4P1gKnGUpmtra31uXQ3lrJKpVLXvj9tnmlB82G5MXfKVibemqk8n8/XfUS20+Z2zfcLCwuUy2VOtcXxLAuZOoC2cAPaBmFuGpk8gF4OnKfdVQclNISSyGK5rmizsoGJQrS0oVaX0VLt+GMj+J1d6NLBm1/BVwlKr16n+T1PvixlLQovFotx8uRJNE2rO0NPTk4ihKg7eT9M4FJKPXKZr5PiP6M8DWEUUUQQug2eAMtEy0ukFkGLCpSoIFOdaGLhwXG4swg8mtUsUp1Ft94AQLOv4scPI7w4evl1pNmP7tzFjx5FaDn0ymW0/BWMljN1ra/jOAwMDNRTnwwPDxONRusDxkZJf8P0RiEhbw3ry0iuH3d0XcfzPO7fv082m+XcuXN17ZJw/hS98kso0YsgAf4MZS9Jk3IAG7zXAn9Mb4SSygIxwMfz7iDlIJo2g9BeQGmHmbcvETWOg1xEq07DFfcNovohLDmNr38BY5XPEdU6EETIuXfq0eWtxmly3nVQSTKyi6IV+F8u2CM0653kvEW6IwdZckYZiB1j1rpDi3GEz2Qm2BuvumNVNaKZcgYEZJ1s8N3LMBjdx82sx4Jv4zk5AJbs4O+qUwAg7wY5NV3p063tY7YQzINNZiBQ9saamK3kGEi08onFUb564NhjuX7ryxJblkU6na5b2JqamupzztMUNB1nhVLl2zDJkjBdLKXTpjto+n6cyPfXA7hqNAZM7d27FyllfS6dnp6mWCwyNjZW1+RuR7vp+/4zkzP72ejFOraTG3On1N5UN2rLsiyuX79OR0cH586d49VXX91Wm9sxnXuex9LSErFYjAsXLmD/398GwBmZJtbdinSC/njT06hEFL2lHef+FJGDB1DzI8ilOfSeXjy9E1kM1pXLSygEKlOtvhCNwNwiWqwVPdWOc28U3gJBs0btgd7IGbqxykIsFqu/fTYm8X3UAUGb/l9E/CzoBkKA7yXRVnWE0DBiRYiDspNoeiDIYw2hjAHQb6D0PgxnAgBduGCZCFJAGoFCuCZa4TYCD6m1gz+HwEGT88jIEJGZ/4B1/MP1vtQqOLS1tdWT/tZKZW6W9LdYLO7YxCGE+ErgPxGkoPh1pdRPr1veCnwYGCJ4zv+9Uuq/7fzshoS8PagFkvq+v6niwnVd8vk87e3tnD9/PlhHVdAq/wnh3QA5h8YMnv4SvpI0xV8Hn7q53JV5LO0gnvdZwETXj+D79/A8F11vwTNbsNFReLhyDkES2x+p1y4Xop0FW+H4rxHXe6n4C3VzuSYCITFv3ydunOK2yJFQJmV/hf7oMebsO7SY3RT8lbpyouzn8UsHuWTNgxJMVaZIaAmmK9MkZIKMliGlpVj1V2n1WpFOklHPZMbL0EsLC26e/fFuxitL9aCfwVgHU9YKhxODjGcVJcei4OVI6iYjhVUMNGYreQCKns1fzt97bILmemKx2Jo8l8Visa4VzOfzeJ5HT0/PjixsNXbrmmc7w5Qr300Ui1a9QMZNkjJtlPnPcaLfsq02GkthAly6dIm2trZ6pH6tvnktUn+9XPMk3AofhWdO0Nxubswa2xVSNhMKV1ZWuHfvHkePHq1HwW2XrQTNYrHI9evXaWpqoqenJ6gkMXEvWOi6yKYDuJNVzZpjUe7oJ2EmgBLSaagF1dRL5fVJ0HT0RBxVyKP1D6DmZ9B6+jCyKyhNYPR14hcqeDMVKrfHiB8/sKPjedyYpkl3dzfd3d312uS1B6Uxia/rujty8l5DZYXI9IfQpY1qKiGLLeiqiIj5SDuKqHoQCFmsb6J5q2jlMWRkD15THzABgFICvTSJ0rpQRhYhJMLRUeZpcF9Ht2/iR/ahueO40S9Csy00bwlj+sN4e4K8tRtFB8bjceLx+IZJf3/yJ3+S2dlZ/uIv/oKv/uqvpre3d8tDFkLowC8D7yWo5HBZCPHHSqnbDav9C+C2UuprhBBdwD0hxG8rpZzdneiQkOeXrXJjwoMMI5FIhEOHgmBAvFH0yk+heUG54FoCduV9GoBc6TCtyWGU+xq2+W4qzkcAga6fxPdvYttLaFqSSCTOfGkAwTWEiGOIXjy5QMK8QNm9jOOPY+jvYMSaAr8XZWSJ6l1U/AWK3nhVq3kX3etHi+5hxW/CESu0aUnwoeQH5vJlexyTGIvOGN2RF5iqmBR8SZlMUDqyPEav1ss00/Ql+xitjNIebadiV2iOvcCn0hMcjAQvvboP6GBU66I36cFg2mYmiYk4VrmFqeIsZ1MDvJGZ5Xiqh6uZOU609nArt0ifHmeksIrleWRti7bo9t25dkNjoZKhoSFu3bpFKpUin8/vyMJWYzcKkFLlk3juT2IKiYHHotdFlApL4l+Qin7TIx1bY6zE+lzYNatZe3t73Tq2GyvwVgqM6jrvBn4eMIEVpdS7tmr3mRE0lVJYllU3I27nJG03YTq8uQylUoqRkRGy2Sznz5/fVT3whwma8/PzjI+Pc+rUKVZXV1FKoSol5OJMfR03bYMRBSpBH7MFnFxg0vFmpjG7O6CwilvSUUJH+D5azx7k5AgiEkUBWjIJ+Tzu4EGEiKCUA76DdfXOWyZobueBbKxNPjg4uCaN0sLCAkIIisXijkwDANErP4Qm83haBD1jIHARbdXrbJqAhfIEJIN0UkprRVQ1mJozjZ5NIBMvoHGfsttHs7sALOJFzoCYRMvcRmhxVKwVIQOnfCleQi8tYZRH8SMnMJY+hjfwdaCZWzptr0/6++EPf5j3vOc9zM3N8U3f9E380R/90Xb8ai4CI0qpsWqbvwe8j1rqggAFNIvgwjQBacDb1kkNCXmbUNNyeZ5HPB7fULiQUjI8PEypVOLChQu89tprAAjrD9ArPwXYSP00SpbwhALvlWoJySu0JoeR+hdQkst4zkfQjVP43jV8fwrXbcU0M2C8l0X7sxCdJaofwvZHMI0X8LwFyu4VTH0fNgMUZQJP2eh6EdDIOjeJ64NU/BlM+yAysoyKHudm+RZJvR2UxrI7RpPesc5cfhxbuqy6PUxZ9+kkEE4qfjDP5PzADL7sLiMQlH2LotXPmDNHROjMelmiwmBZLxFBZ8pewUAwWpzHQMOxdP5mMUdn1ed91QnM6BUvmLv06lzQJAxSkQQDopO/mhrjH71w/Ild581obW2lvxocu97CFo1G6xa4jcpk7tQvslj5n/juL6FjIhDkZDNCKS5nv5B379+9kLkR60tl1qxmExMT5PN5fuEXfgHf9xkfH2f//v3banM7CgwhRBvwK8BXKqWmhBDbyi/5TAiaNVN5LpdjdnaWkydPbmu7mvC4HaGkUSismcrXmEd2wYY1zKsVhCzLqte+TafTwRv1xAREY2AFDzyxNlSkDQpZAHwjhmZ2IsiDUtDSi9AFpRuTGPsGUDNTyFIQ2OIvzIFh4PlRcjMJNAmlsRm07i7Mrh7EYho/V0RvfTaDTBrTKAkhiEajmKa5Jonv+jRKb2pj5q8QlTm0uIOqGGhxD9/TEYDyQMQCLab0kmjRwLdIGnsx3BvB/1onujWMsmP4bQfx3Af3kV68hZc8g8klkCV87Qy6fB1kDFHJozsT+PFDgVkNG/Pur+Ief/+OB6dapP4P//AP7+Q+HACmG77PAC+vW+eXgD8mqFPbDHydUurx5wMLCXlGqQWSLi4uIqVk7969b1qnXC5z/fp1enp6OHLkSOACpFnopQ8g3FdRxkmEdyNIwE4eaAcc8K+CcY5sYRFiN9H1QUDie/fxZQ+6tkgkegqLGBn7E0T109j+dRQeoFHxrhM1TuDLDCV1hDn7NXQRxxStuMYqrcZJct5NdBVoF41olAlvkKxzm1ajm5y3RKvcQ06fps3soeivVi1gAkc28UpmkpjmYmKyqq3SpDUxb8+T0lJkZIaB2ACz1iyHYqf49MoyQ4kWKlaeY02D3CnO1Cv8HEn0c688x9HkIBOVRYbkfj61uMKQlmDKKrI32sJkKcOeeCv3Cyu0R+IM51eIaQauVMhChGmjyJ/bI2+5oLleAdJoYQPWWNhqUd81165oNLojjWau9F/A+22iAnRssrKJNq3In+beTWflq57E4a2h0WpWk3Pe//738/73v59kMsnv/d7vbaeZ7SgwvgH4A6XUFIBSamk7DT91QbPRVG4Yxhqt41bspIZ5TSitRRLuxlS+1f4ty+LatWtvqiBUE0jt4RHoOACztwBwCzbu3AqJrhZUMY+rN6GXJTUjsje/gOjuAzVNqVAmAfjzC9DWgl4q4A2dpnR5Cno7UHPLiFgEM5XAmlqhUPAxjg/T/hVnH+kYt8PjyKO5Po2SbdtrnLyTyWR9EIjH4yB9zHu/iTA9/HInIpoNGqtaZ6QVQU/YKAWqdS94N6t7eyAEKmMPsIpQFlo+jS5bqJ985aIVH1xbvXQrCNhaHUHFg3QdXtuX4HX8XfDLmLd/GewHlTB2cuy7YKMdrG/oKwhC5t8DHAQ+IoT4tFIqv5sdhoQ8TzQGkhqGQaVSedM6NavTiRMnaG2t5oj07nB84D+DryFUGuXmcI3zKLkAcg5YAP0syruCpRQlqZFQK3heCSH2odQESnaAfoCsLCC04EXfk7MoGcNhgrh5nor7GooUk04BV71Gk3GAojdGa+QIaecqtr8CSlD07xHX38n1yiS90SNk/QxJo4Oct4QngmNadiYwiJL1FkloF/hsZpI9sT1MW9McTBxktDxK0klSNIp0xDvIlDLEtBiD0RNMlnXK0sOXwbzrVAuJWNUKP7XvutDB7iFXzZ2ZamllKlsmqQcDZsxVSBQDkWZuOEt8UeoAnx6d42BbK3czq3i+ZKlcojvx1gU9bjUvxeNxBgYGGBgYWFMms1ZOsrm5eU1Vn83IFH4YQ36aFt3GxGXVb6dFq/D7ua9EeSc5pm8dWPwwam6E20XTNI4cOUJ/fz9/8id/spM5ZjsKjMOAKYT4JIEC4z8ppT60VcNPTdDcKDfmTgXN9ebwhyGEYGpqCsuy1kQSPgqNgmZNgD127NibItZr1Ybc0TGcsSmSe7tRhSzu7DJ4PqptLxRvQ9pCZtOIob4gSbvrUFj0MIBoJg/JBFTKyOYUZbONylSBKCA1ge75RA8O4Myv4OdsogN9FF6fIvXlZ556LrGt2GhAiEajb0qjlE6nGR4exrZtjpb/ku5KBuVo4BfREx5Kaoiog5+Oo7wEytHQDAnxCkrfj2zuQPiFBzuRDyzJSmshUpCothgCCxk5jLF0Fa/tJLp7E6EclL8HTU6jSrexh74br/sb6ts7L/4E+vRHgK19LNezC1+aGWBPw/dBAs1lI98C/LQKRpkRIcQ4cBS4tOMOhoQ8J2wUSLp+nvB9nzt37uB5HhcuXKj7hwv7D9Arv0p70wL44Ovn8JQD3meAKOinwb+O9CepGF+A436CWDSCph1CyhFsu4xpRjFjPeT9GBX/VTSZwRDdeGoJ3z6KEb+L442C/sUMV26Ripwm41xHqyZLzzq3EbIJS1sg6h+hEmljScWQyLof5qI9QlxrocQKKX2QjD/Dntg5bhbytFSjvmvJ17OVLAB2zAYP5qw5mvVmVqwYd/IZXOXRVM2JmTKSjJUXaDebmCgv0kyUCWuZ44l9vDZfQqAz66/QbEQYLqwQ1XRm3RI6grwhwYOsXeaQbGNiJoerIFKNru5NNvGXU6N809GdVa57FHaiANmoTObS0hKZTIYrV66gaVpd0dHS0lLNOOOTK347BsNENPCUQVEmKcgEf1r4YhbsJr4pdQY3Yz3Scew2h2YtZd4O5pbtKDAM4BzwpUAceEUI8apSavhhDT96OPcuqUUANk6yhmHgedt3I9uuoGnbNsvLy0gpty1kbuctoCZAjo2NMTo6umnuTSEEyvNwJidBKjw9hdbZD17Qd2t0Hq1nEJENfF1UtA2AclMXXi10w/fRuvsAMLQo/nCRSLqIikXQVrIoTVDO55D5EuZQJ1pMx51fpfDG5JbH8ag86cpANb/GoaEhXnzxRc6f2E9H7irSBU2UkdW3aqfYglppRvcEmuaiGRJpptCsGfTSHHp6BX1+Gl87hxJJNGu8vg8puoirZZQ8EfzgB2/eWjmLwkAaHRgr15F6Cr/lPF7X16/tpBFDth1D83Y2qCildqPVvAy8IITYL4SIAP8vgZm8kSmCwQAhRA9wBBjb6Y5CQp4npJRrErDD2nmlUChw6dIlWltbefHFFwMhUznoxe/FKP8oqBWypRdwxGk8/zbIMdCPADb4t3H1d5JXNo77Cpp+CE1z8Lwsvh8nEsnhm+9i3r5KyXsNU98XJF3XAx9BPXafiHGcvNpPXgYCYdmbR2CSd+/TbBxC4oDViSF7yJtd3K9MsWjdJ661kvMW6Ym8gK9cOiLBe6ZOhK7ICe4UPRadPDOVGQwMpipTxFWcVbVKs99M1ssyFBsiqTejyRd4I7vIwWQfnpLsi3cF2sh4Bwroj3UgUXRpzRyMDJEpJ8i6Dvub2nGkz8GmTiq+y5HmLnKuxeGWLhatIsdbukmoFrK2wbRTIS40RnMZNGAqm+FP7t/Fsh5N6NoJjzIv6bpOa2srzc3NnD9/npMnTxKLxZibm+Py5ctcu/FZltJfh66G0dCxZZys38Sil+KPcl/BgtPEqZYXaBaJR86as9tqc7tImbcdBcYM8BdKqZJSagX4a+DFrRp+aoKmpmlomrbmRtiJhnK766+urvLaa6+RSqXo6+vb1gXbyPdyI6SUTE1N4TgO58+f31SA1TQNFhehmrvNHpnFNx8IpMp2cM0HmjB7YgZPjyDzAm0xg2huCfZXLINpUpiwMXq7wPWIDvaiOR7aYBfmah7RFMNTHtb4HPZShvmPXd3QbPQssdMBQb/0a2hYaEaQzkiLKJylJpSloeHi+waaGQxoMjbwYD/RHoSSGEs3kfYRlP6gpJpwAn9OPXcDXz+NnpsAQHMWkJHTKG0fwi8jIwexh74fNuivSh0i6mR2dOyO4+w4EE0p5QHfBfwlcAf4faXULSHEtwshvr262k8A7xRC3AA+BnygOjCEhLxtqWkx188rnucxPT3NjRs3OHnyJHv27Hmwjojgx9+PjLwPpQQ+EqkWgFZQWfAnUdoxKvppiu7nEFoKsFAyh+cl0LQVzOhZcgyyYn+CqH4U8NCqfjgV7ypR/RiuvYeM38eyO0nWvU1Ua8eWy6QiwcutV1U8oMeY9FJMWKN0Rw/i49ERGQRAVuP50u4MmjIpuUluFlzm7AUGYgNUZIXB6CASSXck8EVMEAQXxrQU19KCQlXoLvrBGJnxgrGvliNzxckT1UxsO8anF7KsWEGln0w16KfsB9oPrzpHRjSdvlgLTU4zNxfTDDQ140rJYDROyfc41t7FkmORd20+ff0aly9fZnh4mJWVlR3N9zvlcSpAIpEIvb29HDt2jJde7GfPnp8mrq9gKh/XlSjpkHaT/EH2Xcw5Ek0JvrTj5V0JievZrUZzF4LmdhQYfwR8kRDCEEIkCEzrd7Zq+Kn7aDay3Uo7NR4maCqlGBsbY3V1lXPnzjE3N7ftm7pmEn/YDVJLmdDR0cHRo0cf2p4QAjE7u+Y3p7Q2nY+dVUhNR5N+IJAefAF5JYhQ17r68At5/IUltBeO4l6aJXasA1hGOg0aYKmI7enCGlvA03TiBzpxlrLce+0GThTa2tpob2+nra3tsSZyfdScXTsZENTifcyVq0jHwOwoIj0DVQHDkMhqBSDfi2OI4P9CsVQv9yl9l/rj6kcRORfZdQDhLWIUpur7EGUN/AfHpBXnqZb/RcX2omJDmx6HZzaB74C+vUoYNf/TnaKU+jPgz9b99sGG/+eAL99xwyEhzzEbjSNKKVZXVxFC8PLLL288aev78ZM/iTLfR9T/FwiVB9EC2n6kzFIGfH8BKKNkDmhFqWVc7yCa2cyycwNTPwQopCoCBrZ/n7h5lop7BU/0M6ddBedq3R8zYR7DdtIUvWlQOhWmiBhfwg3u0qMfpujlUCqYs5adCXQiLDvjtBl9OKqCtE9xzZ/lheQL5LwcUS14Yc2UM6BDjiC6PKNl6DdO8NHFBaJahNHSPO2RZibKi/RG2pi10vRH25mz0wzGOqn4Dp1yH68VlhiKtTJVzrIn3sp4KUN/rJn7hRU6owmGC8s0G1GkVJRWBXdJI4DFciCY2tXYQ7M6j/Y1tzKVjPKeo6fI5XKk02nGx8e3Ffi5Gx5V0NxIBrDdu5St9xPXXNr1HKt+G51GmTcqx/gfiydwPRsU7DWGcPM2nuc9FY1mLXn9TlBKeUKImgJDB36jpsCoLv+gUuqOEOIvgOsEs+KvK6Vubt5qwFPTaMLOgiY2YjNB03EcXn/9dXzfr2sadxI4tNW6s7Oz3Lp1i6GhoW1dTE3TEIsNwVmRCIUbUxhDQdoBEYtRvjdHpa0hU4CMoaouE+5iBoVAJJNY+UCAcWZXUELDnV5AJWIwv4KIR5HlCnpbC9Eje9ENDRZz9C0Izp07R2dnJ9lslitXrnDlyhUmJycpFAqPLCg+atWmnQwI+ud+A5SGiGooH9xiM7oh8T0NPR5ojEVDubPW6ANtrio9ECZ9K49wi4jlPH70NIIH11upGL7+IMGwMnuQ+l6U0HEGvnHTvkkp8aOtbOzqsjFhnfOQkCdHLpfj5s2bRCIRTp48uaVmSEQucH/+J5FiEFQeV7RQFO243lUUZSCFUstYVgcQxSFO1tfxVRlPziNI4soZEmYQhOnJNLZ4J6OVq+j2vmAfdX/MW0REB45cJaFOUBKnWfYDxUHWn0XHZNmZIGUMYMsSvbEgt2dS72einCItgxK6C9YCGhoT5QliKkZOz9Ed6SbrZjmYOIRd6WHVieAqn/3JbiSKwVgQCNsVDaw67WYwBnWbKWYyMaQKFBGpSFCNrjsWLO+Lt6CAoUQKT0nONA9ybSLLQFMrq1aFI6kOpot59jS1MGNXSEVjDGfTRDSNtFXhzuxyvbDHoUOHuHDhAsePHycSiTA1NcWlS5e4desW8/Pz256vN+NxaDQbBbyS9VdUKv+CiHCJCYtFr4u4cPh46QJ/VngnkWgTZjxGLDLIe7rOsrKywvj4OHNzc4801z6qj+ZOUEr9mVLqsFLqoFLq31Z/++A6JcbPKqWOK6VOKqV+fjvtPlVB81HZSNBMp9NcvnyZvXv3cvjw4fqNshOz/GaCpu/73Lx5k5WVFS5cuEAikdjWwyCEwJmzoXqzGN294EsqKy4IgVb9rrJO3fO2NJrBHAzMJd5qFr2vH9kxiDUTCJ0yX8Yc6gWpoKsNPB/z0AGysyaZxSYKc4L5zxbxO/ZQHF6qOzNv9HAXi0Xu3LnD/Pw8jvPW5/Pe7oCgZq5DdhzhlpBSw8u3IozgnMrG1ESp6m9GG5o9H/wf6SVCYCJSGBiVQFss3BKVBYmnNZjRc4toq7fwzX3B+g6Iwgxex5eiYn2b9q8+IOjbTz4flp8MCXn8KKUYHx/nzp07nDp1akcFISS92MYHsY33UHRfQ6ks0IqSizhOO0pBPG5R1t9JxbyLq8bQRApPLhM3gxQ+lneLqPESc66JTSCsSSML6BSq/pgKF7/SQky8wKyIMGMvsmCPklAd2KpEb+wFAOJGkOKo6K3SGXmRV7LL2FKxolZo19op+AU6ZAcSyZ5k4GLXarbSE+kjbbUx5lWwZDCuZ9xA27hoZwGYtQIt5LS1wpHYfl6dL1BwHMaKgW/lZCUb+FiWg/XnrSBpRdapcDo+yMyKFRh/qhNXwgjOc08iiQQOtLRR9lzOd/XhpiUTSzkmM7k157sW+HnixAkuXrzI0NAQtm1jWRaXL1/m/v37rK6u7tjM/jg0mrXt8+XfxHd+Eh2BQLDqt+MonY+WvoBP5o9Rcm00ZVCyWjncvI8DvYMcPnyYvXv30tfXt0aQvnnzJnNzc9t2aXsLTedPjLeNoKmUYnR0lPv373P27Nl6LdQaO02FtH7dcrnM5cuXaW5u5vTp0xiGse02VaGMHF1G2xMMHMoMBh5nPoMYGCKXDwYBPV9B9Qyi9/bhLBeR4oFmTkWS5G6l8bPFQMAERE2gqTjYPXvJTkjsxQqxvmbKoysYLTGU0smO2qQvrTXdNz7cTU1NDA4OYts2N2/e5PLly4yMjNTzfz5ptl3d6ZXfRKkgv5kqeWjKQRPVij9akHrUVX0orR/XOIdrvoQXP48fP4SM9tTbkfF9aLj171FrmUqhDal0KqILzVpBIFFOE0pvQcuOojkZ3K5/8ND+vYVO2yEhIRsghMBxHN544w1s2+bixYv1NDXbRdM0PNmFmfhehEgi5RyIAZSCSGQUzfwylvwyRfcNkCkUBaJGYJ0qu1cwtUE0/RQrXgclP03evYchmlFGlvbIKSCwuqEEZrKb+47BkjNLX/QwoIgRCJYFbxWARWuEJr0TR/YzXTGxpM1gPFBCxKtCrBEJNJBpN4hM96TBtbTgam6aOCbj5UU6Iy3MVFYYiHWwaGfZl+gh7RY4lOgjJfpYLBqsOhWOtHSRdSvsNVvIuhaHm7tYtku80NTBXKXAydYeZMlkIWNzP5emIxbnbmaVJsPkfjaNLgSzxWpNdMfhZKoLL6dYzJVIxWL85fDoQ69fc3Mze/fuJZFIcPbsWdrb20mn07zxxhtcuXKlrhzZSjv4uEznudJ/Qrn/lQgaEVyKMkqLVuJV6x18Jr8PgUFcTzJVNPCkztf0vbimjfWC9L59+/A8j+HhYS5dusS9e/dYXl7Gdd2H9mMnPGuWsqfqo7lZ0M1Oykp6nofjONy4cYOmpiYuXLiw4UXRdX3bEW+1aPIay8vLDA8Pc+LECdra2rbs/3r8yUUA8jeWaNmTwi080BrmZ4uYmkltb56tY7Q1ASUqo3PEO5qRhQK+H6H2XiAigS+OPbmIZhrYNFOe8pG5FfTWOO5KAaQisb8Nay5Had5h6WMTdLw8uGH/ag93W1tb/SHIZrMsLy8zMjKyZQWFR2U711uOXUGsZjATeZxyO7GmNL6rE2mxUL7A9lpgOQKdvYiJu0HS9q6TiPTdYPuuM3iJM+jl6yit5UG7ZidmZQUTKCWPEImaQPDWrudHyDYdo03dxo8PIFMPT83xVpo4QkJC3ozv+7z++uscPHiwnpgbduZHXlNgGMYLJJt+jkL+nyG4jaZdwNV0Vu3PYWipoFa5GkCRoeJeIaIfxpUzOOIkk5XLCHTieh8Vf75er7zkzYLScMUKGO/mWvkug7ETlK0sVrVMblbMECFJ3lukO3KAiiziyyNcKwyzL74PgLSTBgWL/iIREWHBWyBlpsh6WfZGzvHRxUmONe/hTmGaPaKNcbVKf6ydFSdPR6SZWWuVJiNGymhCc1K8sjTLi23VrCbVlESGFozJMT0QE5rMKPsT7cQqSa6sznG+u4/ZUoH9LW28tjTPiY5OriwvcrK9i5vpZfrNKG16lPn5IpNWjrhhMJXNk61YfNvLW+d3FkKg6zodHR31nNeWZZFOp5mYmKBUKtWTrLe3t9eLXzRe80cSNJUk0vTzCO8GKd1Gx2fVbyellfk/ha/kbqUNhcRTguVyDF1ILrTvo7WqSII3C4mNleGGhoaQUtb9VaemAteuWo3z1tbWuiyym3llO+WM3yqeqWAgaHzIt+6aYRjkcjkuX77MCy+8sGZgWc9ufDRrWtJMJsOFCxfedCNvt01/IjDfKsfDi/RiTy3Wl5laDL0thb8aDDL+zDJlWc0w4Eu0nj5kuUR+pIA52IszMoU1sYgeMVC2g376KIWPLxI50onMVIgPtVO8MUtsqAM/V8FZKtJ0oBt7Po+9WibasWV5wzclT19fo7ylpaWeU2zXNcob2Jag+cr/RsfHs5OIagohiYGTj+MVYsRbSyBAmQ+ukXCzD/7PzyMWlvA7DqP8B9dMRvrRq07zifQ4ftfaqlRRP45Ugml1islq9oL29vb6ILCmj7t02g41miEhjwdd13n55ZcfKQCjNgd5nsfdu520tX0NzU2fo0gZyyuhqKBr+3DlHEofRldH8MU9NNHKqm+Qdy7TbLxAwbtPVO+g4s+Tc++An8BmmSZxnnG/hFn1x1x2gvrkGXeWLnMfy+4ErWIfy2oEQ2vnds7F1BYQCKYqU7ToLay6q6RkioyeqSdl7470UnK7WLADodqt5gkuEPhyzlmBtnOyvISGoGw7zK9EGJXzRNC4m18irhncK6yQ0EymnCJRoTNcWCEiNDSpMTPvsGpkEMBcKZiz0tVKd3Y1al7XNExNo0fFuHZ/ibMDvSwVFzjd1831+SVS8RjDy6sc7tq8YMpmLwaxWIz+/n76+/vXJFm/efMmvu/Xx+eaQmi3gqbveyjeT0tkmpgQOMrEkk0UZYzfL3w5E1YcgcQUSaYLGq50iOvmGm0mbD0naJpWFyzhQZnMpaUl7t+/TzQaRdd14vH4jgTnZ81S9syZzrebS1MpxfLyMsvLy5w9e/ahQibs3EfTtm1ef/11pJScP3/+TUJmbb3tCJpeVdAEcPISt/WBRk1vb6ey7NbT5YjOFL54cIPYsxmMoSGclQpeMVCtK8slMtSP3pWiMB9cQj8TPOxeIRDCIqk41nSGWH8zZrOONZVh/k9HtnX866lVUDh16hTnz5+nt7eXYrHI9evXef3117Ftm1wut2sz+1YPkHfts2iZ+WA910VPVo9ZNYGlg/EgrZRwA5ON0iOIYuAuoCItaOVqMNbqHMzl8BOBGwOyoVKQMGGlhNIC4VkZSSLLd5GJE3Sf/Se8+OKLtLS0sLS0xGuvvca1a9fWmHFCjWZIyNNnp8/gRtsXi0UuXbpEV1cXQ0M/S44hCt49tOrYbHl3iJtnAJDkMLSLjFgzaFrNZSsYC7POLeL6IL6yEFY3Me1FxqQk7eVYtEdpNXqxZZmeWFBtTNcCBUteLZLSz/Cp1WniehN5L8++xD4kkoQTKAsSkeBvyS/RGx3gbk5yL59htDRHXIswVlqgM9LCiirSH02x4uQ5kOgl55U5auzjc/Nl+ps6sJG80NSBLX0GtDi29NgTacJWPoeS7Vi+x8WW/bw6tsKBllQ96GeuVOBASxtj+Sx9ySaGs6u0RaIslUscNTqZTgdzUbpcnZuq80NT1OQvhx89pW8tyfq+ffs4e/YsZ86coa2tjZWVFV577TXK5TLT09OUSqUdabQ9d4VC6euJaDPomk5Fxsn4Laz47fzvzHuYtpqICJOIaGUsrzDQSeoRzrUcoj2yVrjbqfKhVibzyJEjXLx4kcOHDwNB7MmlS5e4ffs28/Pz2Lb90HaetXnlmYs6345AWPPB8TyPnp6eoCThFuxEo+m6Lnfv3mVoaIjDhw9vKgRtp02lFO7kQv17QUq8vAl6cOo9W2DNZInsD1Lm+IkWSvcW0JLBIOKl89hucPPakyvonW3Beo6k4qUo3VuGhIm/VCLa34Y1sYrZ2YQ9mwYNoj1NVEZX8Io2+esLjxxhrmkabW1tHDhwgHPnznH69GmEEPVEtjdu3GB2dnZHiXm3EjTlK3+MkBWEAlDoRhkr24bulBBC4FdTPClNrwuXsmkAUU0NIhP9D/bV1I8oZ1BTK/jJo4jyg2wAdmQALT+PnzhV3W4/Qvko1YJK9GOaJl1dXWsGAcMwmJiY4NKlS4yPj1OpVLYcBBp51gaEkJDPdwqFAlNTU5w+fZr+/n6EiNDT8oOAhu3fI2GeB8D1Z0A1U/YHSKtmPOVgy1VAo+CN0mIeBRS+ZSKUSUk0c6dSJOPO0xsNUiEl9UCTlXUXAMGiPUYzfZScAZa9GAroiFTNxm4wphbNIgLBgr9AjBgR0cp0sZmx8iovJPuxpcfBpj4kiv5YkK85ZQRjTFyP0Of3M5Xz8QBRNZPLqpncTARzqV8djkvlMnu8NuZXgiAivSo01YJ+UrFg/YFkM55SnGrvRssKIkon73q80NHORCZHX3OS+8tpmiMRxtNZPnr/4YLmbszeNUvc4cOHuXjxYj3bzNjYGJcuXeLOnTssLi4+NODVtscolr8FQ60Q13yQGhHhUJBx/ij3ZaT9OK7yUH6ChZKOKQxKvgN2kr/d9+Za7o+aRzMej9Pc3MzQ0BAXL15kz549OI7D7du31+QjXa+c2828IoT4SiHEPSHEiBDiX22w/N1CiJwQ4mr18yPbbfuZNZ1vRjab5datWxw6dIhoNMrsuvyUu20Xgpt7ZmaGdDq9pSketpf305lbRXkP9hvTE1QWl4lc2I8zMkZ5MguAlZFogL3ioFwfvX8Qef8+eqoFO//gMuntKfyVLEpEqCw4KE8SGWjHvb+C0Z7EnssS7WuleGOWxIFu3EwJoz1BNNWCl6+Q/twcHe8Y4HFhmiaRSIRjx46hlKJcLtfLcbquS2tra93Mvpmm4WGDinvpY2hOHsdtI26u4Kk4zlIUw9TRzeC8mm1VDWRzP6JcrfYTaXjItAcJ0VUkhWAeIT38BRutrRlYDpZVExszO4Ls7ka5AkHg37kR8XiceDxeN+NMT0+zurpar5Xb1tZGKpV6aN7SUqlEX9/mkewhISE7YyPf+dpvDxNefN/n9u3bWJbF3r1710zUCfMl2hPfRLr8W9jeCIJmwCTvnSTNdSJeGxpxKv48qciLZJxreNWE6MooYomXmdZH6Y8cY865gyuDZYv2feJaC0V/ld7oC1jSIlvqZcydol8PhLiZygw6OvPuPCkjRcbLsDe+l5nKDK3+QT6xtMipln1QWakfX8GrVNvPAkFUecpIMrXoMGHZCE3QpEe4m1+i2YgyXFimzYwxXFgmZcYZt7IMmU1YpSg5y6Xi5YkLjbury0SEYDiziiEEU4XA7WixXOJUqpvCisNyoUxPtaZ5UzQYm/tbmpkvlDjRkeLq/CL7U23cml3mxMDaoN3HiaZpa2qZ5/N50uk0MzMzKKXe5AZl2VepWN9PTPiktCyrXisps8Q15yh/nL1IyXMxhYHyWpm0JFLZxLUI0klyoLWbvkTzm/ogpXxkDXtNWK3FUtSCpXzfr/t3TkxM1M3wnuftWNAUQc6tXwbeS1D957IQ4o+VUrfXrfpppdRX7/QYnhvTuVKKiYkJ7t69y5kzZ+jp6XksKYtq+L7PjRs3yGazDAwMbMv3MKh3+nCNZv7mHHbHg4hndyHwa8nfz2MO9uEXAu1XZTKNHBrAnQ2WlyczKE1D6+qmeG8JrbWq1ZzJgGmwOuoRGQzeVv1ycL7s+RwKcFeLRPd348Y6mL4C+UqK9LzJ/G2Y/dQD/9DHjRCCZDLJ0NAQL730EmfPnq3n7qxFDG6UT+xhE4D36seRHqjqPeGU40QMD6ccbK8kGFoQvEOs4UGXDzSqtao/we8N1yvajT9fRsaCFwrNCtYT0sNXvYhMkALJH/jCbR17JBKho6ODM2fO1KMls9ksV69e5Y033mB8fJxcLrfm2Mvl8o59abZ686yu8+7qW+ctIcSndrSDkJC3GVvNFTVTeSqVYmhoaEMFQnfyu9G1DnyVJWK+zKSjk2UYTTXhyCxtkSD3bsWfB3TKcoIm7R2Mes041QwiaW8WDZNVd5qOyFC16k/gky9I8UbOZ9JbxMBgzpqjO9JNRVboJhijOiOB37yOiecMcd8KqvWMlxcx0BkpzdNiJJgsL9EbbWPRztKrtZIUcbx0K8NWhWOpXmzpc7i1C09JDjV14CvFgaZ2fKXY39TO4WQXsXKC6UKJQ23tuEpytLMbW0kOtaQoei6DkRjLlTIHks1063EqKy53FlfoTMQZXkkT1QRj6SyagIVCoBGteB57WltI2AZ/ee3+ptfjUQN51iOEoLW1lf3793Pu3DleeumlNW5Qd4Z/kXLp/Zj4mMJlzutBF4qP5c/yv9LncKVORI+QsxIsWYFmuM1MspQVFB2fv7d346Itvu8/scpAjflIa2UyE4kEH/rQh/jEJz7BBz7wAX7lV36FQqGwnd1cBEaUUmNKKQf4PeB9j9TxBp45QXOjAcF1Xa5cuUKlUuHixYskEolN191JuzVKpRKXLl2ivb29nnNtO2b2rYRX13WZ+OwNrNtFvO4URmcbXq7qr5Kt4Mc616xvOw9cALxMici+IYqTFsqXRPq667+bLxzCXrRwVgNhypvJI1Ix3JUS8f2dyGSK1fk4K6+l0Uwds8kgfy8Lukb6ZoHywltTknKrxLy3b99mYWEB3/c3HFTsVz4BxTzSkhgxhVVOoftB34UWnHc/0YVQHo7ZhhTNuK1ncFvOIGlBNu1DCaNuTgcQpeX6/0oZCKuEX2zB01swiw1J9Ss+fqQX2bIP1fTA9P4wGgeEWrRk4yAQj8eZm5vj0qVL3Lhxg0984hOsrKzsSNBsePP8KuA48PVCiOPr1mkDfgX4u0qpE8A/3PYOQkLehtTKUG7E3Nwc169f5+TJkwwODm6Y3g5A15rpSX4fQv9Chss30UUzEouIDCxEeXcYnSSWv0TE2U9Uf5kpX1CRFRat+0RkEkvm6YsGiddNEfiWZ9x5mrSzfCo9Scpsx1Y2PaKqnKgO1SIajI9z9hwD0b1cyTisOh7LfoG9iS6KXoXDzf14ymdfIpgruqNtADS5Ca4v+USTgYbLq1bsKXmBCbngBcqOXNU0H1URbk3lybvBfFl0g/UsL4gR0Kq5i1ubW4hoGj0kuDG2QlT6Qa30pgSO7zOYjJOzbI50dTKbL7C3rRUDgZ6R3J5a4jN3J/HfgvR5G2EYRt0N6siJa/T3/D66CK77spVESp+P547ziexRfKVjSZey1YItTSQKz1dkshpNRowX23s50JzacD+PowTldrWikUiEnp4efuInfoLjx4/zoz/6o8C2A6IGgOmG7zPV39bzBUKIa0KIPxdCnNhOw/Ac+GjmcjkuXbpEf38/x44dW3PRHodGc3FxkatXr3L8+HEGqwnShRDbavdhgmaxWOTy5ctEFoORorygo3eujbIrr4Le+kDIcHICeh7UQPc8k8pcoGWrzOZRgDB0Stng7bgynSXS3wYK9M4m0ASyuYPZz+SJdibwii6tR1MUhjPoEY2WfUlKM0VGf398y2N7EqzPJzY4OIhlWRQKBa5fv16P8K9F/Lt/80mkDxo2suKgbBczHgx6kWYfpUCl9lJ2DyBnJHJyDjk8hj+bQd65j3s/i+2dwms6jjLigdm8svqgQ5Vq4uDMIkX/4Jp6PtJoRlkR/L53bPv4HjaoNNbKvXjxIgcOHGB+fp7PfOYzfM/3fA/f9m3fxvT09IbbrmM7b57fAPyBUmoKQCm1REjI5wnb9f2vFeBYXl6u59uEB2nzNqIt/rWs+C4Kl7gRCHSWNkpU68RTRYTVi6aasGP9XC9Ps+xM0G7uwccjqQIzccnPALBoj9AZ2U/G7SXnB0JnqxkUjijJQAOYM3JERIQ5O9BudphDrFjtrDhl+qPBXNFsVP35qz7p6WrN8jkrzYDs57WcjUBjuLBCkx7hXm6JNjPOcH6ZrmiSkeIqPdEmpss5zif38tej83QnmpiulOiOxrmfTdMdS3Avm6Y9GudeZpVmM8JSucRho4ORpQKagHx1KlwtrY1CrzkN7W9uZWx4hZ6WJsq2S3tzgtfH5zY8z49bo7kZ2dK/Q3gfpkmTtBgVXBFjIJbnb0oX+Fh6Hznbwi7aLGejzJRKVDyXJhGnXIxS8DyKnsPX7Dm8afuPq9b5TtuoVCq8+OKLfOd3fud2Tegbnez1av03gL1KqReBXwT+cLv9eSY1mp7n1U3ld+7c4cyZMxvmhHoUjaaUknv37jEzM8OFCxdobW1ds+52NZobmVgWFhaCN+Sjx3Gng0FFZV1s2eg3KCiMZtB7gjdXYepUJkp4okGrKaNEBgLh1FkuonrbYLCb9BvL6MlA2DRSQZt+2sI8tJfFz+VAF5SnAnOyQOGXPdqOpyjPFKjMl1i9sor0Hy0o6FFpjBhsbm7m5MmTa0wZw7/7e8hsBl13kFocJXWkpyEEeK6G7xtUrD3IrI2WXsGLJBClIH0HzQ2aYi2GHB7HznXitRyp/yyNBBQeBGmpksBuOvBgu1IRkZ7C63nnto9pu1HnNReDb/iGb+DFF1/kwx/+MN/8zd9cn+i2YDtvnoeBlBDik0KI14UQ/2S7xxAS8nbEMIw143/NitXa2lovwNG47mbjvxAaR1q+HYCMc5MY/SA8IgTjuBk3WJL7Ga7cryZgh4gWjOkFbR6dCFlvge7IAdrN/WSdQSYqq1SqlprpyjQmJlmRpSfSg61shuJDmMIkqe3jE0vLuLX65+7/n70/D5JsTc86wd9Z3Y/va+wRGZEZGbnnzZvLrU2lrtIIIQSiRCMBakDNdKtpGQKBGdbQ3TZdbTNqxhrDpgcDITRDzwyLpgENiEWN0F6lkqrqVu77Evu++L67n/WbP86J8MibW0TeW1WXSzz/uIfH8c/P+n7P9y7P69v4hfYWIUllvrVNWouy3itzwhimWzco91S6uJyM554Ll5+IZ/1WktEUAJPRNCNeDrvnU4LRqG+LRqIxf7tEEk8IppIpbM/jnewgVCEs1D2v5U6rzYlMmo12h+F4lM2eSVzXWKhUOaVHePJsG8+DWkBEJeA37r9avP3bCc/zqDZ/Btn9VeKyhSH1aHlxknKXX2p8iTvdMQw1TDyUoOAl8VDRXQnRcJndbNHumUQVlSvJEc5nBl/7O9+u0Pnr0Ol0DlQkvQ/rwPi+v8eA51YBQoiGEKIVvP9VQJMk6fmw7CvwsSOaqqpiWRZ3796l0+k8Fyr/IN62f/mudJGiKFy+fPmt9TE/mKMphGB2dpaNjQ2uXbuGUuwi7H3e2fkuoWP+KlgfyeK2bCp3i2i5BPrYAML0MOdrqPk0yBK1uRZE+uRU0aM01gXC9nCy/gq4vVxFACJqUFsT2A2LxOk0ZrFLfCZN42kFLakjLJveTpfUmRRe22bjt16+knwbfNhKdiHECxXdAysLuI6CjEWvpyFLAkIqQkDXzOI1JKRmHanph8LdWKo/oKLuHxwAqdXAKcvYiUsISUZER5FE/9rJnTZeoYtQIwgtCtVNRCgGuekDH8fbdnBIp9N89rOffa4ZwGtwkJWnClwB/jDwB4H/QZKkVy+7j3CETzj2h863tra4d+8e586dY3x8/AXP2QcbdnwQg8bnSesXAYEWNH9ous8w5E/xoNcmrPrEY1eAfcf0O/s4kklWOeb/hjTIt2ptlnvrfj6muekTS88kJ/y5Ox60nrSFi+0c4/3KFioKC60tsnqcktNkVEnRdS1OxEb8FpRGnmE9Q62kMN/tkTT8iJn4QLi8Zvlkr9hrMxXJUKl4zJXrbAXamNsd/7UQ5ICWuv5r3exxMT1Au2RRbnVxA/uqB0QoGfYLL4cTcTwBpwdyHA+liChRal2LsVSU5VKdtKHzbLPM9fl1etaLHXG+nR5N1+nRaP0ZNHEPFYmuCFNwslTdCP9b7Y/yqJPEFA62C8VOhJASwpElEuE0lpwgH/VJt1O1GK5Ze519XuYF/06GzvdDCHHY79wATkqSNCVJkg78KeDf7t9AkqQhKbgokiS9h88fyy+M9BJ87ELnpmmysrLC0NAQZ8+efaPY6UFJzu621WqVmzdvMjU1xfT09Ev34aBEc/92lmVx69YtJEni8uXLaJpGe7avnyl0hfZag1ZFB0VGDrxXwhGQzCL0YPUhgESW0MQAZqlH7XEBDJ8IC1fBaQcyFI7/mVPr4YzHKTzwEDH/xpID6SQ1qiIcj8R0ksZsjVAuhB6RqT6qsPIrBwrTfkfwQaPS+r33kTotFEOh08uhBn2TBIJ6NYvbFUgSeNEEdILwt7pvsWC1++871f77bgt3bhHbuICQ+ykLQjPQWhXkTgvHmMGLjSMJgRi5BNLBH5G3WXm2Wq3DylC8ceUZbPNrQoi2EKIEfA14hyMc4T8CvCp0bts2jx49Ymdnh/fee49EIvGSbx8sUjaT+K8An2BK1hAoVyiKGC4uVXsDGYWqvcGAPoXAI6kFYXavhS5d4vcqS6S0NB23w7GITz5FUOBoaz7xWu2tMhE+zq2yRc9VaDldTsZH8BCMhv1Ily75RauW53/HMj0ebnusezYy8KxRJITMXLtCUgvvhcsXWmVGjQRpNYJdV3lcLjMZT7LRbjKZSLHeajIajrDZaXMsnmC5WWcsGiejGFR3ejwplMkYBrPFMjFdY65UQZdllqt+b/TtZpusriG3BHOr5b2lcDbh27qJfBrH80iHVf7hr/4Ojx49Ymtr67XSQx8FLHODZvvPoIgtFCRcodLxQvREiH9T/0+Y7YVAgCEl2WiHabgWnucRJ0mh4dF1HUzhMqSmmEwP8We/8AUGBgZoNBrcvXuXW7duPVf0+d0Inb+N40cI4QB/Efh14AnwS0KIR5Ik/ZQkST8VbPajwENJku4Bfwf4U+KAP/ax8WgKIVhdXWVjY4OBgYGPXPJFCIFpmjx79myvGvpVOCzRbDQa3Lx5k4mJCU6ePLln6Lrr9f7vZwzwoLXSJHRyEqfbvz6Ve0W6+/hQ41EBUwm8uLbAmPSLUUwzRPhY0K1nuY4+7BtKOZTF60J3tYOQoPakjGTINGarSLqMXfeTvBNnMriKSuLSAFZPUF/aV439XcQHiWbvd76G13OwWy50e+h6F8eRMSsqumehRX0yZ4X3eboDcikkCep+SFxoBjR8j6cnyVD3K+69pSUcK4YISKSIj+65Cd3lBVzhLwK8sUuHOo63DXEcMGS+izeuPIF/A3xekiRVkqQI8Cl843GEI/xHCdd1efbsGbFYjHfeeee1necOQjR16xRqbwqVPFXrGM+6qxTMBUJSlI5bYyjsBxD82j0omIvExDCrvShNV0cg9vQx66Y/T9S0GiEpRMkpkSHDkH6CYi9N3THJ6IF3M+j2s236E8aGUyUk+b3MJxnnK1t1RqIpanaPM8lBuq7NVDjpV5cH4fJjsTQyEifDQ9xcqpAJ+XY0Z/iv2UAbMxVE+nJGlJCiMBPOcHduh9FEHE8IJjNJbM9jOpuhY9vMDOSodHvM5LPENI1EW+bewjb5eIS57QqxkMZSsYYiSxQagb1WNEpemImJCUzT5OHDh9y8eZPl5WUcx3nrJiAvg2nN0en9JLpUYUCtoeIRl9u0PYP/X+2HqLsxFBQUYiw2BLqkElNC2L0wG3ULCcjoBqGuRqHe5fuOTaIoCul0mhMnTnD16lUuXLhAJBLZK/rsdDpsbW3R7b59Ae7bzCuSJB3aIyyE+FUhxIwQ4oQQ4m8En/2CEOIXgvc/J4Q4J4R4RwjxaSHENw469seCaDqOw71792g2m2/0Yn6Y8T3P47333ntj7sJhQue2bfPw4UMuXrz4gu7mxtdKhKf8z7x9cknFu3W6lf7KTUtHMd19HjbHpVzp/35rvYWai1G636Sz0el/L5sgMjNI8XoHKazg1m0Sp7NgCyInErhtB3lMpyt59LJZVm6ZzP5Gk3ZLYfVGm7v/r5U3HuNB8GFDHPuJZudbdxDtFsJzUGQPIal4nkS7PUg4bON5EprsJ7tHEoFXGAj1fMPb05NIQRWlSAwi7S6lE0MQhI0EEu78Mk7CF2YXcv9+kAS4LRmBhBi9dKjjeJvV62FzaQ6y8hRCPAF+DbgPXAf+VyHEw0Pt2BGO8AnB9vY229vbDA8Pc+zYsTfaqzcRzfX1dR49esTp7M8wb0fYUdeIKzlsYZIPTQLQcWoA7JgLJNQBUtoUJXOYgtNEBDZpVx+z5JYY1AexhMV4ZBxd0hFmnq8UijTs5+WLFtrbZPU4BbPOsXAeC4dTsVGi3TyNrj/HZMP+XKLKwYI8CJvvVpXXrR4z2giPtnybudbycz2XG3UkYCV43ex2kPDD5cdEkoUt/5iKLX+fal1/vO5uyDhwbg2EI6wvVDFUFQGMZhLYrsuJwQyNrsnMcJatWovJfIqYqvH0wRaepO11+Ll06RKxWAzTNLl58yb3799nY2PjQ5G1jvl1ur3/Gl0yiUgdSk4aXbK525vhl2p/kB3LpuP2kNw4Wx0FWYK2a+N2DYSrEdd0JCQ6VRcciclkii8eO/bC7+xWfu8Wfeq6jud5zM7Ocv369VcKrL8Oh00jEEJ86HS2jxrf9dB5o9Hg+vXrDAwMcO7cOTRNO3CBz0Gwv5WYYRgHIgIHIZqe5+2Jkr/33nsvhD+drk1rvkJlSUJNGDj7nhEtE0MYfTkEfShN5V4ROe97KKXBKO6KQA77hsPcaSEPjYAHva02kRO+V7Oz0qCyqeCZHqFJ37hIgfSEbEmoMQ09NcTG+xJSWKW93sM4ptDYaNLe7FG6X8dqHfyG/3Zi90Fq/Orvgm1i9Qxk4fr7XUvhtn3y6IXjSMGqXgqqK71IGsX1/x9K9xOzW2b/PnL3C7jHB8Hq4c4u42YuIDr9iyOMJN7SPO745yDSVwA4CN5m5fkWuTRvXHkGf/8tIcRZIcR5IcTfPtQPHOEInwB4nseTJ0/Y2tri+PHjL20j/DK8imjuVqlXKhWuXbvGsfRnSGpjIAkSQWi8bK0ho1JzthjQjyMhEZZP8fVqhZrn26u17hppNU3X6+7JGO3lY3oubWuU+2YNQ9ZZ7RYZDWf3wuZiX9jckHUyRFnfsnnW6VGXfLu40CyjIPG0XiCiaCybDZJqiPlmmfPJYZpViUbbYbPd5EQiTaHbYSaZodTrcDLlv86ks1Rti8upPO0dC9WT2Gq2mEonWas3GE8mWKzUGIrFmCtVSBth5soVPjUwzMMn28hIFNsmElBq+sS0E+RiKpKMBBxLxHn2YJt8Ksbv3Oq3R1ZVlUwmQzwe59q1a0xPT79A1srl8oF5QqvzT3HM/w5F+HNM0U1jihDXe5f4V9V3aDsehmJgW0kW2zYdxyIk6ajdGDXToWb1sF0PoxdCRaXnOHzvxPhel6RXQZIkFEVhfHycd955hytXruzpSu9qKy8vL9NoNN5IDA9DNE3TJBwOv3nD7yC+q0Sz1+vx6NGjvVZfcLhK8l286iLtVn9fuHCB0dGDd8N5E9HczcfUNA3DMF4ahmk+KSFcQa9s4iYGcYv9hGctHaNws4Jx3Je7sC0ZBLQCIQgjm8NuWBjTQfqALNGq9z2iQvMNpjacRtptVdkOVq1Pq8gRFbPUxUrlWfrtKqGMjrVhI8mC1FCc7rpNbEqnUWrw2//365im+aFWix8V2refYpeaeKiohv9gmVUPBRtV9++J0EhA/mQZISSc/AXayjhNc4KOeQyrl8ZOXsDNnSYW7YfWe92+gLup9EmnPb+NcPpETyR8w+8qr+8K9TIcNmn747bqPMIRPgmQJIlOp8ONGzcwDINLly6h6/qHksLbHS+RSHDhwoU9m38t9ccAv+AnLMXoeg2GwicBUKQQgnPcqK8QkkI0RIMheQiBQOsF9jzgvmu9NY6FT3KjZOJ5OhYuJ6K+/d8Nmzuev/+7YXPL8lit6Dyx2uRDUdY7dY7HstSsLmdSg5iew6lkHg/BMSPF2cQQ4V6EtXqTgaDINLrXUtI/nlgwt0RVjdORJFJTotzuEQ/5xCUdRF/ygW0dScbwhOBENs2pSAav7dE2bWaGszRMh+mhDOuVBuOZBPPbFXJxg+VSjcsDAzx9vIMsQbHa4jev94nmB69lJBJ5gaxVKhVu377N3bt3WV1dfaGf+e77RucX8Oy/Twgw5B5dT2dYLXPXPMlvNt5BlsJYwqHeM2jYCgk1TEKNsFUT1C0XXVYYCseRGjLlVhfHcxmPJfjBEwcvEt3FywTWw+Ew6+vrXL9+nYcPH7K5uXmo9s0vQ6vVOnQTkG83vqstKMPhMJ/+9KefY+uv6gz0Kuwahf0T/K50Ua/X49q1a891+TmIG/p18kb1ep2HDx8yMzNDPp9nZ+flnXbqj/vShZ2ii5uPoaz4uTiO5f9+u64iyxK1OX+l6yyZMBmjvubfaM3VDrIsEZ3Os/p+ieREDGunReNphUjGYOexTXjINwy9lS6x4Qi9nQ7piwNsLwi0UBjhtEjNxNl5v0z2QorKowZqVCE5GGXzepXmdUHi+2B+fh7LskilUmSzWVKp1IdunXVY1H7l95AlF7cLerJHx80R0isIIQhH/bC3rHiIwWlsK4b3ZA5oIEZHkaoNPADNwC0GRVi5QUKDF1GqT4mKPtHfL+1khZOwYxMK6SieBcJ/JKSJM4fe/7fRO3ubXJojHOEIr0aj0eDOnTucO3duT8nhg/JGr8MHn8dCocDc3Nxz4+3iZPTThJ00PbXKUPgk671HdJwaGe0YD5sWAjA9k+nINPOdeX8fJGjpLRRP2dPHDEk5Cr0wTbfKhBFh3SzTDCSPljs7qMgstLfIaDGKZoMZ6RhfK1Q5oSWZtxsci6Upmm3SIQNavtcQoOf6c2nI07i7VmIo6p+DlWbNH7vVQALmahW/eKhSQpUkdFfh6XqbsGqiSBJLlSqyBMs1P6y+3vDnrJ1mm1wkgtqGB0tFZoZ8b+su5zP0IJwfj7BWaTCVT9PY6SBb0GibnJrI8Wy1hKYqLG9VmRxOB99/+Ty9S9YyGd/h0Ov1qFQqLC0t7eW7Z7NZkskkqdw/BPs+cdnBkHpsOXnySp1/2/wB3m8OYAsTXdJx7Bw1y6Xn2ggRwmqpJFWNutwiIukUC12iqk4yrBFD5TP5UUIfwdy4q608NDSEEIJ2u02lUuHJkyd7LYwzmcyhHRJv0+f8243veuj8gzfTYT2aH9y+1+tx48YNQqEQly5deo5kHqbI52X7sLGxwePHj3n33XfJ51/fo7X+qN+BRsvFaDwUhMdSADRXgjaUCy20M2PY9YAECbCNOO01P9TQ224TPTWMLcIgQBsIilQsD21qmE7BovqohpLSQEB4NAESdN0w5dkerXXfUHULPnFVNQmn45K/kKD0oIYWU1Elic59iQsXLnDlyhWy2ezeavHevXusra3R6XRee7N/FJ651r0lnI0dBApCVui1dHplD0kC0wojSw4k0pgNnfaDEmLf5ZECqQ5kBVEJ+pYbUUSxQO/hKh1zDKH2vZshZ19lo5FAajSpCd+TaVdKvvzR2Mtbir0Ob1MdeOTVPMIRPlrEYjGuXbv2HCl8XWegV2FXrm51dfWF8XYhywpDncsAVOx1ZBQ0Oc9mL0/ZbpHRfUJUtX0vZIkSSTVJx/OrzUNyCEOa5KvFAg3bt2OLAbFc6RQYDmdoOl1OxkbxEIwbeVLmIDttCYGE7S+v2e76xG9/2DyqaCy1KpxXBvnGaomhaJyNVpPjiRSFTpupaJyGY3M6naXtOpzO5HCE4B0tw+25bUYiYVq2zclsmlrP5HQ+S6XTZSaXpdBqM51NoSsKQ26YO/NbDKWizO9USEfDzG1XCKsyCzsVNEVmrVxnNBXHrlisrlXp9IIuQ4G9TMbC/Pq3Zg91fcB3Vo2MjHD+/HmuXr3KyMgIrVaD7dJPkI3dRhIyptDZdAawhM6/aPww7zeH0OQQcSXBalNju9cDAWk1TrcVpmFb1KweIVfBbkJE0WnbNjFPxWu4/OHzH71SnCRJxGIxJiYmnmthXKlU6HQ6r2zf/DK02+2PnUfzY1EMtB9vQzR3yWOlUuHWrVtMT09z/Pjxl+qjvU1rSc/zePz4McVikWvXrr1S13M/6o/6Hk2BDA50ugbh0SRm2dz7X7Xkohh9x7LjKoTH+uLxZkuicM83IrWnDeSwiqRIVNaCXt+uwBj3CWhrtUXs4hALv1ElOhKmtdYheSpOY7FN4kSM8sM6elLDqtm4PY/BqylcATvv9/ZyBbPZLCdPnuTatWvMzMwgyzLz8/PcuHGDZ8+eUSqVPtIcWvANeumf/Q7CEyh2B1eoeK6MrAfXTw9hRibo1OLYS0E7SSl42GQJteEbcSmTg2AFL6f2i7YbtJ/UcQfOI9Qw1PrXRsFfmUZKNez8aZRmjV48z837j3j69Okr9dFehcMQzV6vd1hR3SMc4QhvgKIoL+RjHnZe8TyPmzdvIkkSV65ceW1+Z757npAcw/K6pLTP8PXqDnJQbb7R3UBDo2yXyZFDSIKB0G5ajkLTHOVblU10Sd3Lx+x6FiP4c0Be9/P2PTzyWpLFLZPH7S5rThtdUli1W+ReETa/kBphyMvhmP6+jMb8sTTbt2eZQJQ9FOgOR1WNcZEA4R9rKHDSOIHk0O5rWPPHG4nGKa009sLtw0m/Gv1YLoXtuowkwkEYPUcuGiHn6jxbLDI+mGJpq0IuGWF+vUzM0FnarPC7txdwXX/efRsdTVmWiUYgk/8ymdg2uqoikKnZYTzX5l8VrnC7FsP2HGxPsNnSiCgRIrJORIqyXLaxXJeEHmJAidFueNQtCyEEQ0qEVs3kM9MTRHTtzTvDh3PA7M7FJ06cIBqNvtC+eVcOyjTNF757RDRfgpeRwcNcoN12YUtLS8zNze155V6GgxqbD4q737x5E8Mw3iiLsQuzZuJ2+6HaTuBRrM+3kQae7yKg2BGip/pdj7oV8ZxIO6EQxrhvdJymTfRkjtiZAYr3GsRPpfzxN0wEoBgqlS0/3zM+4d9oesI3AkZOx7M8cucTKCkd/Z0Mi4+73P9ajcKiy/bj5gvHYRgGo6OjXLx4katXrzIwMECtVuP27dvcuXPnpbkxbwN5uYJbrmDZYUDgtAUKHrphIwT0ugbWah0lue+8dPxKSTmTRQrIpRTdJxOk70uGDkfBE3Tvb2Cn33lO3tyr9PVm3XYYtBCRmctcvXqVoaGhF/TRDpK4fVB8HA3CEY7wScRhiGa1WqXT6TA5OfmcXN0rx0bn3cSXaDnTLAeexdXuKkk1Sdfrknb8cLCh+YvKbXOb8dAJvlFsYXkKbbfHdOz5fEwr0A5e7RaRkbAsj62SzqzZ5kQ8S9uxOJ3II4DJmD9+OuSPr0gyx6NZuk2ZuVKNWtCrfKXmL8gLnhOEy8soksRsrcKpZJadzTaFWpu5UgVDVVlttggrMhudHmFVYa3VQZMkZgslzhhRHj3ewnE8Vst+OH2r5kfqKi3fM9uz/Tk0petszJbRgnBzKhZGCBjNJ7Edl6mRDK2uxWg+yZ1H6we6Ri+DbW/Q6vwEqthiQG1gyDaG7KIrMv+8+UMseSkcz8FtSyztCErtFpVeC90zqDYhpYXxBIQdjXrNxpAV0qEwYUuhXukSVlX+6MVTb96RAB+F6PxuWuAH2zfvykE9fvyYGzduMD8/T6VSwXXdtwqdS5L0g5IkPZMkaV6SpP/2NdtdkyTJlSTpRw8z/nc1R/Ntsf8CSpLE48eP9yrU3iTwfhiPZq1W49GjR5w6deq1upsfRPlemQ4pQoYDUj9UDtAoesiDIbwdE1lXqD7z/5cZjeD0HBpLJl1ssicT9DYadOrgyf3VdLtgYTpBHmGwsupt94jNRKg1Qyhx/7P6chskqDxuoIRlqk+apC+kKFVh5Uad8c+kqa12GbmYoLLd4ut/b5k/+f/oV8K/7Jyk02nSaX+b3dyYxcVFut0uT58+JZvNkk6nD0TG90P96hKuKaNpJh07jWHU8TyJkNSh3hwkkvKgDXJYDfIwVUSl5J+DWBxR282T3UcA7X54XDj9a27VQc2dRSs9hmgSyn2CLTwVNz2NNn4aSZZJpVJ74TLLsqhWq6yvr9NsNolGo3u5QrsVfocloB/HpO0jHOGTiIPkaO5qOW9tbRGJRA5l80/Hv49f3PgdPDyGQ8NsmVskRII6dTAAGzbtTSJESCoTbHVV2m6d49EkO2aVXiC4vpuPuU2DnJ6gZDU4rUzy1e0K76ZHKVY3SQWE1QnsXaHrzyGLQdhc8WR2dhzmrG1yYYO1TotBPcxOr8N0Ms18vcrZbJ7H5SIXsgMonoTSlFiq17g4PMD9rQLvDA1wb7vAmWyaJ+Xq3ueXhgeReuC1HVpmm2OpCCu1DuPpKGtVX7JouVhjNJNgq9rgM+Mj3L+zQTSss7BeJqyrrGxXUWSJzZLvLKi3eowPJJFqNr/6G4+4enHi0CStZz2i1/vLaJJHWLKoOkkUHOatQX6n9UWqjkJE9VCUKE97FiFDJeJJdDsSC80GjgQhVWNYSWKZAkWSqdkOOVPBtT3CusZ7k6Mkgs5HB8G3qyuQJEnE43Hi8TiTk5O4rku1WqVUKvHLv/zL/ON//I/J5/M8fPiQc+fOvfE8Bs/F3wP+AH6zjxuSJP1bIcTjD/yuAvxNfGm9Q+G77tF8KwQPVrPZpFQqkclkOHPmzBsv6mE8mt1ud6/P+usMjiRJLxCM0t0y1dk20tAgkYkU7OO25YUmth1HUiSikyncnofb81DzacLjSfAkhCeQYnH0jEHhfoPSvQrhEX+FIofUPeJZflBHS/nv3WiY0tMupft19KRKZ6tH5lwSu+WQuZAidipJzVFZu1Fn4Gyc7XsN9LiCokp0dzwqCx3qGwevPN/NjdkVqN3v/bt9+/aB80maD9eQK128ngWui9N2kCUPVzGo1zPg2tD2DRJBLqaSy8LugkHe9xB1+oTeq1f23ovGPuF826X3eB1n4Bwknr+ubrONObuBGH1x1bqrj3b27Fnee+89JicncRyHp0+fcuPGDebm5nAc51DhuY9j0vYRjvAfOl5VRPK6FJhdreVWq8V77713aJm9tJbmYuIiAEagy1t0i8jIFOwCQ6EhNEkjZE3wu8WdvSXxareIgsxie5sBPUXT6TId8xVYRsNZctYw6w2BQKIc2L/ZZhFVknnWKBCXVFY7NSajaepWj8+lTvCtxRLHkxlfVD0ReDtV3wGRCsTYw4qKBOSVCI/nS3tTlBOErq3AvtrBq+N6pMIh4o7K4/kdlKD7XDzu26+44S+2ZdcnzKmQwlTIwGu7OK7H5FCanuVwYjRLo21ycjxHsdbmxGiGiK5iNARPnm6zvFqhXN3X2e0AaHV/Dav30yjBXFNz47S8EA/bo/xK4wtsmg4tpwtulM2OQlwNIwDXjdByQ6TicYZjSYyuxtpOne1qFafXI2OqtNsmbcsiLCl86cLBvZnwdq0jP4iD5P0rikIul2NmZoaf/Mmf5Md//MeJx+P87M/+LP/kn/yTN/7G9evXAeaFEItCCAv4Z8CXXrLpXwL+JVB4yf9ei+860Xwr17KqsTX/lAcPHjAwMHDQHtFvpY/5pnzMD/Y7Byjf90nO1s3Gcz245YSCU/JoLHaJXxhBjvTDu9vXq1huP/ejdKdC+MQAwsMvBMrthlRCiCCnxrM9YidSaCmNzdsOoZSKa3qkTvuhdkX3L69n6Dz8nTpO19/PcELF7riMXEiwdbdOZFDGbrp87e8uvfZYX3cOUqnUXneEc+fOoes6KysrXL9+nSdPnrCzs4Ntv9jTduMffhM8kDQF21aRIiGEkCiuh9CwCI8HaRASeGXfiynH9l2TbtBhQpYRVf//IhKDQIRYhAxEvd92yav677sP17Cl1N7nrqLiFYvIA8PI4Tdf893E7UuXLnH58mXS6TSu6z6XVtBqtV5LtI9C50c4wncGr3My7NdaPnfuHLIsHyrUvuts+GLuiwAsd5YxMOjR45jhi3on1AyV3gALpl/oOd/aIq3FqNttTgbEciicAsBDkBBhFrd6PGh1WLGbxNUQK+0qx6JpmrbJ2eQgrhAMBUWOA+E4M9oIlYZPpnsBqV6v+XNRKSCAC7UKChKrzTpX4iPcmNvEUJW9VpLPSmUSoRCzpTJxTWOx1iAVDtG2bAYcg9uzW8QNndktv9PP/HYFQ1NZLjfQVZlS1yETDSM1PTY3O6xt+alJpbrvBNjta75rFgfjUVbvF0jE/XD6QD7Gb3716d55fROanX+KZ/3PhCWHhNLE9hRG1DIr9jj/tPQObUfCUMJIbpqllkvN6tFzHSJuCsfWCMkKtuvhtGQUSWcolWQ8k0VqybS7Dma3R8hyOBmKoEveoaJWb6NC8rIxDktWNU3ji1/8Iv/8n/9zfuInfuKN229sbADs70m9DjynBylJ0ijwx4Bf4C3wXSear8KrCKHneTyZX6S2scK1a9cwDOPABuFNxmO3Yj0WixEOhw90gV9GXsv3+nl/5VUXfdoniYmpfu7o+jcbdBv7blpZorlfK9MTdM19xPNuhehkgo0bTYr36oQH/JVpY7mDPJLAqnqkTvkEs73lJwiXHtTJfCbPg39XJjVpsPOgSXI8zPbdOuGkSnOzh/AgNqRQeNJi9f0q7fKH7zW7m09y/vx53nvvPUZGRmi329y/f/+5XMfKnXXMpQIaJt1eCNl1kKwulWaeSNCGWAtyTJVsCno9Xz9TNXBHzmImT9Euh6mZI3QTZ7DTM4jRGeRcv32plMr1rVokjmg09v7XXbch5z9PZiQFnkCZent9NMMwuHbtGmfOnEFVVZaXl7l+/TqPHz9me3v7hT6+H8dcmiMc4ZOAg+b+b21tvVRr+TBEc3cOyPayJN0knuQxFh0DwBY24+FpvllqUrVsqqLDiegQHh7jhh9R8fY6BZWRAMt2qdRizJodTiXyWJ7LTMJXOckHXX92j6Tp2YwaSapVl0fbZZ5UShiKytNKiYSssm31GDEilMweM6ksVbPH1cERUr0QmGA6LjO5rN9KMpfB9XxNTNcTTCR8jcwLAwM01tukwmEcz+N4Po3tuhwfzNCzHU4OZemYNjNDWRLhECdCCRZWa4xkwlTbNuMDcTZLLbJxncWNCpl4mIWNMlcnh3h0Yw0jpLK8WkbXFNY3a/zmV58e6NzXW/8Lwv55DNklLnWoumkG1Dr/rvVpfr1+BUQIS9g0egaFLkTVEAN6nF47zFqjQ9XqgICUHUUVMo4QWLaLW3NJRyLoqsJIKkPICvH97xxjeXmZGzdu8OTJEwqFwksdJ/vx7QqdvwmHbWv8CvL8wQ//NvDXhRBvVQn8sczR3M2n+eBF6na73Lt3j6GhISY+8wXEzjKKcnB9tNd5NKvVKo8fP+bMmTNkMhk2NzffaszWepte0S/+EUB1voGwBdlJHSH1bxhZk2m1+6c/cTLF6o0GmXMR3JUOxlCEpd8qkz0WpbPZxjU9pFwS4ZYBgTEWo1foIqkyjbp/nppB6Lu+1CZ3Jo6S0Gh2fIObGA1TW+6SnIhQX+sxcSXF8tcrjLyToLLVYvTzSRxN5jf+/gJ/7P90cA3JN0n0SJJEMpkkmfRJsGVZVCoV1tfXqf/d62iehOMahEMOnpBwvDCK0yEcC0hZ1/cAKKkkZDK0F+rIc03cUhV1MIsoVZEAL52jM+tfM+3kFFr+LKq1jRTaV9WdykDNr1oXsoKzU6DTChFJRHFlHQ1QJk8c+Nj3Y//KczetYGRkBCEEzWaTcrnMw4cP8TyPdDpNJBKhXq8fyqP5ncilOcIR/mPA67SW4fBEc3FxkXq9zvePfz//svAvKVtlJCSEl+RZ06JmdzkbHeNxe52Q7P/WrvD6fGuLlBalYjc5o07y1a0KJ9QERccmovoL7fqu9FHT17t82igQV0PonoLcjvC4WuZsJs/jSpHzqQwPaxVOZnPcKm6TD0fY7HZIhELMpLJobYXVUoPkkB9RM4Pj3O3c0wwqmZu2zYV0hvJGi47p0Oj4n7dM3zZ3g+13vadRTWdzo4I75OcxakF4PRWPslZoMjqQodzcZjAdJS1kmtt1LMtl8kSa2YUSZ2aGeDK7zcz0ALfvbzDwisZsQghqrb+K6l1HkkI4QrDmDCAj8yvdP8DXGnlst+e3+nTyNG2Bh4vluJTbCpKnkA6FMGSNStGk4LTRFIWUFkJpQde26XoOEU/Cqli8d3qCcyeP7903u/Z8bc13AmYyGbLZLPF4/LkFzkdBNN/GK9rpdA6kjLOLsbExgPH9HwEfJEBXgX8WHF8O+CFJkhwhxL8+yG981z2ar8qn+eBDXiqVuH37NqdOnWJychJZDyFaVRTP/VAezd0E8GfPnu1pVx0GH1wp7/dmqjkVt+XhmYJGTadT6nu04ieSbN9pkrnsS11IEf/h7NRlkCTCowk8R6DlfY+XpEpsPzVRDP+SlR81UAwFkYzieUH7xpUumbO+KzA0EObx+01qgZZm4XELWZcoPGqihCRqKx3CaRV9OMRq1aYlBA++UuTBbxRoVQ/n1TxM+sOuSO2wm0ZvuOAKnK6MLnVoNCOonokjhVEkD2QJr1xGnpym24tRv72N23NxyzUAlMS+h2nfPgjTpv1gi/qChCPFYXdFqPZTFeRMHmwHt9bGCo0h2f59oUwe3qMJr155SpJEIpFgampqr49vIpHgq1/9Kl/+8pf55V/+ZX7+53/+QAub70QuzRGO8EnHbuQqHA6/oLW8i9c17dgPx3FotVpYlsWVK1f4nvz3oEs6Pc9kQH2Xr5V2GAj5i+ym6zsg5ttbROUQBbPO8cggHh7HjAEGnBHW6gIPiXpQHPSsXiAsq8w3y4waCSpWhzPJQWzP5UpygqWiTSpYTO+KiLcDoli1/NeNjp9epHoS2ytNHmzuEFYVnhZLxHSt30KyVCEXMVgoVxmKx0gKjfJ2h4VClaFkjKWi/7q4U2UgEWV+u0I+EWF+u8J7x4Z5cn8TXVGZXysRM3Q2K12MkMrCRhldlVneqpKOG+g9ma3VJt1Amada850J5YqfS2+ZNu/fWH7pvOI4XWqtP48mbhGWBToWXVcnqzb5/e6n+UZjGEM2iMtRtlohVjsduo5FWNLxujFUVEzPRfIkSsUeIVklbRgMhqI0d3q0TZuQqpJVQvTqLkgSP/zpvqayLMskk0mOHz/OlStXuHjxIpFIZK+7z37ZoY+KaB7Wo9lqtQ7l0bx27RrASUmSpiRJ0oE/Bfzb/dsIIaaEEJNCiEngXwB/4aAkEz4GRPNl2E8IhRAsLCywtLTE1atX96qeAeQTlwgv3ntrj+Zu79p6vb4Xhj8sPpijWV1s753V2Ghq73O7LWHtEw0nqMzeuN9BT+rUVn0j1Fu3SVwcoLHtG5rtm1XCQ1HS5zJU5zukz/vHbzUcMlfyLH+zTulhm9BQUIkeUtBiKqtzJmpIobbSZeBCgl7VZuTdFL2azfC7SSJDIZSZCDd+fYdITmH7aQs1JKHpMr/xcwsHPv63lfpZ+vkbOC0bQQg5JGGJCJLmk20v0GlzUgnaap7qrSKi6RtLbTC1FwqXlP2FQJ29t25gsHA82s+qdNVjkEghzH0EOtJ/EM35HWwvjJTNI8cTb3U8B115qqpKPp/nx3/8x/mZn/kZfuzHfgwhBIuLi2/87ncil+YIR/gk4FWL33K5zK1btzh58iRTU1Ov3O5VTTv2Yze30zAM3/khyxiKweez30epk6Nq+3ZqpVNAQWatVyJHFMtzOB7zJe0MJURGi7G6bXKv0WbVbhFVNApej6lYho5rczrpOyOGg3wiXVZ5JzLBcqGNh8RqUOz4pFxAlyRWex2yYYPFepXxWIKK2eW92AC3n24znc3QtR1ODeSwXY+ZfBZXCKbSKQQwkU4S1TVORVLMLlcZjPtz4lDKd3gMp2MIYDQdRwBjmQTvDg8iNT1s2+PYUArb9ZgayWC7ghOjWTo9m5PjeaJhnePROLNPtpmeylMstTh+LEex3GFiLE2h1GUwH8WzLeZvrrK4sP2cbrNj12i1/3M0b5603CYkWThCxVBM/mn9h7nTztLzbDqOw1Y7hIZBSo2QURNsVqDQ62A6Dlk1Ai0FXVZp2TaGUGgXu6QiYTRJxrBlnKZLSJX59KkxsvFXewc1TXuuSHRiYgLLsnj8+DFPnjyh0WhQrVYPtGh5Gd6GrHY6nUOlZAUqMX8RPwL2BPglIcQjSZJ+SpKknzrUj78CH0uiuduG0rZtbt++jeM4XLlyhVDoeWkBWdMRjoTXqL5ipOexn8B2u11u3LhBMpnk/Pnzb10dtp+8CiG4+y9W4FgUSQZJ7o+pD2usfrNB5qpvNOob/nKuV3UInchRX+pXfLfKHpUln3h6jkAfjNHt+pequtiBgGC1exJCSCBAH/BX5cW7daLnUhQXOwxc8MmUEg7akTVsJBlIqNy5WcXqeggB8ZxCq2wzdSXD8s0q939jh3rh4P1WD1vQVb2zSXe1iutJKFYbFEGnoSGCVXz6WBj12BgYg9irTYQM1rZf6OOF+ukGou2TSyGDVw5E26MRvKA9GkYYt1LHWqvQ2gkjvH1ez/2dhTIZ3JUeysz5Qx3HfrzNyrPb7XL8+HF++qd/mu/5nu954/bfiVyaIxzhkwghBKZpMj8/z5UrV94YuXpT6HxnZ2cvtzMWiz237YX4VbbMNnOtTRJqhLrTYSbmrwdj+HNYzfZtV8ey2CmGedxrczyWCfqT+3NERvcJjun5oem1dp2MHqHVEDzeqjBXq5BRNXY6bcZ1g57ncS7vFwkdT/oOibF4gjNaBqsVRGyCcPZudfluGLza3dW+dMjZYda2fPJabPrzwHagkblVDV5rLcKaSsiUePxwi2LNdwRUGkH6Vsv/Xqvrjx9SZKzNDlYn0DwO5gxN8/cnGvFTBCaHM+w8qZLNJbh3s9TXbb7/76k2/wRtr8eKO87Xzc/z71uf55F1nH9c+2Eetw0kIZFQUlS7CRq2TcMzkT2NzbpLOmSQ1SNklSjFYo9at4sQgmEtilWzsT1B27RICx2362G7LhFk/si1g3eI25UdOnbsGO+++y7Hjx8nHA5TKBS4efMm9+/fZ319nW734OoubzOvvE3uvxDiV4UQM0KIE0KIvxF89gtCiBccFkKIPyeE+BeHGf+7TjRfFTpvNBpcv36dsbExTp069UpWL114D+3Otw70W7ukcLfF4qlTp5iYmPhQoqq7YzqOw60bt6g/6VK47RK7MERnZx9ZCx6oha83SV/IUlvse+B6PZlEIL4OoCZDpC72C4fqKx1qW/4D294yyV5MEZswePqbZXLv+GSyPmuhRhUy5xO0Hf946ms9BLB5p050MER1oU3uezPc+I0CI2fjrN9vMDgdpfTUJpbTKS11kFUJXZX5d/+3ubc+J2/Cs797G8l2kPQQSGD3VGQ8oqEgHzMeo3y3ucunCQ1nkALDaJv+QyoksAt+moIbj4MTGNJs3+Ot5PqTiZB1ak96SCN+Kopb6+tnSvE4suXiZY699TG9zcqz3W5/O3NploEfBX5ekqQfOdSOHeEInyDYts2dO3eQJIlLly7t6d6+Dq8imrttKdfX17l27RrxePyFSNnp+BjHI0M4wmUy4pNGNxBg36GJisxat8gpbZJvbXUZjftFQemAWDZt3wmx207yWb1INhQhqugMOVkeFyqczvjFQbkghzMbhErtwE5Wel2GIzHMmsPcdp3VRgtFknhWKGOoKs+KZZLh0F64fKla5/LQEIWVBrILG9UmI6koxVaXqXyK7XqLqXya7XqL4wNpLMflQjLLvUebTA6l2So1mRhMsV6sMz6YYnWnRjaus7xV5erJEeZubxEN6ywul8imIywsF0mlDBaWSiQTBgvLJS5ND/Hw60tEoyFWlsrMPi4zNDjGuQsK2Ylf4qk5zc3GGLfKA7xfjTLfjfN+6xpFK4oiKahShMdVF9N1iSg6SS9OuSVhuR4ls4PhaTRqNpmwQSpsEHc1ysU2jidIGmFiPYV6tYsnBClZZyYdI5V4+85tu+okp06d4r333mN62k/Lmp2d5fr168zOzr6x097bzisfN9m87zrRfBna7TZLS0tcunSJwcHB126rGAbCEZjLbw49yrJMqVTa6yC0Pwz/MhwkLCzLMp1Oh+vXrxNppXB7/nfWbrdQ8/2L3av4BsDtCToYKOH+KqXX8mg2BJIa5FoWHTbvNdCSvpcyMh4jNNwvGmkXHaSMAUJit/DN6Qiy76RYWzXZedJE1iRqq12GL/m5npmZKOHzcRpd/6bWI/7vx3M6rg0jMzFqWz2mP5OFqMy9OztszL/YLehl5+gwRL14fZv2ShNbhMDsUm3HMbDo2iqyJFBPTVN5fxs8cGt+hbia6j/sIctfESu5FFKQhG7r+1Z8Wl/cXto3ocjpFMK0qT/pIY1N4VX2SR65/jXTT7w90fyk5NIc4QifBOzapF2HxcjICPF4/MCpPi8jmpZlcevWLWRZ5vLly3u5nS/L5/xDQ1cBKJi+Z3C+tU1ai9HFZiY+xpA7wnZN4AJd4duxuWYRTZKZa5bISDo1u8vp1CAeggvxEZY2uqiyH9HpOb7hLwWNKRYaNTRZ5mmlRCoURpMUUt0QD9eLTKUStGyHM4N5eo4fNnc8j+OZNAI4lk7x7uAQoY5Es2MxkPDnmqgaaGWGfZuaMPzXfCxCuCmQgtMTj/pe2mTMt7ep4DUR0Xh3cgip7uDYLoN5v0Xl8FAS1xWMDadwXI9jY2mm8ymkroNtuRybzGKZLtl8hN/+yv/OhvmLrLk5TDWGrY9iG1kiWpztdoS5WoVyq4rTVVhvKCQ0/7c9K8RG08N0HGKqzqicpN10sT2PcrdH1FHxOh5JI0RYVbHLFrInYYQ04kJFNeHq2YML9r8MHySJkUiEsbEx3nnnHa5evUoul3uh094HJfG+Ux7Nbzc+VkTTdV0ePHiAaZpMT08fqCJXURRal67R+ZV//cax19fXMU2Ta9euvXFV+zIh9peh1+sxOzvL+fPnsRf7pzNxIs7T366Se28ALarSWu2LBVumIHne97YpIZntR02qC22S72TRMgrbj5qYdYfoyRQAxaUe6zdqREd9wmV3XNqmb0gLD5pEjvkGz1Zl6jsWnbLN8Lt+Po8AkKAjwcLDOit36sTyOqt36qRGwizfrBHJyaw/aHD8ezOsbDe5c2OHXsvjH/6P9994/IfFs5+7i4zA7Tp4sooceHrViIqTm8AOtHrliI5TrPnvg77mUljfKwTSUn2CJu/rRNSq1fbee+Y++QnFP0fCcmiVDeR9IvxutYUXDqEO5d/6uN7GIHwcc2mOcIRPCtbX13n06BGXLl1iaGjoUJXkH9y20Whw48YNJiYmmJ6efm5x/bJ8zu8feIeQrLFtVpk0/IKfMSNHROhUih536m12hImCxFyjyHA4TsM29/Ixc0HhoirJXI4fY26rheV6zFbKaFJAKFWNimtzIpmmaVuczeZxhMfV7AgrSzXSgR5wLOjTrgT7bAYL9IZpIgERofL48TablaB9ZtknxzutHrIEy6U6iiSxWKhydjjH+lyZZtNkcaOCpsosbj7/urRZIawraKZg/t4WK2sVFEVidcPvCLS2UUORJdY3ayQTYby6ydKjLTbWqiiKxMa6/xpOP6EX+/+yZSt0BFScLFUXHFxKbhw9lCIfzxJWB1lsSxTadYqNGrRUWm2PhKoRUTW8tsR2uU3PcYhpOiMYtJsmbcvGsl1CHQlNkrEcl5hQcZsOX/jUCUL626XT7eJ13khZlslkMkxPT3Pt2jXOnj37nCTeroSSZVlvRTQP48D4TuC7TjR3H9hdr2AymWR0dPTAybOKouBoOpJh0P7m+y/dZnfsRCJBNps9kCv6TeLuQgiWlpZoNpvMzMyQSCTYvN7vRqMaPvl5/DtVMu8Nwr78wPJSh/mvVcm9myF9OrknpL5xq4k8FvLjwsDG9Tr597JUVnp4jiA04hsOYypKt9k3bJFclMSxCA+/Wmb0SgqAdsU3Jlv3Ggx/Ic39r5U4djmJa3kMnYrjuYLsZATPEaSOqejHdNrCYX2+yamrWVafNGiUTG7/1vZrz9NhPJrrv71Bc76O3fUQioTVllAVByFARCJ05uooqk8qQyOJvexDr9ECCdSxYZSp40jHTmLLKbzhGRifwSKEPDgAkoSxr92kWe57La3WvrwY3aC5oyLF40gRA69SxxvJf6gUircNcRxWsP3bnUtzhCN8ErC4uEilUuG9997be8Z2c/8Pgv1Ec2NjY4+wDgwMvLDty+aKmGrwuawvExdVfY+fadmUa1HudVpkdIOq1eVMctAvrommgH7Cdck1iak6bkfh8UaV5UaNyUSKpm0xEY7gAdNZf2GcDvcjPp9Kj7K52cT1BOt1PyK0XKv7kkjFEhFNZbZYJmMYbNabvJcd5vqDNcazCbbrLSZzScqtLsdzSRo9m5mRHI2uyamRHCdzGUItqNS7TI9lafcspkeztLsW02M52l2Lk+M5hBC8OzzI2kKT6ak8zZbJyakBGs0eJ48PUG90OXl8AE1VOJ6MM3t/k+mZQWrVDtOnhqhVO3zmBxvMfPYpvXiS7YLFhhml4TpokkGxl6Fu2zTcNqYVo2Qq5IwE48k8EWmAkiVRNrtUe12ckoXXdUmFQsQ0HatqUa33kJEYiEbQW9BqmciSRMJR6FZ6pBJhvv+zMwe6T16Hw8wJoVCIkZERzp8/z7Vr1xgZGaHVarGzs8Pi4uKe9vRBnF/dbvdA6SHfSXzXiSZAoVDgzp07nD17lomJiQP1pd3FrkGIfunH6Pz2b73wwJdKJe7cucOZM2cYGBg4FIF91ba7ntdOp8Pw8PDeimPrel/aqFsLvGlColTxiE4H4YeJCM1AUH39aReMvrSG3XFp77ODruVh7+utun69RupUnMVbdQpPW6TP+cRz41YdaTCE64AZhMZLc20GLyQYuZaiYfrH0Sz4YZa1h3X0iMzq7RqTn0mysNShVOyycKdKPKuz+qROJKFSXO3w//kf7+2N+WHx5Oce4noSqmciJAVJeISkLgUngdby8zO93eryWBCWyiRwIxlazjCddpTStypUbpbobHSp3StRuV3CftKjdN+mLU8gkoPIiRgYIZTmvkr0wDsK0Gt2sCtdeuSQ83kQEt7Y61M03oS3DXF83FaeRzjCJwGTk5NcuHDhuWfybTyajx8/plgscu3atVcuCl817g8OXgFgsb3NCXWUr2+2iMghPATHY34OvhwsbtfbNQCe1gsktTCyJHFMDHJns8hM2t82o/tzgR7y55JSoDG8UKuQ0HXktsz8WoX5coXheIztZovpXJqmZTOZiO2Js7tCcCqXYVSKIQVCHLm4f2xK0EEoFnSt02QFRZbIhwye3N/aOzYvIDzObqtKOyjyEZAXOo2yv29WkOpkBv83g781VcbdadOs+Q6AdtvfkWajx8jJAkMX7tNLRGl3XO6vejiejiLFeNoE0/OIKgaSnafQ9eh5Nk3bpFSDri1IhgxGI0lyXhwHjbplUW626O00USyXsCIRVTUa2x00WSZuhJAbLliCSFjjD33uNLL89k6HvXP0lvJG+yWU8vk8J06ceE5C6eHDh3sSSq8b4+OE7/re1Go1VldXuXbt2p6o99sYBC2fww1nqP/vvkb1rsdxcXGRq1evkkql3qrbwwfR6/W4efMmqVSKc+fOoSgKQghaRRNlwEBWJWRNpjzX77vdKllsrbjEJgyio/3ij07Zpmn3L4GR19m8YRE66RtHJSzz7PfKpE/74VXhChjQMFvBfgUC8AMX4vSC52LrUZOBcz550RIqDx/WWLpdI5rRKC52mLiUpFtzGLuUZPhygobi0K65jJyIYnZcJk4laFVtpi6kqO30yE9F+MX/5cErz9NBPZqL/3KZ7lYLCUFbTqA6PWxNo+YmMKIqwnSQDRVrK/BCyhKMn6Dj5Cl/q4RV7sHutZME9k4NAH0giWQH5yNkUL5eorxqII3PIOk+WZXTKaR9YXSv4pPZ7lKVWi/oFT/yoqfiMPikJG0f4QifBCiK8oJdOoz93021MgyDd955Zzdt5aV4lRTSpeRxRsNZMk6eQk3BASJSINbe8+eHJ4Hw+navyUzcD32/kxylXpGRPN++t4I8zPmq3zlovlEjoeksN2oMqDqGqnFWy/NorcB0zielo0k/dSoR8gmjFPhKa+02E4k4vbLF2naNraAocqngR+MKXQdVlpjbLhNSFVbLdS5mcty5s0YsEmJurUQyGmZ+vUw6HmZhvUI2GWFhs8K5Y3nKCzXcnsvSaplkXGNptcxALsbSSpnhgQRLq2XePTvC4s11Eokwq8tlxicyrK9WODaVpd1b47M/tkI7HMYyNVZ7MZS4QmnHZqMbJiSHkZBZachsdC0c4ZJQIoTtNAoakiQhCSiVTNo9h5CqMp5IMSQnkOUQPU+g2B6N9RqOadFq91CbDqonoSAxlYpz5dLEoWsPXoaPSkczFAo9J6E0OTm5J6F08+ZN5ufn9ySU3lZu8E0d5yRJ+pIkSfclSborSdJNSZLeLJOyD991oplMJrly5Qq63i/ieNsQR+pLP0TzqzcwW23u3btHr9fj6tWre7JIB+l1vouXGY9arbanwTYxMQH0dTRXvlnm8dcqGGdTZM8lcHr+72hRhdJsC7slqHUEltW/EVJTEea+WmLgM75xSE7HEJ6E2dRQwhLxGZ1e06Vh+tXrkgILD+qkTvihku0HTfIXE5RbDss3a8Ty/jmUwwpqWGZ9p0NiKIzd8xgOhNw9x/99EZa4e7vA4p0aRkJm4U6N9FCI2RsV8uMGxbUOU9+T4rd/Y5Wv/rs1HlwvHui8vQxCCO7/whyOJePhYZkuMoK2qaK3XcJ536Aa4wkkWUY/NUXxnknlVhUt3r8vnKpPEPWBJF7PJ45Kuu9lkINkdWG5dCoyTWsQZXQEOZXsb5OIQ6uvBuBVFczBAbYVsZeQ3W63D/3AHnk0j3CEjzcOGimrVqvMz8+TTCZfq7W5i1dFv2zb5kR7nJu1FgReyDWnRVhWWe/UOB7LYnsuJ4P2kjFN50pygpWdLh3HY65eQZNkZqtlMqpOw3U4k8ljex4nM36O+bAWxiw4uIFdbwdtbjcDibf5UgVFklhv94hoKhFVxy5YPF4rkouG2K61GE1GqHVMZoYyNHsWp0ZydC2HixND5DwdzZWxXY/jI36LysmRNJ4nmBhK4wnB+ECK0+N5YqZMvdZlcCCOEJDPxfzXrL+YTqcNzk8P4lVNbNMhEWh0RoJiIj0suPhHZ7EMlfKOxLYXxbNlqiWNR2WLhtXG9QQdM01IjhJXQySVKKtlj412i5rVQ0NB7+iktDBhRSWmapS32pimQySkMxJJILUVVN0gFYsS7Ug0qi3MVhOn2ORzn5vAdd2PDdH84Bi7ley7EkqXLl0ilUpRKBS4ceMGf+JP/Ak8z2NpaenAv7Gv49wfAs4CPy5J0tkPbPbbwDtCiEvAfwH8r4c5ju860ZRl+UOtPPeTx/DJSQQST//OPyKfz3PmzJnnLtKH8WhubGzw5MkT3n333ec02Ha3W3nfXxEu3qzjJHXCGX/lmjoZ2yN3jW2Lhg2y5h/vbnHP0s060QmDTpB32djokbmcwRVB+7EFh+gZDWNaplUQuEafBGlZna25No7pkT3lP9Drt2sMfS7F+nyL2EBg4B7UCcUU1h82OPkHM3zrq1uMnAljdT2mLmRwTI+hYzFcWzByJs5qtUm52kO4Atty+Z//0jdo1l/sGHSQB/LOzz3DLHcQro1jquiGoKlEiMR8L4Hs+osKNWlgGkNU53o4tYAMBnKQsqFhF/0kdTXTJ5eS2r++Yl9+pnAEVqFD8V4PV0/1r1em/x5Jwt1pYncTjE1N7vUoX1xc5MaNGzx9+pRisXigRc/b6mh+3HJpjnCETwJeJZv3umd5f5e406dPv7Rj0Mvwsnml2Wxy8+ZNvnT8MhJ+RflQOI6Jt1fwk9Z9+9+wu+iyAqbKneUy87UKA3qYlm0xaUQRwImsTyzDgWe1aZlcy42wXbRo9qw92aK5YpmBWJTNRpPjmRQN0+T0QA7TdfnU0CgL8xWO5f35ayQTCMBLu8nwu01SYDKXQqq7bG7W97Qwa00/zF0KNDO3yz6Z1ZBYubfD2kYNSYKllRKyDDvFDpoqs7xWIRRS0VxYvb/FwuwOsViI+dkdkimDuWfb5PIxIue/SXJKYnMb2qkEruJik6JkaYTcMOYOrLfCrHdalMwmkqdQaEhkQhHy4Shj4SRWHQqtDjXTRENC1DwyhoEiS8SESqdiEjF0MlEDUbExdJ2RbIYEBp/77DS67nL79m3u3buHZVlv5XTYxXeiM5CqquRyOU6dOsWnPvUpvvzlL9Pr9fjLf/kv86f/9J8+0G8cpOOcEKIl+iciyov6za/Fd51ovgyHJYS7x18sFimdOU5saYt89MUOL4f1aHqeh+d5PH36lEKhwLVr117QPdzdbvkb/UKgatnBjGtEB0Oo0X7IJTkdYeF6ldxVX1apVfEfYLvrIhI6m08ae9sWl9o06/1wb6ssQPN/e+dhj/gJHUmFp4/L5M74Bmv5do1IVmPoYoJykPOydLNKejRMp24zfinJsc+n2dzx82dqGw6qLjF3q0JqKMzS/Rpnvj/HV39rjWMzCZYe17n8uQxKb4OZ6RY//+Xfx7btQ3U5sDo2T//RMrLjYskaquMgZBe7qRAye/4dWOpgnBmlWZBoLbcxhvpE0qn4IabQcL84SFL6t63X7uepONV+uoIdfA8PGss2YmwaFBnU/uShDaTwuhbKhF8gttuj/MKFC1y9epWhoSEajQZ3797l9u3brKys0Gw2X2p4Pkw+zhGOcIRvP143r+zm3TcajT07/7ZOie3tbR48eMDFixe5OH6c93ITfhedoODHDBbW880SqiRTtXrMqKN8a3WHM0GBTy7Ix1TUIP+/7duzp5USUVUjTZjtzTZV02Yml9mTLRLAeBA2TxlB5boscyUzRHG7BQJKQe76SpC3XjI9VFlipdJCVyS6zRbdjRYP57fIJA2WNisMZmKs7tQYG0iyUWwwOZymWG3zuekxHr6/yoljWaq1DiMDETpdh5kTg34R0PEBbNvl3eODPPnWKsenB7Asl4mpLI7jMTKWwvMEU1dbjJxpU2lEqekRhK1SqkQpKzJSAno9h7myi+qq5EIxhrQM9ZZG13Yo9zponsLWTgtdkslFDIY0A6/uUe+atHomGSmM3XRAgOQJvIqFpiiEFRW73CWfjfFHv3Rlrwr85MmTyLLMwsICN27c4NmzZ2/UvPwgvh0ezTfh+PHj5HI5fuVXfoVf/MVfPNB3DtJxDkCSpD8mSdJT4N/hezUPjFcnnnwX8aaV5wex26ayUqlw8Sd+lO17/1e2/8G/YeK/+TMvjHsY42FZFrdv3yaVSnHp0qWXrpJlWcbqOqzfrgEgyVCYbWG2HLLjYfR2//f0tH+6n/x+hYtfzDL3tX7xkBJRGHgvw9bv+4Q1ORmhUrEQCCQkwvEQJPskSTHCjHwqyt1vlAklgoTsjkv8fIj1jTaVnR4DkxFKy13SEwbVjR6eCvduFLC6HuOnY2w8bXH2czkef73E2EycjVKLze0WId3hs8ev89986Sn5XJPhfAvPg2ovQvff/wOSF38Ea/AHEYrxxvP51b/+ALvnAjIh2aYrS+htlex0DHetTXg8ih2NUvl6g3iQJqnoUnBONKxCoKUZ19ml3V4nIJeSwC4E593QsIuNF94LwNxu0F20SJ6fQur0vbJKMgZrTeTJF5UIZFkmlUqRSqUAME2TSqXCysoK7XZ7T8EgnU6jadqhPZofRWjmCEc4wsGhqiqW9WJUptPpcP/+fUZHRxkf9/shHLZOYDc/bn5+fo+s7npEf2T8PN8qrbIWFPw8axTJhaKUzDafy03xcK2GGve33S2u2ej6XsP5VoOEHmK91eB4Mk2x0+ZKfJhvzK1zZWyEnWaLSPA7u7JFOy2flC6Wa2SMMF7DYWmnQceyyccjrJXrDER1Cm2Lk0NZ5rbLnBvL82i9yBemJ7h+Y5Uzx3I8Xi6SCstU6pCK6uxUIJuIsF6ok4yGOTeQpVsNbHGw+A4bBtDZKwKybIeJRIytxSAHdLuBJMHGWg1Nk1leLDM0HiZz+RtsVQzaKmgRhfWihoiGcVouup5gqyMhhSXWdkrMjEwyW+kSllUMVWWAGL2mR1QL0XUc0nKYrVKLsCyTjBpILY9qqYOuKiR0Dads4UoyEVnGq5nEwxp//D99F03r0yFN0zAMg4sXL+J5HvV6nXK5zNLSEpqmkc1myWQyRCKRV9pxz/PeuuPgLg47r+xXMjno/HLAjnMIIf4V8K8kSfpe4GeB7z/ofn3X3SkvOxmHqTp3HIdut4tt23ttKkNXP4U9v0hnfuu5bQ/j0XQchydPnjA+Pv6CbtoH93/7TgvX8sfNzcQwW/5D1m44bOx0SYz7HsdWuU+eK12XzNl+fl636zH3jQrZM/5n22sdNh81GbwWhDfyOst360Rzfii8MNeiGYQ6inM9Rt/18xBtRaLTsxAeqAEBXbhR5eQXsnzz9zYZmPYfpt2V8sqjOuPnEjxdqmAKl+nYHf7h3/hNfupHvsaFEwW2iong3MHiWozh+Abhhb9P4s5fIlz4TSrlMoqiYNs2juM8d34r8002fq+IJLlYroTsurjxCIolMNIKSkRDyqVo3rOIjMZwmv4k4LZ84xUei/dv9/2FQAG51LIJvIA46gPpvW33v9cGknvb1B5WMO0YBMcuAhkp6VjujavGUCjE8PAw58+f57333tuTn7h//z63bt2iXq/T6/UOFWY5IptHOMJ3Di8jj7uqJKdPn94jma/a9lWQZXmv+5AQ4jkxd4DvH54hqurs9JqMq1E8BJPRNJeSo9SrHqVOl9VmDYAnlSIxWaHuOkwnUjiet1d1PmzEyJoR6g3fPm43/dD1XLmCrsg8C2SL1utNJtMp4iGdk1qK2dUy00NZhIDBhB8VGwpSiCL6LrmSuDI8RGnDFwxvdv1lfdv27dN2pY0EzK4WSEZ0eoU26wtl5peKRAyVxdUKyYTB0kqFXDbG4kqZU9ODdLdaYLpsbdY4fnKAUrHJzOlh6rUOJ08PE4uFOPuHlljv6niZMK4jUW5ksGQNT/ZwHYM1V8JSBL2WibsBmxs98qEIIUUlbOusF9pUej1Mx2FEjeK0XKKqhuMJpJaHZ3rEDJ20HsIqmqiKTFJRkFouEVXm6jtjTEw9Xwzqed6ebZZlmXQ6veftPH369IG8na7rfsc9mq1W69CSeQfsOLcHIcTXgBOSJB1Y0f67TjRfhoM+5K1Wi+vXr6Np2t7FB8j/ye/HbEls/sK/fqtxC4UCpVKJycnJN3YmkmWZzSdt4sN+mCKS78sRZWdilNd7VC2PxAmd0vw+uR0BWxtdoqMhwimN1Qd1PFdQb9lkz/qeSICt2S7pKYO5O1XMlkNqxjcUo1dTlLZ7u4XntNs2A6djPL5eY+ysH5rffNQjNaERG5RZq5YQAorLLtGExvLDOieupEkPGcgDMrVSjb/yR36d//N/+XVatT75OTlex3b88zqRbwTH7LFZ1jCe/i0Si3+XMzNTe1Weruti2zaWZfGrf+UedsPBsiUUQ9AIxxgMerLjONiRNHbDJ9+RoaA6UgFzswb0JY60fByhhgidOoZ+5iTq2Aihk+Ooozk/HA7I0f553/9eTferuvWBBNU7ZRg8BpKEXe34/08Zh1o1SpK0Jz9x5coVLly4gCzL7OzscP36dR4/fsz29vZLvSe72G/IjnCEI3y0eFOOphCCxcXF51RJPrjtQYmmaZrs7OwwMjLCzMzMC79tqBo/MHIKgLCsIiOhuyFuLJZ5WCqS0EPsdNpMRWK4QnA655OeSJDmUzd7nEvn2VhvsFNr8bRQImWE2ag3GYmEaVs2p/M5PCGYCgjkeDxOa7O7VyTUCXqab1V9G75WaSJLMLtdJhMNo3Q81pcrLG6WGUjHWNupMT6QZKfS4sRohnrb5NREnnQ8wlQkxupSlYFsCNt2yWfCfnHQmF8cNDyQYGI0TdyB4kYdIxoUqQbnpR2kO3muh6Jvs6X7neJaJY9CKE5DtlHDMlY1QhsDr+xgoNJraTRCOiuVCsVOm6QXxu4KBiIRcoZBwtUpFltUO11czyPnhcASWLZLTFJxazayLBFFwWlahCQYycb5/j966YVrKoR4JcELh8OMjo5y8eJFrl69ysDAwF6Hn7t377K2tka73f5IiCYc3DMJb6fNfJCOc5IkTUvBjkiSdBnQgfIHx3oVPhZE822KgQqFAvfv3+fChQtomvacJ0kxdPRjk/TWq5S+0pfmedMF2zU+KysrjI2N7VWrvw6yLPPoKzW2uyajV1P0Ov39lkP+6a1u9zCTMkbeXz1KCmw9bdKu2NgRhYELiT2DUFntYib6uZnduk3sVAw7qGJfeL/C0DtxlufrFJc7TH3aT+wuLnZQR1SEgPkbFdKjYYQH6ZEYDeGy9sgiPxGm23RIH/PPg1A85ndqrNxf5m/+xW/x6ZkFAE4OVeha/rHHQj1mN/y8oXzKZG7DX8Qotu8tHrRuEr3/s2iig67r6LqOpmk8/Beb1GdbOAroHRc1FSLUcekuNwgPGlRWPOrzHawtP0QkK/7xR8YSCEdgnBzEFFHqziCFFYO1rzRY/1qLVklh4/earP9+h0bJoFzO0ogPIPQIUrA6F84+r6LUJ5Bq2vcWV+9WkadOYG3XMGZGPnQuze4x7/a0HRsbo9fr8fDhQ27evMni4iL1ev25e7Tb7R6qzznAr/3ar/EGCYo/HUhQ3Jck6RuSJL3z1gd1hCN8wrA7rziOw927d7Es6zlVkv04aPSrUCgwNzdHMplkaGjoldt9afwcAEWny2lthN9d3OB4Mu1XkKd8G24ovv2qBiojC40auiyTVg3aRYvNeovTAzlcIZjO+t+JBxJubmBbSp0OVwaHmJ8v0TNtnm2ViIY05rcrpA2dcsdiaiBNtd3l1HCeeDjE6XiaufkiUyMZhICRnG8nM4H30wgq5uOGjrnRwQ7aLPcCBZVWMOctLReQJLBNi9ZylacPN4nFQsw93SaTjTI/u8PIWJr11QqXr06wemuZgf+sghv10EJhtnoxFCuE6Ep07Bg7skRLtxFJhdqmh6pFoGqTslXMZy1qdZOmZVHsdNC64HZckobBYDyG3BDU6iZCCDKKTrvYwxOCiCvhtiwMSSapqfyJ/+NnX8oLDhptep23s1KpsLy8fOjczg+Dt5HMO2DHuT8OPJQk6S5+hfqfFIcI330siOYHsb/A54MQQjA3N8fq6ipXr14lHo+/1CgM/+QfRNgeO7/09QOFM13X5f79+/R6Pa5cubKXd/cmeA6s32vTrjvcu1dGTijIin+Dllf7HkxPVqnjoGckktM63bq/si7MtTGj+9qZabD51GH0mh8Kl2SYf1hj7EoyOH7Q8hr1kr8qXHtcJ5xUmfx0mqVnDbSwjGN5pEcNJAkKzQZaXEJ4kMj6IfzNZzbTn0py92GRk6d6/J0//1XSob7kT0j3eLiQotBI8v69YVo7cVobSbxijG4pxaMHgywux1ko5JFw2d4so3zjr4Ld8mWhbME3/tYCwvUQsoc2GcFd7pE5FUXPh5EHk7Q3ekRGwthBjo9dbqPEdOTBLA0vx+o3TaqPW1hVG2NfCF3e1xbMbdt4poc571J4YFFt5NBmpnAa/S5AbqvvVRRy/7vtgow+PYlxavQjTdqWJIlEIsHk5CSXL1/mnXfeIRaLsbm5uSe2u7Gxwdzc3KFWnq7r8tM//dPwegmKJeA/EUJcxM+h+X9+qIM6whE+QVAUBdM0uX79OkNDQ89FwT6IgzglFhYWWFlZ4eLFi2+MiFzJjHE5PYbcMhCW/5uZoKPPds3XDl7pddBlmYV6laFwBNN1+J7cBHefbTMSyKCpQQSn0gkiXl3T7/pTKBHXNTJo1LY7VJpdZoZzWI7LUCyEACYHAxk9wyfW8bCOVHFoBqH4ct2fr9YLdSRgcbOCqsjMrRV59/gQs7c20FWFxZUS6aROodRhfDRNudpleipPq+NwaWaQpVubpNM6lukwMp7E8wTDIykAEokw584O01ipYFypYbs27VKIpZ6OlAFTsfBIUy67RF0dedtBbsSwVQ1b9tDSYWpFk44nUS40SOohJqQYbs/D8Twcx8UqmhiKSiysYdgyTtMhEtIImQLZ8ojKEhEJ/tRPfo5Yot9VaT/edk7Y7+1MJBLP9TO/e/fuW8vnHRRvq838po5zQoi/KYQ4J4S4JIT4jBDi9w8z/seSaL4Ktm1z+/ZthBDPaW++zAMaPT6AlMpgFdus/+PXn5Nut8uNGzfIZrOcPXsWWZYPvKJdv9fCCVZ4w6cS3PrdHeIXogycjlFZDQiPJCgudWkVXJy4RjjbX0FrcYm7v71N6pK/mh27lKJVs9lYaBIb1Bm7nKK82aWw0SGUUFB1mblHNY5/1l/Rtqs2o5eSPHlUobrdY+qa//nc9QrDnw6x+LSNJGsgCebvVJm+nGboeIy25KFLPf7qF36L8XyLqUyV7Zqfj1lsROhUDdJdjytDbc7ny3jC37/RWIXjaZNPDbVpFBJcfziC1amhtua49w/+Cv/tX/1NfvYLv0l5q0ur65LPh0kNx0BAJKNRK6l7N110JAiXR2TkTIJKOUa7KOgVLfSUjln0DZ8W6ydpu+0+cext+TlKQpPobbWw6zbbNzuUNwxCJ8cQkoS5Vd/b3mn0K9TlaIjtbzUIzYx/W2UoNE1jYGCAM2fO7IntFotFfuZnfoZ79+7x3//3/z23b99+4/jXr19nenqaN0hQfEMIsdt38338XJsjHOE/OryMKFarVarVKhcuXGB4ePitx3Ych3v37u3VBYTD4Tc6JSRJ4lrsODtdEyvIrZ+rlJCBDavHaDRO27Y4m/XD5kNhgxNSilqwEN9sBFXnBb+N5GKlymgyTsO0ODOYJ6ypnIukeTxfIoTvxPCC6nY3sLjbNX+MhUKVi2ODLD0u4NkeCxtl8qko64U6E4MpSvUOJ8dzNDt+uPzcaB615esfjw77Do+BnD9XxGNBdbwi8c70EK2tDsITWKZ//jfXa8gKzD7dIhLVUDyXymKRlaUthv94i1pdpp1I4DVl9I5Bp5Om6nl4EehZNk09Rs11UWM6YaESKoDaEdC0MHdalBZqFKpterZDXNeJdCQ8V9A1bSK2hNTzEJ5A77rItofuCMKSxI/+559hYLQvU/hBvC50flAIIZ7rZ3769GkURflQlexvwtuEzr8T+FgQzYO4qJvNJjdu3GB0dPSFPJhXCeYO/MnPIzkm2//2Pnb35fly1WqV27dvc+rUqd2kWODgoZP5r9f23keyPvFduF/DG1bJnPRDDwOn47TK/u+XV7s0bIER6GzmT0fxHFh7YJI4pdIIVqrtqk1oSKcb3IT1HZPB8wnGr6ao7vRYvF8jHmhkdhyHxKD/wM/dqpAc0slMqhSrNiBYm21w+tNB3q4ssVZr8OTWNv/Dn3vGsYFdSSWJejvJ/eVh9JbKp0abLBX8lZGmwoMV/33ScHm86a+ux+J1LuWaRDsed5dzXBqe5/u0f0/nSRc9KjNzOU2vLeO1TSJjUQpPTLpFG6fiH6OseMgTBowNsvrVJnbTxSz55DI6vu9hcfoPYm/TJ5d6PrJXPKTkQuAFVY8jCXoFk/Xf7yJPndyTQhKyjLnZl49yTdfvjX5i4CMhmgcJteyK7V66dIm/9/f+Hl/4whf41Kc+xerq6hvH39jYeK5YgVdIUOzDfwn8+wPs+hGO8InE7vMohGB2dpbt7W1isdiHapLQ6XS4ceMG+Xx+zyN60HzOL504DcBcvUpaD1G3Lc5m/LSkkZi/T47nMR5L0K25LBUbPC2USIZDbDaaTOfSfhvJvO+ZHAo8V4aqMuAY1Bp+ylXVFEjAUrFOSJFYKTfIRkNs1ZqcGEwzk82gNjxaHYvjo0G4PB9IIsUCSSRVRlVkUqrOk1sbVGu+XV5d89Py1rca6JrC/GKRdDKCZgmKixVWlkqMH8uws93g5KlBWk2L02dG8Dw4eSzFs28uoRuQ+cEGtWqEaiiCJbkQhm0RpukKrK5D1AnRLqhEPR2t4xHtSfQqHg085HwEB1DaEnaxg9S0GIzG6OyYdE0XXZEJtRzMposkSYR7HsJ20S2PqAo/+hOfYXz69bUXH0UO/QfnlTfldn7Q2/k2Xs9Wq/Wx7Db3sSCab8J+XbKX5cG8qgXYwA9cQFIVsE0W/vZXXvj/2toaz5494/Lly6TT6RfGPBDR/P3a3vtmpe8xa7dsVrdaDF9NEMn1KxAHT8VYuFVFGlDR4zLVQPxWeNA1JVr7mp3Xyx2ccP+4Fm5VaeP/3W06JI8ZDJ+Oc/ebO/gOR4HVddFzgqrlsj7b4cynfUO2MltneDrKwmaN8ZMJ/sofesRMfAvT9r1wridRXIcJrYehBTk49DvqJKP9m143/HBD2uixVEmRDdu4rSTzO2NMJwp88QcWiLT9qm6zbmE2HFwtRGutQyit0lpposY1SlWbnXsqepD0rsVVupv++VCM/q2569kMDUZxglB4aGCfaHu0f37VfZ2Eui2VuplFH80QGkrimf1z29tqEZ3OooTUj4RowuGTttPpNF/60pf4kR/5kTduf1AJimA/vohPNP/6gXfoCEf4BMKyLG7duoUkSVy+fPlDhSx3K9TPnj3L6Gh/jXfQuWIikeR0LIkrBMOaT+iUYCG81gwKLYWEUpNYKjc5nkrgeB7TOd/ztttOshv0DV+r1TmZSbO5XKfe6LJUrDKSjlNpdxlNGtie4MzYIAIYTESRJYmY6fD4/uZeb/Ja0CVto9hAAhY2KuiqwmaxwblshjvfWmYwH2Njq04+G6bZtpk5MUC7Y3Hy+ACapnBqKMXsnXUGh32yutvpx7ICJ0m9y/GRJEt3t4jEQmwXq4izKiUho8oyTkWh1U3RK1pongQ1QaGn4mR1GqqDEQ1RK9mEJAW17cBGi7QdQigSHc+lvlph4cYa8XAIQ1PobDSIh6JkU1HUho0mSYRsD8U0+U//s08xOJHGdd3XXrNvt/PhZbmdH/R2FovFQ5Pdj2tb448t0dytYH727Bmbm5tcu3btlSfwdSvK2Bc+g7Ac6t9cpLPte8Nc1+Xx48dUKhWuXbuGYbyYp3EQ49Fp2LQ9h/igipFU2Xzqj69oEmtPG5gdl0d3yniR/s0SDbyQm7NNpHFBc7tv+BITEUxZIpz0Q8WJMYPZWzWSkz4ZHL5gsLJYxwj+v3CrijaiIIDVJ3WmAikkJRoiNex7U1ee1YlndBzbIz4VprDdYax3mz98eY1E2Ga5PITtyjxayHF5qMuT9b7QfVbrewCPJVqs11PMFZN0W10qbZ/cdV3/eI6lG5zUayhymB/+ka8w8wMehds1Bi4kqFcgEmiIZqajxE4mqUs6jfv+NXPb/ko8fiy2R51EL+gWFNMwd3zyGcr3r5Oi77t1912m5wqBZJnuVo/tZwrKYF+JQc1Esatd4mf9MNVHRTQPg8MahLGxMdbW1p77iJdIUEiSdBG/PdiXhBAHrgo8whE+aWg0Gty4cYOJiQlOnjyJoiiHJppCCIQQLC8v71WoJ5PJ57Z5XU3Bfti2zdWw/8y3gyybJ+USCU1nu9Pii4OTzM6XGIn7NjgcyLDVuj4ZnC+VUWWJ2WKZfDTCaCxBuClRbnSY3s2/DPl2Np3wPaTNnr8wb9suZxJp1je76KrM4maFaFhhdbvGUCZKqdbm5HiOds/i4okhkpZCSFIQApJxnzjmsv5xe0H0yHZc0kJh6WkBRZFYnCsQiejMPd0ml4uzslTi1NlhlLaJLkGnbTJ1ahD+gI1p6CBJeF2dYiRKXbHx0gqdko1txJGbLnFHJVEDc8MmpCl0bZuYHkLWDUzXQZNklEIHu+7nZs7dXab0YJuIFkZTVKiaSK6gvVKmsVbmJ/7K9zN1bmwvAuq6LpZlvSDLt3vdPwpVkIOO8TJvZ7Vapd1uHyq3s9PpfCzbGn8siObLLoYkSdy+fRtFUXj33Xdf2w7sdURz4r/4NLZn4Fkmj778mwDcunWLcDj82iTuV4Xj9+P+7+7w5E6VjXqXyc9n2GVJI2fjmIFQe2okzPXf2mL0c0lkBQr7CoRimRjxaQM15B9/cbNDYaVD/LhBNK2x8KiB50LPlInlNDY3OtQLJpEgwj95Ncmzh1ViaZ/sLT6sc+rzGe7eKFHc6RCKKDSrFiMn42SmDb7+2+t88fMSf+kHHvb3QeqxtD3Iqawfzk7va2+ZDpv8zqM8j1ZHaBVTrCwmGXMlzoRkCtvDLC/nqFVkyh2DtNFhp5xhamCbQmGca5d/nXBew3EkOjsmwnSQZPAiKss3LeJ53+BKCrRXglZm8f616G36+USR8f5DI+8jl06nX5nvNfueSrPULwSyg5aZbteltq1inPW9EPqAP2b8nB8++W4RzcPk0ly7do25uTneIEExAfwy8GeFELMf6Q4f4Qj/AUEIwdraGpcuXWJgYODNX3gJFEXBsiwePHhAu91+ZYX6QdBqtbhx4wbfNzyBLsusNOpMJlJYnsupTI5ryRG6dQdP9At9lmpNQorCQrnKaCLm52MO+AvmC5k8jx9vEw6qzlu78kX1QO9yq0xE11jYqXB6OIdc95As6PRsTk7k8QRMj/nnJWEEgu+9LqOZKHapR2GrwU7Rt8vrW3VUVWZ+qUQsGmJhuci5U0NU5stEdJVqpc3JU0N0uzZT03k8TzAwnGBwKEHYcthcKFIpNP3C1rVNlHddTM9CcSIUezpGV0WueIRqIbpuGMsVkNCwSj06ioZlKLiKTLgjEA2PGDJu28LaamHE4hixEOZWA6ViY7ZsSgtFVr8+z8r9NdZuLCG1Tf67v/3jTJ4cQVEUdF0nHA6j6/puxfWeLJ9t27iu+5FJE70Ndr2dExMTZDKZQ+V2ttvtQ6uZfCfwsSCaH0Sj0aDVajE8PPxasfRdvI5oahEdfWocyzFoz21R+90txsbGOH78+GvHlSTpjUTz9m/5Ej+2JShWu4ROhMidjKLvK17JT/lk4tE3Swx/T4pasU+E6lWLpfs1sudjjF6Ms7Pke+4W79UY+UwKM5CNqG73GL6coFrwjcnGY5PJT8VZXKrSKJtEh3xyaMR06o6/TWmzy4lLfsjFVQWeBqrs8QND99FV/7g8AesbBvVy/zaYSLbZaka4v55geT2LbkWZCrUxFI+Y0SeCWyUYDDtcSXdp7ORYXJ3CtKOARHsLdLXNyXcfUH7cQAlJ9Io9lMkEWw+a4EmEI/45Sk5FcTpB8nrgxQwPGSiGSux0DjUbJ3ZxlNiFUQgZRGfy6Pko5k7QYlKT8Ur+il82VHpbweeyRGe9ube/vZLJ6tfaGGfHEIGMSOK7SDQPm0ujqio/93M/B6+XoPgykAV+XpKku5Ik3fyo9/sIR/gPAZIkcf78+Q9dGHHr1i3S6TTnzp17axtRLBb3pPiGMxk+k/cLkfJGhFQoTNhUuLe4w2yxjK7ILFaqDEcjdB2H0wNBPmY8WJgj8U5ygOUVv+ZvfrtCSFVY3KmQjYWpdf1uP6bjcnIoy4l8moyrsr3TwAi8nWbQtWcnaNO7WfF7kkeNCG7RYna24FeVF5uMDEb9lpJBK8mpiSwnJ/OEOh6NSgc9kJRrNf20sfXVKpomY3YttJbJoxvLTJzIU9yqc/riOM4XWmiOit2KsiN0emGXpmaDrVMQMmoyjKLIxOsybldGLptEXAl5u4ui6FiqoGFZJD2NEDqKK3BrXcJKGE1WULs23bU6sushNU1GB2L87D/6SXLDz6fGgU/oNE0jFArtkc7dSGa320UI8cYQ+7cTu/PSYXI7W63WoT2a3wnZvI8d0dzc3OThw4fPtf97E96UjH36r34PstnBNBWUr9RIJd887kESvG/+mh+5FAjWZxtszDVZXKnhhgW7Sjrter8IqdpooA7KxAd1sscM1p/6oen5O1XC46G97yAJnj6sMP05nyjKisT8sxqnPpfdG0s2VMJBPuL6U5OJSxHktM3994ucvOLfaPe/UeDyDw7xrW9ssjJX57/64gZXhioslP2V7M35HGcyJqrbJ9xdW+HRcobpEAyFHSaT/f0fDdUxXX8nj+f7XkTHjTGsVwn1HCqVLIPjFQyvy/FTS0T0CtETGuWaR3W9h73jn9Ne4HncFbgP5cJghFFPDOOk8yw/UJj/mkV5VTD/2y3mf6fF4ldbzP++TaEUp1RJIE2O4k3GkFT/Ng4P92WQwiNxPNP/LSmk0Fn3jerq11p4SggtYxAe8UNUH5Zovk3ieKfTOXQuzQ/90A/xBgmKnxRCpAMJiktCiKuH+oEjHOEIAFQqFZrNJlNTUx8swjswhBAsLS2xtLT0nBTfHxieAKBj2yTaOt9a2GQ4HqNlWZweCDSLo75XynZ9krNWb5KLGFhVm/XNGhvVBlP5FB3LZjjuyxcdy/lkKhyQv4iqUlyssbrlyxXNrZeJhDQWNnxR9u1KkxOjGVpdi09Nj7F8d4fx4SAfNJhb1CB8X6r4c5UiBGt3N5l7uk0kqjM/u8PAYJz1tQonTg5Qr3W49O4Em/fXyQRRK0Xzx1gtbSNfcOm2wtQkDbtmEXdCuMsSnhJBa7hopkCrCRpdDzlrYMdVpIpFJBHHa5joXRej7tHtuMhRDUwHueHhdR0028MsdohGQ6hdh/HRJP/TP/nzxFNvXmzIsoyqqui6Tr1ep1QqMTw8vEc2d72d30nS+TIlk9fldv61v/bXuHXrFvfu3aPdbh/4N74TsnkfC6K56z18+vQpOzs7vPfeeweSjNjF60ihEIIduYaTiCIJcJvw+G9ef+OYb8q7WbxXpbTuh8EHpkI0gqry7LjBt76yRexkmLGLCVYe9+V1mkVBYaVHR3LJzfTd2+GEyq3f3WLsahIkwdSVNKWNDg+/VWTySooTV9PsrLV58M0ixy+nSA+FuXe9gOlaqEFf8FAsTNfyb8rFh02yoxpDx3Vu3NgglQsxpFX40ullAOKezdPSIBeDcPmJdI/tdpTtVpitQopxxQH8cZOaxbOSnxsZVmGt7ZOzAaNLxfQf4IjiexRTsTbdokGznadWjpM0Onzfn72Dq2l0ih7RUX//tLhMc7mFpEooUQ15coBqL8rsr9fZuN58LueysxlUoY8Y2E0/XB4djtAtO2xe7+D08lSaaYxzE2iZvkFR0+G998ZoHOEG11KRWf29BqnPz+z9/6Mgmof9/sc1afsIR/gk402RKiEEq6urzM7Oks1m3/oZ9TyPhw8f0ul0uHr16p4UnyzLXE3n+NzgOBsrDTLhoNNbMlj0BnPOZssnCrv6mGFZZkKKs7RZ5cSgTwajAaHUdH+xvh6QwdmtMu9NjHD31hrZeIRyIFdkWg7T434ryuFAlN0IaVyeGKKy3kAIwXbBn68KpR4hXWF9q0kmFaFY7nB+MsPjry8zNBLF7Nkcm8rieYJcfnfBLjh3dpjVO6t4rsfcw01SmShLT7cZnEjQudLC7qQpdD0kGYQMpYZENxOhoTnIg2GszR4OKorj4RY75NoqRsjAavVQojpewwVPJhEL4263cUo2sipjCIFieiSTEaSWxenTQ/yNX/yvCYX7xaEHwdbWFqurq1y+fJloNPqct3N/57vdEPu3k3geZF7Z7+382Z/9WdLpNI8ePeILX/gC6+vrb/yN75Rs3seCaJqmya1bt9A0jUuXLqGq6qFagL1q290OEI7jcPKnvhcjZCI7Ntu/s0FzpfGSkfp4VSX7Lq7/7gZTn0ohyYLcSL+Axgg89KuzDUzDYuxKDCEJhk9FKW/6hKxW6LG4WGfiHT+5evxCErPr8vh6iclPpWn3fELluYKl2SrdoNLc8wQr83Uy02HMnktp3eLE5QzZYYMHD0rImoQelrFMj9RAlLrlUq/YxFKCv/p/mEWRfSNWb8qUNyR2ySRIbNSTuLUQg7rDUNRlvds3sK7WJ3CW019htexAEsOo0DV9Y9cxIyS9Oo1qlESkSa9iMmj46YLppD9mbCpM6JRBHZ35rzfYvN0iPtLPfbICL3A4F6Jb8M9ZZLhfCOQp/YdbRsJsuCx9tUGlGCZyfszvob6vI5AS648dGY/hdj1I9MMLH1bK4lUamq/Dx1Xv7AhH+KTgVW0oX2XXPc/j0aNH1Ot1rl27hq7rhyISu44J0zS5ceMGyWTyhZC7oihIwEw4S8dy0IKq8/W6Px/tyhmVOl1O5bN4wPlMlspqi07Tj8qUm0GKVaGKKkssFGrk4hEKjTanR3KczWSh6YKAwaxv57TAM1lv+SHu1e0akZCG0vVYmy2ytFJmIBejVG4zNZGh23OYnhrA8wRjI2nOTeSRgqwvGT+nc22ljCz7GpnJlEFUV+juNCgXmsycH8O2HAbH/QnR0gTm6Tg7jgMRBbPjoFpJvA7ETJm0pcFcD00P43ZsNENHsWQsScJSJVzbRV7rEI8YhMIqnbUauqcSj4dJKBqaI6EjYdU6TJ2I8af+2udpNpuHKv5aX19na2vrhZqQXW/nLunUNO25giLbtl8oKPooBNkPO6+Ew2FkWebLX/4yN27ceE6u8VX4TsnmfSyIZr1eZ3JykhMnTuwZhw9LNHf1zgYGBjh9+jSjf+QUnhqCkIxdt3j/r339tWO+rupcCMGv/m9z3LyxTfi4jrOP+DTL/RusVuny8GaFxEkZfV+h4uQ7KTaXWjx9XGb6sxkKW303d61uosYVdm3k+Pkki/M18uP+yjc9GmJ2vkQs5T8ID98vMnwxRrtps7bQ5MQ7GUKGQrXdIzscAQQXlDUmA+9lx5JRRZicJu9KTzJXDhOpecT21VuVmvskg2yHby4lebI1iFLXqW2nqG+nsCshVjfH2ayMs1MKKiVDPUAin++yNDeEEXGYnnyGLLu0N7vkP5WFSIz1b7lomoZZ8kPw7Y5vRCUFmkv++/h4n1zKWv9W7VT7BVXdYr+jUWujy+JXmlS7SYTa33/Rj/KjJX1PZ/JCem9VCoeTJvog3taj+XGsDjzCET7JeNW80uv1uHHjBrFYjPPnz6MoyhudDfshSRJCCBqNBjdv3mR6epqJiYkXttudV374rN/7/GmhRFTT2G62OJnN4HgeJ7I+OTM0lWuDw5S2u9iuYKdtoysya5UmmbBGx3aZyiXxhGA8myQe1hlUDJ482abV8Rfrazs1JAlm10rEIiFWtquMDSQRwIV8ltmH20xO+AVGQcMgNC1ohVnvEI3oeA2TpYdbzD/bIZ2JsrZaYXIqR6tpcerMCELA6ECYp99YwLJ8Iru1VkbTFWYfbJAfTtL5rIRtSch1l0hXpdMMURceIq7iahJdS8KO6ZghCUIKrHVJGQZOsY273SQuhSESxvIEFLvEjAh6WMMrdTCrXXQBquXyxe87zf/l//0XiMfjrK2t8f777/Po0SN2dnb2+ty/DLutIt955529AqGXYVc3VdO0vYIiRVGe83buVrJ/1DqcB8FhI2XfKdm8jwXRHBwcJJ/PP/eZqqqvvTH244MV4uVymTt37nDmzJk9vTNJksj84Wu0q2AYFs25Ks/+6fwrx3wZ0dzN11h+VmHhUc3fTpH4xu9vkj4f4fT3Ztle8UljPKeyvRg8dEsm6zsdBs8E1X2uT45cR1Bt9UiOhNi9tnpc4f77BU58KoOiwdZGm0bFpOe6JPIa1U6HWsEhNRpGC8mc/Wyeb/z2BjNB4c+D60XOf1+exbkaD28W+d7vTfHn3t1moe6f3yebCTKqw0DEZaGRZLEaIiN0BiMeT8p9YpeXu2y1Q9xZz5LtKAxrEcZki0HNou7EkCXIqg3idEg5TVwrweyzEaIxE9PSiOhdFFtBC+vk0k0+/aPb1E2Zx1+p0d4KQu2TfY+ebvohjui4jmv6592hnx9qNfrvvYDMK4ZCe90/31pMpR2E2bs1h7nfbBI6NYpiqHS3+8RUCAlJlclfGkBRFDqdDp7nvXRVelC8rUfzKHR+hCN8Z/GyeaVWq3Hr1i2mp6eZnJzcIwiqqh7K2bFbX/Duu++SzWZfut3uvHJuaIAT2ecF2KMhf36odLposoxuyczOFVgt15nIJulYNuMp3+FwbMgnh57w7VWpUiPZlbj3eAMjpLK0VWE4G6fS6HJqPI/tuJwIOuEMp+NEW4JO0PBia8ePiharFiHdF2HPZWP0TJuT2QSz9zY4OTOI63qMjPkkWAtaATcbPaaG4izf3SaRjrC9Wmf4WIpauU1uLIoswcBEhNXhJq2QDZrCdltCjRpge8TQcBa6iJJJ3JZRij1iLRk9HaHWMwklwmiuite0iMgSWtMBW0a44BbauG2bqKYidx3+wB+5wF/4n34MTdMYGvr/s/ff8XHd15k//r5lem/olQAJsDeJpKrlFvdI7ilOZDuO7RRnE2/qz3Hi7CZZfzdeJ042Tt1UJxsXOY5tKS6RbckqFMUGEgAJAkRv03u79ffHYIYgBZIABSnyCs/rpZcgaObizr13zuf5nPOc57SwZ88ejh07Rnt7O/l8ntOnT3Pq1ClmZmYaGsb6KNF8Pr+uUaJr3U+LxYLVar0q25lOp5Fl+T9lXdlIAuPFss17SRDNtbCRjGZ951nX10xMTHD48OHnNBMNfmAvsiiTKTqRRJ1zf3SOcqZ63WNemwo3DAPDMHj0yzON3weaahmyy6Npimh03u7F0yQR6bJR3yz07Q8RnS0zfrHI9vuCLE1d6TyvGhVOPxml9/YALX1uLp6q3cNzx2PselUz8RUD8/hiCXeXQGUl+Xl5NMP2I0FGzsfQdZOZiQxd273svDPMo9+YYd/RWsPPUWMIp8Wg1Sjy1JSfXYErtkBK1YatasO+UlK3WupEWGCp7Ced8tNv1ZBEgVj5itYlX60RUkk0SVdqqVqfNUerv0Q1aWdqqkZqyxUrDr1M2fDQFr5MfqmAzSuRnqhlLGW5FtAtLoncCkH3tq4iX8rKBRRMspO10pKjzY66MgHD3e1mJc7i7rriwent9mCoJrNP5Ki4Q4iWK1/W0nIJ/6Afq8uGoihcuHChkcGA59pcrCdAGIaxVTrfwhZeYlhP6Xx+fp4LFy6sSQ7Xm9E0TZNKpcLS0hJHjhy5ob3M6nWlntUsKjXCN5FIYxVF0uUKB30RhsaW2NFaI5QBV22dMVckQTOJDAIwncyzr6OJSlzDabFSVXWavbVYHVjxvxTEFfu8dJEdHWGWxhIUchUmpxL4vFaSqTLbusOUVkzYDdOkuz2AlK6ilGukPJlcKdePR3G6rIyPRdm+oxmhUMYmiShVjY7e2rkKK5KsUkajs9PDM+YMjpKIMK+jl12IFQFKKl6s5GMqYrMb1SNT1nWsFgcmAmZFw17SMebKtayh24ayUEDPKDjsFuS8gtNqxWu3IlV03vpjR/iJX37Tc663IAj4/X76+/s5cuQIu3fvRpIkxsfHefrpp3nmmWfIZrON0dPPB/VsZz6fZ3Z2ll27dj2vdeVWiGa1Wm3ogdeDF8s27/8JoilJEpqmMTIyQiaT4bbbbsNutz/ndRaPFcftEWQJikUZs1Lhuz97fM1jrg4Iq0mmIAiceSq68hqYGa8RIEGAqbEM50/GWc5WsAcdOLy1FLy26qFSdANbi5WWPjehNgezF2rZtpFnE8hhBYev9mDJVoGRc3F6DwaQLGBzCcxPK7gCVjx+K2ASz5bp3uMHTEoFDZtPYilawDRh6HSMN98jcV9vBoAqFrSCg7ous6CIGBmBknFFv9guVZguuljKBOk1ddKlKw+5V76STXeIVzICirrS8W1RSBXdWCQDCRvTE214whqyqFNOioTccXbtmSKy/Qo5LK3oLwN9rivNOsYVcllZXNFqttkxqytjudxXrqXsllb9fKVUbvVf+UymbGduQsK7K4zFb6O8WCJ4IEKhUGhYjvh8vqtsLiwWS+P+X0+Dsxq34rm2VTrfwhZefNTXFcMwuHDhAolE4rrkcD1rUL0PAGDXrl03LLvC1evKm3ZuRxQExhMpmtwuCorC4fY2fGULolaLJ9WVCT4TywlEAaaTOSIeJ6lCmYG2MHtam3CWRQpFBZ+n9hkEuRb/ZqNZRAHGZuJ4nVaCTjtyWiWZLNLXE8EwTSKh2mbXsrIZT2VKbO+JMH9+iUpB4fKlKE3NXqJLWfoHmimXVbb1NdHS6sMNLE0mGh6Z48ML+EJOFmfS7D7ciUcWsFolivfZ0EoCWY+bvMXEDFkQdCiVQNRM9GQZvyrhSBrYNBNBM9CTZdBk7EE3elXFmMlhtdlxBVxYSzoWScKiGVh1gx//8L289UOvWsfdr+kYOzo62L9/Px6PB4fDgdPp5MSJEwwNDbGwsEC1unbyaT2Ix+NcvnyZgwcP4nA4briuKIpyQ9J5q02qG3nPi2Wb95IgmmvtPDdSOjcMozHHdu/evTfcBXQ+2ItFV8AwySQEkmdijP7f6ee8rl6OX+2lJQgCZ45HeezxWVr3ujn0mlbSKxrBvr2+xs9d27088eg8FYvO7ldEmDifqn1OEWYnc8xP5pleyNJ10NfoMgy22LlwpohhNQl1WmgdsJJYLjNyKkF4m52+QyGyqSqzl3O4Qlb2vaKJsfNJzh6PsueOJvxhK1NzWYpFhdZOF4am88Mt443PM7HsYJdPZ6HqwjBhLuuh1Q7J4hVSNlt2E0/7CK6IGltXeRM3yUVKK41AATmHoteInVO6oi+taLU3BP0FQp4y1ZyVbNZBc1OO5dkIvduWsa8k8Ww+mexUEXvAgqPFTvhoGN+hMEVVQugKYN3VRNnpRmnxUA3Z8B5sIngogr8l2Ph7pfyVkni1cCU4GPoVUizZZdSCzviTVVy7ar6Zzp3uxkjTa8vX9V3palPftTQ4qwPErew8b8XeaAtb2MLzgyzLVCoVTp06hc1mY//+/Tcc2nEjolkul3n22Wdpbm7G5/OtqwGkTjRM0yTksHOksw0T6PR52RkOo6ZVoqkC0/EMogDjy0l8NpmiojPYViOHHSsTepodLi6dXyaersXgibnEStk8TVvYS6GsMtBdy1BuD3u5fGYJre6znMgAEEuUkWWR8ckYoYCToMeBlK2SThTp29GMaUJ4ZcCFsjLCV1U0tHiO4ROTtHQGGx6ZqqLjCdiItHgpxbLEZuOctSxjT1nJFSV8igVHwcSdMCEjYhQVLA4LUkmnWjLBb6eg6xiZKh67G7sBWqaEpQxOtxOnVUZbyqOVFKxVHacAH/i11/O6H7tzXfe+DsMwOH/+PE6nk3379jE4OMixY8fo7+9HVVXOnz/PiRMnuHz5Mtlsdt2NPbFYjKmpKQ4ePPicrOJa64osy2vaJ93qunKr04xeDNu8lwTRXAvrzWjmcjkuXryIy+W6Sl9zPTh7PDgG/KiqhssjUq0InPzUMMXk1buYetlE0zRM00QURQRB4Mv/MAbAxeEUy6ki9naZviNeqtqVcrhjJbuWTVUp6Sr+bXZ69vgYOBwivrQyt9su89T35una78PfZKNlmxtNNUjFqpQUE7vnil6yUKwyM5/CF6o9vIqmM7dUINxSe83ZE8v0HgqSSZZJRMuUyhrvvU8im689sNNlHzs8OiBQKMiciXrostSubZdVo6SJnFx2EKqImMUruyufqJLQartkURCIV31Ei27mCyHOTwaZTjWTLruYSwSpqhJWqVbStstVklknHkuF+dkIqmbFUARkySBsnSBywEf4WBCj1cXMks7ynMrwoxlmh4tc/n6GxeEiuikSu1gmcUFFVN2MfSfPyKMF5icM8rIH995mXD4PwsoTXFy4cv1zK56ZAMrK1CBTh3RMwrU3QtQWZ//+/esqXV9Pg7N6V6qq6oa/4Bs1bN/CFrawMaz1nVRVlfHxcXp6em46tONGa1A6neb06dPs3LmTtra2da9XoiiiaVqjWaRePrciMj2eZHQuRsDpIF0s0xP0YpjQu6LHrJ9rPFfkYFMzZ87M4XFaWUzk6GkNUFE0+jtqr42seEcahsn+tiaiMwUEYDlWwm4TiacqhIM2cvkK27qCGIbJQFeYS8dnGhmxWDSHIMD4xWV8fgez00kOH+5i9vQMbZ1BTBM8K82Vc1MxZIsIuoTXKjB1fp7+/Z1kBl0krTa0oIW8w8BhWsgYIppHRnfI6PEqHocHuaSix4t4qyaoIgompiRgr4BZUJENgfJ8FtEApy7glEV+4b89wF1vOHDTa74auq4zNDSEz+e76v4LgtDgELfddhsHDx7E7Xavu6EoGo0yMzNz0ymGq5+Dtczi65yjXkXb6LqyWaMzNxs/0ERzaWmJ4eFhdu3ata6bWz9u8zu6CLg0TFXDME2KKZWvvuepxmvqpXLTNBkZGSEWi6FpGoloiW98+TIAkWYHo2cTLC8UmZrKMLessPvuCB39Hi6cSQBgtYuMj6aZHs9yfiSO5BcJrZDDvj1+yiWNC0NJZL+Ial75rK19Lk4+HWXwiB9RAqfXweJ0GU3QiXRaUIQq0+NZVNOkq9/L7mNNPPbtWQb2hXG4ZHxekbvlWVoFmemMDWvxyrFzOQGrduW2WwWTJ2fd7LDKiIJAr1MnZ1zZjWUUGzN5N5OZZgoZF7aijLds4LK58KsqQcMkHXVTTPrIJO3MJ2pi8cKKptMq6xTSPiSnhUiwjNc5zfDJHIWsQXyyjCBA6nJtRx7svUL8qpUrxLEUr20CBAkyk0UKMZXZs0XOfaNAweYjcLQFVqSnslumslx7vQmkJ69MByqlKsydr3Dbq2+7pTFda+1KRVEkFovhcDg2pMGpVqu3PM5uC1vYwsaxtLRELBajo6PjOc2na+F6a9D8/DxjY2NX9QHcyKWkDtM0sVgsZDIZLl68SDKZ5L5t3dzZ0s7pcwv0hgPohkl3pJaxFFZE58vZ2sZ5bClBW8CDR5VQ8wqqprOtraYr9ThrsSRfqsW+ycUUAbcdsaCTWsyTTBXp7Q6iagbbelZM4VcM3nP5Mt1BO8NPT2G1Slwej9Lc6iMRy7NjZyuqqtPRFWLPrlaycynUqsbsRAybw8L48CKRdg+FbJX9R3qJj81TKVYRBDhZiGL6HIhpBb9uwT6jUE6ruMoGQrJKoCzhlO2UqlUErw2paFAtmnhcduRCFXOxgqqaOFw2hHQZt8eJXTPw2CR+5X+9m313XvFCXg/qMoempia6u7tv+FqLxUJzc3Ojoaijo2PNhiLTNFlaWmJubm7dJPNarDaLr/9jGAbpdBqr1bruhqLna9P3QuIHkmiapsmlS5ca4mu3272hxiHPkRC+/c2oVhOHw4CqRnQow/d+b/gqPeaRI0fo7u6mWCxy6tQp/uRT36F7pxurTaSjz4u+UqLdtiNENl3lmScX8bRb6bstSHOXi8FDYXLp2he/f0+AJx6dJ5otsvcVESYn0o1z8obsnDy+zOCREB39Ls6fjAMwdCLBwVc3k1yZopNOKDT1+vGFaiQpGSuDUyG9EoiGz8TZNujjtS0pAhYdq2ASKzXht9bOM61INEk2dPMKobtU9dBpd7PaU3O5UgtaMyUX5ZwLb8VCQFXw6pWGhNItXCGCVqeAKEDEoVIteZidbsJYEa03RwpYUKhmdQTTxCaohAI5SonadQn1uRpZR6vzSplAzda+VLJDJDNVywL7e11o5dp99vXWsoHZBYVkTCCWt+O/rQlfv7fRFOTucqGvZGhNoUZSI4d8txQMroeLFy8SCoVobW1dU9t5I9L5nzVLdwtbeDnBNE3GxsZYWlqit7f3pjrKOq5dg+q6zmQyye23335VH8DNEiP1dcVisXDs2DFaWlpIJpOcO30K+4oVkcteO6+FRG1tmMuU8NitLGcK9DcHafK46LV5mJ5J4bDVNvLJXC02TswnsVtlppdq9kUOq8wOn5/p8TitzTXruUqlJu2KJ2rz0Cem4kTCbnyiFasmUylrdHT5ME2w2WpBNJctIYoCkmEwf26e6bEoPTuaKeQqbBtsAWpyhMF97Yw8NorLY2fhcoydt20jfqcbTQbJZ6MYraJ7nFTdElWPjL0KqimCJCBUNMzpPC67A5fTRjmeR8+ZOBxW/HYrcl5FFAXMXAmfU+YX/9fb6Nu9Mc9wVVU5c+YM7e3tDSea9UIQBHw+35oNRU888QTj4+N0d3dvSjyvrx/Dw8P09fXh9/vX3VBUKpVesg2mL4mV7nrdgWulqTVN48yZMwAcPHjwlszdDQz8R7chSy7SGR2LS0CyCpz9u1mmnoo3dgaiKOL1eunr62PH9v386/9dYmgoieQ3iWYTtPbY8PqtjJ6tZTCdbpnRoSQnn15iNppDlQ26B1Z2p1LtM1YrOqpuoAomu49GaOt1c+7ZWnPR2RNRTLdK357aTjMQqRFQxTQYPBiid5efE08tcu50goN3NdM76GNivMTF0Sw7DrhxekTSiSSvcsUAmM3LdKlVRrIODBMWUnYcQJupEddsjOYdtJRMArrOfPlK8LUhMZEL4SvJNGtV8it6TIdskqjUMrIOUSWj1gipTy41CKhhyHgdGn5R4+JUE7oBiYyLkEdhPtlB2F9k5444yYmVLvOWK1m9SroWcCW7QGGulqIMrmoUckWuZFqtqxuB7CLljMbot3PkBQfBg7VdviNyRX5gbZUwq+DZbePUqVPPsbnYKOo6H7/f3wgy9Wxn/R9JktbU4LxUyxtb2ML/SxAEAVVVOXXqFJIkcfDgQWw228bWipXFXFVVTp8+jdVqXdMG52a+y6t1/pIkEQwGGRgY4NixY7z9jtro6LHFBLIA8WKVrpAPRdfpW9GkR9xOlOUKsUQtqTA+n8BpszAfy9Ld4qdcVdneWSubtwU9kFDIZ2rEcnI6jijCcqxMOOQmniywvb8Jt8vGtoCHqdFlbCvWSrmciiDA4nwBr89ObDnHtg4no98fp623FleNlbGYEyOLePwOgn4XZqFEpVAl2FJb784nlyFgQRIl3CkBUxEQsgquKlinyzjtDshXUNIl7IYF2eXEsEhUEgXc2HDarVgMk0q0iGgK2KsGrREP//UP34ZiFjl+/Dijo6PE4/Gb3s9qtcqZM2fo6emhpaVlXff+Rqg3FIXDYZxOJ4ODgySTSZ555hnOnj37vBqK6oS4t7eXSCTynBL7jcziX8pOJuvb2r0IqBve1rGWh1mxWGRoaIje3l5aW1sbv19P2eLa1w78+DZO/69RbGEP+YyGjIZaMvnXnz7Fh59+BXb31WXNP/zdZygVa8Q32CRzYbj2hT90ewClrJFagN7tPs48UyOdew5HOP79mh3VXa9qJ5eqkShf0MbouQTFvEo8WuLoK9uQ7SKTFzJ07rBzYagAFDh4pBlJEjl9fBlQUVSdXYfDWKZF9LLO+MUU7X1egmE7S/NFLo8V2XVbmHsr4zhkE8MEQbQhYhBSRU4sOdjrupK1vBS3sctmUHeGrwhOIMe85kZICtjdVyYHZXQ7nhX9Za4k0rTC38qmAz9V7BaDRN5OxFvBJtcynZIIqDKpVIhC2aQZ0Io6sbKPbd0pTp4wAAFTXfHEtEByvFbmDu/wkDhf6+a3+1dlH1dpstVVcoBK7sqGpJTSuHymQM+RMKyyNfK3+yjPpdnzxgGaDwaoVCokEgnGx8epVCoEAgHC4TCBQOCmO9NrSea1qL+//u96hny1rjOZTG6RzS1s4QVE3YS9r6+P5uZaI+D1EhhroZ7AqDtUrD7O9V57LUzTbPy9teKKIAjcuXMbrX43S5kCO1tDXFhKYl2ZBhdP59jbEmZ8eBnDMBvEcmY5w96+Vs5fXsK7Yn2UK1bY3dXE7HAUpawylU0SCjpIpsrs3N7MhfEorU1eEskCNlnCklGYTESRZZGJS1EizR7i0TwDu1oZG12iuzdMKZpDXZnUNjW2jMNlYfZynJZuD9G5AoO7Wnn2kbP4wm4cLhsTQ3PsONjNd3cU8BgyuaUKWUPE4rWhlBSkR/ETeAAAem1JREFUEshBN5lKrRHIVQCtquDyOBCKCoImo+o6dkOnmq7idFixFBWaWz38t7/9AE53bfExDKMxk/zy5cvYbDbC4TCRSOSqTHO5XGZoaIgdO3YQDAbZLMzOzpJMJjlw4ACSJNHU1IRpmpRKJeLxOOfPn8cwDILBIJFIBK/Xe9N4fy3JvBb156duGF9fT+obmdnZWTKZzKZ9xs3ESyKjuRau/eImEgnOnj3L7t27ryKZcPO55Gsd1x600f/2LtyiiVTUKekyVcFEzWj8/Tuevep4x59e4PRIlJ2Hg7T32Bi/WMuCtba5GT6XY3g4T0XUSRSLdA3acDgFJsfrpXGT5aUiQ0Mx2nZ42HMkQqlQI207D4R54rvzjFxM0rPPid11RTeoCyYjF+Lsv6MJQYCeAR9PfHceT9jG4P4QgRYHp08sk0pVuP2uFrp3+pg4MUdENzBMmFLdhFeGhpcECxbxSuNJXJdp1ZxUVu0zAprGhBLAnZVwyRKz6StfCkm9QuI9jiv3RKiuInhmLdvotVQoKrXjqrqIHRWLIRDLevHYioQcFUzBQmdbzS80MbHij9khYax4stu9V85Lq17524XolSlA6ZVyOisl8Wt/P30iz9yMgn1H7bxMHWSnRGRvbcdd35UeOHCA22+/nVAoRDwe55lnnrmhzUWdZPp8vpvqfOpYrcERRZEPfehDvP71r1/Xe7ewhS3cGmw2GwcOHLiKHG7Un7lUKjE0NMTevXuvSzLrr7022VFv7KhXx66HpaUlDjbX4nP9zKJFBYskErY6yM7nKZZV2oK19aFOLLOF2qa+XjYPOhwo0TLZbIW+FR1mwFcjZsVyLbhOziQY2NbE3NklnHYL2WyZ7YMtGIZJZGVmeT5XIRhykZ9Pk17KsjCdpH93G2pVp2NbLWuqVk1aW+08++9naekNkU0U6NnVBsB0PIHZ7yITrSJ5nRgWEbWsECjJuAQZMV3GUzaQFyvoCNiCLirLOaoJBckAlylgUcDvcyAUqvRtC/H7//ThBsmsX+9AIMD27ds5duwYAwMDjZ6KZ555homJCZaXlzl79iw7d+7cVJI5PT1NOp1+jmPBWg1FqycUDQ8PE41GUVX1Oce8GclcC6sbVYvFIr/2a7/GO9/5zk37nJuJl0xG81rUA4JpmszMzBCLxbjtttuedwPF6oCw+wPbGfunKZoO+JkfL2JURDSrQWwozd+9/yTv+9vbWVzI87Mf/CaLiwVkGbb1Bejf78JukRA0WFqsZTZ7+gM8+8wSAHfc1UK5pCBZDfwBK2MjNdKp6waPfnualg4XXZ1elhevECSX18XpE1EO3tlMNlllfCxFLqtw4ukl7nltJ4vztWzf4lyB5g4noinjD9rIpquUVY1iUeVDu0X6LBIXCn4iZhUk0EyoVuy06CYJq4xDNKjm7XiB6aKF3W6dqg5LihcloxF21Ah22G2Blck8IalK1ZRI5CVU0U404STolhAMg+m8HdMwyasgEMYhFDBtdlxkcdtr7/e7VIoVJxWbhCnoOIQqe49mUTPbKcTKaB4dJWSiI2GzWSjbBEJ3BJHFWsLV1WJDLelkp2sk0tvpIDu3Ml1om4tUvQzf6SA9Wwu+FrdI/GKJuAmDrwhTWCrRfDiAKD834EuSRDgcJhwOY5omxWKRRCLR2JWGQiHC4TBut5uRkRF8Ph89PT0bfvY0TeMDH/gAR48e5Td+4zc2/P4tbGEL64cgCM9p+lsv0TRNk8XFRfL5PPfcc89NTbBXH/da3+XrZbLqU2mKxSI/9cZX8O+XPs/4cpKIx0W2XOGOjjaePTPH/v5W4rkllJXTvjQbwyIJzEYzdDb5WEjkuGt7JyefmmL3YCvzixliK/ZF80t5HHYLs/NpujoCeBxWrEWdUrFKd2+IxYUM6RUz9vGxZfwBB6Zh0uZ1cPH0DDsPdpFLz1LMVUCAyyPLtPeGkFUNl8vOogm6qiOIcOHZKToHIszusWJZMDEUEyNRwuewU8ko6E4R3TRrvtJVCbvXiaDqaLM5rIIVm8+OraJhVnUsooCZq7Bnbzsf+/MHb1plcjqddHV10dXVhaZpDSN+q9XK/Pw81WqVYDC4bn3u9TA1NUU+n2fv3r03Pad6Q1Fzc3NjPGk8HmdmZgZJkgiFQkQiESwWC2fPnt0QyVyNbDbLu9/9bj72sY/x1re+9VY/2guKlwzRvLZ0vloUKwgCt91226aIbVcTWN8ODy13RSgtlbEVDTSHhKqBbhGZejTGX/38s/zbxBRNLVYsVgeRiJeTK3rKO+5s5+SZJXYfihAJOTh1YhmAnl4vJ5+NoSoG/oANr0Vm5yEf02M5FK2CrpsszBVo6XQRzeTZc7sfU5M5dXwZXTc5+fQSOw+F2L4nyPhwinCLkye+P4eq6Bw62oLTaeH736uNjPJ4rNz7hi4e+84MraLGwT21DFw+I1PAYF9QZUp102oAgkC0YseoGLSv6EUjhkheF0iU3ARViIkWoJal9OkqOdmCoOksFJwoZZFup4kNKEsWHFqN6OVEO36xjEsyMQoCguQiW7ZTlkXa/FmqmgWbqFI0bfirCst5G31NGUrxEhWtyuzICnkM+ViczAAasdkKatHE02KhuFzb/fXdGcQF2DCx2KQG0XQ12RpE091mbxBNW6tI+VJtQzE/VsYVsrD7vqabPh+CIOB2u3G73fT09KCqKslkktnZWRKJBE6nk+bmZjRN21DQ0nWdD3/4w+zevZvf+I3f2Cqbb2ELLzBu1Z/ZMAxGRkYwTROPx7OuSSuiKKKq6rpJpq7rjIyM4HA42LdvX22N623n2ckFeiJ+ctESmZUm0MnFFLIkMBfL0Rb2spjIsas7wuhMHFnQ6HbYmRuvNZBOTMaxWgQSqQrdnUFm5lLs2dnG8IVF2oIeTn93nKZm74ptURR/wMHyUpbtg82MX4zS39/E2FOXsYRqGdaJkQX8YTdLcyk6+gMU0gohj5Vzj09hc1gJNHmJz2fYdWQbk8PziFaByUhNmy67HBg5hUpGw+5xUEmXkBWDgOCgqlQx0RBzKk6HA1E30eMFyoqBx2FFLGscPNrLRz/1oze99teiWCxeNaUpm80Sj8eZmprCYrEQiUQIh8M4HI6bH2wFpmkyOTlJuVxmz549G+Yi9YYin69WUatLty5dukQqlSIYDDY4z0aOnc/nede73sUv/uIvvmRJJryEiOa1qFQqlEolOjo66Orq2rSFuX4z6//s+qk+vvP+4zQdCGCYIosXiuRKBklNJ/6Pc5i+CnOOEp2dfqanchw91obDIXH8+CKKYhCNFZmcylAqq+y7rQm/z0YyVUFVFHr7/Jw5uUJM72mnUtGwOCxoVYWTzyxhGDAykqa53c3eoxFi8yXautw8/eQCAG0dbsJtDqLxApmqjqYbPH18gdvubGV6IkP3dj/f+PdJmpqd/FyPiWjCYkWg3RQxBAczppWmitnQYabzVprsJnUyKQoiM+Uw7Wot8xg2DIqGgEs0KWoii6qbcEknLAgkrCKwUkrWTViRTlYVAaw1n82cYCdAGZum4jAF4skgqYrOYGsWrawhucEq2oimnVglA7+yAPgQgPiKxVF4m5PkZI18+tpsDaJZrpSZPF0jl9vuCeI55MdumldLJsQrz4ivyUPmUi2T7O1yMHcig39vYMPPi8VioampiVgsRk9PD4FAgEQiwfT0NLIsNzKhNxJh67rORz7yEbq7u/nEJz6xRTK3sIUXCdcmMG6W0axWq5w9e5aWlhba29s5eXJ9Q1AkSaJSqTSSGDcimdVqlXPnztHW1nZVB/SbDw2wlM5TjleYm0uBAGGfk0S2xK7eZkanooT9LhYTOUqKRsDjwF61sBzNUqlqRIJ24qkK27r8TM5mcDpWOtNTBfb2NHHu+5fxB53Eojm2D7YwfnGZ9s4QmfQ8lbLK4GALY09fxmKRWJxJsn1P+8q0HzuZRAGLZMWqFzn3+Bjb93cyPjRHe18T6ViOxckYvQNNPKUk8FTtVIoKgmLglxxohoaSKuKVrZQ1nZJkYHXbkOPlmiuI24IRK4Ju4nXYoKhx96t28KHfedu6rv1qpFIpLl26xIEDBxpE0u/3N2yoyuUyiUSCCxcuoKpqQ0Pp8/lumHmemJhAURR27969KfHbbrfT3NzM4uIie/bsQZZl4vE4ly5dwuFwNNaVtSYc1lEsFnn3u9/Nhz70Id71rnc973N6IfGSJJrZbJbh4WFsNtu6dXCwPrNSURQpFosUi8Vauv2H2vAcbUUUwcip+DscNAVthNIKl+dytJRc6Eg4rRa6ujxIssBj35vD6bRw7yvaEEQ4cyqKrhsgwKPfmcFiEXnl67rIZxU8PiutrS6eOb6Iqhp4vBbCYQv7jzQxO5kj3Gxl9HyGyYkMA7v9ZEpVdu+PMDaawO2z8vj35nA6Ze59TRfjl9JUKzrPPLXIsXvaUTWd9k43/nyeHWaNBKqiA0kwwYSpaQsHQjVSOYeNDlUmLpiEbRoFDdKqi2pJA+/KtUEgJTqIKya2ghXREJCttaygV9PRJZAECEgaulFr+HHKqz06dQI+cEg66YpEwK6jle3MJqw4rDlME7xyiULJjsWm0GlJchofkW1Okpdru3dfq71BNO2OK5kEo3pFCxOfzpKbq32ursM+Wu4MkjiTIbNwRYpQzV05L9EiIsoCnUc2TjTrWXWv19sol9dn566nocgwDD760Y8SDAb5vd/7vS2SuYUt/CfiRkQzl8tx/vx5BgcHCYVCjezkeiCKIrlcjkqlcsNMWT6fZ2RkZM3mlFfu7uX/fOk4l1NZtneGGZ9L0N7kI5EtoWq1c55cSGKRRTTNoF1ycPlynN2DrYxcXMLhqC3nuUItcTA2ESXot+PSTfSCUntPR5BMqkS1UtvAT1yK4nbb8LlsKKkC5XyV3kNdjKZnyaaLtWl2l5LsOdzF1MnLdA+0EptOkFjK4nDZmByeZ//d21m4sMDSRJTsu1vQBQO/w05ZgBIgW22wXKBSUXA5LZiKhrasYiLi9jmRcwqC04asGghllTe84zA/9ouvW9d1X414PM7k5GTDXWAtOBwOOjs76ezsRNM0UqkUCwsLXLhwAY/HQyQSIRQKNapVdStFwzDYtWvXpsVvVVU5e/YsPT09NDXVKm31Z67eUDQyMoKu62s2FJVKJX7kR36EBx98kPe85z2bck4vJF5yRHNxcbHhsF+fIbse1DOVNxrZZJomkiTR0dHBpUuXUBSl5oH4igDf//gE3h1uZJcF09ApJor0dHswXVaa8kUyBYW4w2RiNM1dx9qx2ERGLiSJRUu4XDL3vqKTSkWnudlJe4eHRx+dQddN2jvcOHxWDhxuZuxCgkiThcvjJaYmSxy7s41CQeXQkRbi0QJzcwXyuVoAOHJHBMGUcXutBIN2nj25RLGgcuD2ZnxeK995dBYAp1Pmvf12CobCQkmgQ6jt3qcNK/2yzLygY6+WsJUkEAUiCsyKEqLhwKMIeGSZlAhBQ6MoiMzOSuxw1h4LHyZ5RDwYWEWBFBYiqMjAclmi3aXjQqGoS7gkHY/1SlAumxYC6PgdGg4DlKKLuZJOV7hIvmLFKwt4rEVkScfX6mgQTUO7kn3ILdUymIIokJmp/WzzSOQXVnw3vQLTp7JMA752mbDfQFoSMHSzYZ8EUIhVad3vw+ra2ONeJ5kej2dNTWa9oaijowNd10mn041dqSRJPPnkk0xNTWG32/nUpz615Zu5hS38J+N6RHN5eZnJyUkOHDjQqE6sl1Touo7X6yWfzzM8PAxAJBKhqanpKo1ofQ723r1716yA2Cwyd+7u5t++P4pFrq1j87EsggAT8wmagm5iqQJ37Ozk4qkFWrtrjTmxeBaApVgZj9tOIlVi+7YI8USBbr+LkVMLNLXUzuPyeBSHw8LsdJKevjCzU0kO7u3i5LdGG40+48OLBCJuYgsZtu1qQkKiGEtTzJYZOz1NS0+I5ekkg4d7yKUKzI/MYbHKTDkM7KaAllQwdfDZZAqZIpQM3E43phuqioqcVHDabcgCmKkShilg08GqGzzw4DEe+On1zS2/9v7Nzc1x6NChdfsky7JMU1NTo2P8Wg1lOBwmn8/XfEIHBzeVZNbtluoks456Q1G9qUhVVVKpFHNzc+TzefL5PDMzM3z961/nXe96F+9973s35ZxeaLykiObFixcpl8vcfvvtyLKMIAjr1izUA8j1iGbdx0wUxQY50DSNZDJJ/o5lZLeAaFFZPFXA1iXh6fIiyiKllIrTkHB5PXREfHSEPSTyFRLxMmpJ47Wv7UXTDE6eXCSfVzl2RxvJZJkjx9rI5arkcwrPnqg1Ce3Z60UUbNx+zIehGzz7zBK6buL12WhqdTLQGqZYVPC4LZx4uqb5bG614gtLyHYH4xerSBaRb39nhr7tfpojTjzJLDuKBkt5F5IbMHRSpkioLIIA1pRAQnTSuXINVQTSqpduta5TEohlTIoOGbngoFMUKMgGbq02sjKHBc9KyTyXN4l4IVMVySgSmiGjamD32UllSzhtGgVVwm3RcTpqX0q3VSen2nFJKqmSm+mohCTpOEWdhYyDnqYsejXcuE/JlYYfZ8BCcqWDPNLvIn6pRhwjfS7mztYCa/MOHzMnM7VP4TCYOKPhbZLo3elh4fFaN7vNK5O6XOSOn99202doNVaTzN7e3pu+/tqGouXlZY4fP87Q0BDt7e388z//8w/EznMLW/h/CWtp/1f/d70smsvluP322zc0zGG1HlOWZXp6eujp6aFarRKPxxkbG2skMwzDIJfLcfjw4Rv+jTfdtZN/+/4o47Nx3E4byWyJga4IY7NxWoMeWrwusnN5KmWViekENqtIPFmitzvE1EySwe3NnB9dxGGzYCtozCSSWG0SseUSbR1+FuczdPV4mZ1WMXSN/q4AI09O4PLYmZ9M0L+7jYmRRZwemXQcXHY7kycvU8yVGTjczdipGgkTJYFKqYrHaWFhOEWkI0juVc2Y0TI2rwdFUSkbGgHJTsVakziZJQV3VUC3WJFECWU+iyyJ2GUZWde444299N/RRDQavSqreDMsLCywvLzc8NW+FVyroSyXywwPD1OtVpFlmfHx8UaJ/fkkDNbKZN4I1zYUnT9/nk9/+tPMzc3xhS98gcHBQV7xilfc8vm8WHjJEM3x8XFkWebAgQONnUOdPK6XaK5V5riROFuW5cZNzPy0hWf+6DKOFgHZBovPZrF32fB2OPBYrBi6SSGuEQk6cPmsBBw23FYLakFjdiFHT5efQNCOouokEmVME/J5BVkS2Lffh8Mh8+yJJIYBu3aHmJ3NM7AnhMdtoVrVOXWqpuU8dmcbU1NZjt7VRj6vkEqVOXWqZgV08LCXcqVEJGInES+jKFU+YBhgFanYnFgTBlF3kVxVoq0+r1a0Y9UFkCvopsmSbieUE1myKrRaxdoIzooVj2bBuuKbuZQ12L6y4RZLOopTYC4voagSC4qEFRGHJODQNBxAKiYQkZ0YVViQLDitKlavQRUFGzoVyYLLVLE7DDy6RMFqBap4PBJ9boHLokTn7X4wIX6x1l0f6XMxt0IiPRFbg2ha3VceWYv9yqYi2OwnPZEiF9OJdiqI20WsOQFXxEJpWKPn7tBNn6E66s0A6yWZa+Ev//IvCYVCTE1NUSgUiMfjt3ScLWxhCy8MNE3j/PnzOJ1ODh06tKGM1Y3WFZvN1khmKIrC+fPnKZfLSJLE5cuXaWpqwu/3r7mu7eiKNMrmu9qDDI0vIQg1mb3NEBk9u4Cum7S1+FhcztK/LcjEZAqrpRYX5xcy9PeEmR1axOu2k84X2LW3ndHzC7jdNb1fJq3i8zsw8hXyZYVyUWHbriYmRyvk0kUQYHE6y8Ej3Zz51nl23t7LhWenWJiI4Q06Wbgc47ZXDXLmW+eQZYmmrhCzahG7HsF0WdGyZRxWC0aiQlURcPmdCFWdSt6koteafbRoAbvDirVq4BAFfvr/dz9HXr27kVWcnp5eV+POtX6Wm4G6G0AgEKCvrw/DMEilUiwtLXHx4kXcbnejxL6RjUmdZHZ3d6+LZF4LTdP45Cc/yf33389HP/pRlpaWNnyM/yy8ZIhmf3//c7ww60RzvUPqry2J1INBnaxeL5AYhoH/tTrinwq09PiZPJ4mstOJZujMPJNGCgl4uuzYfXb0sokkCPgcdqSgQKGq0d3sI52pIGiQWC6xazBEPqcQDjmYmU6iqjLnhpL4AzZuv72VTKaKpupMTWbo6vZy8UKK3XvCtLW7GToTJRYrY+gGNpuMzSZzx53tWG0Cj313HoBA0EpLq8wgAn0KlAUBR8bELkosaH5aZBUMk0tlg1ZNBAQm7OCwO/Dna8HNtDlQzCqzZStNqpUFvUqfrXZ9goKEgUZKF8ipdipZCc+K9ZdiAauqY9dNCrKI2zRwY6CbNf1muagS0IGyyHjVhy9iolRKhLzgMRUUXcJd0bmY87MjnKFaFXn2xCK6KTB4R5i5UoVwuwOxSabrniBqRkXXVpXks1c8yFJLhSu/X2XabhFtTI+XsDhEBndJCBIk7NPIl4uEw+EbmufWSabb7b4lkmmaJp/85CeZn5/nH/7hH5Ak6aqd8ha2sIX/fJTLZc6ePUtXV9eGRxLWDbJv1vSjqirDw8MEg0F6enowTZN0Ok00GmVsbAyPx0NTUxOhUOgqkvTmu3byh//yfWKpWnybWkpzuKOF88/OsnN7CxfGl5Gl2lpXKNTi3vhkjKDfSUvYg6WgMpuv0t0dYnkpSzyaq3WZjy3T3OpDVTR6mr2ce3KCnh3NxMkzfzmF02sltpileyCExRRITNUmzF08NU3n9mbmxqP07+ukY1sTp/79LD272pk8N4fb70Q51Ixoihi6gSkKqIkKst2OxWOhmCxgy2jYLBbcLhtmTsPmtmNmqnidFj7yu29lz5E+gEas7O/vp1wuE4/HG407dTsgr7fWVFDfxO/fv3/TZEn1+O9yudi2rVYFkySJSCRCJBLBNE3y+TzxeJzZ2VlEUWyQ4Rs1hG4Gyfypn/opjh49ykc/+lEEQaCtre2WP+eLjZcM0VxrYsN6rChWv3810VwdDG5EMlVV5fz58wTaA+x5dwfn/3keX6cdmyQTGy3RdchPVdNZuJBHcxaxhgVcTXZMQ0I0BDx2KxZJwG6TEK0CuWSFUMCB3VoTh1dVMAyRY3e2YbPKfGeVdrOnx4eqGnh9VrxeK9/+5jSCAEePtuJwWhgbSzE3l6G5xcVj351n+44ATU12FhezXLpY4sF2G9hEFjWBVlGkgIkzLTGPgcelEDGc1Kf7KIYLb1q/MtI8azCiynSJtYYbt14bzSkiUEJgNmOhXbfhRmDJqOKy1QJhIqfhXimLp8oGbjs1/aYOEdkkaKkN8BEA1RSw5UA0HFxSDLoDJZJViVanhlK2MBH34g2IdPvKTGacjVGTiaUyFrfE0ngBAQi32Wk67MZpk8muNApJdsjM1Er6sk0gdmmFdAom8cnaz2rZYHnJpPV1TRy55xDJZLKhdfH5fITD4auC/GaQzD/8wz9kbGyMf/7nf960HfYWtrCFzYOmaZw+fZrdu3c3upFvhNVNpuslmeVymXPnztHT09MwehcEgVAo1Gj6yOVyxGIxJicnsdvtNDU1EQ6Hec3t2/mzf32apWSeXT3NGOkqYrUWG4ulmlY9Gq/gclpZjuXo740wMRVnsDvMye+O09FRazKaGIvi8zuIx/IM7mrl4ugSrS0+5s7NMZMqYLFKTF+K0jvQzNRYlEiHH61qYDFgfnSOSlGla1cTs6MxqmUFi03GahUxqwqGZhCbTdLUGWQxlUPpaEetqBiKjidvIslWZETK82lckgPJZ8NqgBorIcsSkqrj81r5lU//KD2DaxMmh8NxlTfm6vgNYLVaN51k1odxXM8nWRAEvF5vYzR1XSaxuiE0EolclbF+viSzbo23d+9efv3Xf/0HsqFUWO9EnXXilg9Wn6KwGsPDw3R2dq4rGzQ6OkprayuBQOCWg0FivMAXP3gGW8BCKati88sYOqQWy8gemXJJY36ugOAxEX0mOExMi4jVY6Vc1cEioBoGhqhzeSpBOq0zuDuMZuiUKhrD5xNs2+anp9dLOl3hzOnajvHOu9rJZKr4fDaKRYXlpSKxWAlBgFe8sgulqrO4mAdM0qky2azGG7oDvMGuYSg69rKMKIhcrkKLbsPAZMkJ3SvBackq4ExZiNur9MsCeYtAMW+hajdpWTX1Z4EKuioT0uzEUOlaIZd5QyO80sSXN3RCK44LadMkItfen7HJhFZskvKijMfQSGsQWNnKpEwZu6FRFBW2B6rEihb8VshZRVJZg29cDuMP28klqjh9MuW8hmlAc6+L+FStbN6528fixRydOxx4/RLRE1V01aRtr5eFlZGV4W1Ooiuvt7klymWDV/3sNt75P/Y0Pqdpmg1vtVQq1SjRJJNJvF5vYye7EZimyZ/+6Z/y9NNP8/nPf35d3nu3iB+8KLOFLTw/3PK6omnaVQmIupH3XXfd9Rwz97XwzDPPcPjw4cZI5Jv5YwJkMhkuXLjArl271l3JKBaLxGIxEokEgiDwtZPLXJhN0+fxcvbsPH6fg1y+gmGYtDZ7WYrm2LuzlfMXltje14TdFJi/EEXTdKoVjd6+CFOX4+ze18HIuXla2/047BYSl5Zxu+3EFjPsOtTF6OlZmjt8ROezePwOOls8jB6faJTLHW4bslWikCnTv6+JS09OIVkk2vuamb24SKjNT+7uFuaUCjZZRlAEdKVmX2QtKOg5E0HVcYgiSqqCwyZjqeoE/Q4+/mc/SXPH+iVNUIuzo6OjaJqGw+EglUpht9sbWcVbHehiGAbnzp0jEAhsyOlmNVY3hGYyGVwuF8FgkIWFhas2HBs95kc+8hHa2tpeaNeSF3RdeclkNNfCRsaF1V+7OhjcaKezVjAIb3djb7Uz8nAUR7MVS1JiYSJP711BpsZy+Lvs9N8ZRFdN5mdzCKKAKJksj+coKiqBVjtzi0X8EYliwuSOOzvQMXjsu7OEI07uuasD2Sry/cfnUVWDvv4APb0+FuZzXLyQYteeMAtzeYIhO3dub8dml/juSnf5jgEfpZLCzl0RcukqdyQs6BkLF/USe70iGYtES6l2OxdlEV/Cwri9gN8lYU9ZAIFQxcqEvYwz58COiEUxSFp1ApLIAqBrLiJa7ZqFBQuqbGLRTDyiTNFm4KoaeESJrGAgmyYWi0RUMREBQTQp6eCUIF828NhqJLOig10C0SJhUwxU1c503kKbo4CiWXFVdIoCtPa5iF6uZStbt3u4fLLmgRlstTeIpstvQddNpi+UGLw7TMlfZftgAJt8JXPobbM3iGZku5vpM1kGX3Gl2Qhqu9LV3mqlUolz586haRrVahXDMNY9nxZqwe+v/uqvePzxx3nooYdeSJK5hS1s4RZgGAZjY2NUq1W8Xu+6tXX1Slu9MfVmJHNpaYm5uTkOHjx4Qw/Ea+Fyuejt7aW3t5dqtUrFtHP+mXnOTeVxOS1ksmU6Wl3MLxUJBlwsRXMsx/I47DJyWSeTKFIsVBt6THHFU/jyeBSX24rfa4dcmVKuQmdPmNhihpnxGHanheh8lr1HeoheXKCQrlWDLp6apmughdmxZfr3ddLUonLpyUl69rYxfX6R2HyCYJsPT7OTYbeAqNnQYiqSJOF226ks5lAqApJNximKUDHwe+1Uk2Va2rz89l+9H1/IfaNL8hzUK04Oh+Mqq6FisdiYL26aZmPmucvlWlf81nWdc+fOEQ6H6ezs3NA5rca1DaHZbJbz588jiiJzc3OUy+VGiX0951W3xguFQvzu7/7uD2Qms46XDNG81SkOddQnMzzfYPCaX9nO+X9bJtLl4tLTSfqPBZk7l0O0gd0mc+bRKOFtThw+K5MTGXr3+encFqSsqahGhUhYwrQI+P1WsqkS588k2dbrp73Hw+x8jvFLaXp6fXRv85JKVXj029MA3PuKTlRVR+r2MjeXw+WyMPxkguZmJ9sHPMSiRZaXqmTSCV4f9uNRIWET6Mn5mMko6IKGS4aEFXyZ2m214SSeUGivNwYJOtWKgyA1YiYgEtdMSqqMsyoDJjmbhteUEE2BpbJCl0WmKsFMSsVmSrhkG4lUlQ6pdt3iqLRKtb83Jxg4JYGirKIKGkEXaBawqyrWlSm+bhlyZRvzFRGnTycoKOiKlRZ/mejKPbBYr2wQNPVKMiMdv6LJzKcUskmFk0/G6Dnoo+0uP6WZCqpyJUNrdcmIskD/ndffNdcnPjQ1NbFt27ZGiWZ+fp5cLofX622U2NfqaDRNk7/7u7/jG9/4Bl/5ylee94jULWxhC5sLVVUZGhoiEAgwODjImTNn1q39rxNNSZJuOk5ycnKSfD7PoUOHnteoQ5vNxt237+ELLRcYn4wRCTkollSUlerT+OUYbrcNRdXY1Rri/MlZdu1pI7qUJbqcRRQFLo/H6OgMMD+X5tiRHk5+a4TWjiCCAJeGF2jtCrI0m6JnMIxSMkhNRsknC8SKVXbe1sOFk9OUC1UCTR6UfAm3txbvlyYSdA60sjQVJxh2ctGuI0aLWKsidpcdHajMZpEtNhx+C9aqAWUNWRIxcwp9PX5++29+GodzY3FS13XOnz+P3+9/Tll7tR2QoigkEgkuX75MqVRqeFBer/lK1/WrDPo3C7quMz4+zo4dO2hubqZarZJMJhvnVS+xr/ZcXg3DMPi1X/s17HY7f/AHf/ADb433kimdG4bxnGHzk5OTOBwOWltbb/xHTZPZ2VmWl5fp6OggHA5flxRMTk6Sy+XYu3fvdYPBX9x/nPHvJXC22TA0k3SqQuchP6PHE3Qe9pOOV0hlyvTu93NpOIUzbEWw6szM5Bk4GGboZIwdB/zML2UJNMsgCpw5k8HukNl7IILVJvH9x+bRNIOdu0O0dro5dzZGNFqirc2Nz2/D7bai6QamUeXcUAbDgO4eLz3tHn7ogoZVM8kj4VBELusqYd2G0KwhJATsSFRlk3QBJFkgaDfJWU3MpIyESNlToVmVmdSquDU7ss3EqdYe5KxLo1kVUUWTWUXBgYxbs1LBwC3WTN2Lpo5vZWZ4wlRpWbmOy4a2QjpNFMHEjkDcVAiGTAJU0Q0RlwSzJZE2m0DOIROyF1CRycsOvnfZSiWn422WyUU1RBGcnpqMQbICCOiKidUpoqomumoi2wRMQK0ayBaBfXdEyFwskYtWCW134Q7Z+NX/uOe6z83IyAhOp3PNcnl9V5pIJEgmk1gslsZuud4F+bnPfY4vfOELfPWrX11XKW4T8IO7rd3CFm4Nt7yuZLNZTp8+TV9fX6N0OTQ0RF9fH273jTNq9figaRqtra2NMYHXQtd1RkdHsVqt7NixY9MyT994dITP/OX38HpsFIpKrWze5GYpVqCvy0N2poDHZWdhLoPFIuFwWsllywzubuPiyCI7drZiNQ1mzy0giFDMVxnY18HYuXlaun0sz2Tp29lCNZZl/nKUXUe2MXpiEqfbjs1pxTRNureFOPudUURRoHdvB5eH5gi1+Wlp93Pu+xfIvHMnos2JUdWQBLBmFCyGhGmCmFMwyxpetx2hpNHXF+Ljf/W+DZNwXdcZGhqiqamJjo6Odb/PMIxGKTudTuNyuRoldovFgqZpnD17lra2tk1trNE0jTNnztDV1bVmufza83I6nY3zslqtGIbBxz/+ccrlMp/97GdfLJL5gq4rL2miWTdOvdHDVddjGobR0Lkkk0msVitNTU1EIhGsVuuGgsHU8RR/8uon6T4aYPyZFNvuDnLxyQTNez2kYxUKVZX2QS/DJ+LsuCPI/HwGq0ck2OqhommYIuRKCjOTWXp2+Hj2mWUCEQutXVYWlyosL1ZrPpitLpLZCufPxREEuPe+TkwDLowmiMfL7Nvv4+KFPLt2R3B7LMSiJbqmK7zJ7mHZIeDPSGTsIGckTGBWV7FaDTplKykEbMXaAzpnK9NWtSNS+++SXaOKjrtU21UmxArdK01BMVNB8smISREJEfxgr2mv0bwmzkLtFlftBi5VQMdElEwsCGQlHb9Ry5YWXeApmVRNE6sgYJgGKblKf8AgXTEJyxJVA1RNQPSUsJsCfzltY+BACIdFwqzqaBWN2MWa7rNlwM7yWE0I33PQz+SZDADd+3xMnav93LrDzfx4Hqtd4sCRCAunc7z6Z/v44d8cXPO5qZdh+vr6rvssrEZ9fFk8Hudzn/sci4uLzM3N8dhjjzU6IV8EbBHNLbzccMvrSiwWQxRFPB5P43fr0f7X1xVd1xtNO+l0Grfb3WjakSQJRVEYGhqipaXleZVdr4WiKJw8dYZP/+UQxZLK4PZmLo5H2T3QQqmkoidKxJayGLpJuMlJIlZix2CESxfjtLT6SKWKbGv1UUgUWJ5LsftwNyOnZgg1eUgn8xg6HLpjG0OPnqd7ewuTIwuIkkj7tghz41H2HN3GwoV5UksZdh7p48KJy9icVroGWsjHs2SiWaRDHcy6JKwWCzaHBSVRARUsVhkhUUTUwWaREMsqe/d38LHPvnfDJLzeSNPR0XHThNONYJpmw2auroOtVCp0dXXdsiZzLdyMZK51XvXSfyKR4DOf+QylUgmbzcZDDz30vDLjG8TLQ6O51gO4Vif6alzbWV7vBuvv72+QzrNnzyIIAtVqlba2tnU1evQeC7L9vjDRSwX6XxFEF6HnvgBVRUfURNoiXi6dT9F/d4CzJ2K09DuIx1TKaoF8XsEVsLA4l2fHgRCnTyxz76s6qRo6T3xvjkDQzuHbwlTUKs+eWMQ04bZDTXgDdp54Yh6lamC3Sxw45EMQZIIhB+WyyvR0Bi2r8bpAhIwFXBkBxTRQCxIyAlG7Tjhvx6wanKsW6aO2W485NDwFBymvTrgoskwVCjKC78qtDxlWoi6dUsHArdtIZKq0UiuVpPMKrdRIaCav4BRq5SbFIuBSQUIgbzUJKODVJSoY2AURc+W22QSBnGjiNURE3UY8JlCxV/DLYBMhowv4Sy5yUplmm4nFKXPmqVqT1N67IsgVhXDAit125fkQrVfWHYfnSvnL12RjfjyPUtHJVBQKdo1dPxRZ87nZKMmEq8eXjY2N8dd//dfs3buXu+66i2984xubWnrZwha28PwRCoWes4bcTPtft8SDmnwrGAwSDAavmh4zNTWFLMuUy+VGeXSzUNeM79jezxteo/Olr56hUq0lYQQTKvNZkoliI3MZDHpJxErMTKex2USymSL97R4unZqlf3ctUzcxuogn4CAZy7N9bysWUWTu/AyCCZMjC+w42M2lMzNUKyo9O9uYOjNJ92AbqaUM42en6d3TQSFdoJjMYbXJFHNlsn4bVq8dTdEw5/OISHg8DoSihuiwI+sm5CvsPtjK6963l2effbZhE7QenaKiKBsyN78RBEHA4/Hg8Xjo7Ozk9OnThEKhhj9m3TrpRjPPb4aNksz6ebndbtxuNz09PfT393Pq1Cm8Xi/33HMPTz755A982RxeQhlN0zRRFOWq3y0vL1MsFtckA/UsJnDDG1EoFDh37hzBYJBisYiu643xYDfyvRo/nuR3XvsYPQf9jJ9JMXBHiJHjcXbdHWHoiRj9t/sZO5uiud9JbKGCr8VGMl4h2GZnbirHziNhFEOnqurMz+dYWiyy50AEJBNFMxi/lGLv/gixeAG7S2B4OEsgaGVgwE+pVOHcUK2L+uChZspljWDQTtt5ne0ZGzNGFbsoYI9IBJISaauOXJQQEZmmTFi3I4RNVM3AkpUAAUM0iYtlwmqtvGtgYogahgxlE8qaQZtZy3DqkokVkA0BAxMkA5sgkjE1NDRsTgu5gopFAqtVplRVcVoE7FYJySrgNwQsqokggGTCsq7RIsnoAugaSIJAyQduvURRE2i1iCxUDaKmTqE/zKUzKQCae2xEp2sWRu19HtBMWpsdKHmVxZFadjPcayM2Vfu564CPqaEMAAPHQsxeyPJ3U/cjyVeej1slmavx9a9/nT/6oz/i4YcfJhAIrEsXvInYymhu4eWGTa2UjY+P4/f7iUSu3oTeyIT9WiSTSS5evEgoFCKXyyFJUmOc4fPRadebVPfs2YPH4yGWyPO+j/wjhmFyZE8HZx+/zO69VzrJlxYyCAI0t/hYXspy4FAXy2NLoOkklmulqKZ2H7GFLO19PhYns+zZ38H00DT5dIldR7cx+swkbp8DURaJtAWwSSYjT44jCAL9B7sZPz1N985WrLLA2InLWOwWQvdsZzJgRS8pyAUDu8MOgoCYKCIYAm5ZgrLGK163i5/62A8DNPST8Xj8pvrJSqXC2bNn2b59O6HQxjrTb4Q6ee3t7W3cf13XSSaTxOPxhi4/EokQDAbXnVGsl+E7OjpoaWnZ8HnVrfHOnz/PP/3TPyHL8rqnIm4SXh6l87WIZl3DsGPHjqtet5FgMD4+zp49exp6nPrDHo1GqVarhMNhmpqa8Hg8zznW/3zbk5z7dpSO/V6mz2VoGXSzPFXA02IjEy9j81tQFRPTCqqiE+i0Y/dZwGry/UfnOXhHM2dPRxFFkb2HI6jonDkdZXBXiFyuSrmsYXPISJKAx28lFi+Qy1ZIJlWamu3s2hVkaanC2MUUXW4nP5oLk7LouCsWim4QcwIJsYxVFmnSbKS9BpZ07cFckMoIJrSbDjSrSRoNowp+SUbWBTKCguoWcOdlhJVnTHAZOFbK7aWATjmnItolJIeEJSEgIFBxqXiKtSyi6q693sBEkEHSBDIohLCioZOTFVoCVkRVI6ivaEAtAu4qpGVwV02KNoVuO5R0k6op8PUKKBUdp0ekXDQwDQi22Ekt18hksMVOOlph+84AAa+N6VMZ1KqJbAMd0JTaI+hrtjFwNMSvfu6uq56d0dFR7Hb7LZPMb37zm3zyk5/kkUce2dQAuAFsEc0tvNzwgmv/N7KuzM3NEY1G2bdvX8Nhom4uHovFME1zzVnnN0M0GmV6epr9+/df1aT6+3/4TbKxPGZRZWx0CbfbhqrqVKsa/TuambgUZXB3G/lsGTIlcqkC5aLS0GO2dvtZmskgySI927xcPjHLwKFuxk7PYLHKhFp9LM8kOfyKAU5/awhDM9h5tI8Lz1zGYrOw8/Yexo5fQlN1evd2cunZSarvPFBLQhQMjLKOy25BXcojmiIem4xFM3jj2w/x7o/80JqfVdd1UqkU8XicbDaLx+NpTNtRFIVz584xODi4Lp/T9aJarXL27Fn6+voIh8NrvuZa6zur1drQ5V/PRWAzSGbdGu8LX/jChqYNbSJeHqXztbCWCftGgsHy8jKHDh26ym7GarU2xL/1DuOZmRkKhQLBYLAxHkwQBN758V2c+3YUvVTLnAq6gK4aYKpoVWj22zEsJu6IjdmFHMvLRcSUQGypyG3HWjj59DJdfV7CbQ4mJ7PIFpEdO4KcORXl0JEWXF4DVTUYPhdn194g6XSZvr4gbR0mDrvA9767CEDvNhevTgUwBTCrAroE5ZyOAwmLw4ZYEBizlWlK13bSi5YKXnWlK9yvQkbAunKrs069NtIsJyMXYFmo0GrWGltKkkHZZ6JWTPS0iR0LUlFEKxqIgIyApEiYmAgIqLqOAxERgbyk4dNkvFhQBQOLKSGYMkpcAkTGHRoONEzNxC1acekmgiDirtqZFjTarCqaLOPKV1GAtn43E2dqWd22Xk+DaNZ/vjSaZtexMEWXya7bg0iYjD5Zy4T62yXSCxUG7vQ2doWbQTK/853v8Pu///s8/PDD/1kkcwtb2MLzxK2uK6ZpcunSJRRF4eDBg1cNZFhtLq4oylWzzuvJDLfbveaxTdNkZmaGVCrV8Oxcjbe9bh+/9gv/F0kSCYZcpJJFdu9rZ+TcAopSkwXoioaUK7M4l2L3oS5GTs+SjOWQJIGlmQwD+9pRMkUqyTIAY6dnaN0WZGkyhSiJ7Lq9h5OPnGH3HdsZeXqcS6en6dvXhSiajJ+YoH17CxOnp7n07CR9P3yAs5qGFKsCIl6vAyNTxeVyIJZUZMXgne+/ize/d+0mzPo9WD1tp66DvXz5ckM7eb2xk7eCeoZ0x44dBIPB675uLeu7RCLByMgIuq43Suz1xNRmkMy/+qu/4vvf/z5f+tKX/rNI5guOlwzRvJ5Gsx4Q1mvCvjoYHDp06IbTWVbPOr92nqnP56Ops4kjD7Rx4iuL7LwjzOjTCboOOhBFG217bZx8cone3X6e+M48AweCzE5kCUTsNLe7Ofd0jHtf18nMfJaTzyxz4PZmTh5fwhoTeeWru5ibzzM2ViNGd9zTQjpTQNcFzp6Jc/i2FibG0xw91gYCqJdKRFIS02aFFtNJwqrhUmVSHg1bTiYhVHFUbRTsoLt0PMmaaXvKrmDLSBguA1kRScsqUkGkbNEICzVS6nRayNo0Kmkda16iZFXwKzZEAVSfiZwBGZGkUKHZdGBRRZJClbBpw16WqYo6NlNCXrkdIgIpUyWCFZ9pQcdEQkCyWhCzFkqoJMMC3pJJ2tQICjL5kklMteJoEdjdauHZtI4sXfnCKdUri8Jq+yJDh1ymyvGnlth3V4T2o160tE4wYiezmKB1r8kzzzyD2+1u+Ofdihk7wOOPP85v//Zv8/DDDz9vvdD1kMlk+MAHPsDw8DCCIPA3f/M33HHHHS/I39rCFl4O2Kx1pT4X3efz3bSZ1Gq10t7eTnt7O5qmkUgkmJqaolgsEgqFaGpqamgBTdNkbGwMXdc5cODAmqXSwV2tDOxqZWx0idb2AKlkkcX5WoZydjrJbbd1cf67Y/TvqukxL19cxu11kFjO0bU9SCZRgUqV+YsLqIrO4G09XDw5TTmvYHNaEEWVQrLmWzz6zATbD/Uwfnoau0OmlClQzJaYHJplz90D6JrGs7E0osuF1efCKogIqTIWRGyKjlUWePAXX8O9bzm8oXtUvx6JRIK9e/dSKpVu2RfzWtRJ5sDAAIFAYEPvdTqdjQ2EqqpXJaa8Xi+5XI7u7u5bJpkvhjXeS2FdecmUzqFW1l59PsVikfHxcfbv37+hYFAnFLeqmTNNk0wmQywWY2o4xj9/IE6o1wJeiC7VusqTsTJtO9xMXsiw+1iEoeMx9hyJcP7ZGIO3hRDdAk9+b4HBvSGiS0WSiTJH7m6laug883QtU7n/UBM2FzzxxDIAwaCdffubyGWrjIzE6esPsDCb595MEK/LgoBIQVUxyyZWh4i9aCVnUZE0CUGElKRgV2RMv4la0rGrMqZgovhMkpkKTYIDAQHDZlKx6Wg5AxsyFTS8WBBNAVM0MQ0TCxKG06RUUpAsIg6PjKlBqahiiAZWQ0LXTQzJwCVZ0BQdSTDxWi0gmAQrtSxySlAImlbKso5DW5k0JOvYNKhYFXokC2ldx4eFoqlSsSs8ZtXo7PXhcVkpLFdJzldQKjo2R21ue7WsI8kCVqdMMVcriwVb7CSXa7v121/Zit9t4zc+dzeGYTA0NISmaRiGgSzLjZ30enfMTz31FL/yK7/C17/+9Re04efBBx/knnvu4QMf+ACKolAqldYqHW2VzrfwcsMLov2v++bCjXX+lUqFc+fO0dXVdUuEoo56uTgWi5HL5fD5fBQKBUKh0E3Xq6efGOeTn/gaNrsFiyxSKFTZuacN2TApRXPMTMQQRIHmdj/Lc2l6BiNMX4zTuS0MhRJzl5bZfXQbI89M4vTYsdotFDIl9t+xjZP/PgRA955WZoaXkK0SOw61M/zdMWSrzPbDvVx4epzdd25nOpoh29+CUdFwWC1UY0VkScRlirgsIh/+zTdz6BU7N3xt0uk0Y2Nj7N+//6q4vFrXWS6Xr9J1rmd9L5fLDA0NbXoZXlEUTp06hc1mo1qtPseiaD34x3/8R774xS++4NZ4L4V15SVNNCuVCiMjI+zbtw9YXzDo7Ox8XjYI10LTND7zS9/h0X9I0rnHxvRwha6dbqYu5Am3OckVK1QrOu3bvVQ1naZuJ499exaHS6Z7u49zZ+OEInZ2Hgrzne/MoGkGh29vIZevUtUVJiby9PX7aW5xkctWGT6fAODI0VZ03aBpyULLZZm8zUCvmhgICG4BpWiAH3TdQCxBSddxYkHxGSgFA0QTyS2g5k0kQ8QQTeSQgFoyMFZ8zy0+ETELhh2qkoagC1SqGqIF3Gptd1UQFAJG7eeMUCVk2mt32QVSUcC0gKjWMpm6z8Sard0j3WGgl3VMSafNYsNekajIBnZNJF7XcVpMFE3HZdFxShI2XSRhqCR2W3hmpHYd9t4eIZuq0trixinLDH2v1pHetz/A+FBtF96x3cPceK3M7g/bSCcrvO9j+/mJX97L6OgoNpuNvr6+hqVFPB4nHo+jqmqjFHK9KUAnTpzgF3/xF/nqV79KV1fXpj1X1yKXy7F//34mJydvFkC3iOYWXm7YVKJZtyqqk7sbfd+y2Syjo6Ps3LlzU4lKpVLh9OnT2Gw2FEXB4/HQ1NREKBRaswpnGCY//1N/x8Jcmt37OrgwvMCB3W2MPDmOrpts29nC5IVl+ne1MjG6hCgJDO7rYPbsNB19ES6enK7pMVt8LM8m2XGgC7VYZvLsDLuO9TN6fALZKtE10IoswcTpKZp6gyxejAEmB169m9mRORa6msBlxymJ6KkqDquMmasS9Nr4pf/xdgYO9W74WtQN1q/Vpl6La3Wd9aad612zUqnE0NDQhkaBrgfXlsuvtSgCGskMp9O55vP1+c9/nr//+7/n4YcfvmFT8vPFS2VdeckSTdM0UVWV48ePEwqFaG5uvu4u5oUKBnWPNL+nid960ylyySptO9zMjuXp2mtn8nyZnj1uSmUNd5ONxWiR+ek8B481c+ZEbc7N7fe1MruYZXwszaEjLUxOZvD6raQLJZqaHRQLJoZuoqgGqWSZXbvDBEN2zp2NU4hVeYfSQc6u4yrLlJwGoiFQ1gwUUQdDoGRqGKaJ3SehmQZUBXRZx9BAU0GRNbw+G5V0rVSkWXQcdguqZmDqJrpgIpdXCLwLLIXaz0VUgtRIpegRkPKgYyBbRERVII+Cv96l7jWx5kR0wUQ0a6X2kkPDWZZrjUISGLpOFY12mw2LJiDqteaiDBoeJFSfTqQEcVOHJgvfjtW+sLsPRxg5FQdg35EmcukqzREXDlnm7GM10rnvriaGnqxd7z13RDj3dIy/efrNlM3Fq0jmtahrdOPxOPl8Hp/P1+g2lCSJ06dP83M/93N85Stfobd34wF0Izh79iwf/OAH2bVrF0NDQxw+fJjPfOYzawWhLaK5hZcbnte6Uq1WrxxoRQ84NDTUkE1dTztZb87Zt2/fpuoFC4UCw8PDDb3gao1iMpnE4XA0vDpXa/a+860RPvM/v4k/4KQ14GT81Aw7D3Ry4ewc7T0hFqaTALT3BrDbbIiVCuNnZxEEga6BFmYuLtHe10QxW8Jll/EFXYw8PY5kkegebGPm4iLb97ZRKVSZHJpBEAR23rGdSrnE5ZMzGEEXHNuB3RSgqCMJIOQqBDw2fv2PfoyuHRtP8ESjUWZmZjhw4MCGRveubtpJJpPYbLbGNbPZbBSLRc6dO9fo3t8s1Elme3v7dRNa12Zh61OA6t31X/7yl/mLv/gLHnnkkU09t7XwUllXXlJEsz5CcrU42zRN0uk0sViMbDaL3++nqampMbrphQoGxWKR8+fPN+wVvvkPl/nMR07Q2utmeaGAIAh07vJQMVUqZpmL54oEIjZESSAerbDntjCiXeD0ySg7dgaZmcuSTlY4fEcLxUqRCxdzVCoGu3aHsFgk7HaJsYspdu4O8/STCwgCvN3dja0gQBnybh2pIpLTVQwZREMgJyhYkcArUClpCE5QNR2n34psF7A5wTB1LHYJq92K02WjmNMolzQEEaoFnWJeoZRXsdlkdNUEESpZFYss4fRaUAs6laqOKIDLbsGQwWIKGJoJAugVE9MwiLgd6EUTySXgLMjogglmzWczQ5UgNjTZQNIEFHSsNoNw1UbWquJXrFRsBmbFxOHQsWoi/0YKt9dCtaqjVA1sDglRECiXahOD/CEHLe0uXBYLxZTKwkTNyqNvf4BKSePX/77/hiTzWqwOXI8++iif//znicVifO5zn+Ouu+666fufL06ePMmxY8d48sknOXr0KP/lv/wXvF4v//2///drX7pFNLfwcsOmEM3V60rd0iYWi1EqlRrayfrghenpadLpNHv37t3UBo1UKsWlS5euckJZjXp2LBaLkUgkkGW5MXhEli388s/9M0a2hM9jY+TULIGwm0KujKrotG/zszCZ4cCRbs5/dxRd1dlxsItLZ2aJtAfIpQp4/C7aOn0MffdCbdrPnk4un5vFF3bTvaOJs4+OIFtldty2jctnp2nvbyY6E6OpJ8xUyA9VHS2vYreIWKoGQZ+d3/6r99HUfv0Gm+thcXGRxcVF9u/f/7yv8eqMoqZpVKtVdu3a9RwLq+eD+rjKtra2dVdNdV1vTAH63Oc+x+nTp1laWuLb3/72phrFXw8vlXXlJUc06/6Ya3UAGobR0E6m0+nG/zt48OCmCmmv9TKDWgD41Tc8ysjTcfa9oomyprEQKxBfLlIqaOy+PcTQs3GCEQs2r4guCxiGQCGvEo+WCQRt7L49zLe/NQOAP2Dj8JFWRi8kmJ/LI4pw5Fg7mXSFQMCOKy1iuWhQrGhIbhE9DyVRw+aRqRZ0dLuB1SkhOUW6d/sIt8H+uz284W1HriojmKZJPp+/amJSPa1fv2amaRJdLPDUdxY4+cQSscUiqcUK2XiFSkXDIojYbDIUAQ00q4FNkTBkE6sugQF5FLxY0TAQRAFTN3E6JXymFVM1sa6MuMytvE7xGJA30dFoE+2IukBe1HAYImLQ5IJaJHTIx5mnapnKfUeaOHeilsEc3B/i4lBt997d7yWZrDC4K4iaNZgezfL6B1t428/1rJtkXovR0VF+9md/lvvuu4+TJ0/y4IMP8uCDD97aw7ROLC8vc+zYMaanpwH4/ve/zyc/+Ukefvjha1+6RTS38HLD866U1cnlWjr/1aQzn89jmiYul4s9e/bcsJl0o1haWmJ+fp59+/ate70ql8vEYjHi8XhthPK5LF/47NPYnVZkWaKQKzO4v52LQwv4gk46u4IMf2+Unbf3cuHZKXwhN7qmU8iWOXjvDiaenSCfLDb8MW1OK507WiilcsRnk3TtbGf89BRun5PefR0sTkVJzKRwDbZRCPsxCyoulw0zV6Wl2c1Pfuw+FK2M2+1uaBTX4z05NzdHPB5n//79m3qN8/k858+fp6WlhVwuR6VSabjJPB8z9lshmdfiG9/4Bp/61Ke4++67efzxx/mjP/ojjh07dkvHWi9eKuvKS4poKoqCqqo3bfoxDIPR0VE0TcPhcJBKpZ4zGuxWsby8zOzsLPv27XuOXmR2LMsff/RZLlxKEGiyMz6SZs9tEc6fjCFZRLbt9iM6RBaX8+iGzvxsEZdHoqvXScWA0ZE0ff1eXC4bdpeF48cXEEWBvfsihMNOJiczTE9luONQO84noSCouF1WqkUdzWYg2kUUzaB5wMXuY2Huf/8A3dt9XLhwAVmW1zVnt1QqNQIXcEO/t4X5JR7+8jDpRSfnT8aJLZWo5jT0ioHDbUEp6rhcFpSkgU0UkSURVMgLCj7TBlYQFBPdNLD7Ldg1ERkBa15Ex0TDxIJIVq7i0AQkIGLaiQkVipKOeYeMRbCwOJ6npc3N2Lkaudx3tIlzz9RI58G7mjn1ZK2Z6tCdzaTiBX7p93dzz2v23lJQGRsb48EHH+Sf/umf2Lt374bf/3xwzz338Nd//dcMDAzwiU98gmKxyB/8wR9c+7ItormFlxued0az7qV5I51/3b/R6XQ2ytnXVtBuBaZpMjU1RS6XY+/evbe8PlWrVZaXo/z3D3+RdKzEtl1NTI7GsNolrDYrXZ1+BFVl5JlJHG4bNoeVTDzPjoNdqFWNpQvzdA22MnZyCrvLRqjNTzlfwWGXEEWBmZF5BEFg3307Sc4nmbtYa1oduGM7CzYHqiFgwUTPlOnuCvLf/vansDlsjWRGPaO4VjJjNVZfi800JK9L6Pbv399Yz65nxn49Xeda2AyS+Z3vfIff+Z3f4ZFHHtnULOt68FJYV14yRFNVVd70pjfxmte8hgceeID29vY1iYKiKJw/f55IJEJnZ2fDIqKetUskEg2NS63csD4Hp9VeZvv27bvu+/7+0+f48/92mlCLg2pFI5dROHhXMxNjaSLbXFQUjZGhBG6PlZ5+H+lMmVy1gtsDiZhKNqty4PYmkskqzc0ulpbyOJ1WLowmEQWBO+9oQzhpYEdC1ATKko7pBEM22XVPmAf/6376d9XKFLquMzw8jNfrpaenZ8PEqu73FovFUBSlUT7yeDwsLy+zsLDwnLKGomg89A8XOf30MhfPJknOlbHYJdSsgWADs2pilSUCdhtmwaQkqHgMK4qsY9UkDMNEcps4DBmLRcaSFcii4MYCFhND1QiZVjQZviEsoQomTS1WPF4bkYCbXEwhvlhCqeiIEniDdlLxWrd5e68Du0Pmi0++65ZI5uXLl/nxH/9x/uEf/oEDBw5s+P3PF2fPnm10Bm7bto2//du/XcuOY4tobuHlhlteV8bHx/mFX/gF7r//ft785jdf10OxLpXq6+trEIF6BS0ajZLJZPB6vY2GnfUSJMMwuHDhApIkMTAwsCnTwx5/5Dyf+fhXkGQRh1umXNDYPhDg4pNTyBaJYIuP2FyKbXs6mByeZ8eBTkRN48IztXnlobYAixNRtu3pAF1l4vQ0VoeFvgM9JBdTqGWFcrFC5842ZFlmPlUh73bisVkwSho7djTxsT//yeuukaVSqdFwudq83uFwMDEx0ShrbybJzGQyXLx48Tld66tRl0fFYjFSqRR2u71BiK+nD90Mkvn444/zsY99jIcffvh5uRbcKl4K68pLhmgCzM/P8+Uvf5l//dd/pVqt8uY3v5n777+/QaLqIurVweA5J7CicYlGo43dVZ10Xu9hMgyDsbExTNNkcHDwhl8AXTf48Bv+neETcXbsD9Zmnh8MIrkFjj++iNUmMbg3yNmTMfbcFsa06pw5GUNVweu1sv9wmJHRBPFYlWDIistlRRRF2lo9eN0WlAkV66KAYjUpKhqOkMzd93fy0795ELv9CuHTNK0haO/o6Hg+l71xvHr5qC5LGBwcvGlQLeSrfPXz4zz69SmmL+QwNRM1baCgI+sioghBnx2xDBVFx6nLjfK5hoEpmgRMG5JFQKwIZIUqNlPE67ZwuZTnslTg8LFmTh2vldAH97pQygLhoAunbOHUShNQc4ed6HyF3/jUnbzrA7s2/PlnZmb4kR/5Ef7P//k/3Hbbbbd2EV8cbBHNLbzc8LzWlZGRER566CG+/vWv4/P5uP/++3nLW95COBxGEITGBLndu3dftzmjTlKi0ei6K2iapnHu3DlCoRBdXV2bNqLWNE1+8d1/xvzlJAP726kkcsxeWCTc7iU+l6W5J0B0Jg0m3P7qQZ79+hlki0ykM8jiRBRvyE17X4SpM1MANHeHmTo/R/v2FhxuK5lklvhUiv5DvcxcXKS6vQuPy4ZY0th/sINf/uP3rPuzrE5mZLNZ7HY7O3fuvK7Lx62gbo104MCBG3atX4u6rnN1da/u1wmbQzKfeuopfvVXf5Wvfe1rL6g13ibg5UM0GwcxTWKxGF/+8pf58pe/TDab5cCBA1y4cIEvfvGLDcH2elAXVsfj8TXn0da9N/1+/7qzgkuzBd77iq9RLWsceHUz33hkCkGAg0ebOX08iijC3a/v5BvfnEQ3TNo73LS1u8jkFS5eSCEIcOdd7YBBPF6gkFMI+mxkFjS6ql4ME2whiTf8ZB8/+Sv7nkP06vNau7u7aW5u3tC1vRmmp6fJZDK0t7eTSCTIZDI3td5YjcuX0nz+b0c49cQy+aSCmtOpVDRkTUSQwG6VcIoWjLKJRRPJouAxrUh+ATNjYBVFnLqMbjUpGSozoTLFkkKloiNJApFmJ8uLRQB6+hzIsoRdFnHaLMyMlfnWhR/F5Vl/9yLUNjjvete7+LM/+7MX1Mi2p6cHj8eDJEnIsszJkydv5TBbRHMLLzds2royMTHBQw89xFe/+lVsNhudnZ0oisJnP/vZdZOUegUtGo1e1SW+uoJWqVQYGhqip6dnU2O0aZpMTk4yfHKar/3NOWy6itNpYXJkkbZtEZZnEhi6Se+eFtRqlcWRZSKdAZYnE/ibauQu1OwhvZhCskgsT8YQRYFDr9nD2LOXySVqTZX7X7mbSrFC0mqnYgiYhSp33jfAz//+Ozd8znWpm8ViwefzkUgkyOfzBAKBxiS+W81uplKphtf2RkjmtahWqyQSCWKxGNVqlUAgQDqdprOz85YJYt0a72tf+xqdnZ23fG43wiatKfByJJrX4jOf+Qz/+3//b7Zv304sFuMNb3gD999/Pzt37tzQrmi1sBogGAwSi8Xo7u7e8I7l6f+Y5/d+/UmmLme57a4WnnlyCUGAI3e3kilXOXMqyrZ+F6XyykWRBSRJoKXVRbWiMXk5SzZbpbvLCxokFkrss4fQRJ29P+TmQ7+9n5aWludoXOoGtPVu+M2CaZqN8V+ryxp1rVJdf2O32xs7+ZvZUei6wVe/eIl/+79jzI2n0QoimmIgVUREB0iGgNtmRciBaYCCjgi47DKekoWMpOA55KBg15i8kGb7ziCnjtf0mL3b/UyNZwBwukRESeBNb23j53/t8HNsQW6EpaUl3vGOd/CZz3yGe++995av33rQ09PDyZMnrztnd53YIppbeLlh09cVXdf5uZ/7OY4fP47X68U0Td7ylrfcULa15omtUUHzer1Eo1F27dq1qXZ7hmFw8eJFRFFkYGCAP/6Vz/P4v54i0h4gHcuhqTq7j27jwslpBvZ3kI9mmLu0jDfsQlV1ytkKg0e6iI7HSC6mcXoddA62YRoGl89MYbHL9OzuwuG2szixDHYLlWAIqhqvesMeHvy1N9/SOdeHqKy2iDMMo9GNnU6nG7PON9JjkUwmmZiY4MCBA5vaDFw3Y5dlGU3TnmN7tx68WNZ4m7SmwMudaJqmyWc/+1ne97734XQ6SafTfO1rX+Ohhx5idnaW1772tbz1rW/dsLA4lUoxPDyM1VorXdcznRtx6P+7Pz3HH/zmcQAO39XCzHQO02bi8sD4WA6lajKwO4QvbGN8LEU0WuLQoWZGRhP4vDZ27w5TyCjIgoA0LdDc7+Q3//Je/GHpqk7Dusal/qXdbAPa+hi0unTgRkF2dblBEISr9DdroVAocP78efbu3cv8TIXP/eUwwyfjZJeqaIqBUABF0nGIMm6HBTEjUEJFNkXcLgta0eCEHMPjtTCwM4xVEpm9nKO93c2507UNw5G7Wjl1fJl/e+x+rI4yiUTiqlm61zu3aDTK29/+dj71qU/xqle96vlfyJtgi2huYQu3hE1fV8rlMn/zN3/Dz/zMzyAIAouLizz00EP867/+K5VKpSHb6u3t3VAyY35+nsuXL2Oz2a6SbT1fIqTremMEZr3yllzK8Auv+xSVYpVdR7cx+swkdpeNHbvbGPruCIFmH6qiUUgXad0WwRdyMPr4GO6gE5vLSnIuw+DRPsqFEsV8ifhUij13DzL8xEVsbhuOgW0IArzlXUd4+89uPD7qus7Q0BDhcPiGwy7WSmbcTDsZj8eZmprasP/mes757NmztLa20tbW1pgSGI/HSaVSOByOm04AOnfuHB/84Ad56KGH2L59+6ad21rYIpovAnK5HA8//DAPPfQQ4+PjvPrVr+aBBx7g0KFDNySd13qZXdsUUydPa/mcXYtPffw4f/u/z7F9XwBHQOap7y9gmtDa7qZ/wM/TzyxSKmmIosCrXtVFqayhqjouh7XWvW2X0ZZ03vUzO3ngJwefc/xqtUo8HmdxcZF8Pt+YoXs9k+GNwjRNRkdHsVqt9Pf3b+iY9XOLxWKoqko4HG5cN0EQyOVyjclO1xrEplMl/vEvhnnq0QVi0wX0Khh5kwoabtGCx2mFHJRllQWjyM67wxx/qtYFuWdfmFyhTNBnpZoXSEYrvO6Ht/HJP3ll4/jXTgCqz8v1eDyNmbpve9vb+L3f+z1e97rXPe/ruB709vYSCAQQBIEPfehDfPCDH7yVw2wRzS283PCirStrybbe+MY38sADD7B9+/Ybxsf5+XmWl5fZt28fVqu1UUGLxWIIgtBIZmy0xFsfHNLe3k5bW9tV/+/rf/t9/vZ3v4ooiWzb0041W6SQzKNUVAqZEp07WonNJ9m2q5X0UppitkQ2nsdik9lxrIcLT4yjKwYIsPvugVoXuttBsqhTEWXe/dP38Mb3bNxHWFVVhoaGaGtre8453ww3S2bEYrGGyftmepxeSzKvxbUTgARBaKx59QTV6Ogo73//+/nCF77A4OBz1/PNxiatKbBFNNeHUqnEI488wpe+9CVGRka47777eOCBBzhy5GpfycXFRRYWFq7rZaaqakOrUS6XGw9SnaCshb/4w9P8f//jaTTNZMdOH9mUSsc2HyeeXWRbn59gyIHdJvHY9+YAuPfODibHMgwOBBnoCfKR37kdf/D6ZvP1EV27d+9udNfX574+H38wwzAYHh7G4/HcUtf6amia1rhuxWIRl8tFLpfj4MGDNx2xVa1q/MvfXuDRr06yPFVAyRmoRQPDNHEi4/ZYYK/I9GSWakXD5hKJRisAHLujjWJB5R//+S20tK29MVBVtWFxMTw8zCOPPMLExASf+MQneOtb33rLn3mjWFxcpK2tjVgsxmtf+1r+5E/+5FbK9VtEcwsvN/ynrSuJRIKvfOUrfPnLXyYWi/H617+eBx544CrZVl12VCqV2L1795rl1Wq12iCdhmHc0FZuNepSqf7+/jWzVoZh8Ns//hcsTccJBh0sTcQoZkv07ulgdmwJTJN9d/Uz/P0LVIsKgWYf/mYvDpedkScu4go66R5sR5AFojMJZIeMOxwgo0i8/5dfx11vPLDha7aZPQTXJjPsdjulUonDhw9veiZzaGiIlpaWdRPj+rnF43G+973vMTo6yokTJ3jooYcaY7NfaGzSmgJbRHPjqFQqfOtb3+KLX/wiZ86c4e677+aHf/iH+d73vsd9993HPffcsy6tha7rJBIJotEoxWKxYf9zLbGrVqv8z9//Nn/357OoqsGxe9tQDZMLIwlyuSq3H23jmacX8fmsHNrbzIXzSV5xbxdv/5FB7n39jedn101+9+/ff9UX61qT4Y36vem6flVH5GYilUoxOjqKz+ejUChsyLvMNE0e+qeLfP1fJojOFCksKxgY5FSVgltlYKcHTEindHwBO+eHYvzeJ1/B+z+wf13nFo1Gef/734/T6WR+fp4Pf/jD/MzP/MxmfOwN4ROf+ARut5tf/uVf3uhbt4jmFl5ueEmsK2vJtt74xjfyL//yL3zgAx9Yd8/A6gratZWg1cjn8wwPD99UKhWbT/HffuRPWZxYpm9/F5PnZjFN2Hmkj2qhyMSpKToH2shni+QTebYf6qFULFPMlcjHCnQMtHH5zDQtvU14Ij5KViuv/tHdtA+ErpqYtJ7PVq1WOXv2LH19fZtRzr0K8/PzzM7O4nK5KJVKBIPBq0Y73irqJLO5ufmWG3+Ghob4pV/6JSKRCNPT03z605/mta997S2f063geawpsEU0nx8UReEb3/gGv/zLv4zFYuHo0aO89a1v5d57791Q2l3XdVKpFLFYjFwu1+iYs1qtDA8PMzAwwPKizmf/92m++IWLALjdFg7d1lLTIorgtVjRVJPbbm/hfT+/H6//xrqd2dlZEonEDX09YW1h9Y26xOvWSC0tLZtuuXCt1cS1M2nrGpdIJHLT62+aJl/5lzH+7Z8usTxVxHRoxCpllpYq7NwVQtMMXv+GbXzst9ZX2snlcrzjHe/gF37hF3jXu97VKIWsRyLxfFEsFjEMA4/HQ7FY5LWvfS2/9Vu/xetf//qNHmqLaG7h5YaX3LqSy+X4/Oc/z8c//nG6u7u56667uP/++zl8+PCGSM/1KmiKojAxMcG+ffvW1Tdw4pvn+P/e+5eYpsnOo33MXlwkEHBgd9mYOj+LWtUINPvo3dfJ6W8NYRrg8jlp629BUzV8YS+xhQz+nibe/4m3sn1vVyPREo/H19UlXs++DgwMrOXT+LywsLDA8vIyBw4cQJIkDMNorMfZbPaWjNhhc0jmtdZ4mqahquqmjsReC5u4psAW0Xz++OM//mMMw+Bnf/Znefzxx/nSl77EE088weHDh7n//vt55StfuSGxdp3Yzc3NkUwmCYfDtLe3EwwGEUWR7zw6zZc+f5FEoszjj83RFHZy+/5W+gcCvPsndrJtx42/hHULi2KxyJ49ezYUuOrC6vrIybr1Rr0Tu6736erq2nRrpJt1Aa7WuNTtpuolpBvplmo60gt895EoiaTI7Gwe3TTZf6iZX/yvtyOKN/+OFAoF3vnOd/LTP/3TvOc973len/NWMDk52SjTa5rGj/3Yj/Gxj33sVg61RTS38HLDS3Jd+chHPsLrXvc6XvWqV/HII4/w0EMPMTw8zH333cf999/P0aNHN0x6EokEMzMz5PP5hn/jeqVRX/j0v/Mv//PrBJq8dG2PcOY/hgHo2NGKKIlgGMyMzhNo9dG1swMBSMeyuAMeJKuMvz3Ej/7am2nrfq5HdX3Ni0ajDWK32ry+WCxy7ty5TW9UhZuPq7zVZMZmkMy6Nd6f//mfv+DjJK/FJq4psEU0nz/qIy1XQ9d1nnjiCb70pS/x3e9+l7179/LAAw/wmte8Zl07kVgsxtTUFPv27aNSqRCNRtfMJtav70bsMi5erGVEb9YBvp5jrbbekCSJcrlMf3//LRvQXg91HenBgwfXrZ2pN+zEYjF0XW/s5l0u11X6p7GxMQRBWNeIzbVQKpV417vexU/8xE/wvve9b8Pvf4lhi2hu4eWGH5h1ZS3Z1gMPPMCdd965ril109PTpNNpdu3aRS6XIxqNXpVNrDd+XA//8N//le9+7nHSy1kGj/UzOTSD0+PA5bUj2UXysQKyRUbXDZILaXYc6UeyyHTv7+bHf/1+vMEb6+nrn7s+YSeZTGKz2SgUCuzfv3/TSebs7GxjWt96Ey6FQuE5yYxr3Uc2g2S+mNZ4LwK2iOYLDV3XOX78OA899BD/8R//wY4dO3jrW9/KD/3QD63ZyFLvLrx2PGM9m1g38nW5XDQ3NxMKhdYVZOrNOS6Xi23btm3a5ASolTXOnDlDIBCgUCisy5povdgMq4lrS0h1/c3y8jKiKN4yyaxUKvzIj/wIb3/72/ngBz+4qdf0Wui6zm233UZ7eztf//rXX6g/s0U0t/Byww/kuqIoCo8++ihf+tKXOH78OMeOHeOBBx5YU7ZlmiaXLl1C0zR27tx5Fam6Npvo8/lobm6+rh7/7z7+Bb7yx98AYMdtvUiSyOhTlwBo394KgonVZiXYHmT+cpR733kH7/qvb8Rq23gHdzqdZnR0lFAoRDabXdckvvVienqabDb7vGair5XMCIVCTExMPC/p2ItljfcirSmwRTRfXBiGwenTp/niF7/IN7/5TXp6erj//vt5wxvegNvt5vjx47hcLvbs2XPDsohpmhQKhUY20W6309zcfF0z8fq4spt5jt0K6nN8d+7c2dhxru7m0zRtzWziehCNRpmdnd1Uq4m6HnZ8fBxFURqBayOGuVD7jO95z3t4/etfz8///M+/oCQT4NOf/jQnT54kl8ttEc0tbGHz8AO/rqiqymOPPdaQbR06dIgHHniAV77ylRiGwYkTJ2hvb6evr++Gcco0TdLpdGNUsMfjobm5+Tmx8bEvPM1X//RbRKdj5JMF2ne00NzdRClfRikp+FsDGIbB3e84xmt/fOP2RUBjdOfq0Y+rpVGiKK5LGrUWJicnKRQKG5aO3QiqqhKLxZiYmEAQBFpaWm7JteXFtMZ7kdYU2CKa/3moG6R/8Ytf5JFHHqFardYmMvzxHxMMBjd0rEKhQCwWI5FIIMsyzc3NjV1fXTfZ0dGx6SXteufi3r17r9v0cm02cb2dhktLSywsLHDgwIF1ZWzXi/ruHmD79u0N/U0qlcLpdDYMc29EbBVF4b3vfS/33HMPH/3oR19wkjk/P8+DDz7Ixz72MT796U9vEc0tbGHz8P/UurJatvUf//EfqKrKW97yFn7zN39zQ9Wla0vY9QpafbrOwtQif/Nb/8zYY5O0bGtmengOtaJy6If2E+kK8/ZfegPNa+gx14NYLMb09PQNq1jXZhPrpPNGdnerJ9Tt3r17U+N2vVze1NREa2srqVSKeDzeyBKvJ5mRSqV429vexm//9m/zpje9adPObS28iGsKbBHN/3xomsbb3vY2+vr68Pv9PPzwwwQCAX74h3+YN7/5zUQiG/uylkqlqyb/VKvVF0Q3mclkuHjxInv37r2pl2Ud19omXa/TcHFxkaWlJfbv3/+CkEzTNBkYGLgq0NSzxHXDXFmWG/qb1TtmTdN4//vfz+HDh/n1X//1F5xkArzjHe/gN37jN8jn83zqU5/aIppb2MLm4f/JdSWRSPCmN72J+++/n8T/v717D4ryvv4H/n4E8YYgF1lErEiIYlQwCjomBjUXEuWyi2JGnXwlSsy0mgQVq/ZHJi2ZZkzSxtbKaGtMbYymVZeLyOLdUdFRTEywQ8AEVBxAuQmLgLvs7fP7A5+nXBbdXZ5ll93zmmGmGP3sR+k+5+znck5Dg3BsSyaTITo62qxqGHz/9c6LGY8ePUJYWBhGjvRA1S/30Vz3ECO9hmPc5LFwHWz5M5svuWfOLpZGoxEWM9RqtdH61Hwveq1Wa3Z76afhy/mNHj0agYGBXf5b54T9SYsZSqUSS5YswebNm/ul/nI/xhSAEk378MMPP2DGjBkA/veGkMvlyM3NxbBhwxAfH4/4+HhIJBKT3yBtbW24ceMGfHx80NLSAsaY0D2ir+cm+e5Hnbc1zMWfDaqrq4NSqRRuGqpUHW0ee7sFaKknJZnGqFQqYZvGYDBAq9XCzc0Nu3fvRmhoKD766KN+STLz8vKQn5+PXbt24fz585RoEiIuh4wrOp0OJSUlQnFvY8e24uPjsXDhQrMu2Tx48AA3b96Er68vmpubMXjwYNHOTVZVVaG2trZPCww6nU5YzGhtbRXO49fV1ZnUBtlcT0oyu+Mv0HZO2JubmzF69Ghs3LhRKI1nbf0cUwBKNO0bYwwVFRVCn1wXFxfExcVBJpMhICCg1zdMc3MzSkpKumxpdz83acpWgzH85Zzw8PA+99jl8Z/6bt26hebmZvj4+AjbNGKsaJqbZHan0Whw7tw5pKeno7a2FklJSVi9ejUmTZrU57k9ze9+9zt88803cHV1hVqtxsOHD7F48WIcOHDAGi9HiSZxNk4XV/hjW3K5HPn5+ZBIJJBKpYiNjX1ijcra2lqhPSOfVHbeQRs0aJCwmGFubKioqIBSqcS0adNEW2AwGAzCWU/+PL6fn59QKlCM8W/cuGFSkmmMSqXCwYMHsWPHDri4uODtt99GcnKy6KUBu+vnmAJQojlwMMZQXV0tJJ0ajQZxcXGQSqUYP368kDzxb6zw8PBeVy61Wi3q6+tRW1sLjUbTo494b2pqalBZWSl6H1igozBtU1MTpk2bJjy8Ghoa+nzTsK9JJtDxQFm/fj08PT2Rnp6Os2fPYuzYsYiIiDB7rL6gFU1CROf0caW0tBRyuRx5eXkYNWqUkHR2PrZlymqjWq0WWmGauoPG13XmW2yKdTmHH7ukpARubm545plnumxhu7u7C6UCLVnM6GuSCXQtjRcfHw+FQoEFCxZg3LhxFo1nCVrR7MmpHwidMcZQW1uLrKwsZGVloaWlBTExMXB1dYVGo8H69etNTsr4PuK1tbVPvKwjxrZGb+7cuYOWlhajtwA7f2LmOE54eJmyZc8YQ1lZGQwGQ5+SzM2bN8PFxQU7duwQ9UFoLko0CREdxZXHjB3biouLQ1lZGWbNmoUlS5aYvNpoyg4avwig1+tFPzdpMBhQUlKCYcOG9Sjn1/3M6dChQ4XFDFMWUPgk09fX1+KkkC+Nl5iYiDVr1vTLMSxjKNHsyeLBTpw4gZSUFOj1erzzzjvYunWrmPOyufr6eqSmpgorbW+88Qbi4+PNfvPyl3Vqa2uF8y0SiQRKpRJNTU0ICwsT/dykOZ9mzblpyCeZer3e4nM5BoMBH374IdRqNXbt2mXTJLOfUKJJnA3FFSP4Z/OqVatQU1MDf39/k45tGdPbDtrdu3fh5uaGZ599VvQks7i4GO7u7ggODn7q7+fPTfJF2Pmk09hihhhJJl8ab+HChVi3bp3Nksx+5PiJpl6vx8SJE3H69GkEBgYiMjIS//73v/Hcc8+JOTebqqmpwaZNm7B3716oVCrk5uYiMzMTVVVVeO2115CQkGB2zTD+fMutW7egUqkgkUjg7+/fay9ac/GlJtrb2/Hcc8+Z/WbjH17GbhoC6HOSyRhDeno66uvrsXfvXlETbJ5arUZUVBTa29uh0+mQmJiI9PR00V/HDA7/xCOkG4orvbh06RIUCgU++eQT3Lt3r8uxrdjYWEilUgQFBZn1fNXpdEK9ScYYAgICIJFIutwQ7wv+/KmnpyeCgoLM/vP89j9/CZRfzBg+fLgoSaZGo0FSUhLmzZuHDRs2WCXJdLa4YheJ5pUrV/CHP/wBJ0+eBABs27YNQMeBWEfHF2LNzMxEeXk5Xn31VchkMjz//PNPTRb5FUGdTodJkyZBqVR2uSHOF/K1JOnsPLYYWyZ8H1/+piHHcRg6dKhZrcW6z2/btm2oqKjA119/bZUkk3+dtrY2uLu7Q6vVYu7cudixY0e/97XthBJN4mworpih+7Gthw8fIiYmBjKZDCEhIU99lvO3tL29vREYGNjluc3voJlb5Lz72D4+PqI0JtFoNMJiRnt7O/R6Pfz8/Ez6exqj1WqRnJyMiIgIbNmyxWormc4WV8Q9yGeh6urqLp8+AgMDUVhYaMMZ9R8PDw+sWLECK1asQGtrK44fP46MjAyUlpZi/vz5kMlkiIyM7JFI8QfEXVxchETQx8cHPj4+YIwJSWdZWVmP/utPw/cXByDauRwXFxdIJBL4+fmhrKwMbW1tcHNzQ2FhoVAs18fHx6SkkzGG7du3o6ysDAcPHrRakgl09KjnqwJotVpotVpn2EYhZMBz1rjCd71Zu3Yt1q5di/r6euTk5GDr1q2or6/HwoULIZVKjT7bdTqd0AOcv0AjkUggkUiEHbTq6mqUlpb2WmO5N50Lplt6Oac7Nzc3jB07FmPGjEFRURGGDBkClUqFq1evCncZTE2KdTodfv3rX2PatGlWTTIB54srdpFoGltVdeR/9N64u7tj6dKlWLp0KVQqFU6dOoV9+/bhgw8+wEsvvQSZTIY5c+ZAr9fj+++/h7+/v9Ge6BzHwcvLC15eXkL/9bq6Oty+fRvDhw+Hn59fr2WJ+ATW1dVV9HM5/EF2nU6H6dOng+O4LklxeXn5U28aMsaQkZGBH374AYcPHxb90pMxer0eM2fORHl5OdatW4fZs2db/TUJIX1DcaXD6NGjsWbNGqxZswZNTU3Izc3Fxx9/jMrKSkRHRwvHtvhqKMHBwfD39+8xDt9ScvTo0V36r//8889P3UHT6/UoKirqU3/x3hgMBqFOJv/Bgm9jzCfFo0aNgp+fX6/94fV6Pd5//31MmDCh3+ovO1NcsYtEMzAwEJWVlcL3VVVVCAgIsOGMbG/YsGGQSqWQSqVob2/H2bNncejQIeHMyOuvv47f//73T31DcBwHT09PeHp6IiQkRGiFyR/y5lthDh48WCg1MWTIkKf23DVXb10fuifF/E3DO3fuYMiQIUKtTjc3NzDGsGfPHqF9m9jlm3rj4uKCoqIiKJVKJCQkoLi4GFOnTu2X1yaEWIbiSk9eXl5ISkpCUlKScGzrT3/6E0pLS6FWq5GammrS9u2gQYNM3kHT6XQoKioSVh7FxCeZ3t7eXVavXVxcuiTF/Px++eWXHvMzGAzYsGEDRo8ejT/+8Y/99mHEmeKKXZzR1Ol0mDhxonAjOzIyEt9++y2mTJli8hirV69GXl4e/Pz8UFxcbMk07F5bWxtkMhmmTJkCtVqNS5cuISIiAlKpFPPnzze7AG/3m3w6nQ5eXl5WW8k0t7VY5/l99dVXMBgMqK6uxokTJyzudtRX6enpGDFiBDZt2mST1wed0STOxyZxxRliCgBUVlYKne1u3ryJkpISLFiwAFKpFLNmzTLraFLnHbQHDx5g6NChaGtrQ1BQkNVWMr29vU0+79l5fvX19fjLX/6CQYMGwd/fH//4xz9sVrXE0eOKXSSaAJCfn4/169dDr9dj9erVSEtLM+vPX7x4Ee7u7li5cqXDPhS0Wi0KCgrw8ssvA+h4kPKre+fPn0dYWBhkMhleeeUVs1pY8jf1GGPQ6/Vm18J8ErH612ZkZODw4cMYOXIktFotFAqFWW3ZLFVfX4/Bgwdj1KhRUKlUiI6OxpYtWxAbG2v11+4FJZrE2dgkrjhDTAE6GojcuXNHaG6hVqtx8uRJyOVy/Pjjj5g7dy5kMhleeOEFs44qaTQaXL9+HSNGjIBKpcKQIUPMqoX5JPzNdS8vL4svFRkMBmzcuBElJSXQ6/UICAiAXC7vlxVNZ4srdpNoiqGiogKxsbEO/VDojV6vx9WrVyGXy3HmzBmEhoZCJpMhOjr6iS0s+U+FXl5eGD9+PICutTD58hESicTs/ut8eSSNRtOnJPPQoUP4+uuvoVAoMGLECDQ2NsLLy6tfHgj//e9/kZSUBL1eD4PBgDfffBMfffSR1V/3CSjRJM7GZnHFmWMKAOHYllwuR2FhIebMmQOZTIaXXnrpicmiRqNBUVERJkyYIHQv6rxD5erqKixmmNtNzpKVzO6MlcZrbGyEt7e3ReOZy9niCiWaDshgMOD69es4cuQITp48ieDgYEilUrzxxhvw8PAQfh9fauJJNcc6l4/QarXw9fWFRCJ5av91sZLMrKws7NmzBwqFQqi/6eQo0STOhhJNO6DVanH+/HlkZmaioKAAERERkMlkPY5ttbe3o6ioCCEhIfDx8TE6lkqlQm1trdB/na+F+bQdNDFWMvnSeHfv3sW//vUvq1YtGUAo0TQVPRR64j/9HTlyBMePH0dAQACkUinmzZuHffv2YdWqVSaXmtBqtUIrTL4Au0Qi6dF/va+F3nnHjh3D3/72NygUCowaNcqiMeyBwWAQ8+wPJZrE2VCiaWd6O7b1zDPPQKFQYPXq1SavDhorwG5sB41PMkeNGiXsvpmLL41XXFyMgwcP9kvVEmsZSHGFEs3HKisrsXLlStTU1GDQoEF49913kZKSYoVZ2g5/q/zgwYP48ssvMX36dCQkJCA2Nha+vr5mjaXT6YRWmI8ePRJqlo0cORK3b9/uc5J54sQJfP7551AoFL1+Ku4ra/3MlUol9Ho9XFxcuiTIhYWFUKvViIyMxPDhwy0dnhJN4mwGbKLpDHGFP7b1z3/+E9nZ2Zg3bx4SExOfemzLGI1Gg7q6uh7914cNGyZKkpmRkYHCwkIcOnTIalVLKK4YGZwSzQ7379/H/fv3MWPGDLS0tGDmzJnIyclxqHZlvOXLlyMuLg4RERGQy+U4duyYUE4pLi4OEonEov7r/E3DwYMHIzQ01OJzlGfPnsXHH3+M/Px84XyPNVjjZ15TU4MFCxYgIiICbm5uWLduHWbMmIGcnBwcOHAA8+fPh7e3N1asWGHpS1CiSZzNgE00nSWu6HQ6REVF4YsvvoCrqyuOHDmCU6dOYcKECYiPj8fChQu7HNsyRef+63y3u4kTJ/bYQTMFXxrv3LlzyMzMNPtcqDkorhgZ3FESzeXLl+P8+fNoaGiARCJBeno6kpOTLR5PKpXivffew2uvvSbiLO2DSqXqsi3BGMOdO3eQmZmJnJwcuLq6Ii4uDjKZDGPGjDHpTc1vl6vVavj7+6Ourg7Nzc3w9PSERCLptVBudxcvXkRaWhoUCoXRosHW1NefucFgQEpKCsaOHYsNGzbg73//OwoLC/H++++jpKQEixYtwr1791BWVoZly5ZBq9Va8qmaEk3ibGwSV8SOKYBzxRX+2JZcLkd+fj7GjBkDqVSKmJgYeHl5mTQmv13u4eGBYcOGoa6urssOmoeHx1PjE2MM+/btg0KhQHZ2dr+XxqO44kCJppgqKioQFRWF4uJisz+FDXSMMVRVVSEzMxPZ2dnQ6XSIi4uDVCrFr371q17f1HyS2Xm7nDGGpqYm1NXVoampCR4eHkKhXGNJ5+XLl7F582bk5eWJXnPtacT6mX/xxRdYtGgRJk+ejPj4eFRXV+Pdd9/FqlWr4Obmhjt37uDy5ctobm7GlClTMH/+fHNfghJN4mworgxw/LEtuVyOvLw8eHt7QyqVPvHYFp9kenp6IigoSPj1zjtoLS0t8Pb2FlphGotP+/fv77Jz158orjwenBLNrlpbWzFv3jykpaVh8eLFtp6OTTHGUFNTg6ysLGRnZ6O1tRUxMTGQSqVdOgcZSzKNjdXc3Cxsr/OtJn19feHi4oJr165h/fr1OHbsWK834K1FjJ85Ywwcx2Hbtm3QarVobGyESqXCvHnzsHPnTpw4cQKenp746aefsHTpUiQnJyM1NdWSl6JEkzgbiisOhDGGsrKyJx7bMhgMQnLWOcnszmAwoLGxUdhB695q8j//+Q/2798vlMbrTxRXOg1Oieb/aLVaxMbG4vXXX8fGjRttPR27U19fj+zsbGRlZeHBgwdYtGgRKisrMXv2bLz11lsmn5vp3GoyOzsbp06dwr1795CTk4Pw8HAr/y26EvtnrlQqMXfuXEgkEpw9exYAsHTpUixZsgTLli1DaWkpTp8+jQ8++ADA/x4kZqBEkzgbiisOqvuxLRcXF8TExODChQvYsmULIiMjTR6rc6vJ3bt3o7y8HHV1dbhw4YLZl137iuJKt8Ep0ezAGENSUhK8vb3x17/+1aIx1Go1oqKi0N7eDp1Oh8TERKSnp4s7UTvR2NiI5ORkFBcXY+TIkYiOjkZCQgKmTJliVsmFGzduICUlBXPmzMGVK1fwm9/8BqtWrbLizP9HjJ959/E4jsOePXvQ0NCAxYsXIzQ0FJ9++ilCQkKQmJjY5ffzNwjNRIkmcTZOG1ecKaYwxlBRUSGs/g0fPhyxsbGQSqUYP368WYnT0aNHsXPnTsyYMQMFBQXYtWsXXnzxRWtNvQuKK0YwxsT8GrAKCgoYADZt2jQWHh7OwsPDmUKhMGsMg8HAWlpaGGOMaTQaNmvWLHblyhVrTNfmbt26xdasWcN0Oh1TKpXswIEDLCEhgYWHh7PU1FRWUFDAWlpaWFtbW69f3333HZs6dSorLS0VxtVqtf32dxDjZ25MWVkZS0lJYampqWz79u1s6tSpLD8/X4QZM8bEfb/SF30NhK8Bq6/PGGeKKYwxdvz4cfbZZ58xg8HA7t27xzIyMtjLL7/MZs2axdLT01lRURFrbW19YlzJzMxks2fPZg0NDYyxjn9DnU7Xb38Hiis9v2hF00oePXqEuXPnYvfu3Zg9e7atp9NvWltbkZ+fD7lcjps3b2LBggWQyWSIjIzsstJ58+ZNvP322/j2228xdepUG87YOm7duoWrV6/i7NmzeOGFF/DOO++INTStaBJnQ3EFzhtTgI5jWzk5OcjMzERDQwMWLVoEqVSK0NDQLiud/VUaz1YGalyhRFNker0eM2fORHl5OdatW4fPPvvM1lOyGZVKhZMnT0Iul6OoqAhRUVGQyWTw8/PDypUrsX//fkyfPt3W0+w3jJl9bsYYSjSJs3HquEIxpavGxkbk5uYiMzMT1dXVwrGtxsZGfPjhhzYpjWdLAyGuUKJpJUqlEgkJCdi5c6dDrtiZq729HWfOnMGRI0dw9OhRnDp1yqyD3uZavXo18vLy4Ofn52jt4yjRJM6G4goophjT3NyMvLw8HDp0CFevXkVRURECAgKs9noUVywcnBJN60lPT8eIESOwadMmW0/Fruh0Oqv3mL148SLc3d2xcuVKeiAQMrBRXHmMYkrvKK70iVXjimgd2UnHORKlUgmgY9v4zJkzCA0NNXscvV6P559/HrGxsSLP0D5Y+2EAAFFRUfD29rb66xBCiLWIFVMAiitioLhiGev/ZJzI/fv3kZSUBL1eD4PBgDfffNOiN/WOHTswefJkPHz40AqzJIQQMhCIFVMAiivEdijRFFFYWBh+/PHHPo1RVVUFhUKBtLQ0bN++XaSZEUIIGWjEiCkAxRViW7R1bmfWr1+Pzz//3Kyi54QQQkhvKK4QW6L/19kR/jbbzJkzbT0VQgghDoDiCrE1SjTtyOXLl5Gbm4ugoCAsW7YM586dw1tvvWXRWEFBQZg2bRqmT5+OiIgIkWdq/5YvX445c+bg559/RmBgIL766itbT4kQQvodxRXxUFyxDJU3soBIBVKf6Pz58/jzn/+MvLw8i/58UFAQvv/+e/j6+oo8M2JjVN6IOBuKKyKhuEJ6QeWN7A3Hcbh7966tp0EIIcRBUFwhjooSTRPxK783b97Erl27sHbtWjz77LP48ssvrfJ68+fPt/hTJ9Dx0IqOjsbMmTOxZ88eEWdmeydOnMCkSZMQEhKCTz/91NbTIYQQi1BcsR8UV6yIMSbml8NLTExkWVlZjDHGDh8+zH77298ylUpl41n1VF1dzRhjrLa2loWFhbELFy7YeEbi0Ol0LDg4mN26dYu1t7ezsLAw9tNPP9l6Wv1J7PcsfdGXvX85PIortkVxxbrvYVrRNNGjR4+wZ88e5OfngzGGxsZGTJkyBXfv3kVbW5utp9cD3+/Vz88PCQkJuHbtmo1nJI5r164hJCQEwcHBcHNzw7Jly3D06FFbT4sQQsxGccU+UFyxLko0TXTp0iWUl5cjLS0Np0+fxty5c5GcnAx/f3/4+PgInRvsQVtbG1paWoT/ferUKUydOtWisZRKJRITExEaGorJkyfjypUrYk7VbNXV1Rg3bpzwfWBgIKqrq204I0IIsYwzxhV7iykAxRVrE/vWucPiOG4rAB2ADMaYmuO4dwG8+vj7i7adXVccxwUDyH78rSuAbxljn1g41tcAChhjezmOcwMwnDGmFGemFs1nKYDXGWPvPP7+/wDMYoy9b6s5EUKIJZwxrthbTHk8J4orVkQtKE3AddScUAIY8/hhIAGQCmALgJ85jvsQgB+Aj2z9hgEAxthtAOF9HYfjOA8AUQDefjyuBoCmr+P2URWAcZ2+DwRwz0ZzIYQQizhjXLHTmAJQXLEqSjRNwBhjHMfdA5DGcdxIAO4AMhljOQDAcdwuAN/Yw8NAZMEA6gHs4zguHMB1ACmMMVseHvoOwLMcx00AUA1gGYAVNpwPIYSYzUnjij3GFIDiilXRGU0TMcZyAUjR8SlnF2Ps/3X6zy8CuAEAHMc50r+pK4AZAHYzxp4H0AZgqy0nxBjTAXgPwEkApQAOM8Z+suWcCCHEEk4YV+wupgAUV6yNzmj2AcdxgwEYAHwC4Ahj7DrHcRxzkH9UjuP8AVxljAU9/v4lAFsZYzE2nRghhDgoR44rFFOck6N8SuoX3GOdfskDwG4AKwEEAB3bIbaYmzUwxmoAVHIcN+nxL70CoMSGUyKEEIfiTHGFYopzohVNEXAc9xyAEYyx72w9F7FxHDcdwF4AbgBuA1jFGGuy6aQIIcTBOWpcoZjifCjR7ANH2c4ghBBiHyiuEEdDiSYhhBBCCLEKOqNJCCGEEEKsghJNQgghhBBiFZRoEkIIIYQQq6BEkxBCCCGEWAUlmoQQQgghxCoo0SSEEEIIIVZBiSYhhBBCCLEKSjQJIYQQQohV/H8DvWaq4vPwIQAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 960x288 with 2 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    },
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "主程序段总共运行了 4.053140163421631 秒\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 引入必要的 package\n",
-    "from matplotlib import cm\n",
-    "from mpl_toolkits.mplot3d import Axes3D\n",
-    "from matplotlib.ticker import LinearLocator, FormatStrFormatter\n",
-    "\n",
-    "time_start = time.time()\n",
-    "N = 2\n",
-    "\n",
-    "# 设置图像比例 竖：横 = 0.3 \n",
-    "fig = plt.figure(figsize=plt.figaspect(0.3))\n",
-    "\n",
-    "# 生成 x, y 轴上的点\n",
-    "X = np.linspace(0, 2*np.pi, 80)\n",
-    "Y = np.linspace(0, 2*np.pi, 80)\n",
-    "\n",
-    "# 生成 2D 网格 (mesh)\n",
-    "xx, yy = np.meshgrid(X, Y)\n",
-    "\n",
-    "\n",
-    "# 定义必要的逻辑门\n",
-    "def rx(theta):\n",
-    "    mat = np.array([[np.cos(theta/2), -1j*np.sin(theta/2)],\n",
-    "                    [-1j*np.sin(theta/2), np.cos(theta/2)]])\n",
-    "    return mat\n",
-    "\n",
-    "def ry(theta):\n",
-    "    mat = np.array([[np.cos(theta/2), -1*np.sin(theta/2)],\n",
-    "                    [np.sin(theta/2), np.cos(theta/2)]])\n",
-    "    return mat\n",
-    "\n",
-    "def rz(theta):\n",
-    "    mat = np.array([[np.exp(-1j*theta/2), 0],\n",
-    "                    [0, np.exp(1j*theta/2)]])\n",
-    "    return mat\n",
-    "\n",
-    "def CNOT():\n",
-    "    mat = np.array([[1,0,0,0],[0,1,0,0],[0,0,0,1],[0,0,1,0]])\n",
-    "    return mat\n",
-    "\n",
-    "# ============= 第一张图 =============\n",
-    "# 我们可视化第二层是 kron(Ry, Ry) 的情况\n",
-    "ax = fig.add_subplot(1, 2, 1, projection='3d')\n",
-    "\n",
-    "# 向前传播计算损失函数：\n",
-    "def cost_yy(para):\n",
-    "    L1 = np.kron(ry(np.pi/4), ry(np.pi/4))\n",
-    "    L2 = np.kron(ry(para[0]), ry(para[1]))\n",
-    "    U = np.matmul(np.matmul(L1, L2), CNOT())\n",
-    "    H = np.zeros((2 ** N, 2 ** N))\n",
-    "    H[0, 0] = 1\n",
-    "    val = (U.conj().T @ H@ U).real[0][0]\n",
-    "    return val\n",
-    "\n",
-    "# 画出图像\n",
-    "Z = np.array([[cost_yy([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))\n",
-    "surf = ax.plot_surface(xx, yy, Z, cmap='plasma')\n",
-    "#cset = ax.contourf(xx, yy, Z, zdir='z', offset=np.min(Z), cmap='viridis')\n",
-    "ax.set_xlabel(r\"$\\theta_1$\")\n",
-    "ax.set_ylabel(r\"$\\theta_2$\")\n",
-    "ax.set_title(\"Optimization Landscape for Ry-Ry Layer\")\n",
-    "#fig.colorbar(surf, shrink=0.5, aspect=5)\n",
-    "\n",
-    "# ============= 第二张图 =============\n",
-    "# 我们可视化第二层是 kron(Rx, Rz) 的情况\n",
-    "ax = fig.add_subplot(1, 2, 2, projection='3d')\n",
-    "\n",
-    "def cost_xz(para):\n",
-    "    L1 = np.kron(ry(np.pi/4), ry(np.pi/4))\n",
-    "    L2 = np.kron(rx(para[0]), rz(para[1]))\n",
-    "    U = np.matmul(np.matmul(L1, L2), CNOT())\n",
-    "    H = np.zeros((2 ** N, 2 ** N))\n",
-    "    H[0, 0] = 1\n",
-    "    val = (U.conj().T @ H@ U).real[0][0]\n",
-    "    return val\n",
-    "\n",
-    "Z = np.array([[cost_xz([x, y]) for x in X] for y in Y]).reshape(len(Y), len(X))\n",
-    "surf = ax.plot_surface(xx, yy, Z, cmap='viridis')\n",
-    "#cset = ax.contourf(xx, yy, Z, zdir='z', offset=np.min(Z), cmap='viridis')\n",
-    "ax.set_xlabel(r\"$\\theta_1$\")\n",
-    "ax.set_ylabel(r\"$\\theta_2$\")\n",
-    "ax.set_title(\"Optimization Landscape for Rx-Rz Layer\")\n",
-    "\n",
-    "\n",
-    "plt.show()\n",
-    "\n",
-    "time_span = time.time() - time_start        \n",
-    "print('主程序段总共运行了', time_span, '秒')"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 更多的量子比特\n",
-    "\n",
-    "接着我们再看看不断的增加量子比特的数量，会对我们的梯度带来什么影响。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 5,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stderr",
-     "output_type": "stream",
-     "text": [
-      "100% |########################################################################|\n",
-      "100% |########################################################################|\n",
-      "100% |########################################################################|\n",
-      "100% |########################################################################|\r"
-     ]
-    },
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "主程序段总共运行了 424.13999366760254 秒\n"
-     ]
-    },
-    {
-     "name": "stderr",
-     "output_type": "stream",
-     "text": [
-      "\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 超参数设置\n",
-    "selected_qubit = [2, 4, 6, 8]\n",
-    "samples = 300\n",
-    "grad_val = []\n",
-    "means, variances = [], []\n",
-    "\n",
-    "# 记录运算时长\n",
-    "time_start = time.time()\n",
-    "\n",
-    "# 不断增加量子比特数量\n",
-    "for N in selected_qubit:\n",
-    "    grad_info = []\n",
-    "    THETA_SIZE = N\n",
-    "    pbar = ProgressBar()\n",
-    "    for i in pbar(range(samples)):\n",
-    "        class manual_gradient(fluid.dygraph.Layer):\n",
-    "            # 初始化一个长度为 THETA_SIZE 的可学习参数列表\n",
-    "            def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
-    "                low=0.0, high=2 * np.pi, seed=1),dtype='float64'):\n",
-    "                super(manual_gradient, self).__init__()\n",
-    "\n",
-    "                # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "                self.H = fluid.dygraph.to_variable(\n",
-    "                         density_op(N))\n",
-    "\n",
-    "            # 定义损失函数和前向传播机制    \n",
-    "            def forward(self):\n",
-    "\n",
-    "                # 初始化三个 theta 参数列表\n",
-    "                theta_np = np.random.uniform(\n",
-    "                    low=0., high= 2 * np.pi, size=(THETA_SIZE))\n",
-    "                theta_plus_np = np.copy(theta_np) \n",
-    "                theta_minus_np = np.copy(theta_np) \n",
-    "\n",
-    "                # 修改用以计算解析梯度\n",
-    "                theta_plus_np[0] += np.pi/2\n",
-    "                theta_minus_np[0] -= np.pi/2\n",
-    "\n",
-    "                # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "                theta = fluid.dygraph.to_variable(theta_np)\n",
-    "                theta_plus = fluid.dygraph.to_variable(theta_plus_np)\n",
-    "                theta_minus = fluid.dygraph.to_variable(theta_minus_np)\n",
-    "\n",
-    "                # 生成随机目标，在 rand_circuit 中随机选取电路门\n",
-    "                target = np.random.choice(3, N)      \n",
-    "                \n",
-    "                U = rand_circuit(theta, target, N)\n",
-    "                U_dagger = dagger(U) \n",
-    "\n",
-    "                U_plus = rand_circuit(theta_plus, target, N)\n",
-    "                U_plus_dagger = dagger(U_plus) \n",
-    "\n",
-    "                U_minus = rand_circuit(theta_minus, target, N)\n",
-    "                U_minus_dagger = dagger(U_minus) \n",
-    "\n",
-    "                # 计算解析梯度\n",
-    "                grad = ( matmul(matmul(U_plus_dagger, self.H), \n",
-    "                                U_plus).real[0][0]  \n",
-    "                        - matmul(matmul(U_minus_dagger, self.H), \n",
-    "                                 U_minus).real[0][0])/2  \n",
-    "                return grad      \n",
-    "            \n",
-    "           \n",
-    "        # 定义主程序段    \n",
-    "        def main():\n",
-    "            # 初始化paddle动态图机制\n",
-    "            with fluid.dygraph.guard():\n",
-    "\n",
-    "                sampling = manual_gradient(shape=[THETA_SIZE])\n",
-    "                \n",
-    "                # 采样获得梯度信息\n",
-    "                grad = sampling()\n",
-    "                \n",
-    "            return grad.numpy()\n",
-    "        \n",
-    "        if __name__ == '__main__':\n",
-    "            grad = main()\n",
-    "            grad_info.append(grad)\n",
-    "            \n",
-    "    # 记录采样信息\n",
-    "    grad_val.append(grad_info) \n",
-    "    means.append(np.mean(grad_info))\n",
-    "    variances.append(np.var(grad_info))\n",
-    "    \n",
-    "time_span = time.time() - time_start        \n",
-    "print('主程序段总共运行了', time_span, '秒')"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 6,
-   "metadata": {
-    "scrolled": true
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "我们接着画出这个采样出来的梯度的统计结果：\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAzEAAAEWCAYAAABWoBknAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAABSG0lEQVR4nO3dd5iU5dXH8e/ZAktbQAHpogIrvYpdQaJiBY3G3hW7kmJsiRKN0SSm2KJBUTQqaIwFlFesaIwBEcQgRcEKigoIwlKknfeP+9llWGZ3Z9mZnRn297muuXaefmZ2du49z93M3REREREREckWOekOQEREREREpCqUxIiIiIiISFZREiMiIiIiIllFSYyIiIiIiGQVJTEiIiIiIpJVlMSIiIiIiEhWURIjOzQz29/M5ptZsZkNS3c86WZmn5nZj2r62O241nVm9kAmxCIimSP6Lt893XEkwoKHzGy5mb2T7njSzczONrO3avrY7bxeuZ+zmo5FyqckRqok+udxvZk1K7N+ppm5mXVIU2jluQm4290buvuzZTea2aNmttjMVprZR2Z2fpntg81snpmtMbPXzWzXmG1mZr83s2XR4w9mZql/STs+d/+du59f+Z7VY2YjzezRVF9HpDYys0lmdlOc9UPN7Gszy6vqOaPv8k+SE2HKHQAcCrR19wFlN5rZIDObZWYrojLkGTNrE7O9rpk9GJVPX5vZz8oc39vMpkfl03Qz653yV1RL1NTnLPq/qWOqr7OjUhIj2+NT4JSSBTPrAdRLXzgV2hWYXcH2W4EO7l4IHAv81sz6AUSJ2tPAr4GdgHeBJ2KOHQ4MA3oBPYGjgQuTHP8OZ3v+cRGRrDQGOCPOzZ0zgMfcfWOiJ8rS741dgc/cfXU52+cAh7t7E6A1MB+4N2b7SKBTdJ5BwC/NbAiAmdUBngMeBZoCDwPPReulAln6WZI4lMTI9vgHcGbM8lnAI7E7RHeQbjezL8zsGzO7z8zqRduamtnzZrYkqmZ/3szaxhw72cxuNrP/mNkqM3upbM1PmWtdYGYLzOw7MxtvZq2j9R8DuwMToqrhumWPdffZ7v5DyWL02CNaPh6Y7e7/dPd1hAKll5ntGfO6/+Tui9z9S+BPwNnlxFgQ1fosi+66TTOzXaJt55jZ3Oi1fmJmF8YcN9DMFpnZL83s26jWaJiZHRnVHH1nZtfF7D/SzJ4ysyei880ws17lxJRjZteY2cdRXE+a2U4x288ws8+jbdeX9/5H++5sZhOiO4bTzOy3FlPdHt1tutTM5hMKaszsDjNbGB0z3cwOLPM6Ho1ZLjeWil6HmXWIrn1W9FlcWnJ89M/AdcBJ0efj/Ypeo4hU2bOEG0Cxf9tNCTd8HjGzAWb23+g7cbGZ3R37T3g53xuld67N7Cgzey/6DlloZiNjji33bz/anmuh2erH0XfldDNrF23b08xejr5fPzSzn5T3As2sdVTufBeVQxdE688DHgD2jb5fflP2WHf/xt2/ilm1CYi9K38mcLO7L3f3ucD9bCljBgJ5wF/d/Qd3vxMw4JBy4jzSzOZEr/VLM/tFye/DKi+Pf2tmb0evY0L0ff9YzPd9hzK/sysslGVLzeyPZhb3f82K3ufoGuOja7zDlnI5LjM7M6aM+LXFNDm2LeXio2a2Ejg7wc9eyeeswlgqeR1jzOweM3sheu+nmtke0bY3o93ej97bkyp6jRKHu+uhR8IP4DPgR8CHQBcgF1hIuFPkhFoNgL8C4wkFWCNgAnBrtG1n4MdA/WjbP4FnY64xGfgY6Eyo4ZkM3FZOPIcAS4G+QF3gLuDNsvFW8pr+BqyJ4p8BNIzW3wHcW2bfD4AfR8+/B/aO2dYfWFXONS6M3oP60XvWDyiMth1F+FI04OAolr7RtoHARuAGIB+4AFgCPB69d92AdcDu0f4jgQ3ACdH+vyDUnOWXfT+AEcAUoG303v0dGBtt6woUAwdF2/4cxRH3vQTGRY/60bELgbditjvwcvR5qBetOz36LOQBPwe+BgpiXsejicRSyevoEF37fsJnqRfwA9Cl7HX00EOP5D+iv70HYpYvBGZGz/sB+0TfAR2AucCImH3jfW840DF6PhDoQbgh2xP4BhgWbavsb/8qYBZQRPju7RV9HzWIvr/OieLqSyhjupXz+t4glCEFQG/C9/PgaNvZsd+D5RzfHlgBbCZ8d58drW8axb9LzL4nALOi5z8F/q/MuZ4Hfl7OdRYDB8acu6SMSaQ8XkAooxoTao8+IvwfkEe4gflQmd/Z69HvrH207/ll34/K3mdCefJktF934Mvy3ku2lBEHAHWA26P3sqSMGBktD4s+K/VI7LPXsbJYEngdY4DvgAHR9seAcfGuo8d2fL+kOwA9suvBliTmV4SmWEMIhUxe9MfYgVAgrAb2iDluX+DTcs7ZG1geszwZ+FXM8iXAi+UcOxr4Q8xyw+jLqkNsvAm8rtzoC/BXbPmHfzRlkifgP2wpZDYBe8Zs6xS9Bxbn/OcCbwM9E4jlWeDK6PlAYC2QGy03iq4RmzxNZ0vBPRKYErMth60Lr9L3I/rSHhyzb6vovcsjJE2xX7QNgPXx3svovdsAFMWs+y3bJjGHVPK6lwO9Yl5HSRJTYSyVvI4O0bXbxmx/Bzi57HX00EOP5D+i79Xv2ZKE/Af4aTn7jgCeiVne5nuDCv7pI9w8+0v0vLK//Q+BoXHOcRLw7zLr/g7cGGffdoRyoFHMuluBMdHzs6kkiYk5bifgamCfmHM70Y2daN2hhOZpEJo5jytzjseAkeWc/wtCAllYSRy92bY8vj5m+U/EJE/AMURJaczvZ0jM8iXAq2Xfj4reZ7aUKbHl6+/Key8JZcTYmOX6bF1GjCTm5mYVPnsdK4ulss8LIYmJTeKPBOYl8nnWo/KHmpPJ9voHcCrhS+mRMtuaE75EpkdVtSuAF6P1mFl9M/t7VPW7EngTaGJmuTHn+Drm+RpCchJPa+DzkgV3LwaWAW3K2T8ud9/k7m8R7uZfHK0uBgrL7FoIrCpneyFQ7NE3Uxn/ACYB48zsKwuDAOQDmNkRZjYlqopeQfiSi20+t8zdN0XP10Y/v4nZvpat35+FMa9rM7CI8D6VtSvwTMzvaC6hQN4l2j/2PKsJ72s8zQkJw8KYdQvj7LfVOjP7uYVmdN9H12/M1q+7RGWxVPQ6SiT6eRKRJIq+V5cAQy2M9rQXoSYZM+scNV/6OioLfse23wHxvkuIjt/bwoArS8zse+CiOMeX97ffjlDjX9auwN4l3yfRd8ppQMs4+7YGvnP3VTHrPqeK5Q+Au3/Hln4teYTyBbYtY8orf8puL+vHhLLlczN7w8z2hYTL47LlTUXlD2z9O/uc8suf8t7neGXK59ueolTZMmIN25ZXZcufRD57JBBLIp8XlT8poiRGtou7f05opnQkofN7rKWEL7Zu7t4kejR295I/3J8TqvD39tCh/qBo/faM7PUV4UsknMCsAaF6/MvtOBeEL6uS9q6zCU0MYs+9B1sGCthqe/Q87iAC7r7B3X/j7l2B/Qhtws+00E/nX4Tq7108dPCcyPa9FyXaxcScQ0jMvoqz30LgiJjfURN3L/DQv2dxmfPUJ7yv8SwhNO9qG7OuXZz9SpM7C/1frgZ+AjSNXvf3xH/dlcVS0euoTLyEU0SS6xFC/44zgJfcveSf4HuBeUCnqCy4jm2/Ayr6G32c0Gy5nbs3Bu6Lc3x5FhK/n8VC4I0y3ycN3f3iOPt+BexkZo1i1rWneuVPC0JtyXLCd195ZcxsoKfZVoMm9KT8Mmiauw+Nzv8soXkUJLc8LhH7/d+e8suf8t7nkjKl7HnKs5iY8sdC/9uy5VXZz1Einz0SiKUqnxdJMiUxUh3nEar6txp5Jbr7fz/wFzNrAWBmbczs8GiXRoQkZ4WFDtg3ViOGx4FzLAw1WZdwN2Wqu39W2YFm1sLMTjazhhY6eR5OGHXttWiXZ4DuZvZjMysgVFn/z93nRdsfAX4WvbbWhMJgTDnXGmRmPaK7WysJ1dObCO136xJ9UZrZEcBh2/E+xOpnZsdHd/NGENqBT4mz333ALRYNG21mzc1saLTtKeBoMzsg6ux4E+V8X0S1RE8DI6O7enuy9cAP8TQiFAxLgDwzu4Ft7yqWqCyWil5HZb4BOlg5HU9FJCkeITRDvoBQ21CiEeH7sDj63qjqP36NCDUh68xsAKF1QKIeAG42s04W9DSznQn9SjpbGEwkP3rsZWZdyp7A3RcSmgnfamHwlp6EcvGxRAKIvqeLLAxO0pzQ3++9qFYGwvv2Kwud7/ckvH9jom2TCWXIFRYG0rksWv8aZZhZHTM7zcwau/sGwnteUrufzPK4xFVRzO2AK9l6VM8S5b7PccqUroSBdMrzFHCMme0XlRG/ofIkLKHPXgKxJPx5Kcc3hAGIZDuo4Jbt5u4fu/u75Wy+mtAZcEpUVfsK4W4PhHbL9Qg1NlMITc22N4ZXCW2D/0W4G7MHcHKihxO+uBYR+mPcTujY91x07iWEKvhbou17lzn33wmd9WcROvy/EK2LpyXhi3YlobnTG4S+GKuAKwh3xZYTCuHxCcZfnucI7XSXE+58Hh8VXGXdEV3rJTNbRfhd7A1h1DbgUkKSuDg616IKrnkZoTnY14Smc2MJyVN5JgH/R+j0+TlhcIK4zUYSiKXc15GAf0Y/l5nZjASPEZEqiG4qvU3ozxb7/fYLwnfeKsKNr3j/7FbkEuCm6O/+BrbULiTiz9H+LxG+l0cT+u2sItxIOplQg/A18HvCzaZ4TiH0v/mKcOPrRnd/OcEY2hDKv1WEcmQzcFzM9hsJTd4+J5QZf3T3FwHcfT2ho/qZhIEBziX0jVxfzrXOAD6LyuOLCAOrQBLL4xjPEfpqziSUi6PL7pDA+3wZodnV14TE7aHyLhaVEZcTOuAvJryf31JxGVSVz165sWzH56WskcDDUVO0ckfBk/gsfvN9EclGFoYY7ejup1e2b4rj+D3Q0t0runsmIiI7EDNzQhOtBWmMoSEhsevk7p+mKw5JPdXEiEi1WRgnv2fULGMAoUnFM+mOS0REdnxmdkzU3KsBoVXFLMJonLIDy6gkxsyGWJgoaIGZXRNnu5nZndH2/5lZ35htTSxMZjTPwohH+9Zs9CK1WiNCu+HVhCYafyI0KRDJWma2u5mNNrOn0h2LiFRoKKE511eE6Q5OLmekUNmBZExzsqjD80eEcdAXAdOAU9x9Tsw+RxLaPR5JaPN+h7vvHW17mDBW9wNRx6767r6iZl+FiIhkAjN7kDAK4Lfu3j1m/RBCP6pcwvwNtyVwrqfc/YSUBSsiIlWWl+4AYgwAFrj7JwBmNo6QWc+J2Wco8EiUXU+Jal9aEe7+HkSYs6Skw1t5ndtERGTHNwa4m5h5rKKbZfcQc7PMzMYTEppbyxx/rrt/WzOhiohIVWVSEtOGrUcnWsS2IwzF26cNW4ZqfcjMehFGxbiy7NC/AGY2HBgOUFBQ0K99+4qGHs8MmzdvJicno1r+xZUtcUL2xKo4ky9bYs2WOD/66KOl7t483XGU5e5vmlmHMqvj3ixz91sJtTbbReVK6mRLnJA9sSrO5MqWOCF7Yk20XMmkJCbemN5l27qVt08e0Be43N2nmtkdwDWEoXe33tl9FDAKoKioyD/88MNqBV0TJk+ezMCBA9MdRqWyJU7InlgVZ/JlS6zZEqeZVTSTdqZJ5GZZqWjekFuAPmZ2bZTsbEPlSupkS5yQPbEqzuTKljghe2JNtFzJpCRmEVvPiBpvlvHy9nFgkbtPjdY/RUhiRERESiRys2zLBvdlhDk1REQkw2RSndI0oJOZ7RZ1zD+ZbSf9Gw+cGY1Stg/wvbsvdvevgYVmVjKZ4mC27ksjIiKSyM0yERHJAhlTE+PuG83sMsJM3rnAg+4+28wuirbfB0wkjEy2AFgDnBNzisuBx6IE6JMy20REREpvlgFfEm6WnZqME5vZMcAxrVu3TsbpRESkEhmTxAC4+0RCohK77r6Y5w5cWs6xM4H+qYxPRESyg5mNBQYCzcxsEXCju4+Od7MsGddz9wnAhKKioguScT4Rqb4NGzawaNEi1q1bl7JrNG7cmLlz56bs/MmUabEWFBTQtm1b8vPzt+v4jEpiREREksHdTyln/TY3y0Rkx7Ro0SIaNWpEhw4dMIvXJa76Vq1aRaNGjVJy7mTLpFjdnWXLlrFo0SJ222237TpHJvWJERERyUpmdoyZjSouLk53KCISWbduHTvvvHPKEhjZfmbGzjvvXK1aMiUxIiIi1eTuE9x9eMOGDdMdiojEUAKTuar7u1ESIyIiIiIiWUVJjIiIiIhICtxyyy1069aNnj170rt3b6ZODVMaDhw4kHfffbfG4vj0008ZNGgQnTp14qSTTmL9+vXb7PP666/Tu3fv0kdBQQHPPvssEPqwXH/99XTu3JkuXbpw5513lh43efJkevfuTbdu3Tj44IO3OuemTZvo06cPRx99dNJfkzr2i4iIiIgk2X//+1+ef/55ZsyYQd26dVm6dGnc5KEmXH311Vx66aWcc845XHTRRYwePZqLL754q30GDRrEzJkzAfjuu+/o2LEjhx12GABjxoxh4cKFzJs3j5ycHL799lsAVqxYwSWXXMKLL75I+/btS9eXuOOOO+jSpQsrV65M+mtSTYyIiEg1qWO/iJS1ePFimjVrRt26dQFo1qwZ8eaSGjt2LD169KB79+5cffXVpesbNmzIz3/+c/r27cvgwYNZsmQJAB9//DFDhgyhX79+HHjggcybN6/CONyd1157jWHDhgFw1llnldawlOepp57iiCOOoH79+gDce++93HDDDeTkhNShRYsWADz++OMcf/zxtG/ffqv1EEaHe+GFFzj//PMrvNb2UhIjIiJSTerYL5IFBg7c9vG3v4Vta9bE3z5mTNi+dOm22ypx2GGHsXDhQjp37swll1zCG2+8sc0+X331FVdffTWvvfYaM2fOZNq0aaUJxurVq+nbty8zZszg4IMP5je/+Q0Aw4cP56677mL69OncfvvtXHLJJRXGsWzZMpo0aUJeXmiA1bZtW7788ssKjxk3bhynnLJlpPqPP/6YJ554gv79+3PEEUcwf/58AD766COWL1/OwIED6devH4888kjpMSNGjOAPf/hDaeKTbEpiRERERESSrGHDhkyfPp1Ro0bRvHlzTjrpJMaUJEWRadOmMXDgQJo3b05eXh6nnXYab775JgA5OTmcdNJJAJx++um89dZbFBcX8/bbb3PiiSfSu3dvLrzwQhYvXlxhHGGu+K1VNDLY4sWLmTVrFocffnjpuh9++IGCggLeffddLrjgAs4991wANm7cyPTp03nhhReYNGkSN998Mx999BHPP/88LVq0oF+/fgm9V9tDfWJEREREZMc3eXL52+rXr3h7s2YVby9Hbm4uAwcOZODAgfTo0YOHH36Ys88+u3R7vASjPGbG5s2badKkSWnflfIcfvjhfPPNN/Tv35/777+fFStWsHHjRiA084rXrK3Ek08+yXHHHUd+fn7purZt2/LjH/8YgOOOO45zzjmndH2zZs1o0KABDRo04KCDDuL9999nxowZjB8/nokTJ7Ju3TpWrlzJ6aefzqOPPprw662MamJERESqSX1iRKSsDz/8sLTZFcDMmTPZddddt9pn77335o033mDp0qVs2rSJsWPHlo7wtXnzZp566ikg9D054IADKCwsZLfdduOf//wnEJKg999/f5trT5o0iZkzZ/LAAw9gZgwaNKi0mdrDDz/M0KFDy4177NixWzUlAxg2bBivvfYaAG+88QadO3cGYOjQofz73/9m48aNrFmzhqlTp9KlSxduvfVWFi1axGeffca4ceM45JBDkprAgJIYERGRalOfGBEpq7i4mLPOOouuXbvSs2dP5syZw8iRI7fap1WrVtx6660MGjSIXr160bdv39IEo0GDBsyePZt+/frx2muvccMNNwDw2GOPMXr0aHr16kW3bt147rnnKo3l97//PXfffTcdO3Zk2bJlnHfeeQC8++67W3W8/+yzz1i4cOE2QyVfc801/Otf/6JHjx5ce+21PPDAAwB06dKFIUOG0LNnTwYMGMD5559P9+7dt/s9qwo1JxMRERERSbJ+/frx9ttvx902OaZp2qmnnsqpp54ad7+bb76Zm2++eat1u+22Gy+++GKVYtl9992ZPHkyjRo12mp9//79SxMSgA4dOsTt9N+kSRNeeOGFuOe+6qqruOqqq8q9dklzumRTTYyIiIiIiGQVJTEiIiIiIhlGfewqpiRGRERERHZIVRn9S2pWdX83SmJERESqSaOTiWSegoICli1bpkQmA7k7y5Yto6CgYLvPoY79IiIi1eTuE4AJRUVFF6Q7FhEJ2rZty6JFi1iyZEnKrrFu3bpq/SNekzIt1oKCAtq2bbvdxyuJEREREZEdTn5+PrvttltKrzF58mT69OmT0mskSzbFmgg1JxMRERERkayiJEZERERERLKKkhgREREREckqSmJERERERCSrKIkRERGpJg2xLCJSs5TEiIiIVJO7T3D34Q0bNkx3KCIitYKSGBERERERySpKYkREREREJKtkVBJjZkPM7EMzW2Bm18TZbmZ2Z7T9f2bWt8z2XDN7z8yer7moRURERESkJuWlO4ASZpYL3AMcCiwCppnZeHefE7PbEUCn6LE3cG/0s8SVwFygsEaCFhERyRJH3vFv5ixeuWXFiy8A0LVVIROvPDBNUYmIbJ9MqokZACxw90/cfT0wDhhaZp+hwCMeTAGamFkrADNrCxwFPFCTQYuIiGSDvu2bkJ9rW63LzzX67to0TRGJiGy/TEpi2gALY5YXResS3eevwC+BzSmKT0REJGtdMbgTObZ1EpNrxhWDO6YpIhGR7ZcxzckAi7POE9nHzI4GvnX36WY2sMKLmA0HhgM0b96cyZMnVz3SGlZcXKw4kyxbYlWcyZctsWZLnJI9WhQWcGK/tjzx7kI2bHLyc40T+rejRaOCdIcmIlJlmZTELALaxSy3Bb5KcJ8TgGPN7EigACg0s0fd/fSyF3H3UcAogKKiIh84cGDSXkCqTJ48GcWZXNkSq+JMvmyJNVvilMDMjgGOad26dbpDqdAVgzvxz+mLAFctjIhktUxqTjYN6GRmu5lZHeBkYHyZfcYDZ0ajlO0DfO/ui939Wndv6+4douNei5fAiIiIpEK2THZZUhtz6X+f5IK2qBZGRLJWxtTEuPtGM7sMmATkAg+6+2wzuyjafh8wETgSWACsAc5JV7wiIiLZaMQe+TT87xPUnTIOPh0B118PhRrUU0SySybVxODuE929s7vv4e63ROvuixIYolHJLo2293D3d+OcY7K7H13TsYuIiGSDZj33ZMZj/8BOOQX+8Afo1Anuvx82bUp3aCIiCcuoJEZERERSb33z5jBmDLzzTkhifvUrWL063WGJiCRMSYyIiEhttdde8O9/w9SpoUnZxo0wYgR8/HG6IxMRqZCSGBERkdrMDDp0CM/ffx8eeAC6doWrr4aVK9MamohIeZTEiIiISNCvH8yfD6eeqv4yIpLRlMSIiIjIFq1awUMPwbvvQufOcNdd4GXnnhYRSS8lMSIiIrKtfv3gzTfhlVcgLw++/x7OOgsWLEh3ZCIiSmJERESkHGbQokV4Pn06PP106C/zy1+GpEZEJE2UxIiIiEjlDjkEPvoIzjgDbr899Jf5+9/V1ExE0kJJjIiIiCSmVSsYPTr0l+nSBSZMCLU1IiI1TEmMiIhINZnZMWY2qri4ON2h1Iy+fWHyZBg7Nix//DGccEIY2UxEpAYoiREREakmd5/g7sMbNmyY7lBqjhk0ahSez5oFkyZBt27wi1/AihVpDU1EdnxKYkRERKR6hg0LtTBnngl//nPoL/PAA+mOSkR2YEpiREREpPpatgyJy/TpYQSz999Pd0QisgNTEiMiIiLJ06dP6C9z++1h+a234Nhjw8hmIiJJoiRGREREkssM6tYNzz//PCQ13brBz36m/jIikhRKYkRERCR1Tjst1MKcfTb89a/QsSOMGZPmoEQk2ymJERERkdRq2RLuvx9mzIDu3eG778J6TZQpIttJSYyIiIjUjN694fXX4corw/Kjj8Ixx8CHH6Y1LBHJPkpiREREpOaYQW5ueL5uHbzxRqid+elPYfny9MYmIllDSYyIiIikxwUXhPllzj0X7rgj9JcZOzbdUYlIFlASIyIiIumzyy7w97/De+9Bz55QUBDWb96c3rhEJKPlpTsAERGRWGZmwGnA7u5+k5m1B1q6+ztpDk1SqVcveO21Lcu//S09/u//wkhmRUVpC0tEMpNqYkREJNP8DdgXOCVaXgXck75wpMaYhQfATjvReNas0F9mxIgtI5qJiKAkRkREMs/e7n4psA7A3ZcDddIbktS4yy5j6j/+AeedB3fdBZ06wbPPpjsqEckQSmJERCTTbDCzXMABzKw5oA4StdCGpk3hvvtCf5l+/aBdu7Bh/fr0BiYiaackRkREMs2dwDNACzO7BXgL+F16Q5K06tkTXnopJDIAF14IRx4Jc+emNy4RSRslMSIiklHc/THgl8CtwGJgmLv/M71RSUbp2RPefht69IArrlB/GZFaSEmMiIhkHHef5+73uPvd7q7b7bK1n/40zC9zwQVwzz1hfpmXX053VCJSgzIqiTGzIWb2oZktMLNr4mw3M7sz2v4/M+sbrW9nZq+b2Vwzm21mV9Z89CIikgxm9rCZNYlZbmpmD6YhjmFmdr+ZPWdmh9X09aUSzZvDvffCzJlwwAHQtWtYX1yc1rBEpGZkTBITdeK8BzgC6AqcYmZdy+x2BNApegwH7o3WbwR+7u5dgH2AS+McKyIi2aGnu68oWYhGJ+tTlROY2YNm9q2ZfVBmfYU3y2K5+7PufgFwNnBSVa4vNahHDxg/Htq0AXc4+mgYMgTmzEl3ZCKSQgknMWZW18xONbPrzOyGkkcSYxkALHD3T9x9PTAOGFpmn6HAIx5MAZqYWSt3X+zuMwDcfRUwF2iTxNhERKTm5JhZ05IFM9uJqk/OPAYYEruivJtlZtbDzJ4v82gRc+iv0Dw12WHzZhg6FKZMCf1mLr8cli1Ld1QikgLm7ontaPYi8D0wHdhUst7d/5SUQMxOAIa4+/nR8hmEuQIui9nneeA2d38rWn4VuNrd343ZpwPwJtDd3VfGuc5wQi0OzZs37/fkk08mI/yUKi4upmHDhukOo1LZEidkT6yKM/myJdZsiXPQoEHT3b1/Ms9pZmcC1wElnflPBH7n7o9U8TwdgOfdvXu0vC8w0t0Pj5avBXD3W8s53oDbgJfd/ZUKrqNyJUW2N878FSvoMGYMrSdMYGP9+sz6/e9Z2TW1DTR29Pe0pinO5MuWWBMuV9w9oQfwQaL7bs+DUEg9ELN8BnBXmX1eAA6IWX4V6Bez3JCQZB2fyDU7d+7s2eD1119PdwgJyZY43bMnVsWZfNkSa7bECbzrqSkTugKXRY+u23mODrFlF3BCnHLm7gqOvyIqU+4DLkrkmipXkqvacc6a5X7aae7FxWF5yRL3zZurHVc8teY9rSGKM/myJdZEy5Wq9Il528x6VGH/qloEtItZbgt8leg+ZpYP/At4zN2fTmGcIiKSQmZWF+gNFAI7ASckqfmyxVlXbnMEd7/T3fu5+0Xufl8Sri81rXt3ePRRaNAAfvgB9tkHjjgCZs9Od2QiUk1VSWIOAKZHHSL/Z2azzOx/SYxlGtDJzHYzszrAycD4MvuMB86MRinbB/je3RdHVf6jgbnu/uckxiQiIjXvOUIfyI3A6phHdSVys2y7mNkxZjaqWCNjZa6cHLjsMpg6FXr1Cs+XLk13VCKynarSUfKIlEUBuPtGM7sMmATkAg+6+2wzuyjafh8wETgSWACsAc6JDt+f0CxglpnNjNZd5+4TUxmziIikRFt3H1L5blVWerMM+JJws+zUZJzY3ScAE4qKii5IxvkkBfLzYcQIOP10GDkS7rsPHnssTJrZpUu6oxORKko4iXH3z6PRYjoBBTGbPk9WMFHSMbHMuvtinjtwaZzj3iJ+MwEREck+b5tZD3eftb0nMLOxwECgmZktAm5099HxbpYlJWLJHs2awd13w8UXw6hRUFQU1n/xBbRrB6Z/J0SyQcJJjJmdD1xJqH6fSZiP5b/AISmJTEREaqsDgLPN7FPgB8JNKnf3nomewN1PKWf9NjfLpJbq1g3uuCM8X7o0NDEbMAD+/OewTUQyWlX6xFwJ7AV87u6DCBOPLUlJVCIiUpuVTGx8GHAMcHT0M2OpT0yWa9w4NDF7550wv8yll6q/jEiGq0qfmHXuvs7MMLO67j7PzIpSFpmIiNRKNdF8OdnUJybL5efDlVdu6S9z773w+OMwdy60bFnuYUfe8W/mLI6Zku7FFwDo2qqQiVcemOKgRWq3qtTELDKzJsCzwMtm9hxJGtVFRESkRNR8+U1C35XfRD9HpjMmqSV23hnuugv+9z+45potCczs2RBncvC+7ZuQn7t1H5r8XKPvrk1rIlqRWi3hJMbdj3P3Fe4+Evg1YUjjYSmKS0REai81X5b06toVrr46PP/ww9Bf5rDDYNbWY01cMbgTOWUGAsg144rBHWsqUpFaK+EkJpqb5XQzu8Hd3yB07u+dqsBERKTWWufu64DS5stARjdfVp+YHdjuu8Nf/gLTp0Pv3nDJJbAk5NQtCgs4sV/b0tqY/FzjhP7taNGooIITikgyVKU52d+AfYGSEV9WAfckPSIREantsq75srtPcPfhDRs2THcokmz5+XD55bBgQZggc9Qo6N4d1qwBtq6NUS2MSM2pSsf+vd29r5m9B+Duy82sToriEhGRWsrdj4uejjSz14HGwItpDEkEdtopDMl80UUwdSrUrw9Ai9nvcWLfNjz2zkLVwojUoKokMRvMLBdwADNrDmxOSVQiIiJA1HxZJHN06RIeAG+8AQMHcsPBg1jS+wSuGDw4vbGJ1CJVaU52J/AM0MLMbgHeAn6XkqhERKTWMbO3op+rzGxlzGOVma2s7HiRGrfffnDXXdSZ9T733XU5La4aAd9+m+6oRGqFqoxO9hjwS+BWYDEwzN3/marARESkdnH3A8zMgG7uXhjzaOTuhemOryLq2F9L5eeHfjILFvDlccfB6NGw776waVO6IxPZ4VWlJgZ3n+fu97j73e4+N1VBiYhI7eTuTqj1zyrq2F/LNW3KgssuC0Mw33UX5OaGRGbSpLjzy4hI9VXaJ8bMxle03d2PTV44IiIiTDGzvdx9WroDEamSPfcMD4Bx4+D002HQoDBEc69e6Y1NZAeTSMf+fYGFwFhgKmAV7y4iIlItg4ALzexzYDWh3HF375nesESq4KSTYMUKuOEG6NMHzj8fbr4Zdtkl3ZGJ7BASSWJaAocS5oc5FXgBGOvus1MZmIiI1FpHpDsAkWrLy4NLL4VTT4WbboK774b//Q+mTEl3ZCI7hEr7xLj7Jnd/0d3PAvYBFgCTzezylEcnIiK1jrt/DqwEdgF2jXmIZJ+mTUNzsg8+gDvvDOtWroTnnlN/GZFqSKhjv5nVNbPjgUeBSwnDLT+dysBERKR2MrPzgTeBScBvop8j0xlTZTQ6mVSqqAgGDAjPR42CYcNg8GB4//20hiWSrSpNYszsYeBtoC/wG3ffy91vdvcvUx6diIjURlcCewGfu/sgoA+wJL0hVUyjk0mVjBgBf/tbaF7Wpw8MHw7ffJPuqESySiI1MWcAnQmFytuafKzmPPvel+x/22uc/eJq9r/tNZ59T3mjiNQK69x9HYSWAO4+DyhKc0wiyZOXBxdfDAsWwE9/Cg89FJZFJGGVdux39yrNJSPJ8ex7X3Lt07NYuyFMmPXlirVc+/QsAIb1aZPO0EREUm2RmTUBngVeNrPlwFdpjUgkFZo0gT/9CS68EHKif7c+/xzefReOPx5MA8KKlEcJSob646QPSxOYEms3bOJ3E+eyYdPmNEUlIpJ67n6cu69w95HAr4HRwLC0BiWSSp07Q8eO4fk998AJJ4T5Zd57L71xiWSwRIZYljT4asXauOu/XfUDXW94kY4tGtGlVSO6tCxkz1aN6NKqkGYN69ZwlCIiyWNmdwOPu/vbJevc/Y00hiRS8373O9h9d/j1r6FfPzj3XPjtb6Fly3RHJpJRVBOToVo3qRd3fdP6+Zx7wG60aFSX/yxYyi0T53LG6He46p9bRje55/UFTPlkWU2FKiKSLPOBP5nZZ2b2ezPrne6ARGpcXh5cdBHMnw8/+xk88gjccku6oxLJOKqJyVBXHV60VZ8YgHr5udx4TLet+sR8t3o98xavpE5eyEfXbdjEXa/N55KBHdln951Zvno9J4+aQpdWjdizVSF7tmxE11aFNG9UF1NbWxHJIO5+B3CHme0KnAw8ZGYFwFhgnLt/lNYAK2BmxwDHtG7dOt2hyI6iSRO4/fbQX6ZJk7Bu2rTQZ+bHP1Z/Gan1EkpizKwpcAxwHGGksk+B54Dx7q4xAVOgJFH546QP+XLFWto0qcdVhxdt06l/pwZ12K9js9LlgvxcPhh5OOujfjPFP2ykTdN6TP30O56d+dVWx3Vp1Yg9W4bE5sBOzWnZuKAGXpmISMWiyS5/D/zezPoADwI3ArlpDawC7j4BmFBUVHRBumORHUynTlue33MPPPwwHHRQmECzb9/0xSWSZpUmMWb2NNAUeAG42t0/MrP2wFDgH2ZWx90HpjbM2mlYnzYM69OGyZMnM3DgwISPy8vNIS831My026k+D569FwAr1qxn3termLt4JfMWr2Le1yt5bOrnrNuwmftO78uQxq2Yteh7Rv37E355eBHtdqrPhk2bycsx1dqISI0xs3xgCKE2ZjDwBmHSS5Ha7YEHYN994Ve/gv794ZxzQn+ZVq3SHZlIjUukJuZcd18Ru8LdvwDuAu6KhsGULNCkfh322X1n9tl959J1mzY7ny1bTYtGYVCAb1etY8bny8mPkqAH3/qUe9/4mD1bhlqbrq3CQAKdd2lEQX7G3hQVkSxkZocCpwBHAe8A44Dh7r46rYGJZIq8vNC87OSTQ/Jyxx1QVAS//GW6IxOpcYnME7PCzPYk1Ly0AZwwXv94d59bNsGpDjMbAtxBaDLwgLvfVma7RduPBNYAZ7v7jESOlfhyc4w9mm+ZYXpwl10Y3GWX0uWurQs5onsr5i5eyRPTFpb20ckx6NCsAV1aFdKlZSOGH7RHjccuIjuc64DHgV+4+3fpDkYkYzVuDH/8Y0ho2rYN655/HtauDcMzq/WE1AKJNCe7mnBnbBzhzhhAW2CsmY1LVrJgZrnAPcChwCJgmpmNd/c5MbsdAXSKHnsD9wJ7J3isbIcDOzXnwE7NAdi82fniuzXM+3olcxavYt7ilcxa9D1vzV/KpYPC+PYjx8/m21Xr+Ntp/QD4bOlqWhTWpX4djSGxI3r2vS+39Nua8lrcflsiiXL3QemOQSSrlMwtAzBqFEyYAAccAH/9axieWWQHlsh/lucB3dx9Q+xKM/szMBtIVo3HAGCBu38SnX8cofYnNhEZCjzi7g5MMbMmZtYK6JDAsVJNOTlGh2YN6NCsAUO6b2l/u27DptI+My0K65KXs+UO0LkPT+PTpavpsHOD0iZpXaJ5bdo2rae+Nlns2fe+3GoEvS9XrOXap2cBKJGpBiWGIrJdnnkGHnwQrr8e9toLzjorDM2sEfNkB5VIErMZaA18XmZ9q2hbsrQBFsYsLyLUtlS2T5sEjwXAzIYDwwGaN2/O5MmTqxV0TSguLs6aOLs2XAQNYfLkbwE4pt1Gvmicz8JV65jxyRpe/OBrPNq/IBfaNcphQKs8Dt01H4AfNjl1c1Of2GTTe5oJcbo76zbB2o3O2g2wZqNz53vrWLth6/3WbtjEzc+9z9ovP2TBik3kGOSakWOhCWJuDhiQa6Ep426Nc6iXZ6z8wVm6bjPtG+WQl2OsXO+sXu9b9s8hOoeRa5Ser04OVU6EM+U9jeftrzYw5oP1rI++Wb9csZZf/nMmc+bOYb/W+ekNTkQyW24uXHAB/OQnYcLMv/4VhgyBk05Kd2QiKZFIEjMCeNXM5rMlUWgPdAQuS2Is8f4T8QT3SeTYsNJ9FDAKoKioyKsy6le6VHV0snSJF+fAMvus/mEjH32zirnR6GhzF69k59bNGDiwM+s2bKLHyEn84rAiLjx4D9as38ibHy1hz5aFtN+pPjk5yUtusvk9rSp3Z836Taxat5FV6zawMvq5at1GurQqpGOLhiz+fi33Tv6Yk/ZqR7fWjZn22Xfc8NzssP/aDRT/sJHNcf+itvXdOmdz8z0Y/dYHle474bID6NG2MY9P/YKbnpnF1OsGs0thAX95+SPueGt+pceX7H/HK/O587X5zP/tEeTkGDdNmMPT7y0iL8fIzTFyzcjNNfJycli3NofChjnk5BgTrzgAM+O+Nz5mxufLGXVmfwD++spHzFr0PTk5tuUc0aNkuXG9OlxzxJ4APPnuQtb8sJGz998NgCemfcHS4vVbHZuXYzHny2HnBnUYtGcLAN7+eCn18nN5Ycp7pQlMifWb4YUvcrnu1IGJ/QJEpHZr3Bh+/3u49FJo1y6su//+sP7EE9Mbm0gSJdKx/0Uz60xo7tWGkDAsAqa5+6YKD66aRUC7mOW2hAEEEtmnTgLHSgZoUDePPu2b0qd90222bdzsXHFIJ/p3CNvmfLWSix6dAUD9OrkUlY6QFibuLGrZiMKCHfvutLuz+oeNcROQVes20mmXhuzVYSfWrN/Ir575gGN6tWbQni34bOlqznhwKivXbqT4h41sKicD+dVRXejYoiFr129i/PtfcUDHZnRr3Zj6dXJp06QehQWNaFSQR2G9fBoV5NGoYMvPXzz5PkuKf9jmnK2b1GNY7zYc1Kk5m93ZuNnZVOaxcbOz2Z3dmzcA4OCi5jx4dn8a1wu/zyN7tGL35g227Lt52/Ns3Ow0rBu+wvp3aMrFB+9Rmuj2ateYjZs3b3296Ofib9ax884N2OReWouTa0ZeTA3gyrUb+WbVOjZu8rivYeNmZ+cGW5KYV+Z8w7LV60uTmIff/pw5i1dW+Lvt2bZxaRLz2+fn0rpJPb5asTbuvuWt3xFl67xkmuxSMk779uGnOzzyCLz1Ftx5J43OOAOy4CaeSGUS6m3t7puBKSmOZRrQycx2A74kzA9wapl9xgOXRX1e9ga+d/fFZrYkgWMlwzWsm8flg7dM6tW9TWOeu3T/qMYmzG8zcdZixr7zRek+bZrU408/6cU+u+/M8tXrWb5mPbvu3IDccmptarK/gbuzdkPZGpAtScjKtRto27Q+R/UM/YuuGPsee3Voyhn7dmDt+k3se9urrFy7gc2TJpV7jbP23ZW9OuxEXk4O73z2HXvtthMADQvy6L/rTlHCkUdhQX5MAhKSkMKCPHaJJjjdvXlDZt5wWOl5u7VuzANn9a/w9V1/VJet+sQA1MvP5arDi2hQN48GdRMfzKFNk3q0aVKvdLmoZSOKWjZK+Pj9OzZj/5hJX4f2bsPQ3vF/r6F2a+sOrxcctPtWyzcc0zXhawOlNTglxl+2P5t82wQqNhGK/YzedWof8nKMuYtX8mWchKV1zHuzI8vmeck02aVkLDOYPBkeegiuv55+F10E//1vaHKmpFuyWCKjk7VP8Fwr3L3iW48VcPeNZnYZMIkwTPKD7j7bzC6Ktt8HTCQMr7yAMMTyORUdu72xSGYoyM+lV7sm9GrXpHSdu/P1ynXMW7yKOYtXMu/rVexSGP4Rf3H211z79CzevGoQ7Xeuz38WLGXBt8WlAwq8/uG3VeqIvm7DJlau3bb2IyQkYblxvXzOPzD8A3z1U/+jUUEevzo6/AO8z62v8s3KbWsqYh2yZ4vSJOa71etZ9cPG6LXncGyv1nz3zVd0L9pjq1qQwpjnTerVAaBOXg5vXX1I6XmbNazLX07qXdW3vEpK3rPSpLBJPXVCj+Tl5iR2hyhSMsz5VYcXlZsY1hKal0wkFXJz4fzz4Sc/4YuLLqL9E0/AJZcoiZGslkg5+3AC+zgwBnikOsG4+0RCohK77r6Y5w5cmuixsuMxM1o1rkerxvVKm+KUOKBjM/54Qk/aNg13rSfN/ppH/rtlPIpcg01lWlWt3bCJP076kGF92vDb5+fw6dLVjD57LwBOHjWFmQtXVBAL9GzTuDSJqZufQ528nNLt5x2wGxs3e1QLklf6M7ZGpEHM0NOPnr93zLmNm4Z2Z/LkpQw8OHPn4BnWpw3D+rTJmj5Gma62J4Y1OS+ZSK1UWMgnw4fT/s47oVlUe33DDdC1axgAQCOGShZJJIm5EJgfJRAiGavdTvVpt1P90uXfHNuNSwd1ZG5UY3Pb/82Le1xJf4OWjQvYFPMxP++A3VixdkNU87F1f5DCKAGJHWzgpqHdtzqvJgCV7VGbE8OampdMpNYrSWDWr4eJE+Hmm+Guu8KIZnvtldbQRBKVSBLzNNDOzD4CZgH/K/np7ktSGZxIdZgZuxQWsEthAQOLWvCP/35eYX+DkhqVEsf0UjW7SA2rqXnJRASgTh2YOhXGjAnzywwYAGeeGUY3a9ky3dGJVCinsh3cvTvQAriEMGLMHsB1wCwz+zq14Ykkz1WHF1EvP3erdbWsv4FIpiuZl6ysZM9LJiIlcnPhvPPgo4/gmmtg/PhQQyOS4RIdnewHYJqZFbv75SXro6EwRbJCbe9vIJIFRlAz85KJSFmFhXDrraFGpmHDMDTzuefCoYfCKaeov4xknKoMoANlJpB09+VJjEUk5WpzfwORTFeD85KJSHkahtESWbEC3n8/NDUr6S+z994VHChSsyptTmZmd5vZeWbWh1CgiIiIpIS7b3b3Ke7+L3d/KnquBEakpjVtCtOmwYMPwmefwT77wBlnwNKl6Y5MBEisJuZ/QB/gTKCRmc0hdLCcA8xx9ydSGJ+IiNQSNTUvmYgkKDcXzjkHTjgBbrsNHn8c6tZNd1QiQAJJjLuPil02s7ZAT6AHcDSgJEZERJKhxuYlE5EqaNQIbrkFbrwxjGi2YQMceSScfXboL5NTacMekaSrap8Y3H0RoY2yJpYUEZFk0rxkIpmsTp3w85tvYPlyOP30Lf1l9tknraFJ7ZNIn5j2CT4KayJgERHZYT0NrDCzaWb2oJmNMLPBZtY83YFVxsyOMbNRxcXF6Q5FJPXatoV33oGHHoLPP4d994XTToOVauUpNSeRmhhV74uISMq5e3czq0tosjwRWE2Yn6ybmeHuGTv7nrtPACYUFRVdkO5YRGpETk5oTlbSX+bVV6FBg7DNXUMyS8ol0idmUE0EIiIionnJRLJMw4bw29/Cb34TBgJYvhwGDYKrrlJ/GUmphD5ZZranmV1tZnea2R3R8z1THZyIiNRampdMJJvk5oafS5ZAfn7oL7PffjBlSnrjkh1WIn1irgbGEeaIeQeYFj0fZ2bXpDY8ERGpLTQvmcgOoHNnmDoVHn4YvvhiS3+Z9evTHZnsYBLpE3Me0M3dN8SuNLM/E+aLuS0VgYmISK2jeclEdgQ5OXDmmXD88fCHP8D8+VtGNtu0aUutjUg1JNKcbDPQOs76VtE2ERGRanP3Ue5+mbsf7O7NgMOAh4A1hHnJRCSbNGwIN90UJsmEkMx07AiPPAKb9S+kVE8iNTEjgFfNbD6wMFrXHugIXJaiuEREpJbTvGQiO4iSkcrWrYPmzeGss+Duu8P8Mvvtl9bQJHslMjrZi2bWGRgAtCG0U14ETHP3TSmOT0REagkza5/grivcXRNSiGSbHj1CR//HHoNrroH994czzgj9ZzQks1RRpUmMmeW4+2Yg7vASMdtFRESqQ/OSiezocnJC4lLSX2b9+i0JzA8/QN266Y1PskYizcleNrOlwLPAC+6+0szqA0OA44DuhI6YIiIi203zkonUIg0ahLllSrz+ehiW+dZbw0+RSiTSnGywmXUFhgIvmFkdQof+ScBf3H1GimMUEZFaIpqDbCih+bIDXwHPufu8tAYmIqlVWAht24b+MnfdReGZZ8LAgemOSjJYQpNduvscd7/V3Q8EDnb3fd19pBIYERFJFs1LJlKL9esH//0v/OMfsHgxfa+4Ai6+ON1RSQZLpDlZWdeZWS4wE5jp7vOTG5KIiNRSmpdMpDbLyQlNyY47js8uvZQOvXuH9Zs3w5o1YchmkUhCNTGx3P0G4E5gFfBjM7s/6VGJiEhtpHnJRAQaNOCzs8+GCy8My488Ap07w5gxml9GSiUyOlkH4FJgD+A7Qg3MBHd/EXgxlcGJiEitMgLNSyYiZXXrBu3bwznnhPll/vIXOPDAdEclaZZITcxzwDzgHuBQoBfwppndY2YaB09ERJIiujnWGfgNYfCYl4CRQFG0TURqo732grffhkcfha+/hoMOgquuSndUkmaJ9InJdffRAGb2nbtfYGZ5wE+BUcBZqQxQRERqB81LJiLlysmB006DYcPg9tuhf/+wfs0a2LQJGjVKa3hS8xKpiXnFzEqq8R3A3Te6+x+BfZMRhJntZGYvm9n86GfTcvYbYmYfmtmC2JFqzOyPZjbPzP5nZs+YWZNkxCUiIjXqZTN7wsxOMbNCADOrb2bHm9k/gOk1GYyZdTGz+8zsKTPTMEkimaBBA7jxRjjqqLB8222hv8xDD6m/TC2TSBLzM6Cxmb0LtDGz4WZ2upndAyxLUhzXAK+6eyfg1Wh5K9GIaPcARwBdgVOi+WsAXga6u3tP4CPg2iTFJSIiNcTdBxOaknUgzEs2lVAm9CTMS5bwxMpm9qCZfWtmH5RZH/dmWDnxzHX3i4CfAP2r+HJEpCYcdRR06ADnnhuanb35ZrojkhpSaRLj7pvd/RbgIOACoCXQF/iAkFAkw1Dg4ej5w8CwOPsMABa4+yfuvp4wl8DQKMaX3H1jtN8UoG2S4hIRkRqUxHnJxgBDYleUdzPMzHqY2fNlHi2iY44F3iIkUyKSafbeO/SXefxxWLIEDj4Ybrkl3VFJDTB3r3yn0IH/l8B+QDEwA3jS3T9OShBmK9y9SczycndvWmafE4Ah7n5+tHwGsLe7X1ZmvwnAE+7+aDnXGg4MB2jevHm/J598MhkvIaWKi4tpmAVjo2dLnJA9sSrO5MuWWLMlzkGDBk1395TUUpjZTcB2z0sWja75vLt3j5b3BUa6++HR8rUA7n5rAud6wd2PKmebypUUyZY4IXti3ZHjzFm3jnZPPsnS/fZjdceO5H//PZvz89lUv36Kosye9xOyJ9aEyxV3r/RBmBfmAcLIZH8BbgfeAE5P5PjoHK8Qam/KPoYCK8rsuzzO8ScCD8QsnwHcVWaf64FniJKzyh6dO3f2bPD666+nO4SEZEuc7tkTq+JMvmyJNVviBN71BMuB7XkAuxBqVK4B7q/isR2AD2KWT4hTjtxdwfEDo/Lv78CliVxT5UpyZUuc7tkTa62K8/TT3XfZxX30aPeNG6t/vjiy5f10z55YEy1XEhmdjCh5GeruK8xsgLvvH9XOTAbi1njESZZ+VN42M/vGzFq5+2IzawV8G2e3RUC7mOW2wFcx5zgLOBoYHL0BIiKSRWpgXjKLs67c8sLdJxPKORHJRpdfDh9/DOedF+aX+etfw/DMskNIpGM/wB9j9l1qZn8mDK2crGEgxrNlqOazCHPTlDUN6GRmu5lZHeDk6DjMbAhwNXCsu69JUkwiIlKzUj0vWYU3w0RkBzNgAPznPzB2LCxdGvrL/O1v6Y5KkiShJMbdn3f376LFE4F3gYbR82S4DTg0mqX50GgZM2ttZhOjGDYSZmyeBMwl9MmZHR1/N9CIMDznTDO7L0lxiYhIzcl199Hu/irwnbtfQKiV+YwwL1l1lXszrLrM7BgzG1VcXJyM04lIspjBySfDhx+GDv/HHRfWf/oprFyZ3tikWhJtTlbKw8hgjyczCHdfBgyOs/4r4MiY5YnAxDj7dUxmPCIikhavmNll7n43MfOSAX80s4+qciIzG0vo09LMzBYBN7r76Gjes0mEAQMejLkZVi3uPgGYUFRUdEEyzidSGx15x7+ZszgmsXjxBQC6tipk4pUHVu/k9erBdddtWT7rrC2JzTnnQG5u9c4vNS7R5mQiIiKplrR5ydz9FHdv5e757t7W3UdH6ye6e2d338PD9AEikiH6tm9Cfu7WXdfyc42+u8adA716/vQn6NgRLrgA+vWDyZOTfw1JKSUxIiKSEbxm5iVLCTUnE6m+KwZ3Ise2TmJyzbhicAoa3Oy1F7z1FowbB8uXw6BB8MQTyb+OpIySGBERyRhRB/6fAxcDPYAlwEvuviKdcVXG3Se4+/BsmINBJFO1KCzgxH5tS2tj8nONE/q3o0WjgtRc0AxOOgnmzQs1M8ceG9a//776y2QBJTEiIpJJ/gjsSpgXZhGwM/CgmZ2e1qhEpEbE1sakrBamrHr14Gc/Cz83bYIf/xg6dYL77w/LkpGUxIiISCbpBfzC3d8HBrj7L4DDCPPHiMgOrqQ2xiC1tTDlyc0Nzco6d4bhw6FvX3j99ZqNQRKiJEZERDJJquclE5EMd8XgTnRqmlMztTDx9OsHb74JTz4J338PhxyiRCYDKYkREZGMUQPzkqWEOvaLJE+LwgKu27tezdfCxDKDE0+EuXNDs7KDDw7r33gjJDaSdkpiREQkI7n7end/3N3/HM0blrHUsV9kB1WvHpx/PuTkwOrVMGxY6C8zapT6y6SZkhgRERERkco0aACvvgp77gkXXgh9+9Jkxox0R1VrKYkREREREUlE376hSdlTT8HKlfT++c9hzpx0R1UrKYkRERGpJvWJEalFzMIwzHPn8sHNN0PXrmH900/DihVpDa02URIjIiJSTeoTI1ILFRSw9IADwvPFi+Hkk0N/mfvug40b0xtbLaAkRkRERESkOlq1gilTQq3MxRdDnz6h/4ykjJIYEREREZHq6tsXJk8O/WVWr4ajjoKvv053VDssJTEiIiIiIslQ0l9mzhyYNAlatgzrR41Sf5kkUxIjIiIiIpJMBQVbJsj84AO46CLo2BHuvVf9ZZJESYyIiEg1aXQyESlX9+4wY0b4eckl0Ls3vPxyuqPKekpiREREqkmjk4lIhXr3htdfD8Mwr10Lp50W+s3IdlMSIyIiIiKSamZw3HGhv8zLL0ODBqFp2e9+B8uXpzu6rKMkRkRERESkptStC716hedvvQW//nWYX+aee9RfpgqUxIiIiIiIpMPAgaG/TM+ecNllIbl56aV0R5UV8tIdgIiIiIhIrdWrV5gY87nn4Be/gJ/9DN5/H3Jzq33qI+/4N3MWr9yy4sUXAOjaqpCJVx5Y7fOnk2piRERERETSyQyGDYPZs2H8+JDAfP89XHtttfrL9G3fhPxc22pdfq7Rd9em1Qw4/ZTEiIiIVJOGWBaRpKhbF3bfPTx/5RX4wx/C/DLb2V/misGdyLGtk5hcM64Y3DEZ0aaVkhgREZFq0hDLIpJ0P/4xvPdeGJ65pL/MpElVOkWLwgJO7Ne2tDYmP9c4oX87WjQqSEHANUtJjIiIiIhIJurZM9TIPPccrF8Pd9xR5VPE1sbsKLUwoCRGRERERCRzmcGxx4b+MmPGhHWffgojRsB331V6eEltjMEOUwsDGZLEmNlOZvaymc2PfsbtbWRmQ8zsQzNbYGbXxNn+CzNzM2uW+qhFRERERGpInTrQokV4/tprcNddob/MXXfBhg0VHnrF4E50apqzw9TCQIYkMcA1wKvu3gl4NVreipnlAvcARwBdgVPMrGvM9nbAocAXNRKxiIiIiEg6nHcezJwJffvCFVeEZmcvvlju7i0KC7hu73o7TC0MZE4SMxR4OHr+MDAszj4DgAXu/om7rwfGRceV+AvwS8BTGKeIiIiISPr16AEvvxyGZN60CSZMSHdENSpTkphd3H0xQPSzRZx92gALY5YXResws2OBL939/VQHKiIiIiKSEczgmGPggw/gttvCuv/8By6/HJYtS29sKZZXUxcys1eAlnE2XZ/oKeKsczOrH53jsATjGA4MB2jevDmTJ09O8PLpU1xcrDiTLFtiVZzJly2xZkucIiKSAerUCQ+AqVPhb3+DRx+FkSPhkksgPz+t4aVCjSUx7v6j8raZ2Tdm1srdF5tZK+DbOLstAtrFLLcFvgL2AHYD3rcwfFxbYIaZDXD3r+PEMQoYBVBUVOQDBw7czldUcyZPnoziTK5siVVxJl+2xJotcUpgZscAx7Ru3TrdoYhIbfezn8Fhh8FPfxpGMLv33jA0c9266Y4sqTKlOdl44Kzo+VnAc3H2mQZ0MrPdzKwOcDIw3t1nuXsLd+/g7h0IyU7feAmMiIhIKmiySxHJKN27w0svhX4ymzeH5mY7mExJYm4DDjWz+YQRxm4DMLPWZjYRwN03ApcBk4C5wJPuPjtN8YqIiIiIZC4zOProkMBcfnm6o0m6GmtOVhF3XwYMjrP+K+DImOWJwMRKztUh2fGJiIiIiGSlkr4yO5hMqYkRERERERFJiJIYERERERHJKkpiREREREQkqyiJERERERGRrKIkRkREREREsoqSGBERERERySpKYkREREREJKsoiRERERERkayiJEZERERERLKKkhgREZFqMrNjzGxUcXFxukMREakVlMSIiIhUk7tPcPfhDRs2THcoIiK1gpIYERERERHJKkpiREREREQkqyiJERERERGRrKIkRkREREREsoqSGBERERERySpKYkREREREJKsoiRERERERkayiJEZERERERLKKkhgREREREckqSmJERERERCSrKIkREREREZGsoiRGRERERESyipIYERERERHJKkpiREREREQkqyiJERERERGRrKIkRkREREREsoqSGBERERERySoZkcSY2U5m9rKZzY9+Ni1nvyFm9qGZLTCza8psuzzaNtvM/lAzkYuIyI7MzBqY2XQzOzrdsYiIyBYZkcQA1wCvunsn4NVoeStmlgvcAxwBdAVOMbOu0bZBwFCgp7t3A26vqcBFRCTzmNmDZvatmX1QZn25N8PKcTXwZGqiFBGR7ZUpScxQ4OHo+cPAsDj7DAAWuPsn7r4eGBcdB3AxcJu7/wDg7t+mNlwREclwY4AhsSvKuxlmZj3M7PkyjxZm9iNgDvBNTQcvIiIVy0t3AJFd3H0xgLsvNrMWcfZpAyyMWV4E7B097wwcaGa3AOuAX7j7tHgXMrPhwPBo8Yeyd+kyVDNgabqDSEC2xAnZE6viTL5siTVb4ixKdwDxuPubZtahzOrSm2EAZjYOGOrutwLbNBeLavkbEBKetWY20d03x9lP5UrqZEuckD2xKs7kypY4IXtiTahcqbEkxsxeAVrG2XR9oqeIs86jn3lAU2AfYC/gSTPb3d19mwPcRwGjopjedff+CV4/bRRn8mVLrIoz+bIl1myKM90xVEFFN8O24e7XA5jZ2cDSeAlMtJ/KlRTJljghe2JVnMmVLXFC9sSaaLlSY0mMu/+ovG1m9o2ZtYpqYVoB8ZqDLQLaxSy3Bb6K2fZ0lLS8Y2abCdnmkuRELyIiO4CKboaVy93HJD8UERGpjkzpEzMeOCt6fhbwXJx9pgGdzGw3M6sDnBwdB/AscAiAmXUG6pAd1WUiIlJzKroZJiIiWSRTkpjbgEPNbD5waLSMmbU2s4kA7r4RuAyYBMwFnnT32dHxDwK7R+2QxwFnxWtKFseo5L6MlFGcyZctsSrO5MuWWBVn8lV0MyxZsuX9UJzJly2xKs7kypY4IXtiTShOS+x/fRERkexhZmOBgYSmxd8AN7r7aDM7EvgrkAs86O63pC1IERHZbkpiREREREQkq2RKczIREREREZGE1MokpryZnDONmbUzs9fNbK6ZzTazK9MdUzxmVmBm75jZ+1Gcv0l3TBUxs1wze8/Mnk93LBUxs8/MbJaZzczkYWzNrImZPWVm86LP6r7pjqksMyuK3seSx0ozG5HuuOIxs59Gf0cfmNlYMytId0zlMbMrozhnZ+r7WVNUriSXypXky5YyBVSuJFu2lCtVLVNqZXMyMzsIKAYecffu6Y6nPNFw063cfYaZNQKmA8PcfU6aQ9uKmRnQwN2LzSwfeAu40t2npDm0uMzsZ0B/oNDdt5ngLlOY2WdAf3fP6JH2zOxh4N/u/kDUWbq+u69Ic1jlsjBr+5fA3u7+ebrjiWVmbQh/P13dfa2ZPQlMzMQhfs2sO2EglQHAeuBF4GJ3n5/WwNJE5UpyqVxJvmwpU0DlSjJlS7myPWVKrayJcfc3ge/SHUdl3H2xu8+Inq8ijMrWJr1RbcuD4mgxP3pkZHZsZm2Bo4AH0h3LjsDMCoGDgNEA7r4+kwuayGDg40wraGLkAfXMLA+oT+YOAdwFmOLua6LRI98AjktzTGmjciW5VK7UXipXUiIbypUqlym1MonJRmbWAegDTE1zKHFFVekzCROVvuzuGRknYVSiXwJxZ97OMA68ZGbTzWx4uoMpx+6ESWUfippSPGBmDdIdVCVOBsamO4h43P1L4HbgC2Ax8L27v5TeqMr1AXCQme1sZvWBI9l6DhbJcCpXkuavZEe5kg1lCqhcSaosKleqXKYoickCZtYQ+Bcwwt1XpjueeNx9k7v3JkweNyCqFswoZnY08K27T093LAna3937AkcAl0bNVTJNHtAXuNfd+wCrgWvSG1L5omYJxwL/THcs8ZhZU2AosBvQGmhgZqenN6r43H0u8HvgZUK1//vAxrQGJQlTuZIcWVauZEOZAipXkipbypXtKVOUxGS4qC3wv4DH3P3pdMdTmajKdzIwJL2RxLU/cGzULngccIiZPZrekMrn7l9FP78FniG0E800i4BFMXdInyIUPpnqCGCGu3+T7kDK8SPgU3df4u4bgKeB/dIcU7ncfbS793X3gwhNqWplf5hso3IlqbKmXMmSMgVUriRb1pQrVS1TlMRksKhj42hgrrv/Od3xlMfMmptZk+h5PcIfzLy0BhWHu1/r7m3dvQOh6vc1d8+4uxEAZtYg6nRLVI1+GKGqNaO4+9fAQjMrilYNBjKqg3AZp5ChVf6RL4B9zKx+9Pc/mNBnISOZWYvoZ3vgeDL7vRVUriRbtpQr2VKmgMqVFMiacqWqZUpeTQSVaSxmJmczW0Q0k3N6o4prf+AMYFbULhjgOnefmL6Q4moFPByNzpEDPOnuGTvMZJbYBXgmfN+QBzzu7i+mN6RyXQ48FlWpfwKck+Z44ora2B4KXJjuWMrj7lPN7ClgBqEa/T1gVHqjqtC/zGxnYANwqbsvT3dA6aJyJelUriRXNpUpoHIlabKsXKlSmVIrh1gWEREREZHspeZkIiIiIiKSVZTEiIiIiIhIVlESIyIiIiIiWUVJjIiIiIiIZBUlMSIiIiIiklWUxIikgJm1NbPnzGy+mX1iZnebWd0EjisuZ/1NZvaj6PmIaFjHis5zuJmNNLOmZpZpQ6eKiEgVqVwR2ZqSGJEkiyaTehp41t07AZ2AesAftvec7n6Du78SLY4AKixsgAOBfwMHAf/Z3uuKiEj6qVwR2ZbmiRFJMjMbTJjo7qCYdYXA50A74ASgv7tfFm17Hrjd3SdHd8z+DgwClgMnu/sSMxsDPA+0Bm4HPgSWuvugMtc+CbgW2D263i7ASmCOux+bulctIiKponJFZFuqiRFJvm7A9NgV7r4S+AzoWMmxDYAZ7t4XeAO4scx57gS+AgaVLWii7U8AfYEP3L0H8AHQRwWNiEhWU7kiUoaSGJHkMyBeFaclcOxm4Ino+aPAAdtx/U7Ax9Hz+u6+ajvOISIimUPlikgZSmJEkm820D92RVTtvwuhun4jW//tFVRwriq19zSzd4FJwCAzmwMUmdlMMzuwKucREZGMonJFpAwlMSLJ9ypQ38zOBDCzXOBPwN3uvpZQ/d/bzHLMrB0wIObYHELbZoBTgbfinH8V0Cjehd29P/ACMJTQ4fN6d+/t7v+u9qsSEZF0UbkiUoaSGJEk8zBaxnHACWY2H1gGbHb3W6Jd/gN8CswidKacEXP4aqCbmU0HDgFuinOJUcD/mdnr5YTQF5hJGEnmjeq9GhERSTeVKyLb0uhkIilmZvsBY4Hj3X16ZfuLiIhUROWKiJIYERERERHJMmpOJiIiIiIiWUVJjIiIiIiIZBUlMSIiIiIiklWUxIiIiIiISFZREiMiIiIiIllFSYyIiIiIiGSV/wcKPnfrEyx0IgAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 960x288 with 2 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "grad = np.array(grad_val)\n",
-    "means = np.array(means)\n",
-    "variances = np.array(variances)\n",
-    "n = np.array(selected_qubit)\n",
-    "print(\"我们接着画出这个采样出来的梯度的统计结果：\")\n",
-    "fig = plt.figure(figsize=plt.figaspect(0.3))\n",
-    "\n",
-    "\n",
-    "# ============= 第一张图 =============\n",
-    "# 统计出随机采样的梯度平均值和量子比特数量的关系\n",
-    "plt.subplot(1, 2, 1)\n",
-    "plt.plot(n, means, \"o-.\")\n",
-    "plt.xlabel(r\"Qubit #\")\n",
-    "plt.ylabel(r\"$ \\partial \\theta_{i} \\langle 0|H |0\\rangle$ Mean\")\n",
-    "plt.title(\"Mean of {} sampled graident\".format(samples))\n",
-    "plt.xlim([1,9])\n",
-    "plt.ylim([-0.06, 0.06])\n",
-    "plt.grid()\n",
-    "\n",
-    "# ============= 第二张图 =============\n",
-    "# 统计出随机采样的梯度的方差和量子比特数量的关系\n",
-    "plt.subplot(1, 2, 2)\n",
-    "plt.semilogy(n, variances, \"v\")\n",
-    "\n",
-    "# 多项式拟合\n",
-    "fit = np.polyfit(n, np.log(variances), 1)\n",
-    "slope = fit[0] \n",
-    "intercept = fit[1] \n",
-    "plt.semilogy(n, np.exp(n*slope  + intercept), \"r--\", label=\"Slope {:03.4f}\".format(slope))\n",
-    "plt.xlabel(r\"Qubit #\")\n",
-    "plt.ylabel(r\"$ \\partial \\theta_{i} \\langle 0|H |0\\rangle$ Variance\")\n",
-    "plt.title(\"Variance of {} sampled graident\".format(samples))\n",
-    "plt.legend()\n",
-    "plt.xlim([1,9])\n",
-    "plt.ylim([0.0001, 0.1])\n",
-    "plt.grid()\n",
-    "\n",
-    "plt.show()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "要注意的是，在理论上，只有当我们选取的网络结构还有损失函数满足一定条件时 (2-design)详见论文 [[1]](https://arxiv.org/abs/1803.11173), 才会出现这种效应。接着我们不妨可视化一下不同量子比特数量对的优化曲面的影响：\n",
-    "\n",
-    "<img src=\"figures/qubit_landscape_compare.png\" width=\"1000\" >\n",
-    "\n",
-    "**图 1.** &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;\n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;\n",
-    "(a). 2-量子比特 \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;\n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;\n",
-    "(b). 4-量子比特 \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;\n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;\n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; \n",
-    "(c). 6-量子比特\n",
-    "\n",
-    "画图时 $\\theta_1$ 和 $\\theta_2$ 是前两个电路参数, 剩余参数全部固定为 $\\pi$。不然我们画不出这个高维度的流形。\n",
-    "结果不出所料，陡峭程度随着 $n$ 的增大越来越小了，**注意到 Z 轴尺度的极速减小**。相对于2量子比特的情况，6量子比特的优化曲面已经非常扁平了。\n",
-    "\n",
-    "<hr/>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 参考文献\n",
-    "\n",
-    "[1] [McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 9, 4812 (2018).](https://www.nature.com/articles/s41467-018-07090-4)\n",
-    "\n",
-    "\n",
-    "[2] [Cerezo, M., Sone, A., Volkoff, T., Cincio, L. & Coles, P. J. Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks. arXiv:2001.00550 (2020).](https://arxiv.org/abs/2001.00550)"
-   ]
-  }
- ],
- "metadata": {
-  "kernelspec": {
-   "display_name": "Python 3",
-   "language": "python",
-   "name": "python3"
-  },
-  "language_info": {
-   "codemirror_mode": {
-    "name": "ipython",
-    "version": 3
-   },
-   "file_extension": ".py",
-   "mimetype": "text/x-python",
-   "name": "python",
-   "nbconvert_exporter": "python",
-   "pygments_lexer": "ipython3",
-   "version": "3.6.10"
-  }
- },
- "nbformat": 4,
- "nbformat_minor": 4
-}

tutorial/Gibbs/GIBBS_Tutorial_CN.ipynb → tutorial/Gibbs/GibbsState_CN.ipynb

@@ -4,9 +4,14 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# 吉布斯态的制备 （Gibbs State Preparation）\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+    "# 吉布斯态的制备"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
    ]
   },
   {
@@ -14,28 +19,71 @@
    "metadata": {},
    "source": [
     "## 概览\n",
-    "- 在这个案例中，我们将展示如何通过Paddle Quantum训练量子神经网络来制备量子吉布斯态。\n",
     "\n",
-    "- 让我们通过下面几行代码引入必要的library和package。"
+    "在本案例中，我们将展示如何通过 Paddle Quantum 训练量子神经网络（quantum neural network, QNN）来制备量子吉布斯态。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 背景\n",
+    "\n",
+    "量子计算中的前沿方向包含量子机器学习和量子优化，在这两个方向中，特定量子态的制备是非常重要的问题。特别的，吉布斯态（Gibbs state）的制备是实现诸多量子算法所必须的步骤并且广泛应用于：\n",
+    "\n",
+    "- 量子机器学习中受限波尔兹曼机的学习 [1]\n",
+    "- 解决凸优化和半正定规划等优化问题 [2]\n",
+    "- 组合优化问题 [3]\n",
+    "\n",
+    "具体的吉布斯态定义如下：给定一个 $n$ 量子比特的哈密顿量 $H$（一般来说这是一个$2^n\\times2^n$的厄米矩阵），其在温度 $T$ 下的吉布斯态为 "
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "$$\n",
+    "\\rho_G = \\frac{{{e^{ - \\beta H}}}}{{\\text{tr}({e^{ - \\beta H}})}},\n",
+    "\\tag{1}\n",
+    "$$"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "其中 ${e^{ - \\beta H}}$ 是矩阵 $ - \\beta H$ 的矩阵指数，$\\beta  = \\frac{1}{{kT}}$ 是系统的逆温度参数，$T$ 是温度参数，$k$ 是玻尔兹曼常数 (这篇教程中我们取 $k = 1$)。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Paddle Quantum 实现"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "首先通过下面几行代码引入必要的 library 和 package。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 1,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:50.083834Z",
+     "start_time": "2021-01-09T10:26:46.286098Z"
     }
    },
    "outputs": [],
    "source": [
     "import scipy\n",
-    "\n",
     "from numpy import array, concatenate, zeros\n",
     "from numpy import pi as PI\n",
     "from numpy import trace as np_trace\n",
-    "\n",
     "from paddle import fluid\n",
     "from paddle.complex import matmul, trace\n",
     "from paddle_quantum.circuit import UAnsatz\n",
@@ -45,74 +93,57 @@
   },
   {
    "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "name": "#%% md\n"
-    }
-   },
+   "metadata": {},
    "source": [
-    "## 背景\n",
-    "\n",
-    "量子计算中的前沿方向包括量子机器学习和量子优化，在这两个方向中，特定量子态的制备是非常重要的问题。特别的，吉布斯态（Gibbs state）的制备是实现诸多量子算法所必须的一个步骤并且广泛应用于：\n",
-    "- 量子机器学习中受限波尔兹曼机的学习 [1]\n",
-    "- 解决凸优化和半正定规划等优化问题 [2]\n",
-    "- 组合优化问题 [3]\n",
+    "作为一个上手的例子，这里我们考虑一个 3 量子比特的哈密顿量及其吉布斯态：\n",
     "\n",
-    "具体的吉布斯态定义如下：给定一个 $n$ 量子位的哈密顿量 $H$（一般来说这是一个$2^n\\times2^n$的厄米矩阵），其在温度 $T$ 下的吉布斯态为 \n",
     "$$\n",
-    "\\rho_G = \\frac{{{e^{ - \\beta H}}}}{{tr({e^{ - \\beta H}})}}\n",
-    "$$\n",
-    "\n",
-    "其中 ${e^{ - \\beta H}}$ 是矩阵 $ - \\beta H$ 的矩阵指数，$\\beta  = \\frac{1}{{kT}}$ 是系统的逆温度参数，其中 $T$ 是温度参数，$k$ 是玻尔兹曼常数 (这个例子中我们取 $k = 1$)。作为一个上手的例子，这里我们首先考虑一个3量子比特的哈密顿量及其吉布斯态。\n",
-    "\n",
-    "$$\n",
-    "H = -Z \\otimes Z \\otimes I - I \\otimes Z \\otimes Z - Z \\otimes I \\otimes Z,\\,\n",
-    "I=\\left [\n",
+    "H = -Z \\otimes Z \\otimes I - I \\otimes Z \\otimes Z - Z \\otimes I \\otimes Z, \\quad I=\\left [\n",
     "\\begin{matrix}\n",
     "1 & 0  \\\\\n",
     "0 & 1  \\\\\n",
     "\\end{matrix} \n",
-    "\\right ],\n",
+    "\\right ], \\quad \n",
     "Z=\\left [\n",
     "\\begin{matrix}\n",
     "1 & 0  \\\\\n",
     "0 & -1  \\\\\n",
     "\\end{matrix} \n",
-    "\\right ].$$\n",
-    "\n",
+    "\\right ].\n",
+    "\\tag{2}\n",
+    "$$\n",
     "\n",
-    "这个例子中，我们将逆温度参数设置为 $\\beta = 1.5$。此外，为了方便测试结果，我们按照定义提前生成好了理想情况的吉布斯态。"
+    "这个例子中，我们将逆温度参数设置为 $\\beta = 1.5$。此外，为了方便测试结果，我们按照定义提前生成好了理想情况的吉布斯态 $\\rho_G$。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 2,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%% \n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:50.115012Z",
+     "start_time": "2021-01-09T10:26:50.087603Z"
     }
    },
    "outputs": [],
    "source": [
     "N = 4        # 量子神经网络的宽度\n",
     "N_SYS_B = 3  # 用于生成吉布斯态的子系统B的量子比特数   \n",
-    "SEED = 14    # 固定随机种子"
+    "SEED = 14    # 固定随机种子\n",
+    "beta = 1.5   # 设置逆温度参数 beta"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 3,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:50.142645Z",
+     "start_time": "2021-01-09T10:26:50.122554Z"
     }
    },
    "outputs": [],
    "source": [
-    "beta = 1.5   # 设置逆温度参数 beta\n",
-    "\n",
     "# 生成用泡利字符串表示的特定的哈密顿量\n",
     "H = [[-1.0, 'z0,z1'], [-1.0, 'z1,z2'], [-1.0, 'z0,z2']]\n",
     "\n",
@@ -131,42 +162,39 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 搭建量子神经网络\n",
-    "\n",
-    "- 在这个案例中，我们将通过训练量子神经网络QNN（也可以理解为参数化量子电路）来训练吉布斯态。这里，我们提供一个简单的4量子位的量子电路如下：\n",
-    "![Ugibbs.jpg](https://release-data.cdn.bcebos.com/PIC%2FUgibbs.jpg)\n",
-    "\n",
-    "- 我们需要预设一些电路的参数，比如电路有4量子比特，其中第1个量子位是辅助系统，第2-4个量子位是用以产生吉布斯态的子系统。\n",
-    "\n",
-    "- 初始化其中的变量参数，${\\bf{\\theta }}$ 代表我们量子神经网络中的参数组成的向量。\n",
-    "         "
+    "### 搭建量子神经网络"
    ]
   },
   {
    "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "name": "#%% md\n"
-    }
-   },
+   "metadata": {},
    "source": [
-    "接下来我们根据上图中的电路设计，通过 Paddle Quantum 的 `UAnsatz` 函数和内置的 `real_entangled_layer(theta, D)` 电路模板来高效搭建量子神经网络。      "
+    "- 在这个案例中，我们将通过训练量子神经网络（也可以理解为参数化量子电路）来制备吉布斯态。这里，我们提供一个简单的 4 量子比特的量子电路如下：\n",
+    "\n",
+    "  ![Ugibbs.jpg](https://release-data.cdn.bcebos.com/PIC%2FUgibbs.jpg)\n",
+    "\n",
+    "- 我们需要预设一些电路的参数，比如电路有 4 个量子比特，其中第 1 个量子比特是辅助系统，第 2-4 个量子比特是用以产生吉布斯态的子系统。\n",
+    "\n",
+    "- 初始化其中的变量参数，$\\theta$ 代表我们量子神经网络中的参数组成的向量。\n",
+    "         \n",
+    "\n",
+    "接下来我们根据上图中的电路设计，通过 Paddle Quantum 的 `UAnsatz` 类和内置的 `real_entangled_layer(theta, D)` 电路模板来高效搭建量子神经网络。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 4,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:50.162257Z",
+     "start_time": "2021-01-09T10:26:50.152881Z"
     }
    },
    "outputs": [],
    "source": [
     "def U_theta(initial_state, theta, N, D):\n",
     "    \"\"\"\n",
-    "    Quantum Neural Network\n",
+    "    量子神经网络\n",
     "    \"\"\"\n",
     "    \n",
     "    # 按照量子比特数量/网络宽度初始化量子神经网络\n",
@@ -175,7 +203,7 @@
     "    # 内置的 {R_y + CNOT} 电路模板\n",
     "    cir.real_entangled_layer(theta[:D], D)\n",
     "    \n",
-    "    # 铺上最后一列 R_y 旋转门\n",
+    "    # 铺上最后一层 R_y 旋转门\n",
     "    for i in range(N):\n",
     "        cir.ry(theta=theta[D][i][0], which_qubit=i)\n",
     "        \n",
@@ -187,45 +215,51 @@
   },
   {
    "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "name": "#%% md\n"
-    }
-   },
+   "metadata": {},
+   "source": [
+    "### 配置训练模型——损失函数"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
    "source": [
-    "## 配置训练模型 - 损失函数\n",
     "- 现在我们已经有了数据和量子神经网络的架构，我们将进一步定义合适的训练参数、模型和损失函数来达到我们的目标。\n",
-    "- 具体的我们参考的是论文[4]中的方法，核心思想是利用吉布斯态达到了最小自由能的性质。\n",
-    "- 通过作用量子神经网络 $U(\\theta)$ 在初始态上，我们可以得到输出态 $\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle $, 其在第2-4个量子位的态记为 $\\rho_B(\\theta)$。\n",
-    "- 设置训练模型中的的损失函数。在吉布斯态学习中，我们利用冯诺依曼熵函数的截断来进行自由能的估计，相应的损失函数参考[4]可以设为 \n",
-    "$loss= {L_1} + {L_2} + {L_3}$，其中 ${L_1}= tr(H\\rho_B)$, ${L_2} = 2{\\beta^{-1}}{tr}(\\rho_B^2)$ , $L_3 = - {\\beta ^{ - 1}}\\big(tr(\\rho_B^3) + 3\\big)/2$。"
+    "\n",
+    "- 具体的我们参考的是论文 [4] 中的方法，核心思想是**利用吉布斯态达到了最小自由能**的性质。\n",
+    "\n",
+    "- 通过作用量子神经网络 $U(\\theta)$ 在初始态上，我们可以得到输出态 $\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle $，其在第 2-4 个量子比特的态记为 $\\rho_B(\\theta)$。\n",
+    "\n",
+    "- 设置训练模型中的的损失函数。在吉布斯态学习中，我们利用冯诺依曼熵函数的截断来进行自由能的估计，相应的损失函数参考 [4] 可以设为 $loss= {L_1} + {L_2} + {L_3}$，其中 \n",
+    "\n",
+    "$$\n",
+    "{L_1}= \\text{tr}(H\\rho_B), \\quad {L_2} = 2{\\beta^{-1}}{\\text{tr}}(\\rho_B^2), \\quad L_3 = - {\\beta ^{ - 1}}\\big(\\text{tr}(\\rho_B^3) + 3\\big)/2.\n",
+    "\\tag{3}\n",
+    "$$"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 5,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:58.251869Z",
+     "start_time": "2021-01-09T10:26:58.241912Z"
     }
    },
    "outputs": [],
    "source": [
     "class Net(fluid.dygraph.Layer):\n",
-    "    \"\"\"\n",
-    "    Construct the model net\n",
-    "    \"\"\"\n",
-    "\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2*PI, seed=SEED),\n",
-    "                 dtype='float64'):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2*PI, seed=SEED), dtype='float64'):\n",
     "        super(Net, self).__init__()\n",
     "        \n",
     "        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.theta = self.create_parameter(shape=shape, \n",
+    "                     attr=param_attr, dtype=dtype, is_bias=False)\n",
     "        \n",
     "        # 初始化 rho = |0..0><0..0| 的密度矩阵\n",
-    "        self.initial_state = fluid.dygraph.to_variable(density_op(N))\n",
+    "        self.initial_state=fluid.dygraph.to_variable(density_op(N))\n",
     "\n",
     "    # 定义损失函数和前向传播机制\n",
     "    def forward(self, H, N, N_SYS_B, D):\n",
@@ -252,18 +286,23 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 配置训练模型 - 模型参数\n",
-    "\n",
-    "在进行量子神经网络的训练之前，我们还需要进行一些训练的超参数设置，主要是学习速率 (LR, learning rate)、迭代次数(ITR, iteration)和量子神经网络计算模块的深度 (D, Depth)。这里我们设定学习速率为0.5, 迭代次数为50次。读者不妨自行调整来直观感受下超参数调整对训练效果的影响。"
+    "### 配置训练模型——模型参数"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "在进行量子神经网络的训练之前，我们还需要进行一些训练的超参数设置，主要是学习速率（learning rate, LR）、迭代次数（iteration, ITR）和量子神经网络计算模块的深度（depth, D）。这里我们设定学习速率为 0.5，迭代次数为 50 次。读者不妨自行调整来直观感受下超参数调整对训练效果的影响。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 6,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:59.447344Z",
+     "start_time": "2021-01-09T10:26:59.431177Z"
     }
    },
    "outputs": [],
@@ -277,21 +316,26 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 进行训练\n",
-    "\n",
-    "- 当训练模型的各项参数都设置完成后，我们将数据转化为Paddle动态图中的变量，进而进行量子神经网络的训练。\n",
-    "- 训练过程中我们用的是[Adam Optimizer](https://www.paddlepaddle.org.cn/documentation/docs/zh/api_cn/optimizer_cn/AdagradOptimizer_cn.html)，也可以调用Paddle中提供的其他优化器。\n",
+    "### 进行训练"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "- 当训练模型的各项参数都设置完成后，我们将数据转化为 Paddle 动态图中的变量，进而进行量子神经网络的训练。\n",
+    "- 训练过程中我们用的是 [Adam Optimizer](https://www.paddlepaddle.org.cn/documentation/docs/zh/api_cn/optimizer_cn/AdagradOptimizer_cn.html)，也可以调用 Paddle 中提供的其他优化器。\n",
     "- 我们将训练过程中的结果依次输出。\n",
-    "- 特别的我们依次输出了我们学习到的量子态$\\rho_B(\\theta)$与吉布斯态$\\rho_G$的保真度，保真度越高说明QNN输出的态越接近于吉布斯态。\n"
+    "- 特别地，我们依次输出了我们学习到的量子态 $\\rho_B(\\theta)$ 与吉布斯态 $\\rho_G$ 的保真度，保真度越高说明QNN输出的态越接近于吉布斯态。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 7,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%% \n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:27:03.596048Z",
+     "start_time": "2021-01-09T10:27:00.320786Z"
     }
    },
    "outputs": [
@@ -299,15 +343,10 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "iter: 5 loss: -2.5615 fid: 0.8631\n",
       "iter: 10 loss: -3.1189 fid: 0.9504\n",
-      "iter: 15 loss: -3.3290 fid: 0.9732\n",
       "iter: 20 loss: -3.3502 fid: 0.9846\n",
-      "iter: 25 loss: -3.3446 fid: 0.9868\n",
       "iter: 30 loss: -3.3630 fid: 0.9873\n",
-      "iter: 35 loss: -3.3937 fid: 0.9916\n",
       "iter: 40 loss: -3.4087 fid: 0.9948\n",
-      "iter: 45 loss: -3.4108 fid: 0.9954\n",
       "iter: 50 loss: -3.4110 fid: 0.9953\n"
      ]
     }
@@ -322,8 +361,10 @@
     "    # 确定网络的参数维度\n",
     "    net = Net(shape=[D + 1, N, 1])\n",
     "\n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，\n",
+    "    # 当然你可以改成SGD或者是RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, \n",
+    "                          parameter_list=net.parameters())\n",
     "\n",
     "     # 优化循环\n",
     "    for itr in range(1, ITR + 1):\n",
@@ -341,31 +382,43 @@
     "        fid = state_fidelity(rho_B, rho_G)\n",
     "        \n",
     "        # 打印训练结果\n",
-    "        if itr % 5 == 0:\n",
-    "            print('iter:', itr, 'loss:', '%.4f' % loss.numpy(), 'fid:', '%.4f' % fid)"
+    "        if itr % 10 == 0:\n",
+    "            print('iter:', itr, 'loss:', '%.4f' % loss.numpy(), \n",
+    "                                 'fid:', '%.4f' % fid)"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 总结\n",
-    "根据上面训练得到的结果，通过大概50次迭代，我们就能达到高于99.5%保真度的高精度吉布斯态，高效并精确地完成了吉布斯态的制备。我们可以通过print函数来输出学习到的量子神经网络的参数和它的输出态。"
+    "## 总结"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 参考文献\n",
-    "\n",
-    "[1] [Kieferová, M. & Wiebe, N. Tomography and generative training with quantum Boltzmann machines. Phys. Rev. A 96, 062327 (2017).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.96.062327)\n",
+    "根据上面训练得到的结果，通过大概 50 次迭代，我们就能达到高于 99.5% 保真度的高精度吉布斯态，高效并精确地完成了吉布斯态的制备。我们可以通过 print 函数来输出学习到的量子神经网络的参数和它的输出态。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 参考文献"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "[1] Kieferová, M. & Wiebe, N. Tomography and generative training with quantum Boltzmann machines. [Phys. Rev. A 96, 062327 (2017).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.96.062327)\n",
     "\n",
-    "[2] [Brandao, F. G. S. L. & Svore, K. M. Quantum Speed-Ups for Solving Semidefinite Programs. in 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS) 415–426 (IEEE, 2017). ](https://ieeexplore.ieee.org/abstract/document/8104077)\n",
+    "[2] Brandao, F. G. S. L. & Svore, K. M. Quantum Speed-Ups for Solving Semidefinite Programs. [in 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS) 415–426 (IEEE, 2017). ](https://ieeexplore.ieee.org/abstract/document/8104077)\n",
     "\n",
-    "[3] [Somma, R. D., Boixo, S., Barnum, H. & Knill, E. Quantum Simulations of Classical Annealing Processes. Phys. Rev. Lett. 101, 130504 (2008).](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.101.130504)\n",
+    "[3] Somma, R. D., Boixo, S., Barnum, H. & Knill, E. Quantum Simulations of Classical Annealing Processes. [Phys. Rev. Lett. 101, 130504 (2008).](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.101.130504)\n",
     "\n",
-    "[4] [Wang, Y., Li, G. & Wang, X. Variational quantum Gibbs state preparation with a truncated Taylor series. arXiv:2005.08797 (2020).](https://arxiv.org/pdf/2005.08797.pdf)"
+    "[4] Wang, Y., Li, G. & Wang, X. Variational quantum Gibbs state preparation with a truncated Taylor series. [arXiv:2005.08797 (2020).](https://arxiv.org/pdf/2005.08797.pdf)"
    ]
   }
  ],
@@ -385,9 +438,22 @@
    "name": "python",
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
-   "version": "3.7.7"
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
   }
  },
  "nbformat": 4,
- "nbformat_minor": 1
+ "nbformat_minor": 4
 }

tutorial/Gibbs/GibbsState_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Gibbs State Preparation"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Overview"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "This tutorial will show how to train a quantum neural network (QNN) through Paddle Quantum to prepare a quantum Gibbs state.\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Background"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "The frontiers of quantum computing include quantum machine learning and quantum optimization. In these two areas, the preparation of specific quantum states is a fundamental problem. In particular, the preparation of Gibbs state is a necessary step to realize many quantum algorithms and is widely used in:\n",
+    "- Learning of restricted Boltzmann machines in quantum machine learning [1]\n",
+    "- Solving optimization problems such as convex optimization and positive semidefinite programming [2]\n",
+    "- Combinatorial optimization problem [3]\n",
+    "\n",
+    "The Gibbs state is defined as follows: Given the Hamiltonian $H$ of an $n$-qubit system (generally this is a Hermitian matrix of $2^n\\times2^n$), the Gibbs state at temperature $T$ is\n",
+    "$$\n",
+    "\\rho_G = \\frac{{{e^{-\\beta H}}}}{{\\text{tr}({e^{-\\beta H}})}},\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "where ${e^{-\\beta H}}$ is the matrix exponential of matrix $-\\beta H$. $\\beta = \\frac{1}{{kT}}$ is the inverse temperature parameter of the system, where $T $ Is the temperature parameter and $k$ is Boltzmann's constant (in this tutorial, we take $k = 1$)."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Paddle Quantum Implementation"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "First, let us import the necessary libraries and packages through the following code."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:18.115601Z",
+     "start_time": "2021-01-09T10:26:14.563581Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import scipy\n",
+    "from numpy import array, concatenate, zeros\n",
+    "from numpy import pi as PI\n",
+    "from numpy import trace as np_trace\n",
+    "from paddle import fluid\n",
+    "from paddle.complex import matmul, trace\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.state import density_op\n",
+    "from paddle_quantum.utils import state_fidelity, partial_trace, pauli_str_to_matrix"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "As a hands-on example, here we consider a 3-qubit Hamiltonian and its Gibbs state:\n",
+    "\n",
+    "$$\n",
+    "H = -Z \\otimes Z \\otimes I - I \\otimes Z \\otimes Z - Z \\otimes I \\otimes Z, \\quad I=\\left [\n",
+    "\\begin{matrix}\n",
+    "1 & 0  \\\\\n",
+    "0 & 1  \\\\\n",
+    "\\end{matrix} \n",
+    "\\right ], \\quad \n",
+    "Z=\\left [\n",
+    "\\begin{matrix}\n",
+    "1 & 0  \\\\\n",
+    "0 & -1  \\\\\n",
+    "\\end{matrix} \n",
+    "\\right ].\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "In this example, we set the inverse temperature parameter to $\\beta = 1.5$. Besides, to test the final results, we have generated the ideal Gibbs state $\\rho_G$ in advance according to the definition."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:18.156435Z",
+     "start_time": "2021-01-09T10:26:18.118621Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "N = 4        # The width of the QNN\n",
+    "N_SYS_B = 3  # The number of qubits of subsystem B used to generate the Gibbs state\n",
+    "SEED = 14    # Fixed random seed\n",
+    "beta = 1.5   # Set the inverse temperature parameter beta"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:18.185219Z",
+     "start_time": "2021-01-09T10:26:18.161336Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Generate a specific Hamiltonian represented by a Pauli string\n",
+    "H = [[-1.0,'z0,z1'], [-1.0,'z1,z2'], [-1.0,'z0,z2']]\n",
+    "\n",
+    "# Generate matrix information of Hamiltonian\n",
+    "hamiltonian = pauli_str_to_matrix(H, N_SYS_B)\n",
+    "\n",
+    "# Generate the ideal target Gibbs state rho\n",
+    "rho_G = scipy.linalg.expm(-1 * beta * hamiltonian) / np_trace(scipy.linalg.expm(-1 * beta * hamiltonian))\n",
+    "\n",
+    "# Set to the data type supported by Paddle Quantum\n",
+    "hamiltonian = hamiltonian.astype(\"complex128\")\n",
+    "rho_G = rho_G.astype(\"complex128\")"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Building a quantum neural network"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "- In this example, we will prepare the Gibbs state by training the QNN (also can be understood as a parameterized quantum circuit). Here, we provide a simple 4-qubit quantum circuit as follows:\n",
+    "\n",
+    "  ![Ugibbs.jpg](https://release-data.cdn.bcebos.com/PIC%2FUgibbs.jpg)\n",
+    "\n",
+    "- We need to preset some circuit parameters. For example, the circuit has 4 qubits. The first qubit is the ancillary system, and the 2-4th qubits are the subsystems used to generate the Gibbs state.\n",
+    "- Initialize the variable ${\\bf{\\theta }}$ that represents the vector of parameters in our QNN.\n",
+    "         \n",
+    "\n",
+    "Next, we use Paddle Quantum's `UAnsatz` class and the built-in `real_entangled_layer(theta, D)` circuit template to build a QNN based on the circuit design in the above figure."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:18.202627Z",
+     "start_time": "2021-01-09T10:26:18.188216Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def U_theta(initial_state, theta, N, D):\n",
+    "    \"\"\"\n",
+    "    Quantum Neural Network\n",
+    "    \"\"\"\n",
+    "    \n",
+    "    # Initialize the QNN according to the number of qubits/network width\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Built-in {R_y + CNOT} circuit template\n",
+    "    cir.real_entangled_layer(theta[:D], D)\n",
+    "    \n",
+    "    # Add the last layer of R_y rotation gates\n",
+    "    for i in range(N):\n",
+    "        cir.ry(theta=theta[D][i][0], which_qubit=i)\n",
+    "        \n",
+    "    # The QNN acts on a given initial state\n",
+    "    final_state = cir.run_density_matrix(initial_state)\n",
+    "\n",
+    "    return final_state"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Configuring the training model: loss function"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "- Now that we have the data and QNN architecture, we also need to define appropriate training parameters, models, and loss functions to achieve our goals.\n",
+    "\n",
+    "- Specifically, we refer to the method in the paper [4]. The core idea is to use the Gibbs state to achieve the minimum free energy.\n",
+    "\n",
+    "- By applying the QNN $U(\\theta)$ on the initial state, we can get the output state $\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle $. Its state in the 2-4th qubits is recorded as $\\rho_B(\\theta)$.\n",
+    "\n",
+    "- Set the loss function in the training model. In Gibbs state learning, we use the truncation of the von Neumann entropy function to estimate the free energy, and the corresponding loss function, as in reference [4], can be set as $loss = {L_1} + {L_2} + {L_3} $, where\n",
+    "\n",
+    "$$\n",
+    "{L_1}= \\text{tr}(H\\rho_B), \\quad {L_2} = 2{\\beta^{-1}}{\\text{tr}}(\\rho_B^2), \\quad L_3 = - {\\beta ^{ - 1}}\\big(\\text{tr}(\\rho_B^3) + 3\\big)/2.\n",
+    "\\tag{3}\n",
+    "$$"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:18.589450Z",
+     "start_time": "2021-01-09T10:26:18.574464Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class Net(fluid.dygraph.Layer):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2*PI, seed=SEED), dtype='float64'):\n",
+    "        super(Net, self).__init__()\n",
+    "        \n",
+    "        # Initialize parameters theta with the uniform distribution of [0, 2*pi]\n",
+    "        self.theta = self.create_parameter(shape=shape,\n",
+    "                     attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        \n",
+    "        # Initialize the density matrix rho = |0..0><0..0|\n",
+    "        self.initial_state=fluid.dygraph.to_variable(density_op(N))\n",
+    "\n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self, H, N, N_SYS_B, D):\n",
+    "\n",
+    "        # Apply QNN\n",
+    "        rho_AB = U_theta(self.initial_state, self.theta, N, D)\n",
+    "\n",
+    "        # Calculate partial trace to obtain the quantum state rho_B of subsystem B\n",
+    "        rho_B = partial_trace(rho_AB, 2 ** (N-N_SYS_B), 2 ** (N_SYS_B), 1)\n",
+    "        \n",
+    "        # Calculate the three parts of the loss function\n",
+    "        rho_B_squre = matmul(rho_B, rho_B)\n",
+    "        loss1 = (trace(matmul(rho_B, H))).real\n",
+    "        loss2 = (trace(rho_B_squre)).real * 2 / beta\n",
+    "        loss3 =-((trace(matmul(rho_B_squre, rho_B))).real + 3) / (2 * beta)\n",
+    "        \n",
+    "        # Final loss function\n",
+    "        loss = loss1 + loss2 + loss3\n",
+    "\n",
+    "        return loss, rho_B"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Configure training model: model parameters"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Before training the QNN, we also need to set some training hyperparameters, mainly the learning rate (LR), the number of iterations (ITR), and the depth (D) of the QNN. Here we set the learning rate to 0.5 and the number of iterations to 50. Readers may wish to adjust by themselves to explore the influence of hyperparameter adjustment on the training effect."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:20.193223Z",
+     "start_time": "2021-01-09T10:26:20.180849Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "ITR = 50 # Set the total number of iterations of training\n",
+    "LR = 0.5 # Set the learning rate\n",
+    "D = 1 # Set the depth of the QNN"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Training"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "- After all the training model parameters are set, we convert the data into variables in the PaddlePaddle dynamic graph and then train the QNN.\n",
+    "- During training, we use [Adam Optimizer](https://www.paddlepaddle.org.cn/documentation/docs/en/api/optimizer/AdamOptimizer.html). Other optimizers are also provided in PaddlePaddle.\n",
+    "- We output the results of the training process in turn.\n",
+    "- In particular, we sequentially output the fidelity of the quantum state $\\rho_B(\\theta)$ and Gibbs state $\\rho_G$ we learned. The higher the fidelity, the closer the QNN output state is to Gibbs state."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:26:24.585128Z",
+     "start_time": "2021-01-09T10:26:21.249352Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 10 loss: -3.1189 fid: 0.9504\n",
+      "iter: 20 loss: -3.3502 fid: 0.9846\n",
+      "iter: 30 loss: -3.3630 fid: 0.9873\n",
+      "iter: 40 loss: -3.4087 fid: 0.9948\n",
+      "iter: 50 loss: -3.4110 fid: 0.9953\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Initialize PaddlePaddle dynamic graph mechanism\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # Convert Numpy array to variable supported in PaddlePaddle dynamic graph mode\n",
+    "    H = fluid.dygraph.to_variable(hamiltonian)\n",
+    "\n",
+    "    # Determine the parameter dimension of the network\n",
+    "    net = Net(shape=[D + 1, N, 1])\n",
+    "\n",
+    "    # Generally speaking, we use Adam optimizer to get relatively good convergence\n",
+    "    # Of course, it can be changed to SGD or RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR,\n",
+    "                          parameter_list=net.parameters())\n",
+    "\n",
+    "     # Optimization loops\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "        \n",
+    "        # Run forward propagation to calculate the loss function and return the generated quantum state rho_B\n",
+    "        loss, rho_B = net(H, N, N_SYS_B, D)\n",
+    "        \n",
+    "        # Under the dynamic graph mechanism, run back propagation to minimize the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "\n",
+    "        # Convert to Numpy array to calculate the fidelity of the quantum state F(rho_B, rho_G)\n",
+    "        rho_B = rho_B.numpy()\n",
+    "        fid = state_fidelity(rho_B, rho_G)\n",
+    "        \n",
+    "        # Print training results\n",
+    "        if itr% 10 == 0:\n",
+    "            print('iter:', itr,'loss:','%.4f'% loss.numpy(),\n",
+    "                                 'fid:','%.4f'% fid)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Conclusion"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "According to the results obtained from the above training, after about 50 iterations, we can achieve a high-precision Gibbs state with a fidelity higher than 99.5% and complete the preparation of the Gibbs state efficiently and accurately. We can output the QNN's learned parameters and its output state through the print function."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## References"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "[1] Kieferová, M. & Wiebe, N. Tomography and generative training with quantum Boltzmann machines. [Phys. Rev. A 96, 062327 (2017).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.96.062327)\n",
+    "\n",
+    "[2] Brandao, F. G. S. L. & Svore, K. M. Quantum Speed-Ups for Solving Semidefinite Programs. [in 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS) 415–426 (IEEE, 2017). ](https://ieeexplore.ieee.org/abstract/document/8104077)\n",
+    "\n",
+    "[3] Somma, R. D., Boixo, S., Barnum, H. & Knill, E. Quantum Simulations of Classical Annealing Processes. [Phys. Rev. Lett. 101, 130504 (2008).](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.101.130504)\n",
+    "\n",
+    "[4] Wang, Y., Li, G. & Wang, X. Variational quantum Gibbs state preparation with a truncated Taylor series. [arXiv:2005.08797 (2020).](https://arxiv.org/pdf/2005.08797.pdf)"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/Q-Autoencoder/Quantum_Autoencoder_Tutorial_CN.ipynb → tutorial/Q-Autoencoder/Q-Autoencoder_CN.ipynb

@@ -4,36 +4,60 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# 量子变分自编码器 （Quantum Autoencoder）\n",
-    "\n",
-    "<em> Copyright (c) Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>\n",
+    "# 量子变分自编码器\n",
     "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "## 概览\n",
     "\n",
-    "在这个案例中，我们将展示如何训练量子自编码器来压缩和重建给定的量子态（混合态）[1]。量子自编码器的形式与经典自编码器非常相似，同样由编码器 $E$（encoder）和解码器 $D$（decoder）组成。对于输入的 $N$ 量子比特系统的量子态 $\\rho_{in}$（这里我们采用量子力学的密度算符表示来描述混合态），先用编码器 $E = U(\\theta)$ 将信息编码到其中的部分量子比特上。这部分量子比特记为**系统 $A$**。对剩余的量子比特 （这部分记为**系统 $B$**）进行测量并丢弃后，我们就得到了压缩后的量子态 $\\rho_{encode}$！压缩后的量子态维度和量子系统 $A$ 的维度大小保持一致。假设我们需要 $N_A$ 个量子比特来描述系统 $A$ ，那么编码后量子态 $\\rho_{encode}$ 的维度就是 $2^{N_A}\\times 2^{N_A}$。 这里比较特殊的是, 对应我们这一步测量并丢弃的操作的数学操作是 partial trace。读者在直观上可以理解为张量积 $\\otimes$ 的逆运算。\n",
+    "在这个案例中，我们将展示如何训练量子自编码器来压缩和重建给定的量子态（混合态）[1]。\n",
+    "\n",
+    "### 原理\n",
+    "\n",
+    "量子自编码器的形式与经典自编码器非常相似，同样由编码器 $E$（encoder）和解码器 $D$（decoder）组成。对于输入的 $N$ 量子比特系统的量子态 $\\rho_{in}$（这里我们采用量子力学的密度算符表示来描述混合态），先用编码器 $E = U(\\theta)$ 将信息编码到其中的部分量子比特上。这部分量子比特记为**系统 $A$**。对剩余的量子比特 （这部分记为**系统 $B$**）进行测量并丢弃后，我们就得到了压缩后的量子态 $\\rho_{encode}$！压缩后的量子态维度和量子系统 $A$ 的维度大小保持一致。假设我们需要 $N_A$ 个量子比特来描述系统 $A$ ，那么编码后量子态 $\\rho_{encode}$ 的维度就是 $2^{N_A}\\times 2^{N_A}$。 这里比较特殊的是, 对应我们这一步测量并丢弃的操作的数学操作是 partial trace。读者在直观上可以理解为张量积 $\\otimes$ 的逆运算。\n",
     "\n",
-    "我们不妨来看一个具体的例子来理解：\n",
-    "给定一个由 $N_A$ 个量子比特描述的量子态 $\\rho_A$ 和另外一个由 $N_B$ 个量子比特描述的量子态 $\\rho_B$, 那么由 $A、B$ 两个子系统构成的的整体量子系统 $N = N_A+ N_B$ 的量子态就可以描述为: $\\rho_{AB} = \\rho_A \\otimes \\rho_B$。现在我们让整个量子系统在酉矩阵 $U$ 的作用下演化一段时间后，得到了一个新的量子态 $\\tilde{\\rho_{AB}} = U\\rho_{AB}U^\\dagger$。 那么如果这时候我们只想得到量子子系统 $A$ 所处于的新的量子态 $\\tilde{\\rho_A}$， 我们该怎么做呢？很简单，只需要测量量子子系统 $B$ 然后丢弃测量结果。运算上这一步由 partial trace 来完成 $\\tilde{\\rho_A} = \\text{Tr}_B (\\tilde{\\rho_{AB}})$。在量桨上，我们可以用内置的 `partial_trace(rho_AB, 2**N_A, 2**N_B, 2)` 指令来完成这一运算。**注意：** 其中最后一个输入为2，表示我们想丢弃量子系统 $B$ 的量子态。\n",
+    "我们不妨看一个具体的例子来理解。给定 $N_A$ 个量子比特上的一个量子态 $\\rho_A$ 和 $N_B$ 个量子比特上的一个量子态 $\\rho_B$, 那么由 $A、B$ 两个子系统构成的的整体量子系统 $N = N_A+ N_B$ 的量子态就可以描述为: $\\rho_{AB} = \\rho_A \\otimes \\rho_B$。现在我们让整个量子系统在酉矩阵 $U$ 的作用下演化一段时间后，得到了一个新的量子态 $\\tilde{\\rho_{AB}} = U\\rho_{AB}U^\\dagger$。 那么如果这时候我们只想得到量子子系统 A 所处于的新的量子态 $\\tilde{\\rho_A}$， 我们该怎么做呢？很简单，只需要测量量子子系统 $B$ 然后将其丢弃。运算上这一步由 partial trace 来完成 $\\tilde{\\rho_A} = \\text{Tr}_B (\\tilde{\\rho_{AB}})$。在量桨上，我们可以用内置的 `partial_trace(rho_AB, 2**N_A, 2**N_B, 2)` 指令来完成这一运算。**注意：** 其中最后一个参数为 2，表示我们想丢弃量子系统 $B$ 的量子态。\n",
     "\n",
-    "<img src=\"figures/encoder_pipeline.png\" width=\"950\" >\n",
+    "![QA-fig-encoder_pipeline](./figures/QA-fig-encoder_pipeline.png \"**图 1.** 量子变分自编码器流程图\")\n",
     "\n",
-    "在讨论完编码的过程后，我们来看看如何解码。为了解码量子态 $\\rho_{encode}$，我们需要引入与系统 $B$ 维度相同的系统 $C$ 并且初始态取为全0态。再用解码器 $D = U^\\dagger(\\theta)$ 作用在整个量子系统 $A+C$ 上对系统 $A$ 中压缩的信息进行解码。我们希望最后得到的量子态 $\\rho_{out}$ 与 $\\rho_{in}$ 尽可能相似并用 Uhlmann-Josza 保真度 $F$ （Fidelity）来衡量他们之间的相似度。\n",
+    "在讨论完编码的过程后，我们来看看如何解码。为了解码量子态 $\\rho_{encode}$，我们需要引入与系统 $B$ 维度相同的系统 $C$ 并且初始态取为 $|0\\dots0\\rangle$ 态。再用解码器 $D = U^\\dagger(\\theta)$ 作用在整个量子系统 $A+C$ 上对系统 A 中压缩的信息进行解码。我们希望最后得到的量子态 $\\rho_{out}$ 与 $\\rho_{in}$ 尽可能相似并用 Uhlmann-Josza 保真度 $F$ （Fidelity）来衡量他们之间的相似度。\n",
+    "\n",
+    "$$\n",
+    "F(\\rho_{in}, \\rho_{out}) = \\left(\\operatorname{tr} \\sqrt{\\sqrt{\\rho_{in}} \\rho_{out} \\sqrt{\\rho_{in}}} \\right)^{2}.\n",
+    "\\tag{1}\n",
+    "$$\n",
     "\n",
-    "$$ F(\\rho_{in}, \\rho_{out}) = \\left(\\operatorname{tr} \\sqrt{\\sqrt{\\rho_{in}} \\rho_{out} \\sqrt{\\rho_{in}}} \\right)^{2}$$\n",
+    "最后，通过优化编码器里的参数，我们就可以尽可能地提高 $\\rho_{in}$ 与 $\\rho_{out}$ 的保真度。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Paddle Quantum 实现\n",
     "\n",
-    "最后，通过优化编码器里的参数，我们就可以尽可能地提高 $\\rho_{in}$ 与 $\\rho_{out}$ 的保真度。这里我们先引入必要的 package。"
+    "下面我们通过一个简单的例子来展示量子自编码器的工作流程和原理。这里我们先引入必要的 package。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 1,
-   "metadata": {},
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:17:21.098395Z",
+     "start_time": "2021-01-09T09:17:20.543481Z"
+    }
+   },
    "outputs": [],
    "source": [
     "import numpy as np\n",
     "from numpy import diag\n",
     "import scipy\n",
-    "\n",
     "import paddle\n",
     "from paddle import fluid\n",
     "from paddle_quantum.circuit import UAnsatz\n",
@@ -45,19 +69,19 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 生成初始态\n",
-    "\n",
-    "下面我们通过一个简单的例子来展示量子自编码器的工作流程和原理。\n",
+    "### 生成初始态\n",
     "\n",
-    "我们考虑 $N = 3$ 个量子比特上的量子态 $\\rho_{in}$。我们先通过编码器将其信息编码到下方的两个量子比特（系统 $A$），之后对第一个量子比特（系统 $B$）测量并丢弃，之后引入一个处于0态的量子比特（新的参考系统 $C$）来替代丢弃的量子比特 $B$ 的维度。最后通过解码器，将 $A$ 中压缩的信息复原成 $\\rho_{out}$。在这里，我们假设初态是一个混合态并且 $\\rho_{in}$ 的特征谱为 $\\lambda_i \\in \\{0.4， 0.2， 0.2， 0.1， 0.1, \\,0, \\,0, \\,0 \\}$，然后通过作用一个随机的酉变换来生成初态 $\\rho_{in}$。\n",
-    "\n"
+    "我们考虑 $N = 3$ 个量子比特上的量子态 $\\rho_{in}$。我们先通过编码器将其信息编码到下方的两个量子比特（系统 $A$），之后对第一个量子比特（系统 $B$）测量并丢弃，之后引入一个处于 $|0\\rangle$ 态的量子比特（新的参考系统 $C$）来替代丢弃的量子比特 $B$ 的维度。最后通过解码器，将 A 中压缩的信息复原成 $\\rho_{out}$。在这里，我们假设初态是一个混合态并且 $\\rho_{in}$ 的本征谱为 $\\lambda_i \\in \\{0.4， 0.2， 0.2， 0.1， 0.1, \\,0, \\,0, \\,0 \\}$，然后通过作用一个随机的酉变换来生成初态 $\\rho_{in}$。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 2,
    "metadata": {
-    "scrolled": true
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:17:37.603403Z",
+     "start_time": "2021-01-09T09:17:37.590987Z"
+    }
    },
    "outputs": [],
    "source": [
@@ -69,9 +93,9 @@
     "V = scipy.stats.unitary_group.rvs(2**N)         # 随机生成一个酉矩阵\n",
     "D = diag([0.4, 0.2, 0.2, 0.1, 0.1, 0, 0, 0])    # 输入目标态rho的谱\n",
     "V_H = V.conj().T                                # 进行厄尔米特转置\n",
-    "rho_in = (V @ D @ V_H).astype('complex128')      # 生成 rho_in\n",
+    "rho_in = (V @ D @ V_H).astype('complex128')     # 生成 rho_in\n",
     "\n",
-    "# 将 C 量子系统初始化为\n",
+    "# 初始化量子系统 C\n",
     "rho_C = np.diag([1,0]).astype('complex128')"
    ]
   },
@@ -79,15 +103,21 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 搭建量子神经网络\n",
+    "### 搭建量子神经网络\n",
     "\n",
-    "在这里，我们用量子神经网络来作为编码器和解码器。假设系统 $A$ 有 $N_A$ 个量子比特，系统 $B$ 和 $C$ 分别有$N_B$ 个量子比特，量子神经网络的深度为 D。编码器 $E$ 作用在系统 $A$ 和 $B$ 共同构成的总系统上，解码器 $D$ 作用在$A$ 和 $C$ 共同构成的总系统上。在我们的问题里，$N_{A} = 2$，$N_{B} = 1$。"
+    "在这里，我们用量子神经网络来作为编码器和解码器。假设系统 A 有 $N_A$ 个量子比特，系统 $B$ 和 $C$ 各有$N_B$ 个量子比特，量子神经网络的深度为 $D$。编码器 $E$ 作用在系统 A 和 B 共同构成的总系统上，解码器 $D$ 作用在 $A$ 和 $C$ 共同构成的总系统上。在我们的问题里，$N_{A} = 2$，$N_{B} = 1$。\n",
+    "\n"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 3,
-   "metadata": {},
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:17:54.275730Z",
+     "start_time": "2021-01-09T09:17:54.266539Z"
+    }
+   },
    "outputs": [],
    "source": [
     "# 设置电路参数\n",
@@ -120,38 +150,42 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 配置训练模型-损失函数\n",
+    "### 配置训练模型——损失函数\n",
     "\n",
     "在这里，我们定义的损失函数为 \n",
     "\n",
     "$$\n",
-    "Loss = 1 - \\langle 0...0|\\rho_{trash}|0...0\\rangle\n",
+    "Loss = 1 - \\langle 0...0|\\rho_{trash}|0...0\\rangle,\n",
+    "\\tag{2}\n",
     "$$\n",
     "\n",
-    "其中 $\\rho_{trash}$ 是经过编码后丢弃的 $B$ 系统的量子态。接着我们通过飞桨的自动微分框架来训练量子神经网络，最小化损失函数。如果损失函数最后达到 0，则输入态和输出态完全相同。这就意味着我们完美地实现了压缩和解压缩，这时初态和末态的保真度为  $F(\\rho_{in}, \\rho_{out}) = 1$。"
+    "其中 $\\rho_{trash}$ 是经过编码后丢弃的 $B$ 系统的量子态。接着我们通过飞桨训练量子神经网络，最小化损失函数。如果损失函数最后达到 0，则输入态和输出态完全相同。这就意味着我们完美地实现了压缩和解压缩，这时初态和末态的保真度为  $F(\\rho_{in}, \\rho_{out}) = 1$。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 4,
    "metadata": {
-    "scrolled": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:18:38.173148Z",
+     "start_time": "2021-01-09T09:18:20.214869Z"
+    }
    },
    "outputs": [
     {
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "iter: 10 loss: 0.1795 fid: 0.8076\n",
-      "iter: 20 loss: 0.1374 fid: 0.8573\n",
-      "iter: 30 loss: 0.1149 fid: 0.8812\n",
-      "iter: 40 loss: 0.1073 fid: 0.8886\n",
-      "iter: 50 loss: 0.1044 fid: 0.8910\n",
-      "iter: 60 loss: 0.1029 fid: 0.8921\n",
-      "iter: 70 loss: 0.1019 fid: 0.8927\n",
-      "iter: 80 loss: 0.1013 fid: 0.8931\n",
-      "iter: 90 loss: 0.1009 fid: 0.8933\n",
-      "iter: 100 loss: 0.1006 fid: 0.8935\n"
+      "iter: 10 loss: 0.1716 fid: 0.8214\n",
+      "iter: 20 loss: 0.1381 fid: 0.8550\n",
+      "iter: 30 loss: 0.1124 fid: 0.8813\n",
+      "iter: 40 loss: 0.1037 fid: 0.8901\n",
+      "iter: 50 loss: 0.1019 fid: 0.8927\n",
+      "iter: 60 loss: 0.1007 fid: 0.8935\n",
+      "iter: 70 loss: 0.1003 fid: 0.8938\n",
+      "iter: 80 loss: 0.1001 fid: 0.8942\n",
+      "iter: 90 loss: 0.1000 fid: 0.8943\n",
+      "iter: 100 loss: 0.1000 fid: 0.8942\n"
      ]
     }
    ],
@@ -165,22 +199,19 @@
     "SEED = 14      # 固定初始化参数用的随机数种子\n",
     "\n",
     "class NET(fluid.dygraph.Layer):\n",
-    "    \"\"\"\n",
-    "    Construct the model net\n",
-    "    \"\"\"\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
-    "        low=0.0, high=2 * np.pi, seed = SEED), dtype='float64'):\n",
+    "\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * np.pi, seed = SEED), dtype='float64'):\n",
     "        super(NET, self).__init__()\n",
     "        \n",
-    "        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
+    "        # 将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
     "        self.rho_in = fluid.dygraph.to_variable(rho_in)\n",
     "        self.rho_C = fluid.dygraph.to_variable(rho_C)\n",
-    "        self.theta = self.create_parameter(shape=shape, \n",
-    "                     attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
     "    \n",
     "    # 定义损失函数和前向传播机制\n",
     "    def forward(self):\n",
-    "        # 生成初始的编码器 E 和解码器 D\\n\",\n",
+    "      \n",
+    "        # 生成初始的编码器 E 和解码器 D\n",
     "        E = Encoder(self.theta)\n",
     "        E_dagger = dagger(E)\n",
     "        D = E_dagger\n",
@@ -198,7 +229,6 @@
     "        rho_out = matmul(matmul(D, rho_CA), D_dagger)\n",
     "        \n",
     "        # 通过 rho_trash 计算损失函数\n",
-    "        \n",
     "        zero_Hamiltonian = fluid.dygraph.to_variable(np.diag([1,0]).astype('complex128'))\n",
     "        loss = 1 - (trace(matmul(zero_Hamiltonian, rho_trash))).real\n",
     "\n",
@@ -211,9 +241,9 @@
     "    # 生成网络\n",
     "    net = NET([theta_size])\n",
     "\n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdagradOptimizer(learning_rate=LR, \n",
-    "                          parameter_list=net.parameters())\n",
+    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛\n",
+    "    # 当然你可以改成SGD或者是RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
     "\n",
     "    # 优化循环\n",
     "    for itr in range(1, ITR + 1):\n",
@@ -237,18 +267,27 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 总结\n",
-    "\n",
-    "如果系统 $A$ 的维度为 $d_A$，容易证明量子自编码器能实现的压缩重建最大保真度为 $\\rho_{in}$ 最大的 $d_A$ 个本征值之和。在我们的示例里 $d_A = 4$，最大保真度为 \n",
-    "\n",
-    "$$ F_{limit} = 0.4 + 0.2 + 0.2 + 0.1 = 0.9$$\n",
+    "如果系统 A 的维度为 $d_A$，容易证明量子自编码器能实现的压缩重建最大保真度为 $\\rho_{in}$ 最大的 $d_A$ 个本征值之和。在我们的示例里 $d_A = 4$，理论最大保真度为 \n",
     "\n",
-    "通过 100 次迭代，我们训练出的量子自编码器保真度达到 0.89 以上，和最优情况非常接近。\n",
+    "$$\n",
+    "F_{\\text{max}}(\\rho_{in}, \\rho_{out})  = \\sum_{j=1}^{d_A} \\lambda_j(\\rho_{in})= 0.4 + 0.2 + 0.2 + 0.1 = 0.9.\n",
+    "\\tag{3}\n",
+    "$$\n",
     "\n",
+    "通过 100 次迭代，我们训练出的量子自编码器保真度达到 0.89 以上，和理论最大值非常接近。\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
     "\n",
     "## 参考文献\n",
     "\n",
-    "[1] [Romero, J., Olson, J. P. & Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. Quantum Sci. Technol. 2, 045001 (2017).](https://iopscience.iop.org/article/10.1088/2058-9565/aa8072)"
+    "[1] Romero, J., Olson, J. P. & Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. [Quantum Sci. Technol. 2, 045001 (2017).](https://iopscience.iop.org/article/10.1088/2058-9565/aa8072)\n",
+    "\n"
    ]
   }
  ],
@@ -268,7 +307,20 @@
    "name": "python",
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
-   "version": "3.7.7"
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
   }
  },
  "nbformat": 4,

tutorial/Q-Autoencoder/Q-Autoencoder_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Quantum Autoencoder\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Overview\n",
+    "\n",
+    "This tutorial will show how to train a quantum autoencoder to compress and reconstruct a given quantum state (mixed state) [1].\n",
+    "\n",
+    "### Theory\n",
+    "\n",
+    "The form of the quantum autoencoder is very similar to the classical autoencoder, which is composed of an encoder $E$ and a decoder $D$. For the input quantum state $\\rho_{in}$ of the $N$ qubit system (here we use the density operator representation of quantum mechanics to describe the mixed state), first use the encoder $E = U(\\theta)$ to encode information into some of the qubits in the system. This part of qubits is denoted by **system $A$**. After measuring and discarding the remaining qubits (this part is denoted by **system $B$**), we get the compressed quantum state $\\rho_{encode}$! The dimension of the compressed quantum state is the same as the dimension of the quantum system $A$. Suppose we need $N_A$ qubits to describe the system $A$, then the dimension of the encoded quantum state $\\rho_{encode}$ is $2^{N_A}\\times 2^{N_A}$. Note that the mathematical operation corresponding to the measure-and-discard operation in this step is partial trace. The reader can intuitively treat it as the inverse operation of the tensor product $\\otimes$.\n",
+    "\n",
+    "Let us look at a specific example. Given a quantum state $\\rho_A$ of $N_A$ qubits and another quantum state $\\rho_B$ of $N_B$ qubits, the quantum state of the entire quantum system composed of subsystems $A$ and $B$ is $\\rho_{AB} = \\rho_A \\otimes \\rho_B$, which is a state of $N = N_A + N_B$ qubits. Now we let the entire quantum system evolve under the action of the unitary matrix $U$ for some time to get a new quantum state $\\tilde{\\rho_{AB}} = U\\rho_{AB}U^\\dagger$. So if we only want to get the new quantum state $\\tilde{\\rho_A}$ of quantum subsystem A at this time, what should we do? We simply measure the quantum subsystem $B$ and then discard it. This step of the operation is completed by partial trace $\\tilde{\\rho_A} = \\text{Tr}_B (\\tilde{\\rho_{AB}})$. With Paddle Quantum, we can call the built-in function `partial_trace(rho_AB, 2**N_A, 2**N_B, 2)` to complete this operation. **Note:** The last parameter is 2, which means that we want to discard quantum system $B$.\n",
+    "\n",
+    "![QA-fig-encoder_pipeline](./figures/QA-fig-encoder_pipeline.png)\n",
+    "\n",
+    "After discussing the encoding process, let us take a look at how decoding is done. To decode the quantum state $\\rho_{encode}$, we need to introduce an ancillary system $C$ with the same dimension as the system $B$ and take its initial state as the $|0\\dots0\\rangle$ state. Then use the decoder $D = U^\\dagger(\\theta)$ to act on the entire quantum system $A+C$ to decode the compressed information in system A. We hope that the final quantum state $\\rho_{out}$ and $\\rho_{in}$ are as similar as possible and use Uhlmann-Josza fidelity $F$ to measure the similarity between them.\n",
+    "\n",
+    "$$\n",
+    "F(\\rho_{in}, \\rho_{out}) = \\left(\\operatorname{tr} \\sqrt{\\sqrt{\\rho_{in}} \\rho_{out} \\sqrt{\\rho_{in}}} \\right)^{2}.\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "Finally, by optimizing the encoder's parameters, we can improve the fidelity of $\\rho_{in}$ and $\\rho_{out}$ as much as possible."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Paddle Quantum Implementation\n",
+    "\n",
+    "Next, we will use a simple example to show the workflow of the quantum autoencoder. Here we first import the necessary packages."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:12:23.184162Z",
+     "start_time": "2021-01-09T09:12:22.345158Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import numpy as np\n",
+    "from numpy import diag\n",
+    "import scipy\n",
+    "import paddle\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle.complex import matmul, trace, kron\n",
+    "from paddle_quantum.utils import dagger, state_fidelity, partial_trace"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Generating the initial state\n",
+    "\n",
+    "Let us consider the quantum state $\\rho_{in}$ of $N = 3$ qubits. We first encode the information into the two qubits below (system $A$) through the encoder then measure and discard the first qubit (system $B$). Secondly, we introduce another qubit (the new reference system $C$) in state $|0\\rangle$ to replace the discarded qubit $B$. Finally, through the decoder, the compressed information in A is restored to $\\rho_{out}$. Here, we assume that the initial state is a mixed state and the spectrum of $\\rho_{in}$ is $\\lambda_i \\in \\{0.4, 0.2, 0.2, 0.1, 0.1, 0, 0, 0\\}$, and then generate the initial state $\\rho_{in}$ by applying a random unitary transformation.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:12:38.828744Z",
+     "start_time": "2021-01-09T09:12:38.798795Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "N_A = 2            # Number of qubits in system A\n",
+    "N_B = 1            # Number of qubits in system B\n",
+    "N = N_A + N_B      # Total number of qubits\n",
+    "\n",
+    "scipy.random.seed(1)                         # Fixed random seed\n",
+    "V = scipy.stats.unitary_group.rvs(2**N)      # Generate a random unitary matrix\n",
+    "D = diag([0.4, 0.2, 0.2, 0.1, 0.1, 0, 0, 0]) # Enter the spectrum of the target state rho\n",
+    "V_H = V.conj().T                             # Apply Hermitian transpose\n",
+    "rho_in = (V @ D @ V_H).astype('complex128')  # Generate rho_in\n",
+    "\n",
+    "# Initialize the quantum system C\n",
+    "rho_C = np.diag([1,0]).astype('complex128')"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Building a quantum neural network\n",
+    "\n",
+    "Here, we use quantum neural networks (QNN) as encoders and decoders. Suppose system A has $N_A$ qubits, both system $B$ and $C$ have $N_B$ qubits, and the depth of the QNN is $D$. Encoder $E$ acts on the total system composed of systems A and B, and decoder $D$ acts on the total system composed of $A$ and $C$. In this example, $N_{A} = 2$ and $N_{B} = 1$."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:12:57.894565Z",
+     "start_time": "2021-01-09T09:12:57.866300Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Set circuit parameters\n",
+    "cir_depth = 6                       # Circuit depth\n",
+    "block_len = 2                       # The length of each block\n",
+    "theta_size = N*block_len*cir_depth  # The size of the circuit parameter theta\n",
+    "\n",
+    "\n",
+    "# Build the encoder E\n",
+    "def Encoder(theta):\n",
+    "\n",
+    "    # Initialize the network with UAnsatz\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Build the network by layers\n",
+    "    for layer_num in range(cir_depth):\n",
+    "        \n",
+    "        for which_qubit in range(N):\n",
+    "            cir.ry(theta[block_len*layer_num*N + which_qubit], which_qubit)\n",
+    "            cir.rz(theta[(block_len*layer_num + 1)*N+ which_qubit], which_qubit)\n",
+    "\n",
+    "        for which_qubit in range(N-1):\n",
+    "            cir.cnot([which_qubit, which_qubit + 1])\n",
+    "        cir.cnot([N-1, 0])\n",
+    "\n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Configuring the training model: loss function\n",
+    "\n",
+    "Here, we define the loss function to be\n",
+    "\n",
+    "$$\n",
+    "Loss = 1-\\langle 0...0|\\rho_{trash}|0...0\\rangle,\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "where $\\rho_{trash}$ is the quantum state of the system $B$ discarded after encoding. Then we train the QNN through PaddlePaddle to minimize the loss function. If the loss function reaches 0, the input state and output state will be exactly the same state. This means that we have achieved compression and decompression perfectly, in which case the fidelity of the initial and final states is $F(\\rho_{in}, \\rho_{out}) = 1$."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:15:02.004745Z",
+     "start_time": "2021-01-09T09:14:42.039212Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 10 loss: 0.1716 fid: 0.8214\n",
+      "iter: 20 loss: 0.1381 fid: 0.8550\n",
+      "iter: 30 loss: 0.1124 fid: 0.8813\n",
+      "iter: 40 loss: 0.1037 fid: 0.8901\n",
+      "iter: 50 loss: 0.1019 fid: 0.8927\n",
+      "iter: 60 loss: 0.1007 fid: 0.8935\n",
+      "iter: 70 loss: 0.1003 fid: 0.8938\n",
+      "iter: 80 loss: 0.1001 fid: 0.8942\n",
+      "iter: 90 loss: 0.1000 fid: 0.8943\n",
+      "iter: 100 loss: 0.1000 fid: 0.8942\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Set hyper-parameters\n",
+    "N_A = 2        # Number of qubits in system A\n",
+    "N_B = 1        # Number of qubits in system B\n",
+    "N = N_A + N_B  # Total number of qubits\n",
+    "LR = 0.2       # Set the learning rate\n",
+    "ITR = 100      # Set the number of iterations\n",
+    "SEED = 14      # Fixed random number seed for initializing parameters\n",
+    "\n",
+    "class NET(fluid.dygraph.Layer):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * np.pi, seed = SEED), dtype='float64'):\n",
+    "        super(NET, self).__init__()\n",
+    "        \n",
+    "        # Convert Numpy array to variable supported in PaddlePaddle's dynamic graph mode\n",
+    "        self.rho_in = fluid.dygraph.to_variable(rho_in)\n",
+    "        self.rho_C = fluid.dygraph.to_variable(rho_C)\n",
+    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "    \n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self):\n",
+    "      \n",
+    "        # Generate initial encoder E and decoder D\n",
+    "        E = Encoder(self.theta)\n",
+    "        E_dagger = dagger(E)\n",
+    "        D = E_dagger\n",
+    "        D_dagger = E\n",
+    "\n",
+    "        # Encode the quantum state rho_in\n",
+    "        rho_BA = matmul(matmul(E, self.rho_in), E_dagger)\n",
+    "        \n",
+    "        # Take partial_trace() to get rho_encode and rho_trash\n",
+    "        rho_encode = partial_trace(rho_BA, 2 ** N_B, 2 ** N_A, 1)\n",
+    "        rho_trash = partial_trace(rho_BA, 2 ** N_B, 2 ** N_A, 2)\n",
+    "\n",
+    "        # Decode the quantum state rho_out\n",
+    "        rho_CA = kron(self.rho_C, rho_encode)\n",
+    "        rho_out = matmul(matmul(D, rho_CA), D_dagger)\n",
+    "        \n",
+    "        # Calculate the loss function with rho_trash\n",
+    "        zero_Hamiltonian = fluid.dygraph.to_variable(np.diag([1,0]).astype('complex128'))\n",
+    "        loss = 1-(trace(matmul(zero_Hamiltonian, rho_trash))).real\n",
+    "\n",
+    "        return loss, self.rho_in, rho_out\n",
+    "\n",
+    "\n",
+    "# Initialize PaddlePaddle's dynamic graph mechanism\n",
+    "with fluid.dygraph.guard():\n",
+    "\n",
+    "    # Generate network\n",
+    "    net = NET([theta_size])\n",
+    "\n",
+    "    # Generally speaking, we use Adam optimizer to get relatively good convergence\n",
+    "    # Of course, it can be changed to SGD or RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "\n",
+    "    # Optimization loops\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "        \n",
+    "        # Forward propagation for calculating loss function\n",
+    "        loss, rho_in, rho_out = net()\n",
+    "        \n",
+    "        # Under the dynamic graph mechanism, use back propagation to minimize the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "        \n",
+    "        # Calculate and print fidelity\n",
+    "        fid = state_fidelity(rho_in.numpy(), rho_out.numpy())\n",
+    "\n",
+    "        if itr% 10 == 0:\n",
+    "            print('iter:', itr,'loss:','%.4f'% loss,'fid:','%.4f'% np.square(fid))"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "If the dimension of system A is denoted by $d_A$, it is easy to prove that the maximum fidelity can be achieved by quantum autoencoder is the sum of $d_A$ largest eigenvalues ​​of $\\rho_{in}$. In our case $d_A = 4$ and the maximum fidelity is\n",
+    "\n",
+    "$$\n",
+    "F_{\\text{max}}(\\rho_{in}, \\rho_{out})  = \\sum_{j=1}^{d_A} \\lambda_j(\\rho_{in})= 0.4 + 0.2 + 0.2 + 0.1 = 0.9.\n",
+    "\\tag{3}\n",
+    "$$\n",
+    "\n",
+    "After 100 iterations, the fidelity achieved by the quantum autoencoder we trained reaches above 0.89, which is very close to the optimal value."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## References\n",
+    "\n",
+    "[1] Romero, J., Olson, J. P. & Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. [Quantum Sci. Technol. 2, 045001 (2017).](https://iopscience.iop.org/article/10.1088/2058-9565/aa8072)\n",
+    "\n"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/Q-Classifier/Quantum_Classifier_Tutorial_CN.ipynb

-{
- "cells": [
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "# 量子分类器 （Quantum Classifier）\n",
-    "\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 概览\n",
-    "\n",
-    "在本教程中我们一起来学习下如何利用量子神经网络来完成**两分类**任务（后续我们会补充难度更大的多分类任务）。这类方法早期工作的主要代表是 Mitarai et al.(2018) 的 [Quantum Circuit Learning](https://arxiv.org/abs/1803.00745) [1] 还有 Schuld et al.(2018) 的 [Circuit-centric quantum classifiers](https://arxiv.org/abs/1804.00633) [2]。本教程重点复现了前者的理论工作, 请读者跟随我们一起探索其中的奥秘。有经典机器学习基础的读者不妨参考下图思考一下，这个框架和经典的方法有什么异同。\n",
-    "\n",
-    "<img src=\"figures/pipeline.png\" width=\"900\" >\n",
-    "\n",
-    "\n",
-    "\n",
-    "首先我们还是引入需要的 library和 package："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 1,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "import time\n",
-    "import matplotlib\n",
-    "import numpy as np\n",
-    "from numpy import pi as PI\n",
-    "from matplotlib import pyplot as plt\n",
-    "\n",
-    "from paddle import fluid\n",
-    "from paddle.fluid.framework import ComplexVariable\n",
-    "from paddle.complex import matmul, transpose\n",
-    "from paddle_quantum.circuit import UAnsatz\n",
-    "from paddle_quantum.utils import pauli_str_to_matrix"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 2,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 这是教程中会用到的几个主要函数，下面我们来逐一分析\n",
-    "__all__ = [\n",
-    "    \"circle_data_point_generator\",\n",
-    "    \"data_point_plot\",\n",
-    "    \"heatmap_plot\",\n",
-    "    \"myRy\",\n",
-    "    \"myRz\",\n",
-    "    \"Observable\",\n",
-    "    \"U_theta\",\n",
-    "    \"Net\",\n",
-    "    \"QClassifier\",\n",
-    "    \"main\",\n",
-    "]"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 数据集的生成\n",
-    "\n",
-    "对于监督学习来说，我们绕不开的一个问题就是 -- `作者采用的数据集是什么样的` ？在这个教程中我们按照论文里所提及方法生成简单的圆形决策边界二分数据集 $\\{(x^{(i)}, y^{(i)})\\}$。其中数据点 $x^{(i)}\\in \\mathbb{R}^{2}$，标签 $y^{(i)} \\in \\{0,1\\}$。\n",
-    "\n",
-    "<img src=\"figures/data.png\" width=\"600\" >\n",
-    "\n",
-    "具体的生成方式和可视化请见如下代码："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 3,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 圆形决策边界两分类数据集生成器\n",
-    "def circle_data_point_generator(Ntrain, Ntest, boundary_gap, seed_data):\n",
-    "    \"\"\"\n",
-    "    :param Ntrain: number of train samples\n",
-    "    :param Ntest: number of test samples\n",
-    "    :param boundary_gap: value in (0, 0.5), means the gap between two classes\n",
-    "    :param seed_data: random seed\n",
-    "    :return: 'Ntrain' samples for training and 'Ntest' samples for testing\n",
-    "    \"\"\"\n",
-    "    train_x, train_y = [], []\n",
-    "    num_samples, seed_para = 0, 0\n",
-    "    while num_samples < Ntrain + Ntest:\n",
-    "        np.random.seed((seed_data + 10) * 1000 + seed_para + num_samples)\n",
-    "        data_point = np.random.rand(2) * 2 - 1\n",
-    "        # 如果数据点的模小于(0.7 - gap)，标为0\n",
-    "        if np.linalg.norm(data_point) < 0.7 - boundary_gap / 2:\n",
-    "            train_x.append(data_point)\n",
-    "            train_y.append(0.)\n",
-    "            num_samples += 1\n",
-    "        # 如果数据点的模大于(0.7 + gap)，标为1\n",
-    "        elif np.linalg.norm(data_point) > 0.7 + boundary_gap / 2:\n",
-    "            train_x.append(data_point)\n",
-    "            train_y.append(1.)\n",
-    "            num_samples += 1\n",
-    "        else:\n",
-    "            seed_para += 1\n",
-    "\n",
-    "    train_x = np.array(train_x).astype(\"float64\")\n",
-    "    train_y = np.array([train_y]).astype(\"float64\").T\n",
-    "    print(\"训练集的维度大小 x {} 和 y {}\".format(np.shape(train_x[0:Ntrain]),\n",
-    "          np.shape(train_y[0:Ntrain])))\n",
-    "    print(\"测试集的维度大小 x {} 和 y {}\".format(np.shape(train_x[Ntrain:]),\n",
-    "          np.shape(train_y[Ntrain:])), \"\\n\")\n",
-    "    return train_x[0:Ntrain], train_y[0:Ntrain], train_x[Ntrain:], train_y[Ntrain:]\n",
-    "\n",
-    "\n",
-    "# 用以可视化生成的数据集\n",
-    "def data_point_plot(data, label):\n",
-    "    \"\"\"\n",
-    "    :param data: shape [M, 2], means M 2-D data points\n",
-    "    :param label: value 0 or 1\n",
-    "    :return: plot these data points\n",
-    "    \"\"\"\n",
-    "    dim_samples, dim_useless = np.shape(data)\n",
-    "    plt.figure(1)\n",
-    "    for i in range(dim_samples):\n",
-    "        if label[i] == 0:\n",
-    "            plt.plot(data[i][0], data[i][1], color=\"r\", marker=\"o\")\n",
-    "        elif label[i] == 1:\n",
-    "            plt.plot(data[i][0], data[i][1], color=\"b\", marker=\"o\")\n",
-    "    plt.show()"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 4,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "训练集的维度大小 x (200, 2) 和 y (200, 1)\n",
-      "测试集的维度大小 x (100, 2) 和 y (100, 1) \n",
-      "\n",
-      "训练集 200 个数据点的可视化：\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAD4CAYAAADhNOGaAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAApn0lEQVR4nO2df6xexXnnP4+vYydu1Ma89mYdwNeQZZuQ3QrCVZSkUpqkJCHuClOVtiSG3qRUXm6b7kpRqxhZ6kZsrdL+Q6gSRCxKcLlXCQlVFLclYoGEXWk3kFx2AfNDxsYJYErCxQ6RIigJZvaPc974+PX5/XPOe74fafSeM+fX886ZM8/MPM/MmHMOIYQQw2VV1wIIIYToFikCIYQYOFIEQggxcKQIhBBi4EgRCCHEwFndtQBl2LBhg9uyZUvXYgghRK944IEHXnDObZyM76Ui2LJlC8vLy12LIYQQvcLMnoqLV9eQEEIMHCkCIYQYOFIEQggxcKQIhBBi4EgRCCHEwKlFEZjZzWb2vJk9knDczOxvzeyQmT1sZu+MHJs3s4NhmK9DHiHKsLQEW7bAqlXB79JS1xL5ic/p5JNsPsmSiXOucgDeB7wTeCTh+Fbgm4AB7wbuD+NPAw6Hv+vD7fVZz7vgggtcn1lcdG521jmz4HdxsWuJxOKic+vWOQcnwrp1ejeTNJVOdXwTPr1Dn2SJAiy7uDI6LrJMALakKIIvAh+L7B8ANgEfA76YdF5S6LMiiMsgZs4tLHQtWbP4rvxmZ09+J+MwO9u1ZH7RRDrVVWj69A59kiVKkiJoy0ZwOvBMZP9IGJcUfwpmtsPMls1seWVlpTFBm2bXLnjppZPjnIMbb6y/6ehL03RpCXbsgKeeCv7rU08F+z41lZ9+ulj8UHkqdjhStXSK+yZeeimIL4JP79AnWfLQG2Oxc26Pc27OOTe3ceMpI6R7Q9KH5FzxjJ+GT4VvXR96k2zeXCy+SXxR4JMsLYFZ/LEy6TT+n3UpF5/eoU+y5KEtRfAscGZk/4wwLil+akn6kKDe2oJPhW8fake7d8O6dSfHrVsXxLeJTwp8kl27ApkmMSueTtH/mUTRQrPKO6yifOOu9SU/5Sauv6hMIN1G8FucbCz+rjthLP4+gaF4fbh9Wtaz6rARdNVnHddvGNd/WFU+s/hnmNX4Z3Lia3/pJD7YMZpMq6byFBSXJel/VjWsLi46NxqduM9olH2fKjaKtGt9yE+T0KSxGPgy8Bzwc4J+/iuBq4CrwuMGfAF4EtgPzEWu/UPgUBg+med5VRVBlxb9tMw/fn4d8vlU+PrqQeEjTSlw3/JUmlKpUmiW+Z9V/pdP31keGlUEbYeqiiDp5c3MNK+9o7WVaPilX8qWr0jm6qrwTaoF+Vg78pGmChbf8pRP/zOP8k3Kv1Wu7QIpgghptZGmC83FRefWrDn5WWvWnPysumqFbWdA1fyr01Qa+panfPqfWcojTdYq13aBFEGErP7Jppt3WR9T35qbY/oqt280ocB9fDe+/M+swjrtnlWu7QIpgghxL6+O2lJd+FaLyItPBmpxMnXnKR+6O+JkKPs/0/5PVr6ucm3bSBFMsLgY2AS6aBHkla/rD60ovtV+xMn43q1Tlwx1fzvTZEyWIoghy1bQh8LXJ3woIETz+FC4tSlDU+6lXSBFEEOarWA0quURXtFGK6OPLRlRDB+6O9qWoUq+9umbkCKIIc6DB5x73eumrwDzrWYi+svQWgRJ+FTA5yVJEfRmrqEm2L4dbr4ZRqMTcaMRfOlLwbFpwqcpJ0S/8WH6hK5l8HkqkDJYoCT6xdzcnFteXu5ajF6xalWQYScxg9dea18e0W+WloJKxNNPB3MC7d7dfuWpSxmSJsubnYUf/KAdGcpgZg845+ZOiZciGAZ9zbhC+EhfK1ZJimDQXUNp+DoVcFm6bkoLMU1UmWbax7JFiiCGNvr/imSGOjLO9u2wZ0/QAjALfvfsmT5biBBtULZi5a1tIc6C7HtoeqnKpj0SinjwyNtHiPop4/Ezec3CQvF7dO3thNxH89O0j3KRzNB1xhFi2shTuYor9OuokHU9BiNJEchYHEPThtUihqa+GqWE8JWs73vcfRN1tzaL/w6LlgldO200aiw2s4vM7ICZHTKznTHHrzOzB8PwhJm9GDl2PHJsXx3yVKVpw2oRQ1NZo5SPBikhmqJIfs9aOjVuzE1SfbnocqveOm3ENROKBGCGYOWxs4E1wEPAuSnn/ylwc2T/p0Wf2XTXkHPNjhps2kYgu4IYEkXze1Z3a571Sqp00XY5IpmmbATAe4A7I/tXA1ennP9/gA9F9r1UBE1TJDMUzTiyK4ghUTS/l11DYFJB9LFy1aQiuBS4KbJ/BfD5hHNnCdY2nonEvQosA/cBl+R55jQogibp2iAlRJuUye9plaskRTH2EoITU9j3ZY6hMUmKoO1xBJcBtzvnjkfiZl1gvPg48Dkze2vchWa2w8yWzWx5ZWWlDVl7S5XBLkL0jTL5ffv2wDj72mvBb3Q8TdKYmxtuONHHfzwswbwZB1CROhTBs8CZkf0zwrg4LgO+HI1wzj0b/h4G7gXOj7vQObfHOTfnnJvbuHFjVZmngiQDmbcGKSEaoIn8nqQoyk7e2PYA0sLENROKBGA1cBg4ixPG4nfEnPc24AeE8xuFceuBteH2BuAgKYbmcVDXUHY/Zx+nyBWiLHXk9zz3KNsN5csAUpocUAZsBZ4g8B7aFcZdA1wcOeezwLUT170X2B8qj/3AlXmeJ0UQLJwjg7AQyRR1yMhTAJdxxPBpAGmjiqDtMHRFsLgYn1lkEBYioG6X0rL3dS5/K6KN7zpJEWjSuRR8HZSV1h8pg7AQxfvy0waZRcuBXbtgfr7Y5I15jNnj0cxF71EbcdrB99DWgDJfB2WlDXjxQT4huqZoX35Si2A0ql4OxJUla9YE9x53WyV19bZlI1CLIAGfl3ZMqh2MRppWWggo7lKa5HkE1cuBSXfU0Sgo4o8eDX6feirYTqKN6eKlCBLImo+kS5Iy7fXXdyOPEL5R1KU0aezAsWPx5xctB6LuqG98I/z85/mum51tp3InRZBAWo2ia9uBFpkRIp0y30jc2IEmBmfmVSKtjv2J6y/yPXRpI6hrXnIhhP80YStMs0fEubvWOSYI2QiKkVSjuOMOf20HQoh6aaL1nda1G22RAGzYAJdf3vzSllIEMYy7fq64Iti/9dYTTUWfbQdCiPpJm5eoTDdxknKBE/fasAE++cl4I3ITFU8pggmyFpfWhG5CCKi2EP2kcoGT73X0aLpBue6K5yAVQZoWz3IbrWuCq64NzkKIatTpYh53rzRqr3jGGQ58D1WMxVnGnzwDUaoab3werCaEyEed634UWRWtSlmBFq8PyFo8uo3FpbtewFoIUZ06v+Oke00yGgVG5bLG6kYXr+8TWcbeNubyl8FZiP5TZ1kRd681a4KCf2xQXlyEF15oZrzQ4BRBlrG3jcFaMjgL0X/qLCvi7nXzzUHBH+etVDtx/UW+hyZtBHWSZEuQjUCIYeDbAlFoPYITtPFytIKYEMPGxwpfo4oAuAg4ABwCdsYc/wSwAjwYhj+KHJsnWKLyIDCf53l9WJim6ZWGhBB+U6QMaKtimKQIVlftWjKzGeALwIeAI8D3zGyfc+6xiVNvc859auLa04D/BswBDnggvPbHVeXqGhmEhRg2ecuA8cC08TiC8cA0aG8iyTqMxe8CDjnnDjvnfgZ8BdiW89qPAHc5546Fhf9dBK2L3iODsBDDJm8ZkDUwrY3Bp3UogtOBZyL7R8K4SX7HzB42s9vN7MyC12JmO8xs2cyWV1ZWahC7WdpwQxVC+EveMiBrmcyy01gUoS330X8Etjjnfo2g1r+36A2cc3ucc3POubmNGzfWLmDdaM0AIYbN9u3B+sYzM8H+zEywP1kGpLUc2lopsQ5F8CxwZmT/jDDuFzjnjjrnXgl3bwIuyHttn0mbtVAIMd0sLcHevXD8eLB//HiwP1mbT2s5tGVrrEMRfA84x8zOMrM1wGXAvugJZrYpsnsx8Hi4fSfwYTNbb2brgQ+HcUII0Wvy1ubTeg/asjVW9hpyzr1qZp8iKMBngJudc4+a2TUErkr7gP9iZhcDrwLHCNxJcc4dM7P/TqBMAK5xziWsEiqEEP0hae6guPjt2+N7DHbvPtmjCJqxNQ5u0jkhhGiD1atPdAtFmZmBV1/Nf5+lpaAV8fTTQUtg9+76J52r3CIQQghxKnFKIC0+iaTWQp0MbtI5IYRog9nZYvFdIkUghBAN0KexRFIEYrqpa1im1hYVBenTWCIpghj0zU8JdQ3LbGt4p5g6+jKWSF5DE0xOAAVBc85XTS5SqGstQa0tKqYELVWZk7aGdIsWKDIsM60ZqKlkxZQjRTCBvnkPKdtXl3dYZlbXj6aSFVOOFMEE+uY9o0r/fF63jaxmYJ/cP4QogRTBBPrmPaNKX11et42sZmDd7h/yRhAZtJ5F4pYt8z00vVSl1hP2CLP49f7M6ntGm+uK+riQrfCKJrMICUtVqkUQQ19cvgZBHX11WdWrss3AMtU2eSOIDDrJInHawffQh8XrRU1UrR7lvT6pGZgWX0auNlo4otc0mUVIaBF0XqiXCVIEA6NKX12Vbp+0wr7sfdvshhK9pMkskqQI1DUk/CGpq6VKX10Vf+C0NnrZ+8obQWTQRRaRIhB+0NQ0DlVsDGmFfdn79mkCGtEJnWSRuGZC0QBcBBwADgE7Y45/GngMeBi4B5iNHDsOPBiGfXmep66hKaSp9nAVG0OaTPL+ET2EprqGzGwG+ALwUeBc4GNmdu7Eaf8PmHPO/RpwO/A3kWMvO+fOC8PFVeURPaWpId1VqldpbfS0+9bhBK6xBqJN4rRDkQC8B7gzsn81cHXK+ecD/zuy/9Oiz1SLYArxwYgaZ5Quaqiuo6Wg1oZoCBo0Fp8OPBPZPxLGJXEl8M3I/uvNbNnM7jOzS5IuMrMd4XnLKysrlQQWHtK1ETXJRgHFDNV1OIHX6UiuloXIQ5x2KBKAS4GbIvtXAJ9POPdy4D5gbSTu9PD3bOAHwFuznqkWwZTS9pDu6PNmZuppkdThBJ50DygmS56WhYbRDwqaGkdAzq4h4ELgceDfpNzrFuDSrGdKEQyQMgVWWlfPuHBOKnDLjuKpo4sr6R5m9Y6hUBfU4GhSEawGDgNnAWuAh4B3TJxzPvAkcM5E/Ppx6wDYABwEzs16phRBDylb81xcdG40OrUwyyqw4gq5NWuce93rsgv/pAI8z3+oy0aQpKSKKJSs1okPdhnRKo0pguDebAWeCAv7XWHcNcDF4fbdwI+YcBMF3gvsD5XHfuDKPM+TIugZZQvHuOvyFlhJhVyREJWxyH+oo7uljhZKVkGv6S4GR6OKoO0gRdAz6p6OIU+BlafbJy2sWnVyAd527TnP87IUzsJC/D0WFrr5T6JzkhSBRhaL5ik7RiBuneAoaaN4q64k9NprJ++3vXRdkhfV1q2B948ZXHFF+kjsO+6Iv/c4vmtPLeENUgSiecpOxzAzk3wsq8DavTsoLKsQdddse+m6uAFr8/Owd+8JBencyddMupi2veCO6C9xzQTfg7qGekZZG0Fa102efvesbqXZ2eTuk8muJx88bPLYPaIyq+tHTIC6hkRnlK15zs4mx+eptaZdPx4gdsMNMBrFnxet7ftQe87TDRWVWV0/Ii9x2sH3oBbBQGhzUZqua/t5yGoRFFlwRwwS5DUkeknVgizv9X0oMOMU1tg7qk2Z+5BWIhYpAjFdDLUw6vp/96X1JGJJUgQWHOsXc3Nzbnl5uWsxRFeMJ4iLTsy2bp08XppmaSnwXDp+/NRjs7OBzUV4jZk94Jybm4yXsVj0jzpn5xT5GCvfOCUAzY2nEK0gRSC6p+hUyW0P7ppm8qZ9nPKN4pymue4xUgSiW8qsVdz24C6fqbLeQJG0z6Nk61pnWrRPnOHA9yBj8RRRZtBTnwyWTRp3s9Ih69lF0r7IJH4asOYtyGtIeEnZGTC79p7JQ9MKK60gz/PsImmfNRNskXcnOiNJEchrSHTLli3xk8tNgxdK0/9t1apT5xuCYOTz5s3Zzy4q39JSYCt4+ung/j/9KRw9mv960TnyGhJ+Ms3TIDRt1E6zleR5dtG037795PWbr79+et/dwJAiEN3S5Rw+TS/s3rRRO60gz/PsImkfl1Y+zL8k6iGuv6hoAC4CDgCHgJ0xx9cCt4XH7we2RI5dHcYfAD6S53l12Aj60MUsGqSNhd3bMGonyVjns/tknBep0OCaxTMES1SezYk1i8+dOOePgRvD7cuA28Ltc8Pz1xKsefwkMJP1zKqKQPlatLawe5c1jjqevbjo3MxMelqJ3pCkCCobi83sPcBnnXMfCfevDlsafxU5587wnO+Y2Wrgh8BGYGf03Oh5ac+saiyeZvukyEmaofW115RJIH4qjyjjtBK9oUlj8enAM5H9I2Fc7DnOuVeBnwCjnNcCYGY7zGzZzJZXVlYqCayBqSKzD71KJmna9tAWWaOJhziAb0rpjbHYObfHOTfnnJvbuHFjpXtpYKrI9Jgpm0nKjJT2lTSlJ++gqaIORfAscGZk/4wwLvacsGvoV4CjOa+tnWn2WPQW32rJWR4vZTPJNE2Il6T0ZmaCtAK/3qkoT5zhoEgAVgOHCYy9Y2PxOybO+RNONhZ/Ndx+Bycbiw/TgrHYOXkNtUoZw6sPL2hh4YShdGYm2M+i7EhpH0l7b/K46CU0OcUEsBV4gsDrZ1cYdw1wcbj9euBrBG6i3wXOjly7K7zuAPDRPM/TFBOeklR4F51PyIdCpqwM07ZgfNF3OjOj2pXHNKoI2g5SBB6SVnAWrSX7UJiWlcEXJdZ0ayrpnaqF4DVJikBzDYl6SHO3hGKumFmunW1QRYbJOXl2725vtG1bq7clve9JhuRu2wM015BoljR3y6KGVx/curJkSDN+T87J0+aUC0nG6ssvr9egG/dO45BPdj+Iayb4HtQ15CF5Rurm7a7wpXuliKEUnBuNuu8KyeqyqTMdo+9Uo497AbIRiEapu/D2wWuoqKHUh37xPAvINFE4+6C8RSZSBKJ5fCi82yCr1t1lLTjvAjJNPXsI77/HJCkC2QhEfXTZN94mWbaKLvvFowPlkpiZSb9H0cF/4/OvuCLYv/XW6X7/U4gUgRBFyTKUdj1XyVghJ3H8ePKxolNkTNOUGh7R9kB8KQIhspj8KiGodY9Gp57b5lwlWaVFUqsgrbVQdIqMaZpSwxM60a1x/UW+B9kIRCPE9XFnGUG76hfPu7BOUQNu2uC/uP86TVNqeEKT4ynRgDIhUkgaiPWGN/i5QHve9RKKDm5Luu9oBC+/3J/06TFNjqfUgDIxDMp2riZ1ccQVctD9QKm86yUUNeAnDf6D+PSJHo+er6l8S9PFeEopAjE9VOlcLVqwd20Qbqq0SJqe+9ix+POPHdMC9jXTyTT5cf1FvgfZCEQsVTpXk64djaoNlCpjQ8hzTdsDuHyYCHDKib720SgIdZue0IAyMfVUMVxmTSlRxiBcprBeWDj1fyRd06ahWiOHG6Wt5JUiENNP1Vpr3QVrmXUYkpSZDzVvjRxujLYaXEmKQF5Dwn/yer60NQVzXoq6f6RN7dzmFNyiddqaeb0RryEzO83M7jKzg+Hv+phzzjOz75jZo2b2sJn9fuTYLWb2fTN7MAznVZFHTCFFDMBZ6xC3TVGDbprBumvjtGiUrmder+o1tBO4xzl3DnBPuD/JS8AfOOfeAVwEfM7M3hQ5/ufOufPC8GBFecS0UXTkqk/zHdW1DoOZ3DGnnE48hSJUVQTbgL3h9l7gkskTnHNPOOcOhtv/AjwPbKz4XNF38vr75/WX94Xo/9q1C+bn87dQ4koDM7jqqmA7Kb3anphG1E7njdk4w0HeALwY2bbofsL57wIeB1aF+7cQLFr/MHAdsDbl2h3AMrC8efPmei0ool2KuEj0yW2xDtePotNcyJtnKmjLDk9ZryHgbuCRmLBtsuAHfpxyn01hof/uiTgD1hK0KP4iSx4nr6H+U6Rw71NB15TSSrtvnxSliKXN6axKK4K0EBbsm1ykoE8475eB/wtcmnKv9wP/lOe5UgQ9p6i/f1/cFpuagC3tvpr0rfek6fK660FJiqCqjWAfMB9uzwPfmDzBzNYAXwf+3jl3+8SxTeGvEdgXHqkoj+gDRVwkik6a1iVNuX6k3bdrdxNRmTQzWFuzfFdVBNcCHzKzg8CF4T5mNmdmN4Xn/B7wPuATMW6iS2a2H9gPbAD+sqI8og/kdZGoY2L2Ng2pTbl+pN23SFrKoOwlabq8NV+JuGaC70FdQ1NAnu6eOkYKt21faKobK+2+Wc/sk51lgKS9nrpNQGhksegdScMtITk+St45+6cdpYP3JPWA1j1YXusRxKDWsuekDbCqMrW0r2MQmkLp4D1J4yDH4wuiq6K+4Q31P3+wikBrbveA3buDQn8S5/JZy2RIDVA69J6XXz6xffRo/WXVYBWB1tzuAdu3J3cB5anNdj1uvwnKNGOnMR0GRBtl1WAVgVrLPWF2Nj4+T22283H7NVO2GTtt6TAw2iirBmsslv2sJ/g2tXSXKNMOkjpfu4zFE6i13BNUmz2BmrGDpI2yarCKQOVLj/BpaukukdF3kLRRVg1WEUBy+SK3UuElasZOHXnLmqbrQqvrvV3/meySHtvjYLgVUeEJ4wzYl7mXRCo+lTWDNRYnIXucEKINuihrZCzOiexxQog28KmskSKYQPY4IUQb+FTWSBFMIHucEKINfCprpAgmkFupEKINfCpr5DUUw/btKviFEM3g46J7lVoEZnaamd1lZgfD3/UJ5x2PrE62LxJ/lpndb2aHzOy2cFlLIYToBUXHHPk663HVrqGdwD3OuXOAe8L9OF52zp0Xhosj8X8NXOec+3fAj4ErK8ojhBCtUKZQ93XW46qKYBuwN9zeS7AAfS7CBes/CIwXtC90vRBCdEmZQj3LZbSrWQ2qKoI3O+eeC7d/CLw54bzXm9mymd1nZpeEcSPgRefcq+H+EeD0pAeZ2Y7wHssrKysVxRZCiGqUGQeQ5jLaZbdRpiIws7vN7JGYsC16XrgwctIw5dlwNNvHgc+Z2VuLCuqc2+Ocm3POzW3cuLHo5UIIUStlxgGkuYx22W2UqQiccxc65/5DTPgG8CMz2wQQ/j6fcI9nw9/DwL3A+cBR4E1mNvZcOgN4tvI/EkKIFigzDiDNZbTLkcZVu4b2AfPh9jzwjckTzGy9ma0NtzcAvw48FrYgvg1cmna9EEL4SN5xAJP9/hA/k2iXI42rKoJrgQ+Z2UHgwnAfM5szs5vCc94OLJvZQwQF/7XOucfCY58BPm1mhwhsBn9XUR4hhGiEOENu1vTQRfr9Ox1p7JzrXbjgggtcURYXnZuddc4s+F1cLHyLXPep6zlCiO4Zf88QfNNBcR6Edeuyv+/xtZNhdjb9eU2VH8CyiylTOy/Uy4SiimBxMXhp0Rdh5tzCQqHbxN4nmhmyjgsh+kPc95y3QB8zqTyi5U8XJCmCQaxHkDTvtxncemv+4d1Z84drLQMhpoek7zmKWdAtVPQeXZUJg16PIMnq7lwx16wsq75P84sLIaqR57vNMuQm9ftv3erXcriDUARpL6tIIZ1l1fdpfnEhRDWyvts8htw4z6L5edi716/5hgahCHbvDl5CHEUK6Syrvk/ziwshqhH3PY/LkSJTRk96Ft1xh4fzDcUZDnwPZbyGFhbSrf4LC87NzATxMzPJhmR5DQkxHJr4nrs0IDNkr6ExSS91YSH+xRT1KqoDKRIhpoOkb7moS2mdJCmCQXgNZbF6NRw/fmr8zAy8+uqp8U0xHnwSbTauW6cV0oToG2nfMnT3nQ/aayiLOCWQFt8Uvs5VLoTIJjryeH4++Vv2aYnKMWoR4E+LYNWqoJE4SZavshCiW+JaAHF0/S2rRZDCjh3F4ptC7qdC9JO41nwcvn7LUgTADTfAwkLQAoDgd2EhiB/TxspBcj8VohpdrfCVZzxS2rfcldy/IM6C7Hso6zVUljxzDNXl6SOvISHK0eVcX0meQFGPoCQ52pQbeQ2VJ22+kN275ekjhA90Oa/P0hJcfnn8MZ/mI0qyEUgR5CDNiLt5c/xLHI3ghReal00IEZD0nULwPR47Fnyvu3c3U0nbsAGOHj01PqtAb9NJpBFjsZmdZmZ3mdnB8Hd9zDkfMLMHI+FfxwvYm9ktZvb9yLHzqsjTFGlG3KS+waNHu59ISoghkWaIPXq0+Xl9rr++nI3PByeRqsbincA9zrlzgHvC/ZNwzn3bOXeec+484IPAS8D/iJzy5+PjzrkHK8rTCGlG3LSXJf9/Idoj7juNo6mxOWXHB3jhJBJnOMgbgAPApnB7E3Ag4/wdwFJk/xbg0qLPbdtY7FyyEXdxMdlAFDd3SPQ+o1EQZBgWoh7SvkcfFoZJoi0nEZqYawh4MbJt0f2E878F/KfI/i2hMnkYuA5Ym+e5XSiCNEajZE+BKFkrHjXp4SBvJDEUsjx4xhNLDvEbKK0IgLuBR2LCtsmCH/hxyn02ASvA6ybiDFgL7AX+IuX6HcAysLx58+YWkiw/ed2/8mTQJiae0hKaYkjkWWJyqN9AUy2C3F1DwH8F9qQcfz/wT3me61uLwLl8Ne6k6WebbrJ2OduhEF0w2QW7apW+AeeSFUFVY/E+YD7cnge+kXLux4AvRyPMbFP4a8AlBC2NXjK5+EScgSiPF0ATngJaQlP0gTpH10a/xxdeSHYr1TcQUFURXAt8yMwOAheG+5jZnJndND7JzLYAZwL/c+L6JTPbD+wHNgB/WVEer8nyamjKU8AH9zQh0hhP2tbU8o36BjKIayb4HnzsGspLF15DshEI36mj+zKte9b3b6DXXkNdhT4rgq6Q15DwmarLN+Yp6BcXT/bwG438+A4011BJ2p5iQgjRLFXn28lzva8rAJadmqIMWo9ACOEtVUfX5nGI8HEFwKWleCUA7RqypQiEEJ1TdfnGNGPw2BsprsUA3XoOpSmhPs01JGqi84UphKiJsnk5jwt2Ekktiq1bT3gjJdGl51CaEmpzriEpAg9o2nWuTaTQppO877WrvJzUorjjjvQlJLteATBJCY1GLdst4izIvodp8xqalpG/vrvoiXIUea++5eW00fw+eM+1/c0g91F/qeo65wu+FQKiHoq8V1/y8thduok5vep2xW7TtTtJEahrqEPGzW2X4MHbt1GPmspiOinyXn0YwRvtnoqjSndQE11fVWwjdSFF0BFNZtbJ57TVZ+9DISDqp8h77XqRlaUlmJ9PtgsU9UaaxEcX1FqIayb4Hqahayir2VpH87Dt/kfZCKaTou81b1dHE10sadNP19E95UvXV1mQjcAv2shQXfTZayqL6aSNQrtqpSFrvY868n3f7WBSBJ7RRobqe+1F1I8virqJ/J/mIVRXy7Tvrd4kRSAbQUe00ZeqPnu/aXvMhU/jVZpwLEjK1zMz9c0nVHUEtLfEaQffwzS0CJxrvnbW99rLNNPFu6lSC687rzbRIlB+zwZ1DU03SR9qnR9wW90KvnRfNEkXfc1luwqbKGCbKrSHkHeq0IgiAH4XeBR4DZhLOe8igvWNDwE7I/FnAfeH8bcBa/I8V4rgZNqoCaU9o25lM4RaXRf2m7LKpymlpUK7fZpSBG8HfhW4N0kRADPAk8DZwBrgIeDc8NhXgcvC7RuBhTzPlSI4mTZql0nPGI3qLbj77pWRl648usq8KzkdTA9JiqCSsdg597hz7kDGae8CDjnnDjvnfgZ8BdgWLlj/QeD28Ly9BAvYi4K0MaI36V5Hj9Y7wGYoo5O7GHhV1tApp4Pppw2vodOBZyL7R8K4EfCic+7VifhYzGyHmS2b2fLKykpjwvaRNj7UovcqW3APpdDpyvukzHQGXY8WFs2TqQjM7G4zeyQmbGtDwDHOuT3OuTnn3NzGjRvbfLT3tPGhJj1jNIo/v2zBPaRCx4c5ZvIwtS6T4heszjrBOXdhxWc8C5wZ2T8jjDsKvMnMVoetgnG8KMj4g9y1K6iJb94cFJx1fqhJz4D4dWDLFtxt/BdRnO3b9Q6mmVoWrzeze4E/c86dsqK8ma0GngB+k6Cg/x7wcefco2b2NeAfnHNfMbMbgYedczdkPU+L1/vF0pIKbiH6QCOL15vZb5vZEeA9wD+b2Z1h/FvM7A6AsLb/KeBO4HHgq865R8NbfAb4tJkdIrAZ/F0VeUQ39KWLQwgRTy0tgrZRi0AIIYrTSItACCFE/5EiEEKIgSNFIIQQA0eKQAghBk4vjcVmtgIkrPabygbghZrFqQPJVRxfZZNcxfFVtmmUa9Y5d8qI3F4qgrKY2XKcxbxrJFdxfJVNchXHV9mGJJe6hoQQYuBIEQghxMAZmiLY07UACUiu4vgqm+Qqjq+yDUauQdkIhBBCnMrQWgRCCCEmkCIQQoiBM3WKwMx+18weNbPXzCzRxcrMLjKzA2Z2yMx2RuLPMrP7w/jbzGxNTXKdZmZ3mdnB8Hd9zDkfMLMHI+FfzeyS8NgtZvb9yLHz2pIrPO945Nn7IvGNpFde2czsPDP7TvjOHzaz348cqzXNkvJM5PjaMA0OhWmyJXLs6jD+gJl9pIocJeT6tJk9FqbPPWY2GzkW+15bkusTZrYSef4fRY7Nh+/9oJnN1ylXTtmui8j1hJm9GDnWSJqZ2c1m9ryZPZJw3Mzsb0OZHzazd0aOVUuvuIWM+xyAtwO/CtwLzCWcMwM8CZwNrAEeAs4Nj30VuCzcvhFYqEmuvwF2hts7gb/OOP804BiwLty/Bbi0gfTKJRfw04T4RtIrr2zAvwfOCbffAjwHvKnuNEvLM5Fz/hi4Mdy+DLgt3D43PH8tcFZ4n5kW5fpAJB8tjOVKe68tyfUJ4PMx154GHA5/14fb69uUbeL8PwVubiHN3ge8E3gk4fhW4JuAAe8G7q8rvaauReCce9w5dyDjtHcBh5xzh51zPwO+AmwzMwM+CNwenrcXuKQm0baF98t730uBbzrnXso4rypF5foFDadXLtmcc0845w6G2/8CPA80sZZpbJ5Jkfd24DfDNNoGfMU594pz7vvAofB+rcjlnPt2JB/dR7AaYNPkSa8kPgLc5Zw75pz7MXAXcFGHsn0M+HKNz4/FOfe/CCp/SWwD/t4F3EewwuMmakivqVMEOTkdeCayfySMGwEvumAxnWh8HbzZOfdcuP1D4M0Z51/GqZlvd9gkvM7M1rYs1+vNbNnM7ht3V9FsehWRDQAzexdBDe/JSHRdaZaUZ2LPCdPkJwRplOfaJuWKciVBrXJM3HttU67fCd/P7WY2XtK2yfQqdP+wG+0s4FuR6KbSLIskuSunV+aaxT5iZncD/zbm0C7n3DfalmdMmlzRHeecM7NEv91Qy/9HglXdxlxNUBiuIfAj/gxwTYtyzTrnnjWzs4Fvmdl+goKuEjWn2a3AvHPutTC6dJpNI2Z2OTAH/EYk+pT36px7Mv4OtfOPwJedc6+Y2X8maE19sKVn5+Uy4Hbn3PFIXJdp1gi9VATOuQsr3uJZ4MzI/hlh3FGC5tbqsEY3jq8sl5n9yMw2OeeeCwut51Nu9XvA151zP4/ce1wzfsXMvgT8WZtyOeeeDX8PW7BG9fnAP1AhveqSzcx+GfhngorAfZF7l06zGJLyTNw5RyxYq/tXCPJUnmublAszu5BAuf6Gc+6VcXzCe62jUMuUyzl3NLJ7E4FNaHzt+yeuvbcGmXLLFuEy4E+iEQ2mWRZJcldOr6F2DX0POMcCj5c1BC97nwssL98m6J8HmAfqamHsC++X576n9EmGBeG4X/4SINazoAm5zGz9uFvFzDYAvw481nB65ZVtDfB1gr7T2yeO1ZlmsXkmRd5LgW+FabQPuMwCr6KzgHOA71aQpZBcZnY+8EXgYufc85H42PfaolybIrsXE6xpDkFL+MOhfOuBD3Ny67hx2UL53kZgfP1OJK7JNMtiH/AHoffQu4GfhJWd6unVhPW7ywD8NkEf2SvAj4A7w/i3AHdEztsKPEGgyXdF4s8m+EgPAV8D1tYk1wi4BzgI3A2cFsbPATdFzttCoOFXTVz/LWA/QWG2CLyxLbmA94bPfij8vbLp9Cog2+XAz4EHI+G8JtIsLs8QdDVdHG6/PkyDQ2GanB25dld43QHgozXn+Sy57g6/hXH67Mt6ry3J9VfAo+Hzvw28LXLtH4bpeAj4ZJ1y5ZEt3P8scO3EdY2lGUHl77kwPx8hsOdcBVwVHjfgC6HM+4l4RVZNL00xIYQQA2eoXUNCCCFCpAiEEGLgSBEIIcTAkSIQQoiBI0UghBADR4pACCEGjhSBEEIMnP8PNRUZ2fYpuekAAAAASUVORK5CYII=\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    },
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "测试集 100 个数据点的可视化：\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAD4CAYAAADhNOGaAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAh60lEQVR4nO3de8wd9X3n8ffHpia1UBvbeAkB/Bi2pAltuiQ86yQbaZsLCYSVMNmSxKmTddJEXtKQlTbaFUZIm4hda2n3D9SqUbsWSXDwswFKFeFuyLJct380pDxI3AwCGwgXlwTHTiJZUK7f/WPmxOPjc33O3OfzkkbnnJk55/zOzJz5/uZ3G0UEZmbWXcuqToCZmVXLgcDMrOMcCMzMOs6BwMys4xwIzMw67riqE7AUJ554Yqxfv77qZJiZNcp99933s4hY2z+/kYFg/fr1LC4uVp0MM7NGkfT0oPkuGjIz6zgHAjOzjnMgMDPrOAcCM7OOcyAwM+u4XAKBpG9JekHSw0OWS9KfS9on6UFJ784s2yJpbzptySM9ZjabhQVYvx6WLUseFxaqTpEVKa8rgmuB80cs/xhwZjptBf4SQNJq4GvAe4ANwNckrcopTWa2BAsLsHUrPP00RCSPW7c6GLRZLoEgIv4OODRilY3AdyJxD/BmSScD5wG3RcShiPg5cBujA0rtOSdlTXfFFfDii0fPe/HFZL61U1kdyk4Bns28fi6dN2z+MSRtJbmaYN26dcWkcka9nFTvT9TLSQFs3lxdusym8cwz08235mtMZXFE7IiI+YiYX7v2mB7StdCUnJSvWqpV9+0/LJ9V0/zXzKrYH3U7Bsq6ItgPnJZ5fWo6bz/wgb75d5eUptw1ISflq5Zq1X37LyzA4cPHzl+5ErZvLz89Ratif9TyGIiIXCZgPfDwkGX/BvgBIOC9wD+k81cDTwGr0ukpYPW47zrnnHOijubmIpLqtaOn5csjdu2qOnWJYWmcm8v3e3btSj5TSh7r8vurVtb2X4pduyJWrjw2bWvWtHf/TbI/8jqWe58z6PvKOgaAxRh0jh40c9oJ+C7wPPAqSTn/F4BLgEvS5QK+ATwBPATMZ977R8C+dPr8JN+XRyAo4kQ17I8Eyfw6/JmkwemT8vuOQduhLr+/amVs/6Wqc5Ca1bD/+7j9kdexPOrcUOYxUGggKHuaNRAUeaLatSu5AqjrH6qMP3ubTyizqvO2qXOQmsWo//u4/ZHX/hp1JdCaK4Kyp1kDQdF/xjr/ocrIrdf591etzldLdQ5Ssxj1u8btj7yO5WGfU/Yx4ECQUfSJqu5/qKLL7+v++6tW1/qTooNUVb97kuKfYekq44qgzG3hQJBR9Imqzrm+MnT99zdZUSfrKo+JWf7vRdYRVPGfcCDIKGOn1DXXV5au/347WpVXibP+3/NuNVTlf2JYIFCyrFnm5+dj1ltVLiwkHb2eeSbpKHPBBXDLLUdeb99ej3bdZm2wbFlyCu4nwRtvFP/9/f/3rv6/Jd0XEfP98xvTszhvmzfDj3+cHITbt8POnfkOslVGz8G69U40G6bq3srZ//uPf9zNIDBKZwNBVt5DQ5QxeqNHiLQm2b496Z2cNai3sjM3FRlUXlT3Ke+exXm3Ilpqeeg0ZYhumWNNM+74rkuFapvhOoLh1q9PctT95uaSy8hpLaU8tH/8EUhyTDt2DL6MrbrM1Sxvef8P7ViuIxhh0svWSS2lPHTa4qmqy1zN8taEQRvbyoGAJMe9Y0eS85CSx2E58UksJbBM+yfIO3iZVc2Zm+o4EKTybFWwlMAy7Z8g7+BlVrWiMjeugJ7AoIqDuk91HYZ6Fq4oM8u/05X/V0djSGWxrwhqwjl8s/zb+1d518AmXYm41ZCZtVZVreumbQVYFrcaMrPOqaoCuin3L+/JJRBIOl/SY5L2Sdo2YPnVku5Pp8cl/SKz7PXMst15pMfMDKprXde0prAz37xe0nKS21B+hOQ2lfdK2h0Rj/TWiYj/mFn/K8C7Mh/xUkScPWs6zMz69Yphyh5wbt26wZ3j6toUNo8rgg3Avoh4MiJeAa4HNo5Y/9Mk9ziutSIreppUiWTWdFUMONe0fj55BIJTgGczr59L5x1D0hxwOnBnZvabJC1KukfSRcO+RNLWdL3FAwcO5JDs4Yoc0M2DxZm1X9NaAc7cakjSxcD5EfHF9PVngfdExKUD1r0MODUivpKZd0pE7Jd0BkmA+HBEPDHqO4tuNVTkmCceT8XMqlJkq6H9wGmZ16em8wbZRF+xUETsTx+fBO7m6PqDUvWKbAadqCGfip6mVSKZWfvlEQjuBc6UdLqkFSQn+2Na/0h6O7AK+GFm3ipJx6fPTwTeDzzS/94yZItshsmjosfjqZhZ3cwcCCLiNeBS4FbgUeDGiNgj6UpJF2ZW3QRcH0eXRb0DWJT0AHAXcFW2tVGZBrX7zcqroqdplUhmVp2yGpbM3HwUICJuAW7pm/df+l5/fcD7/h54Zx5pmNWoopm5uXybnP36rx8JOmvWwJ/9WX0rkcysGv29k3sNSyD/84V7FqeGFc30KnHz2PC9HXvw4JF5L700++eaWfuU2TvZgSBVRpFN07qdm1l1ymxY4kCQKqPdr1sMmdmkymxY4kCQUXQPRLcYMrNJldmwxIGgRG4xZGaTKrN3ci6thmwyVQ2AZWbNtHlzOecHXxGUrIoBsMysHE0dUNJXBGZmOSiz3X/efEVgZpaDJjcPdyAwM8tBk5uHOxCYmeVg9erp5teJA4GZWcc5EJiZ5eDQoenm14kDgZlZDiYdOaCOTUwdCMzMcjDJyAF1vWe5A8GU6hjNzax6kwwJUdcmprkEAknnS3pM0j5J2wYs/5ykA5LuT6cvZpZtkbQ3nbbkkZ6i1DWam1k9jBs5oK5NTGcOBJKWA98APgacBXxa0lkDVr0hIs5Op2vS964Gvga8B9gAfE3SqlnTVJS6RnMza4a6jkCcxxXBBmBfRDwZEa8A1wMbJ3zvecBtEXEoIn4O3Aacn0OaClHXaG5mzVDXEYjzCASnAM9mXj+Xzuv3B5IelHSTpNOmfC+StkpalLR44MCBHJI9vbpGczNrhjKHlp5GWZXFfwusj4jfI8n175z2AyJiR0TMR8T82rVrc0/gJOoazc2sOeo4AnEegWA/cFrm9anpvF+JiIMR8XL68hrgnEnfWyd1jeZmZrPIIxDcC5wp6XRJK4BNwO7sCpJOzry8EHg0fX4r8FFJq9JK4o+m82qrjtHcasjtjK1BZr4fQUS8JulSkhP4cuBbEbFH0pXAYkTsBv6DpAuB14BDwOfS9x6S9F9JggnAlRHRgA7ZZiM0eWB66yRFRNVpmNr8/HwsLi5WnQyzwdavT07+/ebmkstIs4pIui8i5vvnu2exWd7cztgaxoHALG9uZ2wN40Bglje3M7aGcSAwy5vbGVvDOBCYFWFUO2M3LbWambn5qJlNwU1LrYZ8RWA2Tp45eA9hazXkQGA2St43oRjXtNTFRlYBBwKzUfLOwY9qWuo7H1lFHAismcrKOefdOWxU01IXG1lFHAisecrMOefdOWxU01L3SLaKOBBY85SZcy6ic9iwpqXukWwVcSCw5ikz51xE57BhxVrukWwVcT8Ca5516waP7llUznnz5vza+E/Sj+CKK5Kgtm5dEgTcv8AK5isCa4ZsLvrwYVix4ujlTck5jyvW8p2PLKOsNhEOBFZ//ZXDBw8mj2vWHCmu2bIlOZnWvf29K4RtQmW2icglEEg6X9JjkvZJ2jZg+VclPSLpQUl3SJrLLHtd0v3ptLv/vWYDc9GvvgonnJDknLdvh507m9H+vogKYXdCa6VSWxNHxEwTye0pnwDOAFYADwBn9a3zQWBl+vxLwA2ZZYen/c5zzjknrEOkiOQUf/QkJcvn5gYvn5urMtWD7doVsXLl0elcuTKZP+3n9H53//ZZyudZ7Yw77JeC5PbBx5xT87gi2ADsi4gnI+IV4HpgY1+wuSsierHtHuDUHL43V85U1di4XHSTilvyaIWULTOA5PyQ5U5orVBma+I8AsEpwLOZ18+l84b5AvCDzOs3SVqUdI+ki4a9SdLWdL3FAwcOzJTgfu7ZX3PjmlU2rf39rBXCg8oM+k0bBJ0Tqp1SWxMPukyYZgIuBq7JvP4s8BdD1v0MyRXB8Zl5p6SPZwA/Bv75uO/Mu2ioSSULndUrCpGSx2zRR17FLWWkNQ/DygyWevAO2n4QsWaNi5gqlvehxJCioTwCwfuAWzOvLwcuH7DeucCjwD8b8VnXAheP+868A0ERZXFWsqJPvtOko+igNCznstTvG/V5rm+oXJ6HdpGB4DjgSeB0jlQW/07fOu8iqVA+s2/+qt7VAXAisJe+iuZBk68IrLbKOJgGBZtebmYpZ4pxVxj+I1Qm73zFsEAwcx1BRLwGXArcmub4b4yIPZKulHRhutr/AE4A/rqvmeg7gEVJDwB3AVdFxCOzpmla7tlvuSmj4npQhfN11yXniaXUOYyrS6ljpXtHlNWEVEmQaJb5+flYXFzM9TMXFtyz33Kwfv3g4S/m5pKTdB31D3vRr85pb7lly45tFAZJ/H/jjek/T9J9ETF/zPcsJXFt5J79losmXl72rjDWrDl2Wd3T3nJlNYhzIDDryaMJZRGjlZZh82b42c9g167mpb3FyspXuGjIDAYXj6xc6ROhVS7PYuthRUMOBGbQzLJ9sym5jsBslCYNU2GWMwcC67ZevcCwK+O6DlPRz0NE2Ax8hzLrrnHNJpvSYmaSu56ZjeArAuuuUYO3NanFTKkD11sb+YrAumtY+b/UrApi12/YjHxFYN3VtOGrh2nL77DKOBBYdzWxF/Agk/wOVybbCA4E1l159wKu6mQ77nf4zks2hjuUmeWhzj2T3VnOUu5QZlakOrfccWWyjeFAYJaHOp9sXZlsYzgQmOWhzifbKirFXTndKLkEAknnS3pM0j5J2wYsP17SDenyH0lan1l2eTr/MUnn5ZEes9LVuQVS2UNju3K6cWauLJa0HHgc+AjwHHAv8OnsLScl/THwexFxiaRNwMcj4lOSzgK+C2wA3grcDrwtIl4f9Z2uLLZa8m3uEq6crq0iK4s3APsi4smIeAW4HtjYt85GYGf6/Cbgw5KUzr8+Il6OiKeAfennmTWPb3OXqHN9iQ2URyA4BXg28/q5dN7AddKb3f8SWDPhewGQtFXSoqTFAwcO5JBsswZoYll7netLbKDGVBZHxI6ImI+I+bVr11adHLPiNbWsvc71JTZQHoFgP3Ba5vWp6byB60g6DvhN4OCE77Wua2KuOA917pswSlPv29xheVQWH0dSWfxhkpP4vcAfRsSezDpfBt6ZqSz+txHxSUm/A/wvjlQW3wGc6cpi+5U699gt2rJlg2+YIyX1EGZTKqyyOC3zvxS4FXgUuDEi9ki6UtKF6WrfBNZI2gd8FdiWvncPcCPwCPB/gC+PCwLWMU3NFefBZe1WEo81ZPXW5Vxxl6+GrBAea8iaqcu5Ype1W0kcCKzeBrVA+bVfg8OHu1F57L4JVgIHAqu3/lzxmjXJ48GDzWpSaTaBqhrIORBY/WVzxSecAK+8cvTyulQed7WZq+Wiym4jDgTWLHUbvqB38pfgs59tXuevaTjQFarKBnIOBNYsdao8zmbh4NjWTXW5UslDU3s5N8igcfpGzc+TAwHO6DRKnYYvGJSF69eWgda63J+jJMuXTzc/T50PBM7oNMywJpVQfjSf5CTflmaudSuSa6HXh3SlHTY/T50PBM7oNFB/k0qoJpqPO8m3aaC1OhXJtdTc3HTz89T5QOCMTgtUFc0HFVNJyWPbOn/VqUiupS644Mjh01PWJu58IHBGpwWqiuaDiqmuuy65Kmlb5y/3ci7UwgLs3Hl0ewMJtmwpZxN3fqwhD+fSAr41ojVcWYewxxoawhmdFnCxhTVc1UXUnQ8E4OFcGs/R3Bqu6iJqBwJrB0dza7CqL2pnCgSSVku6TdLe9HHVgHXOlvRDSXskPSjpU5ll10p6StL96XT2LOkxK5V7IlpOqr6onamyWNKfAoci4ipJ24BVEXFZ3zpvAyIi9kp6K3Af8I6I+IWka4H/HRE3TfO9vjGNVc6tDKyBiqos3gjsTJ/vBC7qXyEiHo+IvenzfwReANbO+L1m1XJPRGuRWQPBSRHxfPr8J8BJo1aWtAFYATyRmb09LTK6WtLxM6bHrBxVN/Mwy9HYQCDpdkkPD5g2ZteLpIxpaDmTpJOB64DPR0TvZrOXA28H/iWwGrhsyNuRtFXSoqTFAwcOjP9lZkWqupmHWY7GBoKIODcifnfAdDPw0/QE3zvRvzDoMyT9BvB94IqIuCfz2c9H4mXg28CGEenYERHzETG/dq1LlqxiVTfzMMvRrEVDu4Et6fMtwM39K0haAXwP+E5/pXAmiIikfuHhGdNjVo6qm3lYq5XdIG3WVkNrgBuBdcDTwCcj4pCkeeCSiPiipM+Q5Pb3ZN76uYi4X9KdJBXHAu5P33N43Pe61ZCZtVWRDdKGtRrq/FhD4ywsJA1BnnkmKf7dvt2ZPjMrTpHjDnmsoSXwTWtawh2/rEGqaJDmQDCCm4q3gKO5NUwVDdIcCEZwU/EWcDS3hqmiQZoDwQhuKl5zkxT5tCmau4irE6pokOZAMIKbitfYpEU+bYnmLuLqlLIH03UgGMFNxWts0iKftkRzF3FZgdx81Jpp2bKjb/DaIyXZqKw2tAGe5veaDTGs+ehxVSTGbGbr1g1ubD2oyGfz5uad+PtN83vNpuSiIWumthT5TKprv9dK5UBgzdS1Cpyu/V4rlesIctCGImgzaz8PMdEnrybZbtVnZk3XyUCQ58nbrfrMrOk6GQjyPHm3qeOqmXVTJwNBnifvtnRcNbPu6mQgyPPk7VZ9ZtZ0MwUCSasl3SZpb/q4ash6r0u6P512Z+afLulHkvZJuiG9rWXh8jx5u1WfmTXdrFcE24A7IuJM4I709SAvRcTZ6XRhZv6fAFdHxG8BPwe+MGN6JpL3ybvsAaLMzPI06z2LHwM+EBHPpzeivzsifnvAeocj4oS+eQIOAG+JiNckvQ/4ekScN+5769aPwMysCYrqR3BSRDyfPv8JcNKQ9d4kaVHSPZIuSuetAX4REa+lr58DTpkxPWZmNqWxg85Juh14y4BFRzW2jIiQNOzyYi4i9ks6A7hT0kPAL6dJqKStwFaAdW6SY2aWm7GBICLOHbZM0k8lnZwpGnphyGfsTx+flHQ38C7gb4A3SzouvSo4Fdg/Ih07gB2QFA2NS7eZmU1m1qKh3cCW9PkW4Ob+FSStknR8+vxE4P3AI5FUTtwFXDzq/WZmVqxZA8FVwEck7QXOTV8jaV7SNek67wAWJT1AcuK/KiIeSZddBnxV0j6SOoNvzpgeMzOb0kyBICIORsSHI+LMiDg3Ig6l8xcj4ovp87+PiHdGxL9IH7+Zef+TEbEhIn4rIj4RES/P9nOqMckAdr7vuJnVle9QNqPeAHa9sYt6A9jBkf4Ek6xjZlaVzgwxUVSOfJIB7DxCqZnVWSeuCIrMkU8ygJ1HKDWzOuvEFUGROfJJBrDzCKVm7dWG+r9OBIIic+TjBrBbWIDDh499n0coNWu+ttyhsBOBoMgc+agB7HoHycGDR79nzRqPUGrWBm2p/+vEzev76wggyZEXfTJevz7JIfSbm0tGKTWzZlu2LLkS6CcloxHXTadvXl/VPQNcSWzWbm2p/+tEIIBq7hnQloPEzAab9iZXS61YLrpCujOBoAq+jaVZu01T2rDUiuUyKqQ7UUdQpYWFpOLomWeSK4Ht211JbNZFS60zzLOucVgdgQOBmVkJllqxnGeFdKcri9ukDZ1XzLpoqXWGZdQ1OhA0SFs6r5h10VLrDMuoa3QgaJC2dF4x66KlNmMvo/m76wgapGmdV8ysXgqpI5C0WtJtkvamj6sGrPNBSfdnpn+SdFG67FpJT2WWnT1LetrO/RLMrAizFg1tA+6IiDOBO9LXR4mIuyLi7Ig4G/gQ8CLwfzOr/Ofe8oi4f8b0tJr7JZhZEWYNBBuBnenzncBFY9a/GPhBRLw4Zj0boKqhMsys3WYNBCdFxPPp858AJ41ZfxPw3b552yU9KOlqScfPmJ7Wq2KoDDNrt7F3KJN0O/CWAYuOaqsSESFpaM2zpJOBdwK3ZmZfThJAVgA7gMuAK4e8fyuwFWCdC8XNzHIz9oogIs6NiN8dMN0M/DQ9wfdO9C+M+KhPAt+LiFczn/18JF4Gvg1sGJGOHRExHxHza9eunfT3mZktWVc6cM5aNLQb2JI+3wLcPGLdT9NXLJQJIiKpX3h4xvSYmU1s1Im+Sx04Zw0EVwEfkbQXODd9jaR5Sdf0VpK0HjgN+H9971+Q9BDwEHAi8N9mTI+N0JXcjdkkxp3ou9SB0x3KxuiNHvr007B8Obz+etJap2mjiFZ1lzazuho3qmcbO3B60LklyOYYIAkC0MxLxC7lbswmMeoOggsLSSAYpKi2KlVesfuKYIRhOYaeJt17uI25G7NZDPt/r1kDL710bMYJiruKLuuK3VcESzDu3sJNuvewh6cwS/Ry3k8/nWSEsno99wcFgeXLiwsCW7ZUe8XuQDDCUscJryMPT2F2bHFvxJFg0Oupf+jQ4Pe+8cZ0QWCSop5eenrFzv1Ky2xGROOmc845J8qwa1fEypURyeFy9LRyZbK8SXbtipibi5CSx6al32xWc3OD/89zc9OtM86gc8egc8aw71rKd04CWIwB59TKT+pLmcoKBBFHTp4QsXz5kZ1T1UnUJ3OzpZMGn3ClI+tMehIfZdJgMiw9RWU2HQhaII8DtGoOZFalSU/Qsx6nkwScUelZvryY/4YDQQvkccmaVfZJuQ2BzJqtrGNwmoBT5n/CgaAFJs1lTKKKk3LegcxsKcrIAE3z/yozQzYsELgfQYOM6wlZ1WdNyn0ZrEt6oxI880zSwrAOoxG4H0EL5NkEdFSvyqK4L4N1SZPuHeJA0CB53qGsipPyoEAmwQUXFPedZjaeA0HD5JXLGHd1UcS4J5s3Jz0os705I2DnzmaN29QGHonWjjKo4qDuU1cri/M2rJKqyIrkulQYd7kZaxtbb3V5f04DtxoqXlsOxiJP1nm2fFqqNp4Ip1GXYJyXru/PaQwLBC4aykmb7mZUZEVyHSqMuz4k97T7t+7FSG3cn6Vv80HRYdIJ+ASwB3gDmB+x3vnAY8A+YFtm/unAj9L5NwArJvneOl4RtCmXVeRvqUPurQ5XJVWaZv/WYX+N07b9WeQ2p4iiIeAdwG8Ddw8LBMBy4AngDGAF8ABwVrrsRmBT+vyvgC9N8r11DARtOhiL/vNXXYTWpqC9FNPs3yZsqyakcRpF/p5CAsGvPmR0IHgfcGvm9eXpJOBnwHGD1hs11TEQtO1grPpkXaQm5HKLNun+bUIGp237s8htPiwQlFFHcArwbOb1c+m8NcAvIuK1vvmN1Lbx/pvUGWZaefbHaKpJ928d6nTGadv+rGKbjw0Ekm6X9PCAaWNxyRqYjq2SFiUtHjhwoMyvnkjbDsa2a3Ogy1NTMjht2p9VbPPjxq0QEefO+B37gdMyr09N5x0E3izpuPSqoDd/WDp2ADsgGWtoxjQVYvPmZh+AZv16x3Pdxsxpsyq2+dhAkIN7gTMlnU5yot8E/GFSFqa7gIuB64EtwM0lpMfMpuAMTvnK3uYz1RFI+rik50gqer8v6dZ0/lsl3QKQ5vYvBW4FHgVujIg96UdcBnxV0j6SOoNvzpIeMzObnoehNjPrCA9DbWZmAzkQmJl1nAOBmVnHNbKOQNIBYMCNFidyIkmP5rpxuqZT13RBfdPmdE2vrmlbarrmImJt/8xGBoJZSFocVFlSNadrOnVNF9Q3bU7X9OqatrzT5aIhM7OOcyAwM+u4LgaCHVUnYAinazp1TRfUN21O1/TqmrZc09W5OgIzMztaF68IzMwsw4HAzKzjWhkIJH1C0h5Jb0ga2sRK0vmSHpO0T9K2zPzTJf0onX+DpBU5pWu1pNsk7U0fVw1Y54OS7s9M/yTponTZtZKeyiw7u6x0peu9nvnu3Zn5VW6vsyX9MN3fD0r6VGZZrttr2PGSWX58+vv3pdtjfWbZ5en8xySdN0s6lpCur0p6JN0+d0iayywbuE9LTNvnJB3IpOGLmWVb0n2/V9KWktN1dSZNj0v6RWZZYdtM0rckvSDp4SHLJenP03Q/KOndmWVL316DblvW9ImK7qU8Qbr+FNiWPt8G/MmY9VcDh4CV6etrgYsL2F4TpQs4PGR+ZdsLeBtwZvr8rcDzwJvz3l6jjpfMOn8M/FX6fBNwQ/r8rHT944HT089ZXmK6Ppg5hr7US9eofVpi2j4H/MWA964GnkwfV6XPV5WVrr71vwJ8q6Rt9q+BdwMPD1l+AfADklv9vhf4UR7bq5VXBBHxaEQ8Nma1DcC+iHgyIl4huSfCRkkCPgTclK63E7gop6RtTD9v0s+9GPhBRLyY0/cPM226fqXq7RURj0fE3vT5PwIvAMf0nMzBwONlRHpvAj6cbp+NwPUR8XJEPAXsSz+vlHRFxF2ZY+gekptAlWGSbTbMecBtEXEoIn4O3AacX1G6Pg18N6fvHiki/o4k8zfMRuA7kbiH5OZeJzPj9mplIJhQFfdSPikink+f/wQ4acz6mzj2ANyeXhJeLen4ktP1JiW3C72nV1xFjbaXpA0kObwnMrPz2l7DjpeB66Tb45ck22eS9xaZrqwvkOQoewbt07xMmrY/SPfRTZJ6dzOsxTZLi9FOB+7MzC5ym40zLO0zba8y7lBWCEm3A28ZsOiKiKjsTmej0pV9EREhaWjb3TTKv5Pkhj49l5OcEFeQtCO+DLiyxHTNRcR+SWcAd0p6iORkt2Q5b6/rgC0R8UY6e8nbq40kfQaYB34/M/uYfRoRTwz+hEL8LfDdiHhZ0r8nuaL6UInfP84m4KaIeD0zr+ptlrvGBoKoyb2Up0mXpJ9KOjkink9PXC+M+KhPAt+LiFczn93LHb8s6dvAfyozXRGxP318UtLdwLuAv6Hi7SXpN4Dvk2QC7sl89pK31wDDjpdB6zwn6TjgN0mOp0neW2S6kHQuSXD9/Yh4uTd/yD7N66Q2Nm0RcTDz8hqSeqHeez/Q9967y0pXxibgy9kZBW+zcYalfabt1eWioV/dS1lJK5dNwO5Ial5691KGfO+lvDv9vEk+95hyyfRk2CuXvwgY2LKgiHRJWtUrWpF0IvB+4JGqt1e6775HUm56U9+yPLfXwONlRHovBu5Mt89uYJOSVkWnA2cC/zBDWqZKl6R3Af8TuDAiXsjMH7hPc0rXpGk7OfPyQpLb2UJyJfzRNI2rgI9y9NVxoelK0/Z2korXH2bmFb3NxtkN/Lu09dB7gV+mGZ7ZtldRtd9VTsDHScrIXgZ+Ctyazn8rcEtmvQuAx0mi+RWZ+WeQ/FH3AX8NHJ9TutYAdwB7gduB1en8eeCazHrrSSL8sr733wk8RHJC2wWcUFa6gH+VfvcD6eMX6rC9gM8ArwL3Z6azi9heg44XkqKmC9Pnb0p//750e5yRee8V6fseAz6W8/E+Ll23p/+D3vbZPW6flpi2/w7sSdNwF/D2zHv/KN2W+4DPl5mu9PXXgav63lfoNiPJ/D2fHtPPkdTpXAJcki4X8I003Q+RaRU5y/byEBNmZh3X5aIhMzPDgcDMrPMcCMzMOs6BwMys4xwIzMw6zoHAzKzjHAjMzDru/wPTby8hcT1iEgAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    },
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "\n",
-      " 读者不妨自己调节数据集的参数设置来生成属于自己的数据集吧！\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 数据集参数设置\n",
-    "Ntrain=200        # 规定训练集大小\n",
-    "Ntest=100         # 规定测试集大小\n",
-    "boundary_gap=0.5  # 设置决策边界的宽度\n",
-    "seed_data=2       # 固定随机种子\n",
-    "\n",
-    "# 生成自己的数据集\n",
-    "train_x, train_y, test_x, test_y = circle_data_point_generator(\n",
-    "        Ntrain, Ntest, boundary_gap, seed_data)\n",
-    "print(\"训练集 {} 个数据点的可视化：\".format(Ntrain))\n",
-    "data_point_plot(train_x, train_y)\n",
-    "print(\"测试集 {} 个数据点的可视化：\".format(Ntest))\n",
-    "data_point_plot(test_x, test_y)\n",
-    "print(\"\\n 读者不妨自己调节数据集的参数设置来生成属于自己的数据集吧！\")"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 数据的预处理\n",
-    "\n",
-    "与经典机器学习不同的是，量子分类器在实际工作的时候需要考虑数据的预处理。我们需要多加一个步骤将经典的数据转化成量子信息才能放在量子计算机上跑。接下来我们看看具体是怎么完成的。首先我们确定需要使用的量子比特数量。因为我们的数据 $\\{x^{(i)} = (x^{(i)}_0, x^{(i)}_1)\\}$ 是二维的, 按照 Mitarai (2018) 论文中的编码方式我们至少需要2个量子比特。接着准备一系列的初始量子态 $\\lvert {00}\\rangle$。然后将经典信息 $\\{x^{(i)}\\}$ 编码成一系列量子门 $U(x^{(i)})$ 并作用在初始量子态上。最终得到一系列的量子态 $\\lvert {\\psi^{(i)}}\\rangle = U(x^{(i)})\\lvert {00}\\rangle$。这样我们就完成从经典信息到量子信息的编码了！给定 $m$ 个量子比特去编码二维的经典数据点，则量子门的构造为：\n",
-    "\n",
-    "$$\n",
-    "U(x^{(i)}) = \\otimes_{j=0}^{m-1} R_j^z\\big[\\arccos(x^{(i)}_{j \\, \\text{mod} \\, 2}\\cdot x^{(i)}_{j \\, \\text{mod} \\, 2})\\big] R_j^y\\big[\\arcsin(x^{(i)}_{j \\, \\text{mod} \\, 2}) \\big]\n",
-    "$$\n",
-    "\n",
-    "注意：这种表示下，我们将第一个量子比特编号为 $j = 0$。下标 $j$ 表示旋转门 $R_z$ 或者 $R_y$ 作用在第 $j+1$ 个量子比特上。论文中作者并没有提及为何要这么编码经典信息，更多编码方式见 [Robust data encodings for quantum classifiers](https://arxiv.org/pdf/2003.01695.pdf)。这里我们也欢迎读者自己创新尝试全新的编码方式！由于这种编码的方式看着比较复杂，我们不妨来举一个简单的例子。假设我们给定一个数据点 $x = (x_0, x_1)= (1,0)$, 显然这个数据点的标签应该为 1，对应上图**蓝色**的点。同时数据点对应的2比特量子门 $U(x)$ 是\n",
-    "\n",
-    "$$\n",
-    "U(x) = \n",
-    "\\bigg( R_0^z\\big[\\arccos(x_{0}\\cdot x_{0})\\big] R_0^y\\big[\\arcsin(x_{0}) \\big]  \\bigg)\n",
-    "\\otimes \n",
-    "\\bigg( R_1^z\\big[\\arccos(x_{1}\\cdot x_{1})\\big] R_1^y\\big[\\arcsin(x_{1}) \\big] \\bigg)\n",
-    "$$\n",
-    "\n",
-    "把具体的数值带入我们就能得到：\n",
-    "$$\n",
-    "U(x) = \n",
-    "\\bigg( R_0^z\\big[0\\big] R_0^y\\big[\\pi/2 \\big]  \\bigg)\n",
-    "\\otimes \n",
-    "\\bigg( R_1^z\\big[\\pi/2\\big] R_1^y\\big[0 \\big] \\bigg)\n",
-    "$$\n",
-    "\n",
-    "我们回忆一下常用的旋转门的矩阵形式：\n",
-    "\n",
-    "\n",
-    "$$ \n",
-    "R_x(\\theta) := \n",
-    "\\begin{bmatrix} \n",
-    "\\cos \\frac{\\theta}{2} &-i\\sin \\frac{\\theta}{2} \\\\ \n",
-    "-i\\sin \\frac{\\theta}{2} &\\cos \\frac{\\theta}{2} \n",
-    "\\end{bmatrix}\n",
-    ",\\quad \n",
-    "R_y(\\theta) := \n",
-    "\\begin{bmatrix}\n",
-    "\\cos \\frac{\\theta}{2} &-\\sin \\frac{\\theta}{2} \\\\ \n",
-    "\\sin \\frac{\\theta}{2} &\\cos \\frac{\\theta}{2} \n",
-    "\\end{bmatrix}\n",
-    ",\\quad \n",
-    "R_z(\\theta) := \n",
-    "\\begin{bmatrix}\n",
-    "e^{-i\\frac{\\theta}{2}} & 0 \\\\ \n",
-    "0 & e^{i\\frac{\\theta}{2}}\n",
-    "\\end{bmatrix}\n",
-    "$$\n",
-    "\n",
-    "那么这个两比特量子门 $U(x)$ 的矩阵形式可以写为：\n",
-    "\n",
-    "$$\n",
-    "U(x) = \n",
-    "\\bigg(\n",
-    "\\begin{bmatrix}\n",
-    "1 & 0 \\\\ \n",
-    "0 & 1\n",
-    "\\end{bmatrix}\n",
-    "\\begin{bmatrix}\n",
-    "\\cos \\frac{\\pi}{4} &-\\sin \\frac{\\pi}{4} \\\\ \n",
-    "\\sin \\frac{\\pi}{4} &\\cos \\frac{\\pi}{4} \n",
-    "\\end{bmatrix}\n",
-    "\\bigg)\n",
-    "\\otimes \n",
-    "\\bigg(\n",
-    "\\begin{bmatrix}\n",
-    "e^{-i\\frac{\\pi}{4}} & 0 \\\\ \n",
-    "0 & e^{i\\frac{\\pi}{4}}\n",
-    "\\end{bmatrix}\n",
-    "\\begin{bmatrix}\n",
-    "1 &0 \\\\ \n",
-    "0 &1\n",
-    "\\end{bmatrix}\n",
-    "\\bigg)\n",
-    "$$\n",
-    "\n",
-    "化简后我们作用在零初始化的 $\\lvert {00}\\rangle$ 量子态上可以得到编码后的量子态 $\\lvert {\\psi}\\rangle$，\n",
-    "\n",
-    "$$\n",
-    "\\lvert {\\psi}\\rangle =\n",
-    "U(x)\\lvert {00}\\rangle = \\frac{1}{2}\n",
-    "\\begin{bmatrix}\n",
-    "1-i &0 &-1+i &0 \\\\ \n",
-    "0 &1+i &0  &-1-i \\\\\n",
-    "1-i &0 &1-i  &0 \\\\\n",
-    "0 &1+i &0  &1+i \n",
-    "\\end{bmatrix}\n",
-    "\\begin{bmatrix}\n",
-    "1 \\\\\n",
-    "0 \\\\\n",
-    "0 \\\\\n",
-    "0\n",
-    "\\end{bmatrix}\n",
-    "= \\frac{1}{2}\n",
-    "\\begin{bmatrix}\n",
-    "1-i \\\\\n",
-    "0 \\\\\n",
-    "1-i \\\\\n",
-    "0\n",
-    "\\end{bmatrix}\n",
-    "$$\n",
-    "\n",
-    "接着我们来看看代码上怎么实现这种编码方式。需要注意的是：代码中使用了一个张量积的小技巧\n",
-    "\n",
-    "$$\n",
-    "(U_1 \\lvert {0}\\rangle)\\otimes (U_2 \\lvert {0}\\rangle) = (U_1 \\otimes U_2) \\lvert {0}\\rangle\\otimes\\lvert {0}\\rangle\n",
-    "= (U_1 \\otimes U_2) \\lvert {00}\\rangle\n",
-    "$$"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 5,
-   "metadata": {
-    "scrolled": true
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "作为测试我们输入以上的经典信息:\n",
-      "(x_0, x_1) = (1, 0)\n",
-      "编码后输出的2比特量子态为:\n",
-      "[[[0.5-0.5j 0. +0.j  0.5-0.5j 0. +0.j ]]]\n"
-     ]
-    }
-   ],
-   "source": [
-    "def myRy(theta):\n",
-    "    \"\"\"\n",
-    "    :param theta: parameter\n",
-    "    :return: Y rotation matrix\n",
-    "    \"\"\"\n",
-    "    return np.array([[np.cos(theta / 2), -np.sin(theta / 2)],\n",
-    "                     [np.sin(theta / 2), np.cos(theta / 2)]])\n",
-    "\n",
-    "def myRz(theta):\n",
-    "    \"\"\"\n",
-    "    :param theta: parameter\n",
-    "    :return: Z rotation matrix\n",
-    "    \"\"\"\n",
-    "    return np.array([[np.cos(theta / 2) - np.sin(theta / 2) * 1j, 0],\n",
-    "                     [0, np.cos(theta / 2) + np.sin(theta / 2) * 1j]])\n",
-    "\n",
-    "# 经典 -> 量子数据编码器\n",
-    "def datapoints_transform_to_state(data, n_qubits):\n",
-    "    \"\"\"\n",
-    "    :param data: shape [-1, 2]\n",
-    "    :param n_qubits: the number of qubits to which the data transformed\n",
-    "    :return: shape [-1, 1, 2 ^ n_qubits]\n",
-    "    \"\"\"\n",
-    "    dim1, dim2 = data.shape\n",
-    "    res = []\n",
-    "    for sam in range(dim1):\n",
-    "        res_state = 1.\n",
-    "        zero_state = np.array([[1, 0]])\n",
-    "        for i in range(n_qubits):\n",
-    "            if i % 2 == 0:\n",
-    "                state_tmp=np.dot(zero_state, myRy(np.arcsin(data[sam][0])).T)\n",
-    "                state_tmp=np.dot(state_tmp, myRz(np.arccos(data[sam][0] ** 2)).T)\n",
-    "                res_state=np.kron(res_state, state_tmp)\n",
-    "            elif i % 2 == 1:\n",
-    "                state_tmp=np.dot(zero_state, myRy(np.arcsin(data[sam][1])).T)\n",
-    "                state_tmp=np.dot(state_tmp, myRz(np.arccos(data[sam][1] ** 2)).T)\n",
-    "                res_state=np.kron(res_state, state_tmp)\n",
-    "        res.append(res_state)\n",
-    "\n",
-    "    res = np.array(res)\n",
-    "    return res.astype(\"complex128\")\n",
-    "\n",
-    "print(\"作为测试我们输入以上的经典信息:\")\n",
-    "print(\"(x_0, x_1) = (1, 0)\")\n",
-    "print(\"编码后输出的2比特量子态为:\")\n",
-    "print(datapoints_transform_to_state(np.array([[1, 0]]), n_qubits=2))"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 构造量子神经网络 （QNN）\n",
-    "\n",
-    "那么在完成上述从经典数据到量子数据的编码后，我们现在可以把这些量子态输入到量子计算机里面了。在那之前，我们还需要设计下我们所采用的网络结构。\n",
-    "\n",
-    "<img src=\"figures/classifier_circuit.png\" width=\"600\" >\n",
-    "\n",
-    "为了方便，我们统一将上述参数化的量子神经网络称为 $U(\\boldsymbol{\\theta})$。这个 $U(\\boldsymbol{\\theta})$ 是我们分类器的关键组成部分，他需要一定的复杂结构来拟合我们的决策边界。这一点和传统的神经网络是类似的。我们还是拿原来提过的这个数据点 $x = (x_0, x_1)= (1,0)$ 来举例子，编码过后我们已经得到了一个量子态 $\\lvert {\\psi}\\rangle$，\n",
-    "\n",
-    "$$\n",
-    "\\lvert {\\psi}\\rangle =\n",
-    "\\frac{1}{2}\n",
-    "\\begin{bmatrix}\n",
-    "1-i \\\\\n",
-    "0 \\\\\n",
-    "1-i \\\\\n",
-    "0\n",
-    "\\end{bmatrix}\n",
-    "$$\n",
-    "\n",
-    "接着我们把这个量子态输入进我们的量子神经网络（QNN），也就是把一个酉矩阵乘以一个向量。得到处理过后的量子态 $\\lvert {\\varphi}\\rangle$\n",
-    "\n",
-    "$$\n",
-    "\\lvert {\\varphi}\\rangle = U(\\boldsymbol{\\theta})\\lvert {\\psi}\\rangle\n",
-    "$$\n",
-    "\n",
-    "如果我们把所有的参数 $\\theta$ 都设置为 $\\theta = \\pi$, 那么我们就可以写出具体的矩阵了：\n",
-    "\n",
-    "$$\n",
-    "\\lvert {\\varphi}\\rangle = \n",
-    "U(\\boldsymbol{\\theta} =\\pi)\\lvert {\\psi}\\rangle=\n",
-    "\\begin{bmatrix}\n",
-    "0  &0 &-1 &0 \\\\ \n",
-    "-1 &0 &0  &0 \\\\\n",
-    "0  &1 &0  &0 \\\\\n",
-    "0  &0 &0  &1 \n",
-    "\\end{bmatrix}\n",
-    "\\cdot\n",
-    "\\frac{1}{2}\n",
-    "\\begin{bmatrix}\n",
-    "1-i \\\\\n",
-    "0 \\\\\n",
-    "1-i \\\\\n",
-    "0\n",
-    "\\end{bmatrix}\n",
-    "= \\frac{1}{2}\n",
-    "\\begin{bmatrix}\n",
-    "-1+i \\\\\n",
-    "-1+i \\\\\n",
-    "0 \\\\\n",
-    "0\n",
-    "\\end{bmatrix}\n",
-    "$$"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 6,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 模拟搭建量子神经网络\n",
-    "def U_theta(theta, n, depth):  \n",
-    "    \"\"\"\n",
-    "    :param theta: dim: [n, depth + 3]\n",
-    "    :param n: number of qubits\n",
-    "    :param depth: circuit depth\n",
-    "    :return: U_theta\n",
-    "    \"\"\"\n",
-    "    # 初始化网络\n",
-    "    cir = UAnsatz(n)\n",
-    "    \n",
-    "    # 先搭建广义的旋转层\n",
-    "    for i in range(n):\n",
-    "        cir.rz(theta[i][0], i)\n",
-    "        cir.ry(theta[i][1], i)\n",
-    "        cir.rz(theta[i][2], i)\n",
-    "\n",
-    "    # 默认深度为 depth = 1\n",
-    "    # 搭建纠缠层和 Ry旋转层\n",
-    "    for d in range(3, depth + 3):\n",
-    "        for i in range(n-1):\n",
-    "            cir.cnot([i, i + 1])\n",
-    "        cir.cnot([n-1, 0])\n",
-    "        for i in range(n):\n",
-    "            cir.ry(theta[i][d], i)\n",
-    "\n",
-    "    return cir.U"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "# 测量与损失函数\n",
-    "\n",
-    "当我们在量子计算机上（QPU）用 QNN 处理过初始量子态 $\\lvert {\\psi}\\rangle$ 后， 我们需要重新测量这个新的量子态 $\\lvert {\\varphi}\\rangle$ 来获取经典信息。这些处理过后的经典信息可以用来计算损失函数 $\\mathcal{L}(\\boldsymbol{\\theta})$。最后我们再通过经典计算机（CPU）来不断更新QNN参数 $\\boldsymbol{\\theta}$ 并优化损失函数。这里我们采用的测量方式是测量泡利 $Z$ 算符在第一个量子比特上的期望值。 具体来说，\n",
-    "\n",
-    "$$\n",
-    "\\langle Z \\rangle = \n",
-    "\\langle \\varphi |Z\\otimes I\\cdots \\otimes I| \\varphi\\rangle\n",
-    "$$\n",
-    "\n",
-    "复习一下，泡利 $Z$ 算符的矩阵形式为：\n",
-    "\n",
-    "$$ Z := \\begin{bmatrix} 1 &0 \\\\ 0 &-1 \\end{bmatrix}$$\n",
-    "\n",
-    "继续我们前面的2量子比特的例子，测量过后我们得到的期望值就是：\n",
-    "\n",
-    "$$\n",
-    "\\langle Z \\rangle = \n",
-    "\\langle \\varphi |Z\\otimes I| \\varphi\\rangle = \n",
-    "\\frac{1}{2}\n",
-    "\\begin{bmatrix}\n",
-    "-1-i \\quad\n",
-    "-1-i \\quad\n",
-    "0   \\quad\n",
-    "0\n",
-    "\\end{bmatrix}\n",
-    "\\begin{bmatrix}\n",
-    "1  &0 &0  &0 \\\\ \n",
-    "0  &1 &0  &0 \\\\\n",
-    "0  &0 &-1 &0 \\\\\n",
-    "0  &0 &0  &-1 \n",
-    "\\end{bmatrix}\n",
-    "\\cdot\n",
-    "\\frac{1}{2}\n",
-    "\\begin{bmatrix}\n",
-    "-1+i \\\\\n",
-    "-1+i \\\\\n",
-    "0 \\\\\n",
-    "0\n",
-    "\\end{bmatrix}\n",
-    "= 1\n",
-    "$$\n",
-    "\n",
-    "好奇的读者就会问了，咦？这个测量结果好像就是我们原来的标签1啊，这是不是意味着我们已经成功的分类这个数据点了？其实并不然，因为 $\\langle Z \\rangle$ 的取值范围通常在 $[-1,1]$之间。 为了对应我们的标签范围 $y^{(i)} \\in \\{0,1\\}$, 我们还需要将区间上下限映射上。这个映射最简单的做法就是让\n",
-    "\n",
-    "$$\n",
-    "\\tilde{y}^{(i)} = \\frac{\\langle Z \\rangle}{2} + \\frac{1}{2} + bias \\quad \\in [0, 1]\n",
-    "$$\n",
-    "\n",
-    "其中加入偏置（bias）是机器学习中的一个小技巧，目的就是为了让决策边界不受制于原点或者一些超平面。一般我们默认偏置初始化为0，并且优化器在迭代过程中会类似于参数 $\\theta$ 一样不断更新偏置确保 $\\tilde{y}^{(i)} \\in [0, 1]$。当然读者也可以选择其他复杂的映射比如说 sigmoid 函数。映射过后我们就可以把 $\\tilde{y}^{(i)}$ 看作是我们估计出的标签（label）了。如果 $\\tilde{y}^{(i)}< 0.5$ 就对应标签 0，如果 $\\tilde{y}^{(i)}> 0.5$  就对应标签 1。 我们稍微复习一下整个流程，\n",
-    "\n",
-    "\n",
-    "$$\n",
-    "x^{(i)} \\rightarrow \\lvert {\\psi}\\rangle^{(i)} \\rightarrow U(\\boldsymbol{\\theta})\\lvert {\\psi}\\rangle^{(i)} \\rightarrow\n",
-    "\\lvert {\\varphi}\\rangle^{(i)} \\rightarrow ^{(i)}\\langle \\varphi |Z\\otimes I\\cdots \\otimes I| \\varphi\\rangle^{(i)}\n",
-    "\\rightarrow \\langle Z \\rangle  \\rightarrow \\tilde{y}^{(i)}\n",
-    "$$\n",
-    "\n",
-    "最后我们就可以把损失函数定义为平方损失函数：\n",
-    "\n",
-    "$$\n",
-    "\\mathcal{L} = \\sum_{(i)} |y^{(i)} - \\tilde{y}^{(i)}|^2\n",
-    "$$"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 7,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 生成只作用在第一个量子比特上的泡利 Z 算符\n",
-    "# 其余量子比特上都作用单位矩阵\n",
-    "def Observable(n):\n",
-    "    \"\"\"\n",
-    "    :param n: number of qubits\n",
-    "    :return: local observable: Z \\otimes I \\otimes ...\\otimes I\n",
-    "    \"\"\"\n",
-    "    Ob = pauli_str_to_matrix([[1.0, 'z0']], n)\n",
-    "    return Ob"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 8,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 搭建整个优化流程图\n",
-    "class Net(fluid.dygraph.Layer):\n",
-    "    \"\"\"\n",
-    "    Construct the model net\n",
-    "    \"\"\"\n",
-    "    def __init__(self,\n",
-    "                 n,      # number of qubits\n",
-    "                 depth,  # circuit depth\n",
-    "                 seed_paras=1,\n",
-    "                 dtype='float64'):\n",
-    "        super(Net, self).__init__()\n",
-    "\n",
-    "        self.n = n\n",
-    "        self.depth = depth\n",
-    "        \n",
-    "        # 初始化参数列表 theta，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "        self.theta = self.create_parameter(\n",
-    "            shape=[n, depth + 3],\n",
-    "            attr=fluid.initializer.Uniform(\n",
-    "                low=0.0, high=2*PI, seed=seed_paras),\n",
-    "            dtype=dtype,\n",
-    "            is_bias=False)\n",
-    "        \n",
-    "        # 初始化偏置 (bias)\n",
-    "        self.bias = self.create_parameter(\n",
-    "            shape=[1],\n",
-    "            attr=fluid.initializer.NormalInitializer(\n",
-    "                scale=0.01, seed=seed_paras + 10),\n",
-    "            dtype=dtype,\n",
-    "            is_bias=False)\n",
-    "\n",
-    "    # 定义向前传播机制、计算损失函数 和交叉验证正确率\n",
-    "    def forward(self, state_in, label):\n",
-    "        \"\"\"\n",
-    "        Args:\n",
-    "            state_in: The input quantum state, shape [-1, 1, 2^n]\n",
-    "            label: label for the input state, shape [-1, 1]\n",
-    "        Returns:\n",
-    "            The loss:\n",
-    "                L = ((<Z> + 1)/2 + bias - label)^2\n",
-    "        \"\"\"\n",
-    "        \n",
-    "        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "        Ob = fluid.dygraph.to_variable(Observable(self.n))\n",
-    "        label_pp = fluid.dygraph.to_variable(label)\n",
-    "\n",
-    "        # 按照随机初始化的参数 theta \n",
-    "        Utheta = U_theta(self.theta, n=self.n, depth=self.depth)\n",
-    "        \n",
-    "        # 因为 Utheta是学习得到的，我们这里用行向量运算来提速而不会影响训练效果\n",
-    "        state_out = matmul(state_in, Utheta)  # 维度 [-1, 1, 2 ** n]\n",
-    "        \n",
-    "        # 测量得到泡利 Z 算符的期望值 <Z>\n",
-    "        E_Z = matmul(matmul(state_out, Ob),\n",
-    "                     transpose(ComplexVariable(state_out.real, -state_out.imag),\n",
-    "                               perm=[0, 2, 1]))\n",
-    "        \n",
-    "        # 映射 <Z> 处理成标签的估计值 \n",
-    "        state_predict = E_Z.real[:, 0] * 0.5 + 0.5 + self.bias\n",
-    "        loss = fluid.layers.reduce_mean((state_predict - label_pp) ** 2)\n",
-    "        \n",
-    "        # 计算交叉验证正确率\n",
-    "        is_correct = fluid.layers.where(\n",
-    "            fluid.layers.abs(state_predict - label_pp) < 0.5).shape[0]\n",
-    "        acc = is_correct / label.shape[0]\n",
-    "\n",
-    "        return loss, acc, state_predict.numpy()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 训练效果与调参\n",
-    "\n",
-    "好了， 那么定义完以上所有的概念之后我们不妨来看看实际的训练效果！"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 9,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "def heatmap_plot(net, N):\n",
-    "    # generate data points x_y_\n",
-    "    Num_points = 30\n",
-    "    x_y_ = []\n",
-    "    for row_y in np.linspace(0.9, -0.9, Num_points):\n",
-    "        row = []\n",
-    "        for row_x in np.linspace(-0.9, 0.9, Num_points):\n",
-    "            row.append([row_x, row_y])\n",
-    "        x_y_.append(row)\n",
-    "    x_y_ = np.array(x_y_).reshape(-1, 2).astype(\"float64\")\n",
-    "\n",
-    "    # compute the prediction: heat_data\n",
-    "    input_state_test = fluid.dygraph.to_variable(\n",
-    "        datapoints_transform_to_state(x_y_, N))\n",
-    "    loss_useless, acc_useless, state_predict = net(state_in=input_state_test,\n",
-    "                                                   label=x_y_[:, 0])\n",
-    "    heat_data = state_predict.reshape(Num_points, Num_points)\n",
-    "\n",
-    "    # plot\n",
-    "    fig = plt.figure(1)\n",
-    "    ax = fig.add_subplot(111)\n",
-    "    x_label = np.linspace(-0.9, 0.9, 3)\n",
-    "    y_label = np.linspace(0.9, -0.9, 3)\n",
-    "    ax.set_xticks([0, Num_points // 2, Num_points - 1])\n",
-    "    ax.set_xticklabels(x_label)\n",
-    "    ax.set_yticks([0, Num_points // 2, Num_points - 1])\n",
-    "    ax.set_yticklabels(y_label)\n",
-    "    im = ax.imshow(heat_data, cmap=plt.cm.RdBu)\n",
-    "    plt.colorbar(im)\n",
-    "    plt.show()\n",
-    "\n",
-    "def QClassifier(Ntrain, Ntest, gap, N, D, EPOCH, LR, BATCH, seed_paras, seed_data,):\n",
-    "    \"\"\"\n",
-    "    Quantum Binary Classifier\n",
-    "    \"\"\"\n",
-    "    # 初始化paddle动态图机制\n",
-    "    with fluid.dygraph.guard():\n",
-    "        \n",
-    "        # 生成数据集\n",
-    "        train_x, train_y, test_x, test_y = circle_data_point_generator(\n",
-    "            Ntrain=Ntrain, Ntest=Ntest, boundary_gap=gap, seed_data=seed_data)\n",
-    "        \n",
-    "        # 读取训练集的维度\n",
-    "        N_train = train_x.shape[0]\n",
-    "        \n",
-    "        # 定义优化图\n",
-    "        net = Net(n=N, depth=D, seed_paras=seed_paras)\n",
-    "        \n",
-    "        # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMSprop\n",
-    "        opt = fluid.optimizer.AdamOptimizer(\n",
-    "            learning_rate=LR, parameter_list=net.parameters())\n",
-    "        \n",
-    "        # 初始化寄存器存储正确率 acc 等信息\n",
-    "        summary_iter, summary_test_acc = [], []\n",
-    "        \n",
-    "        # 优化循环\n",
-    "        for ep in range(EPOCH):\n",
-    "            for itr in range(N_train // BATCH):\n",
-    "                \n",
-    "                # 将经典数据编码成量子态 |psi>, 维度 [-1, 2 ** N]\n",
-    "                input_state = fluid.dygraph.to_variable(\n",
-    "                    datapoints_transform_to_state(\n",
-    "                    train_x[itr * BATCH:(itr + 1) * BATCH], N))\n",
-    "                \n",
-    "                # 前向传播计算损失函数\n",
-    "                loss, train_acc, state_predict_useless \\\n",
-    "                    = net(state_in=input_state,\n",
-    "                          label=train_y[itr * BATCH:(itr + 1) * BATCH])\n",
-    "                if itr % 10 == 0:\n",
-    "                    # 计算测试集上的正确率 test_acc\n",
-    "                    input_state_test = fluid.dygraph.to_variable(\n",
-    "                        datapoints_transform_to_state(test_x, N))\n",
-    "                    loss_useless, test_acc, state_predict_useless \\\n",
-    "                        = net(state_in=input_state_test,\n",
-    "                              label=test_y)\n",
-    "                    print(\"epoch:\", ep, \"iter:\", itr,\n",
-    "                          \"loss: %.4f\" % loss.numpy(),\n",
-    "                          \"train acc: %.4f\" % train_acc,\n",
-    "                          \"test acc: %.4f\" % test_acc)\n",
-    "                    \n",
-    "                    # 存储正确率 acc 等信息\n",
-    "                    summary_iter.append(itr + ep * N_train)\n",
-    "                    summary_test_acc.append(test_acc)\n",
-    "                    \n",
-    "                # 在动态图机制下，反向传播极小化损失函数\n",
-    "                loss.backward()\n",
-    "                opt.minimize(loss)\n",
-    "                net.clear_gradients()\n",
-    "\n",
-    "        # 画出 heatmap 表示的决策边界\n",
-    "        heatmap_plot(net, N=N)\n",
-    "\n",
-    "    return summary_test_acc"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 10,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "训练集的维度大小 x (200, 2) 和 y (200, 1)\n",
-      "测试集的维度大小 x (100, 2) 和 y (100, 1) \n",
-      "\n",
-      "epoch: 0 iter: 0 loss: 0.0249 train acc: 1.0000 test acc: 0.5200\n",
-      "epoch: 0 iter: 10 loss: 0.5726 train acc: 0.0000 test acc: 0.5700\n",
-      "epoch: 0 iter: 20 loss: 0.0702 train acc: 1.0000 test acc: 0.6500\n",
-      "epoch: 0 iter: 30 loss: 0.0947 train acc: 1.0000 test acc: 0.6900\n",
-      "epoch: 0 iter: 40 loss: 0.2799 train acc: 0.0000 test acc: 0.7100\n",
-      "epoch: 0 iter: 50 loss: 0.1501 train acc: 1.0000 test acc: 0.7500\n",
-      "epoch: 0 iter: 60 loss: 0.1587 train acc: 1.0000 test acc: 0.8400\n",
-      "epoch: 0 iter: 70 loss: 0.1633 train acc: 1.0000 test acc: 0.9500\n",
-      "epoch: 0 iter: 80 loss: 0.2033 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 90 loss: 0.1852 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 100 loss: 0.1369 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 110 loss: 0.1306 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 120 loss: 0.1341 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 130 loss: 0.1072 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 140 loss: 0.0822 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 150 loss: 0.0838 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 160 loss: 0.1581 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 170 loss: 0.1007 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 180 loss: 0.1596 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 0 iter: 190 loss: 0.1123 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 0 loss: 0.1815 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 10 loss: 0.0504 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 20 loss: 0.1949 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 30 loss: 0.1756 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 40 loss: 0.0438 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 50 loss: 0.1355 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 60 loss: 0.1786 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 70 loss: 0.1217 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 80 loss: 0.2004 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 90 loss: 0.0691 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 100 loss: 0.0649 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 110 loss: 0.1367 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 120 loss: 0.0856 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 130 loss: 0.0660 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 140 loss: 0.0495 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 150 loss: 0.0781 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 160 loss: 0.1616 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 170 loss: 0.1413 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 180 loss: 0.1501 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 1 iter: 190 loss: 0.1235 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 0 loss: 0.1762 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 10 loss: 0.0502 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 20 loss: 0.1897 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 30 loss: 0.1797 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 40 loss: 0.0395 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 50 loss: 0.1357 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 60 loss: 0.1772 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 70 loss: 0.1269 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 80 loss: 0.1983 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 90 loss: 0.0622 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 100 loss: 0.0608 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 110 loss: 0.1372 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 120 loss: 0.0882 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 130 loss: 0.0722 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 140 loss: 0.0474 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 150 loss: 0.0761 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 160 loss: 0.1618 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 170 loss: 0.1443 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 180 loss: 0.1495 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 2 iter: 190 loss: 0.1243 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 0 loss: 0.1759 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 10 loss: 0.0554 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 20 loss: 0.1893 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 30 loss: 0.1803 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 40 loss: 0.0390 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 50 loss: 0.1329 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 60 loss: 0.1754 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 70 loss: 0.1275 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 80 loss: 0.1969 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 90 loss: 0.0617 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 100 loss: 0.0603 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 110 loss: 0.1366 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 120 loss: 0.0900 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 130 loss: 0.0789 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 140 loss: 0.0470 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 150 loss: 0.0741 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 160 loss: 0.1613 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 170 loss: 0.1443 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 180 loss: 0.1487 train acc: 1.0000 test acc: 1.0000\n",
-      "epoch: 3 iter: 190 loss: 0.1231 train acc: 1.0000 test acc: 1.0000\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAATQAAAD5CAYAAACpgMlBAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAdqklEQVR4nO3dbYxj93Xf8e8hORzOzM4+eEeKVUm2lWZjV03TtBHkFn5ht6qKdV5ITZQ2stE2LtwIaK20SOoCFlAIgYrCdpvWcAEhwEZRKwdo5UAvgjW6qNpaNlKksbFb2DEgBXIWahytLEva1T7NzgOH5OkLcgV6wnPuJYezpK5+H4DYIf/3aXjvnL33/s89f3N3RESqoDbrDRARmRYFNBGpDAU0EakMBTQRqQwFNBGpDAU0EamMxrgzmNlx4ItAHXjC3T+3q/29wJPATcCbwN9393OFy2203BZXg3UWxF2zidoKlzvhOpOtyVuz36N4wRPal4WWMGG60F6yjNIUpbgtXWVR2lPSnqZMeW+y+ZJ5vb2Od7b2tMNrB29zOlulpvXNC8+6+/G9rG9cYwU0M6sDjwP3AueA02Z20t1fGJrs14EvuftTZvY3gc8C/6Bw2YurNO/8uZFt9eZSOm+t0YzbFuK2ejKf1erpOrP2/WgDsHrePgmrzeYk3XvxH2w6X7e7h3XG807a1uu003X2snl34nm77c2J19ltjw44nRdPpvOV0tmi8f77Sk268+3/tLb3FY5n3KP5buCsu7/k7m3gaeD+XdPcCTw3+PlrI9pF5O3KDKvVS71mYdyAdivw8tD7c4PPhv0hcP1U62eBVTM7Otnmich8MWqNZqnXLOzH9cangQ+b2beADwOvACPPu83sITM7Y2ZnvOR1uYjM0JyfoY3bKfAKcPvQ+9sGn73F3b/P4AzNzA4AD7j7pVELc/cTwAmA2spNeqhUZM4Z+3Mvd1rGDWingWNmdgf9QPYg8PHhCcxsDXjT3XvAI/R7PEWkCsyozejsq4yxApq7d8zsYeBZ+mkbT7r782b2GHDG3U8CHwE+a2YO/B7wqTLLXjxwiPd96GdGtq0cbKXztlYWkrb4Wv7AYvzrH2jlX81yM96pS0lbsxFf5S8183XWa3GP+2Ky3Gy+IpPO2+1NfsLd7sQ9oJ1kudl8AJvtTtIW90ZuJG2XN3bSdV7ZjNvbSdvGetyTuX4pvz2zfv61kZ+f/95X0/nKmtXlZBlj56G5+yng1K7PHh36+Rngmb1vmojMncE9tHk1dkATkXcuw6g14iuiWVNAE5HydIYmIlWigCYi1WBWqbQNEXkHM3SGJiJVYbW0qMOszU1Aay42eM+x0Q/nf+DPjS4rdN1t71oO225K8tCOLMW9NasFOWEHFpM8tEaSh1aP87oaBTlfC0l7PXmILVtqraBkUVFFo0hRhZteMkE3mbebzNfJZgTaSQ7bdiduu7wd569d3srz0C4keWqvXonzyb53/lrY9sevXk3XeX5p9LF7sTmFQGQ6QxORijDUyykiFTLPAU0luEWkvClW2zCz42b2opmdNbPPjGh/j5l9zcy+ZWbfMbPRz0YO0RmaiIxhOpecJatf/yvgd9z9N8zsTvqPXL4vW64CmoiUZmZpWfsxvFX9erDc69WvhwOaAwcHPx8Cvl+0UAU0ESlvvEef1szszND7E4MaiDC6+vUHd83/a8D/MLNfBlaAv1W0wrkJaMuLDe760XeNbLvz3XnaxnsOxeWF1paT8kHN+BZi1gawlKRfWHsjbutsJ20FVXvbcUkZ68bpAdaL0w6y0YVKtYcrLRqpK273WnxYej1OtfGFvMyUL8aD7fjBA2HbZi8+htbb+fdzNSk99IOr8fbckpTMyspTAfzfIM2knpSYGscYAe28u9+1h1V9DPjP7v7vzeyvA79tZj8xqLU40twENBF5e6jtob7ekMLq18AngeMA7v4HZtYC1oDXw22bxpaJyDuDmWG1cq8Cb1W/NrMm/erXu8fZ+1PgnsF6/wLQAt7IFqozNBEZSz17LKWkktWv/wXwm2b2K/Q7CD7hBaMsK6CJSHlGmbOvUkpUv34B+NA4y1RAE5HS+tU2phPQ9oMCmoiMwQoLGszS3AS01kKNYzetjGz7wNroz6+7ORn16Ugr7mJe2L4SttWuXE7XWduOKx74Rrxc34jn612L5wPwdpzW4dtJWzZfL04r6G/UhGkbtfw+iyUlaCypWW9L8bFQa+XHSW0lTv+pHRydMgRQbx0K25aXj6TrPHggXudSkkaR9SRu7OT77KXXR1fqaEzh3tc0Lzn3w9wENBF5e1BAE5FKMIN6QwFNRCrCdA9NRKrAzKb1pMC+UEATkbHoHpqIVIYCWgkLtRq3BhUGji7nm3nTUpyaUbv6WthWX48fC+tdDJ9/BWAnae9dvRS2da/Ebe2rcZUOgJ1rcfpFdyuu4tHZiqt0eDdPyyhqj1hBikDW3mjFKR2NlbhCRXM1HiwHoHn4YNhWz9I21m6Jt2ft1nSdS6s/ErYdXToatrWTAV9eX8/rkd10cHHk542kQkxpVjywzizNTUATkflnGLUplSHaDwpoIlKeTa180L5QQBORsShtQ0Qqof9w+qy3IqaAJiLl6ZJTRKrDqE3jIfd9ooAmIqWZztDKadQsHKHp0GI+ykwtySerJ3lo3Ve/F7Z1LryarrP9RpyHtnUhLgO0fSkuH9S+kuehdTbiPLT2epxr1tmKR33qJflOAF7QHrGCnKd6MqpWoxWXD2quxDlYzYN5Htri4Xhkp6WbL4Vtra14vzR24u8d+rWlw+1pjM4XA1htxvl22UhmAIeXR39/9SkFIiXWikglmE0vMO4HBTQRGYsCmohUgmEKaCJSDWbQ1KNPIlIFZv0OvHmlgCYipRm6h1ZKrQYrQVf+kuWj3NQ2LoZt3Te+H7Z13nglbNv6wQ/SdV579UI8b5K2sXlhPWzbvhKXACpq72zGqRlZ2ka3nZcH6k1YPqgo+TJP24gPy8WgNA7A4qHRox1dt3w0Tr+YtMTSUtHoVtkoVYvxiFArB+P5DiXfD8ChIK1jKoHIdA9NRCqif4ame2giUhE6QxORSqiZqZdTRKqjrnpoIlIFevRJRCpFAa2EGkYr6OqvbcVpEAC2cTls612J0yvaF86HbZuvx6kgAJtvXArbrr0WV9TYvBCnDmxfySs3bF2O0zbaGzvxOpOKGe1eXk2j65NV2yi6LGkmfxQrC/E9muw7al2LUzqgOEUlUluI/0wWVkaPVHZd/VA8slPj8M1h22It/t6Xku8HYDVI65hGIFJirYhUhqFOARGpCN1DE5HK0KNPIlIdOkMTkapQPTQRqRQFtBLMoBkMrGHJIBUAvY04TaJ39VLYtn0prnyxmVTMANg8n80bb+/G+c14vovxICgA13bitIP1Tty2laRmzGPaRva7HEraJq0MAnn1j3orHpSkdTiumAGwsHYpbtyKq4NYOz6GmrU8PaUZpD9NIwzVpljg0cyOA1+kP5bME+7+uV3tXwD+xuDtMnCzux/Oljk3AU1E3gamdA/NzOrA48C9wDngtJmddPcXrk/j7r8yNP0vA3+laLnzm1AiInPHMOpW7lXgbuCsu7/k7m3gaeD+ZPqPAf+1aKE6QxORsdSm83D6rcDLQ+/PAR8cNaGZvRe4A3iuaKEKaCJSmgEFY0gPWzOzM0PvT7j7iQlW+yDwjLvnpatRQBORcRjUyt9DO+/udwVtrwC3D72/bfDZKA8CnyqzQgU0ESnNgIXplOA+DRwzszvoB7IHgY//mfWZfQA4AvxBmYUqoIlIaWNecobcvWNmDwPP0k/beNLdnzezx4Az7n5yMOmDwNPu5fKH5iagpXlonbg0DkBvM87n6a7HOWqda3FOWOdanhOWlbGZtO1KO79FcCXJwcpyt95u5YMOJHlOaabZel5+qd6sx9uzEs+7dCQ+FtpX85Gm0hzJLA+tE5eKatTzkkWLwfc3lZv5ZuNccqbc/RRwatdnj+56/2vjLHNuApqIzD9jar2c+0IBTUTGMo1Lzv2igCYipZnBQsEg0rOkgCYipemSU0QqRZecIlIJhukMrYw0v6Wbd8d7O+5W72zF8+4kqRnta/k6O1txKkl7PW7b2O6EbdeS9ArIUzPmLW0jS8voL3eyP4rs7KBVsM7la8k+S/Z3O0kHyY4vgN5WfIz5dpIa1IuPk3oj/z0Xgu9hKnFIFWtFpCr699BmvRUxBTQRKW2Kjz7tCwU0ESnPYI6zNhTQRKQ8pW2ISIWUqkY7MwpoIlKaztBKykZktqQLG8A7cdd5byeeN2vrFlS+2NlM5t2J583SJIpSKCaddy/rnHQcpW5BCkrWXLf9+V06yX7pJSNqZfuz186PzW5yjJFUkcmO+aLE1v1Mq+g/+qSAJiIVMccnaApoIjKe2lRG+NwfCmgiUpqhMzQRqRA9KSAi1WA6QxORijDloZUXfk1ekDzQjbvVvRvP20vavDdpwgJ4kpOQpSsUVbYoyISojOx7yL6Doj2WzpsdC8mMRcdJdvx5Lz5uLVluUR5Y1D6tMKRLThGpjDmOZwpoIlKenhQQkUqZ43imgCYi45nj6kEKaCJSnqkEt4hUiS45RaQSDF1yvuNYUl4lq7xSlLA4x1Vbpmq/Ejez7682z3Wl54zN8SmaApqIlGdKrBWRikjHz50DCmgiMhZdcopIJWigYRGplDmOZwpoIjIOq96znGZ2HPgiUAeecPfP7WpfBL4E/DRwAfgFd/+TouWGRVqsoEu9Xo+3NemOry/Ev359IV4mQL2ZrDM5J29O2LaXefdSdqiopFGkKPVi0t8la1so+DurJfNm+6yWHAu15BgCqDfjdqslx1htTtNI5rzA49jfmpnVgceBjwJ3Ah8zszt3TfZJ4KK7/xjwBeDze91QEZk9c8d63VKvWZjkv4G7gbPu/pK7t4Gngft3TXM/8NTg52eAe2yeu0ZEpDTzXqnXLEwS0G4FXh56f27w2chp3L0DXAaOTrKBIjJPvF9BusyrgJkdN7MXzeysmX0mmObvmdkLZva8mf2XomXOtFPAzB4CHgK4/fbbZ7kpIlLWhPdVhw3durqX/knRaTM76e4vDE1zDHgE+JC7XzSzm4uWO8kZ2ivAcPS5bfDZyGnMrAEcot858EPc/YS73+Xud62trU2wKSJyQ/nUztDK3Lr6JeBxd7/YX7W/XrTQSQLaaeCYmd1hZk3gQeDkrmlOAr84+PnngefcpxDWRWTmpnQPrcytqx8HftzMft/MvjHIrkiNfcnp7h0zexh4ln7axpPu/ryZPQaccfeTwG8Bv21mZ4E36Qe9fLlALwp5BWkb1miGbfVW3FZLutSztAzI0zoWluLltrY6cVtBfkV7wooQdYuX2w6/9L5ZpG0sJQ8LHmjE38FSwffTaMX7pZHss2x/ZscQFKR1NBbituSYL9onvaB9OmcUDr34GN5lzczODL0/4e4nxlhZAzgGfIT+leDvmdlfcvdL2Qxjc/dTwKldnz069PMW8HcnWbaIzDGn1A3/gfPuflfQVubW1Tngm+6+A/w/M/su/QB3OlrhnGbvich8cuj1yr1yZW5d/S79szPMbI3+JehL2UL16JOIjGUaOWYlb109C/xtM3sB6AL/0t3/TOfiMAU0ERnPlJJmS9y6cuBXB69SFNBEpDx3mNFjTWUooInIWGb1WFMZCmgiMgaf2iXnfpirgBbl13g9ziUDsGYrbGskeWgLK0tJ22K6zuaB7bCtsxXP223HB8OhXrzMIlmd92ZtL3lo098eKMpDizvfV5IFryZ5ZgCtQ/F+aa7Ex0mjFeeLLSzHxxCALcbHZtaWHfPdgniyE+y0qaW2K6CJSCW4ztBEpCIM3UMTkcpw6KqXU0SqYLxHn244BTQRGYsuOUWkItQpUIo7dIIUAq8nZVbIu79rSyth28JyPF9zdTldZ2urHbZlqRm9pM/dCnIdalfitI6lTjzvZpJ7UZS2MemhW1T1YNLyQcuLSWmmI3mqzeLBOBWidSQ5Fg7Gx8LCSjwfQK0VH39ZWyc55rsFuTSTlnwqTQFNRCpBjz6JSHU43tmZ9UaEFNBEpDxHZ2giUg2O48pDE5FKcMpUo50ZBTQRGYM6BUpxkioBCwVd48urcdvq4bBt8cjlsG1nYytdZ3cnHvnGk271LDWjaKSpbPSh5np8o3ZlJz4Au+384OwVpHVEaklaBuS/azY6U3MlTmdYPJinbWSpGa0jcWpG6+iheJ2HD6TrzI4/krSN7Jhvt/N9st0ZfQYVjQY1FlengIhUhuM6QxORSlAvp4hUh6tTQEQqwlHahohUhXo5RaQq1MtZjntc+cEXCgaiWD4YttUOHA7bGoevhm1L7Tgto0gtGeRj0nQFgJ1r8YG0eDBuy6p/FKVt+IRpG7ZPaRuNJHWlOG0jTs1YuulwPN/R+PiqH35Xus7a6pGwzRfi7enW4sog7W5c6QVgM0jTmXBX7qIzNBGpCvVyikhVOI6rl1NEKkFnaCJSGe74Tn4Pb5YU0ERkDEqsFZEq0SWniFSC6+H0UnrubHeCPLTlvERLbzEpH3ToaNhWb8clghYLdpoluWa1hSSPKhklaGF1I11n51q8vZ2tLA8tKR+UlBbaC6vl4z7VkjJKWa5ZoxXnZxWN1LV4JD5Oslyz1s03hW31Izen66wnx1+nFW/PZlACqN+W77ONYH9PpXwQqJdTRCrCHU+GYpw1BTQRKc3d6SXFTWdNAU1EynN0hiYi1aGAJiKV4O705rgeWt4VJSKyi/d6pV5FzOy4mb1oZmfN7DMj2j9hZm+Y2bcHr39ctMy5OUPrOWzsjP4SNoJ0jusOtOIud1vdDtvq2Zdey0dgWmwm6Rcrcbmj9pVrcdvVPG2juxU/ctLZin/PXlIKaVY3eLPUllozbltYjr/bhSQlBvIRmuoHD8dtR989URtAdylebm8pHk1qczs+5i9v5fvs8sbo46Q7jfpBU+rlNLM68DhwL3AOOG1mJ939hV2TftndHy673LkJaCIy/6bYy3k3cNbdXwIws6eB+4HdAW0suuQUkbH0ur1SrwK3Ai8PvT83+Gy3B8zsO2b2jJndXrRQBTQRKW+QtlHmBayZ2Zmh10Njru0rwPvc/SeB/wk8VTSDLjlFpLzx7qGdd/e7grZXgOEzrtsGnw2tyi8MvX0C+LdFK9QZmoiU5kytl/M0cMzM7jCzJvAgcHJ4AjO7ZejtfcAfFS1UZ2giUp572mtefjHeMbOHgWeBOvCkuz9vZo8BZ9z9JPDPzOw+oAO8CXyiaLlzE9C67lzeHv1FrbfzzVxajru/6cVffnZ62kjSMgB6Sytx27XD8ToPxiNNLW7FKR0Avc24Pet56iYHYNH/pJN20WfVSCCvxlFP0jbqrXhkJ2vF+wSgtno4bktGB8sqZviBuA2gtxyP+rTpcWrQerLPor+Tt+YN0jqmUm3DoTelahvufgo4teuzR4d+fgR4ZJxlzk1AE5H556jahohUhYPP8aNPCmgiMgYNYyciVaHyQSJSFe6edjLNmgKaiIxBl5yldHvOxc3RA32sryyk8za34wE3Dq0k3eq1+Ne3RpweAFBbjAfkqB2Mq2Z4kpqRpWUAeDKoC514kBTvJAPDFtzgnfTgLRokhXqcsmCNeCAUS9JpLEmlAagtx4OSkKR8ZIPwZGkZANsLcYWPrGpG1hb9nVx3aWN0e7c7nbQNXXKKSDU4+DQC4z5RQBOR0hwvU0ljZhTQRKQ8B59Goch9ooAmIqW55wNXz5oCmoiU5657aCJSHT0FNBGpBKVtlNNJ8tAuBHk119UtzkPLSqasNOPRohYX85ymXjvONbOdzaQtziWrdfPf07pJPllSJsmS76DwQePehPdLCkbNsiQPzbN5k9xBbxSUfFqIcwt9Ic4r7LXiPLTNXnzsAVzdir+/K9txYHjtWjyK1+tX4zaAN6+NPk46U7iZ70BPnQIiUgnu6hQQkWpwJdaKSGUooIlIdehJARGpCj0pICJV4SgPrZSdXo9Xr4xOaTjQzFMA8uXGpYc2O/GOWWrk3fGtRtyV31yM00HSxWZpGYB1k8J6WdpGlnrhM7p8sLi80ORpG3HZIYCuxfNuJ3+km0l6xeZO3uN3eTtufy1IrwD4wXqcmvHqpTgtCGAjSOuYSrqFOz31copIFbjrDE1EKkQVa0WkGtx1hiYiFaE8NBGpCkcPp4tIVbjTbSugFdrp9Dj35ugKFksFaRs7SXf01aSLeTVZ7oFm/tUsJvkXzVrc1qjHbXXLf8+svV6LK01kWRB5csr+yS5ashOAbrKvu8mgWADtpJpJO1nu5k68QdnoTABvbsXrfH09Ttv40+BvAeDcm3naxmaw3Glk+LvnFWxmbW4Cmoi8PXQV0ESkChyY4z4BBTQRGY/O0ESkEnqe32+cNQU0ERmLLjlFpBIc1yVnGe2Oh93R9SQNAuBq0nV+dCWuwLC8EOczZG0ASwtxtYhWI25bqCVtSUpH0bxJUzpfkaLvPpKlV0De9Z/9wewkpwdZ+g7AdidO4dnqxCkN60nqz3o7T9u4mAzwk1XNyFIzzicpHQCbV4O0jSkNkqIzNBGpDAU0EakEd/VyikhFOPPdyzn5zRURece5fg+tzKuImR03sxfN7KyZfSaZ7gEzczO7q2iZOkMTkbFM45LTzOrA48C9wDngtJmddPcXdk23Cvxz4JtllqszNBEpzUuenZU4Q7sbOOvuL7l7G3gauH/EdP8a+DxQUHqgb6yAZn3/cXCK+B0z+6vBdL8waH/ezD4/zjpEZL513Uu9CtwKvDz0/tzgs7cM4svt7v7fym7buJecHwWODV4fBH5j8O/wRhwF/h3w0+7+hpk9ZWb3uPtXswV3uj0uBPk17SRHCOBCUoZltRX/igeStqWC8kHLSemhZpKHlrUV5YtleWp1i9smTCXbV9l95eyPIctfy3LUANpJ+ZzNJNcsy3NcT8oDQX5svpm0XQ1GQANYv5SfrGxcvjzy815376M1OTBGEaI1Mzsz9P6Eu58oM6OZ1YD/AHxijM0bO6DdD3zJ3R34hpkdNrNb3P3VoWl+FPhjd39j8P5/AQ8AaUATkfnn+Di9nOfdPbqR/wpw+9D72wafXbcK/ATwdev/Z/1u4KSZ3efuw0Hyh4wb0KLTxOGAdhZ4v5m9b9D+d4B8wEQReVvo93JOJW3jNHDMzO6gH8geBD7+1nrcLwNr19+b2deBT2fBDPahl9PdL5rZPwG+TP/s9P8Af37UtGb2EPAQQPPwzdPeFBGZtpIpGYWLce+Y2cPAs0AdeNLdnzezx4Az7n5ykuUWBjQz+xTwS4O3p8lPE69v7FeArwzmfwgYefE+uJ4+AXDgtvfPb7aeiABTPUPD3U8Bp3Z99mgw7UfKLLOwl9PdH3f3n3L3nwJ+F/iHg97OvwZc3nX/DAAzu3nw7xHgnwJPlNkYEZl/00qs3Q/jXnKeAn6G/n2yDeAfXW8ws28Pgh7AF83sLw9+fszdv7vXDRWR2esx348+mc/Jg6Zm9gbwvcHbNeD8DDdHxqd9Np+G98t73f2mvSzMzP47QzfrC5x39+N7Wd+45iagDTOzM0l3r8wh7bP59E7bL3r0SUQqQwFNRCpjXgNaqccjZK5on82nd9R+mct7aCIik5jXMzQRkbHNNKCpHNHbT1GVUTNbNLMvD9q/OXimV/ZRiX3yXjP76uBv6OtmdtsstvNGmPUZ2nA5oofolyP6IUPliO5x978IvNvM7rmhWynAD1UZ/ShwJ/AxM7tz12SfBC66+48BX6BfnE/2Scl98uv0q+T8JPAY8Nkbu5U3zqwD2lvliNz9G8BhM7tl1zRROSK58cpUGb0feGrw8zPAPWZJsTbZqzL75E7gucHPXxvRXhmzDmiFVSsZKkdkZg365YhuR2ahzP56axp37wCXgaM3ZOvemcrskz8Efm7w888Cq4Mrn8qZdUAr5O4XgevliP438CcE1TtEZKRPAx82s28BH6ZfIaeSf0M3fNSn/SxHJPuuqMro8DTnBmfUh4ALN2bz3pEK94m7f5/BGZqZHQAecPdLN2oDb6QbfoamckRva29VGTWzJv0qo7sL8Z0EfnHw888Dz7mSHfdT4T4xs7VBjX6AR4Anb/A23jCzvuQ8BbxE/z7Zb9IPVkC/HNHQdF80sxeA3wc+p3JEszG4J3a9yugfAb9zvcqomd03mOy3gKNmdhb4VSAcQFb2ruQ++Qjwopl9F/gR4N/MZGNvAD0pICKVMeszNBGRqVFAE5HKUEATkcpQQBORylBAE5HKUEATkcpQQBORylBAE5HK+P91xYus8LBdxQAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 432x288 with 2 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    },
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "主程序段总共运行了 52.354016065597534 秒\n"
-     ]
-    }
-   ],
-   "source": [
-    "def main():\n",
-    "    \"\"\"\n",
-    "    main\n",
-    "    \"\"\"\n",
-    "    time_start = time.time()\n",
-    "    acc = QClassifier(\n",
-    "        Ntrain = 200,        # 规定训练集大小\n",
-    "        Ntest = 100,         # 规定测试集大小\n",
-    "        gap = 0.5,           # 设定决策边界的宽度\n",
-    "        N = 4,               # 所需的量子比特数量\n",
-    "        D = 1,               # 采用的电路深度\n",
-    "        EPOCH = 4,           # 训练 epoch 轮数\n",
-    "        LR = 0.01,           # 设置学习速率\n",
-    "        BATCH = 1,           # 训练时 batch 的大小\n",
-    "        seed_paras = 19,     # 设置随机种子用以初始化各种参数\n",
-    "        seed_data = 2,       # 固定生成数据集所需要的随机种子\n",
-    "    )\n",
-    "    \n",
-    "    time_span = time.time() - time_start\n",
-    "    print('主程序段总共运行了', time_span, '秒')\n",
-    "\n",
-    "if __name__ == '__main__':\n",
-    "    main()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "<hr/>\n",
-    "\n",
-    "# 参考文献\n",
-    "\n",
-    "[1] [Mitarai, K., Negoro, M., Kitagawa, M. & Fujii, K. Quantum circuit learning. Phys. Rev. A 98, 032309 (2018).](https://arxiv.org/abs/1803.00745)\n",
-    "\n",
-    "[2] [Schuld, M., Bocharov, A., Svore, K. M. & Wiebe, N. Circuit-centric quantum classifiers. Phys. Rev. A 101, 032308 (2020).](https://arxiv.org/abs/1804.00633)"
-   ]
-  }
- ],
- "metadata": {
-  "kernelspec": {
-   "display_name": "Python 3",
-   "language": "python",
-   "name": "python3"
-  },
-  "language_info": {
-   "codemirror_mode": {
-    "name": "ipython",
-    "version": 3
-   },
-   "file_extension": ".py",
-   "mimetype": "text/x-python",
-   "name": "python",
-   "nbconvert_exporter": "python",
-   "pygments_lexer": "ipython3",
-   "version": "3.7.7"
-  }
- },
- "nbformat": 4,
- "nbformat_minor": 4
-}

tutorial/Q-GAN/QGAN_Tutorial_CN.ipynb → tutorial/Q-GAN/QGAN_CN.ipynb

@@ -4,100 +4,195 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# 量子生成对抗网络（Quantum GAN）\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+    "# 量子生成对抗网络"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 1. 经典生成对抗网络\n",
-    "\n",
-    "### 生成对抗网络简介\n",
-    "\n",
-    "生成对抗网络（Generative Adversarial Network, GAN）是生成模型的一种，是深度学习在近些年中一个重要的发展[1]。它分为两个部分：生成器 $G$（Generator）和判别器 $D$ (Discriminator)。生成器接受随机的噪声信号，以此为输入来生成我们期望得到的数据。判别器判断接收到的数据是不是来自真实数据，通常输出一个 $P(x)$，表示输入数据 $x$ 是真实数据的概率。\n",
-    "\n",
-    "### 纳什均衡\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 经典生成对抗网络"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 生成对抗网络简介"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "生成对抗网络（Generative Adversarial Network, GAN）是生成模型的一种，是深度学习在近些年中一个重要的发展[1]。它分为两个部分：生成器 $G$（Generator）和判别器 $D$ (Discriminator)。生成器接受随机的噪声信号，以此为输入来生成我们期望得到的数据。判别器判断接收到的数据是不是来自真实数据，通常输出一个 $P(x)$，表示输入数据 $x$ 是真实数据的概率。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 纳什均衡"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "在这里，我们用纳什均衡的思想来探讨 GAN 的收敛问题。\n",
     "\n",
     "纳什均衡（Nash equilibrium）是指在包含两个或以上参与者的非合作博弈（Non-cooperative game）中，假设每个参与者都知道其他参与者的均衡策略的情况下，没有参与者可以通过改变自身策略使自身受益时的一个概念解。在博弈论中，如果每个参与者都选择了自己的策略，并且没有玩家可以通过改变策略而其他参与者保持不变而获益，那么当前的策略选择的集合及其相应的结果构成了纳什均衡。\n",
     "\n",
-    "GAN 采用了纳什均衡的思想。在 GAN 中，生成器和判别器在进行非合作博弈。在双方博弈过程中，不论生成器的策略是什么，判别器最好的策略就是尽量做出判别；而无论判别器的策略是什么，生成器最好的策略就是尽量使判别器无法判别。因此博弈的两个当事人的策略组合及其相应的结果就构成了纳什均衡。**当达到纳什均衡时，生成器就具备了生成真实数据的能力，而判别器也无法区分生成数据和真实数据了**。\n",
-    "\n",
-    "### 优化目标\n",
-    "\n",
+    "我们可以把GAN的训练过程视为生成器和判别器的博弈过程。在这个博弈过程中，无论生成器的策略是什么，判别器最好的策略就是尽量判别出真实数据和生成数据。而无论判别器的策略是什么，生成器最好的策略就是使判别器无法判别出来。我们不难发现，这种博弈是零和博弈（一种非合作博弈），即一方有所得则另一方必有所失。因此生成器和判别器的博弈存在这种纳什均衡策略。而当真实数据的样本足够多，双方的学习能力足够强时，最终就会达到一种纳什均衡点。**生成器具备了生成真实数据的能力，而判别器也无法再区分生成数据和真实数据。**"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 优化目标"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "在 GAN 中，我们重点想要得到的是一个优秀的生成器（但是只有优秀的判别器才能准确判断生成器是否优秀），所以我们训练的理想结果是判别器无法识别出数据是来自真实数据还是生成数据。\n",
     "\n",
     "因此我们的目标函数如下：\n",
     "\n",
-    "$$\\min_{G}\\max_{D} V(G,D)= \\min_{G}\\max_{D}\\mathbb{E}_{x\\sim P_{data}}[\\log D(x)]+\\mathbb{E}_{z\\sim P_{z}}[\\log(1-D(G(z)))]$$\n",
-    "\n",
-    "这里，$G$ 表示生成器的参数，$D$ 表示判别器的参数。实际过程中，通常采用交替训练的方式，即先固定 $G$，训练 $D$，然后再固定 $D$，训练 $G$，不断往复。当两者的性能足够时，模型会收敛，两者达到纳什均衡。\n",
-    "\n",
-    "### 优点\n",
+    "$$\n",
+    "\\min_{G}\\max_{D} V(G,D)= \\min_{G}\\max_{D}\\mathbb{E}_{x\\sim P_{data}}[\\log D(x)]+\\mathbb{E}_{z\\sim P_{z}}[\\log(1-D(G(z)))]. \\tag{1}\n",
+    "$$\n",
     "\n",
+    "这里，$G$ 表示生成器的参数，$D$ 表示判别器的参数。实际过程中，通常采用交替训练的方式，即先固定 $G$，训练 $D$，然后再固定 $D$，训练 $G$，不断往复。当两者的性能足够时，模型会收敛，两者达到纳什均衡。\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 优点"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "- 相对其他生成模型，GAN 的生成效果更好。\n",
     "- 理论上，只要是可微分函数都可以用于构建生成器和判别器，因此能够与深度神经网络结合做深度生成模型。\n",
     "- GAN 相对其他生成模型来说，不依赖先验假设，我们事先不需要假设数据的分布和规律。\n",
-    "- GAN 生成数据的形式也很简单，只需要通过生成器进行前向传播即可。\n",
-    "\n",
-    "### 缺点\n",
-    "\n",
+    "- GAN 生成数据的形式也很简单，只需要通过生成器进行前向传播即可。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 缺点"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "- GAN 无需预先建模，因此过于自由导致训练难以收敛而且不稳定。\n",
     "- GAN 存在梯度消失问题，即很可能会达到这样一种状态，判别器的效果特别好，生成器的效果特别差。在这种情况下，判别器的训练没有任何损失，因此也没有有效的梯度信息去回传给生成器让它优化自己。\n",
-    "- GAN 的学习过程可能发生崩溃问题，生成器开始退化，总是生成同样的样本点，无法继续学习。而此时，判别器也会对相似的样本点指向相似的方向，模型参数已经不再更新，但是实际效果却很差。"
+    "- GAN 的学习过程可能出现模式崩溃（model collapse）问题。生成器发生退化，总是生成同样的样本点，无法继续学习。而此时，判别器也会对相似的样本点指向相似的方向，模型参数已经不再更新，但是实际效果却很差。"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 2. 量子生成对抗网络\n",
-    "\n",
-    "量子生成对抗网络与经典的类似，只不过不再用于生成经典数据，而是生成量子态[2-3]。在实践中，如果我们有一个量子态，其在观测后会坍缩为某一本征态，无法恢复到之前的量子态，因此我们如果有一个方法可以根据已有的目标量子态生成出很多与之相同（或相近）的量子态，会很方便我们的实验。\n",
+    "## 量子生成对抗网络"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "量子生成对抗网络与经典的类似，只不过不再用于生成经典数据，而是生成量子态[2-3]。在实践中，如果我们有一个量子态，其在观测后会坍缩为某一本征态，无法恢复到之前的量子态。因此如果我们有一个方法可以根据已有的目标量子态生成出很多与之相同（或相近）的量子态，会很方便我们的实验。\n",
     "\n",
-    "假设我们已有的目标量子态都来自一个混合态，它们属于同一个系综，其密度算符为$\\rho$。然后我们需要有一个生成器 $G$，它的输入是一个噪声数据，我们用一个系综 $\\rho_{z}=\\sum_{i}p_{i}|z_{i}\\rangle\\langle z_{i}|$ 来表示。因此我们每次取出一个随机噪声样本 $|z_{i}\\rangle$，通过生成器后得到生成的量子态 $|x\\rangle=G|z_{i}\\rangle$，我们期望生成的 $|x\\rangle$ 与目标量子态相近。\n",
+    "假设我们已有的目标量子态是一个混合态，它们属于同一个系综，其密度算符为$\\rho$。然后我们需要有一个生成器 $G$，它的输入是一个噪声数据，我们用一个系综 $\\rho_{z}=\\sum_{i}p_{i}|z_{i}\\rangle\\langle z_{i}|$ 来表示。因此我们每次取出一个随机噪声样本 $|z_{i}\\rangle$，通过生成器后得到生成的量子态 $|x\\rangle=G|z_{i}\\rangle$，我们期望生成的 $|x\\rangle$ 与目标量子态$\\rho$相近。\n",
     "\n",
     "值得注意的是，对于上文中提到的目标态的系综和噪声数据的系综，我们都认为有一个已有的物理设备可以生成出一个该系综下的量子态，而由于量子物理的相关性质，我们每次可以得到一个真正随机的量子态。但是在计算机程序中，我们仍然只能模拟这一过程。\n",
     "\n",
-    "对于判别器，我们期望判别器可以判断我们输入的量子态是已有的目标态还是生成的量子态，这一过程需要由测量给出。"
+    "对于判别器，我们期望判别器可以判断我们输入的量子态是已有的目标态还是生成的量子态，这一过程可以由测量给出。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 一个简单的例子"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 问题描述"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 3. 一个简单的例子\n",
-    "\n",
-    "### 简介\n",
-    "\n",
     "简单起见，我们假设已有的目标量子态是一个纯态，且生成器接受的输入为$|0\\rangle$。\n",
     "\n",
     "制备已有的目标量子态的线路：\n",
-    "\n",
-    "<img src=\"figures/target_state.png\" width=\"400\" >\n",
-    "\n",
+    "![QGAN-fig-target_state](figures/QGAN-fig-target_state.png)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "生成器的线路为：\n",
-    "\n",
-    "<img src=\"figures/generator.png\" width=\"600\" >\n",
-    "\n",
+    "![QGAN-fig-generator](figures/QGAN-fig-generator.png)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "判别器的线路为：\n",
-    "\n",
-    "<img src=\"figures/discriminator.png\" width=\"700\" >\n",
-    "\n",
-    "通过对判别器输出的量子态进行测量，我们可以得到将目标态判断为目标态的概率 $P_{T}$ 和将生成态判断为目标态的概率 $P_{G}$（通过对判别器连接目标态和生成器这两个不同的输入得到）。\n",
-    "\n",
-    "\n",
-    "### 具体过程\n",
-    "\n",
+    "![QGAN-fig-discriminator](figures/QGAN-fig-discriminator.png)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "通过对判别器输出的量子态进行测量，我们可以得到将目标态判断为目标态的概率 $P_{T}$ 和将生成态判断为目标态的概率 $P_{G}$（通过对判别器连接目标态和生成器这两个不同的输入得到）。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 具体过程"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
     "假设已有的目标量子态为 $|\\psi\\rangle$，生成器生成的量子态为 $|x\\rangle=G|00\\rangle$（生成器采用两量子比特线路，其中第0个量子比特认为是生成的量子态）。\n",
     "\n",
     "判别器对数据进行判别并得到量子态$|\\phi\\rangle$，那么当输入为目标态时，$|\\phi\\rangle=D(|\\psi\\rangle\\otimes |00\\rangle)$；当输入为生成态时，$|\\phi\\rangle=D(G\\otimes I)|000\\rangle$。\n",
     "\n",
     "对于判别器得到的量子态，我们还需要采用泡利 Z 门对第3个量子比特进行测量，从而得到判别器对输入量子态的判断结果（即判别器认为输入是目标态的概率）。首先有 $M_{z}=I\\otimes I\\otimes\\sigma_{z}$，而测量结果为 $\\text{disc_output}=\\langle\\phi|M_{z}|\\phi\\rangle$，所以测量结果为目标态的概率是 $P=(\\text{disc_output}+1)/2$。\n",
     "\n",
-    "我们定义判别器的损失函数为 $\\mathcal{L}_{D}=P_{G}(\\text{gen_theta}, \\text{disc_phi})-P_{T}(\\text{disc_phi})$，生成器的损失函数为 $\\mathcal{L}_{G}=-P_{G}(\\text{gen_theta}, \\text{disc_phi})$。这里的 $P_{G}$ 和 $P_{T}$ 分别是输入量子态为生成态和目标态时，$P=(\\text{disc_output}+1)/2$ 的表达式，gen_theta 和 disc_phi 分别是生成器和判别器线路的参数。\n",
+    "我们定义判别器的损失函数为 $\\mathcal{L}_D=P_{G}(\\text{gen_theta}, \\text{disc_phi})-P_{T}(\\text{disc_phi})$，生成器的损失函数为 $\\mathcal{L}_{G}=-P_{G}(\\text{gen_theta}, \\text{disc_phi})$。这里的 $P_{G}$ 和 $P_{T}$ 分别是输入量子态为生成态和目标态时，$P=(\\text{disc_output}+1)/2$ 的表达式，gen_theta 和 disc_phi 分别是生成器和判别器线路的参数。\n",
     "\n",
     "因此我们只需要分别优化目标函数 $\\min_{\\text{disc_phi}}\\mathcal{L}_{D}$ 和 $\\min_{\\text{gen_theta}}\\mathcal{L}_{G}$ 即可交替训练判别器和生成器。"
    ]
@@ -106,7 +201,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 4. 在 paddle quantum 上的实现"
+    "## 在 Paddle Quantum 上的实现"
    ]
   },
   {
@@ -118,7 +213,7 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 11,
+   "execution_count": 1,
    "metadata": {},
    "outputs": [],
    "source": [
@@ -140,20 +235,28 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 12,
+   "execution_count": 3,
    "metadata": {},
    "outputs": [],
    "source": [
     "class QGAN(fluid.dygraph.Layer):\n",
     "    def __init__(self):\n",
     "        super(QGAN, self).__init__()\n",
+    "        \n",
     "        # 用以制备目标量子态的角度\n",
     "        target_omega_0 = 0.9 * np.pi\n",
     "        target_omega_1 = 0.2 * np.pi\n",
-    "        self.target_omega = fluid.dygraph.to_variable(np.array([target_omega_0, target_omega_1], np.float64))\n",
+    "        self.target_omega = fluid.dygraph.to_variable(\n",
+    "        np.array([target_omega_0, target_omega_1], np.float64))\n",
+    "        \n",
     "        # 生成器和判别器电路的参数\n",
-    "        self.gen_theta = self.create_parameter([9], dtype=\"float64\", attr=fluid.initializer.Uniform(low=0.0, high=np.pi, seed=7))\n",
-    "        self.disc_phi = self.create_parameter([9], dtype=\"float64\", attr=fluid.initializer.Uniform(low=0.0, high=np.pi, seed=8))\n",
+    "        self.gen_theta = self.create_parameter([9], \n",
+    "        dtype=\"float64\", attr=fluid.initializer.Uniform(\n",
+    "                            low=0.0, high=np.pi, seed=7))\n",
+    "        self.disc_phi = self.create_parameter([9], \n",
+    "        dtype=\"float64\", attr=fluid.initializer.Uniform(\n",
+    "                            low=0.0, high=np.pi, seed=8))\n",
+    "        \n",
     "        # 制备目标量子态\n",
     "        cir = UAnsatz(3)\n",
     "        cir.ry(self.target_omega[0], 0)\n",
@@ -191,6 +294,7 @@
     "        # 判别器电路\n",
     "        cir = self.discriminator(self.disc_phi)\n",
     "        cir.run_state_vector(self.target_state)\n",
+    "        \n",
     "        # 判别器对目标态的判断结果\n",
     "        target_disc_output = cir.expecval([[1.0, 'z2']])\n",
     "        prob_as_target = (target_disc_output + 1) / 2\n",
@@ -202,7 +306,8 @@
     "        判别器将生成态判断为目标态的概率\n",
     "        \"\"\"\n",
     "        # 得到生成器生成的量子态\n",
-    "        gen_state = self.generator(self.gen_theta).run_state_vector()\n",
+    "        gen_state = self.generator(\n",
+    "                    self.gen_theta).run_state_vector()\n",
     "        # 判别器电路\n",
     "        cir = self.discriminator(self.disc_phi)\n",
     "        cir.run_state_vector(gen_state)\n",
@@ -214,10 +319,12 @@
     "\n",
     "    def forward(self, model_name):\n",
     "        if model_name == 'gen':\n",
-    "            # 计算生成器的损失函数，loss值的区间为[-1, 0]，0表示生成效果极差，为-1表示生成效果极好\n",
+    "            # 计算生成器的损失函数，loss值的区间为[-1, 0]，\n",
+    "            # 0表示生成效果极差，为-1表示生成效果极好\n",
     "            loss =  -1 * self.disc_gen_as_target()\n",
     "        else:\n",
-    "            # 计算判别器的损失函数，loss值的区间为[-1, 1]，为-1表示完美区分，为0表示无法区分，为1表示区分颠倒\n",
+    "            # 计算判别器的损失函数，loss值的区间为[-1, 1]，\n",
+    "            # 为-1表示完美区分，为0表示无法区分，为1表示区分颠倒\n",
     "            loss = self.disc_gen_as_target() - self.disc_target_as_target()\n",
     "\n",
     "        return loss\n",
@@ -228,7 +335,8 @@
     "        \"\"\"\n",
     "        state = self.target_state\n",
     "        state = complex.reshape(state, [1] + state.shape)\n",
-    "        density_matrix = complex.matmul(dagger(state), state)\n",
+    "        density_matrix = complex.matmul(\n",
+    "                         dagger(state), state)\n",
     "        state = partial_trace(density_matrix, 2, 4, 2)\n",
     "\n",
     "        return state.numpy()\n",
@@ -237,9 +345,11 @@
     "        \"\"\"\n",
     "        得到生成态的密度矩阵表示\n",
     "        \"\"\"\n",
-    "        state = self.generator(self.gen_theta).run_state_vector()\n",
+    "        state = self.generator(\n",
+    "                self.gen_theta).run_state_vector()\n",
     "        state = complex.reshape(state, [1] + state.shape)\n",
-    "        density_matrix = complex.matmul(dagger(state), state)\n",
+    "        density_matrix = complex.matmul(\n",
+    "                         dagger(state), state)\n",
     "        state = partial_trace(density_matrix, 2, 4, 2)\n",
     "\n",
     "        return state.numpy()"
@@ -249,19 +359,19 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "接下来我们使用 paddle 的动态图机制来训练我们的模型。"
+    "接下来我们使用 PaddlePaddle 的动态图机制来训练我们的模型。"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 13,
+   "execution_count": 4,
    "metadata": {},
    "outputs": [
     {
      "name": "stderr",
      "output_type": "stream",
      "text": [
-      "Training: 100% |##########################| Elapsed Time: 0:01:30 Time: 0:01:30\r"
+      "Training: 100% |##########################| Elapsed Time: 0:01:57 Time: 0:01:57\r"
      ]
     },
     {
@@ -276,9 +386,9 @@
       "[[0.01664936+0.j         0.03736201+0.11797786j]\n",
       " [0.03736201-0.11797786j 0.98335064+0.j        ]] \n",
       "\n",
-      "the distance between these two quantum states is 0.016958549205174953 \n",
+      "the distance between these two quantum states is 0.0169585492051749 \n",
       "\n",
-      "the fidelity between these two quantum states is 0.9952202072599429\n"
+      "the fidelity between these two quantum states is 0.9952202066208862\n"
      ]
     },
     {
@@ -303,29 +413,38 @@
     "loss_history = list()\n",
     "with fluid.dygraph.guard():\n",
     "    gan_demo = QGAN()\n",
-    "    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=LR, parameter_list=gan_demo.parameters())\n",
-    "    widgets = ['Training: ', Percentage(), ' ', Bar('#'), ' ', Timer(), ' ', ETA()]\n",
+    "    optimizer = fluid.optimizer.SGDOptimizer(\n",
+    "      learning_rate=LR, parameter_list=gan_demo.parameters())\n",
+    "    widgets = ['Training: ', Percentage(), ' ', \n",
+    "               Bar('#'), ' ', Timer(), ' ', ETA()]\n",
     "    pbar = ProgressBar(widgets=widgets, maxval=ITR * 70).start()\n",
     "    for itr0 in range(ITR):\n",
+    "      \n",
     "        # 记录判别器loss值的变化\n",
     "        loss_disc_history = list()\n",
+    "        \n",
     "        # 训练判别器\n",
     "        for itr1 in range(ITR1):\n",
     "            pbar.update(itr0 * (ITR1 + ITR2) + itr1)\n",
     "            loss_disc = gan_demo('disc')\n",
     "            loss_disc.backward()\n",
-    "            optimizer.minimize(loss_disc, parameter_list=[gan_demo.disc_phi], no_grad_set=[gan_demo.gen_theta])\n",
+    "            optimizer.minimize(loss_disc, parameter_list\n",
+    "                               =[gan_demo.disc_phi], \n",
+    "                               no_grad_set=[gan_demo.gen_theta])\n",
     "            gan_demo.clear_gradients()\n",
     "            loss_disc_history.append(loss_disc.numpy()[0])\n",
     "\n",
     "        # 记录生成器loss值的变化\n",
     "        loss_gen_history = list()\n",
+    "        \n",
     "        # 训练生成器\n",
     "        for itr2 in range(ITR2):\n",
     "            pbar.update(itr0 * (ITR1 + ITR2) + ITR1 + itr2)\n",
     "            loss_gen = gan_demo('gen')\n",
     "            loss_gen.backward()\n",
-    "            optimizer.minimize(loss_gen, parameter_list=[gan_demo.gen_theta], no_grad_set=[gan_demo.disc_phi])\n",
+    "            optimizer.minimize(loss_gen, parameter_list\n",
+    "                               =[gan_demo.gen_theta], \n",
+    "                               no_grad_set=[gan_demo.disc_phi])\n",
     "            gan_demo.clear_gradients()\n",
     "            loss_gen_history.append(loss_gen.numpy()[0])\n",
     "\n",
@@ -334,14 +453,18 @@
     "    \n",
     "    # 得到目标量子态\n",
     "    target_state = gan_demo.get_target_state()\n",
+    "    \n",
     "    # 得到生成器最终生成的量子态\n",
     "    gen_state = gan_demo.get_generated_state()\n",
     "    print(\"the density matrix of the target state:\")\n",
     "    print(target_state, \"\\n\")\n",
     "    print(\"the density matrix of the generated state:\")\n",
     "    print(gen_state, \"\\n\")\n",
-    "    # 计算两个量子态之间的距离，这里的距离定义为tr[(target_state-gen_state)^2]\n",
-    "    distance = np.trace(np.matmul(target_state-gen_state, target_state-gen_state)).real\n",
+    "    \n",
+    "    # 计算两个量子态之间的距离，\n",
+    "    # 这里的距离定义为tr[(target_state-gen_state)^2]\n",
+    "    distance = np.trace(np.matmul(target_state-gen_state, \n",
+    "                                  target_state-gen_state)).real\n",
     "    # 计算两个量子态的保真度\n",
     "    fidelity = state_fidelity(target_state, gen_state)\n",
     "    print(\"the distance between these two quantum states is\", distance, \"\\n\")\n",
@@ -359,20 +482,21 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 5. 训练过程的可视化\n",
-    "接下来我们观察一下，在训练过程中，判别器和生成器的 loss 曲线变化过程。"
+    "## 训练过程的可视化"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
+    "接下来我们观察一下，在训练过程中，判别器和生成器的 loss 曲线变化过程。\n",
+    "\n",
     "首先安装所需要的 package。"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 14,
+   "execution_count": 5,
    "metadata": {},
    "outputs": [],
    "source": [
@@ -390,12 +514,12 @@
   },
   {
    "cell_type": "code",
-   "execution_count": 15,
+   "execution_count": 6,
    "metadata": {},
    "outputs": [
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZgAAAEXCAYAAACQ3VJYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAlO0lEQVR4nO3de7xU1X338c9XwDtKjGgQJNgUL2gU5RQ1mkRFrUFT1CT1UpW0VqIvTb2lltY+SVpt42M0Vp9aKUlUTIxGDUaiVPASa0iMcgkiiALiDSGCNyCaiMbf88deB4fDzDkz58yePefwfb9e85q9115r79/MWXN+s/eevbYiAjMzs3rbrOgAzMysZ3KCMTOzXDjBmJlZLpxgzMwsF04wZmaWCycYMzPLhRNMk5J0s6TLJX1a0rM5rP93kv6kk20XSDqsvhGZWU/jBNPkIuIXEbFHDuvdNiKWdrLt3hHxSFdjkPRlSTO6uh6zRnB/rZ0TzCZGUu+iY6iXnvRarFiN6EubYn91gmkSkvaXNEfSWkk/BrZM5YdJWlZS7x8kvZLqPStpVCrvJemfJD2Xls2WtGtaFpLOlbQYWFxS9qdp+mZJ/yXpf9Khs19K+pik/5D0pqRnJO1fEsMLko5M09+UdIekW9J2F0hqKak7viSmpyWdkMr3AiYAB6dtvpXKt0/rWiXpRUn/LGmztOzLKbZrJL0BfDOnP4c1mKQDJP0m9ZM7Jf1Y0uVp2XGS5kp6S9KvJO1b0u4FSV+TNE/S6tRuy5LlHbX9B0nzgLcl9XZ/rbOI8KPgB7A58CJwIdAH+CLwHnA5cBiwLNXbA3gZ2CXNDwE+kab/Hngq1RGwH/DRtCyAB4AdgK1Kyv40Td8MvAaMIEtsDwPPA2cAvVIcPy+J9wXgyDT9TeAPwOhU91vAr0vqfgnYhezLzEnA28CAtOzLwIw278UtwD1A3/T6FgFnltR/H/gq0Lv1tfjRvR8l/f/81P9PBNalfncAsBI4MPWvsan/bVHSF59IfWwHYCFwdlpWTdu5wK4lnwv313r+bYsOwI8A+AywHFBJ2a/YOMH8afrAHAn0abOOZ4ExFdYfwBFlykoTzHdLln0VWFgy/0ngrZL5F9gwwTxYsmwY8Pt2Xuvc1jjbfmDTP4F3gWElZV8BHimp/1LRfy8/6vtI/f+VNv1/Rur/NwCXtan/LPDZNP0CcFrJsiuBCWm6mrZ/00Fs7q9dePgQWXPYBXglUq9MXmxbKSKWABeQ/VNfKel2SbukxbsCz7WzjZc7iOHVkunfl5nftp22vy2ZfgfYsvV4s6QzSg5RvAXsA+xYYT078uG32VYvAgNL5jt6Hdb9lOv/rX/njwMXt/af1Id2TW1ate1/29bQdoP+5P5aX04wzWEFMFCSSsoGl6sYET+KiEPJPjwB/N+06GXgE+1so+HDZkv6OPBd4Dyyw3X9gPlkh/DKxfQa2aHBj5eUDSb7dtvKw3/3POX6/67p+WXg3yKiX8lj64i4rYr1VtN2fX9yf60/J5jm8BjZsdq/SycaTwRGtq0kaQ9JR0jaguy8x++BP6bF3wMukzRUmX0lfbRRL6CCbcg+YKsAJP012TfCVq8CgyRtDhARfwTuAP5NUt/0gb8I+GFDo7ZGe4ysH5+X+v8YPuz/3wXOlnRg6tfbSDpWUt8q1ltrW/fXOnOCaQIRsY7sxOaXgTfJTi5OLlN1C+AKsm9OvwV2Av4pLfsOWWefDqwBvg9slWfcHYmIp4Gryf6BvEp2LueXJVUeBhYAv5X0Wir7KtmJ1aVkx+F/BNzYqJit8Ur6/5nAW8BpwL3AuxExCzgL+E+yz8YSss9JNeutqa37a/1pw8OeZmbFk/Q42cn6m4qOxTrPezBmVjhJn1V27VVvSWOBfYH7i47LuqbwBCPpRkkrJc2vsFySrpO0JF1MdUDJsmOUXWy4RNL4xkVt1nkd9dv2+nwPtgfwJLAauBj4YkSsKDYk66rCD5FJ+gzwO+CWiNinzPLRZMc5R5NdMHVtRBwoqRfZRU1HAcuAmcAp6TiqWVOqpt9W6vMFhGvWJYXvwUTEo8Ab7VQZQ5Z8IiJ+DfSTNIDsVyZLImJpOkl4e6pr1syq6beV+rxZt9IdBl8byIYXKy1LZeXKy37LkzQOGAewzTbbjNhzzz3zidQ2ebNnz34tIvq3U6Waflupz29wyMj92hqpir69ke6QYFSmLNop37gwYiIwEaClpSVmzZpVv+jMSkjaaASGtlXKlLXtt1X1bfdra6Qq+vZGukOCWcaHV/UCDCIbt2vzCuVmzaxSf661jlnTK/wcTBWmAGekX9YcBKxOvy6ZCQyVtFu6svbkVNesmVXTbyv1ebNupfA9GEm3kY0YvKOy+558g2zIbiJiAjCV7Nc0S8gGsvvrtOx9SecB08hGNb0xIhY0/AWY1aBSv5V0dlpesc+bdTeFJ5iIOKWD5QGcW2HZVLIPo1m3Ua7fpsTSOl2xz5t1J93hEJmZmXVDTjBmZpYLJxgzM8uFE4yZmeXCCcbMzHLhBGNmZrlwgjEzs1w4wZiZWS6cYMzMLBdOMGZmlgsnGDMzy4UTjJmZ5cIJxszMcuEEY2ZmuXCCMTOzXDjBmJlZLpxgzMwsF04wZmaWi8ITjKRjJD0raYmk8WWW/72kuekxX9IfJe2Qlr0g6am0bFbjozczs0p6F7lxSb2A64GjgGXATElTIuLp1joR8W3g26n+54ELI+KNktUcHhGvNTBsMzOrQtF7MCOBJRGxNCLWAbcDY9qpfwpwW0MiMzOzLik6wQwEXi6ZX5bKNiJpa+AY4CclxQFMlzRb0rjcojQzs5oVeogMUJmyqFD388Av2xweOyQilkvaCXhA0jMR8ehGG8mSzziAwYMHdzVmMzOrQtF7MMuAXUvmBwHLK9Q9mTaHxyJieXpeCdxNdshtIxExMSJaIqKlf//+XQ7azMw6VnSCmQkMlbSbpM3JksiUtpUkbQ98FrinpGwbSX1bp4GjgfkNidrMzDpU6CGyiHhf0nnANKAXcGNELJB0dlo+IVU9AZgeEW+XNN8ZuFsSZK/jRxFxf+OiNzOz9hR9DoaImApMbVM2oc38zcDNbcqWAvvlHJ6ZmXVS0YfIzMysh3KCMTOzXDjBmJlZLpxgzMwsF04wZmaWCycYMzPLhROMmZnlwgnGzMxy4QRj1iCSdpD0gKTF6fkjZersKunnkhZKWiDp/CJiNasHJxizxhkPPBQRQ4GH0nxb7wMXR8RewEHAuZKGNTBGs7pxgjFrnDHApDQ9CTi+bYWIWBERc9L0WmAhFe6RZNbsnGDMGmfniFgBWSIBdmqvsqQhwP7A4xWWj5M0S9KsVatW1TtWsy4rfLBLsx5md0nlbhtxaS0rkbQt2d1bL4iINeXqRMREYCJAS0tLpRv1mRXGCcasvhZFREu5BZJelTQgIlZIGgCsrFCvD1lyuTUiJucYq1mufIjMrHGmAGPT9FhKbqDXStkNjr4PLIyI7zQwNrO6c4Ixa5wrgKMkLQaOSvNI2kVS6z2RDgFOB46QNDc9RhcTrlnX+BCZWYNExOvAqDLly4HRaXoGoAaHZpYL78GYmVkunGDMzCwXhScYScdIelbSEkkbXdks6TBJq0uOR3+92rZmZlacQs/BSOoFXE92wnMZMFPSlIh4uk3VX0TEcZ1sa2ZmBSh6D2YksCQilkbEOuB2suE08m5rZmY5KzrBDAReLplfRvlxlw6W9KSk/5G0d41tPaSGmVkBik4w5X6O2XbIiznAxyNiP+D/AT+toW1WGDExIloioqV///6djdXMzGpQdIJZBuxaMj8IWF5aISLWRMTv0vRUoI+kHatpa2ZmxSk6wcwEhkraTdLmwMlkw2msJ+ljafgMJI0ki/n1atqamVlxCv0VWUS8L+k8YBrQC7gxIhZIOjstnwB8EThH0vvA74GTIyKAsm0LeSFmZraRwoeKSYe9prYpm1Ay/Z/Af1bb1szMmkPRh8jMzKyHcoIxM7NcOMGYmVkunGDMzCwXTjBmZpYLJxgzM8uFE4yZmeXCCcbMzHLhBGNmZrlwgjEzs1w4wZiZWS6cYMzMLBdOMGZmlgsnGDMzy4UTjJmZ5cIJxszMcuEEY2ZmuXCCMTOzXBSeYCQdI+lZSUskjS+z/K8kzUuPX0nar2TZC5KekjRX0qzGRm5mZu3pXeTGJfUCrgeOApYBMyVNiYinS6o9D3w2It6U9DlgInBgyfLDI+K1hgVtZmZVKXoPZiSwJCKWRsQ64HZgTGmFiPhVRLyZZn8NDGpwjGZm1glFJ5iBwMsl88tSWSVnAv9TMh/AdEmzJY2r1EjSOEmzJM1atWpVlwI2M7PqFHqIDFCZsihbUTqcLMEcWlJ8SEQsl7QT8ICkZyLi0Y1WGDGR7NAaLS0tZddvZmb1VfQezDJg15L5QcDytpUk7Qt8DxgTEa+3lkfE8vS8Erib7JCbWVOStIOkByQtTs8faaduL0m/kXRvI2M0q6eiE8xMYKik3SRtDpwMTCmtIGkwMBk4PSIWlZRvI6lv6zRwNDC/YZGb1W488FBEDAUeSvOVnA8sbEhUZjkpNMFExPvAecA0sg/THRGxQNLZks5O1b4OfBT4rzY/R94ZmCHpSeAJ4L6IuL/BL8GsFmOASWl6EnB8uUqSBgHHku21m3VbRZ+DISKmAlPblE0omf5b4G/LtFsK7Ne23KyJ7RwRKwAiYkU6d1jOfwCXAH3bW1n6Ycs4gMGDB9cxTLP6KPoQmVlPs7uk+WUeYzpuCpKOA1ZGxOyO6kbExIhoiYiW/v37dzlws3orfA/GrIdZFBEt5RZIelXSgLT3MgBYWabaIcBfSBoNbAlsJ+mHEXFajjGb5aLqPRhJ50vaTpnvS5oj6eg8gzPrYaYAY9P0WOCethUi4h8jYlBEDCH70cvDTi7WXdVyiOxvImIN2a+1+gN/DVyRS1RmTeDOO+9k7dq1AFx++eWceOKJzJkzpyurvAI4StJisuGRrgCQtIukqe22NOuGakkwrRdFjgZuiognKX+hpFmPcNlll9G3b19mzJjBtGnTGDt2LOecc06n1xcRr0fEqIgYmp7fSOXLI2J0mfqPRMRxXXgJZoWqJcHMljSdLMFMS9egfJBPWGbF69WrFwD33Xcf55xzDmPGjGHdunUFR2XWfdSSYM4kuzDszyLiHaAP2WEysx5p4MCBfOUrX+GOO+5g9OjRvPvuu3zwgb9TmVWrlgRzMPBsRLwl6TTgn4HV+YRlVrw77riDP//zP+f++++nX79+vPHGG3z7298uOiyzbqOWBHMD8E664dclwIvALblEZdYEVqxYwbHHHsvQoUN55JFHuPPOOxk50sPdmVWrlgTzfkQE2XAX10bEtXRwpbFZd/aFL3yBXr16sWTJEs4880yef/55Tj311KLDMus2akkwayX9I3A6cF+6G2WffMIyK95mm21G7969mTx5MhdccAHXXHMNK1asKDoss26jlgRzEvAu2fUwvyW7MZgPSFuP1adPH2677TZuueUWjjsu+7Xwe++9V3BUZt1H1QkmJZVbge3TeEl/iAifg7Ee66abbuKxxx7j0ksvZbfdduP555/ntNN8Ub1ZtWoZKuYvyYbF/xLwl8Djkr6YV2BmRRs2bBhXXXUVn/zkJ5k/fz6DBg1i/Pj2buFiZqVqGezyUrJrYFYCSOoPPAjclUdgZkV75JFHGDt2LEOGDCEiePnll5k0aRKf+cxnig7NrFuoJcFs1ppcktfxcP/Wg1188cVMnz6dPfbYA4BFixZxyimnMHt2hyPpmxm1JZj7JU0DbkvzJ9HmRmFmPcl77723PrkA7L777j7Jb1aDqhNMRPy9pC+Q3a9CwMSIuDu3yMwK1tLSwplnnsnpp58OwK233sqIESMKjsqs+6jpEFdE/CQiLoqIC+uVXCQdI+lZSUskbXQGNd1/5rq0fJ6kA6pta9YVN9xwA3vvvTfXXXcd1157LcOGDWPChAkdNzQzoIo9GElrgSi3CIiI2K6zG08Xa15Pdm+MZcBMSVMi4umSap8DhqbHgWRD1hxYZdvyotzLWR9Up16L9TxbbLEFF110ERdddFHRoZh1Sx0mmIioajgYSR+JiDdr3P5IYElELE3ruJ1sKJrSJDEGuCUNU/NrSf3S7WaHVNF2Y7Nnw2Y5/Taho+TUdnnpfK1ta1lez7YdzRcVV0fLa4j7k6tXt3ujo3lPPgl7793+9s2sppP8HXkIOKDDWhsaCLxcMr+MbC+lozoDq2wLgKRxwDiAvbbfHi68sHw07e3ZdLS81ral813Zbr3jam9ZR/NFxdXR8lrijuDeNWvaX3+/fu0vNzOgvgmmM8eWyrVp++mvVKeatllhxERgIkBLS0vwjW/UEqNtYj5eZb2DDz6Yxx57LNdYzLqzeiaYDr5WlrUM2LVkfhCwvMo6m1fR1iw3f/jDH4oOwaypFX2h5ExgqKTdJG0OnAxMaVNnCnBG+jXZQcDqiFhRZVuz3Mg/CDFrV6GHyCLifUnnAdOAXsCNEbFA0tlp+QSyizlHA0uAd0i3aa7Uti6vxMzMuqzqBJP2HhZExNo03xcYFhGPpyqjOhNAREylzYgAKbG0TgdwbrVtzRolOvqxgdkmrtZbJv+uZP7tVAZARLxRr6DMuoMf/OAHRYdg1tRqSTCKkq9sEfEB9T3EZtZUJk+ezNChQ9l+++3Zbrvt6Nu3L9tt9+F1xfvss0+B0Zk1v1oSzFJJfyepT3qcDyzNKzCzol1yySVMmTKF1atXs2bNGtauXcuajq6RMbP1akkwZwOfAl7hw4sax+URlFkz2Hnnndlrr72KDsOs26plNOWVZD8FNtsktLS0cNJJJ3H88cezxRZbrC8/8cQTC4zKrPuo5VdkVwKXA78H7gf2Ay6IiB/mFJtZodasWcPWW2/N9OnT15dJcoIxq1ItJ+mPjohLJJ1AdojsS8DPAScY65FuuummokMw69ZqOQfTJz2PBm7zz5Ktp1u0aBGjRo1a/2uxefPmcfnllxcclVn3UUuC+ZmkZ4AW4CFJ/QEPxmQ91llnncW3vvUt+vTJvlvtu+++3H777QVHZdZ9VJ1gImI8cDDQEhHvkV1oOSavwMyK9s477zBy5MgNynr39qVfZtWq5o6WR0TEw5JOLCkrrTI5j8DMirbjjjvy3HPPre/vd911FwMGDCg4KrPuo5qvY58BHgY+z4f3YSl9doKxHun6669n3LhxPPPMMwwcOJDddtuNW2+9teiwzLqNahLMWkkXAfPZ8EZfHunPerSf/vSnjB49msMPP5wPPviAbbbZhgcffJARI0YwfPjwosMza3rVnIPZFugLjADOAQYAu5Bd2T8sv9DMijVr1iwmTJjAm2++yVtvvcXEiRN55JFHOOuss7jyyitrXp+kHSQ9IGlxev5IhXr9JN0l6RlJCyUd3OUXY1aADhNMRPxLRPwLsCNwQER8LSIuJks4g/IO0Kwor7/+OnPmzOGqq67i6quvZtasWaxatYpHH32Um2++uTOrHA88FBFDgYfSfDnXAvdHxJ5kFzQv7MzGzIpWy8+UBwPrSubXAUPqGo1ZE3nppZfYfPPN18/36dOHF198ka222mqDoWNqMAaYlKYnAce3rSBpO7Lznt8HiIh1EfFWZzZmVrRafnP5A+AJSXeTnX85gQ8/LGY9zqmnnspBBx3EmDHZr/F/9rOfccopp/D2228zbFinjg7vnG73TUSskLRTmTp/AqwCbpK0HzAbOD8i3m5bUdI40oCzgwcP7kw8ZrlSLXflk3QA8Ok0+2hE/CaXqHLU0tISs2bNKjoM6yZmz57NjBkziAgOPfRQWlpa2q0vaS3wUplFlwKTIqJfSd03I2KD8zCSWoBfA4dExOOSrgXWRMT/aW+77teWN0mzI6L9D0AbNV01FhFzgDk1RVWBpB2AH5MdZnsB+MuIeLNNnV2BW4CPAR8AEyPi2rTsm8BZZN/2AP4p3ULZrG5GjBjBiBEjammyqNKHUNKrkgakvZcBwMoy1ZYBy0puRX4Xlc/VmDW1Ws7B1Fs1JzzfBy6OiL2Ag4BzJZUem7gmIoanh5OLNbspwNg0PRa4p22FiPgt8LKkPVLRKODpxoRnVl9FJpgOT3hGxIq010RErCX7Nc3ARgVoVmdXAEdJWgwcleaRtIuk0i9IXwVulTQPGA78e6MDNauHIgdWquaE53qShgD7A4+XFJ8n6QxgFtmezpsV2vpkqBUuIl4n2yNpW76cbJTy1vm5ZIPKmnVrue7BSHpQ0vwyj5oGyZS0LfATshuctd4U/QbgE2Tf8FYAV1dqHxETI6IlIlr69+/fuRdjZmY1yXUPJiKOrLSsyhOeSOpDllxujYj1455FxKsldb4L3Fu/yM3MrKuKPAfT4QlPZcPYfh9YGBHfabOsdFjbE8jGSjMzsyZRZIKp5oTnIcDpwBGS5qZH67HqKyU9lU6EHg5c2OD4zcysHYWd5K/mhGdEzODD0Zvb1js91wDNzKxLityDMTOzHswJxszMcuEEY2ZmuXCCMTOzXDjBmJlZLpxgzMwsF04wZmaWCycYMzPLhROMmZnlwgnGzMxy4QRjZma5cIIxM7NcOMGYmVkunGDMzCwXTjBmZpYLJxgzM8uFE4yZmeXCCcbMzHJRWIKRtIOkByQtTs8fqVDvBUlPSZoraVat7c3MrBhF7sGMBx6KiKHAQ2m+ksMjYnhEtHSyvZmZNViRCWYMMClNTwKOb3B7MzPLUZEJZueIWAGQnneqUC+A6ZJmSxrXifZmZlaA3nmuXNKDwMfKLLq0htUcEhHLJe0EPCDpmYh4tMY4xgHjAAYPHlxLUzMz66RcE0xEHFlpmaRXJQ2IiBWSBgArK6xjeXpeKeluYCTwKFBV+9R2IjARoKWlJTr/iszMrFpFHiKbAoxN02OBe9pWkLSNpL6t08DRwPxq25uZWXGKTDBXAEdJWgwcleaRtIukqanOzsAMSU8CTwD3RcT97bU3M7PmkOshsvZExOvAqDLly4HRaXopsF8t7c3MrDn4Sn4zM8uFE4yZmeXCCcasQWoYHulCSQskzZd0m6QtGx2rWT04wZg1TofDG0kaCPwd0BIR+wC9gJMbGqVZnTjBmDVOtcMb9Qa2ktQb2BpYnn9oZvXnBGPWOB0ObxQRrwBXAS8BK4DVETG93MokjZM0S9KsVatW5Ri2Wec4wZjV1+7p3Enbx5hqGqfzMmOA3YBdgG0knVaubkRMjIiWiGjp379//V6BWZ0Udh2MWQ+1qM1tJdarcnikI4HnI2JVajMZ+BTww9wiNsuJ92DMGqea4Y1eAg6StLUkkV1MvLBB8ZnVlROMWeN0ODxSRDwO3AXMAZ4i+4xOLCZcs67xITKzBqlmeKQ0/w3gGw0MzSwX3oMxM7NcOMGYmVkunGDMzCwXTjBmZpYLJxgzM8uFE4yZmeXCCcbMzHJRWIKp5t4YkvaQNLfksUbSBWnZNyW9UrJs9EYbMTOzwhS5B9PhvTEi4tmIGB4Rw4ERwDvA3SVVrmldHhFTGxG0mZlVp8gEU+29MVqNAp6LiBfzDMrMzOqjyATT4b0x2jgZuK1N2XmS5km6sdLtZ83MrBi5JhhJD3bl3hgl69kc+AvgzpLiG4BPAMPJbsx0dTvtfWMmM7MGy3Wwy4g4stKyKu+N0epzwJyIeLVk3eunJX0XuLedOCaSRqRtaWmJGl6CmZl1UpGHyKq5N0arU2hzeCwlpVYnAPPrGp2ZmXVJkQmmw3tjpPmt0/LJbdpfKekpSfOAw4ELGxO2mZlVo7D7wdRwb4x3gI+WqXd6rgGamVmX+Ep+MzPLhROMmZnlwgnGzMxy4QRjZma5cIIxM7NcOMGYmVkunGDMzCwXTjBmZpYLJxgzM8uFE4yZmeXCCcbMzHLhBGNmZrlwgjEzs1w4wZiZWS6cYMzMLBdOMGZmlgsnGDMzy4UTjJmZ5cIJxszMclFYgpH0JUkLJH0gqaWdesdIelbSEknjS8p3kPSApMXp+SONidysc7ra5826m94Fbns+cCLw35UqSOoFXA8cBSwDZkqaEhFPA+OBhyLiivQhHA/8Q/5hm3VaV/t8RWvXwsMPl66n0vo7Lu9K22rKG7GNzsRUdNu8tt2V9Q8aBP36dbzeSgpLMBGxEEDtvysjgSURsTTVvR0YAzydng9L9SYBj+AEY02sDn2+okWLYNSoOgVqltxyC5x+eufbF7kHU42BwMsl88uAA9P0zhGxAiAiVkjaqdJKJI0DxqXZdyXNzyPYLtoReK3oIMpwXLXZo4vt2+vzG2jbr6Gwfl3U36LIPrBJvOYzzsgeSc19O9cEI+lB4GNlFl0aEfdUs4oyZVFrHBExEZiYYpoVERWPfxfFcdWmieNaU+ELTN37fLP066K27dfc+G3X2ibXBBMRR3ZxFcuAXUvmBwHL0/SrkgakvZcBwMoubsusHhZ18R9Ae33erFtp9p8pzwSGStpN0ubAycCUtGwKMDZNjwWq+XZo1uza6/Nm3UqRP1M+QdIy4GDgPknTUvkukqYCRMT7wHnANGAhcEdELEiruAI4StJisl/cXFHlpifW8WXUk+OqTbeLqw59vlPbbYCitu3X3OTbVkTNpzTMzMw61OyHyMzMrJtygjEzs1xsMgmmmYffkPSCpKckze3MTwHrGMeNklaW/sy2GYbkqRDXNyW9kt6zuZJGNzimXSX9XNLCNPzL+am84e9XI/t2UX2kqPdb0paSnpD0ZNruvzRiuyXb7yXpN5LubfB2N/qf1JltbxIJpmT4jc8Bw4BTJA0rNqqNHB4Rwwu+tuNm4Jg2Za1D8gwFHkrzjXYzG8cFcE16z4ZHxNQGx/Q+cHFE7AUcBJyb+lRD368C+vbNFNNHinq/3wWOiIj9gOHAMZIOasB2W51P9mOPVo3sX23/J9W87U0iwVAy/EZErANah9+wEhHxKPBGm+IxZEPxkJ6Pb2RMUDGuQkXEioiYk6bXkv0TGEjj36+G9u2i+khR73dkfpdm+6RH5L1dAEmDgGOB75UUF/l5rHnbm0qCKTf8xsCCYikngOmSZqfhP5rJBkPyABWH5CnAeZLmpcM2hY2mLWkIsD/wOI1/v5qhbzf0NTf6/U6HqeaSXcz9QEQ06u/8H8AlwAclZY16r8v9T6p525tKgqnLkDM5OiQiDiA7zHGupM8UHVA3cAPwCbLDFiuAq4sIQtK2wE+ACyJiTREhlClrpr5dV0W83xHxx4gYTjaqwkhJ++S9TUnHASsjYnbe26qgLv+TNpUE09TDb0TE8vS8Erib7LBHs3hV2VA8qImG5ImIV9MH/wPguxTwnknqQ/bP7taImJyKG/1+NUPfbshrLvr9joi3yEZtP6YB2z0E+AtJL5Ad9jxC0g8bsF2g4v+kmre9qSSYph1+Q9I2kvq2TgNHk903pFk05ZA8rR09OYEGv2eSBHwfWBgR3ylZ1Oj3qxn6du6vuaj3W1J/Sf3S9FbAkcAzeW83Iv4xIgZFxBCyv+nDEXFa3tuFdv8n1b7tiNgkHsBoYBHwHNnItoXHlOL6E+DJ9FhQZGzAbWSHm94j+2Z8JvBRsl+MLE7POzRJXD8AngLmpY4/oMExHUp2KGoeMDc9RhfxfjWybxfVR4p6v4F9gd+k7c4Hvp7KG/Z3Jrvv1b2N2m6l/0md2baHijEzs1xsKofIzMyswZxgzMwsF04wZmaWCycYMzPLhROMmZnlwgnGzMxy4QTTg6Uh7b8m6V8lHVmndf4qPQ+RdGo91mlWNGW3rb4rTQ9Xg2//0FM5wWwCIuLrEfFgndb1qTQ5BKgpwaSh5c2aTkQsj4gvptnhZBdxVk1S77oH1QM4wfQwki5NN596ENgjld0s6Ytp+gpJT6dRiK9KZTtLujvdVOlJSZ9qZ/2tQ5dfAXw63ZDowjTi7LclzUzr/kqqf5iyG0X9iOzKe7NOk/R/JD2Tbnh1W9pD/4Sk+9PIv7+QtGeqe7Ok6yT9StLS1s9AhfUOkTQ/Dbfzr8BJqW+flIZOuTH17d9IGpPafFnSnZJ+BkxvyBvQzTjr9iCSRpCNW7Q/2d92DjC7ZPkOZON27RkR0TrGEnAd8L8RcULay9i2is2NB74WEceldY8DVkfEn0naAvilpNYP3Uhgn4h4vssv0jZZklqAL7Bx/54InB0RiyUdCPwXcERqNoBsmJk9yYYUuqu9bUTEOklfB1oi4ry03X8nGwvsb9Jn5on0BQ7gYGDfiGiq+xU1CyeYnuXTwN0R8Q6ApLaDHq4B/gB8T9J9wL2p/AjgDMiGJgdWd2LbRwP7lnxL3B4YCqwDnnBysTo4FLgnIn4PkPYctgQ+BdyZjYcJwBYlbX4a2YjbT0vauZPbPZpsZOOvpfktgcFp+gEnl8qcYHqeioPLRcT7kkYCo8j2dM7jw296XSXgqxExbYNC6TDg7TptwzZt5e59sxnwVmT3aynn3Q7aV7vdL0TEsxsUZntL7tvt8DmYnuVR4ARJW6Xhtj9fulDZzZq2j+z+9ReQncyEbGTUc1KdXpK2q2Jba4G+JfPTgHOU3bMDSbunob7N6mUG8HlJW6a+fCzwDvC8pC9BNqy/pP26uJ1yffur6ZYBSNq/i+vfZDjB9CCR3bP8x2RDmf8E+EWbKn2BeyXNA/4XuDCVnw8cLukpsmPae1exuXnA++lHAReS3Tf8aWCOpPnAf+M9ZKujiJhJdh7lSWAyMIvscO5fAWdKah1efkwXN/VzYFjrSX7gMqAPMC/17cu6uP5NhofrN7NuQ9K2EfE7SVuT7bGPS1+srAn5G6aZdScTJQ0jO9E+ycmluXkPxjYiqfXOdW2NiojXGx2PWb1I+iTZ3VBLvRsRBxYRT0/nBGNmZrnwSX4zM8uFE4yZmeXCCcbMzHLhBGNmZrn4/y021HZPqXzrAAAAAElFTkSuQmCC\n",
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZgAAAEXCAYAAACQ3VJYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Il7ecAAAACXBIWXMAAAsTAAALEwEAmpwYAAAmkElEQVR4nO3de5gdVZnv8e+PJASEcOdgTAiJEi4RMEAbRAZUbnKAMYAoF9HgAK2MMA6oXA5zEAGPCM7o8MgAkVtAhlsGNCoSEi6DIGA6GEISJAkBJ4mBIAQIIuH2nj9qNVY6u7v37t61a3fn93me/XTVqlVV7969ut9dt7UUEZiZmdXbOmUHYGZm/ZMTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgmpSk6yRdKGlvSU8VsP3XJH2wh+vOlfTJ+kZkZv2NE0yTi4jfRMT2BWx3w4hY1MN1PxwR9/c2BknHS3qwt9sxawS319o5waxlJA0sO4Z66U/vxcrViLa0NrZXJ5gmIWlXSY9JWinpFmC9VP5JSUty9c6UtDTVe0rSfql8gKT/I+nptGympK3TspD0NUkLgAW5sm3T9HWS/kPSr9Ops4ckvV/SjyStkPQHSbvmYnhW0v5p+jxJt0q6Pu13rqSWXN2zcjHNk3R4Kt8RuALYM+3z5VS+cdrWC5L+KOlfJK2Tlh2fYvuhpBeB8wr6dViDSdpN0u9TO7lN0i2SLkzLDpU0S9LLkn4raZfces9K+qak2ZJeSeutl1ve3bpnSpoN/EXSQLfXOosIv0p+AesCfwROAwYBRwJvARcCnwSWpHrbA4uBD6T5kcCH0vS3gCdSHQEfATZPywKYBmwGrJ8r2zZNXwf8GdidLLHdCzwDfAkYkOK4Lxfvs8D+afo84A3g4FT3e8AjubqfAz5A9mXmKOAvwNC07HjgwQ6fxfXAz4Eh6f3NB07I1X8bOBUY2P5e/Orbr1z7/3pq/0cAb6Z2tyuwHNgjta8Jqf0NzrXF36U2thnwJPDVtKyadWcBW+f+Ltxe6/m7LTsAvwJgH+BPgHJlv2XNBLNt+oPZHxjUYRtPAeM72X4A+1YoyyeYn+SWnQo8mZvfGXg5N/8sqyeY6bllY4C/dvFeZ7XH2fEPNv0TeBMYkyv7CnB/rv7/lP378qu+r9T+l3Zo/w+m9n85cEGH+k8Bn0jTzwLH5ZZdDFyRpqtZ9x+6ic3ttRcvnyJrDh8AlkZqlckfO1aKiIXAP5P9U18u6WZJH0iLtwae7mIfi7uJ4fnc9F8rzG/YxbrP5aZfB9ZrP98s6Uu5UxQvAzsBW3SynS3IvsHm3/sfgWG5+e7eh/U9ldp/++95G+Ab7e0ntaGt0zrtOra/DWtYd7X25PZaX04wzWEZMEyScmUjKlWMiP+MiL8j++MJ4Ptp0WLgQ13so+HdZkvaBvgJcArZ6bpNgDlkp/AqxfRnslOD2+TKRpB9u23n7r/7n0rtf+v0czHw3YjYJPd6X0TcVMV2q1n3vfbk9lp/TjDN4WGyc7X/JGmQpCOAcR0rSdpe0r6SBpNd9/gr8G5afBVwgaTRyuwiafNGvYFObED2B/YCgKQvk30jbPc8MFzSugAR8Q5wK/BdSUPSH/zpwE8bGrU12sPAO8Ap6UL7eP7W/n8CfFXSHqldbyDpEElDqthureu6vdaZE0wTiIg3yS5sHg+8RHZx8fYKVQcDF5F9c3oO+F/A2WnZv5E19ruBV4GrgfWLjLs7ETEP+FeyfyDPk13LeShX5V5gLvCcpD+nslPJLqwuIjsP/5/ANY2K2Rov1/5PAF4GjgN+CayKiDbgJODHwApgIdnfSTXbrWldt9f60+qnPc3MyifpUbKL9deWHYv1nI9gzKx0kj6h7NmrgZImALsAd5Udl/VO6QlG0jWSlkua08lySbpU0sL0MNVuuWUTJC1IrwmNi9qs5yQdpOwh2YWSzqqwfHB6YHChpEcljSwhzEbbHnic7BTZN4AjI2JZqRFZr5V+ikzSPsBrwPURsVOF5QeTnec8mOyBqX+PiD0kbQa0AS1kF+ZmArtHxIqGBW9WI0kDyB7GOwBYAswAjknn/9vr/COwS0R8VdLRwOERcVQpAZv1QulHMBHxANmF7c6MJ0s+ERGPAJtIGgp8GpgWES+lpDINOKj4iM16ZRywMCIWpYvbN5O18bzxwKQ0PRnYr8MtvGZ9Ql/ofG0Yqz+stCSVdVa+BkmtQCvABhtssPsOO+xQTKS21ps5c+afI2LLLqpUard7dFYnIt6W9AqwOdndg+9xu7ZGqqJtr6EvJJhei4iJwESAlpaWaGtrKzki668krdEDQ1Hcrq2RetK2Sz9FVoWl/O2pXoDhqayzcrNmVk27fa9O6nJnY+DFhkRnVkd9IcFMAb6U7ib7GPBKurtkKnCgpE0lbQocmMrMmtkMYLSkUemJ8KPJ2njeFLKefyHrWfveKPtuHLMeKP0UmaSbyHoM3kLZuCffJutAjoi4AriT7A6yhWQd2X05LXtJ0gVkf7AA50dEVzcLmJUuXVM5hezL0ADgmoiYK+l8oC0ippD1wnCDpIVkN8AcXV7EZj1XeoKJiGO6WR7A1zpZdg3ulsH6mIi4k+yLU77s3Nz0G2Tjkpj1aX3hFJmZmfVBTjBmZlYIJxgzMyuEE4yZmRXCCcbMzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWiNITjKSDJD0laaGksyos/6GkWek1X9LLuWXv5JZNaWjgZmbWpYFl7lzSAOAy4ABgCTBD0pSImNdeJyJOy9U/Fdg1t4m/RsTYBoVrZmY1KPsIZhywMCIWRcSbwM3A+C7qHwPc1JDIzMysV8pOMMOAxbn5JalsDZK2AUYB9+aK15PUJukRSYcVFqWZmdWs1FNkNToamBwR7+TKtomIpZI+CNwr6YmIeLrjipJagVaAESNGNCZaM7O1XNlHMEuBrXPzw1NZJUfT4fRYRCxNPxcB97P69Zl8vYkR0RIRLVtuuWVvYzYzsyqUnWBmAKMljZK0LlkSWeNuMEk7AJsCD+fKNpU0OE1vAewFzOu4rpmZlaPUU2QR8bakU4CpwADgmoiYK+l8oC0i2pPN0cDNERG51XcErpT0LlmivCh/95mZmZWr9GswEXEncGeHsnM7zJ9XYb3fAjsXGpyZmfVY2afIzMysn3KCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVwgnGzMwK4QRj1iCSNpM0TdKC9HPTCnXGSnpY0lxJsyUdVUasZvXgBGPWOGcB90TEaOCeNN/R68CXIuLDwEHAjyRt0rgQzerHCcasccYDk9L0JOCwjhUiYn5ELEjTfwKWA+4C3PokJxizxtkqIpal6eeArbqqLGkcsC6wxhhHaXlrGnCv7YUXXqhvpGZ1UHpnl2b9zHaS5lQoPyc/ExEhKSrUA0DSUOAGYEJEvFupTkRMBCYCtLS0dLots7I4wZjV1/yIaKm0QNLzkoZGxLKUQJZ3Um8j4FfAORHxSIGxmhXKp8jMGmcKMCFNTwB+3rFCGnjvDuD6iJjcwNjM6s4JxqxxLgIOkLQA2D/NI6lF0lWpzueBfYDjJc1Kr7GlRGvWSz5FZtYgEfEisF+F8jbgxDT9U+CnDQ7NrBA+gjEzs0I4wZiZWSFKTzCSDpL0lKSFktZ4slnS8ZJeyJ2PPjG3bELqdmOBpAkd1zUzs/KUeg1G0gDgMuAAYAkwQ9KUiJjXoeotEXFKh3U3A74NtAABzEzrrmhA6GZm1o2yj2DGAQsjYlFEvAncTNadRjU+DUyLiJdSUplG1neTmZk1gbITzDBgcW5+SSrr6LOpZ9nJkraucV13qWFmVoKyE0w1fgGMjIhdyI5SJnVTfw0RMTEiWiKiZcst3W+gmVkjlJ1glgJb5+aHp7L3RMSLEbEqzV4F7F7tumZmVp6yE8wMYLSkUamLjKPJutN4T+qzqd1ngCfT9FTgQEmbpoGbDkxlZmbWBEq9iywi3pZ0ClliGABcExFzJZ0PtEXEFOCfJH0GeBt4CTg+rfuSpAvIkhTA+RHxUsPfhJmZVVR6VzERcSdwZ4eyc3PTZwNnd7LuNcA1hQZoZmY9UvYpMjMz66ecYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVwgnGzMwK4QRjZmaFcIIxM7NCOMGYmVkhnGDMzKwQpScYSQdJekrSQklnVVh+uqR5kmZLukfSNrll70ialV5TGhu5mZl1ZWCZO5c0ALgMOABYAsyQNCUi5uWq/R5oiYjXJZ0MXAwclZb9NSLGNjJmMzOrTtlHMOOAhRGxKCLeBG4GxucrRMR9EfF6mn0EGN7gGM3MrAfKTjDDgMW5+SWprDMnAL/Oza8nqU3SI5IO62wlSa2pXtsLL7zQq4DNzKw6pZ4iq4Wk44AW4BO54m0iYqmkDwL3SnoiIp7uuG5ETAQmArS0tERDAjYzW8uVfQSzFNg6Nz88la1G0v7AOcBnImJVe3lELE0/FwH3A7sWGaxZb0jaTNI0SQvSz027qLuRpCWSftzIGM3qqewEMwMYLWmUpHWBo4HV7gaTtCtwJVlyWZ4r31TS4DS9BbAXkL85wKzZnAXcExGjgXvSfGcuAB5oSFRmBSk1wUTE28ApwFTgSeDWiJgr6XxJn0nVLgE2BG7rcDvyjkCbpMeB+4CLOtx9ZtZsxgOT0vQk4LBKlSTtDmwF3N2YsMyKUfo1mIi4E7izQ9m5uen9O1nvt8DOxUZnVldbRcSyNP0cWRJZjaR1gH8FjgMqtv1c3VagFWDEiBH1jdSsDkpPMGb9zHaS5lQoPyc/ExEhqdINJ/8I3BkRSyR1uSPfvGLNzgnGrL7mR0RLpQWSnpc0NCKWSRoKLK9QbU9gb0n/SHZqeF1Jr0VEV9drzJpS1ddgJH093dkiSVdLekzSgUUGZ9bPTAEmpOkJwM87VoiIL0TEiIgYCXwTuN7JxfqqWi7y/0NEvAocCGwKfBG4qJCozJrAbbfdxsqVKwG48MILOeKII3jsscd6s8mLgAMkLSC7vnIRgKQWSVf1Nl6zZlNLgmk/IXwwcENEzM2VmfU7F1xwAUOGDOHBBx9k+vTpnHDCCZx88sk93l5EvBgR+0XE6IjYPyJeSuVtEXFihfrXRcQpvXgLZqWqJcHMlHQ3WYKZKmkI8G4xYZmVb8CAAQD86le/orW1lUMOOYQ333yz5KjM+o5aEswJZA+GfTR1PjkI+HIhUZk1gWHDhvGVr3yFW265hYMPPphVq1bx7rv+TmVWrVoSzJ7AUxHxcuoX7F+AV4oJy6x8t956K5/+9KeZOnUqm2yyCS+99BKXXHJJ2WGZ9Rm1JJjLgdclfQT4BvA0cH0hUZk1gWXLlnHIIYcwevRo7r//fm677TbGjRtXdlhmfUYtCebtiAiy7i5+HBGXAUOKCcusfJ/97GcZMGAACxcupLW1lcWLF3PssceWHZZZn1FLglkp6Wyy25N/lbq0GFRMWGblW2eddRg4cCC33347p556KpdccgnLli3rfkUzA2pLMEcBq8ieh3mOrGt9n5C2fmvQoEHcdNNNXH/99Rx66KEAvPXWWyVHZdZ3VJ1gUlK5EdhY0qHAGxHhazDWb1177bU8/PDDnHPOOYwaNYpnnnmGL37xi2WHZdZn1NJVzOeB3wGfAz4PPCrpyKICMyvbmDFj+MEPfsDOO+/MnDlzGD58OGeeeWbZYZn1GbV0dnkO2TMwywEkbQlMByYXEZhZ2e6//34mTJjAyJEjiQgWL17MpEmT2GeffcoOzaxPqCXBrJMfURJ4kfJHxDQrzDe+8Q3uvvtutt9+ewDmz5/PMcccw8yZM0uOzKxvqCXB3CVpKnBTmj+KDgOFmfUnb7311nvJBWC77bbzRX6zGlSdYCLiW5I+C+yViiZGxB3FhGVWvpaWFk488USOO+44AG688UZaWioO9WJmFdR0iisi/isiTk+vuiQXSQdJekrSQklrjHshabCkW9LyRyWNzC07O5U/JenT9YjHrN3ll1/OmDFjuPTSS7n00ksZM2YMl19+edlhmfUZ3R7BSFoJVBqOVWQjv27U051LGgBcBhwALAFmSJoSEfNy1U4AVkTEtpKOBr4PHCVpDHA08GHgA8B0SdtFxDvd7ji6GF22m2Fqbe0xePBgTj/9dE4//fSyQzHrk7pNMBFRVXcwkjaNiBU17n8csDAiFqVt3EzWFU0+wYwHzkvTk4EfKxusfDxwc0SsAp6RtDBt7+Eu9zhzJqxT0L0J3SWn/PKOdWtZtzf77e22myXuWtetIe6dX3mly4GOZq9YAUPcS5JZd2q5yN+de4DdalxnGLA4N78E2KOzOhHxtqRXgM1T+SMd1h1WaSeSWoFWgB033hhOO61yNF0d2XS1rNblHev2Ztv1jKu7Zc0Sd63r1hJ3BL989dWutz+wnn82Zv1XPf9SmvbcUkRMBCYCtLS0BN/+dskRWTPbpsp6e+65Jw8/3PUBs9narJ7nirr5WlnRUmDr3PzwVFaxjqSBwMZkz+BUs65ZYd54442yQzBramU/KDkDGC1plKR1yS7aT+lQZwowIU0fCdybhg2YAhyd7jIbBYwm68rGrCHkG0LMulTqKbJ0TeUUYCowALgmIuZKOh9oi4gpwNXADeki/ktkSYhU71ayGwLeBr5W1R1kZmbWEFUnGEkfA+ZGxMo0vxGwY0Q8mqrs15MAIuJOOvQIEBHn5qbfIOtgs9K63wW+25P9mvVWdHezgdlartYhk1/Lzb+WygCIiJfqFZRZX3DDDTeUHYJZU6slwShyX9ki4l3qe4rNrKncfvvtjB49mo033piNNtqIIUOGsNFGf3uueKeddioxOrPmV0uCWSTpnyQNSq+vA4uKCsysbGeccQZTpkzhlVde4dVXX2XlypW82t0zMmb2nloSzFeBj5PdCtz+QGRrEUGZNYOtttqKHXfcsewwzPqsWnpTXk66g8tsbdDS0sJRRx3FYYcdxuDBg98rP+KII0qMyqzvqOUusouBC4G/AncBuwCnRcRPC4rNrFSvvvoq73vf+7j77rvfK5PkBGNWpVou0h8YEWdIOhx4FjgCeABwgrF+6dprry07BLM+rZZrMO3J6BDgtoh4pYB4zJrG/Pnz2W+//d67W2z27NlceOGFJUdl1nfUkmB+KekPwO7APZK2BNwZk/VbJ510Et/73vcYNGgQALvssgs333xzyVGZ9R1VJ5iIOIvsLrKWiHgL+AvZmCxm/dLrr7/OuHHjVisb6K76zapWzYiW+0bEvZKOyJXlq9xeRGBmZdtiiy14+umn32vvkydPZujQoSVHZdZ3VPN1bB/gXuDvybrkV4efTjDWL1122WW0trbyhz/8gWHDhjFq1ChuvPHGssMy6zOqSTArJZ0OzOFviQV6Nv6LWZ/xs5/9jIMPPphPfepTvPvuu2ywwQZMnz6d3XffnbFjx5YdnlnTq+YazIbAELKL+ycDQ4EPkD3ZX+sQyWZ9RltbG1dccQUrVqzg5Zdf5sorr+Suu+7ipJNO4uKLL655e5I2kzRN0oL0c9NO6o2QdLekJyXNkzSyt+/FrAzdHsFExHcAJD0A7Jbrrv884FeFRmdWoiVLlvDYY4+x4YYbAvCd73yHQw45hAceeIDdd9+dM844o9ZNngXcExEXSTorzZ9Zod71wHcjYpqkDYF3e/E2zEpTy23KWwFv5ubfTGVm/dLy5ctX6yJm0KBBPP/886y//vqrlddgPDApTU8CDutYQdIYYGBETAOIiNci4vWe7MysbLXcc3k98DtJd6T5w4Dr6h2QWbP4whe+wB577MH48dnd+L/4xS849thj+ctf/sKYMWN6ssmtImJZmn6Oyl/QtgNelnQ7MAqYDpxVabRWSa2kDmdHjBjRk3jMCqVaRuWTtBuwd5p9ICJ+X0hUBWppaYm2trayw7A+oq2tjYceegiAvfbai5aWli7rS1oJ/E+FRecAkyJik1zdFRGx2nUYSUeSDRO+a9rOLcCdEXF1V/t1u7aiSZoZEV3/AXRQ01NjEfEY8FhNUXVC0mZkfzwjyfo2+3xErOhQZyzZqJkbAe+QnZe+JS27DvgE0N5lzfERMasesZm1a2lp6TapdDC/sz9CSc9LGhoRyyQNBZZXqLYEmBURi9I6PwM+RpZ0zPqUWq7B1Fv7Bc/RwD1pvqPXgS9FxIeBg4AfSdokt/xbETE2vWYVHbBZL00BJqTpCcDPK9SZAWySumIC2BeY14DYzOquzATT7QXPiJgfEQvS9J/IvvFt2bGeWR9xEXCApAXA/mkeSS2SrgJI11q+Sdbf3xNkz539pKR4zXqlzI6Vqrng+R5J44B1gadzxd+VdC7pCCgiVnWyri+GWuki4kVgvwrlbcCJuflpZOMtmfVphR7BSJouaU6F12qdZEZ2p0Gndxuk89U3AF+OiPZnAs4GdgA+CmxG5ecJ2rc/MSJaIqJlyy19AGRm1giFHsFExP6dLavygieSNiJ7oPOciHgkt+32o59Vkq4lO61gZmZNosxrMN1e8JS0LnAHcH1ETO6wbGj6KbLrN3OKDNbMzGpTZoLp9oIn8Hmy3pyPlzQrvcamZTemi6BPAFsAHmrQzKyJlHaRv5oLnhHxU+Cnnay/b6EBmplZr5R5BGNmZv2YE4yZmRXCCcbMzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVorQEI2kzSdMkLUg/N+2k3juSZqXXlFz5KEmPSloo6RZJ6zYuejMz606ZRzBnAfdExGjgnjRfyV8jYmx6fSZX/n3ghxGxLbACOKHYcM3MrBZlJpjxwKQ0PQk4rNoVJQnYF5jck/XNzKx4ZSaYrSJiWZp+Dtiqk3rrSWqT9Iikw1LZ5sDLEfF2ml8CDCsuVDMzq9XAIjcuaTrw/gqLzsnPRERIik42s01ELJX0QeBeSU8Ar9QYRyvQCjBixIhaVjUzsx4qNMFExP6dLZP0vKShEbFM0lBgeSfbWJp+LpJ0P7Ar8F/AJpIGpqOY4cDSLuKYCEwEaGlp6SyRmZlZHZV5imwKMCFNTwB+3rGCpE0lDU7TWwB7AfMiIoD7gCO7Wt/MzMpTZoK5CDhA0gJg/zSPpBZJV6U6OwJtkh4nSygXRcS8tOxM4HRJC8muyVzd0OjNzKxLhZ4i60pEvAjsV6G8DTgxTf8W2LmT9RcB44qM0czMes5P8puZWSGcYMzMrBBOMGYNUkP3SBdLmivpSUmXpgeLzfocJxizxum2eyRJHye7W3IXYCfgo8AnGhmkWb04wZg1TjXdIwWwHrAuMBgYBDzfiODM6s0Jxqxxuu0eKSIeJrslf1l6TY2IJyttTFJr6kap7YUXXigqZrMeK+02ZbN+ajtJcyqUV9U9kqRtyZ7/Gp6KpknaOyJ+07Gue6iwZucEY1Zf8yOipdKCKrtHOhx4JCJeS+v8GtgTWCPBmDU7nyIza5xuu0cC/gf4hKSBkgaRXeCveIrMrNk5wZg1TjXdI00GngaeAB4HHo+IX5QRrFlv+RSZWYNU2T3SO8BXGhyaWSF8BGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFaK0BFPN2BiSPiVpVu71hqTD0rLrJD2TWza20e/BzMw6V+YRTLdjY0TEfRExNiLGAvsCrwN356p8q315RMxqQMxmZlalMhNMNWNj5B0J/DoiXi8yKDMzq48yE0y3Y2N0cDRwU4ey70qaLemHkgbXPUIzM+uxQvsikzQdeH+FRVWNjZHbzlBgZ2BqrvhsssS0LtmYGGcC53eyfivQCjBixIga3oGZmfVUoQkmIvbvbFmVY2O0+zxwR0S8ldt2+9HPKknXAt/sIg4PzGRm1mBlniKrZmyMdsfQ4fRYSkpIEtn1m0qjCJqZWUnKTDDVjI2BpJHA1sB/d1j/RklPkI2bsQVwYSOCNjOz6pQ2Hkw1Y2Ok+WeBYRXq7VtkfGZm1jt+kt/MzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVwgnGzMwK4QRjZmaFcIIxM7NClJZgJH1O0lxJ70pq6aLeQZKekrRQ0lm58lGSHk3lt0hatzGRm/VMb9u8WV8zsMR9zwGOAK7srIKkAcBlwAHAEmCGpCkRMQ/4PvDDiLhZ0hXACcDlxYdt1mO9bfOdWrkS7r03v53Ott99eW/W7U152ftu1nXrsX53dTorHzUKNtig++12prQEExFPAqjrT2UcsDAiFqW6NwPjJT0J7Ascm+pNAs7DCcaaWG/aPNBlgpk/H/bbr06BmiUPPAB7793z9cs8gqnGMGBxbn4JsAewOfByRLydKx/W2UYktQKtaXaVpDkFxNpbWwB/LjuIChxXbbbv5fqdtfk1dGzXUFq7Lut3UWYbWCve8z77rDZbc9suNMFImg68v8KicyLi50XuOy8iJgITU0xtEdHp+e+yOK7aNHFcr3byBabubb5Z2nVZ+/Z7bvy+a12n0AQTEfv3chNLga1z88NT2YvAJpIGpqOY9nKzss3v5T+Aztq8WZ/T7LcpzwBGpzvG1gWOBqZERAD3AUemehOAhh0RmRWoYpsvOSazHinzNuXDJS0B9gR+JWlqKv+ApDsB0tHJKcBU4Eng1oiYmzZxJnC6pIVk12SurnLXE+v4NurJcdWmz8VVhzbfo/02QFn79ntu8n0rOxgwMzOrr2Y/RWZmZn2UE4yZmRVirUkwzdr9hqRnJT0haVZPbgOscyzXSFqev81W0maSpklakH5u2iRxnSdpafrcZkk6uMExbS3pPknzUvcvX0/lDf+8Gtm2y2ojZX3ektaT9DtJj6f9fieVN6SrKkkDJP1e0i8bvN81/i/15LNeKxKM/tb9xv8GxgDHSBpTblSr+VREjG2C5zquAw7qUHYWcE9EjAbuSfONdh1rxgVZV0Fj0+vOBsf0NvCNiBgDfAz4WmpTDf28Smjb11FOGynr814F7BsRHwHGAgdJ+hh/66pqW2AFWVdVRfg62c0e7Rq1X1jz/1LNn/VakWDIdb8REW8C7d1vWE5EPAC81KF4PFlXPKSfhzUyJug0rlJFxLKIeCxNryT7JzCMxn9eDW3bZbWRsj7vyLyWZgelV5B1VTW5qP0CSBoOHAJclebViP12oebPem1JMJW63+i0a5kGC+BuSTOVdf3RbLaKiGVp+jlgqzKD6eAUSbPTaZuGn7prJ2kksCvwKI3/vJqhbTf0PTf6806nqWYBy4FpwNPU0FVVL/wIOAN4N83X1EVWL1X6v1TzZ722JJhm9ncRsRvZKY6vSdqnuxXKkh5wbZb72i8HPkR22mIZ8K9lBCFpQ+C/gH+OiFfzy5rs82qIot9zGZ93RLwTEWPJelUYB+xQ7310JOlQYHlEzCx6X53o8v9StZ/12pJgmrb7jYhYmn4uB+4ga8DN5HlJQwHSz+UlxwNARDyf/vDfBX5CCZ+bpEFk/+xujIjbU3GjP69maNsNec9lf94R8TJZDyJ7krqqSouK+Mz3Aj4j6Vmy0577Av/egP0Cnf5fqvmzXlsSTFN2vyFpA0lD2qeBA8nGDGkmU8i64oEm6pKnvaEnh9Pgzy2dD78aeDIi/i23qNGfVzO07cLfc1mft6QtJW2SptcnG6fnSQruqioizo6I4RExkux3em9EfKHo/UKX/5dq/6wjYq14AQcD88nOn55Tdjwppg8Cj6fX3LLjAm4iO930Ftn53RPIzvveAywApgObNUlcNwBPALNTwx/a4Jj+juwUwWxgVnodXMbn1ci2XVYbKevzBnYBfp/2Owc4N5V/EPgdsBC4DRhc4Gf+SeCXjdpvZ/+XevJZu6sYMzMrxNpyiszMzBrMCcbMzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMP1Y6tL+m5LOl7R/nbb52/RzpKRj67FNs7IpG7Z6cpoeqwYP/9BfOcGsBSLi3IiYXqdtfTxNjgRqSjC5Li7MmkpE/Cki2p+QH0v2EGfV3LYrc4LpZySdI2m+pAeB7VPZdZKOTNMXpUGbZkv6QSrbStIdaVClxyV9vIvtt3ddfhGwdxqQ6LTU4+wlkmakbX8l1f+kpN9ImgLMK/K9W/8n6f8qG1ztQUk3pSP0D0m6K/X8+xtJO6S610m6VNJvJS1q/xvoZLsjJc1J3e2cDxyV2vZRqeuUa5QNPPZ7SePTOsdLmiLpXrIn3K0DZ91+RNLuZP0WjSX73T4GzMwt35ys364dIiLa+1gCLgX+OyIOVzaA1YZV7O4s4JsRcWjadivwSkR8VNJg4CFJd6e6uwE7RcQzvX2PtvaS9FHgs8BHyMZlaW/fE4GvRsQCSXsA/0HWOSTAULJuZnYg61Jocsft5kXEm5LOBVoi4pS03/9H1hfYP6S/md9Jaj8jsBuwS0Q01XhFzcIJpn/ZG7gjIl4HSEcNea8AbwBXKxuC9ZepfF/gS5B1TZ7q1epAYJfct8SNgdHAm8DvnFysDvYCfh4RbwBvSPoFsB7wceC2rD9MAAbn1vlZZD1uz5PU07FiDiTr2fibaX49YESanubk0jknmLVIRLwtaRywH1mPrKfwt296vSXg1IiYulqh9EngL3Xah1lH65ANwjW2k+WrctPqpE53BHw2Ip5arTA7WnLb7oKvwfQvDwCHSVo/dbf99/mFygZr2jiy8etPIzvVANn545NTnQGSNq5iXyuBIbn5qcDJacwOJG2Xuvo2q5eHgL+XtF5qy4cCrwPPSPocZN36S/pIVxupQqW2fWoaMgBJu/Zy+2sNJ5h+JLIxy28h62b712RjheQNAX4paTbwIHB6Kv868ClJT5Cd0x5Txe5mA++kmwJOIxs3fB7wmKQ5wJX4CNnqKCJmkF1HmU3Wvp8gO537BeAESe3dy4/v5a7uA8a0X+QHLiC75jNb0tw0b1Vwd/1m1mdI2jAiXpP0PrIj9tb0xcqakL9hmllfMlHSGLIL7ZOcXJqbj2BsDel25kr39e8XES82Oh6zepG0M9loqHmrImKPMuLp75xgzMysEL7Ib2ZmhXCCMTOzQjjBmJlZIZxgzMysEP8fpQayYYKX+OAAAAAASUVORK5CYII=\n",
       "text/plain": [
        "<Figure size 432x288 with 2 Axes>"
       ]
@@ -429,7 +553,8 @@
     "        axes[0].plot(disc_x_data, disc_data, color='red')\n",
     "        axes[1].plot(gen_x_data, gen_data, color='blue')\n",
     "        camera.snap()\n",
-    "    animation = camera.animate(interval=600, repeat=True, repeat_delay=800)\n",
+    "    animation = camera.animate(interval=600, \n",
+    "                               repeat=True, repeat_delay=800)\n",
     "    animation.save(\"./figures/loss.gif\")\n",
     "draw_pic(loss_history)\n",
     "clear_output()"
@@ -439,9 +564,7 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "这是我们所绘制的loss曲线的变化过程：\n",
-    "\n",
-    "![needed_rerun_after_drawing](./figures/loss.gif)"
+    "![QGAN-fig-loss](figures/loss.gif)"
    ]
   },
   {
@@ -455,14 +578,18 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 参考文献\n",
-    "\n",
-    "\n",
-    "[1] [Goodfellow, I. J. et al. Generative Adversarial Nets. Proc. 27th Int. Conf. Neural Inf. Process. Syst. (2014).](https://papers.nips.cc/paper/5423-generative-adversarial-nets)\n",
+    "## 参考文献"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "[1] Goodfellow, I. J. et al. Generative Adversarial Nets. [Proc. 27th Int. Conf. Neural Inf. Process. Syst. (2014).](https://papers.nips.cc/paper/5423-generative-adversarial-nets)\n",
     "\n",
-    "[2] [Lloyd, S. & Weedbrook, C. Quantum Generative Adversarial Learning. Phys. Rev. Lett. 121, 040502 (2018).](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.040502)\n",
+    "[2] Lloyd, S. & Weedbrook, C. Quantum Generative Adversarial Learning. [Phys. Rev. Lett. 121, 040502 (2018).](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.040502)\n",
     "\n",
-    "[3] [Benedetti, M., Grant, E., Wossnig, L. & Severini, S. Adversarial quantum circuit learning for pure state approximation. New J. Phys. 21, (2019).](https://iopscience.iop.org/article/10.1088/1367-2630/ab14b5)\n"
+    "[3] Benedetti, M., Grant, E., Wossnig, L. & Severini, S. Adversarial quantum circuit learning for pure state approximation. [New J. Phys. 21, (2019).](https://iopscience.iop.org/article/10.1088/1367-2630/ab14b5)"
    ]
   }
  ],
@@ -482,7 +609,20 @@
    "name": "python",
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
-   "version": "3.7.7"
+   "version": "3.8.5"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
   }
  },
  "nbformat": 4,

tutorial/Q-GAN/QGAN_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Quantum Generative Adversarial Network"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Classical Generative Adversarial Network"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Introduction to Generative Adversarial Network"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Generative Adversarial Network (GAN) is a generative model, which is a breakthrough in deep learning in recent years [1]. It contains two parts: the generator $G$ and the discriminator $D$. The generator accepts a random noise signal and uses it as input to generate the data we expect. The discriminator evaluates the received data $x$ and outputs a probability $P(x)$ that the data $x$ is real."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Nash Equilibrium"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Here we use the idea of Nash equilibrium to discuss the convergence problem of GAN.\n",
+    "\n",
+    "Nash equilibrium refers to a non-cooperative game involving two or more participants, assuming that each participant knows other participants' equilibrium strategies. No participant can change one's strategy to benefit. In the game theory, if each participant chooses his strategy, and no player can benefit by changing the strategy while other participants remain the same, then the current set of strategy choices and their corresponding results constitute Nash Equilibrium.\n",
+    "\n",
+    "We can regard the training process of GAN as a game process between generator and discriminator. No matter what the generator's strategy is, the best strategy of the discriminator is to try to distinguish the real data and the generated data. And regardless of the strategy of the discriminator, the best strategy for the generator is to make the discriminator unable to distinguish. This game is a zero-sum game, which is one of non-cooperative game. That is, one party gains while the other party must lose. Therefore, there exists the Nash equilibrium strategy in the game between the generator and the discriminator. When there are enough samples of real data and the learning ability of both parties is strong enough, a Nash equilibrium point will eventually be reached. **The generator has the ability to generate real data, and the discriminator can no longer distinguish between generated data and real data.** \n",
+    "\n",
+    "GAN adopts the idea of Nash equilibrium. In GAN, the generator and the discriminator are playing a non-cooperative game. No matter what strategies the generator adopts, the best strategy of the discriminator is to discriminate as much as possible; and no matter what strategies the discriminator adopts, the best strategy of the generator is to make the discriminator unable to discriminate as much as possible. Therefore, the two parties' strategic combination in the game and the corresponding results constitute the Nash equilibrium. **When the Nash equilibrium is reached, the generator can to generate real data, and the discriminator cannot distinguish between the generated data and the real data**."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Optimization goal"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "In GAN, we want to get an excellent generator (but only an excellent discriminator can accurately determine whether the generator is excellent). Our training's ideal result is that the discriminator cannot identify whether the data comes from real data or generated data.\n",
+    "\n",
+    "Therefore, our objective function is as follows:\n",
+    "\n",
+    "$$\n",
+    "\\min_{G}\\max_{D} V(G,D)= \\min_{G}\\max_{D}\\mathbb{E}_{x\\sim P_{data}}[\\log D(x)] +\\mathbb{E}_{z\\sim P_{z}}[\\log(1-D(G(z)))]. \\tag{1}\n",
+    "$$\n",
+    "\n",
+    "Here, $G$ represents the parameters of the generator and $D$ represents the parameters of the discriminator. In the actual process, the alternate training method is usually adopted; that is, first fix $G$, train $D$, then fix $D$, train $G$, and repeat. When the two's performance is sufficient, the model will converge, and the two will reach the Nash equilibrium."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Advantages"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "- Compared with other generative models, GAN generates better results.\n",
+    "- Theoretically, as long as it is a differentiable function, it can be used to build generators and discriminators, so it can be combined with deep neural networks to make deep generative models.\n",
+    "- Compared with other generative models, GAN does not rely on prior assumptions, and we do not need to assume the probability distribution and law of the data in advance.\n",
+    "- The form of data generated by GAN is also very simple, just forward propagation through the generator."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Disadvantages"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "- GAN does not require pre-modeling. Too much freedom makes training difficult to converge and unstable.\n",
+    "- GAN has a vanishing gradient problem. In this case, there is no loss in the training of the discriminator, so there is no adequate gradient information to pass back to the generator to optimize itself.\n",
+    "- There may be a problem of model collapse in the learning process of GAN. The generator degenerates, always generating the same sample points, and cannot continue learning. The discriminator also points to similar sample points in similar directions, and the model parameters are no longer updated, but the actual effect is feeble."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Quantum Generative Adversarial Network"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "The quantum generative adversarial network is similar to the classical one, except that it is no longer used to generate classical data but generate quantum states [2-3]. In practice, if we have a quantum state, it will collapse to a certain eigenstate after observation and cannot be restored to the previous quantum state. Therefore, if we have a method that generates many identical (or similar) quantum states based on the existing target quantum state, it will be very convenient for our experiments.\n",
+    "\n",
+    "Assuming that our existing target quantum states all come from a mixed state, they belong to the same ensemble, and their density operator is $\\rho$. Then we need to have a generator $G$ whose input is noise data, denoted by the ensemble $\\rho_{z}=\\sum_{i}p_{i}|z_{i}\\rangle\\langle z_ {i}|$. Therefore, we take out a random noise sample $|z_{i}\\rangle$ every time and get the generated quantum state $|x\\rangle=G|z_{i}\\rangle$ after passing through the generator. We expect the generated $| x\\rangle$ that is close to the target quantum state $\\rho$.\n",
+    "\n",
+    "It is worth noting that for the ensemble of the target state and the ensemble of the noise data mentioned above, we think that there exists a physical device that can generate a quantum state from the ensemble. According to quantum physics, We can get a genuinely random quantum state every time. However, in computer programs, we need to simulate this process.\n",
+    "\n",
+    "We expect the discriminator to judge whether the quantum state we input is an existing target state or a generated quantum state. This process needs to be given by measurement.\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## A simple example"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Problem Description"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "For simplicity, we assume that the existing target quantum state is a pure state, and the input state for the generator is $|0\\rangle$.\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "The circuit to prepare the existing target quantum state:\n",
+    "![QGAN-fig-target_state](figures/QGAN-fig-target_state.png)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "The circuit of the generator is:\n",
+    "![QGAN-fig-generator](figures/QGAN-fig-generator.png)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "The circuit of the discriminator is:\n",
+    "![QGAN-fig-discriminator](figures/QGAN-fig-discriminator.png)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "By measuring the quantum state output by the discriminator, we can get the probability of judging the target state as the target state $P_{T}$ and the probability of judging the generated state as the target state $P_{G}$."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Specific process"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Assuming that the existing target quantum state is $|\\psi\\rangle$, the quantum state generated by the generator is $|x\\rangle=G|00\\rangle$ (the generator uses a two-qubit circuit, of which the 0th qubit is a generated quantum state).\n",
+    "\n",
+    "The discriminator discriminates the data and obtains the quantum state $|\\phi\\rangle$ when the input is the target state, $|\\phi\\rangle=D(|\\psi\\rangle\\otimes |00\\rangle)$; When the input is generated state, $|\\phi\\rangle=D(G\\otimes I)|000\\rangle$.\n",
+    "\n",
+    "For the quantum state obtained by the discriminator, we also need to use the Pauli Z gate to measure the third qubit so as to obtain the judgment result of the input quantum state by the discriminator (that is, the probability that the discriminator thinks the input is the target state). First there is $M_{z}=I\\otimes I\\otimes\\sigma_{z}$, and the measurement result is $\\text{disc_output}=\\langle\\phi|M_{z}|\\phi\\rangle$, so the probability of the measurement that the result is the target state is $P=(\\text{disc_output}+1)/2$.\n",
+    "\n",
+    "We define the loss function of the discriminator as $\\mathcal{L}_{D}=P_{G}(\\text{gen_theta}, \\text{disc_phi})-P_{T}(\\text{disc_phi})$, The loss function of the generator is $\\mathcal{L}_{G}=-P_{G}(\\text{gen_theta}, \\text{disc_phi})$. Here, $P_{G}$ and $P_{T}$ are the expressions of $P=(\\text{disc_output}+1)/2$, when the input quantum state is the generated state and the target state, respectively. gen_theta and disc_phi are the parameters of the generator and discriminator circuits.\n",
+    "\n",
+    "So we only need to optimize the objective function $\\min_{\\text{disc_phi}}\\mathcal{L}_{D}$ and $\\min_{\\text{gen_theta}}\\mathcal{L}_{G}$ respectively. The discriminator and generator can be alternately trained."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Paddle Quantum Implementation"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "First import the relevant packages."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:49:41.308412Z",
+     "start_time": "2021-01-09T10:49:38.115680Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import numpy as np\n",
+    "import paddle\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import partial_trace, dagger, state_fidelity\n",
+    "from paddle import complex\n",
+    "from progressbar import *"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Then define our network model QGAN."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:49:43.091496Z",
+     "start_time": "2021-01-09T10:49:43.060879Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class QGAN(fluid.dygraph.Layer):\n",
+    "    def __init__(self):\n",
+    "        super(QGAN, self).__init__()\n",
+    "        \n",
+    "        # The angle used to prepare the target quantum state\n",
+    "        target_omega_0 = 0.9 * np.pi\n",
+    "        target_omega_1 = 0.2 * np.pi\n",
+    "        self.target_omega = fluid.dygraph.to_variable(\n",
+    "        np.array([target_omega_0, target_omega_1], np.float64))\n",
+    "        \n",
+    "        # Generator and discriminator circuit parameters\n",
+    "        self.gen_theta = self.create_parameter([9], \n",
+    "        dtype=\"float64\", attr=fluid.initializer.Uniform(\n",
+    "                            low=0.0, high=np.pi, seed=7))\n",
+    "        self.disc_phi = self.create_parameter([9], \n",
+    "        dtype=\"float64\", attr=fluid.initializer.Uniform(\n",
+    "                            low=0.0, high=np.pi, seed=8))\n",
+    "        \n",
+    "        # Prepare target quantum state\n",
+    "        cir = UAnsatz(3)\n",
+    "        cir.ry(self.target_omega[0], 0)\n",
+    "        cir.rz(self.target_omega[1], 0)\n",
+    "        self.target_state = cir.run_state_vector()\n",
+    "\n",
+    "    def generator(self, theta):\n",
+    "        \"\"\"\n",
+    "        Generator quantum circuit\n",
+    "        \"\"\"\n",
+    "        cir = UAnsatz(3)\n",
+    "        cir.u3(*theta[:3], 0)\n",
+    "        cir.u3(*theta[3:6], 1)\n",
+    "        cir.cnot([0, 1])\n",
+    "        cir.u3(*theta[6:], 0)\n",
+    "\n",
+    "        return cir\n",
+    "\n",
+    "    def discriminator(self, phi):\n",
+    "        \"\"\"\n",
+    "        Quantum circuit of the discriminator\n",
+    "        \"\"\"\n",
+    "        cir = UAnsatz(3)\n",
+    "        cir.u3(*phi[:3], 0)\n",
+    "        cir.u3(*phi[3:6], 2)\n",
+    "        cir.cnot([0, 2])\n",
+    "        cir.u3(*phi[6:], 0)\n",
+    "\n",
+    "        return cir\n",
+    "\n",
+    "    def disc_target_as_target(self):\n",
+    "         \"\"\"\n",
+    "         The probability that the discriminator judges the target state as the target state\n",
+    "         \"\"\"\n",
+    "         # Discriminator circuit\n",
+    "         cir = self.discriminator(self.disc_phi)\n",
+    "         cir.run_state_vector(self.target_state)\n",
+    "        \n",
+    "         # The judgment result of the discriminator on the target state\n",
+    "         target_disc_output = cir.expecval([[1.0,'z2']])\n",
+    "         prob_as_target = (target_disc_output + 1) / 2\n",
+    "\n",
+    "         return prob_as_target\n",
+    "\n",
+    "    def disc_gen_as_target(self):\n",
+    "         \"\"\"\n",
+    "         The probability that the discriminator judges the generated state as the target state\n",
+    "         \"\"\"\n",
+    "         # Get the quantum state generated by the generator\n",
+    "         gen_state = self.generator(\n",
+    "                     self.gen_theta).run_state_vector()\n",
+    "         # Discriminator circuit\n",
+    "         cir = self.discriminator(self.disc_phi)\n",
+    "         cir.run_state_vector(gen_state)\n",
+    "         # The judgment result of the discriminator on the generated state\n",
+    "         gen_disc_output = cir.expecval([[1.0,'z2']])\n",
+    "         prob_as_target = (gen_disc_output + 1) / 2\n",
+    "        \n",
+    "         return prob_as_target\n",
+    "\n",
+    "    def forward(self, model_name):\n",
+    "         if model_name =='gen':\n",
+    "             # Calculate the loss function of the generator, the interval of the loss value is [-1, 0],\n",
+    "             # 0 means extremely poor generation effect, -1 means excellent generation effect\n",
+    "             loss = -1 * self.disc_gen_as_target()\n",
+    "         else:\n",
+    "             # Calculate the loss function of the discriminator, the loss value range is [-1, 1],\n",
+    "             # -1 means perfect distinction, 0 means indistinguishable, 1 means inverted distinction\n",
+    "             loss = self.disc_gen_as_target() - self.disc_target_as_target()\n",
+    "\n",
+    "         return loss\n",
+    "\n",
+    "    def get_target_state(self):\n",
+    "         \"\"\"\n",
+    "         Get the density matrix representation of the target state\n",
+    "         \"\"\"\n",
+    "         state = self.target_state\n",
+    "         state = complex.reshape(state, [1] + state.shape)\n",
+    "         density_matrix = complex.matmul(\n",
+    "                          dagger(state), state)\n",
+    "         state = partial_trace(density_matrix, 2, 4, 2)\n",
+    "\n",
+    "         return state.numpy()\n",
+    "\n",
+    "    def get_generated_state(self):\n",
+    "         \"\"\"\n",
+    "         Get the density matrix representation of the generated state\n",
+    "         \"\"\"\n",
+    "         state = self.generator(\n",
+    "                 self.gen_theta).run_state_vector()\n",
+    "         state = complex.reshape(state, [1] + state.shape)\n",
+    "         density_matrix = complex.matmul(\n",
+    "                          dagger(state), state)\n",
+    "         state = partial_trace(density_matrix, 2, 4, 2)\n",
+    "\n",
+    "         return state.numpy()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Next, we use PaddlePaddle's dynamic graph mechanism to train our model."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:52:15.221809Z",
+     "start_time": "2021-01-09T10:49:55.308722Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stderr",
+     "output_type": "stream",
+     "text": [
+      "Training:100%|##############################|Elapsed Time: 0:02:19Time: 0:02:19\r"
+     ]
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "the density matrix of the target state:\n",
+      "[[0.02447174+0.j         0.125     +0.09081782j]\n",
+      " [0.125     -0.09081782j 0.97552826+0.j        ]] \n",
+      "\n",
+      "the density matrix of the generated state:\n",
+      "[[0.01664936+0.j         0.03736201+0.11797786j]\n",
+      " [0.03736201-0.11797786j 0.98335064+0.j        ]] \n",
+      "\n",
+      "the distance between these two quantum states is 0.01695854920517497 \n",
+      "\n",
+      "the fidelity between these two quantum states is 0.9952202063690136\n"
+     ]
+    },
+    {
+     "name": "stderr",
+     "output_type": "stream",
+     "text": [
+      "\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Learning rate\n",
+    "LR = 0.1\n",
+    "# Total number of iterations\n",
+    "ITR = 15\n",
+    "# In each iteration, the number of iterations of the discriminator\n",
+    "ITR1 = 20\n",
+    "# In each iteration, the number of generator iterations\n",
+    "ITR2 = 50\n",
+    "\n",
+    "# Used to record the change of loss value\n",
+    "loss_history = list()\n",
+    "with fluid.dygraph.guard():\n",
+    "    gan_demo = QGAN()\n",
+    "    optimizer = fluid.optimizer.SGDOptimizer(\n",
+    "      learning_rate=LR, parameter_list=gan_demo.parameters())\n",
+    "    widgets = ['Training:', Percentage(), '',\n",
+    "               Bar('#'), '', Timer(),'', ETA()]\n",
+    "    pbar = ProgressBar(widgets=widgets, maxval=ITR * 70).start()\n",
+    "    for itr0 in range(ITR):\n",
+    "      \n",
+    "        # Record the change in the loss value of the discriminator\n",
+    "        loss_disc_history = list()\n",
+    "        \n",
+    "        # Train the discriminator\n",
+    "        for itr1 in range(ITR1):\n",
+    "            pbar.update(itr0 * (ITR1 + ITR2) + itr1)\n",
+    "            loss_disc = gan_demo('disc')\n",
+    "            loss_disc.backward()\n",
+    "            optimizer.minimize(loss_disc, parameter_list\n",
+    "                               =[gan_demo.disc_phi],\n",
+    "                               no_grad_set=[gan_demo.gen_theta])\n",
+    "            gan_demo.clear_gradients()\n",
+    "            loss_disc_history.append(loss_disc.numpy()[0])\n",
+    "\n",
+    "        # Record the change of the generator loss value\n",
+    "        loss_gen_history = list()\n",
+    "        \n",
+    "        # Training generator\n",
+    "        for itr2 in range(ITR2):\n",
+    "            pbar.update(itr0 * (ITR1 + ITR2) + ITR1 + itr2)\n",
+    "            loss_gen = gan_demo('gen')\n",
+    "            loss_gen.backward()\n",
+    "            optimizer.minimize(loss_gen, parameter_list\n",
+    "                               =[gan_demo.gen_theta],\n",
+    "                               no_grad_set=[gan_demo.disc_phi])\n",
+    "            gan_demo.clear_gradients()\n",
+    "            loss_gen_history.append(loss_gen.numpy()[0])\n",
+    "\n",
+    "        loss_history.append((loss_disc_history, loss_gen_history))\n",
+    "    pbar.finish()\n",
+    "    \n",
+    "    # Get the target quantum state\n",
+    "    target_state = gan_demo.get_target_state()\n",
+    "    \n",
+    "    # Get the final quantum state generated by the generator\n",
+    "    gen_state = gan_demo.get_generated_state()\n",
+    "    print(\"the density matrix of the target state:\")\n",
+    "    print(target_state, \"\\n\")\n",
+    "    print(\"the density matrix of the generated state:\")\n",
+    "    print(gen_state, \"\\n\")\n",
+    "    \n",
+    "    # Calculate the distance between two quantum states,\n",
+    "    # The distance here is defined as tr[(target_state-gen_state)^2]\n",
+    "    distance = np.trace(np.matmul(target_state-gen_state,\n",
+    "                                  target_state-gen_state)).real\n",
+    "    # Calculate the fidelity of two quantum states\n",
+    "    fidelity = state_fidelity(target_state, gen_state)\n",
+    "    print(\"the distance between these two quantum states is\", distance, \"\\n\")\n",
+    "    print(\"the fidelity between these two quantum states is\", fidelity)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "We compare the target quantum state's density matrix $\\rho_\\text{target}$ and  the generated quantum state's density matrix $\\rho_\\text{gen}$ and calculate the distance between them $\\text{tr}[(\\rho_\\text{target}-\\rho_\\text{gen})^2]$ and fidelity. We can know that our generator generates a quantum state very close to the target state."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Visualization of the training process"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Next, let's observe the change of the discriminator and generator's loss curve during the training process.\n",
+    "\n",
+    "First install the required packages."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 11,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "from IPython.display import clear_output\n",
+    "!pip install celluloid\n",
+    "clear_output()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Next, we draw the change of the loss curve."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 12,
+   "metadata": {},
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZgAAAEXCAYAAACQ3VJYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Il7ecAAAACXBIWXMAAAsTAAALEwEAmpwYAAAmkElEQVR4nO3de5gdVZnv8e+PJASEcOdgTAiJEi4RMEAbRAZUbnKAMYAoF9HgAK2MMA6oXA5zEAGPCM7o8MgAkVtAhlsGNCoSEi6DIGA6GEISJAkBJ4mBIAQIIuH2nj9qNVY6u7v37t61a3fn93me/XTVqlVV7969ut9dt7UUEZiZmdXbOmUHYGZm/ZMTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgmpSk6yRdKGlvSU8VsP3XJH2wh+vOlfTJ+kZkZv2NE0yTi4jfRMT2BWx3w4hY1MN1PxwR9/c2BknHS3qwt9sxawS319o5waxlJA0sO4Z66U/vxcrViLa0NrZXJ5gmIWlXSY9JWinpFmC9VP5JSUty9c6UtDTVe0rSfql8gKT/I+nptGympK3TspD0NUkLgAW5sm3T9HWS/kPSr9Ops4ckvV/SjyStkPQHSbvmYnhW0v5p+jxJt0q6Pu13rqSWXN2zcjHNk3R4Kt8RuALYM+3z5VS+cdrWC5L+KOlfJK2Tlh2fYvuhpBeB8wr6dViDSdpN0u9TO7lN0i2SLkzLDpU0S9LLkn4raZfces9K+qak2ZJeSeutl1ve3bpnSpoN/EXSQLfXOosIv0p+AesCfwROAwYBRwJvARcCnwSWpHrbA4uBD6T5kcCH0vS3gCdSHQEfATZPywKYBmwGrJ8r2zZNXwf8GdidLLHdCzwDfAkYkOK4Lxfvs8D+afo84A3g4FT3e8AjubqfAz5A9mXmKOAvwNC07HjgwQ6fxfXAz4Eh6f3NB07I1X8bOBUY2P5e/Orbr1z7/3pq/0cAb6Z2tyuwHNgjta8Jqf0NzrXF36U2thnwJPDVtKyadWcBW+f+Ltxe6/m7LTsAvwJgH+BPgHJlv2XNBLNt+oPZHxjUYRtPAeM72X4A+1YoyyeYn+SWnQo8mZvfGXg5N/8sqyeY6bllY4C/dvFeZ7XH2fEPNv0TeBMYkyv7CnB/rv7/lP378qu+r9T+l3Zo/w+m9n85cEGH+k8Bn0jTzwLH5ZZdDFyRpqtZ9x+6ic3ttRcvnyJrDh8AlkZqlckfO1aKiIXAP5P9U18u6WZJH0iLtwae7mIfi7uJ4fnc9F8rzG/YxbrP5aZfB9ZrP98s6Uu5UxQvAzsBW3SynS3IvsHm3/sfgWG5+e7eh/U9ldp/++95G+Ab7e0ntaGt0zrtOra/DWtYd7X25PZaX04wzWEZMEyScmUjKlWMiP+MiL8j++MJ4Ptp0WLgQ13so+HdZkvaBvgJcArZ6bpNgDlkp/AqxfRnslOD2+TKRpB9u23n7r/7n0rtf+v0czHw3YjYJPd6X0TcVMV2q1n3vfbk9lp/TjDN4WGyc7X/JGmQpCOAcR0rSdpe0r6SBpNd9/gr8G5afBVwgaTRyuwiafNGvYFObED2B/YCgKQvk30jbPc8MFzSugAR8Q5wK/BdSUPSH/zpwE8bGrU12sPAO8Ap6UL7eP7W/n8CfFXSHqldbyDpEElDqthureu6vdaZE0wTiIg3yS5sHg+8RHZx8fYKVQcDF5F9c3oO+F/A2WnZv5E19ruBV4GrgfWLjLs7ETEP+FeyfyDPk13LeShX5V5gLvCcpD+nslPJLqwuIjsP/5/ANY2K2Rov1/5PAF4GjgN+CayKiDbgJODHwApgIdnfSTXbrWldt9f60+qnPc3MyifpUbKL9deWHYv1nI9gzKx0kj6h7NmrgZImALsAd5Udl/VO6QlG0jWSlkua08lySbpU0sL0MNVuuWUTJC1IrwmNi9qs5yQdpOwh2YWSzqqwfHB6YHChpEcljSwhzEbbHnic7BTZN4AjI2JZqRFZr5V+ikzSPsBrwPURsVOF5QeTnec8mOyBqX+PiD0kbQa0AS1kF+ZmArtHxIqGBW9WI0kDyB7GOwBYAswAjknn/9vr/COwS0R8VdLRwOERcVQpAZv1QulHMBHxANmF7c6MJ0s+ERGPAJtIGgp8GpgWES+lpDINOKj4iM16ZRywMCIWpYvbN5O18bzxwKQ0PRnYr8MtvGZ9Ql/ofG0Yqz+stCSVdVa+BkmtQCvABhtssPsOO+xQTKS21ps5c+afI2LLLqpUard7dFYnIt6W9AqwOdndg+9xu7ZGqqJtr6EvJJhei4iJwESAlpaWaGtrKzki668krdEDQ1Hcrq2RetK2Sz9FVoWl/O2pXoDhqayzcrNmVk27fa9O6nJnY+DFhkRnVkd9IcFMAb6U7ib7GPBKurtkKnCgpE0lbQocmMrMmtkMYLSkUemJ8KPJ2njeFLKefyHrWfveKPtuHLMeKP0UmaSbyHoM3kLZuCffJutAjoi4AriT7A6yhWQd2X05LXtJ0gVkf7AA50dEVzcLmJUuXVM5hezL0ADgmoiYK+l8oC0ippD1wnCDpIVkN8AcXV7EZj1XeoKJiGO6WR7A1zpZdg3ulsH6mIi4k+yLU77s3Nz0G2Tjkpj1aX3hFJmZmfVBTjBmZlYIJxgzMyuEE4yZmRXCCcbMzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWiNITjKSDJD0laaGksyos/6GkWek1X9LLuWXv5JZNaWjgZmbWpYFl7lzSAOAy4ABgCTBD0pSImNdeJyJOy9U/Fdg1t4m/RsTYBoVrZmY1KPsIZhywMCIWRcSbwM3A+C7qHwPc1JDIzMysV8pOMMOAxbn5JalsDZK2AUYB9+aK15PUJukRSYcVFqWZmdWs1FNkNToamBwR7+TKtomIpZI+CNwr6YmIeLrjipJagVaAESNGNCZaM7O1XNlHMEuBrXPzw1NZJUfT4fRYRCxNPxcB97P69Zl8vYkR0RIRLVtuuWVvYzYzsyqUnWBmAKMljZK0LlkSWeNuMEk7AJsCD+fKNpU0OE1vAewFzOu4rpmZlaPUU2QR8bakU4CpwADgmoiYK+l8oC0i2pPN0cDNERG51XcErpT0LlmivCh/95mZmZWr9GswEXEncGeHsnM7zJ9XYb3fAjsXGpyZmfVY2afIzMysn3KCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVwgnGzMwK4QRj1iCSNpM0TdKC9HPTCnXGSnpY0lxJsyUdVUasZvXgBGPWOGcB90TEaOCeNN/R68CXIuLDwEHAjyRt0rgQzerHCcasccYDk9L0JOCwjhUiYn5ELEjTfwKWA+4C3PokJxizxtkqIpal6eeArbqqLGkcsC6wxhhHaXlrGnCv7YUXXqhvpGZ1UHpnl2b9zHaS5lQoPyc/ExEhKSrUA0DSUOAGYEJEvFupTkRMBCYCtLS0dLots7I4wZjV1/yIaKm0QNLzkoZGxLKUQJZ3Um8j4FfAORHxSIGxmhXKp8jMGmcKMCFNTwB+3rFCGnjvDuD6iJjcwNjM6s4JxqxxLgIOkLQA2D/NI6lF0lWpzueBfYDjJc1Kr7GlRGvWSz5FZtYgEfEisF+F8jbgxDT9U+CnDQ7NrBA+gjEzs0I4wZiZWSFKTzCSDpL0lKSFktZ4slnS8ZJeyJ2PPjG3bELqdmOBpAkd1zUzs/KUeg1G0gDgMuAAYAkwQ9KUiJjXoeotEXFKh3U3A74NtAABzEzrrmhA6GZm1o2yj2DGAQsjYlFEvAncTNadRjU+DUyLiJdSUplG1neTmZk1gbITzDBgcW5+SSrr6LOpZ9nJkraucV13qWFmVoKyE0w1fgGMjIhdyI5SJnVTfw0RMTEiWiKiZcst3W+gmVkjlJ1glgJb5+aHp7L3RMSLEbEqzV4F7F7tumZmVp6yE8wMYLSkUamLjKPJutN4T+qzqd1ngCfT9FTgQEmbpoGbDkxlZmbWBEq9iywi3pZ0ClliGABcExFzJZ0PtEXEFOCfJH0GeBt4CTg+rfuSpAvIkhTA+RHxUsPfhJmZVVR6VzERcSdwZ4eyc3PTZwNnd7LuNcA1hQZoZmY9UvYpMjMz66ecYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVwgnGzMwK4QRjZmaFcIIxM7NCOMGYmVkhnGDMzKwQpScYSQdJekrSQklnVVh+uqR5kmZLukfSNrll70ialV5TGhu5mZl1ZWCZO5c0ALgMOABYAsyQNCUi5uWq/R5oiYjXJZ0MXAwclZb9NSLGNjJmMzOrTtlHMOOAhRGxKCLeBG4GxucrRMR9EfF6mn0EGN7gGM3MrAfKTjDDgMW5+SWprDMnAL/Oza8nqU3SI5IO62wlSa2pXtsLL7zQq4DNzKw6pZ4iq4Wk44AW4BO54m0iYqmkDwL3SnoiIp7uuG5ETAQmArS0tERDAjYzW8uVfQSzFNg6Nz88la1G0v7AOcBnImJVe3lELE0/FwH3A7sWGaxZb0jaTNI0SQvSz027qLuRpCWSftzIGM3qqewEMwMYLWmUpHWBo4HV7gaTtCtwJVlyWZ4r31TS4DS9BbAXkL85wKzZnAXcExGjgXvSfGcuAB5oSFRmBSk1wUTE28ApwFTgSeDWiJgr6XxJn0nVLgE2BG7rcDvyjkCbpMeB+4CLOtx9ZtZsxgOT0vQk4LBKlSTtDmwF3N2YsMyKUfo1mIi4E7izQ9m5uen9O1nvt8DOxUZnVldbRcSyNP0cWRJZjaR1gH8FjgMqtv1c3VagFWDEiBH1jdSsDkpPMGb9zHaS5lQoPyc/ExEhqdINJ/8I3BkRSyR1uSPfvGLNzgnGrL7mR0RLpQWSnpc0NCKWSRoKLK9QbU9gb0n/SHZqeF1Jr0VEV9drzJpS1ddgJH093dkiSVdLekzSgUUGZ9bPTAEmpOkJwM87VoiIL0TEiIgYCXwTuN7JxfqqWi7y/0NEvAocCGwKfBG4qJCozJrAbbfdxsqVKwG48MILOeKII3jsscd6s8mLgAMkLSC7vnIRgKQWSVf1Nl6zZlNLgmk/IXwwcENEzM2VmfU7F1xwAUOGDOHBBx9k+vTpnHDCCZx88sk93l5EvBgR+0XE6IjYPyJeSuVtEXFihfrXRcQpvXgLZqWqJcHMlHQ3WYKZKmkI8G4xYZmVb8CAAQD86le/orW1lUMOOYQ333yz5KjM+o5aEswJZA+GfTR1PjkI+HIhUZk1gWHDhvGVr3yFW265hYMPPphVq1bx7rv+TmVWrVoSzJ7AUxHxcuoX7F+AV4oJy6x8t956K5/+9KeZOnUqm2yyCS+99BKXXHJJ2WGZ9Rm1JJjLgdclfQT4BvA0cH0hUZk1gWXLlnHIIYcwevRo7r//fm677TbGjRtXdlhmfUYtCebtiAiy7i5+HBGXAUOKCcusfJ/97GcZMGAACxcupLW1lcWLF3PssceWHZZZn1FLglkp6Wyy25N/lbq0GFRMWGblW2eddRg4cCC33347p556KpdccgnLli3rfkUzA2pLMEcBq8ieh3mOrGt9n5C2fmvQoEHcdNNNXH/99Rx66KEAvPXWWyVHZdZ3VJ1gUlK5EdhY0qHAGxHhazDWb1177bU8/PDDnHPOOYwaNYpnnnmGL37xi2WHZdZn1NJVzOeB3wGfAz4PPCrpyKICMyvbmDFj+MEPfsDOO+/MnDlzGD58OGeeeWbZYZn1GbV0dnkO2TMwywEkbQlMByYXEZhZ2e6//34mTJjAyJEjiQgWL17MpEmT2GeffcoOzaxPqCXBrJMfURJ4kfJHxDQrzDe+8Q3uvvtutt9+ewDmz5/PMcccw8yZM0uOzKxvqCXB3CVpKnBTmj+KDgOFmfUnb7311nvJBWC77bbzRX6zGlSdYCLiW5I+C+yViiZGxB3FhGVWvpaWFk488USOO+44AG688UZaWioO9WJmFdR0iisi/isiTk+vuiQXSQdJekrSQklrjHshabCkW9LyRyWNzC07O5U/JenT9YjHrN3ll1/OmDFjuPTSS7n00ksZM2YMl19+edlhmfUZ3R7BSFoJVBqOVWQjv27U051LGgBcBhwALAFmSJoSEfNy1U4AVkTEtpKOBr4PHCVpDHA08GHgA8B0SdtFxDvd7ji6GF22m2Fqbe0xePBgTj/9dE4//fSyQzHrk7pNMBFRVXcwkjaNiBU17n8csDAiFqVt3EzWFU0+wYwHzkvTk4EfKxusfDxwc0SsAp6RtDBt7+Eu9zhzJqxT0L0J3SWn/PKOdWtZtzf77e22myXuWtetIe6dX3mly4GOZq9YAUPcS5JZd2q5yN+de4DdalxnGLA4N78E2KOzOhHxtqRXgM1T+SMd1h1WaSeSWoFWgB033hhOO61yNF0d2XS1rNblHev2Ztv1jKu7Zc0Sd63r1hJ3BL989dWutz+wnn82Zv1XPf9SmvbcUkRMBCYCtLS0BN/+dskRWTPbpsp6e+65Jw8/3PUBs9narJ7nirr5WlnRUmDr3PzwVFaxjqSBwMZkz+BUs65ZYd54442yQzBramU/KDkDGC1plKR1yS7aT+lQZwowIU0fCdybhg2YAhyd7jIbBYwm68rGrCHkG0LMulTqKbJ0TeUUYCowALgmIuZKOh9oi4gpwNXADeki/ktkSYhU71ayGwLeBr5W1R1kZmbWEFUnGEkfA+ZGxMo0vxGwY0Q8mqrs15MAIuJOOvQIEBHn5qbfIOtgs9K63wW+25P9mvVWdHezgdlartYhk1/Lzb+WygCIiJfqFZRZX3DDDTeUHYJZU6slwShyX9ki4l3qe4rNrKncfvvtjB49mo033piNNtqIIUOGsNFGf3uueKeddioxOrPmV0uCWSTpnyQNSq+vA4uKCsysbGeccQZTpkzhlVde4dVXX2XlypW82t0zMmb2nloSzFeBj5PdCtz+QGRrEUGZNYOtttqKHXfcsewwzPqsWnpTXk66g8tsbdDS0sJRRx3FYYcdxuDBg98rP+KII0qMyqzvqOUusouBC4G/AncBuwCnRcRPC4rNrFSvvvoq73vf+7j77rvfK5PkBGNWpVou0h8YEWdIOhx4FjgCeABwgrF+6dprry07BLM+rZZrMO3J6BDgtoh4pYB4zJrG/Pnz2W+//d67W2z27NlceOGFJUdl1nfUkmB+KekPwO7APZK2BNwZk/VbJ510Et/73vcYNGgQALvssgs333xzyVGZ9R1VJ5iIOIvsLrKWiHgL+AvZmCxm/dLrr7/OuHHjVisb6K76zapWzYiW+0bEvZKOyJXlq9xeRGBmZdtiiy14+umn32vvkydPZujQoSVHZdZ3VPN1bB/gXuDvybrkV4efTjDWL1122WW0trbyhz/8gWHDhjFq1ChuvPHGssMy6zOqSTArJZ0OzOFviQV6Nv6LWZ/xs5/9jIMPPphPfepTvPvuu2ywwQZMnz6d3XffnbFjx5YdnlnTq+YazIbAELKL+ycDQ4EPkD3ZX+sQyWZ9RltbG1dccQUrVqzg5Zdf5sorr+Suu+7ipJNO4uKLL655e5I2kzRN0oL0c9NO6o2QdLekJyXNkzSyt+/FrAzdHsFExHcAJD0A7Jbrrv884FeFRmdWoiVLlvDYY4+x4YYbAvCd73yHQw45hAceeIDdd9+dM844o9ZNngXcExEXSTorzZ9Zod71wHcjYpqkDYF3e/E2zEpTy23KWwFv5ubfTGVm/dLy5ctX6yJm0KBBPP/886y//vqrlddgPDApTU8CDutYQdIYYGBETAOIiNci4vWe7MysbLXcc3k98DtJd6T5w4Dr6h2QWbP4whe+wB577MH48dnd+L/4xS849thj+ctf/sKYMWN6ssmtImJZmn6Oyl/QtgNelnQ7MAqYDpxVabRWSa2kDmdHjBjRk3jMCqVaRuWTtBuwd5p9ICJ+X0hUBWppaYm2trayw7A+oq2tjYceegiAvfbai5aWli7rS1oJ/E+FRecAkyJik1zdFRGx2nUYSUeSDRO+a9rOLcCdEXF1V/t1u7aiSZoZEV3/AXRQ01NjEfEY8FhNUXVC0mZkfzwjyfo2+3xErOhQZyzZqJkbAe+QnZe+JS27DvgE0N5lzfERMasesZm1a2lp6TapdDC/sz9CSc9LGhoRyyQNBZZXqLYEmBURi9I6PwM+RpZ0zPqUWq7B1Fv7Bc/RwD1pvqPXgS9FxIeBg4AfSdokt/xbETE2vWYVHbBZL00BJqTpCcDPK9SZAWySumIC2BeY14DYzOquzATT7QXPiJgfEQvS9J/IvvFt2bGeWR9xEXCApAXA/mkeSS2SrgJI11q+Sdbf3xNkz539pKR4zXqlzI6Vqrng+R5J44B1gadzxd+VdC7pCCgiVnWyri+GWuki4kVgvwrlbcCJuflpZOMtmfVphR7BSJouaU6F12qdZEZ2p0Gndxuk89U3AF+OiPZnAs4GdgA+CmxG5ecJ2rc/MSJaIqJlyy19AGRm1giFHsFExP6dLavygieSNiJ7oPOciHgkt+32o59Vkq4lO61gZmZNosxrMN1e8JS0LnAHcH1ETO6wbGj6KbLrN3OKDNbMzGpTZoLp9oIn8Hmy3pyPlzQrvcamZTemi6BPAFsAHmrQzKyJlHaRv5oLnhHxU+Cnnay/b6EBmplZr5R5BGNmZv2YE4yZmRXCCcbMzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVorQEI2kzSdMkLUg/N+2k3juSZqXXlFz5KEmPSloo6RZJ6zYuejMz606ZRzBnAfdExGjgnjRfyV8jYmx6fSZX/n3ghxGxLbACOKHYcM3MrBZlJpjxwKQ0PQk4rNoVJQnYF5jck/XNzKx4ZSaYrSJiWZp+Dtiqk3rrSWqT9Iikw1LZ5sDLEfF2ml8CDCsuVDMzq9XAIjcuaTrw/gqLzsnPRERIik42s01ELJX0QeBeSU8Ar9QYRyvQCjBixIhaVjUzsx4qNMFExP6dLZP0vKShEbFM0lBgeSfbWJp+LpJ0P7Ar8F/AJpIGpqOY4cDSLuKYCEwEaGlp6SyRmZlZHZV5imwKMCFNTwB+3rGCpE0lDU7TWwB7AfMiIoD7gCO7Wt/MzMpTZoK5CDhA0gJg/zSPpBZJV6U6OwJtkh4nSygXRcS8tOxM4HRJC8muyVzd0OjNzKxLhZ4i60pEvAjsV6G8DTgxTf8W2LmT9RcB44qM0czMes5P8puZWSGcYMzMrBBOMGYNUkP3SBdLmivpSUmXpgeLzfocJxizxum2eyRJHye7W3IXYCfgo8AnGhmkWb04wZg1TjXdIwWwHrAuMBgYBDzfiODM6s0Jxqxxuu0eKSIeJrslf1l6TY2IJyttTFJr6kap7YUXXigqZrMeK+02ZbN+ajtJcyqUV9U9kqRtyZ7/Gp6KpknaOyJ+07Gue6iwZucEY1Zf8yOipdKCKrtHOhx4JCJeS+v8GtgTWCPBmDU7nyIza5xuu0cC/gf4hKSBkgaRXeCveIrMrNk5wZg1TjXdI00GngaeAB4HHo+IX5QRrFlv+RSZWYNU2T3SO8BXGhyaWSF8BGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFaK0BFPN2BiSPiVpVu71hqTD0rLrJD2TWza20e/BzMw6V+YRTLdjY0TEfRExNiLGAvsCrwN356p8q315RMxqQMxmZlalMhNMNWNj5B0J/DoiXi8yKDMzq48yE0y3Y2N0cDRwU4ey70qaLemHkgbXPUIzM+uxQvsikzQdeH+FRVWNjZHbzlBgZ2BqrvhsssS0LtmYGGcC53eyfivQCjBixIga3oGZmfVUoQkmIvbvbFmVY2O0+zxwR0S8ldt2+9HPKknXAt/sIg4PzGRm1mBlniKrZmyMdsfQ4fRYSkpIEtn1m0qjCJqZWUnKTDDVjI2BpJHA1sB/d1j/RklPkI2bsQVwYSOCNjOz6pQ2Hkw1Y2Ok+WeBYRXq7VtkfGZm1jt+kt/MzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMGZmVggnGDMzK4QTjJmZFcIJxszMCuEEY2ZmhXCCMTOzQjjBmJlZIZxgzMysEE4wZmZWCCcYMzMrhBOMmZkVwgnGzMwK4QRjZmaFcIIxM7NClJZgJH1O0lxJ70pq6aLeQZKekrRQ0lm58lGSHk3lt0hatzGRm/VMb9u8WV8zsMR9zwGOAK7srIKkAcBlwAHAEmCGpCkRMQ/4PvDDiLhZ0hXACcDlxYdt1mO9bfOdWrkS7r03v53Ott99eW/W7U152ftu1nXrsX53dTorHzUKNtig++12prQEExFPAqjrT2UcsDAiFqW6NwPjJT0J7Ascm+pNAs7DCcaaWG/aPNBlgpk/H/bbr06BmiUPPAB7793z9cs8gqnGMGBxbn4JsAewOfByRLydKx/W2UYktQKtaXaVpDkFxNpbWwB/LjuIChxXbbbv5fqdtfk1dGzXUFq7Lut3UWYbWCve8z77rDZbc9suNMFImg68v8KicyLi50XuOy8iJgITU0xtEdHp+e+yOK7aNHFcr3byBabubb5Z2nVZ+/Z7bvy+a12n0AQTEfv3chNLga1z88NT2YvAJpIGpqOY9nKzss3v5T+Aztq8WZ/T7LcpzwBGpzvG1gWOBqZERAD3AUemehOAhh0RmRWoYpsvOSazHinzNuXDJS0B9gR+JWlqKv+ApDsB0tHJKcBU4Eng1oiYmzZxJnC6pIVk12SurnLXE+v4NurJcdWmz8VVhzbfo/02QFn79ntu8n0rOxgwMzOrr2Y/RWZmZn2UE4yZmRVirUkwzdr9hqRnJT0haVZPbgOscyzXSFqev81W0maSpklakH5u2iRxnSdpafrcZkk6uMExbS3pPknzUvcvX0/lDf+8Gtm2y2ojZX3ektaT9DtJj6f9fieVN6SrKkkDJP1e0i8bvN81/i/15LNeKxKM/tb9xv8GxgDHSBpTblSr+VREjG2C5zquAw7qUHYWcE9EjAbuSfONdh1rxgVZV0Fj0+vOBsf0NvCNiBgDfAz4WmpTDf28Smjb11FOGynr814F7BsRHwHGAgdJ+hh/66pqW2AFWVdVRfg62c0e7Rq1X1jz/1LNn/VakWDIdb8REW8C7d1vWE5EPAC81KF4PFlXPKSfhzUyJug0rlJFxLKIeCxNryT7JzCMxn9eDW3bZbWRsj7vyLyWZgelV5B1VTW5qP0CSBoOHAJclebViP12oebPem1JMJW63+i0a5kGC+BuSTOVdf3RbLaKiGVp+jlgqzKD6eAUSbPTaZuGn7prJ2kksCvwKI3/vJqhbTf0PTf6806nqWYBy4FpwNPU0FVVL/wIOAN4N83X1EVWL1X6v1TzZ722JJhm9ncRsRvZKY6vSdqnuxXKkh5wbZb72i8HPkR22mIZ8K9lBCFpQ+C/gH+OiFfzy5rs82qIot9zGZ93RLwTEWPJelUYB+xQ7310JOlQYHlEzCx6X53o8v9StZ/12pJgmrb7jYhYmn4uB+4ga8DN5HlJQwHSz+UlxwNARDyf/vDfBX5CCZ+bpEFk/+xujIjbU3GjP69maNsNec9lf94R8TJZDyJ7krqqSouK+Mz3Aj4j6Vmy0577Av/egP0Cnf5fqvmzXlsSTFN2vyFpA0lD2qeBA8nGDGkmU8i64oEm6pKnvaEnh9Pgzy2dD78aeDIi/i23qNGfVzO07cLfc1mft6QtJW2SptcnG6fnSQruqioizo6I4RExkux3em9EfKHo/UKX/5dq/6wjYq14AQcD88nOn55Tdjwppg8Cj6fX3LLjAm4iO930Ftn53RPIzvveAywApgObNUlcNwBPALNTwx/a4Jj+juwUwWxgVnodXMbn1ci2XVYbKevzBnYBfp/2Owc4N5V/EPgdsBC4DRhc4Gf+SeCXjdpvZ/+XevJZu6sYMzMrxNpyiszMzBrMCcbMzArhBGNmZoVwgjEzs0I4wZiZWSGcYMzMrBBOMP1Y6tL+m5LOl7R/nbb52/RzpKRj67FNs7IpG7Z6cpoeqwYP/9BfOcGsBSLi3IiYXqdtfTxNjgRqSjC5Li7MmkpE/Cki2p+QH0v2EGfV3LYrc4LpZySdI2m+pAeB7VPZdZKOTNMXpUGbZkv6QSrbStIdaVClxyV9vIvtt3ddfhGwdxqQ6LTU4+wlkmakbX8l1f+kpN9ImgLMK/K9W/8n6f8qG1ztQUk3pSP0D0m6K/X8+xtJO6S610m6VNJvJS1q/xvoZLsjJc1J3e2cDxyV2vZRqeuUa5QNPPZ7SePTOsdLmiLpXrIn3K0DZ91+RNLuZP0WjSX73T4GzMwt35ys364dIiLa+1gCLgX+OyIOVzaA1YZV7O4s4JsRcWjadivwSkR8VNJg4CFJd6e6uwE7RcQzvX2PtvaS9FHgs8BHyMZlaW/fE4GvRsQCSXsA/0HWOSTAULJuZnYg61Jocsft5kXEm5LOBVoi4pS03/9H1hfYP6S/md9Jaj8jsBuwS0Q01XhFzcIJpn/ZG7gjIl4HSEcNea8AbwBXKxuC9ZepfF/gS5B1TZ7q1epAYJfct8SNgdHAm8DvnFysDvYCfh4RbwBvSPoFsB7wceC2rD9MAAbn1vlZZD1uz5PU07FiDiTr2fibaX49YESanubk0jknmLVIRLwtaRywH1mPrKfwt296vSXg1IiYulqh9EngL3Xah1lH65ANwjW2k+WrctPqpE53BHw2Ip5arTA7WnLb7oKvwfQvDwCHSVo/dbf99/mFygZr2jiy8etPIzvVANn545NTnQGSNq5iXyuBIbn5qcDJacwOJG2Xuvo2q5eHgL+XtF5qy4cCrwPPSPocZN36S/pIVxupQqW2fWoaMgBJu/Zy+2sNJ5h+JLIxy28h62b712RjheQNAX4paTbwIHB6Kv868ClJT5Cd0x5Txe5mA++kmwJOIxs3fB7wmKQ5wJX4CNnqKCJmkF1HmU3Wvp8gO537BeAESe3dy4/v5a7uA8a0X+QHLiC75jNb0tw0b1Vwd/1m1mdI2jAiXpP0PrIj9tb0xcqakL9hmllfMlHSGLIL7ZOcXJqbj2BsDel25kr39e8XES82Oh6zepG0M9loqHmrImKPMuLp75xgzMysEL7Ib2ZmhXCCMTOzQjjBmJlZIZxgzMysEP8fpQayYYKX+OAAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 432x288 with 2 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "import matplotlib.pyplot as plt\n",
+    "from celluloid import Camera\n",
+    "def draw_pic(loss_history):\n",
+    "    fig, axes = plt.subplots(nrows=1, ncols=2)\n",
+    "    camera = Camera(fig)\n",
+    "    axes[0].set_title(\"discriminator\")\n",
+    "    axes[0].set_xlabel(\"disc_iter\")\n",
+    "    axes[0].set_ylabel(\"disc_loss\")\n",
+    "    axes[0].set_xlim(0, 20)\n",
+    "    axes[0].set_ylim(-1, 1)\n",
+    "    axes[1].set_title(\"generator\")\n",
+    "    axes[1].set_xlabel(\"gen_iter\")\n",
+    "    axes[1].set_ylabel(\"gen_loss\")\n",
+    "    axes[1].set_xlim(0, 50)\n",
+    "    axes[1].set_ylim(-1, 0)\n",
+    "    for loss in loss_history:\n",
+    "        disc_data, gen_data = loss\n",
+    "        disc_x_data = range(0, len(disc_data))\n",
+    "        gen_x_data = range(0, len(gen_data))\n",
+    "        axes[0].plot(disc_x_data, disc_data, color='red')\n",
+    "        axes[1].plot(gen_x_data, gen_data, color='blue')\n",
+    "        camera.snap()\n",
+    "    animation = camera.animate(interval=600, \n",
+    "                               repeat=True, repeat_delay=800)\n",
+    "    animation.save(\"./figures/loss.gif\")\n",
+    "draw_pic(loss_history)\n",
+    "clear_output()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "![QGAN-fig-loss](./figures/loss.gif)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "In this dynamic picture, each frame represents an iterative process. In an iteration, the red line on the left represents the loss curve of the discriminator, and the blue line on the right represents the loss curve of the generator. It can be seen that at the initial stage, the discriminator and generator can gradually learn from a poor discriminant ability and generation ability to a better discrimination ability and generation ability in the current situation. As the learning progresses, the generator’s generation ability is getting stronger and stronger, and the discriminator’s ability is getting stronger and stronger. However, the discriminator can not distinguish the real data and the generated data because the generator has generated data close to real data. At this time, the model has converged."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## References"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "[1] Goodfellow, I. J. et al. Generative Adversarial Nets. [Proc. 27th Int. Conf. Neural Inf. Process. Syst. (2014).](https://papers.nips.cc/paper/5423-generative-adversarial-nets)\n",
+    "\n",
+    "[2] Lloyd, S. & Weedbrook, C. Quantum Generative Adversarial Learning. [Phys. Rev. Lett. 121, 040502 (2018).](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.040502)\n",
+    "\n",
+    "[3] Benedetti, M., Grant, E., Wossnig, L. & Severini, S. Adversarial quantum circuit learning for pure state approximation. [New J. Phys. 21, (2019).](https://iopscience.iop.org/article/10.1088/1367-2630/ab14b5)\n"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.8.5"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/QAOA/QAOA.ipynb

-{
- "cells": [
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "\n",
-    "# 量子近似优化算法 (QAOA)\n",
-    "\n",
-    "## 简体中文 | [English](./QAOA_En.ipynb)\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "# 准备\n",
-    "\n",
-    "本文档演示 Paddle Quantum 上量子近似优化算法（QAOA，Quantum Approximate Optimization Algorithm）的工作流程 [1]。\n",
-    "\n",
-    "开始之前完成准备工作：\n",
-    "\n",
-    "   - 调用飞桨 paddlepaddle\n",
-    "\n",
-    "   - 调用常用的库, 例如画图工具库 networkx 和 matplotlib.pyplot\n",
-    "\n",
-    "   - 调用自定义函数 "
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 1,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "from paddle import fluid\n",
-    "\n",
-    "import os\n",
-    "import numpy as np\n",
-    "import matplotlib.pyplot as plt\n",
-    "import networkx as nx\n",
-    "\n",
-    "from paddle_quantum.circuit import UAnsatz\n",
-    "from paddle_quantum.utils import pauli_str_to_matrix"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "# 背景\n",
-    "\n",
-    "\n",
-    "量子近似优化算法（QAOA，Quantum Approximate Optimization Algorithm）是可以在近期有噪中等规模（NISQ，Noisy Intermediate-Scale Quantum）量子计算机上运行且具有广泛应用前景的量子算法。例如，QAOA 可以用来处理压缩图信号和二次优化等领域常见的离散组合优化问题。这类优化问题通常可以归结为下面的数学模型：\n",
-    "\n",
-    "\n",
-    " $$F=\\max_{z_i\\in\\{-1,1\\}} \\sum_{i,j} q_{ij}(1-z_iz_j)=-\\min_{z_i\\in\\{-1,1\\}} \\sum_{i,j} q_{ij}z_iz_j+ \\sum_{i,j} q_{ij}. $$\n",
-    "\n",
-    "\n",
-    "其中, $z_i \\in \\{-1 ,1\\} $ 是待求的二元参数，系数 $q_{ij}$ 是 $z_i z_j$ 的权重 (weight)。一般地，精确求解该问题对于经典计算机是 NP-hard 的，而 QAOA 被认为对近似求解这类困难问题具有潜在速度优势。\n",
-    "\n",
-    "QAOA 的工作原理是把上述经典优化问题（例如组合优化问题）甚至量子优化问题（例如量子多体系统中 Ising 模型的求解）等价地转化为求解一个物理系统哈密顿量（Hamiltonian）的基态能量（对应优化问题的最优值）及其相应的基态（对应于优化问题的最优解）。接下来，我们通过图的最大割问题 （Max-Cut problem）来展示 QAOA 算法的工作流程和原理。在解决最大割问题时，QAOA 在数学形式上等价于求解一个实对角矩阵 $H$ 的最小特征值及其对应的特征向量。\n",
-    "\n",
-    "和另外一种常见的变分量子特征求解器(VQE, Variational Quantum Eigensolver) 一样，QAOA 也是一种量子-经典混杂算法。 然而 QAOA 参数化量子电路的实现更简单，仅需两个可以调节参数的量子电路模块组成。"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "\n",
-    "# 示例\n",
-    "\n",
-    "##  1. Max-Cut 问题\n",
-    "\n",
-    "图的 Max-Cut 问题可以描述为：对于一个给定的包含 $N$ 个顶点 （nodes or vertices）和 $M$ 条边 (edges) 的无向图，找到一种分割方案将图的顶点集合分割成两个无交子集合 $S$ 和 $S^\\prime$，使得连接这两个顶点集合之间边的数目尽可能多。如图所示，我们考虑含4个顶点且具有环形结构的图： \n",
-    "\n",
-    " ![ring4.png](https://release-data.cdn.bcebos.com/PIC%2FMaxCut.png) \n",
-    "\n",
-    "Max-Cut 问题建模：在做分割时，若顶点 $i$ 属于集合 $S$ 时，赋值 $z_i=1$；若顶点 $j$ 属于 $S^\\prime$ 时，则令 $z_j=-1$。那么对于图的任意连接顶点 $(i, j)$ 的边则满足：若顶点属于同一集合 $S$ 或 $S^\\prime$ 时，$z_iz_j=1$; 若顶点分别属于不同集合时，$z_izj=-1$。于是 Max-Cut 问题转化为如下优化问题：\n",
-    "\n",
-    "$$ F=\\min_{z_i\\in\\{-1, 1\\}} z_1 z_2+z_2z_3+z_3z_4+z_4z_1.$$\n",
-    "\n",
-    "这里所有 $q_{ij}$ 均设置为 1，表示每条边的权重相等。该问题的所有可行解由比特串 $ \\boldsymbol{z}=z_1z_2z_3z_4 \\in \\{-1, 1\\}^4$ 组成，而且通常需要遍历所有比特串才能得到问题的最小值（最优解）。容易看出，比特串的数目是顶点数目 $N$ 的指数级别，即 $2^N$。因此，随着顶点数目的增加，搜索的代价也会呈指数级别增加。\n",
-    "\n",
-    "接下来，我们提供两种方法来预处理编码经典优化问题的图，即如何通过 Paddle Quantum 输入和可视化无权（或带权重）图：\n",
-    "\n",
-    "- 方法1是通过指定图的顶点和相应的边（及其权重）\n",
-    "- 方法2是通过直接输入图的邻接矩阵。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 2,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "def generate_graph(N, GRAPHMETHOD):\n",
-    "    \"\"\"\n",
-    "    It plots an N-node graph which is specified by Method 1 or 2.\n",
-    "    \n",
-    "    Args:\n",
-    "        N: number of nodes (vertices) in the graph\n",
-    "        METHOD: choose which method to generate a graph\n",
-    "    Returns:\n",
-    "        the specific graph and its adjacency matrix\n",
-    "    \"\"\"\n",
-    "    # Method 1 generates a graph by self-definition\n",
-    "    if GRAPHMETHOD == 1:\n",
-    "        print(\"Method 1 generates the graph from self-definition using EDGE description\")\n",
-    "        graph = nx.Graph()\n",
-    "        graph_nodelist=range(N)\n",
-    "        graph.add_edges_from([(0, 1), (1, 2), (2, 3), (3, 0)])\n",
-    "        graph_adjacency = nx.to_numpy_matrix(graph, nodelist=graph_nodelist)\n",
-    "    # Method 2 generates a graph by using its adjacency matrix directly\n",
-    "    elif GRAPHMETHOD == 2:\n",
-    "        print(\"Method 2 generates the graph from networks using adjacency matrix\")\n",
-    "        graph_adjacency = np.array([[0, 1, 0, 1], [1, 0, 1, 0], [0, 1, 0, 1], [1, 0, 1, 0]])\n",
-    "        graph = nx.Graph(graph_adjacency)\n",
-    "    else:\n",
-    "        print(\"Method doesn't exist \")\n",
-    "\n",
-    "    return graph, graph_adjacency"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "这里指定方法1来预处理图：\n",
-    "\n",
-    "- 图的顶点数目 $N=4$\n",
-    "- 图的输入方法 GRAPHMETHOD = 1 \n",
-    "\n",
-    "注意：上述两种方法给出的图的顶点均从 $0$ 开始计数。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 3,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "Method 1 generates the graph from self-definition using EDGE description\n",
-      "[[0. 1. 0. 1.]\n",
-      " [1. 0. 1. 0.]\n",
-      " [0. 1. 0. 1.]\n",
-      " [1. 0. 1. 0.]]\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAb4AAAEuCAYAAADx63eqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAXBklEQVR4nO3df2yc9WHH8c/9sH12bNfBceJA6KAxxCUrzghCqVbyQ6yrmu4HTEFtCRIwCkPJWIdWTSihI3RBidRuYq5AqBUJ6g9oISN07Wg7aJMorYhKkyXuD0wILSVmsWM7cS52cr9vfzjn+HJ39v14nrvneb7vl1QV+R4/evjDz4f3+e7sS6fTaQEAYAh/rS8AAIBqYvgAAEZh+AAARmH4AABGYfgAAEZh+AAARmH4AABGYfgAAEZh+AAARmH4AABGCdb6AgCTjIxHtevggPoHwwpHEmoNBdXd2arbly9Se3NDrS8PMIKPz+oE7Hfk+Jie3HtM+44OS5KiidTUY6GgX2lJq5d0aMOqLvVc2VabiwQMwfABNvvWgXf1+Cv9iiSSmumnzeeTQsGANq/t1p0rrqra9QGm4alOwEaTo/emzsdTsx6bTkvn40k9/sqbksT4ATah+ACbHDk+ps98/YDOx5NTXwu/8T2N972q+Mh7UjqlD/zpZ9V28/qc722sC+i796/Q9YvaqnjFgBl4VSdgkyf3HlMkkcz6WmzwmPyhZgVa5s34vZFEUk/tPWbn5QHGYvgAG4yMR7Xv6HDO7/Tm/eU/qXP9dtUv+NCM359OS3veGtboeNTGqwTMxPABNth1cKDic/gk7TpU+XkAZGP4ABv0D4az3rJQjkgipf4TZy26IgAZDB9gg3AkYdF54pacB8BFDB9gg9aQNe8Uag3VWXIeABfxPj7ABt2dLQr6Ukqks//b8uyRHyt6/LeKDb0jSTr39gElzpxU07Ur1HTtR7OObQj61L2wpWrXDJiC4gMsNjAwoP/8yj8rHs99ujN6/Lea+PVPlAxPfnRZ/OTvNfHrnyg29LucYyORqOYM/cr26wVMwxvYAYuk02nt3LlTDz30kMLhsObdtklN16yQz1/6f1+mUymde/t1jezepjvuuEO9vb1qb2+34aoB81B8gAUGBga0du1a3XvvvQqHw5Kk8OsvKp2MlXW+dDKm8OsvSpKee+45LV26VC+//LJVlwsYjeEDKpBOp7Vjxw4tXbpUP/rRj7Ieiw2+rXnv7VND0FfSOQNK6syenYoNXvzklqGhId12221av369RkdHLbl2wFQMH1CmfJWX0dTUpN7eXv3yO0/oi5+6To11Aflm2T+fb/IzOh/76+u175mt6unpyTmG+gMqx+/4gBJd+ru8S61cuVI7duzQ4sWLp77WNzCmp/Ye0563huXT5JvTMzJ/j2/Nkg5tWN019cHUsVhM27Zt09atW5VI5L5Qht/9AeVh+IASDAwM6L777st5WlOarLzt27dr48aN8hd4QcvoeFS7Dg2o/8RZhSNxtYbq1L2wRetuKPwX2A8fPqy7775bR44cyXlswYIFevrpp3XrrbdW9O8FmIThA4pQTuVZifoDrMPwAbOotPKsRP0BlePFLUABM71iU5qsvL6+Pj344INVGT1JWrZsmX7xi19oy5YtCgazP3iJV34CxaH4gDycVHmFUH9AeSg+YBonVl4h1B9QHooPuMANlVcI9QcUz3k/wUCVuanyCqH+gOJRfDCamyuvEOoPmJl7fpoBC3mh8gqh/oCZUXwwjhcrrxDqD8jl/p9soEherrxCqD8gF8UHI5hUeYVQf8Ak7/6UAzKz8gqh/oBJFB88i8orjPqDycz7iYfnUXmzo/5gMooPnkLllY76g2n46YcnUHnlo/5gGooPrkflWYf6gwm4E8C1qDzrUX8wAcUHV6Ly7Ef9wau4K8BVqLzqof7gVRQfXIPKqx3qD17CHQKOR+XVHvUHL6H44GhUnvNQf3A77hZwJCrPuag/uB3FB8eh8tyD+oMbceeAY1B57kP9wY0oPjgCled+1B/cgrsIaorK8w7qD25B8aFmqDzvov7gZNxRUHVUnvdRf3Ayig9VReWZh/qD03B3QVVQeeai/uA0FB9sR+Uhg/qDE3CngW2oPFyK+oMTUHywBZWH2VB/qBXuOrAUlYdiUX+oFYoPlqHyUC7qD9XEHQgVo/JQKeoP1UTxoSJUHqxG/cFu3I1QFioPdqH+YDeKDyWj8lAt1B/swJ0JRaPyUG3UH+xA8aEoVB5qjfqDVbhLYUZUHpyC+oNVKD4UROXBqag/VII7FnJQeXA66g+VoPiQhcqD21B/KBV3L0ii8uBe1B9KRfGByoNnUH8oBncyg1F58BrqD8Wg+AxF5cHrqD8Uwl3NMFQeTEH9oRCKzyBUHkxF/WE67nAGoPJgOuoP01F8HkflAdmoP3C38ygqD8iP+gPF50FUHlAc6s9M3Pk8hMoDSkP9mYni8wgqD6gM9WcO7oIuR+UB1qD+zEHxuRiVB9iD+vM27oguROUB9qL+vI3icxkqD6gu6s97uDu6BJUH1Ab15z0UnwtQeYAzUH/ewJ3Swag8wFmoP2+g+ByKygOcjfpzL+6aDkPlAe5A/bkXxecgVB7gTtSfu3AHdQAqD3A36s9dKL4ao/IAb6H+nI+7aY1QeYA3UX/OR/HVAJUHmIH6cyburFVE5QFmof6cieKrEioPMBv15xzcZW1G5QGQqD8nofhsROUByIf6qy3uuDag8gDMhPqrLYrPYlQegFJQf9XH3dciVB6AclB/1UfxWYDKA2AF6q86uBNXgMoDYCXqrzoovjJReQDsRP3Zh7tyiag8ANVA/dmH4isBlQegFqg/a3GHLgKVB6CWqD9rUXyzoPIAOAn1Vznu1gVQeQCciPqrHMWXB5UHwA2ov/Jw556GygPgJtRfeSi+C6g8AG5G/RXP+Ls4lQfAC6i/4hldfFQeAC+i/mZm5B2dygPgZdTfzIwrPioPgEmov1zG3N2pPAAmov5yGVF8VB4AUH8Znr7TU3kAcBH1N8mzxUflAUBhJtef5+76VB4AzM7k+vNU8VF5AFA60+rPEwtA5QFA+UyrP9cXH5UHANYxof5cuwZUHgBYz4T6c2XxUXkAYD+v1p+rloHKA4Dq8Wr9uab4qDwAqB0v1Z/jV4LKA4Da81L9Obr4qDwAcB63158jF4PKAwDncnv9Oa74qDwAcA831p/twzcyHtWugwPqHwwrHEmoNRRUd2erbl++SO3NDVPHpdNp7dy5Uw899JDC4XDOeVauXKkdO3Zo8eLFdl4uAKBEsVhM27Zt09atW5VIJHIev+OOO9Tb26v29vacx4rdCCvZNnxHjo/pyb3HtO/osCQpmkhNPRYK+pWWtHpJhzas6lK7b5zKAwCXK6X+StmInivbLL1OW4bvWwfe1eOv9CuSSGqms/t8UlBpje3ZoZEDu3Mep/IAwF2Kqb+b/3az/mPfe0VtRCgY0Oa13bpzxVWWXaPlwzc5em/qfDw1+8EXpGIRnf7pMxo//ENJVB4AuF2h+mte9klddsvn5Ksr/mnMxjq/Nq/9sGXjZ+nwHTk+ps98/YDOx5NTXxt9pVeR93+rZHhEvkCd6i+/VnPX3KP6jquyvjcVj2jo2w9rxbWXU3kA4AGX1l995zVasH6b/HWhqWPSiZhO/3SHJvr3Kx07r/oFizX3ls+p4fIlWedqrAvou/ev0PWL2iq+Lktz6sm9xxRJJLO+Nt73P/I3zNGc61bK19CkyO8O6uQLjyqdiGUd5wvU6+YHtmrPnj2MHgB4QH19vR599FG98cYb6unpUetHb5cvUJ91zKnXvqazh36gwJw2NV6zQtH3+zX0nUeUPHcm67hIIqmn9h6z5LqCsx9SnJHxqPYdHc55vrbz7ifU0NklSUqMDen9p+9V8uyoYiPvTX1dknx+v44nWnX6XNy2V/IAAKpv2bJl+uFPf6aPfXmPktN6KzkxpvG+1ySfXws+87gCc9o04g9o4jd7dPbgD9R28/qpY9Npac9bwxodj1a8EZYV366DA3m/Pn3c0qkLv+j0+RVoviznWJ+kXYfynwcA4F7f+9VQzpvd4yPvSamEAq0dCsxpkyTVX9iM2Mnf55zDqo2wbPj6B8NZL0e9VCp2XqP//YQkqfWmWxXMM3yRREr9J85adUkAAIfItxHJidOSJH/9xd/5+S78c+ax6azaCMue6gxHcl+2mpE8d0YnX9ii2ODbau75hNpW3zPDeeJWXRIAwCHybURgzlxJk6/sz0hf+OfMY7nnqXwjLBu+1lD+UyXOnNTQd7+oxKn31frR2zV31V2znKfOqksCADhEvo2om3el5A8qGR5WcuK0AnPmKnriqCSpfv7VBc5T+UZYNnzdna1qCA7mpOzgN7+g5PgpBVo7lI5Hdeq1r0mS5ly3KuflqqGgX90LW6y6JACAQzScH5USMSl48VWdgTlz1fyRWzR+5Mcaen6z6jr+SOfe/Jl89Y1qWf4XOeewaiMs+x3fuuWL8n49OX5q8v/Dwzr7y/+a+l985HjOsZFoVB9uOJPzdQCAO01MTOjzn/+8/u3vb1e+N43P/bP71XzDp5ScGNO5owfUcMUSLfj0lxRo+kDOsWlJ627IvzWlsPQN7Pd/85d69c2hGT+CppB0KqVzb7+use9/WY888og2bdqkujqe9gQAt9q/f7/uuecevfPOO5KkebdtUtM1K+Qr4xO5fD7pE9ct0NN33ljxdVn6BvaNq7sUCgbK+t50Mqbw6y8qkUhoy5Ytuummm/J+0CkAwNkylbdq1aqp0ZOk8OsvKp2MzfCdhYWCAW1Y3TX7gUWwdPh6rmzT5rXdaqwr7bT+VEKnf/KMYoMX35V/+PBh3XjjjXrssccUj/NKTwBwg/3796unp0e9vb269AnFKxoTuusjLSVvxORndXZb8nFlkg1/gf3OFVdp89oPq7EuIJ9v5mN9vsnPX/vSbT36xr/cp/nz52c9Tv0BgDsUqryMjRs3qq+vT/9615+XvBFWfkC1ZOPf4+sbGNNTe49pz1vD8mnyjYcZmb+1tGZJhzas7ppa8dHRUT344IN6/vnnc84XDAb53R8AONClv8ub7uqrr9YzzzyjNWvWZH29nI2wiu1/gX10PKpdhwbUf+KswpG4WkN16l7YonU3FP7rurt379YDDzygkydP5jy2bNkyPfvss+rp6bHzsgEAs5iYmNCmTZv01a9+NedpTWmy8rZv367m5uaC5yhnIypl+/CVi/oDAOcqp/KcwrHDl0H9AYBzWFF5teb44ZOoPwBwAjdX3nSuGL4M6g8Aqs8LlTedq4ZPov4AoJq8UnnTuW74Mqg/ALCP1ypvOtcOn0T9AYAdvFh507l6+DKoPwConJcrbzpPDJ9E/QFAJbxeedN5ZvgyqD8AKJ4plTed54ZPov4AoBgmVd50nhy+DOoPAHKZWHnTeXr4JOoPAKYztfKm8/zwZVB/AExmeuVNZ8zwSdQfADNRedmMGr4M6g+ACai8/IwcPon6A+BtVF5hxg5fBvUHwEuovNkZP3wS9QfAG6i84jB801B/ANyIyisNw3cJ6g+Am1B5pWP4CqD+ADgZlVc+hm8G1B8AJ6LyKsPwFYH6A+AEVJ41GL4iUX8AaonKsw7DVyLqD0A1UXnWY/jKQP0BqAYqzx4MXwWoPwB2oPLsxfBViPoDYCUqz34Mn0WoPwCVoPKqh+GzEPUHoBxUXnUxfDag/gAUg8qrDYbPJtQfgJlQebXD8NmM+gMwHZVXewxfFVB/ACQqzykYviqi/gAzUXnOwvBVGfUHmIXKcx6Gr0aoP8DbqDznYvhqiPoDvInKczaGzwGoP8AbqDx3YPgcgvoD3I3Kcw+Gz2GoP8BdqDz3YfgciPoD3IHKcyeGz8GoP8CZqDx3Y/gcjvoDnIXKcz+GzyWoP6C2qDzvYPhchPoDaoPK8xaGz4WoP6A6qDxvYvhcivoD7EXleRfD53LUH2AtKs/7GD4PoP4Aa1B5ZmD4PIT6A8pD5ZmF4fMY6g8oDZVnHobPo6g/YGZUnrkYPg+j/oD8qDyzMXwGoP6ASVQeJIbPGNQfTEflIYPhMwz1B9NQebgUw2cg6g+moPKQD8NnMOoPXkXlYSYMn+GoP3gNlYfZMHyQRP3B/ag8FIvhwxTqD25F5aEUDB9yUH9wCyoP5WD4kBf1B6ej8lAuhg8zov7gNFQeKsXwYVbUH5yCyoMVGD4UjfpDrVB5sBLDh5JQf6g2Kg9WY/hQFuoPdqPyYBeGD2Wj/mAXKg92YvhQMeoPVqHyUA0MHyxB/aFSVB6qheGDpag/lIrKQ7UxfLAc9YdiUXmoBYYPtqH+UAiVh1pi+GAr6g+XovJQawwfqoL6A5UHp2D4UDXUn7moPDgJw4eqo/7MQeXBiRg+1AT1531UHpyK4UNNUX/eQ+XB6Rg+1Bz15x1UHtyA4YNjUH/uReXBTRg+OAr15z5UHtyG4YMjUX/OR+XBrRg+OBb151xUHtyM4YPjUX/OQeXBCxg+uAL1V3tUHryC4YOrUH/VR+XBaxg+uA71Vz1UHryI4YNrUX/2ofLgZQwfXI36sx6VB69j+OAJ1F/lqDyYguGDZ1B/5aPyYBKGD55D/RWPyoOJGD54EvU3OyoPpmL44GnUXy4qD6Zj+OB51N9FVB7A8MEgJtcflQdcxPDBKCbWH5UHZGP4YCQT6o/KA/Jj+GAsL9cflQcUxvDBeF6qPyoPmB3DB8gb9UflAcVh+IBp3Fh/VB5QGoYPuISb6o/KA0rH8AEFOLn+qDygfAwfMAMn1h+VB1SG4QOK4IT6o/IAazB8QJFqWX9UHmAdhg8oUTXrj8oDrMfwAWUot/5GxqPadXBA/YNhhSMJtYaC6u5s1e3LF6m9uSHrWCoPsAfDB1Sg2Po7cnxMT+49pn1HhyVJ0URq6rhQ0K+0pNVLOrRhVZe6Lquj8gAbMXxAhWarv3UPP6H/9X1I0URKM/20+XxSnU+Kv/GC3n31GzmPU3mANfy1vgDA7drb2/Xcc8/ppZde0vz587MeC/3xx/Xz852KxGcePUlKp6VYSkp+5K/UvOyTWY9t3LhRfX19jB5gAYoPsND0+qvvvEYL1m+Tvy6UdczID/5dkXcPK3k+LH99k+o7uzR31V2q71w8dUwqHtHQtx/WFY1JKg+wGMMH2GD37t36hxd+Jf8H/0Q+f/YTK4PffliBlnb5G5oU+UOfEqfeV6C1Q4s27Jw6Jp1KaWHypF7b8ml+lwdYLFjrCwC86OaPr1XjwQbFkrn/Xdm5fvvUP0cHj2nw2X9U8uyo0smEfIHJH0mf36/T9Zcrqjoxe4C1GD7ABrsODsjn80nK/4RK+OD3FR85rsgfjkiSWm+6dWr0MnySdh0a0N+tXJznDADKxfABNugfDGe9ZeFS5/p/rujxX0uSAi3z1HDFdTnHRBIp9Z84a9s1AqbiVZ2ADcKRxIyPd67frg9+4SV1/M0jSo6f0vDL25Q4k/tewHAkbtclAsZi+AAbtIbyP5mSikeVTiUlSb5gvRo/tFy++pCUSioxNpjnPLX/m3+A1/BUJ2CD7s5WNQQHc57ujP3fWxr5/lfUcOVS+UPNih7/jdLRc/I3fUD1C7J/lxcK+tW9sKWalw0YgeIDbLBu+aK8Xw+0tCs493JFfn9Y40deVSoyrqbuj2nBZx+XPzQn69i0pHU35D8PgPJRfIAN5jU3aNW1HXr1zaGsT2ypu+yKrLczFOLzSWuWdOR8cDWAylF8gE02ru5SKBgo63tDwYA2rO6y+IoASAwfYJueK9u0eW23GutK+zFrrPNr89puXb+ozZ4LAwzHU52Aje5ccZUk6fFX+hVJJGf96wyhYECb13ZPfR8A6/FZnUAV9A2M6am9x7TnrWH5NPnm9IzM3+Nbs6RDG1Z3UXqAzRg+oIpGx6PadWhA/SfOKhyJqzVUp+6FLVp3Q+5fYAdgD4YPAGAUXtwCADAKwwcAMArDBwAwCsMHADAKwwcAMArDBwAwCsMHADAKwwcAMArDBwAwyv8DNCq8HtksmZQAAAAASUVORK5CYII=\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {},
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "# number of qubits or number of nodes in the graph\n",
-    "N=4  \n",
-    "classical_graph, classical_graph_adjacency= generate_graph(N, GRAPHMETHOD=1)\n",
-    "print(classical_graph_adjacency)\n",
-    "\n",
-    "pos = nx.circular_layout(classical_graph)\n",
-    "nx.draw(classical_graph, pos, width=4, with_labels=True, font_weight='bold')\n",
-    "plt.show()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 2. 编码量子优化问题\n",
-    "\n",
-    "接下来需要把上述经典优化问题映射为量子优化问题。利用替代关系 $z=1\\rightarrow |0\\rangle = \\begin{bmatrix}1 \\\\ 0\\end{bmatrix}$ 和 $z=-1\\rightarrow |1\\rangle = \\begin{bmatrix}0 \\\\ 1\\end{bmatrix}$, 我们把二元参数 $z_i\\in\\{-1, 1\\}$ 对应为描述量子比特的 Pauli-Z 算符 $Z_i=\\begin{bmatrix} 1 & 0\\\\ 0 & -1\\end{bmatrix}$ 的两个本征值。于是经典优化问题里的目标函数相应地编码为一个描述系统哈密顿量的矩阵\n",
-    "\n",
-    "$$H_{c}= Z_1Z_2+Z_2Z_3+Z_3Z_4+Z_4Z_1.$$\n",
-    "\n",
-    "其中 $Z_iZ_{j}$ 是 tensor product 运算，表示 Pauli-Z 算符分别作用在量子比特 $i$ 和 $j$ 上，而其余的量子比特上作用单位算符 $I=\\begin{bmatrix} 1 & 0\\\\ 0 & 1\\end{bmatrix}$ ，例如 $Z_1Z_2 =Z_1\\otimes Z_2\\otimes I_3\\otimes I_4$。经过上述操作，我们把经典优化问题转化为求解矩阵 $H_{c}$ 的最小特征值 $F$ 及其对应的向量 $|\\psi\\rangle$, 即\n",
-    "\n",
-    "$$ F=\\min_{|\\psi\\rangle} \\langle \\psi| H_c |\\psi\\rangle.$$\n",
-    "\n",
-    "这里，$|\\psi\\rangle$ 记为一个模长为1的 $2^4=16$ 维复向量，$\\langle \\psi|$ 是其共轭转置。\n",
-    "\n",
-    "Paddle Quantum 中通过函数 H_generator 完成编码任务："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 4,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [],
-   "source": [
-    "def H_generator(N, adjacency_matrix):\n",
-    "    \"\"\"\n",
-    "    This function maps the given graph via its adjacency matrix to the corresponding Hamiltiona H_c.\n",
-    "    \n",
-    "    Args:\n",
-    "        N: number of qubits, or number of nodes in the graph, or number of parameters in the classical problem\n",
-    "        adjacency_matrix:  the adjacency matrix generated from the graph encoding the classical problem\n",
-    "    Returns:\n",
-    "        the problem-based Hmiltonian H's list form generated from the graph_adjacency matrix for the given graph\n",
-    "    \"\"\"\n",
-    "    H_list = []\n",
-    "    # Generate the Hamiltonian H_c from the graph via its adjacency matrix\n",
-    "    for row in range(N):\n",
-    "        for col in range(N):\n",
-    "            if adjacency_matrix[row, col] and row < col:\n",
-    "                # Construct the Hamiltonian in the list form for the calculation of expectation value\n",
-    "                H_list.append([1.0, 'z'+str(row) + ',z' + str(col)])\n",
-    "\n",
-    "    return H_list"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "我们可以查看生成矩阵 $H_c $ 的具体形式，并且获取它的特征值信息："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 5,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "[ 4.  0.  0.  0.  0. -4.  0.  0.  0.  0. -4.  0.  0.  0.  0.  4.]\n",
-      "H_max: 4.0   H_min: -4.0\n"
-     ]
-    }
-   ],
-   "source": [
-    "# Convert the Hamiltonian's list form to matrix form\n",
-    "H_matrix = pauli_str_to_matrix(H_generator(N, classical_graph_adjacency), N)\n",
-    "\n",
-    "H_diag = np.diag(H_matrix).real\n",
-    "H_max = np.max(H_diag)\n",
-    "H_min = np.min(H_diag)\n",
-    "\n",
-    "print(H_diag)\n",
-    "print('H_max:', H_max, '  H_min:', H_min)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 3. 搭建 QAOA 电路\n",
-    "\n",
-    "通过交替地摆放两个参数可调的电路模块，我们得以搭建QAOA电路\n",
-    "\n",
-    "$$U_x(\\beta_P)U_c(\\gamma_P)\\dots U_x(\\beta_1)U_c(\\gamma_1),$$\n",
-    "\n",
-    "其中放置的次数记为 $P$。具体地，模块一是由描述问题哈密顿量的矩阵生成，即\n",
-    "\n",
-    "$$U_c(\\gamma)=e^{-i \\gamma H_c },$$\n",
-    "\n",
-    "其中 $i= \\sqrt{-1}$ 是虚数单位， $\\gamma\\in [0, \\pi]$ 是可以调节的参数。模块二是\n",
-    "\n",
-    "$$U_x(\\beta)=e^{-i \\beta H_x },$$\n",
-    "\n",
-    "由描述驱动哈密顿量的另一个矩阵生成 \n",
-    "\n",
-    "$$H_x =X_1+X_2+X_3+X_4. $$\n",
-    "\n",
-    "$\\beta\\in [0, \\pi]$ 也是一个可调参数，算符 $X=\\begin{bmatrix} 0 & 1\\\\ 1 & 0\\end{bmatrix}$ 是作用在量子比特上的 Pauli-X 门，例如 $X_1$ 实际数学表达式为 $X_1\\otimes I_2\\otimes I_3\\otimes I_4$。\n",
-    "\n",
-    "QAOA 电路的每一模块可以进一步分解为若干个作用在单比特和两比特上的含参的量子门，如图所示:\n",
-    "\n",
-    "\n",
-    "<!--\n",
-    "![QAOA.png](https://release-data.cdn.bcebos.com/PIC%2FQAOACir.png) \n",
-    "-->\n",
-    "\n",
-    "<img src=\"./figures/QAOAcircuit.png\" width=\"600\" >\n",
-    "\n",
-    "其中，模块 $U_x(\\beta)$ 可以分解为在每个量子比特上作用绕 $X$ 方向转动的量子门 $R_x(\\beta)= e^{-i\\beta X}$，而模块 $U_c(\\gamma)$ 则可分解为作用在两比特上的 $ZZ$ 门 $R_{zz}(\\gamma)= e^{-i\\gamma Z\\otimes Z}$。\n",
-    "\n",
-    "此外，我们可以设置交叉放置两个模块的次数，记为 QAOA 电路的层数 $P$。于是输入\n",
-    "\n",
-    "- 量子电路的初始状态\n",
-    "- 经典问题的邻接矩阵\n",
-    "- 电路比特数目\n",
-    "- 电路层数\n",
-    "\n",
-    "构建标准的 QAOA 量子电路："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 6,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "def circuit_QAOA(theta, adjacency_matrix, N, P):\n",
-    "    \"\"\"\n",
-    "    This function constructs the parameterized QAOA circuit which is composed of P layers of two blocks:\n",
-    "    one block is based on the problem Hamiltonian H which encodes the classical problem,\n",
-    "    and the other is constructed from the driving Hamiltonian describing the rotation around Pauli X\n",
-    "    acting on each qubit. It outputs the final state of the QAOA circuit.\n",
-    "    \n",
-    "    Args:\n",
-    "        theta: parameters to be optimized in the QAOA circuit\n",
-    "        adjacency_matrix:  the adjacency matrix of the graph encoding the classical problem\n",
-    "        N: number of qubits, or equivalently, the number of parameters in the original classical problem\n",
-    "        P: number of layers of two blocks in the QAOA circuit\n",
-    "    Returns:\n",
-    "        the QAOA circuit\n",
-    "    \"\"\"\n",
-    "\n",
-    "    cir = UAnsatz(N)\n",
-    "    \n",
-    "    #prepare the input state in the uniform superposition of 2^N bit-strings in the computational basis\n",
-    "    cir.superposition_layer()\n",
-    "    # This loop defines the QAOA circuit with P layers of two blocks\n",
-    "    for layer in range(P):\n",
-    "        # The second and third loops construct the first block which involves two-qubit operation\n",
-    "        #  e^{-i\\gamma Z_iZ_j} acting on a pair of qubits or nodes i and j in the circuit in each layer.\n",
-    "        for row in range(N):\n",
-    "            for col in range(N):\n",
-    "                if adjacency_matrix[row, col] and row < col:\n",
-    "                    cir.cnot([row, col])\n",
-    "                    cir.rz(theta[layer][0], col)\n",
-    "                    cir.cnot([row, col])\n",
-    "        # This loop constructs the second block only involving the single-qubit operation e^{-i\\beta X}.\n",
-    "        for i in range(N):\n",
-    "            cir.rx(theta[layer][1], i)\n",
-    "\n",
-    "    return cir"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "在标准 QAOA 的基础上，我们还支持对电路结构进行扩展，进一步探索 QAOA 更多可能性。例如，可以将模块二的驱动哈密顿量 $H_x$ 中的的绕单比特 X 方向转动 $R_x(\\beta)$ 扩展为绕任意方向转动，即量桨中的$U3(\\beta_1, \\beta_2, \\beta_3)$门："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 7,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "def circuit_extend_QAOA(theta, adjacency_matrix, N, P):\n",
-    "    \"\"\"\n",
-    "    This is an extended version of the QAOA circuit, and the main difference is the block constructed\n",
-    "    from the driving Hamiltonian describing the rotation around an arbitrary direction on each qubit.\n",
-    "\n",
-    "    Args:\n",
-    "        theta: parameters to be optimized in the QAOA circuit\n",
-    "        input_state: input state of the QAOA circuit which usually is the uniform superposition of 2^N bit-strings\n",
-    "                     in the computational basis\n",
-    "        adjacency_matrix:  the adjacency matrix of the problem graph encoding the original problem\n",
-    "        N: number of qubits, or equivalently, the number of parameters in the original classical problem\n",
-    "        P: number of layers of two blocks in the QAOA circuit\n",
-    "    Returns:\n",
-    "        the extended QAOA circuit\n",
-    "\n",
-    "    Note:\n",
-    "        If this circuit_extend_QAOA function is used to construct QAOA circuit, then we need to change the parameter layer\n",
-    "        in the Net function defined below from the Net(shape=[D, 2]) for circuit_QAOA function to Net(shape=[D, 4])\n",
-    "        because the number of parameters doubles in each layer in this QAOA circuit.\n",
-    "    \"\"\"\n",
-    "    cir = UAnsatz(N)\n",
-    "\n",
-    "    #prepare the input state in the uniform superposition of 2^N bit-strings in the computational basis\n",
-    "    cir.superposition_layer()\n",
-    "    for layer in range(P):\n",
-    "        for row in range(N):\n",
-    "            for col in range(N):\n",
-    "                if adjacency_matrix[row, col] and row < col:\n",
-    "                    cir.cnot([row, col])\n",
-    "                    cir.rz(theta[layer][0], col)\n",
-    "                    cir.cnot([row, col])\n",
-    "\n",
-    "        for i in range(N):\n",
-    "            cir.u3(*theta[layer][1:], i)\n",
-    "\n",
-    "    return cir"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "搭建 QAOA 量子电路的工作完成后，此时量子电路的输出状态为\n",
-    "\n",
-    "$$|\\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)\\rangle=U_x(\\beta_P)U_c(\\gamma_P)\\dots U_x(\\beta_1)U_c(\\gamma_1)|+\\rangle_1\\dots|+\\rangle_N.$$\n",
-    "\n",
-    "其中每个量子比特的初始状态处于量子叠加态 $|+\\rangle=\\frac{1}{\\sqrt{2}}\\left(|0\\rangle+|1\\rangle\\right)$ 。最终，我们得到量子优化问题的损失函数\n",
-    "\n",
-    "$$F_P=\\min_{\\boldsymbol{\\beta},\\boldsymbol{\\gamma}} \\langle \\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)| H_c|\\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)\\rangle.$$\n",
-    "\n",
-    "因为 QAOA 是一个量子-经典混杂算法，所以搭建完成 QAOA 电路且得到相应的损失函数后，我们可以进一步利用经典的优化算法寻找最优参数 $\\boldsymbol{\\beta},\\boldsymbol{\\gamma}$，从而形成一个完整的闭环网络。\n",
-    "\n",
-    "下面的函数给出了通过 Paddle Quantum 搭建的完整 QAOA 网络："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 8,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "class Net(fluid.dygraph.Layer):\n",
-    "    \"\"\"\n",
-    "    It constructs the net for QAOA which combines the  QAOA circuit with the classical optimizer which sets rules\n",
-    "    to update parameters described by theta introduced in the QAOA circuit.\n",
-    "\n",
-    "    \"\"\"\n",
-    "    def __init__(\n",
-    "        self,\n",
-    "        shape,\n",
-    "        param_attr=fluid.initializer.Uniform(low=0.0, high=np.pi, seed=1024),\n",
-    "        dtype=\"float64\",\n",
-    "    ):\n",
-    "        super(Net, self).__init__()\n",
-    "\n",
-    "        self.theta = self.create_parameter(\n",
-    "            shape=shape, attr=param_attr, dtype=dtype, is_bias=False\n",
-    "        )\n",
-    "\n",
-    "    def forward(self, adjacency_matrix, N, P, METHOD):\n",
-    "        \"\"\"\n",
-    "        This function constructs the loss function for the QAOA circuit.\n",
-    "\n",
-    "        Args:\n",
-    "            adjacency_matrix: the adjacency matrix generated from the graph encoding the classical problem\n",
-    "            N: number of qubits\n",
-    "            P: number of layers\n",
-    "            METHOD: which version of QAOA is chosen to solve the problem, i.e., standard version labeled by 1 or\n",
-    "            extended version by 2.\n",
-    "        Returns:\n",
-    "            the loss function for the parameterized QAOA circuit and the circuit itself\n",
-    "        \"\"\"\n",
-    "        \n",
-    "        # Generate the problem_based quantum Hamiltonian H_problem based on the classical problem in paddle\n",
-    "        H_problem = H_generator(N, adjacency_matrix)\n",
-    "\n",
-    "        # The standard QAOA circuit: the function circuit_QAOA is used to construct the circuit, indexed by METHOD 1.\n",
-    "        if METHOD == 1:\n",
-    "            cir = circuit_QAOA(self.theta, adjacency_matrix, N, P)\n",
-    "        # The extended QAOA circuit: the function circuit_extend_QAOA is used to construct the net, indexed by METHOD 2.\n",
-    "        elif METHOD == 2:\n",
-    "            cir = circuit_extend_QAOA(self.theta, adjacency_matrix, N, P)\n",
-    "        else:\n",
-    "            raise ValueError(\"Wrong method called!\")\n",
-    "\n",
-    "        cir.run_state_vector()\n",
-    "        loss = cir.expecval(H_problem)\n",
-    "\n",
-    "        return loss, cir"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 4. 训练网络\n",
-    "\n",
-    "我们开始训练整个 QAOA 网络，即通过优化参数向量 $\\boldsymbol{\\beta}=(\\beta_1,\\beta_2,\\beta_3,\\beta_4)$ 和 $\\boldsymbol{\\gamma}=(\\gamma_1,\\gamma_2,\\gamma_3, \\gamma_4)$ 来达到求解 $H_c$ 最小特征值的目的。\n",
-    "\n",
-    "与经典机器学习算法一样，首先设置 QAOA 网络里的超参数:\n",
-    "\n",
-    "- 电路比特数目 N\n",
-    "- 电路的层数 P\n",
-    "- 迭代次数 ITR\n",
-    "- 学习步长 LR"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 9,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "N = 4 # number of qubits, or number of nodes in the graph\n",
-    "P = 4 # number of layers \n",
-    "ITR = 120  # number of iteration steps\n",
-    "LR = 0.1  # learning rate"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "然后，灵活调用：\n",
-    "\n",
-    "- 量子电路初始状态：通过调用`superposition_layer()`使每个量子比特处于相干叠加态 $\\frac{1}{\\sqrt{2}}\\left(|0\\rangle+|1\\rangle\\right)$\n",
-    "- 采用标准 QAOA （记为 METHOD=1）或者扩展 QAOA （记为 METHOD = 2）\n",
-    "- 经典优化器 Adam optimizer \n",
-    "\n",
-    "最后，训练模型并保存结果："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 10,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "def Paddle_QAOA(classical_graph_adjacency, N, P, METHOD, ITR, LR):\n",
-    "    \"\"\"\n",
-    "    This is the core function to run QAOA.\n",
-    "\n",
-    "     Args:\n",
-    "         classical_graph_adjacency: adjacency matrix to describe the graph which encodes the classical problem\n",
-    "         N: number of qubits (default value N=4)\n",
-    "         P: number of layers of blocks in the QAOA circuit (default value P=4)\n",
-    "         METHOD: which version of the QAOA circuit is used: 1, standard circuit (default); 2, extended circuit\n",
-    "         ITR: number of iteration steps for QAOA (default value ITR=120)\n",
-    "         LR: learning rate for the gradient-based optimization method (default value LR=0.1)\n",
-    "     Returns:\n",
-    "         the optimized QAOA circuit\n",
-    "    \"\"\"\n",
-    "    with fluid.dygraph.guard():\n",
-    "        # Construct the net or QAOA circuits based on the standard modules\n",
-    "        if METHOD == 1:\n",
-    "            net = Net(shape=[P, 2])\n",
-    "        # Construct the net or QAOA circuits based on the extended modules\n",
-    "        elif METHOD == 2:\n",
-    "            net = Net(shape=[P, 4])\n",
-    "        else:\n",
-    "            raise ValueError(\"Wrong method called!\")\n",
-    "\n",
-    "        # Classical optimizer\n",
-    "        opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
-    "\n",
-    "        # Gradient descent loop\n",
-    "        summary_iter, summary_loss = [], []\n",
-    "        for itr in range(1, ITR + 1):\n",
-    "            loss, cir = net(\n",
-    "                classical_graph_adjacency, N, P, METHOD\n",
-    "            )\n",
-    "            loss.backward()\n",
-    "            opt.minimize(loss)\n",
-    "            net.clear_gradients()\n",
-    "\n",
-    "            if itr % 10 == 0:\n",
-    "                print(\"iter:\", itr, \"  loss:\", \"%.4f\" % loss.numpy())\n",
-    "            summary_loss.append(loss[0][0].numpy())\n",
-    "            summary_iter.append(itr)\n",
-    "\n",
-    "        theta_opt = net.parameters()[0].numpy()\n",
-    "        print(\"Optmized parameters theta:\\n\", theta_opt)\n",
-    "        \n",
-    "        os.makedirs(\"output\", exist_ok=True)\n",
-    "        np.savez(\"./output/summary_data\", iter=summary_iter, energy=summary_loss)\n",
-    "\n",
-    "    return cir"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "调用模型训练结果，输出得到的最优参数向量 $\\boldsymbol{\\beta}^*$ 和 $\\boldsymbol{\\gamma}^*$，并且将 QAOA 的输出结果和真实结果进行比较："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 11,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "Method 1 generates the graph from self-definition using EDGE description\n",
-      "iter: 10   loss: -3.8531\n",
-      "iter: 20   loss: -3.9626\n",
-      "iter: 30   loss: -3.9845\n",
-      "iter: 40   loss: -3.9944\n",
-      "iter: 50   loss: -3.9984\n",
-      "iter: 60   loss: -3.9996\n",
-      "iter: 70   loss: -3.9999\n",
-      "iter: 80   loss: -4.0000\n",
-      "iter: 90   loss: -4.0000\n",
-      "iter: 100   loss: -4.0000\n",
-      "iter: 110   loss: -4.0000\n",
-      "iter: 120   loss: -4.0000\n",
-      "Optmized parameters theta:\n",
-      " [[0.24726127 0.53087308]\n",
-      " [0.94954664 1.9974811 ]\n",
-      " [1.14545257 2.27267827]\n",
-      " [2.98845718 2.84445401]]\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAA2HklEQVR4nO3deXxU5b348c93ZrITSAibEJaAgOwBAmorRdCLWK2o1VbFIr9ea221VVutCwqttrcLtra2Uveder0uFbWKqAWX63UJiCwKIpsEZEtYErIn398f52SYJJPJZJmcJHzfr9e8yDlzlu+TM8w353nO8zyiqhhjjDEN8XkdgDHGmPbNEoUxxpiILFEYY4yJyBKFMcaYiCxRGGOMiSjgdQCtrUePHjpo0CCvwzDGmA5l5cqV+1W1Z7j3Ol2iGDRoELm5uV6HYYwxHYqIbG/oPU+qnkTkDhFZIyKrRWSZiPRtYLvLRGST+7qsreM0xhjjXRvFQlUdq6rZwMvA/LobiEh3YAFwIjAZWCAi6W0apTHGGG8ShaoeDllMAcJ1Dz8DeF1VC1T1APA6MLMt4jPGGHOUZ20UIvIbYA5wCJgWZpN+wI6Q5Tx3XbhjXQFcATBgwIDWDdSYKFVUVJCXl0dpaanXoRjToMTERDIzM4mLi4t6n5glChF5A+gT5q15qrpEVecB80TkZuBqnGqmZlHV+4H7AXJycmzwKuOJvLw8UlNTGTRoECLidTjG1KOq5Ofnk5eXR1ZWVtT7xSxRqOrpUW66GHiF+oliJ3BqyHImsKLFgRkTI6WlpZYkTLsmImRkZLBv374m7efVU09DQxZnARvCbPYaMENE0t1G7BnuOmPaLUsSpr1rzmfUqzaK34nIcKAa2A5cCSAiOcCVqnq5qhaIyB3AR+4+t6tqgTfhGmPMscuTRKGq325gfS5wecjyw8DDbRFT0boi9i7eS/LIZPp8L1zTijHGHJs6Xc/s5qoqquLIuiP4Umz4K2OMCWXfii7xu/V2Vd7GYUxLdenSJebnuPvuuxkxYgSzZ89uleMdPHiQRYsW1Vr3ta99rVWOXWP69OlUVlZG3KakpISpU6dSVeV8ETz55JNkZWWRkJDAxIkTWbVqFQDl5eV84xvfqHW8U089lW3btgFw33338aMf/ajWsUePHs1nn31Wb9tYxHPgwAHOO++8Ro8fLUsUrppEoZX2dK0xjVm0aBGvv/46ixcvbpXjhUsU7733XqscG2D9+vVkZGQQCESuRHn44Yc5//zz8fv97Nixg7lz55KamsrChQvZvHkzl1xyCQDx8fGcdtppPP3002GPs3btWiZMmBBcLi0tZdu2bQwbNqxJcTc3nvT0dAoKCsjPz2/S+RpiicIlATdRVFuiMK1j7bfWNvjKX3r0P3D+0vyI27aGP/3pT4wePZrRo0fz5z//GYAjR45w1llnMW7cOEaPHs3TTz8ddl1dV155JVu2bOHMM8/krrvuYvTo0cH37rzzTn75y18CsG3bNkaMGMEPfvADRo0axYwZMygpKQHg8ccfZ+zYsYwbN47vfe973HTTTWzevJns7GxuuOEGoPadUbj4Ix2/riVLlnDuuecGl8ePH8/u3bu59dZbefTRR3nrrbe46KKLWLx4MbNmzQLgmWeeoaqqiltuuYVLLrmEOXPmsHHjxuBf8eeee26DiXLNmjW1EsXatWsZNmwYfr+/3rYNxQK0KJ6zzjqLl156KWx8TWVtFDXclGl3FKazWblyJY888ggffPABqsqJJ57I1KlT2bJlC3379uVf//oXAIcOHWLp0qX11tV17733snTpUpYvX05RUREPPfRQg+fetGkTTz31FA888ADf+c53eO655xg/fjy//vWvee+99+jRowcFBQUcPnyYdevWsXr16qjjT09PD3v8Sy+9tN4xXnnlFV5++WUAKisrKSgooE+fPnzyySdccMEFvP3224wYMYIVK1ZQM01BTdXQxRdfXOtY27dvZ8KECYwePZqPPvqIcNavX8/5558ffBS1qKiIs88+u952DcUybtw4ysvL2bJlS7PjmTVrFjfeeCNz584NG2NTWKJwBe8oqixRmNYx5qUxUW2XMTODjJkZMYvj3Xff5bzzziMlJQWA888/n3feeYeZM2fy85//nBtvvJGzzz6bKVOmMGbMmHrrWiIrK4vs7GwAJk6cyLZt2zhw4AAXXnghPXr0AKB79+4cPny4wWM0FP8555wT9vh1FRcXU15eTlpaGgAbNmzghBNOAODTTz9l5MiR/PWvf2X69OnBbcDpxQzwl7/8hZEjR/KPf/yDRx55JLje7/cTHx9PYWEhqampwf127NhBz5492bDhaPewq6++OmxP6IZiOf/889m/f3+L4hk+fDgbN25s8PfaFFb15Ap0C9DtG91IHZ/a+MbGdALDhg1j1apVjBkzhltvvZXbb7897LpIAoEA1dXVweW641wlJCQEf/b7/Y02JjdVNMdPTk5GRCgqKgJg48aNDB8+nIKCArp06UJ8fDy5ubmcfvrpteKv+Us+PT2d008/OtDEwIEDgz+XlZWRmJhY63xr165l1KhRtdZ9+umnjB07tl5sDcUyadIkkpKSWhTP9u3bmzRMRySWKFwJxyUw4IYB9J7d2+tQjGlVU6ZM4YUXXqC4uJgjR47wz3/+kylTprBr1y6Sk5O59NJLueGGG1i1alXYdZH07t2bvXv3kp+fT1lZWbB6J5Lp06fzzDPPBBtaCwoKSE1NpbCwsEnxN8UZZ5zB0qVLAafhd8OGDeTm5jJu3DiefPJJBg0aRO/evamqqgp+OV944YX4/X7mzZvHb3/7W5544gmGDRsWbHvIz8+nR48e9QbXW7NmDSNHjqy1bv369YwZU/8Os6FYevXqRXp6eoviWbJkSbB9o6UsURjTyRQXF5OZmRl8rVixgrlz5zJ58mROPPFELr/8csaPH8/atWuZPHky2dnZ/OpXv+LWW28Nuy6SuLg45s+fz+TJk/mP//iPYDVKJKNGjWLevHlMnTqVcePG8bOf/YyMjAy+/vWvM3r06GBjdo0JEyaEjb8pZs2axQsvvADAzJkzOeGEE5g9ezYrVqwgNzeXxx9/HIAZM2bw7rvvAs5I1I888gg+n48FCxYwbtw4nnrqqWC7w/LlyznrrLPqnWvt2rW1EkVBQQGqSp8+9TvyRoqlpfG89NJLrZYoUNVO9Zo4caI2R1VFlZbsKNHSvNJm7W/Mp59+6nUIJoIxY8ZoRUVFcHnu3Lm6bNmyWtusXLlSL7300qiOd9555+nGjRuDy1OnTtWtW7dGtW/dbcPF0pJ4CgoKdMqUKQ1uG+6zCuRqA9+rdkfhqthXwaYfbWLrgq1eh2KMiYE1a9bU6kexZs2aeu0GEyZMYNq0acEObg0pLy/n3HPPbXK/iEixhWvDaG486enpvP32260SG9hTT0E1Tz1Zz2xjjg0rV64Mu/773/9+o/vGx8czZ86cWuvmzp1b6ymlSOpu21AsLYmnNVmicAV7ZtvjscaYZmhKf4XW6NvQlqzqyWVDeBhjTHiWKFw2hIcxxoRniaKGOwSL3VEYY0xtlihcNsy4McaEZ43ZLgkIWb/NOpowjDHGAHZHESQidBndhZQRKV6HYkyz5Ofnk52dTXZ2Nn369KFfv35kZ2eTlpZWb0iJpvjlL3/JnXfe2YqR1rZixYqwI6vGQltM6hTOo48+ytVXXw3ACy+8wKeffupJHM1licKYTiIjI4PVq1ezevVqrrzySq677rrgss93bP9XV9VagxfGap9oWKLo4HY/tptd9++iurz1PxzGeKmqqirsBD+bN29m5syZTJw4kSlTptQaGjvUJ598wsknn8zQoUN54IEHgusXLlzIpEmTGDt2LAsWLAAiTyj0xRdfcPrppzNu3DgmTJjA5s2bAWe+hgsuuCA47pG6Q2cPGjSIm2++mezsbHJycli1ahVnnHEGQ4YM4d577w3ue9pppzFhwgTGjBnDkiVLgnEMHz6cOXPmMHr0aHbs2BGMe//+/Zx88snBeTdqhNsnXBkbmuBp0KBB7N+/H4Dc3FxOPfXUWsd/7733ePHFF7nhhhvIzs4Olr/da2hsj476au5YT6qq6767TtecvUYrCisa39iYOuqOn3P22c4r1K9+5az74IOj61591Vn3178eXZef76ybM6d5sSxYsEAXLlyoqqpbt25Vv9+vH3/8saqqXnjhhfrEE0+oqur06dP1888/V1XV999/X6dNmxb2WGPHjtXi4mLdt2+fZmZm6s6dO/W1117TH/zgB1pdXa1VVVV61lln6VtvvRXxfJMnT9bnn39eVVVLSkr0yJEjunz5cu3atavu2LFDq6qq9KSTTtJ33nlHVVUHDhyoixYtUlXVa6+9VseMGaOHDx/WvXv3aq9evVRVtaKiQg8dOqSqqvv27dMhQ4ZodXW1bt26VUVE/+///i9YlpSUFN29e7dOnjw57NhKdfdpqIzPPvusXn755cH9Dh48GIx33759qqr60Ucf6dSpU1VV9ZFHHtGrrrpKVVUvu+wyfeaZZ6K4irHT1LGerDE7hPjsySfTOYWb4KeoqIj33nuPCy+8MLhdWVlZ2P1nzZpFUlISSUlJTJs2jQ8//JB3332XZcuWBUdyLSoqYtOmTQwYMCDs+QoLC9m5cyfnnXceQK15HCZPnkxmZiYA2dnZbNu2jVNOOQWAc845B4AxY8ZQVFREamoqqampJCQkcPDgQVJSUrjlllt4++238fl87Ny5kz179gDOXA0nnXRS8DwVFRWcdtpp3HPPPUydOjVsWUP3WbZsWdgyTpkypVUneGrvLFGEsFnuTGsKN13x/Pn1182c6bxCde8efv/mqjvBT0lJCdXV1aSlpYWdfrSumqGsQ5dVlZtvvpkf/vCHtd7btm1b2PM1Jb7QCYhq3vP5fLW28/l8VFZWsnjxYvbt28fKlSuJi4tj0KBBwTkcambFqxEIBJg4cSKvvfZag4kidJ+GygiwatUqXnnlFW699VZOO+005s+fX2sip7qTOHVk1kYRwsZ7MseSrl27kpWVxTPPPAM4X4qffPJJ2G2XLFlCaWkp+fn5rFixgkmTJnHGGWfw8MMPB2eO27lzJ3v37m3wfKmpqWRmZgbnhSgrK6O4uLjF5Th06BC9evUiLi6O5cuXs3379ga3FREefvhhNmzYwO9///tGj91QGRua4GnQoEHBAf6ee+65sMeMNElTe2WJIlRN72xLFOYYsXjxYh566CHGjRvHqFGjgg3BdY0dO5Zp06Zx0kkncdttt9G3b19mzJjBJZdcwsknn8yYMWO44IILGv0CfOKJJ7j77rsZO3YsX/va19i9e3eLyzB79mxyc3MZM2YMjz/+eKOTJ/n9fp566in+/e9/s2jRoojbNlTGhiZ4WrBgAddccw05OTn4/f6wx7zoootYuHAh48eP7zCN2aLaub4Uc3JyNDc3t1n7bvzhRsp3lTPs3mEk9EtofAdjQnz22WeMGDHC6zCMaVS4z6qIrFTVnHDbWxtFiIS+CU71k91nGWNMkCWKEIMWDPI6BGOMaXfsb2djWlFnq8o1nU9zPqOWKIxpJYmJieTn51uyMO2WqpKfn1+rD0s0PKl6EpE7gFlANbAXmKuqu+pskw38HeiK0wXuN6r6dCzj2jp/K0fWHSHrjixSRtnggKZpMjMzycvLY9++fV6HYkyDEhMTg50bo+VVG8VCVb0NQER+CswHrqyzTTEwR1U3iUhfYKWIvKaqB2MVlFYpWqE2eZFplri4OLKysrwOw5hW50miUNXDIYspQL1vZlX9POTnXSKyF+gJHIxVXDVDeFg/CmOMOcqzp55E5DfAHOAQMK2RbScD8UDY3ikicgVwBcCAAQOaH5MN4WGMMfXErDFbRN4QkXVhXrMAVHWeqvYHFgNXRzjOccATwP9T1bDjf6vq/aqao6o5PXv2bH7Q1jPbGGPqidkdhaqeHuWmi4FXgAV13xCRrsC/gHmq+n4rhhdWcKwna6MwxpggTx6PFZGhIYuzgHqzpYhIPPBP4HFVfbZN4grYMOPGGFOXV20UvxOR4TiPx27HfeJJRHKAK1X1cuA7wDeADBGZ6+43V1VXxyqotGlpJA9PJnFI054xNsaYzswGBTTGGBNxUEDrmW2MMSYiGxQwRPGmYsp2lJE0NInE/lb9ZIwx0MQ7ChFJEZHvici/YhWQlw4uP0jeXXkUrSryOhRjjGk3Gk0UIhIvIueJyDPAV8B04N6YR+aBYIe76s7VbmOMMS3RYNWTiMwALgZmAMuBx4FJqvr/2ii2Nmf9KIwxpr5IdxRLgcHAKap6qaq+hPM4a+dlPbONMaaeSI3ZE4CLgDdEZAvw3wS/SjunmjsK63BnjDFHNXhHoaqrVfUmVR2CM7xGNhAnIq+6g/B1Olb1ZIwx9UX11JOqvqeqPwEygbuAk2IalUds9FhjjKkvYj8KEekFXAWMcletBxap6rJYB+aFjHMyyDg742gVlDHGmIbvKETk68BH7uLj7gvgA/e9TscX8OGL91miMMaYEJHuKP4InKuqH4ese1FE/gncB5wY08iMMca0C5HaKLrWSRKA08gNpMYsIg8dzj3M5l9sZu/Te70OxRhj2o1IiUJEJD3Myu6N7NdhVR2uovizYsp2lnkdijHGtBuRvvDvApaJyFQRSXVfpwKvAn9ug9jaXPDxWHvqyRhjghpso1DV+0VkF3AHzlNPCnwK/Nrtpd35WM9sY4ypJ+Ljsar6MvBy6DoRSRSRC1X1mZhG5gHrcGeMMfVF1dYgIn4R+aaIPIEzdel3YxuWN4JzZnfuEa2MMaZJGutwNxW4BPgm8CHwdSBLVYvbILY2Jz67ozDGmLoiDTOeB3wJ/B24XlULRWRrZ00SAHE94kiblkbiQJvdzhhjakS6o3gWOBenmqlKRJbgNGh3WokDE+n/s/5eh2GMMe1KpNFjrwWycHponwpsBHqKyHdEpEubRGeMMcZzERuz1bFcVa/ASRqXALOAbW0QW5urLq+mdEcpZbusw50xxtSI2JgNICLJwPHu4jJVfUlEkmIbljfK8sr44povSMxKZOjdQ70Oxxhj2oVIo8fGicifgTzgEeBRYIuI3KSqJSKS3SYRtiHrR2GMMfU1NnpsMjBQVQsBRKQrcKeI/B2YiVMd1XnU9MyutkRhjDE1IiWKbwJDVTX4ramqh0XkR8B+4MxYB9fW7I7CGGPqi9SYXR2aJGqoahWwT1Xfj11Y3gj2zK7yNg5jjGlPIiWKT0VkTt2VInIp8FnsQvKOjR5rjDH1Rap6ugp4XkS+D6x01+UAScB5sQ7MC1b1ZIwx9UUaZnwncKKITMcZZhzgFVV9s00i84Avxcfg3w1G4mzObGOMqdFoPwpV/Tfw7zaIxXO+gI+UUSleh2GMMe2KJ1OaisgdIrJGRFaLyDIR6Rth264ikicif2vLGI0xxji8mvt6oaqOVdVsnImR5kfY9g7g7bYISlXZ9cAudt23qy1OZ4wxHULEROFOWLS8tU+qqodDFlNoYFRaEZkI9AaWtXYMDcl/MZ/8l/MJ82SwMcYckxobFLAKqBaRbq19YhH5jYjsAGYT5o5CRHw4vcOvj+JYV4hIrojk7tu3ryUxBftS2COyxhjjiKbqqQhYKyIPicjdNa/GdhKRN0RkXZjXLABVnaeq/YHFwNVhDvFjnKes8ho7l6rer6o5qprTs2fPKIoUgfsbsUdkjTHG0ehTT8Dz7qtJVPX0KDddDLwCLKiz/mRgioj8GOgCxItIkare1NRYmkICgpar9c42xhhXNI/HPiYi8cAwd9VGVa1oyUlFZKiqbnIXZwEbwpx3dsj2c4GcWCcJsN7ZxhhTVzTzUZwKPIYzWZEA/UXkMlVtyZNIvxOR4UA1sB240j1XDnClql7egmO3iPXONsaY2qKpevojMENVNwKIyDDgKWBic0+qqt9uYH0uUC9JqOqjOPNhxFxC/wT83fxOSjTGGBNVooirSRIAqvq5iMTFMCZPDf6vwV6HYIwx7Uo0iSJXRB4EnnSXZwO5sQvJGGNMexJNovgRzkiyP3WX3wEWxSwiY4wx7UqDiUJE3lTV04DbVfVG4E9tF5Z3vrj+C0q+KOH4u44nKSvJ63CMMcZzke4ojhORrwHniMh/U6d5V1VXxTQyr1Q5L3vqyRhjHJESxXzgNiCT+ncTCkyPVVCe8rv/VnsahTHGtBuRJi56FnhWRG5T1TvaMCZPWT8KY4yprdGxno6lJAHWM9sYY+ryaj6KdssShTHG1GaJoi63jcKqnowxxhFNPwpExI8zgVBwe1X9MlZBeSnjzAxSc1JJHJDodSjGGNMuRDMo4E9whgDfw9FngRQYG8O4PNP1xK5eh2CMMe1KNHcU1wDDVTU/1sEYY4xpf6Jpo9gBHIp1IO3Fkc+OUPBGAWW7yrwOxRhj2oVo7ii2ACtE5F9A8NtTVTvlkB4FrxVw8M2D9PtpPxL6JngdjjHGeC6aRPGl+4p3X52aBOzxWGOMCRXNVKi/AhCRLu5yUayD8lJNPwqbM9sYYxyNtlGIyGgR+RhYD6wXkZUiMir2oXnDOtwZY0xt0TRm3w/8TFUHqupA4OfAA7ENyztW9WSMMbVFkyhSVHV5zYKqrgBSYhaRx+yOwhhjaovqqScRuQ14wl2+FOdJqM6pZphxa6MwxhggukTxfeBXwPPu8jvuuk6p10W96PXdXsEqKGOMOdZF89TTAY7Ol93p+QI2TqIxxoSKNGf2n1X1WhF5CWdsp1pU9ZyYRmaMMaZdiHRHUdMmcWdbBNJeHHz3IPlL8ul2Sjd6zOrhdTjGGOO5SFOhrnR/zFbVv4S+JyLXAG/FMjCvVB6opHhDMYlDbJhxY4yB6B6PvSzMurmtHEe7EWzEtqeejDEGiNxGcTFwCZAlIi+GvJUKFMQ6MK9YPwpjjKktUhvFe8BXQA/gjyHrC4E1sQzKS8FEYVOhGmMMELmNYjuwXURmA7tUtRRARJKATGBbm0TY1mrmzLY7CmOMAaJro/gfjk6BCk7t/TOxCcd7NtaTMcbUFk3P7ICqltcsqGq5iHTaeSnie8eTNj2NpKFJXodijDHtQjSJYp+InKOqLwKIyCxgf0tOKiJ3ALNw7lT2AnNVdVeY7QYADwL9cTr9fVNVt7Xk3I1JHppM8nXJsTyFMcZ0KNFUPV0J3CIiX4rIDuBG4IctPO9CVR2rqtnAy8D8BrZ73N12BDAZJ6kYY4xpQ9GM9bQZOKk1Z7hT1cMhiymEGSJEREbiVHu93lrnjUZVaRUVeyqQeCHhOJsz2xhjGk0UIpIAfBsYBARE3MZe1dtbcmIR+Q0wBzgETAuzyTDgoIg8D2QBbwA3qWq9rnAicgVwBcCAAQNaEhYlm0rYestWUkanMPi3g1t0LGOM6QyiqXpagtOeUAkcCXlFJCJviMi6MK9ZAKo6T1X7A4uBq8McIgBMAa4HJgGDaaBHuKrer6o5qprTs2fPKIoUIe6A9aMwxphQ0TRmZ6rqzKYeWFVPj3LTxcArwII66/OA1aq6BUBEXgBOAh5qaixNIT57PNYYY0JFc0fxnoiMac2TisjQkMVZwIYwm30EpIlIzS3CdODT1owjbGzWj8IYY2qJ5o7iFGCuiGwFygABVFXHtuC8vxOR4TiPx27HebIKEckBrlTVy1W1SkSuB94Up2FkJfBAC84ZHeuZbYwxtUSTKM5s7ZOq6rcbWJ8LXB6y/DrQkoTUZDbWkzHG1BZNojimvjFtmHFjjKktmkTxL5xkIUAizqOqG4FRMYzLM3EZcQz+w2B8CTZ3tjHGQHQd7mo1ZIvIBODHMYvIY754HykjUrwOwxhj2o0m/9msqquAE2MQizHGmHYomp7ZPwtZ9AETgHoD+HUW1eXV7H50N+IXjvvP47wOxxhjPBfNHUVqyCsBp81iViyD8pJWKfkv5VOwtNPO9mqMMU0Sac7sJ1T1e8BBVf1LG8bkKZsz2xhjaot0RzFRRPoC3xeRdBHpHvpqqwDbmvWjMMaY2iK1UdwLvIkzGN9KnMdja6i7vvOpSZ0KqkrNaLnGGHOsavCOQlXvdicMelhVB6tqVsircyYJcBKDDeNhjDFBjTZmq+qP2iKQ9qSm+sl6ZxtjTHQ9s485iYMS0QpF1e4ojDHGEkUYx//xeK9DMMaYdqPRqicRSRERn/vzMBE5R0TiYh+aMcaY9iCaDndvA4ki0g9YBnwPeDSWQRljjGk/okkUoqrFwPnAIlW9kE46cmyNjVduZO05aynfU+51KMYY47moEoWInAzMxhm+A4IPkHZS1Tj9KOzxWGOMiSpRXAvcDPxTVdeLyGBgeUyj8pgN42GMMUdFMx/FW8BbAG6j9n5V/WmsA/NSzSx3liiMMSa6p57+ISJdRSQFWAd8KiI3xD40D9X0zLbxnowxJqqqp5Gqehg4F3gVZyrU78UyKK/ZwIDGGHNUNIkizu03cS7woqpW4AwK2GkF0p0auYr9FR5HYowx3oumZ/Z9wDbgE+BtERkIHI5lUF7rfkZ3uk7qSvKwZK9DMcYYz0XTmH03cHfIqu0iMi12IXmv66SuXodgjDHtRjSN2d1E5E8ikuu+/giktEFsxhhj2oFo2igeBgqB77ivw8AjsQyqPTiw/AC7H9tNdWW116EYY4ynommjGKKq3w5Z/pWIrI5RPO3Gnif3ULG3grTT0kjMTPQ6HGOM8Uw0dxQlInJKzYKIfB0oiV1I7UNC/wQAyr4s8zgSY4zxVjR3FFcCj4tIN3f5AHBZ7EJqHxIHJFK0soiyHZYojDHHtmieevoEGCciXd3lwyJyLbAmxrF5quaOonRHqceRGGOMt6KpegKcBOH20Ab4WYziaTcSBzjtEnZHYYw51kWdKOqQlpxURO4QkTUislpElolI3wa2+4OIrBeRz0TkbhFp0XmbIiHTbaPIK0OrO3VHdGOMiai5iaKl35wLVXWsqmYDLwPz624gIl8Dvg6MBUYDk4CpLTxv1PwpfuKPiychM4Gqwqq2Oq0xxrQ7DbZRiEgh4ROCAEktOWlIFRY4nffCnUeBRCDePWccsKcl522qYfcNow1vYowxpl1qMFGoamosTywivwHmAIeAekOCqOr/ichy4CucRPE3Vf2sgWNdAVwBMGDAgNaMsdWOZYwxHVVzq54aJSJviMi6MK9ZAKo6T1X7A4uBq8PsfzwwAsgE+gHTRWRKuHOp6v2qmqOqOT179mzVcqgqVUes6skYc+yKph9Fs6jq6VFuuhh4BVhQZ/15wPuqWgQgIq8CJwPvtFqQjSjZWsKWX2whrlccw+4Z1lanNcaYdiVmdxSRiMjQkMVZwIYwm30JTBWRgDsfxlQgbNVTrCT0TwBxemeX7y1vy1MbY0y74UmiAH7nVkOtAWYA1wCISI6IPOhu8yywGViLMxfGJ6r6UlsG6Qv4SJ3oNNUc/qBTT8FhjDENilnVUyR1BhkMXZ8LXO7+XAX8sC3jCid1ciqH3j1E4YeF9PhWD6/DMcaYNufVHUWHkZqTCj4oWltkjdrGmGOSJYpGBFIDpIxMgSooXFXodTjGGNPmLFFEIXWy005xZO2RJu1XUVBByZZOPyK7MaaT86SNoqNJOzWNlDEpJA2JvkO6qrJ1/lbKtpeRmpNKn7l9SBxoEyAZYzoeu6OIQlx6HMnHJzepp7aI0O/qfgAU5hay6SebKHitIFYhGmNMzFiiaKLqivBzaB989yDbfr2Nz3/8OarO0FUpJ6Qw4skRdD+zOyjs+cceG4nWGNPhWKKIUsWBCjbftJlNV20KJoIaReuK2PH7HRR+UEjZjjLKdx3tnBfoFqDvj/oSf1w8lQWVFH1S1NahG2NMi1iiiFKgW4CyvDLKvyqndPvRWe+qy6rZefdOALqf1Z2hfx9K/HHxtfYVEdKmpwFw4M0DbRazMca0BksUURKf0HVyVwAKPzj6mOyexXso/6qchIEJHHf5cSRmJiK++m0Z6dPTSRqWRJexXdosZmOMaQ2WKJqg64lOoqgZzqN4YzH7X9gPApnXZOILNPzrjO8Vz/F/PJ7uM7q3SazGGNNa7PHYJuiS3QWJF0o2lVCRX0HF/grEL2R8K4Pkocleh2eMMTFhiaIJfAk+Uiekcvj9wxz+4DAZ38wgrmcciVnR948o/bKUA28eIOOsDOJ7xTe+gzHGeMyqnpqo60ldSRiQEGzQTh6WjC8u+l/jnn/sYf/z+yn62J5+MsZ0DJYomih1cipVR6roenLXZu3fZYzTmH1kXdOGAzHGGK9Y1VMTBVIDHH/X8fgSmpdjU0anAM5otKpq83IbY9o9u6Nohrj0OPzJ/mbtmzAgAX+qn8r8Ssp326x5xpj2zxJFGxMRUsY4dxVW/WSM6QgsUXigpvqpqcOWG2OMFyxReCBldApxPeIIpFkTkTGm/bNvKg8kDkpk+MPDrSHbGNMhWKLwgCUIY0xHYlVPHqosrKRks02Vaoxp3yxReKR0RymfXfIZ2+7YVm9+C2OMaU8sUXgkITOBQPcAlfmVlG4tbXyHEBUHKsh/NZ99/9xHRUFFjCI0xhiHtVF4RERInZjKgdcPUJhbSNLgpEb3KdtZxs5FO53Hat2bkKJPisj6ZVaMozXGHMvsjsJDqZNTATj84eFGty3ZVsLmGzdzZM0RxC+kTkql69e60uNbPYLbVJVWWTWWMabV2R2Fh7pkd0ECQsnnJVQeqiTQLfzlKM0rZestW6kqrKJLdhcG3DQAf0rtIURUlby78qg6UkX/6/sTlxbXFkUwxhwD7I7CQ/5Ev9NLW6FwZWGD28X3iidpSBKpk1IZeNvAekkCoCK/giPrj3DkkyNsvm4zxZuKYxm6MeYYYonCY6mTU0Gc9oeG+OJ9DLx1IANuGYAvPvwli+8Rz9C/DiV5RDIV+yvYcuMWDiw/EKuwjTHHEEsUHkufns6IJ0fQ53t9aq1XVQpeK6C6shpwZteLNCc3OKPaZv1XFt1ndkcrlLw/5bH36b3WbmGMaRFro/BYuGokgD1P7GHfM/s4/P5hBi0YFPXxfAEf/a7qR8KABL564Cv2PLmHQFqA7md0b1JcJdtKOPjvgxz630NUF7vJKtFHypgUes/pTXwPm8bVmGOFJYp2QlX56sGv6DK+C6WbS9n3zD7wQfezmvYFX6PHt3oQ3yue/FfySZuW1qR9D75zkB1/2FFvfVVRFQffOkjfH/YNrivZUkJ8n/hmz89hjGn/PE0UIvJz4E6gp6ruD/P+ZcCt7uKvVfWxtoyvLR3630Pkv5hP/sv5UA0I9L++P11zmjflKkDXE7uSOjk1OLZUxYEKtt+xnaQhSSQNTyLQLYA/2U/lwUoqCiqCj9p2PbErCf0TSBmTQtq0NBL6JQBQWVBJ6bbS4F2QVinbfrmNqsIqkkcmkzImhYTMBBIyE4jrEYc/xd+sca2qy6upyK+g8lAlWqlQDb4kH/G94/GnNu+Yxpjm8yxRiEh/YAbwZQPvdwcWADk43ctWisiLqtopW2i7fb0bxd8qJv+lfAAyr8kkbUpai48b+qW673/2UbKphJJNJbC0znbxQvczu+ML+PDF+xh6z9B6X8iB1ACJAxODyxUHKog/Lp7ig8UcWXOEI2tqz6/R/xf9g2UoWlNE0cdF+FKc41eXVVNdWk1VURX+ZD99LnPaaKorq1l/wfpgh8K6el/Wm14X9AKcu5nCVYUEUgNIgiAB9+UXxOd0aKxRsq0ELVe0Sqkuq0bLNRhDQmYCKSOcOUIqCio49M4h8IHEOcfzJfjwJfrwJfhIGpaEP9FJlOX7y6k+Ug0CCIhPwO/8K/ESfERZVSnLK0OrnKSn1VqrfPF94gmkOv8VKwsrqTxY6RzL5x7TPT5CrSq/ykOVzjFDqXM+X6KPQBfnmNXl1VQerKxzwd0XEEgLBNu/qo5UUV1WfXSbkH8lIMFjqiqVB+ocM4S/iz/44EVVaRXVJdX1z4/z+Qx9LLyysNL5Q8k9Ryhfgg9/kvO7r66sdn73Ec4vfgmWSSsb+ED5qVWmqsNVDR7Tl+QLlqnms9OQhspUl8RL88pUXIVW1C+Tv2ts/pDy8o7iLuAXwJIG3j8DeF1VCwBE5HVgJvBULIP61recf1966ei622+Hjz6C226DyZOddUuXwj33wBlnwNVXO+sKCuCyy6B7d3gs5N7n2mth82a46y44/nhn3T/+AU89BRdfDJdc4vyHOTLtOG54pAeDs2DRaUe/EC67zDn2Y485xwb429/gtdfgqqtg5kxn3Ycfwh13wKRJMH9+/TItea4P3U7pRvGGYn53Xxyrt8dz1eQCxg+uIHl4Mq/+S7n3wZoySRRliueuu4YwonclRR8XsXix8vyKBM7MPMiZGQcIpAf44gu47jroUyr8NHFfcP95qzM5VO7nN9l59Ojvo89lfdwy+TinNI0pA44QSAuwZl8i97yXzuiMUq4YtJu4HnHBMpXv8XNn7z3BY977eS/WHUzih0P3MrZnKaP/OTp4ncYfKuTCbs62h8r9zFudSbd45TfZO8n4VgYpI1K49lr4fLVwlS+fASnONLX/2tmNV3emcWa/g5zV7xDH//V4dlYmcd110OtQGdd22xa2TMeNS2DIH4bwt7/B0lfhrP1fcUqvIgDWHkjivk29GJ1WwpXD9pL5s0zSp6U7ZdpdzZ19NoUvU+9SRj8XUqaDBVyYVrdMVfwmO4+MWRn0vbyvW6ZqrvJtbbBMQxcNJa8s0S1TccNlyk5gyO9Dy5QXZZmquLPPxpaX6ZwM+v4gtEybY1CmHVGWqbJdlmn5ji5IfCdJFCIyC9ipqp9EyH79gNCK8jx3XbjjXQFcATBgwIBWjLRtiQhxPeKJ7xWb4/vifaSMSiFlVArd1kNyAmT+JJksN/n5l0bevyGB1ABp30gjPQ+Sd0Hfi5MZdUlf5y/Czc42cb3i6D2rN1VFVVSXV5NYkEBpqZ/ec3vTa2Dtj2HmzzI54Uw3UX0IyQcgY1IKo+Zn1Por05/so8f5PagqdI6ZUJpAQAIkj0ymy4Daxwx0D5A0OAnxCxVVfgLbAsR38ZF+ejrJJyQHt5N4IW1qGt0zKqEKUt5PJK4kjqSsJFKGVeLv4oeD7u8z0UdCf6daTqsV30YfPvERyAjUnpRKIC4jQMKABMQvxCfH49/lJ5ARIOn4JPypR9t3JADx/eKDdx6+nT58xT4CaQHiMmp3opREIZAeAAV/uQ9fvOCLF6faL7TNyCcEMgLEpTq/u8DhAL54H/4ufgLdA8G/Up3zHz0muHdVKvi6+uo9eOHv4ne2BfxVfnxxgi/JRyA9gMSF/L/2Uev3IYmCxAm+Lr56nUwlQfB3c87jK/M5549z1vkSQ576E8GX6gv+7nwFzra+JB/+bn7nTiykTDXHbKxMvhTf0fNXuOdPdPavWyZ/N//R35N7R+tL8RHo2oIydalTpoBbpq5hytS1TpmqY1clK7F6dFJE3gD6hHlrHnALMENVD4nINiCnbhuFiFwPJKrqr93l24ASVb0z0nlzcnI0Nze3NYpgjDHHDBFZqao54d6L2R2Fqp7eQDBjgCyg5m4iE1glIpNVdXfIpjuBU0OWM4EVMQnWGGNMg9q8w52qrlXVXqo6SFUH4VQpTaiTJABeA2aISLqIpOM0fL/WxuEaY8wxr131zBaRHBF5EMBtxL4D+Mh93V7TsG2MMabteN7hzr2rqPk5F7g8ZPlh4GEPwjLGGONqV3cUxhhj2h9LFMYYYyKyRGGMMSYiSxTGGGMiilmHO6+IyD5gexN36wHUG5Swg7KytF+dqTxWlvapJWUZqKo9w73R6RJFc4hIbkM9EjsaK0v71ZnKY2Vpn2JVFqt6MsYYE5ElCmOMMRFZonDc73UArcjK0n51pvJYWdqnmJTF2iiMMcZEZHcUxhhjIrJEYYwxJqJjPlGIyEwR2SgiX4jITV7H0xQi0l9ElovIpyKyXkSucdd3F5HXRWST+2+617FGS0T8IvKxiLzsLmeJyAfu9XlaROIbO0Z7ICJpIvKsiGwQkc9E5OSOel1E5Dr387VORJ4SkcSOdF1E5GER2Ssi60LWhb0W4rjbLdcaEZngXeT1NVCWhe7nbI2I/FNE0kLeu9kty0YROaO55z2mE4WI+IF7gDOBkcDFIjLS26iapBL4uaqOBE4CrnLjvwl4U1WHAm+6yx3FNcBnIcu/B+5S1eOBA8B/ehJV0/0FWKqqJwDjcMrU4a6LiPQDfoozC+VowA9cRMe6Lo8CM+usa+hanAkMdV9XAH9voxij9Sj1y/I6MFpVxwKfAzcDuN8FFwGj3H0Wud95TXZMJwpgMvCFqm5R1XLgv4FZHscUNVX9SlVXuT8X4nwZ9cMpw2PuZo8B53oSYBOJSCZwFvCguyzAdOBZd5MOURYR6QZ8A3gIQFXLVfUgHfS64ExHkCQiASAZ+IoOdF1U9W2g7lw2DV2LWcDj6ngfSBOR49ok0CiEK4uqLlPVSnfxfZzZQMEpy3+rapmqbgW+wPnOa7JjPVH0A3aELOe56zocERkEjAc+AHqr6lfuW7uB3l7F1UR/Bn4BVLvLGcDBkP8EHeX6ZAH7gEfcarQHRSSFDnhdVHUncCfwJU6COASspGNel1ANXYuO/p3wfeBV9+dWK8uxnig6BRHpAjwHXKuqh0PfU+f553b/DLSInA3sVdWVXsfSCgLABODvqjoeOEKdaqYOdF3Scf4yzQL6AinUr/ro0DrKtWiMiMzDqY5e3NrHPtYTxU6gf8hypruuwxCROJwksVhVn3dX76m5XXb/3etVfE3wdeAcEdmGUwU4HaeeP82t8oCOc33ygDxV/cBdfhYncXTE63I6sFVV96lqBfA8zrXqiNclVEPXokN+J4jIXOBsYLYe7RzXamU51hPFR8BQ9wmOeJyGnxc9jilqbh3+Q8BnqvqnkLdeBC5zf74MWNLWsTWVqt6sqpnu1LgXAf9W1dnAcuACd7OOUpbdwA4RGe6uOg34lA54XXCqnE4SkWT381ZTlg53Xepo6Fq8CMxxn346CTgUUkXVLonITJwq23NUtTjkrReBi0QkQUSycBroP2zWSVT1mH4B38R5UmAzMM/reJoY+yk4t8xrgNXu65s4dftvApuAN4DuXsfaxHKdCrzs/jzY/XB/ATwDJHgdX5RlyAZy3WvzApDeUa8L8CtgA7AOeAJI6EjXBXgKp32lAudu7z8buhaA4DwJuRlYi/O0l+dlaKQsX+C0RdR8B9wbsv08tywbgTObe14bwsMYY0xEx3rVkzHGmEZYojDGGBORJQpjjDERWaIwxhgTkSUKY4wxEVmiMO2eiKiI/DFk+XoR+WUrHftREbmg8S1bfJ4L3VFkl9dZ31dEnnV/zhaRb7biOdNE5MfhzmVMU1iiMB1BGXC+iPTwOpBQIT2To/GfwA9UdVroSlXdpao1iSobpx9Ma8WQBgQTRZ1zGRM1SxSmI6jEmQv4urpv1L0jEJEi999TReQtEVkiIltE5HciMltEPhSRtSIyJOQwp4tIroh87o45VTMvxkIR+cgd5/+HIcd9R0RexOmhXDeei93jrxOR37vr5uN0jnxIRBbW2X6Qu208cDvwXRFZLSLfFZEUd/6BD93BBWe5+8wVkRdF5N/AmyLSRUTeFJFV7rlrRkD+HTDEPd7CmnO5x0gUkUfc7T8WkWkhx35eRJaKM1fDH0J+H4+6sa4VkXrXwnReTfmLyBgv3QOsqfniitI4YATOsMxbgAdVdbI4Ezz9BLjW3W4QzvDLQ4DlInI8MAdn+IZJIpIA/K+ILHO3n4Az/v/W0JOJSF+ceRom4szRsExEzlXV20VkOnC9quaGC1RVy92EkqOqV7vH+y+coUy+L85kNB+KyBshMYxV1QL3ruI8VT3s3nW97yaym9w4s93jDQo55VXOaXWMiJzgxjrMfS8bZyTiMmCjiPwV6AX0U2dOCiRkchzT+dkdhekQ1BkV93GcSXSi9ZE6c3aU4QxjUPNFvxYnOdT4H1WtVtVNOAnlBGAGzpg/q3GGbs/AGSsH4MO6ScI1CVihzgB6NaN4fqMJ8dY1A7jJjWEFkAgMcN97XVVr5iUQ4L9EZA3OcBT9aHwI81OAJwFUdQOwHahJFG+q6iFVLcW5axqI83sZLCJ/dccWOhzmmKaTsjsK05H8GVgFPBKyrhL3Dx4R8QGhU3KWhfxcHbJcTe3Pft1xbBTny/cnqvpa6BsicirOsOFtQYBvq+rGOjGcWCeG2UBPYKKqVogzAm9iC84b+nurAgKqekBExgFnAFcC38GZ+8AcA+yOwnQY7l/Q/0PtaTe34VT1AJwDxDXj0BeKiM9ttxiMM4Daa8CPxBnGHREZJs7kQ5F8CEwVkR7iTDl5MfBWE+IoBFJDll8DfiIi4sYwvoH9uuHM5VHhtjUMbOB4od7BSTC4VU4DcModllul5VPV54Bbcaq+zDHCEoXpaP4IhD799ADOl/MnwMk076/9L3G+5F8FrnSrXB7EqXZZ5TYA30cjd+DqDEd9E84Q3J8AK1W1KcNvLwdG1jRmA3fgJL41IrLeXQ5nMZAjImtx2lY2uPHk47StrKvbiA4sAnzuPk8Dc90quob0A1a41WBP4s7LbI4NNnqsMcaYiOyOwhhjTESWKIwxxkRkicIYY0xEliiMMcZEZInCGGNMRJYojDHGRGSJwhhjTET/H4PHImkhifUHAAAAAElFTkSuQmCC\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "classical_graph, classical_graph_adjacency = generate_graph(N, 1)\n",
-    "\n",
-    "opt_cir = Paddle_QAOA(classical_graph_adjacency, N =4, P=4, METHOD=1, ITR=120, LR=0.1)\n",
-    "\n",
-    "# Load the data of QAOA\n",
-    "x1 = np.load('./output/summary_data.npz')\n",
-    "\n",
-    "H_min = np.ones([len(x1['iter'])]) * H_min\n",
-    "\n",
-    "# Plot loss\n",
-    "loss_QAOA, = plt.plot(x1['iter'], x1['energy'], \\\n",
-    "                                        alpha=0.7, marker='', linestyle=\"--\", linewidth=2, color='m')\n",
-    "benchmark, = plt.plot(x1['iter'], H_min, alpha=0.7, marker='', linestyle=\":\", linewidth=2, color='b')\n",
-    "plt.xlabel('Number of iterations')\n",
-    "plt.ylabel('Loss function for QAOA')\n",
-    "\n",
-    "plt.legend(handles=[\n",
-    "    loss_QAOA,\n",
-    "    benchmark\n",
-    "],\n",
-    "    labels=[\n",
-    "            r'Loss function $\\left\\langle {\\psi \\left( {\\bf{\\theta }} \\right)} '\n",
-    "            r'\\right|H\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle $',\n",
-    "            'The benchmark result',\n",
-    "    ], loc='best')\n",
-    "\n",
-    "# Show the plot\n",
-    "plt.show()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "\n",
-    "## 5. 解码量子答案\n",
-    "\n",
-    "当求得损失函数 $\\langle \\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)| H_{\\rm Cut}|\\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)\\rangle$ 的最小值以及相对应的一组参数 $(\\boldsymbol{\\beta}^*,\\boldsymbol{\\gamma}^*)$ 后，我们的任务还没有完成。为了进一步求得 Max-Cut 问题的解，需要从 QAOA 输出的量子态 \n",
-    "\n",
-    "$$|\\psi(\\boldsymbol{\\beta}^*,\\boldsymbol{\\gamma}^*, P)\\rangle=\\sum_{i=1}^{2^4}\\lambda_i |\\boldsymbol{x}_i\\rangle$$\n",
-    "\n",
-    "中解码出经典优化问题的答案。上式中  $\\boldsymbol{x}_i=x_1x_2x_3 x_4\\in \\{0, 1\\}^4$，对应着经典问题的一个可行解。物理上，解码量子态需要对量子态进行测量，然后统计测量结果的概率分布：\n",
-    "                 \n",
-    "$$ p(\\boldsymbol{x})=|\\langle \\boldsymbol{x}|\\psi(\\boldsymbol{\\beta}^*,\\boldsymbol{\\gamma}^*,P)\\rangle|^2.$$\n",
-    "              \n",
-    "\n",
-    "多数情况下，某个比特串出现的概率越大，意味着其对应的 Max-Cut 问题最优解的可能性越大。\n",
-    "\n",
-    "此外，Paddle Quantum 提供了查看 QAOA 量子电路输出状态的测量结果概率分布的函数："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 12,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    },
-    "scrolled": true
-   },
-   "outputs": [
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEWCAYAAABrDZDcAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAbM0lEQVR4nO3de9hcZX3u8e+dcBRQQRAtCYbWUMUDqAHZtdsDgg1bDVBROSkqNraSCpe2CluLgnZv1MqubAI1ioh2S/BsqhGwKnZrt5iAKASMpAgSFI0iB2UDRu7+sVZgmMw775r3XWtm8q77c11zZdbpt34TwvxmPetZzyPbREREe80adQIRETFaKQQRES2XQhAR0XIpBBERLZdCEBHRcikEEREtt9WoExjUrrvu6nnz5o06jYiILcqVV175S9u79dq2xRWCefPmsXr16lGnERGxRZF080Tb0jQUEdFyKQQRES2XQhAR0XIpBBERLZdCEBHRcikEEREtl0IQEdFyKQQRES23xT1QFlu2ead8ecrH3nTmi2vMJCI2yRVBRETLpRBERLRco4VA0kJJayWtk3RKj+2vkbRB0tXl6/VN5hMREZtr7B6BpNnAUuAQYD2wStIK29d17Xqx7SVN5REREf01eUVwALDO9o227weWA4c1eL6IiJiCJgvBHsAtHcvry3XdXibpB5I+I2lur0CSFktaLWn1hg0bmsg1IqK1Rn2z+F+AebafDnwVuLDXTraX2V5ge8Fuu/WcVyEiIqaoyUJwK9D5C39Oue5Btn9l+75y8SPAsxrMJyIiemiyEKwC5kvaS9I2wFHAis4dJD2+Y3ERcH2D+URERA+N9RqyvVHSEuBSYDbwUdtrJJ0BrLa9AniTpEXARuB24DVN5RMREb01OsSE7ZXAyq51p3W8PxU4tckcIiKiv1HfLI6IiBHLoHMRLZJB/6KXXBFERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES03KSFQNJzJO1Qvj9O0lmSnlAluKSFktZKWifplD77vUySJS2onnpERNShyhXBecA9kvYF3gL8B/DxyQ6SNBtYChwK7AMcLWmfHvvtBJwEXDFA3hERUZMqhWCjbQOHAefYXgrsVOG4A4B1tm+0fT+wvIzR7d3Ae4F7K+YcERE1qlII7pZ0KvAq4MuSZgFbVzhuD+CWjuX15boHSXomMNf2lyvmGxERNatSCF4J3Ae8zvZtwBzg/dM9cVlQzqJobpps38WSVktavWHDhumeOiIiOkxaCMov/88C25arfgl8vkLsW4G5HctzynWb7AQ8Fbhc0k3AgcCKXjeMbS+zvcD2gt12263CqSMioqoqvYb+AvgM8KFy1R7AFyrEXgXMl7SXpG2Ao4AVmzbavtP2rrbn2Z4HfAdYZHv1YB8hIiKmo0rT0InAc4C7AGzfADx2soNsbwSWAJcC1wOfsr1G0hmSFk095YiIqNNWFfa5z/b9kgCQtBXgKsFtrwRWdq07bYJ9n18lZkRE1KvKFcE3Jf13YHtJhwCfBv6l2bQiImJYqhSCU4ANwDXAGyh+4b+jyaQiImJ4Jm0asv0A8OHyFRERM8yEhUDSp2y/QtI19LgnYPvpjWYWERFD0e+K4KTyz5cMI5GIiBiNCe8R2P5Z+faNtm/ufAFvHE56ERHRtCo3iw/pse7QuhOJiIjR6HeP4K8ofvn/oaQfdGzaCfh204lFRMRw9LtH8EngK8D/pOhCusndtm9vNKuIiBiafoXAtm+SdGL3Bkm7pBhERMwMk10RvAS4kqL7qDq2GfjDBvOKiIghmbAQ2H5J+edew0snIiKGrd/N4mf2O9D2VfWnExERw9avaegDfbYZOKjmXCIiYgT6NQ29YJiJRETEaPRrGjrI9tcl/Xmv7bY/11xaERExLP2ahp4HfB14aY9tBlIIIiJmgH5NQ+8s/3zt8NKJiIhhqzJ5/WMknS3pKklXSvqgpMcMI7mIiGhelUHnllPMUPYy4Mjy/cVNJhUREcNTZfL6x9t+d8fyeyS9sqmEIiJiuKpcEVwm6ShJs8rXK4BLm04sIiKGo1/30bt5aIyhk4F/LjfNAn4D/E3TyUVERPP69RraaZiJRETEaFS5R4CknYH5wHab1tn+t6aSioiI4Zm0EEh6PcVE9nOAq4EDgf9HxhqKiJgRqtwsPgnYH7i5HH/oGcAdTSYVERHDU6UQ3Gv7XgBJ29r+IfDHzaYVERHDUuUewXpJjwa+AHxV0q+Bm5tMKiIihmfSQmD7iPLtuyR9A3gUcEmjWUVExNBU7TX0TOBPKZ4r+Lbt+xvNKiIihqbKoHOnARcCjwF2BS6Q9I4qwSUtlLRW0jpJp/TY/peSrpF0taRvSdpn0A8QERHTU+WK4Fhg344bxmdSdCN9T7+DJM0GlgKHAOuBVZJW2L6uY7dP2v6ncv9FwFnAwkE/RERETF2VXkM/peNBMmBb4NYKxx0ArLN9Y9mUtBw4rHMH23d1LO5A0fQUERFD1G+sof9N8cV8J7BG0lfL5UOA71aIvQdwS8fyeuDZPc5zIvBmYBvykFpExND1axpaXf55JfD5jvWX15mA7aXAUknHAO8Aju/eR9JiYDHAnnvuWefpIyJar9+gcxduei9pG2DvcnGt7d9ViH0rMLdjeQ79m5SWA+dNkMsyYBnAggUL0nwUEVGjKr2Gng/cQHHj91zgR5KeWyH2KmC+pL3KQnIUsKIr9vyOxReX54mIiCGq0mvoA8CLbK8FkLQ3cBHwrH4H2d4oaQnFJDazgY/aXiPpDGC17RXAEkkHA78Dfk2PZqGIiGhWlUKw9aYiAGD7R5K2rhLc9kpgZde60zren1Q10YiIaEaVQnClpI/w0Axlx/LQjeSIiNjCVSkEfwmcCLypXP6/FPcKIiJiBuhbCMqng79v+0kUT/1GRMQM07fXkO3fA2slpfN+RMQMVaVpaGeKJ4u/C/x200rbixrLKiIihqZKIfi7xrOIiIiR6TfW0HYUN4qfCFwDnG9747ASi4iI4eh3j+BCYAFFETiU4sGyiIiYYfo1De1j+2kAks6n2oijERGxhel3RfDgwHJpEoqImLn6XRHsK2nTxDECti+XBdj2IxvPLiIiGtdvGOrZw0wkIiJGo8pUlRERMYOlEEREtFwKQUREy6UQRES0XL8ni+8GJpwfOL2GIiJmhn69hnYCkPRu4GfAJyi6jh4LPH4o2UVEROOqNA0tsn2u7btt32X7POCwphOLiIjhqFIIfivpWEmzJc2SdCwdw1FHRMSWrUohOAZ4BfDz8vXycl1ERMwAk85HYPsm0hQUETFjTXpFIGlvSV+TdG25/HRJ72g+tYiIGIYqTUMfBk6lHI3U9g+Ao5pMKiIihqdKIXiE7e65CDIsdUTEDFGlEPxS0h9RPlwm6UiK5woiImIGqDJ5/YnAMuBJkm4FfkzxUFlERMwAfQuBpNnAG20fLGkHYJbtu4eTWkREDEPfQmD795L+tHyfh8giImagKk1D35O0Avg0HU8U2/5cY1lFRMTQVCkE2wG/Ag7qWGcghSAiYgao8mTxa6caXNJC4IPAbOAjts/s2v5m4PUU3VE3AK+zffNUzxcREYObtBBIuoAe8xLYft0kx80GlgKHAOuBVZJW2L6uY7fvAQts3yPpr4D3Aa8cIP+IiJimKk1DX+p4vx1wBPDTCscdAKyzfSOApOUUYxY9WAhsf6Nj/+8Ax1WIGxERNarSNPTZzmVJFwHfqhB7D+CWjuX1wLP77H8C8JUKcSMiokZVrgi6zQceW2cSko4DFgDPm2D7YmAxwJ577lnnqSMiWq/KPYLuuYtvA95WIfatwNyO5Tnluu74BwNvB55n+75egWwvo3i6mQULFkw4j3JERAyuStPQTlOMvQqYL2kvigJwFF0T2kh6BvAhYKHtX0zxPBERMQ1V5iN4Tjm8BJKOk3SWpCdMdpztjcAS4FLgeuBTttdIOkPSonK39wM7Ap+WdHX54FpERAxRlXsE5wH7StoXeAvwEeDjTNCe38n2SmBl17rTOt4fPFC2ERFRuyrDUG+0bYqun+fYXgpMtbkoIiLGTJUrgrslnUrRx/+5kmYBWzebVkREDEuVK4JXAvcBJ9i+jaL3z/sbzSoiIoamSq+h24CzOpZ/QnGPICIiZoAqvYYOlLRK0m8k3S/p95LuHEZyERHRvCpNQ+cARwM3ANtTjBZ6bpNJRUTE8FQpBNheB8y2/XvbFwALm00rIiKGpUqvoXskbQNcLel9wM+oWEAiImL8VflCf1W53xKKqSrnAi9rMqmIiBieKr2Gbpa0PfB426cPIaeIiBiiKr2GXgpcDVxSLu+XMYEiImaOKk1D76KYbewOANtXA3s1llFERAxVlULwO9vdzw1kToCIiBmiSq+hNZKOAWZLmg+8Cfj3ZtOKiIhhqXJF8NfAUyjGG7oIuAs4ucGcIiJiiKr0GrqHYirJtzefTkREDNuEhWCynkG2F/XbHhERW4Z+VwT/BbiFojnoCkBDySgiIoaqXyF4HHAIxYBzxwBfBi6yvWYYiUVExHBMeLO4HGDuEtvHAwcC64DLJS0ZWnYREdG4vjeLJW0LvJjiqmAecDbw+ebTioiIYel3s/jjwFOBlcDptq8dWlYRETE0/a4IjqMYbfQk4E3Sg/eKBdj2IxvOLSIihmDCQmA7cw5ERLRAvuwjIlouhSAiouVSCCIiWi6FICKi5VIIIiJaLoUgIqLlUggiIlqu0UIgaaGktZLWSTqlx/bnSrpK0kZJRzaZS0RE9NZYIZA0G1gKHArsAxwtaZ+u3X4CvAb4ZFN5REREf1XmLJ6qA4B1tm8EkLQcOAy4btMOtm8qtz3QYB4REdFHk01De1BMbLPJ+nJdRESMkS3iZrGkxZJWS1q9YcOGUacTETGjNFkIbgXmdizPKdcNzPYy2wtsL9htt91qSS4iIgpNFoJVwHxJe0naBjgKWNHg+SIiYgoaKwS2NwJLgEuB64FP2V4j6QxJiwAk7S9pPfBy4EOSMh9yRMSQNdlrCNsrKWY461x3Wsf7VRRNRhERMSJbxM3iiIhoTgpBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMulEEREtFwKQUREy6UQRES0XApBRETLNVoIJC2UtFbSOkmn9Ni+raSLy+1XSJrXZD4REbG5xgqBpNnAUuBQYB/gaEn7dO12AvBr208E/hfw3qbyiYiI3pq8IjgAWGf7Rtv3A8uBw7r2OQy4sHz/GeCFktRgThER0WWrBmPvAdzSsbweePZE+9jeKOlO4DHALzt3krQYWFwu/kbS2kYyhl27zz0mseqOt0XG0uDXi1vk5xxhrL7x8vc/lHh159bpCRNtaLIQ1Mb2MmBZ0+eRtNr2gnGLVXe8NsSqO14bYtUdrw2x6o5Xd25VNdk0dCswt2N5Trmu5z6StgIeBfyqwZwiIqJLk4VgFTBf0l6StgGOAlZ07bMCOL58fyTwddtuMKeIiOjSWNNQ2ea/BLgUmA181PYaSWcAq22vAM4HPiFpHXA7RbEYpTqbn+puyhrX3MY1Vt3x2hCr7nhtiFV3vMabwHtRfoBHRLRbniyOiGi5FIKIiJZLIYiIaLkUgoiIltsiHihrSjmcxQEUTzhD8VzDd+vswirpSbZ/OOAxjwIWduV1qe07aszrENtfncJxY5mbpCdRDFnSmdcK29fXmNdrbV9QV7yIcdHaXkOSXgScC9zAQw+6zQGeCLzR9mU1necntvccYP9XA+8ELuvK6xDgdNsfH0Ve45ybpLcBR1OMZ7W+I6+jgOW2zxxFXh3HjWXxLI8bywI6jLymkdufAYd35fZF25fUmNdpts+oK96k52txIbgeONT2TV3r9wJW2n7yALHOnmgTcLztRw4Qay3w7O4vCUk7A1fY3nuAWN0P8HXmdZDtHarGGufcJP0IeIrt33Wt3wZYY3v+ALF+0CevvW1vWzVWGW8si2d5zFgW0GHlNcXc/hHYG/h4V26vBm6wfdIo8pquNjcNbcVD/yE73QpsPWCs1wJvAe7rse3oAWMJ6FWdHyi3DeK/AscBv+lxjgMGjLXpuHHM7QHgD4Cbu9Y/vtw2iN2BPwN+3SOvfx8wFsDbgWdNVDwpvlAqmaR4PmYKuZ1A7wJ6FrAGqPyFO0kB3X1UeTWQ23/r9YNH0sXAj4DKhUDSXX3y2n7AvKalzYXgo8AqSct5aJTUuRS/Os4fMNYq4Frbm31RSHrXgLH+HrhK0mUdee1J8Qvy3QPG+g5wj+1v9shrKiO4jmtuJwNfk3RDV15PBJYMGOtLwI62r+6R1+UDxoLxLZ6bchjHAlpnXnXndq+k/W2v6lq/P3DvgLHuAPa3/fPuDZJu2Xz35rS2aQignChnEZu3Q143YJxdgHtt31NTXjtT/MPtblPu/oc8dOOam6RZbH7jf5Xt348uK5B0PHAaRdPQZsXT9scGiPUV4H22v9Fj27/Zfu6AuS0EzqG4T7ZZAR2kzVvS+cAFtr/VY9snbR8zirwayO2ZwHnATjzUojAXuBM40faVA8R6D8X3zXd7bHuv7bdVjTVdrS4Em5Rf5Ni+fZxijStJu9PxhdvrF80oYk0Qf0fb3b+ghxprXIsnjHUBHcu8NpH0OB7+7/a2UeYzXa0tBJL2BN4HHERRzQU8Evg6cEr3TeSKsV5Icbk35ViTnOca208bVSxJ+wH/RDFc+HqKzzmH4jO/0fZVA8R6BsUvq0fx8JuoA8ea5Dy13XSbTqwtqXiW5xhpAa27a/e4dhUfRqwq2nyP4GLgH4FjN/3KUDHP8sspeiscOIpYkv58ok3A4wbIqdZYpY8Bb7B9Rdd5DgQuAPYdINYFdcWS9OaJNgE7DpBTrbHKePvRo3hKuoOaiudUYlVwHUVzzNBj9evaLWngrt11x+vjMur7O6sz1qTaXAh2tX1x54ryS3y5pEFvfNYZ62Lg/9D7BuN2I4wFsEP3FzeA7e9IGqgras2x/gfwfmBjj22DPj1fZywY0+JZHjeuBfSDwMETde0GKnftrjveJF3FHz1IUnXGmq42F4IrJZ0LXMjDew0dD3xvhLF+APyD7Wu7N0g6eISxAL4i6csUXR47P+ergUEfpqkz1lXAF3rdqJP0+hHGgvEtnjC+BbTOrt11x6uzq3idsaalzYXg1RT9lU+nq9cQg3cfrTPWycBE/YuPGGEsbL9J0qFs/sTnUtsrRxWL4n+oiaY4HXT+1zpjwfgWTxjfAlpn1+6649XZVbzOWNPS2pvFEcMyQcFbMYWCV3esPwZut72hx7bdB7kJXWes8pgn0/tzDtS1u+54dXYVr7vb+bRyaWshkLQVxa/4w+kaMwQ4v/upxhHEOoLioZqxiFXhXMtsL06siC1PmwvBRRRdFS/k4WOGHA/sYvuVibVZvF0m2gR83/acxNos3qOAUyl+je5OceP+FxTF+MzuoSeGFasr3uHAY2vKbdqxJjnPV2wfWkesuuONa6wq2nyP4FnefMyQ9cB3VAxillib20Dx2H/n0Agulx+bWD19iuJ5khdseuiofBjpNeW2F40oVme853fFO34auU07Vvn0bs9NwH4D5FR7vHGNNV1tLgS3S3o58FnbD8CDTzO+nM3HJEmswo3AC23/pHuDBh8bpQ2xAObZfm/nivKL8kxJrx1hrH7x3ivpdSOMtQr4Jg8vxps8esBYdccb11jTY7uVL2AeRT/7X1CMGvij8v3FwF6J1TPeicC+E2z768TqecxlwFuB3TvW7Q68DfjXUcUa59yAa4H5E2y7ZQqfs7Z44xpruq/W3iOACXsSfNFTmPyiDbHKeLVNGNKSWDsDp5TxNjUt/Zyia/GZHmC8oTpjjXNuko4ErrG92Si0kg63/YWqseqON66xpqu1cxarmPzikxTtv1eUL4CLJJ2SWD3jvZViyAwB3y1fmmJuMz4WgO1f236b7SfZ3qV8PdnFyJKHjyrWOOdm+zO9vhxLOw8Sq+544xpr2oZ5+TFOL4pmkq17rN+GYqahxNpCchvXWBXO9ZNxjDXOueVzNvNq883iOie/aEOscc5tXGOhGmfHqjNW3fHGNVbd8cY11nS1uRCcTH2zWrUh1jjnNq6xoN7ZseqeRnNcc8vnnNrnnLLWFgLbl0jamxomv2hDrHHObVxjleqc+rLuaTTHNbd8zql9zilrda+hiIhoca+hiIgopBBERLRcCkHMaJLmSPqipBsk3SjpHEnbVjiu5xy7ks5QOamPpJMlPWKC/V4i6XuSvi/pOklvKNcfLmmfCuevtF9EHVIIYsaSJOBzFBOmzAfmA9sD75tqTNun2f7XcvFkYLNCIGlrYBnwUtv7As8ALi83Hw5U+YKvul/EtOVmccxYkl4IvNP2czvWPZLiGYG5wJHAAttLym1fopja8/LyiuDDFKNm3gYcZXuDpI9R9Pb4A+AfgLXAL22/oOMcuwA/BJ5g+/93rP+T8tg7y9fLgIOAxRQPrK0DXkUx8mT3fgBLgd2Ae4C/sP3DWv6iovVyRRAz2VOAh02daPsu4CaK5wL62QFYbfspFCNEvrMrztnATymGhH5B17bbKcbYuVnSRZKOlTTLxZSEK4C/tb2f7f8APmd7//LK4XrghAn2W0Yx6N2zgL8Bzh34byNiAq19jiBiEg9QjNIK8M8UTUyV2X69pKcBB1N8cR9CMW9At6dKeg/FsMM7Apd27yBpR+BPgE8XrV0ATHqfI6KqFIKYya6jaP55UNk09DiKJp2n8vCr4u36xBq4DdX2NcA1kj4B/JjeheBjwOG2vy/pNcDze+wzC7jD9n6D5hBRRZqGYib7GvAISa8GkDQb+ABwTtl2fxOwn6RZkuZSPE28ySweKiLHAN/qEf9uYKfulZJ2lPT8jlX78dDYRd3H7AT8rLzBfGyv2GVz1o9VTDKECvv2++ARg0ghiBnLRU+II4Ajy7GDfgU8YPvvy12+TfFL/TrgbOCqjsN/Cxwg6VqKG7pn9DjFMuASSd/oWi/grZLWSroaOJ2HrgaWA39bdi39I+DvKIYH/zbFDWYm2O9Y4ARJ3wfWUIz7H1GL9BqK1ih77VwEHGH7qsn2j2iLFIKIiJZL01BERMulEEREtFwKQUREy6UQRES0XApBRETLpRBERLRcCkFERMv9J2lfuxp4ZulDAAAAAElFTkSuQmCC\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "with fluid.dygraph.guard():\n",
-    "    # Measure the output state of the QAOA circuit for 1024 shots by default\n",
-    "    prob_measure = opt_cir.measure(plot=True)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "最后，再次利用参数代换 $|x \\rangle\\rightarrow z=2x-1\\in\\{-1, 1\\}$，可以从量子答案中解码得到 Max-Cut 问题的可行解。 此时，记 $z_i=-1$ 的顶点属于集合 $S^\\prime$ 以及 $z_j=1$ 的顶点属于集合 $S$，这两个顶点集合之间存在的边就是该图的一个可能得最大割方案。 \n",
-    "\n",
-    "选取测量结果中出现几率最大的比特串，然后将其映射回经典解，并且画出对应的最大割方案：\n",
-    "\n",
-    "- 蓝色顶点属于集合 $S$\n",
-    "- 红色顶点属于集合 $S^\\prime$\n",
-    "- 虚线表示被割的边"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 13,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    },
-    "scrolled": true
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "The output bitstring: ['0101']\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAb4AAAEuCAYAAADx63eqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAqN0lEQVR4nO3dfVhUdfo/8PcIM8pAaqJg9tPETDdhmfEBtlTMHqyvZutDtqW2is8kYqF5rWiG7FpqD6ZorrZfEHNTs02o1l1bCx/QvBQRBk2/66qZUisYKsqgDjjn98c4yDBnhgFm5syZ835dlxdyzhHv3St5c5/z+dxHJQiCACIiIoVoIXUBRERE3sTgIyIiRWHwERGRojD4iIhIURh8RESkKAw+IiJSFAYfEREpCoOPiIgUhcFHRESKEih1AURKc/YscPEiYDIB994L9OwJtGoldVVEysHgI/KCGzeATz8Fli8HfvwR0Ggsx81mQBCAKVOApCTgwQelrZNICVSc1UnkWf/4B/DSS5aAq6wUv0atBgICgBdeADIyLJ8TkWcw+Ig86K9/BaZPt3R8rggKAmJigF277naFROReDD4iD9m7Fxg61PXQswoKAn77W2DrVs/URaR0XNVJ5CEzZ4qF3koA0QACAKgALLb7czduAF99BRQXe7hAIoVi8BF5QEEBcO6c6BkA7QB0dvrnb90CPvjA/XUREYOPyCNWrLCEl71NAPYA0Dv987dvW1aBXrvm9tKIFI/BR+QBu3ZZwqs5NBrg0CH31ENEdzH4iDzg+vXmfw1BAK5caf7XISJbDD4iD2jhpn9ZgRwxQeR2DD4iD2jb1j1fp31793wdIrqLwUfkAePGCQgMrBE5878A4gEcvfN5zp3Pc+yubNECePRRj5RHpGgMPiI3KykpQX7+RNTUVIuc3Q9gI4ALdz433Pm8yOaqli2B3/2uFH//e7YnSyVSJAYfkZsIgoDMzExERkZi795NAA4AqN/1ZQEQRH4ttrlKpRJw4MAEjB49GuPGjUN5ebmnyydSDI4sI3KDkpISTJs2DTt37qxzNAKWDev3NuprabXAwIG78K9/PV17LCwsDOvWrcOoUaPcUi+RkjH4iJrp2rVr6Natm2hX1rv3VJw+vQ5GYwDM5oa/llYLTJlyA5mZHWA0Gu3Ojx07FqtXr0ZoaKg7SidSJN7qJGqm1q1bIyEhweaYVqtFeno6jhxZj8LCAPTrZxk+7Wh7wj33WF5Ku2oVkJ4ehAMHDkCv19tdt2XLFvTq1QvZ2Xz2R9RU7PiI3ODWrVvo168fjh8/jkGDBiEzMxMP1nur7MmTwMqVwJYtlvfytWgBqFRAnz7A/PnAc8/ZBmN1dTXefvttLFmyBDU19itE2f0RNQ2Dj6gRBEGASqUSPVdQUIADBw5g1qxZaNHADvaaGsuvVq0a/jsNBgPi4+NRVFRkd47P/ogaj8FH5AJBELBhwwZs27YNO3bsQEBAgFf/fnZ/RO7D4CNqQP0Vm++88w7mzZsnSS3Our/w8HAUFxcjLCzM+4URyQgXtxA5UHdfXt1tCosWLcLJkyclqUmn0+Hw4cNYvHgxAuutlBkyZAhDj8gFDD4iESUlJRg2bBimTJmCa/VeiteiRQscP35cosoAtVqN1NRUHDlypHblZ8eOHbFq1SrJaiKSE97qJKrD+iwvOTnZLvAAIC4uDpmZmejevbsE1dmzPvvr06cPnnvuOanLIZIFBh/RHeLTVyyCgoKwbNkyl1Zs+hJBEDBz5kw888wzGDlypNTlEPkE+fwLJvIQR8/yrAYNGoTi4mLMnj1bVqEHANu2bavd7jB+/HjO/CQCOz5SOGddnlarxbJly5CYmCi7wAOA0tJSREZG2oRdeHg41q1bx+6PFE1+/5qJ3GjRokVOu7ykpCRZhh4A5OXloaKiwuZYaWkpuz9SPHZ8pGiXLl1CZGQkLl26BED+XV59RUVFiI+Ph8FgsDvH7o+USv7/somaoUOHDli7di0A/+jy6tPr9Q73/bH7I6Vix0eKcPnyZbRr187h+R07dmDo0KF+E3hi2P0RWfjvv3Ii3F2xGRER4fRVPs8++6xfhx7A7o/Iih0f+a36KzbDwsJw4sQJDnKG8+5vxIgRyMnJ8X5RRF7i3z/ikiI52pdXVlaGpKQkCSvzHY66v5YtW2L58uUSVkbkeQw+8ivOZmxqtVo8+uij4E0OC41Gg9TUVOTn50On0wEAlixZgp49e0pcGZFn8VYn+YWGZmw6eis6WZhMJmRlZWHKlCkO3zV469YttGzZ0suVEbkfOz6SvYa6vPT0dOzevZuh54RGo8H06dMdht7hw4fRrVs3pwuEiOSCHR/JFrs877h58yb69OlT+w5Cvu2d5I4dH8kSuzzvSUtLs3nx7pYtW9CrVy92fyRbDD6SpatXryI3N9fuuD9OX5FaSEiI3b6/srIyjB49GuPGjeO+P5IdfmcgWYqKikJqamrt5+zyPGfhwoU2b3uvi90fyRGf8ZFs1dTU4JFHHkFwcDCf5XmB9W3vS5YsQU1Njd15PvsjuWDwkU+7cOECKisr8fDDD4uev3TpEkJDQ3lb04sMBgPi4+NRVFRkdy4sLKz2xbdEvorfLcgnCYKAjIwMREVF4aWXXoLJZBK9rkOHDgw9L9PpdA5nfvLZH8kBv2OQz7lw4QKGDRuGqVOn4tq1ayguLsZbb70ldVlUh1qtRmpqqtNnf4WFhd4vjMgFvNVJPsM6Y3POnDl2WxQCAwNRXFzs8JYnSUfs2d/06dOxfv16iSsjEsfgI59Q/00KdfnbW9H9lfXZ3+XLl3Hs2DG0bt1a6pKIRDH4SFKcvuJfqqurce7cOTz00EOi5y9evAi1Ws2VnyQp/vhMkuH0Ff+jVqsdhp4gCJg0aRIiIyP5vj+SFIOPvM7R+/KsOH3FP2VlZWHnzp182ztJjrc6yatMJhNGjBjBZ3kK89NPPyEyMhIVFRU2x8PDw7Fu3TqMHDlSmsJIkfjdhbxKo9GgY8eOdsfZ5fm3Dh06IDk52W7fH7s/kgI7PvK6q1evIioqCj/99BO7PIUpKipCfHw8DAaD3Tl2f+Qt/E5DXte2bVt89NFH7PIUSK/XO5z6wu6PvIUdH3lESUkJPv74Y6SkpEClUoleIwiCw3Pk/9j9kVT4Yza5Vd0VmwsXLsTmzZsdXsvQUzZXu7+qqiqJKiR/xeAjtxHbl5eUlISLFy9KXBn5Ko1Gg9TUVOTn50On09mdv3jxIlq1aiVBZeTPGHzUbM725V25cgUffvihRJWRXIh1f8HBwcjIyODzX3I7PuOjZuGMTXI367O/GTNm4JVXXpG6HPJDDD5qEs7YJE8ymUwIDAx0+APTpk2bMGzYMM78pCbhj+HUaJyxSZ6m0Wgcht6+ffswYcIE9OrVC9nZ2V6ujPwBOz5yGbs8kprRaER0dDTOnj1be2zs2LFYvXo1uz9yGTs+ctnChQvZ5ZGkVq9ebRN6gOVt7+z+qDHY8ZHLTp8+jejoaNy4caP2GLs88iaxt73Xxe6PXMGOj1zWvXt3LF26FAC7PJKGWq1Gamoqjhw5Ar1eb3ee3R+5gh0fNYrZbMbrr7+OxMREBh5Jit0fNRWDj2yUlJQgISEBCxYsQP/+/aUuh6hBBoMB8fHxKCoqsjsXFhaGdevWYdSoUd4vjHwWb3USANvpKzt27MCkSZNsnuUR+SqdTudw5mdZWRlGjx6NlJQUiaojX8TgI9F9eadOncKiRYskrozINc6e/alUKgwfPlyawsgnMfgUzNmMTQAoKCgQfXZC5KvEur/XXnsNAwYMkLgy8iV8xqdQnLFJ/s5gMGDJkiXYuHEjtFqt1OWQD2HwKQynrxBZnDlzBkuWLMF7773HlZ8Kwx/nFYQzNokszGYzJk+ejKysLERGRiInJ0fqksiLGHwK0NCzvEGDBqG4uBhJSUm8tUmKsHbtWuzbtw/A3be9jxs3DuXl5RJXRt7AW50KUFhYiD59+tgd57M8UiJBEBAXF4cDBw7YneO+P2XgdzsF6N27N2bOnGlzjF0eKZVKpUJubq7TfX/s/vwbOz6FqKysRHR0NEpLS9nlEd1hfdu7wWCwO8fuz38x+PyIIAiorKzEPffcI3o+Pz8f7dq14+IVojpMJhOWLl3KmZ8KwuDzE9Z9ebdv38bXX38NlUoldUlEssKZn8rBe10yV3/F5q5du/CXv/xF6rKIZMeVmZ979+6VqDpyJ3Z8MuZo+kpISAiOHz+OBx54QKLKiORNrPsbPnw4vvzyS95N8QPs+GSooX15ffr0AX+eIWq6+t1f27ZtsX79eoaen2DHJzMlJSWYPn06/vnPf9qd4748IvczGAy4cOGCwzc81NTU2N0aJd/G4JMJQRCQlZWF5ORkVFRU2J3njE0iaUydOhVVVVVc+SkjDD4ZYJdH5Jt27tyJoUOHAuDKTzlh8Pmwhrq8uLg4bNiwgV0ekQQqKioQFRWFkpISm+Pc9+f72CL4uK1bt9qFXlBQEFatWoU9e/Yw9IgkUl5ejvbt29sd37JlC3r16oXs7GwJqiJXsOPzcefPn0dUVBSuX78OwNLlZWZmonv37hJXRkTV1dV4++23HU59GTduHNLT09n9+Rh2fD6uS5cuWLFihU2Xx9Aj8g1qtRqpqak4cuQI9Hq93fnNmzfzfX8+iB2fDxAEAQcPHkT//v0dni8pKUHnzp29XBkRuYrdn3yw45PYhQsXMGzYMAwYMAC5ubmi16hUKoYekY9j9ycf7PgkYp2+MmfOHFy7dg0A0LVrVxw7dgwhISESV0dEzeHsjQ9RUVEoLCzkpncJseOTgLXLmzp1am3oAcC5c+ewcOFCCSsjInfQaDRITU1Ffn4+dDpd7fGAgABkZWUx9CTG4PMiQRCQkZGBqKgo0RmbgwYNwuzZsyWojIg8Qa/X28z8TElJQd++faUuS/F4q9NLHL1JAeD0FSIlOHbsGHr27AmNRiN6/syZM9yX6yX8LuthDb1JYdCgQSguLkZSUhJDj8iP/frXv3YYeidPnkRkZCTGjRuH8vJyL1emPPxO60ElJSUYNmwYpkyZYvMsD7B0eenp6di9ezd/yiNSsJqaGsTHx+PWrVuc+uIlDD4Pyc7OZpdHRA1asWIFDh8+XPu59W3v7P48h991PeS+++5DZWWlzTF2eURU3zPPPCO674/dn+cw+DzkkUcewdy5c2s/Z5dHRGLqv+29LnZ/nsFVnR508+ZNDBw4EBMnTuSKTSJqkMFgQHx8PIqKiuzO8X1/7sPgawbr+/IGDhyIhx56SPQas9nMwCMilzU085Pv+2s+Bl8T1d2XN2DAAOzduxcBAQFSl0VEfqKh7i8zMxPPPvus9wvzA2xFGklsX96BAweQnp4ucWVE5E8aevZ38+ZNiSqTP3Z8jeBs+kpoaCh+/PFHBAcHS1AZEfmz+t3fiy++iK1bt0pblIyx43OBK9NXDh06xNAjIo+o2/3df//9WL16tdQlyRo7vgZcuHAB06dP54xNIvIJVVVV0Gq1oud++eUXHDhwACNGjPByVfLC79YOuPImBe7LIyJvcxR6AJCUlISRI0dy318D2PGJYJdHRHKzfft2PP/887Wfc9+fYwy+en744Qfo9Xq7odKApcvLzMzkuDEi8ikmkwndunXDTz/9ZHeO+/7ssWWpp2vXrnjiiSdsjnHGJhH5Mo1Ggx07dnDmp4vY8Ym4ePEiIiMjcfnyZXZ5RCQbnPriGgafA9u2bUNpaSmf5RGR7HDmp3OKDD5BELBhwwYUFhZyPwwR+SV2f44pLvjqT1/56quvMHz4cImrIiLyjIa6v7179+JXv/qV9wuTkGLu4TmavjJ9+nRcuXJFwsqIiDzH2czPLl26oHv37hJVJh1FBF9JSQmGDRuGKVOm2G1TqKiowJEjRySqjIjI89RqNVJTU3HkyJHalZ8ajQZZWVl2YagEfn2r0/osLzk5mfvyiIhw99lfcHAwXn/9danLkYTfBp+zNylw+goRkWMffPABIiIiMHLkSKlL8Qi/Cz52eURETVdYWIjY2FjU1NRg3LhxSE9P97uVn34VfOzyiIiazmQyISYmBsXFxbXHwsPDsW7dOr/q/vwq+AYPHoy9e/faHWeXR0TUsD179mDIkCF+v+/Pr1qflStX2qxQ4oxNIiLXDR48GPn5+dDpdHbn/Gnmp18Fn16vx8KFCwHwfXlERE2h1+sd7vsrKyvD6NGjZf++P1ne6rxx4waCgoJEz5lMJmzduhUvv/wyA4+IqBmKiooQHx8Pg8Fgd07OMz9llQzW6SsPPPAAjh8/LnqNRqPBhAkTGHpERM2k1+uRn5/vd92fbDq++is2+/bti4MHD0KtVktcGRGR/3M287Nv377Iz8+HSqXyfmFN4PNtkaMZmwUFBXjnnXckrIyISDmczfz805/+JJvQA3w8+JzN2NRqtWjXrp1ElRERKY/YzM9JkyZh6NCh0hbWSD55q5PTV4iIfFt1dTVWrlyJadOmoW3btqLXmM1mn1xv4fngu3IFOHwYuHoVUKuB8HDgN78BHEwE5/QVIiL5++9//4snn3wSb731lvOVn2fOAP/3f8C1a0BwMPDgg0BkpGeLEzzlyBFBeOklQWjVShDatBGEe+4RhNatLR9DQwXhj38UhIsXay83m81CRkaG0Lp1awGA3a9BgwYJp0+f9li5RETkHmazWXjuuedqv3+PHTtW+OWXX+5eUF0tCNnZgvCb3whCUNDdjGjTRhC0WkHo1UsQNm4UhBs3PFKf+zu+GzeAF14Adu8Gbt4EzGbx61q1snxcuRIlzz7LLo+IyE/89a9/xe9//3ubY7X7/nQ64IkngMuXgevXHX+RkBBAowH+9S+gb1+31ufeNxDeuAHExQEnTlh+78zNm5aPc+bg2v79oqHHZ3lERPJTVlaGwMBAm5mfZWVlmD96NJ5Wq6G9fRsqR02RVWWl5eOgQZbwGzDAbfW5t+MbMQLYtavh0KtPq0V6nz54df/+O5+yyyMikrP6+/7aAjgBIAxAQGO/WOvWQFEREBHhltrclyoGg2joTQXwMIAQAKEAhgGwm7lSVYVZp08jPCyMMzaJiPxA/X1/0wC0gX3o3QSQBEsgBgEYAOBQ/S9WVQW8/bbbanNfxzdxIvDJJ8Dt27Z/AYBHAEQB+AbAOQD3AzgNoFXdC0NC8PPateg4fjwDj4jIjxgKC3F/bCzai7zuKAHAelgyIgrAp7A0SmcBtK97oVYLlJZanv01k3sS5to1YNs2u9ADgCMADgL4C4Ddd479BEvLa6OyEp02bWLoERH5GV1pKUJbtbI7XgYgE5Yg+hbAFgDjAVwHsKb+xSoVsGmTW+pxT8oYDEDLlqKn6q7FMd35GADgPrGLDx50SzlERORD8vKgsi5WqeN7ANUAusByqxMA+t35WFT/YqMR+Pprt5TjnuC7cgVo4I5pJYBJd34/Bw6Cr7GLYoiIyPeVloofvvOx7s3L4DsfL4r9ATe9BcI9wafRWNpQBy4BeBzAdwCmAVju6MKARq/1ISIiXydymxMAwu98rNsLWn/fUewPOLiz2FjuCb6OHUWf7wHAjwAGwvKsLwXAR7AseBF1771uKYeIiHxIly6WkZX19AKgBnAed7u//DsfdfUvVqksX8cN3BN8Oh3Qpo3oqf4ATsFyD7cKwGt3fh2ud11NQABu19vpT0REfuCFF3Bb5K5gOIB4AGYATwJ4CZYFLiEAZtW/WKsFJk2qf7RJ3BN8KhUwb56lsHp+vvPxPIBVdX7VX9VZc/s2hu3YIfqSQyIikiej0YhXV65Enskken4VgJmwdHw5sGx/+xeADvUvbN8eGDjQLTW5bx/f1atAp05NWqBSDctWh2cABAYG4o033kBKSgo0Go1bSiMiIu/Ly8vDpEmTcObMGfwPgM9gu5DFZVot8O67wMyZbqnLfZvm2rYFsrJEuz5nzAAqcHfFZ01NDRYvXozY2Fh2f0REMmQ0GvHqq6/isccew5kzZwAAOwH8DYCxsV+sZUsgNhaYPt1t9bn/7Qzr1gFz5rjW+QUEwNymDeY/+ije3bHD7rRWq8X58+cRGhrq1hKJiMhzJk6ciI8//tjuePeuXXGgc2eEHT1q2ZfXkKAgQK+3DKl2w8QWK/ePSUlIALKzgYcesrxUUGwSS6tWlhR/5hm0KC7GO3//O7KzsxEeHm5z2R/+8AeGHhGRzLz55pvQ1rv7l5iYiMJjxxC2dy+waJHlLuE994h/geBgy6+EBGDPHreGHuDJN7ALguXN6++9Zym8stLy1vV77wXi4y3/gzp1svkj5eXlmD17NjZv3ozevXvj0KFDUIssgSUiIt+2evVqzJ49GxEREcjIyMDjjz9ue0F1NfDFF5aMOHXKMoi6VSvLloXkZODFFxv96MxVngu+ZsjJyUG3bt0QHR0ter6mpgaBge59lSARETWOs+/FZrMZ6enpmDp1KkLc3LE1l08GnzPV1dWIi4vD0KFDufKTiEgieXl5mDp1KjIzMzHAjS+J9QbZvQph2bJlOHToEFd+EhFJoO6KzVOnTmHSpEmoqqqSuqxGkVXHV1xcjH79+qG6urr2GPf9ERF5R919eXUlJydjxYoVElXVeLLq+C5duoR27drZHOO+PyIizxLbl1dXTU0NZNRDySv4nnzySXz//fcYN26c3TmDwYCYmBikpaXZdIRERNR0eXl50Ol0SE9Ptwu3iIgI5ObmIj09HSonb+jxNbK61VlXTk4OEhISUCrynie9Xo+srCzodHbzvYmIyAVGoxELFizA6tWrRbu5xMRELFu2zOdWbLpCtsEH2O77q8/67G/BggXcC0hE1AiOnuUBcLwvT0ZkHXxWOTk5mDFjBsrKyuzOsfsjInKNP3d5dflF8AGW7i8pKQlbtmyxOzdx4kRkZWV5vygiIhnZv38/4uLi7I77Q5dXl6wWtzgTGhqKzZs3Y/v27QgLC6s93rFjR1ktsyUiksrAgQMxa5btK2ATExNRXFzsN6EH+FHHV1fd7u/LL7/Ec889J3VJRESyYDQaER0dDUEQ/KrLq8svg88qPz8fMTExoucEQcC5c+cQERHh5aqIiKRlNBpRWVlp90Ycq5MnT6Jz586yf5bniN/c6hTjKPQAYNu2bejRowfS0tJgMpm8WBURkXSs+/LGjx/vcNP5ww8/7LehB/h5x+dIWVkZevXqhfLycgCATqdDVlYW9Hq9tIUREXmI2IrNP//5z0hISJC4Mu9TZPCNGTMGn3/+uc0xzvwkIn/laF9eSEgIjh07hq5du0pTmET8+lanIy+//LLdvW3O/CQif9PQjM2JEyeiffv2ElQmLUV2fIBrU1/Y/RGRXPn79JXmUGzwWTmb+clnf0QkN0qZvtIcig8+gN0fEfmHffv2YfLkyezyGsDgq6Oh7u+TTz5BZGSkBJURETlmMpkwb948pKeni55nl2dLkYtbHBk5cqTD9/39+9//RmBgoARVERE5p1arcerUKbvjERER2L17N9asWcPQq4PBV09oaCg++eQTZGdn26z8XLJkCXr27ClhZURE4lQqFT766CO0bt269tisWbNQXFyMwYMHS1eYj+KtTiesz/7OnTuHffv2ISAgQOqSiIgcysjIwFtvvYXMzEwGnhMMPhcYjUYEBweLnissLIRKpeLKTyLyOKPRiB07duB3v/ud6HlBEHDjxg1otVovVyYvvNXpAkehd/PmTYwfPx4xMTGc+UlEHmWdsfniiy/im2++Eb1GpVIx9FzA4GuGxYsX4+TJk5z6QkQeIzZ9ZerUqbh+/brElckXg6+JTp8+jXfffdfmmMFgYPdHRG5j7fLS09NtNqP/+OOPWLp0qYSVyRuDr4m6d++Ozz//nDM/icjtGpqxmZiYiAULFkhQmX/g4pZm4tQXInInztj0PAafm3DmJxE1B2dseg+Dz43Y/RFRU7DL8y4Gnwc46/70ej2+++47BAUFSVAZEfma999/H/PmzWOX50Vc3OIBzmZ+xsbGMvSIqFZcXBxUKpXNsYiICOTm5nLGpocw+DxEbOZnly5d7LZAEJGyxcbGYt68ebWfJyYmori4mLc2PYi3Or3A+uxv0qRJeOqpp6Quh4h8zM2bNzFmzBjMnTuXgecFDD4fIAgC5s6di4kTJ0Kn00ldDhG5mdFoxJtvvokZM2agR48eUpejeLzV6QM2bNiADz74AP369UNaWhqqq6ulLomI3MQ6fWXFihWYNGkSbt++LXVJiseOT2IlJSWIjIzEtWvXao/p9XpkZWWx+yOSMUf78t5//33MmTNHwsqIHZ/EPv30U5vQA4CioiJ2f0Qy5mjGJmB5Z15NTY1ElRHA4JPc3LlzsX37doSFhdkcrzvz02AwSFQdETWGKzM2Dx06hMDAQAmqIyve6vQR5eXlSEpKwpYtW+zOWae+LFiwAGq1WoLqiKghnL4iHww+H5OdnY2EhASUlZXZneOzPyLfwxmb8sPg80Hs/ojkgV2ePDH4fJiz7i8xMRFr1qyRoCoiAoDCwkL07duXXZ4MMfh8nFj3FxISgmPHjqFr167SFUakcIIgYMyYMdi+fXvtMXZ58sBVnT4uNDQUmzdvtln5+e677zL0iCSmUqmwdu1ahIaGAuCMTTlhxycj5eXl+OijjzB//ny7ae5WZrMZLVrw5xkid3L27+qrr75CSEgIA09GGHx+ZO/evUhOTkZmZibf9k7kBtYVm1evXsXGjRulLofchMHnJ4xGI6Kjo3H27Fm+7Z3IDeqv2Pziiy/w29/+VuKqyB14T8xPpKSk4OzZswBsp74UFRVJWxiRzDiavjJjxgxcvnxZwsrIXRh8fsBsNuPKlSt2xw0GA2JiYpCWlgaTySRBZUTy4mzGZlBQEEpKSiSqjNyJwecHWrRogU2bNtm87d2KMz+JGubKjM3i4mJER0dLUB25G5/x+Rnr2943b95sd45TX4jscfqK8jD4/FROTg4SEhJQWlpqd44zP4k4Y1PJGHx+jDM/icSxy1M2Bp8COJr5qVKpcOjQIcTExEhUGZH3CYKAmJgYFBQU2J1jl6cMXNyiAKNGjcKJEycwduxYm+OvvfYaQ48UR6VSITMz0+ZlsBEREcjNzcWaNWsYegrAjk9hrN1fmzZtUFRUBK1WK3VJRJL44x//iNTUVHZ5CsTgU6Dy8nJcvHgRkZGRoucvXbqEtm3b8tkfyd7PP/+MTp06iZ6rrq5Gfn4++vfv7+WqSGq81alAoaGhDkPPbDZjzJgx3PdHsmbdl9etWzcUFxeLXqNWqxl6CsXgIxsffvgh9u3bh6KiIvTr1w9paWmorq6Wuiwil9WdvnLr1i3Ex8fzv2GyweCjWmfOnMH8+fNrP+fUF5ITR9NXCgsLsWzZMgkrI1/D4KNabdu2xYgRI+yOs/sjX+dsxmZERAQGDhwoUWXki7i4hew42vcHcOoL+RZOX6GmYPCRKFemvvB9fyQlTl+hpmLwkVPOuj+dToesrCy+7Z28il0eNReDjxrUUPe3cOFCLFq0CAEBARJUR0ry3XffYcKECezyqFm4uIUaFBoais2bN2P79u2i7/srKChAixb8T4k8r7y83On78hh65Ap2fNQo9d/317ZtW3z//fcOp2MQuduECROwadMmAOzyqGkYfNQk1vf9vfPOO5gwYYLU5ZCCXLlyBVFRURg1ahSf5VGTMPioySoqKtC6dWuoVCrR81988QWGDh3KlZ/UaHl5eejRo4fdrXWriooKtGnTxstVkb/ggxlqsjZt2jgMvZ07d2LkyJGIjY1FUVGRdwsj2ao7fWXmzJmiqzYBMPSoWdjxkdtVVFQgKioKJSUlALjvj1wjti9v69atePHFFyWsivwRg4/cLjk5GStXrrQ7zn1/JMbZvrwOHTrghx9+QHBwsETVkT/irU5yuzfeeMPube8AYDAYEBMTg7S0NJhMJgkqI1/T0IzNTz/9lKFHbseOjzyGU1/IEU5fISkx+MijOPOT6uOMTZIag4+8gt0fscsjX8HgI69pqPtbu3Ytpk2bJkFl5Gnnz5/HE088wS6PfAIXt5DX1J35GRYWZnNOEAT06dNHosrI0+6//37RzeicsUlSYPCR140aNQonTpywWfmZkpKCvn37SlgVeVJAQAAyMzPRqlUrAJYuLzc3F2vWrOGtTfI63uokSWVnZ2Pt2rXYsWMHF7gowAcffIAzZ87wWR5JisFHPu3kyZP47LPPkJKSArVaLXU51IC8vDwUFBTgtddek7oUIocYfOSzampqMGDAABw+fBh6vR5ZWVnQ6XRSl0UiqqqqsGDBAqSnp0OlUuHgwYOIjY2VuiwiUXzGRz7r/fffx+HDhwEARUVF6NevH9LS0lBdXS1xZVRXXl4eoqOjsWrVKgiCALPZjPj4eNy8eVPq0ohEseMjn3Tr1i306NED58+ftzvH7s83NLQvLycnByNGjJCgMiLn2PGRT2rZsiWOHj0qOvOT3Z/0nM3Y7Nq1K3Jzcxl65LPY8ZHPczb1hd2fdzXU5c2cORPLly/nik3yaQw+kgVXZn4uWLCAKz89iDM2yV8w+EhW2P15H2dskr9h8JHsNNT9HT9+HD179pSgMv/01FNP4dtvv7U7zi6P5IqLW0h2nM38fP755xl6bjZ//ny7Y5yxSXLGjo9krW7316FDB5w4cQLt27eXuiy/k5CQgPXr17PLI7/A4CO/kJ2dDbVajeHDh4ueFwQBKpXKy1XJi7P/j65fv47ly5dj/vz5fJZHssfgI0WYMGECHnzwQa78dCAvLw/JycnIzs5G586dpS6HyKP4jI/83ueff45NmzZh8eLFiI2NhcFgkLokn2E0GvHqq6/iscceQ0FBAaZNmya6cpPIn7DjI7/2yy+/IDIy0mb7A/f9WTjal5eRkYHJkydLVBWR57HjI792+vRpu2M1NTWK7v7qdnlim9H/85//SFAVkfcw+MivPfLII3Zve7dS4sxPZzM2rW9FX7p0qUTVEXkHb3WSYih56gunrxDdxeAjRVHizE/O2CSyxeAjRVJC98cuj0gcg48Uy1n3179/f+zfv1/Wm943btyI+Ph4u+Ps8kjpGHykePW7P41Gg6NHjyIyMlLiyprHbDZjyJAhyM3NrT3GLo+IqzqJMGrUKJuVn4sXL5Z96AFAixYtkJGRgeDg4NoVm2vWrGHokeKx4yOqY9euXXj88ccRGBgoev7SpUvo0KGDl6tyzmg0QqVSQavVip7Py8tD7969GXhEd7DjI6pjyJAhDkPv6NGjeOCBB5CWlgaTyeTlysTt27cPOp1O9NVBVnFxcQw9ojrY8RG5wGQyoV+/fjh27BgAQKfTISsrC3q9XpJ6rCs209PTa4/t2bMHjz32mCT1EMkJOz4iFyxZsqQ29ADAYDAgJiZGku7P2uXVDT0AmDx5MoxGo1drIZIjBh+RC/r27Yvw8HCbY3VnfhYVFXm8hoZmbA4bNszjNRD5A97qJHJReXk5Zs+ejc2bN9uds059SUlJgUajcfvf3dD0lczMTAwePNjtfy+RP2LwETVSTk4OEhISUFpaaneuoWd/VVXA118DFy8CJhNw771A//5A9+7if1dD01dmzZqFpUuXcvEKUSMw+IiaoLHd36lTwMqVwMaNQGAgUF0NmM2AWg3U1AC9ewN/+APw7LOW8wC7PCJPYfARNUPD3d9G7NypQ1oacPu2JfAcCQkBHnwQ+PLLKrz/fgpnbBJ5CIOPqJmcdX9jxpzGP/7xIKqqXPtaGg0QHm6GRvMIzpzJtznHGZtE7sFVnUTNFBoaik8++QTZ2dk2Kz/j4tY3KvQAy3O/0tIWUKu/BXB3QHZiYiKKi4sZekRuwI6PyI2s3d+ePftgNv+IixfFfracCOAbAL8AuAdAPwBLAfSuvSIkBBg6dC2OHHmPXR6RmzH4iDzgs8+uYvLktqisFDs7GEAnAG0A5AI4BaALgB9rr1CpgKefvo2//e0Gn+URuRmDj8gDnn4a2LXLlSuPAugLy1OHmwDuvvm9ZUvghx+A++7zSIlEiiU+jZeImqWgoKEr1gA4AeDbO5/PRd3QA4BWrQCDgcFH5G4MPiIPaHhk5t8A7L3z+/8HYIDdFWYzcPWqW8siInBVJ5FHNDy1bA+AGwByAPwMYAzqPuMDLM/5goLcXxuR0jH4iDwgLMzRmRsAbt/5fSsA/wMgBEANgLM2V5rNwP33e6hAIgVj8BF5wCuvAOIvRD8EoDOAlwC8AsvClmsAOgDoY3PlvfcCfft6tk4iJWLwEXnA5MmWjs1eJwA9AOwCkAHgCoAXYNnW0Kb2Kq0WmDfPcruTiNyL2xmIPOTll4HPPrNMY2ms4GDgp5+ANm0avpaIGocdH5GHfPih5RldYCPXTgcFAZ9+ytAj8hQGH5GHtGkD7N8PPPCAZTO6K4KCgIwMy+uJiMgzGHxEHtSpE3D0qOWZn1ZruYVZn1pt2az+6KPAN98AY8d6v04iJeEzPiIvMRqBrVuB9euB0lLLu/latwaeegp49VXgoYekrpBIGRh8RESkKLzVSUREisLgIyIiRWHwERGRojD4iIhIURh8RESkKAw+IiJSFAYfEREpCoOPiIgUhcFHRESKwuAjIiJF+f/jygxD70htaAAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {},
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "# Find the max value in measured probability of bitstrings\n",
-    "max_prob = max(prob_measure.values())\n",
-    "# Find the bitstring with max probability\n",
-    "solution_list = [result[0] for result in prob_measure.items() if result[1] == max_prob]\n",
-    "print(\"The output bitstring:\", solution_list)\n",
-    "\n",
-    "# Draw the graph representing the first bitstring in the solution_list to the MaxCut-like problem\n",
-    "head_bitstring = solution_list[0]\n",
-    "\n",
-    "node_cut = [\"blue\" if head_bitstring[node] == \"1\" else \"red\" for node in classical_graph]\n",
-    "\n",
-    "edge_cut = [\n",
-    "    \"solid\" if head_bitstring[node_row] == head_bitstring[node_col] else \"dashed\"\n",
-    "    for node_row, node_col in classical_graph.edges()\n",
-    "    ]\n",
-    "nx.draw(\n",
-    "        classical_graph,\n",
-    "        pos,\n",
-    "        node_color=node_cut,\n",
-    "        style=edge_cut,\n",
-    "        width=4,\n",
-    "        with_labels=True,\n",
-    "        font_weight=\"bold\",\n",
-    ")\n",
-    "plt.show()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "source": [
-    "# 参考文献\n",
-    "\n",
-    "[1] [Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv:1411.4028 (2014).](https://arxiv.org/abs/1411.4028)"
-   ]
-  }
- ],
- "metadata": {
-  "kernelspec": {
-   "display_name": "Python 3",
-   "language": "python",
-   "name": "python3"
-  },
-  "language_info": {
-   "codemirror_mode": {
-    "name": "ipython",
-    "version": 3
-   },
-   "file_extension": ".py",
-   "mimetype": "text/x-python",
-   "name": "python",
-   "nbconvert_exporter": "python",
-   "pygments_lexer": "ipython3",
-   "version": "3.7.7"
-  },
-  "pycharm": {
-   "stem_cell": {
-    "cell_type": "raw",
-    "metadata": {
-     "collapsed": false
-    },
-    "source": []
-   }
-  }
- },
- "nbformat": 4,
- "nbformat_minor": 2
-}

tutorial/QAOA/QAOA_CN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# 量子近似优化算法\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 概览\n",
+    "\n",
+    "量子近似优化算法（Quantum Approximate Optimization Algorithm, QAOA）是可以在近期的有噪中等规模量子（Noisy Intermediate-Scale Quantum, NISQ）设备上运行且具有广泛应用前景的量子算法。QAOA 由 Edward Farhi 等人于 2014 年提出[1]，其目的是近似地求解组合优化问题（combinatorial optimization problems）。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 组合优化问题\n",
+    "\n",
+    "在应用数学和理论计算机科学的领域中，组合优化是在一个有限的对象集中找出最优对象的一类课题。简单来说，组合优化问题是指问题的所有解是由离散变量组成的，然后在离散的解集中寻找最优解。组合优化问题涉及的范围很广，且常见于实际生活中，例如飞机航线的设计、快递物流路线的规划等。\n",
+    "\n",
+    "具体来说，一个组合优化问题可以由 $n$ 个比特（bit）和 $m$ 个子句（clause）描述。每个比特的取值为 $0$ 或 $1$，我们用 $z_j$ 表示第 $j$ 个比特的取值。因此，这 $n$ 个比特的取值可以由比特串 $z=z_1z_2\\dots z_n$ 表示。每个子句都是对部分比特的一个限制条件，例如一个子句可以要求第 $2$ 个比特的取值为 $0$，或者可以要求第 $3$ 个比特和第 $5$ 个比特的取值相同，等等。对于第 $j$ 个子句，我们定义一个与之相关的函数\n",
+    "\n",
+    "$$\n",
+    "C_j(z)=\n",
+    "\\begin{cases}\n",
+    "1 & \\text{如果 $n$ 个比特的取值 $z$ 满足子句 $j$ 表明的条件}\\\\\n",
+    "0 & \\text{如果 $n$ 个比特的取值 $z$ 不满足子句 $j$ 表明的条件}\n",
+    "\\end{cases}.\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "例如，如果第一个子句要求第二个比特的取值为 0，那么我们有 $C_1(z_10z_3\\dots z_n)=1$ 和 $C_1(z_11z_3\\dots z_n)=0$。\n",
+    "\n",
+    "由公式（1）中我们对于每个子句定义的函数 $C_j$，我们可以定义该组合优化问题的目标函数（objective function）\n",
+    "\n",
+    "$$\n",
+    "C(z)=\\sum_{j=1}^m w_jC_j(z),\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "其中 $w_j$ 是第 $j$ 个子句的权重（weight）。组合优化问题就是要找到一个取值 $z$ 使得目标函数 $C(z)$ 的值最大，即\n",
+    "\n",
+    "$$\n",
+    "\\underset{z}{\\operatorname{argmax}} C(z).\n",
+    "\\tag{3}\n",
+    "$$"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 量子近似优化算法\n",
+    "\n",
+    "在实际生活中，许多组合优化问题都属于 NP 完全（NP-complete）问题甚至是 NP 困难（NP-hard）问题，这意味着计算机很可能无法高效地解决这样的问题。此时，一种替代方案便是寻找这类问题的近似最优解，而这样的任务通常是可以高效完成的。QAOA 就是一个可以寻找到一个组合优化问题的近似最优解的量子算法。\n",
+    "\n",
+    "#### 编码组合优化问题\n",
+    "\n",
+    "对于上述的一个组合优化问题，有 $n$ 个比特和 $m$ 个子句。QAOA 算法将这个问题转化为了在 $n$ 个量子比特系统上的优化问题，该量子系统的每个计算基态 $|z\\rangle \\in \\{0,1\\}^n$ 对应着原问题中 $n$ 个比特的一种取值 $z$。同时，对于原问题中的第 $j$ 个子句，我们定义一个对角（diagonal）哈密顿量 $H_{C_j}$ 使其满足\n",
+    "\n",
+    "$$\n",
+    "H_{C_j}|z\\rangle = C_j(z)|z\\rangle.\n",
+    "\\tag{4}\n",
+    "$$\n",
+    "\n",
+    "具体我们可以通过下式来构造哈密顿量 $H_{C_j}$：\n",
+    "\n",
+    "$$\n",
+    "H_{C_j} = \\sum_{z\\in\\{0,1\\}^n} C_j(z)|z\\rangle\\langle z|.\n",
+    "\\tag{5}\n",
+    "$$\n",
+    "\n",
+    "例如，假设满足第 $j$ 个子句的取值有 $z^{(1)}$ 和 $z^{(2)}$，那么我们可以定义\n",
+    "\n",
+    "$$\n",
+    "H_{C_j} = |z^{(1)}\\rangle\\langle z^{(1)}| + |z^{(2)}\\rangle\\langle z^{(2)}|.\n",
+    "\\tag{6}\n",
+    "$$\n",
+    "\n",
+    "由此，QAOA 将组合优化问题的目标函数 $C$ 编码成了 $n$ 个量子比特系统上的哈密顿量\n",
+    "\n",
+    "$$\n",
+    "H_C = \\sum_{j=1}^m w_jH_{C_j},\n",
+    "\\tag{7}\n",
+    "$$\n",
+    "\n",
+    "并且\n",
+    "\n",
+    "$$\n",
+    "H_C|z\\rangle = \\sum_{j=1}^m w_jH_{C_j}|z\\rangle = \\sum_{j=1}^m w_jC_j(z)|z\\rangle = C(z)|z\\rangle.\n",
+    "\\tag{8}\n",
+    "$$\n",
+    "\n",
+    "值得注意的是，假设原问题的一个最优解是 $z_\\text{opt}$，那么我们有\n",
+    "\n",
+    "$$\n",
+    "\\langle z_\\text{opt}|H_C|z_\\text{opt}\\rangle = \\langle z_\\text{opt}|C(z_\\text{opt})|z_\\text{opt}\\rangle = C(z_\\text{opt})\\langle z_\\text{opt}|z_\\text{opt}\\rangle = C(z_\\text{opt}).\n",
+    "\\tag{9}\n",
+    "$$\n",
+    "\n",
+    "因此，原组合优化问题的最优解是哈密顿量 $H_C$ 的一个拥有最大本征值（eigenvalue）的本征态（eigenstate）。此外，对于任意量子态 $|\\psi\\rangle$，\n",
+    "\n",
+    "$$\n",
+    "\\langle\\psi|H_C|\\psi\\rangle \\leq C(z_\\text{opt}),\n",
+    "\\tag{10}\n",
+    "$$\n",
+    "\n",
+    "且该式取等号当且仅当 $|\\psi\\rangle$ 是几个最优解的叠加态。由式（9）和式（10）可以得到，\n",
+    "\n",
+    "$$\n",
+    "\\max_{|\\psi\\rangle} \\langle\\psi|H_C|\\psi\\rangle = C(z_\\text{opt})，\n",
+    "\\tag{11}\n",
+    "$$\n",
+    "\n",
+    "并且寻找原组合优化问题的最优解等同于寻找哈密顿量 $H_C$ 的一个拥有最大本征值的本征态，即寻找一个量子态 $|\\psi\\rangle$ 使得\n",
+    "\n",
+    "$$\n",
+    "H_c|\\psi\\rangle = C(z_\\text{opt})|\\psi\\rangle.\n",
+    "\\tag{12}\n",
+    "$$\n",
+    "\n",
+    "找到这样一个量子态 $|\\psi\\rangle$ 后，它很可能并不是一个计算基态，而是几个计算基态的叠加，这其中的每个计算基态都是原组合优化问题的一个最优解。因此，我们对 $|\\psi\\rangle$ 进行计算基上的测量，便能得到原组合优化问题的一个最优解。\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### 寻找近似最优解\n",
+    "\n",
+    "尽管将要解决的组合优化问题的目标函数编码成一个量子系统的哈密顿量 $H_C$ 较为简单，但想要根据式（11）从偌大的希尔伯特空间中找到代表最优解的量子态 $|\\psi\\rangle$ 并不容易。为了找到这样一个量子态，我们需要借助另一个哈密顿量\n",
+    "\n",
+    "$$\n",
+    "H_B = \\sum_{j=1}^n X_j,\n",
+    "\\tag{13}\n",
+    "$$\n",
+    "\n",
+    "其中 $X_j$ 表示作用在第 $j$ 个量子比特上的 Pauli $X$ 门。Pauli $X$ 门的两个本征态分别是 $|+\\rangle$ 和 $|-\\rangle$，它们对应的本征值分别是 $1$ 和 $-1$：\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "X|+\\rangle &=\n",
+    "\\begin{bmatrix}\n",
+    "0&1\\\\1&0\n",
+    "\\end{bmatrix}\n",
+    "\\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "1\\\\1\n",
+    "\\end{bmatrix}\n",
+    "= \\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "1\\\\1\n",
+    "\\end{bmatrix}\n",
+    "= |+\\rangle,\\tag{14}\\\\\n",
+    "X|-\\rangle &=\n",
+    "\\begin{bmatrix}\n",
+    "0&1\\\\1&0\n",
+    "\\end{bmatrix}\n",
+    "\\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "1\\\\-1\n",
+    "\\end{bmatrix}\n",
+    "= \\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "-1\\\\1\n",
+    "\\end{bmatrix}\n",
+    "= -|-\\rangle.\\tag{15}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "因此，$H_B$ 的拥有最大本征值的本征态为\n",
+    "\n",
+    "$$\n",
+    "|s\\rangle \\equiv \\underbrace{|+\\rangle\\otimes\\cdots\\otimes|+\\rangle}_{\\text{共 $n$ 个 }|+\\rangle} = |+\\rangle^{\\otimes n}.\n",
+    "\\tag{16}\n",
+    "$$\n",
+    "\n",
+    "我们将把这个量子态 $|s\\rangle$ 作为算法的初始态。构造出哈密顿量 $H_C$ 和 $H_B$ 后，我们就可以开始寻找原组合优化问题的一个近似最优解了。根据哈密顿量 $H_C$ 和 $H_B$，分别定义酉变换\n",
+    "\n",
+    "$$\n",
+    "U_C(\\gamma) = e^{-i\\gamma H_C}\n",
+    "\\tag{17}\n",
+    "$$\n",
+    "\n",
+    "和酉变换\n",
+    "\n",
+    "$$\n",
+    "U_B(\\beta) = e^{-i\\beta H_B},\n",
+    "\\tag{18}\n",
+    "$$\n",
+    "\n",
+    "其中 $\\gamma$ 和 $\\beta$ 是实数，为可调节的参数。给定任意一个整数 $p\\geq1$ 以及参数 $\\vec{\\gamma}=(\\gamma_1,\\dots,\\gamma_p)$ 和 $\\vec{\\beta}=(\\beta_1,\\dots,\\beta_p)$，我们定义\n",
+    "\n",
+    "$$\n",
+    "|\\vec{\\gamma},\\vec{\\beta}\\rangle = U_B(\\beta_p)U_C(\\gamma_p)\\cdots U_B(\\beta_1)U_C(\\gamma_1)|s\\rangle.\n",
+    "\\tag{19}\n",
+    "$$\n",
+    "\n",
+    "可以看到，整数 $p$ 表示用到的 $U_C,U_B$ 的层数，即分别将 $U_C$ 和 $U_B$ 交替地作用在初始态 $|s\\rangle$ 上 $p$ 次。我们记 $F_p(\\vec{\\gamma},\\vec{\\beta})$ 为哈密顿量 $H_C$ 在式（19）的量子态下的期望值，\n",
+    "\n",
+    "$$\n",
+    "F_p(\\vec{\\gamma},\\vec{\\beta}) = \\langle\\vec{\\gamma},\\vec{\\beta}|H_C|\\vec{\\gamma},\\vec{\\beta}\\rangle.\n",
+    "\\tag{20}\n",
+    "$$\n",
+    "\n",
+    "通过调整参数 $\\vec{\\gamma},\\vec{\\beta}$，我们可以得到\n",
+    "\n",
+    "$$\n",
+    "M_p = \\max_{\\vec{\\gamma},\\vec{\\beta}} F_p(\\vec{\\gamma},\\vec{\\beta})\n",
+    "\\tag{21}\n",
+    "$$\n",
+    "\n",
+    "作为给定层数 $p$ 下的近似最优解。至此，我们将寻找量子态 $|\\psi\\rangle$ 的问题转变为了搜寻参数 $\\vec{\\gamma},\\vec{\\beta}$ 的问题。值得注意的是，$p$ 层酉变换 $U_C,U_B$ 的表达能力强于 $p-1$ 层的表达能力，因此\n",
+    "\n",
+    "$$\n",
+    "M_p \\geq M_{p-1}.\n",
+    "\\tag{22}\n",
+    "$$\n",
+    "\n",
+    "事实上，当 $p$ 足够大时，\n",
+    "\n",
+    "$$\n",
+    "\\lim_{p\\to\\infty} M_p = \\max_z C(z).\n",
+    "\\tag{23}\n",
+    "$$\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### 解码量子答案\n",
+    "\n",
+    "在上一段中，尽管我们将寻找量子态 $|\\psi\\rangle$ 转变为了寻找参数化量子态 $|\\vec{\\gamma},\\vec{\\beta}\\rangle$ 以方便我们的搜索，但同时我们也缩小了搜索的空间，也就是说，在给定层数 $p$ 的情况下，可能并不存在参数 $\\vec{\\gamma},\\vec{\\beta}$ 使得 $F_p(\\vec{\\gamma},\\vec{\\beta}) = C(z_\\text{opt})$。假设参数 $\\vec{\\gamma}^*$ 和 $\\vec{\\beta}^*$ 使得 $F_p$ 最大，即 $F_p(\\vec{\\gamma}^*,\\vec{\\beta}^*) = M_p$，那么在理想情况下量子态 $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ 包含了最优解的信息。但要注意的是，这里只使用了 $p$ 层，因此很可能 $M_p < C(z_\\text{opt})$。因此，一般情况下 $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ 只包含了近似最优解的信息。进一步地，我们假设量子态 $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ 是 $l$ 个计算基态的叠加态，即\n",
+    "\n",
+    "$$\n",
+    "|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle = c_1|z^{(1)}\\rangle + \\cdots + c_l|z^{(l)}\\rangle.\n",
+    "\\tag{24}\n",
+    "$$\n",
+    "\n",
+    "通常情况下，一个态 $|z^{(j)}\\rangle$ 在计算基上测量得到的概率 $|c_j|^2$ 越大，意味着其对应的比特串 $z^{(j)}$ 是最优解的可能性越大。那么我们制备 $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ 并测量，得到一个比特串 $z$ 并计算 $C(z)$ 的值。重复多次这个过程，便能得到一个 $z$ 使得 $C(z)$ 接近甚至超过 $M_p$。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### 绝热定理\n",
+    "\n",
+    "为什么可以用上述的方法来构造量子态 $|\\vec{\\gamma},\\vec{\\beta}\\rangle$？ QAOA 试图找到一个优化问题的近似最优解，一个与之类似的算法是量子绝热算法 [2]（Quantum Adiabatic Algorithm, QAA）。但不同的是，QAA 是为了找到优化问题的最优解而非近似最优解。与 QAOA 类似，QAA 将一个优化问题转化为了求一个哈密顿量的基态的问题，并利用绝热定理（adiabatic theorem）对其求解。考虑一个量子系统的哈密顿量\n",
+    "\n",
+    "$$\n",
+    "H(t) = (1-\\frac tT)H_B + \\frac tT H_C,\n",
+    "\\tag{25}\n",
+    "$$\n",
+    "\n",
+    "初始时，时间 $t=0$，该系统的哈密顿量为 $H(0) = H_B$。随着时间的流逝，该系统的哈密顿量逐渐由 $H_B$ 变为 $H_C$。当 $t=T$ 时，该系统的哈密顿量变为 $H(T) = H_C$。量子力学中的绝热定理告诉我们，如果初始时该系统处于 $H_B$ 的一个本征态，那么只要时间 $T$ 足够长，当系统的哈密顿量完全演化为 $H_C$ 时，该系统会处于 $H_C$ 的对应能级的本征态。因此，如果初始时该系统处于 $|s\\rangle$，即 $H_B$ 拥有最大本征值的本征态，经过足够长的演化时间 $T$，该系统的量子态会变为 $H_C$ 拥有最大本征值的本征态。[3]\n",
+    "\n",
+    "一种模拟哈密顿量 $H(t)$ 随着时间 $t$ 演化的方法便是交替地在该量子系统上作用酉变换 $U_C(\\gamma)$ 和 $U_B(\\beta)$，而模拟的精度取决于 $\\gamma,\\beta$ 的取值。另外，为了让系统的演化遵循绝热定理，需要足够长的演化时间，所以要求 $p$ 的取值足够大。因此，结合公式（22）可以推出公式（23）中的结论。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 示例：QAOA 求解最大割问题\n",
+    "\n",
+    "最大割问题（Max-Cut Problem）是图论中常见的一个组合优化问题，在统计物理学和电路设计中都有重要应用。最大割问题是一个 NP 完全问题，因此目前并不存在一个高效的算法能完美地解决该问题。\n",
+    "\n",
+    "#### 最大割问题\n",
+    "\n",
+    "在图论中，一个图是由一对集合 $G=(V, E)$ 表示，其中集合 $V$ 中的元素为该图的顶点，集合 $E$ 中的每个元素是一对顶点，表示连接这两个顶点的一条边。例如下方图片中的图可以由 $V=\\{0,1,2,3\\}$ 和 $E=\\{(0,1),(1,2),(2,3),(3,0)\\}$ 表示。\n",
+    "\n",
+    "![G](figures/qaoa-fig-maxcut_g.png \"图 1：一个有四个顶点和四条边的图\")\n",
+    "<div style=\"text-align:center\">图 1：一个有四个顶点和四条边的图 </div>\n",
+    "\n",
+    "\n",
+    "一个图上的割（cut）是指将该图的顶点集 $V$ 分割成两个互不相交的集合的一种划分，每个割都对应一个边的集合，这些边的两个顶点被划分在不同的集合中。于是我们可以将这个割的大小定义为这个边的集合的大小，即被割开的边的条数。最大割问题就是要找到一个割使得被割开的边的条数最多。图 2 展示了图 1 中图的一个最大割，该最大割的大小为 $4$，即割开了图中所有的边。\n",
+    "\n",
+    "![Max cut on G](figures/qaoa-fig-maxcut_cut.png \"图 2：图 1 中图的一个最大割\")\n",
+    "<div style=\"text-align:center\">图 2：图 1 中图的一个最大割 </div>\n",
+    "\n",
+    "\n",
+    "假设输入的图 $G=(V, E)$ 有 $n=|V|$ 个顶点和 $m=|E|$ 条边，那么我们可以将最大割问题描述为 $n$ 个比特和 $m$ 个子句的组合优化问题。每个比特对应图 $G$ 中的一个顶点 $v$，其取值 $z_v$ 为 $0$ 或 $1$，分别对应该顶点属于集合 $S_{0}$ 或 $S_{1}$，因此这 $n$ 个比特的每种取值 $z$ 都对应一个割。每个子句则对应图 $G$ 中的一条边 $(u,v)$，一个子句要求其对应的边连接的两个顶点的取值不同，即 $z_u\\neq z_v$，表示该条边被割开。也就是说，当该条边连接这的两个顶点被割划分到不同的集合上时，我们说该子句被满足。因此，对于图 $G$ 中的每条边 $(u,v)$，我们有\n",
+    "\n",
+    "$$\n",
+    "C_{(u,v)}(z) = z_u+z_v-2z_uz_v,\n",
+    "\\tag{26}\n",
+    "$$\n",
+    "\n",
+    "其中 $C_{(u,v)}(z) = 1$ 当且仅当该条边被割开。否则，该函数等于 $0$。整个组合优化问题的目标函数是\n",
+    "\n",
+    "$$\n",
+    "C(z) = \\sum_{(u,v)\\in E}C_{(u,v)}(z) = \\sum_{(u,v)\\in E}z_u+z_v-2z_uz_v.\n",
+    "\\tag{27}\n",
+    "$$\n",
+    "\n",
+    "因此，解决最大割问题就是要找到一个取值 $z$ 使得公式（27）中的目标函数最大。\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### 编码最大割问题\n",
+    "\n",
+    "这里我们以最大割问题为例来进一步阐述 QAOA。为了将最大割问题转化为一个量子问题，我们要用到 $n$ 个量子比特，每个量子比特对应图 $G$ 中的一个顶点。一个量子比特处于量子态 $|0\\rangle$ 或 $|1\\rangle$，表示其对应的顶点属于集合 $S_{0}$ 或 $S_{1}$。值得注意的是，$|0\\rangle$ 和 $|1\\rangle$ 是 Pauli $Z$ 门的两个本征态，并且它们的本征值分别为 $1$ 和 $-1$，即\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "Z|0\\rangle&=|0\\rangle,\\tag{28}\\\\\n",
+    "Z|1\\rangle&=-|1\\rangle.\\tag{29}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "因此我们可以使用 Pauli $Z$ 门来构建该最大割问题的哈密顿量 $H_C$。因为通过映射 $f(x):x\\to(x+1)/2$ 可以将 $-1$ 映射到 $0$ 上 并且仍将 $1$ 映射到 $1$ 上，所以我们可以将式（27）中的 $z$ 替换为 $(Z+I)/2$（$I$ 是单位矩阵），得到原问题目标函数对应的哈密顿量\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "H_C &= \\sum_{(u,v)\\in E} \\frac{Z_u+I}{2} + \\frac{Z_v+I}{2} - 2\\cdot\\frac{Z_u+I}{2}\\frac{Z_v+I}{2}\\tag{30}\\\\\n",
+    "&= \\sum_{(u,v)\\in E} \\frac{Z_u+Z_v+2I - (Z_uZ_v+Z_u+Z_v+I)}{2}\\tag{31}\\\\\n",
+    "&= \\sum_{(u,v)\\in E} \\frac{I - Z_uZ_v}{2}.\\tag{32}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "该哈密顿量关于一个量子态 $|\\psi\\rangle$ 的期望值为\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "\\langle\\psi|H_C|\\psi\\rangle &= \\langle\\psi|\\sum_{(u,v)\\in E} \\frac{I - Z_uZ_v}{2}|\\psi\\rangle\\tag{33}\\\\\n",
+    "&= \\langle\\psi|\\sum_{(u,v)\\in E} \\frac{I}{2}|\\psi\\rangle - \\langle\\psi|\\sum_{(u,v)\\in E} \\frac{Z_uZ_v}{2}|\\psi\\rangle\\tag{34}\\\\\n",
+    "&= \\frac{|E|}{2} - \\frac{1}{2}\\langle\\psi|\\sum_{(u,v)\\in E} Z_uZ_v|\\psi\\rangle.\\tag{35}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "如果我们记\n",
+    "\n",
+    "$$\n",
+    "H_D = -\\sum_{(u,v)\\in E} Z_uZ_v,\n",
+    "\\tag{36}\n",
+    "$$\n",
+    "\n",
+    "那么找到量子态 $|\\psi\\rangle$ 使得 $\\langle\\psi|H_C|\\psi\\rangle$ 最大等价于找到量子态 $|\\psi\\rangle$ 使得 $\\langle\\psi|H_D|\\psi\\rangle$ 最大。\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Paddle Quantum 实现\n",
+    "\n",
+    "我们以最大割问题为例，用量桨实现 QAOA 算法求解最大割问题。有许多方法可以找到参数 $\\vec{\\gamma},\\vec{\\beta}$，我们这里使用经典机器学习中的梯度下降方法。\n",
+    "\n",
+    "要在量桨上实现 QAOA，首先要做的便是加载需要用到的包。其中 `networkx` 包可以帮助我们方便地处理图。\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:00:43.231250Z",
+     "start_time": "2021-01-09T07:00:38.262611Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# 加载量桨、飞桨的相关模块\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import pauli_str_to_matrix\n",
+    "\n",
+    "# 加载额外需要用到的包\n",
+    "import numpy as np\n",
+    "import matplotlib.pyplot as plt\n",
+    "%config InlineBackend.figure_format = 'svg'\n",
+    "import networkx as nx"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "接下来，我们生成该最大割问题中的图 $G$。为了运算方便，这里的顶点从 $0$ 开始计数。\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:01:12.884308Z",
+     "start_time": "2021-01-09T07:01:12.683078Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"231.84pt\" version=\"1.1\" viewBox=\"0 0 349.2 231.84\" width=\"349.2pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T15:01:12.860328</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 231.84 \n",
+       "L 349.2 231.84 \n",
+       "L 349.2 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:none;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"LineCollection_1\">\n",
+       "    <path clip-path=\"url(#pede19378b3)\" d=\"M 294.171429 115.92 \n",
+       "L 174.599995 38.262857 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#pede19378b3)\" d=\"M 294.171429 115.92 \n",
+       "L 174.600001 193.577143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#pede19378b3)\" d=\"M 174.599995 38.262857 \n",
+       "L 55.028571 115.920007 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#pede19378b3)\" d=\"M 55.028571 115.920007 \n",
+       "L 174.600001 193.577143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"PathCollection_1\">\n",
+       "    <defs>\n",
+       "     <path d=\"M 0 22.36068 \n",
+       "C 5.930122 22.36068 11.618159 20.004617 15.811388 15.811388 \n",
+       "C 20.004617 11.618159 22.36068 5.930122 22.36068 0 \n",
+       "C 22.36068 -5.930122 20.004617 -11.618159 15.811388 -15.811388 \n",
+       "C 11.618159 -20.004617 5.930122 -22.36068 0 -22.36068 \n",
+       "C -5.930122 -22.36068 -11.618159 -20.004617 -15.811388 -15.811388 \n",
+       "C -20.004617 -11.618159 -22.36068 -5.930122 -22.36068 0 \n",
+       "C -22.36068 5.930122 -20.004617 11.618159 -15.811388 15.811388 \n",
+       "C -11.618159 20.004617 -5.930122 22.36068 0 22.36068 \n",
+       "z\n",
+       "\" id=\"m71159471ec\" style=\"stroke:#1f78b4;\"/>\n",
+       "    </defs>\n",
+       "    <g clip-path=\"url(#pede19378b3)\">\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"294.171429\" xlink:href=\"#m71159471ec\" y=\"115.92\"/>\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"174.599995\" xlink:href=\"#m71159471ec\" y=\"38.262857\"/>\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"55.028571\" xlink:href=\"#m71159471ec\" y=\"115.920007\"/>\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"174.600001\" xlink:href=\"#m71159471ec\" y=\"193.577143\"/>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_1\">\n",
+       "    <g clip-path=\"url(#pede19378b3)\">\n",
+       "     <!-- 0 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(287.213616 121.43875)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46 36.53125 \n",
+       "Q 46 50.203125 43.4375 55.78125 \n",
+       "Q 40.875 61.375 34.8125 61.375 \n",
+       "Q 28.765625 61.375 26.171875 55.78125 \n",
+       "Q 23.578125 50.203125 23.578125 36.53125 \n",
+       "Q 23.578125 22.703125 26.171875 17.03125 \n",
+       "Q 28.765625 11.375 34.8125 11.375 \n",
+       "Q 40.828125 11.375 43.40625 17.03125 \n",
+       "Q 46 22.703125 46 36.53125 \n",
+       "z\n",
+       "M 64.796875 36.375 \n",
+       "Q 64.796875 18.265625 56.984375 8.421875 \n",
+       "Q 49.171875 -1.421875 34.8125 -1.421875 \n",
+       "Q 20.40625 -1.421875 12.59375 8.421875 \n",
+       "Q 4.78125 18.265625 4.78125 36.375 \n",
+       "Q 4.78125 54.546875 12.59375 64.375 \n",
+       "Q 20.40625 74.21875 34.8125 74.21875 \n",
+       "Q 49.171875 74.21875 56.984375 64.375 \n",
+       "Q 64.796875 54.546875 64.796875 36.375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-48\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-48\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_2\">\n",
+       "    <g clip-path=\"url(#pede19378b3)\">\n",
+       "     <!-- 1 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(167.642182 43.781607)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 11.71875 12.984375 \n",
+       "L 28.328125 12.984375 \n",
+       "L 28.328125 60.109375 \n",
+       "L 11.28125 56.59375 \n",
+       "L 11.28125 69.390625 \n",
+       "L 28.21875 72.90625 \n",
+       "L 46.09375 72.90625 \n",
+       "L 46.09375 12.984375 \n",
+       "L 62.703125 12.984375 \n",
+       "L 62.703125 0 \n",
+       "L 11.71875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-49\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-49\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_3\">\n",
+       "    <g clip-path=\"url(#pede19378b3)\">\n",
+       "     <!-- 2 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(48.070759 121.438757)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 28.8125 13.8125 \n",
+       "L 60.890625 13.8125 \n",
+       "L 60.890625 0 \n",
+       "L 7.90625 0 \n",
+       "L 7.90625 13.8125 \n",
+       "L 34.515625 37.3125 \n",
+       "Q 38.09375 40.53125 39.796875 43.609375 \n",
+       "Q 41.5 46.6875 41.5 50 \n",
+       "Q 41.5 55.125 38.0625 58.25 \n",
+       "Q 34.625 61.375 28.90625 61.375 \n",
+       "Q 24.515625 61.375 19.28125 59.5 \n",
+       "Q 14.0625 57.625 8.109375 53.90625 \n",
+       "L 8.109375 69.921875 \n",
+       "Q 14.453125 72.015625 20.65625 73.109375 \n",
+       "Q 26.859375 74.21875 32.8125 74.21875 \n",
+       "Q 45.90625 74.21875 53.15625 68.453125 \n",
+       "Q 60.40625 62.703125 60.40625 52.390625 \n",
+       "Q 60.40625 46.4375 57.328125 41.28125 \n",
+       "Q 54.25 36.140625 44.390625 27.484375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-50\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-50\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_4\">\n",
+       "    <g clip-path=\"url(#pede19378b3)\">\n",
+       "     <!-- 3 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(167.642189 199.095893)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46.578125 39.3125 \n",
+       "Q 53.953125 37.40625 57.78125 32.6875 \n",
+       "Q 61.625 27.984375 61.625 20.703125 \n",
+       "Q 61.625 9.859375 53.3125 4.21875 \n",
+       "Q 45.015625 -1.421875 29.109375 -1.421875 \n",
+       "Q 23.484375 -1.421875 17.84375 -0.515625 \n",
+       "Q 12.203125 0.390625 6.6875 2.203125 \n",
+       "L 6.6875 16.703125 \n",
+       "Q 11.96875 14.0625 17.15625 12.71875 \n",
+       "Q 22.359375 11.375 27.390625 11.375 \n",
+       "Q 34.859375 11.375 38.84375 13.953125 \n",
+       "Q 42.828125 16.546875 42.828125 21.390625 \n",
+       "Q 42.828125 26.375 38.75 28.9375 \n",
+       "Q 34.671875 31.5 26.703125 31.5 \n",
+       "L 19.1875 31.5 \n",
+       "L 19.1875 43.609375 \n",
+       "L 27.09375 43.609375 \n",
+       "Q 34.1875 43.609375 37.640625 45.828125 \n",
+       "Q 41.109375 48.046875 41.109375 52.59375 \n",
+       "Q 41.109375 56.78125 37.734375 59.078125 \n",
+       "Q 34.375 61.375 28.21875 61.375 \n",
+       "Q 23.6875 61.375 19.046875 60.34375 \n",
+       "Q 14.40625 59.328125 9.8125 57.328125 \n",
+       "L 9.8125 71.09375 \n",
+       "Q 15.375 72.65625 20.84375 73.4375 \n",
+       "Q 26.3125 74.21875 31.59375 74.21875 \n",
+       "Q 45.796875 74.21875 52.84375 69.546875 \n",
+       "Q 59.90625 64.890625 59.90625 55.515625 \n",
+       "Q 59.90625 49.125 56.53125 45.046875 \n",
+       "Q 53.171875 40.96875 46.578125 39.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-51\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-51\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"pede19378b3\">\n",
+       "   <rect height=\"217.44\" width=\"334.8\" x=\"7.2\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "# n 是图 G 的顶点数，同时也是量子比特的个数\n",
+    "n = 4\n",
+    "G = nx.Graph()\n",
+    "V = range(n)\n",
+    "E = [(0, 1), (1, 2), (2, 3), (3, 0)]\n",
+    "G.add_edges_from(E)\n",
+    "\n",
+    "# 将生成的图 G 打印出来\n",
+    "pos = nx.circular_layout(G)\n",
+    "options = {\n",
+    "    \"with_labels\": True,\n",
+    "    \"font_size\": 20,\n",
+    "    \"font_weight\": \"bold\",\n",
+    "    \"font_color\": \"white\",\n",
+    "    \"node_size\": 2000,\n",
+    "    \"width\": 2\n",
+    "}\n",
+    "nx.draw_networkx(G, pos, **options)\n",
+    "ax = plt.gca()\n",
+    "ax.margins(0.20)\n",
+    "plt.axis(\"off\")\n",
+    "plt.show()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 编码哈密顿量\n",
+    "\n",
+    "量桨中，哈密顿量可以以 `list` 的形式输入。这里我们构建式（36）中的哈密顿量 $H_D$。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:01:33.911138Z",
+     "start_time": "2021-01-09T07:01:33.901933Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "[[-1.0, 'z0,z1'], [-1.0, 'z1,z2'], [-1.0, 'z2,z3'], [-1.0, 'z3,z0']]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# 以 list 的形式构建哈密顿量 H_D\n",
+    "H_D_list = []\n",
+    "for (u, v) in E:\n",
+    "    H_D_list.append([-1.0, 'z'+str(u) + ',z' + str(v)])\n",
+    "print(H_D_list)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "可以看到，在这个例子中，哈密顿量 $H_D$ 为\n",
+    "\n",
+    "$$\n",
+    "H_D = -Z_0Z_1 - Z_1Z_2 - Z_2Z_3 - Z_3Z_0.\n",
+    "\\tag{37}\n",
+    "$$\n",
+    "\n",
+    "我们可以查看哈密顿量 $H_D$ 的矩阵形式，并且获取它的本征值信息："
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:01:57.485432Z",
+     "start_time": "2021-01-09T07:01:57.475788Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "[-4.  0.  0.  0.  0.  4.  0.  0.  0.  0.  4.  0.  0.  0.  0. -4.]\n",
+      "H_max: 4.0\n"
+     ]
+    }
+   ],
+   "source": [
+    "# 将哈密顿量 H_D 从 list 形式转为矩阵形式\n",
+    "H_D_matrix = pauli_str_to_matrix(H_D_list, n)\n",
+    "# 取出 H_D 对角线上的元素\n",
+    "H_D_diag = np.diag(H_D_matrix).real\n",
+    "# 获取 H_D 的最大本征值\n",
+    "H_max = np.max(H_D_diag)\n",
+    "\n",
+    "print(H_D_diag)\n",
+    "print('H_max:', H_max)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 搭建 QAOA 电路\n",
+    "\n",
+    "前面我们介绍了 QAOA 需要将两个酉变换 $U_C(\\gamma)$ 和 $U_B(\\beta)$ 交替地作用在初始态 $|s\\rangle = |+\\rangle^{\\otimes n}$ 上。在这里，我们使用量桨中提供的量子门和量子电路模板搭建出一个量子电路来实现这一步骤。要注意的是，在最大割问题中，我们将最大化哈密顿量 $H_C$ 的期望值的问题简化为了最大化哈密顿量 $H_D$ 的期望值的问题，因此要用到的酉变换也就变成了 $U_D(\\gamma)$ 和 $U_B(\\beta)$。通过交替地摆放两个参数可调的电路模块，我们得以搭建QAOA电路\n",
+    "\n",
+    "$$\n",
+    "U_B(\\beta_p)U_D(\\gamma_p)\\cdots U_B(\\beta_1)U_D(\\gamma_1),\n",
+    "\\tag{38}\n",
+    "$$\n",
+    "\n",
+    "其中，$U_D(\\gamma) = e^{-i\\gamma H_D}$ 可以由下图中的电路搭建实现。另一个酉变换 $U_B(\\beta)$ 则等价于在每个量子比特上作用一个 $R_x$ 门。\n",
+    "\n",
+    "![U_D circuit](figures/qaoa-fig-cir_ud.png \"图 3：酉变换 $e^{i\\gamma Z\\otimes Z}$ 的量子电路实现\")\n",
+    "<div style=\"text-align:center\">图 3：酉变换 $e^{i\\gamma Z\\otimes Z}$ 的量子电路实现 </div>\n",
+    "\n",
+    "\n",
+    "因此，实现一层酉变换 $U_B(\\beta)U_D(\\gamma)$ 的量子电路如图 4 所示。\n",
+    "\n",
+    "![U_BU_D circuit](figures/qaoa-fig-cir_ubud.png \"图 4：酉变换 $U_B(\\beta)U_D(\\gamma)$ 的量子电路实现\")\n",
+    "<div style=\"text-align:center\">图 4：酉变换 $U_B(\\beta)U_D(\\gamma)$ 的量子电路实现 </div>\n",
+    "\n",
+    "量桨中，电路运行前每个量子比特默认的初始状态为 $|0\\rangle$（可以通过输入参数来自定义初始状态），我们可以通过添加一层 Hadamard 门使每个量子比特的状态由 $|0\\rangle$ 变为 $|+\\rangle$，由此得到 QAOA 要求的初始态 $|s\\rangle = |+\\rangle^{\\otimes n}$。在量桨中，可以通过调用 `superposition_layer()` 在量子电路中添加一层 Hadamard 门。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:02:33.523693Z",
+     "start_time": "2021-01-09T07:02:33.508316Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def circuit_QAOA(p, gamma, beta):\n",
+    "    # 初始化 n 个量子比特的量子电路\n",
+    "    cir = UAnsatz(n)\n",
+    "    # 制备量子态 |s>\n",
+    "    cir.superposition_layer()\n",
+    "    # 搭建 p 层电路\n",
+    "    for layer in range(p):\n",
+    "        # 搭建 U_D 的电路\n",
+    "        for (u, v) in E:\n",
+    "            cir.cnot([u, v])\n",
+    "            cir.rz(gamma[layer], v)\n",
+    "            cir.cnot([u, v])\n",
+    "\n",
+    "        # 搭建 U_B 的电路，即添加一层 R_x 门\n",
+    "        for v in V:\n",
+    "            cir.rx(beta[layer], v)\n",
+    "\n",
+    "    return cir"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "搭建 QAOA 量子电路的工作完成后，如果运行该量子电路，得到的输出态为\n",
+    "\n",
+    "$$\n",
+    "|\\vec{\\gamma},\\vec{\\beta}\\rangle = U_B(\\beta_p)U_D(\\gamma_p)\\cdots U_B(\\beta_1)U_D(\\gamma_1)|s\\rangle.\n",
+    "\\tag{39}\n",
+    "$$\n",
+    "\n",
+    "### 计算损失函数\n",
+    "\n",
+    "由上一步搭建的电路的输出态，我们可以计算最大割问题的目标函数\n",
+    "\n",
+    "$$\n",
+    "F_p(\\vec{\\gamma},\\vec{\\beta}) = \\langle\\vec{\\gamma},\\vec{\\beta}|H_D|\\vec{\\gamma},\\vec{\\beta}\\rangle.\n",
+    "\\tag{40}\n",
+    "$$\n",
+    "\n",
+    "要最大化该目标函数等价于最小化 $-F_p$。因此我们定义 $L(\\vec{\\gamma},\\vec{\\beta}) = -F_p(\\vec{\\gamma},\\vec{\\beta})$ 为损失函数，即要最小化的函数，然后利用经典的优化算法寻找最优参数 $\\vec{\\gamma},\\vec{\\beta}$。下面的代码给出了通过量桨和飞桨搭建的完整 QAOA 网络："
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:03:00.576339Z",
+     "start_time": "2021-01-09T07:03:00.564735Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class Net(fluid.dygraph.Layer):\n",
+    "    def __init__(\n",
+    "        self,\n",
+    "        p,\n",
+    "        param_attr=fluid.initializer.Uniform(low=0.0, high=np.pi, seed=1024),\n",
+    "        dtype=\"float64\",\n",
+    "    ):\n",
+    "        super(Net, self).__init__()\n",
+    "\n",
+    "        self.p = p\n",
+    "        self.gamma = self.create_parameter(shape=[self.p], attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.beta = self.create_parameter(shape=[self.p], attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "\n",
+    "    def forward(self):\n",
+    "        # 定义 QAOA 的量子电路\n",
+    "        cir = circuit_QAOA(self.p, self.gamma, self.beta)\n",
+    "        # 运行该量子电路\n",
+    "        cir.run_state_vector()\n",
+    "        # 计算损失函数\n",
+    "        loss = -cir.expecval(H_D_list)\n",
+    "\n",
+    "        return loss, cir"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 训练量子神经网络\n",
+    "定义好了用于 QAOA 的量子神经网络后，我们使用梯度下降的方法来更新其中的参数，使得式（40）的期望值最大。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:03:34.844845Z",
+     "start_time": "2021-01-09T07:03:34.829959Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "p = 4      # 量子电路的层数\n",
+    "ITR = 120  # 训练迭代的次数\n",
+    "LR = 0.1   # 基于梯度下降的优化方法的学习率"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "这里，我们在飞桨动态图中优化上面定义的网络。\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 8,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:04:33.677212Z",
+     "start_time": "2021-01-09T07:03:53.962377Z"
+    },
+    "scrolled": true
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 10   loss: -3.7473\n",
+      "iter: 20   loss: -3.9696\n",
+      "iter: 30   loss: -3.9539\n",
+      "iter: 40   loss: -3.9710\n",
+      "iter: 50   loss: -3.9930\n",
+      "iter: 60   loss: -3.9991\n",
+      "iter: 70   loss: -3.9984\n",
+      "iter: 80   loss: -3.9998\n",
+      "iter: 90   loss: -3.9998\n",
+      "iter: 100   loss: -4.0000\n",
+      "iter: 110   loss: -4.0000\n",
+      "iter: 120   loss: -4.0000\n",
+      "优化后的参数 gamma:\n",
+      " [0.70063329 0.45026914 1.17355432 2.13276803]\n",
+      "优化后的参数 beta:\n",
+      " [-0.02466894 -0.20348931  1.12024105  0.61099467]\n"
+     ]
+    }
+   ],
+   "source": [
+    "with fluid.dygraph.guard():\n",
+    "    net = Net(p)\n",
+    "    # 使用 Adam 优化器\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    # 梯度下降循环\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "        # 运行上面定义的网络\n",
+    "        loss, cir = net()\n",
+    "        # 计算梯度并优化\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "        if itr % 10 == 0:\n",
+    "            print(\"iter:\", itr, \"  loss:\", \"%.4f\" % loss.numpy())\n",
+    "\n",
+    "    gamma_opt = net.gamma.numpy()\n",
+    "    print(\"优化后的参数 gamma:\\n\", gamma_opt)\n",
+    "    beta_opt = net.beta.numpy()\n",
+    "    print(\"优化后的参数 beta:\\n\", beta_opt)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 解码量子答案\n",
+    "当求得损失函数的最小值以及相对应的一组参数 $\\vec{\\gamma}^*,\\vec{\\beta}^*$ 后，我们的任务还没有完成。为了进一步求得 Max-Cut 问题的近似解，需要从 QAOA 输出的量子态 $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ 中解码出经典优化问题的答案。物理上，解码量子态需要对量子态进行测量，然后统计测量结果的概率分布：\n",
+    "\n",
+    "$$\n",
+    "p(z)=|\\langle z|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle|^2.\n",
+    "\\tag{41}\n",
+    "$$\n",
+    "\n",
+    "通常情况下，某个比特串出现的概率越大，意味着其对应 Max-Cut 问题最优解的可能性越大。\n",
+    "\n",
+    "Paddle Quantum 提供了查看 QAOA 量子电路输出状态的测量结果概率分布的函数："
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 9,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:04:38.467066Z",
+     "start_time": "2021-01-09T07:04:38.094519Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"277.968125pt\" version=\"1.1\" viewBox=\"0 0 385.78125 277.968125\" width=\"385.78125pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T15:04:38.342915</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 277.968125 \n",
+       "L 385.78125 277.968125 \n",
+       "L 385.78125 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:none;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"patch_2\">\n",
+       "    <path d=\"M 43.78125 224.64 \n",
+       "L 378.58125 224.64 \n",
+       "L 378.58125 7.2 \n",
+       "L 43.78125 7.2 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_3\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 58.999432 224.64 \n",
+       "L 74.410249 224.64 \n",
+       "L 74.410249 224.64 \n",
+       "L 58.999432 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_4\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 78.262953 224.64 \n",
+       "L 93.67377 224.64 \n",
+       "L 93.67377 224.64 \n",
+       "L 78.262953 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_5\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 97.526474 224.64 \n",
+       "L 112.937291 224.64 \n",
+       "L 112.937291 224.64 \n",
+       "L 97.526474 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_6\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 116.789996 224.64 \n",
+       "L 132.200813 224.64 \n",
+       "L 132.200813 224.64 \n",
+       "L 116.789996 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_7\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 136.053517 224.64 \n",
+       "L 151.464334 224.64 \n",
+       "L 151.464334 224.64 \n",
+       "L 136.053517 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_8\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 155.317038 224.64 \n",
+       "L 170.727855 224.64 \n",
+       "L 170.727855 17.554286 \n",
+       "L 155.317038 17.554286 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_9\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 174.58056 224.64 \n",
+       "L 189.991377 224.64 \n",
+       "L 189.991377 224.64 \n",
+       "L 174.58056 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_10\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 193.844081 224.64 \n",
+       "L 209.254898 224.64 \n",
+       "L 209.254898 224.64 \n",
+       "L 193.844081 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_11\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 213.107602 224.64 \n",
+       "L 228.518419 224.64 \n",
+       "L 228.518419 224.64 \n",
+       "L 213.107602 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_12\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 232.371123 224.64 \n",
+       "L 247.78194 224.64 \n",
+       "L 247.78194 224.64 \n",
+       "L 232.371123 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_13\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 251.634645 224.64 \n",
+       "L 267.045462 224.64 \n",
+       "L 267.045462 24.708879 \n",
+       "L 251.634645 24.708879 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_14\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 270.898166 224.64 \n",
+       "L 286.308983 224.64 \n",
+       "L 286.308983 224.64 \n",
+       "L 270.898166 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_15\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 290.161687 224.64 \n",
+       "L 305.572504 224.64 \n",
+       "L 305.572504 224.64 \n",
+       "L 290.161687 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_16\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 309.425209 224.64 \n",
+       "L 324.836026 224.64 \n",
+       "L 324.836026 224.64 \n",
+       "L 309.425209 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_17\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 328.68873 224.64 \n",
+       "L 344.099547 224.64 \n",
+       "L 344.099547 224.64 \n",
+       "L 328.68873 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_18\">\n",
+       "    <path clip-path=\"url(#p5520171445)\" d=\"M 347.952251 224.64 \n",
+       "L 363.363068 224.64 \n",
+       "L 363.363068 224.64 \n",
+       "L 347.952251 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_1\">\n",
+       "    <g id=\"xtick_1\">\n",
+       "     <g id=\"line2d_1\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L 0 3.5 \n",
+       "\" id=\"mc1fc8c99ed\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"66.70484\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_1\">\n",
+       "      <!-- 0000 -->\n",
+       "      <g transform=\"translate(69.464215 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 31.78125 66.40625 \n",
+       "Q 24.171875 66.40625 20.328125 58.90625 \n",
+       "Q 16.5 51.421875 16.5 36.375 \n",
+       "Q 16.5 21.390625 20.328125 13.890625 \n",
+       "Q 24.171875 6.390625 31.78125 6.390625 \n",
+       "Q 39.453125 6.390625 43.28125 13.890625 \n",
+       "Q 47.125 21.390625 47.125 36.375 \n",
+       "Q 47.125 51.421875 43.28125 58.90625 \n",
+       "Q 39.453125 66.40625 31.78125 66.40625 \n",
+       "z\n",
+       "M 31.78125 74.21875 \n",
+       "Q 44.046875 74.21875 50.515625 64.515625 \n",
+       "Q 56.984375 54.828125 56.984375 36.375 \n",
+       "Q 56.984375 17.96875 50.515625 8.265625 \n",
+       "Q 44.046875 -1.421875 31.78125 -1.421875 \n",
+       "Q 19.53125 -1.421875 13.0625 8.265625 \n",
+       "Q 6.59375 17.96875 6.59375 36.375 \n",
+       "Q 6.59375 54.828125 13.0625 64.515625 \n",
+       "Q 19.53125 74.21875 31.78125 74.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-48\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_2\">\n",
+       "     <g id=\"line2d_2\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"85.968362\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_2\">\n",
+       "      <!-- 0001 -->\n",
+       "      <g transform=\"translate(88.727737 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 12.40625 8.296875 \n",
+       "L 28.515625 8.296875 \n",
+       "L 28.515625 63.921875 \n",
+       "L 10.984375 60.40625 \n",
+       "L 10.984375 69.390625 \n",
+       "L 28.421875 72.90625 \n",
+       "L 38.28125 72.90625 \n",
+       "L 38.28125 8.296875 \n",
+       "L 54.390625 8.296875 \n",
+       "L 54.390625 0 \n",
+       "L 12.40625 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-49\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_3\">\n",
+       "     <g id=\"line2d_3\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"105.231883\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_3\">\n",
+       "      <!-- 0010 -->\n",
+       "      <g transform=\"translate(107.991258 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_4\">\n",
+       "     <g id=\"line2d_4\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"124.495404\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_4\">\n",
+       "      <!-- 0011 -->\n",
+       "      <g transform=\"translate(127.254779 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_5\">\n",
+       "     <g id=\"line2d_5\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"143.758925\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_5\">\n",
+       "      <!-- 0100 -->\n",
+       "      <g transform=\"translate(146.5183 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_6\">\n",
+       "     <g id=\"line2d_6\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"163.022447\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_6\">\n",
+       "      <!-- 0101 -->\n",
+       "      <g transform=\"translate(165.781822 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_7\">\n",
+       "     <g id=\"line2d_7\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"182.285968\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_7\">\n",
+       "      <!-- 0110 -->\n",
+       "      <g transform=\"translate(185.045343 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_8\">\n",
+       "     <g id=\"line2d_8\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"201.549489\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_8\">\n",
+       "      <!-- 0111 -->\n",
+       "      <g transform=\"translate(204.308864 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_9\">\n",
+       "     <g id=\"line2d_9\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"220.813011\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_9\">\n",
+       "      <!-- 1000 -->\n",
+       "      <g transform=\"translate(223.572386 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_10\">\n",
+       "     <g id=\"line2d_10\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"240.076532\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_10\">\n",
+       "      <!-- 1001 -->\n",
+       "      <g transform=\"translate(242.835907 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_11\">\n",
+       "     <g id=\"line2d_11\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"259.340053\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_11\">\n",
+       "      <!-- 1010 -->\n",
+       "      <g transform=\"translate(262.099428 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_12\">\n",
+       "     <g id=\"line2d_12\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"278.603575\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_12\">\n",
+       "      <!-- 1011 -->\n",
+       "      <g transform=\"translate(281.36295 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_13\">\n",
+       "     <g id=\"line2d_13\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"297.867096\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_13\">\n",
+       "      <!-- 1100 -->\n",
+       "      <g transform=\"translate(300.626471 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_14\">\n",
+       "     <g id=\"line2d_14\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"317.130617\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_14\">\n",
+       "      <!-- 1101 -->\n",
+       "      <g transform=\"translate(319.889992 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_15\">\n",
+       "     <g id=\"line2d_15\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"336.394138\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_15\">\n",
+       "      <!-- 1110 -->\n",
+       "      <g transform=\"translate(339.153513 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_16\">\n",
+       "     <g id=\"line2d_16\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"355.65766\" xlink:href=\"#mc1fc8c99ed\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_16\">\n",
+       "      <!-- 1111 -->\n",
+       "      <g transform=\"translate(358.417035 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_17\">\n",
+       "     <!-- Qubit State -->\n",
+       "     <g transform=\"translate(182.728906 268.688437)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 39.40625 66.21875 \n",
+       "Q 28.65625 66.21875 22.328125 58.203125 \n",
+       "Q 16.015625 50.203125 16.015625 36.375 \n",
+       "Q 16.015625 22.609375 22.328125 14.59375 \n",
+       "Q 28.65625 6.59375 39.40625 6.59375 \n",
+       "Q 50.140625 6.59375 56.421875 14.59375 \n",
+       "Q 62.703125 22.609375 62.703125 36.375 \n",
+       "Q 62.703125 50.203125 56.421875 58.203125 \n",
+       "Q 50.140625 66.21875 39.40625 66.21875 \n",
+       "z\n",
+       "M 53.21875 1.3125 \n",
+       "L 66.21875 -12.890625 \n",
+       "L 54.296875 -12.890625 \n",
+       "L 43.5 -1.21875 \n",
+       "Q 41.890625 -1.3125 41.03125 -1.359375 \n",
+       "Q 40.1875 -1.421875 39.40625 -1.421875 \n",
+       "Q 24.03125 -1.421875 14.8125 8.859375 \n",
+       "Q 5.609375 19.140625 5.609375 36.375 \n",
+       "Q 5.609375 53.65625 14.8125 63.9375 \n",
+       "Q 24.03125 74.21875 39.40625 74.21875 \n",
+       "Q 54.734375 74.21875 63.90625 63.9375 \n",
+       "Q 73.09375 53.65625 73.09375 36.375 \n",
+       "Q 73.09375 23.6875 67.984375 14.640625 \n",
+       "Q 62.890625 5.609375 53.21875 1.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-81\"/>\n",
+       "       <path d=\"M 8.5 21.578125 \n",
+       "L 8.5 54.6875 \n",
+       "L 17.484375 54.6875 \n",
+       "L 17.484375 21.921875 \n",
+       "Q 17.484375 14.15625 20.5 10.265625 \n",
+       "Q 23.53125 6.390625 29.59375 6.390625 \n",
+       "Q 36.859375 6.390625 41.078125 11.03125 \n",
+       "Q 45.3125 15.671875 45.3125 23.6875 \n",
+       "L 45.3125 54.6875 \n",
+       "L 54.296875 54.6875 \n",
+       "L 54.296875 0 \n",
+       "L 45.3125 0 \n",
+       "L 45.3125 8.40625 \n",
+       "Q 42.046875 3.421875 37.71875 1 \n",
+       "Q 33.40625 -1.421875 27.6875 -1.421875 \n",
+       "Q 18.265625 -1.421875 13.375 4.4375 \n",
+       "Q 8.5 10.296875 8.5 21.578125 \n",
+       "z\n",
+       "M 31.109375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-117\"/>\n",
+       "       <path d=\"M 48.6875 27.296875 \n",
+       "Q 48.6875 37.203125 44.609375 42.84375 \n",
+       "Q 40.53125 48.484375 33.40625 48.484375 \n",
+       "Q 26.265625 48.484375 22.1875 42.84375 \n",
+       "Q 18.109375 37.203125 18.109375 27.296875 \n",
+       "Q 18.109375 17.390625 22.1875 11.75 \n",
+       "Q 26.265625 6.109375 33.40625 6.109375 \n",
+       "Q 40.53125 6.109375 44.609375 11.75 \n",
+       "Q 48.6875 17.390625 48.6875 27.296875 \n",
+       "z\n",
+       "M 18.109375 46.390625 \n",
+       "Q 20.953125 51.265625 25.265625 53.625 \n",
+       "Q 29.59375 56 35.59375 56 \n",
+       "Q 45.5625 56 51.78125 48.09375 \n",
+       "Q 58.015625 40.1875 58.015625 27.296875 \n",
+       "Q 58.015625 14.40625 51.78125 6.484375 \n",
+       "Q 45.5625 -1.421875 35.59375 -1.421875 \n",
+       "Q 29.59375 -1.421875 25.265625 0.953125 \n",
+       "Q 20.953125 3.328125 18.109375 8.203125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 75.984375 \n",
+       "L 18.109375 75.984375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-98\"/>\n",
+       "       <path d=\"M 9.421875 54.6875 \n",
+       "L 18.40625 54.6875 \n",
+       "L 18.40625 0 \n",
+       "L 9.421875 0 \n",
+       "z\n",
+       "M 9.421875 75.984375 \n",
+       "L 18.40625 75.984375 \n",
+       "L 18.40625 64.59375 \n",
+       "L 9.421875 64.59375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-105\"/>\n",
+       "       <path d=\"M 18.3125 70.21875 \n",
+       "L 18.3125 54.6875 \n",
+       "L 36.8125 54.6875 \n",
+       "L 36.8125 47.703125 \n",
+       "L 18.3125 47.703125 \n",
+       "L 18.3125 18.015625 \n",
+       "Q 18.3125 11.328125 20.140625 9.421875 \n",
+       "Q 21.96875 7.515625 27.59375 7.515625 \n",
+       "L 36.8125 7.515625 \n",
+       "L 36.8125 0 \n",
+       "L 27.59375 0 \n",
+       "Q 17.1875 0 13.234375 3.875 \n",
+       "Q 9.28125 7.765625 9.28125 18.015625 \n",
+       "L 9.28125 47.703125 \n",
+       "L 2.6875 47.703125 \n",
+       "L 2.6875 54.6875 \n",
+       "L 9.28125 54.6875 \n",
+       "L 9.28125 70.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-116\"/>\n",
+       "       <path id=\"DejaVuSans-32\"/>\n",
+       "       <path d=\"M 53.515625 70.515625 \n",
+       "L 53.515625 60.890625 \n",
+       "Q 47.90625 63.578125 42.921875 64.890625 \n",
+       "Q 37.9375 66.21875 33.296875 66.21875 \n",
+       "Q 25.25 66.21875 20.875 63.09375 \n",
+       "Q 16.5 59.96875 16.5 54.203125 \n",
+       "Q 16.5 49.359375 19.40625 46.890625 \n",
+       "Q 22.3125 44.4375 30.421875 42.921875 \n",
+       "L 36.375 41.703125 \n",
+       "Q 47.40625 39.59375 52.65625 34.296875 \n",
+       "Q 57.90625 29 57.90625 20.125 \n",
+       "Q 57.90625 9.515625 50.796875 4.046875 \n",
+       "Q 43.703125 -1.421875 29.984375 -1.421875 \n",
+       "Q 24.8125 -1.421875 18.96875 -0.25 \n",
+       "Q 13.140625 0.921875 6.890625 3.21875 \n",
+       "L 6.890625 13.375 \n",
+       "Q 12.890625 10.015625 18.65625 8.296875 \n",
+       "Q 24.421875 6.59375 29.984375 6.59375 \n",
+       "Q 38.421875 6.59375 43.015625 9.90625 \n",
+       "Q 47.609375 13.234375 47.609375 19.390625 \n",
+       "Q 47.609375 24.75 44.3125 27.78125 \n",
+       "Q 41.015625 30.8125 33.5 32.328125 \n",
+       "L 27.484375 33.5 \n",
+       "Q 16.453125 35.6875 11.515625 40.375 \n",
+       "Q 6.59375 45.0625 6.59375 53.421875 \n",
+       "Q 6.59375 63.09375 13.40625 68.65625 \n",
+       "Q 20.21875 74.21875 32.171875 74.21875 \n",
+       "Q 37.3125 74.21875 42.625 73.28125 \n",
+       "Q 47.953125 72.359375 53.515625 70.515625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-83\"/>\n",
+       "       <path d=\"M 34.28125 27.484375 \n",
+       "Q 23.390625 27.484375 19.1875 25 \n",
+       "Q 14.984375 22.515625 14.984375 16.5 \n",
+       "Q 14.984375 11.71875 18.140625 8.90625 \n",
+       "Q 21.296875 6.109375 26.703125 6.109375 \n",
+       "Q 34.1875 6.109375 38.703125 11.40625 \n",
+       "Q 43.21875 16.703125 43.21875 25.484375 \n",
+       "L 43.21875 27.484375 \n",
+       "z\n",
+       "M 52.203125 31.203125 \n",
+       "L 52.203125 0 \n",
+       "L 43.21875 0 \n",
+       "L 43.21875 8.296875 \n",
+       "Q 40.140625 3.328125 35.546875 0.953125 \n",
+       "Q 30.953125 -1.421875 24.3125 -1.421875 \n",
+       "Q 15.921875 -1.421875 10.953125 3.296875 \n",
+       "Q 6 8.015625 6 15.921875 \n",
+       "Q 6 25.140625 12.171875 29.828125 \n",
+       "Q 18.359375 34.515625 30.609375 34.515625 \n",
+       "L 43.21875 34.515625 \n",
+       "L 43.21875 35.40625 \n",
+       "Q 43.21875 41.609375 39.140625 45 \n",
+       "Q 35.0625 48.390625 27.6875 48.390625 \n",
+       "Q 23 48.390625 18.546875 47.265625 \n",
+       "Q 14.109375 46.140625 10.015625 43.890625 \n",
+       "L 10.015625 52.203125 \n",
+       "Q 14.9375 54.109375 19.578125 55.046875 \n",
+       "Q 24.21875 56 28.609375 56 \n",
+       "Q 40.484375 56 46.34375 49.84375 \n",
+       "Q 52.203125 43.703125 52.203125 31.203125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-97\"/>\n",
+       "       <path d=\"M 56.203125 29.59375 \n",
+       "L 56.203125 25.203125 \n",
+       "L 14.890625 25.203125 \n",
+       "Q 15.484375 15.921875 20.484375 11.0625 \n",
+       "Q 25.484375 6.203125 34.421875 6.203125 \n",
+       "Q 39.59375 6.203125 44.453125 7.46875 \n",
+       "Q 49.3125 8.734375 54.109375 11.28125 \n",
+       "L 54.109375 2.78125 \n",
+       "Q 49.265625 0.734375 44.1875 -0.34375 \n",
+       "Q 39.109375 -1.421875 33.890625 -1.421875 \n",
+       "Q 20.796875 -1.421875 13.15625 6.1875 \n",
+       "Q 5.515625 13.8125 5.515625 26.8125 \n",
+       "Q 5.515625 40.234375 12.765625 48.109375 \n",
+       "Q 20.015625 56 32.328125 56 \n",
+       "Q 43.359375 56 49.78125 48.890625 \n",
+       "Q 56.203125 41.796875 56.203125 29.59375 \n",
+       "z\n",
+       "M 47.21875 32.234375 \n",
+       "Q 47.125 39.59375 43.09375 43.984375 \n",
+       "Q 39.0625 48.390625 32.421875 48.390625 \n",
+       "Q 24.90625 48.390625 20.390625 44.140625 \n",
+       "Q 15.875 39.890625 15.1875 32.171875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-101\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-81\"/>\n",
+       "      <use x=\"78.710938\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"142.089844\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"205.566406\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"233.349609\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"272.558594\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"304.345703\" xlink:href=\"#DejaVuSans-83\"/>\n",
+       "      <use x=\"367.822266\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"407.03125\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"468.310547\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"507.519531\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_2\">\n",
+       "    <g id=\"ytick_1\">\n",
+       "     <g id=\"line2d_17\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L -3.5 0 \n",
+       "\" id=\"m8c08098b29\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m8c08098b29\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_18\">\n",
+       "      <!-- 0.0 -->\n",
+       "      <g transform=\"translate(20.878125 228.439219)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 10.6875 12.40625 \n",
+       "L 21 12.40625 \n",
+       "L 21 0 \n",
+       "L 10.6875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-46\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_2\">\n",
+       "     <g id=\"line2d_18\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m8c08098b29\" y=\"183.938316\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_19\">\n",
+       "      <!-- 0.1 -->\n",
+       "      <g transform=\"translate(20.878125 187.737535)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_3\">\n",
+       "     <g id=\"line2d_19\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m8c08098b29\" y=\"143.236633\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_20\">\n",
+       "      <!-- 0.2 -->\n",
+       "      <g transform=\"translate(20.878125 147.035852)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 19.1875 8.296875 \n",
+       "L 53.609375 8.296875 \n",
+       "L 53.609375 0 \n",
+       "L 7.328125 0 \n",
+       "L 7.328125 8.296875 \n",
+       "Q 12.9375 14.109375 22.625 23.890625 \n",
+       "Q 32.328125 33.6875 34.8125 36.53125 \n",
+       "Q 39.546875 41.84375 41.421875 45.53125 \n",
+       "Q 43.3125 49.21875 43.3125 52.78125 \n",
+       "Q 43.3125 58.59375 39.234375 62.25 \n",
+       "Q 35.15625 65.921875 28.609375 65.921875 \n",
+       "Q 23.96875 65.921875 18.8125 64.3125 \n",
+       "Q 13.671875 62.703125 7.8125 59.421875 \n",
+       "L 7.8125 69.390625 \n",
+       "Q 13.765625 71.78125 18.9375 73 \n",
+       "Q 24.125 74.21875 28.421875 74.21875 \n",
+       "Q 39.75 74.21875 46.484375 68.546875 \n",
+       "Q 53.21875 62.890625 53.21875 53.421875 \n",
+       "Q 53.21875 48.921875 51.53125 44.890625 \n",
+       "Q 49.859375 40.875 45.40625 35.40625 \n",
+       "Q 44.1875 33.984375 37.640625 27.21875 \n",
+       "Q 31.109375 20.453125 19.1875 8.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-50\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_4\">\n",
+       "     <g id=\"line2d_20\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m8c08098b29\" y=\"102.534949\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_21\">\n",
+       "      <!-- 0.3 -->\n",
+       "      <g transform=\"translate(20.878125 106.334168)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 40.578125 39.3125 \n",
+       "Q 47.65625 37.796875 51.625 33 \n",
+       "Q 55.609375 28.21875 55.609375 21.1875 \n",
+       "Q 55.609375 10.40625 48.1875 4.484375 \n",
+       "Q 40.765625 -1.421875 27.09375 -1.421875 \n",
+       "Q 22.515625 -1.421875 17.65625 -0.515625 \n",
+       "Q 12.796875 0.390625 7.625 2.203125 \n",
+       "L 7.625 11.71875 \n",
+       "Q 11.71875 9.328125 16.59375 8.109375 \n",
+       "Q 21.484375 6.890625 26.8125 6.890625 \n",
+       "Q 36.078125 6.890625 40.9375 10.546875 \n",
+       "Q 45.796875 14.203125 45.796875 21.1875 \n",
+       "Q 45.796875 27.640625 41.28125 31.265625 \n",
+       "Q 36.765625 34.90625 28.71875 34.90625 \n",
+       "L 20.21875 34.90625 \n",
+       "L 20.21875 43.015625 \n",
+       "L 29.109375 43.015625 \n",
+       "Q 36.375 43.015625 40.234375 45.921875 \n",
+       "Q 44.09375 48.828125 44.09375 54.296875 \n",
+       "Q 44.09375 59.90625 40.109375 62.90625 \n",
+       "Q 36.140625 65.921875 28.71875 65.921875 \n",
+       "Q 24.65625 65.921875 20.015625 65.03125 \n",
+       "Q 15.375 64.15625 9.8125 62.3125 \n",
+       "L 9.8125 71.09375 \n",
+       "Q 15.4375 72.65625 20.34375 73.4375 \n",
+       "Q 25.25 74.21875 29.59375 74.21875 \n",
+       "Q 40.828125 74.21875 47.359375 69.109375 \n",
+       "Q 53.90625 64.015625 53.90625 55.328125 \n",
+       "Q 53.90625 49.265625 50.4375 45.09375 \n",
+       "Q 46.96875 40.921875 40.578125 39.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-51\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-51\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_5\">\n",
+       "     <g id=\"line2d_21\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m8c08098b29\" y=\"61.833266\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_22\">\n",
+       "      <!-- 0.4 -->\n",
+       "      <g transform=\"translate(20.878125 65.632484)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 37.796875 64.3125 \n",
+       "L 12.890625 25.390625 \n",
+       "L 37.796875 25.390625 \n",
+       "z\n",
+       "M 35.203125 72.90625 \n",
+       "L 47.609375 72.90625 \n",
+       "L 47.609375 25.390625 \n",
+       "L 58.015625 25.390625 \n",
+       "L 58.015625 17.1875 \n",
+       "L 47.609375 17.1875 \n",
+       "L 47.609375 0 \n",
+       "L 37.796875 0 \n",
+       "L 37.796875 17.1875 \n",
+       "L 4.890625 17.1875 \n",
+       "L 4.890625 26.703125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-52\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-52\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_6\">\n",
+       "     <g id=\"line2d_22\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m8c08098b29\" y=\"21.131582\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_23\">\n",
+       "      <!-- 0.5 -->\n",
+       "      <g transform=\"translate(20.878125 24.930801)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 10.796875 72.90625 \n",
+       "L 49.515625 72.90625 \n",
+       "L 49.515625 64.59375 \n",
+       "L 19.828125 64.59375 \n",
+       "L 19.828125 46.734375 \n",
+       "Q 21.96875 47.46875 24.109375 47.828125 \n",
+       "Q 26.265625 48.1875 28.421875 48.1875 \n",
+       "Q 40.625 48.1875 47.75 41.5 \n",
+       "Q 54.890625 34.8125 54.890625 23.390625 \n",
+       "Q 54.890625 11.625 47.5625 5.09375 \n",
+       "Q 40.234375 -1.421875 26.90625 -1.421875 \n",
+       "Q 22.3125 -1.421875 17.546875 -0.640625 \n",
+       "Q 12.796875 0.140625 7.71875 1.703125 \n",
+       "L 7.71875 11.625 \n",
+       "Q 12.109375 9.234375 16.796875 8.0625 \n",
+       "Q 21.484375 6.890625 26.703125 6.890625 \n",
+       "Q 35.15625 6.890625 40.078125 11.328125 \n",
+       "Q 45.015625 15.765625 45.015625 23.390625 \n",
+       "Q 45.015625 31 40.078125 35.4375 \n",
+       "Q 35.15625 39.890625 26.703125 39.890625 \n",
+       "Q 22.75 39.890625 18.8125 39.015625 \n",
+       "Q 14.890625 38.140625 10.796875 36.28125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-53\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_24\">\n",
+       "     <!-- Measured Probabilities -->\n",
+       "     <g transform=\"translate(14.798438 172.470781)rotate(-90)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 24.515625 72.90625 \n",
+       "L 43.109375 23.296875 \n",
+       "L 61.8125 72.90625 \n",
+       "L 76.515625 72.90625 \n",
+       "L 76.515625 0 \n",
+       "L 66.890625 0 \n",
+       "L 66.890625 64.015625 \n",
+       "L 48.09375 14.015625 \n",
+       "L 38.1875 14.015625 \n",
+       "L 19.390625 64.015625 \n",
+       "L 19.390625 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-77\"/>\n",
+       "       <path d=\"M 44.28125 53.078125 \n",
+       "L 44.28125 44.578125 \n",
+       "Q 40.484375 46.53125 36.375 47.5 \n",
+       "Q 32.28125 48.484375 27.875 48.484375 \n",
+       "Q 21.1875 48.484375 17.84375 46.4375 \n",
+       "Q 14.5 44.390625 14.5 40.28125 \n",
+       "Q 14.5 37.15625 16.890625 35.375 \n",
+       "Q 19.28125 33.59375 26.515625 31.984375 \n",
+       "L 29.59375 31.296875 \n",
+       "Q 39.15625 29.25 43.1875 25.515625 \n",
+       "Q 47.21875 21.78125 47.21875 15.09375 \n",
+       "Q 47.21875 7.46875 41.1875 3.015625 \n",
+       "Q 35.15625 -1.421875 24.609375 -1.421875 \n",
+       "Q 20.21875 -1.421875 15.453125 -0.5625 \n",
+       "Q 10.6875 0.296875 5.421875 2 \n",
+       "L 5.421875 11.28125 \n",
+       "Q 10.40625 8.6875 15.234375 7.390625 \n",
+       "Q 20.0625 6.109375 24.8125 6.109375 \n",
+       "Q 31.15625 6.109375 34.5625 8.28125 \n",
+       "Q 37.984375 10.453125 37.984375 14.40625 \n",
+       "Q 37.984375 18.0625 35.515625 20.015625 \n",
+       "Q 33.0625 21.96875 24.703125 23.78125 \n",
+       "L 21.578125 24.515625 \n",
+       "Q 13.234375 26.265625 9.515625 29.90625 \n",
+       "Q 5.8125 33.546875 5.8125 39.890625 \n",
+       "Q 5.8125 47.609375 11.28125 51.796875 \n",
+       "Q 16.75 56 26.8125 56 \n",
+       "Q 31.78125 56 36.171875 55.265625 \n",
+       "Q 40.578125 54.546875 44.28125 53.078125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-115\"/>\n",
+       "       <path d=\"M 41.109375 46.296875 \n",
+       "Q 39.59375 47.171875 37.8125 47.578125 \n",
+       "Q 36.03125 48 33.890625 48 \n",
+       "Q 26.265625 48 22.1875 43.046875 \n",
+       "Q 18.109375 38.09375 18.109375 28.8125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 20.953125 51.171875 25.484375 53.578125 \n",
+       "Q 30.03125 56 36.53125 56 \n",
+       "Q 37.453125 56 38.578125 55.875 \n",
+       "Q 39.703125 55.765625 41.0625 55.515625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-114\"/>\n",
+       "       <path d=\"M 45.40625 46.390625 \n",
+       "L 45.40625 75.984375 \n",
+       "L 54.390625 75.984375 \n",
+       "L 54.390625 0 \n",
+       "L 45.40625 0 \n",
+       "L 45.40625 8.203125 \n",
+       "Q 42.578125 3.328125 38.25 0.953125 \n",
+       "Q 33.9375 -1.421875 27.875 -1.421875 \n",
+       "Q 17.96875 -1.421875 11.734375 6.484375 \n",
+       "Q 5.515625 14.40625 5.515625 27.296875 \n",
+       "Q 5.515625 40.1875 11.734375 48.09375 \n",
+       "Q 17.96875 56 27.875 56 \n",
+       "Q 33.9375 56 38.25 53.625 \n",
+       "Q 42.578125 51.265625 45.40625 46.390625 \n",
+       "z\n",
+       "M 14.796875 27.296875 \n",
+       "Q 14.796875 17.390625 18.875 11.75 \n",
+       "Q 22.953125 6.109375 30.078125 6.109375 \n",
+       "Q 37.203125 6.109375 41.296875 11.75 \n",
+       "Q 45.40625 17.390625 45.40625 27.296875 \n",
+       "Q 45.40625 37.203125 41.296875 42.84375 \n",
+       "Q 37.203125 48.484375 30.078125 48.484375 \n",
+       "Q 22.953125 48.484375 18.875 42.84375 \n",
+       "Q 14.796875 37.203125 14.796875 27.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-100\"/>\n",
+       "       <path d=\"M 19.671875 64.796875 \n",
+       "L 19.671875 37.40625 \n",
+       "L 32.078125 37.40625 \n",
+       "Q 38.96875 37.40625 42.71875 40.96875 \n",
+       "Q 46.484375 44.53125 46.484375 51.125 \n",
+       "Q 46.484375 57.671875 42.71875 61.234375 \n",
+       "Q 38.96875 64.796875 32.078125 64.796875 \n",
+       "z\n",
+       "M 9.8125 72.90625 \n",
+       "L 32.078125 72.90625 \n",
+       "Q 44.34375 72.90625 50.609375 67.359375 \n",
+       "Q 56.890625 61.8125 56.890625 51.125 \n",
+       "Q 56.890625 40.328125 50.609375 34.8125 \n",
+       "Q 44.34375 29.296875 32.078125 29.296875 \n",
+       "L 19.671875 29.296875 \n",
+       "L 19.671875 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-80\"/>\n",
+       "       <path d=\"M 30.609375 48.390625 \n",
+       "Q 23.390625 48.390625 19.1875 42.75 \n",
+       "Q 14.984375 37.109375 14.984375 27.296875 \n",
+       "Q 14.984375 17.484375 19.15625 11.84375 \n",
+       "Q 23.34375 6.203125 30.609375 6.203125 \n",
+       "Q 37.796875 6.203125 41.984375 11.859375 \n",
+       "Q 46.1875 17.53125 46.1875 27.296875 \n",
+       "Q 46.1875 37.015625 41.984375 42.703125 \n",
+       "Q 37.796875 48.390625 30.609375 48.390625 \n",
+       "z\n",
+       "M 30.609375 56 \n",
+       "Q 42.328125 56 49.015625 48.375 \n",
+       "Q 55.71875 40.765625 55.71875 27.296875 \n",
+       "Q 55.71875 13.875 49.015625 6.21875 \n",
+       "Q 42.328125 -1.421875 30.609375 -1.421875 \n",
+       "Q 18.84375 -1.421875 12.171875 6.21875 \n",
+       "Q 5.515625 13.875 5.515625 27.296875 \n",
+       "Q 5.515625 40.765625 12.171875 48.375 \n",
+       "Q 18.84375 56 30.609375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-111\"/>\n",
+       "       <path d=\"M 9.421875 75.984375 \n",
+       "L 18.40625 75.984375 \n",
+       "L 18.40625 0 \n",
+       "L 9.421875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-108\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-77\"/>\n",
+       "      <use x=\"86.279297\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"147.802734\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"209.082031\" xlink:href=\"#DejaVuSans-115\"/>\n",
+       "      <use x=\"261.181641\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"324.560547\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"363.423828\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"424.947266\" xlink:href=\"#DejaVuSans-100\"/>\n",
+       "      <use x=\"488.423828\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"520.210938\" xlink:href=\"#DejaVuSans-80\"/>\n",
+       "      <use x=\"578.763672\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"617.626953\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"678.808594\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"742.285156\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"803.564453\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"867.041016\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"894.824219\" xlink:href=\"#DejaVuSans-108\"/>\n",
+       "      <use x=\"922.607422\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"950.390625\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"989.599609\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"1017.382812\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"1078.90625\" xlink:href=\"#DejaVuSans-115\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"patch_19\">\n",
+       "    <path d=\"M 43.78125 224.64 \n",
+       "L 43.78125 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_20\">\n",
+       "    <path d=\"M 378.58125 224.64 \n",
+       "L 378.58125 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_21\">\n",
+       "    <path d=\"M 43.78125 224.64 \n",
+       "L 378.58125 224.64 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_22\">\n",
+       "    <path d=\"M 43.78125 7.2 \n",
+       "L 378.58125 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"p5520171445\">\n",
+       "   <rect height=\"217.44\" width=\"334.8\" x=\"43.78125\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "with fluid.dygraph.guard():\n",
+    "    # 模拟重复测量电路输出态 1024 次\n",
+    "    prob_measure = cir.measure(plot=True)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "通过测量，找到出现几率最高的比特串。 此时，记其在该比特串中对应的比特取值为 $0$ 的顶点属于集合 $S_0$ 以及对应比特取值为 $1$ 的顶点属于集合 $S_1$，这两个顶点集合之间存在的边就是该图的一个可能的最大割方案。\n",
+    "\n",
+    "下面的代码选取测量结果中出现几率最大的比特串，然后将其映射回经典解，并且画出对应的最大割方案：\n",
+    "- 红色顶点属于集合 $S_0$，\n",
+    "- 蓝色顶点属于集合 $S_1$，\n",
+    "- 虚线表示被割的边。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 10,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:04:50.540864Z",
+     "start_time": "2021-01-09T07:04:50.399744Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "找到的割的比特串形式： 0101\n"
+     ]
+    },
+    {
+     "data": {
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"302.4pt\" version=\"1.1\" viewBox=\"0 0 446.4 302.4\" width=\"446.4pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T15:04:50.508349</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 302.4 \n",
+       "L 446.4 302.4 \n",
+       "L 446.4 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"LineCollection_1\">\n",
+       "    <path clip-path=\"url(#p51cca9015d)\" d=\"M 377.485714 151.2 \n",
+       "L 223.199993 48.342857 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p51cca9015d)\" d=\"M 377.485714 151.2 \n",
+       "L 223.200002 254.057143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p51cca9015d)\" d=\"M 223.199993 48.342857 \n",
+       "L 68.914286 151.200009 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p51cca9015d)\" d=\"M 68.914286 151.200009 \n",
+       "L 223.200002 254.057143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"PathCollection_1\">\n",
+       "    <defs>\n",
+       "     <path d=\"M 0 22.36068 \n",
+       "C 5.930122 22.36068 11.618159 20.004617 15.811388 15.811388 \n",
+       "C 20.004617 11.618159 22.36068 5.930122 22.36068 -0 \n",
+       "C 22.36068 -5.930122 20.004617 -11.618159 15.811388 -15.811388 \n",
+       "C 11.618159 -20.004617 5.930122 -22.36068 0 -22.36068 \n",
+       "C -5.930122 -22.36068 -11.618159 -20.004617 -15.811388 -15.811388 \n",
+       "C -20.004617 -11.618159 -22.36068 -5.930122 -22.36068 0 \n",
+       "C -22.36068 5.930122 -20.004617 11.618159 -15.811388 15.811388 \n",
+       "C -11.618159 20.004617 -5.930122 22.36068 0 22.36068 \n",
+       "z\n",
+       "\" id=\"C0_0_370df0a5fc\"/>\n",
+       "    </defs>\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <use style=\"fill:#ff0000;stroke:#ff0000;\" x=\"377.485714\" xlink:href=\"#C0_0_370df0a5fc\" y=\"151.2\"/>\n",
+       "    </g>\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <use style=\"fill:#0000ff;stroke:#0000ff;\" x=\"223.199993\" xlink:href=\"#C0_0_370df0a5fc\" y=\"48.342857\"/>\n",
+       "    </g>\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <use style=\"fill:#ff0000;stroke:#ff0000;\" x=\"68.914286\" xlink:href=\"#C0_0_370df0a5fc\" y=\"151.200009\"/>\n",
+       "    </g>\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <use style=\"fill:#0000ff;stroke:#0000ff;\" x=\"223.200002\" xlink:href=\"#C0_0_370df0a5fc\" y=\"254.057143\"/>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_1\">\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <!-- 0 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(370.527902 156.71875)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46 36.53125 \n",
+       "Q 46 50.203125 43.4375 55.78125 \n",
+       "Q 40.875 61.375 34.8125 61.375 \n",
+       "Q 28.765625 61.375 26.171875 55.78125 \n",
+       "Q 23.578125 50.203125 23.578125 36.53125 \n",
+       "Q 23.578125 22.703125 26.171875 17.03125 \n",
+       "Q 28.765625 11.375 34.8125 11.375 \n",
+       "Q 40.828125 11.375 43.40625 17.03125 \n",
+       "Q 46 22.703125 46 36.53125 \n",
+       "z\n",
+       "M 64.796875 36.375 \n",
+       "Q 64.796875 18.265625 56.984375 8.421875 \n",
+       "Q 49.171875 -1.421875 34.8125 -1.421875 \n",
+       "Q 20.40625 -1.421875 12.59375 8.421875 \n",
+       "Q 4.78125 18.265625 4.78125 36.375 \n",
+       "Q 4.78125 54.546875 12.59375 64.375 \n",
+       "Q 20.40625 74.21875 34.8125 74.21875 \n",
+       "Q 49.171875 74.21875 56.984375 64.375 \n",
+       "Q 64.796875 54.546875 64.796875 36.375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-48\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-48\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_2\">\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <!-- 1 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(216.242181 53.861607)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 11.71875 12.984375 \n",
+       "L 28.328125 12.984375 \n",
+       "L 28.328125 60.109375 \n",
+       "L 11.28125 56.59375 \n",
+       "L 11.28125 69.390625 \n",
+       "L 28.21875 72.90625 \n",
+       "L 46.09375 72.90625 \n",
+       "L 46.09375 12.984375 \n",
+       "L 62.703125 12.984375 \n",
+       "L 62.703125 0 \n",
+       "L 11.71875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-49\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-49\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_3\">\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <!-- 2 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(61.956473 156.718759)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 28.8125 13.8125 \n",
+       "L 60.890625 13.8125 \n",
+       "L 60.890625 0 \n",
+       "L 7.90625 0 \n",
+       "L 7.90625 13.8125 \n",
+       "L 34.515625 37.3125 \n",
+       "Q 38.09375 40.53125 39.796875 43.609375 \n",
+       "Q 41.5 46.6875 41.5 50 \n",
+       "Q 41.5 55.125 38.0625 58.25 \n",
+       "Q 34.625 61.375 28.90625 61.375 \n",
+       "Q 24.515625 61.375 19.28125 59.5 \n",
+       "Q 14.0625 57.625 8.109375 53.90625 \n",
+       "L 8.109375 69.921875 \n",
+       "Q 14.453125 72.015625 20.65625 73.109375 \n",
+       "Q 26.859375 74.21875 32.8125 74.21875 \n",
+       "Q 45.90625 74.21875 53.15625 68.453125 \n",
+       "Q 60.40625 62.703125 60.40625 52.390625 \n",
+       "Q 60.40625 46.4375 57.328125 41.28125 \n",
+       "Q 54.25 36.140625 44.390625 27.484375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-50\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-50\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_4\">\n",
+       "    <g clip-path=\"url(#p51cca9015d)\">\n",
+       "     <!-- 3 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(216.242189 259.575893)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46.578125 39.3125 \n",
+       "Q 53.953125 37.40625 57.78125 32.6875 \n",
+       "Q 61.625 27.984375 61.625 20.703125 \n",
+       "Q 61.625 9.859375 53.3125 4.21875 \n",
+       "Q 45.015625 -1.421875 29.109375 -1.421875 \n",
+       "Q 23.484375 -1.421875 17.84375 -0.515625 \n",
+       "Q 12.203125 0.390625 6.6875 2.203125 \n",
+       "L 6.6875 16.703125 \n",
+       "Q 11.96875 14.0625 17.15625 12.71875 \n",
+       "Q 22.359375 11.375 27.390625 11.375 \n",
+       "Q 34.859375 11.375 38.84375 13.953125 \n",
+       "Q 42.828125 16.546875 42.828125 21.390625 \n",
+       "Q 42.828125 26.375 38.75 28.9375 \n",
+       "Q 34.671875 31.5 26.703125 31.5 \n",
+       "L 19.1875 31.5 \n",
+       "L 19.1875 43.609375 \n",
+       "L 27.09375 43.609375 \n",
+       "Q 34.1875 43.609375 37.640625 45.828125 \n",
+       "Q 41.109375 48.046875 41.109375 52.59375 \n",
+       "Q 41.109375 56.78125 37.734375 59.078125 \n",
+       "Q 34.375 61.375 28.21875 61.375 \n",
+       "Q 23.6875 61.375 19.046875 60.34375 \n",
+       "Q 14.40625 59.328125 9.8125 57.328125 \n",
+       "L 9.8125 71.09375 \n",
+       "Q 15.375 72.65625 20.84375 73.4375 \n",
+       "Q 26.3125 74.21875 31.59375 74.21875 \n",
+       "Q 45.796875 74.21875 52.84375 69.546875 \n",
+       "Q 59.90625 64.890625 59.90625 55.515625 \n",
+       "Q 59.90625 49.125 56.53125 45.046875 \n",
+       "Q 53.171875 40.96875 46.578125 39.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-51\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-51\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"p51cca9015d\">\n",
+       "   <rect height=\"288\" width=\"432\" x=\"7.2\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "# 找到测量结果中出现几率最大的比特串\n",
+    "cut_bitstring = max(prob_measure, key=prob_measure.get)\n",
+    "print(\"找到的割的比特串形式：\", cut_bitstring)\n",
+    "\n",
+    "# 在图上画出上面得到的比特串对应的割\n",
+    "node_cut = [\"blue\" if cut_bitstring[v] == \"1\" else \"red\" for v in V]\n",
+    "\n",
+    "edge_cut = [\n",
+    "    \"solid\" if cut_bitstring[u] == cut_bitstring[v] else \"dashed\"\n",
+    "    for (u, v) in E\n",
+    "    ]\n",
+    "nx.draw(\n",
+    "        G,\n",
+    "        pos,\n",
+    "        node_color=node_cut,\n",
+    "        style=edge_cut,\n",
+    "        **options\n",
+    ")\n",
+    "ax = plt.gca()\n",
+    "ax.margins(0.20)\n",
+    "plt.axis(\"off\")\n",
+    "plt.show()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "可以看到，在这个例子中 QAOA 找到了图上的一个最大割。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## 参考文献\n",
+    "\n",
+    "[1] Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm. [arXiv:1411.4028 (2014).](https://arxiv.org/abs/1411.4028)\n",
+    "\n",
+    "[2] Farhi, E., Goldstone, J., Gutmann, S. & Sipser, M. Quantum computation by adiabatic evolution. [arXiv:quant-ph/0001106 (2000).](https://arxiv.org/abs/quant-ph/0001106)\n",
+    "\n",
+    "[3] Duan, R. Quantum Adiabatic Theorem Revisited. [arXiv:2003.03063 (2020).](https://arxiv.org/abs/2003.03063)\n",
+    "\n",
+    "\n"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/QAOA/QAOA_En.ipynb

@@ -2,159 +2,602 @@
  "cells": [
   {
    "cell_type": "markdown",
-   "metadata": {},
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-06T07:10:17.389768Z",
+     "start_time": "2021-01-06T07:10:17.379639Z"
+    }
+   },
    "source": [
-    "# Quantum Approximate Optimization Algorithm (QAOA)\n",
+    "# Quantum Approximate Optimization Algorithm\n",
     "\n",
-    "## English | [简体中文](./QAOA.ipynb)\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# Preparation\n",
-    "\n",
-    "This document provides an interactive experience to show how the quantum approximate optimization algorithm (QAOA) [1] works in the Paddle Quantum. \n",
+    "## Overview\n",
     "\n",
-    "To get started, let us import some necessary libraries and functions："
+    "Quantum Approximate Optimization Algorithm (QAOA) is a quantum algorithm that can run on recent Noisy Intermediate-Scale Quantum (NISQ) devices and has a wide range of applications. QAOA was proposed by Edward Farhi et al. in 2014 [1], and its purpose is to solve combinatorial optimization problems approximately."
    ]
   },
   {
-   "cell_type": "code",
-   "execution_count": 1,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
+   "cell_type": "markdown",
+   "metadata": {},
    "source": [
-    "from paddle import fluid\n",
+    "### Combinatorial optimization problem\n",
     "\n",
-    "import os\n",
-    "import numpy as np\n",
-    "import matplotlib.pyplot as plt\n",
-    "import networkx as nx\n",
+    "In applied mathematics and theoretical computer science, combinatorial optimization is a type of topic that finds the optimal object in a limited set of objects. In simple terms, the combinatorial optimization problem means that all solutions of the problem are composed of discrete variables, and the optimal solution is to be found in the discrete solution set. Combinatorial optimization problems involve a wide range of areas and are common in real life, such as the design of aircraft routes and the planning of express delivery routes.\n",
     "\n",
-    "from paddle_quantum.circuit import UAnsatz\n",
-    "from paddle_quantum.utils import pauli_str_to_matrix"
+    "Specifically, a combinatorial optimization problem can be described by $n$ bits and $m$ clauses. The value of each bit is $0$ or $1$, and we use $z_j$ to denote the value of the $j$th bit. Therefore, the value of these $n$ bits can be represented by the bit string $z=z_1z_2\\dots z_n$. Each clause is a restriction on some bits. For example, a clause can require the value of the $2$nd bit to be $0$, or it can require the value of the $3$rd bit and the $5$th bit to be the same. For the $j$th clause, we define a function\n",
+    "\n",
+    "$$\n",
+    "C_j(z)=\n",
+    "\\begin{cases}\n",
+    "1 & \\text{If the value $z$ of $n$ bits satisfies the condition indicated by clause $j$}\\\\\n",
+    "0 & \\text{if the value $z$ of $n$ bits does not satisfy the condition indicated by clause $j$}\n",
+    "\\end{cases}.\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "For example, if the first clause requires the value of the second bit to be 0, then we have $C_1(z_10z_3\\dots z_n)=1$ and $C_1(z_11z_3\\dots z_n)=0$.\n",
+    "\n",
+    "From the definition of $C_j$ in equation (1), we can define the objective function of the combinatorial optimization problem\n",
+    "\n",
+    "$$\n",
+    "C(z)=\\sum_{j=1}^m w_jC_j(z),\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "where $w_j$ is the weight of the $j$th clause. The combinatorial optimization problem is to find a value $z$ that maximizes the value of the objective function $C(z)$, namely\n",
+    "\n",
+    "$$\n",
+    "\\underset{z}{\\operatorname{argmax}} C(z).\n",
+    "\\tag{3}\n",
+    "$$\n"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# Background\n",
+    "### Quantum approximate optimization algorithm\n",
+    "\n",
+    "Many combinatorial optimization problems are NP-complete or even NP-hard problems, which means that computers may not be able to solve such problems efficiently. An alternative is to find the approximate optimal solution to such problems, and this task can usually be completed efficiently. QAOA is a quantum algorithm that can find an approximate optimal solution to a combinatorial optimization problem.\n",
+    "\n",
+    "#### Encoding combination optimization problem\n",
+    "\n",
+    "For the above combinatorial optimization problem, there are $n$ bits and $m$ clauses. The QAOA algorithm transforms this problem into an optimization problem on an $n$-qubit system. Each computational basis state $|z\\rangle \\in \\{0,1\\}^n$ of the quantum system corresponds to a value $z$ of $n$ bits in the original problem. At the same time, for the $j$th clause in the original problem, we define a diagonal Hamiltonian $H_{C_j}$ satisfying\n",
+    "\n",
+    "$$\n",
+    "H_{C_j}|z\\rangle = C_j(z)|z\\rangle.\n",
+    "\\tag{4}\n",
+    "$$\n",
+    "\n",
+    "Specifically, we can construct the Hamiltonian $H_{C_j}$ through the following equation:\n",
+    "\n",
+    "$$\n",
+    "H_{C_j} = \\sum_{z\\in\\{0,1\\}^n} C_j(z)|z\\rangle\\langle z|.\n",
+    "\\tag{5}\n",
+    "$$\n",
+    "\n",
+    "For example, assuming that $z^{(1)}$ and $z^{(2)}$ are the values ​​satisfying the $j$th clause, then we can define\n",
+    "\n",
+    "$$\n",
+    "H_{C_j} = |z^{(1)}\\rangle\\langle z^{(1)}| + |z^{(2)}\\rangle\\langle z^{(2)}|.\n",
+    "\\tag{6}\n",
+    "$$\n",
+    "\n",
+    "Therefore, QAOA encodes the objective function $C$ of the combinatorial optimization problem into the Hamiltonian $H_C$ on a system with $n$ qubits, where\n",
+    "\n",
+    "$$\n",
+    "H_C = \\sum_{j=1}^m w_jH_{C_j},\n",
+    "\\tag{7}\n",
+    "$$\n",
+    "\n",
+    "and\n",
+    "\n",
+    "$$\n",
+    "H_C|z\\rangle = \\sum_{j=1}^m w_jH_{C_j}|z\\rangle = \\sum_{j=1}^m w_jC_j(z)|z\\rangle = C(z)|z\\rangle .\n",
+    "\\tag{8}\n",
+    "$$\n",
+    "\n",
+    "It is worth noting that if an optimal solution to the original problem is $z_\\text{opt}$, then we have\n",
+    "\n",
+    "$$\n",
+    "\\langle z_\\text{opt}|H_C|z_\\text{opt}\\rangle = \\langle z_\\text{opt}|C(z_\\text{opt})|z_\\text{opt}\\rangle = C( z_\\text{opt})\\langle z_\\text{opt}|z_\\text{opt}\\rangle = C(z_\\text{opt}).\n",
+    "\\tag{9}\n",
+    "$$\n",
+    "\n",
+    "Therefore, an optimal solution of the original combinatorial optimization problem is an eigenstate with the largest eigenvalue of the Hamiltonian $H_C$. In addition, for any quantum state $|\\psi\\rangle$,\n",
+    "\n",
+    "$$\n",
+    "\\langle\\psi|H_C|\\psi\\rangle \\leq C(z_\\text{opt}),\n",
+    "\\tag{10}\n",
+    "$$\n",
+    "\n",
+    "and the equation takes the equal sign if and only if $|\\psi\\rangle$ is a superposition state of optimal solutions. It can be obtained from equation (9) and equation (10) that\n",
+    "\n",
+    "$$\n",
+    "\\max_{|\\psi\\rangle} \\langle\\psi|H_C|\\psi\\rangle = C(z_\\text{opt}),\n",
+    "\\tag{11}\n",
+    "$$\n",
+    "\n",
+    "and finding the optimal solution of the original combinatorial optimization problem is equivalent to finding an eigenstate with the largest eigenvalue of the Hamiltonian $H_C$, that is, finding a quantum state $|\\psi\\rangle$ such that\n",
+    "\n",
+    "$$\n",
+    "H_c|\\psi\\rangle = C(z_\\text{opt})|\\psi\\rangle.\n",
+    "\\tag{12}\n",
+    "$$\n",
+    "\n",
+    "When we find such a quantum state $|\\psi\\rangle$, it is probably not a computational basis state, but a superposition of several computational basis states, each of which is an optimal solution of the original combinatorial optimization problem. Therefore, we can obtain an optimal solution to the original combinatorial optimization problem by performing computational basis measurements on $|\\psi\\rangle$.\n",
+    "\n",
+    "#### Finding an approximate optimal solution\n",
+    "\n",
+    "Although it is relatively simple to encode the objective function of the combinatorial optimization problem to be solved into the Hamiltonian $H_C$ of a quantum system, finding the quantum state $|\\psi\\rangle$ representing an optimal solution from the huge Hilbert space according to equation (11) is not easy. In order to find such a quantum state, we need another Hamiltonian\n",
+    "\n",
+    "$$\n",
+    "H_B = \\sum_{j=1}^n X_j,\n",
+    "\\tag{13}\n",
+    "$$\n",
+    "\n",
+    "where $X_j$ represents the Pauli $X$ gate acting on the $j$th qubit. The two eigenstates of Pauli $X$ gate are $|+\\rangle$ and $|-\\rangle$, and their corresponding eigenvalues ​​are $1$ and $-1$, respectively:\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "X|+\\rangle &=\n",
+    "\\begin{bmatrix}\n",
+    "0&1\\\\1&0\n",
+    "\\end{bmatrix}\n",
+    "\\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "1\\\\1\n",
+    "\\end{bmatrix}\n",
+    "= \\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "1\\\\1\n",
+    "\\end{bmatrix}\n",
+    "= |+\\rangle,\\tag{14}\\\\\n",
+    "X|-\\rangle &=\n",
+    "\\begin{bmatrix}\n",
+    "0&1\\\\1&0\n",
+    "\\end{bmatrix}\n",
+    "\\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "1\\\\-1\n",
+    "\\end{bmatrix}\n",
+    "= \\frac{1}{\\sqrt{2}}\n",
+    "\\begin{bmatrix}\n",
+    "-1\\\\1\n",
+    "\\end{bmatrix}\n",
+    "= -|-\\rangle.\\tag{15}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "Therefore, the eigenstate with the largest eigenvalue of $H_B$ is\n",
+    "\n",
+    "$$\n",
+    "|s\\rangle \\equiv \\underbrace{|+\\rangle\\otimes\\cdots\\otimes|+\\rangle}_\\text{$n$ terms} = |+\\rangle^{\\otimes n }.\n",
+    "\\tag{16}\n",
+    "$$\n",
+    "\n",
+    "We will use this quantum state $|s\\rangle$ as the initial state for the algorithm. After constructing the Hamiltonian $H_C$ and $H_B$, we can start to find an approximate optimal solution to the original combinatorial optimization problem. According to the Hamiltonian $H_C$ and $H_B$, respectively define the unitary transformation\n",
+    "\n",
+    "$$\n",
+    "U_C(\\gamma) = e^{-i\\gamma H_C}\n",
+    "\\tag{17}\n",
+    "$$\n",
+    "\n",
+    "and unitary transformation\n",
+    "\n",
+    "$$\n",
+    "U_B(\\beta) = e^{-i\\beta H_B},\n",
+    "\\tag{18}\n",
+    "$$\n",
+    "\n",
+    "where $\\gamma$ and $\\beta$ are adjustable real parameters. Given any integer $p\\geq1$ and the parameters $\\vec{\\gamma}=(\\gamma_1,\\dots,\\gamma_p)$ and $\\vec{\\beta}=(\\beta_1,\\dots,\\beta_p) $, we define\n",
+    "\n",
+    "$$\n",
+    "|\\vec{\\gamma},\\vec{\\beta}\\rangle = U_B(\\beta_p)U_C(\\gamma_p)\\cdots U_B(\\beta_1)U_C(\\gamma_1)|s\\rangle.\n",
+    "\\tag{19}\n",
+    "$$\n",
+    "\n",
+    "It can be seen that the integer $p$ represents the number of layers of $U_C, U_B$, that is, the $U_C$ and $U_B$ are alternately applied to the initial state $|s\\rangle$ $p$ times. Let us denote $F_p(\\vec{\\gamma},\\vec{\\beta})$ as the expected value of the Hamiltonian $H_C$ in the quantum state of equation (19):\n",
+    "\n",
+    "$$\n",
+    "F_p(\\vec{\\gamma},\\vec{\\beta}) = \\langle\\vec{\\gamma},\\vec{\\beta}|H_C|\\vec{\\gamma},\\vec{\\beta}\\rangle .\n",
+    "\\tag{20}\n",
+    "$$\n",
     "\n",
-    "QAOA is one of quantum algorithms which can be implemented on near-term quantum processors, also called as noisy intermediate-scale quantum (NISQ) processors, and may have wide applications in solving hard computational problems.  For example, it could be applied to tackle a large family of optimization problems, named as the quadratic unconstrained binary optimization (QUBO) which is ubiquitous in the computer science and operation research. Basically, this class can be modeled with the form of\n",
+    "By adjusting the parameters $\\vec{\\gamma},\\vec{\\beta}$, we can get\n",
     "\n",
-    "$$F=\\max_{z_i\\in\\{-1,1\\}} \\sum_{i,j} q_{ij}(1-z_iz_j)=-\\min_{z_i\\in\\{-1,1\\}} \\sum_{i,j} q_{ij}z_iz_j+ \\sum_{i,j} q_{ij} $$\n",
+    "$$\n",
+    "M_p = \\max_{\\vec{\\gamma},\\vec{\\beta}} F_p(\\vec{\\gamma},\\vec{\\beta})\n",
+    "\\tag{21}\n",
+    "$$\n",
     "\n",
+    "as the approximate optimal solution under a given number of layers $p$. So far, we have transformed the problem of searching for the quantum state $|\\psi\\rangle$ into a problem of searching for the parameters $\\vec{\\gamma},\\vec{\\beta}$. It is worth noting that the search space given by $p$ layers of $U_C, U_B$ is larger than that of $p-1$ layers, so\n",
     "\n",
-    "where $z_i$s are binary parameters and coefficients $q_{ij}$ refer to the weight associated to $x_i x_j$. Indeed, it is usually extremely difficult for classical computers to give the exact optimal solution, while QAOA provides an alternative approach which may have a speedup advantage over classical ones to solve these hard problems.\n",
+    "$$\n",
+    "M_p \\geq M_{p-1}.\n",
+    "\\tag{22}\n",
+    "$$\n",
     "\n",
-    "QAOA works as follows: The above optimization problem is first mapped to another problem of finding the ground energy or/and the corresponding ground state for a complex many-body Hamiltonian, e.g., the well-known Ising model or spin-glass model in many-body physics. In this tutorial, we use the Max-Cut problem in graph theory to explain how QAOA works. Essentially, the Max-cut problem is transformed into a problem of finding the smallest eigenvalue and the corresponding eigenvector(s) for a real diagonal matrix $H$. Then, QAOA designates a specific routine with adjustable parameters to approximately find the best solution. Moreover, to accomplish the task, these parameters could be updated via some rules set by fast classical algorithms, such as gradient-free or gradient-based methods. Thus, it is also a quantum-classical hybrid algorithm just as the variational quantum eigensolver (VQE)."
+    "In fact, when $p$ is large enough,\n",
+    "\n",
+    "$$\n",
+    "\\lim_{p\\to\\infty} M_p = \\max_z C(z).\n",
+    "\\tag{23}\n",
+    "$$\n",
+    "\n",
+    "#### Decoding the quantum solution\n",
+    "\n",
+    "In the previous paragraph, we simplify the search for the quantum state $|\\psi\\rangle$ into the search for the parameterized quantum state $|\\vec{\\gamma},\\vec{\\beta}\\rangle$, but at the same time, we have also reduced the search space. That is to say, given the number of layers $p$, there may be no parameters $\\vec{\\gamma},\\vec{\\beta}$ such that $F_p(\\vec{\\gamma},\\vec{\\beta}) = C(z_\\text{opt})$. Suppose that the parameters $\\vec{\\gamma}^*$ and $\\vec{\\beta}^*$ make $F_p$ the largest, that is, $F_p(\\vec{\\gamma}^*,\\vec{\\beta}^* ) = M_p$. Then under ideal circumstances, the quantum state $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ contains the information of an optimal solution. But it should be noted that only $p$ layers are used here, so it is very likely that $M_p < C(z_\\text{opt})$. Therefore, in general $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ only contains information about an approximate optimal solution. Furthermore, we assume that the quantum state $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ is the superposition state of $l$ computational basis state, namely\n",
+    "\n",
+    "$$\n",
+    "|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle = c_1|z^{(1)}\\rangle + \\cdots + c_l|z^{(l)}\\rangle.\n",
+    "\\tag{24}\n",
+    "$$\n",
+    "\n",
+    "Normally, the larger the probability $|c_j|^2$ that a state $|z^{(j)}\\rangle$ is measured on the computational basis, the more likely that the corresponding bit string $z^{(j) }$ is an optimal solution. Thus, we prepare $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ and measure it to get a bit string $z$ and calculate the value of $C(z)$. Repeat this process many times, and we can get a bit string $z$ that makes $C(z)$ close to or even exceed $M_p$.\n",
+    "\n",
+    "#### Adiabatic theorem\n",
+    "\n",
+    "Why do we use the above method to construct the quantum state $|\\vec{\\gamma},\\vec{\\beta}\\rangle$? QAOA tries to find an approximate optimal solution to an optimization problem. A similar algorithm is the quantum adiabatic algorithm [2] (QAA). The difference is that QAA is designed to find an optimal solution to the optimization problem rather than an approximate one. Similar to QAOA, QAA transforms an optimization problem into a problem of finding the ground state of a Hamiltonian, and uses the adiabatic theorem to solve it. Consider the Hamiltonian\n",
+    "\n",
+    "$$\n",
+    "H(t) = (1-\\frac tT)H_B + \\frac tT H_C,\n",
+    "\\tag{25}\n",
+    "$$\n",
+    "\n",
+    "of a quantum system. At initial, time $t=0$, and the Hamiltonian of the system is $H(0) = H_B$. As time passes, the Hamiltonian of the system gradually changes from $H_B$ to $H_C$. When $t=T$, the Hamiltonian of the system becomes $H(T) = H_C$. The adiabatic theorem in quantum mechanics tells us that if the system is in an eigenstate of $H_B$ at the beginning, then as long as the evolution time $T$ is long enough, the system will be in the eigenstate of the corresponding energy level of $H_C$ when the Hamiltonian of the system completely evolves to $H_C$. Therefore, if the system is initially in $|s\\rangle$, that is, the eigenstate with the largest eigenvalue of $H_B$, after a sufficiently long evolution time $T$, the quantum state of the system will become the eigenstate with the largest eigenvalue of $H_C$. [3]\n",
+    "\n",
+    "One way to simulate the evolution of the Hamiltonian $H(t)$ over time $t$ is to alternately apply the unitary transformations $U_C(\\gamma)$ and $U_B(\\beta)$ on the quantum system, and the accuracy of simulation depends on the value of $\\gamma,\\beta$. In addition, in order for the evolution of the system to follow the adiabatic theorem, a sufficiently long evolution time is required, so the value of $p$ is required to be large enough. Therefore, combining equation (22) we can deduce the conclusion in equation (23).\n",
+    "\n"
    ]
   },
   {
    "cell_type": "markdown",
-   "metadata": {},
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-06T07:12:18.621281Z",
+     "start_time": "2021-01-06T07:12:18.308211Z"
+    }
+   },
    "source": [
+    "### Example: applying QAOA to solve the Max-Cut Problem\n",
+    "\n",
+    "The Max-Cut Problem is a common combinatorial optimization problem in graph theory, and it has important applications in statistical physics and circuit design. The maximum cut problem is an NP-complete problem, so there is no efficient algorithm that can solve this problem perfectly.\n",
+    "\n",
+    "#### Max-Cut Problem\n",
+    "\n",
+    "In graph theory, a graph is represented by a pair of sets $G=(V, E)$, where the elements in the set $V$ are the vertices of the graph, and each element in the set $E$ is a pair of vertices, representing an edge connecting these two vertices. For example, the graph in the figure below is represented by $V=\\{0,1,2,3\\}$ and $E=\\{(0,1),(1,2),(2,3),(3, 0)\\}$.\n",
+    "\n",
+    "![G](figures/qaoa-fig-maxcut_g.png \"Figure 1: A graph with four vertices and four edges\")\n",
+    "<div style=\"text-align:center\">Figure 1: A graph with four vertices and four edges </div>\n",
+    "\n",
+    "A cut on a graph refers to a partition of the graph's vertex set $V$ into two disjoint sets. Each cut corresponds to a set of edges, in which the two vertices of each edge are divided into different sets. So we can define the size of this cut as the size of this set of edges, that is, the number of edges being cut. The Max-Cut Problem is to find a cut that maximizes the number of edges being cut. Figure 2 shows a maximum cut of the graph in Figure 1. The size of the maximum cut is $4$, which means that all edges in the graph are cut.\n",
     "\n",
-    "# Example\n",
+    "![Max cut on G](figures/qaoa-fig-maxcut_cut.png \"Figure 2: A maximum cut of the graph in Figure 1\")\n",
+    "<div style=\"text-align:center\">Figure 2: A maximum cut of the graph in Figure 1 </div>\n",
     "\n",
-    "##  1. Max-Cut problem\n",
+    "Assuming that the input graph $G=(V, E)$ has $n=|V|$ vertices and $m=|E|$ edges, we can describe the Max-Cut Problem as a combinatorial optimization problem with $n$ bits and $m$ clauses. Each bit corresponds to a vertex $v$ in the graph $G$, and its value $z_v$ is $0$ or $1$, corresponding to the vertex belonging to the set $S_{0}$ or $S_{1}$, respectively. Thus, each value $z$ of these $n$ bits corresponds to a distinct cut. Each clause corresponds to an edge $(u,v)$ in the graph $G$. A clause requires that the two vertices connected by its corresponding edge take different values, namely $z_u\\neq z_v$, which means the edge is cut. In other words, when the two vertices connected by the edge are divided into different sets, we say that the clause is satisfied. Therefore, for each edge $(u,v)$ in the graph $G$, we have\n",
     "\n",
-    "Given a graph $G$ composed of $N$ nodes and $M$ edges, the problem is to find a cut protocol which divides the node set into two complementary subsets $S$ and $S^\\prime$ such that the number of edges between these sets is as large as possible. For example, consider the ring case with four nodes as shown in the figure.\n",
+    "$$\n",
+    "C_{(u,v)}(z) = z_u+z_v-2z_uz_v,\n",
+    "\\tag{26}\n",
+    "$$\n",
     "\n",
-    " ![ring4.png](https://release-data.cdn.bcebos.com/PIC%2FMaxCut.png) \n",
-    " \n",
+    "where $C_{(u,v)}(z) = 1$ if and only if the edge is cut. Otherwise, the function is equal to $0$. The objective function of the entire combinatorial optimization problem is\n",
     "\n",
-    "Thus, given a cut protocol, if the node $i$ belongs to the set $S$, then it is assigned to $z_i =1$, while $z_j= -1$ for $j \\in S^\\prime$. Then, for any edge connecting nodes $i$ and $j$, if both nodes are in the same set $S$ or $S^\\prime$, then there is $z_iz_j=1$; otherwise, $z_iz_j=-1$. Hence, the cut problem can be formulated as the optimization problem \n",
+    "$$\n",
+    "C(z) = \\sum_{(u,v)\\in E}C_{(u,v)}(z) = \\sum_{(u,v)\\in E}z_u+z_v-2z_uz_v.\n",
+    "\\tag{27}\n",
+    "$$\n",
     "\n",
-    "$$ F=\\min_{z_i\\in\\{-1, 1\\}} z_1 z_2+z_2z_3+z_3z_4+z_4z_1.$$\n",
+    "Therefore, to solve the maximum cut problem is to find a value $z$ that maximizes the objective function in equation (27).\n",
     "\n",
-    "Here, the weight $q_{ij}s$ are set to $1$ for all edges. Indeed, any feasible solution to the above problem can be described by a bitstring $ \\boldsymbol{z}=z_1z_2z_3z_4 \\in \\{-1, 1\\}^4$. Moreover, we need to search over all possible bitstrings of $2^N$ to find its optimal solution, which becomes computionally hard for classical algorithms.\n",
+    "#### Encoding Max-Cut Problem\n",
+    "\n",
+    "Here we take the Max-Cut Problem as an example to further elaborate on QAOA. In order to transform the Max-Cut Problem into a quantum problem, we need to use $n$ qubits, where each qubit corresponds to a vertex in the graph $G$. A qubit being in a quantum state $|0\\rangle$ or $|1\\rangle$ indicates that its corresponding vertex belongs to the set $S_{0}$ or $S_{1}$, respectively. It is worth noting that $|0\\rangle$ and $|1\\rangle$ are the two eigenstates of Pauli $Z$ gate, and their eigenvalues ​​are respectively $1$ and $-1$, namely\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "Z|0\\rangle&=|0\\rangle,\\tag{28}\\\\\n",
+    "Z|1\\rangle&=-|1\\rangle.\\tag{29}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "Therefore, we can use Pauli $Z$ gate to construct the Hamiltonian $H_C$ of the Max-Cut Problem. Because mapping $f(x):x\\to(x+1)/2$ maps $-1$ to $0$ and $1$ to $1$, we can replace $z$ in equation (27) with $(Z+I)/2$ ($I$ is the identity matrix) to get the Hamiltonian corresponding to the objective function of the original problem:\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "H_C &= \\sum_{(u,v)\\in E} \\frac{Z_u+I}{2} + \\frac{Z_v+I}{2}-2\\cdot\\frac{Z_u+I}{2} \\frac{Z_v+I}{2}\\tag{30}\\\\\n",
+    "&= \\sum_{(u,v)\\in E} \\frac{Z_u+Z_v+2I-(Z_uZ_v+Z_u+Z_v+I)}{2}\\tag{31}\\\\\n",
+    "&= \\sum_{(u,v)\\in E} \\frac{I-Z_uZ_v}{2}.\\tag{32}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "The expected value of this Hamiltonian for a quantum state $|\\psi\\rangle$ is\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "\\langle\\psi|H_C|\\psi\\rangle &= \\langle\\psi|\\sum_{(u,v)\\in E} \\frac{I-Z_uZ_v}{2}|\\psi\\rangle\\tag{33} \\\\\n",
+    "&= \\langle\\psi|\\sum_{(u,v)\\in E} \\frac{I}{2}|\\psi\\rangle-\\langle\\psi|\\sum_{(u,v)\\in E} \\frac{Z_uZ_v}{2}|\\psi\\rangle\\tag{34}\\\\\n",
+    "&= \\frac{|E|}{2}-\\frac{1}{2}\\langle\\psi|\\sum_{(u,v)\\in E} Z_uZ_v|\\psi\\rangle.\\tag{35}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "If we define\n",
+    "\n",
+    "$$\n",
+    "H_D = -\\sum_{(u,v)\\in E} Z_uZ_v,\n",
+    "\\tag{36}\n",
+    "$$\n",
+    "\n",
+    "then finding the quantum state $|\\psi\\rangle$ that maximizes $\\langle\\psi|H_C|\\psi\\rangle$ is equivalent to finding the quantum state $|\\psi\\rangle$ such that $\\langle\\psi|H_D|\\psi \\rangle$ is the largest."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Paddle Quantum Implementation\n",
     "\n",
-    "Two methods are provided to pre-process this optimization problem, i.e., to input the given graph with/without weights: \n",
+    "Let's take the Max-Cut Problem as an example and use the QAOA algorithm to solve it with Paddle Quantum. There are many ways to find the parameters $\\vec{\\gamma},\\vec{\\beta}$. Here we use the gradient descent method in classical machine learning.\n",
     "\n",
-    "- Method 1 generates the graph via its full description of nodes and edges,\n",
-    "- Method 2 specifies the graph via its adjacency matrix.\n",
+    "To implement QAOA on Paddle Quantum, the first thing to do is to import the required packages. Among them, the `networkx` package can help us handle graphs conveniently.\n",
     "\n"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 2,
-   "metadata": {},
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:54:37.202331Z",
+     "start_time": "2021-01-09T06:54:32.649071Z"
+    }
+   },
    "outputs": [],
    "source": [
-    "def generate_graph(N, GRAPHMETHOD):\n",
-    "    \"\"\"\n",
-    "    It plots an N-node graph which is specified by Method 1 or 2.\n",
-    "    \n",
-    "    Args:\n",
-    "        N: number of nodes (vertices) in the graph\n",
-    "        METHOD: choose which method to generate a graph\n",
-    "    Returns:\n",
-    "        the specific graph and its adjacency matrix\n",
-    "    \"\"\"\n",
-    "    # Method 1 generates a graph by self-definition\n",
-    "    if GRAPHMETHOD == 1:\n",
-    "        print(\"Method 1 generates the graph from self-definition using EDGE description\")\n",
-    "        graph = nx.Graph()\n",
-    "        graph_nodelist=range(N)\n",
-    "        graph.add_edges_from([(0, 1), (1, 2), (2, 3), (3, 0)])\n",
-    "        graph_adjacency = nx.to_numpy_matrix(graph, nodelist=graph_nodelist)\n",
-    "    # Method 2 generates a graph by using its adjacency matrix directly\n",
-    "    elif GRAPHMETHOD == 2:\n",
-    "        print(\"Method 2 generates the graph from networks using adjacency matrix\")\n",
-    "        graph_adjacency = np.array([[0, 1, 0, 1], [1, 0, 1, 0], [0, 1, 0, 1], [1, 0, 1, 0]])\n",
-    "        graph = nx.Graph(graph_adjacency)\n",
-    "    else:\n",
-    "        print(\"Method doesn't exist \")\n",
-    "\n",
-    "    return graph, graph_adjacency"
+    "# Import related modules from Paddle Quantum and PaddlePaddle\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import pauli_str_to_matrix\n",
+    "\n",
+    "# Import additional packages needed\n",
+    "import numpy as np\n",
+    "import matplotlib.pyplot as plt\n",
+    "%config InlineBackend.figure_format = 'svg'\n",
+    "import networkx as nx"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "In this notebook, Method 1 is used to process and then visualize the given graph. Note that the node label starts from $0$ to $ N-1$ in both methods for an $N$-node graph. \n",
-    "\n",
-    "Here, we need to specify:\n",
-    "\n",
-    "- number of nodes: $N=4$\n",
-    "- which method to preprocess the graph: GRAPHMETHOD = 1 "
+    "Next, we generate the graph $G$ in the Max-Cut Problem. For the convenience of computation, the vertices here are labeled starting from $0$."
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 3,
+   "execution_count": 2,
    "metadata": {
-    "pycharm": {
-     "is_executing": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:54:37.384183Z",
+     "start_time": "2021-01-09T06:54:37.204886Z"
     }
    },
    "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "Method 1 generates the graph from self-definition using EDGE description\n",
-      "[[0. 1. 0. 1.]\n",
-      " [1. 0. 1. 0.]\n",
-      " [0. 1. 0. 1.]\n",
-      " [1. 0. 1. 0.]]\n"
-     ]
-    },
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAb4AAAEuCAYAAADx63eqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAXC0lEQVR4nO3df2yc9WHH8c/9sH12bNfBcexAaKExxJAVZwShVCv5oa6rmu4HTEFtCVKhFIaSsQ6tmlBC29AFJVK7rXMFQq1IUH9AWzJC1462gzaJ0oqoNFns/ogJoaXELHZsJ87FTu7O92N/OOf4cnf2/Xieu+d5vu+XVBX5Hj96+MPPh/f57uxLpVIpAQBgCH+1LwAAgEpi+AAARmH4AABGYfgAAEZh+AAARmH4AABGYfgAAEZh+AAARmH4AABGYfgAAEYJVvsCAJOMjEe1+9CA+gfDCkfiag4F1dXRrDtXLFZrY121Lw8wgo/P6gTs13tiTE/sO679x4YlSdF4cvqxUNCvlKQ1S9u0cXWnuq9uqc5FAoZg+ACbfevgW3r8pX5F4gnN9tPm80mhYEBb1nXp7pXXVOz6ANPwVCdgo6nRO6oLk8k5j02lpAuTCT3+0lFJYvwAm1B8gE16T4zp418/qAuTiemvhV/7vsb7XtbkyNtSKql3/dkn1HLbhqzvra8J6LsPrNRNi1sqeMWAGXhVJ2CTJ/YdVySeyPhabPC4/KFGBZoWzPq9kXhCT+47buflAcZi+AAbjIxHtf/YcNbv9Bb81T+pY8MO1ba/d9bvT6Wkva8Pa3Q8auNVAmZi+AAb7D40UPY5fJJ2Hy7/PAAyMXyADfoHwxlvWShFJJ5U/8lzFl0RgDSGD7BBOBK36DyTlpwHwCUMH2CD5pA17xRqDtVYch4Al/A+PsAGXR1NCvqSiqcy/9vyXO9PFD3xO8WG3pQknX/joOJnT6nh+pVquP79GcfWBX3qWtRUsWsGTEHxARYbGBjQf375nzU5mf10Z/TE7zTxm58qEZ766LLJU3/QxG9+qtjQ77OOjUSimjf0a9uvFzANb2AHLJJKpbRr1y49/PDDCofDWnDHZjVct1I+f/H/fZlKJnX+jVc1sme77rrrLvX09Ki1tdWGqwbMQ/EBFhgYGNC6det03333KRwOS5LCrz6vVCJW0vlSiZjCrz4vSXr22We1bNkyvfjii1ZdLmA0hg8oQyqV0s6dO7Vs2TL9+Mc/zngsNviGFry9X3VBX1HnDCihs3t3KTZ46ZNbhoaGdMcdd2jDhg0aHR215NoBUzF8QIlyVV5aQ0ODenp69KvvfEWf++iNqq8JyDfH/vl8U5/R+djf3KT9T29Td3d31jHUH1A+fscHFOny3+VdbtWqVdq5c6eWLFky/bW+gTE9ue+49r4+LJ+m3pyelv57fGuXtmnjms7pD6aOxWLavn27tm3bpng8+4Uy/O4PKA3DBxRhYGBA999/f9bTmtJU5e3YsUObNm2SP88LWkbHo9p9eED9J88pHJlUc6hGXYuatP7m/H+B/ciRI7rnnnvU29ub9Vh7e7ueeuop3X777WX9ewEmYfiAApRSeVai/gDrMHzAHMqtPCtRf0D5eHELkMdsr9iUpiqvr69PDz30UEVGT5KWL1+uX/7yl9q6dauCwcwPXuKVn0BhKD4gBydVXj7UH1Aaig+YwYmVlw/1B5SG4gMuckPl5UP9AYVz3k8wUGFuqrx8qD+gcBQfjObmysuH+gNm556fZsBCXqi8fKg/YHYUH4zjxcrLh/oDsrn/JxsokJcrLx/qD8hG8cEIJlVePtQfMMW7P+WAzKy8fKg/YArFB8+i8vKj/mAy837i4XlU3tyoP5iM4oOnUHnFo/5gGn764QlUXumoP5iG4oPrUXnWof5gAu4EcC0qz3rUH0xA8cGVqDz7UX/wKu4KcBUqr3KoP3gVxQfXoPKqh/qDl3CHgONRedVH/cFLKD44GpXnPNQf3I67BRyJynMu6g9uR/HBcag896D+4EbcOeAYVJ77UH9wI4oPjkDluR/1B7fgLoKqovK8g/qDW1B8qBoqz7uoPzgZdxRUHJXnfdQfnIziQ0VReeah/uA03F1QEVSeuag/OA3FB9tReUij/uAE3GlgGyoPl6P+4AQUH2xB5WEu1B+qhbsOLEXloVDUH6qF4oNlqDyUivpDJXEHQtmoPJSL+kMlUXwoC5UHq1F/sBt3I5SEyoNdqD/YjeJD0ag8VAr1BztwZ0LBqDxUGvUHO1B8KAiVh2qj/mAV7lKYFZUHp6D+YBWKD3lReXAq6g/l4I6FLFQenI76QzkoPmSg8uA21B+Kxd0Lkqg8uBf1h2JRfKDy4BnUHwrBncxgVB68hvpDISg+Q1F58DrqD/lwVzMMlQdTUH/Ih+IzCJUHU1F/mIk7nAGoPJiO+sNMFJ/HUXlAJuoP3O08isoDcqP+QPF5EJUHFIb6MxN3Pg+h8oDiUH9movg8gsoDykP9mYO7oMtReYA1qD9zUHwuRuUB9qD+vI07ogtReYC9qD9vo/hchsoDKov68x7uji5B5QHVQf15D8XnAlQe4AzUnzdwp3QwKg9wFurPGyg+h6LyAGej/tyLu6bDUHmAO1B/7kXxOQiVB7gT9ecu3EEdgMoD3I36cxeKr8qoPMBbqD/n425aJVQe4E3Un/NRfFVA5QFmoP6ciTtrBVF5gFmoP2ei+CqEygPMRv05B3dZm1F5ACTqz0koPhtReQByof6qizuuDag8ALOh/qqL4rMYlQegGNRf5XH3tQiVB6AU1F/lUXwWoPIAWIH6qwzuxGWg8gBYifqrDIqvRFQeADtRf/bhrlwkKg9AJVB/9qH4ikDlAagG6s9a3KELQOUBqCbqz1oU3xyoPABOQv2Vj7t1HlQeACei/spH8eVA5QFwA+qvNNy5Z6DyALgJ9Vcaiu8iKg+Am1F/hTP+Lk7lAfAC6q9wRhcflQfAi6i/2Rl5R6fyAHgZ9Tc744qPygNgEuovmzF3dyoPgImov2xGFB+VBwDUX5qn7/RUHgBcQv1N8WzxUXkAkJ/J9ee5uz6VBwBzM7n+PFV8VB4AFM+0+vPEAlB5AFA60+rP9cVH5QGAdUyoP9euAZUHANYzof5cWXxUHgDYz6v156ploPIAoHK8Wn+uKT4qDwCqx0v15/iVoPIAoPq8VH+OLj4qDwCcx+3158jFoPIAwLncXn+OKz4qDwDcw431Z/vwjYxHtfvQgPoHwwpH4moOBdXV0aw7VyxWa2Pd9HGpVEq7du3Sww8/rHA4nHWeVatWaefOnVqyZImdlwsAKFIsFtP27du1bds2xePxrMfvuusu9fT0qLW1NeuxQjfCSrYNX++JMT2x77j2HxuWJEXjyenHQkG/UpLWLG3TxtWdavWNU3kA4HLF1F8xG9F9dYul12nL8H3r4Ft6/KV+ReIJzXZ2n08KKqWxvTs1cnBP1uNUHgC4SyH1d9untug/9r9d0EaEggFtWdelu1deY9k1Wj58U6N3VBcmk3MffFEyFtGZnz2t8SM/kkTlAYDb5au/xuUf0RUf/LR8NYU/jVlf49eWdTdYNn6WDl/viTF9/OsHdWEyMf210R/1KDpwVPHwsHyBGtVeeb3mr/2Uatvek/G9ycmIhr79iFZefyWVBwAecHn91XZcp/YN2+WvCU0fk4rHdOZnOzXRf0Cp2AXVti/R/A9+WnVXLs04V31NQN99YKVuWtxS9nVZmlNP7DuuSDyR8bXx3v+Rr65B825cJV9dgyK/P6RT3/u8UvFYxnG+QK1ue3Cb9u7dy+gBgAfU1tbqC1/4gl577TV1d3er+f13yheozTjm9Ctf07nDP1RgXovqr1up6Dv9GvrOo0qcP5txXCSe0JP7jltyXcG5DynMyHhU+48NZz1f2373lxRafIMkKT42pHeeuk+Jc6OKjbytuo7O6eN8fr9OxJt15vykba/kAQBU3vLly/Wjn/1cH/jSXiVm9FZiYkzjfa9IPr/aP/64AvNaNOIPaOK3e3Xu0A/VctuG6WNTKWnv68MaHY+WvRGWFd/uQwM5v54ePUlKJS/+otPnV6DxiqxjfZJ2H859HgCAe33/10NZb3afHHlbSsYVaG5TYF6LJKn2YhDFTv0h6xxWbYRlw9c/GM54OerlkrELGv3vf5ckNd96u4I5hi8ST6r/5DmrLgkA4BC5NiIxcUaS5K+99Ds/38V/Tj82k1UbYdlTneFI9stW0xLnz+rU81sVO/mGGrs/rJY1985ynkmrLgkA4BC5NiIwb76kqVf2p6Uu/nP6sezzlL8Rlg1fcyj3qeJnT2nou59T/PQ7al65XvPX3DPHeWqsuiQAgEPk2oiaBVdL/qAS4WElJs4oMG++oiePSZJqF16b5zzlb4Rlw9fV0ay64GBWyg5+87NKjJ9WoLlNqXhMp1/5miRp3o2rs16uGgr61bWoyapLAgA4RN2FUSkek4KXXtUZmDdfje/7oMZ7f6Kh57aopu09On/05/LV1qtpxV9mncOqjbDsd3zrVyzO+fXE+Omp/w8P69yv/mv6f5MjJ7KOjUSjuqHubNbXAQDuNDExoc985jP617+/U7neND7/zx9Q480fVWJiTOePHVTdVUvV/rEvKtDwrqxjU5LW35x7a4ph6RvYH/jmr/Ty0aFZP4Imn1QyqfNvvKqxH3xJjz76qDZv3qyaGp72BAC3OnDggO699169+eabkqQFd2xWw3Ur5SvhE7l8PunDN7brqbtvKfu6LH0D+6Y1nQoFAyV9byoRU/jV5xWPx7V161bdeuutOT/oFADgbOnKW7169fToSVL41eeVSsRm+c78QsGANq7pnPvAAlg6fN1Xt2jLui7V1xR3Wn8yrjM/fVqxwUvvyj9y5IhuueUWPfbYY5qc5JWeAOAGBw4cUHd3t3p6enT5E4pX1cf1yfc1Fb0RU5/V2WXJx5VJNvwF9rtXXqMt625QfU1APt/sx/p8U5+/9sU7uvWNz9+vhQsXZjxO/QGAO+SrvLRNmzapr69P//LJvyh6I6z8gGrJxr/H1zcwpif3Hdfe14fl09QbD9PSf2tp7dI2bVzTOb3io6Ojeuihh/Tcc89lnS8YDPK7PwBwoMt/lzfTtddeq6efflpr167N+HopG2EV2/8C++h4VLsPD6j/5DmFI5NqDtWoa1GT1t+c/6/r7tmzRw8++KBOnTqV9djy5cv1zDPPqLu7287LBgDMYWJiQps3b9ZXv/rVrKc1panK27FjhxobG/Oeo5SNKJftw1cq6g8AnKuUynMKxw5fGvUHAM5hReVVm+OHT6L+AMAJ3Fx5M7li+NKoPwCoPC9U3kyuGj6J+gOASvJK5c3kuuFLo/4AwD5eq7yZXDt8EvUHAHbwYuXN5OrhS6P+AKB8Xq68mTwxfBL1BwDl8HrlzeSZ4Uuj/gCgcKZU3kyeGz6J+gOAQphUeTN5cvjSqD8AyGZi5c3k6eGTqD8AmMnUypvJ88OXRv0BMJnplTeTMcMnUX8AzETlZTJq+NKoPwAmoPJyM3L4JOoPgLdRefkZO3xp1B8AL6Hy5mb88EnUHwBvoPIKw/DNQP0BcCMqrzgM32WoPwBuQuUVj+HLg/oD4GRUXukYvllQfwCciMorD8NXAOoPgBNQedZg+ApE/QGoJirPOgxfkag/AJVE5VmP4SsB9QegEqg8ezB8ZaD+ANiByrMXw1cm6g+Alag8+zF8FqH+AJSDyqschs9C1B+AUlB5lcXw2YD6A1AIKq86GD6bUH8AZkPlVQ/DZzPqD8BMVF71MXwVQP0BkKg8p2D4Koj6A8xE5TkLw1dh1B9gFirPeRi+KqH+AG+j8pyL4asi6g/wJirP2Rg+B6D+AG+g8tyB4XMI6g9wNyrPPRg+h6H+AHeh8tyH4XMg6g9wByrPnRg+B6P+AGei8tyN4XM46g9wFirP/Rg+l6D+gOqi8ryD4XMR6g+oDirPWxg+F6L+gMqg8ryJ4XMp6g+wF5XnXQyfy1F/gLWoPO9j+DyA+gOsQeWZgeHzEOoPKA2VZxaGz2OoP6A4VJ55GD6Pov6A2VF55mL4PIz6A3Kj8szG8BmA+gOmUHmQGD5jUH8wHZWHNIbPMNQfTEPl4XIMn4GoP5iCykMuDJ/BqD94FZWH2TB8hqP+4DVUHubC8EES9Qf3o/JQKIYP06g/uBWVh2IwfMhC/cEtqDyUguFDTtQfnI7KQ6kYPsyK+oPTUHkoF8OHOVF/cAoqD1Zg+FAw6g/VQuXBSgwfikL9odKoPFiN4UNJqD/YjcqDXRg+lIz6g12oPNiJ4UPZqD9YhcpDJTB8sAT1h3JReagUhg+Wov5QLCoPlcbwwXLUHwpF5aEaGD7YhvpDPlQeqonhg62oP1yOykO1MXyoCOoPVB6cguFDxVB/5qLy4CQMHyqO+jMHlQcnYvhQFdSf91F5cCqGD1VF/XkPlQenY/hQddSfd1B5cAOGD45B/bkXlQc3YfjgKNSf+1B5cBuGD45E/TkflQe3YvjgWNSfc1F5cDOGD45H/TkHlQcvYPjgCtRf9VF58AqGD65C/VUelQevYfjgOtRf5VB58CKGD65F/dmHyoOXMXxwNerPelQevI7hgydQf+Wj8mAKhg+eQf2VjsqDSRg+eA71VzgqDyZi+OBJ1N/cqDyYiuGDp1F/2ag8mI7hg+dRf5dQeQDDB4OYXH9UHnAJwwejmFh/VB6QieGDkUyoPyoPyI3hg7G8XH9UHpAfwwfjean+qDxgbgwfIG/UH5UHFIbhA2ZwY/1ReUBxGD7gMm6qPyoPKB7DB+Th5Pqj8oDSMXzALJxYf1QeUB6GDyiAE+qPygOswfABBapm/VF5gHUYPqBIlaw/Kg+wHsMHlKDU+hsZj2r3oQH1D4YVjsTVHAqqq6NZd65YrNbGuoxjqTzAHgwfUIZC66/3xJie2Hdc+48NS5Ki8eT0caGgXylJa5a2aePqTnVeUUPlATZi+IAyzVV/6x/5iv7X915F40nN9tPm80k1Pmnyte/prZe/kfU4lQdYw1/tCwDcrrW1Vc8++6xeeOEFLVy4MOOx0J98SL+40KHI5OyjJ0mplBRLSon3/bUal38k47FNmzapr6+P0QMsQPEBFppZf7Ud16l9w3b5a0IZx4z88N8UeeuIEhfC8tc2qLajU/NXf1K1HUumj0lORjT07Ud0VX2CygMsxvABNtizZ4/+4Xu/lv/dfyqfP/OJlcFvP6JAU6v8dQ2K/LFP8dPvKNDcpsUbd00fk0omtShxSq9s/Ri/ywMsFqz2BQBedNuH1qn+UJ1iiez/ruzYsGP6n6ODxzX4zD8qcW5UqURcvsDUj6TP79eZ2isVVY2YPcBaDB9gg92HBuTz+STlfkIlfOgHmhw5ocgfeyVJzbfePj16aT5Juw8P6O9WLclxBgClYvgAG/QPhjPesnC58/2/UPTEbyRJgaYFqrvqxqxjIvGk+k+es+0aAVPxqk7ABuFIfNbHOzbs0Ls/+4La/vZRJcZPa/jF7YqPDeU4z6RdlwgYi+EDbNAcyv1kSnIyqlQyIUnyBWtV/94V8tWGpGRC8bPZw9ccqv7f/AO8hqc6ARt0dTSrLjiY9XRn7P9e18gPvqy6q5fJH2pU9MRvlYqel7/hXaptz/xdXijoV9eipkpeNmAEig+wwfoVi3N+PdDUquD8KxX5wxGN976sZGRcDV0fUPsnHpc/NC/j2JSk9TfnPg+A0lF8gA0WNNZp9fVtevnoUMYnttRccVXG2xny8fmktUvbsj64GkD5KD7AJpvWdCoUDJT0vaFgQBvXdFp8RQAkhg+wTffVLdqyrkv1NcX9mNXX+LVlXZduWtxiz4UBhuOpTsBGd6+8RpL0+Ev9isQTc/51hlAwoC3ruqa/D4D1+KxOoAL6Bsb05L7j2vv6sHyaenN6Wvrv8a1d2qaNazopPcBmDB9QQaPjUe0+PKD+k+cUjkyqOVSjrkVNWn9z9l9gB2APhg8AYBRe3AIAMArDBwAwCsMHADAKwwcAMArDBwAwCsMHADAKwwcAMArDBwAwCsMHADDK/wPoP7wlap6kMgAAAABJRU5ErkJggg==\n",
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"231.84pt\" version=\"1.1\" viewBox=\"0 0 349.2 231.84\" width=\"349.2pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T14:54:37.352699</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 231.84 \n",
+       "L 349.2 231.84 \n",
+       "L 349.2 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:none;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"LineCollection_1\">\n",
+       "    <path clip-path=\"url(#p8c02f84376)\" d=\"M 294.171429 115.92 \n",
+       "L 174.599995 38.262857 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p8c02f84376)\" d=\"M 294.171429 115.92 \n",
+       "L 174.600001 193.577143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p8c02f84376)\" d=\"M 174.599995 38.262857 \n",
+       "L 55.028571 115.920007 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p8c02f84376)\" d=\"M 55.028571 115.920007 \n",
+       "L 174.600001 193.577143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-width:2;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"PathCollection_1\">\n",
+       "    <defs>\n",
+       "     <path d=\"M 0 22.36068 \n",
+       "C 5.930122 22.36068 11.618159 20.004617 15.811388 15.811388 \n",
+       "C 20.004617 11.618159 22.36068 5.930122 22.36068 0 \n",
+       "C 22.36068 -5.930122 20.004617 -11.618159 15.811388 -15.811388 \n",
+       "C 11.618159 -20.004617 5.930122 -22.36068 0 -22.36068 \n",
+       "C -5.930122 -22.36068 -11.618159 -20.004617 -15.811388 -15.811388 \n",
+       "C -20.004617 -11.618159 -22.36068 -5.930122 -22.36068 0 \n",
+       "C -22.36068 5.930122 -20.004617 11.618159 -15.811388 15.811388 \n",
+       "C -11.618159 20.004617 -5.930122 22.36068 0 22.36068 \n",
+       "z\n",
+       "\" id=\"mb1b023645b\" style=\"stroke:#1f78b4;\"/>\n",
+       "    </defs>\n",
+       "    <g clip-path=\"url(#p8c02f84376)\">\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"294.171429\" xlink:href=\"#mb1b023645b\" y=\"115.92\"/>\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"174.599995\" xlink:href=\"#mb1b023645b\" y=\"38.262857\"/>\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"55.028571\" xlink:href=\"#mb1b023645b\" y=\"115.920007\"/>\n",
+       "     <use style=\"fill:#1f78b4;stroke:#1f78b4;\" x=\"174.600001\" xlink:href=\"#mb1b023645b\" y=\"193.577143\"/>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_1\">\n",
+       "    <g clip-path=\"url(#p8c02f84376)\">\n",
+       "     <!-- 0 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(287.213616 121.43875)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46 36.53125 \n",
+       "Q 46 50.203125 43.4375 55.78125 \n",
+       "Q 40.875 61.375 34.8125 61.375 \n",
+       "Q 28.765625 61.375 26.171875 55.78125 \n",
+       "Q 23.578125 50.203125 23.578125 36.53125 \n",
+       "Q 23.578125 22.703125 26.171875 17.03125 \n",
+       "Q 28.765625 11.375 34.8125 11.375 \n",
+       "Q 40.828125 11.375 43.40625 17.03125 \n",
+       "Q 46 22.703125 46 36.53125 \n",
+       "z\n",
+       "M 64.796875 36.375 \n",
+       "Q 64.796875 18.265625 56.984375 8.421875 \n",
+       "Q 49.171875 -1.421875 34.8125 -1.421875 \n",
+       "Q 20.40625 -1.421875 12.59375 8.421875 \n",
+       "Q 4.78125 18.265625 4.78125 36.375 \n",
+       "Q 4.78125 54.546875 12.59375 64.375 \n",
+       "Q 20.40625 74.21875 34.8125 74.21875 \n",
+       "Q 49.171875 74.21875 56.984375 64.375 \n",
+       "Q 64.796875 54.546875 64.796875 36.375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-48\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-48\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_2\">\n",
+       "    <g clip-path=\"url(#p8c02f84376)\">\n",
+       "     <!-- 1 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(167.642182 43.781607)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 11.71875 12.984375 \n",
+       "L 28.328125 12.984375 \n",
+       "L 28.328125 60.109375 \n",
+       "L 11.28125 56.59375 \n",
+       "L 11.28125 69.390625 \n",
+       "L 28.21875 72.90625 \n",
+       "L 46.09375 72.90625 \n",
+       "L 46.09375 12.984375 \n",
+       "L 62.703125 12.984375 \n",
+       "L 62.703125 0 \n",
+       "L 11.71875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-49\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-49\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_3\">\n",
+       "    <g clip-path=\"url(#p8c02f84376)\">\n",
+       "     <!-- 2 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(48.070759 121.438757)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 28.8125 13.8125 \n",
+       "L 60.890625 13.8125 \n",
+       "L 60.890625 0 \n",
+       "L 7.90625 0 \n",
+       "L 7.90625 13.8125 \n",
+       "L 34.515625 37.3125 \n",
+       "Q 38.09375 40.53125 39.796875 43.609375 \n",
+       "Q 41.5 46.6875 41.5 50 \n",
+       "Q 41.5 55.125 38.0625 58.25 \n",
+       "Q 34.625 61.375 28.90625 61.375 \n",
+       "Q 24.515625 61.375 19.28125 59.5 \n",
+       "Q 14.0625 57.625 8.109375 53.90625 \n",
+       "L 8.109375 69.921875 \n",
+       "Q 14.453125 72.015625 20.65625 73.109375 \n",
+       "Q 26.859375 74.21875 32.8125 74.21875 \n",
+       "Q 45.90625 74.21875 53.15625 68.453125 \n",
+       "Q 60.40625 62.703125 60.40625 52.390625 \n",
+       "Q 60.40625 46.4375 57.328125 41.28125 \n",
+       "Q 54.25 36.140625 44.390625 27.484375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-50\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-50\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_4\">\n",
+       "    <g clip-path=\"url(#p8c02f84376)\">\n",
+       "     <!-- 3 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(167.642189 199.095893)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46.578125 39.3125 \n",
+       "Q 53.953125 37.40625 57.78125 32.6875 \n",
+       "Q 61.625 27.984375 61.625 20.703125 \n",
+       "Q 61.625 9.859375 53.3125 4.21875 \n",
+       "Q 45.015625 -1.421875 29.109375 -1.421875 \n",
+       "Q 23.484375 -1.421875 17.84375 -0.515625 \n",
+       "Q 12.203125 0.390625 6.6875 2.203125 \n",
+       "L 6.6875 16.703125 \n",
+       "Q 11.96875 14.0625 17.15625 12.71875 \n",
+       "Q 22.359375 11.375 27.390625 11.375 \n",
+       "Q 34.859375 11.375 38.84375 13.953125 \n",
+       "Q 42.828125 16.546875 42.828125 21.390625 \n",
+       "Q 42.828125 26.375 38.75 28.9375 \n",
+       "Q 34.671875 31.5 26.703125 31.5 \n",
+       "L 19.1875 31.5 \n",
+       "L 19.1875 43.609375 \n",
+       "L 27.09375 43.609375 \n",
+       "Q 34.1875 43.609375 37.640625 45.828125 \n",
+       "Q 41.109375 48.046875 41.109375 52.59375 \n",
+       "Q 41.109375 56.78125 37.734375 59.078125 \n",
+       "Q 34.375 61.375 28.21875 61.375 \n",
+       "Q 23.6875 61.375 19.046875 60.34375 \n",
+       "Q 14.40625 59.328125 9.8125 57.328125 \n",
+       "L 9.8125 71.09375 \n",
+       "Q 15.375 72.65625 20.84375 73.4375 \n",
+       "Q 26.3125 74.21875 31.59375 74.21875 \n",
+       "Q 45.796875 74.21875 52.84375 69.546875 \n",
+       "Q 59.90625 64.890625 59.90625 55.515625 \n",
+       "Q 59.90625 49.125 56.53125 45.046875 \n",
+       "Q 53.171875 40.96875 46.578125 39.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-51\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-51\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"p8c02f84376\">\n",
+       "   <rect height=\"217.44\" width=\"334.8\" x=\"7.2\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
       "text/plain": [
        "<Figure size 432x288 with 1 Axes>"
       ]
@@ -164,13 +607,27 @@
     }
    ],
    "source": [
-    "# number of qubits or number of nodes in the graph\n",
-    "N=4  \n",
-    "classical_graph, classical_graph_adjacency= generate_graph(N, GRAPHMETHOD=1)\n",
-    "print(classical_graph_adjacency)\n",
-    "\n",
-    "pos = nx.circular_layout(classical_graph)\n",
-    "nx.draw(classical_graph, pos, width=4, with_labels=True, font_weight='bold')\n",
+    "# n is the number of vertices in the graph G, which is also the number of qubits\n",
+    "n = 4\n",
+    "G = nx.Graph()\n",
+    "V = range(n)\n",
+    "E = [(0, 1), (1, 2), (2, 3), (3, 0)]\n",
+    "G.add_edges_from(E)\n",
+    "\n",
+    "# Print out the generated graph G\n",
+    "pos = nx.circular_layout(G)\n",
+    "options = {\n",
+    "    \"with_labels\": True,\n",
+    "    \"font_size\": 20,\n",
+    "    \"font_weight\": \"bold\",\n",
+    "    \"font_color\": \"white\",\n",
+    "    \"node_size\": 2000,\n",
+    "    \"width\": 2\n",
+    "}\n",
+    "nx.draw_networkx(G, pos, **options)\n",
+    "ax = plt.gca()\n",
+    "ax.margins(0.20)\n",
+    "plt.axis(\"off\")\n",
     "plt.show()"
    ]
   },
@@ -178,64 +635,58 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 2. Encoding\n",
-    "\n",
-    "This step encodes the classical optimization problem to its quantum version. Using the transformation $z=1\\rightarrow |0\\rangle = \\begin{bmatrix}1 \\\\ 0\\end{bmatrix}$ and $z=-1\\rightarrow |1\\rangle = \\begin{bmatrix}0 \\\\ 1\\end{bmatrix}$, the binary parameter $z$ is encoded as the eigenvalues of the Pauli-Z operator acting on the single qubit, i.e., $z\\rightarrow Z=\\begin{bmatrix} 1 & 0\\\\ 0 & -1\\end{bmatrix}$. It yields that the objective function in the classical optimization problem is transformed to the Hamiltonian\n",
-    "\n",
-    "$$H_c= Z_1Z_2+Z_2Z_3+Z_3Z_4+Z_4Z_1.$$\n",
+    "### Encoding Hamiltonian\n",
     "\n",
-    "Here, for simplicity $Z_iZ_{j}$ stands for the tensor product $Z_i\\otimes Z_j$ which represents that Pauli-Z operator acts on each qubit $i, j$ and the identity operation is imposed on the rest. And the Max-Cut problem is mapped to the following quantum optimization problem\n",
-    "\n",
-    "$$ F=\\min_{|\\psi\\rangle}\\, \\langle \\psi| H_c |\\psi\\rangle$$\n",
-    "\n",
-    "where the state vector $|\\psi\\rangle$ describes a $4$-dimensional complex vector which is normalized to $1$, and $\\langle \\psi|$ is its conjugate transpose form. It is equivalent to find the smallest eigenvalue $F$ and the corresponding eigenstate(s) for the matrix $H_c$."
+    "In Paddle Quantum, a Hamiltonian can be input in the form of `list`. Here we construct the Hamiltonian $H_D$ in equation (36)."
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 4,
+   "execution_count": 3,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:54:37.397513Z",
+     "start_time": "2021-01-09T06:54:37.390477Z"
     }
    },
-   "outputs": [],
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "[[-1.0, 'z0,z1'], [-1.0, 'z1,z2'], [-1.0, 'z2,z3'], [-1.0, 'z3,z0']]\n"
+     ]
+    }
+   ],
    "source": [
-    "def H_generator(N, adjacency_matrix):\n",
-    "    \"\"\"\n",
-    "    This function maps the given graph via its adjacency matrix to the corresponding Hamiltiona H_c.\n",
-    "    \n",
-    "    Args:\n",
-    "        N: number of qubits, or number of nodes in the graph, or number of parameters in the classical problem\n",
-    "        adjacency_matrix:  the adjacency matrix generated from the graph encoding the classical problem\n",
-    "    Returns:\n",
-    "        the problem-based Hmiltonian H's list form generated from the graph_adjacency matrix for the given graph\n",
-    "    \"\"\"\n",
-    "    H_list = []\n",
-    "    # Generate the Hamiltonian H_c from the graph via its adjacency matrix\n",
-    "    for row in range(N):\n",
-    "        for col in range(N):\n",
-    "            if adjacency_matrix[row, col] and row < col:\n",
-    "                # Construct the Hamiltonian in the list form for the calculation of expectation value\n",
-    "                H_list.append([1.0, 'z'+str(row) + ',z' + str(col)])\n",
-    "\n",
-    "    return H_list"
+    "# Construct the Hamiltonian H_D in the form of list\n",
+    "H_D_list = []\n",
+    "for (u, v) in E:\n",
+    "    H_D_list.append([-1.0,'z'+str(u) +',z' + str(v)])\n",
+    "print(H_D_list)"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "The explicit form of the matrix $H_c$, including its maximal and minimal eigenvalues, can be imported, which later could be used to benchmark the performance of QAOA. "
+    "As you can see, in this example, the Hamiltonian $H_D$ is\n",
+    "\n",
+    "$$\n",
+    "H_D = -Z_0Z_1-Z_1Z_2-Z_2Z_3-Z_3Z_0.\n",
+    "\\tag{37}\n",
+    "$$\n",
+    "\n",
+    "We can view the matrix form of the Hamiltonian $H_D$ and get information of its eigenvalues:"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 5,
+   "execution_count": 4,
    "metadata": {
-    "pycharm": {
-     "is_executing": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:54:37.412726Z",
+     "start_time": "2021-01-09T06:54:37.402304Z"
     }
    },
    "outputs": [
@@ -243,109 +694,77 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "[ 4.  0.  0.  0.  0. -4.  0.  0.  0.  0. -4.  0.  0.  0.  0.  4.]\n",
-      "H_max: 4.0   H_min: -4.0\n"
+      "[-4.  0.  0.  0.  0.  4.  0.  0.  0.  0.  4.  0.  0.  0.  0. -4.]\n",
+      "H_max: 4.0\n"
      ]
     }
    ],
    "source": [
-    "# Convert the Hamiltonian's list form to matrix form\n",
-    "H_matrix = pauli_str_to_matrix(H_generator(N, classical_graph_adjacency), N)\n",
-    "\n",
-    "H_diag = np.diag(H_matrix).real\n",
-    "H_max = np.max(H_diag)\n",
-    "H_min = np.min(H_diag)\n",
-    "\n",
-    "print(H_diag)\n",
-    "print('H_max:', H_max, '  H_min:', H_min)"
+    "# Convert Hamiltonian H_D from list form to matrix form\n",
+    "H_D_matrix = pauli_str_to_matrix(H_D_list, n)\n",
+    "# Take out the elements on the diagonal of H_D\n",
+    "H_D_diag = np.diag(H_D_matrix).real\n",
+    "# Get the maximum eigenvalue of H_D\n",
+    "H_max = np.max(H_D_diag)\n",
+    "\n",
+    "print(H_D_diag)\n",
+    "print('H_max:', H_max)"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 3. Building\n",
-    "\n",
-    "This part is to build up the parameterized quantum circuit of QAOA to perform the computation process. Particularly, the QAOA circuit is constructed by alternatively placing two parameterized modules\n",
-    "\n",
-    "$$U_x(\\beta_P)U_c(\\gamma_P)\\dots U_x(\\beta_1)U_c(\\gamma_1)$$\n",
-    "\n",
-    "where $P$ is the number of layers to place these two modules. Particularly, one is governed by the encoding matrix $H_c$ via the unitary transformation\n",
-    "\n",
-    "$$U_c(\\gamma)=e^{-i \\gamma H_c }$$\n",
-    "\n",
-    "where $i$ is the imaginary unit, and $\\gamma\\in [0, \\pi]$ is to be optimized. The other one is \n",
-    "\n",
-    "$$U_x(\\beta)=e^{-i \\beta H_x },$$\n",
+    "### Building the QAOA circuit\n",
     "\n",
-    "where $\\beta\\in [0, \\pi]$ and the driving Hamiltonian or matrix $H_x$ adimits an explicit form of\n",
+    "Earlier we introduced that QAOA needs to apply two unitary transformations $U_C(\\gamma)$ and $U_B(\\beta)$ alternately on the initial state $|s\\rangle = |+\\rangle^{\\otimes n}$. Here, we use the quantum gates and quantum circuit templates provided in Paddle Quantum to build a quantum circuit to achieve this step. It should be noted that in the Max-Cut Problem, we simplify the problem of maximizing the expected value of the Hamiltonian $H_C$ to the problem of maximizing the expected value of the Hamiltonian $H_D$, so the unitary transformations to be used are $U_D(\\gamma)$ and $U_B(\\beta)$. By alternately placing two circuit modules with adjustable parameters, we are able to build a QAOA circuit\n",
     "\n",
-    "$$H_x =X_1+X_2+X_3+X_4 $$\n",
+    "$$\n",
+    "U_B(\\beta_p)U_D(\\gamma_p)\\cdots U_B(\\beta_1)U_D(\\gamma_1),\n",
+    "\\tag{38}\n",
+    "$$\n",
     "\n",
-    "where the operator $X=\\begin{bmatrix} 0 & 1\\\\ 1& 0\\end{bmatrix}$ defines the Pauli-X operation acting on the qubit.\n",
+    "where $U_D(\\gamma) = e^{-i\\gamma H_D}$ can be constructed with the circuit in the figure below. Another unitary transformation $U_B(\\beta)$ is equivalent to applying a $R_x$ gate to each qubit.\n",
     "\n",
+    "![U_D circuit](figures/qaoa-fig-cir_ud.png \"Figure 3: Quantum circuit of unitary transformation $e^{i\\gamma Z\\otimes Z}$\")\n",
+    "<div style=\"text-align:center\">Figure 3: Quantum circuit of unitary transformation $e^{i\\gamma Z\\otimes Z}$</div>\n",
     "\n",
+    "Therefore, the quantum circuit that realizes a layer of unitary transformation $U_B(\\beta)U_D(\\gamma)$ is shown in Figure 4.\n",
     "\n",
-    "Further, each module in the QAOA circuit can be decomposed into a series of operations acting on single qubits and two qubits. In particular, the first has the decomposition of $U_c(\\gamma)=\\prod_{(i, j)}e^{-i \\gamma Z_i\\otimes Z_j }$ while there is $U_x(\\beta)=\\prod_{i}e^{-i \\beta X_i}$ for the second. This is illustrated in the following figure.\n",
+    "![U_BU_D circuit](figures/qaoa-fig-cir_ubud.png \"Figure 4: Quantum circuit of unitary transformation $U_B(\\beta)U_D(\\gamma)$\")\n",
+    "<div style=\"text-align:center\">Figure 4: Quantum circuit of unitary transformation $U_B(\\beta)U_D(\\gamma)$  </div>\n",
     "\n",
-    " <!--\n",
-    "![Circ](https://release-data.cdn.bcebos.com/PIC%2FQAOACir.png) \n",
-    "-->\n",
-    "<img src=\"./figures/QAOAcircuit.png\" width=\"600\" >\n",
-    "\n",
-    "Then, based on\n",
-    "\n",
-    "- initial state of QAOA circuits \n",
-    "- adjacency matrix describing the graph\n",
-    "- number of qubits\n",
-    "- number of layers\n",
-    "\n",
-    "we are able to construct the standard QAOA circuit:"
+    "In Paddle Quantum, the default initial state of each qubit is $|0\\rangle$ (the initial state can be customized by input parameters). We can add a layer of Hadamard gates to change the state of each qubit from $|0\\rangle$ to $|+\\rangle$ so that we get the initial state $|s\\rangle = |+\\rangle^{\\otimes n}$ required by QAOA. In Paddle Quantum, we can add a layer of Hadamard gates to the quantum circuit by calling `superposition_layer()`.\n",
+    "\n"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 6,
+   "execution_count": 5,
    "metadata": {
-    "pycharm": {
-     "is_executing": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:54:37.438826Z",
+     "start_time": "2021-01-09T06:54:37.416589Z"
     }
    },
    "outputs": [],
    "source": [
-    "def circuit_QAOA(theta, adjacency_matrix, N, P):\n",
-    "    \"\"\"\n",
-    "    This function constructs the parameterized QAOA circuit which is composed of P layers of two blocks:\n",
-    "    one block is based on the problem Hamiltonian H which encodes the classical problem,\n",
-    "    and the other is constructed from the driving Hamiltonian describing the rotation around Pauli X\n",
-    "    acting on each qubit. It outputs the final state of the QAOA circuit.\n",
-    "    \n",
-    "    Args:\n",
-    "        theta: parameters to be optimized in the QAOA circuit\n",
-    "        adjacency_matrix:  the adjacency matrix of the graph encoding the classical problem\n",
-    "        N: number of qubits, or equivalently, the number of parameters in the original classical problem\n",
-    "        P: number of layers of two blocks in the QAOA circuit\n",
-    "    Returns:\n",
-    "        the QAOA circuit\n",
-    "    \"\"\"\n",
-    "\n",
-    "    cir = UAnsatz(N)\n",
-    "    \n",
-    "    #prepare the input state in the uniform superposition of 2^N bit-strings in the computational basis\n",
+    "def circuit_QAOA(p, gamma, beta):\n",
+    "    # Initialize the quantum circuit of n qubits\n",
+    "    cir = UAnsatz(n)\n",
+    "    # Prepare quantum state |s>\n",
     "    cir.superposition_layer()\n",
-    "    # This loop defines the QAOA circuit with P layers of two blocks\n",
-    "    for layer in range(P):\n",
-    "        # The second and third loops construct the first block which involves two-qubit operation\n",
-    "        #  e^{-i\\gamma Z_iZ_j} acting on a pair of qubits or nodes i and j in the circuit in each layer.\n",
-    "        for row in range(N):\n",
-    "            for col in range(N):\n",
-    "                if adjacency_matrix[row, col] and row < col:\n",
-    "                    cir.cnot([row, col])\n",
-    "                    cir.rz(theta[layer][0], col)\n",
-    "                    cir.cnot([row, col])\n",
-    "        # This loop constructs the second block only involving the single-qubit operation e^{-i\\beta X}.\n",
-    "        for i in range(N):\n",
-    "            cir.rx(theta[layer][1], i)\n",
+    "    # Build a circuit with p layers\n",
+    "    for layer in range(p):\n",
+    "        # Build the circuit of U_D\n",
+    "        for (u, v) in E:\n",
+    "            cir.cnot([u, v])\n",
+    "            cir.rz(gamma[layer], v)\n",
+    "            cir.cnot([u, v])\n",
+    "\n",
+    "        # Build the circuit of U_B, that is, add a layer of R_x gates\n",
+    "        for v in V:\n",
+    "            cir.rx(beta[layer], v)\n",
     "\n",
     "    return cir"
    ]
@@ -354,130 +773,61 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Indeed, the QAOA circuit could be extended to other structures by replacing the modules in the above standard circuit to improve QAOA performance. Here, we provide one candidate extension in which the Pauli-X rotation $R_x(\\beta) $ on each qubit in the driving matrix $H_x$ is replaced by an arbitrary rotation described by $U3(\\beta_1,\\beta_2,\\beta_3)$. "
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 7,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "def circuit_extend_QAOA(theta, adjacency_matrix, N, P):\n",
-    "    \"\"\"\n",
-    "    This is an extended version of the QAOA circuit, and the main difference is the block constructed\n",
-    "    from the driving Hamiltonian describing the rotation around an arbitrary direction on each qubit.\n",
-    "\n",
-    "    Args:\n",
-    "        theta: parameters to be optimized in the QAOA circuit\n",
-    "        input_state: input state of the QAOA circuit which usually is the uniform superposition of 2^N bit-strings\n",
-    "                     in the computational basis\n",
-    "        adjacency_matrix:  the adjacency matrix of the problem graph encoding the original problem\n",
-    "        N: number of qubits, or equivalently, the number of parameters in the original classical problem\n",
-    "        P: number of layers of two blocks in the QAOA circuit\n",
-    "    Returns:\n",
-    "        the extended QAOA circuit\n",
-    "\n",
-    "    Note:\n",
-    "        If this circuit_extend_QAOA function is used to construct QAOA circuit, then we need to change the parameter layer\n",
-    "        in the Net function defined below from the Net(shape=[D, 2]) for circuit_QAOA function to Net(shape=[D, 4])\n",
-    "        because the number of parameters doubles in each layer in this QAOA circuit.\n",
-    "    \"\"\"\n",
-    "    cir = UAnsatz(N)\n",
-    "\n",
-    "    #prepare the input state in the uniform superposition of 2^N bit-strings in the computational basis\n",
-    "    cir.superposition_layer()\n",
-    "    for layer in range(P):\n",
-    "        for row in range(N):\n",
-    "            for col in range(N):\n",
-    "                if adjacency_matrix[row, col] and row < col:\n",
-    "                    cir.cnot([row, col])\n",
-    "                    cir.rz(theta[layer][0], col)\n",
-    "                    cir.cnot([row, col])\n",
-    "\n",
-    "        for i in range(N):\n",
-    "            cir.u3(*theta[layer][1:], i)\n",
+    "After running the constructed QAOA quantum circuit, we obtain the output state\n",
     "\n",
-    "    return cir"
+    "$$\n",
+    "|\\vec{\\gamma},\\vec{\\beta}\\rangle = U_B(\\beta_p)U_D(\\gamma_p)\\cdots U_B(\\beta_1)U_D(\\gamma_1)|s\\rangle.\n",
+    "\\tag{39}\n",
+    "$$"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Finally, the QAOA circuit outputs\n",
-    "\n",
-    "$$|\\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)\\rangle=U_x(\\beta_P)U_c(\\gamma_P)\\dots U_x(\\beta_1)U_c(\\gamma_1)|+\\rangle_1\\dots|+\\rangle_N$$\n",
-    "\n",
-    "where each qubit is initialized as the superposition state $|+\\rangle=\\frac{1}{\\sqrt{2}}\\left(|0\\rangle+|1\\rangle\\right)$. And we are able to obtain the loss function for the QAOA circuit\n",
+    "### Calculating the loss function\n",
     "\n",
-    "$$F_P=\\min_{\\boldsymbol{\\beta},\\boldsymbol{\\gamma}} \\langle \\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)| H_c|\\psi(\\boldsymbol{\\beta},\\boldsymbol{\\gamma}, P)\\rangle.$$\n",
+    "From the output state of the circuit built in the previous step, we can calculate the objective function of the maximum cut problem\n",
     "\n",
-    "Additionally, we may tend to fast classical algorithms to update the parameter vectors $\\boldsymbol{\\beta},\\boldsymbol{\\gamma}$ to achieve the optimal value for the above quantum optimization problem. \n",
+    "$$\n",
+    "F_p(\\vec{\\gamma},\\vec{\\beta}) = \\langle\\vec{\\gamma},\\vec{\\beta}|H_D|\\vec{\\gamma},\\vec{\\beta}\\rangle.\n",
+    "\\tag{40}\n",
+    "$$\n",
     "\n",
-    "In Paddle Quantum, this process is accomplished in the Net function:"
+    "To maximize the objective function is equivalent to minimizing $-F_p$. Therefore, we define $L(\\vec{\\gamma},\\vec{\\beta}) = -F_p(\\vec{\\gamma},\\vec{\\beta})$ as the loss function, that is, the function to be minimized. Then, we use a classical optimization algorithm to find the optimal parameters $\\vec{\\gamma},\\vec{\\beta}$. The following code shows a complete QAOA network built with Paddle Quantum and PaddlePaddle:"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 8,
+   "execution_count": 6,
    "metadata": {
-    "pycharm": {
-     "is_executing": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:54:39.039309Z",
+     "start_time": "2021-01-09T06:54:39.027860Z"
     }
    },
    "outputs": [],
    "source": [
     "class Net(fluid.dygraph.Layer):\n",
-    "    \"\"\"\n",
-    "    It constructs the net for QAOA which combines the  QAOA circuit with the classical optimizer which sets rules\n",
-    "    to update parameters described by theta introduced in the QAOA circuit.\n",
-    "\n",
-    "    \"\"\"\n",
     "    def __init__(\n",
     "        self,\n",
-    "        shape,\n",
+    "        p,\n",
     "        param_attr=fluid.initializer.Uniform(low=0.0, high=np.pi, seed=1024),\n",
     "        dtype=\"float64\",\n",
     "    ):\n",
     "        super(Net, self).__init__()\n",
     "\n",
-    "        self.theta = self.create_parameter(\n",
-    "            shape=shape, attr=param_attr, dtype=dtype, is_bias=False\n",
-    "        )\n",
-    "\n",
-    "    def forward(self, adjacency_matrix, N, P, METHOD):\n",
-    "        \"\"\"\n",
-    "        This function constructs the loss function for the QAOA circuit.\n",
-    "\n",
-    "        Args:\n",
-    "            adjacency_matrix: the adjacency matrix generated from the graph encoding the classical problem\n",
-    "            N: number of qubits\n",
-    "            P: number of layers\n",
-    "            METHOD: which version of QAOA is chosen to solve the problem, i.e., standard version labeled by 1 or\n",
-    "            extended version by 2.\n",
-    "        Returns:\n",
-    "            the loss function for the parameterized QAOA circuit and the circuit itself\n",
-    "        \"\"\"\n",
-    "        \n",
-    "        # Generate the problem_based quantum Hamiltonian H_problem based on the classical problem in paddle\n",
-    "        H_problem = H_generator(N, adjacency_matrix)\n",
-    "\n",
-    "        # The standard QAOA circuit: the function circuit_QAOA is used to construct the circuit, indexed by METHOD 1.\n",
-    "        if METHOD == 1:\n",
-    "            cir = circuit_QAOA(self.theta, adjacency_matrix, N, P)\n",
-    "        # The extended QAOA circuit: the function circuit_extend_QAOA is used to construct the net, indexed by METHOD 2.\n",
-    "        elif METHOD == 2:\n",
-    "            cir = circuit_extend_QAOA(self.theta, adjacency_matrix, N, P)\n",
-    "        else:\n",
-    "            raise ValueError(\"Wrong method called!\")\n",
+    "        self.p = p\n",
+    "        self.gamma = self.create_parameter(shape=[self.p], attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.beta = self.create_parameter(shape=[self.p], attr=param_attr, dtype=dtype, is_bias=False)\n",
     "\n",
+    "    def forward(self):\n",
+    "        # Define QAOA's quantum circuit\n",
+    "        cir = circuit_QAOA(self.p, self.gamma, self.beta)\n",
+    "        # Run the quantum circuit\n",
     "        cir.run_state_vector()\n",
-    "        loss = cir.expecval(H_problem)\n",
+    "        # Calculate the loss function\n",
+    "        loss = -cir.expecval(H_D_list)\n",
     "\n",
     "        return loss, cir"
    ]
@@ -486,121 +836,41 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 4. Training\n",
-    "\n",
-    "In this part, the QAOA circuit is trained to find the \"optimal\" solution to the optimization problem.\n",
+    "### Training quantum neural network\n",
     "\n",
-    "First, let us specify some parameters:\n",
-    "\n",
-    "- number of qubits: N\n",
-    "- number of layes: P\n",
-    "- iteration steps: ITR\n",
-    "- learning rate: LR"
+    "After defining the quantum neural network for QAOA, we use the gradient descent method to update the parameters in the network to maximize the expected value in equation (40)."
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 9,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
-   "outputs": [],
-   "source": [
-    "N = 4 # number of qubits, or number of nodes in the graph\n",
-    "P = 4 # number of layers \n",
-    "ITR = 120  # number of iteration steps\n",
-    "LR = 0.1  # learning rate"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "Then, with the following inputs\n",
-    "\n",
-    "- initial state: each qubit is initialized as $\\frac{1}{\\sqrt{2}}\\left(|0\\rangle+|1\\rangle\\right)$ by calling `cir.superposition_layer()`\n",
-    "- Standard QAOA circuit (METHOD = 1) or Extended QAOA (METHOD = 2) \n",
-    "- Classical optimizer: Adam optimizer\n",
-    "\n",
-    "we are able to train the whole net："
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 10,
+   "execution_count": 7,
    "metadata": {
-    "pycharm": {
-     "is_executing": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:54:40.191271Z",
+     "start_time": "2021-01-09T06:54:40.187047Z"
     }
    },
    "outputs": [],
    "source": [
-    "def Paddle_QAOA(classical_graph_adjacency, N, P, METHOD, ITR, LR):\n",
-    "    \"\"\"\n",
-    "    This is the core function to run QAOA.\n",
-    "\n",
-    "     Args:\n",
-    "         classical_graph_adjacency: adjacency matrix to describe the graph which encodes the classical problem\n",
-    "         N: number of qubits (default value N=4)\n",
-    "         P: number of layers of blocks in the QAOA circuit (default value P=4)\n",
-    "         METHOD: which version of the QAOA circuit is used: 1, standard circuit (default); 2, extended circuit\n",
-    "         ITR: number of iteration steps for QAOA (default value ITR=120)\n",
-    "         LR: learning rate for the gradient-based optimization method (default value LR=0.1)\n",
-    "     Returns:\n",
-    "         the optimized QAOA circuit\n",
-    "    \"\"\"\n",
-    "    with fluid.dygraph.guard():\n",
-    "        # Construct the net or QAOA circuits based on the standard modules\n",
-    "        if METHOD == 1:\n",
-    "            net = Net(shape=[P, 2])\n",
-    "        # Construct the net or QAOA circuits based on the extended modules\n",
-    "        elif METHOD == 2:\n",
-    "            net = Net(shape=[P, 4])\n",
-    "        else:\n",
-    "            raise ValueError(\"Wrong method called!\")\n",
-    "\n",
-    "        # Classical optimizer\n",
-    "        opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
-    "\n",
-    "        # Gradient descent loop\n",
-    "        summary_iter, summary_loss = [], []\n",
-    "        for itr in range(1, ITR + 1):\n",
-    "            loss, cir = net(\n",
-    "                classical_graph_adjacency, N, P, METHOD\n",
-    "            )\n",
-    "            loss.backward()\n",
-    "            opt.minimize(loss)\n",
-    "            net.clear_gradients()\n",
-    "\n",
-    "            if itr % 10 == 0:\n",
-    "                print(\"iter:\", itr, \"  loss:\", \"%.4f\" % loss.numpy())\n",
-    "            summary_loss.append(loss[0][0].numpy())\n",
-    "            summary_iter.append(itr)\n",
-    "\n",
-    "        theta_opt = net.parameters()[0].numpy()\n",
-    "        print(\"Optmized parameters theta:\\n\", theta_opt)\n",
-    "        \n",
-    "        os.makedirs(\"output\", exist_ok=True)\n",
-    "        np.savez(\"./output/summary_data\", iter=summary_iter, energy=summary_loss)\n",
-    "\n",
-    "    return cir"
+    "p = 4      # Number of layers in the quantum circuit\n",
+    "ITR = 120  # Number of training iterations\n",
+    "LR = 0.1   # Learning rate of the optimization method based on gradient descent"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "After the completion of training, the QAOA outputs the results, including the optimal parameters $\\boldsymbol{\\beta}^*$ and $\\boldsymbol{\\gamma}^*$. By contrast, its performance can be evaluated with the true value of the optimization problem."
+    "Here, we optimize the network defined above in PaddlePaddle's dynamic graph."
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 11,
+   "execution_count": 8,
    "metadata": {
-    "pycharm": {
-     "is_executing": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:55:09.934656Z",
+     "start_time": "2021-01-09T06:54:41.756374Z"
     }
    },
    "outputs": [
@@ -608,104 +878,1158 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "Method 1 generates the graph from self-definition using EDGE description\n",
-      "iter: 10   loss: -3.8531\n",
-      "iter: 20   loss: -3.9626\n",
-      "iter: 30   loss: -3.9845\n",
-      "iter: 40   loss: -3.9944\n",
-      "iter: 50   loss: -3.9984\n",
-      "iter: 60   loss: -3.9996\n",
-      "iter: 70   loss: -3.9999\n",
-      "iter: 80   loss: -4.0000\n",
-      "iter: 90   loss: -4.0000\n",
-      "iter: 100   loss: -4.0000\n",
-      "iter: 110   loss: -4.0000\n",
-      "iter: 120   loss: -4.0000\n",
-      "Optmized parameters theta:\n",
-      " [[0.24726127 0.53087308]\n",
-      " [0.94954664 1.9974811 ]\n",
-      " [1.14545257 2.27267827]\n",
-      " [2.98845718 2.84445401]]\n"
+      "iter: 10 loss: -3.7473\n",
+      "iter: 20 loss: -3.9696\n",
+      "iter: 30 loss: -3.9539\n",
+      "iter: 40 loss: -3.9710\n",
+      "iter: 50 loss: -3.9930\n",
+      "iter: 60 loss: -3.9991\n",
+      "iter: 70 loss: -3.9984\n",
+      "iter: 80 loss: -3.9998\n",
+      "iter: 90 loss: -3.9998\n",
+      "iter: 100 loss: -4.0000\n",
+      "iter: 110 loss: -4.0000\n",
+      "iter: 120 loss: -4.0000\n",
+      "Optimized parameters gamma:\n",
+      " [0.70063329 0.45026914 1.17355432 2.13276803]\n",
+      "Optimized parameters beta:\n",
+      " [-0.02466894 -0.20348931  1.12024105  0.61099467]\n"
      ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAA19UlEQVR4nO3deXxU5b348c93lqwkJOxCCAEE2QmL4FJFxJ9StaBWe61Ypf5aaxXrUr0uVGjr9XftxaqtV2utihtq3SpuBa4WtNbrAoigCCKbBGRLgBCyZ76/P87JZJLMDBPIZLJ836/XvMg585xzvk+A+c5znvM8j6gqxhhjTCSeRAdgjDGmdbNEYYwxJipLFMYYY6KyRGGMMSYqSxTGGGOi8iU6gHjo1q2b5uXlJToMY4xpM1asWLFXVbuHe69dJoq8vDyWL1+e6DCMMabNEJGtkd5LyK0nEblTRFaLyCoRWSIivSOUmyoi60XkaxG5taXjNMYYk7g+inmqOkpV84E3gDkNC4iIF3gQ+C4wDPihiAxr0SiNMcYkJlGoanHIZjoQbnj4BOBrVd2kqpXA88D0lojPGGNMnYT1UYjIXcBlwAFgcpgifYBtIdsFwMQo57sSuBIgNze3+QI1JkZVVVUUFBRQXl6e6FCMiSglJYWcnBz8fn/Mx8QtUYjI20CvMG/NVtWFqjobmC0itwGzgLkNTxHm2IgTU6nqI8AjAOPHj7cJrEyLKygoICMjg7y8PETC/fM1JrFUlcLCQgoKCujfv3/Mx8UtUajqGTEWfRZ4k8aJogDoG7KdA+xohtCMiYvy8nJLEqZVExG6du3Knj17mnRcop56GhSyOQ1YF6bYJ8AgEekvIknAxcBrLRGfMUfKkoRp7Y7k32ii+ijuFpHjgACwFbgKwH1M9lFVPVtVq0VkFrAY8AKPq+oXCYrXGGM6rIQkClX9foT9O4CzQ7bfAt5qiZgqtlew/b+3k3RMEjm/yGmJSxpjTJvQLkdmH4lARYBDnx+ipqQm0aEYY0yrYpMCusTr3LfTGntgyrRtnTp1ivs1/vjHPzJ06FBmzJjRLOfbv38/Dz30UL19J510UrOcu9bpp59OdXV11DJlZWVMmjSJmhrnC+MzzzxD//79SU5OZty4caxcuRKAyspKTj311HrnO+2009iyZQsAf/7zn7n66qvrnXv48OGsW7euUdl4xLNv3z7OP//8w54/VpYoXOKzRGFMrB566CHeeustFixY0CznC5coPvjgg2Y5N8AXX3xB165d8fmi30R5/PHHueCCC/B6vWzbto2ZM2eSkZHBvHnz2LhxI5dccgkASUlJTJkyhb/+9a9hz7N69WrGjBkT3C4vL+ebb75h0KBBYcs3dzzZ2dkUFRVRWFjYpOtFYomiltf5wxKFaS5rvrcm4qtwUd1/4MJFhVHLNod7772XESNGMGLECO6//34ADh06xDnnnMPo0aMZMWIEf/3rX8Pua+iqq65i06ZNTJs2jfvuu48RI0YE37vnnnv49a9/DcCWLVsYOnQoP/3pTxk+fDhnnnkmZWVlADz11FOMGjWK0aNH86Mf/Yhbb72VjRs3kp+fz8033wzUbxmFiz/a+RtauHAh5513XnA7Pz+fXbt28atf/Yonn3ySZcuWcfHFF7NgwQKmT3cmgHjxxRepqanhxhtv5JJLLuGyyy5j/fr1wW/x5513XsREuWbNGsaOHVtve/DgwXi93kZlI8UCHFU855xzDq+//nrY+JrK+ihctbeesC4K086sWLGC+fPn89FHH6GqTJw4kUmTJrFp0yZ69+7Nm2++CcCBAwdYtGhRo30NPfzwwyxatIilS5dSUlLCY489FvHaGzZs4LnnnuMvf/kLP/jBD3j55ZcZM2YMd911F//617/o1q0bRUVFFBcX8/nnn7Nq1aqY48/Ozg57/ksvvbTROd566y3eeOMNAKqrqykqKqJnz5589tlnXHjhhbz33nsMHTqUZcuWUbtEQe2toR//+Mf1zrV161bGjh3LiBEj+OSTT8LW+4svvuCCCy4IPopaUlLCueee26hcpFhGjx5NZWUlmzZtOuJ4pk+fzi233MLMmTPDxtgUlihcwT6KamtRmOYx8vWRMZXrOrUrXad2jVsc77//Pueffz7p6ekAXHDBBfzzn/9k6tSp3HTTTdxyyy2ce+65nHLKKYwcObLRvqPRv39/8vPzARg3bhxbtmxh3759XHjhhXTr1g2ALl26UFxcHPEckeKfNm1a2PM3VFZWRmVlJVlZWQCsW7eOoUOHArB27VqGDRvGAw88wOmnnx4sA84oZoA//OEPDBs2jGeffZb58+cH93u9XpKSkjh48CAZGRnB47Zt20b37t2D/REAs2bNYsCAAY1iixTLBRdcwN69e48qnuOOO47169dH/L02hd16cnlSPHQ+tTOZJ2UmOhRjmlXtB0lDgwcPZsWKFYwcOZLbbruN3/72t2H3RePz+QgEAsHthvNcJScnB3/2er1UV1ejqk0a9BUp/kjnbyg1NRURoaSkBID169dz3HHHUVRURKdOnUhKSmL58uWcccYZ9eKv/SafnZ3NGWfUTTTRr1+/4M8VFRWkpKTUu97q1asZPnx4vX1r165l5MjGXxwixTJ+/HhSU1OPKp6tW7c2aZqOaCxRuLxpXnJvzqXPz/skOhRjmtWpp57Kq6++SmlpKYcOHeJvf/sbp5xyCjt27CAtLY1LL72Um266iZUrV4bdF03Pnj3ZvXs3hYWFVFRUBG/vRDNlyhReeOGFYEdrUVERGRkZHDx4sEnxN8VZZ53FokWLAKfjd926dSxfvpzRo0fzzDPPkJeXR8+ePampqQl+OF900UV4vV5mz57Nf/7nf/L0008zePDgYN9DYWEh3bt3bzS53po1axg2rP6KCF988QWjRo1qFFe0WLKzs48qnoULFwb7N46WJQpj2pnS0lJycnKCr2XLljFz5kwmTJjAxIkT+clPfsKYMWNYs2YNEyZMID8/n7vuuotf/epXYfdF4/f7mTNnDhMnTuTcc89lyJAhh41v+PDhzJ49m0mTJjF69GhuvPFGunbtysknn8yIESOCndm1xo4dGzb+ppg+fTqvvvoqAFOnTmXIkCHMmDGDZcuWsXz5cp566ikAzjzzTN5//33AmYV6/vz5eDwe5s6dy+jRo3nuueeCraGlS5dy9tlnN7pWw0RRVFSEqtKzZ89GZaPFcrTxvP7660ybNq1Jv6eIVLXdvcaNG6dNFQgEtLygXMu2ljX5WGNUVdeuXZvoEEwUo0aN0qqqquD2zJkzdcmSJfXKrFy5Ui+99NKYznf++efrunXrgtuTJk3SzZs3x3Rsw7LhYjmaeIqKivSUU06JWDbcv1VguUb4TLUWRS2Fr676ig2zNiQ6EmNMHHz22Wf1xlGsXr260e2gMWPGMHny5OAAt0gqKys577zzOO6445oltnCxHE082dnZvPfee80SG9hTT0HiEWcFDKXJnW3GmLZnxYoVYfdfccUVhz02KSmJyy67rN6+mTNn1ntKKZqGZSPFcjTxNCdLFCHEK2i1otWK+C1RGGNi15TxCs0xtqEl2a2nUDY62xhjGrFEEaJ2vicbnW2MMXUsUYQQj43ONsaYhixRhLAZZI0xpjHrzA6Re1suKHgzGs/waIwxHZW1KEKkD00nfVg6Hr/9WkzbU1hYSH5+Pvn5+fTq1Ys+ffqQn59PVlZWoyklmuLXv/4199xzTzNGWt+yZcvCzqwaDy2xqFM4TzzxBLNmzQLg1VdfZe3atQmJ40jZJ6Ix7UTXrl1ZtWoVq1at4qqrruKGG24Ibns8Hfu/uqrWm7wwXsfEwhJFG7fnlT3seGQHVYVViQ7FmGZVU1MTdoGfjRs3MnXqVMaNG8cpp5xSb2rsUJ999hmnn346gwYN4i9/+Utw/7x58zj++OMZNWoUc+fOBaIvKPT1119zxhlnMHr0aMaOHcvGjRsBZ72GCy+8MDjvkbozxubl5XH77bdz4oknMn78eFauXMlZZ53FwIEDefjhh4PHTpkyhbFjxzJy5EgWLlxYL46rr76asWPHsm3btmDce/fu5cQTTwyuu1Er3DHh6hhpgae8vDz27t0LwPLlyznttNPqnf+DDz7gtdde4+abbyY/Pz9Y/1Yv0twebfl1JHM9qap+de1Xuvrc1Vq6sfSIjjcdW8P5c84913mF+s1vnH0ffVS37+9/d/Y98EDdvsJCZ99llx1ZLHPnztV58+apqurmzZvV6/Xqp59+qqqqF110kT799NOqqnr66afrV199paqqH374oU6ePDnsuUaNGqWlpaW6Z88ezcnJ0e3bt+vixYv1pz/9qQYCAa2pqdFzzjlH33333ajXmzBhgr7yyiuqqlpWVqaHDh3SpUuXamZmpm7btk1ramr0hBNO0H/+85+qqtqvXz996KGHVFX1+uuv15EjR2pxcbHu3r1bu3fvrqqqVVVVeuDAAVVV3bNnjw4cOFADgYBu3rxZRUT/93//N1iX9PR03blzp06YMCHs3EoNj4lUx5deekl/8pOfBI/bv39/MN49e/aoquonn3yikyZNUlXV+fPn6zXXXKOqqpdffrm++OKLMfwtxk9T53qyzuwQwcWL7Kkn086EW+CnpKSEDz74gIsuuihYrqKiIuzx06dPJzU1ldTUVCZPnszHH3/M+++/z5IlS4IzuZaUlLBhwwZyc3PDXu/gwYNs376d888/H6DeOg4TJkwgJycHcJYG3bJlC9/5zncAgjOgjhw5kpKSEjIyMsjIyCAlJYX9+/eTnp7O7bffznvvvYfH42H79u3s2rULcNZqOOGEE4LXqaqqYsqUKTz44INMmjQpbF1Dj1myZEnYOp5yyinNusBTa2eJIpSNzDbNKNxyxXPmNN43darzCtWlS/jjj1TDBX7KysoIBAJkZWWFXX60oYZzn4kIqsptt93Gz372s3rvbdmyJez19AgXIKp9z+Px1Cvn8Xiorq5mwYIF7NmzhxUrVuD3+8nLywuu4VC7Kl4tn8/HuHHjWLx4ccREEXpMpDqCMz/TW2+9xW233caZZ57JnDlz6i3k1HARp7bM+ihC2HKopiPJzMykf//+vPjii4DzofjZZ5+FLbtw4ULKy8spLCxk2bJlHH/88Zx11lk8/vjjwZXjtm/fzu7du6NeLycnJ7guREVFBaWlpUddjwMHDtCjRw/8fj9Lly5l69atEcuKCI8//jjr1q3j7rvvPuy5I9Ux0gJPeXl5wQn+Xn755bDnjLZIU2tliSJEcAqP5n/QwZhWacGCBTz22GOMHj2a4cOHBzuCG5owYQLnnHMOJ5xwAnfccQe9e/fmzDPP5JJLLuHEE09k5MiRXHjhhYf9AHz66af54x//yKhRozjppJPYuXPnUddhxowZweVDFyxYcNjFk7xeL88//zxLly7loYceilo2Uh0jLfA0d+5crrvuOk455RS83vDjsS6++GLmzZvHmDFj2kxntkRrDrZV48eP1+XLlzf5uM13bKZkVQl5v8kjY2zG4Q8wJsSXX37J0KFDEx2GMYcV7t+qiKxQ1fHhyluLIoS/p5/kvslIkk0xbowxtawzO0TOrJxEh2CMMa2OtSiMaUbt8VauaV+O5N+oJQpjmklKSgqFhYWWLEyrpaoUFhbWG8MSi4TcehKRO4HpOM8X7QZmquqOBmX6Ak8Bvdxyj6jqH+IZV8EDBexfup8+1/Yhe3J2PC9l2qGcnBwKCgrYs2dPokMxJqKUlJTg4MZYJaqPYp6q3gEgIr8A5gBXNShTDfxSVVeKSAawQkT+R1XjN5tWALRKbRyFOSJ+v5/+/fsnOgxjml1Cbj2panHIZjrQ6JNZVb9V1ZXuzweBL4E+cQ3MRmYbY0wjCXvqSUTuAi4DDgCTD1M2DxgDfBSlzJXAlQC5ublHFpONzDbGmEbi1qIQkbdF5PMwr+kAqjpbVfsCC4BZUc7TCXgZuL5BS6QeVX1EVcer6vju3bsfWcy1I7NrjuhwY4xpl+LWolDVM2Is+izwJjC34Rsi4sdJEgtU9ZVmDC8smz3WGGMaS0gfhYgMCtmcBjRaLUWc6SofA75U1XtbJC679WSMMY0kqo/ibhE5Duex1624TzyJSG/gUVU9GzgZ+BGwRkRWucfdrqpvxSuojOMz8GX5SBuWFq9LGGNMm5OQRKGq34+wfwdwtvvz+0CLTrqUPiyd9GHphy9ojDEdiI3MNsYYE5VNChiifFs5ZRvKSM5JJm2w3X4yxhhoYotCRNJF5FIReTNeASVSycoSCu4rYP+7+xMdijHGtBqHTRQikiQi54nIC8C3wBTg4bhHlgg2MtsYYxqJeOtJRP4P8EPgLGAp8DQwQVV/3EKxtbjax2NtwJ0xxtSJ1kexGPgn8B1V3QwgInGdvTXRakdm2zgKY4ypEy1RjAMuBt4WkU3A8wRvzrRP4rGR2cYY01DEPgpV/VRVb1HVgcCvcSblSxKRv7sT8LU7wRaFJQpjjAmK6aknVf2Xqs7Cmeb7fuDEeAaVMNaZbYwxjUQdRyEiPYBrgOE4a0asBR5S1cUtEFuLyzwhk+EvDW/nN9iMMaZpIrYoRORk4BN38yngGffnj9z32h2Pz4Mn2YPHZwPWjTGmVrQWxe+B81T105B9C0Xkb8CfgYlxjcwYY0yrEO2rc2aDJAGAqq4CMuIWUQKVbSxj4y0b2f7w9kSHYowxrUa0FoWISLaq7muwswvtdDLBmrIaSteWtvCctcYY07pF+8C/D1giIpNEJMN9nQb8HefJp3bHFi4yxpjGIrYoVPUREdkB3En9p57+Q1Vfb6H4WlRwzexAYuMwxpjWJOrjsar6BvBG6D4RSRGRi1T1xbhGlgDWojDGmMZi6msQEa+IfFdEnsJZuvTf4htWYgQThQ24M8aYoMMNuDsVuAQ4B/gYZx3r/qpa2gKxtTwbmW2MMY1Em2a8APgG+BNws6oeFJHN7TZJAN50L1mnZeHrYgv/GWNMrWifiC8D5+HcZqoRkYU4Hdrtlj/bT99f9k10GMYY06pEmz32OiAPuBeYDHwFdBeRH4hIp5YJzxhjTKJF7cxWxz9U9ac4SWMGTitjS9wjSwANKOXbyinfVp7oUIwxptU47M14EUkDjnU3F6vqayKSGt+wEqOmtIYNV2/Ak+5h+PPDEx2OMca0CtFmj/WLyP1AATAfeBLYJCK3qmqZiIxpoRhbjC2FaowxjR1u9tg0oJ+qHgQQkUzgHhH5EzAV6B//EFtO7VKo1CQ2DmOMaU2iJYqzgUGqGvx6rarFIvJzYC/w3XgH19JsKVRjjGksWmd2IDRJ1FLVGmCPqn4Yv7ASQzzizByrEKbqxhjTIUVLFGtF5LKGO0XkUuDL+IWUWDbfkzHG1Bft1tM1wCsicgWwAmew3fFAKnB+C8SWGF6g2r395E90MMYYk3jRphnfDkwUkdNxphkX4O+q+k5LBZcI/e/sDwIef7tcm8kYY5rssOMoVPUfwD9aIJZWIX1oeqJDMMaYViUhX5tF5E4RWS0iq0RkiYj0jlLWKyKfisgbkcoYY4yJn0TdX5mnqqNUNR9nYaQ5UcpeRwt2nu96bhfbH95O9cHqlrqkMca0alEThftt/u3mvqiqFodsphNhVloRycFZC+PR5o4hkn1v76PozSJqDtmoO2OMgcMvhVojIqUi0llVDzTnhUXkLuAy4ADO7LTh3A/8O5ARw/muBK4EyM3NPfK4fDY62xhjQsVy66kcWCMij4nIH2tfhztIRN4Wkc/DvKYDqOpsVe0LLABmhTn+XGC3qq6IpSKq+oiqjlfV8d27d4/lkPBx23KoxhhTTyxLub3pvppEVc+Iseiz7vnnNth/MjBNRM4GUoBMEXlGVS9taixNYQPujDGmvlgej31SRJKAwe6u9apadTQXFZFBqrrB3ZwGrAtz3duA29zypwE3xTtJALZutjHGNBDLehSn4UwxvgVn0F1fEblcVd87iuveLSLHAQFgK3CVe63ewKOqevZRnPuo2MSAxhhTXyy3nn4PnKmq6wFEZDDwHDDuSC+qqt+PsH8Hzqy1DfcvA5Yd6fWaIvmYZALlARuZbYwxrlgShb82SQCo6lci0m5nQer7y76JDsEYY1qVWBLFchF5DHja3Z6BM0mgMcaYDiCWRPFznJlkf4HTR/Ee8FA8gzLGGNN6REwUIvKOqk4BfquqtwD3tlxYifPN776h+MNicm/NJXNiZqLDMcaYhIvWojhGRCbhjGV4Hqc1EaSqK+MaWYJoQNFqtXEUxhjjipYo5gC3Ajk0bk0ocHq8gkokG5ltjDH1RVu46CXgJRG5Q1XvbMGYEsrGURhjTH2HHSzQkZIEEPyNWKIwxhiHjSprINiisD4KY4wBLFE0UttHYdOMG2OMI5ZxFIiIF+gZWl5Vv4lXUInU+eTOJOckkzY8LdGhGGNMqxDLpIDX4kwBvgtnEj9wnnoaFce4EqbTqE50GtUp0WEYY0yrEUuL4jrgOFUtjHcwxhhjWp9YEsU2nOVKO4SyzWWUbyonpX8KqQNSEx2OMcYkXCyJYhOwTETeBCpqd6pqu5zSo/jDYnY/u5seF/ewRGGMMcSWKL5xX0nuq12zkdnGGFNfLEuh/gZARDKcTS2Je1QJZGtmG2NMfYcdRyEiI0TkU+Bz4AsRWSEiw+MfWmIEB9wFLFEYYwzENuDuEeBGVe2nqv2AXwJ/iW9YCeR1/rAWhTHGOGJJFOmqurR2w12/Oj1uESWYjcw2xpj6YnrqSUTuoG4p1EuBzfELKbFs9lhjjKkvlkRxBfAb4BXqlkL9cTyDSqSsyVlkTcoKJgxjjOnoYnnqaR/Oetkdgsdn8yQaY0yoaGtm36+q14vI6zhzO9WjqtPiGpkxxphWIVqLorZP4p6WCKS1KPm8hF1P7SJtaBrH/PiYRIdjjDEJF20p1BXuj/mq+ofQ90TkOuDdeAaWKIHSAKVfluLt5E10KMYY0yrEckP+8jD7ZjZzHK2GTeFhjDH1Reuj+CFwCdBfRF4LeSsDaL9TjtuAO2OMqSdaH8UHwLdAN+D3IfsPAqvjGVQi2TgKY4ypL1ofxVZgq4jMAHaoajmAiKQCOcCWFomwhdnIbGOMqS+WPooXqFsCFZyP0BfjE07iWR+FMcbUF8vIbJ+qVtZuqGqliLTbdSl8WT6yJmeR1KvdVtEYY5oklhbFHhEJDq4TkenA3qO5qIjcKSKrRWSViCwRkd4RymWJyEsisk5EvhSRE4/murFI6pFE3xv70vOSnvG+lDHGtAmxJIqrgNtF5BsR2QbcAvzsKK87T1VHqWo+8AYwJ0K5PwCLVHUIMBr48iiva4wxpolimetpI3CCiHQCRFUPHu1FVbU4ZDOdMFOEiEgmcCrumA339ldlw3LNLVAdoHJ7JXggpW9KvC9njDGt3mEThYgkA98H8gCfiNvZq/rbo7mwiNwFXAYcACaHKTIA2APMF5HRwArgOlU9FOF8VwJXAuTm5h5xXNVF1WyYtQF/dz9DHh9yxOcxxpj2IpZbTwuB6UA1cCjkFZWIvC0in4d5TQdQ1dmq2hdYAMwKcwofMBb4k6qOca95a6TrqeojqjpeVcd37949hmpFiNueejLGmHpieeopR1WnNvXEqnpGjEWfBd4E5jbYXwAUqOpH7vZLREkUzaZ2ZLYlCmOMAWJrUXwgIiOb86IiMihkcxqwrmEZVd0JbBOR49xdU4C1zRlH2NhqWxQ2hYcxxgCxtSi+A8wUkc1ABc4qd6qqo47iune7CSAAbMV5sgr3MdlHVfVst9y1wAJ33MYmWmBlveDKdjYy2xhjgNgSxXeb+6Kq+v0I+3cAZ4dsrwLGN/f1o7E+CmOMqS+WRNGhPjHt1pMxxtQXS6J4EydZCJAC9AfWA8PjGFfieGDA7wbUTQ5ojDEdXCwD7up1ZIvIWI5+ZHarJSKkD0tPdBjGGNNqxPLUUz2quhI4Pg6xGGOMaYViGZl9Y8imB2cQ3J64RdQKfPvEtwTKAhxzxTF4kpucS40xpl2J5VMwI+SVjNNnMT2eQSXaviX7KHqriEBF4PCFjTGmnYu2ZvbTqvojYL+q/qEFY0o8N33aI7LGGBO9RTFORPoBV4hItoh0CX21VICJYOtmG2NMnWh9FA8Di3BmcV2B83hsLXX3t0u2brYxxtSJ2KJQ1T+q6lDgcVUdoKr9Q17tNkmAjc42xphQh+3MVtWft0QgrYklCmOMqRPLyOwOJzknGfEJ4rHR2cYYY4kijH6z+yU6BGOMaTUOe+tJRNJFxOP+PFhEpomIP/6hGWOMaQ1iGXD3HpAiIn2Ad3DWhHginkEZY4xpPWJJFKKqpcAFwAOqej4wLL5hJdbmOzazZvoaSlaXJDoUY4xJuJgShYicCMzAmb4DOkLfRgA0YE89GWNMLInieuA24G+q+oWIDACWxjWqRPM6f9jiRcYYE9t6FO8C7wK4ndp7VfUX8Q4skWxktjHG1InlqadnRSRTRNKBtcB6Ebk5/qEljs31ZIwxdWK59TRMVYuB84C3gFzgR/EMKtFqB9rZrSdjjIktUfjdcRPnAQtVtQpnUsB2y5ft3JGr2luV4EiMMSbxYnl66c/AFuAz4D136vHieAaVaJ2/05nknGTSR9ra2cYYI6pNbxyIiE9Vq+MQT7MYP368Ll++PNFhGGNMmyEiK1R1fLj3YunM7iwi94rIcvf1e8C+ahtjTAcRSx/F48BB4AfuqxiYH8+gWoPij4rZtWAXVfutn8IY07HF0kcxUFW/H7L9GxFZFad4Wo29r+7l0OeHSBuShn+czYFojOm4YmlRlInId2o3RORkoCx+IbUOybnJAJRvK09wJMYYk1ixtCiuAp4Skc7u9j7g8viF1Dok93USRcU3FQmOxBhjEiuWKTw+A0aLSKa7XSwi1wOr4xxbQqXkpgBQUWCJwhjTscVy6wlwEoQ7QhvgxjjF02rUtijKvynnSB4hNsaY9iLmRNHAUS0mLSJ3ishqEVklIktEpHeEcjeIyBci8rmIPCciKUdz3abwZfnwdvISOBSgel+rHTJijDFxd6SJ4mi/Ys9T1VGqmg+8AcxpWMBdUe8XwHhVHYEz+ffFR3ndmIkIKQNSSM5NprrYEoUxpuOK2EchIgcJnxAESD2ai4bcwgJn8F6kxOMDUkWkCkgDdhzNdZuq/3/0R+SoGk/GGNPmRUwUqpoRzwuLyF3AZcABYHKY628XkXuAb3Aex12iqkuinO9K4EqA3Nzc5oqxWc5jjDFt2ZHeejosEXnb7Vto+JoOoKqzVbUvsACYFeb4bGA60B/oDaSLyKWRrqeqj6jqeFUd371792arh6pSXWK3nowxHVfc1r5W1TNiLPoszlrccxvsPwPYrKp7AETkFeAk4JlmC/Iwqg9W89WVX6GqDFswrG7lO2OM6UDi1qKIRkQGhWxOA9aFKfYNcIKIpIlzD2gK8GVLxFfLl+HDl+UjcCjAoS8PteSljTGm1UhIogDudm9DrQbOBK4DEJHeIvIWgKp+BLwErATWuLE+0tKBZkx0umoOfnSwpS9tjDGtQtxuPUXTYJLB0P07gLNDtufS+JZUi8qckMnel/dS/FExva7oZR3cxpgOJ1EtijYjbUga3gwvld9W2nQexpgOyRLFYYhHyDjeuf1U/FG7XgHWGGPCskQRg8yJmQAc+rxpHdrVJdWUri+1uaKMMW1aQvoo2ppOYzsx4O4BpA1Ja9JxBb8v4ODyg6QNSaPXFb1IH2oryBpj2h5rUcTAm+IlfXh6k8dR9L7KmeuwdF0pm/59Ezuf2RmP8IwxJq4sUTRRoCoQdn/J6hK23r2V9Veup/qAM5I7qWcSw14YRo+Le4DA3lf22ihvY0ybY4kiRoHqAJt/vZl1l60jUFk/WVRsr2DLb7ZQ/K9iKr+tpGxT3Uqx3lQvPWf0JH1UOlqlHHj/QEuHbowxR8USRYw8Pg81B2qoKamhZFVJcL+qUvDHArRSyTwpk2MfOJb0kY37IrKnZAOw/x/7WypkY4xpFpYomqB2lHbxh3WPyRa9VUTp2lJ8WT76zOpDal4qHl/jX2vmiZmkDkolc2KmPQVljGlTLFE0QeYJzmOyxR8XowGlclclO59wOqh7/7w3vozID5F5U7wce++xdP9+dxvdbYxpU+zx2CZI6ZeCv4efqt1VlK4vdZZb8kDmyZl0PqlzosMzxpi4sBZFE4gImSe6rYqPikkfls7A/xpIzrU5MZ+jclclu57fRelXpfEK0xhjmpW1KJooc2ImBz86SOWOSsBpZTRF4ZuF7P3bXrRKSRvctAF8xhiTCNaiaKL0YekgBFsWTT7efSLq0Bpb38IY0zZYi6KJxCsMvHcghB93d1i1iaZsQxmBigCeZMvVxpjWzT6ljoCvkw9f5pHlWG+6l5QBKWi1UrrO+imMMa2fJYoE6DSyEwAla0oOU9IYYxLPEkUCpI9w+ymaOG25McYkgiWKBEgbnoYv20dSjyQbpW2MafWsMzsBfJ18DHlyiI3QNsa0CdaiSBBLEsaYtsISRQLVlNY4U4EYY0wrZreeEqSmtIYvZ3wJwNDnhuJN8SY4ImOMCc9aFAniTfOSMtAZTxG6vkUsag7VsO+dfex+YTcVOyriFKExxjisRZFAmcdnUra+jIOfHKTzCYeffbZqXxU7HtrBweUH0Wrnaan9y/Yz6MFB1udhjIkbSxQJlHF8Brue2eV88KtG/bCv3FvJ5l9tpnJ7JQikj0rH39VP+oj04HGBqgAIYRdOMsaYI2WJIoFS+qfg6+qjurCa8k3lpA5MDVuuan8Vm27dRNWuKlIGpJA3Jw9/V3+jcrue3kXJZyXk3pJLcu/keIdvjOkg7KtnAokIGePd5VU/KY5YztfZR/qwdFIHpdL/P/qHTRI15TUUf1hM+aZyvr7xaw6uOBi3uI0xHYsligTLPN6Zrrx2fYtwRISc63Lof1f/iMutelO8HHv/sWSekEngUIAtv9nCnpf32MhvY8xRs0SRYJ3GdOK4+cfR98a+jd7b94991JTWAM705t7U6I/QetO85N6eS48ZPUBh5xM72fHQDrTGkoUx5shZH0WCeZI8JHVLarS/cFEhOx7cQUpeCgPvGxhzB7WI0PPinqTkprDt99soWlSEN9NLrx/1alJcFd9WsH/pfva/t5+aA26y8gtpw9LocXEPUvPC96cYY9ofSxStyO6XduPL9CE+YcdDOwDock6XI3qKqfNJnfF18bFz/k66ndetSceWri9l400bw75X/K9iel7SM7hdvq0cX+cjX5/DGNP6JfR/t4jcBMwDuqvq3jDvTwX+AHiBR1X17hYOscWUbihl15O7nA0BFHpd0YuuU7se8TnTh6Qz4O4BdY/PVgbYMncL/p5+0oak4e/ix5PmIXAoQPnWcnr8oAcAqYNTSRuaRlKvJLKnZJMywFkXvOZgDYe+OERy37onqgruK6Ds6zJSB6fSaXQnUnJTSM5Jxt/djzfDe0TjOwJVAaqLqqneX+088qtOy8vfw48vy2djRoxpYQlLFCLSF/g/wDcR3vcCD7plCoBPROQ1VV3bclG2nLRBafS6ohc7H98JCj1m9KD7+d2P+ryhH6qFbxY6a2B8Dvvf2d+obNbpWSR1S0JEGPC7AY0+kH0ZvnqP3QYqAng7eRGvULa+jLL1ZfXK97y8Jz0udJJP2aYy9r+7H28nL54UD4GKAIHyAIFDAQKVAXKuzQke99WVX1G1typsfbpM7UKfa/oAULmr0jlnphdPsgfxC+ITxCOIV0gfmY4nyWmNVWyvoOZQDVqjaKUSqAwEY/B38ZMx1nn6rKa8hn2L94EH51w+wZPswZPivFLyUoKtp6r9Vc5tOQEExCPOcV7n+qFPp1Vsr3CSXgA0oBDSbeTv6sffxSlbU1ZD1d6qunN5xDk/zjX8Xf3OPqD6YDVa1aD/SUFV8fg9+Do7cWqNUlXY4Pfpxgzgy/QFf081ZTUEygJ1ZUL+FI/UazlW7a+KuCSwJ80TnJYmUBmg5lBN4+vj/Pv0ZtZ9oag5VBMcTNrwQQyP34M33TmnBpSagw3O2eD6Hr9bp/IatCJCP51Qr07VB6ojnlOSpa5OVQECpZHXQ45Up0bn9Emz1qn2/2NzS2SL4j7g34GFEd6fAHytqpsAROR5YDoQ10Txve85f77+et2+3/4WPvkE7rgDJkxw9i1aBA8+CGedBbNmOfuKiuDyy6FLF3jyybrjr78eNm6E++6DY4919j37LDz3HPzwh3DJJc6+AyO7c/O+LPJ61fCnf6v7QL78cufcTz7pnBvgv/8bFi+Ga66BqVOdfR9/DHfeCccfD3PmNK7Twr91JX1EOqXrSvnPB/2s2uznmolF5PetJG1wGkuWevjzU7V1khjq5OG++/ozNKeGklUlLHhSeWVZEt/NOcDUrkX4s/18/TXccAP08cA1gbpG4+xVORyo9HJXfgGdk2voM6sPDz4oLF4M56dkclK3YnzZPlbvTeHBD7IZ0a2cnw3Yhb+7P1in6v3Cf2XtCp7z4a968Pn+VH42aDcjs8sY8uQQlnzs4cEHYXyghAs8zu28A5VeZq/KoXOSclf+djImZpAxNoPrr4cNXwpXVxWSm+48hfbm9s78fXsW3+2zn3P6HKDfHf3Y3SWTG26AXlWV/MK/KWyduh4jDH1iaPDv6dySnZzUyXkEes2+VP68oQcjssq4avBueszoQc+Le/K970HVvgDzsjdErNPQZ4by9v/6nDrV7OcC77cN6lTDXfkFZJ6QSb/Z/dw6KVdXbY5cp7n92J1VW6fyiHXq1tvDkPlD6up0aAcnpcdSpxrmZa+LsU77ItYpY2IGeb/KC6nTxjjUaXuz1GnI00N450N/i9dp8YokUnJSaG4JSRQiMg3YrqqfRbmN0AfYFrJdAEyMcs4rgSsBcnNzmynSlufP9pOS4yced1c8Pg9pg9JIG5RG508hzQ85s9IY4CY/36IjO683xUvnEzqTtQlSC+CYH6Yx/JJjUFUK3a4Ob5aPnt/rSU1JDYHyAClFyZSXeel5eU+69/HW+2Z6zBXHMOS7vQEo+hjS9kHX49MZNqdrvW+ZnmQP3S/sTnVxNVqpJJcn4xMfacPS6HSM08qo5evsJbVXKnigKuDDt8VHUicPWVOySD22rmNevELWqVl07eZ8C0z/MAV/uZ/UAamkD67Gl133X8aT5HFuwynO7bH1HjziwdfVh79L/X4lfzc/yT2SEa+QlJaEd4cXX1cfqcemBlsTtddP6pMUbHl4tnvwlHnwZfnwd/PXfcsHJNnjPC6t4K304EkSPEmCv5tz26+uIE5MGc7vzlfstCC8nZwYalsTtdf3ZfuCLR7xC6KCJ9NT/5w467/X/j68NV48fsGT6sGX7cOTEnJOj+DLqvu9SYogfsHTyYO3c/1zihsXgKfCbSX6BW9nb/Cbd/D3n1EXk6fIKetJdc4pvrpflHil3nWi1inNGyzrqXKvn+IcH/rvSQSnXO3vKdltfaZ76rUmmlynTg3q5HPrlBmmTpkN6hSQYGuzuUm8nrMXkbeBcI/azAZuB85U1QMisgUY37CPQkQuAs5S1Z+42z8CJqjqtYe79vjx43X58uVHWwVjjOkwRGSFqo4P917cWhSqekaEYEYC/YHa1kQOsFJEJqjqzpCiBUDo4IIcYEecwjXGGBNBi996UtU1QI/a7UgtCuATYJCI9Ae2AxcDl7RUnMYYYxytamS2iPQWkbcAVLUamAUsBr4EXlDVLxIZnzHGdEQJHyWlqnkhP+8Azg7Zfgt4KwFhGWOMcbWqFoUxxpjWxxKFMcaYqCxRGGOMicoShTHGmKjiNuAukURkD7C1CYd0AxpNSthGtae6QPuqj9WldbK6OPqpatgJ5tplomgqEVkeaURiW9Oe6gLtqz5Wl9bJ6nJ4duvJGGNMVJYojDHGRGWJwvFIogNoRu2pLtC+6mN1aZ2sLodhfRTGGGOishaFMcaYqCxRGGOMiarDJwoRmSoi60XkaxG5NdHxNIWI9BWRpSLypYh8ISLXufu7iMj/iMgG98/sRMcaKxHxisinIvKGu90m6yIiWSLykoisc/9+TmzDdbnB/ff1uYg8JyIpbakuIvK4iOwWkc9D9kWMX0Rucz8P1ovIWYmJOrwIdZnn/jtbLSJ/E5GskPeapS4dOlGIiBd4EPguMAz4oYgMS2xUTVIN/FJVhwInANe48d8KvKOqg4B33O224jqcaeVrtdW6/AFYpKpDgNE4dWpzdRGRPsAvcNaMGQF4cdaGaUt1eQKY2mBf2Pjd/z8XA8PdYx5yPydaiydoXJf/AUao6ijgK+A2aN66dOhEAUwAvlbVTapaCTwPTE9wTDFT1W9VdaX780GcD6M+OHV40i32JHBeQgJsIhHJAc4BHg3Z3ebqIiKZwKnAYwCqWqmq+2mDdXH5gFQR8QFpOCtNtpm6qOp7QFGD3ZHinw48r6oVqroZ+Brnc6JVCFcXVV3irt8D8CHOaqDQjHXp6ImiD7AtZLvA3dfmiEgeMAb4COipqt+Ck0wIWVGwlbsf+HcgELKvLdZlALAHmO/eRntURNJpg3VR1e3APcA3wLfAAVVdQhusSwOR4m/rnwlXAH93f262unT0RCFh9rW554VFpBPwMnC9qhYnOp4jISLnArtVdUWiY2kGPmAs8CdVHQMconXfmonIvXc/HWed+95Auohcmtio4qrNfiaIyGyc29ELaneFKXZEdenoiaIA6BuynYPTrG4zRMSPkyQWqOor7u5dInKM+/4xwO5ExdcEJwPT3DXUnwdOF5FnaJt1KQAKVPUjd/slnMTRFutyBrBZVfeoahXwCnASbbMuoSLF3yY/E0TkcuBcYIbWDY5rtrp09ETxCTBIRPqLSBJOx89rCY4pZiIiOPfBv1TVe0Peeg243P35cmBhS8fWVKp6m6rmuEvjXgz8Q1UvpW3WZSewTUSOc3dNAdbSBuuCc8vpBBFJc/+9TcHpC2uLdQkVKf7XgItFJFlE+gODgI8TEF/MRGQqcAswTVVLQ95qvrqoaod+4azR/RWwEZid6HiaGPt3cJqSq4FV7utsoCvOkxwb3D+7JDrWJtbrNOAN9+c2WRcgH1ju/t28CmS34br8BlgHfA48DSS3pboAz+H0r1ThfMv+v9HiB2a7nwfrge8mOv4Y6vI1Tl9E7WfAw81dF5vCwxhjTFQd/daTMcaYw7BEYYwxJipLFMYYY6KyRGGMMSYqSxTGGGOiskRhWj0RURH5fcj2TSLy62Y69xMicmFznOsw17nInUV2aYP9vUXkJffnfBE5uxmvmSUiV4e7ljFNYYnCtAUVwAUi0i3RgYRq4kyc/xe4WlUnh+5U1R2qWpuo8nHGwTQlBl+Ut7OAYKJocC1jYmaJwrQF1ThrAd/Q8I2GLQIRKXH/PE1E3hWRF0TkKxG5W0RmiMjHIrJGRAaGnOYMEfmnW+5c93ivO8//J+48/z8LOe9SEXkWWBMmnh+65/9cRH7n7puDMzjyYRGZ16B8nls2Cfgt8G8iskpE/k1E0t31Bz5xJxec7h4zU0ReFJHXgSUi0klE3hGRle61a2dAvhsY6J5vXu213HOkiMh8t/ynIjI55NyviMgicdZq+K+Q38cTbqxrRKTR34Vpv6J9GzGmNXkQWF37wRWj0cBQnGmZNwGPquoEcRZ4uha43i2XB0wCBgJLReRY4DKcmVKPF5Fk4F8issQtPwFn/v/NoRcTkd7A74BxwD6cD/HzVPW3InI6cJOqLg8XqKpWugllvKrOcs/3/3CmMrlCnMVoPhaRt91DTgRGqWqR26o4X1WL3VbXhyLyGs5EhCNUNd89X17IJa9xrztSRIa4sQ5238vHmYm4AlgvIg/gzK7aR501KZCQxXFM+2ctCtMmqDMr7lM4i+jE6hN11uyowJnGoPaDfg1Ocqj1gqoGVHUDTkIZApwJXCYiq3Cmbu+KM1cOwMcNk4TreGCZOhPo1c7ieWoT4m3oTOBWN4ZlQAqQ6773P6pauy6BAP9PRFYDb+NMJd3zMOf+Ds50HKjqOmArUJso3lHVA6pajjNHVT+c38sAEXnAnVuoTc5SbI6MtShMW3I/sBKYH7KvGvcLjztpXVLIexUhPwdCtgPU/7ffcB4bxfnwvVZVF4e+ISKn4UwbHk64aZ2PhgDfV9X1DWKY2CCGGUB3YJyqVokzA29KDOeOJPT3VgP4VHWfiIwGzsJpjfwAZ+0D0wFYi8K0Ge436BdwOoZrbcG51QPOugn+Izj1RSLicfstBuBMoLYY+Lk407gjIoPFWXwomo+ASSLSze3o/iHwbhPiOAhkhGwvBq51EyAiMibCcZ1x1vKocvsa+kU4X6j3cBIM7i2nXJx6h+Xe0vKo6svAHTjTppsOwhKFaWt+D4Q+/fQXnA/nj4GG37RjtR7nA/3vwFXuLZdHcW67rHQ7gP/MYVrg6qyUdhuwFPgMWKmqTZl+eykwrLYzG7gTJ/GtdmO4M8JxC4DxIrIc58N/nRtPIU7fyucNO9GBhwCviKwB/grMdG/RRdIHWObeBnvCrafpIGz2WGOMMVFZi8IYY0xUliiMMcZEZYnCGGNMVJYojDHGRGWJwhhjTFSWKIwxxkRlicIYY0xU/x92yCbSdvU3awAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
     }
    ],
    "source": [
-    "classical_graph, classical_graph_adjacency = generate_graph(N, 1)\n",
-    "\n",
-    "opt_cir = Paddle_QAOA(classical_graph_adjacency, N =4, P=4, METHOD=1, ITR=120, LR=0.1)\n",
-    "\n",
-    "# Load the data of QAOA\n",
-    "x1 = np.load('./output/summary_data.npz')\n",
-    "\n",
-    "H_min = np.ones([len(x1['iter'])]) * H_min\n",
-    "\n",
-    "# Plot loss\n",
-    "loss_QAOA, = plt.plot(x1['iter'], x1['energy'], \\\n",
-    "                                        alpha=0.7, marker='', linestyle=\"--\", linewidth=2, color='m')\n",
-    "benchmark, = plt.plot(x1['iter'], H_min, alpha=0.7, marker='', linestyle=\":\", linewidth=2, color='b')\n",
-    "plt.xlabel('Number of iterations')\n",
-    "plt.ylabel('Loss function for QAOA')\n",
-    "\n",
-    "plt.legend(handles=[\n",
-    "    loss_QAOA,\n",
-    "    benchmark\n",
-    "],\n",
-    "    labels=[\n",
-    "            r'Loss function $\\left\\langle {\\psi \\left( {\\bf{\\theta }} \\right)} '\n",
-    "            r'\\right|H\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle $',\n",
-    "            'The benchmark result',\n",
-    "    ], loc='best')\n",
-    "\n",
-    "# Show the plot\n",
-    "plt.show()"
+    "with fluid.dygraph.guard():\n",
+    "    net = Net(p)\n",
+    "    # Use Adam optimizer\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    # Gradient descent iteration\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "        # Run the network defined above\n",
+    "        loss, cir = net()\n",
+    "        # Calculate the gradient and optimize\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "        if itr% 10 == 0:\n",
+    "            print(\"iter:\", itr, \"loss:\", \"%.4f\"% loss.numpy())\n",
+    "\n",
+    "    gamma_opt = net.gamma.numpy()\n",
+    "    print(\"Optimized parameters gamma:\\n\", gamma_opt)\n",
+    "    beta_opt = net.beta.numpy()\n",
+    "    print(\"Optimized parameters beta:\\n\", beta_opt)"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
+    "### Decoding the quantum solution\n",
     "\n",
-    "## 5. Decoding \n",
-    "\n",
-    "However, the output of optimized QAOA circuits \n",
-    "\n",
-    "$$|\\psi(\\boldsymbol{\\beta}^*,\\boldsymbol{\\gamma}^*, P)\\rangle=\\sum_{i=1}^{2^4}\\lambda_i |\\boldsymbol{x}_i\\rangle$$\n",
+    "After obtaining the minimum value of the loss function and the corresponding set of parameters $\\vec{\\gamma}^*,\\vec{\\beta}^*$, our task has not been completed. In order to obtain an approximate solution to the Max-Cut Problem, it is necessary to decode the solution to the classical optimization problem from the quantum state $|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle$ output by QAOA. Physically, to decode a quantum state, we need to measure it and then calculate the probability distribution of the measurement results:\n",
     "\n",
-    "does not give us the answer to the Max-Cut problem directly. Instead, each bitstring $\\boldsymbol{x}_i=x_1x_2x_3 x_4\\in \\{0, 1\\}^4$ in the state $|\\psi(\\boldsymbol{\\beta}^*,\\boldsymbol{\\gamma}^*, P)\\rangle$ represents a possible classical solution. Thus, we need to decode the ouptut of QAOA circuits. \n",
+    "$$\n",
+    "p(z)=|\\langle z|\\vec{\\gamma}^*,\\vec{\\beta}^*\\rangle|^2.\n",
+    "\\tag{41}\n",
+    "$$\n",
     "\n",
-    "The task of decoding quantum answer can be accomplished via measurement. Given the output state, the measurement statistics for each bitstring obeys the probability distribution\n",
+    "Usually, the greater the probability of a certain bit string, the greater the probability that it corresponds to an optimal solution of the Max-Cut problem.\n",
     "\n",
-    "$$ p(\\boldsymbol{x})=|\\langle \\boldsymbol{x}|\\psi(\\boldsymbol{\\beta}^*,\\boldsymbol{\\gamma}^*,P)\\rangle|^2.$$\n",
-    "              \n",
-    "And this distribution is plotted using the following function:"
+    "Paddle Quantum provides a function to view the probability distribution of the measurement results of the state output by the QAOA quantum circuit:"
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 12,
+   "execution_count": 9,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    },
-    "scrolled": true
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:55:10.320339Z",
+     "start_time": "2021-01-09T06:55:09.938137Z"
+    }
    },
    "outputs": [
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEWCAYAAABrDZDcAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZPElEQVR4nO3de7QkdXnu8e/DCIqKUYSogUGIDioaQR2JuSxvgQiJCkSiXLxrCCpe1jmJ4DkejcasSBJdYuSSifdkBdSoOEdBvMeTmOgMBOTmyIggw0XBGyAKgu/5o3qg3bN379p7unr37Pp+1upFd1X12+/00v10/arqV6kqJEn9td1SNyBJWloGgST1nEEgST1nEEhSzxkEktRzBoEk9dzdlrqBhdpll11qzz33XOo2JGmbcu65595QVbvOtm6bC4I999yT9evXL3UbkrRNSXLlXOscGpKknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSem6bu6BM0uLtecKnFv3eK976h2PsRNPEPQJJ6rlOgyDJQUk2JNmY5IRZ1j85yY+TnD94vKHLfiRJW+psaCjJCuBk4EBgE7AuydqqumTGpv+vqp7eVR+SpNG63CPYH9hYVZdX1W3AGcAhHX6eJGkRugyC3YCrhl5vGiyb6beSXJDk7CSPnK1QkmOSrE+y/vrrr++iV0nqrS6DILMsqxmvzwMeXFX7An8PnDlboapaU1Wrq2r1rrvOOp22JGmRugyCTcDKode7A9cMb1BVN1bVzYPnZwHbJ9mlw54kSTN0GQTrgFVJ9kqyA3AEsHZ4gyQPTJLB8/0H/Xy/w54kSTN0dtZQVd2e5DjgHGAF8N6qujjJsYP1pwGHAy9LcjvwU+CIqpo5fCRJ6lCnVxYPhnvOmrHstKHn7wLe1WUPmi5e2SpNH68slqSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSes4gkKSeMwgkqecMAknqOYNAknrOIJCknjMIJKnnDAJJ6rlOgyDJQUk2JNmY5IQR2z0+yR1JDu+yH0nSluYNgiS/k+Reg+fPTfL2JA9u8b4VwMnAwcA+wJFJ9pljuxOBcxbavCRp67XZIzgVuCXJvsBrgSuBD7Z43/7Axqq6vKpuA84ADpllu1cCHwW+165lSdI4tQmC26uqaP6In1RVJwE7tXjfbsBVQ683DZbdKcluwGHAae3alSSNW5sguCnJ64DnAZ8aDOVs3+J9mWVZzXj9DuD4qrpjZKHkmCTrk6y//vrrW3y0JKmtNkHwHOBW4MVVdR3Nr/q/bfG+TcDKode7A9fM2GY1cEaSK4DDgVOSHDqzUFWtqarVVbV61113bfHRkqS27jbfBlV1XZKPAqsGi24APt6i9jpgVZK9gKuBI4CjZtTea/PzJO8HPllVZ7bqXJI0Fm3OGvoT4F+Bfxgs2g04c773VdXtwHE0ZwNdCny4qi5OcmySYxfdsSRprObdIwBeQXMG0FcBquqyJL/apnhVnQWcNWPZrAeGq+qFbWpKksarzTGCWwenfwKQ5G5sedBXkrSNahME/5bkfwE7JjkQ+Ajwf7ttS5I0KW2C4ATgeuBC4E9phnpe32VTkqTJaXPW0C+Afxw8JEnLzJxBkOTDVfXsJBcyyzGBqnp0p51JkiZi1B7Bqwf/ffokGpEkLY05jxFU1bWDpy+vqiuHH8DLJ9OeJKlrbQ4WHzjLsoPH3YgkaWmMOkbwMppf/r+e5OtDq3YC/qPrxiRJkzHqGMG/AGcDf01zCulmN1XVDzrtSpI0MaOCoKrqiiSvmLkiyc6GgSQtD/PtETwdOJfm9NHh+wsU8Osd9iVJmpA5g6Cqnj74715zbSNJ2vaNOlj82FFvrKrzxt+OJGnSRg0NvW3EugKeOuZeJElLYNTQ0FMm2YgkaWmMGhp6alV9Ickfzba+qj7WXVuSpEkZNTT0JOALwDNmWVeAQSBJy8CooaE3Dv77osm1I0matDY3r79/kncmOS/JuUlOSnL/STQnSepem0nnzqC5Q9mzgMMHzz/UZVOSpMmZ9w5lwM5V9ZdDr9+S5NCO+pEkTVibPYIvJjkiyXaDx7OBT3XdmCRpMkadPnoTd80x9D+Afx6s2g64GXhj591Jkjo36qyhnSbZiCRpabQ5RkCS+wGrgHtsXlZVX+6qKUnS5MwbBEleSnMj+92B84EnAP+Jcw1J0rLQ5mDxq4HHA1cO5h96DM0ppJKkZaBNEPysqn4GkOTuVfUN4GHdtiVJmpQ2xwg2JbkvcCbw2SQ/BK7psilJ0uTMGwRVddjg6V8k+SLwK8CnO+1KkjQxbYaGSPLYJK8CHg1sqqrbWr7voCQbkmxMcsIs6w9J8vUk5ydZn+R3F9a+JGlrtZl07g3AB4D7A7sA70vy+hbvWwGcDBwM7AMcmWSfGZt9Hti3qvYDXgy8e0HdS5K2WptjBEcCjxk6YPxW4DzgLfO8b39gY1VdPnjfGcAhwCWbN6iqm4e2vxfNlcySpAlqMzR0BUMXkgF3B77V4n27AVcNvd40WPZLkhyW5Bs08xe9uEVdSdIYjZpr6O9pfqHfClyc5LOD1wcC/96idmZZtsUv/qr6OPDxJE8E/hI4YJZejgGOAdhjjz1afLQkqa1RQ0PrB/89F/j40PIvtay9CVg59Hp3Rpx2WlVfTvKQJLtU1Q0z1q0B1gCsXr3a4SNJGqNRk859YPPzJDsAew9ebqiqn7eovQ5YlWQv4GrgCOCo4Q2SPBT4VlVVkscCOwDfX9g/QZK0NdrMNfRkmrOGrqAZ7lmZ5AXzTTpXVbcnOQ44B1gBvLeqLk5y7GD9aTR3PXt+kp8DPwWeU1X+4pekCWpz1tDbgN+vqg0ASfYGTgceN98bq+os4KwZy04ben4icOJCGpYkjVebs4a23xwCAFX1TWD77lqSJE1Smz2Cc5O8B/inweujaQ4gS5KWgTZBcCzwCuBVNMcIvgyc0mVTkqTJGRkESbYDzq2qRwFvn0xLkqRJGnmMoKp+AVyQxKu4JGmZajM09CCaK4u/Bvxk88KqemZnXUmSJqZNELyp8y4kSUtm1FxD96A5UPxQ4ELgPVV1+6QakyRNxqhjBB8AVtOEwME0F5ZJkpaZUUND+1TVbwAMriP42mRakiRN0qg9gjsnlnNISJKWr1F7BPsmuXHwPMCOg9cBqqru03l3kqTOjZqGesUkG5EkLY02k85JkpYxg0CSes4gkKSeMwgkqedGXVl8EzDnbSM9a0iSlodRZw3tBJDkzcB1NDemCc2NaXaaSHeSpM61GRp6WlWdUlU3VdWNVXUqzU3nJUnLQJsguCPJ0UlWJNkuydHAHV03JkmajDZBcBTwbOC7g8cfD5ZJkpaBee9HUFVXAId034okaSnMu0eQZO8kn09y0eD1o5O8vvvWJEmT0GZo6B+B1zGYjbSqvg4c0WVTkqTJaRME96yqmfcicFpqSVom2gTBDUkewuDisiSHA9d22pUkaWLa3Lz+FcAa4OFJrga+TXNRmSRpGRgZBElWAC+rqgOS3AvYrqpumkxrkqRJGBkEVXVHkscNnv9kMi1JkiapzdDQfydZC3wEuDMMqupjnXUlSZqYNkGwM/B94KlDywowCCRpGWhzZfGLFls8yUHAScAK4N1V9dYZ648Gjh+8vJnmeMQFi/08SdLCzRsESd7HLPclqKoXz/O+FcDJwIHAJmBdkrVVdcnQZt8GnlRVP0xyMM3ZSb+5gP4lSVupzdDQJ4ee3wM4DLimxfv2BzZW1eUASc6gmbPoziCoqq8Mbf9fwO4t6kqSxqjN0NBHh18nOR34XIvauwFXDb3exOhf+y8Bzm5RV5I0Rm32CGZaBezRYrvMsmzWW18meQpNEPzuHOuPAY4B2GOPNh8tSWqrzTGCmfcuvo67DvCOsglYOfR6d2YZUkryaODdwMFV9f3ZClXVGprjB6xevXrO+yhLkhauzdDQYu9PvA5YlWQv4GqaGUt/6YY2SfagOQ31eVX1zUV+jiRpK7S5H8HvDKaXIMlzk7w9yYPne19V3Q4cB5wDXAp8uKouTnJskmMHm70BuD9wSpLzk6xf9L9EkrQobY4RnArsm2Rf4LXAe4APAk+a741VdRZw1oxlpw09fynw0oU0LEkarzbTUN9eVUVz6udJVXUSsNjhIknSlGmzR3BTktcBzwWeOLhQbPtu25IkTUqbPYLnALcCL6mq62iuD/jbTruSJE1Mm7OGrgPePvT6OzTHCCRJy0Cbs4aekGRdkpuT3JbkjiQ/nkRzkqTutRkaehdwJHAZsCPNWT4nd9mUJGlyWk0xUVUbk6yoqjuA9yX5yrxvkiRtE9oEwS1JdgDOT/I3wLXAvbptS5I0KW2Ghp432O44mltVrgSe1WVTkqTJaXPW0JVJdgQeVFVvmkBPkqQJanPW0DOA84FPD17vN7iZvSRpGWgzNPQXNHcb+xFAVZ0P7NlVQ5KkyWo715DXDUjSMtXmrKGLkhwFrEiyCngV4OmjkrRMtNkjeCXwSJr5hk4HbgRe02FPkqQJanPW0C3A/x48JEnLzJxBMN+ZQVX1zPG3I0matFF7BL8FXEUzHPRVIBPpSJI0UaOC4IHAgTQTzh0FfAo4vaounkRjkqTJmPNgcVXdUVWfrqoXAE8ANgJfSvLKiXUnSercyIPFSe4O/CHNXsGewDuBj3XfliRpUkYdLP4A8CjgbOBNVXXRxLqSJE3MqD2C59HMNro38KrkzmPFAaqq7tNxb5KkCZgzCKqqzcVmkqRtnH/sJannDAJJ6jmDQJJ6ziCQpJ4zCCSp5wwCSeo5g0CSeq7TIEhyUJINSTYmOWGW9Q9P8p9Jbk3yZ132IkmaXZtbVS5KkhXAyTQzmG4C1iVZW1WXDG32A5pbXx7aVR+SpNG63CPYH9hYVZdX1W3AGcAhwxtU1feqah3w8w77kCSN0GUQ7EZzY5vNNg2WSZKmSJdBMNsdzWpRhZJjkqxPsv7666/fyrYkScO6DIJNwMqh17sD1yymUFWtqarVVbV61113HUtzkqRGl0GwDliVZK8kOwBHAGs7/DxJ0iJ0dtZQVd2e5DjgHGAF8N6qujjJsYP1pyV5ILAeuA/wiySvAfapqhu76kuS9Ms6CwKAqjoLOGvGstOGnl9HM2QkSVoiXlksST1nEEhSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPWcQSBJPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSzxkEktRzBoEk9ZxBIEk9ZxBIUs8ZBJLUcwaBJPVcp0GQ5KAkG5JsTHLCLOuT5J2D9V9P8tgu+5EkbamzIEiyAjgZOBjYBzgyyT4zNjsYWDV4HAOc2lU/kqTZdblHsD+wsaour6rbgDOAQ2ZscwjwwWr8F3DfJA/qsCdJ0gx367D2bsBVQ683Ab/ZYpvdgGuHN0pyDM0eA8DNSTaMt9U77QLcMIW1xl1vm6yVE8dbz1oLq7eMvv9x15vWWjM9eK4VXQZBZllWi9iGqloDrBlHU6MkWV9Vq6et1rjr9aHWuOv1oda4601rrXHXm9ZaC9Hl0NAmYOXQ692BaxaxjSSpQ10GwTpgVZK9kuwAHAGsnbHNWuD5g7OHngD8uKqunVlIktSdzoaGqur2JMcB5wArgPdW1cVJjh2sPw04C/gDYCNwC/CirvppaZzDT+MeyprW3qa11rjr9aHWuOtNa61x15vWWq2laosheUlSj3hlsST1nEEgST1nEEhSzxkEktRzXV5QNvWSPA04lOZq5qK5huETVfXpMX7GG6rqzdPW1zT3Nq19LbY3adr19qyhJO8A9gY+SHNhGzQXtD0fuKyqXj2mz/lOVe0xbX1Nc2/T2tdiehu8Z2pDymCfzt4m/YOjz0Hwzarae5blAb5ZVasWUOvGuVYBO1ZV6z2vcfY1zb1Na18d9PYOpjSkDPbp7W0xPzi2Rp+Hhn6WZP+q+tqM5Y8HfrbAWj8CHl9V3525IslVW24+sb6mubdp7Wvcvf3BHCH1IeCbwIL+cMwXUkvV27T2Nc29jbmvrdLnIHghcGqSnbgr2VcCNw7WLcQHaWb22+IPB/AvS9jXNPc2rX2Nu7dpDimDffl8Z1ult0NDmyV5IM1YX4BNVXXdErcETG9fML29TWNfg7vunQrMFlIvr6pzF1jvLcDaWf4QkeTEqjp+KXqb1r6mubdx9rW1eh0EgzHk/fnlgz5fq0V8KeOsNeIzHl5V31jKen5ni6s3jSG12bT2Nq19wXT3thi9DYIkvw+cAlwGXD1YvDvwUJpk/8xS1Jrnc8Z6AGkRB8r8zhZ31tBYA29bC9Cl/sHRRb05PmNJv7Ot0edjBCcBB1TVFcMLk+xFMyvqI5aiVpJ3zrUKuO8Ceuqint/ZAuuNCrwkCw68cdcb4TPAuAJ0QbX8zsZea159DoK7cdcY37Crge2XsNaLgP8J3DrLuiMXWGvc9fzOFl5vnOE51npjDrxp/cEx1npT/J1tlT4HwXuBdUnO4K77Jq+kuYHOe5aw1jrgoqr6yswVSf5igbXGXc/vbOH1xhl44643zsCb1h8c4643rd/ZVuntMQKAJPsAz2TooA/NUfxLlqpWkp2Bn1XVLQvtYUL1HgEcwni+s7HUmubvLMnrgGcDswXeh6vqr5eqXpIvAK+fI/C+XVV7LVEtv7MF1tpavQ4CaRLG+YNjnPXGHHhT+4NjnPWm+Tvbql76GgRJfgV4Hc2cIbsOFn8P+ATw1qr60bZeq4t6Iz7n7Ko6eDnX6qKeNA36fIzgw8AXgCdvPgd4cG7wC4GPAAdOWa0XLKLWWOsNLqaZdRWw30KamtZa4643zcE+rbXm+ZypDfZprdXq83q8R7Chqh620HXbUq0OersD+DeaP4gzPaGqWs+PMq21OujtHJog/sAsPxJ+r6oWFOzjrDei1gtozrJZqlqjgviTVfWgtrXGXW9aa22tPgfBZ4DP0fwP97uDZQ+g+T/UgVV1wLZeq4PeLgIOq6rLZll3VVWt3NZrddDbNAf7tNaa5mCfylpbrap6+QDuB5wIXAr8YPC4dLBs5+VQq4PeDgceNse6Q5dDrQ56+wzwWuABQ8seABwPfG4RvY2t3hTXughYNce6qxbxnY2t3rTW2tpHb/cIYIszCYZvMHHpcqnVQW8Pn6XW2uVUa5z1ktwPOGFQ61cHi78LrKUZO//hUtWb4lqHAxdW1YZZ1h1aVWe2rTXuetNaa2v19p7FSY6nmVK4gK8Cm2cAPD3JCcuhVge9vZbmXOwM6qwbPF82tcZdr6p+WFXHV9XDq2rnweMR1cwseehCextnvSmu9a+z/XEcuN9Cao273rTW2mqT3P2YpgfNTSS2n2X5DjR3Gtrma01zb9Naq4t6Iz7nO+OqNe56fag1zb2N+98536PPp4/+Avg14MoZyx80WLccak1zb9Naa6z1knx9rlU0Y+gLMs56fag17nrTWmtr9TkIXgN8Psll3HXZ+R400yAft0xqTXNv01pr3PUeADwNmDlGHmCLqQUmXK8Ptaa5t3H/Oxett0FQVZ9Osjd3zVG++bLzdVV1x3KoNc29TWutDup9Erh3VZ0/c0WSLy20tzHX60Otae5t3P/ORev1WUOSpB6fNSRJahgEktRzBoGWtSS7J/lEksuSXJ7kXUnu3uJ9N8+x/M1JDhg8f02Se86x3dOT/HeSC5JckuRPB8sPTTON9Hyf32o7aRwMAi1bSQJ8DDizqlYBq4Adgb9ZbM2qekNVfW7w8jXAFkGQZHtgDfCMqtoXeAzwpcHqQ4E2f+DbbidtNQ8Wa9lK8nvAG6vqiUPL7kNzfcBKmjmFVlfVcYN1nwT+rqq+NNgj+AfgKTSn9x1RVdcneT/N2R6/BvwdsAG4oaqeMvQZOwPfAB5cVT8dWv7bg/f+ePB4FvBU4Biai9U2As+jmep65nYAJ9NM8XwL8CdV9Y2xfFHqPfcItJw9Ejh3eEFV3QhcQXNNwCj3As6rqsfSzBD5xhl13kkz/9BThkNgsO4HNHPsXJnk9CRHJ9mumlsSrgX+vKr2q6pvAR+rqscP9hwuBV4yx3ZrgFdW1eOAPwNOWfC3Ic2ht9cRqBdCM8fSbMvn8wvgQ4Pn/0wzxNRaVb00yW8AB9D84T6QZurvmR6V5C3AfYF7A+ds0Wxyb+C3gY80o10AzHucQ2rLINBydjF3DasAdw4NPYBmSOdR/PJe8T1G1FrwGGpVXQhcmOSfgG8zexC8n2Zq6wuSvBB48izbbAf8qKr2W2gPUhsODWk5+zxwzyTPB0iyAngb8K7B2P0VwH5JtkuykuZK4s22ozmGAHAU8O+z1L8J2GnmwiT3TvLkoUX7cde8RTPfsxNw7eAA89Gz1R4MZ307yR8P6ifJvqP+4dJCGARatqo5E+Iw4PDBvEHfB35RVX812OQ/aH6pX0hz4Pe8obf/BHhkknNpDui+eZaPWAOcneSLM5YHeG2SDUnOB97EXXsDZwB/Pji19CHA/6GZHvyzNAeYmWO7o4GXJLmAZk/nkAV9GdIInjWk3hictXM68EdVde5820t9YRBIUs85NCRJPWcQSFLPGQSS1HMGgST1nEEgST1nEEhSzxkEktRz/x8RAEcj1XBTZwAAAABJRU5ErkJggg==\n",
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"277.968125pt\" version=\"1.1\" viewBox=\"0 0 385.78125 277.968125\" width=\"385.78125pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T14:55:10.216565</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 277.968125 \n",
+       "L 385.78125 277.968125 \n",
+       "L 385.78125 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:none;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"patch_2\">\n",
+       "    <path d=\"M 43.78125 224.64 \n",
+       "L 378.58125 224.64 \n",
+       "L 378.58125 7.2 \n",
+       "L 43.78125 7.2 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_3\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 58.999432 224.64 \n",
+       "L 74.410249 224.64 \n",
+       "L 74.410249 224.64 \n",
+       "L 58.999432 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_4\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 78.262953 224.64 \n",
+       "L 93.67377 224.64 \n",
+       "L 93.67377 224.64 \n",
+       "L 78.262953 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_5\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 97.526474 224.64 \n",
+       "L 112.937291 224.64 \n",
+       "L 112.937291 224.64 \n",
+       "L 97.526474 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_6\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 116.789996 224.64 \n",
+       "L 132.200813 224.64 \n",
+       "L 132.200813 224.64 \n",
+       "L 116.789996 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_7\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 136.053517 224.64 \n",
+       "L 151.464334 224.64 \n",
+       "L 151.464334 224.64 \n",
+       "L 136.053517 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_8\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 155.317038 224.64 \n",
+       "L 170.727855 224.64 \n",
+       "L 170.727855 27.039128 \n",
+       "L 155.317038 27.039128 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_9\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 174.58056 224.64 \n",
+       "L 189.991377 224.64 \n",
+       "L 189.991377 224.64 \n",
+       "L 174.58056 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_10\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 193.844081 224.64 \n",
+       "L 209.254898 224.64 \n",
+       "L 209.254898 224.64 \n",
+       "L 193.844081 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_11\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 213.107602 224.64 \n",
+       "L 228.518419 224.64 \n",
+       "L 228.518419 224.64 \n",
+       "L 213.107602 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_12\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 232.371123 224.64 \n",
+       "L 247.78194 224.64 \n",
+       "L 247.78194 224.64 \n",
+       "L 232.371123 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_13\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 251.634645 224.64 \n",
+       "L 267.045462 224.64 \n",
+       "L 267.045462 17.554286 \n",
+       "L 251.634645 17.554286 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_14\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 270.898166 224.64 \n",
+       "L 286.308983 224.64 \n",
+       "L 286.308983 224.64 \n",
+       "L 270.898166 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_15\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 290.161687 224.64 \n",
+       "L 305.572504 224.64 \n",
+       "L 305.572504 224.64 \n",
+       "L 290.161687 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_16\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 309.425209 224.64 \n",
+       "L 324.836026 224.64 \n",
+       "L 324.836026 224.64 \n",
+       "L 309.425209 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_17\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 328.68873 224.64 \n",
+       "L 344.099547 224.64 \n",
+       "L 344.099547 224.64 \n",
+       "L 328.68873 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_18\">\n",
+       "    <path clip-path=\"url(#p1913dbb0ed)\" d=\"M 347.952251 224.64 \n",
+       "L 363.363068 224.64 \n",
+       "L 363.363068 224.64 \n",
+       "L 347.952251 224.64 \n",
+       "z\n",
+       "\" style=\"fill:#1f77b4;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_1\">\n",
+       "    <g id=\"xtick_1\">\n",
+       "     <g id=\"line2d_1\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L 0 3.5 \n",
+       "\" id=\"mb21437fbbb\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"66.70484\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_1\">\n",
+       "      <!-- 0000 -->\n",
+       "      <g transform=\"translate(69.464215 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 31.78125 66.40625 \n",
+       "Q 24.171875 66.40625 20.328125 58.90625 \n",
+       "Q 16.5 51.421875 16.5 36.375 \n",
+       "Q 16.5 21.390625 20.328125 13.890625 \n",
+       "Q 24.171875 6.390625 31.78125 6.390625 \n",
+       "Q 39.453125 6.390625 43.28125 13.890625 \n",
+       "Q 47.125 21.390625 47.125 36.375 \n",
+       "Q 47.125 51.421875 43.28125 58.90625 \n",
+       "Q 39.453125 66.40625 31.78125 66.40625 \n",
+       "z\n",
+       "M 31.78125 74.21875 \n",
+       "Q 44.046875 74.21875 50.515625 64.515625 \n",
+       "Q 56.984375 54.828125 56.984375 36.375 \n",
+       "Q 56.984375 17.96875 50.515625 8.265625 \n",
+       "Q 44.046875 -1.421875 31.78125 -1.421875 \n",
+       "Q 19.53125 -1.421875 13.0625 8.265625 \n",
+       "Q 6.59375 17.96875 6.59375 36.375 \n",
+       "Q 6.59375 54.828125 13.0625 64.515625 \n",
+       "Q 19.53125 74.21875 31.78125 74.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-48\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_2\">\n",
+       "     <g id=\"line2d_2\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"85.968362\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_2\">\n",
+       "      <!-- 0001 -->\n",
+       "      <g transform=\"translate(88.727737 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 12.40625 8.296875 \n",
+       "L 28.515625 8.296875 \n",
+       "L 28.515625 63.921875 \n",
+       "L 10.984375 60.40625 \n",
+       "L 10.984375 69.390625 \n",
+       "L 28.421875 72.90625 \n",
+       "L 38.28125 72.90625 \n",
+       "L 38.28125 8.296875 \n",
+       "L 54.390625 8.296875 \n",
+       "L 54.390625 0 \n",
+       "L 12.40625 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-49\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_3\">\n",
+       "     <g id=\"line2d_3\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"105.231883\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_3\">\n",
+       "      <!-- 0010 -->\n",
+       "      <g transform=\"translate(107.991258 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_4\">\n",
+       "     <g id=\"line2d_4\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"124.495404\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_4\">\n",
+       "      <!-- 0011 -->\n",
+       "      <g transform=\"translate(127.254779 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_5\">\n",
+       "     <g id=\"line2d_5\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"143.758925\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_5\">\n",
+       "      <!-- 0100 -->\n",
+       "      <g transform=\"translate(146.5183 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_6\">\n",
+       "     <g id=\"line2d_6\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"163.022447\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_6\">\n",
+       "      <!-- 0101 -->\n",
+       "      <g transform=\"translate(165.781822 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_7\">\n",
+       "     <g id=\"line2d_7\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"182.285968\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_7\">\n",
+       "      <!-- 0110 -->\n",
+       "      <g transform=\"translate(185.045343 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_8\">\n",
+       "     <g id=\"line2d_8\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"201.549489\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_8\">\n",
+       "      <!-- 0111 -->\n",
+       "      <g transform=\"translate(204.308864 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_9\">\n",
+       "     <g id=\"line2d_9\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"220.813011\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_9\">\n",
+       "      <!-- 1000 -->\n",
+       "      <g transform=\"translate(223.572386 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_10\">\n",
+       "     <g id=\"line2d_10\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"240.076532\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_10\">\n",
+       "      <!-- 1001 -->\n",
+       "      <g transform=\"translate(242.835907 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_11\">\n",
+       "     <g id=\"line2d_11\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"259.340053\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_11\">\n",
+       "      <!-- 1010 -->\n",
+       "      <g transform=\"translate(262.099428 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_12\">\n",
+       "     <g id=\"line2d_12\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"278.603575\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_12\">\n",
+       "      <!-- 1011 -->\n",
+       "      <g transform=\"translate(281.36295 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_13\">\n",
+       "     <g id=\"line2d_13\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"297.867096\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_13\">\n",
+       "      <!-- 1100 -->\n",
+       "      <g transform=\"translate(300.626471 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_14\">\n",
+       "     <g id=\"line2d_14\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"317.130617\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_14\">\n",
+       "      <!-- 1101 -->\n",
+       "      <g transform=\"translate(319.889992 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_15\">\n",
+       "     <g id=\"line2d_15\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"336.394138\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_15\">\n",
+       "      <!-- 1110 -->\n",
+       "      <g transform=\"translate(339.153513 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_16\">\n",
+       "     <g id=\"line2d_16\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"355.65766\" xlink:href=\"#mb21437fbbb\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_16\">\n",
+       "      <!-- 1111 -->\n",
+       "      <g transform=\"translate(358.417035 257.09)rotate(-90)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"190.869141\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_17\">\n",
+       "     <!-- Qubit State -->\n",
+       "     <g transform=\"translate(182.728906 268.688437)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 39.40625 66.21875 \n",
+       "Q 28.65625 66.21875 22.328125 58.203125 \n",
+       "Q 16.015625 50.203125 16.015625 36.375 \n",
+       "Q 16.015625 22.609375 22.328125 14.59375 \n",
+       "Q 28.65625 6.59375 39.40625 6.59375 \n",
+       "Q 50.140625 6.59375 56.421875 14.59375 \n",
+       "Q 62.703125 22.609375 62.703125 36.375 \n",
+       "Q 62.703125 50.203125 56.421875 58.203125 \n",
+       "Q 50.140625 66.21875 39.40625 66.21875 \n",
+       "z\n",
+       "M 53.21875 1.3125 \n",
+       "L 66.21875 -12.890625 \n",
+       "L 54.296875 -12.890625 \n",
+       "L 43.5 -1.21875 \n",
+       "Q 41.890625 -1.3125 41.03125 -1.359375 \n",
+       "Q 40.1875 -1.421875 39.40625 -1.421875 \n",
+       "Q 24.03125 -1.421875 14.8125 8.859375 \n",
+       "Q 5.609375 19.140625 5.609375 36.375 \n",
+       "Q 5.609375 53.65625 14.8125 63.9375 \n",
+       "Q 24.03125 74.21875 39.40625 74.21875 \n",
+       "Q 54.734375 74.21875 63.90625 63.9375 \n",
+       "Q 73.09375 53.65625 73.09375 36.375 \n",
+       "Q 73.09375 23.6875 67.984375 14.640625 \n",
+       "Q 62.890625 5.609375 53.21875 1.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-81\"/>\n",
+       "       <path d=\"M 8.5 21.578125 \n",
+       "L 8.5 54.6875 \n",
+       "L 17.484375 54.6875 \n",
+       "L 17.484375 21.921875 \n",
+       "Q 17.484375 14.15625 20.5 10.265625 \n",
+       "Q 23.53125 6.390625 29.59375 6.390625 \n",
+       "Q 36.859375 6.390625 41.078125 11.03125 \n",
+       "Q 45.3125 15.671875 45.3125 23.6875 \n",
+       "L 45.3125 54.6875 \n",
+       "L 54.296875 54.6875 \n",
+       "L 54.296875 0 \n",
+       "L 45.3125 0 \n",
+       "L 45.3125 8.40625 \n",
+       "Q 42.046875 3.421875 37.71875 1 \n",
+       "Q 33.40625 -1.421875 27.6875 -1.421875 \n",
+       "Q 18.265625 -1.421875 13.375 4.4375 \n",
+       "Q 8.5 10.296875 8.5 21.578125 \n",
+       "z\n",
+       "M 31.109375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-117\"/>\n",
+       "       <path d=\"M 48.6875 27.296875 \n",
+       "Q 48.6875 37.203125 44.609375 42.84375 \n",
+       "Q 40.53125 48.484375 33.40625 48.484375 \n",
+       "Q 26.265625 48.484375 22.1875 42.84375 \n",
+       "Q 18.109375 37.203125 18.109375 27.296875 \n",
+       "Q 18.109375 17.390625 22.1875 11.75 \n",
+       "Q 26.265625 6.109375 33.40625 6.109375 \n",
+       "Q 40.53125 6.109375 44.609375 11.75 \n",
+       "Q 48.6875 17.390625 48.6875 27.296875 \n",
+       "z\n",
+       "M 18.109375 46.390625 \n",
+       "Q 20.953125 51.265625 25.265625 53.625 \n",
+       "Q 29.59375 56 35.59375 56 \n",
+       "Q 45.5625 56 51.78125 48.09375 \n",
+       "Q 58.015625 40.1875 58.015625 27.296875 \n",
+       "Q 58.015625 14.40625 51.78125 6.484375 \n",
+       "Q 45.5625 -1.421875 35.59375 -1.421875 \n",
+       "Q 29.59375 -1.421875 25.265625 0.953125 \n",
+       "Q 20.953125 3.328125 18.109375 8.203125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 75.984375 \n",
+       "L 18.109375 75.984375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-98\"/>\n",
+       "       <path d=\"M 9.421875 54.6875 \n",
+       "L 18.40625 54.6875 \n",
+       "L 18.40625 0 \n",
+       "L 9.421875 0 \n",
+       "z\n",
+       "M 9.421875 75.984375 \n",
+       "L 18.40625 75.984375 \n",
+       "L 18.40625 64.59375 \n",
+       "L 9.421875 64.59375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-105\"/>\n",
+       "       <path d=\"M 18.3125 70.21875 \n",
+       "L 18.3125 54.6875 \n",
+       "L 36.8125 54.6875 \n",
+       "L 36.8125 47.703125 \n",
+       "L 18.3125 47.703125 \n",
+       "L 18.3125 18.015625 \n",
+       "Q 18.3125 11.328125 20.140625 9.421875 \n",
+       "Q 21.96875 7.515625 27.59375 7.515625 \n",
+       "L 36.8125 7.515625 \n",
+       "L 36.8125 0 \n",
+       "L 27.59375 0 \n",
+       "Q 17.1875 0 13.234375 3.875 \n",
+       "Q 9.28125 7.765625 9.28125 18.015625 \n",
+       "L 9.28125 47.703125 \n",
+       "L 2.6875 47.703125 \n",
+       "L 2.6875 54.6875 \n",
+       "L 9.28125 54.6875 \n",
+       "L 9.28125 70.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-116\"/>\n",
+       "       <path id=\"DejaVuSans-32\"/>\n",
+       "       <path d=\"M 53.515625 70.515625 \n",
+       "L 53.515625 60.890625 \n",
+       "Q 47.90625 63.578125 42.921875 64.890625 \n",
+       "Q 37.9375 66.21875 33.296875 66.21875 \n",
+       "Q 25.25 66.21875 20.875 63.09375 \n",
+       "Q 16.5 59.96875 16.5 54.203125 \n",
+       "Q 16.5 49.359375 19.40625 46.890625 \n",
+       "Q 22.3125 44.4375 30.421875 42.921875 \n",
+       "L 36.375 41.703125 \n",
+       "Q 47.40625 39.59375 52.65625 34.296875 \n",
+       "Q 57.90625 29 57.90625 20.125 \n",
+       "Q 57.90625 9.515625 50.796875 4.046875 \n",
+       "Q 43.703125 -1.421875 29.984375 -1.421875 \n",
+       "Q 24.8125 -1.421875 18.96875 -0.25 \n",
+       "Q 13.140625 0.921875 6.890625 3.21875 \n",
+       "L 6.890625 13.375 \n",
+       "Q 12.890625 10.015625 18.65625 8.296875 \n",
+       "Q 24.421875 6.59375 29.984375 6.59375 \n",
+       "Q 38.421875 6.59375 43.015625 9.90625 \n",
+       "Q 47.609375 13.234375 47.609375 19.390625 \n",
+       "Q 47.609375 24.75 44.3125 27.78125 \n",
+       "Q 41.015625 30.8125 33.5 32.328125 \n",
+       "L 27.484375 33.5 \n",
+       "Q 16.453125 35.6875 11.515625 40.375 \n",
+       "Q 6.59375 45.0625 6.59375 53.421875 \n",
+       "Q 6.59375 63.09375 13.40625 68.65625 \n",
+       "Q 20.21875 74.21875 32.171875 74.21875 \n",
+       "Q 37.3125 74.21875 42.625 73.28125 \n",
+       "Q 47.953125 72.359375 53.515625 70.515625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-83\"/>\n",
+       "       <path d=\"M 34.28125 27.484375 \n",
+       "Q 23.390625 27.484375 19.1875 25 \n",
+       "Q 14.984375 22.515625 14.984375 16.5 \n",
+       "Q 14.984375 11.71875 18.140625 8.90625 \n",
+       "Q 21.296875 6.109375 26.703125 6.109375 \n",
+       "Q 34.1875 6.109375 38.703125 11.40625 \n",
+       "Q 43.21875 16.703125 43.21875 25.484375 \n",
+       "L 43.21875 27.484375 \n",
+       "z\n",
+       "M 52.203125 31.203125 \n",
+       "L 52.203125 0 \n",
+       "L 43.21875 0 \n",
+       "L 43.21875 8.296875 \n",
+       "Q 40.140625 3.328125 35.546875 0.953125 \n",
+       "Q 30.953125 -1.421875 24.3125 -1.421875 \n",
+       "Q 15.921875 -1.421875 10.953125 3.296875 \n",
+       "Q 6 8.015625 6 15.921875 \n",
+       "Q 6 25.140625 12.171875 29.828125 \n",
+       "Q 18.359375 34.515625 30.609375 34.515625 \n",
+       "L 43.21875 34.515625 \n",
+       "L 43.21875 35.40625 \n",
+       "Q 43.21875 41.609375 39.140625 45 \n",
+       "Q 35.0625 48.390625 27.6875 48.390625 \n",
+       "Q 23 48.390625 18.546875 47.265625 \n",
+       "Q 14.109375 46.140625 10.015625 43.890625 \n",
+       "L 10.015625 52.203125 \n",
+       "Q 14.9375 54.109375 19.578125 55.046875 \n",
+       "Q 24.21875 56 28.609375 56 \n",
+       "Q 40.484375 56 46.34375 49.84375 \n",
+       "Q 52.203125 43.703125 52.203125 31.203125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-97\"/>\n",
+       "       <path d=\"M 56.203125 29.59375 \n",
+       "L 56.203125 25.203125 \n",
+       "L 14.890625 25.203125 \n",
+       "Q 15.484375 15.921875 20.484375 11.0625 \n",
+       "Q 25.484375 6.203125 34.421875 6.203125 \n",
+       "Q 39.59375 6.203125 44.453125 7.46875 \n",
+       "Q 49.3125 8.734375 54.109375 11.28125 \n",
+       "L 54.109375 2.78125 \n",
+       "Q 49.265625 0.734375 44.1875 -0.34375 \n",
+       "Q 39.109375 -1.421875 33.890625 -1.421875 \n",
+       "Q 20.796875 -1.421875 13.15625 6.1875 \n",
+       "Q 5.515625 13.8125 5.515625 26.8125 \n",
+       "Q 5.515625 40.234375 12.765625 48.109375 \n",
+       "Q 20.015625 56 32.328125 56 \n",
+       "Q 43.359375 56 49.78125 48.890625 \n",
+       "Q 56.203125 41.796875 56.203125 29.59375 \n",
+       "z\n",
+       "M 47.21875 32.234375 \n",
+       "Q 47.125 39.59375 43.09375 43.984375 \n",
+       "Q 39.0625 48.390625 32.421875 48.390625 \n",
+       "Q 24.90625 48.390625 20.390625 44.140625 \n",
+       "Q 15.875 39.890625 15.1875 32.171875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-101\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-81\"/>\n",
+       "      <use x=\"78.710938\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"142.089844\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"205.566406\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"233.349609\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"272.558594\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"304.345703\" xlink:href=\"#DejaVuSans-83\"/>\n",
+       "      <use x=\"367.822266\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"407.03125\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"468.310547\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"507.519531\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_2\">\n",
+       "    <g id=\"ytick_1\">\n",
+       "     <g id=\"line2d_17\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L -3.5 0 \n",
+       "\" id=\"m4322a873f8\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m4322a873f8\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_18\">\n",
+       "      <!-- 0.0 -->\n",
+       "      <g transform=\"translate(20.878125 228.439219)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 10.6875 12.40625 \n",
+       "L 21 12.40625 \n",
+       "L 21 0 \n",
+       "L 10.6875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-46\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_2\">\n",
+       "     <g id=\"line2d_18\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m4322a873f8\" y=\"184.171341\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_19\">\n",
+       "      <!-- 0.1 -->\n",
+       "      <g transform=\"translate(20.878125 187.97056)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_3\">\n",
+       "     <g id=\"line2d_19\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m4322a873f8\" y=\"143.702683\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_20\">\n",
+       "      <!-- 0.2 -->\n",
+       "      <g transform=\"translate(20.878125 147.501901)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 19.1875 8.296875 \n",
+       "L 53.609375 8.296875 \n",
+       "L 53.609375 0 \n",
+       "L 7.328125 0 \n",
+       "L 7.328125 8.296875 \n",
+       "Q 12.9375 14.109375 22.625 23.890625 \n",
+       "Q 32.328125 33.6875 34.8125 36.53125 \n",
+       "Q 39.546875 41.84375 41.421875 45.53125 \n",
+       "Q 43.3125 49.21875 43.3125 52.78125 \n",
+       "Q 43.3125 58.59375 39.234375 62.25 \n",
+       "Q 35.15625 65.921875 28.609375 65.921875 \n",
+       "Q 23.96875 65.921875 18.8125 64.3125 \n",
+       "Q 13.671875 62.703125 7.8125 59.421875 \n",
+       "L 7.8125 69.390625 \n",
+       "Q 13.765625 71.78125 18.9375 73 \n",
+       "Q 24.125 74.21875 28.421875 74.21875 \n",
+       "Q 39.75 74.21875 46.484375 68.546875 \n",
+       "Q 53.21875 62.890625 53.21875 53.421875 \n",
+       "Q 53.21875 48.921875 51.53125 44.890625 \n",
+       "Q 49.859375 40.875 45.40625 35.40625 \n",
+       "Q 44.1875 33.984375 37.640625 27.21875 \n",
+       "Q 31.109375 20.453125 19.1875 8.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-50\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_4\">\n",
+       "     <g id=\"line2d_20\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m4322a873f8\" y=\"103.234024\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_21\">\n",
+       "      <!-- 0.3 -->\n",
+       "      <g transform=\"translate(20.878125 107.033243)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 40.578125 39.3125 \n",
+       "Q 47.65625 37.796875 51.625 33 \n",
+       "Q 55.609375 28.21875 55.609375 21.1875 \n",
+       "Q 55.609375 10.40625 48.1875 4.484375 \n",
+       "Q 40.765625 -1.421875 27.09375 -1.421875 \n",
+       "Q 22.515625 -1.421875 17.65625 -0.515625 \n",
+       "Q 12.796875 0.390625 7.625 2.203125 \n",
+       "L 7.625 11.71875 \n",
+       "Q 11.71875 9.328125 16.59375 8.109375 \n",
+       "Q 21.484375 6.890625 26.8125 6.890625 \n",
+       "Q 36.078125 6.890625 40.9375 10.546875 \n",
+       "Q 45.796875 14.203125 45.796875 21.1875 \n",
+       "Q 45.796875 27.640625 41.28125 31.265625 \n",
+       "Q 36.765625 34.90625 28.71875 34.90625 \n",
+       "L 20.21875 34.90625 \n",
+       "L 20.21875 43.015625 \n",
+       "L 29.109375 43.015625 \n",
+       "Q 36.375 43.015625 40.234375 45.921875 \n",
+       "Q 44.09375 48.828125 44.09375 54.296875 \n",
+       "Q 44.09375 59.90625 40.109375 62.90625 \n",
+       "Q 36.140625 65.921875 28.71875 65.921875 \n",
+       "Q 24.65625 65.921875 20.015625 65.03125 \n",
+       "Q 15.375 64.15625 9.8125 62.3125 \n",
+       "L 9.8125 71.09375 \n",
+       "Q 15.4375 72.65625 20.34375 73.4375 \n",
+       "Q 25.25 74.21875 29.59375 74.21875 \n",
+       "Q 40.828125 74.21875 47.359375 69.109375 \n",
+       "Q 53.90625 64.015625 53.90625 55.328125 \n",
+       "Q 53.90625 49.265625 50.4375 45.09375 \n",
+       "Q 46.96875 40.921875 40.578125 39.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-51\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-51\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_5\">\n",
+       "     <g id=\"line2d_21\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m4322a873f8\" y=\"62.765365\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_22\">\n",
+       "      <!-- 0.4 -->\n",
+       "      <g transform=\"translate(20.878125 66.564584)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 37.796875 64.3125 \n",
+       "L 12.890625 25.390625 \n",
+       "L 37.796875 25.390625 \n",
+       "z\n",
+       "M 35.203125 72.90625 \n",
+       "L 47.609375 72.90625 \n",
+       "L 47.609375 25.390625 \n",
+       "L 58.015625 25.390625 \n",
+       "L 58.015625 17.1875 \n",
+       "L 47.609375 17.1875 \n",
+       "L 47.609375 0 \n",
+       "L 37.796875 0 \n",
+       "L 37.796875 17.1875 \n",
+       "L 4.890625 17.1875 \n",
+       "L 4.890625 26.703125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-52\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-52\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_6\">\n",
+       "     <g id=\"line2d_22\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"43.78125\" xlink:href=\"#m4322a873f8\" y=\"22.296707\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_23\">\n",
+       "      <!-- 0.5 -->\n",
+       "      <g transform=\"translate(20.878125 26.095925)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 10.796875 72.90625 \n",
+       "L 49.515625 72.90625 \n",
+       "L 49.515625 64.59375 \n",
+       "L 19.828125 64.59375 \n",
+       "L 19.828125 46.734375 \n",
+       "Q 21.96875 47.46875 24.109375 47.828125 \n",
+       "Q 26.265625 48.1875 28.421875 48.1875 \n",
+       "Q 40.625 48.1875 47.75 41.5 \n",
+       "Q 54.890625 34.8125 54.890625 23.390625 \n",
+       "Q 54.890625 11.625 47.5625 5.09375 \n",
+       "Q 40.234375 -1.421875 26.90625 -1.421875 \n",
+       "Q 22.3125 -1.421875 17.546875 -0.640625 \n",
+       "Q 12.796875 0.140625 7.71875 1.703125 \n",
+       "L 7.71875 11.625 \n",
+       "Q 12.109375 9.234375 16.796875 8.0625 \n",
+       "Q 21.484375 6.890625 26.703125 6.890625 \n",
+       "Q 35.15625 6.890625 40.078125 11.328125 \n",
+       "Q 45.015625 15.765625 45.015625 23.390625 \n",
+       "Q 45.015625 31 40.078125 35.4375 \n",
+       "Q 35.15625 39.890625 26.703125 39.890625 \n",
+       "Q 22.75 39.890625 18.8125 39.015625 \n",
+       "Q 14.890625 38.140625 10.796875 36.28125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-53\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_24\">\n",
+       "     <!-- Measured Probabilities -->\n",
+       "     <g transform=\"translate(14.798438 172.470781)rotate(-90)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 24.515625 72.90625 \n",
+       "L 43.109375 23.296875 \n",
+       "L 61.8125 72.90625 \n",
+       "L 76.515625 72.90625 \n",
+       "L 76.515625 0 \n",
+       "L 66.890625 0 \n",
+       "L 66.890625 64.015625 \n",
+       "L 48.09375 14.015625 \n",
+       "L 38.1875 14.015625 \n",
+       "L 19.390625 64.015625 \n",
+       "L 19.390625 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-77\"/>\n",
+       "       <path d=\"M 44.28125 53.078125 \n",
+       "L 44.28125 44.578125 \n",
+       "Q 40.484375 46.53125 36.375 47.5 \n",
+       "Q 32.28125 48.484375 27.875 48.484375 \n",
+       "Q 21.1875 48.484375 17.84375 46.4375 \n",
+       "Q 14.5 44.390625 14.5 40.28125 \n",
+       "Q 14.5 37.15625 16.890625 35.375 \n",
+       "Q 19.28125 33.59375 26.515625 31.984375 \n",
+       "L 29.59375 31.296875 \n",
+       "Q 39.15625 29.25 43.1875 25.515625 \n",
+       "Q 47.21875 21.78125 47.21875 15.09375 \n",
+       "Q 47.21875 7.46875 41.1875 3.015625 \n",
+       "Q 35.15625 -1.421875 24.609375 -1.421875 \n",
+       "Q 20.21875 -1.421875 15.453125 -0.5625 \n",
+       "Q 10.6875 0.296875 5.421875 2 \n",
+       "L 5.421875 11.28125 \n",
+       "Q 10.40625 8.6875 15.234375 7.390625 \n",
+       "Q 20.0625 6.109375 24.8125 6.109375 \n",
+       "Q 31.15625 6.109375 34.5625 8.28125 \n",
+       "Q 37.984375 10.453125 37.984375 14.40625 \n",
+       "Q 37.984375 18.0625 35.515625 20.015625 \n",
+       "Q 33.0625 21.96875 24.703125 23.78125 \n",
+       "L 21.578125 24.515625 \n",
+       "Q 13.234375 26.265625 9.515625 29.90625 \n",
+       "Q 5.8125 33.546875 5.8125 39.890625 \n",
+       "Q 5.8125 47.609375 11.28125 51.796875 \n",
+       "Q 16.75 56 26.8125 56 \n",
+       "Q 31.78125 56 36.171875 55.265625 \n",
+       "Q 40.578125 54.546875 44.28125 53.078125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-115\"/>\n",
+       "       <path d=\"M 41.109375 46.296875 \n",
+       "Q 39.59375 47.171875 37.8125 47.578125 \n",
+       "Q 36.03125 48 33.890625 48 \n",
+       "Q 26.265625 48 22.1875 43.046875 \n",
+       "Q 18.109375 38.09375 18.109375 28.8125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 20.953125 51.171875 25.484375 53.578125 \n",
+       "Q 30.03125 56 36.53125 56 \n",
+       "Q 37.453125 56 38.578125 55.875 \n",
+       "Q 39.703125 55.765625 41.0625 55.515625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-114\"/>\n",
+       "       <path d=\"M 45.40625 46.390625 \n",
+       "L 45.40625 75.984375 \n",
+       "L 54.390625 75.984375 \n",
+       "L 54.390625 0 \n",
+       "L 45.40625 0 \n",
+       "L 45.40625 8.203125 \n",
+       "Q 42.578125 3.328125 38.25 0.953125 \n",
+       "Q 33.9375 -1.421875 27.875 -1.421875 \n",
+       "Q 17.96875 -1.421875 11.734375 6.484375 \n",
+       "Q 5.515625 14.40625 5.515625 27.296875 \n",
+       "Q 5.515625 40.1875 11.734375 48.09375 \n",
+       "Q 17.96875 56 27.875 56 \n",
+       "Q 33.9375 56 38.25 53.625 \n",
+       "Q 42.578125 51.265625 45.40625 46.390625 \n",
+       "z\n",
+       "M 14.796875 27.296875 \n",
+       "Q 14.796875 17.390625 18.875 11.75 \n",
+       "Q 22.953125 6.109375 30.078125 6.109375 \n",
+       "Q 37.203125 6.109375 41.296875 11.75 \n",
+       "Q 45.40625 17.390625 45.40625 27.296875 \n",
+       "Q 45.40625 37.203125 41.296875 42.84375 \n",
+       "Q 37.203125 48.484375 30.078125 48.484375 \n",
+       "Q 22.953125 48.484375 18.875 42.84375 \n",
+       "Q 14.796875 37.203125 14.796875 27.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-100\"/>\n",
+       "       <path d=\"M 19.671875 64.796875 \n",
+       "L 19.671875 37.40625 \n",
+       "L 32.078125 37.40625 \n",
+       "Q 38.96875 37.40625 42.71875 40.96875 \n",
+       "Q 46.484375 44.53125 46.484375 51.125 \n",
+       "Q 46.484375 57.671875 42.71875 61.234375 \n",
+       "Q 38.96875 64.796875 32.078125 64.796875 \n",
+       "z\n",
+       "M 9.8125 72.90625 \n",
+       "L 32.078125 72.90625 \n",
+       "Q 44.34375 72.90625 50.609375 67.359375 \n",
+       "Q 56.890625 61.8125 56.890625 51.125 \n",
+       "Q 56.890625 40.328125 50.609375 34.8125 \n",
+       "Q 44.34375 29.296875 32.078125 29.296875 \n",
+       "L 19.671875 29.296875 \n",
+       "L 19.671875 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-80\"/>\n",
+       "       <path d=\"M 30.609375 48.390625 \n",
+       "Q 23.390625 48.390625 19.1875 42.75 \n",
+       "Q 14.984375 37.109375 14.984375 27.296875 \n",
+       "Q 14.984375 17.484375 19.15625 11.84375 \n",
+       "Q 23.34375 6.203125 30.609375 6.203125 \n",
+       "Q 37.796875 6.203125 41.984375 11.859375 \n",
+       "Q 46.1875 17.53125 46.1875 27.296875 \n",
+       "Q 46.1875 37.015625 41.984375 42.703125 \n",
+       "Q 37.796875 48.390625 30.609375 48.390625 \n",
+       "z\n",
+       "M 30.609375 56 \n",
+       "Q 42.328125 56 49.015625 48.375 \n",
+       "Q 55.71875 40.765625 55.71875 27.296875 \n",
+       "Q 55.71875 13.875 49.015625 6.21875 \n",
+       "Q 42.328125 -1.421875 30.609375 -1.421875 \n",
+       "Q 18.84375 -1.421875 12.171875 6.21875 \n",
+       "Q 5.515625 13.875 5.515625 27.296875 \n",
+       "Q 5.515625 40.765625 12.171875 48.375 \n",
+       "Q 18.84375 56 30.609375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-111\"/>\n",
+       "       <path d=\"M 9.421875 75.984375 \n",
+       "L 18.40625 75.984375 \n",
+       "L 18.40625 0 \n",
+       "L 9.421875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-108\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-77\"/>\n",
+       "      <use x=\"86.279297\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"147.802734\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"209.082031\" xlink:href=\"#DejaVuSans-115\"/>\n",
+       "      <use x=\"261.181641\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"324.560547\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"363.423828\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"424.947266\" xlink:href=\"#DejaVuSans-100\"/>\n",
+       "      <use x=\"488.423828\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"520.210938\" xlink:href=\"#DejaVuSans-80\"/>\n",
+       "      <use x=\"578.763672\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"617.626953\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"678.808594\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"742.285156\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"803.564453\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"867.041016\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"894.824219\" xlink:href=\"#DejaVuSans-108\"/>\n",
+       "      <use x=\"922.607422\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"950.390625\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"989.599609\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"1017.382812\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"1078.90625\" xlink:href=\"#DejaVuSans-115\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"patch_19\">\n",
+       "    <path d=\"M 43.78125 224.64 \n",
+       "L 43.78125 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_20\">\n",
+       "    <path d=\"M 378.58125 224.64 \n",
+       "L 378.58125 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_21\">\n",
+       "    <path d=\"M 43.78125 224.64 \n",
+       "L 378.58125 224.64 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_22\">\n",
+       "    <path d=\"M 43.78125 7.2 \n",
+       "L 378.58125 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"p1913dbb0ed\">\n",
+       "   <rect height=\"217.44\" width=\"334.8\" x=\"43.78125\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
       "text/plain": [
        "<Figure size 432x288 with 1 Axes>"
       ]
@@ -718,29 +2042,29 @@
    ],
    "source": [
     "with fluid.dygraph.guard():\n",
-    "    # Measure the output state of the QAOA circuit for 1024 shots by default\n",
-    "    prob_measure = opt_cir.measure(plot=True)"
+    "    # Repeat the simulated measurement of the circuit output state 1024 times\n",
+    "    prob_measure = cir.measure(plot=True)"
    ]
   },
   {
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "Again, using the relation $|x \\rangle\\rightarrow z=2x-1$, we are able to obtain a classical answer from the quantum state. Specifically, assume that $z_i=-1$ for $i \\in S$ and $z_j=-1$ for $j \\in S^\\prime$. Thus, one bistring sampled from the output state of QAOA corresponds to one feasible cut to the given graph. And it is highly possible that the higher probability the bitstring is, the more likely it gives rise to the max cut protocol.\n",
-    "\n",
-    "The bistring with the largest probability is picked up, and then mapped back to solution to the Max-Cut problem ：\n",
+    "After measurement, we can find the bit string with the highest probability of occurrence. Let the vertices whose bit values are $0$ in the bit string belong to the set $S_0$ and the vertices whose bit values are $1$ belong to the set $S_1$. The set of edges between these two vertex sets is a possible maximum cut of the graph.\n",
     "\n",
-    "- the node set $S$ is in blue color\n",
-    "- the node set $S^\\prime$ is in red color\n",
-    "- the dashed lines represent the cut edges "
+    "The following code selects the bit string with the greatest chance of appearing in the measurement result, then maps it back to the classic solution, and draws the corresponding maximum cut:\n",
+    "- The red vertex belongs to the set $S_0$,\n",
+    "- The blue vertex belongs to the set $S_1$,\n",
+    "- The dashed line indicates the edge being cut."
    ]
   },
   {
    "cell_type": "code",
-   "execution_count": 13,
+   "execution_count": 10,
    "metadata": {
-    "pycharm": {
-     "is_executing": false
+    "ExecuteTime": {
+     "end_time": "2021-01-09T06:55:10.459840Z",
+     "start_time": "2021-01-09T06:55:10.334585Z"
     }
    },
    "outputs": [
@@ -748,12 +2072,221 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "The output bitstring: ['1010']\n"
+      "The bit string form of the cut found: 1010\n"
      ]
     },
     {
      "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAb4AAAEuCAYAAADx63eqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAqK0lEQVR4nO3dfVhUdf438PcIM8JAaqJgdmtippuwzPgAWypmD9ZPs/Uh21JbxWcSsci8VjRDdi21B1M0V9sbxNzUbBOqddfWwgc0b0WEQdPfumqm2AqGijKKA865/xgHGebMDMjMnDlz3q/r8kLOOeKnvVbefM75fj9HJQiCACIiIoVoIXUBRERE3sTgIyIiRWHwERGRojD4iIhIURh8RESkKAw+IiJSFAYfEREpCoOPiIgUhcFHRESKEih1AUSKc/o0cOECYDIB994L9OgBBAVJXRWRYjD4iLzhxg3gs8+ApUuBn34CNBrLcbMZEARg8mQgORl48EFp6yRSABVndRJ52D/+Abz0kiXgqqrEr1GrgYAA4IUXgMxMy+dE5BEMPiJP+utfgWnTLB1fYwQHA7GxwI4dd7pCInIrBh+Rp+zeDQwZ0vjQswoOBn77W2DzZs/URaRwXNVJ5CkzZtiF3nIAMQACAKgALBT7czduAF9/DZSUeLhAImVi8BF5QmEhcOaM/WEAbQF0cvXnb94EPvzQ/XUREYOPyCOWLbOEVwMbAOwCoHf152/dsqwCvXrV7aURKR2Dj8gTduywhFdzaDTAgQPuqYeI6jD4iDzh2rXmfw1BAC5fbv7XISIbDD4iT2jhpn9agZwxQeRuDD4iT2jTxj1fp10793wdIqrD4CPyAGHsWNSKdGv/F0ACgMO3P8+9/Xmu2Bdp0QJ49FFPlEekaAw+IjcrLS3FhIIC1NTW2p3bC2A9gHO3Pzfc/ry44YUtW6Lsd79Dzt//7sFKiZSJwUfkJoIgICsrC1FRUdiwezf2AWgYfdkABJFfCxt+LZUK4/ftw6hRozB27FhUVFR4uHoi5eDIMiI3KC0txdSpU7F9+/a6Y5GwbFi/t6lfTKvFjgED8PS//lV3KDw8HGvWrMHIkSPdUS6RojH4iJrp6tWr6Nq1q2hXNqVXL6w5eRIBRqPlFUSuaLW4MXky2mdlwWg02p0eM2YMVq5cibCwMHeUTqRIvNVJ1EytWrVCYmKizTGtVouMjAysPXQIAUVFQN++luHTjrYn3HOP5aW0K1YgOCMD+/btg16vt7ts06ZN6NmzJ3JycjzwX0KkDOz4iNzg5s2b6Nu3L44ePYqBAwciKysLDzZ8qezx48Dy5cCmTZb38rVoAahUQO/ewNy5wHPP2QRjTU0N3nnnHSxatAi1Igtl2P0R3R0GH1ETCIIAlUoleq6wsBD79u3DzJkz0cLVBvbaWsuvoCCXf6fBYEBCQgKKi4vtzvHZH1HTMfiIGkEQBKxbtw5btmzBtm3bEBAQ4NW/n90fkfsw+IhcaLhi891338WcOXMkqcVZ9xcREYGSkhKEh4d7vzAiGeHiFiIH6u/Lq79NYcGCBTh+/LgkNel0Ohw8eBALFy5EYIOFMoMHD2boETUCg49IRGlpKYYOHYrJkyfjaoN34rVo0QJHjx6VqDJArVYjLS0Nhw4dqlv52aFDB6xYsUKymojkhLc6ieqxPstLSUmxCzwAiI+PR1ZWFrp16yZBdfasz/569+6N5557TupyiGSBwUd0m9j0Favg4GAsWbKkcSs2fYggCJgxYwaeeeYZjBgxQupyiHyCfP4FE3mIo2d5VgMHDkRJSQlmzZolq9ADgC1bttRtdxg3bhxnfhKBHR8pnLMuT6vVYsmSJUhKSpJd4AFAWVkZoqKibMIuIiICa9asYfdHiia/f81EbrRgwQKnXV5ycrIsQw8A8vPzUVlZaXOsrKyM3R8pHjs+UrSLFy8iKioKFy9eBCD/Lq+h4uJiJCQkwGAw2J1j90dKJf9/2UTN0L59e6xevRqAf3R5Den1eof7/tj9kVKx4yNFuHTpEtq2bevw/LZt2zBkyBC/CTwx7P6ILPz3XzkR7qzYjIyMdPoqn2effdavQw9g90dkxY6P/FbDFZvh4eE4duwYBznDefc3fPhw5Obmer8oIi/x7x9xSZEc7csrLy9HcnKyhJX5DkfdX8uWLbF06VIJKyPyPAYf+RVnMza1Wi0effRR8CaHhUajQVpaGgoKCqDT6QAAixYtQo8ePSSujMizeKuT/IKrGZsO34pOAACTyYTs7GxMnjzZ4bsGb968iZYtW3q5MiL3Y8dHsueqy8vIyMDOnTsZek5oNBpMmzbNYegdPHgQXbt2dbpAiEgu2PGRbLHL847q6mr07t277h2EfNs7yR07PpIldnnek56ebvPi3U2bNqFnz57s/ki2GHwkS1euXEFeXp7dcX+cviK10NBQu31/5eXlGDVqFMaOHct9fyQ7/M5AshQdHY20tLS6z9nlec78+fNt3vZeH7s/kiM+4yPZqq2txSOPPIKQkBA+y/MC69veFy1ahNraWrvzfPZHcsHgI5927tw5VFVV4eGHHxY9f/HiRYSFhfG2phcZDAYkJCSguLjY7lx4eHjdi2+JfBW/W5BPEgQBmZmZiI6OxksvvQSTySR6Xfv27Rl6XqbT6RzO/OSzP5IDfscgn3Pu3DkMHToUU6ZMwdWrV1FSUoK3335b6rKoHrVajbS0NKfP/oqKirxfGFEj8FYn+QzrjM3XX3/dbotCYGAgSkpKHN7yJOmIPfubNm0a1q5dK3FlROIYfOQTGr5JoT5/eyu6v7I++7t06RKOHDmCVq1aSV0SkSgGH0mK01f8S01NDc6cOYOHHnpI9PyFCxegVqu58pMkxR+fSTKcvuJ/1Gq1w9ATBAETJ05EVFQU3/dHkmLwkdc5el+eFaev+Kfs7Gxs376db3snyfFWJ3mVyWTC8OHD+SxPYc6fP4+oqChUVlbaHI+IiMCaNWswYsQIaQojReJ3F/IqjUaDDh062B1nl+ff2rdvj5SUFLt9f+z+SArs+Mjrrly5gujoaJw/f55dnsIUFxcjISEBBoPB7hy7P/IWfqchr2vTpg0+/vhjdnkKpNfrHU59YfdH3sKOjzyitLQUn3zyCVJTU6FSqUSvEQTB4Tnyf+z+SCr8MZvcqv6Kzfnz52Pjxo0Or2XoKVtju7/r169LVCH5KwYfuY3Yvrzk5GRcuHBB4srIV2k0GqSlpaGgoAA6nc7u/IULFxAUFCRBZeTPGHzUbM725V2+fBkfffSRRJWRXIh1fyEhIcjMzOTzX3I7PuOjZuGMTXI367O/6dOn45VXXpG6HPJDDD66K5yxSZ5kMpkQGBjo8AemDRs2YOjQoZz5SXeFP4ZTk3HGJnmaRqNxGHp79uzB+PHj0bNnT+Tk5Hi5MvIH7Pio0djlkdSMRiNiYmJw+vTpumNjxozBypUr2f1Ro7Hjo0abP38+uzyS1MqVK21CD7C87Z3dHzUFOz5qtJMnTyImJgY3btyoO8Yuj7xJ7G3v9bH7o8Zgx0eN1q1bNyxevBgAuzyShlqtRlpaGg4dOgS9Xm93nt0fNQY7PmoSs9mMN954A0lJSQw8khS7P7pbDD6yUVpaisTERMybNw/9+vWTuhwilwwGAxISElBcXGx3Ljw8HGvWrMHIkSO9Xxj5LN7qJAC201e2bduGiRMn2jzLI/JVOp3O4czP8vJyjBo1CqmpqRJVR76IwUei+/JOnDiBBQsWSFwZUeM4e/anUqkwbNgwaQojn8TgUzBnMzYBoLCwUPTZCZGvEuv+XnvtNfTv31/iysiX8BmfQnHGJvk7g8GARYsWYf369dBqtVKXQz6EwacwnL5CZHHq1CksWrQI77//Pld+Kgx/nFcQztgksjCbzZg0aRKys7MRFRWF3NxcqUsiL2LwKYCrZ3kDBw5ESUkJkpOTeWuTFGH16tXYs2cPgDtvex87diwqKiokroy8gbc6FaCoqAi9e/e2O85neaREgiAgPj4e+/btszvHfX/KwO92CtCrVy/MmDHD5hi7PFIqlUqFvLw8p/v+2P35N3Z8ClFVVYWYmBiUlZWxyyO6zfq2d4PBYHeO3Z//YvD5EUEQUFVVhXvuuUf0fEFBAdq2bcvFK0T1mEwmLF68mDM/FYTB5yes+/Ju3bqFb775BiqVSuqSiGSFMz+Vg/e6ZK7his0dO3bgL3/5i9RlEclOY2Z+7t69W6LqyJ3Y8cmYo+kroaGhOHr0KB544AGJKiOSN7Hub9iwYfjqq694N8UPsOOTIVf78nr37g3+PEN09xp2f23atMHatWsZen6CHZ/MlJaWYtq0afjnP/9pd4778ojcz2Aw4Ny5cw7f8FBbW2t3a5R8G4NPJgRBQHZ2NlJSUlBZWWl3njM2iaQxZcoUXL9+nSs/ZYTBJwPs8oh80/bt2zFkyBAAXPkpJww+H+aqy4uPj8e6devY5RFJoLKyEtHR0SgtLbU5zn1/vo8tgo/bvHmzXegFBwdjxYoV2LVrF0OPSCIVFRVo166d3fFNmzahZ8+eyMnJkaAqagx2fD7u7NmziI6OxrVr1wBYurysrCx069ZN4sqIqKamBu+8847DqS9jx45FRkYGuz8fw47Px3Xu3BnLli2z6fIYekS+Qa1WIy0tDYcOHYJer7c7v3HjRr7vzwex4/MBgiBg//796Nevn8PzpaWl6NSpk5crI6LGYvcnH+z4JHbu3DkMHToU/fv3R15enug1KpWKoUfk49j9yQc7PolYp6+8/vrruHr1KgCgS5cuOHLkCEJDQyWujoiaw9kbH6Kjo1FUVMRN7xJixycBa5c3ZcqUutADgDNnzmD+/PkSVkZE7qDRaJCWloaCggLodLq64wEBAcjOzmboSYzB50WCICAzMxPR0dGiMzYHDhyIWbNmSVAZEXmCXq+3mfmZmpqKPn36SF2W4vFWp5c4epMCwOkrREpw5MgR9OjRAxqNRvT8qVOnuC/XS/hd1sNcvUlh4MCBKCkpQXJyMkOPyI/9+te/dhh6x48fR1RUFMaOHYuKigovV6Y8/E7rQaWlpRg6dCgmT55s8ywPsHR5GRkZ2LlzJ3/KI1Kw2tpaJCQk4ObNm5z64iUMPg/Jyclhl0dELi1btgwHDx6s+9z6tnd2f57D77oect9996GqqsrmGLs8ImromWeeEd33x+7Pcxh8HvLII49g9uzZdZ+zyyMiMQ3f9l4fuz/P4KpOD6qursaAAQMwYcIErtgkIpcMBgMSEhJQXFxsd47v+3MfBl8zWN+XN2DAADz00EOi15jNZgYeETWaq5mffN9f8zH47lL9fXn9+/fH7t27ERAQIHVZROQnXHV/WVlZePbZZ71fmB9gK9JEYvvy9u3bh4yMDIkrIyJ/4urZX3V1tUSVyR87viZwNn0lLCwMP/30E0JCQiSojIj8WcPu78UXX8TmzZulLUrG2PE1QmOmrxw4cIChR0QeUb/7u//++7Fy5UqpS5I1dnwunDt3DtOmTeOMTSLyCdevX4dWqxU998svv2Dfvn0YPny4l6uSF363dqAxb1Lgvjwi8jZHoQcAycnJGDFiBPf9ucCOTwS7PCKSm61bt+L555+v+5z7/hxj8DXw448/Qq/X2w2VBixdXlZWFseNEZFPMZlM6Nq1K86fP293jvv+7LFlaaBLly544oknbI5xxiYR+TKNRoNt27Zx5mcjseMTceHCBURFReHSpUvs8ohINjj1pXEYfA5s2bIFZWVlfJZHRLLDmZ/OKTL4BEHAunXrUFRUxP0wROSX2P05prjgazh95euvv8awYcMkroqIyDNcdX+7d+/Gr371K+8XJiHF3MNzNH1l2rRpuHz5soSVERF5jrOZn507d0a3bt0kqkw6igi+0tJSDB06FJMnT7bbplBZWYlDhw5JVBkRkeep1WqkpaXh0KFDdSs/NRoNsrOz7cJQCfz6Vqf1WV5KSgr35RER4c6zv5CQELzxxhtSlyMJvw0+Z29S4PQVIiLHPvzwQ0RGRmLEiBFSl+IRfhd87PKIiO5eUVER4uLiUFtbi7FjxyIjI8PvVn76VfCxyyMiunsmkwmxsbEoKSmpOxYREYE1a9b4VffnV8E3aNAg7N692+44uzwiItd27dqFwYMH+/2+P79qfZYvX26zQokzNomIGm/QoEEoKCiATqezO+dPMz/9Kvj0ej3mz58PgO/LIyK6G3q93uG+v/LycowaNUr27/uT5a3OGzduIDg4WPScyWTC5s2b8fLLLzPwiIiaobi4GAkJCTAYDHbn5DzzU1bJYJ2+8sADD+Do0aOi12g0GowfP56hR0TUTHq9HgUFBX7X/cmm42u4YrNPnz7Yv38/1Gq1xJUREfk/ZzM/+/Tpg4KCAqhUKu8Xdhd8vi1yNGOzsLAQ7777roSVEREph7OZn3/6059kE3qAjwefsxmbWq0Wbdu2lagyIiLlEZv5OXHiRAwZMkTawprIJ291cvoKEZFvq6mpwfLlyzF16lS0adNG9Bqz2eyT6y08HnyXLwMHDwJXrgBqNRARAfzmN4CjgeCcvkJEJH///e9/8eSTT+Ltt992uvLz1Cngf/8XuHoVCAkBHnwQiIrycHGChxw6JAgvvSQIQUGC0Lq1INxzjyC0amX5GBYmCH/8oyBcuHDnerPZLGRmZgqtWrUSANj9GjhwoHDy5ElPlUtERG5iNpuF5557ru7795gxY4Rffvml7nxNjSDk5AjCb34jCMHBdzKidWtB0GoFoWdPQVi/XhBu3PBMfW7v+G7cAF54Adi5E6iuBsxm8euCgiwfly8Hnn2WXR4Rkb/461//it///vc2x6z7/nS6kXjiCeDSJeDaNcdfIzQU0GiAf/0L6NPHvfW59Q2EN24A8fHAsWOW3ztTXW35+PrrwN69V0VDj8/yiIjkp7y8HIGBgTYzPy37/uZCrX4at25pYTY7XwVaVWX5OHCgJfz693dffW7t+IYPB3bscB16DWm1QO/eGdi799Xbn7PLIyKSM/t9f20AHAMQDiCgSV+rVSuguBiIjHRPbW5LFYPBUehNBdATQCiAMABDAfxgc8X168DJkzMRHh7BGZtERH7Aft/fVACtYR961QCSYQnEYAD9ARywueL6deCdd9xXm9s6vgkTgE8/BW7dsvsrAPwGwK8BfAvgDID7AZwEEFR3VWgosHr1zxg3rgMDj4jIjxQVGRAXdz9qa9uJnE0EsBZA9O1fn8HSKJ0GcOd6rRYoK7NkRXO5JWGuXgW2bBELPQDYB+D/AfgLgJ23j52HpeW9o6oK2LChI0OPiMjPlJXpEBQk9h6/cgBZsETRdwA2ARgH4BqAVTZXqlTAhg3uqcctKWMwAC1bOjrbr97vTfX+2vvsrty/3x3VEBGRL8nPB6qqxBaz/ACgBkBnWG51AkDf2x+Lba40GoFvvnFPPW4JvsuXAdc3TKsAJNz+/WyIBV9TF8UQEZHvKytzeOb2x/r3L0Nuf7xgd7W7XgLhluDTaCxtqGO/AHgCwH5YHnAuFb0qoGkLfYiISAaCghydibj9sareMevvO9hd7fjOYtO4Jfg6dHD0fA8AfoJllU4BgLkAPoZlwYu9e+91RzVERORLOne2jKy01xOAGsBZ3On+Cm5/1NlcqVJZvo47uCX4dDqgdWtHZ/sBOAHLPdwbAF67/eugzVUBAbX4/e8dpicREcnUCy8AKpXY9/cIWB6BmQE8CeAlWBa4hAKYaXOlVgtMnOieetwSfCoVMGeOpTB7P9/+eBbAinq/bFd13rpVi23bhoq+5JCIiOTJaDRi+fJXYTLlO7hiBYAZsHR8uQAeAfAvAO1trmrXDhgwwD01uW0f35UrQMeOd7tApQaWrQ7PIDAwEG+++SZSU1Oh0WjcURoREUkgPz8fEydOxKlTpwD8D4DPYbuQpXG0WuC994AZM9xTl9s2zbVpA2RnO+r6nDEDqARg6WFra2uxcOFCxMXFsfsjIpIho9GIV199FY899tjt0AOA7QD+BsDYpK/VsiUQFwdMm+a++tz+doY1ayyDpxvT+QUEAK1bm/Hoo3Oxbdt7due1Wi3Onj2LsDCxjY9EROSLJkyYgE8++cTueJcu3dCp0z4cPhwOYyPyLzgY0OstQ6rdMbHFyu1jUhITgZwc4KGHLC8VFBvEEhRkSfFnngFKSlrg739/Fzk5OYiIiLC57g9/+ANDj4hIZt566y1oG9z+S0pKwpEjRdi9OxwLFljuEt5zj/ifDwmx/EpMBHbtcm/oAR58A7sgWN68/v77lsKrqixvXb/3XiAhwfIf1LGj7Z+pqKjArFmzsHHjRvTq1QsHDhyAWnwNLBER+bCVK1di1qxZiIyMRGZmJh5//HGb8zU1wJdfWjLixAnLIOqgIMuWhZQU4MUX7+bRWeN4LPiaIzc3F127dkVMTIzo+dra2tvTvomISCrOvhebzWZkZGRgypQpCHV3y9ZMPhl8ztTU1CA+Ph5Dhgzhyk8iIonk5+djypQpyMrKQn93viXWC2T3KoQlS5bgwIEDXPlJRCSB+is2T5w4gYkTJ+L69etSl9Uksur4SkpK0LdvX9TU1NQd474/IiLvsN2Xd0dKSgqWLVsmUVVNJ6uO7+LFi2jbtq3NMe77IyLyLPF9eXfU1tZCRj2UvILvySefxA8//ICxY8fanTMYDIiNjUV6erpNR0hERHcvPz8fOp0OGRkZduEWGRmJvLw8ZGRkQOX8FT0+RVa3OuvLzc1FYmIiykRe9KTX65GdnQ2dTifyJ4mIyBWj0Yh58+Zh5cqVot1cUlISlixZ4nMrNhtDtsEH2O77a8j67G/evHncC0hE1ASOnuUBcLgvT05kHXxWubm5mD59OsrLy+3OsfsjImocf+7y6vOL4AMs3V9ycjI2bdpkd27ChAnIzs72flFERDKyd+9exMfH2x33hy6vPlktbnEmLCwMGzduxNatWxEeHl53vEOHDrJaZktEJJUBAwZg5kzbF8AmJSWhpKTEb0IP8KOOr7763d9XX32F5557TuqSiIhkwWg0IiYmBoIg+FWXV59fBp9VQUEBYmNjRc8JgoAzZ84gMjLSy1UREUnLaDSiqqrK7o04VsePH0enTp1k/yzPEb+51SnGUegBwJYtW9C9e3ekp6fDZDJ5sSoiIulY9+WNGzfO4abzhx9+2G9DD/Dzjs+R8vJy9OzZExUVFQAAnU6H7Oxs6PV6aQsjIvIQsRWbf/7zn5GYmChxZd6nyOAbPXo0vvjiC5tjnPlJRP7K0b680NBQHDlyBF26dJGmMIn49a1OR15++WW7e9uc+UlE/sbVjM0JEyagXbt2ElQmLUV2fEDjpr6w+yMiufL36SvNodjgs3I285PP/ohIbpQyfaU5FB98ALs/IvIPe/bswaRJk9jlucDgq8dV9/fpp58iKipKgsqIiBwzmUyYM2cOMjIyRM+zy7OlyMUtjowYMcLh+/7+/e9/IzAwUIKqiIicU6vVOHHihN3xyMhI7Ny5E6tWrWLo1cPgayAsLAyffvopcnJybFZ+Llq0CD169JCwMiIicSqVCh9//DFatWpVd2zmzJkoKSnBoEGDpCvMR/FWpxPWZ39nzpzBnj17EBAQIHVJREQOZWZm4u2330ZWVhYDzwkGXyMYjUaEhISInisqKoJKpeLKTyLyOKPRiG3btuF3v/ud6HlBEHDjxg1otVovVyYvvNXZCI5Cr7q6GuPGjUNsbCxnfhKRR1lnbL744ov49ttvRa9RqVQMvUZg8DXDwoULcfz4cU59ISKPEZu+MmXKFFy7dk3iyuSLwXeXTp48iffee8/mmMFgYPdHRG5j7fIyMjJsNqP/9NNPWLx4sYSVyRuD7y5169YNX3zxBWd+EpHbuZqxmZSUhHnz5klQmX/g4pZm4tQXInInztj0PAafm3DmJxE1B2dseg+Dz43Y/RHR3WCX510MPg9w1v3p9Xp8//33CA4OlqAyIvI1H3zwAebMmcMuz4u4uMUDnM38jIuLY+gRUZ34+HioVCqbY5GRkcjLy+OMTQ9h8HmI2MzPzp07222BICJli4uLw5w5c+o+T0pKQklJCW9tehBvdXqB9dnfxIkT8dRTT0ldDhH5mOrqaowePRqzZ89m4HkBg88HCIKA2bNnY8KECdDpdFKXQ0RuZjQa8dZbb2H69Ono3r271OUoHm91+oB169bhww8/RN++fZGeno6amhqpSyIiN7FOX1m2bBkmTpyIW7duSV2S4rHjk1hpaSmioqJw9erVumN6vR7Z2dns/ohkzNG+vA8++ACvv/66hJUROz6JffbZZzahBwDFxcXs/ohkzNGMTcDyzrza2lqJKiOAwSe52bNnY+vWrQgPD7c5Xn/mp8FgkKg6ImqKxszYPHDgAAIDAyWojqx4q9NHVFRUIDk5GZs2bbI7Z536Mm/ePKjVagmqIyJXOH1FPhh8PiYnJweJiYkoLy+3O8dnf0S+hzM25YfB54PY/RHJA7s8eWLw+TBn3V9SUhJWrVolQVVEBABFRUXo06cPuzwZYvD5OLHuLzQ0FEeOHEGXLl2kK4xI4QRBwOjRo7F169a6Y+zy5IGrOn1cWFgYNm7caLPy87333mPoEUlMpVJh9erVCAsLA8AZm3LCjk9GKioq8PHHH2Pu3Ll209ytzGYzWrTgzzNE7uTs39XXX3+N0NBQBp6MMPj8yO7du5GSkoKsrCy+7Z3IDawrNq9cuYL169dLXQ65CYPPTxiNRsTExOD06dN82zuRGzRcsfnll1/it7/9rcRVkTvwnpifSE1NxenTpwHYTn0pLi6WtjAimXE0fWX69Om4dOmShJWRuzD4/IDZbMbly5ftjhsMBsTGxiI9PR0mk0mCyojkxdmMzeDgYJSWlkpUGbkTg88PtGjRAhs2bLB527sVZ34SudaYGZslJSWIiYmRoDpyNz7j8zPWt71v3LjR7hynvhDZ4/QV5WHw+anc3FwkJiairKzM7hxnfhJxxqaSMfj8GGd+Eoljl6dsDD4FcDTzU6VS4cCBA4iNjZWoMiLvEwQBsbGxKCwstDvHLk8ZuLhFAUaOHIljx45hzJgxNsdfe+01hh4pjkqlQlZWls3LYCMjI5GXl4dVq1Yx9BSAHZ/CWLu/1q1bo7i4GFqtVuqSiCTxxz/+EWlpaezyFIjBp0AVFRW4cOECoqKiRM9fvHgRbdq04bM/kr2ff/4ZHTt2FD1XU1ODgoIC9OvXz8tVkdR4q1OBwsLCHIae2WzG6NGjue+PZM26L69r164oKSkRvUatVjP0FIrBRzY++ugj7NmzB8XFxejbty/S09NRU1MjdVlEjVZ/+srNmzeRkJDA/w+TDQYf1Tl16hTmzp1b9zmnvpCcOJq+UlRUhCVLlkhYGfkaBh/VadOmDYYPH253nN0f+TpnMzYjIyMxYMAAiSojX8TFLWTH0b4/gFNfyLdw+grdDQYfiWrM1Be+74+kxOkrdLcYfOSUs+5Pp9MhOzubb3snr2KXR83F4COXXHV/8+fPx4IFCxAQECBBdaQk33//PcaPH88uj5qFi1vIpbCwMGzcuBFbt24Vfd9fYWEhWrTg/5XI8yoqKpy+L4+hR43Bjo+apOH7/tq0aYMffvjB4XQMIncbP348NmzYAIBdHt0dBh/dFev7/t59912MHz9e6nJIQS5fvozo6GiMHDmSz/LorjD46K5VVlaiVatWUKlUoue//PJLDBkyhCs/qcny8/PRvXt3u1vrVpWVlWjdurWXqyJ/wQczdNdat27tMPS2b9+OESNGIC4uDsXFxd4tjGSr/vSVGTNmiK7aBMDQo2Zhx0duV1lZiejoaJSWlgLgvj9qHLF9eZs3b8aLL74oYVXkjxh85HYpKSlYvny53XHu+yMxzvbltW/fHj/++CNCQkIkqo78EW91ktu9+eabdm97BwCDwYDY2Fikp6fDZDJJUBn5GlczNj/77DOGHrkdOz7yGE59IUc4fYWkxOAjj+LMT2qIMzZJagw+8gp2f8Quj3wFg4+8xlX3t3r1akydOlWCysjTzp49iyeeeIJdHvkELm4hr6k/8zM8PNzmnCAI6N27t0SVkafdf//9opvROWOTpMDgI68bOXIkjh07ZrPyMzU1FX369JGwKvKkgIAAZGVlISgoCICly8vLy8OqVat4a5O8jrc6SVI5OTlYvXo1tm3bxgUuCvDhhx/i1KlTfJZHkmLwkU87fvw4Pv/8c6SmpkKtVktdDrmQn5+PwsJCvPbaa1KXQuQQg498Vm1tLfr374+DBw9Cr9cjOzsbOp1O6rJIxPXr1zFv3jxkZGRApVJh//79iIuLk7osIlF8xkc+64MPPsDBgwcBAMXFxejbty/S09NRU1MjcWVUX35+PmJiYrBixQoIggCz2YyEhARUV1dLXRqRKHZ85JNu3ryJ7t274+zZs3bn2P35Blf78nJzczF8+HAJKiNyjh0f+aSWLVvi8OHDojM/2f1Jz9mMzS5duiAvL4+hRz6LHR/5PGdTX9j9eZerLm/GjBlYunQpV2yST2PwkSw0ZubnvHnzuPLTgzhjk/wFg49khd2f93HGJvkbBh/Jjqvu7+jRo+jRo4cElfmnp556Ct99953dcXZ5JFdc3EKy42zm5/PPP8/Qc7O5c+faHeOMTZIzdnwka/W7v/bt2+PYsWNo166d1GX5ncTERKxdu5ZdHvkFBh/5hZycHKjVagwbNkz0vCAIUKlUXq5KXpz9b3Tt2jUsXboUc+fO5bM8kj0GHynC+PHj8eCDD3LlpwP5+flISUlBTk4OOnXqJHU5RB7FZ3zk97744gts2LABCxcuRFxcHAwGg9Ql+Qyj0YhXX30Vjz32GAoLCzF16lTRlZtE/oQdH/m1X375BVFRUTbbH7jvz8LRvrzMzExMmjRJoqqIPI8dH/m1kydP2h2rra1VdPdXv8sT24z+n//8R4KqiLyHwUd+7ZFHHrF727uVEmd+OpuxaX0r+uLFiyWqjsg7eKuTFEPJU184fYXoDgYfKYoSZ35yxiaRLQYfKZISuj92eUTiGHykWM66v379+mHv3r2y3vS+fv16JCQk2B1nl0dKx+AjxWvY/Wk0Ghw+fBhRUVESV9Y8ZrMZgwcPRl5eXt0xdnlEXNVJhJEjR9qs/Fy4cKHsQw8AWrRogczMTISEhNSt2Fy1ahVDjxSPHR9RPTt27MDjjz+OwMBA0fMXL15E+/btvVyVc0ajESqVClqtVvR8fn4+evXqxcAjuo0dH1E9gwcPdhh6hw8fxgMPPID09HSYTCYvVyZuz5490Ol0oq8OsoqPj2foEdXDjo+oEUwmE/r27YsjR44AAHQ6HbKzs6HX6yWpx7piMyMjo+7Yrl278Nhjj0lSD5GcsOMjaoRFixbVhR4AGAwGxMbGStL9Wbu8+qEHAJMmTYLRaPRqLURyxOAjaoQ+ffogIiLC5lj9mZ/FxcUer8HVjM2hQ4d6vAYif8BbnUSNVFFRgVmzZmHjxo1256xTX1JTU6HRaNz+d7uavpKVlYVBgwa5/e8l8kcMPqImys3NRWJiIsrKyuzOuXz2d/068M03wIULgMkE3Hsv0K8f0K2b6OWupq/MnDkTixcv5uIVoiZg8BHdhSZ3fydOAMuXA+vXA4GBQE0NYDYDajVQWwv06gX84Q/As89azoNdHpGnMPiImsFV97c+Oxu67duB9HTg1i1L4DkSGgo8+CCuf/UVUj/4gDM2iTyEwUfUTM66v5OjR+PBf/zDcouzMTQamCMi8IhGg4IGnR5nbBK5B1d1EjVTWFgYPv30U+Tk5Nis/FwbH9+00AMAkwktysrwnVqN+uOxk5KSUFJSwtAjcgN2fERuZO3+9uzahZ/MZrS4cMHumgkAvgXwC4B7APQFsBhAr/oXhYZi9ZAheP/QIXZ5RG7G4CPygCuff442kyYBVVV25wYB6AigNYA8ACcAdAbwU/2LVCrcevpp3Pjb3/gsj8jNGHxEnvD008COHS4vOwygDyzPHKoB2Lz3vWVL4Mcfgfvu80iJREolPo2XiJqnsNDp6VUAjgH47vbns9Eg9AAgKAgwGBh8RG7G4CPyBBczM/8GYPft3/8fAP3FLjKbgStX3FoWEXFVJ5FnuBhbtgvADQC5AH4GMBrAmYYXqVRAcLDbSyNSOgYfkSeEh4sevgHg1u3fBwH4HwChAGoB/NjwYrMZuP9+DxVIpFwMPiJPeOUVQOSN6AcAdALwEoBXYFnYchVAewC9G158771Anz6erZNIgRh8RJ4waZKlY2ugI4DuAHYAyARwGcALsGxraF3/Qq0WmDPHcruTiNyK2xmIPOXll4HPP7e8haGpQkKA8+eB1q1dX0tETcKOj8hTPvrI8owusImLp4ODgc8+Y+gReQiDj8hTWrcG9u4FHnjAshm9MYKDgcxMy+uJiMgjGHxEntSxI3D4sOWZn1ZruYXZkFpt2az+6KPAt98CY8Z4v04iBeEzPiJvMRqBzZuBtWuBsjLLu/latQKeegp49VXgoYekrpBIERh8RESkKLzVSUREisLgIyIiRWHwERGRojD4iIhIURh8RESkKAw+IiJSFAYfEREpCoOPiIgUhcFHRESKwuAjIiJF+f9DFAxHVSZdhQAAAABJRU5ErkJggg==\n",
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"302.4pt\" version=\"1.1\" viewBox=\"0 0 446.4 302.4\" width=\"446.4pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T14:55:10.428597</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 302.4 \n",
+       "L 446.4 302.4 \n",
+       "L 446.4 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"LineCollection_1\">\n",
+       "    <path clip-path=\"url(#p98894c64dc)\" d=\"M 377.485714 151.2 \n",
+       "L 223.199993 48.342857 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p98894c64dc)\" d=\"M 377.485714 151.2 \n",
+       "L 223.200002 254.057143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p98894c64dc)\" d=\"M 223.199993 48.342857 \n",
+       "L 68.914286 151.200009 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "    <path clip-path=\"url(#p98894c64dc)\" d=\"M 68.914286 151.200009 \n",
+       "L 223.200002 254.057143 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-dasharray:7.4,3.2;stroke-dashoffset:0;stroke-width:2;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"PathCollection_1\">\n",
+       "    <defs>\n",
+       "     <path d=\"M 0 22.36068 \n",
+       "C 5.930122 22.36068 11.618159 20.004617 15.811388 15.811388 \n",
+       "C 20.004617 11.618159 22.36068 5.930122 22.36068 -0 \n",
+       "C 22.36068 -5.930122 20.004617 -11.618159 15.811388 -15.811388 \n",
+       "C 11.618159 -20.004617 5.930122 -22.36068 0 -22.36068 \n",
+       "C -5.930122 -22.36068 -11.618159 -20.004617 -15.811388 -15.811388 \n",
+       "C -20.004617 -11.618159 -22.36068 -5.930122 -22.36068 0 \n",
+       "C -22.36068 5.930122 -20.004617 11.618159 -15.811388 15.811388 \n",
+       "C -11.618159 20.004617 -5.930122 22.36068 0 22.36068 \n",
+       "z\n",
+       "\" id=\"C0_0_c7785b86ce\"/>\n",
+       "    </defs>\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <use style=\"fill:#0000ff;stroke:#0000ff;\" x=\"377.485714\" xlink:href=\"#C0_0_c7785b86ce\" y=\"151.2\"/>\n",
+       "    </g>\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <use style=\"fill:#ff0000;stroke:#ff0000;\" x=\"223.199993\" xlink:href=\"#C0_0_c7785b86ce\" y=\"48.342857\"/>\n",
+       "    </g>\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <use style=\"fill:#0000ff;stroke:#0000ff;\" x=\"68.914286\" xlink:href=\"#C0_0_c7785b86ce\" y=\"151.200009\"/>\n",
+       "    </g>\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <use style=\"fill:#ff0000;stroke:#ff0000;\" x=\"223.200002\" xlink:href=\"#C0_0_c7785b86ce\" y=\"254.057143\"/>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_1\">\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <!-- 0 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(370.527902 156.71875)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46 36.53125 \n",
+       "Q 46 50.203125 43.4375 55.78125 \n",
+       "Q 40.875 61.375 34.8125 61.375 \n",
+       "Q 28.765625 61.375 26.171875 55.78125 \n",
+       "Q 23.578125 50.203125 23.578125 36.53125 \n",
+       "Q 23.578125 22.703125 26.171875 17.03125 \n",
+       "Q 28.765625 11.375 34.8125 11.375 \n",
+       "Q 40.828125 11.375 43.40625 17.03125 \n",
+       "Q 46 22.703125 46 36.53125 \n",
+       "z\n",
+       "M 64.796875 36.375 \n",
+       "Q 64.796875 18.265625 56.984375 8.421875 \n",
+       "Q 49.171875 -1.421875 34.8125 -1.421875 \n",
+       "Q 20.40625 -1.421875 12.59375 8.421875 \n",
+       "Q 4.78125 18.265625 4.78125 36.375 \n",
+       "Q 4.78125 54.546875 12.59375 64.375 \n",
+       "Q 20.40625 74.21875 34.8125 74.21875 \n",
+       "Q 49.171875 74.21875 56.984375 64.375 \n",
+       "Q 64.796875 54.546875 64.796875 36.375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-48\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-48\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_2\">\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <!-- 1 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(216.242181 53.861607)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 11.71875 12.984375 \n",
+       "L 28.328125 12.984375 \n",
+       "L 28.328125 60.109375 \n",
+       "L 11.28125 56.59375 \n",
+       "L 11.28125 69.390625 \n",
+       "L 28.21875 72.90625 \n",
+       "L 46.09375 72.90625 \n",
+       "L 46.09375 12.984375 \n",
+       "L 62.703125 12.984375 \n",
+       "L 62.703125 0 \n",
+       "L 11.71875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-49\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-49\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_3\">\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <!-- 2 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(61.956473 156.718759)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 28.8125 13.8125 \n",
+       "L 60.890625 13.8125 \n",
+       "L 60.890625 0 \n",
+       "L 7.90625 0 \n",
+       "L 7.90625 13.8125 \n",
+       "L 34.515625 37.3125 \n",
+       "Q 38.09375 40.53125 39.796875 43.609375 \n",
+       "Q 41.5 46.6875 41.5 50 \n",
+       "Q 41.5 55.125 38.0625 58.25 \n",
+       "Q 34.625 61.375 28.90625 61.375 \n",
+       "Q 24.515625 61.375 19.28125 59.5 \n",
+       "Q 14.0625 57.625 8.109375 53.90625 \n",
+       "L 8.109375 69.921875 \n",
+       "Q 14.453125 72.015625 20.65625 73.109375 \n",
+       "Q 26.859375 74.21875 32.8125 74.21875 \n",
+       "Q 45.90625 74.21875 53.15625 68.453125 \n",
+       "Q 60.40625 62.703125 60.40625 52.390625 \n",
+       "Q 60.40625 46.4375 57.328125 41.28125 \n",
+       "Q 54.25 36.140625 44.390625 27.484375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-50\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-50\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"text_4\">\n",
+       "    <g clip-path=\"url(#p98894c64dc)\">\n",
+       "     <!-- 3 -->\n",
+       "     <g style=\"fill:#ffffff;\" transform=\"translate(216.242189 259.575893)scale(0.2 -0.2)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 46.578125 39.3125 \n",
+       "Q 53.953125 37.40625 57.78125 32.6875 \n",
+       "Q 61.625 27.984375 61.625 20.703125 \n",
+       "Q 61.625 9.859375 53.3125 4.21875 \n",
+       "Q 45.015625 -1.421875 29.109375 -1.421875 \n",
+       "Q 23.484375 -1.421875 17.84375 -0.515625 \n",
+       "Q 12.203125 0.390625 6.6875 2.203125 \n",
+       "L 6.6875 16.703125 \n",
+       "Q 11.96875 14.0625 17.15625 12.71875 \n",
+       "Q 22.359375 11.375 27.390625 11.375 \n",
+       "Q 34.859375 11.375 38.84375 13.953125 \n",
+       "Q 42.828125 16.546875 42.828125 21.390625 \n",
+       "Q 42.828125 26.375 38.75 28.9375 \n",
+       "Q 34.671875 31.5 26.703125 31.5 \n",
+       "L 19.1875 31.5 \n",
+       "L 19.1875 43.609375 \n",
+       "L 27.09375 43.609375 \n",
+       "Q 34.1875 43.609375 37.640625 45.828125 \n",
+       "Q 41.109375 48.046875 41.109375 52.59375 \n",
+       "Q 41.109375 56.78125 37.734375 59.078125 \n",
+       "Q 34.375 61.375 28.21875 61.375 \n",
+       "Q 23.6875 61.375 19.046875 60.34375 \n",
+       "Q 14.40625 59.328125 9.8125 57.328125 \n",
+       "L 9.8125 71.09375 \n",
+       "Q 15.375 72.65625 20.84375 73.4375 \n",
+       "Q 26.3125 74.21875 31.59375 74.21875 \n",
+       "Q 45.796875 74.21875 52.84375 69.546875 \n",
+       "Q 59.90625 64.890625 59.90625 55.515625 \n",
+       "Q 59.90625 49.125 56.53125 45.046875 \n",
+       "Q 53.171875 40.96875 46.578125 39.3125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Bold-51\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-Bold-51\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"p98894c64dc\">\n",
+       "   <rect height=\"288\" width=\"432\" x=\"7.2\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
       "text/plain": [
        "<Figure size 432x288 with 1 Axes>"
       ]
@@ -763,44 +2296,50 @@
     }
    ],
    "source": [
-    "# Find the max value in measured probability of bitstrings\n",
-    "max_prob = max(prob_measure.values())\n",
-    "# Find the bitstring with max probability\n",
-    "solution_list = [result[0] for result in prob_measure.items() if result[1] == max_prob]\n",
-    "print(\"The output bitstring:\", solution_list)\n",
-    "\n",
-    "# Draw the graph representing the first bitstring in the solution_list to the MaxCut-like problem\n",
-    "head_bitstring = solution_list[0]\n",
+    "# Find the most frequent bit string in the measurement results\n",
+    "cut_bitstring = max(prob_measure, key=prob_measure.get)\n",
+    "print(\"The bit string form of the cut found:\", cut_bitstring)\n",
     "\n",
-    "node_cut = [\"blue\" if head_bitstring[node] == \"1\" else \"red\" for node in classical_graph]\n",
+    "# Draw the cut corresponding to the bit string obtained above on the graph\n",
+    "node_cut = [\"blue\" if cut_bitstring[v] == \"1\" else \"red\" for v in V]\n",
     "\n",
     "edge_cut = [\n",
-    "    \"solid\" if head_bitstring[node_row] == head_bitstring[node_col] else \"dashed\"\n",
-    "    for node_row, node_col in classical_graph.edges()\n",
+    "    \"solid\" if cut_bitstring[u] == cut_bitstring[v] else \"dashed\"\n",
+    "    for (u, v) in E\n",
     "    ]\n",
     "nx.draw(\n",
-    "        classical_graph,\n",
+    "        G,\n",
     "        pos,\n",
     "        node_color=node_cut,\n",
     "        style=edge_cut,\n",
-    "        width=4,\n",
-    "        with_labels=True,\n",
-    "        font_weight=\"bold\",\n",
+    "        **options\n",
     ")\n",
+    "ax = plt.gca()\n",
+    "ax.margins(0.20)\n",
+    "plt.axis(\"off\")\n",
     "plt.show()"
    ]
   },
   {
    "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "is_executing": false
-    }
-   },
+   "metadata": {},
+   "source": [
+    "As you can see, in this example, QAOA has found a maximum cut on the graph.\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
    "source": [
-    "# References\n",
+    "_______\n",
+    "\n",
+    "## References\n",
+    "\n",
+    "[1] Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm. [arXiv:1411.4028 (2014).](https://arxiv.org/abs/1411.4028)\n",
     "\n",
-    "[1] [Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv:1411.4028 (2014).](https://arxiv.org/abs/1411.4028)"
+    "[2] Farhi, E., Goldstone, J., Gutmann, S. & Sipser, M. Quantum computation by adiabatic evolution. [arXiv:quant-ph/0001106 (2000).](https://arxiv.org/abs/quant-ph/0001106)\n",
+    "\n",
+    "[3] Duan, R. Quantum Adiabatic Theorem Revisited. [arXiv:2003.03063 (2020).](https://arxiv.org/abs/2003.03063)\n"
    ]
   }
  ],
@@ -820,18 +2359,27 @@
    "name": "python",
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
-   "version": "3.7.7"
+   "version": "3.6.10"
   },
-  "pycharm": {
-   "stem_cell": {
-    "cell_type": "raw",
-    "metadata": {
-     "collapsed": false
-    },
-    "source": []
-   }
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {
+    "height": "calc(100% - 180px)",
+    "left": "10px",
+    "top": "150px",
+    "width": "426.667px"
+   },
+   "toc_section_display": true,
+   "toc_window_display": true
   }
  },
  "nbformat": 4,
- "nbformat_minor": 2
+ "nbformat_minor": 4
 }

tutorial/SSVQE/SSVQE_Tutorial_CN.ipynb → tutorial/SSVQE/SSVQE_CN.ipynb

@@ -4,35 +4,29 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# 子空间搜索-量子变分特征求解器 (Subspace-Search VQE)\n",
+    "# 子空间搜索-量子变分本征求解器\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>\n",
     "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
     "## 概览\n",
     "\n",
-    "- 在这个案例中，我们将展示如何通过Paddle Quantum训练量子神经网络来求解量子系统的特征。\n",
+    "- 在本案例中，我们将展示如何通过 Paddle Quantum 训练量子神经网络来求解量子系统的整个能量谱。\n",
     "\n",
-    "- 首先，让我们通过下面几行代码引入必要的library和package。"
+    "- 首先，让我们通过下面几行代码引入必要的 library 和 package。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 1,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:59.183983Z",
+     "start_time": "2021-01-09T10:39:55.833348Z"
     }
    },
    "outputs": [],
    "source": [
     "import numpy\n",
-    "\n",
     "from paddle.complex import matmul, transpose\n",
     "from paddle import fluid\n",
     "from paddle_quantum.circuit import UAnsatz\n",
@@ -45,20 +39,25 @@
    "source": [
     "## 背景\n",
     "\n",
-    "- 量子计算在近期内备受瞩目的一个应用就是变分量子特征求解器(VQE, variational quantum eigensolver (VQE)) [1-3].\n",
-    "- VQE是量子化学在近期有噪量子设备（NISQ device）上的核心应用之一，其中一个功能比较强大的版本是SSVQE [4]，其核心是去求解一个物理系统的哈密顿量的基态和**激发态**的性质。数学上，可以理解为求解一个厄米矩阵(Hermitian matrix)的特征值及其对应的特征向量。该哈密顿量的特征值组成的集合我们称其为能谱 (Energy spectrum)。\n",
-    "- 接下来我们将通过一个简单的例子学习如何通过训练量子神经网络解决这个问题，即求解出给定哈密顿量 $H$ 的能谱。\n",
+    "- 量子计算在近期内备受瞩目的一个应用就是变分量子本征求解器（variational quantum eigensolver, VQE）[1-3].\n",
+    "- VQE 是量子化学在近期有噪量子设备（NISQ device）上的核心应用之一，其中一个功能比较强大的版本是 subspace-search VQE（SSVQE） [4]，其核心是去求解一个物理系统的 Hamilton 量（Hamiltonian）的基态和**激发态**的性质。数学上，可以理解为求解一个 Hermite 矩阵（Hermitian matrix）的本征值及其对应的本征向量。该 Hamilton 量的本征值组成的集合我们称其为能谱（energy spectrum）。\n",
+    "- 接下来我们将通过一个简单的例子学习如何通过训练量子神经网络解决这个问题，即求解出给定 Hamilton 量 $H$ 的能谱。\n",
     "\n",
-    "## SSVQE分析物理系统的基态和激发态的能量\n",
+    "## SSVQE 分析物理系统的基态和激发态的能量\n",
     "\n",
-    "- 对于具体需要分析的分子，我们需要其几何构型 (geometry)、电荷 (charge) 以及自旋多重度 (spin multiplicity) 等多项信息来建模获取描述系统的哈密顿量。具体的，通过我们内置的量子化学工具包可以利用 fermionic-to-qubit 映射的技术来输出目标分子的量子比特哈密顿量表示。\n",
-    "- 作为简单的入门案例，我们在这里提供一个简单的随机2量子比特哈密顿量作为例子。 "
+    "- 对于具体需要分析的分子，我们需要其几何构型（geometry）、电荷（charge）以及自旋多重度（spin multiplicity）等多项信息来建模获取描述系统的 Hamilton 量。具体的，通过我们内置的量子化学工具包可以利用 fermionic-to-qubit 映射的技术来输出目标分子的量子比特 Hamilton 量表示。\n",
+    "- 作为简单的入门案例，我们在这里提供一个简单的随机双量子比特 Hamilton 量作为例子。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 2,
-   "metadata": {},
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:59.199187Z",
+     "start_time": "2021-01-09T10:39:59.189011Z"
+    }
+   },
    "outputs": [],
    "source": [
     "N = 2        # 量子比特数/量子神经网络的宽度 \n",
@@ -68,23 +67,28 @@
   {
    "cell_type": "code",
    "execution_count": 3,
-   "metadata": {},
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:59.240622Z",
+     "start_time": "2021-01-09T10:39:59.205845Z"
+    }
+   },
    "outputs": [
     {
      "name": "stdout",
      "output_type": "stream",
      "text": [
       "Random Hamiltonian in Pauli string format = \n",
-      " [[-0.9208973013017021, 'y0,y1'], [0.198490728051139, 'y1'], [0.9587239095910918, 'x1'], [0.07176335076663909, 'x1'], [-0.7920788641602743, 'x1'], [-0.5028229022143014, 'x0'], [-0.14565978959930526, 'z1,y0'], [0.5965836192828249, 'z1,z0'], [0.6251774164147041, 'y1,y0'], [-0.1580838163596252, 'z0,x1']]\n"
+      " [[0.2053246312210153, 'y1'], [0.8007921371055502, 'y0'], [-0.005452633476696667, 'y1'], [0.6584698440348358, 'z0'], [0.8231741294360668, 'y0,x1'], [-0.9500264430442884, 'z1,z0'], [0.500344392541574, 'x1,z0'], [0.26774681450914084, 'z1'], [-0.6560070288135618, 'y0,z1'], [-0.24860662455587024, 'x1']]\n"
      ]
     }
    ],
    "source": [
-    "# 生成用泡利字符串表示的随机哈密顿量\n",
+    "# 生成用泡利字符串表示的随机 Hamilton 量\n",
     "hamiltonian = random_pauli_str_generator(N, terms=10)\n",
     "print(\"Random Hamiltonian in Pauli string format = \\n\", hamiltonian)\n",
     "\n",
-    "# 生成哈密顿量的矩阵信息\n",
+    "# 生成 Hamilton 量的矩阵信息\n",
     "H = pauli_str_to_matrix(hamiltonian, N)"
    ]
   },
@@ -92,20 +96,20 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 搭建量子神经网络（QNN）\n",
+    "## 搭建量子神经网络\n",
     "\n",
-    "- 在实现SSVQE的过程中，我们首先需要设计量子神经网络QNN（也即参数化量子电路）。在本教程中，我们提供一个预设的适用于2量子比特的通用量子电路模板。理论上，该模板具有足够强大的表达能力可以表示任意的2-量子比特逻辑运算 [5]。具体的实现方式是需要 3个 $CNOT$ 门加上任意15个单比特旋转门 $\\in \\{R_y, R_z\\}$。\n",
+    "- 在实现 SSVQE 的过程中，我们首先需要设计量子神经网络（quantum neural network, QNN），也即参数化量子电路。在本教程中，我们提供一个预设的适用于双量子比特的通用量子电路模板。理论上，该模板具有足够强大的表达能力可以表示任意的双量子比特逻辑运算 [5]。具体的实现方式是需要 3 个 $CNOT$ 门加上任意 15 个单比特旋转门 $\\in \\{R_y, R_z\\}$。\n",
     "\n",
-    "- 初始化其中的变量参数，${\\bf{\\theta }}$ 代表我们量子神经网络中的参数组成的向量，一共有15个参数。"
+    "- 初始化其中的变量参数，${\\bf{\\theta}}$ 代表我们量子神经网络中的参数组成的向量，一共有 15 个参数。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 4,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:59.272186Z",
+     "start_time": "2021-01-09T10:39:59.255438Z"
     }
    },
    "outputs": [],
@@ -114,9 +118,8 @@
     "\n",
     "def U_theta(theta, N):\n",
     "    \"\"\"\n",
-    "    Quantum Neural Network\n",
+    "    U_theta\n",
     "    \"\"\"\n",
-    "    \n",
     "    # 按照量子比特数量/网络宽度初始化量子神经网络\n",
     "    cir = UAnsatz(N)\n",
     "    \n",
@@ -131,42 +134,44 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 配置训练模型 - 损失函数\n",
+    "## 配置训练模型——损失函数\n",
+    "\n",
+    "- 现在我们已经有了数据和量子神经网络的架构，我们将进一步定义训练参数、模型和损失函数，具体的理论可以参考 [4]。\n",
+    "\n",
+    "- 通过作用量子神经网络 $U(\\theta)$ 在一组正交的初始态上（方便起见，可以取计算基 $\\{|00\\rangle, |01\\rangle, |10\\rangle, |11\\rangle \\}$），我们将得到输出态 $\\{\\left| {\\psi_1 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle, \\left| {\\psi_2 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle, \\left| {\\psi_3 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle, \\left| {\\psi_4 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle \\}$。\n",
+    "\n",
+    "- 进一步，在 SSVQE 模型中的损失函数一般由每个输出量子态 $\\left| {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right\\rangle$ 关于 Hamilton 量 $H$ 的能量期望值（expectation value）的加权求和给出。这里我们默认权重向量 $\\vec{w} = [4, 3, 2, 1]$。\n",
+    "\n",
+    "- 具体的损失函数（loss function）定义为：\n",
     "\n",
-    "- 现在我们已经有了数据和量子神经网络的架构，我们将进一步定义训练参数、模型和损失函数，具体的理论可以参考 [4].\n",
-    "- 通过作用量子神经网络 $U(\\theta)$ 在1组正交的初始态上 (方便起见，可以取计算基 $\\{|00\\rangle, |01\\rangle, |10\\rangle, |11\\rangle \\}$)，我们将分别得到四个输出态 $\\left| {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right\\rangle (k=0,1,2,3)$。\n",
-    "- 进一步，在SSVQE模型中的损失函数一般由哈密顿量H与量子态 $\\left| {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right\\rangle$ 的内积的加权求和给出。\n",
-    "- 具体的损失函数定义为\n",
-    "$$\\mathcal{L}(\\boldsymbol{\\theta}) = 4\\left\\langle {\\psi_1 \\left( {\\bf{\\theta }} \\right)} \\right|H\\left| {\\psi_1 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle + 3\\left\\langle {\\psi_2 \\left( {\\bf{\\theta }} \\right)} \\right|H\\left| {\\psi_2 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle + 2\\left\\langle {\\psi_3 \\left( {\\bf{\\theta }} \\right)} \\right|H\\left| {\\psi_3 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle + \\left\\langle {\\psi_4 \\left( {\\bf{\\theta }} \\right)} \\right|H\\left| {\\psi_4 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle.$$"
+    "$$\n",
+    "\\mathcal{L}(\\boldsymbol{\\theta}) = \\sum_{k=1}^{2^n}w_k*\\left\\langle {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right|H\\left| {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right\\rangle. \\tag{1}\n",
+    "$$"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 5,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:59.308410Z",
+     "start_time": "2021-01-09T10:39:59.285372Z"
     }
    },
    "outputs": [],
    "source": [
     "class Net(fluid.dygraph.Layer):\n",
-    "    \"\"\"\n",
-    "    Construct the model net\n",
-    "    \"\"\"\n",
-    "\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * numpy.pi, seed=SEED),\n",
-    "                 dtype='float64'):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * numpy.pi, seed=SEED), dtype='float64'):\n",
     "        super(Net, self).__init__()\n",
     "        \n",
     "        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.theta = self.create_parameter(shape=shape, \n",
+    "                     attr=param_attr, dtype=dtype, is_bias=False)\n",
     "    \n",
     "    # 定义损失函数和前向传播机制\n",
     "    def forward(self, H, N):\n",
     "        \n",
-    "        # 施加量子神经网络\n",
+    "        # 构造量子神经网络\n",
     "        U = U_theta(self.theta, N)\n",
     "        \n",
     "        # 计算损失函数\n",
@@ -181,7 +186,8 @@
     "        ]\n",
     "        \n",
     "        # 最终加权求和后的损失函数\n",
-    "        loss = 4 * loss_components[0] + 3 * loss_components[1] + 2 * loss_components[2] + 1 * loss_components[3]\n",
+    "        loss = 4 * loss_components[0] + 3 * loss_components[1]\\\n",
+    "             + 2 * loss_components[2] + 1 * loss_components[3]\n",
     "        \n",
     "        return loss, loss_components"
    ]
@@ -190,18 +196,17 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 配置训练模型 - 模型参数\n",
-    "\n",
-    "在进行量子神经网络的训练之前，我们还需要进行一些训练的超参数设置，主要是学习速率 (LR, learning rate)、迭代次数(ITR, iteration)和量子神经网络计算模块的深度 (D, Depth)。这里我们设定学习速率为0.3, 迭代次数为50次。读者不妨自行调整来直观感受下超参数调整对训练效果的影响。"
+    "## 配置训练模型——模型参数\n",
+    "在进行量子神经网络的训练之前，我们还需要进行一些训练的超参数设置，主要是学习速率（learning rate, LR）、迭代次数（iteration, ITR。这里我们设定学习速率为 0.3，迭代次数为 50 次。读者不妨自行调整来直观感受下超参数调整对训练效果的影响。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 6,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:59.327673Z",
+     "start_time": "2021-01-09T10:39:59.322589Z"
     }
    },
    "outputs": [],
@@ -215,19 +220,18 @@
    "metadata": {},
    "source": [
     "## 进行训练\n",
-    "\n",
-    "- 当训练模型的各项参数都设置完成后，我们将数据转化为Paddle动态图中的变量，进而进行量子神经网络的训练。\n",
-    "- 过程中我们用的是Adam Optimizer，也可以调用Paddle中提供的其他优化器。\n",
-    "- 我们将训练过程中的每一轮loss打印出来。"
+    "- 当训练模型的各项参数都设置完成后，我们将数据转化为 PaddlePaddle 动态图中的变量，进而进行量子神经网络的训练。\n",
+    "- 过程中我们用的是 Adam Optimizer，也可以调用 PaddlePaddle 中提供的其他优化器。\n",
+    "- 我们可以将训练过程中的每一轮 loss 打印出来。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 7,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:40:01.356487Z",
+     "start_time": "2021-01-09T10:39:59.332679Z"
     }
    },
    "outputs": [
@@ -235,11 +239,11 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "iter: 10 loss: -3.8289\n",
-      "iter: 20 loss: -3.9408\n",
-      "iter: 30 loss: -3.9473\n",
-      "iter: 40 loss: -3.9480\n",
-      "iter: 50 loss: -3.9481\n"
+      "iter: 10 loss: -5.3321\n",
+      "iter: 20 loss: -7.4093\n",
+      "iter: 30 loss: -7.6601\n",
+      "iter: 40 loss: -7.8402\n",
+      "iter: 50 loss: -8.0516\n"
      ]
     }
    ],
@@ -247,14 +251,15 @@
     "# 初始化paddle动态图机制\n",
     "with fluid.dygraph.guard():\n",
     "    \n",
-    "    # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
+    "    # 我们需要将 numpy.ndarray 转换成 PaddlePaddle 动态图模式中支持的 variable\n",
     "    hamiltonian = fluid.dygraph.to_variable(H)\n",
     "\n",
     "    # 确定网络的参数维度\n",
     "    net = Net(shape=[THETA_SIZE])\n",
     "\n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdagradOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    # 一般来说，我们利用 Adam 优化器来获得相对好的收敛，\n",
+    "    # 当然你可以改成 SGD 或者是 RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
     "\n",
     "    # 优化循环\n",
     "    for itr in range(1, ITR + 1):\n",
@@ -277,19 +282,20 @@
    "metadata": {},
    "source": [
     "## 测试效果\n",
+    "\n",
     "我们现在已经完成了量子神经网络的训练，我们将通过与理论值的对比来测试效果。\n",
-    "- 理论值由numpy中的工具来求解哈密顿量的各个特征值；\n",
-    "- 我们将训练QNN得到的各个能级的能量和理想情况下的理论值进行比对。\n",
-    "- 可以看到，SSVQE训练输出的值与理想值高度接近。"
+    "- 理论值由 NumPy 中的工具来求解 Hamilton 量的各个本征值；\n",
+    "- 我们将训练 QNN 得到的各个能级的能量和理想情况下的理论值进行比对。\n",
+    "- 可以看到，SSVQE 训练输出的值与理想值高度接近。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 8,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:40:01.398375Z",
+     "start_time": "2021-01-09T10:40:01.375160Z"
     }
    },
    "outputs": [
@@ -297,20 +303,21 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "The estimated ground state energy is:  [-1.07559121]\n",
-      "The theoretical ground state energy:  -1.0756323552750124\n",
-      "The estimated 1st excited state energy is:  [-0.72131763]\n",
-      "The theoretical 1st excited state energy:  -0.7213113808180259\n",
-      "The estimated 2nd excited state energy is:  [0.72132372]\n",
-      "The theoretical 2nd excited state energy:  0.7213113808180256\n",
-      "The estimated 3rd excited state energy is:  [1.07558513]\n",
-      "The theoretical 3rd excited state energy:  1.0756323552750122\n"
+      "The estimated ground state energy is:  [-2.89029006]\n",
+      "The theoretical ground state energy:  -2.914376077505768\n",
+      "The estimated 1st excited state energy is:  [-0.05679422]\n",
+      "The theoretical 1st excited state energy:  -0.07729623846713303\n",
+      "The estimated 2nd excited state energy is:  [0.73281967]\n",
+      "The theoretical 2nd excited state energy:  0.7671454582095175\n",
+      "The estimated 3rd excited state energy is:  [2.21426461]\n",
+      "The theoretical 3rd excited state energy:  2.2245268577633834\n"
      ]
     }
    ],
    "source": [
     "print('The estimated ground state energy is: ', loss_components[0].numpy())\n",
-    "print('The theoretical ground state energy: ', numpy.linalg.eigh(H)[0][0])\n",
+    "print('The theoretical ground state energy: ', \n",
+    "numpy.linalg.eigh(H)[0][0])\n",
     "\n",
     "print('The estimated 1st excited state energy is: ', loss_components[1].numpy())\n",
     "print('The theoretical 1st excited state energy: ', numpy.linalg.eigh(H)[0][1])\n",
@@ -326,18 +333,19 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
+    "_______\n",
     "\n",
     "## 参考文献\n",
     "\n",
-    "[1] [Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
+    "[1] Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. [Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
     "\n",
-    "[2] [McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. C. & Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 92, 015003 (2020).](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003)\n",
+    "[2] McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. C. & Yuan, X. Quantum computational chemistry. [Rev. Mod. Phys. 92, 015003 (2020).](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003)\n",
     "\n",
-    "[3] [Cao, Y. et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 119, 10856–10915 (2019).](https://pubs.acs.org/doi/abs/10.1021/acs.chemrev.8b00803)\n",
+    "[3] Cao, Y. et al. Quantum chemistry in the age of quantum computing. [Chem. Rev. 119, 10856–10915 (2019).](https://pubs.acs.org/doi/abs/10.1021/acs.chemrev.8b00803)\n",
     "\n",
-    "[4] [Nakanishi, K. M., Mitarai, K. & Fujii, K. Subspace-search variational quantum eigensolver for excited states. Phys. Rev. Res. 1, 033062 (2019).](https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.1.033062)\n",
+    "[4] Nakanishi, K. M., Mitarai, K. & Fujii, K. Subspace-search variational quantum eigensolver for excited states. [Phys. Rev. Res. 1, 033062 (2019).](https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.1.033062)\n",
     "\n",
-    "[5] [Vatan, F. & Williams, C. Optimal quantum circuits for general two-qubit gates. Phys. Rev. A 69, 032315 (2004).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.69.032315)\n"
+    "[5] Vatan, F. & Williams, C. Optimal quantum circuits for general two-qubit gates. [Phys. Rev. A 69, 032315 (2004).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.69.032315)"
    ]
   }
  ],
@@ -357,18 +365,22 @@
    "name": "python",
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
-   "version": "3.7.7"
+   "version": "3.6.10"
   },
-  "pycharm": {
-   "stem_cell": {
-    "cell_type": "raw",
-    "metadata": {
-     "collapsed": false
-    },
-    "source": []
-   }
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
   }
  },
  "nbformat": 4,
- "nbformat_minor": 1
+ "nbformat_minor": 4
 }

tutorial/SSVQE/SSVQE_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Subspace-search Variational Quantum Eigensolver\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>\n",
+    "\n",
+    "## Overview\n",
+    "\n",
+    "- In this tutorial, we will show how to train a quantum neural network (QNN) through Paddle Quantum to find the entire energy spectrum of a quantum system.\n",
+    "\n",
+    "- First, import the following packages."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:44.905642Z",
+     "start_time": "2021-01-09T10:39:40.689291Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import numpy\n",
+    "from paddle.complex import matmul, transpose\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import random_pauli_str_generator, pauli_str_to_matrix, dagger"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Background\n",
+    "\n",
+    "- Variational Quantum Eigensolver (VQE) [1-3] is one of the most promising applications for near-term quantum computing. One of the its powerful versions is SSVQE [4], which can be used to find the ground state and the **excited state** of a physical system's Hamiltonian. Mathematically, one can interpret it as solving the eigenvalues and eigenvectors of a Hermitian matrix. The set of eigenvalues of the Hamiltonian is called the energy spectrum.\n",
+    "- Next, we will use a brief example to demonstrate how to solve this problem by training a QNN, that is, to solve the energy spectrum of a given Hamiltonian $H$.\n",
+    "\n",
+    "## Hamiltonian \n",
+    "\n",
+    "- For a specific molecule that needs to be analyzed, we need its geometry, charge, and spin multiplicity to obtain the Hamiltonian (in Pauli products form) describing the system. Specifically, through our built-in quantum chemistry toolkit, fermionic-to-qubit mapping technology can be used to output the qubit Hamiltonian.\n",
+    "- As a simple demonstration of SSVQE, we provide a random 2-qubit Hamiltonian."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:44.922274Z",
+     "start_time": "2021-01-09T10:39:44.908600Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "N = 2       # Number of qubits\n",
+    "SEED = 14   # Fixed random seed"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:44.938897Z",
+     "start_time": "2021-01-09T10:39:44.926267Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "Random Hamiltonian in Pauli string format = \n",
+      " [[0.5288681247649314, 'z1'], [0.9258545165930183, 'z0,z1'], [-0.2323659299902321, 'x0,z1'], [-0.9558751117603583, 'z1'], [-0.619522452161382, 'x1'], [-0.08249108590273635, 'x1,z0'], [0.1662238964776901, 'z0,z1'], [0.3582576655826999, 'x0,x1'], [-0.5987469327681758, 'z1'], [0.4023148129799976, 'x0,y1']]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Generate random Hamiltonian represented by Pauli string\n",
+    "hamiltonian = random_pauli_str_generator(N, terms=10)\n",
+    "print(\"Random Hamiltonian in Pauli string format = \\n\", hamiltonian)\n",
+    "\n",
+    "# Generate matrix representation of Hamiltonian\n",
+    "H = pauli_str_to_matrix(hamiltonian, N)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Building a quantum neural network\n",
+    "\n",
+    "- To implement SSVQE, we first need to design a QNN $U(\\theta)$ (parameterized quantum circuit). In this tutorial, we provide a predefined universal quantum circuit template suitable for 2 qubits. Theoretically, this template has enough expressibility to simulate arbitrary 2-qubit unitary operation [5]. The specific implementation requires 3 $CNOT$ gates plus 15 single-qubit rotation gates $\\in \\{R_y, R_z\\}$.\n",
+    "\n",
+    "- One can randomly initialize the QNN parameters ${\\bf{\\vec{\\theta }}}$ containing 15 parameters."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:44.955929Z",
+     "start_time": "2021-01-09T10:39:44.950527Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "THETA_SIZE = 15 # The number of parameters in the quantum neural network\n",
+    "\n",
+    "def U_theta(theta, N):\n",
+    "    \"\"\"\n",
+    "    U_theta\n",
+    "    \"\"\"\n",
+    "    # Initialize the quantum neural network according to the number of qubits/network width\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Call the built-in quantum neural network template\n",
+    "    cir.universal_2_qubit_gate(theta)\n",
+    "\n",
+    "    # Return the unitary matrix U simulated by the quantum neural network\n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Training model and loss function\n",
+    "\n",
+    "- After setting up the Hamiltonian and the quantum neural network architecture, we will further define the parameters to be trained, the loss function and optimization methods. For a detailed inspection of the theory of SSVQE, please refer to the original paper [4].\n",
+    "\n",
+    "- By acting the quantum neural network $U(\\theta)$ on a set of orthogonal initial states (one can take the computational basis $\\{|00\\rangle, |01\\rangle, |10\\rangle, |11 \\rangle \\}$), we will get the output states $\\{\\left| {\\psi_1 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle, \\left| {\\psi_2 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle, \\left| {\\psi_3 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle, \\left| {\\psi_4 \\left( {\\bf{\\theta }} \\right)} \\right\\rangle \\}$.\n",
+    "\n",
+    "- Further, the loss function in the SSVQE model generally consists of expectation value of each output quantum state $\\left| {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right\\rangle$ given the Hamiltonian $H$. More specifically, it's the weighted summation of the energy expectation value. In this example, the default weight vector is $\\vec{w} = [4, 3, 2, 1]$.\n",
+    "\n",
+    "- The loss function is defined as:\n",
+    "\n",
+    "$$\n",
+    "\\mathcal{L}(\\boldsymbol{\\theta}) = \\sum_{k=1}^{2^n}w_k*\\left\\langle {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right|H\\left| {\\psi_k \\left( {\\bf{\\theta }} \\right)} \\right\\rangle. \\tag{1}\n",
+    "$$"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:44.972097Z",
+     "start_time": "2021-01-09T10:39:44.958878Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class Net(fluid.dygraph.Layer):\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * numpy.pi, seed=SEED), dtype='float64'):\n",
+    "        super(Net, self).__init__()\n",
+    "        \n",
+    "        # Initialize the theta parameter list and fill the initial value with the uniform distribution of [0, 2*pi]\n",
+    "        self.theta = self.create_parameter(shape=shape,\n",
+    "                     attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "    \n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self, H, N):\n",
+    "        \n",
+    "        # Build quantum neural network\n",
+    "        U = U_theta(self.theta, N)\n",
+    "        \n",
+    "        # Calculate the loss function\n",
+    "        loss_struct = matmul(matmul(dagger(U), H), U).real\n",
+    "\n",
+    "        # Enter the computational basis to calculate the expected value \n",
+    "        # which is equivalent to taking the diagonal element of U^dagger*H*U\n",
+    "        loss_components = [\n",
+    "            loss_struct[0][0],\n",
+    "            loss_struct[1][1],\n",
+    "            loss_struct[2][2],\n",
+    "            loss_struct[3][3]\n",
+    "        ]\n",
+    "        \n",
+    "        # Weighted summation of loss function\n",
+    "        loss = 4 * loss_components[0] + 3 * loss_components[1]\\\n",
+    "             + 2 * loss_components[2] + 1 * loss_components[3]\n",
+    "        \n",
+    "        return loss, loss_components"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Hyper-parameters\n",
+    "\n",
+    "Before training the quantum neural network, we also need to set up several hyper-parameters, mainly the learning rate LR, the number of iterations ITR. Here we set the learning rate to be LR = 0.3 and the number of iterations ITR = 50. One can adjust these hyper-parameters accordingly and check how they influence the training performance."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:44.981182Z",
+     "start_time": "2021-01-09T10:39:44.975407Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "ITR = 50  # Set the total number of iterations of training\n",
+    "LR = 0.3  # Set the learning rate"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Training process\n",
+    "\n",
+    "- After setting all the parameters of SSVQE model, we need to convert all the data into variables in the PaddlePaddle dynamic graph, and then train the quantum neural network.\n",
+    "- We use Adam Optimizer in training, and one can also call other optimizers provided in PaddlePaddle."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:46.247964Z",
+     "start_time": "2021-01-09T10:39:44.985154Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 10 loss: -6.6361\n",
+      "iter: 20 loss: -7.2810\n",
+      "iter: 30 loss: -7.5451\n",
+      "iter: 40 loss: -7.6850\n",
+      "iter: 50 loss: -7.7028\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Initialize paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # We need to convert numpy.ndarray to variable supported in Paddle dynamic graph mode\n",
+    "    hamiltonian = fluid.dygraph.to_variable(H)\n",
+    "\n",
+    "    # Determine the parameter dimension of the network\n",
+    "    net = Net(shape=[THETA_SIZE])\n",
+    "\n",
+    "    # We use Adam optimizer for better performance\n",
+    "    # One can change it to SGD or RMSprop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "\n",
+    "    # Optimization loop\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "        \n",
+    "        # Forward propagation calculates the loss function and returns the estimated energy spectrum\n",
+    "        loss, loss_components = net(hamiltonian, N)\n",
+    "        \n",
+    "        # Under the dynamic graph mechanism, use back propagation to minimize the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "        \n",
+    "        # Print training results\n",
+    "        if itr% 10 == 0:\n",
+    "            print('iter:', itr,'loss:','%.4f'% loss.numpy()[0])"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Benchmarking\n",
+    "\n",
+    "We have now completed the training of the quantum neural network, and we will verify the results by comparing them with theoretical values.\n",
+    "- The theoretical Hamiltonian eigenvalues are solved by the linear algebra package in NumPy;\n",
+    "- We compare the energy of each energy level obtained by training QNN with the theoretical value.\n",
+    "- It can be seen that the training output is very close to the exact value."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 8,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:46.288156Z",
+     "start_time": "2021-01-09T10:39:46.253447Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The estimated ground state energy is:  [-2.32236871]\n",
+      "The theoretical ground state energy:  -2.325787163439509\n",
+      "The estimated 1st excited state energy is:  [-0.73748569]\n",
+      "The theoretical 1st excited state energy:  -0.7415874007735302\n",
+      "The estimated 2nd excited state energy is:  [0.73927594]\n",
+      "The theoretical 2nd excited state energy:  0.7415874007735306\n",
+      "The estimated 3rd excited state energy is:  [2.32057845]\n",
+      "The theoretical 3rd excited state energy:  2.325787163439509\n"
+     ]
+    }
+   ],
+   "source": [
+    "print('The estimated ground state energy is: ', loss_components[0].numpy())\n",
+    "print('The theoretical ground state energy: ', \n",
+    "numpy.linalg.eigh(H)[0][0])\n",
+    "\n",
+    "print('The estimated 1st excited state energy is: ', loss_components[1].numpy())\n",
+    "print('The theoretical 1st excited state energy: ', numpy.linalg.eigh(H)[0][1])\n",
+    "\n",
+    "print('The estimated 2nd excited state energy is: ', loss_components[2].numpy())\n",
+    "print('The theoretical 2nd excited state energy: ', numpy.linalg.eigh(H)[0][2])\n",
+    "\n",
+    "print('The estimated 3rd excited state energy is: ', loss_components[3].numpy())\n",
+    "print('The theoretical 3rd excited state energy: ', numpy.linalg.eigh(H)[0][3])"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## References\n",
+    "\n",
+    "[1] Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. [Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
+    "\n",
+    "[2] McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. C. & Yuan, X. Quantum computational chemistry. [Rev. Mod. Phys. 92, 015003 (2020).](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003)\n",
+    "\n",
+    "[3] Cao, Y. et al. Quantum chemistry in the age of quantum computing. [Chem. Rev. 119, 10856–10915 (2019).](https://pubs.acs.org/doi/abs/10.1021/acs.chemrev.8b00803)\n",
+    "\n",
+    "[4] Nakanishi, K. M., Mitarai, K. & Fujii, K. Subspace-search variational quantum eigensolver for excited states. [Phys. Rev. Res. 1, 033062 (2019).](https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.1.033062)\n",
+    "\n",
+    "[5] Vatan, F. & Williams, C. Optimal quantum circuits for general two-qubit gates. [Phys. Rev. A 69, 032315 (2004).](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.69.032315)"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/VQE/VQE_CN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# 变分量子本征求解器\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 概览\n",
+    "\n",
+    "目前普遍认为，量子计算在近期很有前景的一个应用是处理量子化学问题 [1-2]。**变分量子本征求解器** （VQE）作为这个研究方向的核心应用之一，为研究者们提供了可以在目前含噪的中等规模量子设备（NISQ device）上研究量子化学的可能 [1-4]。其核心任务是求解一个量子尺度上封闭物理系统的哈密顿量 $\\hat{H}$ 的基态能量及其对应的量子态。主要的实现方法是通过在量子设备上准备一个参数化的试探波函数 $|\\Psi(\\boldsymbol\\theta)\\rangle$ 然后结合经典机器学习中的优化算法（例如梯度下降法）去不断地调整、优化参数 $\\boldsymbol\\theta$ 使得期望值  $\\langle \\Psi(\\boldsymbol\\theta)|\\hat{H}|\\Psi(\\boldsymbol\\theta)\\rangle$ 最小化。这套方案的基本原理是基于 **Rayleigh-Ritz 变分原理**。 \n",
+    "\n",
+    "$$\n",
+    "E_0 = \\min_{\\boldsymbol\\theta} \\langle \\Psi(\\boldsymbol\\theta)|\\hat{H}|\\Psi(\\boldsymbol\\theta)\\rangle.\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "其中 $E_0$ 表示该系统的基态能量。从数值分析的角度来看，该问题可以被理解为求解一个**离散化**哈密顿量 $H$（厄米矩阵）的最小本征值 $\\lambda_{\\min}$ 和其对应的本征向量 $|\\Psi_0\\rangle$。具体的离散化过程是如何通过建立模型实现的，这属于量子化学的专业领域范畴。精确地解释该过程需要很长的篇幅，这超过了本教程所能处理的范围。我们会在下一节背景知识模块粗略的介绍一下相关知识，感兴趣的读者可以参考 `量子化学: 基本原理和从头计算法`系列丛书 [5]。通常来说，为了能在量子设备上处理量子化学问题，哈密顿量 $H$ 会被表示成为泡利算符 $\\{X,Y,Z\\}$ 的加权求和形式。\n",
+    "\n",
+    "$$\n",
+    "H = \\sum_k c_k ~ \\bigg( \\bigotimes_{j=0}^{M-1} \\sigma_j^{(k)} \\bigg),\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "其中 $c_k$ 表示权重系数, $\\sigma_j^{(k)} \\in \\{I,X,Y,Z\\}$ 并且 $M$ 表示所需的量子比特个数。这样一种哈密顿量的表示形式被称为 **泡利字符串**。以下为一个2量子比特的具体例子，\n",
+    "\n",
+    "$$\n",
+    "H= 0.12~Y_0 \\otimes I_1-0.04~X_0\\otimes Z_1.\n",
+    "\\tag{3}\n",
+    "$$\n",
+    "\n",
+    "在下一节，我们会补充一些关于电子结构问题的背景知识。本质上讨论的就是上述哈密顿量 $H$ 究竟是从哪里来的。对于熟悉相关背景的读者，或者主要关心如何在量桨上实现 VQE 的读者，请直接跳转至第三节分析氢分子（$H_2$）基态的具体例子。 "
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 背景： 电子结构问题\n",
+    "\n",
+    "这本小节，我们集中讨论下量子化学中的一个基本问题 -- **电子结构问题**。更准确的说，我们关心的是给定分子（molecule）的低位能量本征态。这些信息可以帮助我们预测化学反应的速率和分子的稳定结构等等 [6]。假设一个分子由 $N_n$ 个原子核和 $N_e$ 个电子组成，描述该分子系统总能量的哈密顿量算符 $\\hat{H}_{mol}$ 在一次量子化表示下可以写为，\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "\\hat{H}_{\\text{mol}} & = -\\sum_{i}\\frac{\\nabla_{R_i}^2}{2M_i} - \\sum_{i} \\frac{\\nabla_{r_i}^2}{2} -\\sum_{i,j}\\frac{Z_i}{\\lvert R_i - r_j\\lvert} + \\sum_{i,j>i}\\frac{Z_iZ_j}{\\lvert R_i - R_j\\lvert} + \\sum_{i, j>i}\\frac{1}{\\lvert r_i - r_j\\lvert}, \n",
+    "\\tag{4}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "其中 $R_i、M_i$ 和 $Z_i$ 分别表示第 $i$ 个原子核的位置、质量和原子序数（原子核内质子数），第 $i$ 个电子的位置则表示为 $r_i$。以上公式右边前两项分别代表原子核和电子的总动能。第三项表示带正电的质子和带负电的电子之间的库伦相互吸引作用。最后两项则表示原子核-原子核之间，电子-电子之间的相互排斥作用。这里，分子哈密顿量 $\\hat{H}_\\text{mol}$ 使用的是原子单位制能量 **哈特里能量**（Hartree），记为 Ha。1哈特里能量的大小为 $[\\hbar^2/(m_ee^2a_0^2)] = 27.2$ 电子伏或 630 千卡/摩尔，其中 $m_e、e$ 和 $a_0$ 分别表示电子质量、基本电荷和玻尔半径。\n",
+    "\n",
+    "**注释1：** 在这个图景下，我们不考虑自旋-轨道耦合以及超精细结构。如果出于计算需要，可以作为微扰加入。"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 玻恩-奥本海默近似\n",
+    "\n",
+    "由于一般原子核的质量要远大于电子，因而在同样的相互作用下电子的运动速度会比原子核快很多。所以，将原子核所处的位置看成固定 $R_i =$常数 是一种合理的近似。这种通过在时间尺度上将电子行为和原子核行为去耦合的近似处理思想被称为玻恩-奥本海默近似。作为近似的直接结果，公式（4）中原子核的动能项会被消去并且表示原子核-原子核相互排斥作用的项可以被认为是一个能量移位（这个项是与电子位置 $r_i$ 无关的）从而也可以作为常数项被忽略。经过这些步骤后，我们可以把哈密顿量近似为：\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "\\hat{H}_{\\text{electron}} & =  - \\sum_{i} \\frac{\\nabla_{r_i}^2}{2} -\\sum_{i,j}\\frac{Z_i}{\\lvert R_i - r_j\\lvert} + \\sum_{i, j>i}\\frac{1}{\\lvert r_i - r_j\\lvert} \n",
+    "\\tag{5},\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "在经过以上近似后，分子中多电子结构的能级在理论上可以通过求解以下不含时薛定谔方程获得：\n",
+    "\n",
+    "$$\n",
+    "\\hat{H}_{\\text{electron}} |\\Psi_n \\rangle = E_n |\\Psi_n \\rangle,\n",
+    "\\tag{6}\n",
+    "$$\n",
+    "\n",
+    "其中 $n$ 指代能级。值得注意的是，电子哈密顿量中电子-电子相互排斥作用的求和项数会随着电子数 $N_e$ 的增多至 $N_e(N_e-1)/2$ 项。这意味着对于一个含有16个电子的氧分子（$O_2$）我们需要计算多达120项的相互排斥作用项。 一般来说，这样的问题是无法从理论上精确求解的。正如狄拉克在 [Quantum mechanics of many-electron systems](https://royalsocietypublishing.org/doi/10.1098/rspa.1929.0094) [7] 所指出的那样，\n",
+    "\n",
+    "> *The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.* \n",
+    "> \n",
+    "> -- Paul Dirac (1929)\n",
+    "\n",
+    "既然解析的做法因为太复杂了不太可行，那么我们可以采用数值方法来处理。一个最简单的数值方法（离散化方法）就是把上述作用中无限维度希尔伯特空间离散化为等间距排开的立方体晶格点。在这样一个离散化的空间里，主要运算规则为复数域的线性代数。假设空间的每个轴都离散为等间距排开的 $k$ 个点，则 $N$-电子（为了方便去掉下标 $e$）的多体波函数可以写为 [2]：\n",
+    "\n",
+    "$$\n",
+    "|\\Psi \\rangle = \\sum_{\\mathbf{x_1}, \\ldots, \\mathbf{x_N}} \\psi(\\mathbf{x_1}, \\ldots, \\mathbf{x_N}) \\mathcal{A}(|\\mathbf{x_1}, \\ldots, \\mathbf{x_N}\\rangle).\n",
+    "\\tag{7}\n",
+    "$$\n",
+    "\n",
+    "其中坐标 $|\\mathbf{x_j}\\rangle = |r_j\\rangle |\\sigma_j\\rangle$ 记录第 $j$ 个电子的空间位置信息和自旋，$|r_j\\rangle  = |x_j,y_j,z_j\\rangle$ 且 $j\\in \\{1,2,\\cdots,N\\}$, $x_j,y_j,z_j \\in \\{0,1,\\cdots,k-1\\}$ 同时 $\\sigma_j \\in \\{\\downarrow,\\uparrow\\}$ 表示自旋向下和向上。这样一种离散化方式共计需要 $k^{3N}\\times 2^{N}$ 个数据来表示波函数。在这里，$\\mathcal{A}$ 表示反对称化操作（）出于泡利不相容原理）并且 $\\psi(\\mathbf{x_1}, \\mathbf{x_2}, \\ldots, \\mathbf{x_N})=\\langle\\mathbf{x_1}, \\mathbf{x_2}, \\ldots, \\mathbf{x_N}|\\Psi\\rangle$。 可以看出，经典计算机存储这样一个波函数需要的内存是随着电子个数呈指数增长的。这使得基于这种离散化的经典数值方法，无法模拟超过几十个电子的系统。那么，我们是不是能够通过量子设备来存储和准备这样一个波函数然后求解基态能量 $E_0$ 呢？在下一节中，我们将以最简单的分子系统 -- 氢分子（$H_2$）为例，讲解 VQE 算法。\n",
+    "\n",
+    "**注释2：** 关于量子化学和现有数值计算方法的综述也超过了本教程的处理范围，我们推荐感兴趣的读者去查阅以下经典教材 Helgaker 等人撰写的 *'Molecular Electronic-Structure Theory'* [6] 以及 Szabo & Ostlund 撰写的 *'Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory'* [8]。 如果需要弥补量子计算和量子化学之间知识空缺，请参考以下综述文章 [Quantum chemistry in the age of quantum computing](https://pubs.acs.org/doi/10.1021/acs.chemrev.8b00803) [1] 和  [Quantum computational chemistry](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003) [2] 。\n",
+    "\n",
+    "**注释3：** 对于量子化学中的能量计算，我们期望能够达到 **化学精度**（chemical accuracy）$1.6\\times10^{-3}$ Ha 或者 1 千卡/摩尔。\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 氢分子 $H_2$ 基态能量\n",
+    "\n",
+    "### 构造电子哈密顿量\n",
+    "\n",
+    "首先，让我们通过下面几行代码引入必要的 library 和 package。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:23.645493Z",
+     "start_time": "2021-01-09T07:44:20.439467Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import os\n",
+    "import platform\n",
+    "import matplotlib.pyplot as plt\n",
+    "%config InlineBackend.figure_format = 'svg'\n",
+    "from IPython.display import clear_output\n",
+    "\n",
+    "import numpy\n",
+    "from numpy import concatenate\n",
+    "from numpy import pi as PI\n",
+    "from numpy import savez, zeros\n",
+    "\n",
+    "from paddle import fluid\n",
+    "from paddle.complex import matmul, transpose\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import pauli_str_to_matrix\n",
+    "from paddle_quantum.VQE.chemistrysub import H2_generator\n",
+    "clear_output()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "对于具体需要分析的分子，我们需要其**几何构型** (geometry)、**基组**（basis set，例如 STO-3G 基于高斯函数）、**多重度**（multiplicity）以及**分子的净电荷数** (charge) 等多项信息来建模获取描述系统的哈密顿量。具体的，通过我们内置的量子化学工具包可以利用 fermion-to-qubit 映射的技术来输出目标分子的量子比特哈密顿量表示（泡利字符串）。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:23.664668Z",
+     "start_time": "2021-01-09T07:44:23.649741Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "Hamiltonian, N = H2_generator()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "面向更高级的用户，我们这里提供一个简单的生成氢分子 (H2)哈密顿量的教程。先安装以下两个package (**仅Mac/Linux用户可使用，Windows用户暂时不支持**):"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:25.822149Z",
+     "start_time": "2021-01-09T07:44:23.668727Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "!pip install openfermion\n",
+    "clear_output()"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:28.254506Z",
+     "start_time": "2021-01-09T07:44:25.828270Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "!pip install openfermionpyscf\n",
+    "clear_output()"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:29.175345Z",
+     "start_time": "2021-01-09T07:44:28.259368Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The generated h2 Hamiltonian is \n",
+      " (-0.04207897647782281+0j) [] +\n",
+      "(-0.04475014401535161+0j) [X0 X1 Y2 Y3] +\n",
+      "(0.04475014401535161+0j) [X0 Y1 Y2 X3] +\n",
+      "(0.04475014401535161+0j) [Y0 X1 X2 Y3] +\n",
+      "(-0.04475014401535161+0j) [Y0 Y1 X2 X3] +\n",
+      "(0.17771287465139946+0j) [Z0] +\n",
+      "(0.17059738328801055+0j) [Z0 Z1] +\n",
+      "(0.12293305056183798+0j) [Z0 Z2] +\n",
+      "(0.16768319457718958+0j) [Z0 Z3] +\n",
+      "(0.1777128746513994+0j) [Z1] +\n",
+      "(0.16768319457718958+0j) [Z1 Z2] +\n",
+      "(0.12293305056183798+0j) [Z1 Z3] +\n",
+      "(-0.24274280513140456+0j) [Z2] +\n",
+      "(0.17627640804319586+0j) [Z2 Z3] +\n",
+      "(-0.24274280513140456+0j) [Z3]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# 操作系统信息\n",
+    "sysStr = platform.system()\n",
+    "\n",
+    "# 判断操作系统\n",
+    "if sysStr in ('Linux', 'Darwin'):\n",
+    "\n",
+    "    import openfermion\n",
+    "    import openfermionpyscf\n",
+    "\n",
+    "    # 请检查是否正确下载了 h2 的几何构型文件\n",
+    "    geo = 'h2.xyz'\n",
+    "    charge = 0\n",
+    "    multiplicity = 1\n",
+    "\n",
+    "    # 生成哈密顿量\n",
+    "    mol = openfermion.hamiltonians.MolecularData(geo, 'sto-3g', multiplicity, charge)\n",
+    "    openfermionpyscf.run_pyscf(mol)\n",
+    "    terms_molecular_hamiltonian = mol.get_molecular_hamiltonian()\n",
+    "    fermionic_hamiltonian = openfermion.transforms.get_fermion_operator(terms_molecular_hamiltonian)\n",
+    "    qubit_op = openfermion.transforms.jordan_wigner(fermionic_hamiltonian)\n",
+    "\n",
+    "    # 打印结果\n",
+    "    print(\"The generated h2 Hamiltonian is \\n\", qubit_op)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "**注释4：** 生成这个哈密顿量的几何构型中，两个氢原子间的原子间隔（interatomic distance）为 $d = 74$ pm。\n",
+    "\n",
+    "除了氢分子 (H2) 之外, 我们也提供了氟化氢 (HF) 分子的几何构型文件 `hf.xyz`。如果你需要测试更多分子的几何构型，请移步至这个[数据库](http://smart.sns.it/molecules/index.html)。此外，我们还需要把这些本质上由泡利算符表示的哈密顿量转化成量桨支持的数据格式，这里我们提供这个接口。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:29.292390Z",
+     "start_time": "2021-01-09T07:44:29.267116Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def Hamiltonian_str_convert(qubit_op):\n",
+    "    '''\n",
+    "    将上述提供的哈密顿量信息转为量桨支持的泡利字符串\n",
+    "    H = [[1.0, \"z0,x1\"], [-1.0, \"y0,z1\"], ...]\n",
+    "    '''\n",
+    "    info_dic = qubit_op.terms\n",
+    "    \n",
+    "    def process_tuple(tup):\n",
+    "        if len(tup) == 0:\n",
+    "            return 'i0'\n",
+    "        else:\n",
+    "            res = ''\n",
+    "            for ele in tup:\n",
+    "                res += ele[1].lower()\n",
+    "                res += str(ele[0])\n",
+    "                res += ','\n",
+    "            return res[:-1]\n",
+    "    H_info = []\n",
+    "    \n",
+    "    for key, value in qubit_op.terms.items():\n",
+    "        H_info.append([value.real, process_tuple(key)])\n",
+    "    \n",
+    "    return H_info\n",
+    "\n",
+    "if sysStr in ('Linux', 'Darwin'):\n",
+    "    Hamiltonian = Hamiltonian_str_convert(qubit_op)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 搭建量子神经网络（QNN）和试探波函数\n",
+    "\n",
+    "在实现VQE的过程中，我们首先需要设计量子神经网络QNN（也可以理解为参数化量子电路）来准备试探波函数 $|\\Psi(\\boldsymbol\\theta)\\rangle$。这里，我们提供一个预设好的的深度为 $D$ 层的 4-量子比特的量子电路模板，图中的虚线框内为一层：\n",
+    "\n",
+    "![Utheta.jpg](https://release-data.cdn.bcebos.com/PIC%2FUtheta.jpg)\n",
+    "\n",
+    "- 我们预设一些该参数化电路的参数，比如宽度为 $N = 4$ 量子位。\n",
+    "\n",
+    "- 初始化其中的变量参数，${\\bf{\\theta }}$ 代表我们量子神经网络中的参数组成的向量。\n",
+    "\n",
+    "接下来我们根据上图中的电路设计，通过 Paddle Quantum 的 `UAnsatz` 函数和内置的 `real_entangled_layer(theta, D)` 电路模板来高效搭建量子神经网络。 "
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:29.313859Z",
+     "start_time": "2021-01-09T07:44:29.300530Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def U_theta(theta, Hamiltonian, N, D):\n",
+    "    \"\"\"\n",
+    "    Quantum Neural Network\n",
+    "    \"\"\"\n",
+    "    \n",
+    "    # 按照量子比特数量/网络宽度初始化量子神经网络\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # 内置的 {R_y + CNOT} 电路模板\n",
+    "    cir.real_entangled_layer(theta[:D], D)\n",
+    "    \n",
+    "    # 铺上最后一列 R_y 旋转门\n",
+    "    for i in range(N):\n",
+    "        cir.ry(theta=theta[D][i][0], which_qubit=i)\n",
+    "        \n",
+    "    # 量子神经网络作用在默认的初始态 |0000>上\n",
+    "    cir.run_state_vector()\n",
+    "    \n",
+    "    # 计算给定哈密顿量的期望值\n",
+    "    expectation_val = cir.expecval(Hamiltonian)\n",
+    "\n",
+    "    return expectation_val"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 配置训练模型 - 损失函数\n",
+    "\n",
+    "现在我们已经有了数据和量子神经网络的架构，我们将进一步定义训练参数、模型和损失函数。通过作用量子神经网络 $U(\\theta)$ 在初始态 $|0..0\\rangle$ 上，我们将得到输出态 $\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle $。进一步，在VQE模型中的损失函数一般由量子态 $\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle$ 关于哈密顿量 $H$ 的期望值 (能量期望值 expectation value) 给出，\n",
+    "\n",
+    "$$\n",
+    "\\min_{\\boldsymbol\\theta}  \\mathcal{L}(\\boldsymbol \\theta) = \\min_{\\boldsymbol\\theta} \\langle \\Psi(\\boldsymbol\\theta)|H |\\Psi(\\boldsymbol\\theta)\\rangle\n",
+    "= \\min_{\\boldsymbol\\theta} \\sum_k c_k~\\langle \\Psi(\\boldsymbol\\theta)| \\bigotimes_j \\sigma_j^{(k)}|\\Psi(\\boldsymbol\\theta)\\rangle.\n",
+    "\\tag{8}\n",
+    "$$"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 8,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:29.352036Z",
+     "start_time": "2021-01-09T07:44:29.336102Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class StateNet(fluid.dygraph.Layer):\n",
+    "    \"\"\"\n",
+    "    Construct the model net\n",
+    "    \"\"\"\n",
+    "\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * PI), dtype=\"float64\"):\n",
+    "        super(StateNet, self).__init__()\n",
+    "        \n",
+    "        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
+    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        \n",
+    "    # 定义损失函数和前向传播机制\n",
+    "    def forward(self, N, D):\n",
+    "        \n",
+    "        # 计算损失函数/期望值\n",
+    "        loss = U_theta(self.theta, Hamiltonian, N, D)\n",
+    "\n",
+    "        return loss"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 配置训练模型 - 模型参数\n",
+    "\n",
+    "在进行量子神经网络的训练之前，我们还需要进行一些训练的超参数设置，主要是学习速率 (LR, learning rate)、迭代次数(ITR, iteration)和量子神经网络计算模块的深度 (D, Depth)。这里我们设定学习速率为0.5, 迭代次数为50次。读者不妨自行调整来直观感受下超参数调整对训练效果的影响。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 9,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:29.362343Z",
+     "start_time": "2021-01-09T07:44:29.357578Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "ITR = 100  # 设置训练的总迭代次数\n",
+    "LR = 0.2   # 设置学习速率\n",
+    "D = 2      # 设置量子神经网络中重复计算模块的深度 Depth"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 进行训练\n",
+    "\n",
+    "当训练模型的各项参数都设置完成后，我们将数据转化为Paddle动态图中的变量，进而进行量子神经网络的训练。过程中我们用的是Adam Optimizer，也可以调用Paddle中提供的其他优化器。我们将训练过程中的结果存储在summary_data文件中。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 10,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:49.755405Z",
+     "start_time": "2021-01-09T07:44:29.368768Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 20 loss: -0.9230\n",
+      "iter: 20 Ground state energy: -0.9230 Ha\n",
+      "iter: 40 loss: -1.1241\n",
+      "iter: 40 Ground state energy: -1.1241 Ha\n",
+      "iter: 60 loss: -1.1332\n",
+      "iter: 60 Ground state energy: -1.1332 Ha\n",
+      "iter: 80 loss: -1.1359\n",
+      "iter: 80 Ground state energy: -1.1359 Ha\n",
+      "iter: 100 loss: -1.1362\n",
+      "iter: 100 Ground state energy: -1.1362 Ha\n"
+     ]
+    }
+   ],
+   "source": [
+    "# 初始化paddle动态图机制\n",
+    "with fluid.dygraph.guard():\n",
+    "\n",
+    "\n",
+    "    # 确定网络的参数维度\n",
+    "    net = StateNet(shape=[D + 1, N, 1])\n",
+    "\n",
+    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，\n",
+    "    # 当然你可以改成SGD或者是RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(\n",
+    "          learning_rate=LR, parameter_list=net.parameters())\n",
+    "\n",
+    "    # 记录优化结果\n",
+    "    summary_iter, summary_loss = [], []\n",
+    "    \n",
+    "    # 优化循环\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "        \n",
+    "        # 前向传播计算损失函数\n",
+    "        loss = net(N, D)\n",
+    "\n",
+    "        # 在动态图机制下，反向传播极小化损失函数\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "        \n",
+    "        # 更新优化结果\n",
+    "        summary_loss.append(loss.numpy())\n",
+    "        summary_iter.append(itr)\n",
+    "        \n",
+    "        # 打印结果\n",
+    "        if itr % 20 == 0:\n",
+    "            print(\"iter:\", itr, \"loss:\", \"%.4f\" % loss.numpy())\n",
+    "            print(\"iter:\", itr, \"Ground state energy:\", \"%.4f Ha\" \n",
+    "                                                % loss.numpy())\n",
+    "\n",
+    "    # 储存训练结果到 output 文件夹\n",
+    "    os.makedirs(\"output\", exist_ok=True)\n",
+    "    savez(\"./output/summary_data\", iter = summary_iter, \n",
+    "                                   energy=summary_loss)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### 测试效果\n",
+    "我们现在已经完成了量子神经网络的训练，通过 VQE 得到的基态能量的估计值大致为 $E_0 \\approx -1.136$ Ha，这与通过全价构型相互作用（FCI）$E_0 = -1.13618$ Ha 计算得出的值是在化学精度 $\\varepsilon = 1.6 \\times 10^{-3}$ Ha 内相符合的。"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 11,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:44:50.689035Z",
+     "start_time": "2021-01-09T07:44:49.759395Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"262.19625pt\" version=\"1.1\" viewBox=\"0 0 394.160937 262.19625\" width=\"394.160937pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T15:44:50.491460</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 262.19625 \n",
+       "L 394.160937 262.19625 \n",
+       "L 394.160937 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:none;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"patch_2\">\n",
+       "    <path d=\"M 52.160938 224.64 \n",
+       "L 386.960938 224.64 \n",
+       "L 386.960938 7.2 \n",
+       "L 52.160938 7.2 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_1\">\n",
+       "    <g id=\"xtick_1\">\n",
+       "     <g id=\"line2d_1\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L 0 3.5 \n",
+       "\" id=\"m158c43600d\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"64.304739\" xlink:href=\"#m158c43600d\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_1\">\n",
+       "      <!-- 0 -->\n",
+       "      <g transform=\"translate(61.123489 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 31.78125 66.40625 \n",
+       "Q 24.171875 66.40625 20.328125 58.90625 \n",
+       "Q 16.5 51.421875 16.5 36.375 \n",
+       "Q 16.5 21.390625 20.328125 13.890625 \n",
+       "Q 24.171875 6.390625 31.78125 6.390625 \n",
+       "Q 39.453125 6.390625 43.28125 13.890625 \n",
+       "Q 47.125 21.390625 47.125 36.375 \n",
+       "Q 47.125 51.421875 43.28125 58.90625 \n",
+       "Q 39.453125 66.40625 31.78125 66.40625 \n",
+       "z\n",
+       "M 31.78125 74.21875 \n",
+       "Q 44.046875 74.21875 50.515625 64.515625 \n",
+       "Q 56.984375 54.828125 56.984375 36.375 \n",
+       "Q 56.984375 17.96875 50.515625 8.265625 \n",
+       "Q 44.046875 -1.421875 31.78125 -1.421875 \n",
+       "Q 19.53125 -1.421875 13.0625 8.265625 \n",
+       "Q 6.59375 17.96875 6.59375 36.375 \n",
+       "Q 6.59375 54.828125 13.0625 64.515625 \n",
+       "Q 19.53125 74.21875 31.78125 74.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-48\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_2\">\n",
+       "     <g id=\"line2d_2\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"125.792342\" xlink:href=\"#m158c43600d\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_2\">\n",
+       "      <!-- 20 -->\n",
+       "      <g transform=\"translate(119.429842 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 19.1875 8.296875 \n",
+       "L 53.609375 8.296875 \n",
+       "L 53.609375 0 \n",
+       "L 7.328125 0 \n",
+       "L 7.328125 8.296875 \n",
+       "Q 12.9375 14.109375 22.625 23.890625 \n",
+       "Q 32.328125 33.6875 34.8125 36.53125 \n",
+       "Q 39.546875 41.84375 41.421875 45.53125 \n",
+       "Q 43.3125 49.21875 43.3125 52.78125 \n",
+       "Q 43.3125 58.59375 39.234375 62.25 \n",
+       "Q 35.15625 65.921875 28.609375 65.921875 \n",
+       "Q 23.96875 65.921875 18.8125 64.3125 \n",
+       "Q 13.671875 62.703125 7.8125 59.421875 \n",
+       "L 7.8125 69.390625 \n",
+       "Q 13.765625 71.78125 18.9375 73 \n",
+       "Q 24.125 74.21875 28.421875 74.21875 \n",
+       "Q 39.75 74.21875 46.484375 68.546875 \n",
+       "Q 53.21875 62.890625 53.21875 53.421875 \n",
+       "Q 53.21875 48.921875 51.53125 44.890625 \n",
+       "Q 49.859375 40.875 45.40625 35.40625 \n",
+       "Q 44.1875 33.984375 37.640625 27.21875 \n",
+       "Q 31.109375 20.453125 19.1875 8.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-50\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-50\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_3\">\n",
+       "     <g id=\"line2d_3\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"187.279946\" xlink:href=\"#m158c43600d\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_3\">\n",
+       "      <!-- 40 -->\n",
+       "      <g transform=\"translate(180.917446 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 37.796875 64.3125 \n",
+       "L 12.890625 25.390625 \n",
+       "L 37.796875 25.390625 \n",
+       "z\n",
+       "M 35.203125 72.90625 \n",
+       "L 47.609375 72.90625 \n",
+       "L 47.609375 25.390625 \n",
+       "L 58.015625 25.390625 \n",
+       "L 58.015625 17.1875 \n",
+       "L 47.609375 17.1875 \n",
+       "L 47.609375 0 \n",
+       "L 37.796875 0 \n",
+       "L 37.796875 17.1875 \n",
+       "L 4.890625 17.1875 \n",
+       "L 4.890625 26.703125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-52\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-52\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_4\">\n",
+       "     <g id=\"line2d_4\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"248.767549\" xlink:href=\"#m158c43600d\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_4\">\n",
+       "      <!-- 60 -->\n",
+       "      <g transform=\"translate(242.405049 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 33.015625 40.375 \n",
+       "Q 26.375 40.375 22.484375 35.828125 \n",
+       "Q 18.609375 31.296875 18.609375 23.390625 \n",
+       "Q 18.609375 15.53125 22.484375 10.953125 \n",
+       "Q 26.375 6.390625 33.015625 6.390625 \n",
+       "Q 39.65625 6.390625 43.53125 10.953125 \n",
+       "Q 47.40625 15.53125 47.40625 23.390625 \n",
+       "Q 47.40625 31.296875 43.53125 35.828125 \n",
+       "Q 39.65625 40.375 33.015625 40.375 \n",
+       "z\n",
+       "M 52.59375 71.296875 \n",
+       "L 52.59375 62.3125 \n",
+       "Q 48.875 64.0625 45.09375 64.984375 \n",
+       "Q 41.3125 65.921875 37.59375 65.921875 \n",
+       "Q 27.828125 65.921875 22.671875 59.328125 \n",
+       "Q 17.53125 52.734375 16.796875 39.40625 \n",
+       "Q 19.671875 43.65625 24.015625 45.921875 \n",
+       "Q 28.375 48.1875 33.59375 48.1875 \n",
+       "Q 44.578125 48.1875 50.953125 41.515625 \n",
+       "Q 57.328125 34.859375 57.328125 23.390625 \n",
+       "Q 57.328125 12.15625 50.6875 5.359375 \n",
+       "Q 44.046875 -1.421875 33.015625 -1.421875 \n",
+       "Q 20.359375 -1.421875 13.671875 8.265625 \n",
+       "Q 6.984375 17.96875 6.984375 36.375 \n",
+       "Q 6.984375 53.65625 15.1875 63.9375 \n",
+       "Q 23.390625 74.21875 37.203125 74.21875 \n",
+       "Q 40.921875 74.21875 44.703125 73.484375 \n",
+       "Q 48.484375 72.75 52.59375 71.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-54\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-54\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_5\">\n",
+       "     <g id=\"line2d_5\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"310.255152\" xlink:href=\"#m158c43600d\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_5\">\n",
+       "      <!-- 80 -->\n",
+       "      <g transform=\"translate(303.892652 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 31.78125 34.625 \n",
+       "Q 24.75 34.625 20.71875 30.859375 \n",
+       "Q 16.703125 27.09375 16.703125 20.515625 \n",
+       "Q 16.703125 13.921875 20.71875 10.15625 \n",
+       "Q 24.75 6.390625 31.78125 6.390625 \n",
+       "Q 38.8125 6.390625 42.859375 10.171875 \n",
+       "Q 46.921875 13.96875 46.921875 20.515625 \n",
+       "Q 46.921875 27.09375 42.890625 30.859375 \n",
+       "Q 38.875 34.625 31.78125 34.625 \n",
+       "z\n",
+       "M 21.921875 38.8125 \n",
+       "Q 15.578125 40.375 12.03125 44.71875 \n",
+       "Q 8.5 49.078125 8.5 55.328125 \n",
+       "Q 8.5 64.0625 14.71875 69.140625 \n",
+       "Q 20.953125 74.21875 31.78125 74.21875 \n",
+       "Q 42.671875 74.21875 48.875 69.140625 \n",
+       "Q 55.078125 64.0625 55.078125 55.328125 \n",
+       "Q 55.078125 49.078125 51.53125 44.71875 \n",
+       "Q 48 40.375 41.703125 38.8125 \n",
+       "Q 48.828125 37.15625 52.796875 32.3125 \n",
+       "Q 56.78125 27.484375 56.78125 20.515625 \n",
+       "Q 56.78125 9.90625 50.3125 4.234375 \n",
+       "Q 43.84375 -1.421875 31.78125 -1.421875 \n",
+       "Q 19.734375 -1.421875 13.25 4.234375 \n",
+       "Q 6.78125 9.90625 6.78125 20.515625 \n",
+       "Q 6.78125 27.484375 10.78125 32.3125 \n",
+       "Q 14.796875 37.15625 21.921875 38.8125 \n",
+       "z\n",
+       "M 18.3125 54.390625 \n",
+       "Q 18.3125 48.734375 21.84375 45.5625 \n",
+       "Q 25.390625 42.390625 31.78125 42.390625 \n",
+       "Q 38.140625 42.390625 41.71875 45.5625 \n",
+       "Q 45.3125 48.734375 45.3125 54.390625 \n",
+       "Q 45.3125 60.0625 41.71875 63.234375 \n",
+       "Q 38.140625 66.40625 31.78125 66.40625 \n",
+       "Q 25.390625 66.40625 21.84375 63.234375 \n",
+       "Q 18.3125 60.0625 18.3125 54.390625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-56\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-56\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_6\">\n",
+       "     <g id=\"line2d_6\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"371.742756\" xlink:href=\"#m158c43600d\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_6\">\n",
+       "      <!-- 100 -->\n",
+       "      <g transform=\"translate(362.199006 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 12.40625 8.296875 \n",
+       "L 28.515625 8.296875 \n",
+       "L 28.515625 63.921875 \n",
+       "L 10.984375 60.40625 \n",
+       "L 10.984375 69.390625 \n",
+       "L 28.421875 72.90625 \n",
+       "L 38.28125 72.90625 \n",
+       "L 38.28125 8.296875 \n",
+       "L 54.390625 8.296875 \n",
+       "L 54.390625 0 \n",
+       "L 12.40625 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-49\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_7\">\n",
+       "     <!-- Number of iteration -->\n",
+       "     <g transform=\"translate(170.354688 252.916562)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 23.09375 72.90625 \n",
+       "L 55.421875 11.921875 \n",
+       "L 55.421875 72.90625 \n",
+       "L 64.984375 72.90625 \n",
+       "L 64.984375 0 \n",
+       "L 51.703125 0 \n",
+       "L 19.390625 60.984375 \n",
+       "L 19.390625 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-78\"/>\n",
+       "       <path d=\"M 8.5 21.578125 \n",
+       "L 8.5 54.6875 \n",
+       "L 17.484375 54.6875 \n",
+       "L 17.484375 21.921875 \n",
+       "Q 17.484375 14.15625 20.5 10.265625 \n",
+       "Q 23.53125 6.390625 29.59375 6.390625 \n",
+       "Q 36.859375 6.390625 41.078125 11.03125 \n",
+       "Q 45.3125 15.671875 45.3125 23.6875 \n",
+       "L 45.3125 54.6875 \n",
+       "L 54.296875 54.6875 \n",
+       "L 54.296875 0 \n",
+       "L 45.3125 0 \n",
+       "L 45.3125 8.40625 \n",
+       "Q 42.046875 3.421875 37.71875 1 \n",
+       "Q 33.40625 -1.421875 27.6875 -1.421875 \n",
+       "Q 18.265625 -1.421875 13.375 4.4375 \n",
+       "Q 8.5 10.296875 8.5 21.578125 \n",
+       "z\n",
+       "M 31.109375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-117\"/>\n",
+       "       <path d=\"M 52 44.1875 \n",
+       "Q 55.375 50.25 60.0625 53.125 \n",
+       "Q 64.75 56 71.09375 56 \n",
+       "Q 79.640625 56 84.28125 50.015625 \n",
+       "Q 88.921875 44.046875 88.921875 33.015625 \n",
+       "L 88.921875 0 \n",
+       "L 79.890625 0 \n",
+       "L 79.890625 32.71875 \n",
+       "Q 79.890625 40.578125 77.09375 44.375 \n",
+       "Q 74.3125 48.1875 68.609375 48.1875 \n",
+       "Q 61.625 48.1875 57.5625 43.546875 \n",
+       "Q 53.515625 38.921875 53.515625 30.90625 \n",
+       "L 53.515625 0 \n",
+       "L 44.484375 0 \n",
+       "L 44.484375 32.71875 \n",
+       "Q 44.484375 40.625 41.703125 44.40625 \n",
+       "Q 38.921875 48.1875 33.109375 48.1875 \n",
+       "Q 26.21875 48.1875 22.15625 43.53125 \n",
+       "Q 18.109375 38.875 18.109375 30.90625 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 21.1875 51.21875 25.484375 53.609375 \n",
+       "Q 29.78125 56 35.6875 56 \n",
+       "Q 41.65625 56 45.828125 52.96875 \n",
+       "Q 50 49.953125 52 44.1875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-109\"/>\n",
+       "       <path d=\"M 48.6875 27.296875 \n",
+       "Q 48.6875 37.203125 44.609375 42.84375 \n",
+       "Q 40.53125 48.484375 33.40625 48.484375 \n",
+       "Q 26.265625 48.484375 22.1875 42.84375 \n",
+       "Q 18.109375 37.203125 18.109375 27.296875 \n",
+       "Q 18.109375 17.390625 22.1875 11.75 \n",
+       "Q 26.265625 6.109375 33.40625 6.109375 \n",
+       "Q 40.53125 6.109375 44.609375 11.75 \n",
+       "Q 48.6875 17.390625 48.6875 27.296875 \n",
+       "z\n",
+       "M 18.109375 46.390625 \n",
+       "Q 20.953125 51.265625 25.265625 53.625 \n",
+       "Q 29.59375 56 35.59375 56 \n",
+       "Q 45.5625 56 51.78125 48.09375 \n",
+       "Q 58.015625 40.1875 58.015625 27.296875 \n",
+       "Q 58.015625 14.40625 51.78125 6.484375 \n",
+       "Q 45.5625 -1.421875 35.59375 -1.421875 \n",
+       "Q 29.59375 -1.421875 25.265625 0.953125 \n",
+       "Q 20.953125 3.328125 18.109375 8.203125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 75.984375 \n",
+       "L 18.109375 75.984375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-98\"/>\n",
+       "       <path d=\"M 56.203125 29.59375 \n",
+       "L 56.203125 25.203125 \n",
+       "L 14.890625 25.203125 \n",
+       "Q 15.484375 15.921875 20.484375 11.0625 \n",
+       "Q 25.484375 6.203125 34.421875 6.203125 \n",
+       "Q 39.59375 6.203125 44.453125 7.46875 \n",
+       "Q 49.3125 8.734375 54.109375 11.28125 \n",
+       "L 54.109375 2.78125 \n",
+       "Q 49.265625 0.734375 44.1875 -0.34375 \n",
+       "Q 39.109375 -1.421875 33.890625 -1.421875 \n",
+       "Q 20.796875 -1.421875 13.15625 6.1875 \n",
+       "Q 5.515625 13.8125 5.515625 26.8125 \n",
+       "Q 5.515625 40.234375 12.765625 48.109375 \n",
+       "Q 20.015625 56 32.328125 56 \n",
+       "Q 43.359375 56 49.78125 48.890625 \n",
+       "Q 56.203125 41.796875 56.203125 29.59375 \n",
+       "z\n",
+       "M 47.21875 32.234375 \n",
+       "Q 47.125 39.59375 43.09375 43.984375 \n",
+       "Q 39.0625 48.390625 32.421875 48.390625 \n",
+       "Q 24.90625 48.390625 20.390625 44.140625 \n",
+       "Q 15.875 39.890625 15.1875 32.171875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-101\"/>\n",
+       "       <path d=\"M 41.109375 46.296875 \n",
+       "Q 39.59375 47.171875 37.8125 47.578125 \n",
+       "Q 36.03125 48 33.890625 48 \n",
+       "Q 26.265625 48 22.1875 43.046875 \n",
+       "Q 18.109375 38.09375 18.109375 28.8125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 20.953125 51.171875 25.484375 53.578125 \n",
+       "Q 30.03125 56 36.53125 56 \n",
+       "Q 37.453125 56 38.578125 55.875 \n",
+       "Q 39.703125 55.765625 41.0625 55.515625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-114\"/>\n",
+       "       <path id=\"DejaVuSans-32\"/>\n",
+       "       <path d=\"M 30.609375 48.390625 \n",
+       "Q 23.390625 48.390625 19.1875 42.75 \n",
+       "Q 14.984375 37.109375 14.984375 27.296875 \n",
+       "Q 14.984375 17.484375 19.15625 11.84375 \n",
+       "Q 23.34375 6.203125 30.609375 6.203125 \n",
+       "Q 37.796875 6.203125 41.984375 11.859375 \n",
+       "Q 46.1875 17.53125 46.1875 27.296875 \n",
+       "Q 46.1875 37.015625 41.984375 42.703125 \n",
+       "Q 37.796875 48.390625 30.609375 48.390625 \n",
+       "z\n",
+       "M 30.609375 56 \n",
+       "Q 42.328125 56 49.015625 48.375 \n",
+       "Q 55.71875 40.765625 55.71875 27.296875 \n",
+       "Q 55.71875 13.875 49.015625 6.21875 \n",
+       "Q 42.328125 -1.421875 30.609375 -1.421875 \n",
+       "Q 18.84375 -1.421875 12.171875 6.21875 \n",
+       "Q 5.515625 13.875 5.515625 27.296875 \n",
+       "Q 5.515625 40.765625 12.171875 48.375 \n",
+       "Q 18.84375 56 30.609375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-111\"/>\n",
+       "       <path d=\"M 37.109375 75.984375 \n",
+       "L 37.109375 68.5 \n",
+       "L 28.515625 68.5 \n",
+       "Q 23.6875 68.5 21.796875 66.546875 \n",
+       "Q 19.921875 64.59375 19.921875 59.515625 \n",
+       "L 19.921875 54.6875 \n",
+       "L 34.71875 54.6875 \n",
+       "L 34.71875 47.703125 \n",
+       "L 19.921875 47.703125 \n",
+       "L 19.921875 0 \n",
+       "L 10.890625 0 \n",
+       "L 10.890625 47.703125 \n",
+       "L 2.296875 47.703125 \n",
+       "L 2.296875 54.6875 \n",
+       "L 10.890625 54.6875 \n",
+       "L 10.890625 58.5 \n",
+       "Q 10.890625 67.625 15.140625 71.796875 \n",
+       "Q 19.390625 75.984375 28.609375 75.984375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-102\"/>\n",
+       "       <path d=\"M 9.421875 54.6875 \n",
+       "L 18.40625 54.6875 \n",
+       "L 18.40625 0 \n",
+       "L 9.421875 0 \n",
+       "z\n",
+       "M 9.421875 75.984375 \n",
+       "L 18.40625 75.984375 \n",
+       "L 18.40625 64.59375 \n",
+       "L 9.421875 64.59375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-105\"/>\n",
+       "       <path d=\"M 18.3125 70.21875 \n",
+       "L 18.3125 54.6875 \n",
+       "L 36.8125 54.6875 \n",
+       "L 36.8125 47.703125 \n",
+       "L 18.3125 47.703125 \n",
+       "L 18.3125 18.015625 \n",
+       "Q 18.3125 11.328125 20.140625 9.421875 \n",
+       "Q 21.96875 7.515625 27.59375 7.515625 \n",
+       "L 36.8125 7.515625 \n",
+       "L 36.8125 0 \n",
+       "L 27.59375 0 \n",
+       "Q 17.1875 0 13.234375 3.875 \n",
+       "Q 9.28125 7.765625 9.28125 18.015625 \n",
+       "L 9.28125 47.703125 \n",
+       "L 2.6875 47.703125 \n",
+       "L 2.6875 54.6875 \n",
+       "L 9.28125 54.6875 \n",
+       "L 9.28125 70.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-116\"/>\n",
+       "       <path d=\"M 34.28125 27.484375 \n",
+       "Q 23.390625 27.484375 19.1875 25 \n",
+       "Q 14.984375 22.515625 14.984375 16.5 \n",
+       "Q 14.984375 11.71875 18.140625 8.90625 \n",
+       "Q 21.296875 6.109375 26.703125 6.109375 \n",
+       "Q 34.1875 6.109375 38.703125 11.40625 \n",
+       "Q 43.21875 16.703125 43.21875 25.484375 \n",
+       "L 43.21875 27.484375 \n",
+       "z\n",
+       "M 52.203125 31.203125 \n",
+       "L 52.203125 0 \n",
+       "L 43.21875 0 \n",
+       "L 43.21875 8.296875 \n",
+       "Q 40.140625 3.328125 35.546875 0.953125 \n",
+       "Q 30.953125 -1.421875 24.3125 -1.421875 \n",
+       "Q 15.921875 -1.421875 10.953125 3.296875 \n",
+       "Q 6 8.015625 6 15.921875 \n",
+       "Q 6 25.140625 12.171875 29.828125 \n",
+       "Q 18.359375 34.515625 30.609375 34.515625 \n",
+       "L 43.21875 34.515625 \n",
+       "L 43.21875 35.40625 \n",
+       "Q 43.21875 41.609375 39.140625 45 \n",
+       "Q 35.0625 48.390625 27.6875 48.390625 \n",
+       "Q 23 48.390625 18.546875 47.265625 \n",
+       "Q 14.109375 46.140625 10.015625 43.890625 \n",
+       "L 10.015625 52.203125 \n",
+       "Q 14.9375 54.109375 19.578125 55.046875 \n",
+       "Q 24.21875 56 28.609375 56 \n",
+       "Q 40.484375 56 46.34375 49.84375 \n",
+       "Q 52.203125 43.703125 52.203125 31.203125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-97\"/>\n",
+       "       <path d=\"M 54.890625 33.015625 \n",
+       "L 54.890625 0 \n",
+       "L 45.90625 0 \n",
+       "L 45.90625 32.71875 \n",
+       "Q 45.90625 40.484375 42.875 44.328125 \n",
+       "Q 39.84375 48.1875 33.796875 48.1875 \n",
+       "Q 26.515625 48.1875 22.3125 43.546875 \n",
+       "Q 18.109375 38.921875 18.109375 30.90625 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 21.34375 51.125 25.703125 53.5625 \n",
+       "Q 30.078125 56 35.796875 56 \n",
+       "Q 45.21875 56 50.046875 50.171875 \n",
+       "Q 54.890625 44.34375 54.890625 33.015625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-110\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-78\"/>\n",
+       "      <use x=\"74.804688\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"138.183594\" xlink:href=\"#DejaVuSans-109\"/>\n",
+       "      <use x=\"235.595703\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"299.072266\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"360.595703\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"401.708984\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"433.496094\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"494.677734\" xlink:href=\"#DejaVuSans-102\"/>\n",
+       "      <use x=\"529.882812\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"561.669922\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"589.453125\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"628.662109\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"690.185547\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"731.298828\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"792.578125\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"831.787109\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"859.570312\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"920.751953\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_2\">\n",
+       "    <g id=\"ytick_1\">\n",
+       "     <g id=\"line2d_7\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L -3.5 0 \n",
+       "\" id=\"m7a20f2d7ac\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"223.594127\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_8\">\n",
+       "      <!-- −1.2 -->\n",
+       "      <g transform=\"translate(20.878125 227.393345)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 10.59375 35.5 \n",
+       "L 73.1875 35.5 \n",
+       "L 73.1875 27.203125 \n",
+       "L 10.59375 27.203125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-8722\"/>\n",
+       "        <path d=\"M 10.6875 12.40625 \n",
+       "L 21 12.40625 \n",
+       "L 21 0 \n",
+       "L 10.6875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-46\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-50\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_2\">\n",
+       "     <g id=\"line2d_8\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"195.894119\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_9\">\n",
+       "      <!-- −1.0 -->\n",
+       "      <g transform=\"translate(20.878125 199.693338)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_3\">\n",
+       "     <g id=\"line2d_9\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"168.194112\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_10\">\n",
+       "      <!-- −0.8 -->\n",
+       "      <g transform=\"translate(20.878125 171.993331)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-56\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_4\">\n",
+       "     <g id=\"line2d_10\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"140.494104\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_11\">\n",
+       "      <!-- −0.6 -->\n",
+       "      <g transform=\"translate(20.878125 144.293323)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-54\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_5\">\n",
+       "     <g id=\"line2d_11\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"112.794097\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_12\">\n",
+       "      <!-- −0.4 -->\n",
+       "      <g transform=\"translate(20.878125 116.593316)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-52\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_6\">\n",
+       "     <g id=\"line2d_12\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"85.09409\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_13\">\n",
+       "      <!-- −0.2 -->\n",
+       "      <g transform=\"translate(20.878125 88.893308)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-50\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_7\">\n",
+       "     <g id=\"line2d_13\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"57.394082\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_14\">\n",
+       "      <!-- 0.0 -->\n",
+       "      <g transform=\"translate(29.257812 61.193301)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_8\">\n",
+       "     <g id=\"line2d_14\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m7a20f2d7ac\" y=\"29.694075\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_15\">\n",
+       "      <!-- 0.2 -->\n",
+       "      <g transform=\"translate(29.257812 33.493294)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_16\">\n",
+       "     <!-- Energy (Ha) -->\n",
+       "     <g transform=\"translate(14.798437 145.741094)rotate(-90)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 55.90625 72.90625 \n",
+       "L 55.90625 64.59375 \n",
+       "L 19.671875 64.59375 \n",
+       "L 19.671875 43.015625 \n",
+       "L 54.390625 43.015625 \n",
+       "L 54.390625 34.71875 \n",
+       "L 19.671875 34.71875 \n",
+       "L 19.671875 8.296875 \n",
+       "L 56.78125 8.296875 \n",
+       "L 56.78125 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-69\"/>\n",
+       "       <path d=\"M 45.40625 27.984375 \n",
+       "Q 45.40625 37.75 41.375 43.109375 \n",
+       "Q 37.359375 48.484375 30.078125 48.484375 \n",
+       "Q 22.859375 48.484375 18.828125 43.109375 \n",
+       "Q 14.796875 37.75 14.796875 27.984375 \n",
+       "Q 14.796875 18.265625 18.828125 12.890625 \n",
+       "Q 22.859375 7.515625 30.078125 7.515625 \n",
+       "Q 37.359375 7.515625 41.375 12.890625 \n",
+       "Q 45.40625 18.265625 45.40625 27.984375 \n",
+       "z\n",
+       "M 54.390625 6.78125 \n",
+       "Q 54.390625 -7.171875 48.1875 -13.984375 \n",
+       "Q 42 -20.796875 29.203125 -20.796875 \n",
+       "Q 24.46875 -20.796875 20.265625 -20.09375 \n",
+       "Q 16.0625 -19.390625 12.109375 -17.921875 \n",
+       "L 12.109375 -9.1875 \n",
+       "Q 16.0625 -11.328125 19.921875 -12.34375 \n",
+       "Q 23.78125 -13.375 27.78125 -13.375 \n",
+       "Q 36.625 -13.375 41.015625 -8.765625 \n",
+       "Q 45.40625 -4.15625 45.40625 5.171875 \n",
+       "L 45.40625 9.625 \n",
+       "Q 42.625 4.78125 38.28125 2.390625 \n",
+       "Q 33.9375 0 27.875 0 \n",
+       "Q 17.828125 0 11.671875 7.65625 \n",
+       "Q 5.515625 15.328125 5.515625 27.984375 \n",
+       "Q 5.515625 40.671875 11.671875 48.328125 \n",
+       "Q 17.828125 56 27.875 56 \n",
+       "Q 33.9375 56 38.28125 53.609375 \n",
+       "Q 42.625 51.21875 45.40625 46.390625 \n",
+       "L 45.40625 54.6875 \n",
+       "L 54.390625 54.6875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-103\"/>\n",
+       "       <path d=\"M 32.171875 -5.078125 \n",
+       "Q 28.375 -14.84375 24.75 -17.8125 \n",
+       "Q 21.140625 -20.796875 15.09375 -20.796875 \n",
+       "L 7.90625 -20.796875 \n",
+       "L 7.90625 -13.28125 \n",
+       "L 13.1875 -13.28125 \n",
+       "Q 16.890625 -13.28125 18.9375 -11.515625 \n",
+       "Q 21 -9.765625 23.484375 -3.21875 \n",
+       "L 25.09375 0.875 \n",
+       "L 2.984375 54.6875 \n",
+       "L 12.5 54.6875 \n",
+       "L 29.59375 11.921875 \n",
+       "L 46.6875 54.6875 \n",
+       "L 56.203125 54.6875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-121\"/>\n",
+       "       <path d=\"M 31 75.875 \n",
+       "Q 24.46875 64.65625 21.28125 53.65625 \n",
+       "Q 18.109375 42.671875 18.109375 31.390625 \n",
+       "Q 18.109375 20.125 21.3125 9.0625 \n",
+       "Q 24.515625 -2 31 -13.1875 \n",
+       "L 23.1875 -13.1875 \n",
+       "Q 15.875 -1.703125 12.234375 9.375 \n",
+       "Q 8.59375 20.453125 8.59375 31.390625 \n",
+       "Q 8.59375 42.28125 12.203125 53.3125 \n",
+       "Q 15.828125 64.359375 23.1875 75.875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-40\"/>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 19.671875 72.90625 \n",
+       "L 19.671875 43.015625 \n",
+       "L 55.515625 43.015625 \n",
+       "L 55.515625 72.90625 \n",
+       "L 65.375 72.90625 \n",
+       "L 65.375 0 \n",
+       "L 55.515625 0 \n",
+       "L 55.515625 34.71875 \n",
+       "L 19.671875 34.71875 \n",
+       "L 19.671875 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-72\"/>\n",
+       "       <path d=\"M 8.015625 75.875 \n",
+       "L 15.828125 75.875 \n",
+       "Q 23.140625 64.359375 26.78125 53.3125 \n",
+       "Q 30.421875 42.28125 30.421875 31.390625 \n",
+       "Q 30.421875 20.453125 26.78125 9.375 \n",
+       "Q 23.140625 -1.703125 15.828125 -13.1875 \n",
+       "L 8.015625 -13.1875 \n",
+       "Q 14.5 -2 17.703125 9.0625 \n",
+       "Q 20.90625 20.125 20.90625 31.390625 \n",
+       "Q 20.90625 42.671875 17.703125 53.65625 \n",
+       "Q 14.5 64.65625 8.015625 75.875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-41\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-69\"/>\n",
+       "      <use x=\"63.183594\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "      <use x=\"126.5625\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"188.085938\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"227.449219\" xlink:href=\"#DejaVuSans-103\"/>\n",
+       "      <use x=\"290.925781\" xlink:href=\"#DejaVuSans-121\"/>\n",
+       "      <use x=\"350.105469\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"381.892578\" xlink:href=\"#DejaVuSans-40\"/>\n",
+       "      <use x=\"420.90625\" xlink:href=\"#DejaVuSans-72\"/>\n",
+       "      <use x=\"496.101562\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"557.380859\" xlink:href=\"#DejaVuSans-41\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"line2d_15\">\n",
+       "    <path clip-path=\"url(#pbfd4c8560f)\" d=\"M 67.379119 17.083636 \n",
+       "L 70.453499 59.162431 \n",
+       "L 73.52788 79.407506 \n",
+       "L 76.60226 95.210999 \n",
+       "L 79.67664 115.446164 \n",
+       "L 82.75102 131.715299 \n",
+       "L 85.8254 141.174561 \n",
+       "L 88.89978 146.302209 \n",
+       "L 91.974161 149.293451 \n",
+       "L 95.048541 151.575729 \n",
+       "L 98.122921 154.266659 \n",
+       "L 101.197301 157.17722 \n",
+       "L 104.271681 159.795712 \n",
+       "L 107.346061 161.931274 \n",
+       "L 110.420442 163.915613 \n",
+       "L 113.494822 166.376486 \n",
+       "L 116.569202 169.759944 \n",
+       "L 119.643582 174.169725 \n",
+       "L 122.717962 179.458996 \n",
+       "L 125.792342 185.234189 \n",
+       "L 128.866723 190.851049 \n",
+       "L 131.941103 195.617314 \n",
+       "L 135.015483 199.160219 \n",
+       "L 138.089863 201.693139 \n",
+       "L 141.164243 203.707113 \n",
+       "L 144.238623 205.277677 \n",
+       "L 147.313004 206.065487 \n",
+       "L 150.387384 206.009472 \n",
+       "L 153.461764 205.744671 \n",
+       "L 156.536144 206.226523 \n",
+       "L 159.610524 207.918238 \n",
+       "L 162.684904 210.307467 \n",
+       "L 165.759285 212.223385 \n",
+       "L 168.833665 212.775448 \n",
+       "L 171.908045 212.084488 \n",
+       "L 174.982425 211.071191 \n",
+       "L 178.056805 210.636355 \n",
+       "L 181.131185 211.074441 \n",
+       "L 184.205566 212.070507 \n",
+       "L 187.279946 213.082506 \n",
+       "L 190.354326 213.691593 \n",
+       "L 193.428706 213.736827 \n",
+       "L 196.503086 213.341923 \n",
+       "L 199.577466 212.868223 \n",
+       "L 202.651847 212.715921 \n",
+       "L 205.726227 213.035753 \n",
+       "L 208.800607 213.603043 \n",
+       "L 211.874987 214.018049 \n",
+       "L 214.949367 214.061001 \n",
+       "L 218.023747 213.848249 \n",
+       "L 221.098128 213.659017 \n",
+       "L 224.172508 213.664885 \n",
+       "L 227.246888 213.835347 \n",
+       "L 230.321268 214.041707 \n",
+       "L 233.395648 214.193222 \n",
+       "L 236.470028 214.272251 \n",
+       "L 239.544409 214.293527 \n",
+       "L 242.618789 214.282296 \n",
+       "L 245.693169 214.282259 \n",
+       "L 248.767549 214.335711 \n",
+       "L 251.841929 214.437753 \n",
+       "L 254.916309 214.534153 \n",
+       "L 257.99069 214.579094 \n",
+       "L 261.06507 214.580142 \n",
+       "L 264.13945 214.576204 \n",
+       "L 267.21383 214.588764 \n",
+       "L 270.28821 214.612231 \n",
+       "L 273.36259 214.638786 \n",
+       "L 276.436971 214.668014 \n",
+       "L 279.511351 214.693322 \n",
+       "L 282.585731 214.701257 \n",
+       "L 285.660111 214.691601 \n",
+       "L 288.734491 214.683392 \n",
+       "L 291.808871 214.692365 \n",
+       "L 294.883252 214.712222 \n",
+       "L 297.957632 214.725843 \n",
+       "L 301.032012 214.726955 \n",
+       "L 304.106392 214.722567 \n",
+       "L 307.180772 214.720176 \n",
+       "L 310.255152 214.721699 \n",
+       "L 313.329533 214.72684 \n",
+       "L 316.403913 214.733977 \n",
+       "L 319.478293 214.738464 \n",
+       "L 322.552673 214.736764 \n",
+       "L 325.627053 214.732428 \n",
+       "L 328.701433 214.732605 \n",
+       "L 331.775814 214.73841 \n",
+       "L 334.850194 214.743692 \n",
+       "L 337.924574 214.743867 \n",
+       "L 340.998954 214.741263 \n",
+       "L 344.073334 214.740513 \n",
+       "L 347.147714 214.742716 \n",
+       "L 350.222095 214.745901 \n",
+       "L 353.296475 214.748198 \n",
+       "L 356.370855 214.74876 \n",
+       "L 359.445235 214.747765 \n",
+       "L 362.519615 214.746894 \n",
+       "L 365.593995 214.748086 \n",
+       "L 368.668376 214.750921 \n",
+       "L 371.742756 214.752832 \n",
+       "\" style=\"fill:none;stroke:#ff0000;stroke-linecap:square;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"line2d_16\">\n",
+       "    <path clip-path=\"url(#pbfd4c8560f)\" d=\"M 67.379119 214.756364 \n",
+       "L 70.453499 214.756364 \n",
+       "L 73.52788 214.756364 \n",
+       "L 76.60226 214.756364 \n",
+       "L 79.67664 214.756364 \n",
+       "L 82.75102 214.756364 \n",
+       "L 85.8254 214.756364 \n",
+       "L 88.89978 214.756364 \n",
+       "L 91.974161 214.756364 \n",
+       "L 95.048541 214.756364 \n",
+       "L 98.122921 214.756364 \n",
+       "L 101.197301 214.756364 \n",
+       "L 104.271681 214.756364 \n",
+       "L 107.346061 214.756364 \n",
+       "L 110.420442 214.756364 \n",
+       "L 113.494822 214.756364 \n",
+       "L 116.569202 214.756364 \n",
+       "L 119.643582 214.756364 \n",
+       "L 122.717962 214.756364 \n",
+       "L 125.792342 214.756364 \n",
+       "L 128.866723 214.756364 \n",
+       "L 131.941103 214.756364 \n",
+       "L 135.015483 214.756364 \n",
+       "L 138.089863 214.756364 \n",
+       "L 141.164243 214.756364 \n",
+       "L 144.238623 214.756364 \n",
+       "L 147.313004 214.756364 \n",
+       "L 150.387384 214.756364 \n",
+       "L 153.461764 214.756364 \n",
+       "L 156.536144 214.756364 \n",
+       "L 159.610524 214.756364 \n",
+       "L 162.684904 214.756364 \n",
+       "L 165.759285 214.756364 \n",
+       "L 168.833665 214.756364 \n",
+       "L 171.908045 214.756364 \n",
+       "L 174.982425 214.756364 \n",
+       "L 178.056805 214.756364 \n",
+       "L 181.131185 214.756364 \n",
+       "L 184.205566 214.756364 \n",
+       "L 187.279946 214.756364 \n",
+       "L 190.354326 214.756364 \n",
+       "L 193.428706 214.756364 \n",
+       "L 196.503086 214.756364 \n",
+       "L 199.577466 214.756364 \n",
+       "L 202.651847 214.756364 \n",
+       "L 205.726227 214.756364 \n",
+       "L 208.800607 214.756364 \n",
+       "L 211.874987 214.756364 \n",
+       "L 214.949367 214.756364 \n",
+       "L 218.023747 214.756364 \n",
+       "L 221.098128 214.756364 \n",
+       "L 224.172508 214.756364 \n",
+       "L 227.246888 214.756364 \n",
+       "L 230.321268 214.756364 \n",
+       "L 233.395648 214.756364 \n",
+       "L 236.470028 214.756364 \n",
+       "L 239.544409 214.756364 \n",
+       "L 242.618789 214.756364 \n",
+       "L 245.693169 214.756364 \n",
+       "L 248.767549 214.756364 \n",
+       "L 251.841929 214.756364 \n",
+       "L 254.916309 214.756364 \n",
+       "L 257.99069 214.756364 \n",
+       "L 261.06507 214.756364 \n",
+       "L 264.13945 214.756364 \n",
+       "L 267.21383 214.756364 \n",
+       "L 270.28821 214.756364 \n",
+       "L 273.36259 214.756364 \n",
+       "L 276.436971 214.756364 \n",
+       "L 279.511351 214.756364 \n",
+       "L 282.585731 214.756364 \n",
+       "L 285.660111 214.756364 \n",
+       "L 288.734491 214.756364 \n",
+       "L 291.808871 214.756364 \n",
+       "L 294.883252 214.756364 \n",
+       "L 297.957632 214.756364 \n",
+       "L 301.032012 214.756364 \n",
+       "L 304.106392 214.756364 \n",
+       "L 307.180772 214.756364 \n",
+       "L 310.255152 214.756364 \n",
+       "L 313.329533 214.756364 \n",
+       "L 316.403913 214.756364 \n",
+       "L 319.478293 214.756364 \n",
+       "L 322.552673 214.756364 \n",
+       "L 325.627053 214.756364 \n",
+       "L 328.701433 214.756364 \n",
+       "L 331.775814 214.756364 \n",
+       "L 334.850194 214.756364 \n",
+       "L 337.924574 214.756364 \n",
+       "L 340.998954 214.756364 \n",
+       "L 344.073334 214.756364 \n",
+       "L 347.147714 214.756364 \n",
+       "L 350.222095 214.756364 \n",
+       "L 353.296475 214.756364 \n",
+       "L 356.370855 214.756364 \n",
+       "L 359.445235 214.756364 \n",
+       "L 362.519615 214.756364 \n",
+       "L 365.593995 214.756364 \n",
+       "L 368.668376 214.756364 \n",
+       "L 371.742756 214.756364 \n",
+       "\" style=\"fill:none;stroke:#0000ff;stroke-dasharray:1.5,2.475;stroke-dashoffset:0;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_3\">\n",
+       "    <path d=\"M 52.160938 224.64 \n",
+       "L 52.160938 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_4\">\n",
+       "    <path d=\"M 386.960938 224.64 \n",
+       "L 386.960938 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_5\">\n",
+       "    <path d=\"M 52.160938 224.64 \n",
+       "L 386.960938 224.64 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_6\">\n",
+       "    <path d=\"M 52.160938 7.2 \n",
+       "L 386.960938 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"legend_1\">\n",
+       "    <g id=\"patch_7\">\n",
+       "     <path d=\"M 244.220312 44.978125 \n",
+       "L 379.960938 44.978125 \n",
+       "Q 381.960938 44.978125 381.960938 42.978125 \n",
+       "L 381.960938 14.2 \n",
+       "Q 381.960938 12.2 379.960938 12.2 \n",
+       "L 244.220312 12.2 \n",
+       "Q 242.220312 12.2 242.220312 14.2 \n",
+       "L 242.220312 42.978125 \n",
+       "Q 242.220312 44.978125 244.220312 44.978125 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;opacity:0.8;stroke:#cccccc;stroke-linejoin:miter;\"/>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_17\">\n",
+       "     <path d=\"M 246.220312 20.4 \n",
+       "L 266.220312 20.4 \n",
+       "\" style=\"fill:none;stroke:#ff0000;stroke-linecap:square;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_18\"/>\n",
+       "    <g id=\"text_17\">\n",
+       "     <!-- $\\left\\langle {\\psi \\left( {\\theta } \\right)} \\right|H\\left| {\\psi \\left( {\\theta } \\right)} \\right\\rangle $ -->\n",
+       "     <g transform=\"translate(274.220312 23.9)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 8.9375 31.34375 \n",
+       "L 22.703125 75.875 \n",
+       "L 31 75.875 \n",
+       "L 17.234375 31.34375 \n",
+       "L 31 -13.1875 \n",
+       "L 22.703125 -13.1875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-10216\"/>\n",
+       "       <path d=\"M 24.859375 -1.21875 \n",
+       "Q 13.921875 0.59375 9.625 5.328125 \n",
+       "Q 4.34375 11.140625 6.640625 23 \n",
+       "L 12.796875 54.6875 \n",
+       "L 21.875 54.6875 \n",
+       "L 15.765625 23.34375 \n",
+       "Q 14.0625 14.40625 17.484375 10.6875 \n",
+       "Q 20.515625 7.46875 26.421875 6.78125 \n",
+       "L 35.6875 54.6875 \n",
+       "L 44.625 54.6875 \n",
+       "L 35.359375 6.84375 \n",
+       "Q 41.890625 7.515625 45.75 10.75 \n",
+       "Q 50.734375 14.84375 52.390625 23.390625 \n",
+       "L 58.453125 54.6875 \n",
+       "L 67.53125 54.6875 \n",
+       "L 61.375 23.046875 \n",
+       "Q 58.984375 10.75 51.5625 5.375 \n",
+       "Q 44.875 0.53125 33.796875 -1.171875 \n",
+       "L 29.984375 -20.796875 \n",
+       "L 21.046875 -20.796875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Oblique-968\"/>\n",
+       "       <path d=\"M 45.515625 34.671875 \n",
+       "L 14.453125 34.671875 \n",
+       "Q 12.359375 20.0625 14.5 13.875 \n",
+       "Q 17.1875 6.25 24.46875 6.25 \n",
+       "Q 31.78125 6.25 37.359375 13.921875 \n",
+       "Q 42.234375 20.65625 45.515625 34.671875 \n",
+       "z\n",
+       "M 47.015625 42.96875 \n",
+       "Q 48.34375 56.84375 46.625 61.71875 \n",
+       "Q 43.953125 69.4375 36.765625 69.4375 \n",
+       "Q 29.296875 69.4375 23.828125 61.8125 \n",
+       "Q 19.53125 55.671875 16.15625 42.96875 \n",
+       "z\n",
+       "M 38.1875 76.765625 \n",
+       "Q 49.90625 76.765625 54.59375 66.40625 \n",
+       "Q 59.28125 56.109375 55.71875 37.84375 \n",
+       "Q 52.203125 19.625 43.453125 9.28125 \n",
+       "Q 34.765625 -1.125 23.046875 -1.125 \n",
+       "Q 11.28125 -1.125 6.640625 9.28125 \n",
+       "Q 2 19.625 5.515625 37.84375 \n",
+       "Q 9.078125 56.109375 17.71875 66.40625 \n",
+       "Q 26.421875 76.765625 38.1875 76.765625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Oblique-952\"/>\n",
+       "       <path d=\"M 21 76.421875 \n",
+       "L 21 -23.578125 \n",
+       "L 12.703125 -23.578125 \n",
+       "L 12.703125 76.421875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-124\"/>\n",
+       "       <path d=\"M 16.890625 72.90625 \n",
+       "L 26.8125 72.90625 \n",
+       "L 21 43.015625 \n",
+       "L 56.78125 43.015625 \n",
+       "L 62.59375 72.90625 \n",
+       "L 72.515625 72.90625 \n",
+       "L 58.296875 0 \n",
+       "L 48.390625 0 \n",
+       "L 55.171875 34.71875 \n",
+       "L 19.390625 34.71875 \n",
+       "L 12.59375 0 \n",
+       "L 2.6875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Oblique-72\"/>\n",
+       "       <path d=\"M 30.078125 31.34375 \n",
+       "L 16.3125 -13.1875 \n",
+       "L 8.015625 -13.1875 \n",
+       "L 21.78125 31.34375 \n",
+       "L 8.015625 75.875 \n",
+       "L 16.3125 75.875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-10217\"/>\n",
+       "      </defs>\n",
+       "      <use transform=\"translate(0 0.234375)\" xlink:href=\"#DejaVuSans-10216\"/>\n",
+       "      <use transform=\"translate(39.013672 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-968\"/>\n",
+       "      <use transform=\"translate(104.980469 0.234375)\" xlink:href=\"#DejaVuSans-40\"/>\n",
+       "      <use transform=\"translate(143.994141 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-952\"/>\n",
+       "      <use transform=\"translate(205.175781 0.234375)\" xlink:href=\"#DejaVuSans-41\"/>\n",
+       "      <use transform=\"translate(244.189453 0.234375)\" xlink:href=\"#DejaVuSans-124\"/>\n",
+       "      <use transform=\"translate(277.880859 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-72\"/>\n",
+       "      <use transform=\"translate(353.076172 0.234375)\" xlink:href=\"#DejaVuSans-124\"/>\n",
+       "      <use transform=\"translate(386.767578 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-968\"/>\n",
+       "      <use transform=\"translate(452.734375 0.234375)\" xlink:href=\"#DejaVuSans-40\"/>\n",
+       "      <use transform=\"translate(491.748047 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-952\"/>\n",
+       "      <use transform=\"translate(552.929688 0.234375)\" xlink:href=\"#DejaVuSans-41\"/>\n",
+       "      <use transform=\"translate(591.943359 0.234375)\" xlink:href=\"#DejaVuSans-10217\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_19\">\n",
+       "     <path d=\"M 246.220312 35.398437 \n",
+       "L 266.220312 35.398437 \n",
+       "\" style=\"fill:none;stroke:#0000ff;stroke-dasharray:1.5,2.475;stroke-dashoffset:0;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_20\"/>\n",
+       "    <g id=\"text_18\">\n",
+       "     <!-- Ground-state energy -->\n",
+       "     <g transform=\"translate(274.220312 38.898437)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 59.515625 10.40625 \n",
+       "L 59.515625 29.984375 \n",
+       "L 43.40625 29.984375 \n",
+       "L 43.40625 38.09375 \n",
+       "L 69.28125 38.09375 \n",
+       "L 69.28125 6.78125 \n",
+       "Q 63.578125 2.734375 56.6875 0.65625 \n",
+       "Q 49.8125 -1.421875 42 -1.421875 \n",
+       "Q 24.90625 -1.421875 15.25 8.5625 \n",
+       "Q 5.609375 18.5625 5.609375 36.375 \n",
+       "Q 5.609375 54.25 15.25 64.234375 \n",
+       "Q 24.90625 74.21875 42 74.21875 \n",
+       "Q 49.125 74.21875 55.546875 72.453125 \n",
+       "Q 61.96875 70.703125 67.390625 67.28125 \n",
+       "L 67.390625 56.78125 \n",
+       "Q 61.921875 61.421875 55.765625 63.765625 \n",
+       "Q 49.609375 66.109375 42.828125 66.109375 \n",
+       "Q 29.4375 66.109375 22.71875 58.640625 \n",
+       "Q 16.015625 51.171875 16.015625 36.375 \n",
+       "Q 16.015625 21.625 22.71875 14.15625 \n",
+       "Q 29.4375 6.6875 42.828125 6.6875 \n",
+       "Q 48.046875 6.6875 52.140625 7.59375 \n",
+       "Q 56.25 8.5 59.515625 10.40625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-71\"/>\n",
+       "       <path d=\"M 45.40625 46.390625 \n",
+       "L 45.40625 75.984375 \n",
+       "L 54.390625 75.984375 \n",
+       "L 54.390625 0 \n",
+       "L 45.40625 0 \n",
+       "L 45.40625 8.203125 \n",
+       "Q 42.578125 3.328125 38.25 0.953125 \n",
+       "Q 33.9375 -1.421875 27.875 -1.421875 \n",
+       "Q 17.96875 -1.421875 11.734375 6.484375 \n",
+       "Q 5.515625 14.40625 5.515625 27.296875 \n",
+       "Q 5.515625 40.1875 11.734375 48.09375 \n",
+       "Q 17.96875 56 27.875 56 \n",
+       "Q 33.9375 56 38.25 53.625 \n",
+       "Q 42.578125 51.265625 45.40625 46.390625 \n",
+       "z\n",
+       "M 14.796875 27.296875 \n",
+       "Q 14.796875 17.390625 18.875 11.75 \n",
+       "Q 22.953125 6.109375 30.078125 6.109375 \n",
+       "Q 37.203125 6.109375 41.296875 11.75 \n",
+       "Q 45.40625 17.390625 45.40625 27.296875 \n",
+       "Q 45.40625 37.203125 41.296875 42.84375 \n",
+       "Q 37.203125 48.484375 30.078125 48.484375 \n",
+       "Q 22.953125 48.484375 18.875 42.84375 \n",
+       "Q 14.796875 37.203125 14.796875 27.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-100\"/>\n",
+       "       <path d=\"M 4.890625 31.390625 \n",
+       "L 31.203125 31.390625 \n",
+       "L 31.203125 23.390625 \n",
+       "L 4.890625 23.390625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-45\"/>\n",
+       "       <path d=\"M 44.28125 53.078125 \n",
+       "L 44.28125 44.578125 \n",
+       "Q 40.484375 46.53125 36.375 47.5 \n",
+       "Q 32.28125 48.484375 27.875 48.484375 \n",
+       "Q 21.1875 48.484375 17.84375 46.4375 \n",
+       "Q 14.5 44.390625 14.5 40.28125 \n",
+       "Q 14.5 37.15625 16.890625 35.375 \n",
+       "Q 19.28125 33.59375 26.515625 31.984375 \n",
+       "L 29.59375 31.296875 \n",
+       "Q 39.15625 29.25 43.1875 25.515625 \n",
+       "Q 47.21875 21.78125 47.21875 15.09375 \n",
+       "Q 47.21875 7.46875 41.1875 3.015625 \n",
+       "Q 35.15625 -1.421875 24.609375 -1.421875 \n",
+       "Q 20.21875 -1.421875 15.453125 -0.5625 \n",
+       "Q 10.6875 0.296875 5.421875 2 \n",
+       "L 5.421875 11.28125 \n",
+       "Q 10.40625 8.6875 15.234375 7.390625 \n",
+       "Q 20.0625 6.109375 24.8125 6.109375 \n",
+       "Q 31.15625 6.109375 34.5625 8.28125 \n",
+       "Q 37.984375 10.453125 37.984375 14.40625 \n",
+       "Q 37.984375 18.0625 35.515625 20.015625 \n",
+       "Q 33.0625 21.96875 24.703125 23.78125 \n",
+       "L 21.578125 24.515625 \n",
+       "Q 13.234375 26.265625 9.515625 29.90625 \n",
+       "Q 5.8125 33.546875 5.8125 39.890625 \n",
+       "Q 5.8125 47.609375 11.28125 51.796875 \n",
+       "Q 16.75 56 26.8125 56 \n",
+       "Q 31.78125 56 36.171875 55.265625 \n",
+       "Q 40.578125 54.546875 44.28125 53.078125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-115\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-71\"/>\n",
+       "      <use x=\"77.490234\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"116.353516\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"177.535156\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"240.914062\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "      <use x=\"304.292969\" xlink:href=\"#DejaVuSans-100\"/>\n",
+       "      <use x=\"367.769531\" xlink:href=\"#DejaVuSans-45\"/>\n",
+       "      <use x=\"403.853516\" xlink:href=\"#DejaVuSans-115\"/>\n",
+       "      <use x=\"455.953125\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"495.162109\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"556.441406\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"595.650391\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"657.173828\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"688.960938\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"750.484375\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "      <use x=\"813.863281\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"875.386719\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"914.75\" xlink:href=\"#DejaVuSans-103\"/>\n",
+       "      <use x=\"978.226562\" xlink:href=\"#DejaVuSans-121\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"pbfd4c8560f\">\n",
+       "   <rect height=\"217.44\" width=\"334.8\" x=\"52.160938\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "result = numpy.load('./output/summary_data.npz')\n",
+    "\n",
+    "eig_val, eig_state = numpy.linalg.eig(\n",
+    "                     pauli_str_to_matrix(Hamiltonian, N))\n",
+    "min_eig_H = numpy.min(eig_val.real)\n",
+    "min_loss = numpy.ones([len(result['iter'])]) * min_eig_H\n",
+    "\n",
+    "plt.figure(1)\n",
+    "func1, = plt.plot(result['iter'], result['energy'], \n",
+    "                  alpha=0.7, marker='', linestyle=\"-\", color='r')\n",
+    "func_min, = plt.plot(result['iter'], min_loss, \n",
+    "                  alpha=0.7, marker='', linestyle=\":\", color='b')\n",
+    "plt.xlabel('Number of iteration')\n",
+    "plt.ylabel('Energy (Ha)')\n",
+    "\n",
+    "plt.legend(handles=[\n",
+    "    func1,\n",
+    "    func_min\n",
+    "],\n",
+    "    labels=[\n",
+    "        r'$\\left\\langle {\\psi \\left( {\\theta } \\right)} '\n",
+    "        r'\\right|H\\left| {\\psi \\left( {\\theta } \\right)} \\right\\rangle $',\n",
+    "        'Ground-state energy',\n",
+    "    ], loc='best')\n",
+    "\n",
+    "#plt.savefig(\"vqe.png\", bbox_inches='tight', dpi=300)\n",
+    "plt.show()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## 通过 VQE 确定原子间隔\n",
+    "\n",
+    "还记得在前面的注释中提到我们默认使用的两个氢原子间原子间隔为 $74$ pm 吗？VQE 的另一个用法便是通过在不同的原子间隔下多次运行然后观察运行结果的最小值是在什么原子间隔发生的，这个间隔即为估计得真实原子间隔。\n",
+    "\n",
+    "![vqe-fig-dist](figures/vqe-fig-distance.png)\n",
+    "\n",
+    "从上述过程中可以看出，最小值确实发生在 $d = 74$ pm (1 pm = $1\\times 10^{-12}$m) 附近，这是与[实验测得数据](https://cccbdb.nist.gov/exp2x.asp?casno=1333740&charge=0)相符合的 $d_{exp} (H_2) = 74.14$ pm."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## 参考文献\n",
+    "\n",
+    "[1] Cao, Yudong, et al. Quantum chemistry in the age of quantum computing. [Chemical reviews 119.19 (2019): 10856-10915.](https://pubs.acs.org/doi/10.1021/acs.chemrev.8b00803)\n",
+    "\n",
+    "[2] McArdle, Sam, et al. Quantum computational chemistry. [Reviews of Modern Physics 92.1 (2020): 015003.](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003)\n",
+    "\n",
+    "\n",
+    "[3] Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. [Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
+    "\n",
+    "[4] Moll, Nikolaj, et al. Quantum optimization using variational algorithms on near-term quantum devices. [Quantum Science and Technology 3.3 (2018): 030503.](https://iopscience.iop.org/article/10.1088/2058-9565/aab822)\n",
+    "\n",
+    "[5] 徐光宪, 黎乐民, 王德民. 量子化学: 基本原理和从头计算法(上)[M], 第二版. 北京: 科学出版社, 2012; \n",
+    "\n",
+    "[6] Helgaker, Trygve, Poul Jorgensen, and Jeppe Olsen. Molecular electronic-structure theory. John Wiley & Sons, 2014.\n",
+    "\n",
+    "[7] Dirac, Paul Adrien Maurice. Quantum mechanics of many-electron systems. [Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 123.792 (1929): 714-733.](https://royalsocietypublishing.org/doi/10.1098/rspa.1929.0094)\n",
+    "\n",
+    "[8] Szabo, Attila, and Neil S. Ostlund. Modern quantum chemistry: introduction to advanced electronic structure theory. Courier Corporation, 2012."
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/VQE/VQE_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Variational Quantum Eigensolver\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Overview\n",
+    "\n",
+    "It is widely believed that one of the most promising applications of quantum computing in the near future is solving quantum chemistry problems [1-2]. **Variational Quantum Eigensolver** (VQE) is a strong proof to this possibility of studying quantum chemistry with **Noisy Intermediate-Scale Quantum** (NISQ) devices [1-4]. The core task is to solve the energy ground state of any molecular Hamiltonian $\\hat{H}$ by preparing a parametrized wave function ansatz $|\\Psi(\\boldsymbol\\theta)\\rangle$ on a quantum computer and adopt classical optimization methods (e.g. gradient descent) to adjust the parameters $\\boldsymbol\\theta$ to minimize the expectation value $\\langle \\Psi(\\boldsymbol\\theta)|\\hat{H}|\\Psi(\\boldsymbol\\theta)\\rangle$. This approach is based on the **Rayleigh-Ritz variational principle**. \n",
+    "\n",
+    "$$\n",
+    "E_0 = \\min_{\\boldsymbol\\theta} \\langle \\Psi(\\boldsymbol\\theta)|\\hat{H}|\\Psi(\\boldsymbol\\theta)\\rangle.\n",
+    "\\tag{1}\n",
+    "$$\n",
+    "\n",
+    "where $E_0$ denotes the ground state energy. Numerically, it can be understood as finding the smallest eigenvalue $\\lambda_{\\min}$ of a **discretized** Hamiltonian $H$ (hermitian matrix) and its corresponding eigenvector $|\\Psi_0\\rangle$. How such a discretization can be done on a classical computer belongs to the art of quantum chemistry and is far beyond the scope of this tutorial. We will discuss this part with a few words in the background section. In general, such a Hamiltonian $H$ is expressed as a weighted sum of Pauli spin operators $\\{X,Y,Z\\}$ (native to quantum devices) such that this information can be processed on a quantum computer.\n",
+    "\n",
+    "$$\n",
+    "H = \\sum_k c_k ~ \\bigg( \\bigotimes_{j=0}^{M-1} \\sigma_j^{(k)} \\bigg),\n",
+    "\\tag{2}\n",
+    "$$\n",
+    "\n",
+    "where $\\sigma_j^{(k)} \\in \\{I,X,Y,Z\\}$ and $M$ stands for qubit number. We refer this form of Hamiltonian as **Pauli strings**. For example, \n",
+    "\n",
+    "$$\n",
+    "H= 0.12~Y_0 \\otimes I_1-0.04~X_0\\otimes Z_1.\n",
+    "\\tag{3}\n",
+    "$$\n",
+    "\n",
+    "In the next section, we will provide a brief review on the electronic structure problem which essentially tells us where does the Hamiltonian $H$ come from. For those who are already familiar with this topic or only interested in how to implement VQE on Paddle Quantum, please skip this part and jump into the illustrative example of hydrogen molecule $H_2$.\n",
+    "\n",
+    "## Background: the electronic structure problem\n",
+    "\n",
+    "In this section, we focus on one of the fundamental problems in quantum chemistry --  **the electronic structure problem**. To be more specific, we are interested in the low lying energy eigenstates of any given molecule. These knowledge could help predict reaction rates and location of stable structures [5]. Suppose a molecule consists of $N_n$ nuclei and $N_e$ electrons, the first quantized (canonical quantization) Hamiltonian operator $\\hat{H}_{mol}$ describing the total energy of this molecular system can be written as\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "\\hat{H}_{\\text{mol}} & = -\\sum_{i}\\frac{\\nabla_{R_i}^2}{2M_i} - \\sum_{i} \\frac{\\nabla_{r_i}^2}{2} -\\sum_{i,j}\\frac{Z_i}{\\lvert R_i - r_j\\lvert} + \\sum_{i,j>i}\\frac{Z_iZ_j}{\\lvert R_i - R_j\\lvert} + \\sum_{i, j>i}\\frac{1}{\\lvert r_i - r_j\\lvert}, \n",
+    "\\tag{4}\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "where $R_i, M_i,$ and $Z_i$ denote the position, mass and atomic number (the number of protons) of the $i^{th}$ nucleus, and the positions of electrons are $r_i$. The first two sums describe the kinetic energy of nuclei and electrons, respectively. The third sum describes the attractive Coulomb interaction between the positively charged nuclei and the negatively charged electrons. The last two terms represent the repulsive nuclei-nuclei and electron-electron interactions.  Here, the molecular Hamiltonian $\\hat{H}_\\text{mol}$ is already in atomic units of energy, **Hartree**. 1 Hartree is $[\\hbar^2/(m_ee^2a_0^2)] = 27.2$ eV or 630 kcal/mol, where $m_e, e,$ and $a_0$ stand for the mass of electron, charge of electron, and Bohr radius. \n",
+    "\n",
+    "\n",
+    "**Note:** The spin-orbit interaction and hyperfine interaction are not considered in this picture. They can be treated as perturbations if necessary. \n",
+    "\n",
+    "### Born-Oppenheimer approximation\n",
+    "\n",
+    "Since the nuclei are much heavier than electrons, the electrons will move much faster than the nuclei. It is reasonable to treat the positions of nuclei as fixed, $R_i =$ constants. This is known as the Born-Oppenheimer approximation by decoupling the behavior of nuclei and electrons in time scale. Consequently, the kinetic energy term of nuclei will disappear and the nuclei-nuclei repulsive interaction term can be viewed as an energy shift (independent of electron positions $r_i$). We could derive the electronic Hamiltonian $\\hat{H}_{\\text{electron}}$ as\n",
+    "\n",
+    "$$\n",
+    "\\begin{align}\n",
+    "\\hat{H}_{\\text{electron}} & =  - \\sum_{i} \\frac{\\nabla_{r_i}^2}{2} -\\sum_{i,j}\\frac{Z_i}{\\lvert R_i - r_j\\lvert} + \\sum_{i, j>i}\\frac{1}{\\lvert r_i - r_j\\lvert} \n",
+    "\\tag{5},\n",
+    "\\end{align}\n",
+    "$$\n",
+    "\n",
+    "The energy levels of the electrons in the molecule can be found by solving the time independent Schrödinger equation\n",
+    "$$\n",
+    "\\hat{H}_{\\text{electron}} |\\Psi_n \\rangle = E_n |\\Psi_n \\rangle,\n",
+    "\\tag{6}\n",
+    "$$\n",
+    "\n",
+    "where $n$ stands for the energy level. Notice the electron repulsion terms scale as $N_e(N_e-1)/2$ which means for the Oxygen molecule $O_2$ carrying 16 electrons there will be 120 electron repulsion terms in total! In general, this problem cannot be solved analytically. As Dirac concluded in [Quantum mechanics of many-electron systems](https://royalsocietypublishing.org/doi/10.1098/rspa.1929.0094) [6],\n",
+    "\n",
+    "> *The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.*                                                                                                                                                                  \n",
+    ">\n",
+    "> ​\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t-- Paul Dirac (1929)\n",
+    "\n",
+    "A straightforward numerical approach is discretizing the infinite-dimensional Hilbert space into equidistant grid points where linear algebra guides the whole calculation. Suppose each axis of space is discretized into $k$ points, the $N$-electron (drop the subscript e for simplicity) wave function can be written as [2]\n",
+    "\n",
+    "$$\n",
+    "|\\Psi \\rangle = \\sum_{\\mathbf{x_1}, \\ldots, \\mathbf{x_N}} \\psi(\\mathbf{x_1}, \\ldots, \\mathbf{x_N}) \\mathcal{A}(|\\mathbf{x_1}, \\ldots, \\mathbf{x_N}\\rangle).\n",
+    "\\tag{7}\n",
+    "$$\n",
+    "\n",
+    "where coordinate $|\\mathbf{x_j}\\rangle = |r_j\\rangle |\\sigma_j\\rangle$ records the spatial location and spin of the $j^{th}$ electron, $|r_j\\rangle  = |x_j,y_j,z_j\\rangle$ for $j\\in \\{1,2,\\cdots,N\\}$, $x_j,y_j,z_j \\in \\{0,1,\\cdots,k-1\\}$ and  $\\sigma_j \\in \\{\\downarrow,\\uparrow\\}$ for spin down or up.  There will be $k^{3N}\\times 2^{N}$ complex amplitudes in total. Here, $\\mathcal{A}$ denotes anti-symmetrization and a consequence of the Pauli exclusion principle (electrons are fermion), and $\\psi(\\mathbf{x_1}, \\mathbf{x_2}, \\ldots, \\mathbf{x_N})=\\langle\\mathbf{x_1}, \\mathbf{x_2}, \\ldots, \\mathbf{x_N}|\\Psi\\rangle$. One can see that storing such a wave function already requires **exponentially growing memory** with respect to the number of electrons $N$. This would make classical simulation methods based on this naive numerical approach intractable for systems size larger than few tens of electrons. Now, the question becomes can we prepare such a wave function $|\\Psi\\rangle$ directly on a quantum computer and measure the expectation value $E_0$? In the next section, let's take the simplest molecular system -- hydrogen molecule $H_2$ as a concrete example.\n",
+    "\n",
+    "\n",
+    "\n",
+    "**Note:** A detailed review on quantum chemistry and existing classical computational methods are far beyond the scope of this tutorial, we refer the enthusiastic readers to the standard textbooks *'Molecular Electronic-Structure Theory'* [5] by Helgaker and *'Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory'* [7] by Szabo & Ostlund. To bridge to knowledge gap between quantum chemistry and quantum computing, please check the following review papers [Quantum computational chemistry](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003) [2] and [Quantum chemistry in the age of quantum computing](https://pubs.acs.org/doi/10.1021/acs.chemrev.8b00803) [1].\n",
+    "\n",
+    "**Note:** For energy calculation, it is desired to reach the **chemical accuracy** of $1.6\\times10^{-3}$ Hartree or 1 kcal/mol . "
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Energy ground state of the hydrogen molecule $H_2$\n",
+    "\n",
+    "### Building electronic Hamiltonian\n",
+    "\n",
+    "First of all, let us import the necessary libraries and packages.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:04.537224Z",
+     "start_time": "2021-01-09T07:26:00.836470Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import os\n",
+    "import platform\n",
+    "import matplotlib.pyplot as plt\n",
+    "%config InlineBackend.figure_format = 'svg'\n",
+    "from IPython.display import clear_output\n",
+    "\n",
+    "import numpy\n",
+    "from numpy import concatenate\n",
+    "from numpy import pi as PI\n",
+    "from numpy import savez, zeros\n",
+    "\n",
+    "from paddle import fluid\n",
+    "from paddle.complex import matmul, transpose\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import pauli_str_to_matrix\n",
+    "from paddle_quantum.VQE.chemistrysub import H2_generator"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "To analyze specific molecules, we need several key information such as **geometry**, **basis set** (such as STO-3G), **multiplicity**, and **charge** to obtain the discretized Hamiltonian $H$. Specifically, through our built-in quantum chemistry toolkit, fermion-to-qubit mapping technology can be used to output the qubit Hamiltonian of hydrogen molecule $H_2$,"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:04.570840Z",
+     "start_time": "2021-01-09T07:26:04.544640Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "Hamiltonian, N = H2_generator()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "For more advanced users, we provide a simple tutorial on how to generate such a Hamiltonian. Install the following two packages first (**only available for Mac/Linux users, not available to Windows users temporarily**):"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:07.190974Z",
+     "start_time": "2021-01-09T07:26:05.431945Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "!pip install openfermion\n",
+    "clear_output()"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:09.219268Z",
+     "start_time": "2021-01-09T07:26:07.195371Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "!pip install openfermionpyscf\n",
+    "clear_output()"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:10.031901Z",
+     "start_time": "2021-01-09T07:26:09.224389Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The generated h2 Hamiltonian is \n",
+      " (-0.04207897647782281+0j) [] +\n",
+      "(-0.04475014401535161+0j) [X0 X1 Y2 Y3] +\n",
+      "(0.04475014401535161+0j) [X0 Y1 Y2 X3] +\n",
+      "(0.04475014401535161+0j) [Y0 X1 X2 Y3] +\n",
+      "(-0.04475014401535161+0j) [Y0 Y1 X2 X3] +\n",
+      "(0.17771287465139946+0j) [Z0] +\n",
+      "(0.17059738328801055+0j) [Z0 Z1] +\n",
+      "(0.12293305056183798+0j) [Z0 Z2] +\n",
+      "(0.16768319457718958+0j) [Z0 Z3] +\n",
+      "(0.1777128746513994+0j) [Z1] +\n",
+      "(0.16768319457718958+0j) [Z1 Z2] +\n",
+      "(0.12293305056183798+0j) [Z1 Z3] +\n",
+      "(-0.24274280513140456+0j) [Z2] +\n",
+      "(0.17627640804319586+0j) [Z2 Z3] +\n",
+      "(-0.24274280513140456+0j) [Z3]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Operating system information\n",
+    "sysStr = platform.system()\n",
+    "\n",
+    "# Decide which operating system the user is using\n",
+    "if sysStr in ('Linux', 'Darwin'):\n",
+    "\n",
+    "    import openfermion\n",
+    "    import openfermionpyscf\n",
+    "\n",
+    "    # Please check whether the geometric configuration file of h2 is downloaded correctly\n",
+    "    geo = 'h2.xyz'\n",
+    "    charge = 0\n",
+    "    multiplicity = 1\n",
+    "\n",
+    "    # Generate Hamiltonian\n",
+    "    mol = openfermion.hamiltonians.MolecularData(geo, 'sto-3g', multiplicity, charge)\n",
+    "    openfermionpyscf.run_pyscf(mol)\n",
+    "    terms_molecular_hamiltonian = mol.get_molecular_hamiltonian()\n",
+    "    fermionic_hamiltonian = openfermion.transforms.get_fermion_operator(terms_molecular_hamiltonian)\n",
+    "    qubit_op = openfermion.transforms.jordan_wigner(fermionic_hamiltonian)\n",
+    "\n",
+    "    # Print result\n",
+    "    print(\"The generated h2 Hamiltonian is \\n\", qubit_op)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "**Note:** This Hamiltonian is generated with an interatomic distance of $d = 74$ pm. \n",
+    "\n",
+    "In addition to hydrogen molecule $H_2$, we also provide the geometric configuration file of hydrogen fluoride (HF) molecule `hf.xyz`. If you need to test the geometric configuration of more molecules, please check out this [database](http://smart.sns.it/molecules/index.html). In addition, we also need to convert the Hamiltonian into the Pauli string format supported by Paddle Quantum. Here we provide this interface.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:11.884870Z",
+     "start_time": "2021-01-09T07:26:11.875694Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def Hamiltonian_str_convert(qubit_op):\n",
+    "    '''\n",
+    "    Convert the Hamiltonian information provided above into Pauli strings supported by Paddle Quantum\n",
+    "\n",
+    "    H = [[1.0, \"z0,x1\"], [-1.0, \"y0,z1\"], ...]\n",
+    "    '''\n",
+    "    info_dic = qubit_op.terms\n",
+    "    \n",
+    "    def process_tuple(tup):\n",
+    "        if len(tup) == 0:\n",
+    "            return 'i0'\n",
+    "        else:\n",
+    "            res = ''\n",
+    "            for ele in tup:\n",
+    "                res += ele[1].lower()\n",
+    "                res += str(ele[0])\n",
+    "                res += ','\n",
+    "            return res[:-1]\n",
+    "    H_info = []\n",
+    "    \n",
+    "    for key, value in qubit_op.terms.items():\n",
+    "        H_info.append([value.real, process_tuple(key)])\n",
+    "    \n",
+    "    return H_info\n",
+    "\n",
+    "if sysStr in ('Linux', 'Darwin'):\n",
+    "    Hamiltonian = Hamiltonian_str_convert(qubit_op)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Building QNN and trial wave function\n",
+    "\n",
+    "To implement VQE, we firstly need to design a quantum neural network QNN to prepare the wave function ansatz $|\\Psi(\\boldsymbol\\theta)\\rangle$. Here, we provide a 4-qubit quantum circuit template with a depth of $D$ blocks. The dotted frame in the figure below denotes a single block:\n",
+    "\n",
+    "\n",
+    "![Utheta.jpg](https://release-data.cdn.bcebos.com/PIC%2FUtheta.jpg)\n",
+    "\n",
+    "Next, we use the `UAnsatz` class and the built-in `real_entangled_layer(theta, D)` circuit template in Paddle Quantum to realize this QNN.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:13.717206Z",
+     "start_time": "2021-01-09T07:26:13.709627Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "def U_theta(theta, Hamiltonian, N, D):\n",
+    "    \"\"\"\n",
+    "    Quantum Neural Network\n",
+    "    \"\"\"\n",
+    "    \n",
+    "    # Initialize the quantum neural network according to the number of qubits N\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Built-in {R_y + CNOT} circuit template\n",
+    "    cir.real_entangled_layer(theta[:D], D)\n",
+    "    \n",
+    "    # Lay R_y gates in the last row\n",
+    "    for i in range(N):\n",
+    "        cir.ry(theta=theta[D][i][0], which_qubit=i)\n",
+    "        \n",
+    "    # The quantum neural network acts on the default initial state |0000>\n",
+    "    cir.run_state_vector()\n",
+    "    \n",
+    "    # Calculate the expected value of a given Hamiltonian\n",
+    "    expectation_val = cir.expecval(Hamiltonian)\n",
+    "\n",
+    "    return expectation_val"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Setting up the loss function and model\n",
+    "\n",
+    "Now that we have the target Hamiltonian and QNN, we will further define the training model and loss function. By applying the QNN $U(\\theta)$ on the initial state $|0..0\\rangle$, we get the output state $|\\psi(\\boldsymbol\\theta)\\rangle $. Then, the loss function to be minimized is the expectation value, \n",
+    "\n",
+    "\n",
+    "$$\n",
+    "\\min_{\\boldsymbol\\theta}  \\mathcal{L}(\\boldsymbol \\theta) = \\min_{\\boldsymbol\\theta} \\langle \\Psi(\\boldsymbol\\theta)|H |\\Psi(\\boldsymbol\\theta)\\rangle\n",
+    "= \\min_{\\boldsymbol\\theta} \\sum_k c_k~\\langle \\Psi(\\boldsymbol\\theta)| \\bigotimes_j \\sigma_j^{(k)}|\\Psi(\\boldsymbol\\theta)\\rangle.\n",
+    "\\tag{8}\n",
+    "$$"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 8,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:15.661433Z",
+     "start_time": "2021-01-09T07:26:15.654903Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "class StateNet(fluid.dygraph.Layer):\n",
+    "\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * PI), dtype=\"float64\"):\n",
+    "        super(StateNet, self).__init__()\n",
+    "        \n",
+    "        # Initialize the theta parameter list and fill the initial value with a uniform distribution of [0, 2*pi]\n",
+    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        \n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self, N, D):\n",
+    "        \n",
+    "        # Calculate the loss function/expected value\n",
+    "        loss = U_theta(self.theta, Hamiltonian, N, D)\n",
+    "\n",
+    "        return loss"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Hyper-parameters\n",
+    "\n",
+    "Before training the QNN, we also need to set some training hyper-parameters, mainly the learning rate (LR), the number of iterations (ITR), and the depth (D) of repeated blocks. "
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 9,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:17.770511Z",
+     "start_time": "2021-01-09T07:26:17.767150Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "ITR = 100  # Set the number of optimization iterations\n",
+    "LR = 0.2   # Set the learning rate\n",
+    "D = 2      # Set the depth of the repetitive calculation module in QNN"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Training\n",
+    "\n",
+    "After all the training model parameters are set, we convert the data into variables in the Paddle dynamic computational graph, and then train the quantum neural network. The results of the training process is stored in the summary_data file.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 10,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:33.571665Z",
+     "start_time": "2021-01-09T07:26:19.157308Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 20 loss: -0.8523\n",
+      "iter: 20 Ground state energy: -0.8523 Ha\n",
+      "iter: 40 loss: -1.1264\n",
+      "iter: 40 Ground state energy: -1.1264 Ha\n",
+      "iter: 60 loss: -1.1323\n",
+      "iter: 60 Ground state energy: -1.1323 Ha\n",
+      "iter: 80 loss: -1.1360\n",
+      "iter: 80 Ground state energy: -1.1360 Ha\n",
+      "iter: 100 loss: -1.1361\n",
+      "iter: 100 Ground state energy: -1.1361 Ha\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Initialize Paddle dynamic computational graph\n",
+    "with fluid.dygraph.guard():\n",
+    "\n",
+    "\n",
+    "    # Determine the parameter dimension of the network\n",
+    "    net = StateNet(shape=[D + 1, N, 1])\n",
+    "\n",
+    "    \n",
+    "    # Generally speaking, we use Adam optimizer to obtain relatively good convergence,\n",
+    "    # You can change it to SGD or RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(\n",
+    "          learning_rate=LR, parameter_list=net.parameters())\n",
+    "\n",
+    "    # Record optimization results\n",
+    "    summary_iter, summary_loss = [], []\n",
+    "    \n",
+    "    # Optimization loop\n",
+    "    for itr in range(1, ITR + 1):\n",
+    "        \n",
+    "        # Forward propagation to calculate loss function\n",
+    "        loss = net(N, D)\n",
+    "\n",
+    "        # Use back propagation to minimize the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "        \n",
+    "        # Record optimization results\n",
+    "        summary_loss.append(loss.numpy())\n",
+    "        summary_iter.append(itr)\n",
+    "        \n",
+    "        # Print result\n",
+    "        if itr % 20 == 0:\n",
+    "            print(\"iter:\", itr, \"loss:\", \"%.4f\" % loss.numpy())\n",
+    "            print(\"iter:\", itr, \"Ground state energy:\", \"%.4f Ha\" \n",
+    "                                                % loss.numpy())\n",
+    "\n",
+    "    # Save the training results to the output folder\n",
+    "    os.makedirs(\"output\", exist_ok=True)\n",
+    "    savez(\"./output/summary_data\", iter = summary_iter, \n",
+    "                                   energy=summary_loss)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Benchmarking\n",
+    "We have now completed the training of the quantum neural network, and the estimated value of the ground state energy obtained is $E_0 \\approx -1.1361$ Hartree, we compare it with the theoretical value $E_0 = -1.13618$ to benchmark our model. The estimation obtained with VQE agree with a full configuration-interaction (FCI) calculation within chemical accuracy $\\varepsilon = 1.6 \\times 10^{-3}$ Hartree.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 11,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T07:26:42.456121Z",
+     "start_time": "2021-01-09T07:26:41.495984Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/svg+xml": [
+       "<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
+       "<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
+       "  \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
+       "<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
+       "<svg height=\"262.19625pt\" version=\"1.1\" viewBox=\"0 0 394.160937 262.19625\" width=\"394.160937pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
+       " <metadata>\n",
+       "  <rdf:RDF xmlns:cc=\"http://creativecommons.org/ns#\" xmlns:dc=\"http://purl.org/dc/elements/1.1/\" xmlns:rdf=\"http://www.w3.org/1999/02/22-rdf-syntax-ns#\">\n",
+       "   <cc:Work>\n",
+       "    <dc:type rdf:resource=\"http://purl.org/dc/dcmitype/StillImage\"/>\n",
+       "    <dc:date>2021-01-09T15:26:42.336203</dc:date>\n",
+       "    <dc:format>image/svg+xml</dc:format>\n",
+       "    <dc:creator>\n",
+       "     <cc:Agent>\n",
+       "      <dc:title>Matplotlib v3.3.1, https://matplotlib.org/</dc:title>\n",
+       "     </cc:Agent>\n",
+       "    </dc:creator>\n",
+       "   </cc:Work>\n",
+       "  </rdf:RDF>\n",
+       " </metadata>\n",
+       " <defs>\n",
+       "  <style type=\"text/css\">*{stroke-linecap:butt;stroke-linejoin:round;}</style>\n",
+       " </defs>\n",
+       " <g id=\"figure_1\">\n",
+       "  <g id=\"patch_1\">\n",
+       "   <path d=\"M 0 262.19625 \n",
+       "L 394.160937 262.19625 \n",
+       "L 394.160937 0 \n",
+       "L 0 0 \n",
+       "z\n",
+       "\" style=\"fill:none;\"/>\n",
+       "  </g>\n",
+       "  <g id=\"axes_1\">\n",
+       "   <g id=\"patch_2\">\n",
+       "    <path d=\"M 52.160938 224.64 \n",
+       "L 386.960938 224.64 \n",
+       "L 386.960938 7.2 \n",
+       "L 52.160938 7.2 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_1\">\n",
+       "    <g id=\"xtick_1\">\n",
+       "     <g id=\"line2d_1\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L 0 3.5 \n",
+       "\" id=\"mb15aed2d89\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"64.304739\" xlink:href=\"#mb15aed2d89\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_1\">\n",
+       "      <!-- 0 -->\n",
+       "      <g transform=\"translate(61.123489 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 31.78125 66.40625 \n",
+       "Q 24.171875 66.40625 20.328125 58.90625 \n",
+       "Q 16.5 51.421875 16.5 36.375 \n",
+       "Q 16.5 21.390625 20.328125 13.890625 \n",
+       "Q 24.171875 6.390625 31.78125 6.390625 \n",
+       "Q 39.453125 6.390625 43.28125 13.890625 \n",
+       "Q 47.125 21.390625 47.125 36.375 \n",
+       "Q 47.125 51.421875 43.28125 58.90625 \n",
+       "Q 39.453125 66.40625 31.78125 66.40625 \n",
+       "z\n",
+       "M 31.78125 74.21875 \n",
+       "Q 44.046875 74.21875 50.515625 64.515625 \n",
+       "Q 56.984375 54.828125 56.984375 36.375 \n",
+       "Q 56.984375 17.96875 50.515625 8.265625 \n",
+       "Q 44.046875 -1.421875 31.78125 -1.421875 \n",
+       "Q 19.53125 -1.421875 13.0625 8.265625 \n",
+       "Q 6.59375 17.96875 6.59375 36.375 \n",
+       "Q 6.59375 54.828125 13.0625 64.515625 \n",
+       "Q 19.53125 74.21875 31.78125 74.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-48\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_2\">\n",
+       "     <g id=\"line2d_2\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"125.792342\" xlink:href=\"#mb15aed2d89\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_2\">\n",
+       "      <!-- 20 -->\n",
+       "      <g transform=\"translate(119.429842 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 19.1875 8.296875 \n",
+       "L 53.609375 8.296875 \n",
+       "L 53.609375 0 \n",
+       "L 7.328125 0 \n",
+       "L 7.328125 8.296875 \n",
+       "Q 12.9375 14.109375 22.625 23.890625 \n",
+       "Q 32.328125 33.6875 34.8125 36.53125 \n",
+       "Q 39.546875 41.84375 41.421875 45.53125 \n",
+       "Q 43.3125 49.21875 43.3125 52.78125 \n",
+       "Q 43.3125 58.59375 39.234375 62.25 \n",
+       "Q 35.15625 65.921875 28.609375 65.921875 \n",
+       "Q 23.96875 65.921875 18.8125 64.3125 \n",
+       "Q 13.671875 62.703125 7.8125 59.421875 \n",
+       "L 7.8125 69.390625 \n",
+       "Q 13.765625 71.78125 18.9375 73 \n",
+       "Q 24.125 74.21875 28.421875 74.21875 \n",
+       "Q 39.75 74.21875 46.484375 68.546875 \n",
+       "Q 53.21875 62.890625 53.21875 53.421875 \n",
+       "Q 53.21875 48.921875 51.53125 44.890625 \n",
+       "Q 49.859375 40.875 45.40625 35.40625 \n",
+       "Q 44.1875 33.984375 37.640625 27.21875 \n",
+       "Q 31.109375 20.453125 19.1875 8.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-50\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-50\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_3\">\n",
+       "     <g id=\"line2d_3\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"187.279946\" xlink:href=\"#mb15aed2d89\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_3\">\n",
+       "      <!-- 40 -->\n",
+       "      <g transform=\"translate(180.917446 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 37.796875 64.3125 \n",
+       "L 12.890625 25.390625 \n",
+       "L 37.796875 25.390625 \n",
+       "z\n",
+       "M 35.203125 72.90625 \n",
+       "L 47.609375 72.90625 \n",
+       "L 47.609375 25.390625 \n",
+       "L 58.015625 25.390625 \n",
+       "L 58.015625 17.1875 \n",
+       "L 47.609375 17.1875 \n",
+       "L 47.609375 0 \n",
+       "L 37.796875 0 \n",
+       "L 37.796875 17.1875 \n",
+       "L 4.890625 17.1875 \n",
+       "L 4.890625 26.703125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-52\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-52\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_4\">\n",
+       "     <g id=\"line2d_4\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"248.767549\" xlink:href=\"#mb15aed2d89\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_4\">\n",
+       "      <!-- 60 -->\n",
+       "      <g transform=\"translate(242.405049 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 33.015625 40.375 \n",
+       "Q 26.375 40.375 22.484375 35.828125 \n",
+       "Q 18.609375 31.296875 18.609375 23.390625 \n",
+       "Q 18.609375 15.53125 22.484375 10.953125 \n",
+       "Q 26.375 6.390625 33.015625 6.390625 \n",
+       "Q 39.65625 6.390625 43.53125 10.953125 \n",
+       "Q 47.40625 15.53125 47.40625 23.390625 \n",
+       "Q 47.40625 31.296875 43.53125 35.828125 \n",
+       "Q 39.65625 40.375 33.015625 40.375 \n",
+       "z\n",
+       "M 52.59375 71.296875 \n",
+       "L 52.59375 62.3125 \n",
+       "Q 48.875 64.0625 45.09375 64.984375 \n",
+       "Q 41.3125 65.921875 37.59375 65.921875 \n",
+       "Q 27.828125 65.921875 22.671875 59.328125 \n",
+       "Q 17.53125 52.734375 16.796875 39.40625 \n",
+       "Q 19.671875 43.65625 24.015625 45.921875 \n",
+       "Q 28.375 48.1875 33.59375 48.1875 \n",
+       "Q 44.578125 48.1875 50.953125 41.515625 \n",
+       "Q 57.328125 34.859375 57.328125 23.390625 \n",
+       "Q 57.328125 12.15625 50.6875 5.359375 \n",
+       "Q 44.046875 -1.421875 33.015625 -1.421875 \n",
+       "Q 20.359375 -1.421875 13.671875 8.265625 \n",
+       "Q 6.984375 17.96875 6.984375 36.375 \n",
+       "Q 6.984375 53.65625 15.1875 63.9375 \n",
+       "Q 23.390625 74.21875 37.203125 74.21875 \n",
+       "Q 40.921875 74.21875 44.703125 73.484375 \n",
+       "Q 48.484375 72.75 52.59375 71.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-54\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-54\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_5\">\n",
+       "     <g id=\"line2d_5\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"310.255152\" xlink:href=\"#mb15aed2d89\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_5\">\n",
+       "      <!-- 80 -->\n",
+       "      <g transform=\"translate(303.892652 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 31.78125 34.625 \n",
+       "Q 24.75 34.625 20.71875 30.859375 \n",
+       "Q 16.703125 27.09375 16.703125 20.515625 \n",
+       "Q 16.703125 13.921875 20.71875 10.15625 \n",
+       "Q 24.75 6.390625 31.78125 6.390625 \n",
+       "Q 38.8125 6.390625 42.859375 10.171875 \n",
+       "Q 46.921875 13.96875 46.921875 20.515625 \n",
+       "Q 46.921875 27.09375 42.890625 30.859375 \n",
+       "Q 38.875 34.625 31.78125 34.625 \n",
+       "z\n",
+       "M 21.921875 38.8125 \n",
+       "Q 15.578125 40.375 12.03125 44.71875 \n",
+       "Q 8.5 49.078125 8.5 55.328125 \n",
+       "Q 8.5 64.0625 14.71875 69.140625 \n",
+       "Q 20.953125 74.21875 31.78125 74.21875 \n",
+       "Q 42.671875 74.21875 48.875 69.140625 \n",
+       "Q 55.078125 64.0625 55.078125 55.328125 \n",
+       "Q 55.078125 49.078125 51.53125 44.71875 \n",
+       "Q 48 40.375 41.703125 38.8125 \n",
+       "Q 48.828125 37.15625 52.796875 32.3125 \n",
+       "Q 56.78125 27.484375 56.78125 20.515625 \n",
+       "Q 56.78125 9.90625 50.3125 4.234375 \n",
+       "Q 43.84375 -1.421875 31.78125 -1.421875 \n",
+       "Q 19.734375 -1.421875 13.25 4.234375 \n",
+       "Q 6.78125 9.90625 6.78125 20.515625 \n",
+       "Q 6.78125 27.484375 10.78125 32.3125 \n",
+       "Q 14.796875 37.15625 21.921875 38.8125 \n",
+       "z\n",
+       "M 18.3125 54.390625 \n",
+       "Q 18.3125 48.734375 21.84375 45.5625 \n",
+       "Q 25.390625 42.390625 31.78125 42.390625 \n",
+       "Q 38.140625 42.390625 41.71875 45.5625 \n",
+       "Q 45.3125 48.734375 45.3125 54.390625 \n",
+       "Q 45.3125 60.0625 41.71875 63.234375 \n",
+       "Q 38.140625 66.40625 31.78125 66.40625 \n",
+       "Q 25.390625 66.40625 21.84375 63.234375 \n",
+       "Q 18.3125 60.0625 18.3125 54.390625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-56\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-56\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"xtick_6\">\n",
+       "     <g id=\"line2d_6\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"371.742756\" xlink:href=\"#mb15aed2d89\" y=\"224.64\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_6\">\n",
+       "      <!-- 100 -->\n",
+       "      <g transform=\"translate(362.199006 239.238437)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 12.40625 8.296875 \n",
+       "L 28.515625 8.296875 \n",
+       "L 28.515625 63.921875 \n",
+       "L 10.984375 60.40625 \n",
+       "L 10.984375 69.390625 \n",
+       "L 28.421875 72.90625 \n",
+       "L 38.28125 72.90625 \n",
+       "L 38.28125 8.296875 \n",
+       "L 54.390625 8.296875 \n",
+       "L 54.390625 0 \n",
+       "L 12.40625 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-49\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"127.246094\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_7\">\n",
+       "     <!-- Number of iteration -->\n",
+       "     <g transform=\"translate(170.354688 252.916562)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 23.09375 72.90625 \n",
+       "L 55.421875 11.921875 \n",
+       "L 55.421875 72.90625 \n",
+       "L 64.984375 72.90625 \n",
+       "L 64.984375 0 \n",
+       "L 51.703125 0 \n",
+       "L 19.390625 60.984375 \n",
+       "L 19.390625 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-78\"/>\n",
+       "       <path d=\"M 8.5 21.578125 \n",
+       "L 8.5 54.6875 \n",
+       "L 17.484375 54.6875 \n",
+       "L 17.484375 21.921875 \n",
+       "Q 17.484375 14.15625 20.5 10.265625 \n",
+       "Q 23.53125 6.390625 29.59375 6.390625 \n",
+       "Q 36.859375 6.390625 41.078125 11.03125 \n",
+       "Q 45.3125 15.671875 45.3125 23.6875 \n",
+       "L 45.3125 54.6875 \n",
+       "L 54.296875 54.6875 \n",
+       "L 54.296875 0 \n",
+       "L 45.3125 0 \n",
+       "L 45.3125 8.40625 \n",
+       "Q 42.046875 3.421875 37.71875 1 \n",
+       "Q 33.40625 -1.421875 27.6875 -1.421875 \n",
+       "Q 18.265625 -1.421875 13.375 4.4375 \n",
+       "Q 8.5 10.296875 8.5 21.578125 \n",
+       "z\n",
+       "M 31.109375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-117\"/>\n",
+       "       <path d=\"M 52 44.1875 \n",
+       "Q 55.375 50.25 60.0625 53.125 \n",
+       "Q 64.75 56 71.09375 56 \n",
+       "Q 79.640625 56 84.28125 50.015625 \n",
+       "Q 88.921875 44.046875 88.921875 33.015625 \n",
+       "L 88.921875 0 \n",
+       "L 79.890625 0 \n",
+       "L 79.890625 32.71875 \n",
+       "Q 79.890625 40.578125 77.09375 44.375 \n",
+       "Q 74.3125 48.1875 68.609375 48.1875 \n",
+       "Q 61.625 48.1875 57.5625 43.546875 \n",
+       "Q 53.515625 38.921875 53.515625 30.90625 \n",
+       "L 53.515625 0 \n",
+       "L 44.484375 0 \n",
+       "L 44.484375 32.71875 \n",
+       "Q 44.484375 40.625 41.703125 44.40625 \n",
+       "Q 38.921875 48.1875 33.109375 48.1875 \n",
+       "Q 26.21875 48.1875 22.15625 43.53125 \n",
+       "Q 18.109375 38.875 18.109375 30.90625 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 21.1875 51.21875 25.484375 53.609375 \n",
+       "Q 29.78125 56 35.6875 56 \n",
+       "Q 41.65625 56 45.828125 52.96875 \n",
+       "Q 50 49.953125 52 44.1875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-109\"/>\n",
+       "       <path d=\"M 48.6875 27.296875 \n",
+       "Q 48.6875 37.203125 44.609375 42.84375 \n",
+       "Q 40.53125 48.484375 33.40625 48.484375 \n",
+       "Q 26.265625 48.484375 22.1875 42.84375 \n",
+       "Q 18.109375 37.203125 18.109375 27.296875 \n",
+       "Q 18.109375 17.390625 22.1875 11.75 \n",
+       "Q 26.265625 6.109375 33.40625 6.109375 \n",
+       "Q 40.53125 6.109375 44.609375 11.75 \n",
+       "Q 48.6875 17.390625 48.6875 27.296875 \n",
+       "z\n",
+       "M 18.109375 46.390625 \n",
+       "Q 20.953125 51.265625 25.265625 53.625 \n",
+       "Q 29.59375 56 35.59375 56 \n",
+       "Q 45.5625 56 51.78125 48.09375 \n",
+       "Q 58.015625 40.1875 58.015625 27.296875 \n",
+       "Q 58.015625 14.40625 51.78125 6.484375 \n",
+       "Q 45.5625 -1.421875 35.59375 -1.421875 \n",
+       "Q 29.59375 -1.421875 25.265625 0.953125 \n",
+       "Q 20.953125 3.328125 18.109375 8.203125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 75.984375 \n",
+       "L 18.109375 75.984375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-98\"/>\n",
+       "       <path d=\"M 56.203125 29.59375 \n",
+       "L 56.203125 25.203125 \n",
+       "L 14.890625 25.203125 \n",
+       "Q 15.484375 15.921875 20.484375 11.0625 \n",
+       "Q 25.484375 6.203125 34.421875 6.203125 \n",
+       "Q 39.59375 6.203125 44.453125 7.46875 \n",
+       "Q 49.3125 8.734375 54.109375 11.28125 \n",
+       "L 54.109375 2.78125 \n",
+       "Q 49.265625 0.734375 44.1875 -0.34375 \n",
+       "Q 39.109375 -1.421875 33.890625 -1.421875 \n",
+       "Q 20.796875 -1.421875 13.15625 6.1875 \n",
+       "Q 5.515625 13.8125 5.515625 26.8125 \n",
+       "Q 5.515625 40.234375 12.765625 48.109375 \n",
+       "Q 20.015625 56 32.328125 56 \n",
+       "Q 43.359375 56 49.78125 48.890625 \n",
+       "Q 56.203125 41.796875 56.203125 29.59375 \n",
+       "z\n",
+       "M 47.21875 32.234375 \n",
+       "Q 47.125 39.59375 43.09375 43.984375 \n",
+       "Q 39.0625 48.390625 32.421875 48.390625 \n",
+       "Q 24.90625 48.390625 20.390625 44.140625 \n",
+       "Q 15.875 39.890625 15.1875 32.171875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-101\"/>\n",
+       "       <path d=\"M 41.109375 46.296875 \n",
+       "Q 39.59375 47.171875 37.8125 47.578125 \n",
+       "Q 36.03125 48 33.890625 48 \n",
+       "Q 26.265625 48 22.1875 43.046875 \n",
+       "Q 18.109375 38.09375 18.109375 28.8125 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 20.953125 51.171875 25.484375 53.578125 \n",
+       "Q 30.03125 56 36.53125 56 \n",
+       "Q 37.453125 56 38.578125 55.875 \n",
+       "Q 39.703125 55.765625 41.0625 55.515625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-114\"/>\n",
+       "       <path id=\"DejaVuSans-32\"/>\n",
+       "       <path d=\"M 30.609375 48.390625 \n",
+       "Q 23.390625 48.390625 19.1875 42.75 \n",
+       "Q 14.984375 37.109375 14.984375 27.296875 \n",
+       "Q 14.984375 17.484375 19.15625 11.84375 \n",
+       "Q 23.34375 6.203125 30.609375 6.203125 \n",
+       "Q 37.796875 6.203125 41.984375 11.859375 \n",
+       "Q 46.1875 17.53125 46.1875 27.296875 \n",
+       "Q 46.1875 37.015625 41.984375 42.703125 \n",
+       "Q 37.796875 48.390625 30.609375 48.390625 \n",
+       "z\n",
+       "M 30.609375 56 \n",
+       "Q 42.328125 56 49.015625 48.375 \n",
+       "Q 55.71875 40.765625 55.71875 27.296875 \n",
+       "Q 55.71875 13.875 49.015625 6.21875 \n",
+       "Q 42.328125 -1.421875 30.609375 -1.421875 \n",
+       "Q 18.84375 -1.421875 12.171875 6.21875 \n",
+       "Q 5.515625 13.875 5.515625 27.296875 \n",
+       "Q 5.515625 40.765625 12.171875 48.375 \n",
+       "Q 18.84375 56 30.609375 56 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-111\"/>\n",
+       "       <path d=\"M 37.109375 75.984375 \n",
+       "L 37.109375 68.5 \n",
+       "L 28.515625 68.5 \n",
+       "Q 23.6875 68.5 21.796875 66.546875 \n",
+       "Q 19.921875 64.59375 19.921875 59.515625 \n",
+       "L 19.921875 54.6875 \n",
+       "L 34.71875 54.6875 \n",
+       "L 34.71875 47.703125 \n",
+       "L 19.921875 47.703125 \n",
+       "L 19.921875 0 \n",
+       "L 10.890625 0 \n",
+       "L 10.890625 47.703125 \n",
+       "L 2.296875 47.703125 \n",
+       "L 2.296875 54.6875 \n",
+       "L 10.890625 54.6875 \n",
+       "L 10.890625 58.5 \n",
+       "Q 10.890625 67.625 15.140625 71.796875 \n",
+       "Q 19.390625 75.984375 28.609375 75.984375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-102\"/>\n",
+       "       <path d=\"M 9.421875 54.6875 \n",
+       "L 18.40625 54.6875 \n",
+       "L 18.40625 0 \n",
+       "L 9.421875 0 \n",
+       "z\n",
+       "M 9.421875 75.984375 \n",
+       "L 18.40625 75.984375 \n",
+       "L 18.40625 64.59375 \n",
+       "L 9.421875 64.59375 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-105\"/>\n",
+       "       <path d=\"M 18.3125 70.21875 \n",
+       "L 18.3125 54.6875 \n",
+       "L 36.8125 54.6875 \n",
+       "L 36.8125 47.703125 \n",
+       "L 18.3125 47.703125 \n",
+       "L 18.3125 18.015625 \n",
+       "Q 18.3125 11.328125 20.140625 9.421875 \n",
+       "Q 21.96875 7.515625 27.59375 7.515625 \n",
+       "L 36.8125 7.515625 \n",
+       "L 36.8125 0 \n",
+       "L 27.59375 0 \n",
+       "Q 17.1875 0 13.234375 3.875 \n",
+       "Q 9.28125 7.765625 9.28125 18.015625 \n",
+       "L 9.28125 47.703125 \n",
+       "L 2.6875 47.703125 \n",
+       "L 2.6875 54.6875 \n",
+       "L 9.28125 54.6875 \n",
+       "L 9.28125 70.21875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-116\"/>\n",
+       "       <path d=\"M 34.28125 27.484375 \n",
+       "Q 23.390625 27.484375 19.1875 25 \n",
+       "Q 14.984375 22.515625 14.984375 16.5 \n",
+       "Q 14.984375 11.71875 18.140625 8.90625 \n",
+       "Q 21.296875 6.109375 26.703125 6.109375 \n",
+       "Q 34.1875 6.109375 38.703125 11.40625 \n",
+       "Q 43.21875 16.703125 43.21875 25.484375 \n",
+       "L 43.21875 27.484375 \n",
+       "z\n",
+       "M 52.203125 31.203125 \n",
+       "L 52.203125 0 \n",
+       "L 43.21875 0 \n",
+       "L 43.21875 8.296875 \n",
+       "Q 40.140625 3.328125 35.546875 0.953125 \n",
+       "Q 30.953125 -1.421875 24.3125 -1.421875 \n",
+       "Q 15.921875 -1.421875 10.953125 3.296875 \n",
+       "Q 6 8.015625 6 15.921875 \n",
+       "Q 6 25.140625 12.171875 29.828125 \n",
+       "Q 18.359375 34.515625 30.609375 34.515625 \n",
+       "L 43.21875 34.515625 \n",
+       "L 43.21875 35.40625 \n",
+       "Q 43.21875 41.609375 39.140625 45 \n",
+       "Q 35.0625 48.390625 27.6875 48.390625 \n",
+       "Q 23 48.390625 18.546875 47.265625 \n",
+       "Q 14.109375 46.140625 10.015625 43.890625 \n",
+       "L 10.015625 52.203125 \n",
+       "Q 14.9375 54.109375 19.578125 55.046875 \n",
+       "Q 24.21875 56 28.609375 56 \n",
+       "Q 40.484375 56 46.34375 49.84375 \n",
+       "Q 52.203125 43.703125 52.203125 31.203125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-97\"/>\n",
+       "       <path d=\"M 54.890625 33.015625 \n",
+       "L 54.890625 0 \n",
+       "L 45.90625 0 \n",
+       "L 45.90625 32.71875 \n",
+       "Q 45.90625 40.484375 42.875 44.328125 \n",
+       "Q 39.84375 48.1875 33.796875 48.1875 \n",
+       "Q 26.515625 48.1875 22.3125 43.546875 \n",
+       "Q 18.109375 38.921875 18.109375 30.90625 \n",
+       "L 18.109375 0 \n",
+       "L 9.078125 0 \n",
+       "L 9.078125 54.6875 \n",
+       "L 18.109375 54.6875 \n",
+       "L 18.109375 46.1875 \n",
+       "Q 21.34375 51.125 25.703125 53.5625 \n",
+       "Q 30.078125 56 35.796875 56 \n",
+       "Q 45.21875 56 50.046875 50.171875 \n",
+       "Q 54.890625 44.34375 54.890625 33.015625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-110\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-78\"/>\n",
+       "      <use x=\"74.804688\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"138.183594\" xlink:href=\"#DejaVuSans-109\"/>\n",
+       "      <use x=\"235.595703\" xlink:href=\"#DejaVuSans-98\"/>\n",
+       "      <use x=\"299.072266\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"360.595703\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"401.708984\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"433.496094\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"494.677734\" xlink:href=\"#DejaVuSans-102\"/>\n",
+       "      <use x=\"529.882812\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"561.669922\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"589.453125\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"628.662109\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"690.185547\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"731.298828\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"792.578125\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"831.787109\" xlink:href=\"#DejaVuSans-105\"/>\n",
+       "      <use x=\"859.570312\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"920.751953\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"matplotlib.axis_2\">\n",
+       "    <g id=\"ytick_1\">\n",
+       "     <g id=\"line2d_7\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 0 0 \n",
+       "L -3.5 0 \n",
+       "\" id=\"m82ff1f3097\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
+       "      </defs>\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m82ff1f3097\" y=\"183.328577\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_8\">\n",
+       "      <!-- −1.0 -->\n",
+       "      <g transform=\"translate(20.878125 187.127796)scale(0.1 -0.1)\">\n",
+       "       <defs>\n",
+       "        <path d=\"M 10.59375 35.5 \n",
+       "L 73.1875 35.5 \n",
+       "L 73.1875 27.203125 \n",
+       "L 10.59375 27.203125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-8722\"/>\n",
+       "        <path d=\"M 10.6875 12.40625 \n",
+       "L 21 12.40625 \n",
+       "L 21 0 \n",
+       "L 10.6875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-46\"/>\n",
+       "       </defs>\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_2\">\n",
+       "     <g id=\"line2d_8\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m82ff1f3097\" y=\"137.175537\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_9\">\n",
+       "      <!-- −0.8 -->\n",
+       "      <g transform=\"translate(20.878125 140.974756)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-56\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_3\">\n",
+       "     <g id=\"line2d_9\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m82ff1f3097\" y=\"91.022497\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_10\">\n",
+       "      <!-- −0.6 -->\n",
+       "      <g transform=\"translate(20.878125 94.821716)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-54\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"ytick_4\">\n",
+       "     <g id=\"line2d_10\">\n",
+       "      <g>\n",
+       "       <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"52.160938\" xlink:href=\"#m82ff1f3097\" y=\"44.869457\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "     <g id=\"text_11\">\n",
+       "      <!-- −0.4 -->\n",
+       "      <g transform=\"translate(20.878125 48.668676)scale(0.1 -0.1)\">\n",
+       "       <use xlink:href=\"#DejaVuSans-8722\"/>\n",
+       "       <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
+       "       <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
+       "       <use x=\"179.199219\" xlink:href=\"#DejaVuSans-52\"/>\n",
+       "      </g>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"text_12\">\n",
+       "     <!-- Energy (Ha) -->\n",
+       "     <g transform=\"translate(14.798437 145.741094)rotate(-90)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 55.90625 72.90625 \n",
+       "L 55.90625 64.59375 \n",
+       "L 19.671875 64.59375 \n",
+       "L 19.671875 43.015625 \n",
+       "L 54.390625 43.015625 \n",
+       "L 54.390625 34.71875 \n",
+       "L 19.671875 34.71875 \n",
+       "L 19.671875 8.296875 \n",
+       "L 56.78125 8.296875 \n",
+       "L 56.78125 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-69\"/>\n",
+       "       <path d=\"M 45.40625 27.984375 \n",
+       "Q 45.40625 37.75 41.375 43.109375 \n",
+       "Q 37.359375 48.484375 30.078125 48.484375 \n",
+       "Q 22.859375 48.484375 18.828125 43.109375 \n",
+       "Q 14.796875 37.75 14.796875 27.984375 \n",
+       "Q 14.796875 18.265625 18.828125 12.890625 \n",
+       "Q 22.859375 7.515625 30.078125 7.515625 \n",
+       "Q 37.359375 7.515625 41.375 12.890625 \n",
+       "Q 45.40625 18.265625 45.40625 27.984375 \n",
+       "z\n",
+       "M 54.390625 6.78125 \n",
+       "Q 54.390625 -7.171875 48.1875 -13.984375 \n",
+       "Q 42 -20.796875 29.203125 -20.796875 \n",
+       "Q 24.46875 -20.796875 20.265625 -20.09375 \n",
+       "Q 16.0625 -19.390625 12.109375 -17.921875 \n",
+       "L 12.109375 -9.1875 \n",
+       "Q 16.0625 -11.328125 19.921875 -12.34375 \n",
+       "Q 23.78125 -13.375 27.78125 -13.375 \n",
+       "Q 36.625 -13.375 41.015625 -8.765625 \n",
+       "Q 45.40625 -4.15625 45.40625 5.171875 \n",
+       "L 45.40625 9.625 \n",
+       "Q 42.625 4.78125 38.28125 2.390625 \n",
+       "Q 33.9375 0 27.875 0 \n",
+       "Q 17.828125 0 11.671875 7.65625 \n",
+       "Q 5.515625 15.328125 5.515625 27.984375 \n",
+       "Q 5.515625 40.671875 11.671875 48.328125 \n",
+       "Q 17.828125 56 27.875 56 \n",
+       "Q 33.9375 56 38.28125 53.609375 \n",
+       "Q 42.625 51.21875 45.40625 46.390625 \n",
+       "L 45.40625 54.6875 \n",
+       "L 54.390625 54.6875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-103\"/>\n",
+       "       <path d=\"M 32.171875 -5.078125 \n",
+       "Q 28.375 -14.84375 24.75 -17.8125 \n",
+       "Q 21.140625 -20.796875 15.09375 -20.796875 \n",
+       "L 7.90625 -20.796875 \n",
+       "L 7.90625 -13.28125 \n",
+       "L 13.1875 -13.28125 \n",
+       "Q 16.890625 -13.28125 18.9375 -11.515625 \n",
+       "Q 21 -9.765625 23.484375 -3.21875 \n",
+       "L 25.09375 0.875 \n",
+       "L 2.984375 54.6875 \n",
+       "L 12.5 54.6875 \n",
+       "L 29.59375 11.921875 \n",
+       "L 46.6875 54.6875 \n",
+       "L 56.203125 54.6875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-121\"/>\n",
+       "       <path d=\"M 31 75.875 \n",
+       "Q 24.46875 64.65625 21.28125 53.65625 \n",
+       "Q 18.109375 42.671875 18.109375 31.390625 \n",
+       "Q 18.109375 20.125 21.3125 9.0625 \n",
+       "Q 24.515625 -2 31 -13.1875 \n",
+       "L 23.1875 -13.1875 \n",
+       "Q 15.875 -1.703125 12.234375 9.375 \n",
+       "Q 8.59375 20.453125 8.59375 31.390625 \n",
+       "Q 8.59375 42.28125 12.203125 53.3125 \n",
+       "Q 15.828125 64.359375 23.1875 75.875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-40\"/>\n",
+       "       <path d=\"M 9.8125 72.90625 \n",
+       "L 19.671875 72.90625 \n",
+       "L 19.671875 43.015625 \n",
+       "L 55.515625 43.015625 \n",
+       "L 55.515625 72.90625 \n",
+       "L 65.375 72.90625 \n",
+       "L 65.375 0 \n",
+       "L 55.515625 0 \n",
+       "L 55.515625 34.71875 \n",
+       "L 19.671875 34.71875 \n",
+       "L 19.671875 0 \n",
+       "L 9.8125 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-72\"/>\n",
+       "       <path d=\"M 8.015625 75.875 \n",
+       "L 15.828125 75.875 \n",
+       "Q 23.140625 64.359375 26.78125 53.3125 \n",
+       "Q 30.421875 42.28125 30.421875 31.390625 \n",
+       "Q 30.421875 20.453125 26.78125 9.375 \n",
+       "Q 23.140625 -1.703125 15.828125 -13.1875 \n",
+       "L 8.015625 -13.1875 \n",
+       "Q 14.5 -2 17.703125 9.0625 \n",
+       "Q 20.90625 20.125 20.90625 31.390625 \n",
+       "Q 20.90625 42.671875 17.703125 53.65625 \n",
+       "Q 14.5 64.65625 8.015625 75.875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-41\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-69\"/>\n",
+       "      <use x=\"63.183594\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "      <use x=\"126.5625\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"188.085938\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"227.449219\" xlink:href=\"#DejaVuSans-103\"/>\n",
+       "      <use x=\"290.925781\" xlink:href=\"#DejaVuSans-121\"/>\n",
+       "      <use x=\"350.105469\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"381.892578\" xlink:href=\"#DejaVuSans-40\"/>\n",
+       "      <use x=\"420.90625\" xlink:href=\"#DejaVuSans-72\"/>\n",
+       "      <use x=\"496.101562\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"557.380859\" xlink:href=\"#DejaVuSans-41\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "   <g id=\"line2d_11\">\n",
+       "    <path clip-path=\"url(#pd4f85b6dad)\" d=\"M 67.379119 17.083636 \n",
+       "L 70.453499 52.067317 \n",
+       "L 73.52788 73.893781 \n",
+       "L 76.60226 89.403365 \n",
+       "L 79.67664 101.103015 \n",
+       "L 82.75102 106.747158 \n",
+       "L 85.8254 106.460241 \n",
+       "L 88.89978 105.507185 \n",
+       "L 91.974161 108.730875 \n",
+       "L 95.048541 114.828986 \n",
+       "L 98.122921 121.317281 \n",
+       "L 101.197301 127.271118 \n",
+       "L 104.271681 132.722947 \n",
+       "L 107.346061 136.290317 \n",
+       "L 110.420442 136.491529 \n",
+       "L 113.494822 135.229009 \n",
+       "L 116.569202 136.040872 \n",
+       "L 119.643582 139.270694 \n",
+       "L 122.717962 143.632285 \n",
+       "L 125.792342 149.250196 \n",
+       "L 128.866723 156.475322 \n",
+       "L 131.941103 164.321024 \n",
+       "L 135.015483 171.975289 \n",
+       "L 138.089863 180.051056 \n",
+       "L 141.164243 188.816374 \n",
+       "L 144.238623 196.68898 \n",
+       "L 147.313004 201.880479 \n",
+       "L 150.387384 204.341765 \n",
+       "L 153.461764 205.809501 \n",
+       "L 156.536144 207.470168 \n",
+       "L 159.610524 208.717602 \n",
+       "L 162.684904 208.33442 \n",
+       "L 165.759285 206.106599 \n",
+       "L 168.833665 203.368367 \n",
+       "L 171.908045 202.193985 \n",
+       "L 174.982425 203.821426 \n",
+       "L 178.056805 207.6248 \n",
+       "L 181.131185 211.442128 \n",
+       "L 184.205566 213.178232 \n",
+       "L 187.279946 212.501548 \n",
+       "L 190.354326 210.881746 \n",
+       "L 193.428706 209.83521 \n",
+       "L 196.503086 209.713236 \n",
+       "L 199.577466 210.116092 \n",
+       "L 202.651847 210.667376 \n",
+       "L 205.726227 211.253538 \n",
+       "L 208.800607 211.874728 \n",
+       "L 211.874987 212.461954 \n",
+       "L 214.949367 212.89122 \n",
+       "L 218.023747 213.121225 \n",
+       "L 221.098128 213.196632 \n",
+       "L 224.172508 213.159061 \n",
+       "L 227.246888 213.040632 \n",
+       "L 230.321268 212.924493 \n",
+       "L 233.395648 212.956861 \n",
+       "L 236.470028 213.213594 \n",
+       "L 239.544409 213.568351 \n",
+       "L 242.618789 213.799369 \n",
+       "L 245.693169 213.844271 \n",
+       "L 248.767549 213.858923 \n",
+       "L 251.841929 213.990464 \n",
+       "L 254.916309 214.191296 \n",
+       "L 257.99069 214.30897 \n",
+       "L 261.06507 214.272577 \n",
+       "L 264.13945 214.151579 \n",
+       "L 267.21383 214.087872 \n",
+       "L 270.28821 214.171999 \n",
+       "L 273.36259 214.356773 \n",
+       "L 276.436971 214.517026 \n",
+       "L 279.511351 214.588477 \n",
+       "L 282.585731 214.597824 \n",
+       "L 285.660111 214.587599 \n",
+       "L 288.734491 214.580132 \n",
+       "L 291.808871 214.588033 \n",
+       "L 294.883252 214.607926 \n",
+       "L 297.957632 214.624079 \n",
+       "L 301.032012 214.635498 \n",
+       "L 304.106392 214.655124 \n",
+       "L 307.180772 214.683389 \n",
+       "L 310.255152 214.704753 \n",
+       "L 313.329533 214.707474 \n",
+       "L 316.403913 214.697921 \n",
+       "L 319.478293 214.695318 \n",
+       "L 322.552673 214.706996 \n",
+       "L 325.627053 214.716078 \n",
+       "L 328.701433 214.708365 \n",
+       "L 331.775814 214.695788 \n",
+       "L 334.850194 214.696601 \n",
+       "L 337.924574 214.71113 \n",
+       "L 340.998954 214.727622 \n",
+       "L 344.073334 214.736059 \n",
+       "L 347.147714 214.734302 \n",
+       "L 350.222095 214.729354 \n",
+       "L 353.296475 214.728984 \n",
+       "L 356.370855 214.732614 \n",
+       "L 359.445235 214.735857 \n",
+       "L 362.519615 214.737722 \n",
+       "L 365.593995 214.739443 \n",
+       "L 368.668376 214.742204 \n",
+       "L 371.742756 214.746107 \n",
+       "\" style=\"fill:none;stroke:#ff0000;stroke-linecap:square;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"line2d_12\">\n",
+       "    <path clip-path=\"url(#pd4f85b6dad)\" d=\"M 67.379119 214.756364 \n",
+       "L 70.453499 214.756364 \n",
+       "L 73.52788 214.756364 \n",
+       "L 76.60226 214.756364 \n",
+       "L 79.67664 214.756364 \n",
+       "L 82.75102 214.756364 \n",
+       "L 85.8254 214.756364 \n",
+       "L 88.89978 214.756364 \n",
+       "L 91.974161 214.756364 \n",
+       "L 95.048541 214.756364 \n",
+       "L 98.122921 214.756364 \n",
+       "L 101.197301 214.756364 \n",
+       "L 104.271681 214.756364 \n",
+       "L 107.346061 214.756364 \n",
+       "L 110.420442 214.756364 \n",
+       "L 113.494822 214.756364 \n",
+       "L 116.569202 214.756364 \n",
+       "L 119.643582 214.756364 \n",
+       "L 122.717962 214.756364 \n",
+       "L 125.792342 214.756364 \n",
+       "L 128.866723 214.756364 \n",
+       "L 131.941103 214.756364 \n",
+       "L 135.015483 214.756364 \n",
+       "L 138.089863 214.756364 \n",
+       "L 141.164243 214.756364 \n",
+       "L 144.238623 214.756364 \n",
+       "L 147.313004 214.756364 \n",
+       "L 150.387384 214.756364 \n",
+       "L 153.461764 214.756364 \n",
+       "L 156.536144 214.756364 \n",
+       "L 159.610524 214.756364 \n",
+       "L 162.684904 214.756364 \n",
+       "L 165.759285 214.756364 \n",
+       "L 168.833665 214.756364 \n",
+       "L 171.908045 214.756364 \n",
+       "L 174.982425 214.756364 \n",
+       "L 178.056805 214.756364 \n",
+       "L 181.131185 214.756364 \n",
+       "L 184.205566 214.756364 \n",
+       "L 187.279946 214.756364 \n",
+       "L 190.354326 214.756364 \n",
+       "L 193.428706 214.756364 \n",
+       "L 196.503086 214.756364 \n",
+       "L 199.577466 214.756364 \n",
+       "L 202.651847 214.756364 \n",
+       "L 205.726227 214.756364 \n",
+       "L 208.800607 214.756364 \n",
+       "L 211.874987 214.756364 \n",
+       "L 214.949367 214.756364 \n",
+       "L 218.023747 214.756364 \n",
+       "L 221.098128 214.756364 \n",
+       "L 224.172508 214.756364 \n",
+       "L 227.246888 214.756364 \n",
+       "L 230.321268 214.756364 \n",
+       "L 233.395648 214.756364 \n",
+       "L 236.470028 214.756364 \n",
+       "L 239.544409 214.756364 \n",
+       "L 242.618789 214.756364 \n",
+       "L 245.693169 214.756364 \n",
+       "L 248.767549 214.756364 \n",
+       "L 251.841929 214.756364 \n",
+       "L 254.916309 214.756364 \n",
+       "L 257.99069 214.756364 \n",
+       "L 261.06507 214.756364 \n",
+       "L 264.13945 214.756364 \n",
+       "L 267.21383 214.756364 \n",
+       "L 270.28821 214.756364 \n",
+       "L 273.36259 214.756364 \n",
+       "L 276.436971 214.756364 \n",
+       "L 279.511351 214.756364 \n",
+       "L 282.585731 214.756364 \n",
+       "L 285.660111 214.756364 \n",
+       "L 288.734491 214.756364 \n",
+       "L 291.808871 214.756364 \n",
+       "L 294.883252 214.756364 \n",
+       "L 297.957632 214.756364 \n",
+       "L 301.032012 214.756364 \n",
+       "L 304.106392 214.756364 \n",
+       "L 307.180772 214.756364 \n",
+       "L 310.255152 214.756364 \n",
+       "L 313.329533 214.756364 \n",
+       "L 316.403913 214.756364 \n",
+       "L 319.478293 214.756364 \n",
+       "L 322.552673 214.756364 \n",
+       "L 325.627053 214.756364 \n",
+       "L 328.701433 214.756364 \n",
+       "L 331.775814 214.756364 \n",
+       "L 334.850194 214.756364 \n",
+       "L 337.924574 214.756364 \n",
+       "L 340.998954 214.756364 \n",
+       "L 344.073334 214.756364 \n",
+       "L 347.147714 214.756364 \n",
+       "L 350.222095 214.756364 \n",
+       "L 353.296475 214.756364 \n",
+       "L 356.370855 214.756364 \n",
+       "L 359.445235 214.756364 \n",
+       "L 362.519615 214.756364 \n",
+       "L 365.593995 214.756364 \n",
+       "L 368.668376 214.756364 \n",
+       "L 371.742756 214.756364 \n",
+       "\" style=\"fill:none;stroke:#0000ff;stroke-dasharray:1.5,2.475;stroke-dashoffset:0;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_3\">\n",
+       "    <path d=\"M 52.160938 224.64 \n",
+       "L 52.160938 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_4\">\n",
+       "    <path d=\"M 386.960938 224.64 \n",
+       "L 386.960938 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_5\">\n",
+       "    <path d=\"M 52.160938 224.64 \n",
+       "L 386.960938 224.64 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"patch_6\">\n",
+       "    <path d=\"M 52.160938 7.2 \n",
+       "L 386.960938 7.2 \n",
+       "\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
+       "   </g>\n",
+       "   <g id=\"legend_1\">\n",
+       "    <g id=\"patch_7\">\n",
+       "     <path d=\"M 244.220312 44.978125 \n",
+       "L 379.960938 44.978125 \n",
+       "Q 381.960938 44.978125 381.960938 42.978125 \n",
+       "L 381.960938 14.2 \n",
+       "Q 381.960938 12.2 379.960938 12.2 \n",
+       "L 244.220312 12.2 \n",
+       "Q 242.220312 12.2 242.220312 14.2 \n",
+       "L 242.220312 42.978125 \n",
+       "Q 242.220312 44.978125 244.220312 44.978125 \n",
+       "z\n",
+       "\" style=\"fill:#ffffff;opacity:0.8;stroke:#cccccc;stroke-linejoin:miter;\"/>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_13\">\n",
+       "     <path d=\"M 246.220312 20.4 \n",
+       "L 266.220312 20.4 \n",
+       "\" style=\"fill:none;stroke:#ff0000;stroke-linecap:square;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_14\"/>\n",
+       "    <g id=\"text_13\">\n",
+       "     <!-- $\\left\\langle {\\psi \\left( {\\theta } \\right)} \\right|H\\left| {\\psi \\left( {\\theta } \\right)} \\right\\rangle $ -->\n",
+       "     <g transform=\"translate(274.220312 23.9)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 8.9375 31.34375 \n",
+       "L 22.703125 75.875 \n",
+       "L 31 75.875 \n",
+       "L 17.234375 31.34375 \n",
+       "L 31 -13.1875 \n",
+       "L 22.703125 -13.1875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-10216\"/>\n",
+       "       <path d=\"M 24.859375 -1.21875 \n",
+       "Q 13.921875 0.59375 9.625 5.328125 \n",
+       "Q 4.34375 11.140625 6.640625 23 \n",
+       "L 12.796875 54.6875 \n",
+       "L 21.875 54.6875 \n",
+       "L 15.765625 23.34375 \n",
+       "Q 14.0625 14.40625 17.484375 10.6875 \n",
+       "Q 20.515625 7.46875 26.421875 6.78125 \n",
+       "L 35.6875 54.6875 \n",
+       "L 44.625 54.6875 \n",
+       "L 35.359375 6.84375 \n",
+       "Q 41.890625 7.515625 45.75 10.75 \n",
+       "Q 50.734375 14.84375 52.390625 23.390625 \n",
+       "L 58.453125 54.6875 \n",
+       "L 67.53125 54.6875 \n",
+       "L 61.375 23.046875 \n",
+       "Q 58.984375 10.75 51.5625 5.375 \n",
+       "Q 44.875 0.53125 33.796875 -1.171875 \n",
+       "L 29.984375 -20.796875 \n",
+       "L 21.046875 -20.796875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Oblique-968\"/>\n",
+       "       <path d=\"M 45.515625 34.671875 \n",
+       "L 14.453125 34.671875 \n",
+       "Q 12.359375 20.0625 14.5 13.875 \n",
+       "Q 17.1875 6.25 24.46875 6.25 \n",
+       "Q 31.78125 6.25 37.359375 13.921875 \n",
+       "Q 42.234375 20.65625 45.515625 34.671875 \n",
+       "z\n",
+       "M 47.015625 42.96875 \n",
+       "Q 48.34375 56.84375 46.625 61.71875 \n",
+       "Q 43.953125 69.4375 36.765625 69.4375 \n",
+       "Q 29.296875 69.4375 23.828125 61.8125 \n",
+       "Q 19.53125 55.671875 16.15625 42.96875 \n",
+       "z\n",
+       "M 38.1875 76.765625 \n",
+       "Q 49.90625 76.765625 54.59375 66.40625 \n",
+       "Q 59.28125 56.109375 55.71875 37.84375 \n",
+       "Q 52.203125 19.625 43.453125 9.28125 \n",
+       "Q 34.765625 -1.125 23.046875 -1.125 \n",
+       "Q 11.28125 -1.125 6.640625 9.28125 \n",
+       "Q 2 19.625 5.515625 37.84375 \n",
+       "Q 9.078125 56.109375 17.71875 66.40625 \n",
+       "Q 26.421875 76.765625 38.1875 76.765625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Oblique-952\"/>\n",
+       "       <path d=\"M 21 76.421875 \n",
+       "L 21 -23.578125 \n",
+       "L 12.703125 -23.578125 \n",
+       "L 12.703125 76.421875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-124\"/>\n",
+       "       <path d=\"M 16.890625 72.90625 \n",
+       "L 26.8125 72.90625 \n",
+       "L 21 43.015625 \n",
+       "L 56.78125 43.015625 \n",
+       "L 62.59375 72.90625 \n",
+       "L 72.515625 72.90625 \n",
+       "L 58.296875 0 \n",
+       "L 48.390625 0 \n",
+       "L 55.171875 34.71875 \n",
+       "L 19.390625 34.71875 \n",
+       "L 12.59375 0 \n",
+       "L 2.6875 0 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-Oblique-72\"/>\n",
+       "       <path d=\"M 30.078125 31.34375 \n",
+       "L 16.3125 -13.1875 \n",
+       "L 8.015625 -13.1875 \n",
+       "L 21.78125 31.34375 \n",
+       "L 8.015625 75.875 \n",
+       "L 16.3125 75.875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-10217\"/>\n",
+       "      </defs>\n",
+       "      <use transform=\"translate(0 0.234375)\" xlink:href=\"#DejaVuSans-10216\"/>\n",
+       "      <use transform=\"translate(39.013672 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-968\"/>\n",
+       "      <use transform=\"translate(104.980469 0.234375)\" xlink:href=\"#DejaVuSans-40\"/>\n",
+       "      <use transform=\"translate(143.994141 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-952\"/>\n",
+       "      <use transform=\"translate(205.175781 0.234375)\" xlink:href=\"#DejaVuSans-41\"/>\n",
+       "      <use transform=\"translate(244.189453 0.234375)\" xlink:href=\"#DejaVuSans-124\"/>\n",
+       "      <use transform=\"translate(277.880859 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-72\"/>\n",
+       "      <use transform=\"translate(353.076172 0.234375)\" xlink:href=\"#DejaVuSans-124\"/>\n",
+       "      <use transform=\"translate(386.767578 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-968\"/>\n",
+       "      <use transform=\"translate(452.734375 0.234375)\" xlink:href=\"#DejaVuSans-40\"/>\n",
+       "      <use transform=\"translate(491.748047 0.234375)\" xlink:href=\"#DejaVuSans-Oblique-952\"/>\n",
+       "      <use transform=\"translate(552.929688 0.234375)\" xlink:href=\"#DejaVuSans-41\"/>\n",
+       "      <use transform=\"translate(591.943359 0.234375)\" xlink:href=\"#DejaVuSans-10217\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_15\">\n",
+       "     <path d=\"M 246.220312 35.398437 \n",
+       "L 266.220312 35.398437 \n",
+       "\" style=\"fill:none;stroke:#0000ff;stroke-dasharray:1.5,2.475;stroke-dashoffset:0;stroke-opacity:0.7;stroke-width:1.5;\"/>\n",
+       "    </g>\n",
+       "    <g id=\"line2d_16\"/>\n",
+       "    <g id=\"text_14\">\n",
+       "     <!-- Ground-state energy -->\n",
+       "     <g transform=\"translate(274.220312 38.898437)scale(0.1 -0.1)\">\n",
+       "      <defs>\n",
+       "       <path d=\"M 59.515625 10.40625 \n",
+       "L 59.515625 29.984375 \n",
+       "L 43.40625 29.984375 \n",
+       "L 43.40625 38.09375 \n",
+       "L 69.28125 38.09375 \n",
+       "L 69.28125 6.78125 \n",
+       "Q 63.578125 2.734375 56.6875 0.65625 \n",
+       "Q 49.8125 -1.421875 42 -1.421875 \n",
+       "Q 24.90625 -1.421875 15.25 8.5625 \n",
+       "Q 5.609375 18.5625 5.609375 36.375 \n",
+       "Q 5.609375 54.25 15.25 64.234375 \n",
+       "Q 24.90625 74.21875 42 74.21875 \n",
+       "Q 49.125 74.21875 55.546875 72.453125 \n",
+       "Q 61.96875 70.703125 67.390625 67.28125 \n",
+       "L 67.390625 56.78125 \n",
+       "Q 61.921875 61.421875 55.765625 63.765625 \n",
+       "Q 49.609375 66.109375 42.828125 66.109375 \n",
+       "Q 29.4375 66.109375 22.71875 58.640625 \n",
+       "Q 16.015625 51.171875 16.015625 36.375 \n",
+       "Q 16.015625 21.625 22.71875 14.15625 \n",
+       "Q 29.4375 6.6875 42.828125 6.6875 \n",
+       "Q 48.046875 6.6875 52.140625 7.59375 \n",
+       "Q 56.25 8.5 59.515625 10.40625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-71\"/>\n",
+       "       <path d=\"M 45.40625 46.390625 \n",
+       "L 45.40625 75.984375 \n",
+       "L 54.390625 75.984375 \n",
+       "L 54.390625 0 \n",
+       "L 45.40625 0 \n",
+       "L 45.40625 8.203125 \n",
+       "Q 42.578125 3.328125 38.25 0.953125 \n",
+       "Q 33.9375 -1.421875 27.875 -1.421875 \n",
+       "Q 17.96875 -1.421875 11.734375 6.484375 \n",
+       "Q 5.515625 14.40625 5.515625 27.296875 \n",
+       "Q 5.515625 40.1875 11.734375 48.09375 \n",
+       "Q 17.96875 56 27.875 56 \n",
+       "Q 33.9375 56 38.25 53.625 \n",
+       "Q 42.578125 51.265625 45.40625 46.390625 \n",
+       "z\n",
+       "M 14.796875 27.296875 \n",
+       "Q 14.796875 17.390625 18.875 11.75 \n",
+       "Q 22.953125 6.109375 30.078125 6.109375 \n",
+       "Q 37.203125 6.109375 41.296875 11.75 \n",
+       "Q 45.40625 17.390625 45.40625 27.296875 \n",
+       "Q 45.40625 37.203125 41.296875 42.84375 \n",
+       "Q 37.203125 48.484375 30.078125 48.484375 \n",
+       "Q 22.953125 48.484375 18.875 42.84375 \n",
+       "Q 14.796875 37.203125 14.796875 27.296875 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-100\"/>\n",
+       "       <path d=\"M 4.890625 31.390625 \n",
+       "L 31.203125 31.390625 \n",
+       "L 31.203125 23.390625 \n",
+       "L 4.890625 23.390625 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-45\"/>\n",
+       "       <path d=\"M 44.28125 53.078125 \n",
+       "L 44.28125 44.578125 \n",
+       "Q 40.484375 46.53125 36.375 47.5 \n",
+       "Q 32.28125 48.484375 27.875 48.484375 \n",
+       "Q 21.1875 48.484375 17.84375 46.4375 \n",
+       "Q 14.5 44.390625 14.5 40.28125 \n",
+       "Q 14.5 37.15625 16.890625 35.375 \n",
+       "Q 19.28125 33.59375 26.515625 31.984375 \n",
+       "L 29.59375 31.296875 \n",
+       "Q 39.15625 29.25 43.1875 25.515625 \n",
+       "Q 47.21875 21.78125 47.21875 15.09375 \n",
+       "Q 47.21875 7.46875 41.1875 3.015625 \n",
+       "Q 35.15625 -1.421875 24.609375 -1.421875 \n",
+       "Q 20.21875 -1.421875 15.453125 -0.5625 \n",
+       "Q 10.6875 0.296875 5.421875 2 \n",
+       "L 5.421875 11.28125 \n",
+       "Q 10.40625 8.6875 15.234375 7.390625 \n",
+       "Q 20.0625 6.109375 24.8125 6.109375 \n",
+       "Q 31.15625 6.109375 34.5625 8.28125 \n",
+       "Q 37.984375 10.453125 37.984375 14.40625 \n",
+       "Q 37.984375 18.0625 35.515625 20.015625 \n",
+       "Q 33.0625 21.96875 24.703125 23.78125 \n",
+       "L 21.578125 24.515625 \n",
+       "Q 13.234375 26.265625 9.515625 29.90625 \n",
+       "Q 5.8125 33.546875 5.8125 39.890625 \n",
+       "Q 5.8125 47.609375 11.28125 51.796875 \n",
+       "Q 16.75 56 26.8125 56 \n",
+       "Q 31.78125 56 36.171875 55.265625 \n",
+       "Q 40.578125 54.546875 44.28125 53.078125 \n",
+       "z\n",
+       "\" id=\"DejaVuSans-115\"/>\n",
+       "      </defs>\n",
+       "      <use xlink:href=\"#DejaVuSans-71\"/>\n",
+       "      <use x=\"77.490234\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"116.353516\" xlink:href=\"#DejaVuSans-111\"/>\n",
+       "      <use x=\"177.535156\" xlink:href=\"#DejaVuSans-117\"/>\n",
+       "      <use x=\"240.914062\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "      <use x=\"304.292969\" xlink:href=\"#DejaVuSans-100\"/>\n",
+       "      <use x=\"367.769531\" xlink:href=\"#DejaVuSans-45\"/>\n",
+       "      <use x=\"403.853516\" xlink:href=\"#DejaVuSans-115\"/>\n",
+       "      <use x=\"455.953125\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"495.162109\" xlink:href=\"#DejaVuSans-97\"/>\n",
+       "      <use x=\"556.441406\" xlink:href=\"#DejaVuSans-116\"/>\n",
+       "      <use x=\"595.650391\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"657.173828\" xlink:href=\"#DejaVuSans-32\"/>\n",
+       "      <use x=\"688.960938\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"750.484375\" xlink:href=\"#DejaVuSans-110\"/>\n",
+       "      <use x=\"813.863281\" xlink:href=\"#DejaVuSans-101\"/>\n",
+       "      <use x=\"875.386719\" xlink:href=\"#DejaVuSans-114\"/>\n",
+       "      <use x=\"914.75\" xlink:href=\"#DejaVuSans-103\"/>\n",
+       "      <use x=\"978.226562\" xlink:href=\"#DejaVuSans-121\"/>\n",
+       "     </g>\n",
+       "    </g>\n",
+       "   </g>\n",
+       "  </g>\n",
+       " </g>\n",
+       " <defs>\n",
+       "  <clipPath id=\"pd4f85b6dad\">\n",
+       "   <rect height=\"217.44\" width=\"334.8\" x=\"52.160938\" y=\"7.2\"/>\n",
+       "  </clipPath>\n",
+       " </defs>\n",
+       "</svg>\n"
+      ],
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "result = numpy.load('./output/summary_data.npz')\n",
+    "\n",
+    "eig_val, eig_state = numpy.linalg.eig(\n",
+    "                     pauli_str_to_matrix(Hamiltonian, N))\n",
+    "min_eig_H = numpy.min(eig_val.real)\n",
+    "min_loss = numpy.ones([len(result['iter'])]) * min_eig_H\n",
+    "\n",
+    "plt.figure(1)\n",
+    "func1, = plt.plot(result['iter'], result['energy'], \n",
+    "                  alpha=0.7, marker='', linestyle=\"-\", color='r')\n",
+    "func_min, = plt.plot(result['iter'], min_loss, \n",
+    "                  alpha=0.7, marker='', linestyle=\":\", color='b')\n",
+    "plt.xlabel('Number of iteration')\n",
+    "plt.ylabel('Energy (Ha)')\n",
+    "\n",
+    "plt.legend(handles=[\n",
+    "    func1,\n",
+    "    func_min\n",
+    "],\n",
+    "    labels=[\n",
+    "        r'$\\left\\langle {\\psi \\left( {\\theta } \\right)} '\n",
+    "        r'\\right|H\\left| {\\psi \\left( {\\theta } \\right)} \\right\\rangle $',\n",
+    "        'Ground-state energy',\n",
+    "    ], loc='best')\n",
+    "\n",
+    "#plt.savefig(\"vqe.png\", bbox_inches='tight', dpi=300)\n",
+    "plt.show()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Determining the interatomic distance\n",
+    "\n",
+    "Recall the above calculation is done with an interatomic distance $d = 74$ pm between two hydrogen atoms. Another interesting aspect we can try with VQE is determining the true interatomic distance by modifying the `h2.xyz` file. The results are summarize in figure below,\n",
+    "\n",
+    "![VQE-fig-dist](figures/VQE-fig-distance.png)\n",
+    "\n",
+    "The lowest value is found around $d = 74$ pm (1 pm = $1\\times 10^{-12}$m), which is consistent with the [experimental data](https://cccbdb.nist.gov/exp2x.asp?casno=1333740&charge=0) $d_{exp} (H_2) = 74.14$ pm.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "## References\n",
+    "\n",
+    "[1] [Cao, Yudong, et al. Quantum chemistry in the age of quantum computing. Chemical reviews 119.19 (2019): 10856-10915.](https://pubs.acs.org/doi/10.1021/acs.chemrev.8b00803)\n",
+    "\n",
+    "[2] [McArdle, Sam, et al. Quantum computational chemistry. Reviews of Modern Physics 92.1 (2020): 015003.](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003)\n",
+    "\n",
+    "\n",
+    "[3] [Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
+    "\n",
+    "[4] [Moll, Nikolaj, et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Science and Technology 3.3 (2018): 030503.](https://iopscience.iop.org/article/10.1088/2058-9565/aab822)\n",
+    "\n",
+    "[5] Helgaker, Trygve, Poul Jorgensen, and Jeppe Olsen. Molecular electronic-structure theory. John Wiley & Sons, 2014.\n",
+    "\n",
+    "[6] [Dirac, Paul Adrien Maurice. Quantum mechanics of many-electron systems. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 123.792 (1929): 714-733.](https://royalsocietypublishing.org/doi/10.1098/rspa.1929.0094)\n",
+    "\n",
+    "[7] Szabo, Attila, and Neil S. Ostlund. Modern quantum chemistry: introduction to advanced electronic structure theory. Courier Corporation, 2012.\n",
+    "\n"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {
+    "height": "calc(100% - 180px)",
+    "left": "10px",
+    "top": "150px",
+    "width": "426.667px"
+   },
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/VQE/VQE_Tutorial_CN.ipynb

-{
- "cells": [
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "# 变分量子特征求解器（VQE）\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 概览\n",
-    "\n",
-    "- 在这个案例中，我们将展示如何通过Paddle Quantum训练量子神经网络来求解量子系统的能量基态。\n",
-    "\n",
-    "- 首先，让我们通过下面几行代码引入必要的library和package。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 1,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [],
-   "source": [
-    "import os\n",
-    "import numpy\n",
-    "import platform\n",
-    "import matplotlib.pyplot as plt\n",
-    "\n",
-    "from numpy import concatenate\n",
-    "from numpy import pi as PI\n",
-    "from numpy import savez, zeros\n",
-    "from IPython.display import clear_output\n",
-    "from paddle import fluid\n",
-    "from paddle.complex import matmul, transpose\n",
-    "from paddle_quantum.circuit import UAnsatz\n",
-    "from paddle_quantum.utils import pauli_str_to_matrix\n",
-    "from paddle_quantum.VQE.chemistrysub import H2_generator"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 背景\n",
-    "\n",
-    "- 量子计算在近期非常有前景的一个应用就是变分量子特征求解器 (VQE, Variational Quantum Eigensolver) [1-3]。\n",
-    "- VQE作为量子化学在短期内含噪量子设备（NISQ device）上的核心应用之一, 其核心任务是求解一个量子尺度上物理系统的哈密顿量 $H$ 的基态能量及其对应的量子态。数学上，可以理解为求解一个厄米矩阵 (Hermitian matrix) 的最小特征值及其对应的特征向量。\n",
-    "- 接下来我们将通过一个简单的例子学习如何通过训练量子神经网络解决这个问题，我们的目标是通过训练量子神经网络去找到量子态 $\\left| \\phi  \\right\\rangle $ (可以理解为一个归一化的复数向量), 使得 $$\\left\\langle \\phi  \\right|H\\left| \\phi  \\right\\rangle =\\lambda_{\\min}(H)$$ 其中 $\\left\\langle \\phi  \\right|$ 是 $\\left| \\phi  \\right\\rangle$ 的共轭转置，$\\lambda_{\\min}(H)$是矩阵$H$的最小特征值。\n"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## VQE分析氢分子的性质\n",
-    "\n",
-    "- 对于具体需要分析的分子，我们需要其几何构型 (geometry)、电荷 (charge) 以及自旋多重度 (spin multiplicity) 等多项信息来建模获取描述系统的哈密顿量。具体的，通过我们内置的量子化学工具包可以利用 fermionic-to-qubit 映射的技术来输出目标分子的量子比特哈密顿量表示。\n",
-    "- 在这里，作为简单的入门案例，我们提供已经映射好的的氢分子的哈密顿量。 "
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 2,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [],
-   "source": [
-    "Hamiltonian, N = H2_generator()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "面向更高级的用户，我们这里提供一个简单的生成氢分子 (H2)哈密顿量的教程。先安装以下两个package (**仅Mac/Linux用户可使用，Windows用户暂时不支持**):\n"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 3,
-   "metadata": {
-    "scrolled": true
-   },
-   "outputs": [],
-   "source": [
-    "!pip install openfermion\n",
-    "clear_output()"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 4,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "\n",
-      "Collecting openfermionpyscf\n",
-      "  Using cached https://pypi.tuna.tsinghua.edu.cn/packages/cb/6e/01bc7d2e478ea75b9b5dd262c876f5e7d32105e713b588af5b0121def125/openfermionpyscf-0.4.tar.gz (13 kB)\n",
-      "Requirement already satisfied: openfermion>=0.5 in c:\\users\\v_liurenyu\\anaconda3\\envs\\test_paddle\\lib\\site-packages (from openfermionpyscf) (0.11.0)\n",
-      "Collecting pyscf\n",
-      "  Using cached https://pypi.tuna.tsinghua.edu.cn/packages/c0/f1/fe52a94e92acf3fa8c5543d86cfed6fea0526011d2ff2dda352f9cf9eaef/pyscf-1.7.4.tar.gz (7.5 MB)\n"
-     ]
-    }
-   ],
-   "source": [
-    "!pip install openfermionpyscf\n",
-    "clear_output()"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 5,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 操作系统信息\n",
-    "sysStr = platform.system()\n",
-    "\n",
-    "# 判断操作系统\n",
-    "if sysStr in ('Linux', 'Darwin'):\n",
-    "\n",
-    "    import openfermion\n",
-    "    import openfermionpyscf\n",
-    "\n",
-    "    # 请检查是否正确下载了 h2 的几何构型文件\n",
-    "    geo = 'h2.xyz'\n",
-    "    charge = 0\n",
-    "    multiplicity = 1\n",
-    "\n",
-    "    # 生成哈密顿量\n",
-    "    mol = openfermion.hamiltonians.MolecularData(geo, 'sto-3g', multiplicity, charge)\n",
-    "    openfermionpyscf.run_pyscf(mol)\n",
-    "    terms_molecular_hamiltonian = mol.get_molecular_hamiltonian()\n",
-    "    fermionic_hamiltonian = openfermion.transforms.get_fermion_operator(terms_molecular_hamiltonian)\n",
-    "    qubit_op = openfermion.transforms.jordan_wigner(fermionic_hamiltonian)\n",
-    "\n",
-    "    # 打印结果\n",
-    "    print(\"The generated h2 Hamiltonian is \\n\", qubit_op)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "除了氢分子 (H2) 之外, 我们也提供了氟化氢 (HF) 分子的几何构型文件 `hf.xyz`。如果你需要测试更多分子的几何构型，请移步至这个[数据库](http://smart.sns.it/molecules/index.html)。此外，我们还需要把这些本质上由泡利算符表示的哈密顿量转化成 Paddle quantum 支持的数据格式，这里我们提供这个接口。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 6,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "def Hamiltonian_str_convert(qubit_op):\n",
-    "    '''\n",
-    "    将上述提供的哈密顿量信息转为量桨支持的泡利字符串\n",
-    "    H = [[1.0, \"z0,x1\"], [-1.0, \"y0,z1\"], ...]\n",
-    "    '''\n",
-    "    info_dic = qubit_op.terms\n",
-    "    \n",
-    "    def process_tuple(tup):\n",
-    "        if len(tup) == 0:\n",
-    "            return 'i0'\n",
-    "        else:\n",
-    "            res = ''\n",
-    "            for ele in tup:\n",
-    "                res += ele[1].lower()\n",
-    "                res += str(ele[0])\n",
-    "                res += ','\n",
-    "            return res[:-1]\n",
-    "    H_info = []\n",
-    "    \n",
-    "    for key, value in qubit_op.terms.items():\n",
-    "        H_info.append([value.real, process_tuple(key)])\n",
-    "    \n",
-    "    return H_info\n",
-    "\n",
-    "if sysStr in ('Linux', 'Darwin'):\n",
-    "    Hamiltonian = Hamiltonian_str_convert(qubit_op)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 搭建量子神经网络（QNN）\n",
-    "\n",
-    "- 在实现VQE的过程中，我们首先需要设计量子神经网络QNN（也可以理解为参数化量子电路）。这里，我们提供一个预设好的的深度为D层的4量子比特的量子电路模板，图中的虚线框内为一层：\n",
-    "\n",
-    "![Utheta.jpg](https://release-data.cdn.bcebos.com/PIC%2FUtheta.jpg)\n",
-    "\n",
-    "- 我们预设一些该参数化电路的参数，比如宽度为 $N = 4$ 量子位。\n",
-    "\n",
-    "- 初始化其中的变量参数，${\\bf{\\theta }}$ 代表我们量子神经网络中的参数组成的向量。"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "接下来我们根据上图中的电路设计，通过 Paddle Quantum 的 `UAnsatz` 函数和内置的 `real_entangled_layer(theta, D)` 电路模板来高效搭建量子神经网络。 "
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 7,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [],
-   "source": [
-    "def U_theta(theta, Hamiltonian, N, D):\n",
-    "    \"\"\"\n",
-    "    Quantum Neural Network\n",
-    "    \"\"\"\n",
-    "    \n",
-    "    # 按照量子比特数量/网络宽度初始化量子神经网络\n",
-    "    cir = UAnsatz(N)\n",
-    "    \n",
-    "    # 内置的 {R_y + CNOT} 电路模板\n",
-    "    cir.real_entangled_layer(theta[:D], D)\n",
-    "    \n",
-    "    # 铺上最后一列 R_y 旋转门\n",
-    "    for i in range(N):\n",
-    "        cir.ry(theta=theta[D][i][0], which_qubit=i)\n",
-    "        \n",
-    "    # 量子神经网络作用在默认的初始态 |0000>上\n",
-    "    cir.run_state_vector()\n",
-    "    \n",
-    "    # 计算给定哈密顿量的期望值\n",
-    "    expectation_val = cir.expecval(Hamiltonian)\n",
-    "\n",
-    "    return expectation_val"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 配置训练模型 - 损失函数\n",
-    "- 现在我们已经有了数据和量子神经网络的架构，我们将进一步定义训练参数、模型和损失函数.\n",
-    "- 设置训练模型中的的损失函数。通过作用量子神经网络 $U(\\theta)$ 在初始态 $|0..0\\rangle$ 上，我们将得到输出态 $\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle $。进一步，在VQE模型中的损失函数一般由量子态 $\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle$ 关于哈密顿量 $H$ 的期望值 (能量期望值 expectation value) 给出，具体可定义为\n",
-    "\n",
-    "$$\n",
-    "\\mathcal{L}(\\boldsymbol \\theta) =  \\left\\langle {\\psi \\left( {\\bf{\\theta }} \\right)} \\right|H\\left| {\\psi \\left( {\\bf{\\theta }} \\right)} \\right\\rangle\n",
-    "$$"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 8,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [],
-   "source": [
-    "class StateNet(fluid.dygraph.Layer):\n",
-    "    \"\"\"\n",
-    "    Construct the model net\n",
-    "    \"\"\"\n",
-    "\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * PI), dtype=\"float64\"):\n",
-    "        super(StateNet, self).__init__()\n",
-    "        \n",
-    "        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
-    "        \n",
-    "    # 定义损失函数和前向传播机制\n",
-    "    def forward(self, N, D):\n",
-    "        \n",
-    "        # 计算损失函数/期望值\n",
-    "        loss = U_theta(self.theta, Hamiltonian, N, D)\n",
-    "\n",
-    "        return loss"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 配置训练模型 - 模型参数\n",
-    "\n",
-    "在进行量子神经网络的训练之前，我们还需要进行一些训练的超参数设置，主要是学习速率 (LR, learning rate)、迭代次数(ITR, iteration)和量子神经网络计算模块的深度 (D, Depth)。这里我们设定学习速率为0.5, 迭代次数为50次。读者不妨自行调整来直观感受下超参数调整对训练效果的影响。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 9,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [],
-   "source": [
-    "ITR = 80  # 设置训练的总迭代次数\n",
-    "LR = 0.2  # 设置学习速率\n",
-    "D = 2     # 设置量子神经网络中重复计算模块的深度 Depth"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 进行训练\n",
-    "\n",
-    "- 当训练模型的各项参数都设置完成后，我们将数据转化为Paddle动态图中的变量，进而进行量子神经网络的训练。\n",
-    "- 过程中我们用的是Adam Optimizer，也可以调用Paddle中提供的其他优化器。\n",
-    "- 我们将训练过程中的结果存储在summary_data文件中。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 10,
-   "metadata": {
-    "pycharm": {
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "iter: 20 loss: -1.0843\n",
-      "iter: 20 Ground state energy: -1.0843 Ha\n",
-      "iter: 40 loss: -1.1313\n",
-      "iter: 40 Ground state energy: -1.1313 Ha\n",
-      "iter: 60 loss: -1.1356\n",
-      "iter: 60 Ground state energy: -1.1356 Ha\n",
-      "iter: 80 loss: -1.1361\n",
-      "iter: 80 Ground state energy: -1.1361 Ha\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 初始化paddle动态图机制\n",
-    "with fluid.dygraph.guard():\n",
-    "\n",
-    "\n",
-    "    # 确定网络的参数维度\n",
-    "    net = StateNet(shape=[D + 1, N, 1])\n",
-    "\n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
-    "\n",
-    "    # 记录优化结果\n",
-    "    summary_iter, summary_loss = [], []\n",
-    "    \n",
-    "    # 优化循环\n",
-    "    for itr in range(1, ITR + 1):\n",
-    "        \n",
-    "        # 前向传播计算损失函数\n",
-    "        loss = net(N, D)\n",
-    "\n",
-    "        # 在动态图机制下，反向传播极小化损失函数\n",
-    "        loss.backward()\n",
-    "        opt.minimize(loss)\n",
-    "        net.clear_gradients()\n",
-    "        \n",
-    "        # 更新优化结果\n",
-    "        summary_loss.append(loss.numpy())\n",
-    "        summary_iter.append(itr)\n",
-    "        \n",
-    "        # 打印结果\n",
-    "        if itr % 20 == 0:\n",
-    "            print(\"iter:\", itr, \"loss:\", \"%.4f\" % loss.numpy())\n",
-    "            print(\"iter:\", itr, \"Ground state energy:\", \"%.4f Ha\" % loss.numpy())\n",
-    "\n",
-    "    # 储存训练结果到 output 文件夹\n",
-    "    os.makedirs(\"output\", exist_ok=True)\n",
-    "    savez(\"./output/summary_data\", iter=summary_iter, energy=summary_loss)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 测试效果\n",
-    "我们现在已经完成了量子神经网络的训练，得到的基态能量的估计值大致为-1.136 Ha (注: Ha为[哈特里能量](https://baike.baidu.com/item/%E5%93%88%E7%89%B9%E9%87%8C%E8%83%BD%E9%87%8F/13777793?fr=aladdin)，是原子单位制中的能量单位)，我们将通过与理论值的对比来测试效果。\n",
-    "- 训练后得到的QNN作用在初始零态上就是VQE算法的输出态，最后更新的损失函数则为其对应的能量。\n",
-    "- 接下来我们将训练QNN得到的基态能量和理想情况下的理论值。\n",
-    "- 我们可以先求解理论值，即哈密顿量$H$的最小特征值。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 11,
-   "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
-    }
-   },
-   "outputs": [
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAyhUlEQVR4nO3deXhU5dn48e9tQgirYUsgoEAU2WIIEBDkRZBNxQVQqWvdqrbWtZvK2/ZXWvsqdWnrvi/YoqhUBJUKgiC4ExCQVVoIEo0QE3YISeD+/fGchBBmhiHJ5Ewy9+e65jrzzDxzzp1hmHvOc55FVBVjjDEmmOP8DsAYY0x0s0RhjDEmJEsUxhhjQrJEYYwxJiRLFMYYY0KK9zuASGjdurV26tTJ7zCMMabOWLJkyQ+q2ibQc/UyUXTq1Ins7Gy/wzDGmDpDRDYFe86anowxxoRkicIYY0xIliiMMcaE5Ms1ChFpCbwGdAJygB+p6rYgdeOAbOBbVT2vtmI0pq4pKSkhNzeXoqIiv0MxUSwxMZEOHTrQoEGDsF/j18Xsu4F5qjpJRO72yncFqXs7sAZoXlvBGVMX5ebm0qxZMzp16oSI+B2OiUKqSkFBAbm5uXTu3Dns1/nV9DQGmOzdnwyMDVRJRDoA5wLP1U5YxtRdRUVFtGrVypKECUpEaNWq1TGfdfqVKFJUNQ/A2yYHqfd34E7g4NF2KCI3iki2iGTn5+fXWKDG1CWWJMzRVOUzErFEISJzRWRlgNuYMF9/HrBVVZeEU19Vn1HVLFXNatMm4JiRo+0AXnsNli499tcaY0w9FrFrFKo6IthzIrJFRNqpap6ItAO2Bqg2CLhAREYDiUBzEfmnql4ZkYBF4M03Yfhw6NMnIocwxpi6yK+mp5nA1d79q4EZlSuo6gRV7aCqnYBLgQ8iliTKtGgB2wJ2vjLGmJjlV6KYBIwUkfXASK+MiKSKyCyfYoKkJNi+3bfDG1NfDBs2jNLS0pB19u3bx5AhQzhw4AAABw4c4Pbbb6dnz56ceuqpbNiwgeLiYs4444zD9jV06FBycnIAePrpp/n5z39+2H579uzJ2rVrj6hb07Fs27aNcePGhfV+1HW+JApVLVDV4araxdsWeo9/p6qjA9RfUCtjKJKS7IzCmGpatWoVrVq1Ij4+dMv2Cy+8wIUXXkhcXBwA9913H2lpaaxatYrbbruNJ554goSEBIYPH85rr70WcB8rVqygd+/e5eWioiK++eYbunTpckwxVyWWFi1aUFhYSEFBwTEdqy6ql5MCVlmLFrBsmd9RGFN9zz4LGzbU7D7T0uCGG45abcaMGYwdOxaAzMxMZs+ezaOPPkqXLl3o2LEjTz31FFOnTmXKlCm88sorAOzZs4fp06ezZInru9K5c2feffddAMaOHcuECRO44oorjjjWV199xXXXXXdY+ZRTTin/wq8oErGce+65vP3221xzzTXhvIN1liWKipKSYM8eKC6GhAS/ozGmTpo1axbvvPMOpaWlFBYWkpKSwvLly7n44otZuHAhvXr1ori4mA0bNlC2HMDcuXPZvHkzmZmZABQWFjJihOsPk56ezuLFiwMea9WqVVx44YXlXT53797Neecd2fgQqVjGjBnDXXfdZYkiprRo4bbbt0NysKEdxtQBYfzyj4R9+/ZRXFxMUlISK1eupHv37gCsXr2aHj168Oijj3LhhRfyww8/kJSUVP66ZcuW8ac//Ymf/exnAFx//fVkZGQAEBcXR0JCArt27aJZs2blr9m8eTNt2rQpvx4BcMstt5CWlnZEXGvXro1ILF27dmXdunU18M5FN5sUsKKyD4td0DamSho1aoSIsHv3btatW0fXrl0pLCykadOmJCQkkJ2dTVZWFo0aNTpsdPC2bdto3Lgx4H79z5kzh/PPP7/8+f3795OYmHjYsVasWEHPnj0Pe2z16tWceuqpR8QVqVg2bdp0TFNh1FWWKCqqeEZhjKmSs846i/fee4+EhATWrl1LdnY2vXr14p///CedOnUiJSWFFi1acODAgfIv6FNOOYXPPvsMgL/97W+ce+655V/ABQUFtGnT5ohJ7L766it69Ohx2GOrVq0q//VfUaRimTFjBmPGhDWGuE6zRFFR2RmF9XwypsrGjBnDW2+9xdlnn023bt244oorWLBgAdnZ2bz88svl9UaNGsVHH30EwGWXXcbSpUs5+eSTWbFiBX/961/L682fP5/Ro4/oDHlEoigsLERVSUlJOaJupGJ5++23ueCCC6ryNtUtqlrvbn379tUqKS5WPe881alTq/Z6Y3y0evVqv0Mol5GRoSUlJaqqes011+icOXOOqLN06VK98sorj7qvcePG6dq1a8vLQ4YM0Y0bN4YVR+W6NRlLYWGhDh48OKw4ok2gzwqQrUG+U+2MoqIGDaBJEzujMKaali9fXj6OYsWKFQGbg3r37s2ZZ55ZPsgtkOLiYsaOHUvXrl1rJK6ajKVFixYsXLiwRuKKdtbrqbIWLewahTE1qGw8QiAVx0AEkpCQwFVXXXXYY9dcc81hvZRCqVy3pmOJFZYoKrPR2cZEtWMZs1DfxzfUFmt6qszmezLGmMNYoqjMmp6MMeYwligqS0qCvXvdNB7GGGMsURzBBt0ZY8xhLFFUZoPujDHmMJYoKrMzCmOqbMuWLVx++eWkpaXRt29fBg4cyPTp02s1hpycHNLT08Ouv2DBAj755JMaq1cfWaKozM4ojKkSVWXs2LGcccYZbNiwgSVLljB16lRyc3OPqHu01e9qU11MFLX9/lmiqMxmkDWmSj744AMSEhLKp+cG6NixI7feeisAL730EuPHj+f8889n1KhRFBYWMnbsWDIyMhgwYAArVqwAYOLEiTz44IPl+0hPTycnJ4ecnBy6d+/ODTfcQM+ePRk1ahT79u0D3EC6Xr16MXDgQB5//PGgMT7yyCP06NGDjIwMLr30UnJycnjqqaf429/+RmZmJosWLeLtt9/mtNNOo3fv3owYMYItW7YErJefn89FF11Ev3796NevHx9//PERxztw4AC/+c1v6NevHxkZGTz99NOASzpDhw7l4osvLp+Dys2i4f6WIUOG0LdvX8466yzy8vIAt6zr//7v/zJkyBAefvhhFi9eTEZGBgMHDuQ3v/lN+VnU4MGDWVZhAbZBgwaVv7dVFmxuj0jegJbA+8B6b9siSL0c4CtgGSHmIal8q/JcT2Uuu0z1iSeqtw9jalnl+Xvuvlt17lx3v6TElT/4wJWLilx54UJX3r3blT/+2JV37HDlzz935cLCox//4Ycf1jvuuCPo8y+++KK2b99eCwoKVFX1lltu0YkTJ6qq6rx587RXr16qqvqHP/xBH3jggfLX9ezZUzdu3KgbN27UuLg4/fLLL1VVdfz48fqPf/xDVVVPPfVUXbBggaqq/vrXv9aePXsGjKFdu3ZaVFSkqqrbtm0LeLzCwkI9ePCgqqo+++yz+stf/jJgvcsuu0wXLVqkqqqbNm3Sbt26HXG8p59+Wu+55x5VVS0qKtK+ffvqhg0bdP78+dq8eXPdvHmzHjhwQAcMGKCLFi3S4uJiHThwoG7dulVVVadOnarXXnutqrp5q2666abD3pePvX+wu+66q/xvfumll/T2229XVdV169ZpoO/DY53rya+R2XcD81R1kojc7ZXvClL3TFX9ofZCwwbdGVMDbr75Zj766CMSEhLKV4UbOXIkLVu2BOCjjz7iX//6FwDDhg2joKCAHTt2hNxn586dy1ee69u3Lzk5OezYsYPt27czZMgQAH784x/z73//O+DrMzIyuOKKKxg7dmz5cq2V5ebmcskll5CXl0dxcXHQ9Sbmzp3L6tWry8s7d+48YnGlOXPmsGLFCqZNmwbAjh07WL9+PQkJCfTv358OHToAbpnWnJyc8gWfRo4cCbgzknbt2pXv75JLLgFg+/bt7Nq1i9NPPx2Ayy+/nHfeeQeA8ePHc8899/DAAw/wwgsv1MjodL8SxRhgqHd/MrCA4Imi9rVoYdcoTJ13332H7sfHH15u2PDwcpMmh5ebNz+8XNbHI5SePXuWf/EDPP744/zwww9kZWVVOE6T8vvqNbVUJCLEx8dz8ODB8scqLirUsGHD8vtxcXHs27cPVS1fCrWya6+9li+//JLU1FRmzZrFu+++y8KFC5k5cyb33HMPq1atOuI1t956K7/85S+54IILWLBgARMnTgy474MHD/Lpp5/SqFGjgM+X/Y2PPvooZ5111mGPL1iw4Ii/pbS0FFWlZ8+efPrppwH3V/b+BXrvyjRu3JiRI0cyY8YMXn/9dbKzs4PWDZdf1yhSVDUPwNsGW3dUgTkiskREbqy16OyMwphjNmzYMIqKinjyySfLH9u7d2/Q+meccQZTpkwB3Bdn69atad68OZ06dWLp0qUALF26lI0bN4Y8blJSEscff3z5ehJl+wR48cUXWbZsGbNmzeLgwYNs3ryZM888k/vvv5/t27eze/dumjVrxq5du8pfs2PHDtq3bw/A5MmTyx+vXG/UqFE89thj5eWK1wXKnHXWWTz55JOUlJQA8PXXX7Nnz56gf0vXrl3Jz88vTxQlJSUBk1mLFi1o1qxZ+QJLU6dOPez566+/nttuu41+/fqVn8FVR8QShYjMFZGVAW7HshzUIFXtA5wD3CwiZ4Q43o0iki0i2fn5+dUL3s4ojDlmIsJbb73Fhx9+SOfOnenfvz9XX301f/nLXwLWnzhxItnZ2WRkZHD33XeXfylfdNFFFBYWkpmZyZNPPskpp5xy1GO/+OKL3HzzzQwcODDoL/wDBw5w5ZVXcuqpp9K7d29+8YtfkJSUxPnnn8/06dPLL1JPnDiR8ePHM3jwYFq3bl3++sr1HnnkkfL4e/TowVNPPXXEMa+//np69OhBnz59SE9P56c//WnIHksJCQlMmzaNu+66i169epGZmRm0p9Xzzz/PjTfeyMCBA1FVjj/++PLn+vbtS/Pmzbn22muP+t6FQ0KdwkSKiKwDhqpqnoi0AxaoasgJ50VkIrBbVR8MVQ8gKytLq3W6NW0aTJ4Mb7wBldbpNSZarVmzhu7du/sdhqklu3fvpmnTpgBMmjSJvLw8Hn74YQC+++47hg4dytq1aznuuCPPBwJ9VkRkiapmHVEZ/5qeZgJXe/evBmZUriAiTUSkWdl9YBSwslais0F3xpgo9+6775KZmUl6ejqLFi3id7/7HQAvv/wyp512Gv/3f/8XMElUhV8XsycBr4vIT4BvgPEAIpIKPKeqo4EUYLp3kSoeeEVV36uV6CoOumvbtlYOaYwxx+KSSy4p7wVV0VVXXVXjCyz5kihUtQAYHuDx74DR3v0NQK9aDs2xMwpTR4XqAWQMhO4xFYyNzA7EpvEwdVBiYiIFBQVV+iIwsUFVKSgoIPEYr73aUqiBNG/utnZGYeqQDh06kJubS7V7/Zl6LTExsXygX7gsUQQSH++ShSUKU4c0aNAg6ChiY6rDmp6CSUqypidjjMESRXC2drYxxgCWKIKzMwpjjAEsUQRXdkZhPUiMMTHOEkUwSUmwfz9UmLnSGGNikSWKYGzQnTHGAJYogrMlUY0xBrBEEVzZGYVd0DbGxDhLFMGULfZRUOBvHMYY4zNLFME0bw4JCbB1q9+RGGOMryxRBCMCKSmWKIwxMc8SRSjJybBli99RGGOMryxRhJKSYonCGBPzLFGEkpwMu3fDnj1+R2KMMb6xRBFKSorb2vz+xpgY5kuiEJGWIvK+iKz3ti2C1EsSkWkislZE1ojIwFoNtCxRWPOTMSaG+XVGcTcwT1W7APO8ciAPA++pajfc+tlraik+JznZbS1RGGNimF+JYgww2bs/GRhbuYKINAfOAJ4HUNViVd1eS/E5zZtDw4bWRdYYE9P8ShQpqpoH4G2TA9RJA/KBF0XkSxF5TkSa1GaQ5WMp7IzCGBPDIpYoRGSuiKwMcBsT5i7igT7Ak6raG9hD8CYqRORGEckWkewaXVzeEoUxJsbFR2rHqjoi2HMiskVE2qlqnoi0AwK17eQCuar6uVeeRohEoarPAM8AZGVl1dxqQ8nJsHp1je3OGGPqGr+anmYCV3v3rwZmVK6gqt8Dm0Wkq/fQcKD2v7FTUtw4ChtLYYyJUX4liknASBFZD4z0yohIqojMqlDvVmCKiKwAMoF7aztQ6yJrjIl1EWt6CkVVC3BnCJUf/w4YXaG8DMiqvcgCqNhFNi3N11CMMcYPNjL7aMrOKKyLrDEmRlmiOJqmTSEx0ZqejDExyxLF0YhA27Z2RmGMiVmWKMJh61IYY2KYJYpwlA2605obnmGMMXWFJYpwJCfDvn1ubQpjjIkxlijCYT2fjDExzBJFOGzQnTEmhlmiCIetS2GMiWGWKMLRpAk0bmxNT8aYmGSJIhy2LoUxJoZZogiXjaUwxsQoSxThSklxTU82lsIYE2MsUYQrORmKimDXLr8jMcaYWhVymnERSQTOAwYDqcA+YCXwrqquinx4UaRtW7fdsgWaN/c3FmOMqUVBzyhEZCLwMTAQ+Bx4GngdKAUmicj7IpJRG0FGhbKxFHl5/sZhjDG1LNQZxWJVnRjkub+KSDJwYs2HFKVSU932u+/8jcMYY2pZ0EShqu+GeqGqbgViZ2BBQgK0bm2JwhgTc466FKqItAHuAnoAiWWPq+qwCMYVnVJTLVEYY2JOOL2epgBrgM7AH4EcYHF1DioiLb1rHOu9bYsAdbqKyLIKt50ickd1jlttliiMMTEonETRSlWfB0pU9UNVvQ4YUM3j3g3MU9UuwDyvfBhVXaeqmaqaCfQF9gLTq3nc6klNdd1jrYusMSaGhJMoSrxtnoicKyK9gQ7VPO4YYLJ3fzIw9ij1hwP/VdVN1Txu9bRv77Z2VmGMiSHhJIo/i8jxwK+AXwPPAb+o5nFTVDUPwNsmH6X+pcCroSqIyI0iki0i2fn5+dUMLwjr+WSMiUFHvZitqu94d3cAZ4a7YxGZC7QN8NRvw92Ht58E4AJgQqh6qvoM8AxAVlZWZObZaNvWTRBoicIYE0OCJgoReRQI+oWrqreF2rGqjgix7y0i0k5V80SkHaG72Z4DLFVV/2fki493U3lYojDGxJBQZxTZFe7/EfhDDR53JnA1MMnbzghR9zKO0uxUq1JT4dtv/Y7CGGNqTagBd2UXmxGROyqWa8Ak4HUR+QnwDTDeO04q8JyqjvbKjYGRwE9r8NjV0749rF3rZpEV8TsaY4yJuKNeo/DUaJu/qhbgejJVfvw7YHSF8l6gVU0eu9pSU2HfPtixA5KS/I7GGGMizqYZP1bW88kYE2NCXczexaEzicYisrPsKUBVNTbn2q6YKHr08DcWY4ypBaGuUTSrzUDqjORkiIuzC9rGmJgRaj2Kpkd7cTh16p24ODeewpqejDExItQ1ihki8pCInCEiTcoeFJE0EfmJiMwGzo58iFHIJgc0xsSQUE1Pw0VkNK5r6iBvhtdSYB3wLnC1qn5fO2FGmdRUWLHCusgaY2JCyO6xqjoLmFVLsdQdqamwfz8UFkKr6Oq9a4wxNc26x1ZFWc8nu6BtjIkBliiqwsZSGGNiiCWKqmjTBho0sERhjIkJR00UIvKgiPSsjWDqDBHrImuMiRnhnFGsBZ4Rkc9F5GfeIkamfXtLFMaYmHDURKGqz6nqIOAqoBOwQkReEZGwFzGql1JTIS8PDh70OxJjjImosK5RiEgc0M27/QAsB34pIlMjGFt0O+EEKC2FzZv9jsQYYyIqnGsUf8UNshsN3KuqfVX1L6p6PtA70gFGrcxMt1282NcwjDEm0sI5o1gJZKjqT1X1i0rP9Y9ATHVD69aQlmaJwhhT74WzcNEyoJscPlXFDmCTqu6IRFB1Rv/+8NprsGsXNLPJdo0x9VM4ZxRPAJ8BzwDPAp8CU4GvRWRUBGOLfv37u/mesrOPXtcYY+qocBJFDtBbVbNUtS/uusRKYARwf1UOKiItReR9EVnvbVsEqfcLEVklIitF5FURSazK8SLm5JOhRQv4onKLnDHG1B/hJIpuqrqqrKCqq3GJY0M1jns3ME9VuwDzvPJhRKQ9cBuQparpQBxwaTWOWfNEICsLli51PaCMMaYeCidRfC0iT4rIEO/2hPdYQ6CkiscdA0z27k8GxgapFw80EpF4oDEQfSPcTjsN9u6F1av9jsQYYyIinERxNfAf4A7gF8AG4BpckqjqoLsUVc0D8LbJlSuo6rfAg8A3QB6wQ1XnBNuhiNwoItkikp2fn1/FsKqgVy8375M1Pxlj6qmQicIbaPe2qj6kquNUdayqPqiqe1X1oKruDvHaud61hcq3MeEE5l23GAN0BlKBJiJyZbD6qvqMdx0lq02bNuEcomYkJkJGhksUqrV3XGOMqSUhE4WqHgD2VmV+J1UdoarpAW4zgC0i0g7A224NsIsRwEZVzVfVEuBN4PRjjaNW9O/vpvOw9SmMMfVQOE1PRcBXIvK8iDxSdqvmcWfimrTwtjMC1PkGGCAijcUN4hgOrKnmcSOjXz+3teYnY0w9FE6ieBf4PbAQWFLhVh2TgJEish4Y6ZURkVQRmQWgqp8D04ClwFderM9U87iR0aYNdO4Mn3/udyTGGFPjRMNoVxeRRsCJqrou8iFVX1ZWlmbX9iC4adNg8mS4+WY4++zaPbYxxlSTiCxR1axAz4UzKeD5uGk83vPKmSIys0YjrA/GjXNjKp58EpZU94TLGGOiRzhNTxNxk/9tB1DVZbieSKaiuDi46y7o1AkmTYIN1RmPaIwx0SOcRFEaYPI/6wcaSGIi/OEP0LQp/PGP8MMPfkdkjDHVFtY04yJyORAnIl1E5FHgkwjHVXe1bOmSxb59cN99NrbCGFPnhZMobgV6AvuBV4GduFHaJphOneCmm+Drr2HBAr+jMcaYaglnzey9qvpbVe3njXz+raoW1UZwddrQodClC7z8Muzf73c0xhhTZeH0ejpFRJ4RkTki8kHZrTaCq9NE4Lrr3HWKGYHGExpjTN0Qzgp3bwBPAc8BByIbTj2Tng4DBsAbb8DIkW7tCmOMqWPC7fX0pKp+oapLym4Rj6y+uOYaKCmBV17xOxJjjKmScBLF2yLycxFp561M11JEWkY8svqifXsYPRpmz4ZNm/yOxhhjjlm461H8BtcltmyeJ1sk+lhcdhk0bgxTp/odiTHGHLOjXqNQVRuFXV3NmsGQITB3LhQVuYF5xhhTRwQ9oxCROyvcH1/puXsjGVS9NHgwFBfD4sV+R2KMMcckVNPTpRXuT6j0nE2Peqx69HC9nj76yO9IjDHmmIRKFBLkfqCyOZrjjoNBgyA72zU/GWNMHREqUWiQ+4HKJhyDBrnmJ1sJzxhTh4RKFL1EZKeI7AIyvPtl5VNrKb76pUcPN2mgNT8ZY+qQoL2eVDWuNgOJCWXNT++952aXbdTI74iMMeaowhlHUeO8QXvvi8h6bxtwbgsRuV1EVorIKhG5o5bDjIxBg9xIbev9ZIypI3xJFMDdwDxV7QLM88qHEZF04Abc6nq9gPNEpEutRhkJZc1Pixb5HYkxxoTFr0QxBpjs3Z8MjA1QpzvwmTfNeSnwITCudsKLIBF3VrFkCezd63c0xhhzVH4lihRVzQPwtskB6qwEzhCRViLSGBgNnBBshyJyo4hki0h2fn5+RIKuMYMHu+Yn6/1kjKkDwplmvEpEZC7QNsBTvw3n9aq6RkT+ArwP7AaWA6Uh6j8DPAOQlZUV3d13u3WDpCR3nWLoUL+jMcaYkCKWKFR1RLDnRGSLiLRT1TwRaQdsDbKP54HnvdfcC+RGJNjaJgK9e7vBd6qubIwxUcqvpqeZuFlp8bYBl4ATkWRveyJwIW7N7vqhTx/YtQv+8x+/IzHGmJD8ShSTgJEish4Y6ZURkVQRmVWh3r9EZDXwNnCzqm6r/VAjpHdvt/3yS3/jMMaYo4hY01MoqloADA/w+He4i9Zl5cG1GVetOv54SEtzieJHP/I7GmOMCcqvMwoDrvlpzRo3StsYY6KUJQo/9e4NBw7AihV+R2KMMUFZovBT9+7QsKFdpzDGRDVLFH5q0AAyMmDpUr8jMcaYoCxR+K13b8jLg++/9zsSY4wJyBKF3/r0cVtrfjLGRClLFH5LTYXkZEsUxpioZYnCb2XTeSxfDqVBp7IyxhjfWKKIBn36uCnHv/7a70iMMeYIliiiQa9ebpnUJUv8jsQYY45giSIaNGnixlRkZ/sdiTHGHMESRbTIyoING6Cw0O9IjDHmMJYookVWltta85MxJspYoogWHTtCq1bW/GSMiTqWKKKFiDur+PJL6yZrjIkqliiiSb9+bsrxNWv8jsQYY8pZoogmvXpBfLw1PxljooolimiSmAjp6ZYojDFRxZdEISLjRWSViBwUkawQ9c4WkXUi8h8Rubs2Y/RNVhZ88w1s3ep3JMYYA/h3RrESuBBYGKyCiMQBjwPnAD2Ay0SkR+2E5yPrJmuMiTK+JApVXaOq645SrT/wH1XdoKrFwFRgTOSj81lqKrRta81PxpioEc3XKNoDmyuUc73HAhKRG0UkW0Sy8/PzIx5cxJR1k12+HIqL/Y7GGGMilyhEZK6IrAxwC/esQAI8psEqq+ozqpqlqllt2rSpWtDRIisL9u+3NSqMMVEhPlI7VtUR1dxFLnBChXIH4Ltq7rNu6NULjj8e5s+H007zOxpjTIyL5qanxUAXEeksIgnApcBMn2OqHfHxMGQIfPEF7N7tdzTGmBjnV/fYcSKSCwwE3hWR2d7jqSIyC0BVS4FbgNnAGuB1VV3lR7y+GDYMSkrgo4/8jsQYE+Mi1vQUiqpOB6YHePw7YHSF8ixgVi2GFj3S0uCEE+CDD+Dss/2OxhgTw6K56Sm2ibizijVrIC/P72iMMTHMEkU0GzrUJYz58/2OxBgTwyxRRLPWrV0PqA8+AA3aM9gYYyLKEkW0GzYMtmyxqceNMb6xRBHtBg50s8pa85MxxieWKKJdYiKcfjosWgRFRX5HY4yJQZYo6oLRo2HPHnjnHb8jMcbEIEsUdUHXrtC3L7z5Juzd63c0xpgYY4mirrjySti1C2bGxiwmxpjoYYmirjj5ZHdhe/p0lzCMMaaWWKKoSy6/HPbtg7feqrl9bt0KH34IOTlw8GDN7dcYU2/4MteTqaJOnWDwYNf8dMEFbiryqti1Cz7+2HW5Xb360OONG7vrIZmZcO650LBhTURtjKnjLFHUNZdf7rrKTpsGP/nJsb1WFWbPhmefdavnnXAC/PjH0Ls35Oa6pLF2Lbz4outhdcMNMGCAm0bEGBOzLFHUNe3bw/Dh7qzi1FOhf//wXldUBI8/DgsWuMRwzTXQufOhJNClC5x5pru/ciU89RTce6/rbXXjjW4tb2NMTBKth3MIZWVlaXZ2tt9hRM6+ffDb38KmTfCnP0HPnqHrb9oEkybBt9/CFVfAj3509LOE0lJ4912YMsWti3HRRTB+vDVHGVNPicgSVc0K+Jwlijpq5064807Ytg3uu8+tX1FZSYnrJfXaa+76w29+AxkZx3acwkJ46SV3PSM52TVHnXaaNUcZU89YoqivfvjBffmXlMAf/wgdO7plVME1Hz3+uLv28D//45qPWrSo+rHKmqM2bXLJ5pJLXNOXJQxj6gVLFPVZbq47s9i1y31pt2zpekNt2AApKfCzn0FWwH/7Y1daCrNmwRtvwPbt0K2ba8bKyrKEYUwdF3WJQkTGAxOB7kB/VQ34rS4iLwDnAVtVNT3c/cdUogA3FmLZMsjPd7eCAvclfvHFkbmmUFwMc+fCv/7ljt25s7t+MWgQHGdDc4ypi6IxUXQHDgJPA78OkSjOAHYDL1uiiEKlpW6w3rRp7symXTt30Xv48ENNYMaYOiFUovDl55+qrlHVdWHUWwgU1kJIpiri411SeOIJmDABmjSBxx6Dn/7UrcpnI72NqRfqTTuBiNwoItkikp2fn+93OLFFxK2Z8de/wsSJ0KwZ/O1vcMst8OmntoyrMXVcxNoHRGQu0DbAU79V1Rk1fTxVfQZ4BlzTU03v34RBxA3Q69MHPvkE/vEPN2jvhBNg3DgYOhQaNPA7SmPMMYpYolDVEZHat4lyIu7C9oABsHChG8vxyCMucYwe7Z7r0MF6ShlTR9gVRxM5cXFuWpChQ2H5cpcwpkxxt5QU6NfPTSdy8smuW68xJir51etpHPAo0AbYDixT1bNEJBV4TlVHe/VeBYYCrYEtwB9U9fmj7d96PUWx/HzIzobFi13yKC52jyclwUknuUGDKSnu1rYtNG/uLpo3aOASz/79sHu3Gzeya9fh9/fscfsScbcGDVwCatUK2rRxI8sTE337042JZlHXPTbSLFHUEcXFsH69Gxz43/+6W26u63ZbFfHxLkGouh5XgXpdtW3rxn107uymPUlLg9atrRnMxLxQicKanox/EhLchIYVJzVUdfNLbdkC33/vzhJKS900JaWlbgBhs2bQtKm7NW/uts2auf1V/MIvLXX7Kihw053k5cHGjS4xffbZod5YzZq5hHHCCe6so+zso2lTdwbSsKG72dgQE6Psk2+ii4hrKmrVCnr0qN6+4uPdF35y8pHPFRW5Vf3KzmY2bHBjP/buDb6/445zyagscVROVs2bu6RTlsgaNjxUPz7evb6sWawsoZVt4+MP3Ro0cK+xsxwTJSxRmNiUmOimOenW7fDH9+w5NBXK7t3umsj+/S6xFBe7+2XbsusjOTmHrpPU5CDDikkpIcHdGjQ41MQGh7aqh86QjjvO1Su7JSZCo0ZuBuHGjV254i0+3l3/KdsGSlDBmqgrxlH5dYFec9xxh24Vj1l2DaqsHBdn08FEEUsUlUyYACNGuAHHpaXw+9/DqFGu887+/W482ejRbkXSPXvgz3+G889348127nQzfo8b59YT2rYN7r/fTbnUt69r/XjoITfxamama1l5+GG3RER6ulsu4rHH4KqroHt3N1HrU0/Bdde5dYU2bHCL091wg2spWb8eXnjBzfvXsSOsWQMvv+zGubVv7yZ8nTIFbr/dNc0vW+ZmHP/Vr1yz/JIlbvaNO+90E8t+8YXrmDRhgvtx/Mkn8Pbb8LvfuUHXixa5OQEnTnTfXfPnw5w5cM897v/3vHluCqj77nPv5ezZ7jV//rMrz5rljjFxoivPnOmuZ//+9648fbpbYG/CBFeeNs39zXfe6cpTp7r36Fe/cuUpU9z3+R13uPLkye67+pZbXPmFF9y/2U03ufKzz7rtDTe47ZNPur/juutc+bHHoFmzJlx9dRPo1Im//921Ql1xhXv+oYfc+3rppa58//2Q1t39+wLcd6/SrfN+xg3dBnv2cM/Dzel10m4uGJgPJSVMfOFE+nfbwej+BQD87rlODM7YwVlZBXDgABOeTWNExlaG98ijdG8xv3+1B6NOzOHMjhvYv+8gE98bwOi0tQxO/S97ihvw54/P5Pwuazm9/SZ2Fidy3ydDGNd1Nf3bbWbbduH+z07n4k6L6dt8JT9si+Ohr0ZxSbuFZB6/ke+Lknh44wVc0X4B6c2/4dt9LXks5zyu6vAB3ZvlsmlvG57adA7XnfA+XZrmsWFPCs9+cxY3nDibtCZbWL+7HS9sHsnPOv6bjo3zWbOrAy/nDuOWTu/QvlEhK3eeyJRvh3J755m0TdzOsh2dee27wfzqpLdonbCTJdtPYlreIO486V+0SNjDF9u6MP37gUw4+Q2aN9jHJ4XdeHtLf353yus0aVDMosKezNrSl4ndptIwrpT5+enM2ZrJPd1fIf64g8zLP5W5W3txX/oUEGH2lkwWFXTnz+mvuc/e9334ouAkJvZ8w332vu3L8u0d+X33ae6z921/1u5uz4Su091n79uBbNibwp3d3wERpn5zOt/ua8mver7nPns5g8jf35w7esxxn73//g+7ShtxS/d57rO3fjD7D8ZzU/cP3Wdv3Rnus9d1ofvsrRlKw7hSruuyyH32Vg+jWYMirj7pIwD+vnoUbRJ3cUXap+6zt+ps2jfexqVpX4AI9391DmnN8rk4bSmIcN/yc+h2/PeM67UBHnzwiO+16rJEYUxNEXG/0Nu1c+VkIC0ZTvPWCpkLpOP68ZWVewHDvPIHwMCTYDhQCqwCRmXAmcB+YCcw+nQYDOwB/gycPwRO9567Dxg3BPoD24D7gYtHQF/gB+BBhQsvgK77YHMJPNEAzsmCtL3wncCrLeHsbtC5CPIS4M1kOL8rnLgfvm0Ib7WBsV2hQzF80xBmtoYLT4G2+2FDQ/h3G7j4JEgugf82gtmt4dKToVUJfN0Y3m8Jl3WG5sWwphF80ArGJ0OjIljdFD5uA2MbQsP9sCYJslPhgguhYSmsaQ0rOsCYMdDgIKxJga9SYexYiFNYlQKrUt1a8qruua9T4OyzvXIH2JjsyiKw7ATY3BLOO8+Vl5wIecfDeaWu/uKOsLUpjNzvzhK/SIPtjd0YoIMHIf5k2JXoZk5WhQMdoSjB/QJUhaIOUBrvpuJXhV3eCpHp6a68IxUaHDi0PsyO9pBY4garAuzsAE33QZ/9rry9vZsVupdXzm8LLROhR5Hb37dtoM1xcFJkmiut15MxxpjomxTQGGNM3WGJwhhjTEiWKIwxxoRkicIYY0xIliiMMcaEZInCGGNMSJYojDHGhGSJwhhjTEj1csCdiOQDm8Ks3ho3bjXaRGtcYLFVRbTGBdEbW7TGBdEbW3Xi6qiqbQI9US8TxbEQkexgoxH9FK1xgcVWFdEaF0RvbNEaF0RvbJGKy5qejDHGhGSJwhhjTEiWKOAZvwMIIlrjAoutKqI1Loje2KI1Loje2CISV8xfozDGGBOanVEYY4wJyRKFMcaYkGI2UYjI2SKyTkT+IyJ3+xzLCyKyVURWVnispYi8LyLrvW0LH+I6QUTmi8gaEVklIrdHUWyJIvKFiCz3YvtjtMTmxREnIl+KyDtRFleOiHwlIstEJDtaYhORJBGZJiJrvc/bwCiJq6v3XpXddorIHVES2y+8z/5KEXnV+z8RkbhiMlGISBzwOHAO0AO4TER6+BjSS8DZlR67G5inql2AeV65tpUCv1LV7sAA4GbvfYqG2PYDw1S1F5AJnC0iA6IkNoDbgTUVytESF8CZqppZob99NMT2MPCeqnbDLRC7JhriUtV13nuViVtUdi8w3e/YRKQ9cBuQparpQBxwacTiUtWYuwEDgdkVyhOACT7H1AlYWaG8Dmjn3W8HrIuC920GMDLaYgMaA0uB06IhNqCD9590GPBONP17AjlA60qP+Rob0BzYiNe5JlriChDnKODjaIgNaA9sBloC8cA7XnwRiSsmzyg49CaXyfUeiyYpqpoH4G2T/QxGRDoBvYHPiZLYvOadZcBW4H1VjZbY/g7cCRys8Fg0xAWgwBwRWSIiN0ZJbGlAPvCi11z3nIg0iYK4KrsUeNW772tsqvot8CDwDZAH7FDVOZGKK1YThQR4zPoJByEiTYF/AXeo6k6/4ymjqgfUNQl0APqLSLrPISEi5wFbVXWJ37EEMUhV++CaXW8WkTP8Dgj3i7gP8KSq9gb24G/T3BFEJAG4AHjD71gAvGsPY4DOQCrQRESujNTxYjVR5AInVCh3AL7zKZZgtohIOwBvu9WPIESkAS5JTFHVN6MptjKquh1YgLvO43dsg4ALRCQHmAoME5F/RkFcAKjqd952K66tvX8UxJYL5HpnhADTcInD77gqOgdYqqpbvLLfsY0ANqpqvqqWAG8Cp0cqrlhNFIuBLiLS2fulcCkw0+eYKpsJXO3dvxp3faBWiYgAzwNrVPWvURZbGxFJ8u43wv3HWet3bKo6QVU7qGon3OfqA1W90u+4AESkiYg0K7uPa9Ne6Xdsqvo9sFlEunoPDQdW+x1XJZdxqNkJ/I/tG2CAiDT2/p8Ox3UAiExcfl4c8vMGjAa+Bv4L/NbnWF7FtTOW4H5d/QRohbsgut7btvQhrv/BNcmtAJZ5t9FRElsG8KUX20rg/3mP+x5bhRiHcuhitu9x4a4FLPduq8o+91ESWyaQ7f17vgW0iIa4vNgaAwXA8RUe8z024I+4H0crgX8ADSMVl03hYYwxJqRYbXoyxhgTJksUxhhjQrJEYYwxJiRLFMYYY0KyRGGMMSYkSxSmThERFZGHKpR/LSITa2jfL4nIxTWxr6McZ7w3Q+r8So+nisg0736miIyuwWMmicjPAx3LmKOxRGHqmv3AhSLS2u9AKvJmJA7XT4Cfq+qZFR9U1e9UtSxRZeLGrBxLDPEhnk4CyhNFpWMZE5IlClPXlOLWBf5F5ScqnxGIyG5vO1REPhSR10XkaxGZJCJXiFvP4isROanCbkaIyCKv3nne6+NE5AERWSwiK0TkpxX2O19EXgG+ChDPZd7+V4rIX7zH/h9uIONTIvJApfqdvLoJwJ+AS7w1EC7xRlW/4MXwpYiM8V5zjYi8ISJv4yb7ayoi80RkqXfsMd7uJwEneft7oOxY3j4SReRFr/6XInJmhX2/KSLviVvf4P5j/tcy9UKoXyDGRKvHgRXH+MXVC+gOFAIbgOdUtb+4xZhuBe7w6nUChgAnAfNF5GTgKtzsnP1EpCHwsYjM8er3B9JVdWPFg4lIKvAX3BoG23Bf4mNV9U8iMgz4tapmBwpUVYu9hJKlqrd4+7sXNx3Idd7UJV+IyFzvJQOBDFUt9M4qxqnqTu+s6zMRmYmbZC9d3SSKZbMBl7nZO+6pItLNi/UU77lM3KzB+4F1IvKoqlacednEADujMHWOuhlsX8Yt3BKuxaqap6r7cdO2lH3Rf4VLDmVeV9WDqroel1C64eZEukrclOaf46ZJ6OLV/6JykvD0Axaom7StFJgCVGem1lHA3V4MC4BE4ETvufdVtdC7L8C9IrICmIubPj/lKPv+H9wUEKjqWmATUJYo5qnqDlUtws2/1LEaf4Opo+yMwtRVf8ctVvRihcdK8X78eBOlJVR4bn+F+wcrlA9y+P+DynPaKO7L91ZVnV3xCREZipsSO5BAU9lXhwAXqeq6SjGcVimGK4A2QF9VLRE3i21iGPsOpuL7dgD7zohJdkZh6iTvF/TruAvDZXJwTT3g5upvUIVdjxeR47zrFmm4FcNmAzeJm3IdETnFm301lM+BISLS2rvQfRnw4THEsQtoVqE8G7jVS4CISO8grzsetx5GiXetoewMoPL+KlqISzB4TU4n4v5uYwBLFKZuewio2PvpWdyX8xe4ZVGD/doPZR3uC/3fwM+8JpfncM0uS70LwE9zlF/W6lYXmwDMx83WulRVj2XK5/lAj7KL2cA9uMS3wovhniCvmwJkiUg27st/rRdPAe7aysrKF9GBJ4A4EfkKeA24xmuiMwbAZo81xhgTmp1RGGOMCckShTHGmJAsURhjjAnJEoUxxpiQLFEYY4wJyRKFMcaYkCxRGGOMCen/A4+sGRDnBubkAAAAAElFTkSuQmCC\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "result = numpy.load('./output/summary_data.npz')\n",
-    "\n",
-    "eig_val, eig_state = numpy.linalg.eig(pauli_str_to_matrix(Hamiltonian, N))\n",
-    "min_eig_H = numpy.min(eig_val.real)\n",
-    "min_loss = numpy.ones([len(result['iter'])]) * min_eig_H\n",
-    "\n",
-    "plt.figure(1)\n",
-    "func1, = plt.plot(result['iter'], result['energy'], alpha=0.7, marker='', linestyle=\"-\", color='r')\n",
-    "func_min, = plt.plot(result['iter'], min_loss, alpha=0.7, marker='', linestyle=\":\", color='b')\n",
-    "plt.xlabel('Number of iteration')\n",
-    "plt.ylabel('Energy (Ha)')\n",
-    "\n",
-    "plt.legend(handles=[\n",
-    "    func1,\n",
-    "    func_min\n",
-    "],\n",
-    "    labels=[\n",
-    "        r'$\\left\\langle {\\psi \\left( {\\theta } \\right)} '\n",
-    "        r'\\right|H\\left| {\\psi \\left( {\\theta } \\right)} \\right\\rangle $',\n",
-    "        'Ground-state energy',\n",
-    "    ], loc='best')\n",
-    "\n",
-    "#plt.savefig(\"vqe.png\", bbox_inches='tight', dpi=300)\n",
-    "plt.show()"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "name": "#%% md\n"
-    }
-   },
-   "source": [
-    "\n",
-    "## 参考文献\n",
-    "\n",
-    "[1] [Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).](https://www.nature.com/articles/ncomms5213)\n",
-    "\n",
-    "[2] [McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. C. & Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 92, 015003 (2020).](https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.92.015003)\n",
-    "\n",
-    "[3] [Cao, Y. et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 119, 10856–10915 (2019).](https://pubs.acs.org/doi/abs/10.1021/acs.chemrev.8b00803)\n"
-   ]
-  }
- ],
- "metadata": {
-  "kernelspec": {
-   "display_name": "Python 3",
-   "language": "python",
-   "name": "python3"
-  },
-  "language_info": {
-   "codemirror_mode": {
-    "name": "ipython",
-    "version": 3
-   },
-   "file_extension": ".py",
-   "mimetype": "text/x-python",
-   "name": "python",
-   "nbconvert_exporter": "python",
-   "pygments_lexer": "ipython3",
-   "version": "3.7.7"
-  }
- },
- "nbformat": 4,
- "nbformat_minor": 1
-}

tutorial/VQSD/VQSD_Tutorial_CN.ipynb → tutorial/VQSD/VQSD_CN.ipynb

@@ -4,28 +4,24 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "# 变分量子态对角化算法（VQSD）\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
+    "# 变分量子态对角化算法\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>\n",
+    "\n",
     "## 概览\n",
     "\n",
-    "- 在本案例中，我们将通过Paddle Quantum训练量子神经网络来完成量子态的对角化。\n",
+    "- 在本案例中，我们将通过 Paddle Quantum 训练量子神经网络来完成量子态的对角化\n",
     "\n",
-    "- 首先，让我们通过下面几行代码引入必要的library和package。"
+    "- 首先，让我们通过下面几行代码引入必要的 library 和 package。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 1,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:04.699669Z",
+     "start_time": "2021-01-09T10:38:59.947656Z"
     }
    },
    "outputs": [],
@@ -41,26 +37,21 @@
   },
   {
    "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "name": "#%% md\n"
-    }
-   },
+   "metadata": {},
    "source": [
-    "\n",
     "## 背景\n",
-    "量子态对角化算法（VQSD，Variational Quantum State Diagonalization）[1-3] 的目标是输出一个量子态的特征谱，即其所有特征值。求解量子态的特征值在量子计算中有着诸多应用，比如可以用于计算保真度和冯诺依曼熵，也可以用于主成分分析。\n",
+    "量子态对角化算法（Variational Quantum State Diagonalization, VQSD）[1-3] 目标是输出一个量子态的本征谱，即其所有本征值。求解量子态的本征值在量子计算中有着诸多应用，比如可以用于计算保真度和冯诺依曼熵，也可以用于主成分分析。\n",
     "- 量子态通常是一个混合态，表示如下 $\\rho_{\\text{mixed}} = \\sum_i P_i |\\psi_i\\rangle\\langle\\psi_i|$\n",
-    "- 作为一个简单的例子，我们考虑一个2量子位的量子态，它的特征谱为 $(0.5, 0.3, 0.1, 0.1)$, 我们先通过随机作用一个酉矩阵来生成具有这样特征谱的随机量子态。\n"
+    "- 作为一个简单的例子，我们考虑一个 2 量子位的量子态，它的本征谱为 $(0.5, 0.3, 0.1, 0.1)$，我们先通过随机作用一个酉矩阵来生成具有这样本征谱的随机量子态。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 2,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:04.723926Z",
+     "start_time": "2021-01-09T10:39:04.702772Z"
     }
    },
    "outputs": [
@@ -68,24 +59,20 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "[[ 0.25692714+2.79965123e-18j -0.01201165+4.35008229e-02j\n",
-      "  -0.04922153-5.53435795e-03j -0.05482813+6.81592880e-02j]\n",
-      " [-0.01201165-4.35008229e-02j  0.29589652-4.11838221e-18j\n",
-      "   0.10614221-7.12575060e-02j -0.03921986-9.71359495e-02j]\n",
-      " [-0.04922153+5.53435795e-03j  0.10614221+7.12575060e-02j\n",
-      "   0.214462  -3.16199986e-18j  0.02936413-1.13227406e-01j]\n",
-      " [-0.05482813-6.81592880e-02j -0.03921986+9.71359495e-02j\n",
-      "   0.02936413+1.13227406e-01j  0.23271434+4.32784528e-18j]]\n"
+      "[[ 0.2569+0.j     -0.012 +0.0435j -0.0492-0.0055j -0.0548+0.0682j]\n",
+      " [-0.012 -0.0435j  0.2959-0.j      0.1061-0.0713j -0.0392-0.0971j]\n",
+      " [-0.0492+0.0055j  0.1061+0.0713j  0.2145-0.j      0.0294-0.1132j]\n",
+      " [-0.0548-0.0682j -0.0392+0.0971j  0.0294+0.1132j  0.2327+0.j    ]]\n"
      ]
     }
    ],
    "source": [
-    "scipy.random.seed(13)\n",
+    "scipy.random.seed(13)                  # 固定随机种子，方便复现结果\n",
     "V = scipy.stats.unitary_group.rvs(4)   # 随机生成一个酉矩阵\n",
     "D = diag([0.5, 0.3, 0.1, 0.1])         # 输入目标态 rho 的谱\n",
     "V_H = V.conj().T \n",
-    "rho = V @ D @ V_H                      # 生成 rho\n",
-    "print(rho)                             # 打印量子态 rho"
+    "rho = V @ D @ V_H                      # 通过逆向的谱分解生成 rho\n",
+    "print(numpy.around(rho, 4))            # 打印量子态 rho"
    ]
   },
   {
@@ -93,21 +80,20 @@
    "metadata": {},
    "source": [
     "## 搭建量子神经网络\n",
-    "- 在这个案例中，我们将通过训练量子神经网络QNN（也可以理解为参数化量子电路）来学习量子态的特征谱。这里，我们提供一个预设的2量子位量子电路。\n",
+    "- 在这个案例中，我们将通过训练量子神经网络 QNN（也可以理解为参数化量子电路）来学习量子态的本征谱。这里，我们提供一个预设的 2 量子位量子电路。\n",
     "\n",
-    "- 我们预设一些该参数化电路的参数，比如宽度为2量子位。\n",
+    "- 我们预设一些该参数化电路的参数，比如宽度为 2 量子位。\n",
     "\n",
-    "- 初始化其中的变量参数，${\\bf{\\theta }}$代表我们量子神经网络中的参数组成的向量。\n",
-    "         "
+    "- 初始化其中的变量参数，${\\bf{\\theta }}$ 代表我们量子神经网络中的参数组成的向量。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 3,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%% \n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:04.741146Z",
+     "start_time": "2021-01-09T10:39:04.729478Z"
     }
    },
    "outputs": [],
@@ -123,35 +109,29 @@
     "    \n",
     "    # 按照量子比特数量/网络宽度初始化量子神经网络\n",
     "    cir = UAnsatz(N)\n",
-    "    \n",
     "    # 调用内置的量子神经网络模板\n",
     "    cir.universal_2_qubit_gate(theta)\n",
-    "\n",
     "    # 返回量子神经网络所模拟的酉矩阵 U\n",
     "    return cir.U"
    ]
   },
   {
    "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "name": "#%% md\n"
-    }
-   },
+   "metadata": {},
    "source": [
-    "## 配置训练模型 - 损失函数\n",
+    "## 配置训练模型——损失函数\n",
     "- 现在我们已经有了数据和量子神经网络的架构，我们将进一步定义训练参数、模型和损失函数。\n",
-    "- 通过作用量子神经网络$U(\\theta)$在量子态$\\rho$后得到的量子态记为$\\tilde\\rho$，我们设定损失函数为$\\tilde\\rho$与用来标记的量子态$\\sigma=0.1 |00\\rangle\\langle 00| + 0.2 |01\\rangle \\langle 01| + 0.3 |10\\rangle \\langle10| + 0.4 |11 \\rangle\\langle 11|$的推广的内积。\n",
-    "- 具体的，设定损失函数为 $\\mathcal{L}(\\boldsymbol{\\theta})  = \\text{Tr}(\\tilde\\rho\\sigma) .$"
+    "- 通过作用量子神经网络 $U(\\theta)$ 在量子态 $\\rho$ 后得到的量子态记为 $\\tilde\\rho$，我们设定损失函数为 $\\tilde\\rho$ 与用来标记的量子态 $\\sigma=0.1 |00\\rangle\\langle 00| + 0.2 |01\\rangle \\langle 01| + 0.3 |10\\rangle \\langle10| + 0.4 |11 \\rangle\\langle 11|$ 的内积。\n",
+    "- 具体的，设定损失函数为 $\\mathcal{L}(\\boldsymbol{\\theta})  = \\text{Tr}(\\tilde\\rho\\sigma)$。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 4,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:04.763989Z",
+     "start_time": "2021-01-09T10:39:04.749814Z"
     }
    },
    "outputs": [],
@@ -164,16 +144,18 @@
     "    Construct the model net\n",
     "    \"\"\"\n",
     "\n",
-    "    def __init__(self, shape, rho, sigma, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * numpy.pi, seed=SEED),\n",
-    "                 dtype='float64'):\n",
+    "    def __init__(self, shape, rho, sigma, param_attr =fluid.initializer.Uniform(low=0.0, high=2 * numpy.pi, seed=SEED), dtype='float64'):\n",
     "        super(Net, self).__init__()\n",
     "        \n",
-    "        # 将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
+    "        \n",
+    "        \n",
+    "        # 将 numpy.ndarray 转换成 Paddle 动态图模式中支持的 variable\n",
     "        self.rho = fluid.dygraph.to_variable(rho)\n",
     "        self.sigma = fluid.dygraph.to_variable(sigma)\n",
     "        \n",
     "        # 初始化 theta 参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        self.theta = self.create_parameter(\n",
+    "        shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
     "\n",
     "    # 定义损失函数和前向传播机制\n",
     "    def forward(self, N):\n",
@@ -194,26 +176,24 @@
    "cell_type": "markdown",
    "metadata": {},
    "source": [
-    "## 配置训练模型 - 模型参数\n",
+    "## 配置训练模型——模型参数\n",
     "\n",
-    "在进行量子神经网络的训练之前，我们还需要进行一些训练（超）参数的设置，例如学习速率与迭代次数。\n",
-    "- 设定学习速率（learning rate）为 0.1;\n",
-    "- 设定迭代次数为50次。"
+    "在进行量子神经网络的训练之前，我们还需要进行一些训练的超参数设置，主要是学习速率 (learning rate, LR)和迭代次数(iteration, ITR)。这里我们设定学习速率为 0.1，迭代次数为 50 次。读者不妨自行调整来直观感受下超参数调整对训练效果的影响。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 5,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:04.782143Z",
+     "start_time": "2021-01-09T10:39:04.771644Z"
     }
    },
    "outputs": [],
    "source": [
-    "ITR = 50 # 设置训练的总的迭代次数\n",
-    "LR = 0.1 # 设置学习速率"
+    "ITR = 50  # 设置训练的总的迭代次数\n",
+    "LR = 0.1  # 设置学习速率"
    ]
   },
   {
@@ -222,8 +202,8 @@
    "source": [
     "## 进行训练\n",
     "\n",
-    "- 当训练模型的各项参数都设置完成后，我们将数据转化为Paddle动态图中的变量，进而进行量子神经网络的训练。\n",
-    "- 过程中我们用的是Adam Optimizer，也可以调用Paddle中提供的其他优化器。\n",
+    "- 当训练模型的各项参数都设置完成后，我们将数据转化为 Paddle 动态图中的变量，进而进行量子神经网络的训练。\n",
+    "- 过程中我们用的是 Adam Optimizer，也可以调用 Paddle 中提供的其他优化器。\n",
     "- 我们将训练过程中的结果依次输出。"
    ]
   },
@@ -231,9 +211,9 @@
    "cell_type": "code",
    "execution_count": 6,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%% \n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:06.249584Z",
+     "start_time": "2021-01-09T10:39:04.786391Z"
     }
    },
    "outputs": [
@@ -242,10 +222,10 @@
      "output_type": "stream",
      "text": [
       "iter: 0 loss: 0.2354\n",
-      "iter: 10 loss: 0.1912\n",
-      "iter: 20 loss: 0.1844\n",
-      "iter: 30 loss: 0.1823\n",
-      "iter: 40 loss: 0.1813\n"
+      "iter: 10 loss: 0.1883\n",
+      "iter: 20 loss: 0.1817\n",
+      "iter: 30 loss: 0.1814\n",
+      "iter: 40 loss: 0.1809\n"
      ]
     }
    ],
@@ -256,8 +236,9 @@
     "    # 确定网络的参数维度\n",
     "    net = Net(shape=[THETA_SIZE], rho=rho, sigma=sigma)\n",
     "\n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdagradOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    # 一般来说，我们利用 Adam 优化器来获得相对好的收敛\n",
+    "    # 当然你可以改成 SGD 或者是 RMS prop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
     "    \n",
     "    # 优化循环\n",
     "    for itr in range(ITR):\n",
@@ -273,7 +254,7 @@
     "        \n",
     "        # 打印训练结果\n",
     "        if itr % 10 == 0:\n",
-    "            print('iter:', itr, 'loss:', '%.4f' % loss.numpy()[0])\n"
+    "            print('iter:', itr, 'loss:', '%.4f' % loss.numpy()[0])"
    ]
   },
   {
@@ -281,19 +262,17 @@
    "metadata": {},
    "source": [
     "## 总结\n",
-    "根据上面训练得到的结果，通过大概50次迭代，我们就比较好的完成了对角化。\n",
-    "我们可以通过打印\n",
-    "$\\tilde{\\rho} = U(\\boldsymbol{\\theta})\\rho U^\\dagger(\\boldsymbol{\\theta})$\n",
-    "的来验证谱分解的效果。特别的，我们可以验证它的对角线与我们目标谱是非常接近的。"
+    "\n",
+    "根据上面训练得到的结果，通过大概50次迭代，我们就比较好的完成了对角化。我们可以通过打印 $\\tilde{\\rho} = U(\\boldsymbol{\\theta})\\rho U^\\dagger(\\boldsymbol{\\theta})$ 的来验证谱分解的效果。特别的，我们可以验证它的对角线与目标谱非常接近。"
    ]
   },
   {
    "cell_type": "code",
    "execution_count": 7,
    "metadata": {
-    "pycharm": {
-     "is_executing": false,
-     "name": "#%%\n"
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:06.263643Z",
+     "start_time": "2021-01-09T10:39:06.254056Z"
     }
    },
    "outputs": [
@@ -301,7 +280,7 @@
      "name": "stdout",
      "output_type": "stream",
      "text": [
-      "The estimated spectrum is: [0.49401064 0.30357179 0.10224927 0.10016829]\n",
+      "The estimated spectrum is: [0.49951803 0.29739084 0.10256743 0.10052371]\n",
       "The target spectrum is: [0.5 0.3 0.1 0.1]\n"
      ]
     }
@@ -313,19 +292,17 @@
   },
   {
    "cell_type": "markdown",
-   "metadata": {
-    "pycharm": {
-     "name": "#%% md\n"
-    }
-   },
+   "metadata": {},
    "source": [
+    "_______\n",
+    "\n",
     "## 参考文献\n",
     "\n",
-    "[1] [Larose, R., Tikku, A., Neel-judy, É. O., Cincio, L. & Coles, P. J. Variational quantum state diagonalization. npj Quantum Inf. (2019) doi:10.1038/s41534-019-0167-6.](https://www.nature.com/articles/s41534-019-0167-6)\n",
+    "[1] Larose, R., Tikku, A., Neel-judy, É. O., Cincio, L. & Coles, P. J. Variational quantum state diagonalization. [npj Quantum Inf. (2019) doi:10.1038/s41534-019-0167-6.](https://www.nature.com/articles/s41534-019-0167-6)\n",
     "\n",
-    "[2] [Nakanishi, K. M., Mitarai, K. & Fujii, K. Subspace-search variational quantum eigensolver for excited states. Phys. Rev. Res. 1, 033062 (2019).](https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.1.033062)\n",
+    "[2] Nakanishi, K. M., Mitarai, K. & Fujii, K. Subspace-search variational quantum eigensolver for excited states. [Phys. Rev. Res. 1, 033062 (2019).](https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.1.033062)\n",
     "\n",
-    "[3] [Cerezo, M., Sharma, K., Arrasmith, A. & Coles, P. J. Variational Quantum State Eigensolver. arXiv:2004.01372 (2020).](https://arxiv.org/pdf/2004.01372.pdf)\n"
+    "[3] Cerezo, M., Sharma, K., Arrasmith, A. & Coles, P. J. Variational Quantum State Eigensolver. [arXiv:2004.01372 (2020).](https://arxiv.org/pdf/2004.01372.pdf)"
    ]
   }
  ],
@@ -345,18 +322,22 @@
    "name": "python",
    "nbconvert_exporter": "python",
    "pygments_lexer": "ipython3",
-   "version": "3.7.7"
+   "version": "3.6.10"
   },
-  "pycharm": {
-   "stem_cell": {
-    "cell_type": "raw",
-    "metadata": {
-     "collapsed": false
-    },
-    "source": []
-   }
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
   }
  },
  "nbformat": 4,
- "nbformat_minor": 1
+ "nbformat_minor": 4
 }

tutorial/VQSD/VQSD_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Variational Quantum State Diagonalization \n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>\n",
+    "\n",
+    "## Overview\n",
+    "\n",
+    "- In this tutorial, we will train a quantum neural network (QNN) through Paddle Quantum to complete the diagonalization of quantum states.\n",
+    "\n",
+    "- First, import the following packages."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:18.985186Z",
+     "start_time": "2021-01-09T10:39:15.015255Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import numpy\n",
+    "from numpy import diag\n",
+    "import scipy\n",
+    "from paddle import fluid\n",
+    "from paddle_quantum.circuit import UAnsatz\n",
+    "from paddle_quantum.utils import dagger\n",
+    "from paddle.complex import matmul, trace, transpose"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Background\n",
+    "The Variational Quantum State Diagonalization [1-3] aims to output the eigen-spectrum (eigenvalues) of a quantum state. Solving the eigenvalues ​​of quantum states has many applications in quantum computation, such as calculating fidelity and Von Neumann entropy.\n",
+    "\n",
+    "- Quantum state is usually a mixed state which can be expressed as follows: \n",
+    "\n",
+    "$$\n",
+    "\\rho_{\\text{mixed}} = \\sum_i P_i |\\psi_i\\rangle\\langle\\psi_i|. \\tag{1}\n",
+    "$$\n",
+    "\n",
+    "- As an example, we consider a mixed 2-qubit quantum state with eigen-spectrum $[0.5, 0.3, 0.1, 0.1]$."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:19.011525Z",
+     "start_time": "2021-01-09T10:39:18.987897Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "[[ 0.2569+0.j     -0.012 +0.0435j -0.0492-0.0055j -0.0548+0.0682j]\n",
+      " [-0.012 -0.0435j  0.2959-0.j      0.1061-0.0713j -0.0392-0.0971j]\n",
+      " [-0.0492+0.0055j  0.1061+0.0713j  0.2145-0.j      0.0294-0.1132j]\n",
+      " [-0.0548-0.0682j -0.0392+0.0971j  0.0294+0.1132j  0.2327+0.j    ]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Fixed random seed\n",
+    "scipy.random.seed(13) \n",
+    "V = scipy.stats.unitary_group.rvs(4)  # Randomly generate a unitary matrix\n",
+    "D = diag([0.5, 0.3, 0.1, 0.1])        # Input the spectrum of the target state rho\n",
+    "V_H = V.conj().T                      # Conjugate transpose operation\n",
+    "rho = V @ D @ V_H                     # Generate rho by inverse spectral decomposition\n",
+    "print(numpy.around(rho, 4))           # Print quantum state rho"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Building a quantum neural network\n",
+    "\n",
+    "- In this case, we will learn the eigen-spectrum of quantum state $\\rho$ defined above by training a QNN (also known as the parameterized quantum circuit). Here, we provide a predefined 2-qubit quantum circuit.\n",
+    "\n",
+    "- One can randomly initialize the QNN parameters ${\\bf{\\vec{\\theta }}}$ containing 15 parameters."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:19.025782Z",
+     "start_time": "2021-01-09T10:39:19.017838Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "N = 2           # The width of the quantum neural network\n",
+    "SEED = 14       # Fixed random seed\n",
+    "THETA_SIZE = 15 # The number of parameters in the quantum neural network\n",
+    "\n",
+    "def U_theta(theta, N):\n",
+    "    \"\"\"\n",
+    "    Quantum Neural Network\n",
+    "    \"\"\"\n",
+    "    # Initialize the quantum neural network according to the number of qubits/network width\n",
+    "    cir = UAnsatz(N)\n",
+    "    # Call the built-in quantum neural network template\n",
+    "    cir.universal_2_qubit_gate(theta)\n",
+    "    # Return the unitary matrix U simulated by the quantum neural network\n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Training model and loss function\n",
+    "\n",
+    "- After setting up the quantum state and the QNN architecture, we will further define the parameters to be trained, loss function, and optimization methods. \n",
+    "- The quantum state obtained by acting the quantum neural network $U(\\theta)$ on $\\rho$  is denoted by $\\tilde\\rho$, and we set the loss function to be the inner product of the quantum state $\\sigma$ and $\\tilde\\rho$ where\n",
+    "\n",
+    "$$\n",
+    "\\sigma=0.1 |00\\rangle\\langle 00| + 0.2 |01\\rangle \\langle 01| + 0.3 |10\\rangle \\langle10| + 0.4 |11 \\rangle\\langle 11|, \\tag{2}\n",
+    "$$\n",
+    "\n",
+    "- In specific, the loss function is defined as the state overlap \n",
+    "\n",
+    "$$\n",
+    "\\mathcal{L}(\\boldsymbol{\\theta}) = \\text{Tr}(\\tilde\\rho\\sigma). \\tag{3}\n",
+    "$$"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:19.048447Z",
+     "start_time": "2021-01-09T10:39:19.029044Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Enter the quantum state sigma \n",
+    "sigma = diag([0.1, 0.2, 0.3, 0.4]).astype('complex128')\n",
+    "\n",
+    "class Net(fluid.dygraph.Layer):\n",
+    "    \"\"\"\n",
+    "    Construct the model net\n",
+    "    \"\"\"\n",
+    "\n",
+    "    def __init__(self, shape, rho, sigma, param_attr =fluid.initializer.Uniform(low=0.0, high=2 * numpy.pi, seed=SEED), dtype='float64'):\n",
+    "        super(Net, self).__init__()\n",
+    "        \n",
+    "        \n",
+    "        \n",
+    "        # Convert Numpy array to variable supported in Paddle dynamic graph mode\n",
+    "        self.rho = fluid.dygraph.to_variable(rho)\n",
+    "        self.sigma = fluid.dygraph.to_variable(sigma)\n",
+    "        \n",
+    "        # Initialize the theta parameter list and fill the initial value with the uniform distribution of [0, 2*pi]\n",
+    "        self.theta = self.create_parameter(\n",
+    "        shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "\n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self, N):\n",
+    "        \n",
+    "        # Apply quantum neural network\n",
+    "        U = U_theta(self.theta, N)\n",
+    "\n",
+    "        # rho_tilde is the quantum state U*rho*U^dagger \n",
+    "        rho_tilde = matmul(matmul(U, self.rho), dagger(U))\n",
+    "\n",
+    "        # Calculate the loss function\n",
+    "        loss = trace(matmul(self.sigma, rho_tilde))\n",
+    "\n",
+    "        return loss.real, rho_tilde"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Hyper-parameters\n",
+    "\n",
+    "Before training the quantum neural network, we also need to set up several hyper-parameters, mainly the learning rate LR and the number of iterations ITR. Here we set the learning rate to be LR = 0.1 and the number of iterations to ITR = 50. One can adjust these hyper-parameters accordingly and check how they influence the training performance."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:19.110711Z",
+     "start_time": "2021-01-09T10:39:19.061263Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "ITR = 50 # Set the total number of iterations of training\n",
+    "LR = 0.1 # Set the learning rate"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Training process\n",
+    "\n",
+    "- After setting all the parameters of SSVQE model, we need to convert all the data into variables in the PaddlePaddle dynamic graph, and then train the quantum neural network.\n",
+    "- We used Adam Optimizer in training, and one can also call other optimizers provided in Paddle."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:20.745068Z",
+     "start_time": "2021-01-09T10:39:19.142878Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter: 0 loss: 0.2354\n",
+      "iter: 10 loss: 0.1883\n",
+      "iter: 20 loss: 0.1817\n",
+      "iter: 30 loss: 0.1814\n",
+      "iter: 40 loss: 0.1809\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Initialize paddle dynamic graph mechanism\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    # Determine the parameter dimension of the network\n",
+    "    net = Net(shape=[THETA_SIZE], rho=rho, sigma=sigma)\n",
+    "\n",
+    "    # We use Adam optimizer for better performance\n",
+    "    # One can change it to SGD or RMSprop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    \n",
+    "    # Optimization loop\n",
+    "    for itr in range(ITR):\n",
+    "        \n",
+    "        # Forward propagation calculates the loss function and returns the estimated energy spectrum\n",
+    "        loss, rho_tilde = net(N)\n",
+    "        rho_tilde_np = rho_tilde.numpy()\n",
+    "        \n",
+    "        # Under the dynamic graph mechanism, back propagation minimizes the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "        \n",
+    "        # Print training results\n",
+    "        if itr% 10 == 0:\n",
+    "            print('iter:', itr,'loss:','%.4f'% loss.numpy()[0])"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Benchmarking\n",
+    "\n",
+    "After 50 iterations, we have completed the diagonalization procedure. The next step is to verify the results of spectral decomposition by printing out $\\tilde{\\rho} = U(\\boldsymbol{\\theta})\\rho U^\\dagger(\\boldsymbol{\\theta})$. One can see the results are very close to what we expect."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:39:20.757262Z",
+     "start_time": "2021-01-09T10:39:20.747722Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The estimated spectrum is: [0.49951803 0.29739084 0.10256743 0.10052371]\n",
+      "The target spectrum is: [0.5 0.3 0.1 0.1]\n"
+     ]
+    }
+   ],
+   "source": [
+    "print(\"The estimated spectrum is:\", numpy.real(numpy.diag(rho_tilde_np)))\n",
+    "print(\"The target spectrum is:\", numpy.diag(D))"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "\n",
+    "## References\n",
+    "\n",
+    "[1] Larose, R., Tikku, A., Neel-judy, É. O., Cincio, L. & Coles, P. J. Variational quantum state diagonalization. [npj Quantum Inf. (2019) doi:10.1038/s41534-019-0167-6.](https://www.nature.com/articles/s41534-019-0167-6)\n",
+    "\n",
+    "[2] Nakanishi, K. M., Mitarai, K. & Fujii, K. Subspace-search variational quantum eigensolver for excited states. [Phys. Rev. Res. 1, 033062 (2019).](https://journals.aps.org/prresearch/pdf/10.1103/PhysRevResearch.1.033062)\n",
+    "\n",
+    "[3] Cerezo, M., Sharma, K., Arrasmith, A. & Coles, P. J. Variational Quantum State Eigensolver. [arXiv:2004.01372 (2020).](https://arxiv.org/pdf/2004.01372.pdf)"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": false
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/VQSVD/VQSVD_EN.ipynb

+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "# Variational Quantum Singular Value Decomposition\n",
+    "\n",
+    "<em> Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Overview\n",
+    "\n",
+    "In this tutorial, we will go through the concept of classical singular value decomposition (SVD) and the quantum neural network (QNN) version of variational quantum singular value decomposition (VQSVD) [1]. The tutorial consists of the following two parts: \n",
+    "- Decompose a randomly generated $8\\times8$ complex matrix; \n",
+    "- Apply SVD on image compression."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Background\n",
+    "\n",
+    "Singular value decomposition (SVD) has many applications, including principal component analysis (PCA), solving linear equations and recommender systems. The main task is formulated as following:\n",
+    "> Given a complex matrix $M \\in \\mathbb{C}^{m \\times n}$, find the decomposition in form $M = UDV^\\dagger$, where $U_{m\\times m}$ and $V^\\dagger_{n\\times n}$ are unitary matrices, which satisfy the property $UU^\\dagger = VV^\\dagger = I$.\n",
+    "\n",
+    "- The column vectors $|u_j\\rangle$ of the unitary matrix $U$ are called left singular vectors $\\{|u_j\\rangle\\}_{j=1}^{m}$ form an orthonormal basis. These column vectors are the eigenvectors of the matrix $MM^\\dagger$.\n",
+    "- Similarly, the column vectors $\\{|v_j\\rangle\\}_{j=1}^{n}$ of the unitary matrix $V$ are the eigenvectors of $M^\\dagger M$ and form an orthonormal basis.\n",
+    "- The diagonal elements of the matrix $D_{m\\times n}$ are singular values $d_j$ arranged in a descending order.\n",
+    "\n",
+    "For the convenience, we assume that the $M$ appearing below are all square matrices. Let's first look at an example: \n",
+    "\n",
+    "$$\n",
+    "M = 2*X\\otimes Z + 6*Z\\otimes X + 3*I\\otimes I = \n",
+    "\\begin{bmatrix} \n",
+    "3 &6 &2 &0 \\\\\n",
+    "6 &3 &0 &-2 \\\\\n",
+    "2 &0 &3 &-6 \\\\\n",
+    "0 &-2 &-6 &3 \n",
+    "\\end{bmatrix}, \\tag{1}\n",
+    "$$\n",
+    "\n",
+    "Then the singular value decomposition of the matrix can be expressed as:\n",
+    "\n",
+    "$$\n",
+    "M = UDV^\\dagger = \n",
+    "\\frac{1}{2}\n",
+    "\\begin{bmatrix} \n",
+    "-1 &-1 &1 &1 \\\\\n",
+    "-1 &-1 &-1 &-1 \\\\\n",
+    "-1 &1 &-1 &1 \\\\\n",
+    "1 &-1 &-1 &1 \n",
+    "\\end{bmatrix}\n",
+    "\\begin{bmatrix} \n",
+    "11 &0 &0 &0 \\\\\n",
+    "0 &7 &0 &0 \\\\\n",
+    "0 &0 &5 &0 \\\\\n",
+    "0 &0 &0 &1 \n",
+    "\\end{bmatrix}\n",
+    "\\frac{1}{2}\n",
+    "\\begin{bmatrix} \n",
+    "-1 &-1 &-1 &-1 \\\\\n",
+    "-1 &-1 &1 &1 \\\\\n",
+    "-1 &1 &1 &-1 \\\\\n",
+    "1 &-1 &1 &-1 \n",
+    "\\end{bmatrix}. \\tag{2}\n",
+    "$$\n",
+    "\n",
+    "Import packages."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:49:00.623425Z",
+     "start_time": "2021-01-09T09:48:57.424722Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "import time\n",
+    "import numpy as np\n",
+    "from matplotlib import pyplot as plt\n",
+    "%config InlineBackend.figure_format = 'svg'\n",
+    "from scipy.stats import unitary_group\n",
+    "from scipy.linalg import norm\n",
+    "\n",
+    "import paddle.fluid as fluid\n",
+    "from paddle.complex import matmul, transpose, trace\n",
+    "from paddle_quantum.circuit import *\n",
+    "from paddle_quantum.utils import *\n",
+    "\n",
+    "\n",
+    "\n",
+    "# Draw the learning curve in the optimization process\n",
+    "def loss_plot(loss):\n",
+    "    '''\n",
+    "    loss is a list, this function plots loss over iteration\n",
+    "    '''\n",
+    "    plt.plot(list(range(1, len(loss)+1)), loss)\n",
+    "    plt.xlabel('iteration')\n",
+    "    plt.ylabel('loss')\n",
+    "    plt.title('Loss Over Iteration')\n",
+    "    plt.show()"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Classical Singular Value Decomposition\n",
+    "\n",
+    "With the above mathematical definition, one can realize SVD numerically through NumPy."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:49:00.646056Z",
+     "start_time": "2021-01-09T09:49:00.626439Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The matrix M we want to decompose is: \n",
+      "[[ 3.+0.j  6.+0.j  2.+0.j  0.+0.j]\n",
+      " [ 6.+0.j  3.+0.j  0.+0.j -2.+0.j]\n",
+      " [ 2.+0.j  0.+0.j  3.+0.j -6.+0.j]\n",
+      " [ 0.+0.j -2.+0.j -6.+0.j  3.+0.j]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Generate matrix M\n",
+    "def M_generator():\n",
+    "    I = np.array([[1, 0], [0, 1]])\n",
+    "    Z = np.array([[1, 0], [0, -1]])\n",
+    "    X = np.array([[0, 1], [1, 0]])\n",
+    "    Y = np.array([[0, -1j], [1j, 0]])\n",
+    "    M = 2 *np.kron(X, Z) + 6 * np.kron(Z, X) + 3 * np.kron(I, I)\n",
+    "    return M.astype('complex64')\n",
+    "\n",
+    "print('The matrix M we want to decompose is: ')\n",
+    "print(M_generator())"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:49:00.667463Z",
+     "start_time": "2021-01-09T09:49:00.650150Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The singular values of the matrix from large to small are:\n",
+      "[11.  7.  5.  1.]\n",
+      "The decomposed unitary matrix U is:\n",
+      "[[-0.5+0.j -0.5+0.j  0.5+0.j  0.5+0.j]\n",
+      " [-0.5+0.j -0.5+0.j -0.5+0.j -0.5+0.j]\n",
+      " [-0.5+0.j  0.5+0.j -0.5+0.j  0.5+0.j]\n",
+      " [ 0.5+0.j -0.5+0.j -0.5+0.j  0.5+0.j]]\n",
+      "The decomposed unitary matrix V_dagger is:\n",
+      "[[-0.5+0.j -0.5+0.j -0.5+0.j  0.5+0.j]\n",
+      " [-0.5+0.j -0.5+0.j  0.5+0.j -0.5+0.j]\n",
+      " [-0.5+0.j  0.5+0.j  0.5+0.j  0.5+0.j]\n",
+      " [-0.5+0.j  0.5+0.j -0.5+0.j -0.5+0.j]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# We only need the following line of code to complete SVD\n",
+    "U, D, V_dagger = np.linalg.svd(M_generator(), full_matrices=True)\n",
+    "\n",
+    "\n",
+    "# Print decomposition results\n",
+    "print(\"The singular values of the matrix from large to small are:\")\n",
+    "print(D)\n",
+    "print(\"The decomposed unitary matrix U is:\")\n",
+    "print(U)\n",
+    "print(\"The decomposed unitary matrix V_dagger is:\")\n",
+    "print(V_dagger)"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:49:00.680019Z",
+     "start_time": "2021-01-09T09:49:00.671042Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "[[ 3.+0.j  6.+0.j  2.+0.j  0.+0.j]\n",
+      " [ 6.+0.j  3.+0.j  0.+0.j -2.+0.j]\n",
+      " [ 2.+0.j  0.+0.j  3.+0.j -6.+0.j]\n",
+      " [ 0.+0.j -2.+0.j -6.+0.j  3.+0.j]]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Then assemble it back, can we restore the original matrix?\n",
+    "M_reconst = np.matmul(U, np.matmul(np.diag(D), V_dagger))\n",
+    "print(M_reconst)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Surely, we can be restored the original matrix $M$! One can further modify the matrix, see what happens if it is not a square matrix.\n",
+    "\n",
+    "---"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "## Quantum Singular Value Decomposition\n",
+    "\n",
+    "Next, let's take a look at what the quantum version of singular value decomposition is all about. In summary, we transform the problem of matrix factorization into an optimization problem with the variational principle of singular values. Specifically, this is achieved through the following four steps:\n",
+    "\n",
+    "- Prepare an orthonormal basis $\\{|\\psi_j\\rangle\\}$, one can take the computational basis $\\{ |000\\rangle, |001\\rangle,\\cdots |111\\rangle\\}$ (this is in the case of 3 qubits)\n",
+    "- Prepare two parameterized quantum neural networks $U(\\theta)$ and $V(\\phi)$ to learn left/right singular vectors respectively\n",
+    "- Use quantum neural network to estimate singular values $m_j = \\text{Re}\\langle\\psi_j|U(\\theta)^{\\dagger} M V(\\phi)|\\psi_j\\rangle$\n",
+    "- Design the loss function $\\mathcal{L}(\\theta)$ and use PaddlePaddle Deep Learning framework to maximize the following quantity, \n",
+    "\n",
+    "$$\n",
+    "L(\\theta,\\phi) = \\sum_{j=1}^T q_j\\times \\text{Re} \\langle\\psi_j|U(\\theta)^{\\dagger} MV(\\phi)|\\psi_j\\rangle. \\tag{3}\n",
+    "$$\n",
+    "\n",
+    "Where $q_1>\\cdots>q_T>0$ is the adjustable weights (hyperparameter), and $T$ represents the rank we want to learn or the total number of singular values to be learned.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Case 1: Decompose a randomly generated $8\\times8$ complex matrix\n",
+    "\n",
+    "Then we look at a specific example, which can better explain the overall process.\n",
+    "\n",
+    "#### Define matrix $M$"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:49:00.724542Z",
+     "start_time": "2021-01-09T09:49:00.704404Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The matrix M we want to decompose is:\n",
+      "[[6.+1.j 3.+9.j 7.+3.j 4.+7.j 6.+6.j 9.+8.j 2.+7.j 6.+4.j]\n",
+      " [7.+1.j 4.+4.j 3.+7.j 7.+9.j 7.+8.j 2.+8.j 5.+0.j 4.+8.j]\n",
+      " [1.+6.j 7.+8.j 5.+7.j 1.+0.j 4.+7.j 0.+7.j 9.+2.j 5.+0.j]\n",
+      " [8.+7.j 0.+2.j 9.+2.j 2.+0.j 6.+4.j 3.+9.j 8.+6.j 2.+9.j]\n",
+      " [4.+8.j 2.+6.j 6.+8.j 4.+7.j 8.+1.j 6.+0.j 1.+6.j 3.+6.j]\n",
+      " [8.+7.j 1.+4.j 9.+2.j 8.+7.j 9.+5.j 4.+2.j 1.+0.j 3.+2.j]\n",
+      " [6.+4.j 7.+2.j 2.+0.j 0.+4.j 3.+9.j 1.+6.j 7.+6.j 3.+8.j]\n",
+      " [1.+9.j 5.+9.j 5.+2.j 9.+6.j 3.+0.j 5.+3.j 1.+3.j 9.+4.j]]\n",
+      "The singular values of the matrix M are:\n",
+      "[54.83484985 19.18141073 14.98866247 11.61419557 10.15927045  7.60223249\n",
+      "  5.81040539  3.30116001]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# First fix the random seed, in order to reproduce the results at any time\n",
+    "np.random.seed(42)\n",
+    "\n",
+    "# Set the number of qubits, which determines the dimension of the Hilbert space\n",
+    "N = 3\n",
+    "\n",
+    "# Make a random matrix generator\n",
+    "def random_M_generator():\n",
+    "    M = np.random.randint(10, size = (2**N, 2**N)) + 1j*np.random.randint(10, size = (2**N, 2**N))\n",
+    "    return M\n",
+    "\n",
+    "M = random_M_generator()\n",
+    "M_err = np.copy(M)\n",
+    "\n",
+    "\n",
+    "# Output the matrix M\n",
+    "print('The matrix M we want to decompose is:')\n",
+    "print(M)\n",
+    "\n",
+    "# Apply SVD and record the exact singular values\n",
+    "U, D, V_dagger = np.linalg.svd(M, full_matrices=True)\n",
+    "print(\"The singular values of the matrix M are:\")\n",
+    "print(D)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### Hyper-parameters"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:49:01.389789Z",
+     "start_time": "2021-01-09T09:49:01.383262Z"
+    }
+   },
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "The selected weight is:\n",
+      "[24.+0.j 21.+0.j 18.+0.j 15.+0.j 12.+0.j  9.+0.j  6.+0.j  3.+0.j]\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Hyperparameter settings\n",
+    "N = 3       # Number of qubits\n",
+    "T = 8       # Set the number of rank you want to learn\n",
+    "ITR = 100   # Number of iterations\n",
+    "LR = 0.02   # Learning rate\n",
+    "SEED = 14   # Random seed\n",
+    "\n",
+    "# Set the learning weight \n",
+    "weight = np.arange(3 * T, 0, -3).astype('complex128')\n",
+    "print('The selected weight is:')\n",
+    "print(weight)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### Building a quantum neural network\n",
+    "\n",
+    "We design QNN with the following structure:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:49:02.113260Z",
+     "start_time": "2021-01-09T09:49:02.104652Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Set circuit parameters\n",
+    "cir_depth = 40              # circuit depth\n",
+    "block_len = 2               # length of each block\n",
+    "theta_size = N * block_len * cir_depth  # size of the network parameter theta\n",
+    "\n",
+    "\n",
+    "# Define quantum neural network\n",
+    "def U_theta(theta):\n",
+    "\n",
+    "    # Initialize the network with UAnsatz\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Build QNN\n",
+    "    for layer_num in range(cir_depth):\n",
+    "        \n",
+    "        for which_qubit in range(N):\n",
+    "            cir.ry(theta[block_len * layer_num * N + which_qubit], which_qubit)\n",
+    "        \n",
+    "        for which_qubit in range(N):\n",
+    "            cir.rz(theta[(block_len * layer_num + 1) * N + which_qubit], which_qubit)\n",
+    "\n",
+    "        for which_qubit in range(1, N):\n",
+    "            cir.cnot([which_qubit - 1, which_qubit])\n",
+    "        cir.cnot([N - 1, 0])\n",
+    "\n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### Training model and loss function\n",
+    "Then we complete the main part of the algorithm:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 8,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:51:53.804588Z",
+     "start_time": "2021-01-09T09:49:02.916138Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZMAAAEWCAYAAACjYXoKAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAArpElEQVR4nO3de3xcdZ3/8ddnJjNJJpemTdI2vRdaKi0il3KXXRaRy8padUXRRfHK6squt58rrO667i7+cHVXlx8qyy4oeAFZEOkqclOU+6WFCrS1EEpb2rRN2ubW3DPz+f1xTtJJSEraSTKTmffz8ZgHM99zZs73ZGje+V7O95i7IyIikolItisgIiJTn8JEREQypjAREZGMKUxERCRjChMREcmYwkRERDKmMBGRQ2Jm+83siGzXQ3KLwkSmHDPbYmbnZOnYp5vZb8ys3cxazex/zWz5JB5/8NzN7ENm9sgEH++3Zvax9DJ3L3f3zRN5XJl6FCYiY2RmpwH3AXcBc4DFwO+BR8f7L3ULTOi/TzMrmsjPl8KiMJG8YWbFZvZtM2sIH982s+JwW42Z/cLMWsxsn5k9PPDL2sy+aGY7wtbGJjN7yyiH+FfgZnf/D3dvd/d97v5l4AngH8PP2mhmF6bVqcjMmszshPD1qWb2WFiP35vZWWn7/tbMrjKzR4FOYNSAMrOjgeuA08Jup5a0n8E3zWybme02s+vMrDTcdpaZbQ/PdxfwfTObHv5cmsysOXw+L9z/KuBM4NrwGNeG5W5mS8Ln08zs5vD9W83sy2k/1w+Z2SNhfZrN7BUzu2DMX6hMKQoTySdfAk4FjgPeBJwMfDnc9nlgO1ALzAL+DnAzWwZcDpzk7hXAecCW4R9sZgngdOB/RjjubcBbw+e3AO9L23YesMfdnzGzucAvgX8BZgD/B7jDzGrT9v8AcBlQAWwd7UTdfSPwCeDxsNupKtx0NXBU+DNYAswF/iHtrbPDYy8MjxMBvh++XgB0AdeGx/gS8DBweXiMy0eoyv8DphEE3x8DHwQ+nLb9FGATUEMQxjeYmY12XjJ1KUwkn/wF8E/u3ujuTcBXCX45A/QBdcBCd+9z94c9WJguCRQDy80s5u5b3P3lET57BsG/l50jbNtJ8MsS4CfA28PwAXg/QcAAXALc7e53u3vK3e8H1gB/mvZZP3D39e7e7+59h3Ly4S/py4DPhq2mduBrwMVpu6WAr7h7j7t3ufted7/D3TvD/a8iCIWxHC8afvaVYUttC/BvHPiZA2x19/9y9yRwE8F3MOtQzkumBoWJ5JM5DP1rfmtYBvANoB64z8w2m9kVAO5eD3yGoJuq0cxuNbM5vFYzwS/iuhG21QF70j5vI/BnYaC8nSBgIPjr/6Kwi6sl7Jp687DPfPVQTniYWiABrE37/HvC8gFN7t498MLMEmb2n2EXVRvwEFAVBsXrqQFivPZnPjft9a6BJ+7eGT4tP4RzkilCYSL5pIHgF/aABWEZ4V/On3f3Iwh+wX9uYGzE3X/i7m8O3+vA14d/sLt3AI8DF41w3PcAv057PdDVtQrYEAYMBEHxQ3evSnuUufvV6Yc6hPMdvu8egm6qFWmfP83dyw/yns8Dy4BT3L0S+KOw3EbZf/jx+njtz3zHIZyD5AmFiUxVMTMrSXsUEfwS/7KZ1ZpZDcFYwY8AzOxCM1sSdgW1EnRvpcxsmZmdHQ7UdxP8Mk6NcswrgEvN7G/MrCIcvP4X4DSCLrUBtwLnAp/kQKuEsC5/ZmbnmVk0rPdZAwPeh2E3MM/M4gDungL+C/iWmc0Mz3uumZ13kM+oIDjnFjObAXxlhGOMOBEg7Lq6Dbgq/HksBD4XnqcUGIWJTFV3E/wSHHj8I8HA9hrgOeB54JmwDGAp8ACwn6CF8V13f5BgvORqgr+ydwEzgStHOqC7P0IwoP4ugnGSrcDxwJvd/aW0/XaGxzgd+Gla+asErZW/A5oIWipf4PD/Hf4GWA/sMrM9YdkXCbrzngi7rR4gaHmM5ttAKcH5P0HQLZbuP4B3h7Oxrhnh/X8NdACbgUcIwvPGwzobmdJMN8cSEZFMqWUiIiIZU5iIiEjGFCYiIpIxhYmIiGSsYBd6q6mp8UWLFmW7GiIiU8ratWv3uHvt8PKCDZNFixaxZs2abFdDRGRKMbMR14xTN5eIiGRMYSIiIhlTmIiISMYUJiIikjGFiYiIZExhIiIiGVOYiIhIxhQmGdi4s43fvdiU7WqIiGSdwuQwtXb18aHvP8WX7nw+21UREck6hclh+r93b2R3Ww8dPf3ZroqISNYpTA7Dwy81cevTr1JeXERnbzLb1RERybq8CRMzO9/MNplZvZldMVHH6ejp54o7nueImjI+cNpCevpTJFO6W6WIFLa8CBMziwLfAS4AlgPvM7PlE3Gsb9y7iYbWLv713ccyPREDoKtPrRMRKWx5ESbAyUC9u292917gVmDVRByotqKYj595BCsXzaA0Hiy63NmrcRMRKWz5sgT9XODVtNfbgVOG72RmlwGXASxYsOCwDvSpP1ky+DwRiwLQ2ZOEisP6OBGRvJAvLZMxcffr3X2lu6+srX3NvV0OWSIehokG4UWkwOVLmOwA5qe9nheWTajSMEy6+tTNJSKFLV/C5GlgqZktNrM4cDGweqIPmhgcM1HLREQKW16Mmbh7v5ldDtwLRIEb3X39RB9X3VwiIoG8CBMAd78buHsyjznYzaUwEZECly/dXFmhlomISEBhkoGErjMREQEUJhlJqJtLRARQmGQkFo0QixqdWk5FRAqcwiRDpbGoWiYiUvAUJhlKxIs0ZiIiBU9hkqFEPKrZXCJS8BQmGSqNq5tLRERhkiG1TEREFCYZK40XaTaXiBQ8hUmGErEoXRqAF5ECpzDJkLq5REQUJhkrVZiIiChMMhW0TNTNJSKFTWGSodJ4Ed19KVIpz3ZVRESyRmGSocHFHjWjS0QKmMIkQ7qniYiIwiRjA/c00VXwIlLIFCYZGmyZ9GkQXkQKl8IkQ6Xq5hIRUZhkKhHT3RZFRBQmGTpwH3iFiYgULoVJhg50c2nMREQKl8IkQ4PXmahlIiIFTGGSIV1nIiKiMMlYqa6AFxFRmGQqHo0QjdiQMZP+ZIrWzr4s1kpEZHIpTDJkZiRiQ5ehv+WpbfzxNx+kL5nKYs1ERCaPwmQclMajQwbgX9y9n5bOPlq71DoRkcKgMBkHiXiUjrQwaWzvBqBFXV0iUiAUJuOgNF405D7wTe09ALR09marSiIikyrnwsTM/tHMdpjZuvDxp2nbrjSzejPbZGbnpZWfH5bVm9kVk13n4feBbxwME7VMRKQwFGW7AqP4lrt/M73AzJYDFwMrgDnAA2Z2VLj5O8Bbge3A02a22t03TFZlE/Eo7d1By8TdB8OkWS0TESkQOdcyOYhVwK3u3uPurwD1wMnho97dN7t7L3BruO+kKY0dGIBv6+qntz+YxaUBeBEpFLkaJpeb2XNmdqOZTQ/L5gKvpu2zPSwbrfw1zOwyM1tjZmuamprGrbJlxUWD9zNp2t89WK6WiYgUiqyEiZk9YGYvjPBYBXwPOBI4DtgJ/Nt4Hdfdr3f3le6+sra2drw+dsjU4Ma2nsFyjZmISKHIypiJu58zlv3M7L+AX4QvdwDz0zbPC8s4SPmkSL9ocWC8pChitKibS0QKRM51c5lZXdrLdwIvhM9XAxebWbGZLQaWAk8BTwNLzWyxmcUJBulXT2adE/EoXX3JcPA96OZaXFOmqcEiUjBycTbXv5rZcYADW4C/BHD39WZ2G7AB6Ac+5e5JADO7HLgXiAI3uvv6yaxwabwId+juS9HU3kNJLML8GQl2t3W//ptFRPJAzoWJu3/gINuuAq4aofxu4O6JrNfBJNJukNXY3sPMihKqEjE27WrPVpVERCZVznVzTUWlafc0aWzrobaimKrSuLq5RKRgKEzGQSLtniaN7d3MrChmeiJGR29y8JoTEZF8pjAZB+l3W2xq72FmRTFViRgALV1qnYhI/lOYjIPSWDD01NzZS1t3PzMrS6hKxAFdayIihUFhMg4GWibb9nYCUFue1jJRmIhIAVCYjIOBMNmytwOA2spipg+2TNTNJSL5L+emBk9FA7O5toYtk5kVxVSWqGUiIoVDYTIOEvHgxzjYMqkoHizTALyIFAKFyTgY6OZ6dV8nEYPqsmIiFqzP1ayWiYgUAI2ZjIPioghm0Jd0asqLiUYMM6MqEVc3l4gUBIXJODAzErGgdTKzsniwvCoR0wC8iBQEhck4SRQHPYa15WlhUhpTy0RECoLCZJwMjJvMrCgZLKtKxHVPExEpCAqTcVKqbi4RKWAKk3FyoGVyIEymJ9TNJSKFQWEyTgauK6mtSG+ZxOnqS9Ldl8xWtUREJoXCZJwMXAVfO2TMJLgKvlXjJiKS5xQm42Skbq6q0mB9rmaNm4hInlOYjJPEYMtk6JgJaH0uEcl/CpNxsrC6jCNqyigJZ3UBTBsME7VMRCS/aW2ucXLZmUfwkTMWDymbrhtkiUiBUJiMk0jEiEdsSNmBW/cqTEQkv6mbawKVxqLEiyIagBeRvKcwmUBmRlVpjFZ1c4lInlOYTLCqREwtExHJewqTCaZ7mohIIVCYTDAtQy8ihUBhMsGmJ+K6D7yI5D2FyQSr0srBIlIAFCYTrCoRp6c/RVevVg4WkfylMJlgA2t1NbR2vWZbMuWTXR0RkQmhMJlgR80qB+Cl3e1Dyjc0tHH039/Dy037s1EtEZFxlZUwMbOLzGy9maXMbOWwbVeaWb2ZbTKz89LKzw/L6s3sirTyxWb2ZFj+UzOLT+a5vJ6lMyswg027hobGE5v30ptMUd+oMBGRqS9bLZMXgHcBD6UXmtly4GJgBXA+8F0zi5pZFPgOcAGwHHhfuC/A14FvufsSoBn46OScwtiUxqMsnJFg0+62IeXrG4LXe/drppeITH1ZCRN33+jum0bYtAq41d173P0VoB44OXzUu/tmd+8FbgVWmZkBZwO3h++/CXjHhJ/AITpqVgWbdg3r5to5ECY92aiSiMi4yrUxk7nAq2mvt4dlo5VXAy3u3j+sfERmdpmZrTGzNU1NTeNa8YNZNruCLXs7B+8F39ufor4xCJe9HWqZiMjUN2FhYmYPmNkLIzxWTdQxX4+7X+/uK919ZW1t7aQdd9nsCpIpHxxsf6mxnb5kMJNLYSIi+WDC7mfi7uccxtt2APPTXs8LyxilfC9QZWZFYeskff+csWxWBQAv7m5nxZxpg+Ml1WVxdXOJSF7ItW6u1cDFZlZsZouBpcBTwNPA0nDmVpxgkH61uzvwIPDu8P2XAndlod4HtaimjFjUBmd0bWhoIxGPcvyCKg3Ai0heyNbU4Hea2XbgNOCXZnYvgLuvB24DNgD3AJ9y92TY6rgcuBfYCNwW7gvwReBzZlZPMIZyw+SezeuLRSMcWVvOpl1Bi2TDzjbeMLuC2opidXOJSF7Iym173f1O4M5Rtl0FXDVC+d3A3SOUbyaY7ZXTls2uYM2WZtydjQ1trDp+DlWlcfZ19JBKOZFht/wVEZlKxtQyMbNPm1mlBW4ws2fM7NyJrlw+OWpWBTtautiws432nn5WzJlGdXmclOse8SIy9Y21m+sj7t4GnAtMBz4AXD1htcpDb5gdDML//NlgfsDyukqqy4N1uzQILyJT3VjDZKAP5k+BH4bjFeqXOQRHhTO67lrXQMSCbq/qsmDlF42biMhUN9YwWWtm9xGEyb1mVgGkJq5a+WduVSll8SiN7T0cWVtOSSxKdXkYJprRJSJT3FjD5KPAFcBJ7t4JxIAPT1it8lAkYhwVdnUtn1MJQHVZ2M3VoW4uEZnaxhompwGb3L3FzC4Bvgy0Tly18tPAxYvL64IwmZ6IAWqZiMjUN9Yw+R7QaWZvAj4PvAzcPGG1ylMD4yYr5kwDoCgaYXoippaJiEx5Y73OpN/dPVxX61p3v8HMcmqp96nggjfO5sXd7axcNH2wrLq8WC0TEZnyxhom7WZ2JcGU4DPNLEIwbiKHoG5aKVf/+bFDyqrL4prNJSJT3li7ud4L9BBcb7KLYEHFb0xYrQpIdbkWexSRqW9MYRIGyI+BaWZ2IdDt7hozGQfVZVqfS0SmvrEup/IegtV7LwLeAzxpZu8++LtkLKrL47R09tGX1GU7IjJ1jXXM5EsE15g0AphZLfAAB26XK4dpYEmV5s5eZlaUZLk2IiKHZ6xjJpGBIAntPYT3ykEMLqmiGV0iMoWNtWVyT3jPkVvC1+9lhOXg5dApTEQkH4wpTNz9C2b258AZYdH14T1JJEODKwfrwkURmcLGfHMsd78DuGMC61KQarTYo4jkgYOGiZm1Az7SJsDdvXJCalVAKktiRCOmlomITGkHDRN3r5isihSqSMSYURZXy0REpjTNyMoBB1tSpbc/hftIjUMRkdyhMMkBoy2p0trVxylfe4Db127PQq1ERMZOYZIDRltS5f4Nu2nu7GN9Q1sWaiUiMnYKkxxQXR5n3whjJr98rgGAna1dk10lEZFDojDJATXlxbT39NPdlxwsa+ns5eGX9gDQ0NKdraqJiIyJwiQHzAivgt+X1tV13/rd9KecY+ZWqmUiIjlPYZIDqkcIk/99roEFMxKcu3w2e/b3Dmm1iIjkGoVJDhhYUuX5Ha1AECqPvbyXC4+tY05VKQC7WtXVJSK5a8zLqcjEOWZuJcfOm8bf//wFEvEonb1JkinnbcfW0drVB0BDSxeLasqyXFMRkZEpTHJAcVGUH3/sFD520xo+89N1zKwoZnFNGcvrKtm6txOABrVMRCSHqZsrR1SUxLjpIydz9rKZ7G7r4W1vrMPMmD0tuGFWQ4sG4UUkd6llkkNKYlGu+8CJ/PzZHZx/zOzBspryuGZ0iUhOy0rLxMwuMrP1ZpYys5Vp5YvMrMvM1oWP69K2nWhmz5tZvZldY2YWls8ws/vN7KXwv9OzcU7jJRaNcNHK+VSUxAbL5lSVskPXmohIDstWN9cLwLuAh0bY9rK7Hxc+PpFW/j3g48DS8HF+WH4F8Gt3Xwr8OnydV+ZMK2WnurlEJIdlJUzcfaO7bxrr/mZWB1S6+xMeLKF7M/COcPMq4Kbw+U1p5XmjrqqEhpYurR4sIjkrFwfgF5vZs2b2OzM7MyybC6Qvnbs9LAOY5e47w+e7gFmjfbCZXWZma8xsTVNT07hXfKLMrSqlozdJW3d/tqsiIjKiCRuAN7MHgNkjbPqSu981ytt2Agvcfa+ZnQj83MxWjPWY7u5mNuqf7+5+PXA9wMqVK6fMn/l104ILFxtauphWGnudvUVEJt+EhYm7n3MY7+kBesLna83sZeAoYAcwL23XeWEZwG4zq3P3nWF3WGNmNc89c6qC6cE7W7s4uk53ShaR3JNT3VxmVmtm0fD5EQQD7ZvDbqw2Mzs1nMX1QWCgdbMauDR8fmlaed4YWFJFM7pEJFdla2rwO81sO3Aa8Eszuzfc9EfAc2a2Drgd+IS77wu3/RXw30A98DLwq7D8auCtZvYScE74Oq/UlhcTi5ouXBSRnJWVixbd/U7gzhHK7wDuGOU9a4BjRijfC7xlvOuYSyIRY1ZliaYHi0jOyqluLhndnKpS3SRLRHKWwmSKmDOthIZRllS54ZFX+OVzO0fcJiIyGRQmU8ScqlJ2tXaTTA2d0byjpYuv3b2RGx99JUs1ExFRmEwZdVWl9KecPft7hpTf/NgWkimnvnG/rpAXkaxRmEwRc8NrTXakDcJ39PTzk6e2ES+K0NrVx9602/6KiEwmhckUMXAV/M60Qfjb126nvbufvzrrSABebtyflbqJiChMpoiBCxe37O0AIJlybnz0FY5fUMVFK+cDUN+kMBGR7NDNsaaIypIijqgp49/u28TWvR28cV4VW/d28oXzllFXWUJpLMrLjR3ZrqaIFCiFyRRhZtzxydO59sF6fvj4Vm5bs525VaWcv2I2kYhx5MwytUxEJGsUJlPI9LI4f3/hcj50+iKuf2gzf3RULUXRoKfyyNpy1mxpznINRaRQKUymoPkzEvzzO4auLLOktpy71jXQ2dtPIq6vVUQmlwbg88SRM8sB2NykcRMRmXwKkzyxJAyTlzVuIiJZoDDJEwurE0RM15qISHYoTPJEcVGUBTMSo87oqm/cz4N/yLubUIpIjlCY5JElM8tHvNbE3fncbev45I/X0pdMZaFmIpLvFCZ55Mjacl7Z00H/sMB4tH4vz21vpbsvxcadbVmqnYjkM4VJHjlyZjm9yRTbm4fe9+S7v62nsiSYLvzMVl2LIiLjT2GSR46sDWZ01acNwq97tYXHXt7L5WcvYXZlCc9sa8lS7UQknylM8siS2tdOD/7ug/VMK43x/lMWcsLCKp7ZppaJiIw/hUkemZaIUVNezNqtzWxu2s+6V1u4b8NuLj1tIeXFRZywYDrbm7tobNe95EVkfGndjTyzYk4l923YzX0bdgNQGovyoTMWA3D8gioAntnawvnHzM5WFUUkDylM8sw1Fx/Pczta2LO/h6b2HpbOqmBGWRyAFXOmEYsaz25rVpiIyLhSmOSZaYkYZy6tHXFbSSzKijnTeFaD8CIyzjRmUmBOWDCd53a06OJFERlXCpMCc8LCqlEvXvzV8zs5+5u/pbmjNws1E5GpTGFSYE5YMB147cWL9Y3tfP5/fs/mPR08XL8nG1UTkSlMYVJg6qaVMKuyeMjFix09/XziR8+QiEepKC7iMYWJiBwihUmBMTNOWDCdx17ewy1PbeOl3e1c+bPn2dy0n2suPp7Tl1Tz8Et7cPdsV1VEphDN5ipA7zx+Lk9s3suVP3t+sOwL5y3j9CU1vNy0n3vX72bbvk4WVpdlsZYiMpUoTArQuStm89bls3hlTwdrtzazv6efS09bBMAZS2oAeKR+j8JERMYsK91cZvYNM/uDmT1nZneaWVXativNrN7MNpnZeWnl54dl9WZ2RVr5YjN7Miz/qZnFJ/l0piQz44jaci5aOZ8Pn7GYSMQAWFxTxpxpJTyqcRMROQTZGjO5HzjG3Y8FXgSuBDCz5cDFwArgfOC7ZhY1syjwHeACYDnwvnBfgK8D33L3JUAz8NFJPZM8Y2acvqSGx17eSzKlcRMRGZushIm73+fu/eHLJ4B54fNVwK3u3uPurwD1wMnho97dN7t7L3ArsMrMDDgbuD18/03AOybpNPLWm5fU0NLZx4YG3UhLRMYmF2ZzfQT4Vfh8LvBq2rbtYdlo5dVAS1owDZSPyMwuM7M1ZramqalpnKqff05fUg0E4yYjUYtFRIabsDAxswfM7IURHqvS9vkS0A/8eKLqkc7dr3f3le6+srZ25PWrBGZWlLBsVsWI4yarf9/Asf94Lw/+oTELNRORXDVhs7nc/ZyDbTezDwEXAm/xAxc17ADmp+02LyxjlPK9QJWZFYWtk/T9JQNnLKnhR09upaWzl6pEMKfhh49v4R9Wr8cdbn58C3/yhplZrqWI5IqsTA02s/OBvwX+2N070zatBn5iZv8OzAGWAk8BBiw1s8UEYXEx8H53dzN7EHg3wTjKpcBdk3cm+evcFbO48dFXOPlrv+aco2dSU17MzY9v5ZyjZ7FgRoKbHt9CY3s3MytKsl1VEckB2RozuRaoAO43s3Vmdh2Au68HbgM2APcAn3L3ZNjquBy4F9gI3BbuC/BF4HNmVk8whnLD5J5Kfjr1iGpWX34G7z95AU9u3sfNj2/lz0+Yx3WXnMD7T5lPMuWsXteQ7WqKSI6wQl02Y+XKlb5mzZpsV2NK6EumeGn3fo6uqyCYQAerrn2E3qTzq0+fmeXaichkMrO17r5yeHkuzOaSHBeLRlg+p3IwSAD+/MR5bNzZNur04fUNrbR29k1WFUUkyxQmclguPHYOsahx57Pbh5Tvbuvm8p88w9uueYTP3rYuO5UTkUmnMJHDMqMszp8sm8nP1zXQ259ifUMr33mwnrf82++4b8NuTl40g9/8oZEXdrRmu6oiMgm00KMctnedMI/7NuzmTV+9j66+JABnLavlq29fQVUizpuv/g3febCe711yYpZrKiITTWEih+3sN8zkwmPrqCgp4qRFMzhp0Qzmz0gMbr/09EVc+2A9L+5u56hZFVmsqYhMNM3mkgmzr6OXN3/9N5y7fBbfvvh4+pMpfvXCLtZubWZXazc7W7s4dl4V/7RqxZDBfRHJXaPN5lLLRCbMjLI4l5y6kP9+eDPL51Tykye3sWVvJ2XxKHVVpSTiUX74xFZOWFjFO4+f9/ofKCI5S2EiE+pjZy7mB49t4Wt3/4EVcyq57pITOHf5bCIRI5ly3vufj/MPd63n1COqqZtWCgTTip/Z2sxJi2ewbFaFWi0iU4C6uWTCPfRiE0l3zjqq9jXBsGVPBxf8x8OsXDSd73/oJP7zoc186/4X6Q9XJp5ZUcz5x8zmyguOpjQezUb1RSTNaN1cChPJuh8+voW/v2s9C6sTbN3byduOreMzb1nKs6+28LsXm7j7+Z2ctGgGN1y6koqSGACbdrVzzwu7uOTUBVSXF2f5DEQKh8JkGIVJ7nB3Lv3+0zyztZmvvn0F7zph7pAWzP/+voHP/nQdb6ir4JqLj+emx7bwoye3kUw5tRXFfOPdx3LWMq1gLDIZFCbDKExyS29/ip7+5GDLY7gH/9DIJ360lp7+FBGDvzhlIW87to6v3LWeTbvbufS0hXz2rUcNLpc/IJlyohGNuYiMF4XJMAqTqefpLfu45altfPzMIzi6rhKA7r4k/3rPJm589BVKY1Hee9J83nfyAp7b3sJd6xp4YvNeVh03l39+xwoScc03EcmUwmQYhUl++cOuNq5/aDOr1zUMDt4vmJHg+AVVrP59A0tnlvO9S07kyNryLNdUZGpTmAyjMMlPO1u7uPeFXbxpfhXHza/CzHjoxSY+89N19PQlObquku7+JD19KRwoihjRiHHGkhouP3sJlaN0s4lIQGEyjMKksOxs7eKqX26kubOX4qIoxUURzIIxlc7eJI/U76G6LM4XzlvGiQuns3ZrM2u3NhMvinDBMXWcsngGRVGtiyqiMBlGYSLpXtjRyldWr2ft1ubBsqpEjN7+FJ29SarL4vzxUbWsmDuNFXMqqSkvZldrNw0tXQCc/8bZatVIQVCYDKMwkeHcnfs27Ka1s48TF03niJoyuvtS/O7FRn7x3E6efGUfTe09I763NBbl7W+awwVvnE1f0mnp7KWnP8URNWUsm12ha2EkbyhMhlGYyOFobO9mfUMbzR29zKkqZW5VKfs6ernlqW3cta5hcCn+4WrKizlmbiVvnDuNZbMrSKactq4+OnuTrJgzjZWLplMS0xX+kvsUJsMoTGS8tXX38cL2VipKYlQlYhRFjfrG/Wza1c7Gne28sKOVlxrbSY3wT64kFuGkRTOoSsTpT6boSzo15XEW1ZSxqLqMhdUJ5s9IUF6s6c2SXVo1WGSCVZbEOH1JzZCyummlnLm0dvB1V2+SV/Z0UByLUFkSIx6NsHbbPh56cQ9PbN7LjuYuiqJGNBLh2W3N7O3oHfJ5M8riVJYc+Gc7vSzO0XWVLK+rZHZlCf2pFL1Jp6QowvwZCiCZPGqZiOSwtu4+tuzp4NV9XWzb18mrzZ109PQD4A6727rZsLON9u7+UT+joqSIsngRiXiU0niUsngRpfEo5SVF1JYXU1tRTHVZnIgZjmNm1JYXM6uyhJmVxcTCWWxmUB4vIqIVBQqaWiYiU1BlSYxj51Vx7LyqUfdxd3a0dLGvo5dYNEIsanT2JgcDaHdbN129STp6++nsTdLZ209LZy+v7uvkofYe2ntGD6LhIgbTSmNMT8QpjUeJF0WIRSOUxKKUFAX/TcSjJOJFlBVHiUcjRMJreUqKIpSXxKgoKaI0FsUMDKMoapQXF1FWHJRHDMyC95TGopTEIroNwRSgMBGZ4syMedMTzJueGFJ+sABK19WbZF9nL+5BqySVchrbe9jd1k1Te8/gigLuwaSBfZ29NHf00d2XpDeZorc/RVtXH419Sbr7knT1JensCcJrpPGhw1ESi1AUiRAxKAoDM14UobgoSlHEiEUjRCNGLBqEUFEk2KcoGjkQaAYRC8IrCN0IRREjEjEMwvdHiBcFnxUJ94+YESuKEIsEnzdQbsbgcQc+J2JGNAzCorAu0fAzzAjKzML6BNvNgmNHh5QFx48OfGa4zcKgzUUKE5ECVxqPMjdeOqRs/ozEKHuPnbvTn3KSKSflTndfivbuPtq7++nuS+IEXXV9yRT7e/rp6Omnqy+JOzjQn0zR3Zeiq7ef7v4U/cngc/pTKfr6nZ7+IMz6kk5/MjV4rP6k09HfTzLl9Pan6EumSDmkPNieTDl9yRQ9/SlSKSflkHQnlfLB4MxlFoZZEEoMhlMkLYBsYHtaKy9iDO5346UnsaA68+84ncJERCaEWdBSGJjxnIgHEwhymbsH4ZRK4WkB1JcMAqg/6ThhAKUF00BgBvunbUulcHdSqaGBdWB/wkAbuTwZHn8g9FLuuA+UH6hfUM6weoRlPvT9KXeKY+O/moPCREQkZGbEi4w4WjrnUOknJiIiGVOYiIhIxhQmIiKSMYWJiIhkTGEiIiIZy0qYmNk3zOwPZvacmd1pZlVh+SIz6zKzdeHjurT3nGhmz5tZvZldY+GVO2Y2w8zuN7OXwv9Oz8Y5iYgUsmy1TO4HjnH3Y4EXgSvTtr3s7seFj0+klX8P+DiwNHycH5ZfAfza3ZcCvw5fi4jIJMpKmLj7fe4+sCDQE8C8g+1vZnVApbs/4cHKlDcD7wg3rwJuCp/flFYuIiKTJBcuWvwI8NO014vN7FmgDfiyuz8MzAW2p+2zPSwDmOXuO8Pnu4BZox3IzC4DLgtf7jezTYdQzxpgzyHsnw8K8ZyhMM+7EM8ZCvO8Mz3nhSMVTliYmNkDwOwRNn3J3e8K9/kS0A/8ONy2E1jg7nvN7ETg52a2YqzHdHc3s1EX13H364Hrx/p56cxszUjLLuezQjxnKMzzLsRzhsI874k65wkLE3c/52DbzexDwIXAW8KuK9y9B+gJn681s5eBo4AdDO0KmxeWAew2szp33xl2hzWO64mIiMjrytZsrvOBvwXe7u6daeW1ZhYNnx9BMNC+OezGajOzU8NZXB8E7grfthq4NHx+aVq5iIhMkmyNmVwLFAP3hzN8nwhnbv0R8E9m1gekgE+4+77wPX8F/AAoBX4VPgCuBm4zs48CW4H3TFCdD6t7bIorxHOGwjzvQjxnKMzznpBzLtjb9oqIyPjRFfAiIpIxhYmIiGRMYfI6zOx8M9sULuOSt1fXm9l8M3vQzDaY2Xoz+3RYnvfL1ZhZ1MyeNbNfhK8Xm9mT4Xf+UzPL7dsDHgYzqzKz28NljTaa2Wn5/l2b2WfD/7dfMLNbzKwkH79rM7vRzBrN7IW0shG/WwtcE57/c2Z2wuEeV2FyEOHMsu8AFwDLgfeZ2fLs1mrC9AOfd/flwKnAp8JzLYTlaj4NbEx7/XXgW+6+BGgGPpqVWk2s/wDucfc3AG8iOP+8/a7NbC7wN8BKdz8GiAIXk5/f9Q84sNzUgNG+2ws4sETVZQTLVh0WhcnBnQzUu/tmd+8FbiVYviXvuPtOd38mfN5O8MtlLnm+XI2ZzQPeBvx3+NqAs4Hbw13y8ZynEcycvAHA3XvdvYU8/64JZq+WmlkRkCC4SDrvvmt3fwjYN6x4tO92FXCzB54AqsLr9Q6ZwuTg5gKvpr1OX8Ylb5nZIuB44EkOYbmaKerbBNc8pcLX1UBL2tpx+fidLwaagO+H3Xv/bWZl5PF37e47gG8C2whCpBVYS/5/1wNG+27H7XecwkSGMLNy4A7gM+7elr4tXKkgb+aSm9mFQKO7r812XSZZEXAC8D13Px7oYFiXVh5+19MJ/gpfDMwBynhtV1BBmKjvVmFycDuA+Wmv05dxyTtmFiMIkh+7+8/C4t0Dzd48XK7mDODtZraFoAvzbIKxhKqwKwTy8zvfDmx39yfD17cThEs+f9fnAK+4e5O79wE/I/j+8/27HjDadztuv+MUJgf3NLA0nPERJxiwW53lOk2IcKzgBmCju/972qa8Xa7G3a9093nuvojgu/2Nu/8F8CDw7nC3vDpnAHffBbxqZsvCorcAG8jj75qge+tUM0uE/68PnHNef9dpRvtuVwMfDGd1nQq0pnWHHRJdAf86zOxPCfrVo8CN7n5Vdms0MczszcDDwPMcGD/4O4Jxk9uABYTL1aQtcZM3zOws4P+4+4XhunC3AjOAZ4FLwkVI84aZHUcw6SAObAY+TPDHZd5+12b2VeC9BDMXnwU+RjA+kFfftZndApxFsNT8buArwM8Z4bsNg/Vagi6/TuDD7r7msI6rMBERkUypm0tERDKmMBERkYwpTEREJGMKExERyZjCREREMqYwEcmQmT0W/neRmb1/nD/770Y6lkiu0dRgkXGSfq3KIbynKG1tqJG273f38nGonsiEUstEJENmtj98ejVwppmtC++dETWzb5jZ0+G9Iv4y3P8sM3vYzFYTXIWNmf3czNaG99u4LCy7mmCV23Vm9uP0Y4VXLH8jvDfH82b23rTP/m3avUp+HF6YJjKhil5/FxEZoytIa5mEodDq7ieZWTHwqJndF+57AnCMu78Svv5IeEVyKfC0md3h7leY2eXuftwIx3oXcBzBvUhqwvc8FG47HlgBNACPEqxB9ch4n6xIOrVMRCbOuQTrHq0jWJammuAmRABPpQUJwN+Y2e+BJwgW3lvKwb0ZuMXdk+6+G/gdcFLaZ2939xSwDlg0DuciclBqmYhMHAP+2t3vHVIYjK10DHt9DnCau3ea2W+BkgyOm762VBL9O5dJoJaJyPhpByrSXt8LfDJc2h8zOyq8CdVw04DmMEjeQHDb5AF9A+8f5mHgveG4TC3BnROfGpezEDkM+otFZPw8ByTD7qofENwbZRHwTDgI3sTIt4W9B/iEmW0ENhF0dQ24HnjOzJ4Jl8cfcCdwGvB7ghsd/a277wrDSGTSaWqwiIhkTN1cIiKSMYWJiIhkTGEiIiIZU5iIiEjGFCYiIpIxhYmIiGRMYSIiIhn7/0ZAI1Xa6DLeAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "class NET(fluid.dygraph.Layer):\n",
+    "    \n",
+    "    # Initialize the list of learnable parameters, and fill the initial value with the uniform distribution of [0, 2*pi]\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * np.pi), dtype='float64'):\n",
+    "        super(NET, self).__init__()\n",
+    "        \n",
+    "        # Create the parameter theta for learning U\n",
+    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype,is_bias=False)\n",
+    "        \n",
+    "        # Create a parameter phi to learn V_dagger\n",
+    "        self.phi = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        \n",
+    "        # Convert Numpy array to variable supported in Paddle dynamic graph mode\n",
+    "        self.M = fluid.dygraph.to_variable(M)\n",
+    "        self.weight = fluid.dygraph.to_variable(weight)\n",
+    "\n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self):\n",
+    "        \n",
+    "        # Get the unitary matrix representation of the quantum neural network\n",
+    "        U = U_theta(self.theta)\n",
+    "        U_dagger = dagger(U)\n",
+    "        \n",
+    "        \n",
+    "        V = U_theta(self.phi)\n",
+    "        V_dagger = dagger(V)\n",
+    "        \n",
+    "        # Initialize the loss function and singular value memory\n",
+    "        loss = 0\n",
+    "        singular_values = np.zeros(T)\n",
+    "        \n",
+    "        # Define loss function\n",
+    "        for i in range(T):\n",
+    "            loss -= self.weight.real[i] * matmul(U_dagger,matmul(self.M, V)).real[i][i]\n",
+    "            singular_values[i] = (matmul(U_dagger, matmul(self.M, V)).real[i][i]).numpy()\n",
+    "        \n",
+    "        # Function returns two matrices U and V_dagger, learned singular values and loss function\n",
+    "        return U, V_dagger, loss, singular_values\n",
+    "    \n",
+    "# Record the optimization process\n",
+    "loss_list, singular_value_list = [], []\n",
+    "U_learned, V_dagger_learned = [], []\n",
+    "\n",
+    "# Start Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "  \n",
+    "    # Determine the parameter dimension of the network\n",
+    "    net = NET([theta_size])\n",
+    "    \n",
+    "    # We use Adam optimizer for better performance\n",
+    "    # One can change it to SGD or RMSprop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    \n",
+    "    # Optimization cycle\n",
+    "    for itr in range(ITR):\n",
+    "        \n",
+    "        # Forward propagation to calculate loss function\n",
+    "        U, V_dagger, loss, singular_values = net()\n",
+    "        \n",
+    "        # Under the dynamic graph mode, back propagation minimizes the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "\n",
+    "        # Record optimization intermediate results\n",
+    "        loss_list.append(loss[0][0].numpy())\n",
+    "        singular_value_list.append(singular_values)\n",
+    "\n",
+    "    # Record the last two learned unitary matrices\n",
+    "    U_learned = U.real.numpy() + 1j * U.imag.numpy()\n",
+    "    V_dagger_learned = V_dagger.real.numpy() + 1j * V_dagger.imag.numpy()\n",
+    "\n",
+    "# Draw a learning curve\n",
+    "loss_plot(loss_list)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "#### Error analysis\n",
+    "\n",
+    "We will explore the accuracy of the quantum version of singular value decomposition. In the above section, we mentioned that the original matrix can be expressed with less information obtained by decomposition. Specifically, it uses the first $T$ singular values ​​and the first $T$ left and right singular vectors to reconstruct a matrix:\n",
+    "\n",
+    "$$\n",
+    "M_{re}^{(T)} = UDV^{\\dagger}, \\tag{4}\n",
+    "$$\n",
+    "\n",
+    "For matrix $M$ with rank $r$, the error will decreasing dramatically as more and more singular values are used to reconstruct it. The classic singular value algorithm can guarantee:\n",
+    "\n",
+    "$$\n",
+    "\\lim_{T\\rightarrow r} ||M-M_{re}^{(T)}||^2_2 = 0, \\tag{5}\n",
+    "$$\n",
+    "\n",
+    "The distance measurement between the matrices is calculated by the Frobenius-norm,\n",
+    "\n",
+    "$$\n",
+    "||M||_2 = \\sqrt{\\sum_{i,j} |M_{ij}|^2}. \\tag{6}\n",
+    "$$\n",
+    "\n",
+    "The current quantum version of singular value decomposition still needs a lot of efforts to be optimized. In theory, it can only guarantee the reduction of accumulated errors."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 12,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:54:23.390172Z",
+     "start_time": "2021-01-09T09:54:21.827423Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEKCAYAAAAfGVI8AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAABEKElEQVR4nO3dd3hUddbA8e9JIYUWCCGE3gklkECkiEhTQUVUpMiqK+rq2tuLbd1V3CaKBbtrWUUsFBEULIg0CwsIhJ4gYoKUUEMngZTz/nFvQggpE0gyKefzPPNk5t47d85Mkjn310VVMcYYU3X5eDsAY4wx3mWJwBhjqjhLBMYYU8VZIjDGmCrOEoExxlRxft4O4GzUq1dPmzdv7u0wjDGmQlm5cuU+VQ3Lu71CJoLmzZuzYsUKb4dhjDEViohszW+7VQ0ZY0wVZ4nAGGOqOEsExhhTxVXINgJjyoM9e/YwduxYEhISyMrK8nY4xgDg4+NDZGQkzz33HPXr1/foOZYIjDlLY8eOpX///rz77rv4+/t7OxxjAEhPT2fy5MmMHTuWDz74wKPnVJmqoVlxOxj69Kcse6IHVzw9g1lxO7wdkqngEhISuP766y0JmHLF39+fG264gYSEBI+fUyVKBLPidvDYZ+v4i37Ceb6bGHHsYx77rDoAV8U08nJ0pqLKysqyJGDKJX9//2JVV1aJEsGEuZuokb6PEb6L8RFlhO/31Ejfz4S5m7wdmjHGeF2VSAQ7D6Zyr99MfMkEwIdM7vH7jJ0HU70cmTHnxtfXl+joaDp16sQVV1zBwYMHvRbLokWLWLJkSYmdb9asWWzcuDHn8RNPPMF3331XYufP64svvmD8+PEeHXv8+HFCQ0M5fPjwaduvuuoqpk6dCjjxd+7cmcjISDp16sSnn36ac9zSpUvp0aMH0dHRtG/fnnHjxpGUlETjxo3PuJKPjo5m2bJljBs3jkaNGhEdHU2bNm0YNmzYaZ/PuagSiSCqdiojfBfjL84HHCCZjPD9nk6107wcmalKZsXtoPf4BbR49Et6j19QIu1UQUFBrF69mvXr11O3bl1ee+21Eoj07BSWCDIyMop9vryJ4O9//zsXXXTRWcdXlKFDh/Loo496dGxwcDCDBg1i5syZOdsOHTrEjz/+yBVXXMGaNWsYO3Ysn3/+OQkJCcyePZtHHnmElStXAnDjjTfy1ltv5fzuRo4cSfPmzWnatCk//PBDzjkTEhI4cuQIPXr0AOCBBx5g9erVbN68mVGjRjFgwAD27t17zu+9SiSCiRHzEE5fic2HLF6K+NZLEZmqJrudasfBVBTYcTCVxz5bV6KdFnr16sWOHc75tmzZwuDBg+nWrRt9+vTJaTjcvXs3V199NV26dKFLly45X9wvvPACnTp1olOnTkycOBGApKQk2rdvz6233krHjh255JJLSE11StEvv/wyHTp0oHPnzlx77bUkJSXx5ptv8uKLLxIdHc0PP/zAmDFjuP322+nRowcPP/ww48aN47nnnsuJt1OnTiQlJQHwwQcf0LlzZ7p06cINN9zAkiVL+OKLL3jooYeIjo5my5YtjBkzJueqev78+cTExBAVFcXNN9/MiRMnAGf6mSeffJKuXbsSFRWVb4Npz5492bBhQ87jfv36sWLFCt5//33uvvtuAGbPnk2PHj2IiYnhoosuYvfu3WecZ/To0UyZMiXn8cyZMxk0aBDBwcE899xz/OUvf6FFixYAtGjRgr/85S88//zzgNP1OCIiAnBKdR06dMj3nFOmTOHaa6/N9/c9atQoLrnkEj7++ON89xdHlWgsbpm2AeT0K5IAyXC2G1NCRv3nfwXui/v9ICczTy/yp6ZnMm72Bq6KaUTKsZPc8eHK0/ZP/XMvj187MzOT+fPnc8sttwBw22238eabb9KmTRuWLVvGnXfeyYIFC7j33nvp27cvM2fOJDMzk6NHj7Jy5Uree+89li1bhqrSo0cP+vbtS506ddi8eTOffPIJb7/9NiNHjmTGjBlcf/31jB8/nsTERAICAjh48CAhISHcfvvt1KhRg7FjxwLw7rvvsn37dpYsWYKvry/jxo3LN/YNGzbwz3/+kyVLllCvXj1SUlKoW7cuQ4cOZciQIQwfPvy049PS0hgzZgzz58+nbdu2/PGPf+SNN97g/vvvB6BevXqsWrWK119/neeee4533nnntOePGjWKadOm8dRTT5GcnExycjKxsbGsX78+55gLLriApUuXIiK88847PPvsszlf4tkGDRrEn/70J/bv309oaChTpkzJSSQbNmzI+RyyxcbG8sorrwDOlX27du3o168fgwcP5sYbbyQwMJCRI0cSHR3NK6+8gp+fH1OnTmX69OkF/t67du1arN5BBakSJQJu/xHGHYJxhzh49yZOqD9L6w1zthtTBvImgWwHj6ef03lTU1OJjo6mQYMG7N69m4svvpijR4+yZMkSRowYQXR0NH/+859JTk4GYMGCBdxxxx2AcyVau3ZtfvzxR66++mqqV69OjRo1GDZsWE71RIsWLYiOjgagW7duOVfwnTt35rrrruPDDz/Ez6/g68kRI0bg6+tb6HtYsGABI0aMoF69egDUrVu30OM3bdpEixYtaNu2LeBUs3z//fc5+4cNG3ZGvLmNHDkyp2Qxbdq0MxINwPbt2xk0aBBRUVFMmDDhtBJEtmrVqjF06FA+/fRT9u3bR1xcHIMGDSo09mxPPPEEK1asyLmiHzx4MADh4eF06tSJ+fPns3r1avz8/OjUqVOB5ympNeerRIkgt5B6DZgecS+zkusQdSKD6gFV7iMwpaSwK/je4xewI5/OCY1CggCoW71asUoA2bLbCI4fP86gQYN47bXXGDNmDCEhIaxevbrY58srICAg576vr29O1dCXX37J999/z+zZs/nXv/7FunXr8n1+9erVc+77+fmd1hCallY6bXTZMfv6+ubbNtGoUSNCQ0NZu3YtU6dO5c033zzjmHvuuYcHH3yQoUOHsmjRogJLM6NHj+Yf//gHqsqVV16Z0524Q4cOrFy5ki5duuQcu3LlSmJjY3Met2rVijvuuINbb72VsLCwnJJFdvVQeHg4o0ePLvS9xsXFnXbOs1WmJQIRCRGRT0UkQUTiRaSXiNQVkXkistn9Wae042h56d38dKIlX6zZWdovZQwADw1qR5D/6VfGQf6+PDSoXYmcPzg4mJdffpnnn3+e4OBgWrRokVOloKqsWbMGgIEDB/LGG28ATnXSoUOH6NOnD7NmzeL48eMcO3aMmTNn0qdPnwJfKysri23bttG/f3+eeeYZDh06xNGjR6lZsyZHjhwp8HnNmzdn1apVAKxatYrExEQABgwYwPTp09m/fz8AKSkpAAWer127diQlJfHrr78CMHnyZPr27Vusz2vUqFE8++yzHDp0iM6dO5+x/9ChQzRq5IwxmjRpUoHn6devH5s3b+a111477Ut77NixPP300zklkqSkJCZOnMhDDz0EOIk0+2p+8+bN+Pr6EhISAjglmq+++oqpU6cW2D4AMGPGDL799tsik4Unyrpq6CXgG1WNBLoA8cCjwHxVbQPMdx+Xqq5N63Bx2EFOLJxQYkUrYwpzVUwjnh4WRaOQIASnJPD0sKgSHdAYExND586d+eSTT/joo49499136dKlCx07duTzzz8H4KWXXmLhwoVERUXRrVs3Nm7cSNeuXRkzZgzdu3enR48e/OlPfyImJqbA18nMzOT6668nKiqKmJgY7r33XkJCQrjiiiuYOXNmTmNxXtdccw0pKSl07NiRV199Nadqp2PHjjz++OP07duXLl268OCDDwJw7bXXMmHCBGJiYtiyZUvOeQIDA3nvvfcYMWIEUVFR+Pj4cPvttxfrsxo+fDhTpkxh5MiR+e4fN24cI0aMoFu3bjlVVvnx8fFh+PDh7N+//7RkFB0dzTPPPMMVV1xB27Ztadu2LW+88Qbt2jmJf/LkybRr147o6GhuuOEGPvroo5wqtJCQEHr16kV4eDgtW7Y87fWyG+PbtGnDhx9+yIIFCwgLO2OdmWKTsvoiFJHawGqgpeZ6URHZBPRT1WQRiQAWqWqhl0mxsbF6rgvTLJv6DD3i/03isDm06Fzw1Y8xBYmNjbUFkoxHHn30UZYtW8bcuXOpVq1ambxmfn+fIrJSVc+oSyrLEkELYC/wnojEicg7IlIdCFfVZPeYXUB4fk8WkdtEZIWIrCiJfrMdBv2JLL8gWiROPedzGWNMYcaPH8/ChQvLLAkUV1kmAj+gK/CGqsYAx8hTDeSWFPItoqjqW6oaq6qxJVEUqhkSik/nEbB+BqQePOfzGWNMRVWWiWA7sF1Vl7mPP8VJDLvdKiHcn3vKKqCTMWMg/TgrZp/Za8AYY6qKMksEqroL2CYi2fX/A4GNwBfAje62G4HPyyqmak26saFaZzKOHy76YGOMqaTKuhP9PcBHIlIN+A24CScZTRORW4CtQP7N+KWkw6OLEZ+qMa7OGGPyU6aJQFVXA/mNfhhYlnHkJj4+aFYWO5PiadSyo7fCMMYYr7FLYWDZB49Tb1JfUvbYADNTsdg01CWnONNQgzMV9XXXXUdUVBSdOnXiggsu4OjRo/Tv35+5c+eeduzEiRO54447SEpKIigoiJiYGNq3b0/37t15//33S/idFJ8lAqBB92EESDqb5r7l7VBMZXdkF7x3KRw5czbLs2HTUJec4kxDDc7gvPDwcNatW8f69etz1q7OO4MoOLOIZo8AbtWqFXFxccTHxzNlyhQmTpzIe++9V6LvpbgsEQDNO5xHvH9HGv82lazMTG+HYyqzxc/C70th8TMlfmqbhrpsp6FOTk7OmYYCnKkvAgICGD58OF9++SUnT57M+Rx37tyZ77QdLVu25IUXXuDll18u6tdbulS1wt26deumJW3FF2+oPllL134/q8TPbSqnM/4O/3vZmbdlbzn7ThxTfesi1XEhqk/Wcn6+fZHqqg+d/Uf3nflcD1SvXl1VVTMyMnT48OH69ddfq6rqgAED9JdfflFV1aVLl2r//v1VVXXkyJH64osv5jzn4MGDumLFCu3UqZMePXpUjxw5oh06dNBVq1ZpYmKi+vr6alxcnKqqjhgxQidPnqyqqhEREZqWlqaqqgcOHFBV1SeffFInTJiQE9uNN96ol19+uWZkZOS7v2PHjpqYmKjr16/XNm3a6N69e1VVdf/+/TnPnz59+mnnmz59uqampmrjxo1106ZNqqp6ww035LynZs2a6csvv6yqqq+99precsstZ3xmL7zwgj7xxBOqqrpz505t27atqqq+9957etddd6mqakpKimZlZamq6ttvv60PPvjgGeeJi4vTsLAw7dmzpz7++OM5n7eq6uWXX66zZjnfJU8//bT+3//9n6qqJiYmaseOHU87z4EDBzQwMPCM85+r/L4ngRWaz3eqlQhcnS6+gQPU5Niyyd4OxVRWh36H7NlVVOHg7+d8SpuG2nvTUEdHR/Pbb7/x0EMPkZKSwnnnnUd8fDxw+gIzuauF8qPlYL4zm4PZFRBYnY87vsKEOGHh4TTCawV6OyRT0dz0ZcH7ThyGtIOcGjivzuPWbp139dDCn18Am4a64JjLYhrq7MQ5bNgwfHx8+Oqrr2jfvj1XXnklDzzwAKtWreL48eN069atwHjj4uJo37792b3ZEmIlglz697+E41n+TP15m7dDMZXN4mdB8yxOo1kl1lZg01CX/TTUP/30EwcOHADg5MmTbNy4kWbNmgFOgujfvz8333xzoaWBpKQkxo4dyz333FOs+EuaJYJcmterzgON4jn/x5vISD+3laOMOc325ZB58vRtmSed7SXEpqH2XElMQ71lyxb69u2b8znExsZyzTXX5OwfPXo0a9asOSMRbNmyJaf76MiRI7n33nu56aabihV/SSuzaahLUklMQ12QuG/eI2bp/SRfPomI864qldcwlYNNQ23Ks/I6DXWFEDXgD2iNcCI2f+LtUIwxpkxYIsjDr1oAEnMD+stcUvcmejscY4wpdZYI8pHW5QYUWD3Ly4M8TLnm4+NDurUlmXIoPT0dn2JMpmmJIB+B9ZqzvMktVG/d29uhmHIsMjKSyZMnWzIw5Up6ejqTJ08mMjLS4+dYY7ExZ2nPnj2MHTuWhISE0/rHG+NNPj4+REZG8txzz1G/fv3T9hXUWGwDygqxZ0ciicu/pMfVd3s7FFMO1a9fnw8++MDbYRhzzqxqqBCJ896kx5rH+X1z/qMmjTGmMrBEUIhWg+4gQ33YMf8Nb4dijDGlxhJBIepFNGddjd5E7vqCtNTj3g7HGGNKhSWCIlTreSt1OMK676wu2BhTOVkiKEKH3kPYKo1JSljt7VCMMaZUWCIogvj4Mr/fDB7afwUJuw57OxxjjClxlgg8cHVsS6r5+fDZT2cuTmGMMRWdJQIP1KlejRciFnDX2ms4duSQt8MxxpgSZYnAQ21iL6K2HCNj3Qxvh2KMMSXKEoGH2nW/BMIiqb3e1jQ2xlQuZZoIRCRJRNaJyGoRWeFuqysi80Rks/uzTlnG5DERiL0Zdq4iOf5/3o7GGGNKjDdKBP1VNTrXxEePAvNVtQ0w331cLh1vP5xUrcbv8173dijGGFNiysOkc1cC/dz7k4BFwCPeCqYwwbVCWdv/Ddp2tOmpjTGVR1mXCBT4VkRWisht7rZwVU127+8CwvN7oojcJiIrRGTF3r17yyLWfHXuN5w6YRFee31jjClpZZ0ILlDVrsClwF0icmHuneosjpDvAgmq+paqxqpqbFhYWBmEWrC1C6ez/MVRqM1Bb4ypBMo0EajqDvfnHmAm0B3YLSIRAO7PPWUZ09k4mbKN7oe+IWHFAm+HYowx56zMEoGIVBeRmtn3gUuA9cAXwI3uYTcCn5dVTGerw6CbOUoQR396y9uhGGPMOSvLxuJwYKaIZL/ux6r6jYj8DEwTkVuArcDIMozprATXCGF5vUvpsnc2B/btpk69fJs1jDGmQiizEoGq/qaqXdxbR1X9l7t9v6oOVNU2qnqRqqaUVUznov6A2wmQdBK++Y+3QzHGmHNSrEQgIrEiMsqt2smu7ikPXVDLXPMOPZgfNIi5233Jysq3fdsYYyoEjxKBiISLyFJgOfAxp7p4vgA8X0qxlXtHB73I+wej+d9v+70dijHGnDVPSwQvAruBUCD3mo3TcRp9q6TBnRrQJDiDVQs+9XYoxhhz1jyt1hkIDFTVA25jb7YtQNMSj6qCCPDzZUL9uXTbMYW9yZcRFlFlPwpjTAXmaYkgCDiZz/YwIK3kwql4ml18O/6SScimad4OxRhjzoqnieB7YEyuxyoivjhzAs0v6aAqkohWnaF5H/xXTwIbaWyMqYA8TQQPA7eKyDwgAKeBeCPQG3islGKrME7GjIGDvxP/4yxvh2KMMcXmUSJQ1Y1AFLAE+BYIxGkojlHVLaUXXsUg7Yewn9ociLcpJ4wxFY/HYwBUdRfwZCnGUmH5VwvE965lnG+zkhpjKiBPxxHcLSLX57P9ehG5s+TDqnhC3CSQfvKElyMxxpji8bSN4H5gWz7bk4AHSiqYim7Zh+PY83QU6en5dbAyxpjyydNE0BhnQri8trv7DBDUoA2NdDdr50/1dijGGOMxTxPBLiA6n+1dgX0lFk0F17HfSPYQin/c+94OxRhjPOZpIvgYeFlELhYRf/d2CTAR+KjUoqtgfP38SWx2DZ1PrGDblo3eDscYYzziaSJ4EvgJmIsz19Bx4Guc7qR/K53QKqZWl9xJhvqw7bvXvR2KMcZ4xKPuo6qaDowWkSeAGJx1hVer6ubSDK4iqteoBR80GMunuxozLT2TQH9fb4dkjDGFKtZ6BKq6WVWnqep0SwIFa3Xxn1mbWo9v1u/ydijGGFMkjweUicgonFlI65Mngajq0BKOq0Lr1TKUoXWSyPhuNsS86e1wjDGmUJ4OKJsAfAg0Bw4C+/PcTC4+PsL1DXcx/Ngn7P5tjbfDMcaYQnlaIvgjMFpVbQUWD7W/7A70tTcI/2UKtOzi7XCMMaZAnrYR+ACrSzGOSqdmaEOkw1BY/RGkp3o7HGOMKZCnieAt4Iy5hkzhjkXdAGmHWDbnXW+HYowxBfK0aigE+IOIXAysBdJz71TVe0s4rkohuE1f1gd29XYYxhhTKE8TQQdOVQ1F5tmnJRZNJSM+PnR6dKG3wzDGmEJ5OqCsf0m9oLvE5Qpgh6oOEZEWwBQgFFgJ3KCqlWr6zvSTJ9iasJLWnc/3dijGGHOGYg0oKyH3AfG5Hj8DvKiqrYEDwC1eiKlUxb19JxEzrubwoRRvh2KMMWfwOBGISH8ReUtEvhGRBblvxThHY+By4B33sQADgOxuqZOAqzyOvoKo2+t6qksaG+Zao7ExpvzxdEDZGJxJ5moC/YC9QB2caaiLM83mROBhIMt9HAocVNUM9/F2oFEBMdwmIitEZMXevXuL8ZLe1zqmH7/5tqB+wkdoVlaRxxtjTFnytEQwFrhbVUfj9Bh6TFVjcEYbH/XkBCIyBNijqivPJlBVfUtVY1U1Niws7GxO4T0ipLS/nlZZiSSstMZjY0z54mkiaAl8594/AdRw778KjPHwHL2BoSKShNM4PAB4CQgRkexG68bADg/PV6F0GHQLxzSQ5P9N83YoxhhzGk8TwX6caiFwvqg7ufdDgSBPTqCqj6lqY1VtDlwLLFDV64CFwHD3sBuBzz2MqUIJrlmHdzv8lzv2DCXlWKXqFGWMqeA8TQQ/AJe496fhrFb2HvAJMO8cY3gEeFBEfsVJLJW2RXVQ3ws5kQEzVmzzdijGGJPD0wFldwOB7v2ngQycqp5pwD+L+6KqughY5N7/Dehe3HNURO0a1OSvYT/SY/E/yLpgCT6+3ui9a4wxp/N0QFlKrvtZOH3/zVno2roRUXHxpCQsom7HAd4OxxhjPO4+miki9fPZHioimSUfVuUVPfgmNLA2deM/8nYoxhgDeN5GIAVsDwCs5bMYfAKqI11Goxs/5+j+nd4OxxhjCq8aEpEH3bsK3C4iuccM+AJ9gIRSiq3SOtzxemote5M1c16n943FbmIxxpgSVVQbwT3uTwH+BOSuBjoJJAG3l3xYlVutplEsa3EX9bsM8nYoxhhTeCJQ1RYAIrIQGKaqB8okqiqgx43/9nYIxhgDeNhGoKr98yYBEWktIoEFPccU7bf1S1k69Vlvh2GMqeI87TX0bxG50b0vIvId8AuQLCI9SjPAymzfkg+J3fg0O7dt8XYoxpgqzNNeQ9cBm9z7lwJdgJ7AB8D4UoirSmhy8Z34SRaJ377p7VCMMVWYp4kgHGeKaIDLgGmquhx4BYgpjcCqgogWHVgf2I3W22aQnm69cI0x3lGcSeeaufcvAea79/0oeIyB8UBWt5sIZz9rF0z3dijGmCrK00QwA/hYROYBdYG57vZo4NdSiKvK6NhvFEnSiDXxNhzDGOMdniaCB4GXcVYju1hVj7nbI4A3SiOwqsLXvxqze8/k77t6krjvWNFPMMaYEuZp99EMVX1eVe9T1bhc219U1XdKL7yqYVT3Zvj6wJwffvZ2KMaYKqjAAWUi0hVYrapZ7v0CqeqqEo+sCqlfK5B3wqYRtWYhaZduIjDQo7V+jDGmRBQ2sngF0ADY495X8m8YVpx5h8w5iIgdSr35szgW/yXEDC/6CcYYU0IKqxpqAezNdb+l+zPvrWVpBlhVRPa+Cmo3pfraSd4OxRhTxRRYIlDVrfndN6XEx5esrjfis/Af7Ph1DY1ad/F2RMaYKsLTKSZaisiDIvKqiLwiIg+ISIvSDq6qORw5inT1Jem7t70dijGmCilyqUoR+T+cdYp9cdoLBAgDnhGRR1T1xdINseoICW9CwmUfE9vlQm+HYoypQgotEYjIBcCzwAQgTFUjVLUBUB94HpggIr1LP8yqI7LHYAICg70dhjGmCimqaugO4ANVfTzPAvb7VfUx4EPgztIMsCpaMfMVfn7uam+HYYypIopKBD2B9wvZ/757jClBmnqA844u4PZ/vMiyJ3pwxdMzmBW3w9thGWMqqaISQQPgt0L2b8GZZsKUoN+bXskJ9ef+9Hc4TzYx4tjHPPbZOksGxphSUVQiCAJOFLL/JBDgyQuJSKCILBeRNSKyQUSecre3EJFlIvKriEwVkWqehV55vfDjfr7LiqGdbMdHlBG+31MjfT8T5m4q+snGGFNMRfYaAi4XkUMF7AspxmudAAao6lER8Qd+FJGvcSa0e1FVp4jIm8AtVPGJ7HYeTEX8NOexD1nc4/cZTx682YtRGWMqK08SwbtF7Nci9jsHqSpw1H3o794UGAD8wd0+CRhHFU8EUbVTGZC2GnEn9AiQDEb6LuaAbyiHDl9I7Vo1vRugMaZSKbRqSFV9PLh5PM+QiPiKyGqc8QjzcNoYDqpqhnvIdqBRAc+9TURWiMiKvXv35ndIpTExYh6SJ7/6kcl9MhW/17rCiv9CZrqXojPGVDaerkdQIlQ1U1WjgcZAdyCyGM99S1VjVTU2LCystEIsF1qmbSBAMk7b5idZnKzVnKCwZjDnAY4+H8N3n0wkIyPTS1EaYyoLT6qGSpyqHhSRhUAvIERE/NxSQWPAusbc/mO+m6sBqMLmeRz67C+E//YZvr73AZCVpfj42KqhxpjiK7MSgYiEiUiIez8IuBiIBxYC2fMu3wh8XlYxVUgi0PYSGj28nFZ3fYqIsH/Hb8T/swfzP5/EifSMos9hjDG5lGXVUASwUETWAj8D81R1DvAI8KCI/AqEUnTjtAHw8SE4pD4AqSnbCJXDDIy7l83/7sX8L6eRnpnl5QCNMRWFOJ15KpbY2FhdsWKFt8MoVzTjJL/O+w91fp5Ivax9/OzThd8v/YAruzbFz7dMm4KMMeWUiKxU1di82+0bopIQv2q0ufQeQh9bzy9d/8rWaq34vxkbuOTF75n301KysipewjfGlA2PGotFpA5O//7+ODOPnpZAVLV+iUdmzor4B9F26EO0uUKpsWE3s7/5ioHfPkj8z33p+IdnoL7HHbWMMVWEp72GPgA64gz42o2Hg8iM94gIgzs14JKWw9j8xWYit0yC13tyrN0w1rS+g16xsYhYLyNjjIdtBCJyBOirqqtKP6SiWRvBWTi2H36aSPr//sOxLH8y799AaJ0Qb0dljClD59pGsKUYx5ryqHooXPIPuG81+we9QmidEDQri3lvPcbKDQnejs4Y40WefrnfBzwtIl1ExOMpJUz54x/SkFbnDwNg/5aV9N/5Ju2nXcgXz9/Gms2JXo7OGOMNniaCX3GmpF4FnBSRzNy30gvPlKZ6bc4j8/al7GzQnyFHptHiw17MfPEe1ift8nZoxpgy5Glj8SdAbeBerLG4Uglo0I7Wd0zl+La17Pv8b/TY9zX93hxIvw6NefDiNkRG1PZ2iMaYUuZpIogFuqvq+tIMxnhPcJPOtLz7c44c3M9dK1L44IcETvx6K3OaXMmQmx4DP4/WHzLGVECeVg1tBGqVZiCmfKgZEsp9F7Vh4R1R1A0JYciOF+GVbmStnMTvew97OzxjTCnwNBH8FXhBRC4SkXARqZv7VpoBGu+o1aA5TR5YADfMhBr18Zl9L5mvnsfGX2y5TGMqG0+rhr5yf37L6e0D4j62nkSVkQi0GgAt+3Nw9eekLZtBZKs2ACz7+X80axNNg5AgLwdpjDlXniaC/qUahSnfRAiJuYqQmKsAOHFoN1FfXsUWbcj8NneT2XIAny5eyeOpE/hn0MPcMrgnV8Xku9CcMaYcKjIRuAvNPwv8UVWtXsAQUCOU/ReNp9Hi8UT9+iDLfonkrqzqnOe7iRHHPuaxz6oDWDIwpoIoso1AVdOBFliXUZPN14/QC26i7iPreMbnVlrKTgb5rcRHlBG+31MjfT/jv7HRysZUFJ42Fk8Cbi3NQEwF5FeNN4/3Z15mN9LVaSbyIYsPq/2LG469z/7tvwCQaVNgG1OuedpGUB24TkQuBlYCx3LvVNV7SzowUzFE1U5lWNqP+LsDzAMkg9bspLXfDnzfmQ2tL+KtYxeyqWYvJv7hPC9Ha4zJj6eJoD3O9BIALfPss8u9KmxixDwk8fQ/gQx82d34Mpq26gCrJnHHkXksDboHOI+sLOWOj1bSq2UogztF0KB2oHcCN8bk8CgRqKr1GjL5apm2ASTjtG0BkkHTjEToPxkufAh++YaejboCcGj1F9yw9Q3ejO/HU7M70q1ZKJdGRXBppwY0tK6oxnhFsdYsFpFAoDVOKWCLqqaVVmCFsfUIKrC4j2De3+D4fg4GNuZTuZjXD/QghVrENA3h8qgIBndqQOM6wd6O1JhK55zWIxARfxGZABwA1gDrgAMi8qzbvdQYz8RcBw/GwzXvEhLejD+lvsfSiOd56JK2nMzI4p9fxnPBMwuJT3ams8jIzPJywMZUfp62ETwDjAZuB350t/UBnsZJJmNLPjRTafkFQNRw57YnnmpHdnFXqzbc1acJae8NZXXNfkSGnA/AuNkb+GX3Uabe1tOW1jSmlHiaCP4A3KyqX+XatkVE9gLvYInAnK367Z0bwJGdBJJOz03PwAuvQKdr6BN8OXVatMxJAvdNiaNteE0u7dSAlmE1vBi4MZWHp4mgNs5ylXltAUJKLBpTtdVtCbcthJ1xsOI9WDedQemTGXTbIgCOn8xgW8pxPl+9kwlzNxHZoCaXRUVwWVQEretbUjDmbHm6eP1SYKWq3pVn+xtAtKr28uAcTYAPgHCcxua3VPUld/bSqUBzIAkYqaoHCjuXNRZXEWmHYNPX0HmUMwHevCfg5HH2tPsDc3bV4at1yazY6vyptA2vkZMU2obX9HLgxpRPBTUWe5oILsSZgXQHsNTd3BNoCFyqqj8W9Nxc54gAIlR1lYjUxBmYdhUwBkhR1fEi8ihQR1UfKexclgiqqDkPQtyHkHkCmvSE2JvZ1XgQ3yQc4Kv1u/g5KQVVmHRzd/q2DSM9Mws/H7G2BWNc55QI3BM0BO4CIt1N8cDrqrrzLAP6HHjVvfVT1WQ3WSxS1XaFPdcSQRV2bD+s+RhW/BdSfoMed8Cl4wHYcySNuRt2M6JbYwL9fXnpu818sWYHX97bh0B/ZwqMWXE7mDB3EzsPptIwJIiHBrWzyfFMlVFQIvC0jQD3C//xEgqmORADLAPCVTXZ3bULp+oov+fcBtwG0LRp05IIw1RE1UPh/Hug512Q9D3UbuJs/30Z9Rf9mxtibwafhoAvbcNr0K9d/ZwkMPrt//Fz4gEy3LmPdhxM5bHP1gE2U6qp2gpNBJ6uPqaqKZ6+oIjUAGYA96vq4dzFdlVVEcm3iKKqbwFvgVMi8PT1TCXl4wMt+516fHw/7PsVpv0RaoRD1z9yadcbuTSqAwBZWcqqrQdzkkC21PRMJsxNsERgqrSiBpTtA/YWcdvj6Yu5g89mAB+p6mfu5t1ulVB2O4LH5zMmR+RlcP9aGD0VIqLh++fg7f6Q6Ux/4eMjnMzIf3DajoNpvDjvF37dc7QMAzam/Ci0jUBE+hby3MHAfUCGqha5sL04l/6TcBqG78+1fQKwP1djcV1Vfbiwc1kbgSnSwd9h7yZoczFkZcHkq/jPtsa8c7Q3oLxa7RXuPnkvewmhmp8P6ZlZqMJL10ZzZXQjVNUamU2lc1ZtBKq6OJ8TxQATcEYW/wf4h4cx9AZuANaJyGp321+A8cA0EbkF2AqM9PB8xhQspKlzA0h1ai7/nPERNwdMYYeG0lT2cq/fDP4tt/H0sCh6tQrlq3XJXNC6HgCfLN/GtBXbmHRTd2oH2ywqpnLzuLFYRFoA/wJGAJ8BHVQ1v0Fm+XK7mBZ0iTXQ0/MYU2zV68GNX8C+X9k2+xlabJ2GAKP8FlNv0BNcGlkd/OCm3i1ynlIryI+I2oHUCnL+Rf6zeAvBAX5c2qkB9WoEeOmNGFM6PFmzOBR4AmeeoZ+A81X159IOzJgSV681LcNqwvZqkHmSar4+XLr/A1hSB5a9Ca0vgsgh0PYShnRuyJDODQFQVb7duJuVWw8w7osNnN8qlCs6N2RQxwZWWjCVQlFtBI8DD+GM+H1UVb8po7gKZW0E5qwc2QUvdYGMXLOn+wXC8Pdg87ew6Ss4uht8/KHtIBj1oTOiGScZbNp9hDlrkpm9didb9x/H31fo2zaMIZ0bclGHcGoEeFzANsYrzmpAmYhkAanAQqDA+YBVdWhJBOkpSwTmrMx5EOImQ+bJU9t8q0HMDTDkBadRefvPkDAHMtNzBqox606o19YpLdRrjaqybsch5qxNZs6anew8lEaAnw8TRnRhaJeG3nlvxnjgbAeUfYAtRWkqi+3LT08C4Dzevty57+MDTXs4t2wnj8OejbD6I/juSQiLRCIvp3Pna+l8WXseHRzJqt8PMHvNTjpEOJ3nFv+yl5mrtvO3IR0ItfYEUwEU1WtoTBnFYUzpu73IKbHOVC0YblsEB7c5VUcJc+DHiVCnBYS1xef4PmKzNhA7pDf4Ou0Fuw6lsmb7IWoFOY+/WZ9M9QA/erUMxc/Xo7WgjClTxVqqsrywqiHjVcdTnCqlgBqw/G34aiwEhkDbwRB5ObQeiPoH54xDuPSlH4hPPkxo9WpcFhXBkM4RnNe8Lj4+Nk7BlK1znnSuPLFEYMqNk8dhywJI+BJ++RpSD4B/MPxfAgTWhqws0jKVRZv2MHtNMvMTdpOWnkWDWoFc3jmCK7o0pEvj2jZ4zZQJSwTGlLbMDNj6EySvgd73Ots+vhZOHnUamiMv41hQQ76L383sNcks/mUP6ZlKk7pB/PXyDgzq2MC78ZtK75xnHzXGFMHXD1r2dW7ZGnWF9Z/BN4/AN49QPaILV3b/M1feeB2Hjqczd+Mu5qxNplag054Qn3yYuRt2Meb85oQEV7Nps02ZsJYrY0pT34fhrqVwzyq4+O/gG+CMVQBq+51kZMpbfHBRFr1ahACwPDGFNxZtQUSYFbeDR2asZcfBVJRT02bPitvhvfdjKiWrGjKmrKk6A9W2LoFJQyErHaqHQbvLIHIIhyLOp3bNGvQev4AdB1MJ48Bpk+Q1Cgnkp0dtVhZTfAVVDVmJwJiylt0w3Ox8ePg3uOZdaH4BrJ8BH4+g9rFEADIO7qQGx7nXbybnySbu8XNmbt9xMI3HPlvH/PjdpJ7M9Na7MJWIlQiMKS8yTjiNzS37gwhz/nE1l2QswhfFV5Q09afPiZc44l8XXxGOncwkwM+HBy5uy+19W3k7elMBWInAmPLOLwBaDcgpMdTofRtbaIKPO7g/gHSmBzzF+GGdWfXExUy+pTujuzelVVgNALbuP8aQV34g7vcDXnsLpmKyXkPGlFP9zosh88ddiDvLlwg0lf00b+0HPkKf5XfSp9n5ED4UCOdQajqBfr6EVnemtZi7YReLNu1hQGQ4F7SuR1A1X++9GVOuWSIwprxa/Cy+eZbw9vHxgcXPOL2Rju2F78Y5t/BOdG5/BZ+O/gOEBAOwLeU4s9ck88nybQT4+dC7dT0GRNZnYPv6RNQOKvv3Y8otayMwprx68wLYte7M7Q2iTs2bdPB3iJ8D8V/A70vh+k+ddRUO/g7H9nGyfheWJx3gu/jdzE/YzbaUVAA6NqzFwMj6XNQhnM6NQ8ruPRmvspHFxlR2R3ZBcKgz+d13T8GPL0DtJtD+Cmh/Bdq4O7/uS+W7+D0sSHAW2unWrA7Tbz8fgJ+TUujYsBbB1ayioLKyRGBMVXI8BX75BjZ+4cyFlHnCmTH1nlXOdNtAyrGT7D96gjbhNTmclk7Xv8/j1gtb8sjgSNIzs9h75AQNQ6wKqTKxKSaMqUqC60L0H5zbiSPOCmxHduckAd4fQt3aTajbYSjU7U+QfzU+uLl7zhf/8sQUrntnGR0iajGwfX0Gtg+nc6PaNmNqJWUlAmOqmoyT8MU9sOlrOHEIqtWANpdA99ugWS8Akg+l8vnqnSyI38OKrSlkKdSrEcCAyDAGtg+nT5t6VoVUAVnVkDHmdBknIel7iJ/tTKN90VMQcx0cTobfFkG7wRBUhwPHTrLolz3Mj9/D4l/2ciQtg2p+PvRqGcpr13XNWavZJsgr/6xqyBhzOr9qTg+j1hfB5S9AljtdxS9fw5wHwMcPWlxInfZDuTrycq6O6Up6ZhY/J6YwP2EPv+w+QnV3bMKfP1jB/IQ9ZGQ5F5bZE+QBlgwqACsRGGNOl5UFO+Mg/nOnsflAopMUHvoVguo4JQm/aqc9JfJvX5OWnnXGqWoE+PHXy9vTpG4wjesE0TAkCH9brtNrvF4iEJH/AkOAParayd1WF5gKNAeSgJGqauPjjfEmHx9o3M25XfQU7N4AO1Y6SQDgk1GQdsjtljoUQltxwk0CeWdKPXoig0c/OzUWwkegQa1AGtcNZnjXxow8rwlZWcrypBTahdekTvVq+UVkSllZpub3gcF5tj0KzFfVNsB897ExprwQgQadoNuNp7a1GuBMpf3dOHilK7x+PrfW+AngjJlSG4YE8sPD/fnk1p48O7wzdw9oQ8+WoaCQluFURe09eoJr31rKnLU7Afht71Gue2cpj3y6llcXbGZW3A5Wbk1hz+E0srIqXg1GRVBmJQJV/V5EmufZfCXQz70/CVgEPFJWMRljzsL59zi3g9sgYQ5s/IKhbQP5Zt1hRvgsxkeUUb6LeF+u5N5BA2lSN5gmdYPpRWi+p6sd5M/kW7rT0p087/jJTI6fzGR+wh72HT1x2rHV/HxoXCeIxnWCuW9ga7o1q8vB4ydJ2n+cyAY1CfT3fD4la9w+pUzbCNxEMCdX1dBBVQ1x7wtwIPtxYayNwJhyRpXfJt1Ok6Tp+ONc6Wfhg0/LC6FFX2c8Q83ir8mcejKTHQePsy0lle0HjrPtgPszJZUnr+hAbPO6fLUumTs/WsVX9/ahQ8NafL0umekrt9PETRhN6ro/6wRTO9hZEnRW3A4e+2wdqemn1nMI8vfl6WFRlToZeL2NoCiqqiJSYFYSkduA2wCaNm1aZnEZYzxwdDctt88CTn2x+ojAoZ0w/ylod6mTCJJ+gj0boWU/CG19apGeAgRV86V1/Zq0rl+zwGPOa16Xt/8YS4t61QGnyin5UBo/J6Zw5ETGacfWDPSjcZ1gEvceJS3j9Mbt1PRMJszdVKkTQUG8nQh2i0iEqiaLSASwp6ADVfUt4C1wSgRlFaAxxgOLnwXN02vIxxda9IGbvnSW4gRnvMLS15z7NRtCy75OiaHzqFOjnosprGYAF3cIz3l8dUxjro5pDMCh4+lsO3A8pxSRXaqITz6c77l2Hkzlm/XJpKVn0T6iFi3DqleJXk7eTgRfADcC492fn3s3HGPMWdm+HDJPnr4t86SzvUb9U9sG/QvOuwUSF8Nvi+GXuc6sqdGjnf1xH0JgiLN0Z1DIOYdVO9if2sG16dSo9mnbs9eDzqthSBD//TGJ5UkpAFTz9aFNeA06RNSivXvrEFErp4qpsiizNgIR+QSnYbgesBt4EpgFTAOaAltxuo+mFHUuayMwppLIyoKju6BWQ6cn0kudnSm0xQcaxjilhcjLofEZ1drnpLA2gss7R/Db3mPEJx8mPvkwG5MPE5985LSG637twnj/pu4ALNmyj6Z1g2lcJ7hEYywNXm8jUNXRBewaWFYxGGPKGR8fJwmA015w90rYscKZ4uK3xbDkZWct58axkJkO/3sVml8IDaOdqqezlN0OUFCvoXYNatKuQc3T2gv2HjmRkxhqBTolAlXlzx+s5MqYhvzzqigyMrN4avZG2jaoSYeImrRrUCtnCo7yzEYWG2PKrxNHnERQvR7sXA1v9XW2B9R2qo9a9oMOQ8+qR1JJyMpSNuw8THCAL63CarDjYCqXTvyew2mnGqmbhQafVrXUPqImjUKCkCIaykuDTTpnjKn4ju6BxO+dEkPiYqca6cY5TqP07g2QvNZpgM4uZXiBqrLzUBrxO52qpfhdTtVS0v5jZH/d/vOqTlzfsxl7jqSxMGEPA9uHU69GQIHnLKkxD16vGjLGmHNWoz5EDXduACmJUMv9QtwwC75/1rkf2sZJCC37QdvBzqptZUREaBQSRKOQIC7K1Zvp2IkMEnYdIT75ML1b1wNgZdIBHpmxjtl316ZejQAWJOxmVtzOnJJDh4ha/PTrPv4yc31Oe0ZpTOhnJQJjTOWQlQV7NjhtC78tgq1LwNcPHk502hMSvgL/IGja0/kJzvKen94Ew9+HmuGFnb2UQla2phynUUgQ1fx8mPbzNl6av/m0Hk0+AvnNrNEoJIifHh1QrNezqiFjTNWScdKZOTWsnfP49V7OYDbfAGjS3Skx7FrnrMfQ7SYY8oJ3483l0PF0t0rpME/N3pjvMQIkjr+8WOe1qiFjTNXiV+1UEgC45VvY+j93DMMiWPBPp5uqZsHqj6B2E2h7CYS1P+vBbSWldrA/PVuG0rNlKO/8kFjgmIeSYiUCY0zVNPMOWDcdstLBx9/5CRBcz2l8bnEhtL0UakV4NcySnBepoBJB5R87bYwxeR3ZBRs+O/Xln5UOfgEw6GlnxbbflzqrtG1b6uw/kASrP4FDO8o81KtiGvH0sCinyylO20BJT45nVUPGmKonv7mRVGH/rzDsP+79LacakDd9A9+4M+TXbeWUFlr2dXok+ZdcFU1BroppVKqT4VkiMMZUPYXNjQTOKOd6rU/t636bM4AtcbEzjmHdpxA3GR7Z6uz/9Ttn5HOz3hBYq2zeQwmyRGCMqXpu/7F4x/v4OCu1NegEve6CzAzY9wsEOIvp8NPLTpIQX3eOpAuh9UAneVQAlgiMMaa4fP0gvMOpx3+YBtt/dkoLid87cyQlrz6VCH5+F8I7QsOuTm+mcsYSgTHGnCv/QLenUR/gcThxFI7vc/alHYavHgLNBP/q0KyXU2KIHAKhrbwadjZLBMYYU9ICapyqNgqsBQ/9Ckk/nioxzHsC/IOdRHBkN2z83EkOYe2KXLWtNFgiMMaY0hZc15kltcNQ5/GRXU53VYCtP8HXDzn3a4Q7CaHFhdDhSgjMtaBOKU6HYYnAGGPKWu5pszsNg0ZdT5UWEr93Brq1GugkgsTvnSSwZYEzvmHxMyU+HYYlAmOM8bY6zZ1b1z+eGsNQ2x03EPchrJ166tjVH0HfR0q0VGAji40xpjzJO4bhqjeg/ZVO11RwBsItfqZEX9ISgTHGlGfH9sLmuU6vI3AGvq3+yGlkLiGWCIwxpjzLdzqMki0VWCIwxpjyrKjpMEqANRYbY0x5VtzpMM6ClQiMMaaKs0RgjDFVnCUCY4yp4iwRGGNMFWeJwBhjqrgKuXi9iOwFtp7l0+sB+0ownNJWkeK1WEtPRYq3IsUKFSvec421maqG5d1YIRPBuRCRFaoa6+04PFWR4rVYS09FircixQoVK97SitWqhowxpoqzRGCMMVVcVUwEb3k7gGKqSPFarKWnIsVbkWKFihVvqcRa5doIjDHGnK4qlgiMMcbkYonAGGOquCqTCETkvyKyR0TWezuWoohIExFZKCIbRWSDiNzn7ZgKIyKBIrJcRNa48T7l7ZiKIiK+IhInInO8HUtRRCRJRNaJyGoRWeHteAojIiEi8qmIJIhIvIj08nZMBRGRdu5nmn07LCL3ezuugojIA+7/13oR+UREAkvs3FWljUBELgSOAh+oaidvx1MYEYkAIlR1lYjUBFYCV6nqRi+Hli8REaC6qh4VEX/gR+A+VV3q5dAKJCIPArFALVUd4u14CiMiSUCsqpb7QU8iMgn4QVXfEZFqQLCqHvRyWEUSEV9gB9BDVc92sGqpEZFGOP9XHVQ1VUSmAV+p6vslcf4qUyJQ1e+BFG/H4QlVTVbVVe79I0A80Mi7URVMHUfdh/7urdxeYYhIY+By4B1vx1KZiEht4ELgXQBVPVkRkoBrILClPCaBXPyAIBHxA4KBnSV14iqTCCoqEWkOxADLvBxKodyqltXAHmCeqpbneCcCDwNZRRxXXijwrYisFJHbvB1MIVoAe4H33Gq3d0SkureD8tC1wCfeDqIgqroDeA74HUgGDqnqtyV1fksE5ZiI1ABmAPer6mFvx1MYVc1U1WigMdBdRMpl9ZuIDAH2qOpKb8dSDBeoalfgUuAut5qzPPIDugJvqGoMcAx41LshFc2twhoKTPd2LAURkTrAlTjJtiFQXUSuL6nzWyIop9y69hnAR6r6mbfj8ZRbFbAQGOzlUArSGxjq1rtPAQaIyIfeDalw7tUgqroHmAl0925EBdoObM9VGvwUJzGUd5cCq1R1t7cDKcRFQKKq7lXVdOAz4PySOrklgnLIbXx9F4hX1Re8HU9RRCRMRELc+0HAxUCCV4MqgKo+pqqNVbU5TnXAAlUtsSurkiYi1d0OA7jVLJcA5bLnm6ruAraJSDt300CgXHZwyGM05bhayPU70FNEgt3vh4E4bYclosokAhH5BPgf0E5EtovILd6OqRC9gRtwrlazu7Zd5u2gChEBLBSRtcDPOG0E5b5bZgURDvwoImuA5cCXqvqNl2MqzD3AR+7fQjTwb++GUzg3uV6Mc4VdbrmlrE+BVcA6nO/uEptuosp0HzXGGJO/KlMiMMYYkz9LBMYYU8VZIjDGmCrOEoExxlRxlgiMMaaKs0RQhYnIIhF51UuvrSIy3Buv7YnyHl9JcGexHOfBcQtF5I9lEFJ+r13o78Gd9faasoypMrJEUEm5g7xed6cwPiEiu0VkvohcnOuwYcBj3oqxpIlIV/eLo08B+6eKyJKyjqswBX3Ricj75WGKbBG5HGgCfJRrW5Ibt4pIqjvl9EPuQKey9g9gvIjYd9k5sA+v8pqBMxXBLUBbYAjwNRCafYCqprizm1Y4IuKX94vHnbF1NXBzPseHAldhM44W133A+6qamWf733EGErbHmQzt34A3JsT7CqiJM02EOUuWCCohd7qHPsCjqjpfVbeq6s+q+pyqTsl13GlVQ+6V3l9F5D/uIh3bReShPOduKyKLRSRNRDaJyGUiclRExrj7m7tXirF5nldUEX+8e75UN45ncy+8ISLj3KqMMSKyBTgB5Dez5TvACHfCvtyud58zVUQGi8gPInJARFJEZK6ItC8kNo/ek4g0EpEp7nkPiMiXItKmoPMWh4gME5G17ueT4v4OwnPtv0Kc2UnTRCRRRP4lzmRq2fvri8jn7vO3isgZyTKf1wzDmeNmdj67j6jqLlVNUtV3gLU4019kP7eV+3q7ROSYiKwSZ8K/3Ocv8u8tn5geEZF9ItITnMkOcZLB6KLejymYJYLK6ah7GyrFX8XoAZwh7F2BZ4BnxV1lyi1+zwQygJ7AGOBJIKAEYj6GcyXfHrgTZx6gx/Mc0wL4AzAC6AKk5XOejwBfYFSe7bcAU1X1GE4CmYhTYuoHHAJm5/7iLC4RCcaZbC8N6Av0wpku+Dt331kTkQY4E+RNwvl8LgQm59o/COd9vwp0xPkch3P69A7vA61xvtivAv4INC/ipS/ASZ4Fzm0kjn5uXOm5dtXAKYFejPO7mgF8JiKReU5R4N9bPq/zHM4UFn3zLHq0HOczN2dLVe1WCW/ANTgL8aThzLH0HM7qS7mPWQS8mutxEvBJnmM2A3917w/CSQKNcu0/H2e+/DHu4+bu49g851FgeEGP84n/duDXXI/H4XzRhHvw3j8EluR6fJ77ej0KOL46kIkz3fMZ8XnynnC+fDfjTtvibvMF9gMjC4k1388B54t7jnu/q3tcswLO8T3wtzzbrsK5GBCcqkEFeufa38x9z+MKie1+YGs+25NwEsRR4KR77lTg/CJ+L0uz/5Y8+XvL9fmMAt4DfsnvM8CZQjoL8Cvr/7PKcrMSQSWlqjNw5i2/AufK7HxgqYj8pYinrs3zeCdQ370fCexUd1pk18+UwAIvIjJcRH50qxKOAi8CTfMctl09myr4HaBXrqvPm4H16k6P7FZbfCwiW0TkMLAbp3Sc9/WKoxtOieWIW1V2FKekUQdodQ7nBVgDfAesF5EZInKHW22T+7Ufz35d97U/xklwDXCu1rNwrpwBUGclrqJWuAoi/1IXwAs4k8r1xSkJPaWqOQ3x4sya+qw4624fcGOK5czPuLC/t2zP4ZTcLtD8VxBLxUl4JbaGb1VjiaASU9U0VZ2nqn9X1fNxprYeV0QVSHqex0rx/k6yk0JOQ644aysUyK3vnQLMxUlcMcBfcZa8zO2YhzEsBn4FbhZnWuzRuMsnuuYAYcCfgR7u62UABX0unrwnH5yG6ug8t7bAfwqJ9QhQO5/tITiJBHXqwS9xb2txqrk2i0iXXK/9VJ7X7Qy0wVkxLFtxZ5jch5PI8rNfVX9V1f/hlD7Hikj/XPufw6nC+xtOsojGSUR5P2NP/t7m4SS0gmbgrQuk6anlUk0x+Xk7AFOmNuL8zgNxivTFlQA0FJGGqpp9NRnL6f+42V88Ebm2RRdx3t7ADlX9R/YGEWl2FvEBzhrKIvJfnB4vCThXtpPd84bilGzuVNWF7rauFP6/4Ml7WoWTcPZp8dbp3YRzRZ+TqMRZSL0LTnVIznvCqeL7n4j8HdiAU2Wyxn3tSFX9Nb8XEJEEnN9Rd2CJu60pTomxMHFAmIjUU9V9BR2kqgfE6XTwoojEuLFeAHzglkxx26pa4VTvFNdXONNETxcRVdVJefZ3wvkMzFmyEkElJCKhIrJARK4Xkc4i0kJERuCs0ztfz37Zy3k4X1yTRKSLeyX/As7VtFOhq5qKUxf8iIh0FJHzca4OC/ML0EhErhORliJyB+feC2QSUM997Vmqut/dfgDnSvdWEWktIn2BN933kC8P39NHOFVMn4tIX/czv1BEni+i59ALOCWXu8TpkRWNM898XfcnItLT7V1znvsFPhSnb3/2oi9/B/4gIn8XkU4iEulWtT3rxr8J+Ab4j4j0cl/jfZwqlcLE4axBfUERxwG8DrTDKQWA8zu9WpyxHVE47TZnXXWjzvoWI4A35czBbX1w3p85S5YIKqejOF9c9+FUk2zA6UHyMWf2pvGYqmYBV+P0ElqO82X7L5wkkLsuObtr4s841SJ/LeK8s4EJOD151uL0NHnibON0z7kT50qyDrnGDrjvYRRO1cl64DWc6osTRZyy0PekqsdxevP8hrP2bQLO51MHJ/kUFOcnwE3ubQXOF1oDoI86K36BU0XUG6dKazPwPPAPVf3QPcdc4HKgP87vZTnOWsG/53qpMUAisACnO+jHOI21BXKrpP4LXFfYce6xe3BKXePc3mUP4iSRH3DaqJa698+amwxG4iS0P4LTZRen/eu9wp5rCmcL05hz4tZTr8bpUVORFoQ3HhCR+jglj/NUNdHb8eQlIhOA2qrqjcFslYa1EZhiEZGrcRptN+N0q3yBU/XUppJR1T3iDD5rilOiKG/2UHTVoymClQhMsbhF8r/i1FEfwBmL8ICH3TqNMeWQJQJjjKnirLHYGGOqOEsExhhTxVkiMMaYKs4SgTHGVHGWCIwxpor7fy4MfkGRGO/QAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "singular_value = singular_value_list[-1]\n",
+    "err_subfull, err_local, err_SVD = [], [], []\n",
+    "U, D, V_dagger = np.linalg.svd(M, full_matrices=True)\n",
+    "\n",
+    "\n",
+    "# Calculate the Frobenius-norm error\n",
+    "for i in range(T):\n",
+    "    lowrank_mat = np.matrix(U[:, :i]) * np.diag(D[:i])* np.matrix(V_dagger[:i, :])\n",
+    "    recons_mat = np.matrix(U_learned[:, :i]) * np.diag(singular_value[:i])* np.matrix(V_dagger_learned[:i, :])\n",
+    "    err_local.append(norm(lowrank_mat - recons_mat)) \n",
+    "    err_subfull.append(norm(M_err - recons_mat))\n",
+    "    err_SVD.append(norm(M_err- lowrank_mat))\n",
+    "\n",
+    "\n",
+    "# Plot\n",
+    "fig, ax = plt.subplots()\n",
+    "ax.plot(list(range(1, T+1)), err_subfull, \"o-.\", \n",
+    "        label = 'Reconstruction via VQSVD')\n",
+    "ax.plot(list(range(1, T+1)), err_SVD, \"^--\", \n",
+    "        label='Reconstruction via SVD')\n",
+    "plt.xlabel('Singular Value Used (Rank)', fontsize = 14)\n",
+    "plt.ylabel('Norm Distance', fontsize = 14)\n",
+    "leg = plt.legend(frameon=True)\n",
+    "leg.get_frame().set_edgecolor('k')\n",
+    "# plt.savefig(\"vqsvd-fig-error.png\", bbox_inches='tight', dpi=600)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "---\n",
+    "### Case 2: Image compression\n",
+    "\n",
+    "In order to fulfill image processing tasks, we first import the necessary package.\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 13,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:55:17.832481Z",
+     "start_time": "2021-01-09T09:55:17.822888Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Image processing package PIL\n",
+    "from PIL import Image\n",
+    "\n",
+    "# Open the picture prepared in advance\n",
+    "img = Image.open('./figures/MNIST_32.png')\n",
+    "imgmat = np.array(list(img.getdata(band=0)), float)\n",
+    "imgmat.shape = (img.size[1], img.size[0])\n",
+    "imgmat = np.matrix(imgmat)/255"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 14,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:55:19.530630Z",
+     "start_time": "2021-01-09T09:55:18.663734Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAEICAYAAACZA4KlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAUsUlEQVR4nO3dbWxcVXoH8P8fx46NHSW2A4mdOC+khGAqNomsQEVAdOkugS8EtOLlA2Il1KwqkIq0+wFRbZdWVctWBUSliioUtNmKQtgFRFqhdilaKUVasWvSxCREJCE4L7bjJMRJnMRxYufph7nZOtF9jsczd2Zsn/9Psjw+z5yZx9fz+I7v8TmHZgYRmf6uqXQCIlIeKnaRSKjYRSKhYheJhIpdJBIqdpFIqNhFIqFil6KR/D7JUZJnxnzcXem85EozKp2ATBu/MbO1lU5CfDqzT3Mku0n+iGQXyVMkN5OsrXReUn4q9jg8DGAdgKUAbgXw/bQ7kVxL8mTgI3TmXkXyOMk9JH9MUu8aJxn9QOLwj2bWCwAk/x3AyrQ7mdknAOYU8PhbAfwhgAMAbgGwGcAIgL8r4LGkRHRmj8ORMbfPAWjI8sHNbL+ZfW1ml8zscwB/DeB7WT6HFE/FLr9H8s6rrqhf/XFnng9lAFjKXGXi9DZefs/M/gcFnPVJ3gdgm5n1k1wB4McAfpF1flIcndklC/cA6CJ5FsCHAN4D8LeVTUmuRi1eIRIHndlFIqFiF4mEil0kEip2kUiUdeitsbHRWltby/mUmbrmmvTfjV47AJD+cHPo4ujo6GhBsUIuuBaafyh26dKlCbUD4dxnzPBfqlVVVW7MU2gek11vby8GBgZSfzBFFTvJdQBeAVAF4F/M7IXQ/VtbW7F58+ZinrKiZs6cmdpeX1/v9qmpqXFjFy5ccGOnTp1yY6dPn3Zjw8PDqe2hgq6rq3Nj3vcMhAtwaGgotX1wcNDtMzIy4saam5sLinmFe+7cObfPxYsX3dhk98gjj7ixgt/Gk6wC8E8A7gPQDuAxku2FPp6IlFYxf7OvAbAv+b/oCwDeBvBANmmJSNaKKfYFAA6N+fpw0nYFkhtIdpLsHBgYKOLpRKQYJb8ab2YbzazDzDoaGxtL/XQi4iim2HsAtI35emHSJiKTUDHF/jsAN5JcSrIGwKMAtmSTlohkreChNzMbIfk0gP9CbujtDTPblVlmIpKposbZzexD5KY0isgkp3+XFYmEil0kEip2kUio2EUioWIXiYSKXSQSKnaRSKjYRSKhYheJhIpdJBIqdpFIqNhFIqFiF4mEil0kEip2kUio2EUioWIXiYSKXSQSKnaRSKjYRSKhYheJhIpdJBIqdpFIqNhFIqFiF4lEUTvCkOwGMAhgFMCImXVkkZSIZK+oYk/8sZkdz+BxRKSE9DZeJBLFFrsB+BXJz0huSLsDyQ0kO0l2DgwMFPl0IlKoYot9rZmtBnAfgKdI3nX1Hcxso5l1mFlHY2NjkU8nIoUqqtjNrCf5fBTA+wDWZJGUiGSv4GInWU9y1uXbAL4LYGdWiYlItoq5Gj8PwPskLz/Ov5nZf2aSlYhkruBiN7P9AL6VYS4iUkIaehOJhIpdJBIqdpFIqNhFIpHF/8ZH49SpU6ntPT09bp/z58+7sZkzZ7qx2bNnu7Frr73WjY2Ojqa29/f3u33OnDkz4ccDgAsXLrixwcHBCedx+PBhN1ZVVeXG2tvb3diKFStS2xcuXOj2qaurc2NTmc7sIpFQsYtEQsUuEgkVu0gkVOwikSj71XgzK/dTZubIkSOp7bt27XL7dHd3u7Ha2lo31tTUVFA/78p6b2+v2+fYsWNuzBuBAIChoSE35uWYzKVIdfDgQTe2f/9+N7ZkyRI3tn79+tT2e++91+2zYMECNzaV6cwuEgkVu0gkVOwikVCxi0RCxS4SCRW7SCQ0EWYCzp07l9p+6NAht09XV5cbO336tBsLTQoJDYd5Q17XXXed26ehocGNhSbJjIyMuLGlS5dOqH28PELHOBTzJt4MDw+7faYrndlFIqFiF4mEil0kEip2kUio2EUioWIXiURZh95IoqamppxPmam2trbU9jvvvNPts2jRIjfmzaIDgJ07/Z20+vr63Nj8+fNT2++44w63z2233TbhxwOAa67xzxXe8OCePXvcPlu3bnVjt9xyixsLDeetXbs2tb2lpcXtM5Vfo6FZheOe2Um+QfIoyZ1j2ppIfkRyb/JZ27OKTHL5vI3/GYB1V7U9C+BjM7sRwMfJ1yIyiY1b7Ga2FcCJq5ofALApub0JwPps0xKRrBV6gW6emV3+w/EIcju6piK5gWQnyc6BgYECn05EilX01XjLrTPlrjVlZhvNrMPMOhob9ae9SKUUWuz9JFsAIPl8NLuURKQUCh162wLgCQAvJJ8/yLfjVF5w0tt2KbRA4Zw5c9zY6tWr3dhDDz2Ud15jedtNXbx40e0TynHu3LlurL6+3o1dunQptf3Eiasv//y/vXv3urHQDLvQ8Oa8eel/YVZXV7t9pvJrNCSfobe3APwGwE0kD5N8Erki/w7JvQD+JPlaRCaxcc/sZvaYE7on41xEpIT077IikVCxi0RCxS4SCRW7SCS019sEeDOKQsM4M2fOdGOhPdtCC0SGZmWdPXs2tT20SGUoxxkz/JfI6OioG/P2gQstshmKeUN5QHj2XSjmmcqv0RCd2UUioWIXiYSKXSQSKnaRSKjYRSKhYheJhIbeMhAa3gkNXVVVVbmx0FBTSF1dXWp7KMdQHqHhtdBiJL29vanthexTB/gzDoHwrL3QsKhnOr5GAZ3ZRaKhYheJhIpdJBIqdpFIqNhFIlHWq/FmVvBV5sksdDU7NGkl1C+05lroGHpX42fNmuX2CV1xD109P3DggBvbt2/fhB8vtN5daJ0/b505wD8eIVP5NRoaSdCZXSQSKnaRSKjYRSKhYheJhIpdJBIqdpFIaCLMBHi5e2vTAeHhtVC/0HZNoWE5b+JHQ0OD28fbMgoADh8+7Ma++uorN7Z///7U9tA6c83NzW5syZIlBfULra/nmcqv0ZB8tn96g+RRkjvHtD1Psofk9uTj/tKmKSLFyudt/M8ArEtpf9nMViYfH2ablohkbdxiN7OtAPytN0VkSijmAt3TJLuSt/mN3p1IbiDZSbIztNiBiJRWocX+KoBlAFYC6APwondHM9toZh1m1tHY6P5OEJESK6jYzazfzEbN7BKA1wCsyTYtEclaQUNvJFvMrC/58kEAO0P3ny68obLQ8FooFhriCQ2HhdaT84blQn2Gh4fdWE9Pjxv74osv3Jg39BZaS2758uVubNWqVW4sNFvOm3VYyLZQU924xU7yLQB3A5hL8jCAnwC4m+RKAAagG8APSpeiiGRh3GI3s8dSml8vQS4iUkLxvZcRiZSKXSQSKnaRSKjYRSJR9llvoZlek503VBYaQgt9v6F+oZlthSxGGVpEcWhoyI0dP37cjYWG5fr7+1Pb29ra3D5NTU1u7Prrr3djoUUlve879HOZyq/REJ3ZRSKhYheJhIpdJBIqdpFIqNhFIqFiF4lEWYfeSE7p2UaFDL2FhI5FocfJG0Y7duyY2+fQoUNurLu7240dOXLEjV24cCG1PbTnXGtrqxsL7ecWGooMDSt6pvJrNDRsOHW/KxGZEBW7SCRU7CKRULGLRELFLhIJTYTJQKETYUJXfUPbFs2Y4f/Yzpw5M6F2APjyyy/dWOhqfGgrp9ra2tT20ISW+fPnu7HZs2cXlEdoLT/PdHyNAjqzi0RDxS4SCRW7SCRU7CKRULGLRELFLhKJfHaEaQPwcwDzkNsBZqOZvUKyCcBmAEuQ2xXmYTOLcpvW0NBbKBbaGsrbtggIDw2dPHkytf3rr792++zZs8eNhSa7hIYAvSG2lpYWt09okkzI6OioGytkDbrpKp8z+wiAH5pZO4DbATxFsh3AswA+NrMbAXycfC0ik9S4xW5mfWa2Lbk9CGA3gAUAHgCwKbnbJgDrS5SjiGRgQn+zk1wCYBWATwHMG7OT6xHk3uaLyCSVd7GTbADwLoBnzOyK/0+03B+mqX+cktxAspNk54kTJ4pKVkQKl1exk6xGrtDfNLP3kuZ+ki1JvAXA0bS+ZrbRzDrMrCO0CYCIlNa4xc7cZcvXAew2s5fGhLYAeCK5/QSAD7JPT0Syks+stzsAPA7gc5Lbk7bnALwA4B2STwI4AODhkmQ4iXjDaKGtlUJCQ1ehWV7e+m6AP0utq6vL7bNt2zY3dvRo6hs2AOHtmtrb21Pbb7rpJrdPQ0ODGwvNXhseHnZj3rBcaNhzuhq32M3sEwDeoOQ92aYjIqWi/6ATiYSKXSQSKnaRSKjYRSKhYheJRNkXnCx0q6TJwBtiCw29hb7fUL/Q0NDFixfdWE9PT2r7jh073D6hBSdDM9FWrFjhxtauXZvafuutt7p9QotserP5AGBwcNCNeUKLfU7l12iIzuwikVCxi0RCxS4SCRW7SCRU7CKRULGLRKKsQ29mVvAMscnAW6QwtHhhKBYa4hkZGXFjQ0NDbswbhgoNT4XyaG5udmPLly93Y97stnnz/AWNQnu2hfaqC80CrK6uTm0vdEh0sgt9Xzqzi0RCxS4SCRW7SCRU7CKRULGLRKLsE2Gmo0InVYSuIn/zzTdurK+vz42dOnUqtb22ttbt09ra6sZuuOEGN7Zs2bIJP2Z9fb3bx8sdCE/+CfF+Ntr+SUSmLRW7SCRU7CKRULGLRELFLhIJFbtIJMYdeiPZBuDnyG3JbAA2mtkrJJ8H8KcAjiV3fc7MPixVopNBIRNhvO2HgPDEj+PHj7sxb4snAOjv709tb2xsdPssXrzYjd18881urK2tzY15a9eF1tYrdEJRiDf0Fhouna7yGWcfAfBDM9tGchaAz0h+lMReNrN/KF16IpKVfPZ66wPQl9weJLkbwIJSJyYi2ZrQexmSSwCsAvBp0vQ0yS6Sb5D03yeKSMXlXewkGwC8C+AZMzsN4FUAywCsRO7M/6LTbwPJTpKdAwMDxWcsIgXJq9hJViNX6G+a2XsAYGb9ZjZqZpcAvAZgTVpfM9toZh1m1hG6SCQipTVusTN3GfR1ALvN7KUx7S1j7vYggJ3ZpyciWcnnavwdAB4H8DnJ7UnbcwAeI7kSueG4bgA/KEF+k4o3XFPoemahLY12797txvbu3evGvJl0CxcudPuE1pJbtGiRG2toaHBj58+fT20PDUWGhsNCs/ZCM+JmzEh/icc46y2fq/GfAEg7MtN6TF1kuonvPwtEIqViF4mEil0kEip2kUio2EUioQUnSyw0LOcNTwHAoUOH3NjBgwfdWFNTU2p7aIZae3u7G5szZ44bC/H+W9IbChtPaOgtNIzmzbILDfNN5e2fQnRmF4mEil0kEip2kUio2EUioWIXiYSKXSQSGnrLQGgmV2g/t8HBQTfW29vrxg4cOODGvGGo6upqt8/s2bPdWF1dnRsbGRlxY96wYmgILRQLLVQZGirzYjEuOBnfdywSKRW7SCRU7CKRULGLRELFLhIJFbtIJDT0NgHeME5o6G14eNiNnT171o0dO3asoNjcuXNT20OzzUILR4b6hb43bxHI0JBXTU2NGwsNr4UWnPSGIjX0JiLTlopdJBIqdpFIqNhFIqFiF4nEuFfjSdYC2ApgZnL/X5rZT0guBfA2gGYAnwF43Mz8WR+RKsU2Q6FJId5kktAV9/r6ejcWWkMvNAoxNDTkxjyFXo2PcSunQuRzZh8G8G0z+xZy2zOvI3k7gJ8CeNnM/gDAAIAnS5aliBRt3GK3nDPJl9XJhwH4NoBfJu2bAKwvRYIiko1892evSnZwPQrgIwBfAThpZpcnNB8GsKAkGYpIJvIqdjMbNbOVABYCWANgRb5PQHIDyU6Snd5a4iJSehO6Gm9mJwH8GsAfAZhD8vIFvoUAepw+G82sw8w6Ghsbi8lVRIowbrGTvI7knOR2HYDvANiNXNF/L7nbEwA+KFGOIpKBfCbCtADYRLIKuV8O75jZf5D8AsDbJP8GwP8CeL2EeU4K3uSJ0NppoeGp5uZmN7Z48eKCHnPRokWp7aFtnELr04WeKzTk5Q2VhSbPhGKhCTmhdfK8YcpQ7qHveSobt9jNrAvAqpT2/cj9/S4iU4D+g04kEip2kUio2EUioWIXiYSKXSQSDM1qyvzJyGMALu9dNBfA8bI9uU95XEl5XGmq5bHYzK5LC5S12K94YrLTzDoq8uTKQ3lEmIfexotEQsUuEolKFvvGCj73WMrjSsrjStMmj4r9zS4i5aW38SKRULGLRKIixU5yHckvSe4j+Wwlckjy6Cb5OcntJDvL+LxvkDxKcueYtiaSH5Hcm3wu+UofTh7Pk+xJjsl2kveXIY82kr8m+QXJXST/PGkv6zEJ5FHWY0KyluRvSe5I8virpH0pyU+TutlM0l+ON42ZlfUDQBVya9jdAKAGwA4A7eXOI8mlG8DcCjzvXQBWA9g5pu3vATyb3H4WwE8rlMfzAH5U5uPRAmB1cnsWgD0A2st9TAJ5lPWYACCAhuR2NYBPAdwO4B0Ajybt/wzgzybyuJU4s68BsM/M9ltunfm3ATxQgTwqxsy2AjhxVfMDyK3SC5RptV4nj7Izsz4z25bcHkRuJaQFKPMxCeRRVpaT+YrOlSj2BQAOjfm6kivTGoBfkfyM5IYK5XDZPDPrS24fATCvgrk8TbIreZtf1oUDSS5BbrGUT1HBY3JVHkCZj0kpVnSO/QLdWjNbDeA+AE+RvKvSCQG53+zI/SKqhFcBLENuQ5A+AC+W64lJNgB4F8AzZnZ6bKycxyQlj7IfEytiRWdPJYq9B0DbmK/dlWlLzcx6ks9HAbyPyi6z1U+yBQCSz0crkYSZ9ScvtEsAXkOZjgnJauQK7E0zey9pLvsxScujUsckee6TmOCKzp5KFPvvANyYXFmsAfAogC3lToJkPclZl28D+C6AneFeJbUFuVV6gQqu1nu5uBIPogzHhLnVH18HsNvMXhoTKusx8fIo9zEp2YrO5brCeNXVxvuRu9L5FYC/qFAONyA3ErADwK5y5gHgLeTeDl5E7m+vJ5HbIPNjAHsB/DeApgrl8a8APgfQhVyxtZQhj7XIvUXvArA9+bi/3MckkEdZjwmAW5FbsbkLuV8sfznmNftbAPsA/ALAzIk8rv5dViQSsV+gE4mGil0kEip2kUio2EUioWIXiYSKXSQSKnaRSPwffyIxG32ku9UAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAEICAYAAACZA4KlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAUkklEQVR4nO3df4xV5Z3H8fe3yK/KYBGmgIgDAroCRSATUiq2rm4t2jTaZNNWN103caXp1mSbdP8w3WTrbvaPdrNt081u3NDV1DZdqbaauhvaqtQGTS064AhYrfwoWJAfQwUB5YcD3/3jHrID3u8zM+f+muH5vJLJ3Hm+99zzzJn7nXPv+d7neczdEZHz3/ta3QERaQ4lu0gmlOwimVCyi2RCyS6SCSW7SCaU7CKZULLLoJnZfDP7hZkdMLP3fFDDzC42s8fM7G0z22lmt7ein3I2JbuU8S7wMHBnEP8P4CQwGfgL4D4zm9ekvknA9Am684uZ7QD+HfhLoAP4OXCHux9vwL5mA1vc3fq0XQgcBOa7+2tF2w+A3e5+T737IAOnM/v56TPAcmAmsAD4q2p3MrNlZnYo8bWsxL6vAHrPJHrhJUBn9ha7oNUdkIb4N3d/A8DM/gdYWO1O7v4s8IE673sccPictreAtjrvRwZJZ/bz094+t9+hkoDNchQYf07beOBIE/sgVSjZM2Zm15rZ0cTXtSUe9jXgAjOb06ftauDl+vRaytLL+Iy5+zOUOOubmQGjgVHFz2MqD+cn3P1tM3sU+Ccz+2sqbyFuAT5St45LKTqzSxkdwDH+/2x9DPhdn/jfAGOB/cBDwBfdXWf2FlPpTSQTOrOLZELJLpIJJbtIJpTsIploault0qRJ3tHR0cxdimRl586dHDhwwKrFakp2M1sOfAcYAfyXu389df+Ojg5+/etf17LLIalSdq4uVe1Ixco+ZpnHSynbx2Y9Xn+PWe99DXUf+Uj8cYbSL+PNbASVoYw3AXOB28xsbtnHE5HGquU9+xJgq7tvd/eTwCoqn5QSkSGolmSfBvyhz8+7irazmNkKM+sys66enp4adicitWj41Xh3X+nune7e2d7e3ujdiUiglmTfDUzv8/OlRZuIDEG1JPsLwBwzm2lmo4DPAY/Xp1siUm+lS2/u3mtmdwO/oFJ6e0Ajm0SGrprq7O6+Glhdp76ISAPp47IimVCyi2RCyS6SCSW7SCaU7CKZULKLZELJLpIJJbtIJpTsIplQsotkQskukgklu0gmlOwimVCyi2RCyS6SCSW7SCaU7CKZULKLZELJLpIJJbtIJpTsIplQsotkQskukgklu0gmlOwimahpRRgz2wEcAU4Bve7eWY9OiUj91ZTshT919wN1eBwRaSC9jBfJRK3J7sATZrbezFZUu4OZrTCzLjPr6unpqXF3IlJWrcm+zN0XAzcBXzKzj557B3df6e6d7t7Z3t5e4+5EpKyakt3ddxff9wOPAUvq0SkRqb/SyW5mF5pZ25nbwI3A5np1TETqq5ar8ZOBx8zszOP8t7v/vC69EpG6K53s7r4duLqOfRGRBlLpTSQTSnaRTCjZRTKhZBfJRD0+G5+Nt956a1DtAO97X/z/dObMmWHs+PHjYWzEiBFh7MiRI1Xbd+3aFW5z+vTpMHby5Mkwtn379jB29OjRqu2p45E6jtu2bQtjF1wQP43nz59ftX3ZsmXhNrNmzQpjw5nO7CKZULKLZELJLpIJJbtIJpTsIplo+tV4d2/2Lutmx44dVdufe+65cJt9+/aFsblz55bqx6lTpwa9v9///vfhNqm/yeHDh8PY66+/HsaKMRPvceGFF4bbpK7Gd3d3h7He3t4wduutt1Ztv+KKK8JtLr/88jA2nOnMLpIJJbtIJpTsIplQsotkQskukgklu0gmNBBmEKLS0Pr168Ntfvazn4Wxt99+O4yNGTMmjKVKb9GgkPHjx5faV2pAzrhx48LYpZdeWrV9ypQp4TYTJkwIY1HZE9Ilu2hG44kTJ4bbnK90ZhfJhJJdJBNKdpFMKNlFMqFkF8mEkl0kE00vvaXmIBvqFi9eXLU9NZIrNbpq3bp1YSw12iy1v6iP119/fbjN7Nmzw1iqZJdalfeiiy6q2j569Ohwm9WrV4exX/3qV2Fs3rx5YeyGG26o2p6a/284P0dT+v2tzOwBM9tvZpv7tF1sZk+a2Zbie1wgFZEhYSD/wr4HLD+n7R5gjbvPAdYUP4vIENZvsrv7WuDNc5pvAR4sbj8I3FrfbolIvZV9czLZ3fcUt/dSWdG1KjNbYWZdZtZ14MCBkrsTkVrVfCXCK3MahfMauftKd+90985JkybVujsRKalssu8zs6kAxff99euSiDRC2dLb48AdwNeL7z8d6IbDecLJqJy0aNGicJtUiee2224LY2XLP1FpKzVCLVUOS42wmz59ehiLlqhKTRy5atWqMBYtJwWwdOnSMHbZZZeFschwfo6mDKT09hDwHHClme0yszupJPnHzWwL8GfFzyIyhPV7Znf36PRT/dMKIjIknZ8fFRKR91Cyi2RCyS6SCSW7SCa01tsgROWw1ISNqUkU29rawtjYsWPD2MmTJ8NYdHxHjhwZbpNy4sSJMJYafRdNpvnqq6+G22zYsCGMRWvHQbq8+cEPfrBq+6hRo8JtTp8+HcaGM53ZRTKhZBfJhJJdJBNKdpFMKNlFMqFkF8mE1nobhN7e3qrtqbJQKhaNDIPyJcrU/iKpUlNq9F2qj9u2bava/vzzz4fbHDp0KIwtXLgwjM2dOzeMRaXP1O+l0puIDGtKdpFMKNlFMqFkF8mEkl0kE02/Gl/mavFQEV2NT129TQ1AueCC+PC/++67YSx1DKOrzKk+puaZSw3IiQa7AKxfv75q+7PPPhtukzpWN910Uxj70Ic+FMai/qeOx3B+jqbozC6SCSW7SCaU7CKZULKLZELJLpIJJbtIJjQQZhCiElWqjJMqr6UGY6TKYan506LHTJXyUlKDdfbs2RPGotLb1q1bw21SSzUtWbIkjLW3t4exSFRGhfTvPJwNZPmnB8xsv5lt7tN2r5ntNrPu4uvmxnZTRGo1kJfx3wOWV2n/trsvLL5W17dbIlJv/Sa7u68F3mxCX0SkgWq5QHe3mW0sXuaHk6Ob2Qoz6zKzrp6enhp2JyK1KJvs9wGzgIXAHuCb0R3dfaW7d7p7Z5kLKSJSH6WS3d33ufspdz8NfBeIL5WKyJBQqvRmZlPd/Uzd5dPA5tT9zxdlllBKlddS5bDUdqlRWVEZMFXKSy1fdezYsTD29NNPh7ForrmJEyeG23z2s58NYwsWLAhjKWXmDTxf9ZvsZvYQcB0wycx2AV8DrjOzhYADO4AvNK6LIlIP/Sa7u99Wpfn+BvRFRBpIH5cVyYSSXSQTSnaRTCjZRTKhUW+DEI2GKjt6LTXyKjVaLlU2ivZXtpT3xz/+MYx1d3eHsR07dlRtv+SSS8JtUss4tbW1hbHUcYyWqEodj/NVfr+xSKaU7CKZULKLZELJLpIJJbtIJpTsIplQ6a0OUhNORqUfSJd/yq4DF0lNUnn06NEw9swzz4SxF154IYxFI+mWLl0abjNv3rwwlhpxePLkyTAWlRVzHPWmM7tIJpTsIplQsotkQskukgklu0gmdDV+EKKr7qkr7qlYI5aGKjNY54033ghjq1fH63+89tprYWz+/PlV26+77rpwm46OjjCWqnikrqxHv3dqm9TfbDjTmV0kE0p2kUwo2UUyoWQXyYSSXSQTSnaRTAxkRZjpwPeByVRWgFnp7t8xs4uBHwEzqKwK8xl3P9i4rrZeVJJJlWpSJZ5ULDWvWqqMFsUOHoz/NC+++GKpWKr/V1111aDaAUaPHh3GUstQpQbJRMfjfC2vpQzkzN4LfMXd5wIfBr5kZnOBe4A17j4HWFP8LCJDVL/J7u573H1DcfsI8AowDbgFeLC424PArQ3qo4jUwaDes5vZDGARsA6Y3Gcl171UXuaLyBA14GQ3s3HAT4Avu/vhvjGvvAGq+ibIzFaYWZeZdfX09NTUWREpb0DJbmYjqST6D9390aJ5n5lNLeJTgf3VtnX3le7e6e6d7e3t9eiziJTQb7Jb5ZLr/cAr7v6tPqHHgTuK23cAP61/90SkXgYy6u0a4PPAJjPrLtq+CnwdeNjM7gR2Ap9pSA+HgVQJKhqFBumRXO+8804YmzBhQhiLRsS9/PLL4TaPPPJIGHv11VfD2NVXXx3Grr322qrts2bNCrcpOy9cmRFsZUfRDWf9Jru7PwtEv/0N9e2OiDSKPkEnkgklu0gmlOwimVCyi2RCyS6SCU04OQipkWhlpMpyZZc7ikpsqfLamjVrwlhbW1sY+8QnPhHGrrnmmqrt48ePD7dJLUOVmpyzzFJZZUcqDmc6s4tkQskukgklu0gmlOwimVCyi2RCyS6SCZXeBiFVKisjtWZbavLFVAnw9ddfr9qemjjyyJEjYezGG28MYx/72MfC2CWXXFK1PTXaLKXs2nc5TiwZ0ZldJBNKdpFMKNlFMqFkF8mEkl0kE02/Gj+cr45GAy5SAydSV4pTsdRAmP37q07kC8CmTZuqtkdX6QFmzJgRxj71qU+FsdQcdKNGjaranppbL9oG0sf4xIkTYSz6m6Wu7g/n52iKzuwimVCyi2RCyS6SCSW7SCaU7CKZULKLZKLf0puZTQe+T2VJZgdWuvt3zOxe4C7gzNKsX3X31Y3q6PkoVf6J5k4D+M1vfhPGfvnLX1ZtT83vdvvtt4ex5cuXh7EpU6aEsagclhoIU2Yuuf5Ex7hsuXQ4G0idvRf4irtvMLM2YL2ZPVnEvu3u/9q47olIvQxkrbc9wJ7i9hEzewWY1uiOiUh9Deo9u5nNABYB64qmu81so5k9YGbx0qIi0nIDTnYzGwf8BPiyux8G7gNmAQupnPm/GWy3wsy6zKyrp6en2l1EpAkGlOxmNpJKov/Q3R8FcPd97n7K3U8D3wWWVNvW3Ve6e6e7d7a3t9er3yIySP0mu1UuW94PvOLu3+rTPrXP3T4NbK5/90SkXgZyNf4a4PPAJjPrLtq+CtxmZguplON2AF8YyA6H89I6Ufmn7Lxq73//+8PY3r17w9hTTz0Vxrq7u6u2X3nlleE2d911Vxi77LLLwtixY8fCWGTs2LFhLFVeS8VS8/VFz7fU32w4P0dTBnI1/lmg2m+vmrrIMKJP0IlkQskukgklu0gmlOwimVCyi2RCyz8NQlSSSS0LlZo4MjX54hNPPBHGNm+OP9IwbVr1YQuf/OQnw22uuuqqMFZ2dFg0eWTq8VLltdRxTI0ePHnyZNX21KSS9V7ma6jQmV0kE0p2kUwo2UUyoWQXyYSSXSQTSnaRTKj0NghlSm+pstCbb74ZxtauXRvGtmzZEsY6Ojqqtk+dOrVqO6TLUPUuUaVGm6WOVSpWdj29iEpvIjKsKdlFMqFkF8mEkl0kE0p2kUwo2UUy0fTSW6qUM9RF5Z9UOenw4cNhLDV6bcOGDWHs4MGDYWzBggVV21Olt9Ros2j0GqRLVGUm4Uyt9ZYqoaWeU6n+R8pOIDrU6cwukgklu0gmlOwimVCyi2RCyS6SiX6vxpvZGGAtMLq4/4/d/WtmNhNYBUwE1gOfd/fqE36d51JXilNX43fu3BnGUivetrW1hbFomafZs2eH25S9qp7arkzVpRGDXaLlplL9O3HiRBgbzgZyZj8BXO/uV1NZnnm5mX0Y+AbwbXefDRwE7mxYL0WkZv0mu1ccLX4cWXw5cD3w46L9QeDWRnRQROpjoOuzjyhWcN0PPAlsAw65e29xl11A9TmMRWRIGFCyu/spd18IXAosAf5koDswsxVm1mVmXan3oSLSWIO6Gu/uh4CngaXAB8zszAW+S4HdwTYr3b3T3Tvb29tr6auI1KDfZDezdjP7QHF7LPBx4BUqSf/nxd3uAH7aoD6KSB0MZCDMVOBBMxtB5Z/Dw+7+v2b2W2CVmf0z8CJw/0B2mFr+Z6iL+j5mzJhwm8mTJ4exOXPmhLEpU6aEsdSAkUWLFlVtnzlzZrhNyvHjx0v1IyrL9fb2Vm2HdAkttfxTqox29OjRqu1l5w0czvpNdnffCLznGeTu26m8fxeRYeD8/BcmIu+hZBfJhJJdJBNKdpFMKNlFMmHNnBPOzHqAM0O9JgEHmrbzmPpxNvXjbMOtHx3uXvXTa01N9rN2bNbl7p0t2bn6oX5k2A+9jBfJhJJdJBOtTPaVLdx3X+rH2dSPs503/WjZe3YRaS69jBfJhJJdJBMtSXYzW25mvzOzrWZ2Tyv6UPRjh5ltMrNuM+tq4n4fMLP9Zra5T9vFZvakmW0pvk9oUT/uNbPdxTHpNrObm9CP6Wb2tJn91sxeNrO/LdqbekwS/WjqMTGzMWb2vJm9VPTjH4v2mWa2rsibH5nZ4Bayc/emfgEjqMxhdzkwCngJmNvsfhR92QFMasF+PwosBjb3afsX4J7i9j3AN1rUj3uBv2vy8ZgKLC5utwGvAXObfUwS/WjqMQEMGFfcHgmsAz4MPAx8rmj/T+CLg3ncVpzZlwBb3X27V+aZXwXc0oJ+tIy7rwXePKf5Fiqz9EKTZusN+tF07r7H3TcUt49QmQlpGk0+Jol+NJVX1H1G51Yk+zTgD31+buXMtA48YWbrzWxFi/pwxmR331Pc3gvEU9w03t1mtrF4md/wtxN9mdkMKpOlrKOFx+ScfkCTj0kjZnTO/QLdMndfDNwEfMnMPtrqDkHlPzuVf0StcB8wi8qCIHuAbzZrx2Y2DvgJ8GV3P2spnWYekyr9aPox8RpmdI60Itl3A9P7/BzOTNto7r67+L4feIzWTrO1z8ymAhTf97eiE+6+r3iinQa+S5OOiZmNpJJgP3T3R4vmph+Tav1o1TEp9n2IQc7oHGlFsr8AzCmuLI4CPgc83uxOmNmFZtZ25jZwI7A5vVVDPU5lll5o4Wy9Z5Kr8GmacEysMpPn/cAr7v6tPqGmHpOoH80+Jg2b0blZVxjPudp4M5UrnduAv29RHy6nUgl4CXi5mf0AHqLycvBdKu+97qSyQOYaYAvwFHBxi/rxA2ATsJFKsk1tQj+WUXmJvhHoLr5ubvYxSfSjqccEWEBlxuaNVP6x/EOf5+zzwFbgEWD0YB5XH5cVyUTuF+hEsqFkF8mEkl0kE0p2kUwo2UUyoWQXyYSSXSQT/weYte4bQI3fgAAAAABJRU5ErkJggg==\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAEICAYAAACZA4KlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAASZUlEQVR4nO3df4xdZZ3H8feH2h9AK6XbsU5K6ZS2AmWBgYxdQQS2VoP800o2YmOUjWRrNpBogskSN1nZxGR1s2rchLgpP2I1rsiKRlzrQiEutEJopy5Oi0VoaRFK2xki/QHdpbT97h/3NE7rec7M3J/tPJ9XMpk7z/eee74c+plz5zz3nKOIwMzGvzM63YCZtYfDbpYJh90sEw67WSYcdrNMOOxmmXDYzTLhsNuYSfpzSY9Iel3Sn3xQQ9J/S/o/SW8WX7/rRJ92Iofd6vEO8CBwa8Vzbo+IqcXXhW3qyyo47OOMpJ2SvihpQNJ+ST+UNKWZ64iI30XEfcBzzXxday2HfXz6BHADMA+4DPjrsidJukbSvoqvaxro4Z+Kt/m/knR9A69jTfKuTjdgLfGvEfEagKSfAb1lT4qI9cD0Fqz/74DfAoeBTwI/k9QbEdtbsC4bJe/Zx6c9wx4fAqa2c+UR8UxEHIyItyNiNfAr4MZ29mB/ymHPmKQPDTtiXvb1oSatKgA16bWsTn4bn7GIWEcde31JAiYDk4qfp9ReLt6WNB34C+AJ4AhwM3At8PkmtW11ctitHnOBHcN+/l/gZaAHmAh8BbgIOAo8DyyPiBfa3KOdRL54hVke/De7WSYcdrNMOOxmmXDYzTLR1qPxM2fOjJ6ennau0iwrO3fu5PXXXy/9TENDYZd0A/AtYAJwb0R8ter5PT09bNy4sZFVmlmF97///cla3W/jJU0A7gY+BiwCVkhaVO/rmVlrNfI3+2JgW0S8FBGHgQeAZc1py8yarZGwzwZeGfbzq8XYCSStlNQvqX9oaKiB1ZlZI1p+ND4iVkVEX0T0dXV1tXp1ZpbQSNh3AXOG/XxeMWZmp6BGwr4RWChpnqRJ1C5S8HBz2jKzZqt76i0ijki6HXiE2tTb/RHha5KZnaIammePiDXAmib1YmYt5I/LmmXCYTfLhMNulgmH3SwTDrtZJhx2s0w47GaZcNjNMuGwm2XCYTfLhMNulgmH3SwTDrtZJhx2s0w47GaZcNjNMuGwm2XCYTfLhMNulgmH3SwTDrtZJhx2s0w47GaZcNjNMuGwm2WioTvCSNoJHASOAkcioq8ZTZlZ8zUU9sJfRsTrTXgdM2shv403y0SjYQ/gUUmbJK0se4KklZL6JfUPDQ01uDozq1ejYb8mIq4EPgbcJunak58QEasioi8i+rq6uhpcnZnVq6GwR8Su4vsg8BNgcTOaMrPmqzvsks6WNO34Y+CjwJZmNWZmzdXI0fhZwE8kHX+df4+I/2pKV2bWdHWHPSJeAi5vYi9m1kKeejPLhMNulgmH3SwTDrtZJprx2fhsHDx4sHT8wIEDyWXOOCP9+7S7u7uuPooZkFJvvPFG6fiuXbvqWlfqvxnglVdeGfNyx44dSy5TtR137NiRrFW95mWXXVY6vmTJkuQyCxcuTNZOZ96zm2XCYTfLhMNulgmH3SwTDrtZJnw0fgy2b99eOr5u3brkMnv27EnWFi1a1HBPJ3vttddKx1O9j2T//v3JWtUR8tQsxNSpU5PL7Nu3L1nbtGlTshYRydqyZctKxy+++OLkMj4ab2anNYfdLBMOu1kmHHazTDjsZplw2M0y4am3MRgcHCwdr5p6e/TRR5O1w4cPN9zTySZPnlw6XjXlNXHixGSt6kSeqtrcuXPHNA4wffr0ZG3btm3J2qFDh5K1888/v3R81qxZyWXGK+/ZzTLhsJtlwmE3y4TDbpYJh90sEw67WSY89TYGS5cuLR2fM2dOcplLL700WVu/fn2yduTIkdE3NszixeW320ud/QUwf/78utZVdbbZWWedVTpeNd34xBNPJGtV2+q9731vsnbdddeVjr/vfe9LLjNejbhnl3S/pEFJW4aNzZC0VtKLxfdzW9ummTVqNG/jvwPccNLYncDjEbEQeLz42cxOYSOGPSKeBP5w0vAyYHXxeDWwvLltmVmz1XuAblZE7C4e76F2R9dSklZK6pfUPzQ0VOfqzKxRDR+Nj9pRmuSRmohYFRF9EdHX1dXV6OrMrE71hn2vpG6A4nv5GSJmdsqod+rtYeAW4KvF9582raNTWOosrwULFiSXue2225K1z372s3X1Uc+U19lnn51cZtKkSXX1USW1rQYGBpLL3Hvvvcla1cUoly9fnqylptiqbqE1Xo1m6u0HwNPAhZJelXQrtZB/RNKLwNLiZzM7hY24Z4+IFYnSh5vci5m1kD8ua5YJh90sEw67WSYcdrNM+Ky3Jqi6YOOMGTPa2MmpI3URyOeffz65TH9/f7L2zjvvJGuXXHJJsvae97yndLxq6q1qavN05j27WSYcdrNMOOxmmXDYzTLhsJtlwmE3y4Sn3k5D9UwbtXuqafv27aXjVffFO3DgQLLW29ubrF1++eXJ2rvf/e5kLTfes5tlwmE3y4TDbpYJh90sEw67WSZ8NP40VM/R81Ycca+6RVXqpJbHHnssuczkyZOTtZtuuilZu+iii5K1M888s3R8vJ7sUsV7drNMOOxmmXDYzTLhsJtlwmE3y4TDbpYJT71Z3fbs2ZOsbdiwoXT8hRdeSC5zwQUXJGtLlixJ1qZNm5as5TjFljKa2z/dL2lQ0pZhY3dJ2iXp2eLrxta2aWaNGs3b+O8AN5SMfzMieouvNc1ty8yabcSwR8STwB/a0IuZtVAjB+hulzRQvM0/N/UkSSsl9UvqHxoaamB1ZtaIesP+bWA+0AvsBr6eemJErIqIvojo6+rqqnN1ZtaousIeEXsj4mhEHAPuARY3ty0za7a6pt4kdUfE7uLHjwNbqp5v49OaNenjsuvXry8d7+7uTi7zqU99KlmrusVT1dly9kcjhl3SD4DrgZmSXgW+DFwvqRcIYCfwuda1aGbNMGLYI2JFyfB9LejFzFrIH5c1y4TDbpYJh90sEw67WSZ81ptVnhlWdUumjRs3Jms7duwoHe/p6UkuU3UbpylTpiRrNjres5tlwmE3y4TDbpYJh90sEw67WSYcdrNMeOptnJFUOl41vVZ1z7Zf/OIXyVrqfm6Qvsfa4sXps6GvuOKKZO2MM7xfapS3oFkmHHazTDjsZplw2M0y4bCbZcJH48eZ1FH3o0ePJpcZHBxM1h566KFkrepWTpdeemnp+NKlS5PLzJ07N1mzxnnPbpYJh90sEw67WSYcdrNMOOxmmXDYzTIxmjvCzAG+C8yidgeYVRHxLUkzgB8CPdTuCvOJiHijda3acamTXSA99fbWW28ll3nqqaeSteeeey5ZqzqBZtGiRaXjvb29yWWstUazZz8C3BERi4APALdJWgTcCTweEQuBx4ufzewUNWLYI2J3RPy6eHwQ2ArMBpYBq4unrQaWt6hHM2uCMf3NLqkHuAJ4Bpg17E6ue6i9zTezU9Sowy5pKvAQ8IWIOOFi4lH7Q7H0j0VJKyX1S+ofGhpqqFkzq9+owi5pIrWgfz8iflwM75XUXdS7gdIPWEfEqojoi4i+rq6uZvRsZnUYMeyqHfq9D9gaEd8YVnoYuKV4fAvw0+a3Z2bNMpqz3j4IfBrYLOnZYuxLwFeBByXdCrwMfKIlHdqfqLqeXGpa7ve//31ymbvvvjtZS93GCWD+/PnJ2nXXXVc6fuGFFyaXsdYaMewRsR5ITex+uLntmFmr+BN0Zplw2M0y4bCbZcJhN8uEw26WCV9wcgyqzjZLqZomq3ddVa85MDBQOn7PPfckl9m0aVOy9vbbbydrK1asSNauv/760vEJEyYkl2n3tsqN9+xmmXDYzTLhsJtlwmE3y4TDbpYJh90sE556G4N2TuPUc2YbpM9ue/rpp5PLHDp0KFm7+uqrk7XU9BrAeeedVzreim3o6bXR8Z7dLBMOu1kmHHazTDjsZplw2M0y4aPxLdaKkzT27t2brG3evLl0/OWXX04ukzpyDvCZz3wmWbv44ouTtXe9q/yflk926Rzv2c0y4bCbZcJhN8uEw26WCYfdLBMOu1kmRpx6kzQH+C61WzIHsCoiviXpLuBvgOO3Zv1SRKxpVaOnq3qnhY4dO5asrVu3Lllbs6b8f0HVteSWL1+erN10003JWtWNOlP/3fVOoXl6rXGjmWc/AtwREb+WNA3YJGltUftmRPxL69ozs2YZzb3edgO7i8cHJW0FZre6MTNrrjH9zS6pB7gCeKYYul3SgKT7JZ3b7ObMrHlGHXZJU4GHgC9ExAHg28B8oJfanv/rieVWSuqX1D80NFT2FDNrg1GFXdJEakH/fkT8GCAi9kbE0Yg4BtwDLC5bNiJWRURfRPRVHdAxs9YaMeyqHT69D9gaEd8YNt497GkfB7Y0vz0za5bRHI3/IPBpYLOkZ4uxLwErJPVSm47bCXyuBf2Na1XTSfv370/WHnnkkWQtdSunSy65JLnMHXfckayde64PxYwXozkavx4omxz1nLrZacSfoDPLhMNulgmH3SwTDrtZJhx2s0z4gpMtVnWW19GjR5O1tWvXJmsbN25M1s4///zS8Ztvvjm5zPz585O11IUjob5bVLX77LVTpY9TgffsZplw2M0y4bCbZcJhN8uEw26WCYfdLBOeemuxqgtHvvnmm8naz3/+82Rt+/btydqCBQtKx6vOXqt3eq1Ksy84Wa8cp9hSvGc3y4TDbpYJh90sEw67WSYcdrNMOOxmmfDU2xhUTRulvPXWW8naU089laxt2LAhWauasjvnnHNKx2fNmpVcpt3TYc12uvffLt6zm2XCYTfLhMNulgmH3SwTDrtZJkY8Gi9pCvAkMLl4/o8i4suS5gEPAH8GbAI+HRGHW9lsp9VzZPfw4fQm2bp1a7K2b9++ZG3q1KnJ2sKFC0vHq27/1Ioj1u289puPuI/OaPbsbwNLIuJyardnvkHSB4CvAd+MiAXAG8CtLevSzBo2Ytij5vjE7sTiK4AlwI+K8dXA8lY0aGbNMdr7s08o7uA6CKwFtgP7IuJI8ZRXgdkt6dDMmmJUYY+IoxHRC5wHLAYuGu0KJK2U1C+pf2hoqL4uzaxhYzoaHxH7gF8CVwHTJR0/wHcesCuxzKqI6IuIvq6urkZ6NbMGjBh2SV2SphePzwQ+AmylFvq/Kp52C/DTFvVoZk0wmhNhuoHVkiZQ++XwYET8p6TfAg9I+grwP8B9LezztHXWWWcla1dffXWyNnPmzGRt9uz04ZGrrrqqdHzevHnJZeqdumr2CSitOKHFt3/6oxHDHhEDwBUl4y9R+/vdzE4D/gSdWSYcdrNMOOxmmXDYzTLhsJtlQu2cgpA0BLxc/DgTeL1tK09zHydyHyc63fqYGxGln15ra9hPWLHUHxF9HVm5+3AfGfbht/FmmXDYzTLRybCv6uC6h3MfJ3IfJxo3fXTsb3Yzay+/jTfLhMNulomOhF3SDZJ+J2mbpDs70UPRx05JmyU9K6m/jeu9X9KgpC3DxmZIWivpxeL7uR3q4y5Ju4pt8qykG9vQxxxJv5T0W0nPSfp8Md7WbVLRR1u3iaQpkjZI+k3Rxz8W4/MkPVPk5oeSJo3phSOirV/ABGrXsLsAmAT8BljU7j6KXnYCMzuw3muBK4Etw8b+GbizeHwn8LUO9XEX8MU2b49u4Mri8TTgBWBRu7dJRR9t3SaAgKnF44nAM8AHgAeBTxbj/wb87VhetxN79sXAtoh4KWrXmX8AWNaBPjomIp4E/nDS8DJqV+mFNl2tN9FH20XE7oj4dfH4ILUrIc2mzdukoo+2ipqmX9G5E2GfDbwy7OdOXpk2gEclbZK0skM9HDcrInYXj/cA6Xsst97tkgaKt/kt/3NiOEk91C6W8gwd3CYn9QFt3iatuKJz7gforomIK4GPAbdJurbTDUHtNzu1X0Sd8G1gPrUbguwGvt6uFUuaCjwEfCEiDgyvtXOblPTR9m0SDVzROaUTYd8FzBn2c/LKtK0WEbuK74PAT+jsZbb2SuoGKL4PdqKJiNhb/EM7BtxDm7aJpInUAvb9iPhxMdz2bVLWR6e2SbHufYzxis4pnQj7RmBhcWRxEvBJ4OF2NyHpbEnTjj8GPgpsqV6qpR6mdpVe6ODVeo+Hq/Bx2rBNVLsq5H3A1oj4xrBSW7dJqo92b5OWXdG5XUcYTzraeCO1I53bgb/vUA8XUJsJ+A3wXDv7AH5A7e3gO9T+9rqV2g0yHwdeBB4DZnSoj+8Bm4EBamHrbkMf11B7iz4APFt83djubVLRR1u3CXAZtSs2D1D7xfIPw/7NbgC2Af8BTB7L6/rjsmaZyP0AnVk2HHazTDjsZplw2M0y4bCbZcJhN8uEw26Wif8HhJAtV2Fb+ucAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "# Then we look at the effect of the classic singular value decomposition\n",
+    "U, sigma, V = np.linalg.svd(imgmat)\n",
+    "\n",
+    "for i in range(5, 16, 5):\n",
+    "    reconstimg = np.matrix(U[:, :i]) * np.diag(sigma[:i]) * np.matrix(V[:i, :])\n",
+    "    plt.imshow(reconstimg, cmap='gray')\n",
+    "    title = \"n = %s\" % i\n",
+    "    plt.title(title)\n",
+    "    plt.show()"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 15,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:55:24.681157Z",
+     "start_time": "2021-01-09T09:55:24.669666Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Hyper-parameters\n",
+    "N = 5           # Number of qubits\n",
+    "T = 8           # Set the number of rank you want to learn\n",
+    "ITR = 200       # Number of iterations\n",
+    "LR = 0.02       # Learning rate\n",
+    "SEED = 14       # Random number seed\n",
+    "\n",
+    "# Set the learning weight\n",
+    "weight = np.arange(2 * T, 0, -2).astype('complex128')\n",
+    "\n",
+    "# Convert the image into numpy array\n",
+    "def Mat_generator():\n",
+    "    imgmat = np.array(list(img.getdata(band=0)), float)\n",
+    "    imgmat.shape = (img.size[1], img.size[0])\n",
+    "    lenna = np.matrix(imgmat)\n",
+    "    return lenna.astype('complex128')\n",
+    "\n",
+    "M_err = Mat_generator()\n",
+    "U, D, V_dagger = np.linalg.svd(Mat_generator(), full_matrices=True)\n",
+    "\n",
+    "# Set circuit parameters\n",
+    "cir_depth = 40 # Circuit depth\n",
+    "block_len = 1 # The length of each module\n",
+    "theta_size = N * block_len * cir_depth # The size of the network parameter theta"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 16,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T09:55:31.997970Z",
+     "start_time": "2021-01-09T09:55:31.988769Z"
+    }
+   },
+   "outputs": [],
+   "source": [
+    "# Define quantum neural network\n",
+    "def U_theta(theta):\n",
+    "\n",
+    "    # Initialize the network with UAnsatz\n",
+    "    cir = UAnsatz(N)\n",
+    "    \n",
+    "    # Build a hierarchy:\n",
+    "    for layer_num in range(cir_depth):\n",
+    "        \n",
+    "        for which_qubit in range(N):\n",
+    "            cir.ry(theta[block_len * layer_num * N + which_qubit], which_qubit)\n",
+    "\n",
+    "        for which_qubit in range(1, N):\n",
+    "            cir.cnot([which_qubit - 1, which_qubit])\n",
+    "\n",
+    "    return cir.U"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 18,
+   "metadata": {
+    "ExecuteTime": {
+     "end_time": "2021-01-09T10:06:45.142151Z",
+     "start_time": "2021-01-09T09:59:56.016358Z"
+    }
+   },
+   "outputs": [
+    {
+     "data": {
+      "text/plain": [
+       "<matplotlib.image.AxesImage at 0x143718be0>"
+      ]
+     },
+     "execution_count": 18,
+     "metadata": {},
+     "output_type": "execute_result"
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD5CAYAAADhukOtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAYS0lEQVR4nO2dX2xd1ZXGv5WQkDhx/thJwDFJXEjQEKoJfwwUUSqmVSumqkSRRogiIR5QU42KNJU6D4iRBkaaBzoaqPow6igdoqajTilTWoEqNANElVAfCjUNOGlCAjUGnDhx3DiJQ8j/NQ/3RBjmrO/a+957bmB/PynK9V7e5+y7vT/f6/3dtba5O4QQn35mtXsAQohqkNiFyASJXYhMkNiFyASJXYhMkNiFyISLGulsZrcD+AGA2QD+w90fZd/f1dXlvb29pTFmAZpZafvZs2fDPrNmxb/H2L1S+rE+p0+fDmPR8wLSn9vcuXNnfK8zZ86EsZMnT874XgAwZ86cGY+D3YuNMboXwOeq2bB11WyLO7re6OgoJiYmSic5WexmNhvAvwH4MoARAL83s2fdfWfUp7e3F88880xpjP2gL7qofJiTk5Nhn3nz5oUxJsCOjo4wFi24zs7OsM++ffvCWPS8AODo0aNhjD231atXl7YzYR48eDCMvf3222Es+sXNYmwce/bsCWPj4+NJ44jmavbs2WEfxrlz58IY+wXN1nfKL6RoLd5zzz3xfWZ8lw+5EcBb7j7k7qcAPAngjgauJ4RoIY2IvRfAe1O+HinahBAXIC3/g8bMNprZgJkNHDp0qNW3E0IENCL2vQBWTfn6sqLtI7j7Jnfvd/f+rq6uBm4nhGiERsT+ewDrzOwzZjYXwN0Anm3OsIQQzSZ5N97dz5jZAwD+FzXrbbO7/7FOn3AXke1kpsCux2LMIol2cNmu+sUXXxzG2M4/27WeP39+GItsqImJibAPi33wwQdhLGVH+9ixY2HsxIkTYYw5EGweo/lga4DtuJ86dSqMsXXA1hW7X0Q098zabMhnd/fnADzXyDWEENWgT9AJkQkSuxCZILELkQkSuxCZILELkQkN7cbPFDMLP/TPbIuoD0sgYLYQsydSssNYRhYbB0uOYHbY4cOHw1hkKbHMMJbIw5KNjh8/HsaOHDlS2s5swyVLloSxVAswsrVSrV62TpmFxtZVSiJMil2nV3YhMkFiFyITJHYhMkFiFyITJHYhMqHS3Xgg3pVkO5LN7APwHVVGdE22q85gSRUsYYSNP9ohZzvu7HosAYXNcfTcWEIImw+288/6RWNMqXnYSCx1Fz8iZQdfr+xCZILELkQmSOxCZILELkQmSOxCZILELkQmVGq9uXt4Ggs7pSVKdGCWC4NZHaz2W5Q8sWDBgrAPs9DYvbq7u8MYs10WLVoUxiKYdchiLHGFWXYRbK6abZWxRBh2vdQTYdhaTaknFyVf0aPNwogQ4lOFxC5EJkjsQmSCxC5EJkjsQmSCxC5EJjRkvZnZMIBJAGcBnHH3/jrfn3RkUGRBMHuH2VOpx/REsGOL2PNldgyrM8eIrsmOoWKWEevHrKHISmXWFYuxGnRs/qPae+xebH2kZkwym7WZ12vZ8U8Ff+Xu4024jhCihehtvBCZ0KjYHcDzZvaqmW1sxoCEEK2h0bfxn3f3vWa2AsALZvaGu7809RuKXwIbAWDlypUN3k4IkUpDr+zuvrf4fwzArwDcWPI9m9y93937u7q6GrmdEKIBksVuZgvMrPP8YwBfAbCjWQMTQjSXRt7GXwLgV8VW/0UA/svd/4d1cPcwW4fZPylZb+y4o5R7AbFdw2wVdjQUsw47OjpmPA52TWYZMbuGzRV7blE/Nr8se5Bl87Hsu8gCZNl8bH6ZNcvmKiWrMzX7LiJZ7O4+BGBDan8hRLXIehMiEyR2ITJBYhciEyR2ITJBYhciEyovOMnsiYioz/z582fcpx7MTorsk4mJibAPy9ZKPWONWX2RJXP06NGwz4EDB8IY67dz584wFmWiMbt0//79YYxZTVdeeWUYu/zyy0vbL7300rAPswBZNiVbc8wKjqw3dj2d9SaECJHYhcgEiV2ITJDYhcgEiV2ITKh0N/7cuXPhET8pNdJWrFgR9mE75GxnlNV+O378eGn7K6+8EvZhjgE77mjx4sVhjDkG+/btK21nddoOHjwYxhYuXBjGdu3aFcai58bmnu38Dw0NhbG+vr4wduedd5a233bbbWGfnp6eMMbWabQ+AJ6sEzkNqYleEXplFyITJHYhMkFiFyITJHYhMkFiFyITJHYhMqHyRJgomYTZSRHMqmE2CKvtxRJXjhw5Utoe2V0Ar1n25ptvhrG9e/eGMfbcogSaq666KuzDEi4mJyfD2HvvvRfGVq9eXdq+YUNcyYwld2zevDmMjYyMhLEouYZZkWxdMSuVrR1m2b3//vul7UwT0VzR5JkwIoT4VCGxC5EJErsQmSCxC5EJErsQmSCxC5EJda03M9sM4GsAxtz9s0VbF4CfA+gDMAzgLneP08wK5syZE9b+YhZPBLMmWJ02Rnd3dxiLbJdbb7017LN79+4wlnLUFMBrpPX395e233TTTWEfZiexzCtWx2358uWl7ePj42GfLVu2hDFmXV1//fVh7IYbbihtX7VqVdgntQYdyxBk/aL5Z+s7so+ZrTydV/YfA7j9Y20PAtjq7usAbC2+FkJcwNQVe3He+qGPNd8B4Pyv4S0Avt7cYQkhmk3q3+yXuPto8Xg/aie6CiEuYBreoPPa50HDz4Sa2UYzGzCzgUOHPv4GQQhRFaliP2BmPQBQ/D8WfaO7b3L3fnfv7+rqSrydEKJRUsX+LID7isf3AXimOcMRQrSK6VhvPwNwG4BlZjYC4GEAjwJ4yszuB/AOgLumczMzCy0xZndEmWPMZmDWFcsMYkcyRUX+WPE/Zl2tX78+jLGCiMuWLQtja9asKW1nx0kxOyzKyAJ4UczISmVW5LZt28IYWx/r1q0LY5dddllpe2dnZ9iHxRhsXbFY9LOJMkSBWBPMzq0rdnf/RhD6Ur2+QogLB32CTohMkNiFyASJXYhMkNiFyASJXYhMqLzgJLPEZgrLJGKFHpm9xvpFVh+z3phlxD5kxM4GY9ZbZIexIpUsu4plxLEsr6ho4+joaGk7AAwPD4exkydPhjGW4Rj9bFJ+zvVizF5jRHYZux4bR4Re2YXIBIldiEyQ2IXIBIldiEyQ2IXIBIldiEyo1Ho7d+4czaKKiKwhZrmknB0HcEsmskiYlccKWDJ7raOjI4wxSyY6j46dQ8bsNZYtx+Y4Oqvu3XffTRpHX19fGFu7dm0YizLY2NjZXDHLi60dlsEW2dEsY5LZvRF6ZRciEyR2ITJBYhciEyR2ITJBYhciEyrdjWekHEHEkkxOnDgRxtiOKtuljXbdWZLGypUrwxh7zuy4o8OHD4exgwcPlraz57VixYowxhyPPXv2hLEXX3yxtP13v/td2Ift/LMjnqI6c0C8RlitNgZzXlhiFrtfNMdsnUZuDRuDXtmFyASJXYhMkNiFyASJXYhMkNiFyASJXYhMmM7xT5sBfA3AmLt/tmh7BMA3AZz3eR5y9+fqXcvdQ5uKfbA/so1Sj9thSQnMuohsF2ZPMQuNWW/smszqi2q/Meutp6cnjDGiewFxIkxkDQLcpmRHZTHrMMWiSjl2CeA/M3bNlBp0KbUcp/PK/mMAt5e0f9/dryn+1RW6EKK91BW7u78EQAerC/EJp5G/2R8ws0Ez22xmS5s2IiFES0gV+w8BXAHgGgCjAB6LvtHMNprZgJkNTExMJN5OCNEoSWJ39wPuftbdzwH4EYAbyfducvd+d+9fulRvAIRoF0liN7Op27d3AtjRnOEIIVrFdKy3nwG4DcAyMxsB8DCA28zsGgAOYBjAt6Z7w8jyYNYbszsiWJZRs4+GOnbsWNL1onpxALdqWL/ofuzIKDZXQ0NDYez5558PY9u3by9tZ/PR398fxpgtx64ZzSOzRNn6SD1yjK3vyEZjWW/R86JrO4x82PkbJc1P1OsnhLiw0CfohMgEiV2ITJDYhcgEiV2ITJDYhciESgtOuntYPJJl+EQZW8zOSLlePSIrhN2LjZHZa+yazOqLilEyy2jx4sVhjFk54+PjYWxkZKS0nVlerOAky8xjGWDRPLI1wK6XWqgy5ZpsjCnj0Cu7EJkgsQuRCRK7EJkgsQuRCRK7EJkgsQuRCZVab2YWWlHMmogK+bHCiykZQ+xeQHzmHMu6YueyMfuEWVQsA2zNmjWl7ex5jY2NhTF2Nts777wTxlavXl3avmHDhrAPi7E5fv/998NYBJtfBrMwo/WRCrtX9JyZZatXdiEyQWIXIhMkdiEyQWIXIhMkdiEyodLdeIDvMEakJKCwnW42BraLHzkGbDc4tdYZ233u7OwMY0uWLCltZ27H4OBgGNu2bVsYe+ONN8JY5ApceeWVYZ+rr746jLGfZ8oxScydSFkD9cbBxh+5Sik7/7R+XhgRQnyqkNiFyASJXYhMkNiFyASJXYhMkNiFyITpHP+0CsBPAFyC2nFPm9z9B2bWBeDnAPpQOwLqLndPPqaVfoA/wa5jMGuFjSOKMRuHwWy5rq6uMMZqtUV1y4aHh8M+zEJjiTyXXnppGLvqqqtK2/v6+sI+rOZaas049rOOYLZnK8YRre+m9wkjH3IGwHfdfT2AzwH4tpmtB/AggK3uvg7A1uJrIcQFSl2xu/uou/+heDwJYBeAXgB3ANhSfNsWAF9v0RiFEE1gRu+PzawPwLUAXgZwibuPFqH9qL3NF0JcoExb7Ga2EMDTAL7j7kenxrz2Gb3Sz+mZ2UYzGzCzAfb3nxCitUxL7GY2BzWh/9Tdf1k0HzCzniLeA6C03Im7b3L3fnfvjz63LYRoPXXFbrXtvScA7HL3x6eEngVwX/H4PgDPNH94QohmMZ2st1sA3Atgu5m9VrQ9BOBRAE+Z2f0A3gFwV70LzZo1K7SbmGUQWSHMukrNXGK2S8oxPal18hgp9diY9bZ9+/Yw9vbbb4exRYsWhbEog41ltrFjqFi9O5Z1GI2RHcvFrM0PPvggjKVmMUb9mOWcpKMw8uFAfgsgusKX6vUXQlwY6BN0QmSCxC5EJkjsQmSCxC5EJkjsQmRCpQUnz549i2PHjpXGmG0RZZWlZq8xq4wd4RNdkxUTnD9/fhhbsGBBGGO2IrPzdu/eXdq+devWsA/LemMZfbfccksYu+mmm0rbly9fHvZhsH4dHR1hLPrZsJ8zWx/sU6Cp2Y8RzHpLuZde2YXIBIldiEyQ2IXIBIldiEyQ2IXIBIldiEyo/Ky3CGajRbYcy05i9hSzNJhlF9kd7HrMemPjZ9bK/v37w1hko+3atSvswzKy1q9fH8ZuvfXWMLZs2bLS9vHx8bDP8ePHw1h3d3cYY9ZbtK7Y+mAwm5Vl0rF1Fc0/y86Mzvtja1Gv7EJkgsQuRCZI7EJkgsQuRCZI7EJkQqW78bNmzUr6AH+0A8p2ulOuB/B6ZtHOLkviYTu0rJ5ZlDAEADt27AhjUT25Q4cOhX3YMU6rV68OY6wG3enTp0vbU4/5Yo4Bm8eUo8NSE5tYPxaLNMF246N11ejxT0KITwESuxCZILELkQkSuxCZILELkQkSuxCZUNd6M7NVAH6C2pHMDmCTu//AzB4B8E0AB4tvfcjdn2PXcvfQTkg5rolZXsy2YLBrRjYOs4VYLbkTJ06EMZbsMjg4GMYi6+3IkSNhn5tvvjmM3XDDDWGMHeU0MTFR2j46OlraDvDkn6VLl4YxZm+mWIBRH4CvKzZ+ds1o7accU9bQ8U8AzgD4rrv/wcw6AbxqZi8Use+7+79O4xpCiDYznbPeRgGMFo8nzWwXgN5WD0wI0Vxm9De7mfUBuBbAy0XTA2Y2aGabzSx+nyWEaDvTFruZLQTwNIDvuPtRAD8EcAWAa1B75X8s6LfRzAbMbCD6O04I0XqmJXYzm4Oa0H/q7r8EAHc/4O5n3f0cgB8BuLGsr7tvcvd+d+9nmyxCiNZSV+xW2957AsAud398SnvPlG+7E0CcnSGEaDvT2Y2/BcC9ALab2WtF20MAvmFm16Bmxw0D+NZ0bhjZCSw7KerD6ogx24LZICl2HrPe2DiY9TYyMhLGhoaGwlhUx23NmjVhH2avrV27NoyxTK7omCSWVcje+XV1dYUxZqOlWL2p9QsZ7EipaPzseUVjZOt3OrvxvwVQNjPUUxdCXFjoE3RCZILELkQmSOxCZILELkQmSOxCZEKlBSfNLMwMSjn+KRVmGaVYK6w4JLNcWAbYzp07w9i+ffvC2MKFC0vbr7322rAPO+Ipuh4A/PnPfw5jR48eLW1nc79gwYIwNjY2FsbYJzOZzRrB1iLLsGNrh2XEpWRoRs+LZm3O+C5CiE8kErsQmSCxC5EJErsQmSCxC5EJErsQmVC59RZliLEMH2bXpPRh1sqpU6fCWDRGdj12DhnLAIuy1wBgcnIyjEUwy4jNVUdHRxibN29eGIueN8soY8+ZzSOLRc871UJj/ZjtlXoeYERKEVa9sguRCRK7EJkgsQuRCRK7EJkgsQuRCRK7EJlQqfXm7tRii4gyx1i2EIsxayUl641ZP+ysN2bzHThwIOl+S5YsKW1fuXJl2Ke3Nz7gh9lC4+PjYSyyFdn89vT0hDFWnJNZhynrjWXKsXuxuUqxZ1PXcNhnxj2EEJ9IJHYhMkFiFyITJHYhMkFiFyIT6u7Gm9k8AC8BuLj4/l+4+8Nm9hkATwLoBvAqgHvdPd5eRm0HMUqeYDugUfIM261ku6YsxmrGsd3ziCNHjoQxVruOPTe269vd3V3avmLFirAPgyWuMBYvXlzazpJnoiOjAGB4eDiMsbnq7OwsbV+0aFHYhzkoLDGIrWG2Gx/dL8VtajQR5iSAL7r7BtSOZ77dzD4H4HsAvu/uawFMALh/GtcSQrSJumL3GudfguYU/xzAFwH8omjfAuDrrRigEKI5TPd89tnFCa5jAF4A8CcAh939/HveEQDxJzOEEG1nWmJ397Pufg2AywDcCOAvpnsDM9toZgNmNnDo0KG0UQohGmZGu/HufhjAbwDcDGCJmZ3fObsMwN6gzyZ373f3fnbGthCitdQVu5ktN7MlxeP5AL4MYBdqov+b4tvuA/BMi8YohGgC00mE6QGwxcxmo/bL4Sl3/7WZ7QTwpJn9M4BtAJ6odyF3D60tlrAQfeif2UKRXQdwCy2lNhmzapgdE9lCALfKmCWzbt260vYrrrgi7LN06dIwxqxDduwSS1yJYEdNsTGm1HdjiSTMfmUxNg62vtk1I1Kst7pid/dBAP/voDB3H0Lt73chxCcAfYJOiEyQ2IXIBIldiEyQ2IXIBIldiEwwtlXf9JuZHQTwTvHlMgBxEbPq0Dg+isbxUT5p41jj7svLApWK/SM3Nhtw9/623Fzj0DgyHIfexguRCRK7EJnQTrFvauO9p6JxfBSN46N8asbRtr/ZhRDVorfxQmRCW8RuZreb2W4ze8vMHmzHGIpxDJvZdjN7zcwGKrzvZjMbM7MdU9q6zOwFM3uz+D9O82rtOB4xs73FnLxmZl+tYByrzOw3ZrbTzP5oZn9XtFc6J2Qclc6Jmc0zs1fM7PViHP9UtH/GzF4udPNzM5s7owu7e6X/AMxGrazV5QDmAngdwPqqx1GMZRjAsjbc9wsArgOwY0rbvwB4sHj8IIDvtWkcjwD4+4rnowfAdcXjTgB7AKyvek7IOCqdEwAGYGHxeA6AlwF8DsBTAO4u2v8dwN/O5LrteGW/EcBb7j7ktdLTTwK4ow3jaBvu/hKAj9fougO1wp1ARQU8g3FUjruPuvsfiseTqBVH6UXFc0LGUSleo+lFXtsh9l4A7035up3FKh3A82b2qpltbNMYznOJu48Wj/cDuKSNY3nAzAaLt/kt/3NiKmbWh1r9hJfRxjn52DiAiuekFUVec9+g+7y7XwfgrwF828y+0O4BAbXf7Kj9ImoHPwRwBWpnBIwCeKyqG5vZQgBPA/iOux+dGqtyTkrGUfmceANFXiPaIfa9AFZN+TosVtlq3H1v8f8YgF+hvZV3DphZDwAU/4+1YxDufqBYaOcA/AgVzYmZzUFNYD91918WzZXPSdk42jUnxb0PY4ZFXiPaIfbfA1hX7CzOBXA3gGerHoSZLTCzzvOPAXwFwA7eq6U8i1rhTqCNBTzPi6vgTlQwJ1Y7G+kJALvc/fEpoUrnJBpH1XPSsiKvVe0wfmy38auo7XT+CcA/tGkMl6PmBLwO4I9VjgPAz1B7O3gatb+97kftzLytAN4E8CKArjaN4z8BbAcwiJrYeioYx+dRe4s+COC14t9Xq54TMo5K5wTAX6JWxHUQtV8s/zhlzb4C4C0A/w3g4plcV5+gEyITct+gEyIbJHYhMkFiFyITJHYhMkFiFyITJHYhMkFiFyITJHYhMuH/APv77k5dLXd9AAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 432x288 with 1 Axes>"
+      ]
+     },
+     "metadata": {
+      "needs_background": "light"
+     },
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "class NET(fluid.dygraph.Layer):\n",
+    "    \n",
+    "    # Initialize the list of learnable parameters, and fill the initial value with the uniform distribution of [0, 2*pi]\n",
+    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(\n",
+    "        low=0.0, high=2 * np.pi), dtype='float64'):\n",
+    "        super(NET, self).__init__()\n",
+    "        \n",
+    "        # Create the parameter theta for learning U\n",
+    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        \n",
+    "        # Create a parameter phi to learn V_dagger\n",
+    "        self.phi = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
+    "        \n",
+    "        # Convert Numpy array to variable supported in Paddle dynamic graph mode\n",
+    "        self.M = fluid.dygraph.to_variable(Mat_generator())\n",
+    "        self.weight = fluid.dygraph.to_variable(weight)\n",
+    "\n",
+    "    # Define loss function and forward propagation mechanism\n",
+    "    def forward(self):\n",
+    "        \n",
+    "        # Get the unitary matrix representation of the quantum neural network\n",
+    "        U = U_theta(self.theta)\n",
+    "        U_dagger = dagger(U)\n",
+    "        \n",
+    "        \n",
+    "        V = U_theta(self.phi)\n",
+    "        V_dagger = dagger(V)\n",
+    "        \n",
+    "        # Initialize the loss function and singular value memory\n",
+    "        loss = 0\n",
+    "        singular_values = np.zeros(T)\n",
+    "        \n",
+    "        # Define loss function\n",
+    "        for i in range(T):\n",
+    "            loss -= self.weight.real[i]* matmul(U_dagger, matmul(self.M, V)).real[i][i]\n",
+    "            singular_values[i] = (matmul(U_dagger, matmul(self.M, V)).real[i][i]).numpy()\n",
+    "        \n",
+    "        # Function returns two matrices U and V_dagger, learned singular values and loss function\n",
+    "        return U, V_dagger, loss, singular_values\n",
+    "\n",
+    "# Record the optimization process\n",
+    "loss_list, singular_value_list = [], []\n",
+    "U_learned, V_dagger_learned = [], []\n",
+    "\n",
+    "\n",
+    "# Start Paddle dynamic graph mode\n",
+    "with fluid.dygraph.guard():\n",
+    "    \n",
+    "    net = NET([theta_size])\n",
+    "    \n",
+    "    # We use Adam optimizer for better performance\n",
+    "    # One can change it to SGD or RMSprop.\n",
+    "    opt = fluid.optimizer.AdamOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
+    "    \n",
+    "    # Optimization loop\n",
+    "    for itr in range(ITR):\n",
+    "        \n",
+    "        # Forward propagation to calculate loss function\n",
+    "        U, V_dagger, loss, singular_values = net()\n",
+    "        \n",
+    "        # Under the dynamic graph mode, back propagation minimizes the loss function\n",
+    "        loss.backward()\n",
+    "        opt.minimize(loss)\n",
+    "        net.clear_gradients()\n",
+    "\n",
+    "        # Record optimization intermediate results\n",
+    "        loss_list.append(loss[0][0].numpy())\n",
+    "        singular_value_list.append(singular_values)\n",
+    "\n",
+    "    # Record the last two unitary matrices learned\n",
+    "    U_learned = U.real.numpy() + 1j * U.imag.numpy()\n",
+    "    V_dagger_learned = V_dagger.real.numpy() + 1j*V_dagger.imag.numpy()\n",
+    "\n",
+    "singular_value = singular_value_list[-1]\n",
+    "mat = np.matrix(U_learned.real[:, :T]) * np.diag(singular_value[:T])* np.matrix(V_dagger_learned.real[:T, :])\n",
+    "\n",
+    "reconstimg = mat\n",
+    "plt.imshow(reconstimg, cmap='gray')"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "_______\n",
+    "\n",
+    "\n",
+    "## References:\n",
+    "\n",
+    "[1] Wang, X., Song, Z. & Wang, Y. Variational Quantum Singular Value Decomposition. [arXiv:2006.02336 (2020).](https://arxiv.org/abs/2006.02336)\n",
+    "\n"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.10"
+  },
+  "toc": {
+   "base_numbering": 1,
+   "nav_menu": {},
+   "number_sections": true,
+   "sideBar": true,
+   "skip_h1_title": false,
+   "title_cell": "Table of Contents",
+   "title_sidebar": "Contents",
+   "toc_cell": false,
+   "toc_position": {},
+   "toc_section_display": true,
+   "toc_window_display": true
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}

tutorial/VQSVD/VQSVD_Tutorial_CN.ipynb

-{
- "cells": [
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "# 变分量子奇异值分解 (VQSVD)\n",
-    "\n",
-    "<em> Copyright (c) 2020 Institute for Quantum Computing, Baidu Inc. All Rights Reserved. </em>\n",
-    "\n",
-    "\n",
-    "## 概览\n",
-    "\n",
-    "在本教程中，我们一起学习下经典奇异值分解（SVD）的概念以及我们自主研发的量子神经网络版本的量子奇异值分解 （VQSVD，Variational Quantum Singular Value Decomposition）[1] 是如何运作的。主体部分包括两个具体案例：\n",
-    "\n",
-    "- 分解随机生成的 8x8 复数矩阵\n",
-    "- 应用在图像压缩上的效果\n",
-    "\n",
-    "## 背景\n",
-    "\n",
-    "奇异值分解（SVD）有非常多的应用包括 -- 主成分分析（PCA）、求解线性方程组和推荐系统。其主要任务是给定一个复数矩阵 $M \\in \\mathbb{C}^{m \\times n}$, 找到分解形式：\n",
-    "\n",
-    "$$\n",
-    "M = UDV^\\dagger\n",
-    "$$\n",
-    "\n",
-    "其中 $U_{m\\times m}$ 和 $V^\\dagger_{n\\times n}$ 是酉矩阵（Unitary matrix）, 满足性质 $UU^\\dagger = VV^\\dagger = I$。 \n",
-    "- 矩阵 $U$ 的列向量 $\\lvert {u_j}\\rangle$ 被称为左奇异向量（left singular vectors）, $\\{\\lvert {u_j}\\rangle\\}_{j=1}^{m}$ 组成一组正交向量基。这些列向量本质上是矩阵 $MM^\\dagger$ 的特征向量。\n",
-    "- 类似的，矩阵 $V$ 的列向量 $\\{\\lvert {v_j}\\rangle\\}_{j=1}^{n}$ 是 $M^\\dagger M$ 的特征向量也组成一组正交向量基。\n",
-    "- 中间矩阵 $D_{m\\times n}$ 的对角元素上存储着由大到小排列的奇异值 $d_j$。 \n",
-    "\n",
-    "我们不妨先来看个简单的例子：（为了方便讨论，我们假设以下出现的 $M$ 都是方阵）\n",
-    "\n",
-    "$$\n",
-    "M = 2*X\\otimes Z + 6*Z\\otimes X + 3*I\\otimes I = \n",
-    "\\begin{bmatrix} \n",
-    "3 &6 &2 &0 \\\\\n",
-    "6 &3 &0 &-2 \\\\\n",
-    "2 &0 &3 &-6 \\\\\n",
-    "0 &-2 &-6 &3 \n",
-    "\\end{bmatrix}\n",
-    "$$\n",
-    "\n",
-    "那么该矩阵的奇异值分解可表示为:\n",
-    "\n",
-    "$$\n",
-    "M = UDV^\\dagger = \n",
-    "\\frac{1}{2}\n",
-    "\\begin{bmatrix} \n",
-    "-1 &-1 &1 &1 \\\\\n",
-    "-1 &-1 &-1 &-1 \\\\\n",
-    "-1 &1 &-1 &1 \\\\\n",
-    "1 &-1 &-1 &1 \n",
-    "\\end{bmatrix}\n",
-    "\\begin{bmatrix} \n",
-    "11 &0 &0 &0 \\\\\n",
-    "0 &7 &0 &0 \\\\\n",
-    "0 &0 &5 &0 \\\\\n",
-    "0 &0 &0 &1 \n",
-    "\\end{bmatrix}\n",
-    "\\frac{1}{2}\n",
-    "\\begin{bmatrix} \n",
-    "-1 &-1 &-1 &-1 \\\\\n",
-    "-1 &-1 &1 &1 \\\\\n",
-    "-1 &1 &1 &-1 \\\\\n",
-    "1 &-1 &1 &-1 \n",
-    "\\end{bmatrix}\n",
-    "$$\n",
-    "\n",
-    "首先，让我们通过下面几行代码引入必要的 library和 package。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 1,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "import time\n",
-    "import numpy as np\n",
-    "from progressbar import ProgressBar\n",
-    "from matplotlib import pyplot as plt\n",
-    "from scipy.stats import unitary_group\n",
-    "from scipy.linalg import norm\n",
-    "\n",
-    "import paddle.fluid as fluid\n",
-    "from paddle.complex import matmul, transpose, trace\n",
-    "from paddle_quantum.circuit import *\n",
-    "from paddle_quantum.utils import *\n",
-    "\n",
-    "\n",
-    "# 画出优化过程中的学习曲线\n",
-    "def loss_plot(loss):\n",
-    "    '''\n",
-    "    loss is a list, this function plots loss over iteration\n",
-    "    '''\n",
-    "    plt.plot(list(range(1, len(loss)+1)), loss)\n",
-    "    plt.xlabel('iteration')\n",
-    "    plt.ylabel('loss')\n",
-    "    plt.title('Loss Over Iteration')\n",
-    "    plt.show()\n"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 经典奇异值分解\n",
-    "\n",
-    "那么在了解一些简单的数学背景之后， 我们来学习下如何用 Numpy 完成矩阵的奇异值分解。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 2,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "我们想要分解的矩阵 M 是：\n",
-      "[[ 3.+0.j  6.+0.j  2.+0.j  0.+0.j]\n",
-      " [ 6.+0.j  3.+0.j  0.+0.j -2.+0.j]\n",
-      " [ 2.+0.j  0.+0.j  3.+0.j -6.+0.j]\n",
-      " [ 0.+0.j -2.+0.j -6.+0.j  3.+0.j]]\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 生成矩阵 M\n",
-    "def M_generator():\n",
-    "    I = np.array([[1, 0], [0, 1]])\n",
-    "    Z = np.array([[1, 0], [0, -1]])\n",
-    "    X = np.array([[0, 1], [1, 0]])\n",
-    "    Y = np.array([[0, -1j], [1j, 0]])\n",
-    "    M = 2 *np.kron(X, Z) + 6 * np.kron(Z, X) + 3 * np.kron(I, I)\n",
-    "    return M.astype('complex64')\n",
-    "\n",
-    "print('我们想要分解的矩阵 M 是：')\n",
-    "print(M_generator())"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 3,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "矩阵的奇异值从大到小分别是:\n",
-      "[11.  7.  5.  1.]\n",
-      "分解出的酉矩阵 U 是:\n",
-      "[[-0.5+0.j -0.5+0.j  0.5+0.j  0.5+0.j]\n",
-      " [-0.5+0.j -0.5+0.j -0.5+0.j -0.5+0.j]\n",
-      " [-0.5+0.j  0.5+0.j -0.5+0.j  0.5+0.j]\n",
-      " [ 0.5+0.j -0.5+0.j -0.5+0.j  0.5+0.j]]\n",
-      "分解出的酉矩阵 V_dagger 是:\n",
-      "[[-0.5+0.j -0.5+0.j -0.5+0.j  0.5+0.j]\n",
-      " [-0.5+0.j -0.5+0.j  0.5+0.j -0.5+0.j]\n",
-      " [-0.5+0.j  0.5+0.j  0.5+0.j  0.5+0.j]\n",
-      " [-0.5+0.j  0.5+0.j -0.5+0.j -0.5+0.j]]\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 我们只需要以下一行代码就可以完成 SVD \n",
-    "U, D, V_dagger = np.linalg.svd(M_generator(), full_matrices=True)\n",
-    "\n",
-    "# 打印分解结果\n",
-    "print(\"矩阵的奇异值从大到小分别是:\")\n",
-    "print(D)\n",
-    "print(\"分解出的酉矩阵 U 是:\")\n",
-    "print(U)\n",
-    "print(\"分解出的酉矩阵 V_dagger 是:\")\n",
-    "print(V_dagger)"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 4,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "[[ 3.+0.j  6.+0.j  2.+0.j  0.+0.j]\n",
-      " [ 6.+0.j  3.+0.j  0.+0.j -2.+0.j]\n",
-      " [ 2.+0.j  0.+0.j  3.+0.j -6.+0.j]\n",
-      " [ 0.+0.j -2.+0.j -6.+0.j  3.+0.j]]\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 再组装回去， 能不能复原矩阵？\n",
-    "M_reconst = np.matmul(U, np.matmul(np.diag(D), V_dagger))\n",
-    "print(M_reconst)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "那当然是可以复原成原来的矩阵 $M$ 的！读者也可以自行修改矩阵，试试看不是方阵的情况。\n",
-    "<hr>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 量子奇异值分解\n",
-    "\n",
-    "接下来我们来看看量子版本的奇异值分解是怎么一回事。简单的说，我们把矩阵分解这一问题巧妙的转换成了优化问题。通过以下四个步骤：\n",
-    "\n",
-    "- 准备一组正交向量基 $\\{\\lvert {\\psi_j}\\rangle\\}$, 不妨直接取计算基 $\\{ \\lvert {000}\\rangle, \\lvert {001}\\rangle,\\cdots \\lvert {111}\\rangle\\}$ （这是3量子比特的情形）\n",
-    "- 准备两个参数化的量子神经网络 $U(\\theta)$ 和 $V(\\phi)$ 分别用来学习左/右奇异向量\n",
-    "- 利用量子神经网络估算奇异值 $m_j = \\text{Re}\\langle{\\psi_j} \\lvert U(\\theta)^{\\dagger} M V(\\phi)\\lvert {\\psi_j}\\rangle$\n",
-    "- 设计损失函数并且利用飞桨来优化\n",
-    "\n",
-    "$$\n",
-    "L(\\theta,\\phi) = \\sum_{j=1}^T q_j\\times \\text{Re} \\langle{\\psi_j} \\lvert U(\\theta)^{\\dagger} M V(\\phi)\\lvert {\\psi_j}\\rangle\n",
-    "$$\n",
-    "\n",
-    "其中 $q_1>\\cdots>q_T>0$ 是可以调节的权重（超参数）, $T$ 表示我们想要学习到的阶数（rank），或者可以解释为总共要学习得到的奇异值个数。"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "### 案例1：分解随机生成的 8x8 复数矩阵\n",
-    "\n",
-    "接着我们来看一个具体的例子，这可以更好的解释整体流程。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 5,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "我们想要分解的矩阵 M 是：\n",
-      "[[6.+1.j 3.+9.j 7.+3.j 4.+7.j 6.+6.j 9.+8.j 2.+7.j 6.+4.j]\n",
-      " [7.+1.j 4.+4.j 3.+7.j 7.+9.j 7.+8.j 2.+8.j 5.+0.j 4.+8.j]\n",
-      " [1.+6.j 7.+8.j 5.+7.j 1.+0.j 4.+7.j 0.+7.j 9.+2.j 5.+0.j]\n",
-      " [8.+7.j 0.+2.j 9.+2.j 2.+0.j 6.+4.j 3.+9.j 8.+6.j 2.+9.j]\n",
-      " [4.+8.j 2.+6.j 6.+8.j 4.+7.j 8.+1.j 6.+0.j 1.+6.j 3.+6.j]\n",
-      " [8.+7.j 1.+4.j 9.+2.j 8.+7.j 9.+5.j 4.+2.j 1.+0.j 3.+2.j]\n",
-      " [6.+4.j 7.+2.j 2.+0.j 0.+4.j 3.+9.j 1.+6.j 7.+6.j 3.+8.j]\n",
-      " [1.+9.j 5.+9.j 5.+2.j 9.+6.j 3.+0.j 5.+3.j 1.+3.j 9.+4.j]]\n",
-      "矩阵的奇异值从大到小分别是:\n",
-      "[54.83484985 19.18141073 14.98866247 11.61419557 10.15927045  7.60223249\n",
-      "  5.81040539  3.30116001]\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 先固定随机种子， 为了能够复现结果\n",
-    "np.random.seed(42)\n",
-    "\n",
-    "# 设置量子比特数量，确定希尔伯特空间的维度\n",
-    "N = 3\n",
-    "\n",
-    "# 制作随机矩阵生成器\n",
-    "def random_M_generator():\n",
-    "    M = np.random.randint(10, size = (2**N, 2**N))\\\n",
-    "    + 1j*np.random.randint(10, size = (2**N, 2**N))\n",
-    "    M1 = np.random.randint(10, size = (2**N, 2**N)) \n",
-    "    return M\n",
-    "\n",
-    "M = random_M_generator()\n",
-    "M_err = np.copy(M)\n",
-    "\n",
-    "\n",
-    "# 打印结果\n",
-    "print('我们想要分解的矩阵 M 是：')\n",
-    "print(M)\n",
-    "\n",
-    "U, D, V_dagger = np.linalg.svd(M, full_matrices=True)\n",
-    "print(\"矩阵的奇异值从大到小分别是:\")\n",
-    "print(D)"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 6,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "选取的等差权重为：\n",
-      "[24.+0.j 21.+0.j 18.+0.j 15.+0.j 12.+0.j  9.+0.j  6.+0.j  3.+0.j]\n"
-     ]
-    }
-   ],
-   "source": [
-    "# 超参数设置\n",
-    "N = 3           # 量子比特数量\n",
-    "T = 8           # 设置想要学习的阶数\n",
-    "ITR = 100       # 迭代次数\n",
-    "LR = 0.02       # 学习速率\n",
-    "SEED = 1        # 随机数种子\n",
-    "\n",
-    "# 设置等差的学习权重\n",
-    "weight = np.arange(3 * T, 0, -3).astype('complex128')\n",
-    "print('选取的等差权重为：')\n",
-    "print(weight)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "### 量子神经网络的构造\n",
-    "\n",
-    "我们搭建如下的结构：\n"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 7,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 设置电路参数\n",
-    "cir_depth = 40                           # 电路深度\n",
-    "block_len = 2                            # 每个模组的长度\n",
-    "theta_size = N * block_len * cir_depth   # 网络参数 theta 的大小\n",
-    "\n",
-    "\n",
-    "# 定义量子神经网络\n",
-    "def U_theta(theta):\n",
-    "\n",
-    "    # 用 UAnsatz 初始化网络\n",
-    "    cir = UAnsatz(N)\n",
-    "    \n",
-    "    # 搭建层级结构：\n",
-    "    for layer_num in range(cir_depth):\n",
-    "        \n",
-    "        for which_qubit in range(N):\n",
-    "            cir.ry(theta[block_len * layer_num * N + which_qubit], \n",
-    "                                              which_qubit)\n",
-    "        \n",
-    "        for which_qubit in range(N):\n",
-    "            cir.rz(theta[(block_len * layer_num + 1) * N + which_qubit], \n",
-    "                                                    which_qubit)\n",
-    "\n",
-    "        for which_qubit in range(1, N):\n",
-    "            cir.cnot([which_qubit - 1, which_qubit])\n",
-    "        cir.cnot([N - 1, 0])\n",
-    "\n",
-    "    return cir.U"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 8,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stderr",
-     "output_type": "stream",
-     "text": [
-      "100% |########################################################################|\r"
-     ]
-    },
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "主程序段总共运行了 216.55158972740173 秒\n"
-     ]
-    },
-    {
-     "name": "stderr",
-     "output_type": "stream",
-     "text": [
-      "\n"
-     ]
-    }
-   ],
-   "source": [
-    "class NET(fluid.dygraph.Layer):\n",
-    "    \n",
-    "    # 初始化长度为 theta_size 的可学习参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * np.pi), dtype='float64'):\n",
-    "        super(NET, self).__init__()\n",
-    "        \n",
-    "        # 创建用来学习 U 的参数 theta\n",
-    "        self.theta = self.create_parameter(shape=shape, \n",
-    "                     attr=param_attr, dtype=dtype, is_bias=False)\n",
-    "        \n",
-    "        # 创建用来学习 V_dagger 的参数 phi\n",
-    "        self.phi = self.create_parameter(shape=shape, \n",
-    "                    attr=param_attr, dtype=dtype, is_bias=False)\n",
-    "        \n",
-    "        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "        self.M = fluid.dygraph.to_variable(M)\n",
-    "        self.weight = fluid.dygraph.to_variable(weight)\n",
-    "\n",
-    "    # 定义损失函数和前向传播机制\n",
-    "    def forward(self):\n",
-    "        \n",
-    "        # 获取量子神经网络的酉矩阵表示\n",
-    "        U = U_theta(self.theta)\n",
-    "        U_dagger = dagger(U)\n",
-    "        \n",
-    "        \n",
-    "        V = U_theta(self.phi)\n",
-    "        V_dagger = dagger(V)\n",
-    "        \n",
-    "        # 初始化损失函数和奇异值存储器\n",
-    "        loss = 0 \n",
-    "        singular_values = np.zeros(T)\n",
-    "        \n",
-    "        # 定义损失函数\n",
-    "        for i in range(T):\n",
-    "            loss -= self.weight.real[i] * matmul(U_dagger, matmul(self.M, V)).real[i][i]\n",
-    "            singular_values[i] = (matmul(U_dagger, matmul(self.M, V)).real[i][i]).numpy()\n",
-    "        \n",
-    "        # 函数返回两个矩阵 U 和 V_dagger、 学习的奇异值以及损失函数    \n",
-    "        return U, V_dagger, loss, singular_values\n",
-    "    \n",
-    "# 记录优化中间过程\n",
-    "loss_list, singular_value_list = [], []\n",
-    "U_learned, V_dagger_learned = [], []\n",
-    "\n",
-    "time_start = time.time()\n",
-    "# 启动 Paddle 动态图模式\n",
-    "with fluid.dygraph.guard():\n",
-    "    \n",
-    "    # 确定网络的参数维度\n",
-    "    net = NET([theta_size])\n",
-    "    \n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdagradOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
-    "    \n",
-    "    # 优化循环\n",
-    "    pbar = ProgressBar()\n",
-    "    for itr in pbar(range(ITR)):\n",
-    "        \n",
-    "        #  前向传播计算损失函数\n",
-    "        U, V_dagger, loss, singular_values = net()\n",
-    "        \n",
-    "        # 在动态图机制下，反向传播极小化损失函数\n",
-    "        loss.backward()\n",
-    "        opt.minimize(loss)\n",
-    "        net.clear_gradients()\n",
-    "\n",
-    "        # 记录优化中间结果\n",
-    "        loss_list.append(loss[0][0].numpy())\n",
-    "        singular_value_list.append(singular_values)\n",
-    "\n",
-    "    # 记录最后学出的两个酉矩阵    \n",
-    "    U_learned = U.real.numpy() + 1j * U.imag.numpy()\n",
-    "    V_dagger_learned = V_dagger.real.numpy() + 1j * V_dagger.imag.numpy()\n",
-    "\n",
-    "time_span = time.time() - time_start        \n",
-    "print('主程序段总共运行了', time_span, '秒')"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 9,
-   "metadata": {},
-   "outputs": [
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZQAAAEWCAYAAABBvWFzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAojUlEQVR4nO3deXxU9b3/8dcnk2SyExLCFgIIAipUQIJ1q3rVW7Ha2vZqpb0u3a61t6u1i9b+utzf9Xfr1V5b21ut1bq0WrVal7au1VKVugUXwAUFZAlr2ENClkk+vz/OCQwQIMBMTjLzfj4e88g53zNnzufLMu98z2rujoiIyMHKiboAERHJDAoUERFJCQWKiIikhAJFRERSQoEiIiIpoUAREZGUUKCIyH4xs61mNibqOqTvUaBIv2NmS8zstIi2fZyZPW1mjWa22cz+ZGZH9OL2t/fdzD5tZs+leXuzzOzzyW3uXuLui9O5XemfFCgiPWRmxwJPAA8Bw4FDgNeB2an+jd0Caf3/aWa56fx8yT4KFMkYZhY3s5+a2crw9VMzi4fLBpnZn81sk5ltMLNnu76wzew7ZrYiHHUsMLNT97CJ/wbucPefuXuju29w9+8BLwA/DD/rLTM7K6mmXDNbZ2ZHhfPHmNk/wjpeN7OTk947y8yuMrPZQDOwx5Ays8OBG4Fjw11Qm5L+DK41s2VmtsbMbjSzwnDZyWZWH/Z3NXCrmQ0M/1wazGxjOD0ifP9VwAeAX4Tb+EXY7mZ2aDg9wMzuCNdfambfS/pz/bSZPRfWs9HM3jOzM3r8Fyr9jgJFMsmVwDHAFGAycDTwvXDZZUA9UAUMAb4LuJlNAL4MTHf3UuB0YMmuH2xmRcBxwB+62e69wD+H078HPpm07HRgnbu/YmbVwF+A/wQqgG8C95tZVdL7LwAuBkqBpXvqqLu/BVwCPB/ugioPF10NjA//DA4FqoHvJ606NNz2qHA7OcCt4fxIYBvwi3AbVwLPAl8Ot/Hlbkr5OTCAIPxOAi4EPpO0/P3AAmAQQSDfYma2p35J/6ZAkUzyr8B/uPtad28AfkTwBQ3QDgwDRrl7u7s/68GN7DqAOHCEmeW5+xJ3X9TNZ1cQ/H9Z1c2yVQRfmAB3AR8JAwjgU2EbwPnAI+7+iLt3uvuTQB3woaTPus3d33D3hLu370/nwy/qfwMuDUdPjcD/A2Ymva0T+IG7t7r7Nndf7+73u3tz+P6rCIKhJ9uLAecBV4QjtiXAT9jxZw6w1N1/7e4dwO0EfwdD9qdf0n8oUCSTDGfn3+qXhm0A1wALgSfMbLGZXQ7g7guBrxPsslprZneb2XB2t5Hgy3hYN8uGAeuSPu8t4MNhqHyEHYEyCjg33N21KdxNdcIun7l8fzq8iyqgCJiT9PmPhe1dGty9pWvGzIrM7Ffh7qotwDNAeRgW+zIIyGf3P/PqpPnVXRPu3hxOluxHn6QfUaBIJllJ8KXdZWTYRvgb9GXuPgb4MPCNrmMl7n6Xu58QrusEu4124u5NwPPAud1s9xPAU0nzXbu9zgbeDEMGgrD4rbuXJ72K3f3HyZvaj/7u+t51BLusJiZ9/gB3L9nLOpcBE4D3u3sZcGLYbnt4/67ba2f3P/MV+9EHySAKFOmv8sysIOmVS/BF/j0zqzKzQQTHDn4HYGZnmdmh4W6hLQS7ujrMbIKZnRIevG8h+ELu2MM2LwcuMrOvmllpeED7P4FjCXavdbkb+CDwRXaMTghr+bCZnW5msbDuk7sOgh+ANcAIM8sHcPdO4NfAdWY2OOx3tZmdvpfPKCXo8yYzqwB+0M02uj05INyNdS9wVfjnMQr4RthPyUIKFOmvHiH4Iux6/ZDgYHcdMBeYB7wStgGMA/4KbCUYafzS3WcRHD/5McFv26uBwQQH7Hfj7s8RHGT/OMFxk6XAVOAEd3836X2rwm0cB9yT1L6cYNTyXaCBYMTyLQ78/+HTwBvAajNbF7Z9h2DX3gvhLqy/EoxA9uSnQCFB/18g2EWW7GfAOeFZWtd3s/5XgCZgMfAcQYD+5oB6I/2e6QFbIiKSChqhiIhISihQREQkJRQoIiKSEgoUERFJiay9OdygQYN89OjRUZchItKvzJkzZ527V3W3LGsDZfTo0dTV1UVdhohIv2Jme7zHnHZ5iYhISihQREQkJRQoIiKSEgoUERFJCQWKiIikhAJFRERSQoEiIiIpoUDZTy8v2cDVj72N7tIsIrIzBcp+mlu/mRtmLWLLtkTUpYiI9CkKlP1UVRoHoGFryz7eKSKSXRQo+6mqJAiUtY2tEVciItK3KFD2U1VpPgANChQRkZ0oUPZTVUkBoEAREdmVAmU/lRXmkh/LoWGrAkVEJJkCZT+ZGVWlcY1QRER2oUA5AINK46zb2hZ1GSIifYoC5QBUlWiEIiKyKwXKAdAuLxGR3SlQDkBVaZwNTa10dOr2KyIiXRQoB6CqNE6nw/omjVJERLpkTKCY2QwzW2BmC83s8nRuq+tqee32EhHZISMCxcxiwP8CZwBHAJ80syPStT1dLS8isruMCBTgaGChuy929zbgbuDsdG1MV8uLiOwuUwKlGlieNF8ftu3EzC42szozq2toaDjgjQ3qGqHoankRke0yJVCsm7bdTsFy95vcvdbda6uqqg54Y0X5uZTEc3cboeisLxHJZpkSKPVATdL8CGBlOjdYtcvV8nOWbuTw7z/Gik3b0rlZEZE+K1MC5WVgnJkdYmb5wEzg4XRuMLhafsdDtp57dx1tiU7ea2hK52ZFRPqsjAgUd08AXwYeB94C7nX3N9K5zV2vlp+3YjOga1NEJHvlRl1Aqrj7I8AjvbW9qtI4z767Izzmh4GysUk3jRSR7JQxgdLbqkrjbGlJ0NLeQWNLgtVbgt1fGxQoIpKlFCgHqOtq+XVbW3l37dbt7esVKCKSpTLiGEoUqkp33H5lfn2wu2toWYFGKCKStTRCOUCDku7nNW/FZsYMKmZQSVyBIiJZSyOUA7R9hLK1lfkrNjOpegADi/MUKCKStRQoB6iyJLj9yjurG1m5uYVJ1WVUFGuEIiLZS7u8DlBeLIeK4nz+tiC4J9ik6gFs2ZZgY3MbnZ1OTk53d4MREclcGqEchKqSOMs2NAMwcfgAKorz6XTYtK094spERHqfAuUgdB1HGVVZxIDCPCqKg91g2u0lItlIgXIQugJlUvUAAAWKiGQ1BcpB6AqU9+0WKLqfl4hkHwXKQei6Wn7S8CBQus780tXyIpKNFCgHYfohFUypKWfKyHIABhYFgaIbRIpINtJpwwdhSk05D37p+O3zBXkxivNjGqGISFbSCCXFKkrydVBeRLKSAiXFdLW8iGQrBUqKVRbns36rAkVEso8CJcUqivPZ2KxAEZHso0BJsYrifNY3teHuUZciItKrFCgpVlGcT1uik6a2jqhLERHpVQqUFNt+tbyOo4hIllGgpFhlV6DoOIqIZBkFSorpfl4ikq0UKCnWFSg6dVhEso0CJcV0C3sRyVYKlBQrieeSH8tRoIhI1lGgpJiZUVGs+3mJSPZRoKSBAkVEspECJQ26rpYXEckmCpQ00AhFRLKRAiUNKorz9dRGEck6fS5QzOyHZrbCzF4LXx9KWnaFmS00swVmdnpS+zQzmxcuu97MLJrqA5XF+TS2JmhN6H5eIpI9+lyghK5z9ynh6xEAMzsCmAlMBGYAvzSzWPj+G4CLgXHha0YENW9XUdL1bPn2KMsQEelVfTVQunM2cLe7t7r7e8BC4GgzGwaUufvzHtwz/g7goxHWSUVReLW8br8iIlmkrwbKl81srpn9xswGhm3VwPKk99SHbdXh9K7tuzGzi82szszqGhoa0lE3AFWlcQDWbGlJ2zZERPqaSALFzP5qZvO7eZ1NsPtqLDAFWAX8pGu1bj7K99K+e6P7Te5e6+61VVVVB9+RPZgwtBQzmFu/OW3bEBHpa3Kj2Ki7n9aT95nZr4E/h7P1QE3S4hHAyrB9RDftkSktyGP84FJeW74pyjJERHpVn9vlFR4T6fIxYH44/TAw08ziZnYIwcH3l9x9FdBoZseEZ3ddCDzUq0V3Y+rIcl5dtkmPAhaRrNHnAgX47/AU4LnAPwGXArj7G8C9wJvAY8CX3L3rvNwvAjcTHKhfBDza61XvYkpNOZu3tfPeuqaoSxER6RWR7PLaG3e/YC/LrgKu6qa9DpiUzrr219SRwbkEry3fxJiqkoirERFJv744QskIhw4uoTg/xqvLNkVdiohIr1CgpEksx5hcU64D8yKSNRQoaTSlppy3Vm1hW5tuwSIimU+BkkZTRw4k0enMX6nrUUQk8ylQ0mhKTTkAr+k4iohkAQVKGlWVxhkxsJBXl2+MuhQRkbRToKTZ1JEDNUIRkaygQEmzKTXlrNzcohtFikjGU6Ck2dSR5QDMWardXiKS2RQoafa+6gGUxHN59t11UZciIpJWCpQ0y4vlcNzYSp55p0E3ihSRjKZA6QUnTahixaZtLGrYGnUpIiJpo0DpBSeOCx7m9fd3tNtLRDKXAqUX1FQUMbaqmL+/k77HDouIRE2B0ktOHF/Fi4vX09Ku+3qJSGZSoPSSk8ZX0Zro5IXF66MuRUQkLRQoveSYMZXEc3N4RsdRRCRDKVB6SUFejKMPqeDv76yNuhQRkbRQoPSik8ZXsaihieUbmqMuRUQk5RQovejkCcHpw0+/rVGKiGQeBUovGltVwmFDS/njK/VRlyIiknIKlF5kZpwzbQSv12/mnTWNUZcjIpJSCpRe9rGp1eTmGH+oWx51KSIiKaVA6WWVJXFOOWwwD7y6gvaOzqjLERFJGQVKBM6trWHd1jZmLdCtWEQkcyhQInDyhCoGleRrt5eIZBQFSgTyYjl8bGo1T7+9lnVbW6MuR0QkJRQoETm3toZEp/PgqyuiLkVEJCUUKBEZP6SUyTXl3Fu3XE9yFJGMoECJ0MzpNbyzZiuvLd8UdSkiIgdNgRKhs44cRmFejHte1sF5Een/IgkUMzvXzN4ws04zq91l2RVmttDMFpjZ6Unt08xsXrjsejOzsD1uZveE7S+a2ehe7s4BKy3I48wjh/Gn11fS1JqIuhwRkYPSo0Axs6+ZWZkFbjGzV8zsgwex3fnAx4FndtnOEcBMYCIwA/ilmcXCxTcAFwPjwteMsP1zwEZ3PxS4Drj6IOrqdedNr6GprYO/zFsVdSkiIgelpyOUz7r7FuCDQBXwGeDHB7pRd3/L3Rd0s+hs4G53b3X394CFwNFmNgwoc/fnPTiCfQfw0aR1bg+n7wNO7Rq99Ae1owYypqqYe7XbS0T6uZ4GStcX9IeAW9399aS2VKoGkr9Z68O26nB61/ad1nH3BLAZqOzuw83sYjOrM7O6hoa+cZW6mXFebQ11SzeycK1uGCki/VdPA2WOmT1BECiPm1kpsNcbUZnZX81sfjevs/e2Wjdtvpf2va2ze6P7Te5e6+61VVVVeyu/V338qBHk5hi/f0mjFBHpv3J7+L7PAVOAxe7ebGYVBLu99sjdTzuAeuqBmqT5EcDKsH1EN+3J69SbWS4wANhwANuOTFVpnBmThnLvy8u59J/HUxLv6V+LiEjf0dMRyrHAAnffZGbnA98j2LWUag8DM8Mztw4hOPj+kruvAhrN7Jjw+MiFwENJ61wUTp8DPO398ErBz51wCI2tCd3fS0T6rZ4Gyg1As5lNBr4NLCU4MH5AzOxjZlZPEFR/MbPHAdz9DeBe4E3gMeBL7t4RrvZF4GaCA/WLgEfD9luASjNbCHwDuPxA64rS1JEDOWpkObfOXkJHZ7/LQxERrCe/zJvZK+5+lJl9H1jh7rd0taW/xPSora31urq6qMvYyV/mruJLd73Cry6YxukTh0ZdjojIbsxsjrvXdrespyOURjO7AriAYEQRA/JSVaAETp84hOryQm557r2oSxER2W89DZTzgFaC61FWE5yqe03aqspSubEcPn3caF56bwPzV6TjEJWISPr0KFDCELkTGGBmZwEt7n7Ax1Bkz847uobi/Bi/0ShFRPqZnt565RPAS8C5wCeAF83snHQWlq3KCvI4Z9oI/jx3lR6+JSL9Sk93eV0JTHf3i9z9QuBo4P+kr6zsdsGxo2nr6OTul5ZFXYqISI/1NFBy3H1t0vz6/VhX9tOhg0v4wLhB/O6FZbR37PWGBCIifUZPQ+ExM3vczD5tZp8G/gI8kr6y5MJjR7N6SwtPvLEm6lJERHqkpwflvwXcBBwJTAZucvfvpLOwbHfKYYMZMbCQ259fEnUpIiI90uObRrn7/cD9aaxFksRyjAuOGcV/Pfo2b63awuHDyqIuSURkr/Y6QjGzRjPb0s2r0cy29FaR2eq86TXEc3O4bfaSqEsREdmnvQaKu5e6e1k3r1J316/MaVZelM8500bwwKsrWL25JepyRET2Smdq9XFfOHEsHe7c/OziqEsREdkrBUofN7KyiI9MHs6dLy5jQ1Nb1OWIiOyRAqUf+PeTx7KtvYPbZut2LCLSdylQ+oFxQ0o5feIQbvvHEhpb2qMuR0SkWwqUfuLL/zSOLS0JfveCbsciIn2TAqWfeN+IAZw4vopbnlvMtraOfa8gItLLFCj9yFdOOZR1W9v4vW4aKSJ9kAKlH5k+uoL3H1LBr55ZRGtCoxQR6VsUKP3MV08dx5otrfyhrj7qUkREdqJA6WeOG1vJ1JHl3DBrkW5tLyJ9igKlnzEzvnrKOFZs2sYDr66IuhwRke0UKP3QyROqmFRdxi+eXkhbQqMUEekbFCj9kJlx2QcnsGxDM799YWnU5YiIAAqUfuvk8VV8YNwgrn/qXTY36+p5EYmeAqWfMjO++6HD2dLSzs+ffjfqckREFCj92eHDyjh32ghuf34Jy9Y3R12OiGQ5BUo/d9kHJ5Cbk8PVj70ddSkikuUUKP3ckLICvnDSGP4ybxUvLl4fdTkiksUUKBngCyeOpbq8kB88/AYJXewoIhFRoGSAwvwY3zvzcN5e3agbR4pIZCIJFDM718zeMLNOM6tNah9tZtvM7LXwdWPSsmlmNs/MFprZ9WZmYXvczO4J2180s9ERdClyMyYN5bixlVz7xDts1KOCRSQCUY1Q5gMfB57pZtkid58Svi5Jar8BuBgYF75mhO2fAza6+6HAdcDV6Su77zIzfvDhiWxtTfCTJxdEXY6IZKFIAsXd33L3Hn/rmdkwoMzdn3d3B+4APhouPhu4PZy+Dzi1a/SSbSYMLeWCY0Zx54vLmLN0Q9TliEiW6YvHUA4xs1fN7O9m9oGwrRpIvl97fdjWtWw5gLsngM1AZXcfbGYXm1mdmdU1NDSkp/qIffP0CQwfUMg3/zBXT3YUkV6VtkAxs7+a2fxuXmfvZbVVwEh3nwp8A7jLzMqA7kYc3rWpvSzbudH9Jnevdffaqqqq/elOv1ESz+Wac47kvXVNXPuEdn2JSO/JTdcHu/tpB7BOK9AaTs8xs0XAeIIRyYikt44AVobT9UANUG9mucAAIKv39xx36CDOP2Ykv5n9HjMmDWX66IqoSxKRLNCndnmZWZWZxcLpMQQH3xe7+yqg0cyOCY+PXAg8FK72MHBROH0O8HR4nCWrXXHG4VSXF/LNP7xOU2si6nJEJAtEddrwx8ysHjgW+IuZPR4uOhGYa2avExxgv8Tdu0YbXwRuBhYCi4BHw/ZbgEozW0iwm+zyXupGn1Ycz+XacyezbEMz//fPb0ZdjohkAcvWX+Zra2u9rq4u6jLS7urH3uaGWYu48fyjmDFpWNTliEg/Z2Zz3L22u2V9apeXpN6lp43nfdUDuPyP81i9uSXqckQkgylQMlx+bg4/mzmF1vZOvnHva3R0ZueIVETST4GSBcZUlfCjj0zkH4vWc92T70RdjohkKAVKlji3dgQzp9fwi78t5JF5q6IuR0QykAIlS5gZPzp7IkeNLOeye1/nrVVboi5JRDKMAiWLxHNj3Hj+NMoKc7n4t3Vs0F2JRSSFFChZZnBZATeeP401W1q5+I46Wtp1vy8RSQ0FShaaOnIg131iCnVLN/Kt++bSqTO/RCQF0nYvL+nbzjxyGMs2HMbVj71NzcBCvj3jsKhLEpF+ToGSxS45aQzLNjTxy1mLGFwa59PHHxJ1SSLSjylQspiZ8R9nT2Ld1jZ++Kc3iefF+OTRI6MuS0T6KR1DyXJ5sRx+8ampnDS+iu8+MI8HXq3f90oiIt1QoAjx3Bi/umAax46p5LJ7X+eh11ZEXZKI9EMKFAGgIC/GzRfVMn10BV+/5zX+ULc86pJEpJ9RoMh2Rfm53PaZoznh0EF867653Pni0qhLEpF+RIEiOynMj/HrC2s55bDBXPnAfG78+yKy9Zk5IrJ/FCiym4K84BYtZx05jB8/+jbfe3A+iY7OqMsSkT5Opw1Lt/Jzc7h+5lSqBxbyq78vZtXmFn7+yakUx/VPRkS6pxGK7FFOjnHFGYfznx+dxKwFa/mXG/7B8g3NUZclIn2UAkX26fxjRnHrZ45m5aZtnP2/s3lh8fqoSxKRPkiBIj1y0vgqHvzS8ZQX5XH+zS9y6+z3dLBeRHaiQJEeG1NVwoNfOp6TJ1Txoz+9yRd+O4fNze1RlyUifYQCRfZLWUEev76wlu+deTh/W7CWD13/LHOWboi6LBHpAxQost/MjM9/YAz3XXIcOTlw7o3Pc+3jC2hL6NRikWymQJEDNrmmnEe++gH+5agR/OJvC/n4DbN5Z01j1GWJSEQUKHJQSgvyuObcyfzqgmms3NTCmdc/y3VPvkNrQo8WFsk2ChRJidMnDuWJS0/kzPcN42dPvcsZP3tWpxeLZBkFiqTMoJI4P505lds+M522RCczb3qBr9/9Kmu2tERdmoj0AgWKpNzJEwbz5KUn8dVTDuWR+as55dpZ3DBrES3t2g0mkskUKJIWhfkxvvHBCTx56YkcO7aSqx97m1OuncV9c+rp6NQFkSKZSIEiaTWqspibL5rOXf/2fgaVxvnmH17nzOuf5bH5q3WlvUiGiSRQzOwaM3vbzOaa2QNmVp607AozW2hmC8zs9KT2aWY2L1x2vZlZ2B43s3vC9hfNbHTv90j25bixg3jw34/n55+cSluik0t+N4ezfv4cf31zjYJFJENENUJ5Epjk7kcC7wBXAJjZEcBMYCIwA/ilmcXCdW4ALgbGha8ZYfvngI3ufihwHXB1b3VC9k9OjvHhycN54tIT+cm5k2lsSfD5O+o442fP8sCr9bTrmSsi/VokgeLuT7h7Ipx9ARgRTp8N3O3ure7+HrAQONrMhgFl7v68B7/O3gF8NGmd28Pp+4BTu0Yv0jflxnL4l2kjeOqyk/ifT0ym051L73mdk6+Zxa+fWczmbbo/mEh/1BeOoXwWeDScrgaWJy2rD9uqw+ld23daJwypzUBldxsys4vNrM7M6hoaGlLWATkwebEcPn7UCB772oncclEt1QMLueqRtzj2v57i+w/N11X3Iv1M2h6/Z2Z/BYZ2s+hKd38ofM+VQAK4s2u1bt7ve2nf2zq7N7rfBNwEUFtbqx33fUROjnHq4UM49fAhzF+xmVtnL+Hul5Zzx/NLmT56IJ96/0jOmDSMgrzYvj9MRCKTtkBx99P2ttzMLgLOAk71HUdl64GapLeNAFaG7SO6aU9ep97McoEBgG5/209Nqh7ATz4xme9+6DDuf6We37+0nEvveZ3vP/QGH548nHOmjWBqTTnaqynS90TygHAzmwF8BzjJ3ZOfKfswcJeZ/Q8wnODg+0vu3mFmjWZ2DPAicCHw86R1LgKeB84BnnadNtTvVZbEufjEsXz+hDG88N567qur54+v1HPXi8sYVVnEh48czkemDGf8kNKoSxWRkEXx3WtmC4E40HWzpxfc/ZJw2ZUEx1USwNfd/dGwvRa4DSgkOObyFXd3MysAfgtMJRiZzHT3xfuqoba21uvq6lLaL0mvxpZ2Hp23modfX8k/Fq2j02Hc4BLOmDSUM943jMOGlmrkIpJmZjbH3Wu7XZatv8wrUPq3tY0tPDpvNY/MW8XLSzbQ6VBTUchphw/htMOHMH10Bfm5feGcE5HMokDphgIlczQ0tvLEm6t56q21zF64jtZEJyXxXI4bW8lJE6o4cVwVNRVFUZcpkhEUKN1QoGSm5rYEsxeuZ9aCtcxa0MCKTduAYPRy/NhBHDu2kvcfUsnQAQURVyrSPylQuqFAyXzuzqKGrTz37jpmL1rPC4vX09gSXE87qrKIo0dXMG3UQGpHD2RsVYmOv4j0gAKlGwqU7NPR6by5cgsvvreeFxZvYM7SDWxsDq7KH1CYx+SacqbUlDOlZgDvqy6nqjQeccUifY8CpRsKFHF3Fq9rYs6SjbyybCOvLd/EO2sa6bq7/tCyAiZVD2Di8DKOGF7GEcPKGDGwUCMZyWp7C5RIrkMR6QvMjLFVJYytKuET04PraZtaE8xfsZl5KzZv//nU22vo+r2rJJ7L+CElTBhaxvghJYwfUsq4wSVUlcYVNJL1NEIR2YfmtgQLVjfy5qotLFjdyNurG1mwunGnm1iWFuRuD6cxVcUcMih4jaosoihfv7dJ5tAIReQgFOXnMnXkQKaOHLi9zd1p2NrKu2u28u6aRhY1NAUnACxs4P5X6ndaf3BpnFGVRYysKGZkRRE1FYXUVBRRXV7IkLICYjka2UhmUKCIHAAzY3BpAYNLCzj+0EE7LWtqTbBkfROLG5pYtqGZJeuaWLq+mdkL13H/lpad3psXM4YOKGD4gEKqBxYyfEBhMF9ewNCyQoYNKKC8KE+706RfUKCIpFhxPJeJwwcwcfiA3Za1tHdQv3EbKzZto35jM8s3bGPlpuD1/KL1rNnSsv2kgC7x3ByGlBUwpCwehFhZnKrScLo0zqCSYL6iOF+jHYmUAkWkFxXkxTh0cAmHDi7pdnmio5OGra2s3NTCmi0trNoc/Fy9uYW1jS28tWoLsxa00NTWsdu6OQYVxflUFsepLMmnsiROZXE+lcX5DEz6WVGcz8CifMqL8siL6fY0kjoKFJE+JDeWw7ABhQwbULjX9zW1JmhobKVhayvrwp8Nja2s29rG+q2trNvayrz6Tazf2kZja2KPn1Maz6W8OI+BRfkMKMyjvCif8sK8cDr4OaAwj7Kkn2UFuZTEc7UbTnajQBHph4rjuRTHcxk9qHif721NdLCpuZ31W9vY0NTGxuY2NjW3saGpffv0xuZ2Nm9rZ/mGZjY2t7OlpZ29nQCaY8Ep1GWFeZQW5FFakEtZQe726ZJ4MF1SkEtpPJgvCduD2mOUxHMpzIspmDKIAkUkw8VzYwwpizGkrOf3L+vsdBpbE2zZFgTN9p8t7WzZlmDztnYaW9ppbEkEbS0JVmxqYWtrI40tCRpbEnTsejCoGzkGxfm5FMVjFIfBU5QfC9tyKc6PUbh9PkZRXoyi/FwK82MUhcuK8oN1CvOC+cK8GAV5MR1PioACRUR2k5Nj23d31ez77btxd1raO2lsaWdrayJ4tQQ/m9oSbG3toKk1QVO4rLm1g61twXxzWwdrGltoWtdBc1uwrKktsdvJCvsSz83ZHjBdIVOQl7NT6HS1FeQmTefFiOfFKMjN2ek98dyk5bnBfDx3x3yOAkyBIiKpZ2bBF3d+jMEp+Dx3pzXRyba2IFy2tXXQHL62tSfY1tZJc1uCbe0d25e1JDpo2f6eDlraO2lpD0JqY1P79uUtiaB9W3vHXnfz7UtezLaHTDw3h/yu0MnL2R5A+bk55MeCZfm7vG/7fNLyvK7p2I73bm9PWha02U7Logg4BYqI9Hlmtn20MLA4Py3bcHfaOjppae+ktb2D1jBoWto7aU3sCKTWxI751sSO97UlOnebbk3smN7W3sHmbe3hfPJ7OmlLdNLW0ZnS/sRyLAiZ2I4QCl7G104bz0cmD0/p9kCBIiICBKEVjDBiUJjX69vvCrS2pIBpS3TS3pEUOru0t3X4julweXtnJ+0Jp62jg/ZweVtHJ4mOzmC+o5PyNPVPgSIi0gfsFGj9lK5qEhGRlFCgiIhISihQREQkJRQoIiKSEgoUERFJCQWKiIikhAJFRERSQoEiIiIpYX4wN6/px8ysAVi6H6sMAtalqZy+LBv7nY19huzsdzb2GQ6u36Pcvaq7BVkbKPvLzOrcvTbqOnpbNvY7G/sM2dnvbOwzpK/f2uUlIiIpoUAREZGUUKD03E1RFxCRbOx3NvYZsrPf2dhnSFO/dQxFRERSQiMUERFJCQWKiIikhAKlB8xshpktMLOFZnZ51PWkg5nVmNnfzOwtM3vDzL4WtleY2ZNm9m74c2DUtaaamcXM7FUz+3M4nw19Ljez+8zs7fDv/NhM77eZXRr+255vZr83s4JM7LOZ/cbM1prZ/KS2PfbTzK4Iv9sWmNnpB7NtBco+mFkM+F/gDOAI4JNmdkS0VaVFArjM3Q8HjgG+FPbzcuApdx8HPBXOZ5qvAW8lzWdDn38GPObuhwGTCfqfsf02s2rgq0Ctu08CYsBMMrPPtwEzdmnrtp/h//GZwMRwnV+G33kHRIGyb0cDC919sbu3AXcDZ0dcU8q5+yp3fyWcbiT4gqkm6Ovt4dtuBz4aSYFpYmYjgDOBm5OaM73PZcCJwC0A7t7m7pvI8H4TPPK80MxygSJgJRnYZ3d/BtiwS/Oe+nk2cLe7t7r7e8BCgu+8A6JA2bdqYHnSfH3YlrHMbDQwFXgRGOLuqyAIHWBwhKWlw0+BbwOdSW2Z3ucxQANwa7ir72YzKyaD++3uK4BrgWXAKmCzuz9BBvd5F3vqZ0q/3xQo+2bdtGXsudZmVgLcD3zd3bdEXU86mdlZwFp3nxN1Lb0sFzgKuMHdpwJNZMaunj0KjxmcDRwCDAeKzez8aKvqE1L6/aZA2bd6oCZpfgTBUDnjmFkeQZjc6e5/DJvXmNmwcPkwYG1U9aXB8cBHzGwJwa7MU8zsd2R2nyH4N13v7i+G8/cRBEwm9/s04D13b3D3duCPwHFkdp+T7amfKf1+U6Ds28vAODM7xMzyCQ5gPRxxTSlnZkawT/0td/+fpEUPAxeF0xcBD/V2beni7le4+wh3H03w9/q0u59PBvcZwN1XA8vNbELYdCrwJpnd72XAMWZWFP5bP5XgOGEm9znZnvr5MDDTzOJmdggwDnjpQDeiK+V7wMw+RLCvPQb8xt2virai1DOzE4BngXnsOJ7wXYLjKPcCIwn+U57r7rse8Ov3zOxk4JvufpaZVZLhfTazKQQnIuQDi4HPEPyCmbH9NrMfAecRnNH4KvB5oIQM67OZ/R44meAW9WuAHwAPsod+mtmVwGcJ/ly+7u6PHvC2FSgiIpIK2uUlIiIpoUAREZGUUKCIiEhKKFBERCQlFCgiIpISChSRg2Rm/wh/jjazT6X4s7/b3bZE+iKdNiySIsnXsuzHOjF379jL8q3uXpKC8kTSTiMUkYNkZlvDyR8DHzCz18Jnb8TM7Boze9nM5prZF8L3nxw+e+YuggtJMbMHzWxO+LyOi8O2HxPcHfc1M7szeVsWuCZ8tsc8Mzsv6bNnJT3r5M7wynCRtMuNugCRDHI5SSOUMBg2u/t0M4sDs83sifC9RwOTwluGA3zW3TeYWSHwspnd7+6Xm9mX3X1KN9v6ODCF4Fkmg8J1ngmXTSV4vsVKYDbBPcueS3VnRXalEYpI+nwQuNDMXiO4hU0lwb2SAF5KChOAr5rZ68ALBDfrG8fenQD83t073H0N8HdgetJn17t7J/AaMDoFfRHZJ41QRNLHgK+4++M7NQbHWpp2mT8NONbdm81sFlDQg8/ek9ak6Q70/1x6iUYoIqnTCJQmzT8OfDF8LABmNj58kNWuBgAbwzA5jOARzF3au9bfxTPAeeFxmiqCJzAe8F1iRVJBv7mIpM5cIBHuurqN4Lnto4FXwgPjDXT/iNnHgEvMbC6wgGC3V5ebgLlm9oq7/2tS+wPAscDrBA9E+ra7rw4DSSQSOm1YRERSQru8REQkJRQoIiKSEgoUERFJCQWKiIikhAJFRERSQoEiIiIpoUAREZGU+P+ZSjJOwy8ECgAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "# 绘制学习曲线\n",
-    "loss_plot(loss_list)"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "接着我们来探究下量子版本的奇异值分解的精度问题。在上述部分，我们提到过可以用分解得到的更少的信息来表达原矩阵。具体来说，就是用前 $T$ 个奇异值和前 $T$ 列左右奇异向量重构一个矩阵：\n",
-    "\n",
-    "$$\n",
-    "M_{re}^{(T)} = U_{m \\times T} * D_{T \\times T} * V^{\\dagger}_{T \\times m}\n",
-    "$$\n",
-    "\n",
-    "并且对于一个本身秩 (rank) 为 $r$ 的矩阵 $M$, 误差随着使用奇异值的数量变多会越来越小。经典的奇异值算法可以保证：\n",
-    "\n",
-    "$$\n",
-    "\\lim_{T\\rightarrow r} ||M - M_{re}^{(T)}||^2_2 = 0\n",
-    "$$\n",
-    "\n",
-    "其中矩阵间的距离测量由 2-norm 来计算,\n",
-    "\n",
-    "$$\n",
-    "||M||_2 = \\sqrt{\\sum_{i,j} |M_{ij}|^2}\n",
-    "$$\n",
-    "\n",
-    "目前量子版本的奇异值分解还需要很长时间的优化，理论上只能保证上述误差不断减小。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 10,
-   "metadata": {},
-   "outputs": [
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEKCAYAAAAfGVI8AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAABGDUlEQVR4nO3dd3iUZdbA4d9JIyGUUALEANIJJZBAFBUQsCAqICKgrAWsa1l3VxZX1F1ld79dG/Z17aJiQWxgb1QBAem9iATphJJAIIGQnO+PZxKSkDIhZZLMua9rrsy8M/POmRDmzNPOI6qKMcYY/xXg6wCMMcb4liUCY4zxc5YIjDHGz1kiMMYYP2eJwBhj/FyQrwM4HQ0bNtQWLVr4OgxjjKlSlixZsk9VI/Mfr5KJoEWLFixevNjXYRhjTJUiIlsLOm5dQ8YY4+csERhjjJ+zRGCMMX6uSo4RGFNZ7N27l7Fjx7J+/XqysrJ8HY4xBAQEEBMTw4QJE2jUqJFXz7FEYEwpjB07ln79+vH6668THBzs63CMISMjg0mTJjF27Fjefvttr57jN11DU5ftYPAjH7HwoR4MeuRjpi7b4euQTDWwfv16rrvuOksCptIIDg7m+uuvZ/369V4/xy9aBFOX7eD+T1bxgL7PWYEbGH7kPe7/JByAIfHRPo7OVGVZWVmWBEylExwcXKKuSr9oETzx7QZqZexjeOBsAkQZHjiHWhn7eeLbDb4OzRhjfM4vEsHO5DT+GPQpgbgMGUgmdwd9ws7kNB9HZkzpBQYGEhcXR+fOnRk0aBDJyck+i2XWrFnMnz+/zM43depU1q5dm3P7oYce4ocffiiz8+f32Wef8eijj3r12CNHjtCgQQNSUlLyHB8yZAhTpkwBXPxdunQhJiaGzp0789FHH+U8bsGCBfTo0YO4uDg6dOjA+PHjSUxMpGnTpqd8m4+Li2PRokWMHz+e6Oho4uLiaNu2LUOHDs3z+zldfpEIYuumMTxwNsGSCUCIZDI8cA6d66b7ODLjb6Yu20HPR2fQctyX9Hx0RpmMVYWFhbF8+XJWr15N/fr1eeGFF8og0tNTVCI4ceJEic+XPxH885//5KKLLjrt+IozePBgxo0b59Vjw8PD6d+/P1OnTs05lpKSwty5cxk4cCArVqxg7NixTJs2jfXr1/P5559z3333sWTJEgBGjRrFK6+8kvNvN2LECFq0aEGzZs348ccfc865fv16Dh8+zNlnnw3APffcw/Lly9m0aRNXX301F1xwAUlJSaV6336RCJ6J+h4h705sAWTxbNR3PorI+KPssaodyWkosCM5jfs/WVWmExfOPfdcduxw59u8eTMDBgyge/fu9O7dO2fwcM+ePVx55ZV07dqVrl275nxwP/XUU3Tu3JnOnTvzzDPPAJCYmEiHDh249dZb6dSpE/379yctzbWkn3vuOTp27EiXLl245pprSExM5KWXXuLpp58mLi6OH3/8kdGjRzNmzBj69evHfffdx/jx45kwYUJOvJ07dyYxMRGAt99+my5dutC1a1euv/565s+fz2effca9995LXFwcmzdvZvTo0TnfqqdPn058fDyxsbHcdNNNHDt2DHAlaB5++GG6detGbGxsgYOmPXr0YM2aNTm3+/bty5IlS3jzzTf5wx/+AMDnn39Ojx49iI+P56KLLmLPnj2nnGfkyJFMnjw55/ann37KgAEDqFmzJhMmTOCBBx6gZcuWALRs2ZIHHniAJ598EnBTj6OiogDXquvYsWOB55w8eTIjR44s8N/76quvpn///rz33nsF3u8tvxgsbpW+BiTvt5EacsIdN6YMXf3yT4Xet+y3ZI5n5m3yp2VkMv7zNQyJj+bAkePc8c6SPPd/8PtzvX7tzMxMpk+fzs033wzAbbfdxksvvUTbtm1ZuHAhd955JzNmzOCPf/wjffr04dNPPyUzM5PU1FSWLFnCxIkTWbhwIapKjx496NOnD/Xq1WPTpk28//77vPrqq4wYMYKPP/6Y6667jkcffZQtW7ZQo0YNkpOTiYiI4Pbbb6dWrVqMHTsWgNdff52NGzfyww8/EBgYyPjx4wuMfc2aNfz73/9m3rx5NGzYkAMHDlC/fn0GDx7MwIEDGTZsWJ7Hp6enM3r0aKZPn067du244YYbePHFF/nzn/8MQMOGDVm6dCn/+9//mDBhAq+99lqe519zzTVMmTKFf/zjH+zatYudO3fSvXt3Vq1alfOYXr16sWDBAkSE1157jccffzznQzzbgAEDuOWWW9i/fz8NGjRg8uTJ3H333TnvKfv3kC0hIYHnn38ecN/s27dvT9++fRkwYACjRo0iNDSUESNGEB8fz/PPP09QUBAffPABH374YaH/7t26dSvRDKGC+EWLgNvnwvgUGJ9C1oNJ7JN6/BxyljtuTAXJnwSyJR/NKNV509LSiIuLo0GDBhw4cICLL76Y1NRU5s+fz/Dhw4mLi+P3v/89u3btAmDGjBnccccdgPsmWrduXebOncuVV15JeHg4tWrVYujQoTndEy1btiQuLg6A7t2753yD79KlC9deey3vvPMOQUGFf6ccPnw4gYGBRb6HGTNmMGzYMBo2bAhA/fr1i3z8hg0baNmyJe3atQNcN8ucOXNy7h86dOgp8eY2YsSInA/XKVOmMHz48FMes337di655BJiY2N54okn8rQgsoWEhDB48GA++ugj9u3bx/Lly+nfvz8AqoqI5Hl87j3iH3roIRYvXpzzjX7AgAEANGnShE6dOjF9+nSWL19OcHAwnTt3LvR3URb7zvtFiyC3gOAQ1nT6K28sTWbMtmS6NovwdUimGinqG3zPR2ewo4AJCtERYQDUDw8pUQsgW/YYQUpKCgMHDuSFF15g9OjRREREsHz5cq/OUdSHSY0aNXKuBwYG5nQNffnll8yZM4fPPvuMf/3rXwV+UILrS88WFBSUZyA0PT095/Xzf2iebry5Yw4MDCxwbCI6OpoGDRqwcuVKPvjgA15++eVTHnP33XczZswYBg8ezKxZswptzYwcOZL/+7//Q1W54oorcqYTd+rUicWLF9OlS5ecxy5dupSEhISc261bt+aOO+7g1ltvJTIyMqdlkd091Lhx40K7hbItW7YszzlPR4W2CEQkQkQ+EpH1IrJORM4Vkfoi8r2IbPL8rFfecXQbeCuLg7rx9k8FVmQ1plzce0l7woLzfjMOCw7k3kval8n569aty3PPPceECRMICwujZcuWOd96VZUVK1YAcOGFF/Liiy8Crjvp0KFDnH/++UydOpWjR49y5MgRPv30U3r37l3oa2VlZbFt2zb69evH448/TnJyMqmpqdSuXZvDhw8X+rwWLVqwdOlSwH0obtmyJSemKVOmsH//fgAOHDgAUOj5YmJiSExM5JdffgFg0qRJ9OnTp0S/r2uuuYbHH3+clJQUYmNjT7k/JSWF6Gi3zuitt94q9Dz9+vVj06ZNvPDCC3k+tMeOHcsjjzyS0yJJTEzkmWee4d577wVcIs1OaJs2bSIwMJCIiAgArrrqKr766is++OADrrnmmkJf++OPP+a7774rNlkUp6K7hp4FvlHVGKArsA4YB0xX1bbAdM/tclU7NJgbOwfRYvWz7E9JLe+XMwZwixcfGRpLdEQYgmsJPDI0tkwXNcbHx9O1a1cmT57Mu+++y+uvv07Xrl3p1KkT06ZNA+DZZ59l5syZxMbG0r17d9asWUO3bt0YPXo0Z599Nj169OCWW24hPj6+0NfJzMzkuuuuIzY2lvj4eO655x4iIiIYNGgQn376ac5gcX5XXXUVBw4cIC4ujhdffDGna6dTp048+OCD9OnTh65duzJmzBjAfVg/8cQTxMfHs3nz5pzzhIaGMnHiRIYPH05sbCwBAQHcfvvtJfpdDRs2jMmTJzNixIgC7x8/fjzDhw+nd+/eOV1WBQkICOCqq65i//79nH/++TnH4+LieOyxxxg0aBDt2rWjXbt2vPjii7Rv7xL/pEmTaN++PXFxcVx//fW8++67OV1oERERnHPOOTRu3DhnsDlb9mB827Zteeedd5gxYwaRkafsNVMiUhb9S169kEgdYAXQSnO9qIhsAPqq6i4RiQJmqWqRX5ESEhK0tBvT7Fg0leivRjG765P0ufKWUp3L+K+EhATbJMl4Zdy4cSxcuJBvv/2WkJCQcn+9gv42RWSJqp7Sj1SRLYJWQBIwUUSWichrIhIONFbVXQCenwWWyxOR20RksYgsLu2cWYDohEEcrxXN+Yc+K/W5jDGmOI8++igzZ86skCRQUhWZCIKAbsCLqhoPHKEE3UCq+oqqJqhqQmmbQQAEBBJy9o3Iltmw75fSn88YY6qoikwE24HtqrrQc/sjXGLY4+kSwvNzb4VFFH89mRLId5O8W1JujDHVUYUlAlXdDWwTkez+/wuBtcBnwCjPsVHAtIqKidpN2NKoP6GSQUYhc7yNMaa6q+h1BHcD74pICPArcCMuGU0RkZuB34BTV3aUoza3v0+bEsxfNsaY6qZCE4GqLgcKWvlwYUXGkYcnCWzesJJGZ3agdqjVljfG+Bf/KDFRjN1z36b1+735YfYsX4diTIlZGeqyU5Iy1ABHjx7l2muvJTY2ls6dO9OrVy9SU1Pp27cv3377bZ7HPvPMM9x5550kJiYSFhZGfHw8HTp04Oyzzy5ywVpFsEQANIm/nOMEo4snkpVVMesqjB87vBsmXgqHT61meTqsDHXZKUkZanCL8xo3bsyqVatYvXp1zt7V+SuIQt4qoq1bt2bZsmWsW7eOyZMn8/TTTzNx4sQyfS8lYYkAILwBe5oO4KLjM5i3/jdfR2Oqu9mPw28LYPZjZX5qK0NdsWWod+3alVOGAqB9+/bUqFGDYcOG8cUXX+TElJiYyM6dO+nVq9cp52jVqhVPPfUUzz33XHH/vOVHVavcpXv37lrWjv86T/XhOvrGc/8o83Ob6uuUv8U3Ljv1svAVd9+xI6qvXKQ6PkL14Tru56sXqS59x92fuu/U53ohPDxcVVVPnDihw4YN06+//lpVVS+44ALduHGjqqouWLBA+/Xrp6qqI0aM0KeffjrnOcnJybp48WLt3Lmzpqam6uHDh7Vjx466dOlS3bJliwYGBuqyZctUVXX48OE6adIkVVWNiorS9PR0VVU9ePCgqqo+/PDD+sQTT+TENmrUKL388sv1xIkTBd7fqVMn3bJli65evVrbtWunSUlJqqq6f//+nOd/+OGHec734YcfalpamjZt2lQ3bNigqqrXX399zns688wz9bnnnlNV1RdeeEFvvvnmU35nTz31lD700EOqqrpz505t27atqqpOnDhR77rrLlVVPXDggGZlZamq6quvvqpjxow55TzLli3TyMhIPeecc/TBBx/M+X2rql522WU6depUVVV95JFHdOzYsaqqumXLFu3UqVOe8xw8eFBDQ0NPOX9pFPQ5CSzWAj5TrUXgEdziXPbVbE2npC/5bf9RX4djqquU3yC7wooqJJe+BWplqH1XhjouLo5ff/2Ve++9lwMHDnDWWWexbt06IO8GM0VtLgNlU0q6NPyuDHWhROCq17j19V8ZsSCRBy/v6OuITFV045eF33fsEKQnQ85ueeput/H0eYc3KPr5hbAy1IXHXBFlqLMT59ChQwkICOCrr76iQ4cODBkyhDFjxrB06VLS0tLo1q1bofEuW7aMDh06FPmeypO1CHJp2LobvTq14oOft5F2PNPX4ZjqZvbjoPkWLmpWmY0VWBnqii9DPW/ePA4ePAjA8ePHWbt2LWeeeSbgEkTfvn256aabimwNJCYmMnbs2JydzXzBEkE+f2i1mzey/sZXP5du6zdjTrF9EWQez3ss87g7XkasDLX3yqIM9ebNm+nTp0/O7yEhIYGrrroq5/6RI0eyYsWKU/YU2Lx5c8700REjRnD33Xdz4403lij+slRhZajLUlmUoS6M7liKvNqP+e3Hcd7I+8vlNUz1YWWoTWVVWctQVwkS3Q2NiuO8g5+dHNQzxphqzBJBASThJti7lt+Wz/R1KMYYU+4sERSk81UcCwxn6SdPsjsl3dfRmEosICCAjIwMX4dhTB4ZGRkEBHj/8W6JoCA1anH0vL8SlTCIiJpWhM4ULiYmhkmTJlkyMJVGRkYGkyZNIiYmxuvn2GCxMaWwd+9exo4dy/r16/PMjzfGVwICAoiJiWHChAk0apR359/CBottQVkRjh/ax8Iv3yAj7gYu6NDE1+GYSqhRo0a8/fbbvg7DmFKxrqEiBP36Pb03/JtZ337s61CMMabcWCIoQkCnIaQH1+Xs/dNYtT3F1+EYY0y5sERQlOAwJO53XBKwmE/nLPF1NMYYUy4sERSjRo9bCJZMaq2bzIEjx4t/gjHGVDGWCIrTsA1HonvTTHfxwc/bfB2NMcaUOUsEXgi/8WM+af4g7yzYSqZtZWmMqWYsEXgjqAajzjuTw8n7mL6ubPaZNcaYysISgZcuPjGbxaF38MWPZVcy2BhjKgNLBF4KPPNcgslkTIMFvg7FGGPKlCUCb9U7E2l7MS22fgyZVlfGGFN9VGgiEJFEEVklIstFZLHnWH0R+V5ENnl+1qvImEok4SZI3c2nH7zG4XRLBsaY6sEXLYJ+qhqXq/DROGC6qrYFpntuV05t+3M8/AwarH+XnxMP+DoaY4wpE5Wh6NwVQF/P9beAWcB9vgqmSAGBhAx7hY4hZ9AwurGvozHGmDJR0S0CBb4TkSUicpvnWGNV3QXg+dmooCeKyG0islhEFiclJVVQuAVo2ZuG0a0ByMi0ssPGmKqvohNBT1XtBlwK3CUi53v7RFV9RVUTVDUhMjKy/CL0xrafWf7kFfzxHZtBZIyp+io0EajqTs/PvcCnwNnAHhGJAvD83FuRMZ2WY4eIOzyL4I1fsu3AUV9HY4wxpVJhiUBEwkWkdvZ1oD+wGvgMGOV52ChgWkXFdNpa9eNE3RZcG/gD7yzc6utojDGmVCqyRdAYmCsiK4BFwJeq+g3wKHCxiGwCLvbcrtwCAgg6+yZ6BKzn50XzSc/I9HVExhhz2iosEajqr6ra1XPppKr/9hzfr6oXqmpbz8+qMS8z7lqyAkIYlPEtny3f6etojDHmtJUoEYhIgohc7enaye7uqQxTUCteeEPk3DtJrdWSN+cnompVSY0xVZNXiUBEGovIQlyXznu4bh6Ap4Anyym2Sk8u/gf1+93J2l2HWPrbQV+HY4wxp8XbFsHTwG6gAZB7msyHuEFfvzWkcwMGhi7nrfk2aGyMqZq8TQQXAg+qav6vvZuB5mUbUtUSvuZ9/svj7NmwgKPHT/g6HGOMKTFvE0EYUNCGvZFAetmFUwXFDkODwni761pqhvjncIkxpmrzNhHMAUbnuq0iEoirCTS9rIOqUsLqIZ2vosbaj9H0FLJsK0tjTBXjbSL4K3CriHwP1MANEK8FegL3l1NsVUfCTZBxhBeee5QvVu3ydTTGGFMiXiUCVV0LxALzge+AUNxAcbyqbi6/8KqI6G5oky6cLWsJCw70dTTGGFMiXndqq+pu4OFyjKXqEkGun8rZNeuDiK+jMcaYEvF2HcEfROS6Ao5fJyJ3ln1YVVB4AxAh9Wga83/Z5+tojDHGa96OEfwZ2FbA8UTgnrIKpspb9RE8FcOf35xJ8tGCJlkZY0zl420iaAoUtGJqu+c+AxDZnlonkhmos/ng54LypjHGVD7eJoLdQFwBx7sB1g+SrUksND2Lm0NnMumnRDJtKqkxpgrwNhG8BzwnIheLSLDn0h94Bni33KKrihJuIjpzO00PLWXm+sq/x44xxnibCB4G5gHf4moNHQW+xk0n/Xv5hFZFdboSDa3LzaEzeeunRF9HY4wxxfJq+qiqZgAjReQhIN5zeKmq/lJukVVVwWHIoOfY90sQP/60j81JqbSOrOXrqIwxplAl2o9AVTep6hTPxZJAYToN4aILLiYkMIBJP1lVUmNM5eb1gjIRuRpXhbQR+RKIqg4u47iqvMgjG3m10Uf8Yckwxl7Snlo1rCCdMaZy8nZB2RPAO0ALIBnYn+9i8tu3kT4HP+Lahr+wP/WYr6MxxphCefs19QZgpKp+VJ7BVCsxg6BmQ8ZFLoAGd/s6GmOMKZS3YwQBwPJyjKP6CQqBbtfDhq9J2vErW/Yd8XVExhhTIG8TwSvAKbWGTDG6jQLN5NPXH+WRr9b5OhpjjCmQt11DEcDvRORiYCWQkftOVf1jGcdVPdRvCbHDuTCgGZec38HX0RhjTIG8TQQdOdk1FJPvPqujUJSrXqO1r2MwxpgieLugrF9ZvaBni8vFwA5VHSgi9YEPcDOSEoERqnqwrF6vUsjK4peV83h+fS0eu6oLobZ5jTGmEinRgrIy8icgd4f5OGC6qrbF7X88zgcxla8FL9B66iCWrljG5yt2+joaY4zJw+tEICL9ROQVEflGRGbkvpTgHE2By4HXch2+AnjLc/0tYIi356syOg0FEe6sPZe3fkpE1XrTjDGVh7cLykbjiszVBvoCSUA9XBnqtSV4vWeAvwJZuY41VtVdAJ6fjQqJ4TYRWSwii5OSkkrwkpVA3Wik3aVcyQw27DjAsm3Jvo7IGGNyeNsiGAv8QVVH4mYM3a+q8bjVxqnenEBEBgJ7VXXJ6QSqqq+oaoKqJkRGRp7OKXwr4SZCjx/kihpLeWt+oq+jMcaYHN4mglbAD57rx4Dscpr/BUZ7eY6ewGARSQQmAxeIyDvAHhGJAvD8rJ5F/FtfABHNubHeCr5atYu9h9N9HZExxgDeJ4L9uG4hgB1AZ8/1BkCYNydQ1ftVtamqtgCuAWao6nXAZ8Aoz8NGAdO8jKlqCQiA66cSNvJNMjKVyYtsK0tjTOXgbSL4EejvuT4Ft1vZROB94PtSxvAocLGIbAIu9tyunhq0plXjCM5v25B3F24lIzOr+OcYY0w58zYR/AH3oQ/wCPAErjUwBbilpC+qqrNUdaDn+n5VvVBV23p+Hijp+aqUNVP536E/kHzoMN+t2ePraIwxxusFZQdyXc8CHiu3iKq7mg2olbKR17tvo2Pry30djTHGeD19NFNETpnWKSINRCSz7MOqxlr0ggZt6ZXyOfXDQ3wdjTHGeN01JIUcrwEcL6NY/IMIJNwI2xcxZ85MXpmz2dcRGWP8XJFdQyIyxnNVgdtFJPeagUCgN7C+nGKrvrqOhB/+QfDyN5mqt3BLr1YEBBSWa40xpnwVN0aQvbWW4AaFc3cDHccVibu97MOq5mrWh/7/R1y9tnzRppclAWOMTxWZCFS1JYCIzASGVruqoL7U47acBRhpxzMJCQog0BKCMcYHvBojUNV++ZOAiLQRkdDyCctPHPiVPd88zjn/+YHZG6vngmpjTOXn7ayh/4jIKM91EZEfgI3ALhHpUZ4BVmubZ9B4wb+JD/yVt+Zv9XU0xhg/5e2soWuBDZ7rlwJdgXOAt6nOK4HLW+wICA7n3gbzmL0xiV+TvKrfZ4wxZcrbRNAY2O65fhkwRVUXAc8D8eURmF8IrQNdhtPxwA80CDzCpAXWKjDGVLySFJ0703O9P5C9GU0Qha8xMN5IuAk5kcYD0Sv5aPF2jhw74euIjDF+xttE8DHwnoh8D9QHvvEcjwN+KYe4/EdUVzizJ+dGCYePneDTZTt8HZExxs94VWsIGANsBZoDf1XVI57jUcCL5RGYXxn1BVEidN4+l7d/SuTaHs0RsYaWMaZieFt07gTwZAHHny7ziPxRQAAC/D6uBnd/mcRPv+7nvNYNfR2VMcZPFNo1JCLdRCQg1/VCLxUXbjU27zkGzrqcVmFHmffLPl9HY4zxI0W1CBYDTXBbRy7G1RsqqL9CcXWHTGm07Y98/3c+P/83wi8Y7utojDF+pKhE0BJIynXdlKdGMdD8PMJXTYK+93A8C0KCvB3LN8aY01foJ42qblVVzXW90EvFhVvNJdwEB7fw7ReT6fPETNIzbKsHY0z582qwWERaAUOAVriuoF+Baar6a/mF5oc6DoZvGtD9wJe0jrybfhNmsTslnTMiwrj3kvYMiY/2dYTGmGqo2EQgIn/B7VMciBsvECASeExE7rOZQ2UoqAb8bgoLdtZhyee/kuZpEexITuP+T1YBWDIwxpS5IjuhRaQn8Dhus/pIVY1S1SZAI9x00ic8jzFlpWkCj8zYnpMEsqVlZPLEtxsKeZIxxpy+4kYj7wTeVtUH821gv19V7wfe8TzGlKGYQ/N4M/gxAsjKc3xncpqPIjLGVGfFJYJzgDeLuP9Nz2NMGWocHkDfwBVcETCXD0L+SSTJgBucGTNlOat3pPg0PmNM9VJcImiCGxguzGZcmQlThnoMuJa9Wo+/BH3IWbKBu4M+oUZQAL3bNOCb1bsZ+Pxchr80ny9X7uJEZlbxJzTGmCIUlwjCgGNF3H8cqOHNC4lIqIgsEpEVIrJGRP7hOV5fRL4XkU2en/W8C736uqJ7C1JaDyI6YD8BoowImsMzl0cx6ZZz+On+C/nb5R3YfSidu95byrJtyb4O1xhTxXkzffRyESmsLyKiBK91DLhAVVNFJBiYKyJfA0OB6ar6qIiMA8YB95XgvNVS21on829oIFy6/20gjrphwdzSuxU39mzJ/M37SDjT5c1HvlrHsRNZPDyooxWsM8aUiDeJ4PVi7ldvXsizOC17C65gz0WBK4C+nuNvAbPw90RweDesnXbyduZxWP4u1G4CPX4PoXUJDBB6t43MecjxzCyOZ2blJIGfEw/QvXk9AgIsKRhjiiaexcMV82IigcASoA3wgqreJyLJqhqR6zEHVfWU7iERuQ24DaB58+bdt26txguavxgDyya5BJAtIAiyTkBoBPT8k0sIIeF5nqaqiAird6Qw8Pm5tGwYzqhzz2RYQjNq1fC24rgxproSkSWqmpD/eIUWs1HVTFWNA5oCZ4tI5xI89xVVTVDVhMjIyOKfUJVtX5Q3CYBLAg3aQLOzYfo/4Nk4WPASnDj5uOzWQPsmtXluZDwRNYMZ//lazv3PdP75+Vq27j+CMcbkV6EtgjwvLPIwcAS4FeirqrtEJAqYparti3puQkKCLl68uCLCrJx+WwAz/g8O7YS7FkFg4d/2l29LZuK8LXy5cheZqlwY04gbe7bkvNYNbCzBGD9TWIugwhKBiEQCGaqaLCJhwHfAY0AfYH+uweL6qvrXos7l94kAQBWOHoDwBnAsFd4ZCgk3Q+wwCDi1KvieQ+m8s2Ar7y38jf1HjnN2y/p8cNs5lgyM8SOFJYKK7DiOAt7yjBMEAFNU9QsR+QmYIiI3A78BVozfGyIuCYAbXM44Cp/eBnOfgn4PQMwgCDjZ89e4Tih/6d+eu/q14fMVO0nLyEREyMpSXp7zK0PizyCqbpiP3owxxpd81jVUGtYiKEBWFqybBjP/A/s2QpMuMOozCCt6WcbqHSkM/u9cnhoRx5D4aE5kZhEYINZSMKYaqgwtAlOeAgKg05XQYTCs+hC2zHEzjAAObIH6Be8t1Dm6LrPv7UfjOqEAvPrjFr5atYsbe7bg8i5R1AiyzeeMqe68mjUkIvVE5FkRWSkiu0Vkb+5LeQdpSiAgELpeA0P+57qPDu2EF3rAW4Nh288FPqVZ/Zo5u6GdERHK0eMnGDNlBT0fnckzP2wk6XBRi8uNMVWdV11DIvI50Am34GsP+RaRqerL5RJdIaxrqAQy0mHxG/Djk3B0H7QbAP0ehKguhT4lK0v58Zd9TJy3hVkbkggJDGBg1yhu6tmSztF1KzB4Y0xZKtWsIRE5DPRR1aXlEVxJWSI4DcdSYdHLMO9Zd/2eNVCn+HqBm5NSeWt+Ih8t2c7R45mc1aIefx0Qw1kt6ldA0MaYslTaMYLNVPDiM1PGatSC3n9xU0y3zD6ZBBa9Cm0uKnQMoXVkLf55RWf+0r89Hy7expvzEzmW4SqeHjhynACBWRuSeOLbDexMTrNtNY2pgrxtEfQB/gaMBVarqk93VbcWQRk5vAee7QpZGRB/PZx/L9Qt+gM8M0sJELeK+V9frOWdBYmICOkZJ8thhwUH8sjQWEsGxlQypS0x8QuuJPVS4LiIZOa+lGWgpgLVbgx/XAbdR8Oyd+C5ePjmfrdQrRC5p5YOT2hKWHBQniQAblvNR75eR1ZW1ZuabIw/8rZFMAeoB7xEwYPFH5dLdIWwFkE5OLgVZj8O6z+Hu5e5xWqqbuZREVqO+7LQ8rO1Q4Po0rQusdERdGlaly5N6xIdEWZrFIzxkdKOESQAZ6vq6rINy1Qa9c6EIS9A+n8gtK5LApOGwJk94Zw7oEbtAp92RkQYOwrYSzkiLJjLu0SxcnsKr8/9lYxMly5u79OacZfGcPxEFrM3JnFWi3pE1Awpz3dmjCmGt4lgLVCnPAMxlUSoZ3roscMQUgtm/hsWvgS97oGzboHgvGUo7r2kPfd/soq0jJM9hGHBgYwf3ClnjODYiUw27D7Miu0pdIxyf0Ybdh/m1rcX89/fxTOwyxn8sjeVr1ftokuzCLpE16VeuCUHYyqKt11DA4DxuAHjVUBG7vtVtfBO5XJgXUMVaMcSV+l08wyo1QSu/wQad8rzkKnLdpR41lB6Riard6TQplEtImqG8PGS7fzlwxU59zerH0YXT5dSbNO6dI6uS53Q4HJ5i8b4i9KuI8g9Gpj7CYLbfKxC6xBYIvCBxHnw86tw5csQVAP2b4aIM4ssgV1Sh9IzWL0jhVXbU1i5PYWVO5LZduBkt1OryHDeu+UcmtQNZX/qMcJCAqkZYlVSjPFWaccI+pVxPKaqadHTXQBOHHMlK4JDoe/90GkoHNkLH90Iw950s5FOQ53QYM5r3ZDzWjfMOXbgyHFW7Uhh5bZk1u46RMNarsvomR828dmKnSx/6GJEhJ8276dmSCAxUbWtPpIxJVRsiyB7o3ngBlXdUCFRFcNaBD6mCuu/dOMHe9dCo05ugdrmGdD9Rhj4VLmHsGjLAbbsS+Xqs5oDcNmzP7J21yGCA4WYJnWIbVqXLtF16dI0graNaxEceHKm9Ol0ZRlTHZS2a2gv0EtVN5ZHcCVliaCSyMqCNZ/A9H9CsmcP6aBQ+NPK024VnK4dyWms3JbMyh0prNyezMrtKRxOPwFAjaAAOp1Rh8tio2hYq0aBg9u2AM74g9J2Db2F21Ly3jKNylRtAQFuR7TEubBskttXWbPg/auh6VmuddC4Y4WEEh0RRnREGJfGutIZWVnK1gNHWbk9OWfMYe/hY0ycl5gnCYBbAPfQNDcz+oyIMM6ICKVxndA8rQhjqjNvWwT/A64FtgBLcHsN51DVP5ZLdIWwFkElcni3K1NxIv3kMQkECXClK5qfCwk3uX0SgkN9F6dHUQvgcgsQaFQ7lDMiQj3JIYzLYqOIaxbB8RNZpB47Qb2awbY4zlQppW0RdMCVlwBole8+qyPgz2Y/7loBuQUEQuwIaBTjSmB/cit0nw+DnvFJiLkVtgAuqm4ok27uwc7kNHalpLEjOT3n+pqdh/hu7R7aNa5NXLMI1u46xJAX5vHaDQlc1LExy7cl897CrS5h1A3LaVWcERFGaLANXJvKz6tEoKo2a8gUbPsiyDye91jmcdi9wq1UPucuSJwDtTxjBrtWwvd/d1VQ218KgRW7NqCwBXD3DYihTaNatGlUq8DnqSqZntpJTeqE8tDAjnSKdovjdqekMXtjEnsPHyN/A7t+eAhnRIQSVTeMcZfG0DqyFrtS0tiZnE5sdN2cDYEKYwPbpiKUaBK2iIQCbXCtgM2qml7MU0x1d/vcou8PCIBWfU/ePrwb9v0CU653C9S63eAuEc3KNcxs2R+iJf1wFRGCAl03UJO6odzU62TZ7gGdoxjQOYrjJ7LYcyidHclpntbEyetb9x8h0NON9NWq3fzri7Us+/vFhASF8PrcLXy7endOKyIqIozoiFDW7z7Mc9M35RT125Gcxv2frMrzPowpC96OEQQD/wH+AITgFpIdA54HHlTVjCKeXuZsjKCKy8qETd+7bqNN30FoHRi7yS1U8wN7DqWzduch+raPRER4d+FWpi3fya6UNHYlp3OimKqt0RFhzBt3QQVFa6qT0k4ffQoYCYzDrSkA6A08AryrqmPLMNZiWSKoRg5uhT1rIOYytz7hvRHQrIfbH6GCp6BWBplZyr7UY+xMTuPK/80v9HG39GrJ3wZWzIwsU32UdrD4d8BNqvpVrmObRSQJeA23YY0xJVfvTHcBSE92s49m/AtmPQIdBrkZRy16F1sOu7oIDBAa13HTV6MLGdgODwnM+XWoKrdNWkKX6Lr0i2lEx6g6BAT4x+/KlB1vE0Fd3HaV+W0GIsosGuPfwurBqM9h3yZY8qbbLGfNpzBiEnQc7OvoKlxhA9v/vvLk4rfkoxnsPZTOk2v38OT3G2lYqwZ920fSt30kvdtGUjfMCvWZ4nnbNbQAWKKqd+U7/iIQp6rnenGOZsDbQBMgC3hFVZ8VkfrAB0ALIBEYoaoHizqXdQ35iYw0WPsZdBrixg8WvAi7VrhWQtOz/KKV4O2soX2px5izMYmZG5KYszGJlLQMAgOE7s3r0ad9JFfGR3NGRFgBr2D8SWnHCM4HvgJ2Aj/hZg2dC5wBXKqqxUwdARGJAqJUdamI1MYtTBsCjAYOqOqjIjIOqKeq9xV1LksEfmr2EzDvGTieCo07Q8KNbr1CqG2VkduJzCxWbE9m5vokZm3cy+odh5jy+3M5u2V9Nu45zOa9qVzQoZEV5/NDpUoEnhOcAdwFxOBmDa0F/qeqO08zoGnAfz2Xvqq6y5MsZqlq+6Kea4nAjx07DKs+gsWvw+5V0P5yGPmer6Oq1PYeSqd+eAhBgQE88vU6Js5NZPnDF1MzJIglWw9Qq0Yw7RrXslXSfqDUiaCMg2kBzAE6A7+pakSu+w6qar0CnnMbcBtA8+bNu2/durVigjWVkyrsWOrWKZwRD8nb4KOboPto6HQlhNT0dYSVUkZmFpuTUolp4lpRQ16Yx/JtyZxRN5Q+7RvRr30kPds0JLyG7fNQHZ1WIvD03xerJDuUiUgtYDbwb1X9RESSvUkEuVmLwJxi2yKYdhfs2+i22+z6O9d1FFlk49Lv7UpJY/aGJGZu2Mu8X/aTeuwEIYEBnNWyHv3aN6Jv+0haR1probo43USQRfG1hFRVvfr64FmY9gXwrao+5Tm2AesaMmVBFbbOcwvV1n4GqFuoVtOr7zN+7/iJLBZvPcCsDUnM2rCXjXtSAbixZwseHtQJVSU9I4uwEBtbqKpOdx1BUTWGBgB/Ak54GYAArwPrspOAx2fAKOBRz89p3pzPmFOIQIte7pKaBL/9dDIJfHQTRDR3XUf1WrhSF6XcUa26CQkKyNkh7oHLOrD94FFmb0yiTaSrv7Q56QiXPfsj/7u2Gxd1bExmlhIg5GktWG2kqqnEYwQi0g14DDgfeBn4l6omefG8XsCPwCrc9FGAB4CFwBSgOfAbMLy4riZrEZgSOXHcfehv+Mq1Gtpc6H7+OrPCdlSrDrYdOMpb8xO5sVdLoiPC+ODn33hh5mb6tY+kb0wj9h0+xkPT1timP5VYWcwaagn8GxgOfAI8oKoFLTIrd5YIzGlJ2eE20Pn5DTiyxx0LCoU7F0B4Q6hR27fxVTGzNybx9vxE5m3el1MYryBWG6nyOO0SEyLSAHgIuB2YB5yrqvYpbKqeutHQd5zrFsq9o9q0P8D2n12V1JjLof1lUCvS19FWen3aRdKnXSTpGZks3HKAUW8sKvBxOz1lMmZt2EtIYADntWlYkWEaLxSZCETkAeCvuBW/V6jqNxURlDHl5vBuWPG+SwLg9k7Y/jN0HQm/zoBN38Lnf3I7q13/CQTbatzihAYH0qddZKG1kbJXND/zwyZqhgTmJILb3l5McGAArSPDad2oFq0ja9EqMpyaITZ1taIV9xv/PyAN2A7cKSJ3FvQgVfW/QjCmaipoRzXU7ar2p5Vukdr6L2H/LyeTwHd/g+Bw11poEusXpS1OR2G1ke69xE0CnDj6LFKPuQSsqgSIsGZnCl+v3kXuytvREWG0igynTaNa9G7bkAtibDC/vBWXCN7GtqI01UlhO6ptX+Q+4KO6uEs2Vdi7Dn6ZDrMfdTOPYgZC7HCI7laxsVdyxW36Uy88hHrhIYCbafTS9d0BOHYik8R9R9mclMrmvanuZ9IRPvh5G6pwQUxjMjKzOOc/0/nzxe24/pwzSTueyY+bkmjTqBbN69ckKLDond5M0YpMBKo6uoLiMKZiFLejWn4icN3Hbjrqxq9da+Hn1yGklksEGelu9lGrvtaNhEsGJZ0hVCMokPZNatO+Sd7BelXl2AnXekvLyOSy2ChaNHArxjfuOcxtk5YAEBwonNkgnNaeVkTryJPdTLVDC6++alNdT/JJiYnSsllDxqeOHYbMDLdGYeO3bjOd4HA3LTVmILTr70pqm3KTnpHJ+t2Hc1oQv3h+bt1/NM8Ob/+7thuXxUbx2/6jzNywl4FdomhQqwZTl+0osBuruk91Le3GNMaYbLmnmbbqB9d94loK67+EdZ9BQBDcMd+Vt8jKcvWQTJkKDQ4krlkEcc0i8hzPyMzitwNHcxJD5zPqAvBz4gEe/mwN57eLpEGtGoz/LO96B3Ctjke+XsflXaII9rOuJmsRGFNWsrJgxxLYPB3O/6tLAF/+BXYucy2FmIEQ2c7XUfolVSXp8DEa1KpBYIDQYtyXhT42QKBxnVDOiAjjjVFnUbdmMKt3pLAv9Rh92kVW6bpL1iIwprwFBECzs9wlW6OOrkrq9H+4S8N2EH8d9PyT7+L0QyJCozqhObcLm+oaERbMDee1YMfBNHalpFEr1H1EvrvwN75ds5ulf78YgHEfr2TVjhSiI8KIrhdGdEQYTeuFER1Rk+h6YdSrGVylEoYlAmPK01k3u0vKDlfiYt3ncNBTQl0VfhgPrfrAmb0gKMSnofqTwqa6jh/cqcAxgr/0b8d15zTPud2iYTi7D6WzZd8R5v6yj6PH83Yz1QwJJL55BO/ecg4AX6zcSXiNIPq1bwS4FkpJE0V5Dm5b15AxFU3VzUY6mAj/OxcyjkKNutDuErdWoc1FUKPWycdbgbxyUVYfrKpK8tEMdiSnsf1gGjuS09hxMI2wkADuvSQGgEuenkOz+jV5bZTrlen56AxEyGlRNM1pWbgWRVTdUEKDT1Z5LavB7Uq1MU1pWSIw1UZGGmyeCeu/gA1fQ9oBuOY9lxCO7AcUZv4Hlky0AnlV2JFjJzh6PJPI2jVQVZ78biPbDh5lhydx7DmUnmdRHcDIs5vzyNBYAGIf/pbDx04t9FzSOk42RmBMZRQcBjGXuUvmCVc6u6nn/+nPr8GsR1zrQbNg+TvQ5z5rFVRB4TWCcnZ9ExHGXpJ3y5WMzCx2p6TntCZ2JKfRppFrFaYdzywwCcDJOk6lZYnAmMoiMAha9j55u+MVblxh13J3+8QxeLk3jFlvU1KrmeDAAJrVr0mz+qdusRoWEsgZEaHsTE4/5b7sOk6lZX9NxlRWYRGQtD7vsaP74Yhn+49Pfu+6jXavduMOptr66yUxhAXn3Rkudx2n0rJEYExlVVCBPAmA2Y+51sGhHTDnCXipJzzfDb5/yNVFMtXOkPhoHhkaS3REGIIbGyjLVdDWNWRMZVVUgbygGjD6C0jde3JF808vuG04G3WAowdg71pXTjvA9hiuDk6njpO3bNaQMdVF2kFX3qJGbVg8Eb74M9Rs6GYgdRwMLc63tQp+zmYNGVPd5S50FzvcjTGs+xxWfwxL34LQCPjTCnfcmFwsERhTHdWoBZ2udJfsUtk7l59MAh/f4rqZOgx2C9lsv2a/ZonAmOouOBTaX+ou2cIjYdVHsHYaBNaA1hdA91F5H2P8hs0aMsYfDXgE/rIebvzG1ULas9q1GMCtdv75dTi8x6chmopjg8XGGLcO4cQx13r45Qd45ypAoPk50GGQu0Q0L/Y0pnIrbLDYWgTGGFfGIthTprn1hXDHT9D3frcb27cPwDOxsGetu//E8cLPY6qkChsjEJE3gIHAXlXt7DlWH/gAaAEkAiNU9WBFxWSMKYAINO7oLn3vg/2bYdP3bn0CwFdjYfvPnpbCYGjcyT0nm1VLrXIqskXwJjAg37FxwHRVbQtM99w2xlQmDVrDObef/LBvfg6E1T+5qvm5eJj79MnHz34cflvgVkCbKqHCEoGqzgEO5Dt8BfCW5/pbwJCKiscYc5rifgc3fgl/2QiDnoX6reDQLndfyk5Y+qanWuq7NuBcRfh6+mhjVd0FoKq7RKSRj+MxxnirViR0H+0u2ZNOvn8Isjybp5xIh5d6Q8KN0GWEa1mYSqnKDBaLyG0islhEFiclJfk6HGNMbiJubGD953mPH9nruoj2/+Ju71kL85+HXSshK+vU8xif8HWLYI+IRHlaA1HA3sIeqKqvAK+Amz5aUQEaY7xUULXUwGDXGmjV193eMge++5u7XrMBtOjt7utyNYScWovfVAxftwg+A0Z5ro8CpvkwFmNMaRRWLXXXClctFdyg8z1rYchL0OZi2LYQvrn/ZIXUtdPciudUa/VXpApbUCYi7wN9gYbAHuBhYCowBWgO/AYMV9X8A8qnsAVlxlQTqnBoJ9T1lFd+cyAk/uiuN+rkWgvt+p9sUZhS8Xn1UVUdWchdF1ZUDMaYSkbkZBIAuGGa25rz19nw6yxY/Dokbz2ZCH56AaLioOlZVlK7DPl6jMAYY04KCITo7u7Se4yrnJrmWWN6ZJ8bX9AsCK7pNt1p1cctbKvfyrdxV3GWCIwxlVdwKARHuevhDeGvWyBxLmzxtBi+f8htvlO/FaRsh03fQcs+7nbu1c6mSJYIjDFVR1gEdBjoLuDGF0JqueubZ8IX97jrdZtDq/OhZV+IuQxCwn0QbNXh61lDxhhz+uqcAaF13PX46+APi+GyCXBGV7c72ye3uO4lcFNXN3wN6YdOPv/wbph4qd+vgLYWgTGmehCBhm3d5exb3QrnpA0Q3sDd/9MLsPEbEM84RKs+boFbdl2kgU/5Nn4fskRgjKmeAgJdBdVsw99y6xa2zHazkuZM8Nyhri5Sw3ZuNlJUVwj0r49G25jGGOOfpt4FKz+ArAwIDIHME0AW1KgLLXpCy/Pdfs7VaEaSbUxjjDHZDu+G1R+5JABuBXRQCAx8GjoNgb3r4JtxbpwB3BTWxRPd3gxV8Mtzcfyr/WOMMVBwXSTNgt2rYfBz7nbyb269AsDWn+CLP7vrdZq61kLL86H9pW4mUxVnLQJjjP8prC7S9kUnb0c0d2sXwH3g/2EJXP4UNO3uBp2n3u4WuQFsWwRrPj15u4qxFoExxv/cPrdkjxeBhm3c5aybXQntvWtP7rGw9G1YNsldbxx7ssXQ7pIqsbDNEoExxpRUQAA06Xzy9sCnodsoNyNpyxxXI2nTt9Deszvvig+gViO3zWdwmG9iLoIlAmOMKa3AYGh2lrucP9YtYju0w92nCt89CEeS3OykZj08rYUBENXFt3F7WCIwxpiyFhx6sttIBP64zC1c+3WWazHM/A8cO+wSwYnjsOhlt0lPk9iTezNUIEsExhhT3mrUhrYXuwvA0QOQ6Zm6unvlyV3bQiOgRS9XOK/jFVC7cd7zHN4NH90Iw9489b5SsFlDxhhT0WrWP/lB3jQBxqyHoa+6Ynq7VsLX98LBLe7+XSvcYPTBrW7aa3ZJjDJkLQJjjPG1OlFub+cuI9ztg4lQx7Nhz7rPYc4T7roEuvUOy9+FPveVWavAWgTGGFPZ1GvhBqAB+j0Idy6EZueenIqqWWXaKrBEYIwxlZmIW728axlknXDHMo+7VkEZlc+2RGCMMZVdYSUxyqhVYInAGGMqO29KYpSCDRYbY0xlV9KSGCVkLQJjjPFzlgiMMcbPWSIwxhg/Z4nAGGP8nCUCY4zxc1Vy83oRSQK2nubTGwJVaRuhqhRvVYoVqla8VSlWqFrxVqVYoXTxnqmqkfkPVslEUBoislhVE3wdh7eqUrxVKVaoWvFWpVihasVblWKF8onXuoaMMcbPWSIwxhg/54+J4BVfB1BCVSneqhQrVK14q1KsULXirUqxQjnE63djBMYYY/LyxxaBMcaYXCwRGGOMn/ObRCAib4jIXhFZ7etYiiMizURkpoisE5E1IvInX8dUFBEJFZFFIrLCE+8/fB1TcUQkUESWicgXvo6lOCKSKCKrRGS5iCz2dTxFEZEIEflIRNZ7/n7P9XVMhRGR9p7fafblkIj82ddxFUZE7vH8/1otIu+LSGiZndtfxghE5HwgFXhbVTv7Op6iiEgUEKWqS0WkNrAEGKKqa30cWoFERIBwVU0VkWBgLvAnVV3g49AKJSJjgASgjqoO9HU8RRGRRCBBVSv9oicReQv4UVVfE5EQoKaqJvs4rGKJSCCwA+ihqqe7WLXciEg07v9VR1VNE5EpwFeq+mZZnN9vWgSqOgc44Os4vKGqu1R1qef6YWAdEO3bqAqnTqrnZrDnUmm/YYhIU+By4DVfx1KdiEgd4HzgdQBVPV4VkoDHhcDmypgEcgkCwkQkCKgJ7CyrE/tNIqiqRKQFEA8s9HEoRfJ0tSwH9gLfq2pljvcZ4K9AVjGPqywU+E5ElojIbb4OpgitgCRgoqfb7TURCfd1UF66Bnjf10EURlV3ABOA34BdQIqqfldW57dEUImJSC3gY+DPqnrI1/EURVUzVTUOaAqcLSKVsvtNRAYCe1V1ia9jKYGeqtoNuBS4y9PNWRkFAd2AF1U1HjgCjPNtSMXzdGENBj70dSyFEZF6wBVAS+AMIFxEriur81siqKQ8fe0fA++q6ie+jsdbnq6AWcAA30ZSqJ7AYE+/+2TgAhF5x7chFU1Vd3p+7gU+Bc72bUSF2g5sz9Ua/AiXGCq7S4GlqrrH14EU4SJgi6omqWoG8AlwXlmd3BJBJeQZfH0dWKeqT/k6nuKISKSIRHiuh+H+aNf7NKhCqOr9qtpUVVvgugNmqGqZfbMqayIS7pkwgKebpT9QKWe+qepuYJuItPccuhColBMc8hlJJe4W8vgNOEdEano+Hy7EjR2WCb9JBCLyPvAT0F5EtovIzb6OqQg9getx31azp7Zd5uugihAFzBSRlcDPuDGCSj8ts4poDMwVkRXAIuBLVf3GxzEV5W7gXc/fQhzwH9+GUzQRqQlcjPuGXWl5WlkfAUuBVbjP7jIrNeE300eNMcYUzG9aBMYYYwpmicAYY/ycJQJjjPFzlgiMMcbPWSIwxhg/Z4nAj4nILBH5r49eW0VkmC9e2xuVPb6y4KliOd6Lx80UkRsqIKSCXrvIfwdP1duhFRlTdWSJoJryLPL6n6eE8TER2SMi00Xk4lwPGwrc76sYy5qIdPd8cPQq5P4pIjKvouMqSmEfdCLyZmUokS0ilwPNgHdzHUv0xK0ikuYpOX2vZ6FTRfsX8JiI2GdZKdgvr/r6GFeK4GagHTAQ+BpokP0AVT3gqW5a5YhIUP4PHk/9oGW495z/8Q1w9WRer5gIq40/AW+qama+4//ELSTsgCuG9h/AFwXxvgJq48pEmNNkiaAa8pR76A2MU9XpqrpVVX9W1QmqOjnX4/J0DXm+6f1NRF72bNKxXUTuzXfudiIyW0TSRWSDiFwmIqkiMtpzfwvPN8WEfM8rron/qOd8aZ44Hs+98YaIjPd0ZYwWkc3AMaCgypavA8M9Bftyuw7IAD4QkQEi8qOIHBSRAyLyrYh0KCI2r96TiESLyGTPeQ+KyJci0raw85aEiAwVkZWe388Bz79B41z3DxJXnTRdRLaIyL/FFVPLvr+RiEzzPH+riNzkxWtG4sqFfFbA3YdVdbeqJqrqa8BKXPmL7Oe29rzebhE5IiJLxRX8y33+Yv/eCojpPhHZJyI9wBU7xCWDkcW9H1M4SwTVU6rnMlhKvovRPbgl7N2Ax4DHxbPLlKf5/SlwAjgHGA08DNQog5iPADfhvmHeiasD9GC+x7QEfgcMB7oC6QWc510gELg63/GbgMmqegSXQJ7BtZj6AinA57k/OEtKXKmCmZ6Y+gDn4soF/+C577SJSBNcgby3cL+f84FJue6/BPe+/wt0wr3XYeQt7/Am0Ab3wT4EuAFoUcxL98Il3DVFxCYi0tcTV0auu2rhWqAX4/6tPgY+EZGYfKco9O+tgNeZgCth0SdfmfNFuN+5OV2qapdqeAGuwm3Ek46rsTQBt/tS7sfMAv6b63Yi8H6+x2wC/ua5fgkuCUTnuv88XL380Z7bLTy3E/KdR4Fhhd0uIP7bgV9y3R6P+6Bp7MV7fweYn+v2WZ7X61HI48OBTKBXQfF5855wH76b8JRt8RwLBPYDI4qItcDfA+6D+wvP9W6ex51ZyDnmAH/Pd2wI7suA4LoGFVfOOvv+Mz3veXwRsf0Z2FrA8URcgkgFjnvOnQacV8y/y4LsvyVv/t5y/X6uBiYCG4EWBZx3MG5viSBf/F+rDhdrEVRTqvoxrm75INw3s/OABSLyQDFPXZnv9k6gked6DLBT3SYZ2X6mDDZ4EZFhIjLX05WQCjwNNM/3sO3qXang14Fzc337vAlYrZ5vkZ5ui/dEZLOIHAL24FrH+V+vJLrjWiyHPV1lqbiWRj2gdSnOC7AC+AFYLSIfi8gdnm6b3K/9YPbrel77PVyCa4L7tp6F++YMgLqduIrb4SqMgltdAE/hisr1wbWE/qGq87PvFFc19XERWevpJkvFbQ2a/3dc1N9btgm4llsvVU0sIJY0XMIrsz18/Y0lgmpMVdNV9XtV/aeqnof7gBxfTBdIRr7bysm/E6H4LSizk0LOQK64vRUKJSLn4Lo+vsUlrnjgb7gtL3M7UsxrZ5sF/ALcJK4s9kjyDhJ/DkQCvwd6eF7vBFDY78Wb9xQALMd9OOa+tANeLiLWw0DdAo5H4BIJ6vrB+3suK3GD4ZtEpGuu1/5HvtftArTF7Rh2urN59uESWUH2q+ovqvoTrvU5VkT65bp/Aq4L7++4ZBGHS0T5f8dF/b1l+x6X0AqrwFsfSNeT26WaEgrydQCmQq3F/ZuH4pr0JbUOiBaRM9SzWQruW17u/7hJnp9RuY7FFXPensAOVf1X9gEROfM04gPcHsoi8gZuxst63DfbSZ7zNsB9Q75LVWd6jnWj6P8L3rynpbiEs09Ltk/vBtw3+pxEJW4j9a647pCc94Tr4vtJRP6J67e/GtdaWArEqOovBb2AiKzD/RudBcz3HGuOazEWZRkQKSINVXVfYQ9S1YPiJh08LSLxnlh7AW97WqZ4xqpa47p3SuorXJnoD0VEVfWtfPd3xv0OzGmyFkE1JCINRGSGiFwnIl1EpKWIDMft0ztdT3/by+9xH1xviUhXzzf5p3Dfpl2Hrmoari/4PhHpJCLn4b4dFmUjLsFcKyKtROQOSj8L5E2goee1p6rqfs/xg7hvureKSBsR6QO85HkPBfLyPb2L62KaJiJ9PL/z80XkyWJmDj2Fa7ncJW5GVhyuznx9z09E5BzP7JqzPB/gg3Fz+7M3ffkn8DsR+aeIdBaRGE9X2+Oe+DcA3wAvi8i5ntd4E9elUpRluD2oC1yXkc8LQHtcKwDcv+mVItJNRGJx4zan3XWjbn+L4cBLcuritt6492dOkyWC6ikV98H1J2A27tvjf3D9xvln03hNVbOAK3GzhBbhZrH8G5cEcvclZ09N/BnXLfK3Ys77OfAEbibPStxMk4dON07POXfhvknWA17L9x6uxnWdrMZ9gP0dN/hZlCLfk6oexc3m+RW39+163O+nHi75FBbn+8CNnsti3AdaE6C3uh2/wHUR9QS+wA2mPgn8S1Xf8ZzjW+ByoB/u32URbq/g33K91GhgCzAD1zX2Hm6wtlCeLqk3gGuLepznsUm4Vtd4z+yyMbgk8iNujGqB5/pp8ySDEbiEdgO4Kbu48a+JRT3XFM02pjGl4umnXo6bUVOVNoQ3XhCRRriWx9mq+quv48lPRJ4A6qqqLxazVRs2RmBKRESuxA3absJNq3yKk/3UpppR1b3iFp81w7V2Kpu9FN/1aIphLQJTIp4m+d9wHwwHcTN07vFyWqcxphKyRGCMMX7OBouNMcbPWSIwxhg/Z4nAGGP8nCUCY4zxc5YIjDHGz/0/eYjewdb4YeMAAAAASUVORK5CYII=\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "singular_value = singular_value_list[-1]\n",
-    "err_subfull, err_local, err_SVD = [], [], []\n",
-    "U, D, V_dagger = np.linalg.svd(M, full_matrices=True)\n",
-    "\n",
-    "# 计算 2-norm 误差\n",
-    "for i in range(T):\n",
-    "    lowrank_mat = np.matrix(U[:, :i]) * np.diag(D[:i])* np.matrix(V_dagger[:i, :])\n",
-    "    recons_mat = np.matrix(U_learned[:, :i]) * np.diag(singular_value[:i])* np.matrix(V_dagger_learned[:i, :])\n",
-    "    err_local.append(norm(lowrank_mat - recons_mat)) \n",
-    "    err_subfull.append(norm(M_err - recons_mat))\n",
-    "    err_SVD.append(norm(M_err- lowrank_mat))\n",
-    "\n",
-    "# 画图 \n",
-    "fig, ax = plt.subplots()\n",
-    "ax.plot(list(range(1, T+1)), err_subfull, \"o-.\", label = 'Reconstruction via VQSVD')\n",
-    "ax.plot(list(range(1, T+1)), err_SVD, \"^--\", label='Reconstruction via SVD')\n",
-    "plt.xlabel('Singular Value Used (Rank)', fontsize = 14)\n",
-    "plt.ylabel('Norm Distance', fontsize = 14)\n",
-    "leg = plt.legend(frameon=True)\n",
-    "leg.get_frame().set_edgecolor('k')"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "### 案例2：图像压缩\n",
-    "\n",
-    "为了做图像处理，我们先引入必要的 package。"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 11,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 图像处理包 PIL\n",
-    "from PIL import Image\n",
-    "\n",
-    "# 打开提前准备好的图片\n",
-    "img = Image.open('./figures/MNIST_32.png')\n",
-    "imgmat = np.array(list(img.getdata(band=0)), float)\n",
-    "imgmat.shape = (img.size[1], img.size[0])\n",
-    "imgmat = np.matrix(imgmat)/255"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 12,
-   "metadata": {
-    "scrolled": false
-   },
-   "outputs": [
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAEICAYAAACZA4KlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAUb0lEQVR4nO3db2yVVZ4H8O/X0tLaEmiLQgvlj0TEOnGANGgCGnfdGdE3otnR8cXEScwyLzRZk5kXxs3suPti192sTtxkY4KrGWbjOrirRndjdseQ3bAmxp3KQgVZAbFAaSkgBQqUQtvfvrgPs4V5fqe39z733rbn+0ma3p7fPfeePtwfz+3zu+ccmhlEZOa7odIDEJHyULKLRELJLhIJJbtIJJTsIpFQsotEQskuEgkluxSN5A9JjpI8P+7rvkqPS641q9IDkBnjEzPbUOlBiE9n9hmOZDfJn5DsInmW5DaStZUel5Sfkj0OjwHYCGA5gDsB/DDtTiQ3kDwT+AqdudeQPEVyP8mfktS7xilG/yBx+Fsz6wUAkv8CYHXanczsYwDzCnj8HQC+BeAwgDsAbAMwAuAvC3gsKRGd2eNwfNztiwAasnxwMztkZl+b2ZiZfQ7gzwH8YZbPIcVTsstvkbznuivq13/dk+dDGQCWcqwyeXobL79lZv+FAs76JB8EsNPM+kmuAvBTAP+U9fikODqzSxbuB9BF8gKADwG8C+AvKjskuR61eIVIHHRmF4mEkl0kEkp2kUgo2UUiUdbSW2Njo7W2tpbzKTN1ww3p/zd67QBA+uXm0MXR0dHRgmKFXHAtdPyh2NjY2KTagfDYZ83yX6pVVVVuzFPoOKa63t5eDAwMpP7DFJXsJDcCeAVAFYC/N7MXQ/dvbW3Ftm3binnKipo9e3Zqe319vdunpqbGjV2+fNmNnT171o2dO3fOjQ0PD6e2hxK6rq7OjXm/MxBOwKGhodT2wcFBt8/IyIgba25uLijmJe7FixfdPleuXHFjU93jjz/uxgp+G0+yCsDfAXgQQDuAJ0i2F/p4IlJaxfzNvg7AweRz0ZcB/ArAw9kMS0SyVkyyLwJwdNzPPUnbNUhuJtlJsnNgYKCIpxORYhST7GkXAX7nDyQz22JmHWbW0djYWMTTiUgxikn2HgBt435eDKC3uOGISKkUk+y/AXAryeUkawB8H8AH2QxLRLJWcOnNzEZIPgPg35Ervb1hZnszG5mIZKqoOruZfYjclEYRmeL0cVmRSCjZRSKhZBeJhJJdJBJKdpFIKNlFIqFkF4mEkl0kEkp2kUgo2UUioWQXiYSSXSQSSnaRSCjZRSKhZBeJhJJdJBJKdpFIKNlFIqFkF4mEkl0kEkp2kUgo2UUioWQXiYSSXSQSSnaRSBS1IwzJbgCDAEYBjJhZRxaDEpHsFZXsid8zs1MZPI6IlJDexotEothkNwC/JvkZyc1pdyC5mWQnyc6BgYEin05EClVssq83s7UAHgTwNMl7r7+DmW0xsw4z62hsbCzy6USkUEUlu5n1Jt9PAHgPwLosBiUi2Ss42UnWk5xz9TaA7wLYk9XARCRbxVyNXwDgPZJXH+cfzezfMhmViGSu4GQ3s0MAvp3hWESkhFR6E4mEkl0kEkp2kUgo2UUikcVn46Nx9uzZ1PZjx465fS5duuTGZs+e7cbmzp3rxm688UY3Njo6mtre39/v9jl//vykHw8ALl++7MYGBwcnPY6enh43VlVV5cba29vd2KpVq1LbFy9e7Papq6tzY9OZzuwikVCyi0RCyS4SCSW7SCSU7CKRKPvVeDMr91Nm5vjx46nte/fudft0d3e7sdraWjfW1NRUUD/vynpvb6/b5+TJk27Mq0AAwNDQkBvzxpjMpUh15MgRN3bo0CE3tmzZMje2adOm1PYHHnjA7bNo0SI3Np3pzC4SCSW7SCSU7CKRULKLRELJLhIJJbtIJDQRZhIuXryY2n706FG3T1dXlxs7d+6cGwtNCgmVw7yS10033eT2aWhocGOhSTIjIyNubPny5ZNqn2gcoWMcinkTb4aHh90+M5XO7CKRULKLRELJLhIJJbtIJJTsIpFQsotEoqylN5Koqakp51Nmqq2tLbX9nnvucfssWbLEjXmz6ABgzx5/J62+vj43tnDhwtT29evXu33uuuuuST8eANxwg3+u8MqD+/fvd/vs2LHDjd1xxx1uLFTO27BhQ2p7S0uL22c6v0ZDswonPLOTfIPkCZJ7xrU1kfyI5IHku7ZnFZni8nkb/wsAG69rew7AdjO7FcD25GcRmcImTHYz2wHg9HXNDwPYmtzeCmBTtsMSkawVeoFugZn1AUDy/WbvjiQ3k+wk2TkwMFDg04lIsUp+Nd7MtphZh5l1NDbqT3uRSik02ftJtgBA8v1EdkMSkVIotPT2AYAnAbyYfH8/347TecFJb9ul0AKF8+bNc2Nr1651Y48++mje4xrP227qypUrbp/QGOfPn+/G6uvr3djY2Fhq++nT11/++X8HDhxwY6EZdqHy5oIFC1Lbq6ur3T7T+TUakk/p7S0AnwC4jWQPyaeQS/LvkDwA4DvJzyIyhU14ZjezJ5zQ/RmPRURKSB+XFYmEkl0kEkp2kUgo2UUiob3eJsGbURQq48yePduNhfZsCy0QGZqVdeHChdT20CKVoTHOmuW/REZHR92Ytw9caJHNUMwr5QHh2XehmGc6v0ZDdGYXiYSSXSQSSnaRSCjZRSKhZBeJhJJdJBIqvWUgVN4Jla6qqqrcWKjUFFJXV5faHhpjaByh8lpoMZLe3t7U9kL2qQP8GYdAeNZeqCzqmYmvUUBndpFoKNlFIqFkF4mEkl0kEkp2kUiU9Wq8mRV8lXkqC13NDk1aCfULrbkWOobe1fg5c+a4fUJX3ENXzw8fPuzGDh48OOnHC613F1rnz1tnDvCPR8h0fo2GKgk6s4tEQskuEgklu0gklOwikVCyi0RCyS4SCU2EmQRv7N7adEC4vBbqF9quKVSW8yZ+NDQ0uH28LaMAoKenx4199dVXbuzQoUOp7aF15pqbm93YsmXLCuoXWl/PM51foyH5bP/0BskTJPeMa3uB5DGSu5Kvh0o7TBEpVj5v438BYGNK+8/NbHXy9WG2wxKRrE2Y7Ga2A4C/9aaITAvFXKB7hmRX8ja/0bsTyc0kO0l2hhY7EJHSKjTZXwWwAsBqAH0AXvLuaGZbzKzDzDoaG93/E0SkxApKdjPrN7NRMxsD8BqAddkOS0SyVlDpjWSLmfUlPz4CYE/o/jOFVyoLlddCsVCJJ1QOC60n55XlQn2Gh4fd2LFjx9zYF1984ca80ltoLbmVK1e6sTVr1rix0Gw5b9ZhIdtCTXcTJjvJtwDcB2A+yR4APwNwH8nVAAxAN4AflW6IIpKFCZPdzJ5IaX69BGMRkRKK772MSKSU7CKRULKLRELJLhKJss96C830muq8UlmohBb6fUP9QjPbClmMMrSI4tDQkBs7deqUGwuV5fr7+1Pb29ra3D5NTU1u7Oabb3ZjoUUlvd879O8ynV+jITqzi0RCyS4SCSW7SCSU7CKRULKLRELJLhKJspbeSE7r2UaFlN5CQsei0OPkldFOnjzp9jl69Kgb6+7udmPHjx93Y5cvX05tD+0519ra6sZC+7mFSpGhsqJnOr9GQ2XD6ftbicikKNlFIqFkF4mEkl0kEkp2kUhoIkwGCp0IE7rqG9q2aNYs/5/t/Pnzk2oHgC+//NKNha7Gh7Zyqq2tTW0PTWhZuHChG5s7d25B4wit5eeZia9RQGd2kWgo2UUioWQXiYSSXSQSSnaRSCjZRSKRz44wbQB+CWAhgDEAW8zsFZJNALYBWIbcrjCPmVmU27SGSm+hWGhrKG/bIiBcGjpz5kxq+9dff+322b9/vxsLTXYJlQC9EltLS4vbJzRJJmR0dNSNFbIG3UyVz5l9BMCPzex2AHcDeJpkO4DnAGw3s1sBbE9+FpEpasJkN7M+M9uZ3B4EsA/AIgAPA9ia3G0rgE0lGqOIZGBSf7OTXAZgDYBPASy4upNr8t3/aJSIVFzeyU6yAcA7AJ41M//zib/bbzPJTpKdp0+fLmSMIpKBvJKdZDVyif6mmb2bNPeTbEniLQBOpPU1sy1m1mFmHaFNAESktCZMduYuW74OYJ+ZvTwu9AGAJ5PbTwJ4P/vhiUhW8pn1th7ADwB8TnJX0vY8gBcBvE3yKQBHAHyvJCOcQrwyWmhrpZBQ6So0y8tb3w3wZ6l1dXW5fXbu3OnGTpxIfcMGILxdU3t7e2r7bbfd5vZpaGhwY6HZa8PDw27MK8uFyp4z1YTJbmYfA/CKkvdnOxwRKRV9gk4kEkp2kUgo2UUioWQXiYSSXSQSZV9wstCtkqYCr8QWKr2Fft9Qv1Bp6MqVK27s2LFjqe27d+92+4QWnAzNRFu1apUb27BhQ2r7nXfe6fYJLbLpzeYDgMHBQTfmCS32OZ1foyE6s4tEQskuEgklu0gklOwikVCyi0RCyS4SibKW3sys4BliU4G3SGFo8cJQLFTiGRkZcWNDQ0NuzCtDhcpToXE0Nze7sZUrV7oxb3bbggUL3D6hPdtCe9WFZgFWV1enthdaEp3qQr+XzuwikVCyi0RCyS4SCSW7SCSU7CKRKPtEmJmo0EkVoavI33zzjRvr6+tzY2fPnk1tr62tdfu0tra6sVtuucWNrVixYtKPWV9f7/bxxg6EJ/+EeP822v5JRGYsJbtIJJTsIpFQsotEQskuEgklu0gkJiy9kWwD8EsACwGMAdhiZq+QfAHAHwE4mdz1eTP7sFQDnQoKmQjjbT8EhCd+nDp1yo15WzwBQH9/f2p7Y2Oj22fp0qVu7Pbbb3djbW1tbsxbuy60tl6hE4pCvNJbqFw6U+VTZx8B8GMz20lyDoDPSH6UxH5uZn9TuuGJSFby2eutD0BfcnuQ5D4Ai0o9MBHJ1qTey5BcBmANgE+TpmdIdpF8g6T/PlFEKi7vZCfZAOAdAM+a2TkArwJYAWA1cmf+l5x+m0l2kuwcGBgofsQiUpC8kp1kNXKJ/qaZvQsAZtZvZqNmNgbgNQDr0vqa2RYz6zCzjtBFIhEprQmTnbnLoK8D2GdmL49rbxl3t0cA7Ml+eCKSlXyuxq8H8AMAn5PclbQ9D+AJkqsBGIBuAD8qwfimFK9cU+h6ZqEtjfbt2+fGDhw44Ma8mXSLFy92+4TWkluyZIkba2hocGOXLl1KbQ+VIkPlsNCsvdCMuFmz0l/iMc56y+dq/McA0o7MjK6pi8w08X2yQCRSSnaRSCjZRSKhZBeJhJJdJBJacLLEQmU5rzwFAEePHnVjR44ccWNNTU2p7aEZau3t7W5s3rx5bizE+7SkVwqbSKj0FiqjebPsQmW+6bz9U4jO7CKRULKLRELJLhIJJbtIJJTsIpFQsotEQqW3DIRmcoX2cxscHHRjvb29buzw4cNuzCtDVVdXu33mzp3rxurq6tzYyMiIG/PKiqESWigWWqgyVCrzYjEuOBnfbywSKSW7SCSU7CKRULKLRELJLhIJJbtIJFR6mwSvjBMqvQ0PD7uxCxcuuLGTJ08WFJs/f35qe2i2WWjhyFC/0O/mLQIZKnnV1NS4sVB5LbTgpFeKVOlNRGYsJbtIJJTsIpFQsotEQskuEokJr8aTrAWwA8Ds5P7/bGY/I9kEYBuAZcht//SYmWmb1uuUYpuh0KQQbzJJ6Ip7fX29GwutoReqQgwNDbkxT6FX42PcyqkQ+ZzZhwH8vpl9G7ntmTeSvBvAcwC2m9mtALYnP4vIFDVhslvO+eTH6uTLADwMYGvSvhXAplIMUESyke/+7FXJDq4nAHxkZp8CWGBmfQCQfL+5ZKMUkaLllexmNmpmqwEsBrCO5LfyfQKSm0l2kuz01hIXkdKb1NV4MzsD4D8BbATQT7IFAJLvJ5w+W8ysw8w6GhsbixutiBRswmQneRPJecntOgB/AOB/AXwA4Mnkbk8CeL9EYxSRDOQzEaYFwFaSVcj95/C2mf0ryU8AvE3yKQBHAHyvhOOcErzJE6G100LlqebmZje2dOnSgh5zyZIlqe2hbZxC69OFnitU8vJKZaHJM6FYaEJOaJ08r0wZGnvod57OJkx2M+sCsCal/RsA95diUCKSPX2CTiQSSnaRSCjZRSKhZBeJhJJdJBIMzWrK/MnIkwCu7l00H8Cpsj25T+O4lsZxrek2jqVmdlNaoKzJfs0Tk51m1lGRJ9c4NI4Ix6G38SKRULKLRKKSyb6lgs89nsZxLY3jWjNmHBX7m11Eyktv40UioWQXiURFkp3kRpJfkjxIsmILVZLsJvk5yV0kO8v4vG+QPEFyz7i2JpIfkTyQfC/5Sh/OOF4geSw5JrtIPlSGcbSR/A+S+0juJfnHSXtZj0lgHGU9JiRrSf43yd3JOP4saS/ueJhZWb8AVAH4CsAtAGoA7AbQXu5xJGPpBjC/As97L4C1APaMa/trAM8lt58D8FcVGscLAH5S5uPRAmBtcnsOgP0A2st9TALjKOsxAUAADcntagCfAri72ONRiTP7OgAHzeyQmV0G8CvkVqqNhpntAHD6uuayr9brjKPszKzPzHYmtwcB7AOwCGU+JoFxlJXlZL6icyWSfRGAo+N+7kEFDmjCAPya5GckN1doDFdNpdV6nyHZlbzNL+vCgSSXIbdYSkVXML5uHECZj0kpVnSuRLKnrQdUqfrfejNbC+BBAE+TvLdC45hKXgWwArkNQfoAvFSuJybZAOAdAM+a2blyPW8e4yj7MbEiVnT2VCLZewC0jft5MYDeCowDZtabfD8B4D3k/sSolLxW6y01M+tPXmhjAF5DmY4JyWrkEuxNM3s3aS77MUkbR6WOSfLcZzDJFZ09lUj23wC4leRykjUAvo/cSrVlRbKe5JyrtwF8F8CecK+SmhKr9V59MSUeQRmOCXOrP74OYJ+ZvTwuVNZj4o2j3MekZCs6l+sK43VXGx9C7krnVwD+pEJjuAW5SsBuAHvLOQ4AbyH3dvAKcu90ngLQjNyeeQeS700VGsc/APgcQFfy4mopwzg2IPenXBeAXcnXQ+U+JoFxlPWYALgTwP8kz7cHwJ8m7UUdD31cViQS+gSdSCSU7CKRULKLRELJLhIJJbtIJJTsIpFQsotE4v8AZj022F13GxAAAAAASUVORK5CYII=\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAEICAYAAACZA4KlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAUS0lEQVR4nO3dfYyV5ZnH8e9V5K0ytAgjIOKAgIaXIpAJqUVbV7cWbRrtH33RTddNXGl2a7JNun+YbrJ196/uZtumm92Y0NWUNq3WbjV1N7TVUg2aWnTAUTBQEQuUgjAoCigwDlz7x3nIDniue2ae8zYz9++TTM6Z+zrPee55OBfPOc917vs2d0dERr8PtLoDItIcSnaRTCjZRTKhZBfJhJJdJBNKdpFMKNlFMqFklyEzsyVm9iszO2xm7/uihpldZGaPmtk7ZrbHzG5vRT/lXEp2KeM94GHgziD+n0AvMB34C+A+M1vcpL5JwPQNutHFzHYD/wH8JdAB/BK4w91PNmBf84Gd7m792i4EjgBL3P2Vou2HwJ/c/Z5690EGT2f20enzwGpgLrAU+KtqDzKza8zsrcTPNSX2fQVw+myiF14EdGZvsQta3QFpiH939/0AZvY/wLJqD3L3Z4AP13nfk4C3z2t7G2ir835kiHRmH51e73f/XSoJ2CzHgcnntU0GjjWxD1KFkj1jZnatmR1P/Fxb4mlfAS4wswX92q4CXq5Pr6UsvY3PmLs/TYmzvpkZMB4YV/w+ofJ0fsrd3zGzR4B/NrO/pvIR4hbgY3XruJSiM7uU0QGc4P/P1ieA3/eL/y0wETgEPAj8jbvrzN5iKr2JZEJndpFMKNlFMqFkF8mEkl0kE00tvU2bNs07OjqauUuRrOzZs4fDhw9btVhNyW5mq4HvAmOA/3L3b6Ye39HRwW9/+9tadjksVcrO1aWqHalY2ecs83wpZfvYrOcb6Dnrva/h7mMfi7/OUPptvJmNoTKU8SZgEXCbmS0q+3wi0li1fGZfCbzq7q+5ey/wEJVvSonIMFRLss8C/tjv931F2znMbI2ZdZlZV09PTw27E5Fa1JLs1T70vO/Dk7uvdfdOd+9sb2+vYXciUotakn0fMLvf75cC+2vrjog0Si3J/jywwMzmmtk44IvAY/XplojUW+nSm7v3mdndwK+olN4e0MgmkeGrpjq7u68H1tepLyLSQPq6rEgmlOwimVCyi2RCyS6SCSW7SCaU7CKZULKLZELJLpIJJbtIJpTsIplQsotkQskukgklu0gmlOwimVCyi2RCyS6SCSW7SCaU7CKZULKLZELJLpIJJbtIJpTsIplQsotkQskukgklu0gmaloRxsx2A8eA00Cfu3fWo1MiUn81JXvhz9z9cB2eR0QaSG/jRTJRa7I78LiZbTazNdUeYGZrzKzLzLp6enpq3J2IlFVrsq9y9xXATcBXzOzj5z/A3de6e6e7d7a3t9e4OxEpq6Zkd/f9xe0h4FFgZT06JSL1VzrZzexCM2s7ex+4EdhWr46JSH3VcjV+OvComZ19nh+7+y/r0isRqbvSye7urwFX1bEvItJAKr2JZELJLpIJJbtIJpTsIpmox3fjs/H2228PqR3gAx+I/z+dO3duGDt58mQYGzNmTBg7duxY1fZ9+/aF25w5cyaM9fb2hrHXXnstjB0/frxqe+p4pI7jrl27wtgFF8Qv4yVLllRtv+aaa8Jt5s2bF8ZGMp3ZRTKhZBfJhJJdJBNKdpFMKNlFMtH0q/Hu3uxd1s3u3burtj/77LPhNgcPHgxjixYtKtWP06dPD3l/f/jDH8JtUv8mR48eDWN79+4NY8WYife58MILw21SV+O7u7vDWF9fXxi79dZbq7ZfccUV4TaXX355GBvJdGYXyYSSXSQTSnaRTCjZRTKhZBfJhJJdJBMaCDMEUWlo8+bN4Ta/+MUvwtg777wTxiZMmBDGUqW3aFDI5MmTS+0rNSBn0qRJYezSSy+t2j5jxoxwmylTpoSxqOwJ6ZJdNKPx1KlTw21GK53ZRTKhZBfJhJJdJBNKdpFMKNlFMqFkF8lE00tvqTnIhrsVK1ZUbU+N5EqNrtq0aVMYS402S+0v6uP1118fbjN//vwwlirZpVbl/dCHPlS1ffz48eE269evD2NPPfVUGFu8eHEYu+GGG6q2p+b/G8mv0ZQB/yoze8DMDpnZtn5tF5nZE2a2s7iNC6QiMiwM5r+w7wOrz2u7B9jg7guADcXvIjKMDZjs7r4RePO85luAdcX9dcCt9e2WiNRb2Q8n0939AEBxe3H0QDNbY2ZdZtZ1+PDhkrsTkVo1/EqEu691905375w2bVqjdycigbLJftDMZgIUt4fq1yURaYSypbfHgDuAbxa3Px/shiN5wsmonLR8+fJwm1SJ57bbbgtjZcs/UWkrNUItVQ5LjbCbPXt2GIuWqEpNHPnQQw+FsWg5KYCrr746jF122WVhLDKSX6Mpgym9PQg8C1xpZvvM7E4qSf5JM9sJfLL4XUSGsQHP7O4enX6qf1tBRIal0flVIRF5HyW7SCaU7CKZULKLZEJrvQ1BVA5LTdiYmkSxra0tjE2cODGM9fb2hrHo+I4dOzbcJuXUqVNhLDX6LppMc8eOHeE2W7ZsCWPR2nGQLm9efHH1L3eOGzcu3ObMmTNhbCTTmV0kE0p2kUwo2UUyoWQXyYSSXSQTSnaRTGittyHo6+ur2p4qC6Vi0cgwKF+iTO0vkio1pUbfpfq4a9euqu3PPfdcuM1bb70VxpYtWxbGFi1aFMai0mfq71LpTURGNCW7SCaU7CKZULKLZELJLpKJpl+NL3O1eLiIrsanrt6mBqBccEF8+N97770wljqG0VXmVB9T88ylBuREg10ANm/eXLX9mWeeCbdJHaubbropjH3kIx8JY1H/U8djJL9GU3RmF8mEkl0kE0p2kUwo2UUyoWQXyYSSXSQTGggzBFGJKlXGSZXXUoMxUuWw1Pxp0XOmSnkpqcE6Bw4cCGNR6e3VV18Nt0kt1bRy5cow1t7eHsYiURkV0n/zSDaY5Z8eMLNDZratX9u9ZvYnM+sufm5ubDdFpFaDeRv/fWB1lfbvuPuy4md9fbslIvU2YLK7+0bgzSb0RUQaqJYLdHeb2UvF2/xwcnQzW2NmXWbW1dPTU8PuRKQWZZP9PmAesAw4AHwreqC7r3X3TnfvLHMhRUTqo1Syu/tBdz/t7meA7wHxpVIRGRZKld7MbKa7n627fBbYlnr8aFFmCaVUeS1VDkttlxqVFZUBU6W81PJVJ06cCGNPPvlkGIvmmps6dWq4zRe+8IUwtnTp0jCWUmbewNFqwGQ3sweB64BpZrYP+AZwnZktAxzYDXy5cV0UkXoYMNnd/bYqzfc3oC8i0kD6uqxIJpTsIplQsotkQskukgmNehuCaDRU2dFrqZFXqdFyqbJRtL+ypbw33ngjjHV3d4ex3bt3V22/5JJLwm1Syzi1tbWFsdRxjJaoSh2P0Sq/v1gkU0p2kUwo2UUyoWQXyYSSXSQTSnaRTKj0VgepCSej0g+kyz9l14GLpCapPH78eBh7+umnw9jzzz8fxqKRdFdffXW4zeLFi8NYasRhb29vGIvKijmOetOZXSQTSnaRTCjZRTKhZBfJhJJdJBO6Gj8E0VX31BX3VKwRS0OVGayzf//+MLZ+fbz+xyuvvBLGlixZUrX9uuuuC7fp6OgIY6mKR+rKevR3p7ZJ/ZuNZDqzi2RCyS6SCSW7SCaU7CKZULKLZELJLpKJwawIMxv4ATADOAOsdffvmtlFwE+AOVRWhfm8ux9pXFdbLyrJpEo1qRJPKpaaVy1VRotiR47E/zQvvPBCqViq/wsXLhxSO8D48ePDWGoZqtQgmeh4jNbyWspgzux9wNfcfSHwUeArZrYIuAfY4O4LgA3F7yIyTA2Y7O5+wN23FPePAduBWcAtwLriYeuAWxvURxGpgyF9ZjezOcByYBMw/exKrsXtxXXvnYjUzaCT3cwmAT8DvuruR4ew3Roz6zKzrp6enjJ9FJE6GFSym9lYKon+I3d/pGg+aGYzi/hM4FC1bd19rbt3untne3t7PfosIiUMmOxWueR6P7Dd3b/dL/QYcEdx/w7g5/XvnojUy2BGva0CvgRsNbPuou3rwDeBh83sTmAv8LmG9HAESJWgolFokB7J9e6774axKVOmhLFoRNzLL78cbvPTn/40jO3YsSOMXXXVVWHs2muvrdo+b968cJuy88KVGcFWdhTdSDZgsrv7M0D0199Q3+6ISKPoG3QimVCyi2RCyS6SCSW7SCaU7CKZ0ISTQ5AaiVZGqixXdrmjqMSWKq9t2LAhjLW1tYWxT33qU2Fs1apVVdsnT54cbpNahio1OWeZpbLKjlQcyXRmF8mEkl0kE0p2kUwo2UUyoWQXyYSSXSQTKr0NQapUVkZqzbbU5IupEuDevXurtqcmjjx27FgYu/HGG8PYJz7xiTB2ySWXVG1PjTZLKbv2XY4TS0Z0ZhfJhJJdJBNKdpFMKNlFMqFkF8lE06/Gj+Sro9GAi9TAidSV4lQsNRDm0KGqE/kCsHXr1qrt0VV6gDlz5oSxz3zmM2EsNQfduHHjqran5taLtoH0MT516lQYi/7NUlf3R/JrNEVndpFMKNlFMqFkF8mEkl0kE0p2kUwo2UUyMWDpzcxmAz8AZgBngLXu/l0zuxe4Czi7NOvX3X19ozo6GqXKP9HcaQC/+93vwthvfvObqu2p+d1uv/32MLZ69eowNmPGjDAWlcNSA2HKzCU3kOgYly2XjmSDqbP3AV9z9y1m1gZsNrMnith33P3fGtc9EamXwaz1dgA4UNw/ZmbbgVmN7piI1NeQPrOb2RxgObCpaLrbzF4yswfMLF5aVERabtDJbmaTgJ8BX3X3o8B9wDxgGZUz/7eC7daYWZeZdfX09FR7iIg0waCS3czGUkn0H7n7IwDuftDdT7v7GeB7wMpq27r7WnfvdPfO9vb2evVbRIZowGS3ymXL+4Ht7v7tfu0z+z3ss8C2+ndPROplMFfjVwFfAraaWXfR9nXgNjNbBjiwG/jyYHY4kpfWico/ZedV++AHPxjGXn/99TD261//Oox1d3dXbb/yyivDbe66664wdtlll4WxEydOhLHIxIkTw1iqvJaKpebri15vqX+zkfwaTRnM1fhngGp/vWrqIiOIvkEnkgklu0gmlOwimVCyi2RCyS6SCS3/NARRSSa1LFRq4sjU5IuPP/54GNu2Lf5Kw6xZ1YctfPrTnw63WbhwYRgrOzosmjwy9Xyp8lrqOKZGD/b29lZtT00qWe9lvoYLndlFMqFkF8mEkl0kE0p2kUwo2UUyoWQXyYRKb0NQpvSWKgu9+eabYWzjxo1hbOfOnWGso6OjavvMmTOrtkO6DFXvElVqtFnqWKViZdfTi6j0JiIjmpJdJBNKdpFMKNlFMqFkF8mEkl0kE00vvaVKOcNdVP5JlZOOHj0axlKj17Zs2RLGjhw5EsaWLl1atT1VekuNNotGr0G6RFVmEs7UWm+pElrqNZXqf6TsBKLDnc7sIplQsotkQskukgklu0gmlOwimRjwaryZTQA2AuOLx/+3u3/DzC4CfgLMobL80+fdPb5MPIqlrhSnrsbv2bMnjKVWvG1rawtj0TJP8+fPD7cpe1U9tV2ZqksjBrtEy02l+nfq1KkwNpIN5sx+Crje3a+isjzzajP7KHAPsMHdFwAbit9FZJgaMNm94njx69jix4FbgHVF+zrg1kZ0UETqY7Drs48pVnA9BDzh7puA6e5+AKC4vbhhvRSRmg0q2d39tLsvAy4FVprZksHuwMzWmFmXmXWlPoeKSGMN6Wq8u78FPAWsBg6a2UyA4vZQsM1ad+9098729vbaeisipQ2Y7GbWbmYfLu5PBP4c2AE8BtxRPOwO4OcN6qOI1MFgBsLMBNaZ2Rgq/zk87O7/a2bPAg+b2Z3AXuBzg9lhavmf4S7q+4QJE8Jtpk+fHsYWLFgQxmbMmBHGUgNGli9fXrV97ty54TYpJ0+eLNWPqCzX19cXbpMqoaWWf0qV0Y4fP161vey8gSPZgMnu7i8B73sFufsbwA2N6JSI1N/o/C9MRN5HyS6SCSW7SCaU7CKZULKLZMKaOSecmfUAZ4d6TQMON23nMfXjXOrHuUZaPzrcveq315qa7Ofs2KzL3TtbsnP1Q/3IsB96Gy+SCSW7SCZamexrW7jv/tSPc6kf5xo1/WjZZ3YRaS69jRfJhJJdJBMtSXYzW21mvzezV82sZRNVmtluM9tqZt1m1tXE/T5gZofMbFu/tovM7Akz21ncTmlRP+41sz8Vx6TbzG5uQj9mm9mTZrbdzF42s78r2pt6TBL9aOoxMbMJZvacmb1Y9OOfivbajoe7N/UHGAPsAi4HxgEvAoua3Y+iL7uBaS3Y78eBFcC2fm3/CtxT3L8H+JcW9eNe4O+bfDxmAiuK+23AK8CiZh+TRD+aekwAAyYV98cCm4CP1no8WnFmXwm86u6vuXsv8BCVmWqz4e4bgTfPa276bL1BP5rO3Q+4+5bi/jFgOzCLJh+TRD+ayivqPqNzK5J9FvDHfr/vowUHtODA42a22czWtKgPZw2n2XrvNrOXirf5Df840Z+ZzaEyWUpLZzA+rx/Q5GPSiBmdW5Hs1eZ2alX9b5W7rwBuAr5iZh9vUT+Gk/uAeVQWBDkAfKtZOzazScDPgK+6e7yUTvP70fRj4jXM6BxpRbLvA2b3+/1SYH8L+oG77y9uDwGPUvmI0SqDmq230dz9YPFCOwN8jyYdEzMbSyXBfuTujxTNTT8m1frRqmNS7Psthjijc6QVyf48sMDM5prZOOCLVGaqbSozu9DM2s7eB24EtqW3aqhhMVvv2RdT4bM04ZhYZSbP+4Ht7v7tfqGmHpOoH80+Jg2b0blZVxjPu9p4M5UrnbuAf2hRHy6nUgl4EXi5mf0AHqTydvA9Ku907gSmUlkzb2dxe1GL+vFDYCvwUvHimtmEflxD5aPcS0B38XNzs49Joh9NPSbAUuCFYn/bgH8s2ms6Hvq6rEgm9A06kUwo2UUyoWQXyYSSXSQTSnaRTCjZRTKhZBfJxP8Bg73z2LgfrqwAAAAASUVORK5CYII=\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAEICAYAAACZA4KlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAASJUlEQVR4nO3dbYxc5XnG8f+F4xfATsD1YlbGeME4YBNgQRs3gQSo40QOX+wgJcSKEqqgOh9AKhKRilKpoVKlplWTKJVQJPOiOBVNggoopHEKDmrADgh7nRLb1ARwbN78skuDX8AtxvbdD3OsrM08Z8czZ2bW+1w/aTUzzz1nz50TX5zZ88w5RxGBmY1/p3W7ATPrDIfdLBMOu1kmHHazTDjsZplw2M0y4bCbZcJht5Mm6SOSHpP0pqT3fVFD0q8k/Z+kt4uf33WjTzuew27NeA94ELil5D23RcTU4ufiDvVlJRz2cUbSDklfl7RJ0j5JP5E0pcp1RMTvIuI+4Pkqf6+1l8M+Pn0BWAJcAFwO/Hm9N0n6hKS9JT+faKGHvy8+5v9a0vUt/B6ryAe63YC1xT9HxE4AST8D+uu9KSLWAWe1Yf1/Bfw3cAj4IvAzSf0Rsa0N67IGec8+Pu0e8fwgMLWTK4+IZyPiQES8GxGrgF8DN3SyB3s/hz1jkj454oh5vZ9PVrSqAFTR77Im+WN8xiJiLU3s9SUJmAxMKl5Pqf26eFfSWcCfAk8Ch4GbgGuB26vp2prlsFsz5gDbR7z+X+AVoA+YCPwdcAlwBHgBWBYRnmvvMvniFWZ58N/sZplw2M0y4bCbZcJhN8tER4/Gz5gxI/r6+jq5SrOs7NixgzfffLPudxpaCrukJcD3gAnAvRHxrbL39/X1sWHDhlZWaWYlPvrRjyZrTX+MlzQBuBv4LLAAWC5pQbO/z8zaq5W/2RcCL0fE7yPiEPBjYGk1bZlZ1VoJ+yzgtRGvXy/GjiNphaRBSYPDw8MtrM7MWtFK2OsdBHjf1/EiYmVEDETEQE9PTwurM7NWtBL214HZI16fB+xsrR0za5dWwr4BmCfpAkmTqF2k4NFq2jKzqjU99RYRhyXdBjxGbert/ojwNcnMxqiW5tkjYjWwuqJezKyN/HVZs0w47GaZcNjNMuGwm2XCYTfLhMNulgmH3SwTDrtZJhx2s0w47GaZcNjNMuGwm2XCYTfLhMNulgmH3SwTDrtZJhx2s0w47GaZcNjNMuGwm2XCYTfLhMNulgmH3SwTDrtZJhx2s0y0dEcYSTuAA8AR4HBEDFTRlJlVr6WwF/4sIt6s4PeYWRv5Y7xZJloNewCPS9ooaUW9N0haIWlQ0uDw8HCLqzOzZrUa9msi4irgs8Ctkq498Q0RsTIiBiJioKenp8XVmVmzWgp7ROwsHoeAR4CFVTRlZtVrOuySzpQ07dhz4DPAlqoaM7NqtXI0fibwiKRjv+dfI+I/KunKzCrXdNgj4vfAFRX2YmZt5Kk3s0w47GaZcNjNMuGwm2Wiiu/GZ+PAgQN1x/fv359c5rTT0v897e3tbaqPYgakrrfeeqvu+BtvvNHUulL/mwFee+21k17u6NGjyWXKtuP27duTtbLfefnll9cdX7RoUXKZefPmJWunMu/ZzTLhsJtlwmE3y4TDbpYJh90sEz4afxK2bdtWd3zt2rXJZXbv3p2sLViwoOWeTrRz586646neR7Nv375krewIeWoWYurUqcll9u7dm6xt3LgxWYuIZG3p0qV1x+fPn59cxkfjzeyU5rCbZcJhN8uEw26WCYfdLBMOu1kmPPV2EoaGhuqOl029Pf7448naoUOHWu7pRJMnT647XjblNXHixGSt7ESestqcOXNOahzgrLPOStZefvnlZO3gwYPJ2vnnn193fObMmcllxivv2c0y4bCbZcJhN8uEw26WCYfdLBMOu1kmPPV2EhYvXlx3fPbs2cllLrvssmRt3bp1ydrhw4cbb2yEhQvr324vdfYXwNy5c5taV9nZZmeccUbd8bLpxieffDJZK9tW5557brJ23XXX1R3/8Ic/nFxmvBp1zy7pfklDkraMGJsuaY2kl4rHs9vbppm1qpGP8T8AlpwwdifwRETMA54oXpvZGDZq2CPiKeAPJwwvBVYVz1cBy6pty8yq1uwBupkRsQugeDwn9UZJKyQNShocHh5ucnVm1qq2H42PiJURMRARAz09Pe1enZklNBv2PZJ6AYrH+meImNmY0ezU26PAzcC3isefVtbRGJY6y+uiiy5KLnPrrbcma1/96leb6qOZKa8zzzwzucykSZOa6qNMaltt2rQpucy9996brJVdjHLZsmXJWmqKrewWWuNVI1NvPwKeAS6W9LqkW6iF/NOSXgI+Xbw2szFs1D17RCxPlD5VcS9m1kb+uqxZJhx2s0w47GaZcNjNMuGz3ipQdsHG6dOnd7CTsSN1EcgXXnghuczg4GCy9t577yVrl156abJ2zjn1v9xZNvVWNrV5KvOe3SwTDrtZJhx2s0w47GaZcNjNMuGwm2XCU2+noGamjTo91bRt27a642X3xdu/f3+y1t/fn6xdccUVydoHP/jBZC033rObZcJhN8uEw26WCYfdLBMOu1kmfDT+FNTM0fN2HHEvu0VV6qSWX/7yl8llJk+enKzdeOONydoll1ySrJ1++ul1x8fryS5lvGc3y4TDbpYJh90sEw67WSYcdrNMOOxmmfDUmzVt9+7dydr69evrjr/44ovJZS688MJkbdGiRcnatGnTkrUcp9hSGrn90/2ShiRtGTF2l6Q3JD1X/NzQ3jbNrFWNfIz/AbCkzvh3I6K/+FldbVtmVrVRwx4RTwF/6EAvZtZGrRygu03SpuJj/tmpN0laIWlQ0uDw8HALqzOzVjQb9u8Dc4F+YBfw7dQbI2JlRAxExEBPT0+TqzOzVjUV9ojYExFHIuIocA+wsNq2zKxqTU29SeqNiF3Fy88BW8reb+PT6tXp47Lr1q2rO97b25tc5ktf+lKyVnaLp7Kz5eyPRg27pB8B1wMzJL0OfBO4XlI/EMAO4Gvta9HMqjBq2CNieZ3h+9rQi5m1kb8ua5YJh90sEw67WSYcdrNM+Kw3Kz0zrOyWTBs2bEjWtm/fXne8r68vuUzZbZymTJmSrFljvGc3y4TDbpYJh90sEw67WSYcdrNMOOxmmfDU2zgjqe542fRa2T3bfvGLXyRrqfu5QfoeawsXps+GvvLKK5O1007zfqlV3oJmmXDYzTLhsJtlwmE3y4TDbpYJH40fZ1JH3Y8cOZJcZmhoKFl76KGHkrWyWzlddtlldccXL16cXGbOnDnJmrXOe3azTDjsZplw2M0y4bCbZcJhN8uEw26WiUbuCDMb+CFwLnAUWBkR35M0HfgJ0EftrjBfiIi32teqHZM62QXSU2/vvPNOcpmnn346WXv++eeTtbITaBYsWFB3vL+/P7mMtVcje/bDwB0RMR/4GHCrpAXAncATETEPeKJ4bWZj1Khhj4hdEfGb4vkBYCswC1gKrCretgpY1qYezawCJ/U3u6Q+4ErgWWDmsTu5Fo/nVN6dmVWm4bBLmgo8BNweEemLib9/uRWSBiUNDg8PN9OjmVWgobBLmkgt6A9ExMPF8B5JvUW9F6j7BeuIWBkRAxEx0NPTU0XPZtaEUcOu2qHf+4CtEfGdEaVHgZuL5zcDP62+PTOrSiNnvV0DfBnYLOm5YuwbwLeAByXdArwKfL4tHdr7lF1PLjUt9+qrryaXufvuu5O11G2cAObOnZusXXfddXXHL7744uQy1l6jhj0i1gGpid1PVduOmbWLv0FnlgmH3SwTDrtZJhx2s0w47GaZ8AUnT0LZ2WYpZdNkza6r7Hdu2rSp7vg999yTXGbjxo3J2rvvvpusLV++PFm7/vrr645PmDAhuUynt1VuvGc3y4TDbpYJh90sEw67WSYcdrNMOOxmmfDU20no5DROM2e2QfrstmeeeSa5zMGDB5O1q6++OllLTa8BnHfeeXXH27ENPb3WGO/ZzTLhsJtlwmE3y4TDbpYJh90sEz4a32btOEljz549ydrmzZvrjr/yyivJZVJHzgG+8pWvJGvz589P1j7wgfr/tHyyS/d4z26WCYfdLBMOu1kmHHazTDjsZplw2M0yMerUm6TZwA+Bc4GjwMqI+J6ku4C/AI7dmvUbEbG6XY2eqpqdFjp69Giytnbt2mRt9er6/xeUXUtu2bJlydqNN96YrJXdqDP1v7vZKTRPr7WukXn2w8AdEfEbSdOAjZLWFLXvRsQ/ta89M6tKI/d62wXsKp4fkLQVmNXuxsysWif1N7ukPuBK4Nli6DZJmyTdL+nsqpszs+o0HHZJU4GHgNsjYj/wfWAu0E9tz//txHIrJA1KGhweHq73FjPrgIbCLmkitaA/EBEPA0TEnog4EhFHgXuAhfWWjYiVETEQEQNlB3TMrL1GDbtqh0/vA7ZGxHdGjPeOeNvngC3Vt2dmVWnkaPw1wJeBzZKeK8a+ASyX1A8EsAP4Whv6G9fKppP27duXrD322GPJWupWTpdeemlymTvuuCNZO/tsH4oZLxo5Gr8OqDc56jl1s1OIv0FnlgmH3SwTDrtZJhx2s0w47GaZ8AUn26zsLK8jR44ka2vWrEnWNmzYkKydf/75dcdvuumm5DJz585N1lIXjoTmblHV6bPXxkofY4H37GaZcNjNMuGwm2XCYTfLhMNulgmH3SwTnnprs7ILR7799tvJ2s9//vNkbdu2bcnaRRddVHe87Oy1ZqfXylR9wclm5TjFluI9u1kmHHazTDjsZplw2M0y4bCbZcJhN8uEp95OQtm0Uco777yTrD399NPJ2vr165O1sim7D33oQ3XHZ86cmVym09NhVTvV++8U79nNMuGwm2XCYTfLhMNulgmH3SwTox6NlzQFeAqYXLz/3yLim5KmAz8B+qjd/ukLEfFW+1rtvmaO7B46dChZ27p1a7K2d+/eZG3q1KnJ2rx58+qOl93+qR1HrDt57TcfcW9MI3v2d4FFEXEFtdszL5H0MeBO4ImImAc8Ubw2szFq1LBHzbGJ3YnFTwBLgVXF+CpgWTsaNLNqNHp/9gnFHVyHgDUR8SwwMyJ2ARSP57StSzNrWUNhj4gjEdEPnAcslPSRRlcgaYWkQUmDw8PDTbZpZq06qaPxEbEX+BWwBNgjqRegeBxKLLMyIgYiYqCnp6e1bs2saaOGXVKPpLOK56cDi4EXgEeBm4u33Qz8tE09mlkFGjkRphdYJWkCtf84PBgR/y7pGeBBSbcArwKfb2Ofp6wzzjgjWbv66quTtRkzZiRrs2bNStY+/vGP1x2/4IILkss0O3VV9Qko7Tihxbd/+qNRwx4Rm4Ar64z/D/CpdjRlZtXzN+jMMuGwm2XCYTfLhMNulgmH3SwT6uQUhKRh4JXi5QzgzY6tPM19HM99HO9U62NORNT99lpHw37ciqXBiBjoysrdh/vIsA9/jDfLhMNuloluhn1lF9c9kvs4nvs43rjpo2t/s5tZZ/ljvFkmHHazTHQl7JKWSPqdpJclde1ClZJ2SNos6TlJgx1c7/2ShiRtGTE2XdIaSS8Vj2d3qY+7JL1RbJPnJN3QgT5mS/pPSVslPS/pL4vxjm6Tkj46uk0kTZG0XtJviz7+thhvbXtEREd/gAnANuBCYBLwW2BBp/soetkBzOjCeq8FrgK2jBj7R+DO4vmdwD90qY+7gK93eHv0AlcVz6cBLwILOr1NSvro6DYBBEwtnk8EngU+1ur26MaefSHwckT8PiIOAT+mdqXabETEU8AfThju+NV6E310XETsiojfFM8PAFuBWXR4m5T00VFRU/kVnbsR9lnAayNev04XNmghgMclbZS0oks9HDOWrtZ7m6RNxcf8tv85MZKkPmoXS+nqFYxP6AM6vE3acUXnboS93nWCujX/d01EXAV8FrhV0rVd6mMs+T4wl9oNQXYB3+7UiiVNBR4Cbo+I/Z1abwN9dHybRAtXdE7pRthfB2aPeH0esLMLfRARO4vHIeARan9idEtDV+ttt4jYU/xDOwrcQ4e2iaSJ1AL2QEQ8XAx3fJvU66Nb26RY915O8orOKd0I+wZgnqQLJE0CvkjtSrUdJelMSdOOPQc+A2wpX6qtxsTVeo/9Yyp8jg5sE9WuCnkfsDUivjOi1NFtkuqj09ukbVd07tQRxhOONt5A7UjnNuCvu9TDhdRmAn4LPN/JPoAfUfs4+B61Tzq3AH9C7Z55LxWP07vUx78Am4FNxT+u3g708Qlqf8ptAp4rfm7o9DYp6aOj2wS4HPivYn1bgL8pxlvaHv66rFkm/A06s0w47GaZcNjNMuGwm2XCYTfLhMNulgmH3SwT/w9vmDMUFyve2wAAAABJRU5ErkJggg==\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "# 然后我们看看经典奇异值的分解效果\n",
-    "U, sigma, V = np.linalg.svd(imgmat)\n",
-    "\n",
-    "for i in range(5, 16, 5):\n",
-    "    reconstimg = np.matrix(U[:, :i]) * np.diag(sigma[:i]) * np.matrix(V[:i, :])\n",
-    "    plt.imshow(reconstimg, cmap='gray')\n",
-    "    title = \"n = %s\" % i\n",
-    "    plt.title(title)\n",
-    "    plt.show()"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 13,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 然后我们再来看看量子版本的分解效果：\n",
-    "time_start = time.time()\n",
-    "\n",
-    "# 超参数设置\n",
-    "N = 5           # 量子比特数量\n",
-    "T = 8           # 设置想要学习的阶数\n",
-    "D = 80          # 量子神经网络的深度\n",
-    "ITR = 200       # 迭代次数\n",
-    "LR = 0.02       # 学习速率\n",
-    "SEED = 14       # 随机数种子\n",
-    "\n",
-    "# 设置等差的学习权重\n",
-    "weight = np.arange(2 * T, 0, -2).astype('complex128')\n",
-    "\n",
-    "\n",
-    "def Mat_generator():\n",
-    "    imgmat = np.array(list(img.getdata(band=0)), float)\n",
-    "    imgmat.shape = (img.size[1], img.size[0])\n",
-    "    lenna = np.matrix(imgmat)\n",
-    "    return lenna.astype('complex128')\n",
-    "\n",
-    "M_err = Mat_generator()\n",
-    "U, D, V_dagger = np.linalg.svd(Mat_generator(), full_matrices=True)"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 14,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "# 设置电路参数\n",
-    "cir_depth = 80                           # 电路深度\n",
-    "block_len = 1                            # 每个模组的长度\n",
-    "theta_size = N * block_len * cir_depth   # 网络参数 theta 的大小\n",
-    "\n",
-    "# 定义量子神经网络\n",
-    "def U_theta(theta):\n",
-    "\n",
-    "    # 用 UAnsatz 初始化网络\n",
-    "    cir = UAnsatz(N)\n",
-    "    \n",
-    "    # 搭建层级结构：\n",
-    "    for layer_num in range(cir_depth):\n",
-    "        \n",
-    "        for which_qubit in range(N):\n",
-    "            cir.ry(theta[block_len * layer_num * N + which_qubit], which_qubit)\n",
-    "\n",
-    "        for which_qubit in range(1, N):\n",
-    "            cir.cnot([which_qubit - 1, which_qubit])\n",
-    "\n",
-    "    return cir.U"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 15,
-   "metadata": {},
-   "outputs": [],
-   "source": [
-    "class NET(fluid.dygraph.Layer):\n",
-    "    \n",
-    "    # 初始化长度为 theta_size 的可学习参数列表，并用 [0, 2*pi] 的均匀分布来填充初始值\n",
-    "    def __init__(self, shape, param_attr=fluid.initializer.Uniform(low=0.0, high=2 * np.pi), dtype='float64'):\n",
-    "        super(NET, self).__init__()\n",
-    "        \n",
-    "        # 创建用来学习 U 的参数 theta\n",
-    "        self.theta = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
-    "        \n",
-    "        # 创建用来学习 V_dagger 的参数 phi\n",
-    "        self.phi = self.create_parameter(shape=shape, attr=param_attr, dtype=dtype, is_bias=False)\n",
-    "        \n",
-    "        # 我们需要将 Numpy array 转换成 Paddle 动态图模式中支持的 variable\n",
-    "        self.M = fluid.dygraph.to_variable(Mat_generator())\n",
-    "        self.weight = fluid.dygraph.to_variable(weight)\n",
-    "\n",
-    "    # 定义损失函数和前向传播机制\n",
-    "    def forward(self):\n",
-    "        \n",
-    "        # 获取量子神经网络的酉矩阵表示\n",
-    "        U = U_theta(self.theta)\n",
-    "        U_dagger = dagger(U)\n",
-    "        \n",
-    "        \n",
-    "        V = U_theta(self.phi)\n",
-    "        V_dagger = dagger(V)\n",
-    "        \n",
-    "        # 初始化损失函数和奇异值存储器\n",
-    "        loss = 0 \n",
-    "        singular_values = np.zeros(T)\n",
-    "        \n",
-    "        # 定义损失函数\n",
-    "        for i in range(T):\n",
-    "            loss -= self.weight.real[i] * matmul(U_dagger, matmul(self.M, V)).real[i][i]\n",
-    "            singular_values[i] = (matmul(U_dagger, matmul(self.M, V)).real[i][i]).numpy()\n",
-    "        \n",
-    "        # 函数返回两个矩阵 U 和 V_dagger、 学习的奇异值以及损失函数    \n",
-    "        return U, V_dagger, loss, singular_values"
-   ]
-  },
-  {
-   "cell_type": "code",
-   "execution_count": 17,
-   "metadata": {},
-   "outputs": [
-    {
-     "name": "stderr",
-     "output_type": "stream",
-     "text": [
-      "100% |########################################################################|\n"
-     ]
-    },
-    {
-     "name": "stdout",
-     "output_type": "stream",
-     "text": [
-      "主程序段总共运行了 1971.4076132774353 秒\n"
-     ]
-    },
-    {
-     "data": {
-      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD5CAYAAADhukOtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAYhklEQVR4nO2dW2xdZXbH/ysmF0icm52LyQUnjiEBBAGZiIiCaBmGFI0EPICGh4EHNJmHQSrS9AFRqdA3WhVGPFRIoYTJVJQBlUGgCrWDoiKEqCAGcqMOmASHOHbs3OOQBEi8+nB2JAN7/e3s47OPh+//kyI73zrf3ut8ey+fc77/WWuZu0MI8eNnUr0dEEKUg4JdiERQsAuRCAp2IRJBwS5EIijYhUiEi6qZbGbrADwDoAHAv7r7k+zxs2fP9paWlnxHLopdieRBJhueO3cutE2aFP+NYzYzyx1nvjPOnj0b2r7++uvQVsTHyZMnh3OGh4dD27fffnvB5wJiH7/55ptCx5s6dWpomzZtWmiLzsfuHXZd2NqzY7J5RY4X2fr6+nDs2LHchSwc7GbWAOBfANwOoBfAFjN7w93/L5rT0tKCF154Idc2b9688FzR4rMb8ejRo6GtsbExtLEbp6GhIXec+c4u8sDAQGj74osvQtvFF18c2qZMmZI7Hv2RBYCvvvoqtPX19V3wuQDgkksuyR3fu3dvoeOtWLEitK1cuTK09fT05I6zF4PDhw+HNvZHh92P0XoA8R859ocxOtcDDzwQzqnmbfwaAJ+7+x53/wbAHwDcVcXxhBA1pJpgXwRg34j/92ZjQogJSDXBnvfe4wcfJMxsvZl1mlnnsWPHqjidEKIaqgn2XgBLRvx/MYAffMBz9w3u3uHuHbNnz67idEKIaqgm2LcAaDezZWY2BcDPAbwxPm4JIcabwrvx7n7WzB4G8N+oSG8b3f0TNqehoQHRq3tvby+dlweTk5qbm0Mb24kdGhoKbXPmzMkdHxwcDOdEvgN8Z/fSSy8NbYcOHQptkdLAVIFZs2aFthkzZoS2AwcOhLZIDbn88svDOUVlrW3btoW26LkdP348nMPuHabysHVkH2Ej6ZNJutHuPlvDqnR2d38TwJvVHEMIUQ76Bp0QiaBgFyIRFOxCJIKCXYhEULALkQhV7cZfKO5Ov9wfESVIMOmNyRYsYYFlm0W+s+QZllF26tSp0MZgkl0kvRR5XgB/biwhp4hcymQtBpMHIz+YRMWuC/P/9OnToY3JvZGsWDRzM5xzwTOEEH+WKNiFSAQFuxCJoGAXIhEU7EIkQqm78WZGd5Ijot1ilmRStM4c232OVAG20818nD59emhju/gsqeLEiRMXfDyW+DFz5szQxspZRTvrTCUpojIAfBc8Shhh68FUhmh9gWIlzYC4LBWryVcEvbILkQgKdiESQcEuRCIo2IVIBAW7EImgYBciEUpPhImSUM6cORPOi2p7sbpkRWUL5keRRBjWSogloLAkCCYNRZ1f2PEOHjwY2piPbP0XLFiQO97U1BTOYR1ymLxZpDUUk/JYohST0Iq284rWkSXdKBFGCBGiYBciERTsQiSCgl2IRFCwC5EICnYhEqEq6c3MegAMATgH4Ky7d7DHu3soT7Bm9UVq0DFZiMlQjChTiskxDCbHMGmFyYpRWyMmC7EMsKLPLVpjljXGWm+x58wahkbPjR2PXRd2zzHZls2LKNoOK2I8dPa/dPe4+ZgQYkKgt/FCJEK1we4A/mRmH5rZ+vFwSAhRG6p9G3+Tu/eZ2XwAb5nZLnd/Z+QDsj8C64H4q5xCiNpT1Su7u/dlPwcBvAZgTc5jNrh7h7t3sI0UIURtKRzsZjbdzBrP/w7gpwB2jpdjQojxpZq38QsAvJZJGBcB+Hd3/6/RJkUSEGvhE8k4LCOLFSFkRQ9ZEchIPmEyDstQY/IJy0RjEk8kG7GiklFWIQCcPHkytDEZLVp/JgGytZo/f35oY+8YIzmPXTMmRbL7ismUkXzMYH5ExT7ZnMLB7u57AFxbdL4QolwkvQmRCAp2IRJBwS5EIijYhUgEBbsQiVBqwcmLLroICxcuzLX19PSE8yKJisl1TGpi2VVM1jp16lTu+I4dO8I5jKgoI8C/bbhv377QFvWBY+vb2toa2pgUuXXr1tD2wQcf5I4vXbo0nMOkKyZ5sQKRa9euzR2fM2dOOKe9vT209ff3h7a5c+eGNtafL8puKyLl0R6HoUUI8aNCwS5EIijYhUgEBbsQiaBgFyIRSt2NB+JECFaDLkqEYbuV0c458wHgtcKindhdu3aFc44cORLaWAJHpFoAwOHDh0Nb1EKpt7e3kB9sjZkqsH///tzx7u7ucA67LtHxAGDmzJmhLdqdvvnmm8M5UZIJwOsXFk2+ipJyWKJUkUQYvbILkQgKdiESQcEuRCIo2IVIBAW7EImgYBciEUqV3oaHh8O6cUxmKNLqhsEkHkYko/X19YVzdu/eHdpYDT0moTAZLZJ/WA00VvuNrRW7LlFdu8suu6zQubZv3x7aDhw4ENpuuOGG3HFWW4/JayzRhMmU7FpH52PXLJrDrole2YVIBAW7EImgYBciERTsQiSCgl2IRFCwC5EIo0pvZrYRwM8ADLr71dnYXAAvA2gF0APgPnc/Wo0jTAqZNm1a7jiTp4pk0QG8VtiiRYtyx1kGFZOaWHYVy5ZramoKbW1tbbnjq1atCuew2mmszh9r/xRdz8bGxnBOV1dXaGMZZUw6vP3223PHWY1CdjxW7461lIracrFjsuNF68jkv7G8sv8OwLrvjT0KYLO7twPYnP1fCDGBGTXYs37r33+ZuQvApuz3TQDuHl+3hBDjTdHP7AvcvR8Asp9xi00hxISg5ht0ZrbezDrNrPPo0ao+1gshqqBosA+YWQsAZD8Howe6+wZ373D3DlaYXwhRW4oG+xsAHsx+fxDA6+PjjhCiVoxFensJwK0Ams2sF8DjAJ4E8IqZPQTgSwD3juVkZhZKA0wyiGSGohlIkZQH8IKT0bzly5eHc5gEyDKUpk6dGtrY847kQTbn+PHjoY3JUEyWO3jwYO44Kxy5c+fO0Ma46qqrQlvURosV2WTSLLsuTB6kkhi5NhHRfcrkulGD3d3vD0y3jckrIcSEQN+gEyIRFOxCJIKCXYhEULALkQgKdiESofSCk5E8waSQSPJiBQpZ9hqTQYpIZUzKY7IKy4RivcGiYo5s3pkzZ8I5TF5jfrDnHUlAn376aTiH9Y5j2YNXXHFFaIuuNXvOLAOTFYEcGhoKbeyaRT6y+yOKI/V6E0Io2IVIBQW7EImgYBciERTsQiSCgl2IRChVejOzMFuHFV+M5rCsMZa9xuaxgoKRjMYkEmZjfjCJh8lhUYYgW49Tp06FNgaTqCLpk2ZlkefFeqWxrL358/OLKDHZlvnBpC2WEccy6aL7gN0fbB0j9MouRCIo2IVIBAW7EImgYBciERTsQiRCqbvx586dQ1ROur29PZwX7Razml89PT2hbd68eaGNVcCNzsfaJ7HjRXXaAN5aiR0zqvHGdopZLbmBgYHQxna0o53kjz/+OJzDkpfWrl0b2m655ZbQ1t/fnzs+ffr0cA5LyGHtq9g1a21tDW2RUsJUhiiO2K6/XtmFSAQFuxCJoGAXIhEU7EIkgoJdiERQsAuRCGNp/7QRwM8ADLr71dnYEwB+CeC8dvSYu7852rEmTZoUyjyDg2FvyFBOYIkCTJ5iNeiYnBclQTAJjcFquLGafEXq5LH6aEXbFjGpLJIAo/ZUAH/OzI/u7u7QFq0VS+Jh9eJYotTMmTNDG1vj6JhMRotq6LGah2N5Zf8dgHU5479199XZv1EDXQhRX0YNdnd/B8CREnwRQtSQaj6zP2xm281so5mp8boQE5yiwf4sgDYAqwH0A3gqeqCZrTezTjPrjL7iJ4SoPYWC3d0H3P2cuw8DeA7AGvLYDe7e4e4dbNNMCFFbCgW7mY3scH8PgJ3j444QolaMRXp7CcCtAJrNrBfA4wBuNbPVABxAD4BfVesIy8qKsolYHS7W7qhoS6NICmGyCpPJmJzEMspYvb5Dhw7ljrO1YhlgrD7dgQMHQluUbcbkpGXLloW2tra20MYy0aLadTQ7jMhX7Lqwa81qAEb3IztXVNuQydGjBru7358z/Pxo84QQEwt9g06IRFCwC5EICnYhEkHBLkQiKNiFSIRSC042NDSEWW+suF6UscUkI/YFniKSBhBLZawoI/Ojubk5tLGimJGsBcRSGcvyYj6yTDSWSRcV/Fy+fHk4Z+XKlaGNFcVkxUWj9k9sPRYvXhzamBTJsuWYXBrBpNlaZb0JIX4EKNiFSAQFuxCJoGAXIhEU7EIkgoJdiEQoVXpz97C4HpMMooy4olljLAOMZQ1Fx4xkEIA/LybHMD+iwpdAXPSQ+bh3797QtmfPntDW19cX2iLJjvXFY9IVy4osYmOZj6yoJJvHYNesCOwejtAruxCJoGAXIhEU7EIkgoJdiERQsAuRCBNmN57tqLJ6YREsYYEl0EyZMiW0RUkyrG4dOx5TDFhyDVuraPef1UfbtWtXaHvvvfdC25Ejce+QKAGF7bgvXbo0tLE1Zjvd0X3AdtXZ/cZ2wZk6xGrQFdmpL9ISTa/sQiSCgl2IRFCwC5EICnYhEkHBLkQiKNiFSISxtH9aAuD3ABYCGAawwd2fMbO5AF4G0IpKC6j73J22aR0eHg7lKyZbRFIZqxdXi/Y+USuhKPmEzQHitlYAl95Ym6RI8mLS2+effx7atmzZEtoWLlwY2lasWJE7HvkH8GvGWmyxY0ZSFJMvWeswJqWya83ktWgeu08jCZBJg2N5ZT8L4DfuvgrAjQB+bWZXAngUwGZ3bwewOfu/EGKCMmqwu3u/u3+U/T4EoAvAIgB3AdiUPWwTgLtr5KMQYhy4oM/sZtYK4DoA7wNY4O79QOUPAoD4vZQQou6MOdjNbAaAVwE84u7xh80fzltvZp1m1nn0KP1IL4SoIWMKdjObjEqgv+juf8yGB8ysJbO3ABjMm+vuG9y9w907WDMCIURtGTXYrbK99zyALnd/eoTpDQAPZr8/COD18XdPCDFejCXr7SYAvwCww8y2ZmOPAXgSwCtm9hCALwHcO9qB3D2UNVhWUFTPjNUKK1pnrkhdO9aaiLW1KppBxWS0SK5h8trbb78d2j755JPQxiTAa665JnecSVdM8mL3B6trF0l2LIvuwIEDoa2pqSm0sSzAIlmd7P6O7g92b48a7O7+LoDorrxttPlCiImBvkEnRCIo2IVIBAW7EImgYBciERTsQiRCqQUnJ02aFMpGLNuMFY+MYJloTPJitkj+YZILk5OYvMb8379/f2jbvXt37nh3d3c4h7WGWr16dWibN29eaBsaGsodX758eTiHPWfWKou1oWKZkRGsICmDyWvsvoqKXxaRiKvNehNC/AhQsAuRCAp2IRJBwS5EIijYhUgEBbsQiVCq9DY8PBwW12NZSJGNSXK05xUp5Mfkk0jGYf3L2LlYVhOzseKFURHLzz77LJxz+PDh0MZqEFx77bWhLcp6YwVMItkQ4HIYk/MOHTqUO84yB/v7+0MbkymjcwFcpoykN3Z/q9ebECJEwS5EIijYhUgEBbsQiaBgFyIRSk+EiXYzi+w8RruYQFy3DuA7wixxJdpZZzXL2O4o29llLY127NgR2rq6unLHd+3aFc5ZtWpVaLvhhhtC25IlS0JblJzCnldjY2NoY62Venp6QluUvMQUDbbzz1pUsevJ5kWwRKnoeSkRRgihYBciFRTsQiSCgl2IRFCwC5EICnYhEmFU6c3MlgD4PYCFAIYBbHD3Z8zsCQC/BHAwe+hj7v4mO5a7h7XmWCJMJLuwVkJMWmFJJiwRJpLemKzC2haxunsMJvVt27Ytd3zfvn3hnDvuuCO03XZb3PSHPbfIRyZ7suvJZFYmb0b3DktQYjA5jMmDTM6L7rki93BV7Z8AnAXwG3f/yMwaAXxoZm9ltt+6+z+P4RhCiDozll5v/QD6s9+HzKwLwKJaOyaEGF8u6L2MmbUCuA7A+9nQw2a23cw2mpmarwsxgRlzsJvZDACvAnjE3U8AeBZAG4DVqLzyPxXMW29mnWbWeezYsaodFkIUY0zBbmaTUQn0F939jwDg7gPufs7dhwE8B2BN3lx33+DuHe7ewb6vLoSoLaMGu1W+Wf88gC53f3rEeMuIh90DYOf4uyeEGC/Gsht/E4BfANhhZluzsccA3G9mqwE4gB4AvxrtQGYWSihMdjl58uQFzymSvQbwzKVICmG1x5iPLENpcHAwtO3Zsye0RfXTWEbZ9ddfH9ra29tD28DAQGg7fvx47jiT0JYuXRra2DpG52IwiZXVp2P3FZPXmP+RjUm6UUwwxrIb/y6AvLuSaupCiImFvkEnRCIo2IVIBAW7EImgYBciERTsQiRCqQUnWdYby9aJJKqiLZKY5MUKX0aSXdFCg0wy6u7uDm1fffVVaIuksmXLloVz2JedDh48GNpOnz4d2ubOnZs7XjSzjV0XlonGzjfeMP+j1mFAfB+ze7gIemUXIhEU7EIkgoJdiERQsAuRCAp2IRJBwS5EIpQqvZlZKHuxYn2RfEWL6xEZhEl2RXpyseOxopJMjmHrwSSvaE2YPMWeM5N/2PpHxShZ9h2TMFmWF5PlIumNPS927zDYGrP7gK1jRJGCmXplFyIRFOxCJIKCXYhEULALkQgKdiESQcEuRCKUKr2dPXsWUe34tra2cN6JEydyx5nk1dfXF9qamppCGys2GEleCxcuDOdEvgPA3r17Q9u7774b2lj9/VmzZuWOr1ixIpzDZL4tW7aEtpaWltC2ZMmS3PGenp5wDivYyFi1alVoi4pisnOx9S1a5HTGjBmhLZIBi2RMMklRr+xCJIKCXYhEULALkQgKdiESQcEuRCKMuhtvZtMAvANgavb4/3D3x81sLoCXAbSi0v7pPnc/WtQRtgNapEbXtGnTQhtLPGB+FEkyYTu0RVtUsZ3kSNW4+uqrwzlsHdl6MP+jY7IdfAZrh8WSZKLdc5aExK4nI0r+AXiyTnR/s+NF7atYfcWxvLJ/DeCv3P1aVNozrzOzGwE8CmCzu7cD2Jz9XwgxQRk12L3C+T+dk7N/DuAuAJuy8U0A7q6Fg0KI8WGs/dkbsg6ugwDecvf3ASxw934AyH7Or5mXQoiqGVOwu/s5d18NYDGANWYWfwD8Hma23sw6zayzSGtdIcT4cEG78e5+DMDbANYBGDCzFgDIfubuoLj7BnfvcPeO6KucQojaM2qwm9k8M5ud/X4xgJ8A2AXgDQAPZg97EMDrNfJRCDEOjCURpgXAJjNrQOWPwyvu/p9m9r8AXjGzhwB8CeDesZywSEubSAphdb1YcgdLdmGSVyRrsLpqLJmBJeQwG5NkWltbc8ejdkwAcOjQodDGko1YUkiU+MESlFhtPXZdmpubQ9vRo/lqMLsuQ0NDhfwYbzmP3d/RdaF1GUc7obtvB3BdzvhhALeNNl8IMTHQN+iESAQFuxCJoGAXIhEU7EIkgoJdiESwIq1nCp/M7CCA84XXmgHEmk95yI/vIj++y5+bH5e5+7w8Q6nB/p0Tm3W6e0ddTi4/5EeCfuhtvBCJoGAXIhHqGewb6njukciP7yI/vsuPxo+6fWYXQpSL3sYLkQh1CXYzW2dmn5rZ52ZWt9p1ZtZjZjvMbKuZdZZ43o1mNmhmO0eMzTWzt8ysO/s5p05+PGFm+7M12Wpmd5bgxxIz+x8z6zKzT8zsb7LxUteE+FHqmpjZNDP7wMy2ZX78QzZe3Xq4e6n/ADQA2A1gOYApALYBuLJsPzJfegA01+G8twC4HsDOEWP/BODR7PdHAfxjnfx4AsDflrweLQCuz35vBPAZgCvLXhPiR6lrAsAAzMh+nwzgfQA3Vrse9XhlXwPgc3ff4+7fAPgDKsUrk8Hd3wFw5HvDpRfwDPwoHXfvd/ePst+HAHQBWISS14T4USpeYdyLvNYj2BcB2Dfi/72ow4JmOIA/mdmHZra+Tj6cZyIV8HzYzLZnb/Nr/nFiJGbWikr9hLoWNf2eH0DJa1KLIq/1CPa8ci/1kgRucvfrAfw1gF+b2S118mMi8SyANlR6BPQDeKqsE5vZDACvAnjE3eNe1+X7UfqaeBVFXiPqEey9AEY2714MIK5VVEPcvS/7OQjgNVQ+YtSLMRXwrDXuPpDdaMMAnkNJa2Jmk1EJsBfd/Y/ZcOlrkudHvdYkO/cxXGCR14h6BPsWAO1mtszMpgD4OSrFK0vFzKabWeP53wH8FMBOPqumTIgCnudvpox7UMKaWKW43/MAutz96RGmUtck8qPsNalZkdeydhi/t9t4Jyo7nbsB/F2dfFiOihKwDcAnZfoB4CVU3g5+i8o7nYcANKHSRqs7+zm3Tn78G4AdALZnN1dLCX78BSof5bYD2Jr9u7PsNSF+lLomAK4B8HF2vp0A/j4br2o99A06IRJB36ATIhEU7EIkgoJdiERQsAuRCAp2IRJBwS5EIijYhUgEBbsQifD/a7hBdbxhRo0AAAAASUVORK5CYII=\n",
-      "text/plain": [
-       "<Figure size 432x288 with 1 Axes>"
-      ]
-     },
-     "metadata": {
-      "needs_background": "light"
-     },
-     "output_type": "display_data"
-    }
-   ],
-   "source": [
-    "# 记录优化中间过程\n",
-    "loss_list, singular_value_list = [], []\n",
-    "U_learned, V_dagger_learned = [], []\n",
-    "\n",
-    "\n",
-    "# 启动 Paddle 动态图模式\n",
-    "with fluid.dygraph.guard():\n",
-    "    \n",
-    "    net = NET([theta_size])\n",
-    "    # 一般来说，我们利用Adam优化器来获得相对好的收敛，当然你可以改成SGD或者是RMS prop.\n",
-    "    opt = fluid.optimizer.AdagradOptimizer(learning_rate=LR, parameter_list=net.parameters())\n",
-    "    \n",
-    "    # 优化循环\n",
-    "    pbar = ProgressBar()\n",
-    "    for itr in pbar(range(ITR)):\n",
-    "        \n",
-    "        #  前向传播计算损失函数\n",
-    "        U, V_dagger, loss, singular_values = net()\n",
-    "        \n",
-    "        # 在动态图机制下，反向传播极小化损失函数\n",
-    "        loss.backward()\n",
-    "        opt.minimize(loss)\n",
-    "        net.clear_gradients()\n",
-    "\n",
-    "        # 记录优化中间结果\n",
-    "        loss_list.append(loss[0][0].numpy())\n",
-    "        singular_value_list.append(singular_values)\n",
-    "\n",
-    "    # 记录最后学出的两个酉矩阵    \n",
-    "    U_learned = U.real.numpy() + 1j * U.imag.numpy()\n",
-    "    V_dagger_learned = V_dagger.real.numpy() + 1j*V_dagger.imag.numpy()\n",
-    "\n",
-    "singular_value = singular_value_list[-1]\n",
-    "mat = np.matrix(U_learned.real[:, :T]) * np.diag(singular_value[:T])* np.matrix(V_dagger_learned.real[:T, :])\n",
-    "\n",
-    "reconstimg = mat\n",
-    "plt.imshow(reconstimg, cmap='gray')\n",
-    "\n",
-    "time_span = time.time() - time_start        \n",
-    "print('主程序段总共运行了', time_span, '秒')"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "<hr>"
-   ]
-  },
-  {
-   "cell_type": "markdown",
-   "metadata": {},
-   "source": [
-    "## 参考文献：\n",
-    "\n",
-    "[1] [Wang, X., Song, Z. & Wang, Y. Variational Quantum Singular Value Decomposition. arXiv:2006.02336 (2020).](https://arxiv.org/abs/2006.02336)"
-   ]
-  }
- ],
- "metadata": {
-  "kernelspec": {
-   "display_name": "Python 3",
-   "language": "python",
-   "name": "python3"
-  },
-  "language_info": {
-   "codemirror_mode": {
-    "name": "ipython",
-    "version": 3
-   },
-   "file_extension": ".py",
-   "mimetype": "text/x-python",
-   "name": "python",
-   "nbconvert_exporter": "python",
-   "pygments_lexer": "ipython3",
-   "version": "3.7.7"
-  }
- },
- "nbformat": 4,
- "nbformat_minor": 4
-}