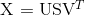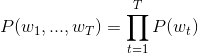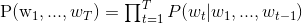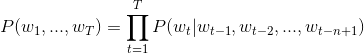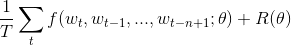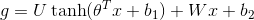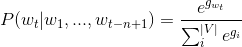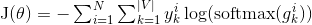Fix the doc of word2vec (#735)
Showing
04.word2vec/image/Eqn1.gif
0 → 100644
397 字节
04.word2vec/image/Eqn2.gif
0 → 100644
991 字节
04.word2vec/image/Eqn3.gif
0 → 100644
1.1 KB
04.word2vec/image/Eqn4.gif
0 → 100644
1.4 KB
04.word2vec/image/Eqn5.gif
0 → 100644
1.2 KB
04.word2vec/image/Eqn6.gif
0 → 100644
982 字节
04.word2vec/image/Eqn7.gif
0 → 100644
1.1 KB
04.word2vec/image/Eqn8.gif
0 → 100644
1.5 KB
04.word2vec/image/Eqn9.gif
0 → 100644
1009 字节