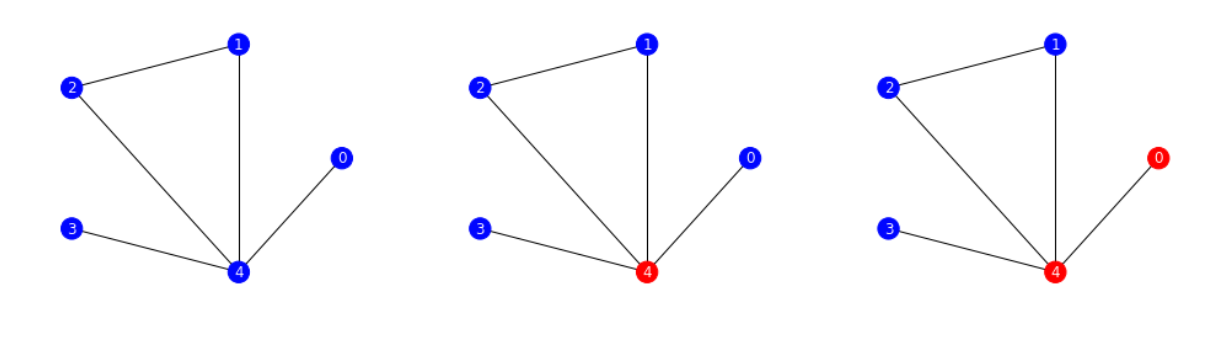
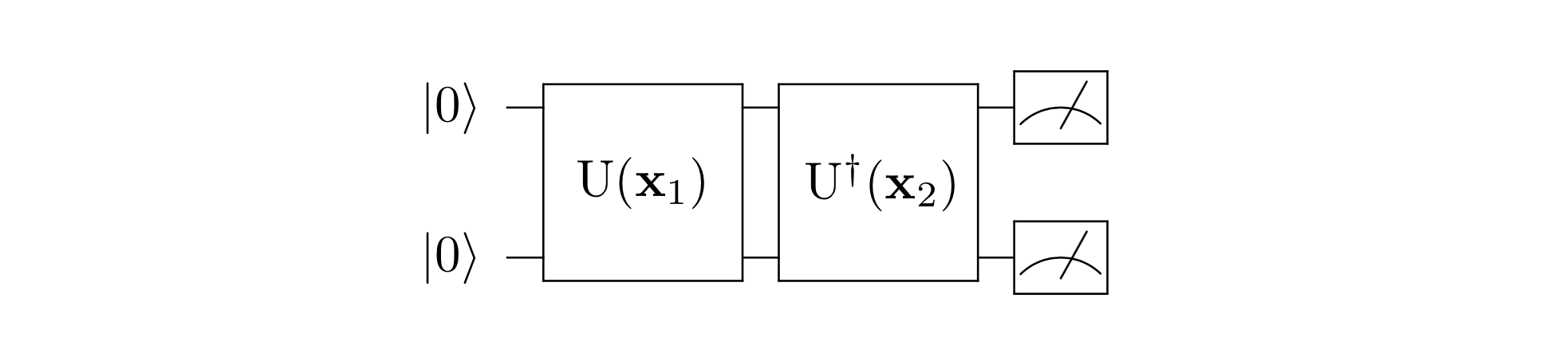
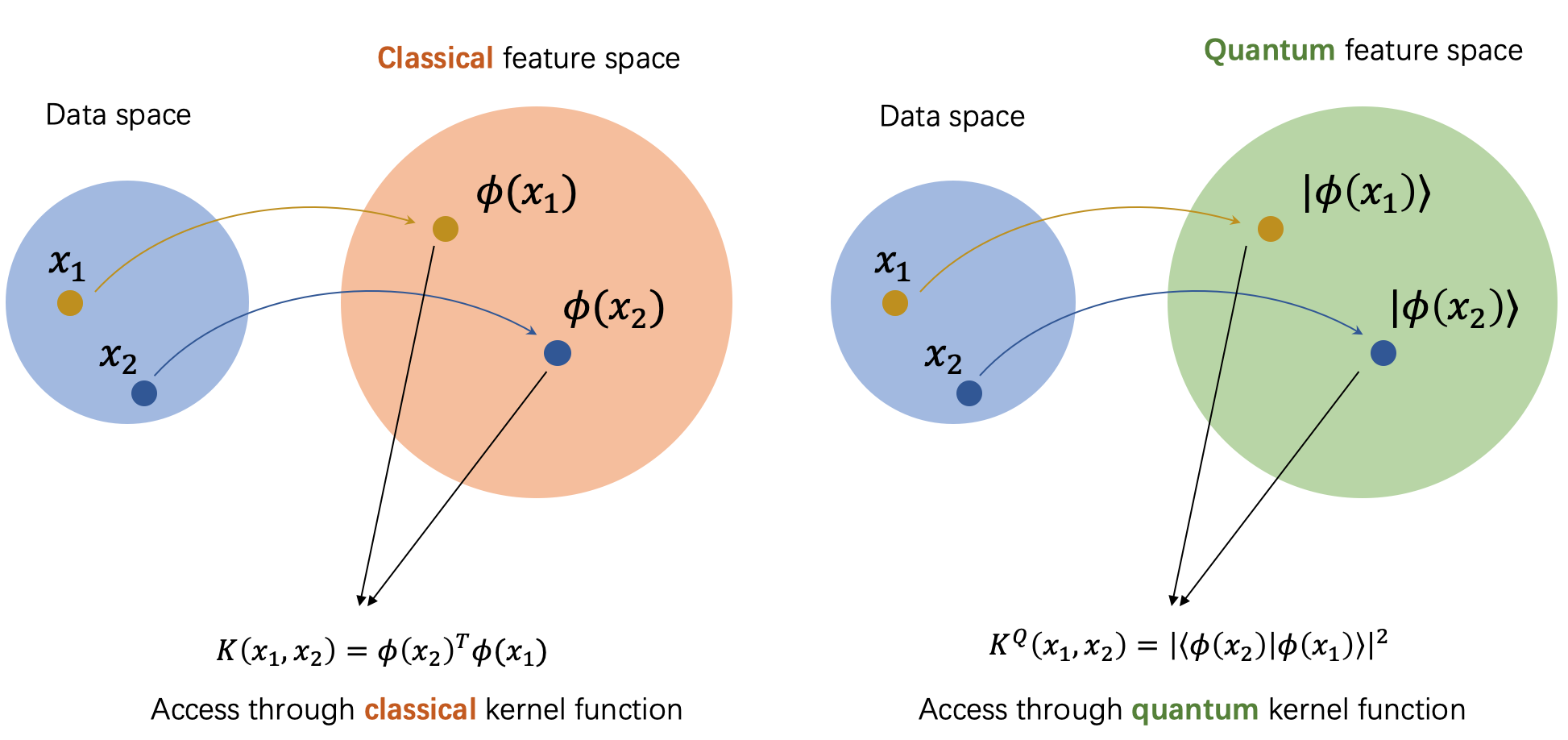
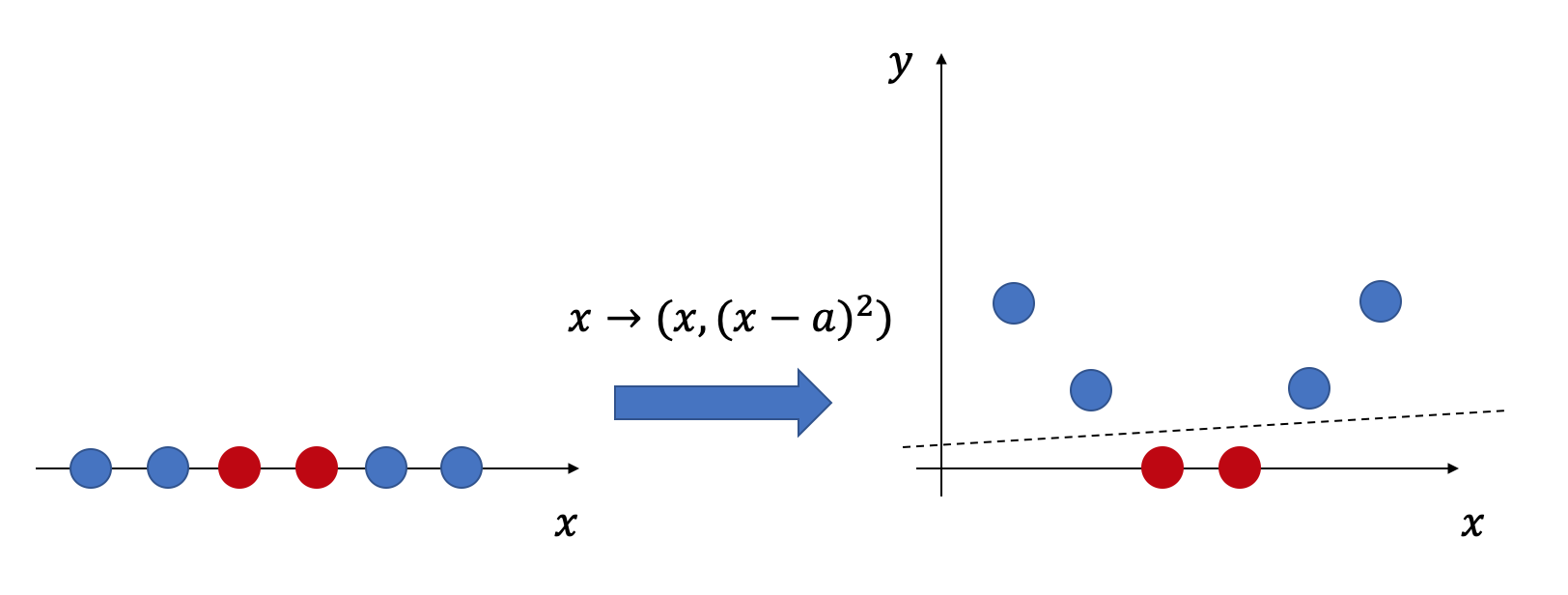update to v2.1.0
Showing
1.2 MB
969.5 KB
paddle_quantum/QAOA/maxcut.py
0 → 100644
paddle_quantum/QAOA/tsp.py
0 → 100644
| paddlepaddle>=2.0.1 | paddlepaddle>=2.0.1 | ||
| scipy | scipy | ||
| networkx | networkx>=2.5 | ||
| matplotlib | matplotlib | ||
| interval | interval | ||
| tqdm | tqdm | ||
| \ No newline at end of file |
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
52.9 KB
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
此差异已折叠。
此差异已折叠。
文件已移动
此差异已折叠。
文件已移动
此差异已折叠。
文件已移动
文件已移动
此差异已折叠。
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
41.6 KB
45.9 KB
199.4 KB
192.8 KB
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
文件已移动
此差异已折叠。
此差异已折叠。