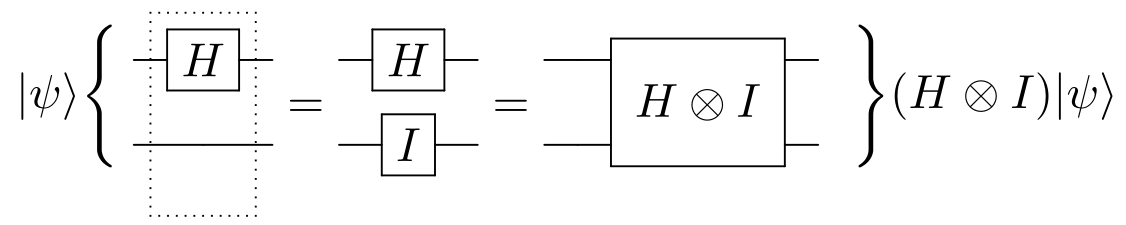update to v1.1.0
Showing
Simulator/main.py
0 → 100644
此差异已折叠。
docs/Makefile
0 → 100644
docs/make.bat
0 → 100644
docs/requirements.txt
0 → 100644
docs/source/_static/logo.png
0 → 100644
12.1 KB
docs/source/conf.py
0 → 100644
docs/source/index.rst
0 → 100644
docs/source/introduction.rst
0 → 100644
docs/source/modules.rst
0 → 100644
docs/source/paddle_quantum.rst
0 → 100644
docs/source/tutorial.rst
0 → 100644
此差异已折叠。
文件已添加
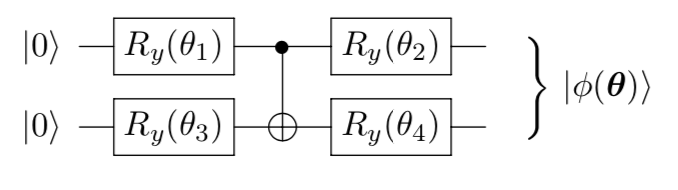
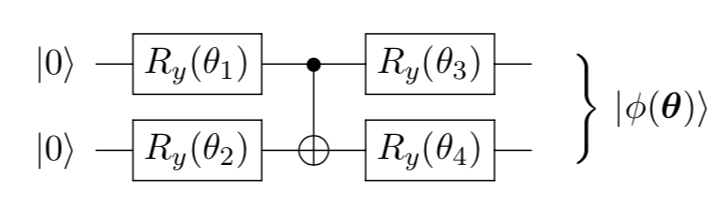
introduction/figures/ansatz1.png
0 → 100644
23.7 KB
introduction/figures/bell2.png
0 → 100644
25.0 KB
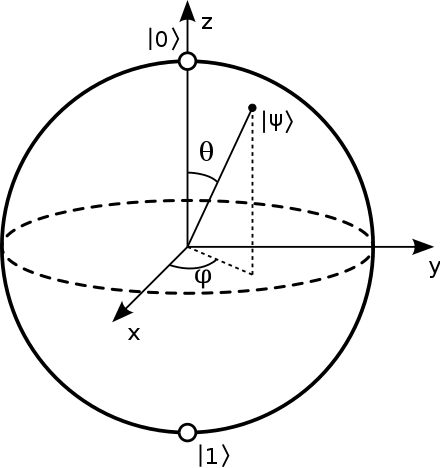
introduction/figures/bloch.png
0 → 100644
15.4 KB
308.3 KB
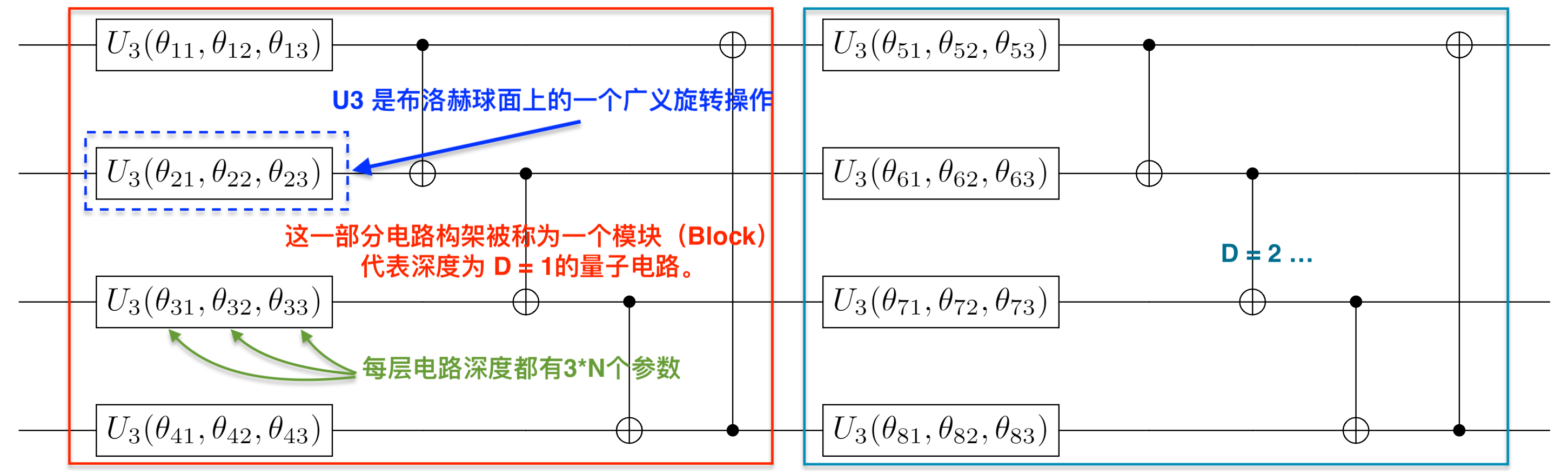
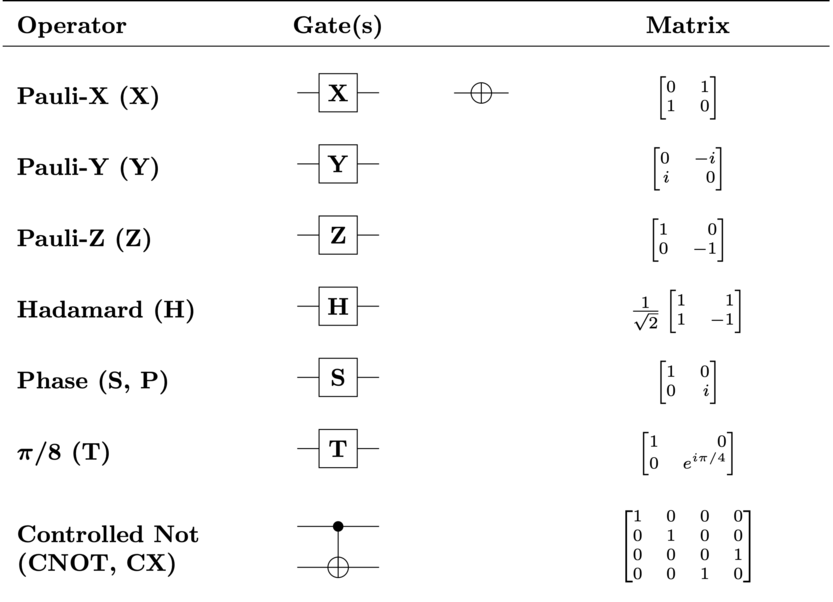
introduction/figures/gate.png
0 → 100644
59.9 KB
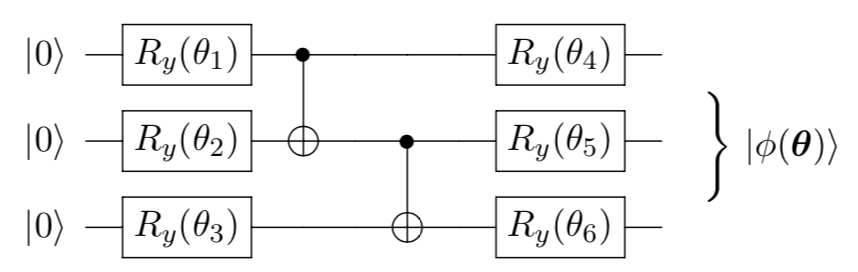
introduction/figures/gate1.png
0 → 100644
26.1 KB
introduction/figures/gate2.png
0 → 100644
36.9 KB
introduction/figures/hardmad.png
0 → 100644
27.1 KB
43.8 KB
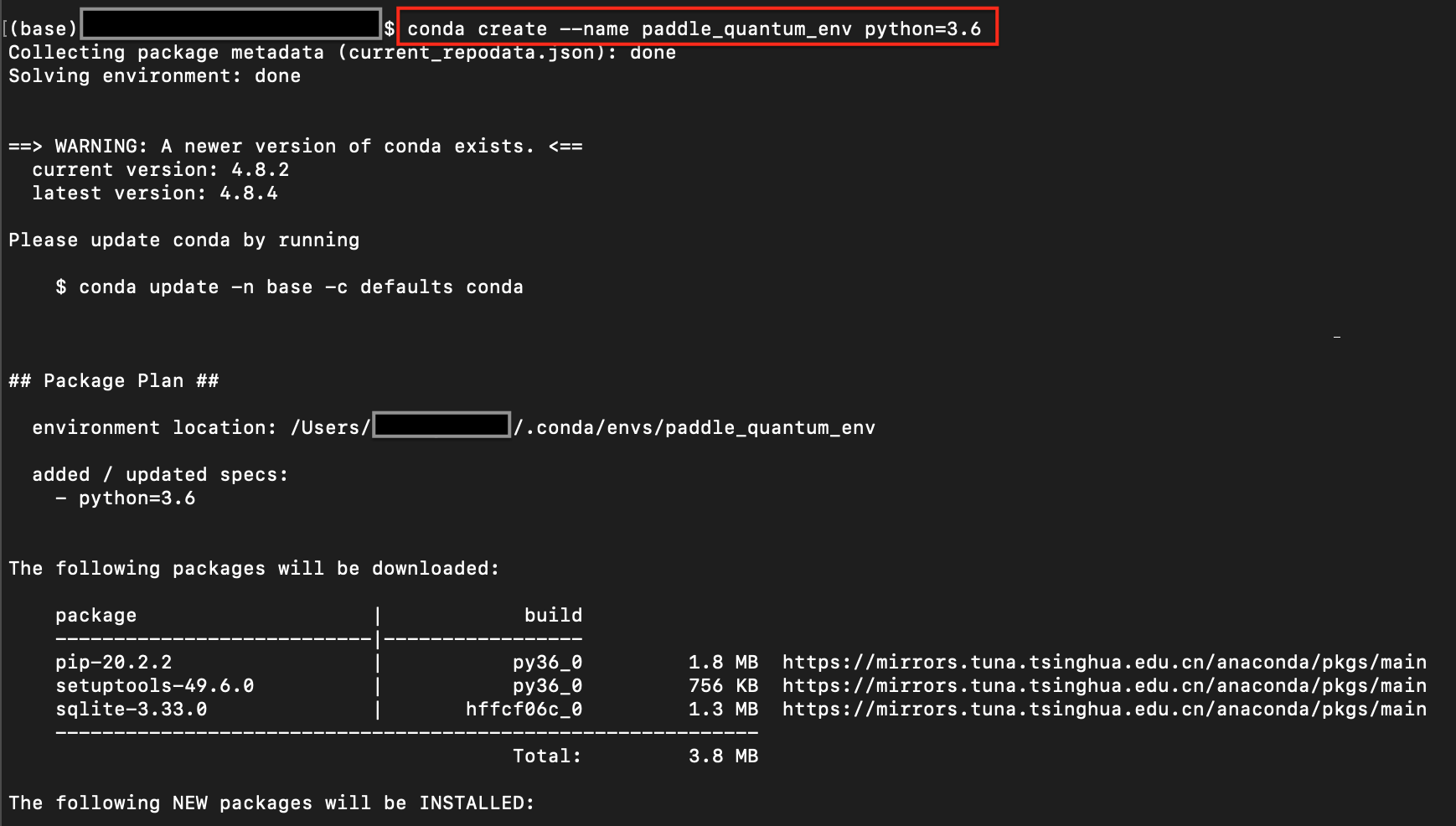
introduction/figures/terminal.png
0 → 100644
150.3 KB
24.9 KB
44.8 KB
paddle_quantum/GIBBS/main.py
已删除
100644 → 0
paddle_quantum/QAOA/main.py
已删除
100644 → 0
paddle_quantum/SSVQE/main.py
已删除
100644 → 0
paddle_quantum/VQE/main.py
已删除
100644 → 0
此差异已折叠。
paddle_quantum/VQSD/main.py
已删除
100644 → 0
此差异已折叠。
paddle_quantum/intrinsic.py
0 → 100644
此差异已折叠。
paddle_quantum/state.py
0 → 100644
此差异已折叠。
| paddlepaddle>=1.8.0 | paddlepaddle>=1.8.3 | ||
| networkx | networkx>=2.4 | ||
| matplotlib | matplotlib>=3.3.0 | ||
| \ No newline at end of file | interval>=1.0.0 | ||
| progressbar>=2.5 | |||
| \ No newline at end of file |
此差异已折叠。
此差异已折叠。
文件已添加
1.8 MB
50.0 KB
1.0 MB
2.1 MB
734.0 KB
1.4 MB
此差异已折叠。
tutorial/GPU/GPU_Tutorial_CN.pdf
0 → 100644
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
tutorial/Q-GAN/figures/loss.gif
0 → 100644
此差异已折叠。
此差异已折叠。
tutorial/QAOA.ipynb
已删除
100644 → 0
此差异已折叠。
tutorial/QAOA/QAOA.ipynb
0 → 100644
此差异已折叠。
tutorial/QAOA/QAOA.pdf
0 → 100644
此差异已折叠。
tutorial/QAOA/QAOA_En.ipynb
0 → 100644
此差异已折叠。
tutorial/QAOA/QAOA_En.pdf
0 → 100644
此差异已折叠。
此差异已折叠。
tutorial/QAOA_En.ipynb
已删除
100644 → 0
此差异已折叠。
此差异已折叠。
tutorial/VQE.ipynb
已删除
100644 → 0
此差异已折叠。
此差异已折叠。
tutorial/VQE/VQE_Tutorial_CN.pdf
0 → 100644
此差异已折叠。
tutorial/VQE/h2.xyz
0 → 100644
此差异已折叠。
tutorial/VQE/hf.xyz
0 → 100644
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。