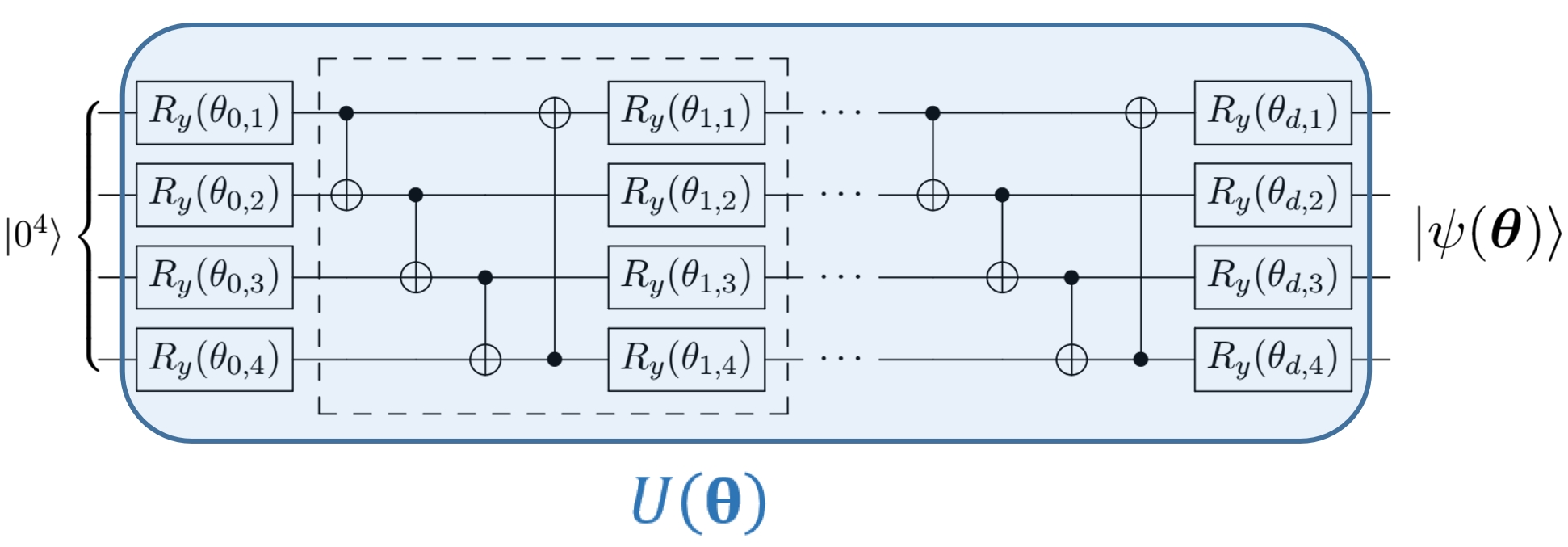
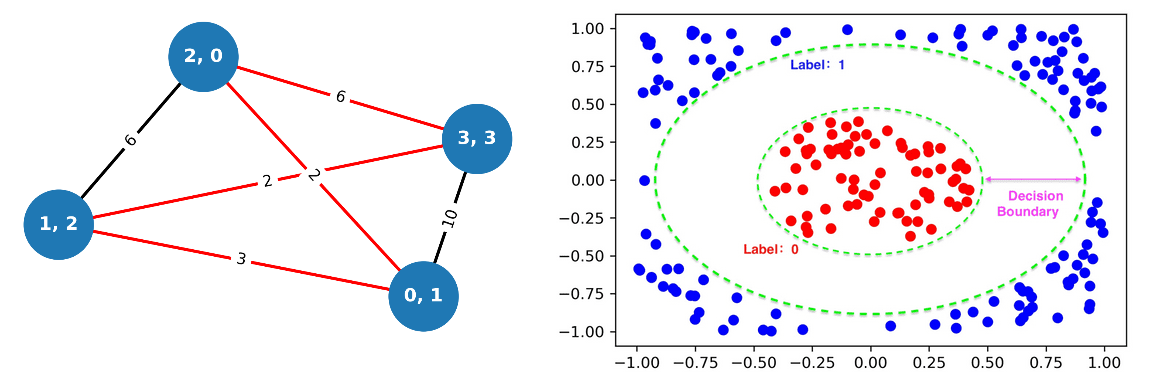
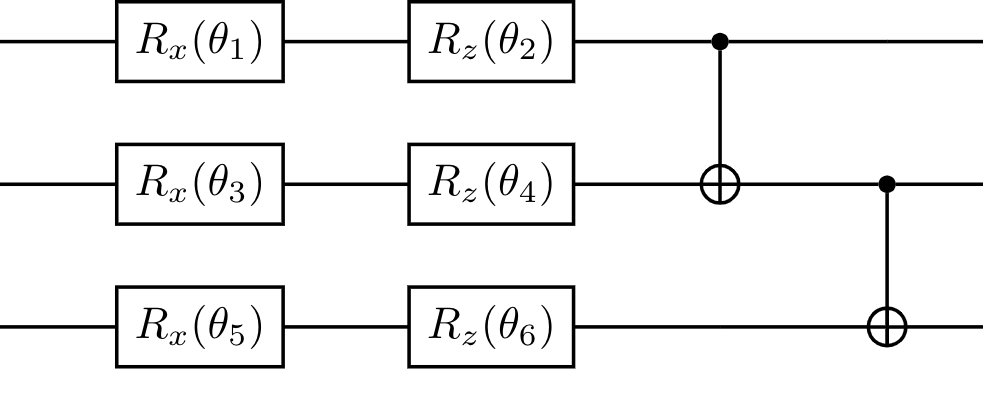
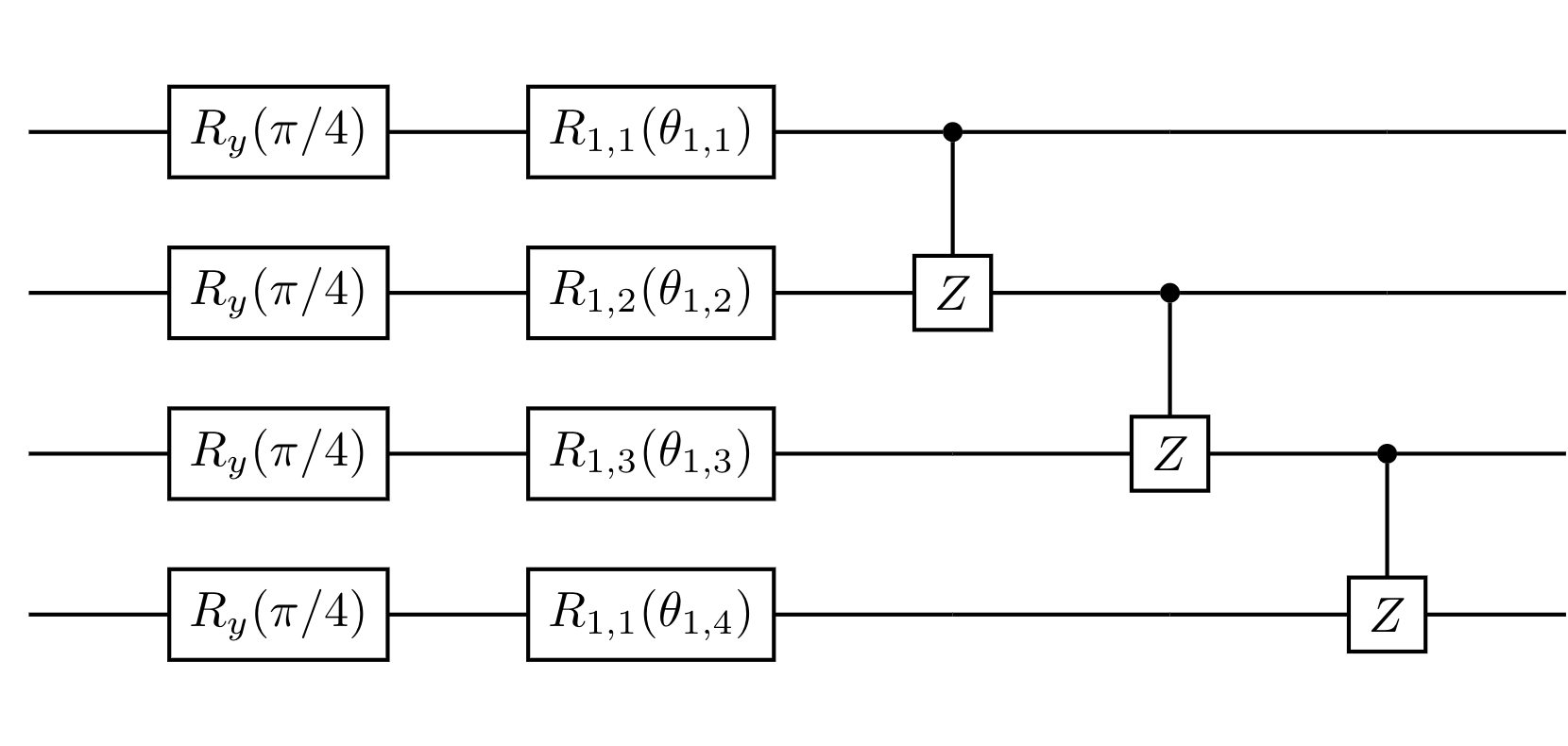
update to v2.1.3
Showing
documents/单测文件.py
已删除
100644 → 0
此差异已折叠。
此差异已折叠。
233.8 KB
229.6 KB
230.4 KB
145.8 KB
29.9 KB
paddle_quantum/dataset.py
0 → 100644
此差异已折叠。
paddle_quantum/gradtool.py
0 → 100644
paddle_quantum/qchem/__init__.py
0 → 100755
paddle_quantum/qchem/layers.py
0 → 100755
paddle_quantum/qchem/linalg.py
0 → 100755
此差异已折叠。
paddle_quantum/qchem/molecule.py
0 → 100755
此差异已折叠。
paddle_quantum/qchem/qmodel.py
0 → 100755
此差异已折叠。
paddle_quantum/qchem/run.py
0 → 100755
此差异已折叠。
此差异已折叠。
此差异已折叠。
test_and_documents/readme.md
已删除
100644 → 0
此差异已折叠。
test_and_documents/test.py
已删除
100644 → 0
此差异已折叠。
test_documents/test.py
已删除
100644 → 0
此差异已折叠。
此差异已折叠。
此差异已折叠。
此差异已折叠。
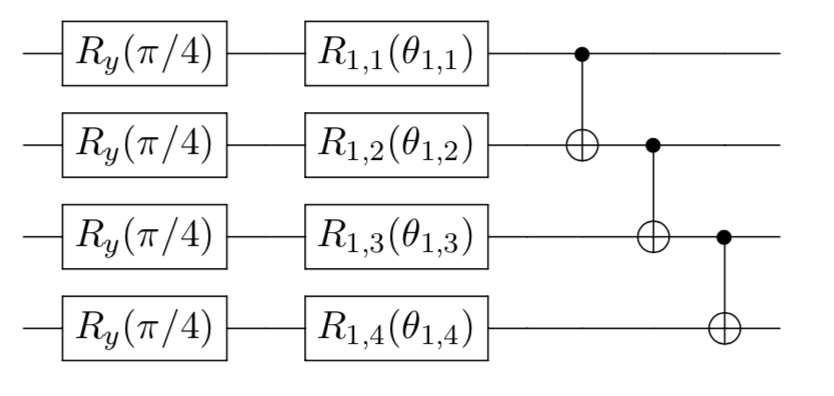
| W: | H:
| W: | H:


此差异已折叠。
此差异已折叠。
此差异已折叠。