Update faq_2021_s1 (#572)
Showing
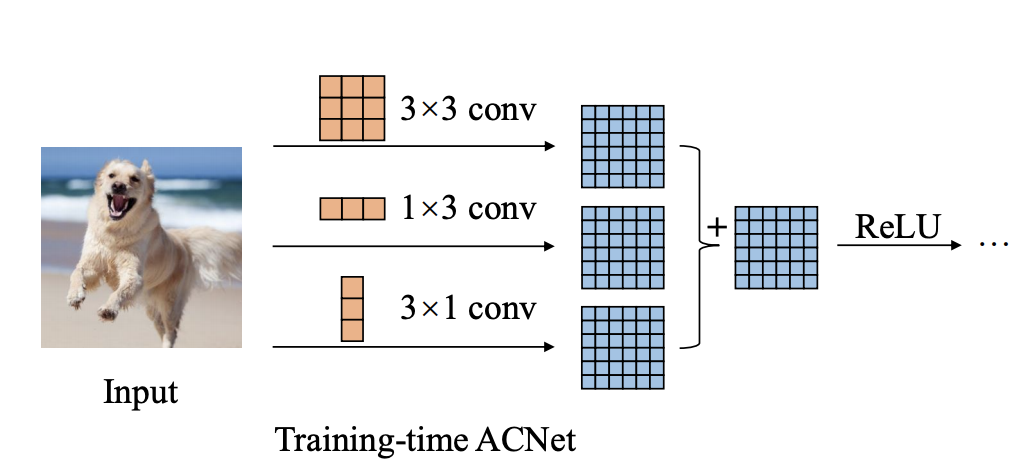
docs/images/faq/ACNetFusion.png
0 → 100644
132.8 KB
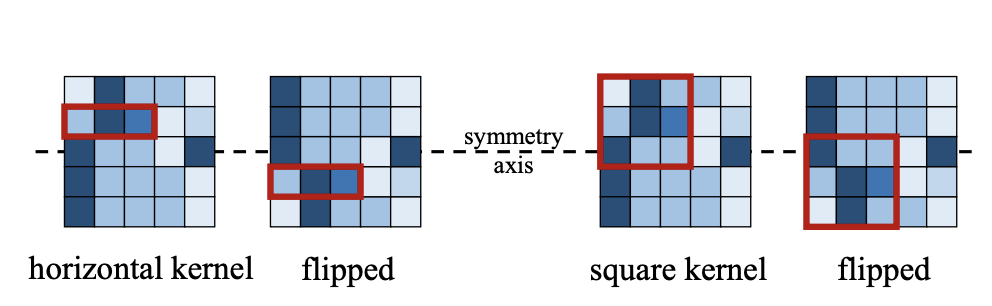
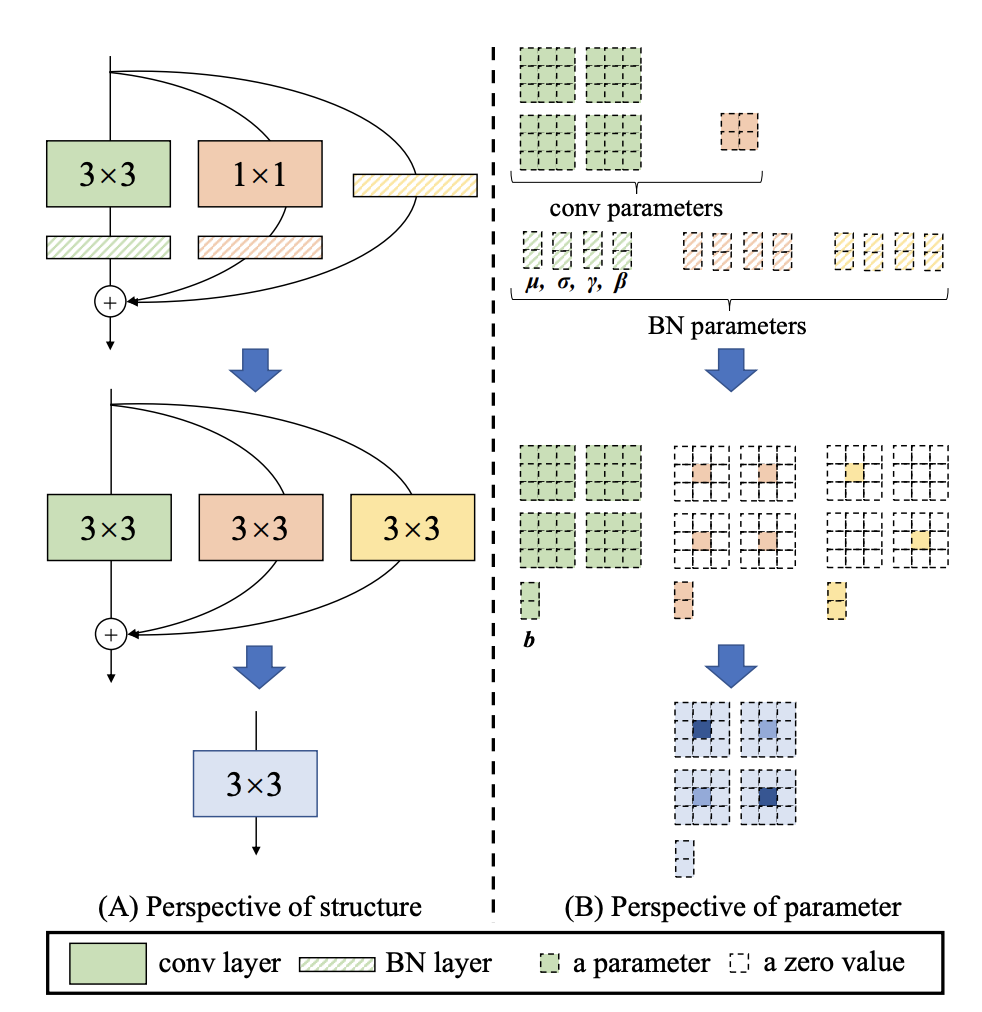
docs/images/faq/ACNetReParams.png
0 → 100644
53.5 KB
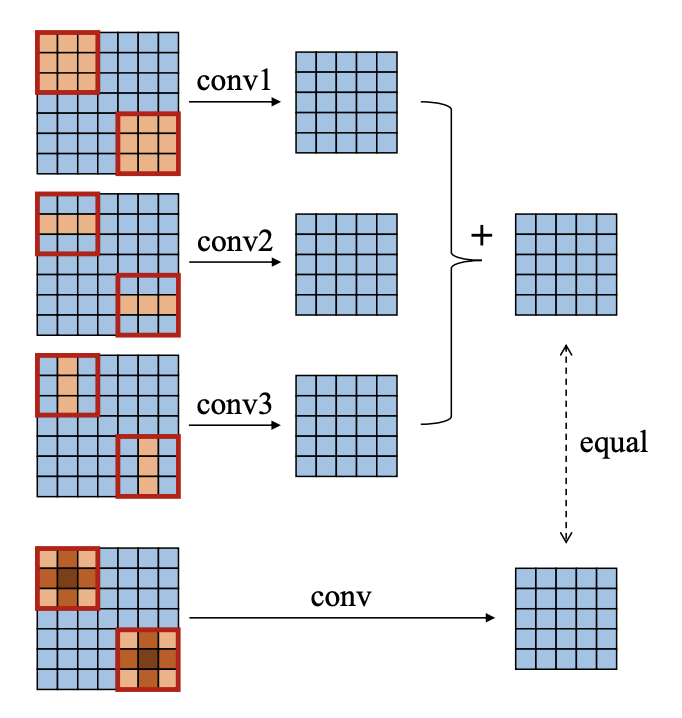
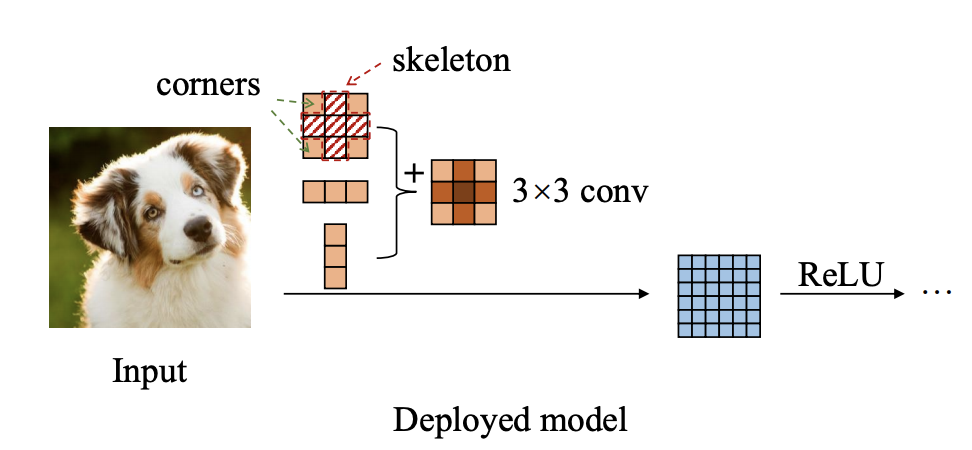
docs/images/faq/DeployedACNet.png
0 → 100644
132.6 KB
33.7 KB
56.6 KB
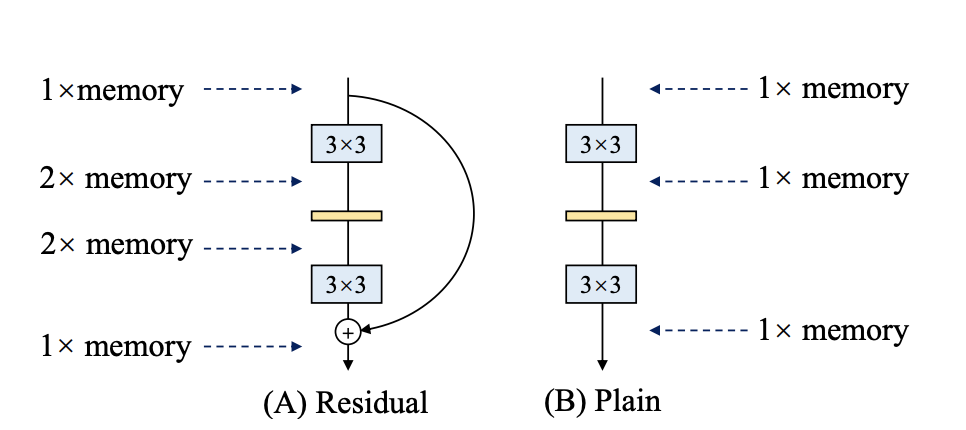
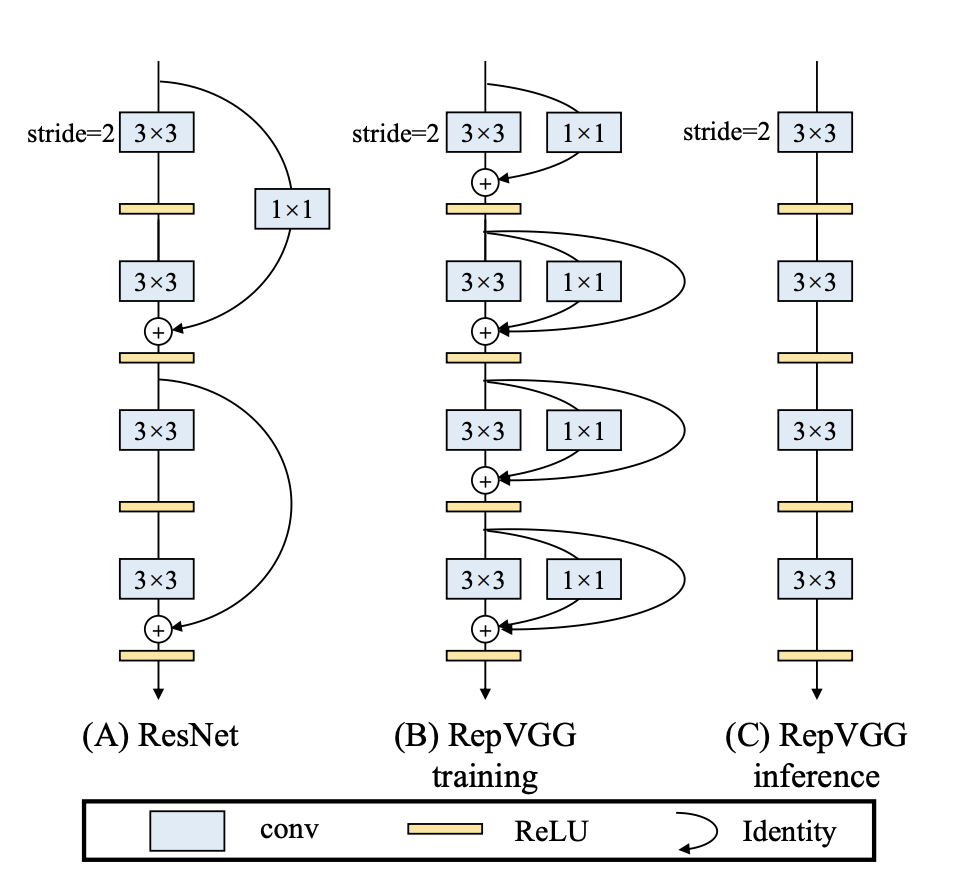
docs/images/faq/RepVGG.png
0 → 100644
106.3 KB
161.9 KB
119.6 KB