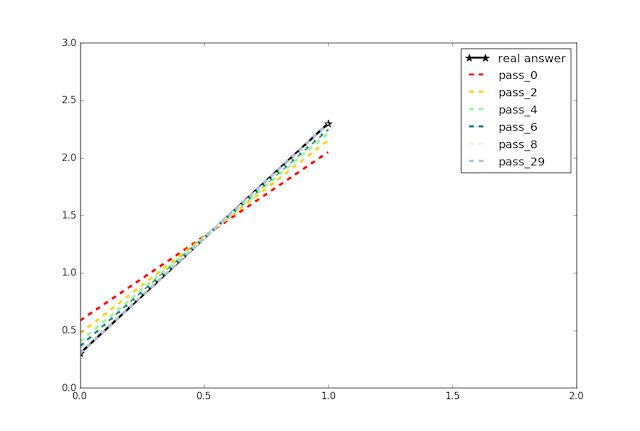
Adding an introduction doc for Paddle to implement simplest linear regression.

demo/introduction/README.md

+This folder contains scripts used in PaddlePaddle introduction.
+- use `bash train.sh` to train a simple linear regression model
+- use `python evaluate_model.py` to read model parameters. You can see that `w` and `b` are very close to [2, 0.3].
+

demo/introduction/dataprovider.py

+# Copyright (c) 2016 Baidu, Inc. All Rights Reserved
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+#     http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from paddle.trainer.PyDataProvider2 import *
+import random
+
+# define data types of input: 2 real numbers
+@provider(input_types=[dense_vector(1), dense_vector(1)],use_seq=False)
+def process(settings, input_file):
+    for i in xrange(2000):
+        x = random.random()
+        yield [x], [2*x+0.3]
+

demo/introduction/evaluate_model.py

+#!/usr/bin/env python
+# -*- coding: UTF-8 -*-
+
+# Copyright (c) 2016 Baidu, Inc. All Rights Reserved
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+#     http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+"""
+Print model parameters in last model
+
+Usage:
+    python evaluate_model.py
+"""
+import numpy as np
+import os
+
+def load(file_name):
+    with open(file_name, 'rb') as f:
+        f.read(16) # skip header for float type.
+        return np.fromfile(f, dtype=np.float32)
+
+def main():
+    print 'w=%.6f, b=%.6f from pass 29' % (load('output/pass-00029/w'),
+            load('output/pass-00029/b'))
+
+if __name__ == '__main__':
+    main()

demo/introduction/train.sh

+#!/bin/bash
+# Copyright (c) 2016 Baidu, Inc. All Rights Reserved
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+#     http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+set -e
+
+paddle train \
+    --config=trainer_config.py \
+    --save_dir=./output \
+    --num_passes=30 \
+    2>&1 |tee 'train.log'

demo/introduction/trainer_config.py

+# Copyright (c) 2016 Baidu, Inc. All Rights Reserved
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+#     http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from paddle.trainer_config_helpers import *
+
+# 1. read data. Suppose you saved above python code as dataprovider.py
+data_file = 'empty.list'
+with open(data_file, 'w') as f: f.writelines(' ')
+define_py_data_sources2(train_list=data_file, test_list=None, 
+        module='dataprovider', obj='process',args={})
+
+# 2. learning algorithm
+settings(batch_size=12, learning_rate=1e-3, learning_method=MomentumOptimizer())
+
+# 3. Network configuration
+x = data_layer(name='x', size=1)
+y = data_layer(name='y', size=1)
+y_predict = fc_layer(input=x, param_attr=ParamAttr(name='w'), size=1, act=LinearActivation(), bias_attr=ParamAttr(name='b'))
+cost = regression_cost(input=y_predict, label=y)
+outputs(cost)
+

doc/index.md

@@ -3,6 +3,7 @@ PaddlePaddle Documentation
 
 User Guide
 ----------
+* [Introduction](introduction/index.md)
 * [Quick Start](demo/quick_start/index_en.md)
 * [Build and Installation](build/index.rst)
 * [Contribute Code](build/contribute_to_paddle.md)

doc/introduction/index.md

+# Introduction
+
+PaddlePaddle is a deep learning platform open-sourced by Baidu. With PaddlePaddle, you can easily train a classic neural network within a couple lines of configuration, or you can build sophisticated models that provide state-of-the-art performance on difficult learning tasks like sentiment analysis, machine translation, image caption and so on.
+
+## 1. A Classic Problem
+
+Now, to give you a hint of what using PaddlePaddle looks like, let's start with a fundamental learning problem - <a href="https://en.wikipedia.org/wiki/Simple_linear_regression">**simple linear regression**</a> : you have observed a set of two-dimensional data points of `X` and `Y`, where `X` is an explanatory variable and `Y` is corresponding dependent variable, and you want to recover the underlying correlation between `X` and `Y`. Linear regression can be used in many practical scenarios. For example, `X` can be a variable about house size, and `Y` a variable about house price. You can build a model that captures relationship between them by observing real estate markets.
+
+## 2. Prepare the Data
+
+Suppose the true relationship can be characterized as `Y = 2X + 0.3`, let's see how to recover this pattern only from observed data. Here is a piece of python code that feeds synthetic data to PaddlePaddle. The code is pretty self-explanatory, the only extra thing you need to add for PaddlePaddle is a definition of input data types.
+
+```python
+# dataprovider.py
+from paddle.trainer.PyDataProvider2 import *
+import random
+
+# define data types of input: 2 real numbers
+@provider(input_types=[dense_vector(1), dense_vector(1)],use_seq=False)
+def process(settings, input_file):
+    for i in xrange(2000):
+        x = random.random()
+        yield [x], [2*x+0.3]
+```
+
+## 3. Train a NeuralNetwork in PaddlePaddle
+
+To recover this relationship between `X` and `Y`, we use a neural network with one layer of linear activation units and a square error cost layer. Don't worry if you are not familiar with these terminologies, it's just saying that we are starting from a random line `Y' = wX + b` , then we gradually adapt `w` and `b` to minimize the difference between `Y'` and `Y`. Here is what it looks like in PaddlePaddle:
+
+```python
+# trainer_config.py
+from paddle.trainer_config_helpers import *
+
+# 1. read data. Suppose you saved above python code as dataprovider.py
+data_file = 'empty.list'
+with open(data_file, 'w') as f: f.writelines(' ')
+define_py_data_sources2(train_list=data_file, test_list=None, 
+        module='dataprovider', obj='process',args={})
+
+# 2. learning algorithm
+settings(batch_size=12, learning_rate=1e-3, learning_method=MomentumOptimizer())
+
+# 3. Network configuration
+x = data_layer(name='x', size=1)
+y = data_layer(name='y', size=1)
+y_predict = fc_layer(input=x, param_attr=ParamAttr(name='w'), size=1, act=LinearActivation(), bias_attr=ParamAttr(name='b'))
+cost = regression_cost(input=y_predict, label=y)
+outputs(cost)
+```
+
+Some of the most fundamental usages of PaddlePaddle are demonstrated:
+
+-  The first part shows how to feed data into PaddlePaddle. In general cases, PaddlePaddle reads raw data from a list of files, and then do some user-defined process to get real input. In this case, we only need to create a placeholder file since we are generating synthetic data on the fly.
+
+-  The second part describes learning algorithm. It defines in what ways adjustments are made to model parameters. PaddlePaddle provides a rich set of optimizers, but a simple momentum based optimizer will suffice here, and it processes 12 data points each time.
+
+-  Finally, the network configuration. It usually is as simple as "stacking" layers. Three kinds of layers are used in this configuration:
+	-  **Data Layer**: a network always starts with one or more data layers. They provide input data to the rest of the network. In this problem, two data layers are used respectively for `X` and `Y`.
+	-  **FC Layer**: FC layer is short for Fully Connected Layer, which connects all the input units to current layer and does the actual computation specified as activation function. Computation layers like this are the fundamental building blocks of a deeper model.
+	-  **Cost Layer**: in training phase, cost layers are usually the last layers of the network. They measure the performance of current model, and provide guidence to adjust parameters.
+
+Now that everything is ready, you can train the network with a simple command line call:
+ ```
+ paddle train --config=trainer_config.py --save_dir=./output --num_passes=30
+ ```
+
+This means that PaddlePaddle will train this network on the synthectic dataset for 30 passes, and save all the models under path `./output`. You will see from the messages printed out during training phase that the model cost is decreasing as time goes by, which indicates we are getting a closer guess.
+
+
+## 4. Evaluate the Model
+
+Usually, a different dataset that left out during training phase should be used to evalute the models. However, we are lucky enough to know the real answer: `w=2, b=0.3`, thus a better option is to check out model parameters directly.
+
+In PaddlePaddle, training is just to get a collection of model parameters, which are `w` and `b` in this case. Each parameter is saved in an individual file in the popular `numpy` array format. Here is the code that reads parameters from last pass.
+
+```python
+import numpy as np
+import os
+
+def load(file_name):
+    with open(file_name, 'rb') as f:
+        f.read(16) # skip header for float type.
+        return np.fromfile(f, dtype=np.float32)
+        
+print 'w=%.6f, b=%.6f' % (load('output/pass-00029/w'), load('output/pass-00029/b'))
+# w=1.999743, b=0.300137
+```
+
+<center> ![](./parameters.png) </center>
+
+Although starts from a random guess, you can see that value of `w` changes quickly towards 2 and `b` changes quickly towards 0.3. In the end, the predicted line is almost identical with real answer.
+
+There, you have recovered the underlying pattern between `X` and `Y` only from observed data.
+
+
+## 5. Where to Go from Here
+
+- <a href="../build/index.html"> Build and Installation </a>
+- <a href="../demo/quick_start/index_en.html">Quick Start</a>
+- <a href="../demo/index.html">Example and Demo</a>
+

doc/introduction/parameters.png

+../../doc_cn/introduction/parameters.png
\ No newline at end of file

doc_cn/index.rst

@@ -3,7 +3,7 @@ PaddlePaddle文档
 
 使用指南
 --------
-
+* `介绍 <introduction/index.html>`_
 * `快速入门 <demo/quick_start/index.html>`_
 * `编译与安装 <build_and_install/index.html>`_
 * `用户接口 <ui/index.html>`_

doc_cn/introduction/index.md

+# 简介
+
+PaddlePaddle 是起源于百度的开源深度学习平台。它是简单易用的：你可以通过简单的十数行配置搭建经典的神经网络模型；它也是高效强大的：PaddlePaddle可以支撑复杂集群环境下超大模型的训练，令你受益于深度学习的前沿成果。在百度内部，已经有大量产品线使用了基于PaddlePaddle的深度学习技术。
+
+这份简短的介绍将像你展示如何利用PaddlePaddle解决一个经典的学习问题。
+
+## 1. 一个经典的任务
+
+让我们从一个基础问题开始：<a href="https://www.baidu.com/s?wd=单变量线性回归">单变量的线性回归</a>。问题假定观测到了一批二维空间上的点`(x, y) `，并且已知 `x` 和 `y` 之间存在着某种线性关系，我们的目标是通过观测数据还原这个线性关系。作为一个简单基础的模型，线性回归却有着广泛的应用场景。比如可以想象一个资产定价的简化场景，其中 `x` 对应于房屋的大小，`y` 对应于房屋价格。我们可以通过观察市场上房屋的情况获得二者之间的关系，从而为新房屋的定价提供参考。
+
+
+## 2. 准备数据
+
+假设变量 `X` 和 `Y` 的真实关系为： `Y = 2X + 0.3`，这里展示如何使用观测数据还原这一线性关系。如下Python代码将随机产生2000个观测点，它们将被用作PaddlePaddle的输入。产生PaddlePaddle的输入数据和写一段普通的Python脚本几乎一样，你唯一需要增加的就是定义输入数据的类型。
+
+```python
+# -*- coding:utf-8 -*-
+# dataprovider.py
+from paddle.trainer.PyDataProvider2 import *
+import random
+
+# 定义输入数据的类型: 2个浮点数
+@provider(input_types=[dense_vector(1), dense_vector(1)],use_seq=False)
+def process(settings, input_file):
+    for i in xrange(2000):
+        x = random.random()
+        yield [x], [2*x+0.3]
+```
+
+## 3. 训练模型
+
+为了还原 `Y = 2X + 0.3`，我们先从一条随机的直线 `Y' = wX + b` 开始，然后利用观测数据调整 `w` 和 `b` 使得 `Y'` 和 `Y` 的差距不断减小，最终趋于相同。这个过程就是模型的训练过程，而 `w` 和 `b` 就是模型的参数，即我们的训练目标。
+
+在PaddlePaddle里，该模型的网络配置如下。
+
+```python
+# -*- coding:utf-8 -*-
+# trainer_config.py
+from paddle.trainer_config_helpers import *
+
+# 1. 定义数据来源，调用上面的process函数获得观测数据
+data_file = 'empty.list'
+with open(data_file, 'w') as f: f.writelines(' ')
+define_py_data_sources2(train_list=data_file, test_list=None, 
+        module='dataprovider', obj='process',args={})
+
+# 2. 学习算法。控制如何改变模型参数 w 和 b
+settings(batch_size=12, learning_rate=1e-3, learning_method=MomentumOptimizer())
+
+# 3. 神经网络配置
+x = data_layer(name='x', size=1)
+y = data_layer(name='y', size=1)
+# 线性计算单元: y_predict = wx + b
+y_predict = fc_layer(input=x, param_attr=ParamAttr(name='w'), size=1, act=LinearActivation(), bias_attr=ParamAttr(name='b'))
+# 损失计算，度量 y_predict 和真实 y 之间的差距
+cost = regression_cost(input=y_predict, label=y)
+outputs(cost)
+```
+这段简短的配置展示了PaddlePaddle的基本用法：
+
+- 首先，第一部分定义了数据输入。一般情况下，PaddlePaddle先从一个文件列表里获得数据文件地址，然后交给用户自定义的函数（例如上面的`process`函数）进行读入和预处理从而得到真实输入。本文中由于输入数据是随机生成的不需要读输入文件，所以放一个空列表（`empty.list`）即可。
+
+- 第二部分主要是选择学习算法，它定义了模型参数如何改变。PaddlePaddle提供了很多优秀的学习算法，但这里使用一个简单的基于momentum的算法就足够了，它每次读取12个数据进行计算和模型更新。
+
+- 最后一部分是神经网络的配置。由于PaddlePaddle已经实现了丰富的网络单元（Layer），所以很多时候你需要做的只是声明正确的网络单元并把它们拼接起来。这里使用了三种网络单元：
+	- **数据层**：数据层 `data_layer` 是神经网络的入口，它读入数据并将它们传输到下游的其它单元。这里数据层有两个，分别对应于变量 `X` 和 `Y`。
+	- **全连接层**：全连接层 `fc_layer` 是基础的计算单元，这里利用它建模变量之间的线性关系。计算单元是神经网络的核心，PaddlePaddle支持大量的计算单元和任意深度的网络连接，从而可以挖掘复杂的数据关系。
+	- **回归损失层**：回归损失层 `regression_cost`是众多损失函数层的一种，它们在训练过程作为网络的出口，用来计算模型的表现，并指导模型参数的改变。
+
+这样定义了网络结构并保存为`trainer_config.py`之后，运行训练命令即可：
+ ```
+ paddle train --config=trainer_config.py --save_dir=./output --num_passes=30
+ ```
+
+PaddlePaddle将在观测数据集上迭代训练30轮，并将每轮的模型结果存放在 `./output` 路径下。从输出日志可以看到，随着轮数增加损失函数的输出在不断的减小，这意味着模型在不断的改进，直到逼近真实解：` Y = 2X + 0.3 `
+
+## 4. 模型检验
+
+训练完成后，我们希望能够检验模型的好坏。一种常用的做法是用模型对另外一组数据进行预测，然后评价预测的效果。但在这个例子中，由于已经知道了真实答案，我们可以直接观察模型的参数是否符合预期来进行检验。
+
+PaddlePaddle将每个模型参数作为一个numpy数组单独存为一个文件，所以可以利用如下方法读取模型的参数。
+
+```python
+import numpy as np
+import os
+
+def load(file_name):
+    with open(file_name, 'rb') as f:
+        f.read(16) # skip header for float type.
+        return np.fromfile(f, dtype=np.float32)
+        
+print 'w=%.6f, b=%.6f' % (load('output/pass-00029/w'), load('output/pass-00029/b'))
+# w=1.999743, b=0.300137
+```
+<center> ![](./parameters.png) </center>
+
+从图中可以看到，虽然 `w` 和 `b` 都使用随机值初始化，但在起初的几轮训练中它们都在快速逼近真实值，并且后续仍在不断改进，使得最终得到的模型几乎与真实模型重合。
+
+这样，我们就完成了对单变量线性回归问题的解决：将数据输入PaddlePaddle，训练模型，最后验证结果。
+
+## 5. 推荐后续阅读
+
+- <a href="../build_and_install/index.html">安装/编译</a>：PaddlePaddle的安装与编译文档。
+- <a href="../demo/quick_start/index.html">快速入门 </a>：使用商品评论分类任务，系统性的介绍如何一步步改进，最终得到产品级的深度模型。
+- <a href="../demo/index.html">示例</a>：各种实用案例，涵盖图像、文本、推荐等多个领域。