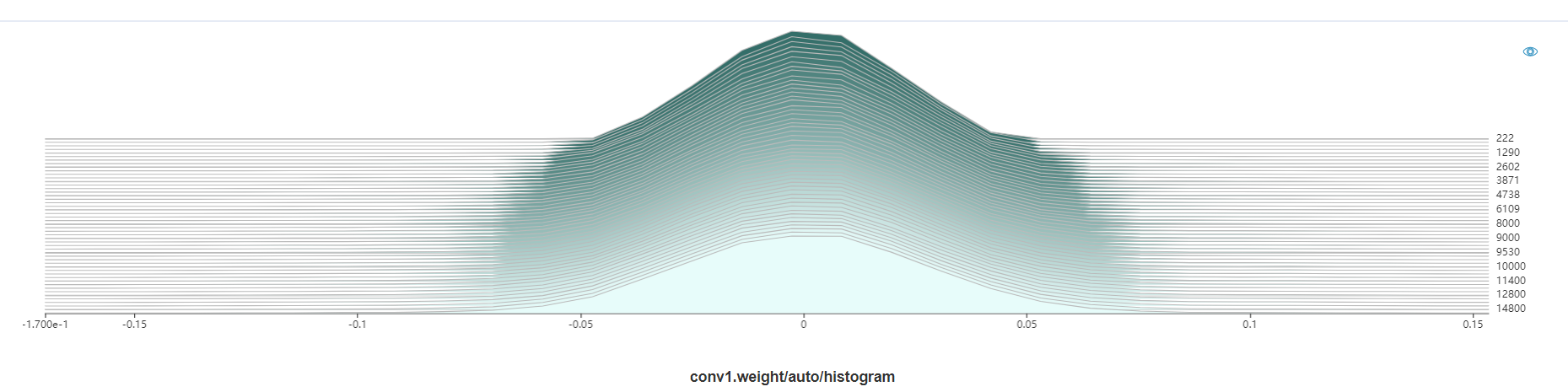
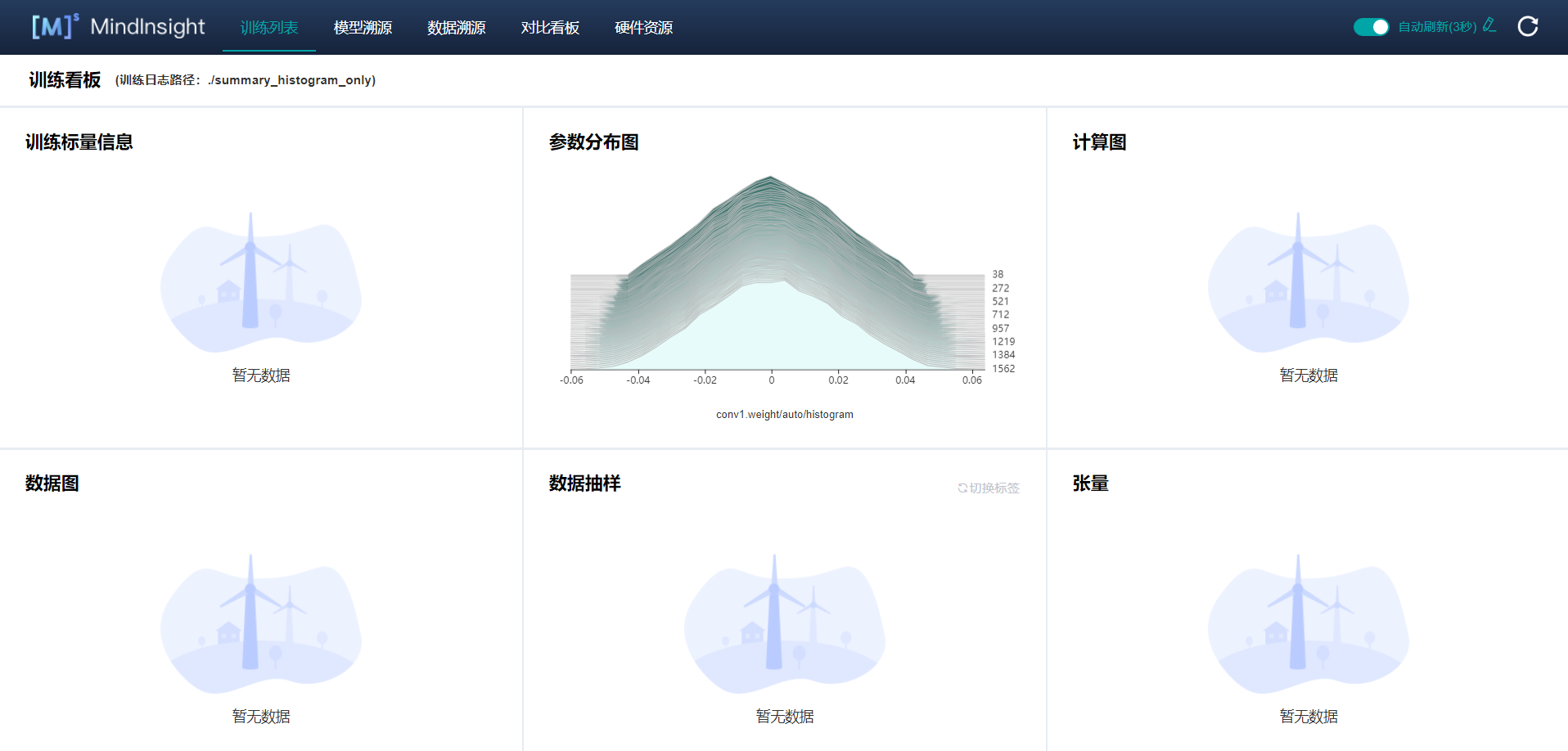
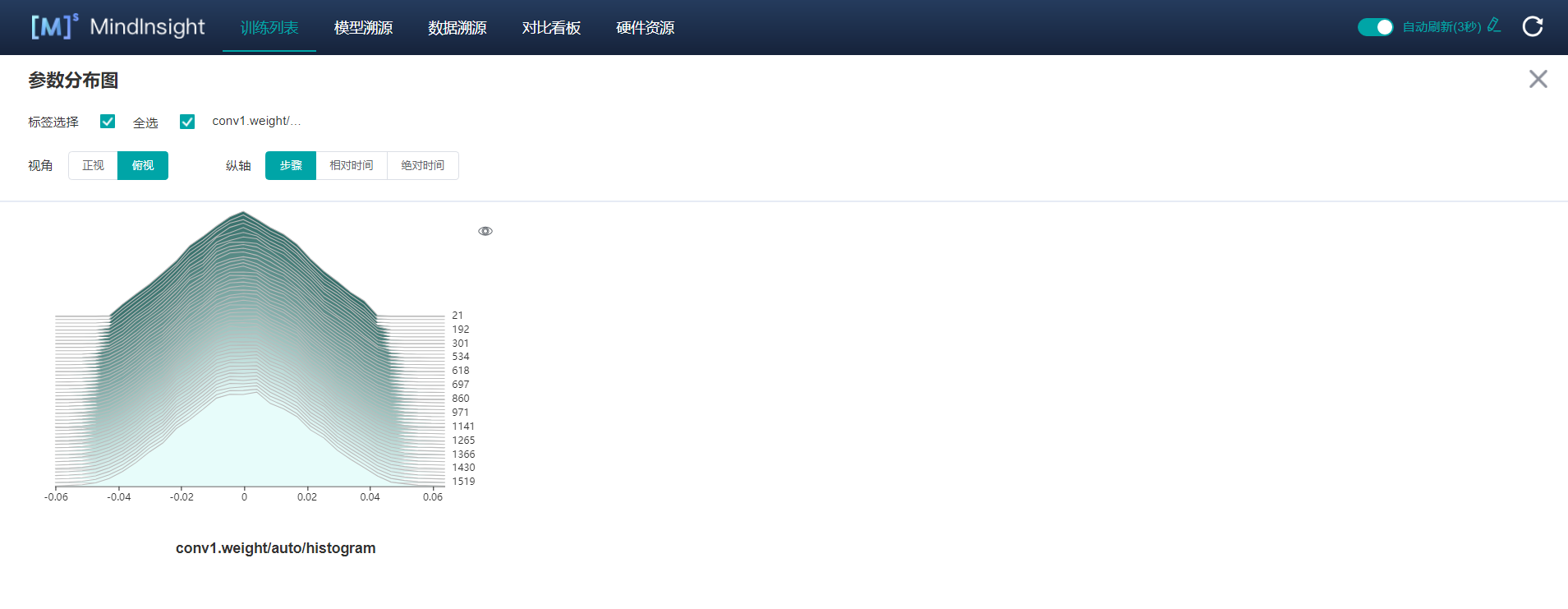
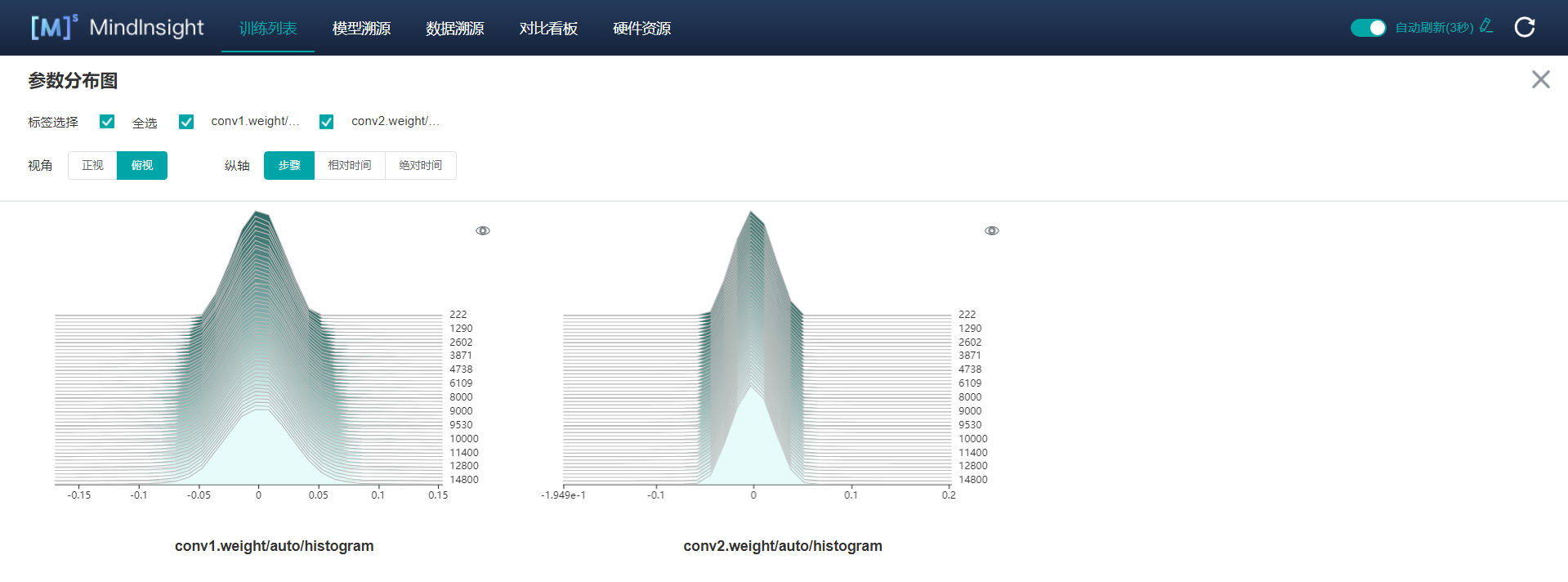
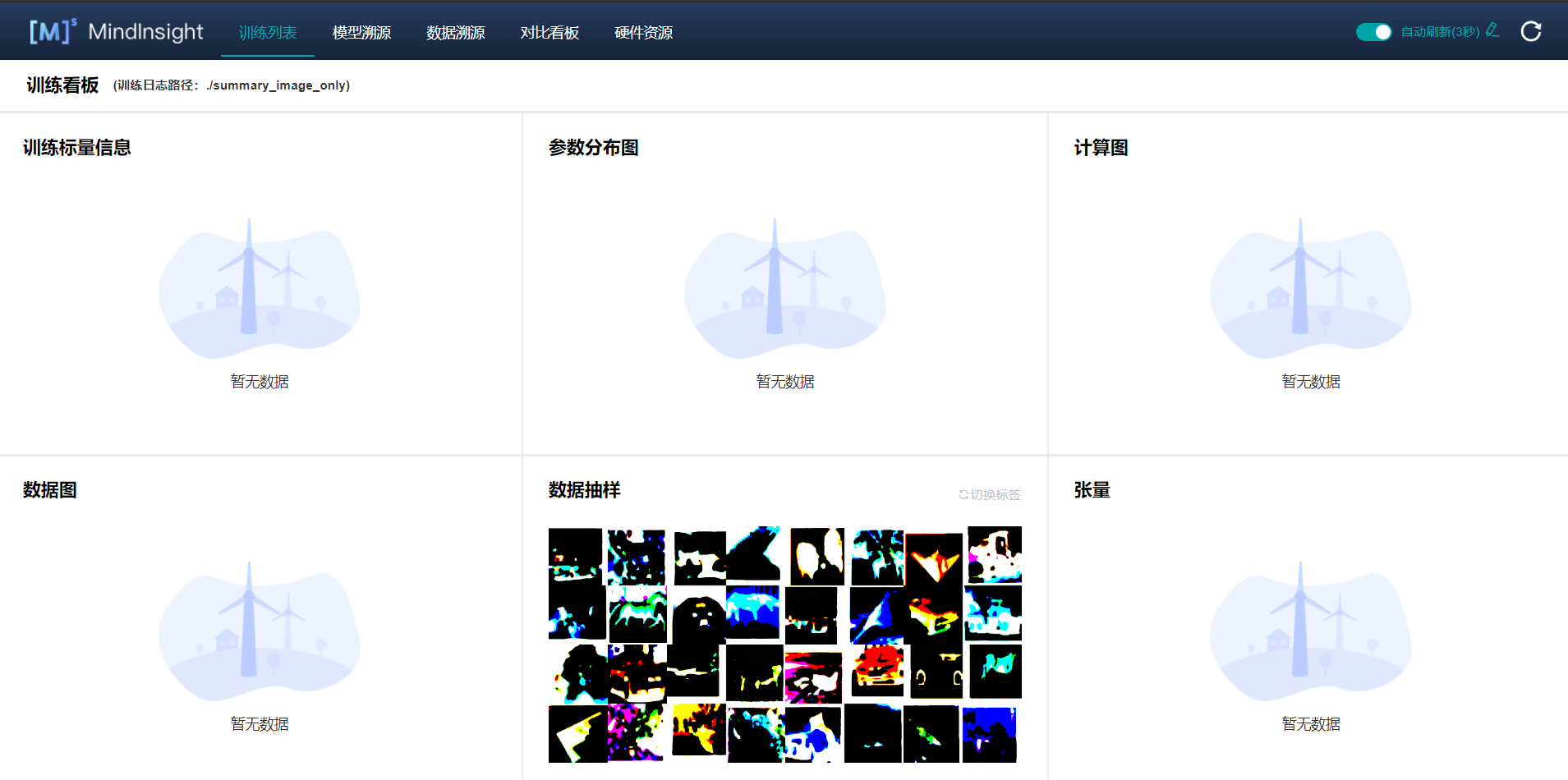
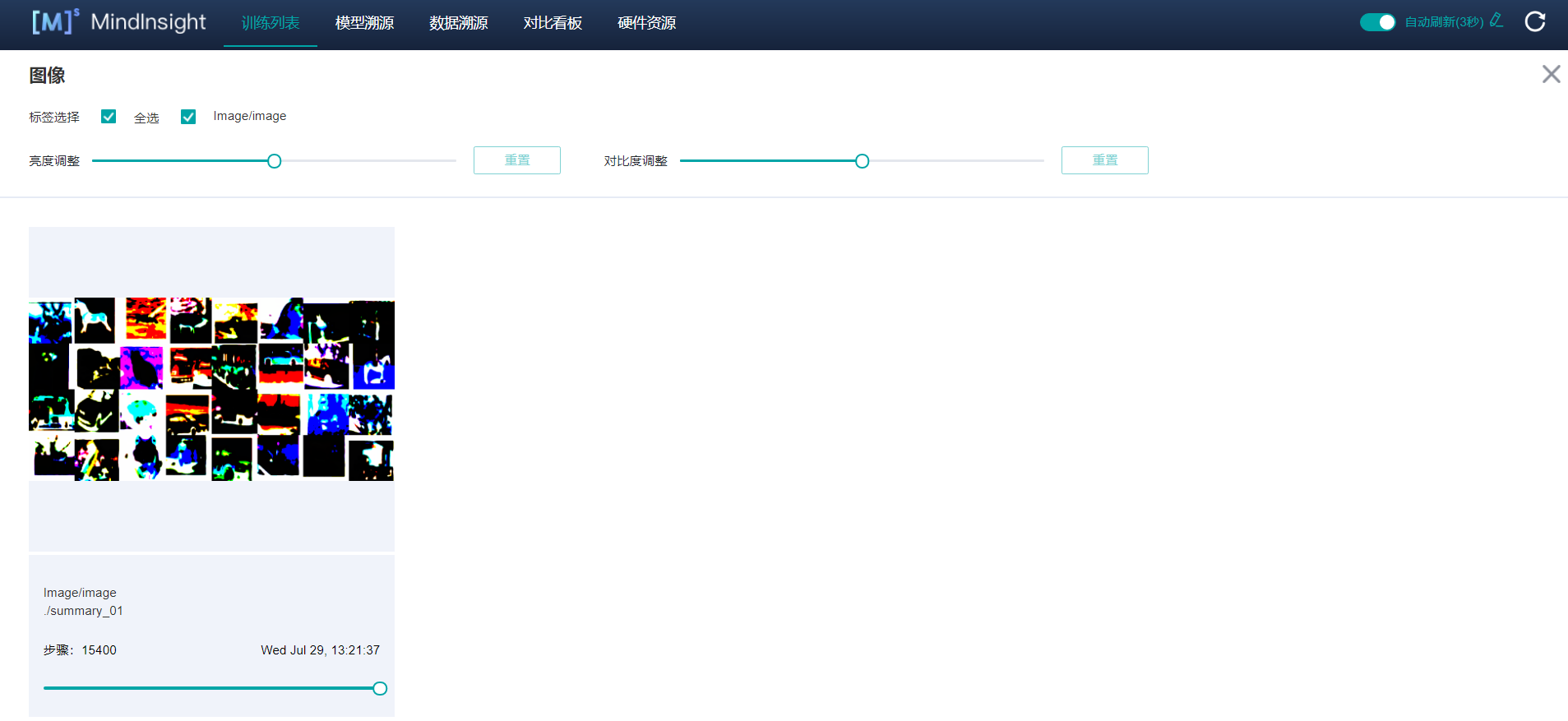
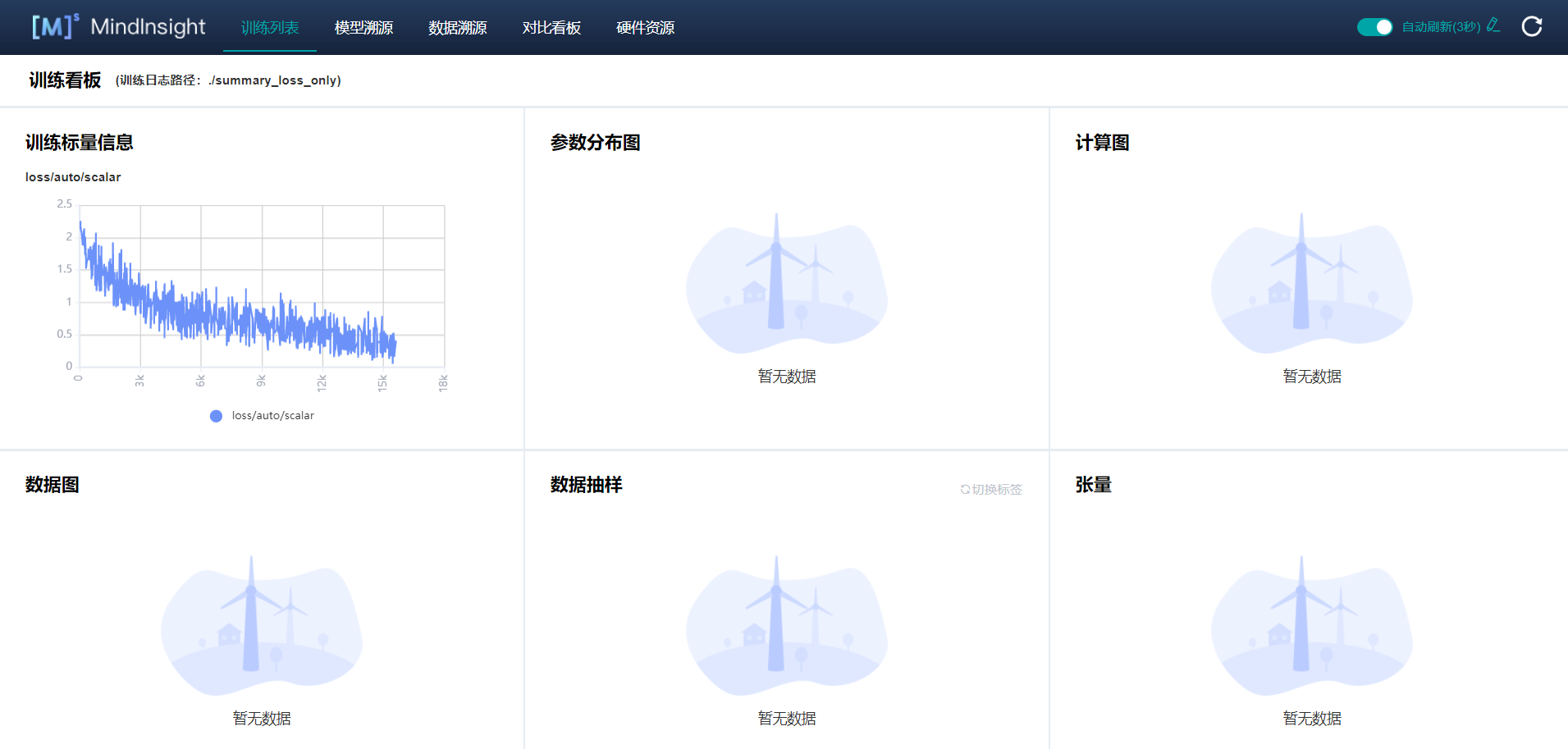
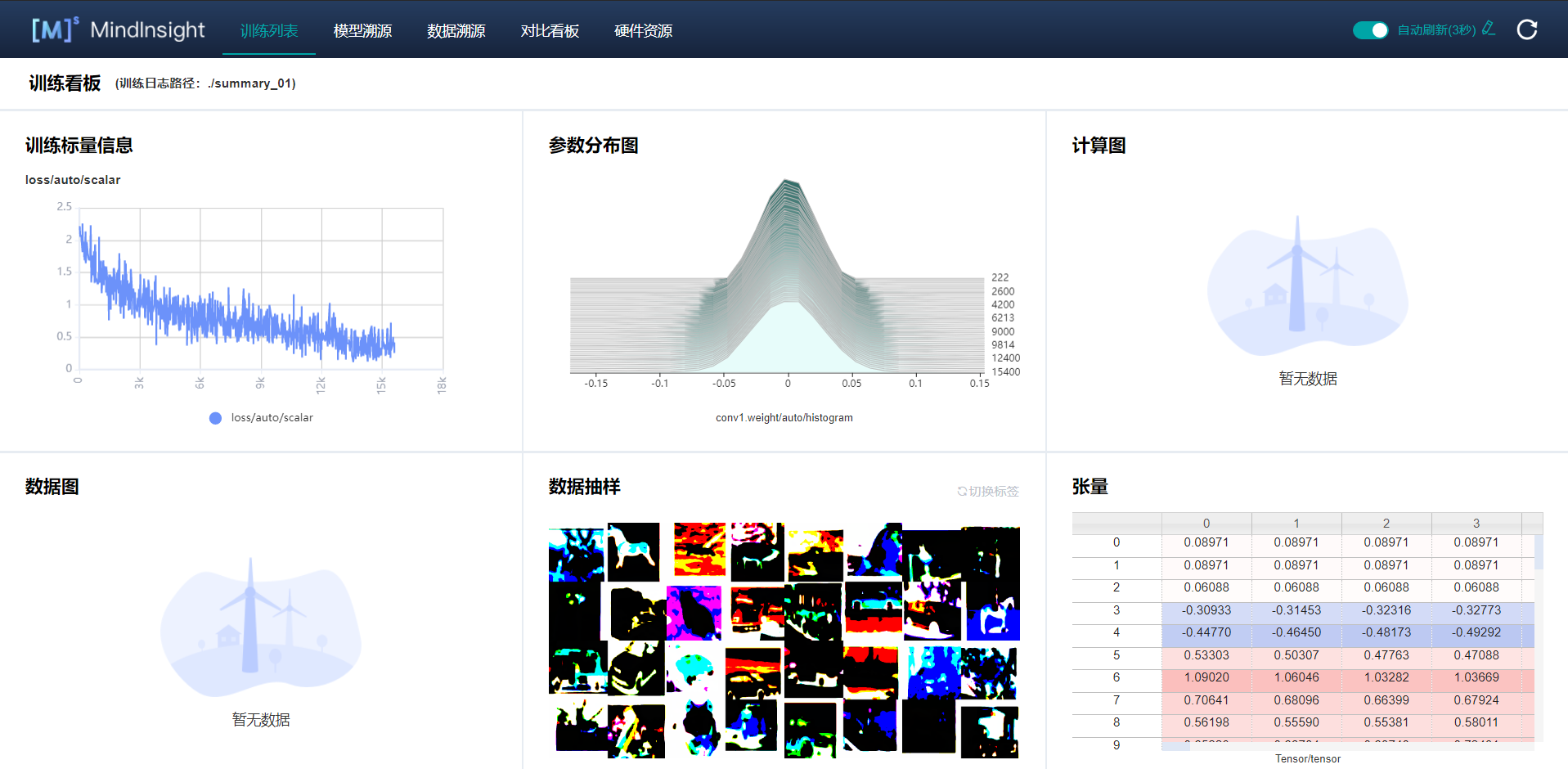
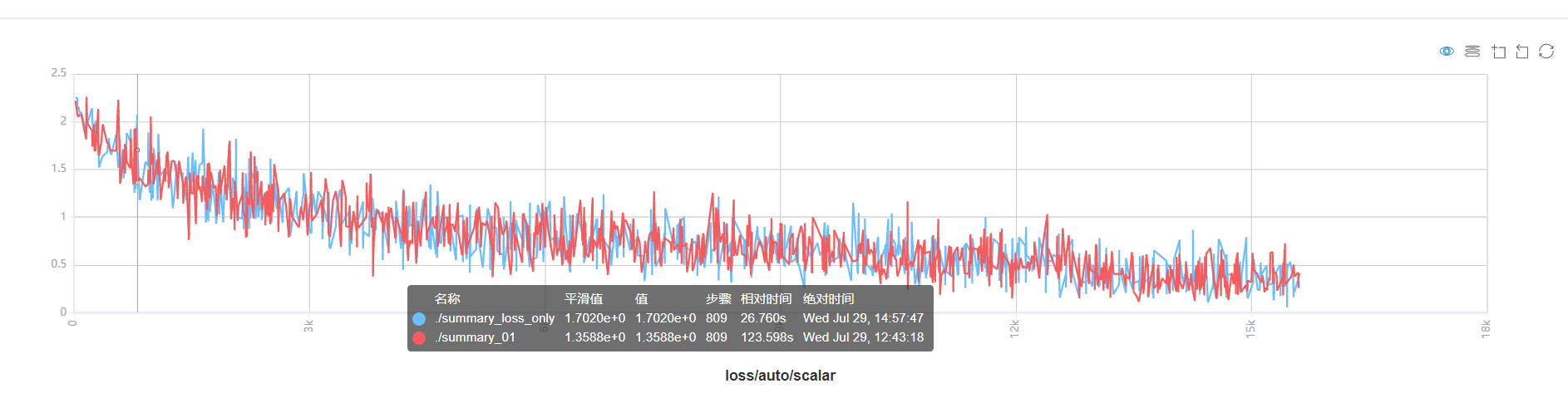
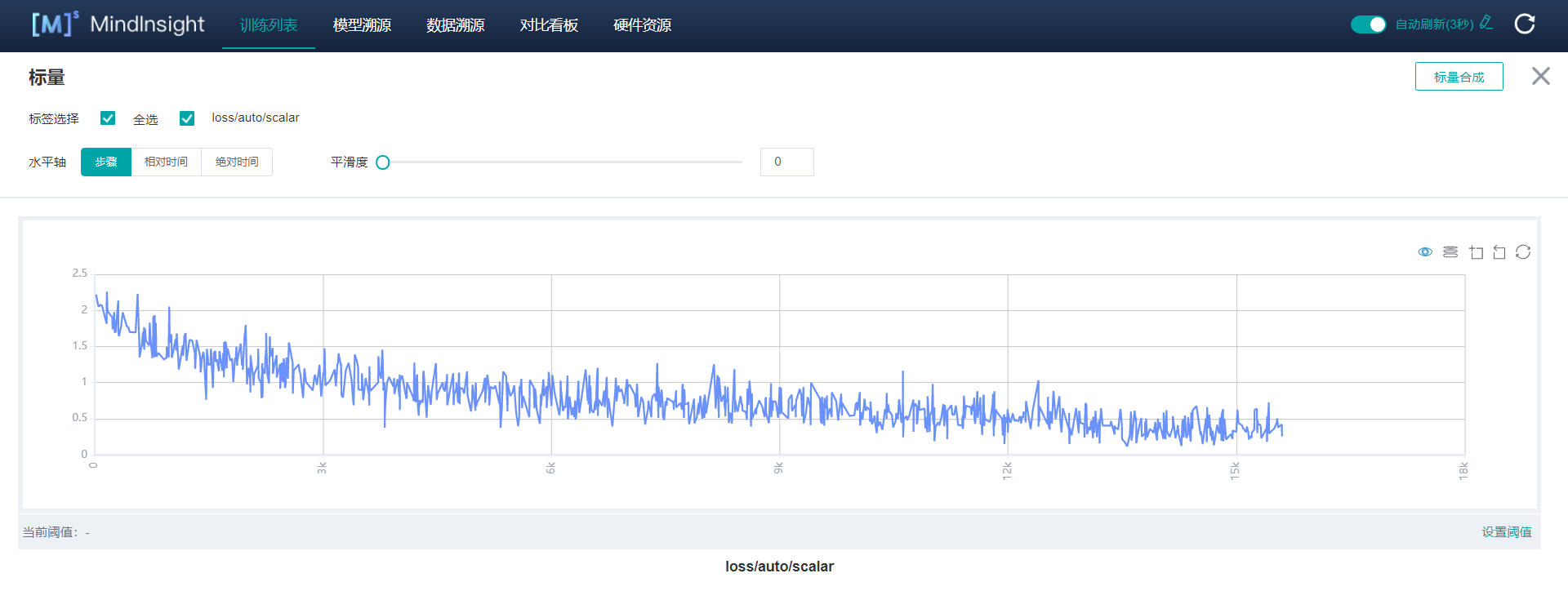
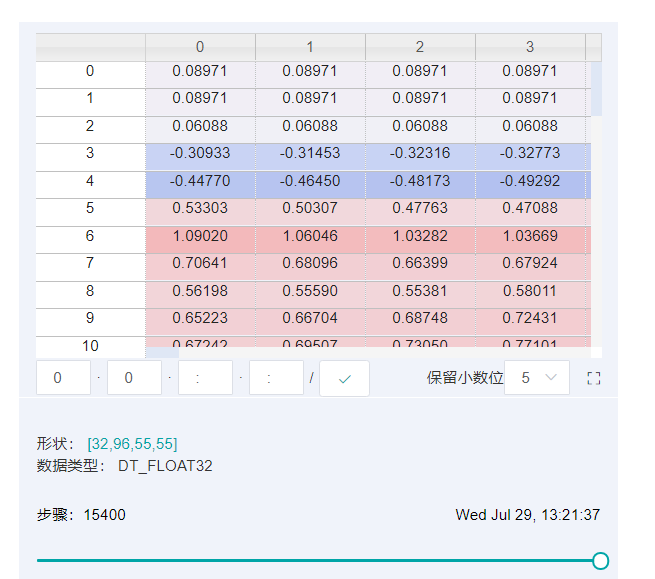
Modify MindInsight'notebook for adding tensor visualization
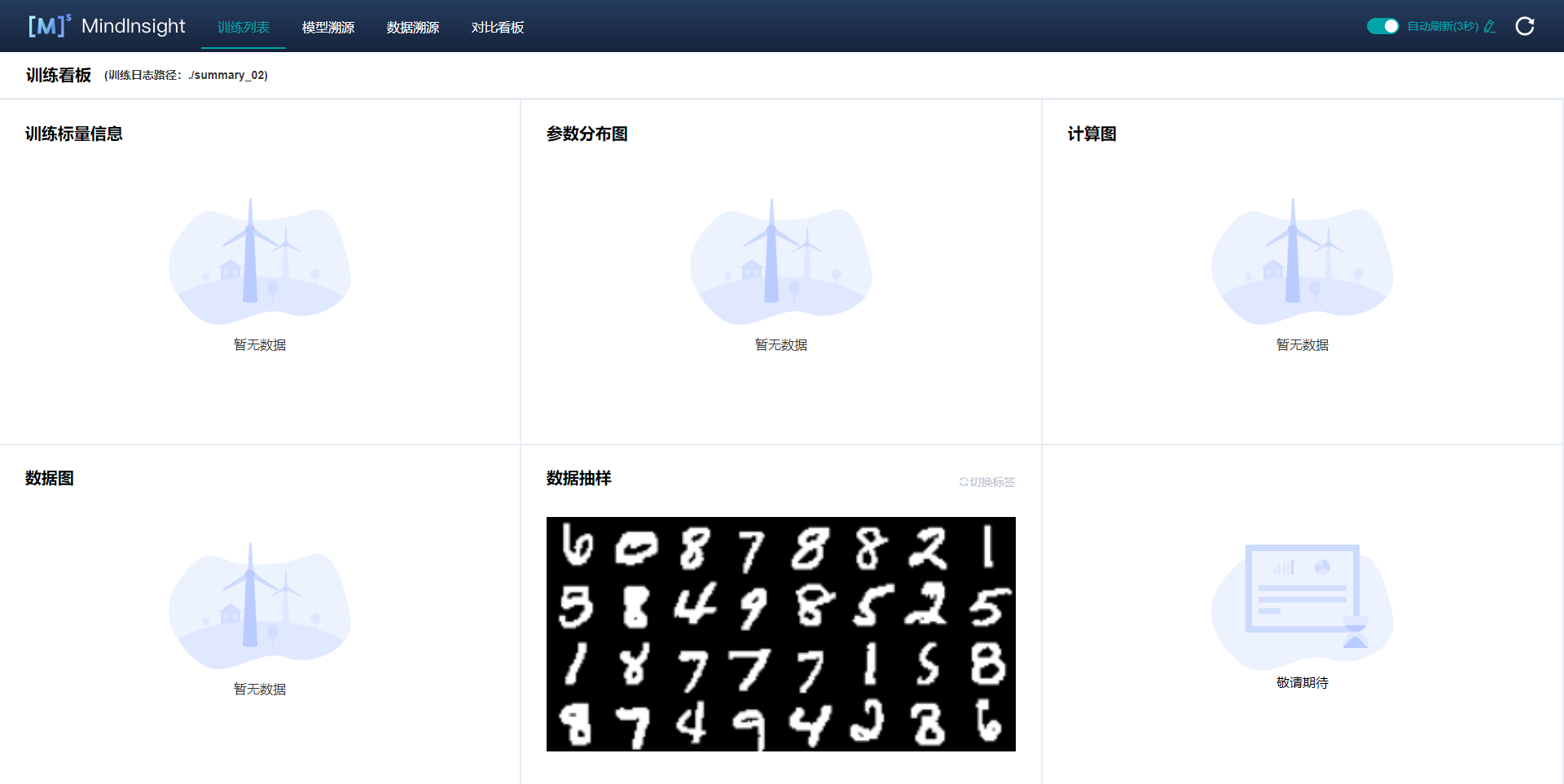
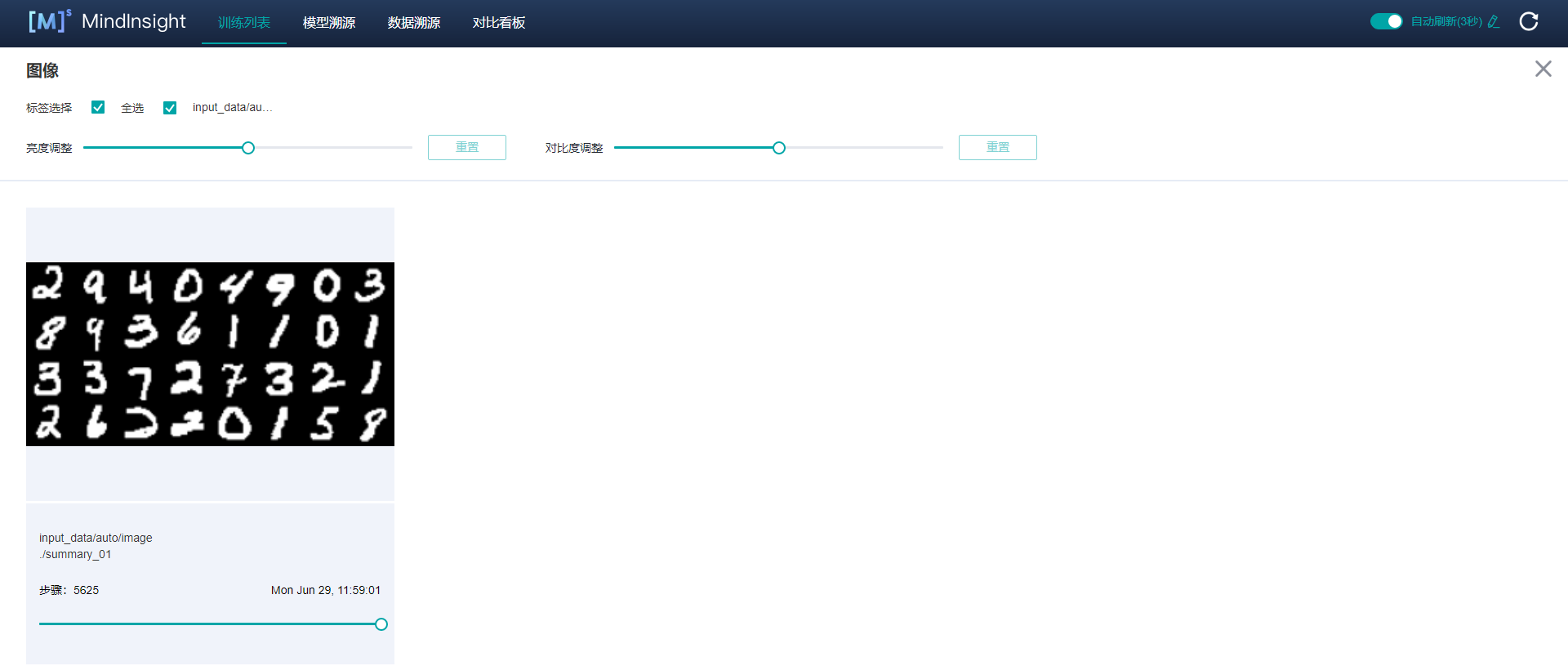
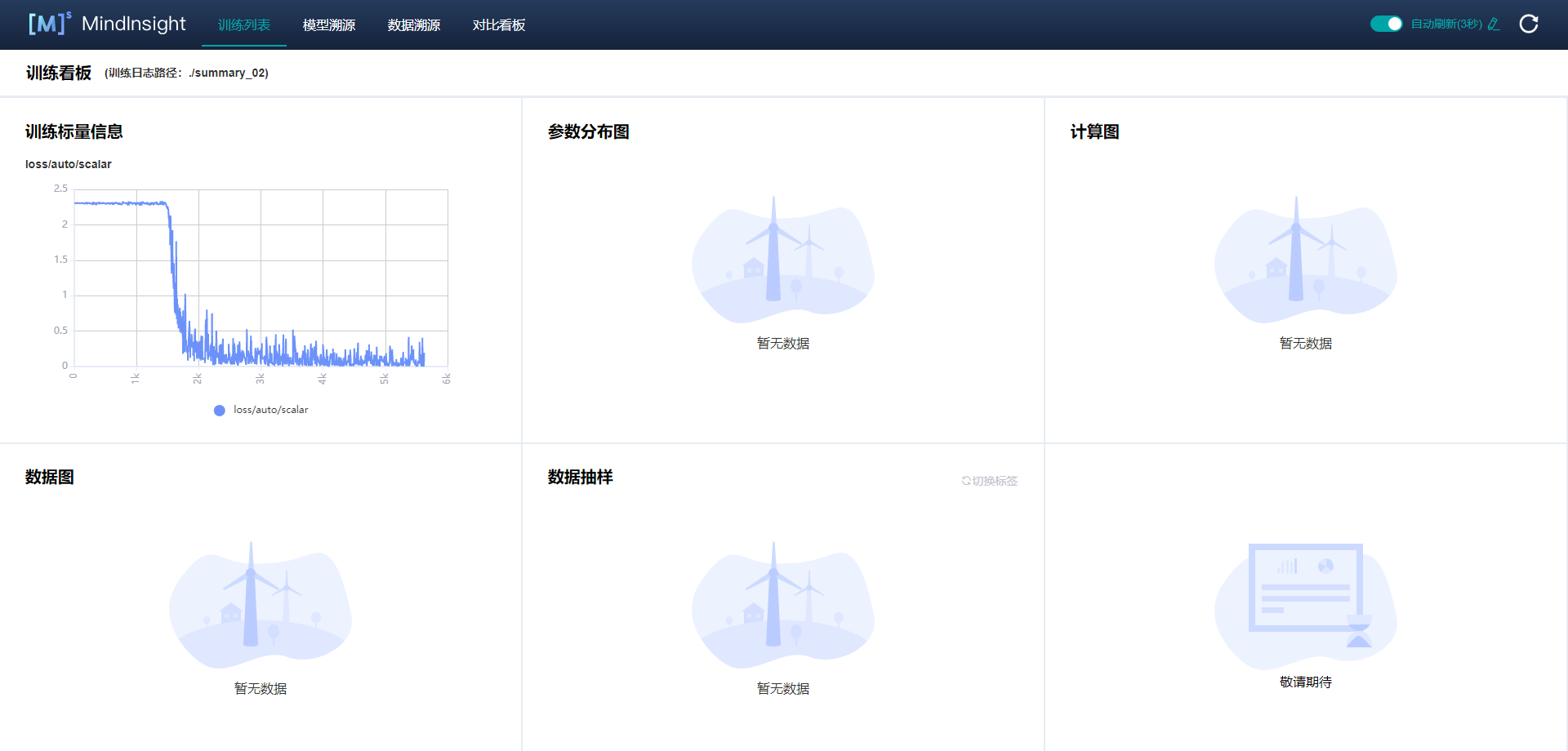
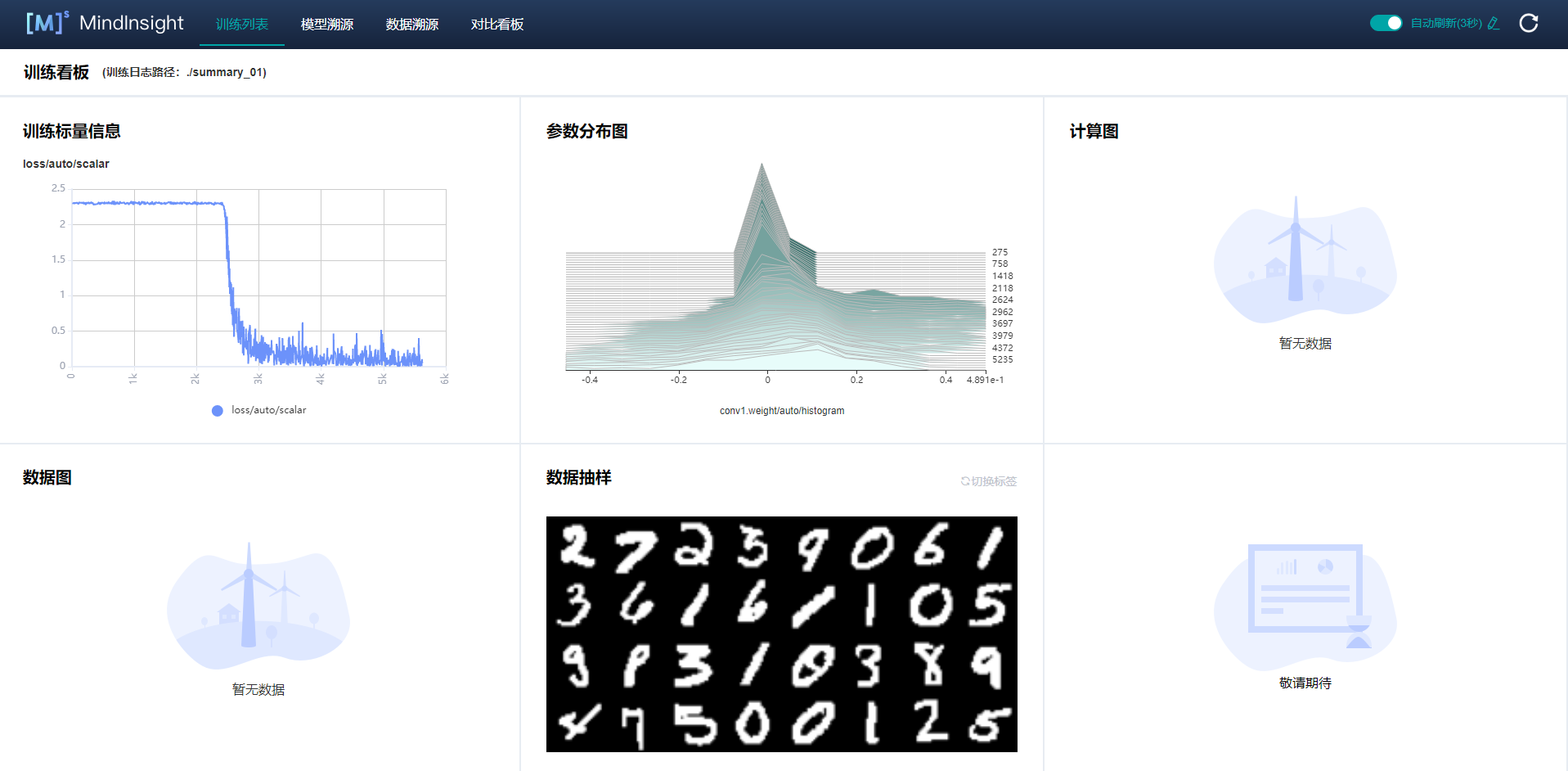
Showing
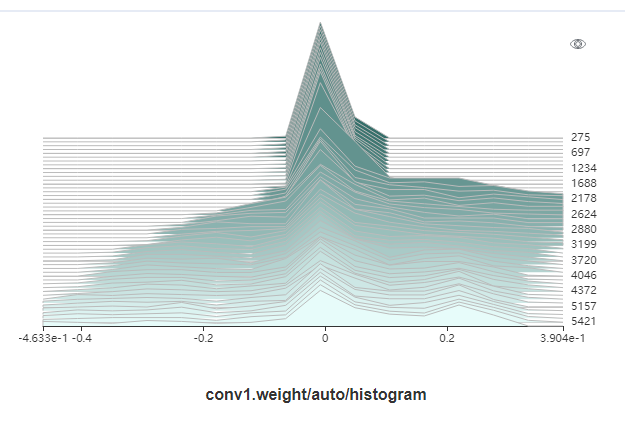
| W: | H:
| W: | H:


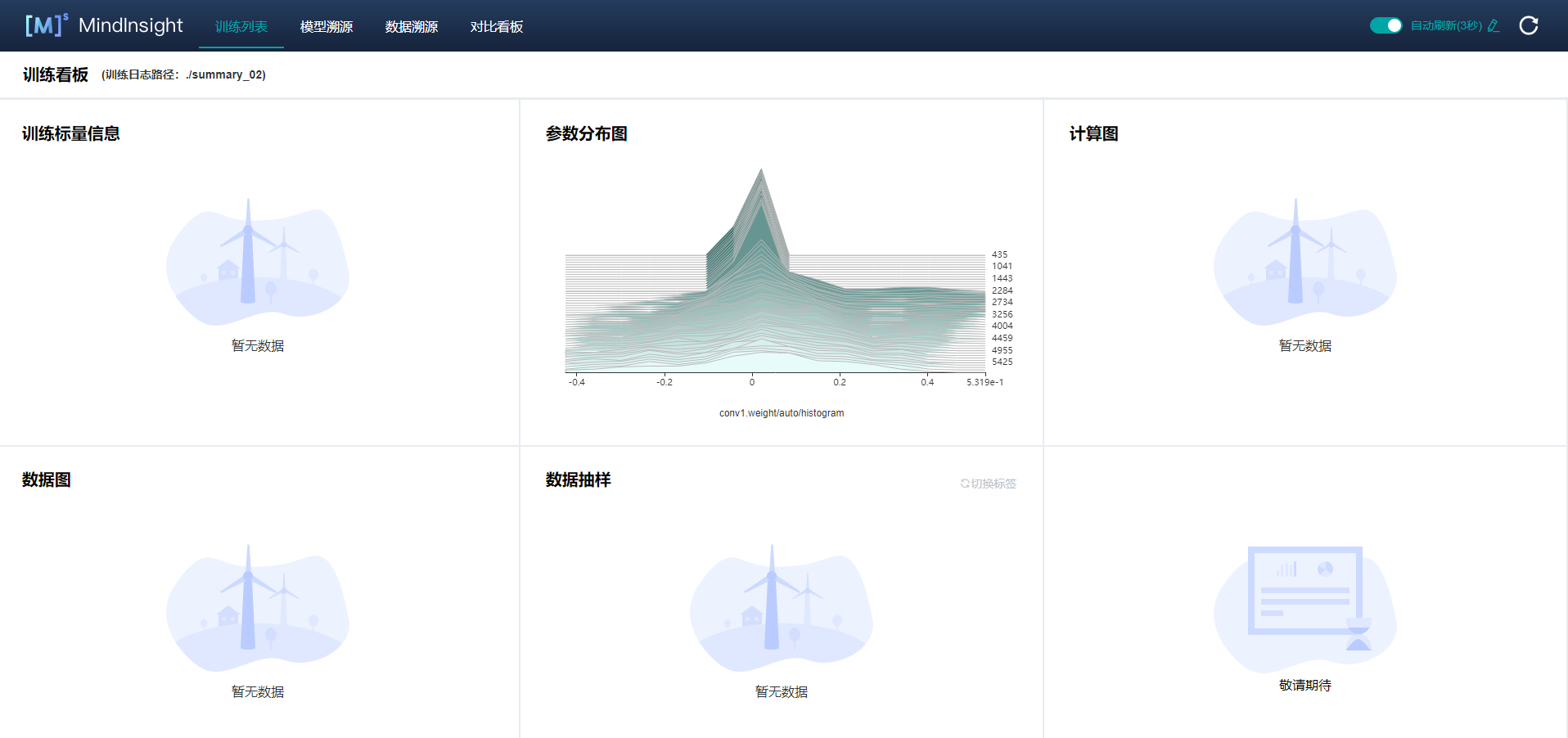
| W: | H:
| W: | H:


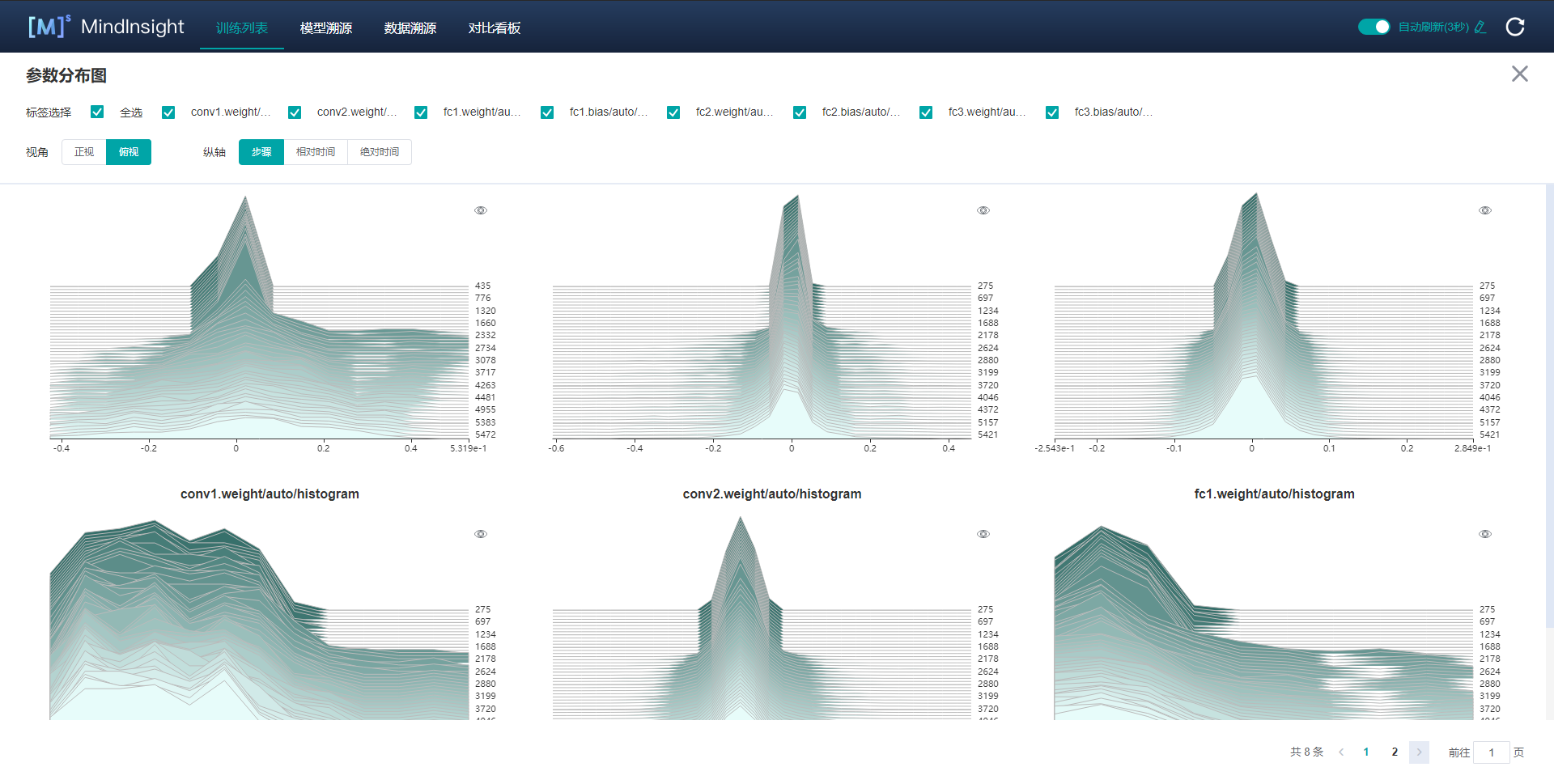
| W: | H:
| W: | H:


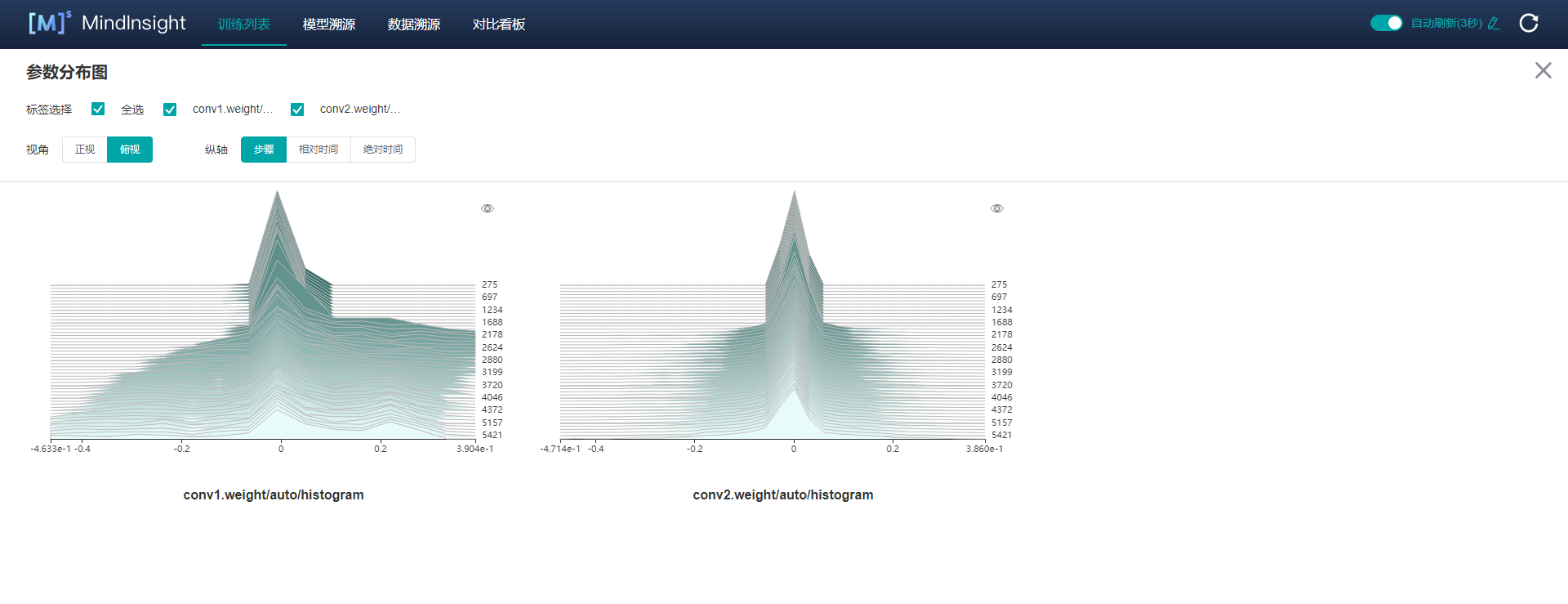
| W: | H:
| W: | H:



| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:



| W: | H:
| W: | H:


| W: | H:
| W: | H:


17.3 KB
| W: | H:
| W: | H:


30.6 KB
5.5 KB
96.6 KB
因为 它太大了无法显示 source diff 。你可以改为 查看blob。