翻译完成
Showing
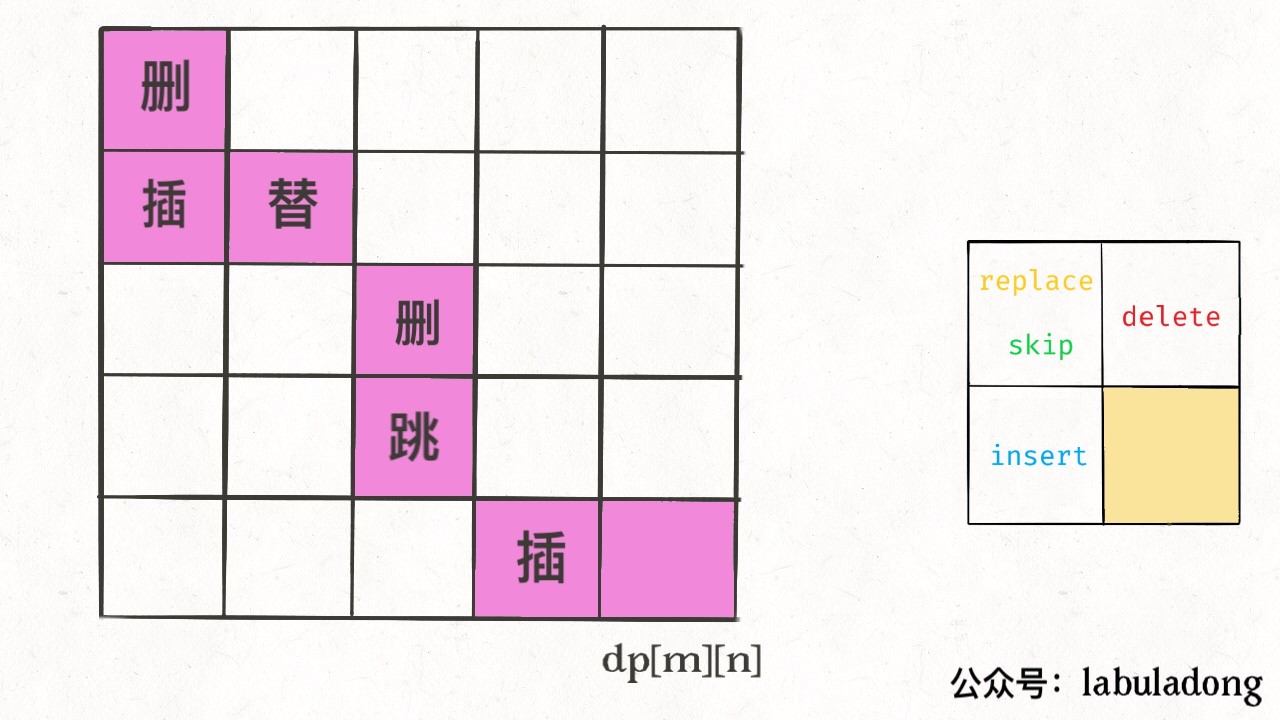
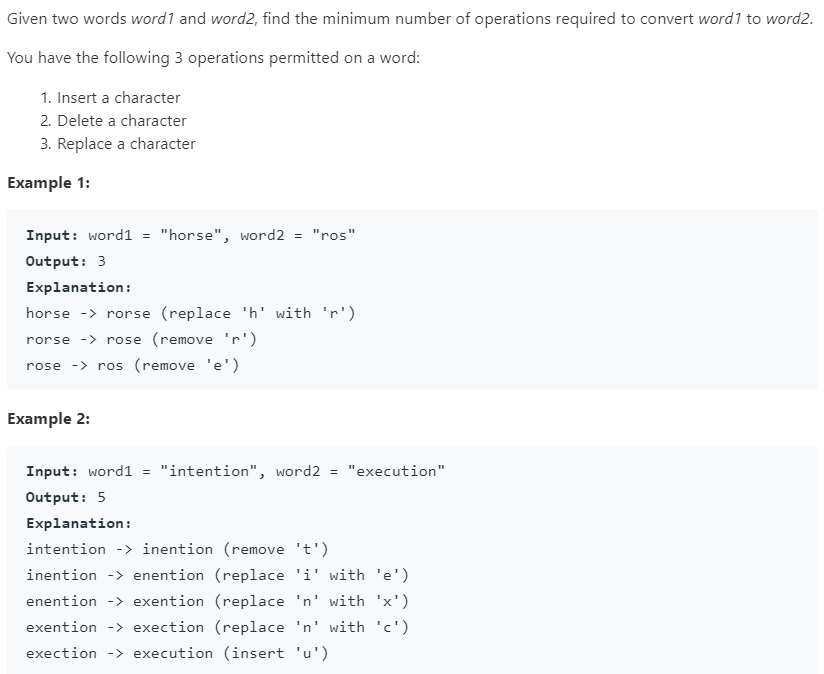
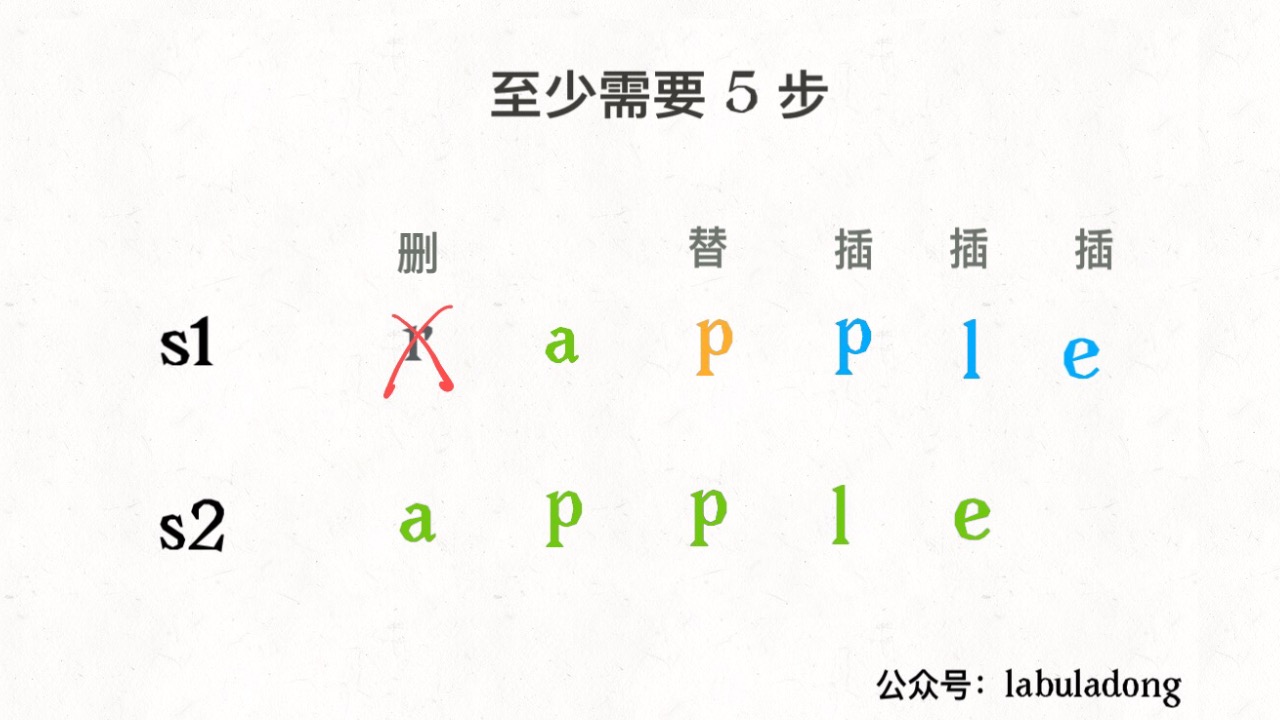
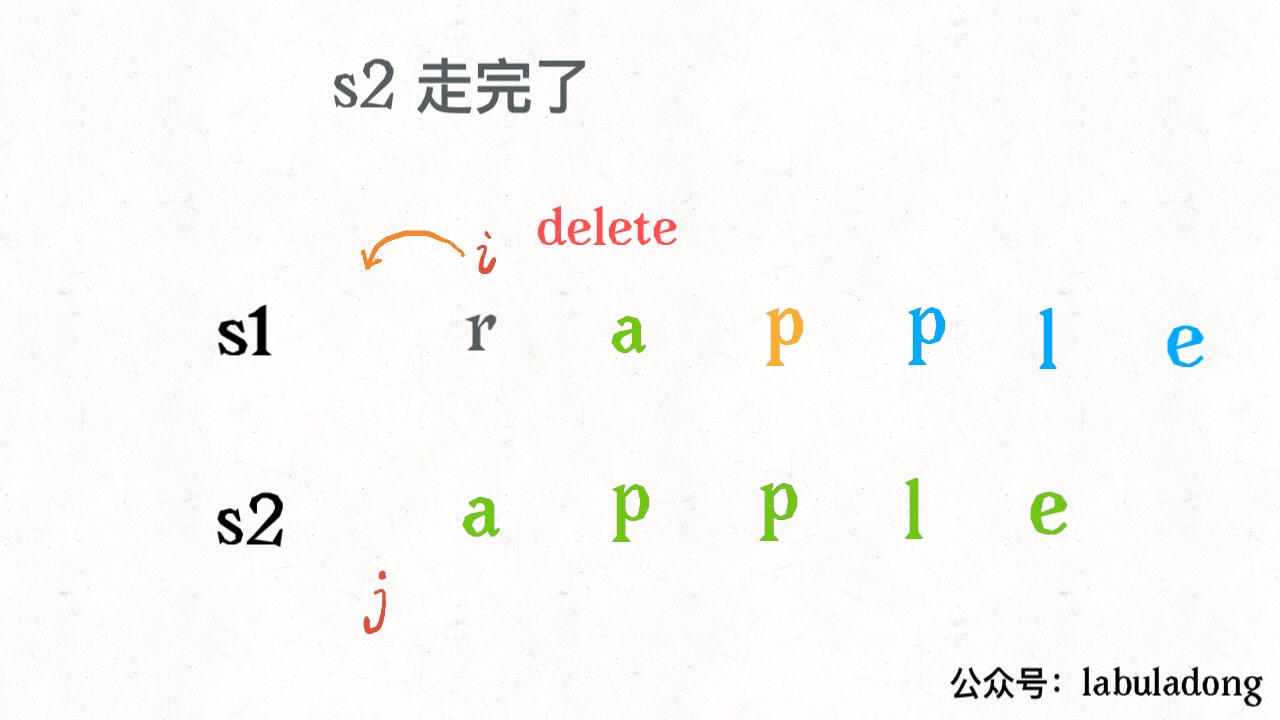
dynamic_programming/编辑距离.md
已删除
100644 → 0
| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:



| W: | H:
| W: | H:



| W: | H:
| W: | H: