Skip to content
体验新版
项目
组织
正在加载...
登录
切换导航
打开侧边栏
CSDN 技术社区
skill_tree_algorithm
提交
2eda9185
S
skill_tree_algorithm
项目概览
CSDN 技术社区
/
skill_tree_algorithm
通知
9
Star
8
Fork
1
代码
文件
提交
分支
Tags
贡献者
分支图
Diff
Issue
1
列表
看板
标记
里程碑
合并请求
0
DevOps
流水线
流水线任务
计划
Wiki
0
Wiki
分析
仓库
DevOps
项目成员
Pages
S
skill_tree_algorithm
项目概览
项目概览
详情
发布
仓库
仓库
文件
提交
分支
标签
贡献者
分支图
比较
Issue
1
Issue
1
列表
看板
标记
里程碑
合并请求
0
合并请求
0
Pages
DevOps
DevOps
流水线
流水线任务
计划
分析
分析
仓库分析
DevOps
Wiki
0
Wiki
成员
成员
收起侧边栏
关闭侧边栏
动态
分支图
创建新Issue
流水线任务
提交
Issue看板
提交
2eda9185
编写于
10月 29, 2021
作者:
每日一练社区
浏览文件
操作
浏览文件
下载
电子邮件补丁
差异文件
update exercises
上级
64162ac5
变更
8
隐藏空白更改
内联
并排
Showing
8 changed file
with
309 addition
and
125 deletion
+309
-125
data/1.算法初阶/1.蓝桥杯/堆的计数/solution.cpp
data/1.算法初阶/1.蓝桥杯/堆的计数/solution.cpp
+1
-1
data/1.算法初阶/1.蓝桥杯/堆的计数/solution.md
data/1.算法初阶/1.蓝桥杯/堆的计数/solution.md
+133
-5
data/1.算法初阶/1.蓝桥杯/大数乘法/solution.md
data/1.算法初阶/1.蓝桥杯/大数乘法/solution.md
+1
-1
data/1.算法初阶/1.蓝桥杯/夺冠概率/desc.md
data/1.算法初阶/1.蓝桥杯/夺冠概率/desc.md
+3
-1
data/1.算法初阶/1.蓝桥杯/夺冠概率/solution.cpp
data/1.算法初阶/1.蓝桥杯/夺冠概率/solution.cpp
+25
-67
data/1.算法初阶/1.蓝桥杯/夺冠概率/solution.md
data/1.算法初阶/1.蓝桥杯/夺冠概率/solution.md
+102
-6
data/1.算法初阶/1.蓝桥杯/等腰三角形/solution.md
data/1.算法初阶/1.蓝桥杯/等腰三角形/solution.md
+4
-4
data/1.算法初阶/1.蓝桥杯/颠倒的价牌/solution.md
data/1.算法初阶/1.蓝桥杯/颠倒的价牌/solution.md
+40
-40
未找到文件。
data/1.算法初阶/1.蓝桥杯/堆的计数/solution.cpp
浏览文件 @
2eda9185
...
...
@@ -44,7 +44,7 @@ int main()
{
if
(
i
*
2
+
1
<=
n
)
{
dp
[
i
]
=
(
C
(
s
[
i
]
-
1
,
s
[
i
*
2
+
1
])
*
dp
[
i
*
2
+
1
])
%
mod
*
dp
[
i
*
2
]
%
mod
;
dp
[
i
]
=
(
C
(
s
[
i
]
,
s
[
i
*
2
])
*
dp
[
i
*
2
])
%
mod
*
dp
[
i
*
2
]
%
mod
;
}
}
cout
<<
dp
[
1
]
<<
endl
;
...
...
data/1.算法初阶/1.蓝桥杯/堆的计数/solution.md
浏览文件 @
2eda9185
...
...
@@ -56,7 +56,31 @@ CPU消耗 < 1000ms
## aop
### before
```
cpp
#include <bits/stdc++.h>
using
namespace
std
;
typedef
long
long
ll
;
const
int
maxn
=
100000
;
ll
s
[
maxn
+
10
],
dp
[
maxn
+
10
],
inv
[
maxn
+
10
],
f
[
maxn
+
10
];
ll
n
;
ll
mod
=
1000000009
;
ll
qPow
(
ll
a
,
ll
b
)
{
ll
ans
=
1
;
while
(
b
!=
0
)
{
if
(
b
&
1
)
{
ans
=
ans
*
a
%
mod
;
}
a
=
a
*
a
%
mod
;
b
>>=
1
;
}
return
ans
%
mod
;
}
ll
C
(
ll
n
,
ll
m
)
{
return
(
f
[
n
]
*
inv
[
f
[
m
]])
%
mod
*
inv
[
f
[
n
-
m
]]
%
mod
;
}
```
### after
```
cpp
...
...
@@ -65,21 +89,125 @@ CPU消耗 < 1000ms
## 答案
```
cpp
int
main
()
{
cin
>>
n
;
f
[
0
]
=
1
;
for
(
int
i
=
1
;
i
<=
maxn
;
i
++
)
{
f
[
i
]
=
(
f
[
i
-
1
]
*
i
)
%
mod
;
inv
[
i
]
=
qPow
(
i
,
mod
-
2
);
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
s
[
i
]
=
(
s
[
i
*
2
+
1
]
<=
n
?
s
[
i
*
2
+
1
]
:
0
)
+
(
s
[
i
*
2
]
<=
n
?
s
[
i
*
2
]
:
0
)
+
1
;
}
for
(
int
i
=
1
;
i
<=
n
;
i
++
)
{
dp
[
i
]
=
1
;
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
if
(
i
*
2
+
1
<=
n
)
{
dp
[
i
]
=
(
C
(
s
[
i
]
-
1
,
s
[
i
*
2
+
1
])
*
dp
[
i
*
2
+
1
])
%
mod
*
dp
[
i
*
2
]
%
mod
;
}
}
cout
<<
dp
[
1
]
<<
endl
;
return
0
;
}
```
## 选项
### A
```
cpp
int
main
()
{
cin
>>
n
;
f
[
0
]
=
1
;
for
(
int
i
=
1
;
i
<=
maxn
;
i
++
)
{
f
[
i
]
=
(
f
[
i
-
1
]
*
i
)
%
mod
;
inv
[
i
]
=
qPow
(
i
,
mod
-
2
);
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
s
[
i
]
=
(
s
[
i
*
2
+
1
]
<=
n
?
s
[
i
*
2
+
1
]
:
0
)
+
(
s
[
i
*
2
]
<=
n
?
s
[
i
*
2
]
:
0
)
+
1
;
}
for
(
int
i
=
1
;
i
<=
n
;
i
++
)
{
dp
[
i
]
=
1
;
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
if
(
i
*
2
+
1
<=
n
)
{
dp
[
i
]
=
(
C
(
s
[
i
]
-
1
,
s
[
i
*
2
-
1
])
*
dp
[
i
*
2
+
1
])
%
mod
*
dp
[
i
*
2
]
%
mod
;
}
}
cout
<<
dp
[
1
]
<<
endl
;
return
0
;
}
```
### B
```
cpp
int
main
()
{
cin
>>
n
;
f
[
0
]
=
1
;
for
(
int
i
=
1
;
i
<=
maxn
;
i
++
)
{
f
[
i
]
=
(
f
[
i
-
1
]
*
i
)
%
mod
;
inv
[
i
]
=
qPow
(
i
,
mod
-
2
);
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
s
[
i
]
=
(
s
[
i
*
2
+
1
]
<=
n
?
s
[
i
*
2
+
1
]
:
0
)
+
(
s
[
i
*
2
]
<=
n
?
s
[
i
*
2
]
:
0
)
+
1
;
}
for
(
int
i
=
1
;
i
<=
n
;
i
++
)
{
dp
[
i
]
=
1
;
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
if
(
i
*
2
+
1
<=
n
)
{
dp
[
i
]
=
(
C
(
s
[
i
]
-
1
,
s
[
i
*
2
-
1
])
*
dp
[
i
*
2
-
1
])
%
mod
*
dp
[
i
*
2
]
%
mod
;
}
}
cout
<<
dp
[
1
]
<<
endl
;
return
0
;
}
```
### C
```
cpp
int
main
()
{
cin
>>
n
;
f
[
0
]
=
1
;
for
(
int
i
=
1
;
i
<=
maxn
;
i
++
)
{
f
[
i
]
=
(
f
[
i
-
1
]
*
i
)
%
mod
;
inv
[
i
]
=
qPow
(
i
,
mod
-
2
);
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
s
[
i
]
=
(
s
[
i
*
2
+
1
]
<=
n
?
s
[
i
*
2
+
1
]
:
0
)
+
(
s
[
i
*
2
]
<=
n
?
s
[
i
*
2
]
:
0
)
+
1
;
}
for
(
int
i
=
1
;
i
<=
n
;
i
++
)
{
dp
[
i
]
=
1
;
}
for
(
int
i
=
n
;
i
>=
1
;
i
--
)
{
if
(
i
*
2
+
1
<=
n
)
{
dp
[
i
]
=
(
C
(
s
[
i
],
s
[
i
*
2
])
*
dp
[
i
*
2
])
%
mod
*
dp
[
i
*
2
]
%
mod
;
}
}
cout
<<
dp
[
1
]
<<
endl
;
return
0
;
}
```
data/1.算法初阶/1.蓝桥杯/大数乘法/solution.md
浏览文件 @
2eda9185
# 大数乘法
对于32位字长的机器,大约超过20亿,用int类型就无法表示了,我们可以选择int64类型,但无论怎样扩展,固定的整数类型总是有表达的极限!如果对超级大整数进行精确运算呢?一个简单的办法是:仅仅使用现有类型,但是把大整数的运算化解为若干小整数的运算,即所谓:“分块法”。

上图表示了分块乘法的原理。可以把大数分成多段(此处为2段)小数,然后用小数的多次运算组合表示一个大数。可以根据int的承载能力规定小块的大小,比如要把int分成2段,则小块可取10000为上限值。注意,小块在进行纵向累加后,需要进行进位校正。
...
...
data/1.算法初阶/1.蓝桥杯/夺冠概率/desc.md
浏览文件 @
2eda9185
...
...
@@ -10,7 +10,9 @@
```
数据含义:甲对乙的取胜概率为0.1,丙对乙的胜率为0.3,...
现在要举行一次锦标赛。双方抽签,分两个组比,获胜的两个队再争夺冠军。(参见【1.jpg】)
现在要举行一次锦标赛。双方抽签,分两个组比,获胜的两个队再争夺冠军。
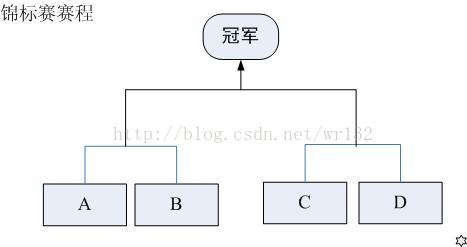
请你进行10万次模拟,计算出甲队夺冠的概率。
data/1.算法初阶/1.蓝桥杯/夺冠概率/solution.cpp
浏览文件 @
2eda9185
#include <
stdio.h
>
#include <stdlib.h>
int
main
(
void
)
{
int
i
,
j
,
k
;
//count
int
randfigure
;
int
awin
=
0
;
#include <
iostream
>
using
namespace
std
;
double
rate
[
4
][
4
]
=
{
{
0
,
0.1
,
0.3
,
0.5
},
{
0.9
,
0
,
0.7
,
0.4
},
{
0.7
,
0.3
,
0
,
0.2
},
{
0.5
,
0.6
,
0.8
,
0
}}
;
for
(
i
=
0
;
i
<
100000
;
i
++
)
int
main
()
{
int
i
,
j
,
k
;
double
time
,
sum
;
time
=
0
;
sum
=
0
;
for
(
i
=
1
;
i
<
4
;
i
++
)
{
randfigure
=
rand
();
if
(
randfigure
%
3
==
0
)
{
//AB together
if
(
randfigure
%
10
<
1
)
{
//A win B
if
(
randfigure
%
10
<
2
)
{
//C win D
if
(
randfigure
%
10
<
3
)
{
//A win C
awin
++
;
}
}
else
{
//D win C
if
(
randfigure
%
10
<
5
)
{
//A win D
awin
++
;
}
}
}
}
else
if
(
randfigure
%
3
==
1
)
{
//AC together
if
(
randfigure
%
10
<
3
)
{
//A win C
if
(
randfigure
%
10
<
4
)
{
//B win D
if
(
randfigure
%
10
<
1
)
{
//A win B
awin
++
;
}
}
else
{
//D win B
if
(
randfigure
%
10
<
5
)
{
//A win D
awin
++
;
}
}
}
}
else
{
//AD together
if
(
randfigure
%
10
<
5
)
{
//A win D
if
(
randfigure
%
10
<
3
)
{
//C win B
if
(
randfigure
%
10
<
3
)
{
//A win C
awin
++
;
}
}
else
{
//B win C
if
(
randfigure
%
10
<
1
)
{
//A win B
awin
++
;
}
for
(
j
=
1
;
j
<
4
;
j
++
)
{
for
(
k
=
1
;
k
<
4
;
k
++
)
{
if
(
j
!=
i
&&
k
!=
i
&&
j
!=
k
)
{
sum
+=
rate
[
0
][
i
]
*
rate
[
j
][
k
];
}
}
}
time
++
;
}
printf
(
"%f
\n
"
,
awin
/
100000.0
);
cout
<<
sum
/
time
;
return
0
;
}
\ No newline at end of file
data/1.算法初阶/1.蓝桥杯/夺冠概率/solution.md
浏览文件 @
2eda9185
...
...
@@ -11,7 +11,9 @@
```
数据含义:甲对乙的取胜概率为0.1,丙对乙的胜率为0.3,...
现在要举行一次锦标赛。双方抽签,分两个组比,获胜的两个队再争夺冠军。(参见【1.jpg】)
现在要举行一次锦标赛。双方抽签,分两个组比,获胜的两个队再争夺冠军。

请你进行10万次模拟,计算出甲队夺冠的概率。
...
...
@@ -20,7 +22,13 @@
## aop
### before
```
cpp
#include <iostream>
using
namespace
std
;
double
rate
[
4
][
4
]
=
{
{
0
,
0.1
,
0.3
,
0.5
},
{
0.9
,
0
,
0.7
,
0.4
},
{
0.7
,
0.3
,
0
,
0.2
},
{
0.5
,
0.6
,
0.8
,
0
}};
```
### after
```
cpp
...
...
@@ -29,21 +37,109 @@
## 答案
```
cpp
int
main
()
{
int
i
,
j
,
k
;
double
time
,
sum
;
time
=
0
;
sum
=
0
;
for
(
i
=
1
;
i
<
4
;
i
++
)
{
for
(
j
=
1
;
j
<
4
;
j
++
)
{
for
(
k
=
1
;
k
<
4
;
k
++
)
{
if
(
j
!=
i
&&
k
!=
i
&&
j
!=
k
)
{
sum
+=
rate
[
0
][
i
]
*
rate
[
j
][
k
]
*
rate
[
0
][
j
];
}
}
}
time
++
;
}
cout
<<
sum
/
time
;
return
0
;
}
```
## 选项
### A
```
cpp
int
main
()
{
int
i
,
j
,
k
;
double
time
,
sum
;
time
=
0
;
sum
=
0
;
for
(
i
=
1
;
i
<
4
;
i
++
)
{
for
(
j
=
1
;
j
<
4
;
j
++
)
{
for
(
k
=
1
;
k
<
4
;
k
++
)
{
if
(
j
!=
i
&&
k
!=
i
&&
j
!=
k
)
{
sum
+=
rate
[
0
][
i
]
*
rate
[
0
][
j
];
}
}
}
time
++
;
}
cout
<<
sum
/
time
;
return
0
;
}
```
### B
```
cpp
int
main
()
{
int
i
,
j
,
k
;
double
time
,
sum
;
time
=
0
;
sum
=
0
;
for
(
i
=
1
;
i
<
4
;
i
++
)
{
for
(
j
=
1
;
j
<
4
;
j
++
)
{
for
(
k
=
1
;
k
<
4
;
k
++
)
{
if
(
j
!=
i
&&
k
!=
i
&&
j
!=
k
)
{
sum
+=
rate
[
j
][
k
]
*
rate
[
0
][
j
];
}
}
}
time
++
;
}
cout
<<
sum
/
time
;
return
0
;
}
```
### C
```
cpp
int
main
()
{
int
i
,
j
,
k
;
double
time
,
sum
;
time
=
0
;
sum
=
0
;
for
(
i
=
1
;
i
<
4
;
i
++
)
{
for
(
j
=
1
;
j
<
4
;
j
++
)
{
for
(
k
=
1
;
k
<
4
;
k
++
)
{
if
(
j
!=
i
&&
k
!=
i
&&
j
!=
k
)
{
sum
+=
rate
[
0
][
i
]
*
rate
[
j
][
k
];
}
}
}
time
++
;
}
cout
<<
sum
/
time
;
return
0
;
}
```
data/1.算法初阶/1.蓝桥杯/等腰三角形/solution.md
浏览文件 @
2eda9185
...
...
@@ -4,7 +4,7 @@
先用1,2,3,…的自然数拼一个足够长的串
用这个串填充三角形的三条边。从上方顶点开始,逆时针填充。
比如,当三角形高度是8时:

输入,一个正整数n(3<n<300),表示三角形的高度
输出,用数字填充的等腰三角形。
...
...
@@ -15,20 +15,20 @@
5
#### 程序应该输出:

### 再例如:
#### 输入:
10
#### 程序应该输出:

### 再例如:
#### 输入:
15
#### 程序应该输出:

## aop
...
...
data/1.算法初阶/1.蓝桥杯/颠倒的价牌/solution.md
浏览文件 @
2eda9185
...
...
@@ -26,15 +26,15 @@ using namespace std;
```
cpp
int
main
()
{
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
//价牌包含的数字
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
//价牌翻转对应的数字
int
profit1
[
1111
][
2
];
//利润1
int
profit2
[
1111
][
2
];
//利润2
int
before_reverse
;
//颠倒前
int
after_reverse
;
//颠倒后
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
int
profit1
[
1111
][
2
];
int
profit2
[
1111
][
2
];
int
before_reverse
;
int
after_reverse
;
int
i
=
0
;
int
j
=
0
;
for
(
int
a
=
1
;
a
<
7
;
a
++
)
//从1开始,第一位数字不可以是0
for
(
int
a
=
1
;
a
<
7
;
a
++
)
{
for
(
int
b
=
0
;
b
<
7
;
b
++
)
{
...
...
@@ -44,16 +44,16 @@ int main()
{
before_reverse
=
num1
[
a
]
*
1000
+
num1
[
b
]
*
100
+
num1
[
c
]
*
10
+
num1
[
d
];
after_reverse
=
num2
[
d
]
*
1000
+
num2
[
c
]
*
100
+
num2
[
b
]
*
10
+
num2
[
a
];
//因为是颠倒之后所以第一位可以是0
if
(
after_reverse
-
before_reverse
>
-
300
&&
after_reverse
-
before_reverse
<
-
200
)
//在200-300范围内,我们以正数为准
{
profit1
[
i
][
0
]
=
before_reverse
;
profit1
[
i
][
1
]
=
after_reverse
-
before_reverse
;
i
++
;
}
else
if
(
after_reverse
-
before_reverse
>
800
&&
after_reverse
-
before_reverse
<
900
)
//在800-900范围内
{
profit1
[
j
][
0
]
=
before_reverse
;
profit2
[
j
][
1
]
=
after_reverse
-
before_reverse
;
...
...
@@ -84,15 +84,15 @@ int main()
```
cpp
int
main
()
{
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
//价牌包含的数字
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
//价牌翻转对应的数字
int
profit1
[
1111
][
2
];
//利润1
int
profit2
[
1111
][
2
];
//利润2
int
before_reverse
;
//颠倒前
int
after_reverse
;
//颠倒后
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
int
profit1
[
1111
][
2
];
int
profit2
[
1111
][
2
];
int
before_reverse
;
int
after_reverse
;
int
i
=
0
;
int
j
=
0
;
for
(
int
a
=
1
;
a
<
7
;
a
++
)
//从1开始,第一位数字不可以是0
for
(
int
a
=
1
;
a
<
7
;
a
++
)
{
for
(
int
b
=
0
;
b
<
7
;
b
++
)
{
...
...
@@ -102,16 +102,16 @@ int main()
{
before_reverse
=
num1
[
a
]
*
1000
+
num1
[
b
]
*
100
+
num1
[
c
]
*
10
+
num1
[
d
];
after_reverse
=
num2
[
d
]
*
1000
+
num2
[
c
]
*
100
+
num2
[
b
]
*
10
+
num2
[
a
];
//因为是颠倒之后所以第一位可以是0
if
(
after_reverse
-
before_reverse
>
-
300
&&
after_reverse
-
before_reverse
<
-
200
)
//在200-300范围内,我们以正数为准
{
profit1
[
i
][
0
]
=
before_reverse
;
profit1
[
i
][
1
]
=
after_reverse
-
before_reverse
;
i
++
;
}
else
if
(
after_reverse
-
before_reverse
>
800
&&
after_reverse
-
before_reverse
<
900
)
//在800-900范围内
{
profit1
[
j
][
0
]
=
before_reverse
;
profit2
[
j
][
1
]
=
after_reverse
-
before_reverse
;
...
...
@@ -141,15 +141,15 @@ int main()
```
cpp
int
main
()
{
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
//价牌包含的数字
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
//价牌翻转对应的数字
int
profit1
[
1111
][
2
];
//利润1
int
profit2
[
1111
][
2
];
//利润2
int
before_reverse
;
//颠倒前
int
after_reverse
;
//颠倒后
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
int
profit1
[
1111
][
2
];
int
profit2
[
1111
][
2
];
int
before_reverse
;
int
after_reverse
;
int
i
=
0
;
int
j
=
0
;
for
(
int
a
=
1
;
a
<
7
;
a
++
)
//从1开始,第一位数字不可以是0
for
(
int
a
=
1
;
a
<
7
;
a
++
)
{
for
(
int
b
=
0
;
b
<
7
;
b
++
)
{
...
...
@@ -159,16 +159,16 @@ int main()
{
before_reverse
=
num1
[
a
]
*
1000
+
num1
[
b
]
*
100
+
num1
[
c
]
*
10
+
num1
[
d
];
after_reverse
=
num2
[
d
]
*
1000
+
num2
[
c
]
*
100
+
num2
[
b
]
*
10
+
num2
[
a
];
//因为是颠倒之后所以第一位可以是0
if
(
after_reverse
-
before_reverse
>
-
300
&&
after_reverse
-
before_reverse
<
-
200
)
//在200-300范围内,我们以正数为准
{
profit1
[
i
][
0
]
=
before_reverse
;
profit1
[
i
][
1
]
=
after_reverse
-
before_reverse
;
i
++
;
}
else
if
(
after_reverse
-
before_reverse
>
800
&&
after_reverse
-
before_reverse
<
900
)
//在800-900范围内
{
profit1
[
j
][
0
]
=
before_reverse
;
profit2
[
j
][
1
]
=
after_reverse
-
before_reverse
;
...
...
@@ -198,15 +198,15 @@ int main()
```
cpp
int
main
()
{
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
//价牌包含的数字
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
//价牌翻转对应的数字
int
profit1
[
1111
][
2
];
//利润1
int
profit2
[
1111
][
2
];
//利润2
int
before_reverse
;
//颠倒前
int
after_reverse
;
//颠倒后
int
num1
[
7
]
=
{
0
,
1
,
2
,
5
,
6
,
8
,
9
};
int
num2
[
7
]
=
{
0
,
1
,
2
,
5
,
9
,
8
,
6
};
int
profit1
[
1111
][
2
];
int
profit2
[
1111
][
2
];
int
before_reverse
;
int
after_reverse
;
int
i
=
0
;
int
j
=
0
;
for
(
int
a
=
1
;
a
<
7
;
a
++
)
//从1开始,第一位数字不可以是0
for
(
int
a
=
1
;
a
<
7
;
a
++
)
{
for
(
int
b
=
0
;
b
<
7
;
b
++
)
{
...
...
@@ -216,16 +216,16 @@ int main()
{
before_reverse
=
num1
[
a
]
*
1000
+
num1
[
b
]
*
100
+
num1
[
c
]
*
10
+
num1
[
d
];
after_reverse
=
num2
[
d
]
*
1000
+
num2
[
c
]
*
100
+
num2
[
b
]
*
10
+
num2
[
a
];
//因为是颠倒之后所以第一位可以是0
if
(
after_reverse
-
before_reverse
>
-
300
&&
after_reverse
-
before_reverse
<
-
200
)
//在200-300范围内,我们以正数为准
{
profit1
[
i
][
0
]
=
before_reverse
;
profit1
[
i
][
1
]
=
after_reverse
-
before_reverse
;
i
++
;
}
else
if
(
after_reverse
-
before_reverse
>
800
&&
after_reverse
-
before_reverse
<
900
)
//在800-900范围内
{
profit1
[
j
][
0
]
=
before_reverse
;
profit2
[
j
][
1
]
=
after_reverse
-
before_reverse
;
...
...
编辑
预览
Markdown
is supported
0%
请重试
或
添加新附件
.
添加附件
取消
You are about to add
0
people
to the discussion. Proceed with caution.
先完成此消息的编辑!
取消
想要评论请
注册
或
登录