Merge pull request #9075 from jacquesqiao/add_distributed_lookup_table_design
Add distributed lookup table design
Showing
doc/design/lookup_table.png
0 → 100644
23.7 KB
88.3 KB
Fork自 PaddlePaddle / Paddle
Add distributed lookup table design
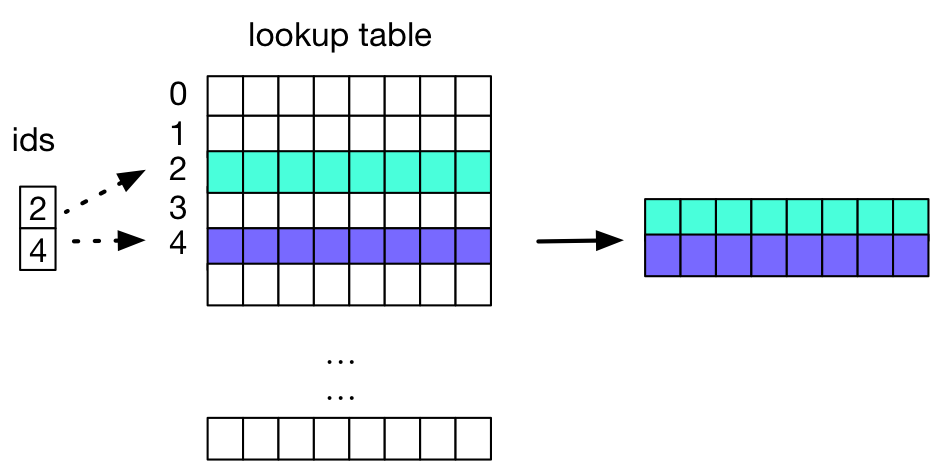
23.7 KB

88.3 KB
