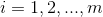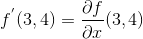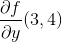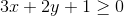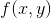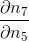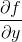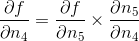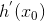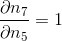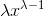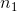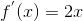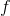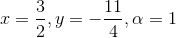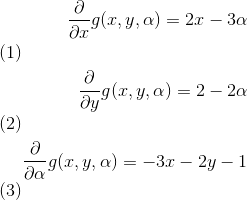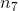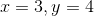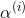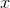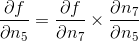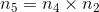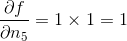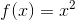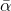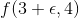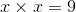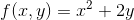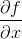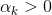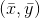c d tex
Showing
467 字节
234 字节
282 字节
875 字节
288 字节
635 字节
609 字节
1.0 KB
422 字节
139 字节
197 字节
145 字节
356 字节
810 字节
552 字节
496 字节
330 字节
379 字节
331 字节
906 字节
137 字节
498 字节
160 字节
244 字节
162 字节
525 字节
244 字节
769 字节
649 字节
611 字节
352 字节
306 字节
313 字节
452 字节
246 字节
156 字节
636 字节
321 字节
160 字节
748 字节
726 字节
861 字节
197 字节
406 字节
390 字节
135 字节
245 字节
623 字节
2.5 KB
165 字节
344 字节
224 字节
124 字节
944 字节
312 字节
685 字节
406 字节
458 字节
358 字节
276 字节
635 字节
435 字节
897 字节
400 字节
133 字节
364 字节
171 字节
572 字节
363 字节
139 字节
400 字节
281 字节
367 字节
813 字节
192 字节
1.0 KB
422 字节
559 字节
313 字节
274 字节
281 字节