style

docs/11.训练深层神经网络.md

@@ -509,7 +509,7 @@ TensorFlow 在 <https://github.com/tensorflow/models> 中有自己的模型动
 
 想象一下，一个保龄球在一个光滑的表面上平缓的斜坡上滚动：它会缓慢地开始，但是它会很快地达到最终的速度（如果有一些摩擦或空气阻力的话）。 这是 Boris Polyak 在 1964 年提出的动量优化背后的一个非常简单的想法。相比之下，普通的梯度下降只需要沿着斜坡进行小的有规律的下降步骤，所以需要更多的时间才能到达底部。
 
-回想一下，梯度下降只是通过直接减去损失函数`J(θ)`相对于权重`θ`的梯度，乘以学习率`η`来更新权重`θ`。 方程是： $\theta := \theta - \eta \nabla_\theta J(\theta)$ 。 它不关心早期的梯度是什么。 如果局部梯度很小，则会非常缓慢。
+回想一下，梯度下降只是通过直接减去损失函数`J(θ)`相对于权重`θ`的梯度，乘以学习率`η`来更新权重`θ`。 方程是：$\theta := \theta - \eta \nabla_\theta J(\theta)$。它不关心早期的梯度是什么。 如果局部梯度很小，则会非常缓慢。
 
 ![](https://img-blog.csdn.net/20171214105924019?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWtvbl93YW5nX2hrYnU=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)
 
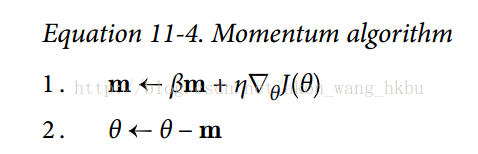
@@ -553,7 +553,7 @@ AdaGrad 算法通过沿着最陡的维度缩小梯度向量来实现这一点（
 
 ![](https://img-blog.csdn.net/20171214121745625?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWtvbl93YW5nX2hrYnU=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)
 
-第一步将梯度的平方累加到矢量`s`中（`⊗`符号表示单元乘法）。 这个向量化形式相当于向量`s`的每个元素`si`计算 $s_i := s_i + (\partial J(\theta) / \partial \theta_i)^2$ 换一种说法，每个 $s_i$ 累加损失函数对参数 $\theta_i$ 的偏导数的平方。 如果损失函数沿着第`i`维陡峭，则在每次迭代时，$s_i$ 将变得越来越大。
+第一步将梯度的平方累加到矢量`s`中（`⊗`符号表示单元乘法）。 这个向量化形式相当于向量`s`的每个元素`si`计算 $s_i := s_i + (\partial J(\theta) / \partial \theta_i)^2$。换一种说法，每个 $s_i$ 累加损失函数对参数 $\theta_i$ 的偏导数的平方。 如果损失函数沿着第`i`维陡峭，则在每次迭代时，$s_i$ 将变得越来越大。
 
 第二步几乎与梯度下降相同，但有一个很大的不同：梯度矢量按比例缩小 ![](https://img-blog.csdn.net/20171214122532613?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWtvbl93YW5nX2hrYnU=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)（`⊘`符号表示元素分割，`ε`是避免被零除的平滑项，通常设置为 ![](https://img-blog.csdn.net/20171214122711809?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWtvbl93YW5nX2hrYnU=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)。 这个矢量化的形式相当于计算 ![](https://img-blog.csdn.net/20171214122927252?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWtvbl93YW5nX2hrYnU=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center) 对于所有参数 $\theta_i$（同时）。
 
@@ -617,7 +617,7 @@ T 代表迭代次数（从 1 开始）。
 
 预定的分段恒定学习率:
 
-例如，首先将学习率设置为 $η_0 = 0.1$ ，然后在 50 个迭代之后将学习率设置为 $η_1= 0.001$ 。虽然这个解决方案可以很好地工作，但是通常需要弄清楚正确的学习速度以及何时使用它们。
+例如，首先将学习率设置为 $η_0 = 0.1$，然后在 50 个迭代之后将学习率设置为 $η_1= 0.001$。虽然这个解决方案可以很好地工作，但是通常需要弄清楚正确的学习速度以及何时使用它们。
 
 性能调度:
 

docs/15.自编码器.md

@@ -132,7 +132,9 @@ with tf.Session() as sess:
 ## 关联权重
 
 当自编码器整齐地对称时，就像我们刚刚构建的那样，一种常用技术是将解码器层的权重与编码器层的权重相关联。 这样减少了模型中的权重数量，加快了训练速度，并限制了过度拟合的风险。
-具体来说，如果自编码器总共具有`N`个层（不计入输入层），并且 $W_[L]$ 表示第`L`层的连接权重（例如，层1是第一隐藏层，则层`N / 2`是编码 层，而层`N`是输出层），则解码器层权重可以简单地定义为： $W_[N-L + 1]= W_[L]T$ （其中`L = 1,2，...，N2`）。
+
+具体来说，如果自编码器总共具有`N`个层（不计入输入层），并且 $W^{[L]}$ 表示第`L`层的连接权重（例如，层 1 是第一隐藏层，则层`N / 2`是编码 层，而层`N`是输出层），则解码器层权重可以简单地定义为：$W^{[N-L + 1]}= W^{[L]T}$（其中`L = 1, 2, ..., N2`）。
+
 不幸的是，使用`fully_connected()`函数在 TensorFlow 中实现相关权重有点麻烦；手动定义层实际上更容易。 代码结尾明显更加冗长：
 
 ```py

docs/2.一个完整的机器学习项目.md

@@ -85,7 +85,7 @@ OK，有了这些信息，你就可以开始设计系统了。首先，你需要
 > *   `m`是测量 RMSE 的数据集中的实例数量。  
 >     例如，如果用一个含有 2000 个街区的验证集求 RMSE，则`m = 2000`。
 > 
-> *   $x^{(i)}$ 是数据集第`i`个实例的所有特征值（不包含标签）的向量， $y^{(i)}$ 是它的标签（这个实例的输出值）。 
+> *   $x^{(i)}$ 是数据集第`i`个实例的所有特征值（不包含标签）的向量，$y^{(i)}$ 是它的标签（这个实例的输出值）。 
 > 
 >     例如，如果数据集中的第一个街区位于经度 –118.29°，纬度 33.91°，有 1416 名居民，收入中位数是 \$38372，房价中位数是 \$156400（不考虑其它特征），则有：  
 >     
@@ -95,18 +95,18 @@ OK，有了这些信息，你就可以开始设计系统了。首先，你需要
 >     
 >     ![](https://upload-images.jianshu.io/upload_images/7178691-e54122a46b09f013.png)
 >     
-> *   `X`是包含数据集中所有实例的所有特征值（不包含标签）的矩阵。每一行是一个实例，第`i`行是 $x^{(i)}$ 的转置，标记为 $x^{(i)T}$ 。
+> *   `X`是包含数据集中所有实例的所有特征值（不包含标签）的矩阵。每一行是一个实例，第`i`行是 $x^{(i)}$ 的转置，标记为 $x^{(i)T}$。
 ? 
 >     例如，仍然是前面的第一区，矩阵`X`就是：  
 >     
 >     ![](https://upload-images.jianshu.io/upload_images/7178691-e159cd4395a29dca.png)
 >     
-> *   `h`是系统的预测函数，也称为假设（hypothesis）。当系统收到一个实例的特征向量 $x^{(i)}$ ，就会输出这个实例的一个预测值 $\hat y^{(i)} = h(x^{(i)})$ （ $\hat y$ 读作`y-hat`）。  
+> *   `h`是系统的预测函数，也称为假设（hypothesis）。当系统收到一个实例的特征向量 $x^{(i)}$，就会输出这个实例的一个预测值 $\hat y^{(i)} = h(x^{(i)})$（$\hat y$ 读作`y-hat`）。  
 > 
->     例如，如果系统预测第一区的房价中位数是 \$158400，则 $\hat y^{(1)} = h(x^{(1)}) = 158400$ 。预测误差是 $\hat y^{(1)} – y^{(1)} = 2000$ 。
+>     例如，如果系统预测第一区的房价中位数是 \$158400，则 $\hat y^{(1)} = h(x^{(1)}) = 158400$。预测误差是 $\hat y^{(1)} – y^{(1)} = 2000$。
 >     `RMSE(X,h)`是使用假设`h`在样本集上测量的损失函数。
 > 
-> 我们使用小写斜体表示标量值（例如 $\it m$ 或 $\it{y^{(1)}}$ ）和函数名（例如 $\it h$ ），小写粗体表示向量（例如 $\bb{x^{(i)}}$ ），大写粗体表示矩阵（例如 $\bb X$ ）。
+> 我们使用小写斜体表示标量值（例如 $\it m$ 或 $\it{y^{(1)}}$）和函数名（例如 $\it h$），小写粗体表示向量（例如 $\bb{x^{(i)}}$），大写粗体表示矩阵（例如 $\bb X$）。
 
 虽然大多数时候 RMSE 是回归任务可靠的性能指标，在有些情况下，你可能需要另外的函数。例如，假设存在许多异常的街区。此时，你可能需要使用平均绝对误差（Mean Absolute Error，也称作平均绝对偏差，见公式 2-2）：
 
@@ -116,9 +116,9 @@ OK，有了这些信息，你就可以开始设计系统了。首先，你需要
 
 RMSE 和 MAE 都是测量预测值和目标值两个向量距离的方法。有多种测量距离的方法，或范数：
 
-*   计算对应欧几里得范数的平方和的根（RMSE）：这个距离介绍过。它也称作`ℓ2`范数，标记为 $\| \cdot \|_2$ （或只是 $\| \cdot \|$ ）。
+*   计算对应欧几里得范数的平方和的根（RMSE）：这个距离介绍过。它也称作`ℓ2`范数，标记为 $\| \cdot \|_2$（或只是 $\| \cdot \|$）。
     
-*   计算对应于`ℓ1`（标记为 $\| \cdot \|_1$ ）范数的绝对值和（MAE）。有时，也称其为曼哈顿范数，因为它测量了城市中的两点，沿着矩形的边行走的距离。
+*   计算对应于`ℓ1`（标记为 $\| \cdot \|_1$）范数的绝对值和（MAE）。有时，也称其为曼哈顿范数，因为它测量了城市中的两点，沿着矩形的边行走的距离。
     
 *   更一般的，包含`n`个元素的向量`v`的`ℓk`范数（K 阶闵氏范数），定义成
     

docs/8.降维.md

@@ -20,7 +20,7 @@
 
 这表明很多物体在高维空间表现的十分不同。比如，如果你在一个正方形单元中随机取一个点（一个`1×1`的正方形），那么随机选的点离所有边界大于 0.001（靠近中间位置）的概率为 0.4%（`1 - 0.998^2`）（换句话说，一个随机产生的点不大可能严格落在某一个维度上。但是在一个 1,0000 维的单位超正方体（一个`1×1×...×1`的立方体，有 10,000 个 1），这种可能性超过了 99.999999%。在高维超正方体中，大多数点都分布在边界处。   
 
-还有一个更麻烦的区别：如果你在一个平方单位中随机选取两个点，那么这两个点之间的距离平均约为 0.52。如果您在单位 3D 立方体中选取两个随机点，平均距离将大致为 0.66。但是，在一个 1,000,000 维超立方体中随机抽取两点呢？那么，平均距离，信不信由你，大概为 408.25（大致 $\sqrt{1,000,000/6}$ ）！这非常违反直觉：当它们都位于同一单元超立方体内时，两点是怎么距离这么远的？这一事实意味着高维数据集有很大风险分布的非常稀疏：大多数训练实例可能彼此远离。当然，这也意味着一个新实例可能远离任何训练实例，这使得预测的可靠性远低于我们处理较低维度数据的预测，因为它们将基于更大的推测（extrapolations）。简而言之，训练集的维度越高，过拟合的风险就越大。  
+还有一个更麻烦的区别：如果你在一个平方单位中随机选取两个点，那么这两个点之间的距离平均约为 0.52。如果您在单位 3D 立方体中选取两个随机点，平均距离将大致为 0.66。但是，在一个 1,000,000 维超立方体中随机抽取两点呢？那么，平均距离，信不信由你，大概为 408.25（大致 $\sqrt{1,000,000/6}$）！这非常违反直觉：当它们都位于同一单元超立方体内时，两点是怎么距离这么远的？这一事实意味着高维数据集有很大风险分布的非常稀疏：大多数训练实例可能彼此远离。当然，这也意味着一个新实例可能远离任何训练实例，这使得预测的可靠性远低于我们处理较低维度数据的预测，因为它们将基于更大的推测（extrapolations）。简而言之，训练集的维度越高，过拟合的风险就越大。  
 
 理论上来说，维数爆炸的一个解决方案是增加训练集的大小从而达到拥有足够密度的训练集。不幸的是，在实践中，达到给定密度所需的训练实例的数量随着维度的数量呈指数增长。如果只有 100 个特征（比 MNIST 问题要少得多）并且假设它们均匀分布在所有维度上，那么如果想要各个临近的训练实例之间的距离在 0.1 以内，您需要比宇宙中的原子还要多的训练实例。  
 
@@ -339,13 +339,13 @@ X_reduced=lle.fit_transform(X)
 图 8-12 使用 LLE 展开瑞士卷  
 
 
-这是LLE的工作原理：首先，对于每个训练实例 $x^{(i)}$ ，该算法识别其最近的`k`个邻居（在前面的代码中`k = 10`中），然后尝试将 $x^{(i)}$ 重构为这些邻居的线性函数。更特殊的，它假设如果 $x^{(j)}$ 不是 $x^{(i)}$ 的`k`个最近邻之一，就找到权重 $w_{i,j}$ 从而使 $x^{(i)}$ 和 $\sum_{j=1}^{m}w_{i,j} x^{(j)}$ 之间的平方距离尽可能的小。因此，LLE 的第一步是方程 8-4 中描述的约束优化问题，其中`W`是包含所有权重 $w_{i,j}$ 的权重矩阵。第二个约束简单地对每个训练实例 $x^{(i)}$ 的权重进行归一化。  
+这是LLE的工作原理：首先，对于每个训练实例 $x^{(i)}$，该算法识别其最近的`k`个邻居（在前面的代码中`k = 10`中），然后尝试将 $x^{(i)}$ 重构为这些邻居的线性函数。更特殊的，它假设如果 $x^{(j)}$ 不是 $x^{(i)}$ 的`k`个最近邻之一，就找到权重 $w_{i,j}$ 从而使 $x^{(i)}$ 和 $\sum_{j=1}^{m}w_{i,j} x^{(j)}$ 之间的平方距离尽可能的小。因此，LLE 的第一步是方程 8-4 中描述的约束优化问题，其中`W`是包含所有权重 $w_{i,j}$ 的权重矩阵。第二个约束简单地对每个训练实例 $x^{(i)}$ 的权重进行归一化。  
 
 公式 8-4 LLE 第一步：对局部关系进行线性建模
 
 ![](https://view.shino.cc/images/2018/04/16/equation8_4.png)
 
-在这步之后，权重矩阵  $\widehat{W}$ （包含权重 $\hat{w_{i,j}}$ 对训练实例的线形关系进行编码。现在第二步是将训练实例投影到一个`d`维空间（`d < n`）中去，同时尽可能的保留这些局部关系。如果 $z^{(i)}$ 是 $x^{(i)}$ 在这个`d`维空间的图像，那么我们想要 $z^{(i)}$ 和 $\sum_{j=1}^{m}\hat{w_{i,j}}\ z^{(j)}$  之间的平方距离尽可能的小。这个想法让我们提出了公式8-5中的非限制性优化问题。它看起来与第一步非常相似，但我们要做的不是保持实例固定并找到最佳权重，而是恰相反：保持权重不变，并在低维空间中找到实例图像的最佳位置。请注意，`Z`是包含所有 $z^{(i)}$ 的矩阵。  
+在这步之后，权重矩阵  $\widehat{W}$（包含权重 $\hat{w_{i,j}}$ 对训练实例的线形关系进行编码。现在第二步是将训练实例投影到一个`d`维空间（`d < n`）中去，同时尽可能的保留这些局部关系。如果 $z^{(i)}$ 是 $x^{(i)}$ 在这个`d`维空间的图像，那么我们想要 $z^{(i)}$ 和 $\sum_{j=1}^{m}\hat{w_{i,j}}\ z^{(j)}$ 之间的平方距离尽可能的小。这个想法让我们提出了公式8-5中的非限制性优化问题。它看起来与第一步非常相似，但我们要做的不是保持实例固定并找到最佳权重，而是恰相反：保持权重不变，并在低维空间中找到实例图像的最佳位置。请注意，`Z`是包含所有 $z^{(i)}$ 的矩阵。  
 
 公式 8-5 LLE 第二步：保持关系的同时进行降维