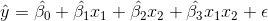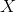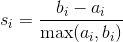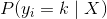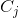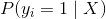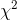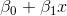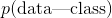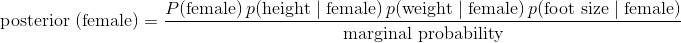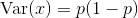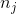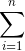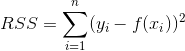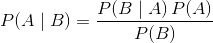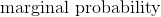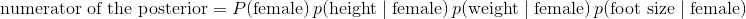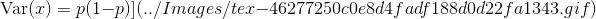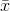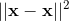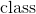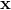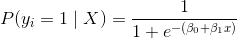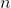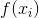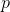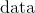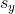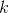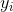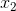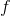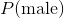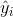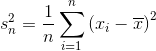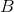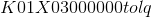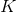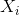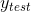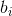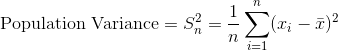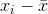tex
Showing
964 字节
152 字节
708 字节
484 字节
387 字节
145 字节
181 字节
158 字节
990 字节
170 字节
178 字节
114 字节
461 字节
176 字节
345 字节
538 字节
130 字节
3.1 KB
137 字节
1.0 KB
580 字节
1.5 KB
166 字节
326 字节
987 字节
1.1 KB
710 字节
182 字节
876 字节
137 字节
1.6 KB
2.5 KB
2.4 KB
376 字节
210 字节
144 字节
128 字节
299 字节
245 字节
131 字节
917 字节
133 字节
129 字节
2.7 KB
273 字节
140 字节
141 字节
117 字节
232 字节
158 字节
133 字节
158 字节
162 字节
135 字节
385 字节
171 字节
838 字节
155 字节
124 字节
539 字节
1.7 KB
395 字节
178 字节
751 字节
157 字节
490 字节
173 字节
1.6 KB
244 字节
169 字节
2.8 KB
407 字节
223 字节
156 字节
1.5 KB
203 字节
1.1 KB
145 字节
298 字节
558 字节
1.4 KB
680 字节
3.0 KB
114 字节
138 字节
172 字节
2.9 KB
994 字节
218 字节
此差异已折叠。
此差异已折叠。
此差异已折叠。
src/process_tex.js
0 → 100644
此差异已折叠。