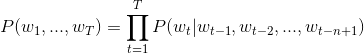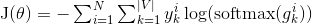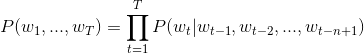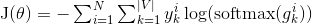diff --git a/04.word2vec/README.cn.md b/04.word2vec/README.cn.md
index bf5d51bec9c1c5d4df82830c7e57fc7710ddbcb7..2f947b7c027cb8c6a9c6786d9e434f7163de0597 100644
--- a/04.word2vec/README.cn.md
+++ b/04.word2vec/README.cn.md
@@ -1,18 +1,18 @@
# 词向量
-本教程源代码目录在[book/word2vec](https://github.com/PaddlePaddle/book/tree/develop/04.word2vec),初次使用请您参考[Book文档使用说明](https://github.com/PaddlePaddle/book/blob/develop/README.cn.md#运行这本书)。
-
-### 说明
-
-1. 本教程可支持在 CPU/GPU 环境下运行
-
-2. Docker镜像支持的CUDA/cuDNN版本
-
- 如果使用了Docker运行Book,请注意:这里所提供的默认镜像的GPU环境为 CUDA 8/cuDNN 5,对于NVIDIA Tesla V100等要求CUDA 9的 GPU,使用该镜像可能会运行失败;
-
-3. 文档和脚本中代码的一致性问题
-
+本教程源代码目录在[book/word2vec](https://github.com/PaddlePaddle/book/tree/develop/04.word2vec),初次使用请您参考[Book文档使用说明](https://github.com/PaddlePaddle/book/blob/develop/README.cn.md#运行这本书)。
+
+### 说明
+
+1. 本教程可支持在 CPU/GPU 环境下运行
+
+2. Docker镜像支持的CUDA/cuDNN版本
+
+ 如果使用了Docker运行Book,请注意:这里所提供的默认镜像的GPU环境为 CUDA 8/cuDNN 5,对于NVIDIA Tesla V100等要求CUDA 9的 GPU,使用该镜像可能会运行失败;
+
+3. 文档和脚本中代码的一致性问题
+
请注意:为使本文更加易读易用,我们拆分、调整了[train.py](https://github.com/PaddlePaddle/book/blob/develop/04.word2vec/train.py)的代码并放入本文。本文中代码与train.py的运行结果一致,可直接运行train.py进行验证。
## 背景介绍
@@ -27,9 +27,9 @@ One-hot vector虽然自然,但是用处有限。比如,在互联网广告系
在机器学习领域里,各种“知识”被各种模型表示,词向量模型(word embedding model)就是其中的一类。通过词向量模型可将一个 one-hot vector映射到一个维度更低的实数向量(embedding vector),如$embedding(母亲节) = [0.3, 4.2, -1.5, ...], embedding(康乃馨) = [0.2, 5.6, -2.3, ...]$。在这个映射到的实数向量表示中,希望两个语义(或用法)上相似的词对应的词向量“更像”,这样如“母亲节”和“康乃馨”的对应词向量的余弦相似度就不再为零了。
词向量模型可以是概率模型、共生矩阵(co-occurrence matrix)模型或神经元网络模型。在用神经网络求词向量之前,传统做法是统计一个词语的共生矩阵$X$。$X$是一个$|V| \times |V|$ 大小的矩阵,$X_{ij}$表示在所有语料中,词汇表$V$(vocabulary)中第i个词和第j个词同时出现的词数,$|V|$为词汇表的大小。对$X$做矩阵分解(如奇异值分解,Singular Value Decomposition \[[5](#参考文献)\]),得到的$U$即视为所有词的词向量:
-
+
- 
+ 
但这样的传统做法有很多问题:
@@ -79,19 +79,19 @@ similarity: -0.0997506977351
对语言模型的目标概率$P(w_1, ..., w_T)$,如果假设文本中每个词都是相互独立的,则整句话的联合概率可以表示为其中所有词语条件概率的乘积,即:
-
+
- 
-
-
+ 
+
+
然而我们知道语句中的每个词出现的概率都与其前面的词紧密相关, 所以实际上通常用条件概率表示语言模型:
- 
+ 
-
+
### N-gram neural model
@@ -99,17 +99,17 @@ similarity: -0.0997506977351
Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models \[[1](#参考文献)\] 中介绍如何学习一个神经元网络表示的词向量模型。文中的神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。因所有的词语都用一个低维向量来表示,用这种方法学习语言模型可以克服维度灾难(curse of dimensionality)。注意:由于“神经概率语言模型”说法较为泛泛,我们在这里不用其NNLM的本名,考虑到其具体做法,本文中称该模型为N-gram neural model。
-我们在上文中已经讲到用条件概率建模语言模型,即一句话中第$t$个词的概率和该句话的前$t-1$个词相关。可实际上越远的词语其实对该词的影响越小,那么如果考虑一个n-gram, 每个词都只受其前面`n-1`个词的影响,则有:
-
+我们在上文中已经讲到用条件概率建模语言模型,即一句话中第$t$个词的概率和该句话的前$t-1$个词相关。可实际上越远的词语其实对该词的影响越小,那么如果考虑一个n-gram, 每个词都只受其前面`n-1`个词的影响,则有:
+
- 
-
+ 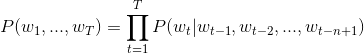
+
给定一些真实语料,这些语料中都是有意义的句子,N-gram模型的优化目标则是最大化目标函数:
-
+
- 
+ 
其中$f(w_t, w_{t-1}, ..., w_{t-n+1})$表示根据历史n-1个词得到当前词$w_t$的条件概率,$R(\theta)$表示参数正则项。
@@ -124,24 +124,24 @@ Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Langu
每个输入词$w_{t-n+1},...w_{t-1}$首先通过映射矩阵映射到词向量$C(w_{t-n+1}),...C(w_{t-1})$。
- - 然后所有词语的词向量拼接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
-
+ - 然后所有词语的词向量拼接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
+
- 
+ 
其中,$x$为所有词语的词向量拼接成的大向量,表示文本历史特征;$\theta$、$U$、$b_1$、$b_2$和$W$分别为词向量层到隐层连接的参数。$g$表示未经归一化的所有输出单词概率,$g_i$表示未经归一化的字典中第$i$个单词的输出概率。
- - 根据softmax的定义,通过归一化$g_i$, 生成目标词$w_t$的概率为:
-
+ - 根据softmax的定义,通过归一化$g_i$, 生成目标词$w_t$的概率为:
+
- 
+ 
- - 整个网络的损失值(cost)为多类分类交叉熵,用公式表示为
-
+ - 整个网络的损失值(cost)为多类分类交叉熵,用公式表示为
+
- 
+ 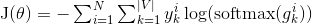
其中$y_k^i$表示第$i$个样本第$k$类的真实标签(0或1),$\text{softmax}(g_k^i)$表示第i个样本第k类softmax输出的概率。
@@ -158,10 +158,10 @@ CBOW模型通过一个词的上下文(各N个词)预测当前词。当N=2时
具体来说,不考虑上下文的词语输入顺序,CBOW是用上下文词语的词向量的均值来预测当前词。即:
-
+
- 
-
+ 
+
其中$x_t$为第$t$个词的词向量,分类分数(score)向量 $z=U*context$,最终的分类$y$采用softmax,损失函数采用多类分类交叉熵。
@@ -246,7 +246,7 @@ from __future__ import print_function
```
-然后,定义参数:
+然后,定义参数:
```python
EMBED_SIZE = 32 # embedding维度
@@ -391,10 +391,10 @@ def train(if_use_cuda, params_dirname, is_sparse=True):
outs = train_test(test_program, test_reader)
print("Step %d: Average Cost %f" % (step, outs[0]))
-
- # 整个训练过程要花费几个小时,如果平均损失低于5.8,
- # 我们就认为模型已经达到很好的效果可以停止训练了。
- # 注意5.8是一个相对较高的值,为了获取更好的模型,可以将
+
+ # 整个训练过程要花费几个小时,如果平均损失低于5.8,
+ # 我们就认为模型已经达到很好的效果可以停止训练了。
+ # 注意5.8是一个相对较高的值,为了获取更好的模型,可以将
# 这里的阈值设为3.5,但训练时间也会更长。
if outs[0] < 5.8:
if params_dirname is not None:
@@ -434,15 +434,15 @@ def infer(use_cuda, params_dirname=None):
exe = fluid.Executor(place)
inference_scope = fluid.core.Scope()
- with fluid.scope_guard(inference_scope):
- # 使用fluid.io.load_inference_model获取inference program,
+ with fluid.scope_guard(inference_scope):
+ # 使用fluid.io.load_inference_model获取inference program,
# feed变量的名称feed_target_names和从scope中fetch的对象fetch_targets
[inferencer, feed_target_names,
fetch_targets] = fluid.io.load_inference_model(params_dirname, exe)
- # 设置输入,用四个LoDTensor来表示4个词语。这里每个词都是一个id,
- # 用来查询embedding表获取对应的词向量,因此其形状大小是[1]。
- # recursive_sequence_lengths设置的是基于长度的LoD,因此都应该设为[[1]]
+ # 设置输入,用四个LoDTensor来表示4个词语。这里每个词都是一个id,
+ # 用来查询embedding表获取对应的词向量,因此其形状大小是[1]。
+ # recursive_sequence_lengths设置的是基于长度的LoD,因此都应该设为[[1]]
# 注意recursive_sequence_lengths是列表的列表
data1 = numpy.asarray([[211]], dtype=numpy.int64) # 'among'
data2 = numpy.asarray([[6]], dtype=numpy.int64) # 'a'
@@ -488,7 +488,7 @@ def infer(use_cuda, params_dirname=None):
[[0.03768077 0.03463154 0.00018074 ... 0.00022283 0.00029888 0.02967956]]
0
the
-```
+```
其中第一行表示预测词在词典上的概率分布,第二行表示概率最大的词对应的id,第三行表示概率最大的词。
整个程序的入口很简单:
diff --git a/04.word2vec/index.cn.html b/04.word2vec/index.cn.html
index 73cbd2ee29d2c243a9dfe1c69930878f54ecb6c6..20ede2195d7f175d250cd91c03f59a1a0eddc769 100644
--- a/04.word2vec/index.cn.html
+++ b/04.word2vec/index.cn.html
@@ -43,18 +43,18 @@
# 词向量
-本教程源代码目录在[book/word2vec](https://github.com/PaddlePaddle/book/tree/develop/04.word2vec),初次使用请您参考[Book文档使用说明](https://github.com/PaddlePaddle/book/blob/develop/README.cn.md#运行这本书)。
-
-### 说明
-
-1. 本教程可支持在 CPU/GPU 环境下运行
-
-2. Docker镜像支持的CUDA/cuDNN版本
-
- 如果使用了Docker运行Book,请注意:这里所提供的默认镜像的GPU环境为 CUDA 8/cuDNN 5,对于NVIDIA Tesla V100等要求CUDA 9的 GPU,使用该镜像可能会运行失败;
-
-3. 文档和脚本中代码的一致性问题
-
+本教程源代码目录在[book/word2vec](https://github.com/PaddlePaddle/book/tree/develop/04.word2vec),初次使用请您参考[Book文档使用说明](https://github.com/PaddlePaddle/book/blob/develop/README.cn.md#运行这本书)。
+
+### 说明
+
+1. 本教程可支持在 CPU/GPU 环境下运行
+
+2. Docker镜像支持的CUDA/cuDNN版本
+
+ 如果使用了Docker运行Book,请注意:这里所提供的默认镜像的GPU环境为 CUDA 8/cuDNN 5,对于NVIDIA Tesla V100等要求CUDA 9的 GPU,使用该镜像可能会运行失败;
+
+3. 文档和脚本中代码的一致性问题
+
请注意:为使本文更加易读易用,我们拆分、调整了[train.py](https://github.com/PaddlePaddle/book/blob/develop/04.word2vec/train.py)的代码并放入本文。本文中代码与train.py的运行结果一致,可直接运行train.py进行验证。
## 背景介绍
@@ -69,9 +69,9 @@ One-hot vector虽然自然,但是用处有限。比如,在互联网广告系
在机器学习领域里,各种“知识”被各种模型表示,词向量模型(word embedding model)就是其中的一类。通过词向量模型可将一个 one-hot vector映射到一个维度更低的实数向量(embedding vector),如$embedding(母亲节) = [0.3, 4.2, -1.5, ...], embedding(康乃馨) = [0.2, 5.6, -2.3, ...]$。在这个映射到的实数向量表示中,希望两个语义(或用法)上相似的词对应的词向量“更像”,这样如“母亲节”和“康乃馨”的对应词向量的余弦相似度就不再为零了。
词向量模型可以是概率模型、共生矩阵(co-occurrence matrix)模型或神经元网络模型。在用神经网络求词向量之前,传统做法是统计一个词语的共生矩阵$X$。$X$是一个$|V| \times |V|$ 大小的矩阵,$X_{ij}$表示在所有语料中,词汇表$V$(vocabulary)中第i个词和第j个词同时出现的词数,$|V|$为词汇表的大小。对$X$做矩阵分解(如奇异值分解,Singular Value Decomposition \[[5](#参考文献)\]),得到的$U$即视为所有词的词向量:
-
+
- 
+ 
但这样的传统做法有很多问题:
@@ -121,19 +121,19 @@ similarity: -0.0997506977351
对语言模型的目标概率$P(w_1, ..., w_T)$,如果假设文本中每个词都是相互独立的,则整句话的联合概率可以表示为其中所有词语条件概率的乘积,即:
-
+
- 
-
-
+ 
+
+
然而我们知道语句中的每个词出现的概率都与其前面的词紧密相关, 所以实际上通常用条件概率表示语言模型:
- 
+ 
-
+
### N-gram neural model
@@ -141,17 +141,17 @@ similarity: -0.0997506977351
Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models \[[1](#参考文献)\] 中介绍如何学习一个神经元网络表示的词向量模型。文中的神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。因所有的词语都用一个低维向量来表示,用这种方法学习语言模型可以克服维度灾难(curse of dimensionality)。注意:由于“神经概率语言模型”说法较为泛泛,我们在这里不用其NNLM的本名,考虑到其具体做法,本文中称该模型为N-gram neural model。
-我们在上文中已经讲到用条件概率建模语言模型,即一句话中第$t$个词的概率和该句话的前$t-1$个词相关。可实际上越远的词语其实对该词的影响越小,那么如果考虑一个n-gram, 每个词都只受其前面`n-1`个词的影响,则有:
-
+我们在上文中已经讲到用条件概率建模语言模型,即一句话中第$t$个词的概率和该句话的前$t-1$个词相关。可实际上越远的词语其实对该词的影响越小,那么如果考虑一个n-gram, 每个词都只受其前面`n-1`个词的影响,则有:
+
- 
-
+ 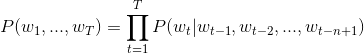
+
给定一些真实语料,这些语料中都是有意义的句子,N-gram模型的优化目标则是最大化目标函数:
-
+
- 
+ 
其中$f(w_t, w_{t-1}, ..., w_{t-n+1})$表示根据历史n-1个词得到当前词$w_t$的条件概率,$R(\theta)$表示参数正则项。
@@ -166,24 +166,24 @@ Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Langu
每个输入词$w_{t-n+1},...w_{t-1}$首先通过映射矩阵映射到词向量$C(w_{t-n+1}),...C(w_{t-1})$。
- - 然后所有词语的词向量拼接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
-
+ - 然后所有词语的词向量拼接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
+
- 
+ 
其中,$x$为所有词语的词向量拼接成的大向量,表示文本历史特征;$\theta$、$U$、$b_1$、$b_2$和$W$分别为词向量层到隐层连接的参数。$g$表示未经归一化的所有输出单词概率,$g_i$表示未经归一化的字典中第$i$个单词的输出概率。
- - 根据softmax的定义,通过归一化$g_i$, 生成目标词$w_t$的概率为:
-
+ - 根据softmax的定义,通过归一化$g_i$, 生成目标词$w_t$的概率为:
+
- 
+ 
- - 整个网络的损失值(cost)为多类分类交叉熵,用公式表示为
-
+ - 整个网络的损失值(cost)为多类分类交叉熵,用公式表示为
+
- 
+ 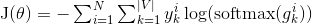
其中$y_k^i$表示第$i$个样本第$k$类的真实标签(0或1),$\text{softmax}(g_k^i)$表示第i个样本第k类softmax输出的概率。
@@ -200,10 +200,10 @@ CBOW模型通过一个词的上下文(各N个词)预测当前词。当N=2时
具体来说,不考虑上下文的词语输入顺序,CBOW是用上下文词语的词向量的均值来预测当前词。即:
-
+
- 
-
+ 
+
其中$x_t$为第$t$个词的词向量,分类分数(score)向量 $z=U*context$,最终的分类$y$采用softmax,损失函数采用多类分类交叉熵。
@@ -288,7 +288,7 @@ from __future__ import print_function
```
-然后,定义参数:
+然后,定义参数:
```python
EMBED_SIZE = 32 # embedding维度
@@ -433,10 +433,10 @@ def train(if_use_cuda, params_dirname, is_sparse=True):
outs = train_test(test_program, test_reader)
print("Step %d: Average Cost %f" % (step, outs[0]))
-
- # 整个训练过程要花费几个小时,如果平均损失低于5.8,
- # 我们就认为模型已经达到很好的效果可以停止训练了。
- # 注意5.8是一个相对较高的值,为了获取更好的模型,可以将
+
+ # 整个训练过程要花费几个小时,如果平均损失低于5.8,
+ # 我们就认为模型已经达到很好的效果可以停止训练了。
+ # 注意5.8是一个相对较高的值,为了获取更好的模型,可以将
# 这里的阈值设为3.5,但训练时间也会更长。
if outs[0] < 5.8:
if params_dirname is not None:
@@ -476,15 +476,15 @@ def infer(use_cuda, params_dirname=None):
exe = fluid.Executor(place)
inference_scope = fluid.core.Scope()
- with fluid.scope_guard(inference_scope):
- # 使用fluid.io.load_inference_model获取inference program,
+ with fluid.scope_guard(inference_scope):
+ # 使用fluid.io.load_inference_model获取inference program,
# feed变量的名称feed_target_names和从scope中fetch的对象fetch_targets
[inferencer, feed_target_names,
fetch_targets] = fluid.io.load_inference_model(params_dirname, exe)
- # 设置输入,用四个LoDTensor来表示4个词语。这里每个词都是一个id,
- # 用来查询embedding表获取对应的词向量,因此其形状大小是[1]。
- # recursive_sequence_lengths设置的是基于长度的LoD,因此都应该设为[[1]]
+ # 设置输入,用四个LoDTensor来表示4个词语。这里每个词都是一个id,
+ # 用来查询embedding表获取对应的词向量,因此其形状大小是[1]。
+ # recursive_sequence_lengths设置的是基于长度的LoD,因此都应该设为[[1]]
# 注意recursive_sequence_lengths是列表的列表
data1 = numpy.asarray([[211]], dtype=numpy.int64) # 'among'
data2 = numpy.asarray([[6]], dtype=numpy.int64) # 'a'
@@ -530,7 +530,7 @@ def infer(use_cuda, params_dirname=None):
[[0.03768077 0.03463154 0.00018074 ... 0.00022283 0.00029888 0.02967956]]
0
the
-```
+```
其中第一行表示预测词在词典上的概率分布,第二行表示概率最大的词对应的id,第三行表示概率最大的词。
整个程序的入口很简单: