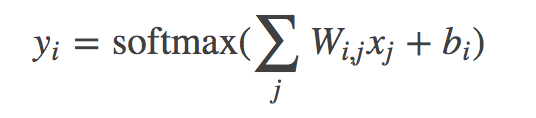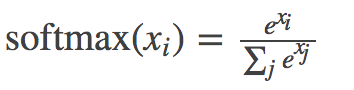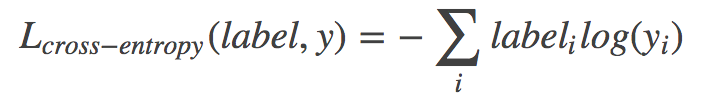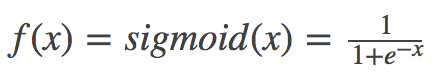update description for book/02 (#722)
* add some description for book/02 * Update README.cn.md * Update README.cn.md * update reademe * update
Showing
02.recognize_digits/image/01.png
0 → 100644
16.1 KB
02.recognize_digits/image/02.png
0 → 100644
12.5 KB
02.recognize_digits/image/03.png
0 → 100644
21.6 KB
02.recognize_digits/image/04.png
0 → 100644
13.5 KB
02.recognize_digits/image/05.png
0 → 100644
13.3 KB