diff --git a/01.fit_a_line/README.cn.md b/01.fit_a_line/README.cn.md
index b028c2fde00f7d06a8fdfb4cf85b6a8a6dab7fc0..16018f0455cbcb82da229a1ee8deb050dc743e48 100644
--- a/01.fit_a_line/README.cn.md
+++ b/01.fit_a_line/README.cn.md
@@ -37,6 +37,12 @@ $$MSE=\frac{1}{n}\sum_{i=1}^{n}{(\hat{Y_i}-Y_i)}^2$$
即对于一个大小为$n$的测试集,$MSE$是$n$个数据预测结果误差平方的均值。
+对损失函数进行优化所采用的方法一般为梯度下降法。梯度下降法是一种一阶最优化算法。如果$f(x)$在点$x_n$有定义且可微,则认为$f(x)$在点$x_n$沿着梯度的负方向$-▽f(x_n)$下降的是最快的。反复调节$x$,使得$f(x)$接近最小值或者极小值,调节的方式为:
+
+$$x_n+1=x_n-λ▽f(x), n≧0$$
+
+其中λ代表学习率。这种调节的方法称为梯度下降法。
+
### 训练过程
定义好模型结构之后,我们要通过以下几个步骤进行模型训练
@@ -131,30 +137,71 @@ test_reader = paddle.batch(
batch_size=BATCH_SIZE)
```
+如果想直接从txt文件中读取数据的话,可以参考以下方式。
+
+feature_names = [
+ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
+ 'PTRATIO', 'B', 'LSTAT', 'convert'
+]
+
+feature_num = len(feature_names)
+
+data = numpy.fromfile(filename, sep=' ') # 从文件中读取原始数据
+
+data = data.reshape(data.shape[0] // feature_num, feature_num)
+
+maximums, minimums, avgs = data.max(axis=0), data.min(axis=0), data.sum(axis=0)/data.shape[0]
+
+for i in six.moves.range(feature_num-1):
+ data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i]) # six.moves可以兼容python2和python3
+
+ratio = 0.8 # 训练集和验证集的划分比例
+
+offset = int(data.shape[0]*ratio)
+
+train_data = data[:offset]
+
+test_data = data[offset:]
+
+train_reader = paddle.batch(
+ paddle.reader.shuffle(
+ train_data, buf_size=500),
+ batch_size=BATCH_SIZE)
+
+test_reader = paddle.batch(
+ paddle.reader.shuffle(
+ test_data, buf_size=500),
+ batch_size=BATCH_SIZE)
+
### 配置训练程序
训练程序的目的是定义一个训练模型的网络结构。对于线性回归来讲,它就是一个从输入到输出的简单的全连接层。更加复杂的结果,比如卷积神经网络,递归神经网络等会在随后的章节中介绍。训练程序必须返回`平均损失`作为第一个返回值,因为它会被后面反向传播算法所用到。
```python
-x = fluid.layers.data(name='x', shape=[13], dtype='float32')
-y = fluid.layers.data(name='y', shape=[1], dtype='float32')
-y_predict = fluid.layers.fc(input=x, size=1, act=None)
+x = fluid.layers.data(name='x', shape=[13], dtype='float32') # 定义输入的形状和数据类型
+y = fluid.layers.data(name='y', shape=[1], dtype='float32') # 定义输出的形状和数据类型
+y_predict = fluid.layers.fc(input=x, size=1, act=None) # 连接输入和输出的全连接层
-main_program = fluid.default_main_program()
-startup_program = fluid.default_startup_program()
+main_program = fluid.default_main_program() # 获取默认/全局主函数
+startup_program = fluid.default_startup_program() # 获取默认/全局启动程序
-cost = fluid.layers.square_error_cost(input=y_predict, label=y)
-avg_loss = fluid.layers.mean(cost)
+cost = fluid.layers.square_error_cost(input=y_predict, label=y) # 利用标签数据和输出的预测数据估计方差
+avg_loss = fluid.layers.mean(cost) # 对方差求均值,得到平均损失
```
+详细资料请参考:
+[fluid.default_main_program](http://www.paddlepaddle.org/documentation/docs/zh/develop/api_cn/fluid_cn.html#default-main-program)
+[fluid.default_startup_program](http://www.paddlepaddle.org/documentation/docs/zh/develop/api_cn/fluid_cn.html#default-startup-program)
### Optimizer Function 配置
-在下面的 `SGD optimizer`,`learning_rate` 是训练的速度,与网络的训练收敛速度有关系。
+在下面的 `SGD optimizer`,`learning_rate` 是学习率,与网络的训练收敛速度有关系。
```python
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.001)
sgd_optimizer.minimize(avg_loss)
-#clone a test_program
+#克隆main_program得到test_program
+#有些operator在训练和测试之间的操作是不同的,例如batch_norm,使用参数for_test来区分该程序是用来训练还是用来测试
+#该api不会删除任何操作符,请在backward和optimization之前使用
test_program = main_program.clone(for_test=True)
```
@@ -163,31 +210,21 @@ test_program = main_program.clone(for_test=True)
```python
use_cuda = False
-place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()
+place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace() # 指明executor的执行场所
+###executor可以接受传入的program,并根据feed map(输入映射表)和fetch list(结果获取表)向program中添加数据输入算子和结果获取算子。使用close()关闭该executor,调用run(...)执行program。
exe = fluid.Executor(place)
```
-
-除此之外,还可以通过画图,来展现`训练进程`:
-
-```python
-# Plot data
-from paddle.utils.plot import Ploter
-
-train_prompt = "Train cost"
-test_prompt = "Test cost"
-plot_prompt = Ploter(train_prompt, test_prompt)
-
-```
+详细资料请参考:
+[fluid.executor](http://www.paddlepaddle.org/documentation/docs/zh/develop/api_cn/fluid_cn.html#permalink-15-executor)
### 创建训练过程
-训练需要有一个训练程序和一些必要参数,并构建了一个获取训练过程中测试误差的函数。
+训练需要有一个训练程序和一些必要参数,并构建了一个获取训练过程中测试误差的函数。必要参数有executor,program,reader,feeder,fetch_list,executor表示之前创建的执行器,program表示执行器所执行的program,是之前创建的program,如果该项参数没有给定的话则默认使用defalut_main_program,reader表示读取到的数据,feeder表示前向输入的变量,fetch_list表示用户想得到的变量或者命名的结果。
```python
num_epochs = 100
-# For training test cost
def train_test(executor, program, reader, feeder, fetch_list):
accumulated = 1 * [0]
count = 0
@@ -195,19 +232,36 @@ def train_test(executor, program, reader, feeder, fetch_list):
outs = executor.run(program=program,
feed=feeder.feed(data_test),
fetch_list=fetch_list)
- accumulated = [x_c[0] + x_c[1][0] for x_c in zip(accumulated, outs)]
- count += 1
- return [x_d / count for x_d in accumulated]
+ accumulated = [x_c[0] + x_c[1][0] for x_c in zip(accumulated, outs)] # 累加测试过程中的损失值
+ count += 1 # 累加测试集中的样本数量
+ return [x_d / count for x_d in accumulated] # 计算平均损失
+
+```
+可以直接输出损失值来观察`训练进程`:
+
+```python
+train_prompt = "train cost"
+test_prompt = "test cost"
+print("%s', out %f" % (train_prompt, out))
+print("%s', out %f" % (test_prompt, out))
+
+```
+
+除此之外,还可以通过画图,来展现`训练进程`:
+
+```python
+from paddle.utils.plot import ploter
+
+plot_prompt = ploter(train_prompt, test_prompt)
```
### 训练主循环
-PaddlePaddle提供了读取数据者发生器机制来读取训练数据。读取数据者会一次提供多列数据,因此我们需要一个Python的list来定义读取顺序。我们构建一个循环来进行训练,直到训练结果足够好或者循环次数足够多。
-如果训练顺利,可以把训练参数保存到`params_dirname`。
+
+给出需要存储的目录名,并初始化一个执行器。
```python
%matplotlib inline
-# Specify the directory to save the parameters
params_dirname = "fit_a_line.inference.model"
feeder = fluid.DataFeeder(place=place, feed_list=[x, y])
naive_exe = fluid.Executor(place)
@@ -215,17 +269,21 @@ naive_exe.run(startup_program)
step = 0
exe_test = fluid.Executor(place)
+```
-# main train loop.
+paddlepaddle提供了reader机制来读取训练数据。reader会一次提供多列数据,因此我们需要一个python的列表来定义读取顺序。我们构建一个循环来进行训练,直到训练结果足够好或者循环次数足够多。
+如果训练迭代次数满足参数保存的迭代次数,可以把训练参数保存到`params_dirname`。
+设置训练主循环
+```python
for pass_id in range(num_epochs):
for data_train in train_reader():
avg_loss_value, = exe.run(main_program,
feed=feeder.feed(data_train),
fetch_list=[avg_loss])
- if step % 10 == 0: # record a train cost every 10 batches
+ if step % 10 == 0: # 每10个批次记录一下训练损失
plot_prompt.append(train_prompt, step, avg_loss_value[0])
plot_prompt.plot()
- if step % 100 == 0: # record a test cost every 100 batches
+ if step % 100 == 0: # 每100批次记录一下测试损失
test_metics = train_test(executor=exe_test,
program=test_program,
reader=test_reader,
@@ -233,18 +291,17 @@ for pass_id in range(num_epochs):
feeder=feeder)
plot_prompt.append(test_prompt, step, test_metics[0])
plot_prompt.plot()
- # If the accuracy is good enough, we can stop the training.
- if test_metics[0] < 10.0:
+ if test_metics[0] < 10.0: # 如果准确率达到要求,则停止训练
break
step += 1
if math.isnan(float(avg_loss_value[0])):
sys.exit("got NaN loss, training failed.")
- if params_dirname is not None:
- # We can save the trained parameters for the inferences later
- fluid.io.save_inference_model(params_dirname, ['x'],
- [y_predict], exe)
+
+ #保存训练参数到之前给定的路径中
+ if params_dirname is not None:
+ fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)
```
## 预测
@@ -264,30 +321,52 @@ inference_scope = fluid.core.Scope()
```python
with fluid.scope_guard(inference_scope):
[inference_program, feed_target_names,
- fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe)
+ fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe) # 载入预训练模型
batch_size = 10
infer_reader = paddle.batch(
- paddle.dataset.uci_housing.test(), batch_size=batch_size)
+ paddle.dataset.uci_housing.test(), batch_size=batch_size) # 准备测试集
infer_data = next(infer_reader())
infer_feat = numpy.array(
- [data[0] for data in infer_data]).astype("float32")
+ [data[0] for data in infer_data]).astype("float32") # 提取测试集中的数据
infer_label = numpy.array(
- [data[1] for data in infer_data]).astype("float32")
+ [data[1] for data in infer_data]).astype("float32") # 提取测试集中的标签
assert feed_target_names[0] == 'x'
results = infer_exe.run(inference_program,
feed={feed_target_names[0]: numpy.array(infer_feat)},
- fetch_list=fetch_targets)
+ fetch_list=fetch_targets) # 进行预测
+```
+
+保存图片
+```python
+def save_result(points1, points2):
+ import matplotlib
+ matplotlib.use('Agg')
+ import matplotlib.pyplot as plt
+ x1 = [idx for idx in range(len(points1))]
+ y1 = points1
+ y2 = points2
+ l1 = plt.plot(x1, y1, 'r--', label='predictions')
+ l2 = plt.plot(x1, y2, 'g--', label='GT')
+ plt.plot(x1, y1, 'ro-', x1, y2, 'g+-')
+ plt.title('predictions VS GT')
+ plt.legend()
+ plt.savefig('./image/prediction_gt.png')
+```
+
+打印预测结果和标签并可视化结果
+```python
+ print("infer results: (House Price)")
+ for idx, val in enumerate(results[0]):
+ print("%d: %.2f" % (idx, val)) # 打印预测结果
- print("infer results: (House Price)")
- for idx, val in enumerate(results[0]):
- print("%d: %.2f" % (idx, val))
+ print("\nground truth:")
+ for idx, val in enumerate(infer_label):
+ print("%d: %.2f" % (idx, val)) # 打印标签值
- print("\nground truth:")
- for idx, val in enumerate(infer_label):
- print("%d: %.2f" % (idx, val))
+save_result(results[0], infer_label) # 保存图片
```
## 总结
diff --git a/01.fit_a_line/image/prediction_gt.png b/01.fit_a_line/image/prediction_gt.png
new file mode 100644
index 0000000000000000000000000000000000000000..69dee8cb479aa878a4ff10b0bbeb97a4774aa2ac
Binary files /dev/null and b/01.fit_a_line/image/prediction_gt.png differ
diff --git a/01.fit_a_line/image/ranges.png b/01.fit_a_line/image/ranges.png
index 916337f0720ef221851e89456c5c295e2e13445f..c6a9e182df89a905a922de63dccaeec028616d42 100644
Binary files a/01.fit_a_line/image/ranges.png and b/01.fit_a_line/image/ranges.png differ
diff --git a/01.fit_a_line/index.cn.html b/01.fit_a_line/index.cn.html
index 5b234e40869cc7e63e339700dfd0b840bf3acd09..1a95a9928f3db196e93828889545c6b9dc56dfcf 100644
--- a/01.fit_a_line/index.cn.html
+++ b/01.fit_a_line/index.cn.html
@@ -79,6 +79,12 @@ $$MSE=\frac{1}{n}\sum_{i=1}^{n}{(\hat{Y_i}-Y_i)}^2$$
即对于一个大小为$n$的测试集,$MSE$是$n$个数据预测结果误差平方的均值。
+对损失函数进行优化所采用的方法一般为梯度下降法。梯度下降法是一种一阶最优化算法。如果$f(x)$在点$x_n$有定义且可微,则认为$f(x)$在点$x_n$沿着梯度的负方向$-▽f(x_n)$下降的是最快的。反复调节$x$,使得$f(x)$接近最小值或者极小值,调节的方式为:
+
+$$x_n+1=x_n-λ▽f(x), n≧0$$
+
+其中λ代表学习率。这种调节的方法称为梯度下降法。
+
### 训练过程
定义好模型结构之后,我们要通过以下几个步骤进行模型训练
@@ -173,30 +179,71 @@ test_reader = paddle.batch(
batch_size=BATCH_SIZE)
```
+如果想直接从txt文件中读取数据的话,可以参考以下方式。
+
+feature_names = [
+ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
+ 'PTRATIO', 'B', 'LSTAT', 'convert'
+]
+
+feature_num = len(feature_names)
+
+data = numpy.fromfile(filename, sep=' ') # 从文件中读取原始数据
+
+data = data.reshape(data.shape[0] // feature_num, feature_num)
+
+maximums, minimums, avgs = data.max(axis=0), data.min(axis=0), data.sum(axis=0)/data.shape[0]
+
+for i in six.moves.range(feature_num-1):
+ data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i]) # six.moves可以兼容python2和python3
+
+ratio = 0.8 # 训练集和验证集的划分比例
+
+offset = int(data.shape[0]*ratio)
+
+train_data = data[:offset]
+
+test_data = data[offset:]
+
+train_reader = paddle.batch(
+ paddle.reader.shuffle(
+ train_data, buf_size=500),
+ batch_size=BATCH_SIZE)
+
+test_reader = paddle.batch(
+ paddle.reader.shuffle(
+ test_data, buf_size=500),
+ batch_size=BATCH_SIZE)
+
### 配置训练程序
训练程序的目的是定义一个训练模型的网络结构。对于线性回归来讲,它就是一个从输入到输出的简单的全连接层。更加复杂的结果,比如卷积神经网络,递归神经网络等会在随后的章节中介绍。训练程序必须返回`平均损失`作为第一个返回值,因为它会被后面反向传播算法所用到。
```python
-x = fluid.layers.data(name='x', shape=[13], dtype='float32')
-y = fluid.layers.data(name='y', shape=[1], dtype='float32')
-y_predict = fluid.layers.fc(input=x, size=1, act=None)
+x = fluid.layers.data(name='x', shape=[13], dtype='float32') # 定义输入的形状和数据类型
+y = fluid.layers.data(name='y', shape=[1], dtype='float32') # 定义输出的形状和数据类型
+y_predict = fluid.layers.fc(input=x, size=1, act=None) # 连接输入和输出的全连接层
-main_program = fluid.default_main_program()
-startup_program = fluid.default_startup_program()
+main_program = fluid.default_main_program() # 获取默认/全局主函数
+startup_program = fluid.default_startup_program() # 获取默认/全局启动程序
-cost = fluid.layers.square_error_cost(input=y_predict, label=y)
-avg_loss = fluid.layers.mean(cost)
+cost = fluid.layers.square_error_cost(input=y_predict, label=y) # 利用标签数据和输出的预测数据估计方差
+avg_loss = fluid.layers.mean(cost) # 对方差求均值,得到平均损失
```
+详细资料请参考:
+[fluid.default_main_program](http://www.paddlepaddle.org/documentation/docs/zh/develop/api_cn/fluid_cn.html#default-main-program)
+[fluid.default_startup_program](http://www.paddlepaddle.org/documentation/docs/zh/develop/api_cn/fluid_cn.html#default-startup-program)
### Optimizer Function 配置
-在下面的 `SGD optimizer`,`learning_rate` 是训练的速度,与网络的训练收敛速度有关系。
+在下面的 `SGD optimizer`,`learning_rate` 是学习率,与网络的训练收敛速度有关系。
```python
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.001)
sgd_optimizer.minimize(avg_loss)
-#clone a test_program
+#克隆main_program得到test_program
+#有些operator在训练和测试之间的操作是不同的,例如batch_norm,使用参数for_test来区分该程序是用来训练还是用来测试
+#该api不会删除任何操作符,请在backward和optimization之前使用
test_program = main_program.clone(for_test=True)
```
@@ -205,31 +252,21 @@ test_program = main_program.clone(for_test=True)
```python
use_cuda = False
-place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()
+place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace() # 指明executor的执行场所
+###executor可以接受传入的program,并根据feed map(输入映射表)和fetch list(结果获取表)向program中添加数据输入算子和结果获取算子。使用close()关闭该executor,调用run(...)执行program。
exe = fluid.Executor(place)
```
-
-除此之外,还可以通过画图,来展现`训练进程`:
-
-```python
-# Plot data
-from paddle.utils.plot import Ploter
-
-train_prompt = "Train cost"
-test_prompt = "Test cost"
-plot_prompt = Ploter(train_prompt, test_prompt)
-
-```
+详细资料请参考:
+[fluid.executor](http://www.paddlepaddle.org/documentation/docs/zh/develop/api_cn/fluid_cn.html#permalink-15-executor)
### 创建训练过程
-训练需要有一个训练程序和一些必要参数,并构建了一个获取训练过程中测试误差的函数。
+训练需要有一个训练程序和一些必要参数,并构建了一个获取训练过程中测试误差的函数。必要参数有executor,program,reader,feeder,fetch_list,executor表示之前创建的执行器,program表示执行器所执行的program,是之前创建的program,如果该项参数没有给定的话则默认使用defalut_main_program,reader表示读取到的数据,feeder表示前向输入的变量,fetch_list表示用户想得到的变量或者命名的结果。
```python
num_epochs = 100
-# For training test cost
def train_test(executor, program, reader, feeder, fetch_list):
accumulated = 1 * [0]
count = 0
@@ -237,19 +274,36 @@ def train_test(executor, program, reader, feeder, fetch_list):
outs = executor.run(program=program,
feed=feeder.feed(data_test),
fetch_list=fetch_list)
- accumulated = [x_c[0] + x_c[1][0] for x_c in zip(accumulated, outs)]
- count += 1
- return [x_d / count for x_d in accumulated]
+ accumulated = [x_c[0] + x_c[1][0] for x_c in zip(accumulated, outs)] # 累加测试过程中的损失值
+ count += 1 # 累加测试集中的样本数量
+ return [x_d / count for x_d in accumulated] # 计算平均损失
+
+```
+可以直接输出损失值来观察`训练进程`:
+
+```python
+train_prompt = "train cost"
+test_prompt = "test cost"
+print("%s', out %f" % (train_prompt, out))
+print("%s', out %f" % (test_prompt, out))
+
+```
+
+除此之外,还可以通过画图,来展现`训练进程`:
+
+```python
+from paddle.utils.plot import ploter
+
+plot_prompt = ploter(train_prompt, test_prompt)
```
### 训练主循环
-PaddlePaddle提供了读取数据者发生器机制来读取训练数据。读取数据者会一次提供多列数据,因此我们需要一个Python的list来定义读取顺序。我们构建一个循环来进行训练,直到训练结果足够好或者循环次数足够多。
-如果训练顺利,可以把训练参数保存到`params_dirname`。
+
+给出需要存储的目录名,并初始化一个执行器。
```python
%matplotlib inline
-# Specify the directory to save the parameters
params_dirname = "fit_a_line.inference.model"
feeder = fluid.DataFeeder(place=place, feed_list=[x, y])
naive_exe = fluid.Executor(place)
@@ -257,17 +311,21 @@ naive_exe.run(startup_program)
step = 0
exe_test = fluid.Executor(place)
+```
-# main train loop.
+paddlepaddle提供了reader机制来读取训练数据。reader会一次提供多列数据,因此我们需要一个python的列表来定义读取顺序。我们构建一个循环来进行训练,直到训练结果足够好或者循环次数足够多。
+如果训练迭代次数满足参数保存的迭代次数,可以把训练参数保存到`params_dirname`。
+设置训练主循环
+```python
for pass_id in range(num_epochs):
for data_train in train_reader():
avg_loss_value, = exe.run(main_program,
feed=feeder.feed(data_train),
fetch_list=[avg_loss])
- if step % 10 == 0: # record a train cost every 10 batches
+ if step % 10 == 0: # 每10个批次记录一下训练损失
plot_prompt.append(train_prompt, step, avg_loss_value[0])
plot_prompt.plot()
- if step % 100 == 0: # record a test cost every 100 batches
+ if step % 100 == 0: # 每100批次记录一下测试损失
test_metics = train_test(executor=exe_test,
program=test_program,
reader=test_reader,
@@ -275,18 +333,17 @@ for pass_id in range(num_epochs):
feeder=feeder)
plot_prompt.append(test_prompt, step, test_metics[0])
plot_prompt.plot()
- # If the accuracy is good enough, we can stop the training.
- if test_metics[0] < 10.0:
+ if test_metics[0] < 10.0: # 如果准确率达到要求,则停止训练
break
step += 1
if math.isnan(float(avg_loss_value[0])):
sys.exit("got NaN loss, training failed.")
- if params_dirname is not None:
- # We can save the trained parameters for the inferences later
- fluid.io.save_inference_model(params_dirname, ['x'],
- [y_predict], exe)
+
+ #保存训练参数到之前给定的路径中
+ if params_dirname is not None:
+ fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)
```
## 预测
@@ -306,30 +363,52 @@ inference_scope = fluid.core.Scope()
```python
with fluid.scope_guard(inference_scope):
[inference_program, feed_target_names,
- fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe)
+ fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe) # 载入预训练模型
batch_size = 10
infer_reader = paddle.batch(
- paddle.dataset.uci_housing.test(), batch_size=batch_size)
+ paddle.dataset.uci_housing.test(), batch_size=batch_size) # 准备测试集
infer_data = next(infer_reader())
infer_feat = numpy.array(
- [data[0] for data in infer_data]).astype("float32")
+ [data[0] for data in infer_data]).astype("float32") # 提取测试集中的数据
infer_label = numpy.array(
- [data[1] for data in infer_data]).astype("float32")
+ [data[1] for data in infer_data]).astype("float32") # 提取测试集中的标签
assert feed_target_names[0] == 'x'
results = infer_exe.run(inference_program,
feed={feed_target_names[0]: numpy.array(infer_feat)},
- fetch_list=fetch_targets)
+ fetch_list=fetch_targets) # 进行预测
+```
+
+保存图片
+```python
+def save_result(points1, points2):
+ import matplotlib
+ matplotlib.use('Agg')
+ import matplotlib.pyplot as plt
+ x1 = [idx for idx in range(len(points1))]
+ y1 = points1
+ y2 = points2
+ l1 = plt.plot(x1, y1, 'r--', label='predictions')
+ l2 = plt.plot(x1, y2, 'g--', label='GT')
+ plt.plot(x1, y1, 'ro-', x1, y2, 'g+-')
+ plt.title('predictions VS GT')
+ plt.legend()
+ plt.savefig('./image/prediction_gt.png')
+```
+
+打印预测结果和标签并可视化结果
+```python
+ print("infer results: (House Price)")
+ for idx, val in enumerate(results[0]):
+ print("%d: %.2f" % (idx, val)) # 打印预测结果
- print("infer results: (House Price)")
- for idx, val in enumerate(results[0]):
- print("%d: %.2f" % (idx, val))
+ print("\nground truth:")
+ for idx, val in enumerate(infer_label):
+ print("%d: %.2f" % (idx, val)) # 打印标签值
- print("\nground truth:")
- for idx, val in enumerate(infer_label):
- print("%d: %.2f" % (idx, val))
+save_result(results[0], infer_label) # 保存图片
```
## 总结
diff --git a/01.fit_a_line/train.py b/01.fit_a_line/train.py
index 5b4625e07e4b00045f9689f061816f5212389ba4..0d567fef5974e845fcfb0ec036c0df5cb60741ef 100644
--- a/01.fit_a_line/train.py
+++ b/01.fit_a_line/train.py
@@ -33,6 +33,21 @@ def train_test(executor, program, reader, feeder, fetch_list):
return [x_d / count for x_d in accumulated]
+def save_result(points1, points2):
+ import matplotlib
+ matplotlib.use('Agg')
+ import matplotlib.pyplot as plt
+ x1 = [idx for idx in range(len(points1))]
+ y1 = points1
+ y2 = points2
+ l1 = plt.plot(x1, y1, 'r--', label='predictions')
+ l2 = plt.plot(x1, y2, 'g--', label='GT')
+ plt.plot(x1, y1, 'ro-', x1, y2, 'g+-')
+ plt.title('predictions VS GT')
+ plt.legend()
+ plt.savefig('./image/prediction_gt.png')
+
+
def main():
batch_size = 20
train_reader = paddle.batch(
@@ -141,6 +156,8 @@ def main():
for idx, val in enumerate(infer_label):
print("%d: %.2f" % (idx, val))
+ save_result(results[0], infer_label)
+
if __name__ == '__main__':
main()
diff --git a/03.image_classification/README.cn.md b/03.image_classification/README.cn.md
index 8531b147342b46bc86bc33e33a217cf961d8ddad..c3ad46c69c877c7d15ca43759c7291ad9de1ba2a 100644
--- a/03.image_classification/README.cn.md
+++ b/03.image_classification/README.cn.md
@@ -10,7 +10,7 @@
图像分类是根据图像的语义信息将不同类别图像区分开来,是计算机视觉中重要的基本问题,也是图像检测、图像分割、物体跟踪、行为分析等其他高层视觉任务的基础。图像分类在很多领域有广泛应用,包括安防领域的人脸识别和智能视频分析等,交通领域的交通场景识别,互联网领域基于内容的图像检索和相册自动归类,医学领域的图像识别等。
-一般来说,图像分类通过手工特征或特征学习方法对整个图像进行全部描述,然后使用分类器判别物体类别,因此如何提取图像的特征至关重要。在深度学习算法之前使用较多的是基于词袋(Bag of Words)模型的物体分类方法。词袋方法从自然语言处理中引入,即一句话可以用一个装了词的袋子表示其特征,袋子中的词为句子中的单词、短语或字。对于图像而言,词袋方法需要构建字典。最简单的词袋模型框架可以设计为**底层特征抽取**、**特征编码**、**分类器设计**三个过程。
+一般来说,图像分类通过手工提取特征或特征学习方法对整个图像进行全部描述,然后使用分类器判别物体类别,因此如何提取图像的特征至关重要。在深度学习算法之前使用较多的是基于词袋(Bag of Words)模型的物体分类方法。词袋方法从自然语言处理中引入,即一句话可以用一个装了词的袋子表示其特征,袋子中的词为句子中的单词、短语或字。对于图像而言,词袋方法需要构建字典。最简单的词袋模型框架可以设计为**底层特征抽取**、**特征编码**、**分类器设计**三个过程。
而基于深度学习的图像分类方法,可以通过有监督或无监督的方式**学习**层次化的特征描述,从而取代了手工设计或选择图像特征的工作。深度学习模型中的卷积神经网络(Convolution Neural Network, CNN)近年来在图像领域取得了惊人的成绩,CNN直接利用图像像素信息作为输入,最大程度上保留了输入图像的所有信息,通过卷积操作进行特征的提取和高层抽象,模型输出直接是图像识别的结果。这种基于"输入-输出"直接端到端的学习方法取得了非常好的效果,得到了广泛的应用。
@@ -48,15 +48,15 @@
在2012年之前的传统图像分类方法可以用背景描述中提到的三步完成,但通常完整建立图像识别模型一般包括底层特征学习、特征编码、空间约束、分类器设计、模型融合等几个阶段。
- 1). **底层特征提取**: 通常从图像中按照固定步长、尺度提取大量局部特征描述。常用的局部特征包括SIFT(Scale-Invariant Feature Transform, 尺度不变特征转换) \[[1](#参考文献)\]、HOG(Histogram of Oriented Gradient, 方向梯度直方图) \[[2](#参考文献)\]、LBP(Local Bianray Pattern, 局部二值模式) \[[3](#参考文献)\] 等,一般也采用多种特征描述子,防止丢失过多的有用信息。
+ 1). **底层特征提取**: 通常从图像中按照固定步长、尺度提取大量局部特征描述。常用的局部特征包括SIFT(Scale-Invariant Feature Transform, 尺度不变特征转换) \[[1](#参考文献)\]、HOG(Histogram of Oriented Gradient, 方向梯度直方图) \[[2](#参考文献)\]、LBP(Local Bianray Pattern, 局部二值模式) \[[3](#参考文献)\] 等,一般也采用多种特征描述,防止丢失过多的有用信息。
- 2). **特征编码**: 底层特征中包含了大量冗余与噪声,为了提高特征表达的鲁棒性,需要使用一种特征变换算法对底层特征进行编码,称作特征编码。常用的特征编码包括向量量化编码 \[[4](#参考文献)\]、稀疏编码 \[[5](#参考文献)\]、局部线性约束编码 \[[6](#参考文献)\]、Fisher向量编码 \[[7](#参考文献)\] 等。
+ 2). **特征编码**: 底层特征中包含了大量冗余与噪声,为了提高特征表达的鲁棒性,需要使用一种特征变换算法对底层特征进行编码,称作特征编码。常用的特征编码方法包括向量量化编码 \[[4](#参考文献)\]、稀疏编码 \[[5](#参考文献)\]、局部线性约束编码 \[[6](#参考文献)\]、Fisher向量编码 \[[7](#参考文献)\] 等。
3). **空间特征约束**: 特征编码之后一般会经过空间特征约束,也称作**特征汇聚**。特征汇聚是指在一个空间范围内,对每一维特征取最大值或者平均值,可以获得一定特征不变形的特征表达。金字塔特征匹配是一种常用的特征聚会方法,这种方法提出将图像均匀分块,在分块内做特征汇聚。
4). **通过分类器分类**: 经过前面步骤之后一张图像可以用一个固定维度的向量进行描述,接下来就是经过分类器对图像进行分类。通常使用的分类器包括SVM(Support Vector Machine, 支持向量机)、随机森林等。而使用核方法的SVM是最为广泛的分类器,在传统图像分类任务上性能很好。
-这种方法在PASCAL VOC竞赛中的图像分类算法中被广泛使用 \[[18](#参考文献)\]。[NEC实验室](http://www.nec-labs.com/)在ILSVRC2010中采用SIFT和LBP特征,两个非线性编码器以及SVM分类器获得图像分类的冠军 \[[8](#参考文献)\]。
+这种传统的图像分类方法在PASCAL VOC竞赛中的图像分类算法中被广泛使用 \[[18](#参考文献)\]。[NEC实验室](http://www.nec-labs.com/)在ILSVRC2010中采用SIFT和LBP特征,两个非线性编码器以及SVM分类器获得图像分类的冠军 \[[8](#参考文献)\]。
Alex Krizhevsky在2012年ILSVRC提出的CNN模型 \[[9](#参考文献)\] 取得了历史性的突破,效果大幅度超越传统方法,获得了ILSVRC2012冠军,该模型被称作AlexNet。这也是首次将深度学习用于大规模图像分类中。从AlexNet之后,涌现了一系列CNN模型,不断地在ImageNet上刷新成绩,如图4展示。随着模型变得越来越深以及精妙的结构设计,Top-5的错误率也越来越低,降到了3.5%附近。而在同样的ImageNet数据集上,人眼的辨识错误率大概在5.1%,也就是目前的深度学习模型的识别能力已经超过了人眼。
@@ -77,7 +77,7 @@ Alex Krizhevsky在2012年ILSVRC提出的CNN模型 \[[9](#参考文献)\] 取得
- 卷积层(convolution layer): 执行卷积操作提取底层到高层的特征,发掘出图片局部关联性质和空间不变性质。
- 池化层(pooling layer): 执行降采样操作。通过取卷积输出特征图中局部区块的最大值(max-pooling)或者均值(avg-pooling)。降采样也是图像处理中常见的一种操作,可以过滤掉一些不重要的高频信息。
- 全连接层(fully-connected layer,或者fc layer): 输入层到隐藏层的神经元是全部连接的。
-- 非线性变化: 卷积层、全连接层后面一般都会接非线性变化层,例如Sigmoid、Tanh、ReLu等来增强网络的表达能力,在CNN里最常使用的为ReLu激活函数。
+- 非线性变化: 卷积层、全连接层后面一般都会接非线性变化函数,例如Sigmoid、Tanh、ReLu等来增强网络的表达能力,在CNN里最常使用的为ReLu激活函数。
- Dropout \[[10](#参考文献)\] : 在模型训练阶段随机让一些隐层节点权重不工作,提高网络的泛化能力,一定程度上防止过拟合。
另外,在训练过程中由于每层参数不断更新,会导致下一次输入分布发生变化,这样导致训练过程需要精心设计超参数。如2015年Sergey Ioffe和Christian Szegedy提出了Batch Normalization (BN)算法 \[[14](#参考文献)\] 中,每个batch对网络中的每一层特征都做归一化,使得每层分布相对稳定。BN算法不仅起到一定的正则作用,而且弱化了一些超参数的设计。经过实验证明,BN算法加速了模型收敛过程,在后来较深的模型中被广泛使用。
@@ -110,7 +110,7 @@ Inception模块如下图7所示,图(a)是最简单的设计,输出是3个卷
图7. Inception模块
-GoogleNet由多组Inception模块堆积而成。另外,在网络最后也没有采用传统的多层全连接层,而是像NIN网络一样采用了均值池化层;但与NIN不同的是,池化层后面接了一层到类别数映射的全连接层。除了这两个特点之外,由于网络中间层特征也很有判别性,GoogleNet在中间层添加了两个辅助分类器,在后向传播中增强梯度并且增强正则化,而整个网络的损失函数是这个三个分类器的损失加权求和。
+GoogleNet由多组Inception模块堆积而成。另外,在网络最后也没有采用传统的多层全连接层,而是像NIN网络一样采用了均值池化层;但与NIN不同的是,GoogleNet在池化层后加了一个全连接层来映射类别数。除了这两个特点之外,由于网络中间层特征也很有判别性,GoogleNet在中间层添加了两个辅助分类器,在后向传播中增强梯度并且增强正则化,而整个网络的损失函数是这个三个分类器的损失加权求和。
GoogleNet整体网络结构如图8所示,总共22层网络:开始由3层普通的卷积组成;接下来由三组子网络组成,第一组子网络包含2个Inception模块,第二组包含5个Inception模块,第三组包含2个Inception模块;然后接均值池化层、全连接层。
@@ -125,7 +125,7 @@ GoogleNet整体网络结构如图8所示,总共22层网络:开始由3层普
### ResNet
-ResNet(Residual Network) \[[15](#参考文献)\] 是2015年ImageNet图像分类、图像物体定位和图像物体检测比赛的冠军。针对训练卷积神经网络时加深网络导致准确度下降的问题,ResNet提出了采用残差学习。在已有设计思路(BN, 小卷积核,全卷积网络)的基础上,引入了残差模块。每个残差模块包含两条路径,其中一条路径是输入特征的直连通路,另一条路径对该特征做两到三次卷积操作得到该特征的残差,最后再将两条路径上的特征相加。
+ResNet(Residual Network) \[[15](#参考文献)\] 是2015年ImageNet图像分类、图像物体定位和图像物体检测比赛的冠军。针对随着网络训练加深导致准确度下降的问题,ResNet提出了残差学习方法来减轻训练深层网络的困难。在已有设计思路(BN, 小卷积核,全卷积网络)的基础上,引入了残差模块。每个残差模块包含两条路径,其中一条路径是输入特征的直连通路,另一条路径对该特征做两到三次卷积操作得到该特征的残差,最后再将两条路径上的特征相加。
残差模块如图9所示,左边是基本模块连接方式,由两个输出通道数相同的3x3卷积组成。右边是瓶颈模块(Bottleneck)连接方式,之所以称为瓶颈,是因为上面的1x1卷积用来降维(图示例即256->64),下面的1x1卷积用来升维(图示例即64->256),这样中间3x3卷积的输入和输出通道数都较小(图示例即64->64)。
@@ -215,7 +215,7 @@ def vgg_bn_drop(input):
3. 最后接两层512维的全连接。
-4. 通过上面VGG网络提取高层特征,然后经过全连接层映射到类别维度大小的向量,再通过Softmax归一化得到每个类别的概率,也可称作分类器。
+4. 在这里,VGG网络首先提取高层特征,随后在全连接层中将其映射到和类别维度大小一致的向量上,最后通过Softmax方法计算图片划为每个类别的概率。
### ResNet
@@ -226,7 +226,6 @@ ResNet模型的第1、3、4步和VGG模型相同,这里不再介绍。主要
- `conv_bn_layer` : 带BN的卷积层。
- `shortcut` : 残差模块的"直连"路径,"直连"实际分两种形式:残差模块输入和输出特征通道数不等时,采用1x1卷积的升维操作;残差模块输入和输出通道相等时,采用直连操作。
- `basicblock` : 一个基础残差模块,即图9左边所示,由两组3x3卷积组成的路径和一条"直连"路径组成。
- - `bottleneck` : 一个瓶颈残差模块,即图9右边所示,由上下1x1卷积和中间3x3卷积组成的路径和一条"直连"路径组成。
- `layer_warp` : 一组残差模块,由若干个残差模块堆积而成。每组中第一个残差模块滑动窗口大小与其他可以不同,以用来减少特征图在垂直和水平方向的大小。
```python
@@ -277,7 +276,7 @@ def layer_warp(block_func, input, ch_in, ch_out, count, stride):
3. 最后对网络做均值池化并返回该层。
-注意:除过第一层卷积层和最后一层全连接层之外,要求三组 `layer_warp` 总的含参层数能够被6整除,即 `resnet_cifar10` 的 depth 要满足 $(depth - 2) % 6 == 0$ 。
+注意:除第一层卷积层和最后一层全连接层之外,要求三组 `layer_warp` 总的含参层数能够被6整除,即 `resnet_cifar10` 的 depth 要满足 $(depth - 2) % 6 = 0$ 。
```python
def resnet_cifar10(ipt, depth=32):
@@ -331,7 +330,7 @@ def train_program():
## Optimizer Function 配置
-在下面的 `Adam optimizer`,`learning_rate` 是训练的速度,与网络的训练收敛速度有关系。
+在下面的 `Adam optimizer`,`learning_rate` 是学习率,与网络的训练收敛速度有关系。
```python
def optimizer_program():
@@ -371,8 +370,7 @@ feed_order = ['pixel', 'label']
main_program = fluid.default_main_program()
star_program = fluid.default_startup_program()
-predict = inference_program()
-avg_cost, acc = train_program(predict)
+avg_cost, acc = train_program()
# Test program
test_program = main_program.clone(for_test=True)
diff --git a/03.image_classification/index.cn.html b/03.image_classification/index.cn.html
index 9449633a0de6d164dbe8a7941f60d61bbcfa9d4b..8944a6384224717ccdc74edbb354703424038839 100644
--- a/03.image_classification/index.cn.html
+++ b/03.image_classification/index.cn.html
@@ -52,7 +52,7 @@
图像分类是根据图像的语义信息将不同类别图像区分开来,是计算机视觉中重要的基本问题,也是图像检测、图像分割、物体跟踪、行为分析等其他高层视觉任务的基础。图像分类在很多领域有广泛应用,包括安防领域的人脸识别和智能视频分析等,交通领域的交通场景识别,互联网领域基于内容的图像检索和相册自动归类,医学领域的图像识别等。
-一般来说,图像分类通过手工特征或特征学习方法对整个图像进行全部描述,然后使用分类器判别物体类别,因此如何提取图像的特征至关重要。在深度学习算法之前使用较多的是基于词袋(Bag of Words)模型的物体分类方法。词袋方法从自然语言处理中引入,即一句话可以用一个装了词的袋子表示其特征,袋子中的词为句子中的单词、短语或字。对于图像而言,词袋方法需要构建字典。最简单的词袋模型框架可以设计为**底层特征抽取**、**特征编码**、**分类器设计**三个过程。
+一般来说,图像分类通过手工提取特征或特征学习方法对整个图像进行全部描述,然后使用分类器判别物体类别,因此如何提取图像的特征至关重要。在深度学习算法之前使用较多的是基于词袋(Bag of Words)模型的物体分类方法。词袋方法从自然语言处理中引入,即一句话可以用一个装了词的袋子表示其特征,袋子中的词为句子中的单词、短语或字。对于图像而言,词袋方法需要构建字典。最简单的词袋模型框架可以设计为**底层特征抽取**、**特征编码**、**分类器设计**三个过程。
而基于深度学习的图像分类方法,可以通过有监督或无监督的方式**学习**层次化的特征描述,从而取代了手工设计或选择图像特征的工作。深度学习模型中的卷积神经网络(Convolution Neural Network, CNN)近年来在图像领域取得了惊人的成绩,CNN直接利用图像像素信息作为输入,最大程度上保留了输入图像的所有信息,通过卷积操作进行特征的提取和高层抽象,模型输出直接是图像识别的结果。这种基于"输入-输出"直接端到端的学习方法取得了非常好的效果,得到了广泛的应用。
@@ -90,15 +90,15 @@
在2012年之前的传统图像分类方法可以用背景描述中提到的三步完成,但通常完整建立图像识别模型一般包括底层特征学习、特征编码、空间约束、分类器设计、模型融合等几个阶段。
- 1). **底层特征提取**: 通常从图像中按照固定步长、尺度提取大量局部特征描述。常用的局部特征包括SIFT(Scale-Invariant Feature Transform, 尺度不变特征转换) \[[1](#参考文献)\]、HOG(Histogram of Oriented Gradient, 方向梯度直方图) \[[2](#参考文献)\]、LBP(Local Bianray Pattern, 局部二值模式) \[[3](#参考文献)\] 等,一般也采用多种特征描述子,防止丢失过多的有用信息。
+ 1). **底层特征提取**: 通常从图像中按照固定步长、尺度提取大量局部特征描述。常用的局部特征包括SIFT(Scale-Invariant Feature Transform, 尺度不变特征转换) \[[1](#参考文献)\]、HOG(Histogram of Oriented Gradient, 方向梯度直方图) \[[2](#参考文献)\]、LBP(Local Bianray Pattern, 局部二值模式) \[[3](#参考文献)\] 等,一般也采用多种特征描述,防止丢失过多的有用信息。
- 2). **特征编码**: 底层特征中包含了大量冗余与噪声,为了提高特征表达的鲁棒性,需要使用一种特征变换算法对底层特征进行编码,称作特征编码。常用的特征编码包括向量量化编码 \[[4](#参考文献)\]、稀疏编码 \[[5](#参考文献)\]、局部线性约束编码 \[[6](#参考文献)\]、Fisher向量编码 \[[7](#参考文献)\] 等。
+ 2). **特征编码**: 底层特征中包含了大量冗余与噪声,为了提高特征表达的鲁棒性,需要使用一种特征变换算法对底层特征进行编码,称作特征编码。常用的特征编码方法包括向量量化编码 \[[4](#参考文献)\]、稀疏编码 \[[5](#参考文献)\]、局部线性约束编码 \[[6](#参考文献)\]、Fisher向量编码 \[[7](#参考文献)\] 等。
3). **空间特征约束**: 特征编码之后一般会经过空间特征约束,也称作**特征汇聚**。特征汇聚是指在一个空间范围内,对每一维特征取最大值或者平均值,可以获得一定特征不变形的特征表达。金字塔特征匹配是一种常用的特征聚会方法,这种方法提出将图像均匀分块,在分块内做特征汇聚。
4). **通过分类器分类**: 经过前面步骤之后一张图像可以用一个固定维度的向量进行描述,接下来就是经过分类器对图像进行分类。通常使用的分类器包括SVM(Support Vector Machine, 支持向量机)、随机森林等。而使用核方法的SVM是最为广泛的分类器,在传统图像分类任务上性能很好。
-这种方法在PASCAL VOC竞赛中的图像分类算法中被广泛使用 \[[18](#参考文献)\]。[NEC实验室](http://www.nec-labs.com/)在ILSVRC2010中采用SIFT和LBP特征,两个非线性编码器以及SVM分类器获得图像分类的冠军 \[[8](#参考文献)\]。
+这种传统的图像分类方法在PASCAL VOC竞赛中的图像分类算法中被广泛使用 \[[18](#参考文献)\]。[NEC实验室](http://www.nec-labs.com/)在ILSVRC2010中采用SIFT和LBP特征,两个非线性编码器以及SVM分类器获得图像分类的冠军 \[[8](#参考文献)\]。
Alex Krizhevsky在2012年ILSVRC提出的CNN模型 \[[9](#参考文献)\] 取得了历史性的突破,效果大幅度超越传统方法,获得了ILSVRC2012冠军,该模型被称作AlexNet。这也是首次将深度学习用于大规模图像分类中。从AlexNet之后,涌现了一系列CNN模型,不断地在ImageNet上刷新成绩,如图4展示。随着模型变得越来越深以及精妙的结构设计,Top-5的错误率也越来越低,降到了3.5%附近。而在同样的ImageNet数据集上,人眼的辨识错误率大概在5.1%,也就是目前的深度学习模型的识别能力已经超过了人眼。
@@ -119,7 +119,7 @@ Alex Krizhevsky在2012年ILSVRC提出的CNN模型 \[[9](#参考文献)\] 取得
- 卷积层(convolution layer): 执行卷积操作提取底层到高层的特征,发掘出图片局部关联性质和空间不变性质。
- 池化层(pooling layer): 执行降采样操作。通过取卷积输出特征图中局部区块的最大值(max-pooling)或者均值(avg-pooling)。降采样也是图像处理中常见的一种操作,可以过滤掉一些不重要的高频信息。
- 全连接层(fully-connected layer,或者fc layer): 输入层到隐藏层的神经元是全部连接的。
-- 非线性变化: 卷积层、全连接层后面一般都会接非线性变化层,例如Sigmoid、Tanh、ReLu等来增强网络的表达能力,在CNN里最常使用的为ReLu激活函数。
+- 非线性变化: 卷积层、全连接层后面一般都会接非线性变化函数,例如Sigmoid、Tanh、ReLu等来增强网络的表达能力,在CNN里最常使用的为ReLu激活函数。
- Dropout \[[10](#参考文献)\] : 在模型训练阶段随机让一些隐层节点权重不工作,提高网络的泛化能力,一定程度上防止过拟合。
另外,在训练过程中由于每层参数不断更新,会导致下一次输入分布发生变化,这样导致训练过程需要精心设计超参数。如2015年Sergey Ioffe和Christian Szegedy提出了Batch Normalization (BN)算法 \[[14](#参考文献)\] 中,每个batch对网络中的每一层特征都做归一化,使得每层分布相对稳定。BN算法不仅起到一定的正则作用,而且弱化了一些超参数的设计。经过实验证明,BN算法加速了模型收敛过程,在后来较深的模型中被广泛使用。
@@ -152,7 +152,7 @@ Inception模块如下图7所示,图(a)是最简单的设计,输出是3个卷
图7. Inception模块
-GoogleNet由多组Inception模块堆积而成。另外,在网络最后也没有采用传统的多层全连接层,而是像NIN网络一样采用了均值池化层;但与NIN不同的是,池化层后面接了一层到类别数映射的全连接层。除了这两个特点之外,由于网络中间层特征也很有判别性,GoogleNet在中间层添加了两个辅助分类器,在后向传播中增强梯度并且增强正则化,而整个网络的损失函数是这个三个分类器的损失加权求和。
+GoogleNet由多组Inception模块堆积而成。另外,在网络最后也没有采用传统的多层全连接层,而是像NIN网络一样采用了均值池化层;但与NIN不同的是,GoogleNet在池化层后加了一个全连接层来映射类别数。除了这两个特点之外,由于网络中间层特征也很有判别性,GoogleNet在中间层添加了两个辅助分类器,在后向传播中增强梯度并且增强正则化,而整个网络的损失函数是这个三个分类器的损失加权求和。
GoogleNet整体网络结构如图8所示,总共22层网络:开始由3层普通的卷积组成;接下来由三组子网络组成,第一组子网络包含2个Inception模块,第二组包含5个Inception模块,第三组包含2个Inception模块;然后接均值池化层、全连接层。
@@ -167,7 +167,7 @@ GoogleNet整体网络结构如图8所示,总共22层网络:开始由3层普
### ResNet
-ResNet(Residual Network) \[[15](#参考文献)\] 是2015年ImageNet图像分类、图像物体定位和图像物体检测比赛的冠军。针对训练卷积神经网络时加深网络导致准确度下降的问题,ResNet提出了采用残差学习。在已有设计思路(BN, 小卷积核,全卷积网络)的基础上,引入了残差模块。每个残差模块包含两条路径,其中一条路径是输入特征的直连通路,另一条路径对该特征做两到三次卷积操作得到该特征的残差,最后再将两条路径上的特征相加。
+ResNet(Residual Network) \[[15](#参考文献)\] 是2015年ImageNet图像分类、图像物体定位和图像物体检测比赛的冠军。针对随着网络训练加深导致准确度下降的问题,ResNet提出了残差学习方法来减轻训练深层网络的困难。在已有设计思路(BN, 小卷积核,全卷积网络)的基础上,引入了残差模块。每个残差模块包含两条路径,其中一条路径是输入特征的直连通路,另一条路径对该特征做两到三次卷积操作得到该特征的残差,最后再将两条路径上的特征相加。
残差模块如图9所示,左边是基本模块连接方式,由两个输出通道数相同的3x3卷积组成。右边是瓶颈模块(Bottleneck)连接方式,之所以称为瓶颈,是因为上面的1x1卷积用来降维(图示例即256->64),下面的1x1卷积用来升维(图示例即64->256),这样中间3x3卷积的输入和输出通道数都较小(图示例即64->64)。
@@ -257,7 +257,7 @@ def vgg_bn_drop(input):
3. 最后接两层512维的全连接。
-4. 通过上面VGG网络提取高层特征,然后经过全连接层映射到类别维度大小的向量,再通过Softmax归一化得到每个类别的概率,也可称作分类器。
+4. 在这里,VGG网络首先提取高层特征,随后在全连接层中将其映射到和类别维度大小一致的向量上,最后通过Softmax方法计算图片划为每个类别的概率。
### ResNet
@@ -268,7 +268,6 @@ ResNet模型的第1、3、4步和VGG模型相同,这里不再介绍。主要
- `conv_bn_layer` : 带BN的卷积层。
- `shortcut` : 残差模块的"直连"路径,"直连"实际分两种形式:残差模块输入和输出特征通道数不等时,采用1x1卷积的升维操作;残差模块输入和输出通道相等时,采用直连操作。
- `basicblock` : 一个基础残差模块,即图9左边所示,由两组3x3卷积组成的路径和一条"直连"路径组成。
- - `bottleneck` : 一个瓶颈残差模块,即图9右边所示,由上下1x1卷积和中间3x3卷积组成的路径和一条"直连"路径组成。
- `layer_warp` : 一组残差模块,由若干个残差模块堆积而成。每组中第一个残差模块滑动窗口大小与其他可以不同,以用来减少特征图在垂直和水平方向的大小。
```python
@@ -319,7 +318,7 @@ def layer_warp(block_func, input, ch_in, ch_out, count, stride):
3. 最后对网络做均值池化并返回该层。
-注意:除过第一层卷积层和最后一层全连接层之外,要求三组 `layer_warp` 总的含参层数能够被6整除,即 `resnet_cifar10` 的 depth 要满足 $(depth - 2) % 6 == 0$ 。
+注意:除第一层卷积层和最后一层全连接层之外,要求三组 `layer_warp` 总的含参层数能够被6整除,即 `resnet_cifar10` 的 depth 要满足 $(depth - 2) % 6 = 0$ 。
```python
def resnet_cifar10(ipt, depth=32):
@@ -373,7 +372,7 @@ def train_program():
## Optimizer Function 配置
-在下面的 `Adam optimizer`,`learning_rate` 是训练的速度,与网络的训练收敛速度有关系。
+在下面的 `Adam optimizer`,`learning_rate` 是学习率,与网络的训练收敛速度有关系。
```python
def optimizer_program():
@@ -413,8 +412,7 @@ feed_order = ['pixel', 'label']
main_program = fluid.default_main_program()
star_program = fluid.default_startup_program()
-predict = inference_program()
-avg_cost, acc = train_program(predict)
+avg_cost, acc = train_program()
# Test program
test_program = main_program.clone(for_test=True)
diff --git a/04.word2vec/README.cn.md b/04.word2vec/README.cn.md
index 660787043bdcff95c5d847f0a7fb79f31fc8ec5f..3b0058112bdd5e5a03d8843755df6ffc25412f4b 100644
--- a/04.word2vec/README.cn.md
+++ b/04.word2vec/README.cn.md
@@ -14,7 +14,7 @@ One-hot vector虽然自然,但是用处有限。比如,在互联网广告系
在机器学习领域里,各种“知识”被各种模型表示,词向量模型(word embedding model)就是其中的一类。通过词向量模型可将一个 one-hot vector映射到一个维度更低的实数向量(embedding vector),如$embedding(母亲节) = [0.3, 4.2, -1.5, ...], embedding(康乃馨) = [0.2, 5.6, -2.3, ...]$。在这个映射到的实数向量表示中,希望两个语义(或用法)上相似的词对应的词向量“更像”,这样如“母亲节”和“康乃馨”的对应词向量的余弦相似度就不再为零了。
-词向量模型可以是概率模型、共生矩阵(co-occurrence matrix)模型或神经元网络模型。在用神经网络求词向量之前,传统做法是统计一个词语的共生矩阵$X$。$X$是一个$|V| \times |V|$ 大小的矩阵,$X_{ij}$表示在所有语料中,词汇表`V`(vocabulary)中第i个词和第j个词同时出现的词数,$|V|$为词汇表的大小。对$X$做矩阵分解(如奇异值分解,Singular Value Decomposition \[[5](#参考文献)\]),得到的$U$即视为所有词的词向量:
+词向量模型可以是概率模型、共生矩阵(co-occurrence matrix)模型或神经元网络模型。在用神经网络求词向量之前,传统做法是统计一个词语的共生矩阵$X$。$X$是一个$|V| \times |V|$ 大小的矩阵,$X_{ij}$表示在所有语料中,词汇表$V$(vocabulary)中第i个词和第j个词同时出现的词数,$|V|$为词汇表的大小。对$X$做矩阵分解(如奇异值分解,Singular Value Decomposition \[[5](#参考文献)\]),得到的$U$即视为所有词的词向量:
$$X = USV^T$$
@@ -26,7 +26,7 @@ $$X = USV^T$$
3) 需要手动去掉停用词(如although, a,...),不然这些频繁出现的词也会影响矩阵分解的效果。
-基于神经网络的模型不需要计算存储一个在全语料上统计的大表,而是通过学习语义信息得到词向量,因此能很好地解决以上问题。在本章里,我们将展示基于神经网络训练词向量的细节,以及如何用PaddlePaddle训练一个词向量模型。
+基于神经网络的模型不需要计算和存储一个在全语料上统计产生的大表,而是通过学习语义信息得到词向量,因此能很好地解决以上问题。在本章里,我们将展示基于神经网络训练词向量的细节,以及如何用PaddlePaddle训练一个词向量模型。
## 效果展示
@@ -77,7 +77,7 @@ $$P(w_1, ..., w_T) = \prod_{t=1}^TP(w_t | w_1, ... , w_{t-1})$$
在计算语言学中,n-gram是一种重要的文本表示方法,表示一个文本中连续的n个项。基于具体的应用场景,每一项可以是一个字母、单词或者音节。 n-gram模型也是统计语言模型中的一种重要方法,用n-gram训练语言模型时,一般用每个n-gram的历史n-1个词语组成的内容来预测第n个词。
-Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models \[[1](#参考文献)\] 中介绍如何学习一个神经元网络表示的词向量模型。文中的神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。用这种方法学习语言模型可以克服维度灾难(curse of dimensionality),即训练和测试数据不同导致的模型不准。注意:由于“神经概率语言模型”说法较为泛泛,我们在这里不用其NNLM的本名,考虑到其具体做法,本文中称该模型为N-gram neural model。
+Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models \[[1](#参考文献)\] 中介绍如何学习一个神经元网络表示的词向量模型。文中的神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。因所有的词语都用一个低维向量来表示,用这种方法学习语言模型可以克服维度灾难(curse of dimensionality)。注意:由于“神经概率语言模型”说法较为泛泛,我们在这里不用其NNLM的本名,考虑到其具体做法,本文中称该模型为N-gram neural model。
我们在上文中已经讲到用条件概率建模语言模型,即一句话中第$t$个词的概率和该句话的前$t-1$个词相关。可实际上越远的词语其实对该词的影响越小,那么如果考虑一个n-gram, 每个词都只受其前面`n-1`个词的影响,则有:
@@ -95,15 +95,15 @@ $$\frac{1}{T}\sum_t f(w_t, w_{t-1}, ..., w_{t-n+1};\theta) + R(\theta)$$
图2展示了N-gram神经网络模型,从下往上看,该模型分为以下几个部分:
- - 对于每个样本,模型输入$w_{t-n+1},...w_{t-1}$, 输出句子第t个词为字典中`|V|`个词的概率。
+ - 对于每个样本,模型输入$w_{t-n+1},...w_{t-1}$, 输出句子第t个词在字典中`|V|`个词上的概率分布。
每个输入词$w_{t-n+1},...w_{t-1}$首先通过映射矩阵映射到词向量$C(w_{t-n+1}),...C(w_{t-1})$。
- - 然后所有词语的词向量连接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
+ - 然后所有词语的词向量拼接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
$$g=Utanh(\theta^Tx + b_1) + Wx + b_2$$
- 其中,$x$为所有词语的词向量连接成的大向量,表示文本历史特征;$\theta$、$U$、$b_1$、$b_2$和$W$分别为词向量层到隐层连接的参数。$g$表示未经归一化的所有输出单词概率,$g_i$表示未经归一化的字典中第$i$个单词的输出概率。
+ 其中,$x$为所有词语的词向量拼接成的大向量,表示文本历史特征;$\theta$、$U$、$b_1$、$b_2$和$W$分别为词向量层到隐层连接的参数。$g$表示未经归一化的所有输出单词概率,$g_i$表示未经归一化的字典中第$i$个单词的输出概率。
- 根据softmax的定义,通过归一化$g_i$, 生成目标词$w_t$的概率为:
@@ -111,7 +111,7 @@ $$\frac{1}{T}\sum_t f(w_t, w_{t-1}, ..., w_{t-n+1};\theta) + R(\theta)$$
- 整个网络的损失值(cost)为多类分类交叉熵,用公式表示为
- $$J(\theta) = -\sum_{i=1}^N\sum_{c=1}^{|V|}y_k^{i}log(softmax(g_k^i))$$
+ $$J(\theta) = -\sum_{i=1}^N\sum_{k=1}^{|V|}y_k^{i}log(softmax(g_k^i))$$
其中$y_k^i$表示第$i$个样本第$k$类的真实标签(0或1),$softmax(g_k^i)$表示第i个样本第k类softmax输出的概率。
@@ -213,15 +213,16 @@ from __future__ import print_function
```
-然后,定义参数:
+然后,定义参数:
+
```python
-EMBED_SIZE = 32
-HIDDEN_SIZE = 256
-N = 5
-BATCH_SIZE = 100
-PASS_NUM = 100
+EMBED_SIZE = 32 # embedding维度
+HIDDEN_SIZE = 256 # 隐层大小
+N = 5 # ngram大小,这里固定取5
+BATCH_SIZE = 100 # batch大小
+PASS_NUM = 100 # 训练轮数
-use_cuda = False # set to True if training with GPU
+use_cuda = False # 如果用GPU训练,则设置为True
word_dict = paddle.dataset.imikolov.build_dict()
dict_size = len(word_dict)
@@ -269,13 +270,13 @@ def inference_program(words, is_sparse):
return predict_word
```
-- 基于以上的神经网络结构,我们可以如下定义我们的`训练`方法
+- 基于以上的神经网络结构,我们可以如下定义我们的训练方法
```python
def train_program(predict_word):
- # The declaration of 'next_word' must be after the invoking of inference_program,
- # or the data input order of train program would be [next_word, firstw, secondw,
- # thirdw, fourthw], which is not correct.
+ # 'next_word'的定义必须要在inference_program的声明之后,
+ # 否则train program输入数据的顺序就变成了[next_word, firstw, secondw,
+ # thirdw, fourthw], 这是不正确的.
next_word = fluid.layers.data(name='nextw', shape=[1], dtype='int64')
cost = fluid.layers.cross_entropy(input=predict_word, label=next_word)
avg_cost = fluid.layers.mean(cost)
@@ -357,11 +358,11 @@ def train(if_use_cuda, params_dirname, is_sparse=True):
outs = train_test(test_program, test_reader)
print("Step %d: Average Cost %f" % (step, outs[0]))
-
- # it will take a few hours.
- # If average cost is lower than 5.8, we consider the model good enough to stop.
- # Note 5.8 is a relatively high value. In order to get a better model, one should
- # aim for avg_cost lower than 3.5. But the training could take longer time.
+
+ # 整个训练过程要花费几个小时,如果平均损失低于5.8,
+ # 我们就认为模型已经达到很好的效果可以停止训练了。
+ # 注意5.8是一个相对较高的值,为了获取更好的模型,可以将
+ # 这里的阈值设为3.5,但训练时间也会更长。
if outs[0] < 5.8:
if params_dirname is not None:
fluid.io.save_inference_model(params_dirname, [
@@ -377,7 +378,7 @@ def train(if_use_cuda, params_dirname, is_sparse=True):
train_loop()
```
-- `train_loop`将会开始训练。期间打印返回的监控情况如下:
+- `train_loop`将会开始训练。期间打印训练过程的日志如下:
```text
Step 0: Average Cost 7.337213
@@ -400,23 +401,16 @@ def infer(use_cuda, params_dirname=None):
exe = fluid.Executor(place)
inference_scope = fluid.core.Scope()
-
- inference_scope = fluid.core.Scope()
- with fluid.scope_guard(inference_scope):
- # Use fluid.io.load_inference_model to obtain the inference program desc,
- # the feed_target_names (the names of variables that will be feeded
- # data using feed operators), and the fetch_targets (variables that
- # we want to obtain data from using fetch operators).
+ with fluid.scope_guard(inference_scope):
+ # 使用fluid.io.load_inference_model获取inference program,
+ # feed变量的名称feed_target_names和从scope中fetch的对象fetch_targets
[inferencer, feed_target_names,
fetch_targets] = fluid.io.load_inference_model(params_dirname, exe)
- # Setup inputs by creating 4 LoDTensors representing 4 words. Here each word
- # is simply an index to look up for the corresponding word vector and hence
- # the shape of word (base_shape) should be [1]. The recursive_sequence_lengths,
- # which is length-based level of detail (lod) of each LoDTensor, should be [[1]]
- # meaning there is only one level of detail and there is only one sequence of
- # one word on this level.
- # Note that recursive_sequence_lengths should be a list of lists.
+ # 设置输入,用四个LoDTensor来表示4个词语。这里每个词都是一个id,
+ # 用来查询embedding表获取对应的词向量,因此其形状大小是[1]。
+ # recursive_sequence_lengths设置的是基于长度的LoD,因此都应该设为[[1]]
+ # 注意recursive_sequence_lengths是列表的列表
data1 = [[211]] # 'among'
data2 = [[6]] # 'a'
data3 = [[96]] # 'group'
@@ -433,8 +427,8 @@ def infer(use_cuda, params_dirname=None):
assert feed_target_names[2] == 'thirdw'
assert feed_target_names[3] == 'fourthw'
- # Construct feed as a dictionary of {feed_target_name: feed_target_data}
- # and results will contain a list of data corresponding to fetch_targets.
+ # 构造feed词典 {feed_target_name: feed_target_data}
+ # 预测结果包含在results之中
results = exe.run(
inferencer,
feed={
@@ -453,17 +447,16 @@ def infer(use_cuda, params_dirname=None):
key for key, value in six.iteritems(word_dict)
if value == most_possible_word_index
][0])
-
-
```
-由于词向量矩阵本身比较稀疏,训练的过程如果要达到一定的精度耗时会比较长。为了能简单看到效果,教程只设置了经过很少的训练就结束并得到如下的预测。我们的模型预测 `among a group of` 的下一个词是`the`。这比较符合文法规律。如果我们训练时间更长,比如几个小时,那么我们会得到的下一个预测是 `workers`。
+由于词向量矩阵本身比较稀疏,训练的过程如果要达到一定的精度耗时会比较长。为了能简单看到效果,教程只设置了经过很少的训练就结束并得到如下的预测。我们的模型预测 `among a group of` 的下一个词是`the`。这比较符合文法规律。如果我们训练时间更长,比如几个小时,那么我们会得到的下一个预测是 `workers`。预测输出的格式如下所示:
```text
[[0.03768077 0.03463154 0.00018074 ... 0.00022283 0.00029888 0.02967956]]
0
the
-```
+```
+其中第一行表示预测词在词典上的概率分布,第二行表示概率最大的词对应的id,第三行表示概率最大的词。
整个程序的入口很简单:
diff --git a/04.word2vec/index.cn.html b/04.word2vec/index.cn.html
index b271e3428bcf416d58603b4056eec664b390f61c..9ef79aab5759ef8163010d98f1ff4240ff2ecd0b 100644
--- a/04.word2vec/index.cn.html
+++ b/04.word2vec/index.cn.html
@@ -56,7 +56,7 @@ One-hot vector虽然自然,但是用处有限。比如,在互联网广告系
在机器学习领域里,各种“知识”被各种模型表示,词向量模型(word embedding model)就是其中的一类。通过词向量模型可将一个 one-hot vector映射到一个维度更低的实数向量(embedding vector),如$embedding(母亲节) = [0.3, 4.2, -1.5, ...], embedding(康乃馨) = [0.2, 5.6, -2.3, ...]$。在这个映射到的实数向量表示中,希望两个语义(或用法)上相似的词对应的词向量“更像”,这样如“母亲节”和“康乃馨”的对应词向量的余弦相似度就不再为零了。
-词向量模型可以是概率模型、共生矩阵(co-occurrence matrix)模型或神经元网络模型。在用神经网络求词向量之前,传统做法是统计一个词语的共生矩阵$X$。$X$是一个$|V| \times |V|$ 大小的矩阵,$X_{ij}$表示在所有语料中,词汇表`V`(vocabulary)中第i个词和第j个词同时出现的词数,$|V|$为词汇表的大小。对$X$做矩阵分解(如奇异值分解,Singular Value Decomposition \[[5](#参考文献)\]),得到的$U$即视为所有词的词向量:
+词向量模型可以是概率模型、共生矩阵(co-occurrence matrix)模型或神经元网络模型。在用神经网络求词向量之前,传统做法是统计一个词语的共生矩阵$X$。$X$是一个$|V| \times |V|$ 大小的矩阵,$X_{ij}$表示在所有语料中,词汇表$V$(vocabulary)中第i个词和第j个词同时出现的词数,$|V|$为词汇表的大小。对$X$做矩阵分解(如奇异值分解,Singular Value Decomposition \[[5](#参考文献)\]),得到的$U$即视为所有词的词向量:
$$X = USV^T$$
@@ -68,7 +68,7 @@ $$X = USV^T$$
3) 需要手动去掉停用词(如although, a,...),不然这些频繁出现的词也会影响矩阵分解的效果。
-基于神经网络的模型不需要计算存储一个在全语料上统计的大表,而是通过学习语义信息得到词向量,因此能很好地解决以上问题。在本章里,我们将展示基于神经网络训练词向量的细节,以及如何用PaddlePaddle训练一个词向量模型。
+基于神经网络的模型不需要计算和存储一个在全语料上统计产生的大表,而是通过学习语义信息得到词向量,因此能很好地解决以上问题。在本章里,我们将展示基于神经网络训练词向量的细节,以及如何用PaddlePaddle训练一个词向量模型。
## 效果展示
@@ -119,7 +119,7 @@ $$P(w_1, ..., w_T) = \prod_{t=1}^TP(w_t | w_1, ... , w_{t-1})$$
在计算语言学中,n-gram是一种重要的文本表示方法,表示一个文本中连续的n个项。基于具体的应用场景,每一项可以是一个字母、单词或者音节。 n-gram模型也是统计语言模型中的一种重要方法,用n-gram训练语言模型时,一般用每个n-gram的历史n-1个词语组成的内容来预测第n个词。
-Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models \[[1](#参考文献)\] 中介绍如何学习一个神经元网络表示的词向量模型。文中的神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。用这种方法学习语言模型可以克服维度灾难(curse of dimensionality),即训练和测试数据不同导致的模型不准。注意:由于“神经概率语言模型”说法较为泛泛,我们在这里不用其NNLM的本名,考虑到其具体做法,本文中称该模型为N-gram neural model。
+Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models \[[1](#参考文献)\] 中介绍如何学习一个神经元网络表示的词向量模型。文中的神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。因所有的词语都用一个低维向量来表示,用这种方法学习语言模型可以克服维度灾难(curse of dimensionality)。注意:由于“神经概率语言模型”说法较为泛泛,我们在这里不用其NNLM的本名,考虑到其具体做法,本文中称该模型为N-gram neural model。
我们在上文中已经讲到用条件概率建模语言模型,即一句话中第$t$个词的概率和该句话的前$t-1$个词相关。可实际上越远的词语其实对该词的影响越小,那么如果考虑一个n-gram, 每个词都只受其前面`n-1`个词的影响,则有:
@@ -137,15 +137,15 @@ $$\frac{1}{T}\sum_t f(w_t, w_{t-1}, ..., w_{t-n+1};\theta) + R(\theta)$$
图2展示了N-gram神经网络模型,从下往上看,该模型分为以下几个部分:
- - 对于每个样本,模型输入$w_{t-n+1},...w_{t-1}$, 输出句子第t个词为字典中`|V|`个词的概率。
+ - 对于每个样本,模型输入$w_{t-n+1},...w_{t-1}$, 输出句子第t个词在字典中`|V|`个词上的概率分布。
每个输入词$w_{t-n+1},...w_{t-1}$首先通过映射矩阵映射到词向量$C(w_{t-n+1}),...C(w_{t-1})$。
- - 然后所有词语的词向量连接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
+ - 然后所有词语的词向量拼接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
$$g=Utanh(\theta^Tx + b_1) + Wx + b_2$$
- 其中,$x$为所有词语的词向量连接成的大向量,表示文本历史特征;$\theta$、$U$、$b_1$、$b_2$和$W$分别为词向量层到隐层连接的参数。$g$表示未经归一化的所有输出单词概率,$g_i$表示未经归一化的字典中第$i$个单词的输出概率。
+ 其中,$x$为所有词语的词向量拼接成的大向量,表示文本历史特征;$\theta$、$U$、$b_1$、$b_2$和$W$分别为词向量层到隐层连接的参数。$g$表示未经归一化的所有输出单词概率,$g_i$表示未经归一化的字典中第$i$个单词的输出概率。
- 根据softmax的定义,通过归一化$g_i$, 生成目标词$w_t$的概率为:
@@ -153,7 +153,7 @@ $$\frac{1}{T}\sum_t f(w_t, w_{t-1}, ..., w_{t-n+1};\theta) + R(\theta)$$
- 整个网络的损失值(cost)为多类分类交叉熵,用公式表示为
- $$J(\theta) = -\sum_{i=1}^N\sum_{c=1}^{|V|}y_k^{i}log(softmax(g_k^i))$$
+ $$J(\theta) = -\sum_{i=1}^N\sum_{k=1}^{|V|}y_k^{i}log(softmax(g_k^i))$$
其中$y_k^i$表示第$i$个样本第$k$类的真实标签(0或1),$softmax(g_k^i)$表示第i个样本第k类softmax输出的概率。
@@ -255,15 +255,16 @@ from __future__ import print_function
```
-然后,定义参数:
+然后,定义参数:
+
```python
-EMBED_SIZE = 32
-HIDDEN_SIZE = 256
-N = 5
-BATCH_SIZE = 100
-PASS_NUM = 100
+EMBED_SIZE = 32 # embedding维度
+HIDDEN_SIZE = 256 # 隐层大小
+N = 5 # ngram大小,这里固定取5
+BATCH_SIZE = 100 # batch大小
+PASS_NUM = 100 # 训练轮数
-use_cuda = False # set to True if training with GPU
+use_cuda = False # 如果用GPU训练,则设置为True
word_dict = paddle.dataset.imikolov.build_dict()
dict_size = len(word_dict)
@@ -311,13 +312,13 @@ def inference_program(words, is_sparse):
return predict_word
```
-- 基于以上的神经网络结构,我们可以如下定义我们的`训练`方法
+- 基于以上的神经网络结构,我们可以如下定义我们的训练方法
```python
def train_program(predict_word):
- # The declaration of 'next_word' must be after the invoking of inference_program,
- # or the data input order of train program would be [next_word, firstw, secondw,
- # thirdw, fourthw], which is not correct.
+ # 'next_word'的定义必须要在inference_program的声明之后,
+ # 否则train program输入数据的顺序就变成了[next_word, firstw, secondw,
+ # thirdw, fourthw], 这是不正确的.
next_word = fluid.layers.data(name='nextw', shape=[1], dtype='int64')
cost = fluid.layers.cross_entropy(input=predict_word, label=next_word)
avg_cost = fluid.layers.mean(cost)
@@ -399,11 +400,11 @@ def train(if_use_cuda, params_dirname, is_sparse=True):
outs = train_test(test_program, test_reader)
print("Step %d: Average Cost %f" % (step, outs[0]))
-
- # it will take a few hours.
- # If average cost is lower than 5.8, we consider the model good enough to stop.
- # Note 5.8 is a relatively high value. In order to get a better model, one should
- # aim for avg_cost lower than 3.5. But the training could take longer time.
+
+ # 整个训练过程要花费几个小时,如果平均损失低于5.8,
+ # 我们就认为模型已经达到很好的效果可以停止训练了。
+ # 注意5.8是一个相对较高的值,为了获取更好的模型,可以将
+ # 这里的阈值设为3.5,但训练时间也会更长。
if outs[0] < 5.8:
if params_dirname is not None:
fluid.io.save_inference_model(params_dirname, [
@@ -419,7 +420,7 @@ def train(if_use_cuda, params_dirname, is_sparse=True):
train_loop()
```
-- `train_loop`将会开始训练。期间打印返回的监控情况如下:
+- `train_loop`将会开始训练。期间打印训练过程的日志如下:
```text
Step 0: Average Cost 7.337213
@@ -442,23 +443,16 @@ def infer(use_cuda, params_dirname=None):
exe = fluid.Executor(place)
inference_scope = fluid.core.Scope()
-
- inference_scope = fluid.core.Scope()
- with fluid.scope_guard(inference_scope):
- # Use fluid.io.load_inference_model to obtain the inference program desc,
- # the feed_target_names (the names of variables that will be feeded
- # data using feed operators), and the fetch_targets (variables that
- # we want to obtain data from using fetch operators).
+ with fluid.scope_guard(inference_scope):
+ # 使用fluid.io.load_inference_model获取inference program,
+ # feed变量的名称feed_target_names和从scope中fetch的对象fetch_targets
[inferencer, feed_target_names,
fetch_targets] = fluid.io.load_inference_model(params_dirname, exe)
- # Setup inputs by creating 4 LoDTensors representing 4 words. Here each word
- # is simply an index to look up for the corresponding word vector and hence
- # the shape of word (base_shape) should be [1]. The recursive_sequence_lengths,
- # which is length-based level of detail (lod) of each LoDTensor, should be [[1]]
- # meaning there is only one level of detail and there is only one sequence of
- # one word on this level.
- # Note that recursive_sequence_lengths should be a list of lists.
+ # 设置输入,用四个LoDTensor来表示4个词语。这里每个词都是一个id,
+ # 用来查询embedding表获取对应的词向量,因此其形状大小是[1]。
+ # recursive_sequence_lengths设置的是基于长度的LoD,因此都应该设为[[1]]
+ # 注意recursive_sequence_lengths是列表的列表
data1 = [[211]] # 'among'
data2 = [[6]] # 'a'
data3 = [[96]] # 'group'
@@ -475,8 +469,8 @@ def infer(use_cuda, params_dirname=None):
assert feed_target_names[2] == 'thirdw'
assert feed_target_names[3] == 'fourthw'
- # Construct feed as a dictionary of {feed_target_name: feed_target_data}
- # and results will contain a list of data corresponding to fetch_targets.
+ # 构造feed词典 {feed_target_name: feed_target_data}
+ # 预测结果包含在results之中
results = exe.run(
inferencer,
feed={
@@ -495,17 +489,16 @@ def infer(use_cuda, params_dirname=None):
key for key, value in six.iteritems(word_dict)
if value == most_possible_word_index
][0])
-
-
```
-由于词向量矩阵本身比较稀疏,训练的过程如果要达到一定的精度耗时会比较长。为了能简单看到效果,教程只设置了经过很少的训练就结束并得到如下的预测。我们的模型预测 `among a group of` 的下一个词是`the`。这比较符合文法规律。如果我们训练时间更长,比如几个小时,那么我们会得到的下一个预测是 `workers`。
+由于词向量矩阵本身比较稀疏,训练的过程如果要达到一定的精度耗时会比较长。为了能简单看到效果,教程只设置了经过很少的训练就结束并得到如下的预测。我们的模型预测 `among a group of` 的下一个词是`the`。这比较符合文法规律。如果我们训练时间更长,比如几个小时,那么我们会得到的下一个预测是 `workers`。预测输出的格式如下所示:
```text
[[0.03768077 0.03463154 0.00018074 ... 0.00022283 0.00029888 0.02967956]]
0
the
-```
+```
+其中第一行表示预测词在词典上的概率分布,第二行表示概率最大的词对应的id,第三行表示概率最大的词。
整个程序的入口很简单:
diff --git a/06.understand_sentiment/README.cn.md b/06.understand_sentiment/README.cn.md
index 5a60edd6695569c091fb5c06db25cd7fa8423b08..d7b80d80264828aa43e5333d6976504f8716e9ca 100644
--- a/06.understand_sentiment/README.cn.md
+++ b/06.understand_sentiment/README.cn.md
@@ -28,7 +28,12 @@
我们在[推荐系统](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system)一节介绍过应用于文本数据的卷积神经网络模型的计算过程,这里进行一个简单的回顾。
-对卷积神经网络来说,首先使用卷积处理输入的词向量序列,产生一个特征图(feature map),对特征图采用时间维度上的最大池化(max pooling over time)操作得到此卷积核对应的整句话的特征,最后,将所有卷积核得到的特征拼接起来即为文本的定长向量表示,对于文本分类问题,将其连接至softmax即构建出完整的模型。在实际应用中,我们会使用多个卷积核来处理句子,窗口大小相同的卷积核堆叠起来形成一个矩阵,这样可以更高效的完成运算。另外,我们也可使用窗口大小不同的卷积核来处理句子,[推荐系统](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system)一节的图3作为示意画了四个卷积核,不同颜色表示不同大小的卷积核操作。
+对卷积神经网络来说,首先使用卷积处理输入的词向量序列,产生一个特征图(feature map),对特征图采用时间维度上的最大池化(max pooling over time)操作得到此卷积核对应的整句话的特征,最后,将所有卷积核得到的特征拼接起来即为文本的定长向量表示,对于文本分类问题,将其连接至softmax即构建出完整的模型。在实际应用中,我们会使用多个卷积核来处理句子,窗口大小相同的卷积核堆叠起来形成一个矩阵,这样可以更高效的完成运算。另外,我们也可使用窗口大小不同的卷积核来处理句子,[推荐系统](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system)一节的图3作为示意画了四个卷积核,既文本图1,不同颜色表示不同大小的卷积核操作。
+
+
+
+图1. 卷积神经网络文本分类模型
+
对于一般的短文本分类问题,上文所述的简单的文本卷积网络即可达到很高的正确率\[[1](#参考文献)\]。若想得到更抽象更高级的文本特征表示,可以构建深层文本卷积神经网络\[[2](#参考文献),[3](#参考文献)\]。
@@ -38,16 +43,16 @@
-图1. 循环神经网络按时间展开的示意图
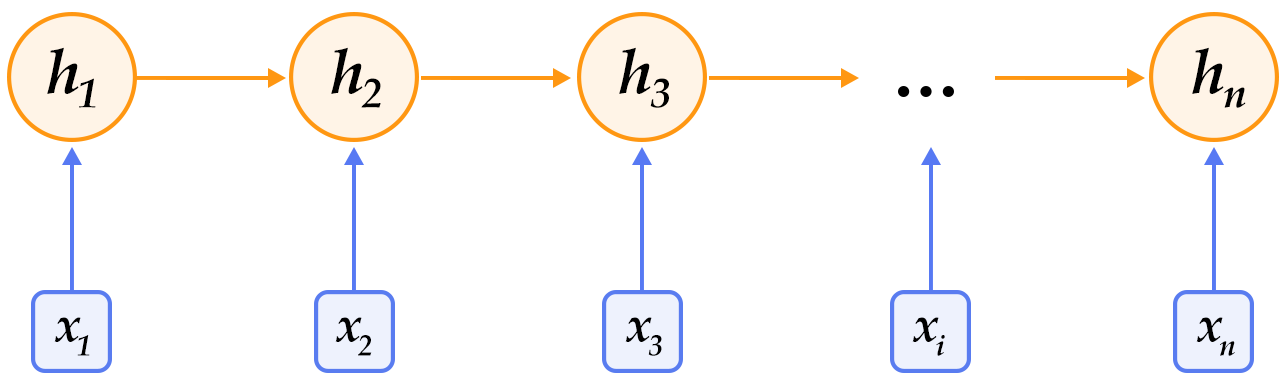
+图2. 循环神经网络按时间展开的示意图
-循环神经网络按时间展开后如图1所示:在第$t$时刻,网络读入第$t$个输入$x_t$(向量表示)及前一时刻隐层的状态值$h_{t-1}$(向量表示,$h_0$一般初始化为$0$向量),计算得出本时刻隐层的状态值$h_t$,重复这一步骤直至读完所有输入。如果将循环神经网络所表示的函数记为$f$,则其公式可表示为:
+循环神经网络按时间展开后如图2所示:在第$t$时刻,网络读入第$t$个输入$x_t$(向量表示)及前一时刻隐层的状态值$h_{t-1}$(向量表示,$h_0$一般初始化为$0$向量),计算得出本时刻隐层的状态值$h_t$,重复这一步骤直至读完所有输入。如果将循环神经网络所表示的函数记为$f$,则其公式可表示为:
$$h_t=f(x_t,h_{t-1})=\sigma(W_{xh}x_t+W_{hh}h_{t-1}+b_h)$$
其中$W_{xh}$是输入到隐层的矩阵参数,$W_{hh}$是隐层到隐层的矩阵参数,$b_h$为隐层的偏置向量(bias)参数,$\sigma$为$sigmoid$函数。
-在处理自然语言时,一般会先将词(one-hot表示)映射为其词向量(word embedding)表示,然后再作为循环神经网络每一时刻的输入$x_t$。此外,可以根据实际需要的不同在循环神经网络的隐层上连接其它层。如,可以把一个循环神经网络的隐层输出连接至下一个循环神经网络的输入构建深层(deep or stacked)循环神经网络,或者提取最后一个时刻的隐层状态作为句子表示进而使用分类模型等等。
+在处理自然语言时,一般会先将词(one-hot表示)映射为其词向量表示,然后再作为循环神经网络每一时刻的输入$x_t$。此外,可以根据实际需要的不同在循环神经网络的隐层上连接其它层。如,可以把一个循环神经网络的隐层输出连接至下一个循环神经网络的输入构建深层(deep or stacked)循环神经网络,或者提取最后一个时刻的隐层状态作为句子表示进而使用分类模型等等。
### 长短期记忆网络(LSTM)
@@ -63,11 +68,11 @@ $$ f_t = \sigma(W_{xf}x_t+W_{hf}h_{t-1}+W_{cf}c_{t-1}+b_f) $$
$$ c_t = f_t\odot c_{t-1}+i_t\odot tanh(W_{xc}x_t+W_{hc}h_{t-1}+b_c) $$
$$ o_t = \sigma(W_{xo}x_t+W_{ho}h_{t-1}+W_{co}c_{t}+b_o) $$
$$ h_t = o_t\odot tanh(c_t) $$
-其中,$i_t, f_t, c_t, o_t$分别表示输入门,遗忘门,记忆单元及输出门的向量值,带角标的$W$及$b$为模型参数,$tanh$为双曲正切函数,$\odot$表示逐元素(elementwise)的乘法操作。输入门控制着新输入进入记忆单元$c$的强度,遗忘门控制着记忆单元维持上一时刻值的强度,输出门控制着输出记忆单元的强度。三种门的计算方式类似,但有着完全不同的参数,它们各自以不同的方式控制着记忆单元$c$,如图2所示:
+其中,$i_t, f_t, c_t, o_t$分别表示输入门,遗忘门,记忆单元及输出门的向量值,带角标的$W$及$b$为模型参数,$tanh$为双曲正切函数,$\odot$表示逐元素(elementwise)的乘法操作。输入门控制着新输入进入记忆单元$c$的强度,遗忘门控制着记忆单元维持上一时刻值的强度,输出门控制着输出记忆单元的强度。三种门的计算方式类似,但有着完全不同的参数,它们各自以不同的方式控制着记忆单元$c$,如图3所示:

-图2. 时刻$t$的LSTM [7]
+图3. 时刻$t$的LSTM [7]
LSTM通过给简单的循环神经网络增加记忆及控制门的方式,增强了其处理远距离依赖问题的能力。类似原理的改进还有Gated Recurrent Unit (GRU)\[[8](#参考文献)\],其设计更为简洁一些。**这些改进虽然各有不同,但是它们的宏观描述却与简单的循环神经网络一样(如图2所示),即隐状态依据当前输入及前一时刻的隐状态来改变,不断地循环这一过程直至输入处理完毕:**
@@ -80,11 +85,11 @@ $$ h_t=Recrurent(x_t,h_{t-1})$$
对于正常顺序的循环神经网络,$h_t$包含了$t$时刻之前的输入信息,也就是上文信息。同样,为了得到下文信息,我们可以使用反方向(将输入逆序处理)的循环神经网络。结合构建深层循环神经网络的方法(深层神经网络往往能得到更抽象和高级的特征表示),我们可以通过构建更加强有力的基于LSTM的栈式双向循环神经网络\[[9](#参考文献)\],来对时序数据进行建模。
-如图3所示(以三层为例),奇数层LSTM正向,偶数层LSTM反向,高一层的LSTM使用低一层LSTM及之前所有层的信息作为输入,对最高层LSTM序列使用时间维度上的最大池化即可得到文本的定长向量表示(这一表示充分融合了文本的上下文信息,并且对文本进行了深层次抽象),最后我们将文本表示连接至softmax构建分类模型。
+如图4所示(以三层为例),奇数层LSTM正向,偶数层LSTM反向,高一层的LSTM使用低一层LSTM及之前所有层的信息作为输入,对最高层LSTM序列使用时间维度上的最大池化即可得到文本的定长向量表示(这一表示充分融合了文本的上下文信息,并且对文本进行了深层次抽象),最后我们将文本表示连接至softmax构建分类模型。
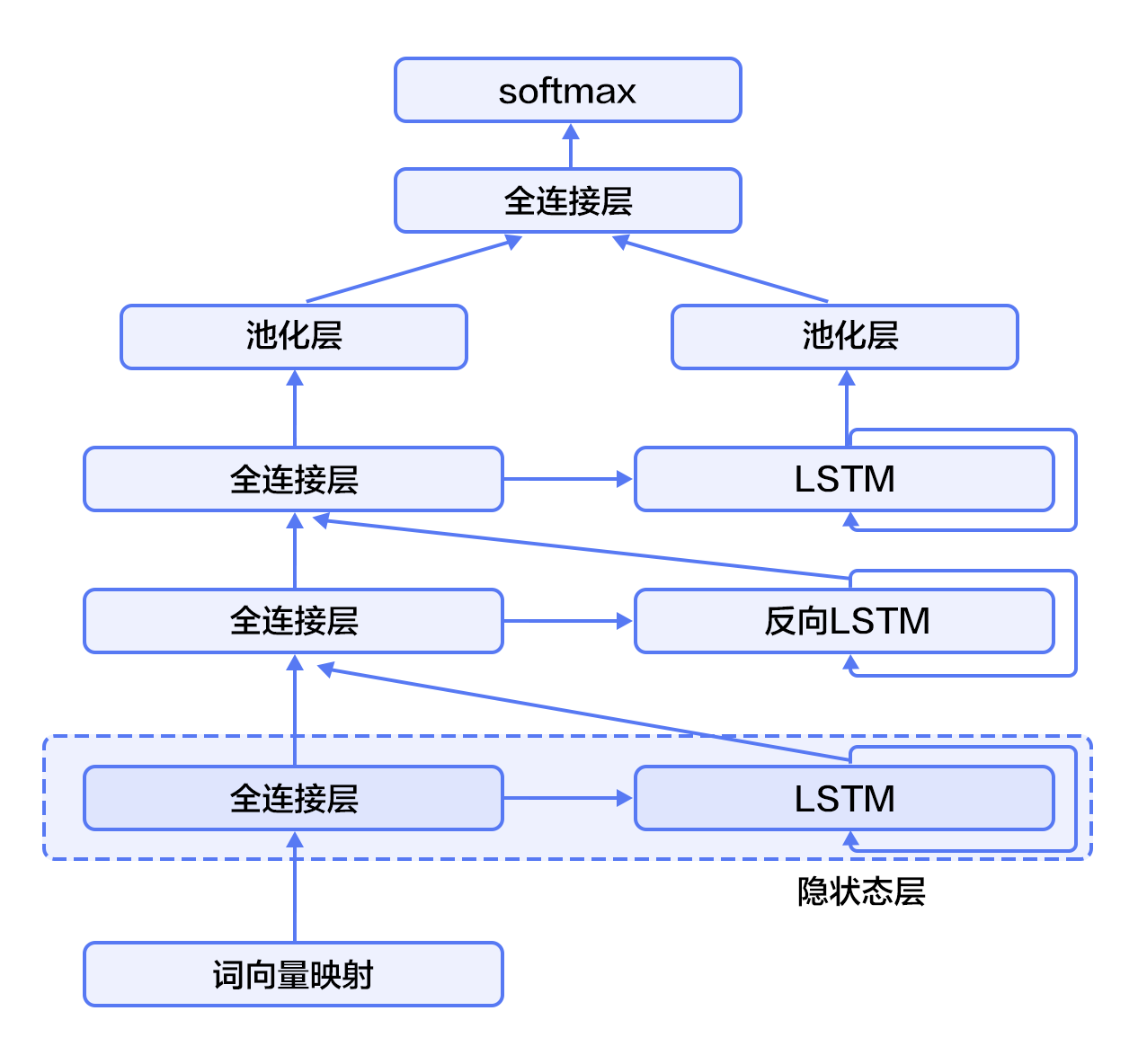
-图3. 栈式双向LSTM用于文本分类
+图4. 栈式双向LSTM用于文本分类
@@ -114,11 +119,11 @@ import numpy as np
import sys
import math
-CLASS_DIM = 2
-EMB_DIM = 128
-HID_DIM = 512
-STACKED_NUM = 3
-BATCH_SIZE = 128
+CLASS_DIM = 2 #情感分类的类别数
+EMB_DIM = 128 #词向量的维度
+HID_DIM = 512 #隐藏层的维度
+STACKED_NUM = 3 #LSTM双向栈的层数
+BATCH_SIZE = 128 #batch的大小
```
@@ -128,6 +133,7 @@ BATCH_SIZE = 128
需要注意的是:`fluid.nets.sequence_conv_pool` 包含卷积和池化层两个操作。
```python
+#文本卷积神经网络
def convolution_net(data, input_dim, class_dim, emb_dim, hid_dim):
emb = fluid.layers.embedding(
input=data, size=[input_dim, emb_dim], is_sparse=True)
@@ -157,32 +163,40 @@ def convolution_net(data, input_dim, class_dim, emb_dim, hid_dim):
栈式双向神经网络`stacked_lstm_net`的代码片段如下:
```python
+#栈式双向LSTM
def stacked_lstm_net(data, input_dim, class_dim, emb_dim, hid_dim, stacked_num):
+ #计算词向量
emb = fluid.layers.embedding(
input=data, size=[input_dim, emb_dim], is_sparse=True)
+ #第一层栈
+ #全连接层
fc1 = fluid.layers.fc(input=emb, size=hid_dim)
+ #lstm层
lstm1, cell1 = fluid.layers.dynamic_lstm(input=fc1, size=hid_dim)
inputs = [fc1, lstm1]
+ #其余的所有栈结构
for i in range(2, stacked_num + 1):
fc = fluid.layers.fc(input=inputs, size=hid_dim)
lstm, cell = fluid.layers.dynamic_lstm(
input=fc, size=hid_dim, is_reverse=(i % 2) == 0)
inputs = [fc, lstm]
+ #池化层
fc_last = fluid.layers.sequence_pool(input=inputs[0], pool_type='max')
lstm_last = fluid.layers.sequence_pool(input=inputs[1], pool_type='max')
+ #全连接层,softmax预测
prediction = fluid.layers.fc(
input=[fc_last, lstm_last], size=class_dim, act='softmax')
return prediction
```
-以上的栈式双向LSTM抽象出了高级特征并把其映射到和分类类别数同样大小的向量上。`paddle.activation.Softmax`函数用来计算分类属于某个类别的概率。
+以上的栈式双向LSTM抽象出了高级特征并把其映射到和分类类别数同样大小的向量上。最后一个全连接层的'softmax'激活函数用来计算分类属于某个类别的概率。
-重申一下,此处我们可以调用`convolution_net`或`stacked_lstm_net`的任何一个。我们以`convolution_net`为例。
+重申一下,此处我们可以调用`convolution_net`或`stacked_lstm_net`的任何一个网络结构进行训练学习。我们以`convolution_net`为例。
接下来我们定义预测程序(`inference_program`)。预测程序使用`convolution_net`来对`fluid.layer.data`的输入进行预测。
@@ -199,9 +213,9 @@ def inference_program(word_dict):
我们这里定义了`training_program`。它使用了从`inference_program`返回的结果来计算误差。我们同时定义了优化函数`optimizer_func`。
-因为是有监督的学习,训练集的标签也在`paddle.layer.data`中定义了。在训练过程中,交叉熵用来在`paddle.layer.classification_cost`中作为损失函数。
+因为是有监督的学习,训练集的标签也在`fluid.layers.data`中定义了。在训练过程中,交叉熵用来在`fluid.layer.cross_entropy`中作为损失函数。
-在测试过程中,分类器会计算各个输出的概率。第一个返回的数值规定为 损耗(cost)。
+在测试过程中,分类器会计算各个输出的概率。第一个返回的数值规定为cost。
```python
def train_program(prediction):
@@ -209,9 +223,9 @@ def train_program(prediction):
cost = fluid.layers.cross_entropy(input=prediction, label=label)
avg_cost = fluid.layers.mean(cost)
accuracy = fluid.layers.accuracy(input=prediction, label=label)
- return [avg_cost, accuracy]
-
+ return [avg_cost, accuracy] #返回平均cost和准确率acc
+#优化函数
def optimizer_func():
return fluid.optimizer.Adagrad(learning_rate=0.002)
```
@@ -224,13 +238,13 @@ def optimizer_func():
```python
-use_cuda = False
+use_cuda = False #在cpu上进行训练
place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()
```
### 定义数据提供器
-下一步是为训练和测试定义数据提供器。提供器读入一个大小为 BATCH_SIZE的数据。paddle.dataset.imdb.train 每次会在乱序化后提供一个大小为BATCH_SIZE的数据,乱序化的大小为缓存大小buf_size。
+下一步是为训练和测试定义数据提供器。提供器读入一个大小为 BATCH_SIZE的数据。paddle.dataset.imdb.word_dict 每次会在乱序化后提供一个大小为BATCH_SIZE的数据,乱序化的大小为缓存大小buf_size。
注意:读取IMDB的数据可能会花费几分钟的时间,请耐心等待。
@@ -244,31 +258,39 @@ train_reader = paddle.batch(
paddle.dataset.imdb.train(word_dict), buf_size=25000),
batch_size=BATCH_SIZE)
```
+word_dict是一个字典序列,是词和label的对应关系,运行下一行可以看到具体内容:
+```python
+word_dict
+```
+每行是如('limited': 1726)的对应关系,该行表示单词limited所对应的label是1726。
-### 构造训练器(trainer)
+### 构造训练器
训练器需要一个训练程序和一个训练优化函数。
```python
exe = fluid.Executor(place)
prediction = inference_program(word_dict)
-[avg_cost, accuracy] = train_program(prediction)
-sgd_optimizer = optimizer_func()
+[avg_cost, accuracy] = train_program(prediction)#训练程序
+sgd_optimizer = optimizer_func()#训练优化函数
sgd_optimizer.minimize(avg_cost)
```
### 提供数据并构建主训练循环
-`feed_order`用来定义每条产生的数据和`paddle.layer.data`之间的映射关系。比如,`imdb.train`产生的第一列的数据对应的是`words`这个特征。
+`feed_order`用来定义每条产生的数据和`fluid.layers.data`之间的映射关系。比如,`imdb.train`产生的第一列的数据对应的是`words`这个特征。
```python
# Specify the directory path to save the parameters
params_dirname = "understand_sentiment_conv.inference.model"
feed_order = ['words', 'label']
-pass_num = 1
+pass_num = 1 #训练循环的轮数
+#程序主循环部分
def train_loop(main_program):
+ #启动上文构建的训练器
exe.run(fluid.default_startup_program())
+
feed_var_list_loop = [
main_program.global_block().var(var_name) for var_name in feed_order
]
@@ -277,12 +299,15 @@ def train_loop(main_program):
test_program = fluid.default_main_program().clone(for_test=True)
+ #训练循环
for epoch_id in range(pass_num):
for step_id, data in enumerate(train_reader()):
+ #运行训练器
metrics = exe.run(main_program,
feed=feeder.feed(data),
fetch_list=[avg_cost, accuracy])
+ #测试结果
avg_cost_test, acc_test = train_test(test_program, test_reader)
print('Step {0}, Test Loss {1:0.2}, Acc {2:0.2}'.format(
step_id, avg_cost_test, acc_test))
@@ -294,7 +319,7 @@ def train_loop(main_program):
if step_id == 30:
if params_dirname is not None:
fluid.io.save_inference_model(params_dirname, ["words"],
- prediction, exe)
+ prediction, exe)#保存模型
return
```
@@ -325,7 +350,7 @@ inference_scope = fluid.core.Scope()
### 生成测试用输入数据
为了进行预测,我们任意选取3个评论。请随意选取您看好的3个。我们把评论中的每个词对应到`word_dict`中的id。如果词典中没有这个词,则设为`unknown`。
-然后我们用`create_lod_tensor`来创建细节层次的张量。
+然后我们用`create_lod_tensor`来创建细节层次的张量,关于该函数的详细解释请参照[API文档](http://paddlepaddle.org/documentation/docs/zh/1.2/user_guides/howto/basic_concept/lod_tensor.html)。
```python
reviews_str = [
diff --git a/06.understand_sentiment/index.cn.html b/06.understand_sentiment/index.cn.html
index b9de3f8b74218e9870aa7889a81624c0453a2b06..f1817c137359047d628e4f1cbe0fe0c6e84096e1 100644
--- a/06.understand_sentiment/index.cn.html
+++ b/06.understand_sentiment/index.cn.html
@@ -70,7 +70,12 @@
我们在[推荐系统](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system)一节介绍过应用于文本数据的卷积神经网络模型的计算过程,这里进行一个简单的回顾。
-对卷积神经网络来说,首先使用卷积处理输入的词向量序列,产生一个特征图(feature map),对特征图采用时间维度上的最大池化(max pooling over time)操作得到此卷积核对应的整句话的特征,最后,将所有卷积核得到的特征拼接起来即为文本的定长向量表示,对于文本分类问题,将其连接至softmax即构建出完整的模型。在实际应用中,我们会使用多个卷积核来处理句子,窗口大小相同的卷积核堆叠起来形成一个矩阵,这样可以更高效的完成运算。另外,我们也可使用窗口大小不同的卷积核来处理句子,[推荐系统](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system)一节的图3作为示意画了四个卷积核,不同颜色表示不同大小的卷积核操作。
+对卷积神经网络来说,首先使用卷积处理输入的词向量序列,产生一个特征图(feature map),对特征图采用时间维度上的最大池化(max pooling over time)操作得到此卷积核对应的整句话的特征,最后,将所有卷积核得到的特征拼接起来即为文本的定长向量表示,对于文本分类问题,将其连接至softmax即构建出完整的模型。在实际应用中,我们会使用多个卷积核来处理句子,窗口大小相同的卷积核堆叠起来形成一个矩阵,这样可以更高效的完成运算。另外,我们也可使用窗口大小不同的卷积核来处理句子,[推荐系统](https://github.com/PaddlePaddle/book/tree/develop/05.recommender_system)一节的图3作为示意画了四个卷积核,既文本图1,不同颜色表示不同大小的卷积核操作。
+
+
+
+图1. 卷积神经网络文本分类模型
+
对于一般的短文本分类问题,上文所述的简单的文本卷积网络即可达到很高的正确率\[[1](#参考文献)\]。若想得到更抽象更高级的文本特征表示,可以构建深层文本卷积神经网络\[[2](#参考文献),[3](#参考文献)\]。
@@ -80,16 +85,16 @@

-图1. 循环神经网络按时间展开的示意图
+图2. 循环神经网络按时间展开的示意图
-循环神经网络按时间展开后如图1所示:在第$t$时刻,网络读入第$t$个输入$x_t$(向量表示)及前一时刻隐层的状态值$h_{t-1}$(向量表示,$h_0$一般初始化为$0$向量),计算得出本时刻隐层的状态值$h_t$,重复这一步骤直至读完所有输入。如果将循环神经网络所表示的函数记为$f$,则其公式可表示为:
+循环神经网络按时间展开后如图2所示:在第$t$时刻,网络读入第$t$个输入$x_t$(向量表示)及前一时刻隐层的状态值$h_{t-1}$(向量表示,$h_0$一般初始化为$0$向量),计算得出本时刻隐层的状态值$h_t$,重复这一步骤直至读完所有输入。如果将循环神经网络所表示的函数记为$f$,则其公式可表示为:
$$h_t=f(x_t,h_{t-1})=\sigma(W_{xh}x_t+W_{hh}h_{t-1}+b_h)$$
其中$W_{xh}$是输入到隐层的矩阵参数,$W_{hh}$是隐层到隐层的矩阵参数,$b_h$为隐层的偏置向量(bias)参数,$\sigma$为$sigmoid$函数。
-在处理自然语言时,一般会先将词(one-hot表示)映射为其词向量(word embedding)表示,然后再作为循环神经网络每一时刻的输入$x_t$。此外,可以根据实际需要的不同在循环神经网络的隐层上连接其它层。如,可以把一个循环神经网络的隐层输出连接至下一个循环神经网络的输入构建深层(deep or stacked)循环神经网络,或者提取最后一个时刻的隐层状态作为句子表示进而使用分类模型等等。
+在处理自然语言时,一般会先将词(one-hot表示)映射为其词向量表示,然后再作为循环神经网络每一时刻的输入$x_t$。此外,可以根据实际需要的不同在循环神经网络的隐层上连接其它层。如,可以把一个循环神经网络的隐层输出连接至下一个循环神经网络的输入构建深层(deep or stacked)循环神经网络,或者提取最后一个时刻的隐层状态作为句子表示进而使用分类模型等等。
### 长短期记忆网络(LSTM)
@@ -105,11 +110,11 @@ $$ f_t = \sigma(W_{xf}x_t+W_{hf}h_{t-1}+W_{cf}c_{t-1}+b_f) $$
$$ c_t = f_t\odot c_{t-1}+i_t\odot tanh(W_{xc}x_t+W_{hc}h_{t-1}+b_c) $$
$$ o_t = \sigma(W_{xo}x_t+W_{ho}h_{t-1}+W_{co}c_{t}+b_o) $$
$$ h_t = o_t\odot tanh(c_t) $$
-其中,$i_t, f_t, c_t, o_t$分别表示输入门,遗忘门,记忆单元及输出门的向量值,带角标的$W$及$b$为模型参数,$tanh$为双曲正切函数,$\odot$表示逐元素(elementwise)的乘法操作。输入门控制着新输入进入记忆单元$c$的强度,遗忘门控制着记忆单元维持上一时刻值的强度,输出门控制着输出记忆单元的强度。三种门的计算方式类似,但有着完全不同的参数,它们各自以不同的方式控制着记忆单元$c$,如图2所示:
+其中,$i_t, f_t, c_t, o_t$分别表示输入门,遗忘门,记忆单元及输出门的向量值,带角标的$W$及$b$为模型参数,$tanh$为双曲正切函数,$\odot$表示逐元素(elementwise)的乘法操作。输入门控制着新输入进入记忆单元$c$的强度,遗忘门控制着记忆单元维持上一时刻值的强度,输出门控制着输出记忆单元的强度。三种门的计算方式类似,但有着完全不同的参数,它们各自以不同的方式控制着记忆单元$c$,如图3所示:

-图2. 时刻$t$的LSTM [7]
+图3. 时刻$t$的LSTM [7]
LSTM通过给简单的循环神经网络增加记忆及控制门的方式,增强了其处理远距离依赖问题的能力。类似原理的改进还有Gated Recurrent Unit (GRU)\[[8](#参考文献)\],其设计更为简洁一些。**这些改进虽然各有不同,但是它们的宏观描述却与简单的循环神经网络一样(如图2所示),即隐状态依据当前输入及前一时刻的隐状态来改变,不断地循环这一过程直至输入处理完毕:**
@@ -122,11 +127,11 @@ $$ h_t=Recrurent(x_t,h_{t-1})$$
对于正常顺序的循环神经网络,$h_t$包含了$t$时刻之前的输入信息,也就是上文信息。同样,为了得到下文信息,我们可以使用反方向(将输入逆序处理)的循环神经网络。结合构建深层循环神经网络的方法(深层神经网络往往能得到更抽象和高级的特征表示),我们可以通过构建更加强有力的基于LSTM的栈式双向循环神经网络\[[9](#参考文献)\],来对时序数据进行建模。
-如图3所示(以三层为例),奇数层LSTM正向,偶数层LSTM反向,高一层的LSTM使用低一层LSTM及之前所有层的信息作为输入,对最高层LSTM序列使用时间维度上的最大池化即可得到文本的定长向量表示(这一表示充分融合了文本的上下文信息,并且对文本进行了深层次抽象),最后我们将文本表示连接至softmax构建分类模型。
+如图4所示(以三层为例),奇数层LSTM正向,偶数层LSTM反向,高一层的LSTM使用低一层LSTM及之前所有层的信息作为输入,对最高层LSTM序列使用时间维度上的最大池化即可得到文本的定长向量表示(这一表示充分融合了文本的上下文信息,并且对文本进行了深层次抽象),最后我们将文本表示连接至softmax构建分类模型。

-图3. 栈式双向LSTM用于文本分类
+图4. 栈式双向LSTM用于文本分类
@@ -156,11 +161,11 @@ import numpy as np
import sys
import math
-CLASS_DIM = 2
-EMB_DIM = 128
-HID_DIM = 512
-STACKED_NUM = 3
-BATCH_SIZE = 128
+CLASS_DIM = 2 #情感分类的类别数
+EMB_DIM = 128 #词向量的维度
+HID_DIM = 512 #隐藏层的维度
+STACKED_NUM = 3 #LSTM双向栈的层数
+BATCH_SIZE = 128 #batch的大小
```
@@ -170,6 +175,7 @@ BATCH_SIZE = 128
需要注意的是:`fluid.nets.sequence_conv_pool` 包含卷积和池化层两个操作。
```python
+#文本卷积神经网络
def convolution_net(data, input_dim, class_dim, emb_dim, hid_dim):
emb = fluid.layers.embedding(
input=data, size=[input_dim, emb_dim], is_sparse=True)
@@ -199,32 +205,40 @@ def convolution_net(data, input_dim, class_dim, emb_dim, hid_dim):
栈式双向神经网络`stacked_lstm_net`的代码片段如下:
```python
+#栈式双向LSTM
def stacked_lstm_net(data, input_dim, class_dim, emb_dim, hid_dim, stacked_num):
+ #计算词向量
emb = fluid.layers.embedding(
input=data, size=[input_dim, emb_dim], is_sparse=True)
+ #第一层栈
+ #全连接层
fc1 = fluid.layers.fc(input=emb, size=hid_dim)
+ #lstm层
lstm1, cell1 = fluid.layers.dynamic_lstm(input=fc1, size=hid_dim)
inputs = [fc1, lstm1]
+ #其余的所有栈结构
for i in range(2, stacked_num + 1):
fc = fluid.layers.fc(input=inputs, size=hid_dim)
lstm, cell = fluid.layers.dynamic_lstm(
input=fc, size=hid_dim, is_reverse=(i % 2) == 0)
inputs = [fc, lstm]
+ #池化层
fc_last = fluid.layers.sequence_pool(input=inputs[0], pool_type='max')
lstm_last = fluid.layers.sequence_pool(input=inputs[1], pool_type='max')
+ #全连接层,softmax预测
prediction = fluid.layers.fc(
input=[fc_last, lstm_last], size=class_dim, act='softmax')
return prediction
```
-以上的栈式双向LSTM抽象出了高级特征并把其映射到和分类类别数同样大小的向量上。`paddle.activation.Softmax`函数用来计算分类属于某个类别的概率。
+以上的栈式双向LSTM抽象出了高级特征并把其映射到和分类类别数同样大小的向量上。最后一个全连接层的'softmax'激活函数用来计算分类属于某个类别的概率。
-重申一下,此处我们可以调用`convolution_net`或`stacked_lstm_net`的任何一个。我们以`convolution_net`为例。
+重申一下,此处我们可以调用`convolution_net`或`stacked_lstm_net`的任何一个网络结构进行训练学习。我们以`convolution_net`为例。
接下来我们定义预测程序(`inference_program`)。预测程序使用`convolution_net`来对`fluid.layer.data`的输入进行预测。
@@ -241,9 +255,9 @@ def inference_program(word_dict):
我们这里定义了`training_program`。它使用了从`inference_program`返回的结果来计算误差。我们同时定义了优化函数`optimizer_func`。
-因为是有监督的学习,训练集的标签也在`paddle.layer.data`中定义了。在训练过程中,交叉熵用来在`paddle.layer.classification_cost`中作为损失函数。
+因为是有监督的学习,训练集的标签也在`fluid.layers.data`中定义了。在训练过程中,交叉熵用来在`fluid.layer.cross_entropy`中作为损失函数。
-在测试过程中,分类器会计算各个输出的概率。第一个返回的数值规定为 损耗(cost)。
+在测试过程中,分类器会计算各个输出的概率。第一个返回的数值规定为cost。
```python
def train_program(prediction):
@@ -251,9 +265,9 @@ def train_program(prediction):
cost = fluid.layers.cross_entropy(input=prediction, label=label)
avg_cost = fluid.layers.mean(cost)
accuracy = fluid.layers.accuracy(input=prediction, label=label)
- return [avg_cost, accuracy]
-
+ return [avg_cost, accuracy] #返回平均cost和准确率acc
+#优化函数
def optimizer_func():
return fluid.optimizer.Adagrad(learning_rate=0.002)
```
@@ -266,13 +280,13 @@ def optimizer_func():
```python
-use_cuda = False
+use_cuda = False #在cpu上进行训练
place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()
```
### 定义数据提供器
-下一步是为训练和测试定义数据提供器。提供器读入一个大小为 BATCH_SIZE的数据。paddle.dataset.imdb.train 每次会在乱序化后提供一个大小为BATCH_SIZE的数据,乱序化的大小为缓存大小buf_size。
+下一步是为训练和测试定义数据提供器。提供器读入一个大小为 BATCH_SIZE的数据。paddle.dataset.imdb.word_dict 每次会在乱序化后提供一个大小为BATCH_SIZE的数据,乱序化的大小为缓存大小buf_size。
注意:读取IMDB的数据可能会花费几分钟的时间,请耐心等待。
@@ -286,31 +300,39 @@ train_reader = paddle.batch(
paddle.dataset.imdb.train(word_dict), buf_size=25000),
batch_size=BATCH_SIZE)
```
+word_dict是一个字典序列,是词和label的对应关系,运行下一行可以看到具体内容:
+```python
+word_dict
+```
+每行是如('limited': 1726)的对应关系,该行表示单词limited所对应的label是1726。
-### 构造训练器(trainer)
+### 构造训练器
训练器需要一个训练程序和一个训练优化函数。
```python
exe = fluid.Executor(place)
prediction = inference_program(word_dict)
-[avg_cost, accuracy] = train_program(prediction)
-sgd_optimizer = optimizer_func()
+[avg_cost, accuracy] = train_program(prediction)#训练程序
+sgd_optimizer = optimizer_func()#训练优化函数
sgd_optimizer.minimize(avg_cost)
```
### 提供数据并构建主训练循环
-`feed_order`用来定义每条产生的数据和`paddle.layer.data`之间的映射关系。比如,`imdb.train`产生的第一列的数据对应的是`words`这个特征。
+`feed_order`用来定义每条产生的数据和`fluid.layers.data`之间的映射关系。比如,`imdb.train`产生的第一列的数据对应的是`words`这个特征。
```python
# Specify the directory path to save the parameters
params_dirname = "understand_sentiment_conv.inference.model"
feed_order = ['words', 'label']
-pass_num = 1
+pass_num = 1 #训练循环的轮数
+#程序主循环部分
def train_loop(main_program):
+ #启动上文构建的训练器
exe.run(fluid.default_startup_program())
+
feed_var_list_loop = [
main_program.global_block().var(var_name) for var_name in feed_order
]
@@ -319,12 +341,15 @@ def train_loop(main_program):
test_program = fluid.default_main_program().clone(for_test=True)
+ #训练循环
for epoch_id in range(pass_num):
for step_id, data in enumerate(train_reader()):
+ #运行训练器
metrics = exe.run(main_program,
feed=feeder.feed(data),
fetch_list=[avg_cost, accuracy])
+ #测试结果
avg_cost_test, acc_test = train_test(test_program, test_reader)
print('Step {0}, Test Loss {1:0.2}, Acc {2:0.2}'.format(
step_id, avg_cost_test, acc_test))
@@ -336,7 +361,7 @@ def train_loop(main_program):
if step_id == 30:
if params_dirname is not None:
fluid.io.save_inference_model(params_dirname, ["words"],
- prediction, exe)
+ prediction, exe)#保存模型
return
```
@@ -367,7 +392,7 @@ inference_scope = fluid.core.Scope()
### 生成测试用输入数据
为了进行预测,我们任意选取3个评论。请随意选取您看好的3个。我们把评论中的每个词对应到`word_dict`中的id。如果词典中没有这个词,则设为`unknown`。
-然后我们用`create_lod_tensor`来创建细节层次的张量。
+然后我们用`create_lod_tensor`来创建细节层次的张量,关于该函数的详细解释请参照[API文档](http://paddlepaddle.org/documentation/docs/zh/1.2/user_guides/howto/basic_concept/lod_tensor.html)。
```python
reviews_str = [








