Merge pull request #1 from PaddlePaddle/develop
pull new commits
Showing
136.8 KB
fit_a_line/image/ranges_en.png
0 → 100644
29.6 KB
fit_a_line/index.en.html
0 → 100644
226.4 KB
135.9 KB
95.9 KB
2.3 MB
此差异已折叠。
此差异已折叠。
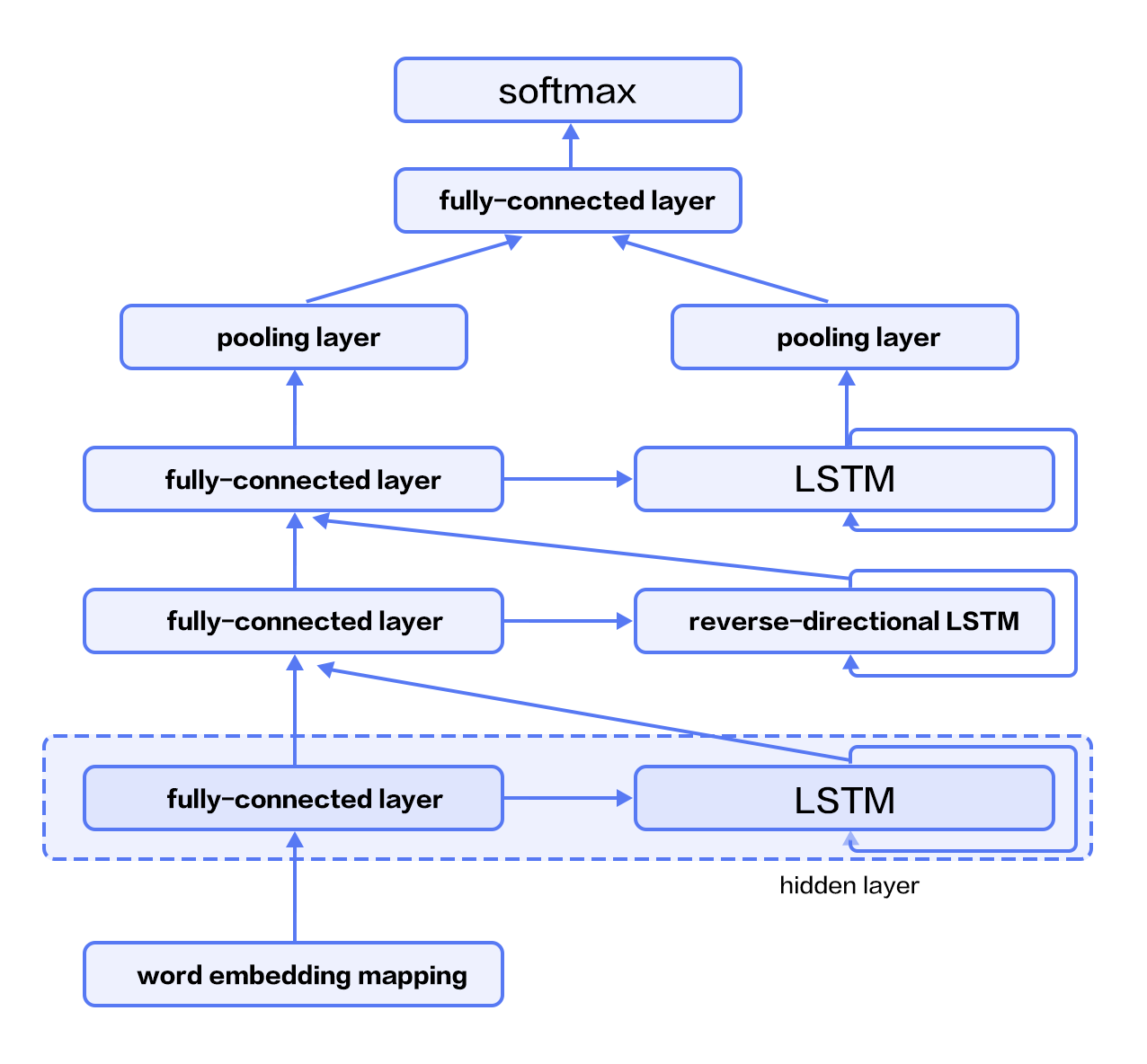
label_semantic_roles/README.en.md
0 → 100644
此差异已折叠。
label_semantic_roles/api_train.py
0 → 100644
此差异已折叠。
176.3 KB
85.7 KB
49.7 KB
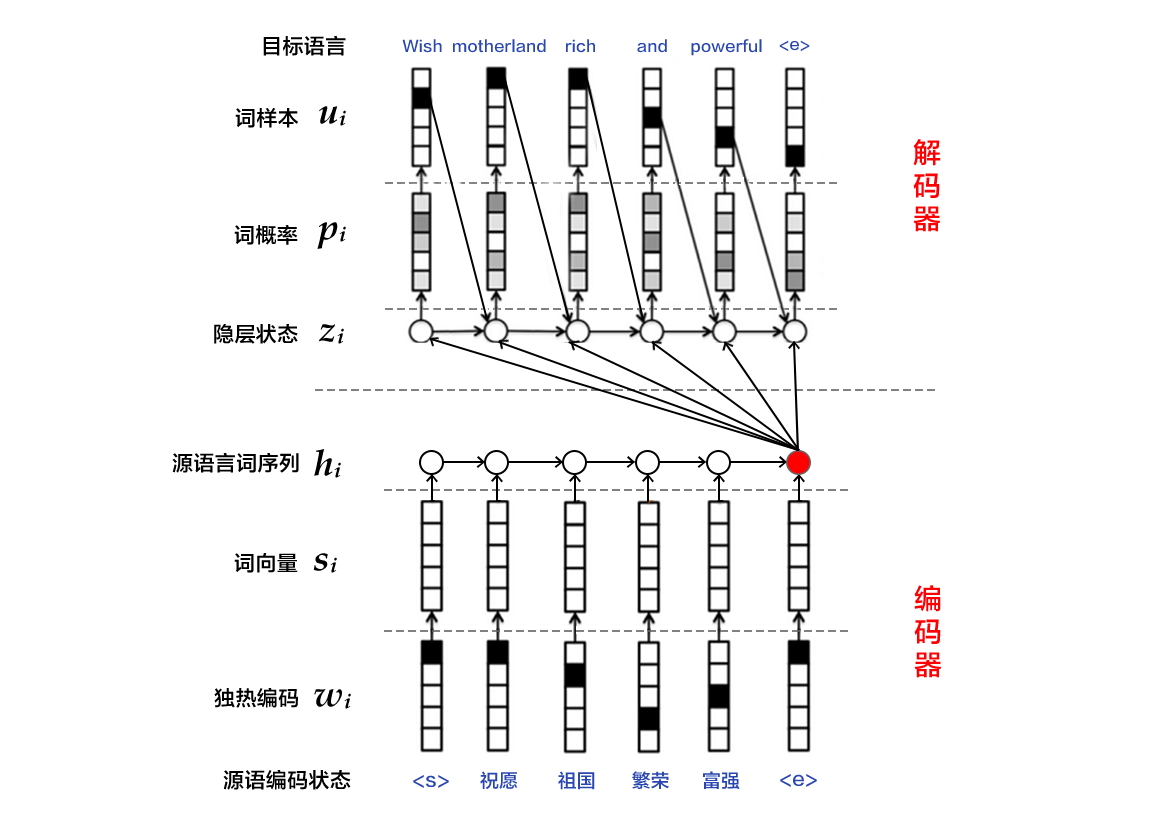
| W: | H:
| W: | H:


130.7 KB
49.2 KB
31.3 KB
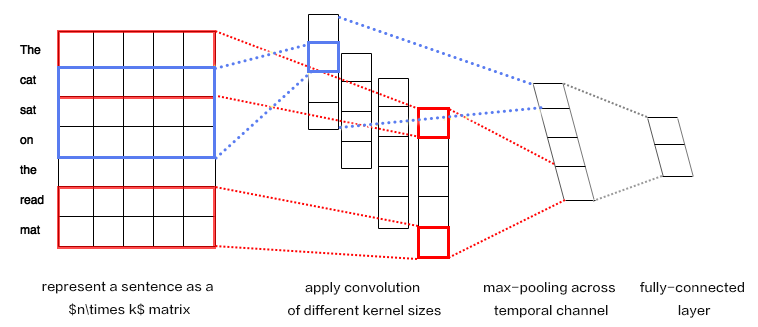
machine_translation/index.en.html
0 → 100644
此差异已折叠。
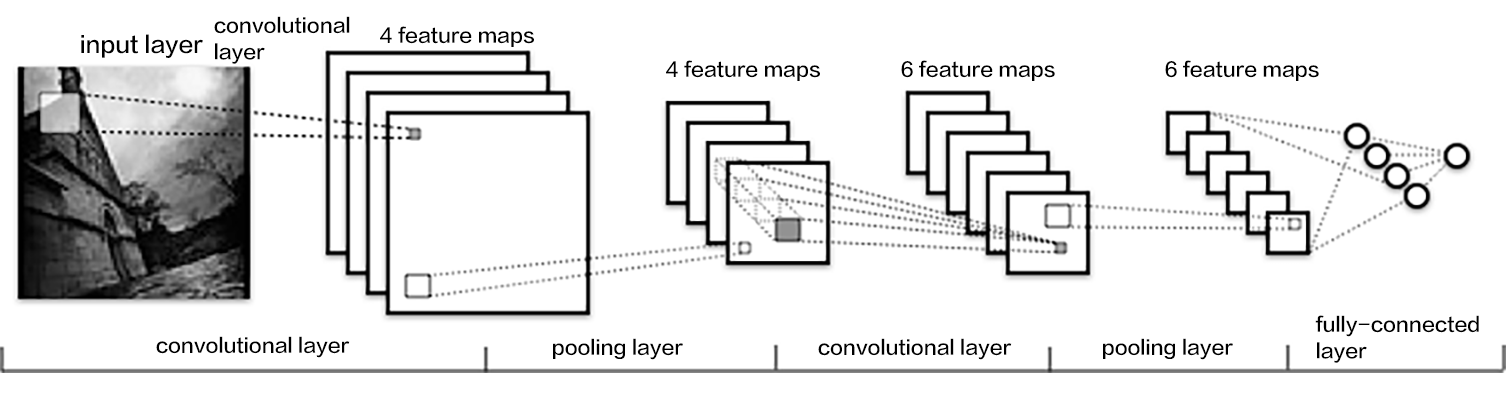
recognize_digits/image/cnn_en.png
0 → 100755
51.0 KB
82.6 KB
248.5 KB
19.5 KB
recognize_digits/image/mlp_en.png
0 → 100755
190.2 KB
142.2 KB
424.5 KB
125.7 KB
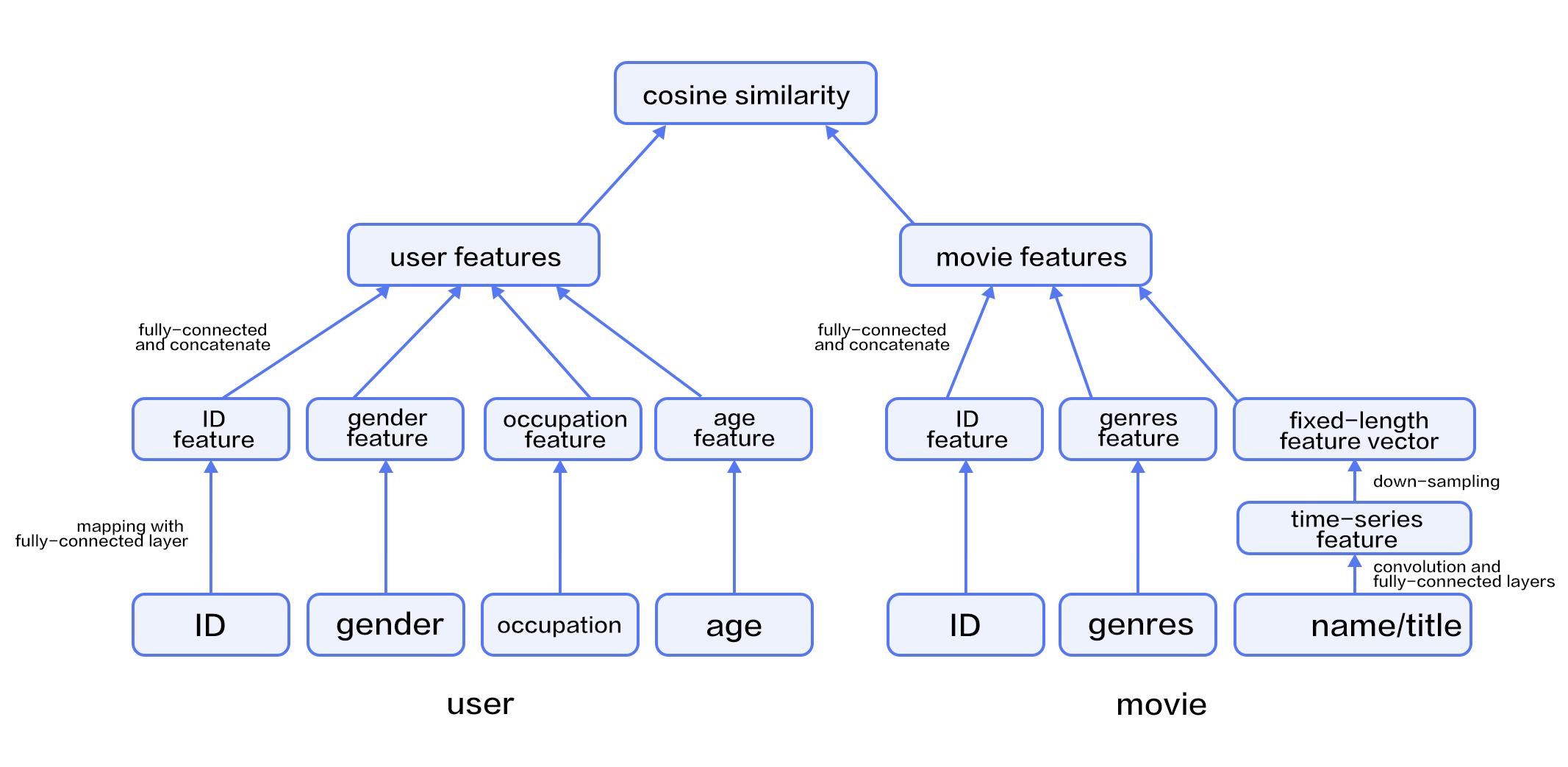
recommender_system/README.en.md
0 → 100644
此差异已折叠。
322.8 KB
264.7 KB
103.0 KB
recommender_system/index.en.html
0 → 100644
此差异已折叠。
89.0 KB
65.9 KB
32.1 KB
此差异已折叠。
此差异已折叠。
word2vec/data/getdata.sh
已删除
100755 → 0
word2vec/dataprovider.py
已删除
100644 → 0
此差异已折叠。
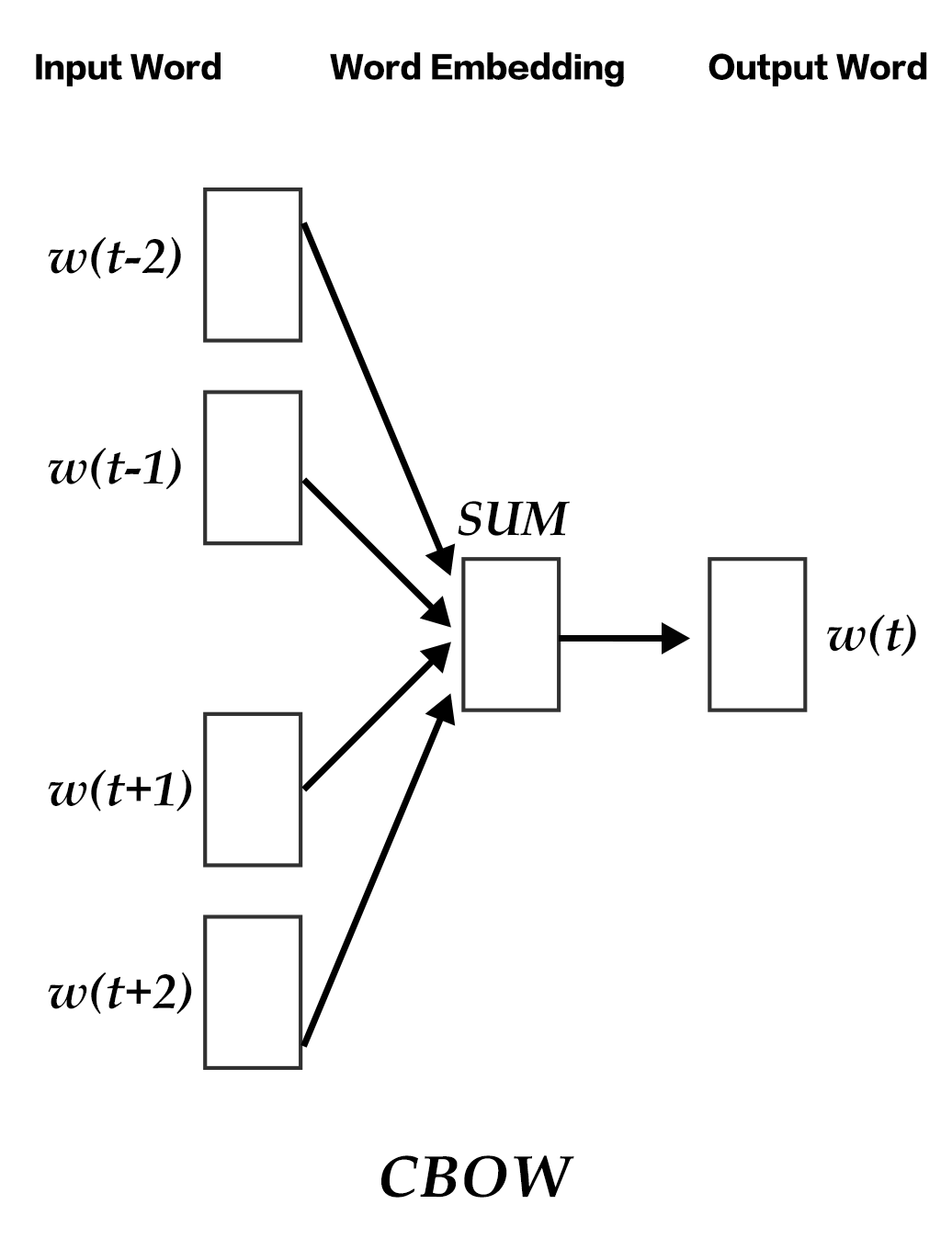
word2vec/image/cbow_en.png
0 → 100755
56.4 KB
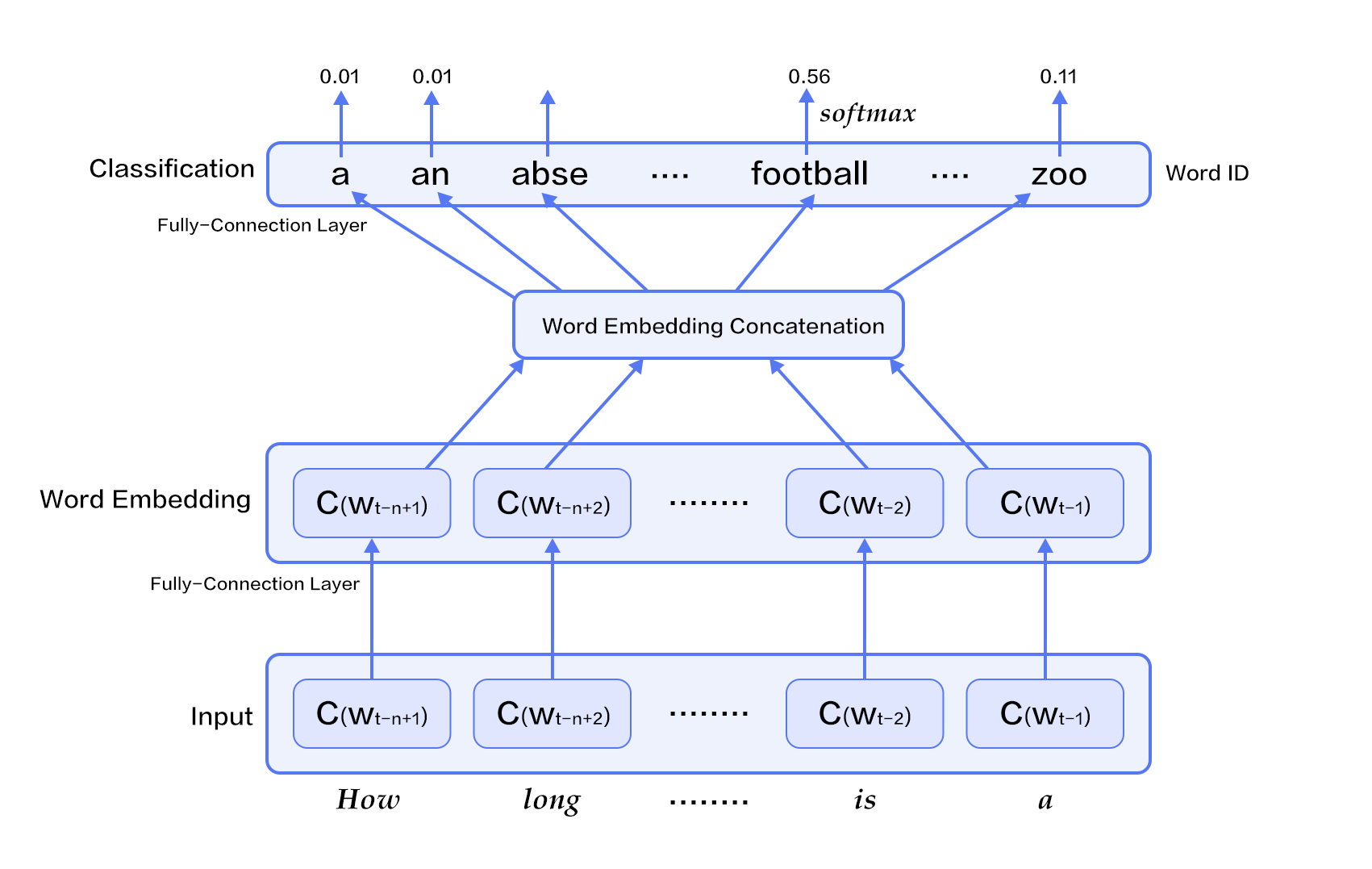
word2vec/image/ngram.en.png
0 → 100755
56.3 KB
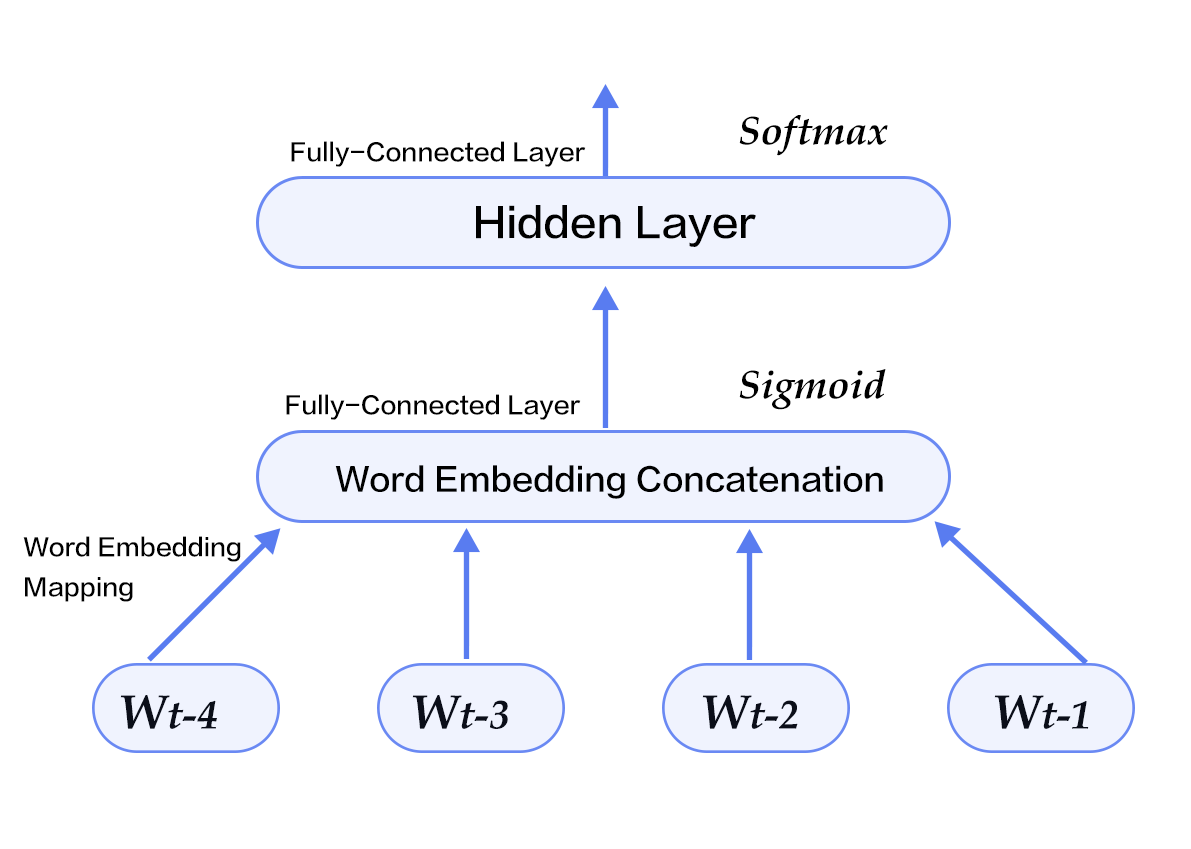
word2vec/image/nnlm_en.png
0 → 100755
82.4 KB
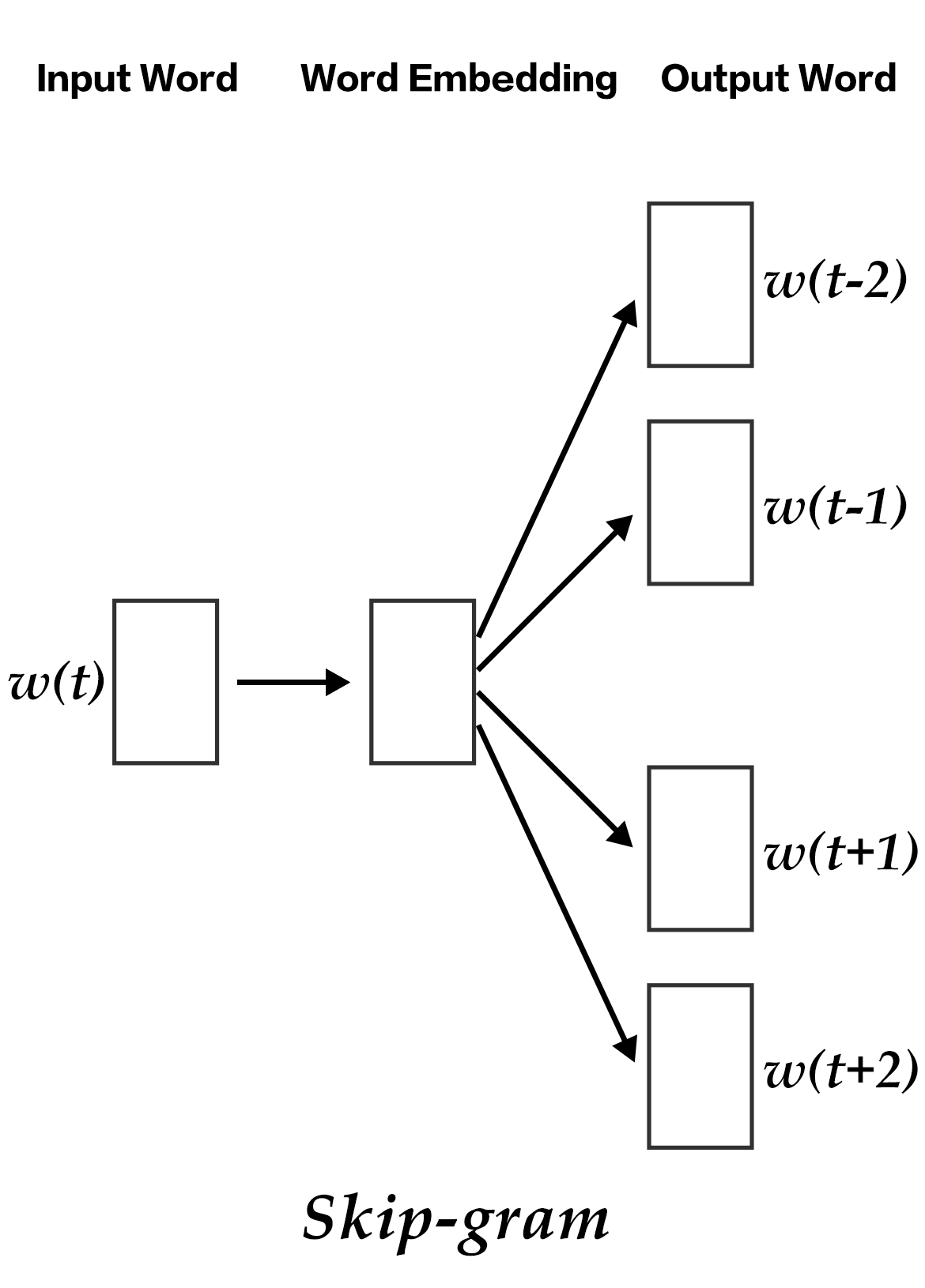
word2vec/image/skipgram_en.png
0 → 100755
67.1 KB
word2vec/index.en.html
0 → 100644
此差异已折叠。
word2vec/ngram.py
已删除
100644 → 0
此差异已折叠。
word2vec/train.py
0 → 100644
此差异已折叠。
word2vec/train.sh
已删除
100755 → 0
此差异已折叠。