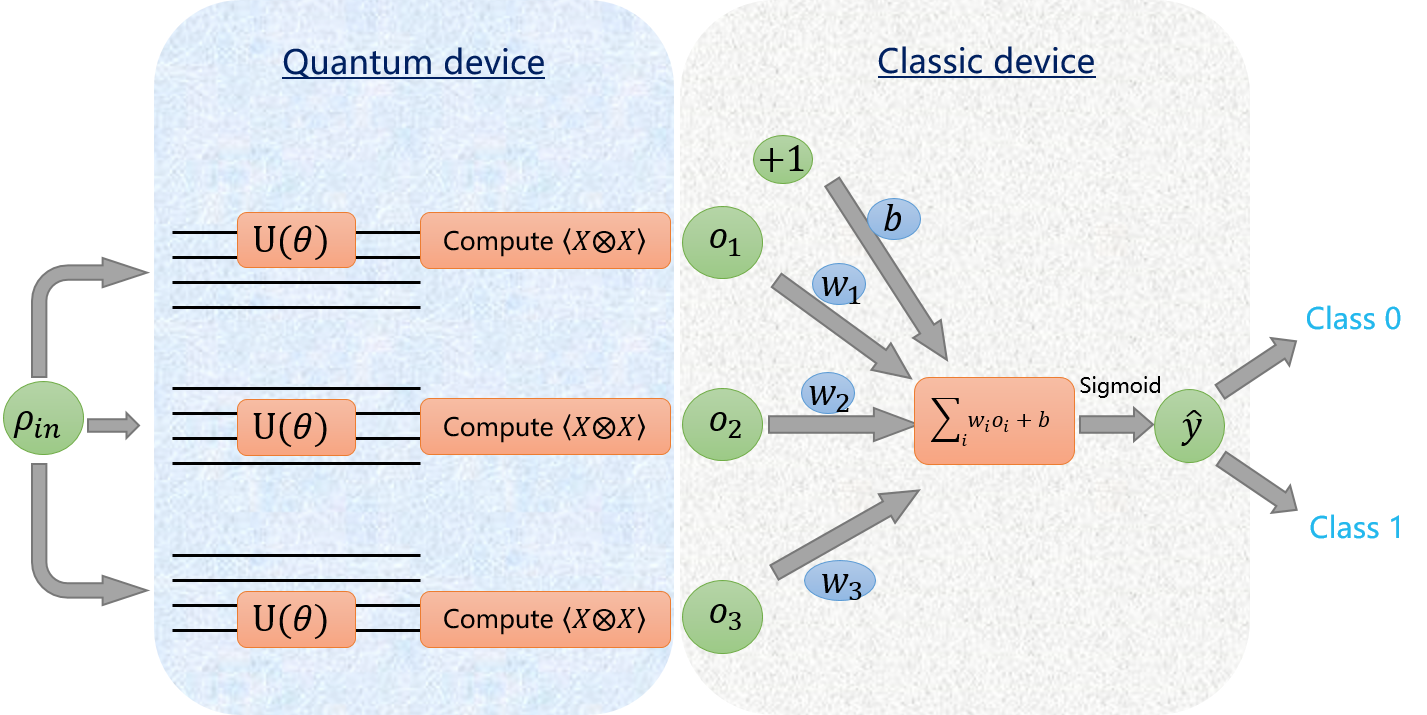
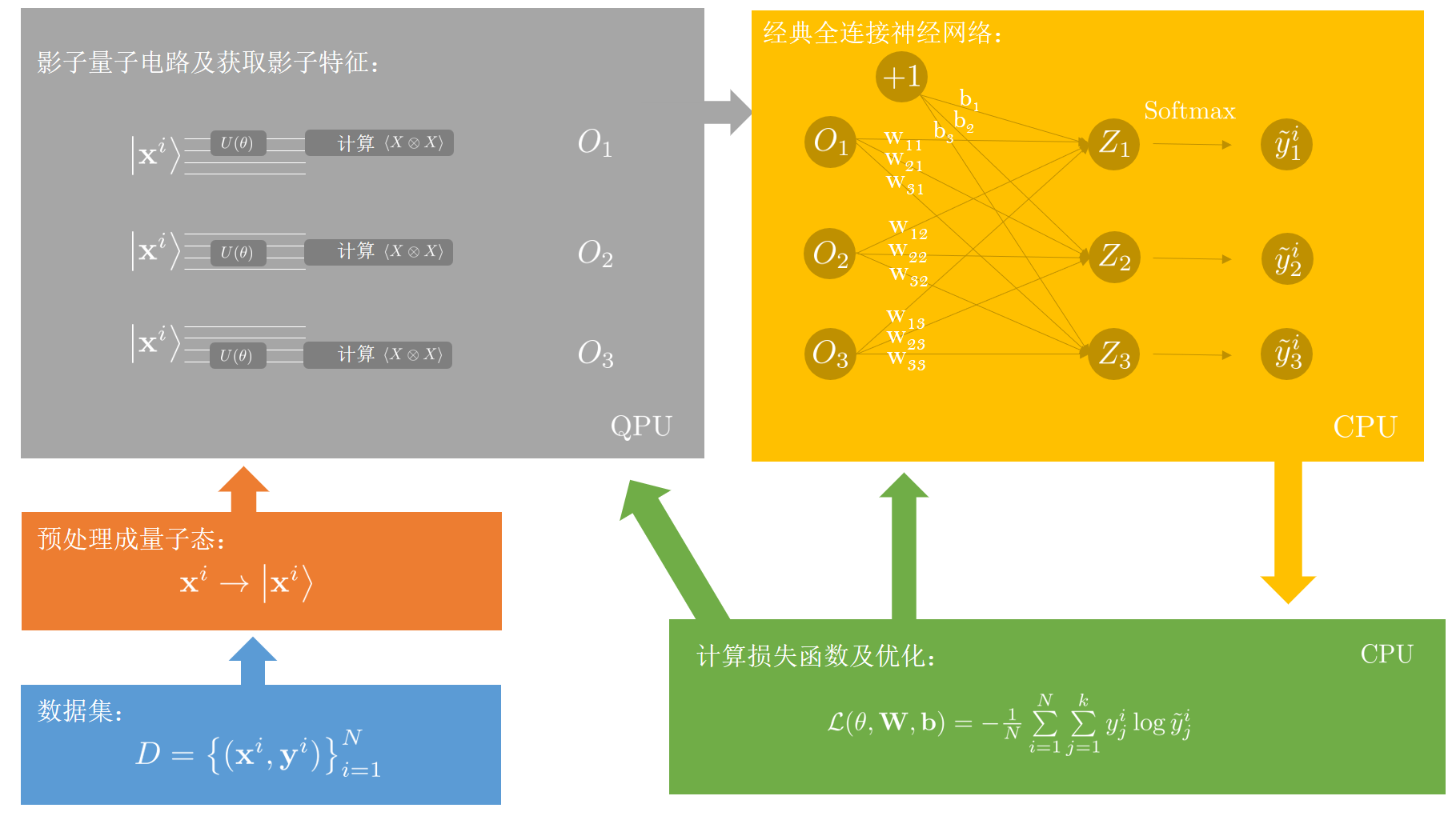
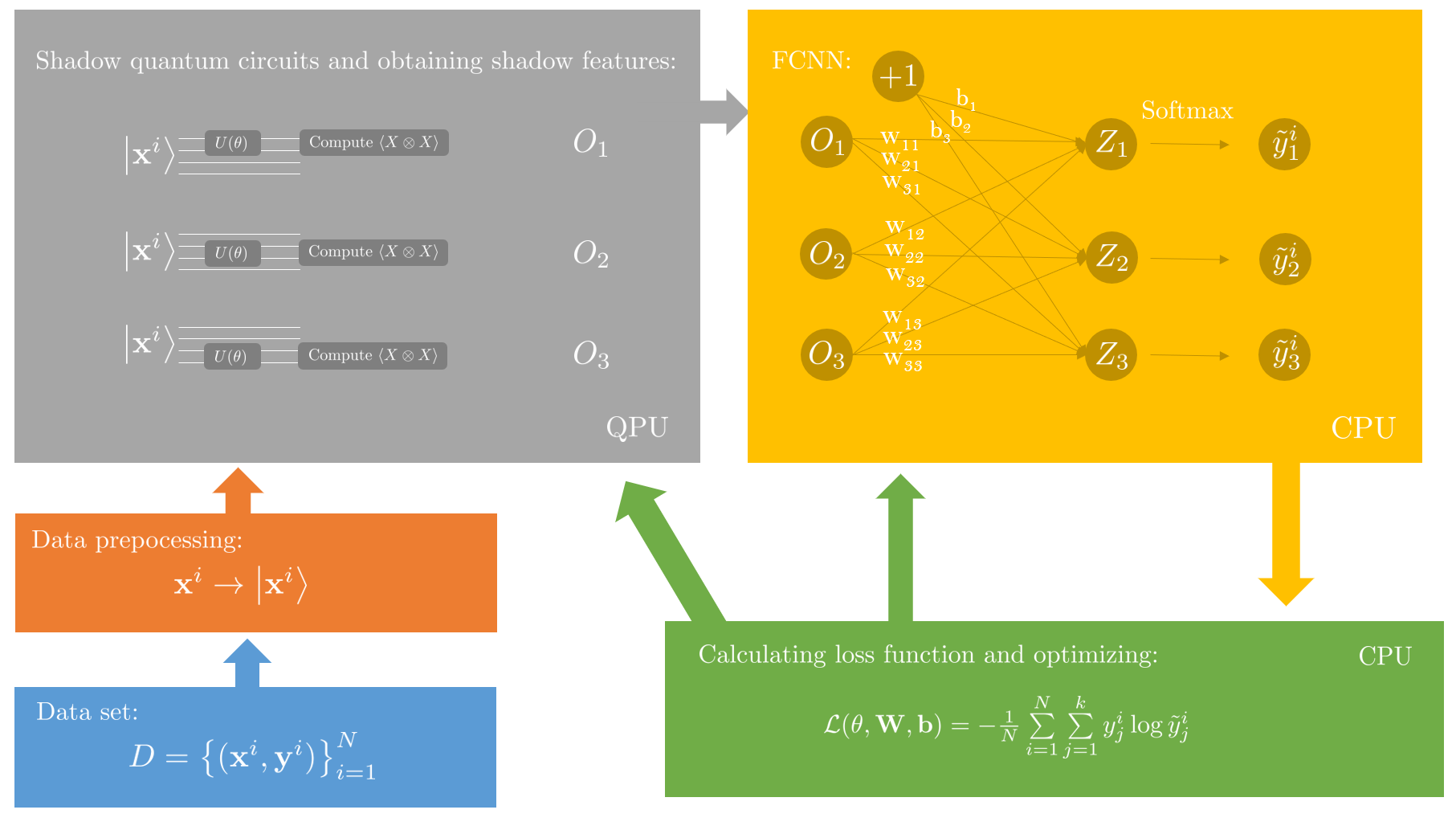
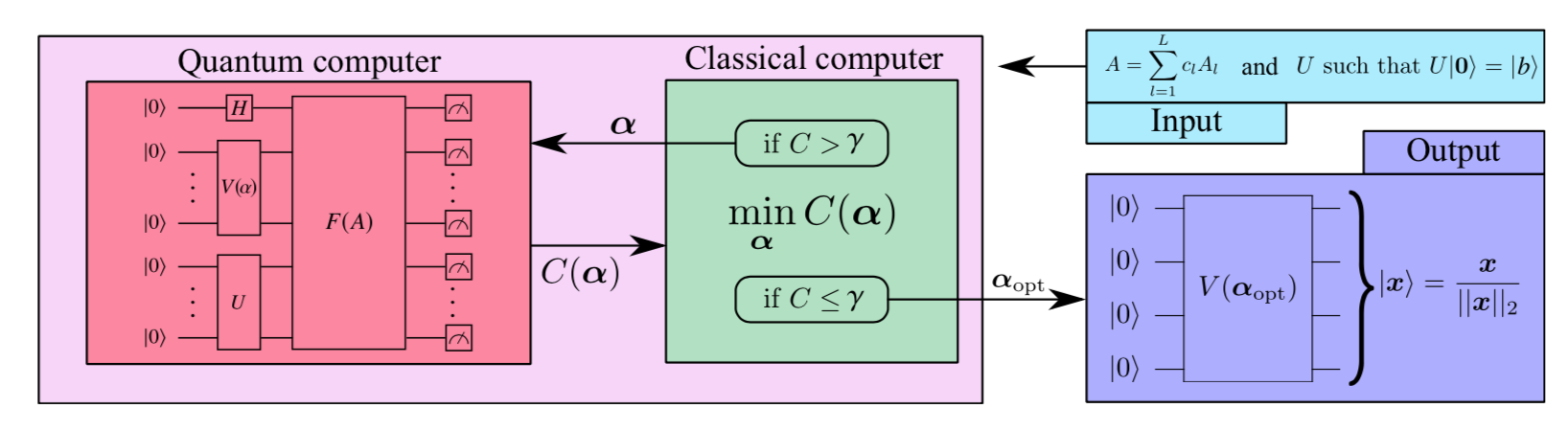
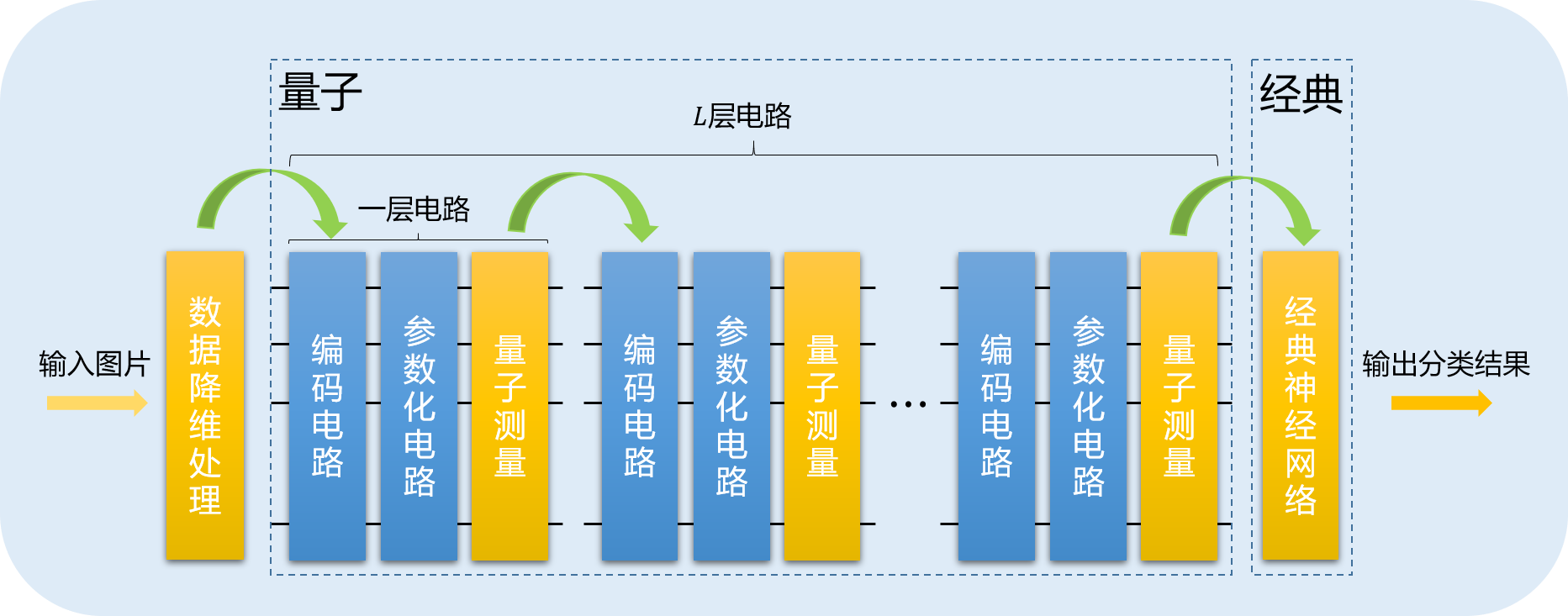
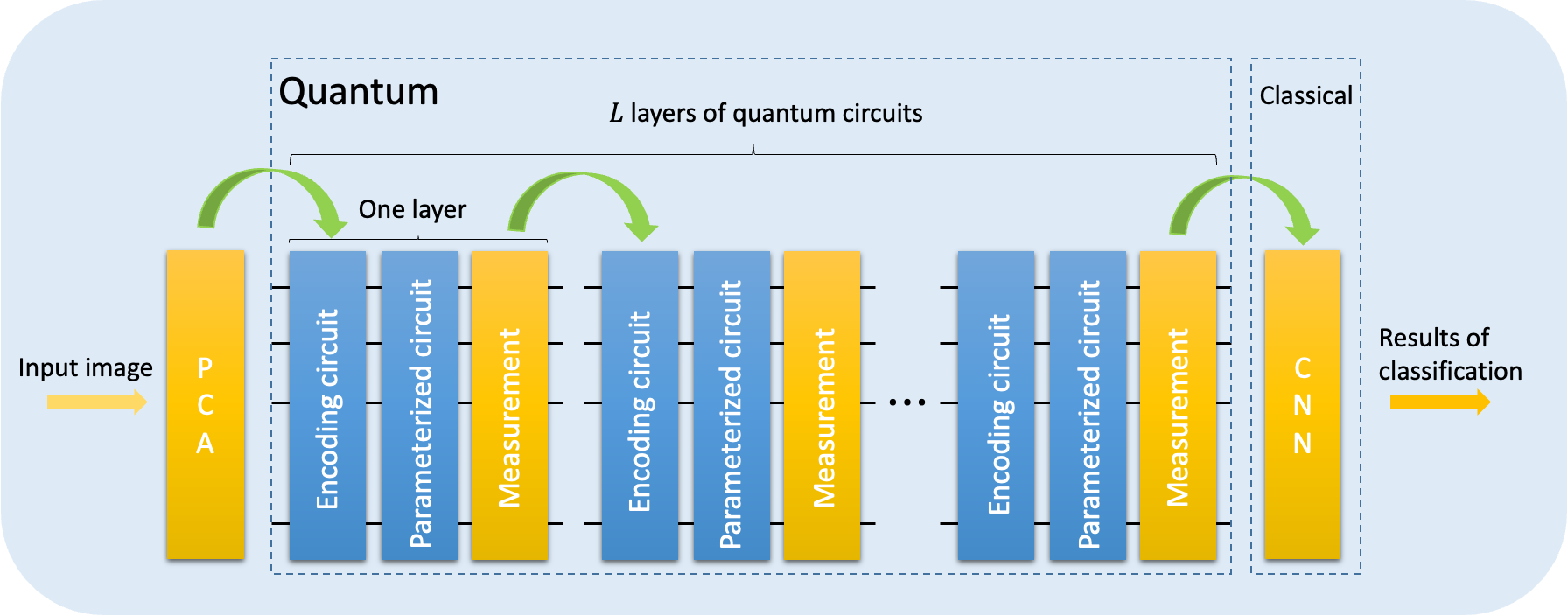
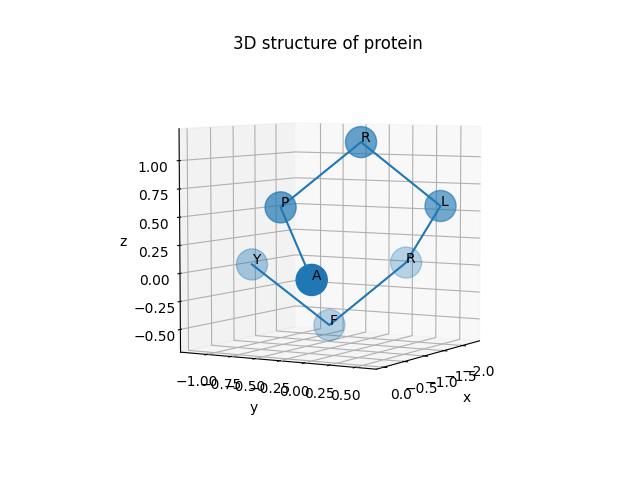
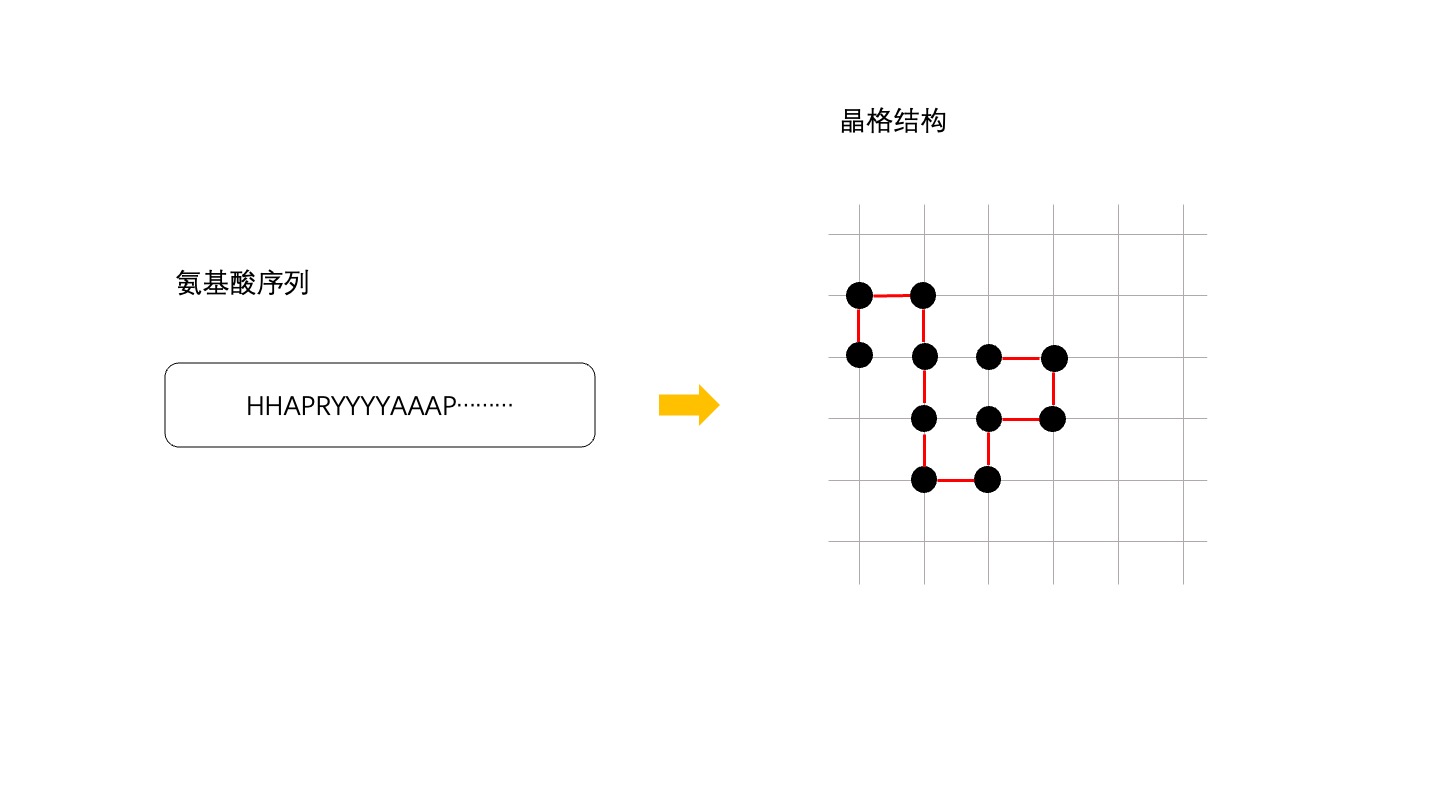
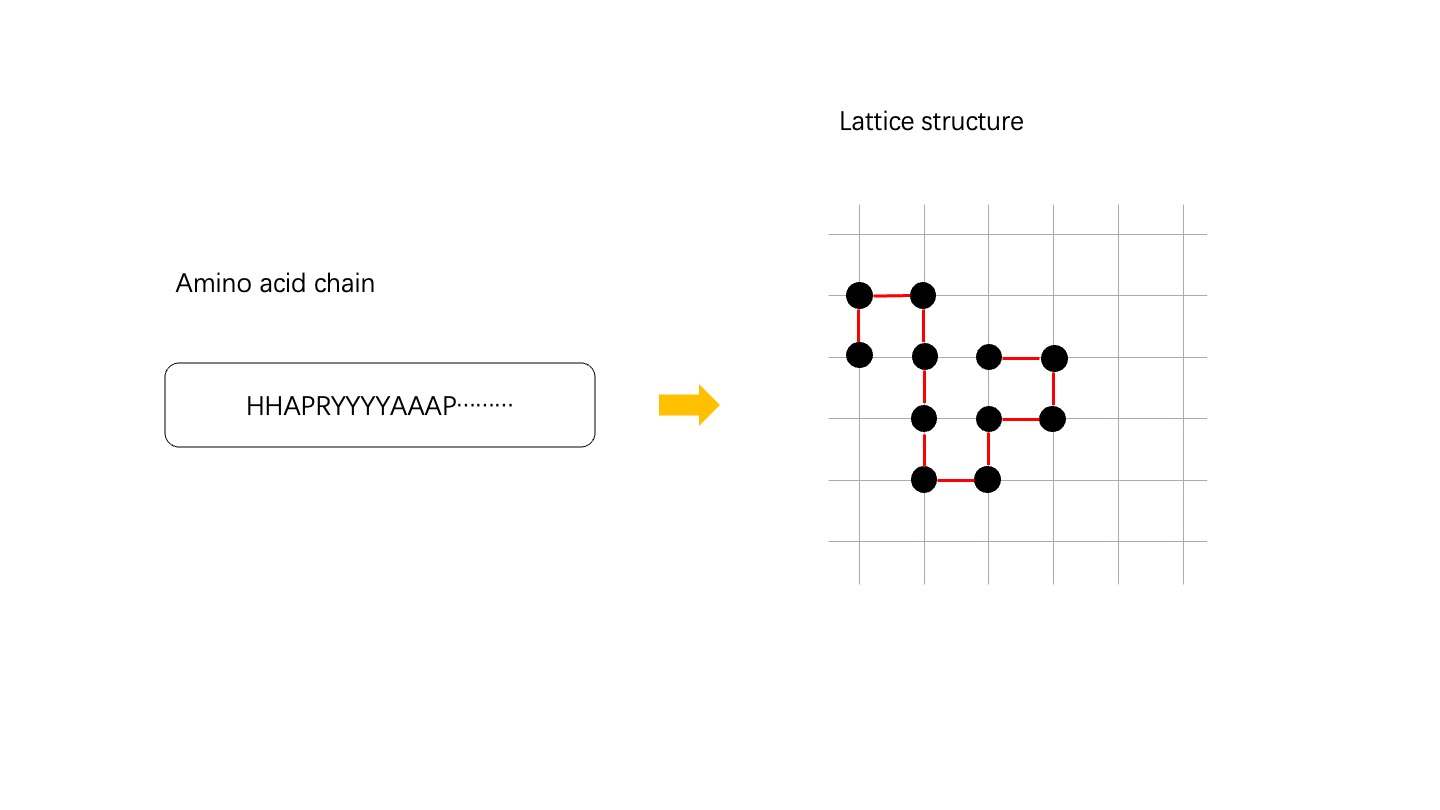
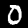update to v2.3.0
290 字节
14.9 KB
499.2 KB
145.7 KB
152.7 KB
114.1 KB
632 字节
507 字节
137.6 KB
114.3 KB
24.1 KB
46.8 KB
47.7 KB
410 字节
414 字节
444 字节
471 字节
519 字节
437 字节
396 字节
419 字节
433 字节
409 字节
412 字节
390 字节
410 字节
442 字节
419 字节
402 字节
399 字节
389 字节
462 字节
467 字节
411 字节
503 字节
441 字节
456 字节
421 字节
494 字节
435 字节
434 字节
415 字节
415 字节
464 字节
458 字节
443 字节
470 字节
452 字节
434 字节
423 字节
444 字节
434 字节
445 字节
457 字节
420 字节
403 字节
432 字节
419 字节
420 字节
485 字节
452 字节
363 字节
444 字节
425 字节
451 字节
485 字节
395 字节
486 字节
453 字节
417 字节
441 字节
429 字节
526 字节
453 字节
466 字节
437 字节
435 字节
413 字节
411 字节
423 字节
417 字节
427 字节
453 字节
446 字节
462 字节
390 字节
440 字节
419 字节
437 字节
441 字节
361 字节
420 字节
413 字节
486 字节
467 字节
424 字节
445 字节
378 字节
473 字节
410 字节
416 字节
428 字节
403 字节
418 字节
368 字节
407 字节
426 字节
392 字节
475 字节
485 字节
439 字节
413 字节
430 字节
574 字节
493 字节
524 字节
525 字节
527 字节
517 字节
529 字节
509 字节
471 字节
427 字节
499 字节
503 字节
480 字节
501 字节
569 字节
583 字节
529 字节
545 字节
466 字节
544 字节
509 字节
525 字节
492 字节
531 字节
534 字节
515 字节
454 字节
535 字节
473 字节
509 字节
491 字节
524 字节
482 字节
499 字节
521 字节
493 字节
537 字节
501 字节
559 字节
468 字节
475 字节
542 字节
543 字节
556 字节
482 字节
511 字节
558 字节
504 字节
521 字节
528 字节
512 字节
541 字节
521 字节
550 字节
513 字节
528 字节
547 字节
499 字节
519 字节
440 字节
492 字节
600 字节
517 字节
462 字节
523 字节
519 字节
522 字节
530 字节
491 字节
500 字节
533 字节
590 字节
564 字节
500 字节
516 字节
518 字节
459 字节
508 字节
514 字节
569 字节
478 字节
510 字节
540 字节
519 字节
475 字节
509 字节
498 字节
472 字节
493 字节
553 字节
497 字节
483 字节
497 字节
510 字节
542 字节
531 字节
517 字节
540 字节
534 字节
514 字节
493 字节
422 字节
457 字节
421 字节
410 字节
482 字节
480 字节
421 字节
464 字节
433 字节
460 字节
400 字节
459 字节
464 字节
469 字节
455 字节
451 字节
441 字节
413 字节
444 字节
439 字节
433 字节
487 字节
426 字节
483 字节
451 字节
470 字节
416 字节
462 字节
420 字节
374 字节
416 字节
409 字节
431 字节
431 字节
433 字节
433 字节
435 字节
446 字节
423 字节
434 字节
391 字节
422 字节
409 字节
467 字节
430 字节
427 字节
448 字节
402 字节
450 字节
395 字节
436 字节
461 字节
426 字节
446 字节
429 字节
465 字节
519 字节
433 字节
471 字节
417 字节
435 字节
493 字节
459 字节
427 字节
464 字节
416 字节
545 字节
421 字节
435 字节
487 字节
466 字节
531 字节
426 字节
434 字节
410 字节
415 字节
438 字节
406 字节
425 字节
425 字节
463 字节
450 字节
424 字节
455 字节
429 字节
409 字节
422 字节
416 字节
462 字节
452 字节
423 字节
441 字节
435 字节
366 字节
441 字节
435 字节
419 字节
396 字节
427 字节
416 字节
478 字节
403 字节
459 字节
448 字节
461 字节
419 字节
419 字节
409 字节
460 字节
461 字节
424 字节
458 字节
423 字节
404 字节
398 字节
446 字节
428 字节
392 字节
484 字节
442 字节
410 字节
450 字节
482 字节
417 字节
450 字节
423 字节
424 字节
461 字节
437 字节
512 字节
385 字节
430 字节
395 字节
398 字节
439 字节
470 字节
478 字节
375 字节
423 字节
468 字节
390 字节
430 字节
409 字节
419 字节
451 字节
440 字节
463 字节
461 字节
411 字节
430 字节
423 字节
399 字节
393 字节
413 字节
471 字节
373 字节
516 字节
445 字节
399 字节
433 字节
418 字节
386 字节
437 字节
447 字节
453 字节
422 字节
525 字节
413 字节
464 字节
473 字节
409 字节
450 字节
405 字节
431 字节
447 字节
375 字节
414 字节
424 字节
434 字节
436 字节
421 字节
430 字节
448 字节
440 字节
458 字节
471 字节
425 字节
418 字节
425 字节
409 字节
393 字节
435 字节
429 字节
448 字节
371 字节
459 字节
401 字节
425 字节
436 字节
424 字节
501 字节
443 字节
434 字节
408 字节
433 字节
442 字节
416 字节
453 字节
439 字节
475 字节
417 字节
441 字节
415 字节
419 字节
440 字节
459 字节
437 字节
406 字节
417 字节
502 字节
421 字节
398 字节
420 字节
474 字节
418 字节
422 字节
407 字节
395 字节
402 字节
421 字节
422 字节
436 字节
426 字节
490 字节
420 字节
483 字节
459 字节
427 字节
427 字节
412 字节
454 字节
397 字节
432 字节
410 字节
428 字节
398 字节
444 字节
437 字节
424 字节
446 字节
448 字节
433 字节
495 字节
414 字节
461 字节
407 字节
435 字节
424 字节
451 字节
475 字节
446 字节
397 字节
503 字节
451 字节
446 字节
403 字节
421 字节
441 字节
432 字节
468 字节
408 字节
463 字节
431 字节
470 字节
469 字节
410 字节
450 字节
366 字节
408 字节
405 字节
421 字节
432 字节
478 字节
475 字节
445 字节
409 字节
407 字节
446 字节
395 字节
413 字节
423 字节
483 字节
411 字节
397 字节
421 字节
436 字节
431 字节
473 字节
416 字节
410 字节
454 字节
391 字节
409 字节
458 字节
425 字节
442 字节
416 字节
482 字节
426 字节
457 字节
433 字节
437 字节
470 字节
419 字节
422 字节
433 字节
432 字节
449 字节
454 字节
413 字节
413 字节
433 字节
435 字节
436 字节
442 字节
420 字节
447 字节
378 字节
398 字节
407 字节
415 字节
387 字节
489 字节
495 字节
431 字节
449 字节
398 字节
437 字节
419 字节
415 字节
428 字节
415 字节
460 字节
459 字节
361 字节
442 字节
375 字节
435 字节
419 字节
442 字节
421 字节
494 字节
386 字节
396 字节
416 字节
445 字节
463 字节
394 字节
415 字节
456 字节
441 字节
408 字节
497 字节
465 字节
462 字节
421 字节
450 字节
373 字节
392 字节
424 字节
461 字节
456 字节
439 字节
434 字节
435 字节
458 字节
378 字节
440 字节
443 字节
409 字节
409 字节
425 字节
473 字节
433 字节
460 字节
410 字节
434 字节
438 字节
468 字节
469 字节
458 字节
403 字节
437 字节
455 字节
476 字节
439 字节
415 字节
453 字节
458 字节
573 字节
511 字节
474 字节
511 字节
516 字节
484 字节
508 字节
458 字节
525 字节
470 字节
501 字节
553 字节
536 字节
550 字节
481 字节
518 字节
523 字节
535 字节
509 字节
546 字节
485 字节
510 字节
570 字节
512 字节
492 字节
554 字节
492 字节
497 字节
569 字节
490 字节
457 字节
516 字节
521 字节
523 字节
547 字节
554 字节
509 字节
455 字节
507 字节
540 字节
503 字节
503 字节
495 字节
530 字节
530 字节
563 字节
489 字节
570 字节
488 字节
531 字节
515 字节
461 字节
514 字节
515 字节
548 字节
525 字节
546 字节
506 字节
506 字节
488 字节
563 字节
500 字节
498 字节
533 字节
536 字节
455 字节
556 字节
470 字节
541 字节
512 字节
543 字节
442 字节
503 字节
486 字节
511 字节
520 字节
527 字节
493 字节
485 字节
524 字节
525 字节
521 字节
556 字节
520 字节
533 字节
519 字节
480 字节
474 字节
548 字节
528 字节
541 字节
538 字节
541 字节
556 字节
564 字节
574 字节
521 字节
539 字节
520 字节
500 字节
541 字节
480 字节
527 字节
483 字节
453 字节
516 字节
503 字节
526 字节
533 字节
533 字节
512 字节
523 字节
522 字节
503 字节
529 字节
510 字节
506 字节
531 字节
484 字节
515 字节
525 字节
517 字节
549 字节
522 字节
532 字节
517 字节
497 字节
579 字节
545 字节
513 字节
498 字节
538 字节
522 字节
512 字节
481 字节
517 字节
497 字节
497 字节
539 字节
583 字节
506 字节
499 字节
501 字节
533 字节
601 字节
516 字节
535 字节
479 字节
482 字节
438 字节
475 字节
528 字节
472 字节
545 字节
548 字节
517 字节
440 字节
541 字节
528 字节
505 字节
512 字节
492 字节
533 字节
515 字节
479 字节
536 字节
529 字节
553 字节
506 字节
493 字节
525 字节
533 字节
591 字节
517 字节
537 字节
523 字节
469 字节
513 字节
503 字节
558 字节
536 字节
536 字节
508 字节
472 字节
513 字节
521 字节
521 字节
495 字节
506 字节
477 字节
512 字节
517 字节
549 字节
480 字节
547 字节
548 字节
526 字节
531 字节
488 字节
552 字节
538 字节
473 字节
516 字节
491 字节
538 字节
504 字节
509 字节
532 字节
503 字节
538 字节
462 字节
499 字节
497 字节
465 字节
593 字节
537 字节
520 字节
511 字节
489 字节
538 字节
477 字节
508 字节
510 字节
526 字节
512 字节
471 字节
538 字节
426 字节
556 字节
584 字节
529 字节
473 字节
545 字节
520 字节
517 字节
544 字节
491 字节
569 字节
492 字节
549 字节
517 字节
517 字节
544 字节
472 字节
509 字节
512 字节
520 字节
523 字节
509 字节
522 字节
542 字节
473 字节
453 字节
442 字节
476 字节
514 字节
538 字节
476 字节
488 字节
563 字节
464 字节
504 字节
522 字节
541 字节
552 字节
514 字节
510 字节
533 字节
517 字节
510 字节
561 字节
446 字节
569 字节
551 字节
487 字节
517 字节
559 字节
515 字节
545 字节
479 字节
520 字节
509 字节
591 字节
475 字节
476 字节
535 字节
511 字节
524 字节
532 字节
539 字节
513 字节
487 字节
471 字节
484 字节
492 字节
537 字节
514 字节
523 字节
537 字节
483 字节
517 字节
520 字节
475 字节
501 字节
475 字节
498 字节
527 字节
461 字节
531 字节
509 字节
499 字节
508 字节
528 字节
438 字节
516 字节
542 字节
564 字节
508 字节
470 字节
488 字节
535 字节
499 字节
504 字节
538 字节
525 字节
497 字节
513 字节
498 字节
528 字节
495 字节
497 字节
478 字节
477 字节
559 字节
539 字节
490 字节
510 字节