# 图像分类常见问题汇总 - 2021 第1季
## 目录
* [第1期](#第1期)(2021.01.05)
* [第2期](#第2期)(2021.01.14)
* [第3期](#第3期)(2020.01.21)
## 第1期
### Q1.1: 在模型导出时,发现导出的inference model预测精度很低,这块是为什么呢?
**A**:可以从以下几个方面排查
* 需要先排查下预训练模型路径是否正确。
* 模型导出时,默认的类别数为1000,如果预训练模型是自定义的类别数,则在导出的时候需要指定参数`--class_num=k`,k是自定义的类别数。
* 可以对比下`tools/infer/infer.py`和`tools/infer/predict.py`针对相同输入的输出class id与score,如果完全相同,则可能是预训练模型自身的精度很差。
### Q1.2: 训练样本的类别不均衡,这个该怎么处理呢?
**A**:有以下几种比较常用的处理方法。
* 从采样的角度出发的话
* 可以对样本根据类别进行动态采样,每个类别都设置不同的采样概率,保证不同类别的图片在同一个minibatch或者同一个epoch内,不同类别的训练样本数量基本一致或者符合自己期望的比例。
* 可以使用过采样的方法,对图片数量较少的类别进行过采样。
* 从损失函数的角度出发的话
* 可以使用OHEM(online hard example miniing)的方法,对根据样本的loss进行筛选,筛选出hard example用于模型的梯度反传和参数更新。
* 可以使用Focal loss的方法,对一些比较容易的样本的loss赋予较小的权重,对于难样本的loss赋予较大的权重,从而让容易样本的loss对网络整体的loss有贡献,但是又不会主导loss。
### Q1.3 在docker中训练的时候,数据路径和配置均没问题,但是一直报错`SystemError: (Fatal) Blocking queue is killed because the data reader raises an exception`,这是为什么呢?
**A**:这可能是因为docker中共享内存太小导致的。创建docker的时候,`/dev/shm`的默认大小为64M,如果使用多进程读取数据,共享内存可能不够,因此需要给`/dev/shm`分配更大的空间,在创建docker的时候,传入`--shm-size=8g`表示给`/dev/shm`分配8g的空间,一般是够用的。
### Q1.4 PaddleClas提供的10W类图像分类预训练模型在哪里下载,应该怎么使用呢?
**A**:基于ResNet50_vd, 百度开源了自研的大规模分类预训练模型,其中训练数据为10万个类别,4300万张图片。10万类预训练模型的下载地址:[下载地址](https://paddle-imagenet-models-name.bj.bcebos.com/ResNet50_vd_10w_pretrained.tar),在这里需要注意的是,该预训练模型没有提供最后的FC层参数,因此无法直接拿来预测;但是可以使用它作为预训练模型,在自己的数据集上进行微调。经过验证,该预训练模型相比于基于ImageNet1k数据集的ResNet50_vd预训练模型,在不同的数据集上均有比较明显的精度收益,最多可达30%,更多的对比实验可以参考:[图像分类迁移学习教程](../application/transfer_learning.md)。
### Q1.5 使用C++进行预测部署的时候怎么进行加速呢?
**A**:可以从以下几个方面加速预测过程。
1. 如果是CPU预测的话,可以开启mkldnn进行预测,同时适当增大运算的线程数(cpu_math_library_num_threads,在`tools/config.txt`中),一般设置为6~10比较有效。
2. 如果是GPU预测的话,在硬件条件允许的情况下,可以开启TensorRT预测以及FP16预测,这可以进一步加快预测速度。
3. 在内存或者显存足够的情况下,可以增大预测的batch size。
4. 可以将图像预处理的逻辑(主要设计resize、crop、normalize等)放在GPU上运行,这可以进一步加速预测过程。
更多的预测部署加速技巧,也欢迎大家补充。
## 第2期
### Q2.1: PaddleClas在设置标签的时候必须从0开始吗?class_num必须等于数据集的类别数吗?
**A**:在PaddleClas中,标签默认是从0开始,所以,尽量从0开始设置标签,当然,从其他值开始设置也可以,这样会导致设置的class_num增大,进而导致分类的FC层参数量较大,权重文件会占用更多的存储空间。在数据集类别连续的情况下,设置的class_num要等于数据集类别数(当然大于数据集类别数也可以,在很多数据集上甚至可以获得更高的精度,但同样会使FC层参数量较大),在数据集类别数不连续的情况下,设置的class_num要等于数据集中最大的class_id+1。
### Q2.2: 当类别数特别多的时候,最后的FC特别大,导致权重文件占用较大的存储空间,该怎么解决?
**A**:最终的FC的权重是一个大的矩阵,大小为C*class_num,其中C为FC前一层的神经单元个数,如ResNet50中的C为2048,可以通过降低C的值来进一步减小FC权重的大小,比如,可以在GAP之后加一层维数较小的FC层,这样可以大大缩小最终分类层的权重大小。
### Q2.3: 为什么使用PaddleClas在自定义的数据集上训练ssld蒸馏没有达到预期?
首先,需要确保Teacher模型的精度是否存在问题,其次,需要确保Student模型是否成功加载了ImageNet-1k的预训练权重以及Teacher模型是否成功加载了训练自定义数据集的权重,最后,要确保初次学习率不应太大,至少保证初始学习率不要超过训练ImageNet-1k的值。
### Q2.4: 移动端或嵌入式端上哪些网络具有优势?
建议使用移动端系列的网络,网络详情可以参考[移动端系列网络结构介绍](../models/Mobile.md)。如果任务的速度更重要,可以考虑MobileNetV3系列,如果模型大小更重要,可以根据移动端系列网络结构介绍中的StorageSize-Accuracy来确定具体的结构。
### Q2.5: 既然移动端网络非常快,为什么还要使用诸如ResNet这样参数量和计算量较大的网络?
不同的网络结构在不同的设备上运行速度优势不同。在移动端,移动端系列的网络比服务器端的网络运行速度更快,但是在服务器端,相同精度下,ResNet等经过特定优化后的网络具有更大的优势,所以需要根据具体情况来选择具体的网络结构。
## 第3期
### Q3.1: 双(多)分支结构与Plain结构,各自有什么特点?
**A**:
以VGG为代表的Plain网络,发展到以ResNet系列(带有残差模块)、Inception系列(多卷积核并行)为代表的的多分支网络结构,人们发现多分支结构在模型训练阶段更为友好,更大的网络宽度可以带来更强的特征拟合能力,而残差结构则可以避免深度网络梯度消失的问题,但是在推理阶段,带有多分支结构的模型在速度上并无优势,即使多分支结构模型的FLOPs要更低,但多分支结构的模型计算密度也更低。例如VGG16模型的FLOPs远远大于EfficientNetB3,但是VGG16模型的推理速度却显著快于EfficientNetB3,因此多分支结构在模型训练阶段更为友好,而Plain结构模型则更适合于推理阶段,那么以此为出发点,可以在训练阶段使用多分支网络结构,以更大的训练时间成本换取特征拟合能力更强的模型,而在推理阶段,将多分支结构转为Plain结构,从而换取更短的推理时间。实现多分支结构到Plain结构的转换,可以通过结构重参数化(structural re-parameterization)技术实现。
另外,Plain结构对于剪枝操作也更为友好。
注:“Plain结构”与“结构重参数化(structural re-parameterization)技术”出自论文“RepVGG: Making VGG-style ConvNets Great Again”。Plain结构网络模型指整个网络不存在分支结构,也即网络中第`i`层layer的输入为第`i-1`层layer的输出,第`i`层layer的输出为第`i+1`层layer的输入。
### Q3.2: ACNet的创新点主要在哪里?
**A**:
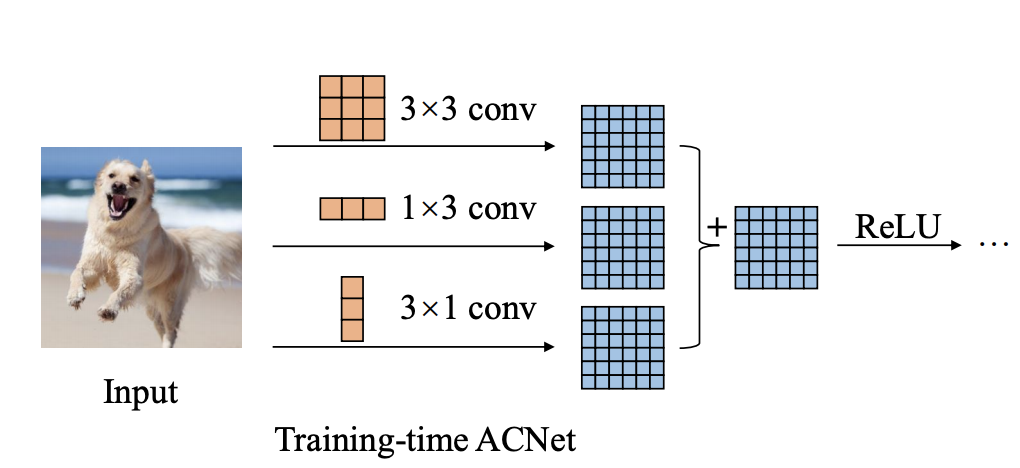
ACNet意为“Asymmetric Convolution Block”,即为非对称卷积模块,该思想出自论文“ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks”,文章提出了以“ACB”结构的三个CNN卷积核为一组,用来在训练阶段替代现有卷积神经网络中的传统方形卷积核。
方形卷积核的尺寸为假设为`d*d`,即宽、高相等均为`d`,则用于替换该卷积核的ACB结构是尺寸为`d*d`、`1*d`、`d*1`的三个卷积核,然后再将三个卷积核的输出直接相加,可以得到与原有方形卷积核相同尺寸的计算结果。
而在训练完成后,将ACB结构换回原有的方形卷积核,方形卷积核的参数则为ACB结构的三个卷积核的参数直接相加(见`Q3.4`,因此还是使用与之前相同的模型结构用于推理,ACB结构只是在训练阶段使用。
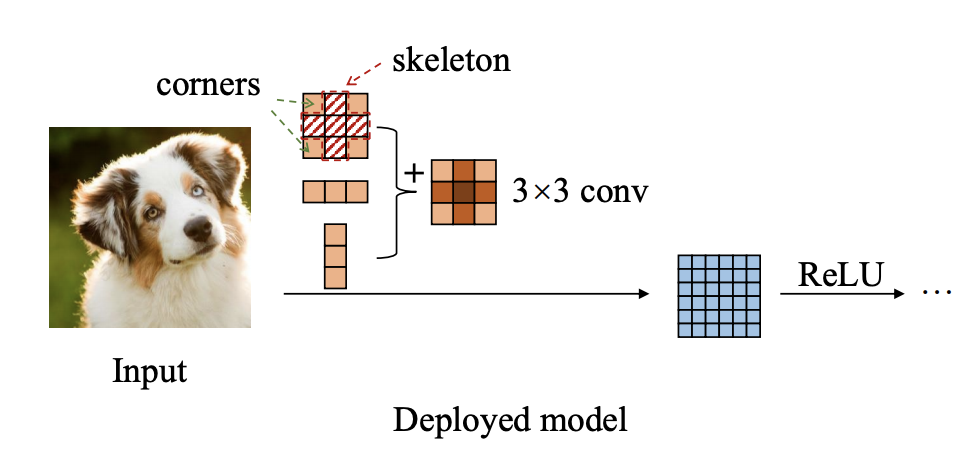
在训练中,通过ACB结构,模型的网络宽度得到了提高,利用`1*d`、`d*1`的两个非对称卷积核提取得到更多的特征用于丰富`d*d`卷积核提取的特征图的信息。而在推理阶段,这种设计思想并没有带来额外的参数与计算开销。如下图所示,分别是用于训练阶段和部署推理阶段的卷积核形式。
文章作者的实验表明,通过在原有网络模型训练中使用ACNet结构可以显著提高模型能力,原作者对此有如下解释:
1. 实验表明,对于一个`d*d`的卷积核,相对于消除卷积核角落位置(如上图中卷积核的`corners`位置)的参数而言,消除骨架位置(如上图中卷积核的`skeleton`位置)的参数会给模型精度带来更大的影响,因此卷积核骨架位置的参数要更为重要,而ACB结构中的两个非对称卷积核增强了方形卷积核骨架位置参数的权重,使之作用更为显著。这种相加是否会因正负数抵消作用而减弱骨架位置的参数作用,作者通过实验发现,网络的训练总是会向着提高骨架位置参数作用的方向发展,并没有出现正负数抵消而减弱的现象。
2. 非对称卷积核对于翻转的图像具有更强的鲁棒性,如下图所示,水平的非对称卷积核对于上下翻转的图像具有更强的鲁棒性。对于翻转前后图像中语义上的同一位置,非对称卷积核提取的特征图是相同的,这一点要强于方形卷积核。
### Q3.3: RepVGG的创新点主要在哪里?
**A**:
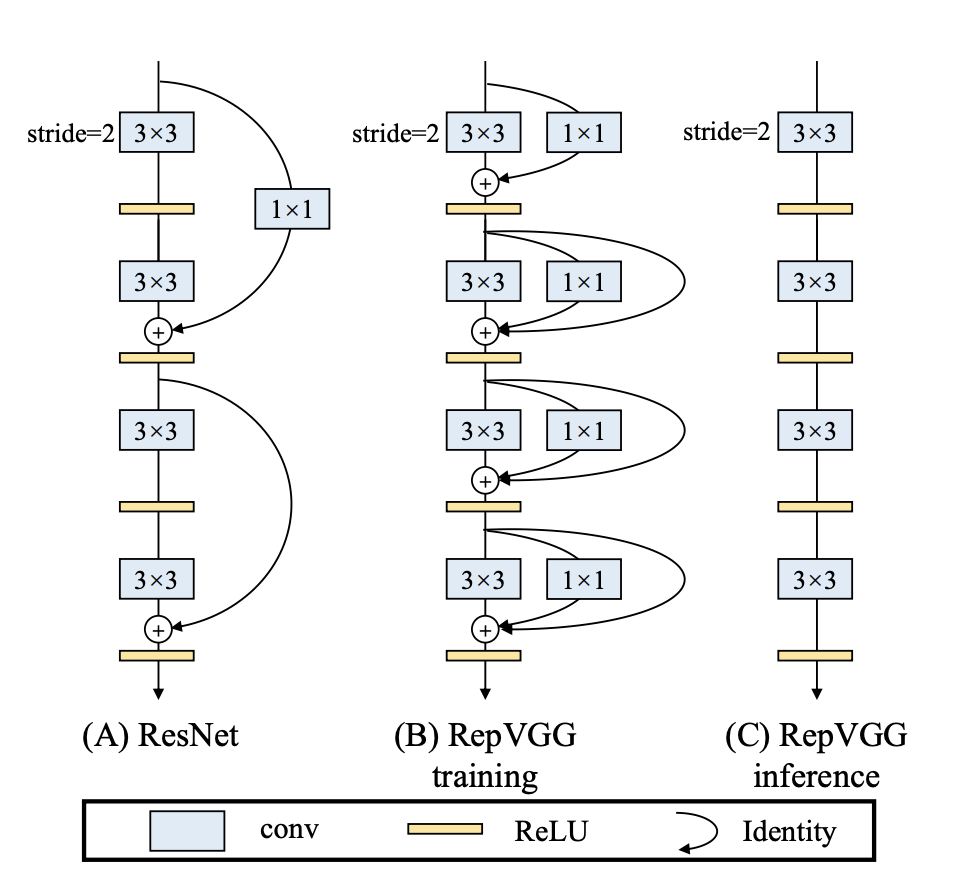
通过Q3.1与Q3.2,我们可以大胆想到,是否可以借鉴ACNet将训练阶段与推理阶段解耦,并且训练阶段使用多分支结构,推理阶段使用Plain结构,这也就是RepVGG的创新点。下图为ResNet、RepVGG训练和推理阶段网络结构的对比。
首先训练阶段的RepVGG采用多分支结构,可以看作是在传统VGG网络的基础上,增加了`1*1`卷积和恒等映射的残差结构,而推理阶段的RepVGG则退化为VGG结构。训练阶段RepVGG到推理阶段RepVGG的网络结构转换使用“结构重参数化”技术实现。
对于恒等映射,可将其视为参数均为`1`的`1*1`卷积核作用在输入特征图的输出结果,因此训练阶段的RepVGG的卷积模块可以视为两个`1*1`卷积和一个`3*3`卷积,而`1*1`卷积的参数又可以直接相加到`3*3`卷积核中心位置的参数上(该操作类似于ACNet中,非对称卷积核参数相加到方形卷积核骨架位置参数的操作),通过上述操作,即可在推理阶段,将网络结构中的恒等映射、`1*1`卷积、`3*3`卷积三个分支合并为一个`3*3`卷积,详见`Q3.4`。
### Q3.4: ACNet与RepVGG中的struct re-parameters有何异同?
**A**:
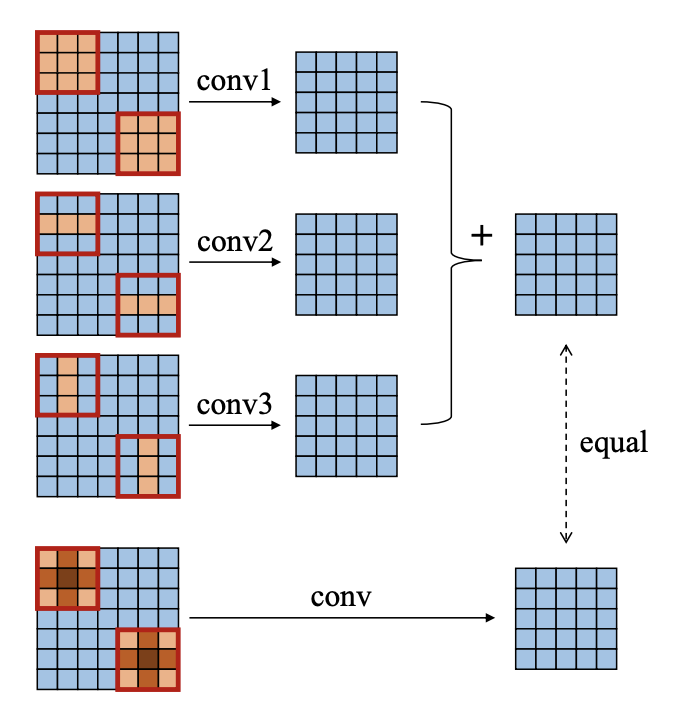
通过上面的了解,可以简单理解RepVGG是更为极端的ACNet。ACNet中的re-parameters操作如下图所示:
观察上图,以其中的`conv2`为例,该非对称卷积可以视为`3*3`的方形卷积核,只不过该方形卷积核的上下六个参数为`0`,`conv3`同理。并且,`conv1`、`conv2`、`conv3`的结果相加,等同于三个卷积核相加再做卷积,以`Conv`表示卷积操作,`+`表示矩阵的加法操作,则:`Conv1(A)+Conv2(A)+Conv3(A) == Convk(A)`,其中`Conv1`、`Conv2`、`Conv3`的卷积核分别为`Kernel1`、`kernel2`、`kernel3`,而`Convk`的卷积核为`Kernel1 + kernel2 + kernel3`。
RepVGG网络与ACNet同理,只不过ACNet的`1*d`非对称卷积变成了`1*1`卷积,`1*1`卷积相加的位置变成了`3*3`卷积的中心。
### Q3.5: 影响模型计算速度的因素都有哪些?参数量越大的模型计算速度一定更慢吗?
**A**:
影响模型计算速度的因素有很多,参数量只是其中之一。具体来说,在不考虑硬件差异的前提下,模型的计算速度可以参考以下几个方面:
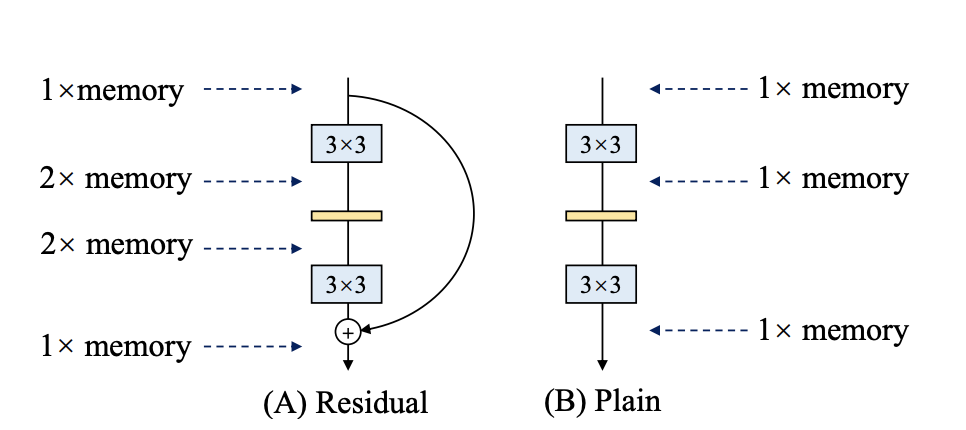
1. 参数量:用于衡量模型的参数数量,模型的参数量越大,模型在计算时对内存(显存)的容量要求一般也更高。但内存(显存)占用大小不完全取决于参数量。如下图中,假设输入特征图内存占用大小为`1`个单位,对于左侧的残差结构而言,由于需要记录两个分支的运算结果,然后再相加,因此该结构在计算时的内存峰值占用是右侧Plain结构的两倍。
2. 浮点运算数量(FLOPs):注意与每秒浮点运算次数(FLOPS)相区分。FLOPs可以简单理解为计算量,通常用来衡量一个模型的计算复杂度。
以常见的卷积操作为例,在不考虑batch size、激活函数、stride操作、bias的前提下,假设input future map尺寸为`Min*Min`,通道数为`Cin`,output future map尺寸为`Mout*Mout`,通道数为`Cout`,conv kernel尺寸为`K*K`,则进行一次卷积的FLOPs可以通过下述方式计算:
1. 输出特征图包含特征点的数量为:`Cout * Mout * Mout`;
2. 对于输出特征图中的每一个特征点的卷积操作而言:
乘法计算数量为:`Cin * K * K`;
加法计算数量为:`Cin * K * K - 1`;
3. 因此计算总量为:`Cout * Mout * Mout * (Cin * K * K + Cin * K * K - 1)`,也即`Cout * Mout * Mout * (2Cin * K * K - 1)`。
3. Memory Access Cost(MAC):内存访问成本,由于计算机在对数据进行运算(例如乘法、加法)前,需要将运算的数据从内存(此处泛指内存,包括显存)读取到运算器的Cache中,而内存的访问是十分耗时的。以分组卷积为例,假设分为`g`组,虽然分组后模型的参数量和FLOPs没有变化,但是分组卷积的内存访问次数成为之前的`g`倍(此处只是简单计算,未考虑多级Cache),因此MAC显著提高,模型的计算速度也相应变慢。
4. 并行度:常说的并行度包括数据并行和模型并行两部分,此处是指模型并行。以卷积操作为例,一个卷积层的参数量通常十分庞大,如果将卷积层中的矩阵做分块处理,然后分别交由多个GPU进行运算,即可达到加速的目的。甚至有的网络层参数量过大,单张GPU显存无法容纳时,也可能将该层分由多个GPU计算,但是能否分由多个GPU并行运算,不仅取决于硬件条件,也受特定的运算形式所限制。当然,并行度越高的模型,其运行速度也越快。