RNN配置¶

本教程将指导你如何在 PaddlePaddle 中配置循环神经网络（RNN）。PaddlePaddle 高度支持灵活和高效的循环神经网络配置。在本教程中，您将了解如何：

配置循环神经网络架构。
使用学习完成的循环神经网络模型生成序列。

我们将使用 vanilla 循环神经网络和 sequence to sequence 模型来指导你完成这些步骤。sequence to sequence 模型的代码可以在 book/08.machine_translation 找到。 wmt14数据的提供文件在 python/paddle/v2/dataset/wmt14.py 。

配置循环神经网络架构¶

简单门控循环神经网络(Gated Recurrent Neural Network)¶

循环神经网络在每个时间步骤顺序地处理序列。下面列出了 LSTM 的架构的示例。

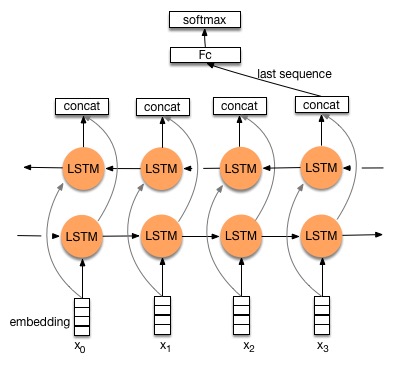
一般来说，循环网络从 \(t=1\) 到 \(t=T\) 或者反向地从 \(t=T\) 到 \(t=1\) 执行以下操作。

\[x_{t+1} = f_x(x_t), y_t = f_y(x_t)\]

其中 \(f_x(.)\) 称为单步函数（即单时间步执行的函数，step function），而 \(f_y(.)\) 称为输出函数。在 vanilla 循环神经网络中，单步函数和输出函数都非常简单。然而，PaddlePaddle 可以通过修改这两个函数来实现复杂的网络配置。我们将使用 sequence to sequence 模型演示如何配置复杂的循环神经网络模型。在本节中，我们将使用简单的 vanilla 循环神经网络作为使用recurrent_group配置简单循环神经网络的例子。注意，如果你只需要使用简单的RNN，GRU或LSTM，那么推荐使用grumemory和lstmemory，因为它们的计算效率比recurrent_group更高。

对于 vanilla RNN，在每个时间步长，单步函数为：

\[x_{t+1} = W_x x_t + W_i I_t + b\]

其中 \(x_t\) 是RNN状态，并且 \(I_t\) 是输入，\(W_x\) 和 \(W_i\) 分别是RNN状态和输入的变换矩阵。\(b\) 是偏差。它的输出函数只需要 \(x_t\) 作为输出。

recurrent_group是构建循环神经网络的最重要的工具。它定义了单步函数，输出函数和循环神经网络的输入。注意，这个函数的step参数需要实现step function（单步函数）和output function（输出函数）：

def simple_rnn(input,
               size=None,
               name=None,
               reverse=False,
               rnn_bias_attr=None,
               act=None,
               rnn_layer_attr=None):
    def __rnn_step__(ipt):
       out_mem = paddle.layer.memory(name=name, size=size)
       rnn_out = paddle.layer.mixed(input = [paddle.layer.full_matrix_projection(input=ipt),
                                             paddle.layer.full_matrix_projection(input=out_mem)],
                                    name = name,
                                    bias_attr = rnn_bias_attr,
                                    act = act,
                                    layer_attr = rnn_layer_attr,
                                    size = size)
       return rnn_out
    return paddle.layer.recurrent_group(name='%s_recurrent_group' % name,
                                        step=__rnn_step__,
                                        reverse=reverse,
                                        input=input)

PaddlePaddle 使用“Memory”（记忆模块）实现单步函数。Memory是在PaddlePaddle中构造循环神经网络时最重要的概念。 Memory是在单步函数中循环使用的状态，例如 \(x_{t+1} = f_x(x_t)\) 。一个Memory包含输出和输入。当前时间步处的Memory的输出作为下一时间步Memory的输入。Memory也可以具有boot layer(引导层)，其输出被用作Memory的初始值。在我们的例子中，门控循环单元的输出被用作输出Memory。请注意，rnn_out层的名称与out_mem的名称相同。这意味着rnn_out (xt + 1)的输出被用作out_memMemory的输出。

Memory也可以是序列。在这种情况下，在每个时间步中，我们有一个序列作为循环神经网络的状态。这在构造非常复杂的循环神经网络时是有用的。其他高级功能包括定义多个Memory，以及使用子序列来定义分级循环神经网络架构。

我们在函数的结尾返回rnn_out。这意味着 rnn_out 层的输出被用作门控循环神经网络的输出函数。

Sequence to Sequence Model with Attention¶

我们将使用 sequence to sequence model with attention 作为例子演示如何配置复杂的循环神经网络模型。该模型的说明如下图所示。

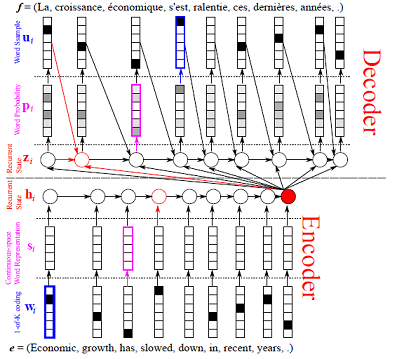
../../_images/encoder-decoder-attention-model.png

在这个模型中，源序列 \(S = \{s_1, \dots, s_T\}\) 用双向门控循环神经网络编码。双向门控循环神经网络的隐藏状态 \(H_S = \{H_1, \dots, H_T\}\) 被称为 编码向量。解码器是门控循环神经网络。当解读每一个 \(y_t\) 时, 这个门控循环神经网络生成一系列权重 \(W_S^t = \{W_1^t, \dots, W_T^t\}\) , 用于计算编码向量的加权和。加权和用来生成 \(y_t\) 。

模型的编码器部分如下所示。它叫做grumemory来表示门控循环神经网络。如果网络架构简单，那么推荐使用循环神经网络的方法，因为它比 recurrent_group 更快。我们已经实现了大多数常用的循环神经网络架构，可以参考 api_trainer_config_helpers_layers 了解更多细节。

我们还将编码向量投射到 decoder_size 维空间。这通过获得反向循环网络的第一个实例，并将其投射到 decoder_size 维空间完成：

# 定义源语句的数据层
src_word_id = paddle.layer.data(
    name='source_language_word',
    type=paddle.data_type.integer_value_sequence(source_dict_dim))
# 计算每个词的词向量
src_embedding = paddle.layer.embedding(
    input=src_word_id,
    size=word_vector_dim,
    param_attr=paddle.attr.ParamAttr(name='_source_language_embedding'))
# 应用前向循环神经网络
src_forward = paddle.networks.simple_gru(
    input=src_embedding, size=encoder_size)
# 应用反向递归神经网络（reverse=True表示反向循环神经网络）
src_backward = paddle.networks.simple_gru(
    input=src_embedding, size=encoder_size, reverse=True)
# 将循环神经网络的前向和反向部分混合在一起
encoded_vector = paddle.layer.concat(input=[src_forward, src_backward])

# 投射编码向量到 decoder_size
encoded_proj = paddle.layer.mixed(
    size=decoder_size,
    input=paddle.layer.full_matrix_projection(encoded_vector))

# 计算反向RNN的第一个实例
backward_first = paddle.layer.first_seq(input=src_backward)

# 投射反向RNN的第一个实例到 decoder size
decoder_boot = paddle.layer.mixed(
   size=decoder_size,
   act=paddle.activation.Tanh(),
   input=paddle.layer.full_matrix_projection(backward_first))

解码器使用 recurrent_group 来定义循环神经网络。单步函数和输出函数在 gru_decoder_with_attention 中定义：

group_input1 = paddle.layer.StaticInput(input=encoded_vector, is_seq=True)
group_input2 = paddle.layer.StaticInput(input=encoded_proj, is_seq=True)
group_inputs = [group_input1, group_input2]
trg_embedding = paddle.layer.embedding(
        input=paddle.layer.data(
            name='target_language_word',
            type=paddle.data_type.integer_value_sequence(target_dict_dim)),
        size=word_vector_dim,
        param_attr=paddle.attr.ParamAttr(name='_target_language_embedding'))
    group_inputs.append(trg_embedding)
group_inputs.append(trg_embedding)

# 对于配备有注意力机制的解码器，在训练中，
# 目标向量（groudtruth）是数据输入，
# 而源序列的编码向量可以被无边界的memory访问
# StaticInput 意味着不同时间步的输入都是相同的值，
# 否则它以一个序列输入，不同时间步的输入是不同的。
# 所有输入序列应该有相同的长度。
decoder = paddle.layer.recurrent_group(
        name=decoder_group_name,
        step=gru_decoder_with_attention,
        input=group_inputs)

单步函数的实现如下所示。首先，它定义解码网络的Memory。然后定义 attention，门控循环单元单步函数和输出函数：

def gru_decoder_with_attention(enc_vec, enc_proj, current_word):
    # 定义解码器的Memory
    # Memory的输出定义在 gru_step 内
    # 注意 gru_step 应该与它的Memory名字相同
    decoder_mem = paddle.layer.memory(
        name='gru_decoder', size=decoder_size, boot_layer=decoder_boot)
    # 计算 attention 加权编码向量
    context = paddle.networks.simple_attention(
        encoded_sequence=enc_vec,
        encoded_proj=enc_proj,
        decoder_state=decoder_mem)
    # 混合当前词向量和attention加权编码向量
     decoder_inputs = paddle.layer.mixed(
        size=decoder_size * 3,
        input=[
            paddle.layer.full_matrix_projection(input=context),
            paddle.layer.full_matrix_projection(input=current_word)
        ])
    # 定义门控循环单元循环神经网络单步函数
     gru_step = paddle.layer.gru_step(
        name='gru_decoder',
        input=decoder_inputs,
        output_mem=decoder_mem,
        size=decoder_size)
    # 定义输出函数
     out = paddle.layer.mixed(
        size=target_dict_dim,
        bias_attr=True,
        act=paddle.activation.Softmax(),
        input=paddle.layer.full_matrix_projection(input=gru_step))
    return out

生成序列¶

训练模型后，我们可以使用它来生成序列。通常的做法是使用beam search 生成序列。以下代码片段定义 beam search 算法。注意，beam_search 函数假设 step 的输出函数返回的是下一个时刻输出词的 softmax 归一化概率向量。我们对模型进行了以下更改。

使用 GeneratedInput 来表示 trg_embedding。 GeneratedInput 将上一时间步所生成的词的向量来作为当前时间步的输入。
使用 beam_search 函数。这个函数需要设置：
- bos_id: 开始标记。每个句子都以开始标记开头。
- eos_id: 结束标记。每个句子都以结束标记结尾。
- beam_size: beam search 算法中的beam大小。
- max_length: 生成序列的最大长度。

代码如下：

group_input1 = paddle.layer.StaticInput(input=encoded_vector, is_seq=True)
group_input2 = paddle.layer.StaticInput(input=encoded_proj, is_seq=True)
group_inputs = [group_input1, group_input2]
# 在生成时，解码器基于编码源序列和最后生成的目标词预测下一目标词。
# 编码源序列（编码器输出）必须由只读Memory的 StaticInput 指定。
# 这里， GeneratedInputs 自动获取上一个生成的词，并在最开始初始化为起始词，如 <s>。
trg_embedding = paddle.layer.GeneratedInput(
        size=target_dict_dim,
        embedding_name='_target_language_embedding',
        embedding_size=word_vector_dim)
group_inputs.append(trg_embedding)
beam_gen = paddle.layer.beam_search(
        name=decoder_group_name,
        step=gru_decoder_with_attention,
        input=group_inputs,
        bos_id=0, # Beginnning token.
        eos_id=1, # End of sentence token.
        beam_size=beam_size,
        max_length=max_length)

return beam_gen

注意，这种生成技术只用于类似解码器的生成过程。如果你正在处理序列标记任务，请参阅 book/06.understand_sentiment 了解更多详细信息。

完整的配置文件在 book/08.machine_translation/train.py 。