# MiniOB B+Tree 实现
## 简介
在基本的逻辑上,MiniOB 的 B+Tree 和 B+Tree 是一致的,查询和插入都是从根逐层定位到叶结点,然后在叶结点内获取或者插入。如果插入过程发生叶结点满的情况,同样会进行分裂,并向上递归这一过程。
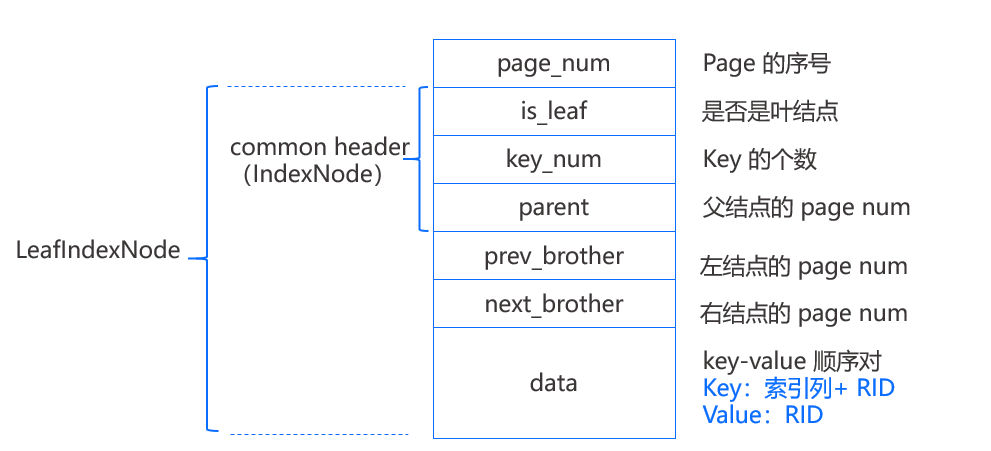 如上图,每个结点组织成一个固定大小的 page,之前介绍过每个 page 首先有一个 page_num 表示 page 在文件中的序号,每个结点 page 都有一个common header 实现为 IndexNode 结构,其中包括 is_leaf(是否为叶结点)、key_num(结点中 key 的个数)、parent(结点父结点的 page num),当 parent=-1 时表示该结点没有父结点。
除此之外,Leaf page 还有 prev_brother(左结点的 page num)和 next_brother(右结点的 page num),这两项用于帮助遍历。最后 page 所剩下的空间就顺序存放键值对,叶结点所存放的 key 是索引列的值加上 RID(该行数据在磁盘上的位置),Value 则为 RID,也就是说键值数据都是存放在叶结点上的,和 B+Tree 中叶结点的值是指向记录的指针不同。
如上图,每个结点组织成一个固定大小的 page,之前介绍过每个 page 首先有一个 page_num 表示 page 在文件中的序号,每个结点 page 都有一个common header 实现为 IndexNode 结构,其中包括 is_leaf(是否为叶结点)、key_num(结点中 key 的个数)、parent(结点父结点的 page num),当 parent=-1 时表示该结点没有父结点。
除此之外,Leaf page 还有 prev_brother(左结点的 page num)和 next_brother(右结点的 page num),这两项用于帮助遍历。最后 page 所剩下的空间就顺序存放键值对,叶结点所存放的 key 是索引列的值加上 RID(该行数据在磁盘上的位置),Value 则为 RID,也就是说键值数据都是存放在叶结点上的,和 B+Tree 中叶结点的值是指向记录的指针不同。
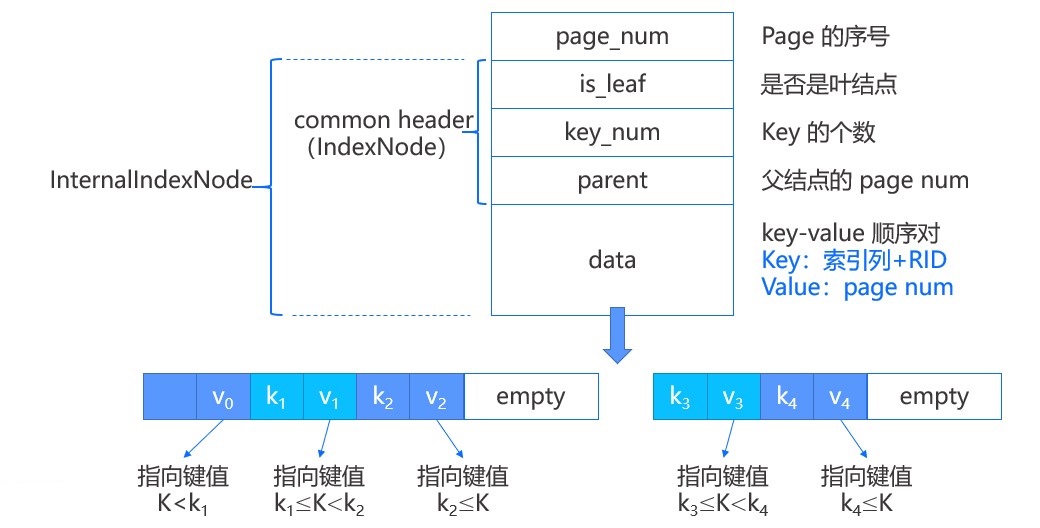 内部结点和叶结点有两点不同,一个是没有左右结点的 page num;另一个是所存放的值是 page num,也就是标识了子结点的 page 位置。如上图所示,键值对在内部结点是这样表示的,第一个键值对中的键是一个无效数据,真正用于比较的只有 k1 和 k2。
内部结点和叶结点有两点不同,一个是没有左右结点的 page num;另一个是所存放的值是 page num,也就是标识了子结点的 page 位置。如上图所示,键值对在内部结点是这样表示的,第一个键值对中的键是一个无效数据,真正用于比较的只有 k1 和 k2。
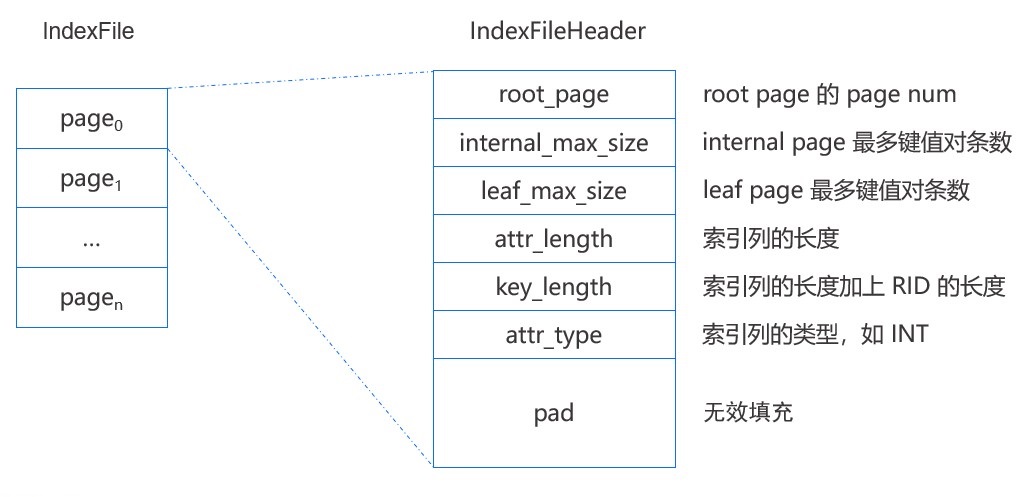 所有的结点(即 page)都存储在外存的索引文件 IndexFile 中,其中文件的第一个 page 是索引文件头,存储了一些元数据,如 root page 的 page num,内部结点和叶子结点能够存储键值对的最大个数等。
所有的结点(即 page)都存储在外存的索引文件 IndexFile 中,其中文件的第一个 page 是索引文件头,存储了一些元数据,如 root page 的 page num,内部结点和叶子结点能够存储键值对的最大个数等。
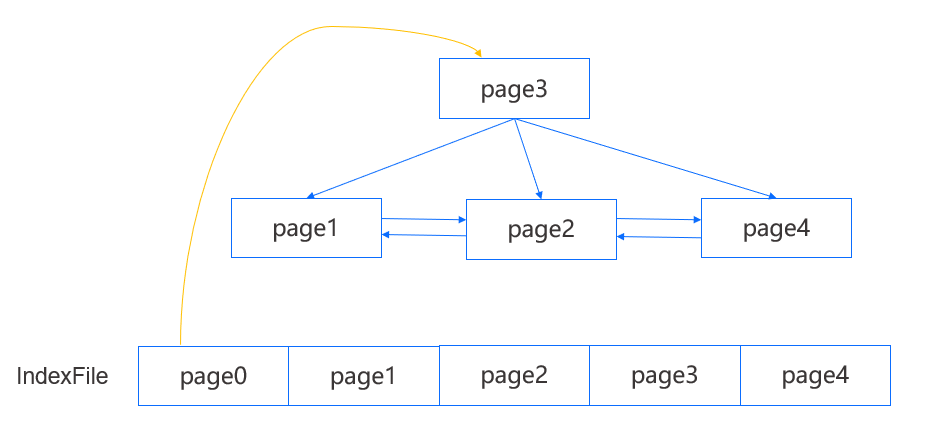 上图是一个简单的 MiniOB B+Tree 示例,其中叶结点能够访问到左右结点,并且每个结点能够访问到父结点。我们能够从 IndexFile 的第一个 page 得到 root page,而在知道一棵 B+Tree 的 root page 以后就足够访问到任意一个结点了。查询时我们会从 root page 开始逐层向下定位到目标叶结点,在每个 page 内遍历搜索查找键。
## 插入
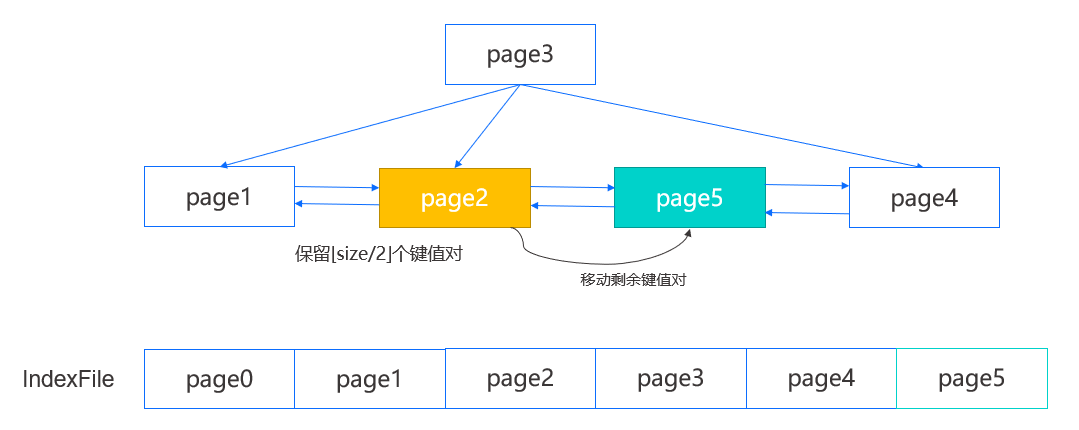
在插入时,我们首先定位到叶结点,如下图中的 page2,然后在结点内定位一个插入位置,如果结点未满,那么将键值对插入指定位置并向后移动部分数据即可;如果结点已满,那么需要对其进行分裂。
我们将先创建一个新的右兄弟结点,即 page5,然后在原结点内保留前一半的键值对,剩余的键值对则移动到新结点,并修改 page2 的后向 page num,page5 的前后向 page num 以及 page4 的前向 page num,再根据之前定位的插入位置判断是插入 page2 还是 page5 ,完成叶结点的插入。
上图是一个简单的 MiniOB B+Tree 示例,其中叶结点能够访问到左右结点,并且每个结点能够访问到父结点。我们能够从 IndexFile 的第一个 page 得到 root page,而在知道一棵 B+Tree 的 root page 以后就足够访问到任意一个结点了。查询时我们会从 root page 开始逐层向下定位到目标叶结点,在每个 page 内遍历搜索查找键。
## 插入
在插入时,我们首先定位到叶结点,如下图中的 page2,然后在结点内定位一个插入位置,如果结点未满,那么将键值对插入指定位置并向后移动部分数据即可;如果结点已满,那么需要对其进行分裂。
我们将先创建一个新的右兄弟结点,即 page5,然后在原结点内保留前一半的键值对,剩余的键值对则移动到新结点,并修改 page2 的后向 page num,page5 的前后向 page num 以及 page4 的前向 page num,再根据之前定位的插入位置判断是插入 page2 还是 page5 ,完成叶结点的插入。
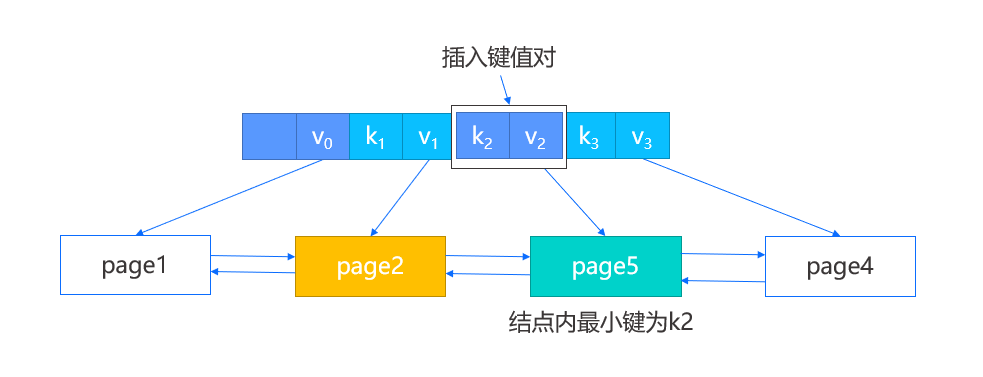
 此外,由于我们新增了结点,我们需要在父结点也插入新的键值对,这一步将涉及到原结点,新结点以及新结点中的最小键,分为以下两种情况:
1. 有父结点,那么直接将新结点中的最小键以及新结点的 page num 作为键值对插入父结点即可。
此外,由于我们新增了结点,我们需要在父结点也插入新的键值对,这一步将涉及到原结点,新结点以及新结点中的最小键,分为以下两种情况:
1. 有父结点,那么直接将新结点中的最小键以及新结点的 page num 作为键值对插入父结点即可。
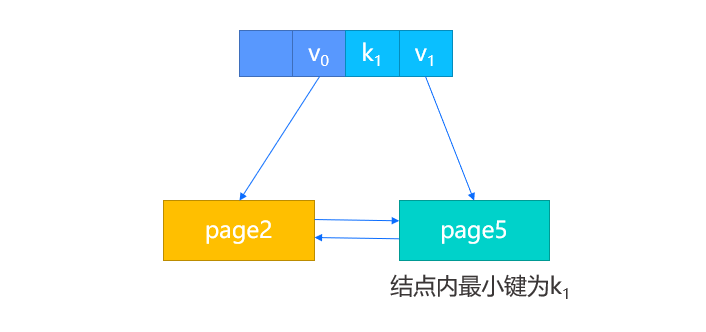
 2. 假设此时没有父结点,那么我们将创建一个新的根结点,除了把新结点键值对插入,还会将原结点的 page num 作为第一个键值对的值进行插入。
2. 假设此时没有父结点,那么我们将创建一个新的根结点,除了把新结点键值对插入,还会将原结点的 page num 作为第一个键值对的值进行插入。
 如果父结点的键值对插入同样触发了分裂,我们将按上述的步骤递归执行。
## 删除
正常的删除操作我们就不再介绍,这里介绍一些涉及结点合并的特殊情况。
首先在结点内删除键值对,然后判断其中的键值对数目是否小于一半,如果是则需要进行特殊处理。比如 page2 中删除一个键值对,导致其键值对数目小于一半,此时通过它的父结点找到该结点的左兄弟,如果是最左边的结点,则找到其右兄弟。
如果父结点的键值对插入同样触发了分裂,我们将按上述的步骤递归执行。
## 删除
正常的删除操作我们就不再介绍,这里介绍一些涉及结点合并的特殊情况。
首先在结点内删除键值对,然后判断其中的键值对数目是否小于一半,如果是则需要进行特殊处理。比如 page2 中删除一个键值对,导致其键值对数目小于一半,此时通过它的父结点找到该结点的左兄弟,如果是最左边的结点,则找到其右兄弟。
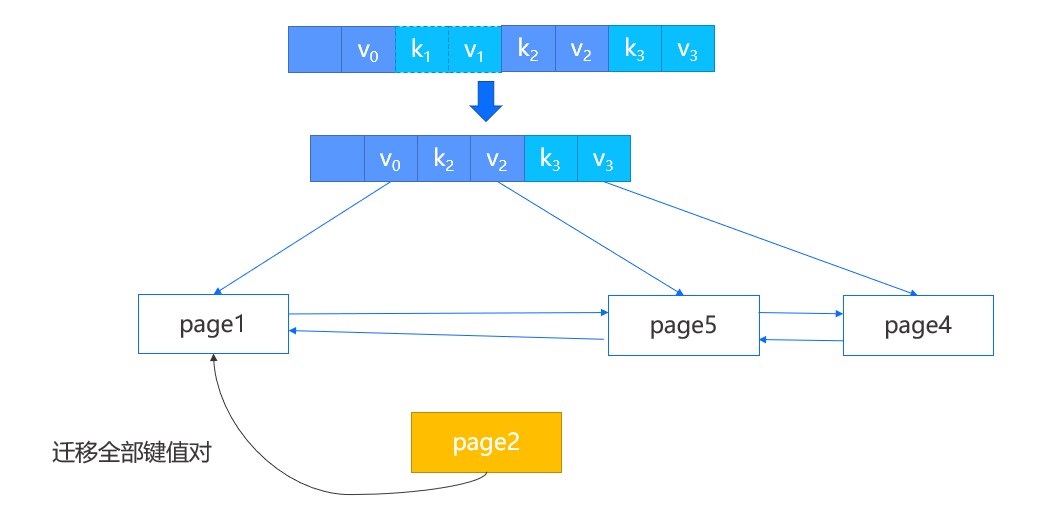
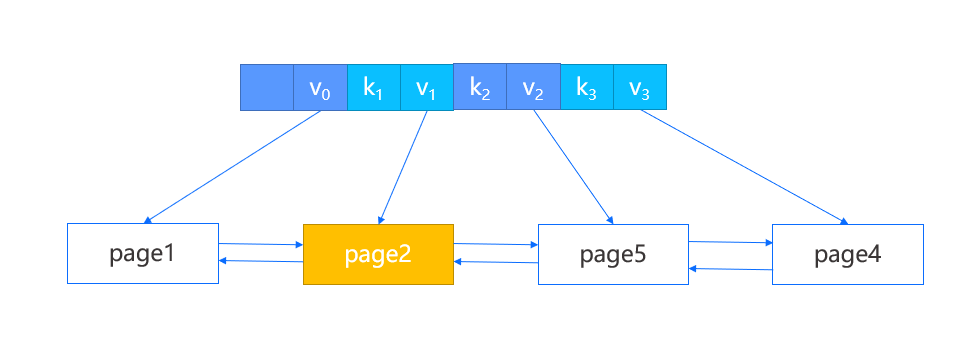 - 如果两个结点的所有键值对能容纳在一个结点内,那么进行合并操作,将右结点的数据迁移到左结点,并删除父结点中指向右结点的键值对。
- 如果两个结点的所有键值对能容纳在一个结点内,那么进行合并操作,将右结点的数据迁移到左结点,并删除父结点中指向右结点的键值对。
 - 如果两个结点的所有键值对不能容纳在一个结点内,那么进行重构操作。
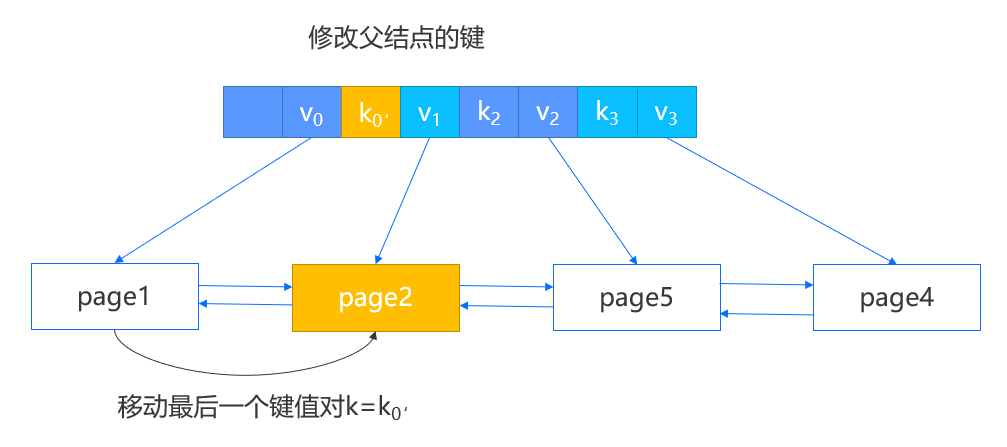
- 当所删除键值对的结点不是第一个结点时,那么选择将左兄弟的最后一个键值对移动到当前结点,并修改父结点中指向当前结点的键。
- 如果两个结点的所有键值对不能容纳在一个结点内,那么进行重构操作。
- 当所删除键值对的结点不是第一个结点时,那么选择将左兄弟的最后一个键值对移动到当前结点,并修改父结点中指向当前结点的键。
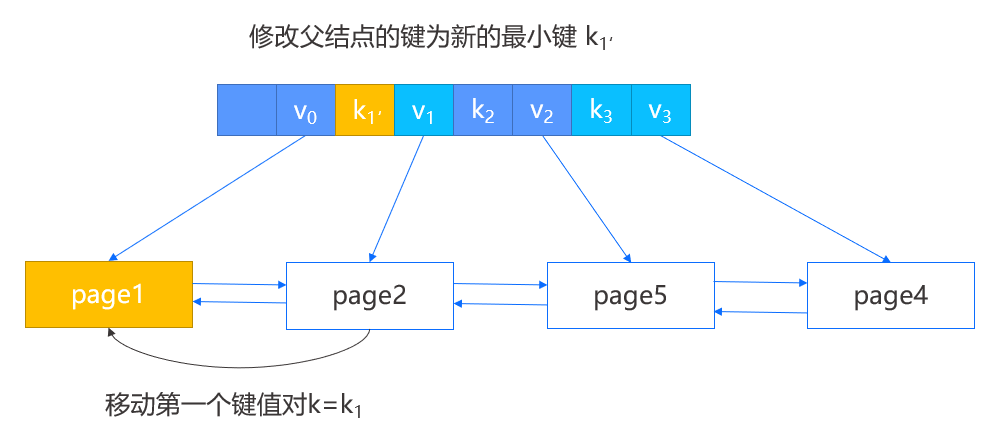
 - 当所删除键值对的结点是第一个结点时,那么选择将右兄弟的第一个键值对移动到当前结点,并修改父结点中指向右兄弟的键。
- 当所删除键值对的结点是第一个结点时,那么选择将右兄弟的第一个键值对移动到当前结点,并修改父结点中指向右兄弟的键。
 在上述两种操作中,合并操作会导致父结点删除键值对,因此会向上递归地去判断是否需要再次的合并与重构。
在上述两种操作中,合并操作会导致父结点删除键值对,因此会向上递归地去判断是否需要再次的合并与重构。
 如上图,每个结点组织成一个固定大小的 page,之前介绍过每个 page 首先有一个 page_num 表示 page 在文件中的序号,每个结点 page 都有一个common header 实现为 IndexNode 结构,其中包括 is_leaf(是否为叶结点)、key_num(结点中 key 的个数)、parent(结点父结点的 page num),当 parent=-1 时表示该结点没有父结点。
除此之外,Leaf page 还有 prev_brother(左结点的 page num)和 next_brother(右结点的 page num),这两项用于帮助遍历。最后 page 所剩下的空间就顺序存放键值对,叶结点所存放的 key 是索引列的值加上 RID(该行数据在磁盘上的位置),Value 则为 RID,也就是说键值数据都是存放在叶结点上的,和 B+Tree 中叶结点的值是指向记录的指针不同。
如上图,每个结点组织成一个固定大小的 page,之前介绍过每个 page 首先有一个 page_num 表示 page 在文件中的序号,每个结点 page 都有一个common header 实现为 IndexNode 结构,其中包括 is_leaf(是否为叶结点)、key_num(结点中 key 的个数)、parent(结点父结点的 page num),当 parent=-1 时表示该结点没有父结点。
除此之外,Leaf page 还有 prev_brother(左结点的 page num)和 next_brother(右结点的 page num),这两项用于帮助遍历。最后 page 所剩下的空间就顺序存放键值对,叶结点所存放的 key 是索引列的值加上 RID(该行数据在磁盘上的位置),Value 则为 RID,也就是说键值数据都是存放在叶结点上的,和 B+Tree 中叶结点的值是指向记录的指针不同。
 内部结点和叶结点有两点不同,一个是没有左右结点的 page num;另一个是所存放的值是 page num,也就是标识了子结点的 page 位置。如上图所示,键值对在内部结点是这样表示的,第一个键值对中的键是一个无效数据,真正用于比较的只有 k1 和 k2。
内部结点和叶结点有两点不同,一个是没有左右结点的 page num;另一个是所存放的值是 page num,也就是标识了子结点的 page 位置。如上图所示,键值对在内部结点是这样表示的,第一个键值对中的键是一个无效数据,真正用于比较的只有 k1 和 k2。
 所有的结点(即 page)都存储在外存的索引文件 IndexFile 中,其中文件的第一个 page 是索引文件头,存储了一些元数据,如 root page 的 page num,内部结点和叶子结点能够存储键值对的最大个数等。
所有的结点(即 page)都存储在外存的索引文件 IndexFile 中,其中文件的第一个 page 是索引文件头,存储了一些元数据,如 root page 的 page num,内部结点和叶子结点能够存储键值对的最大个数等。
 上图是一个简单的 MiniOB B+Tree 示例,其中叶结点能够访问到左右结点,并且每个结点能够访问到父结点。我们能够从 IndexFile 的第一个 page 得到 root page,而在知道一棵 B+Tree 的 root page 以后就足够访问到任意一个结点了。查询时我们会从 root page 开始逐层向下定位到目标叶结点,在每个 page 内遍历搜索查找键。
## 插入
在插入时,我们首先定位到叶结点,如下图中的 page2,然后在结点内定位一个插入位置,如果结点未满,那么将键值对插入指定位置并向后移动部分数据即可;如果结点已满,那么需要对其进行分裂。
我们将先创建一个新的右兄弟结点,即 page5,然后在原结点内保留前一半的键值对,剩余的键值对则移动到新结点,并修改 page2 的后向 page num,page5 的前后向 page num 以及 page4 的前向 page num,再根据之前定位的插入位置判断是插入 page2 还是 page5 ,完成叶结点的插入。
上图是一个简单的 MiniOB B+Tree 示例,其中叶结点能够访问到左右结点,并且每个结点能够访问到父结点。我们能够从 IndexFile 的第一个 page 得到 root page,而在知道一棵 B+Tree 的 root page 以后就足够访问到任意一个结点了。查询时我们会从 root page 开始逐层向下定位到目标叶结点,在每个 page 内遍历搜索查找键。
## 插入
在插入时,我们首先定位到叶结点,如下图中的 page2,然后在结点内定位一个插入位置,如果结点未满,那么将键值对插入指定位置并向后移动部分数据即可;如果结点已满,那么需要对其进行分裂。
我们将先创建一个新的右兄弟结点,即 page5,然后在原结点内保留前一半的键值对,剩余的键值对则移动到新结点,并修改 page2 的后向 page num,page5 的前后向 page num 以及 page4 的前向 page num,再根据之前定位的插入位置判断是插入 page2 还是 page5 ,完成叶结点的插入。
 此外,由于我们新增了结点,我们需要在父结点也插入新的键值对,这一步将涉及到原结点,新结点以及新结点中的最小键,分为以下两种情况:
1. 有父结点,那么直接将新结点中的最小键以及新结点的 page num 作为键值对插入父结点即可。
此外,由于我们新增了结点,我们需要在父结点也插入新的键值对,这一步将涉及到原结点,新结点以及新结点中的最小键,分为以下两种情况:
1. 有父结点,那么直接将新结点中的最小键以及新结点的 page num 作为键值对插入父结点即可。
 2. 假设此时没有父结点,那么我们将创建一个新的根结点,除了把新结点键值对插入,还会将原结点的 page num 作为第一个键值对的值进行插入。
2. 假设此时没有父结点,那么我们将创建一个新的根结点,除了把新结点键值对插入,还会将原结点的 page num 作为第一个键值对的值进行插入。
 如果父结点的键值对插入同样触发了分裂,我们将按上述的步骤递归执行。
## 删除
正常的删除操作我们就不再介绍,这里介绍一些涉及结点合并的特殊情况。
首先在结点内删除键值对,然后判断其中的键值对数目是否小于一半,如果是则需要进行特殊处理。比如 page2 中删除一个键值对,导致其键值对数目小于一半,此时通过它的父结点找到该结点的左兄弟,如果是最左边的结点,则找到其右兄弟。
如果父结点的键值对插入同样触发了分裂,我们将按上述的步骤递归执行。
## 删除
正常的删除操作我们就不再介绍,这里介绍一些涉及结点合并的特殊情况。
首先在结点内删除键值对,然后判断其中的键值对数目是否小于一半,如果是则需要进行特殊处理。比如 page2 中删除一个键值对,导致其键值对数目小于一半,此时通过它的父结点找到该结点的左兄弟,如果是最左边的结点,则找到其右兄弟。
 - 如果两个结点的所有键值对能容纳在一个结点内,那么进行合并操作,将右结点的数据迁移到左结点,并删除父结点中指向右结点的键值对。
- 如果两个结点的所有键值对能容纳在一个结点内,那么进行合并操作,将右结点的数据迁移到左结点,并删除父结点中指向右结点的键值对。
 - 如果两个结点的所有键值对不能容纳在一个结点内,那么进行重构操作。
- 当所删除键值对的结点不是第一个结点时,那么选择将左兄弟的最后一个键值对移动到当前结点,并修改父结点中指向当前结点的键。
- 如果两个结点的所有键值对不能容纳在一个结点内,那么进行重构操作。
- 当所删除键值对的结点不是第一个结点时,那么选择将左兄弟的最后一个键值对移动到当前结点,并修改父结点中指向当前结点的键。
 - 当所删除键值对的结点是第一个结点时,那么选择将右兄弟的第一个键值对移动到当前结点,并修改父结点中指向右兄弟的键。
- 当所删除键值对的结点是第一个结点时,那么选择将右兄弟的第一个键值对移动到当前结点,并修改父结点中指向右兄弟的键。
 在上述两种操作中,合并操作会导致父结点删除键值对,因此会向上递归地去判断是否需要再次的合并与重构。
在上述两种操作中,合并操作会导致父结点删除键值对,因此会向上递归地去判断是否需要再次的合并与重构。