---
title: '两种思路解决单词拼接问题'
tags: ['动态规划', '设计']
---




**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。[第 18 期每日打卡](https://aep.xet.tech/s/2PLO1n) 开始报名。反馈或修正 chatGPT 翻译的多语言代码 [点击这里](https://github.com/labuladong/fucking-algorithm/issues/1113)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
| :----: | :----: | :----: |
| [139. Word Break](https://leetcode.com/problems/word-break/) | [139. 单词拆分](https://leetcode.cn/problems/word-break/) | 🟠
| [140. Word Break II](https://leetcode.com/problems/word-break-ii/) | [140. 单词拆分 II](https://leetcode.cn/problems/word-break-ii/) | 🔴
**-----------**
之前 [手把手带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结) 把递归穷举划分为「遍历」和「分解问题」两种思路,其中「遍历」的思路扩展延伸一下就是回溯算法,「分解问题」的思路可以扩展成动态规划算法。
我在 [手把手带你刷二叉树(思路篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列1) 对一些二叉树问题进行举例,同时给出「遍历」和「分解问题」两种思路的解法,帮大家借助二叉树理解更高级的算法设计思想。
当然,这种思维转换不止局限于二叉树相关的算法,本文就跳出二叉树类型问题,来看看实际算法题中如何把问题抽象成树形结构,从而进行「遍历」和「分解问题」的思维转换,从 [回溯算法](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 顺滑地切换到 [动态规划算法](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)。
先说句题外话,前文 [动态规划核心框架详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 说,**标准的动态规划问题一定是求最值的**,因为动态规划类型问题有一个性质叫做「最优子结构」,即从子问题的最优解推导出原问题的最优解。
但在我们平常的语境中,就算不是求最值的题目,只要看见使用备忘录消除重叠子问题,我们一般都称它为动态规划算法。严格来讲这是不符合动态规划问题的定义的,说这种解法叫做「带备忘录的 DFS 算法」可能更准确些。不过咱也不用太纠结这种名词层面的细节,既然大家叫的顺口,就叫它动态规划也无妨。
本文讲解的两道题目也不是求最值的,但依然会把他们的解法称为动态规划解法,这里提前跟大家说下这里面的细节,免得细心的读者疑惑。其他不多说了,直接看题目吧。
### 单词拆分 I
首先看下力扣第 139 题「单词拆分」:

函数签名如下:
```java
boolean wordBreak(String s, List wordDict);
```
这是一道非常高频的面试题,我们来思考下如何通过「遍历」和「分解问题」的思路来解决它。
**先说说「遍历」的思路,也就是用回溯算法解决本题**。回溯算法最经典的应用就是排列组合相关的问题了,不难发现这道题换个说法也可以变成一个排列问题:
现在给你一个不包含重复单词的单词列表 `wordDict` 和一个字符串 `s`,请你判断是否可以从 `wordDict` 中选出若干单词的排列(可以重复挑选)构成字符串 `s`。
这就是前文 [回溯算法秒杀排列组合问题的九种变体](https://labuladong.github.io/article/fname.html?fname=子集排列组合) 中讲到的最后一种变体:元素无重可复选的排列问题,前文我写了一个 `permuteRepeat` 函数,代码如下:
```java
class Solution {
List> res = new LinkedList<>();
LinkedList track = new LinkedList<>();
// 元素无重可复选的全排列
public List> permuteRepeat(int[] nums) {
backtrack(nums);
return res;
}
// 回溯算法核心函数
void backtrack(int[] nums) {
// base case,到达叶子节点
if (track.size() == nums.length) {
// 收集根到叶子节点路径上的值
res.add(new LinkedList(track));
return;
}
// 回溯算法标准框架
for (int i = 0; i < nums.length; i++) {
// 做选择
track.add(nums[i]);
// 进入下一层回溯树
backtrack(nums);
// 取消选择
track.removeLast();
}
}
}
```
给这个函数输入 `nums = [1,2,3]`,输出是 3^3 = 27 种可能的组合:
```java
[
[1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],
[2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],
[3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
]
```
这段代码实际上就是遍历一棵高度为 `N + 1` 的满 `N` 叉树(`N` 为 `nums` 的长度),其中根到叶子的每条路径上的元素就是一个排列结果:
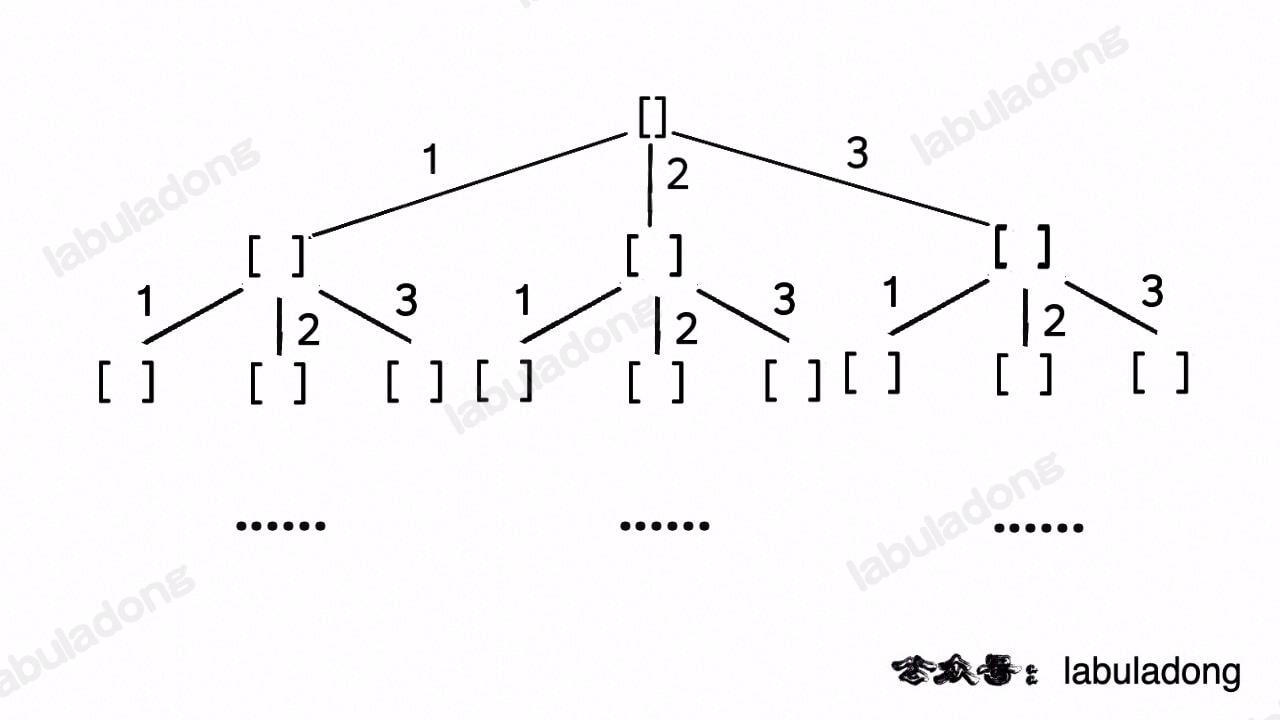
类比一下,本文讲的这道题也有异曲同工之妙,假设 `wordDict = ["a", "aa", "ab"], s = "aaab"`,想用 `wordDict` 中的单词拼出 `s`,其实也面对着类似的一棵 `M` 叉树,`M` 为 `wordDict` 中单词的个数,**你需要做的就是站在回溯树的每个节点上,看看哪个单词能够匹配 `s[i..]` 的前缀,从而判断应该往哪条树枝上走**:
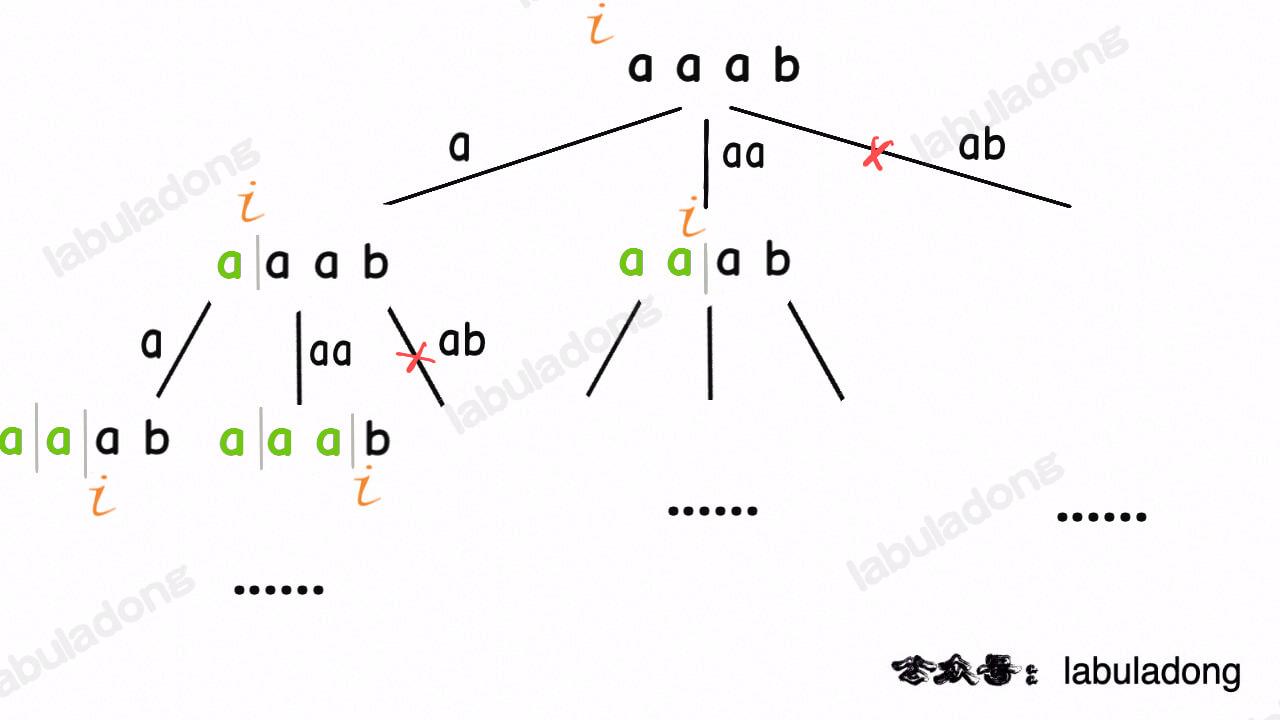
然后,按照前文 [回溯算法框架详解](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 所说,你把 `backtrack` 函数理解成在回溯树上游走的一个指针,维护每个节点上的变量 `i`,即可遍历整棵回溯树,寻找出匹配 `s` 的组合。
回溯算法解法代码如下:
```java
class Solution {
List wordDict;
// 记录是否找到一个合法的答案
boolean found = false;
// 记录回溯算法的路径
LinkedList track = new LinkedList<>();
// 主函数
public boolean wordBreak(String s, List wordDict) {
this.wordDict = wordDict;
// 执行回溯算法穷举所有可能的组合
backtrack(s, 0);
return found;
}
// 回溯算法框架
void backtrack(String s, int i) {
// base case
if (found) {
// 如果已经找到答案,就不要再递归搜索了
return;
}
if (i == s.length()) {
// 整个 s 都被匹配完成,找到一个合法答案
found = true;
return;
}
// 回溯算法框架
for (String word : wordDict) {
// 看看哪个单词能够匹配 s[i..] 的前缀
int len = word.length();
if (i + len <= s.length()
&& s.substring(i, i + len).equals(word)) {
// 找到一个单词匹配 s[i..i+len)
// 做选择
track.addLast(word);
// 进入回溯树的下一层,继续匹配 s[i+len..]
backtrack(s, i + len);
// 撤销选择
track.removeLast();
}
}
}
}
```
这段代码就是严格按照回溯算法框架写出来的,应该不难理解,但这段代码无法通过所有测试用例,我们按照之前 [算法时空复杂度使用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度) 中讲到的方法来分析一下它的时间复杂度。
递归函数的时间复杂度的粗略估算方法就是用递归函数调用次数(递归树的节点数) x 递归函数本身的复杂度。对于这道题来说,递归树的每个节点其实就是对 `s` 进行的一次切割,那么最坏情况下 `s` 能有多少种切割呢?长度为 `N` 的字符串 `s` 中共有 `N - 1` 个「缝隙」可供切割,每个缝隙可以选择「切」或者「不切」,所以 `s` 最多有 `O(2^N)` 种切割方式,即递归树上最多有 `O(2^N)` 个节点。
当然,实际情况可定会好一些,毕竟存在剪枝逻辑,但从最坏复杂度的角度来看,递归树的节点个数确实是指数级别的。
那么 `backtrack` 函数本身的时间复杂度是多少呢?主要的时间消耗是遍历 `wordDict` 寻找匹配 `s[i..]` 的前缀的单词:
```java
// 遍历 wordDict 的所有单词
for (String word : wordDict) {
// 看看哪个单词能够匹配 s[i..] 的前缀
int len = word.length();
if (i + len <= s.length()
&& s.substring(i, i + len).equals(word)) {
// 找到一个单词匹配 s[i..i+len)
// ...
}
}
```
设 `wordDict` 的长度为 `M`,字符串 `s` 的长度为 `N`,那么这段代码的最坏时间复杂度是 `O(MN)`(for 循环 `O(M)`,Java 的 `substring` 方法 `O(N)`),所以总的时间复杂度是 `O(2^N * MN)`。
这里顺便说一个细节优化,其实你也可以反过来,通过穷举 `s[i..]` 的前缀去判断 `wordDict` 中是否有对应的单词:
```java
// 注意,要转化成哈希集合,提高 contains 方法的效率
HashSet wordDict = new HashSet<>(wordDict);
// 遍历 s[i..] 的所有前缀
for (int len = 1; i + len <= s.length(); len++) {
// 看看 wordDict 中是否有单词能匹配 s[i..] 的前缀
String prefix = s.substring(i, i + len);
if (wordDict.contains(prefix)) {
// 找到一个单词匹配 s[i..i+len)
// ...
}
}
```
这段代码和刚才那段代码的结果是一样的,但这段代码的时间复杂度变成了 `O(N^2)`,和刚才的代码不同。
到底哪样子好呢?这要看题目给的数据范围。本题说了 `1 <= s.length <= 300, 1 <= wordDict.length <= 1000`,所以 `O(N^2)` 的结果较小,这段代码的实际运行效率应该稍微高一些,这个是一个细节的优化,你可以自己做一下,我就不写了。
不过即便你优化这段代码,总的时间复杂度依然是指数级的 `O(2^N * N^2)`,是无法通过所有测试用例的,那么问题出在哪里呢?
比如输入 `wordDict = ["a", "aa"], s = "aaab"`,算法无法找到一个可行的组合,所以一定会遍历整棵回溯树,但你注意这里面会存在重复的情况:
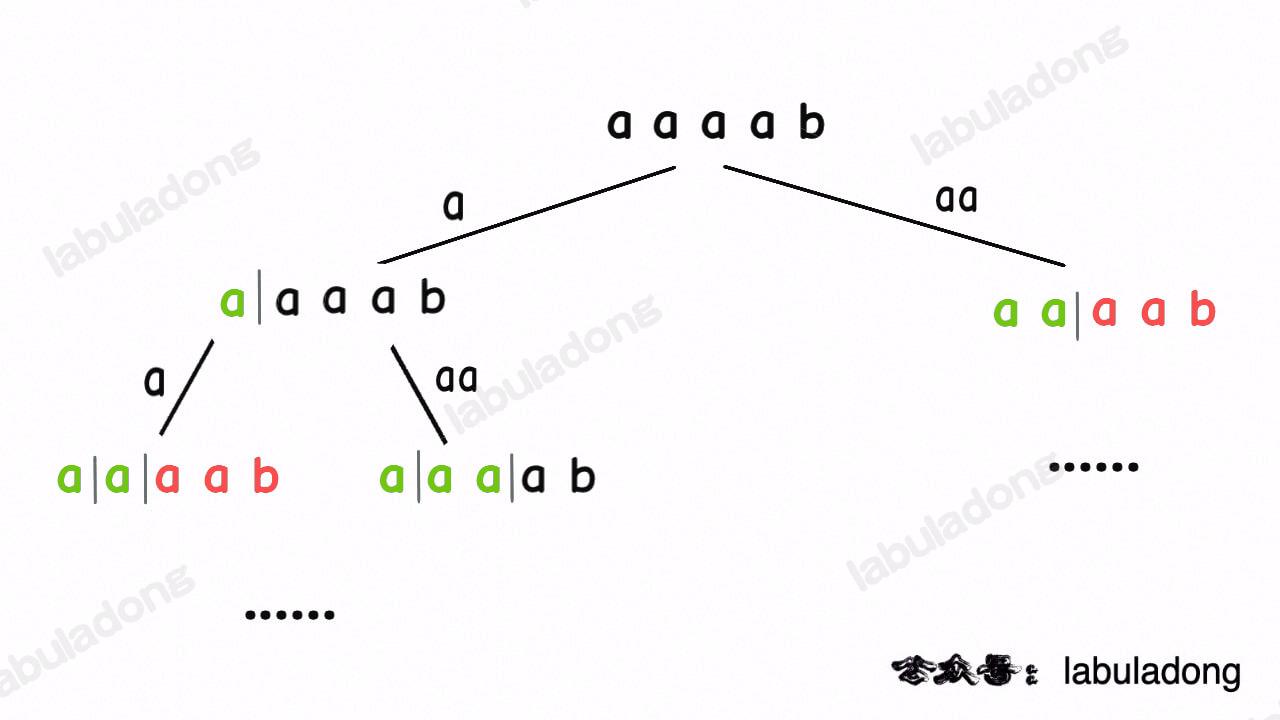
图中标红的这两部分,虽然经历了不同的切分,但是切分得出的结果是相同的,所以这两个节点下面的子树也是重复的,即存在冗余计算,极端情况下会消耗大量时间。
**如何消除冗余计算呢?这就要稍微转变一下思维模式,用「分解问题」的思维模式来考虑这道题**。
我们刚才以排列组合的视角思考这个问题,现在我们换一种视角,思考一下是否能够把原问题分解成规模更小,结构相同的子问题,然后通过子问题的结果计算原问题的结果。
对于输入的字符串 `s`,如果我能够从单词列表 `wordDict` 中找到一个单词匹配 `s` 的前缀 `s[0..k]`,那么只要我能拼出 `s[k+1..]`,就一定能拼出整个 `s`。换句话说,我把规模较大的原问题 `wordBreak(s[0..])` 分解成了规模较小的子问题 `wordBreak(s[k+1..])`,然后通过子问题的解反推出原问题的解。
有了这个思路就可以定义一个 `dp` 函数,并给出该函数的定义:
```java
// 定义:返回 s[i..] 是否能够被拼出
int dp(String s, int i);
// 计算整个 s 是否能被拼出,调用 dp(s, 0)
```
有了这个函数定义,就可以把刚才的逻辑大致翻译成伪码:
```java
List wordDict;
// 定义:返回 s[i..] 是否能够被拼出
int dp(String s, int i) {
// base case,s[i..] 是空串
if (i == s.length()) {
return true;
}
// 遍历 wordDict,看看哪些单词是 s[i..] 的前缀
for (Strnig word : wordDict) {
if word 是 s[i..] 的前缀 {
int len = word.length();
// 只要 s[i+len..] 可以被拼出,s[i..] 就能被拼出
if (dp(s, i + len) == true) {
return true;
}
}
}
// 所有单词都尝试过,无法拼出整个 s
return false;
}
```
类似之前讲的回溯算法,`dp` 函数中的 for 循环也可以优化一下:
```java
// 注意,用哈希集合快速判断元素是否存在
HashSet wordDict;
// 定义:返回 s[i..] 是否能够被拼出
int dp(String s, int i) {
// base case,s[i..] 是空串
if (i == s.length()) {
return true;
}
// 遍历 s[i..] 的所有前缀,看看哪些前缀存在 wordDict 中
for (int len = 1; i + len <= s.length(); len++) {
if wordDict 中存在 s[i..len) {
// 只要 s[i+len..] 可以被拼出,s[i..] 就能被拼出
if (dp(s, i + len) == true) {
return true;
}
}
}
// 所有单词都尝试过,无法拼出整个 s
return false;
}
```
对于这个 `dp` 函数,指针 `i` 的位置就是「状态」,所以我们可以通过添加备忘录的方式优化效率,避免对相同的子问题进行冗余计算。最终的解法代码如下:
```java
class Solution {
// 用哈希集合方便快速判断是否存在
HashSet wordDict;
// 备忘录,-1 代表未计算,0 代表无法凑出,1 代表可以凑出
int[] memo;
// 主函数
public boolean wordBreak(String s, List wordDict) {
// 转化为哈希集合,快速判断元素是否存在
this.wordDict = new HashSet<>(wordDict);
// 备忘录初始化为 -1
this.memo = new int[s.length()];
Arrays.fill(memo, -1);
return dp(s, 0);
}
// 定义:s[i..] 是否能够被拼出
boolean dp(String s, int i) {
// base case
if (i == s.length()) {
return true;
}
// 防止冗余计算
if (memo[i] != -1) {
return memo[i] == 0 ? false : true;
}
// 遍历 s[i..] 的所有前缀
for (int len = 1; i + len <= s.length(); len++) {
// 看看哪些前缀存在 wordDict 中
String prefix = s.substring(i, i + len);
if (wordDict.contains(prefix)) {
// 找到一个单词匹配 s[i..i+len)
// 只要 s[i+len..] 可以被拼出,s[i..] 就能被拼出
boolean subProblem = dp(s, i + len);
if (subProblem == true) {
memo[i] = 1;
return true;
}
}
}
// s[i..] 无法被拼出
memo[i] = 0;
return false;
}
}
```
这个解法能够通过所有测试用例,我们根据 [算法时空复杂度使用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度) 来算一下它的时间复杂度:
因为有备忘录的辅助,消除了递归树上的重复节点,使得递归函数的调用次数从指数级别降低为状态的个数 `O(N)`,函数本身的复杂度还是 `O(N^2)`,所以总的时间复杂度是 `O(N^3)`,相较回溯算法的效率有大幅提升。
### 单词拆分 II
有了上一道题的铺垫,力扣第 140 题「单词拆分 II」就容易多了,先看下题目:

相较上一题,这道题不是单单问你 `s` 是否能被拼出,还要问你是怎么拼的,其实只要把之前的解法稍微改一改就可以解决这道题。
上一道题的回溯算法维护一个 `found` 变量,只要找到一种拼接方案就提前结束遍历回溯树,那么在这道题中我们不要提前结束遍历,并把所有可行的拼接方案收集起来就能得到答案:
```java
class Solution {
// 记录结果
List res = new LinkedList<>();
// 记录回溯算法的路径
LinkedList track = new LinkedList<>();
List wordDict;
// 主函数
public List wordBreak(String s, List wordDict) {
this.wordDict = wordDict;
// 执行回溯算法穷举所有可能的组合
backtrack(s, 0);
return res;
}
// 回溯算法框架
void backtrack(String s, int i) {
// base case
if (i == s.length()) {
// 找到一个合法组合拼出整个 s,转化成字符串
res.add(String.join(" ", track));
return;
}
// 回溯算法框架
for (String word : wordDict) {
// 看看哪个单词能够匹配 s[i..] 的前缀
int len = word.length();
if (i + len <= s.length()
&& s.substring(i, i + len).equals(word)) {
// 找到一个单词匹配 s[i..i+len)
// 做选择
track.addLast(word);
// 进入回溯树的下一层,继续匹配 s[i+len..]
backtrack(s, i + len);
// 撤销选择
track.removeLast();
}
}
}
}
```
这个解法的时间复杂度和前一道题类似,依然是 `O(2^N * MN)`,但由于这道题给的数据规模较小,所以可以通过所有测试用例。
类似的,这个问题也可以用分解问题的思维解决,把上一道题的 `dp` 函数稍作修改即可:
```java
class Solution {
HashSet wordDict;
// 备忘录
List[] memo;
public List wordBreak(String s, List wordDict) {
this.wordDict = new HashSet<>(wordDict);
memo = new List[s.length()];
return dp(s, 0);
}
// 定义:返回用 wordDict 构成 s[i..] 的所有可能
List dp(String s, int i) {
List res = new LinkedList<>();
if (i == s.length()) {
res.add("");
return res;
}
// 防止冗余计算
if (memo[i] != null) {
return memo[i];
}
// 遍历 s[i..] 的所有前缀
for (int len = 1; i + len <= s.length(); len++) {
// 看看哪些前缀存在 wordDict 中
String prefix = s.substring(i, i + len);
if (wordDict.contains(prefix)) {
// 找到一个单词匹配 s[i..i+len)
List subProblem = dp(s, i + len);
// 构成 s[i+len..] 的所有组合加上 prefix
// 就是构成构成 s[i] 的所有组合
for (String sub : subProblem) {
if (sub.isEmpty()) {
// 防止多余的空格
res.add(prefix);
} else {
res.add(prefix + " " + sub);
}
}
}
}
// 存入备忘录
memo[i] = res;
return res;
}
}
```
这个解法依然用备忘录消除了重叠子问题,所以 `dp` 函数递归调用的次数减少为 `O(N)`,但 `dp` 函数本身的时间复杂度上升了,因为 `subProblem` 是一个子集列表,它的长度是指数级的。再加上 Java 中用 `+` 拼接字符串的效率并不高,且还要消耗备忘录去存储所有子问题的结果,所以这个算法的时间复杂度并不比回溯算法低,依然是指数级别。
综上,我们处理排列组合问题时一般使用回溯算法去「遍历」回溯树,而不用「分解问题」的思路去处理,因为存储子问题的结果就需要大量的时间和空间,除非重叠子问题的数量较多的极端情况,否则得不偿失。
以上就是本文的全部内容,希望你能对回溯思路和分解问题的思路有更深刻的理解。
**_____________**
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:



