# 恢复二叉搜索树
给你二叉搜索树的根节点 root ,该树中的两个节点被错误地交换。请在不改变其结构的情况下,恢复这棵树。
进阶:使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗?
示例 1:
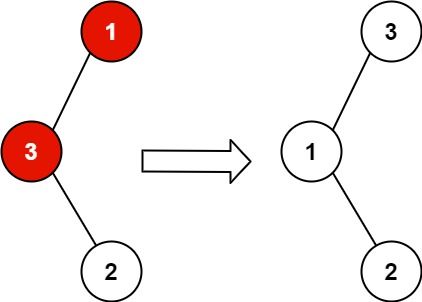
输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:
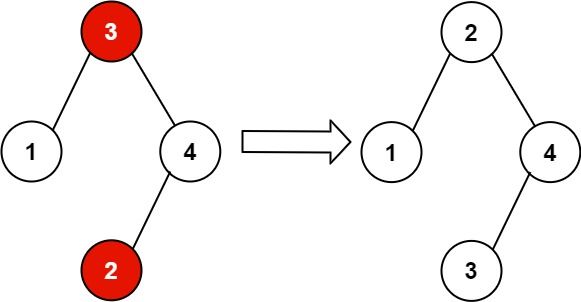
输入:root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示:
- 树上节点的数目在范围
[2, 1000] 内 -231 <= Node.val <= 231 - 1
## template
```cpp
#include
using namespace std;
struct TreeNode
{
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution
{
public:
void recoverTree(TreeNode *root)
{
dfs(root);
int tmp = p0_->val;
p0_->val = p1_->val;
p1_->val = tmp;
}
private:
int wrong_ = 0;
TreeNode *prev_ = nullptr;
TreeNode *p0_ = nullptr;
TreeNode *p1_ = nullptr;
void dfs(TreeNode *root)
{
if (root == nullptr || wrong_ == 2)
{
return;
}
dfs(root->left);
if (prev_ != nullptr && prev_->val > root->val)
{
if (++wrong_ == 1)
{
p0_ = prev_;
p1_ = root;
}
else if (wrong_ == 2)
{
p1_ = root;
}
}
prev_ = root;
dfs(root->right);
}
};
```
## 答案
```cpp
```
## 选项
### A
```cpp
```
### B
```cpp
```
### C
```cpp
``` 
