# 完美矩形
我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。
每个矩形用左下角的点和右上角的点的坐标来表示。例如, 一个单位正方形可以表示为 [1,1,2,2]。 ( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为 (2, 2) )。
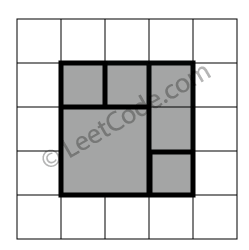
示例 1:
rectangles = [
[1,1,3,3],
[3,1,4,2],
[3,2,4,4],
[1,3,2,4],
[2,3,3,4]
]
返回 true。5个矩形一起可以精确地覆盖一个矩形区域。
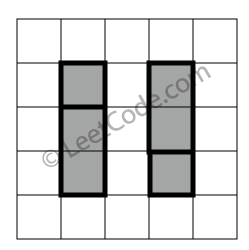
示例 2:
rectangles = [
[1,1,2,3],
[1,3,2,4],
[3,1,4,2],
[3,2,4,4]
]
返回 false。两个矩形之间有间隔,无法覆盖成一个矩形。
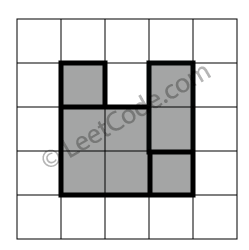
示例 3:
rectangles = [
[1,1,3,3],
[3,1,4,2],
[1,3,2,4],
[3,2,4,4]
]
返回 false。图形顶端留有间隔,无法覆盖成一个矩形。
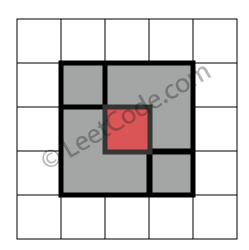
示例 4:
rectangles = [
[1,1,3,3],
[3,1,4,2],
[1,3,2,4],
[2,2,4,4]
]
返回 false。因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
## template
```java
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
int left = Integer.MAX_VALUE;
int right = Integer.MIN_VALUE;
int top = Integer.MIN_VALUE;
int bottom = Integer.MAX_VALUE;
int n = rectangles.length;
Set set = new HashSet<>();
int sumArea = 0;
for (int i = 0; i < n; i++) {
left = Math.min(left, rectangles[i][0]);
bottom = Math.min(bottom, rectangles[i][1]);
right = Math.max(right, rectangles[i][2]);
top = Math.max(top, rectangles[i][3]);
sumArea += (rectangles[i][3] - rectangles[i][1]) * (rectangles[i][2] - rectangles[i][0]);
String lt = rectangles[i][0] + " " + rectangles[i][3];
String lb = rectangles[i][0] + " " + rectangles[i][1];
String rt = rectangles[i][2] + " " + rectangles[i][3];
String rb = rectangles[i][2] + " " + rectangles[i][1];
if (!set.contains(lt))
set.add(lt);
else
set.remove(lt);
if (!set.contains(lb))
set.add(lb);
else
set.remove(lb);
if (!set.contains(rt))
set.add(rt);
else
set.remove(rt);
if (!set.contains(rb))
set.add(rb);
else
set.remove(rb);
}
if (set.size() == 4 && set.contains(left + " " + top) && set.contains(left + " " + bottom)
&& set.contains(right + " " + bottom) && set.contains(right + " " + top)) {
return sumArea == (right - left) * (top - bottom);
}
return false;
}
}
```
## 答案
```java
```
## 选项
### A
```java
```
### B
```java
```
### C
```java
``` 



