# 搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
- 每行中的整数从左到右按升序排列。
- 每行的第一个整数大于前一行的最后一个整数。
示例 1:
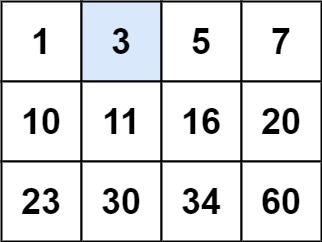
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
示例 2:
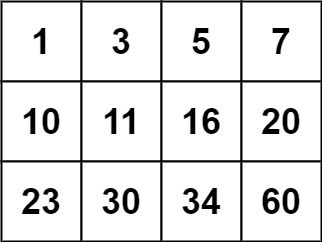
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
## template
```python
class Solution(object):
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if not matrix or not matrix[0]:
return False
rows = len(matrix)
cols = len(matrix[0])
row, col = 0, cols - 1
while True:
if row < rows and col >= 0:
if matrix[row][col] == target:
return True
elif matrix[row][col] < target:
row += 1
else:
col -= 1
else:
return False
# %%
s = Solution()
print(s.searchMatrix(matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3))
```
## 答案
```python
```
## 选项
### A
```python
```
### B
```python
```
### C
```python
``` 
