每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
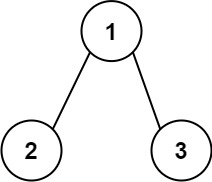
输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径1->2代表数字12从根到叶子节点路径1->3代表数字13因此,数字总和 = 12 + 13 =25
示例 2:
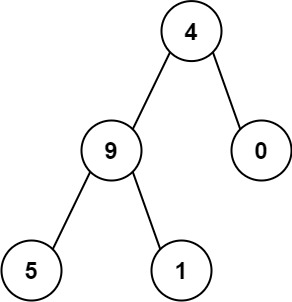
输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径4->9->5代表数字 495 从根到叶子节点路径4->9->1代表数字 491 从根到叶子节点路径4->0代表数字 40 因此,数字总和 = 495 + 491 + 40 =1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10