# 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
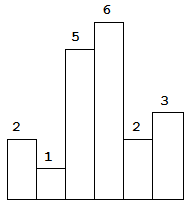
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
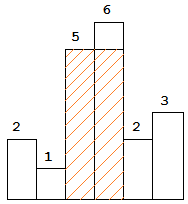
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
以下错误的选项是?
## aop
### before
```c
#include
using namespace std;
```
### after
```c
int main()
{
Solution sol;
vector heights = {2, 1, 5, 6, 2, 3};
int res;
res = sol.largestRectangleArea(heights);
cout << res << endl;
return 0;
}
```
## 答案
```c
class Solution
{
public:
int largestRectangleArea(vector &heights)
{
if (heights.empty())
return 0;
stack st;
heights.push_back(0);
int res = 0;
for (int i = 0; i < heights.size(); i++)
{
while (!st.empty() && heights[i] < heights[st.top()])
{
int curHeight = heights[st.top()];
st.pop();
int width = st.empty() ? i : i - st.top();
if (width * curHeight > res)
res = width * curHeight;
}
st.push(i);
}
return res;
}
};
```
## 选项
### A
```c
class Solution
{
public:
int largestRectangleArea(vector &heights)
{
int sz = heights.size();
int ma = 0;
for (int i = 0; i < sz; i++)
{
int len = 1;
int hei = heights[i];
int sta = i - 1, en = i + 1;
while (sta >= 0 && heights[sta] >= hei)
{
len++;
sta--;
}
while (en < sz && heights[en] >= hei)
{
len++;
en++;
}
ma = max(ma, len * hei);
}
return ma;
}
};
```
### B
```c
class Solution
{
public:
int largestRectangleArea(vector &heights)
{
int n = heights.size();
vector left(n), right(n, n);
stack mono_stack;
for (int i = 0; i < n; ++i)
{
while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i])
{
right[mono_stack.top()] = i;
mono_stack.pop();
}
left[i] = (mono_stack.empty() ? -1 : mono_stack.top());
mono_stack.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i)
{
ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
};
```
### C
```c
class Solution
{
public:
int largestRectangleArea(vector &heights)
{
int n = heights.size();
stack index;
int area = 0;
for (int i = 0; i < heights.size(); i++)
{
if (index.empty() || heights[index.top()] < heights[i])
index.push(i);
else
{
while (!index.empty() && heights[index.top()] >= heights[i])
{
int tmp = index.top();
index.pop();
int length = 0;
if (index.empty())
length = i;
else
length = i - index.top() - 1;
area = max(area, length * heights[tmp]);
}
index.push(i);
}
}
while (!index.empty())
{
int tmp = index.top();
index.pop();
int length = 0;
if (index.empty())
length = n;
else
length = n - index.top() - 1;
area = max(area, length * heights[tmp]);
}
return area;
}
};
```


