# 夺冠概率

足球比赛具有一定程度的偶然性，弱队也有战胜强队的可能。

假设有甲、乙、丙、丁四个球队。根据他们过去比赛的成绩，得出每个队与另一个队对阵时取胜的概率表:
```
    甲   乙  丙  丁   
甲   -  0.1 0.3 0.5
乙 0.9  -   0.7 0.4 
丙 0.7  0.3 -   0.2
丁 0.5  0.6 0.8 -
```
数据含义：甲对乙的取胜概率为0.1，丙对乙的胜率为0.3，...

现在要举行一次锦标赛。双方抽签，分两个组比，获胜的两个队再争夺冠军。

![](https://img-blog.csdn.net/20150228234310457?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvd3IxMzI=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)

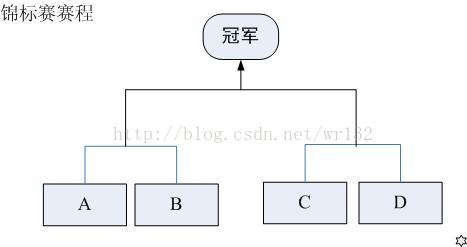
请你进行10万次模拟，计算出甲队夺冠的概率。

以下选项<span style="color:red">错误</span>的是？

## aop

### before

```cpp
#include <bits/stdc++.h>
using namespace std;
```
### after

```cpp

```

## 答案

```cpp
int main()
{
    float a[4][4] = {0, 0.1, 0.3, 0.5, 0.9, 0, 0.7, 0.4, 0.7, 0.3, 0, 0.2, 0.5, 0.6, 0.8, 0};
    float p[3];

    p[0] = a[0][1] * (a[2][3] * a[0][2] + a[3][2] * a[0][3]);

    p[1] = a[0][2] * (a[1][3] * a[0][1] + a[3][1] * a[0][3]);

    p[2] = a[0][3] * (a[1][2] * a[0][1] + a[2][1] * a[0][2]);
    srand(time(0));
    float sum = 0;
    for (int i = 0; i < 10000; i++)
    {
        int r = rand() / 3;
        sum += p[r];
    }
    float pi = sum / 10000;
    cout << pi << endl;
}
```
## 选项


### A

```cpp
int main()
{
    int i, j;
    double a[4][4] = {1.0, 0.1, 0.3, 0.5,
                      0.9, 1.0, 0.7, 0.4,
                      0.7, 0.3, 1.0, 0.2,
                      0.5, 0.6, 0.8, 1.0};
    double p[3], sum = 0.0;
    p[0] = a[0][1] * (a[2][3] * a[0][2] + a[3][2] * a[0][3]);
    p[1] = a[0][2] * (a[1][3] * a[0][1] + a[3][1] * a[0][3]);
    p[2] = a[0][3] * (a[1][2] * a[0][1] + a[2][1] * a[0][2]);
    srand(time(0));
    for (i = 0; i < 100000; i++)
    {
        j = rand() % 3;
        sum += p[j];
    }
    sum /= 100000;
    printf("%lf\n", sum);
    return 0;
}
```

### B

```cpp
double p[3];
int main()
{

    p[0] = 0.1 * 0.8 * 0.5 + 0.1 * 0.2 * 0.3;
    p[1] = 0.3 * 0.6 * 0.5 + 0.3 * 0.4 * 0.1;
    p[2] = 0.5 * 0.7 * 0.1 + 0.5 * 0.3 * 0.3;

    double sum = 0;

    srand(time(NULL));
    for (int i = 1; i <= 100000; i++)
    {
        int r = rand() % 3;
        sum += p[r];
    }
    printf("%f\n", sum / 100000);
    return 0;
}
```

### C

```cpp
double rate[4][4] = {
    {0, 0.1, 0.3, 0.5},
    {0.9, 0, 0.7, 0.4},
    {0.7, 0.3, 0, 0.2},
    {0.5, 0.6, 0.8, 0}};

int main()
{
    int i, j, k;
    double time, sum;
    time = 0;
    sum = 0;
    for (i = 1; i < 4; i++)
    {
        for (j = 1; j < 4; j++)
        {
            for (k = 1; k < 4; k++)
            {
                if (j != i && k != i && j != k)
                {
                    sum += rate[0][i] * rate[j][k] * rate[0][j];
                }
            }
        }
        time++;
    }
    cout << sum / time;
    return 0;
}
```