# 交错字符串
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + ... + snt = t1 + t2 + ... + tm|n - m| <= 1- 交错 是
s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...
提示:a + b 意味着字符串 a 和 b 连接。
示例 1:
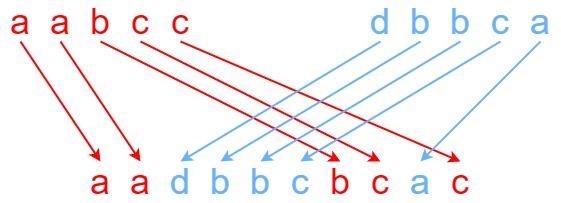
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出:true
示例 2:
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出:false
示例 3:
输入:s1 = "", s2 = "", s3 = ""
输出:true
提示:
0 <= s1.length, s2.length <= 1000 <= s3.length <= 200s1、s2、和 s3 都由小写英文字母组成
以下错误的选项是?
## aop
### before
```c
#include
using namespace std;
```
### after
```c
int main()
{
Solution sol;
bool res;
string s1 = "aabcc";
string s2 = "dbbca";
string s3 = "aadbbcbcac";
res = sol.isInterleave(s1, s2, s3);
cout << res;
return 0;
}
```
## 答案
```c
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
int len1 = s1.length();
int len2 = s2.length();
int len3 = s3.length();
if (len1 + len2 != len3)
return false;
bool f[len1 + 1][len2 + 1];
f[0][0] = true;
for (int i = 0; i < len1 + 1; i++)
{
for (int j = 0; j < len2 + 1; j++)
{
if (j > 0)
{
f[i][j] = f[i][j - 1] && s3[i + j - 1];
}
if (i > 0)
{
f[i][j] = f[i][j] || (f[i - 1][j] && s3[i + j - 1]);
}
}
}
return f[len1][len2];
}
};
```
## 选项
### A
```c
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
if (s1.size() + s2.size() != s3.size())
return false;
int m = s1.size(), n = s2.size(), i, j, k;
vector> dp(m + 1, vector(n + 1, 0));
dp[0][0] = 1;
for (i = 0; i < m; i++)
if (s1[i] == s3[i])
dp[i + 1][0] = 1;
else
break;
for (i = 0; i < n; i++)
if (s2[i] == s3[i])
dp[0][i + 1] = 1;
else
break;
for (i = 1; i <= m; ++i)
for (j = 1; j <= n; j++)
{
k = i + j;
if (s1[i - 1] == s3[k - 1])
dp[i][j] |= dp[i - 1][j];
if (s2[j - 1] == s3[k - 1])
dp[i][j] |= dp[i][j - 1];
}
return dp[m][n];
}
};
```
### B
```c
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
if (s1.size() + s2.size() != s3.size())
return false;
int m = s1.size(), n = s2.size();
vector> dp(m + 1, vector(n + 1, false));
dp[0][0] = true;
for (int i = 1; i <= m; ++i)
dp[i][0] = dp[i - 1][0] && (s1[i - 1] == s3[i - 1]);
for (int i = 1; i <= n; ++i)
dp[0][i] = dp[0][i - 1] && (s2[i - 1] == s3[i - 1]);
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= n; ++j)
{
dp[i][j] = (dp[i - 1][j] && s1[i - 1] == s3[i + j - 1]) || (dp[i][j - 1] && s2[j - 1] == s3[i + j - 1]);
}
return dp[m][n];
}
};
```
### C
```c
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
int s1_len = s1.size();
int s2_len = s2.size();
int s3_len = s3.size();
if (s1_len + s2_len != s3_len)
return false;
if (s1_len == 0 || s2_len == 0)
return s1 + s2 == s3;
vector> dp(s1_len + 1, vector(s2_len + 1));
dp[0][0] = true;
for (int i = 0; i <= s1_len; i++)
{
for (int j = 0; j <= s2_len; j++)
{
if (dp[i][j])
{
if (i < s1_len && s1[i] == s3[i + j])
dp[i + 1][j] = true;
if (j < s2_len && s2[j] == s3[i + j])
dp[i][j + 1] = true;
}
}
}
return dp[s1_len][s2_len];
}
};
```
