add exercises

data/1.算法初阶/1.蓝桥杯-基础/20.星系炸弹/config.json

+{
+  "node_id": "algorithm-7155bf0956dc4133abb9ba64b5e4f6ae",
+  "keywords": [
+    "蓝桥杯",
+    "星系炸弹"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/20.星系炸弹/desc.md

+在X星系的广袤空间中漂浮着许多X星人造“炸弹”，用来作为宇宙中的路标。  
+每个炸弹都可以设定多少天之后爆炸。  
+比如：阿尔法炸弹2015年1月1日放置，定时为15天，则它在2015年1月16日爆炸。  
+有一个贝塔炸弹，2014年11月9日放置，定时为1000天，请你计算它爆炸的准确日期。  

data/1.算法初阶/1.蓝桥杯-基础/20.星系炸弹/solution.cpp

+#include <cstdio>
+int month[13][2] = {{0, 0}, {31, 31}, {28, 29}, {31, 31}, {30, 30}, {31, 31}, {30, 30}, {31, 31}, {31, 31}, {30, 30}, {31, 31}, {30, 30}, {31, 31}};
+
+bool isLeap(int year)
+{
+    return year % 400 == 0 || (year % 4 == 0 && year % 100 != 0);
+}
+
+int main()
+{
+    int y, m, d;
+    int count;
+    scanf("%d-%d-%d", &y, &m, &d);
+    scanf("%d", &count);
+    while (count)
+    {
+        d++;
+        if (d > month[m][isLeap(y)])
+        {
+            d = 1;
+            m++;
+        }
+        if (m > 12)
+        {
+            m = 1;
+            y++;
+        }
+        count--;
+    }
+    printf("%d-%d-%d", y, m, d);
+    return 0;
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/20.星系炸弹/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "880abd1a201c4b02b1c3e75a502c8fcc"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/20.星系炸弹/solution.md

+# 星系炸弹
+
+在X星系的广袤空间中漂浮着许多X星人造“炸弹”，用来作为宇宙中的路标。  
+每个炸弹都可以设定多少天之后爆炸。  
+比如：阿尔法炸弹2015年1月1日放置，定时为15天，则它在2015年1月16日爆炸。  
+有一个贝塔炸弹，2014年11月9日放置，定时为1000天，请你计算它爆炸的准确日期。  
+
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+2017-08-05
+```
+
+## 选项
+
+### A
+
+```cpp
+2017-09-05
+```
+
+### B
+
+```cpp
+2017-08-06
+```
+
+### C
+
+```cpp
+2017-09-06
+```

data/1.算法初阶/1.蓝桥杯-基础/21.蛇形填数/config.json

+{
+  "node_id": "algorithm-f4874378183445fb9edcf1cb372399f7",
+  "keywords": [
+    "蓝桥杯",
+    "蛇形填数"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/21.蛇形填数/desc.md

+如下图所示，小明用从1 开始的正整数“蛇形”填充无限大的矩阵。  
+![](https://img-blog.csdnimg.cn/20210221154521571.png)  
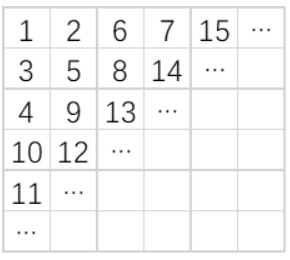
+容易看出矩阵第二行第二列中的数是5。请你计算矩阵中第20 行第20 列的数是多少？

data/1.算法初阶/1.蓝桥杯-基础/21.蛇形填数/solution.cpp

+#include <stdio.h>
+#include <math.h>
+
+int main()
+{
+    int map[50][50];
+    int i, j, cnt = 1;
+    int nowi, nowj;
+    for (i = 1; i <= 40; i++)
+    {
+        if (i & 1)
+        { //若为奇数轮的时候,是从左下角到右上角
+            nowi = i, nowj = 1;
+            for (j = 0; j < i; j++)
+                map[nowi - j][nowj + j] = cnt++;
+        }
+        else
+        { //若为偶数轮的时候,是从右上角到左下角
+            nowi = 1, nowj = i;
+            for (j = 0; j < i; j++)
+                map[nowi + j][nowj - j] = cnt++;
+        }
+    }
+    printf("%d", map[20][20]); //答案:761
+    return 0;
+}

data/1.算法初阶/1.蓝桥杯-基础/21.蛇形填数/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "383bda00ddc5462ab99e42db64e0f076"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/21.蛇形填数/solution.md

+# 蛇形填数
+
+如下图所示，小明用从1 开始的正整数“蛇形”填充无限大的矩阵。  
+![](https://img-blog.csdnimg.cn/20210221154521571.png)  
+容易看出矩阵第二行第二列中的数是5。请你计算矩阵中第20 行第20 列的数是多少？
+
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+761
+```
+
+## 选项
+
+### A
+
+```cpp
+759
+```
+
+### B
+
+```cpp
+760
+```
+
+### C
+
+```cpp
+769
+```

data/1.算法初阶/1.蓝桥杯-基础/22.跑步训练/config.json

+{
+  "node_id": "algorithm-e707e31088ea4929964936a8f8ef15d7",
+  "keywords": [
+    "蓝桥杯",
+    "跑步训练"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/22.跑步训练/desc.md

+小明要做一个跑步训练。  
+初始时，小明充满体力，体力值计为 10000 。如果小明跑步，每分钟损耗 600的体力。如果小明休息，每分钟增加 300 的体力。体力的损耗和增加都是均匀变化的。    
+小明打算跑一分钟、休息一分钟、再跑一分钟、再休息一分钟……如此循环。如果某个时刻小明的体力到达 0 ，他就停止锻炼。  
+请问小明在多久后停止锻炼。为了使答案为整数，请以秒为单位输出答案

data/1.算法初阶/1.蓝桥杯-基础/22.跑步训练/solution.cpp

+#include <iostream>
+using namespace std;
+
+int slove(int n)
+{
+    int m = 0;
+    while (true)
+    {
+        // 体力大于600，还能进行下次循环
+        if (n > 600)
+        {
+            n -= 600; //      跑1分钟消耗600体力
+        }
+        else
+        {
+            // 600/60 每秒钟消耗的体力
+            // n / (600 / 60)  n体力能够跑的时间
+            return m + n / (600 / 60);
+        }
+
+        n += 300;       //      休息1分钟提升300体力
+        m = m + 2 * 60; //      一个循环2分钟
+    }
+}
+
+// 递归算法
+int slove_d(int n)
+{
+    //体力不大于600，结束递归
+    if (n <= 600)
+    {
+        return n / (600 / 60);
+    }
+
+    // 每次循环2分钟， 消耗300体力
+    return 60 * 2 + slove_d(n - 300);
+}
+
+int main()
+{
+    cout << slove(10000) << endl;
+    cout << slove_d(10000) << endl;
+    return 0;
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/22.跑步训练/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "916f0cb3ec744b6a94784acd8f421495"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/22.跑步训练/solution.md

+# 跑步训练
+
+小明要做一个跑步训练。  
+初始时，小明充满体力，体力值计为 10000 。如果小明跑步，每分钟损耗 600的体力。如果小明休息，每分钟增加 300 的体力。体力的损耗和增加都是均匀变化的。    
+小明打算跑一分钟、休息一分钟、再跑一分钟、再休息一分钟……如此循环。如果某个时刻小明的体力到达 0 ，他就停止锻炼。  
+请问小明在多久后停止锻炼。为了使答案为整数，请以秒为单位输出答案
+
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+3880
+```
+
+## 选项
+
+### A
+
+```cpp
+3400
+```
+
+### B
+
+```cpp
+3920
+```
+
+### C
+
+```cpp
+3900
+```

data/1.算法初阶/1.蓝桥杯-基础/23.特别数的和/config.json

+{
+  "node_id": "algorithm-ef2760aef95742c49f78c313d1ff2eb1",
+  "keywords": [
+    "蓝桥杯",
+    "特别数的和"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/23.特别数的和/desc.md

+#### 题目描述
+小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导 0），在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。
+
+请问，在 1 到 n 中，所有这样的数的和是多少？
+
+#### 输入格式
+共一行，包含一个整数 n。
+
+#### 输出格式
+共一行，包含一个整数，表示满足条件的数的和。
+
+#### 数据范围
+```
+1≤n≤10000
+```
+#### 输入样例：
+```
+40
+```
+#### 输出样例：
+```
+574
+```

data/1.算法初阶/1.蓝桥杯-基础/23.特别数的和/solution.cpp

+#include <iostream>
+
+using namespace std;
+
+int ans, n;
+
+bool check(int n)
+{
+    while (n)
+    {
+        int tmpn = n % 10;
+        if (tmpn == 2 || tmpn == 0 || tmpn == 1 || tmpn == 9)
+            return true;
+        n /= 10;
+    }
+    return false;
+}
+
+int main()
+{
+    cin >> n;
+
+    for (int i = 1; i <= n; i++)
+    {
+        if (check(i))
+            ans += i;
+    }
+
+    cout << ans << endl;
+
+    return 0;
+}

data/1.算法初阶/1.蓝桥杯-基础/23.特别数的和/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "17de9b97dbc247aba50ec0c5c0170a68"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/23.特别数的和/solution.md

+# 特别数的和
+
+**题目描述**
+
+小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导 0），在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。
+
+请问，在 1 到 n 中，所有这样的数的和是多少？
+
+**输入格式**
+
+共一行，包含一个整数 n。
+
+**输出格式**
+
+共一行，包含一个整数，表示满足条件的数的和。
+
+**数据范围**
+
+```
+1≤n≤10000
+```
+
+**输入样例：**
+
+```
+40
+```
+
+**输出样例：**
+
+```
+574
+```
+
+以下代码实现了这一功能，请你填补空白处的内容：
+
+```cpp
+#include <iostream>
+
+using namespace std;
+
+int ans, n;
+
+bool check(int n)
+{
+    while (n)
+    {
+        int tmpn = n % 10;
+        if (tmpn == 2 || tmpn == 0 || tmpn == 1 || tmpn == 9)
+            return true;
+        __________________
+    }
+    return false;
+}
+
+int main()
+{
+    cin >> n;
+
+    for (int i = 1; i <= n; i++)
+    {
+        if (check(i))
+            ans += i;
+    }
+
+    cout << ans << endl;
+
+    return 0;
+}
+```
+
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+        n /= 10;
+```
+
+## 选项
+
+### A
+
+```cpp
+        n %= 10;
+```
+
+### B
+
+```cpp
+        break;
+```
+
+### C
+
+```cpp
+        continue;
+```

data/1.算法初阶/1.蓝桥杯-基础/24.切面条/config.json

+{
+  "node_id": "algorithm-530255df51be437b967cbc4524fe66ea",
+  "keywords": [
+    "蓝桥杯",
+    "切面条"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/24.切面条/desc.md

+一根高筋拉面，中间切一刀，可以得到2根面条。  
+如果先对折1次，中间切一刀，可以得到3根面条。  
+如果连续对折2次，中间切一刀，可以得到5根面条。  
+那么，连续对折10次，中间切一刀，会得到多少面条呢？      
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/24.切面条/solution.cpp

+#include <iostream>
+
+using namespace std;
+
+int main()
+{
+    int f[10];
+    f[1] = 3;
+    for (int i = 2; i < 11; i++)
+        f[i] = f[i - 1] * 2 - 1; //等同(f[i-1]-1)*2+1
+    cout << f[10];
+}

data/1.算法初阶/1.蓝桥杯-基础/24.切面条/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "096fc08eabd34865aa1a97820435d66b"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/24.切面条/solution.md

+# 切面条
+
+一根高筋拉面，中间切一刀，可以得到2根面条。  
+如果先对折1次，中间切一刀，可以得到3根面条。  
+如果连续对折2次，中间切一刀，可以得到5根面条。  
+那么，连续对折10次，中间切一刀，会得到多少面条呢？      
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+1025
+```
+
+## 选项
+
+### A
+
+```cpp
+1024
+```
+
+### B
+
+```cpp
+512
+```
+
+### C
+
+```cpp
+513
+```

data/1.算法初阶/1.蓝桥杯-基础/25.日志统计/config.json

+{
+  "node_id": "algorithm-9aea8ae61f274180b9b7172c43ebe69f",
+  "keywords": [
+    "蓝桥杯",
+    "日志统计"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/25.日志统计/desc.md

+#### 题目描述
+小明维护着一个程序员论坛。现在他收集了一份”点赞”日志，日志共有 N 行。  
+
+其中每一行的格式是：  
+ts id  
+表示在 ts 时刻编号 id 的帖子收到一个”赞”。
+
+现在小明想统计有哪些帖子曾经是”热帖”。  
+
+如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞，小明就认为这个帖子曾是”热帖”。
+
+具体来说，如果存在某个时刻 T 满足该帖在 [T,T+D) 这段时间内(注意是左闭右开区间)收到不少于 K 个赞，该帖就曾是”热帖”。
+
+给定日志，请你帮助小明统计出所有曾是”热帖”的帖子编号。
+
+#### 输入格式
+第一行包含三个整数 N,D,K。
+
+以下 N 行每行一条日志，包含两个整数 ts 和 id。
+
+#### 输出格式
+按从小到大的顺序输出热帖 id。
+
+每个 id 占一行。
+
+#### 数据范围
+```
+1≤K≤N≤10E5,
+0≤ts,id≤10E5,
+1≤D≤10000
+```
+#### 输入样例：
+```
+7 10 2
+0 1
+0 10
+10 10
+10 1
+9 1
+100 3
+100 3
+```
+#### 输出样例：
+```
+1
+3
+```
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/25.日志统计/solution.cpp

+#include <iostream>
+#include <algorithm>
+
+using namespace std;
+const int N = 1e5 + 10;
+typedef pair<int, int> PII;
+#define x first
+#define y second
+PII logs[N];
+bool st[N];
+int cnt[N];
+
+int main()
+{
+    int n, d, k;
+    cin >> n >> d >> k;
+    for (int i = 0; i < n; i++)
+        cin >> logs[i].x >> logs[i].y; //时间，编号
+
+    sort(logs, logs + n); //按照时间先排序
+
+    for (int i = 0, j = 0; i < n; i++)
+    {
+        cnt[logs[i].y]++; //目标编号出现次数加1
+        while (logs[i].x - logs[j].x >= d)
+            cnt[logs[j].y]--, j++; //滑动窗口，保证目标区域合法
+        if (cnt[logs[i].y] >= k)
+            st[logs[i].y] = true; //如果编号次数超K则输出
+    }
+
+    for (int i = 0; i < N; i++)
+        if (st[i])
+            cout << i << endl;
+    return 0;
+}

data/1.算法初阶/1.蓝桥杯-基础/25.日志统计/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "55585dfb13104063adb7e4d41384f5a6"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/25.日志统计/solution.md

+# 日志统计
+
+**题目描述**
+
+小明维护着一个程序员论坛。现在他收集了一份”点赞”日志，日志共有 N 行。  
+
+其中每一行的格式是：  
+ts id  
+表示在 ts 时刻编号 id 的帖子收到一个”赞”。
+
+现在小明想统计有哪些帖子曾经是”热帖”。  
+
+如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞，小明就认为这个帖子曾是”热帖”。
+
+具体来说，如果存在某个时刻 T 满足该帖在 [T,T+D) 这段时间内(注意是左闭右开区间)收到不少于 K 个赞，该帖就曾是”热帖”。
+
+给定日志，请你帮助小明统计出所有曾是”热帖”的帖子编号。
+
+**输入格式**
+
+第一行包含三个整数 N,D,K。
+
+以下 N 行每行一条日志，包含两个整数 ts 和 id。
+
+**输出格式**
+
+按从小到大的顺序输出热帖 id。
+
+每个 id 占一行。
+
+**数据范围**
+
+```
+1≤K≤N≤10E5,
+0≤ts,id≤10E5,
+1≤D≤10000
+```
+
+**输入样例：**
+
+```
+7 10 2
+0 1
+0 10
+10 10
+10 1
+9 1
+100 3
+100 3
+```
+
+**输出样例：**
+
+```
+1
+3
+```
+
+下面的程序实现了这一功能，请你补全空白处的内容：
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+const int N = 1e5 + 10;
+typedef pair<int, int> PII;
+#define x first
+#define y second
+PII logs[N];
+bool st[N];
+int cnt[N];
+
+int main()
+{
+    int n, d, k;
+    cin >> n >> d >> k;
+    for (int i = 0; i < n; i++)
+        cin >> logs[i].x >> logs[i].y;
+
+    sort(logs, logs + n);
+
+    for (int i = 0, j = 0; i < n; i++)
+    {
+        cnt[logs[i].y]++;
+        while (logs[i].x - logs[j].x >= d)
+            __________________
+        if (cnt[logs[i].y] >= k)
+            st[logs[i].y] = true;
+    }
+
+    for (int i = 0; i < N; i++)
+        if (st[i])
+            cout << i << endl;
+    return 0;
+}
+```
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+cnt[logs[j].y]--, j++;
+```
+
+## 选项
+
+### A
+
+```cpp
+cnt[logs[j].y]--; j++;
+```
+
+### B
+
+```cpp
+cnt[logs[j].y]++, j++;
+```
+
+### C
+
+```cpp
+cnt[logs[j].y]++; j++;
+```

data/1.算法初阶/1.蓝桥杯-基础/26.神奇算式/config.json

+{
+  "node_id": "algorithm-d98c791357f2416389a36896d0186317",
+  "keywords": [
+    "蓝桥杯",
+    "神奇算式"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/26.神奇算式/desc.md

+由4个不同的数字，组成的一个乘法算式，它们的乘积仍然由这4个数字组成。
+比如： 
+```
+210 x 6 = 1260 
+8 x 473 = 3784
+27 x 81 = 2187 
+```
+都符合要求。  
+如果满足乘法交换律的算式算作同一种情况，那么，包含上边已列出的3种情况，一共有多少种满足要求的算式。

data/1.算法初阶/1.蓝桥杯-基础/26.神奇算式/solution.cpp

+#include <iostream>
+#define MAX_N 1005
+using namespace std;
+
+bool judge1(int n) //判断两个数的乘积是否为4位数
+{
+    int ans = 0;
+    while (n)
+    {
+        ans++;
+        n /= 10;
+    }
+    if (ans == 4)
+        return true;
+    return false;
+}
+
+bool judge2(int i, int j) //判断乘积的数是否为原来的四个数
+{
+    int s1 = 0, s2 = 0;   //和
+    int ss1 = 1, ss2 = 1; //积
+    int tmp = i * j;
+    bool flag1 = true, flag2 = true;
+    while (tmp)
+    {
+        s1 += tmp % 10;
+        if (tmp % 10 == 0)
+            flag1 = false;
+        else
+            ss1 *= tmp % 10;
+        tmp /= 10;
+    }
+    while (j)
+    {
+        s2 += j % 10;
+        if (j % 10 != 0)
+            ss2 *= j % 10;
+        else
+            flag2 = false;
+        j /= 10;
+    }
+    while (i)
+    {
+        s2 += i % 10;
+        if (i % 10 != 0)
+            ss2 *= i % 10;
+        else
+            flag2 = false;
+        i /= 10;
+    }
+    if (s1 == s2 && ss1 == ss2 && flag1 && flag2) //如果没有0的话，是否乘积和和都相等
+        return true;
+    else if ((!flag1 && !flag2) && s1 == s2 && ss1 == ss2) //如果有0的话，是否乘积都相等
+        return true;
+    return false;
+}
+
+bool judge3(int i, int j) //判断两个数中是否全是不同的数
+{
+    int a[4];
+    int ans = 0;
+    while (i)
+    {
+        a[ans] = i % 10;
+        i /= 10;
+        ans++;
+    }
+    while (j)
+    {
+        a[ans] = j % 10;
+        j /= 10;
+        ans++;
+    }
+    for (i = 0; i < 3; i++)
+    {
+        for (j = i + 1; j < 4; j++)
+            if (a[i] == a[j]) //如果有相等的话返回false
+                return false;
+    }
+    return true;
+}
+
+int main()
+{
+    //freopen("data.txt","r",stdin);
+    int i, j;
+    int ans = 0;
+    for (i = 1; i < 10; i++)
+    { //一位数乘以三位数
+        for (j = 123; j < 1000; j++)
+        {
+            if (judge1(i * j) && judge2(i, j) && judge3(i, j))
+                ans++;
+        }
+    }
+    for (i = 10; i < 100; i++)
+    { //两位数乘以两位数
+        for (j = i + 1; j < 100; j++)
+        {
+            if (judge1(i * j) && judge2(i, j) && judge3(i, j))
+                ans++;
+        }
+    }
+    cout << ans;
+    return 0;
+}

data/1.算法初阶/1.蓝桥杯-基础/26.神奇算式/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "aad0e280f4944ea9aff2b9e426aaef21"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/26.神奇算式/solution.md

+# 神奇算式
+
+由4个不同的数字，组成的一个乘法算式，它们的乘积仍然由这4个数字组成。
+比如： 
+```
+210 x 6 = 1260 
+8 x 473 = 3784
+27 x 81 = 2187 
+```
+都符合要求。  
+如果满足乘法交换律的算式算作同一种情况，那么，包含上边已列出的3种情况，一共有多少种满足要求的算式。
+
+以下选项错误的是？
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+int vis[10];
+int ans = 0;
+bool s(int i)
+{
+    while (i)
+    {
+        if (vis[i % 10] == 1)
+            return false;
+        else
+        {
+            vis[i % 10] = 1;
+            i /= 10;
+        }
+    }
+    return true;
+}
+int main()
+{
+    for (int i = 1; i < 999; i++)
+    {
+        for (int j = 1; j < 999; j++)
+        {
+            memset(vis, 0, sizeof(vis));
+            if (s(i) && s(j))
+            {
+                int k = i * j;
+                if (k > 9999 || k < 1000)
+                    continue;
+
+                int t = k;
+                while (k)
+                {
+                    if (vis[k % 10] == 1)
+                    {
+                        vis[k % 10]++;
+
+                        k /= 10;
+                    }
+                    else
+                        break;
+                }
+                if (k == 0 && vis[0] != 1 && vis[1] != 1 && vis[2] != 1 && vis[3] != 1 && vis[4] != 1 && vis[5] != 1 && vis[6] != 1 && vis[7] != 1 && vis[8] != 1 && vis[9] != 1)
+                {
+                    ans++;
+                }
+            }
+        }
+    }
+    cout << ans << endl;
+    return 0;
+}
+```
+
+## 选项
+
+### A
+
+```cpp
+bool isOk(int result, int t1, int t2)
+{
+    bool flag1[10] = {0}, flag2[10] = {0};
+    int i, rNum[4], num[4];
+    for (i = 0; i < 4; i++)
+    {
+        rNum[i] = result % 10;
+        result /= 10;
+        if (flag1[rNum[i]])
+            return false;
+        flag1[rNum[i]] = true;
+    }
+    i = 0;
+    while (t1 > 0)
+    {
+        num[i] = t1 % 10;
+        t1 /= 10;
+        if (flag2[num[i]])
+            return false;
+        flag2[num[i]] = true;
+        i++;
+    }
+    while (t2 > 0)
+    {
+        num[i] = t2 % 10;
+        t2 /= 10;
+        if (flag2[num[i]])
+            return false;
+        flag2[num[i]] = true;
+        i++;
+    }
+    if (i != 4)
+        return false;
+    for (i = 0; i < 10; i++)
+        if (flag1[i] != flag2[i])
+            return false;
+    return true;
+}
+
+int main()
+{
+    int i, j, count = 0;
+    for (i = 1000; i < 10000; i++)
+    {
+
+        for (j = 1; j * j <= i; j++)
+            if (!(i % j) && isOk(i, j, i / j))
+            {
+                count++;
+            }
+    }
+    cout << count << endl;
+
+    return 0;
+}
+```
+
+### B
+
+```cpp
+int main()
+{
+    int v[5], i;
+    int ans = 0;
+    for (i = 1023; i <= 9876; i++)
+    {
+        v[0] = i / 1000;
+        v[1] = i / 10 % 10;
+        v[2] = i / 100 % 10;
+        v[3] = i % 10;
+        int flag1 = 0, flag2 = 0;
+        if (v[0] != v[1] && v[0] != v[2] && v[0] != v[3] && v[1] != v[2] && v[1] != v[3] && v[2] != v[3])
+        {
+            do
+            {
+                if (flag1 != 3 && (v[0] * 100 + v[1] * 10 + v[2]) * v[3] == i)
+                {
+                    flag1 = 1;
+                    ans++;
+                }
+                else if (flag2 != 2 && (v[0] * 10 + v[1]) * (v[2] * 10 + v[3]) == i)
+                {
+                    flag2 = 2;
+                    ans++;
+                }
+                else if (flag1 != 1 && v[0] * (v[1] * 100 + v[2] * 10 + v[3]) == i)
+                {
+                    flag1 = 3;
+                    ans++;
+                }
+            } while (next_permutation(v, v + 4));
+        }
+    }
+    cout << ans;
+    return 0;
+}
+```
+
+### C
+
+```cpp
+#define MAX_N 1005
+
+bool judge1(int n)
+{
+    int ans = 0;
+    while (n)
+    {
+        ans++;
+        n /= 10;
+    }
+    if (ans == 4)
+        return true;
+    return false;
+}
+
+bool judge2(int i, int j)
+{
+    int s1 = 0, s2 = 0;
+    int ss1 = 1, ss2 = 1;
+    int tmp = i * j;
+    bool flag1 = true, flag2 = true;
+    while (tmp)
+    {
+        s1 += tmp % 10;
+        if (tmp % 10 == 0)
+            flag1 = false;
+        else
+            ss1 *= tmp % 10;
+        tmp /= 10;
+    }
+    while (j)
+    {
+        s2 += j % 10;
+        if (j % 10 != 0)
+            ss2 *= j % 10;
+        else
+            flag2 = false;
+        j /= 10;
+    }
+    while (i)
+    {
+        s2 += i % 10;
+        if (i % 10 != 0)
+            ss2 *= i % 10;
+        else
+            flag2 = false;
+        i /= 10;
+    }
+    if (s1 == s2 && ss1 == ss2 && flag1 && flag2)
+        return true;
+    else if ((!flag1 && !flag2) && s1 == s2 && ss1 == ss2)
+        return true;
+    return false;
+}
+
+bool judge3(int i, int j)
+{
+    int a[4];
+    int ans = 0;
+    while (i)
+    {
+        a[ans] = i % 10;
+        i /= 10;
+        ans++;
+    }
+    while (j)
+    {
+        a[ans] = j % 10;
+        j /= 10;
+        ans++;
+    }
+    for (i = 0; i < 3; i++)
+    {
+        for (j = i + 1; j < 4; j++)
+            if (a[i] == a[j])
+                return false;
+    }
+    return true;
+}
+
+int main()
+{
+
+    int i, j;
+    int ans = 0;
+    for (i = 1; i < 10; i++)
+    {
+        for (j = 123; j < 1000; j++)
+        {
+            if (judge1(i * j) && judge2(i, j) && judge3(i, j))
+                ans++;
+        }
+    }
+    for (i = 10; i < 100; i++)
+    {
+        for (j = i + 1; j < 100; j++)
+        {
+            if (judge1(i * j) && judge2(i, j) && judge3(i, j))
+                ans++;
+        }
+    }
+    cout << ans;
+    return 0;
+}
+```

data/1.算法初阶/1.蓝桥杯-基础/27.星期一/config.json

+{
+  "node_id": "algorithm-b788a09cd8e647738a9ac6aea903aadb",
+  "keywords": [
+    "蓝桥杯",
+    "星期一"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/27.星期一/desc.md

+整个20世纪（1901年1月1日至2000年12月31日之间），一共有多少个星期一？(不要告诉我你不知道今天是星期几)
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/27.星期一/solution.cpp

+#include <iostream>
+#include <vector>
+using namespace std;
+
+int a[12] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
+int b[12] = {31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; // 闰年
+int days = 0;                                                 //共多少天
+int rows = 0;                                                 //共多少行
+bool f(int n)                                                 // n是不是闰年
+{
+    if ((n % 4 == 0 && n % 100 != 0) || n % 100 == 0)
+        return true;
+    else
+        return false;
+}
+
+void print(int t[]) //打印那一年
+{
+    for (int i = 0; i < 12; i++)
+    {
+        for (int j = 1; j <= t[i]; j++)
+        {
+            cout << j << "  ";
+            days++;
+            if (days % 7 == 0) //  7天一礼拜
+            {
+                cout << endl;
+                rows++;
+            }
+        }
+    }
+}
+int main()
+{
+    int start = 1901;
+    int end = 2000;
+    for (int i = start; i <= end; i++)
+    {
+        if (f(i) == true) //是闰年,按b数组打印
+            print(b);
+        else //不是，按a数组打印
+            print(a);
+    }
+    cout << "rows is " << endl;
+    cout << rows << endl;
+    return 0;
+}

data/1.算法初阶/1.蓝桥杯-基础/27.星期一/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "d246625d4b1140b3a726569ae37220fb"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/27.星期一/solution.md

+# 星期一
+
+整个20世纪（1901年1月1日至2000年12月31日之间），一共有多少个星期一？(不要告诉我你不知道今天是星期几)
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+5217
+```
+
+## 选项
+
+### A
+
+```cpp
+5218
+```
+
+### B
+
+```cpp
+5216
+```
+
+### C
+
+```cpp
+5210
+```

data/1.算法初阶/1.蓝桥杯-基础/30.生日蜡烛/config.json

+{
+  "node_id": "algorithm-5a3bc1e4f38648379d0f7be6d46a7648",
+  "keywords": [
+    "蓝桥杯",
+    "生日蜡烛"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/30.生日蜡烛/desc.md

+某君从某年开始每年都举办一次生日party，并且每次都要吹熄与年龄相同根数的蜡烛。 现在算起来，他一吹熄了236根蜡烛。  
+请问，他从多少岁开始过生日party的？
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/30.生日蜡烛/solution.cpp

+#include <iostream>
+using namespace std;
+int main()
+{
+    for (int i = 1; i <= 50; i++)
+    {
+        for (int j = 50; j >= i; j--)
+        {
+            if ((i + j) * (j - i + 1) == 472)
+            {
+                cout << i << " " << j << endl;
+            }
+        }
+    }
+    return 0;
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/30.生日蜡烛/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "ff9342bf7bcc48fba2718fdde83d1c0b"
+}
\ No newline at end of file

data/1.算法初阶/1.蓝桥杯-基础/30.生日蜡烛/solution.md

+# 生日蜡烛
+
+某君从某年开始每年都举办一次生日party，并且每次都要吹熄与年龄相同根数的蜡烛。 现在算起来，他一吹熄了236根蜡烛。  
+请问，他从多少岁开始过生日party的？
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+26
+```
+
+## 选项
+
+### A
+
+```cpp
+24
+```
+
+### B
+
+```cpp
+25
+```
+
+### C
+
+```cpp
+27
+```

data/1.算法初阶/2.蓝桥杯-字符串/4.人物相关性分析/config.json

+{
+  "node_id": "algorithm-108089b131c346dabc981230a1cb4fb1",
+  "keywords": [
+    "蓝桥杯",
+    "人物相关性分析"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/2.蓝桥杯-字符串/4.人物相关性分析/desc.md

+小明正在分析一本小说中的人物相关性。
+
+他想知道在小说中 Alice 和 Bob 有多少次同时出现。
+
+更准确的说，小明定义 Alice 和 Bob “同时出现”的意思是：在小说文本中 Alice 和 Bob 之间不超过 K 个字符。
+
+例如以下文本：
+```
+This is a story about Alice and Bob. Alice wants to send a private message to Bob.
+```
+假设 K=20，则 Alice 和 Bob 同时出现了 2 次，分别是 Alice and Bob 和 Bob. Alice。
+
+前者 Alice 和 Bob 之间有 5 个字符，后者有 2 个字符。
+
+注意:
+
+1. Alice 和 Bob 是大小写敏感的，alice 或 bob 等并不计算在内。
+2. Alice 和 Bob 应为单独的单词，前后可以有标点符号和空格，但是不能有字母。例如 Bobbi 並不算出现了 Bob。
+#### 输入格式
+第一行包含一个整数 K。
+
+第二行包含一行字符串，只包含大小写字母、标点符号和空格。长度不超过 1000000。
+
+#### 输出格式
+输出一个整数，表示 Alice 和 Bob 同时出现的次数。
+
+#### 数据范围
+```
+1≤K≤1000000
+```
+#### 输入样例：
+```
+20
+This is a story about Alice and Bob. Alice wants to send a private message to Bob.
+```
+输出样例：
+```
+2
+```
\ No newline at end of file

data/1.算法初阶/2.蓝桥杯-字符串/4.人物相关性分析/solution.cpp

+#include <bits/stdc++.h>
+using namespace std;
+int len;
+string s;
+bool check(int i)
+{
+    if (len - i < 5)
+        return false;
+    return s[i + 1] == 'l' && s[i + 2] == 'i' && s[i + 3] == 'c' && s[i + 4] == 'e';
+}
+bool check2(int i)
+{
+    if (len - i < 3)
+        return false;
+    return s[i + 1] == 'o' && s[i + 2] == 'b';
+}
+int main()
+{
+    int k; //这里绝对不能加关闭流读入，如果这加了getline会直接读不到
+    cin >> k;
+    getchar();
+    getline(cin, s);
+    len = s.length();
+    vector<int> Alice, Bob;
+    for (int i = 0; i < len; i++)
+    {
+        if (s[i] == 'A' && check(i))
+        {
+            Alice.push_back(i);
+            i += 5;
+        }
+        else if (s[i] == 'B' && check2(i))
+        {
+            Bob.push_back(i);
+            i += 3;
+        }
+    }
+    int As = Alice.size(), Bs = Bob.size();
+    int i = 0, j = 0;
+    long long ans = 0;
+    for (int q = 0; q < As; q++)
+    {
+        while (i < Bs && Bob[i] < Alice[q] - k - 3)
+            i++; //左边界已经有些被排除的
+        while (j < Bs && Bob[j] <= Alice[q] + k + 5)
+            j++; //右边界
+        ans += j - i;
+    }
+    cout << ans << "\n";
+    return 0;
+}

data/1.算法初阶/2.蓝桥杯-字符串/4.人物相关性分析/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "f79d5efd471f46ec87d7069fb765f43d"
+}
\ No newline at end of file

data/1.算法初阶/2.蓝桥杯-字符串/4.人物相关性分析/solution.md

+# 人物相关性分析
+
+小明正在分析一本小说中的人物相关性。
+
+他想知道在小说中 Alice 和 Bob 有多少次同时出现。
+
+更准确的说，小明定义 Alice 和 Bob “同时出现”的意思是：在小说文本中 Alice 和 Bob 之间不超过 K 个字符。
+
+例如以下文本：
+```
+This is a story about Alice and Bob. Alice wants to send a private message to Bob.
+```
+假设 K=20，则 Alice 和 Bob 同时出现了 2 次，分别是 Alice and Bob 和 Bob. Alice。
+
+前者 Alice 和 Bob 之间有 5 个字符，后者有 2 个字符。
+
+注意:
+
+1. Alice 和 Bob 是大小写敏感的，alice 或 bob 等并不计算在内。
+2. Alice 和 Bob 应为单独的单词，前后可以有标点符号和空格，但是不能有字母。例如 Bobbi 並不算出现了 Bob。
+
+**输入格式**
+
+第一行包含一个整数 K。
+
+第二行包含一行字符串，只包含大小写字母、标点符号和空格。长度不超过 1000000。
+
+**输出格式**
+
+输出一个整数，表示 Alice 和 Bob 同时出现的次数。
+
+**数据范围**
+
+```
+1≤K≤1000000
+```
+
+**输入样例：**
+
+```
+20
+This is a story about Alice and Bob. Alice wants to send a private message to Bob.
+```
+
+**输出样例：**
+
+```
+2
+```
+
+以下选项错误的是？
+
+## aop
+
+### before
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+int main()
+{
+    int k;
+    scanf("%d", &k);
+    getchar();
+
+    const char *a = "Alice", *b = "Bob";
+    char str[1000000];
+    gets(str);
+
+    int length = strlen(str);
+    int num = 0, i, j, t, flag;
+    char word[20];
+    for (i = 0; i < length; i++)
+    {
+        if (str[i] == 'A' || str[i] == 'B')
+        {
+            j = 0;
+            while (str[i] != ' ' && str[i] != '.')
+                word[j++] = str[i++];
+            word[j] = '\0';
+
+            flag = 0;
+            if (strcmp(word, a) == 0)
+                flag = 1;
+            else if (strcmp(word, b) == 0)
+                flag = 2;
+
+            if (flag == 1)
+            {
+                for (t = i; t < length; t++)
+                {
+                    if (str[t] == 'B')
+                    {
+                        j = 0;
+                        while (str[t] != ' ' && str[t] != '.')
+                            word[j++] = str[t++];
+                        word[j] = '\0';
+
+                        if (strcmp(word, b) == 0)
+                            num++;
+                    }
+                }
+            }
+            else if (flag == 2)
+            {
+                for (t = i; t < length; t++)
+                {
+                    if (str[t] == 'A')
+                    {
+                        j = 0;
+                        while (str[t] != ' ' && str[t] != '.')
+                            word[j++] = str[t++];
+                        word[j] = '\0';
+
+                        if (strcmp(word, a) == 0)
+                            num++;
+                    }
+                }
+            }
+        }
+    }
+    printf("%d\n", num);
+
+    return 0;
+}
+```
+
+## 选项
+
+### A
+
+```cpp
+int cnt, k;
+bool temp = true;
+char f[2][20] = {"Alice", "Bob"};
+bool check(string &a, int &pa, int &pb)
+{
+    bool flage = true;
+    pa = a.find(f[0], ++pa);
+    if (pa == -1)
+        temp = false;
+    if (temp && abs((pa - 1) - pb) < k && pb)
+        cnt++;
+    if (a[pa - 1] != ' ' && a[pa + 6] != ' ')
+        flage = false;
+    pb = a.find(f[1], ++pb);
+    if (pb == -1)
+        temp = false;
+    if (a[pb - 1] != ' ' && a[pb + 6] != ' ')
+        flage = false;
+    return flage;
+}
+int main()
+{
+    string a;
+    cin >> k;
+    getchar();
+    getline(cin, a);
+    int pa = 0, pb = 0;
+    while (1)
+    {
+        if (check(a, pa, pb) && abs(pa - pb) < k && temp)
+        {
+            cnt++;
+        }
+        else if (!temp)
+            break;
+    }
+    cout << cnt;
+    return 0;
+}
+```
+
+### B
+
+```cpp
+#define mem(a, b) memset(a, b, sizeof a)
+#define PII pair<int, int>
+#define ll long long
+#define ull unsigned long long
+#define IOS ios::sync_with_stdio(0), cin.tie(0)
+#define gcd(a, b) __gcd(a, b)
+#define ft first
+#define sd second
+#define endl '\n'
+#define PI acos(-1.0)
+#define lcm(a, b) a / gcd(a, b) * b
+#define INF_INT 0x3f3f3f3f
+#define INF_LONG 4557430888798830399
+const int N = 4e6 + 9;
+int ta, tb;
+int a[N], b[N];
+string s;
+int solve(string ss, int *cnt)
+{
+    int t = 0, n = s.size();
+    for (int i = 0; i < n; i++)
+    {
+        if (s[i] == ss[0])
+        {
+            if (i)
+            {
+                char ch = s[i - 1];
+                if ((ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z'))
+                    continue;
+            }
+            int flag = 1, j;
+            string tmp = "";
+            for (j = i; j < n && j - i < ss.size(); j++)
+            {
+                tmp += s[j];
+            }
+            if (tmp != ss)
+                flag = 0;
+
+            if (j < n && ((s[j] >= 'a' && s[j] <= 'z') || (s[j] >= 'A' && s[j] <= 'Z')))
+                flag = 0;
+            if (flag)
+                cnt[t++] = i;
+        }
+    }
+    return t;
+}
+int main()
+{
+    int k;
+    cin >> k;
+    getchar();
+    getline(cin, s);
+    int ta = solve("Alice", a);
+    int tb = solve("Bob", b);
+    ll ans = 0;
+    for (int i = 0, lp = 0, rp = 0; i < ta; i++)
+    {
+        while (b[lp] < a[i] - 3 - k)
+            lp++;
+        while (b[rp] <= a[i] + k + 5 && rp < tb)
+            rp++;
+
+        if (rp - lp > 0)
+            ans += (ll)(rp - lp);
+    }
+    cout << ans << endl;
+    return 0;
+}
+```
+
+### C
+
+```cpp
+int len;
+string s;
+bool check(int i)
+{
+    if (len - i < 5)
+        return false;
+    return s[i + 1] == 'l' && s[i + 2] == 'i' && s[i + 3] == 'c' && s[i + 4] == 'e';
+}
+bool check2(int i)
+{
+    if (len - i < 3)
+        return false;
+    return s[i + 1] == 'o' && s[i + 2] == 'b';
+}
+int main()
+{
+    int k;
+    cin >> k;
+    getchar();
+    getline(cin, s);
+    len = s.length();
+    vector<int> Alice, Bob;
+    for (int i = 0; i < len; i++)
+    {
+        if (s[i] == 'A' && check(i))
+        {
+            Alice.push_back(i);
+            i += 5;
+        }
+        else if (s[i] == 'B' && check2(i))
+        {
+            Bob.push_back(i);
+            i += 3;
+        }
+    }
+    int As = Alice.size(), Bs = Bob.size();
+    int i = 0, j = 0;
+    long long ans = 0;
+    for (int q = 0; q < As; q++)
+    {
+        while (i < Bs && Bob[i] < Alice[q] - k - 3)
+            i++;
+        while (j < Bs && Bob[j] <= Alice[q] + k + 5)
+            j++;
+        ans += j - i;
+    }
+    cout << ans << "\n";
+    return 0;
+}
+```

data/1.算法初阶/2.蓝桥杯-字符串/5.解码/config.json

+{
+  "node_id": "algorithm-216aba466fa84f069f09de86439271b1",
+  "keywords": [
+    "蓝桥杯",
+    "解码"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/2.蓝桥杯-字符串/5.解码/desc.md

+#### 问题描述
+
+小明有一串很长的英文字母，可能包含大写和小写。在这串字母中，有很多连续的是重复的。小明想了一个办法将这串字母表达得更短：将连续的几个相同字母写成字母 + 出现次数的形式。
+
+例如，连续的 5 个 a，即 aaaaa，小明可以简写成 a5（也可能简写成 a4a、aa3a 等）。对于这个例子：HHHellllloo，小明可以简写成 H3el5o2。为了方便表达，小明不会将连续的超过 9 个相同的字符写成简写的形式。
+现在给出简写后的字符串，请帮助小明还原成原来的串。
+
+#### 输入格式
+
+输入一行包含一个字符串。
+
+#### 输出格式
+
+输出一个字符串，表示还原后的串。
+
+#### 样例输入
+```
+H3el5o2
+```
+#### 样例输出
+```
+HHHellllloo
+```
+#### 评测用例规模与约定
+
+对于所有评测用例，字符串由大小写英文字母和数字组成，长度不超过100。
+
+请注意原来的串长度可能超过 100。
\ No newline at end of file

data/1.算法初阶/2.蓝桥杯-字符串/5.解码/solution.cpp

+#include <bits/stdc++.h>
+using namespace std;
+char s2[100000];
+int main()
+{
+    char s1[150];
+    cin >> s1;
+
+    int top = 0;
+    for (int i = 0; s1[i] != '\0'; i++)
+    {
+        if ((s1[i] >= 'A' && s1[i] <= 'Z') || (s1[i] >= 'a' && s1[i] <= 'z'))
+        {
+            s2[top++] = s1[i];
+        }
+        else
+        {
+            while (s1[i] != '1')
+            {
+                s2[top++] = s1[i - 1];
+                s1[i] = s1[i] - 1;
+            }
+        }
+    }
+    s2[top] = '\0';
+
+    cout << s2;
+    return 0;
+}

data/1.算法初阶/2.蓝桥杯-字符串/5.解码/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "7f65d6a25e334652bfe898316850934e"
+}
\ No newline at end of file

data/1.算法初阶/2.蓝桥杯-字符串/5.解码/solution.md

+# 解码
+
+**问题描述**
+
+小明有一串很长的英文字母，可能包含大写和小写。在这串字母中，有很多连续的是重复的。小明想了一个办法将这串字母表达得更短：将连续的几个相同字母写成字母 + 出现次数的形式。
+
+例如，连续的 5 个 a，即 aaaaa，小明可以简写成 a5（也可能简写成 a4a、aa3a 等）。对于这个例子：HHHellllloo，小明可以简写成 H3el5o2。为了方便表达，小明不会将连续的超过 9 个相同的字符写成简写的形式。
+现在给出简写后的字符串，请帮助小明还原成原来的串。
+
+**输入格式**
+
+输入一行包含一个字符串。
+
+**输出格式**
+
+输出一个字符串，表示还原后的串。
+
+**样例输入**
+
+```
+H3el5o2
+```
+
+**样例输出**
+
+```
+HHHellllloo
+```
+
+**评测用例规模与约定**
+
+对于所有评测用例，字符串由大小写英文字母和数字组成，长度不超过100。
+
+请注意原来的串长度可能超过 100。
+
+以下程序实现了这一功能，请你填补空白处内容：
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+char s2[100000];
+int main()
+{
+    char s1[150];
+    cin >> s1;
+
+    int top = 0;
+    for (int i = 0; s1[i] != '\0'; i++)
+    {
+        if ((s1[i] >= 'A' && s1[i] <= 'Z') || (s1[i] >= 'a' && s1[i] <= 'z'))
+        {
+            s2[top++] = s1[i];
+        }
+        else
+        {
+            while (s1[i] != '1')
+            {
+                __________________
+                s1[i] = s1[i] - 1;
+            }
+        }
+    }
+    s2[top] = '\0';
+
+    cout << s2;
+    return 0;
+}
+```
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+s2[top++] = s1[i - 1];
+```
+
+## 选项
+
+### A
+
+```cpp
+s2[++top] = s1[i - 1];
+```
+
+### B
+
+```cpp
+s2[++top] = s1[i + 1];
+```
+
+### C
+
+```cpp
+s2[top++] = s1[i + 1];
+```

data/1.算法初阶/3.蓝桥杯-递归/6.取数位/config.json

+{
+  "node_id": "algorithm-9e407b7a4ec844019c7a4db5b61ee004",
+  "keywords": [
+    "蓝桥杯",
+    "取数位"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/3.蓝桥杯-递归/6.取数位/desc.md

+求1个整数的第k位数字有很多种方法。
+
+以下的方法就是一种。
+

data/1.算法初阶/3.蓝桥杯-递归/6.取数位/solution.cpp

+#include <stdio.h>
+int len(int x)
+{
+    if (x < 10)
+        return 1;
+    return len(x / 10) + 1;
+}
+// 取x的第k位数字
+int f(int x, int k)
+{
+    if (len(x) - k == 0)
+        return x % 10;
+    return f(x / 10, k); //填空
+}
+int main()
+{
+    int x = 23574;
+    printf("%d\n", f(x, 3));
+    return 0;
+}
\ No newline at end of file

data/1.算法初阶/3.蓝桥杯-递归/6.取数位/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "4f854873186048839ba4c2a7da47f366"
+}
\ No newline at end of file

data/1.算法初阶/3.蓝桥杯-递归/6.取数位/solution.md

+# 取数位
+
+求1个整数的第k位数字有很多种方法。
+
+以下的方法就是一种。请你填补空白处的内容：
+
+```cpp
+#include <stdio.h>
+int len(int x)
+{
+    if (x < 10)
+        return 1;
+    return len(x / 10) + 1;
+}
+
+int f(int x, int k)
+{
+    if (len(x) - k == 0)
+        return x % 10;
+    __________________
+}
+int main()
+{
+    int x = 23574;
+    printf("%d\n", f(x, 3));
+    return 0;
+}
+```
+
+
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+    return f(x / 10, k);
+```
+
+## 选项
+
+### A
+
+```cpp
+    return f(x % 10, k);
+```
+
+### B
+
+```cpp
+    return f(x, k);
+```
+
+### C
+
+```cpp
+    return f(x, k / 10);
+```

data/1.算法初阶/3.蓝桥杯-递归/7.逆波兰表达式/config.json

+{
+  "node_id": "algorithm-b40b51c853e940adadaf01b5a205aa0c",
+  "keywords": [
+    "蓝桥杯",
+    "逆波兰表达式"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/3.蓝桥杯-递归/7.逆波兰表达式/desc.md

+正常的表达式称为中缀表达式，运算符在中间，主要是给人阅读的，机器求解并不方便。  
+例如：3 + 5 * (2 + 6) - 1  
+而且，常常需要用括号来改变运算次序。  
+相反，如果使用逆波兰表达式（前缀表达式）表示，上面的算式则表示为：  
+```
+- + 3 * 5 + 2 6 1
+```
+不再需要括号，机器可以用递归的方法很方便地求解。
+为了简便，我们假设：
+1. 只有 $ + - * $ 三种运算符
+2. 每个运算数都是一个小于10的非负整数  
+
+下面的程序对一个逆波兰表示串进行求值。  
+其返回值为一个数组：其中第一元素表示求值结果，第二个元素表示它已解析的字符数。 

data/1.算法初阶/3.蓝桥杯-递归/7.逆波兰表达式/solution.cpp

+#include <iostream>
+using namespace std;
+
+struct EV
+{
+    int result; //计算结果
+    int n;      //消耗掉的字符数
+};
+
+struct EV evaluate(char *x)
+{
+    struct EV ev = {0, 0};
+    struct EV v1;
+    struct EV v2;
+
+    if (*x == 0)
+        return ev;
+
+    if (x[0] >= '0' && x[0] <= '9')
+    {
+        ev.result = x[0] - '0'; //字符转数字
+        ev.n = 1;
+        return ev;
+    }
+
+    v1 = evaluate(x + 1);
+    v2 = evaluate(x + v1.n + 1);
+
+    if (x[0] == '+')
+        ev.result = v1.result + v2.result;
+    if (x[0] == '*')
+        ev.result = v1.result * v2.result;
+    if (x[0] == '-')
+        ev.result = v1.result - v2.result;
+    ev.n = 1 + v1.n + v2.n;
+
+    return ev;
+}
+
+int main(int argc, char **argv)
+{
+    string str = "-+3*5+261";
+    const EV &ev = evaluate((char *)(str.c_str()));
+    cout << ev.result << endl;
+    return 0;
+}
\ No newline at end of file

data/1.算法初阶/3.蓝桥杯-递归/7.逆波兰表达式/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "c29652154669434cb71e4f036b690fef"
+}
\ No newline at end of file

data/1.算法初阶/3.蓝桥杯-递归/7.逆波兰表达式/solution.md

+# 逆波兰表达式
+
+正常的表达式称为中缀表达式，运算符在中间，主要是给人阅读的，机器求解并不方便。  
+例如：3 + 5 * (2 + 6) - 1  
+而且，常常需要用括号来改变运算次序。  
+相反，如果使用逆波兰表达式（前缀表达式）表示，上面的算式则表示为：  
+```
+- + 3 * 5 + 2 6 1
+```
+不再需要括号，机器可以用递归的方法很方便地求解。
+为了简便，我们假设：
+1. 只有 $ + - * $ 三种运算符
+2. 每个运算数都是一个小于10的非负整数  
+
+下面的程序对一个逆波兰表示串进行求值。  
+其返回值为一个数组：其中第一元素表示求值结果，第二个元素表示它已解析的字符数。 
+请你补全代码：
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+struct EV
+{
+    int result;
+    int n;
+};
+
+struct EV evaluate(char *x)
+{
+    struct EV ev = {0, 0};
+    struct EV v1;
+    struct EV v2;
+
+    if (*x == 0)
+        return ev;
+
+    if (x[0] >= '0' && x[0] <= '9')
+    {
+        ev.result = x[0] - '0';
+        ev.n = 1;
+        return ev;
+    }
+
+    v1 = evaluate(x + 1);
+    __________________
+
+    if (x[0] == '+')
+        ev.result = v1.result + v2.result;
+    if (x[0] == '*')
+        ev.result = v1.result * v2.result;
+    if (x[0] == '-')
+        ev.result = v1.result - v2.result;
+    ev.n = 1 + v1.n + v2.n;
+
+    return ev;
+}
+
+int main(int argc, char **argv)
+{
+    string str = "-+3*5+261";
+    const EV &ev = evaluate((char *)(str.c_str()));
+    cout << ev.result << endl;
+    return 0;
+}
+```
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+v2 = evaluate(x + v1.n + 1);
+```
+
+## 选项
+
+### A
+
+```cpp
+v2 = evaluate(x + v1.n);
+```
+
+### B
+
+```cpp
+v2 = evaluate(v1.n);
+```
+
+### C
+
+```cpp
+v2 = evaluate(v1.n + 1);
+```

data/1.算法初阶/5.蓝桥杯-模拟/11.跑步锻炼/config.json

+{
+  "node_id": "algorithm-e41cd4349f6d4bbdb1801a6cdc95b57a",
+  "keywords": [
+    "蓝桥杯",
+    "跑步锻炼"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/5.蓝桥杯-模拟/11.跑步锻炼/desc.md

+小蓝每天都锻炼身体。  
+正常情况下，小蓝每天跑1千米。如果某天是周一或者月初（1日），为了激励自己，小蓝要跑2千米。如果同时是周一或月初，小蓝也是跑2千米。  
+小蓝跑步已经坚持了很长时间，从2000年1月1日周六（含）到2020年10月1日周四（含）。请问这段时间小蓝总共跑步多少千米？
\ No newline at end of file

data/1.算法初阶/5.蓝桥杯-模拟/11.跑步锻炼/solution.cpp

+#include <bits/stdc++.h>
+using namespace std;
+int M[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
+int main()
+{
+    int y = 2000, m = 1, d = 1, w = 6, ans = 2;
+    while (y != 2020 || m != 10 || d != 1)
+    {
+        if ((y % 4 == 0 && y % 100 != 0) || y % 400 == 0)
+            M[2] = 29;
+        else
+            M[2] = 28;
+        d++;
+        w = (w + 1) % 7;
+        if (d > M[m])
+        {
+            d = 1;
+            m++;
+            if (m > 12)
+            {
+                y++;
+                m = 1;
+            }
+        }
+        if (d == 1 || w == 1)
+            ans++;
+        ans++;
+    }
+    cout << ans;
+}

data/1.算法初阶/5.蓝桥杯-模拟/11.跑步锻炼/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "ebc12c88b5f049f684c3e7b63f44b6d7"
+}
\ No newline at end of file

data/1.算法初阶/5.蓝桥杯-模拟/11.跑步锻炼/solution.md

+# 跑步锻炼
+
+小蓝每天都锻炼身体。  
+正常情况下，小蓝每天跑1千米。如果某天是周一或者月初（1日），为了激励自己，小蓝要跑2千米。如果同时是周一或月初，小蓝也是跑2千米。  
+小蓝跑步已经坚持了很长时间，从2000年1月1日周六（含）到2020年10月1日周四（含）。请问这段时间小蓝总共跑步多少千米？
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+8879
+```
+
+## 选项
+
+### A
+
+```cpp
+8888
+```
+
+### B
+
+```cpp
+8880
+```
+
+### C
+
+```cpp
+8808
+```

data/1.算法初阶/6.蓝桥杯-搜索/10.跳蚱蜢/config.json

+{
+  "node_id": "algorithm-daed047610e942a6bb5548f7acacdf3b",
+  "keywords": [
+    "蓝桥杯",
+    "跳蚱蜢"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/10.跳蚱蜢/desc.md

+有 9 只盘子，排成 1 个圆圈。
+
+其中 8 只盘子内装着 8 只蚱蜢，有一个是空盘，我们把这些蚱蜢顺时针编号为 1 ~ 8
+
+每只蚱蜢都可以跳到相邻的空盘中，也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。
+
+请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，
+
+并且保持空盘的位置不变（也就是 1-8 换位，2-7 换位,…），至少要经过多少次跳跃？
+
+![](https://img-blog.csdnimg.cn/20200530104930106.png)
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/10.跳蚱蜢/solution.cpp

+#include <iostream>
+#include <unordered_map>
+#include <queue>
+using namespace std;
+
+int dir[] = {1, -1, 2, -2};
+unordered_map<string, int> dist;
+string S = "12345678X", T = "87654321X";
+
+int bfs()
+{
+    queue<string> q;
+    q.push(S);
+    dist[S] = 0;
+
+    while (q.size())
+    {
+        string t = q.front();
+        q.pop();
+
+        if (t == T)
+            return dist[t];
+
+        int k = t.find('X'), distance = dist[t];
+        for (int i = 0; i < 4; i++)
+        {
+            swap(t[k], t[(k + dir[i] + 9) % 9]);
+            if (!dist.count(t))
+            {
+                q.push(t);
+                dist[t] = distance + 1;
+            }
+            swap(t[k], t[(k + dir[i] + 9) % 9]);
+        }
+    }
+
+    return -1;
+}
+
+int main()
+{
+    cout << bfs() << endl;
+    return 0;
+}

data/1.算法初阶/6.蓝桥杯-搜索/10.跳蚱蜢/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "f6527d9cc83345379fe1fedfa52a3b6a"
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/10.跳蚱蜢/solution.md

+# 跳蚱蜢
+
+有 9 只盘子，排成 1 个圆圈。
+
+其中 8 只盘子内装着 8 只蚱蜢，有一个是空盘，我们把这些蚱蜢顺时针编号为 1 ~ 8
+
+每只蚱蜢都可以跳到相邻的空盘中，也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。
+
+请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，
+
+并且保持空盘的位置不变（也就是 1-8 换位，2-7 换位,…），至少要经过多少次跳跃？
+
+![](https://img-blog.csdnimg.cn/20200530104930106.png)
+
+以下选项错误的是？
+
+## aop
+
+### before
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+const int MAXN = 1e7;
+
+int arr[9] = {4, 3, 2, 1, 0, 8, 7, 6, 5};
+
+int tar[9] = {5, 6, 7, 8, 0, 1, 2, 3, 4};
+
+int que[MAXN][9];
+
+int dist[MAXN];
+
+int pos[MAXN];
+
+struct cmp
+{
+    bool operator()(int a, int b)
+    {
+        return memcmp(que[a], que[b], sizeof(int) * 9) < 0;
+    }
+};
+
+set<int, cmp> vis;
+
+void set_init()
+{
+    vis.clear();
+}
+
+bool inset_check(int a)
+{
+    if (vis.find(a) == vis.end())
+    {
+        vis.insert(a);
+        return true;
+    }
+    return false;
+}
+
+int bfs()
+{
+
+    int front = 1;
+    int rear = 2;
+    pos[front] = 4;
+    dist[front] = 0;
+    memcpy(que[front], arr, sizeof(int) * 9);
+
+    while (front < rear)
+    {
+        int *a = que[front];
+
+        if (memcmp(a, tar, sizeof(int) * 9) == 0)
+            return front;
+
+        for (int i = -2; i <= 2; i++)
+        {
+            if (i == 0)
+                continue;
+
+            int new_pos = (pos[front] + i + 9) % 9;
+            int *t = que[rear];
+            memcpy(t, a, sizeof(int) * 9);
+            dist[rear] = dist[front];
+
+            t[new_pos] = a[pos[front]];
+            t[pos[front]] = a[new_pos];
+            pos[rear] = new_pos;
+
+            if (inset_check(rear))
+                rear++;
+        }
+        front++;
+    }
+    return 0;
+}
+
+int main()
+{
+    int ans = bfs();
+    printf("%d\n", dist[ans]);
+
+    return 0;
+}
+```
+
+## 选项
+
+### A
+
+```cpp
+string start = "012345678";
+string e = "087654321";
+int main()
+{
+    queue<pair<string, int>> q;
+    q.push(make_pair(start, 0));
+    set<string> s;
+    s.insert(start);
+    while (!q.empty())
+    {
+        string a = q.front().first;
+        int level = q.front().second;
+        if (a == e)
+        {
+            cout << level;
+            break;
+        }
+        q.pop();
+        int pos = 0;
+        while (a[pos] != '0')
+            pos++;
+        int posi[4];
+        posi[0] = (pos + 8) % 9;
+        posi[1] = (pos + 1) % 9;
+        posi[2] = (pos + 7) % 9;
+        posi[3] = (pos + 2) % 9;
+        for (int i = 0; i < 4; i++)
+        {
+            string b = a;
+            b[pos] = b[posi[i]];
+            b[posi[i]] = '0';
+            if (s.count(b) == 0)
+            {
+                s.insert(b);
+                q.push(make_pair(b, level + 1));
+            }
+        }
+    }
+    return 0;
+}
+```
+
+### B
+
+```cpp
+struct node
+{
+    string str;
+    int pos;
+    int step;
+    node(string str, int pos, int step) : str(str), pos(pos), step(step) {}
+};
+int N = 9;
+set<string> visited;
+queue<node> q;
+void insertq(node no, int i)
+{
+    string s = no.str;
+    swap(s[no.pos], s[(no.pos + i + 9) % 9]);
+
+    if (visited.count(s) == 0)
+    {
+        visited.insert(s);
+        node n(s, (no.pos + i + 9) % 9, no.step + 1);
+        q.push(n);
+    }
+}
+int main()
+{
+    node first("012345678", 0, 0);
+    q.push(first);
+
+    while (!q.empty())
+    {
+        node temp = q.front();
+        if (temp.str == "087654321")
+        {
+            cout << temp.step;
+            break;
+        }
+        else
+        {
+
+            insertq(temp, 1);
+            insertq(temp, -1);
+            insertq(temp, 2);
+            insertq(temp, -2);
+            q.pop();
+        }
+    }
+}
+```
+
+### C
+
+```cpp
+int dir[] = {1, -1, 2, -2};
+unordered_map<string, int> dist;
+string S = "12345678X", T = "87654321X";
+
+int bfs()
+{
+    queue<string> q;
+    q.push(S);
+    dist[S] = 0;
+
+    while (q.size())
+    {
+        string t = q.front();
+        q.pop();
+
+        if (t == T)
+            return dist[t];
+
+        int k = t.find('X'), distance = dist[t];
+        for (int i = 0; i < 4; i++)
+        {
+            swap(t[k], t[(k + dir[i] + 9) % 9]);
+            if (!dist.count(t))
+            {
+                q.push(t);
+                dist[t] = distance + 1;
+            }
+            swap(t[k], t[(k + dir[i] + 9) % 9]);
+        }
+    }
+
+    return -1;
+}
+
+int main()
+{
+    cout << bfs() << endl;
+    return 0;
+}
+```

data/1.算法初阶/6.蓝桥杯-搜索/11.网络分析/config.json

+{
+  "node_id": "algorithm-268291e6cb264bce97c6919f98c2c8f0",
+  "keywords": [
+    "蓝桥杯",
+    "网络分析"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/11.网络分析/desc.md

+#### 问题描述
+小明正在做一个网络实验。
+他设置了 n 台电脑，称为节点，用于收发和存储数据。初始时，所有节点都是独立的，不存在任何连接。  
+小明可以通过网线将两个节点连接起来，连接后两个节点就可以互相通信了。两个节点如果存在网线连接，称为相邻。  
+小明有时会测试当时的网络，他会在某个节点发送一条信息，信息会发送到每个相邻的节点，之后这些节点又会转发到自己相邻的节点，直到所有直接或间接相邻的节点都收到了信息。所有发送和接收的节点都会将信息存储下来。
+一条信息只存储一次。  
+给出小明连接和测试的过程，请计算出每个节点存储信息的大小。  
+
+#### 输入格式
+输入的第一行包含两个整数 n, m，分别表示节点数量和操作数量。节点从1 至 n 编号。  
+接下来 m 行，每行三个整数，表示一个操作。  
+如果操作为 1 a b，表示将节点 a 和节点 b 通过网线连接起来。当 a = b时，表示连接了一个自环，对网络没有实质影响。  
+如果操作为 2 p t，表示在节点 p 上发送一条大小为 t 的信息。  
+
+#### 输出格式
+输出一行，包含 n 个整数，相邻整数之间用一个空格分割，依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
+
+#### 样例输入
+```
+4 8
+1 1 2
+2 1 10
+2 3 5
+1 4 1
+2 2 2
+1 1 2
+1 2 4
+2 2 1
+```
+#### 样例输出
+```
+13 13 5 3
+```
+#### 评测用例规模与约定
+```
+对于 30% 的评测用例，1 ≤ n ≤ 20，1 ≤ m ≤ 100。
+对于 50% 的评测用例，1 ≤ n ≤ 100，1 ≤ m ≤ 1000。
+对于 70% 的评测用例，1 ≤ n ≤ 1000，1 ≤ m ≤ 10000。
+对于所有评测用例，1 ≤ n ≤ 10000，1 ≤ m ≤ 100000，1 ≤ t ≤ 100。
+```

data/1.算法初阶/6.蓝桥杯-搜索/11.网络分析/solution.cpp

+#include <iostream>
+#include <cstdio>
+#include <cstring>
+
+using namespace std;
+const int maxn = 10005;
+int a[maxn][maxn];
+int dfs_vis[maxn];
+int n, m;
+
+struct Node
+{
+    int data;
+} Point[maxn];
+
+void DFS(int a[maxn][maxn], int x, int y)
+{
+    Point[x].data += y;
+    dfs_vis[x] = 1;
+    for (int i = 1; i <= n; i++)
+    {
+        if (a[x][i] == 1 && dfs_vis[i] == 0)
+        {
+            DFS(a, i, y);
+        }
+    }
+}
+int main()
+{
+    cin >> n >> m;
+    cin.get();
+
+    for (int i = 1; i <= m; i++)
+    {
+        int flag, x1, x2;
+        scanf("%d %d %d", &flag, &x1, &x2);
+        if (flag == 1)
+        {
+            a[x1][x2] = a[x2][x1] = 1;
+        }
+        else if (flag == 2)
+        {
+            memset(dfs_vis, 0, sizeof(dfs_vis));
+            DFS(a, x1, x2);
+        }
+    }
+    for (int i = 1; i <= n; ++i)
+    {
+        cout << Point[i].data << " ";
+    }
+    return 0;
+}

data/1.算法初阶/6.蓝桥杯-搜索/11.网络分析/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "1cd422764c9f4e5f9842a3195b91a919"
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/11.网络分析/solution.md

+# 网络分析
+
+
+**问题描述**
+
+小明正在做一个网络实验。
+他设置了 n 台电脑，称为节点，用于收发和存储数据。初始时，所有节点都是独立的，不存在任何连接。  
+小明可以通过网线将两个节点连接起来，连接后两个节点就可以互相通信了。两个节点如果存在网线连接，称为相邻。  
+小明有时会测试当时的网络，他会在某个节点发送一条信息，信息会发送到每个相邻的节点，之后这些节点又会转发到自己相邻的节点，直到所有直接或间接相邻的节点都收到了信息。所有发送和接收的节点都会将信息存储下来。
+一条信息只存储一次。  
+给出小明连接和测试的过程，请计算出每个节点存储信息的大小。  
+
+
+**输入格式**
+
+输入的第一行包含两个整数 n, m，分别表示节点数量和操作数量。节点从1 至 n 编号。  
+接下来 m 行，每行三个整数，表示一个操作。  
+如果操作为 1 a b，表示将节点 a 和节点 b 通过网线连接起来。当 a = b时，表示连接了一个自环，对网络没有实质影响。  
+如果操作为 2 p t，表示在节点 p 上发送一条大小为 t 的信息。  
+
+
+**输出格式**
+
+输出一行，包含 n 个整数，相邻整数之间用一个空格分割，依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
+
+
+**样例输入**
+
+```
+4 8
+1 1 2
+2 1 10
+2 3 5
+1 4 1
+2 2 2
+1 1 2
+1 2 4
+2 2 1
+```
+
+**样例输出**
+
+```
+13 13 5 3
+```
+
+**评测用例规模与约定**
+
+```
+对于 30% 的评测用例，1 ≤ n ≤ 20，1 ≤ m ≤ 100。
+对于 50% 的评测用例，1 ≤ n ≤ 100，1 ≤ m ≤ 1000。
+对于 70% 的评测用例，1 ≤ n ≤ 1000，1 ≤ m ≤ 10000。
+对于所有评测用例，1 ≤ n ≤ 10000，1 ≤ m ≤ 100000，1 ≤ t ≤ 100。
+```
+
+以下选项错误的是？
+
+## aop
+
+### before
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+int main()
+{
+    int n = 0;
+    int m = 0;
+    cin >> n;
+    cin >> m;
+    int ar[n + 1][n + 1];
+
+    for (int i = 0; i < n + 1; i++)
+        for (int j = 0; j < n + 1; j++)
+            ar[i][j] = 0;
+
+    bool arJudge[n + 1];
+
+    for (int i = 0; i < n + 1; i++)
+        arJudge[i] = 0;
+
+    vector<int> v(n, 0);
+    for (int i = 0; i <= n; ++i)
+    {
+        for (int j = 0; j <= n; ++j)
+        {
+            ar[i][j] = 0;
+        }
+    }
+
+    int a = 0, b = 0, c = 0;
+    for (int i = 0; i < m; ++i)
+    {
+        cin >> a;
+        cin >> b;
+        cin >> c;
+        if (a == 1)
+        {
+            if (ar[b][c] == 0)
+            {
+                ar[b][c] = 1;
+            }
+
+            if (ar[c][b] == 0)
+            {
+                ar[c][b] = 1;
+            }
+        }
+        if (a == 2)
+        {
+            queue<int> que;
+            que.push(b);
+            while (!que.empty())
+            {
+                int size = que.size();
+
+                for (int i = 0; i < size; ++i)
+                {
+                    int temp = que.front();
+                    que.pop();
+                    if (arJudge[temp] == 0)
+                    {
+                        v[temp - 1] += c;
+                        arJudge[temp] = 1;
+                    }
+                    for (int j = 1; j <= n; ++j)
+                    {
+                        if (ar[temp][j] != 0)
+                        {
+                            que.push(j);
+                        }
+                    }
+                }
+            }
+        }
+        for (int i = 0; i <= n; ++i)
+        {
+            arJudge[i] = 0;
+        }
+    }
+
+    for (int i = 1; i <= n; ++i)
+    {
+        for (int j = 1; j <= n; ++j)
+        {
+            cout << ar[i][j] << " ";
+        }
+        cout << endl;
+    }
+    for (int i = 0; i < n; ++i)
+    {
+        cout << v[i] << " ";
+    }
+    cout << endl;
+    return 0;
+}
+```
+
+## 选项
+
+### A
+
+```cpp
+int const N = 10010;
+using namespace std;
+int n, m;
+int i, j, k;
+int num[N];
+
+int f[N];
+
+int r[N];
+
+void init()
+{
+    for (i = 1; i <= n; i++)
+    {
+        f[i] = i;
+        r[i] = 1;
+    }
+}
+
+int find(int x)
+{
+    return f[x] == x ? x : (f[x] = find(f[x]));
+}
+
+void send(int x, int y)
+{
+    int tempx, tempy;
+
+    tempx = find(x);
+    tempy = find(y);
+    if (r[tempx] >= r[tempy])
+    {
+
+        f[tempy] = tempx;
+    }
+    else
+    {
+        f[tempx] = tempy;
+    }
+    if (r[tempx] == r[tempy] && tempx != tempy)
+    {
+        r[tempx]++;
+    }
+}
+void count(int x, int y)
+{
+    int tempx;
+    tempx = find(x);
+    for (i = 1; i <= n; i++)
+    {
+        if (tempx == find(i))
+        {
+            num[i] += y;
+        }
+    }
+}
+int main()
+{
+    cin >> n >> m;
+    init();
+    while (m--)
+    {
+        int x, y, z;
+        cin >> x >> y >> z;
+        if (x == 1)
+        {
+            send(y, z);
+        }
+        if (x == 2)
+        {
+            count(y, z);
+        }
+    }
+    for (i = 1; i <= n; i++)
+    {
+        cout << num[i] << " ";
+    }
+    return 0;
+}
+```
+
+### B
+
+```cpp
+const int N = 10010;
+int p[N], d[N];
+int find(int x)
+{
+    if (p[x] == x || p[p[x]] == p[x])
+        return p[x];
+    int r = find(p[x]);
+    d[x] += d[p[x]];
+    p[x] = r;
+    return r;
+}
+int main()
+{
+    int n, m;
+    cin >> n >> m;
+    for (int i = 1; i <= n; i++)
+        p[i] = i;
+    while (m--)
+    {
+        int t, a, b;
+        cin >> t >> a >> b;
+        if (t == 1)
+        {
+            a = find(a), b = find(b);
+            if (a != b)
+            {
+                d[a] -= d[b];
+                p[a] = b;
+            }
+        }
+        else
+        {
+            a = find(a);
+            d[a] += b;
+        }
+    }
+    for (int i = 1; i <= n; i++)
+        if (i == find(i))
+            cout << d[i] << " ";
+        else
+            cout << d[i] + d[find(i)] << " ";
+    cout << endl;
+    return 0;
+}
+```
+
+### C
+
+```cpp
+const int maxn = 10005;
+int a[maxn][maxn];
+int dfs_vis[maxn];
+int n, m;
+
+struct Node
+{
+    int data;
+} Point[maxn];
+
+void DFS(int a[maxn][maxn], int x, int y)
+{
+    Point[x].data += y;
+    dfs_vis[x] = 1;
+    for (int i = 1; i <= n; i++)
+    {
+        if (a[x][i] == 1 && dfs_vis[i] == 0)
+        {
+            DFS(a, i, y);
+        }
+    }
+}
+int main()
+{
+    cin >> n >> m;
+    cin.get();
+
+    for (int i = 1; i <= m; i++)
+    {
+        int flag, x1, x2;
+        scanf("%d %d %d", &flag, &x1, &x2);
+        if (flag == 1)
+        {
+            a[x1][x2] = a[x2][x1] = 1;
+        }
+        else if (flag == 2)
+        {
+            memset(dfs_vis, 0, sizeof(dfs_vis));
+            DFS(a, x1, x2);
+        }
+    }
+    for (int i = 1; i <= n; ++i)
+    {
+        cout << Point[i].data << " ";
+    }
+    return 0;
+}
+```

data/1.算法初阶/6.蓝桥杯-搜索/8.李白打酒/config.json

+{
+  "node_id": "algorithm-57652e0b6b054bb7871b0ec49edf5814",
+  "keywords": [
+    "蓝桥杯",
+    "李白打酒"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/8.李白打酒/desc.md

+话说大诗人李白，一生好饮。幸好他从不开车。  
+一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：  
+无事街上走，提壶去打酒。  
+逢店加一倍，遇花喝一斗。  
+这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。   
+请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。

data/1.算法初阶/6.蓝桥杯-搜索/8.李白打酒/solution.cpp

+#include <iostream>
+using namespace std;
+
+int sum = 0;               //注意这里的sum需要是全局变量，否则在函数体内会每次都被初始化为0，无法达到计数效果
+int f(int a, int b, int c) //a代表遇到的是店，b代表遇到的是花，c代表酒的总量
+{
+    if (a > 0)
+        f(a - 1, b, 2 * c); //逢店加一倍，同时遇到的店个数 -1
+    if (b > 0)
+        f(a, b - 1, c - 1);         //遇花喝一斗，同时遇到的花个数 -1
+    if (a == 0 && b == 0 && c == 1) //这里的c为1，是因为最后遇到的是花，所以最后遇到花的情况在这里不考虑，那么遇到
+        sum += 1;                   //花之前还剩1斗
+    return sum;                     //因为需要多次调用这个函数，所以不能在函数体里输出sum
+}
+int main(void)
+{
+    cout << f(5, 9, 2) << endl;
+    return 0;
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/8.李白打酒/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "cd0ddced79924660889797a1875dd99c"
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/8.李白打酒/solution.md

+# 李白打酒
+
+话说大诗人李白，一生好饮。幸好他从不开车。  
+一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：  
+无事街上走，提壶去打酒。  
+逢店加一倍，遇花喝一斗。  
+这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。   
+请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。
+
+以下错误的一项是？
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+int main()
+{
+    int a[15] = {-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 2, 2, 2, 2, 2};
+
+    int n = 0;
+    do
+    {
+        int sum = 2;
+
+        for (int i = 0; i < 15; i++)
+        {
+            if (a[i] == -1)
+            {
+                sum += a[i];
+            }
+            else
+            {
+                sum *= a[i];
+            }
+        }
+
+        if (a[14] == -1)
+        {
+            n += 1;
+        }
+
+    } while (next_permutation(a, a + 15));
+
+    cout << n << endl;
+    return 0;
+}
+```
+
+## 选项
+
+### A
+
+```cpp
+int res = 0;
+
+void f(int dian, int hua, int jiu)
+{
+    if (dian == 0 && hua == 0 && jiu == 1)
+    {
+        res++;
+    }
+    if (dian > 0)
+        f(dian - 1, hua, jiu * 2);
+    if (hua > 0)
+        f(dian, hua - 1, jiu - 1);
+}
+
+int main(int argc, char **argv)
+{
+
+    f(5, 9, 2);
+    cout << res << endl;
+    return 0;
+}
+```
+
+### B
+
+```cpp
+int main()
+{
+    int ans = 0;
+    for (int i = 0; i < (1 << 14); ++i)
+    {
+        int tot_1 = 0;
+        int tot_0 = 0;
+        int num = 2;
+        for (int j = 0; j < 14; ++j)
+        {
+            if (i & (1 << j))
+            {
+                tot_1++;
+                num = num * 2;
+            }
+            else
+            {
+                tot_0++;
+                num = num - 1;
+            }
+        }
+        if (tot_1 == 5 && tot_0 == 9 && num == 1)
+        {
+            ++ans;
+        }
+    }
+    cout << ans;
+}
+```
+
+### C
+
+```cpp
+int cnt;
+
+void dfs(int a, int b, int sum, int u, int flag)
+{
+    if (u == 15)
+    {
+        if (a == 5 && b == 10 && sum == 0 && flag == 0)
+        {
+            cnt++;
+            return;
+        }
+    }
+    else
+    {
+        dfs(a + 1, b, sum * 2, u + 1, 1);
+        dfs(a, b + 1, sum - 1, u + 1, 0);
+    }
+}
+int main()
+{
+    dfs(0, 0, 2, 0, 0);
+    cout << cnt;
+    return 0;
+}
+```

data/1.算法初阶/6.蓝桥杯-搜索/9.迷宫/config.json

+{
+  "node_id": "algorithm-8a4019c4beb049c4ab7accb34629f72d",
+  "keywords": [
+    "蓝桥杯",
+    "迷宫"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/9.迷宫/desc.md

+#### 问题描述
+下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可 以通行的地方。
+```
+010000
+000100
+001001
+110000
+```
+迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这 个它的上、下、左、右四个方向之一。 对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫， 一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫（30 行 50 列），请找出一种通过迷宫的方式， 其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。 请注意在字典序中D<L<R<U。（如果你把以下文字复制到文本文件中，请务 必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt， 内容与下面的文本相同）
+
+#### 题目数据
+```
+01010101001011001001010110010110100100001000101010
+00001000100000101010010000100000001001100110100101
+01111011010010001000001101001011100011000000010000
+01000000001010100011010000101000001010101011001011
+00011111000000101000010010100010100000101100000000
+11001000110101000010101100011010011010101011110111
+00011011010101001001001010000001000101001110000000
+10100000101000100110101010111110011000010000111010
+00111000001010100001100010000001000101001100001001
+11000110100001110010001001010101010101010001101000
+00010000100100000101001010101110100010101010000101
+11100100101001001000010000010101010100100100010100
+00000010000000101011001111010001100000101010100011
+10101010011100001000011000010110011110110100001000
+10101010100001101010100101000010100000111011101001
+10000000101100010000101100101101001011100000000100
+10101001000000010100100001000100000100011110101001
+00101001010101101001010100011010101101110000110101
+11001010000100001100000010100101000001000111000010
+00001000110000110101101000000100101001001000011101
+10100101000101000000001110110010110101101010100001
+00101000010000110101010000100010001001000100010101
+10100001000110010001000010101001010101011111010010
+00000100101000000110010100101001000001000000000010
+11010000001001110111001001000011101001011011101000
+00000110100010001000100000001000011101000000110011
+10101000101000100010001111100010101001010000001000
+10000010100101001010110000000100101010001011101000
+00111100001000010000000110111000000001000000001011
+10000001100111010111010001000110111010101101111000
+
+```
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/9.迷宫/solution.cpp

+#include <cstdio>
+#include <cstdlib>
+#include <cstring>
+#include <cmath>
+#include <iostream>
+#include <algorithm>
+#include <string>
+#include <vector>
+#include <queue>
+#include <set>
+using namespace std;
+
+#define N 30
+#define M 50
+
+char map[N][M];
+int dir[4][2] = {{1, 0}, {0, -1}, {0, 1}, {-1, 0}}; //D<L<R<U
+char ch[4] = {'D', 'L', 'R', 'U'};
+int vis[N][M] = {0};
+
+struct point
+{
+    int x, y;
+    string road;
+    point(int a, int b)
+    {
+        x = a;
+        y = b;
+    }
+};
+
+void bfs()
+{
+    queue<point> q;
+    point p(0, 0);
+    p.road = "";
+    q.push(p);
+    vis[0][0] = 1;
+    while (!q.empty())
+    {
+        point t = q.front();
+        q.pop();
+        if (t.x == N - 1 && t.y == M - 1)
+        {
+            cout << t.road << endl;
+            break;
+        }
+        for (int i = 0; i < 4; i++)
+        {
+            int dx = t.x + dir[i][0];
+            int dy = t.y + dir[i][1];
+            if (dx >= 0 && dx < N && dy >= 0 && dy < M)
+            {
+                if (map[dx][dy] == '0' && !vis[dx][dy])
+                {
+                    point tt(dx, dy);
+                    tt.road = t.road + ch[i]; //记录路径
+                    q.push(tt);
+                    vis[dx][dy] = 1;
+                }
+            }
+        }
+    }
+}
+
+int main()
+{
+    for (int i = 0; i < N; i++)
+    {
+        for (int j = 0; j < M; j++)
+            scanf("%c", &map[i][j]);
+        getchar(); //读掉回车
+    }
+    bfs();
+    return 0;
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/9.迷宫/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "7ccd50fabede40e8a54a998c04c8bb42"
+}
\ No newline at end of file

data/1.算法初阶/6.蓝桥杯-搜索/9.迷宫/solution.md

+# 迷宫
+
+**问题描述**
+
+下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可 以通行的地方。
+```
+010000
+000100
+001001
+110000
+```
+迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这 个它的上、下、左、右四个方向之一。 对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫， 一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫（30 行 50 列），请找出一种通过迷宫的方式， 其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。 请注意在字典序中D<L<R<U。（如果你把以下文字复制到文本文件中，请务 必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt， 内容与下面的文本相同）
+
+**题目数据**
+
+```
+01010101001011001001010110010110100100001000101010
+00001000100000101010010000100000001001100110100101
+01111011010010001000001101001011100011000000010000
+01000000001010100011010000101000001010101011001011
+00011111000000101000010010100010100000101100000000
+11001000110101000010101100011010011010101011110111
+00011011010101001001001010000001000101001110000000
+10100000101000100110101010111110011000010000111010
+00111000001010100001100010000001000101001100001001
+11000110100001110010001001010101010101010001101000
+00010000100100000101001010101110100010101010000101
+11100100101001001000010000010101010100100100010100
+00000010000000101011001111010001100000101010100011
+10101010011100001000011000010110011110110100001000
+10101010100001101010100101000010100000111011101001
+10000000101100010000101100101101001011100000000100
+10101001000000010100100001000100000100011110101001
+00101001010101101001010100011010101101110000110101
+11001010000100001100000010100101000001000111000010
+00001000110000110101101000000100101001001000011101
+10100101000101000000001110110010110101101010100001
+00101000010000110101010000100010001001000100010101
+10100001000110010001000010101001010101011111010010
+00000100101000000110010100101001000001000000000010
+11010000001001110111001001000011101001011011101000
+00000110100010001000100000001000011101000000110011
+10101000101000100010001111100010101001010000001000
+10000010100101001010110000000100101010001011101000
+00111100001000010000000110111000000001000000001011
+10000001100111010111010001000110111010101101111000
+```
+
+下面的程序实现了这一功能，请你补全空白处：
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+char mp[55][55];
+int book[55][55];
+int block[55][55];
+int minns[55][55];
+int minn = 100000;
+int dx[4] = {1, 0, 0, -1};
+int dy[4] = {0, -1, 1, 0};
+char dir[4] = {'D', 'L', 'R', 'U'};
+char road[1000];
+char roadans[1000];
+int step;
+
+void dfs(int x, int y, int step)
+{
+    if (x == 29 && y == 49)
+    {
+        if (step < minn)
+        {
+            minn = step;
+            for (int i = 0; i < minn; i++)
+                roadans[i] = road[i];
+        }
+        return;
+    }
+
+    for (int i = 0; i < 4; i++)
+    {
+        int tx = x + dx[i];
+        int ty = y + dy[i];
+        if (tx >= 0 && tx < 30 && ty >= 0 && ty < 50 && book[tx][ty] == 0 && block[tx][ty] == 0 && step + 1 < minns[tx][ty])
+        {
+            book[tx][ty] = 1;
+            road[step] = dir[i];
+            minns[tx][ty] = step + 1;
+            __________________
+            book[tx][ty] = 0;
+        }
+    }
+    return;
+}
+
+int main()
+{
+    for (int i = 0; i < 30; i++)
+    {
+        for (int j = 0; j < 50; j++)
+        {
+            char c;
+            cin >> c;
+            mp[i][j] = c;
+            minns[i][j] = 10000;
+            if (c == '1')
+                block[i][j] = 1;
+        }
+    }
+    book[0][0] = 1;
+    dfs(0, 0, 0);
+    for (int i = 0; i < minn; i++)
+        cout << roadans[i];
+
+    return 0;
+}
+```
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+            dfs(tx, ty, step + 1);
+```
+
+## 选项
+
+### A
+
+```cpp
+            dfs(tx, ty, step);
+```
+
+### B
+
+```cpp
+            dfs(tx + 1, ty + 1, step + 1);
+```
+
+### C
+
+```cpp
+            dfs(tx - 1, ty - 1, step + 1);
+```

data/1.算法初阶/7.蓝桥杯-动态规划/5.组合数问题/config.json

+{
+  "node_id": "algorithm-10be8e52e39c4281a5a4bcba071261fa",
+  "keywords": [
+    "蓝桥杯",
+    "组合数问题"
+  ],
+  "children": [],
+  "export": []
+}
\ No newline at end of file

data/1.算法初阶/7.蓝桥杯-动态规划/5.组合数问题/desc.md

+#### 问题描述
+给 n, m, k， 求有多少对(i, j)满足 1 ≤ i ≤ n, 0 ≤ j ≤ min(i, m) 且$C_i^j$≡0(mod k)，k 是质数。其中$C_i^j$是组合数，表示从 i 个不同的数中选出 j 个组成一个集合的方案数。
+#### 输入格式
+第一行两个数 t, k，其中 t 代表该测试点包含 t 组询问，k 的意思与上文中相同。
+接下来 t 行每行两个整数 n, m，表示一组询问。
+#### 输出格式
+输出 t 行，每行一个整数表示对应的答案。由于答案可能很大，请输出答案除以 109 + 7 的余数。
+#### 样例输入
+```
+1 2
+3 3
+```
+#### 样例输出
+```
+1
+```
+#### 样例说明
+在所有可能的情况中，只有 $C_2^1$ 是 2 的倍数。
+#### 样例输入
+```
+2 5
+4 5
+6 7
+```
+#### 样例输出
+```
+0
+7
+```
+#### 样例输入
+```
+3 23
+23333333 23333333
+233333333 233333333
+2333333333 2333333333
+```
+#### 样例输出
+```
+851883128
+959557926
+680723120
+```
+#### 数据规模和约定
+```
+对于所有评测用例，1 ≤ k ≤ 108, 1 ≤ t ≤ 105, 1 ≤ n, m ≤ 1018，且 k 是质数。评测时将使用 10 个评测用例测试你的程序
+```
\ No newline at end of file

data/1.算法初阶/7.蓝桥杯-动态规划/5.组合数问题/solution.cpp

+#include <bits/stdc++.h>
+using namespace std;
+#define modk(x) (((x) >= k) ? ((x)-k) : (x))
+const int maxn = 2005;
+int c[maxn][maxn], n, m, k, T;
+void init()
+{
+    ///预处理C(i,j)
+    c[0][0] = 1;
+    for (int i = 1; i < maxn; i++)
+    {
+        c[i][0] = 1 % k;
+        for (int j = 1; j <= i; j++)
+        {
+            c[i][j] = modk(c[i - 1][j] + c[i - 1][j - 1]);
+        }
+    }
+    ///处理C(i,j)是否为k 的倍数
+    for (int i = 0; i < maxn; i++)
+    {
+        for (int j = 0; j <= i; j++)
+        {
+            if (c[i][j] == 0)
+                c[i][j] = 1;
+            else
+                c[i][j] = 0;
+        }
+    }
+    ///将二维数组C处理成区域前缀和
+    for (int i = 1; i < maxn; i++)
+    {
+        int s = 0;
+        for (int j = 0; j < maxn; j++)
+        {
+            s += c[i][j];
+            c[i][j] = c[i - 1][j] + s;
+        }
+    }
+}
+int main()
+{
+    scanf("%d%d", &T, &k);
+    init();
+    while (T--)
+    {
+        scanf("%d%d", &n, &m);
+        printf("%d\n", c[n][m]);
+    }
+    return 0;
+}

data/1.算法初阶/7.蓝桥杯-动态规划/5.组合数问题/solution.json

+{
+  "type": "code_options",
+  "author": "CSDN.net",
+  "source": "solution.md",
+  "exercise_id": "3c3985435f414d7f9a8bbdcf42a42d46"
+}
\ No newline at end of file

data/1.算法初阶/7.蓝桥杯-动态规划/5.组合数问题/solution.md

+# 组合数问题
+
+
+**问题描述**
+
+给 n, m, k， 求有多少对(i, j)满足 1 ≤ i ≤ n, 0 ≤ j ≤ min(i, m) 且$C_i^j$≡0(mod k)，k 是质数。其中$C_i^j$是组合数，表示从 i 个不同的数中选出 j 个组成一个集合的方案数。
+
+**输入格式**
+
+第一行两个数 t, k，其中 t 代表该测试点包含 t 组询问，k 的意思与上文中相同。
+接下来 t 行每行两个整数 n, m，表示一组询问。
+
+**输出格式**
+
+输出 t 行，每行一个整数表示对应的答案。由于答案可能很大，请输出答案除以 109 + 7 的余数。
+
+**样例输入**
+
+```
+1 2
+3 3
+```
+
+**样例输出**
+
+```
+1
+```
+
+**样例说明**
+
+在所有可能的情况中，只有 $C_2^1$ 是 2 的倍数。
+
+**样例输入**
+
+```
+2 5
+4 5
+6 7
+```
+
+**样例输出**
+
+```
+0
+7
+```
+
+**样例输入**
+
+```
+3 23
+23333333 23333333
+233333333 233333333
+2333333333 2333333333
+```
+
+**样例输出**
+
+```
+851883128
+959557926
+680723120
+```
+
+**数据规模和约定**
+
+```
+对于所有评测用例，1 ≤ k ≤ 108, 1 ≤ t ≤ 105, 1 ≤ n, m ≤ 1018，且 k 是质数。评测时将使用 10 个评测用例测试你的程序
+```
+
+以下选项错误的是？
+
+## aop
+
+### before
+
+```cpp
+
+```
+
+### after
+
+```cpp
+
+```
+
+## 答案
+
+```cpp
+其他三项都是错的
+```
+
+## 选项
+
+### A
+
+```cpp
+const int Mod = 1e9 + 7;
+int c[2010][2010];
+int main()
+{
+    int n, m, t, k;
+    cin >> t >> k;
+    int nn = 2000, mm = 2000;
+    for (int i = 0; i <= nn; i++)
+    {
+        c[i][0] = 1;
+        c[i][i] = 1;
+    }
+    for (int i = 1; i <= nn; i++)
+        for (int j = 1; j <= mm; j++)
+            c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % k;
+    while (t--)
+    {
+        cin >> n >> m;
+        int ans = 0;
+        for (int j = 0; j <= m; j++)
+            for (int i = j; i <= n; i++)
+                if (c[i][j] == 0)
+                    ans++;
+        cout << ans % Mod;
+    }
+    return 0;
+}
+```
+
+### B
+
+```cpp
+#define modk(x) (((x) >= k) ? ((x)-k) : (x))
+const int maxn = 2005;
+int c[maxn][maxn], n, m, k, T;
+void init()
+{
+
+    c[0][0] = 1;
+    for (int i = 1; i < maxn; i++)
+    {
+        c[i][0] = 1 % k;
+        for (int j = 1; j <= i; j++)
+        {
+            c[i][j] = modk(c[i - 1][j] + c[i - 1][j - 1]);
+        }
+    }
+
+    for (int i = 0; i < maxn; i++)
+    {
+        for (int j = 0; j <= i; j++)
+        {
+            if (c[i][j] == 0)
+                c[i][j] = 1;
+            else
+                c[i][j] = 0;
+        }
+    }
+
+    for (int i = 1; i < maxn; i++)
+    {
+        int s = 0;
+        for (int j = 0; j < maxn; j++)
+        {
+            s += c[i][j];
+            c[i][j] = c[i - 1][j] + s;
+        }
+    }
+}
+int main()
+{
+    scanf("%d%d", &T, &k);
+    init();
+    while (T--)
+    {
+        scanf("%d%d", &n, &m);
+        printf("%d\n", c[n][m]);
+    }
+    return 0;
+}
+```
+
+### C
+
+```cpp
+const int Mod = 1e9 + 7;
+const int inv_2 = 5e8 + 4;
+
+long long cal(long long x, long long y)
+{
+    if (x < y)
+    {
+        x %= Mod;
+        return (x + 2) * (x + 1) % Mod * inv_2 % Mod;
+    }
+    x %= Mod, y %= Mod;
+    return ((y + 2) * (y + 1) % Mod * inv_2 % Mod + (x - y) * (y + 1) % Mod) % Mod;
+}
+long long cal_1(long long x, long long y)
+{
+    return min(x, y) + 1;
+}
+long long cal_2(long long x, long long y)
+{
+    if (x < y)
+    {
+        return 0;
+    }
+    return x - y + 1;
+}
+
+int main()
+{
+    int t, k;
+    cin >> t >> k;
+    long long n, m;
+    int a[100], b[100];
+    for (int turn = 0; turn < t; ++turn)
+    {
+        cin >> n >> m;
+        if (m > n)
+            m = n;
+        long long ans = cal(n, m);
+        int len_a = 0, len_b = 0;
+        while (n)
+        {
+            a[len_a++] = n % k;
+            n /= k;
+        }
+        while (m)
+        {
+            b[len_b++] = m % k;
+            m /= k;
+        }
+        int len = max(len_a, len_b);
+        vector<vector<long long>> dp(len + 1, vector<long long>(4));
+        dp[len][3] = 1;
+        for (int i = len - 1; i >= 0; --i)
+        {
+            dp[i][0] = dp[i + 1][0] * cal(k - 1, k - 1) + dp[i + 1][1] * cal(a[i] - 1, k - 1) + dp[i + 1][2] * cal(k - 1, b[i] - 1) + dp[i + 1][3] * cal(a[i] - 1, b[i] - 1);
+            dp[i][1] = dp[i + 1][1] * cal_1(a[i], k - 1) + dp[i + 1][3] * cal_1(a[i], b[i] - 1);
+            dp[i][2] = dp[i + 1][2] * cal_2(k - 1, b[i]) + dp[i + 1][3] * cal_2(a[i] - 1, b[i]);
+            dp[i][3] = dp[i + 1][3] & (a[i] >= b[i]);
+            dp[i][0] %= Mod, dp[i][1] %= Mod;
+            dp[i][2] %= Mod, dp[i][3] %= Mod;
+        }
+        ans -= dp[0][0] + dp[0][1] + dp[0][2] + dp[0][3];
+        ans %= Mod;
+        if (ans < 0)
+            ans += Mod;
+        cout << ans << endl;
+    }
+    return 0;
+}
+```

data_backup/3.蓝桥杯/10.特别数的和/solution.md

@@ -32,6 +32,43 @@
 574
 ```
 
+以下代码实现了这一功能，请你填补空白处的内容：
+
+```cpp
+#include <iostream>
+
+using namespace std;
+
+int ans, n;
+
+bool check(int n)
+{
+    while (n)
+    {
+        int tmpn = n % 10;
+        if (tmpn == 2 || tmpn == 0 || tmpn == 1 || tmpn == 9)
+            return true;
+        __________________
+    }
+    return false;
+}
+
+int main()
+{
+    cin >> n;
+
+    for (int i = 1; i <= n; i++)
+    {
+        if (check(i))
+            ans += i;
+    }
+
+    cout << ans << endl;
+
+    return 0;
+}
+```
+
 
 ## aop
 
@@ -50,7 +87,7 @@
 ## 答案
 
 ```cpp
-
+        n /= 10;
 ```
 
 ## 选项
@@ -58,17 +95,17 @@
 ### A
 
 ```cpp
-
+        n %= 10;
 ```
 
 ### B
 
 ```cpp
-
+        break;
 ```
 
 ### C
 
 ```cpp
-
+        continue;
 ```

data_backup/3.蓝桥杯/11.逆波兰表达式/solution.md

@@ -14,7 +14,55 @@
 
 下面的程序对一个逆波兰表示串进行求值。  
 其返回值为一个数组：其中第一元素表示求值结果，第二个元素表示它已解析的字符数。 
-
+请你补全代码：
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+struct EV
+{
+    int result;
+    int n;
+};
+
+struct EV evaluate(char *x)
+{
+    struct EV ev = {0, 0};
+    struct EV v1;
+    struct EV v2;
+
+    if (*x == 0)
+        return ev;
+
+    if (x[0] >= '0' && x[0] <= '9')
+    {
+        ev.result = x[0] - '0';
+        ev.n = 1;
+        return ev;
+    }
+
+    v1 = evaluate(x + 1);
+    __________________
+
+    if (x[0] == '+')
+        ev.result = v1.result + v2.result;
+    if (x[0] == '*')
+        ev.result = v1.result * v2.result;
+    if (x[0] == '-')
+        ev.result = v1.result - v2.result;
+    ev.n = 1 + v1.n + v2.n;
+
+    return ev;
+}
+
+int main(int argc, char **argv)
+{
+    string str = "-+3*5+261";
+    const EV &ev = evaluate((char *)(str.c_str()));
+    cout << ev.result << endl;
+    return 0;
+}
+```
 
 ## aop
 
@@ -33,7 +81,7 @@
 ## 答案
 
 ```cpp
-
+v2 = evaluate(x + v1.n + 1);
 ```
 
 ## 选项
@@ -41,17 +89,17 @@
 ### A
 
 ```cpp
-
+v2 = evaluate(x + v1.n);
 ```
 
 ### B
 
 ```cpp
-
+v2 = evaluate(v1.n);
 ```
 
 ### C
 
 ```cpp
-
+v2 = evaluate(v1.n + 1);
 ```

data_backup/3.蓝桥杯/12.李白打酒/solution.md

@@ -7,13 +7,15 @@
 这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。   
 请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。
 
+以下错误的一项是？
 
 ## aop
 
 ### before
 
 ```cpp
-
+#include <bits/stdc++.h>
+using namespace std;
 ```
 
 ### after
@@ -25,7 +27,37 @@
 ## 答案
 
 ```cpp
-
+int main()
+{
+    int a[15] = {-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 2, 2, 2, 2, 2};
+
+    int n = 0;
+    do
+    {
+        int sum = 2;
+
+        for (int i = 0; i < 15; i++)
+        {
+            if (a[i] == -1)
+            {
+                sum += a[i];
+            }
+            else
+            {
+                sum *= a[i];
+            }
+        }
+
+        if (a[14] == -1)
+        {
+            n += 1;
+        }
+
+    } while (next_permutation(a, a + 15));
+
+    cout << n << endl;
+    return 0;
+}
 ```
 
 ## 选项
@@ -33,17 +65,87 @@
 ### A
 
 ```cpp
-
+int res = 0;
+
+void f(int dian, int hua, int jiu)
+{
+    if (dian == 0 && hua == 0 && jiu == 1)
+    {
+        res++;
+    }
+    if (dian > 0)
+        f(dian - 1, hua, jiu * 2);
+    if (hua > 0)
+        f(dian, hua - 1, jiu - 1);
+}
+
+int main(int argc, char **argv)
+{
+
+    f(5, 9, 2);
+    cout << res << endl;
+    return 0;
+}
 ```
 
 ### B
 
 ```cpp
-
+int main()
+{
+    int ans = 0;
+    for (int i = 0; i < (1 << 14); ++i)
+    {
+        int tot_1 = 0;
+        int tot_0 = 0;
+        int num = 2;
+        for (int j = 0; j < 14; ++j)
+        {
+            if (i & (1 << j))
+            {
+                tot_1++;
+                num = num * 2;
+            }
+            else
+            {
+                tot_0++;
+                num = num - 1;
+            }
+        }
+        if (tot_1 == 5 && tot_0 == 9 && num == 1)
+        {
+            ++ans;
+        }
+    }
+    cout << ans;
+}
 ```
 
 ### C
 
 ```cpp
-
+int cnt;
+
+void dfs(int a, int b, int sum, int u, int flag)
+{
+    if (u == 15)
+    {
+        if (a == 5 && b == 10 && sum == 0 && flag == 0)
+        {
+            cnt++;
+            return;
+        }
+    }
+    else
+    {
+        dfs(a + 1, b, sum * 2, u + 1, 1);
+        dfs(a, b + 1, sum - 1, u + 1, 0);
+    }
+}
+int main()
+{
+    dfs(0, 0, 2, 0, 0);
+    cout << cnt;
+    return 0;
+}
 ```

data_backup/3.蓝桥杯/13.迷宫/solution.md

@@ -46,6 +46,76 @@
 10000001100111010111010001000110111010101101111000
 ```
 
+下面的程序实现了这一功能，请你补全空白处：
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+char mp[55][55];
+int book[55][55];
+int block[55][55];
+int minns[55][55];
+int minn = 100000;
+int dx[4] = {1, 0, 0, -1};
+int dy[4] = {0, -1, 1, 0};
+char dir[4] = {'D', 'L', 'R', 'U'};
+char road[1000];
+char roadans[1000];
+int step;
+
+void dfs(int x, int y, int step)
+{
+    if (x == 29 && y == 49)
+    {
+        if (step < minn)
+        {
+            minn = step;
+            for (int i = 0; i < minn; i++)
+                roadans[i] = road[i];
+        }
+        return;
+    }
+
+    for (int i = 0; i < 4; i++)
+    {
+        int tx = x + dx[i];
+        int ty = y + dy[i];
+        if (tx >= 0 && tx < 30 && ty >= 0 && ty < 50 && book[tx][ty] == 0 && block[tx][ty] == 0 && step + 1 < minns[tx][ty])
+        {
+            book[tx][ty] = 1;
+            road[step] = dir[i];
+            minns[tx][ty] = step + 1;
+            __________________
+            book[tx][ty] = 0;
+        }
+    }
+    return;
+}
+
+int main()
+{
+    for (int i = 0; i < 30; i++)
+    {
+        for (int j = 0; j < 50; j++)
+        {
+            char c;
+            cin >> c;
+            mp[i][j] = c;
+            minns[i][j] = 10000;
+            if (c == '1')
+                block[i][j] = 1;
+        }
+    }
+    book[0][0] = 1;
+    dfs(0, 0, 0);
+    for (int i = 0; i < minn; i++)
+        cout << roadans[i];
+
+    return 0;
+}
+```
+
 ## aop
 
 ### before
@@ -63,7 +133,7 @@
 ## 答案
 
 ```cpp
-
+            dfs(tx, ty, step + 1);
 ```
 
 ## 选项
@@ -71,17 +141,17 @@
 ### A
 
 ```cpp
-
+            dfs(tx, ty, step);
 ```
 
 ### B
 
 ```cpp
-
+            dfs(tx + 1, ty + 1, step + 1);
 ```
 
 ### C
 
 ```cpp
-
+            dfs(tx - 1, ty - 1, step + 1);
 ```

data_backup/3.蓝桥杯/15.切面条/solution.md

@@ -22,7 +22,7 @@
 ## 答案
 
 ```cpp
-
+1025
 ```
 
 ## 选项
@@ -30,17 +30,17 @@
 ### A
 
 ```cpp
-
+1024
 ```
 
 ### B
 
 ```cpp
-
+512
 ```
 
 ### C
 
 ```cpp
-
+513
 ```

data_backup/3.蓝桥杯/16.循环节长度/solution.md

@@ -3,6 +3,37 @@
 两个整数做除法，有时会产生循环小数，其循环部分称为：循环节。   
 比如，11/13=6=>0.846153846153….. 其循环节为[846153] 共有6位。   
 下面的方法，可以求出循环节的长度。  
+请你填补空白处的内容：
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+int f(int n, int m)
+{
+    n = n % m;
+    vector<int> v;
+    for (;;)
+    {
+        v.push_back(n);
+        n *= 10;
+        n = n % m;
+        if (n == 0)
+            return 0;
+        if (find(v.begin(), v.end(), n) != v.end())
+        {
+            __________________
+        }
+    }
+}
+int main()
+{
+    int n, m;
+    cin >> n >> m;
+    cout << f(n, m) << endl;
+    return 0;
+}
+```
 
 ## aop
 
@@ -21,7 +52,7 @@
 ## 答案
 
 ```cpp
-
+return v.size() - (find(v.begin(), v.end(), n) - v.begin());
 ```
 
 ## 选项
@@ -29,17 +60,17 @@
 ### A
 
 ```cpp
-
+return v.size() - (find(v.begin(), v.end(), n) + v.begin());
 ```
 
 ### B
 
 ```cpp
-
+return v.size() + (find(v.begin(), v.end(), n) - v.begin());
 ```
 
 ### C
 
 ```cpp
-
+return v.size() - find(v.begin(), v.end(), n) - v.begin();
 ```

data_backup/3.蓝桥杯/17.日志统计/solution.md

@@ -56,6 +56,45 @@ ts id
 3
 ```
 
+下面的程序实现了这一功能，请你补全空白处的内容：
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+const int N = 1e5 + 10;
+typedef pair<int, int> PII;
+#define x first
+#define y second
+PII logs[N];
+bool st[N];
+int cnt[N];
+
+int main()
+{
+    int n, d, k;
+    cin >> n >> d >> k;
+    for (int i = 0; i < n; i++)
+        cin >> logs[i].x >> logs[i].y;
+
+    sort(logs, logs + n);
+
+    for (int i = 0, j = 0; i < n; i++)
+    {
+        cnt[logs[i].y]++;
+        while (logs[i].x - logs[j].x >= d)
+            __________________
+        if (cnt[logs[i].y] >= k)
+            st[logs[i].y] = true;
+    }
+
+    for (int i = 0; i < N; i++)
+        if (st[i])
+            cout << i << endl;
+    return 0;
+}
+```
+
 ## aop
 
 ### before
@@ -73,7 +112,7 @@ ts id
 ## 答案
 
 ```cpp
-
+cnt[logs[j].y]--, j++;
 ```
 
 ## 选项
@@ -81,17 +120,17 @@ ts id
 ### A
 
 ```cpp
-
+cnt[logs[j].y]--; j++;
 ```
 
 ### B
 
 ```cpp
-
+cnt[logs[j].y]++, j++;
 ```
 
 ### C
 
 ```cpp
-
+cnt[logs[j].y]++; j++;
 ```

data_backup/3.蓝桥杯/18.跳蚱蜢/solution.md

@@ -12,12 +12,15 @@
 
 ![](https://img-blog.csdnimg.cn/20200530104930106.png)
 
+以下选项错误的是？
+
 ## aop
 
 ### before
 
 ```cpp
-
+#include <bits/stdc++.h>
+using namespace std;
 ```
 
 ### after
@@ -29,7 +32,88 @@
 ## 答案
 
 ```cpp
+const int MAXN = 1e7;
+
+int arr[9] = {4, 3, 2, 1, 0, 8, 7, 6, 5};
+
+int tar[9] = {5, 6, 7, 8, 0, 1, 2, 3, 4};
+
+int que[MAXN][9];
+
+int dist[MAXN];
+
+int pos[MAXN];
+
+struct cmp
+{
+    bool operator()(int a, int b)
+    {
+        return memcmp(que[a], que[b], sizeof(int) * 9) < 0;
+    }
+};
+
+set<int, cmp> vis;
+
+void set_init()
+{
+    vis.clear();
+}
+
+bool inset_check(int a)
+{
+    if (vis.find(a) == vis.end())
+    {
+        vis.insert(a);
+        return true;
+    }
+    return false;
+}
+
+int bfs()
+{
+
+    int front = 1;
+    int rear = 2;
+    pos[front] = 4;
+    dist[front] = 0;
+    memcpy(que[front], arr, sizeof(int) * 9);
+
+    while (front < rear)
+    {
+        int *a = que[front];
 
+        if (memcmp(a, tar, sizeof(int) * 9) == 0)
+            return front;
+
+        for (int i = -2; i <= 2; i++)
+        {
+            if (i == 0)
+                continue;
+
+            int new_pos = (pos[front] + i + 9) % 9;
+            int *t = que[rear];
+            memcpy(t, a, sizeof(int) * 9);
+            dist[rear] = dist[front];
+
+            t[new_pos] = a[pos[front]];
+            t[pos[front]] = a[new_pos];
+            pos[rear] = new_pos;
+
+            if (inset_check(rear))
+                rear++;
+        }
+        front++;
+    }
+    return 0;
+}
+
+int main()
+{
+    int ans = bfs();
+    printf("%d\n", dist[ans]);
+
+    return 0;
+}
 ```
 
 ## 选项
@@ -37,17 +121,139 @@
 ### A
 
 ```cpp
-
+string start = "012345678";
+string e = "087654321";
+int main()
+{
+    queue<pair<string, int>> q;
+    q.push(make_pair(start, 0));
+    set<string> s;
+    s.insert(start);
+    while (!q.empty())
+    {
+        string a = q.front().first;
+        int level = q.front().second;
+        if (a == e)
+        {
+            cout << level;
+            break;
+        }
+        q.pop();
+        int pos = 0;
+        while (a[pos] != '0')
+            pos++;
+        int posi[4];
+        posi[0] = (pos + 8) % 9;
+        posi[1] = (pos + 1) % 9;
+        posi[2] = (pos + 7) % 9;
+        posi[3] = (pos + 2) % 9;
+        for (int i = 0; i < 4; i++)
+        {
+            string b = a;
+            b[pos] = b[posi[i]];
+            b[posi[i]] = '0';
+            if (s.count(b) == 0)
+            {
+                s.insert(b);
+                q.push(make_pair(b, level + 1));
+            }
+        }
+    }
+    return 0;
+}
 ```
 
 ### B
 
 ```cpp
+struct node
+{
+    string str;
+    int pos;
+    int step;
+    node(string str, int pos, int step) : str(str), pos(pos), step(step) {}
+};
+int N = 9;
+set<string> visited;
+queue<node> q;
+void insertq(node no, int i)
+{
+    string s = no.str;
+    swap(s[no.pos], s[(no.pos + i + 9) % 9]);
 
+    if (visited.count(s) == 0)
+    {
+        visited.insert(s);
+        node n(s, (no.pos + i + 9) % 9, no.step + 1);
+        q.push(n);
+    }
+}
+int main()
+{
+    node first("012345678", 0, 0);
+    q.push(first);
+
+    while (!q.empty())
+    {
+        node temp = q.front();
+        if (temp.str == "087654321")
+        {
+            cout << temp.step;
+            break;
+        }
+        else
+        {
+
+            insertq(temp, 1);
+            insertq(temp, -1);
+            insertq(temp, 2);
+            insertq(temp, -2);
+            q.pop();
+        }
+    }
+}
 ```
 
 ### C
 
 ```cpp
+int dir[] = {1, -1, 2, -2};
+unordered_map<string, int> dist;
+string S = "12345678X", T = "87654321X";
+
+int bfs()
+{
+    queue<string> q;
+    q.push(S);
+    dist[S] = 0;
+
+    while (q.size())
+    {
+        string t = q.front();
+        q.pop();
+
+        if (t == T)
+            return dist[t];
+
+        int k = t.find('X'), distance = dist[t];
+        for (int i = 0; i < 4; i++)
+        {
+            swap(t[k], t[(k + dir[i] + 9) % 9]);
+            if (!dist.count(t))
+            {
+                q.push(t);
+                dist[t] = distance + 1;
+            }
+            swap(t[k], t[(k + dir[i] + 9) % 9]);
+        }
+    }
+
+    return -1;
+}
 
+int main()
+{
+    cout << bfs() << endl;
+    return 0;
+}
 ```

data_backup/3.蓝桥杯/19.人物相关性分析/solution.md

@@ -48,12 +48,15 @@ This is a story about Alice and Bob. Alice wants to send a private message to Bo
 2
 ```
 
+以下选项错误的是？
+
 ## aop
 
 ### before
 
 ```cpp
-
+#include <bits/stdc++.h>
+using namespace std;
 ```
 
 ### after
@@ -65,7 +68,72 @@ This is a story about Alice and Bob. Alice wants to send a private message to Bo
 ## 答案
 
 ```cpp
-
+int main()
+{
+    int k;
+    scanf("%d", &k);
+    getchar();
+
+    const char *a = "Alice", *b = "Bob";
+    char str[1000000];
+    gets(str);
+
+    int length = strlen(str);
+    int num = 0, i, j, t, flag;
+    char word[20];
+    for (i = 0; i < length; i++)
+    {
+        if (str[i] == 'A' || str[i] == 'B')
+        {
+            j = 0;
+            while (str[i] != ' ' && str[i] != '.')
+                word[j++] = str[i++];
+            word[j] = '\0';
+
+            flag = 0;
+            if (strcmp(word, a) == 0)
+                flag = 1;
+            else if (strcmp(word, b) == 0)
+                flag = 2;
+
+            if (flag == 1)
+            {
+                for (t = i; t < length; t++)
+                {
+                    if (str[t] == 'B')
+                    {
+                        j = 0;
+                        while (str[t] != ' ' && str[t] != '.')
+                            word[j++] = str[t++];
+                        word[j] = '\0';
+
+                        if (strcmp(word, b) == 0)
+                            num++;
+                    }
+                }
+            }
+            else if (flag == 2)
+            {
+                for (t = i; t < length; t++)
+                {
+                    if (str[t] == 'A')
+                    {
+                        j = 0;
+                        while (str[t] != ' ' && str[t] != '.')
+                            word[j++] = str[t++];
+                        word[j] = '\0';
+
+                        if (strcmp(word, a) == 0)
+                            num++;
+                    }
+                }
+            }
+        }
+    }
+    printf("%d\n", num);
+
+    return 0;
+}
 ```
 
 ## 选项
@@ -73,17 +141,171 @@ This is a story about Alice and Bob. Alice wants to send a private message to Bo
 ### A
 
 ```cpp
-
+int cnt, k;
+bool temp = true;
+char f[2][20] = {"Alice", "Bob"};
+bool check(string &a, int &pa, int &pb)
+{
+    bool flage = true;
+    pa = a.find(f[0], ++pa);
+    if (pa == -1)
+        temp = false;
+    if (temp && abs((pa - 1) - pb) < k && pb)
+        cnt++;
+    if (a[pa - 1] != ' ' && a[pa + 6] != ' ')
+        flage = false;
+    pb = a.find(f[1], ++pb);
+    if (pb == -1)
+        temp = false;
+    if (a[pb - 1] != ' ' && a[pb + 6] != ' ')
+        flage = false;
+    return flage;
+}
+int main()
+{
+    string a;
+    cin >> k;
+    getchar();
+    getline(cin, a);
+    int pa = 0, pb = 0;
+    while (1)
+    {
+        if (check(a, pa, pb) && abs(pa - pb) < k && temp)
+        {
+            cnt++;
+        }
+        else if (!temp)
+            break;
+    }
+    cout << cnt;
+    return 0;
+}
 ```
 
 ### B
 
 ```cpp
-
+#define mem(a, b) memset(a, b, sizeof a)
+#define PII pair<int, int>
+#define ll long long
+#define ull unsigned long long
+#define IOS ios::sync_with_stdio(0), cin.tie(0)
+#define gcd(a, b) __gcd(a, b)
+#define ft first
+#define sd second
+#define endl '\n'
+#define PI acos(-1.0)
+#define lcm(a, b) a / gcd(a, b) * b
+#define INF_INT 0x3f3f3f3f
+#define INF_LONG 4557430888798830399
+const int N = 4e6 + 9;
+int ta, tb;
+int a[N], b[N];
+string s;
+int solve(string ss, int *cnt)
+{
+    int t = 0, n = s.size();
+    for (int i = 0; i < n; i++)
+    {
+        if (s[i] == ss[0])
+        {
+            if (i)
+            {
+                char ch = s[i - 1];
+                if ((ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z'))
+                    continue;
+            }
+            int flag = 1, j;
+            string tmp = "";
+            for (j = i; j < n && j - i < ss.size(); j++)
+            {
+                tmp += s[j];
+            }
+            if (tmp != ss)
+                flag = 0;
+
+            if (j < n && ((s[j] >= 'a' && s[j] <= 'z') || (s[j] >= 'A' && s[j] <= 'Z')))
+                flag = 0;
+            if (flag)
+                cnt[t++] = i;
+        }
+    }
+    return t;
+}
+int main()
+{
+    int k;
+    cin >> k;
+    getchar();
+    getline(cin, s);
+    int ta = solve("Alice", a);
+    int tb = solve("Bob", b);
+    ll ans = 0;
+    for (int i = 0, lp = 0, rp = 0; i < ta; i++)
+    {
+        while (b[lp] < a[i] - 3 - k)
+            lp++;
+        while (b[rp] <= a[i] + k + 5 && rp < tb)
+            rp++;
+
+        if (rp - lp > 0)
+            ans += (ll)(rp - lp);
+    }
+    cout << ans << endl;
+    return 0;
+}
 ```
 
 ### C
 
 ```cpp
-
+int len;
+string s;
+bool check(int i)
+{
+    if (len - i < 5)
+        return false;
+    return s[i + 1] == 'l' && s[i + 2] == 'i' && s[i + 3] == 'c' && s[i + 4] == 'e';
+}
+bool check2(int i)
+{
+    if (len - i < 3)
+        return false;
+    return s[i + 1] == 'o' && s[i + 2] == 'b';
+}
+int main()
+{
+    int k;
+    cin >> k;
+    getchar();
+    getline(cin, s);
+    len = s.length();
+    vector<int> Alice, Bob;
+    for (int i = 0; i < len; i++)
+    {
+        if (s[i] == 'A' && check(i))
+        {
+            Alice.push_back(i);
+            i += 5;
+        }
+        else if (s[i] == 'B' && check2(i))
+        {
+            Bob.push_back(i);
+            i += 3;
+        }
+    }
+    int As = Alice.size(), Bs = Bob.size();
+    int i = 0, j = 0;
+    long long ans = 0;
+    for (int q = 0; q < As; q++)
+    {
+        while (i < Bs && Bob[i] < Alice[q] - k - 3)
+            i++;
+        while (j < Bs && Bob[j] <= Alice[q] + k + 5)
+            j++;
+        ans += j - i;
+    }
+    cout << ans << "\n";
+    return 0;
+}
 ```

data_backup/3.蓝桥杯/2.星系炸弹/solution.md

@@ -23,7 +23,7 @@
 ## 答案
 
 ```cpp
-
+2017-08-05
 ```
 
 ## 选项
@@ -31,17 +31,17 @@
 ### A
 
 ```cpp
-
+2017-09-05
 ```
 
 ### B
 
 ```cpp
-
+2017-08-06
 ```
 
 ### C
 
 ```cpp
-
+2017-09-06
 ```

data_backup/3.蓝桥杯/20.神奇算式/solution.md

@@ -10,6 +10,7 @@
 都符合要求。  
 如果满足乘法交换律的算式算作同一种情况，那么，包含上边已列出的3种情况，一共有多少种满足要求的算式。
 
+以下选项错误的是？
 
 ## aop
 
@@ -28,7 +29,57 @@
 ## 答案
 
 ```cpp
+int vis[10];
+int ans = 0;
+bool s(int i)
+{
+    while (i)
+    {
+        if (vis[i % 10] == 1)
+            return false;
+        else
+        {
+            vis[i % 10] = 1;
+            i /= 10;
+        }
+    }
+    return true;
+}
+int main()
+{
+    for (int i = 1; i < 999; i++)
+    {
+        for (int j = 1; j < 999; j++)
+        {
+            memset(vis, 0, sizeof(vis));
+            if (s(i) && s(j))
+            {
+                int k = i * j;
+                if (k > 9999 || k < 1000)
+                    continue;
 
+                int t = k;
+                while (k)
+                {
+                    if (vis[k % 10] == 1)
+                    {
+                        vis[k % 10]++;
+
+                        k /= 10;
+                    }
+                    else
+                        break;
+                }
+                if (k == 0 && vis[0] != 1 && vis[1] != 1 && vis[2] != 1 && vis[3] != 1 && vis[4] != 1 && vis[5] != 1 && vis[6] != 1 && vis[7] != 1 && vis[8] != 1 && vis[9] != 1)
+                {
+                    ans++;
+                }
+            }
+        }
+    }
+    cout << ans << endl;
+    return 0;
+}
 ```
 
 ## 选项
@@ -36,17 +87,209 @@
 ### A
 
 ```cpp
+bool isOk(int result, int t1, int t2)
+{
+    bool flag1[10] = {0}, flag2[10] = {0};
+    int i, rNum[4], num[4];
+    for (i = 0; i < 4; i++)
+    {
+        rNum[i] = result % 10;
+        result /= 10;
+        if (flag1[rNum[i]])
+            return false;
+        flag1[rNum[i]] = true;
+    }
+    i = 0;
+    while (t1 > 0)
+    {
+        num[i] = t1 % 10;
+        t1 /= 10;
+        if (flag2[num[i]])
+            return false;
+        flag2[num[i]] = true;
+        i++;
+    }
+    while (t2 > 0)
+    {
+        num[i] = t2 % 10;
+        t2 /= 10;
+        if (flag2[num[i]])
+            return false;
+        flag2[num[i]] = true;
+        i++;
+    }
+    if (i != 4)
+        return false;
+    for (i = 0; i < 10; i++)
+        if (flag1[i] != flag2[i])
+            return false;
+    return true;
+}
+
+int main()
+{
+    int i, j, count = 0;
+    for (i = 1000; i < 10000; i++)
+    {
 
+        for (j = 1; j * j <= i; j++)
+            if (!(i % j) && isOk(i, j, i / j))
+            {
+                count++;
+            }
+    }
+    cout << count << endl;
+
+    return 0;
+}
 ```
 
 ### B
 
 ```cpp
-
+int main()
+{
+    int v[5], i;
+    int ans = 0;
+    for (i = 1023; i <= 9876; i++)
+    {
+        v[0] = i / 1000;
+        v[1] = i / 10 % 10;
+        v[2] = i / 100 % 10;
+        v[3] = i % 10;
+        int flag1 = 0, flag2 = 0;
+        if (v[0] != v[1] && v[0] != v[2] && v[0] != v[3] && v[1] != v[2] && v[1] != v[3] && v[2] != v[3])
+        {
+            do
+            {
+                if (flag1 != 3 && (v[0] * 100 + v[1] * 10 + v[2]) * v[3] == i)
+                {
+                    flag1 = 1;
+                    ans++;
+                }
+                else if (flag2 != 2 && (v[0] * 10 + v[1]) * (v[2] * 10 + v[3]) == i)
+                {
+                    flag2 = 2;
+                    ans++;
+                }
+                else if (flag1 != 1 && v[0] * (v[1] * 100 + v[2] * 10 + v[3]) == i)
+                {
+                    flag1 = 3;
+                    ans++;
+                }
+            } while (next_permutation(v, v + 4));
+        }
+    }
+    cout << ans;
+    return 0;
+}
 ```
 
 ### C
 
 ```cpp
+#define MAX_N 1005
+
+bool judge1(int n)
+{
+    int ans = 0;
+    while (n)
+    {
+        ans++;
+        n /= 10;
+    }
+    if (ans == 4)
+        return true;
+    return false;
+}
+
+bool judge2(int i, int j)
+{
+    int s1 = 0, s2 = 0;
+    int ss1 = 1, ss2 = 1;
+    int tmp = i * j;
+    bool flag1 = true, flag2 = true;
+    while (tmp)
+    {
+        s1 += tmp % 10;
+        if (tmp % 10 == 0)
+            flag1 = false;
+        else
+            ss1 *= tmp % 10;
+        tmp /= 10;
+    }
+    while (j)
+    {
+        s2 += j % 10;
+        if (j % 10 != 0)
+            ss2 *= j % 10;
+        else
+            flag2 = false;
+        j /= 10;
+    }
+    while (i)
+    {
+        s2 += i % 10;
+        if (i % 10 != 0)
+            ss2 *= i % 10;
+        else
+            flag2 = false;
+        i /= 10;
+    }
+    if (s1 == s2 && ss1 == ss2 && flag1 && flag2)
+        return true;
+    else if ((!flag1 && !flag2) && s1 == s2 && ss1 == ss2)
+        return true;
+    return false;
+}
+
+bool judge3(int i, int j)
+{
+    int a[4];
+    int ans = 0;
+    while (i)
+    {
+        a[ans] = i % 10;
+        i /= 10;
+        ans++;
+    }
+    while (j)
+    {
+        a[ans] = j % 10;
+        j /= 10;
+        ans++;
+    }
+    for (i = 0; i < 3; i++)
+    {
+        for (j = i + 1; j < 4; j++)
+            if (a[i] == a[j])
+                return false;
+    }
+    return true;
+}
+
+int main()
+{
 
+    int i, j;
+    int ans = 0;
+    for (i = 1; i < 10; i++)
+    {
+        for (j = 123; j < 1000; j++)
+        {
+            if (judge1(i * j) && judge2(i, j) && judge3(i, j))
+                ans++;
+        }
+    }
+    for (i = 10; i < 100; i++)
+    {
+        for (j = i + 1; j < 100; j++)
+        {
+            if (judge1(i * j) && judge2(i, j) && judge3(i, j))
+                ans++;
+        }
+    }
+    cout << ans;
+    return 0;
+}
 ```

data_backup/3.蓝桥杯/21.解码/solution.md

@@ -33,6 +33,41 @@ HHHellllloo
 
 请注意原来的串长度可能超过 100。
 
+以下程序实现了这一功能，请你填补空白处内容：
+
+```cpp
+#include <bits/stdc++.h>
+using namespace std;
+
+char s2[100000];
+int main()
+{
+    char s1[150];
+    cin >> s1;
+
+    int top = 0;
+    for (int i = 0; s1[i] != '\0'; i++)
+    {
+        if ((s1[i] >= 'A' && s1[i] <= 'Z') || (s1[i] >= 'a' && s1[i] <= 'z'))
+        {
+            s2[top++] = s1[i];
+        }
+        else
+        {
+            while (s1[i] != '1')
+            {
+                __________________
+                s1[i] = s1[i] - 1;
+            }
+        }
+    }
+    s2[top] = '\0';
+
+    cout << s2;
+    return 0;
+}
+```
+
 ## aop
 
 ### before
@@ -50,7 +85,7 @@ HHHellllloo
 ## 答案
 
 ```cpp
-
+s2[top++] = s1[i - 1];
 ```
 
 ## 选项
@@ -58,17 +93,17 @@ HHHellllloo
 ### A
 
 ```cpp
-
+s2[++top] = s1[i - 1];
 ```
 
 ### B
 
 ```cpp
-
+s2[++top] = s1[i + 1];
 ```
 
 ### C
 
 ```cpp
-
+s2[top++] = s1[i + 1];
 ```

data_backup/3.蓝桥杯/22.星期一/solution.md

@@ -19,7 +19,7 @@
 ## 答案
 
 ```cpp
-
+5217
 ```
 
 ## 选项
@@ -27,17 +27,17 @@
 ### A
 
 ```cpp
-
+5218
 ```
 
 ### B
 
 ```cpp
-
+5216
 ```
 
 ### C
 
 ```cpp
-
+5210
 ```

data_backup/3.蓝桥杯/25.网络分析/solution.md

@@ -53,13 +53,15 @@
 对于所有评测用例，1 ≤ n ≤ 10000，1 ≤ m ≤ 100000，1 ≤ t ≤ 100。
 ```
 
+以下选项错误的是？
 
 ## aop
 
 ### before
 
 ```cpp
-
+#include <bits/stdc++.h>
+using namespace std;
 ```
 
 ### after
@@ -71,7 +73,98 @@
 ## 答案
 
 ```cpp
-
+int main()
+{
+    int n = 0;
+    int m = 0;
+    cin >> n;
+    cin >> m;
+    int ar[n + 1][n + 1];
+
+    for (int i = 0; i < n + 1; i++)
+        for (int j = 0; j < n + 1; j++)
+            ar[i][j] = 0;
+
+    bool arJudge[n + 1];
+
+    for (int i = 0; i < n + 1; i++)
+        arJudge[i] = 0;
+
+    vector<int> v(n, 0);
+    for (int i = 0; i <= n; ++i)
+    {
+        for (int j = 0; j <= n; ++j)
+        {
+            ar[i][j] = 0;
+        }
+    }
+
+    int a = 0, b = 0, c = 0;
+    for (int i = 0; i < m; ++i)
+    {
+        cin >> a;
+        cin >> b;
+        cin >> c;
+        if (a == 1)
+        {
+            if (ar[b][c] == 0)
+            {
+                ar[b][c] = 1;
+            }
+
+            if (ar[c][b] == 0)
+            {
+                ar[c][b] = 1;
+            }
+        }
+        if (a == 2)
+        {
+            queue<int> que;
+            que.push(b);
+            while (!que.empty())
+            {
+                int size = que.size();
+
+                for (int i = 0; i < size; ++i)
+                {
+                    int temp = que.front();
+                    que.pop();
+                    if (arJudge[temp] == 0)
+                    {
+                        v[temp - 1] += c;
+                        arJudge[temp] = 1;
+                    }
+                    for (int j = 1; j <= n; ++j)
+                    {
+                        if (ar[temp][j] != 0)
+                        {
+                            que.push(j);
+                        }
+                    }
+                }
+            }
+        }
+        for (int i = 0; i <= n; ++i)
+        {
+            arJudge[i] = 0;
+        }
+    }
+
+    for (int i = 1; i <= n; ++i)
+    {
+        for (int j = 1; j <= n; ++j)
+        {
+            cout << ar[i][j] << " ";
+        }
+        cout << endl;
+    }
+    for (int i = 0; i < n; ++i)
+    {
+        cout << v[i] << " ";
+    }
+    cout << endl;
+    return 0;
+}
 ```
 
 ## 选项
@@ -79,17 +172,184 @@
 ### A
 
 ```cpp
-
+int const N = 10010;
+using namespace std;
+int n, m;
+int i, j, k;
+int num[N];
+
+int f[N];
+
+int r[N];
+
+void init()
+{
+    for (i = 1; i <= n; i++)
+    {
+        f[i] = i;
+        r[i] = 1;
+    }
+}
+
+int find(int x)
+{
+    return f[x] == x ? x : (f[x] = find(f[x]));
+}
+
+void send(int x, int y)
+{
+    int tempx, tempy;
+
+    tempx = find(x);
+    tempy = find(y);
+    if (r[tempx] >= r[tempy])
+    {
+
+        f[tempy] = tempx;
+    }
+    else
+    {
+        f[tempx] = tempy;
+    }
+    if (r[tempx] == r[tempy] && tempx != tempy)
+    {
+        r[tempx]++;
+    }
+}
+void count(int x, int y)
+{
+    int tempx;
+    tempx = find(x);
+    for (i = 1; i <= n; i++)
+    {
+        if (tempx == find(i))
+        {
+            num[i] += y;
+        }
+    }
+}
+int main()
+{
+    cin >> n >> m;
+    init();
+    while (m--)
+    {
+        int x, y, z;
+        cin >> x >> y >> z;
+        if (x == 1)
+        {
+            send(y, z);
+        }
+        if (x == 2)
+        {
+            count(y, z);
+        }
+    }
+    for (i = 1; i <= n; i++)
+    {
+        cout << num[i] << " ";
+    }
+    return 0;
+}
 ```
 
 ### B
 
 ```cpp
-
+const int N = 10010;
+int p[N], d[N];
+int find(int x)
+{
+    if (p[x] == x || p[p[x]] == p[x])
+        return p[x];
+    int r = find(p[x]);
+    d[x] += d[p[x]];
+    p[x] = r;
+    return r;
+}
+int main()
+{
+    int n, m;
+    cin >> n >> m;
+    for (int i = 1; i <= n; i++)
+        p[i] = i;
+    while (m--)
+    {
+        int t, a, b;
+        cin >> t >> a >> b;
+        if (t == 1)
+        {
+            a = find(a), b = find(b);
+            if (a != b)
+            {
+                d[a] -= d[b];
+                p[a] = b;
+            }
+        }
+        else
+        {
+            a = find(a);
+            d[a] += b;
+        }
+    }
+    for (int i = 1; i <= n; i++)
+        if (i == find(i))
+            cout << d[i] << " ";
+        else
+            cout << d[i] + d[find(i)] << " ";
+    cout << endl;
+    return 0;
+}
 ```
 
 ### C
 
 ```cpp
-
+const int maxn = 10005;
+int a[maxn][maxn];
+int dfs_vis[maxn];
+int n, m;
+
+struct Node
+{
+    int data;
+} Point[maxn];
+
+void DFS(int a[maxn][maxn], int x, int y)
+{
+    Point[x].data += y;
+    dfs_vis[x] = 1;
+    for (int i = 1; i <= n; i++)
+    {
+        if (a[x][i] == 1 && dfs_vis[i] == 0)
+        {
+            DFS(a, i, y);
+        }
+    }
+}
+int main()
+{
+    cin >> n >> m;
+    cin.get();
+
+    for (int i = 1; i <= m; i++)
+    {
+        int flag, x1, x2;
+        scanf("%d %d %d", &flag, &x1, &x2);
+        if (flag == 1)
+        {
+            a[x1][x2] = a[x2][x1] = 1;
+        }
+        else if (flag == 2)
+        {
+            memset(dfs_vis, 0, sizeof(dfs_vis));
+            DFS(a, x1, x2);
+        }
+    }
+    for (int i = 1; i <= n; ++i)
+    {
+        cout << Point[i].data << " ";
+    }
+    return 0;
+}
 ```

data_backup/3.蓝桥杯/27.组合数问题/solution.md

@@ -69,6 +69,8 @@
 对于所有评测用例，1 ≤ k ≤ 108, 1 ≤ t ≤ 105, 1 ≤ n, m ≤ 1018，且 k 是质数。评测时将使用 10 个评测用例测试你的程序
 ```
 
+以下选项错误的是？
+
 ## aop
 
 ### before
@@ -86,7 +88,7 @@
 ## 答案
 
 ```cpp
-
+其他三项都是错的
 ```
 
 ## 选项
@@ -94,17 +96,158 @@
 ### A
 
 ```cpp
-
+const int Mod = 1e9 + 7;
+int c[2010][2010];
+int main()
+{
+    int n, m, t, k;
+    cin >> t >> k;
+    int nn = 2000, mm = 2000;
+    for (int i = 0; i <= nn; i++)
+    {
+        c[i][0] = 1;
+        c[i][i] = 1;
+    }
+    for (int i = 1; i <= nn; i++)
+        for (int j = 1; j <= mm; j++)
+            c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % k;
+    while (t--)
+    {
+        cin >> n >> m;
+        int ans = 0;
+        for (int j = 0; j <= m; j++)
+            for (int i = j; i <= n; i++)
+                if (c[i][j] == 0)
+                    ans++;
+        cout << ans % Mod;
+    }
+    return 0;
+}
 ```
 
 ### B
 
 ```cpp
-
+#define modk(x) (((x) >= k) ? ((x)-k) : (x))
+const int maxn = 2005;
+int c[maxn][maxn], n, m, k, T;
+void init()
+{
+
+    c[0][0] = 1;
+    for (int i = 1; i < maxn; i++)
+    {
+        c[i][0] = 1 % k;
+        for (int j = 1; j <= i; j++)
+        {
+            c[i][j] = modk(c[i - 1][j] + c[i - 1][j - 1]);
+        }
+    }
+
+    for (int i = 0; i < maxn; i++)
+    {
+        for (int j = 0; j <= i; j++)
+        {
+            if (c[i][j] == 0)
+                c[i][j] = 1;
+            else
+                c[i][j] = 0;
+        }
+    }
+
+    for (int i = 1; i < maxn; i++)
+    {
+        int s = 0;
+        for (int j = 0; j < maxn; j++)
+        {
+            s += c[i][j];
+            c[i][j] = c[i - 1][j] + s;
+        }
+    }
+}
+int main()
+{
+    scanf("%d%d", &T, &k);
+    init();
+    while (T--)
+    {
+        scanf("%d%d", &n, &m);
+        printf("%d\n", c[n][m]);
+    }
+    return 0;
+}
 ```
 
 ### C
 
 ```cpp
-
+const int Mod = 1e9 + 7;
+const int inv_2 = 5e8 + 4;
+
+long long cal(long long x, long long y)
+{
+    if (x < y)
+    {
+        x %= Mod;
+        return (x + 2) * (x + 1) % Mod * inv_2 % Mod;
+    }
+    x %= Mod, y %= Mod;
+    return ((y + 2) * (y + 1) % Mod * inv_2 % Mod + (x - y) * (y + 1) % Mod) % Mod;
+}
+long long cal_1(long long x, long long y)
+{
+    return min(x, y) + 1;
+}
+long long cal_2(long long x, long long y)
+{
+    if (x < y)
+    {
+        return 0;
+    }
+    return x - y + 1;
+}
+
+int main()
+{
+    int t, k;
+    cin >> t >> k;
+    long long n, m;
+    int a[100], b[100];
+    for (int turn = 0; turn < t; ++turn)
+    {
+        cin >> n >> m;
+        if (m > n)
+            m = n;
+        long long ans = cal(n, m);
+        int len_a = 0, len_b = 0;
+        while (n)
+        {
+            a[len_a++] = n % k;
+            n /= k;
+        }
+        while (m)
+        {
+            b[len_b++] = m % k;
+            m /= k;
+        }
+        int len = max(len_a, len_b);
+        vector<vector<long long>> dp(len + 1, vector<long long>(4));
+        dp[len][3] = 1;
+        for (int i = len - 1; i >= 0; --i)
+        {
+            dp[i][0] = dp[i + 1][0] * cal(k - 1, k - 1) + dp[i + 1][1] * cal(a[i] - 1, k - 1) + dp[i + 1][2] * cal(k - 1, b[i] - 1) + dp[i + 1][3] * cal(a[i] - 1, b[i] - 1);
+            dp[i][1] = dp[i + 1][1] * cal_1(a[i], k - 1) + dp[i + 1][3] * cal_1(a[i], b[i] - 1);
+            dp[i][2] = dp[i + 1][2] * cal_2(k - 1, b[i]) + dp[i + 1][3] * cal_2(a[i] - 1, b[i]);
+            dp[i][3] = dp[i + 1][3] & (a[i] >= b[i]);
+            dp[i][0] %= Mod, dp[i][1] %= Mod;
+            dp[i][2] %= Mod, dp[i][3] %= Mod;
+        }
+        ans -= dp[0][0] + dp[0][1] + dp[0][2] + dp[0][3];
+        ans %= Mod;
+        if (ans < 0)
+            ans += Mod;
+        cout << ans << endl;
+    }
+    return 0;
+}
 ```

data_backup/3.蓝桥杯/29.生日蜡烛/solution.md

@@ -20,7 +20,7 @@
 ## 答案
 
 ```cpp
-
+26
 ```
 
 ## 选项
@@ -28,17 +28,17 @@
 ### A
 
 ```cpp
-
+24
 ```
 
 ### B
 
 ```cpp
-
+25
 ```
 
 ### C
 
 ```cpp
-
+27
 ```

data_backup/3.蓝桥杯/5.蛇形填数/solution.md

@@ -22,7 +22,7 @@
 ## 答案
 
 ```cpp
-
+761
 ```
 
 ## 选项
@@ -30,17 +30,17 @@
 ### A
 
 ```cpp
-
+759
 ```
 
 ### B
 
 ```cpp
-
+760
 ```
 
 ### C
 
 ```cpp
-
+769
 ```

data_backup/3.蓝桥杯/7.跑步训练/solution.md

@@ -23,7 +23,7 @@
 ## 答案
 
 ```cpp
-
+3880
 ```
 
 ## 选项
@@ -31,17 +31,17 @@
 ### A
 
 ```cpp
-
+3400
 ```
 
 ### B
 
 ```cpp
-
+3920
 ```
 
 ### C
 
 ```cpp
-
+3900
 ```

data_backup/3.蓝桥杯/8.取数位/solution.md

@@ -2,7 +2,30 @@
 
 求1个整数的第k位数字有很多种方法。
 
-以下的方法就是一种。
+以下的方法就是一种。请你填补空白处的内容：
+
+```cpp
+#include <stdio.h>
+int len(int x)
+{
+    if (x < 10)
+        return 1;
+    return len(x / 10) + 1;
+}
+
+int f(int x, int k)
+{
+    if (len(x) - k == 0)
+        return x % 10;
+    __________________
+}
+int main()
+{
+    int x = 23574;
+    printf("%d\n", f(x, 3));
+    return 0;
+}
+```
 
 
 
@@ -23,7 +46,7 @@
 ## 答案
 
 ```cpp
-
+    return f(x / 10, k);
 ```
 
 ## 选项
@@ -31,17 +54,17 @@
 ### A
 
 ```cpp
-
+    return f(x % 10, k);
 ```
 
 ### B
 
 ```cpp
-
+    return f(x, k);
 ```
 
 ### C
 
 ```cpp
-
+    return f(x, k / 10);
 ```

data_backup/3.蓝桥杯/9.跑步锻炼/solution.md

@@ -21,7 +21,7 @@
 ## 答案
 
 ```cpp
-
+8879
 ```
 
 ## 选项
@@ -29,17 +29,17 @@
 ### A
 
 ```cpp
-
+8888
 ```
 
 ### B
 
 ```cpp
-
+8880
 ```
 
 ### C
 
 ```cpp
-
+8808
 ```