
现在开始用Q-Learning算法解决冰湖挑战问题。前面说过,冰湖挑战是一个4×4的迷宫,共有16个状态(0~15)。在每个状态中,有上、下、左、右4种选择(也就是智能体的4种可能的移动方向,其中左、下、右、上分别对应0、1、2、3)。因此Q-table就形成了一个16×4的矩阵。
下面就导入Gym库:
import gym # 导入Gym库
import numpy as np # 导入Num Py库
初始化冰湖挑战的环境:
env = gym.make('Frozen Lake-v0', is_slippery=False) # 生成冰湖挑战的环境
env.reset() # 初始化冰湖挑战的环境
print("状态数:", env.observation_space.n)
print("动作数:", env.action_space.n)
状态数:16
动作数:4
随机走20步:
for _ in range(20): # 随机走20步
env.render() # 生成环境
env.step(env.action_space.sample()) # 随机乱走
env.close() # 关闭冰湖挑战的环境
这一盘试玩中,到了第7步之后,就掉进了冰窟窿,游戏结束,如下所示:

这个问题,我们唯一的目标,就是对该环境创建一个有用的Q-Table,以作为未来冰湖挑战者的行动指南和策略地图。
首先,来初始化Q-Table:
# 初始化Q-Table
Q = np.zeros([env.observation_space.n, env.action_space.n])
print(Q)
输出结果如下:
[[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]]
此时Q-Table是16×4的全0值矩阵。
下面来实现Q-Learning算法:
# 初始化参数
alpha = 0.6 # 学习速率
gamma = 0.75 # 奖励折扣
episodes = 500 # 游戏盘数
r_history = [] # 奖励值的历史信息
j_history = [] # 步数的历史信息
for i in range(episodes):
s = env.reset() # 重置环境
r All = 0
d = False
j = 0
#Q-Learning算法的实现
while j < 99:
j+=1
# 通过Q-Table选择下一个动作, 但是增加随机噪声, 该噪声随着盘数的增加而减小
# 所增加的随机噪声其实就是ε-Greedy策略的实现, 通过它在探索和利用之间平衡
a = np.argmax(Q[s, :] +
np.random.randn(1, env.action_space.n)*(1./(i+1)))
# 智能体执行动作, 并从环境中得到新的状态和奖励
s1, r, d, _ = env.step(a)
# 通过贪心策略更新Q-Table, 选择新状态中的最大Q值
Q[s, a] = Q[s, a] + alpha*(r + gamma*np.max(Q[s1, :]) - Q[s, a])
r All += r
s = s1
if d == True:
break
j_history.append(j)
r_history.append(r All)
print(Q)
其中两个最重要的,就是智能体动作的选择和Q-Table的更新这两段代码。
■智能体动作的选择,采用的是ε-Greedy策略,力图在探索和利用之间平衡。ε值在此处实际上是一个随机值。
■Q-Table的更新,则采用贪心策略,总是选择长期奖励最大Q值来更新Q-Table。
200盘游戏过后,Q-Table如下:
[[0.00896807 0.23730469 0. 0.0110088 ]
[0.00697516 0. 0. 0. ]
[0. 0. 0. 0. ]
[0. 0. 0. 0. ]
[0.03321506 0.31640625 0. 0.00498226 ]
[0. 0. 0. 0. ]
[0. 0. 0. 0. ]
[0. 0. 0. 0. ]
[0. 0. 0.421875 0. ]
[0. 0. 0.5625 0. ]
[0. 0.75 0. 0. ]
[0. 0. 0. 0. ]
[0. 0. 0. 0. ]
[0. 0. 0. 0. ]
[0. 0. 1. 0. ]
[0. 0. 0. 0. ]]
Q-Table里面的内容,就是强化学习学到的经验,也就是后续盘中智能体的行动指南。可以看出,越是接近冰湖挑战终点的状态,Q值越大。这是因为γ值的存在(γ=0.75),Q值逆向传播的过程呈现出逐步的衰减。
还可以绘制出游戏的奖惩值随迭代次数而变化的曲线,以及每盘游戏的步数:
import matplotlib.pyplot as plt # 导入Matplotlib库
plt.figure(figsize=(16, 5))
plt.subplot(1, 2, 1)
plt.plot(r_history)
plt.subplot(1, 2, 2)
plt.plot(j_history)
绘制出的曲线如下图所示。
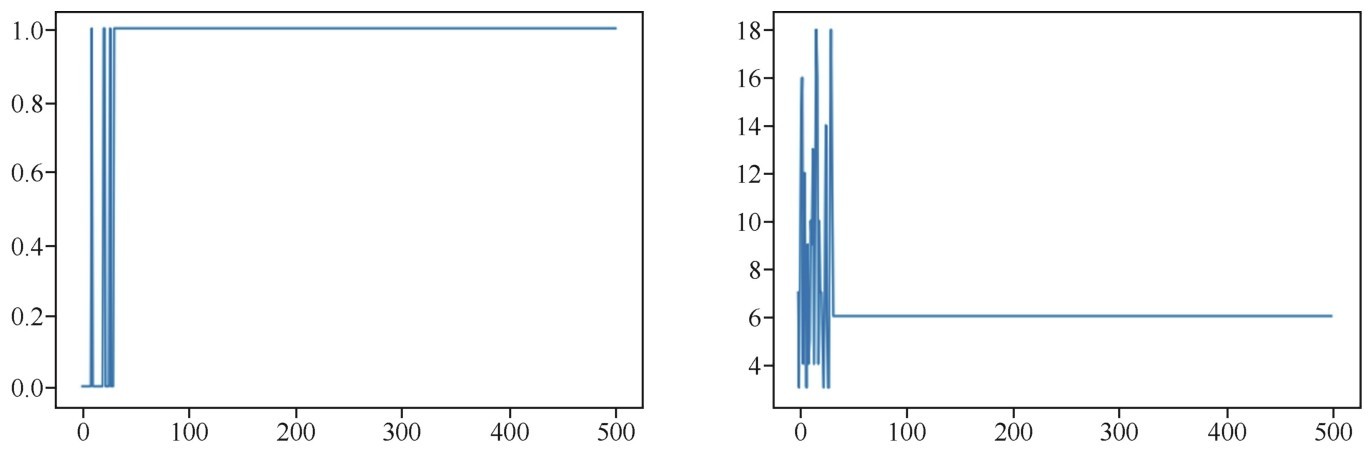
Q-Learing算法中Q-Table的收敛很快
左图告诉我们的信息是,开始的时候,智能体只是盲目地走动,有时走运,可以得到1分,大部分是得到0分,直到Q-Table里面的知识比较丰富了,几乎每盘游戏都得到1分。而右图告诉我们的信息是,智能体没有知识的初期,游戏的步数摇摆不定,要么很快掉进冰窟窿,要么来回地乱走。但是到了大概50盘之后,Q-Table的知识积累完成了,这以后,智能体可以保证每次都得到奖励,而且按照6步的速度迅速地走到飞盘所在地,完成冰湖挑战。
下面详细地看一下Q-Table的更新过程。
在开始阶段,智能体将做出大量尝试(甚至可能是10次、100次的尝试),然而,因为没有任何方向感和Q-Table作为指引,智能体的知识空间如同一张白纸。这时智能体处于婴儿态,经常性地坠入冰窟窿,而且得不到系统的任何奖赏。因为在冰湖挑战的环境设定中,掉进冰窟窿只是结束游戏,并没有惩罚分数,因此初始很多盘的尝试并不能带来Q-Table的更新。
如果用env.render方法显示出所有的环境状态,可以看出智能体的探索过程。
第1盘:

第2盘:

第3盘:

直到终于有一天,奇迹发生了,智能体达到了状态14(如第N盘的输出所示),并且随机地选择出了正确的动作,它终于可以得到它梦寐以求的奖励—就好像抓来抓去的婴儿终于抓到了一颗能吃的糖果。
第N盘:

第一个Q-Table状态的更新可以称之为奇点:
[[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.0.]
[0.0.0.75 0.]
[0.0.0.0.]]
此时Q[14,2]被更新为0.75(加了γ折扣的奖励值)。以后,有了这个值做引导,Q-Table自身更新的能力被增强不少:
Q[s, a] = Q[s, a] + lr*(r + y*np.max(Q[s1, :]) - Q[s, a])
因为在Q-Table的更新策略中,任何奖励r或者Q[s1,:]的值都会带来之前状态Q[s,a]的更新。也就是说,当智能体未来有朝一日,从状态10或13踩进状态14,都会带来状态10或13中Q值的更新,智能体也能够根据Q-Table的指引从状态14走到终点。之后开始发生蝴蝶效应,第一个奖励值就像波浪一样,它荡起的涟漪越传越远,从后面的状态向前传递。
 咖哥发言
咖哥发言
冰湖挑战的环境设定的一些细节如下。
第一,环境初始化时有一个is_slippery开关,默认是Ture值,这代表冰面很滑,此时智能体不能顺利地走到自己想去的方向。这种设定大大增加了随机性和游戏的难度。为了降低难度,我把这个开关,设为False,以演示Q-Table的正常更新过程。同学们可以尝试设置is_slippery=Ture,重新进行冰湖挑战。
第二,冰湖挑战设定所有的状态Q值的最大值为1。也就是说,当累积得到的奖励分大于1时,就不继续增加该状态Q[s,a]的Q值了。