二维到一维的PCA—平面到直线的投影
降维是把高维的数据降到低维的空间或平面上进行处理,也就是让特征数量减少,同时保留特征中的主要信息,从而简化数据集的空间结构,更易于可视化。
最常见的降维算法是主成分分析(Principal Component Analysis,PCA),它是通过正交变换将可能相关的原始变量转换为一组各维度线性无关的变量值,可用于提取数据的主要特征分量,以达到压缩数据或提高数据可视化程度的目的。
主成分分析这个名字也许让人觉得和“降维”不沾边,其实所谓“成分”,指的不是“地主”或者“贫下中农”,而是“特征”(即“变量”)。主成分分析,意思是抓主要特征,也就是降低特征维度。
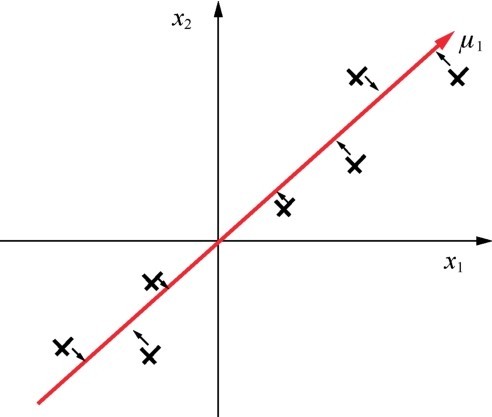
简单说说PCA算法是怎么降低数据特征的维度的。先看从二维到一维的情况。下图中的叉号代表一个含有两个特征的数据集,这些数据点分散在二维平面中。那么如何把二维的数据用一维的方式进行表达,同时又保留数据集中特征的性质呢?

二维到一维的PCA—平面到直线的投影
可以通过扭转坐标轴的方向,令新坐标轴μ1均匀地穿过这些数据点,同时使这些数据点以最小的距离降落在新坐标轴周围,然后,就可以用新的一维空间(直线)来展示原来的二维数据集。这就是PCA算法的原理。
 咖哥发言
咖哥发言
从示意图上看,二维到一维的PCA看起来好像是在解决线性回归问题,但其意义是不同的。回归问题是找各点到模型的最小损失,而PCA是找各点到新坐标轴的欧氏距离。
类推到三维数据集的情况,也可以用同样的方式把三维的数据映射到二维的平面(如下图所示),同时这个二维平面将力求最大程度保留原来的数据特性,在尽可能保存信息的同时降低数据的复杂度。

三维到二维的PCA—空间到平面的投影
PCA算法本质上是将数据集方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”。那么PCA算法的主要局限在于,它假设数据各主特征分布在正交方向上,如果在非正交方向上存在几个方差较大的方向,PCA算法的效果就“大打折扣”了。
 咖哥发言
咖哥发言
对于同样的数据,PCA由谁来做都会得到相同的结果。因此,PCA是一种通用实现,不存在个性化的优化。
PCA算法的理论也许比较抽象,让我们来看一个通过PCA算法进行数据可视化的案例。这个案例非常直观,很易于理解。
1.问题定义:给手语数字数据集降维
这是一个手语数字数据集,它是土耳其Ankara Ayranci Anadolu中学创建的,同学们可以在Kaggle中搜索关键字Sign Language找到这个数据集。
数据集中有2 062张64px×64px的图像,内容是各种各样的手语,代表0~9的数字。可以看出该组图像有实际意义的区域都集中在图像中部的手指区域,而外面的信息都可以视为噪声,如下图所示。

对分类有意义的图像区域
对于图像数据集来说,如何减少机器学习的处理时间、提升处理效率是很重要的,因为图像通常容量大,特征的维度也大。如果可以压缩图像数据集的特征空间,又不毁掉图像中太多有意义的内容,那么就很好地执行了降维。
因此,希望通过PCA算法,在为特征空间降维的同时,还能极大程度地保留有效特征,甚至突出有效特征。
下面就看一看PCA算法可以带来什么样的效果。
2.导入数据并显示部分数据
首先导入数据并显示部分数据:
import numpy as np # 导入Num Py库
import pandas as pd # 导入pandas库
import matplotlib.pyplot as plt # 导入Matplotlib库
x_load = np.load('../input/sign-language-digits-dataset/X.npy') # 导入特征
y_load = np.load('../input/sign-language-digits-dataset/Y.npy') # 导入标签
img_size = 64 # 设定显示图像的大小
image_index_list = [299, 999, 1699, 699, 1299, 1999, 699, 499, 1111, 199]
for each in range(10): # 每个手语数字选取一张展示
plt.subplot(2, 5, each+1)
plt.imshow(x_load[image_index_list[each]].reshape(img_size, img_size))
plt.axis('off')
title = "Sign " + str(each)
plt.title(title)
plt.show() # 显示图像
手语数字图像如下图所示。

手语数字图像
3.进行降维模型的拟合
下面使用Sklearn中decomposition模块的PCA工具进行数据的降维,并显示出降维后的结果:
from sklearn.decomposition import PCA # 导入Sklearn中decomposition模块的PCA工具
X = x_load.reshape((len(x_load), -1)) # Reshaple张量X
n_components = 5 # 设定因子个数, 因子越多, 模型越复杂
(n_samples, n_features) = X.shape
pca = PCA(n_components=n_components, # PCA工具
svd_solver='randomized', whiten=True)
X_pca = pca.fit_transform(X) # PCA降维拟合
components_ = pca.components_ # 保留的主要成分因子(也就是被简化的模型)
images = components_[:n_components] # 显示降维之后的特征图
plt.figure(figsize=(6, 5))
for i, comp in enumerate(images):
vmax = max(comp.max(), -comp.min())
plt.imshow(comp.reshape((64, 64)),
interpolation='nearest', vmin=-vmax, vmax=vmax)
plt.xticks(())
plt.yticks(())
plt.savefig('graph.png')
plt.show()
通过降维得到的特征图显示,这个数据集的特征空间中的主要成分是手指的形状(如下图所示),也就是说所保留的特征将聚集于手指部分,并会忽略其他对手语数字判断来说并不重要的噪声。

降维后的特征图
上面的fit方法只是进行拟合,如果要在拟合的同时给数据集X降维,使用fit_transform方法即可:
X_pca = pca.fit_transform(X)
print (X.shape)
print (X_pca.shape)
输出数据集张量的形状,新数据集的特征维度为5:
(2062, 4096)
(2062, 5)
降维之后的图像库因为特征数的减少,训练速度将得到显著的提高。
那么大家是否注意到,在上面这个主要特征的学习、寻找过程中,完全没有标签集介入,这5个手指都是机器根据输入的特征图自己发现的。是不是很有意思?这就是为什么PCA是一种无监督的自我学习过程。