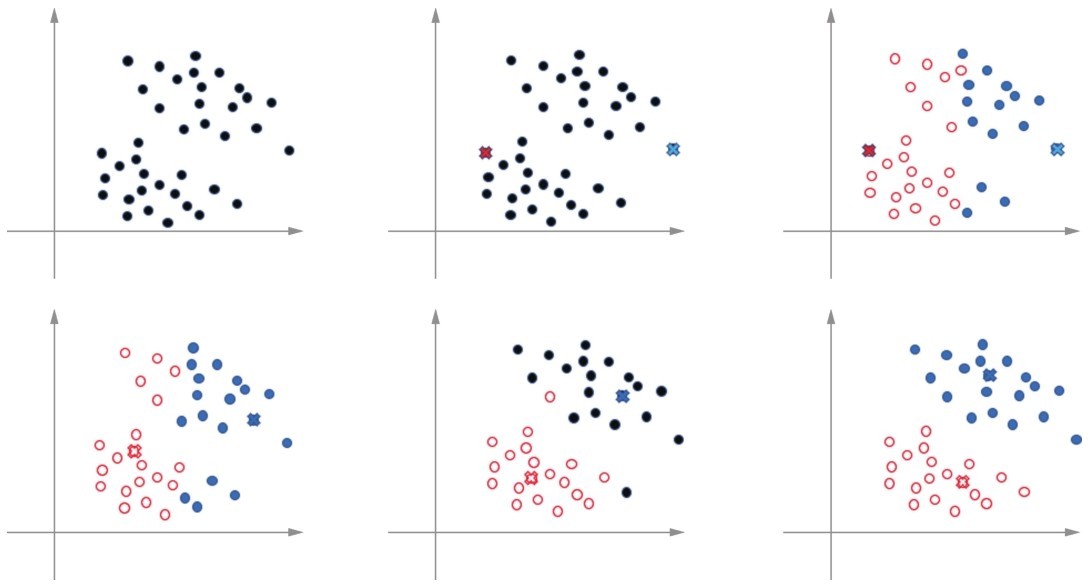
聚类中质心的移动和簇形成的过程
聚类是最常见的无监督学习算法。人有归纳和总结的能力,机器也有。聚类就是让机器把数据集中的样本按照特征的性质分组,这个过程中没有标签的存在。
聚类和监督学习中的分类问题有些类似,其主要区别在于:传统分类问题“概念化在前”。也就是说,在对猫狗图像分类之前,我们心里面已经对猫、狗图像形成了概念。这些概念指导着我们为训练集设定好标签。机器首先是学习概念,然后才能够做分类、做判断。分类的结果,还要接受标签,也就是已有概念的检验。
而聚类不同,虽然本质上也是“分类”,但是“概念化在后”或者“不概念化”,在给一堆数据分组时,没有任何此类、彼类的概念。譬如,漫天繁星,彼此之间并没有关联,也没有星座的概念,当人们看到它们,是先根据星星在广袤苍穹中的位置将其一组一组地“聚集”起来,然后才逐渐形成星座的概念。人们说,这一组星星是“大熊座”,那一组星星是“北斗七星”。这个先根据特征进行分组,之后再概念化的过程就是聚类。
聚类也有好几种算法,K均值(K-means)是其中最常用的一种。
K均值算法是最容易理解的无监督学习算法。算法简单,速度也不差,但需要人工指定K值,也就是分成几个聚类。
具体算法流程如下。
(1)首先确定K的数值,比如5个聚类,也叫5个簇。
(2)然后在一大堆数据中随机挑选K个数据点,作为簇的质心(centroid)。这些随机质心当然不完美,别着急,它们会慢慢变得完美。
(3)遍历集合中每一个数据点,计算它们与每一个质心的距离(比如欧氏距离)。数据点离哪个质心近,就属于哪一类。此时初始的K个类别开始形成。
(4)这时每一个质心中都聚集了很多数据点,于是质心说,你们来了,我就要“退役”了(这个是伟大的“禅让制度”啊!),选一个新的质心吧。然后计算出每一类中最靠近中心的点,作为新的质心。此时新的质心会比原来随机选的靠谱一些(等会儿用图展示质心的移动)。
(5)重新进行步骤(3),计算所有数据点和新的质心的距离,在新的质心周围形成新的簇分配(“吃瓜群众”随风飘摇,离谁近就跟谁)。
(6)重新进行步骤(4),继续选择更好的质心(一代一代地“禅让”下去)。
(7)一直重复进行步骤(5)和(6),不断更新簇中的数据点,不断找到新的质心,直至收敛。
小冰说:“不好意思,这里的收敛是什么意思?”
咖哥说:“就是质心的移动变化后来很小很小了,已经在一个阈值之下,或者固定不变了,算法就可以停止了。这个无监督学习算法是不是超好理解?算法真的是很奇妙的东西,有点像变魔术。没有告诉你们其中奥秘之前,你们觉得怎么可能做得到呢?一旦揭秘之后,会有一种恍然大悟的感觉。”
“哦,原来是这样!”小冰点头说道
通过下面这个图,可以看到聚类中质心的移动和簇形成的过程。

聚类中质心的移动和簇形成的过程
聚类问题的关键在于K值的选取。也就是说,把一批数据划分为多少个簇是最合理的呢?当数据特征维度较少、数据分布较为分散时,可通过数据可视化的方法来人工确定K值。但当数据特征维度较多、数据分布较为混乱时,数据可视化帮助不大。
当然,也可以经过多次实验,逐步调整,使簇的数目逐渐达到最优,以符合数据集的特点。
这里我介绍一种直观的手肘法(elbow method)进行簇的数量的确定。手肘法是基于对聚类效果的一个度量指标来实现的,这个指标也可以视为一种损失。在K值很小的时候,整体损失很大,而随着K值的增大,损失函数的值会在逐渐收敛之前出现一个拐点。此时的K值就是比较好的值。
大家看下面的图,损失随着簇的个数而收敛的曲线有点像只手臂,最佳K值的点像是手肘,因此取名为手肘法。
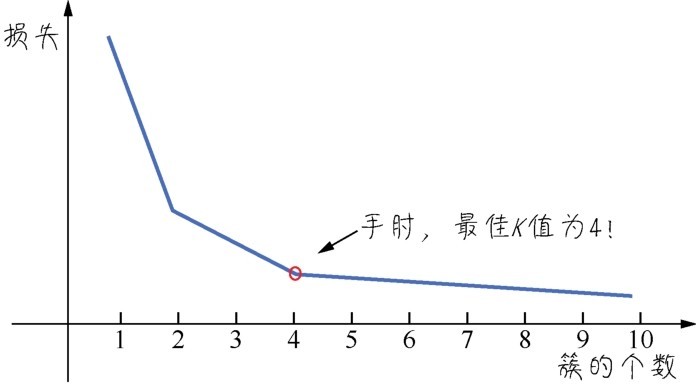
手肘法—确定最佳K值
同学们认真地观察着图中被称为“手臂”的曲线,并没觉得特别像。
咖哥忽然发现小冰的手已经举了好久了。咖哥说:“小冰,有什么问题,说吧。”
小冰说:“咖哥啊,这个聚类问题太适合帮我给客户分组了!这样我才好对隶属于不同‘簇’的客户进行有针对性的营销啊!”
咖哥说:“完全可以啊。看一下你的数据。”
1.问题定义:为客户分组
小冰打开她收集的数据集,如下图所示。小冰攒到了200个客户的信息,主要信息有以下4个方面。
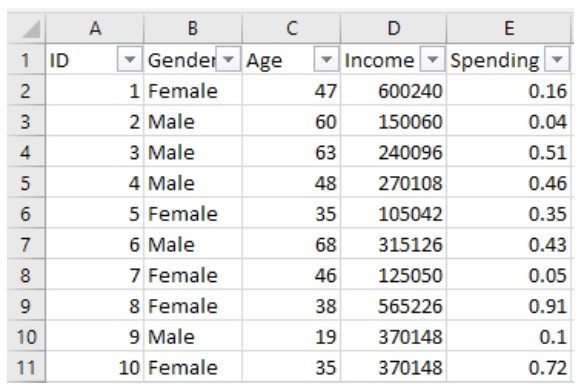
小冰收集的客户数据(未显示完)
■Gender:性别。
■Age:年龄。
■Income年收入(这可是很不好收集的信息啊!)。
■Spending Score:消费分数。这是客户们在我的网店里面花费多少、购物频率的综合指标。这是我从后台数据中整理出来的,已经归一化成一个0~1的分数。
那么这个案例的目标如下。
(1)通过这个数据集,理解K均值算法的基本实现流程。
(2)通过K均值算法,给小冰的客户分组,让小冰了解每类客户消费能力的差别。
2.数据读入
参考第10课源码包中的“教学用例1客户聚类”目录下的数据文件,创建Customer Cluster数据集,或在Kaggel中根据关键字Customer Cluster搜索该数据集。这里只选择两个特征,即年收入和消费分数,并对进行聚类。
示例代码如下:
import numpy as np # 导入Num Py库
import pandas as pd # 导入pandas库
dataset = pd.read_csv('../input/customer-cluster/Customers Cluster.csv')
dataset.head() # 显示一些数据
# 只针对两个特征进行聚类, 以方便二维展示
X = dataset.iloc[:, [3, 4]].values
3.聚类的拟合
下面尝试用不同的K值进行聚类的拟合:
from sklearn.cluster import KMeans # 导入聚类模型
cost=[] # 初始化损失(距离)值
for i in range(1, 11): # 尝试不同的K值
kmeans = KMeans(n_clusters= i, init='k-means++', random_state=0)
kmeans.fit(X)
cost.append(kmeans.inertia_) #inertia_是我们选择的方法, 其作用相当于损失函数
4.绘制手肘图
下面绘制手肘图:
import matplotlib.pyplot as plt # 导入Matplotlib库
import seaborn as sns # 导入Seaborn库
# 绘制手肘图找到最佳K值
plt.plot(range(1, 11), cost)
plt.title('The Elbow Method')#手肘法
plt.xlabel('No of clusters')#聚类的个数
plt.ylabel('Cost')#成本
plt.show()
生成的手肘图如下图所示。

生成的手肘图
从手肘图上判断,肘部数字大概是3或4,我们选择4作为聚类个数:
kmeansmodel = KMeans(n_clusters= 4, init='k-means++') # 选择4作为聚类个数
y_kmeans= kmeansmodel.fit_predict(X) # 进行聚类的拟合和分类
5.把分好的聚类可视化
下面把分好的聚类可视化:
# 下面把分好的聚类可视化
plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1],
s = 100, c = 'cyan', label = 'Cluster 1')#聚类1
plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1],
s = 100, c = 'blue', label = 'Cluster 2')#聚类2
plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1],
s = 100, c = 'green', label = 'Cluster 3')#聚类3
plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1],
s = 100, c = 'red', label = 'Cluster 4')#聚类4
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
s = 200, c = 'yellow', label = 'Centroids')#质心
plt.title('Clusters of customers')#客户形成的聚类
plt.xlabel('Income')#年收入
plt.ylabel('Spending Score')#消费分数
plt.legend()
plt.show()
客户形成的聚类如下图所示。
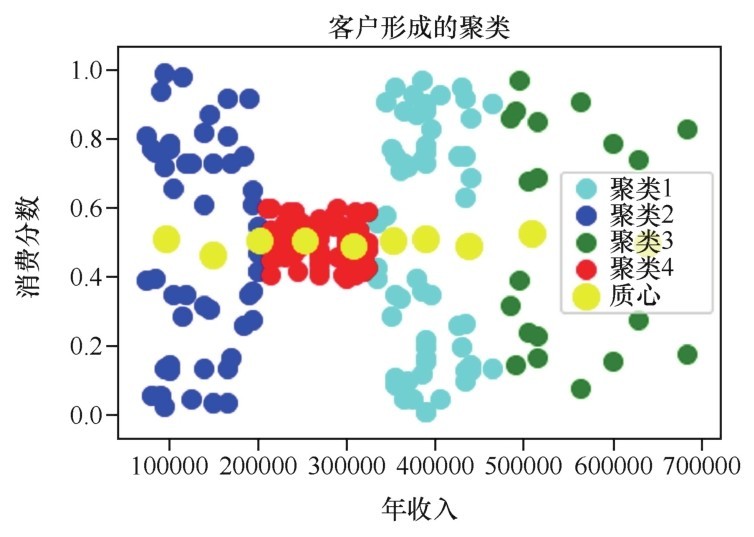
客户形成的聚类
(请见340页彩色版插图)
这个客户的聚类问题就解决了。其中,黄色高亮的大点是聚类的质心,可以看到算法中的质心并不止一个。