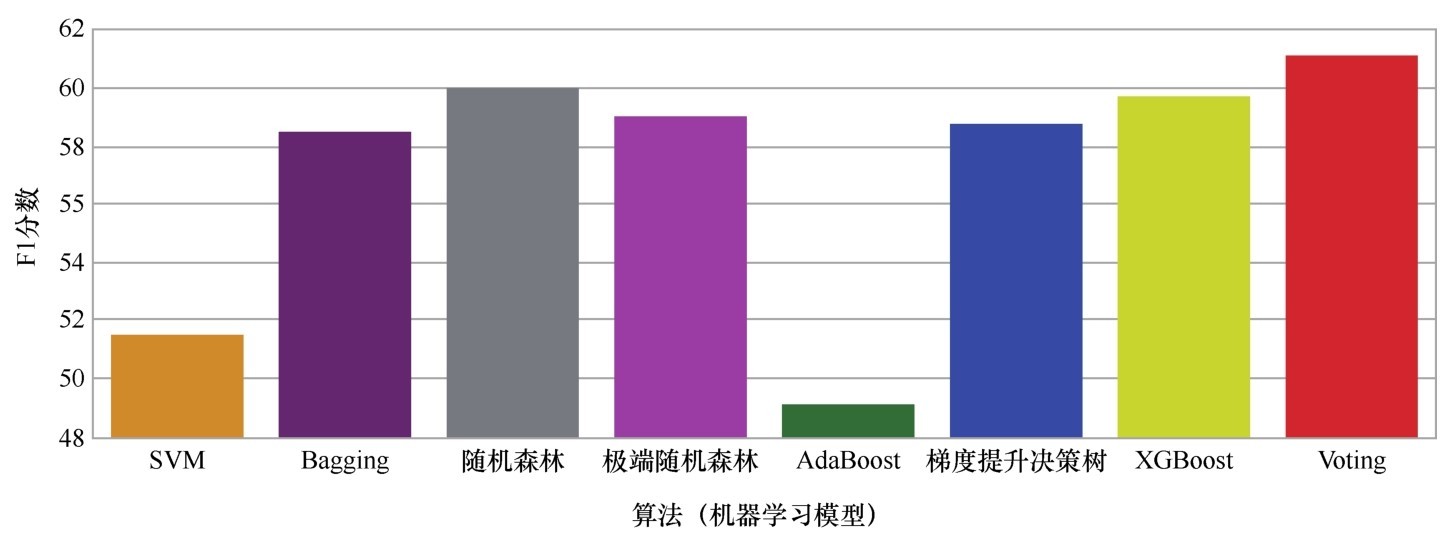
Voting后得到的F1分数最高
下面再接着说另外两种常见的异质集成算法—Voting和Averaging,它们的思路是直接集成各种基模型的预测结果。
Voting就是投票的意思。这种集成算法一般应用于分类问题。思路很简单。假如用6种机器学习模型来进行分类预测,就拥有6个预测结果集,那么6种模型,一种模型一票。如果是猫狗图像分类,4种模型被认为是猫,2种模型被认为是狗,那么集成的结果会是猫。当然,如果出现票数相等的情况(3票对3票),那么分类概率各为一半。
下面就用Voting算法集成之前所做的银行客户流失数据集,看一看Voting的结果能否带来F1分数的进一步提升。截止目前,针对这个问题我们发现的最好算法是随机森林和GBDT,随后的次优算法是极端随机森林、树的聚合和XGBoost,而SVM和Ada Boost对于这个问题来说稍微弱一些,但还是比逻辑回归强很多(从这里也可以看出“集成学习算法家族”的整体实力是非常强的)。
把上述这些比较好的算法放在一起进行Voting—这也可以算是集成的集成吧。
具体代码如下:
from sklearn.ensemble import Voting Classifier # 导入Voting模型
# 把各种模型的预测结果进行Voting。同学们还可以加入更多模型如SVM, KNN等
voting = Voting Classifier(estimators=[('rf', rf_gs),
('gb', gb_gs),
('ext', ext_gs),
('xgb', xgb_gs),
('ada', ada_gs)],
voting='soft', n_jobs=10)
voting = voting.fit(X_train, y_train) # 拟合模型
y_pred = voting.predict(X_test) # 进行预测
print("Voting测试准确率: {:.2f}%", voting.score(X_test, y_test)*100)
print("Voting测试F1分数:{:.2f}%", f1_score(y_test, y_pred)*100)
输出结果显示,集成这几大算法的预测结果之后,准确率进一步小幅上升至87.00%,而更为重要的F1分数居然提高到61.53%。对于这个预测客户流失率的问题而言,这个F1分数已经几乎是我们目前可以取得的最佳结果。
Voting测试准确率: 87.00%
Voting测试F1分数: 61.53%
如果显示各种模型F1分数的直方图,会发现Voting后的结果最为理想,而次优算法是机器学习中的“千年老二”—随机森林算法。

Voting后得到的F1分数最高
最后,还有一种更为简单粗暴的结果集成算法—Averaging,就是完全独立地进行几种机器学习模型的训练,训练好之后生成预测结果,最后把各个预测结果集进行平均:
model1.fit(X_train, y_train)
model2.fit(X_train, y_train)
model3.fit(X_train, y_train)
pred_m1=model1.predict_proba(X_test)
pred_m2=model2.predict_proba(X_test)
pred_m3=model3.predict_proba(X_test)
pred_final=(pred_m1+pred_m2+pred_m3)/3
是不是很直接?
你们可能会问,如果觉得几个基模型中一种模型比另一种更好怎么办?那也无妨,你们在取均值的时候可以给你们觉得更优秀的算法进行加权。
pred_final = (pred_m1*0.5+pred_m2*0.3+pred_m3*0.2)
一开始的时候我曾以为这种思路并没有什么实用价值,后来在Kaggle的官方文档中读到了一个Notebook—Minimal LSTM + NB-SVM baseline ensemble,其中所推荐的协作算法正是Averaging集成。
在通过Averaging集成之前,这个Notebook的作者已经通过LSTM和SVM两种算法训练机器,对维基百科中的评论进行分类鉴定,分别得到了两个可提交的CSV格式的文件。
这个Notebook中,并没有新的模型训练过程,只是读取了两个CSV的数据,然后加起来,除以2,重新生成可提交的预测结果文件:
p_res[label_cols] = (p_nbsvm[label_cols] + p_lstm[label_cols]) / 2
p_res.to_csv('submission.csv', index=False)
不偏不倚,就是简单平均而已。
与通常只用于分类问题的Voting相比较,Averaging的优点在于既可以处理分类问题,又可以处理回归问题。分类问题是将概率值进行平均,而回归问题是将预测值进行平均,而且在平均的过程中还可以增加权重。