有放回的随机抽取数据样本
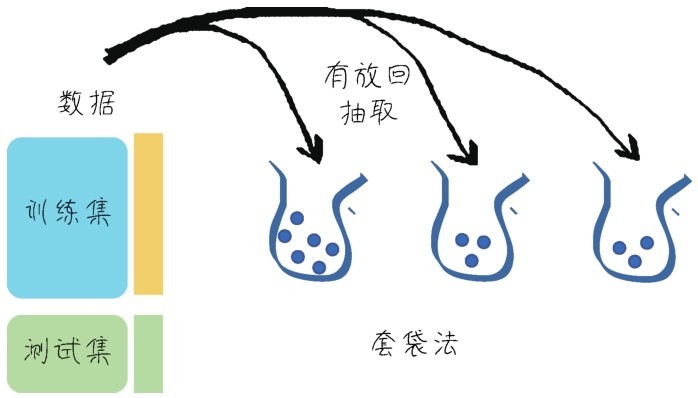
Bagging是我们要讲的第一种集成学习算法,是Bootstrap Aggregating的缩写。有人把它翻译为套袋法、装袋法,或者自助聚合,没有统一的叫法,就直接用它的英文名称。其算法的基本思想是从原始的数据集中抽取数据,形成K个随机的新训练集,然后训练出K个不同的模型。具体过程如下。
(1)从原始样本集中通过随机抽取形成K个训练集(如下图所示):每轮抽取n个训练样本(有些样本可能被多次抽取,而有些样本可能一次都没有被抽取,这叫作有放回的抽取)。这K个训练集是彼此独立的—这个过程也叫作bootstrap(可译为自举或自助采样),它有点像K折验证,但不同之处是其样本是有放回的。

有放回的随机抽取数据样本
(2)每次使用一个训练集通过相同的机器学习算法(如决策树、神经网络等)得到一个模型,K个训练集共得到K个模型。我们把这些模型称为基模型(base estimator),或者基学 习器。
基模型的集成有以下两种情况。
■对于分类问题,K个模型采用投票的方式得到分类结果。
■对于回归问题,计算K个模型的均值作为最后的结果。
这个过程如下图所示。

Bagging的过程
小冰发言:“咖哥,我怎么觉得这个Bagging上节课你已经讲过一遍了?”
咖哥说:“很好,你还记得,就代表上一课我没有白讲。多数情况下的Bagging,都是基于决策树的,构造随机森林的第一个步骤其实就是对多棵决策树进行Bagging,我们把它称为树的聚合(Bagging of Tree)。”
树这种模型,具有显著的低偏差、高方差的特点。也就是受数据的影响特别大,一不小心,训练集准确率就接近100%了。但是这种效果不能够移植到其他的数据集。这是很明显的过拟合现象。集成学习的Bagging算法,就从树模型开始,着手解决它太过于精准,又不易泛化的问题。
当然,Bagging的原理,并不仅限于决策树,还可以扩展到其他机器学习算法。因为通过随机抽取数据的方法减少了可能的数据干扰,所以经过Bagging的模型将会具有低方差。
在Sklearn的集成学习库中,有Bagging Classifier和Bagging Regressor这两种Bagging模型,分别适用于分类问题和回归问题。
现在把树的Bagging Classifier应用于第5课中预测银行客户是否会流失的案例,看一看其效果如何。数据读入和特征工程部分的代码不再重复,同学们可参考第5课中的代码段或源码包中的内容。
示例代码如下:
# 对多棵决策树进行聚合(Bagging)
from sklearn.ensemble import Bagging Classifier #导入Bagging分类器
from sklearn.tree import Decision Tree Classifier #导入决策树分类器
from sklearn.metrics import (f1_score, confusion_matrix) # 导入评估指标
dt = Bagging Classifier(Decision Tree Classifier()) # 只使用一棵决策树
dt.fit(X_train, y_train) # 拟合模型
y_pred = dt.predict(X_test) # 进行预测
print("决策树测试准确率: {:.2f}%".format(dt.score(X_test, y_test)*100))
print("决策树测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
bdt = Bagging Classifier(Decision Tree Classifier()) #树的Bagging
bdt.fit(X_train, y_train)# 拟合模型
y_pred = bdt.predict(X_test) # 进行预测
print("决策树Bagging测试准确率: {:.2f}%".format(bdt.score(X_test, y_test)*100))
print("决策树Bagging测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
上面代码中的Bagging Classifier指定了Decision Tree Classifier决策树分类器作为基模型的类型,默认的基模型的数量是10,也就是在Bagging过程中会用Bootstrap算法生成10棵树。
输出结果如下:
决策树测试准确率: 84.00%
决策树测试F1分数: 53.62%
决策树Bagging测试准确率: 85.75%
决策树Bagging测试F1分数: 58.76%
在这里比较了只使用一棵决策树和经过Bagging之后的树这两种算法的预测效果,可以看到决策树Bagging的准确率及F1分数明显占优势。在没有调参的情况下,其验证集的F1分数达到58.76%。当然,因为Bagging过程的随机性,每次测试的分数都稍有不同。
如果用网格搜索再进行参数优化:
from sklearn.model_selection import Grid Search CV # 导入网格搜索工具
# 使用网格搜索优化参数
bdt_param_grid = {
'base_estimator__max_depth' : [5, 10, 20, 50, 100],
'n_estimators' : [1, 5, 10, 50]}
bdt_gs = Grid Search CV(Bagging Classifier(Decision Tree Classifier()),
param_grid = bdt_param_grid, scoring = 'f1',
n_jobs= 10, verbose = 1)
bdt_gs.fit(X_train, y_train) # 拟合模型
bdt_gs = bdt_gs.best_estimator_ # 最佳模型
y_pred = bdt.predict(X_test) # 进行预测
print("决策树Bagging测试准确率: {:.2f}%".format(bdt_gs.score(X_test, y_test)*100))
print("决策树Bagging测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
F1分数可能会进一步提升:
决策树Bagging测试准确率: 86.75%
决策树Bagging测试F1分数: 59.47%
其中,base_estimator__max_depth中的base_estimator表示Bagging的基模型,即决策树分类器Decision Tree Classifier。因此,两个下划线后面的max_depth参数隶属于决策树分类器,指的是树的深度。而n_estimators参数隶属于Bagging Classifier,指的是Bagging过程中树的个数。
准确率为何会提升?其中的关键正是降低了模型的方差,增加了泛化能力。因为每一棵树都是在原始数据集的不同子集上进行训练的,这是以偏差的小幅增加为代价的,但是最终的模型应用于测试集后,性能会大幅提升。
当我们说到集成学习,最关键的一点是各个基模型的相关度要小,差异性要大。异质性越强,集成的效果越好。两个准确率为99%的模型,如果其预测结果都一致,也就没有提高的余地了。
那么对树的集成,关键在于这些树里面每棵树的差异性是否够大。
在树的聚合中,每一次树分叉时,都会遍历所有的特征,找到最佳的分支方案。而随机森林在此算法基础上的改善就是在树分叉时,增加了对特征选择的随机性,而并不总是考量全部的特征。这个小小的改进,就在较大程度上进一步提高了各棵树的差异。
假设树分叉时选取的特征数为m,m这个参数值通常遵循下面的规则。
■对于分类问题,m可以设置为特征数的平方根,也就是如果特征是36,那么m大概是6。
■对于回归问题,m可以设置为特征数的1/3,也就是如果特征是36,那么m大概是12。
在Sklearn的集成学习库中,也有Random Forest Classifier和Random Forest Regressor两种随机森林模型,分别适用于分类问题和回归问题。
下面用随机森林算法解决同样的问题,看一下预测效率:
from sklearn.ensemble import Random Forest Classifier # 导入随机森林模型
rf = Random Forest Classifier() # 随机森林模型
# 使用网格搜索优化参数
rf_param_grid = {"max_depth": [None],
"max_features": [1, 3, 10],
"min_samples_split": [2, 3, 10],
"min_samples_leaf": [1, 3, 10],
"bootstrap": [True, False],
"n_estimators" :[100, 300],
"criterion": ["gini"]}
rf_gs = Grid Search CV(rf, param_grid = rf_param_grid,
scoring="f1", n_jobs= 10, verbose = 1)
rf_gs.fit(X_train, y_train) # 拟合模型
rf_gs = rf_gs.best_estimator_ # 最佳模型
y_pred = rf_gs.predict(X_test) # 进行预测
print("随机森林测试准确率: {:.2f}%".format(rf_gs.score(X_test, y_test)*100))
print("随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
输出测结果如下:
随机森林测试准确率: 86.65%
随机森林测试F1分数: 59.48%
这个结果显示出随机森林的预测效率比起树的聚合更好。
从树的聚合到随机森林,增加了树生成过程中的随机性,降低了方差。顺着这个思路更进一步,就形成了另一个算法叫作极端随机森林,也叫更多树(extra tree)。
这么多种“树”让小冰和同学们听得有点呆了。
咖哥笑道:“虽然决策树这个算法本身不突出,但是经过集成,衍生出了许多强大的算法。而且这儿还没说完,后面还有。”
前面说过,随机森林算法在树分叉时会随机选取m个特征作为考量,对于每一次分叉,它还是会遍历所有的分支,然后选择基于这些特征的最优分支。这本质上仍属于贪心算法(greedy algorithm),即在每一步选择中都采取在当前状态下最优的选择。而极端随机森林算法一点也不“贪心”,它甚至不去考量所有的分支,而是随机选择一些分支,从中拿到一个最优解。
下面用极端随机森林算法来解决同样的问题:
from sklearn.ensemble import Extra Trees Classifier # 导入极端随机森林模型
ext = Extra Trees Classifier() # 极端随机森林模型
# 使用网格搜索优化参数
ext_param_grid = {"max_depth": [None],
"max_features": [1, 3, 10],
"min_samples_split": [2, 3, 10],
"min_samples_leaf": [1, 3, 10],
"bootstrap": [True, False],
"n_estimators" :[100, 300],
"criterion": ["gini"]}
ext_gs = Grid Search CV(et, param_grid = ext_param_grid, scoring="f1",
n_jobs= 4, verbose = 1)
ext_gs.fit(X_train, y_train) # 拟合模型
ext_gs = ext_gs.best_estimator_ # 最佳模型
y_pred = ext_gs.predict(X_test) # 进行预测
print("极端随机森林测试准确率: {:.2f}%".format(ext_gs.score(X_test, y_test)*100))
print("极端随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
输出结果如下:
极端随机森林测试准确率: 86.10%
极端随机森林测试F1分数: 56.97%
关于随机森林和极端随机森林算法的性能,有以下几点需要注意。
(1)随机森林算法在绝大多数情况下是优于极端随机森林算法的。
(2)极端随机森林算法不需要考虑所有分支的可能性,所以它的运算效率往往要高于随机森林算法,也就是说速度比较快。
(3)对于某些数据集,极端随机森林算法可能拥有更强的泛化功能。但是很难知道具体什么情况下会出现这样的结果,因此不妨各种算法都试试。
刚才的示例代码使用的都是上述算法的分类器版本。咱们再用一个实例来比较决策树、树的聚合、随机森林,以及极端随机森林在处理回归问题上的优劣。
处理回归问题要选择各种工具的Regressor(回归器)版本,而不是Classifier(分类器)。
这个示例是从Yury Kashnitsky[1]发布在Kaggle上的一个Notebook的基础上修改后形成的,其中展示了4种树模型拟合一个随机函数曲线(含有噪声)的情况,其目的是比较4种算法中哪一种对原始函数曲线的拟合效果最好。
案例的完整代码如下:
# 导入所需的库
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.ensemble import (Random Forest Regressor,
Bagging Regressor,
Extra Trees Regressor)
from sklearn.tree import Decision Tree Regressor
# 生成需要拟合的数据点—多次函数曲线
def compute(x):
return 1.5 * np.exp(-x ** 2) + 1.1 * np.exp(-(x - 2) ** 2)
def f(x):
x = x.ravel()
return compute(x)
def generate(n_samples, noise):
X = np.random.rand(n_samples) * 10 - 4
X = np.sort(X).ravel()
y = compute(X) + np.random.normal(0.0, noise, n_samples)
X = X.reshape((n_samples, 1))
return X, y
X_train, y_train = generate(250, 0.15)
X_test, y_test = generate(500, 0.15)
# 用决策树回归模型拟合
dtree = Decision Tree Regressor().fit(X_train, y_train)
d_predict = dtree.predict(X_test)
plt.figure(figsize=(20, 12))
# ax.add_gridspec(b=False)
plt.grid(b=None)
plt.subplot(2, 2, 1)
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, d_predict, "g", lw=2)
plt.title("Decision Tree, MSE = %.2f" % np.sum((y_test - d_predict) ** 2))
# 用树的聚合回归模型拟合
bdt = Bagging Regressor(Decision Tree Regressor()).fit(X_train, y_train)
bdt_predict = bdt.predict(X_test)
# plt.figure(figsize=(10, 6))
plt.subplot(2, 2, 2)
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, bdt_predict, "y", lw=2)
plt.title("Bagging for Trees, MSE = %.2f" % np.sum((y_test - bdt_predict) ** 2));
# 用随机森林回归模型拟合
rf = Random Forest Regressor(n_estimators=10).fit(X_train, y_train)
rf_predict = rf.predict(X_test)
# plt.figure(figsize=(10, 6))
plt.subplot(2, 2, 3)
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, rf_predict, "r", lw=2)
plt.title("Random Forest, MSE = %.2f" % np.sum((y_test - rf_predict) ** 2));
# 用极端随机森林回归模型拟合
et = Extra Trees Regressor(n_estimators=10).fit(X_train, y_train)
et_predict = et.predict(X_test)
# plt.figure(figsize=(10, 6))
plt.subplot(2, 2, 4)
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, et_predict, "purple", lw=2)
plt.title("Extra Trees, MSE = %.2f" % np.sum((y_test - et_predict) ** 2));
从下图的输出中不难看出,曲线越平滑,过拟合越小,机器学习算法也就越接近原始函数曲线本身,损失也就越小。

4种算法的比较
对于后3种集成学习算法,每次训练得到的均方误差都是不同的,因为算法内部均含有随机成分。经过集成学习后,较之单棵决策树,3种集成学习算法都显著地降低了在测试集上的均方误差。
总结一下:Bagging,是并行地生成多个基模型,利用基模型的独立性,然后通过平均或者投票来降低模型的方差。