 咖哥发言
咖哥发言小冰问道:“偏差和方差?上节课讲决策树和随机森林时你好像提到过它们,当时你没有细说。”
“对。”咖哥说,“在深入介绍集成学习算法之前,先要了解的是偏差和方差这两个概念在机器学习项目优化过程中的指导意义。”
方差是从统计学中引入的概念,方差定义的是一组数据距离其均值的离散程度。而机器学习里面的偏差用于衡量模型的准确程度。
 咖哥发言
咖哥发言
注意,机器学习内部参数w和b中的参数b,英文也是bias,它是线性模型内部的偏置。而这里的bias是模型准确率的偏差。两者英文相同,但不是同一个概念。
同学们看下面的图。
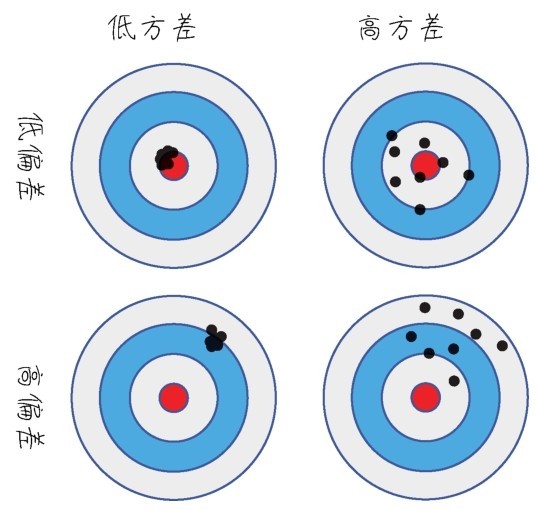
偏差和方差都低,是我们对模型的追求
偏差评判的是机器学习模型的准确度,偏差越小,模型越准确。它度量了算法的预测与真实结果的离散程度,刻画了学习算法本身的拟合能力 。也就是每次打靶,都比较靠近靶心。
方差评判的是机器学习模型的稳定性(或称精度),方差越小,模型越稳定。它度量了训练集变动所导致的学习性能变化,刻画了数据扰动所造成的影响。也就是每次打靶,不管打得准不准,击中点都比较集中。
 咖哥发言
咖哥发言
其实机器学习中的预测误差还包含另一个部分,叫作噪声。噪声表达的是在当前任务上任何学习算法所能达到的泛化误差的下界,也可以说刻画了学习问题本身的难度,属于不可约减的误差 (irreducible error),因此就不在我们关注的范围内。
低偏差和低方差,是我们希望达到的效果,然而一般来说,偏差与方差是鱼与熊掌不可兼得的,这被称作偏差-方差窘境 (bias-variance dilemma)。
■给定一个学习任务,在训练的初期,模型对训练集的拟合还未完善,能力不够强,偏差也就比较大。正是由于拟合能力不强,数据集的扰动是无法使模型的效率产生显著变化的—此时模型处于欠拟合的状态,把模型应用于训练集数据,会出现高偏差。
■随着训练的次数增多,模型的调整优化,其拟合能力越来越强,此时训练数据的扰动也会对模型产生影响。
■当充分训练之后,模型已经完全拟合了训练集数据,此时数据的轻微扰动都会导致模型发生显著变化。当训练好的模型应用于测试集,并不一定得到好的效果—此时模型应用于不同的数据集,会出现高方差,也就是过拟合的状态。
其实,在第4课的正则化、欠拟合和过拟合一节中,我们已经探讨过这个道理了。机器学习性能优化领域的最核心问题,就是不断地探求欠拟合-过拟合之间,也就是偏差-方差之间的最佳平衡点,也是训练集优化和测试集泛化的平衡点。
如右图所示,如果同时为训练集和测试集绘制损失曲线,大概可以看出以下内容。
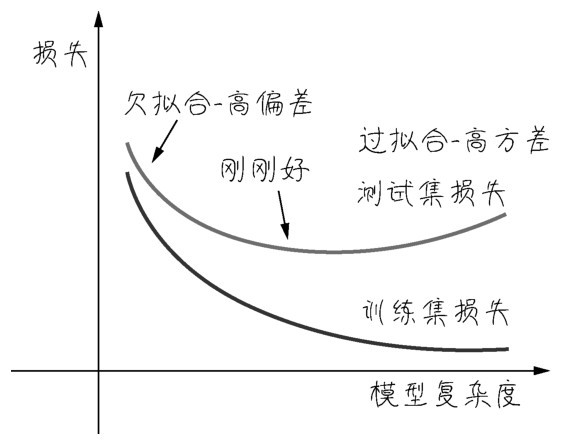
损失、偏差、方差与模型复杂度之间的关系
■在训练初期,当模型很弱的时候,测试集和训练集上,损失都大。这时候需要调试的是机器学习的模型,或者甚至选择更好算法。这是在降低偏差。
■在模型或者算法被优化之后,损失曲线逐渐收敛。但是过了一段时间之后,发现损失在训练集上越来越小,然而在测试集上逐渐变大。此时要集中精力降低方差。
因此,机器学习的性能优化是有顺序的,一般是先降低偏差,再聚焦于降低方差。
咖哥发问:“刚才画出了损失与模型复杂度之间的关系曲线,以评估偏差和方差的大小。还有另外一种的方法,能判断机器学习模型当前方差的大致状况,你们能猜出来吗?”
小冰想了想:“刚才你说到……数据的扰动……”
“不错啊”咖哥很惊讶,“没想到你的思路还挺正确。看来你经过坚持学习,能力都有提升了。答案正是通过调整数据集的大小来观测损失的情况,进而判定是偏差还是方差影响着机器学习效率。”
高方差,意味着数据扰动对模型的影响大。那么观察数据集的变化如何能够发现目前模型的偏差和方差状况?
你们看下面的图:左图中的模型方差较低,而右图中的模型方差较高。
这是因为,数据集越大,越能够降低过拟合的风险。数据集越大,训练集和测试集上的损失差异理论上应该越小,因为更大的数据集会导致训练集上的损失值上升,测试集上的损失值下降。
■如果随着数据集逐渐增大,训练集和测试集的误差的差异逐渐减小,然后都稳定在一个值附近。这说明此时模型的方差比较小。如果这个模型准确率仍然不高,需要从模型的性能优化上调整,减小偏差。

损失、偏差、方差与模型复杂度之间的关系
■如果随着数据集的增大,训练集和测试集的误差的差异仍然很大,此时就说明模型的方差大。也就是模型受数据的影响大,此时需要增加模型的泛化能力。
小冰想了想,又问:“你煞费苦心,绘制出来上面这样的曲线,又有什么意义,我们拿来做什么啊?”
咖哥回答:“当然是为了确定目前的模型是偏差大还是方差大。”
小冰接着问:“然后呢?”
咖哥又答:“很重要。知道偏差大还是方差大,就知道应该把模型往哪个方向调整。回到下面要谈的集成学习算法的话,就是选择什么算法优化模型。我们需要有的放矢。”
“不同的模型,有不同的复杂度,其预测空间大小不同、维度也不同。一个简单的线性函数,它所能够覆盖的预测空间是比较有限的,其实也可以说简单的函数模型方差都比较低。这是好事儿。那么如果增加变量的次数,增加特征之间的组合,函数就变复杂了,预测空间就随着特征空间的变化而增大。再发展到很多神经元非线性激活之后组成神经网络,可以包含几十万、几百万个参数,它的预测空间维度特别大。这个时候,方差也会迅速增大。”
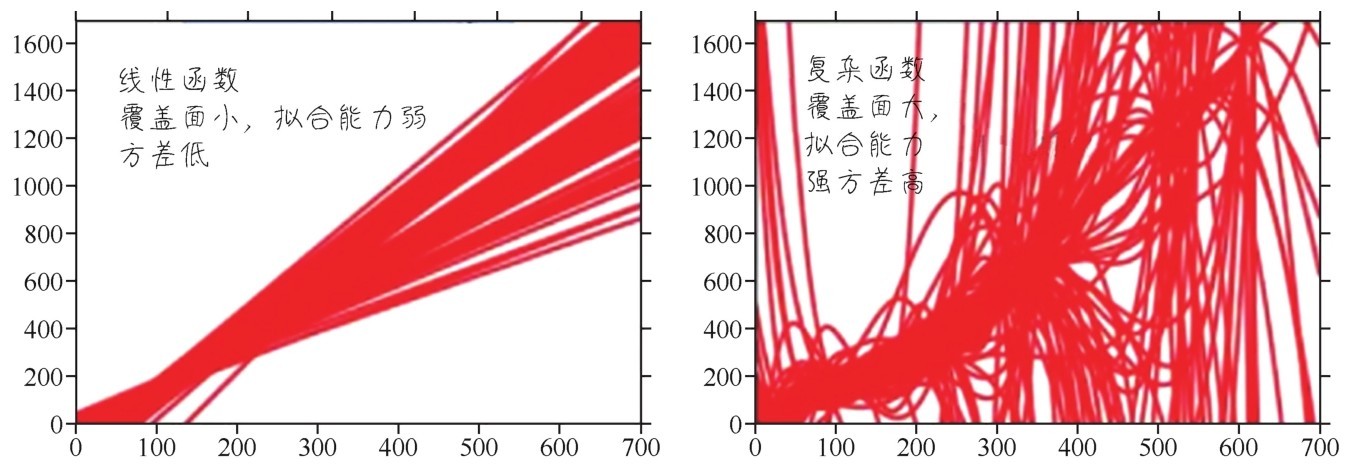
函数复杂度的提升,拟合能力的增强会带来高方差
小冰刚想说话,咖哥说:“我知道你想问,为什么我们还要不断增加预测空间,增加模型的复杂度?因为现实世界中的问题的确就是这么复杂。简单的线性函数虽然方差低,但是偏差高,对于稍微复杂的问题,根本不能解决。那么只能用威力比较大的、覆盖面比较大的‘大杀器’来解决问题了。而神经网络就像是原子弹,一旦被发射,肯定能够把要打击的目标击倒。但是如何避免误伤无辜,降低方差,就又回到如何提高精度的问题了。这样,偏差-方差窘境就又出现了。”
“不过,集成学习之所以好,是因为它通过组合一些比较简单的算法来保留这些算法低方差的优势。在此基础之上,它又能引入复杂的模型来扩展简单算法的预测空间。这样,我们就能理解为何集成学习是同时降低方差和偏差的大招。”
下面逐个来看每一种集成学习算法。