
根据相亲数据集所生成的决策树
咖哥问 :“同学们,你们玩过‘20 个问题’这个游戏吗?”
小冰说 :“我知道你说的这个游戏。就是一群人在一起,出题者心里面想一个东西或者一个人,然后让其他人随便猜。其他人可以随便问出题者问题,出题者只能回答是或者不是,不给出其他信息,直到最后猜中出题者心里所想。你说的是这个吧?—咦,你问这个做什么?”
“对。”咖哥说,“一个人心里面想的东西范围那么广,可以说太难猜了,为什么正确答案最后却总是能够被猜中?其实答题者应用的策略就是决策树算法。决策树(Decision Trees,DT),可以应用于回归或者分类问题,所以有时候也叫分类与回归树(Classification And Regression Tree,CART)。这个算法简单直观,很容易理解。它有点像是将一大堆的if…else语句进行连接,直到最后得到想要的结果。算法中的各个节点是根据训练数据集中的特征形成的。大家要注意特征节点的选择不同时,可以生成很多不一样的决策树。”
“下图所示是一个相亲数据集和根据该数据集而形成的决策树。此处我们设定一个根节点,作为决策的起点,从该点出发,根据数据集中的特征和标签值给树分叉。”

根据相亲数据集所生成的决策树
此时咖哥发问:“大家说说这里为什么要选择相貌这个特征作为这棵决策树的根节点?”
小冰说:“呃……这个……你有你的标准,我有我的标准……”
咖哥有些沉重地说:“还是熵啊!”小冰心里很诧异。伤什么伤,这个标准很伤你心吗?
此“熵”非彼“伤”。
在信息学中,熵(entropy),度量着信息的不确定性,信息的不确定性越大,熵越大。信息熵和事件发生的概率成反比。比如,“相亲者会认为咖哥很帅”这一句话的信息熵为0,因为这是事实。
这里有几个新概念,下面介绍一下。
■信息熵代表随机变量的复杂度,也就是不确定性。
■条件熵代表在某一个条件下,随机变量的复杂度。
■信息增益等于信息熵减去条件熵,它代表了在某个条件下,信息复杂度(不确定性)减少的程度。
因此,如果一个特征从不确定到确定,这个过程对结果影响比较大的话,就可以认为这个特征的分类能力比较强。那么先根据这个特征进行决策之后,对于整个数据集而言,熵(不确定性)减少得最多,也就是信息增益最大。相亲的时候你们最看中什么,就先问什么,如果先问相貌,说明你们觉得相貌不合格则后面其他所有问题都不用再问了,当然你们的妈妈可能一般会先问收入。
 咖哥发言
咖哥发言
除了熵之外,还有Gini不纯度等度量信息不确定性的指标。
决策树算法有以下两个特点。
(1)由于if…else可以无限制地写下去,因此,针对任何训练集,只要树的深度足够,决策树肯定能够达到100%的准确率。这听起来像是个好消息。
(2)决策树非常容易过拟合。也就是说,在训练集上,只要分得足够细,就能得到100%的正确结果,然而在测试集上,准确率会显著下降。
这种过拟合的现象在下图的这个二分类问题中就可以体现出来。决策树算法将每一个样本都根据标签值成功分类,图中的两种颜色就显示出决策树算法生成的分类边界。
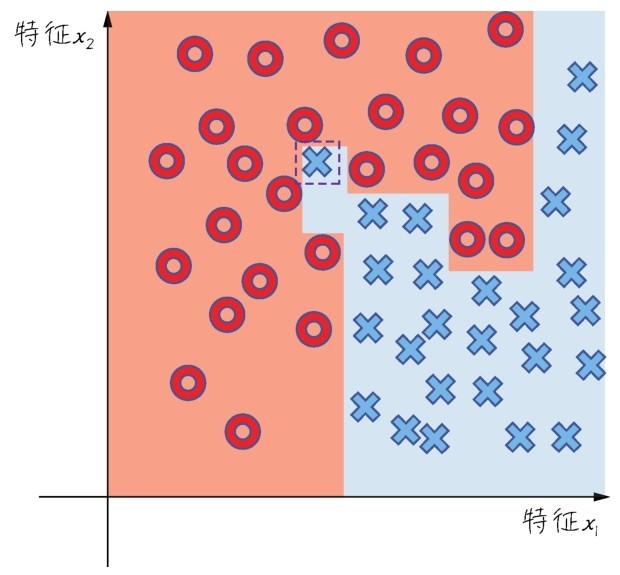
一个过拟合的决策树分类结果
而实际上,当分类边界精确地绕过了每一个点时,过拟合已经发生了。根据直觉,那个被圆圈包围着的叉号并不需要被考虑,它只是一个特例。因此,树的最后几个分叉,也就是找到虚线框内叉号的决策过程都应该省略,才能够提高模型的泛化功能。
解决的方法是为决策树进行剪枝(pruning),有以下两种形式。
■先剪枝:分支的过程中,熵减少的量小于某一个阈值时,就停止分支的创建。
■后剪枝:先创建出完整的决策树,然后尝试消除多余的节点。
整体来说,决策树算法很直观,易于理解,因为它与人类决策思考的习惯是基本契合的,而且模型还可以通过树的形式可视化。此外,决策树还可以直接处理非数值型数据,不需要进行哑变量的转化,甚至可以直接处理含缺失值的数据。因此,决策树算法是应用较为广泛的算法。
然而,它的缺点明显。首先,对于多特征的复杂分类问题效率很一般,而且容易过拟合。节点很深的树容易学习到高度不规则的模式,造成较大的方差,泛化能力弱。此外,决策树算法处理连续变量问题时效果也不太好。
因为这些缺点,决策树很少独立作为一种算法被应用于实际问题。然而,一个非常微妙的事是,决策树经过集成的各种升级版的算法—随机森林、梯度提升树算法等,都是非常优秀的常用算法。这些算法下一课还要重点介绍。
下面用决策树算法解决心脏病的预测问题:
from sklearn.tree import Decision Tree Classifier # 导入决策树模型
dtc = Decision Tree Classifier()
dtc.fit(X_train, y_train)
dtc_acc = dtc.score(X_test, y_test)*100
y_pred = dtc.predict(X_test) # 预测心脏病结果
print("Decision Tree Test Accuracy {:.2f}%".format(dtc_acc))
print("决策树 预测准确率: {:.2f}%".format(dtc.score(X_test, y_test)*100))
print("决策树 预测F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
print('决策树 混淆矩阵:\n', confusion_matrix(y_pred, y_test))
不出所料,单纯使用决策树算法时的预测准确率和F1分数相对于其他算法偏低:
决策树 预测准确率: 77.05%
决策树 预测F1分数: 78.79%
决策树 混淆矩阵:
[[21 8]
[ 6 26]]