SVM:超平面的确定
下面说说在神经网络重回大众视野之前,一个很受推崇的分类算法:支持向量机(Support Vector Machine,SVM)。“支持向量机”这个名字,总让我联想起工厂里面的千斤顶之类的工具,所以下面我还是直接用英文SVM。
和神经网络不同,SVM有非常严谨的数学模型做支撑,因此受到学术界和工程界人士的共同喜爱。
下面,在不进行数学推导的前提下,我简单讲一讲它的原理。
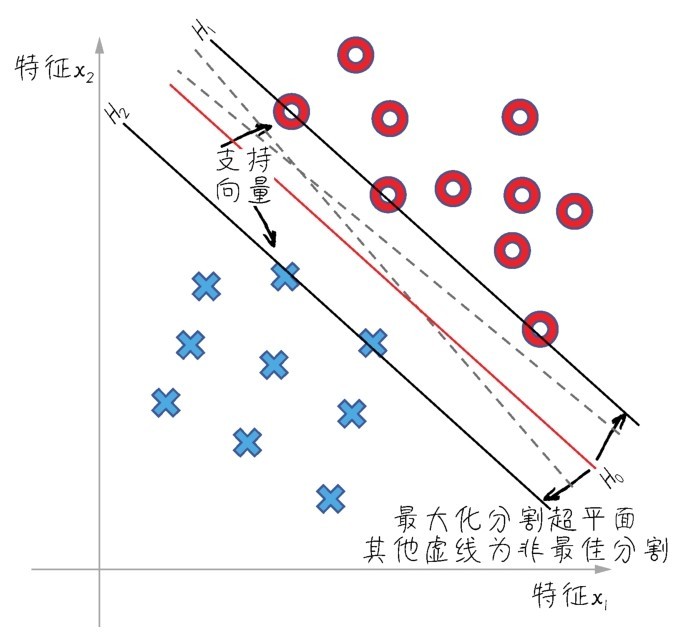
主要说说超平面(hyperplane)和支持向量(support vector)这两个概念。超平面,就是用于特征空间根据数据的类别切分出来的分界平面。如下图所示的两个特征的二分类问题,我们就可以用一条线来表示超平面。如果特征再多一维,可以想象切割线会延展成一个平面,以此类推。而支持向量,就是离当前超平面最近的数据点,也就是下图中被分界线的两条平行线所切割的数据点,这些点对于超平面的进一步确定和优化最为重要。
如下图所示,在一个数据集的特征空间中,存在很多种可能的类分割超平面。比如,图中的H0实线和两条虚线,都可以把数据集成功地分成两类。但是你们看一看,是实线分割较好,还是虚线分割较好?

SVM:超平面的确定
答案是实线分割较好。为什么呢?
因为这样的分界线离两个类中的支持向量都比较远。SVM算法就是要在支持向量的帮助之下,通过类似于梯度下降的优化方法,找到最优的分类超平面—具体的目标就是令支持向量到超平面之间的垂直距离最宽,称为“最宽街道”。
那么目前的特征空间中有以下3条线。
■H0就是目前的超平面。
■与之平行的H1/H2线上的特征点就是支持向量。
这3条线,由线性函数和其权重、偏置的值所确定:
H0=w·x+b=0
H1=w·x+b=1
H2=w·x+b=−1
然后计算支持向量到超平面的垂直距离,并通过机器学习算法调整参数w和b,将距离(也就是特征空间中的这条街道宽度)最大化。这和线性回归寻找最优函数的斜率和截距的过程很相似。
下面用SVM算法来解决同样的问题:
from sklearn.svm import SVC # 导入SVM模型
svm = SVC(random_state = 1)
svm.fit(X_train, y_train)
y_pred = svm.predict(X_test) # 预测心脏病结果
svm_acc = svm.score(X_test, y_test)*100
print("SVM预测准确率:: {:.2f}%".format(svm.score(X_test, y_test)*100))
print("SVM预测F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
print('SVM混淆矩阵:\n', confusion_matrix(y_pred, y_test))
输出结果显示,采用默认值的情况下,预测准确率为86.89%,略低于KNN算法的最优解:
SVM预测准确率:: 86.89%
SVM预测F1分数: 88.24%
SVM混淆矩阵:
[[23 4]
[ 4 30]]
[[22 5]
普通的SVM分类超平面只能应对线性可分的情况,对于非线性的分类,SVM要通过核方法(kernel method)解决。核方法是机器学习中的一类算法,并非专用于SVM。它的思路是,首先通过某种非线性映射(核函数)对特征粒度进行细化,将原始数据的特征嵌入合适的更高维特征空间;然后,利用通用的线性模型在这个新的空间中分析和处理模式,这样,将在二维上线性不可分的问题在多维上变得线性可分,那么SVM就可以在此基础上找到最优分割超平面。