
根据KNN算法来确定支持者
咖哥说:“本课要介绍的第一个算法—K最近邻算法,简称KNN。它的简称中也有个‘NN’,但它和神经网络没有关系,它的英文是K-Nearest Neighbor,意思是K个最近的邻居。这个算法的思路特别简单,就是随大流。对于需要贴标签的数据样本,它总是会找几个和自己离得最近的样本,也就是邻居,看看邻居的标签是什么。如果它的邻居中的大多数样本都是某一类样本,它就认为自己也是这一类样本。参数K,是邻居的个数,通常是3、5、7等不超过20的数字。”
“举例来说,右图是某高中选班长的选举地图,选举马上开始,两个主要候选人(一个是小冰,另一个是咖哥,他们是高中同学)的支持者都已经确定了,A是小冰的支持者, B则是咖哥的支持者。从这些支持者的座位分布上并不难看出,根据KNN算法来确定支持者,可靠率还是蛮高的。因为每个人都有其固定的势力范围。”

根据KNN算法来确定支持者
小冰发问:“那么数据样本也不是选民的座位,怎么衡量距离的远和近呢?”
“好问题。”咖哥说,“这需要看特征向量在特征空间中的距离。我们说过,样本的特征可以用几何空间中的向量来表示。特征的远近,就代表样本的远近。如果样本是一维特征,那就很容易找到邻居。比如一个分数,当然59分和60分是邻居,99分和100分是邻居。那么如果100分是A类,99分也应是A类。如果特征是多维的,也是一样的道理。”
 咖哥发言
咖哥发言
说说向量的距离。在KNN和其他机器学习算法中,常用的距离计算公式包括欧氏距离和曼哈顿距离。两个向量之间,用不同的距离计算公式得出来的结果是不一样的。
欧氏距离是欧几里得空间中两点间的“普通”(即直线)距离。在欧几里得空间中,点x=(x1,…,xn)和点y=(y1,…,yn)之间的欧氏距离为:
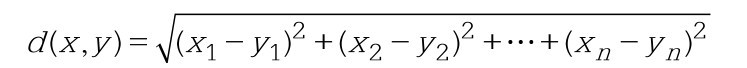
曼哈顿距离,也叫方格线距离或城市区块距离,是两个点在标准坐标系上的绝对轴距的总和。在欧几里得空间的固定直角坐标系上,曼哈顿距离的意义为两点所形成的线段对轴产生的投影的距离总和。在平面上,点x=(x1,…, xn)和点y=(y1,…,yn)之间的曼哈顿距离为:
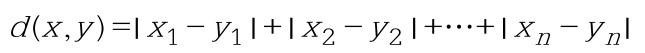
这两种距离的区别,是不是像极了MSE和MAE误差计算公式之间的区别呢?其实这两种距离也就是向量的L1范数(曼哈顿)和L2范数(欧氏)的定义。
右图的两个点之间,1、2与3线表示的各种曼哈顿距离长度都相同,而4线表示的则是欧氏距离。
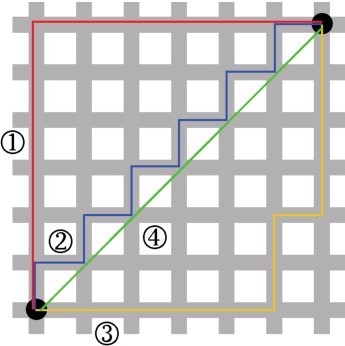
欧氏距离和曼哈顿距离
下图中的两个特征,就形成了二维空间,图中心的问号代表一个未知类别的样本。如何归类呢,它是圆圈还是叉号?如果K=3,叉号所占比例大,问号样本将被判定为叉号类;如果K=7,则圆圈所占比例大,问号样本将被判定为圆圈类。

KNN算法示意
因此,KNN算法的结果和K的取值有关系。要注意的是,KNN要找的邻居都是已经“站好队的人”,也就是已经正确分类的对象。
原理很简单,下面直接进入实战。咱们重用第4课中的案例,根据调查问卷中的数据推断客户是否有心脏病。
用下列代码读取数据:
import numpy as np # 导入Num Py库
import pandas as pd # 导入Pandas库
df_heart = pd.read_csv("../input/heart-dataset/heart.csv") # 读取文件
df_heart.head() # 显示前5行数据
那么数据分析、特征工程部分的代码不再重复(同学们可参考第4课中的代码段或源码包中的内容),直接定义KNN分类器。而这个分类器,也不需要自己做,Scikit-Learn库里面有,直接使用即可。
示例代码如下:
from sklearn.neighbors import KNeighbors Classifier # 导入KNN模型
K = 5 # 设定初始K值为5
KNN = KNeighbors Classifier(n_neighbors = K) # KNN模型
KNN.fit(X_train, y_train) # 拟合KNN模型
y_pred = KNN.predict(X_test) # 预测心脏病结果
from sklearn.metrics import (f1_score, confusion_matrix) # 导入评估指标
print("{}NN预测准确率: {:.2f}%".format(K, KNN.score(X_test, y_test)*100))
print("{}NN预测F1分数: {:.2f}%".format(K, f1_score(y_test, y_pred)*100))
print('KNN混淆矩阵:\n', confusion_matrix(y_pred, y_test))
预测结果显示,KNN算法在这个问题上的准确率为85.25%:
5NN预测准确率: 85.25%
5NN预测F1分数: 86.15%
KNN混淆矩阵:
[[24 6]
[ 3 28]]
怎么知道K值为5是否合适呢?
这里,5只是随意指定的。下面让我们来分析一下到底K取何值才是此例的最优选择。请看下面的代码。
# 寻找最佳K值
f1_score_list = []
acc_score_list = []
for i in range(1, 15):
KNN = KNeighbors Classifier(n_neighbors = i) # n_neighbors means K
KNN.fit(X_train, y_train)
acc_score_list.append(KNN.score(X_test, y_test))
y_pred = KNN.predict(X_test) # 预测心脏病结果
f1_score_list.append(f1_score(y_test, y_pred))
index = np.arange(1, 15, 1)
plt.plot(index, acc_score_list, c='blue', linestyle='solid')
plt.plot(index, f1_score_list, c='red', linestyle='dashed')
plt.legend(["Accuracy", "F1 Score"])
plt.xlabel("k value")
plt.ylabel("Score")
plt.grid('false')
plt.show()
KNN_acc = max(f1_score_list)*100
print("Maximum KNN Score is {:.2f}%".format(KNN_acc))
这个代码用于绘制出1~12,不同K值的情况下,模型所取得的测试集准确率和F1分数。通过观察这个曲线(如下图所示),就能知道针对当前问题,K的最佳取值。

不同K值时,模型所取得的测试集准确率和F1分数
就这个案例而言,当K=3时,F1分数达到89.86%。而当K=7或K=8时,准确率虽然也达到峰值88%左右,但是此时的F1分数不如K=3时高。
很简单吧。如果你们觉得不过瘾,想要看看KNN算法的实现代码,可以进入Sklearn官网,单击source之后,到Git Hub里面看Python源码,如下图所示。而且官网上也有这个库的各种参数的解释,课堂上不赘述了。
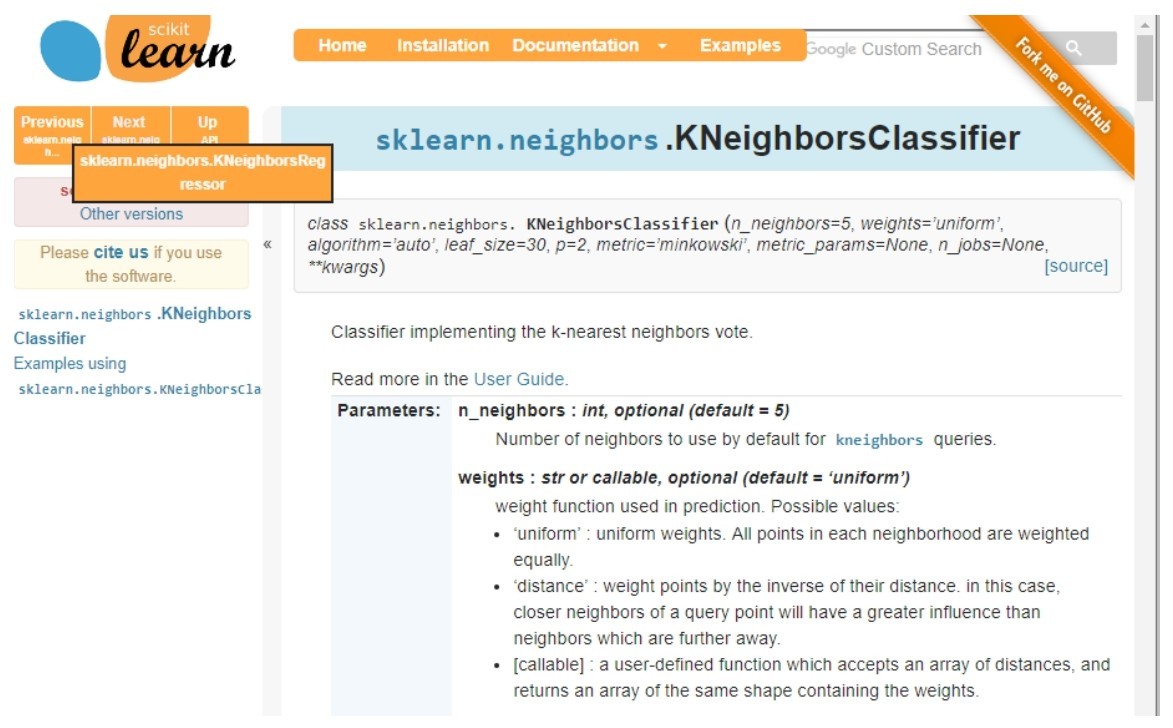
单击source,可以看KNN算法的实现代码
KNN算法的实现代码
KNN算法在寻找最近邻居时,要将余下所有的样本都遍历一遍,以确定谁和它最近。因此,如果数据量特别大,它的计算成本还是比较高的。