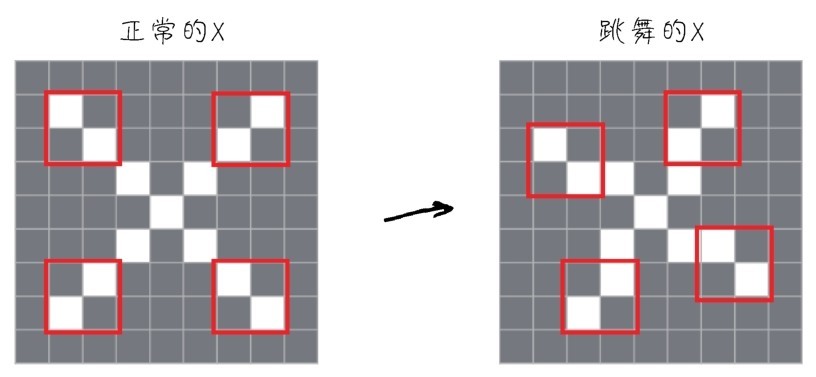
字母X中的“小模式”—变形后,模式还在
卷积网络是通过卷积层(Conv2D层)中的过滤器(filter)用卷积计算对图像核心特征进行抽取,从而提高图像处理的效率和准确率。
机器是通过模式(pattern)进行图像的识别。举例来说,有一个字母X,这个X由一堆像素组成,可以把X想象成一个个小模式的组合,如下图所示,X的形状好像上面有两只手,下面长了两只脚,中间是躯干部分。如果机器发现一个像下面左图这样中规中矩的X,就能识别出来。但是无论是手写数字,还是照片扫描进计算机的时候,都可能出现噪声(noise)。那么这个X可能变样了,手脚都变了位置,好像手舞足蹈的样子(如下面右图所示)。但是肉眼一看,还是X。

字母X中的“小模式”—变形后,模式还在
普通的全连接网络也可以进行上面的图像识别,但是全连接网络每一次都会全面地侦测每一个像素点,把图像作为一个整体进行评估判断。而卷积网络的思路则不同,它聚焦于“小模式”,只要两只手、两只脚、中间的躯干这些小模式还在,就会增加“X开关”的权重。这种思路对于模式识别来说,既省力,又高效。
上面这个模式识别原理就是卷积网络最基本的思路。它的好处是不仅使模式识别变得更加准确了,而且通过对这些“模式特征组”的权重共享减少了很多所需要调节的神经元的参数数量,因而大幅度减少了计算量。这使得神经网络不仅效能提高了,而且还变得“轻量级”了。
这种“小模式”识别的另一个优越性是平移不变性(translation invariance),意思是一旦卷积神经网络在图像中学习到某个模式,它就可以在任何地方识别这个模式,不管模式是出现在左上角、中间,还是右下角。
你们看下图中的飞鸟,无论放到哪里,都是一只鸟,这是人脑处理图像的方式,这种技术也被卷积神经网络学到了。而对于全连接网络,如果模式出现在新的位置,那么它只能重新去学习这个模式—这肯定要花费更多力气。

模式的平移不变性
因此,卷积网络在处理图像时和人脑的策略很相似,智能度更高,可以高效利用数据。它通过训练较少的样本就可以学到更具有泛化能力的数据表示,而且,模式学到的结果还可以保存,把知识迁移至其他应用。
卷积操作是如何实现的呢?它是通过滑动窗口一帧一帧地抽取局部特征,也就是一块一块地抠图实现的。直观地说,这个分解过程,就像是人眼在对物体进行从左到右、从上到下、火眼金睛般的审视。
所谓图像,对计算机来说就是一个巨大的数字矩阵,里面的值都代表它的颜色或灰度值。下图所示,在卷积网络的神经元中,一张图像将被以3px×3px,或者5px×5px的帧进行一个片段一个片段的特征抽取处理。
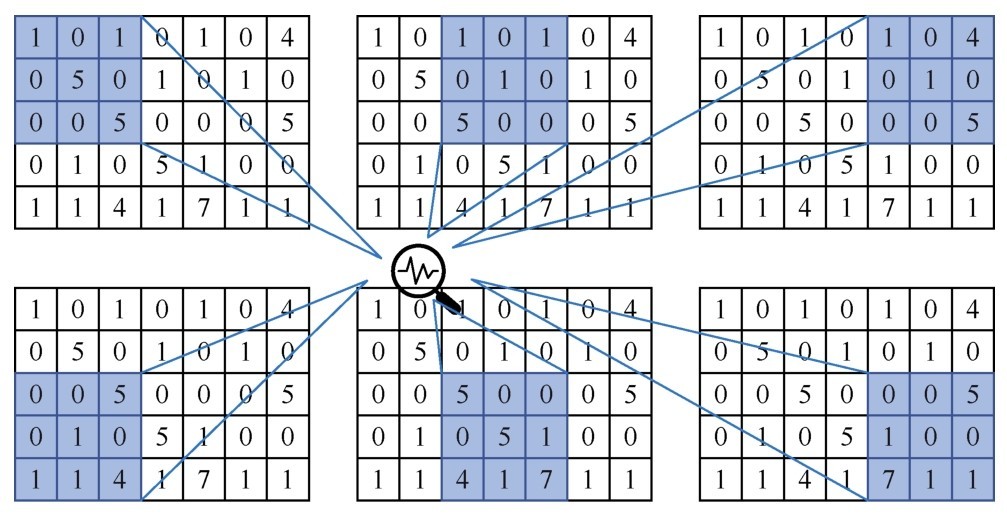
通过滑动窗口一帧一帧地局部特征抽取的过程
这个过程就是模式的寻找:分析局部的模式,找出其特征特点,留下有用的信息。
一帧一帧抽取的每个局部特征,我们拿来做什么呢?
是要与过滤器进行卷积计算,进行图像特征的提取(也就是模式的识别)。在MNIST图像数据集的示例代码中,参数filters=32即指定了该卷积层中有32个过滤器,参数kernel_size=(3, 3)表示每一个过滤器的大小均为3px×3px:
model.add(Conv2D(filters=32, # 添加Conv2D层, 指定过滤器的个数, 即通道数
kernel_size=(3, 3), # 指定卷积核的大小
activation='relu', # 指定激活函数
input_shape=(28, 28, 1))) # 指定输入数据样本张量的类型
卷积网络中的过滤器也叫卷积核(convolution kernel),是卷积层中带着一组组固定权重的神经元,大家同样可以把它想象成人类的眼睛。刚才说一帧一帧地抽取局部特征的过程就好像是人眼审视东西,那么不同过滤器就是不同人的眼睛。通常正常人的眼睛和孙悟空的眼睛不同,看到的东西也可能是不同的。所以,刚才抽取的同样的特征(局部图像),会被不同权重的过滤器进行放大操作,有的过滤器像火眼金睛一般,能发现这个模式背后有特别的含义。
下图所示,左边是输入图像,中间有两个过滤器,卷积之后,产生不同的输出,也许有的侧重颜色深浅,有的则侧重轮廓。这样就有利于提取图像的不同类型的特征,也有利于进一步的类别判断。

不同的过滤器抽取不同类型的特征
对于MNIST来说,第一个卷积层接收的是形状为(28,28,1)的输入特征图(feature map),并输出一个大小为(26,26,32) 的特征图,如下图所示。也就是说,这个卷积层有32个过滤器,形成了32个输出通道。这32个通道中,每个通道都包含一个26×26(为什么从28×28变成26×26了?等会儿揭秘)的矩阵。它们都是过滤器对输入的响应图(response map),表示这个过滤器对输入中不同位置抠取下来的每一帧的响应,其实也就是提取出来的特征,即输出特征图。
32个输入特征图中,每一个特征图都有自己负责的模式,各有不同功能,未来整合在一起后,就会实现分类任务。

MNIST案例中第一个卷积层的输入特征图和输出特征图
经过两层卷积之后的输出形状为(11,11,64),也就是形成了64个输出特征图,如下图所示。因此,随着卷积过程的进行,图像数字矩阵的大小逐渐缩小(这是池化的效果),但是深度逐渐增加,也就是特征图的数目越来越多了。

MNIST案例中第二个卷积层的输入特征图和输出特征图
那么过滤器是如何对输入特征图进行卷积运算,从而提取出输出特征图的呢?
这个过程中有以下两个关键参数。
■卷积核的大小,定义了从输入中所提取的图块尺寸,通常是3px×3px或5px×5px。这里以3px×3px为例。
■输出特征图的深度,也就是本层的过滤器数量。示例中第一层的深度为32,即输出32个特征图;第二层的深度为64,即输出64个特征图。
具体运算规则就是卷积核与抠下来的数据窗口子区域的对应元素相乘后求和,求得两个矩阵的内积,如下图所示。

卷积运算示意—黑白图像
在输入特征图上滑动这个3×3的窗口,每个可能的位置会形成特征图块(形状为(3,3,1))。然后这些图块与同一个权重矩阵,也就是卷积核进行卷积运算,转换成形状为(1,) 的1D张量。最后按照原始空间位置对这些张量进行组合,形成形状为(高,宽,特征图深度) 的3D输出特征图。
那么,如果不是深度为1的黑白或灰度图像,而是深度为3的RGB图像,则卷积之后的1D向量形状为(3,),经过组合之后的输出特征图形状仍为(高,宽,特征图深度),如下图所示。
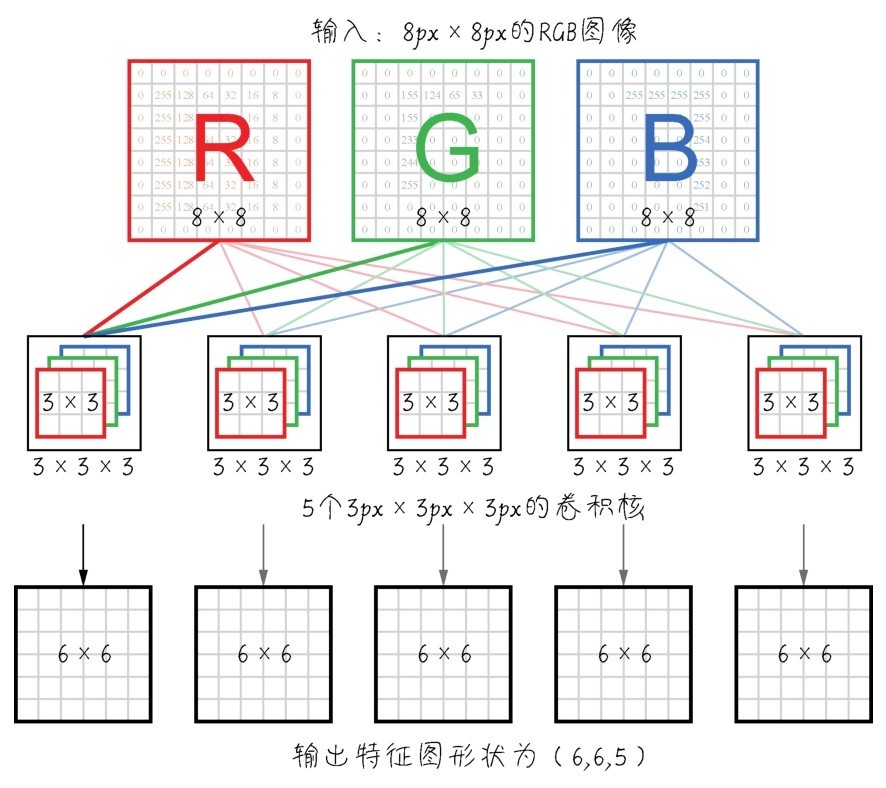
卷积过程示意—RGB图像
上述卷积运算的细节当然不需要我们编写代码去实现。这里要注意的实际上是输入输出张量的维度和形状。
经过这样的卷积过程,卷积神经网络就可以逐渐学到模式的空间层级结构。举例来说,第一个卷积层可能是学习较小的局部模式(比如图像的纹理),第二个卷积层将学习由第一层输出的各特征图所组成的更大的模式,以此类推。
层数越深,特征图将越来越抽象,无关的信息越来越少,而关于目标的信息则越来越多。这样,卷积神经网络就可以有效地学习到越来越抽象、越来越复杂的视觉概念。特征组合由浅入深,彼此叠加,产生良好的模式识别效果。
这种将视觉输入抽象化,并将其转换为更高层的视觉概念的思路,和人脑对影像的识别判断过程是有相似之处的。所以,卷积神经网络就是这样实现了对原始数据信息的提纯。
再介绍一下卷积层中的填充和步幅这两个概念。
1.边界效应和填充
填充并不一定存在于每一个卷积网络中,它是一个可选操作。
在不进行填充的情况下,卷积操作之后,输出特征图的维度中,高度和宽度将各减少2维。原本是4px×4px的黑白图像,卷积之后特征图就变成2px×2px。如果初始输入的特征是28×28(不包括深度维),卷积之后就变成26×26,这个现象叫作卷积过程中的边界效应,如右图所示。

输入特征维度为28×28,输出特征维度为26×26
如果我们非要输出特征图的空间维度与输入的相同,就可以使用填充(padding)操作。填充就是在输入特征图的边缘添加适当数目的空白行和空白列,使得每个输入块都能作为卷积窗口的中心,然后卷积运算之后,输出特征图的维度将会与输入维度保持一致。
■对于3×3的窗口,在左右各添加一列,在上下各添加一行。
■对于5×5的窗口,则各添加两行和两列。

填充后,卷积层输入输出的高度和宽度将不变
填充操作并不是一个必需选项。如果需要,可以通过Conv2D层的padding参数设置:
model.add(Conv2D(filters=32, #过滤器
kernel_size=(3, 3), # 卷积核大小
strides=(1, 1), # 步幅
padding='valid')) # 填充
2.卷积的步幅
影响输出尺寸的另一个因素是卷积操作过程中,窗口滑动抽取特征时候的步幅(stride)。以刚才的滑动窗口示意为例,步幅的大小为2(如下图所示),它指的就是两个连续窗口之间的距离。

步幅为2的步进卷积
步幅大于1的卷积,叫作步进卷积(strided convolution),其作用是使输出特征图的高度和宽度都减半。这个效果叫作特征的下采样(subsampling),能使特征抽取的效率加快。然而,在实践中,步进卷积很少使用在卷积层中,大多数情况下的步幅为默认值1。