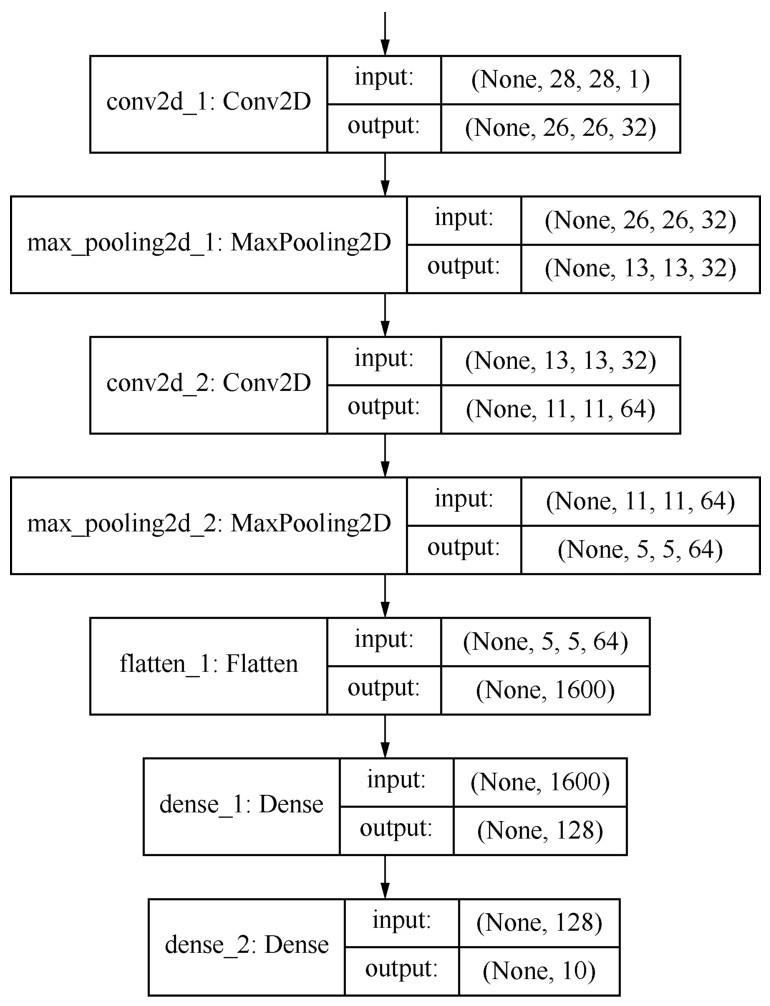
程序编译出来的卷积网络的结构信息
其实,卷积网络我们已经见过并使用过了,在第1课介绍机器学习项目实战架构时,我特别给出了一个通过卷积网络识别MNIST图像的例子,一是因为想强调它作为常用深度网络的重要性,二是因为它的结构并不复杂。
复习一下该程序的完整代码,并通过model.summary方法显示网络的结构:
from keras import models # 导入Keras模型和各种神经网络的层
from keras.layers import Dense, Dropout, Flatten, Conv2D, Max Pooling2D
model = models.Sequential() # 序贯模型
model.add(Conv2D(filters=32, # 添加Conv2D层, 指定过滤器的个数, 即通道数
kernel_size=(3, 3), # 指定卷积核的大小
activation='relu', # 指定激活函数
input_shape=(28, 28, 1))) # 指定输入数据样本张量的类型
model.add(Max Pooling2D(pool_size=(2, 2))) # 添加Max Pooling2D层
model.add(Conv2D(64, (3, 3), activation='relu')) # 添加Conv2D层
model.add(Max Pooling2D(pool_size=(2, 2))) # 添加Max Pooling2D层
model.add(Dropout(0.25)) # 添加Dropout层
model.add(Flatten()) # 添加展平层
model.add(Dense(128, activation='relu')) # 添加全连接层
model.add(Dropout(0.5)) # 添加Dropout层
model.add(Dense(10, activation='softmax')) # Softmax分类激活, 输出10维分类码
model.compile(optimizer='rmsprop', # 指定优化器
loss='categorical_crossentropy', # 指定损失函数
metrics=['accuracy']) # 指定评估指标
model.summary() # 显示网络模型
运行代码,输出网络结构如下:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 26, 26, 32) 320
_________________________________________________________________
max_pooling2d_1 (Max Pooling2 (None, 13, 13, 32) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 11, 11, 64) 18496
_________________________________________________________________
max_pooling2d_2 (Max Pooling2 (None, 5, 5, 64) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 1600) 0
_________________________________________________________________
dense_1 (Dense) (None, 128) 204928
_________________________________________________________________
dense_2 (Dense) (None, 10) 1290
=================================================================
Total params: 225, 034
Trainable params: 225, 034
Non-trainable params: 0
还可以用下页图形的方式显示出这个有225 034个参数、用序贯方式生成的卷积网络的形状:
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
SVG(model_to_dot(ann, show_shapes = True ).create(prog='dot', format='svg'))

程序编译出来的卷积网络的结构信息
下图更直观地显示了卷积网络的典型架构。它实现了一个图像分类功能:输入的是图像,输出的是图像的类别标签。
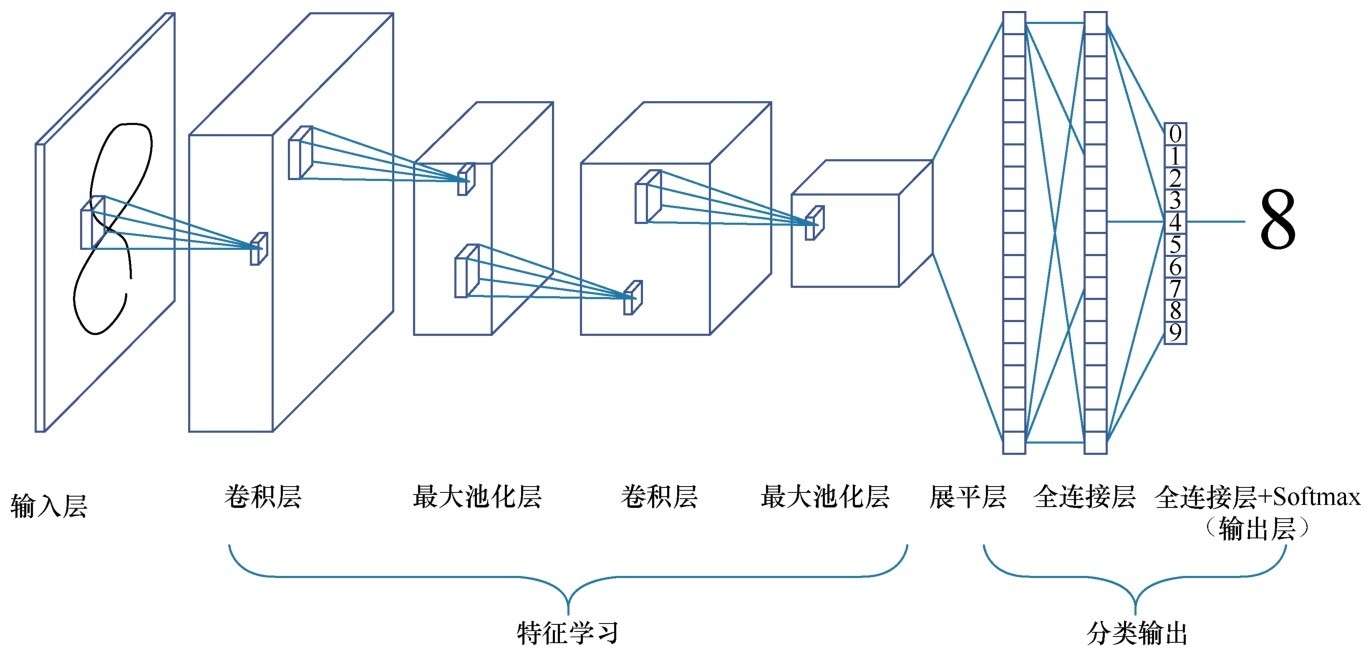
卷积网络的典型架构
卷积网络也是多层的神经网络,但是层内和层间神经元的类型和连接方式与普通神经网络不同。卷积神经网络由输入层、一个或多个卷积层和输出层的全连接层组成。
(1)网络左边仍然是数据输入部分,对数据做一些初始处理,如标准化、图片压缩、降维等工作,最后输入数据集的形状为 (样本,图像高度,图像宽度,颜色深度)。
(2)中间是卷积层,这一层中,也有激活函数的存在,示例中用的是Re LU。
(3)一般卷积层之后接一个池化层,池化层包括区域平均池化或最大池化。
(4)通常卷积+池化的架构会重复几次,形成深度卷积网络。在这个过程中,图片特征张量的尺寸通常会逐渐减小,而深度将逐渐加深。如上一张图所示,特征图从一张扁扁的纸片形状变成了胖胖的矩形。
(5)之后是一个展平层,用于将网络展平。
(6)展平之后接一个普通的全连接层。
(7)最右边的输出层也是全连接层,用Softmax进行激活分类输出层,这与普通神经网络的做法一致。
(8)在编译网络时,使用了Adam优化器,以分类交叉熵作为损失函数,采用了准确率作为评估指标。
卷积网络的核心特点就是卷积+池化的架构,要注意到“卷积层”中的参数,其实是远少于全连接层的(本例中两个卷积层中的参数加起来不到2万个,而全连接层则贡献了其他20多万个参数)。这是因为,卷积网络中各层的神经元之间,包括输入层的特征和卷积层之间,不是彼此全部连接的,而是以卷积的方式有选择性的局部连接,如下图所示。这种结构除了能大大减少参数的数量之外,还有其他一些特殊优势。下面讲一讲这其中的道理。
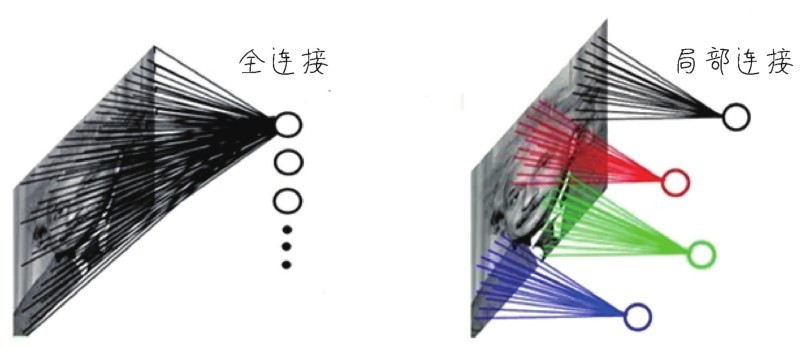
全连接和局部连接的示意