神经元
咖哥一下子讲了那么多原理，讲累了，喝了一口水，接着说：“神经网络由神经元组成，最简单的神经网络只有一个神经元，叫感知器。”
所谓“道生一，一生二，二生三，三生万物”，万事万物都是从简单到复杂的演进。神经网络也是。前面说到，感知器是神经网络的雏形，最初的神经网络也就是只有一个神经元的感知器。
右图中的圆圈就代表一个神经元，它可以接收输入，并根据输入提供一个输出。
神经元
这个简单的感知器可以做什么呢？
首先它可以成为一个“与门”。与门我们很熟悉，它的逻辑就是只有当所有输入值都为1时，输出才为1，否则输出为0。这个与门逻辑通过感知器的实现如下图所示。
设定了权重，感知器可以用来做“与”逻辑判断
小冰说：“这个感知器看起来的确有点像是逻辑回归。”
咖哥说：“小冰，你说得很对，这就是一个逻辑回归分类器。但它太简单了，只有两个特征（x1和x2），而且输入也简单，只有0、1两种可能，共4组数据。因为数据量太小，所以很容易拟合。很多权重值的组合都可以实现这个拟合，如果我们随意分配两个简单的权重（w1=20， w2=20）和一个偏置（b=−30）值，就能够通过一个线性函数（y=20x1+20x2−30）加一个激活函数（Sigmiod（z）），对4组数据进行简单的‘与’逻辑判断，其实也就是为一个小小的数据集进行分类。这些都是在逻辑回归里面讲过的内容。”
咖哥发言
Sigmiod函数，在逻辑回归中叫逻辑函数，在神经网络中则称为激活函数，用以类比人类神经系统中神经元的“激活”过程。
如果换其他数据，比如再给4组符合“或”规则的数据（只要输入中有一个值为1，输出就为1，否则输出为0），感知器能不能够完成这个新的逻辑判断呢？当然可以。通过调整感知器的权重和偏置，比如设置w1=20，w2=20，b=−10后，就成功地实现了新规则（如下图所示）。这样，根据不同的数据输入，感知器适当地调整权重，在不同的功能之间切换（也就是拟合），形成了一个简单的自适应系统，人们就说它拥有了“感知”事物的能力。
通过调整权重，感知器从“与门”变成了“或门”
单神经元，也就是感知器，通过训练可以用作逻辑回归分类器，那么它是如何进化成更为复杂的多层神经网络呢？
要理解从单层到多层这一“跃迁”的意义，我们需要重温几个概念。前面讲过，机器学习中数据的几何映射是空间；向量，也可以看作一个多维空间中的点。由此，对输入空间、输出空间、特征空间、假设空间进行如下的定义。
■输入空间：x，输入值的集合。
■输出空间：y，输出值的集合。通常，输出空间会小于输入空间。
■特征空间：每一个样本被称作一个实例，通常由特征向量表示，所有特征向量存在的空间称为特征空间。特征空间有时候与输入空间相同，有时候不同。因为有时候经过特征工程之后，输入空间可通过某种映射生成新的特征空间。
■假设空间：假设空间一般是对于学习到的模型（即函数）而言的。模型表达了输入到输出的一种映射集合，这个集合就是假设空间。假设空间代表着模型学习过程中能够覆盖的最大范围。
因为模型本身就是对特征的一种函数化的表达，一个基本的原则是：模型的假设空间，一定要大到能覆盖特征空间，否则，模型就不可能精准地完成任务。某些回归问题，一定需要曲线模型进行拟合，如果坚持使用线性模型，就会因为其特征空间覆盖面有限，无论怎么调整权重和偏置都不可能达到理想效果。下面的示意图就描绘出函数的复杂度和其所能够覆盖的假设空间范围之间的关系：函数越复杂，假设空间的覆盖面越大，拟合能力就越强。
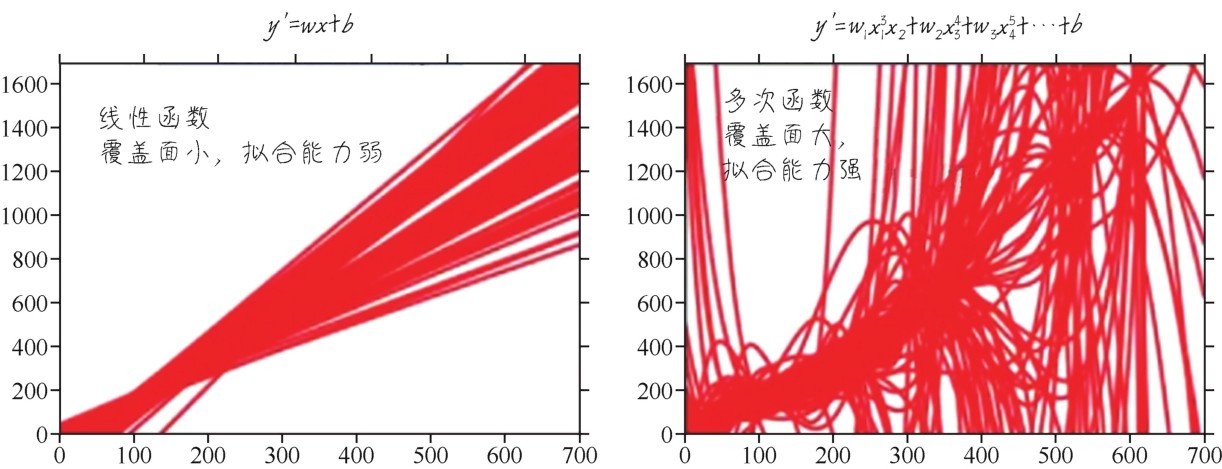
模型的假设空间越大，拟合复杂数据集的能力就越强[1]
其实，从拓扑结构来看，感知器，也就是说神经网络中的单个神经元所能够解决的问题是线性可分的。刚才我们成功拟合的“与”和“或”两个数据集，它们的输入空间都满足线性可分这个条件，如下图所示。因此，如果模型的假设空间能够覆盖输入空间，就可以搞定它们。
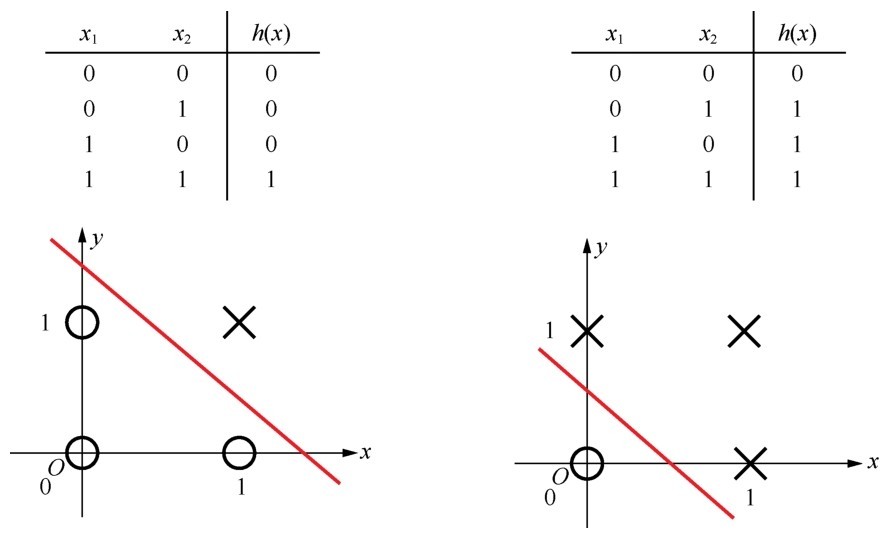
“与”和“或”的线性分界平面
但是，感知器没有办法拟合非线性的空间。再看看下图中这个符合“同或”（XOR）逻辑的数据集，也是只有2个特征，4组数据而已。两个输入值不同时，输出为0。反之，输出为1。数据集虽然简单，但“同或”逻辑是线性不可分的，我们再怎么画直线，也无法分割出一个平面来为其分界。因此，这个问题也就没有办法通过一个单节点感知器处理—无论我们如何调整感知器的权重和偏置，都无法拟合“同或”数据集从特征到标签的逻辑。
无论怎么调整感知器的权重和偏置，都无法解决同或问题
所以，感知器是有局限性的。它连同或这样简单的任务都完成不了，又如何去模拟现实世界中更为复杂的关系？难怪感知器当年“红火”一阵子后就消失在人们的视野了。
那么，机器学习如何解决这个问题？
有以下两个思路。
■第一个思路，进行手工特征工程，就是对x1、x2进行各种各样的组合变形，形成新的特征，比如x3、x4。然后对新特征x3、x4做线性回归。这种特征工程本质上改变了数据集原本的特征空间，目标是降低其维度，使其线性回归算法可解。
■第二个思路，就是将神经网络分层。人们发现，如果在感知器的激活函数后面再多加入一个新的神经网络层，以上一层神经元激活后的输出作为下一层神经元的输入，此时模型的假设空间就会被扩展，神经网络就会从线性模型跃迁至非线性模型（如下图所示），从而将本来线性不可分的函数图像拟合成功！
同或问题的特征空间并不是线性可分的，需要引入非线性模型
第二个思路较之于第一个思路的优势是什么？省去了特征工程。因为特征的变换，特征之间的组合的种种逻辑都是人工决定的，相当耗时耗力。所以，对特征量巨大，而且特征之间无明显关联的非结构化数据做特征工程是不实际的。
神经网络隐层的出现把手工的特征工程工作丢给了神经网络，网络第一层的权重和偏置自己去学，网络第二层的权重和偏置自己去学，网络其他层的权重和偏置也是自己去学。我们除了提供数据以及一些网络的初始参数之外，剩下的事情全部都让网络自己完成。
因此，神经网络的自我学习功能实在是懒人的福音。
下图展示的就是神经网络解决这个非线性的“同或”问题的具体过程。这个网络不但多出一层，每层还可以有多个神经元，具有充分的灵活性。哪怕特征数量再大，特征空间再复杂，神经网络通过多层架构也可以将其搞定。
咖哥发言
注意神经网络的上下标符号规则。神经网络中因为层数多，每层中节点（即神经元）数目也多，因此其中节点、权重的标号规则变得复杂起来。举例来说，此处，
中，中括号里面的上标的数字代表第几层；下标有两个，第一个代表权重属于哪一个特征，即特征的维度，第二个代表其所连接到的下层神经元的维度。
还要注意的就是每层会有多个权重，但每层只有1个偏置。
再多说一句，对于数据集的特征x来说，有时候也会出现这样比较复杂的标号
，这里的下标1代表特征的维度，1就是第1个特征；而圆括号里面的上标的数字代表的是样本的维度， 1也就是第1个样本。
加入网络隐层之后，同或数据集变得可以拟合了