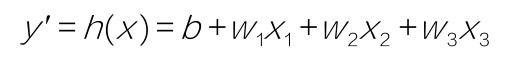
多元,即多变量,也就是特征是多维的。我们用下标(例如w1和x1)代表特征的编号,即特征的维度。多个特征,可以用来表示更复杂的机器学习模型。同学们不要忘了,小冰给咱们带来的原始数据集,本来就是具有3个特征的模型。只是为了简化教学,才只选择了微信公众号广告投放金额作为唯一的特征,构建单变量线性回归模型。现在重新引入x2代表微博广告投放金额, x3代表其他类型广告投放金额,采用以下多元(多变量)的线性方程式来构造假设函数:
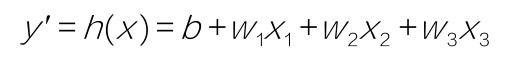
在机器学习的程序设计中,这个公式可以被向量化地实现,以表示任意维的特征:
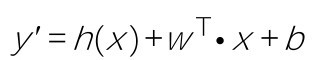
其中,w T·x就是 。
。
点积前面讲过:如果w是一个向量,x也是一个向量,两个向量做乘法,会得到一个标量,也就是数值y'。两个向量,你点积我,我点积你,结果是相同的。因此wT·x等于x·wT。
但是,为什么公式里面有一个矩阵转置符号T呢?这是因为w和x这两个张量的实际形状为(N,1)的矩阵,它们直接相乘是不行的。其中一个需要先转置为(1,N),才能进行点积操作,这就是为什么公式中特别强调用wT。
而且,要注意以下几点。
■张量形状(1,N)点积(N,1),就得到1×1的标量。
■张量形状(N,1)点积(1,N),那就得到(N,N)的矩阵,就不是我们想要的y'。
■张量形状(1,N)点积(1,N),或者(N,1)点积(N,1),就会出错。
 咖哥发言
咖哥发言
要注意输入张量的维度和目标张量的维度,维度的错误会导致得不到想要的结果。公式里的y'是一个值,也就是标量。而在本例的程序代码中,因为整个数据集是一起进行向量化运算的,所以y'应该是一个形状为(200,1)的张量,里面包含200个值。调试程序时要记得多输出张量的形状。
还可以把公式进一步简化,就是把b也看作权重w0,那么需要引入x0,这样公式就是:
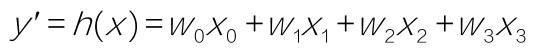
引入x0,就是给数据集添加一个新的哑(dummy)特征,值为1,b和这个哑特征相乘,值不变:
w0x0=b×1=b
新的公式变为:
y'=h(x)=wTx
习惯上,对于多元参数,会把W和X大写,突出它们是一个数组,而非标量:
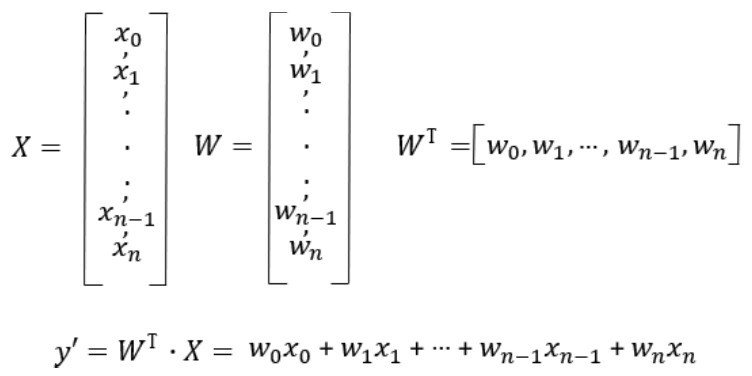
上面的表述形式令多元回归的程序实现过程更为简洁。多元回归的代码实现和刚才的单变量回归非常相似,只有几个部分需要注意(下面只给出重点代码段,完整代码参阅代码包中的源代码)。
首先,在构建特征数据集时,保留所有字段,包括wechat、weibo、others,然后用Num Py的delete方法删除标签字段:
X = np.array(df_ads) # 构建特征集, 包含全部特征
X = np.delete(X, [3], axis = 1) # 删除标签
y = np.array(df_ads.sales) #构建标签集, 销售额
print ("张量X的阶:", X.ndim)
print ("张量X的维度:", X.shape)
print (X)
输出结果如下:
张量X的阶: 2
张量X的维度: (200, 3)
[[ 304.4 93.6 294.4]
[1011.9 34.4 398.4]
… …
[ 343.5 86.4 48.]
[ 796.7 180. 252.]]
因为X特征集已经是2阶的,不需要再进行reshape操作,所以只需要把标签张量y进行reshape操作:
y = y.reshape(-1, 1) #通过reshape方法把向量转换为矩阵, -1等价于len(y), 返回样本个数
目前输入数据集是2D矩阵,包含两个轴,样本轴和特征轴,其中样本轴共200行数据,特征轴中有3个特征。
多变量线性回归实现过程中的重点就是W和X点积运算的实现,因为W不再是一个标量,而是变成了一个1D向量[w0,w1,w2,w3]。此时,假设函数f(x)在程序中的实现就变成了一个循环,其伪代码如下:
for i in N: # N为特征的个数
y_hat = y_hat + weight[i]*X[i]
y_hat = y_hat + bias
但是,我们已经知道,Num Py工具集中的点积运算可以避免类似的循环语句出现。
而且,有以下两种实现思路。
■一种是W和X点积,再加上偏置。
■另一种是给X最前面加上一列(一个新的维度),这个维度所有数值全都是1,是一个哑特征,然后把偏置看作w0。
第二种实现的代码比较整齐。为X训练集添加x0维特征的代码如下:
x0_train = np.ones((len(X_train), 1)) # 构造X长度的全1数组配合对偏置的点积
X_train = np.append(x0_train, X_train, axis=1) #把X增加一系列的1
print ("张量X的形状:", X_train.shape)
print (X_train)
输出结果如下:
张量X的形状: (160, 4)
[[1. 0.39995488 0.1643002 0.42568162]
[1. 0.72629521 0.83975659 0.34564644]
[1. 0.22746071 0.31845842 0.35620053]
--- ---
[1. 0.31949771 0.14807302 0.06068602]]
类似的x0维特征也需要添加至测试集。
损失函数也通过向量化来实现:
def loss_function(X, y, W): # 手工定义一个均方误差函数, W此时是一个向量
y_hat = X.dot(W.T) # 点积运算h(x)=w0x0+w1x1+w2x2+w3x3
loss = y_hat.reshape((len(y_hat), 1))-y # 中间过程, 求出当前W和真值的差值
cost = np.sum(loss**2)/(2*len(X)) # 这是平方求和过程, 均方误差函数的代码实现
return cost # 返回当前模型的均方误差值
梯度下降的公式仍然是:
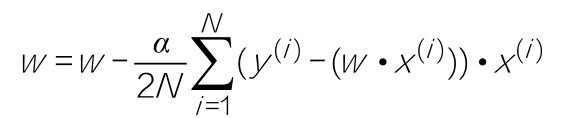
封装进一个梯度下降函数:
def gradient_descent(X, y, W, lr, iter): # 定义梯度下降函数
l_history = np.zeros(iter) # 初始化记录梯度下降过程中损失的数组
W_history = np.zeros((iter, len(W))) # 初始化记录梯度下降过程中权重的数组
for i in range(iter): # 进行梯度下降的迭代, 就是下多少级台阶
y_hat = X.dot(W) # 这是向量化运算实现的假设函数
loss = y_hat.reshape((len(y_hat), 1))-y # 中间过程, 求出y_hat和y真值的差值
derivative_W = X.T.dot(loss)/(2*len(X)) #求出多项式的梯度向量
derivative_W = derivative_W.reshape(len(W))
W = W - alpha*derivative_W # 结合学习速率更新权重
l_history[i] = loss_function(X, y, W) # 梯度下降过程中损失的历史记录
W_history[i] = W # 梯度下降过程中权重的历史记录
return l_history, W_history # 返回梯度下降过程中的数据
在训练机器之前,构建一个线性回归函数,把梯度下降和训练过程封装至一个函数。这可以通过调用线性回归模型来训练机器,代码显得比较整齐:
# 定义线性回归模型
def linear_regression(X, y, weight, alpha, iterations):
loss_history, weight_history = gradient_descent(X, y,
weight,
alpha, iterations)
print("训练最终损失:", loss_history[-1]) # 输出最终损失
y_pred = X.dot(weight_history[-1]) # 进行预测
traning_acc = 100 - np.mean(np.abs(y_pred - y))*100 # 计算准确率
print("线性回归训练准确率: {:.2f}%".format(traning_acc)) # 输出准确率
return loss_history, weight_history # 返回训练历史记录
这个模型中调用了梯度下降函数来训练机器,同时计算了最终损失并基于训练集给出了在训练集上的预测准确率。
下面初始化权重,这时候weight变成了一个数组,bias变成了其中的w[0]:
#首先确定参数的初始值
iterations = 300;# 迭代300次
alpha = 0.15;#学习速率设为0.15
weight = np.array([0.5, 1, 1, 1]) # 权重向量, w[0] = bias
#计算一下初始值的损失
print ('当前损失:', loss_function(X_train, y_train, weight))
下面通过调用前面定义好的线性回归模型训练机器,并给出最终损失,以及基于训练集的预测准确率:
# 调用刚才定义的线性回归模型
loss_history, weight_history = linear_regression(X_train, y_train,
weight, alpha, iterations) #训练机器
输出结果如下:
训练最终损失: 0.004334018335124016
线性回归训练准确率: 74.52%
还可以输出返回的权重历史记录以及损失历史记录:
print("权重历史记录:", weight_history)
print("损失历史记录:", loss_history)
损失历史记录显示,迭代200次之后,基本收敛。迭代300次之后,weight的值如下:
[-0.04161205 0.6523009 0.24686767 0.37741512]
这表示w0约为 −0.004,w1约为0.65,w2约为0.25,w3约为0.38。
最后,回答本课开始时,小冰同学提出的问题:在未来的某周,当我将各种广告投放金额做一个分配(比如,我决定用250元、50元、50元)来进行一周的广告投放时,我将大概实现多少元的商品销售额?
X_plan = [250,50,50] # 要预测的X特征数据
X_train,X_plan = scaler(X_train_original,X_plan) # 对预测数据也要归一化缩放
X_plan = np.append([1], X_plan ) # 加一个哑特征X0 = 1
y_plan = np.dot(weight_history[-1],X_plan) # [-1] 即模型收敛时的权重
# 对预测结果要做反向缩放,才能得到与原始广告费用对应的预测值
y_value = y_plan*23.8 + 3.2 #23.8是当前y_train中最大值和最小值的差,3.2是最小值
print ("预计商品销售额:",y_value, "千元")
通过上面的机器学习函数给出的预测参数向量,可以计算出预计商品销售额约为6千元:
预计商品销售额:6.088909584694067千元
同学们都转头去看小冰,眼神很诧异。咖哥也忍不住了,开口问道:“350元的广告费用,就能卖出6千多元的商品,你真的确定你需要学AI才能养家糊口吗?”小冰白了咖哥一眼:“咖哥,人家这个是商品销售额,不是利润。这6千元里面,大部分是成本。”
小冰接着说:“再说,这个模型预测得就一定很准吗?”