
还没有开始机器学习之前:随机选择初始参数时的函数图像
下面继续通过Python代码实现回归模型并调试模型。
在线性回归中,权重和偏置的初始值的选择可以是随机的,这对结果的影响不大,因为我们知道无论怎么选择,梯度下降总会带领机器“走”到最优结果(差别只是步数的多少而已)。通过下面的代码设置初始参数值:
# 首先确定参数的初始值
iterations = 100;# 迭代100次
alpha = 1;# 初始学习速率设为1
weight = -5 # 权重
bias = 3 # 偏置
# 计算一下初始权重和偏置值所带来的损失
print ('当前损失:', loss_function(X_train, y_train, weight, bias))
上面的代码设定各个参数的初始值并通过损失函数loss_function,求出初始损失:
当前损失:1.343795534906634
下面画出当前回归函数的图像:
# 绘制当前的函数模型
plt.plot(X_train, y_train, 'r.', label='Training data') # 显示训练数据
line_X = np.linspace(X_train.min(), X_train.max(), 500) # X值域
line_y = [weight*xx + bias for xx in line_X] # 假设函数y_hat
plt.plot(line_X, line_y, 'b--', label='Current hypothesis' ) #显示当前假设函数
plt.xlabel('wechat') # x轴标签
plt.ylabel('sales') # y轴标签
plt.legend() # 显示图例
plt.show() # 显示函数图像
输出函数图像如下所示。

还没有开始机器学习之前:随机选择初始参数时的函数图像
“哇!”一位同学看了一愣,“咖哥,这个好像和刚才你手绘的L-W线有很大差异!”
咖哥哈哈大笑,说:“因为初始权重和偏置的值都是随机选择的。而且我是故意让当前这个拟合结果显得很离谱,目的就是在后面的步骤中更好地显示出梯度下降的效果。”
下面就基于这个平均损失比较大的初始参数值,进行梯度下降,也就是开始训练机器,拟合函数。调用刚才已经定义好的梯度下降函数gradient_descent,并迭代100次(在上一节参数初始化的代码中已设定),也就是下100级台阶:
# 根据初始参数值, 进行梯度下降, 也就是开始训练机器, 拟合函数
loss_history, weight_history, bias_history = gradient_descent(
X_train, y_train, weight, bias, alpha, iterations)
在训练机器的过程中,已经通过变量loss_history记录了每一次迭代的损失值。下面把损失大小和迭代次数的关系通过函数图像显示出来,看看损失是不是如同所预期的那样,随着梯度下降而逐渐减小并趋近最佳状态。通过下面的代码绘制损失曲线:
plt.plot(loss_history, 'g--', label='Loss Curve') # 显示损失曲线
plt.xlabel('Iterations') # x轴标签
plt.ylabel('Loss') # y轴标签
plt.legend() # 显示图例
plt.show() # 显示损失曲线
代码运行后,发现很奇怪的现象,图中(如下图所示)显示出来的损失竟随着梯度下降的迭代而变得越来越大,从很小的值开始,越来越大,后来达到好几万。
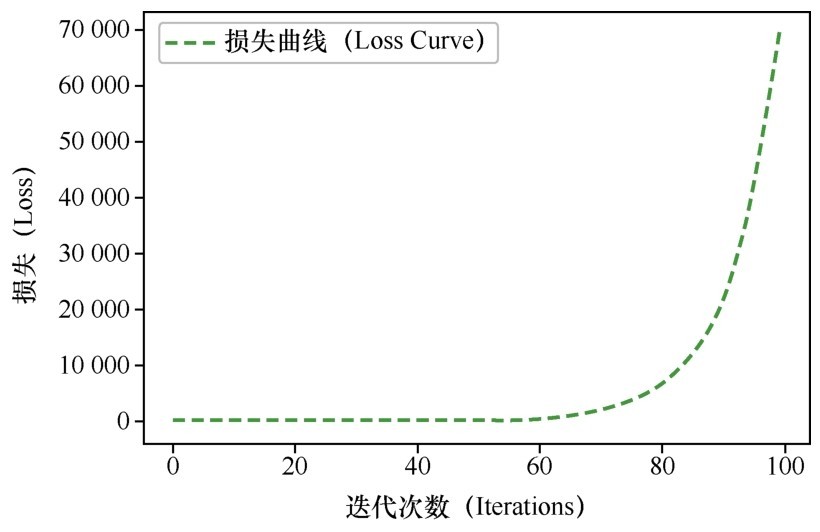
损失值竟然越来越大
如果在这时画出当前的线性函数图像,也会特别离谱,根本就没有与数据集形成拟合:
# 绘制当前的函数模型
plt.plot(X_train, y_train, 'r.', label='Training data') # 显示训练数据
line_X = np.linspace(X_train.min(), X_train.max(), 500) # X值域
# 关于weight_history[-1], 这里的索引[-1], 就代表迭代500次后的最后一个W值
line_y = [weight_history[-1]*xx + bias_history[-1] for xx in line_X] # 假设函数
plt.plot(line_X, line_y, 'b--', label='Current hypothesis' ) # 显示当前假设函数
plt.xlabel('wechat') # x轴标签
plt.ylabel('sales') # y轴标签
plt.legend() # 显示图例
plt.show() # 显示函数图像

不成功的拟合
梯度下降并没有得到我们所期望的结果。原因何在呢?
咖哥说:“考验咱们的经验和解决问题的能力的时刻来了!同学们说一说自己的看法吧。”
此时,同学们却都沉默了。
咖哥说:“其实,根据刚刚讲过的内容,应该可以猜出问题大概出在哪里。这个数据集比较简单,没有什么潜在的数据问题。而且模型也比较简单,如果损失函数、梯度下降代码和求导过程都没有出现错误的话,那么此处基本上可以确定,问题出在学习速率α的设定方面。”
现在的α值,也就是梯度下降的速率在参数初始化时设定为1,这个值可能太大了。我们可以在0到1之间进行多次尝试,以找到最合适的α值。
当把α从1调整为0.01后,损失开始随着迭代次数而下降,但是似乎下降的速度不是很快,迭代100次后没有出现明显的收敛现象,如下面左图所示。反复调整α,发现在α=0.5的情况下损失曲线在迭代80~100次之后开始出现比较好的收敛现象,如下面右图所示。此时梯度已经极为平缓,接近凸函数的底部最优解,对权重求导时斜率几乎为0,因此继续增加迭代次数,损失值也不会再发生什么大的变化。

调整学习速率:α = 0.01,α = 0.5
将α设为0.5,迭代100次后,绘制新的线性函数图像,就呈现出了比较好的拟合状态,如下图所示。

终于得到成功的拟合
看到这条漂亮的虚线,同学们一颗颗原本悬着的小心脏都落了地。
对迭代次数进行调试的主要目的是确认损失值已经收敛,因为收敛之后再继续迭代下去,损失值的变化已经微乎其微。
确定损失值已经收敛的主要方法是观察不同迭代次数下形成的损失曲线。下图是α = 0.5时,迭代20次、100次、500次的损失曲线图像。
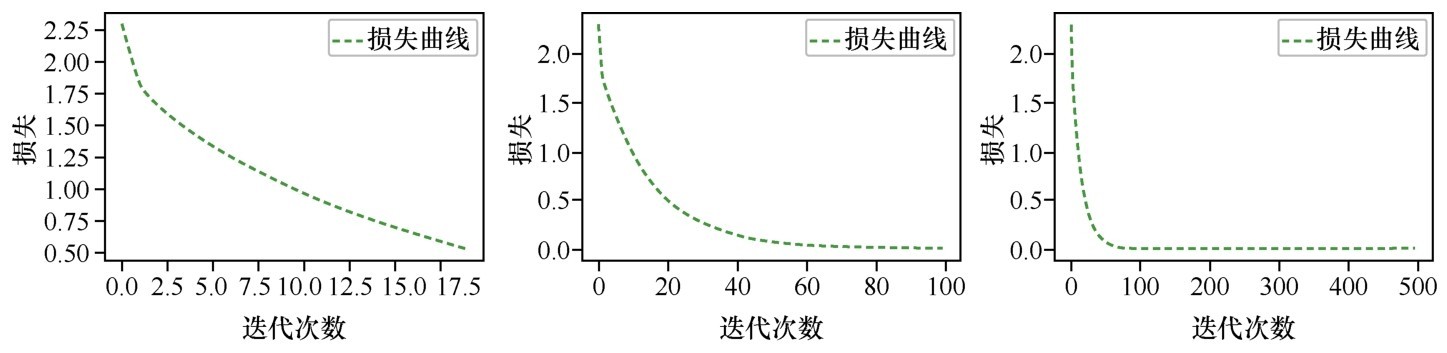
将迭代次数从100次增加至500次后,损失并没有明显减小
从图像显示可知,迭代20次显然太少了,损失值还在持续减少,训练不应停止。大概在迭代80~100次之后,损失已经达到了比较小的值,继续迭代下去没有太大意义,只是浪费资源,所以迭代500次没有什么必要。
就此例而言,以0.5的学习速率来说,为了安全起见,我们迭代100~200次差不多就可以了,最后确定迭代200次吧。
下面就输出α=0.5时,迭代200次之后的损失值,以及参数w和b的值:
print ('当前损失:', loss_function(X_train, y_train,
weight_history[-1], bias_history[-1]))
print ('当前权重:', weight_history[-1])
print ('当前偏置:', bias_history[-1])
这里的索引[-1],前面讲过,是相对索引,它代表迭代200次后的最后一次的w和b值,这两个值就是机器学习基于训练数据集得到的结果:
当前损失:0.00465780405531404
当前权重:0.6552253409192808
当前偏置:0.17690341009472488
现在,在迭代200次之后,我们认为此时机器学习已经给出了足够好的结果,对于训练集的均方误差函数的损失值已经非常小,几乎接近0。那么,是不是在测试集上,这个函数模型效果也一样好呢?
下面在测试集上进行预测和评估:
print ('测试集损失:', loss_function(X_test, y_test,
weight_history[-1], bias_history[-1]))
输出结果如下:
测试集损失:0.00458180938024721
结果显示当前的测试集的损失值约为0.00458,甚至还要好过训练集。测试集损失比训练集损失还低,这种情形并不是机器学习的常态,但在比较小的数据集上是有可能出现的。
我们还可以同时描绘出训练集和测试集随着迭代次数而形成的损失曲线,如下图所示。

同时显示测试集与训练集的损失曲线
结果显示,测试集与训练集的损失随迭代次数的增加,呈现相同的下降趋势,说明我们的机器学习模型是成功的。在训练的初期,训练集上的损失明显小于测试集上的损失,但是这种差距会随着学习的过程而逐渐变小,这也是机器学习过程正确性的体现。
因此,最终确定了一个适合预测小冰的网店销售额的最佳线性回归模型:
w = 0.6608381748731955
b = 0.17402747570052432
函数模型:y'=0.66x+0.17
而我们刚才所做的全部工作,就是利用机器学习的原理,基于线性回归模型,通过梯度下降,找到了两个最佳的参数值而已。
至此,机器学习建模过程已经完成。这里我再多讲一个辅助性的工具,叫作轮廓图(contour plot)。损失曲线描绘的是损失和迭代次数之间的关系,而轮廓图则描绘的是L、w和b这3者之间的关系,这样才能够清楚地知道损失值是怎样随着w和b的变化而逐步下降的。
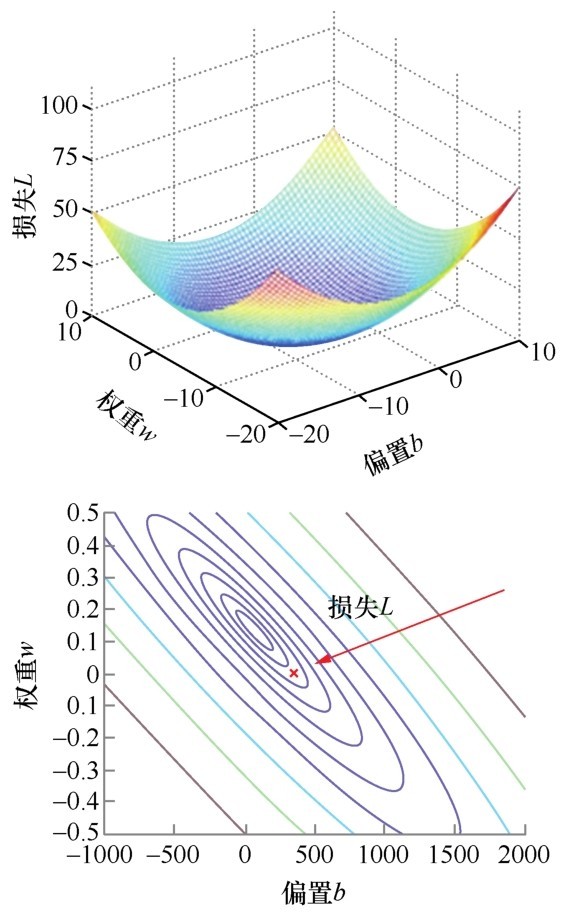
从损失曲线到轮廓图
这个轮廓图,其实大概就是等高线+地形图。
小冰插嘴:“等高线和地形图地理课学过啊,我知道是怎么回事。”
咖哥说:“那就比较容易理解了。”
介绍梯度下降的时候,我们反复讲全局最低点,如果只有一个参数w,那么损失函数的图像就是二次函数曲线。
如果考虑两个参数w和b,就是类似于右侧上图的一个三维立体图像,像一个碗。而轮廓图,就是这个三维的碗到二维平面的投影,如右侧下图所示。
在轮廓图中,每一个圈圈上的各个点,损失值都相同,也就是说,这些点所对应的w和b,带来的L是等值的。而L的最小值,就投影到了同心椭圆的中心点,也就是全局最优解,此时只有一个最优的w和b的组合。
因此,这个轮廓图可以方便、直观地观察损失函数和模型内部参数之间关系。
小冰突然发问:“如果参数超过两个呢?又怎么画轮廓图?”
咖哥“痛苦”地回答:“轮廓图,费了好大的力气,把三维的关系降到二维平面上进行显示,你又想再多加一维,那是又在挑战人类的极限了。这里请理解一下,不要钻牛角尖了。其实在纸面上是比较难画出更多个参数的轮廓图的。”
针对这个案例,我在训练机器的过程中绘制出了轮廓图,代码比较长,基于篇幅,我就不进行展示了,你们可以去源码包里面看一看。代码显示了线性函数图像从初始状态到最优状态的渐变和损失在轮廓图中逐渐下降到最低点的轨迹,这把训练机器的过程描绘得非常直观,如下图所示。
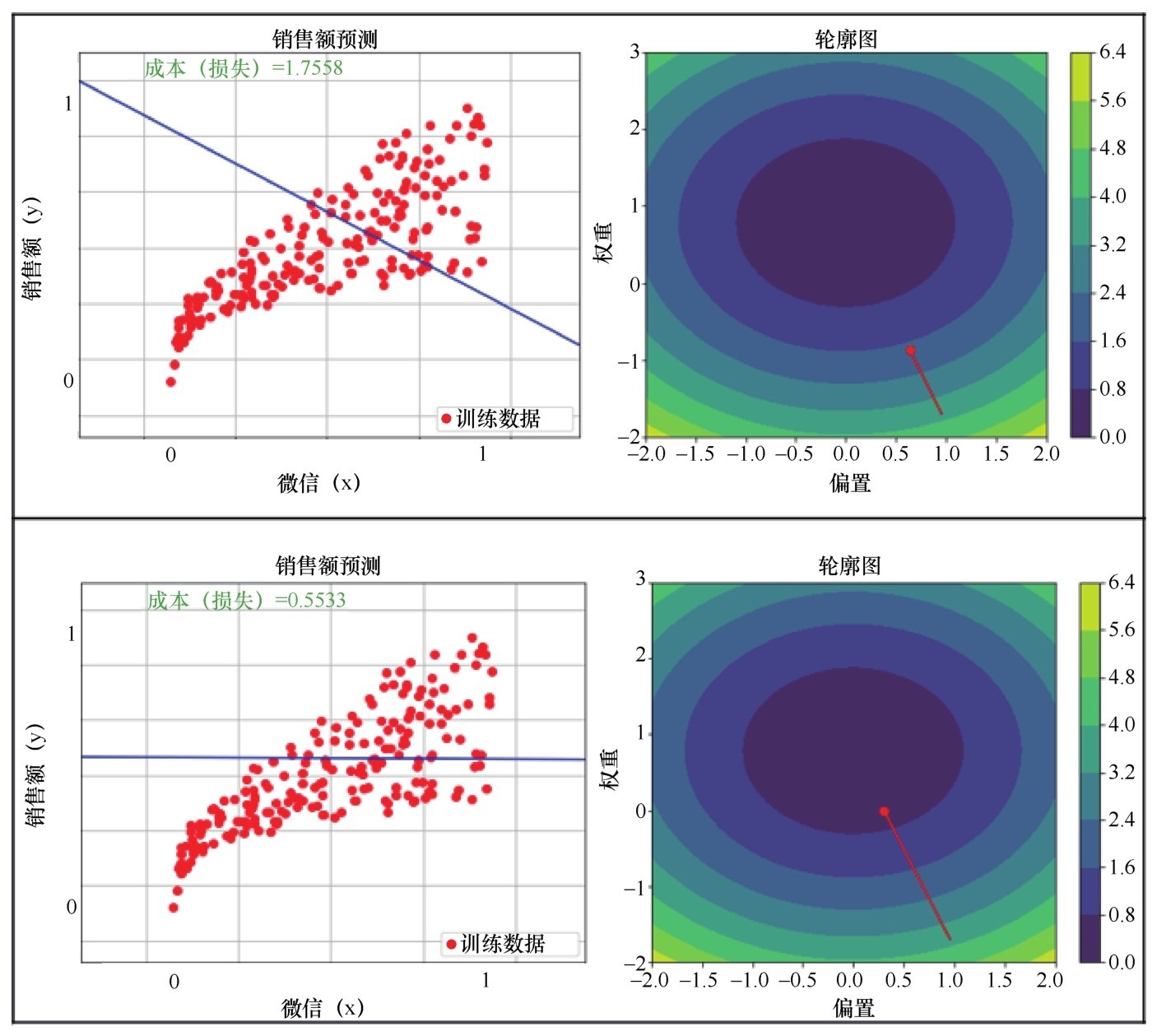
随着参数的拟合过程,损失越来越小,最终下降到轮廓图的中心点

随着参数的拟合过程,损失越来越小,最终下降到轮廓图的中心点(续)
从图中可以分析出,当w在0.66附近,b在0.17附近时,L值接近轮廓图颜色最深的底部中心点,也就是最优解。
“休息10分钟,”咖哥说,“之后讲如何实现多变量的线性回归。”