一元线性函数
机器学习模型的确立过程中有两个主要环节。
(1)确定选用什么类型的模型。
(2)确定模型的具体参数。
先聚焦于第一个问题。
对于这个案例,使用什么模型我们早就心中有数了。虽然上图中的函数直线并未精确无误地穿过每个点,但已经能够反映出特征(也就是微信公众号广告投放金额)和标签(也就是商品销售额)之间的关系,拟合程度还是挺不错的。
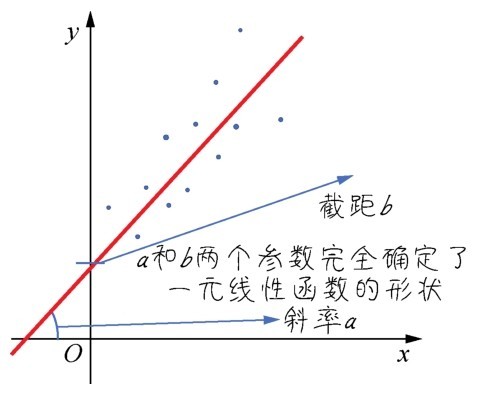
这个简单的模型就是一元线性函数(如右图所示):

一元线性函数
y=ax+b
其中,参数a的数学含义是直线的斜率(陡峭程度),b则是截距(与y轴相交的位置)。
在机器学习中,会稍微修改一下参数的代号,把模型表述为:
y=wx+b
此处,方程式中的a变成了w,在机器学习中,这个参数代表权重。因为在多元变量(多特征)的情况下,一个特征对应的w参数值越大,就表示权重越大。而参数b,在机器学习中称为偏置。
不要小看这个简单的线性函数,在后续的机器学习过程中,此函数会作为一个基本运算单元反复地发挥威力。
 咖哥发言
咖哥发言
小冰提问:“咖哥,说到模型的参数,我也看过一些文档,经常听见有人说西塔、西塔(θ)什么的,这是怎么一回事儿?”
咖哥解释:“有些机器学习教程中,用θ(读作theta)表示机器学习的参数,也会使用θ0和θ1来代表此处的w和b,还有用其他字母表示机器学习参数的情况。我觉得此处使用w和b来表示这些参数会使它们的意义更清晰一些:weight是权重,bias是偏置,各取首字母。你们看其他机器学习资料的时候,要懂得θ0、θ1和这里的w、b其实是一回事儿。”
确定以线性函数作为机器学习模型之后,我们接着介绍假设函数的概念。先来看一个与线性函数稍有差别的方程式:
y'=wx+b
也可以写成:
h(x)=wx+b
其中,需要注意以下两点。
■y'指的是所预测出的标签,读作y帽(y-hat)或y撇。
■h(x)就是机器学习所得到的函数模型,它能根据输入的特征进行标签的预测。
我们把它称为假设函数,英文是hypothesis function(所以选用首字母h作为函数符号)。
小冰疑惑了:“这不就是线性函数吗?为什么又要叫假设函数h(x)?”
咖哥笑答:“这的确就是线性函数。不过,机器学习的过程,是一个不断假设、探寻、优化的过程,在找到最佳的函数f(x)之前,现有的函数模型不一定是很准确的。它只是很多种可能的模型之中的一种—因此我们强调,假设函数得出的结果是y',而不是y本身。所以假设函数有时也被叫作预测函数(predication function)。在机器学习中看到h(x)、f(x)或者p(x),基本上它们所要做的都是一回事,就是根据微信公众号广告投放金额x推断(或预测)销售额y'。”
所以,机器学习的具体目标就是确定假设函数h(x)。
■确定b,也就是y轴截距,这里称为偏置,有些机器学习文档中,称它为w0(或θ0)。
■确定w,也就是斜率,这里称为特征x的权重,有些机器学习文档中,称它为w1(或θ1)。
一旦找到了参数w和b的值,整个函数模型也就被确定了。那么这些参数w和b的具体值怎么得到呢?
在继续寻找最优参数之前,需要先介绍损失和损失函数。
如果现在已经有了一个假设函数,就可以进行标签的预测了。那么,怎样才能够量化这个模型是不是足够好?比如,一个模型是3x+5,另一个是100x+1,怎样评估哪一个更好?
这里就需要引入损失(loss)这个概念。
损失,是对糟糕预测的惩罚。损失也就是误差,也称为成本(cost)或代价。名字虽多,但都是一个意思,也就是当前预测值和真实值之间的差距的体现。它是一个数值,表示对于单个样本而言模型预测的准确程度。如果模型的预测完全准确,则损失为0;如果不准确,就有损失。在机器学习中,我们追求的当然是比较小的损失。
不过,模型好不好还不能仅看单个样本,而是要针对所有数据样本找到一组平均损失“较小”的函数模型。样本的损失的大小,从几何意义上基本上可以理解为y和y'之间的几何距离。平均距离越大,说明误差越大,模型越离谱。如右图所示,左边模型所有数据点的平均损失很明显大过右边模型。

左边是平均损失较大的模型,右边是平均损失较小的模型
因此,针对每一组不同的参数,机器都会针对样本数据集算一次平均损失。计算平均损失是每一个机器学习项目的必要环节。
损失函数(loss function)L(w,b)就是用来计算平均损失的。
 咖哥发言
咖哥发言
有些地方把损失函数记作J(θ),也叫代价函数、成本函数(cost function)。刚才说过, θ就是w和b,J(θ)就是L(w,b),符号有别,但意思相同。
这里要强调一下:损失函数L是参数w和b的函数,不是针对x的函数。我们会有一种思维定势,总觉得函数一定是表示x和y之间的关系。现在需要大家换一个角度去思考问题,暂时忘掉x和y,聚焦于参数。对于一个给定的数据集来说,所有的特征和标签都是已经确定的,那么此时损失值的大小就只随着参数w和b而变。也就是说,现在x和y不再是变量,而是定值,而w和b在损失函数中成为了变量。
“这里有点不好理解,大家能听得懂吗?”咖哥问。
其中一位同学思考了一下,说:“大概还跟得上你的思路,接着讲吧。”
计算数据集的平均损失非常重要,简而言之就是:如果平均损失小,参数就好;如果平均损失大,模型或者参数就还要继续调整。
这个计算当前假设函数所造成的损失的过程,就是前面提到过的模型内部参数的评估的过程。
机器学习中的损失函数很多,主要包括以下几种。
■用于回归的损失函数。
□均方误差(Mean Square Error,MSE)函数,也叫平方损失或L2损失函数。
□平均绝对误差(Mean Absolute Error,MAE)函数,也叫L1损失函数。
□平均偏差误差(mean bias error)函数。
■用于分类的损失函数。
□交叉熵损失(cross-entropy loss)函数。
□多分类SVM损失(hinge loss)函数。
一般来说,选择最常用的损失函数就可以达到评估参数的目的。下面给出线性回归模型的常用损失函数—均方误差函数的实现过程。
■首先,对于每一个样本,其预测值和真实值的差异为(y−y'),而y'=wx+b,所以损失值与参数w和b有关。
■如果将损失值(y−y')夸张一下,进行平方(平方之后原来有正有负的数值就都变成正数),就变成(y−y')2。我们把这个值叫作单个样本的平方损失。
■然后,需要把所有样本(如本章示例一共记录了200周的数据,即200个样本)的平方损失都相加,即(y(x(1))−y'(x(1)))2+(y(x(2))−y'(x(2)))2+…+(y(x(200)))−y'(x(200)))2。
写成求和的形式就是:

 咖哥发言
咖哥发言
同学们注意一下,此处公式里带小括号的上标x(1),代表样本的维度索引,即整个数据集中的第几个样本。那么大家是否还记得x1中的下标代表什么?那是标签的维度索引,即第几个标签。这个例子中目前只有一个标签,因此省略了下标。
■最后,根据样本的数量求平均值,则损失函数L为:

关于以上公式,说明以下几点。
■(x,y)为样本,x是特征(微信公众号广告投放金额),y是标签(销售额)。
■h(x)是假设函数wx+b,也就是y'。
■D指的是包含多个样本的数据集。
■N指的是样本数量(此例为200)。N前面还有常量2,是为了在求梯度的时候,抵消二次方后产生的系数,方便后续进行计算,同时增加的这个常量并不影响梯度下降的最效结果。
■而L呢,对于一个给定的训练样本集而言,它是权重w和偏置b的函数,它的大小随着w和b的变化而变。
下面用Python定义一个MSE函数,并将其封装起来,以后会调用它。
 咖哥发言
咖哥发言
其实,MSE函数也不需要我们自己写代码来实现,直接调用Python数学库函数也是可以的,但这是我们的第一个项目,多练练手吧。
还有一点要告诉大家的,使用MSE函数做损失函数的线性回归算法,有时被称为最小二乘法。
下面是本例的核心代码段之一:
def loss_function(X, y, weight, bias): # 手工定义一个均方误差函数
y_hat = weight*X + bias # 这是假设函数, 其中已经应用了Python的广播功能
loss = y_hat-y # 求出每一个y'和训练集中真实的y之间的差异
cost = np.sum(loss**2)/2*len(X) # 这是均方误差函数的代码实现
return cost # 返回当前模型的均方误差值
其中,利用了Python的广播功能以及向量化运算。下面是代码中涉及的内容。
■在weight*X + bias中,X是一个2D张量,共200行,1列,但是此处X可以直接与标量weight相乘,并与标量bias相加,之后仍然得到形状为(200,1)的2D张量。在运行期间weight和bias自动复制自身,形成X形状匹配的张量。这就是上一课中讲过的广播。
■y_hat是上面广播计算的结果,形状与标签集y相同。同学们如果对当前张量形状有疑惑,可以通过shape方法输出其形状。y_hat可以和y进行直接的向量化的加减运算,不需要任何for循环参与。这种向量化运算既减少了代码量,又提高了运算效率。
■损失函数代码中的loss或者cost,都代表当前模型的误差(或称为损失、成本) 值。
np.sum(loss**2)/2*len(X)是MSE函数的实现,其中包含以下内容。
■loss**2代表对误差值进行平方。
■sum(loss**2)是对张量所有元素求和。
■len(X)则返回数据集大小,例如200。
有了这个损失函数,我们就可以判断不同参数的优与劣了。MSE函数值越小越好,越大就说明误差越大。
下面随便设定了两组参数,看看其均方误差大小:
print ("当权重为5, 偏置为3时, 损失为:",
loss_function(X_train, y_train, weight=5, bias=3))
print ("当权重为100, 偏置为1时, 损失为:",
loss_function(X_train, y_train, weight=100, bias=1))
调用刚才定义好的损失函数,运行后结果如下:
当权重为5,偏置为3时,损失为:25.592781941560116
当权重为100,偏置为1时,损失为:3155.918523006111
因此,线性函数y=3x+5相对于线性函数y=100x+1而言是更优的模型。
同学们纷纷表示基本理解了损失函数的重要性。但小冰提出一个疑问:“这个MSE函数,为什么非要平方呢?y−y'就是预测误差,取个绝对值之后直接相加不就行了吗?”
咖哥表扬道:“好问题,这个疑惑我以前也曾经有过。均方损失函数,并不是唯一可用的损失函数。为什么这里要选用它呢?如果目的仅是计算损失,把误差的绝对值加起来取平均值就足够了(即平均绝对误差函数)。但是之所以还要平方,是为了让L(w,b)形成相对于w和b而言的凸函数,从而实现梯度下降。下面马上就要讲到这个关键之处了。”